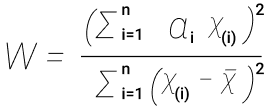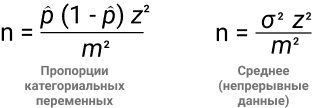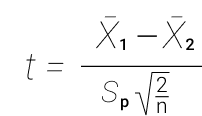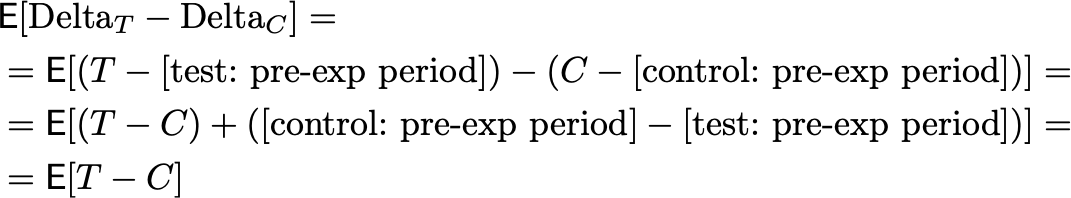A b тестирование ошибка первого рода - Не ошибается лишь тот, кто ничего не делает!

В Учи.ру мы стараемся даже небольшие улучшения выкатывать A/B-тестом, только за этот учебный год их было больше 250. A/B-тест — мощнейший инструмент тестирования изменений, без которого сложно представить нормальное развитие интернет-продукта. В то же время, несмотря на кажущуюся простоту, при проведении A/B-теста можно допустить серьёзные ошибки как на этапе дизайна эксперимента, так и при подведении итогов. В этой статье я расскажу о некоторых технических моментах проведения теста: как мы определяем срок тестирования, подводим итоги и как избегаем ошибочных результатов при досрочном завершении тестов и при тестировании сразу нескольких гипотез.

Типичная схема A/B-тестирования у нас (да и у многих) выглядит так:

Разрабатываем фичу, но перед раскаткой на всю аудиторию хотим убедиться, что она улучшает целевую метрику, например, вовлечённость.
Определяем срок, на который запускается тест.
Случайно разбиваем пользователей на две группы.
Одной группе показываем версию продукта с фичей (экспериментальная группа), другой — старую (контрольная).
В процессе мониторим метрику, чтобы вовремя прекратить особо неудачный тест.
По истечении срока теста сравниваем метрику в экспериментальной и контрольной группах.
Если метрика в экспериментальной группе статистически значимо лучше, чем в контрольной, раскатываем протестированную фичу на всех. Если же статистической значимости нет, завершаем тест с отрицательным результатом.

Всё выглядит логично и просто, дьявол, как всегда, в деталях.

Статистическая значимость, критерии и ошибки

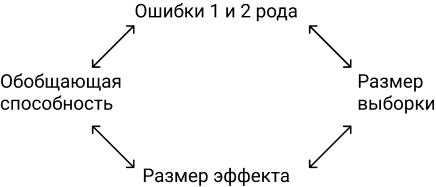
В любом A/B-тесте присутствует элемент случайности: метрики групп зависят не только от их функционала, но и от того, какие пользователи в них попали и как они себя ведут. Чтобы достоверно сделать выводы о превосходстве какой-то группы, нужно набрать достаточно наблюдений в тесте, но даже тогда вы не застрахованы от ошибок. Их различают два типа:

Ошибка первого рода происходит, если мы фиксируем разницу между группами, хотя на самом деле её нет. В тексте также будет встречаться эквивалентный термин — ложноположительный результат. Статья посвящена именно таким ошибкам.
Ошибка второго рода происходит, если мы фиксируем отсутствие разницы, хотя на самом деле она есть.

При большом количестве экспериментов важно, чтобы вероятность ошибки первого рода была мала. Её можно контролировать с помощью статистических методов. Например, мы хотим, чтобы в каждом эксперименте вероятность ошибки первого рода не превышала 5% (это просто удобное значение, для собственных нужд можно брать другое). Тогда мы будем принимать эксперименты на уровне значимости 0.05:

Есть A/B-тест с контрольной группой A и экспериментальной — B. Цель — проверить, что группа B отличается от группы A по какой-то метрике.
Формулируем нулевую статистическую гипотезу: группы A и B не отличаются, а наблюдаемые различия объясняются шумом. По умолчанию всегда считаем, что разницы нет, пока не доказано обратное.
Проверяем гипотезу строгим математическим правилом — статистическим критерием, например, критерием Стьюдента.
В результате получаем величину p-value. Она лежит в диапазоне от 0 до 1 и означает вероятность увидеть текущую или более экстремальную разницу между группами при условии верности нулевой гипотезы, то есть при отсутствии разницы между группами.
Значение p-value сравнивается с уровнем значимости 0.05. Если оно больше, принимаем нулевую гипотезу о том, что различий нет, иначе считаем, что между группами есть статистически значимая разница.

Проверить гипотезу можно параметрическим или непараметрическим критерием. Параметрические опираются на параметры выборочного распределения случайной величины и обладают большей мощностью (реже допускают ошибки второго рода), но предъявляют требования к распределению исследуемой случайной величины.

Самый распространенный параметрический тест — критерий Стьюдента. Для двух независимых выборок (случай A/B-теста) его иногда называют критерием Уэлча. Этот критерий работает корректно, если исследуемые величины распределены нормально. Может показаться, что на реальных данных это требование почти никогда не удовлетворяется, однако на самом деле тест требует нормального распределения выборочных средних, а не самих выборок. На практике это означает, что критерий можно применять, если у вас в тесте достаточно много наблюдений (десятки-сотни) и в распределениях нет совсем уж длинных хвостов. При этом характер распределения исходных наблюдений неважен. Читатель самостоятельно может убедиться, что критерий Стьюдента работает корректно даже на выборках, сгенерированных из распределений Бернулли или экспоненциального.

Из непараметрических критериев популярен критерий Манна — Уитни. Его стоит применять, если ваши выборки очень малого размера или есть большие выбросы (метод сравнивает медианы, поэтому устойчив к выбросам). Также для корректной работы критерия в выборках должно быть мало совпадающих значений. На практике нам ни разу не приходилось применять непараметрические критерии, в своих тестах всегда пользуемся критерием Стьюдента.

Проблема множественного тестирования гипотез

Самая очевидная и простая проблема: если в тесте кроме контрольной группы есть несколько экспериментальных, то подведение итогов с уровнем значимости 0.05 приведёт к кратному росту доли ошибок первого рода. Так происходит, потому что при каждом применении статистического критерия вероятность ошибки первого рода будет 5%. При количестве групп

и уровне значимости

$alpha$ вероятность, что какая-то экспериментальная группа выиграет случайно, составляет:

$P(any false positive) = 1 − (1 − alpha) ^ {ngroups}$

Например, для трёх экспериментальных групп получим 14.3% вместо ожидаемых 5%. Решается проблема поправкой Бонферрони на множественную проверку гипотез: нужно просто поделить уровень значимости на количество сравнений (то есть групп) и работать с ним. Для примера выше уровень значимости с учётом поправки составит 0.05/3 = 0.0167 и вероятность хотя бы одной ошибки первого рода составит приемлемые 4.9%.

Метод Холма — Бонферрони

Искушенный читатель знает и о методе Холма — Бонферрони, который всегда обладает большей мощностью, чем поправка Бонферрони, то есть реже совершает ошибки второго рода. В этом методе мы сортируем

гипотез по возрастанию значений p-value и начинаем их сравнивать по порядку с требуемым уровнем значимости, который увеличивается в зависимости от номера шага

по формуле:

$alpha_{step} = frac {alpha} {ngroups − step_number + 1}$

P-value первой гипотезы сравнивается с уровнем статистический значимости

. Если гипотеза принимается, то переходим ко второй и сравниваем её p-value с уровнем статистической значимости

, и так далее. Как только какая-то гипотеза отвергается, процесс останавливается и все оставшиеся гипотезы так же отвергаются. Самое жёсткое требование (и такое же, как в поправке Бонферрони) накладывается на гипотезу с наименьшим p-value, а большая мощность достигается за счёт менее жёстких условий для последующих гипотез. Цель A/B-теста — выбрать одного единственного победителя, поэтому методы Бонферрони и Холма — Бонферрони абсолютно идентичны в этом приложении.

Строго говоря, сравнения групп по разным метрикам или срезам аудитории тоже подвержены проблеме множественного тестирования. Формально учесть все проверки довольно сложно, потому что их количество сложно спрогнозировать заранее и подчас они не являются независимыми (особенно если речь идёт про разные метрики, а не срезы). Универсального рецепта нет, полагайтесь на здравый смысл и помните, что если проверить достаточно много срезов по разным метрикам, то в любом тесте можно увидеть якобы статистически значимый результат. А значит, надо с осторожностью относиться, например, к значимому приросту ретеншена пятого дня новых мобильных пользователей из крупных городов.

Проблема подглядывания

Частный случай множественного тестирования гипотез — проблема подглядывания (peeking problem). Смысл в том, что значение p-value по ходу теста может случайно опускаться ниже принятого уровня значимости. Если внимательно следить за экспериментом, то можно поймать такой момент и ошибочно сделать вывод о статистической значимости.

Предположим, что мы отошли от описанной в начале поста схемы проведения тестов и решили подводить итоги на уровне значимости 5% каждый день (или просто больше одного раза за время теста). Под подведением итогов я понимаю признание теста положительным, если p-value ниже 0.05, и его продолжение в противном случае. При такой стратегии доля ложноположительных результатов будет пропорциональна количеству проверок и уже за первый месяц достигнет 28%. Такая огромная разница кажется контринтуитивной, поэтому обратимся к методике A/A-тестов, незаменимой для разработки схем A/B-тестирования.

Идея A/A-теста проста: симулировать на исторических данных много A/B-тестов со случайным разбиением на группы. Разницы между группами заведомо нет, поэтому можно точно оценить долю ошибок первого рода в своей схеме A/B-тестирования. На гифке ниже показано, как изменяются значения p-value по дням для четырёх таких тестов. Равный 0.05 уровень значимости обозначен пунктирной линией. Когда p-value опускается ниже, мы окрашиваем график теста в красный. Если бы в этом время подводились итоги теста, он был бы признан успешным.

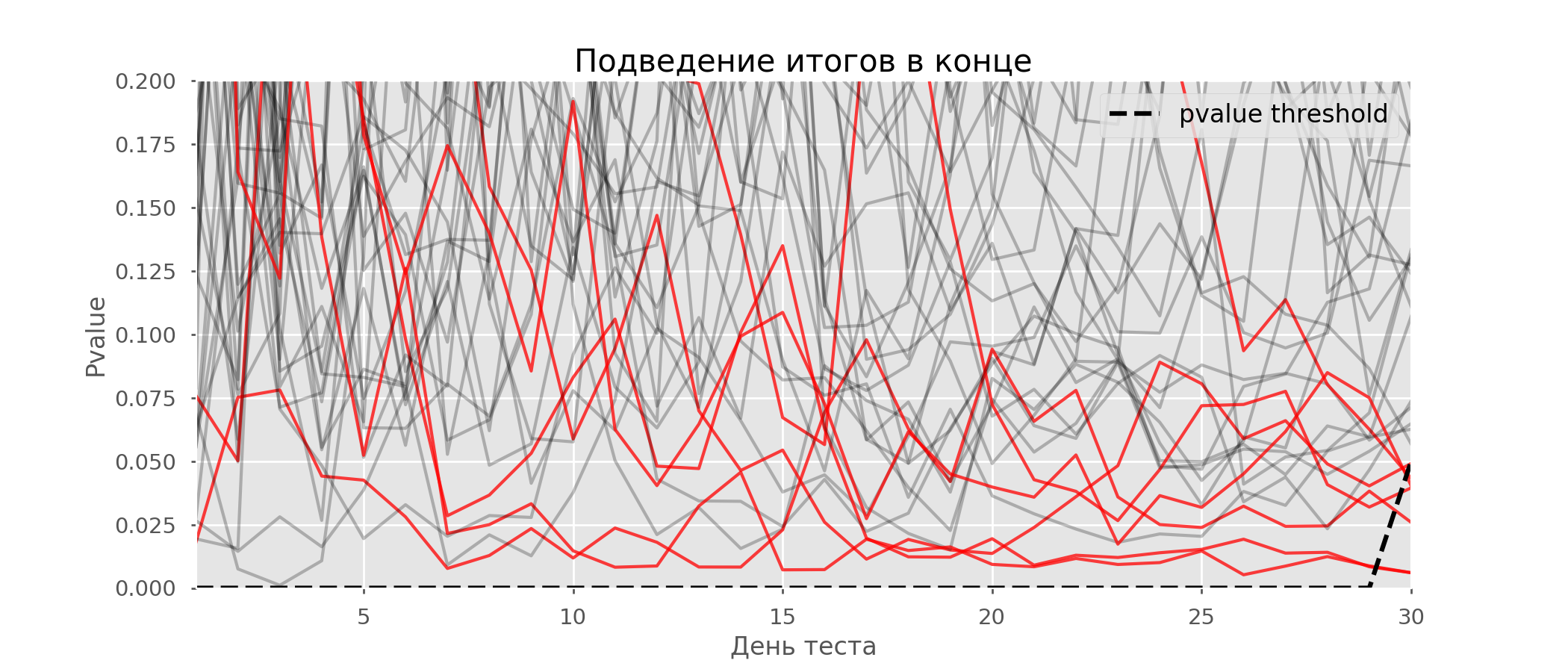
Рассчитаем аналогично 10 тысяч A/A-тестов продолжительностью в один месяц и сравним доли ложноположительных результатов в схеме с подведением итогов в конце срока и каждый день. Для наглядности приведём графики блуждания p-value по дням для первых 100 симуляций. Каждая линия — p-value одного теста, красным выделены траектории тестов, в итоге ошибочно признанных удачными (чем меньше, тем лучше), пунктирная линия — требуемое значение p-value для признания теста успешным.

На графике можно насчитать 7 ложноположительных тестов, а всего среди 10 тысяч их было 502, или 5%. Хочется отметить, что p-value многих тестов по ходу наблюдений опускались ниже 0.05, но к концу наблюдений выходили за пределы уровня значимости. Теперь оценим схему тестирования с подведением итогов каждый день:

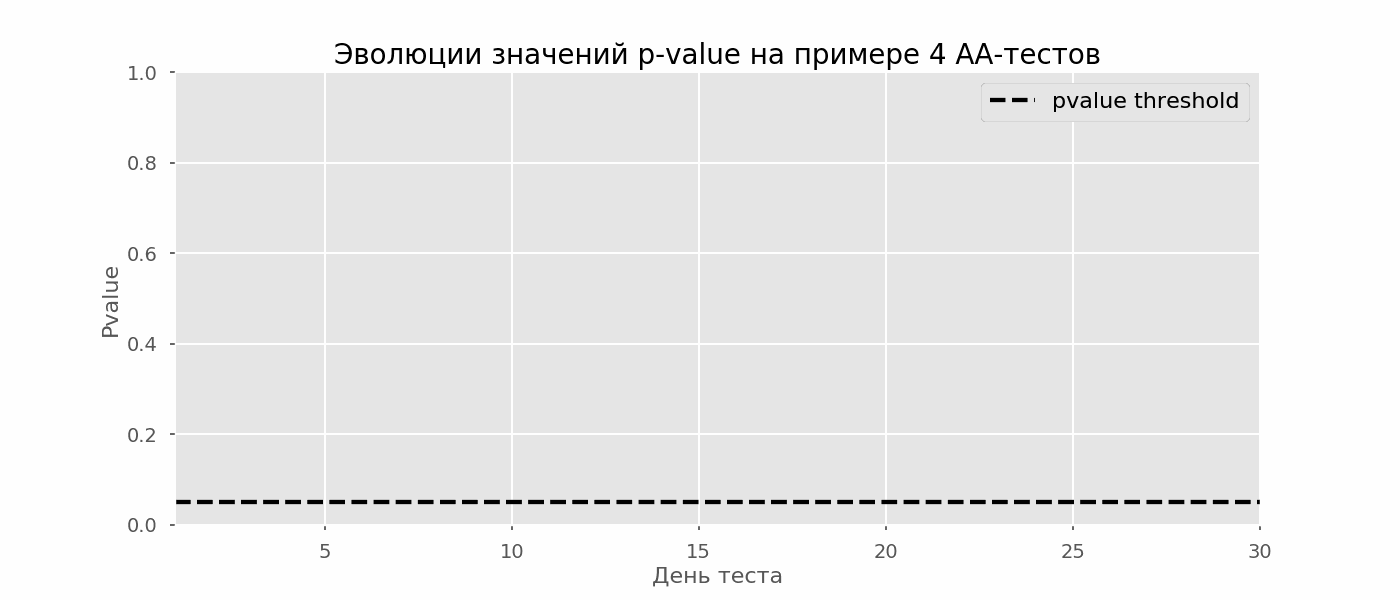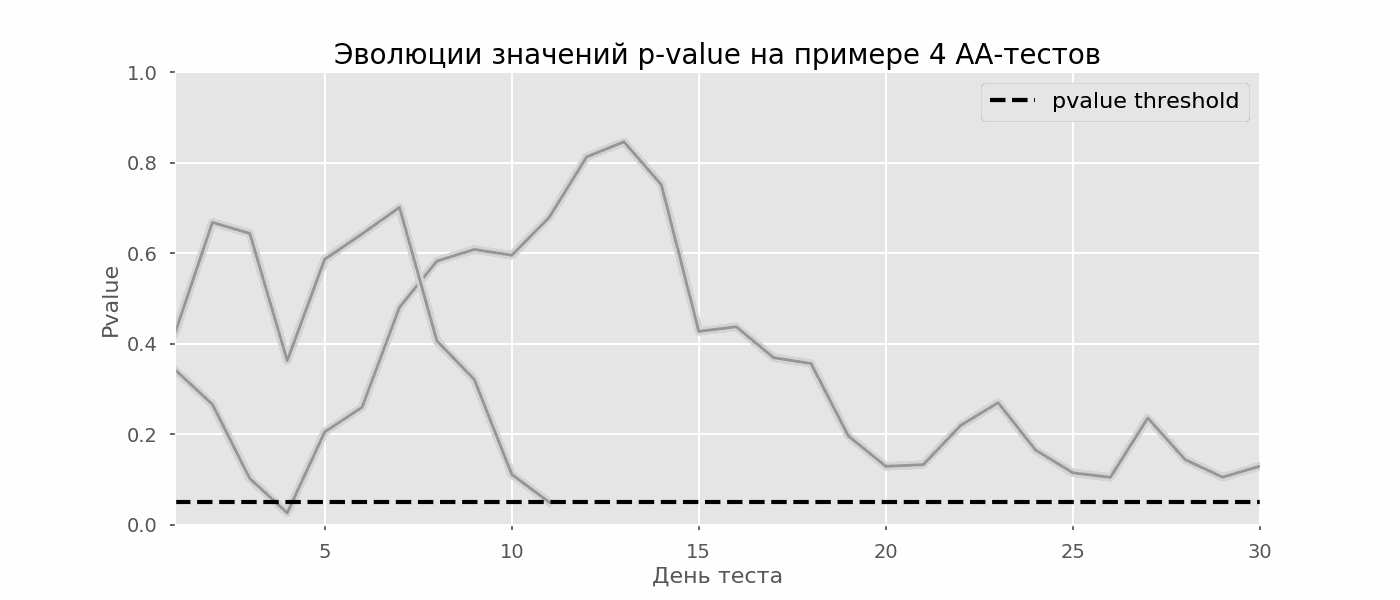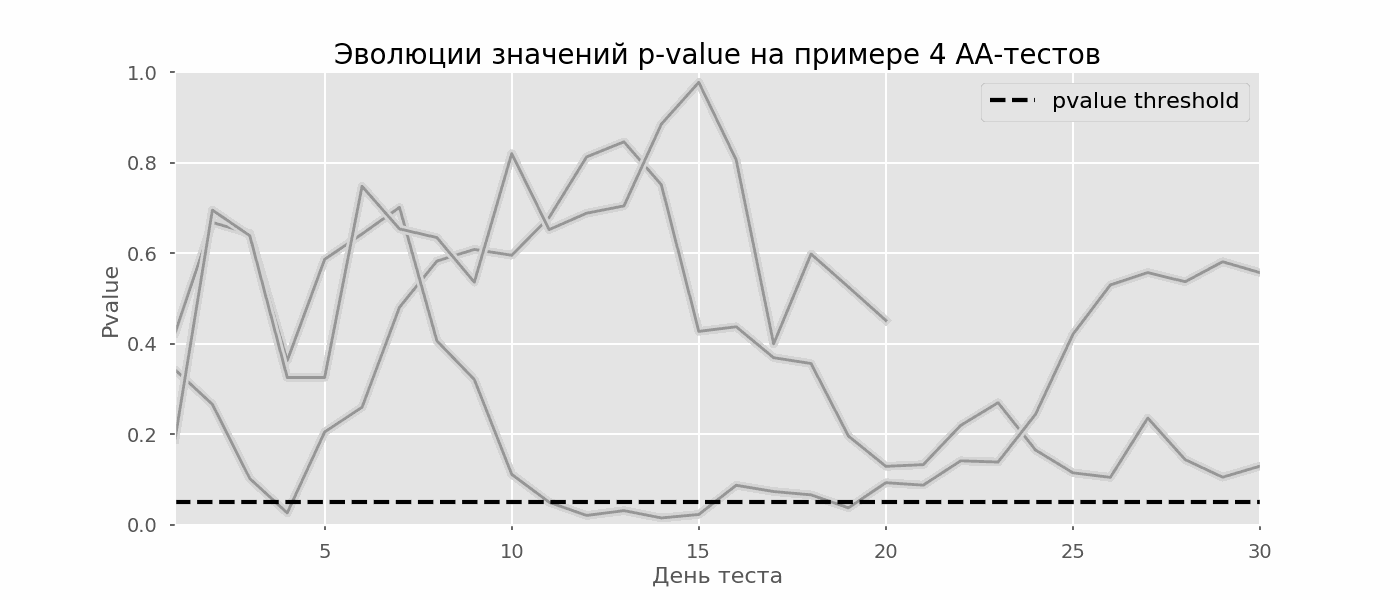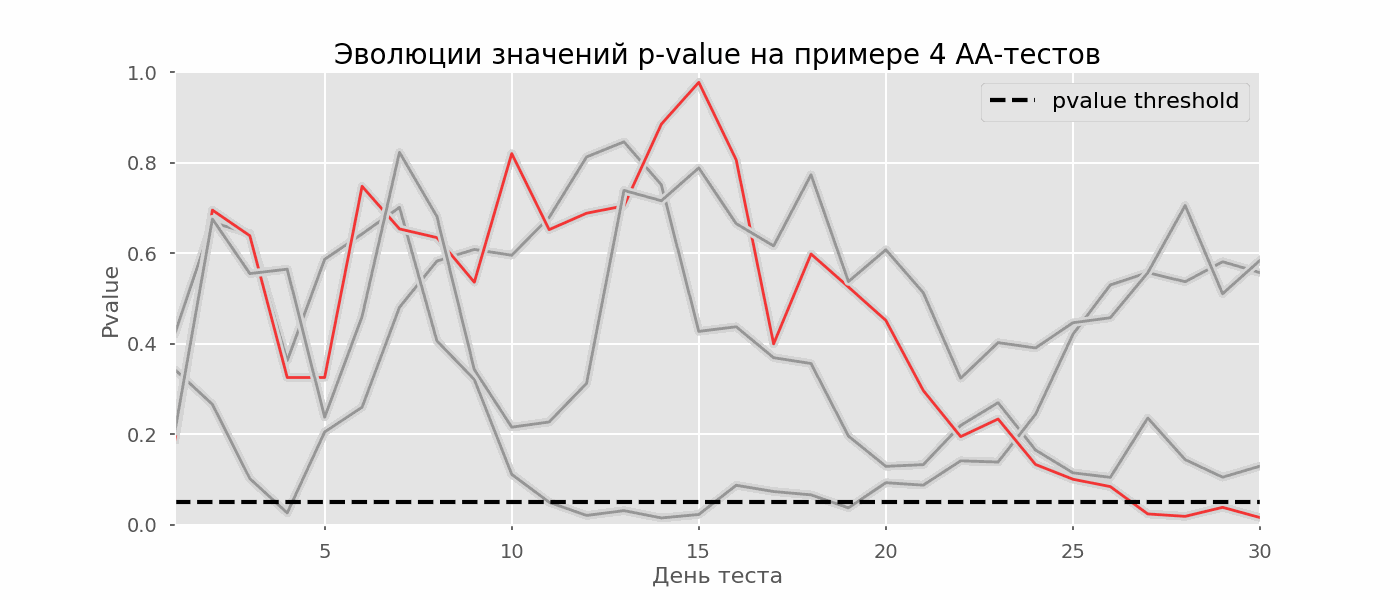
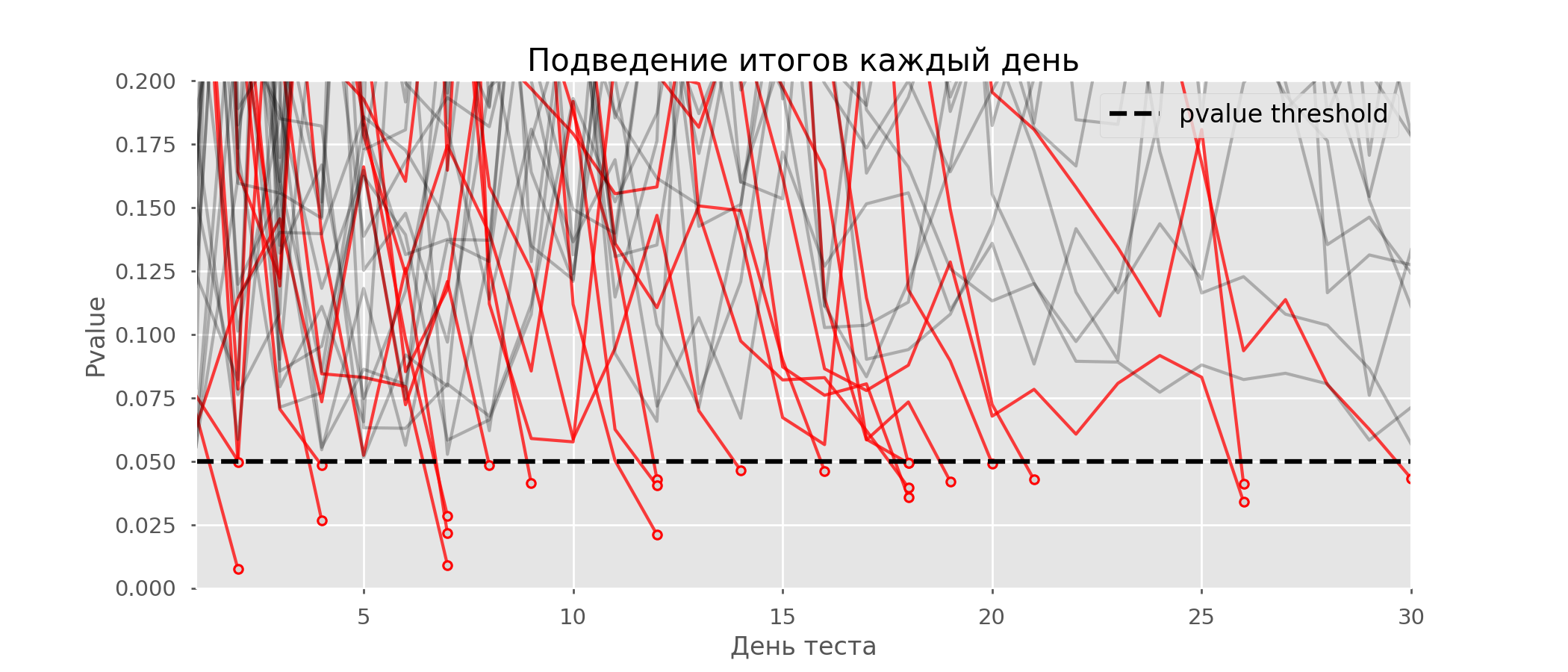
Красных линий настолько много, что уже ничего не понятно. Перерисуем, обрывая линии тестов, как только их p-value достигнут критического значения:

Всего будет 2813 ложноположительных тестов из 10 тысяч, или 28%. Понятно, что такая схема нежизнеспособна.

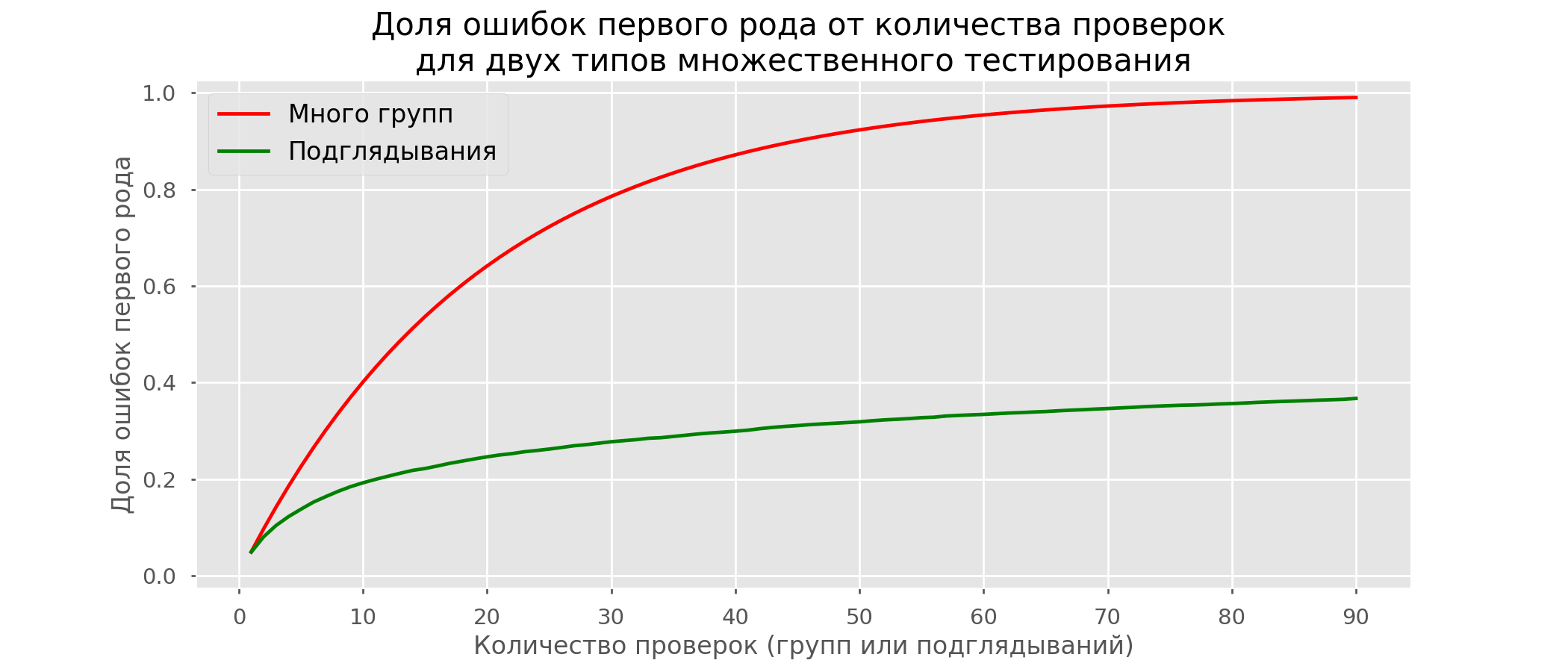
Хоть проблема подглядывания — это частный случай множественного тестирования, применять стандартные поправки (Бонферрони и другие) здесь не стоит, потому что они окажутся излишне консервативными. На графике ниже — доля ложноположительных результатов в зависимости от количества тестируемых групп (красная линия) и количества подглядываний (зелёная линия).

Хотя на бесконечности и в подглядываниях мы вплотную приблизимся к 1, доля ошибок растёт гораздо медленнее. Это объясняется тем, что сравнения в этом случае независимыми уже не являются.

Байесовский подход и проблема подглядывания

Можно встретить мнение, что Байесовский подход к анализу A/B-тестов избавляет от проблемы подглядывания. Это не так, хотя и его можно настроить соответствующим образом. Отличную статью с дополнительными материалами можно почитать здесь.

Методы досрочного завершения теста

Есть варианты тестирования, позволяющие досрочно принять тест. Расскажу о двух из них: с постоянным уровнем значимости (поправка Pocock’a) и зависимым от номера подглядывания (поправка O’Brien-Fleming’a). Строго говоря, для обеих поправок нужно заранее знать максимальный срок теста и количество проверок между запуском и окончанием теста. Причём проверки должны происходить примерно через равные промежутки времени (или через равные количества наблюдений).

Pocock

Метод заключается в том, что мы подводим итоги тестов каждый день, но при сниженном (более строгом) уровне значимости. Например, если мы знаем, что сделаем не больше 30 проверок, то уровень значимости надо выставить равным 0.006 (подбирается в зависимости от количества подглядываний методом Монте-Карло, то есть эмпирически). На нашей симуляции получим 4% ложноположительных исходов — видимо, порог можно было увеличить.

Несмотря на кажущуюся наивность, некоторые крупные компании пользуются именно этим способом. Он очень прост и надёжен, если вы принимаете решения по чувствительным метрикам и на большом трафике. Например, в «Авито» по умолчанию уровень значимости принят за 0.005.

O’Brien-Fleming

В этом методе уровень значимости изменяется в зависимости от номера проверки. Надо заранее определить количество шагов (или подглядываний) в тесте и рассчитать уровень значимости для каждого из них. Чем раньше мы пытаемся завершить тест, тем более жёсткий критерий будет применён. Пороговые значения статистики Стьюдента

$Z_{step}$ (в том числе значение на последнем шаге

$Z_{last_step}$ ), соответствующие нужному уровню значимости, зависят от номера проверки

(принимает значения от 1 до общего количества проверок

включительно) и рассчитываются по эмпирически полученной формуле:

$Z_{last_step} = 2.2471 + frac {0.3373} {total_steps} − frac {0.6331} {sqrt {total_steps}} \ Z_{step} = Z_{last_step} {sqrt { frac {total_steps} {step_number}}}$

Код для воспроизведения коэффициентов

from sklearn.linear_model import LinearRegression
from sklearn.metrics import explained_variance_score
import matplotlib.pyplot as plt

# datapoints from https://www.aarondefazio.com/tangentially/?p=83
total_steps = [
    2, 3, 4, 5, 6, 8, 10, 15, 20, 25, 30, 50, 60
]
last_z = [
    1.969, 1.993, 2.014, 2.031, 2.045, 2.066, 2.081, 
    2.107, 2.123, 2.134, 2.143, 2.164, 2.17
]
features = [
    [1/t, 1/t**0.5] for t in total_steps
]
lr = LinearRegression()
lr.fit(features, last_z)
print(lr.coef_)  # [ 0.33729346, -0.63307934]
print(lr.intercept_)  # 2.247105015502784
print(explained_variance_score(lr.predict(features), last_z))  # 0.999894

total_steps_extended = np.arange(2, 80)
features_extended = [ [1/t, 1/t**0.5] for t in total_steps_extended ]
plt.plot(total_steps_extended, lr.predict(features_extended))
plt.scatter(total_steps, last_z, s=30, color='black')
plt.show()

Соответствующие уровни значимости вычисляются через перцентиль

$perc$ стандартного распределения, соответствующий значению статистики Стьюдента

$Z$ :

perc = scipy.stats.norm.cdf(Z)
pval_thresholds = (1 − perc) * 2

На тех же симуляциях это выглядит так:

Ложноположительных результатов получилось 501 из 10 тысяч, или ожидаемые 5%. Обратите внимание, что уровень значимости не достигает значения в 5% даже в конце, так как эти 5% должны «размазаться» по всем проверкам. В компании мы пользуемся именно этой поправкой, если запускаем тест с возможностью ранней остановки. Прочитать про эти же и другие поправки можно по ссылке.

Метод Optimizely

Метод Optimizely хорош тем, что позволяет вообще не фиксировать дату окончания теста, а требуемый уровень значимости рассчитывается на каждый момент времени как функция от количества наблюдений в тесте. Интуитивно лично мне их метод нравится меньше, так как в нём жёсткость критерия увеличивается по ходу теста. То есть она минимальна в первые дни, когда случайный шум оказывает наибольшее влияние на метрики. В методе O’Brien-Fleming’a ситуация противоположная.

Калькулятор A/B-тестов

Специфика нашего продукта такова, что распределение любой метрики очень сильно меняется в зависимости от аудитории теста (например, номера класса) и времени года. Поэтому не получится принять за дату окончания теста правила в духе «тест закончится, когда в каждой группе наберётся 1 млн пользователей» или «тест закончится, когда количество решённых заданий достигнет 100 млн». То есть получится, но на практике для этого надо будет учесть слишком много факторов:

какие классы попадают в тест;
тест раздаётся на учителей или учеников;
время учебного года;
тест на всех пользователей или только на новых.

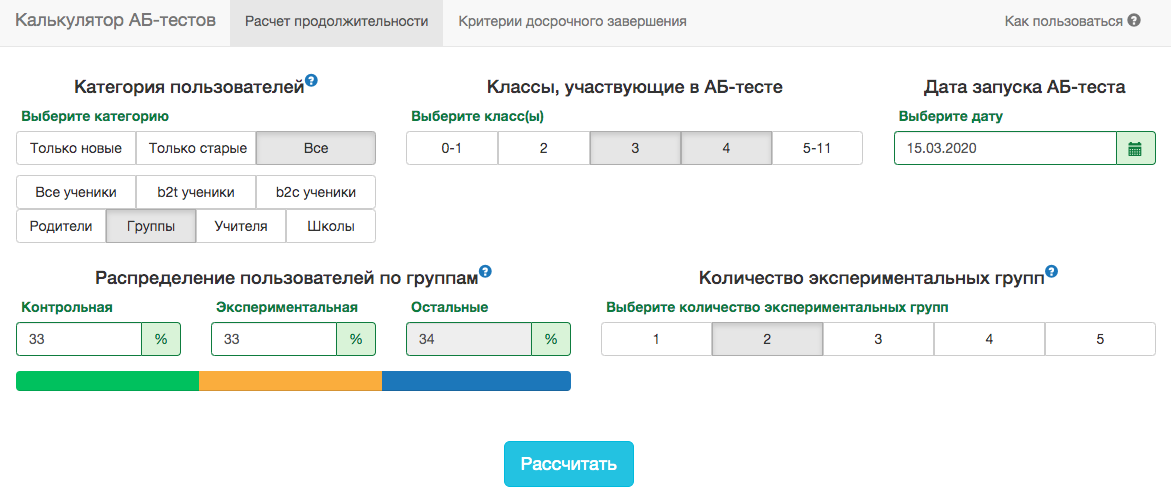
Тем не менее, в наших схемах A/B-тестирования всегда нужно заранее фиксировать дату окончания. Для прогноза продолжительности теста мы разработали внутреннее приложение — калькулятор A/B-тестов. Основываясь на активности пользователей из выбранного сегмента за прошлый год, приложение рассчитывает срок, на который надо запустить тест, чтобы значимо зафиксировать аплифт в X% по выбранной метрике. Также автоматически учитывается поправка на множественную проверку и рассчитываются пороговые уровни значимости для досрочной остановки теста.

Все метрики у нас рассчитываются на уровне объектов теста. Если метрика — количество решённых задач, то в тесте на уровне учителей это будет сумма решённых задач его учениками. Так как мы пользуемся критерием Стьюдента, можно заранее рассчитать нужные калькулятору агрегаты по всем возможным срезам. Для каждого дня со старта теста нужно знать количество людей в тесте

, среднее значение метрики

и её дисперсию

. Зафиксировав доли контрольной группы

, экспериментальной группы

и ожидаемый прирост от теста

в процентах, можно рассчитать ожидаемые значения статистики Стьюдента

и соответствующее p-value на каждый день теста:

$ttest_stat_precursor = frac{metric_mean sqrt {users_cnt}}{metric_std} \ ttest_stat_value = frac {ttest_stat_precursor} {sqrt{ frac{1} {control_group_share} + frac {1} {exp_group_share}}} * uplift_expected / 100$

Далее легко получить значения p-value на каждый день:

pvalue = (1 − scipy.stats.norm.cdf(ttest_stat_value)) * 2

Зная p-value и уровень значимости с учетом всех поправок на каждый день теста, для любой продолжительности теста можно рассчитать минимальный аплифт, который можно задетектировать (в англоязычной литературе — MDE, minimal detectable effect). После этого легко решить обратную задачу — определить количество дней, необходимое для выявления ожидаемого аплифта.

Заключение

В качестве заключения хочу напомнить основные посылы статьи:

Если вы сравниваете средние значения метрики в группах, скорее всего, вам подойдёт критерий Стьюдента. Исключение — экстремально малые размеры выборки (десятки наблюдений) или аномальные распределения метрики (на практике я таких не встречал).
Если в тесте несколько групп, пользуйтесь поправками на множественное тестирование гипотез. Подойдёт простейшая поправка Бонферрони.
Сравнения по дополнительным метрикам или срезам групп тоже подвержены проблеме множественного тестирования.
Выбирайте дату завершения теста заранее. Вместо даты также можно зафиксировать количество наблюдений в группе.
Не подводите итоги теста раньше этой даты. Это можно делать, только если вы заранее решили пользоваться методами, подразумевающими досрочное завершение, например, методом O’Brien-Fleming.
Когда вносите изменения в схему A/B-тестирования, всегда проверяйте её жизнеспособность A/A-тестами.

Несмотря на всё вышенаписанное, бизнес и здравый смысл не должны страдать в угоду математической строгости. Иногда можно выкатить на всех функционал, не показавший значимого прироста в тесте, какие-то изменения неизбежно происходят вообще без тестирования. Но если вы проводите сотни тестов в год, их аккуратный анализ особенно важен. Иначе есть риск, что количество ложноположительных тестов будет сравнимо с реально полезными.

Источник

Сегодня новая статья в рубрике #чтопочитать , где поговорим о статистике, науке о данных и на простом примере разберем A/B тестирование (проверку статистических гипотез).

Замаскированная проверка гипотез

Если вы уже имели дело со статистикой, вы возможно задавались вопросом: «Разве A/B тестирование не тоже самое, что проверка статистических гипотез?». Так и есть! Поэтому давайте узнаем побольше об A/B тестировании, разобрав на простом примере принцип работы проверки статистических гипотез.

Представьте, что наш клиент — владелец очень успешного приложения для работы с личными финансами. Он обратился к нам со следующей проблемой:

Тони, новый дизайн нашего приложения должен помочь пользователям сэкономить больше денег. Но приводит ли он к этому на самом деле? Пожалуйста помоги нам определить это, чтобы мы могли принять решение о внедрении этого дизайна.

Наша цель — определить, экономят ли пользователи лучше благодаря новому дизайну приложения. Для начала, нам надо узнать, имеем ли мы необходимое нам количество данных, поэтому мы задаем вопрос: «Какие потенциально полезные данные вы уже собрали?»

Оказывается, наш клиент уже провел эксперимент и собрал некоторые данные:

Шесть месяцев назад, наш клиент выбрал 1000 новых пользователей и разделил их на две группы: 500 в контрольной группе и 500 в экспериментальной группе.
Контрольной группе был предоставлен текущий дизайн приложения.
В то же время, экспериментальной группе был предоставлен новый дизайн.
Все пользователи начали с 0% экономии.
1000 пользователей составляют лишь маленькую часть всего количества пользователей данного приложения.

Через шесть месяцев, наш клиент фиксирует процент экономии всех 1000 пользователей. Процент экономии (дословно «норма сбережений») представляет собой процент, который конкретный пользователь экономит от расчетного чека за каждый месяц. Наш клиент узнает следующую информацию:

В контрольной группе среднее значение процента экономии составило 12% со стандартным (среднеквадратическим) отклонением в 5%.
В экспериментальной группе среднее значение процента экономии составило 13% со стандартным (среднеквадратическим) отклонением в 5%.

Результаты нашего эксперимента на гистограмме выглядят следующим образом:

Создается впечатление, что по окончании шести месяцев представители экспериментальной группы имели более высокий процент экономии, чем представители контрольной группы. Можем ли мы просто построить данную гистограмму, показать её клиенту и считать работу законченной?

Нет, потому что мы не можем быть уверены в том, что данный рост экономии был вызван новым дизайном. Возможно, нам просто не повезло при выборе пользователей для эксперимента, и все люди с желанием экономить больше попали в экспериментальную группу.

Для решения этой проблемы нам необходимо задать следующий вопрос:

Какова вероятность того, что данный результат мы получили только из-за случайного стечения обстоятельств?

Суть проверки статистических гипотез (и А/В тестирования) как раз и заключается в ответе на данный вопрос.

Нулевая гипотеза

Давайте представим альтернативную ситуацию, в которой новый дизайн не помог пользователям экономить лучше. Даже в таком случае, несмотря на то что новый дизайн получился бесполезным, мы все еще можем наблюдать рост процента экономии при проведении нашего эксперимента.

Как такое могло произойти? Это может произойти из-за того, что мы используем выборку. Приведу пример: если я случайном образом выберу 100 людей из десяти тысячной толпы и вычислю их средний рост, результат составит, например, 170 см. Но проведя данный эксперимент еще несколько раз, результат будет 177 см, 168 см и так далее.

Так как мы вычисляем статистику используя выборки, а не всё целое, средние значения каждой выборки будут различаться.

Зная, что использование выборок приводит к вариациям, мы можем переформулировать предыдущий вопрос:

В случае если новый дизайн на самом деле никак не влияет на экономию пользователей, какова вероятность того, что мы обнаружим настолько же высокий рост экономии, как и при случайном стечении обстоятельств?

Формально говоря, мы формулируем нулевую гипотезу следующим образом: рост процента экономии контрольной группы равен росту процента экономии экспериментальной группы.

Теперь наша работа заключается в проверке данной нулевой гипотезы. Мы можем сделать это проведя мысленный эксперимент.

Многочисленное проведение эксперимента

Представьте, что мы можем проводить наш эксперимент снова и снова. При этом, мы все еще рассматриваем ситуацию, в которой новый дизайн никак не влияет на экономию пользователей. Что мы будем наблюдать?

Для тех, кому интересно, вот как мы это представляем:

Для каждой группы генерируем 500 нормально распределенных случайных величин с такими же статистическими характеристиками, как и у контрольной группы (среднее значение = 12%, среднеквадратическое отклонение = 5%). Теперь у нас есть контрольная группа и экспериментальная группа (средние значения одинаковы, так как мы рассматриваем ситуацию, в которой новый дизайн не имеет никакого эффекта). Технически, правильнее было бы использовать распределение Пуассона, но мы используем нормальное распределение для простоты примера.
Вычисляем разность средних значений процентов экономии двух групп (например, мы можем вычесть из среднего значения процента экономии контрольной группы среднее значение процента экономии экспериментальной группы).
Проделываем данные шаги 10 000 раз.
Строим гистограмму, показывающую разности средних значений экономии двух групп.

В итоге, мы получаем гистограмму, приведенную ниже. Данная гистограмма показывает, насколько сильно среднее значение процента экономии между группами различается из-за случайного стечения обстоятельств (обусловленное использованием выборки).

Красная вертикальная линия показывает тот результат, который получил наш клиент при проведении эксперимента (1%). Для нас важен процент количества значений справа от красной линии — он показывает вероятность того, что при проведении эксперимента мы получим разность, равную 1% или выше (мы используем односторонний критерий, потому что он легче для понимания).

В данном случае это значение очень маленькое — из 10 000 экспериментов только в 9 мы получили разность процентов экономии групп, равную 1% или выше.

Это означает, что результат, который наш клиент получил при проведении эксперимента, по случайному стечению обстоятельств может быть получен с вероятностью лишь 0.09%!

Данная вероятность, 0.09%, является нашим p-значением. «Каким значением? Хватит забрасывать меня какими-то случайными терминами!» — вы можете подумать. И правда, когда дело доходит до проверки статистических гипотез, приходится использовать много различных терминов, и, мы, пожалуй, оставим их разъяснение Википедии.

Наша задача, как и всегда, состоит в построении интуитивного понимания того, как работают эти инструменты статистики и для чего они пользуются, поэтому по возможности мы постараемся избегать использования терминологии в пользу простоты объяснении. Однако, p-значение является крайне необходимым термином, с которым вы еще не раз встретитесь в мире науки о данных, поэтому его мы должны обсудить. P-значение (в нашем случае 0.09%) представляет собой:

Вероятность получения, наблюдаемого нами результата, в случае если нулевая гипотеза правильна.

Соответственно, мы можем использовать p-значение для проверки справедливости нулевой гипотеза. Основываясь на определении, кажется, что мы хотим, чтобы это значение было минимальным, так как, чем меньше p-значение, тем менее вероятно то, что результат нашего эксперимента был случайным. Но на практике, мы введем уровень значимости для p-значения (называемый «альфа»), и, в случае если p-значение меньше альфа, мы отвергаем нулевую гипотезу и делаем вывод, что полученный результат и эффект реальны (статистически значимы).

Теперь давайте рассмотрим способ быстрого вычисления p-значения.

Центральная предельная теорема

Время поговорить об одной из фундаментальных концепций статистики. Центральная предельная теорема утверждает, что при сложении независимых случайных величин, их сумма стремится к нормальному распределению по мере сложения всё большего количества величин. Центральная предельная теорема работает даже в случае, если случайные величины не имеют нормального распределения.

Другими словами, если мы вычислим средние значения набора выборок (подразумевая, что все наши наблюдения независимы друг от друга, как, например, друг от друга не зависят броски монетки), распределение всех этих выборок будет близко к нормальному.

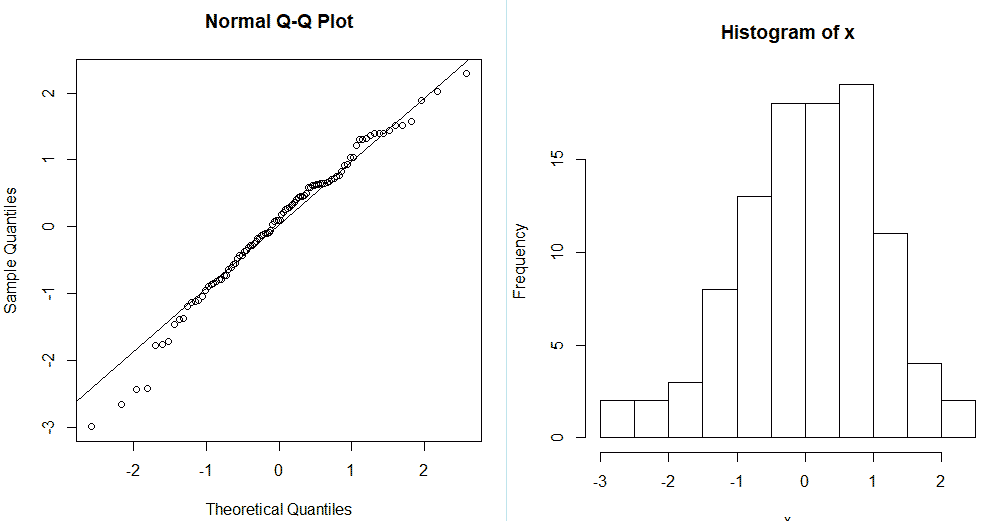
Взгляните на гистограмму, которую мы построили ранее. Выглядит как нормальное распределение, не так ли? Мы можем проверить нормальность с помощью КК (квантиль-квантиль) графика, который сравнивает квантиль нашего распределения с другим квантилем (в нашем случае, с нормальным распределением). Если наше распределение нормальное, то КК график будет близок к красной линии, находящейся под углом в 45°. И именно так и получается, здорово!

Значит, когда мы проводили наш эксперимент снова и снова, это был пример работы центральной предельной теоремы!

Так почему же это так важно?

Помните, как мы проверяли нашу нулевую гипотезу, проводя 10 000 экспериментов? Звучит очень утомительно, не так ли? На практике, это и утомительно, и дорого. Но благодаря центральной предельной теореме мы можем это избежать!

Теперь мы знаем, что распределение наших повторяющихся экспериментов будет нормальным, и мы можем использовать это знание для определения того, как распределяться наши 10 000 экспериментов без их проведения!

Давайте обобщим пройденное:

Мы знаем, что разность средних значений процента экономий экспериментальной группы и контрольной группы составляет 1%, и мы хотим узнать, является ли эта разность оправданной.
Важно помнить, что мы провели эксперимент лишь на маленькой части от всего количества пользователей приложения. Если мы проведем эксперимент заново, результат немного изменится.
Так как нас волнует возможность того, что новый дизайн не имеет никакого эффекта на экономию, мы формулируем нулевую гипотезу: разность средних значений экономии двух групп — 0%.
Согласно центральной предельной теореме, при повторном проведении данного эксперимента, его результаты будут нормально распределены.
Из основных формул статистики, мы также знаем, что дисперсия разности двух независимых случайных величин равна сумме дисперсий данных величин:

Завершающие шаги

Здорово! Теперь у нас есть всё, что нам требуется для проверки гипотезы. Давайте завершим работу для нашего клиента.

Перед тем как взглянуть на имеющиеся данные, нам надо выбрать уровень значимости, называемый альфа (если полученное p-значение меньше альфа, мы отвергаем нулевую гипотезу и делаем вывод, что новый дизайн привел к росту экономии). Значение альфа соответствует вероятности допущения ошибки первого рода — отвержения правильной нулевой гипотезы. Обычно специалисты используют значение 0.05, поэтому его мы и используем.
Далее нам надо вычислить тестовую статистику. Тестовая статистика является числовым эквивалентом вышеприведенной гистограммы и обозначает среднеквадратическое отклонение нашего наблюдаемого значения (1%) от значения нулевой гипотезы (в нашем случае 0%). Вычислить мы её можем по формуле:

Стандартная ошибка — это среднеквадратическое отклонение разности средне арифметических значений экономии экспериментальной группы и экономии контрольной группы. На графике выше, стандартная ошибка обозначена шириной синей гистограммы. Помните, что дисперсия разности двух случайных величин равна сумме дисперсий данных величин (а среднеквадратическое отклонение — это квадратный корень дисперсии). Зная это, мы с легкостью можем вычислить стандартную ошибку:

Среднеквадратическое отклонение равно 5% как для контрольной группы, так и для экспериментальной группы, поэтому наша выборочная дисперсия равна 0.0025. N — это количество наблюдений в каждой группе, поэтому N равно 500. Подставляем числа в формулу и получаем стандартную ошибку, равную 0.316%.
В формуле тестовой статистики наблюдаемое значение — 1%, а значение гипотезы — 0% (так как наша нулевая гипотеза, предполагает, что эффекта нет). Подставляя данные значения вместе со значением стандартной ошибки в формулу тестовой статистики, мы получаем результат 3,16.
Это значение довольно велико. Мы можем использовать приведенный ниже Python код для вычисления p-значения (для двустороннего критерия). Получится p-значение, равное 0.0016. Важно понимать, что мы используем двусторонний критерий, потому что мы не можем заранее быть уверенными в том, что новый дизайн или лучше текущего, или не имеет эффекта — новый дизайн может также иметь негативное влияние, и двусторонний критерий учитывает такую возможность.

from scipy.stats import norm

#Двусторонний критерий

print(‘The p-value is: ‘ + str(round((1 — norm.cdf(3.16))*2,4)))

P-значение (0.0016) меньше альфа (0.05), поэтому мы отвергаем нулевую гипотезу и говорим клиенту, что новый дизайн на самом деле помогает пользователям лучше экономить. Ура, победа!

Но обратите еще внимание на то, что p-значение, которое мы вычислили аналитически (0.0016), отличается от значения 0.0009, которое мы получили ранее. Связано это с тем, что наша симуляция была односторонней (односторонний тест более легок для понимания и визуализации). Мы можем удвоить данное значение для получения 0.0018, примерно равного настоящему 0.0016.

Подведем итоги

В реальной жизни A/B тестирование не настолько легко как в нашем выдуманном примере. Скорее всего, наш клиент не будет обладать готовыми данными, и нам придется самим искать нужные данные. Приведу несколько трудных моментов, с которыми вы можете встретиться при A/B тестировании:

Сколько данных вам нужно? Сбор данных требует много времени и денег. Плохо проведенный эксперимент может даже негативно повлиять на пользовательский опыт. Но недостаточное количество информации приведет к тому, что результаты вашей работы будут не очень надежными. Поэтому вам придется соблюдать баланс между преимуществами большего количества данных и возрастающими затратами на их сбор.
Что хуже — отвержение правильной нулевой гипотезы (ошибка первого рода) или принятие неправильной нулевой гипотезы (ошибка второго рода)? В нашем примере ошибка первого рода означала принятие нового дизайна, в то время как он не имеет никакого эффекта. Ошибка второго рода означала отказ от нового дизайна, хотя он помог бы людям экономить лучше. Мы находим подходящий баланс между вероятностями ошибки первого рода и ошибки второго рода выбирая уровень значимости (альфа). Более высокое значение альфа увеличит риск ошибки первого рода, меньшее значение увеличит риск ошибки второго рода.

Источник

A/B-тесты это основной способ решения споров об интерфейсах в команде. Но часто эти споры решаются неверно, потому что ключевая ошибка при анализе результатов A/B теста это сравнение двух средних, без подбора критерия, оценки выборки. Беглый визуальный анализ отчетов в GA по принципу «где график выше, та версия и лучше» приводит к ошибочным выводам и стоит бизнесу кучу денег. Если до этого момента вы обходились знаниями, что онлайн-калькуляторы должны показать «p < 0.05» и «нормальное распределение похоже на колокол», то в этой статье я постараюсь расширить ваш кругозор.

Все примеры будут продемонстрированы для R-Studio. Общий процесс анализа: экспериментальный дизайн → сырые данные → обработанные данные → выбор статистической модели → суммарная статистика → p value. С экспериментальным дизайном дизайнеры справляются, про остальные шаги давайте говорить подробнее.

Формируем гипотезу

При формировании гипотезы руководствоваться лучше простыми понятиями: цели бизнеса, как эти цели достигаются клиентами и как это можно измерить (Single A/B test или Multi A/B test). Не менее важно понимать, как данные будут собираться и валидироваться, и как будут вноситься изменения по результатам теста. При этом предполагается, что проблема репрезентативности и достаточности объёма выборки решена. По умолчанию в данном уроке мы будем считать, что стандартное отклонение (корень из дисперсии) не зависит от размера выборки, так как выборка репрезентативна.

Но будем честны, часто задача будет ставиться по принципу: «у нас упала прибыль, посмотри, че там такое». Или приходит продукт-менеджер или гейм-дизайнер, рассказывает про уже реализованную фичу на проде, и просит узнать эффективность этой фичи. При этом нет информации, на что эта фича была направлена, на каких данных ее исследовать, как ее операционализировать. В случае столь слабо формализованных задач нужно придумывать гипотезы самостоятельно и думать, откуда взять данные для формирования этих гипотез. Помогает консолидация данных из разных источников.

Либо, в качестве источника гипотезы банальный спор менеджеров продукта и проекта, результат коридорного опроса, желание оптимизировать CRO. Я не люблю тестировать фичи, которые очевидно улучшат конверсию, это достаточно бесполезная работа. Лучше тестировать фичи, у которых отдача бизнесу непредсказуема. В таких фичах обычно кроется рост всех ключевых метрик: CTR (Click Through Rate), конверсия, CPA, ROAS, CPI. Должен сказать, что при малом количестве данных очень сложно оценивать небинарные метрики (средний чек, выручка), результаты обычно очень шумные: работает принцип garbage in garbage out. А вот A/B тесты для бинарных задач проводить просто (выполнено/не выполнено). Но в любом случае самый первый шаг это определиться с целевой метрикой.

Далее мы должны определиться с математикой. Например, у нас частотный подход, а не Байес. Выбираем класс критериев. Если распределение нормальное, то параметрические критерии (Стьюдент, Anova для равенства средних; F-test, Бартлетта, Левана на равенство дисперсий; тест пропорций для биномиальных метрик; формальные тесты на принадлежность распределению). Они считают свою статистику на основе информации об оригинальной функции распределения, т.е. мы должны задать некие переменные. Если сравниваем средние и данных не много, то Bootstrap (траты внутри приложения). Последняя инстанция это непараметрические тесты, им нужна только информация из выборки. Есть подклассы: критерии случайности, симметрии, корреляции, сдвига и масштаба, сдвига. Они не такие мощные, но применимы везде. Так, Манна-Уитни и Краскала-Уоллисана наличие сдвига, для зависимых выборок тест Фридмана и «знаковый» критерий Уилкоксона, Bootstrap для сравнения распределения характеристик по квантилям и хи-квадрат Пирсона для изменения функций распределения.

Отличная практика для реальных данных со смещением влево, это сравнить две выборки непараметрикой, и сравнить эти же выборки после логарифма t-test’ом. Двойная проверка результата.

Хорошая гипотеза учитывает принципы индукции и фальсифицируемости. Индукция это отрицание гипотезы, возможность сформулировать негативного суждения. Древнегреческие боги были? Нет, не было. Фальсифицируемость же про попытки опровергнуть гипотезу, и если не получилось, тогда гипотезу можно принять. Докажи что не было Древнегреческих богов, а до тех пор считаем, что они были.

При проверке гипотезы помним, что нулевая гипотеза про отсутствие отличий, для ее доказательства нужна вся популяция, а не выборка. Альтернативная гипотеза говорит о значимости различий. Все отличия в выборках это всегда альтернативная гипотеза, а проверяется всегда нулевая. Ошибка первого рода (α, false positive) происходит, когда мы отклоняем нулевую гипотезу в пользу альтернативной гипотезы, при условии что справедлива нулевая гипотеза. H0 считается верной, пока не доказано обратное, и если она отвергается, значит нам пора бежать предпринимать действия. Это та самая альфа 0,05, которая говорит что в одном случае из 20 будет ошибка первого рода. Ошибка второго рода (false negative) происходит, когда верна альтернативная гипотеза, но было принято решение принять нулевую гипотезу. Другими словами, во время дизайна теста мы задаем уровень значимости. который показывает вероятность верности нулевой гипотезы. На основе significance level мы принимаем или отвергаем гипотезу с полученным p-value, это вероятность совершить ошибку первого рода. Вероятность ошибки второго рода это 1 — power, шанс не заметить значимые изменения. Поэтому нет смысла делать дизайна тестов базируясь только на ошибке первого рода. Низкое значение уровня значимости уменьшает шанс совершить ошибку первого рода, но растет шанс совершить ошибку второго рода, поэтому значение p-value подбирается исходя из критичности допуска ошибок. Например, нельзя допустить ошибку второго рода в таком кейсе: не сработать сигнализацией при попытке угона машины, это критично. При работе с калькуляторами вроде evanmiller для расчёта доверительных интервалов разницы мы не учитываем ошибку второго рода.

Возможно, некоторым будет проще понять так: p-value это соответствие площадей двух гипотез, дисперсии равны.

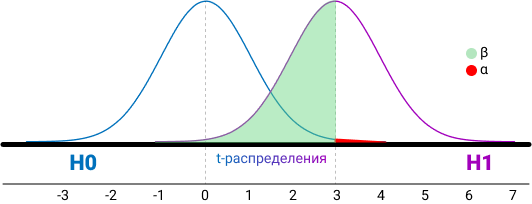
Доверительные интервалы всегда считаются по результатам теста и куда информативнее, чем размер выборки и мощность. Доверительные интервалы это способ смотреть на соответствие реальных и теоретических данных. Выборка из нормального распределения, и выборочное среднее не может быть равно мат. ожиданию. Поэтому нам нужно знать интервал, в который попадает значение оцениваемого параметра.

Итак, summary: если человек болен и мы это подтвердили — true positive (TP). Если человек не болен и мы это подтвердили — true negative (TN). Ошибка первого рода — здоровому человеку сказали, что он болен (FP). Или ошибка второго рода, сказали больному человеку что он здоров (FN).

Ошибки будут всегда, и для определения их существенности есть две метрики: полнота и точность (recall и precision), они про количество ошибок первого и второго рода. Recall = TP/(TP+FN), Precision = TP/(TP+FP). Метрики между собой конкурируют, поэтому надо учитывать обе метрики по интегральной характеристике.

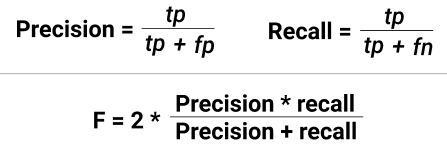
И вернемся к метрикам бизнеса, нельзя про них забывать в ходе погружения в техническую часть. Надо видеть картину целиком. Если игнорировать LTV (lifetime value или сколько денег принес клиент за свой жизненный цикл) и ROI (return on investment или окупилась ли сумма привлечения клиента), то в краткосрочной перспективе можно хорошо поднять метрики ARPU diary, ARPU month и процент платящих, чем часто пользуются продуктовые менеджеры, бегающие из компании в компанию. Для краткосрочного поднятия ARPU достаточно ввести дополнительные регулярные акции. Но в долгосрочной перспективе такой подход приведет к финансовым проблемам, так как каннибализирует остальные механики привлечения денег, и это будет видно на LTV 6 month. Еще можно выполнить краткосрочный KPI если uplift-нуть CTR одной кнопки, и каннибализировать CTR других кнопок. Или остановить трафик для мобильного приложения, очень краткосрочно подрастет ROI. В общем, любые временные изменения в базовой экономике всегда ведут к временному увеличению метрик с дальнейшей трагической просадкой. Можно привести более наглядный пример: промо-ловушка из продуктовых магазинов. Покупатель думает, что цены растут и доходы снижаются, значит нужно меньше тратить. Продавцы это видят и снижают цены в рамках акций, это увеличивает выручку на короткий промежуток времени. Покупатели привыкают к акциям и идут в магазин целенаправленно в поисках товаров по скидке, продавец вынужден еще раз снижать цену, и далее делать это постоянно. При чем тут тесты? Бизнес после запуска разовой акции видит, что прибыль пошла вверх, трафик увеличился, клиентов стало больше, но вы как аналитик должны сказать, что не смотря на это выгода/маржа/грязный вал в разрезе трех месяцев упали. Это вечная дилема: выполнить план и получить просадку по марже, или не выполнить план, разово увеличить прибыль, но просесть по выручке. Говорите бизнесу про положительную EBITDA, тогда они вас будут слушать

Я буду приводить p-value = 0,05, так как это общепринятое значение. В реальных проектах p-value куда меньше.

Либо вы идете к разработчику и он каким то образом все делает за вас, и при работе с мобилками это основной способ проведения A/B теста. Либо используете GTM или Google Optimize, где разделяем трафик, готовите визуальное представление гипотезы и задаете условия ее отображения (сегменты и тому подобное). В результате будет возможность менять не только цвет и тексты на странице, но и создавать новые функциональные сущности или развивать имеющиеся, а также успешно сегментировать гипотезы еще на этапе запуска. Это дает большое преимущество в условиях ограниченных технических и финансовых ресурсов крупного бизнеса.

С Optimize надо быть осторожным, нельзя полагаться на автоматику. Так, предположим что у вас есть два варианта страницы, но только второй вариант проходит через переадресацию. Тогда latency и частота отказов у второго варианта будет больше, как следствие, когорта меньше. Если смотреть более глобально на вопрос «в какой момент пользователь должен попасть в свою группу во время теста», то очевидным ответом будет «чем раньше, тем лучше». Тесты могут быть exposed и non-exposed, в первом случае мы сталкиваем пользователя с изменениями на сайте и тем самым уменьшаем дисперсию (не факт), во втором — глобально делим на когорты, тем самым экстраполируем эффект на весь трафик. Кейс из практики: мы устанавливаем виджет с такси только на главную страницу нашего сайта и только для пользователей, у кого накопилось более 20 000 баллов. Тогда используем exposed тест, считаем A2C, получаем бОльший эффект, чем при подсчете метрики глобально.

Вот как все происходит в подавляющем большинстве случаев: случайно делите весь новый трафик из новичков на тест и контроль. На основании опыта или теории получаем ожидаемый размер эффекта, и от него считаем выборку. Получив результаты, проверяем их на статистическую значимость. Дополнительно, можно провести АAB-тест, это позволит убедиться, что различия только на уровне поведения пользователей, а не на уровне багов системы, изменения погоды и прочих факторов. Аудиторию перед тестом можно раскидывать простым рандомом, а можно престратификацией (CUPED). Если почти все пользователи новые, то CUPED с дополнительной ковариатой.

В идеальном случае после запуска теста через определенное время тест проверяется, и делается переоценка кол-ва дней, нужных для сбора данных. Торопиться при сборе данных не надо, средний цикл оформления банковской услуги это 2 недели, значит, это минимальный срок для сбора данных. Данные влияют на качество валидации гипотез, обязательно проверяем стабильность данных (отсутствие шума), исходя из исторических данных.

Данные не обязательно собирать самостоятельно, основные источники данных это:
1. Данные из собственных приложений, сайтов, расширений и т.д (CRM, ERP, транзакции, метрика, Amplitude).
2. Снифферинг незашифрованного траффика на крупных узлах обмена данными.
3. Покупка данных сторонних поставщиков — создателей приложений, расширений, рекламных/баннерных сетей, малвари, червей и т.д., как легитимным, так и не очень образом.
4. Открытые данные рынка и исследования агентств (Росстат, GFK).
5. Сырые events из продукта.
6. Покупка данных о посещаемости каких-нибудь ресурсов, которые готовы продать данные.
7. Хантинг людей, опросы и исследования, фокус-группы.

Характеристика и нормализация данных

Предположим, данные готовы, они могут быть в формате csv или Excel. Их может быть много или мало, плотность распределения вероятностей среднего значения выборки может быть нормальной и ненормальной. Проверка на нормальность данных нужна, чтобы центральная предельная теорема выполнялась на малых выборках. Если выборки большие и наблюдения независимые, то предположение о нормальном распределении для теста Стьюдента не нужно (т.к. работает центральная предельная теорема). На 1000 пользователях не удастся отследить мелкие изменения (1-2%), но изменения в 20-30% можно. Проще говоря, при большой выборке результаты теста будут точные, при маленькой выборке не факт, что есть смысл проводить A/B тест.

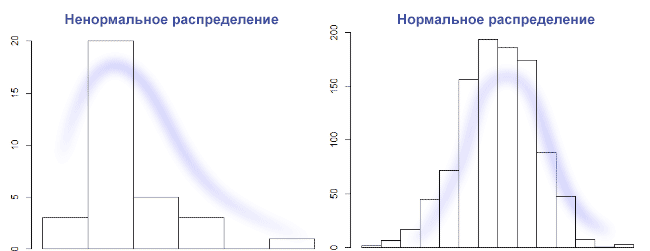
Предположим, что данных мало, значит, нужна проверка о типе распределения данных. Не факт, что удастся отличить равномерное распределение от нормального на очень маленькой выборке. В общем случае, нужно построить график столбчатой диаграммы и посмотреть его форму. Нормальное распределение выглядит как колокол с тремя сигмами с каждой стороны. Правило трех сигм: каждая сигма это одно стандартное отклонение, данные нормально распределены, и 99,7% выборки попадает влево по графику на три сигмы, и вправо по графику на 3 сигмы. Если выборки гомогенные и распределение нормальное, то наш выбор это t-Критерий Стьюдента. На Стьюденте сложно контролировать мощность, и значит, растет шанс совершить ошибку второго рода. Если же по графику видно, что распределение с отклонением на левую сторону графика, то используется хи-квадрат Пирсона, это непараметрический критерий. Он хорошо подходит для проверки равномерного налива трафика, но требует сгруппировать данные по бакетам (создать таблицу сопряженности). Если распределение отлично от нормального, то правило трех сигм — не лучший выбор, если наше распределение вырожденное. Но на картинке ниже слева распределение вполне может быть логнормальное, и можно отрезать по квантилям.

Встречается еще мультимодальное или бимодальное распределение, но чаще после ресемплинга. Если мы говорим про оценку средних, то при достаточном кол-ве наблюдений данные будут распределены нормально. Это большой плюс работы над крупным продуктом, в котором всегда много данных: при любом распределении исходных величин распределение выборочных средних будет стремиться к нормальному. Результат попросту зависит от мощности, т.е. от размера выборки. Идеально нормальных данных быть не может, если под реальной жизнью не понимать результат работы функции rnorm(). Да и данные в нашем случае дискретны и являются набором точек. Поэтому на большой выборке shapiro-wilk всегда будет значимым. А вот на выборках 10-15 значений он всегда незначимый из-за недостаточной мощности. В статистике мощность асимптотически стремится к 1.

Мощность это вероятность допустить ошибку первого рода, то есть отклонить нулевую гипотезу, хотя она верна.

Стратификация (выделение суб-группы из выборки и рандомом деллим на 2 группы) не плохо работает для однородности. Страта это группа наблюдений, подчиняющихся единому правилу. Стратифицированный метод предпочтителем, когда мы сначала делим людей по какому-то признаку (например, по полу), а затем берем людей из этих групп в равной пропорции. Если люди распределяются между двумя группами полностью случайно, то ни о какой статистической значимости речи быть не может.

Сегментация нужна. Хотя бы на уровне киты/планктон и рандомом, сверяясь на A/A-тесте. Или по странам, месяцу регистрации. Если нет параметрического критерия, тогда делим данные на две одинаковые группы, задаем α — уровень значимости, n — размер выборки, mde — эффект. Одну из групп сдвигаем на mde, применяем критерий и бутстрэп.

Итоговый процент принятия нулевых гипотез будет 1 — β. По завершению A/A-теста важно посмотреть на распределения p-value. Оно должно быть равномерным. Если наблюдается скос, то значит, есть сильные зависимости между данными и анализ делать нельзя. А вот для a/b такой подход не пойдёт.

И даже так выборки могут быть с нестабильным по времени и с дисбалансом. Поэтом важно выбрать подходящий критерий для таких выборок. Ресемплинг поможет для оценки, как и моральная подготовка к перезапуску теста при наличии скачков данных на ретроспективе.

Выбросы надо смотреть на box-plot и удалять ручками, как и дубли. Если мы работает с финансовыми метриками и удалять выбросы невозможно, то значит увеличивается разброс значений и доверительные интервалы также увеличиваются. Применяется правило трех сигм: убрать все значения, которые выходят за три стандартных отклонения и посмотреть, как изменятся наши данные. Но будет большая потеря данных, что может быть критично. Другой способ это метод трансформации по Боксу-Коксу. При этом надо понимать, что удаление выбросов только для применения того или иного критерия—не верный подход. Прагматичнее для начала посмотреть срезы, где явно будут видны различия.

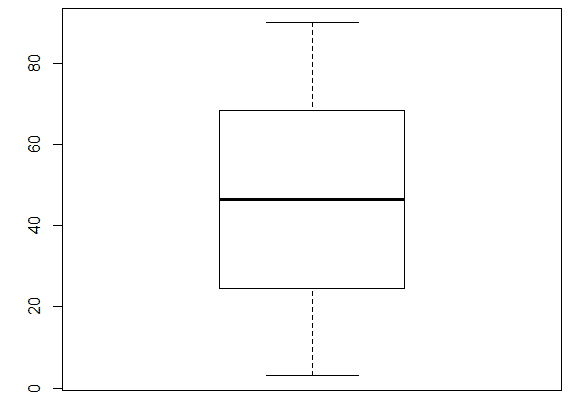
Давайте сгенерируем данные таким способом usersExport <- data.frame(n = 3:90) и построим график boxplot(usersExport). Мы получим практически идеальный график, на котором есть квантили.

Как читать график boxplot: точка или линия соответствуют средней арифметической, эту точку окружает квадрат, его длина соответствует точности оценки генерального параметра. Усы от квадрата соответствуют своей длиной одному из показателей разброса или точности. Для формирования boxplot нужно написать комманду boxplot(имя переменной). Можно для эксперимента создать дырки в данных usersExport <- usersExport[-sample(3:90, 23), ] и посмотреть, как изменится график boxplot.

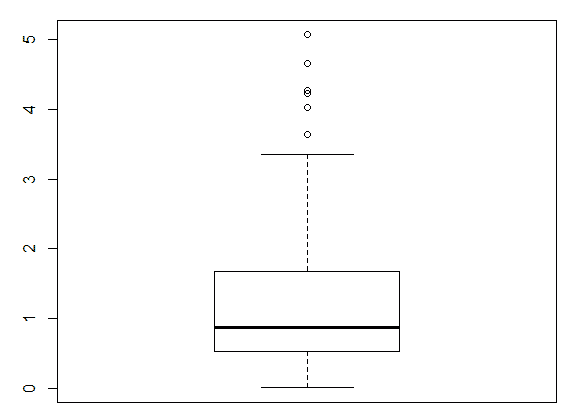
Вот пример графика с выбросами:

Проверить данные на нормальность можно простым взглядом по qqplot(). При больших объемах тесты практически всегда покажут отклонения от нормального распределения. Поэтому, если данные получились очень ненормальные, например у времени, проведенного за смартфоном или финансовых показателей всегда есть ограничение снизу, то нужна нормализация или хотя бы удаление выбросов. Переходя к цифрам, различие в 5% не такое уж и большое. На большой выборке будет совсем близко к 0,05. Кроме того, многие тесты устойчивы к умеренным отклонениям от нормального распределения. Даже очень небольшие отклонения от нормальности будут значимы на больших выборках, но это справедливо для всех стат. тестов.

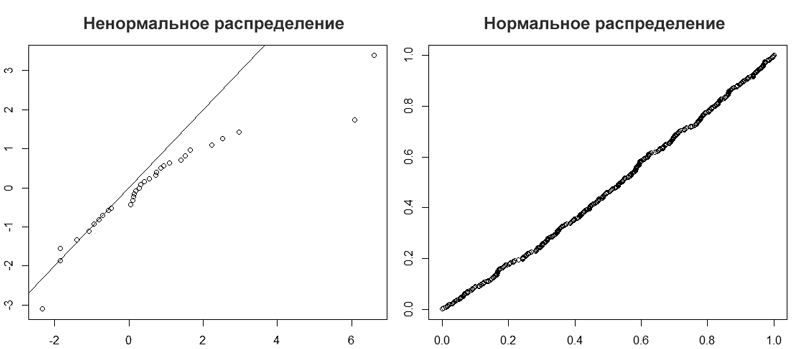
qqplot(rt(a,df=3), x, main="t(3) Q-Q Plot")
abline(0,1)

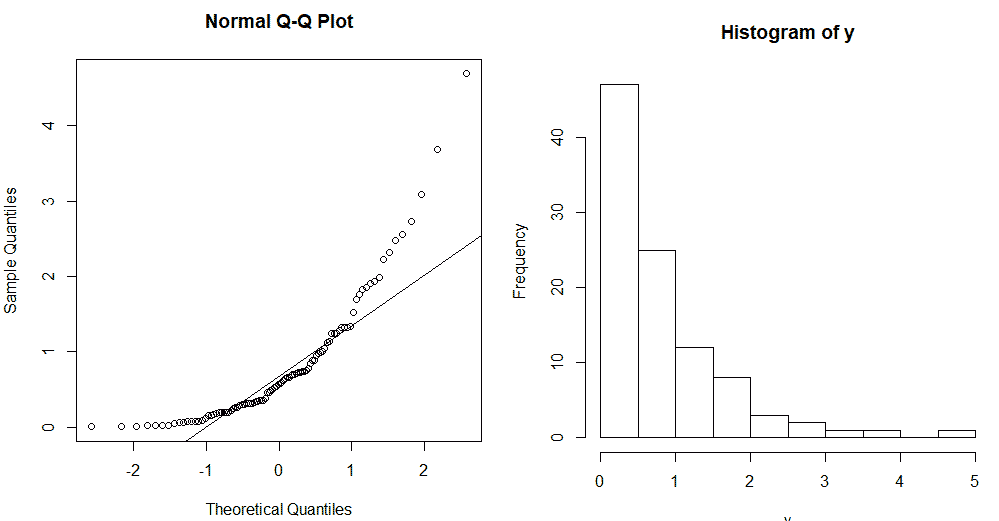
Мы видим, что R-Studio нарисовал график Q-Q (слева). На таком графике отображаются данные в отсортированном порядке по сравнению с квантилями из стандартного нормального распределения. За исключением выбросов, точки расположены более менее по прямой, хотя и скашиваются. Значит, наши данные искажены. На это также указывает, что точки расположены вдоль линии в середине графика, но отгибаются в конце. Такое поведение характеризует наличие в выборке более высокие значений, чем ожидалось от нормального распределения. Пример нормального распределения показан на графике Q-Q справа.

Еще один пример нормальных данных: вводим команду для генерирования данных x <- rnorm(100). Строим график с линией qqline(x), и добивает гистаграммой hist(x).

Пример ненормальных данных: y <- rgamma(100, 1), затем qqnorm(y); qqline(y), и гистограмма hist(y).

Выбираем победителя

В зависимости от количества и нормальности данных мы выбираем разные критерии для выявления победителя. Если данные нормально распределены, то используем бернулевский тест, гаусовские расчеты. Смотрим степени свободы, победил вариант, не победил вариант.

Тест на нормальность (Шапиро — Уилка)

Для начала рассмотрим тест Шапиро-Уилка как критерий для определения нормальности, он очень мощный. Критерий Шапиро-Уилка это W-критерий, который также позволяет оценить нормальность. Если W=1, то выборка точно нормально распределена. Так, нулевая гипотеза = выборка принадлежит нормальному распределению. Если Шапиро-Уилка дает маленький p-value, то значит есть выбросы. Все, что выше 0,75, можно считать нормальным распределением. Для выполнения теста Шапиро-Уилка предназначена функция shapiro.test(x), принимающая на вход выборку x объема не меньше 3 и не больше 5000. Генерируем нормальные данные, x <- rnorm(4600), и используем тест shapiro.test(x). Мы видим следующий текст:

Shapiro-Wilk normality test
data: x
W = 0.99947, p-value = 0.222

Смотрим на p-value = 0.222 и принимаем нулевую гипотезу.

W это значение статистики теста, в данном случае это 0.99947, что считается отличным результатом, т.к. выборка изначально имеет нормально распределенные данные. Чтобы отклонить нулевую гипотезу, p-value должно быть не выше альфы 0,05 (максимум 0,1). Проверим на ненормальных данных: y <- rgamma(100, 1), shapiro.test(y).

Shapiro-Wilk normality test
data: y
W = 0.9829, p-value < 2.2e-16

P-value < 2.2e-16, что намного меньше 0.05, практически 0. И это при том, что R сообщает только значения p-value выше порога 2.2×10−16. Мы отклоняем нулевую гипотезу. Сначала смотрим, меньше ли 0.05, потом сравниваем средние или медианы. На несимметричных данных медиана значительно лучше отразит центральную тенденцию, чем обычное среднее. Если распределение одной из выборок заметно отличается от нормального, то в качестве центра берется медиана и соответственно, критерий Уилкоксона — Манна-Уитни, непараметрический и хорошая замена Хи-квадрату Пирсона. Если у данных положительный длинный хвост (прибыль) и ненормальное распределение, то это Манна-Уитни, перестановочные тесты или бутстреп. Перестановочные тесты про гипотезу о схожести распределений двух выборок.

Если же распределение всех выборок нормальное, то среднее арифметическое это наш выбор, и какой-либо из Стьюдентов (критерий сдвига).

Проблема это ограничение на 5000 наблюдений. Если наша выборка больше, то применяем Shapiro-francia w’ test. Или Anderson-Darling test, его попроще найти в готовом виде, он может проверить данные на любые распределения. Либо тест Колмогорова-Смирнова (критерий согласия), но для решения реальных задач лучше его не использовать.

A/B-тесты подразумевают два набора данных, поэтому тест нужно проводить для обоих выборок. Это не обязательно тест Шапиро-Уилка, это может быть и непараметрический ранговый U-критерий Уилкоксона — Манна-Уитни. Проверяет гипотезу сдвига, кушает любые выборки, но понятное дело, что обе выборки должны быть примерно схожи по распределению. Тест робастый, оперирует рангами. Сдвиг это не про проверку медианы, а про проверку «скошенности» данных относительно друг друга. Если в одной выборке у нас значения [2,3,4,5], а во второй [5,6,7,8], то это явно сдвиг.

Если данные непрерывные, то в простых случаях хорошо работают критерии Уилкоксона — Манна-Уитни/Краскела-Уоллиса, в которых нулевые гипотезы на сравнения распределений и медианы. Распределение 50 на 50 подразумевает использование формулы Бернулли, а может быть и Байесовский многорукий бандит. Если же использовалось сплит-тестирование, то нужно использовать непараметрический дисперсионный анализ — критерий Краскела-Уоллиса. Для сравнения дисперсий хороший вариант Fligner-Killeen и Brown–Forsythe. Рассмотрим с примерами.

Подход Байеса рекомендуется при большом количестве данных, альтернатива частотному подходу. Частотный подход про нулевую гипотезу и про частоту событий, Байес — про принятие нулевой гипотезы, позволяет работать с событиями и причинами. Нельзя применять Байеса и частотный подходы одновременно, это ведёт к «парадоксу Линди».

Частотный подход не позволяет сделать предположение заранее, предлагается полагаться на данные тестовой выборки. Мы повторяем эксперимент бесконечное количество раз для получения гистограммы объективной неопределенности. Сама гипотеза проверяется по классическому p-value. Важно зафиксировать размер выборки до эксперимента, вот две формулы для этого:

В числителе находим дисперсию (α2), в знаменателе mde.
z — стандартная ошибка, 1,96 при 95% уровне значимости.
σ — стандартное отклонение.

Обратите внимание, что практически все переменные взаимосвязаны. Чем меньше эффект, который мы хотим поймать, тем больше размер выборки.

Обобщающая способность. Если мы возьмем гомогенную выборку, то дисперсия будет меньше, функция плотности вероятности будет более сконцентрированная, чем при 100% доступных данных. Но и выводы по гомогенной выборке будутрелевантны выборке, а не всем данным. Вывод: меньше дисперсия = меньше обобщающая способность.

Давайте на примере. Нужно найти размер выборки для теста пропорции категориальных данных. α = 95%, mde = 0.05, p = 70%, z = 1.96. Так, n = 1.96^2 * 0.7 * (1 — 0.7) / 0.05^2 = 3.8416 * 0.7 * 0.3 / 0.0025 = 322.

Идея Байеса в получении 500 раз выпадение орла из 1000 бросаний монетки, и считается по формуле C500(1000) * 0.5^(500) * 0.5^(500), т.к. броски друг от друга никак не зависят. Если бы мы знали все возможные параметры монетки, мы могли бы предсказать результат. Но так как это невозможно, то проводим множество наблюдений. Байес позволяет ответить на задачу индукции, какой из вариантов лучше и на сколько. У Байаса всегда есть априорное распределение, а значит, нужно иметь свои представления о параметрах исследуемового процесса. Что, в принципе, является основой образа мышления дизайнера. Для Байеса можно не считать мощность и значимость, но пропадает понимание эффекта. Если по каким то причинам не нравится Байеc, то можно использовать Стьюдента или Бернулли для больших выборок. Если результаты 0 и 1, то точно Бернулли и биномиальное распределение. А с ним легко работать, интерпретировать, визуализировать.

Критерий Стьюдента

Стьюдент. T-тест или определение t-критерия Стьюдента является простейшим способом проверки точности среднего значения для данных с естественными значениями. Выборки должны быть независимыми (не парными) и нормально распределенными (чем больше результатов, тем ближе распределение к нормальному). Это гарантирует концентрацию плотности значений вокруг среднего значения, что позволяет делать выводы о генеральной совокупности, имея только информацию о выборке. Провести тест легко: x = rnorm(1000000) и y = rnorm(1000000). Команда t.test(x,y). Получаем следующие данные:

data: x and y
t = -1.1696, df = 2e+06, p-value = 0.2422
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-0.004424298 0.001117388
sample estimates:
mean of x mean of y 
-0.0007571144 0.0008963404

И проверяем:

m = length(x); n = length(y)
t = ( mean(x) - mean(y) ) / sqrt( var(x)/m + var(y)/n ); t

В обоих случаях получаем t = -1.1696, и p-value = 0.2422. Так как мы всегда обеспокоены тем, является ли p больше или меньше 0,05, то при 0.2422 > 0.05 есть основания не отвергать нулевую гипотезу. P-Value это достигнутый уровень значимости (пи-величина)—наименьшая величина уровня значимости, при которой нулевая гипотеза отвергается для данного значения статистики. По P-Value происходит проверки (и отклонения) «нулевой гипотезы». Чем меньше значение Р, найденное для набора результатов, тем меньше вероятность того, что результаты случайны. Результаты считаются «статистически значимыми», когда это значение ниже 0,05 (или 5%). Если удастся довести значение до 0,005, то уже хорошо, сильно уменьшится количество позитивных неправильных результатов. При 0,05 считается нормой 1/3 неправильных выводов. В идеальном мире даже 0,005 должно быть лишь приблизительной наводкой на финальное решение. В физике или при исследовании генов используется 0.0000003. Чем ниже значение p, тем выше перевес в пользу альтернативной гипотезы.

В примере ниже я визуализировал, как границы меняются в зависимости от входных данных, и в момент выхода за границы принимаем H1 о наличие различий. Различия могут быть на уровне среднего значения, медианы, и не только. Не обязательно делать динамические границы, можно и статичные.

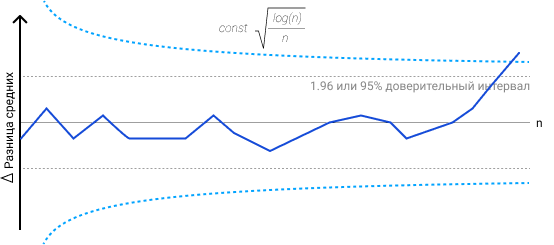
Нулевая гипотеза всегда про отсутствие статистической значимости в результатах, т.е. о равенстве значения генеральной совокупности относительно выбранного критерия. Она зовется нулевой, так как отрицание это ноль, а согласие это единица. Например, все пользователи видят баннер. Альтернативная гипотеза скажет, что не все пользователи видят баннер, т.е. нет утверждения о равенстве параметра генеральной совокупности заранее заданному значению.

Парный t-тест имеет уменьшенное количество степеней свободы, но при этом устраняется влияние индивидуальных различий. Нужен для сравнения зависимых выборок, он мощнее непарного t-теста. Зависимые выборки это когда элемент из контрольной группы имеет соответствующий ему элемент во второй группе. Например, при тесте одинаковой главной страницы в сентябре 2018 года и в сентябре 2019, или навыки дизайнеров до и после курсов. при зависимых выборках нас интересует, как изменения в одной группе повлияют на другую.

leftGroup <- c(12, 13, 11, 15, 19, 15, 17)
rightGroup <- c(14, 14, 16, 16, 18, 14, 15)
t.test(leftGroup, rightGroup, var.equal=TRUE)
t.test(leftGroup, rightGroup, paired=TRUE)

Получаем p-value = 0.5648 в первом случае и p-value = 0.4539 во втором. Очевидно, что дискриминационная способность у парного теста больше.

Второй по популярности — z-тест пропорций. Это параметрический тест, проверяет равенство средних. Видим биномиальное распределение, применяем z-тест. Например, для метрик отношения/конверсии. Тестируется биномиальная случайная величина (орел или решка, 1 или 0, Да или Нет), значит, z-тест. Нужна независимость выборок. Если же задача в сравнении равенства дисперсий, то наш выбор это Levene, тест Бартлетта. Они параметрические, тест Бартлетта будет помощнее, но и требует более нормальное распределение, чем Levene.

Следующий критерий, Уилкоксона — Манна-Уитни, позволяет протестировать, что результаты случайных наблюдений из одной группы могут быть выше, чем в другой. Это непараметрический критерий, альтернатива t-test. Идея такая: для t-test нужны нормально распределенные данные (нормальность среднего распределения) и его результаты легко интерпретировать, но он чувствителен к выбросам. Если у нас нет информации о нормальности распределения, используем критерий Манна-Уитни, имея ввиду, что он не покажет тонких различий между выборками и его сложнее интерпретировать. Причина в том, что t-критерий работает на основе сравнения средних из фактических наблюдений, в то время как критерий Манна-Уитни использует сравнение рангов (номеров наблюдения в упорядоченной выборке), что позволяет ему быть устойчивым к выбросам. Но при этом критерий Манна-Уитни весьма чувствителен к различию дисперсий, и на больших выборках это становится очень заметно.

Поэтому на практике допускается использовать t-test для оценки средних на большой выборке, так как нормальность обеспечивается «сжиманием» крайних значений по ЦПД (чем больше элементов в выборке, тем меньше дисперсия среднего арифметического). Но при этом помним, что чем больше отклонения от нормальности, тем хуже тест сравнивает выборки. Так что t-test не подойдет для небольших выборок из ненормального распределения, но подойдет для большой выборки из ненормального распределения.

T-test чувствителен к выбросам, и если есть длинный хвост в данных (а он почти всегда есть на реальных финансовых данных), то такой хвост сильно скажется на среднем, и за счет большой дисперсии получим плохой результат работы критерия. Любые популярные метрики, вроде ARPU, количество сессий, время чего-либо, ARPPU, средний чек это не биномиальное распределения. И зачастую они не поддаются анализу параметрическими тестами, длинные хвосты и значит, большее количество денег мы получаем от небольшого кол-ва пользователей. Это можно решить за счет техники бакетов, но опять же, нужна большая выборка. Если маленькая выборка, тогда у нас выбор: либо U-критерий Манна-Уитни, считаем p-value внутри дней с поправкой на множественное сравнение, теряя в мощности. Если можно избежать применения поправок — лучше избежать. Либо накопительный p-value. Либо bootstrap как самое простое решение, получим распределение выборочного среднего и посмотрим на пересечение квантилей с заданным уровнем значимости. Либо CUPED преобразует данные в нормальные, уменьшив отклонения от среднего, и T-Test с поправкой Уэлча. Либо mood’s median test, но понадобится таблица сопряженности.

Используем команду wilcox.test(mpg ~ am, data=mtcars) получаем сообщение, “не могу подсчитать точное p-значение при наличии повторяющихся наблюдений”. Если вас смущает это сообщение, измените команду на wilcox.test(mpg ~ am, data=mtcars, exact=FALSE). Это объяснит программе, что мы все понимаем, и не ждем точного расчета p-value. Получилось W = 42, p-value = 0.001871. Напомню, P-Value должно быть не выше 0,05.

А теперь возьмем два набора наблюдений и протестируем:

a = c(123, 105, 147, 142, 119, 129, 130, 87 ,301, 92, 177, 141, 137, 112, 138, 128, 114, 197, 198, 210, 101, 125, 134, 214, 110, 100, 152, 122, 144, 148 ,153 ,212)
b = c(154, 512, 120 ,131 ,124 ,118 ,178 ,140 ,136, 68, 162, 127, 78 ,106, 133, 655 ,155 ,169 ,199 ,108 ,143, 341 ,121 ,139, 166, 174, 184, 98, 135, 132, 146, 209)

 wilcox.test(a,b)

На выходе получаем:

data: a and b
W = 455, p-value = 0.4507
alternative hypothesis: true location shift is not equal to 0

У нас есть наше любимое P-Value, которое куда больше, чем 0,05. Мы принимаем нулевую гипотезу. W является статистической статистикой Уилкоксона и, как следует из названия, является суммой рангов в одной из двух групп.

Если р < 0,05, то нулевая гипотеза про отсутствие отличий отвергается.

С Бернулли схожая история, берет два вида данных (орел/решка, мальчик/девочка, красное/черное). rbinom(200, size = 1, p = 0.68) где p это шанс получить 1. Грубо говоря, rbinom скажет, сколько будет орлов, если сыграть определенное кол-во раз в монетку. Пример показывает сразу 200 испытаний Бернулли. Посмотрим, как мы можем сравнить два испытания Бернулли, т.к. данные очень похоже на результат бинарного A/B теста:

varA <- rbinom(200, 20, 0.5) varB <- rbinom(200, 20, 0.25)

И используем hist(varB, probability = TRUE, col = gray(0.9)) для двух наборов данных. На графиках мы видим 200 биномиально распределенных случайных чисел для испытаний размером = 20 и с разной вероятностью возникновения интересующего нас события p = 0,25 и 0,50.

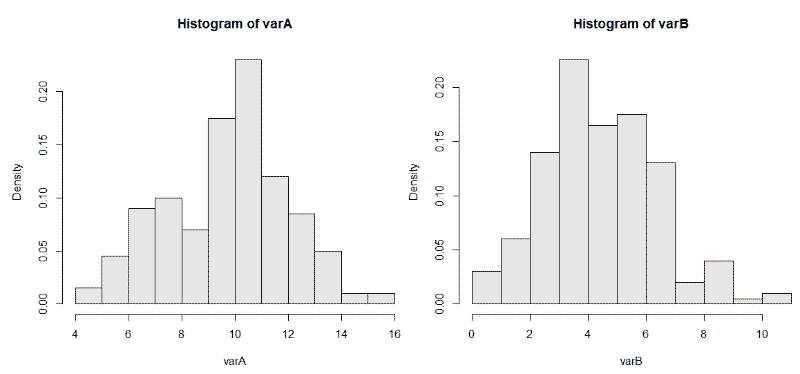
Биномиальные критерии это сравнение пропорций. Позволяют проверить гипотезу про коэффициент удаления приложения. Если выборка маленькая (100), конверсия в покупку 12%, то биномиальный тест лучший выбор. Стьюдент может быть применен к распределению Бернулли, но выборка маловата, должно быть > 200. В данном примере, с бутстрепом будет аналогичная история.

Говоря о типичных финансовых данных, где есть пик-скопление небольших платежей + длинный хвост, и нас не пугает работать с логарифмом от некой велечины (но не от 0), то методом Бокса-Кокса можно транформировать данные в нормально распределенные. Простой логарифм от числа, который тем не менее усложняет интерпретацию результатов. После этого берем привычный параметрический тест (t-критерий Стьюдента), смотрим p-value и оцениваем уровень значимости для закрытия эксперимента.

Процесс выглядит так: узнаем про выбросы с помощью boxplot, проверяем выборку на нормальность с помощью теста Шапиро Уилко, охарактеризовать распределение с помощью QQnorm, и выбрать метод анализа. Если данные нормальные, используем Бернулли, Гаусса, Стьюдента. Ненормальные (график сглажен по одной из сторон): Хи-квадрат, Байес, Пуассон. Обычно данные выглядят как диапазон от 0 до десятков в кучей выбросов до нескольких сотен, и это распределение Пуассона. Распределение Пуассона применяется в теории массового обслуживания. После этого оцениваем параметры, учитываем их при запуске теста хи-квадрат к выборке и распределению Пуассона, и получаем ответ про правильность гипотезы при распределение Пуассона.

Итак, тест прошёл. На что мы можем посмотреть? В первую очередь, нельзя подгонять новые гипотезы по факту завершения эксперимента под найденную разницу, хотя очень хочется. Называется это P-hacking, когда сначала идет сбор данных, проверяют множество разных гипотез, и те, которые соответствуют p<0.05, публикуют в научных журналах. Если вы работаете в науке и нужно собирать гранты на новые научные изыскания, то все на вашей совести. Но в бизнесе такой подход недопустим.

Могло показаться, что t-test это участь исключительно научной работы и он не применим для бизнес-задач. Но вот пример: возьмем метрику отношения (ratio metric), например CTR. Посчитаем соотношение суммы кликов и суммы просмотров, их отношение это конверсия в клик. В таком примере данные зависимы и не можем использовать t-test.

Другой тип метрик это поюзерная метрика. Смотрим на среднее значение, т.е. был ли открыт лутбокс, или нет. Здесь у нас одинаково распределенные, независимые случайные величины, и мы можем применить t-test. А теперь магия: мы можем использовать линеризацию для превращения метрик отношения в поюзерные метрики. При этом не теряется чувствительность и метрика сонаправлена с изначальной.

После теста проверяем, все ли пользователи завершили целевое действие. Например, среднее время жизни пользователя сервиса для генерации временных e-mail адресов составляет 5 дней. В выборке не должно быть тех, кто начал пользоваться сервисом за 5 дней до конца эксперимента.

Нельзя допускать аномальных всплесков в ходе эксперимента, они могут внести статистически значимый вклад в результат.

Если у нас биномиальная метрика, то надо смотреть на изменение мощности. Например, обе наблюдаемые группы резко скатились вниз, и это сказывается на мощности. Ближе к концу эксперимента можно пересчитать и сделать вывод, сильно ли отличается мощность в конце и начале эксперимента. Сильно отличается в худшую сторону? Продолжаем эксперимент, ждём нужную мощность.

P-value тоже имеет свой доверительный интервал. Если провести 10000 A/A-тестов при p-value=0.05, то мы ожидаем, что 500 прокрасится. Даже у этих 500 есть доверительный интервал, некий доверительный интервал доверительного интервала. Помогает вероятностный подход: классическая теорема Байеса.

Не только R

Сейчас любой аналитик (не важно, UX, бизнес, дашбордист, ресерчер, разработчик) должен уметь в R и Python. Но базовый навык работы в Excel по прежнему помогает быстро решать многие задачи. При работе над продуктом требуются быстрые выводы по популярным метрикам, dau/mau, конверсия в регистрацию, и показатели метрик часто меняются. Распространенная практика это использовать среднее для всех первичных KPI, если распределение нормальное. Это позволяет делать первичные выводы очень быстро. Понять тип распределение можно с помощью стандартного/среднеквадратичного отклонения. в Excel для этого используется функция =сроткл. Формула выглядит как STD=√[(∑(x-x)²)/n], и расшифровывается как корень из суммы квадратов разниц между элементами выборки и средним, деленной на количество элементов в выборке.

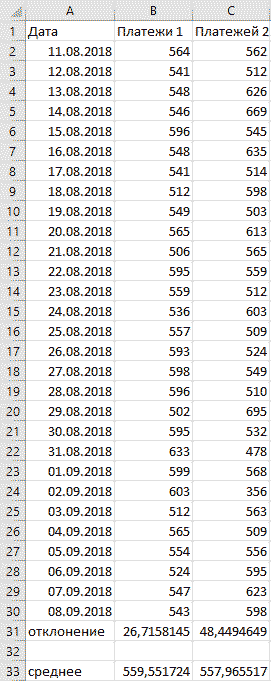
В примере выше видно, что, не смотря на практически одинаковые средние значения, видны огромные колебания данных вокруг среднего значения второго варианта. Первый вариант заслуживает больше доверия.

В Excel еще много замечательных способов визуализировать данные, особенно полезны сводные таблицы. Работают по принципу вирутальной группировки строчек с одинаковыми названиями товаров. Берется группа и считается для нее сумма, очень удобно. Такие таблицы используются для агрегирования данных и получения отчета.

Главное при проведении тестов это умение делать выводы из цифр, критически мыслить, делать выводы на основе исторических данных, генерировать гипотезы, рассуждать, чувство рациональности и нерациональности. Математический анализ лишь помогает не принять вымысел за правду, но окончательное бизнес-решение принимает по прежнему специалист.

Источник

Время на прочтение
24 мин

Количество просмотров 13K

Всем привет! Меня зовут Дима Лунин, и я аналитик в Авито. Как и в большинстве компаний, наш основной инструмент для принятия решений — это A/B-тесты. Мы уделяем им большое внимание: проверяем на корректность все используемые критерии, пытаемся сделать результаты более интерпретируемыми, а также увеличиваем мощность критериев. Про это всё мы уже написали две статьи на Хабр, вот первая часть, а вот — вторая.

В текущем посте я хочу рассказать, как ещё сильнее увеличить мощность критериев для A/B-тестирования, используя машинное обучение. В некоторых моментах буду ссылаться на две предыдущие статьи, так что если вы их ещё не читали, самое время это исправить.

Кратко, о чём я собираюсь рассказать:

Что такое CUPED-метод.
Как улучшить CUPED-алгоритм. CUPAC, CUNOPAC и CUMPED — подробно про каждый из них.
Как использовать Uplift-модель в качестве статистического критерия. Здесь я продемонстрирую все прелести bootstrap-технологий.
Как использовать все модели сразу для достижения лучшей мощности.
Насколько эти методы вместе с парной стратификацией лучше, чем обычный CUPED.

Отдельно отмечу, что такие методы, как CUNOPAC, CUMPED, критерий на основе Uplift-модели и критерий, объединяющий несколько критериев, были разработаны и придуманы нашей командой.

Задачи для проверки критериев

Прежде чем приступить к рассказу о критериях, хочу показать, для каких задач годятся описанные далее алгоритмы.

Поюзерные A/B-тесты. Здесь вы одним пользователям показываете новый дизайн, новые фишки и так далее, а в другой группе оставляете всё как было. Ждёте какой-то срок и смотрите с помощью статистического критерия, прокрашен тест или нет.

Конечно, в таких экспериментах хочется иметь наиболее мощный критерий: так мы сможем проверить больше гипотез за меньшее время. Ещё примеры, зачем может потребоваться большая мощность у критерия, можно найти в статьях выше.

Но бывают случаи, когда такое не получается сделать. Например, вы тестируете новую рекламу на билбордах или телевидении. Тогда вы не можете одним пользователям в Москве показывать новую рекламу, а вторым в этот момент завязать глаза.

То же самое с новыми продуктами. Мы в Авито тестировали в своё время новые услуги продвижения. Если бы мы проводили обычный поюзерный A/B-тест, то в поисковой выдаче были бы два типа объявлений: с новыми услугами продвижения и со старыми. И это нарушило бы чистоту эксперимента: при раскатке у нас все объявления будут с новыми услугами в поисковой выдаче, а результаты A/B мы получили на смешанной поисковой выдаче. Здесь поможет другой тип экспериментов.

Региональные A/B-тесты. Давайте перейдём к новой статистической единице — региону. Например, будем показывать нашу рекламу или введём новые услуги только в половине регионов России. Тогда всё честно: рекламу в одном регионе не увидят пользователи из других регионов (а точнее число тех, кто увидит, будет пренебрежимо мало). И выдача объявлений не пересекается по регионам. Так что пользователям Ростовской области можно разрешить купить новые услуги продвижения, а в Краснодарском крае — нет, они друг на друга не влияют.

С точки зрения математики это означает, что вместо гигантского количества пользователей в A/B-тесте у нас будет примерно 85 элементов-регионов: 42 из них — в тесте и 43 — в контроле. В этом случае мы также можем применять статкритерии, которые используются для поюзерных экспериментов. Но элементов всего 85, нормально ли они себя покажут? Не будут ли критерии строить некорректный доверительный интервал?

Главный минус таких тестов — они слишком шумные. Чтобы задетектировать хоть какой-то эффект, надо, чтобы он был огромным. Поэтому если будет алгоритм, который сможет очень сильно увеличить мощность критерия, или, что эквивалентно, сократить доверительный интервал для эффекта, это будет мегаполезно для бизнеса.

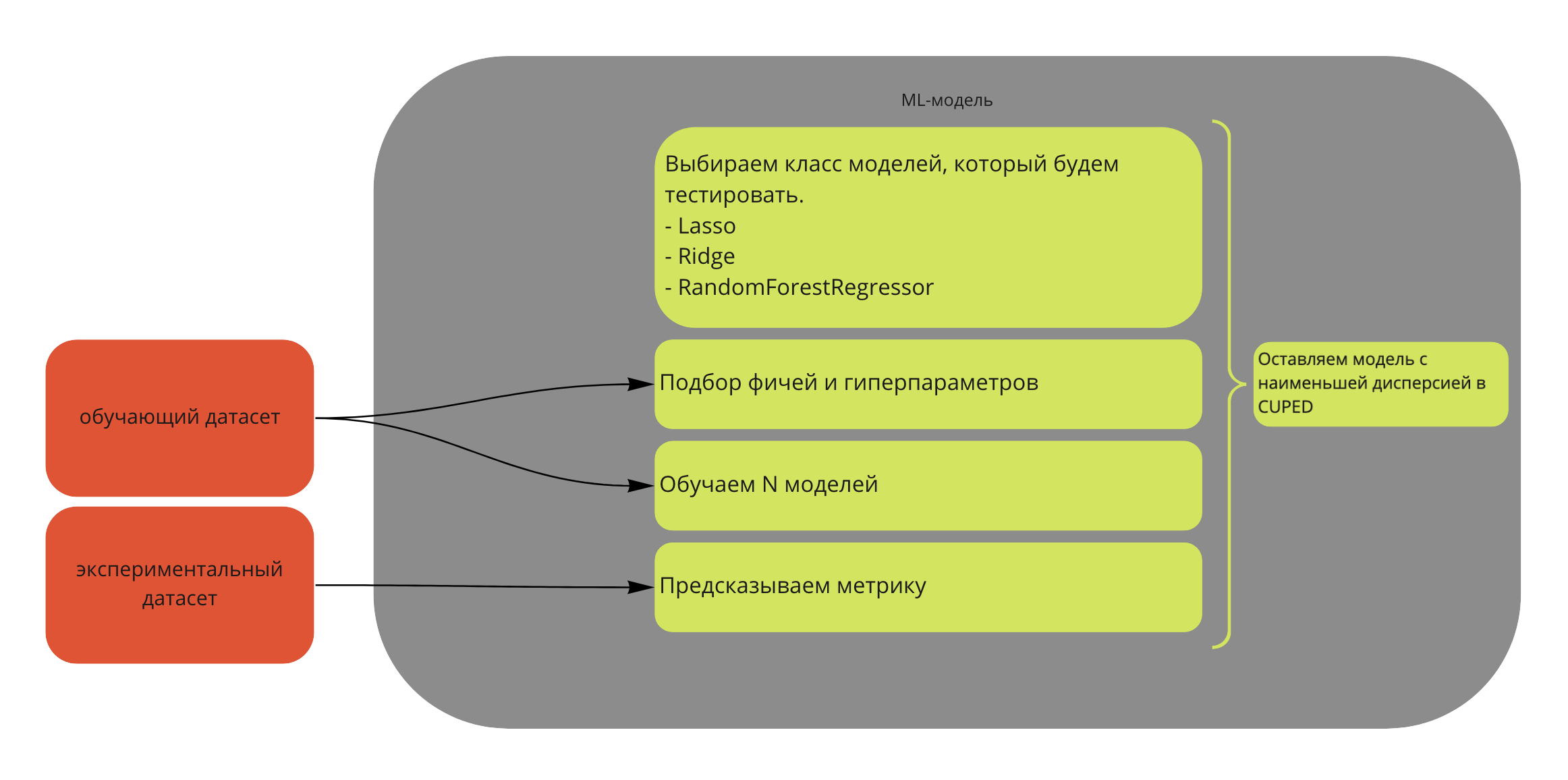
На этих двух задачах я и буду тестировать все представленные далее критерии и на них же покажу результаты. Теперь предлагаю перейти к сути статьи. Начнём с CUPED-алгоритма.

CUPED

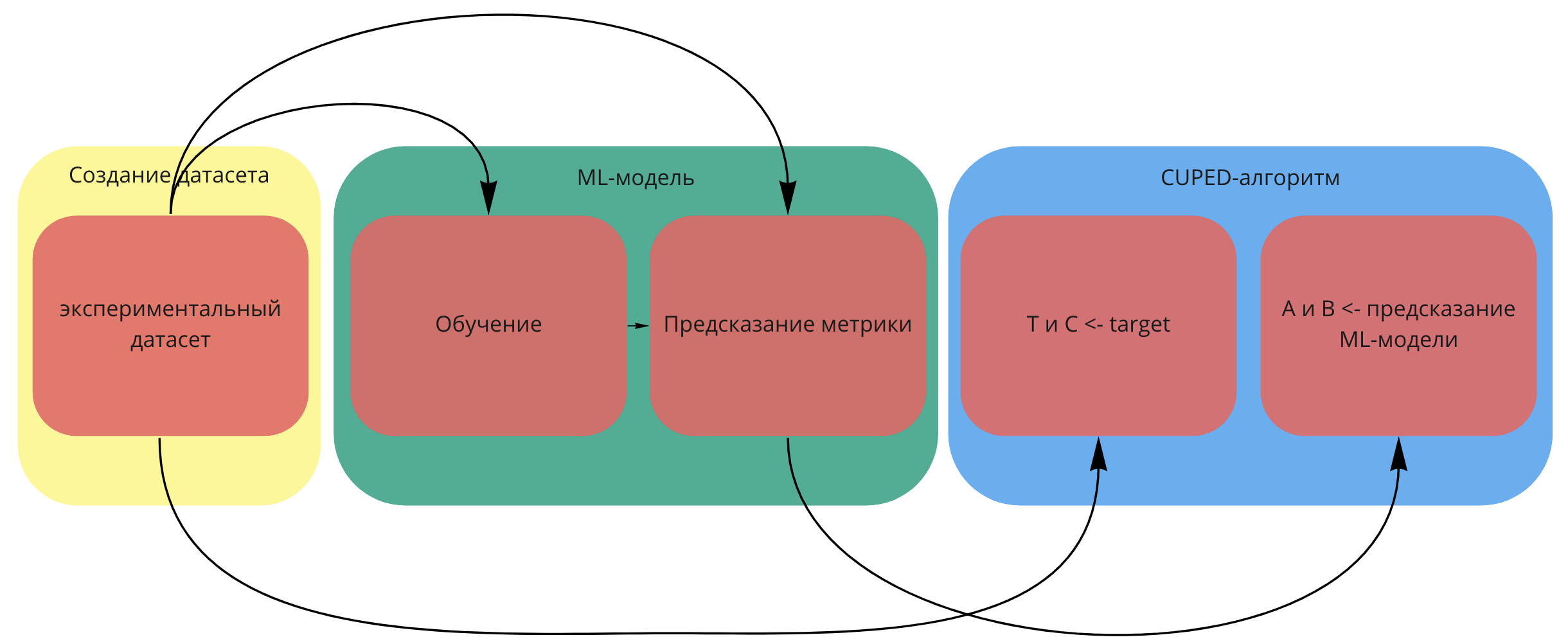
CUPED (Controlled-experiment Using Pre-Experiment Data) — очень популярный в последнее время метод уменьшения вариации. Чтобы понять, как он работает, рассмотрим искусственный пример.

Пусть ваша метрика — выручка, и эксперимент длится месяц. Вы собрали данные во время эксперимента, какая выручка от пользователей в тесте и в контроле:

В итоге метрики очень шумные: в тесте даже на трёх точках видно, что значения разнятся от 50 до 150, а в контроле — от 20 до 200 рублей. С помощью T-test получились следующие результаты: +10±20 ₽ на одного пользователя, результат не статзначим. Как это исправить?

Давайте добавим информацию с предпериода: сколько эти пользователи тратили в среднем в месяц до начала эксперимента. При правильном сетапе теста матожидание этой величины одинаково в тесте и в контроле. Тогда:

Будем теперь смотреть на дельту. Это разница выручки на экспериментальном периоде минус средняя выручка на предпериоде в месяц.

Во-первых, почему так можно? В тесте и в контроле мы вычитаем с точки зрения матожидания одно и то же, потому что в правильно проведённом A/B-тесте контроль и тест ничем не отличаются на предпериоде. Поэтому, когда мы смотрим на разницу, эти вычитаемые величины нивелируются.

Здесь:

T — экспериментальная метрика в тесте.
C — экспериментальная метрика в контроле.

Во-вторых, зачем нам всё это?

Посмотрим на разброс значений в delta: в контроле от -10 до 6 рублей, а в тесте от -10 до 20 рублей. Это намного меньше того разброса, что мы видели ранее. Поэтому и доверительный интервал сократится: результат станет +15±5 ₽ для одного пользователя, и он уже статзначим! Почему дисперсия уменьшилась? Потому что мы смогли объяснить часть данных в эксперименте с помощью предпериода.

А теперь посмотрим на CUPED более формально.

Основная идея CUPED-метода: давайте вычтем что-то из теста и из контроля так, чтобы матожидание разницы новых величин осталось таким же, как и было. Но дисперсия при этом уменьшилась бы:

Где A и B — некоторые случайные величины (ковариаты). Тогда утверждается, что если θ будет такой, как указано в формулах далее, то дисперсия будет минимально возможной для таких статистик.

В примере выше θ я взял равной 1, но на самом деле, лучше было подобрать значение по этой формуле. Тогда формула для дисперсии получается такой:

Поэтому, чем больше корреляция по модулю, тем меньше будет дисперсия.

Также важно помнить: чтобы метод работал корректно, достаточно, чтобы матожидания A и B совпадали:

Ещё больше интересных и нетривиальных моментов про CUPED расписано в прошлой статье. В частности, там есть информация о том, как построить относительный CUPED-критерий.

Осталось понять, что брать в роли A и B. Чаще всего для них берут значения той же метрики, но на предэкспериментальном периоде. В примере выше мы брали среднюю выручку за месяц. Чем хорош такой способ:

Матожидание метрики на предпериоде будет одним и тем же в тесте и в контроле — иначе у вас некорректно поставлен A/B-тест. А значит, CUPED даст правильный результат.
В большинстве случаев метрика на предпериоде сильно коррелирует с экспериментальным периодом. Отсюда получается, что и дисперсия сильно уменьшится.

Но кроме значения метрики на предпериоде можно использовать результаты ML-модели, обученной предсказывать истинные значения метрик без влияния тритмента. С хорошей моделью можно достичь большего уменьшения дисперсии. Давайте поговорим о том, как это сделать.

CUPAC

CUPAC (Controlled-experiment Using Prediction As Covariate) — первая вариация на тему CUPED с ML. Как я уже писал выше, давайте попробуем использовать предсказание в качестве ковариаты. Распишу сам предлагаемый алгоритм на примере определённой задачи. Для ваших задач вы сможете переиспользовать алгоритм по аналогии.

Пусть у нас есть A/B-тест, где:

Дата начала — 1 июня.
Длительность теста составляет 1 месяц.
Наша ключевая метрика — выручка.
1 месяц уже прошёл.

Чтобы оценить такой тест, мы проделаем следующую операцию из трёх основных шагов:

Соберём датасет для предсказания (или «экспериментальный датасет») и обучения.
На обучающем датасете обучим нашу модель, подберём гиперпараметры, а на экспериментальном будем предсказывать таргет, используя фичи с предпериода.
Мы получили новую ковариату и запускаем обычный CUPED-алгоритм.

На схеме это можно изобразить так:

Как собрать экспериментальный и обучающий датасеты?

На иллюстрации сине-красный датасет — экспериментальный, а бирюзовый — обучающий, собранный до 1 июня. Одним цветом отмечено, что пользователи друг от друга в среднем ничем не отличаются, разными цветами — между ними есть разница.

Теперь опишем сам алгоритм в тексте. Повторим в цикле, пока не жалко:

Вычитаем из текущей даты длительность эксперимента. Начинаем с 1 июня, потом получим дату 1 мая, потом — 1 апреля и так далее.
Теперь собираем таргет. Для каждого юзера сохраняем его суммарные траты у нас на сайте за этот месяц. Для 1 июня это экспериментальная выручка за июнь (и уже за июнь вся выручка известна), для мая это выручка за май, когда ещё не было никаких отличий между тестом и контролем, и так далее.
- Тут у нас получатся один сине-красный датасет с экспериментальной выручкой (и она отлична у теста с контролем) и много бирюзовых датасетов, где пользователи в среднем неразличимы.
И теперь собираем датасет фичей. Главная особенность состоит в том, что фичи должны быть собраны до текущей рассматриваемой даты. То есть для 1 июня все фичи должны быть собраны по данным до 1 июня, аналогично для остальных дат.
- Например, количество заходов на сайт за N месяцев до рассматриваемой даты (за 2 месяца до 1 июня; за 2 месяца до 1 мая и так далее).
- Выручка от пользователя за разные промежутки времени (за 1 месяц, за 2 месяца и так далее).
- Сколько месяцев назад зарегистрировался пользователь.
Ни в одном из датасетов нет фичи тестовая или контрольная группа. Важно, чтобы пользователи по обучающим фичам в тесте и в контроле были полностью идентичны.

Что важно проверить: нужно, чтобы матожидания новых ковариат совпадали. А для этого достаточно, чтобы признаки ML-модели в среднем не отличались в тесте и в контроле. Далее идёт теоретическое пояснение этому факту.

Теоретическое пояснение

Обозначим X и Y — фичи пользователей в тесте и в контроле. То есть наша случайная величина — это вектор фичей. Тогда, если тест и контроль подобраны корректно (случайно или с помощью парной стратификации):

Что произойдет, когда мы обучим модель? Она просто преобразует вектор признаков одного пользователя в число с помощью некоторой функции F. Тогда:

Обозначим A := F(X), B := F(Y). Тогда, как я писал выше в CUPED, метод будет корректен.

Вот и всё! Это полный пайплайн работы CUPAC-алгоритма. Теперь я попытаюсь объяснить, зачем нужен тот или иной шаг.

Вопросы и ответы к методу

Зачем нужен обучающий датасет?

Чтобы не было переобучения. Если объяснять простыми словами, то это приводит к тому, что доверительный интервал заужается и становится некорректным. И ошибка первого рода будет не 5, а, например, 15%. А теперь поподробней.

Допустим, мы бы обучались прямо на экспериментальном датасете и на нём же предсказывали. Рассмотрим пример:

Пусть у нас есть один признак для обучения, и функция выручки пользователя зависит от признака рыжей линией на рисунке. Допустим, мы возьмём какую-то легко переобучаемую модель: например, полином 10-й степени. Обучим её на синих точках-примерах (экспериментальном датасете в терминах CUPAC). В таком случае текущая модель практически идеально предскажет их значения.

Подставим в CUPED предсказание, получим эффект 0 и дисперсию 0, потому что модель везде всё верно предсказала. Имеет ли это какое-то отношение к реальной картине? Нет! Видно даже, что в реальности синие точки не лежат на рыжей линии, а значит, некоторый шум в данных точно есть.

Мы видим, что в других точках, где модель не обучалась, она ведёт себя совершенно не так, как истинная функция выручки. Это значит, что если бы мы насемплировали другую выборку пользователей, то эффект и дисперсия в CUPED были бы другими! Итого, мы обучились не на генеральную совокупность, а на частичный, увиденный в обучении, пример. Это и есть проблема переобучения.

Почему нельзя собирать обучающие фичи на том же периоде, на котором мы и предсказываем?

Во время эксперимента так делать нельзя, потому что мы могли повлиять на этот признак тестируемым тритментом. И тогда фичи в тесте и в контроле будут различны в этих группах, а полученные на таких данных ковариаты будут иметь разное матожидание в зависимости от группы. А значит, CUPED применять нельзя.

На обучающем датасете мы тоже не можем использовать такие признаки, потому что тогда обучающий и экспериментальный датасеты будут различны по структуре.

Зачем лезть так далеко в историю? Не достаточно ли для обучающего датасета взять датасет, собранный, например, для 1 мая?

В принципе, такой вариант подойдёт, но чем больше обучающий датасет, тем лучше обучится модель. Плюс мы можем добавить временные признаки в качестве обучающих фичей: номер года, категорийную фичу месяца, сезон.

А что, если наша метрика — конверсия?

Так вместо задачи регрессии у нас задача классификации. И можно использовать вероятность модели в качестве ковариаты. При этом можно точно также оставить регрессионную модель.

Как обучать модель?

Об этом я расскажу дальше.

Про результаты работы критерия: как и ранее, я буду сравнивать алгоритмы по метрике «ширина доверительного интервала». Чем она меньше, тем лучше.

На поюзерных тестах: уменьшение доверительного интервала на 1000 A/A-тестах в среднем на 4% относительно CUPED.
На региональных тестах: уменьшение доверительного интервала на 1000 A/A-тестах в среднем на 22% относительно CUPED.

Если вы решите реализовать этот или любой другой алгоритм из статьи, то обязательно проверьте его корректность!

Это всё, что здесь можно рассказать. Теперь перейдём к «нечестному» CUPAC и избавимся от большинства шагов в алгоритме.

CUNOPAC

CUNOPAC (Controlled-experiment Using Not Overfitted Prediction As Covariate) — чуть более простая, чуть менее корректная и чуть более мощная модель, чем CUPAC. В вопросах к CUPAC я писал, что обучающий датасет нам нужен, ведь иначе может возникнуть проблема переобучения. Но я предлагаю забыть про эту проблему!

Главное, о чём надо помнить в таком случае — вы можете построить некорректный критерий! Он будет строить зауженный доверительный интервал, и вместо 95% случаев будет покрывать лишь 85%. Но об этом я расскажу далее.

Алгоритм работы критерия такой:

Соберём экспериментальный датасет для предсказания.
На нём обучим нашу модель, подберём гиперпараметры, и на нём будем предсказывать таргет, используя фичи с предпериода. Обучаемся на всем датасете сразу! И предсказываем весь датасет. Ничего не откладываем на валидацию (да, метод рискованный).
Мы получили новую ковариату и запускаем обычный CUPED-алгоритм.

На схеме это можно изобразить так:

Датасет собираем также, как и в CUPAC-алгоритме, только обучающий датасет больше не нужен:

Теперь вопрос: как подобрать модель, которая не переобучится? Мы решили этот вопрос так: отбираем небольшое количество фичей и используем только линейные модели.

Рассмотрим пример: что, если взять CatBoost-алгоритм или линейную регрессию в качестве ML-алгоритма внутри критерия? Посмотрим на реальный уровень значимости (или False Positive Rate), полученный при проверке метода на 1000 А/А-тестах:

Линейные модели: 0.055 (при alpha=0.05), результат статзначимо не отличается от теоретического alpha.
CatBoost: 0.14 (при alpha=0.05), результат статзначимо отличается от теоретического alpha!

То есть CatBoost ошибается примерно в 3 раза чаще, чем должен был! Он переобучается, заужает доверительный интервал и поэтому критерий некорректен. Что это значит на практике? Что вы в 3 раза чаще будете катить изменение, которое на самом деле не имеет никакого эффекта. Поэтому CatBoost нельзя использовать внутри CUNOPAC, а линейные модели можно. При этом я не говорю, что CatBoost плохой алгоритм! Он отличный, просто он легче переобучается.

Есть ли переобучение у линейной модели? Наверняка есть, но оно настолько мало, что не влияет на эффект.

А почему качество CUNOPAC лучше, чем у CUPAC?

Возникает вопрос: а почему качество может стать лучше, чем у CUPAC?

В предыдущей модели CUNOPAC мы обучаемся на исторических данных, и в этот момент не учитываем текущие тренды и сезонность, а в текущей CUNOPAC эти недостатки убраны.
Наша цель — найти наиболее скоррелированную метрику с T-C, ведь в таком случае дисперсия уменьшится максимально возможным способом. А так как в CUPAC при обучении вообще никак не участвует метрика T (а лишь значения метрики без какого-либо тритмента), то результат вполне ожидаемо будет менее скоррелирован, чем у модели, которая обучалась в том числе и на значениях метрики T. Поэтому, качество у CUNOPAC должно быть лучше, чем у CUPAC.
Ну и наконец, как показали наши эксперименты, в CUPAC лучше всего также сработали линейные модели (что было для нас удивительно, бустинги и деревья показали себя хуже). CUNOPAC дал буст по качеству, так как тоже использует линейные модели.

Что ещё хочется отметить: это очень опасная модель! Если модель переобучиться, вы будете заужать доверительный интервал и ошибка будет больше заявленной. Поэтому снова предупреждаю: обязательно проверьте ваш критерий!

Результаты работы критерия:

На поюзерных тестах: уменьшение доверительного интервала на 9% относительно CUPED.
На региональных тестах: не удалось использовать, реальный уровень значимости сильно больше тестируемых 5%, слишком мало регионов. Модель просто всегда переобучается.

Проверено на 1000 A/А-тестах.

А теперь обсудим, как построить пайплайн обучения модели для этих двух критериев.

Автоматизация ML-части критериев

Поговорим про основную часть алгоритмов. Что у нас есть: обучающий и экспериментальный датасеты, которые мы будем скармливать модели. В случае CUNOPAC это один и тот же датасет. Расскажу, как я воплотил ML-часть алгоритмов, но это не значит, что у меня получилась идеальная автоматизация: возможно, вы сможете придумать лучше. При этом, если вы плохо понимаете идеи и алгоритмы машинного обучения, то можете пропустить эту часть. Она никак не повлияет на осознание всех алгоритмов далее.

Краткая иллюстрация:

Шаг 1. Выбираем класс моделей, который будем тестировать. Например, я использовал:

Для CUPAC: Lasso, Ridge, ARDRegression, CatBoostRegressor, RandomForestRegressor, SGD, XGBRegressor.

Для CUNOPAC: Lasso, ARDRegression, Ridge.

Дополнительно: для адекватности я нормирую все признаки с помощью StandardScaler.

Шаг 2. Выбираем фичи для обучения. Ограничим сверху количество используемых фичей и воспользуемся одним из алгоритмов подбора признаков:

Жадный алгоритм добавления/удаления признаков (например, SequentialFeatureSelector из библиотеки scikit-learn на Python).
Алгоритм на основе feature_importance параметра фичей у модели (SelectFromModel из библиотеки scikit-learn на Python). Самый быстрый из алгоритмов.
Add-del алгоритм (добавляем фичи, пока качество улучшается, потом выкидываем фичи, пока качество улучшается, повторим процедуру снова, пока не сойдёмся).
Всё, что ещё найдёте или придумаете.

Единственное замечание: если у алгоритма отбора фичей можно задать функцию оценки для качества модели, то стоит использовать специальную функцию-скоррер:

def cuped_std_loss_func(y_true, y_pred):
    theta = np.cov(y_true, y_pred)[0, 1] / (np.var(y_pred) + 1e-5)
    cuped_metric = y_true - theta *  y_pred
    return np.std(cuped_metric)

Так вы будете оценивать ровно ту величину, которую вы хотите оптимизировать — ширину доверительного интервала у CUPED-метрики.

Шаг 3. Следующая остановка — выбор гиперпараметров. Мы считаем в этот момент, что все обучающие признаки уже выбраны. Есть следующие варианты:

Перебор по GridSearchCV.
Перебор по RandomizedSearchCV.
Жадный перебор по одному параметру:
- сначала подбираем по функции cuped_std_loss_func первый в списке гиперпараметр;
- потом подбираем второй в списке, при учёте выбранного первого гиперпараметра и т.д. Пример с кодом:

start_params = {
    'random_state': [0, 2, 5, 7, 229, 13],
    'loss': ['squared_loss', 'huber'],
    'alpha': np.logspace(-4, 2, 200),
    'l1_ratio': np.linspace(0, 1, 20),
} # Пример перебора параметров для SGD
def create_best_model_with_grid_search(pipeline, start_params, X, y):
        final_params = {}
        params = []
        for param in start_params.items():
            params_dict = {}
            params_dict[param[0]] = param[1]
            params.append(params_dict)
         
        score = make_scorer(cuped_std_loss_func, greater_is_better=False)
        for param in params:
            search_model = GridSearchCV(pipeline, param, cv = 2, n_jobs = -1,
                                        scoring = score)
            search_model.fit(X, y)
            final_params = {**final_params, **search_model.best_params_}
            pipeline.set_params(**final_params)
        return pipeline, final_params

Плюс такого метода: скорость по сравнению с первым методом. Вместо всех возможных комбинаций здесь перебирается линейное количество вариантов. Все значения гиперпараметров будут рассмотрены по сравнению со вторым методом.

Минус: GridSearchCV даст лучшее качество, но работать будет сильно дольше.

Ещё, конечно, можно объединить предыдущий шаг с этим: для каждого набора фичей подобрать гиперпараметры и измерять качество по cuped_std_loss_func. Но это работает очень долго. Можно также устроить сходящуюся процедуру из этих двух шагов: выбираем признаки, выбираем гиперпараметры, снова выбираем признаки с подобранными значениями гиперпараметра и так далее.

Шаг 4. Отлично, после обучения у нас есть N моделей с первого шага с подобранными гиперпараметрами и обучающими признаками для каждой из них. Отберём из них одну модель, которая даёт наилучшее качество на экспериментальном датасете по cuped_std_loss_func. Почему так можно сделать, я расскажу, когда буду описывать Frankenstein-критерий.

А пока перейдём к третьему критерию, который, грубо говоря, не является ML-критерием.

CUMPED

Почему нам вообще нужна только одна ковариата? Почему нельзя использовать сразу N ковариат? Именно на этой идее построен алгоритм CUMPED (Controlled-experiment Using Multiple Pre-Experiment Data).

Ранее в CUPED было так:

А теперь в CUMPED будет так:

При этом не обязательно использовать только две ковариаты, их может быть сколько угодно!

Зачем нам вообще может потребоваться N ковариат? Почему одной недостаточно?

Как я писал в CUPED-алгоритме, из-за того, что часть метрик T и C описывается данными из ковараиты, мы и сокращаем дисперсию. А если признаков будет не один, а сразу несколько, то мы лучше опишем нашу метрику T и C, а значит сильнее сократим дисперсию. Это то же самое, что и в машинном обучении: что лучше, использовать один признак для обучения или несколько различных фичей? Обычно выбирают второе.

Теперь опишем первую версию предлагаемого алгоритма CUMPED:

Соберём один экспериментальный датасет, как сделали это в CUNOPAC.
В цикле по всем признакам, которые использовались ранее для предсказания метрики:
- Образуем CUPED-метрику T’, С’, используя в качестве ковариат текущие признаки в цикле.
- В следующий раз в качестве изначальных метрик будут использоваться новые CUPED-метрики. То есть на следующей итерации цикла вместо текущих метрик T и C будут использоваться полученные сейчас T’, C’.

Если расписать формулами, то:

Где наша итоговая CUMPED-метрика это T^N, C^N, а A_i, B_i — это признаки пользователя, собранные на предпериоде. Раньше мы на них обучали модель, а сейчас используем в качестве ковариат. Коэффициенты тета подбираются следующим образом:

Вот и весь алгоритм. Но! Если бы вы его реализовали, то он, вероятно, показал бы себя хуже, чем обычный CUPED-алгоритм. Почему?

В этом алгоритме есть одна беда:

Порядок применения ковариат важен! Если сначала вычесть ковариату A_1, а потом ковариату А_2, то дисперсия может быть больше, нежели в случае, когда вы сначала вычтете A_2, а потом A_1. Вы можете сами расписать формулы, и увидеть, что две эти случайные величины будут иметь разную дисперсию.

Поэтому предлагается применять ковариаты в «жадном» порядке: сначала ищем наилучшую ковариату, уменьшающую дисперсию сильнее всего, потом следующую ковариату, уменьшающую дисперсию лучше всего для T^1, C^1 и т. д. То есть в первой версии алгоритма мы берём не случайную ковариату, а ту, которая на текущий момент сильнее всего уменьшает доверительный интервал.

На рисунке представлен итоговый алгоритм CUMPED:

Иллюстрация подбора наилучшей ковариаты:

Вопросы и ответы к методу

Можно ли подобрать коэффициенты theta_1, theta_2, … theta_N в алгоритме неким другим способом, чтобы дисперсия была меньше?

Да, можно. Текущий алгоритм не является оптимальным, потому что если решать задачу,

то оптимум у коэффициентов будет другим! Но для этого надо взять производную N раз по каждой theta, приравнять производные к 0 и решить N уравнений относительно N неизвестных. Не самая приятная задача, хотя есть методы, которые могут численно найти ответ для неё. Также я не считаю, что дисперсия в таком решении сильно уменьшится относительно того, что я получил описанным жадным алгоритмом. Я не реализовывал такой вариант, так что буду рад, если кто-то решит сравнить эти два алгоритма.

А алгоритм может остановиться? Если признаков в обучающем датасете будет бесконечно много, то как понять, что пора остановиться?

Никак. Если посмотреть на CUPED-алгоритм, то дисперсия в новых CUPED-метриках не больше изначальной дисперсии. Поэтому в теории можно использовать бесконечно много ковариат, просто большинство из них будут иметь нулевой коэффициент theta.

На практике всё не так радужно: к сожалению, мы не знаем истинной ковариаты, а лишь её состоятельную оценку, полученную на текущих данных. А оценка, как известно, практически всегда отличается от настоящего значения. Поэтому в реальности посчитанный коэффициент theta в алгоритме всегда будет не нулём, и мы всё время будем уменьшать выборочную дисперсию, даже если метрика и ковариата не скоррелированны. А это может привести к тому, что мы заузим доверительный интервал. А значит и ошибка первого рода будет больше заявленной.

В качестве примера рассмотрим на искусственных данных первый шаг алгоритма: насколько он уменьшит дисперсию. Пример будет показан на одновыборочном CUPED-критерии.

import scipy.stats as sps
import numpy as np
import seaborn as sns
 
sample_size = 100
 
sample = sps.norm(scale=10).rvs(sample_size)
 
cumpled_std_samples = []
# генерируем эксперимент 100 раз, чтобы получить какое-то распределение для оценки дисперсии
for _ in range(100):
    # истинная оценка стандартного отклонения
    estimated_mean_sample_std = np.std(sample) / np.sqrt(sample_size)
    # признаки-ковариаты в CUMPED, никак не скоррелированны с sample
    feature_matrix = sps.norm().rvs((5000, sample_size))
    # 1 шаг алгоритма
    for covariate in feature_matrix:
        # CUPED part
        theta = np.cov(sample, covariate)[0, 1] / np.var(covariate)
        sample_std = np.std(sample - theta * covariate) / np.sqrt(sample_size)
         
        # Выбор наилучшей ковариаты по уменьшению std у CUPED-метрики. Первый шаг алгоритма.
        if sample_std < estimated_mean_sample_std:
            estimated_mean_sample_std = sample_std
    cumpled_std_samples.append(estimated_mean_sample_std)
 
sns.distplot(cumpled_std_samples)

Получилось, что оценка алгоритмом стандартного отклонения в каждом случае из 100 была меньше теоретического значения 1 — стандартное отклонение равно 10, а размер выборки равен 100, значит стандартное отклонение для среднего равно 1. А это лишь первый шаг алгоритма!

А теперь хорошие новости: чем больше выборка, тем меньше будет это различие. Рассмотрим на примере, когда размер выборки равен 10000. В этом случае мы всё также будем заужать дисперсию, но в процентном соотношении сильно меньше: например в случае, когда выборка была размера 100, средний процент заужения доверительного интервала составлял 8%. А когда выборка стала размером 10000, то процент заужения относительно истинного стандартного отклонения составил 0,1%!

Поэтому во втором случае заужением доверительного интервала можно пренебречь: ничего плохо не произойдёт. Да, возможно ошибка первого рода будет не 5%, а 5,1%, но это и не страшно. Плюс в реальности размеры выборок чаще всего ещё больше.

Итого, исходя из вышесказанного, CUMPED отлично работает в случае, если выборка большого размера: и с точки зрения теории, и на проведенных 1000 A/A-тестах. То есть на поюзерных тестах его можно использовать. Но на региональных тестах с ним надо быть осторожным: в нашем случае он заработал только тогда, когда мы ограничили количество шагов алгоритма до 1.

Результаты работы критерия:

На поюзерных тестах: уменьшение доверительного интервала на 14% относительно CUPED. Это наилучший результат среди всех представленных здесь алгоритмов.
На региональных тестах: уменьшение доверительного интервала на 21% относительно CUPED. Но можно использовать лишь одну ковариату! Почему так, я ответил в скрытом разделе с вопросами.

Проверено на 1000 A/А-тестах.

Uplift-критерий

Всё, забыли про CUPED и всё, что с ним связано. В этом разделе я покажу, как из Uplift-модели сделать настоящий критерий. Но для начала о том, что такое Uplift-модель.

Давайте соберём датасет так же, как ранее это делали в CUNOPAC и в CUMPED, но в этот раз добавим фичу: какая группа пользователя. 1 — пользователь в тесте, 0 — в контроле.

Теперь посмотрим, как работает алгоритм:

Разделим датасет на K частей.
Будем в цикле размера K выбирать часть пользователей, которым будем предсказывать их метрику. На оставшейся части обучим ML-алгоритм. Эти два шага в ML зовутся кросс-валидацией.
Теперь для каждого пользователя на тестовой части предскажем его выручку, если бы он был в тесте и если бы он был в контроле. Как мы это сделаем? Поменяем в датасете фичу группы пользователя: на 1, если предсказываем выручку от него в тесте, и на 0, если предсказываем его выручку в контроле. Обозначим эти значения T_p и C_p. Теперь оценка Uplift для пользователя — это предсказанная выручка, если пользователь в тесте минус предсказанная выручка, если пользователь в контроле.
Повторим K раз и получим Uplift для всех пользователей.

На рисунке я кратко описал то же самое. Возможно, так будет понятней:

Мы смогли получить численную оценку эффекта для каждого пользователя. Однако есть несколько «но»:

Как из оценки построить доверительный интервал?
А если модель смещённая или некорректная? Например, она никак не учитывает группу пользователя внутри себя: тогда Uplift будет равен 0, что может быть не так. А если для тестовых юзеров он постоянно занижает предсказание, а для контрольных юзеров завышает?

Чтобы решить обе проблемы, введём ошибку предсказания:

Тогда:

То есть наш Uplift будет равен разнице предсказаний + разнице ошибок предсказаний в тесте и в контроле. Отличие по сравнению со старой формулой в том, что теперь мы добавляем ошибку предсказания: если мы занижаем предсказание на тестовых юзерах, то ошибка предсказания на тесте будет положительной. То же самое для контрольных юзеров.

Тогда численную оценку Uplift можно представить следующим образом:

Но и здесь есть проблема: размер выборок у трёх слагаемых разный! Давайте посмотрим, а что мы вообще можем посчитать для каждого пользователя.

Для пользователя в тесте:

Значение метрики в тесте (или T в формулах выше).
Предсказание модели, если пользователь в тесте (или T_p в формулах выше).
Предсказание модели, если пользователь в контроле (или C_p в формулах выше).
Ошибку предсказания модели, если пользователь в тесте (или ε_T в формулах выше).

Для пользователя в контроле:

Значение метрики в контроле (или C в формулах выше).
Предсказание модели, если пользователь в тесте (или T_p в формулах выше).
Предсказание модели, если пользователь в контроле (или C_p в формулах выше).
Ошибку предсказания модели, если пользователь в контроле (или ε_C в формулах выше).

Поэтому, размер выборок на самом деле будет таким:

T_p, С_p: их размер равен количеству пользователей в тесте и в контроле, или |T| + |C| .
ε_C: размер этой выборки равен количеству пользователей в контроле, или |C|.
ε_T: размер выборки равен количеству пользователей в тесте, или |T|.

Вкратце это выглядит так:

Выпишем формулу Uplift с учётом всех вводных:

Так, а теперь вопрос. Как для такой статистики построить доверительный интервал? Ведь T_p, C_p, ε_T, ε_C ещё и коррелируют между собой? Как я упоминал в предыдущих статьях, если не знаете, как что-то посчитать теоретически, то используйте bootstrap. В данном случае достаточно забутстрапить каждого пользователя в тесте и в контроле по отдельности, а точнее их метрики T_p, С_p, ε_C, ε_T. Далее на каждой итерации внутри бутстрапа посчитаем оценку Uplift для них по формуле выше, и по этим данным построим доверительный интервал.

Замечание

В предложении выше есть небольшой подвох: на самом деле, мы должны не просто забутсрапить пользователей, но и каждый раз заново обучать модель. Когда мы обучаем модель, наши предсказания на тесте становятся зависимыми от пользователей в обучении. Если мы обучимся на одних пользователях, то предсказание будет одно, а если на других, то предсказание изменится.

Поэтому, по логике работы бутстрапа, когда мы бутстрапим пользователей для построения доверительного интервала, мы должны использовать не те значения, которые были посчитаны в первый раз на изначальном датасете, а заново обучить модель K раз (K — параметр кросс-валидации) и использовать новые метрики.

Но на практике работает и описанный выше алгоритм, поэтому можете провести обучение один раз и не заморачиваться.

Результаты работы критерия:

На поюзерных тестах: уменьшение доверительного интервала на 4% относительно CUPED.
На региональных тестах: уменьшение доверительного интервала на 40% относительно CUPED. Это наилучший результат — обыгрывает CUPAC, CUMPED в 2 раза.

Почему произошло столь сильное сокращение на региональных тестах? Потому что на самом деле мы увеличили датасет в 2 раза. Если ранее размер выборки был примерно 42 на 43 (если регионов 85), то сейчас, так как модель предсказывает значения в тесте и в контроле для каждого региона, размер датасета стал 85 на 85. Есть, конечно, оговорка, что мы так увеличили только T_p и C_p, но как видим, это отлично работает.

Проверено на 1000 A/А-тестах.

Frankenstein-критерий

Вот у нас есть четыре критерия, а когда какой стоит использовать? Ранее я писал, что CUMPED лучше всего работает для поюзерных тестов, а Uplift — для региональных. ~~А зачем я рассказывал про все остальные?~~ Но ведь они лучше всего работают в среднем, а не всегда. На самом деле когда-то лучше может сработать CUPED, а когда-то — CUPAC или CUNOPAC. И как в каждом A/B-тесте выбрать, какой критерий сейчас лучше всего использовать?

Для ответа на этот вопрос был придуман критерий-Франкенштейн. Посмотрим на следующую схему:

Суть метода проста: берём N критериев и из них выбираем тот, который на текущий момент даёт наименьший доверительный интервал.

Какие критерии использовать внутри? У нас получилась следующая картина.

Для поюзерных тестов стоит использовать:

CUNOPAC.
CUMPED.
CUPED.

CUPAC и Uplift-критерий не стоит использовать, так как они всегда работают хуже, чем CUNOPAC и CUMPED.

А для региональных тестов стоит использовать:

Uplift-критерий.
CUPAC.
CUMPED.
CUPED.

Почему критерий валиден?

Вопрос 1. Почему нет проблемы множественной проверки гипотез? Мы же провели на самом деле N тестов, и по-хорошему должны применить поправку Бонферрони/Холма. Ведь когда мы выбираем критерий с наиболее узким доверительным интервалом, мы можем как-то влиять на эффект.

Ответа два. Во-первых, проверено на 1000 А/А-тестах. Реальный уровень значимости (или ошибка первого рода) всегда был равен заданному теоретическому значению. Во-вторых, есть теоретическое объяснение. Если совсем просто, то мы смотрим не на p-value, а на ширину доверительного интервала, поэтому множественную проверку гипотез применять не надо. А теперь чуть более формально:

Выборочное среднее и выборочная дисперсия независимы (в предположении, что CUPED-выборка из нормального распределения). Когда мы выбираем какой-то критерий, то мы выбираем его на самом деле по выборочной дисперсии. И в этот момент, если наша метрика была бы из нормального распределения, то можно было бы утверждать, что оценка эффекта никак не зависит от выборочной дисперсии. А значит, выбирая критерий по выборочной дисперсии, мы никак не влияем на оценённый эффект, то есть применять множественную проверку гипотез не надо. Можно считать, что на самом деле мы проверили результаты только одним критерием. Единственное «но»: всё это верно, если данные из нормального распределения, что на самом деле не так.
В общем случае можно утверждать, что корреляция между выборочным средним и выборочной дисперсией стремится к 0 при увеличении размера выборки. Зависимость может и есть, но здесь играют роль три фактора: если даже она и есть, то нелинейная. Поэтому сложно придумать адекватную ситуацию на практике, когда при наиболее узком доверительном интервале будет наибольший/наименьший эффект. Хотя с точки зрения теории это вполне возможно. Далее, для нормальных случайных величин выборочное среднее и дисперсия независимы, отсюда есть шанс полагать, что и на ваших данных нет зависимости. Ну и в-третьих, у нас всё было проверено. Вы также можете проверить критерий у себя на данных и удостовериться, что всё хорошо.

Вопрос 2. Не заужаем ли мы доверительный интервал?

Для начала допустим, что на самом деле все критерии описывают одно и то же распределение, но полученное из разных семплирований. Например, пусть CUPAC и CUNOPAC строят ковариату из одного и того же распределения, просто она получилась разной в двух алгоритмах (получились разные выборки из одного распределения).

И вот здесь ответ неутешительный: да, мы можем заузить доверительный интервал. Представьте себе, что у нас N критериев, которые оперируют с нормальным распределением Norm(0, 1). Каждый из них как-то оценивает его дисперсию, и из всех этих оценок мы берём не любую, а наименьшую! Если среди этих N критериев хотя бы один критерий оценил дисперсию меньше, чем она есть на самом деле, то мы заузили доверительный интервал. При этом очевидно, что чем больше критериев, тем более вероятно, что хотя бы раз мы получим оценку дисперсии меньше реальной и ошибёмся. В качестве примера приведу код:

import scipy.stats as sps
import numpy as np
import matplotlib.pyplot as plt
 
small_number_of_criteria_std = []
large_number_of_criteria_std = []
 
# генерируем эксперимент 1000 раз, чтобы получить какое-то распределение для оценки дисперсии
for i in range(1000):
    # small_number_of_criteria, 5 критериев внутри критерия Франкенштейна
    current_std_array = []
    for i in range(5):
        # текущий критерий
        sample = sps.norm().rvs(100)
        # сохраняем std, полученное от критерия
        current_std_array.append(np.std(sample))
    # сохраняем текущее std, полученное от критерия Франкенштейна
    small_number_of_criteria_std.append(min(current_std_array))
     
    # large_number_of_criteria_std, 500 критериев внутри критерия Франкенштейна
    current_std_array = []
    for i in range(500):
        # текущий критерий
        sample = sps.norm().rvs(100)
        # сохраняем std, полученное от критерия
        current_std_array.append(np.std(sample))
    # сохраняем текущее std, полученное от критерия Франкенштейна
    large_number_of_criteria_std.append(min(current_std_array))
 
 
plt.hist(small_number_of_criteria_std, label='small number of criteria', bins='auto')
plt.hist(large_number_of_criteria_std, label='large number of criteria', bins='auto')
plt.xlabel('std')
plt.legend()
plt.show()

Мы видим, что чем больше критериев, тем сильнее дисперсия смещена в меньшую сторону. Так что если использовать очень много критериев, мы можем заузить доверительный интервал и создать некорректный критерий.

Но на практике, во-первых, во всех критериях распределения всё же разные, во-вторых, у нас всего 3 или 4 критерия. При этом, на наших проверках, реальный уровень значимости каждый раз был заявленные alpha%. Мы проверили критерий на 1000 А/А- и A/B-тестах, как поюзерных, так и региональных, везде всё было корректно. Так что предложенный Frankenstein-критерий корректен. Но когда будете реализовывать его у себя, не забудьте дополнительно его проверить!

Результаты

Поюзерные тесты:

Сокращение доверительного интервала на 14% относительно CUPED.
С использованием парной стратификации: на 21%.

Региональные тесты:

Сокращение доверительного интервала в 1,5 раза относительно CUPED.
С использованием парной стратификации: в 2 раза .

Получились отличные результаты! Особенно для региональных тестов.

Итого, в данной статье я постарался рассказать про такие методы, как:

CUPED.
CUPAC, CUNOPAC, CUNOPAC — три вариации на тему CUPED.
Uplift-критерий — как из Uplift-модели сделать критерий.
Frankenstein-критерий — как из нескольких критериев сделать один.

Если у вас остались вопросы, обязательно пишите. Постараюсь ответить. Также мне можно писать в соц. сетях:

тг: @dimon2016
linkedin

Источник

A/B-тестирование — это неотъемлемая часть процесса работы над продуктом. Это эксперимент, который позволяет сравнить две версии чего-либо, чтобы проверить гипотезы и определить, какая версия лучше. Должны ли кнопки быть черными или белыми, какая навигация лучше, какой порядок прохождения регистрации меньше всего отпугивает пользователей? Продуктовый дизайнер из Сан-Франциско Лиза Шу рассказывает о простой последовательности шагов, которые помогут провести базовое тестирование.

Кому нужно A/B-тестирование

— Продакт-менеджеры могут тестировать изменения ценовых моделей, направленные на повышение доходов, или оптимизацию части воронки продаж для увеличения конверсии.

— Маркетологи могут тестировать изображения, призывы к действию (call-to-action) или практически любые другие элементы маркетинговой кампании или рекламы с точки зрения улучшения метрик.

— Продуктовые дизайнеры могут тестировать дизайнерские решения (например, цвет кнопки оформления заказа) или использовать результаты тестирования для того, чтобы перед внедрением определить, будет ли удобно пользоваться новой функцией.

Вот шесть шагов, которые нужно пройти, чтобы провести тестирование. В некоторые из пунктов включены примеры тестирования страницы регистрации выдуманного стартапа.

1. Определите цели

Определите основные бизнес-задачи вашей компании и убедитесь, что цели A/B-тестирования с ними совпадают.

Пример: Допустим, вы менеджер продукта в «компании X» на стадии стартапа. Руководству нужно добиться роста количества пользователей. В частности, компания стремится к росту количества активных пользователей (метрика DAU), определяемых как среднее количество зарегистрированных пользователей сайта в день за последние 30 дней. Вы предполагаете, что этого можно добиться либо путем улучшения показателей удержания (процент пользователей, возвращающихся для повторного использования продукта), либо путем увеличения числа новых регистрирующихся пользователей.

В процессе исследования воронки вы замечаете, что 60% пользователей уходят до завершения регистрации. Это означает, что можно повысить количество регистраций, изменив страницу регистрации, что, в свою очередь, должно помочь увеличить количество активных пользователей.

2. Определите метрику

Затем вам нужно определить метрику, на которую вы будете смотреть, чтобы понять, является ли новая версия сайта более успешной, чем изначальная. Обычно в качестве такой метрики берут коэффициент конверсии, но можно выбрать и промежуточную метрику вроде показателя кликабельности (CTR).

Пример: В нашем примере в качестве метрики вы выбираете долю зарегистрированных пользователей (registration rate), определяемую как количество новых пользователей, которые регистрируются, поделенное на общее количество новых посетителей сайта.

3. Разработайте гипотезу

Затем нужно разработать гипотезу о том, что именно поменяется, и, соответственно, что вы хотите проверить. Нужно понять, каких результатов вы ожидаете и какие у них могут быть обоснования.

Пример: Допустим, на текущей странице регистрации есть баннер и форма регистрации. Есть несколько пунктов, которые вы можете протестировать: поля формы, позиционирование, размер текста, но баннер на главной странице визуально наиболее заметен, поэтому сначала надо узнать, увеличится ли доля регистраций, если изменить изображение на нём.

Общая гипотеза заключается в следующем: «Если изменить главную страницу регистрации, то больше новых пользователей будут регистрироваться внутри продукта, потому что новое изображение лучше передает его ценности».

Нужно определить две гипотезы, которые помогут понять, является ли наблюдаемая разница между версией A (изначальной) и версией B (новой, которую вы хотите проверить) случайностью или результатом изменений, которые вы произвели.

— Нулевая гипотеза предполагает, что результаты, А и В на самом деле не отличаются и что наблюдаемые различия случайны. Мы надеемся опровергнуть эту гипотезу.

— Альтернативная гипотеза — это гипотеза о том, что B отличается от A, и вы хотите сделать вывод об её истинности.

Решите, будет ли это односторонний или двусторонний тест. Односторонний тест позволяет обнаружить изменение в одном направлении, в то время как двусторонний тест позволяет обнаружить изменение по двум направлениям (как положительное, так и отрицательное).

4. Подготовьте эксперимент

Для того, чтобы тест выдавал корректные результаты сделайте следующее:

— Создайте новую версию (B), отражающую изменения, которые вы хотите протестировать.

— Определите контрольную и экспериментальную группы. Каких пользователей вы хотите протестировать: всех пользователей на всех платформах или только пользователей из одной страны? Определите группу испытуемых, отобрав их по типам пользователей, платформе, географическим показателям и т. п. Затем определите, какой процент исследуемой группы составляет контрольная группа (группа, видящая версию A), а какой процент — экспериментальная группа (группа, видящая версию B). Обычно эти группы одинакового размера.

— Убедитесь, что пользователи будут видеть версии A и B в случайном порядке. Это значит, у каждого пользователя будет равный шанс получить ту или иную версию.

— Определите уровень статистической значимости (α). Это уровень риска, который вы принимаете при ошибках первого рода (отклонение нулевой гипотезы, если она верна), обычно α = 0.05. Это означает, что в 5% случаев вы будете обнаруживать разницу между A и B, которая на самом деле обусловлена случайностью. Чем ниже выбранный вами уровень значимости, тем ниже риск того, что вы обнаружите разницу, вызванную случайностью.

— Определите минимальный размер выборки. Калькуляторы есть здесь и здесь, они рассчитывают размер выборки, необходимый для каждой версии. На размер выборки влияют разные параметры и ваши предпочтения. Наличие достаточно большого размера выборки важно для обеспечения статистически значимых результатов.

— Определите временные рамки. Возьмите общий размер выборки, необходимый вам для тестирования каждой версии, и разделите его на ваш ежедневный трафик, так вы получите количество дней, необходимое для проведения теста. Как правило, это одна или две недели.

Пример: На существующем сайте в разделе регистрации мы изменим главную страницу — это и будет нашей версией B. Мы решаем, что в эксперименте будут участвовать только новые пользователи, заходящие на страницу регистрации. Мы также обеспечиваем случайную выборку, то есть каждый пользователь будет иметь равные шансы получить A или B, распределенные случайным образом.

Важно определить временные рамки. Допустим, ежедневно на нашу страницу регистрации в среднем приходит трафик от 10 000 новых пользователей, это означает, что только 5000 пользователей могут увидеть каждую версию. Тогда минимальный размер выборки составляет около 100 000 просмотров каждой версии. 100 000/ 5000 = 20 дней — столько должен продлиться эксперимент.

5. Проведите эксперимент

Помните о важных шагах, которые необходимо выполнить:

— Обсудите параметры эксперимента с исполнителями.

— Выполните запрос на тестовой закрытой площадке, если она у вас есть. Это поможет проверить данные. Если ее нет, проверьте данные, полученные в первый день эксперимента.

— В самом начале проведения тестирования проверьте, действительно ли оно работает.

— И, наконец, не смотрите на результаты! Преждевременный просмотр результатов может испортить статистическую значимость. Почему? Читайте здесь.

6. Анализируйте результаты. Наконец-то самое интересное

Вам нужно получить данные и рассчитать значения выбранной ранее метрики успеха для обеих версий (A и B) и разницу между этими значениями. Если не было никакой разницы в целом, вы также можете сегментировать выборку по платформам, типам источников, географическим параметрам и т. п., если это применимо. Вы можете обнаружить, что версия B работает лучше или хуже для определенных сегментов.

Проверьте статистическую значимость. Статистическая теория, лежащая в основе этого подхода, объясняется здесь, но основная идея в том, чтобы выяснить, была ли разница в результатах между A и B связана с изменениями или это результат случайности или естественных изменений. Это определяется путем сравнения тестовых статистических данных (и полученного p-значения) с вашим уровнем значимости.

Если p-значение меньше уровня значимости, то можно отвергнуть нулевую гипотезу, имея доказательства для альтернативы.

Если p-значение больше или равно уровню значимости, мы не можем отвергнуть нулевую гипотезу о том, что A и B не отличаются друг от друга.

A/B-тестирование может дать следующие результаты:

— Контрольная версия, А выигрывает или между версиями нет разницы. Если исключить причины, которые могут привести к недействительному тестированию, то проигрыш новой версии может быть вызван, например, плохим сообщением и брендингом конкурентного предложения или плохим клиентским опытом.

В этом сценарии вы можете углубиться в данные или провести исследование пользователей, чтобы понять, почему новая версия не работает так, как ожидалось. Это, в свою очередь, поможет собрать информацию для следующих тестов.

— Версия B выигрывает. A/B-тест подтвердил вашу гипотезу о лучшей производительности версии B по сравнению с версией A. Отлично! Опубликовав результаты, вы можете провести эксперимент на всей аудитории и получить новые результаты.

Заключение

Независимо от того, был ли ваш тест успешным или нет, относитесь к каждому эксперименту как к возможности для обучения. Используйте то, чему вы научились, для выработки вашей следующей гипотезы. Вы можете, например, использовать предыдущий тест или сконцентрироваться на другой области, требующей оптимизации. Возможности бесконечны.

Источник

Статистическая значимость, критерии и ошибки

Проблема множественного тестирования гипотез

Проблема подглядывания

Методы досрочного завершения теста

Pocock

O’Brien-Fleming

Калькулятор A/B-тестов

Заключение

Замаскированная проверка гипотез

Нулевая гипотеза

Многочисленное проведение эксперимента

Центральная предельная теорема

Давайте обобщим пройденное:

Завершающие шаги

Подведем итоги

Формируем гипотезу

Характеристика и нормализация данных

Выбираем победителя

Не только R

Задачи для проверки критериев

CUPED

CUPAC

CUNOPAC

Автоматизация ML-части критериев

CUMPED

Uplift-критерий

Frankenstein-критерий

Результаты

Кому нужно A/B-тестирование

1. Определите цели

2. Определите метрику

3. Разработайте гипотезу

4. Подготовьте эксперимент

5. Проведите эксперимент

6. Анализируйте результаты. Наконец-то самое интересное

Заключение

Не пропустите эти материалы по теме: