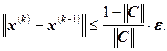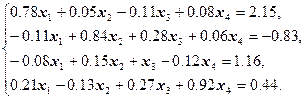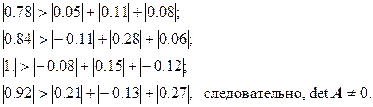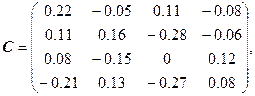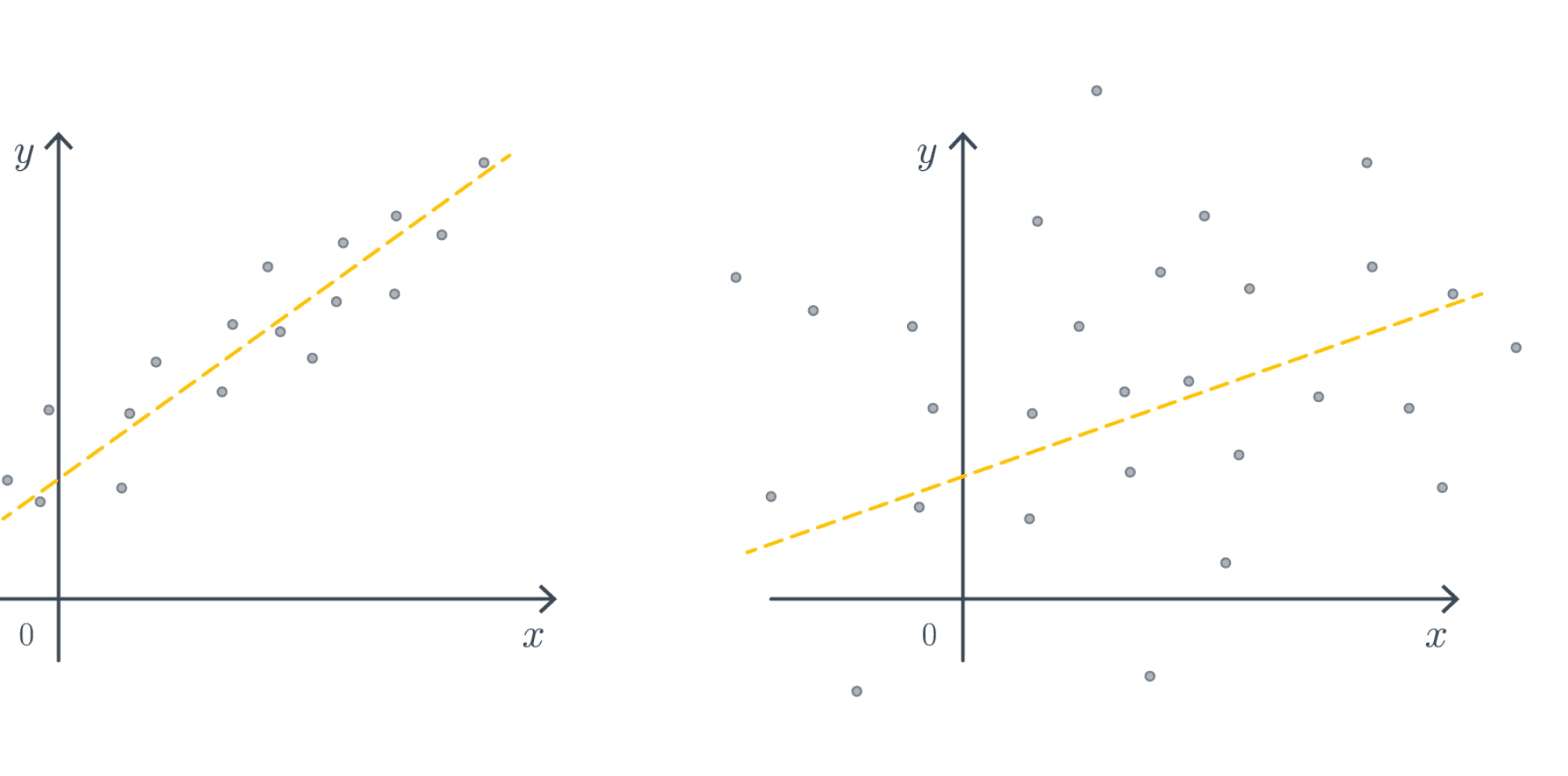Априорные и апостериорные ошибки

48

1.1. Определение погрешности

Физические величины
почти всегда известны приближенно, с
погрешностью, если только речь не идет
о целочисленных величинах или физических
эталонах.

Погрешность
(ошибка)
некоторой величины— это разность между приближенными точнымзначениями некоторой величины.

.
(1.1)

Абсолютная погрешность
величины
— абсолютная величина погрешности:.

Относительная
погрешность
величины
— это отношение абсолютной погрешности
к абсолютной величине приближенного
значения:

(1.2)

В соответствии с
определением (1.1) погрешность бывает
известна точно только тогда, когда
известно точное значение интересующей
нас величины. В практических расчетах
такая ситуация лишена смысла и поэтому
обычно погрешность находят приближенно.
Как правило, достаточно знать значение
погрешности, округленное до первой
значащей цифры. Более того, часто
достаточно указать порядок величины
абсолютной погрешности или оценку
сверху и проводить исследования с
запасом
точности.

Под понятием
точность
понимают количество верных значащих
цифр в значении величины.

Приближенную величину

можно рассматривать как переменную,
принимающую значения в некоторой
окрестности точки
.
Тогда, если задана некоторая функция
,
то оценить ее погрешность можно с помощью
формулы для дифференциала:

.
(1.3)

Аналогично для функции,
зависящей от нескольких переменных
,
погрешность имеет вид

.
(1.4)

1.2. Источники погрешности

В теоретических
исследованиях выделяют следующие
источники погрешности:

— погрешность
исходных данных;

— погрешность
математической модели,
связанную с тем, что не рассматриваются
факторы и явления, мало влияющие на
исследуемые процессы;

— погрешность
метода, связанную
с тем, что идеальные математические
объекты и операции могут заменяться их
приближенными аналогами (производная
— на отношение разностей, интеграл — на
конечную сумму и т.п.);

— погрешность
округления,
связанную с количеством удерживаемых
значащих цифр в расчетах, которая при
машинном счете зависит от типа используемых
переменных.

Считается рациональным,
если каждый из этапов преобразования
данных несущественно увеличивает
погрешность. Поэтому погрешность каждого
из перечисленных типов должна быть
меньше погрешности предыдущего типа.

После получения
результатов расчетов следует сравнить
их погрешность с допустимой погрешностью,
которая обычно диктуется конкретными
условиями. Если погрешность велика
(больше допустимой), то нужно найти
главный источник погрешности и, устранив
его, повторить исследование.

При оформлении
результатов расчетов числовые данные
следует записывать с количеством
значащих цифр, соответствующим точности
исходных данных.

1.3. Способы оценки погрешности

Различают априорную
и апостериорную оценки погрешности.

Априорная оценка
погрешности
— та, которая может быть получена до
решения задачи. Она позволяет сначала
определить, при каких параметрах
математической модели может быть
получена удовлетворительная точность
и только после этого провести решение
поставленной задачи. Такая последовательность
действий является наиболее рациональной.
Однако на практике получить априорную
оценку погрешности удается нечасто.

Апостериорная
оценка погрешности
— та, которая получается после (в
результате) решения задачи. Для этого,
как правило, необходимо получить
несколько решений задачи с различными
параметрами математической модели.
Такой подход более трудоемок, но обычно
он бывает единственно возможным.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Пусть ищется решение системы линейных уравнений  с невырожденной матрицей  A ().

Так как , следовательно, система линейных уравнений  имеет единственное решение.

Преобразуем систему линейных уравнений  к виду: , где  – квадратная матрица,  – вектор. Причем системы являются эквивалентными, то есть их решения совпадают. В дальнейшем мы будем рассматривать систему .

Выбирается вектор начального приближения:

.

Строится итерационный процесс:

.

Итерационный процесс прекращается при выполнении условия:

,

где  – точное решение системы линейных уравнений. В этом случае  – приближенное решение системы линейных уравнений с точностью , полученное методом итераций.

Естественно, возникает ряд вопросов:

· При каких условиях последовательность  сходится к точному решению системы линейных уравнений?

· Как выбирать начальное приближение ?

· Как сформулировать условия остановки итерационного процесса?

Последовательно будем отвечать на эти вопросы.

Теорема о сходимости

Пусть система линейных уравнений  имеет единственное решение. Для сходимости последовательности приближений  к точному решению системы линейных уравнений  достаточно, чтобы . При выполнении этого условия последовательность  сходится к точному решению при любом векторе начального приближения .

Оценка погрешности. Для метода итераций удается получить две оценки погрешности: априорную и апостериорную.

Априорная оценка погрешности – это оценка погрешности , которую можно получить до начала вычислений, зная только  и .

Апостериорная оценка погрешности – это оценка погрешности , которую получают, используя вычислительные приближения   и зная .

Теорема (априорная оценка погрешности)

Пусть система линейных уравнений  имеет единственное решение. Пусть . Тогда имеет место неравенство:

,   ,

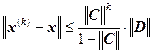
где  – k-е приближение, полученное методом итераций;  – точное решение системы линейных уравнений .

Отметим, что априорная оценка погрешности позволяет до вычислений оценить число шагов k, необходимых для достижения точности :

,        ,  следовательно, .

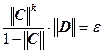
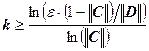
Следствие. Пусть система линейных уравнений  имеет единственное решение. Пусть , тогда для числа итераций k, необходимых для достижения точности e, справедливо следующее неравенство:

.

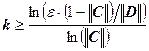
Отметим, что все нормы, входящие в это неравенство, должны быть согласованы. То есть если мы выбираем первую норму матрицы С, то должны взять и первую норму вектора D. Как правило, число шагов k, полученное из этой оценки, является заметно завышенным.

Теорема (апостериорная оценка погрешности)

Пусть система линейных уравнений  имеет единственное решение. Пусть , тогда имеет место неравенство:

. 

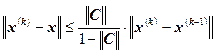
Следствие. Если выполняется условие , то . То есть, для того чтобы получить приближенное решение с точностью e, необходимо использовать следующее условие остановки итерационного процесса:

Сформулируем алгоритм метода итераций

1) Задана система линейных уравнений с невырожденной матрицей.

Преобразуем систему линейных уравнений  к виду: , где C – квадратная матрица, D – вектор. Причем системы являются эквивалентными и .

2) Выбираем произвольный вектор начального приближения:   .

3) Строим последовательность:   .

4) Эта последовательность сходится к точному решению системы линейных уравнений . При выполнении условия остановки итерационного процесса вычисления прекращаются.

Пример 1

Построить и обосновать алгоритм решения системы линейных уравнений  методом итераций с точностью :

Решение

Прежде всего, необходимо обосновать, что , если это не заданно в условии задачи. В нашем случае можно воспользоваться следующей теоремой:

Теорема

Если для матрицы А выполняются n неравенств 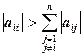 , то   матрица А невырожденная. 

Это свойство называется диагональным преобладанием: модуль диагонального элемента больше, чем сумма модулей внедиагональных элементов строки.

Эту теорему можно сформулировать и в другом виде, используя перенумерацию строк (столбцов). Определитель матрицы А не равен нулю, если в каждой строке (столбце) А имеется преобладающий элемент и эти элементы расположены в различных столбцах (строках).

В нашем случае:

В общем случае, нахождение матрицы C – сложная задача. Но в нашем примере очень легко найти матрицу C, удовлетворяющую всем условиям. Достаточно взять , тогда :

,             – эти системы эквивалентны.

.

Найдем С и докажем, что :

.

Вычислим первую норму С:

2. Выбираем вектор начального приближения:

Так как , то итерационный процесс:  сходится для любого     начального приближения.

3. Формула метода: .

4. Условие остановки итерационного процесса:

;

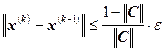
, следовательно, .

При выполнении этого условия  считается приближенным решением система линейных уравнений с точностью , полученным методом итераций.

Пример 2

Оценить число шагов, необходимых для достижения точности , при решении системы линейных уравнений  методом итераций.

Решение

Рассмотрим ту же систему линейных уравнений. Воспользуемся следствием из априорной оценкой погрешности. Условие на матрицу C выполнено:

, следовательно, метод итераций сходится и справедливо неравенство:

.

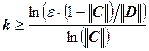
Мы вычисляли первую норму матрицы С, следовательно, и у вектора D также необходимо вычислять первую норму:

,

,

следовательно, .

Оценку сложности алгоритма метода итераций (по времени) мы получаем из априорной оценки погрешности

На каждом шаге итерационного процесса мы выполняем О(n²) арифметических действий, где n – порядок матрицы, следовательно, общее число арифметических действий: kО(n²).

Для реализации алгоритма метода итераций на каждом шаге необходимо хранить матрицу С, ,  и D, следовательно, требуется памяти О(n²).

Если ||C|| < 1, то алгоритм метода итераций для решения система линейных уравнений является устойчивым по отношению к вычислительной погрешности.

Недостатки метода итераций для решения систем линейных уравнений

1) Нет общего приема для перехода от матрицы А к матрице С таким образом, чтобы .

2) Метод итераций медленно сходится, если  близка к 1.

Существующие, приборы,
системы и традиционные методы определения места судна имеют значительные
недостатки. Так, например, погрешности определения счислимых координат за­висят
от точности работы лага и компаса, от гидрометеороло­гических условий
‘плавания, ‘погрешности определения счислимых координат растут с течением
времени. Методы мореходной аст­рономии зависят от погодных условий, имеют
ограниченную точность, а также требуют значительного времени для полу­чения
обсервованных координат. Визуальные методы опреде­ления места судна имеют
ограниченный район применения, и их использование также зависит от погодных
условий. Радио­пеленгование имеет ограниченный район использования и низ­кую
точность. Почти все радионавигационные системы имеют ограниченный район
использования, а глобальные радионавига­ционные системы имеют и низкую
точность. Спутниковые на­вигационные системы на низких орбитах обладают
значитель­ной дискретностью определения места. Радиолокационные стан­ции имеют
ограниченный район использования и необходимость опознания ориентиров.

Список можно продолжить,
но уже совершенно очевидно, что недостатки традиционных методов и средств
определения места судна в значительной мере снижают безопасность море­плавания.

1.6 
Априорная и
апостериорная оценка точности обсервации.

В соответствии с хорошей
практикой любой инженерный расчет должен сопровождаться оценкой точности
полученного результата: отыскание математического ожидания искомых параметров и
их дисперсии. В судовождении при определении места судна рассчитывают
координаты и оценивают их точность либо через ковариационную матрицу, либо
через одну из ее геометрических интерпретаций, например в виде эллипса
погрешностей.

Измерения проводятся с
погрешностями, поэтому и обсервованные координаты вычисляются тоже с
погрешностями.

1.6.1 
Правило переноса
погрешностей

Особенностью определения
координат является тот факт, что измерения косвенные, то есть измеряются
навигационные параметры, и допущенные погрешности затем переносятся в
погрешности координат.

1.6.2 
Априорная оценка
точности обсервации

Для оценки точности
обсервации используются вероятно-статистические методы, которые устанавливают
границы некоторой доверительной области, в которой с заданной вероятностью
может находиться истинное место судна. При этом делаются следующие допущения:

1. В измерениях отсутствуют
   промахи, т.е. грубые погрешности;
2. Систематические
   погрешности измерений определены и компенсированы поправкой;
3. Вычислительные
   погрешности и погрешности графики пренебрежительно малы;
4. Статистические числовые
   характеристики погрешностей измерений (дисперсия и СКП) и законы их
   распределения заданы априорно, т.е. по результатам предыдущих
   экспериментов (обсерваций). Эти априорные данные имеют приближенные
   средние значения и базируются на том, что все эксперименты, проведенные
   ранее с такими же приборами на судах, имеют сходные условия, что и текущая
   обсервация.

Рассмотрим этот вопрос на
примере ОМС по двум измерениям. В этом случае линеаризованная система принимает
вид.

A DX = DU(75)

Так как измерения с
погрешностями, то перепишем систему в виде

A (DX+dx) = DU+du.(76)

Тогда 

A dx = du.

Откуда

dx = A^-1 du.                                                                                              (77)

Погрешности измерений
могут быть статистически зависимы. Такая зависимость существует хотя бы потому,
что обычно используются как минимум одни и те же инструменты.  Эта
статистическая зависимость определяется коэффициентом корреляции, а общее
описание такой зависимости дает ковариационная матрица погрешностей измерений.

Формирование
ковариационной матрицы погрешности измерений выполняется по формуле

D(Du)=du du^T .                                    (78)

Для двумерного случая это
выглядит так:

На главной диагонали
находятся дисперсии измеряемых навигационных параметров, а вне диагонали —
ковариационные моменты, которые характеризуют статистическую связь между измерениями.

Структура ковариационной
матрицы погрешностей измерений определяет название МНК: если матрица
диагональна и все ее компоненты равны, то алгоритм носит название МНК, если
компоненты не равны, то это метод взвешенных наименьших квадратов; если матрица
не диагональна, то это обобщенный МНК.

Погрешности измерений в
процедуре расчета трансформируются в погрешности координат. В качестве такого
преобразователя погрешностей используется матрица коэффициентов A.

Определим ковариационную
матрицу погрешностей определяемых параметров, используя правила (A B)^-1
= B^-1 A^-1  и  (B^-1)^T=(B^T)^-1

D(Dx)=dx dx^T =
(A^-1 du) (A^-1 du)^T =A^-1 du du^T
(A^-1)^T =

A^-1 D(Du) (A^-1)^T = (A^Т (D(Du))^-1  A)^-1.

В дальнейшем при написании
ковариационных матриц, где это не вносит двузначности, будем опускать аргумент

Обозначим ковариационную
матрицу погрешностей координат через

N= D(Dx) = (A^Т D^-1 A)^-1.                                                                       (79)

Для двумерного случая
матрица N имеет вид:

,

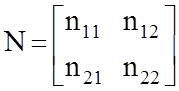
где n₁₁ —
дисперсия по широте

n₂₂ — дисперсия
по отшествию.

n₁₂ = n₂₁
— ковариационные моменты.

Вся информация о
погрешностях содержится в матрице N . В судовождении часто используется ее
геометрическая интерпретация в виде эллипса погрешностей. Установим связь между
элементами матрицы N и параметрами эллипса: полуосями и углом ориентации.

В общем случае такая
задача рассматривалась Хоттелингом Г. в 1933 г. Было показано, что для
ковариационной матрицы существуют векторы, направлениям которых соответствуют
максимальные и минимальные значения рассеивания (погрешностей). Численно эти
значения соответствуют собственным числам матрицы. Направления собственных
векторов, указывающие на направление максимального и минимального рассеивания
(дисперсии), соответствуют направлениям полуосей эллипса. Собственные числа —
это экстремальные значения дисперсий. Для перехода к линейным величинам —
полуосям эллипса (гипер — эллипса для n-мерного пространства), необходимо
извлечь квадратный корень.

Уважаемый посетитель!

Чтобы распечатать файл, скачайте его (в формате Word).

Ссылка на скачивание — внизу страницы.

Начнём с простого вопроса: как нам внести в модель априорные знания.

А зачем, собственно?

Представьте, что мы обучаем модель линейной регрессии $ysim langle x, wrangle + varepsilon$, $varepsilonsimmathcal{N}(0,sigma^2)$. С помощью MLE мы получили некоторую оценку $widehat{w}$ на веса $w$ – всякие ли их значения мы встретим с покорностью и смирением? Наверное, мы удивимся, если какие-то компоненты вектора $widehat{w}$ будут очень большими по сравнению с элементами $X$: пожалуй, наша физическая интуиция будет бунтовать против этого, мы задумаемся о том, что из-за потенциальных ошибок сокращения вычисление предсказаний $(x_i, widehat{w})$ окажутся неточным – в общем, хотелось бы по возможности избежать этого. Но как?

Будь мы приверженцами чисто инженерного подхода, мы бы сделали просто: прибавили бы к функции потерь слагаемое $+alpha|w|^2$, или $+alpha vert w vert^2$, или ещё что-то такое – тогда процедура обучения стала бы компромиссом между минимизацией исходного лосса и этой добавки, что попортило бы слегка близость $ysim langle x, w rangle$, но зато позволило бы лучше контролировать масштаб $widehat{w}$. Надо думать, вы узнали в этой конструкции старую добрую регуляризацию.

Но наша цель – зашить наше априорное знание о том, что компоненты $w$ не слишком велики по модулю, в вероятностную модель. Введение в модель априорного знания соответствует введению априорного распределения на $w$. Какое распределение выбрать? Ну, наверное, компоненты $w$ будут независимыми (ещё нам не хватало задавать взаимосвязи между ними!), а каждая из них будет иметь какое-то непрерывное распределение, в котором небольшие по модулю значения более правдоподобны, а совсем большие очень неправдоподобны. Мы знаем такие распределения? Да, и сразу несколько. Например, нормальное. Логично было бы определить

$$p(w) = prod_{i=1}^Dmathcal{N}(w_i vert 0,tau^2)$$

где $tau^2$ – какая-то дисперсия, которую мы возьмём с потолка или подберём по валидационной выборке. Отметим, что выбор нормального распределение следует и из принципа максимальной энтропии: ведь у него наибольшая энтропия среди распределений на всей числовой оси с нулевым матожиданием и дисперсией $tau^2$.

Контроль масштаба весов – это, вообще говоря, не единственное, что мы можем потребовать. Например, мы можем из каких-то физических соображений знать, что тот или иной вес в линейной модели непременно должен быть неотрицательным. Тогда в качестве априорного на этот вес мы можем взять, например, показательное распределение (которое, напомним, обладает максимальной энтропией среди распределений на положительных числах с данным матожиданием).

Оцениваем не значение параметра, а его распределение

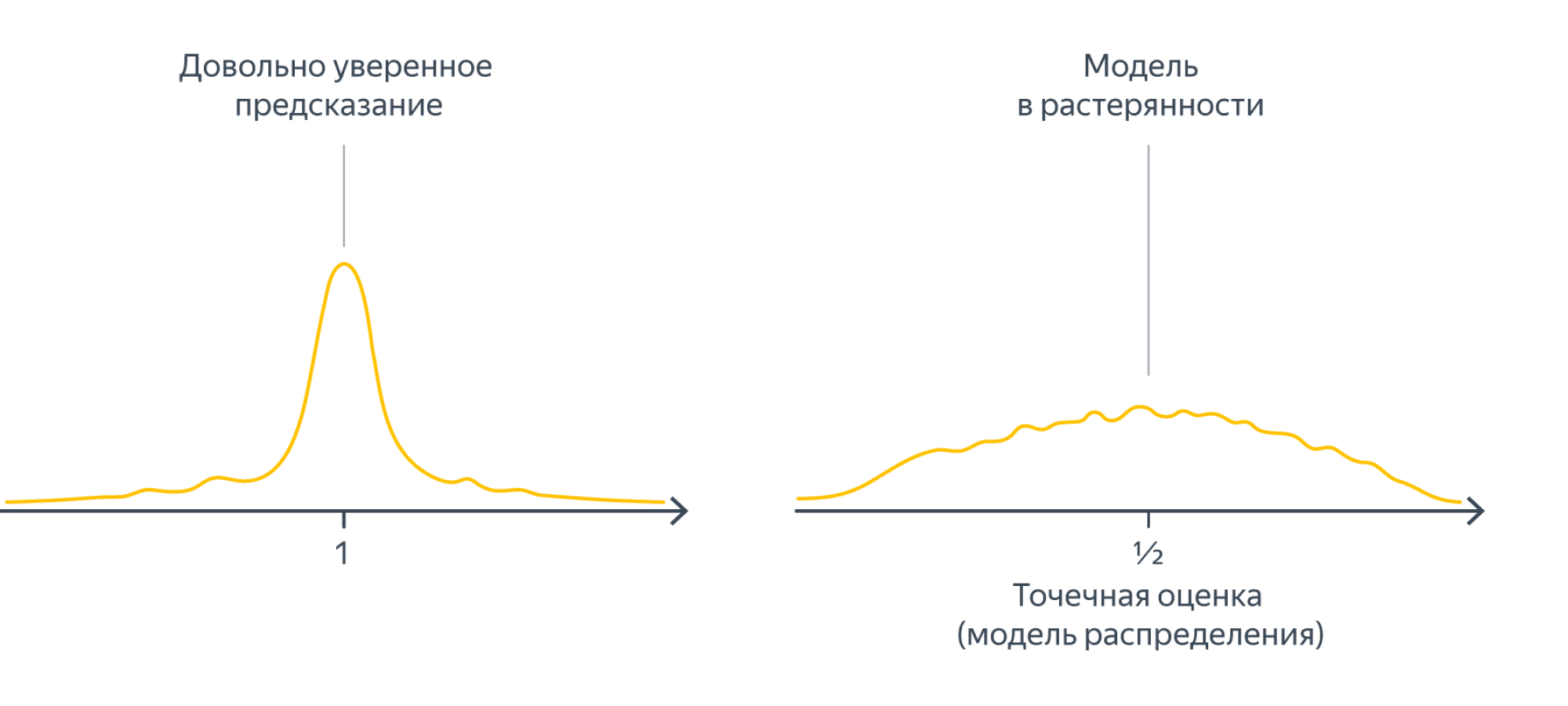
Раз уж мы начали говорить о распределении на веса $w$, то почему бы не пойти дальше. Решая задачу классификации, мы уже столкнулись с тем, что может быть важна не только предсказанная метка класса, но и вероятности. Аналогичное верно и для задачи регрессии. Давайте рассмотрим две следующих ситуации, в каждой из коорых мы пытаемся построить регрессию $ysim ax + b$:

Несмотря на то, что в каждом из случаев »точная формула» или градиентный спуск выдадут нам что-то, степень нашей уверенности в ответе совершенно различная. Один из способов выразить (не)уверенность – оценить распределение параметров. Так, для примеров выше распределения на параметр $a$ могли бы иметь какой-то такой вид:

Дальше мы постараемся формализовать процесс получения таких оценок.

Построение апостериорного распределения

Давайте ненадолго забудем про линейную регрессию и представим, что мы подобрали с полу монету, которая выпадает орлом с некоторой неизвестной пока вероятностью $theta$. До тех пор, пока мы не начали её подкидывать, мы совершенно ничего не знаем о $theta$, эта вероятность может быть совершенно любой – то есть априорное распределение на $theta$ является равномерным (на отрезке $[0,1]$):

$$p(theta) = mathbb{I}_{[0;1]}(theta)$$

Теперь представим, что мы подкинули её $n$ раз, получив результаты $Y = (y_1,ldots,y_n)$ ($0$ – решка, $1$ – орёл), среди которых $n_0 = n — sum_{i=1}^ny_i$ решек и $n_1=sum_{i=1}^ny_i$ орлов. Определённо наши познания о числе $p$ стали точнее: так, если $n_1$ мало, то можно заподозрить, что и $p$ невелико (уже чувствуете, запахло распределением!). Распределение мы посчитаем с помощью формулы Байеса:

$$color{#348FEA}{p(theta vert Y) = frac{p(theta , Y)}{p(Y)} = frac{p(Y vert theta)p(theta)}{
int p(Y vert psi)p(psi)dpsi
}}$$

в нашем случае:

$$p(theta vert Y) = frac{prod_{i=1}^ntheta^{x_i}(1 — theta)^{1 — x_i}mathbb{I}_{[0,1]}(theta)}{
int_0^1prod_{i=1}^npsi^{x_i}(1 — psi)^{1 — x_i}dpsi} =
$$

$$=frac{theta^{n_1}(1 — theta)^{n_0}mathbb{I}_{[0,1]}(theta)}{
int_0^1psi^{n_1}(1 — psi)^{n_0}dpsi}
$$

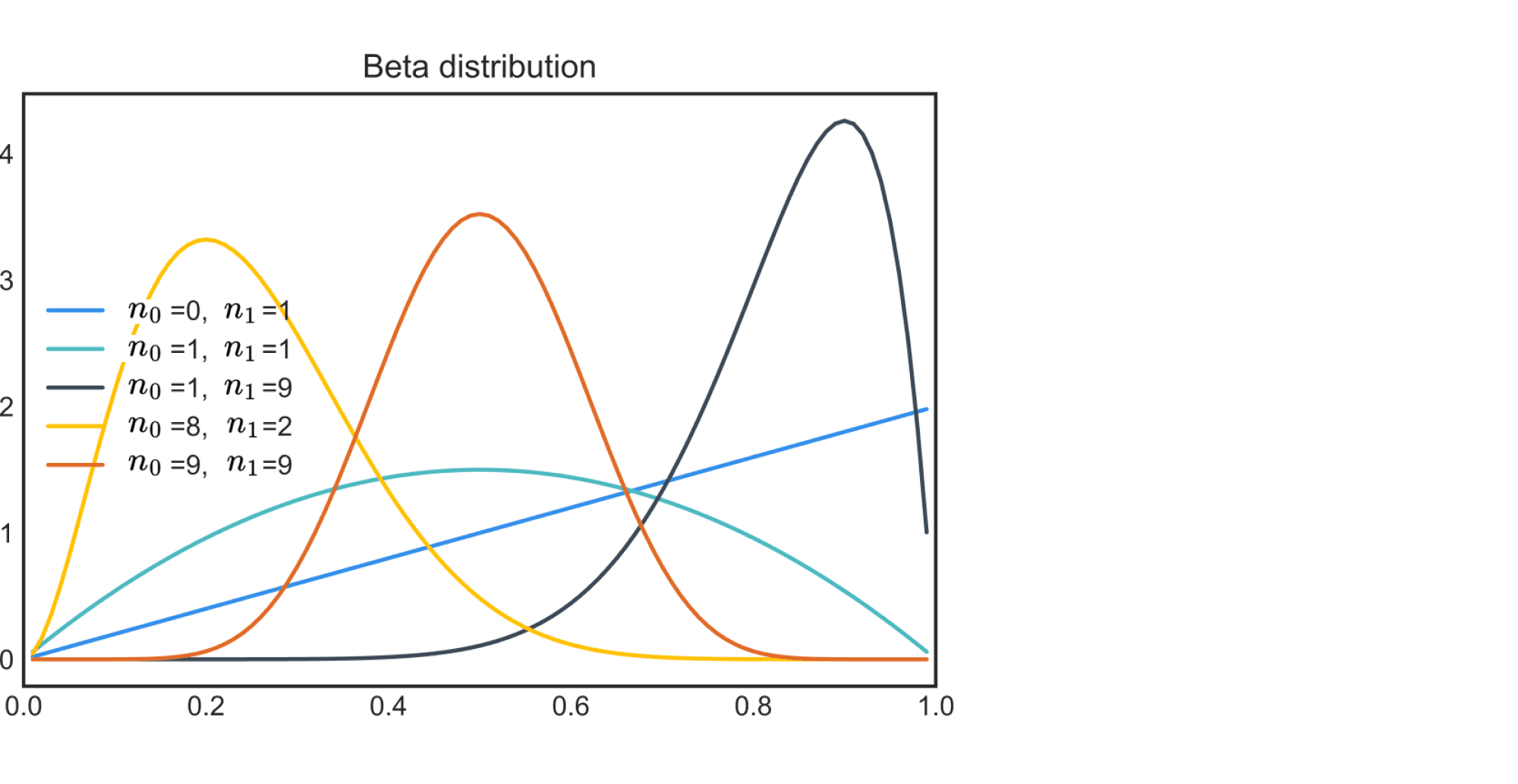
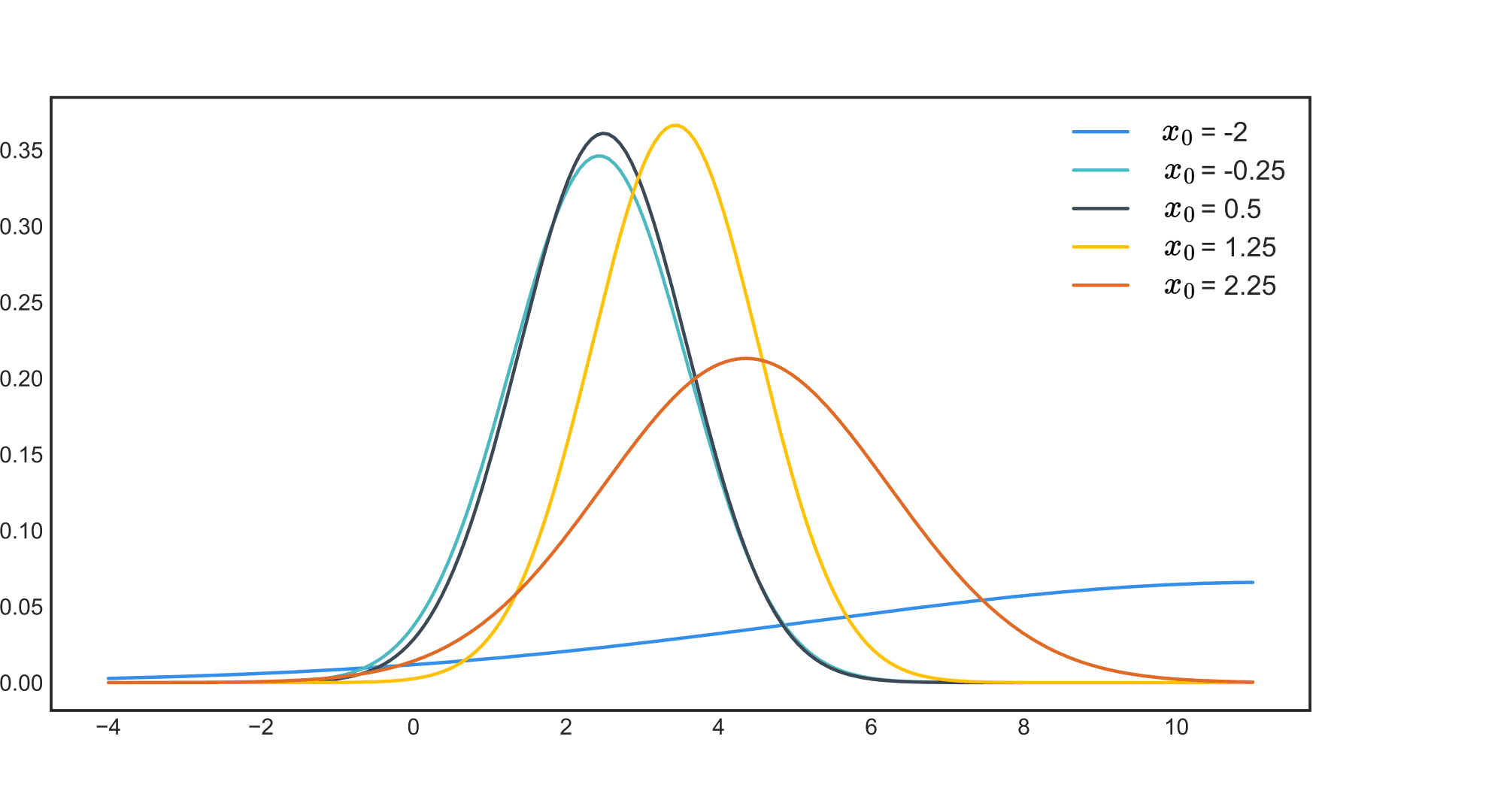
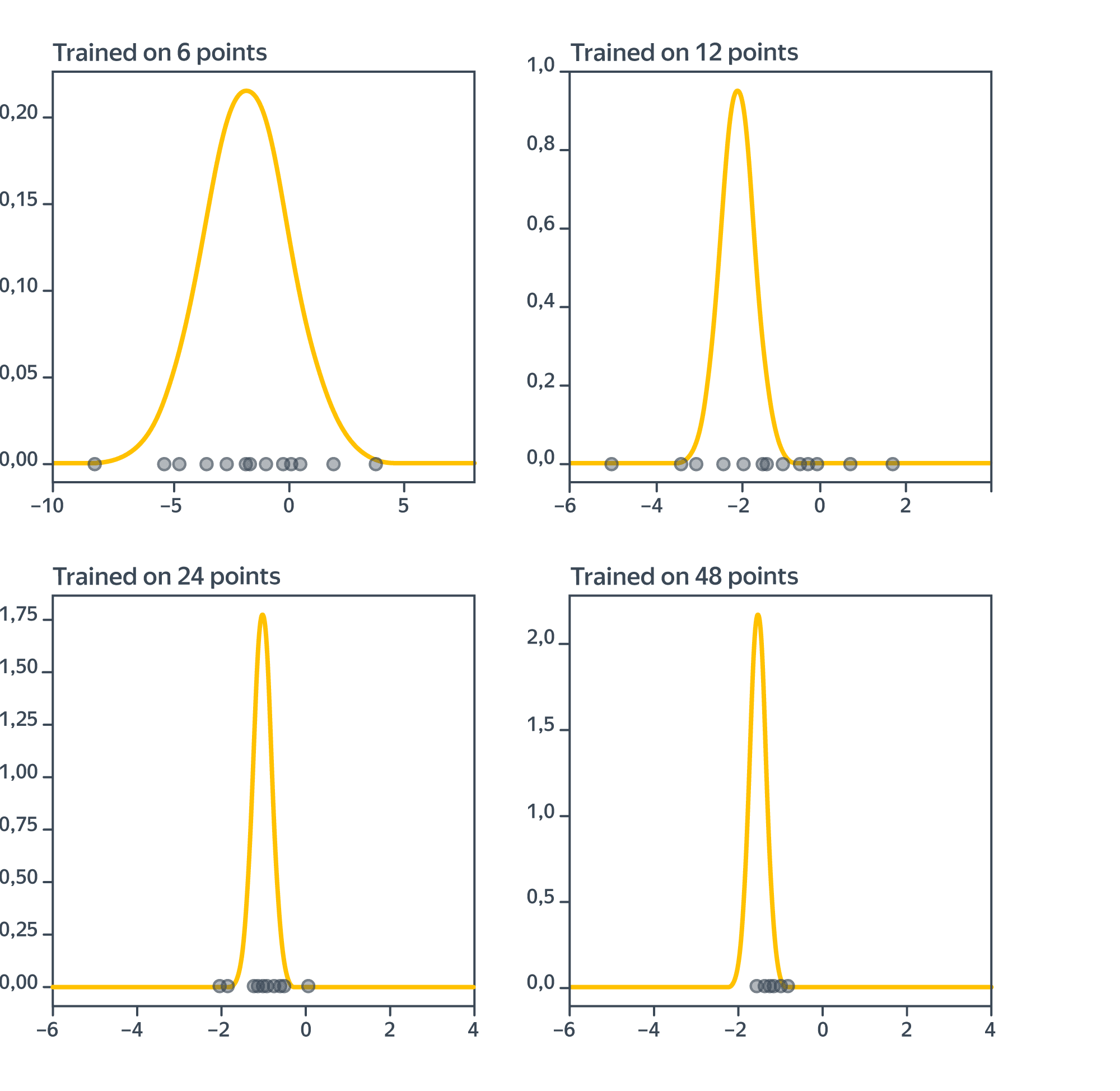
В этом выражении нетрудно узнать бета-распределение: $text{Beta}(n_1 + 1, n_0 + 1)$. Давайте нарисует графики его плотности для нескольких конкретных значений $n_0$ и $n_1$:

Как можно заметить, с ростом $n$ мы всё лучше понимаем, каким может быть $theta$, при этом если орёл выпадал редко, то пик оказывается ближе к нулю, и наоборот. Ширина пика в каком-то смысле отражает нашу уверенность в том, какими могут быть значения параметра, и не случайно чем больше у нас данных – тем уже будет пик, то есть тем больше уверенности.

Распределение $p(thetavert Y)$ параметра, полученное с учётом данных, называется апостериорным. Переход от априорного распределения к апостериорному отражает обновление нашего представления о параметрах распределения с учётом полученной информации, и этот процесс является сердцем байесовского подхода. Отметим, что если нам придут новые данные $Y’ = (y_1′,ldots,y_m’)$, в которых $m_0$ решек и $m_1$ орлов, мы сможем ещё раз обновить распределение по той же формуле Байеса:

$$p(theta vert Ycup Y’) = p([thetavert Y]vert Y’) = frac{p(Y’verttheta)p(thetavert Y)}{p(Y’)}=
$$

$$=frac{theta^{m_1}(1 — theta)^{m_0}frac{theta^{n_1}(1 — theta)^{n_0}}{B(n_1 + 1, n_0 + 1)}mathbb{I}_{[0,1]}(theta)}{
text{злой интеграл}} =
$$

$$=frac{theta^{n_1 + m_1}(1 — theta)^{n_0 + m_0}}{text{константа}}simtext{Beta}(n_1 + m_1 + 1, n_0 + m_0 + 1)$$

Вопрос на подумать. Пусть $p(yvertmu) = mathcal{N}(yvertmu,sigma^2)$ – нормальное распределение с фиксированной дисперсией $sigma^2$, а для параметра $mu$ в качестве априорного выбрано также нормальное распределение $mathcal{N}(yvert lambda,theta^2)$. Каким будет апостериорное распределение при условии данных $Y = (y_1,ldots,y_n)$?

Попробуйте посчитать сами, прежде чем смотреть решение.

Сопряжённые распределения

В двух предыдущих примерах нам очень сильно повезло, что апостериорные распределения оказались нашими добрыми знакомыми. Если же взять случайную пару распределений $p(yverttheta)$ и $p(theta)$, результат может оказаться совсем не таким приятным. В самом деле, нет никакой проблемы в том, чтобы посчитать числитель формулы Байеса, но вот интеграл в знаменателе может и не найтись. Поэтому выбирать распределения нужно с умом. Более того, поскольку апостериорное распределение само станет априорным, когда придут новые данные, хочется, чтобы априорное и апостериорное распределения были из одного семейства; пары (семейств) распределений $p(yverttheta)$ и $p(theta)$, для которых это выполняется, называются сопряжёнными ($ptheta)$ называется сопряжённым к $p(yverttheta)$). Полезно помнить несколько наиболее распространённых пар сопряжённых распределений:

• $p(yverttheta)$ – распределение Бернулли с вероятностью успеха $theta$, $p(theta)$ – бета распределение;
• $p(yvertmu)$ – нормальное с матожиданием $mu$ и фиксированной дисперсией $sigma^2$, $p(theta)$ также нормальное;
• $p(yvertlambda)$ – показательное с параметром $lambda$, $p(lambda)$ – гамма распределение;
• $p(yvertlambda)$ – пуассоновское с параметром $lambda$, $p(lambda)$ – гамма распределение;
• $p(yverttheta)$ – равномерное на отрезке $[0,theta]$, $p(theta)$ – Парето;

Возможно, вы заметили, что почти все указанные выше семейства распределений (кроме равномерного и Парето) относятся к экспоненциальному классу. И это не случайность! Экспоненциальный класс и тут лучше всех: оказывается, что для $p(yverttheta)$ из экспоненциального класса можно легко подобрать сопряжённое $p(theta)$. Давайте же это сделаем.

Пусть $p(yverttheta)$ имеет вид

$$p(yverttheta) = frac1{h(theta)}g(y)exp(theta^Tu(y))$$

Положим

$$p(theta) = frac1{h^{nu}(theta)}exp(eta^Ttheta)cdot f(eta, nu)$$

где $f(eta, nu)$ – множитель, обеспечивающий равенство единице интеграла от этой функции. Найдём апостериорное распределение:

$$p(thetavert Y) = frac{left[prod_{i=1}^nfrac1{h(theta)}g(y_i)exp(theta^Tu(y_i))right]frac1{h^{nu}(theta)}exp(eta^Ttheta)cdot f(eta, nu)}{text{злой интеграл}} = $$

$$= frac{frac1{h^{nu + n}(theta)}expleft(theta^Tleft[eta + sum_{i=1}^nu(y_i)right]right)}{text{что-то, где нет }theta}$$

Это распределение действительно из того же семейства, что и $p(theta)$, только с новыми параметрами:

$$eta_{new} = eta + sum_{i=1}^nu(y_i),quadnu_{new} = nu + n$$

Пример. Пусть $p(yvert q) = q^y(1 — q)^{1 — y}$ подчиняется распределению Бернулли. Напомним, что оно следующим образом представляется в привычном для экспоненциального класса виде:

$$p(yvert q) = underbrace{(1 — q)}_{=frac1{h(q)}}expleft(underbrace{y}_{=u_1(y)}underbrace{log{frac{q}{1 — q}}}_{=theta}right)$$

Предлагается брать априорное распределение вида

$$p(q) = frac{(1 — q)^{nu}expleft(etalog{frac{q}{1-q}}right)}{text{что-то, где нет}q}$$

Тогда апостериорное распределение будет иметь вид (проверьте, посчитав по формуле Байеса!)

$$p(qvert Y) = frac{(1 — q)^{nu + n}expleft(left[eta + sum_{i=1}^ny_iright]log{frac{q}{1-q}}right)}{text{что-то, где нет}q}$$

Превратив логарифм частного в сумму, а экспоненту суммы в произведение, легко убедиться, что получается то самое бета распределение, которое мы уже получали выше.

Оценка апостериорного максимума (MAP)

Апостериорное распределение – это очень тонкий инструмент анализа данных, но иногда надо просто сказать число (или же интеграл в знаменателе не берётся и мы не можем толком посчитать распределение). В качестве точечной оценки логично выдать самое вероятное значение $thetavert Y$ (интеграл в знаменателе от $theta$ не зависит, поэтому на максимизацию не влияет):

$$color{blue}{widehat{theta}_{MAP} = underset{theta}{operatorname{argmax}}{p(theta vert Y)} = underset{theta}{operatorname{argmax}}{p(Y vert theta)p(theta)}}$$

Это число называется оценкой апостериорного максимума (MAP).

Если же в формуле выше перейти к логарифмам, то мы получим кое-что, до боли напоминающее старую добрую регуляризацию (и не просто так, как мы вскоре убедимся!):

$$underset{theta}{operatorname{argmax}}{p(Y vert theta)p(theta)} = underset{theta}{operatorname{argmax}}log(p(Y vert theta)p(theta)) = $$

$$=underset{theta}{operatorname{argmax}}left(vphantom{frac12}log{p(Y vert theta)} + log{p(theta)}right)$$

Пример. Рассмотрим снова распределение Бернулли $p(yvert q)$ и априорное распределение $p(q)simtext{Beta}(qvert a, b)$. Тогда MAP-оценка будет равна

$$underset{q}{operatorname{argmax}}{p(Y vert q)p(q)} = underset{q}{operatorname{argmax}}{q^{sum_{i=1}^ny_i}(1 — q)^{n — sum_{i=1}^ny_i}cdot q^{a — 1}(1 — q)^{b — 1}} = $$

$$underset{q}{operatorname{argmax}}left((a — 1 + sum_{i=1}^ny_i)log{q} + (b — 1 + n — sum_{i=1}^ny_i)log(1 — q)right)$$

Дифференцируя по $q$ и приравнивая производную к нулю, мы получаем

$$q = frac{a + sum_{i=1}^ny_i — 1}{a + b + n — 2}$$

В отличие от оценки максимального правдоподобия $frac{sum_{i=1}^ny_i}{n}$ мы здесь используем априорное знание: параметры $(a — 1)$ и $(b — 1)$ работают как «память о воображаемых испытаниях», как будто бы до того, как получить данные $y_i$, мы уже имели $(a — 1)$ успехов и $(b — 1)$ неудач.

Связь MAP- и MLE-оценок

Оценка максимального правдоподобия является частным случаем апостериорной оценки. В самом деле, если априорное распределение является равномерным, то есть $p(theta)$ не зависит $theta$ (если веса $theta$ вещественные, могут потребоваться дополнительные усилия, чтобы понять, как такое вообще получается), и тогда

$$widehat{theta}_{MAP} = underset{theta}{operatorname{argmax}}log{p(Y vert theta)p(theta)} = underset{theta}{operatorname{argmax}}left(log{p(Y vert theta)} + underbrace{log{p(theta)}}_{=const}right) =$$

$$= underset{theta}{operatorname{argmax}}log{p(y vert theta)} = widehat{theta}_{MLE}$$

Байесовские оценки для условных распределений

В предыдущих разделах мы разобрали, как байесовский подход работает для обычных, не условных распределений. Теперь вернёмся к чему-то более близкому к машинному обучению, а именно к распределениям вида $yvert x,w$, и убедимся, что для них байесовских подход работает точно так же, как и для обычных распределений.

Имея некоторое распределение $p(yvert x, w)$, мы подбираем для него априорное распределение на веса $p(w)$ (и да, оно не зависит от $x$: ведь априорное распределение существует ещё до появления данных) и вычисляем апостериорное распределение на веса:

$$p(w vert X, y)$$

Вычислять его мы будем по уже привычной формуле Байеса:

$$color{blue}{p(w vert X, y) = frac{p(y, w vert X)}{p(y)} = frac{p(y vert X, w)p(w)}{p(y)}}$$

Повторим ещё разок, в чём суть байесовского подхода: у нас было некоторое априорное представление $color{blue}{p(w)}$ о распределении весов $color{blue}{w}$, а теперь, посмотрев на данные $(x_i, y_i)_{i=1}^n$, мы уточняем своё понимание, формулируя апостериорное представление $p(w vert X, y)$.

Если же нам нужна только точечная оценка, мы можем ограничиться оценкой апостериорного максимума (MAP): $$color{blue}{widehat{w}_{MAP} = underset{w}{operatorname{argmax}}{p(w vert X,y)} = underset{w}{operatorname{argmax}}{p(y vert X, w)p(w)}} = $$

$$=underset{w}{operatorname{argmax}}left(vphantom{frac12}log{p(y vert X, w)} + log{p(w)}right)$$

что уже до неприличия напоминает регуляризованную модель

Пример: линейная регрессия с $L^2$-регуляризацией как модель с гауссовским априорным распределением на веса

В модели линейной регрессии $y = langle x, wrangle + varepsilon$, $varepsilonsimmathcal{N}(0, sigma^2)$ введём априорное распределение на веса вида

$$color{blue}{p(w) = mathcal{N}(w vert 0, tau^2I) = prod_{j=1}^D mathcal{N}(w_j vert 0, tau^2) = prod_{j=1}^D p(w_j)}$$

Тогда $widehat{w}_{MAP}$ является точкой минимума следующего выражения:

$$-log{p(y vert X, w)} — log{p(w)} =-sum_{i=1}^Np(y_i vert x_i, w) — sum_{j=1}^Dp(w_j) =$$

$$=-sum_{i=1}^Nleft(-frac12log(2pisigma^2) — frac{(y_i — (w, x_i))^2}{2sigma^2}right)
-sum_{j=1}^Dleft(-frac12log(2pitau^2) — frac{w_j^2}{2tau^2}right)=$$

$$= frac1{2sigma^2}sum_{i=1}^N(y_i — (w, x_i))^2 + frac1{2tau^2}sum_{j=1}^D w_j^2+mbox{ не зависящие от $w$ члены}$$

Получается, что

$$color{blue}{widehat{w}_{MAP} = underset{w}{operatorname{argmin}}left(vphantom{frac12}sum_{i=1}^N(y_i — (w, x_i))^2 + frac{sigma^2}{tau^2}|w|^2right)}$$

а это же функция потерь для линейной регрессии с $L^2$-регуляризацией! Напомним на всякий случай, что у этой задачи есть »точное» решение

$$color{blue}{widehat{w}_{MAP} = left(X^TX + frac{sigma^2}{tau^2}Iright)^{-1}X^Ty}$$

Для этого примера мы можем вычислить и апостериорное распределение $p(w vert X, y)$. В самом деле, из написанного выше мы можем заключить, что

$$log{p(w vert X, y)} = log(p(y vert X, w)p(w)) — log{p(y)} = $$

$$ =frac1{2sigma^2}(y — Xw)^T(y — Xw) + frac1{2tau^2}w^Tw+mbox{ не зависящие от $w$ члены}$$

Таким образом, $log{p(w vert X, y)}$ – это квадратичная функция от $w$, откуда следует, что апостериорное распределение является нормальным. Чтобы найти его параметры, нужно немного преобразовать полученное выражение:

$$ ldots=frac1{2sigma^2}(y^Ty — w^TX^Ty — y^TWx + w^TX^TXw) + frac1{2tau^2}w^Tw+mathrm{const}(w) =$$

$$=w^Tleft(frac1{2sigma^2}X^TX + frac1{2tau^2}Iright)w — frac{1}{2sigma^2}w^TX^Ty — frac1{2sigma^2}y^TWx + mathrm{const}(w) =$$

$$=frac12left(w — widehat{w}_{MAP}right)^Tleft(frac1{sigma^2}X^TX + frac1{tau^2}Iright)left(w — widehat{w}_{MAP}right) + mathrm{const}(w)=$$

Таким образом,

$$color{blue}{p(w vert X,y) = mathcal{N}left(widehat{w}_{MAP}, left(frac1{sigma^2}X^TX + frac1{tau^2}Iright)^{-1} right)}$$

Как видим, от априорного распределения оно отличается корректировкой как матожидания $0mapstowidehat{w}_{MAP}$, так и ковариационной матрицы $left(frac1{tau^2}Iright)^{-1}mapstoleft(frac1{sigma^2}X^TX + frac1{tau^2}Iright)^{-1}$. Отметим, что $X^TX$ – это, с точностью до численного множителя, оценка ковариационной матрицы признаков нашего датасета (элементы матрицы $X^TX$ – это скалярные произведения столбцов $X$, то есть столбцов значений признаков).

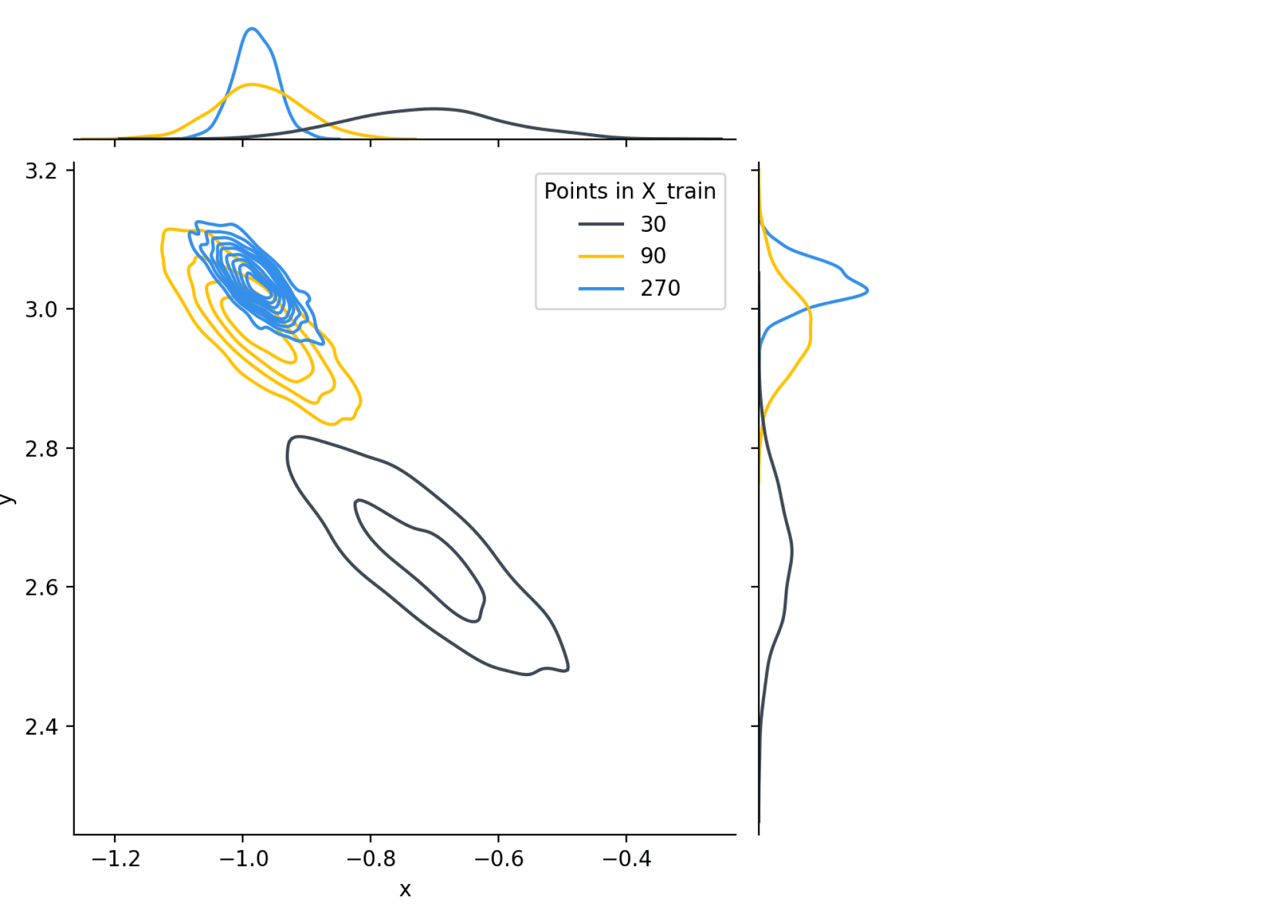
Иллюстрация. Давайте на простом примере (датасет с двумя признаками) посмотрим, как меняется апостериорное распределение $w$ с ростом размера обучающей выборки:

Как видим, не только мода распределения, то есть $widehat{w}_{MAP}$ приближается к своему истинному значению, но и дисперсия распределения постепенно уменьшается.

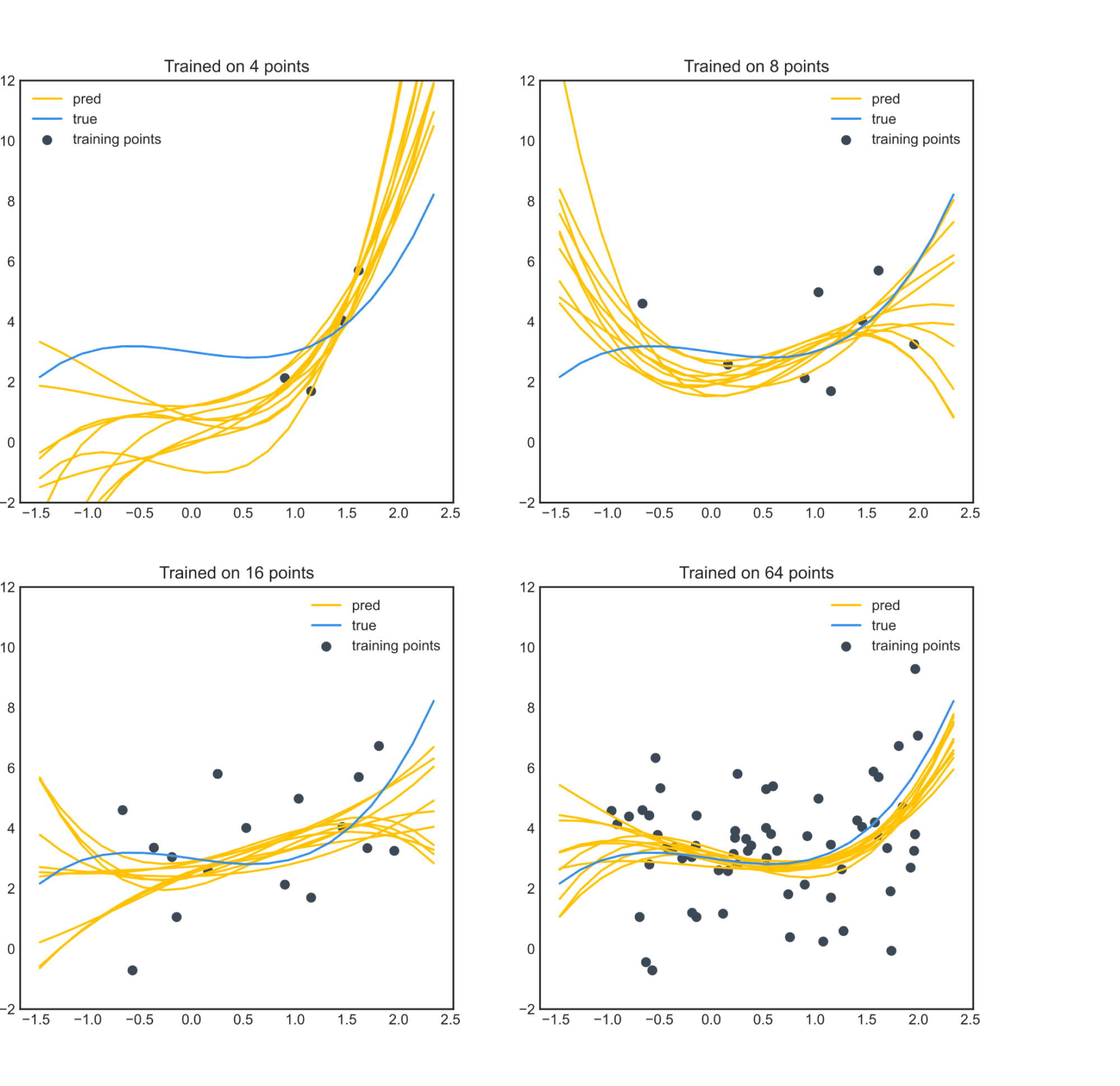
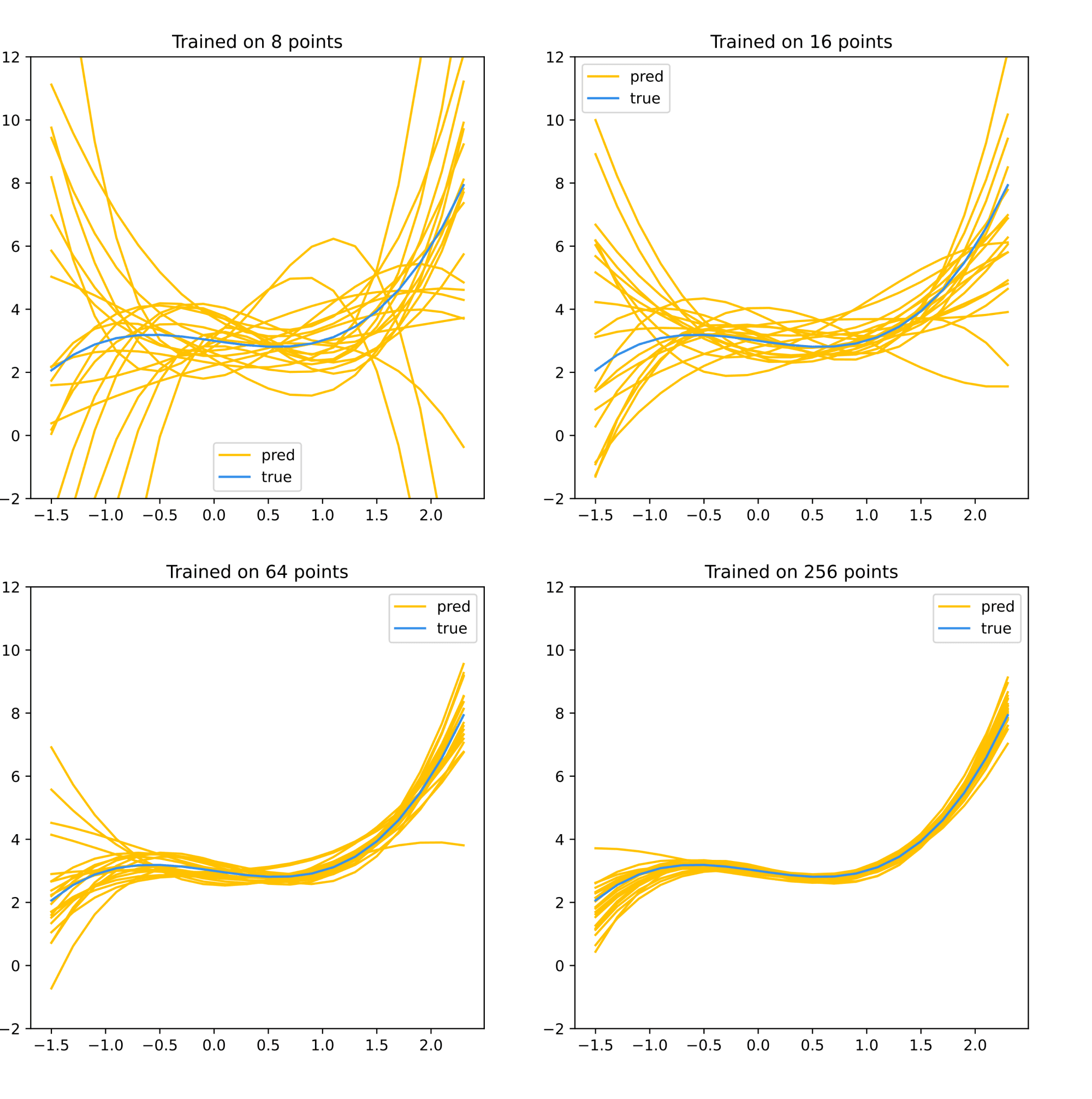
Ещё иллюстрация. Теперь рассмотрим задачу аппроксимации неизвестной функции одной переменной (чьи значения в обучающей выборке искажены нормальным шумом) многочленом третьей степени. Её, разумеется, тоже можно решать, как задачу линейной регрессии на коэффициенты многочлена. Давайте нарисуем, как будут выглядеть функции, сгенерированные из распределения ${p(w vert X,y)}$ для разного объёма обучающей выборки:

Тут тоже видим, что функции не только становятся ближе к истинной, но и разброс их уменьшается.

Пример: линейная регрессия с $L^1$-регуляризацией как модель с лапласовским априорным распределением на веса

Другим распределением, которое тоже может кодировать наше желание, чтобы небольшие по модулю значения $w_j$ были правдоподобными, а большие не очень, является распределение Лапласа. Посмотрим, что будет, если его взять в качестве априорного распределения на веса.

$$color{blue}{p(w) = prod_{j=1}^D p(w_j) = prod_{j=1}^Dfrac{lambda}{2}exp(-lambda|w_m|)}$$

Проводя такое же вычисление, получаем, что

$$color{blue}{widehat{w}_{MAP} = underset{w}{operatorname{argmin}}left(vphantom{frac12}sum_{i=1}^N(y_i — (w, x_i))^2 + lambdasum_{j=1}^D|w_j|right)}$$

а это же функция потерь для линейной регрессии с $L^1$-регуляризацией!

Если мы нашли распределение $w$, как делать предсказания?

Все изложенные выше рассуждения проводились в ситуации, когда $X = X_{train}$ – обучающая выборка. Для неё мы можем посчитать

$$p(w vert X_{train}, y_{train}) = frac{(y vert X,w)p(w)}{p(y)}$$

и точечную апостериорную оценку $widehat{w}_{MAP} = underset{w}{operatorname{argmax}}{p(y vert X,w)p(y)}$. А теперь пусть нам дан новый объект $x_0inmathbb{X}$. Какой таргет $y_0$ мы для него предскажем?

Было бы естественным, раз уж мы предсказываем распределение для $w$, и для $y_0$ тоже предсказывать распределение. Делается это следующим образом:

$$p(y_0 vert x_0, X_{train}, y_{train}) = int{p(y_0 vert x_0,w)p(w vert X_{train}, y_{train})}dw$$

Надо признать, что вычисление этого интеграла не всегда является посильной задачей, поэтому зачастую приходится »просто подставлять $widehat{w}_{MAP}$». В вероятностных терминах это можно описать так: вместо сложного апостериорного распределения $p(w vert X_{train}, y_{train})$ мы берём самое грубое на свете приближение

$$p(w vert X_{train}, y_{train})approxdelta(w — widehat{w}_{MAP}),$$

где $delta(t)$ – дельта-функция, которая не является честной функцией (а является тем, что математики называют обобщёнными функциями), которая определяется тем свойством, что $int f(t)delta(t)dt = f(0)$ для достаточно разумных функций $f$. Если не мудрствовать лукаво, то это всё значит, что

$$p(y_0 vert x_0,X_{train}, y_{train})approx p(y_0 vert x_0,widehat{w}_{MAP})$$

Пример. Пусть $ysim Xw + varepsilon$, $varepsilonsimmathcal{N}(0,sigma)^2$ – модель линейной регрессии с априорным распределением $p(w) = mathcal{N}(0,tau^2)$ на параметры. Тогда, как мы уже видели раньше,

$$p(w vert X,y) = mathcal{N}left(w vert widehat{w}_{MAP}, left(frac1{sigma^2}X^TX + frac1{tau^2}Iright)^{-1} right)$$

Попробуем для новой точки $x_0$ посчитать распределение на $y_0$. Рекомендуем читателю попробовать самостоятельно посчитать интеграл или же обратиться к пункту 7.6.2 книжки »Machine Learning A Probabilistic Perspective» автора Kevin P. Murphy, убедившись, что

$$p(y_0 vert x_0, X_{train}, y_{train}) = mathcal{N}left(y_0 vert x_0widehat{w}_{MAP},
sigma^2 + sigma^2x_0^Tleft(X^TX + frac{sigma^2}{tau^2}Iright)^{-1}x_0right)$$

что, очевидно, более содержательно, чем оценка, полученная с помощью приближения $p(w vert X_{train}, y_{train})approxdelta(w — widehat{w}_{MAP})$:

$$p(y_0 vert x_0, widehat{w}_{MAP}) = mathcal{N}left(y_0left vert x_0widehat{w}_{MAP},
sigma^2right.right)$$

Собственно, видно, что в этом случае

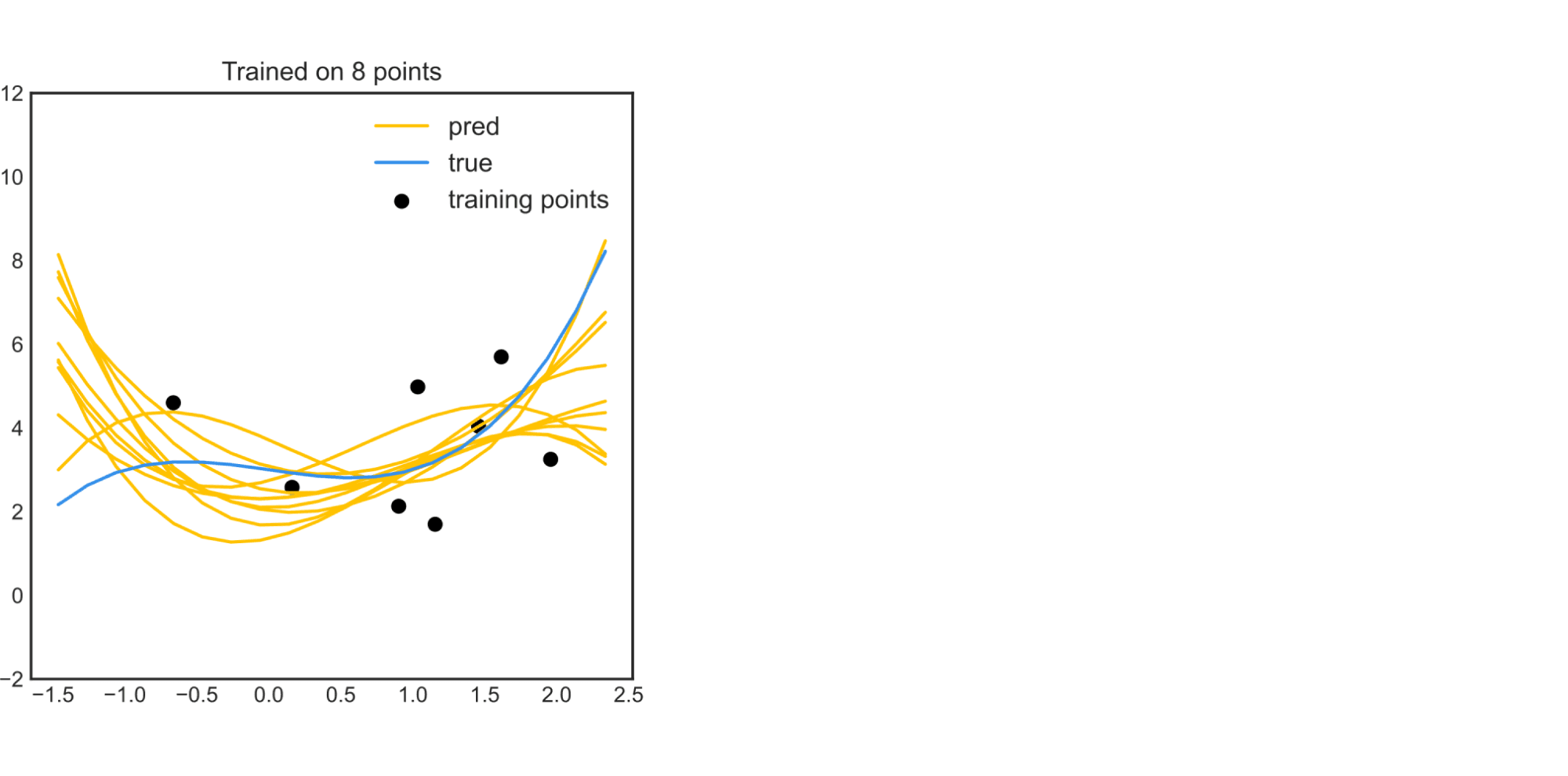
Пример в примере. Рассмотрим полюбившуюся уже нам задачу приближения функции многочленом степени не выше $3$ (в которой мы строим модели с $sigma^2 = tau^2 = 1$). Для $N = 8$ мы получали такую картинку:

Если оценить по приведённым выше формулам $p(y_0 vert x_0, X_{train}, y_{train})$ для разных $x_0$, то можно убедиться, что модель в большей степени уверена в предсказаниях для точек из областей, где было больше точек из обучающей выборки:

Байесовский подход и дообучение моделей

До сих пор мы в основном рассуждали о моделях машинного обучения как о чём-то, что один раз обучается и дальше навсегда застывает в таком виде, но в жизни такое скорее редкость. Мы пока не будем обсуждать изменчивость истинных зависимостей во времени, но даже если истина неизменна, к нам могут поступать новые данные, которые очень хотелось бы использовать для дообучения модели.

Обычные, не байесовские вероятностные модели не предоставляют таких инструментов. Оценку максимального правдоподобия придётся пересчитывать заново (хотя, конечно, можно схитрить, использовав старое значение в качестве начального приближения при итеративной оптимизации). Байесовский же подход позволяет оформить дообучения в виде простой и элегантной формулы: при добавлении новых данных $(x_{N+1}, y_{N+1}),ldots,(x_M, y_M)$ имеем

$$pleft(wvert (x_i, y_i)_{i=1}^Mright) = frac{pleft((y_i)_{i=N+1}^Mvert (x_i)_{i=N+1}^Mright) pleft(wvert (x_i, y_i)_{i=1}^Nright)}{pleft( (y_i)_{i=N+1}^M right)}$$

Байесовский подход к выбору модели: мотивация

Нам часто приходится выбирать: дерево или случайный лес, линейная модель или метод ближайших соседей; да, собственно, и внутри наших вероятностных моделей есть параметры (скажем, дисперсия шума $sigma^2$ и $tau^2$), которые надо бы подбирать. Но как?

В обычной ситуации мы выбираем модель, обученную на выборке $(X_{train}, y_{train})$ в зависимости от того, как она себя ведёт на валидационной выборке $(X_{val}, y_{val})$ (сравниваем правдоподобие или более сложные метрики) – или же делаем кросс-валидацию. Но как сравнивать модели, выдающие распределение?

Ответим вопросом на вопрос: а как вообще сравнивать модели? Назначение любой модели – объяснять мир вокруг нас, и её качество определяется именно тем, насколько хорошо она справляется с этой задачей. Тестовая выборка – это хороший способ оценки, потому что она показывает, насколько вписываются в модель новые данные. Но могут быть и другие соображения, помогающие оценить качество модели.

Пример

Аналитик Василий опоздал на работу. Своему руководителю он может предложить самые разные объяснения – и это будет выработанная на одном обучающем примере модель, описывающая причины опоздания (и потенциально позволяющая руководителю принять решение о том, карать ли Василия). Конечно, руководитель мог бы принять изложенную Василием модель к сведению, подождать, пока появятся другие опоздавшие, и оценить её, так скажем, на тестовой выборке, но стоит ли? Давайте рассмотрим несколько конкретных примеров:

• Модель »Василий опоздал, потому что так получилось», то есть факт опоздания – это просто ни от чего не зависящая случайная величина. Такая модель плоха тем, что (а) не предлагает, на самом деле, никакого объяснения тому факту, что Василий опоздал, а его коллега Надежда не опоздала и (б) совершенно не помогает решить, наказывать ли за опоздание. Наверное, такое не удовлетворит руководителя.

• Модель »Василий опоздал, потому что рядом с его домом открылся портал в другой мир, где шла великая битва орков с эльфами, и он почувствовал, что посто обязан принять в ней участие на стороне орков, которых привёл к победе, завоевав руку и сердце орочьей принцессы, после чего был перенсён обратно в наш скучный мир завистливым шаманом». Чем же она плоха? Битва с эльфами – это, безусловно, важное и нужное дело, и на месте руководителя мы бы дружно согласились, что причина уважительная. Но заметим, что в рамках этой модели можно объяснить множество потенциальных исходов, среди которых довольно маловероятным представляется наблюдаемый: тот, в котором Василий не погиб в бою, не остался со своей принцессой и не был порабощён каким-нибудь завистливым шаманом. Отметим и другой недостаток этой модели: её невозможно провалидировать. Если в совершенно случайной модели можно оценить вероятность опоздания и впоследствии, когда накопятся ещё примеры, проверить, правильно ли мы её посчитали, то в мире, где открываются порталы и любой аналитик может завоевать сердце орочьей принцессы, возможно всё, и даже если больше никто не попадёт в такую ситуацию, Василий всё равно сможет бить себя в грудь кулаком и говорить, что он избранный. Так что, наверное, это тоже не очень хорошая модель.

• Модель »Василий опоздал, потому что проспал» достаточно проста, чтобы в неё поверить, и в то же время даёт руководителю возможность принять решение, что делать с Василием.

Пример

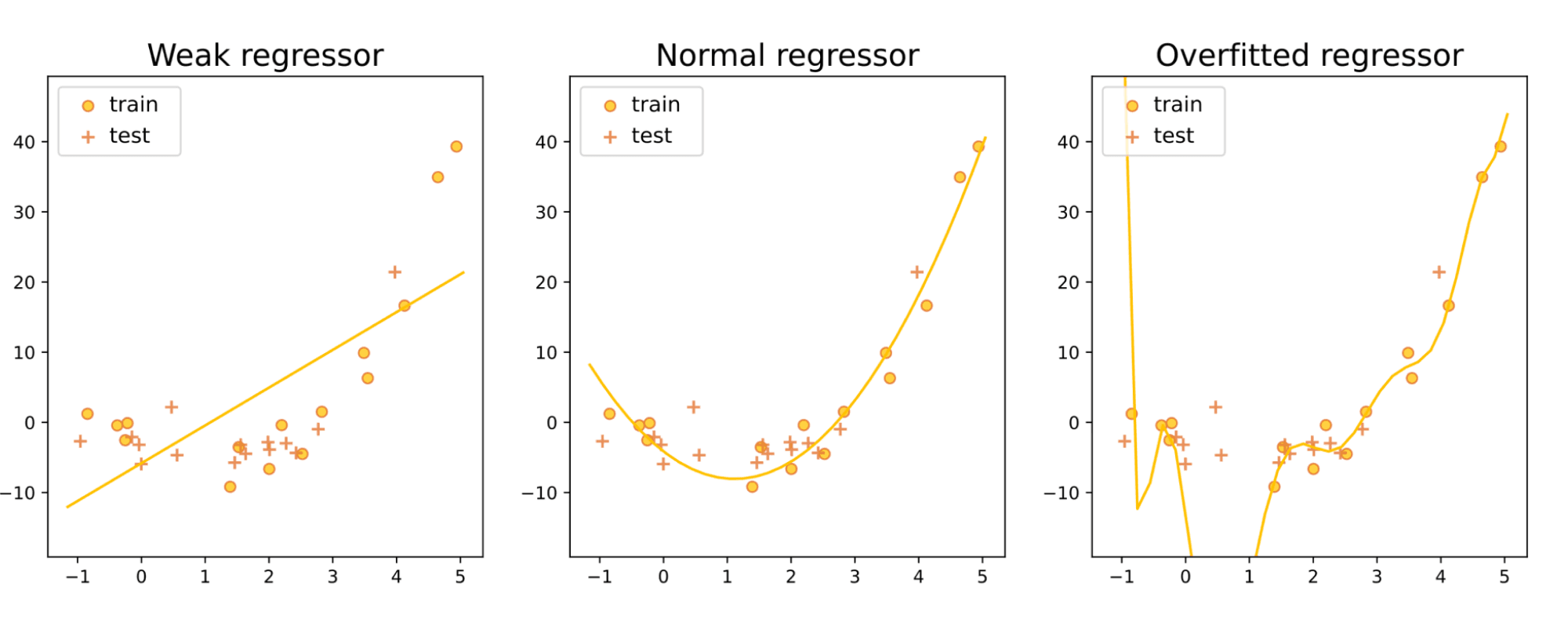
Обратимся к примеру из машинного обучения. Сравним три модели линейной регрессии:

Даже и не заправшивая тестовую выборку, мы можем сделать определённые выводы о качестве этих моделей. Средняя (квадратичная) явно лучше левой (линейной), потому что она лучше объясняет то, что мы видим: тот факт, что облако точек обучающей выборки выглядит вогнутым вниз.

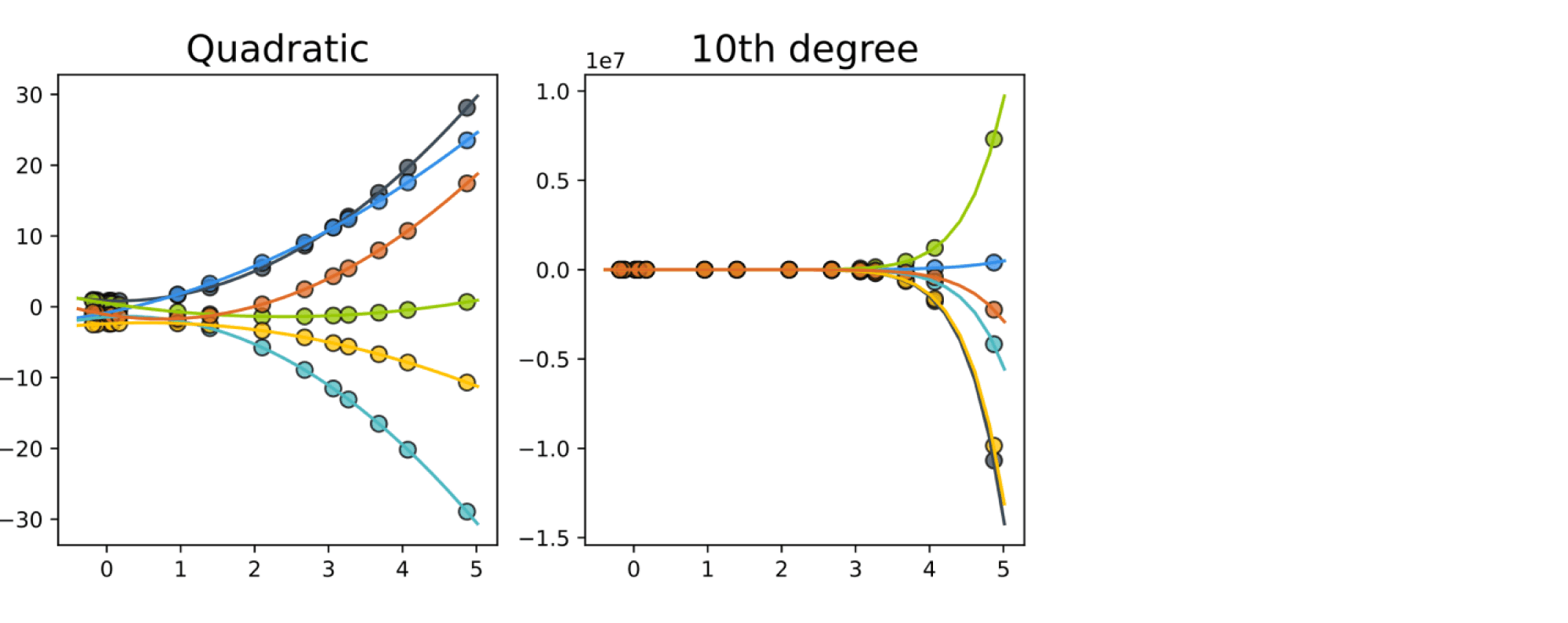
А что с правым, почему мы можем утверждать, что он хуже? Есть много причин критиковать его. Остановимся вот на какой. На средней картинке у нас приближение квадратичной функцией, а на правой – многочленом довольно большой степени (на самом деле, десятой). А ради интереса: как выглядит график квадратичной функции и как – многочлена десятой степени со случайно сгенерированными коэффициентами? Давайте сгенерируем несколько и отметим их значения в точках обучающей выборки:

Обратите внимание на масштаб на графиках справа. И какова вероятность, что нам достался именно тот многочлен десятой степени, у которого значения в обучающих точках по модулю в пределах сотни? Очевидно, она очень мала. Поэтому мы можем сказать, что выбор в качестве модели многочлена десятой степени не очень обоснован.

Попробуем резюмировать

Слишком простая модель плохо объясняет наблюдаемые нами данные, тогда как слишком сложная делает это хорошо, но при этом описывает слишком многообразный мир, в котором имеющиеся у нас данные оказываются уже слишком частным случаем. В каком-то смысле наш способ выбора модели оказывается переформулировкой бритвы Оккама: из моделей, пристойно описывающих наблюдаемые явления, следует выбирать наиболее минималистичную.

Байесовский подход к выбору модели: формализация

Пусть у нас есть некоторое семейство моделей $mathcal{J}$ и для каждого $jinmathcal{J}$ задана какая-то своя вероятностная модель. В духе байесовского подхода было бы оценить условное распределение моделей

$$p(j vert y, X) = frac{p(y vert X,j)p(j)}{sumlimits_{jinmathcal{J}}p(j, y vert X)}$$

и в качестве наилучшей модели взять её моду. Если же считать все модели равновероятными, то мы сводим всё к максимизации только лишь $p(y vert X,j) = p_j(y vert X)$:

$$color{blue}{widehat{jmath} = underset{j}{operatorname{argmax}}int{p_j(y vert X,w)p_j(w)}dw =underset{j}{operatorname{argmax}}p_j(y vert X)}$$

Величина $p_j(y vert X)$ называется обоснованностью (evidence, marginal likelihood) модели.

Отметим, что такое определение вполне согласуется с мотивацией из предыдущего подраздела. Слишком простая модель плохо описывает наблюдаемые данные, и потому будет отвергнута. В свою очередь, слишком сложная модель способна описывать гораздо большее многообразие явлений, чем нам было бы достаточно. Таким образом, компромисс между качеством описания и сложностью и даёт нам оптимальную модель.

Пример

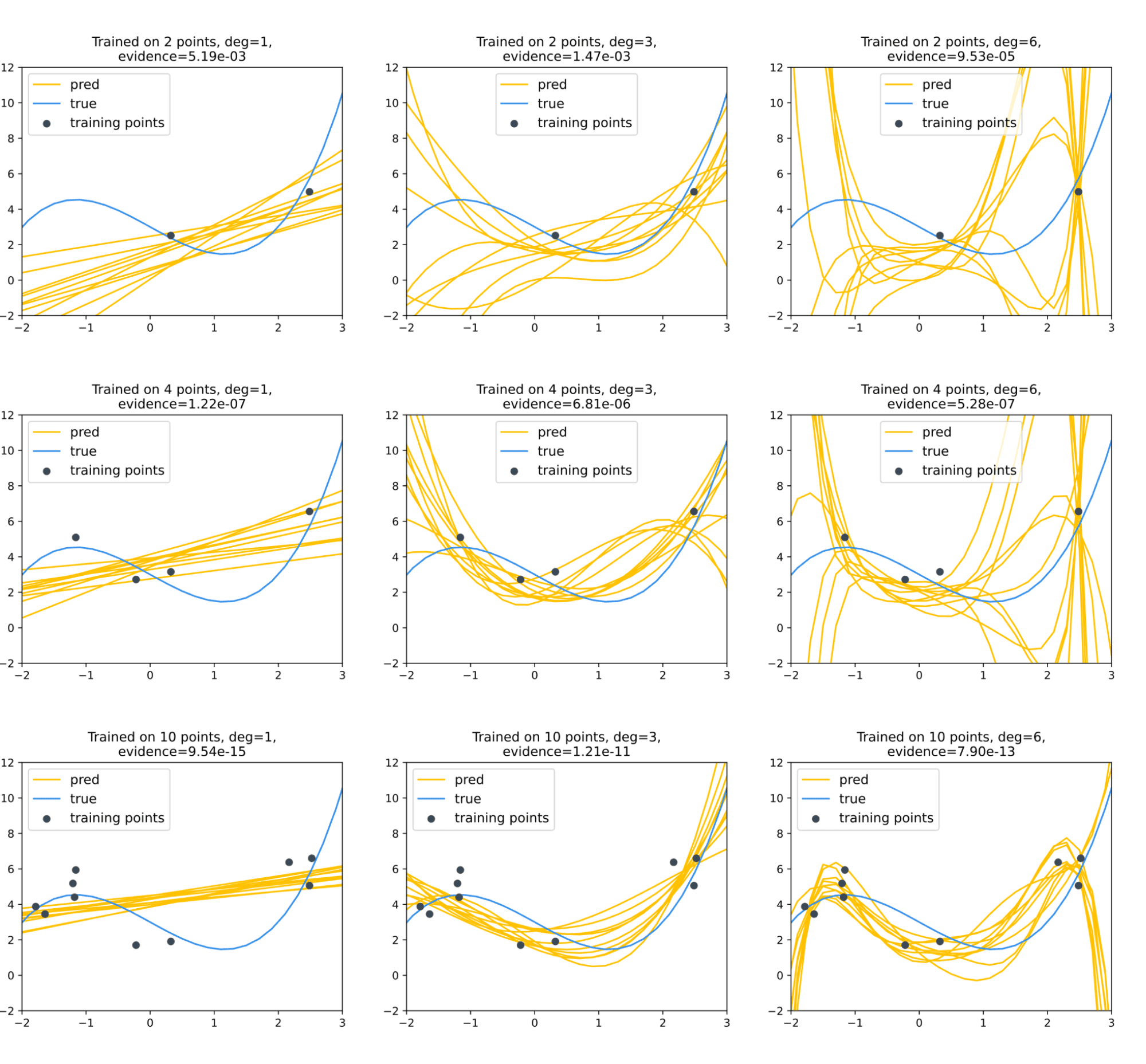
Вернёмся к нашей любимой задаче аппроксимации функции одной переменной многочленом небольшой степени по нескольким точкам, значение в которых было искажено нормальным шумом. Построим несколько моделей, приближающих многочленом степени не выше некоторого $mathrm{deg}$ (будет принимать значения 1, 3 и 6), положив в вероятностной модели $sigma^2 = tau^2 = 1$.

Мы не будем приводить полный вывод обоснованности для задачи регрессии $p(y vert X,w) = mathcal{N}(y vert Xw,sigma^2I)p(w vert tau^2I)$, а сразу выпишем ответ:

$$p(y vert X) = mathcal{N}left(0, sigma^2I + tau^2XX^Tright)$$

Посмотрим, какой будет обоснованность для разного числа обучающих точек:

Можно убедиться, что для регрессии по двум точкам наиболее обоснованной является линейная модель (и неудивительно), тогда как с ростом числа точек более обоснованной становится модель с многочленом третьей степени; слишком сложная же модель шестой степени всегда плетётся в хвосте.

Аппроксимация обоснованности и байесовский информационный критерий

Точно вычислить обоснованность может быть трудной задачей (попробуйте проделать это сами хотя бы для линейной регрессии!). Есть разные способы посчитать её приближённо; мы рассмотрим самый простой. Напомним, что

$$p(y vert X) = int{p(y vert X,w)p(w)}dw $$

Воспользуемся приближением Лапласа, то есть разложим $p(y vert X,w)$ (как функцию от $w$) вблизи своего максимума, то есть вблизи $widehat{w} := widehat{w}_{MLE}$ в ряд Тейлора:

$$log{p(y vert X,w)} approx log{p(y vert X,widehat{w})} — frac12(w — widehat{w})^TI_N(widehat{w})(w — widehat{w}),$$

где линейный член отсутствует, поскольку разложение делается в точке локального экстремума, а $I(widehat{w})$ – знакомая нам матрица Фишера $I_N(widehat{w}) = -mathbb{E}nabla^2_wlog{p(y vert X,w)}vert_{widehat{w}} = NI_1(widehat{w})$.

Далее, $p(w)$ мы можем с точностью до второго порядка приблизить $p(widehat{w}_{MAP})$. Получается, что

$$p(y vert X)approxint e^{log{p(y vert X,widehat{w})} — frac{N}2(w — widehat{w})^TI_1(widehat{w})(w — widehat{w})}p(widehat{w}_{MAP})dw =$$

$$= e^{log{p(y vert X,widehat{w})}}p(widehat{w}_{MAP})int e^{ — frac{N}{2}(w — widehat{w})^TI_1(widehat{w})(w — widehat{w})}dw = $$

$$= e^{log{p(y vert X,widehat{w})}}p(widehat{w}_{MAP})cdot (2pi)^{D/2}frac{|I_1(widehat{w})|^{-frac12}}{N^{D/2}} =$$

$$=expleft(log{p(y vert X,widehat{w})} — frac{D}2log{N} + mbox{всякие штуки}right)$$

Несмотря на то, что $p(widehat{w}_{MAP})$ и $vert I_1(widehat{w})vert^{-frac12}$, сгруппированные нами во »всякие штуки», существенным образом зависят от модели, при больших $N$ они вносят в показатель гораздо меньше вклада, чем первые два слагаемых. Таким образом, мы можем себе позволить вместо трудновычисляемых $p(y vert X)$ использовать для сравнения модели $ color{blue} { mbox{байесовский информационный критерий (BIC)}:} $

$$color{blue}{BIC = Dlog{N} — 2log{p(y vert X,widehat{w})}}$$

Фреквентисты против байесиан: кто кого?

Мы с вами познакомились с двумя парадигмами оценивания:

• фреквентистской (frequentist, от слова «frequency», частота) – в которой считается, что данные являются случайным (настоящая случайность!) семплом из некоторого фиксированного распределения, которое мы стараемся оценить по этому семплу, и
• байесовской – в которой данные считаются данностью и в которой мы используем данные для обновления наших априорных представлений о распределении параметров (здесь случайности нет, а есть лишь нехватка знания).

У обеих есть свои достоинства и недостатки, поборники и гонители. К недостаткам байесовской относится, безусловно, её вычислительная сложность: возможно, вы помните, в пучину вычислений сколь мрачных нас низвергла банальная задача линейной регрессии, и дальше становиться только ещё трудней. Если мы захотим байесовский подход применять к более сложным моделям, например, нейросетям, нам придётся прибегать к упрощениям, огрублениям, приближениям, что, разумеется, ухудшает наши оценки. Но, если простить ему эту вынужденную неточность, он логичнее и честней, и мы продемонстрируем это на следующем примере.

Одним известным свойством оценки максимального правдоподобия является асимптотическая нормальность. Если оценивать наши веса $w$ по различным наборам из $N$ обучающих примеров, причём считать, что наборы выбираются случайно (не будем уточнять, как именно), то оценка $widehat{w}_{MLE}$ тоже превращается в случайную величину, которая как-то распределена. Теория утверждает, что при $Nrightarrowinfty$

$$ quad widehat{w}_{MLE}simmathcal{N}left(w^{ast}, I_N({w}^{ast})^{-1}right)$$

где $w^{ast}$ – истинное значение весов, а $I_N({w}^{ast})$ – матрица информации Фишера, которая определяется как

$$I_N({w}^{ast}) = mathbb{E}left[left(left.frac{partial}{partial w_i}log{p(y vert X,w)}right|_{w^{ast}}right)left(left.frac{partial}{partial w_j}log{p(y vert X,w)}right|_{w^{ast}}right)right]$$

что при некоторых не слишком обременительных ограничениях равно

$$I_N({w}^{ast}) = -mathbb{E}left[left.frac{partial^2}{partial w_ipartial w_j}log{p(y vert X,w)}right|_{w^{ast}}right]$$

При этом поскольку $log{p(y vert X,w)} = sum_{i=1}^Nlog{p(y vert X,w)}$, матрица тоже распадается в сумму, и получается, что $I_N({w}^{ast}) = NI_1(w^{ast})$, то есть с ростом $N$ ковариация $(NI_1(w^{ast}))^{-1}$ оценки максимального правдоподобия стремится к нулю.

На интуитивном уровне можно сказать, что матрица информации Фишера показывает, сколько информации о весах $w$ содержится в $X$.

Поговорим о проблемах. В реальной ситуации мы не знаем $w^{ast}$ и тем более не можем посчитать матрицу Фишера, то есть мы с самого начала вынуждены лукавить. Ясно, что вместо $w^{ast}$ можно взять просто $widehat{w}$, а вместо $I_N(w^{ast})$ – матрицу $I_N(widehat{w})$, которую можно даже при желании определить как

$$-left(left.frac{partial^2}{partial w_ipartial w_j}log(p(y vert X, w))right|_{w^{ast}}right)$$

безо всякого математического ожидания. Итак, хотя мы можем теперь построить доверительный интервал для оцениваемых параметров, по ходу нами было сделано много упрощений: мы предположили, что асимптотическая оценка распределения уже достигнута, от $w^{ast}$ перешли к $widehat{w}$, а для полноты чувств ещё и избавились от математического ожидания. В байесовском подходе мы такого себе не позволяем.

Если вам интересно, посмотрите, как это будет выглядеть для линейной регрессии.