-
Что такое эффект наложения частот?
Эффект
наложения – признак нарушения условий
теоремы отсчетов. Эффект состоит в том,
что при выборе недостаточно высокой
частоты дискретизации некоторые
частотные составляющие становятся
неразличимыми. Из-за эффекта наложения
спектры «маскируются». [Пример приведен
в вопросе 10]
-
Как на практике использовать теорему отсчётов в задачах цифровой обработки сигналов?
В
практических задачах цифровой обработки
сигналов использование теоремы отсчетов
можно сформулировать в виде следующих
основных рекомендаций:
—
частота дискретизации (Fs)
должна выбираться так, чтобы она превышала
верхнюю частоту информативных составляющих
сигнала (берется с запасом не менее чем
в 2 — 3 раза);
—
перед аналого-цифровым преобразованием
полоса частот исходного аналогового
сигнала должна быть ограничена с помощью
ФНЧ с Fсреза
Fs/2.
—
рассмотрение частотных свойств
дискретизованного сигнала допустимо
для частот меньших Fs/2.
-
Что такое ошибка квантования и чем она вызвана?
Ошибка
квантования – накопительная ошибка
округления значений.
Ошибка
квантования вызвана низкой разрядностью
АЦП и, в следствие, маленьким числом
уровней квантования.
|
|
Пусть В Данное |
-
Чему равны
максимальное и минимальное значения
ошибки квантования?
Максимальная
ошибка квантования зависит от принципа
работы АЦП и равняется
для АЦП, присваивающего значение
ближайшего уровня квантования, где
α-шаг квантования. [Как в примере в
вопросе 13].
-
Что такое
динамический диапазон АЦП?
Динамический
диапазон (А) – один из параметров АЦП,
задающий пределы измерения входного
сигнала.
Динамический
диапазон – разность между наибольшим
и наименьшим измеряемым значением
непрерывного сигнала на входе АЦП.
А
= Аmax
— Amin
-
Что такое шаг
квантования и число уровней квантования
АЦП?
Параметры
АЦП: динамический диапазон (А) [вопрос
15];
шаг квантования;
число уровней
квантования.
Число
уровней квантования (К)
K=2k,
где k
– разрядность АЦП
(число
двоичных разрядов выходного сигнала).
Шаг
квантования – дистанция между соседними
уровнями квантования.
-
Какая связь
между разрядностью АЦП, динамическим
диапазоном АЦП и ошибкой квантования?
Как уже
отмечалось, квантование – это
присваивание отсчету цифрового значения,
соответствующего некоторому фиксированному
уровню сигнала.
Точность
квантования сигнала с использованием
аналого-цифрового преобразователя
определяется двумя параметрами:
– динамическим
диапазоном, задающим пределы измерения
входного сигнала;
– разрядностью,
определяющей число двоичных разрядов
выходного кода АЦП.
Обозначим
размах динамического диапазона как A
= Amax – Amin,
где AmaxиAmin
– наименьшее и наибольшее измеряемые
значения непрерывного сигнала на входе
АЦП соответственно. Если далее обозначить
разрядность АЦП как k,
то наибольшее возможное число уровней
квантования K =
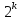
а величина a =
A/Kсоответствует
дистанции между соседними уровнями
квантования и называется шагом
квантования.
Шаг квантования
определяет точность представления
входного аналогового сигнала в виде
цифровых отсчетов. Максимальная ошибка
квантования зависит от принципа работы
АЦП и равняется ±a/2
для АЦП, присваивающего значение
ближайшего уровня квантования. Нетрудно
показать [2.24], что среднеквадратическая
ошибка квантования при этом будет
составлять a/
0.29a.
Для оптимального
выбора динамического диапазона АЦП и
его разрядности необходима информация
о диапазоне возможного изменения сигнала
на входе АЦП и о требуемой точности
представления цифрового сигнала.
Отметим, что повышение точности за счет
увеличения разрядности ограничено
точностью представления самого
аналогового сигнала (например, уровнем
собственных шумов усилителя, если на
входе АЦП измеряется напряжение или
ток).
5.1. Цифровые сигналы: дискретизация, квантование, кодирование
5.2. Цифровые иерархии
5.1. Цифровые сигналы: дискретизация, квантование, кодирование
В настоящее время во всём мире развивается цифровая форма передачи сигналов: цифровая телефония, цифровое кабельное телевидение, цифровые системы коммутации и системы передачи, цифровые сети связи. Качество цифровой связи значительно выше, чем аналоговой, так как цифровые сигналы гораздо более помехоустойчивы: нет накопления шумов, легко обрабатываются, цифровые сигналы можно «сжимать», что позволяет в одной полосе частот организовать больше каналов с высокой скоростью передачи и отличным качеством.
Цифровой сигнал – это последовательность импульсов. Общепринято импульсную последовательность представлять как чередование двух символов: 0 и 1. «Binary Digit» – «двоичная цифра». Отсюда и пошло понятие бит, то есть одна позиция в цифровом сигнале есть 1 бит; это может быть либо 0, либо 1. Восемь позиций в цифровом сигнале определяется понятием байт [1].
При передаче цифровых сигналов вводится понятие скорости передачи – это количество бит, передаваемых в единицу времени (в секунду).
Для передачи непрерывных сообщений цифровыми методами необходимо произвести преобразование этих сообщений в дискретные, которое осуществляется путём дискретизации непрерывных сигналов во времени и квантования их по уровню, и преобразования квантованных отсчётов в цифровой сигнал [6].
Дискретизация сигналов заключается в замене непрерывного сообщения uк(t) последовательностью его отсчётов, то есть последовательностью импульсов, модулированных по амплитуде (смотри рисунок 5.1, а). Частота дискретизации Fд выбирается из условия (4.4.1). Полученный аналоговый АИМ сигнал uАИМ(iTд), где i = 1, 2, 3 …, приведённый на рисунке 5.1, а, затем подвергается операции квантования, которая состоит в замене отсчётов мгновенных значений сигнала uАИМ (iTд) дискретными значениями u0, u1, u2 … u7 разрешённых уровней uкв (iTд). В процессе квантования мгновенные значения АИМ сигнала уровней uАИМ(iTд) заменяются ближайшими разрешёнными уровнями сигнала uкв(iTд) (смотри рисунок 5.1, а).
Рисунок 5.1. Принцип ИКМ: а – дискретизация; б – ошибка квантования; в – цифровой сигнал с ИКМ
Такое преобразование первичных сигналов можно называть квантованной амплитудно-импульсной модуляцией (КАИМ). Особенностью такого сигнала является то, что все его уровни можно пронумеровать и тем самым свести передачу КАИМ-сигнала к передаче последовательностей номеров уровней, которые этот сигнал принимает в моменты i∙tд.
Расстояние между ближайшими разрешёнными уровнями квантования (u0 … u7 на рисунке 5.1, а) ∆ называется шагом квантования. Шкала квантования называется равномерной, если все шаги квантования равны между собой ∆j = ∆0 [5].
Если в момент взятия i-го отсчёта мгновенное значение непрерывного сообщения uк(ti) удовлетворяет условию
uj – ∆j/2 ≤ uАИМ(iTд) ≤ uj + ∆j/2, (5.1)
то квантованному импульсу uкв(iTд) присваивается амплитуда разрешённого uj уровня квантования (смотри рисунок 5.1, а). При этом возникает ошибка квантования δкв, представляющая разность между передаваемой квантованной величиной uкв(iTд) и истинным значением непрерывного сигнала в данный момент времени uАИМ(iTд) (смотри рисунок 5.1, б):
δкв(iTд) = uкв(iTд) – uАИМ(iTд). (5.2)
Как следует из рисунков 5.1, б и (5.1), ошибка квантования лежит в пределах
–∆0/2 ≤ δкв ≤ ∆0/2. (5.3)
Амплитудная характеристика квантующего устройства при равномерной шкале квантования приведена на рисунке 5.2, а. Она имеет ступенчатую форму, и при изменении непрерывного сообщения uк(t) и соответствующего ему АИМ сигнала uАИМ(iTд) в пределах одной ступени выходной сигнал остаётся постоянным, а при достижении границы этой ступени изменяется скачком на величину шага квантования. При этом ошибка квантования зависит от uк(t) и имеет вид, изображённый на рисунке 5.2, б.
Рисунок 5.2. Амплитудная характеристика квантователя (а) и зависимость ошибки квантования от амплитуды импульсов (б)
Как следует из рисунка 5.2, б, из-за нелинейности амплитудной характеристики квантователя ошибка квантования δкв представляет собой функцию с большим числом резких скачков, частота следования которых существенно выше частоты исходного сообщения uк(t), то есть при квантовании происходит расширение спектра сигнала. При этом соседние боковые полосы будут накладываться друг на друга и в полосу пропускания ФНЧ на выходе канала попадут составляющие спектра искажений от квантования, распределение которых в полосе ФНЧ считается равномерным. Поскольку практически все дискретные значения непрерывного сообщения находятся в пределах зоны квантования от –uогр до +uогр, то при равномерной шкале квантования ∆j = ∆0 и тогда:
Ркв = (1/12) ∆20. (5.4)
Из выражения (5.4) видно, что при равномерной шкале квантования мощность шума квантования не зависит от уровня квантуемого сигнала и определяется только шагом квантования ∆0.
Рассмотрим теперь кодирование и декодирование сигналов. Следующий шаг в преобразовании сигнала состоит в переводе квантованного АИМ-сигнала в цифровой. Эта операция называется кодированием АИМ-сигнала. Кодом называется закон, устанавливающий соответствие между квантованной амплитудой и структурой кодовой группы [8].
Различают равномерный и неравномерный коды. Если все кодовые группы состоят из равного числа символов, то код называется равномерным. Если же кодовые группы состоят из различного числа символов, то код называется неравномерным. В системах передачи с импульсно-кодовой модуляцией, как правило, используется равномерный двоичный код.
Для определения структуры двоичной кодовой комбинации на выходе кодера в простейшем случае необходимо в двоичном коде записать амплитуду АИМ отсчётов, выраженную в шагах квантования
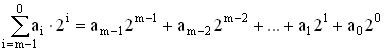
где ai = {0,1} – состояние соответствующего разряда комбинации; 2i – вес соответствующего разряда в шагах квантования.
Если в десятичной системе «вес» каждой позиции числа равен числу десять в некоторой степени, то в двоичной системе вместо числа десять используют число два. «Веса» первых тринадцати позиций двоичного числа имеют следующие значения:
Таблица – 5.1
|
212 |
211 |
210 |
29 |
28 |
27 |
26 |
25 |
24 |
23 |
22 |
21 |
20 |
|
4096 |
2048 |
1024 |
512 |
256 |
128 |
64 |
32 |
16 |
8 |
4 |
2 |
1 |
По принципу действия кодеры делятся на кодеры счётного типа, матричные, взвешивающего типа и другие. Наиболее часто используются кодеры взвешивающего типа, простейшим из которых является кодер поразрядного взвешивания (рисунок 5.3), реализующий функцию (5.5) с формирования натурального двоичного кода [5]. Принцип работы такого кодера заключается в уравновешивании кодируемых АИМ отсчётов суммой эталонных напряжений. Схема линейного кодера поразрядного взвешивания содержит восемь ячеек (при m = 8), обеспечивающих формирование значения коэффициента аi соответствующего разряда (5.5). В состав каждой ячейки (за исключением последней, соответствующей младшему по весу разряду) входит схема сравнения СС и схема вычитания СВ.
Схема сравнения обеспечивает сравнение амплитуды поступающего АИМ сигнала с эталонными сигналами, амплитуды которых равны весам соответствующих разрядов
Uэт8 = 27∆ = 128∆; Uэт7 = 26∆ = 64∆; … Uэт1 = 20∆ = 1∆.
Если на входе ССi амплитуда поступающего АИМ сигнала равна или превышает Uэтi, то на выходе схемы сравнения формируется «1», а в СВi из входного сигнала вычитается Uэтi, после чего он поступает на вход следующей ячейки. Если же амплитуда АИМ сигнала на входе ССi меньше Uэтi, то на выходе ССi формируется «0» и АИМ сигнал проходит через СВi без изменений. После окончания процесса кодирования текущего отсчёта на выходе кодера получается восьмиразрядный параллельный код, кодер устанавливается в исходное состояние и начинается кодирование следующего отсчёта.
Рисунок 5.3. Линейный кодер поразрядного действия
Если, например, на вход кодера поступил АИМ отсчёт с амплитудой UАИМ = 185∆, то СС8 формирует Р8 = 1 и на вход седьмой ячейки поступил сигнал с амплитудой UАИМ = 185∆ – 128∆ = 57∆. На выходе СС7 сформируется Р7 = 0 и на вход шестой ячейки кодера поступит сигнал с той же амплитудой UАИМ = 57∆. На выходе СС6 сформируется Р6 = 1 и на вход следующей ячейки поступит сигнал с амплитудой UАИМ = 57∆ – 32∆ = 25∆ и так далее. В результате будет сформирована кодовая комбинация 10111001.
В процессе декодирования сигнала m – разрядные кодовые комбинации преобразуются в АИМ отсчёты соответствующей амплитуды [4]. Сигнал на выходе декодера получается в результате суммирования эталонных сигналов Uэтi тех разрядов кодовой комбинации, значения которых равно 1 (рисунок 5.4). Так, если на вход декодера поступила кодовая комбинация 10111001, то амплитуда АИМ отсчёта на его выходе будет равна UАИМ = 128∆ + 32∆ + 16∆ + 8∆ + 1∆ = 185∆.
В линейном декодере (рисунок 5.4) под воздействием управляющих сигналов, поступающих от генераторного оборудования, в регистр сдвига записывается очередная восьмиразрядная кодовая комбинация. В момент прихода импульса считывания замыкаются только те ключи Кл1 … Кл8, которые соответствуют разрядам, имеющим значения «1». В результате в сумматоре объединяются соответствующие эталонные напряжения и на его выходе получается соответствующая амплитуда АИМ отсчёта.
Рисунок 5.4. Линейный декодер взвешивающего типа
Рассмотренная схема кодера (рисунок 5.3) поразрядного взвешивания содержит большое число схем сравнения, которые являются относительно сложными устройствами. На практике чаще используется кодер взвешивающего типа с одной схемой сравнения и цепью обратной связи, содержащей декодер. Как следует из выражения (5.4), мощность шума квантования при линейном кодировании будет равной при различных амплитудах квантованных сигналов. Для синусоидальных сигналов отношение сигнал/шум квантования, рассчитывается по формуле:
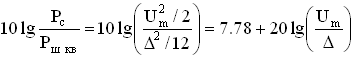
где Um – амплитуда квантуемого сигнала.
Из формулы видно, что для слабых входных сигналов это отношение гораздо хуже, чем для сигналов большой амплитуды. Для устранения этого недостатка было предложено использовать неравномерное квантование, то есть изменять шаг квантования пропорционально изменению амплитуды входного сигнала.
Для кодирования с неравномерной шкалой квантования могут быть использованы:
- прямое нелинейное кодирование, при котором кодер сочетает в себе функции аналого-цифрового преобразования (АЦП) и компрессора;
- аналоговое компандирование, при котором компрессирование сигнала осуществляется перед линейным кодером и экспандирование сигнала после линейного декодера;
- преобразование на основе линейного кодирования, при котором кодирование сигнала осуществляется в линейном кодере с большим числом разрядов с последующим цифровым компандированием [5].
Переменную величину шага квантования можно получить с помощью устройства с нелинейной амплитудной характеристикой (рисунок 5.5) (которая называется компрессором, поскольку сжимает динамический диапазон входного сигнала) и равномерного квантователя (смотри рисунок 5.2). На приёмной стороне осуществляется расширение динамического диапазона экспандером, имеющим характеристику, противоположную компрессору, что обеспечивает линейность системы передачи. Совокупность операций сжатия динамического диапазона компрессором и расширение его экспандером называется компадированием сигнала.
В настоящее время в системах ВРК с ИКМ применяется характеристика компадирования типа А (рисунок 5.5).
Рисунок 5.5. Характеристика компрессирования типа А
На этом рисунке сегментированная характеристика компрессии типа А для положительных сигналов (для отрицательных сигналов характеристика имеет аналогичный вид). Общее число сегментов характеристики Nс = 16, однако четыре центральных сегмента (по два в положительной и отрицательной областях) имеют одинаковый шаг квантования и фактически образуют один сегмент, вследствие чего число сегментов равно Nс = 13. Поэтому такая характеристика получила название типа А = 87.16/13. В центральном сегменте (Nс =1 или 2) значение ∆0 минимально (то есть равно ∆0) и соответствует равномерной двенадцатиразрядной шкале (m = 12), а в каждом последующем сегменте к краям характеристики шаг квантования увеличивается вдвое.
Представление ИКМ сигнала восьмиразрядными кодовыми комбинациями использует формат «знак – абсолютное значение», где один разряд отображает полярность АИМ сигнала П, а остальные – определяют его абсолютное значение. Семь разрядов, отображающих абсолютное значение, подразделяются на определитель номера сегмента С из трёх разрядов и определитель шага квантования К из четырёх разрядов (рисунок 5.6).
Рисунок 5.6. Формат восьмиразрядной ИКМ комбинации
Для реализации такого кодера необходимо задать величины эталонных напряжений для нижней границы каждого сегмента и при кодировании внутри сегмента (таблица 5.2).
Схемы и принцип действия нелинейных кодеков взвешивающего типа в основном те же, что и у линейных кодеков. Отличие заключается в последовательности включения эталонных напряжений в процессе кодирования исходного сигнала [5].
Таблица 5.2. Эталонные напряжения для нелинейного кодека
|
Номер сегмента Nс |
Эталонное напряжение нижней границы сегмента |
Эталонные напряжения при кодировании в пределах сегмента |
|||
|
8∆i(A) |
4∆i(B) |
2∆iI(С) |
∆i(D) |
||
|
0 |
0 |
8∆0 |
4∆0 |
2∆0 |
1∆0 |
|
1 |
16∆0 |
8∆0 |
4∆0 |
2∆0 |
1∆0 |
|
2 |
32∆0 |
16∆0 |
8∆0 |
4∆0 |
2∆0 |
|
3 |
64∆0 |
32∆0 |
16∆0 |
8∆0 |
4∆0 |
|
4 |
128∆0 |
64∆0 |
32∆0 |
16∆0 |
8∆0 |
|
5 |
256∆0 |
128∆0 |
64∆0 |
32∆0 |
16∆0 |
|
6 |
512∆0 |
256∆0 |
128∆0 |
64∆0 |
32∆0 |
|
7 |
1024∆0 |
512∆0 |
256∆0 |
128∆0 |
64∆0 |
Таким образом, максимальный шаг квантования (в седьмом сегменте) в 64 раза превышает минимальный шаг квантования, а отношение сигнал/шум квантования (для максимального значения синусоидального сигнала) может быть определено по выражению (5.6) и составит: для второго сегмента
Рс – Рш кв = 7.78 + 20lg(А/∆) = 7.78 + 20 lg(32∆0/∆0) = 37.88 дБ;
Для седьмого сегмента
Рс – Рш кв = 7.78 + 20 lg(2048∆0/64∆0) = 37.88 дБ.
Зависимость отношения сигнал/шум квантования от уровня входного сигнала при компадировании по закону А = 87.6/13 приведена на рисунке 5.7. Для сигналов в пределах нулевого и первого сегментов осуществляется равномерное квантование с шагом ∆0, поэтому Рс – Рш кв увеличивается с ростом рс. При переходе ко второму сегменту шаг квантования увеличивается в два раза, вследствие чего Рс – Рш кв резко уменьшается на 6 дБ, а затем в пределах данного сегмента возрастает с ростом рс, поскольку внутри сегмента осуществляется равномерное квантование. После попадания сигнала в зону ограничения отношение сигнал/шум резко уменьшается за счёт перегрузки кодера.
Рисунок 5.7. Зависимость Рс/Рш кв = f(рс)
На рисунке 5.8 представлена упрощённая схема нелинейного кодера взвешивающего типа, реализующего прямое кодирование АИМ сигнала.
Рисунок 5.8. Нелинейный кодер взвешивающего типа
Кодирование осуществляется за восемь тактовых интервалов, в каждом из которых формируется один из символов кодовой комбинации (рисунок 5.6). В первом такте определяется знак поступившего на вход кодера отсчёта. Если отсчёт положительный, то в знаковом разряде формируется «1» и к схеме переключения и суммирования эталонов СПСЭ подключается формирователь положительных эталонных напряжений ФЭ1, в противном случае формируется «0» и к схеме подключается ФЭ2. Затем происходит формирование кода номера сегмента методом деления их числа пополам (рисунок 5.9).
Рисунок 5.9. Алгоритм формирования кода номера сегмента
Во втором такте управляющая логическая схема УЛС и СПСЭ обеспечивают подачу на вход схемы сравнения эталонного сигнала Uэт = 128 ∆0, соответствующего нижней границе четвёртого (среднего) сегмента. Если амплитуда отсчёта UАИМ ≥ Uэт = 128 ∆0, то принимается решение, что амплитуда отсчёта попадёт в один из четырёх вышележащих сегментов и формируется очередной символ X = 1, который по цепи обратной связи поступает на вход УЛС. В противном случае принимается решение, что амплитуда отсчёта попадает в один из нижележащих сегментов и формируется X = 0.
В третьем такте в зависимости от значения предыдущего символа X уточняется номер сегмента, в который попадает амплитуда кодируемого отсчёта. Если X = 1, то УЛС и СПСЭ подают на вход СС эталонное напряжение Uэт = 512 ∆0, соответствующего нижней границе шестого сегмента. При этом, если UАИМ ≥ Uэт = 512 ∆0 то принимается решение, что отсчёт попадает в один из двух вышележащих сегментов и формируется очередной символ Y = 1. В противном случае, если UАИМ ≤ Uэт = 512 ∆0, принимается решение, что отсчёт попадает в два нижележащих сегмента и формируется Y = 0.
Если же X = 0, то УЛС с помощью СПСЭ обеспечивает подачу на вход СС эталонного напряжения Uэт = 32 ∆0, соответствующего нижней границе второго сегмента. Если UАИМ ≥ Uэт = 32 ∆0, то принимается решение, что отсчёт попадает во второй и третий сегменты и формируется Y = 1. Если UАИМ ≤ Uэт = 32 ∆0, то принимается решение, что отсчёт попадает в два нижележащих сегмента и формируется Y = 0.
В четвёртом такте аналогичным образом формируется символ Z и окончательно формируется код номера сегмента. В результате, после четырёх тактов кодирования, сформируется четыре символа восьмиразрядной кодовой комбинации PXYZ (рисунок 5.6) и к СС подключается одно из восьми эталонных напряжений, соответствующих нижней границе сегмента, в котором находится кодируемый отсчёт.
В оставшихся четырёх тактах последовательно формируются символы ABCD кодовой комбинации, значения которых зависят от номера шага квантования внутри сегмента, соответствующего амплитуде кодируемого отсчёта. Поскольку внутри любого сегмента осуществляется равномерное квантование, то процесс кодирования реализуется, как и в линейных кодерах взвешивающего типа, путём последовательного включения эталонных напряжений соответствующих данному сегменту (таблица 5.2).
Практикум на применение нелинейного кодера при компадировании по закону А = 87.6/13:
Например, если на вход кодера поступил положительный отсчёт с амплитудой UАИМ = 889 ∆0, то после первых четырёх тактов сформируются символы PXYZ = 1110 и к СС подключится эталонное напряжение Uэт = 512 ∆0, соответствующее нижней границе шестого сегмента, поскольку кодируемый сигнал находится в этом сегменте. В пятом такте к этому эталонному сигналу добавляется максимальное эталонное напряжение Uэт = 256 ∆0, соответствующее символу А в определителе шага квантования К (рисунок 5.6) шестого сегмента (таблица 5.2). Так как UАИМ > Uэт = (512 +256) ∆0, то формируется символ А = 1 и это эталонное напряжение остаётся включенным. В шестом такте подключается эталонное напряжение соответствующее символу В в определителе шага квантования Uэт = 128 ∆0 и так как UАИМ > Uэт = (512 +256 + 128) ∆0, то на выходе СС формируется символ В = 1 и это эталонное напряжение остаётся включенным. В седьмом такте подключается эталонное напряжение соответствующее символу С в определителе шага квантования Uэт = 64 ∆0 и так как UАИМ < Uэт = (512 +256 + 128 + 64) ∆0, то на выходе СС формируется символ С = 0. В восьмом такте вместо Uэт = 64 ∆0 подключается эталонное напряжение соответствующее символу D в определителе шага квантования Uэт = 32 ∆0 и так как UАИМ < Uэт = (512 +256 + 128 + 32) ∆0, то на выходе СС формируется символ D = 0 и это эталонное напряжение отключается и на этом процесс кодирования очередного отсчёта заканчивается. При этом на выходе кодера сформирована кодовая комбинация PXYZABCD = 11101100, соответствующая амплитуде уравновешивающего АИМ сигнала на входе СС UАИМ = 896 ∆0. Разница между входным и уравновешивающим АИМ сигналами на входах СС представляет ошибку квантования δкв = UАИМ – UАИМ = 7∆0.
5.2. Цифровые иерархии
При выборе иерархии ЦСП должны учитываться следующие требования: стандартизированные скорости передачи цифровых потоков должны выбираться с учётом возможности использования цифровых и аналоговых систем передачи и электрических характеристик существующих и перспективных линий связи; обеспечение возможности как синхронного, так и асинхронного объединения, разделения и транзита цифровых потоков и сигналов в цифровой форме. Кроме того, ЦСП высшего порядка должна удовлетворять требованию независимости скорости передачи в групповом цифровом сигнале от видов передаваемой информации и способа формирования этого сигнала [21].
Указанным требованиям удовлетворяет европейская иерархия ЦСП, которая базируется на первичной ЦСП ИКМ-30 со скоростью передачи группового цифрового сигнала 2048 кбит/с (Fт = 2048 кГц) (рисунок 5.10) [1].
Рисунок 5.10. Европейская иерархия цифровых систем передачи
Относительное возрастание скорости передачи в каждой последующей ступени иерархии по отношению к предыдущей связано с необходимостью увеличения объёма служебной информации при увеличении числа каналов.
Иерархия ЦСП с ИКМ. Упрощенная структурная схема аппаратуры ВРК с ИКМ приведена на рисунке 5.11, где для простоты показано индивидуальное оборудование одного канала.
Рисунок 5.11. Упрощенная структурная схема аппаратуры объединения (АО) и разделения (АР) при ВРК с ИКМ
Телефонное сообщение uк(t) через дифференциальную систему (ДС) фильтр нижних частот (ФНЧ), который ограничивает спектр сигнала частотой 3.4 кГц, подается на вход модулятора АИМ (МАИМ). В модуляторе непрерывный сигнал дискретизируется, то есть превращается в последовательность модулированных по амплитуде импульсов, которые имеют частоту Fд=8 кГц.
Сигналы с АИМ всех каналов объединяются в групповой АИМ сигнал (смотри рисунок 5.1, в), который поступает на компрессор (Км). После компрессии групповой АИМ сигнал квантуется и кодируется в кодере (Кд). С выхода Кд двухуровневый цифровой сигнал подается на устройство объединения (УО), куда поступают импульсы от передатчика (П) СУВ и от передатчика циклового синхросигнала (ПЦС). Таким образом, в УО формируется групповой цифровой сигнал, структура цикла которого показана на рисунке 5.12.
Рисунок 5.12. Структура цикла группового сигнала ВРК с ИКМ
Параметры двоичного цифрового сигнала плохо согласуются с параметрами реальных линий передачи, не пропускающих низкочастотные составляющие спектра такого сигнала. Поэтому двоичный сигнал подвергается перекодированию в преобразователе кода (ПКп) в так называемый код линии, у которого низкочастотные компоненты ослаблены и характеристики вследствие этого лучше сочетаются с параметрами линии. Работа всех блоков АО синхронизируется сигналами, вырабатываемыми распределителем каналов передачи (РКп).
На приёмной стороне ИКМ сигнал подвергается обратному преобразованию в АИМ квантованный сигнал (декодированию). Для этого непрерывный поток символов должен быть разделён на кодовые группы, каждая из которых соответствует одному отсчёту квантованного сигнала. Декодированный сигнал аналогичен квантованным отсчётам исходного сигнала uкв(iTд) (смотри рисунок 5.1, а), которые в своём спектре имеют составляющие с частотами Ωн … Ωв передаваемого сообщения uк(t). Поэтому из импульсной последовательности u*кв(iТд) принятое сообщение u*к(t) выделяется с помощью ФНЧ.
На стороне приёма сигнал по кабелю поступает на преобразователь кода приёма (ПКпр), где код линии преобразуется в двоичный и поступает в устройство разделения (УР). С выхода УР цикловой синхросигнал и СУВ поступают на свои приёмники, а кодовые группы речевых сигналов в декодере (Дк) преобразуются в групповой АИМ сигнал, который после экспандера (Эк) поступает на временные селекторы (ВС), открывающиеся поочерёдно и пропускающие импульсы АИМ, относящиеся к данному каналу. Демодуляция сигнала в канале осуществляется в ФНЧ.
Управление работой АР осуществляет распределитель каналов приёма (РКпр), синхронизация которого производится тактовой частотой, выделяемой из группового цифрового сигнала узкополосным фильтром, расположенным на выходе ПКпр, и цикловой синхронизацией.
Рассмотрим методы синхронизации. Для согласованной работы АО, АР и регенераторов необходимо обеспечить равенство скоростей обработки сигналов, правильное распределение АИМ сигналов и СУВ. Это осуществляется путём синхронизации регенераторов, генераторного оборудования АР по тактовой частоте и по циклам принимаемого цифрового сигнала [3].
При Nгр канальных интервалах и m разрядах в информационных кодовых группах тактовая частота группового цифрового сигнала
Fт = Fд ∙ m ∙ Nгр. (5.7)
Так, для системы ИКМ-30, рассчитанной на Nгр = 32 канальных интервала при восьмиразрядной кодовой группе, Fт = 8∙8∙32 = 2048 кГц. Групповой цифровой сигнал uИКМ(t) представляет собой случайную последовательность двоичных импульсов (рисунок 5.1, в). Эту последовательность можно представить в виде суммы периодической и случайной последовательностей. Периодическая последовательность импульсов имеет дискретный спектр и при τи, равной Т и Т/2, дискретные составляющие будут иметь частоты F=0; Fт и так далее (смотри рисунок 5.13, где эти составляющие отмечены точками). Случайная биполярная последовательность определяет непрерывный спектр (рисунок 5.13) исходной двоичной последовательности.
Рисунок 5.13. Энергетический спектр случайной последовательности двоичных импульсов (а, б) и сигнала с ЧПИ (в) (составляющие дискретного спектра отмечены точками)
Из рисунка 5.13 следует, что максимальную энергию тактовой частоты имеет случайная двоичная последовательность с τи = T/2. Колебания с тактовой частотой Fт выделяются из такой последовательности узкополосным фильтром и используются в регенераторе для синхронизации работы решающего устройства.
Система цикловой синхронизации определяет начало цикла передачи и обеспечивает согласованное с АО распределение декодированных на приемном конце отсчетных значений аналоговых сигналов по своим каналам. Неточность работы цикловой синхронизации приводит к увеличению вероятности ошибки в информационных каналах. Для увеличения помехоустойчивости в качестве циклового синхросигнала (рисунок 5.12) используется группа символов постоянной структуры с частотой следования 4 кГц, то есть ЦС передаются через цикл передачи.
Рассмотрим объединение ЦСП на базе асинхронного ввода цифровых сигналов. Необходимость объединения цифровых потоков возникает при формировании группового цифрового сигнала из цифровых потоков систем более низкого порядка, из различных сигналов, передаваемых в цифровом виде, а также при вводе в групповой цифровой сигнал дискретных сигналов от различных источников информации (рисунок 5.14). Цифровые потоки формируются в ЦСП, задающие генераторы которых могут быть синхронизированы или несинхронизированы с задающим генератором оборудования объединения. В соответствии с этим производится синхронное или асинхронное объединение цифровых потоков.
Рисунок 5.14. Упрощенная структурная схема (а) посимвольное (б) и поканальное (в) объединение цифровых потоков
Для временного объединения асинхронных цифровых потоков необходимо предварительно согласовать их скорости, то есть «привязать» их к одной опорной частоте [3]. На приёме суммарный сигнал распределяется по соответствующим выходам. Приходящие на вход системы передачи биты из четырёх информационных потоков записываются в ячейки памяти запоминающего устройства (ЗУ), а затем считываются с них и направляются в линию. Если содержимое ячеек памяти считалось быстрее, сформировался «пустой» временной интервал для вставки синхроимпульсов. Строгая периодичность синхросигнала – одно из важнейших свойств для его распознавания.
Если же генератор окажется нестабильным, то появится смещение во времени «пустых» интервалов и нарушится строгая периодичность их повторения. Может произойти сбой в работе системы синхронизации и всей аппаратуры в целом. Во избежание этого применяют процедуру выравнивания скоростей или, как часто называют, согласования скоростей.
Специальный контроллер следит за взаимным положением импульсов записи и считывания и, если импульсы считывания начали следовать быстрее (расстояние между соседними парами этих импульсов уменьшается), то контролер сигнализирует, что «пустой» интервал появился раньше времени. Другое устройство вводит в пустой интервал ложный импульс, не несущий никакой информации. В данном случае мы имеем дело с положительным согласованием скоростей.
Описанная выше процедура согласования скоростей называется стаффинг (от английского «staffing» — вставка). На приёмную станцию подаётся команда, что произошло согласование скоростей для ликвидации ложного импульса. Для надёжности команду согласования скоростей многократно дублируют, например, посылают её три раза.
Если же генератор вырабатывает импульсы считывания реже и в цифровом потоке уже должен появиться «пустой» интервал, а тактовые импульсы ещё не считали из ЗУ предшествующий ему информационный импульс, то придётся исключить из цифрового потока лишний бит и предоставить временной интервал для передачи очередного синхроимпульса. Такое согласование получило название отрицательного.
Таким образом, на приёмную станцию необходимо сообщить, какое согласование произошло: положительное или отрицательное. Для этой цели вводят команду «Вид согласования», посылая по другому служебному каналу 1 при положительном согласовании и 0 при отрицательном. Её также повторяют три раза. Таким образом, информация об изъятии или добавлении импульса передается в специально выделенных импульсных позициях, и на основе этой информации, на приемной стороне при разделении цифровых потоков происходит восстановление их скоростей (рисунок 5.14). Объединение потоков с выравниванием скоростей получило название плезиохронного, то есть почти синхронного, а существующая иерархия скоростей передачи цифровых потоков, а, значит, и систем передачи типа ИКМ – плезиохронной цифровой иерархией (по-английски PDH- Plesiohronous Digital Hierarhy).
При асинхронном способе объединения в блоках цифрового сопряжения БЦСпер (рисунок 5.14) скорости цифровых потоков объединяемых систем приводятся в соответствие с их соотношением с тактовой частотой объединенного потока и устанавливаются необходимые временные положения сигналов объединяемых потоков (КЦП – коллектор цифрового потока, РЦП – распределитель цифрового потока). Для синхронизации тракта передачи и приема по групповому цифровому потоку он разбивается на циклы, в начале которых вводится сигнал синхронизации (рисунок 5.14, б и в). При поканальном объединении цифровых потоков сужаются и распределяются во времени интервалы, отводимые для кодовых групп (рисунок 5.14, в).
Указанные иерархии, известные под общим названием PDH, или ПЦИ, сведены в таблицу 5.3.
Таблица 5.3 – Сравнение иерархий
|
Уровень цифровой |
Скорости передач, соответствующие |
||
|
AC: 1544 Кбит/с |
ЯС: 1544 Кбит/с |
EC: 2048 Кбит/с |
|
|
0 |
64 |
64 |
64 |
|
1 |
1544 |
1544 |
2048 |
|
2 |
6312 |
6312 |
8448 |
|
3 |
44736 |
32064 |
34368 |
|
4 |
– |
97728 |
139264 |
Где: АС – американская схема;
ЯС – японская схема;
ЕС – европейская схема.
Но PDH обладала рядом недостатков, а именно:
- затруднённый ввод/вывод цифровых потоков в промежуточных пунктах;
- отсутствие средств сетевого автоматического контроля и управления;
- многоступенчатое восстановление синхронизма требует достаточно большого времени;
Также можно считать недостатком наличие трёх различных иерархий.
Указанные недостатки PDH, а также ряд других факторов привели к разработке в Европе аналогичной синхронной цифровой иерархии SDH.
Синхронная цифровая иерархия.
Новая цифровая иерархия SDH – это способ мультиплексирования различных цифровых данных в единый блок, называемый синхронным транспортным модулем (STM), с целью передачи этого модуля по линии связи [21]. Упрощённая структура STM показана на рисунке 5.15:
Рисунок 5.15 – Структура синхронного транспортного модуля STM-1
Модуль представляет собой фрейм (рамку) 9∙270 = 2430 байт. Кроме передаваемой информации (называемой в литературе полезной нагрузкой), он содержит в 4-й строке указатель (Pointer, PTR), определяющий начало записи полезной нагрузки.
Чтобы определить маршрут транспортного модуля, в левой части рамки записывается секционный заголовок (Section Over Head – SOH). Нижние 5∙9 = 45 байтов (после указателя) отвечают за доставку информации в то место сети, к тому мультиплексору, где этот транспортный модуль будет переформировываться. Данная часть заголовка так и называется: секционный заголовок мультиплексора (MSOH). Верхние 3∙9 = 27 байтов (до указателя) представляют собой секционный заголовок регенератора (RSOH), где будут осуществляться восстановление потока, «поврежденного» помехами, и исправление ошибок в нем.
Один цикл передачи включает в себя считывание в линию такой прямоугольной таблицы. Порядок передачи байтов – слева направо, сверху вниз (так же, как при чтении текста на странице). Продолжительность цикла передачи STM-1 составляет 125 мкс, т.е. он повторяется с частотой 8 кГц. Каждая клеточка соответствует скорости передачи 8 бит ∙ 8 кГц = 64 кбит/с. Значит, если тратить на передачу в линию каждой прямоугольной рамки 125 мкс, то за секунду в линию будет передано 9∙270∙64 Кбит/с = 155520 Кбит/с, т.е. 155 Мбит/с.
Таблица 5.4 – Синхронная цифровая иерархия
|
Уровень |
Тип синхронного |
Скорость передачи, Мбит/с |
|
1 |
STM-1 |
155,520 |
|
2 |
STM-4 |
622,080 |
|
3 |
STM-16 |
2488,320 |
|
4 |
STM-64 |
9953,280 |
Для создания более мощных цифровых потоков в SDH-системах формируется следующая скоростная иерархия (таблица 5.4): 4 модуля STM-1 объединяются путем побайтного мультиплексирования в модуль STM-4, передаваемый со скоростью 622,080 Мбит/с; затем 4 модуля STM-4 объединяются в модуль STM-16 со скоростью передачи 2488,320 Мбит/с; наконец 4 модуля STM-16 могут быть объединены в высокоскоростной модуль STM-64 (9953,280 Мбит/с).
На рисунке 5.17 показано формирование модуля STM-16. Сначала каждые 4 модуля STM-1 с помощью мультиплексоров с четырьмя входами объединяются в модуль STM-4, затем четыре модуля STM-4 мультиплексируются таким же четырёхвходовым мультиплексором в модуль STM-16. Однако существует мультиплексор на 16 входов, с помощью которого можно одновременно объединить 16 модулей STM-1 в один модуль STM-16.
Рисунок 5.16– Формирование синхронного транспортного модуля STM–16
Формирование модуля STM-1. В сети SDH применены принципы контейнерных перевозок. Подлежащие транспортировке сигналы предварительно размещаются в стандартных контейнерах (Container – С). Все операции с контейнерами производятся независимо от их содержания, чем и достигается прозрачность сети SDH, т.е. способность транспортировать различные сигналы, в частности, сигналы PDH [1].
Наиболее близким по скорости к первому уровню иерархии SDH (155,520 Мбит/с) является цифровой поток со скоростью 139,264 Мбит/с, образуемый на выходе аппаратуры плезиохронной цифровой иерархии ИКМ-1920. Его проще всего разместить в модуле STM-1. Для этого поступающий цифровой сигнал сначала «упаковывают» в контейнер (т.е. размещают на определенных позициях его цикла), который обозначается С-4.
Рамка контейнера С-4 содержит 9 строк и 260 однобайтовых столбцов. Добавлением слева еще одного столбца – маршрутного или трактового заголовка (Path Over Head – РОН) – этот контейнер преобразуется в виртуальный контейнер VC-4.
Наконец, чтобы поместить виртуальный контейнер VC-4 в модуль STM-1, его снабжают указателем (PTR), образуя таким образом административный блок AU-4 (Administrative Unit), а последний помещают непосредственно в модуль STM-1 вместе с секционным заголовком SOH (рисунок 5.17 и рисунок 5.18).
Синхронный транспортный модуль STM-1 можно загрузить и плезиохронными потоками со скоростями 2,048 Мбит/с. Такие потоки формируются аппаратурой ИКМ-30, они широко распространены в современных сетях. Для первоначальной «упаковки» используется контейнер С12. Цифровой сигнал размещается на определенных позициях этого контейнера. Путем добавления маршрутного, или транспортного, заголовка (РОН) образуется виртуальный контейнер VC-12. Виртуальные контейнеры формируются и расформировываются в точках окончаниях трактов [1].
Рисунок 5.17. Размещение контейнеров в модуле STM-1
В модуле STM-1 можно разместить 63 виртуальных контейнера VC-12. При этом поступают следующим образом. Виртуальный контейнер VC-12 снабжают указателем (PTR) и образуют тем самым транспортный блок TU-12 (Tributary Unit). Теперь цифровые потоки разных транспортных блоков можно объединять в цифровой поток 155,520 Мбит/с (рисунок 5.18). Сначала три транспортных блока TU-12 путем мультиплексирования объединяют в группу транспортных блоков TUG-2 (Tributary Unit Group), затем семь групп TUG-2 мультиплексируют в группы транспортных блоков TUG-3, а три группы TUG-3 объединяют вместе и помещают в виртуальный контейнер VC-4. Далее путь преобразований известен.
На рисунке 5.18 показан также способ размещения в STM-N, N=1,4,16 различных цифровых потоков от аппаратуры плезиохронной цифровой иерархии. Плезиохронные цифровые потоки всех уровней размещаются в контейнерах С с использованием процедуры выравнивания скоростей (положительного, отрицательного и двухстороннего).
Наличие большого числа указателей (PTR) позволяет совершенно четко определить местонахождение в модуле STM-N любого цифрового потока со скоростями 2,048; 34,368 и 139,264 Мбит/с. Выпускаемые промышленностью мультиплексоры ввода-вывода (Add/Drop Multiplexer – ADM) позволяют ответвлять и добавлять любые цифровые потоки.
Рисунок 5.18. Ввод плезиохронных цифровых потоков в синхронный транспортный модуль STM-N
Важной особенностью аппаратуры SDH является то, что в трактовых и сетевых заголовках помимо маршрутной информации создается много информации, позволяющей обеспечить наблюдение и управление всей сетью в целом, осуществлять дистанционные переключения в мультиплексорах по требованию клиентов, осуществлять контроль и диагностику, своевременно обнаруживать и устранять неисправности, реализовать эффективную эксплуатацию сети и сохранить высокое качество предоставляемых услуг.
Иерархии PDH и SDH взаимодействуют через процедуры мультиплексирования и демультиплексирования потоков PDH в системы SDH.
Основным отличием системы SDH от системы PDH является переход на новый принцип мультиплексирования. В системе SDH производится синхронное мультиплексирование/демультиплексирование, которое позволяет организовывать непосредственный доступ к каналам PDH, которые передаются в сети SDH. Это довольно важное и простое нововведение в технологии привело к тому, что в целом технология мультиплексирования в сети SDH намного сложнее, чем технология в сети PDH, усилились требования по синхронизации и параметрам качества среды передачи и системы передачи, а также увеличилось количество параметров, существенных для работы сети.
Контрольные вопросы:
- Что такое цифровой сигнал?
- Перечислите основные преимущества цифровой связи перед аналоговой?
- Дайте понятие скорости передачи?
- С какой частотой следует дискретизировать аналоговый сигнал?
- Поясните суть квантования?
- Как определить ошибку квантования сигнала?
- Запишите число 859 в двоичной системе счисления.
- Закодируйте положительный отсчёт 358 мА в симметричном восьмиразрядном коде. Чему равна ошибка квантования?
- Дайте понятие плезиохронной цифровой иерархии?
- Для чего необходимо согласование скоростей передачи различных потоков при их объединении в высокоскоростной поток? Как осуществляется согласование?
- Принцип синхронной цифровой иерархии, её преимущества по сравнению с плезиохронной цифровой иерархией?
- Для чего нужен указатель (PTR)?
- Охарактеризуйте структуру синхронного транспортного модуля.
- Как в STM-N размещаются три потока со скоростью 34,368 Мбит/с от аппаратуры плезиохронной цифровой иерархии ИКМ-480.
Ошибка квантования E = em — ea — это разность между реальной продолжительностью события ea и его измеренной продолжительностью em. У вас нет возможности узнать реальную продолжительность события, следовательно, нельзя и обнаружить ошибку квантования, основываясь на отдельном значении. Однако можно доказать наличие ошибки квантования, исследуя группы родственных статистик. Мы уже рассматривали пример, в котором удалось выявить ошибку квантования. В примере 7.5 наличие ошибки квантования удалось определить, заметив, что:
Ошибку квантования легко выявить, исследуя вызов базы данных и выполняемые им события ожидания в системе с низкой загрузкой, где минимизировано влияние других факторов, способных нарушить отношение e и c + Eela.
Рассмотрим фрагмент файла трассировки Oracle8i, который демонстрирует эффект ошибки квантования:
Данный вызов выборки инициировал ровно три события ожидания. Мы знаем, что приведенные значения c, e и ela должны быть связаны таким приблизительным равенством:
В системе с низкой загрузкой величина, на которую отличаются левая и правая части приблизительного равенства, указывает на общую ошибку квантования, присутствующую в пяти измерениях (одно значение c, одно значение e и три значения ela):
С учетом того, что отдельному вызову gettimeofday в большинстве систем соответствует лишь несколько микросекунд ошибки, вызванной влиянием измерителя, получается, что ошибка квантования вносит значительный вклад в «разность» длиной в одну сантисекунду в данных трассировки.
Следующий фрагмент файла трассировки Oracle8i демонстрирует простейший вариант избыточного учета продолжительности, в результате которого возникает отрицательная величина неучтенного времени:
WAIT #96: nam=’db file sequential read’ ela= 0 p1=1 p2=1691 p3=1
FETCH #96:c=1,e=0,p=1,cr=4,cu=0,mis=0,r=1,dep=1,og=4,tim=116694789 В данном случае E = -1 сантисекунда:
При наличии «отрицательной разности» (подобного только что рассмотренному) невозможно все объяснить эффектом влияния измерителя, ведь этот эффект может быть причиной появления только положительных значений неучтенного времени. Можно было бы подумать, что имел место двойной учет использования процессора, но и это не соответствует действительности, т. к. нулевое значение ela свидетельствует о том, что время занятости процессора вообще не учитывалось для события ожидания. В данном случае ошибка квантования имеет преобладающее влияние и приводит к излишнему учету времени для выборки.
В данном случае E = 640 мкс:
В Oracle9i разрешение временной статистики улучшено, но и эта версия отнюдь не защищена от воздействия ошибки квантования, что видно в предложенном ниже фрагменте файла трассировки для E > 0:
Некоторая часть этой ошибки, несомненно, является ошибкой квантования (невозможно, чтобы общее время использования процессора данной выборкой действительно равнялось нулю). Несколько микросекунд следует отнести на счет эффекта влияния измерителя.
Наконец, рассмотрим пример ошибки квантования E < 0 в данных трассировки Oracle9i:
Возможно, в данном случае имел место двойной учет использования процессора. Также вероятно, что именно ошибка квантования внесла основной вклад в полученное время вызова выборки. Избыточный учет 8784 микросекунд говорит о том, что фактический общий расход процессорного времени вызовом базы данных составил, вероятно, всего около (10000 — 8784) мкс = 1,216 мкс.
Диапазон значений ошибки квантования
Величину ошибки квантования, содержащейся во временных статистиках Oracle, нельзя измерить напрямую. Зато можно проанализировать статистические свойства ошибки квантования в данных расширенной трассировки SQL. Во-первых, величина ошибки квантования для конкретного набора данных трассировки ограничена сверху. Легко представить ситуацию, в которой ошибка квантования, вносимая такими характеристиками продолжительности, как e и ela, будет максимальной. Наибольшего значения данная ошибка достигает в том случае, когда в последовательности значений e и ela все отдельные ошибки квантования имеют максимальную величину и их знаки совпадают.
На рис. 7.9 показан пример возникновения описанной ситуации: имеется восемь очень непродолжительных системных вызовов, причем все они попадают на такты интервального таймера. Фактическая длительность каждого события близка к нулю, но измеренная длительность каждого такого события равна одному такту системного таймера. В итоге суммарная фактическая продолжительность всех вызовов близка к нулю, а общая измеренная продолжительность равна 8 тактам. Для такого набора из n = 8 системных вызовов ошибка квантования по существу равна nrx, где rx — это разрешение интервального таймера, с помощью которого измеряется характеристика x.
Думаю, вы обратили внимание, что изображенный на рис. 7.9 случай выглядит надуманно и изобретен исключительно для прояснения вопроса. В реальной жизни подобная ситуация чрезвычайно маловероятна. Вероятность, что n ошибок квантования будут иметь одинаковые знаки, равна всего 0,5n. Вероятность того, что n=8 последовательных
Рис. 7.9. Наихудший вариант накопления ошибки квантования для последовательности измеренных продолжительностей
ошибок квантования будут отрицательными, равна всего 0,00390625 (т. е. приблизительно четыре шанса из тысячи). Для 266 значений шанс совпадения знаков у всех ошибок квантования меньше, чем один из 1080.
Для больших наборов значений длительностей совпадение знаков всех ошибок квантования практически невозможно. Но это не единственное, в чем состоит надуманность ситуации, изображенной на рис. 7.9. Она также предполагает, что абсолютная величина каждой ошибки квантования максимальна. Шансы наступления такого события еще более иллюзорны, чем у совпадения всех знаков ошибок. Например, вероятность того, что величина каждой из n имеющихся ошибок квантования превышает 0,9, равна (1 — 0,9)n. Вероятность того, что величина каждой из n = 266 ошибок квантования превысит 0,9, составляет всего 1 из 10266.
Вероятность того, что все n ошибок квантования имеют одинаковый знак и абсолютная величина всех из них больше m, чрезвычайно мала и равна произведению рассмотренных ранее вероятностей:
P (значения всех n ошибок квантования больше m или меньше -m)=
= (0.5)n(1- m)n
Ошибки квантования для продолжительностей (например, значений e и ela в Oracle) — это случайные числа в диапазоне:
-rx < E < rx где rx — это разрешение интервального таймера, с помощью которого измеряется характеристика x (x- это e или ela).
Так как положительные и отрицательные ошибки квантования возникают c равной вероятностью, средняя ошибка квантования для выбранного набора статистик стремится к нулю даже для больших файлов трассировки. Опираясь на теорему Лапласа (Pierre Simon de Laplace, 1810), можно предсказать вероятность того, что ошибки квантования для статистик e и ela будут превышать указанное пороговое значение для файла трассировки, содержащего определенное количество статистик.
Я начал работать над вычислением вероятности того, что общая ошибка квантования файла трассировки (включая ошибку, вносимую статистикой c) будет превышать заданную величину, однако мое исследование еще не завершено. Мне предстоит получить распределение ошибки квантования для статистики c, что, как я уже говорил, осложняется особенностями получения этой статистики в процессе опроса. Результаты этих изысканий планируется воплотить в одном из будущих проектов.
К счастью, относительно ошибки квантования есть и оптимистические соображения, которые позволяют не слишком расстраиваться по поводу невозможности определения ее величины:
• Во многих сотнях файлов трассировки Oracle, проанализированных нами в hotsos.com, общая продолжительность неучтенного вре-
Что означает «один шанс из десяти в [очень большой] степени»?
Для того чтобы представить себе, что такое «один шанс из 1080», задумайтесь над следующим фактом: ученые утверждают, что в наблюдаемой вселенной содержится всего около 1080 атомов (по данным http:// www.sunspot.noao.edu/sunspot/pr/answerbook/universe.html#q70, http:/ /www.nature.com/nsu/020527/020527-16.html и др.). Это означает, что если бы вам удалось написать на каждом атоме нашей вселенной 266 равномерно распределенных случайных чисел от -1 до +1, то лишь на одном из этих атомов можно было бы ожидать наличия всех 266 чисел с одинаковым знаком.
Представить вторую упомянутую вероятность — «один шанс из 10266»-еще труднее. На этот раз представим себе три уровня вложенных вселенных. То есть что каждый из 1080 атомов нашей вселенной сам по себе является вселенной, состоящей из 1080 вселенных, каждая из которых в свою очередь содержит 1080 атомов. Теперь у нас достаточно атомов для того, чтобы представить себе возможность возникновения ситуации с вероятностью «один из 10240». Даже во вселенных третьего уровня вложенности вероятность появления атома, для которого все 266 его случайных чисел по абсолютной величине больше 0,9, составит один из 100 000 000 000 000 000 000 000 000.
мени в случае корректного сбора данных (см. главу 6) чрезвычайно редко превышала 10% общего времени отклика.
Несмотря на то, что и ошибка квантования, и двойной учет использования процессора могут привести к такому результату, файл трассировки чрезвычайно редко содержит отрицательное неучтенное время, абсолютная величина которого превышала бы 10% общего времени отклика.
В случаях, когда неучтенное время оценивается более чем в 25% времени отклика для корректно собранных данных трассировки, такой объем неучтенного времени почти всегда объясняется одним из двух явлений, описанных в последующих разделах.
Наличие ошибки квантования не лишает нас возможности правильно диагностировать основные причины проблем производительности при помощи файлов расширенной трассировки SQL в Oracle (даже в файлах трассировки Oracle8i, в которых вся статистика приводится с точностью лишь до сотых долей секунды).
Ошибка квантования становится еще менее значимой в Oracle9i благодаря повышению точности измерений.
В некоторых случаях влияние ошибки квантования способно привести к утрате доверия к достоверности данных трассировки Oracle. Наверное, ничто не может так подорвать боевой дух, как подозрение в недостоверности данных, на которые вы полагаетесь. Думаю, что лучшим средством, призванным укрепить веру в получаемые данные, должно служить четкое понимание влияния ошибки квантования.
| Следующая > |
|---|
Sensors
Andrea Colagrossi, … Matteo Battilana, in Modern Spacecraft Guidance, Navigation, and Control, 2023
Quantization errors
Quantization error is a systematic error resulting from the difference between the continuous input value and its quantized output, and it is like round-off and truncation errors. This error is intrinsically associated with the AD conversion that maps the input values from a continuous set to the output values in a countable set, often with a finite number of elements. The quantization error is linked to the resolution of the sensor. Namely, a high-resolution sensor has a small quantization error. Indeed, the maximum quantization error is smaller than the resolution interval of the output, which is associated to the least significant bit representing the smallest variation that can be represented digitally:
LSB=FSR2NBIT
where FSR is the full-scale range of the sensor, and NBIT is the number of bits (i.e., the resolution) used in the AD converter to represent the sensor’s output. Quantization errors are typically not corrected, and the discrete values of the output are directly elaborated by the GNC system, which is designed to operate on digital values.
Fig. 6.9 shows a convenient model block to simulate quantization errors.
Figure 6.9. Quantization error model.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780323909167000068
Digital Filters
Marcio G. Siqueira, Paulo S.R. Diniz, in The Electrical Engineering Handbook, 2005
2.11 Quantization in Digital Filters
Quantization errors in digital filters can be classified as:
- •
-
Round-off errors derived from internal signals that are quantized before or after more down additions;
- •
-
Deviations in the filter response due to finite word length representation of multiplier coefficients; and
- •
-
Errors due to representation of the input signal with a set of discrete levels.
A general, digital filter structure with quantizers before delay elements can be represented as in Figure 2.23, with the quantizers implementing rounding for the granular quantization and saturation arithmetic for the overflow nonlinearity.
FIGURE 2.23. Digital Filter Including Quantizers at the Delay Inputs
The criterion to choose a digital filter structure for a given application entails evaluating known structures with respect to the effects of finite word length arithmetic and choosing the most suitable one.
2.11.1 Coefficient Quantization
Approximations are known to generate digital filter coefficients with high accuracy. After coefficient quantization, the frequency response of the realized digital filter will deviate from the ideal response and eventually fail to meet the prescribed specifications. Because the sensitivity of the filter response to coefficient quantization varies with the structure, the development of low-sensitivity digital filter realizations has raised significant interest (Antoniou, 1993; Diniz et al., 2002).
A common procedure is to design the digital filter with infinite coefficient word length satisfying tighter specifications than required, to quantize the coefficients, and to check if the prescribed specifications are still met.
2.11.2 Quantization Noise
In fixed-point arithmetic, a number with a modulus less than one can be represented as follows:
(2.84)x=b0b1b2b3…bb,
where b0 is the sign bit and where b1b2b3 … bb represent the modulus using a binary code. For digital filtering, the most widely used binary code is the two’s complement representation, where for positive numbers b0 = 0 and for negative numbers b0 = 1. The fractionary part of the number, called x2 here, is represented as:
(2.85)x2={xif b0=0.2−|x|if b0=1.
The discussion here concentrates in the fixed-point implementation.
A finite word length multiplier can be modeled in terms of an ideal multiplier followed by a single noise source e(n) as shown in Figure 2.24.
FIGURE 2.24. Model for the Noise Generated after a Multiplication
For product quantization performed by rounding and for signal levels throughout the filter much larger than the quantization step q = 2−b, it can be shown that the power spectral density of the noise source ei(n) is given by:
(2.86)Pei(z)=q212=2−2b12.
In this case, ei(n) represents a zero mean white noise process. We can consider that in practice, ei(n) and ek(n + l) are statistically independent for any value of n or l (for i ≠ k). As a result, the contributions of different noise sources can be taken into consideration separately by using the principle of superposition.
The power spectral density of the output noise, in a fixed-point digital-filter implementation, is given by:
(2.87)Py(z)=σe2Σi=1KGi(z)Gi(z−1),
where Pei(ejw)=σe2, for all i, and each Gi(z) is a transfer function from multiplier output (gi(n)) to the output of the filter as shown in Figure 2.25. The word length, including sign, is b + 1 bits, and K is the number of multipliers of the filter.
FIGURE 2.25. Digital Filter Including Scaling and Noise Transfer Functions.
2.11.3 Overflow Limit Cycles
Overflow nonlinearities influence the most significant bits of the signal and cause severe distortion. An overflow can give rise to self-sustained, high-amplitude oscillations known as overflow limit cycles. Digital filters, which are free of zero-input limit cycles, are also free of overflow oscillations if the overflow nonlinearities are implemented with saturation arithmetic, that is, by replacing the number in overflow by a number with the same sign and with maximum magnitude that fits the available wordlength.
When there is an input signal applied to a digital filter, overflow might occur. As a result, input signal scaling is required to reduce the probability of overflow to an acceptable level. Ideally, signal scaling should be applied to ensure that the probability of overflow is the same at each internal node of the digital filter. This way, the signal-to-noise ratio is maximized in fixed-point implementations.
In two’s complement arithmetic, the addition of more than two numbers will be correct independently of the order in which they are added even if overflow occurs in a partial summation as long as the overall sum is within the available range to represent the numbers. As a result, a simplified scaling technique can be used where only the multiplier inputs require scaling. To perform scaling, a multiplier is used at the input of the filter section as illustrated in Figure 2.25.
It is possible to show that the signal at the multiplier input is given by:
(2.88)xi(n)=12πj∮cXi(z)zn−1dz=12π∫02πFi(ejω)X(ejω)ejωndω,
where c is the convergence region common to Fi(z) and X(z).
The constant λ is usually calculated by using Lp norm of the transfer function from the filter input to the multiplier input Fi(z), depending on the known properties of the input signal. The Lp norm of Fi(z) is defined as:
(2.89)‖Fi(ejω)‖p=[12π∫02π|Fi(ejω)|pdω]1p,
for each p ≥ 1, such that ∫02π|Fi(ejω)|pdω≤∞. In general, the following inequality is valid:
(2.90)|xi(n)| ≤ ‖Fi‖p‖X‖q, (1p+1q=1),
for p, q = 1, 2 and ∞.
The scaling guarantees that the magnitudes of multiplier inputs are bounded by a number Mmax when |x(n)| ≤ Mmax. Then, to ensure that all multiplier inputs are bounded by Mmax we must choose λ as follows:
(2.91)λ=1Max{‖F1‖p,…,‖F1‖p,…, ‖FK‖p},
which means that:
(2.92)‖F′i(ejω)‖p≤1, for‖X(ejω)‖q ≤ Mmax.
The K is the number of multipliers in the filter.
The norm p is usually chosen to be infinity or 2. The L∞ norm is used for input signals that have some dominating frequency component, whereas the L2 norm is more suitable for a random input signal. Scaling coefficients can be implemented by simple shift operations provided they satisfy the overflow constraints.
In case of modular realizations, such as cascade or parallel realizations of digital filters, optimum scaling is accomplished by applying one scaling multiplier per section.
As an illustration, we present the equation to compute the scaling factor for the cascade realization with direct-form second-order sections:
(2.93)λi=1‖∏j=1i−1Hj(z)Fi(z)‖p,
where:
Fi(z)=1z2+m1iz+m2i.
The noise power spectral density is computed as:
(2.94)Py(z)=σe2[3+3λ12∏i=1mHi(z)Hi(z−1)+5Σj=2m1λj2∏i=jmHi(z)Hi(z−1)],
whereas the output noise variance is given by:
(2.95)σo2=σe2[3+3λ12||∏i=1mHi(ejω)||22+5Σj=2m1λj2||∏i=jmHi(ejω)||22].
As a design rule, the pairing of poles and zeros is performed as explained here: poles closer to the unit circle pair with closer zeros to themselves, such that ||Hi(z)||p is minimized for p = 2 or p = ∞.
For ordering, we define the following:
(2.96)Pi=| |Hi(z)| |∞| |Hi(z)| |2.
For L2 scaling, we order the section such that Pi is decreasing. For L∞ scaling, Pi should be increasing.
2.11.4 Granularity Limit Cycles
The quantization noise signals become highly correlated from sample to sample and from source to source when signal levels in a digital filter become constant or very low, at least for short periods of time. This correlation can cause autonomous oscillations called granularity limit cycles.
In recursive digital filters implemented with rounding, magnitude truncation,72 and other types of quantization, limitcycles oscillations might occur.
In many applications, the presence of limit cycles can be harmful. Therefore, it is desirable to eliminate limit cycles or to keep their amplitude bounds low.
If magnitude truncation is used to quantize particular signals in some filter structures, it can be shown that it is possible to eliminate zero-input limit cycles. As a consequence, these digital filters are free of overflow limit cycles when overflow nonlinearities, such as saturation arithmetic, are used.
In general, the referred methodology can be applied to the following class of structures:
- •
-
State-space structures: Cascade and parallel realization of second-order state-space structures includes design constraints to control nonlinear oscillations (Diniz and Antoniou, 1986).
- •
-
Wave digital filters: These filters emulate doubly terminated lossless filters and have inherent stability under linear conditions as well as in the nonlinear case where the signals are subjected to quantization (Fettweis, 1986).
- •
-
Lattice realization: Modular structures allowing easy limit cycles elimination (Gray and Markel, 1975).
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780121709600500621
Biomedical signals and systems
Sri Krishnan, in Biomedical Signal Analysis for Connected Healthcare, 2021
2.2.1 Noise power
The quantization error (e) or noise tends to have a random behavior, and they could be mathematically represented using statistical variables. Power of a random variable with a probability density function of p(e) could be obtained by computing the second-order statistics of variance, and it is denoted by
σ2=∫−q/2q/2e2p(e)de
A good assumption for p(e) is a uniform probability density function which will have a value of 1/q over the range of −q/2 to q/2.
=∫−q/2q/2e2·1qde=q212
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780128130865000049
Measurement of high voltages
E. Kuffel, … J. Kuffel, in High Voltage Engineering Fundamentals (Second Edition), 2000
Static errors
The quantization error is present because the analogue value of each sample is transformed into a digital word. This A-to-D conversion entails a quantization of the recorder’s measuring range into a number of bands or code bins, each represented by its central value which corresponds to a particular digital code or level. The number of bands is given by 2N, where N is the resolution of the A-to-D converter. The digital output to analogue input relationship of an ideal digitizer is shown diagrammatically in Fig. 3.49. For any input in the range (iΔVav – 0.5 * ΔVav to iΔVav + 0.5 * ΔVav), where iΔVav is the voltage corresponding to the width of each code bin, or one least significant bit (LSB), and iΔVav is the centre voltage corresponding to the i th code, an ideal digitizer will return a value of Ii. Therefore, the response of an ideal digitizer to a slowly increasing linear ramp would be a stairway such as that shown in Fig. 3.50. A quick study of these figures reveals the character of the quantization error associated with the ideal A-to-D conversion process. The maximum error possible is equivalent to a voltage corresponding to ±(½) of an LSB. For an ideal digital recorder, this quantization would be the only source of error in the recorded samples. For a real digital recorder, this error sets the absolute upper limit on the accuracy of the readings. In the case of an 8-bit machine, this upper limit would be 0.39 per cent of the recorder’s full-scale deflection. The corresponding maximum accuracy (lowest uncertainty) of a 10-bit recorder is 0.10 per cent of its full-scale deflection.
Figure 3.49. Analogue input to digital output relation of an ideal A/D converter
Figure 3.50. Response of an ideal A/D converter to a slowly rising ramp
The error caused by discrete time sampling is most easily demonstrated with reference to the recording of sinusoidal signals. As an example we can look at the discrete time sampling error introduced in the measurement of a single cycle of a pure sine wave of frequency f, which is sampled at a rate of four times its frequency. When the sinusoid and the sampling clock are in phase, as shown in Fig. 3.51, a sample will fall on the peak value of both positive and negative half-cycles. The next closest samples will lie at π/2 radians from the peaks. As the phase of the clock is advanced relative to the input sinusoid the sample points which used to lie at the peak values will move to lower amplitude values giving an error (Δ) in the measurement of the amplitude (A) of
Figure 3.51. Sample points with sinusoid and sampling clock in phase. (Error in peak amplitude = 0)
Δ = A(1 − cos ϕ)
where ϕ is the phase shift in the sample points. This error will increase until ϕ – π/4 (Fig. 3.52). For ϕ > π/4 the point behind the peak value will now be closer to the peak and the error will decrease for a ϕ in the range of π/4 to π/2. The maximum per unit value of the discrete time sampling error is given by eqn 3.93,
Figure 3.52. Sample points with sampling clock phase advanced to π/4 with respect to the sinusoid. Error in peak amplitude (Δ) is at a maximum
(3.93)Δmax=I−cos(πfts)
where ts is the recorder’s sampling interval and f the sinewave frequency.
The maximum errors obtained through quantization and sampling when recording a sinusoidal waveform are shown in Fig. 3.53. The plotted quantities were calculated for an 8-bit 200-MHz digitizer.
Figure 3.53. Sampling and quantization errors of an ideal recorder
In a real digital recorder, an additional two categories of errors are introduced. The first includes the instrument’s systematic errors. These are generally due to the digitizer’s analogue input circuitry, and are present to some degree in all recording instruments. They include such errors as gain drift, linearity errors, offset errors, etc. They can be compensated by regular calibration without any net loss in accuracy. The second category contains the digitizer’s dynamic errors. These become important when recording high-frequency or fast transient signals. The dynamic errors are often random in nature, and cannot be dealt with as simply as their systematic counterparts and are discussed below.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780750636346500046
Remaining useful life prediction
Yaguo Lei, in Intelligent Fault Diagnosis and Remaining Useful Life Prediction of Rotating Machinery, 2017
6.3.4.3 RUL Prediction
The constructed indicator WMQE is further input into the RUL prediction module. In this module, a PF-based prediction algorithm is utilized to predict RUL of the rotating machinery whose degradation processes are described using a variant of Paris–Erdogan model. The Paris–Erdogan model is formulated as
(6.96)dxdt=c(Δδ)γ, Δδ=mx
where x represents the semicrack length, t is the number of stress cycles (i.e., the fatigue life), c, γ, and m are material constants which are determined by tests, and Δδ is amplitude of stress intensity factor roughly proportional to the square root of x.
It is seen from Eq. (6.96) that there are several model parameters in the Paris–Erdogan model, that is, c, γ, and m, which are difficult to measure during the operation process of the rotating machinery. For convenient application, the Paris–Erdogan model is transformed into the following format with α=cmγ and β = γ/2.
(6.97)dxdt=αxβ.
Then, the above function is rewritten into the following state space model.
(6.98)xk=xk−1+αk−1xk−1βΔtkαk=αk−1zk=xk+νk,
where αk−1 is a random variable following a normal distribution of Nμα,σα2, β is a constant parameter, Δtk=tk−tk−1, zk is the measured WMQE value at tk and νk is the measurement noise following the normal distribution of N0,σν2. With the transformation of the Paris–Erdogan model, the model parameters are more convenient to estimate according to the measurements. In addition, the state space model inherits the superiority of the Paris–Erdogan model in describing the general degradation processes. Therefore, it is supposed to be a good model for a general degradation process.
After the transformation, the unknown model parameters are changed to be Θ=μα,σα2,β,σν2′, where (·)′ denotes the vector transposition. Then, the measured WMQE values constructed from vibration signals are input into the model, and the model parameters are initialized using MLE. It is assumed that there are a series of measurements z0:M=z0,…,zM′ at ordered times t0,…,tM. According to Eq. (6.98), zk is formulated as follows:
(6.99)zk=xk−1+αkxk−1βΔtk+νk.
The degradation state xk−1 has the following relationship with the measurement zk−1.
(6.100)xk−1=zk−1−νk−1.
The degradation state xk−1 is hard to be acquired in real applications. If the measurement noise νk−1 is small enough compared with the measurement itself, it is negligible and xk−1 is approximated by zk−1. Let T=z0βΔt1,…,zM−1βΔtM′. z1:M=z1,…,zM′ is multivariate normally distributed, which is denoted as follows:
(6.101)z1:M∼Nz0:M−1+μαT,σα2TT′+σν2IM,
where IM is an identity matrix of order M.
Let Δz1:M=z1−z0,…,zM−zM−1′, and the log-likelihood function of the unknown parameters based on the measurements is expressed as
(6.102)ℓΘ|z0:M=−M2ln2π−12lnσα2TT′+σν2IM −12Δz1:M−μαT′σα2TT′+σν2IM−1Δz1:M−μαT =−M2ln2π−M2lnσα2−12lnTT′+σ˜ν2IM −12σα2Δz1:M−μαT′σα2TT′+σν2IM−1Δz1:M−μαT,
with σ~ν2=σν2/σα2. The first partial derivatives of ℓΘ|z0:M with respect to μα and σα2 are calculated and formulated with
(6.103)∂ℓΘ|z0:M∂μα=1σα2T′TT′+σ~ν2IM-1Δz1:M−μαT,
(6.104)∂ℓΘ|z0:M∂σα2=−M2σα2+12σα4Δz1:M−μαT′TT′+σ~ν2IM−1Δz1:M−μαT.
Let ∂ℓΘ|z0:M/∂μα=0 and ∂ℓΘ|z0:M/∂σα2=0. The MLE results of μα and σα2 are
(6.105)μα=T′TT′+σ~ν2IM−1Δz1:MT′TT′+σ~ν2IM−1T,
(6.106)σα2=Δz1:M−μαT′TT′+σ~ν2IM−1Δz1:M−μαTM.
With Eqs. (6.105) and (6.106) substituted into Eq. (6.102), the log-likelihood function is reduced into a two-variable function about β and σ~ν2, which is denoted by
(6.107)ℓΘ|z0:M=−M2ln2π−M2lnσα2−12lnTT′+σ~ν2IM−M2.
The MLE values of β and σ~ν2 are obtained by maximizing the log-likelihood function (6.107) through two-dimensional optimizing. Then the MLE values of β and σ~ν2 are substituted into Eqs. (6.105) and (6.106), and the MLE values of μα and σα2 are acquired. The value of σν2 is calculated with σ~ν2 multiplied by σα2. Finally, all of the unknown parameters Θ=μα,σα2,β,σν2′ are initialized.
After parameter initialization, the model parameters are further updated and the RUL is predicted using a PF-based prediction algorithm. Based on the initialized parameters, a series of initial particles y0nn=1:Ns are sampled from the initial PDF of the system state p(y0n|Θ0)∼N(y0,Q0) with
(6.108)y0=x0μα and Q0=000σα2.
Ns is the number of particles and the weight of each particle is set to be 1/Ns. Then new particles ykni=1:Ns are obtained following
(6.109)ykn=xknμαn=xk−1n+μαnxk−1nβΔtkμαn.
When the new measurement zk at tk is available, each particle weight is updated and normalized by
(6.110)wkn=wk−1npzk|ykn, w~kn=wkn∑n=1Nswkn,
where
(6.111)pzk|ykn=12πσνexp−12zk−xknσν2.
The particles are resampled according to the particle weights and their weights are reset to be 1/Ns. After that, the RUL is predicted based on the resampled particles. The RUL lk at tk is defined as
(6.112)lk=inflk:xlk+tk≥λ|x1:k,
where λ is a prespecified failure threshold. Each particle is transmitted following the transition function of Eq. (6.98) from current state until the state value exceeds the failure threshold, and the RUL lknn=1:Ns predicted using each particle is acquired. Then the PDF of the RUL is approximated by
(6.113)plk|z0:k=∑n=1Nsw~knδlk−lkn.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780128115343000068
Orbit and Attitude Sensors
Enrico Canuto, … Carlos Perez Montenegro, in Spacecraft Dynamics and Control, 2018
Exercise 1
Prove that the quantization error defined by Eq. (8.6) is bounded by |n˜y(i)|≤ρy/2 and under the random assumption has zero mean and variance equal to ρy2/12. □
A typical model of the random error d˜ in Eq. (8.4), which includes quantization errors, is the linear continuous-time stochastic state equation
(8.7)x˜˙(t)=A˜x˜+G˜w˜d˜(t)=C˜x˜+D˜w˜E{w˜(t)}=0,E{w˜(t)w˜T(t+τ)}=S˜w2δ(τ)E{x˜(0)}=x˜0,E{(x˜(0)−x˜0)(x˜(0)−x˜0)T}=P˜0≥0E{(x˜(0)−x˜0)w˜T(0)}=0,
which is similar to the DT Eq. (4.159) of Section 4.8.1. Eq. (8.7) being continuous-time, the eigenvalues of the state matrix A˜ are assumed to lie on the imaginary axis and when equal to zero may be multiple. The statistics in Eq. (8.7) assumes that w˜ is a zero-mean second-order stationary white noise with constant spectral density S˜w2, and impulsive covariance, where δ(τ) denotes a Dirac delta (see Sections 13.2.1 and 13.7.3Section 13.2.1Section 13.7.3). The initial state may be modeled as a random vector with mean value x˜0 and covariance matrix P˜0, but is uncorrelated from any simultaneous white noise as expressed by the last identity in Eq. (8.7). This uncorrelation has been already referred to as the causality constraint. In principle, Eq. (8.7) may be unobservable from the output d˜ and uncontrollable by the noise w˜, because the output d˜ may include polynomial and trigonometric components (deterministic signals) just driven by the initial state x˜0. For instance, a trigonometric component tuned to the angular frequency ω˜ corresponds to a second-order subsystem with eigenvalues ±jω˜. A first-order polynomial corresponds to a second-order subsystem with a pair of zero eigenvalues and a single eigenvector. The mixed case of stochastic processes and deterministic signals can be simplified by assuming that trigonometric and polynomial components are the free response of the equations driven by w˜, and that Eq. (8.7) is observable and controllable.
The simplest model of the class in Eq. (8.7), which is common to inertial sensors (accelerometers in Section 8.4 and gyroscopes in Section 8.5), is the scalar first-order random drift [32]:
(8.8)x˜˙(t)=w˜x,x˜(0)=x˜0d˜(t)=x˜+w˜dE{x˜(0)}=x˜0,var{x˜}=σ02,E{(x˜−x˜0)w˜T(0)}=0w˜=[w˜xw˜d],E{w˜(t)}=0,E{w˜(t)w˜T(t+τ)}=[S˜wx200S˜wd2]δ(τ),
where, if [unit] denotes the unit of measurement of x˜, we find S˜wx2 in [(unit/s)2Hz−1] and S˜wd2 in [unit2Hz−1]. The initial state x˜0 accounts for a constant bias and is uncorrelated with any simultaneous noise; the scalar input noise w˜x and the output noise w˜d in Eq. (8.8) are uncorrelated with each other. The output process d˜ is nonstationary and the autocorrelation is given by
(8.9)R˜d(t,t+τ)=S˜wx2min(t,t+τ)+S˜wd2δ(τ).
Although x˜ is nonstationary, the spectral density S˜x2(f) can be defined through the AS equation x˜˙=−εx˜+w˜x, where ε > 0 must be sufficiently smaller than the cutoff frequency f0 to be defined in the next paragraph. We can write the following identities:
(8.10)S˜d2(f)=S˜x2(f)+S˜wd2=S˜wx2(2πf)2+S˜wd2,f>ε2π=fεσ˜x2=limf→∞∫0fS˜x2νdν<∞,
where if, for f < ε, S˜x2(f) is bounded, also the variance σ˜x2 is bounded. The Bode plot of S˜d(f) is approximately flat for f>f0=2π−1S˜wx/S˜wd>fε and has a −20 dB/decade slope for fε < f < f0. The first PSD in the first row of Eq. (8.10) is a first-order random walk, which is known, in the realm of inertial sensors, as the (long-term) bias instability of the sensor. The name is appropriate because it describes the long-term fluctuations—bounded because of ε—around the mean sensor bias x˜0. The square root of the second term S˜wd corresponds to the minimum-valued profile of the overall spectral density. Let us call it, as already anticipated, noise floor, although the name sometimes refers to the whole instrument noise (here referred to as the background noise). In the realm of inertial sensors, it is known as the velocity random walk in the case of linear accelerometers, the unit being [m/(s2Hz)], and the angular random walk (ARW) in the case of gyroscopes, the unit being[rad/(sHz)]. The name, which may cause same confusion, is justified by the fact that when either of the two measurements (linear acceleration and angular rate) is time integrated for generating either velocity or attitude measurements, the integrated noise floor becomes a random walk. By restricting to gyroscopes, the ARW unit [rad/(sHz)] is usually simplified to [rad/s], de facto to the non-SI unit [degree/hour]. Indeed, the simplified unit is at the same time the unit of S˜wd and the unit of the root mean square (RMS) σ¯w(t,Δt) of the random walk increment w¯d(t,Δt)=∫tt+Δtw˜d(τ)dτ, namely:
(8.11)σ¯w(t,Δt)=E{1Δt(∫tt+Δtw˜d(τ)dτ)2}=S˜wd.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780081007006000088
Sampling Theory
Luis Chaparro, in Signals and Systems Using MATLAB (Second Edition), 2015
8.3.2 Quantization and Coding
Amplitude discretization of the sampled signal xs(t) is accomplished by a quantizer consisting of a number of fixed amplitude levels against which the sample amplitudes {x(nTs)} are compared. The output of the quantizer is one of the fixed amplitude levels that best represents {x(nTs)} according to some approximation scheme. The quantizer is a non-linear system.
Independent of how many levels or, equivalently, of how many bits are allocated to represent each level of the quantizer, in general there is a possible error in the representation of each sample. This is called the quantization error. To illustrate this, consider the 2-bit or four-level quantizer shown in Figure 8.12. The input of the quantizer are the samples {x(nTs)}, which are compared with the values in the bins [-2Δ,-Δ],[-Δ,0],[0,Δ], and [Δ,2Δ]. Depending on which of these bins the sample falls in it is replaced by the corresponding levels -2Δ,-Δ,0, or Δ, respectively. The value of the quantization step Δ for the four-level quantizer is
Figure 8.12. Four-level quantizer and coder.
(8.23)Δ=dynamic range of signal2b=2max|x(t)|22
where b = 2 is number of bits of the code assigned to each level. The bits assigned to each of the levels uniquely represents the different levels [-2Δ,-Δ,0,Δ]. As to how to approximate the given sample to one of these levels, it can be done by rounding or by truncating. The quantizer shown in Figure 8.12 approximates by truncation, i.e., if the sample kΔ≤x(nTs)<(k+1)Δ, for k = −2, −1,0,1, then it is approximated by the level kΔ.
To see how quantization and coding are done, and how to obtain the quantization error, let the sampled signal be
x(nTs)=x(t)|t=nTS
The given four-level quantizer is such that if the sample x(nTs) is such that
(8.24)kΔ≤x(nTs)<(k+1)Δ⇒xˆ(nTs)=kΔk=-2,-1,0,1
The sampled signal x(nTs) is the input of the quantizer and the quantized signal xˆ(nTs) is its output. So that whenever
-2Δ≤x(nTs)<-Δ⇒xˆ(nTs)=-2Δ-Δ≤x(nTs)<0⇒xˆ(nTs)=-Δ0≤x(nTs)<Δ⇒xˆ(nTs)=0Δ≤x(nTs)<2Δ⇒xˆ(nTs)=Δ
To transform the quantized values into unique binary 2-bit values, one could use a code such as
xˆ(nTs)⇒binary code-2Δ10-Δ110Δ00Δ01
which assigns a unique 2 bit binary number to each of the 4 quantization levels. Notice that the first bit of this code can be considered a sign bit, “1” for negative levels and “0” for positive levels.
If we define the quantization error as
ε(nTs)=x(nTs)-xˆ(nTs)
and use the characterization of the quantizer given by Equation (8.24) as
xˆ(nTs)≤x(nTs)≤xˆ(nTs)+Δ
by subtracting xˆ(nTs) from each of the terms gives that the quantization error is bounded as follows
(8.25)0≤ε(nTs)≤Δ
i.e., the quantization error for the four-level quantizer being considered is between 0 and Δ. This expression for the quantization error indicates that one way to decrease the quantization error is to make the quantization step Δsmaller. Increasing the number of bits of the A/D converter makes Δ smaller (see Equation (8.23) where the denominator is 2 raised to the number of bits) which in turn makes smaller the quantization error, and improves the quality of the A/D converter.
In practice, the quantization error is random and so it needs to be characterized probabilistically. This characterization becomes meaningful when the number of bits is large, and when the input signal is not a deterministic signal. Otherwise, the error is predictable and thus not random. Comparing the energy of the input signal to the energy of the error, by means of the so-called signal to noise ratio (SNR), it is possible to determine the number of bits that are needed in a quantizer to get a reasonable quantization error.
Example 8.5
Suppose we are trying to decide between an 8 and a 9 bit A/D converter for a certain application where the signals in this application are known to have frequencies that do not exceed 5 kHz. The dynamic range of the signals is 10 volts, so that the signal is bounded as −5 ≤ x(t) ≤ 5. Determine an appropriate sampling period and compare the percentage of error for the two A/Ds of interest.
Solution
The first consideration in choosing the A/D converter is the sampling period, so we need to get an A/D converter capable of sampling at fs = 1/Ts > 2 fmax samples/second. Choosing fs = 4 fmax = 20 k samples/second then Ts = 1/20 msec/sample or 50 microseconds/sample. Suppose then we look at the 8-bit A/D converter, the quantizer has 28 = 256 levels so that the quantization step is Δ=10/256 volts and if we use a truncation quantizer the quantization error would be
0≤ε(nTs)≤10/256
If we find that objectionable we can then consider the 9-bit A/D converter, with a quantizer of 29 = 512 levels and the quantization step Δ=10/512 or half that of the 8-bit A/D converter, and
0≤ε(nTs)≤10/512
So that by increasing one bit we cut the quantization error in half from the previous quantizer. Inputting a signal of constant amplitude 5 into the 9-bit A/D gives a quantization error of [(10/512)/5] × 100% = (100/256)% ≈ 0.4% in representing the input signal. For the 8-bit A/D it would correspond to 0.8% error. ▪
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780123948120000085
Compression
StéphaneMallat , in A Wavelet Tour of Signal Processing (Third Edition), 2009
Weighted Quantization and Regions of Interest
Visual distortions introduced by quantization errors of wavelet coefficients depend on the scale 2j. Errors at large scales are more visible than at fine scales [481]. This can be taken into account by quantizing the wavelet coefficients with intervals Δj=Δwj that depend on the scale 2j. For R¯≤1 bit/pixel, wj = 2−j is appropriate for the three finest scales. The distortion in (10.34) shows that choosing such weights is equivalent to minimizing a weighted mean-square error.
Such a weighted quantization is implemented like in (10.35) by quantizing weighted wavelet coefficients fB[m]/wj with a uniform quantizer. The weights are inverted during the decoding process. JPEG-2000 supports a general weighting scheme that codes weighted coefficients w[m]fB[m] where w[m] can be designed to emphasize some region of interest Ω ⊂ [0, 1]2 in the image. The weights are set to w[m] = w > 1 for the wavelet coefficients fB[m]=〈f,ψj,p,q1〉 where the support of ψj,p,q1 intersects Ω. As a result, the wavelet coefficients inside Ω are given a higher priority during the coding stage, and the region Ω is coded first within the compressed stream. This provides a mechanism to more precisely code regions of interest in images—for example, a face in a crowd.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780123743701000148
Signal and Image Representation in Combined Spaces
Zoran. Cvetković, Martin. Vetterli, in Wavelet Analysis and Its Applications, 1998
6.1 Two lemmas on frames of complex exponentials
Estimates of bounds on the quantization error in Subsection 4.3 are derived from the next two lemmas [5].
Lemma 1
Letejλnωbe a frame in L2[− σ, σ]. If M is any constant and {μn} is a sequence satisfying |μn − λn| ≤ M, for all n, then there is a number C = C(M, σ, {λn}) such that
(6.1.1)∑n|fμn|2∑n|fλn|2≤C
for every cr-bandlimited signal f(x).
Lemma 2
Letejλnωbe a frame in L2[− σ, σ], with bounds 0 < A ≤ B < ∞ and δ a given positive number. If a sequence { μn } satisfies | λn − μn < δ for all n, then for every σ-bandlimited signal f(x)
(6.1.2)A1−C2||f||2≤∑n|fμn|2≤B(1+C)2||f||2,
where
(6.1.3)C=BAeγδ−12
Remark 1
If δ in the statement of Lemma 2 is chosen small enough, so that C is less then 1, then ejμnω is also a frame in L2[− σ, σ]. Moreover, there exists some δ 1/4 ({λn},σ), such that whenever δ < δ 1/4 ({λn }, σ), ejμnω is a frame with frame bounds A/A and 9B/4.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/S1874608X98800125
Live HDR Video Broadcast Production
I.G. Olaizola, … J. Gorostegui, in High Dynamic Range Video, 2017
1.4.1 Banding
Banding effects are directly related to quantization errors. As the dynamic range increases, the quantization effects become more noticeable and banding artifacts arise. To avoid this, smaller quantization steps must be taken, but this requires a higher bitdepth (from 8 to 10 or 12 in order to have backwards compatibility with existing infrastructures, and ideally 14 or 16 bits) and nonlinear transform functions based on the HVS that minimize the observable banding effects. Nowadays, this is partially solved by the electro-optical transfer function (EOTF) and opto-electronic transfer function (OETF) mapping curves that will be introduced in a further section.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B978012809477800008X
Самый простой способ квантовать сигнал — выбрать значение цифровой амплитуды, наиболее близкое к исходной аналоговой амплитуде. В этом примере показан исходный аналоговый сигнал (зеленый), квантованный сигнал (черные точки), сигнал реконструирован от квантованного сигнала (желтый) и разницы между исходным сигналом и восстановленным сигналом (красный). Разница между исходным сигналом и восстановленным сигналом является ошибкой квантования и, в этой простой схеме квантования, является детерминированной функцией входного сигнала.
Квантование, по математике и цифровая обработка сигналов, представляет собой процесс отображения входных значений из большого набора (часто непрерывного набора) в выходные значения в (счетном) меньшем наборе, часто с конечным количество элементов. Округление и усечение являются типичными примерами процессов квантования. Квантование в некоторой степени участвует почти во всей цифровой обработке сигналов, поскольку процесс представления сигнала в цифровой форме обычно включает округление. Квантование также составляет основу практически всех сжатие с потерями алгоритмы.
Разница между входным значением и его квантованным значением (например, ошибка округления ) упоминается как ошибка квантования. Устройство или алгоритмическая функция который выполняет квантование, называется квантователь. An аналого-цифровой преобразователь является примером квантователя.
Пример
В качестве примера, округление а настоящий номер 

,
где обозначение 
Существенным свойством квантователя является то, что он имеет счетный набор возможных выходных значений, который имеет меньше членов, чем набор возможных входных значений. Члены набора выходных значений могут иметь целые, рациональные или действительные значения. Для простого округления до ближайшего целого числа размер шага 


Когда размер шага квантования (Δ) невелик по сравнению с изменением квантованного сигнала, относительно просто показать, что среднеквадратичная ошибка произведенное такой операцией округления будет приблизительно 
Поскольку набор возможных выходных значений квантователя является счетным, любой квантователь можно разложить на два отдельных этапа, которые можно назвать классификация этап (или прямое квантование этап) и реконструкция этап (или обратное квантование stage), где на этапе классификации входное значение преобразуется в целое число индекс квантования 


,
и этап восстановления для этого примера квантователя просто
.
Это разложение полезно для разработки и анализа поведения квантования, и оно показывает, как квантованные данные могут быть переданы по каналу связи — кодировщик источника может выполнять этап прямого квантования и отправлять индексную информацию по каналу связи, а декодер может выполнять этап реконструкции для получения выходного приближения исходных входных данных. В общем, на этапе прямого квантования может использоваться любая функция, которая отображает входные данные в целочисленное пространство данных индекса квантования, а этап обратного квантования может концептуально (или буквально) быть операцией просмотра таблицы для отображения каждого индекса квантования на соответствующее значение реконструкции. Это двухэтапное разложение одинаково хорошо применимо к вектор а также скалярные квантователи.
Математические свойства
Поскольку квантование — это отображение «многие-к-немногим», оно по своей сути нелинейный и необратимый процесс (то есть, поскольку одно и то же выходное значение используется несколькими входными значениями, в общем случае невозможно восстановить точное входное значение, если задано только выходное значение).
Набор возможных входных значений может быть бесконечно большим и, возможно, непрерывным и, следовательно, бесчисленный (например, набор всех действительные числа, или все действительные числа в некотором ограниченном диапазоне). Набор возможных выходных значений может быть конечный или же счетно бесконечный.[6] Наборы входов и выходов, участвующие в квантовании, можно определить довольно общим образом. Например, векторное квантование представляет собой приложение квантования к многомерным (векторным) входным данным.[7]
Типы
2-битное разрешение с четырьмя уровнями квантования по сравнению с аналоговым.[8]
3-битное разрешение с восемью уровнями.
Аналого-цифровой преобразователь
An аналого-цифровой преобразователь (ADC) можно смоделировать как два процесса: отбор проб и квантование. Выборка преобразует изменяющийся во времени сигнал напряжения в сигнал с дискретным временем, последовательность действительные числа. Квантование заменяет каждое действительное число приближением из конечного набора дискретных значений. Чаще всего эти дискретные значения представлены в виде слов с фиксированной точкой. Хотя возможно любое количество уровней квантования, общая длина слова 8 бит (256 уровней), 16 бит (65 536 уровней) и 24 бит (16,8 млн уровней). Квантование последовательности чисел дает последовательность ошибок квантования, которая иногда моделируется как аддитивный случайный сигнал, называемый шум квантования из-за его стохастический поведение. Чем больше уровней использует квантователь, тем ниже его мощность шума квантования.
Оптимизация скорости и искажений
Оптимизированный коэффициент искажения квантование встречается в исходное кодирование для алгоритмов сжатия данных с потерями, целью которых является управление искажением в пределах скорости передачи данных, поддерживаемой каналом связи или носителем данных. Анализ квантования в этом контексте включает изучение количества данных (обычно измеряемых цифрами, битами или битами). ставка), который используется для представления выходных данных квантователя, и изучения потери точности, вызванной процессом квантования (который называется искажение).
Унифицированные квантователи со средней подступенкой и средней ступенью
Большинство однородных квантователей для входных данных со знаком можно разделить на два типа: средний человек и середина протектора. Терминология основана на том, что происходит в области вокруг значения 0, и использует аналогию с просмотром функции ввода-вывода квантователя как лестница. Квантователи среднего протектора имеют нулевой уровень реконструкции (соответствующий ступать лестницы), в то время как квантователи средней ступени имеют нулевой порог классификации (соответствующий стояк лестницы).[9]
Квантование середины протектора предполагает округление. Формулы для равномерного квантования средней протектора приведены в предыдущем разделе.
Квантование среднего уровня включает усечение. Формула ввода-вывода для равномерного квантователя среднего уровня определяется следующим образом:
,
где правило классификации дается
и правило реконструкции
.
Обратите внимание, что унифицированные квантователи среднего уровня не имеют нулевого выходного значения — их минимальная выходная величина составляет половину размера шага. В отличие от этого, квантователи со средним протектором имеют нулевой выходной уровень. Для некоторых приложений может потребоваться представление нулевого выходного сигнала.
В общем, квантователь со средним подступенком или средним протектором на самом деле не может быть униформа квантователь — то есть размер интервалов классификации квантователя может не быть одинаковым, или интервалы между его возможными выходными значениями могут не быть одинаковыми. Отличительной особенностью квантователя среднего уровня является то, что он имеет значение порога классификации, которое точно равно нулю, а отличительная характеристика квантователя среднего уровня состоит в том, что он имеет значение восстановления, которое точно равно нулю.[9]
Квантователи мертвой зоны
А квантователь мертвой зоны — это тип квантователя среднего уровня с симметричным поведением около 0. Область вокруг нулевого выходного значения такого квантователя называется мертвая зона или же зона нечувствительности. Мертвая зона иногда может служить той же цели, что и шумовые ворота или же хлюпать функция. В частности, для компрессионных приложений ширина мертвой зоны может отличаться от ширины других ступеней. Для однородного квантователя ширина мертвой зоны может быть установлена на любое значение. 
,
где функция 
,
куда 







Очень часто используемый частный случай (например, схема, обычно используемая в финансовом учете и элементарной математике) — это установка 


Характеристики шума и ошибок
Модель аддитивного шума
Распространенное допущение для анализа ошибка квантования в том, что он влияет на систему обработки сигналов аналогично аддитивному белый шум — имеющая пренебрежимо малую корреляцию с сигналом и приблизительно ровную спектральная плотность мощности.[2][6][13][14] Модель аддитивного шума обычно используется для анализа эффектов ошибок квантования в системах цифровой фильтрации и может быть очень полезна в таком анализе. Было показано, что это действительная модель в случаях квантования с высоким разрешением (малые 
Аддитивное шумовое поведение не всегда является верным предположением. Ошибка квантования (для квантователей, определенных как описано здесь) детерминированно связана с сигналом и не полностью от него независима. Таким образом, периодические сигналы могут создавать периодический шум квантования. А в некоторых случаях это может даже вызвать предельные циклы появиться в системах цифровой обработки сигналов. Один из способов гарантировать эффективную независимость ошибки квантования от исходного сигнала — выполнить смущенный квантование (иногда с формирование шума ), который включает добавление случайных (или псевдослучайный ) шум к сигналу до квантования.[6][14]
Модели ошибок квантования
В типичном случае исходный сигнал намного больше одного младший бит (МЗБ). В этом случае ошибка квантования существенно не коррелирует с сигналом и имеет приблизительно равномерное распределение. Когда округление используется для квантования, ошибка квантования имеет иметь в виду нуля и среднеквадратичное значение (RMS) значение — это стандартное отклонение этого распределения, задаваемого 



При более низких амплитудах ошибка квантования становится зависимой от входного сигнала, что приводит к искажению. Это искажение создается после сглаживания фильтра, и, если эти искажения превышают 1/2 частоты дискретизации, они возвращаются в интересующую полосу. Чтобы ошибка квантования не зависела от входного сигнала, сигнал смущенный путем добавления шума к сигналу. Это немного снижает отношение сигнал / шум, но может полностью устранить искажения.
Модель шума квантования
Шум квантования для 2-битного АЦП, работающего на бесконечности частота дискретизации. Разница между синим и красным сигналами на верхнем графике — это ошибка квантования, которая «добавляется» к квантованному сигналу и является источником шума.
Сравнение квантования синусоиды на 64 уровня (6 бит) и 256 уровней (8 бит). Аддитивный шум, создаваемый 6-битным квантованием, на 12 дБ больше, чем шум, создаваемый 8-битным квантованием. Когда спектральное распределение ровное, как в этом примере, разница в 12 дБ проявляется как измеримая разница в минимальном уровне шума.
Шум квантования — это модель ошибки квантования, вызванной квантованием в аналого-цифровое преобразование (АЦП). Это ошибка округления между аналоговым входным напряжением АЦП и выходным цифровым значением. Шум нелинейный и зависит от сигнала. Его можно смоделировать несколькими способами.
В идеальном аналого-цифровом преобразователе, где ошибка квантования равномерно распределена между -1/2 LSB и +1/2 LSB, а сигнал имеет равномерное распределение, охватывающее все уровни квантования, Отношение сигнал / шум квантования (SQNR) можно рассчитать из
где Q — количество битов квантования.
Наиболее распространенные тестовые сигналы, которые соответствуют этому, — это полная амплитуда треугольные волны и пилообразные волны.
Например, 16 бит Максимальное отношение сигнал / шум квантования АЦП составляет 6,02 × 16 = 96,3 дБ.
Когда входной сигнал имеет полную амплитуду синусоидальная волна распределение сигнала больше не является равномерным, и вместо этого соответствующее уравнение
Здесь шум квантования снова предполагается быть равномерно распределенным. Это так, когда входной сигнал имеет высокую амплитуду и широкий частотный спектр.[16] В этом случае 16-битный АЦП имеет максимальное отношение сигнал / шум 98,09 дБ. Разница в соотношении сигнал-шум 1,761 возникает только из-за того, что сигнал представляет собой полномасштабную синусоидальную волну, а не треугольник или пилообразную форму.
Для сложных сигналов в АЦП с высоким разрешением это точная модель. Для АЦП с низким разрешением, сигналов низкого уровня в АЦП с высоким разрешением и для простых сигналов шум квантования распределяется неравномерно, что делает эту модель неточной.[17] В этих случаях на распределение шума квантования сильно влияет точная амплитуда сигнала.
Вычисления относятся к исходной величине. Для сигналов меньшего размера относительное искажение квантования может быть очень большим. Чтобы обойти эту проблему, аналог компандирование можно использовать, но это может привести к искажению.
Дизайн
Гранулярное искажение и искажение при перегрузке
Часто конструкция квантователя включает поддержку только ограниченного диапазона возможных выходных значений и выполнение отсечения для ограничения выхода этим диапазоном всякий раз, когда входной сигнал превышает поддерживаемый диапазон. Ошибка, вызванная этим отсечением, называется перегрузка искажение. В крайних пределах поддерживаемого диапазона величина интервала между выбираемыми выходными значениями квантователя называется его детализация, и ошибка, вызванная этим интервалом, называется гранулированный искажение. При разработке квантователя обычно используется определение надлежащего баланса между зернистым искажением и искажением из-за перегрузки. Для заданного поддерживаемого числа возможных выходных значений уменьшение среднего гранулярного искажения может включать увеличение среднего искажения от перегрузки, и наоборот. Методика управления амплитудой сигнала (или, что то же самое, размером шага квантования 
Конструкция квантователя скорости-искажения
Скалярный квантователь, который выполняет операцию квантования, обычно можно разделить на два этапа:
- Классификация
- Процесс, который классифицирует диапазон входного сигнала на
неперекрывающийся интервалы
, определяя
граница решения значения
, так что
за
, с крайними пределами, определяемыми
и
. Все входы
попадают в заданный интервал
связаны с одним и тем же индексом квантования
.
- Реконструкция
- Каждый интервал
представлен стоимость реконструкции
который реализует отображение
.
Эти два этапа вместе составляют математическую операцию 
Энтропийное кодирование методы могут применяться для передачи индексов квантования от исходного кодера, который выполняет этап классификации, в декодер, который выполняет этап восстановления. Один из способов сделать это — связать каждый индекс квантования 








Предполагая, что источник информации 




.
Результирующий битрейт 
.
Если предположить, что искажение измеряется среднеквадратичная ошибка,[а] искажение D, дан кем-то:
.
Ключевое наблюдение заключается в том, что скорость 





После определения этих двух показателей производительности для квантователя, типичная формулировка «скорость – искажение» для задачи разработки квантователя может быть выражена одним из двух способов:
- Учитывая ограничение максимального искажения
, минимизировать битрейт
- Учитывая ограничение максимальной скорости передачи данных
, минимизировать искажение
Часто решение этих проблем может быть эквивалентно (или приблизительно) выражено и решено путем преобразования формулировки к неограниченной проблеме 

Обратите внимание, что значения реконструкции 


куда
Это наблюдение можно использовать для облегчения анализа — учитывая набор 


Для критерия искажения среднеквадратичной ошибки легко показать, что оптимальный набор значений восстановления 


.
Использование достаточно хорошо продуманных методов энтропийного кодирования может привести к использованию скорости передачи данных, близкой к истинному информационному содержанию индексов. 
и поэтому
.
Использование этого приближения может позволить отделить проблему проектирования энтропийного кодирования от конструкции самого квантователя. Современные методы энтропийного кодирования, такие как арифметическое кодирование может достигать скорости передачи данных, которая очень близка к истинной энтропии источника, учитывая набор известных (или адаптивно оцененных) вероятностей 
В некоторых проектах вместо оптимизации для определенного количества областей классификации 


Пренебрежение ограничением энтропии: квантование Ллойда – Макса
В приведенной выше формулировке, если пренебречь ограничением скорости передачи данных путем установки 

Индексы, производимые 



Предполагая, что FLC с 





.
Нахождение оптимального решения вышеуказанной проблемы приводит к квантователю, который иногда называют решением MMSQE (минимальная среднеквадратическая ошибка квантования), а полученный в результате оптимизированный для pdf (неоднородный) квантователь называется Ллойд – Макс квантователь, названный в честь двух людей, которые независимо разработали итерационные методы[6][21][22] для решения двух систем одновременных уравнений в результате 

,
который помещает каждый порог в середину между каждой парой значений реконструкции, и
который помещает каждое значение реконструкции в центроид (условное ожидаемое значение) соответствующего интервала классификации.
Алгоритм метода Ллойда I, первоначально описанный в 1957 году, может быть просто обобщен для применения в вектор данные. Это обобщение приводит к Линде – Бузо – Грей (LBG) или же k-означает методы оптимизации классификатора. Кроме того, метод может быть дополнительно обобщен прямым способом, чтобы также включить ограничение энтропии для векторных данных.[23]
Равномерное квантование и приближение 6 дБ / бит
Квантователь Ллойда – Макса на самом деле является равномерным квантователем, когда входной PDF-файл равномерно распределен по диапазону 
Симметричный источник X можно смоделировать с помощью 
![{ Displaystyle х в [-X _ { max}, X _ { max}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3cf4bd582eef8f8d55332145bed84a97829c283d)

.
Для кода фиксированной длины с использованием 


или примерно 6 дБ на бит. Например, для 



Однако обычно предполагается, что для многих источников наклон функции SQNR квантователя может быть аппроксимирован как 6 дБ / бит при работе с достаточно высокой скоростью передачи данных. При асимптотически высоких скоростях передачи данных уменьшение размера шага вдвое увеличивает скорость передачи данных примерно на 1 бит на выборку (поскольку 1 бит необходим, чтобы указать, находится ли значение в левой или правой половине предыдущего интервала двойного размера) и уменьшает среднеквадратичная ошибка в 4 раза (т. е. 6 дБ) на основе 
При асимптотически высоких скоростях передачи данных приближение 6 дБ / бит для многих исходных файлов PDF поддерживается строгим теоретическим анализом.[2][3][5][6] Более того, структура оптимального скалярного квантователя (в смысле «скорость – искажение») приближается к структуре равномерного квантователя в этих условиях.[5][6]
В других сферах
Многие физические величины фактически квантуются физическими объектами. Примеры полей, в которых применяется это ограничение, включают электроника (из-за электроны ), оптика (из-за фотоны ), биология (из-за ДНК ), физика (из-за Пределы Планка ) и химия (из-за молекулы ).
Смотрите также
- Аналого-цифровой преобразователь
- Бета-кодировщик
- Цветовое квантование
- Биннинг данных
- Дискретность
- Ошибка дискретизации
- Квантование (обработка изображений)
- Постеризация
- Импульсно-кодовая модуляция
- Квантиль
- Разбавление регрессии — смещение в оценках параметров, вызванное такими ошибками, как квантование в объясняющей или независимой переменной
Примечания
- ^ Можно также рассмотреть другие меры искажения, хотя среднеквадратичная ошибка является популярной.
Рекомендации
- ^ Уильям Флитвуд Шеппард, «О вычислении наиболее вероятных значений частотных постоянных для данных, упорядоченных по равноудаленным делениям шкалы», Труды Лондонского математического общества, Vol. 29, стр. 353–80, 1898.Дои:10.1112 / плмс / с1-29.1.353
- ^ а б c d В. Р. Беннетт «Спектры квантованных сигналов «, Технический журнал Bell System, Vol. 27, стр. 446–472, июль 1948 г.
- ^ а б Б. М. Оливер, Дж. Р. Пирс и Клод Э. Шеннон, «Философия ПКМ», Труды IRE, Vol. 36, стр. 1324–1331, ноябрь 1948 г. Дои:10.1109 / JRPROC.1948.231941
- ^ Сеймур Штайн и Джей Джей Джонс, Принципы современной коммуникации, Макгроу – Хилл, ISBN 978-0-07-061003-3, 1967 (с. 196).
- ^ а б c Герберт Гиш и Джон Н. Пирс, «Асимптотически эффективное квантование», IEEE Transactions по теории информации, Vol. ИТ-14, № 5, с. 676–683, сентябрь 1968 г. Дои:10.1109 / TIT.1968.1054193
- ^ а б c d е ж грамм час я Роберт М. Грей и Дэвид Л. Нойхофф, «Квантование», IEEE Transactions по теории информации, Vol. ИТ-44, № 6, стр. 2325–2383, октябрь 1998 г. Дои:10.1109/18.720541
- ^ Аллен Гершо; Роберт М. Грей (1991). Векторное квантование и сжатие сигналов. Springer. ISBN 978-0-7923-9181-4.
- ^ Ходжсон, Джей (2010). Понимание записей, стр.56. ISBN 978-1-4411-5607-5. По материалам Franz, David (2004). Запись и продюсирование в домашней студии, стр.38-9. Berklee Press.
- ^ а б Аллен Гершо, «Квантование», Журнал IEEE Communications Society, стр. 16–28, сентябрь 1977 г. Дои:10.1109 / MCOM.1977.1089500
- ^ Раббани, Маджид; Джоши, Раджан Л .; Джонс, Пол В. (2009). «Раздел 1.2.3: Квантование в главе 1: Базовая система кодирования JPEG 2000 (Часть 1)». В Шелкенах, Питер; Скодрас, Афанасий; Эбрахими, Турадж (ред.). Пакет JPEG 2000. Джон Уайли и сыновья. стр.22 –24. ISBN 978-0-470-72147-6.
- ^ Таубман, Дэвид С .; Марселлин, Майкл В. (2002). «Глава 3: Квантование». JPEG2000: основы, стандарты и практика сжатия изображений. Kluwer Academic Publishers. п.107. ISBN 0-7923-7519-X.
- ^ а б c Гэри Дж. Салливан, «Эффективное скалярное квантование экспоненциальных и лапласовских случайных величин», IEEE Transactions по теории информации, Vol. ИТ-42, № 5, с. 1365–1374, сентябрь 1996 г. Дои:10.1109/18.532878
- ^ Бернард Видроу, «Исследование грубого квантования амплитуды с помощью теории дискретизации Найквиста», IRE Trans. Теория схем, Vol. СТ-3, стр. 266–276, 1956. Дои:10.1109 / TCT.1956.1086334
- ^ а б Бернард Видроу, «Статистический анализ систем амплитудно-квантованных выборочных данных «, Пер. AIEE Pt. II: Прил. Ind., Vol. 79, стр. 555–568, январь 1961.
- ^ Даниэль Марко и Дэвид Л. Нойхофф, «Достоверность модели аддитивного шума для однородных скалярных квантователей», IEEE Transactions по теории информации, Vol. ИТ-51, № 5, с. 1739–1755, май 2005 г. Дои:10.1109 / TIT.2005.846397
- ^ Полман, Кен С. (1989). Принципы цифрового аудио 2-е издание. САМС. п. 60. ISBN 9780071441568.
- ^ Уоткинсон, Джон (2001). Искусство цифрового аудио, третье издание. Focal Press. ISBN 0-240-51587-0.
- ^ Нариман Фарвардин и Джеймс В. Модестино, «Оптимальная производительность квантователя для класса негауссовских источников памяти», IEEE Transactions по теории информации, Vol. IT-30, № 3, стр. 485–497, май 1982 г. (Раздел VI.C и Приложение B). Дои:10.1109 / TIT.1984.1056920
- ^ Тоби Бергер, «Оптимальные квантователи и коды перестановок», IEEE Transactions по теории информации, Vol. ИТ-18, № 6, с. 759–765, ноябрь 1972 г. Дои:10.1109 / TIT.1972.1054906
- ^ Тоби Бергер, «Квантователи минимальной энтропии и коды перестановок», IEEE Transactions по теории информации, Vol. ИТ-28, № 2, с. 149–157, март 1982 г. Дои:10.1109 / TIT.1982.1056456
- ^ Стюарт П. Ллойд, «Квантование методом наименьших квадратов в PCM», IEEE Transactions по теории информации, Vol. ИТ-28, с. 129–137, № 2, март 1982 г. Дои:10.1109 / TIT.1982.1056489 (работа задокументирована в рукописи, распространенной для комментариев по адресу Bell Laboratories с датой журнала отдела от 31 июля 1957 г., а также представленной на собрании 1957 г. Институт математической статистики, хотя официально не публиковались до 1982 г.).
- ^ Джоэл Макс, «Квантование для минимального искажения», Сделки IRE по теории информации, Vol. ИТ-6, стр. 7–12, март 1960 г. Дои:10.1109 / TIT.1960.1057548
- ^ Филип А. Чоу, Том Лукабо и Роберт М. Грей, «Векторное квантование с ограничениями по энтропии», Транзакции IEEE по акустике, речи и обработке сигналов, Vol. АССП-37, № 1, январь 1989 г. Дои:10.1109/29.17498
- Сайуд, Халид (2005), Введение в сжатие данных, третье издание, Морган Кауфманн, ISBN 978-0-12-620862-7
- Джаянт, Никил С .; Нолл, Питер (1984), Цифровое кодирование сигналов: принципы и приложения к речи и видео, Прентис – Холл, ISBN 978-0-13-211913-9
- Грегг, В. Дэвид (1977), Аналоговая и цифровая связь, Джон Вили, ISBN 978-0-471-32661-8
- Штейн, Сеймур; Джонс, Дж. Джей (1967), Принципы современной коммуникации, Макгроу – Хилл, ISBN 978-0-07-061003-3
внешняя ссылка
- Шум квантования в цифровых вычислениях, обработке сигналов и управлении, Бернард Видроу и Иштван Коллар, 2007.
- Связь динамического диапазона с размером слова данных при обработке цифрового звука
- Дисперсия ошибки округления — вывод мощности шума
для ошибки округления
- Динамическая оценка высокоскоростных цифро-аналоговых преобразователей высокого разрешения Обрисовывает в общих чертах измерения HD, IMD и NPR, также включает вывод шума квантования
- Сигнал к шуму квантования в квантованной синусоидальной


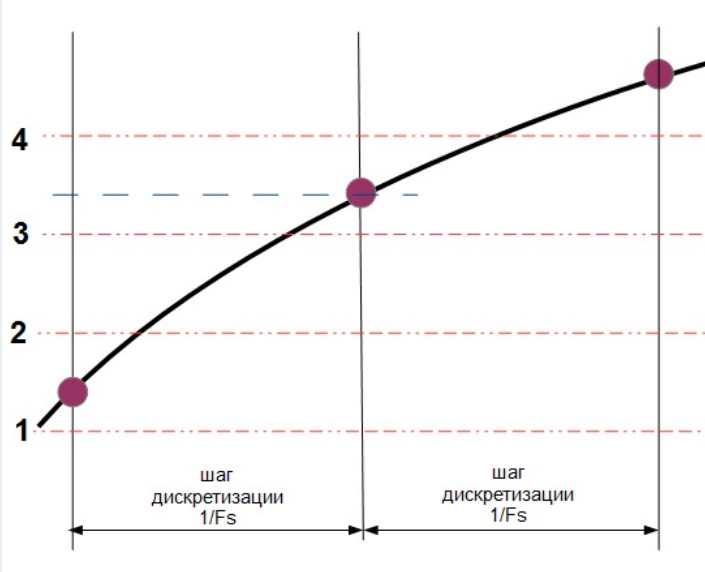


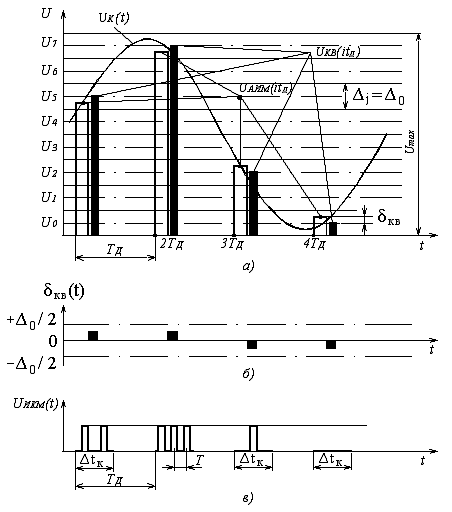
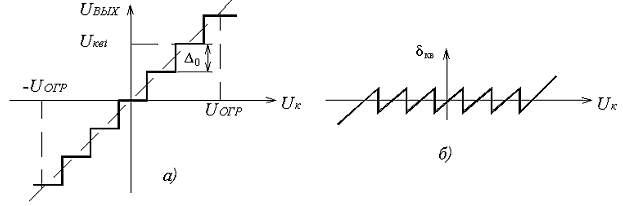
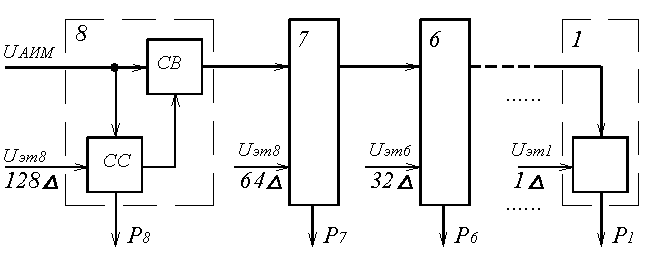
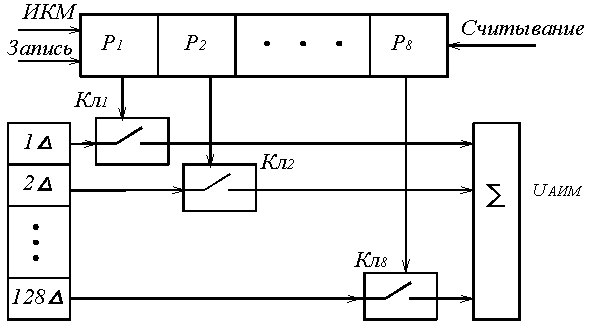
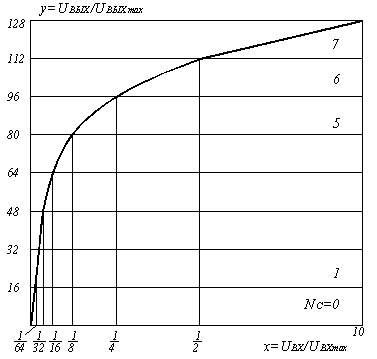
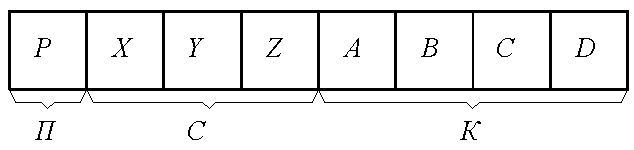
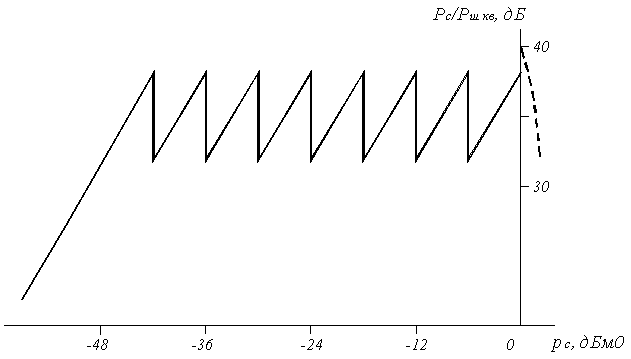
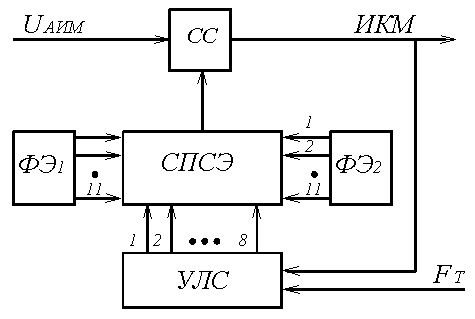
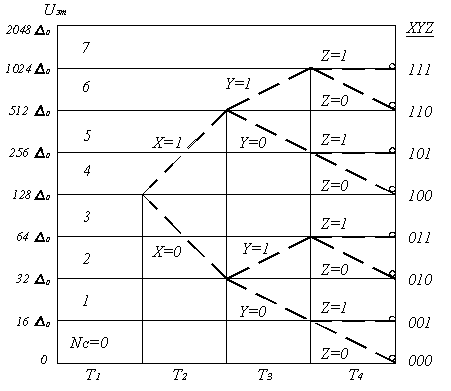
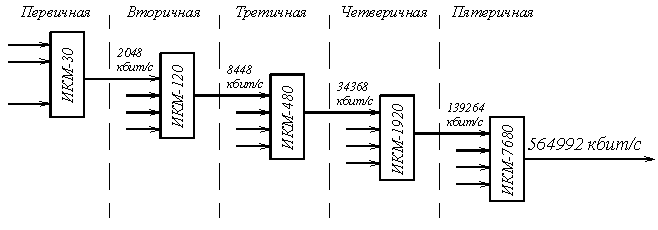
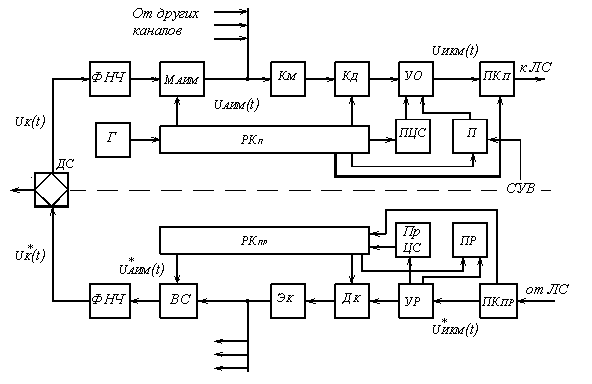

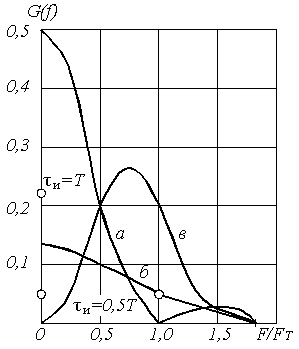
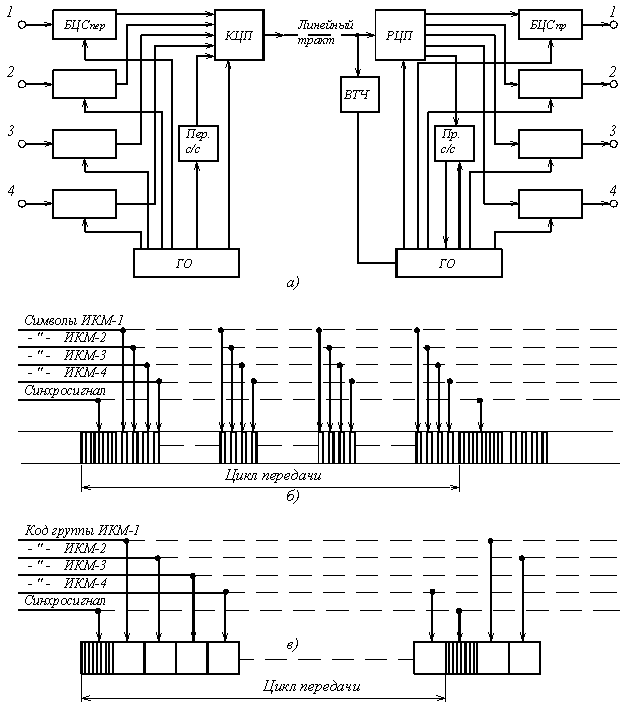
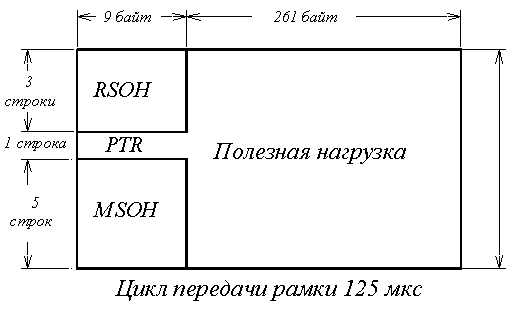
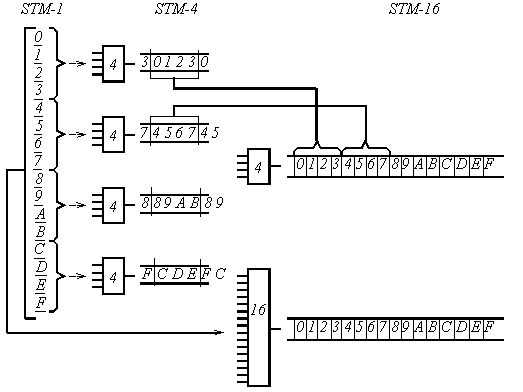
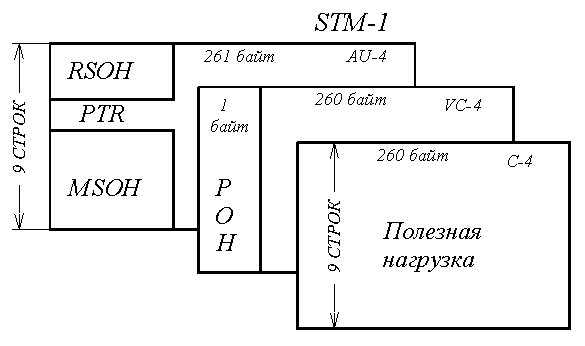
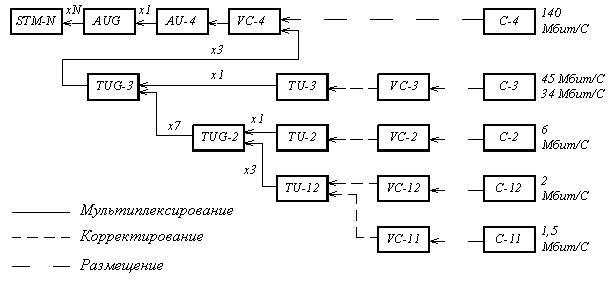

























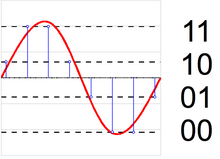
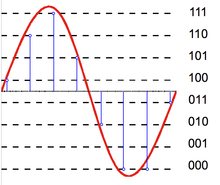





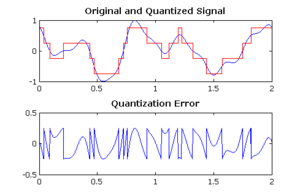
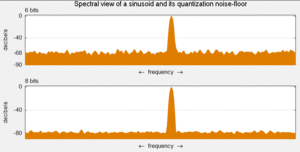









![p_ {k} = P [x in I_ {k}] = int _ {b_ {k-1}} ^ {b_ {k}} f (x) dx](https://wikimedia.org/api/rest_v1/media/math/render/svg/26424325c60e39665f71cb6c4881bb490b08e841)

![D = E [(xQ (x)) ^ {2}] = int _ {- infty} ^ { infty} (xQ (x)) ^ {2} f (x) dx = sum _ {k = 1} ^ {M} int _ {b_ {k-1}} ^ {b_ {k}} (x-y_ {k}) ^ {2} f (x) dx](https://wikimedia.org/api/rest_v1/media/math/render/svg/2292fcf1093dc30c77e2f85e4ad930c2b695ec54)







![D = E [(xQ (x)) ^ {2}] = int _ {- infty} ^ { infty} (xQ (x)) ^ {2} f (x) dx = sum _ {k = 1} ^ {M} int _ {b_ {k-1}} ^ {b_ {k}} (x-y_ {k}) ^ {2} f (x) dx = sum _ {k = 1 } ^ {M} d_ {k}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a11a15b3c5710c31187e8dfd713f12ca0981a65)


