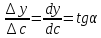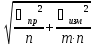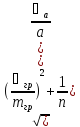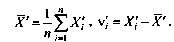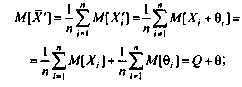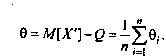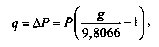1) Кислотно-основного титриметрического определения уксусной кислоты в уксусной эссенции;
2) Гравиметрического определения хроматов в электролите для хромирования.
Абсолютная погрешность аналитических
весов 0,1мг
Абсолютная погрешность (ошибка)
∆x=xi—xист.
Xi-измеренное
значениеXист-истинное
значение ( если истинное значение не
известно – берется среднее)
Абсолютная погрешность не может ясно
охарактеризовать точность измерения,
так как она не связана с измеренным
значением.
Относительная погрешность (ошибка)
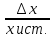
Систематические погрешности (ошибки)– возникают при действии постоянных
причин, их можно выявить устранить или
учесть изменяются по постоянно
действующему закону .
-
Инструментальные погрешности–связанные с инструментами для измерения
аналитического сигнала (весы, посуда)
уменьшить можно периодической проверкой
аналитических приборов. Обычно составляют
небольшую долю . -
Методические ошибки–
обусловлены методом анализа (например
погрешности пробоотбора и пробоподготовки.)
вносят основной вклад в общую погрешность. -
Реактивные– связаны с чистотой
используемых реактивов. -
Оперативные ошибки –зависят
от правильности и точности выполнения
аналитических операций (например,
недостаточное или излишнее промывание
или прокаливания осадков, недостаточное
тщательное перемещение осадка из одной
посуды в другую, неправильный способ
выливания раствора из пипетки и т.д.) -
Индивидуальные ошибки(личные) – это результат некоторых
физических недостатков экспериментатора,
которые мешают ему правильно проводить
известные операции.
Способы выявления систематических
погрешностей
1)варьирование величин пробы
Увеличив размер в кратное число раз
можно обнаружить по изменению найденного
содержания постоянную систематическую
погрешность
2)способ «введено найдено»
Добавить точно известное количество
компонента в той же форме, в которой
находится аналитический объект. Введенная
добавка проводится через все стадии
анализа. Если на конечной стадии
определяется добавка с точностью, то
систематической ошибки нет.
3) сравнение результата анализа с
результатом, полученным другим независимым
методом
4)анализ стандартного образца
Проведение всех стадий анализа, на
стадии обработки сравнивается с
паспортом, если все совпадает , то
систематической ошибки нет.
Типы погрешностей
-
Погрешности известной природы, могут
быть рассчитаны и учтены введение
соответствующей поправки -
Погрешности известной природы, значение
которых может быть оценены в ходе
химического анализа
Релятивизация — способ устранения
систематической погрешности, когда в
идентичных условиях проводят отдельные
аналитические операции таким образом,
что происходит нивелирование
систематической ошибки
-
Погрешность невыясненной природы,
значение который неизвестно, их сложно
выявить и устранить , используют прием
рандомизации
Рандомизация – переведение систематической
ошибки в разряд случайной
Случайные ошибки– обрабатываются
по правилам матемтической статистики,
связаны с влиянием неконтролируемых
параметров, непредвиденны и неучтимы.
Промахи– грубые ошибки, сильно
искажающие результаты анализа (ошибки
при расчётах, неправильный отчёт по
шкале, проливание раствора или просыпание
осадка). Результат с промахом отбрасывается
при выводе среднего значения.
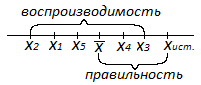
6. Случайные
ошибки. Метрологические характеристики,
отражающие случайные ошибки. Оценка и
критерии воспроизводимости и правильности.
Рассмотрите на примере титриметрического
комплексонометрического определения
меди (II).
Случайные ошибки–отражают
неопределенность результата , присущую
любому измерению, обрабатываются по
правилам матемтической статистики,
связаны с влиянием неконтролируемых
параметров, непредвиденны и неучтимы.
Причины таких погрешностей:
Изменение температуры во время измерения,
ослабление внимания при работе, случайные
потери, загрязнение, использование
разной посуды, весов и тд.
метрологические характеристики:
Правильность— характеризует степень
близости измеренного результата
некоторой величины к её истинному
значению
Воспроизводимость— характеризует
степень близости друг к другу единичный
определений (рассеяние единичных
результатов относительно среднего
значения
Точность— собирательная характеристика
метода или методики , включающая их
правильность и воспроизводимость .
Чувствительность— величина,
определяемая минимальным количеством
вещества, которое можно обнаружить
данным методом
Чувствительность – собирательное
понятие , включающее три характеристики:
1)Коэффициент чувствительности
коэффициент чувствительности sхарактеризует отклик аналитического
сигналаyна содержание
компонентаc,s-
это значение первой производной
градуировочной функции при определенном
содержании компонента, для прямолинейных
градуировочных графиковs– это тангенс угла наклона прямойy=Sc+b
s=
чем больше s, тем меньшие
количества компонента можно обнаружить
, используя один и тот же аналитический
сигнал, чем большеs, тем
точнее можно определить одно и то же
количество вещества
2)предел обнаружения Сminнаименьшее содержание при котором по
данной методике можно обнаружить
присутствие компонента с заданной
доверительной вероятностью, относится
к области качественного анализа и
определяет минимальное содержание
компонента
3)нижняя граница определяемого содержания
Сн
В количественном анализе обычно приводят
интервал определяемых содержаний-
область значений определяемых содержаний,
предусмотренная данной методикой и
ограниченная нижней и верхней границами.
Верхняя граница Свнаибольшее
значение количества или концентрации
компонента, определяемое по данной
методике.
нижняя граница Сн-наименьшее
содержание компонента , определяемое
по данной методике . З нижнюю границу
обычно принимают то минимальное
количество или концентрацию, которые
можно определить с относительным
стандартным отклонением Ϭr≤0,33
Оценка и критерии воспроизводимости
1)Среднее арифметическое

2)Отклонение
di=xi—
3)Медиана— тот единичный результат
, относительно которого число результатов
с большими и меньшими значениями
одинаковое, если количество значений
нечетное, то медиана совпадает с
центральным результатом ранжированной
выборки , если количество значений
четное, то медиана есть среднее
арифметическое между двумя центральными
значениями ранжированной выборки
4)среднее отклонение-среднее
арифметическое единичных отклонений,
без учет знака

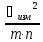
5)Дисперсия
Ϭ2илиs2
Ϭ2=
еслиn>10
Ϭ2=
еслиn≤10
6)стандартное отклонениеϬx=
7)Относительное стандартное отклонение
Ϭr=
Титриметрическое комплексонометрическое
определения меди (II).
Выполнение определениея
1)Титрование исследуемого раствора
стандартным раствором ЭДТА
2)расчет граммового содержания меди
Ход анализа:Титрование исследуемого
раствора стандартным раствором ЭДТА.
Анализируемый раствор помещают в мерную
колбу на 100 мл, довдят водой до метки,
тщательно перемешивают. В коническую
колбу дл титрования берут аликвоту,
добавляют индикатор мурексид на кончике
шпателя и титруют раствором ЭДТА сначала
до грязно-розового цвета, натем добавляют
несколько капель 10%-ного раствора аммиака
до появления изумрудной или желтой
окраски раствора и дотитровывают
раствором ЭДТА до перехода окраски в
фиолетовую.
Формула для расчета граммового содержания
меди:
mCu,г=C(

ЭДТА·Mэкв(Cu)·P·10-3
Формула для расчета процентного
содержания меди:
ωCu=
Возможные причины возникновения
случайных ошибокв комплексонометрическом
титровании меди возникают в процессе
измерения объемов: неточное доведение
до метки мерной колбы, использование
разных пипеток, потеря титранта (капнуло
мимо), использование непромытой посуды.
Так же могут возникать ошибки из-за
неточного определения перехода окраски
, но эти ошибки будут относиться к
категории систематических индивидуальных
ошибок.
7. Гравиметрическое
определение бария в минерале альстонит:
этапы определения, возможные формулы
осадителей, осаждаемой и гравиметрической
формы, механизм образования осадка,
возможные варианты загрязнения осадка,
приемы повышения чистоты осадка,
погрешности определения. Условия
аналитического выделения осадков бария.
Минерал альстонит минерал, безводный
двойной карбонат бария и кальция
BaCa(CO3)2
Этапы определения:
1)взятие навески и её растворение
2)расчет количества осадителя
3)приготовление раствора осадителя
4)осаждение
5)фильтрование и промывание
6)высушивание и прокаливание осадка
7)взвешивание осадка, расчёт содержания
бария
Для количественного определения бария
его осаждают в виде сульфата BaSO4
(осаждаемая форма)
BaCO3+H2SO4=
BaSO4+H2CO3
В качестве осадителя, посташика
сульфат-ионов используют серную кислоту
H2SO4(осадитель)
После прокаливания осадка его формула
не меняется и остается так же в виде
сульфата бария BaSO4
(гравиметрическая форма)
Механизм образования осадка:
В процессе образования осадка различают
три стадии :
1)образование зародышей кристаллов
2)рост кристаллов
3)объединение (агрегация) хаотично
ориентированных кристаллов
Насыщение=>пересыщение=>ПКИ>ПР=>
образование мельчайших зародышей
кристаллов
Осаждение происходит при определенной
степени пересыщения раствора
P=


пересыщение,Q-концентрация
кристаллизующегося вещества в растворе
Центром кристалла может служить твердая
частица этого вещества или любая другая
твердая частица, которую мы вносим в
раствор, твердые частицы могут изначально
присутствовать в растворе как примесь.
Если осаждение происходи из разбавленных
растворов, то появление осадка занимает
время-индукцинный период.
В процессе добавления каждой новой
порции осадителя происходит мгновенное
пересыщение раствора, зародыши растут
быстро за счет окружающих их ионов, как
только зародыш дотиг определенного
размера выпадает осадок
Рост кристаллов идет параллельно 1-ой
стадии, происходит за счет диффузии
ионов к поверхности растущего кристалла.
Число и размер частиц осадка (дисперсность
системы кол-во в единицы объёма) зависит
от соотношения скоростей 1-ой и 2-ой
стадий
V1— скорость образования
зародышейV2-скорость
роста кристаллов
V1>>V2-мелкодисперсный
осадокV1<<V2-крупнокристаллический
осадок
Лимитирующую стадию определяет скорость
осаждения и концентрации ионов
При медленном осаждении лимитирующей
стадией является кристаллизация ,
частица окружена однородным слоем
осаждаемый ионов в результате получается
кристалл правильной форм
При высокой концентрации ионов
лимитирующей стадией становится диффузия
, образуются кристаллы не правильной
формы с большой площадью поверхности
Следует отметить, что на скорость
процесса кристаллизации влияет

влияние
зародышей и на скорость роста кристаллов
В случае образования зародышей
V1=k·(
закон
В случае роста кристаллов V2=k·
При высокой степени

мелкодисперсные осадки, при уменьшении
образуются крупнокристаллические
осадки
Агрегация происходит в гетерогенной
системе, в значительной степени
определяется числом центров кристаллизации.
Чем больше центров кристаллизации , тем
в меньшей степени они укрупняются на
второй стадии , тем хуже структура и тем
выше дисперсность осадков.
К аналитическим свойствам осадка
относятся: растворимость, чистота,
фильтруемость.
Лучшими свойствами обладают
крупнокристаллические осадки.
Загрязнение осадков
В гарвиметрическом определении часто
возникают ошибки , вызванные переходом
осадка в раствор или веществ из раствора
в осадок-соосождение
Соосаждение происходит в процессе
образования осадка
Отрицательная роль : загрязнение осадка
Положительная роль :используется для
концентрирования микропримесей
Существует три типа соосаждения:
1)Адсорбция- соосаждение примесей на
поверхности уже сформированного осадка,
происходит в результате нескомпенсированности
зарядов внутри и на поверхности.
Характеризуется ярко выраженной
избирательность, преимущественно
адсорбируются те ионы, которые входят
в структуру осадка, противоионы-примеси
Адсорбция противоионов подчиняется
правилам Панета-Фаянса-Гана
А)при одинаковых концентрациях
адсорбируются многозарядные ионы
Б)при одинаковых зарядах адсорбируются
те, концентрация которых выше
В)при одинаковых концентрациях и
зарядах-те, которые образуют с ионами
решетки менее растворимое соединение
Г)в кислой среде соосаждение ионов
уменьшается в следствии конкурентной
адсорбции H3O+
Количество адсорбируемой примеси
зависит от величины поверхности осадка,
концентрации адсорбируемой примеси и
температуры ( с ↑ поверхности и ↑
концентрации- адсорбция ↑; с ↑ температуры
адсорбция ↓)
2)Окклюзия- загрязнение осадка в результате
захвата примеси внутрь растущего
кристалла, происходит в процессе
формирования осадка.
Различают 2-х видов: абсорбционная и
механическая
Механическа- случайный захват частиц
маточного раствора внутрь твердой фазы
вследствие нарушения механической
структуры
Характерна при выделении аморфных
осадков.
Окклюзированные примеси равномерно
распределены внутри, но не принимают
участие в построении решетки кристалла.
Адсорбционная-возникает при быстром
росте кристалла, когда ионы на поверхности
обратают кристаллизованным веществом.
Протекает вследствии адсорбции примесей
по микротрещинам кристаллической
структуры.
Окклюзия подчиняется тем же правилам,
что и адсорбция
Общие правила понижения окклюзии–замедление процесса выделения твердой
фазы-осаждение при малом пересыщении
, работают с разбавленными растворами
, осадитель добавляют по каплям, при
постоянном перемешивании.
3)изоморфное соосаждение характерно
для изоморфно кристаллизующегося
веществ, которые могут образовывать
смешанные кристаллы, примесь участвует
в построении кристаллической решетки,
наблюдается лишь в тех случаях, когда
вещества сходны по химическим свойствам
или ионы имеют одинаковые кч и радиус.
Совместное осаждение-выделение в твердую
фазу нескольких веществ, для которых в
услових осаждения достигнуты величины
их Kst
Последовательное осаждение- веделение
примеси на поверхности уже сформированного
осадка
Приемы и методы повышения чистоты
осадка
Зависят от типа соосаждения
1)адсорбционные примеси хорошо удаляются
промыванием осадка, более эффективно
многократное промывание малыми порциями
Выбор промывочной жидкости:
Не увеличивает растворимость осадка и
не ухудшает его фильтруемость, водой
промывают осадки с k~10-11/-12,
не подвергаемых пептизации, кристаллические
осадки с конст, растворимости 10-9/-11промывают разбавленным раствором
осадителя, аморфные осадки промывают
разбавленными растворами электролитов
коагуляторов, чтобы избежать пептизации
Промывние кристаллических осадков
проводят холодной промывочной жидкостью,
чтоб не увеличивать растворимость,
аморфные наоборот горячими
2)окклюзированные примеси , для избавления
от них:
Для кристаллических осадков-старение
Для аморфных-переосаждение
Погрешность гравиметрического
метода анализа
Общая погрешность анализа
Ϭ2=


пробоотбораm-число пробn-число параллельных
определений

измерений
Результат находится по формуле
P,%=
Методическая ошибка, обусловлена
неколичественным выпадением осадка,
её устранить нельзя
Qоб=
г/100мл воды,
фильтрата,
масса гравиметрической формы
Случайные ошибки
Относительное стандартное отклонение


массы гравиметрической формы

гравиметрической формы
Ϭa1-погрешность
взвешивания тары
Ϭa2-погрешность
взвешивания тары с навеской


г Ϭa1= Ϭa2=0,0002г
Суммарная ошибка
n-число проб
m-число измерений

прибора

измерения
8. Гравиметрическое
определение алюминия в каолине: этапы
определения, возможные формулы осадителей,
осаждаемой и гравиметрической формы,
механизм образования осадка, возможные
варианты загрязнения осадка, приемы
повышения чистоты осадка, погрешности
определения. Преимущества органических
осадителей. Условия аналитического
выделения осадков алюминия.
Механизм образования осадка:
В процессе образования осадка различают
три стадии :
1)образование зародышей кристаллов
2)рост кристаллов
3)объединение (агрегация) хаотично
ориентированных кристаллов
Насыщение=>пересыщение=>ПКИ>ПР=>
образование мельчайших зародышей
кристаллов
Осаждение происходит при определенной
степени пересыщения раствора
P=


пересыщение,Q-концентрация
кристаллизующегося вещества в растворе
Центром кристалла может служить твердая
частица этого вещества или любая другая
твердая частица, которую мы вносим в
раствор, твердые частицы могут изначально
присутствовать в растворе как примесь.
Если осаждение происходи из разбавленных
растворов, то появление осадка занимает
время-индукцинный период.
В процессе добавления каждой новой
порции осадителя происходит мгновенное
пересыщение раствора, зародыши растут
быстро за счет окружающих их ионов, как
только зародыш дотиг определенного
размера выпадает осадок
Рост кристаллов идет параллельно 1-ой
стадии, происходит за счет диффузии
ионов к поверхности растущего кристалла.
Число и размер частиц осадка (дисперсность
системы кол-во в единицы объёма) зависит
от соотношения скоростей 1-ой и 2-ой
стадий
V1— скорость образования
зародышейV2-скорость
роста кристаллов
V1>>V2-мелкодисперсный
осадокV1<<V2-крупнокристаллический
осадок
Лимитирующую стадию определяет скорость
осаждения и концентрации ионов
При медленном осаждении лимитирующей
стадией является кристаллизация ,
частица окружена однородным слоем
осаждаемый ионов в результате получается
кристалл правильной форм
При высокой концентрации ионов
лимитирующей стадией становится диффузия
, образуются кристаллы не правильной
формы с большой площадью поверхности
Следует отметить, что на скорость
процесса кристаллизации влияет

влияние
зародышей и на скорость роста кристаллов
В случае образования зародышей
V1=k·(
закон
В случае роста кристаллов V2=k·
При высокой степени

мелкодисперсные осадки, при уменьшении
образуются крупнокристаллические
осадки
Агрегация происходит в гетерогенной
системе, в значительной степени
определяется числом центров кристаллизации.
Чем больше центров кристаллизации , тем
в меньшей степени они укрупняются на
второй стадии , тем хуже структура и тем
выше дисперсность осадков.
К аналитическим свойствам осадка
относятся: растворимость, чистота,
фильтруемость.
Лучшими свойствами обладают
крупнокристаллические осадки.
Загрязнение осадков
В гарвиметрическом определении часто
возникают ошибки , вызванные переходом
осадка в раствор или веществ из раствора
в осадок-соосождение
Соосаждение происходит в процессе
образования осадка
Отрицательная роль : загрязнение осадка
Положительная роль :используется для
концентрирования микропримесей
Существует три типа соосаждения:
1)Адсорбция- соосаждение примесей на
поверхности уже сформированного осадка,
происходит в результате нескомпенсированности
зарядов внутри и на поверхности.
Характеризуется ярко выраженной
избирательность, преимущественно
адсорбируются те ионы, которые входят
в структуру осадка, противоионы-примеси
Адсорбция противоионов подчиняется
правилам Панета-Фаянса-Гана
А)при одинаковых концентрациях
адсорбируются многозарядные ионы
Б)при одинаковых зарядах адсорбируются
те, концентрация которых выше
В)при одинаковых концентрациях и
зарядах-те, которые образуют с ионами
решетки менее растворимое соединение
Г)в кислой среде соосаждение ионов
уменьшается в следствии конкурентной
адсорбции H3O+
Количество адсорбируемой примеси
зависит от величины поверхности осадка,
концентрации адсорбируемой примеси и
температуры ( с ↑ поверхности и ↑
концентрации- адсорбция ↑; с ↑ температуры
адсорбция ↓)
2)Окклюзия- загрязнение осадка в результате
захвата примеси внутрь растущего
кристалла, происходит в процессе
формирования осадка.
Различают 2-х видов: абсорбционная и
механическая
Механическа- случайный захват частиц
маточного раствора внутрь твердой фазы
вследствие нарушения механической
структуры
Характерна при выделении аморфных
осадков.
Окклюзированные примеси равномерно
распределены внутри, но не принимают
участие в построении решетки кристалла.
Адсорбционная-возникает при быстром
росте кристалла, когда ионы на поверхности
обратают кристаллизованным веществом.
Протекает вследствии адсорбции примесей
по микротрещинам кристаллической
структуры.
Окклюзия подчиняется тем же правилам,
что и адсорбция
Общие правила понижения окклюзии–замедление процесса выделения твердой
фазы-осаждение при малом пересыщении
, работают с разбавленными растворами
, осадитель добавляют по каплям, при
постоянном перемешивании.
3)изоморфное соосаждение характерно
для изоморфно кристаллизующегося
веществ, которые могут образовывать
смешанные кристаллы, примесь участвует
в построении кристаллической решетки,
наблюдается лишь в тех случаях, когда
вещества сходны по химическим свойствам
или ионы имеют одинаковые кч и радиус.
Совместное осаждение-выделение в твердую
фазу нескольких веществ, для которых в
услових осаждения достигнуты величины
их Kst
Последовательное осаждение- веделение
примеси на поверхности уже сформированного
осадка
Приемы и методы повышения чистоты
осадка
Зависят от типа соосаждения
1)адсорбционные примеси хорошо удаляются
промыванием осадка, более эффективно
многократное промывание малыми порциями
Выбор промывочной жидкости:
Не увеличивает растворимость осадка и
не ухудшает его фильтруемость, водой
промывают осадки с k~10-11/-12,
не подвергаемых пептизации, кристаллические
осадки с конст, растворимости 10-9/-11промывают разбавленным раствором
осадителя, аморфные осадки промывают
разбавленными растворами электролитов
коагуляторов, чтобы избежать пептизации
Промывние кристаллических осадков
проводят холодной промывочной жидкостью,
чтоб не увеличивать растворимость,
аморфные наоборот горячими
2)окклюзированные примеси , для избавления
от них:
Для кристаллических осадков-старение
Для аморфных-переосаждение
Погрешность гравиметрического
метода анализа
Общая погрешность анализа
Ϭ2=


пробоотбораm-число пробn-число параллельных
определений

измерений
Результат находится по формуле
P,%=
Методическая ошибка, обусловлена
неколичественным выпадением осадка,
её устранить нельзя
Qоб=
г/100мл воды,
фильтрата,
масса гравиметрической формы
Случайные ошибки
Относительное стандартное отклонение


массы гравиметрической формы

гравиметрической формы
Ϭa1-погрешность
взвешивания тары
Ϭa2-погрешность
взвешивания тары с навеской


г Ϭa1= Ϭa2=0,0002г
Суммарная ошибка

n-число проб
m-число измерений
прибора
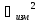
измерения
9. Гравиметрическое
определение железа в руде: этапы
определения, возможные формулы осадителя,
осаждаемой и гравиметрической формулы,
механизм образования коллоидной частицы,
процессы, приводящие к образованию
осадка, возможные варианты загрязнения
осадка, приемы повышения чистоты осадка,
погрешности. Условия аналитического
выделения осадков железа.
Гравиметрическое определение железа(III)
основано на его осаждении в виде
гидроксида железа(III)Fe(OH)3.
Трехвалентное железо осаждают раствором
аммиака, осаждаемой формой являетсяFe(OH)3.
Реакция:Fe(NO3)3+3NH3·H2O=Fe(OH)3+3NH4NO3.
При прокаливании гидроксид железа(III)
превращается в оксид железа(III),
который является гравиметрической
формой:Fe(OH)3=(t°)Fe2O3+3H2O.
Этапы определения:1) взятие навески
и ее растворение; 2) приготовление
раствора осадителя; 3) осаждение; 4)
фильтрование и промывание осадка; 5)
высушивание и прокаливание; 6) взвешивание
осадка, расчет содержания железа.
Расчет ведут по формулам
ωFe2O3=

ωFe
=
Механизм образования коллоидной
частицы:
Fe(NO3)3+3NH4OH(изб.)=Fe(OH)3↓+3NH4NO3
{[Fe(OH)3]m
· nOH—
·(n-x)NH4+}-x
·xNH4+
агрегат плотный слой
диффузный слой Мицелла
Ядро
Коллоидная частица
Вещество в коллоидной системе имеет
большую развитую поверхность и
нескомпенсированный заряд на границе
разлела фаз. Существование
нескомпенсированного силового поля
ведет к адсорбции из раствора молекул
или ионов. Если коллоидная система
возникла в результате проведения
химической реакции осаждения, то частицы
адсорбируют в первую очередь те ионы,
которые могут достраивать кристаллическую
решетку. Адсорбированные ионы сообщают
частице «+» или «-« заряд. Слой
адсорбированных ионов на ядре – это
первичный адсорбционный слой. Заряд,
созданный таким слоем, достаточно высок
и обуславливает электростатическое
взаимодействие с иоами противоположного
знака. В результате образуется слой
противоионов, который выравнивает заряд
первичного слоя. Слой противоионов
имеет диффузный характер. Часть
противоионов, прочно связанных с
первичным слоем – это плотный слой,
остальные противоионы составляют
диффузный слой.
Образование осадкапроисходит
тогда, когда раствор становится
пересыщенным, т.е. [A+]m[B-]n>Ks(ПКИ>ПР). Образование осадков связано
с процессом укрупнения частиц, с
образованием кристаллической решетки
вещества. Этот процесс определяется
числом центров кристаллизации: чем
больше центров, тем в меньшей степени
они укрупняются и тем хуже структура и
выше дисперсность осадка.
Возможные варианты загрязнения:
1)Путем адсорбции ( для конкретного
примера хлорид-ионов на поверхности
осадка); 2)Окклюзия; 3)Изоморфное
соосаждение; 4) Совместное осаждение;
5) Последующее осаждение.
Приемы повышения чистоты осадка:
1) Адсорбированные на поверхности примеси
хорошо удаляются при промывании осадков
на фильтре при помощи промывных жидкостей,
т.к. примеси переходят в промывную
жидкость и уходят через поры фильтра.
Эффективно многократное промывание
небольшими порциями промывной жидкости.
Промывную жидкость выбирают максимально
тщательно, чтобы не увеличивать
растворимость осадка и не ухудшать его
фильтрацию. Кристаллические осадки
промывают холодными промывными
жидкостями, чтобы не увеличить
растворимость осадка, а аморфные –
наоборот горячими. Водой промывают
осадки с низкими константами растворимости
(ниже 10-11-10-12), а также те,
которые не подвергаются пептизации.
Если константа растворимости осадка
10-9-10-11и он кристаллический,
то его промывают разбавленным раствором
осадителя. Аморфные осадки промывают
разбавленными растворами
электролитов-коагулянтов (солиNH4+),
чтобы избежать пептизации(в опыте с
железом осадок промывали растворомNH4NO3).
Повышение температуры также способствует
уменьшению адсорбции (на конкретном
примере горячий раствор, содержащий
10% аммиак разбавляют горячей водой для
уменьшения адсорбции хлорид-ионов на
поверхности осадка). 2) Для очищения
окклюдированных примесей в случае
кристаллических осадков используют
старение, в случае аморфных осадков –
переосаждение.Степень окклюзии в
процессе осаждения можно уменьшить
медленным добавлением осадителя по
каплям, при перемешивании.
Погрешности:
1) Общая погрешность анализа σ2=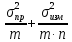
где σпр2– погрешность
пробоотбора, σизм2–
погрешность измерения,m– число проб,n– число
параллельных определений.
2) Методическая ошибка OобOоб=
—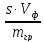
гдеs– растворимость
осадка, г/100 мл воды;Vф
– объем фильтрата и промывных вод,
мл;mгр– масса
полученного осадка, г.
3) Относительное стандартное отклонение


массы гравиметрической формы;mгр– масса гравиметрической формы; σa– дисперсия массы исходной навески;a– масса исходной навески;p– процентное содержание вещества в
исследуемой пробе;n–число
измерений.
4) Погрешность взвешивания тары σa1и тары с навескойσa2σa1=σa2=0,0002
г, σгр=
отклонение с учетом стадий пробоотбора
и пробоподготовки

Fe(OH)3– типичный пример осадка в аморфном
состоянии, легко дающий коллоидный
раствор.
Условия его осаждения следующие:
1)осаждение проводят из горячего раствора
анализируемого вещества горячим
раствором осадителя при перемешивании;
2)осаждение проводят из достаточно
концентрированного исследуемого
раствора концентрированным раствором
осадителя с последующим разбавлением(при
разбавлении устанавливается адсорбционное
равновесие, часть адсорбированных ионов
переходи в раствор, и осадок становится
более чистым); 3)осаждение проводят в
присутствии подходящего
электролита-коагулятора;
4)аморфные осадки почти не требуют
времени для созревания, их необходимо
фильтровать сразу после разбавления
раствора. Аморфные осадки нельзя
оставлять более, чем на несколько минут,
т.к. сильное уплотнение их затрудняет
последующее отмывание примесей, а также
при стоянии увеличивается количество
примесей, адсорбированных поверхностью
осадка.
10. Гравиметрическое определение никеля
в нихромовом сплаве: этапы определения,
возможные формулы осадителей, осаждаемой
и гравиметрической формулы, механизм
образования осадка, возможные варианты
загрязнения осадка, приемы повышения
чистоты осадка, погрешности. Условия
аналитического выделения осадков
никеля.
Гравиметрическое определение никеля
в нихромовом сплаве основано на его
осаждении в виде диметилглиоксимата
никеля Ni(HDMG)2.
Никель осаждают 1 %-ным спиртовым раствором
диметикглиоксимаH2DMG,
осаждаемой формой являетсяNi(HDMG)2.
Реакция:Ni2++2H2DMG=Ni(HDMG)2+2H+.
После высушивания осадка остается сухойNi(HDMG)2,
который является гравиметрической
формой.
Этапы определения:1) взятие навески
и ее растворение; 2) приготовление
раствора осадителя; 3) осаждение; 4)
фильтрование и промывание осадка; 5)
высушивание; 6) взвешивание осадка,
расчет содержания никеля.
Расчет ведут по формуле ωNi=
Механизм образования осадка:в
процессе образования осадка различают
3 параллельных процесса: 1) образование
зародышей кристалла (центров
кристаллизации); 2) рост кристаллов; 3)
объединение (агрегация) хаотично
ориентированных мелких кристаллов. В
начальный момент происходит насыщение
раствора, а затем его пересыщение. В
момент определенной пересыщенности
раствора, начинается выпадение
осадка.Центром кристалла может служить
твердая частица этого вещества или
любая другая твердая частица, которую
мы вносим в раствор, твердые частицы
могут изначально присутствовать в
растворе как примесь.
Если осаждение происходит из разбавленных
растворов, то появление осадка занимает
время-индукционный период.
В процессе добавления каждой новой
порции осадителя происходит мгновенное
пересыщение раствора, зародыши растут
быстро за счет окружающих их ионов, как
только зародыш достиг определенного
размера выпадает осадок.
Рост кристаллов идет параллельно 1-ой
стадии, происходит за счет диффузии
ионов к поверхности растущего кристалла.
Число и размер частиц осадка (дисперсность
системы кол-во в единицы объёма) зависит
от соотношения скоростей 1-ой и 2-ой
стадий (V1— скорость
образования зародышей,V2-скорость
роста кристаллов):V1>>V2-мелкодисперсный
осадок,V1<<V2-крупнокристаллический
осадок. Какая из стадий будет лимитировать
определяет скорость осаждения и
концентрации ионов. При медленном
осаждении лимитирующей стадией является
кристаллизация, частица окружена
однородным слоем осаждаемых ионов в
результате получается кристалл правильной
формы. При высокой концентрации ионов
лимитирующей стадией становится
диффузия, образуются кристаллы
неправильной формы с большой площадью
поверхности. Следует отметить, что на
скорость процесса кристаллизации влияет
влияние
зародышей и на скорость роста кристаллов.
При высокой степени
мелкодисперсные осадки, при уменьшении
осадки. Агрегация происходит в гетерогенной
системе, в значительной степени
определяется числом центров
кристаллизации.Чем больше центров
кристаллизации, тем в меньшей степени
они укрупняются на второй стадии, тем
хуже структура и тем выше дисперсность
осадков.
К аналитическим свойствам осадка
относятся: растворимость, чистота,
фильтруемость.Лучшими свойствами
обладают крупнокристаллические осадки.
Возможные варианты загрязнения: 1)
Путем адсорбции ( для конкретного примера
хлорид-ионов на поверхности осадка); 2)
Окклюзия; 3) Изоморфное соосаждение; 4)
Совместное осаждение; 5) Последующее
осаждение.
Приемы повышения чистоты осадка:
1) Адсорбированные на поверхности примеси
хорошо удаляются при промывании осадков
на фильтре при помощи промывных жидкостей,
т.к. примеси переходят в промывную
жидкость и уходят через поры фильтра.
Эффективно многократное промывание
небольшими порциями промывной жидкости.
Промывную жидкость выбирают максимально
тщательно, чтобы не увеличивать
растворимость осадка и не ухудшать его
фильтрацию. Кристаллические осадки
промывают холодными промывными
жидкостями, чтобы не увеличить
растворимость осадка, а аморфные –
наоборот горячими. Водой промывают
осадки с низкими константами растворимости
(ниже 10-11-10-12), а также те,
которые не подвергаются пептизации.
Если константа растворимости осадка
10-9-10-11и он кристаллический,
то его промывают разбавленным раствором
осадителя. Аморфные осадки промывают
разбавленными растворами
электролитов-коагулянтов (солиNH4+),
чтобы избежать пептизации (в опыте с
железом осадок промывали растворомNH4NO3).
Повышение температуры также способствует
уменьшению адсорбции (на конкретном
примере горячий раствор, содержащий
10% аммиак разбавляют горячей водой для
уменьшения адсорбции хлорид-ионов на
поверхности осадка). 2) Для очищения
окклюдированных примесей в случае
кристаллических осадков используют
старение, в случае аморфных осадков –
переосаждение.Степень окклюзии в
процессе осаждения можно уменьшить
медленным добавлением осадителя по
каплям, при перемешивании.
Погрешности:1) Общая погрешность
анализа σ2=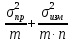
где σпр2– погрешность
пробоотбора, σизм2–
погрешность измерения,m– число проб,n– число
параллельных определений.
2) Методическая ошибка OобOоб=
—
гдеs– растворимость
осадка, г/100 мл воды;Vф
– объем фильтрата и промывных вод,
мл;mгр– масса
полученного осадка, г.
3) Относительное стандартное отклонение


массы гравиметрической формы;mгр– масса гравиметрической формы; σa– дисперсия массы исходной навески;a– масса исходной навески;p– процентное содержание вещества в
исследуемой пробе;n–число
измерений.
4) Погрешность взвешивания тары σa1и тары с навескойσa2σa1=σa2=0,0002
г, σгр=
5) Относительное стандартное отклонение
с учетом стадий пробоотбора и
пробоподготовки


Ni(HDMG)2– кристаллический осадок.
Условия его осаждения следующие:
1) осаждение ведут из достаточно
разбавленного исследуемого раствора
разбавленным раствором осадителя
(концентрации исследуемого раствора и
раствора осадителя должны быть примерно
одинаковыми);
2) раствор осадителя прибавляют медленно,
по каплям, при постоянном перемешивании
стеклянной палочкой (это предотвращает
явление окклюзии);
3) осаждение ведут из подогретого
исследуемого раствора горячим раствором
осадителя (для предотвращения пептизации);
4) к раствору прибавляют вещества,
способствующие повышению растворимости
осадка (увеличивают Iраствора), а затем понижают его
растворимость путем прибавления избытка
осадителя;
5) осадок оставляют на «созревание».
11. Гравиметрическое определение меди:
этапы определения, возможные формулы
осадителей, осаждаемой и гравиметрической
формулы, механизм образования осадка,
возможные варианты загрязнения осадка,
приемы повышения чистоты осадка,
погрешности. Преимущества органических
осадителей. Условия выделения осадков.
При гравиметрическом определении меди
медь из раствора осаждают различными
осадителями: 1) раствор аммиака осаждает
из нагретого раствора осадок Cu(OH)2;
2) Тиокарбонат калияK2CS3осаждает из нагретого раствора осадокCuS, который сушат при
100-110
3) В виде оксалата медь осаждается в
присутствиеCH3COOH;
4) При определении меди в виде
тетророданомеркуриатамедиCu[Hg(SCN)4]
медь осаждают из нагретого до кипения
раствора содержащего серную или азотную
кислоту, действиемK2[Hg(SCN)4].
Метод рекомендован для определения
меди в медных рудах; 5) Соль Рейнеке
(тетрароданодиаминохромат аммония)
NH4[Cr(NH3)2(SCN)4]
является избирательным реагентом для
определения меди в присутствие многих
посторонних ионов. Осаждение проводят
как в кислом, так и в аммиачном растворе
в виде [Cu(NH3)4][Cr(NH3)2(SCN)4]2
после предварительного восстановления
меди до одновалентного состояния
оловом(II). Для осаждения меди используются
также различные органические реагенты:
1) 8- оксихинолин осаждает медь в
уксуснокислом, аммиачном и щелочном
растворах при pH=5.33 — 14.55. Осадок, высушенный
при 105-110°С, соответствует составу
Cu(C9H6ON)2; 2) Медь осаждается
спиртовым раствором β-бензоиноксима в
слабощелочной среде в виде хлопьевидного
зеленого осадка составаCu(C6H5CHOCNOC6H5)2.
Осадок высушивают при 105-110
3) Салицилальдиоксим осаждает Cu (II) в
виде внутрикомплексного соединения
Cu(C7H6O2N)2в
уксуснокислой среде, среде ацетатного
буфера или ацетата аммония; 4) При действии
купферона наCu(II)
образуется купферонат меди (II)
с формулой Cu(C6H5N(NO)O)2;
5) При действии глицина на медь образуется
кристаллический осадок глицината меди
(II)Cu(NH2CH2COO)2.
Рассмотрим гравиметрическое определение
меди на примере осаждения ее
глицином.Реакция:CuO+2NH2CH2COOH=Cu(NH2CH2COO)2+H2OВданном случае глицинNH2CH2COOHявляется
осадителем, глицинат меди (II)Cu(NH2CH2COO)2– осаждаемой формой. При высушивании
получается гравиметрическая форма
сухогоCu(NH2CH2COO)2.
Этапы определения:1) взятие навески
и её растворение;2) приготовление раствора
осадителя;3) осаждение;4) фильтрование
и промывание;5) высушивание осадка;6)
взвешивание осадка, расчёт содержания
меди.
Механизм образования осадка:в
процессе образования осадка различают
3 параллельных процесса: 1) образование
зародышей кристалла (центров
кристаллизации); 2) рост кристаллов; 3)
объединение (агрегация) хаотично
ориентированных мелких кристаллов. В
начальный момент происходит насыщение
раствора, а затем его пересыщение. В
момент определенной пересыщенности
раствора, начинается выпадение осадка.
Центром кристалла может служить твердая
частица этого вещества или любая другая
твердая частица, которую мы вносим в
раствор, твердые частицы могут изначально
присутствовать в растворе как примесь.
Если осаждение происходит из разбавленных
растворов, то появление осадка занимает
время-индукционный период.
В процессе добавления каждой новой
порции осадителя происходит мгновенное
пересыщение раствора, зародыши растут
быстро за счет окружающих их ионов, как
только зародыш достиг определенного
размера выпадает осадок.
Рост кристаллов идет параллельно 1-ой
стадии, происходит за счет диффузии
ионов к поверхности растущего кристалла.
Число и размер частиц осадка (дисперсность
системы кол-во в единицы объёма) зависит
от соотношения скоростей 1-ой и 2-ой
стадий (V1— скорость
образования зародышей,V2-скорость
роста кристаллов):V1>>V2-мелкодисперсный
осадок,V1<<V2-крупнокристаллический
осадок. Какая из стадий будет лимитировать
определяет скорость осаждения и
концентрации ионов. При медленном
осаждении лимитирующей стадией является
кристаллизация, частица окружена
однородным слоем осаждаемых ионов в
результате получается кристалл правильной
формы. При высокой концентрации ионов
лимитирующей стадией становится
диффузия, образуются кристаллы
неправильной формы с большой площадью
поверхности. Следует отметить, что на
скорость процесса кристаллизации влияет
влияние
зародышей и на скорость роста кристаллов.
При высокой степени
мелкодисперсные осадки, при уменьшении
осадки. Агрегация происходит в гетерогенной
системе, в значительной степени
определяется числом центров
кристаллизации.Чем больше центров
кристаллизации, тем в меньшей степени
они укрупняются на второй стадии, тем
хуже структура и тем выше дисперсность
осадков.
К аналитическим свойствам осадка
относятся: растворимость, чистота,
фильтруемость.Лучшими свойствами
обладают крупнокристаллические осадки.
Возможные варианты загрязнения: 1)
Путем адсорбции ( для конкретного примера
хлорид-ионов на поверхности осадка); 2)
Окклюзия; 3) Изоморфное соосаждение; 4)
Совместное осаждение; 5) Последующее
осаждение.
Приемы повышения чистоты осадка:
1) Адсорбированные на поверхности примеси
хорошо удаляются при промывании осадков
на фильтре при помощи промывных жидкостей,
т.к. примеси переходят в промывную
жидкость и уходят через поры фильтра.
Эффективно многократное промывание
небольшими порциями промывной жидкости.
Промывную жидкость выбирают максимально
тщательно, чтобы не увеличивать
растворимость осадка и не ухудшать его
фильтрацию. Кристаллические осадки
промывают холодными промывными
жидкостями, чтобы не увеличить
растворимость осадка, а аморфные –
наоборот горячими. Водой промывают
осадки с низкими константами растворимости
(ниже 10-11-10-12), а также те,
которые не подвергаются пептизации.
Если константа растворимости осадка
10-9-10-11и он кристаллический,
то его промывают разбавленным раствором
осадителя. Аморфные осадки промывают
разбавленными растворами
электролитов-коагулянтов (солиNH4+),
чтобы избежать пептизации (в опыте с
железом осадок промывали растворомNH4NO3).
Повышение температуры также способствует
уменьшению адсорбции (на конкретном
примере горячий раствор, содержащий
10% аммиак разбавляют горячей водой для
уменьшения адсорбции хлорид-ионов на
поверхности осадка). 2) Для очищения
окклюдированных примесей в случае
кристаллических осадков используют
старение, в случае аморфных осадков –
переосаждение.Степень окклюзии в
процессе осаждения можно уменьшить
медленным добавлением осадителя по
каплям, при перемешивании.
Погрешности:1) Общая погрешность
анализа σ2 =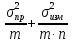
где σпр2– погрешность
пробоотбора, σизм2–
погрешность измерения,m– число проб,n– число
параллельных определений
2) Методическая ошибка OобOоб=
—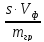
гдеs– растворимость
осадка, г/100 мл воды;Vф
– объем фильтрата и промывных вод,
мл;mгр– масса
полученного осадка, г.
3) Относительное стандартное отклонение


массы гравиметрической формы;mгр– масса гравиметрической формы; σa– дисперсия массы исходной навески;a– масса исходной навески;p– процентное содержание вещества в
исследуемой пробе;n–число
измерений.
4) Погрешность взвешивания тары σa1и тары с навескойσa2σa1=σa2=0,0002
г, σгр=
5) Относительное стандартное отклонение
с учетом стадий пробоотбора и
пробоподготовки


Преимущества органических осадителей:
1. Пользуясь органическими осадителями,
можно осаждать и разделять различные
элементы из очень сложных смесей.
Например, при помощи диметилглиоксима
возможно количественное осаждение
катионов никеля в присутствии многих
других катионов.
2. Осадки, получающиеся с органическими
осадителями, хорошо отфильтровываются
и промываются (например, осадки комплексных
соединений катионов, содержащих в
качестве лигандов пиридин или другие
органические соединения). Это дает
возможность легко отмывать от осадков
примеси, содержащиеся в анализируемом
растворе.
3. Осадки, получающиеся при действии на
катионы или анионы органических
осадителей, отличаются большим
молекулярным весом. Вследствие этого
точность анализа повышается. Например,
определение магния, алюминия и других
катионов проводится с большой точностью
осаждением их в виде оксихинолятов,
обладающих большим молекулярным весом.
4. В составе осадков, являющихся
соединениями неорганических веществ
с органическими компонентами, обычно
содержится мало соосаждающихся пиримесей.
Cu(NH2CH2COO)2– кристаллический осадок, поэтому
условия его выделения следующие:
1) осаждение ведут из достаточно
разбавленного исследуемого раствора
разбавленным раствором осадителя
(концентрации исследуемого раствора и
раствора осадителя должны быть примерно
одинаковыми);
2) раствор осадителя прибавляют медленно,
по каплям, при постоянном перемешивании
стеклянной палочкой (это предотвращает
явление окклюзии);
3) осаждение ведут из подогретого
исследуемого раствора горячим раствором
осадителя (для предотвращения пептизации);
4) к раствору прибавляют вещества,
способствующие повышению растворимости
осадка (увеличивают Iраствора), а затем понижают его
растворимость путем прибавления избытка
осадителя;
5) осадок оставляют на «созревание».
12. Гравиметрическое определение
кремния в силикатных породах: этапы
определения, возможные формулы осадителя,
осаждаемой и гравиметрической формулы,
механизм образования коллоидной частицы,
процессы, приводящие к образованию
осадка, возможные варианты загрязнения
осадка, приемы повышения чистоты осадка,
погрешности. Классификация коллоидных
систем. Условия аналитического выделения
кремнекислоты.
При гравиметрическом определении
кремния растворимый силикат натрия
Na2SiO3,
полученный в результате сплавления не
разлагаемой кремниевой кислоты с содойNa2CO3,
обрабатывается сильной кислотойHCl.
Реакция:Na2SiO3+2HCl=H2SiO3↓+2NaCl.
Осадителем в данном случае являетсяHCl, осаждаемой формой –H2SiO3.
При высушивании и прокаливании получается
гравиметрическая формаSiO2.
Этапы определения:1) взятие навески
и ее растворение; 2) приготовление
раствора осадителя; 3) осаждение; 4)
фильтрование и промывание осадка; 5)
высушивание и прокаливание осадка;; 6)
взвешивание осадка, расчет содержания
кремния.
Механизм образования коллоидной
частицы: Вещество в коллоидной системе
имеет большую развитую поверхность и
нескомпенсированный заряд на границе
разлела фаз. Существование
нескомпенсированного силового поля
ведет к адсорбции из раствора молекул
или ионов. Если коллоидная система
возникла в результате проведения
химической реакции осаждения, то частицы
адсорбируют в первую очередь те ионы,
которые могут достраивать кристаллическую
решетку. Адсорбированные ионы сообщают
частице “+» или “-“ заряд. Слой
адсорбированных ионов на ядре – это
первичный адсорбционный слой. Заряд,
созданный таким слоем, достаточно высок
и обуславливает электростатическое
взаимодействие с иоами противоположного
знака. В результате образуется слой
противоионов, который выравнивает заряд
первичного слоя. Слой противоионов
имеет диффузный характер. Часть
противоионов, прочно связанных с
первичным слоем – это плотный слой,
остальные противоионы составляют
диффузный слой.
Образование осадкапроисходит
тогда, когда раствор становится
пересыщенным, т.е. [A+]m[B-]n>Ks(ПКИ>ПР). Образование осадков связано
с процессом укрупнения частиц, с
образованием кристаллической решетки
вещества. Этот процесс определяется
числом центров кристаллизации: чем
больше центров, тем в меньшей степени
они укрупняются и тем хуже структура и
выше дисперсность осадка.
Возможные варианты загрязнения:1)
Путем адсорбции ( для конкретного примера
хлорид-ионов на поверхности осадка); 2)
Окклюзия; 3) Изоморфное соосаждение; 4)
Совместное осаждение; 5) Последующее
осаждение.
Приемы повышения чистоты осадка:
1) Адсорбированные на поверхности примеси
хорошо удаляются при промывании осадков
на фильтре при помощи промывных жидкостей,
т.к. примеси переходят в промывную
жидкость и уходят через поры фильтра.
Эффективно многократное промывание
небольшими порциями промывной жидкости.
Промывную жидкость выбирают максимально
тщательно, чтобы не увеличивать
растворимость осадка и не ухудшать его
фильтрацию. Кристаллические осадки
промывают холодными промывными
жидкостями, чтобы не увеличить
растворимость осадка, а аморфные –
наоборот горячими. Водой промывают
осадки с низкими константами растворимости
(ниже 10-11-10-12), а также те,
которые не подвергаются пептизации.
Если константа растворимости осадка
10-9-10-11и он кристаллический,
то его промывают разбавленным раствором
осадителя. Аморфные осадки промывают
разбавленными растворами
электролитов-коагулянтов (солиNH4+),
чтобы избежать пептизации (в опыте с
железом осадок промывали растворомNH4NO3).
Повышение температуры также способствует
уменьшению адсорбции (на конкретном
примере горячий раствор, содержащий
10% аммиак разбавляют горячей водой для
уменьшения адсорбции хлорид-ионов на
поверхности осадка). 2) Для очищения
окклюдированных примесей в случае
кристаллических осадков используют
старение, в случае аморфных осадков –
переосаждение.Степень окклюзии в
процессе осаждения можно уменьшить
медленным добавлением осадителя по
каплям, при перемешивании.
Погрешности:
1) Общая погрешность анализа σ2 =
где σпр2– погрешность
пробоотбора, σизм2–
погрешность измерения,m– число проб,n– число
параллельных определений.
2) Методическая ошибка OобOоб=
—
гдеs– растворимость
осадка, г/100 мл воды;Vф
– объем фильтрата и промывных вод,
мл;mгр– масса
полученного осадка, г.
3) Относительное стандартное отклонение


массы гравиметрической формы;mгр– масса гравиметрической формы; σa– дисперсия массы исходной навески;a– масса исходной навески;p– процентное содержание вещества в
исследуемой пробе;n–число
измерений.
4) Погрешность взвешивания тары σa1и тары с навескойσa2σa1=σa2=0,0002
г, σгр=
5) Относительное стандартное отклонение
с учетом стадий пробоотбора и
пробоподготовки


Классификация коллоидных систем. В
зависимости от характера межмолекулярных
сил, которые действуют на границе раздела
фаз коллоидные растворы делят на
лиофильные и лиофобные. Вокруг лиофильной
частицы располагается прочная сольватная
оболочка. В этих оболочках молекулы
ориентированы определенным образом и
образуют более или менее правильные
структуры. Вокруг лиофобной частицы
раствора также имеются сольватные
оболочки, но они непрочные и не предохраняют
молекулы от слипания.
H2SiO3– аморфный осадок, поэтому
условия его осаждения следующие:
1)осаждение проводят из горячего раствора
анализируемого вещества горячим
раствором осадителя при перемешивании;
2)осаждение проводят из достаточно
концентрированного исследуемого
раствора концентрированным раствором
осадителя с последующим разбавлением(при
разбавлении устанавливается адсорбционное
равновесие, часть адсорбированных ионов
переходи в раствор, и осадок становится
более чистым); 3)осаждение проводят в
присутствии подходящего
электролита-коагулятора;
4)аморфные осадки почти не требуют
времени для созревания, их необходимо
фильтровать сразу после разбавления
раствора. Аморфные осадки нельзя
оставлять более, чем на несколько минут,
т.к. сильное уплотнение их затрудняет
последующее отмывание примесей, а также
при стоянии увеличивается количество
примесей, адсорбированных поверхностью
осадка.
Систематические погрешности при повторных измерениях остаются постоянными или изменяются по определенному закону.
Когда судят о погрешности, подразумевают не значение, а интервал значений, в котором с заданной вероятностью находится истинное значение. Поэтому говорят об оценке погрешности. Если бы погрешность оказалась измеренной, т.е. стали бы известны её знак и значение, то её можно было бы исключить из действительного значения измеряемой физической величины и получить истинное значение.
Для получения результатов, минимально отличающихся от истинного значения измеряемой физической величины, проводят многократные наблюдения и проводят математическую обработку полученного массива с целью определения и минимизации случайной составляющей погрешности.
Минимизация систематической погрешности в процессе наблюдений выполняется следующими методами: метод замещения (состоит в замещении измеряемой величины мерой), метод противопоставления (состоит в двух поочерёдных измерениях при замене местами меры и измеряемого объекта), метод компенсации погрешности по знаку (состоит в двух поочерёдных измерениях, при которых влияющая величина становится противоположной).
При многократных наблюдениях возможно апостериорное (после выполнения наблюдений) исключение систематической погрешности в результате анализа рядов наблюдений. Рассмотрим графический анализ. При этом результаты последовательных наблюдений представляются функцией времени либо ранжируются в порядке возрастания погрешности.
Рассмотрим временную зависимость. Будем проводить наблюдения через одинаковые интервалы времени. Результаты последовательных наблюдений являются случайной функцией времени. В серии экспериментов, состоящих из ряда последовательных наблюдений, получаем одну реализацию этой функции. При повторении серии получаем новую реализацию, отличающуюся от первой.
Реализации отличаются преимущественно из-за влияния факторов, определяющих случайную погрешность, а факторы, определяющие систематическую погрешность, одинаково проявляются для соответствующих моментов времени в каждой реализации. Значение, соответствующее каждому моменту времени, называется сечением случайной функции времени. Для каждого сечения можно найти среднее по всем реализациям значение. Очевидно, что эта составляющая и определяет систематическую погрешность. Если через значения систематической погрешности для всех моментов времени провести плавную кривую, то она будет характеризовать временную закономерность изменения погрешности. Зная закономерность изменения, можем определить поправку для исключения систематической погрешности. После исключения систематической погрешности получаем «исправленный ряд результатов наблюдений».
Известен ряд способов исключения систематических погрешностей, которые условно можно разделить па 4 основные группы:
- устранение источников погрешностей до начала измерений;
- исключение почетностей в процессе измерения способами замещения, компенсации погрешностей по знаку, противопоставления, симметричных наблюдений;
- внесение известных поправок в результат измерения (исключение погрешностей начислением);
- оценка границ систематических погрешностей, если их нельзя исключить.
По характеру проявления систематические погрешности подразделяют на постоянные, прогрессивные и периодические.
Постоянные систематические погрешности сохраняют свое значение в течение всего времени измерений (например, погрешность в градуировке шкалы прибора переносится на все результаты измерений).
Прогрессивные погрешности – погрешности, которые в процессе измерении подрастают или убывают (например, погрешности, возникающие вследствие износа контактирующих деталей средств измерения).
И группу систематических погрешностей можно отнести: инструментальные погрешности; погрешности из-за неправильной установки измерительного устройства; погрешности, возникающие вследствие внешних влияний; погрешности метода измерения (теоретические погрешности); субъективные погрешности.
Систематической погрешностью называется составляющая погрешности измерения, остающаяся постоянной или закономерно меняющаяся при повторных измерениях одной и той же величины. При этом предполагается, что систематические погрешности представляют собой определенную функцию неслучайных факторов, состав которых зависит от физических, конструкционных и технологических особенностей средств измерений, условий их применения, а также индивидуальных качеств наблюдателя. Сложные детерминированные закономерности, которым подчиняются систематические погрешности, определяются либо при создании средств измерений и комплектации измерительной аппаратуры, либо непосредственно при подготовке измерительного эксперимента и в процессе его проведения. Совершенствование методов измерения, использование высококачественных материалом, прогрессивная технология — все это позволяет на практике устранить систематические погрешности настолько, что при обработке результатов наблюдений с их наличием зачастую не приходится считаться.
Систематические погрешности принято классифицировать в зависимости от причин их возникновения и по характеру их проявления при измерениях.
В зависимости от причин возникновения рассматриваются четыре вида систематических погрешностей.
1. Погрешности метода, или теоретические погрешности, проистекающие от ошибочности или недостаточной разработки принятой теории метода измерений в целом или от допущенных упрощений при проведении измерений.
Погрешности метода возникают также при экстраполяции свойства, измеренного на ограниченной части некоторого объекта, на весь объект, если последний не обладает однородностью измеряемого свойства. Так, считая диаметр цилиндрического вала равным результату, полученному при измерении в одном сечении и в одном направлении, мы допускаем систематическую погрешность, полностью определяемую отклонениями формы исследуемого вала. При определении плотности вещества по измерениям массы и объема некоторой пробы возникает систематическая погрешность, если проба содержала некоторое количество примесей, а результат измерения принимается за характеристику данного вещества -вообще.
К погрешностям метода следует отнести также те погрешности, которые возникают вследствие влияния измерительной аппаратуры на измеряемые свойства объекта. Подобные явления возникают, например, при измерении длин, когда измерительное усилие используемых приборов достаточно велико, при регистрации быстропротекаюших процессов недостаточно быстродействующей аппаратурой, при измерениях температур жидкостными или газовыми термометрами и т.д.
2. Инструментальные погрешности, зависящие от погрешностей применяемых средств измерений.. Среди инструментальных погрешностей в отдельную группу выделяются погрешности схемы, не связанные с неточностью изготовления средств измерения и обязанные своим происхождением самой структурной схеме средств измерений. Исследование инструментальных погрешностей является предметом специальной дисциплины — теории точности измерительных устройств.
3. Погрешности, обусловленные неправильной установкой и взаимным расположением средств измерения, являющихся частью единого комплекса, несогласованностью их характеристик, влиянием внешних температурных, гравитационных, радиационных и других полей, нестабильностью источников питания, несогласованностью входных и выходных параметров электрических цепей приборов и т.д.
4. Личные погрешности, обусловленные индивидуальными особенностями наблюдателя. Такого рода погрешности вызываются, например, запаздыванием или опережением при регистрации сигнала, неправильным отсчетом десятых долей деления шкалы, асимметрией, возникающей при установке штриха посередине между двумя рисками.
По характеру своего поведения в процессе измерения систематические погрешности подразделяются на постоянные и переменные.
Постоянные систематические погрешности возникают, например, при неправильной установке начала отсчета, неправильной градуировке и юстировке средств измерения и остаются постоянными при всех повторных наблюдениях. Поэтому, если уж они возникли, их очень трудно обнаружить в результатах наблюдений.
Среди переменных систематических погрешностей принято выделять прогрессивные и периодические.
Прогрессивная погрешность возникает, например, при взвешивании, когда одно из коромысел весов находится ближе к источнику тепла, чем другое, поэтому быстрее нагревается и
удлиняется. Это приводит к систематическому сдвигу начала отсчета и к монотонному изменению показаний весов.
Периодическая погрешность присуща измерительным приборам с круговой шкалой, если ось вращения указателя не совпадает с осью шкалы.
Все остальные виды систематических погрешностей принято называть погрешностями, изменяющимися по сложному закону.
В тех случаях, когда при создании средств измерений, необходимых для данной измерительной установки, не удается устранить влияние систематических погрешностей, приходится специально организовывать измерительный процесс и осуществлять математическую обработку результатов. Методы борьбы с систематическими погрешностями заключаются в их обнаружении и последующем исключении путем полной или частичной компенсации. Основные трудности, часто непреодолимые, состоят именно в обнаружении систематических погрешностей, поэтому иногда приходится довольствоваться приближенным их анализом.
Способы обнаружения систематических погрешностей. Результаты наблюдений, полученные при наличии систематических погрешностей, будем называть неисправленными и в отличие от исправленных снабжать штрихами их обозначения (например, Х1, Х2 и т.д.). Вычисленные в этих условиях средние арифметические значения и отклонения от результатов наблюдений будем также называть неисправленными и ставить штрихи у символов этих величин. Таким образом,
Поскольку неисправленные результаты наблюдений включают в себя систематические погрешности, сумму которых для каждого /-го наблюдения будем обозначать через 8., то их математическое ожидание не совпадает с истинным значением измеряемой величины и отличается от него на некоторую величину 0, называемую систематической погрешностью неисправленного среднего арифметического. Действительно,
Если систематические погрешности постоянны, т.е. 0/ = 0, /=1,2, …, п, то неисправленные отклонения могут быть непосредственно использованы для оценки рассеивания ряда наблюдений. В противном случае необходимо предварительно исправить отдельные результаты измерений, введя в них так называемые поправки, равные систематическим погрешностям по величине и обратные им по знаку:
q = -Oi.
Таким образом, для нахождения исправленного среднего арифметического и оценки его рассеивания относительно истинного значения измеряемой величины необходимо обнаружить систематические погрешности и исключить их путем введения поправок или соответствующей каждому конкретному случаю организации самого измерения. Остановимся подробнее на некоторых способах обнаружения систематических погрешностей.
Постоянные систематические погрешности не влияют на значения случайных отклонений результатов наблюдений от средних арифметических, поэтому никакая математическая обработка результатов наблюдений не может привести к их обнаружению. Анализ таких погрешностей возможен только на основании некоторых априорных знаний об этих погрешностях, получаемых, например, при поверке средств измерений. Измеряемая величина при поверке обычно воспроизводится образцовой мерой, действительное значение которой известно. Поэтому разность между средним арифметическим результатов наблюдения и значением меры с точностью, определяемой погрешностью аттестации меры и случайными погрешностями измерения, равна искомой систематической погрешности.
Одним из наиболее действенных способов обнаружения систематических погрешностей в ряде результатов наблюдений является построение графика последовательности неисправленных значений случайных отклонений результатов наблюдений от средних арифметических.
Рассматриваемый способ обнаружения постоянных систематических погрешностей можно сформулировать следующим образом: если неисправленные отклонения результатов наблюдений резко изменяются при изменении условий наблюдений, то данные результаты содержат постоянную систематическую погрешность, зависящую от условий наблюдений.
Систематические погрешности являются детерминированными величинами, поэтому в принципе всегда могут быть вычислены и исключены из результатов измерений. После исключения систематических погрешностей получаем исправленные средние арифметические и исправленные отклонения результатов наблюдении, которые позволяют оценить степень рассеивания результатов.
Для исправления результатов наблюдений их складывают с поправками, равными систематическим погрешностям по величине и обратными им по знаку. Поправку определяют экспериментально при поверке приборов или в результате специальных исследований, обыкновенно с некоторой ограниченной точностью.
Поправки могут задаваться также в виде формул, по которым они вычисляются для каждого конкретного случая. Например, при измерениях и поверках с помощью образцовых манометров следует вводить поправки к их показаниям на местное значение ускорения свободного падения
где Р — измеряемое давление.
Введением поправки устраняется влияние только одной вполне определенной систематической погрешности, поэтому в результаты измерения зачастую приходится вводить очень большое число поправок. При этом вследствие ограниченной точности определения поправок накапливаются случайные погрешности и дисперсия результата измерения увеличивается.
Систематическая погрешность, остающаяся после введения поправок на ее наиболее существенные составляющие включает в себя ряд элементарных составляющих, называемых неисключенными остатками систематической погрешности. К их числу относятся погрешности:
• определения поправок;
• зависящие от точности измерения влияющих величин, входящих в формулы для определения поправок;
• связанные с колебаниями влияющих величин (температуры окружающей среды, напряжения питания и т.д.).
Перечисленные погрешности малы, и поправки на них не вводятся.
Систематические
погрешности не изменяются при увеличении
числа измерений, поскольку согласно
определению остаются постоянными или
изменяются по определенному закону в
процессе измерения. Систематические
погрешности могут быть выявлены на
основе теоретических оценок результатов,
путем сопоставления результатов,
полученных разными методами, на разных
приборах. Имеются возможности определить
систематические погрешности путем
тщательного исследования средства или
метода измерений путем построения
зависимости результатов от какого-либо
изменяющегося параметра, например
времени, климатических условий,
электромагнитных полей, напряжения
питания и т.д. В ряде случаев необходимо
выполнить большой объем исследовательской
работы для того, чтобы выявить условия,
создающие систематические погрешности
и, соответственно, представить либо
график, либо таблицу поправок, либо
определить аналитическую зависимость
систематической погрешности от
какого-либо параметра.
На
результат измерения влияют несколько
факторов, каждый из которых вызывает
свою систематическую погрешность. В
этом случае выявление аналитического
вида погрешности значительно усложняется,
приходится проводить трудоемкие
тщательные исследования, которые иногда
оканчиваются неудачей. Тем не менее,
необнаруженная систематическая
погрешность опаснее случайной, т.к.
последняя может быть минимизирована
соответствующей методикой измерения,
а систематическая невыявленная
погрешность исказит результат
непредсказуемо.
Особую
категорию систематических погрешностей
составляют измеренные с недостаточной
точностью фундаментальные и физические
константы, используемые в процессе
измерения. То же самое относится к
неточностям в стандартных справочных
данных, или к недостаточно точной
аттестации стандартных образцов.
Появление более точных справочных
данных требует пересчета результатов
всех измерений с их использованием, или
переградуировки шкал приборов. Например,
получение более точных данных о давлении
насыщающих паров индивидуальных веществ
может привести к необходимости
переградуировки термометров, манометров,
приборов для измерения концентраций и
т. д.
Уточнения
постоянной
Авогадро приводят к переградуировке
шкал всех приборов в физико-химических
измерениях. Новые исследования свойств
воды могут изменить результаты измерения
огромного числа приборов, т. к. на этих
постоянных строится температурная
шкала, шкала плотности, шкала вязкости.
Рассмотрим
группы систематических погрешностей,
отличающихся одна от другой причиной
возникновения. В основном различают
следующие группы:
-
Инструментальные
погрешности, связанные с несовершенством
конструкции прибора, неправильностью
технологии его изготовления. -
Погрешности
внешних влияний. Особенно часто в
измерительной практике приходится
сталкиваться с влиянием климатических
условий — температуры, давления,
влажности. Кроме того, весьма
распространенным источником такого
рода погрешностей является влияние
внешних электромагнитных полей и
изменения в напряжении сети питания
измерительных приборов. -
Погрешности
метода измерения. Этот вид погрешности
может быть связан как с неточностью
знания свойства объекта измерения, так
и с одинаковым влиянием разных факторов
на датчик измерительного прибора. Сюда
же можно отнести погрешности
пробоподготовки в определении состава
веществ и материалов. -
Субъективные
погрешности, связанные либо с недостаточным
вниманием, либо с невысокой квалификацией
персонала, обслуживающего прибор.
Особенно большое значение этот вид
погрешности имеет при пользовании
приборами с визуальным отсчетом. Большая
часть промахов также может быть связана
с субъективными погрешностями.
Инструментальная
погрешность
Инструментальная
погрешность — это составляющая погрешности,
зависящая от погрешности (класса
точности) средства измерения. Такие
погрешности могут быть выявлены либо
теоретически на основании механического,
электрического, теплового, оптического
расчета конструкции прибора, либо
опытным путем на основе контроля его
показаний по образцовым мерам, по
стандартным образцам, а также
компарированием показаний прибора с
аналогичными измерениями на других
приборах.
Инструментальные
погрешности, присущие конструкции
прибора, могут быть легко выявлены из
рассмотрения кинематической, электрической
или оптической схемы. Например, взвешивание
на весах с коромыслом обязательно
содержит погрешность, связанную с
неравенством длин коромысла от точек
подвеса чашек до средней точки опоры
коромысла. В электрических измерениях
на переменном токе обязательно будут
погрешности от сдвига фаз, который
появляется в любой электрической цепи.
В оптических приборах наиболее частыми
источниками систематической погрешности
являются аберрации оптических систем
и явления параллакса. Общим источником
погрешностей в большинстве приборов
является трение и связанные с ним наличие
люфтов, мертвого хода, свободного хода,
проскальзывания.
Способы
устранения или учета инструментальных
погрешностей достаточно хорошо известны
для каждого типа прибора. В метрологии
процедуры аттестации или испытаний
часто включают в себя исследования
инструментальных погрешностей. В ряде
случаев инструментальную погрешность
можно учесть и устранить за счет методики
измерений. Например, неравноплечесть
весов можно установить, поменяв местами
объект и гири. Аналогичные приемы
существуют практически во всех видах
измерения.
Инструментальные
погрешности, часто связанные с
несовершенством технологии изготовления
измерительного прибора. Особенно это
касается серийных приборов, выпускаемых
большими партиями. При сборке может
иметь место отличие в сигналах с датчиков,
отличие в установке шкал. Подвижные
части приборов могут собираться с разным
натягом, механические детали могут
иметь разные значения допусков и посадок
даже в пределах установленной нормы. В
оптических приборах огромное значение
имеет качество сборки или юстировка
оптической измерительной системы.
Современные оптические приборы могут
иметь десятки и сотни сборочных единиц,
а допуски при сборке составляют дол и
длины волны оптического излучения (λ =
0,4 — 0,7 мкм).
Методы
выявления таких погрешностей чаще всего
состоят в индивидуальной градуировке
измерительного прибора по образцовым
мерам или по образцовым приборам. В
современных приборах коррекция показаний
может быть выполнена не только
переградуировкой шкалы, но и коррекцией
электрического сигнала или компьютерной
обработкой результата. Естественно,
что во всех случаях коррекции должно
предшествовать исследование показаний
прибора.
Инструментальные
погрешности, связанные с износом или
старением средства измерения, имеют
определенные характерные особенности.
Процесс износа, как правило, проявляется
в погрешностях измерения постепенно.
Изменяются зазоры в сопрягаемых деталях,
соприкасающиеся поверхности покрываются
коррозией, изменяются упругости пружин
и т. д. Изменяется масса гирь, уменьшаются
размеры образцовых мер, изменяются
электрические и физико-химические
свойства узлов и деталей приборов, и
все это приводит к изменению показаний
приборов. Старение приборов — это, как
правило, следствие изменений структуры
материалов, из которых сделан прибор.
Изменяются не только механические
характеристики, но и электрические,
оптические, физико-химические. Стареют
металлы и сплавы, изменяя исходную
намагниченность, стареет оптика,
приобретая дополнительное светорассеяние
или центры окраски, стареют датчики
состава веществ. Последнее хорошо
известно тем, кто профессионально
работал с химреактивами, которые могут
сорбировать воду, реагировать с окружающей
средой и с примесями. Использование
химических веществ в измерительной
технике всегда необходимо с учетом
срока годности реактива.
Устранение
погрешностей приборов от старения или
износа, как правило, проводится по
результатам поверки, когда устанавливается
погрешность по истечении какого-либо
длительного времени хранения или
эксплуатации. В ряде случаев достаточно
почистить прибор, но иногда требуется
ремонт или перекалибровка шкалы.
Например, при появлении систематических
погрешностей во взвешивании на весах
удается вернуть им работоспособность
обычным техническим обслуживанием —
регулировкой и смазкой. При более
серьезном старении приходится
переполировывать трущиеся детали или
заменять сопрягаемые детали.
Особенно
важно выявить систематическую погрешность
у приборов, предназначенных для поверки
средств измерений — у образцовых приборов.
Как правило, на образцовых приборах
выполняется меньший объем работы, чем
на рабочих приборах, и по этой причине
систематический временной «уход»
показаний может не так наглядно
проявляться. Вместе с тем невыявленная
в образцовых приборах погрешность
передается другим приборам, которые по
данному образцовому прибору поверяются.
С
целью уменьшения влияния процессов
старения на измерительную технику в
ряде случаев прибегают к искусственному
старению наиболее ответственных узлов.
У оптических приборов — рефрактометров,
интерферометров, гониометров — старение
проявляется часто в том, что несущие
конструкции «ведет», т. е. они изменяют
форму, особенно в тех местах, где есть
сварка или обработка металла резанием.
Для того чтобы свести к минимуму влияние
такого старения, готовые узлы выдерживаются
какое-то время в жестких климатических
условиях или в специальных камерах, где
процесс старения можно ускорить, изменив
температуру, давление или влажность.
Отдельное
место в инструментальных погрешностях
занимает неправильная установка и
исходная регулировка средства измерения.
Многие приборы имеют встроенные указатели
уровня. Это значит, что перед измерением
нужно отгоризонтировать прибор. Причем,
такие требования предъявляются не
только к средствам измерений высокой
точности, но и к рутинным приборам
массового использования. Например,
неправильно установленные весы будут
систематически «обвешивать» покупателя,
на гониометре невозможно работать без
тщательного горизонтирования отсчетного
устройства. В приборах для измерения
магнитного поля весьма существенным
может оказаться ориентация его
относительно силовых линий поля Земли.
Озонометры нужно очень тщательно
ориентировать по Солнцу. Многие приборы
требуют установки по уровню или по
отвесу. Если двухплечие весы не установлены
горизонтально, нарушаются соотношения
длин между коромыслами. Если маятниковые
механизмы или грузопоршневые манометры
установлены не по отвесу, то показания
таких приборов будут сильно отличаться
от истинных.
Погрешности,
возникающие вследствие внешних влияний
Под
категорией
погрешностей,
возникающих вследствие внешних влияний,
обычно понимают изменение показаний
приборов под воздействием температуры,
влажности и давления. Тем не менее, это
лишь часть причин, приводящих к появлению
систематических погрешностей. Сюда же
следует отнести влияние вибраций,
постоянных и переменных ускорений,
влияние электромагнитного поля и
различных излучений: рентгеновского,
ультрафиолетового, ионизирующих
излучений, гамма-излучения. По мере
развития техники и науки появилась
возможность и необходимость проводить
измерения в нестандартных условиях,
например в Космосе или внутри подводной
лодки. Специфичность условий измерения
может доходить до высших категорий,
если ставить задачу измерения погодных
условий на Марсе или на Венере. Такие
же особенности могут иметь место в
реальных жизненно важных для нас
ситуациях. Если речь идет о контроле
параметров ядерного реактора, то условия,
в которых работает измерительный прибор,
могут значительно отличаться от
стандартных.
Влияние
температуры
— наиболее распространенный источник
погрешности при измерениях. Поскольку
от температуры зависит длина тел,
сопротивление проводников, объем
определенного количества газа, давление
насыщенного пара индивидуальных веществ,
то сигналы со всех видов датчиков, где
используются упомянутые физические
явления, будут изменяться с изменением
температуры. Существенно, что сигнал
сдатчика не только зависит от абсолютного
значения температуры, но от градиента
температуры в том месте, где расположен
датчик. Еще одна из причин появления
«температурной» систематической
погрешности — это изменение температуры
в процессе измерения. Указанные причины
существенны при косвенных измерениях,
т. е. в тех случаях, когда нет
необходимости измерять температуру
как физическую величину. Тем не менее
в собственно температурных измерениях
необходимо тщательно исследовать
показания приборов в различных
температурных интервалах. Например,
результаты измерения теплоемкости,
теплопроводности, теплотворной
способности топлива могут сильно
искажаться от различного рода температурных
воздействий.
Учитывая
большое влияние температуры на физические
свойства материалов и, соответственно,
на показания приборов, особое внимание
следует обращать на температурные
условия в тех комнатах, лабораториях и
зданиях, где проводятся градуировочнные
или поверочные работы. Здесь необходимо
тщательно следить за отсутствием
тепловых потоков, градиентов температуры,
однородностью температуры окружающей
среды и измерительного прибора. Для
того чтобы избежать влияния этих факторов
на измерения, приборы длительное время
выдерживают в термостатированном
помещении, прежде чем начинать какие-либо
работы. Для особо точных измерений
иногда используют дистанционные
манипуляторы, чтобы исключить тепловые
помехи, создаваемые операторами.
Для
большинства приборов при испытаниях
на право серийного выпуска программа
испытаний обязательно содержит
исследование показаний прибора (одного
или нескольких образцов) в зависимости
от температуры.
Влияние
магнитных или электрических полей
сказывается не только на средствах
измерения электромагнитных величин. В
зависимости от принципа действия прибора
наведенная ЭДС или токи Фуко могут
исказить показания любого датчика,
выходным сигналом которого служит
напряжение, ток, сопротивление или
электрическая емкость. Таких приборов
существует великое множество, особенно
в тех случаях, когда приборы имеют
цифровой выход. Аналогово-цифровые
преобразователи иногда начинают
регистрировать сигналы радиочастотных
или еще каких-либо электрических полей.
Очень часто электромагнитные помехи
попадают в прибор по сети питания.
Выяснить причины появления таких ложных
сигналов, научиться вводить поправки
в измерения при наличии электромагнитных
помех — это одна из важных проблем
метрологии и измерительной техники.
Особенно
важен рассматриваемый фактор появления
систематических погрешностей в больших
городах, где хорошо поставлена связь,
телевидение, радиовещание и т.п. Уровень
электромагнитного излучения бывает
настолько высоким, что, например, вблизи
мощного телецентра может загореться
низковольтная лампочка, если ее соединить
с проволочным контуром без источника
питания. Тот же эффект можно наблюдать
в зоне действия радиолокаторов вблизи
какого-либо аэропорта. О том, что этот
фактор может существенно влиять на
показания измерительных приборов,
свидетельствует тот факт, что буквально
за последние несколько лет появились
возможности уверенной радиотелефонной
связи, а также уверенного приема
спутникового телевидения. Это означает,
что уровень сигнала в окружающем нас
пространстве достаточно высок и легко
регистрируется соответствующей техникой.
Этот же сигнал будет накладываться на
сигналы, поступающие с датчиков
измерительных приборов.
Еще
один интересный случай появления
систематических погрешностей при
измерениях связан с измерительными
приборами на кораблях. Много лет назад
опытными мореплавателями было установлено,
что если корабль идет долгое время
курсом «норд» или «зюйд» некоторые
приборы начинают показывать неверные
результаты, т. е. приобретают какую-то
систематическую погрешность. Причина
этого была выяснена довольно точно:
корабль намагничивается от магнитного
поля Земли и при дальнейшем изменении
курса сохраняет остаточную намагниченность.
В наше время это хорошо исследованный
эффект. Во время мировой войны суда
специально размагничивали, чтобы
избежать срабатывания магнитных мин.
Сейчас в ряде стран, в том числе и у нас,
созданы корабли науки, которые либо
делаются из немагнитных материалов,
либо персонал тщательно следит за
намагниченностью корпуса. Такие суда
осуществляют дальнюю и космическую
связь, занимаются экологическими
измерениями, исследуют озоновый слой
Земли, исследуют прохождения радиоволн
и выполняют еще целый ряд необходимых
функций.
Влияние
второго климатического фактора — давления
— распространяется на несколько более
узкий круг измерений, чем температура,
но существует целый ряд очень важных
видов измерения, где данные об атмосферном
или внешнем давлении практически
определяют уровень точности измерений.
Так же, как в предыдущем случае, имеет
смысл отдельно рассматривать собственно
показания датчиков в других видах
измерения. Многие типы манометров по
сути своей являются дифференциальными,
т. е. измеряют разность давлений между
двумя различными точками какой-либо
системы. В этом случае любая погрешность
определения абсолютной величины давления
в той точке, относительно которой
измеряется давление, аддитивно
накладывается на результат измерения.
Влияние
давления на сигналы датчиков очень
существенны в рефрактометрии — измерении
показателя преломления — воздуха и
газов. Это относится собственно к
измерениям рефракции, а также к измерениям
с использованием соответствующих
датчиков, например при измерении
концентрации газов и газовых смесей.
От изменения давления меняется не только
показатель преломления газа, но и другие
характеристики, такие как диэлектрическая
постоянная. Соответственно, может
измениться сигнал с любого емкостного
датчика.
В
измерении массы информация о давлении
весьма существенна в связи с тем, что
при точных измерениях массы основной
вклад в систематическую погрешность
дает архимедова сила, выталкивающая
гирю. Силы Архимеда зависят от плотности
среды (плотности воздуха) и, следовательно,
непосредственно зависят от давления,
поскольку число молекул газа в единице
объема
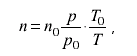
где
n0
— постоянная, называемая числом Лошмита;
р — давление; Т — температура; a p0
и T0
— нормальные значения давления и
температуры.

В
метрологических справочниках всегда
можно найти данные о поправках, которые
необходимо ввести при взвешивании для
учета
силы
Архимеда. Нетрудно показать, что
выталкивающая сила, действующая на
гирю, выражается формулой
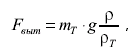
где
ρ — плотность воздуха; ρT
— плотность материала взвешиваемого
тела; mT
— масса тела. Масса взвешиваемого тела
будет равна:
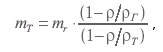
где
ρГ
— плотность материала гири. Если плотность
воздуха считать много меньшей плотности
материалов тела и гири, то массу
взвешиваемого тела можно выразить через
действительную массу гири плюс некоторая
поправка на силу Архимеда
(3.10)
Из
приведенныхформул следует, что при
взвешивании гирями из материала большой
плотности систематическая погрешность
от силы Архимеда меньше, чем при
взвешивании гирями из легкого материала.
В табл. 3.1 представлены поправки на силы
Архимеда, которые необходимо учитывать
при взвешивании для тела массой 100 г.
Таблица
3.1
Поправки
на силы Архимеда, которые нужно делать
при
взвешивании гирями для тела массой 100
г.
|
Плотность |
0,5 |
1 |
1,5 |
2 |
4 |
6 |
8 |
|
Поправка |
230 |
100 |
70 |
50 |
15 |
6 |
0,7 |
Отдельно
следует рассматривать систематические
погрешности при измерении давления в
условиях вакуума. Здесь наиболее
существенным источником погрешностей
является селективность процесса
откачивания воздуха насосами с различными
принципами действия. Этот вопрос очень
сложен с точки зрения анализа физической
сущности процесса вакуумирования.
Насосы ротационные, сорбционные,
магниторазрядные, турбо-молекулярные
создают совершенно разный состав
остаточных газов. В итоге в каждом
отдельном случае при оценке погрешностей
измерения
вакуума
нужно анализировать совместные искажения,
вносимые в состав остаточного газа
насосом, и искажения, вносимые тем или
иным датчиком давления. В ряде случаев
для прояснения картины недостаточна
даже дополнительная калибровка, т. к.
создать достаточно точно ту среду по
составу, в которой будет работать датчик,
очень трудно.
Проблема
создания вакуума и измерения давления
остаточного вакуума является одной из
ключевых проблем современной техники
и науки. Уверенно можно утверждать, что
уровень вакуумной техники определяет
уровень многих технологий, например
технологии изготовления микросхем и
микросборок.
То
же самое относится к наукоемким видам
измерения —
масс-спектометрии
или ЯМР спектометрии. Все метрологические
категории этих видов измерения напрямую
зависят от того, насколько «чистый»
вакуум удается создать и с какой точностью
удается этот вакуум измерить.
Третий
климатический фактор, вносящий
систематические погрешности во многие
измерения, — это влажность, т. е. содержание
молекул воды в том или ином месте
расположения измерительного прибора.
При оценке такой погрешности можно
рассматривать гигрометрию как вид
измерения, т. е. возможные систематические
погрешности в измерении влагосодержания
(абсолютная влажность) и Благосостояния
(относительная влажность). Можно также
оценивать погрешность как следствие
влияния влаги на показания других типов
приборов. Например, наличие влаги
изменяет проводимость или емкость
электрических элементов датчиков. Влага
ухудшает изоляционные свойства
материалов, вызывая токи утечки. Влага
изменяет структуру многих химических
соединений, трансформируясь из свободной
влаги в кристаллизационную и обратно.
С
учетом этого становится очевидным
всеобъемлющий характер учета влажности
при оценке систематических погрешностей.
На
эти трудности накладываются еще
неоднозначности в выражении измеряемых
в гигрометрии величин и единиц. По одной
из версий исходным моментом в гигрометрии
является упругость насыщенного водяного
пара при фиксированной температуре. В
этом случае любое уточнение термодинамических
свойств воды должно привести к пересчету
всех результатов измерений. По другой
версии исходным моментом в
гигрометрии
должно являться число молекул воды в
единице объема. Эти измерения наиболее
точно выполняются радиочастотными
методами, возможности которых и определяют
погрешности гигрометрии.
Вся
проблема влияния влажности на
систематические погрешности в измерениях
обозначена во многих странах и
международных организациях как одна
из наиболее существенных. По этой причине
влияние влажности на показания любого
прибора являются обязательным элементом
любых испытаний и исследований на
предмет выявления систематической
погрешности.
Погрешности
метода измерения или теоретические
погрешности
Любое
измерение имеет предел точности. Какой
бы мы не создали измерительный инструмент,
всегда будут существовать рамки возможной
точности, превзойти которые созданием
совершенных измерительных устройств
невозможно. Всегда при измерениях идут
на допущения, отклонения от идеальных
ситуаций, от функциональных зависимостей,
ограничивая трудоемкость процесса на
основании принципа достаточности
точности измерения для решения
практической задачи. Такие допущения
приходится делать во всех видах измерений.
В
механических измерениях на практике
постоянно присутствующей систематической
погрешностью является сила Архимеда,
по разному действующая на взвешиваемый
предмет и на гири. Учет
силы
Архимеда делается только при взвешивании
на высшем уровне точности при аттестации
мер высшего разряда. Во всех практических
измерениях массы такие поправки не
делаются, ограничивая тем самым точность
определения массы.
В
электрических измерениях постоянным
источником систематической погрешности
являются собственные сопротивления
приборов, собственная распределенная
емкость и индуктивность проводников.
При использовании законов для цепей
постоянного и переменного тока как
правило собственные электрические
параметры не учитываются. Не учитываются
в большинстве случаев и возможные
термоЭДС в цепи или образования
гальванических пар. Можно свести эти
погрешности к минимуму тщательным
исследованием цепей, но в реальных
случаях стремятся работать в таких
ситуациях, когда влияние перечисленных
причин ничтожно в сравнении с необходимой
и достаточной точностью измерений.
Измерения
физико-химических величин в каждой
конкретной задаче имеет определенные
систематические погрешности, специфические
для данного вида измерения. Прежде всего
это порог чувствительности датчика
концентрации какого-либо вещества.
Детектирование отдельных атомов, т. е.
отсутствие порога чувствительности,
имеет место только для весьма специфических
методов и для очень узкого класса
веществ. Второй фактор — вещество,
например вода, может входить как в виде
собственно молекул воды, так и в виде
кристаллизационной воды. Особенно
сложно выявить фактор многообразия
различных форм существования измеряемого
компонента в случае элементного анализа.
Так, водород может встречаться в газе
или в воздухе в виде молекул водорода
Н^, может входить в состав паров воды, в
состав углеводородов и т. д. Если при
измерениях используется метод с
предварительной атомизацией пробы, то
информацию о содержании водорода в
составе какого-либо соединения можно
получить только с использованием
дополнительных усилий, например с
использованием хроматографической
колонки, которая разделит компоненты
пробы по массам.
В
температурных измерениях всегда
существуют погрешности, связанные с
температурными
градиентами, т. е. с неоднородностью
температурного поля. Практически
невозможно реализовать такую ситуацию,
когда все части термометра будут
находиться в одинаковых температурных
условиях, а это приведет к тому, что в
жидкостных термометрах не весь объем
жидкости примет измеряемую температуру,
а термопарный термометр кроме полезного
сигнала зарегистрирует все влияния
температурных градиентов на ЭДС
термопары.
В
оптических измерениях, особенно в
измерении характеристик светового
потока — фотометрии, постоянный источник
систематических погрешностей — это
рассеянный свет в измерительных приборах.
Поскольку не существует идеально
отражающих и идеально поглощающих
поверхностей, в любой ситуации внутри
каждого прибора существует некий
постоянный фон паразитной подсветки.
В прецизионных оптических прибоpax
принимаются специальные меры борьбы с
рассеянным светом: устанавливаются
светофильтры, предварительные
монохроматизаторы излучения,
изготавливаются специфические
дифракционные решетки (голографические).Тем
не менее на каком-то уровне рассеянный
свет присутствует в оптических измерениях
всегда.
В
приборах для измерения показателей
преломления —
рефрактометрах
— систематическая погрешность обычно
связана с влиянием показателя преломления
воздуха. Чтобы исключить эту погрешность,
рефрактометры высокой точности иногда
вакуумируют, т. е. откачивают из объема
прибора воздух. Эта процедура делает
прибор громоздким и дорогим, поэтому
по такому пути идут только при крайней
необходимости. Чаще просто вносят
поправки на преломление воздуха,
используя таблицы показателя преломления
при различных температурах и давлениях.
В
магнитных измерениях источником
систематической погрешности служит,
как уже указывалось, магнитное поле
Земли, а также электромагнитные поля,
создаваемые теле- и радиопередатчиками,
системами связи, линиями электропередач.
В зависимости от расстояния между
измерительным прибором и источником
помех такого рода влияние может быть
очень сильным. Методы борьбы с такими
погрешностями достаточно хорошо освоены:
это либо защита измерительных приборов
экранами, либо измерение уровня помех
другими, более чувствительными и более
точными специальными приборами.
К
систематическим погрешностям метода
измерения относятся не только перечисленные
погрешности, которые можно назвать
инструментальными, поскольку они есть
следствие влияния каких-либо причин на
измерительный прибор, но и систематические
погрешности метода или процедуры
приготовления объекта к измерениям.
Особенно наглядно это видно в измерениях
состава веществ и материалов. Например,
существует распространенный метод
определения влажности зерна путем
взвешивания определенного его количества
до и после сушки. При этом полагается,
во-первых, что испаряется вся влага и,
во-вторых, что ничего, кроме воды, не
испаряется. Понятно, что и то и другое
справедливо только с какими-то допущениями.
Другой пример — измерение содержания
двуокиси серы в дымовых газах. Если в
пробозаборном тракте есть следы влаги,
а сам зонд находится при комнатной
температуре, то сернистый газ по пути
транспортировки от трубы до измерительного
прибора прореагирует с парами воды с
образованием серной кислоты. Естественно,
что прибор покажет неверное, заниженное
значение концентрации двуокиси серы.
Еще
один источник систематической погрешности,
связанный с несовершенством методов
измерения, имеет место в тех случаях,
когда приходится пользоваться при
измерениях какими-либо таблицами или
справочными данными. Любые данные в
справочниках получены с определенной
погрешностью, которая переносится на
объект измерения автоматически. Такого
же рода погрешности появляются при
использовании стандартных образцов.
Погрешности в аттестации стандартного
образца непосредственно ограничиваютточность
измерения в любом методе, когда
используются при калибровке и градуировке
стандартные образцы.
После
перечисления многочисленных причин
появления систематических погрешностей,
заключенных в методе измерения, может
показаться, что точно вообще ничего
измерить невозможно. На самом деле в
большинстве случаев обеспечивается
достаточный запас точности, или проводятся
специальные исследования по выявлению
причин систематических погрешностей.
После этого вносятся поправки либо в
показания шкал приборов, либо в методику
измерений.
Субъективные
систематические погрешности
На
результаты измерений непосредственное
влияние оказывает квалификация персонала
и индивидуальные особенности человека,
работающего на приборе. Для полной
реализации возможностей измерительного
прибора или метода предела для
совершенствования не существует. В
главе, посвященной эталонам, изложена
история совершенствования эталона
длины. На таком уровне обычных инженерных
знаний недостаточно, по этой причине
процесс измерения ставят рядом с
искусством. Понятно, что получить
информацию о результатах измерений
состава атмосферы на Венере, расшифровать
ее и оценить погрешность может только
очень квалифицированный человек. С
другой стороны, некоторые измерения,
например температуры тела человека,
может выполнить любой, даже неграмотный
человек.
На
субъективные погрешности измерений
влияют самые разнообразные особенности
человека. Известно, что время реакции
на звук, на свет, на запах, на тепло у
каждого человека разное. Хорошо известно,
что дискретные кадры в кино или в
телевизоре, следующие 25 раз в секунду,
воспринимаются наблюдателем как
непрерывная картина. Из этого следует,
что между откликом прибора и реакцией
человека временной интервал в 1/25 секунды
не может быть зарегистрирован.
Еще
одним наглядным примером влияния
оператора на результат измерения служат
измерения цвета. Человеческий глаз
имеет два аппарата зрения — дневной и
сумеречный. Дневной аппарат представляет
собой комбинацию из красных, зеленых и
синих рецепторов. У большой части людей
наблюдаются отклонения от средних
статистических характеристик — хорошо
известный дефект, называемый в обиходе
дальтонизмом. У человека может ненормально
функционировать либо какой-нибудь
рецептор, либо какой-нибудь аппарат
зрения. Принято проверять на правильность
цветовосприятия только водителей
транспорта. Обычный персонал, занимающийся
измерениями, никто на цветовосприятие
не проверяет. Это может привести к
неверным измерениям координат цвета
или температуры пирометром, т. е. в тех
случаях, когда используются визуальные
методы оценки яркости или цвета. Известно
также, что у человека цветовосприятие
может измениться с возрастом. Это связано
с тем, что стекловидное тело глаза с
возрастом желтеет, в результате чего
цвет одним и тем же человеком воспринимается
с годами по-разному. Некоторые художники,
восстанавливавшие свои собственные
картины через десятки лет, изображали
все в синих тонах.
Субъективное
восприятие человеком результата
измерения в большой степени определяется
также опытом работы. Например, при
измерении состава сплавов визуальным
стилометром опыт работы является
определяющим в получении достоверного
и точного результата. Опытный оператор
по появлению спектральных линий в поле
зрения прибора может определить не
только тип сплава, но и количественное
содержание в нем многих элементов.
From Wikipedia, the free encyclopedia
«Systematic bias» redirects here. For the sociological and organizational phenomenon, see Systemic bias.
Observational error (or measurement error) is the difference between a measured value of a quantity and its true value.[1] In statistics, an error is not necessarily a «mistake». Variability is an inherent part of the results of measurements and of the measurement process.
Measurement errors can be divided into two components: random and systematic.[2]
Random errors are errors in measurement that lead to measurable values being inconsistent when repeated measurements of a constant attribute or quantity are taken. Systematic errors are errors that are not determined by chance but are introduced by repeatable processes inherent to the system.[3] Systematic error may also refer to an error with a non-zero mean, the effect of which is not reduced when observations are averaged.[citation needed]
Measurement errors can be summarized in terms of accuracy and precision.
Measurement error should not be confused with measurement uncertainty.
Science and experiments[edit]
When either randomness or uncertainty modeled by probability theory is attributed to such errors, they are «errors» in the sense in which that term is used in statistics; see errors and residuals in statistics.
Every time we repeat a measurement with a sensitive instrument, we obtain slightly different results. The common statistical model used is that the error has two additive parts:
- Systematic error which always occurs, with the same value, when we use the instrument in the same way and in the same case.
- Random error which may vary from observation to another.
Systematic error is sometimes called statistical bias. It may often be reduced with standardized procedures. Part of the learning process in the various sciences is learning how to use standard instruments and protocols so as to minimize systematic error.
Random error (or random variation) is due to factors that cannot or will not be controlled. One possible reason to forgo controlling for these random errors is that it may be too expensive to control them each time the experiment is conducted or the measurements are made. Other reasons may be that whatever we are trying to measure is changing in time (see dynamic models), or is fundamentally probabilistic (as is the case in quantum mechanics — see Measurement in quantum mechanics). Random error often occurs when instruments are pushed to the extremes of their operating limits. For example, it is common for digital balances to exhibit random error in their least significant digit. Three measurements of a single object might read something like 0.9111g, 0.9110g, and 0.9112g.
Characterization[edit]
Measurement errors can be divided into two components: random error and systematic error.[2]
Random error is always present in a measurement. It is caused by inherently unpredictable fluctuations in the readings of a measurement apparatus or in the experimenter’s interpretation of the instrumental reading. Random errors show up as different results for ostensibly the same repeated measurement. They can be estimated by comparing multiple measurements and reduced by averaging multiple measurements.
Systematic error is predictable and typically constant or proportional to the true value. If the cause of the systematic error can be identified, then it usually can be eliminated. Systematic errors are caused by imperfect calibration of measurement instruments or imperfect methods of observation, or interference of the environment with the measurement process, and always affect the results of an experiment in a predictable direction. Incorrect zeroing of an instrument leading to a zero error is an example of systematic error in instrumentation.
The Performance Test Standard PTC 19.1-2005 “Test Uncertainty”, published by the American Society of Mechanical Engineers (ASME), discusses systematic and random errors in considerable detail. In fact, it conceptualizes its basic uncertainty categories in these terms.
Random error can be caused by unpredictable fluctuations in the readings of a measurement apparatus, or in the experimenter’s interpretation of the instrumental reading; these fluctuations may be in part due to interference of the environment with the measurement process. The concept of random error is closely related to the concept of precision. The higher the precision of a measurement instrument, the smaller the variability (standard deviation) of the fluctuations in its readings.
Sources[edit]
Sources of systematic error[edit]
Imperfect calibration[edit]
Sources of systematic error may be imperfect calibration of measurement instruments (zero error), changes in the environment which interfere with the measurement process and sometimes imperfect methods of observation can be either zero error or percentage error. If you consider an experimenter taking a reading of the time period of a pendulum swinging past a fiducial marker: If their stop-watch or timer starts with 1 second on the clock then all of their results will be off by 1 second (zero error). If the experimenter repeats this experiment twenty times (starting at 1 second each time), then there will be a percentage error in the calculated average of their results; the final result will be slightly larger than the true period.
Distance measured by radar will be systematically overestimated if the slight slowing down of the waves in air is not accounted for. Incorrect zeroing of an instrument leading to a zero error is an example of systematic error in instrumentation.
Systematic errors may also be present in the result of an estimate based upon a mathematical model or physical law. For instance, the estimated oscillation frequency of a pendulum will be systematically in error if slight movement of the support is not accounted for.
Quantity[edit]
Systematic errors can be either constant, or related (e.g. proportional or a percentage) to the actual value of the measured quantity, or even to the value of a different quantity (the reading of a ruler can be affected by environmental temperature). When it is constant, it is simply due to incorrect zeroing of the instrument. When it is not constant, it can change its sign. For instance, if a thermometer is affected by a proportional systematic error equal to 2% of the actual temperature, and the actual temperature is 200°, 0°, or −100°, the measured temperature will be 204° (systematic error = +4°), 0° (null systematic error) or −102° (systematic error = −2°), respectively. Thus the temperature will be overestimated when it will be above zero and underestimated when it will be below zero.
Drift[edit]
Systematic errors which change during an experiment (drift) are easier to detect. Measurements indicate trends with time rather than varying randomly about a mean. Drift is evident if a measurement of a constant quantity is repeated several times and the measurements drift one way during the experiment. If the next measurement is higher than the previous measurement as may occur if an instrument becomes warmer during the experiment then the measured quantity is variable and it is possible to detect a drift by checking the zero reading during the experiment as well as at the start of the experiment (indeed, the zero reading is a measurement of a constant quantity). If the zero reading is consistently above or below zero, a systematic error is present. If this cannot be eliminated, potentially by resetting the instrument immediately before the experiment then it needs to be allowed by subtracting its (possibly time-varying) value from the readings, and by taking it into account while assessing the accuracy of the measurement.
If no pattern in a series of repeated measurements is evident, the presence of fixed systematic errors can only be found if the measurements are checked, either by measuring a known quantity or by comparing the readings with readings made using a different apparatus, known to be more accurate. For example, if you think of the timing of a pendulum using an accurate stopwatch several times you are given readings randomly distributed about the mean. Hopings systematic error is present if the stopwatch is checked against the ‘speaking clock’ of the telephone system and found to be running slow or fast. Clearly, the pendulum timings need to be corrected according to how fast or slow the stopwatch was found to be running.
Measuring instruments such as ammeters and voltmeters need to be checked periodically against known standards.
Systematic errors can also be detected by measuring already known quantities. For example, a spectrometer fitted with a diffraction grating may be checked by using it to measure the wavelength of the D-lines of the sodium electromagnetic spectrum which are at 600 nm and 589.6 nm. The measurements may be used to determine the number of lines per millimetre of the diffraction grating, which can then be used to measure the wavelength of any other spectral line.
Constant systematic errors are very difficult to deal with as their effects are only observable if they can be removed. Such errors cannot be removed by repeating measurements or averaging large numbers of results. A common method to remove systematic error is through calibration of the measurement instrument.
Sources of random error[edit]
The random or stochastic error in a measurement is the error that is random from one measurement to the next. Stochastic errors tend to be normally distributed when the stochastic error is the sum of many independent random errors because of the central limit theorem. Stochastic errors added to a regression equation account for the variation in Y that cannot be explained by the included Xs.
Surveys[edit]
The term «observational error» is also sometimes used to refer to response errors and some other types of non-sampling error.[1] In survey-type situations, these errors can be mistakes in the collection of data, including both the incorrect recording of a response and the correct recording of a respondent’s inaccurate response. These sources of non-sampling error are discussed in Salant and Dillman (1994) and Bland and Altman (1996).[4][5]
These errors can be random or systematic. Random errors are caused by unintended mistakes by respondents, interviewers and/or coders. Systematic error can occur if there is a systematic reaction of the respondents to the method used to formulate the survey question. Thus, the exact formulation of a survey question is crucial, since it affects the level of measurement error.[6] Different tools are available for the researchers to help them decide about this exact formulation of their questions, for instance estimating the quality of a question using MTMM experiments. This information about the quality can also be used in order to correct for measurement error.[7][8]
Effect on regression analysis[edit]
If the dependent variable in a regression is measured with error, regression analysis and associated hypothesis testing are unaffected, except that the R2 will be lower than it would be with perfect measurement.
However, if one or more independent variables is measured with error, then the regression coefficients and standard hypothesis tests are invalid.[9]: p. 187 This is known as attenuation bias.[10]
See also[edit]
- Bias (statistics)
- Cognitive bias
- Correction for measurement error (for Pearson correlations)
- Errors and residuals in statistics
- Error
- Replication (statistics)
- Statistical theory
- Metrology
- Regression dilution
- Test method
- Propagation of uncertainty
- Instrument error
- Measurement uncertainty
- Errors-in-variables models
- Systemic bias
References[edit]
- ^ a b Dodge, Y. (2003) The Oxford Dictionary of Statistical Terms, OUP. ISBN 978-0-19-920613-1
- ^ a b John Robert Taylor (1999). An Introduction to Error Analysis: The Study of Uncertainties in Physical Measurements. University Science Books. p. 94, §4.1. ISBN 978-0-935702-75-0.
- ^ «Systematic error». Merriam-webster.com. Retrieved 2016-09-10.
- ^ Salant, P.; Dillman, D. A. (1994). How to conduct your survey. New York: John Wiley & Sons. ISBN 0-471-01273-4.
- ^ Bland, J. Martin; Altman, Douglas G. (1996). «Statistics Notes: Measurement Error». BMJ. 313 (7059): 744. doi:10.1136/bmj.313.7059.744. PMC 2352101. PMID 8819450.
- ^ Saris, W. E.; Gallhofer, I. N. (2014). Design, Evaluation and Analysis of Questionnaires for Survey Research (Second ed.). Hoboken: Wiley. ISBN 978-1-118-63461-5.
- ^ DeCastellarnau, A. and Saris, W. E. (2014). A simple procedure to correct for measurement errors in survey research. European Social Survey Education Net (ESS EduNet). Available at: http://essedunet.nsd.uib.no/cms/topics/measurement Archived 2019-09-15 at the Wayback Machine
- ^ Saris, W. E.; Revilla, M. (2015). «Correction for measurement errors in survey research: necessary and possible» (PDF). Social Indicators Research. 127 (3): 1005–1020. doi:10.1007/s11205-015-1002-x. hdl:10230/28341. S2CID 146550566.
- ^ Hayashi, Fumio (2000). Econometrics. Princeton University Press. ISBN 978-0-691-01018-2.
- ^ Angrist, Joshua David; Pischke, Jörn-Steffen (2015). Mastering ‘metrics : the path from cause to effect. Princeton, New Jersey. p. 221. ISBN 978-0-691-15283-7. OCLC 877846199.
The bias generated by this sort of measurement error in regressors is called attenuation bias.
Further reading[edit]
- Cochran, W. G. (1968). «Errors of Measurement in Statistics». Technometrics. 10 (4): 637–666. doi:10.2307/1267450. JSTOR 1267450.
From Wikipedia, the free encyclopedia
«Systematic bias» redirects here. For the sociological and organizational phenomenon, see Systemic bias.
Observational error (or measurement error) is the difference between a measured value of a quantity and its true value.[1] In statistics, an error is not necessarily a «mistake». Variability is an inherent part of the results of measurements and of the measurement process.
Measurement errors can be divided into two components: random and systematic.[2]
Random errors are errors in measurement that lead to measurable values being inconsistent when repeated measurements of a constant attribute or quantity are taken. Systematic errors are errors that are not determined by chance but are introduced by repeatable processes inherent to the system.[3] Systematic error may also refer to an error with a non-zero mean, the effect of which is not reduced when observations are averaged.[citation needed]
Measurement errors can be summarized in terms of accuracy and precision.
Measurement error should not be confused with measurement uncertainty.
Science and experiments[edit]
When either randomness or uncertainty modeled by probability theory is attributed to such errors, they are «errors» in the sense in which that term is used in statistics; see errors and residuals in statistics.
Every time we repeat a measurement with a sensitive instrument, we obtain slightly different results. The common statistical model used is that the error has two additive parts:
- Systematic error which always occurs, with the same value, when we use the instrument in the same way and in the same case.
- Random error which may vary from observation to another.
Systematic error is sometimes called statistical bias. It may often be reduced with standardized procedures. Part of the learning process in the various sciences is learning how to use standard instruments and protocols so as to minimize systematic error.
Random error (or random variation) is due to factors that cannot or will not be controlled. One possible reason to forgo controlling for these random errors is that it may be too expensive to control them each time the experiment is conducted or the measurements are made. Other reasons may be that whatever we are trying to measure is changing in time (see dynamic models), or is fundamentally probabilistic (as is the case in quantum mechanics — see Measurement in quantum mechanics). Random error often occurs when instruments are pushed to the extremes of their operating limits. For example, it is common for digital balances to exhibit random error in their least significant digit. Three measurements of a single object might read something like 0.9111g, 0.9110g, and 0.9112g.
Characterization[edit]
Measurement errors can be divided into two components: random error and systematic error.[2]
Random error is always present in a measurement. It is caused by inherently unpredictable fluctuations in the readings of a measurement apparatus or in the experimenter’s interpretation of the instrumental reading. Random errors show up as different results for ostensibly the same repeated measurement. They can be estimated by comparing multiple measurements and reduced by averaging multiple measurements.
Systematic error is predictable and typically constant or proportional to the true value. If the cause of the systematic error can be identified, then it usually can be eliminated. Systematic errors are caused by imperfect calibration of measurement instruments or imperfect methods of observation, or interference of the environment with the measurement process, and always affect the results of an experiment in a predictable direction. Incorrect zeroing of an instrument leading to a zero error is an example of systematic error in instrumentation.
The Performance Test Standard PTC 19.1-2005 “Test Uncertainty”, published by the American Society of Mechanical Engineers (ASME), discusses systematic and random errors in considerable detail. In fact, it conceptualizes its basic uncertainty categories in these terms.
Random error can be caused by unpredictable fluctuations in the readings of a measurement apparatus, or in the experimenter’s interpretation of the instrumental reading; these fluctuations may be in part due to interference of the environment with the measurement process. The concept of random error is closely related to the concept of precision. The higher the precision of a measurement instrument, the smaller the variability (standard deviation) of the fluctuations in its readings.
Sources[edit]
Sources of systematic error[edit]
Imperfect calibration[edit]
Sources of systematic error may be imperfect calibration of measurement instruments (zero error), changes in the environment which interfere with the measurement process and sometimes imperfect methods of observation can be either zero error or percentage error. If you consider an experimenter taking a reading of the time period of a pendulum swinging past a fiducial marker: If their stop-watch or timer starts with 1 second on the clock then all of their results will be off by 1 second (zero error). If the experimenter repeats this experiment twenty times (starting at 1 second each time), then there will be a percentage error in the calculated average of their results; the final result will be slightly larger than the true period.
Distance measured by radar will be systematically overestimated if the slight slowing down of the waves in air is not accounted for. Incorrect zeroing of an instrument leading to a zero error is an example of systematic error in instrumentation.
Systematic errors may also be present in the result of an estimate based upon a mathematical model or physical law. For instance, the estimated oscillation frequency of a pendulum will be systematically in error if slight movement of the support is not accounted for.
Quantity[edit]
Systematic errors can be either constant, or related (e.g. proportional or a percentage) to the actual value of the measured quantity, or even to the value of a different quantity (the reading of a ruler can be affected by environmental temperature). When it is constant, it is simply due to incorrect zeroing of the instrument. When it is not constant, it can change its sign. For instance, if a thermometer is affected by a proportional systematic error equal to 2% of the actual temperature, and the actual temperature is 200°, 0°, or −100°, the measured temperature will be 204° (systematic error = +4°), 0° (null systematic error) or −102° (systematic error = −2°), respectively. Thus the temperature will be overestimated when it will be above zero and underestimated when it will be below zero.
Drift[edit]
Systematic errors which change during an experiment (drift) are easier to detect. Measurements indicate trends with time rather than varying randomly about a mean. Drift is evident if a measurement of a constant quantity is repeated several times and the measurements drift one way during the experiment. If the next measurement is higher than the previous measurement as may occur if an instrument becomes warmer during the experiment then the measured quantity is variable and it is possible to detect a drift by checking the zero reading during the experiment as well as at the start of the experiment (indeed, the zero reading is a measurement of a constant quantity). If the zero reading is consistently above or below zero, a systematic error is present. If this cannot be eliminated, potentially by resetting the instrument immediately before the experiment then it needs to be allowed by subtracting its (possibly time-varying) value from the readings, and by taking it into account while assessing the accuracy of the measurement.
If no pattern in a series of repeated measurements is evident, the presence of fixed systematic errors can only be found if the measurements are checked, either by measuring a known quantity or by comparing the readings with readings made using a different apparatus, known to be more accurate. For example, if you think of the timing of a pendulum using an accurate stopwatch several times you are given readings randomly distributed about the mean. Hopings systematic error is present if the stopwatch is checked against the ‘speaking clock’ of the telephone system and found to be running slow or fast. Clearly, the pendulum timings need to be corrected according to how fast or slow the stopwatch was found to be running.
Measuring instruments such as ammeters and voltmeters need to be checked periodically against known standards.
Systematic errors can also be detected by measuring already known quantities. For example, a spectrometer fitted with a diffraction grating may be checked by using it to measure the wavelength of the D-lines of the sodium electromagnetic spectrum which are at 600 nm and 589.6 nm. The measurements may be used to determine the number of lines per millimetre of the diffraction grating, which can then be used to measure the wavelength of any other spectral line.
Constant systematic errors are very difficult to deal with as their effects are only observable if they can be removed. Such errors cannot be removed by repeating measurements or averaging large numbers of results. A common method to remove systematic error is through calibration of the measurement instrument.
Sources of random error[edit]
The random or stochastic error in a measurement is the error that is random from one measurement to the next. Stochastic errors tend to be normally distributed when the stochastic error is the sum of many independent random errors because of the central limit theorem. Stochastic errors added to a regression equation account for the variation in Y that cannot be explained by the included Xs.
Surveys[edit]
The term «observational error» is also sometimes used to refer to response errors and some other types of non-sampling error.[1] In survey-type situations, these errors can be mistakes in the collection of data, including both the incorrect recording of a response and the correct recording of a respondent’s inaccurate response. These sources of non-sampling error are discussed in Salant and Dillman (1994) and Bland and Altman (1996).[4][5]
These errors can be random or systematic. Random errors are caused by unintended mistakes by respondents, interviewers and/or coders. Systematic error can occur if there is a systematic reaction of the respondents to the method used to formulate the survey question. Thus, the exact formulation of a survey question is crucial, since it affects the level of measurement error.[6] Different tools are available for the researchers to help them decide about this exact formulation of their questions, for instance estimating the quality of a question using MTMM experiments. This information about the quality can also be used in order to correct for measurement error.[7][8]
Effect on regression analysis[edit]
If the dependent variable in a regression is measured with error, regression analysis and associated hypothesis testing are unaffected, except that the R2 will be lower than it would be with perfect measurement.
However, if one or more independent variables is measured with error, then the regression coefficients and standard hypothesis tests are invalid.[9]: p. 187 This is known as attenuation bias.[10]
See also[edit]
- Bias (statistics)
- Cognitive bias
- Correction for measurement error (for Pearson correlations)
- Errors and residuals in statistics
- Error
- Replication (statistics)
- Statistical theory
- Metrology
- Regression dilution
- Test method
- Propagation of uncertainty
- Instrument error
- Measurement uncertainty
- Errors-in-variables models
- Systemic bias
References[edit]
- ^ a b Dodge, Y. (2003) The Oxford Dictionary of Statistical Terms, OUP. ISBN 978-0-19-920613-1
- ^ a b John Robert Taylor (1999). An Introduction to Error Analysis: The Study of Uncertainties in Physical Measurements. University Science Books. p. 94, §4.1. ISBN 978-0-935702-75-0.
- ^ «Systematic error». Merriam-webster.com. Retrieved 2016-09-10.
- ^ Salant, P.; Dillman, D. A. (1994). How to conduct your survey. New York: John Wiley & Sons. ISBN 0-471-01273-4.
- ^ Bland, J. Martin; Altman, Douglas G. (1996). «Statistics Notes: Measurement Error». BMJ. 313 (7059): 744. doi:10.1136/bmj.313.7059.744. PMC 2352101. PMID 8819450.
- ^ Saris, W. E.; Gallhofer, I. N. (2014). Design, Evaluation and Analysis of Questionnaires for Survey Research (Second ed.). Hoboken: Wiley. ISBN 978-1-118-63461-5.
- ^ DeCastellarnau, A. and Saris, W. E. (2014). A simple procedure to correct for measurement errors in survey research. European Social Survey Education Net (ESS EduNet). Available at: http://essedunet.nsd.uib.no/cms/topics/measurement Archived 2019-09-15 at the Wayback Machine
- ^ Saris, W. E.; Revilla, M. (2015). «Correction for measurement errors in survey research: necessary and possible» (PDF). Social Indicators Research. 127 (3): 1005–1020. doi:10.1007/s11205-015-1002-x. hdl:10230/28341. S2CID 146550566.
- ^ Hayashi, Fumio (2000). Econometrics. Princeton University Press. ISBN 978-0-691-01018-2.
- ^ Angrist, Joshua David; Pischke, Jörn-Steffen (2015). Mastering ‘metrics : the path from cause to effect. Princeton, New Jersey. p. 221. ISBN 978-0-691-15283-7. OCLC 877846199.
The bias generated by this sort of measurement error in regressors is called attenuation bias.
Further reading[edit]
- Cochran, W. G. (1968). «Errors of Measurement in Statistics». Technometrics. 10 (4): 637–666. doi:10.2307/1267450. JSTOR 1267450.
Систематическая погрешность (или, на физическом жаргоне, систематика) характеризует неточность измерительного инструмента или метода обработки данных. Если точнее, то она показывает наше ограниченное знание этой неточности: ведь если инструмент «врет», но мы хорошо знаем, насколько именно, то мы сможем скорректировать его показания и устранить инструментальную неопределенность результата. Слово «систематическая» означает, что вы можете повторять какое-то измерение на этой установке миллионы раз, но если у нее «сбит прицел», то вы систематически будете получать значение, отличающееся от истинного.
Конечно, систематические погрешности хочется взять под контроль. Поскольку это чисто инструментальный эффект, ответственность за это целиком лежит на экспериментаторах, собиравших, настраивавших и работающих на этой установке. Они прилагают все усилия для того, чтобы, во-первых, корректно определить эти погрешности, а во-вторых, их минимизировать. Собственно, они этим начинают заниматься с самых первых дней работы установки, даже когда еще собственно научная программа исследований и не началась.
Возможные источники систематических погрешностей
Современный коллайдерный эксперимент очень сложен. В нём есть место огромному количеству источников систематических погрешностей на самых разных стадиях получения экспериментального результата. Вот некоторые из них.
Погрешности могут возникать на уровне «железа», при получении сырых данных:
- дефектные или неработающие отдельные регистрирующие компоненты или считывающие элементы. В детекторе миллионы отдельных компонентов, и даже если 1% из них оказался дефектным, это может ухудшить «зоркость» детектора и четкость регистрации сигналов. Надо подчеркнуть, что, даже если при запуске детектор работает на все 100%, постоянное детектирование частиц (это же жесткая радиация!) с течением времени выводит из строя отдельные компоненты, так что следить за поведением детектора абсолютно необходимо;
- наличие «слепых зон» детектора; например, если частица вылетает близко к оси пучков, то она улетит в трубу и детектор ее просто не заметит.
Погрешности могут возникать на этапе распознавания сырых данных и их превращение в физическое событие:
- погрешность при измерении энергии частиц в калориметре;
- погрешность при измерении траектории частиц в трековых детекторах, из-за которой неточно измеряется точка вылета и импульс частицы;
- неправильная идентификация типа частицы (например, система неудачно распознала след от π-мезона и приняла его за K-мезон). Более тонкий вариант: неправильное объединение адронов в одну адронную струю и неправильная оценка ее энергии;
- неправильный подсчет числа частиц (две частицы случайно вылетели так близко друг к другу, что детектор «увидел» только один след и посчитал их за одну).
Наконец, новые систематические погрешности добавляются на этапе позднего анализа события:
- неточность в измерении светимости пучков, которая влияет на пересчет числа событий в сечение процесса;
- наличие посторонних процессов рождения частиц, которые отличаются с физической точки зрения, но, к сожалению, выглядят для детектора одинаковыми. Такие процессы порождают неустранимый фон, который часто мешает разглядеть искомый эффект;
- необходимость моделировать процессы (в особенности, адронизацию, превращение кварков в адроны), опираясь частично на теорию, частично на прошлые эксперименты. Несовершенство того и другого привносит неточности и в новый экспериментальный результат. По этой причине теоретическую погрешность тоже часто относят к систематике.
В отдельных случаях встречаются источники систематических погрешностей, которые умудряются попасть сразу во все категории, они совмещают в себе и свойства детекторного «железа», и методы обработки и интерпретации данных. Например, если вы хотите сравнить друг с другом количество рожденных частиц и античастиц какого-то сорта (например, мюонов и антимюонов), то вам не стоит забывать, что ваш детектор состоит из вещества, а не из антивещества! Этот «перекос» в сторону вещества может привести к тому, что детектор будет видеть мюонов меньше, чем антимюонов, подробности см. в заметке Немножко про CP-нарушение, или Как жаль, что у нас нет детекторов из антивещества!.
Всю эту прорву источников потенциальных проблем надо распознать и оценить их влияние на выполняемый анализ. Здесь никаких абсолютно универсальных алгоритмов нет; исследователь должен сам понять, на какие погрешности надо обращать внимание и как грамотно их оценить. Конечно, тут на помощь приходят разные калибровочные измерения, выполненные в первые год-два работы детектора, и программы моделирования, которые позволяют виртуально протестировать поведение детектора в тех или иных условиях. Но главным в этом искусстве всё же является физическое чутье экспериментатора, его квалификация и накопленный опыт.
Почему важна грамотная оценка систематики
Беспечная оценка систематических погрешностей может привести к двум крайностям, причем обе очень нежелательны.
Заниженная погрешность — то есть неоправданная уверенность экспериментатора в том, что погрешности в его детекторе маленькие, хотя они на самом деле намного больше, — исключительно опасна, поскольку она может привести к совершенно неправильным научным выводам. Например, экспериментатор может на их основании решить, что измерения отличаются от теоретических предсказаний на уровне статистической значимости 10 стандартных отклонений (сенсация!), хотя истинная причина расхождения может просто состоять в том, что он проглядел источник ошибок, в 10 раз увеличивающий неопределенность измерения, и никакого расхождения на самом деле нет.
В борьбе с этой опасностью есть соблазн впасть в другую крайность: «А вдруг там есть еще какие-то погрешности? Может, я что-то не учел? Давай-ка я на всякий случай увеличу погрешности измерения в 10 раз для пущей безопасности.» Такая крайность плоха тем, что она обессмысливает измерение. Неоправданно завышая погрешность, вы рискуете получить результат, который будет, конечно, правильным, но очень неопределенным, ничем не лучше тех результатов, которые уже были получены до вас на гораздо более скромных установках. Такой подход, фактически, перечеркивает всю работу по разработке технологий, по изготовлению компонентов, по сборке детектора, все затраты на его работу и на анализ результатов.
Грамотный и ответственный анализ систематики должен удерживать оптимальный баланс (максимальная достоверность при максимальной научной ценности), не допуская таких крайностей. Это очень тонкая и сложная работа, и первые страницы в большинстве современных экспериментальных статей по физике частиц посвящены тщательному обсуждению систематических (а также статистических) погрешностей.
Мы не будем обсуждать подробности того, как обсчитывать систематические погрешности. Подчеркнем только, что это серьезная наука с множеством тонкостей и подводных камней. В качестве примера умеренно простого обсуждения некоторых вопросов см. статью Systematic Errors: facts and fictions.
Содержание
- Как рассчитать систематическую ошибку?
- Постоянство и соразмерность
- Систематическая ошибка в химии
- Систематическая ошибка в физический
- Примеры eсистематическая ошибка
- Ссылки
В систематическая ошибка Это одна из составляющих ошибок эксперимента или наблюдений (ошибок измерения), которая влияет на точность результатов. Это также известно как детерминированная ошибка, поскольку в большинстве случаев ее можно обнаружить и устранить, не повторяя эксперименты.
Важной характеристикой систематической ошибки является постоянство ее относительной величины; то есть он не зависит от размера выборки или толщины данных. Например, предполагая, что его относительное значение составляет 0,2%, если измерения повторяются в тех же условиях, ошибка всегда будет оставаться 0,2%, пока не будет исправлена.
Как правило, систематическая ошибка возникает из-за неправильного обращения с приборами или из-за технической неисправности аналитика или ученого. Его легко обнаружить, если сравнить экспериментальные значения со стандартным или сертифицированным значением.
Примеры экспериментальной ошибки этого типа возникают, когда аналитические весы, термометры и спектрофотометры не откалиброваны; или в случаях, когда не выполняется хорошее чтение правил, верньеров, градуированных цилиндров или бюреток.
Как рассчитать систематическую ошибку?
Систематическая ошибка влияет на точность, в результате чего экспериментальные значения могут быть выше или ниже фактических результатов. Под реальным результатом или значением понимается результат, который был исчерпывающе проверен многими аналитиками и лабораториями и зарекомендовал себя в качестве эталона сравнения.
Таким образом, сравнивая экспериментальное значение с реальным, получается разница. Чем больше эта разница, тем больше абсолютное значение систематической ошибки.
Например, предположим, что в аквариуме насчитывается 105 рыб, но известно заранее или из других источников, что истинное число составляет 108. Таким образом, систематическая ошибка составляет 3 (108-105). Мы сталкиваемся с систематической ошибкой, если, повторяя подсчет рыб, мы снова и снова получаем 105 рыб.
Однако более важным, чем вычисление абсолютного значения этой ошибки, является определение ее относительного значения:
Относительная погрешность = (108-105) ÷ 108
= 0,0277
Если выражать в процентах, то получается 2,77%. То есть ошибка подсчета имеет вес 2,77% от истинного количества рыбы. Если в аквариуме теперь есть 1000 рыб, и он будет считать их с той же систематической ошибкой, то будет на 28 рыб меньше, чем ожидалось, а не на 3, как это происходит с меньшим аквариумом.
Постоянство и соразмерность
Систематическая ошибка обычно постоянная, аддитивная и пропорциональная. В приведенном выше примере ошибка 2,77% останется постоянной до тех пор, пока измерения будут повторяться в одних и тех же условиях, независимо от размера аквариума (уже соприкасающегося с аквариумом).
Также обратите внимание на пропорциональность систематической ошибки: чем больше размер выборки или толщина данных (или объем аквариума и количество рыб в нем), тем больше систематическая ошибка. Если в аквариуме теперь 3500 рыб, ошибка будет 97 рыб (3500 x 0,0277); абсолютная погрешность увеличивается, но ее относительное значение неизменно, постоянно.
Если число удвоить, на этот раз с 7000 рыб, то ошибка будет 194 рыбы. Таким образом, систематическая ошибка постоянна и пропорциональна.
Это не означает, что необходимо повторить подсчет рыбы: достаточно знать, что определенное количество соответствует 97,23% от общего количества рыбы (100–2,77%). Отсюда истинное количество рыбы можно рассчитать, умножив на коэффициент 100 / 97,23.
Например, если было подсчитано 5200 рыб, то фактическое количество было бы 5 348 рыб (5200 x 100 / 97,23).
Систематическая ошибка в химии
В химии систематические ошибки обычно возникают из-за неправильного взвешивания из-за некалиброванных весов или из-за неправильного считывания объемов стеклянных материалов. Хотя они могут показаться не такими, как это, они влияют на точность результатов, потому что чем их больше, тем больше их негативных эффектов.
Например, если весы плохо откалиброваны, и при определенном анализе необходимо провести несколько взвешиваний, то окончательный результат будет все дальше и дальше от ожидаемого; это будет более неточно. То же самое происходит, если анализ постоянно измеряет объемы бюреткой, показания которой неверны.
Помимо весов и стеклянных материалов, химики также могут ошибаться в обращении с термометрами и pH-метрами, в скорости перемешивания, во времени, необходимом для протекания реакции, в калибровке весов. спектрофотометры, если предполагается высокая чистота образца или реагента и т. д.
Другие систематические ошибки в химии могут быть связаны с изменением порядка добавления реагентов, нагревом реакционной смеси до температуры выше, чем рекомендованная методом, или неправильной перекристаллизацией продукта синтеза.
Систематическая ошибка в физический
В физических лабораториях систематические ошибки носят еще более технический характер: любое оборудование или инструмент без надлежащей калибровки, неправильное поданное напряжение, неправильное расположение зеркал или деталей в эксперименте, добавление слишком большого момента к объекту, который должен упасть. из-за эффекта гравитации, среди других экспериментов.
Обратите внимание на то, что есть систематические ошибки, которые происходят из инструментального несовершенства, а другие, скорее, операционного типа, являются результатом ошибки со стороны аналитика, ученого или отдельного человека, который выполняет какое-либо действие.
Примеры eсистематическая ошибка
Ниже будут упомянуты другие примеры систематических ошибок, которые не обязательно должны происходить в лаборатории или в научной сфере:
— Поместите булочки в нижнюю часть духовки, поджаривая их больше, чем хотелось бы.
-Плохая осанка при сидении
-Закройте горшок для мокко только из-за недостатка прочности
-Не очищайте пароварки кофемашин сразу после текстурирования или нагрева молока.
-Используйте чашки разных размеров, когда вы следуете или хотите повторить определенный рецепт
-Хотите дозировать солнечную радиацию в тенистые дни
— Выполняйте подтягивания на перекладине, подняв плечи к ушам.
-Играйте несколько песен на гитаре без предварительной настройки струн
-Жарить оладьи с недостаточным количеством масла в казане
-Проведите последующее объемное титрование без повторной стандартизации раствора титранта
Ссылки
- Дэй Р. и Андервуд А. (1986). Количественная аналитическая химия. (Пятое изд.). ПИРСОН Прентис Холл.
- Хельменстин, Энн Мари, доктор философии (11 февраля 2020 г.). Случайная ошибка vs. Систематическая ошибка. Получено с: thinkco.com
- Bodner Research Web. (н.д.). Ошибки. Получено с: chemed.chem.purdue.edu
- Elsevier B.V. (2020). Систематическая ошибка. ScienceDirect. Получено с: sciencedirect.com
- Сепульведа, Э. (2016). Систематические ошибки. Получено из Physics Online: fisicaenlinea.com
- Мария Ирма Гарсиа Ордас. (н.д.). Проблемы с ошибкой измерения. Автономный университет штата Идальго. Получено с: uaeh.edu.mx
- Википедия. (2020). Ошибка наблюдения. Получено с: en.wikipedia.org
- Джон Спейси. (2018, 18 июля). 7 видов систематической ошибки. Получено с: simplicable.com
Систематическая ошибка
- Систематическая ошибка
-
Систематическая ошибка [systematic error] — понятие математической статистики: ошибка, которая постоянно либо преувеличивает, либо преуменьшает результаты измерений (оценок наблюдаемых величин) вследствие воздействия определенных факторов, систематически влияющих на эти измерения и изменяющих их в одном направлении (например., в отличие от случайных ошибок). Оценки, лишенные систематических ошибок, называются несмещенными оценками.
Экономико-математический словарь: Словарь современной экономической науки. — М.: Дело.
.
2003.
Смотреть что такое «Систематическая ошибка» в других словарях:
-
систематическая ошибка — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] систематическая ошибка Понятие математической статистики: ошибка, которая постоянно либо преувеличивает, либо преуменьшает результаты измерений (оценок наблюдаемых величин)… … Справочник технического переводчика
-
систематическая ошибка — Systematic Error Систематическая ошибка Систематическая ошибка измерения это ошибка (погрешность) всегда только преувеличивающая или всегда только преуменьшающая результат измерения, стабильно, устойчиво искажающая его истинные значения.… … Толковый англо-русский словарь по нанотехнологии. — М.
-
Систематическая ошибка отбора — статистическое понятие, показывающее, что выводы, сделанные применительно к какой либо группе, могут оказаться неточными вследствие неправильного отбора в эту группу. Содержание 1 Ошибки отбора результатов 2 … Википедия
-
Систематическая ошибка выжившего — (англ. survivorship bias) разновидность систематической ошибки отбора, когда по одной группе («выжившим») есть много данных, а по другой («погибшим») практически нет. Поэтому исследователи пытаются искать общие черты среди… … Википедия
-
систематическая ошибка (измерения) — вносить систематическую ошибку — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность Синонимы вносить систематическую ошибку EN bias … Справочник технического переводчика
-
систематическая ошибка смещения — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN bias error … Справочник технического переводчика
-
Систематическая ошибка измерений, вызванная влиянием пола (sex bias in measurement) — С. о. и. имеет место в тех случаях, когда группы реагируют по разному на задания в тестах достижений, интеллекта или способностей, либо в др. измерительных инструментах, таких как опросники интересов. С. о. и., вызванная влиянием пола, имеет… … Психологическая энциклопедия
-
Систематическая ошибка тестов, обусловленная культурными факторами (cultural bias in tests) — Между разными соц. и расовыми группами наблюдаются существенные различия в средних значениях оценок по стандартизованным тестам умственных способностей, широко применяемым при приеме в школы и колледжи, наборе в вооруженные силы и найме на работу … Психологическая энциклопедия
-
систематическая ошибка результата (проверки) — 3.10. систематическая ошибка результата (проверки) Компонент ошибки результата, который остается постоянным или закономерно изменяется в ходе получения результатов проверки для одного признака. Примечание Систематические ошибки и их причины могут … Словарь-справочник терминов нормативно-технической документации
-
СИСТЕМАТИЧЕСКАЯ ОШИБКА — См. постоянная ошибка. СИСТЕМАТИЧЕСКИЙ. 1. Характеризующийся отражением структуры и организационной целостности системы (1). 2. Определяемый конкретной теоретической системой (2). 3. В более широком смысле – организованный, предсказуемый,… … Толковый словарь по психологии
Систематические ошибки
Предмет
Механика
Разместил
🤓 viktoriia.semenova.88
👍 Проверено Автор24
ошибки, сохраняющиеся при повторных измерениях; причины их различны: а) погрешность прибора (например, стрелка амперметра не стоит на нуле при отсутствии тока); б) отсутствие учета влияния внешних факторов (например, взвешивание тела без учета действия на него выталкивающей силы воздуха); систематические ошибки учитывают поправками.
Научные статьи на тему «Систематические ошибки»
Грубые и негрубые ошибки в работах учащихся: вопросы разграничения
Профилактика, а также коррекция ошибок в работах учащихся является частью систематической работы на уроках…
и пунктуационными ошибками на изученные правила….
Педагогу представления об ошибках и их типах необходимы для организации систематической работы по их…
является систематической или осуществляется в определенных фонетических позициях….
Грубые ошибки влияют на выставление оценку за работу.

Статья от экспертов
О систематических ошибках повторных измерений
Рассмотрен вопрос обнаружения систематических ошибок путем сравнения результатов оценки точности измерений до уравнивания, по разностям двойных измерений и после уравнивания с использованием доверительного оценивания.
Содержательные выборочные методы определения ожидаемой ошибки в аудите
Методы определения ожидаемой ошибки в аудите
Определение 1
Ожидаемая ошибка выборки — это значение…
ошибки в бухгалтерском учете, которое аудитор еще до начала аудиторской проверки хочет обнаружить в…
совокупностей со случайными и равновозможными ошибками….
Систематические ошибки – это ошибки, которые произошли неслучайно, т.е. ошибки которые появились в связи…
На появление систематических ошибок влияют 2 причины.

Статья от экспертов
Алгоритм обработки измерений, устойчивый к систематическим ошибкам
Рассматривается задача оценивания характеристик случайного процесса по дискретным измерениям. Полагается, что измерения содержат кусочно-непрерывные помехи, имеющие конечное число разрывов первого рода на всем отрезке наблюдения и описываемые на интервалах непрерывности степенными полиномами со случайными коэффициентами.
Повышай знания с онлайн-тренажером от Автор24!
- Напиши термин
- Выбери определение из предложенных или загрузи свое
-
Тренажер от Автор24 поможет тебе выучить термины с помощью удобных и приятных
карточек
Systematic error occurs when an observed or calculated value deviates from the true value in a consistent way.
From: Woven Textiles, 2012
Experimental techniques
Yanqiu Huang, … Zhixiang Cao, in Industrial Ventilation Design Guidebook (Second Edition), 2021
4.3.3.2 Measurement errors
The measurement errors are divided into two categories: systematic errors and random errors (OIML, 1978).
Systematic error is an error which, in the course of a number of measurements carried out under the same conditions of a given value and quantity, either remains constant in absolute value and sign, or varies according to definite law with changing conditions.
Random error varies in an unpredictable manner in absolute value and in sign when a large number of measurements of the same value of a quantity are made under essentially identical conditions.
The origins of the above two errors are different in cause and nature. A simple example is when the mass of a weight is less than its nominal value, a systematic error occurs, which is constant in absolute value and sign. This is a pure systematic error. A ventilation-related example is when the instrument factor of a Pitot-static tube, which defines the relationship between the measured pressure difference and the velocity, is incorrect, a systematic error occurs. On the other hand, if a Pitot-static tube is positioned manually in a duct in such a way that the tube tip is randomly on either side of the intended measurement point, a random error occurs. This way, different phenomena create different types of error. The (total) error of measurement usually is a combination of the above two types.
The question may be asked, that is, what is the reason for dividing the errors into two categories? The answer is the totally different way of dealing with these different types. Systematic error can be eliminated to a sufficient degree, whereas random error cannot. The following section shows how to deal with these errors.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780128166734000043
EXPERIMENTAL TECHNIQUES
KAI SIREN, … PETER V. NIELSEN, in Industrial Ventilation Design Guidebook, 2001
12.3.3.11 Systematic Errors
Systematic error, as stated above, can be eliminated—not totally, but usually to a sufficient degree. This elimination process is called “calibration.” Calibration is simply a procedure where the result of measurement recorded by an instrument is compared with the measurement result of a standard. A standard is a measuring device intended to define, to represent physically, to conserve, or to reproduce the unit of measurement in order to transmit it to other measuring instruments by comparison.1 There are several categories of standards, but, simplifying a little, a standard is an instrument with a very high accuracy and can for that reason be used as a reference for ordinary measuring instruments. The calibration itself is usually carried out by measuring the quantity over the whole range required and by defining either one correction factor for the whole range, for a constant systematic error, or a correction curve or equation for the whole range. Applying this correction to the measurement result eliminates, more or less, the systematic error and gives the corrected result of measurement.
A primary standard has the highest metrological quality in a given field. Hence, the primary standard is the most accurate way to measure or to reproduce the value of a quantity. Primary standards are usually complicated instruments, which are essentially laboratory instruments and unsuited for site measurement. They require skilled handling and can be expensive. For these reasons it is not practical to calibrate all ordinary meters against a primary standard. To utilize the solid metrological basis of the primary standard, a chain of secondary standards, reference standards, and working standards combine the primary standard and the ordinary instruments. The lower level standard in the chain is calibrated using the next higher level standard. This is called “traceability.” In all calibrations traceability along the chain should exist, up to the instrument with the highest reliability, the primary standard.
The question is often asked, How often should calibration be carried out? Is it sufficient to do it once, or should it be repeated? The answer to this question depends on the instrument type. A very simple instrument that is robust and stable may require calibrating only once during its lifetime. Some fundamental meters do not need calibration at all. A Pitot-static tube or a liquid U-tube manometer are examples of such simple instruments. On the other hand, complicated instruments with many components or sensitive components may need calibration at short intervals. Also fouling and wearing are reasons not only for maintenance but also calibration. Thus the proper calibration interval depends on the instrument itself and its use. The manufacturers recommendations as well as past experience are often the only guidelines.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780122896767500151
Intelligent control and protection in the Russian electric power system
Nikolai Voropai, … Daniil Panasetsky, in Application of Smart Grid Technologies, 2018
3.3.1.2 Systematic errors in PMU measurements
The systematic errors caused by the errors of the instrument transformers that exceed the class of their accuracy are constantly present in the measurements and can be identified by considering some successive snapshots of measurements. The TE linearized at the point of a true measurement, taking into account random and systematic errors, can be written as:
(25)wky¯=∑l∈ωk∂w∂ylξyl+cyl=∑aklξyl+∑aklcyl
where ∑ aklξyl—mathematical expectation of random errors of the TE, equal to zero; ∑ aklcyl—mathematical expectation of systematic error of the TE, ωk—a set of measurements contained in the kth TE.
The author of Ref. [28] suggests an algorithm for the identification of a systematic component of the measurement error on the basis of the current discrepancy of the TE. The algorithm rests on the fact that systematic errors of measurements do not change through a long time interval. In this case, condition (17) will not be met during such an interval of time. Based on the snapshots that arrive at time instants 0, 1, 2, …, t − 1, t…, the sliding average method is used to calculate the mathematical expectation of the TE discrepancy:
(26)Δwkt=1−αΔwkt−1+αwkt
where 0 ≤ α ≤ 1.
Fig. 5 shows the curve of the TE discrepancy (a thin dotted line) calculated by (26) for 100 snapshots of measurements that do not have systematic errors.
Fig. 5. Detection of a systematic error in the PMU measurements and identification of mathematical expectation of the test equation.
It virtually does not exceed the threshold dk = 0.014 (a light horizontal line). Above the threshold, there is a curve of the TE discrepancy (a bold dotted line) that contains a measurement with a systematic error and a curve of nonzero mathematical expectation Δwk(t) ∈ [0.026; 0.03] (a black-blue thick line). However, the nonzero value of the calculated mathematical expectation of the TE discrepancy can only testify to the presence of a systematic error in the PMU measurements contained in this TE, but cannot be used to locate it.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780128031285000039
Measurements
Sankara Papavinasam, in Corrosion Control in the Oil and Gas Industry, 2014
ii Systematic or determinate error
To define systematic error, one needs to understand ‘accuracy’. Accuracy is a measure of the closeness of the data to its true or accepted value. Figure 12.3 illustrates accuracy schematically.4 Determining the accuracy of a measurement is difficult because the true value may never be known, so for this reason an accepted value is commonly used. Systematic error moves the mean or average value of a measurement from the true or accepted value.
FIGURE 12.3. Difference between Accuracy and Precision in a Measurement.4
Reproduced with permission from Brooks/Cole, A Division of Cengage Learning.
Systematic error may be expressed as absolute error or relative error:
- •
-
The absolute error (EA) is a measure of the difference between the measured value (xi) and true or accepted value (xt) (Eqn. 12.5):
(Eqn. 12.5)EA=xi−xt
Absolute error bears a sign:
- •
-
A negative sign indicates that the measured value is smaller than true value and
- •
-
A positive sign indicates that the measured value is higher than true value
The relative error (ER) is the ratio of measured value to true value and it is expressed as (Eqn. 12.6):
(Eqn. 12.6)ER=(xi−xtxt).100
Table 12.2 illustrates the absolute and relative errors for six measurements in determining the concentration of 20 ppm of an ionic species in solution.
Table 12.2. Relative and Absolute Errors in Six Measurements of Aqueous Solution Containing 20 ppm of an Ionic Species
| Measured Value | Absolute Error | Relative Error (Percentage) | Remarks |
|---|---|---|---|
| 19.4 | −0.6 | −3.0 | Experimental value lower than actual value. |
| 19.5 | −0.5 | −2.5 | |
| 19.6 | −0.4 | −2.0 | |
| 19.8 | −0.2 | −1.0 | |
| 20.1 | +0.1 | +0.5 | Experimental value higher than actual value. |
| 20.3 | +0.3 | +1.5 |
Systematic error may occur due to instrument, methodology, and personal error.
Instrument error
Instrument error occurs due to variations that can affect the functionality of the instrument. Some common causes include temperature change, voltage fluctuation, variations in resistance, distortion of the container, error from original calibration, and contamination. Most instrument errors can be detected and corrected by frequently calibrating the instrument using a standard reference material. Standard reference materials may occur in different forms including minerals, gas mixtures, hydrocarbon mixtures, polymers, solutions of known concentration of chemicals, weight, and volume. The standard reference materials may be prepared in the laboratory or may be obtained from standard-making organizations (e.g., ASTM standard reference materials), government agencies (e.g., National Institute of Standards and Technology (NIST) provides about 900 reference materials) and commercial suppliers. If standard materials are not available, a blank test may be performed using a solution without the sample. The value from this test may be used to correct the results from the actual sample. However this methodology may not be applicable for correcting instrumental error in all situations.
Methodology error
Methodology error occurs due to the non-ideal physical or chemical behavior of the method. Some common causes include variation of chemical reaction and its rate, incompleteness of the reaction between analyte and the sensing element due to the presence of other interfering substances, non-specificity of the method, side reactions, and decomposition of the reactant due to the measurement process. Methodology error is often difficult to detect and correct, and is therefore the most serious of the three types of systematic error. Therefore a suitable method free from methodology error should be established for routine analysis.
Personal error
Personal error occurs due to carelessness, lack of detailed knowledge of the measurement, limitation (e.g., color blindness of a person performing color-change titration), judgment, and prejudice of person performing the measurement. Some of these can be overcome by automation, proper training, and making sure that the person overcomes any bias to preserve the integrity of the measurement.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780123970220000121
Experimental Design and Sample Size Calculations
Andrew P. King, Robert J. Eckersley, in Statistics for Biomedical Engineers and Scientists, 2019
9.4.2 Blinding
Systematic errors can arise because either the participants or the researchers have particular knowledge about the experiment. Probably the best known example is the placebo effect, in which patients’ symptoms can improve simply because they believe that they have received some treatment even though, in reality, they have been given a treatment of no therapeutic value (e.g. a sugar pill). What is less well known, but nevertheless well established, is that the behavior of researchers can alter in a similar way. For example, a researcher who knows that a participant has received a specific treatment may monitor the participant much more carefully than a participant who he/she knows has received no treatment. Blinding is a method to reduce the chance of these effects causing a bias. There are three levels of blinding:
- 1.
-
Single-blind. The participant does not know if he/she is a member of the treatment or control group. This normally requires the control group to receive a placebo. Single-blinding can be easy to achieve in some types of experiments, for example, in drug trials the control group could receive sugar pills. However, it can be more difficult for other types of treatment. For example, in surgery there are ethical issues involved in patients having a placebo (or sham) operation.2
- 2.
-
Double-blind. Neither the participant nor the researcher who delivers the treatment knows whether the participant is in the treatment or control group.
- 3.
-
Triple-blind. Neither the participant, the researcher who delivers the treatment, nor the researcher who measures the response knows whether the participant is in the treatment or control group.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780081029398000189
The pursuit and definition of accuracy
Anthony J. Martyr, David R. Rogers, in Engine Testing (Fifth Edition), 2021
Systematic instrument errors
Typical systematic errors (Fig. 19.2C) include the following:
- 1.
-
Zero errors—the instrument does not read zero when the value of the quantity observed is zero.
- 2.
-
Scaling errors—the instrument reads systematically high or low.
- 3.
-
Nonlinearity—the relation between the true value of the quantity and the indicated value is not exactly in proportion; if the proportion of error is plotted against each measurement over full scale, the graph is nonlinear.
- 4.
-
Dimensional errors—for example, the effective length of a dynamometer torque arm may not be precisely correct.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B978012821226400019X
Power spectrum and filtering
Andreas Skiadopoulos, Nick Stergiou, in Biomechanics and Gait Analysis, 2020
5.10 Practical implementation
As suggested by Winter (2009), to cancel the phase shift of the output signal relative to the input that is introduced by the second-order filter, the once-filtered data has to filtered again, but this time in the reverse direction. However, at every pass the −3dB cutoff frequency is pushed lower, and a correction is needed to match the original single-pass filter. This correction should be applied once the coefficients of the fourth-order low-pass filter are calculated. Nevertheless, it should be also checked whether functions of closed source software use the correction factor. If they have not used it, the output of the analyzed signal will be distorted. The format of the recursive second-order filter is given by Eq. (5.36) (Winter, 2009):
(5.36)yk=α0χk+α1χk−1+α2χk−2+β1yk−1+β2yk−2
where y are the filtered output data, x are past inputs, and k the kth sample.The coefficients α0,α1,α2,β1, and β2 for a second-order Butterworth low-pass filter are computed from Eq. (5.37) (Winter, 2009):
(5.37)ωc=tanπfcfsCK1=2ωcK2=ωc2K3=α1K2α0=K21+K1+K2α1=2α0α2=α0β1=K3−α1β2=1−α1-K3
where, ωc is the cutoff angular frequency in rad/s, fc is the cutoff frequency in Hz, and fs is the sampling rate in Hz. When the filtered data are filtered again in the reverse direction to cancel phase-shift, the following correction factor to compensate for the introduced error should be used:
(5.38)C=(21n−1)14
where n≥2 is the number of passes. For a single-pass C=1, and no compensation is needed. For a dual pass, (n=2), a compensation is needed, and the correction factor should be applied. Thus, the ωc term from Eq. (5.37) is calculated as follows:
(5.39)ωc=tan(πfcfs)(212−1)14=tan(πfcfs)0.802
A systematic error is introduced to the signal if the correction factor is not applied. Therefore, remember to check any algorithm before using it. Let us check the correctness of the fourth-order low-pass filter that was built previously in R language. Vignette 5.2 contains the code to perform Winter’s (2009) low-pass filter in R programming language. Because the filter needs two past inputs (two data points) to compute a present filtered output (one data point), the time-series data to be filtered (the raw data) should be padded at the beginning and at the end. Additional data are usually collected before and after the period of interest.
Vignette 5.2
The following vignette contains a code in R programming language that performs the fourth-order zero-phase-shift low-pass filter from Eq. (5.37).
- 1.
-
The first step is to create a sine (or equally a cosine) wave with known amplitude and known frequency. Vignette 5.3 is used to synthesize periodic digital waves. Let us create a simple periodic sine wave s[n] with the following characteristics:
- a.
-
Amplitude A=1 unit (e.g., 1 m);
- b.
-
Frequency f=2 Hz;
- c.
-
Phase θ=0 rad;
- d.
-
Shift a0=0 unit (e.g., 0 m).
Vignette 5.3
The following vignette contains a code in R programming language that synthesizes periodic waveforms from sinusoids.
Let us choose an arbitrary fundamental period T0=2 seconds, which corresponds to a fundamental frequency of f0=1/T0=0.5 Hz. Now, knowing the fundamental frequency, the fourth harmonic that corresponds to a sine wave with frequency of f=2 Hz will be chosen. The periodic sine wave s[n] will be sampled at Fs=40 Hz (Ts=1/40 seconds) (i.e., 20 times the Nyquist frequency, fN=2 Hz). The sine wave will be recorded for a time interval of t=2 s, which corresponds to N=80 data points. Thus, and because ω0=2πf0, we have:
s[n]=sin(2ω0nTs)
which means that the fourth harmonic has frequency f=2
Hz. Fig. 5.14A shows the sine wave created. The first and last 20 data points can be considered as extra points (padded). Additional data at the beginning and end of the signal are needed for the next steps because the filter is does not behave well at the edges. Thus, the signal of interest starts at 0.5
seconds and ends at 1.5
seconds, which corresponds to N=40 data points.
Figure 5.14. (A) Example of a low-pass filter (cutoff frequency=2 Hz) applied to a sine wave sampled at 40 Hz, with amplitude equal to 1 m, and frequency equal to 2 Hz. (B) The signal interpolated by a factor of 2, and filtered with cutoff frequency equal to the frequency of the sine wave (cutoff frequency=2 Hz). (C) Since the amplitude of the filtered signal has been reduced by a ratio of 0.707, the low-pass filter correctly attenuated the signal. The power spectra of the original and reconstructed signal are shown.
- 2.
-
An extra, but not mandatory, step is to interpolate the created sine wave in order to increase the temporal resolution of the created signal (Fig. 5.14B). Of course, when a digital periodic signal is created from scratch, like we are doing using the R code in the vignettes, we can easily sample the signal at higher frequencies. However, if we want to use real biomechanical time series data, that have already been collected, a possible way to increase its temporal resolution is by using the Whittaker–Shannon interpolation formula. With the Whittaker–Shannon interpolation a signal is up-sampled with interpolation using the sinc() function (Yaroslavsky, 1997):
(5.40)s(x)=∑n=0N−1αnsin(π(xΔx−n))Nsin(π(xΔx−n)/N)
The Whittaker–Shannon interpolation formula can be used to increase the temporal resolution after removing the “white” noise from the data. Without filtering, the interpolation results in a noise level equal to that of the original signal before sampling (Marks, 1991). However, the interpolation noise can be reduced by both oversampling and filtering the data before interpolation (Marks, 1991). An alternative, and efficient, method is to run the DFT, zero-pad the signal, and then take the IDFT to reconstruct it. Vignette 5.4 can be used to increase the temporal resolution by a factor of 2, which corresponds to a sampling frequency of 80 Hz.
Vignette 5.4
The following vignette contains a code in R programming language that runs the normalized discrete sinc() function, and the Whittaker–Shannon interpolation function.
- 3.
-
The third step is to filter the previously created sine wave with the fourth-order zero-phase-shift low-pass filter, setting the cutoff frequency equal to the sine wave frequency f=2 Hz. Vignette 5.2 is used for step 3. To cancel any shift (i.e., a zero-phase-shift filter) n=2 passes must be chosen. The interpolated signal has a sampling rate of 80 Hz.
- 4.
-
The fourth step is to investigate the frequency response of the filtered sine wave. The frequency response of the Butterworth filter is given by Eq. (5.41)
(5.41)|AoutAin|=1(1+fsf3dB)2n
where the point at which the amplitude response, Aout, of the input signal, s[n], with frequency, f, and amplitude, Ain, drops off by 3dB and is known as the cutoff frequency, f3dB. When the cutoff frequency is set equal to the frequency of the signal (f3dB=f), the ratio should be equal to 0.707, since:
(5.42)|AoutAin|=12≈0.707
Fig. 5.14C shows the plots of the filtered and interpolated sine wave. Since the ratio of the maximum value of the filtered sine wave to the original sine wave ratio=0.707, the created fourth-order zero-phase-shift low-pass filter works properly. Without the correction factor the amplitude reduces nearly to half (0.51), indicating that the coefficients of the filter needed correction. Fig. 5.15 also shows an erroneously filtered signal. You can try to create Fig. 5.15 by yourself.
Figure 5.15. Example of a recursive low-pass filter applied to a sine wave with amplitude equal to 1 m and cutoff frequency equal to the frequency of the sine wave. Since the amplitude of the filtered signal has been reduced by a ratio of 0.707, the low-pass filter correctly attenuated the signal. However, the function without the correction factor reduced the amplitude by nearly one-half (0.51), indicating that the coefficients need correction.
The same procedure should be applied to check whether the output of the functions from closed source software used the correction factor or not. For example, using the library(signal) of the R computational software, if x is the vector that contains the raw data, then using butter() the Butterworth coefficients can be generated.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780128133729000051
Introduction to coal sampling
Wes B. Membrey, in The Coal Handbook (Second Edition), 2023
4.1.1 Definitions
The following definitions have been adapted from definitions given in the sampling standards.
Accuracy. A measure of the closeness of agreement between an analytical result and the true value or a reference value.
Cut. An increment taken by a sampling device typically from a conveyor belt, screen discharge, or other streams of coal.
Bias. Systematic error which leads to the average value of a series of analytical results being persistently higher or lower than the true value or a reference sample result.
Error. Difference between the measured value and the true value or a value from a reference sample result.
Increment. An amount of coal taken from a body of coal (a truck or barge, etc.) or from a stream of coal (coal on a conveyor, sizing screen or a chute, etc.) in a single operation of the sampling device.
Lot. Defined quantity of coal for which the quality is to be determined.
Particle top size is the nominal top size and is the square aperture size of the smallest sieve through which 95% of the sample passes.
Precision. A statistical term that quantifies how closely repeated experimental values agree. It usually has the value of the 95% confidence level, or 2 standard deviations from the mean of the experimental values.
Representative. A sample is representative when the sampling error, a combination of precision and accuracy, is of an acceptable level.
Sample. Quantity of coal with qualities that are representative of a larger mass (lot) for which the quality is to be determined.
Standard deviation. A measure of the spread of a set of values, equal to the square root of the variance of the results.
Sub lot. A part of a lot that is sampled and tested separately to the entire lot.
Tolerance. The maximum acceptable difference between measurement values or analytical results.
Variance. A measure of the spread of a set of values expressed as the square of the differences between the values and their mean.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780128243282000169
Sensors
Andrea Colagrossi, … Matteo Battilana, in Modern Spacecraft Guidance, Navigation, and Control, 2023
Quantization errors
Quantization error is a systematic error resulting from the difference between the continuous input value and its quantized output, and it is like round-off and truncation errors. This error is intrinsically associated with the AD conversion that maps the input values from a continuous set to the output values in a countable set, often with a finite number of elements. The quantization error is linked to the resolution of the sensor. Namely, a high-resolution sensor has a small quantization error. Indeed, the maximum quantization error is smaller than the resolution interval of the output, which is associated to the least significant bit representing the smallest variation that can be represented digitally:
LSB=FSR2NBIT
where FSR is the full-scale range of the sensor, and NBIT is the number of bits (i.e., the resolution) used in the AD converter to represent the sensor’s output. Quantization errors are typically not corrected, and the discrete values of the output are directly elaborated by the GNC system, which is designed to operate on digital values.
Fig. 6.9 shows a convenient model block to simulate quantization errors.
Figure 6.9. Quantization error model.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780323909167000068
The Systems Approach to Control and Instrumentation
William B. Ribbens, in Understanding Automotive Electronics (Seventh Edition), 2013
Systematic Errors
One example of a systematic error is known as loading errors, which are due to the energy extracted by an instrument when making a measurement. Whenever the energy extracted from a system under measurement is not negligible, the extracted energy causes a change in the quantity being measured. Wherever possible, an instrument is designed to minimize such loading effects. The idea of loading error can be illustrated by the simple example of an electrical measurement, as illustrated in Figure 1.17. A voltmeter M having resistance Rm measures the voltage across resistance R. The correct voltage (vc) is given by
Figure 1.17. Illustration of loading error-volt meter.
(71)vc=V(RR+R1)
However, the measured voltage vm is given by
(72)vm=V(RpRp+R1)
where Rp is the parallel combination of R and Rm:
(73)Rp=RRmR+Rm
Loading is minimized by increasing the meter resistance Rm to the largest possible value. For conditions where Rm approaches infinite resistance, Rp approaches resistance R and vm approaches the correct voltage. Loading is similarly minimized in measurement of any quantity by minimizing extracted energy. Normally, loading is negligible in modern instrumentation.
Another significant systematic error source is the dynamic response of the instrument. Any instrument has a limited response rate to very rapidly changing input, as illustrated in Figure 1.18. In this illustration, an input quantity to the instrument changes abruptly at some time. The instrument begins responding, but cannot instantaneously change and produce the new value. After a transient period, the indicated value approaches the correct reading (presuming correct instrument calibration). The dynamic response of an instrument to rapidly changing input quantity varies inversely with its bandwidth as explained earlier in this chapter.
Figure 1.18. Illustration of instrument dynamic response error.
In many automotive instrumentation applications, the bandwidth is purposely reduced to avoid rapid fluctuations in readings. For example, the type of sensor used for fuel-quantity measurements actually measures the height of fuel in the tank with a small float. As the car moves, the fuel sloshes in the tank, causing the sensor reading to fluctuate randomly about its mean value. The signal processing associated with this sensor is actually a low-pass filter such as is explained later in this chapter and has an extremely low bandwidth so that only the average reading of the fuel quantity is displayed, thereby eliminating the undesirable fluctuations in fuel quantity measurements that would occur if the bandwidth were not restricted.
The reliability of an instrumentation system refers to its ability to perform its designed function accurately and continuously whenever required, under unfavorable conditions, and for a reasonable amount of time. Reliability must be designed into the system by using adequate design margins and quality components that operate both over the desired temperature range and under the applicable environmental conditions.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780080970974000011