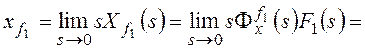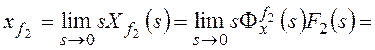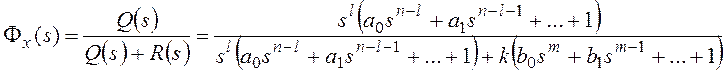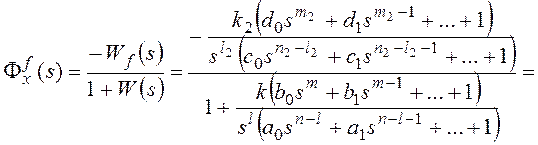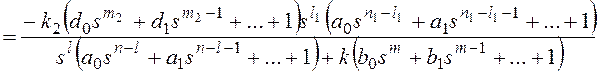Максимальная
динамическая ошибка
– наибольшее
отклонение регулируемой переменной от
заданного значения Узад:
.
(3.1)
В
устойчивой САР максимальным является
первое отклонение. Таким образом,
показатель
характеризует динамическую точность
регулирования [14].
Время
регулирования
tp
–промежуток времени от момента нанесения
возмущающего воздействия до момента,
начиная с которого отклонение регулируемой
переменной от установившегося значения
становится и остается меньше наперед
заданного значения ].
Остаточное
отклонение (остаточная неравномерность)
—
абсолютная статическая ошибка
регулирования, определяемая как разность
между установившимся значением
регулируемой величины и ее заданным
значением:
=Ууст
– Узад.
(3.2)
Показатель
характеризует точность регулирования
в статическом режиме [5].
Во
всех системах регулирования обязательно
имеется статическая ошибка. Ее можно
уменьшать путем увеличения общего
коэффициента усиления регулятора.
Однако она все равно остается, так как
увеличение коэффициента усиления
регулятора всегда ограничено.
Причиной
статической ошибки системы регулирования
является то, что в равновесном состоянии
регулятора положение регулирующего
органа жестко связано с величиной
регулируемой величины [6].
Система
регулирования, которая по принципу
своего действия обладает статической
ошибкой, называется статической
системой, а
регулятор в этом случае называется
статическим
регулятором.
Статический регулятор осуществляет
следующий закон регулирования:
y
= kрегх,
(3.3)
где
х
– отклонение регулируемой величины, у
– регулирующее воздействие регулятора
на объект.
Система
автоматического регулирования, не
обладающая статической ошибкой,
называется астатической
системой автоматического
регулирования,
а регулятор называется астатическим
регулятором [3].
3.2. Критерии устойчивости сар
Понятие
устойчивости САР связано с способностью
системы возвращаться в состояние
равновесия после исчезновения внешних
сил, которые вывели ее из этого состояния.
Устойчивость
систем автоматического управления
является одним из важнейших условий их
работоспособности, так как устойчивость
включает в себя требование затухания
переходных процессов во времени.
Очевидно, что система с расходящимся
процессом была бы неработоспособной.
Рассмотрим
дифференциальное уравнение движения
линеаризованной системы автоматического
регулирования, записанное для регулируемой
величины у(t)
при наличии управляющего воздействия
g(t)
и при равенстве нулю возмущающих
воздействий (см. формулу (2.4)):
.(3.4)
Процесс
регулирования определяется решением
дифференциального уравнения, как сумма
двух решений – частного решения
неоднородного уравнения (3.4)
с правой частью и общего решения уравнения
(3.4)
без правой части [1].
Характеристическое
уравнение САР имеет вид:
.
(3.5)
Корни
характеристического уравнения (3.5)
определяются только видом левой части
уравнения (3.4).
Постоянные интегрирования определяются
также и видом правой части. Поэтому
быстрота затухания и форма переходного
процесса определяются как левой, так и
правой частями исходного дифференциального
уравнения. Однако поскольку в понятие
устойчивости входит только факт наличия
или отсутствия затухания переходного
процесса (независимо от быстроты
затухания и формы переходного процесса),
то устойчивость линейной системы не
зависит от вида правой части
дифференциального уравнения (3.4)
и определяется только характеристическим
уравнением (3.5)
[13].
Так
как получающаяся при решении линейного
дифференциального уравнения (3.4) формула
переходного процесса содержит составляющие
в виде экспонент от вещественных частей
корней характеристического уравнения
САР (3.5) (см. главу 2), то для того, чтобы
САР была устойчивой и переходный процесс
затухал, необходимо, чтобы вещественные
части корней были отрицательными.
Следовательно,
для устойчивости линейной САР необходимо,
чтобы все корни лежали слева от мнимой
оси, в левой полуплоскости комплексных
чисел. Если хотя бы один корень окажется
справа от мнимой оси, то система будет
неустойчивой. Система будет находиться
на границе устойчивости при наличии:
нулевого корня
(
);
пары чисто мнимых корней
;
бесконечного корня
(
).
Во всех трех случаях предполагается,
что все остальные корни имеют отрицательные
вещественные части.
Необходимым
(но не достаточным) условием устойчивости
САР является положительность всех
коэффициентов характеристического
уравнения [7]. Это означает, что система
является неустойчивой, если хотя бы
один из коэффициентов характеристического
уравнения отрицателен. Если все
коэффициенты характеристического
уравнения положительны, то требуются
дополнительные исследования САР на
устойчивость с помощью критериев
устойчивости Гурвица, Михайлова или
Найквиста [3].
В
программе «SAU»
для определения устойчивости САР
используется критерий устойчивости
Гурвица, как наиболее удобный с точки
зрения компьютерной реализации. В методе
Гурвица для характеристического
уравнения (3.5) составляется квадратная
матрица коэффициентов, содержащая n
строк и n
столбцов:
.
(3.6)
Критерий
устойчивости сводится к тому, что при
а0>0
должны быть больше нуля все n
определителей Гурвица, получаемых из
квадратной матрицы коэффициентов.
Определители
Гурвица составляются по следующему
правилу:
;
;
(3.7)
Последний
определитель включает в себя всю матрицу.
Но так как в последнем столбце матрицы
все элементы, кроме нижнего, равны нулю,
то последний определитель Гурвица
выражается через предпоследний следующим
образом:
.
(3.8)
Однако
в устойчивой системе предпоследний
определитель тоже должен быть
положительным. Поэтому условие
положительности последнего определителя
сводится к условию
,
т.е. к положительности свободного члена
характеристического уравнения [1].
Условия
нахождения системы на границе устойчивости
можно получить, приравнивая к нулю
последний определитель (
)
при положительности всех остальных
определителей. Как следует из (3.8),
это условие распадается на два условия:
и
.
Первое
условие соответствует границе устойчивости
первого типа (апериодическая граница
устойчивости), а второе – границе
устойчивости второго типа (колебательная
граница устойчивости).
Для
уравнения второго порядка необходимым
и достаточным условием устойчивости
является положительность всех
коэффициентов характеристического
уравнения. Для уравнений более высокого
порядка необходимо исследование с
помощью составления определителей
Гурвица и проверки их на положительность.
Существенным
недостатком критерия Гурвица является
то, что для уравнений высоких порядков
в лучшем случае можно получить ответ о
том, устойчива или неустойчива система
автоматического регулирования. При
этом в случае неустойчивой системы
критерий не дает ответа на то, каким
образом надо изменять параметры системы,
чтобы сделать ее устойчивой. Это
обстоятельство привело к поискам других
критериев, которые более удобны в
инженерной практике.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Точность системы автоматического управления Статическая ошибка системы
В системах
автоматического управления часто
приходится решать задачу стабилизации
управляемой величины. Точность поддержания
требуемого значения управляемой величины
в такой системе можно оценить как разницу
между заданным значением управляемой
величины и её установившимся значением
в системе после окончания переходного
процесса:
.
Эта величина
получила название статической ошибки
системы. При вычислении статической
ошибки предполагается, что система
находится в статике и все сигналы в ней
имеют постоянные величины. Статическая
ошибка используется для оценки точности
установления в системе заданной
постоянной выходной величины после
окончания переходного процесса.
Используя
передаточную функцию замкнутой системы
по ошибке, для изображения ошибки в
системе можно записать
,
где
передаточная
функция замкнутой системы по ошибке,
изображение
задающего воздействия.
Для статики,
когда все сигналы в системе неизменны,
выражение для ошибки можно перенести
в область оригиналов
.
Поскольку
,
гдеW(p)
– передаточная функция разомкнутой
системы, то статическую ошибку системы
можно вычислить, зная передаточную
функцию разомкнутой системы:
,
где
.
Вместо
абсолютного значения статической ошибки
часто используют относительную
статическую ошибку
.
Если система
статическая (т.е. не содержит интегрирующих
звеньев), то передаточную функцию
разомкнутой системы можно представить
в следующем нормированном виде:
,
гдеK– коэффициент
усиления системы,A*(p),B*(p)
– нормированные полиномыA(p)
иB(p).
При этом
и
.
Тогда
и статическая ошибка в статической
системе
.
Статическая
ошибка в статической системе уменьшается
с увеличением коэффициента усиления
системы. Статическая система всегда
будет иметь некоторую ошибку. Физический
смысл такой ошибки заключается в
необходимости некоторого рассогласования
между задающей и выходной величинами
системы для получения сигнала управления.
Если в системе
управления имеются интегрирующие
звенья, то система будет астатической.
Для астатической системы первого порядка
(содержащей одно интегрирующее звено)
передаточная функция разомкнутой
системы
и передаточная функция замкнутой системы
по ошибке
.
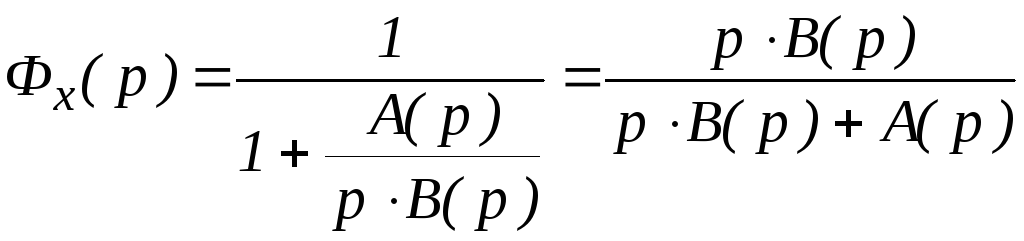
В этом случае всегда
и, следовательно, статическая ошибка
астатической системы будет равна нулю.
Таким образом, статическая ошибка в
астатической системе в принципе
отсутствует, что обуславливает более
высокую точность астатических систем,
по сравнению со статическими системами.
В астатической системе автоматического
управления установившееся значение
управляемой величины равно заданному
значению этой величины.
Вынужденная ошибка системы
Процесс в
системе складывается из свободного
процесса и вынужденного процесса:
.
Для
устойчивой системы свободный процесс
по истечении времениtпзатухает и в системе устанавливается
вынужденный процесс
Точность
поддержания заданного значения
управляемой величины в вынужденном
режиме характеризуется вынужденной
ошибкой системы
.
Вынужденная
ошибка хорошо характеризует работу
системы автоматического управления в
том случае, когда изменения управляющего
воздействия происходят существенно
медленнее собственных переходных
процессов в системе и последними можно
пренебречь.
Рассмотрим
вычисление вынужденной ошибки системы
автоматического управления. Изображение
для вынужденной ошибки
.
В общем случае
является дробно-рациональной функцией
отpи ее можно разложить
в ряд Тейлора по степенямрвблизи
, тогда
и
выражение для вынужденной ошибки системы
примет вид
где
постоянные
коэффициенты.
Для полученного
изображения вынужденной ошибки на
основе свойств преобразования Лапласа
легко находится выражение для оригинала
ошибки
где
,
,
…коэффициенты
ошибок, полученные выше (C0– коэффициент статической ошибки,C1
– коэффициент скоростной ошибки и
т. д.).
Коэффициенты
ошибки могут быть также получены делением
числителя передаточной функции на ее
знаменатель. Полученное выражение для
вынужденной ошибки позволяет оценить
точность системы автоматического
управления в установившемся режиме.
Вынужденная ошибка, например, хорошо
характеризует точность работы следящих
систем автоматического управления.
Соседние файлы в папке ТАУ
- #
- #
- #
Лекция 17. Расчет установившейся ошибки в системах управления.
Структурные признаки астатизма
Установившейся (статической) ошибкой называют
постоянное значение сигнала ошибки x(t)=g(t)-y(t),
которое она приобретает по окончании переходного процесса: 
, рисунок 116.
Очевидно, установившаяся ошибка зависит от законов
изменения и численных характеристик входных сигналов системы. Поэтому при ее
определении принято рассматривать так называемые типовые входные сигналы,
законы изменения которых составляют степенной ряд относительно времени.
Например, для задающего воздействия:
, 
, 
и так
далее.
При наличии нескольких воздействий на линейную систему
для определения xуст используется
принцип суперпозиции – реакция линейной системы на совокупность входных
сигналов совпадает с алгебраической суммой ее реакций на каждый из сигналов в
отдельности:
, где
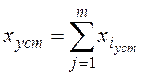
каждое слагаемое, или составляющая сигнала ошибки, 
определяется
для i-го входного сигнала при условии, что остальные
тождественно равны нулю. Такой подход полностью соответствует определению
передаточной функции и позволяет выполнять расчет установившейся ошибки на
основе структурной схемы системы.
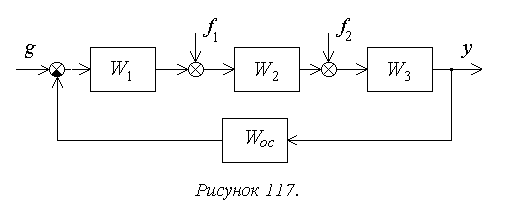
Рассмотрим порядок расчета установившейся ошибки на
следующем достаточно общем примере (рисунок 117).
В соответствии с принципом суперпозиции установившаяся
ошибка будет определяться здесь в виде суммы трех составляющих 
.
Изображение по Лапласу ошибки от задающего воздействия
получают через передаточную функцию замкнутой системы по ошибке 
при известном изображении задающего
воздействия G(s):
, где
F(s) – основная передаточная функция замкнутой системы.
Для структурной схемы на рисунке 117
, где 
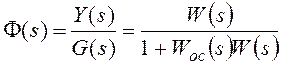
— передаточная функция
разомкнутой системы, или прямой цепи системы, для рассматриваемого примера.
Непосредственно для расчета
установившегося значения ошибки от задающего воздействия используют теорему о
конечном значении для преобразования Лапласа:
В результате:
.
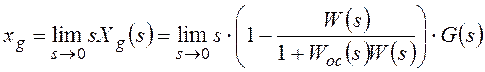
Изображение по Лапласу ошибки от возмущающего
воздействия получают через передаточную функцию замкнутой системы по ошибке от
возмущения 
при известном изображении возмущающего
воздействия F(s):
, где
Ff(s) –передаточная функция замкнутой системы по
возмущающему воздействию,
;
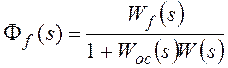
Wf(s)
– передаточная функция разомкнутой системы по возмущению (передаточная функция
участка прямой цепи системы от точки приложения возмущающего воздействия до
выхода системы).
Для структурной схемы на рисунке 8 необходимо
учитывать два возмущающих воздействия, приложенные в различные точки системы.
Для f1:
,
,
.
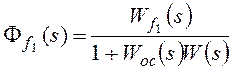
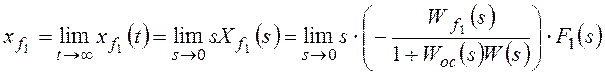
Для f2:
,
,
.
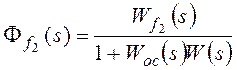
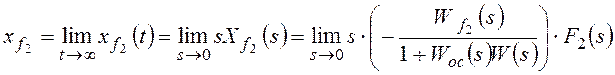
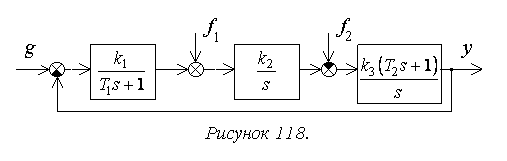
Расчет упрощается для
системы с единичной отрицательной обратной связью (рисунок 118):
,
, где k=k1k2k3 – коэффициент передачи
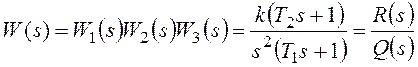
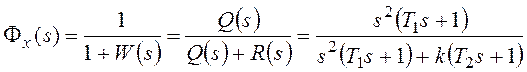
разомкнутой системы.
Найдем установившуюся ошибку
для некоторых типовых вариантов задающего воздействия.
При получим:
.
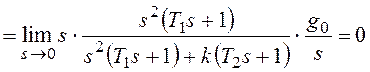
При получим:
.
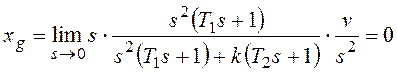
При получим:
.
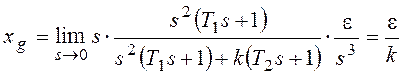
Если установившаяся ошибка
тождественно равна нулю при каком-либо типовом варианте входного сигнала,
независимо от его численных характеристик, систему называют астатической по
рассматриваемому входному сигналу.
Количество типовых вариантов
входного сигнала – членов степенного ряда, при которых установившаяся ошибка
тождественно равна нулю, определяет порядок астатизма.
Рассматриваемая система
обладает свойством астатизма второго порядка по задающему воздействию.
Рассмотрим установившуюся
ошибку от возмущения f1:
,
, где 
–
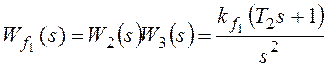
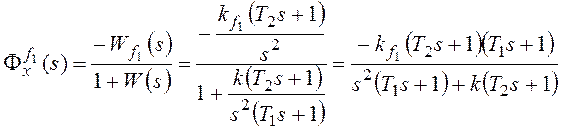
коэффициент передачи разомкнутой системы по возмущению f1.
При 
получим:
.
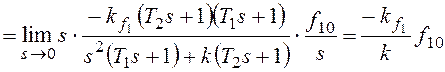
При 
получим:
.
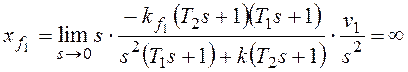
При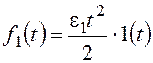 
получим
тот же результат.
Отметим, что по возмущению f1 рассматриваемая система
не является астатической. Кроме того, она не в состоянии отработать два последних
варианта входного сигнала.
Рассмотрим установившуюся
ошибку от возмущения f2:
,
, где 
–
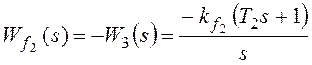
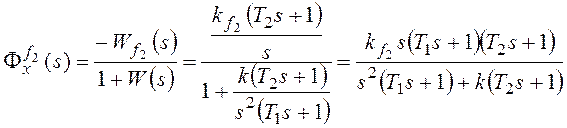
коэффициент передачи разомкнутой системы по возмущению f2.
При 
получим:
.
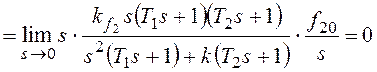
При 
получим:
.
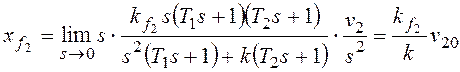
При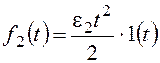 
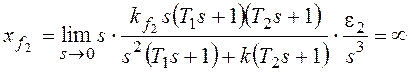
получим:
.
По возмущению f2 рассматриваемая система имеет
астатизм первого порядка. Она не в состоянии отработать возмущающее
воздействие, изменяющееся во времени с постоянным ускорением.
Подведем некоторые итоги:
1. Наличие и глубина
свойства астатизма зависят от точки приложения входного сигнала.
2. Постоянные времени
звеньев системы не влияют на ее точность.
3. Увеличение значения
коэффициента передачи разомкнутой системы приводит к снижению величины
установившейся ошибки.
Для систем с единичной
отрицательной обратной связью существуют достаточно простые структурные
признаки астатизма.
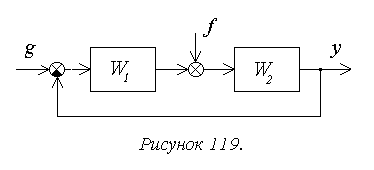
Рассмотрим структуру,
показанную на рисунке 119.
В общем случае передаточная
функция разомкнутой системы может быть представлена в следующей форме:
, где l³0.
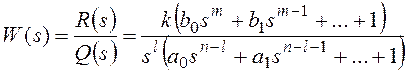
Тогда получим:
и для общего вида задающего воздействия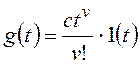 
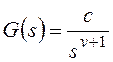
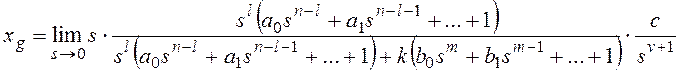
, которому соответствует изображение 
,
.
Результат нахождения этого
предела зависит от соотношения показателей степени:
— при l>v установившаяся
ошибка равна нулю независимо от остальных параметров, то есть имеет место
астатизм;
— при l=v получаем
константу;
— при l<v установившаяся
ошибка стремится к бесконечности, то есть система не в состоянии отработать
входной сигнал.
Учитывая, что минимальное
значение v нулевое,
получаем условие астатизма по задающему воздействию: l>0.
Таким образом, структурный
признак астатизма по задающему воздействию в системе с единичной отрицательной
обратной связью состоит в наличии нулевых корней в знаменателе передаточной
функции разомкнутой системы, или интегрирующих звеньев в прямой цепи системы.
Нетрудно также убедиться,
что положительное значение l совпадает
с порядком астатизма.
Для получения признака
астатизма по возмущающему воздействию представим передаточные функции на
рисунке 10 в форме:
,
, где l1+l2=l,
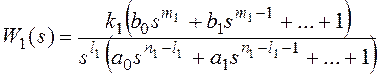
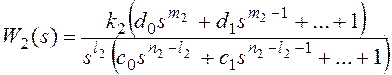
k1k2=k, m1+m2=m,
n1+n2=n,
причем 
и 
.
Тогда получим:
и для общего вида возмущающего воздействия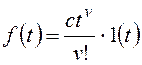 
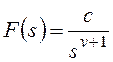
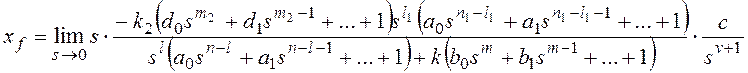
, которому соответствует изображение 
,
.
Все вышеприведенные выводы
можно повторить для показателя степени l1.
Таким образом, структурный
признак астатизма по возмущающему воздействию в системе с единичной
отрицательной обратной связью состоит в наличии нулевых корней в знаменателе
передаточной функции участка системы до точки приложения воздействия, или
интегрирующих звеньев на том же участке.
Величина — статическая ошибка
Cтраница 1
Величина статической ошибки зависит как от настройки регулятора, так и от характеристики и режима работы объекта.
[1]
Стремление уменьшить величину статической ошибки иногда неизбежно приводит к увеличению перерегулирования и времени регулирования. Уменьшение перерегулирования иногда приводит к увеличению статической ошибки.
[2]
В статических системах величина статической ошибки зависит от величины ступенчатой нагрузки. Эта зависимость, называемая статической характеристикой, имеет большое значение для анализа работы САР.
[3]
В астатических системах величина статической ошибки определяется значением нечувствительности регулятора.
[4]
При большом числе компрессоров величина статической ошибки может выйти за допустимые пределы.
[5]
Статическая точность передачи характеризуется величиной статической ошибки, определяемой углом рассогласования между осями датчика и приемника при отсутствии вращения. Величина статической ошибки зависит от нагрузки или момента на валу приемника, а также от собственной погрешности сельсинов.
[6]
Статическая точность передачи характеризуется величиной статической ошибки, определяемой углом пяссогласования между осями датчика и приемника при отсутствии вращения. Величина статической ошибки зависит от нагрузки или момента на валу приемника, а также от собственной погрешности сельсинов.
[7]
По мере увеличения коэффициента усиления величина статической ошибки уменьшается. В то же время степень колебания повышается и соответственно увеличивается динамическая ошибка регулирования. Оптимальная величина должна выбираться как с учетом статической, так и динамической ошибки. Причем статическая ошибка регулирования может быть исключена за счет введения интегральной составляющей в закон регулирования.
[8]
Нужно иметь в виду, что величина статической ошибки зависит как от настройки регулятора, так и от характеристики и режима работы объекта.
[9]
Получается противоречие между требованиями обеспечения устойчивости и величиной статической ошибки.
[10]
Определим границу ОНР, исходя из предположения, что величина статической ошибки не должна превышать величины 0 5 % от входного сигнала при полном перемещении исполнительного механизма.
[11]
Таким образом, давление в приемном канале 2 с точностью до величины статической ошибки, определяемой коэффициентом усиления струйного усилителя, поддерживается постоянным. При постоянном сечении потока этим способом измеряют расход вещества, определяемого как произведение скорости на площадь поперечного сечения потока.
[13]
По оси ординат откладывается отношение максимальной динамической ошибки в переходном процессе к величине статической ошибки, которая имела бы место, если бы в системе использовался пропорциональный регулятор, и была бы равна KLI ( K) при единичном ступенчатом изменении нагрузки. Это значение принято считать наилучшим. Нижняя кривая соответствует декременту затухания, равному 0 46, который получается, если коэффициент усиления выбрать близким к максимальному.
[15]
Страницы:
1
2
3
4
В автоматической системе с симметричной нелинейностью могут иметь место несимметричные автоколебания с некоторой постоянной составляющей 
при приложении постоянного внешнего воздействия. При этом величина амплитуды и частота автоколебаний, существовавших до приложения внешнего воздействия, во многом определяют величину постоянной составляющей. Но, наличие постоянного внешнего воздействия изменяет величину амплитуды и частоты автоколебаний.
Величина 
в случае статической системы определяет собой статическую ошибку, в астатической системе — установившуюся ошибку при постоянной скорости, а в дважды астатической — установившуюся ошибку при постоянном ускорении. Основная задача, таким образом, сводится к определению зависимости между величинами постоянного внешнего воздействия (или постоянной скорости его изменения) и установившейся ошибки, или же к такому выбору параметров системы, например, коэффициента усиления 
при котором величина статической ошибки не превышает заданного значения.
Практический интерес представляет также определение зависимости амплитуды и частоты автоколебаний от величины постоянного внешнего воздействия.
Уравнение нелинейной автоматической системы
где 
— приложенное в любой точке ее внешнее воздействие в данном случае может быть записано в виде
В статической системе будет 
, где 
, а в астатической, когда 
имеем 
, где 
(постоянная скорость изменения внешнего воздействия). В дважды астатической системе 
и при 
будет 
Решение уравнения 
вследствие несимметричности автоколебаний необходимо искать в виде [16], [13]
где 
— постоянная составляющая автоколебаний, х — периодическая (колебательная) составляющая.
Вследствие наличия смещения 
при разложении нелинейной функции 
в ряд Фурье добавится член, характеризующий
постоянную составляющую; при этом выражение для гармонической линеаризации нелинейности приобретает вид
здесь 
— соответственно постоянная составляющая и коэффициенты гармонической линеаризации, определяемые по формулам
где 
В частном случае, когда нелинейность 
является однозначной (не петлевой) 
то формула (Х.59) принимает вид
Определив по формулам 
коэффициенты гармонической линеаризации 
и подставив в уравнение 
вместо 
выражение 
получим гармонически линеаризованное уравнение системы
Это уравнение можно представить в виде системы двух уравнений соответственно для постоянной и колебательной составляющих решения:
Уравнение 
описывает смещение центра колебаний системы в зависимости от величины постоянного внешнего воздействия М. Уравнение (Х.64) описывает периодическое движение системы по координате х относительно центра колебаний, определяемого величиной смещения 
Однако оба уравнения линейно взаимосвязаны, так как коэффициенты 
уравнения 
зависят от величины смещения 
а величина 
в уравнении 
зависит от амплитуды автоколебаний А.
Из уравнения 
можно определить величину статической ошибки в функции от амплитуды автоколебаний А, внешнего воздействия М и параметров системы, например, k:
Подставляя найденное выражение 
в уравнение 
полагая 
и выделяя вещественную и мнимую части, получим два уравнения
Решить аналитически уравнения 
относительно А и 
обычно затруднительно. Целесообразно в данном случае применение какого-либо из графических приемов. Часто бывает удобно из уравнений 
найти выражение для 
. Приравнивая полученные значения 
, получим новое уравнение с тремя неизвестными 
:
Из уравнения 
как правило, можно определить какую-либо из величин как функцию двух остальных. Например,
Полученное уравнение 
дает возможность построить семейство кривых 
при разных значениях М. Затем по одной из формул 
легко определить 
при 
Если какая-либо из искомых величин входит только в одно из уравнений 
то описанное решение значительно упрощается.
Поскольку после построения графиков станет известной зависимость амплитуды автоколебаний 
от значения параметра 
и величины внешнего воздействия М, то из формулы 
определяются искомые зависимости 
при 
или 
при 
Таким образом определяется величина статической ошибки 
в зависимости от величины внешнего воздействия М и значения определяемого параметра системы 
Если полученные значений статической ошибки и амплитуды автоколебаний на входе нелинейного звена 
не являются непосредственно интересующими проектировщика величинами, то пересчет в любую точку системы производится через передаточные функции соответствующих звеньев системы.
Решение уравнений 
возможно и другим способом: подставив в уравнение 
и выделив вещественную и мнимую части, получим два алгебраических уравнения с тремя неизвестными 
Эти уравнения дают возможность определить амплитуду А и частоту 
автоколебаний как функцию постоянной составляющей 
Подставив значения амплитуды и частоты автоколебаний в выражение для 
[первая формула (Х.60)], получим функцию смещения
которая является характеристикой данного нелинейного звена по отношению к постоянной составляющей 
при наличии автоколебаний. Важно отметить, что функция смещения 
не зависит ни от числа внешних воздействий на систему, ни от характера их изменения (он может быть не постоянной, а медленно меняющейся, что рассматривается ниже в § 5).
После определения функции смещения из уравнения 
с подстановкой 
сразу определяется искомая зависимость статической ошибки 
от величины постоянного внешнего воздействия М.
Возможен случай, когда к нелинейной системе приложено несколько внешних воздействий:
Методика расчетов при этом сохраняется. В отличие от линейных систем в данном случае складывать статические ошибки от отдельных воздействий нельзя. Это обусловлено нелинейной зависимостью 
от величины внешнего воздействия, как это следует из уравнения 
которое в данном случае принимает вид
Для облегчения практических расчетов в табл. 1 и 2 приложения IV приведены значения коэффициентов гармонической линеаризации для некоторых типоб нелинейных звеньев. Более полные сведения по гармонической линеаризации при наличии внешнего воздействия приведены в работе [13].
Несимметричные колебания в нелинейных автоматических системах могут возникать не только при наличии внешнего воздействия, но и при несимметричных характеристиках самого нелинейного элемента 
без внешнего воздействия.
В этом случае правая часть уравнения 
равна нулю:
При несимметричных характеристиках нелинейного звена 
возникает постоянная составляющая
Поэтому решение уравнения 
как и прежде, надо искать в виде суммы постоянной и периодической составляющих:
Уравнения 
в данном случае имеют вид
Решение уравнений 
выполняется таким же образом, как это делалось для симметричной характеристики нелинейного звена, при наличии постоянного внешнего воздействия.
Для облегчения использования описанной выше методики в табл. 3 приложения II приведены готовые выражения 
для некоторых типов несимметричных нелинейностей [13].
Пример 4. Для иллюстрации описанной выше методики определения установившихся ошибок в автоколебательных нелинейных системах рассмотрим систему, блок-схема которой приведена на рис. Х.20.
Рис. Х.20. Блок-схема релейной системы автоматического регулирования
Уравнения этой системы имеют вид:
Нелинейность представляет собой характеристику идеального симметричного реле
Уравнение системы будет
Предположим, что функция 
является управляющим воздействием, изменяющимся с постоянной скоростью
которое должна воспроизвести система на выходе. Второе внешнее воздействие 
является возмущающим и имеет постоянную величину (например, постоянная нагрузка на выходном валу системы), т. е.
Необходимо определить установившуюся ошибку на выходе системы. Правая часть характеристического уравнения будет при этом постоянной и установившееся решение для X с учетом автоколебаний следует искать в виде выражений 
Тогда уравнения для постоянных и периодических составляющих будут иметь вид:
В соответствии с изложенной выше методикой из уравнений 
определим
Откуда
или
Для определения амплитуды А периодической составляющей используется уравнение 
для которого запишем характеристическое уравнение
Подставив 
и выделив вещественную и мнимую части, получим 
Из уравнений 
найдем
Исключая из уравнений 
величину 
определим частоту автоколебаний
Подставив полученные значения 
в уравнение 
определим амплитуду автоколебаний
Здесь величина
является амплитудой симметричных автоколебаний при отсутствии внешних воздействий 
Подставив полученное значение амплитуды А в формулу 
определим искомую величину смещения
Из формулы (Х.82) видно, что автоколебания в системе существуют только до тех пор, пока внешние воздействия удовлетворяют условию
причем амплитуда автоколебаний уменьшается 
с увеличением внешних воздействий.
Так, в результате расчета определена величина смещения на входе реле. Однако практически больший интерес представляет установившаяся ошибка на выходе системы. Поскольку на выходе системы должно воспроизводиться внешнее воздействие 
то, согласно рис. Х.20, ошибка данной системы выражается величиной 
Запишем переменную 
через х, которая уже известна.
Из заданных уравнений системы 
имеем
Учитывая, что 
уравнение 
запишем в виде
В соответствии с характером правой части нужно искать установившееся решение этого линейного уравнения в виде
где 
— постоянные величины;
— периодическая составляющая.
Подставляя выражение 
получим три уравнения
Из уравнения (X.87) определим
Затем из уравнения 
найдем
Наконец, из уравнения 
получим
где 
определяются соответственно из формул 
Итак, в системе содержатся все три составляющие ошибки 
зависящие от величины внешних воздействий и от параметров системы. Наиболее нежелательной составляющей ошибки является составляющая 
возрастающая с течением времени. Для исключения этой ошибки необходимо в системе жесткую обратную связь заменить гибкой
Статическая ошибка — регулирование
Cтраница 2
И-регулятор не имеет статической ошибки регулирования, поскольку выход регулятора будет расти при любом малом значении рассогласования. Таким образом, в отличие от системы с П — регулятором системы с И-регулятором не имеют статической ошибки, но динамическая ошибка в этих системах большая. Это объясняется тем, что в начальный момент И-регулятор еще не успевает из-за своих инерционных свойств выработать значительный выходной сигнал.
[16]
И-регулятор не имеет статической ошибки регулирования, поскольку выход регулятора будет расти при любом малом значении рассогласования. Таким образом, в отличие от системы с П — регулято-ром системы с И-регулятором не имеют статической ошибки, но динамическая ошибка в этих системах большая. Это объясняется тем, что в начальный момент И-регулятор еще не успевает из-за своих инерционных свойств выработать значительный выходной сигнал.
[18]
И-регулятор не имеет статической ошибки регулирования, поскольку выход регулятора будет расти при любом малом значении рассогласования. Таким образом, в отличие от системы с П — регулятором системы с И-регулятором не имеют статической ошибки, но динамическая ошибка в этих системах большая.
[20]
Этот коэффициент равен отношению статической ошибки регулирования к установившемуся отклонению того же параметра в случае отсутствия регулятора.
[21]
Изменение скорости б называется статической ошибкой регулирования скорости.
[22]
Почему в статической АСР возникает статическая ошибка регулирования.
[23]
Для пропорционального закона регулирования характерна статическая ошибка регулирования Д, связанная с принципом регулирования — изменением положения регулирующего органа только при отклонении регулируемого параметра от заданной величины.
[25]
ВЫХо и, следовательно, статическая ошибка регулирования бст равна нулю.
[27]
Из этого выражения следует, что статическая ошибка регулирования увеличивается при росте отклонения регулируемой величины при работе без регулятора и уменьшается с ростом коэффициента усилителя разомкнутой системы.
[29]
САР на регулируемом объекте допускается наличие статической ошибки регулирования.
[30]
Страницы:
1
2
3
4
5
Статистическая погрешность — это та неопределенность в оценке истинного значения измеряемой величины, которая возникает из-за того, что несколько повторных измерений тем же самым инструментом дали различающиеся результаты. Возникает она, как правило, из-за того, что результаты измерения в микромире не фиксированы, а вероятностны. Она тесно связана с объемом статистики: обычно чем больше данных, тем меньше статистическая погрешность и тем точнее результат измерения. Среди всех типов погрешностей она, пожалуй, самая безобидная: понятно, как ее считать, и понятно, как с ней бороться.
Статистическая погрешность: чуть подробнее
Предположим, что ваш детектор может очень точно измерить какую-то величину в каждом конкретном столкновении. Это может быть энергия или импульс какой-то родившейся частицы, или дискретная величина (например, сколько мюонов родилось в событии), или вообще элементарный ответ «да» или «нет» на какой-то вопрос (например, родилась ли в этом событии хоть одна частица с импульсом больше 100 ГэВ).
Это конкретное число, полученное в одном столкновении, почти бессмысленно. Скажем, взяли вы одно событие и выяснили, что в нём хиггсовский бозон не родился. Никакой научной пользы от такого единичного факта нет. Законы микромира вероятностны, и если вы организуете абсолютно такое же столкновение протонов, то картина рождения частиц вовсе не обязана повторяться, она может оказаться совсем другой. Если бозон не родился сейчас, не родился в следующем столкновении, то это еще ничего не говорит о том, может ли он родиться вообще и как это соотносится с теоретическими предсказаниями. Для того, чтобы получить какое-то осмысленное число в экспериментах с элементарными частицами, надо повторить эксперимент много раз и набрать статистику одинаковых столкновений. Всё свое рабочее время коллайдеры именно этим и занимаются, они накапливают статистику, которую потом будут обрабатывать экспериментаторы.
В каждом конкретном столкновении результат измерения может быть разный. Наберем статистику столкновений и усредним по ней результат. Этот средний результат, конечно, тоже не фиксирован, он может меняться в зависимости от статистики, но он будет намного стабильнее, он не будет так сильно прыгать от одной статистической выборки к другой. У него тоже есть некая неопределенность (в статистическом анализе она так и называется: «неопределенность среднего»), но она обычно небольшая. Вот эта величина и называется статистической погрешностью измерения.
Итак, когда экспериментаторы предъявляют измерение какой-то величины, то они сообщают результат усреднения этой величины по всей набранной статистике столкновений и сопровождают его статистической погрешностью. Именно такие средние значения имеют физический смысл, только их может предсказывать теория.
Есть, конечно, и иной источник статистической погрешности: недостаточный контроль условий эксперимента при повторном измерении. Если в физике частиц этот источник можно попытаться устранить, по крайней мере, в принципе, то в других разделах естественных наук он выходит на первый план; например, в медицинских исследованиях каждый человек отличается от другого по большому числу параметров.
Как считать статистическую погрешность?
Существует теория расчета статистической погрешности, в которую мы, конечно, вдаваться не будем. Но есть одно очень простое правило, которое легко запомнить и которое срабатывает почти всегда. Пусть у вас есть статистическая выборка из N столкновений и в ней присутствует n событий какого-то определенного типа. Тогда в другой статистической выборке из N событий, набранной в тех же условиях, можно ожидать примерно n ± √n таких событий. Поделив это на N, мы получим среднюю вероятность встретить такое событие и погрешность среднего: n/N ± √n/N. Оценка истинного значения вероятности такого типа события примерно соответствует этому выражению.
Сразу же, впрочем, подчеркнем, что эта простая оценка начинает сильно «врать», когда количество событий очень мало. В науке обсчета маленькой статистики есть много дополнительных тонкостей.
Более серьезное (но умеренно краткое) введение в методы статистической обработки данных в применении к экспериментам на LHC см. в лекциях arXiv.1307.2487.
Именно поэтому эксперименты в физике элементарных частиц стараются оптимизировать не только по энергии, но и по светимости. Ведь чем больше светимость, тем больше столкновений будет произведено — значит, тем больше будет статистическая выборка. И уже это позволит сделать измерения более точными — даже без каких-либо улучшений в эксперименте. Примерная зависимость тут такая: если вы увеличите статистику в k раз, то относительные статистические погрешности уменьшатся примерно в √k раз.
Этот пример — некая симуляция того, как могло бы происходить измерение массы ρ-мезона свыше полувека назад, на заре адронной физики, если бы он был вначале обнаружен в процессе e+e– → π+π–. А теперь перенесемся в наше время.
Сейчас этот процесс изучен вдоль и поперек, статистика набрана огромная (миллионы событий), а значит, и масса ρ-мезона сейчас определена несравнимо точнее. На рис. 3 показано современное состояние дел в этой области масс. Если ранние эксперименты еще имели какие-то существенные погрешности, то сейчас они практически неразличимы глазом. Огромная статистика позволила не только измерить массу (примерно равна 775 МэВ с точностью в десятые доли МэВ), но и заметить очень странную форму этого пика. Такая форма получается потому, что практически в том же месте на шкале масс находится и другой мезон, ω(782), который «вмешивается» в процесс и искажает форму ρ-мезонного пика.
Другой, гораздо более реальный пример влияния статистики на процесс поиска и изучения хиггсовского бозона обсуждался в новости Анимации показывают, как в данных LHC зарождался хиггсовский сигнал.
По наличию статической ошибки — регуляторы статические и астатические. [c.35]
Меняя величину ступенчатой нагрузки, можно получить различные переходные процессы. При этом в статической системе каждой нагрузке будет соответствовать свое значение статической ошибки. Можно построить график (рис. 8, кривая /), показывающий зависимость установившегося значения выходной величины от нагрузки. Такой график называется статической характеристикой системы. [c.17]
Интегральное регулирование допускает, большие изменения нагрузки и исключает возможность появления статической ошибки. Поэтому такая комбинация дает хорошие результаты почти во всех случаях, за исключением процессов с очень резкими возмущающими воздействиями или очень большими запаздываниями. Регуляторы такого типа иногда называют регуляторами с автоматической обратной перестановкой, так как они автоматически сводят к нулю статическую ошибку, возникающую при пропорциональном регулировании. [c.460]
Реализация метода Монте-Карло связана с получением последовательности так называемых случайных чисел с заданным законом распределения. Особое значение имеют последовательности равномерно распределенных случайных величин, поскольку они часто используются при вычислениях и, кроме того, на основе последовательностей равномерно распределенных чисел строятся последовательности с другими законами распределения (нормальным, экспоненциальным и др.). Пусть I — случайная величина, которая может принимать любые (однако с фиксированным числом знаков после запятой) значения в интервале [0,1] О 1. Будем производить испытания над случайной величиной и выберем п значений подряд или любым произвольным образом, в результате чего получим последовательность Ь, 1п = 1п)- Пусть а, й) — некоторый промежуток на отрезке [0,1] 1 (а, Ь) — число элементов из последовательности , принадлежащих промежутку (а, Ь). Если последовательность равномерно распределенная, то при п > 1 значение (а, Ь)1п с точностью до статической ошибки совпадает с величиной Ь — а, как бы мы ни выбирали промежуток (а, Ь). Если интервал [0,1] разделим на равные промежутки, то числа, попадающие в различные промежутки, должны встречаться в среднем в одинаковых пропорциях при этом ни одно из чисел не должно иметь заметной тенденции следовать за каким-либо определенным другим. [c.387]
Введение интеграла (использование ПИ-регулятора) устраняет статическую ошибку, но мало улучшает динамику процесса. Добавление импульса по производной (применение ПИД-регуля-тора) существенно повышает быстродействие системы, но при большом коэффициенте усиления возникает значительное перерегулирование и САР становится более чувствительной к внешним возмущениям. Для устранения этих недостатков возможны два пути усложнение САР (создание многоконтурной системы с дополнительными перекрещивающимися обратными связями) или создание регулятора со специальной характеристикой. При этом передаточная функция регулятора должна иметь вид [21] [c.711]
At/p при установившейся рабочей скорости v — Vp и статическая ошибка позиционирования Ау = Ау,. при рабочей внешней нагрузке Яа = Ир. В некоторых случаях дополнительно учитывают ошибку слежения при фиксированном ускорении выходного звена следящего привода. Точность следящего привода зависит от измерителей рассогласования, передаточного числа приборной зубчатой передачи и минимально необходимой добротности регулирующего контура. [c.320]
В итоге можно сказать, что пропорциональное регулирование обеспечивает хорошие переходные характеристики и может стабилизовать процесс, имеющий характерные временные задержки в таких случаях оно широко используется. Но при изменении нагрузки возникает статическая ошибка выходной величины, так что эти из- менения должны быть малы и редки. Ошибку можно уменьшить,. ограничивая зону пропорциональности или увеличивая коэффициент усиления, но тогда возникают нежелательные незатухающие колебания вы- [c.458]
Как определить относительную статическую ошибку регулирования насоса в режиме постоянной мощности [c.324]
Полезно заметить, что при астатическом объекте (vj ф 0), но статическом регуляторе (vj = 0), как показывает формула (5.85), постоянное возмущающее воздействие создает в системе статическую ошибку, которая не возникает, если объект статический (vx = 0), а регулятор астатический (vj Ф 0). [c.158]
Указанное свойство системы можно обобщить следующим правилом для устранения в системе статической ошибки по какому-либо воздействию интегрирующее звено необходимо включать до места приложения этого воздействия. [c.158]
Изодромные, или пропорционально-инте-тральные, регуляторы (сокращенно ПИ-регуляторы) объединяют в себе положительные свойства пропорциональных и интегральных регуляторов. Как следует из сказанного выше, наличие отрицательной обратной связи благотворно влияет на переходный процесс регулирования, но приводит к остаточному отклонению. В пропорционально-интегральных регуляторах применяется особая обратная связь — упругая, действие которой постепенно исчезает после осуществления пропорционального воздействия. Благодаря этому возникают дополнительные перемещения регулирующего органа, ликвидирующие статическую ошибку. Устройство упругой обратной связи носит название изодрома, откуда и происходит наименование самого регулятора. [c.42]
Величина отклонения параметра в конце процесса регулирования от заданного значения называется остаточной неравномерностью, или статической ошибкой. Она представляет собой отклонение регулируемого параметра в процентах от заданного значения, вызывающее полный ход исполнительного механизма. Например, если степень неравномерности регулятора равна 10%, то это значит, что изменение параметра на I % от шкалы регулятора вызовет перемещение регулирующего органа на Vio его полного хода из одного крайнего положения в другое. Неравномерность, или статическая ошибка, регулирующего органа с чувствительным элементом определяется жесткостью связи. Чем жестче связь, тем большее изменение задания регулируемого параметра вызывает перемещение регулирующего органа на единицу его полного хода. В данном примере жесткость связи определяется положением точки 4 на рычаге 1. Чем больше расстояние между точками 2 я 4, тем жестче связь и больше статическая ошибка. [c.262]
Таким образом, за счет статической ошибки (погрешности) потенциостата потенциал ИЭ всегда несколько отклоняется от заданного значения в сторону ф1=о, причем отклонение это возрастает с увеличением поляризующего тока. [c.64]
Для изменения -производительности установки требуется такое изменение регулируемой величины — температуры, которое приводит к срабатыванию реле температуры. Это неизбежное отклонение от первоначально заданного значения регулируемой величины, вызванное изменением нагрузки в новом установившемся режиме, называют статической ошибкой. [c.229]
Если колебание нагрузки (между максимальным и минимальным значениями) вызывает такую статическую ошибку, что регулируемая величина выходит за требуемые пределы, то можно применить астатическую систему регулирования. [c.229]
У астатических регуляторов (рис. 18, д) малейшее отклонение входного параметра X вызывает непрерывное движение РО с определенной скоростью до предельного значения К акс- Регулирующий орган остановится только при X = Хо. Если при этом окажется МрФ Мн,, то снова возникнет рассогласование X — Хо и РО дополнительно переместится, пока не остановится в положении, при котором Мр == Мн. и X = Хо, т. е. когда статическая ошибка равна нулю. Именно поэтому их и называют астатическими. [c.36]
Диапазон пропорциональности и соответственно коэффициент усиления (чувствительность прибора) зависит от жесткости пружины, площади мембраны и обычно не регулируется. В схеме на рис. 19, а коэффициент усиления зависит также от соотношения плеч рычага ОА и ОБ. Перемещая винтом 2 центр О вправо, можно повысить чувствительность прибора. Характеристика 1 — 2 станет круче. Это уменьшит ДП, а следовательно, и статическую ошибку. Однако в реальных регуляторах увеличение чувствительности ухудшает переходные характеристики. [c.39]
Сиглске [21], анализируя полученные динамические характеристики колпачковой абсорбционной колонны, предположил, что необходимо поддерживать постоянным состав выходящего газа. В результате показано, что по динамике лучше всего воздействовать на состав входящей жидкости (канал состав входящей жидкости—состав выходящего газа является наименее инерционным). Однако из практических соображений удобнее воздействовать на подачу входящей жидкости некоторое ухудшение динамических свойств при этом компенсируется техническими преимуществами. При использовании в этом случае П-регулятора САР устойчива, но передемпфирована она имеет статическую ошибку, и процесс регулирования проходит медленно. [c.711]
На рис. 4.5 показан аксиально-поршневой насос / с валом 2 и регулятором мощности прямого действия. Через отверстия А Б камеру с плунжером 5 поступа<т рабочая жидкость под давлением Рн- Плунжер 5 через промежуточный толкатель 4 поворачивает наклонную шайбу 6, пока сила со стороны пружинного блока 3 не уравновесит силу давления жидкости. Перемещение Ху и поворот шайбы приводят к изменению удельного рабочего объема i7n насоса. Пружинный блок составлен из двух цилиндрических пружин различной длины, поэтому статическая характеристика данного регулятора имеет вид ломаной линии (см. на рис. 4.4, б линию 2). Отклоиеиие ломаной линии 2 от идеальной статической характеристики (линии 1) приводит к появлению статической ошибки регулирования. (Изготовление специальной пружины с заданной нелинейной характеристикой сопряжено со значительными трудностями). [c.283]
Статическая ошибка регулятора прямого действия существенно зависит от силы, возникающей со стороны регулирующего органа насоса, в частности, наклонной шайбы. Сила трения на регулирующем органе насоса приводит к петлевой статической характеристике регулятора прямого действия. Снизить влияние нагрузки на регулятор можно, увеличив эффективную плоы адь плунжера и соответственно жесткость пружинного блока. Однако из-за этого во многих случаях габаритные размеры регулятора мощности прямого действия значительно увеличиваются. [c.284]
Рассматриваемый регулятор имеет дополнительный подвод энергии в виде рабочей жидкости, поступающей от вспомогательного насоса в исполнительный механизм через отверстие Б и уходящей на слив через В. Благодаря вспомогательному следящему приводу, называемому иногда гидроусилителем, нагрузка со стороны регулирующего органа насоса несущественно влияет на статическую характеристику регулятора мощности. Использование в пружинном блоке трех пружин различной жесткости уменьшает статическую ошибку по сравнению с двухпружинным блоком. Демпфирующий поршень снижает колебания регулятора при переходном процессе. [c.285]
Чтобы точность позиционирозания рабочего органа была высокой, необходимо наряду о большой величиной к обеспечить малые ошибки электрических приборов и механических передач. Суммарная статическая ошибка позиционирования следящего привода [c.313]
От точности выполнения размеров основных деталей шагового распределителя, обратной связи и силовой механической передачи зависит точность позиционирования выходного звена шагового гидропривода. Относительная статическая ошибка позиционирования Bnos = At/ /i/шаг может быть опредёлена в виде [c.340]
Соотношение (5.88) показывает, что при отсутствии в системе интегрирующих звеньев (разомкнутая система — статическая) постоянные воздействия и /о вызывают постоянную установив-щуюся ошибку (,, которую называют статической. Эта ошибка будет тем меньше, чем больше коэффициент-усиления К. системы, причем для уменьшения статической ошибки, вызываемой возмущающим воздействием, следует для увеличения К увеличивать коэффициент /Са регулятора, а не К объекта. [c.158]
Критерий статической ошибки. При использовании статических, регуляторов каждому значению величины статичеокого отклонения возмущающего воздействия соответствует определенное отклонение выходного пара-M Tipa объекта. [c.109]
Отклонение выходного параметра от требуемого значения есть величина статической ошибкй, которая тем меньше, чем меньше коэффициент усиления по дйн-ному каналу, т. е. чем выше коэфф ицие Нт усиления uetiH регулированиями ниже так называемая степень нерав- номерности самого регулятора. [c.109]
Регулирование по отклонению, производной и. цкте-гралу. Комбинация из всех трех основных видов регулирования обеспечивает наилучшее возможное управление. Сохраняются преимущества каждого вида—пропорциональное воздействие статического регулирования с исключением статической ошибки благодаря интегральному регулированию и преодолением любых запаздываний благодаря стабилизирующему быстродействующему регулированию по производной. [c.461]
Пропорциональные регуляторы не могут поддерживать постоянное значение регулируемой величины, так как перемещение регулирующего органа в таких системах однозначно связано с изменением входной величины, следовательно, всякому новому его положению, необходимому при изменениях нагрузки, отвечает некоторое новое значение регулируемого параметра. Это неизбежное отклонение называют остаточной неравномерностью регулирования или статической ошибкой. Величина остаточной неравномерности тем менЫне, чем больше коэффициент передачи регулятора по прямому тракту. [c.41]
Кривые переходных процессов по каналу расход сырья — состав верхнего продукта показали, что лучщее качество регулирования обеспечивает схема с использоваипем хроматографа. Первая схема имеет большую статическую ошибку. Применение метода прямого регулирования с ИК-анализаторо.м менее целесообразно вследствие значительного ухудшения частотных характеристик системы. В частности, время переходного процесса прн этом методе в 4 раза больше, чем в системах, основанных на двух других методах регулирования. [c.312]
У астатических регуляторов регулирующий орган перемещается со-скоростью, пропорциональной отклонению регулируемого параметра. Преимуществом регуляторов этого типа является то, что установившееся значение регулируемой величины не зависит от нагруз-ки, и статическая ошибка равна нулю. Однако астатические регуляторы можно применять лишь для управления объектами, обладающими самовыравни-ванием в противном случае система будет неустойчивой. [c.543]
В момент источник питания выключается, а плунжер золотника начинает ускоренно двигаться в прежнем направлении со скоростью Хп = Уподв- Вновь возникает динамическая ошибка, которая со временем переходит в статическую. Если ко времени касания электродов ошибка успевает установиться, то в момент их касания плунжер оказывается смещенным относительно своего нейтрального положения на величину статической ошибки [c.140]
У статических регуляторов (рис. 18,г) установившееся значение вырдного параметра У однозначно ( жестко ) определяется величиной входного параметра X. При регулировании они дают статическую ошибку (см рис. 7, в). [c.35]
Устройство, монтаж и ремонт холодильных установок Издание 4 (1985) — [
c.124
]
Устройство, монтаж и ремонт холодильных установок Издание 4 (1986) — [
c.124
]
Основы автоматизации холодильных установок Издание 3 (1987) — [
c.21
]