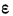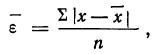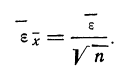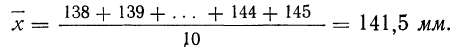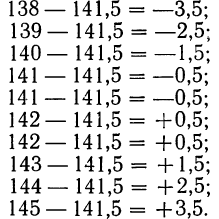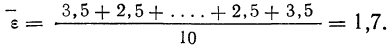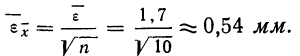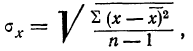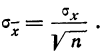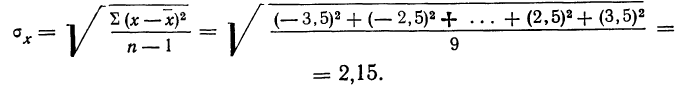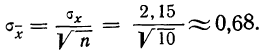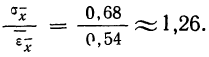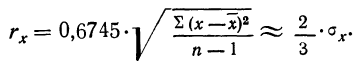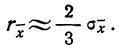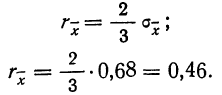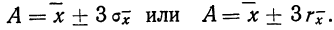Теория
ошибок.
В лабораторном
практикуме студенты при выполнении
работ должны производить измерения, но
при использовании даже очень точных и
чувствительных приборов и наилучших
условий проведения эксперимента во
всяком измерении содержится ошибка
(погрешность) характер и причины которой
могут быть различными. Существуют методы
анализа и учета влияния различных
погрешностей на результаты измерений.
Все погрешности (ошибки) измерений
принято подразделять на систематические
и случайные.
Систематические
ошибки
обусловлены постоянными, но односторонними
внешними воздействиями. Например,
измерение температуры термометром, у
которого нулевая точка смешена, будет
систематически неправильным, пока в
результаты измерений не будет внесена
соответствующая поправка.
Так как
систематическая ошибка имеет одно и
тоже значение, ее нельзя устранить
увеличением числа повторных измерений.
Но можно уменьшить систематическую
ошибку, критически анализируя факторы,
которые могут повлиять на результаты,
проверяя используемые приборы по
соответствующим эталонам, внося поправки
в показания приборов, используя более
точные приборы и инструменты.
Случайные
ошибки
при измерениях обусловлены влиянием
большого числа факторов, случайным
образом изменяющихся в процессе
эксперимента. Например, источником
случайных ошибок при взвешивании на
аналитических весах может явиться
неоднородность в распределении
температуры в различных частях весов,
влияние колебаний стола из-за проезжающего
мимо здания грузовика и т.п.
При повторных
измерениях случайные ошибки с одинаковой
вероятностью приводят к отклонениям
значений измеряемых величин от истинного
значения как в сторону увеличения, так
и в сторону уменьшения, т.е. случайные
ошибки имеют разные численные значения
и знаки.
Полностью
исключить случайные ошибки нельзя, но
их можно уменьшить за счет увеличения
числа измерений при одних и тех же
условиях эксперимента.
Итак, при измерениях
неизбежно возникают погрешности. Теория
погрешностей указывает на то, как следует
вести измерения и их обработку, чтобы
допущенные ошибки были минимальными.
Кроме того, устанавливаются пределы,
внутри которых заключается точное
значение определяемой величины.
Теория погрешностей
I. Погрешности при прямых измерениях
Прямыми измерениями
называются такие, при которых измерение
величины производится непосредственно
по шкале прибора. Например,
2
измерение длины
штангенциркулем, измерение веса тела
на весах, определение промежутков
времени с помощью секундомера. Если
отклонение результатов измерений от
истинного значения измеряемой величины
происходит как в сторону увеличения,
так и в сторону уменьшения результатов
измерений, то наиболее вероятным
значением измеряемой величины будет
среднее арифметическое всех сделанных
измерений:
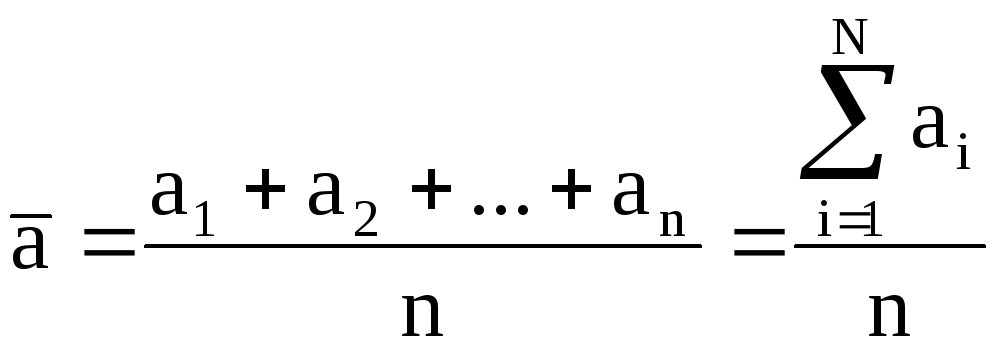
(1)
где
результаты отдельных измерений, n
число измерений.
Для
характеристики степени приближения к
истинному значению измеряемой
величины вводится понятие абсолютной
погрешности
величины, показывающей насколько
найденное (среднее арифметическое)
значение может отличаться от истинного
значения измеряемой величины.
Для
определения абсолютной погрешности
сначала нужно найти отклонения каждого
отдельного измерения от среднего
арифметического:
,
где
отклонение данного измерения, равное
разности между средним значением
измеряемой величины
и результатом этого измерения
.
Случайная погрешность
вычисляется по формуле:

(2)
где
модули отклонений каждого отдельного
измерения от среднего арифметического
значения.
Из
формулы (2) и теории вероятностей следует,
что с увеличением числа измерений n
случайная погрешность будет уменьшаться.
В
качестве систематической погрешности
берется приборная погрешность, равная
половине цены деления шкалы прибора.
Ценой деления прибора называется
минимальная величина, измеряемая
прибором.
В
общем случае необходимо принимать во
внимание как случайные, так и систематические
погрешности прямых измерений. Поэтому
абсолютная погрешность
при прямых измерениях рассчитывается
по формуле:
(3)
где
случайная погрешностей, определяемых
по формуле (2),
3

погрешность прибора, инструмента.
Примечание:
Если случайная погрешность много меньше
систематической, то для повышения
точности результата измерений нет
смысла увеличивать число измерений, а
нужно принять меры к уменьшению
систематической погрешности (например,
использовать более точные приборы).
Пример.
Пусть
измеряется диаметр цилиндрического
стержня с помощью штангенциркуля и
делается 5 измерений: 34.50
мм,
34.65
мм,
34.30
мм,
34.70
мм,
34.55
мм.
Среднее арифметическое
всех сделанных измерений:
Полученное
значение
даёт наиболее вероятное значение
измеряемой величиныD.
Для
нахождения случайной погрешности
нужно найти абсолютное значение
отклонения каждого из 5-ти измерений от
среднего арифметическогои затем определить среднее значение
этих отклонений:
Цена
деления штангенциркуля равна 0.05 мм,
следовательно, систематическая
погрешность равна
.
Абсолютная
погрешность при измерении диаметра
стержня:
Результат
измерений принято записывать следующим
образом:
.
(Результат измерений
34,54 мм и абсолютная погрешность 0,12 мм
должны заканчиваться в одинаковом
разряде)
Для характеристики
точности измерения вводится понятие
относительной погрешности:
Относительная
погрешность ε представляет собой
отношение абсолютной погрешности
к среднему значению измеряемой величины.
В нашем примере относительная погрешность
при измерении диаметра:
4
Относительная
погрешность является безразмерной
величиной. Она показывает, какую часть
измеряемой величины составляет абсолютная
погрешность.
Соседние файлы в папке Отчеты_Погрешность
- #
- #
- #
- #
- #
Свойства физического объекта (явления, процесса) определяются набором
количественных характеристик — физических величин.
Как правило, результат измерения представляет
собой число, задающее отношение измеряемой величины к некоторому эталону.
Сравнение с эталоном может быть как
прямым (проводится непосредственно
экспериментатором), так и косвенным (проводится с помощью некоторого
прибора, которому экспериментатор доверяет).
Полученные таким образом величины имеют размерность, определяемую выбором эталона.
Замечание. Результатом измерения может также служить количество отсчётов некоторого
события, логическое утверждение (да/нет) или даже качественная оценка
(сильно/слабо/умеренно). Мы ограничимся наиболее типичным для физики случаем,
когда результат измерения может быть представлен в виде числа или набора чисел.
Взаимосвязь между различными физическими величинами может быть описана
физическими законами, представляющими собой идеализированную
модель действительности. Конечной целью любого физического
эксперимента (в том числе и учебного) является проверка адекватности или
уточнение параметров таких моделей.
1.1 Результат измерения
Рассмотрим простейший пример: измерение длины стержня
с помощью линейки. Линейка проградуирована производителем с помощью
некоторого эталона длины — таким образом, сравнивая длину
стержня с ценой деления линейки, мы выполняем косвенное сравнение с
общепринятым стандартным эталоном.
Допустим, мы приложили линейку к стержню и увидели на шкале некоторый результат
x=xизм. Можно ли утверждать, что xизм — это длина
стержня?
Во-первых, значение x не может быть задано точно, хотя бы
потому, что оно обязательно округлено до некоторой значащей
цифры: если линейка «обычная», то у неё
есть цена деления; а если линейка, к примеру, «лазерная»
— у неё высвечивается конечное число значащих цифр
на дисплее.
Во-вторых, мы никак не можем быть уверенны, что длина стержня на
самом деле такова хотя бы с точностью до ошибки округления. Действительно,
мы могли приложить линейку не вполне ровно; сама линейка могла быть
изготовлена не вполне точно; стержень может быть не идеально цилиндрическим
и т.п.
И, наконец, если пытаться хотя бы гипотетически переходить к бесконечной
точности измерения, теряет смысл само понятие «длины стержня». Ведь
на масштабах атомов у стержня нет чётких границ, а значит говорить о его
геометрических размерах в таком случае крайне затруднительно!
Итак, из нашего примера видно, что никакое физическое измерение не может быть
произведено абсолютно точно, то есть
у любого измерения есть погрешность.
Замечание. Также используют эквивалентный термин ошибка измерения
(от англ. error). Подчеркнём, что смысл этого термина отличается от
общеупотребительного бытового: если физик говорит «в измерении есть ошибка»,
— это не означает, что оно неправильно и его надо переделать.
Имеется ввиду лишь, что это измерение неточно, то есть имеет
погрешность.
Количественно погрешность можно было бы определить как разность между
измеренным и «истинным» значением длины стержня:
δx=xизм-xист. Однако на практике такое определение
использовать нельзя: во-первых, из-за неизбежного наличия
погрешностей «истинное» значение измерить невозможно, и во-вторых, само
«истинное» значение может отличаться в разных измерениях (например, стержень
неровный или изогнутый, его торцы дрожат из-за тепловых флуктуаций и т.д.).
Поэтому говорят обычно об оценке погрешности.
Об измеренной величине также часто говорят как об оценке, подчеркивая,
что эта величина не точна и зависит не только от физических свойств
исследуемого объекта, но и от процедуры измерения.
Замечание.
Термин оценка имеет и более формальное значение. Оценкой называют результат процедуры получения значения параметра или параметров физической модели, а также иногда саму процедуру. Теория оценок является подразделом математической статистики. Некоторые ее положения изложены в главе 3, но для более серьезного понимания следует обратиться к [5].
Для оценки значения физической величины корректно использовать
не просто некоторое фиксированное число xизм, а интервал (или
диапазон) значений, в пределах которого может лежать её
«истинное» значение. В простейшем случае этот интервал
может быть записан как
где δx — абсолютная величина погрешности.
Эта запись означает, что исследуемая величина лежит в интервале
x∈(xизм-δx;xизм+δx)
с некоторой достаточно большой долей вероятности (более подробно о
вероятностном содержании интервалов см. п. 2.2).
Для наглядной оценки точности измерения удобно также использовать
относительную величину погрешности:
Она показывает, насколько погрешность мала по сравнению с
самой измеряемой величиной (её также можно выразить в процентах:
ε=δxx⋅100%).
Пример. Штангенциркуль —
прибор для измерения длин с ценой деления 0,1мм. Пусть
диаметр некоторой проволоки равен 0,37 мм. Считая, что абсолютная
ошибка составляет половину цены деления прибора, результат измерения
можно будет записать как d=0,40±0,05мм (или
d=(40±5)⋅10-5м).
Относительная погрешность составляет ε≈13%, то
есть точность измерения весьма посредственная — поскольку
размер объекта близок к пределу точности прибора.
О необходимости оценки погрешностей.
Измерим длины двух стержней x1 и x2 и сравним результаты.
Можно ли сказать, что стержни одинаковы или различны?
Казалось бы,
достаточно проверить, справедливо ли x1=x2. Но никакие
два результата измерения не равны друг другу с абсолютной точностью! Таким
образом, без указания погрешности измерения ответ на этот вопрос дать
невозможно.
С другой стороны, если погрешность δx известна, то можно
утверждать, что если измеренные длины одинаковы
в пределах погрешности опыта, если |x2-x1|<δx
(и различны в противоположном случае).
Итак, без знания погрешностей невозможно сравнить между собой никакие
два измерения, и, следовательно, невозможно сделать никаких
значимых выводов по результатам эксперимента: ни о наличии зависимостей
между величинами, ни о практической применимости какой-либо теории,
и т. п. В связи с этим задача правильной оценки погрешностей является крайне
важной, поскольку существенное занижение или завышение значения погрешности
(по сравнению с реальной точностью измерений) ведёт к неправильным выводам.
В физическом эксперименте (в том числе лабораторном практикуме) оценка
погрешностей должна проводиться всегда
(даже когда составители задания забыли упомянуть об этом).
1.2 Многократные измерения
Проведём серию из n одинаковых (однотипных) измерений одной
и той же физической величины (например, многократно приложим линейку к стержню) и получим
ряд значений
Что можно сказать о данном наборе чисел и о длине стержня?
И можно ли увеличивая число измерений улучшить конечный результат?
Если цена деления самой линейки достаточно мала, то как нетрудно убедиться
на практике, величины {xi} почти наверняка окажутся
различными. Причиной тому могут быть
самые разные обстоятельства, например: у нас недостаточно остроты
зрения и точности рук, чтобы каждый раз прикладывать линейку одинаково;
стенки стержня могут быть слегка неровными; у стержня может и не быть
определённой длины, например, если в нём возбуждены звуковые волны,
из-за чего его торцы колеблются, и т. д.
В такой ситуации результат измерения интерпретируется как
случайная величина, описываемая некоторым вероятностным законом
(распределением).
Подробнее о случайных величинах и методах работы с ними см. гл. 2.
По набору результатов 𝐱 можно вычислить их среднее арифметическое:
| ⟨x⟩=x1+x2+…+xnn≡1n∑i=1nxi. | (1.1) |
Это значение, вычисленное по результатам конечного числа n измерений,
принято называть выборочным средним. Здесь и далее для обозначения
выборочных средних будем использовать угловые скобки.
Кроме среднего представляет интерес и то, насколько сильно варьируются
результаты от опыта к опыту. Определим отклонение каждого измерения от среднего как
Разброс данных относительно среднего принято характеризовать
среднеквадратичным отклонением:
| s=Δx12+Δx22+…+Δxn2n=1n∑i=1nΔxi2 | (1.2) |
или кратко
Значение среднего квадрата отклонения s2 называют
выборочной дисперсией.
Будем увеличивать число измерений n (n→∞). Если объект измерения и методика
достаточно стабильны, то отклонения от среднего Δxi будут, во-первых,
относительно малы, а во-вторых, положительные и отрицательные отклонения будут
встречаться примерно одинаково часто. Тогда при вычислении (1.1)
почти все отклонения Δxi скомпенсируются и можно ожидать,
что выборочное среднее при n≫1 будет стремиться к некоторому пределу:
Тогда предельное значение x¯ можно отождествить с «истинным» средним
для исследуемой величины.
Предельную величину среднеквадратичного отклонения при n→∞
обозначим как
Замечание. В общем случае указанные пределы могут и не существовать. Например, если измеряемый параметр
меняется во времени или в результате самого измерения, либо испытывает слишком большие
случайные скачки и т. п. Такие ситуации требуют особого рассмотрения и мы на них не
останавливаемся.
Замечание. Если n мало (n<10), для оценки среднеквадратичного отклонения
математическая статистика рекомендует вместо формулы (1.3) использовать
исправленную формулу (подробнее см. п. 5.2):
sn-12=1n-1∑i=1nΔxi2,
(1.4)
где произведена замена n→n-1. Величину sn-1
часто называют стандартным отклонением.
Итак, можно по крайней мере надеяться на то, что результаты небольшого числа
измерений имеют не слишком большой разброс, так что величина ⟨x⟩
может быть использована как приближенное значение (оценка) истинного значения
⟨x⟩≈x¯,
а увеличение числа измерений позволит уточнить результат.
Многие случайные величины подчиняются так называемому нормальному закону
распределения (подробнее см. Главу 2). Для таких величин
могут быть строго доказаны следующие свойства:
- •
при многократном повторении эксперимента бо́льшая часть измерений
(∼68%) попадает в интервал x¯-σ<x<x¯+σ
(см. п. 2.2). - •
выборочное среднее значение ⟨x⟩ оказывается с большей
вероятностью ближе к истинному значению x¯, чем каждое из измерений
{xi} в отдельности. При этом ошибка вычисления среднего
убывает пропорционально корню из числа опытов n
(см. п. 2.4).
Упражнение. Показать, что
s2=⟨x2⟩-⟨x⟩2.
(1.5)
то есть дисперсия равна разности среднего значения квадрата
⟨x2⟩=1n∑i=1nxi2
и квадрата среднего ⟨x⟩2=(1n∑i=1nxi)2.
1.3 Классификация погрешностей
Чтобы лучше разобраться в том, нужно ли многократно повторять измерения,
и в каком случае это позволит улучшить результаты опыта,
проанализируем источники и виды погрешностей.
В первую очередь, многократные измерения позволяют проверить
воспроизводимость результатов: повторные измерения в одинаковых
условиях, должны давать близкие результаты. В противном случае
исследование будет существенно затруднено, если вообще возможно.
Таким образом, многократные измерения необходимы для того,
чтобы убедиться как в надёжности методики, так и в существовании измеряемой
величины как таковой.
При любых измерениях возможны грубые ошибки — промахи
(англ. miss). Это «ошибки» в стандартном
понимании этого слова — возникающие по вине экспериментатора
или в силу других непредвиденных обстоятельств (например, из-за сбоя
аппаратуры). Промахов, конечно, нужно избегать, а результаты таких
измерений должны быть по возможности исключены из рассмотрения.
Как понять, является ли «аномальный» результат промахом? Вопрос этот весьма
непрост. В литературе существуют статистические
критерии отбора промахов, которыми мы, однако, настоятельно не рекомендуем
пользоваться (по крайней мере, без серьезного понимания последствий
такого отбора). Отбрасывание аномальных данных может, во-первых, привести
к тенденциозному искажению результата исследований, а во-вторых, так
можно упустить открытие неизвестного эффекта. Поэтому при научных
исследованиях необходимо максимально тщательно проанализировать причину
каждого промаха, в частности, многократно повторив эксперимент. Лишь
только если факт и причина промаха установлены вполне достоверно,
соответствующий результат можно отбросить.
Замечание. Часто причины аномальных отклонений невозможно установить на этапе
обработки данных, поскольку часть информации о проведении измерений к этому моменту
утеряна. Единственным способ борьбы с этим — это максимально подробное описание всего
процесса измерений в лабораторном журнале. Подробнее об этом
см. п. 4.1.1.
При многократном повторении измерении одной и той же физической величины
погрешности могут иметь систематический либо случайный
характер. Назовём погрешность систематической, если она повторяется
от опыта к опыту, сохраняя свой знак и величину, либо закономерно
меняется в процессе измерений. Случайные (или статистические)
погрешности меняются хаотично при повторении измерений как по величине,
так и по знаку, и в изменениях не прослеживается какой-либо закономерности.
Кроме того, удобно разделять погрешности по их происхождению. Можно
выделить
- •
инструментальные (или приборные) погрешности,
связанные с несовершенством конструкции (неточности, допущенные при
изготовлении или вследствие старения), ошибками калибровки или ненормативными
условиями эксплуатации измерительных приборов; - •
методические погрешности, связанные с несовершенством
теоретической модели явления (использование приближенных формул и
моделей явления) или с несовершенством методики измерения (например,
влиянием взаимодействия прибора и объекта измерения на результат измерения); - •
естественные погрешности, связанные со случайным
характером
измеряемой физической величины — они являются не столько
«ошибками» измерения, сколько характеризуют
природу изучаемого объекта или явления.
Замечание. Разделение погрешностей на систематические и случайные
не является однозначным и зависит от постановки опыта. Например, производя
измерения не одним, а несколькими однотипными приборами, мы переводим
систематическую приборную ошибку, связанную с неточностью шкалы и
калибровки, в случайную. Разделение по происхождению также условно,
поскольку любой прибор подвержен воздействию «естественных»
случайных и систематических ошибок (шумы и наводки, тряска, атмосферные
условия и т. п.), а в основе работы прибора всегда лежит некоторое
физическое явление, описываемое не вполне совершенной теорией.
1.3.1 Случайные погрешности
Случайный характер присущ большому количеству различных физических
явлений, и в той или иной степени проявляется в работе всех без исключения
приборов. Случайные погрешности обнаруживаются просто при многократном
повторении опыта — в виде хаотичных изменений (флуктуаций)
значений {xi}.
Если случайные отклонения от среднего в большую или меньшую стороны
примерно равновероятны, можно рассчитывать, что при вычислении среднего
арифметического (1.1) эти отклонения скомпенсируются,
и погрешность результирующего значения ⟨x⟩ будем меньше,
чем погрешность отдельного измерения.
Случайные погрешности бывают связаны, например,
- •
с особенностями используемых приборов: техническими
недостатками
(люфт в механических приспособлениях, сухое трение в креплении стрелки
прибора), с естественными (тепловой и дробовой шумы в электрических
цепях, тепловые флуктуации и колебания измерительных устройств из-за
хаотического движения молекул, космическое излучение) или техногенными
факторами (тряска, электромагнитные помехи и наводки); - •
с особенностями и несовершенством методики измерения (ошибка
при отсчёте по шкале, ошибка времени реакции при измерениях с секундомером); - •
с несовершенством объекта измерений (неровная поверхность,
неоднородность состава); - •
со случайным характером исследуемого явления (радиоактивный
распад, броуновское движение).
Остановимся несколько подробнее на двух последних случаях. Они отличаются
тем, что случайный разброс данных в них порождён непосредственно объектом
измерения. Если при этом приборные погрешности малы, то «ошибка»
эксперимента возникает лишь в тот момент, когда мы по своей
воле совершаем замену ряда измеренных значений на некоторое среднее
{xi}→⟨x⟩. Разброс данных при этом
характеризует не точность измерения, а сам исследуемый объект или
явление. Однако с математической точки зрения приборные и
«естественные»
погрешности неразличимы — глядя на одни только
экспериментальные данные невозможно выяснить, что именно явилось причиной
их флуктуаций: сам объект исследования или иные, внешние причины.
Таким образом, для исследования естественных случайных процессов необходимо
сперва отдельно исследовать и оценить случайные инструментальные погрешности
и убедиться, что они достаточно малы.
1.3.2 Систематические погрешности
Систематические погрешности, в отличие от случайных, невозможно обнаружить,
исключить или уменьшить просто многократным повторением измерений.
Они могут быть обусловлены, во-первых, неправильной работой приборов
(инструментальная погрешность), например, сдвигом нуля отсчёта
по шкале, деформацией шкалы, неправильной калибровкой, искажениями
из-за не нормативных условий эксплуатации, искажениями из-за износа
или деформации деталей прибора, изменением параметров прибора во времени
из-за нагрева и т.п. Во-вторых, их причиной может быть ошибка в интерпретации
результатов (методическая погрешность), например, из-за использования
слишком идеализированной физической модели явления, которая не учитывает
некоторые значимые факторы (так, при взвешивании тел малой плотности
в атмосфере необходимо учитывать силу Архимеда; при измерениях в электрических
цепях может быть необходим учет неидеальности амперметров и вольтметров
и т. д.).
Систематические погрешности условно можно разделить на следующие категории.
- 1.
Известные погрешности, которые могут быть достаточно точно вычислены
или измерены. При необходимости они могут быть учтены непосредственно:
внесением поправок в расчётные формулы или в результаты измерений.
Если они малы, их можно отбросить, чтобы упростить вычисления. - 2.
Погрешности известной природы, конкретная величина которых неизвестна,
но максимальное значение вносимой ошибки может быть оценено теоретически
или экспериментально. Такие погрешности неизбежно присутствуют в любом
опыте, и задача экспериментатора — свести их к минимуму,
совершенствуя методики измерения и выбирая более совершенные приборы.Чтобы оценить величину систематических погрешностей опыта, необходимо
учесть паспортную точность приборов (производитель, как правило, гарантирует,
что погрешность прибора не превосходит некоторой величины), проанализировать
особенности методики измерения, и по возможности, провести контрольные
опыты. - 3.
Погрешности известной природы, оценка величины которых по каким-либо
причинам затруднена (например, сопротивление контактов при подключении
электронных приборов). Такие погрешности должны быть обязательно исключены
посредством модификации методики измерения или замены приборов. - 4.
Наконец, нельзя забывать о возможности существования ошибок, о
которых мы не подозреваем, но которые могут существенно искажать результаты
измерений. Такие погрешности самые опасные, а исключить их можно только
многократной независимой проверкой измерений, разными методами
и в разных условиях.
В учебном практикуме учёт систематических погрешностей ограничивается,
как правило, паспортными погрешностями приборов и теоретическими поправками
к упрощенной модели исследуемого явления.
Точный учет систематической ошибки возможен только при учете специфики конкретного эксперимента. Особенное внимание надо обратить на зависимость (корреляцию) систематических смещений при повторных измерениях. Одна и та же погрешность в разных случаях может быть интерпретирована и как случайная, и как систематическая.
Пример.
Калибровка электромагнита производится при помощи внесения в него датчика Холла или другого измерителя магнитного потока. При последовательных измерениях с разными токами (и соотственно полями в зазоре) калибровку можно учитыать двумя различными способами:
•
Измерить значение поля для разных токов, построить линейную калибровочную кривую и потом использовать значения, восстановленные по этой кривой для вычисления поля по току, используемому в измерениях.
•
Для каждого измерения проводить допольнительное измерения поля и вообще не испльзовать значения тока.
В первом случае погрешность полученного значения будет меньше, поскльку при проведении прямой, отдельные отклонения усреднятся. При этом погрешность измерения поля будет носить систематический харрактер и при обработке данных ее надо будет учитывать в последний момент. Во втором случае погрешность будет носить статистический (случайный) харрактер и ее надо будет добавить к погрешности каждой измеряемой точки. При этом сама погрешность будет больше. Выбор той или иной методики зависит от конретной ситуации. При большом количестве измерений, второй способ более надежный, поскольку статистическая ошибка при усреднении уменьшается пропорционально корню из количества измерений. Кроме того, такой способ повзоляет избежать методической ошибки, связанной с тем, что зависимость поля от тока не является линейной.
Пример.
Рассмотрим измерение напряжения по стрелочному вольтметру. В показаниях прибора будет присутствовать три типа погрешности:
1.
Статистическая погрешность, связанная с дрожанием стрелки и ошибкой визуального наблюдения, примерно равная половине цены деления.
2.
Систематическая погрешность, связанная с неправильной установкой нуля.
3.
Систематическая погрешность, связанная с неправильным коэффициентом пропорциональности между напряжением и отклонением стрелки. Как правило приборы сконструированы таким образом, чтобы максимальное значение этой погрешности было так же равно половине цены деления (хотя это и не гарантируется).
Неотъемлемой частью любого измерения является погрешность измерений. С развитием приборостроения и методик измерений человечество стремиться снизить влияние данного явления на конечный результат измерений. Предлагаю более детально разобраться в вопросе, что же это такое погрешность измерений.
Погрешность измерения – это отклонение результата измерения от истинного значения измеряемой величины. Погрешность измерений представляет собой сумму погрешностей, каждая из которых имеет свою причину.
По форме числового выражения погрешности измерений подразделяются на абсолютные и относительные
Абсолютная погрешность – это погрешность, выраженная в единицах измеряемой величины. Она определяется выражением.
(1.2), где X — результат измерения; Х0 — истинное значение этой величины.
Поскольку истинное значение измеряемой величины остается неизвестным, на практике пользуются лишь приближенной оценкой абсолютной погрешности измерения, определяемой выражением
(1.3), где Хд — действительное значение этой измеряемой величины, которое с погрешностью ее определения принимают за истинное значение.
Относительная погрешность – это отношение абсолютной погрешности измерения к действительному значению измеряемой величины:
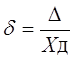
По закономерности появления погрешности измерения подразделяются на систематические, прогрессирующие, и случайные.
Систематическая погрешность – это погрешность измерения, остающаяся постоянной или закономерно изменяющейся при повторных измерениях одной и той же величины.
Прогрессирующая погрешность – это непредсказуемая погрешность, медленно меняющаяся во времени.
Систематические и прогрессирующие погрешности средств измерений вызываются:
- первые — погрешностью градуировки шкалы или ее небольшим сдвигом;
- вторые — старением элементов средства измерения.
Систематическая погрешность остается постоянной или закономерно изменяющейся при многократных измерениях одной и той же величины. Особенность систематической погрешности состоит в том, что она может быть полностью устранена введением поправок. Особенностью прогрессирующих погрешностей является то, что они могут быть скорректированы только в данный момент времени. Они требуют непрерывной коррекции.
Случайная погрешность – это погрешность измерения изменяется случайным образом. При повторных измерениях одной и той же величины. Случайные погрешности можно обнаружить только при многократных измерениях. В отличии от систематических погрешностей случайные нельзя устранить из результатов измерений.
По происхождению различают инструментальные и методические погрешности средств измерений.
Инструментальные погрешности — это погрешности, вызываемые особенностями свойств средств измерений. Они возникают вследствие недостаточно высокого качества элементов средств измерений. К данным погрешностям можно отнести изготовление и сборку элементов средств измерений; погрешности из-за трения в механизме прибора, недостаточной жесткости его элементов и деталей и др. Подчеркнем, что инструментальная погрешность индивидуальна для каждого средства измерений.
Методическая погрешность — это погрешность средства измерения, возникающая из-за несовершенства метода измерения, неточности соотношения, используемого для оценки измеряемой величины.
Погрешности средств измерений.
Абсолютная погрешность меры – это разность между номинальным ее значением и истинным (действительным) значением воспроизводимой ею величины:
(1.5), где Xн – номинальное значение меры; Хд – действительное значение меры
Абсолютная погрешность измерительного прибора – это разность между показанием прибора и истинным (действительным) значением измеряемой величины:
(1.6), где Xп – показания прибора; Хд – действительное значение измеряемой величины.
Относительная погрешность меры или измерительного прибора – это отношение абсолютной погрешности меры или измерительного прибора к истинному
(действительному) значению воспроизводимой или измеряемой величины. Относительная погрешность меры или измерительного прибора может быть выражена в ( % ).
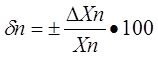
Приведенная погрешность измерительного прибора – отношение погрешности измерительного прибора к нормирующему значению. Нормирующие значение XN – это условно принятое значение, равное или верхнему пределу измерений, или диапазону измерений, или длине шкалы. Приведенная погрешность обычно выражается в ( % ).
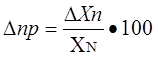
Предел допускаемой погрешности средств измерений – наибольшая без учета знака погрешность средства измерений, при которой оно может быть признано и допущено к применению. Данное определение применяют к основной и дополнительной погрешности, а также к вариации показаний. Поскольку свойства средств измерений зависят от внешних условий, их погрешности также зависят от этих условий, поэтому погрешности средств измерений принято делить на основные и дополнительные.
Основная – это погрешность средства измерений, используемого в нормальных условиях, которые обычно определены в нормативно-технических документах на данное средство измерений.
Дополнительная – это изменение погрешности средства измерений вследствии отклонения влияющих величин от нормальных значений.
Погрешности средств измерений подразделяются также на статические и динамические.
Статическая – это погрешность средства измерений, используемого для измерения постоянной величины. Если измеряемая величина является функцией времени, то вследствие инерционности средств измерений возникает составляющая общей погрешности, называется динамической погрешностью средств измерений.
Также существуют систематические и случайные погрешности средств измерений они аналогичны с такими же погрешностями измерений.
Факторы влияющие на погрешность измерений.
Погрешности возникают по разным причинам: это могут быть ошибки экспериментатора или ошибки из-за применения прибора не по назначению и т.д. Существует ряд понятий которые определяют факторы влияющие на погрешность измерений
Вариация показаний прибора – это наибольшая разность показаний полученных при прямом и обратном ходе при одном и том же действительном значении измеряемой величины и неизменных внешних условиях.
Класс точности прибора – это обобщенная характеристика средств измерений (прибора), определяемая пределами допускаемых основной и дополнительных погрешностей, а также другими свойствами средств измерений, влияющих на точность, значение которой устанавливаются на отдельные виды средств измерений.
Классы точности прибора устанавливают при выпуске, градуируя его по образцовому прибору в нормальных условиях.
Прецизионность — показывает, как точно или отчетливо можно произвести отсчет. Она определяется, тем насколько близки друг к другу результаты двух идентичных измерений.
Разрешение прибора — это наименьшее изменение измеряемого значения, на которое прибор будет реагировать.
Диапазон прибора — определяется минимальным и максимальным значением входного сигнала, для которого он предназначен.
Полоса пропускания прибора — это разность между минимальной и максимальной частотой, для которых он предназначен.
Чувствительность прибора — определяется, как отношение выходного сигнала или показания прибора к входному сигналу или измеряемой величине.
Шумы — любой сигнал не несущий полезной информации.
| Напечатано:: | Гость |
| Дата: | вторник, 31 января 2023, 17:02 |
Описание
1. Понятие о погрешности измерения.
2. Классификация погрешностей измерения.
3. Систематические погрешности
Оглавление
- 1. Понятие о погрешности измерения
- 2. Классификация погрешностей измерения
- 3. Систематические погрешности
1. Понятие о погрешности измерения
Всякий процесс измерения независимо от условий, в которых его проводят, сопряжен с погрешностями, которые искажают представление о действительном значении измеряемой величины.
Погрешностью называют отличие между объективно существующим истинным значением физической величины и найденным в результате измерения действительным значением физической величины.
Истинное значение физической величины идеальным образом отражает соответствующее свойство объекта. Практически получено быть не может.
Действительное значение физической величины находится как результат измерения и приближается к истинному значению настолько, что для данной цели может применяться вместо него.
Источниками появления погрешностей при измерениях могут служить различные факторы, основными из которых являются: несовершенство конструкции средств измерений или принципиальной схемы метода измерения; неточность изготовления средств измерений; несоблюдение внешних условий при измерениях; субъективные погрешности и др.
2. Классификация погрешностей измерения
В зависимости от обстоятельств, при которых проводились измерения, а также в зависимости от целей измерения, выбирается та или иная классификация погрешностей. Иногда используют одновременно несколько взаимно пересекающихся классификаций, желая по нескольким признакам точно охарактеризовать влияющие на результат измерения физические величины. В таком случае рассматривают, например, инструментальную составляющую неисключённой систематической погрешности. При выборе классификаций важно учитывать наиболее весомые или динамично меняющиеся или поддающиеся регулировке влияющие величины. Ниже приведены общепринятые классификации согласно типовым признакам и влияющим величинам.
По виду представления, различают абсолютную, относительную и приведённую погрешности.
Абсолютная погрешность это разница между результатом измерения X и истинным значением Q измеряемой величины. Абсолютная погрешность находится как D = X — Q и выражается в единицах измеряемой величины.
Относительная погрешность это отношение абсолютной погрешности измерения к истинному значению измеряемой величины: d = D / Q = (X – Q) / Q .
Приведённая погрешность это относительная погрешность, в которой абсолютная погрешность средства измерения отнесена к условно принятому нормирующему значению QN , постоянному во всём диапазоне измерений или его части. Относительная и приведённая погрешности – безразмерные величины.
В зависимости от источника возникновения, различают субъективную, инструментальную и методическую погрешности.
Субъективная погрешность обусловлена погрешностью отсчёта оператором показаний средства измерения.
Инструментальная погрешность обусловлена несовершенством применяемого средства измерения. Иногда эту погрешность называют аппаратурной. Метрологические характеристики средств измерений нормируются согласно ГОСТ 8.009 – 84, при этом различают четыре составляющие инструментальной погрешности: основная, дополнительная, динамическая, интегральная. Согласно этой классификации, инструментальная погрешность зависит от условий и режима работы, а также от параметров сигнала и объекта измерения.
Методическая погрешность обусловлена следующими основными причинами:
– отличие принятой модели объекта измерения от модели, адекватно описывающей его метрологические свойства;
– влияние средства измерения на объект измерения;
– неточность применяемых при вычислениях физических констант и математических соотношений.
В зависимости от измеряемой величины, различают погрешность аддитивную и мультипликативную. Аддитивная погрешность не зависит от измеряемой величины. Мультипликативная погрешность меняется пропорционально измеряемой величине.
В зависимости от режима работы средства измерений, различают статическую и динамическую погрешности.
Динамическая погрешность обусловлена реакцией средства измерения на изменение параметров измеряемого сигнала (динамический режим).
Статическая погрешность средства измерения определяется при параметрах измеряемого сигнала, принимаемых за неизменные на протяжении времени измерения (статический режим).
По характеру проявления во времени, различают случайную и систематическую погрешности.
Систематической погрешностью измерения называют погрешность, которая при повторных измерениях одной и той же величины в одних и тех же условиях остаётся постоянной или закономерно меняется.
Случайной погрешностью измерения называют погрешность, которая при повторных измерениях одной и той же величины в одних и тех же условиях изменяется случайным образом.
3. Систематические погрешности
Систематические погрешности при повторных измерениях остаются постоянными или изменяются по определенному закону.
Когда судят о погрешности, подразумевают не значение, а интервал значений, в котором с заданной вероятностью находится истинное значение. Поэтому говорят об оценке погрешности. Если бы погрешность оказалась измеренной, т.е. стали бы известны её знак и значение, то её можно было бы исключить из действительного значения измеряемой физической величины и получить истинное значение.
Для получения результатов, минимально отличающихся от истинного значения измеряемой физической величины, проводят многократные наблюдения и проводят математическую обработку полученного массива с целью определения и минимизации случайной составляющей погрешности.
Минимизация систематической погрешности в процессе наблюдений выполняется следующими методами: метод замещения (состоит в замещении измеряемой величины мерой), метод противопоставления (состоит в двух поочерёдных измерениях при замене местами меры и измеряемого объекта), метод компенсации погрешности по знаку (состоит в двух поочерёдных измерениях, при которых влияющая величина становится противоположной).
При многократных наблюдениях возможно апостериорное (после выполнения наблюдений) исключение систематической погрешности в результате анализа рядов наблюдений. Рассмотрим графический анализ. При этом результаты последовательных наблюдений представляются функцией времени либо ранжируются в порядке возрастания погрешности.
Рассмотрим временную зависимость. Будем проводить наблюдения через одинаковые интервалы времени. Результаты последовательных наблюдений являются случайной функцией времени. В серии экспериментов, состоящих из ряда последовательных наблюдений, получаем одну реализацию этой функции. При повторении серии получаем новую реализацию, отличающуюся от первой.
Реализации отличаются преимущественно из-за влияния факторов, определяющих случайную погрешность, а факторы, определяющие систематическую погрешность, одинаково проявляются для соответствующих моментов времени в каждой реализации. Значение, соответствующее каждому моменту времени, называется сечением случайной функции времени. Для каждого сечения можно найти среднее по всем реализациям значение. Очевидно, что эта составляющая и определяет систематическую погрешность. Если через значения систематической погрешности для всех моментов времени провести плавную кривую, то она будет характеризовать временную закономерность изменения погрешности. Зная закономерность изменения, можем определить поправку для исключения систематической погрешности. После исключения систематической погрешности получаем «исправленный ряд результатов наблюдений».
Известен ряд способов исключения систематических погрешностей, которые условно можно разделить па 4 основные группы:
- устранение источников погрешностей до начала измерений;
- исключение почетностей в процессе измерения способами замещения, компенсации погрешностей по знаку, противопоставления, симметричных наблюдений;
- внесение известных поправок в результат измерения (исключение погрешностей начислением);
- оценка границ систематических погрешностей, если их нельзя исключить.
По характеру проявления систематические погрешности подразделяют на постоянные, прогрессивные и периодические.
Постоянные систематические погрешности сохраняют свое значение в течение всего времени измерений (например, погрешность в градуировке шкалы прибора переносится на все результаты измерений).
Прогрессивные погрешности – погрешности, которые в процессе измерении подрастают или убывают (например, погрешности, возникающие вследствие износа контактирующих деталей средств измерения).
И группу систематических погрешностей можно отнести: инструментальные погрешности; погрешности из-за неправильной установки измерительного устройства; погрешности, возникающие вследствие внешних влияний; погрешности метода измерения (теоретические погрешности); субъективные погрешности.
3.4 Погрешности измерений
Основные понятия и определения.
При анализе измерений следует четко разграничивать два понятия: истинные значения физических величин и их эмпирические проявления – результаты измерений.
Истинные значения физических величин – это значения, идеальным образом отражающие свойства данного объекта как в количественном, так и в качественном отношении. Они не зависят от средств нашего познания и являются абсолютной истиной.
Результаты измерений, напротив, являются продуктами нашего познания. Представляя собой приближенные оценки значений величин, найденные путем измерения, они зависят не только от них, но еще и от метода измерения, от технических средств, с помощью которых проводятся измерения, и от свойств органов чувств наблюдателя, осуществляющего измерения.
Разница между результатами измерения X’ и истинным значением Q измеряемой величины называется погрешностью измерения :
|
|
(3.13) |
Но поскольку истинное значение Q измеряемой величины неизвестно, то неизвестны и погрешности измерения, поэтому для получения хотя бы приближенных сведений о них приходится в формулу (3.13) вместо истинного значения подставлять так называемое действительное значение.
Под действительным значением физической величины мы будем понимать ее значение, найденное экспериментально и настолько приближающееся к истинному, что для данной цели оно может быть использовано вместо него.
Причинами возникновения погрешностей являются: несовершенство методов измерений, технических средств, применяемых при измерениях, и органов чувств наблюдателя. В отдельную группу следует объединить причины, связанные с влиянием условий проведения измерений. Последние проявляются двояко. С одной стороны, все физические величины, играющие какую-либо роль при проведении измерений, в той или иной степени зависят друг от друга. Поэтому с изменением внешних условий изменяются истинные значения измеряемых величин. С другой стороны, условия проведения измерений влияют и на характеристики средств измерений и физиологические свойства органов чувств наблюдателя и через их посредство становятся источником погрешностей измерения.
Описанные причины возникновения погрешностей определяются совокупностью большого числа факторов, под влиянием которых складывается суммарная погрешность измерения – см. формулу (3.13). Их можно объединить в две основные группы.
1. Факторы, проявляющиеся весьма нерегулярно и столь же неожиданно исчезающие или проявляющиеся с интенсивностью, которую трудно предвидеть. К ним относятся, например, перекосы элементов приборов в их направляющих, нерегулярные изменения моментов трения в опорах, малые флюктуации влияющих величин, изменения внимания операторов и др.
Доля, или составляющая, суммарной погрешности измерения (3.13), определяемая действием факторов этой группы, называется случайной погрешностью измерения. Ее основная особенность в том, что она случайно изменяется при повторных измерениях одной и той же величины.
При создании измерительной аппаратуры и организации процесса измерения в целом интенсивность проявления большинства факторов данной группы удается свести к общему уровню, так что все они влияют более или менее одинаково на формирование случайной погрешности. Однако некоторые из них, например внезапное падение напряжения в сети электропитания, могут проявиться неожиданно сильно, в результате чего погрешность примет размеры, явно выходящие за границы, обусловленные ходом эксперимента в целом. Такие погрешности в составе случайной погрешности называютсягрубыми. К ним тесно примыкают промахи – погрешности, зависящие от наблюдателя и связанные с неправильным обращением со средствами измерений, неверным отсчетом показаний или ошибками при записи результатов.
2. Факторы, постоянные или закономерно изменяющиеся в процессе измерительного эксперимента, например плавные изменения влияющих величин или погрешности применяемых при измерениях образцовых мер. Составляющие суммарной погрешности (1), определяемые действием факторов этой группы, называютсясистематическими погрешностями измерения . Их отличительная особенность в том, что они остаются постоянными или закономерно изменяются при повторных измерениях одной и той же величины. До тех пор, пока систематические погрешности больше случайных, их зачастую можно вычислить или исключить из результатов измерений надлежащей постановкой опыта.
Таким образом, мы имеем два типа погрешностей измерения:
- случайные (в том числе грубые погрешности и промахи), изменяющиеся случайным образом при повторных измерениях одной и той же величины;
- систематические погрешности, остающиеся постоянными или закономерно изменяющиеся при повторных измерениях.
В процессе измерения оба вида погрешностей проявляются одновременно, и погрешность измерения можно представить в виде суммы:
|
|
(3.14) |
где – случайная, а
– систематическая погрешности.
Для получения результатов, минимально отличающихся от истинных значений величин, проводят многократные наблюдения за измеряемой величиной с последующей математической обработкой опытных данных. Поэтому наибольшее значение имеет изучение погрешности как функции номера наблюдения, т. е. времени . Тогда отдельные значения погрешностей можно будет трактовать как набор значений этой функции:
В общем случае погрешность является случайной функцией времени, которая отличается от классических функций математического анализа тем, что нельзя сказать, какое значение она примет в момент времениt . Можно указать лишь вероятности появления ее значений в том или ином интервале. В серии экспериментов, состоящих из ряда многократных наблюдений, мы получаем одну реализацию этой функции. При повторении серии при тех же значениях величин, характеризующих факторы второй группы, неизбежно получаем новую реализацию, отличающуюся от первой.
Реализации отличаются друг от друга из-за влияния факторов первой группы, а факторы второй группы, одинаково проявляющиеся при получении каждой реализации, придают им некоторые общие черты (рис.3.2).
Погрешность измерений, соответствующая каждому моменту времени , называется сечением случайной функции
. В каждом сечении в большинстве случаев можно найти среднее значение погрешности
, относительно которого группируются погрешности в различных реализациях. Если через полученные таким образом точки
провести плавную кривую, то она будет характеризовать общую тенденцию изменения погрешности во времени. Нетрудно заметить, что средние значения
определяются действием факторов второй группы и представляют собой систематическую погрешность измерения в момент времени
, а отклонения
от среднего в сечении , соответствующие
-й реализации, дают нам значения случайной погрешности. Последние являются уже представителями случайных величин – объектов изучения классической теории вероятностей.
Предположим, что , т.е. систематические погрешности тем или иным способом исключены из результатов наблюдений, и будем рассматривать только случайные погрешности, средние значения которых равны нулю в каждом сечении. Предположим далее, что случайные погрешности в различных сечениях не зависят друг от друга, т.е. знание случайной погрешности в одном сечении как ординаты одной реализации не дает нам никакой дополнительной информации о значении, принимаемом этой реализацией в любом другом сечении. Тогда случайную погрешность можно рассматривать как случайную величину, а ее значения при каждом из многократных наблюдений одной и той же физической величины – как ее эмпирические проявления, т.е. как результаты независимых наблюдений над ней.
В этих условиях случайная погрешность измерений определяется как разность между исправленным результатом Х измерения и истинным значением Q измеряемой величины:
|
|
(3.15) |
причем исправленным будем называть результат измерений, из которого исключены систематические погрешности.
При проведении измерений целью является оценка истинного значения измеряемой величины, которое до опыта неизвестно. Результат измерения включает в себя помимо истинного значения еще и случайную погрешность, следовательно, сам является случайной величиной. В этих условиях фактическое значение случайной погрешности, полученное при поверке, еще не характеризует точности измерений, поэтому не ясно, какое же значение принять за окончательный результат измерения и как охарактеризовать его точность.
Ответ на эти вопросы можно получить, используя при метрологической обработке результатов измерения методы математической статистики, имеющей дело именно со случайными величинами.
Классификация систематических погрешностей
Систематической погрешностью называется составляющая погрешности измерения, остающаяся постоянной или закономерно меняющаяся при повторных измерениях одной и той же величины . При этом предполагается, что систематические погрешности представляют собой определенную функцию неслучайных факторов, состав которых зависит от физических, конструкционных и технологических особенностей средств измерений, условий их применения, а также индивидуальных качеств наблюдателя. Сложные детерминированные закономерности, которым подчиняются систематические погрешности, определяются либо при создании средств измерений и комплектации измерительной аппаратуры, либо непосредственно при подготовке измерительного эксперимента и в процессе его проведения. Совершенствование методов измерения, использование высококачественных материалов, прогрессивная технология – все это позволяет на практике устранить систематические погрешности настолько, что при обработке результатов наблюдений с их наличием зачастую не приходится считаться.
В предыдущих параграфах, посвященных случайным погрешностям, было показано, что единственно правильным методом их анализа является математическая статистика. Случайные погрешности измерения изучались только в совокупности, без рассмотрения их фактических значений в каждом опыте. Систематические погрешности приходится изучать в каждом случае отдельно.
Систематические погрешности принято классифицировать в зависимости от причин их возникновения и по характеру их проявления при измерениях.
В зависимости от причин возникновения рассматриваются четыре вида систематических погрешностей:
1. Погрешности метода, или теоретические погрешности, проистекающие от ошибочности или недостаточной разработки принятой теории метода измерений в целом или от допущенных упрощений при проведении измерений.
Погрешности метода возникают также при экстраполяции свойства, измеренного на ограниченной части некоторого объекта, на весь объект, если последний не обладает однородностью измеряемого свойства. Так, считая диаметр цилиндрического вала равным результату, полученному при измерении в одном сечении и в одном направлении, мы допускаем систематическую погрешность, полностью определяемую отклонениями формы исследуемого вала. При определении плотности вещества по измерениям массы и объема некоторой пробы возникает систематическая погрешность, если проба содержала некоторое количество примесей, а результат измерения принимается за характеристику данного вещества вообще.
К погрешностям метода следует отнести также те погрешности, которые возникают вследствие влияния измерительной аппаратуры на измеряемые свойства объекта. Подобные явления возникают, например, при измерении длин, когда измерительное усилие используемых приборов достаточно велико, при регистрации быстропротекающих процессов недостаточно быстродействующей аппаратурой, при измерениях температур жидкостными или газовыми термометрами и так далее.
2. Инструментальные погрешности, зависящие от погрешностей применяемых средств измерений. Среди инструментальных погрешностей в отдельную группу выделяются погрешности схемы, не связанные с неточностью изготовления средств измерения и обязанные своим происхождением самой структурной схеме средств измерений. Исследование инструментальных погрешностей является предметом специальной дисциплины – теории точности измерительных устройств.
3. Погрешности, обусловленные неправильной установкой и взаимным расположением средств измерения, являющихся частью единого комплекса, несогласованностью их характеристик, влиянием внешних температурных, гравитационных, радиационных и других полей, нестабильностью источников питания, несогласованностью входных и выходных параметров электрических цепей приборов и так далее.
4. Личные погрешности, обусловленные индивидуальными особенностями наблюдателя. Такого рода погрешности вызываются, например, запаздыванием или опережением при регистрации сигнала, неправильным отсчетом десятых долей деления шкалы, асимметрией, возникающей при установке штриха посередине между двумя рисками.
По характеру своего поведения в процессе измерения систематические погрешности подразделяются на постоянные и переменные.
Постоянные систематические погрешности возникают, например, при неправильной установке начала отсчета, неправильной градуировке и юстировке средств измерения и остаются постоянными при всех повторных наблюдениях. Поэтому, если уж они возникли, их очень трудно обнаружить в результатах наблюдений.
Среди переменных систематических погрешностей принято выделять прогрессивные и периодические.
Прогрессивная погрешность возникает, например, при взвешивании, когда одно из коромысел весов находится ближе к источнику тепла, чем другое, поэтому быстрее нагревается и удлиняется. Это приводит к систематическому сдвигу начала отсчета и к монотонному изменению показаний весов.
Периодическая погрешность присуща измерительным приборам с круговой шкалой, если ось вращения указателя не совпадает с осью шкалы.
Все остальные виды систематических погрешностей принято называть погрешностями, изменяющимися по сложному закону.
В тех случаях, когда при создании средств измерений, необходимых для данной измерительной установки, не удается устранить влияние систематических погрешностей, приходится специально организовывать измерительный процесс и осуществлять математическую обработку результатов. Методы борьбы с систематическими погрешностями заключаются в их обнаружении и последующем исключении путем полной или частичной компенсации. Основные трудности, часто непреодолимые, состоят именно в обнаружении систематических погрешностей, поэтому иногда приходится довольствоваться приближенным их анализом.
Способы обнаружения систематических погрешностей
Результаты наблюдений, полученные при наличии систематических погрешностей, будем называть неисправленными и в отличие от исправленных снабжать штрихами их обозначения (например и т.д.). Вычисленные в этих условиях средние арифметические значения и отклонения от результатов наблюдений будем также называть неисправленными и ставить штрихи у символов этих величин. Таким образом,
|
|
(3.16) |
Поскольку неисправленные результаты наблюдений включают в себя систематические погрешности, сумму которых для каждого -го наблюдения будем обозначать через
, то их математическое ожидание не совпадает с истинным значением измеряемой величины и отличается от него на некоторую величину
, называемую систематической погрешностью неисправленного среднего арифметического. Действительно,


Если систематические погрешности постоянны, т.е. то неисправленные отклонения могут быть непосредственно использованы для оценки рассеивания ряда наблюдений. В противном случае необходимо предварительно исправить отдельные результаты измерений, введя в них так называемые поправки, равные систематическим погрешностям по величине и обратные им по знаку:
.
Таким образом, для нахождения исправленного среднего арифметического и оценки его рассеивания относительно истинного значения измеряемой величины необходимо обнаружить систематические погрешности и исключить их путем введения поправок или соответствующей каждому конкретному случаю организации самoгo измерения. Остановимся подробнее на некоторых способах обнаружения систематических погрешностей.
Постоянные систематические погрешности не влияют на значения случайных отклонений результатов наблюдений от средних арифметических, поэтому никакая математическая обработка результатов наблюдений не может привести к их обнаружению. Анализ таких погрешностей возможен только на основании некоторых априорных знаний об этих погрешностях, получаемых, например, при поверке средств измерений. Измеряемая величина при поверке обычно воспроизводится образцовой мерой, действительное значение которой известно. Поэтому разность между средним арифметическим результатов наблюдения и значением меры с точностью, определяемой погрешностью аттестации меры и случайными погрешностями измерения, равна искомой систематической погрешности.
Ценность полученных при поверке результатов определяется их постоянством в течение некоторого промежутка времени и независимостью от тех изменений внешних условий, которые допустимы при эксплуатации средств измерений с заданной точностью. Тогда полученные при поверке данные могут быть использованы для вычисления поправок, необходимых для исправления результатов наблюдений.
Одним из наиболее действенных способов обнаружения систематических погрешностей в ряде результатов наблюдений является построение графика последовательности неисправленных значений случайных отклонений результатов наблюдений от средних арифметических.
Вначале рассмотрим случай, когда в ряде результатов наблюдений предполагается наличие постоянной систематической погрешности. Для того чтобы удостовериться в этом, исследователь, сделав несколько измерений, заменяет некоторые меры или измерительные приборы, включенные в установку и являющиеся предполагаемыми источниками постоянных систематических погрешностей, другими мерами и измерительными приборами и проводит еще несколько измерений.
Рассматриваемый способ обнаружения постоянных систематических погрешностей можно сформулировать следующим образом: если неисправленные отклонения результатов наблюдений резко изменяются при изменении условий наблюдений, то данные результаты содержат постоянную систематическую погрешность, зависящую от условий наблюдений.
При прогрессивной систематической погрешности последовательность неисправленных отклонений результатов наблюдений обнаруживает тенденцию к возрастанию или убыванию. На рис.3.3 изображена зависимость погрешности измерения от длины измеряемой детали.
Несмотря на большие случайные изменения погрешности тенденция к увеличению ее в отрицательном направлении с ростом измеряемой величины явно обнаруживается. Если бы случайные погрешности были невелики, то значения неисправленных отклонений меняли бы свой знак при некотором среднем значении измеряемой величины. Случайные погрешности несколько искажают эту картину, однако, если они даже одного порядка малости с систематическими погрешностями, в последовательности знаков можно заметить некоторую неравномерность: неисправленные отклонения результатов одного знака чаще встречаются в отрицательной полуплоскости, чем в положительной.
Если же в ряде результатов наблюдений присутствует периодическая систематическая погрешность, то группы знаков плюс и минус в последовательности неисправленных отклонений результатов наблюдений могут периодически сменять друг друга, если, конечно, случайные погрешности не особенно велики.
Обобщая два рассмотренных случая, можно сказать: если последовательность знаков плюс сменяется последовательностью знаков минус или наоборот, то данный ряд результатов наблюдений обнаруживает прогрессивную погрешность, если группы знаков плюс и минус чередуются – периодическую погрешность.
Введение поправок. Неисключенная систематическая погрешность
Систематические погрешности являются детерминированными величинами, поэтому в принципе всегда могут быть вычислены и исключены из результатов измерений. После исключения систематических погрешностей получаем исправленные средние арифметические и исправленные отклонения результатов наблюдении, которые позволяют оценить степень рассеивания результатов.
Для исправления результатов наблюдений их складывают с поправками, равными систематическим погрешностям по величине и обратными им по знаку. Поправку определяют экспериментально при поверке приборов или в результате специальных исследований, обыкновенно с некоторой ограниченной точностью. Для исправления результата наблюдения его складывают только со средним арифметическим значением поправки:
|
|
(3.17) |
где и
– соответственно исправленный и неисправленный результаты наблюдений,
– среднее арифметическое значение поправки, определяемые экспериментально.
Поправки могут задаваться также в виде формул, по которым они вычисляются для каждого конкретного случая. Например, при измерениях и поверках с помощью образцовых манометров следует вводить поправки к их показаниям на местное значение ускорения свободного падения

где – измеряемое давление.
Введением поправки устраняется влияние только одной вполне определенной систематической погрешности, поэтому в результаты измерения зачастую приходится вводить очень большое число поправок. При этом вследствие ограниченной точности определения поправок накапливаются случайные погрешности и дисперсия результата измерения увеличивается.
Действительно, при исправлении неисправленного результата путем введения поправок
по формуле
|
|
(3.18) |
дисперсия становится равной
|
|
(3.19) |
где – оценка дисперсии неисправленных результатов;
– оценка дисперсии
-й поправки.
Поправку имеет смысл вводить до тех пор, пока она уменьшает доверительные границы погрешности, т.е. пока выполняется неравенство
|
|
(3.20) |
При малой дисперсии поправки на основании формулы (62) может показаться, что введение любой поправки повышает достоверность результата. Однако следует помнить, что погрешность результата выражается не более чем двумя значащими цифрами, поэтому поправка, если она меньше пяти единиц разряда, следующего за последним десятичным знаком погрешности результата, будет все равно потеряна при округлении, и вводить ее не имеет смысла.
Систематическая погрешность, остающаяся после введения поправок на ее наиболее существенные составляющие включает в себя ряд элементарных составляющих, называемыхнеисключенными остатками систематической погрешности. К их числу относятся:
- погрешности определения поправок;
- погрешности, зависящие от точности измерения влияющих величин, входящих в формулы для определения поправок;
- погрешности, связанные с колебаниями влияющих величин (температуры окружающей среды, напряжения питания и т.д.).
Перечисленные погрешности малы и поправки на них не вводятся.
Для каждого данного измерения элементарные составляющие систематической погрешности имеют вполне определенные значения, но эти значения нам неизвестны. Известно лишь, что в массе однотипных измерений эти составляющие лежат в определенных границах или имеют определенные средние квадратические отклонения
. В первом случае для неисключенных остатков следует принять равномерное распределение, во втором – нормальное. Дисперсия суммы неисключенных остатков систематической погрешности определяется как сумма их дисперсий и поэтому
|
|
(3.21) |
где m1– число равномерно распределенных и m2 – число нормально распределенных элементарных составляющих.
Обработка результатов прямых равнорассеянных наблюдений
Прямыми называются измерения, в результате которых искомое значение физической величины находят непосредственно из опытных данных. Прямые измерения осуществляются путем многократных наблюдений. Результаты наблюдений называются равнорассеянными, если они являются независимыми, одинаково распределенными случайными величинами. Равнорассеянные результаты получают при измерениях, проводимых одним наблюдателем или группой наблюдателей с помощью одних и тех же методов и средств измерений в неизменных условиях внешней среды.
Обработка результатов наблюдений в соответствии с методикой прямых измерений с многократными наблюдениями производится в следующем порядке:
1. Путем введения поправок исключают известные систематические погрешности из результатов наблюдений.
2. Вычисляют среднее арифметическое исправленных результатов наблюдений, принимая его за оценку истинного значения измеряемой величины.
3. Вычисляют оценку среднеквадратического отклонения результатов наблюдения и оценку
среднеквадратического отклонения среднего арифметического.
4. Проверяют гипотезу о нормальности распределения результатов наблюдения. Если число результатов , используют критерий Пирсона
, при
– составной критерий. Уровень значимости выбирается из интервала 0.02 – 0.10. При
нормальность распределения не проверяется.
5. Если результаты наблюдений распределены нормально, то определяют наличие грубых погрешностей и промахов и если последние обнаружены, соответствующие результаты отбраковывают и повторяют вычисления.
6. Вычисляют доверительные границы случайной погрешности при доверительной вероятности , а также при
, если измерения в дальнейшем повторить нельзя.
7. Определяют границы неисключенной систематической погрешности результата измерений. В качестве составляющих неисключенной систематической погрешности рассматривают погрешности метода, погрешности средств измерений (например пределы допускаемой основной и дополнительных погрешностей, если их случайные составляющие пренебрежимо малы) и погрешности, вызванные другими источниками. При суммировании составляющих неисключенные систематические погрешности средств измерений рассматриваются как случайные величины. Если их распределение неизвестно, то принимается равномерное распределение и тогда границы неисключенной систематической погрешности результата при числе составляющих определяют как
|
|
(3.21) |
где – границы отдельных составляющих общим числом
;
– коэффициент, равный 1.1 при доверительной вероятности
и 1.4 при
.
8. Вычисляют доверительные границы погрешности результата. Если выполняется условие , то систематической погрешностью можно пренебречь и определить доверительные границы погрешности результата как доверительные границы случайной погрешности
при
(и при
); если же выполняется условие
, то можно пренебречь случайной погрешностью и тогда
при
(и
).
Если эти условия не выполняются, то доверительные границы погрешности результата определяют по формуле , где коэффициент
находят из выражения
|
|
(3.22) |
а среднеквадратическое общей погрешности результата находят квадратическим суммированием дисперсии случайной
и систематической
погрешности результата, определяемой формулой (63). Границы случайной
и систематической
погрешности, входящие в формулу (65), необходимо выбирать при одной и той же доверительной вероятности (
или
).
9. Результат измерения записывают в виде , а при отсутствии сведений о виде функции распределения составляющих погрешности и необходимости дальнейшей обработки результатов и анализа погрешностей– в виде
.
Если полученный при измерениях результат в дальнейшем используется для анализа и сопоставления с другими результатами или является промежуточным для нахождения других величин, то необходимо указать раздельно границы систематической погрешности и среднеквадратическое отклонение случайной погрешности: .
В некоторых случаях нас может интересовать не сама измеряемая величина, а связанная с ней функциональной зависимостью. Требуется найти интервальную или точечную оценку ее истинного значения. Решается такая задача следующим образом.
Пусть и f – непрерывная дифференцируемая функция в окрестности точки
.
При проведении точных измерений . Тогда
|
|
(3.23) |
Если
повторять несколько раз измерения одной
и той же физической величины (например,
веса или, скажем, времени падения
грузика), стараясь при этом сохранить
все условия опыта постоянными, то, тем
не менее, полученные результаты будут
обязательно несколько отличаться друг
от друга (если, конечно, для результатов
каждого измерения записать достаточное
количество значащих цифр). Тому существует
множество разных причин, которые
практически невозможно учесть. Как
пример: неточности в фиксации времени
включения и выключения секундомера,
которые, кстати, важны для точного
определения интервалов времени не
только при физических измерениях, но и
во многих других случаях, в частности,
на спортивных соревнованиях. Как уже
указывалось ранее, соответствующие
ошибки называют случайными
ошибками.
Со
случайными изменениями некоторых
величин мы встречаемся и в повседневной
жизни, например, многократно отмечая
время, которое требуется, чтобы доехать
до нужного пункта. Случайные величины
важны для многих разделов естествознания,
например, для молекулярной физики при
измерениях скорости теплового движения
молекул газа или в ядерной физике при
изучении закономерностей радиоактивности.
Для количественного описания всех таких
случайно изменяющихся величин используют
хорошо разработанные методы теории
вероятностей. Эти методы позволяют
строго определить не только средние и
наиболее вероятные значения величин,
но и вероятности отклонений от этих
значений.
Среднее
значение любой случайной величины х,
а в данном случае результатов нескольких
последовательных её измерений (x1,
x2,
x3…xn),
определяют как среднее
арифметическое значение x
по формуле:

(5)
где
n
– число
измерений.
Далее
необходимо установить тот интервал
значений (—x
≤ x
≤
+x),
так называемый доверительный
интервал, в
пределах которого с обусловленной
доверительной
вероятностью
P(Δx)
(определяющей коэффициент надежности
полученных результатов измерения)
должны находиться значения x.
Доверительная
вероятность P(Δx)
в случае непрерывного распределения
значений x
определяется как:

(6)
где ρ(x)
– плотность вероятности реализации
значений x
в диапазоне от x
до x + dx,
причем знаменатель в этом выражении
обычно принимается равным 1 (условие
нормировки).
Еще
важнее, что эти две величины (доверительный
интервал и доверительная вероятность)
однозначно определяют отличие измеренного
значения x
от истинного значения той же физической
величины a.
Именно в их определении и состоит
основная задача математической обработки
результатов измерений.
Для
решения этой задачи необходимо, помимо
,
найтисреднюю
квадратичную ошибку измерений
в
данной серии опытов, которая определяется
по следующей формуле:

(7)
Вычисление
средней квадратичной, а не, как часто
делается, средней арифметической ошибки
измерений:

позволяет
более корректно и просто определить
затем доверительный интервал и
доверительную вероятность, как это
будет показано в дальнейшем.
При
большом числе измерений (n
> 30) можно воспользоваться и более
простым расчётом средней арифметической
ошибки, так как в этом случае: ()ср≈0,8
.
Таким
образом, при n
,
0
и случайную ошибку измерения можно в
принципе сделать столь угодно малой
величиной, что однако потребует бесконечно
долгого процесса измерения.
Определение
доверительного интервала для случайной
ошибки и, соответственно, отличие
среднего значения
от истинного значения этой величиныа
для заданного значения доверительной
вероятности P(x)
очевидно требует знания конкретного
вида функции распределения ρi(xi),
т.е. функции реализации определенных
значений xi.
Рассмотрим
вначале наиболее простой для математической
обработки, но сложный для практического
осуществления случай достаточно большого
числа измерений. Строго говоря, для
этого необходимо, чтобы n
и дискретная функция распределения
ρi(xi)
переходила в непрерывную функцию
плотности вероятности ρ(x).
Однако, как будет показано далее, для
этого достаточно n100
или даже n30.
При этом обычно реализуется функция
нормального распределения или функция
Гаусса, названная так в честь великого
немецкого математика, впервые установившего
вид этой функции:
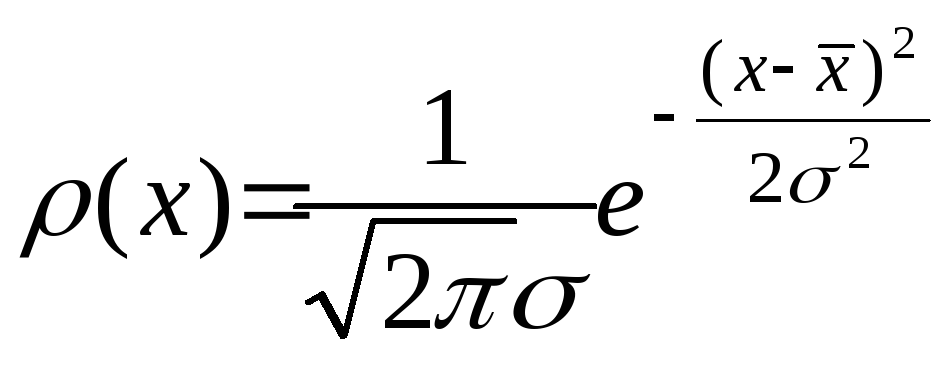
(9)
Здесь
использована новая величина
– среднестатистический предел средней
квадратичной ошибки одного измерения
при очень большом количестве измерений.
Квадрат этой величины 2,
однозначно определяющей ширину функции
распределения для ошибок измерения и
вообще распределения случайных величин,
называют нормой или дисперсией
распределения.
Для
обоснования применимости формулы Гаусса
необходимо выполнение трех положений,
а именно:
— ошибки
измерений могут принимать непрерывный
ряд значений,
— при
достаточно большом числе измерений
ошибки одинаковой абсолютной величины,
но разного знака, встречаются одинаково
часто
— большие
ошибки наблюдается реже, чем меньшие.
Тогда
измеренные значения величины x,
будут находиться внутри доверительного
интервала (-x
≤ x
≤
+x)
с доверительной вероятностью P(x),
определяемой по формуле:

(10)
При
этом, чем больше требуется доверительная
вероятность P(x)
и, соответственно, надежность того, что
измеренные значения x
отличаются
от истинного значения этой величины а
не более, чем на x,
тем шире по отношению к
становится доверительный интервал.
Так, если, например, требуется, чтобы
P(x)
= 0,7; 0,95; 0,98 или 0,999, то соответствующие
доверительные интервалы будут равны
;
2;
2,3
или 3,3.
В учебных лабораториях достаточно
выбирать доверительный интервал не
более 2σ, то есть брать доверительную
вероятность не более 0,95.
Для
выбора конкретного значения доверительной
вероятности P(x),
определяющей значения доверительного
интервала x,
необходимо понимать, насколько опасен
выход за пределы этого интервала,
вероятность которого, очевидно, равна
1 – P(x).
Такие задачи возникают на практике,
например, при отбраковке изделий,
выпускаемых в машиностроительной
промышленности, по их габаритам или
другим параметрам.
Реально
очень трудно осуществить (по причинам
большой длительности и малой продуктивности)
вышеуказанный идеализированный случай,
требующий, чтобы число измерений было,
по крайней мере, больше тридцати. Поэтому
необходимо рассмотреть реальный, но
более сложный для анализа случай
относительно небольшого числа измерений
(3
n
10).
Интуитивно понятно, что в этом случае
возникают повышенные требования к
доверительному интервалу (-x
;
+x)
при заданном значении P(x),
то есть он становится шире. Увеличение
числа измерений, наоборот, сужает этот
интервал.
На
опыте часто измеряют физические величины,
которые могут принимать лишь дискретные
значения, а число этих измерений конечно.
В ряде случаев вероятность реализации
определенных значений таких величин
хорошо описывается распределением
Пуассона (знаменитый французский
математик и физик).
Коэффициенты
Стьюдента .
Таблица №1.
|
n (число измерений) |
Доверительная вероятность |
||||||||||||
|
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
0,95 |
0,98 |
0,99 |
0,999 |
|
|
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21-24 25 26-27 28 29 30 40 60 120
|
0,16 0,14 0,14 0,13 0,13 0,13 0,13 0,13 0,13 0,13 0,13 0,13 0,13 0,13 0,13 0,13 0,13 0,13 0,13 0,13 0,13 0,13 0,13 0,13 0,13 0,13 0,13 0,13 0,13 |
0,33 0,29 0,28 0,27 0,27 0,27 0,26 0,26 0,26 0,26 0,26 0,26 0,26 0,26 0,26 0,26 0,26 0,26 0,26 0,26 0,26 0,26 0,26 0,26 0,26 0,26 0,25 0,25 0,25 |
0,51 0,45 0,42 0,41 0,41 0,40 0,40 0,40 0,40 0,40 0,40 0,40 0,39 0,39 0,39 0,39 0,39 0,39 0,39 0,39 0,39 0,39 0,39 0,39 0,39 0,39 0,39 0,39 0,39 |
0,73 0,62 0,58 0,57 0,56 0,55 0,55 0,54 0,54 0,54 0,54 0,54 0,54 0,54 0,54 0,54 0,53 0,53 0,53 0,53 0,53 0,53 0,53 0,53 0,53 0,53 0,53 0,53 0,52 |
1,00 0,82 0,77 0,74 0,73 0,72 0,71 0,71 0,70 0,70 0,70 0,70 0,69 0,69 0,69 0,69 0,69 0,69 0,69 0,69 0,69 0,68 0,68 0,68 0,68 0,68 0,68 0,68 0,67 |
1,38 1,06 0,98 0,94 0,92 0,90 0,90 0,90 0,88 0,88 0,87 0,87 0,87 0,87 0,87 0,86 0,86 0,86 0,86 0,86 0,86 0,86 0,86 0,86 0,85 0,85 0,85 0,85 0,84 |
2,0 1,3 1,3 1,2 1,2 1,1 1,1 1,1 1,1 1,1 1,1 1,1 1,1 1,1 1,1 1,1 1,1 1,1 1,1 1,1 1,1 1,1 1,1 1,1 1,1 1,1 1,0 1,0 1,0 |
3,1 1,9 1,6 1,5 1,5 1,4 1,4 1,4 1,4 1,4 1,4 1,4 1,4 1,3 1,3 1,3 1,3 1,3 1,3 1,3 1,3 1,3 1,3 1,3 1,3 1,3 1,3 1,3 1,3 |
6,3 2,9 2,4 2,1 2,0 1,9 1,9 1,9 1,8 1,8 1,8 1,8 1,8 1,8 1,8 1,7 1,7 1,7 1,7 1,7 1,7 1,7 1,7 1,7 1,7 1,7 1,7 1,7 1,6 |
12,7 4,3 3,2 2,8 2,6 2,4 2,4 2,3 2,3 2,2 2,2 2,2 2,2 2,1 2,1 2,1 2,1 2,1 2,1 2,1 2,1 2,1 2,0 2,0 2,0 2,0 2,0 2,0 2,0 |
31,8 7,0 4,5 3,7 3,4 3,1 3,0 2,9 2,8 2,8 2,7 2,7 2,7 2,6 2,6 2,6 2,6 2,6 2,5 2,5 2,5 2,5 2,5 2,5 2,5 2,4 2,4 2,4 2,3 |
63,7 9,9 5,8 4,6 4,0 3,7 3,5 3,4 3,3 3,2 3,1 3,1 3,0 3,0 2,9 2,9 2,9 2,9 2,9 2,8 2,8 2,8 2,8 2,8 2,8 2,7 2,7 2,6 2,6 |
636,6 31,6 12,9 8,6 6,9 6,0 5,4 5,0 4,8 4,6 4,5 4,3 4,2 4,1 4,0 4,0 4,0 3,9 3,9 3,8 3,7 3,7 3,7 3,7 3,7 3,6 3,5 3,4 3,3 |
Для
многих лабораторных работ, когда число
измерений не велико, распределение
погрешностей описывается еще более
сложными, специальными гамма–функциями
(распределение Стьюдента или “t”–
распределение. “Стьюдент” – это
псевдоним английского математика
Уильяма Сита Госсета.). Для такого
распределения с высокой точностью
вычислены и затабулированы так называемые
коэффициенты Стьюдента
(таблица №1). Они определяют отношение
доверительного интервала x
к средней квадратичной ошибке
для данной серии измерений и определенных
значенийn
и P(x),
то есть:
.
(11)
Из
таблицы 1 следует, что при доверительной
вероятности P(x)
0,7 доверительный интервал x
всегда несколько превышает значение
,
но дляP(x)=0,7
по мере увеличения числа измерений n
стремится
к этому значению, причем их различие
становится незначительным (меньше 10%)
уже при n
7. Аналогичное, но более медленное
уменьшение
наблюдается и для более высоких значений
P(x)=
0,95; 0,98; 0,999. Для этих значений P,
чтобы достаточно приблизиться к
предельным значениям
(2; 2,3; 3,3), соответствующим функции Гаусса,
необходимо значительно большее число
измерений (n
15,
20 и 40). В большинстве лабораторных работ
число измерений (3
n
10), а доверительная вероятность P(x)
принимается равной 0,95, так что
соответствующие коэффициенты Стьюдента
изменяются от 4,3 до 2,3. Если значения
доверительной вероятности не указаны,
то её обычно выбирают равной 0,7.
Таким
образом, окончательный результат
измерений с указанием доверительной
вероятности P
в лабораторных практикумах следует
представлять в виде:
,
(12)
где за
скобкой указывают единицу измерения
данной величины в общепринятой
международной системе единиц (СИ).
При
этом необходимо, чтобы среднее значение
и доверительный интервалx
были записаны в одних и тех же единицах
и с одинаковой точностью. Доверительный
интервал x
обычно
записывают в виде двух (реже одной)
значащих цифр, округляя последующие
цифры. Если число n
измерений невелико (менее 5 – 6), что
имеет место в большинстве лабораторных
работ, то достаточно округления
доверительного интервала до первой
значащей цифры, и только если она является
единицей – до двух значащих цифр. При
большем числе измерений (n
> 10) одна значащая цифра в доверительном
интервале оставляется только, когда
она больше трёх. При ещё большем числе
измерений (n
30 и более) оставляются две значащие
цифры. Предварительные вычисления
и
следует
проводить, разумеется, с несколько более
высокой точностью.
Таким
же образом округляются и приборные
абсолютная xпр
и относительная
пр
ошибки: с точностью до двух значащих
цифр, если первая значащая цифра равна
1, и до одной значащей цифры, если она
больше единицы.
При
округлении последняя из оставляемых
цифр в доверительном интервале x
всегда увеличивается на 1 (округление
с избытком).
Среднее
значение измеряемой величины
округляется до того же порядка величины,
что и значение x,
при этом
и x
должны быть
выражены в одинаковых единицах измерения.
Если в значении
первая отбрасываемая цифра, следующая
за последней оставляемой, больше или
равна 5 (но только, если за этой пятёркой
есть ещё цифры), то последняя из оставляемых
цифр увеличивается на 1 (округление с
избытком). Если же первая отбрасываемая
цифра меньше 5, то последняя из оставляемых
цифр не изменяется (округление с
недостатком).
Так,
если полученные при вычислении значения
∆x
составляют,
например, в одном случае: 1,255, а в другом
случае: 2,455, то, округляя их, в первом
случае следует записать: x
= 1,3 (округление с избытком до двух
значащих цифр, т.к. первая значащая цифра
— единица), а во втором – x
= 3
(округление с избытком до одной значащей
цифры, т.к. она – больше единицы). Если
при этом результат измерения составил,
скажем,
= 40,71 , то окончательно правильная запись:
в
первом случае x
= 40,7
1,3,
во
втором случае x
= 41
3.
Если
же в полученном результате измерения
первая
отбрасываемая цифра равна 5, а других
цифр после неё нет, то можно как оставить
предыдущую цифру неизменной, так и
увеличить её на 1. Часто для удобства
расчётов делают эту последнюю из
оставленных цифр чётной. Если, скажем,
получено значение тока 2,375 А, а погрешность
0,125 А, то результат удобнее записать
так:
I
= (2,38
0,13) A.
В
случае приборных погрешностей допустима
запись, когда в самой величине и
погрешности не совпадают разряды, в
которых стоят последние оставленные
цифры, например:
I
= (2,38 ± 0,005) А.
Если
случайная ошибка xсл
заметно превосходит приборную xnp
(приблизительно, раза в три и более), то
последней можно пренебречь, и, наоборот.
Если случайные и приборные ошибки
сравнимы, то они складываются по общему
закону сложения всех случайных величин,
а именно:
.
Рассмотрим
как пример расчёта случайных ошибок, а
также учета приборных ошибок и правильной
записи окончательного результата,
измерение величины тока I
через фотоэлемент, возникающего при
его освещении. Опыт повторялся пять раз
(n
= 5) при одинаковых условиях освещения
и были зафиксированы следующие результаты:
I1
= 0,292 мА; I2
= 0,284 мА; I3
= 0,305 мА; I4
= 0,293 мА; I5
= 0,290 мА. Измерения проводились цифровым
миллиамперметром, приборная ошибка
которого составляет единицу последнего
разряда цифрового табло индикатора
миллиамперметра: ∆Iпр
= 0,001 мА
Среднее
значение
= 0,2928 мА. Для доверительной вероятности
P
= 0,95 в таблице находится коэффициент
Стьюдента α = 2,8. Тогда доверительный
интервал: ∆I
= 2,8·
·=0,009594 мА.
Так
как ∆I
>> ∆Iпр,
то окончательный результат с учётом
округления: I
= 0,293±0,010 мА.
Всё
вышесказанное справедливо, прежде
всего, для прямых измерений, когда на
опыте непосредственно измеряется
интересующая нас физическая величина.
При косвенных
измерениях,
когда эта величина определяется по
известной формуле, в которую входят
несколько других измеряемых на опыте
независимых величин, необходимо провести
дополнительный анализ общей ошибки
измерения. Если искомая величина y
= (x1,
x2….xk),
то есть является известной функцией
нескольких непосредственно измеряемых
величин xi,
то её среднее значение определяется,
как.
Если в данном опыте преобладают приборные
ошибки, то
оценку
абсолютной y
ошибки
измерения следует производить по
формуле:
,
(13)
Если,
наоборот, в измерениях преобладают
случайные ошибки, то расчет общей ошибки
производят по формуле:

(14)
Вопрос
о том, какими формулами пользоваться,
решают при анализе результатов измерений.
Если отклонения большинства из результатов
измерений от среднего арифметического
значения не превышает абсолютную ошибку
используемых приборов, то расчет
производят по формуле (13), а в противоположном
случае, по формуле (14).
В
общем случае случайные xсл
и приборные ошибки xnp
складываются по общему закону сложения
всех случайных величин, а именно:
(15)
и расчёт
абсолютной ошибки ∆y
косвенных измерений производят по
формуле (14).
Поэтому,
если одна из этих ошибок в три и более
раз превышает другую ошибку, то последняя
из этих ошибок будет очень слабо влиять
на общую точность измерения. Исходя из
этих соображений, обычно и выбирается
необходимое число измерений n,
поскольку нет никакого смысла стремиться
получить случайную ошибку значительно
меньше приборной ошибки.
Наглядной
иллюстрацией систематических и случайных
ошибок могут служить результаты стрельбы
из различных видов оружия, в том числе
на спортивных соревнованиях. Так, если
имеется только систематическая ошибка
(сбит прицел, неправильное прицеливание
или расчеты), то все пули (снаряды, стрелы,
бомбы и т.д.) попадут в одно и то же место,
но смещенное от центра мишени или цели.
Наоборот, если существуют только
случайные ошибки, то будет значительный
разброс в местах попадания («плохая
кучность»), но усредненное отклонение
от центра мишени (или цели) будет
стремиться к нулю. Реально, конечно,
наблюдаются оба вида ошибок, но один из
них обычно существенно преобладает над
другим.
Разберём
пример нахождения плотности ρ материала
шара по измерениям его массы m
и объёма V
(объём шара находится через его диаметр
D:
V
= πD3/6):
ρ = 6m/πD3.
Если
масса шара была измерена на отъюстированных
рычажных весах с точностью 0,02 г и
составила m
= 11,20 г, то результат измерения запишется:
m
= 11,20 ± 0,02 г.
Диаметр
шара измерялся штангенциркулем, имеющем
погрешность ∆Dпр
= 0,05 мм. Десятикратное (n
= 10) повторение измерений диаметра даёт
среднее значение диаметра

13,615 мм.При
этом для случайных ошибок измерений
доверительный интервал ∆D
находится по формуле (11):
=

гдеn
= 10, и для доверительной вероятности P
= 0,95 по таблице №1 коэффициент Стьюдента
α = 2,3.
Произведённый
подсчёт показывает, что ∆D
= 0,1676 мм, то есть случайная ошибка более
чем в три раза превосходит приборную
ошибку ∆Dпр
= 0,05 мм, и последнюю можно не учитывать:
D
= 13,62 ± 0,17 мм.
Среднее
значение плотности находится из:
= 6m/π
=
8,480 г/см3.
А ошибка в определении плотности
находится по формуле (14):=
.
Подставляя
полученные ранее значения
,
,
,
∆m,
∆D,
находится ∆ρ = 0,1069 г/см3.
Округляя результаты, окончательный
результат записывается: ρ = 8,48 ± 0,11 г/см3.
При
сложении (вычитании) неточных значений
величин в окончательной записи полученной
суммы следует оставлять только те
разряды, которые имеются во всех
складываемых величинах, проводя
соответствующее округление. При умножении
(делении) неточных значений величин в
результате оставляется только то число
значащих цифр, которое имеется в
перемножаемой величине с наименьшим
их количеством.
Как
пример: нужно записать результат
вычислений с неточно полученными
величинами x
= 8,232 + 0,31π = 8,232 + 0,97 = 9,20.
Теория
вероятностей полезна и для правильного
построения
графиков на
основе полученных экспериментальных
данных. Недопустимо рисовать изломанную
кривую, точно проходящую через
экспериментальные точки: следует
провести такую плавную линию, чтобы
отклонение экспериментальных точек от
нее в разные стороны приблизительно
компенсировали друг друга. По методу
наименьших квадратов построение графика
экспериментальной зависимости y=(x)
следует проводить таким образом, чтобы
свести к минимуму сумму квадратичных
отклонений
экспериментальных точек yi
от
проводимой кривой f(xi),
где i
— номер
экспериментальной точки, n
– число
экспериментальных точек.
Для
построения графика кривой по
экспериментальным точкам вначале
подбирается функциональная зависимость
определённого вида (линейная: y=a+bx,
квадратичная: y=a+bx+cx2,
экспоненциальная: y
= a+bex
и т.д.),
которая предположительно наилучшим
образом соответствует экспериментальным
данным, и определяются значения её
параметров a,b,c.
При этих значениях функция S
должна быть минимальна, то есть её
частные производные по этим параметрам
должны быть равны нулю:.
Решая полученную систему уравнений,
сначала находят значения этих параметров,
а затем и значениеS.
Сравнивая значения S,
полученные таким образом для разного
вида функций f(x),
выбирают функцию, для которой S
будет
минимальна – этой функцией и
аппроксимируются полученные
экспериментальные данные.
Следует
отметить, что разработаны способы, с
помощью которых можно достаточно просто
оценить наиболее подходящую функцию y
= f(x)
для описания известных экспериментальных
данных. Кроме того, существует компьютерная
программа Grapher,
которая даёт возможность подбирать
необходимые функции с соответствующими
параметрами для приближения экспериментально
полученных точек xi
и yi.
Добавим, что удобно использовать для
построения графиков такие координаты,
при которых график функции представляет
собой прямую (эти координаты следует
выбирать на основании подобранной
функции y=f(x)).
Методы
теории вероятностей успешно используют
и для планирования различных экспериментов,
например по разработке технологии
синтеза многокомпонентных материалов
с оптимальными свойствами (электрическими,
оптическими, механическими и др.),
требующимися для их практических
применений.
Прогресс
физики и других разделов естествознания
во многом определяется точностью
экспериментов. В настоящее время
достигнута поразительная точность при
измерении ряда физических величин
(расстояние, время и др.). Так, с помощью
молекулярных генераторов и стандартов
частоты удается осуществить такие
молекулярные часы, что их ошибка
составляет всего одну секунду за 106
лет, т.е. относительная погрешность
равна 10-12%.
С
очень высокой точностью измерена и
такая важнейшая физическая величина
как скорость распространения света в
вакууме с = (299792458,0
1,2) м/с. Это позволяет производить очень
точные измерения больших расстояний:
до Луны, планет Солнечной системы и
других космических объектов.
На
смену общеизвестного эталона метра в
виде стержня, изготовленного из
платиноиридиевого сплава и хранящегося
в международной Палате мер и весов
вблизи Парижа, пришел «оптический
эталон». Он равен 1650763,73 длин волн
оранжевой линии излучения атомов
криптона, то есть на одном метре должно
укладываться ровно столько длин волн
этого излучения. Такой эталон примерно
в 100 раз точнее прежнего и может быть
легче воспроизведен в научных лабораториях.
При обычных измерениях, например в
физическом практикуме, конечно, не
удается достичь таких прецизионных
точностей измерений, которые во многом
определяются погрешностью используемых
приборов. Вместе с тем при работе в
практикуме нужно стремиться к уменьшению
ошибок измерения, правильно производить
их оценки и грамотно оформлять
промежуточные и окончательные результаты
измерений.
Навигация по странице:
Ю. Н. Корнилов геодезия топографические съемки
|
Единственный в мире Музей Смайликов |
|
Подборка по базе: Индивидуальное домашнее задание Геодезия 2.docx, КР 1 геодезия Кетова Юлия.docx, Диплом, Геодезия, Орлов.docx, КР геодезия.docx, Курсовая геодезия (2).doc, Инженерная геодезия.docx, Контрольная работа геодезия.docx, Практическая работа №2, Корнилова Н.Г..docx, Рабочая программа.7 класс. Пономарева, Кучменко, Корнилова..docx, Лекция 2 ГЕОДЕЗИЯ.doc
означает сравнить ее с однородной ей величиной Е единицей меры. В результате измерения устанавливают, сколько единиц меры содержится в измеряемой величине. Различают измерения прямые и косвенные В первом случае искомая величина непосредственно сравнивается с единицей меры (например, измерение вместимости ведра цилиндрической формы с помощью воды и литровой банки. Во втором измеряется какая-нибудь другая величина, которая связана с искомой функциональной зависимостью (определение вместимости того же ведра путем измерения его высоты и диаметра дна. В процессе измерений обязательно возникают ошибки. По характеру действия они бывают грубые, случайные и систематические Грубые ошибки возникают вследствие невнимательности исполнителя, неблагоприятных условий или непродуманной методики выполнения работ. Такие ошибки стараются исключить, и эффективным средством для этого являются повторные измерения. Систематические ошибки подчиняются определенным закономерностям. Их источниками являются несовершенство приборов, изменение внешних условий выполнения работ, влияние тех или иных факторов на действия исполнителя. Поэтому систематические ошибки подразделяют на ошибки приборные, внешней среды и личные ошибки наблюдателя. Закономерности, которым подчиняются систематические ошибки, изучают, и это позволяет исключить их из результатов измерений (например, определяют температурный , коэффициент расширения стали для введения поправок в расстояния, измеренные стальной рулеткой. Случайные ошибки возникают из-за воздействия на процесс измерений огромного числа непрерывно меняющихся факторов, учесть, а значит, и исключить влияние которых на результат невозможно. Но возникающие при этом ошибки подчиняются определенным закономерностям, которые особенно четко проявляются при
44
массовом характере измерений. Указанные закономерности называются статистическими и являются предметом изучения таких наук, как теория вероятности и математическая статистика. Пусть / — результат измерения некоторой величины X, истинное значение которой обозначим буквой L. Разность А называется случайной ошибкой измерения. Ее также называют истинной ошибкой (как отклонение результата измерений от истинного значения измеряемой величины) и, кроме того абсолютной ошибкой в отличие от дроби A/L, которую называют относительной ошибкой измерений. В процессе массовых измерений случайные ошибки подчиняются следующим закономерностям
1. При постоянных условиях измерений (при равноточных измерениях) ошибки по абсолютной величине не могут превосходить некоторого предела.
2. Равные по абсолютной величине положительные и отрицательные ошибки равновероятны.
3. Малые по абсолютной величине ошибки встречаются чаще, чем большие.
4. Среднее арифметическое из случайных ошибок равноточ-
ных измерений стремится к нулю, когда число измерений п стремится к бесконечности
lim — -> О, если и->оо. Запись Д равносильна выражению ^ ^ называется гауссовой суммой. Из вышеприведенных рассуждений следует, что сама случайная ошибка не может служить критерием точности измерений.
К.Ф. Гаусс предложил в качестве такого критерия использовать среднюю квадратическую ошибку т вычисляемую по формуле т
= (14) Преимущество средней квадратической ошибки состоит в том, что она стандартна для ряда равноточных измерений (кстати, в статистике она и называется стандартом) и имеет следующий вероятностный смысл.
45
Пусть / — результат измерений. Какова вероятность того, что истинная величина L&[l+m, т или[/+2ш, т или ш, /-Зш]? Теория утверждает, что значения вероятности соответственно равны
68; 95 и 99,7 %. Но это означает, что появление ошибок, превышающих
Зш, маловероятно. Указанное обстоятельство позволило принять эту величину в качестве предельной ошибки и использовать для выявления грубых погрешностей. Иногда в качестве предельной используют удвоенную среднюю квадратическую ошибку. При выполнении косвенных измерений, когда искомая величина Y является функцией измеренной величины X, ошибка результата оценивается по формуле
(15) Если она является функцией нескольких переменныхЛ’ь Х, Х то используют соотношение г
2
/ >
2
/ N
дУ
2
1 Ул+
‘»Л’т
—
— ту) На практике в подавляющем числе случаев истинное значение измеряемой величины неизвестно, и перед исполнителем, выполнившим несколько ее измерений, возникают три следующих вопроса что принять за результат измерений, каковы средняя квадратическая ошибка одного измерения и ошибка результата Для того, чтобы ответить на поставленные вопросы, предположим, что выполнено п измерений одной и той же величины и получено столько же ошибок Сложим левые и правые части равенства, разделим их на число измерений и перейдем к пределам, в результате получим
Urn
= lim — — lim —
П-><Й
л н-х»
fi Левая часть вышеприведенного соотношения стремится к нулю по 4-му свойству случайных ошибок измерений, первое слагаемое правой части (обозначим его буквой Zo) является средним из
46
всех измерений, а второе слагаемое равно L. Таким образом, получается, что среднее стремится к истинному значению измеряемой величины при увеличении числа измерений до бесконечности, и есть все основания принимать егоза результат измерений. Для вычисления ошибки отдельного измерения используется формула Бесселя В ней / = 1 , 2 , . . . , « — отклонения отдельных измерений от среднего значения. Причем если вычисления верны, то сумма отклонений должна равняться нулю. Для оценки точности результата запишем формулу вычисления среднего в виде
1 » 5 , 1 , п п пи воспользуемся соотношением (16) для вычисления ошибки функции нескольких переменных. В результате получим
1 т, п
1
— ш , п ‘
+ …+
1 т, п Примем ошибки отдельных измерений равными, те. тп = ш = …=
= nil,, = nil,
тогда
(17) Таким образом, повторные измерения не только позволяют исключать фубые ошибки, но и повышают точность ре:^льтата измерений.
3.2, ЛИНЕЙНЫЕ ИЗМЕРЕНИЯ. Единица длины
Линейньши
называют измерения расстояний между точками земной поверхности. Выполнять эту работу приходится при построении опорных геодезических сетей, создании съемочного обоснования ив процессе съемки местности. Для исключения грубых ошибок одно и тоже расстояние измеряют дважды. За единицу длины в большинстве стран мира принят метр от греч. laexpov — мера. Эта единица появилась в конце XVII века, после того как французские ученые предложили в качестве единицы длины принять 10-10″^ часть 1/4 дуги Парижского меридиана. Были выполнены точные градусные измерения, изготовлен архивный метр из платиново-иридиевого сплава, а спустя почти 100 лети его копия. Две из них находятся в России. С 1983 года за 1 метр приняли расстояние, которое проходит в вакууме плоская электромагнитная волна за 1/299 792 458 секунды.
3.2.2. Приборы для непосредственного измерения расстояний При непосредственном способе мерный прибор известной длины откладывают в створе линии, длину которой требуется определить Створом называется вертикальная плоскость, проходящая через конечные точки линии. Для измерений используют, прежде всего, рулетки, землемерные ленты и проволоки. Известны случаи измерения расстояний с помощью мерного диска. Рулетки предназначены для измерения сравнительно коротких отрезков в процессе съемки местности, при обмерах зданий и сооружений, выполнении разбивок в строительных работах. Их полотно длиной от 1 дом делают из углеродистой или нержавеющей стали, капрона, стекловолокна или из прочной тесьмы, реже — инвара. Поточности нанесения шкал рулетки делятся натри класса, при этом их цена деления может быгь равна 1 мм или 1 см. В топографо-геодезическом производстве в основном используют стальные метровые рулетки, а при менее точных работах — тесьмяные длиной 10 м. По названию рулетки можно судить о ее характеристиках. Например, рулетка ОПК2-30АНТ/10 — с открытым корпусом, плоская, имеет вытяжное кольцо, го класса точности, метровая, начало шкалы не совпадает с торцом полотна, выполнена из нержавеющей стали, шкала нанесена методом травления, цена деления 10 мм. Ленты землемерные выпускают двух типов — ЛЗ (штриховые) и ЛЗШ (шкаловые). Лента штриховая представляет собой стальную полосу длиной 20 или ( ^ о ООО. ООО Ош Т ^ З ^
24 м, шириной 15-20 мм и ‘ ^ ^ ^ — — L V толщиной 0,3-0,4 мм, на
100 см
20 м- концах которой нанесены штрихи, ограничивающие ее Рис. Штриховая землемерная лента длину (рис. В полотне (показана без ручек) ленты просверлены отверстия через 10 см. Латунные заклепки фиксируют полуметровые интервалы, а пластины с числами — метровые. Закреплены они на обеих сторонах ленты, но значения шкалы возрастают в противоположные стороны. Лента наматывается на кольцо с про-
ушинами. В комплект входят 6 или 11 металлических шпилек. В зависимости от условий местности штриховые ленты обеспечивают точность измерений длины от 1/1 ООО до 1/3 ООО.
Шкаловые ленты используются для измерения расстояний между точками с повышенной точностью. Они представляют собой сплошную полосу со шкалами на концах длиной по 10 см и ценой деления 1 мм. Разбивка на метровые или более мелкие отрезки между шкалами отсутствует. Для линейных измерений с высокой точностью до конца XX века применялся базисный прибор. Например, при измерении базисов в триангуляции го иго классов использовали прибор БП-2. В его комплект входят 4 инварные проволоки пом каждая со шкалами на концах, рулетка с инварной лентой длиной 6 или 12 ми вспомогательное оборудование (штативы с целиками, термометры-
пращи, гири и т.д.). Цена деления шкал 1 мм. Рулетка предназначена для домера остатков измеряемых линий. Ранее базисный прибор был единственным средством высокоточных линейных измерений в плановых государственных геодезических сетях. В ряде производственных организаций при измерении расстояний используют длиномер АД-1М. В комплект прибора входят две стальные проволоки длиной дом, которые натягиваются между конечными точками измеряемого отрезка, и измерительная головка, в
корп)’се которой размещены мерный диск, счетный механизм, два направляющих ролика и тормозное устройство. В процессе измерения диск прокатывается по проволоке, а счетное устройство по числу оборотов фиксирует расстояние с точностью до 1 мм.
49
3.2.3. Измерение расстояний штриховыми землемерными лентами Фактическая длина ленты обычно отличается от номинальной. Чтобы вводить поправки в результаты измерений, необходимо определить, насколько велико это различие. Сделать это можно до начала работ или сразу после их завершения путем сравнения длины ленты с эталоном — нормальной лентой или отрезком (базисом) соответствующей длины, измеренным с высокой точностью. Процесс сравнения длины мерных приборов с эталоном называется компарированием а определенная в результате поправка — поправкой за компарирование Если длина ленты отличается от номинала меньше чем на 1/10 000 ее длины, то поправки не вводятся, в противном случае — вводятся, причем со знаком плюс, когда лента длиннее. При измерении расстояния лента должна укладываться в створе линии. Отклонение от створа приводит к ошибке, поэтому если ошибка велика и профиль местности сложен, створ закрепляют рядом вех. Совокупность действий, связанных сих установкой, называют вешением линий Короткие линии (150-200 м) провешивают на глаз. Для этого две вехи устанавливают наконечных точках. Затем наблюдатель становится на одной из них и руководит рабочим, который устанавливает третью веху так, чтобы все три вехи при визировании перекрывали друг друга. Провешивать линию можно на себя и от себя. Первый вариант точнее. При больших расстояниях провешивание линии выполняют с помощью теодолита. Измерения выполняют два рабочих. Задний рабочий, взяв одну шпильку и передав десять остальных переднему, втыкает шпильку в точку, обозначающую начало линии, вставляет прорезь ленты, расположенную у заднего штриха, в шпильку и направляет переднего так, чтобы он уложил ленту в створе. Передний рабочий, 1 встряхнув ленту, натягивает ее с силой примерно 10 кг, прижимает : ручку к земле и, вставляя шпильку в прорезь против переднего штриха, втыкает ее в землю. Задний рабочий вытаскивает первую : шпильку из земли, и оба передвигаются вдоль линии на длину ленты. Аналогично лента укладывается второй, третий … десятый раз. Затем задний рабочий передает переднему 10 собранных им шпилек, и процесс измерений продолжается. Как правило, длина линий не кратна длине ленты, поэтому лента укладывается нецелое число разв результате образуется остаток При его измерении отсчет берут с точностью до сантиметра, оценивая десятые дециметра на глаз предварительно убедившись в том, что шкала возрастает походу движения. Если при измерении используется метровая лента, то длина всей линии
D = 200«, +20«2 + d .
(18) где /7], «2 и J — соответственно число передач ленты, число шпилек у заднего рабочего в конце измерения и остаток. Для контроля обязательно выполняют измерение ив обратном направлении, а полученные результаты сравнивают. Их разность не должна превышать 1 см на каждую отложенную ленту. Очевидно, что из-за неровностей земной поверхности измеряют наклонные линии, утлы наклона которых, к тому же, как правило, непостоянны. Для последующих вычислений нужны горизонтальные проекции линий, поэтому в процессе измерений линию разбивают на отрезки и определяют угол наклона v каждого из них, а искомые проекции вычисляют по формуле (2). При измерении длины мерной лентой углы наклона определяют для каждого метрового отрезка, причем если значение угла не превышает 6°, то для этой цели используют эклиметр. Общее горизонтальное расстояние получают как сумму горизонтальных проекций отрезков. В настоящее время на производстве наиболее распространен маятниковый эклиметр-высотомер ЭВ (рис. Он предназначен для измерения углов наклона в пределах ±60° с точностью 0,5°, а также для измерения высоты предметов с расстояний 15 им. Прибор представляет собой небольшую металлическую коробочку 1 прямоугольной формы, в которой вокруг горизонтальной оси, закрепленной с помощью двух агатовых подпятников, вращается кольцо 2 с грузом 3. На ободе кольца нанесены две шкалы для измерения углов Рис. 24. Эклиметр (разрез и вид со стороны лупы)
51
наклона и для измерения высоты предметов. На первой из них по обе стороны от нулевого штриха нанесены градусные деления (цена деления. 1 Под действием груза нулевой диаметр кольца устанавливается горизонтально, если прижата стопорная кнопка 4 (арретир, расположенная сверху коробки. С помощью визирного индекса 6 диафрагмы через лупу 5 берется отсчет. Визирование ведется вдоль наружной вертикальной стенки корпуса путем совмещения индекса сточкой визирования. Прежде чем использовать эклиметр, следует определить его место нуля (МО). Местом нуля шкалы любого прибора называется отсчет по шкале при определенных условиях (например, отсчет по шкале весов, когда на них нет груза. Искомая величина (например, масса продукта) в этом случае равна отсчету, полученному в результате измерений, минус МО. Место нуля эклиметра — это отсчет по его шкале при условии, что ось визирования горизонтальна. Получить его можно путем наведения индекса на линию горизонта. Если это невозможно, то следует эклиметром выполнить измерение угла наклона одного итого же отрезка прямо и обратно, тогда место нуля будет равно полусумме полученных отсчетов. Отметим, что в настоящее время горизонтальные расстояния легко вычислить на компьютере или с помощью калькулятора. Но еще совсем недавно их определяли путем введения поправок М, которые находили в таблицах. Значения поправок вычисляли по формуле
AZ) = 2Z)sin^(v/2). (19) Получить эту формулу легко с помощью следующих преобразований
a d = Z) — Z = Z) — £) cos
V
= £)(! — cos
V)
= 2Z)
s i n ^ (V
/ 2).
3.2.4. Принципы измерения расстояний дальномерами Дальномеры —
это приборы для определения расстояний между точками. По принципу действия их можно разделить на две группы оптические дальномеры и дальномеры, основанные на использовании электромагнитных волн (светодальномеры и радиодальномеры.
52
в основу определения расстояний оптическими дальномерами положено решение равнобедренного треугольника АБС (рис. Искомая величина — его высота АЕ, поэтому
Z = 0 , 5 b c t g ( 0 , 5 9 ) . Рис. Схема параллактического треугольника Угол ф называется параллактическим, а отрезок — базисом. В конструкциях дальномеров предусматривается, что одна из величин правой части формулы является постоянной, а вторая — переменной, ее и измеряют. Таким образом, существует два типа оптических дальномеров дальномеры с постоянным параллактическим углом и дальномеры с постоянным базисом. Типичный представитель первого типа — нитяный дальномер. Им снабжены зрительные трубы практически всех геодезических приборов. Представители второго типа -дальномеры двойного изображения, например Д. В свето- и радиодальномерах тем или иным способом определяют либо время т, за которое электромагнитная волна проходит расстояние между точками, либо число N модулированных колебаний (длин волн Я, которое укладывается между точками. Таким образом, волна играет роль мерной ленты. В связи с этим различают дальномеры импульсного и фазового типов. Перед измерением на одном из концов линии устанавливается приемопередатчика на другом — отражатель. У дальномеров импульсного типа расстояние вычисляется по формуле
D = Cxl2, где С — скорость распространения электромагнитной волны, которая зависит от температуры, влажности воздуха и атмосферного давления, поэтому указанные характеристики атмосферы тоже измеряют. В фазовом дальномере формула для определения расстояний имеет вид
53
Величина АД р / 2 я ,
где Д ф — разность фаз модулированных колебаний посланной и отраженной электромагнитных волн, ее и измеряют в дальномерах фазового типа. Нетрудно видеть, что если длина волны дана, тов вышеприведенном уравнении две величины
— N к D,
Содержание:
Ошибки измерения: Опыт убеждает, что измерения объектов не могут быть произведены абсолютно точно и каждое конкретное измерение дает лишь, как правило, приближенное значение величины явления, истинное значение которой (A) нам неизвестно. Ошибки измерения (
Рассмотрим такие измерения, которые производятся одним наблюдателем, одним и тем же инструментом, в одинаковых условиях, т. е. равноточные измерения.
Различают два вида ошибок измерения:
- систематические ошибки, т. е. такие, которые при данных условиях проведения измерения имеют вполне определенное значение (например, ошибка измерительного прибора);
- случайные — такие, которые являются результатом взаимодействия большого числа незначительных в отдельности факторов и имеют в каждом отдельном случае различные значения.
Задача математической статистики — предусмотреть возможность возникновения систематических ошибок и добиться их ликвидации или сведения к минимуму.
Случайные ошибки измерения обладают рядом свойств: при большом числе измерений крупные ошибки встречаются реже мелких и число положительных ошибок примерно равно числу отрицательных, вследствие чего сумма всех ошибок близка к нулю.
Если ошибки получаются весьма малыми по сравнению с величиной явления, то ими просто пренебрегают или считаются с наибольшей возможной ошибкой, чтобы обезопасить себя от влияния случайной неточности.
В теории ошибок изучаются те ошибки, которые, являясь, с одной стороны, ошибками случайного характера, по своему абсолютному значению настолько велики, что ими пренебречь нельзя, а с другой стороны, для них существует закон, позволяющий установить зависимость между величиной ошибки и вероятностью ее появления. Закон случайных ошибок, полученный Гауссом, состоит в том, что случайные ошибки подчиняются закону нормального распределения.
Средняя ошибка сводного результата измерения
Принимая за действительное значение измеряемой величины при равноточном измерении среднюю арифметическую из всех результатов n измерений, можно охарактеризовать точность одного измерения с помощью средней арифметической из абсолютных величин значений ошибок:
где n — число измерений, х — численное значение отдельных измерений, 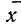
За меру точности соответствия принятой средней арифметической 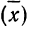
Пример 1. Произведено 10-кратное измерение размера детали (в мм), давшее следующие, расположенные в возрастающем порядке результаты: 138; 139; 140; 141; 141; 142; 142; 143; 144; 145.
Охарактеризуем сначала точность одного измерения, т. е. вычислим среднюю арифметическую из абсолютных значений ошибок. Для этой цели вычислим среднюю арифметическую из результатов измерений:
Найдем ошибки измерения:
Следовательно:
Теперь можно вычислить среднюю ошибку сводного результата измерения:
Значит, мерой точности соответствия 141,5 мм истинной величине размера детали является средняя ошибка, равная 0,54 мм.
Средняя квадратическая ошибка
Если в качестве меры точности одного измерения принять не среднюю арифметическую из абсолютных значений ошибок (средняя ошибка), а среднюю квадратическую из ошибок измерений, т. е.
то средняя квадратическая ошибка найденной средней арифметической из ошибок измерения вычисляется по формуле:
Между средней -квадратической ошибкой и средней ошибкой сводного результата измерения существует связь: 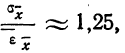
Пример 2. Используя данные предыдущего примера, находим меру точности одного измерения, т. е. среднюю квадратическую ошибку:
Затем исчисляем среднюю квадратическую ошибку найденной средней арифметической, равной 141,5 мм:
Сопоставляя среднюю квадратическую ошибку сводного результата измерения со средней ошибкой, получаем:
Вероятная ошибка
За меру точности одного измерения иногда принимают вероятную ошибку:
Тогда в качестве вероятной ошибки сводного результата измерения используют соотношение:
Пример 3. Используя данные предыдущих примеров, находим вероятную ошибку сводного результата измерения:
Наиболее вероятные границы сводных результатов измерения
Математическое ожидание случайной ошибки равно нулю. В качестве значения измеряемой величины применяется средняя арифметическая всех измерений (если они равноточны). Использование отклонений результатов измерений (х) от средней из них 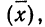
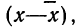
Для этой цели используют удвоенную или утроенную среднюю квадратическую ошибку сводного результата измерения или его вероятную ошибку и получают:
Найденные границы неизвестной истинной величины в случае, если ошибки подчинены нормальному закону распределения Гаусса (чаще всего так и бывает), соблюдаются с большой вероятностью (0,997 и 0,954).
Пример 4. По данным предыдущих примеров находим границы истинного значения размера детали 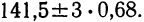
- Методы математической статистики
- Комбинаторика — правила, формулы и примеры
- Классическое определение вероятности
- Геометрические вероятности
- Законы распределения случайных величин
- Дисперсионный анализ
- Математическая обработка динамических рядов
- Корреляция — определение и вычисление



 .
.
 ,
, ,
, .
. ,
, ,
,
 .
.
 Скачать 7.93 Mb.
Скачать 7.93 Mb.