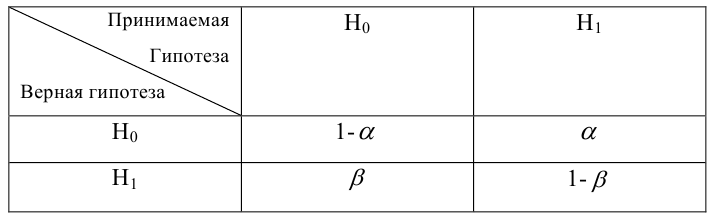
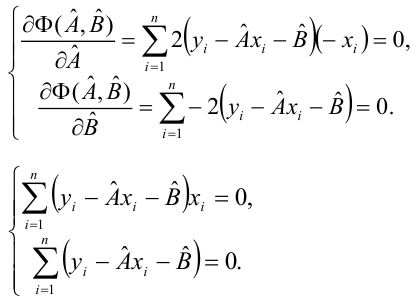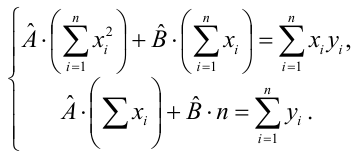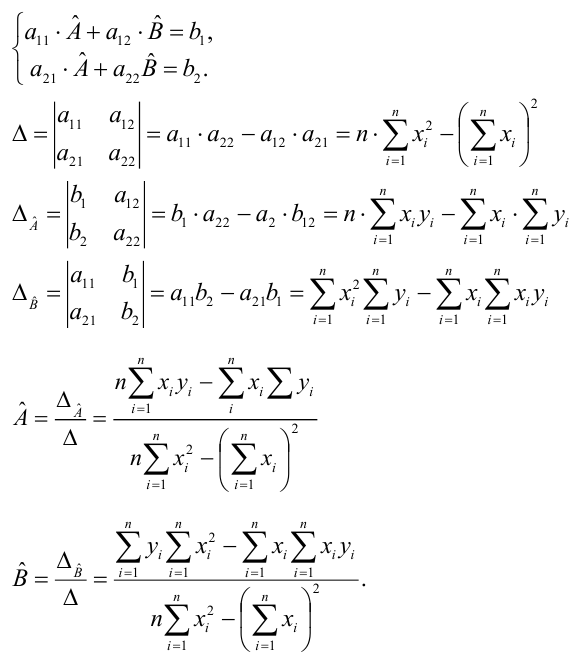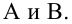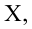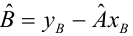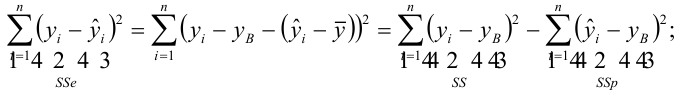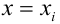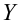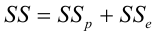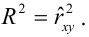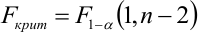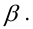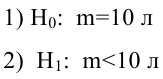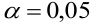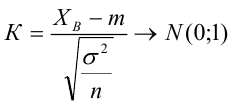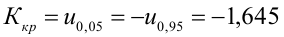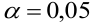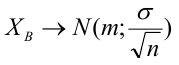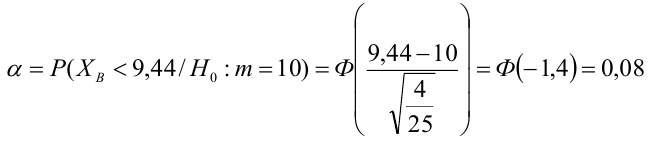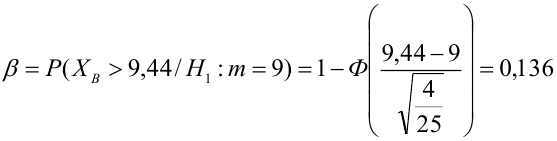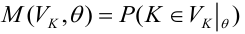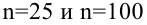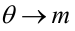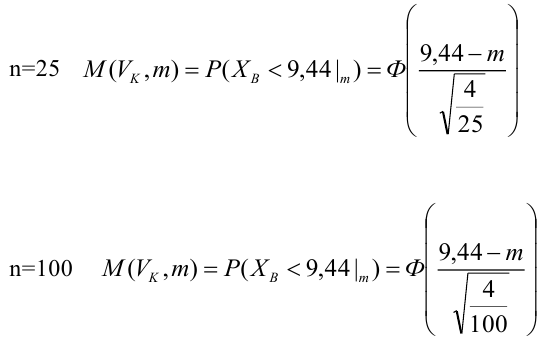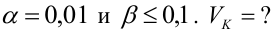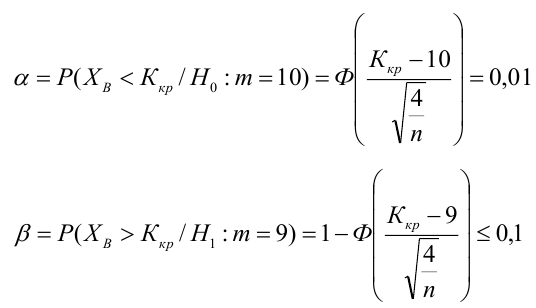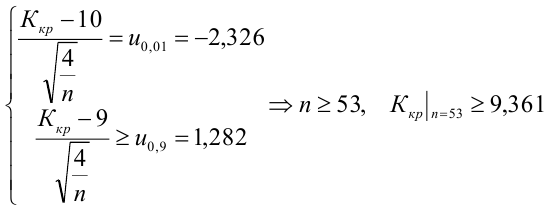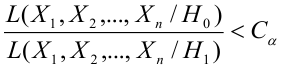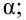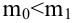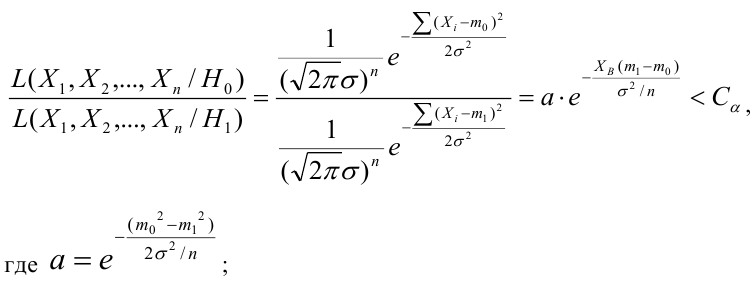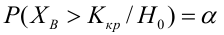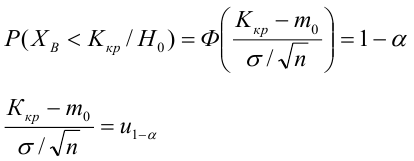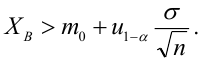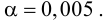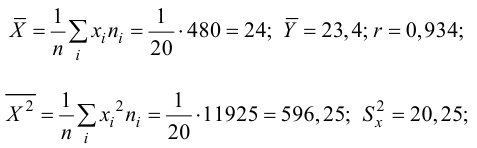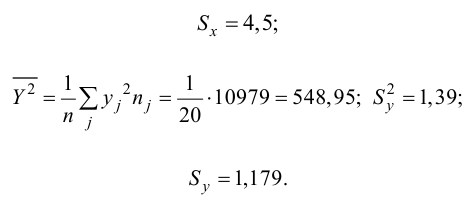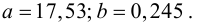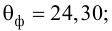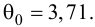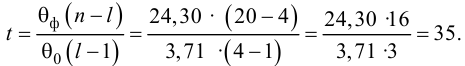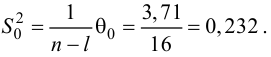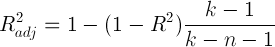Когда мы подгоняем регрессионную модель к набору данных, нас часто интересует, насколько хорошо регрессионная модель «подходит» к набору данных. Две метрики, обычно используемые для измерения согласия, включают R -квадрат (R2) и стандартную ошибку регрессии , часто обозначаемую как S.
В этом руководстве объясняется, как интерпретировать стандартную ошибку регрессии (S), а также почему она может предоставить более полезную информацию, чем R 2 .
Стандартная ошибка по сравнению с R-квадратом в регрессии
Предположим, у нас есть простой набор данных, который показывает, сколько часов 12 студентов занимались в день в течение месяца, предшествующего важному экзамену, а также их баллы за экзамен:
Если мы подгоним простую модель линейной регрессии к этому набору данных в Excel, мы получим следующий результат:
R-квадрат — это доля дисперсии переменной отклика, которая может быть объяснена предикторной переменной. При этом 65,76% дисперсии экзаменационных баллов можно объяснить количеством часов, потраченных на учебу.
Стандартная ошибка регрессии — это среднее расстояние, на которое наблюдаемые значения отклоняются от линии регрессии. В этом случае наблюдаемые значения отклоняются от линии регрессии в среднем на 4,89 единицы.
Если мы нанесем фактические точки данных вместе с линией регрессии, мы сможем увидеть это более четко:
Обратите внимание, что некоторые наблюдения попадают очень близко к линии регрессии, в то время как другие не так близки. Но в среднем наблюдаемые значения отклоняются от линии регрессии на 4,19 единицы .
Стандартная ошибка регрессии особенно полезна, поскольку ее можно использовать для оценки точности прогнозов. Примерно 95% наблюдений должны находиться в пределах +/- двух стандартных ошибок регрессии, что является быстрым приближением к 95% интервалу прогнозирования.
Если мы заинтересованы в прогнозировании с использованием модели регрессии, стандартная ошибка регрессии может быть более полезной метрикой, чем R-квадрат, потому что она дает нам представление о том, насколько точными будут наши прогнозы в единицах измерения.
Чтобы проиллюстрировать, почему стандартная ошибка регрессии может быть более полезной метрикой для оценки «соответствия» модели, рассмотрим другой пример набора данных, который показывает, сколько часов 12 студентов занимались в день в течение месяца, предшествующего важному экзамену, а также их экзаменационная оценка:
Обратите внимание, что это точно такой же набор данных, как и раньше, за исключением того, что все значения s сокращены вдвое.Таким образом, студенты из этого набора данных учились ровно в два раза дольше, чем студенты из предыдущего набора данных, и получили ровно половину экзаменационного балла.
Если мы подгоним простую модель линейной регрессии к этому набору данных в Excel, мы получим следующий результат:
Обратите внимание, что R-квадрат 65,76% точно такой же, как и в предыдущем примере.
Однако стандартная ошибка регрессии составляет 2,095 , что ровно вдвое меньше стандартной ошибки регрессии в предыдущем примере.
Если мы нанесем фактические точки данных вместе с линией регрессии, мы сможем увидеть это более четко:
Обратите внимание на то, что наблюдения располагаются гораздо плотнее вокруг линии регрессии. В среднем наблюдаемые значения отклоняются от линии регрессии на 2,095 единицы .
Таким образом, несмотря на то, что обе модели регрессии имеют R-квадрат 65,76% , мы знаем, что вторая модель будет давать более точные прогнозы, поскольку она имеет более низкую стандартную ошибку регрессии.
Преимущества использования стандартной ошибки
Стандартную ошибку регрессии (S) часто бывает полезнее знать, чем R-квадрат модели, потому что она дает нам фактические единицы измерения. Если мы заинтересованы в использовании регрессионной модели для получения прогнозов, S может очень легко сказать нам, достаточно ли точна модель для прогнозирования.
Например, предположим, что мы хотим создать 95-процентный интервал прогнозирования, в котором мы можем прогнозировать результаты экзаменов с точностью до 6 баллов от фактической оценки.
Наша первая модель имеет R-квадрат 65,76%, но это ничего не говорит нам о том, насколько точным будет наш интервал прогнозирования. К счастью, мы также знаем, что у первой модели показатель S равен 4,19. Это означает, что 95-процентный интервал прогнозирования будет иметь ширину примерно 2*4,19 = +/- 8,38 единиц, что слишком велико для нашего интервала прогнозирования.
Наша вторая модель также имеет R-квадрат 65,76%, но опять же это ничего не говорит нам о том, насколько точным будет наш интервал прогнозирования. Однако мы знаем, что вторая модель имеет S 2,095. Это означает, что 95-процентный интервал прогнозирования будет иметь ширину примерно 2*2,095= +/- 4,19 единиц, что меньше 6 и, следовательно, будет достаточно точным для использования для создания интервалов прогнозирования.
Дальнейшее чтение
Введение в простую линейную регрессию
Что такое хорошее значение R-квадрата?
Содержание:
Регрессионный анализ:
Регрессионным анализом называется раздел математической статистики, объединяющий практические методы исследования корреляционной зависимости между случайными величинами по результатам наблюдений над ними. Сюда включаются методы выбора модели изучаемой зависимости и оценки ее параметров, методы проверки статистических гипотез о зависимости.
Пусть между случайными величинами X и Y существует линейная корреляционная зависимость. Это означает, что математическое ожидание Y линейно зависит от значений случайной величины X. График этой зависимости (линия регрессии Y на X) имеет уравнение
Линейная модель пригодна в качестве первого приближения и в случае нелинейной корреляции, если рассматривать небольшие интервалы возможных значений случайных величин.
Пусть параметры линии регрессии 
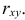
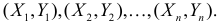
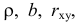
Неизвестная нам линия регрессии 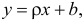

Такие значения 
Решения этой системы уравнений дают оценки называемые оценками по методу наименьших квадратов.
и
Известно, что оценки по методу наименьших квадратов являются несмещенными и, более того, среди всех несмещенных оценок обладают наименьшей дисперсией. Для оценки коэффициента корреляции можно воспользоваться тем, что 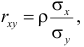
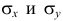
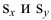
По методу наименьших квадратов можно находить оценки параметров линии регрессии и при нелинейной корреляции. Например, для линии регрессии вида 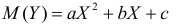
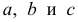
Пример:
По данным наблюдений двух случайных величин найти коэффициент корреляции и уравнение линии регрессии Y на X
Решение. Вычислим величины, необходимые для использования формул (3.7.1)–(3.7.3):
По формулам (3.7.1) и (3.7.2) получим
Итак, оценка линии регрессии имеет вид 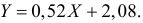
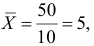
Аналогично, 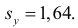
Ответ.
Пример:
Получена выборка значений величин X и Y
Для представления зависимости между величинами предполагается использовать модель 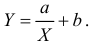
Решение. Рассмотрим сначала задачу оценки параметров этой модели в общем виде. Линия 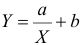
Необходимые условия экстремума приводят к системе из двух уравнений:
Откуда
Решения системы уравнений (3.7.4) и (3.7.5) и будут оценками по методу наименьших квадратов для параметров
На основе опытных данных вычисляем:
В итоге получаем систему уравнений (?????) и (?????) в виде
Эта система имеет решения
Ответ.
Если наблюдений много, то результаты их обычно группируют и представляют в виде корреляционной таблицы.
В этой таблице 
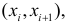
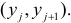
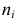
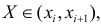
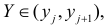
Если величины дискретны, то вместо интервалов указывают отдельные значения этих величин. Для непрерывных случайных величин представителем каждого интервала считают его середину и полагают, что 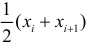
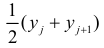
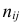
При больших значениях X и Y можно для упрощения вычислений перенести начало координат и изменить масштаб по каждой из осей, а после завершения вычислений вернуться к старому масштабу.
Пример:
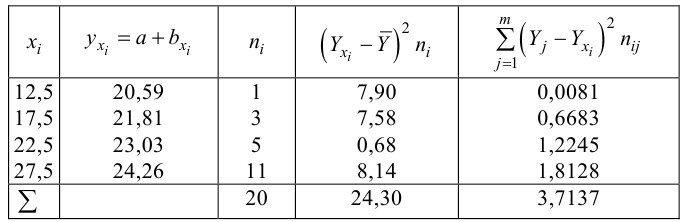
Проделано 80 наблюдений случайных величин X и Y. Результаты наблюдений представлены в виде таблицы. Найти линию регрессии Y на X. Оценить коэффициент корреляции.
Решение. Представителем каждого интервала будем считать его середину. Перенесем начало координат и изменим масштаб по каждой оси так, чтобы значения X и Y были удобны для вычислений. Для этого перейдем к новым переменным 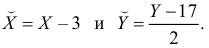
Чтобы иметь представление о виде линии регрессии, вычислим средние значения 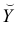
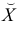
Нанесем эти значения на координатную плоскость, соединив для наглядности их отрезками прямой (рис. 3.7.1).
По виду полученной ломанной линии можно предположить, что линия регрессии Y на X является прямой. Оценим ее параметры. Для этого сначала вычислим с учетом группировки данных в таблице все величины, необходимые для использования формул (3.31–3.33):
Тогда
В новом масштабе оценка линии регрессии имеет вид 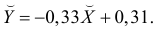
Для оценки 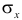
Подобным же образом можно оценить 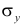
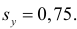
Вернемся к старому масштабу:
Коэффициент корреляции пересчитывать не нужно, так как это величина безразмерная и от масштаба не зависит.
Ответ.
Пусть некоторые физические величины X и Y связаны неизвестной нам функциональной зависимостью 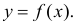
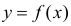
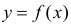
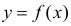
Регрессионный анализ
Основные положения регрессионного анализа:
Основная задача регрессионного анализа — изучение зависимости между результативным признаком Y и наблюдавшимся признаком X, оценка функции регрессий.
Предпосылки регрессионного анализа:
- Y — независимые случайные величины, имеющие постоянную дисперсию;
- X— величины наблюдаемого признака (величины не случайные);
- условное математическое ожидание
можно представить в виде
Выражение (2.1), как уже упоминалось в п. 1.2, называется функцией регрессии (или модельным уравнением регрессии) Y на X. Оценке в этом выражении подлежат параметры 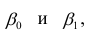
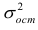
Остаточной дисперсией называется та часть рассеивания результативного признака, которую нельзя объяснить действием наблюдаемого признака; Остаточная дисперсия может служить для оценки точности подбора вида функции регрессии (модельного уравнения регрессии), полноты набора признаков, включенных в анализ. Оценки параметров функции регрессии находят, используя метод наименьших квадратов.
В данном вопросе рассмотрен линейный регрессионный анализ. Линейным он называется потому, что изучаем лишь те виды зависимостей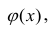
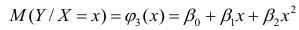
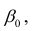
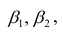
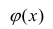
Важное место в линейном регрессионном анализе занимает так называемая «нормальная регрессия». Она имеет место, если сделать предположения относительно закона распределения случайной величины Y. Предпосылки «нормальной регрессии»:
- Y — независимые случайные величины, имеющие постоянную дисперсию и распределенные по нормальному закону;
- X— величины наблюдаемого признака (величины не случайные);
- условное математическое ожидание
можно представить в виде (2.1).
В этом случае оценки коэффициентов регрессии — несмещённые с минимальной дисперсией и нормальным законом распределения. Из этого положения следует что при «нормальной регрессии» имеется возможность оценить значимость оценок коэффициентов регрессии, а также построить доверительный интервал для коэффициентов регрессии и условного математического ожидания M(YX=x).
Линейная регрессия
Рассмотрим простейший случай регрессионного анализа — модель вида (2.1), когда зависимость 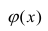
по переменным. Оценки параметров модели (2.1) 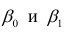
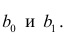
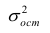
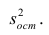
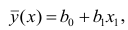
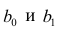
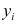
Составим систему нормальных уравнений: первое уравнение
откуда
второе уравнение
откуда
Итак,
Оценки, полученные по способу наименьших квадратов, обладают минимальной дисперсией в классе линейных оценок. Решая систему (2.2) относительно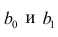
Остаётся получить оценку параметра 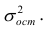
где т — количество наблюдений.
Еслит велико, то для упрощения расчётов наблюдавшиеся данные принята группировать, т.е. строить корреляционную таблицу. Пример построения такой таблицы приведен в п. 1.5. Формулы для нахождения коэффициентов регрессии по сгруппированным данным те же, что и для расчёта по несгруппированным данным, но суммы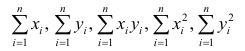
где 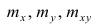
Нелинейная регрессия
Рассмотрим случай, когда зависимость нелинейна по переменным х, например модель вида
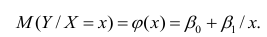
На рис. 2.1 изображено поле корреляции. Очевидно, что зависимость между Y и X нелинейная и её графическим изображением является не прямая, а кривая. Оценкой выражения (2.6) является уравнение регрессии
где 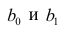
Принцип нахождения коэффициентов тот же — метод наименьших квадратов, т.е.
или
Дифференцируя последнее равенство по 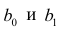
В общем случае нелинейной зависимости между переменными Y и X связь может выражаться многочленом k-й степени от x:
Коэффициенты регрессии определяют по принципу наименьших квадратов. Система нормальных уравнений имеет вид
Вычислив коэффициенты системы, её можно решить любым известным способом.
Оценка значимости коэффициентов регрессии. Интервальная оценка коэффициентов регрессии
Проверить значимость оценок коэффициентов регрессии — значит установить, достаточна ли величина оценки для статистически обоснованного вывода о том, что коэффициент регрессии отличен от нуля. Для этого проверяют гипотезу о равенстве нулю коэффициента регрессии, соблюдая предпосылки «нормальной регрессии». В этом случае вычисляемая для проверки нулевой гипотезы 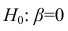
имеет распределение Стьюдента с к= n-2 степенями свободы (b — оценка коэффициента регрессии, 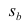
коэффициента регрессии, иначе стандартная ошибка оценки). По уровню значимости а и числу степеней свободы к находят по таблицам распределения Стьюдента (см. табл. 1 приложений) критическое значение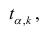
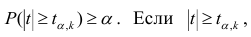
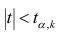
Оценки среднеквадратического отклонения коэффициентов регрессии вычисляют по следующим формулам:
где 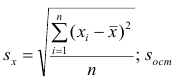
формуле (2.5).
Доверительный интервал для значимых параметров строят по обычной схеме. Из условия
где а — уровень значимости, находим
Интервальная оценка для условного математического ожидания
Линия регрессии характеризует изменение условного математического ожидания результативного признака от вариации остальных признаков.
Точечной оценкой условного математического ожидания 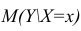
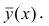
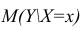
построить доверительный интервал в точке
Известно, что 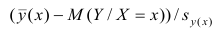
Стьюдента с k=n—2 степенями свободы. Найдя оценку среднеквадратического отклонения для условного среднего, можно построить доверительный интервал для условного математического ожидания
Оценку дисперсии условного среднего вычисляют по формуле
или для интервального ряда
Доверительный интервал находят из условия
где а — уровень значимости. Отсюда
Доверительный интервал для условного математического ожидания можно изобразить графически (рис, 2.2).
Из рис. 2.2 видно, что в точке 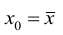
Проверка значимости уравнения регрессии
Оценить значимость уравнения регрессии — значит установить, соответствует ли математическая, модель, выражающая зависимость между Y и X, экспериментальным данным. Для оценки значимости в предпосылках «нормальной регрессии» проверяют гипотезу 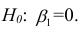
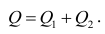
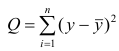
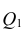
X) и 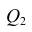
Для проверки нулевой гипотезы вычисляют статистику 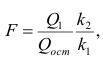
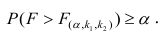
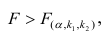
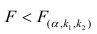
Многомерный регрессионный анализ
В случае, если изменения результативного признака определяются действием совокупности других признаков, имеет место многомерный регрессионный анализ. Пусть результативный признак У, а независимые признаки 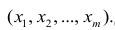
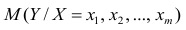
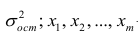
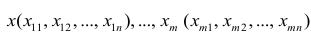
Оценке подлежат параметры 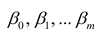
Заменив параметры их оценками, запишем уравнение регрессии
Коэффициенты в этом выражении находят методом наименьших квадратов.
Исходными данными для вычисления коэффициентов 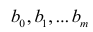

Как и в двумерном случае, составляют систему нормальных уравнений
которую можно решить любым способом, известным из линейной алгебры. Рассмотрим один из них — способ обратной матрицы. Предварительно преобразуем систему уравнений. Выразим из первого уравнения значение 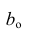
Подставим в остальные уравнения системы вместо 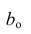
Пусть С — матрица коэффициентов при неизвестных параметрах 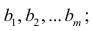
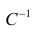
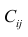
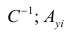
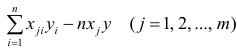
запишем окончательные выражения для параметров:
Оценкой остаточной дисперсии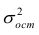
где 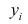
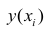
Если выборка получена из нормально распределенной генеральной совокупности, то, аналогично изложенному в п. 2.4, можно проверить значимость оценок коэффициентов регрессии, только в данном случае статистику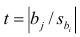
где 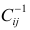
го столбца;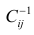
При заданном уровне значимости а и числе степеней свободы к=n— m—1 по табл. 1 приложений находят критическое значение 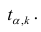
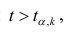
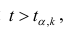
Для значимых коэффициентов регрессии целесообразно построить доверительные интервалы по формуле (2.10). Для оценки значимости уравнения регрессии следует проверить нулевую гипотезу о том, что все коэффициенты регрессии (кроме свободного члена) равны нулю: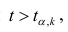
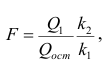
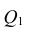
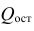
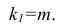
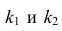
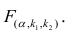
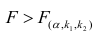
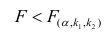
Факторный анализ
Основные положения. В последнее время всё более широкое распространение находит один из новых разделов многомерного статистического анализа — факторный анализ. Первоначально этот метод
разрабатывался для объяснения многообразия корреляций между исходными параметрами. Действительно, результатом корреляционного анализа является матрица коэффициентов корреляций. При малом числе параметров можно произвести визуальный анализ этой матрицы. С ростом числа параметра (10 и более) визуальный анализ не даёт положительных результатов. Оказалось, что всё многообразие корреляционных связей можно объяснить действием нескольких обобщённых факторов, являющихся функциями исследуемых параметров, причём сами обобщённые факторы при этом могут быть и неизвестны, однако их можно выразить через исследуемые параметры.
Один из основоположников факторного анализа Л. Терстоун приводит такой пример: несколько сотен мальчиков выполняют 20 разнообразных гимнастических упражнений. Каждое упражнение оценивают баллами. Можно рассчитать матрицу корреляций между 20 упражнениями. Это большая матрица размером 20><20. Изучая такую матрицу, трудно уловить закономерность связей между упражнениями. Нельзя ли объяснить скрытую в таблице закономерность действием каких-либо обобщённых факторов, которые в результате эксперимента непосредственно, не оценивались? Оказалось, что обо всех коэффициентах корреляции можно судить по трём обобщённым факторам, которые и определяют успех выполнения всех 20 гимнастических упражнений: чувство равновесия, усилие правого плеча, быстрота движения тела.
Дальнейшие разработки факторного анализа доказали, что этот метод может быть с успехом применён в задачах группировки и классификации объектов. Факторный анализ позволяет группировать объекты со сходными сочетаниями признаков и группировать признаки с общим характером изменения от объекта к объекту. Действительно, выделенные обобщённые факторы можно использовать как критерии при классификации мальчиков по способностям к отдельным группам гимнастических упражнений.
Методы факторного анализа находят применение в психологии и экономике, социологии и экономической географии. Факторы, выраженные через исходные параметры, как правило, легко интерпретировать как некоторые существенные внутренние характеристики объектов.
Факторный анализ может быть использован и как самостоятельный метод исследования, и вместе с другими методами многомерного анализа, например в сочетании с регрессионным анализом. В этом случае для набора зависимых переменных наводят обобщённые факторы, которые потом входят в регрессионный анализ в качестве переменных. Такой подход позволяет сократить число переменных в регрессионном анализе, устранить коррелированность переменных, уменьшить влияние ошибок и в случае ортогональности выделенных факторов значительно упростить оценку значимости переменных.
Представление, информации в факторном анализе
Для проведения факторного анализа информация должна быть представлена в виде двумерной таблицы чисел размерностью 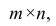
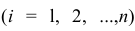
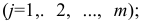
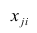
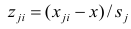
Основная модель факторного анализа. Основная модель факторного анализа имеет вид
где 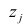
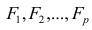
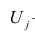
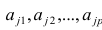
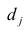
Модель предполагает, что каждый из j признаков, входящих в исследуемый набор и заданных в стандартной форме, может быть представлен в виде линейной комбинации небольшого числа общих факторов 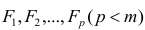
Термин «общий фактор» подчёркивает, что каждый такой фактор имеет существенное значение для анализа всех признаков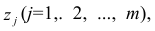
Термин «характерный фактор» показывает, что он относится только к данному j-му признаку. Это специфика признака, которая не может быть, выражена через факторы
Факторные нагрузки 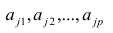
Для j-го признака и i-го объекта модель (2.19) можно записать в. виде
где 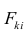
Дисперсию признака 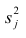
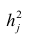
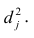
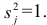
Если общие и характерные факторы не коррелируют между собой, то дисперсию j-го признака можно представить в виде
где 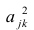
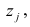
Полный вклад k-го фактора в суммарную дисперсию признаков
Вклад общих факторов в суммарную дисперсию
Факторное отображение
Используя модель (2.19), запишем выражения для каждого из параметров:
Коэффициенты системы (2,21) — факторные нагрузки — можно представить в виде матрицы, каждая строка которой соответствует параметру, а столбец — фактору.
Факторный анализ позволяет получить не только матрицу отображений, но и коэффициенты корреляции между параметрами и
факторами, что является важной характеристикой качества факторной модели. Таблица таких коэффициентов корреляции называется факторной структурой или просто структурой.
Коэффициенты отображения можно выразить через выборочные парные коэффициенты корреляции. На этом основаны методы вычисления факторного отображения.
Рассмотрим связь между элементами структуры и коэффициентами отображения. Для этого, учитывая выражение (2.19) и определение выборочного коэффициента корреляции, умножим уравнения системы (2.21) на соответствующие факторы, произведём суммирование по всем n наблюдениям и, разделив на n, получим следующую систему уравнений:
где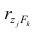
м фактором;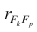
Если предположить, что общие факторы между собой, не коррелированы, то уравнения (2.22) можно записать в виде
элементам структуры.
Введём понятие, остаточного коэффициента корреляции и остаточной корреляционной матрицы. Исходной информацией для построения факторной модели (2.19) служит матрица выборочных парных коэффициентов корреляции. Используя построенную факторную модель, можно снова вычислить коэффициенты корреляции между признаками и сравнись их с исходными Коэффициентами корреляции. Разница между ними и есть остаточный коэффициент корреляции.
В случае независимости факторов имеют место совсем простые выражения для вычисляемых коэффициентов корреляции между параметрами: для их вычисления достаточно взять сумму произведений коэффициентов отображения, соответствующих наблюдавшимся признакам:
где 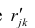
и к-м признаком. Остаточный коэффициент корреляции
Матрица остаточных коэффициентов корреляции называется остаточной матрицей или матрицей остатков
где 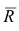
Результаты факторного анализа удобно представить в виде табл. 2.10.
Здесь суммы квадратов нагрузок по строкам — общности параметров, а суммы квадратов нагрузок по столбцам — вклады факторов в суммарную дисперсию параметров. Имеет место соотношение
Определение факторных нагрузок
Матрицу факторных нагрузок можно получить различными способами. В настоящее время наибольшее распространение получил метод главных факторов. Этот метод основан на принципе последовательных приближений и позволяет достичь любой точности. Метод главных факторов предполагает использование ЭВМ. Существуют хорошие алгоритмы и программы, реализующие все вычислительные процедуры.
Введём понятие редуцированной корреляционной матрицы или просто редуцированной матрицы. Редуцированной называется матрица выборочных коэффициентов корреляции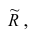
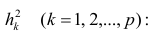
Редуцированная и полная матрицы связаны соотношением
где D — матрица характерностей.
Общности, как правило, неизвестны, и нахождение их в факторном анализе представляет серьезную проблему. Вначале определяют (хотя бы приближённо) число общих факторов, совокупность, которых может с достаточной точностью аппроксимировать все взаимосвязи выборочной корреляционной матрицы. Доказано, что число общих факторов (общностей) равно рангу редуцированной матрицы, а при известном ранге можно по выборочной корреляционной матрице найти оценки общностей. Числа общих факторов можно определить априори, исходя из физической природы эксперимента. Затем рассчитывают матрицу факторных нагрузок. Такая матрица, рассчитанная методом главных факторов, обладает одним интересным свойством: сумма произведений каждой пары её столбцов равна нулю, т.е. факторы попарно ортогональны.
Сама процедура нахождения факторных нагрузок, т.е. матрицы А, состоит из нескольких шагов и заключается в следующем: на первом шаге ищут коэффициенты факторных нагрузок при первом факторе так, чтобы сумма вкладов данного фактора в суммарную общность была максимальной:
Максимум 
где 
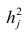
Затем рассчитывают матрицу коэффициентов корреляции с учётом только первого фактора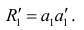
На втором шаге определяют коэффициенты нагрузок при втором факторе так, чтобы сумма вкладов второго фактора в остаточную общность (т.е. полную общность без учёта той части, которая приходится на долю первого фактора) была максимальной. Сумма квадратов нагрузок при втором факторе
Максимум 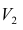
где 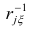
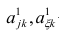
Факторный анализ учитывает суммарную общность. Исходная суммарная общность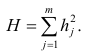
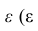
Адекватность факторной модели оценивается по матрице остатков (если величины её коэффициентов малы, то модель считают адекватной).
Такова последовательность шагов для нахождения факторных нагрузок. Для нахождения максимума функции (2.24) при условии (2.25) используют метод множителей Лагранжа, который приводит к системе т уравнений относительно m неизвестных
Метод главных компонент
Разновидностью метода главных факторов является метод главных компонент или компонентный анализ, который реализует модель вида
где m — количество параметров (признаков).
Каждый из наблюдаемых, параметров линейно зависит от m не коррелированных между собой новых компонент (факторов) 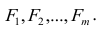
Если для дальнейшего анализа оставить все найденные т компонент, то тем самым будет использована вся информация, заложенная в корреляционной матрице. Однако это неудобно и нецелесообразно. На практике обычно оставляют небольшое число компонент, причём количество их определяется долей суммарной дисперсии, учитываемой этими компонентами. Существуют различные критерии для оценки числа оставляемых компонент; чаще всего используют следующий простой критерий: оставляют столько компонент, чтобы суммарная дисперсия, учитываемая ими, составляла заранее установленное число процентов. Первая из компонент должна учитывать максимум суммарной дисперсии параметров; вторая — не коррелировать с первой и учитывать максимум оставшейся дисперсии и так до тех пор, пока вся дисперсия не будет учтена. Сумма учтённых всеми компонентами дисперсий равна сумме дисперсий исходных параметров. Математический аппарат компонентного анализа полностью совпадает с аппаратом метода главных факторов. Отличие только в исходной матрице корреляций.
Компонента (или фактор) через исходные переменные выражается следующим образом:
где 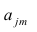
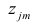
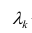
компонент.
Для иллюстрации возможностей факторного анализа покажем, как, используя метод главных компонент, можно сократить размерность пространства независимых переменных, перейдя от взаимно коррелированных параметров к независимым факторам, число которых р
Следует особо остановиться на интерпретации результатов, т.е. на смысловой стороне факторного анализа. Собственно факторный анализ состоит из двух важных этапов; аппроксимации корреляционной матрицы и интерпретации результатов. Аппроксимировать корреляционную матрицу, т.е. объяснить корреляцию между параметрами действием каких-либо общих для них факторов, и выделить сильно коррелирующие группы параметров достаточно просто: из корреляционной матрицы одним из методов
факторного анализа непосредственно получают матрицу нагрузок — факторное решение, которое называют прямым факторным решением. Однако часто это решение не удовлетворяет исследователей. Они хотят интерпретировать фактор как скрытый, но существенный параметр, поведение которого определяет поведение некоторой своей группы наблюдаемых параметров, в то время как, поведение других параметров определяется поведением других факторов. Для этого у каждого параметра должна быть наибольшая по модулю факторная нагрузка с одним общим фактором. Прямое решение следует преобразовать, что равносильно повороту осей общих факторов. Такие преобразования называют вращениями, в итоге получают косвенное факторное решение, которое и является результатом факторного анализа.
Приложения
Значение t — распределения Стьюдента
Понятие о регрессионном анализе. Линейная выборочная регрессия. Метод наименьших квадратов (МНК)
Основные задачи регрессионного анализа:
- Вычисление выборочных коэффициентов регрессии
- Проверка значимости коэффициентов регрессии
- Проверка адекватности модели
- Выбор лучшей регрессии
- Вычисление стандартных ошибок, анализ остатков
Построение простой регрессии по экспериментальным данным.
Предположим, что случайные величины 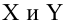
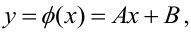
Диаграмма рассеяния (разброса, рассеивания)
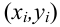
Выборочное уравнение прямой линии регрессии 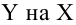
Задача: подобрать 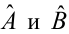
Для того, что бы провести прямую 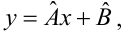
чтобы
Постулаты регрессионного анализа, которые должны выполняться при использовании МНК.
подчинены нормальному закону распределения.
- Дисперсия
постоянна и не зависит от номера измерения.
- Результаты наблюдений
в разных точках независимы.
- Входные переменные
независимы, неслучайны и измеряются без ошибок.
Введем функцию ошибок 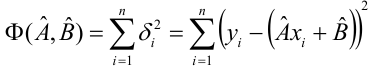
Решив систему, получим искомые значения
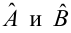
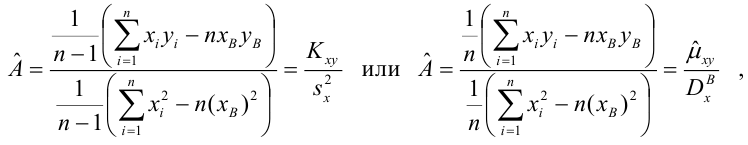
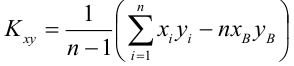
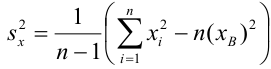
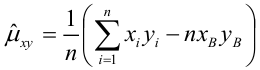
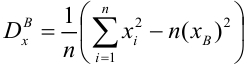
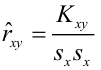
Коэффициент детерминации
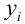
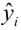
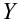
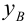
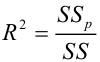
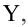
Коэффициент детерминации принимает значения от 0 до 1. Чем ближе значение коэффициента к 1, тем сильнее зависимость. При оценке регрессионных моделей это используется для доказательства адекватности модели (качества регрессии). Для приемлемых моделей предполагается, что коэффициент детерминации должен быть хотя бы не меньше 0,5 (в этом случае коэффициент множественной корреляции превышает по модулю 0,7). Модели с коэффициентом детерминации выше 0,8 можно признать достаточно хорошими (коэффициент корреляции превышает 0,9). Подтверждение адекватности модели проводится на основе дисперсионного анализа путем проверки гипотезы о значимости коэффициента детерминации.
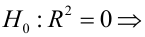
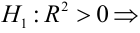
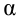
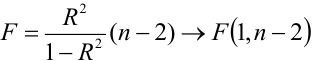
Критическая область — правосторонняя;
Если 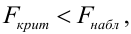
Мощность статистического критерия. Функция мощности
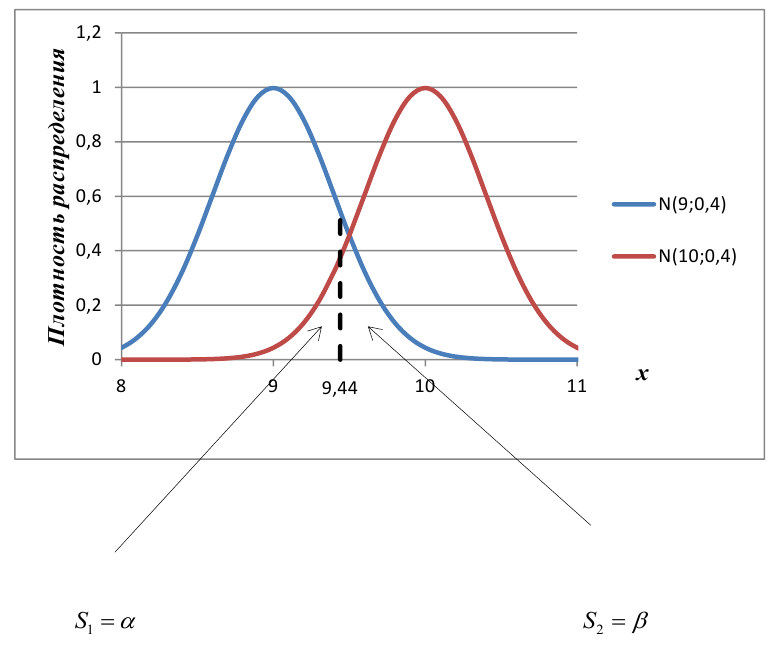
Определение. Мощностью критерия 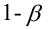
Задача: построить критическую область таким образом, чтобы мощность критерия была максимальной.
Определение. Наилучшей критической областью (НКО) называют критическую область, которая обеспечивает минимальную ошибку второго рода
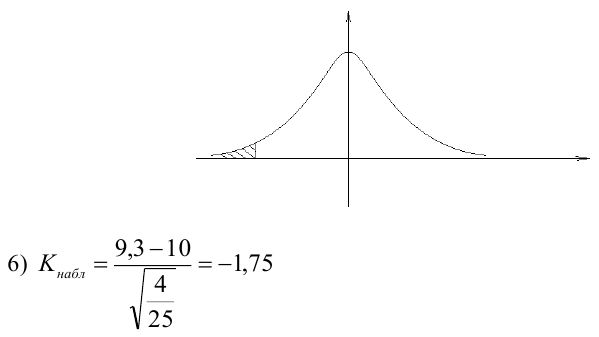
Пример:
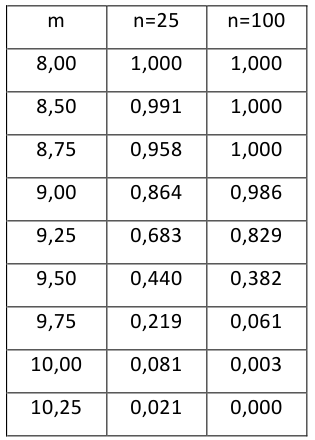
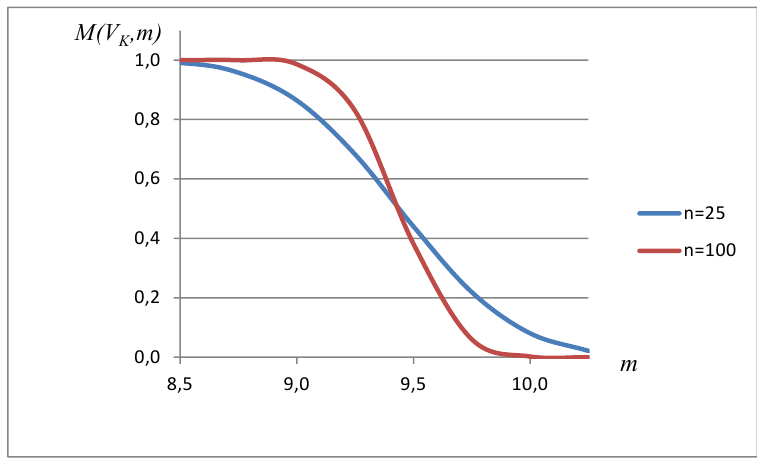
По паспортным данным автомобиля расход топлива на 100 километров составляет 10 литров. В результате измерения конструкции двигателя ожидается, что расход топлива уменьшится. Для проверки были проведены испытания 25 автомобилей с модернизированным двигателем; выборочная средняя расхода топлива по результатам испытаний составила 9,3 литра. Предполагая, что выборка получена из нормально распределенной генеральной совокупности с математическим ожиданием 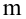
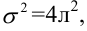
3) Уровень значимости
4) Статистический критерий
5) Критическая область — левосторонняя
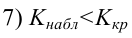
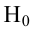
Пример:
В условиях примера 1 предположим, что наряду с 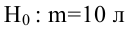
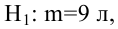
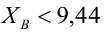
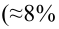
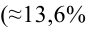
Определение. Пусть проверяется 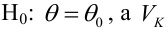
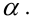
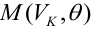
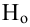
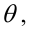
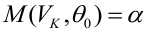
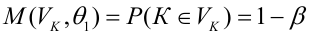
Пример:
Построить график функции мощности из примера 2 для

Пример:
Какой минимальный объем выборки следует взять в условии примера 2 для того, чтобы обеспечить
Лемма Неймана-Пирсона.
При проверке простой гипотезы 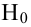
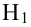
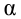
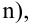
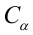
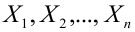
Пример:
Случайная величина 
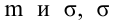
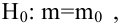
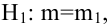
Решение:
Ошибка первого рода:
НКО:
Пример:
Для зависимости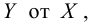
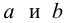
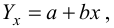
Решение. Воспользуемся предыдущими результатами
Согласно формуле (24), уравнение регрессии будет иметь вид 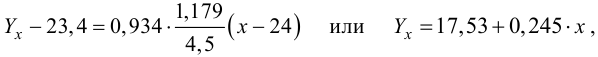
Для выяснения значимости уравнения регрессии вычислим суммы 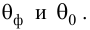
Из (27) и (28) по данным таблицы получим
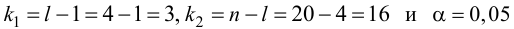
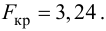
Вычислим статистику
Так как 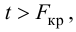
- Корреляционный анализ
- Статистические решающие функции
- Случайные процессы
- Выборочный метод
- Проверка гипотезы о равенстве вероятностей
- Доверительный интервал для математического ожидания
- Доверительный интервал для дисперсии
- Проверка статистических гипотез
Стандартная ошибка уравнения регрессии, Эта статистика SEE представляет собой стандартное отклонение фактических значений теоретических значений У. [c.650]
Что такое стандартная ошибка уравнения регрессии ).Какие допущения лежат в основе парной регрессии 10. Что такое множественная регрессия [c.679]
Следующий этап корреляционного анализа — расчет уравнения связи (регрессии). Решение проводится обычно шаговым способом. Сначала в расчет принимается один фактор, который оказывает наиболее значимое влияние на результативный показатель, потом второй, третий и т.д. И на каждом шаге рассчитываются уравнение связи, множественный коэффициент корреляции и детерминации, /»»-отношение (критерий Фишера), стандартная ошибка и другие показатели, с помощью которых оценивается надежность уравнения связи. Величина их на каждом шаге сравнивается с предыдущей. Чем выше величина коэффициентов множественной корреляции, детерминации и критерия Фишера и чем ниже величина стандартной ошибки, тем точнее уравнение связи описывает зависимости, сложившиеся между исследуемыми показателями. Если добавление следующих факторов не улучшает оценочных показателей связи, то надо их отбросить, т.е. остановиться на том уравнении, где эти показатели наиболее оптимальны.
[c.149]
Прогнозное значение ур определяется путем подстановки в уравнение регрессии ух =а + Ьх соответствующего (прогнозного) значения хр. Вычисляется средняя стандартная ошибка прогноза
[c.9]
В линейной регрессии обычно оценивается значимость не только уравнения в целом, но и отдельных его параметров. С этой целью по каждому из параметров определяется его стандартная ошибка ть и та.
[c.53]
В прогнозных расчетах по уравнению регрессии определяется предсказываемое (ур) значение как точечный прогноз ух при хр =хь т. е. путем подстановки в уравнение регрессии 5 = а + b х соответствующего значения х. Однако точечный прогноз явно не реален. Поэтому он дополняется расчетом стандартной ошибки ух, т. е. Шух, и соответственно интервальной оценкой прогнозного значения (у )
[c.57]
Чтобы понять, как строится формула для определения величин стандартной ошибки ух, обратимся к уравнению линейной регрессии ух = а + b х. Подставим в это уравнение выражение параметра а [c.57]
При прогнозировании на основе уравнения регрессии следует помнить, что величина прогноза зависит не только от стандартной ошибки индивидуального значения у, но и от точности прогноза значения фактора х. Его величина может задаваться на основе анализа других моделей исходя из конкретной ситуации, а также из анализа динамики данного фактора.
[c.61]
В скобках указаны стандартные ошибки параметров уравнения регрессии.
[c.327]
В скобках указаны стандартные ошибки параметров уравнения регрессии. Определим по этому уравнению расчетные значения >>, ,, а затем параметры уравнения регрессии (7.44). Получим следующие результаты [c.328]
Стандартные ошибки коэффициентов уравнения регрессии, t — критерий
[c.7]
На каждом шаге рассматриваются уравнение регрессии, коэффициенты корреляции и детерминации, F-критерий, стандартная ошибка оценки и другие оценочные показатели. После каждого шага перечисленные оценочные показатели сравниваются с
[c.39]
Проблемы с методологией регрессии. Методология регрессии — это традиционный способ уплотнения больших массивов данных и их сведения в одно уравнение, отражающее связь между мультипликаторами РЕ и финансовыми фундаментальными переменными. Но данный подход имеет свои ограничения. Во-первых, независимые переменные коррелируют друг с другом . Например, как видно из таблицы 18,2, обобщающей корреляцию между коэффициентами бета, ростом и коэффициентами выплат для всех американских фирм, быстрорастущие фирмы обычно имеют большой риск и низкие коэффициенты выплат. Обратите внимание на отрицательную корреляцию между коэффициентами выплат и ростом, а также на положительную корреляцию между коэффициентами бета и ростом. Эта мультиколлинеарность делает мультипликаторы регрессии ненадежными (увеличивает стандартную ошибку) и, возможно, объясняет ошибочные знаки при коэффициентах и крупные изменения этих мультипликаторов в разные периоды. Во-вторых, регрессия основывается на линейной связи между мультипликаторами РЕ и фундаментальными переменными, и данное свойство, по всей вероятности, неадекватно. Анализ остаточных явлений, связанных с корреляцией, может привести к трансформациям независимых переменных (их квадратов или натуральных логарифмов), которые в большей степени подходят для объяснения мультипликаторов РЕ. В-третьих, базовая связь между мультипликаторами РЕ и финансовыми переменными сама по себе не является стабильной. Если же эта связь смещается из года в год, то прогнозы, полученные из регрессионного уравнения, могут оказаться ненадежными для более длительных периодов времени. По всем этим причинам, несмотря на полезность регрессионного анализа, его следует рассматривать только как еще один инструмент поиска подлинного значения ценности.
[c.649]
На рисунке 16.6 явно просматривается четкая линейная зависимость объема частного потребления от величины располагаемого дохода. Уравнение парной линейной регрессии, оцененное по этим данным, имеет вид С= -217,6 + 1,007 Yf Стандартные ошибки для свободного члена и коэффициента парной регрессии равны, соответственно, 28,4 и 0,012, а -статистики — -7,7 и 81 9. Обе они по модулю существенно превышают 3, следовательно, их статистическая значимость весьма высока. Впрочем, несмотря на то, что здесь удалось оценить статистически значимую линейную функцию потребления, в ней нарушены сразу две предпосылки Кейнса — уровень автономного потребления С0 оказался отрицательным, а предель-
[c.304]
Стандартные ошибки свободного члена и коэффициента регрессии равны, соответственно, 84,7 и 0,46 их /-статистики — (-21,4 и 36,8). По абсолютной величине /-статистики намного превышают 3, и это свидетельствует о высокой надежности оцененных коэффициентов. Коэффициент детерминации /Р уравнения равен 0,96, то есть объяснено 96% дисперсии объема потребления. И в то же время уже по рисунку видно, что оцененная рефессия не очень хоро-
[c.320]
Эта стандартная ошибка S у, равная 0,65, указывает отклонение фактических данных от прогнозируемых на основании использования воздействующих факторов j i и Х2 (влияние среди покупателей бабушек с внучками и высокопрофессионального вклада Шарика). В то же время мы располагаем обычным стандартным отклонением Sn, равным 1,06 (см. табл.8), которое было рассчитано для одной переменной, а именно сами текущие значения уги величина среднего арифметического у, которое равно 6,01. Легко видеть, что S у< Sn следовательно, ошибки прогнозирования, как правило, оказываются меньшими, если использовать уравнение регрессии (учитывается вклад факторов j i и Х2), а не ограничиваться только значением у.
[c.64]
Эти два выражения показывают, как возникает ковариация между [52 и Рз в СИЛУ присутствия 2ыу в каждом из выражений для ошибок Р2 и (33. Положительное и большое значение ос приводит, как мы видим, к большим противоположным значениям ошибок J32 и(33- Если (32 оценивает значение р 2 снизу, то р3 оценивает значение ps сверху, и наоборот. Очень важным является то обстоятельство, что стандартные ошибки могут служить одним из индикаторов наличия мульти-коллинеарности. Формула (5.84) показывает, что истинное значение стандартной ошибки возрастает с увеличением а, однако эта формула содержит неизвестный параметр а . В оцененной величине стандартной ошибки значение а заменяется на Ее2/(п — /г), где 2е2 — сумма квадратов остатков после подгонки уравнения регрессии к эмпирическим данным. Как было показано в (5.19),
[c.162]
С помощью парной регрессии устанавливается математическая зависимость (в виде уравнения) между метрической зависимой (критериальной) переменной и метрической независимой переменной (предиктором). Уравнение описывает прямую линиию, и для его вывода используют метод наименьших В случае построения регрессии с нормированными данными отрезок, отсекаемый на оси OY, принимает значение, равное 0, и коэффициенты регрессии называют взвешенными Силу тесноты связи измеряют ко-детерминации который получают, вычисляя отношение к Стандартную ошибку уравнения регрессии используют для оценки точности предсказания, и ее можно интерпретировать как род средней ошибки, сделанной при теоретическом предсказании Y, исходя из уравнения регрессии.
[c.678]
В скобках указаны стандартные ошибки коэффициентов регрессии. «Коэффициенты детерминации рассчитаны по линеаризованным уравнениям регрессии. [c.237]
Это уравнение намного лучше, чем (5). Все коэффициенты статистически значимы, их коэффициенты по абсолютной величине в 7-10 раз превышают свои стандартные ошибки. Уравнение соответствует макроэкономической теории, говорящей об отрицательной зависимости величины реального чистого экспорта от реального ВНП и валютного курса. Взглянув на рис. 18.7, можно отметить, что рассчитанные по уравнению регрессии величины ВНП за 1965-1990 гг. очень близки к фактическим. Единственной проблемой является то, что статистика Дарбина-Уотсона существенно меньше двух, -таким образом, можно попытаться улучшить это уравнение. При этом мы надеемся избавиться от автокорреляции остатков (то есть, получить более близкую к двум DW) и, возможно, увеличить долю объясненной дисперсии RNX, то есть R2.
[c.346]
В скобках указаны стандартные ошибки параметров уравнения регрессии. Применение метода инструментальных переменных привело к статистической незначимости параметра С[ = 0,109 при переменной yf . Это произошло ввиду высокой мультиколлинеарности факторов, иyt v. Несмотря на то что результаты, полученные обычным МНК, на первый взгляд лучше, чем результаты применения метода инструментальных переменных, результатам обычного МНК вряд ли можно доверять вследствие нарушения в данной модели его предпосылок. Поскольку ни один из методов не привел к получению достоверных результатов расчетов параметров, следует перейти к получению оценок параметров данной модели авторегрессии методом максимального правдоподобия.
[c.328]
Нетрудно заметить, что в данном случае не выполняются необходимые предпосылки МНК об отклонениях Si точек наблюдений от линии регрессии (см. параграф 6.1). Эти отклонения явно не обладают постоянной дисперсией и не являются взаимно независимыми. Нарушение необходимых предпосылок делает неточными полученные оценки коэффициентов регрессии, увеличивая их стандартные ошибки, и обычно свидетельствует о неверной спецификации самого уравнения. Поэтому следующим этапом проверки качества уравнения регрессии является проверка выполнимости предпосылок МНК. Причины невыполнимости этих предпосылок, их последствия и методы корректировки будут подробно рассмотрены в последующих главах. В данном разделе мы лишь обозначим эти проблемы, а также обсудим весьма популярную в регрессионном анализе статистику Дарбина— Уотсона.
[c.164]
В скобках указаны стандартные ошибки соответствующих коэффициентов. Можно отметить, что статистическое качество полученного уравнения регрессии практически идеально. Все г-статистики превышают 5 по абсолютной величине (а, грубо говоря, границей для очень хорошей оценки является 3). Очень высока доля дисперсии зависимой переменной, объясненная с помощью уравнения регрессии, — 94,2% — особенно с учетом того, что уравнение регрессии связывает относительные величины, не имеющие выраженного временного тренда. Статистика Дарбина-Уотсона ЯИ очень близка к 2, и, даже не прибегая к таблицам, здесь ясно, что гипотеза об отсутствии автокорреляции остатков первого порядка будет принята при любом разумно малом уровне значимости. Итак, мы имеем хороший пример линейной регрессии, когда можно оценить ее статистическую значимость, не прибегая к таблицам распределений Стьюден-та, Фишера или Дарбина-Уотсона, а лишь по общему порядку полученных статистик.
[c.330]
Это уравнение приемлемо по всем параметрам и статистическим характеристикам. Единственное, что имеет смысл сделать в нем, это замена переменных ER и ER на одну переменную ER(-l). Это можно сделать, поскольку абсолютные величины коэффициентов при ER и ER почти одинаковы. В таком случае можно сделать преобразование (-a-ER+aAER) = (-aER + a(ER — ER(-l))=-aER(-l), и мы можем использовать это равенство для сокращения числа объясняющих переменных.1 Включив снова преобразование AR(l) (для которого коэффициент авторегрессии соседних отклонений et получился равен р=0,71, со стандартной ошибкой 0,16), получаем уравнение регрессии [c.363]
Подобным же образом на основе соответствующих формул рассчитывают стандартные ошибки параметров уравнения регрессии, а затем и t-критерии для каждого параметра. Важно опять-таки проверить, чтобы соблюдалось условие tpa 4 > tTa6n. В противном случае доверять полученной оценке параметра нет оснований.
[c.139]
Для определения профиля посетителей магазинов местного торгового центра, не имеющих определенной цели (browsers), маркетологи использовали три набора независимых переменных демографические, покупательское поведение психологические. Зависимая переменная представляет собой индекс посещения магазина без определенной цели, индекс (browsing index). Методом ступенчатой включающей все три набора переменных, выявлено, что демографические факторы — наиболее сильные предикторы, определяющие поведение покупателей, не преследующих конкретных целей. Окончательное уравнение регрессии, 20 из 36 возможных переменных, включало все демографические переменные. В следующей таблице приведены коэффициенты регрессии, стандартные ошибки коэффициентов, а также их уровни значимости.
[c.668]
Имея
прямую регрессии, необходимо оценить
насколько сильно точки исходных данных
отклоняются от прямой регрессии. Можно
выполнить оценку разброса, аналогичную
стандартному отклонению выборки. Этот
показатель, называемый стандартной
ошибкой оценки, демонстрирует величину
отклонения точек исходных данных от
прямой регрессии в направлении оси Y.
Стандартная ошибка оценки ()
вычисляется по следующей формуле.
Стандартная
ошибка оценки измеряет степень отличия
реальных значений Y от оцененной величины.
Для сравнительно больших выборок следует
ожидать, что около 67% разностей по модулю
не будет превышать
и около 95% модулей разностей будет не
больше 2.
Стандартная
ошибка оценки подобна стандартному
отклонению. Ее можно использовать для
оценки стандартного отклонения
совокупности. Фактически
оценивает стандартное отклонение
слагаемого ошибки
в статистической модели простой линейной
регрессии. Другими словами,
оценивает общее стандартное отклонение
нормального распределения значений Y,
имеющих математические ожидания
для каждого X.
Малая
стандартная ошибка оценки, полученная
при регрессионном анализе, свидетельствует,
что все точки данных находятся очень
близко к прямой регрессии. Если стандартная
ошибка оценки велика, точки данных могут
значительно удаляться от прямой.
2.3 Прогнозирование величины y
Регрессионную
прямую можно использовать для оценки
величины переменной Y
при данных значениях переменной X. Чтобы
получить точечный прогноз, или предсказание
для данного значения X, просто вычисляется
значение найденной функции регрессии
в точке X.
Конечно
реальные значения величины Y,
соответствующие рассматриваемым
значениям величины X, к сожалению, не
лежат в точности на регрессионной
прямой. Фактически они разбросаны
относительно прямой в соответствии с
величиной
.
Более того, выборочная регрессионная
прямая является оценкой регрессионной
прямой генеральной совокупности,
основанной на выборке из определенных
пар данных. Другая случайная выборка
даст иную выборочную прямую регрессии;
это аналогично ситуации, когда различные
выборки из одной и той же генеральной
совокупности дают различные значения
выборочного среднего.
Есть
два источника неопределенности в
точечном прогнозе, использующем уравнение
регрессии.
-
Неопределенность,
обусловленная отклонением точек данных
от выборочной прямой регрессии. -
Неопределенность,
обусловленная отклонением выборочной
прямой регрессии от регрессионной
прямой генеральной совокупности.
Интервальный
прогноз значений переменной Y
можно построить так, что при этом будут
учтены оба источника неопределенности.
Стандартная
ошибка прогноза
дает меру вариативности предсказанного
значения Y
около истинной величины Y
для данного значения X.
Стандартная ошибка прогноза равна:
Стандартная
ошибка прогноза зависит от значения X,
для которого прогнозируется величина
Y.
минимально, когда
,
поскольку тогда числитель в третьем
слагаемом под корнем в уравнении будет
0. При прочих неизменных величинах
большему отличию соответствует большее
значение стандартной ошибки прогноза.
Если
статистическая модель простой линейной
регрессии соответствует действительности,
границы интервала прогноза величины Y
равны:
где
— квантиль распределения Стьюдента с
n-2 степенями свободы ().
Если выборка велика (),
этот квантиль можно заменить соответствующим
квантилем нормального распределения.
Например, для большой выборки 95%-ный
интервал прогноза задается следующими
значениями:
Завершим
раздел обзором предположений, положенных
в основу статистической модели линейной
регрессии.
-
Для
заданного значения X генеральная
совокупность значений Y имеет нормальное
распределение относительно регрессионной
прямой совокупности. На практике
приемлемые результаты получаются
и
тогда, когда значения Y имеют
нормальное распределение лишь
приблизительно. -
Разброс
генеральной совокупности точек данных
относительно регрессионной прямой
совокупности остается постоянным всюду
вдоль этой прямой. Иными словами, при
возрастании значений X в точках данных
дисперсия генеральной совокупности
не увеличивается и не уменьшается.
Нарушение этого предположения называется
гетероскедастичностью. -
Слагаемые
ошибок
независимы между собой. Это предположение
определяет случайность выборки точек
Х-Y.
Если точки данных X-Y
записывались в течение некоторого
времени, данное предположение часто
нарушается. Вместо независимых данных,
такие последовательные наблюдения
будут давать серийно коррелированные
значения. -
В
генеральной совокупности существует
линейная зависимость между X и Y.
По аналогии с простой линейной регрессией
может рассматриваться и нелинейная
зависимость между X и У. Некоторые такие
случаи будут обсуждаться ниже.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Стандартная ошибка оценки по уравнению регрессии
Стандартная ошибка оценки, также известная как стандартная ошибка уравнения регрессии, определяется следующим образом (см. (6.23)) [c.280]
Стандартная ошибка уравнения регрессии, Эта статистика SEE представляет собой стандартное отклонение фактических значений теоретических значений У. [c.650]
Что такое стандартная ошибка уравнения регрессии ).Какие допущения лежат в основе парной регрессии 10. Что такое множественная регрессия [c.679]
Следующий этап корреляционного анализа — расчет уравнения связи (регрессии). Решение проводится обычно шаговым способом. Сначала в расчет принимается один фактор, который оказывает наиболее значимое влияние на результативный показатель, потом второй, третий и т.д. И на каждом шаге рассчитываются уравнение связи, множественный коэффициент корреляции и детерминации, /»»-отношение (критерий Фишера), стандартная ошибка и другие показатели, с помощью которых оценивается надежность уравнения связи. Величина их на каждом шаге сравнивается с предыдущей. Чем выше величина коэффициентов множественной корреляции, детерминации и критерия Фишера и чем ниже величина стандартной ошибки, тем точнее уравнение связи описывает зависимости, сложившиеся между исследуемыми показателями. Если добавление следующих факторов не улучшает оценочных показателей связи, то надо их отбросить, т.е. остановиться на том уравнении, где эти показатели наиболее оптимальны. [c.149]
Прогнозное значение ур определяется путем подстановки в уравнение регрессии ух =а + Ьх соответствующего (прогнозного) значения хр. Вычисляется средняя стандартная ошибка прогноза [c.9]
В линейной регрессии обычно оценивается значимость не только уравнения в целом, но и отдельных его параметров. С этой целью по каждому из параметров определяется его стандартная ошибка ть и та. [c.53]
В прогнозных расчетах по уравнению регрессии определяется предсказываемое (ур) значение как точечный прогноз ух при хр =хь т. е. путем подстановки в уравнение регрессии 5 = а + b х соответствующего значения х. Однако точечный прогноз явно не реален. Поэтому он дополняется расчетом стандартной ошибки ух, т. е. Шух, и соответственно интервальной оценкой прогнозного значения (у ) [c.57]
Чтобы понять, как строится формула для определения величин стандартной ошибки ух, обратимся к уравнению линейной регрессии ух = а + b х. Подставим в это уравнение выражение параметра а [c.57]
При прогнозировании на основе уравнения регрессии следует помнить, что величина прогноза зависит не только от стандартной ошибки индивидуального значения у, но и от точности прогноза значения фактора х. Его величина может задаваться на основе анализа других моделей исходя из конкретной ситуации, а также из анализа динамики данного фактора. [c.61]
В скобках указаны стандартные ошибки параметров уравнения регрессии. [c.327]
В скобках указаны стандартные ошибки параметров уравнения регрессии. Определим по этому уравнению расчетные значения >>, ,, а затем параметры уравнения регрессии (7.44). Получим следующие результаты [c.328]
На каждом шаге рассматриваются уравнение регрессии, коэффициенты корреляции и детерминации, F-критерий, стандартная ошибка оценки и другие оценочные показатели. После каждого шага перечисленные оценочные показатели сравниваются с [c.39]
Проблемы с методологией регрессии. Методология регрессии — это традиционный способ уплотнения больших массивов данных и их сведения в одно уравнение, отражающее связь между мультипликаторами РЕ и финансовыми фундаментальными переменными. Но данный подход имеет свои ограничения. Во-первых, независимые переменные коррелируют друг с другом . Например, как видно из таблицы 18,2, обобщающей корреляцию между коэффициентами бета, ростом и коэффициентами выплат для всех американских фирм, быстрорастущие фирмы обычно имеют большой риск и низкие коэффициенты выплат. Обратите внимание на отрицательную корреляцию между коэффициентами выплат и ростом, а также на положительную корреляцию между коэффициентами бета и ростом. Эта мультиколлинеарность делает мультипликаторы регрессии ненадежными (увеличивает стандартную ошибку) и, возможно, объясняет ошибочные знаки при коэффициентах и крупные изменения этих мультипликаторов в разные периоды. Во-вторых, регрессия основывается на линейной связи между мультипликаторами РЕ и фундаментальными переменными, и данное свойство, по всей вероятности, неадекватно. Анализ остаточных явлений, связанных с корреляцией, может привести к трансформациям независимых переменных (их квадратов или натуральных логарифмов), которые в большей степени подходят для объяснения мультипликаторов РЕ. В-третьих, базовая связь между мультипликаторами РЕ и финансовыми переменными сама по себе не является стабильной. Если же эта связь смещается из года в год, то прогнозы, полученные из регрессионного уравнения, могут оказаться ненадежными для более длительных периодов времени. По всем этим причинам, несмотря на полезность регрессионного анализа, его следует рассматривать только как еще один инструмент поиска подлинного значения ценности. [c.649]
На рисунке 16.6 явно просматривается четкая линейная зависимость объема частного потребления от величины располагаемого дохода. Уравнение парной линейной регрессии, оцененное по этим данным, имеет вид С= -217,6 + 1,007 Yf Стандартные ошибки для свободного члена и коэффициента парной регрессии равны, соответственно, 28,4 и 0,012, а -статистики — -7,7 и 81 9. Обе они по модулю существенно превышают 3, следовательно, их статистическая значимость весьма высока. Впрочем, несмотря на то, что здесь удалось оценить статистически значимую линейную функцию потребления, в ней нарушены сразу две предпосылки Кейнса — уровень автономного потребления С0 оказался отрицательным, а предель- [c.304]
Стандартные ошибки свободного члена и коэффициента регрессии равны, соответственно, 84,7 и 0,46 их /-статистики — (-21,4 и 36,8). По абсолютной величине /-статистики намного превышают 3, и это свидетельствует о высокой надежности оцененных коэффициентов. Коэффициент детерминации /Р уравнения равен 0,96, то есть объяснено 96% дисперсии объема потребления. И в то же время уже по рисунку видно, что оцененная рефессия не очень хоро- [c.320]
Эта стандартная ошибка S у, равная 0,65, указывает отклонение фактических данных от прогнозируемых на основании использования воздействующих факторов j i и Х2 (влияние среди покупателей бабушек с внучками и высокопрофессионального вклада Шарика). В то же время мы располагаем обычным стандартным отклонением Sn, равным 1,06 (см. табл.8), которое было рассчитано для одной переменной, а именно сами текущие значения уги величина среднего арифметического у, которое равно 6,01. Легко видеть, что S у tTa6n. В противном случае доверять полученной оценке параметра нет оснований. [c.139]
Для определения профиля посетителей магазинов местного торгового центра, не имеющих определенной цели (browsers), маркетологи использовали три набора независимых переменных демографические, покупательское поведение психологические. Зависимая переменная представляет собой индекс посещения магазина без определенной цели, индекс (browsing index). Методом ступенчатой включающей все три набора переменных, выявлено, что демографические факторы — наиболее сильные предикторы, определяющие поведение покупателей, не преследующих конкретных целей. Окончательное уравнение регрессии, 20 из 36 возможных переменных, включало все демографические переменные. В следующей таблице приведены коэффициенты регрессии, стандартные ошибки коэффициентов, а также их уровни значимости. [c.668]
Смотреть страницы где упоминается термин Стандартная ошибка уравнения регрессии
Маркетинговые исследования Издание 3 (2002) — [ c.650 ]
Лекции по дисциплине «Эконометрика» (заочное отделение) (стр. 2 )
 |
Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 |
Параметр формально является значением Y при X = 0. Он может не иметь экономического содержания. Интерпретировать можно лишь знак при параметре . Если > 0, то относительное изменение результата происходит медленнее, чем изменение фактора. Иными словами, вариация по фактору X выше вариации для результата Y. Также считают, что включает в себя неучтенные в модели факторы.
По итогам 2008 года были собраны данные по прибыли и оборачиваемости оборотных средств 500 торговых предприятий г. Челябинска. Результаты наблюдения сведены в таблицу.
Годовая прибыль предприятия, млн. руб.
Годовая оборачиваемость оборотных средств, раз
Требуется построить зависимость прибыли предприятий от оборачиваемости оборотных средств и оценить качество полученного уравнения.
Пусть y – прибыль предприятия, x – оборачиваемость оборотных средств.
На основе исходных данных были рассчитаны следующие показатели:
Уровень доверия возьмем q=0,95 или 95%.
1. Стандартные ошибки оценок , . намного больше =0,39, следовательно, низкая точность коэффициента . очень мала по сравнению с , следовательно, высокая точность коэффициента .
2. Интервальные оценки коэффициентов уравнения регрессии.
n – 2 = 500 – 2 = 498;
α: 

β: 

3. Значимость коэффициентов регрессии.


4. Стандартная ошибка регрессии. Se=0,91, по сравнению со средним значением =34,5 ошибка невысокая, точность уравнения хорошая.
5. Коэффициент детерминации. R2 = rxy2=0,782=0,6084 не очень близко к 1, качество подгонки среднее.
6. Средняя ошибка аппроксимации. A=11%, качество подгонки уравнения среднее.
Экономическая интерпретация: при увеличении оборачиваемости оборотных средств предприятия на 1 раз в год средняя годовая прибыль увеличится на 5,86 млн. руб.
Тема 6. Нелинейная парная регрессия
Часто на практике между зависимой и независимыми переменными существует нелинейная форма взаимосвязи. В этом случае существует два выхода:
1) подобрать к анализируемым переменным преобразование, которое бы позволило представить существующую зависимость в виде линейной функции;
2) применить нелинейный метод наименьших квадратов.
Основные нелинейные регрессионные модели и приведение их к линейной форме
1. Экспоненциальное уравнение 
Если прологарифмировать левую и правую части данного уравнения, то получится

Это уравнение является линейным, но вместо y в левой части стоит ln y.
В данном случае параметр β1 имеет следующий экономический смысл: при увеличении переменной x на единицу переменная y в среднем увеличится примерно на 100·β% (более точно: y увеличится в 
2. Логарифмическое уравнение 
Переход к линейному уравнению осуществляется заменой переменной x на X=lnx..
Параметр β1 имеет следующий экономический смысл: для увеличения y на единицу необходимо увеличить переменную x в 

3. Гиперболическое уравнение 
В этом случае необходимо сделать замену переменных x на 
4. Степенное уравнение 
Прологарифмировав левую и правую части данного уравнения, получим

Заменив соответствующие ряды их логарифмами, получится линейная регрессия.
Экономический смысл параметра β1: если значение переменной x увеличить на 1%, то y увеличится на β1%.
5. Показательное уравнение 
Прологарифмировав левую и правую части уравнения, получим

Проведя замены Y=ln y и B1=ln β1, получится линейная регрессия.
Экономический смысл параметра β1: при увеличении переменной x на единицу переменная y в среднем увеличится в β1 раз.
Тема 7. Множественная линейная регрессия: определение и оценка параметров
1. Понятие множественной линейной регрессии
Модель множественной линейной регрессии является обобщением парной линейной регрессии и представляет собой следующее выражение:

где yt – значение зависимой переменной для наблюдения t,
xit – значение i-й независимой переменной для наблюдения t,
εt – значение случайной ошибки для наблюдения t,
n – число наблюдений,
m – число независимых переменных x.
2. Матричная форма записи множественной линейной регрессии
Уравнение множественной линейной регрессии можно записать в матричной форме:

где 



3. Основные предположения
2. 
3. 
4. 
В случае выполнения вышеперечисленных гипотез модель называется нормальной линейной регрессионной.
4. Метод наименьших квадратов
Параметры уравнения множественной регрессии оцениваются, как и в парной регрессии, методом наименьших квадратов (МНК): 
Чтобы найти минимум этой функции необходимо вычислить производные по каждому из параметров и приравнять их к нулю, в результате получается система уравнений, решение которой в матричном виде следующее:



5. Теорема Гаусса-Маркова
Если выполнены предположения 1-5 из пункта 3, то оценки , полученные методом наименьших квадратов, имеют наименьшую дисперсию в классе линейных несмещенных оценок, то есть являются несмещенными, состоятельными и эффективными.
Тема 8. Множественная линейная регрессия: оценка качества
1. Общая схема проверки качества парной регрессии
Адекватность модели – остатки должны удовлетворять условиям теоремы Гаусса-Маркова.
Основные показатели качества коэффициентов регрессии:
1. Стандартные ошибки оценок (анализ точности определения оценок).
2. Интервальные оценки коэффициентов уравнения регрессии (построение доверительных интервалов).
3. Значимость коэффициентов регрессии (проверка гипотез относительно коэффициентов регрессии).
Основные показатели качества уравнения регрессии в целом:
1. Стандартная ошибка регрессии Se (анализ точности уравнения регрессии).
2. Значимость уравнения регрессии в целом (проверка гипотезы относительно всех коэффициентов регрессии).
3. Коэффициент детерминации R2 (проверка качества подгонки уравнения к исходным данным).
4. Скорректированный коэффициент детерминации R2adj (проверка качества подгонки уравнения к исходным данным).
5. Средняя ошибка аппроксимации (проверка качества подгонки уравнения к эмпирическим данным).
2. Стандартные ошибки оценок
Стандартные ошибки коэффициентов регрессии – это средние квадратические отклонения коэффициентов регрессии от их истинных значений.

где



Стандартная ошибка является оценкой среднего квадратического отклонения коэффициента регрессии от его истинного значения. Чем меньше стандартная ошибка тем точнее оценка.
3. Интервальные оценки коэффициентов множественной линейной регрессии
Доверительные интервалы для коэффициентов регрессии определяются следующим образом:
1. Выбирается уровень доверия q (0,9; 0,95 или 0,99).
2. Рассчитывается уровень значимости g = 1 – q.
3. Рассчитывается число степеней свободы n – m – 1, где n – число наблюдений, m – число независимых переменных.
4. Определяется критическое значение t-статистики (tкр) по таблицам распределения Стьюдента на основе g и n – m – 1.
5. Рассчитывается доверительный интервал для параметра 

Доверительный интервал показывает, что истинное значение параметра с вероятностью q находится в данных пределах.
Чем меньше доверительный интервал относительно коэффициента, тем точнее полученная оценка.
4. Значимость коэффициентов регрессии
Процедура оценки значимости коэффициентов осуществляется аналогичной парной регрессии следующим образом:
1. Рассчитывается значение t-статистики для коэффициента регрессии по формуле 
2. Выбирается уровень доверия q ( 0,9; 0,95 или 0,99).
3. Рассчитывается уровень значимости g = 1 – q.
4. Рассчитывается число степеней свободы n – m – 1, где n – число наблюдений, m – число независимых переменных.
5. Определяется критическое значение t-статистики (tкр) по таблицам распределения Стьюдента на основе g и n – m – 1.
6. Если 
t-тесты обеспечивают проверку значимости предельного вклада каждой переменной при допущении, что все остальные переменные уже включены в модель.
5. Стандартная ошибка регрессии
Стандартная ошибка регрессии Se показывает, насколько в среднем фактические значения зависимой переменной y отличаются от ее расчетных значений

Используется как основная величина для измерения качества модели (чем она меньше, тем лучше).
Значения Se в однотипных моделях с разным числом наблюдений и (или) переменных сравнимы.
6. Оценка значимости уравнения регрессии в целом
Уравнение значимо, если есть достаточно высокая вероятность того, что существует хотя бы один коэффициент, отличный от нуля.
Имеются альтернативные гипотезы:
Если принимается гипотеза H0, то уравнение статистически незначимо. В противном случае говорят, что уравнение статистически значимо.
Значимость уравнения регрессии в целом осуществляется с помощью F-статистики.
Оценка значимости уравнения регрессии в целом основана на тождестве дисперсионного анализа:

TSS – общая сумма квадратов отклонений
ESS – объясненная сумма квадратов отклонений
RSS – необъясненная сумма квадратов отклонений
F-статистика представляет собой отношение объясненной суммы квадратов (в расчете на одну независимую переменную) к остаточной сумме квадратов (в расчете на одну степень свободы)
n – число выборочных наблюдений, m – число независимых переменных.
При отсутствии линейной зависимости между зависимой и независимой переменными F-статистика имеет F-распределение Фишера-Снедекора со степенями свободы k1 = m, k2 = n – m –1.
Процедура оценки значимости уравнения осуществляется следующим образом:
7. Рассчитывается значение F-статистики по формуле 
8. Выбирается уровень доверия q ( 0,9; 0,95 или 0,99).
9. Рассчитывается уровень значимости g = 1 – q.
10. Рассчитывается число степеней свободы n – m – 1, где n – число наблюдений, m – число независимых переменных.
11. Определяется критическое значение F-статистики (Fкр) по таблицам распределения Фишера на основе g и n – m – 1.
12. Если 
В парной регрессии F-статистика равна квадрату t-статистики: 
Качество оценки уравнения можно проверить путем расчета коэффициента детерминации R2, который показывает степень соответствия найденного уравнения экспериментальным данным.

Коэффициент R2 показывает долю дисперсии переменной y, объясненную регрессией, в общей дисперсии y.
Коэффициент детерминации лежит в пределах 0 £ R2 £ 1.
Чем ближе R2 к 1, тем выше качество подгонки уравнения к статистическим данным.
Чем ближе R2 к 0, тем ниже качество подгонки уравнения к статистическим данным.
Коэффициенты R2 в разных моделях с разным числом наблюдений и переменных несравнимы.
8. Скорректированный коэффициент детерминации R2adj
Низкое значение R2 не свидетельствует о плохом качестве модели, и может объясняться наличием существенных факторов, не включенных в модель
R2 всегда увеличивается с включением новой переменной. Поэтому его необходимо корректировать, и рассчитывают скорректированный коэффициент детерминации
Если R2adj выходит за пределы интервала [0;1], то его использовать нельзя.
Если при добавлении новой переменной в модель увеличивается не только R2, но и R2adj, то можно считать, что вклад этой переменной в повышение качества модели существенен.
9. Средняя ошибка аппроксимации
Средняя ошибка аппроксимации (средняя абсолютная процентная ошибка) – показывает в процентах среднее отклонение расчетных значений зависимой переменной от фактических значений yi
Если A ≤ 10%, то качество подгонки уравнения считается хорошим. Чем меньше значение A, тем лучше.
10. Использование показателей качества коэффициентов и уравнения регрессии для интерпретации и корректировки модели
В случае незначимости уравнения, необходимо устранить ошибки модели. Наиболее распространенными являются следующие ошибки:
— неправильно выбран вид функции регрессии;
— в модель включены незначимые регрессоры;
— в модели отсутствуют значимые регрессоры.
После устранения ошибок требуется заново оценить параметры уравнения и его качество, продолжая этот процесс до тех пор, пока качество уравнения не станет удовлетворительным. Если после поделанных процедур, мы не достигли требуемого уровня значимости, то необходимо устранять другие ошибки (спецификации, классификации, наблюдения и т. д., см. тему 3, п. 6).
11. Интерпретация множественной линейной регрессии
Коэффициент регрессии 
В апреле 2006 года были собраны данные по стоимости 200 двухкомнатных квартир в Металлургическом районе г. Челябинска, их жилой площади, площади кухни и расстоянии до центра города (пл. Революции). Результаты наблюдения сведены в таблицу.
Оценка результатов линейной регрессии
Введение
Модель линейной регрессии
Итак, пусть есть несколько независимых случайных величин X1, X2, . Xn (предикторов) и зависящая от них величина Y (предполагается, что все необходимые преобразования предикторов уже сделаны). Более того, мы предполагаем, что зависимость линейная, а ошибки рапределены нормально, то есть 
где I — единичная квадратная матрица размера n x n.
Итак, у нас есть данные, состоящие из k наблюдений величин Y и Xi и мы хотим оценить коэффициенты. Стандартным методом для нахождения оценок коэффициентов является метод наименьших квадратов. И аналитическое решение, которое можно получить, применив этот метод, выглядит так: 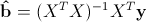
где b с крышкой — оценка вектора коэффициентов, y — вектор значений зависимой величины, а X — матрица размера k x n+1 (n — количество предикторов, k — количество наблюдений), у которой первый столбец состоит из единиц, второй — значения первого предиктора, третий — второго и так далее, а строки соответствуют имеющимся наблюдениям.
Функция summary.lm() и оценка получившихся результатов
Теперь рассмотрим пример построения модели линейной регрессии в языке R:
Таблица gala содержит некоторые данные о 30 Галапагосских островах. Мы будем рассматривать модель, где Species — количество разных видов растений на острове линейно зависит от нескольких других переменных.
Рассмотрим вывод функции summary.lm().
Сначала идет строка, которая напоминает, как строилась модель.
Затем идет информация о распределении остатков: минимум, первая квартиль, медиана, третья квартиль, максимум. В этом месте было бы полезно не только посмотреть на некоторые квантили остатков, но и проверить их на нормальность, например тестом Шапиро-Уилка.
Далее — самое интересное — информация о коэффициентах. Здесь потребуется немного теории.
Сначала выпишем следующий результат: 
при этом сигма в квадрате с крышкой является несмещенной оценкой для реальной сигмы в квадрате. Здесь b — реальный вектор коэффициентов, а эпсилон с крышкой — вектор остатков, если в качестве коэффициентов взять оценки, полученные методом наименьших квадратов. То есть при предположении, что ошибки распределены нормально, вектор коэффициентов тоже будет распределен нормально вокруг реального значения, а его дисперсию можно несмещенно оценить. Это значит, что можно проверять гипотезу на равенство коэффициентов нулю, а следовательно проверять значимость предикторов, то есть действительно ли величина Xi сильно влияет на качество построенной модели.
Для проверки этой гипотезы нам понадобится следующая статистика, имеющая распределение Стьюдента в том случае, если реальное значение коэффициента bi равно 0: 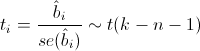
где

Теперь все готово для продолжения разбора вывода функции summary.lm().
Итак, далее идут оценки коэффициентов, полученные методом наименьших квадратов, их стандартные ошибки, значения t-статистики и p-значения для нее. Обычно p-значение сравнивается с каким-нибудь достаточно малым заранее выбранным порогом, например 0.05 или 0.01. И если значение p-статистики оказывается меньше порога, то гипотеза отвергается, если же больше, ничего конкретного, к сожалению, сказать нельзя. Напомню, что в данном случае, так как распределение Стьюдента симметричное относительно 0, то p-значение будет равно 1-F(|t|)+F(-|t|), где F — функция распределения Стьюдента с k-n-1 степенями свободы. Также, R любезно обозначает звездочками значимые коэффициенты, для которых p-значение достаточно мало. То есть, те коэффициенты, которые с очень малой вероятностью равны 0. В строке Signif. codes как раз содержится расшифровка звездочек: если их три, то p-значение от 0 до 0.001, если две, то оно от 0.001 до 0.01 и так далее. Если никаких значков нет, то р-значение больше 0.1.
В нашем примере можно с большой уверенностью сказать, что предикторы Elevation и Adjacent действительно с большой вероятностью влияют на величину Species, а вот про остальные предикторы ничего определенного сказать нельзя. Обычно, в таких случаях предикторы убирают по одному и смотрят, насколько изменяются другие показатели модели, например BIC или Adjusted R-squared, который будет разобран далее.
Значение Residual standart error соответствует просто оценке сигмы с крышкой, а степени свободы вычисляются как k-n-1.
А теперь самая важные статистики, на которые в первую очередь стоит смотреть: R-squared и Adjusted R-squared: 
где Yi — реальные значения Y в каждом наблюдении, Yi с крышкой — значения, предсказанные моделью, Y с чертой — среднее по всем реальным значениям Yi.
Начнем со статистики R-квадрат или, как ее иногда называют, коэффициента детерминации. Она показывает, насколько условная дисперсия модели отличается от дисперсии реальных значений Y. Если этот коэффициент близок к 1, то условная дисперсия модели достаточно мала и весьма вероятно, что модель неплохо описывает данные. Если же коэффициент R-квадрат сильно меньше, например, меньше 0.5, то, с большой долей уверенности модель не отражает реальное положение вещей.
Однако, у статистики R-квадрат есть один серьезный недостаток: при увеличении числа предикторов эта статистика может только возрастать. Поэтому, может показаться, что модель с большим количеством предикторов лучше, чем модель с меньшим, даже если все новые предикторы никак не влияют на зависимую переменную. Тут можно вспомнить про принцип бритвы Оккама. Следуя ему, по возможности, стоит избавляться от лишних предикторов в модели, поскольку она становится более простой и понятной. Для этих целей была придумана статистика скорректированный R-квадрат. Она представляет собой обычный R-квадрат, но со штрафом за большое количество предикторов. Основная идея: если новые независимые переменные дают большой вклад в качество модели, значение этой статистики растет, если нет — то наоборот уменьшается.
Для примера рассмотрим ту же модель, что и раньше, но теперь вместо пяти предикторов оставим два:
Как можно увидеть, значение статистики R-квадрат снизилось, однако значение скорректированного R-квадрат даже немного возросло.
Теперь проверим гипотезу о равенстве нулю всех коэффициентов при предикторах. То есть, гипотезу о том, зависит ли вообще величина Y от величин Xi линейно. Для этого можно использовать следующую статистику, которая, если гипотеза о равенстве нулю всех коэффициентов верна, имеет распределение Фишера c n и k-n-1 степенями свободы: 
Значение F-статистики и p-значение для нее находятся в последней строке вывода функции summary.lm().
Заключение
В этой статье были описаны стандартные методы оценки значимости коэффициентов и некоторые критерии оценки качества построенной линейной модели. К сожалению, я не касался вопроса рассмотрения распределения остатков и проверки его на нормальность, поскольку это увеличило бы статью еще вдвое, хотя это и достаточно важный элемент проверки адекватности модели.
Очень надеюсь что мне удалось немного расширить стандартное представление о линейной регрессии, как об алгоритме который просто оценивает некоторый вид зависимости, и показать, как можно оценить его результаты.
http://pandia.ru/text/78/101/1285-2.php
http://habr.com/ru/post/195146/







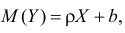
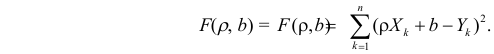
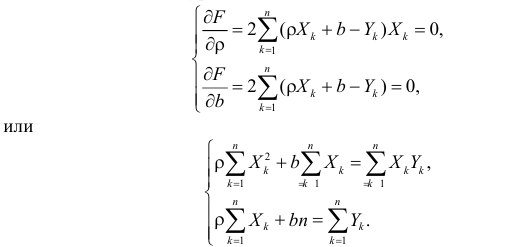
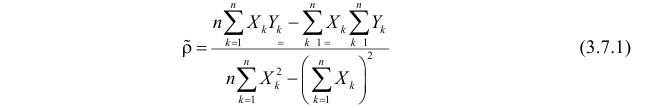
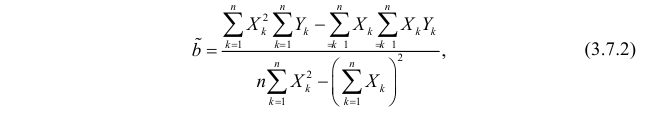
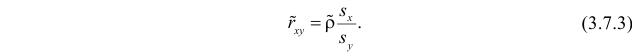
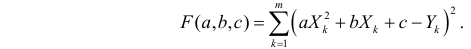

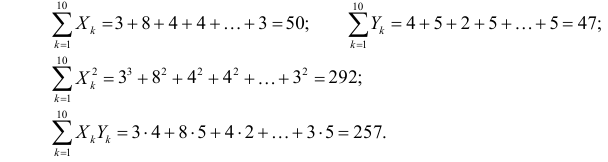
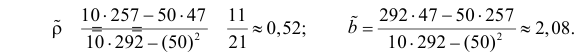
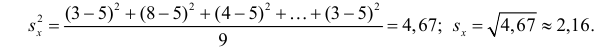
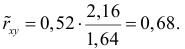
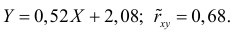

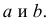
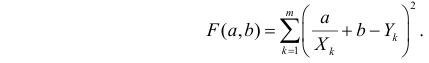
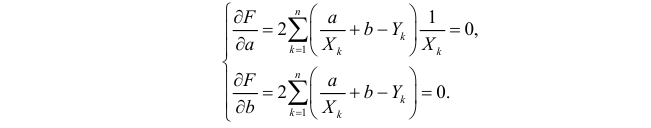
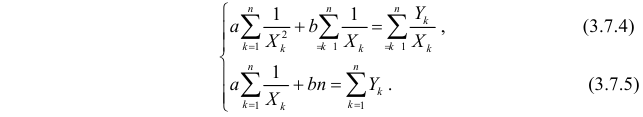
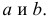
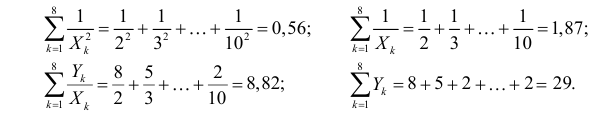
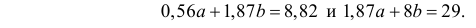
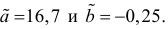
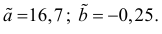

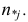



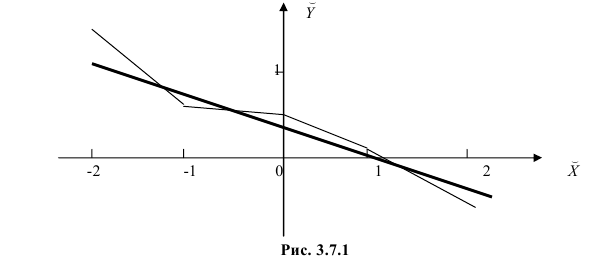
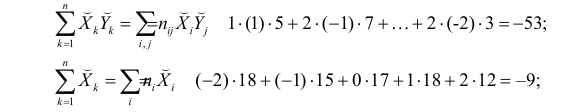
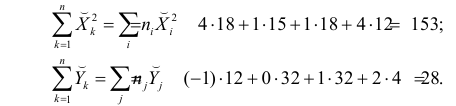
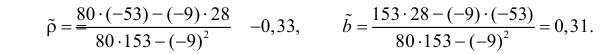
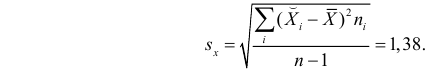
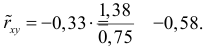
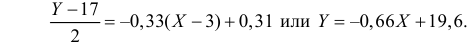
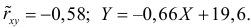
 можно представить в виде
можно представить в виде 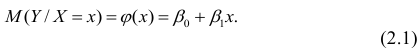
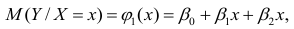
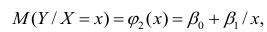
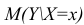 можно представить в виде (2.1).
можно представить в виде (2.1).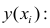
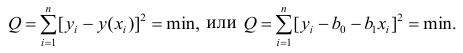
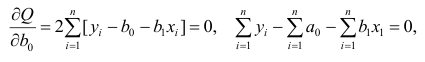
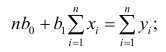
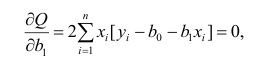
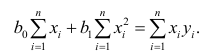
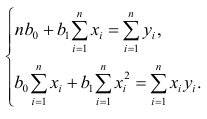
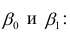
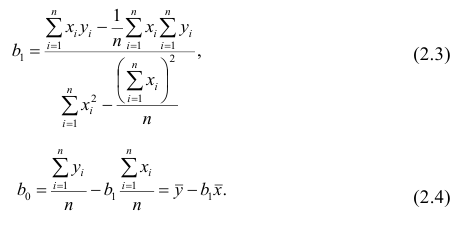
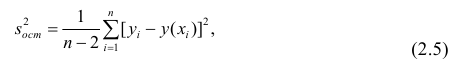
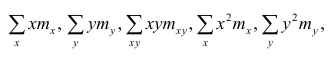
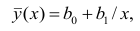
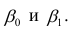
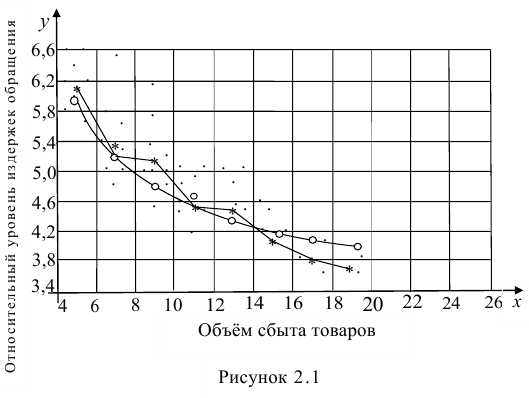
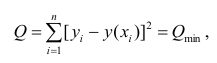
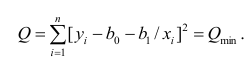
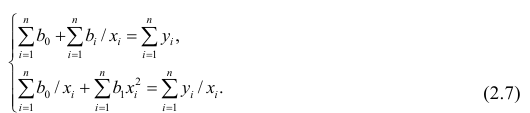
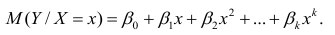
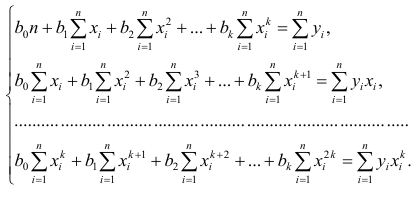

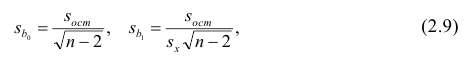
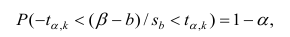

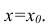
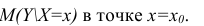
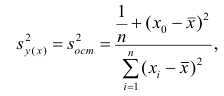
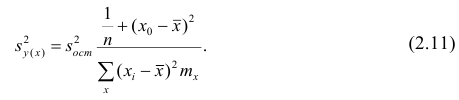
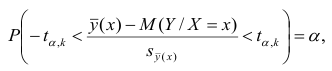
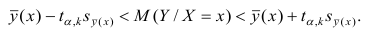
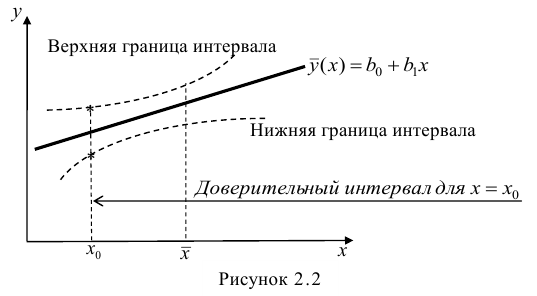
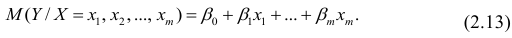
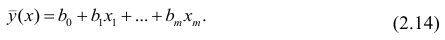
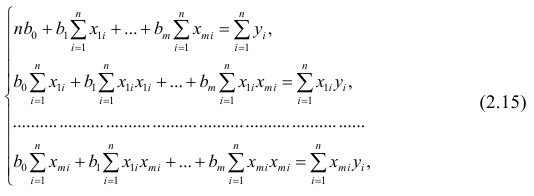
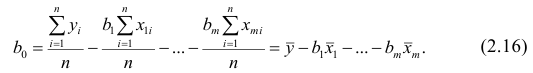
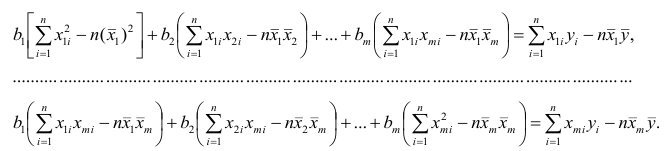
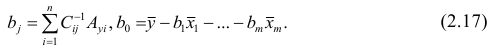
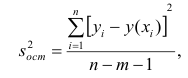
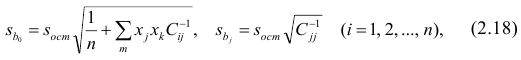
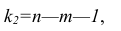
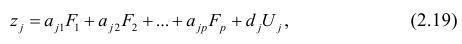
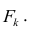
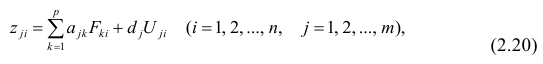
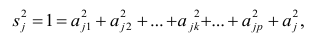
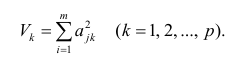
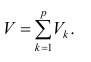
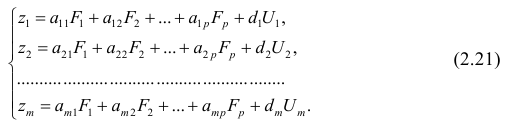
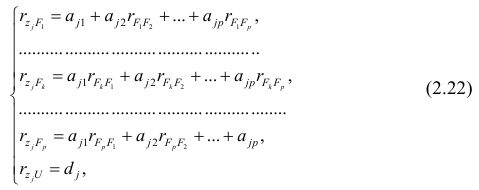
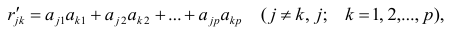
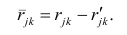
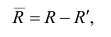

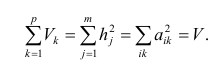
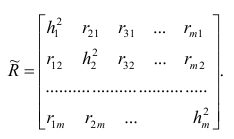


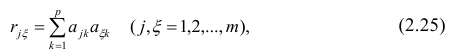

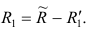

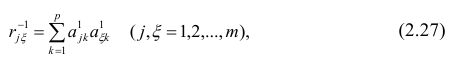
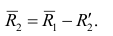
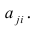
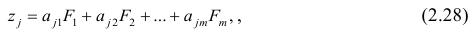
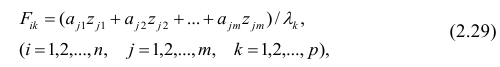
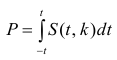
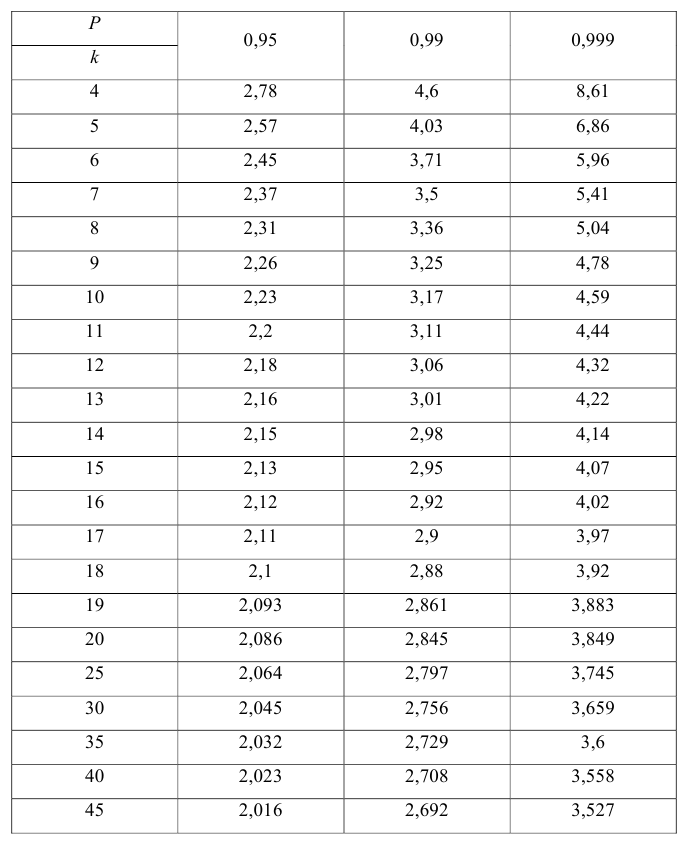
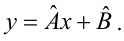
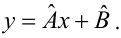
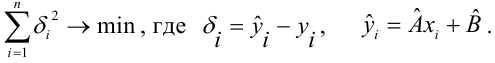
 подчинены нормальному закону распределения.
подчинены нормальному закону распределения.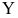 постоянна и не зависит от номера измерения.
постоянна и не зависит от номера измерения.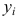 в разных точках независимы.
в разных точках независимы.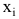 независимы, неслучайны и измеряются без ошибок.
независимы, неслучайны и измеряются без ошибок.