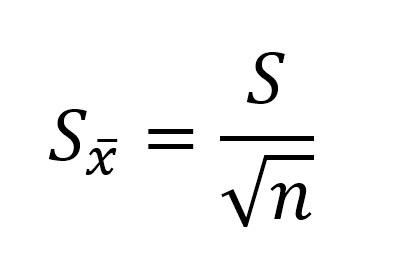Что считать арифметической ошибкой - Не ошибается лишь тот, кто ничего не делает!

Содержание

Расчет ошибки средней арифметической
- Способ 1: расчет с помощью комбинации функций
- Способ 2: применение инструмента «Описательная статистика»
Вопросы и ответы

Стандартная ошибка или, как часто называют, ошибка средней арифметической, является одним из важных статистических показателей. С помощью данного показателя можно определить неоднородность выборки. Он также довольно важен при прогнозировании. Давайте узнаем, какими способами можно рассчитать величину стандартной ошибки с помощью инструментов Microsoft Excel.

Расчет ошибки средней арифметической

Одним из показателей, которые характеризуют цельность и однородность выборки, является стандартная ошибка. Эта величина представляет собой корень квадратный из дисперсии. Сама дисперсия является средним квадратном от средней арифметической. Средняя арифметическая вычисляется делением суммарной величины объектов выборки на их общее количество.

В Экселе существуют два способа вычисления стандартной ошибки: используя набор функций и при помощи инструментов Пакета анализа. Давайте подробно рассмотрим каждый из этих вариантов.

Способ 1: расчет с помощью комбинации функций

Прежде всего, давайте составим алгоритм действий на конкретном примере по расчету ошибки средней арифметической, используя для этих целей комбинацию функций. Для выполнения задачи нам понадобятся операторы СТАНДОТКЛОН.В, КОРЕНЬ и СЧЁТ.

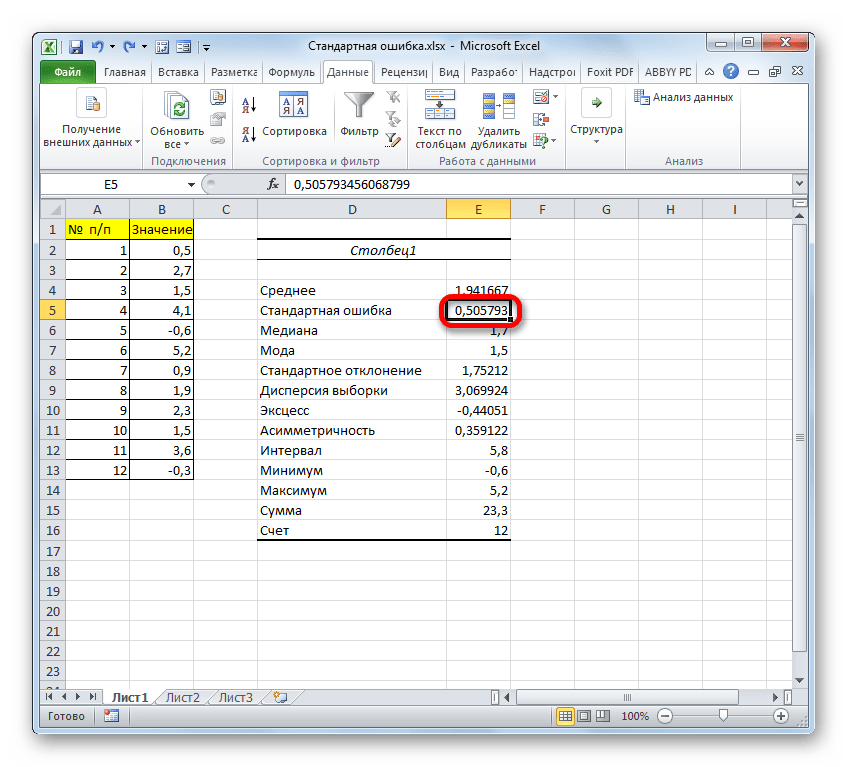
Для примера нами будет использована выборка из двенадцати чисел, представленных в таблице.

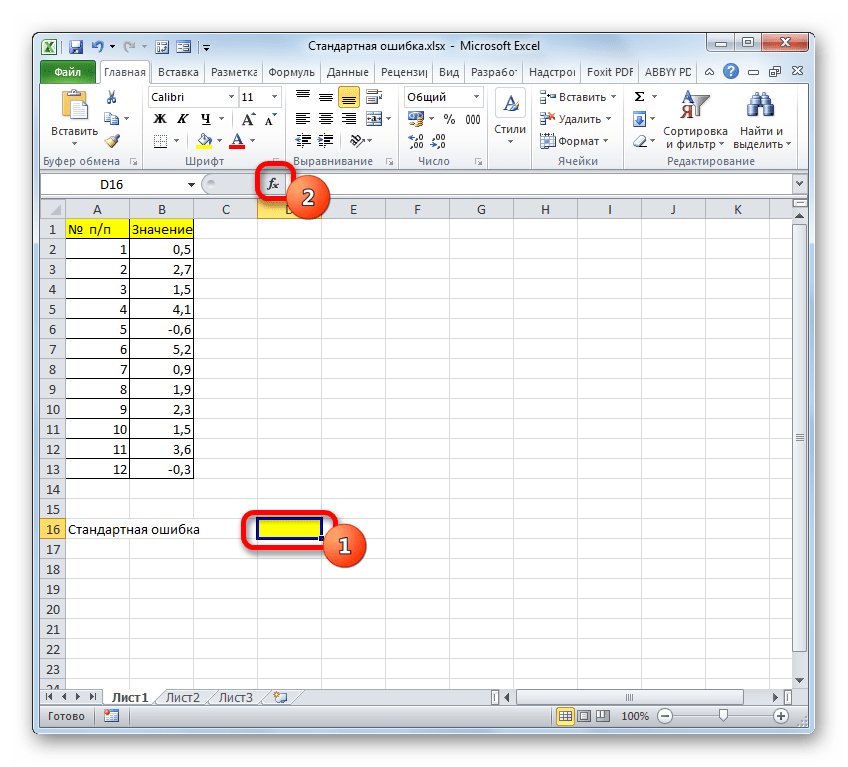
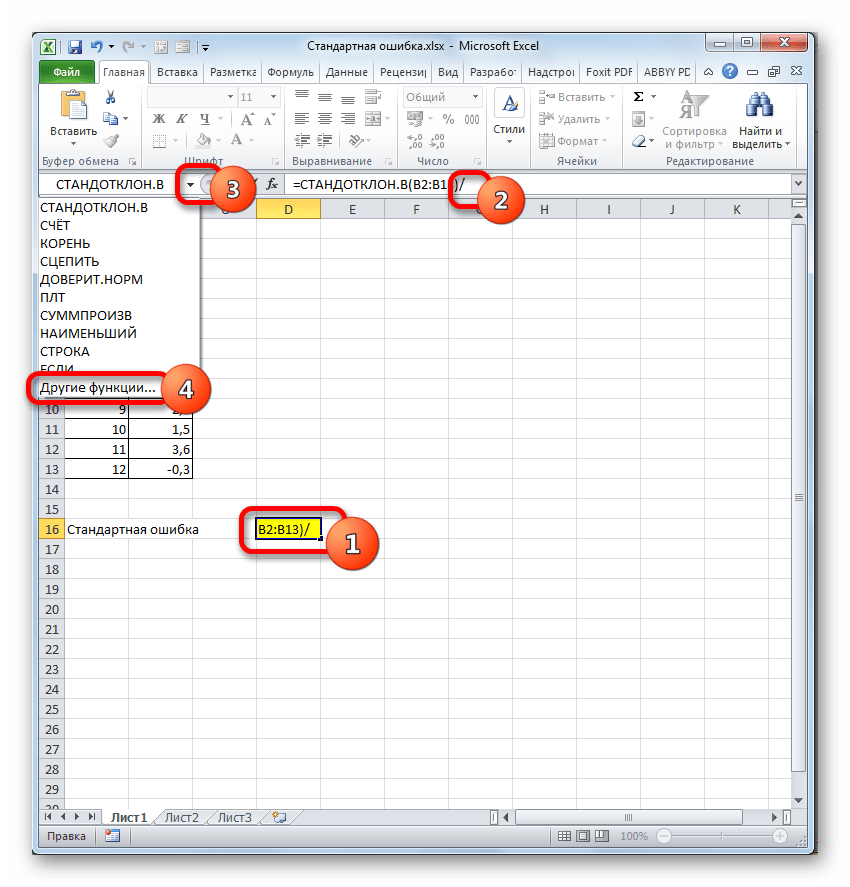
Выделяем ячейку, в которой будет выводиться итоговое значение стандартной ошибки, и клацаем по иконке «Вставить функцию».

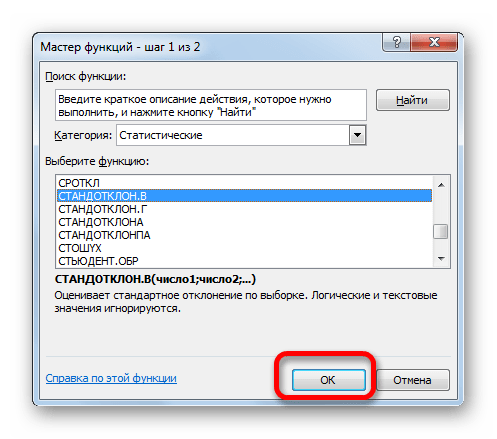
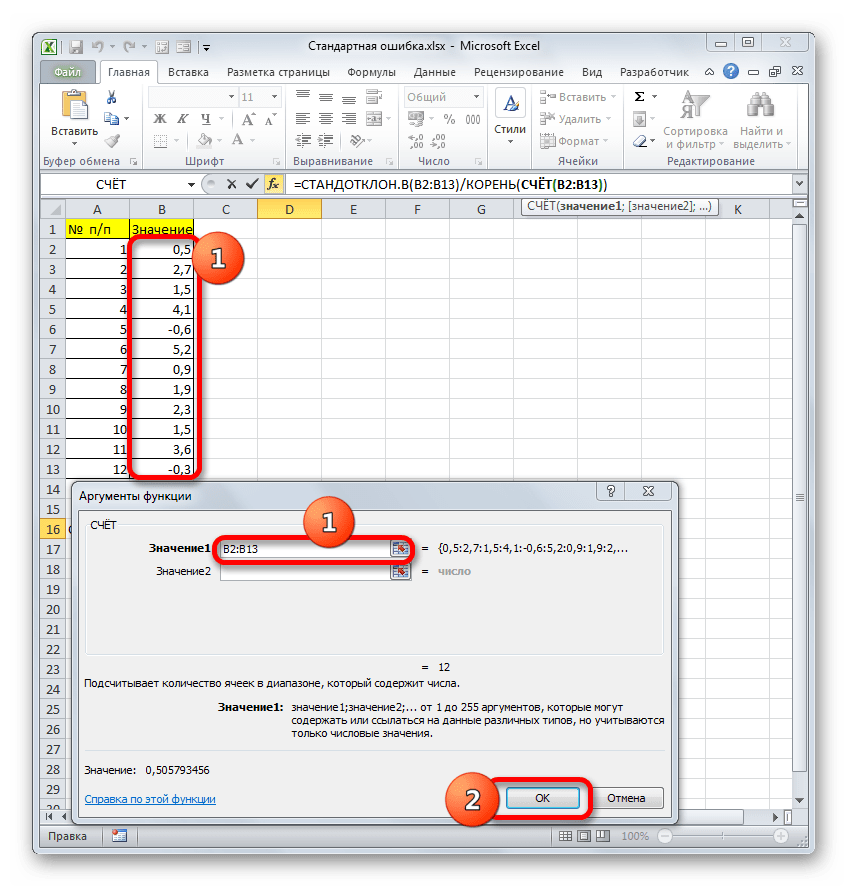
Открывается Мастер функций. Производим перемещение в блок «Статистические». В представленном перечне наименований выбираем название «СТАНДОТКЛОН.В».

Запускается окно аргументов вышеуказанного оператора. СТАНДОТКЛОН.В предназначен для оценивания стандартного отклонения при выборке. Данный оператор имеет следующий синтаксис:
=СТАНДОТКЛОН.В(число1;число2;…)

«Число1» и последующие аргументы являются числовыми значениями или ссылками на ячейки и диапазоны листа, в которых они расположены. Всего может насчитываться до 255 аргументов этого типа. Обязательным является только первый аргумент.

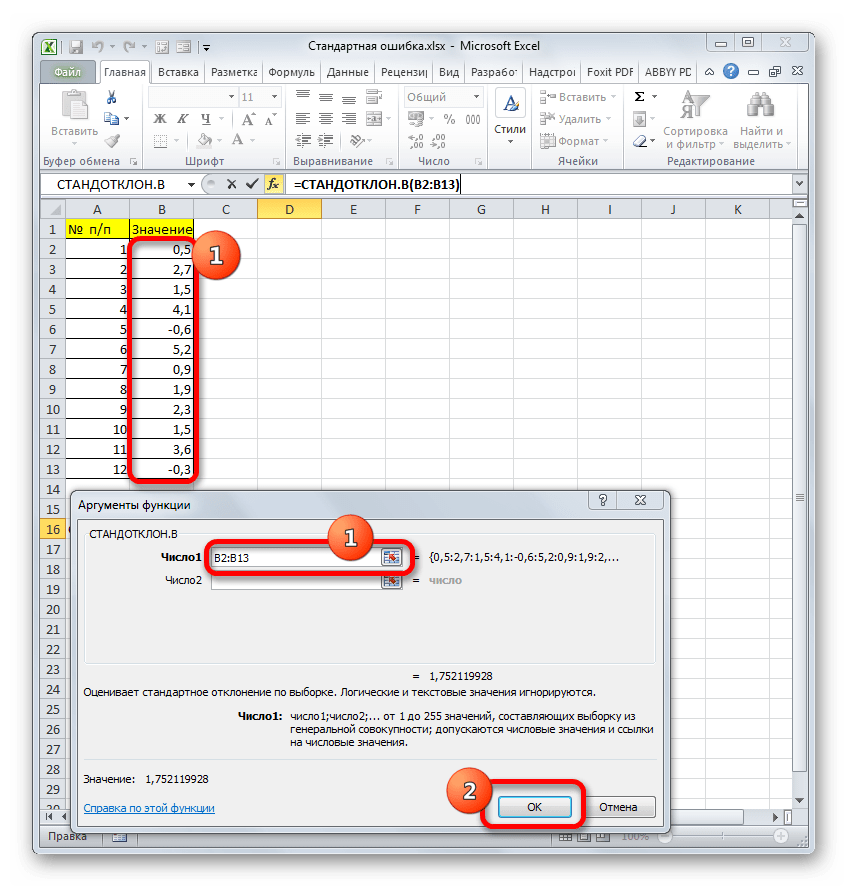
Итак, устанавливаем курсор в поле «Число1». Далее, обязательно произведя зажим левой кнопки мыши, выделяем курсором весь диапазон выборки на листе. Координаты данного массива тут же отображаются в поле окна. После этого клацаем по кнопке «OK».

В ячейку на листе выводится результат расчета оператора СТАНДОТКЛОН.В. Но это ещё не ошибка средней арифметической. Для того, чтобы получить искомое значение, нужно стандартное отклонение разделить на квадратный корень от количества элементов выборки. Для того, чтобы продолжить вычисления, выделяем ячейку, содержащую функцию СТАНДОТКЛОН.В. После этого устанавливаем курсор в строку формул и дописываем после уже существующего выражения знак деления (/). Вслед за этим клацаем по пиктограмме перевернутого вниз углом треугольника, которая располагается слева от строки формул. Открывается список недавно использованных функций. Если вы в нем найдете наименование оператора «КОРЕНЬ», то переходите по данному наименованию. В обратном случае жмите по пункту «Другие функции…».

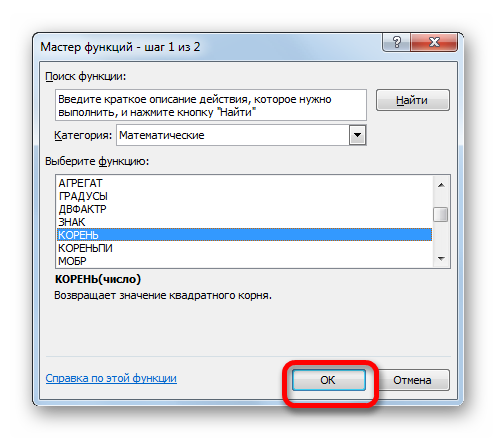
Снова происходит запуск Мастера функций. На этот раз нам следует посетить категорию «Математические». В представленном перечне выделяем название «КОРЕНЬ» и жмем на кнопку «OK».

Открывается окно аргументов функции КОРЕНЬ. Единственной задачей данного оператора является вычисление квадратного корня из заданного числа. Его синтаксис предельно простой:
=КОРЕНЬ(число)

Как видим, функция имеет всего один аргумент «Число». Он может быть представлен числовым значением, ссылкой на ячейку, в которой оно содержится или другой функцией, вычисляющей это число. Последний вариант как раз и будет представлен в нашем примере.

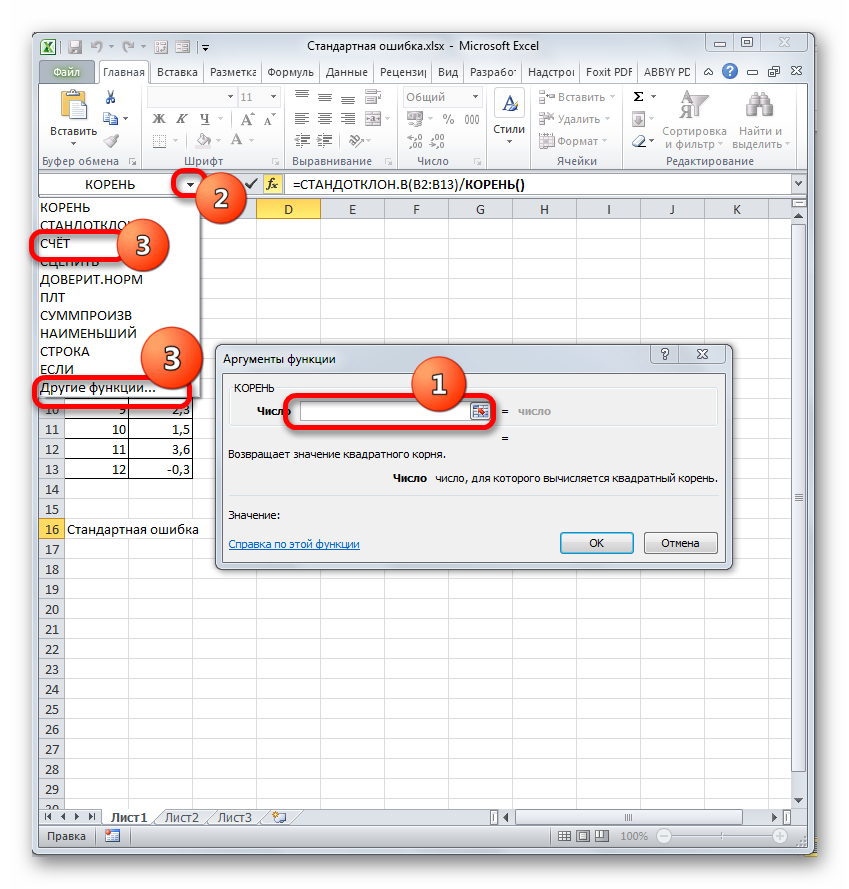
Устанавливаем курсор в поле «Число» и кликаем по знакомому нам треугольнику, который вызывает список последних использованных функций. Ищем в нем наименование «СЧЁТ». Если находим, то кликаем по нему. В обратном случае, опять же, переходим по наименованию «Другие функции…».

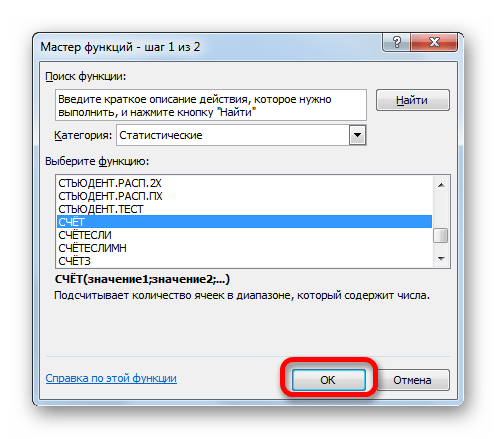
В раскрывшемся окне Мастера функций производим перемещение в группу «Статистические». Там выделяем наименование «СЧЁТ» и выполняем клик по кнопке «OK».

Запускается окно аргументов функции СЧЁТ. Указанный оператор предназначен для вычисления количества ячеек, которые заполнены числовыми значениями. В нашем случае он будет подсчитывать количество элементов выборки и сообщать результат «материнскому» оператору КОРЕНЬ. Синтаксис функции следующий:
=СЧЁТ(значение1;значение2;…)

В качестве аргументов «Значение», которых может насчитываться до 255 штук, выступают ссылки на диапазоны ячеек. Ставим курсор в поле «Значение1», зажимаем левую кнопку мыши и выделяем весь диапазон выборки. После того, как его координаты отобразились в поле, жмем на кнопку «OK».

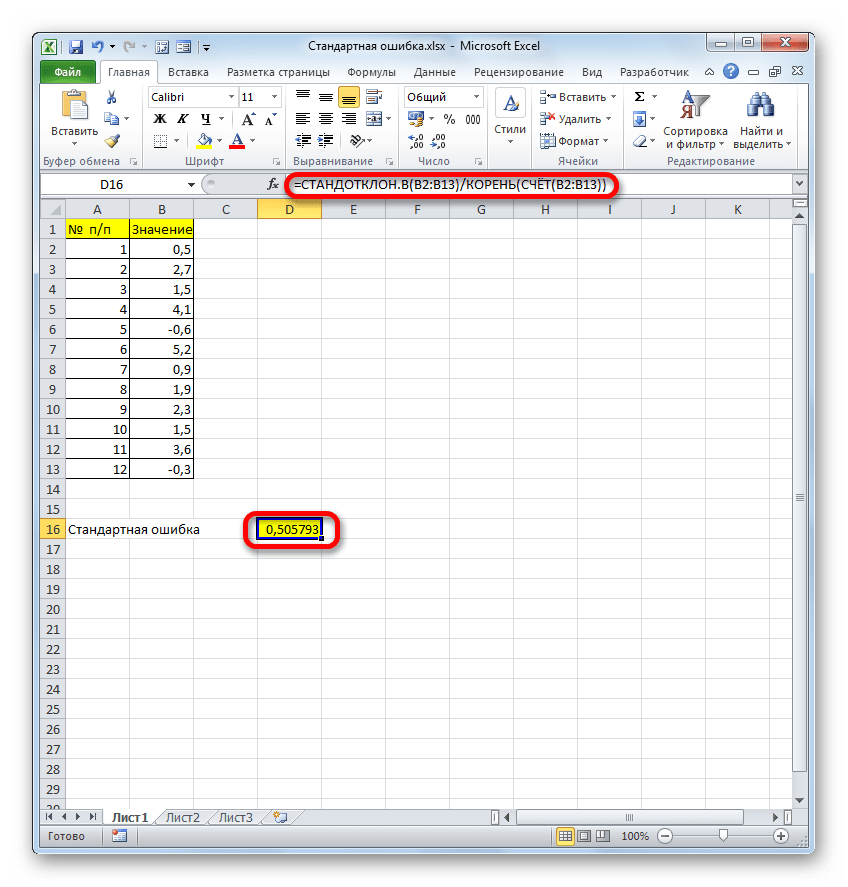
После выполнения последнего действия будет не только рассчитано количество ячеек заполненных числами, но и вычислена ошибка средней арифметической, так как это был последний штрих в работе над данной формулой. Величина стандартной ошибки выведена в ту ячейку, где размещена сложная формула, общий вид которой в нашем случае следующий:
=СТАНДОТКЛОН.В(B2:B13)/КОРЕНЬ(СЧЁТ(B2:B13))

Результат вычисления ошибки средней арифметической составил 0,505793. Запомним это число и сравним с тем, которое получим при решении поставленной задачи следующим способом.

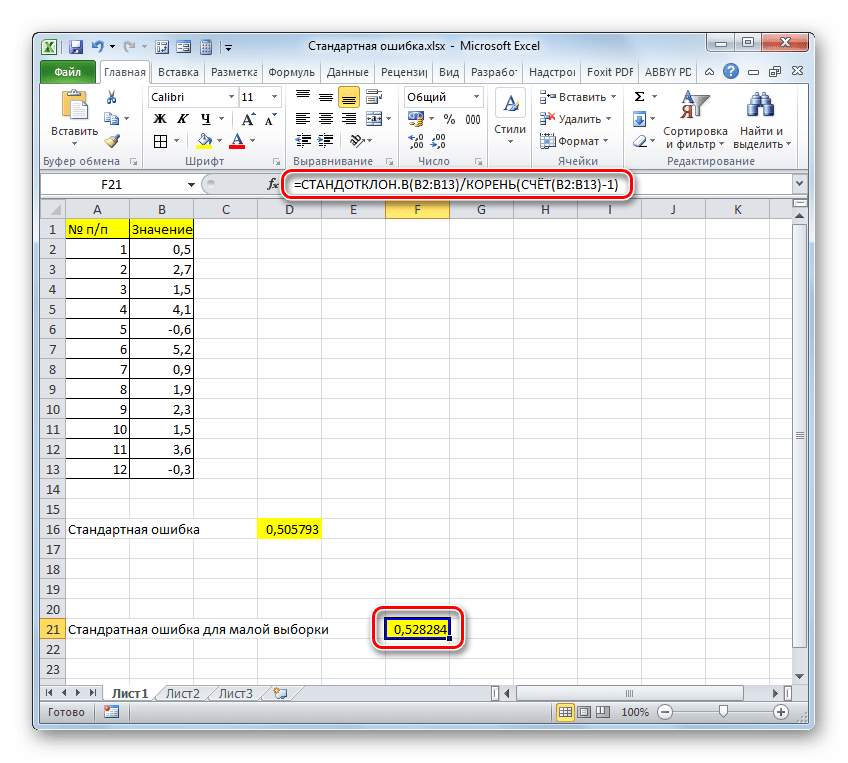
Но дело в том, что для малых выборок (до 30 единиц) для большей точности лучше применять немного измененную формулу. В ней величина стандартного отклонения делится не на квадратный корень от количества элементов выборки, а на квадратный корень от количества элементов выборки минус один. Таким образом, с учетом нюансов малой выборки наша формула приобретет следующий вид:

=СТАНДОТКЛОН.В(B2:B13)/КОРЕНЬ(СЧЁТ(B2:B13)-1)

Урок: Статистические функции в Экселе

Способ 2: применение инструмента «Описательная статистика»

Вторым вариантом, с помощью которого можно вычислить стандартную ошибку в Экселе, является применение инструмента «Описательная статистика», входящего в набор инструментов «Анализ данных» («Пакет анализа»). «Описательная статистика» проводит комплексный анализ выборки по различным критериям. Одним из них как раз и является нахождение ошибки средней арифметической.

Но чтобы воспользоваться данной возможностью, нужно сразу активировать «Пакет анализа», так как по умолчанию в Экселе он отключен.

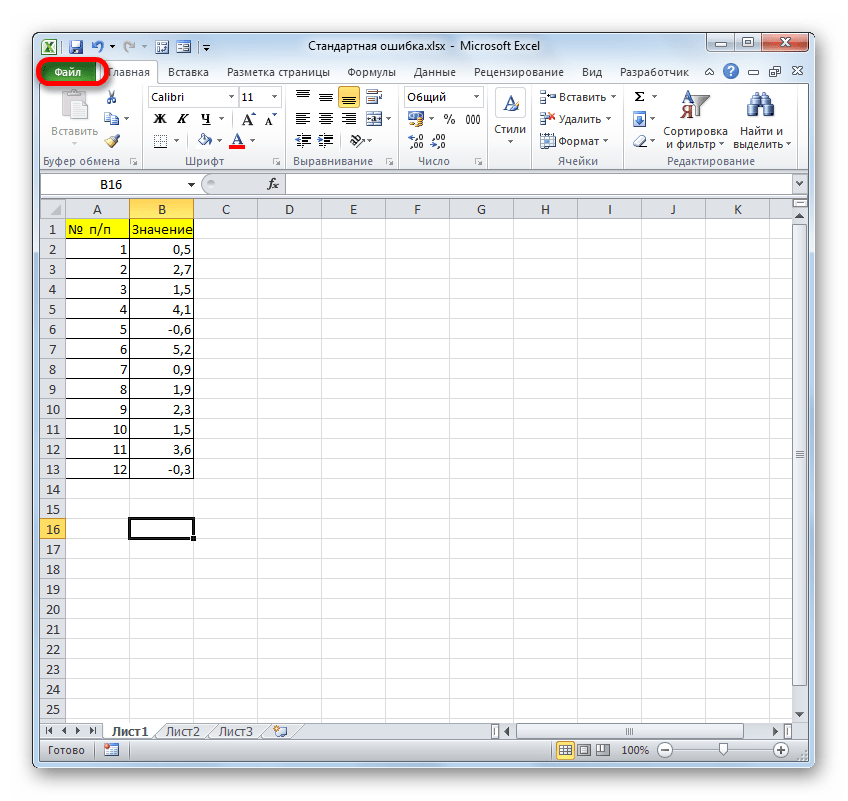
После того, как открыт документ с выборкой, переходим во вкладку «Файл».

Далее, воспользовавшись левым вертикальным меню, перемещаемся через его пункт в раздел «Параметры».

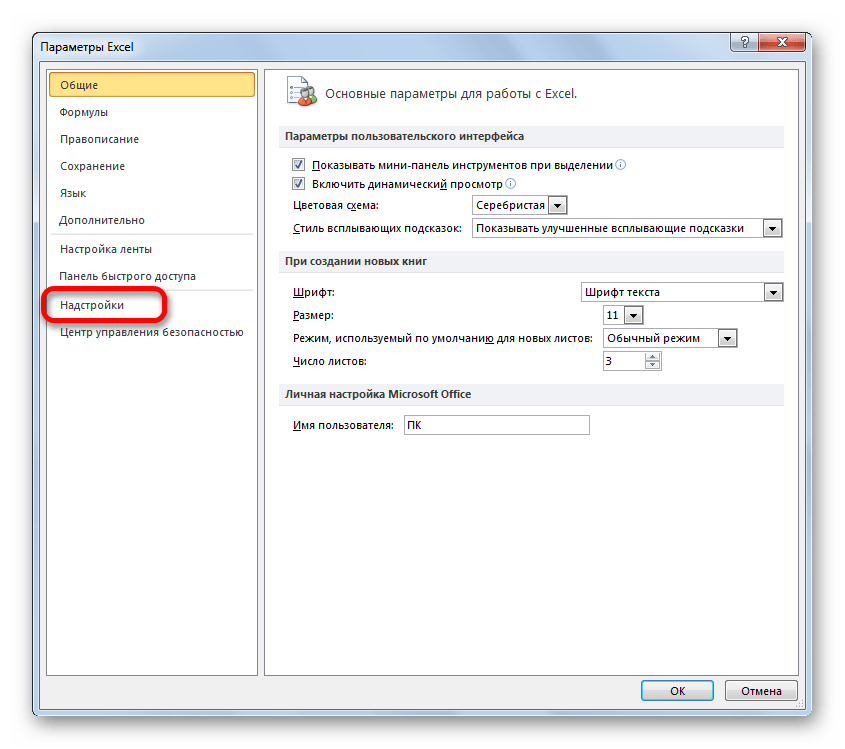
Запускается окно параметров Эксель. В левой части данного окна размещено меню, через которое перемещаемся в подраздел «Надстройки».

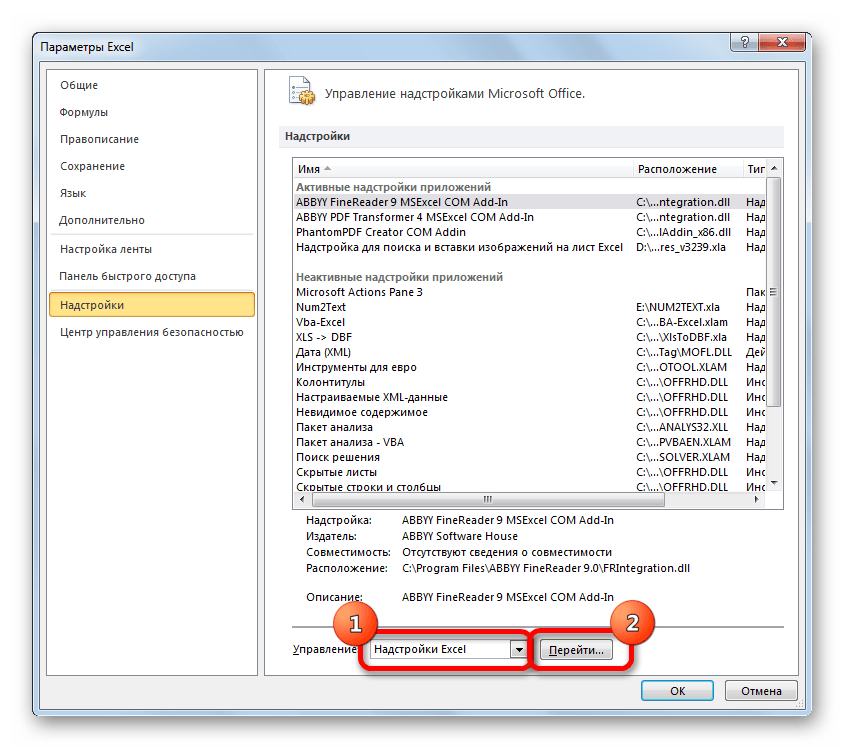
В самой нижней части появившегося окна расположено поле «Управление». Выставляем в нем параметр «Надстройки Excel» и жмем на кнопку «Перейти…» справа от него.

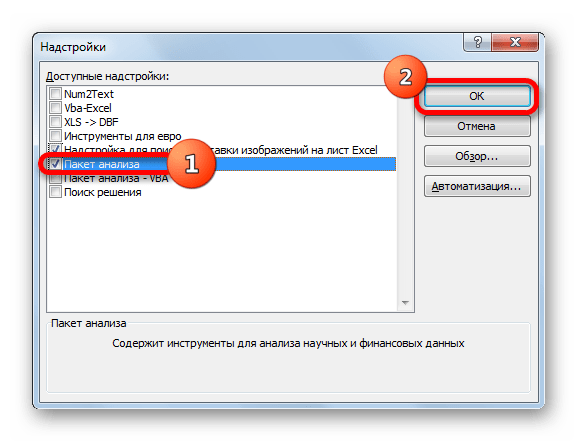
Запускается окно надстроек с перечнем доступных скриптов. Отмечаем галочкой наименование «Пакет анализа» и щелкаем по кнопке «OK» в правой части окошка.

После выполнения последнего действия на ленте появится новая группа инструментов, которая имеет наименование «Анализ». Чтобы перейти к ней, щелкаем по названию вкладки «Данные».

После перехода жмем на кнопку «Анализ данных» в блоке инструментов «Анализ», который расположен в самом конце ленты.

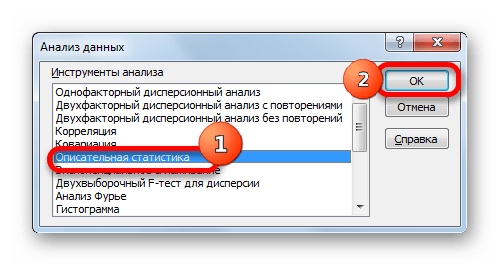
Запускается окошко выбора инструмента анализа. Выделяем наименование «Описательная статистика» и жмем на кнопку «OK» справа.

Запускается окно настроек инструмента комплексного статистического анализа «Описательная статистика».
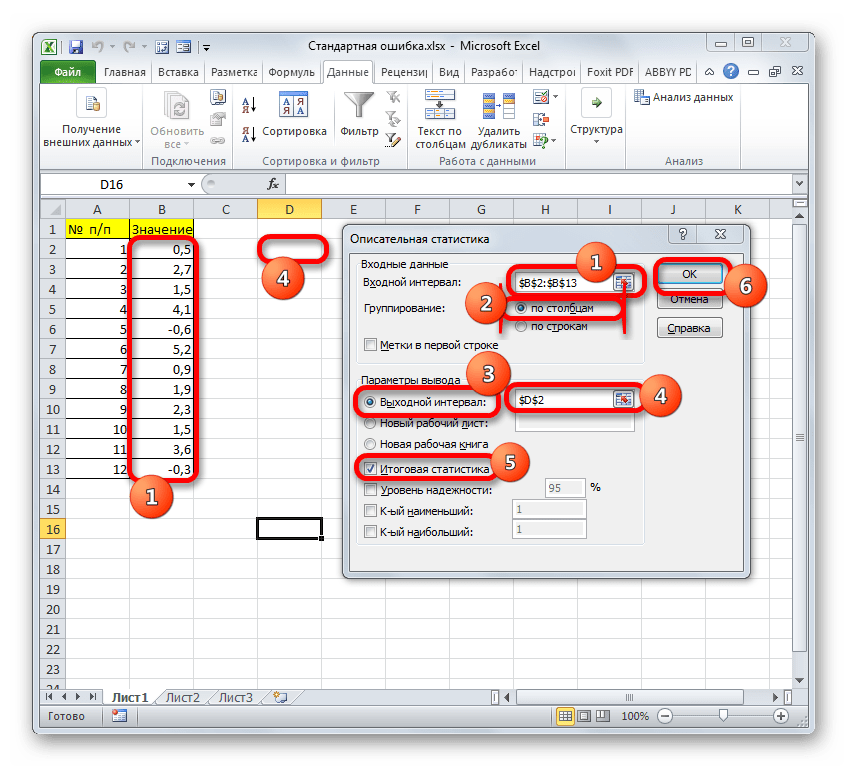
В поле «Входной интервал» необходимо указать диапазон ячеек таблицы, в которых находится анализируемая выборка. Вручную это делать неудобно, хотя и можно, поэтому ставим курсор в указанное поле и при зажатой левой кнопке мыши выделяем соответствующий массив данных на листе. Его координаты тут же отобразятся в поле окна.

В блоке «Группирование» оставляем настройки по умолчанию. То есть, переключатель должен стоять около пункта «По столбцам». Если это не так, то его следует переставить.

Галочку «Метки в первой строке» можно не устанавливать. Для решения нашего вопроса это не важно.

Далее переходим к блоку настроек «Параметры вывода». Здесь следует указать, куда именно будет выводиться результат расчета инструмента «Описательная статистика»:
- На новый лист;
- В новую книгу (другой файл);
- В указанный диапазон текущего листа.
Давайте выберем последний из этих вариантов. Для этого переставляем переключатель в позицию «Выходной интервал» и устанавливаем курсор в поле напротив данного параметра. После этого клацаем на листе по ячейке, которая станет верхним левым элементом массива вывода данных. Её координаты должны отобразиться в поле, в котором мы до этого устанавливали курсор.

Далее следует блок настроек определяющий, какие именно данные нужно вводить:
- Итоговая статистика;
- К-ый наибольший;
- К-ый наименьший;
- Уровень надежности.
Для определения стандартной ошибки обязательно нужно установить галочку около параметра «Итоговая статистика». Напротив остальных пунктов выставляем галочки на свое усмотрение. На решение нашей основной задачи это никак не повлияет.

После того, как все настройки в окне «Описательная статистика» установлены, щелкаем по кнопке «OK» в его правой части.

После этого инструмент «Описательная статистика» выводит результаты обработки выборки на текущий лист. Как видим, это довольно много разноплановых статистических показателей, но среди них есть и нужный нам – «Стандартная ошибка». Он равен числу 0,505793. Это в точности тот же результат, который мы достигли путем применения сложной формулы при описании предыдущего способа.

Урок: Описательная статистика в Экселе

Как видим, в Экселе можно произвести расчет стандартной ошибки двумя способами: применив набор функций и воспользовавшись инструментом пакета анализа «Описательная статистика». Итоговый результат будет абсолютно одинаковый. Поэтому выбор метода зависит от удобства пользователя и поставленной конкретной задачи. Например, если ошибка средней арифметической является только одним из многих статистических показателей выборки, которые нужно рассчитать, то удобнее воспользоваться инструментом «Описательная статистика». Но если вам нужно вычислить исключительно этот показатель, то во избежание нагромождения лишних данных лучше прибегнуть к сложной формуле. В этом случае результат расчета уместится в одной ячейке листа.

Заметили ошибку в решении суда — ничего страшного, всё можно исправить.

Ошибки бывают разные. В зависимости от того, какая ошибка, закон предусматривает разные пути её исправления.

Неумышленная описка в тексте решения или ошибка в расчётах исправляется просто. Сложнее, если суд ошибся в своих суждениях.

Имеет ли судья право на ошибку

Кто ничего не делает, тот и не ошибается — простое и понятное изречение.

Судья каждый день принимает решения и каждое решение несёт риск ошибки.

Можете возразить — судья представляет власть и не должен ошибаться.

Да, не должен, но иногда ошибается и с этим ничего не поделаешь.

Поэтому закон предусматривает многоэтапную проверку судебных решений — апелляция и кассация, в некоторых случаях надзор.

Вероятность ошибиться в нескольких инстанциях крайне низкая, но не нулевая. Ошибаются даже в Верховном Суде. И с этим то же ничего не поделаешь.

Что такое описка в решении суда

Были времена, когда текст судебного решения печатали на механической машинке, иногда писали от руки.

Нельзя было скопировать кусок текста из одного решение и вставить в другой. Мотивировка решения была скудной, а текст решения умещался на одной странице.

Сегодня тексты набирают на компьютере: быстро, удобно, повышает производительность.

Однако ошибались всегда: в рукописном тексте допускали описку, в печатном — опечатку.

В любом случае, описка или опечатка — это неумышленная случайная ошибка из-за невнимательности при подготовке текста.

Отличие от судебной ошибки

Описку в решении суда нужно отличать от судебной ошибки. Это важно, от этого зависит способ исправления дефекта в судебном решении.

Описка — это результат невнимательности: хотели написать одно, получилось другое.

Судья или помощник торопились при составлении текста решения, потом не проверили его, и вот результат.

Судебная же ошибка всегда осознанна — суд ошибается в суждениях, оценке доказательств, выборе и применении закона.

Описка или опечатка — ошибка в букве, слове, предложении. Судебная ошибка — ошибка в мыслях.

Ошибка в арифметике: явная и неявная

У судей нет времени сидеть с калькулятором, делать или проверять сложные расчёты.

Особо сложные, например проверку бухгалтерского или налогового учёта, судьи поручают экспертам.

Расчёт предоставляют участники процесса. Судья либо соглашается с ним, либо делает свой.

Обсчитаться может каждый. Не нужно забывать, что большинство судей гуманитарии не только по образованию, но и по типу мышления.

Арифметическая ошибка — ошибка в математических расчётах.

Неправильно умножили, не там поставили запятую перед десятичным знаком, сложили не те значения, наконец, просто потеряли ноль.

Явная арифметическая ошибка — очевидная, грубая, которую может определить человек со школьным уровнем знаний в арифметике.

Почти все ошибки явные. Поэтому не нужно забивать голову вопросом: «Явную или неявную арифметическую ошибку допустил судья?»

Способы исправления

Исправление описки или арифметической ошибки в тексте решении суда — это НЕ изменение самого решения

При изменении решения меняется его смысловое содержание. Неважно, полностью или частично.

Суд не вправе изменить своё решение. Это запрещено законом и разрешено только вышестоящему суду.

А вот неумышленную описку и ошибку в расчётах исправляет суд, который её допустил.

Отсюда следующее правило:

Судья неумышленно в решении допустил описку (опечатку) или ошибся в математических расчётах — подаём заявление об исправлении
Судья ошибся в суждениях, оценке доказательств, выборе и применении закона (допустил осознанную судебную ошибку) — подаем апелляционную жалобу на решение суда

Когда нужно исправлять решение

«Исправить или оставить как есть» — зависит от конкретной ситуации, от обстоятельств дела.

Важно определить, какие последствия может повлечь такая описка. Лучше, если это сделает юрист.

Немаловажно в какой части решения описка.

Описка в резолютивной части (после «суд решил») — лучше исправить.

В мотивировочной части (где выводы суда) — на усмотрение, опять же в зависимости от возможных последствий.

Арифметические ошибки нужно исправлять, когда обсчёт существенен.

Не нужно тратить силы и время, если судья ошибся на несколько копеек или рублей.

Кстати, исправить описку или ошибку в арифметике можно не только в решении суда, но и в определении, по аналогии.

Кто инициирует, кто исправляет, куда подавать

Исправление описки или арифметической ошибки инициирует тот, кто её обнаружил.

Если заметил судья — исправит по собственной инициативе, если участник процесса — суд на основании его заявления.

Не нужно ждать инициативы от суда — у судей много работы и нет времени на перепроверку своих же решений.

Просто помогите судье — подайте заявление об исправлении, не ждите что это сделает кто-то другой.

Заявление нужно подавать по принципу: кто ошибся, тот и должен исправить — кто должен исправить, тому адресуем и ему же подаём.

Заявление в суд об исправлении описки

Составить самому заявление в суд об исправлении описки не сложно. В Интернете масса образцов, само же заявление — на одну страницу.

Структура заявления проста и состоит из четырёх частей:

Обозначаем описку
Мотивируем, почему это описка
Ссылаемся на статьи 200 и 203.1 ГПК РФ (в арбитраже — статья 179 АПК РФ)
Просим исправить, предлагая свой вариант

В качестве примера. Разъясняя в мотивировочной части решения права истцу, судья перепутал его ФИО с ФИО ответчика.

Просительная часть заявления об исправлении описки будет выглядеть следующим образом:

— Прошу исправить допущенную в первом предложении последнего абзаца мотивировочной части решения суда описку:

«При таких обстоятельствах, Иванов Иван Иванович вправе требовать установления сервитута в отношении застроенного земельного участка»,

изложив его в следующей редакции:

«При таких обстоятельствах, Петров Пётр Петрович вправе требовать установления сервитута в отношении застроенного земельного участка»

Когда лучше привлечь юриста

Заявление не всегда простенький текст на половину страницы. Иногда его нужно дополнить смысловой нагрузкой.

Суд исказил фамилию участника, неправильно указал отчество, ошибся в дате рождения — всё это легко исправимо и не требует участия юриста.

Другое дело, когда не совсем ясно, почему суд допустил описку и описка ли это вообще.

В этом случае за составлением заявления лучше обратиться к юристу или адвокату, минимум — получить консультацию.

Почему меня не вызвали в суд

Раньше суд рассматривал заявление об исправлении описки в решении только в судебном заседании.

Рассмотрение вопроса об исправлении вне судебного заседания считалось процессуальным нарушением.

Сейчас у судьи два варианта:

Не проводить заседание, не извещать участников процесса
Провести заседание, предварительно сообщив участникам время и место проведения

Вариант определяет судья, по своему усмотрению. Сочтёт необходимым — вызовет и проведёт заседание, не сочтёт — рассмотрит не заседая в одиночестве.

Суд отказал в исправлении описки. Что дальше?

Рассмотрев заявление о исправлении, суд выносит определение — либо исправляет, либо отказывает в этом.

Если вопрос рассматривался в судебном заседании с вызовом, обычно копию определения вручают здесь же.

Если суд не проводил заседания, копию высылают в течение трёх дней по почте.

Почтовые отправления — всегда риск. Лучше отследить дело и получить определение в суде.

Судья отказал в исправлении, вы не согласны, позиции разошлись — можно подать частную жалобу

Здесь точно лучше обратиться к юристу.

Представление результатов исследования

В научных публикациях важно представление результатов исследования. Очень часто окончательный результат приводится в следующем виде: M±m, где M – среднее арифметическое, m –ошибка среднего арифметического. Например, 163,7±0,9 см.

Прежде чем разбираться в правилах представления результатов исследования, давайте точно усвоим, что же такое ошибка среднего арифметического.

Ошибка среднего арифметического

Среднее арифметическое, вычисленное на основе выборочных данных (выборочное среднее), как правило, не совпадает с генеральным средним (средним арифметическим генеральной совокупности). Экспериментально проверить это утверждение невозможно, потому что нам неизвестно генеральное среднее. Но если из одной и той же генеральной совокупности брать повторные выборки и вычислять среднее арифметическое, то окажется, что для разных выборок среднее арифметическое будет разным.

Чтобы оценить, насколько выборочное среднее арифметическое отличается от генерального среднего, вычисляется ошибка среднего арифметического или ошибка репрезентативности.

Ошибка среднего арифметического обозначается как m или

Ошибка среднего арифметического рассчитывается по формуле:

где: S — стандартное отклонение, n – объем выборки; Например, если стандартное отклонение равно S=5 см, объем выборки n=36 человек, то ошибка среднего арифметического равна: m=5/6 = 0,833.

Ошибка среднего арифметического показывает, какая ошибка в среднем допускается, если использовать вместо генерального среднего выборочное среднее.

Так как при небольшом объеме выборки истинное значение генерального среднего не может быть определено сколь угодно точно, поэтому при вычислении выборочного среднего арифметического нет смысла оставлять большое число значащих цифр.

Правила записи результатов исследования

В записи ошибки среднего арифметического оставляем две значащие цифры, если первые цифры в ошибке «1» или «2».
В остальных случаях в записи ошибки среднего арифметического оставляем одну значащую цифру.
В записи среднего арифметического положение последней значащей цифры должно соответствовать положению первой значащей цифры в записи ошибки среднего арифметического.

Представление результатов научных исследований

В своей статье «Осторожно, статистика!», опубликованной в 1989 году В.М. Зациорский указал, какие числовые характеристики должны быть представлены в публикации, чтобы она имела научную ценность. Он писал, что исследователь «…должен назвать: 1) среднюю величину (или другой так называемый показатель положения); 2) среднее квадратическое отклонение (или другой показатель рассеяния) и 3) число испытуемых. Без них его публикация научной ценности иметь не будет “с. 52

В научных публикациях в области физической культуры и спорта очень часто окончательный результат приводится в виде: (М±m) (табл.1).

Таблица 1 — Изменение механических свойств латеральной широкой мышцы бедра под воздействием физической нагрузки (n=34)

	Эффективный модуль упругости (Е), кПа	Эффективный модуль вязкости (V), Па с
Этап эксперимента	Рассл.	Напряж.	Рассл.	Напряж.
До ФН	7,0±0,3	17,1±1,4	29,7±1,7	46±4
После ФН	7,7±0,3	18,7±1,4	30,9±2,0	53±6

Литература

Высшая математика и математическая статистика: учебное пособие для вузов / Под общ. ред. Г. И. Попова. – М. Физическая культура, 2007.– 368 с.
Гласс Дж., Стэнли Дж. Статистические методы в педагогике и психологии. М.: Прогресс. 1976.- 495 с.
Зациорский В.М. Осторожно — статистика! // Теория и практика физической культуры, 1989.- №2.
Катранов А.Г. Компьютерная обработка данных экспериментальных исследований: Учебное пособие/ А. Г. Катранов, А. В. Самсонова; СПб ГУФК им. П.Ф. Лесгафта. – СПб.: изд-во СПб ГУФК им. П.Ф. Лесгафта, 2005. – 131 с.
Основы математической статистики: Учебное пособие для ин-тов физ. культ / Под ред. В.С. Иванова.– М.: Физкультура и спорт, 1990. 176 с.

Условное
обозначение средней арифметической
величины через М (от латинского слова
Media) чаще применяется в медицинских и
педагогических исследованиях. В
математической статистике предпочитают
обозначение через .
Средняя арифметическая величина является
производной, обобщающей количественные
признаки ряда однородных показателей
(совокупности). Выражая одним числом
определенную совокупность, она как бы
ослабляет влияние случайных индивидуальных
отклонений, и акцентирует некую обобщенную
количественную характеристику, наиболее
типичное свойство изучаемого ряда
показателей.

Определяя
значение средней арифметической
величины, следует придерживаться
некоторых правил.

1.
Средняя арифметическая величина может
характеризовать только те признаки
изучаемого объекта, которые присущи
всей совокупности, но в разной
количественной мере (например, уровень
развития быстроты движений характерен
для каждого человека, хотя и в разной
количественной мере). Средняя арифметическая
величина не может характеризовать
количественную меру тех признаков,
которые одной части совокупности
присущи, а другой нет, т. е. она не может
отражать присутствие или отсутствие
того или иного признака (например, умение
или неумение выполнять то или иное
двигательное действие).

2.
Средняя арифметическая величина должна
включать все показатели, полученные в
данном исследовании. Произвольное
исключение даже некоторых из них
неизбежно приведет к искажению конечного
результата.

3.
Средняя арифметическая величина обязана
отражать только однородную совокупность.
Нельзя, например, определять средний
уровень физического развития школьников,
не разделив их предварительно по возрасту
и полу.

4.
Средняя арифметическая величина должна
вычисляться на достаточно большой
совокупности, размеры которой определяются
в каждом конкретном случае отдельно
(см. «Подбор исследуемых»).

5.
Необходимо стремиться к тому, чтобы
средняя арифметическая величина имела
четкие и простые свойства, позволяющие
легко и быстро ее вычислять.

6.
Средняя арифметическая величина должна
обладать достаточной устойчивостью к
действию случайных факторов. Только в
этом случае она будет отражать
действительное состояние изучаемого
явления, а не его случайные изменения.

7.
Точность вычисления средней арифметической
величины должна соответствовать
содержанию изучаемого педагогического
явления. В некоторых случаях нет
необходимости в расчетах с большой
точностью, в других — большая точность
нужна при вычислениях, но совершенно
не нужна в выводах. Например, при расчете
средних величин числа подтягиваний на
перекладине можно пользоваться и сотыми
долями целого, но представлять и выводах,
что исследуемые в среднем подтянулись
7,83 раза, было бы неграмотна, так как
невозможно измерение с подобной
точностью. В этом случае необходимо в
выводах представлять числа, округленные
до целых единиц.

В
простейшем случае этот показатель
вычисляется путем сложения всех
полученных значений (которые называются
вариантами) и деления суммы на число
вариант:

где
S — знак суммирования;

V
— полученные в исследовании значения
(варианты);

п
— число вариант.

По
этой формуле вычисляется так называемая
простая средняя арифметическая величина.
Применяется она в тех случаях, когда
имеется небольшое число вариант.

При
большом числе вариант прибегают к
вычислению так называемой взвешенной
средней арифметической величины. С этой
целью строят ряд распределения, или
вариационный ряд, который представляет
собой ряд вариант и их частот,
характеризующих какой-нибудь признак
в убывающем или возрастающем порядке.
Например, в нашем случае измерение
точности попадания мячом в цель дало
125 вариант, т. е. в группе I, где применялась
методика обучения «А», одноразово
исследовалось 125 детей с числовым
выражением от 0 (точное попадание в цель)
до 21,5 см (максимальное отклонение от
цели). Каждое числовое выражение
встречалось в исследовании один и более
раз, например «0» встретился 28 раз.
Другими словами, 28 участников эксперимента
точно попали в цель. Этот показатель
называется числом наблюдений или
частотой вариант и условно обозначается
буквой «Р» (число наблюдений составляет
часть числа вариант).

Для
упрощения числовых операций все 125
вариант разбиваются на классы с величиной
интервала 1,9 см. Число классов зависит
от величины колебаний вариант (разности
между максимальной и минимальной
вариантами), наличия вариант для каждого
класса (если, например, для первого
класса — «0 — 1,9» — нет соответствующих
вариант, т.е. ни один исследуемый не имел
точных попаданий или отклонений от цели
в пределах от 0 до 1,9 см, то подобный класс
не вносится в вариационный ряд) и,
наконец, требуемой точности вычисления,
(чем больше классов, тем точность
вычисления выше). Вполне понятно, что
чем больше величина интервала, тем
меньше число классов при одной и той же
величине колебаний вариант.

После
разбивки вариант по классам в каждом
классе определяется срединная варианта
«V_c»,
и для каждой срединной варианты
проставляется число наблюдений. Пример
этих операций, и дальнейший ход вычислений
приведены в следующей таблице:

Классы	Серединные варианты V_C	Число набл, р	V_CP	V_C-M=d	d²	d²P
0 – 1.9	1	28	28	-4.6	21.16	592.48
2 – 3.9	3	29	87	-2.6	6.76	196.04
4 – 5.9	5	22	110	-0.6	0.36	7.92
6 – 7.9	7	13	91	1.4	1.96	25.48
8 – 9.9	9	11	99	3.4	11.56	127.16
10 – 11.9	11	13	143	5.4	29.16	379.08
12 – 13.9	13	4	52	7.4	54.76	219.04
14 – 15.9	15	2	30	9.4	88.36	176.72
16 – 17.9	17	1	17	11.4	130.00	130.00
18 – 19.9	19	1	19	13.4	179.60	179.60
20 – 21.9	21	1	21	15.4	237.20	237.20
		125	697			2270.72

Очередность
числовых операций:

1)
вычислить сумму числа наблюдений (в
нашем примере она равна 125);

2)
вычислить произведение каждой срединной
варианты на ее частоту (например, 1*28 =
28);

3)
вычислить сумму произведений срединных
вариант на их частоты (в нашем примере
она равна 697);

4)
вычислить взвешенную среднюю арифметическую
величину по формуле:

Средняя
арифметическая величина позволяет
сравнивать и оценивать группы изучаемых
явлений в целом. Однако для характеристики
группы явлений только этой величины
явно недостаточно, так как размер
колебаний вариант, из которых она
складывается, может быть различным.
Поэтому в характеристику группы явлений
необходимо ввести такой показатель,
который давал бы представление о величине
колебаний вариант около их средней
величины.

Вычисление
средней ошибки среднего арифметического.
Условное обозначение средней ошибки
среднего арифметического — т. Следует
помнить, что под «ошибкой» в статистике
понимается не ошибка исследования, а
мера представительства данной величины,
т. е. мера, которой средняя арифметическая
величина, полученная на выборочной
совокупности (в нашем примере — на 125
детях), отличается от истинной средней
арифметической величины, которая была
бы получена на генеральной совокупности
(в нашем примере это были бы все дети
аналогичного возраста, уровня
подготовленности и т. д.). Например, в
приведенном ранее примере определялась
точность попадания малым мячом в цель
у 125 детей и была получена средняя
арифметическая величина примерно равная
5,6 см. Теперь надо установить, в какой
мере эта величина будет характерна,
если взять для исследования 200, 300, 500 и
больше аналогичных детей. Ответ на этот
вопрос и даст вычисление средней ошибки
среднего арифметического, которое
производится по формуле:

Для
приведенного примера величина средней
ошибки среднего арифметического будет
равна:

Следовательно,
M±m = 5,6±0,38. Это означает, что полученная
средняя арифметическая величина (M =
5,6) может иметь в других аналогичных
исследованиях значения от 5,22 (5,6 — 0,38 =
5,22) до 5,98 (5,6+0,38 = 5,98).

Соседние файлы в предмете Ветеринарная генетика

Материал из MachineLearning.

Перейти к: навигация, поиск

Содержание

1 Введение
- 1.1 Постановка вопроса. Виды погрешностей
2 Виды мер точности
3 Предельные погрешности
4 Погрешности округлений при представлении чисел в компьютере
5 Погрешности арифметических операций
6 Погрешности вычисления функций
7 Числовые примеры
8 Список литературы
9 См. также

Введение

Постановка вопроса. Виды погрешностей

Процесс исследования исходного объекта методом математического моделирования и вычислительного эксперимента неизбежно носит приближенный характер, так как на каждом этапе вносятся погрешности. Построение математической модели связано с упрощением исходного явления, недостаточно точным заданием коэффициентов уравнения и других входных данных. По отношению к численному методу, реализующему данную математическую модель, указанные погрешности являются неустранимыми, поскольку они неизбежны в рамках данной модели.

При переходе от математической модели к численному методу возникают погрешности, называемые погрешностями метода. Они связаны с тем, что всякий численный метод воспроизводит исходную математическую модель приближенно. Наиболее типичными погрешностями метода являются погрешность дискретизации и погрешность округления.
При построении численного метода в качестве аналога исходной математической задачи обычно рассматривается её дискретная модель. Разность решений дискретизированной задачи и исходной называется погрешностью дискретизации. Обычно дискретная модель зависит от некоторого параметра (или их множества) дискретизации, при стремлении которого к нулю должна стремиться к нулю и погрешность дискретизации.
Дискретная модель представляет собой систему большого числа алгебраических уравнений. Для её решения используется тот или иной численный алгоритм. Входные данные этой системы, а именно коэффициенты и правые части, задаются в ЭВМ не точно, а с округлением. В процессе работы алгоритма погрешности округления обычно накапливаются, и в результате, решение, полученное на ЭВМ, будет отличаться от точного решения дискретизированной задачи. Результирующая погрешность называется погрешностью округления (вычислительной погрешностью). Величина этой погрешности определяется двумя факторами: точностью представления вещественных чисел в ЭВМ и чувствительностью данного алгоритма к погрешностям округления.

Итак, следует различать погрешности модели, дискретизации и округления. В вопросе преобладания какой-либо погрешности ответ неоднозначен. В общем случае нужно стремиться, чтобы все погрешности имели один и тот же порядок. Например, нецелесообразно пользоваться разностными схемами, имеющими точность 10⁻⁶, если коэффициенты исходных уравнений задаются с точностью 10⁻².

Виды мер точности

Мерой точности вычислений являются абсолютные и относительные погрешности. Абсолютная погрешность определяется формулой

где tilde a – приближение к точному значению .
Относительная погрешность определяется формулой

$delta(tilde a)=frac{|tilde a-a|}{a}.$

Относительная погрешность часто выражается в процентах. Абсолютная и относительная погрешности тесно связаны с понятием верных значащих цифр. Значащими цифрами числа называют все цифры в его записи, начиная с первой ненулевой цифры слева. Например, число 0,000129 имеет три значащих цифры. Значащая цифра называется верной, если абсолютная погрешность числа не превышает половины веса разряда, соответствующего этой цифре. Например, , абсолютная погрешность . Записывая число в виде

имеем , следовательно, число имеет две верных значащих цифр (9 и 3).

В общем случае абсолютная погрешность должна удовлетворять следующему неравенству:

$Delta(tilde a)<0,5cdot10^{m-n+1} ,$

где — порядок (вес) старшей цифры, — количество верных значащих цифр.
В рассматриваемом примере $Delta(tilde a)le0,5cdot10^{3-2+1}le0,5cdot10^2=50$ .

Относительная погрешность связана с количеством верных цифр приближенного числа соотношением:

$delta(tilde a)lefrac{Delta(tilde a)}{alpha_m}10^mlefrac{10^{m-n+1}}{alpha_m10^m}lefrac{1}{alpha_m10^{n-1}},$

где alpha_m — старшая значащая цифра числа.

Для двоичного представления чисел имеем $delta(tilde a)le2^{-n}$ .

Тот факт, что число tilde a является приближенным значением числа с абсолютной погрешностью , записывают в виде

причем числа tilde a и записываются с одинаковым количеством знаков после запятой, например, или $a=2,347pm2cdot10^{-3}$ .

Запись вида

означает, что число tilde a является приближенным значение числа с относительной погрешностью .

Так как точное решение задачи как правило неизвестно, то погрешности приходится оценивать через исходные данные и особенности алгоритма. Если оценка может быть вычислена до решения задачи, то она называется априорной. Если оценка вычисляется после получения приближенного решения задачи, то она называется апостериорной.

Очень часто степень точности решения задачи характеризуется некоторыми косвенными вспомогательными величинами. Например точность решения системы алгебраических уравнений

AX=F

характеризуется невязкой

где tilde X — приближенное решение системы.
Причём невязка достаточно сложным образом связана с погрешностью решения , причём если невязка мала, то погрешность может быть значительной.

Предельные погрешности

Пусть искомая величина является функцией параметров — приближенное значение . Тогда предельной абсолютной погрешностью называется величина

$D(a^*) = suplimits_{(t_1, ldots ,t_n) in Omega } left|{a(t_1, ldots ,t_n) - a^*}right| ,$

Предельной относительной погрешностью называется величина .

Пусть $left|{t_j - t_j^*}right| le Delta (t_j^* ), qquad j = 1 div n$ — приближенное значение . Предполагаем, что — непрерывно дифференцируемая функция своих аргументов. Тогда, по формуле Лагранжа,

$a(t_1, ldots ,t_n) - a^* = sumlimits_{j = 1}^n gamma_j (alpha )(t_j - t_j^*),$

где $gamma_j (alpha ) = a^{prime}_{t_j}(t_1^* + alpha (t_1 - t_1^*), ldots ,t_n^* + alpha (t_n - t_n^*)), qquad 0 le alpha le 1$ .

Отсюда

$left|{a(t_1, ldots ,t_n) - a^*}right| le D_1 (a^*) = sumlimits_{j = 1}^n b_j Delta (t_j^*),$

где $b_j = suplimits_Omega left|{a^{prime}_{t_j}(t_1, ldots ,t_n)}right|$ .

Можно показать, что при малых $rho = sqrt{{(Delta (t_1^* ))}^2 + ldots + {(Delta (t_n^* ))}^2 }$ эта оценка не может быть существенно улучшена. На практике иногда пользуются грубой (линейной) оценкой

$left|{a(t_1, ldots ,t_n) - a^*}right| le D_2 (a^*),$

где $D_2 (a^*) = sumlimits_{j = 1} left|{gamma_j (0)}right| Delta (t^*)$ .

Несложно показать, что:

— предельная погрешность суммы или разности равна сумме предельных погрешностей.
$delta (t_1^* cdots t_m^* cdot d_1^{* - 1} cdots d_m^{* - 1} ) = delta (t_1^* ) + ldots + delta (t_m^*) + delta (d_1^*) + ldots + delta (d_n^*)$ — предельная относительная погрешность произведения или частного приближенного равна сумме предельных относительных погрешностей.

Погрешности округлений при представлении чисел в компьютере

Одним из основных источников вычислительных погрешностей является приближенное представление чисел в компьютере, обусловленное конечностью разрядной сетки (см. Международный стандарт представления чисел с плавающей точкой в ЭВМ). Число , не представимое в компьютере, подвергается округлению, т. е. заменяется близким числом tilde a , представимым в компьютере точно.
Найдем границу относительной погрешности представления числа с плавающей точкой. Допустим, что применяется простейшее округление – отбрасывание всех разрядов числа, выходящих за пределы разрядной сетки. Система счисления – двоичная. Пусть надо записать число, представляющее бесконечную двоичную дробь

$a=underbrace{pm2^p}_{order}underbrace{left(frac{a_1}{2}+frac{a_2}{2^2}+dots+frac{a_t}{2^t}+frac{a_{t+1}}{2^{t+1}}+dotsright)}_{mantissa},$

где $a_j={01$ , — цифры мантиссы.
Пусть под запись мантиссы отводится t двоичных разрядов. Отбрасывая лишние разряды, получим округлённое число

$tilde a=pm2^pleft(frac{a_1}{2}+frac{a_2}{2^2}+dots+frac{a_t}{2^t}right).$

Абсолютная погрешность округления в этом случае равна

$a-tilde a=pm2^pleft(frac{a_{t+1}}{2^{t+1}}+frac{a_{t+2}}{2^{t+2}}+dotsright).$

Наибольшая погрешность будет в случае $a_{t+1}=1, qquad a_{t+2}=1,$ , тогда

$|a-tilde a|lepm2^pfrac{1}{2^{t+1}}underbrace{left(1+frac{1}{2}+frac{1}{2^2}+dotsright)}_{=2}=2^{p-t}.$

Т.к. , где — мантисса числа , то всегда a_1=1 . Тогда $|a|ge2^pcdot2^{-1}=2^{p-1}$ и относительная погрешность равна $frac{|a-tilde a|}{|a|}le2^{-t+1}$ . Практически применяют более точные методы округления и погрешность представления чисел равна

( 1 )

$frac{|a-tilde a|}{|a|}le2^{-t},$

т.е. точность представления чисел определяется разрядностью мантиссы .
Тогда приближенно представленное в компьютере число можно записать в виде , где $|epsilon|le2^{-t}$ – «машинный эпсилон» – относительная погрешность представления чисел.

Погрешности арифметических операций

При вычислениях с плавающей точкой операция округления может потребоваться после выполнения любой из арифметических операций. Так умножение или деление двух чисел сводится к умножению или делению мантисс. Так как в общем случае количество разрядов мантисс произведений и частных больше допустимой разрядности мантиссы, то требуется округление мантиссы результатов. При сложении или вычитании чисел с плавающей точкой операнды должны быть предварительно приведены к одному порядку, что осуществляется сдвигом вправо мантиссы числа, имеющего меньший порядок, и увеличением в соответствующее число раз порядка этого числа. Сдвиг мантиссы вправо может привести к потере младших разрядов мантиссы, т.е. появляется погрешность округления.

Округленное в системе с плавающей точкой число, соответствующее точному числу , обозначается через fl(x) (от англ. floating – плавающий). Выполнение каждой арифметической операции вносит относительную погрешность, не большую, чем погрешность представления чисел с плавающей точкой (1). Верна следующая запись:

где box — любая из арифметических операций, $|epsilon|le2^{-t}$ .

Рассмотрим трансформированные погрешности арифметических операций. Арифметические операции проводятся над приближенными числами, ошибка арифметических операций не учитывается (эту ошибку легко учесть, прибавив ошибку округления соответствующей операции к вычисленной ошибке).

Рассмотрим сложение и вычитание приближенных чисел. Абсолютная погрешность алгебраической суммы нескольких приближенных чисел равна сумме абсолютных погрешностей слагаемых.

Если сумма точных чисел равна

сумма приближенных чисел равна

где — абсолютные погрешности представления чисел.

Тогда абсолютная погрешность суммы равна

Относительная погрешность суммы нескольких чисел равна

( 2 )

$delta(S)=frac{Delta(S)}{S}=frac{a_1}{S}left(frac{Delta(a_1)}{a_1}right)+frac{a_2}{S}left(frac{Delta(a_2)}{a_2}right)+dots=frac{a_1delta(a_1)+a_2delta(a_2)+dots}{S},$

где — относительные погрешности представления чисел.

Из (2) следует, что относительная погрешность суммы нескольких чисел одного и того же знака заключена между наименьшей и наибольшей из относительных погрешностей слагаемых:

При сложении чисел разного знака или вычитании чисел одного знака относительная погрешность может быть очень большой (если числа близки между собой). Так как даже при малых величина может быть очень малой. Поэтому вычислительные алгоритмы необходимо строить таким образом, чтобы избегать вычитания близких чисел.

Необходимо отметить, что погрешности вычислений зависят от порядка вычислений. Далее будет рассмотрен пример сложения трех чисел.

( 3 )

tilde S=(tilde S_1+x_3)(1+delta_2)=(x_1+x_2)(1+delta_1)(1+delta_2)+x_3(1+delta_2).

При другой последовательности действий погрешность будет другой:

tilde S=(x_3+x_2)(1+delta_1)(1+delta_2)+x_1(1+delta_2).

Из (3) видно, что результат выполнения некоторого алгоритма, искаженный погрешностями округлений, совпадает с результатом выполнения того же алгоритма, но с неточными исходными данными. Т.е. можно применять обратный анализ: свести влияние погрешностей округления к возмущению исходных данных. Тогда вместо (3) будет следующая запись:

где

При умножении и делении приближенных чисел складываются и вычитаются их относительные погрешности.

tilde S=a_1cdot a_2(1+delta(a_1))(1+delta(a_2))

≅

с точностью величин второго порядка малости относительно delta .

Тогда .

Если $S=frac{a_1}{a_2}$ , то $Delta(S)=frac{a_1(1+delta_1)}{a_2(1+delta_2)}-frac{a_1}{a_2}=frac{a_1(delta_1-delta_2)}{a_2(1+delta_2)}approx frac{a_1}{a_2}(delta_1-delta_2), qquad delta(S)$ ≅

При большом числе n арифметических операций можно пользоваться приближенной статистической оценкой погрешности арифметических операций, учитывающей частичную компенсацию погрешностей разных знаков:

$delta_Sigma approx delta_{fl} quad sqrt{n},$

где – суммарная погрешность, $|delta_{fl}|leepsilon$ – погрешность выполнения операций с плавающей точкой, epsilon – погрешность представления чисел с плавающей точкой.

Погрешности вычисления функций

Рассмотрим трансформированную погрешность вычисления значений функций.

Абсолютная трансформированная погрешность дифференцируемой функции y=f(x) , вызываемая достаточно малой погрешностью аргумента , оценивается величиной .

Если f(x)>0 , то $delta(y)=frac{|f'(x)|}{f(x)}Delta(x)=left|(ln(f(x)))'right|cdotDelta(x)$ .

Абсолютная погрешность дифференцируемой функции многих аргументов , вызываемая достаточно малыми погрешностями аргументов оценивается величиной:

$Delta(y)=sumlimits_{i=1}^nleft|frac{partial f}{partial x_i}right|Delta(x_i)$

Если , то $delta(y)=sumlimits_{i=1}^nfrac{1}{f}cdotleft|frac{partial f}{partial x_i}right|cdotDelta(x_i)=sumlimits_{i=1}^{n}left|frac{partial l_n(f)}{partial x_i}right|Delta(x_i)$ .

Практически важно определить допустимую погрешность аргументов и допустимую погрешность функции (обратная задача). Эта задача имеет однозначное решение только для функций одной переменной y=f(x) , если f(x) дифференцируема и :

$Delta(x)=frac{1}{|f'(x)|}Delta(y)$ .

Для функций многих переменных задача не имеет однозначного решения, необходимо ввести дополнительные ограничения. Например, если функция наиболее критична к погрешности , то:

$Delta(x_i)=frac{Delta(y)}{left|frac{partial f}{partial x_i}right|}qquad$

(погрешностью других аргументов пренебрегаем).

Если вклад погрешностей всех аргументов примерно одинаков, то применяют принцип равных влияний:

$Delta(x_i)=frac{Delta(y)}{nleft|frac{partial f}{partial x_i}right|},qquad i=overline{1,n}.$

Числовые примеры

Специфику машинных вычислений можно пояснить на нескольких элементарных примерах.

ПРИМЕР 1. Вычислить все корни уравнения

$x^4 - 4x^3 + 8x^2 - 16x + 15.underbrace{99999999}_8 = {(x - 2)}^4 - 10^{- 8} = 0.$

Точное решение задачи легко найти:

$(x - 2)^2 = pm 10^{- 4},$

$x_1= 2,01; x_2= 1,99; x_{3,4}= 2 pm 0,01i.$

Если компьютер работает при $delta _M > 10^{ - 8}$ , то свободный член в исходном уравнении будет округлен до 16,0 и, с точки зрения представления чисел с плавающей точкой, будет решаться уравнение , т.е. $x_{1,2,3,4} = 2$ , что, очевидно, неверно. В данном случае малые погрешности в задании свободного члена $approx10^{-8}$ привели, независимо от метода решения, к погрешности в решении $approx10^{-2}$ .

ПРИМЕР 2. Решается задача Коши для обыкновенного дифференциального уравнения 2-го порядка:

u''(t) = u(t), qquad u(0) = 1, qquad u'(0) = - 1.

Общее решение имеет вид:

$u(t) = 0,5[u(0) + u'(0)]e^t + 0,5[u(0) - u'(0)]e^{- t}.$

При заданных начальных данных точное решение задачи: $u(x) = e^{-t}$ , однако малая погрешность delta в их задании приведет к появлению члена , который при больших значениях аргумента может существенно исказить решение.

ПРИМЕР 3. Пусть необходимо найти решение обыкновенного дифференциального уравнения:

$stackrel{cdot}{u} = 10u,qquad u = u(t), u(t_0) = u_0,qquad t in [0,1].$

Его решение: $u(t) = u_0e^{10(t - t_0 )}$ , однако значение u(t_0) известно лишь приближенно: , и на самом деле $u^*(t) = u_0^*e^{10(t - t_0)}$ .

Соответственно, разность u* - u будет:

$u^* - u = (u_0^* - u_0)e^{10(t - t_0)}.$

Предположим, что необходимо гарантировать некоторую заданную точность вычислений всюду на отрезке . Тогда должно выполняться условие:

$|{u^*(t) - u(t)}| le varepsilon.$

Очевидно, что:

$maxlimits_{t in [0,1]} |{u^*(t) - u(t)}| = |{u*(1) - u(1)}| = |{u_0^* - u_0}|e^{10(1 - t_0)}.$

Отсюда можно получить требования к точности задания начальных данных $delta: qquad|u_0^* - u_0| < delta, qquad delta le varepsilon e^{ - 10}$ при t_0= 0 .

Таким образом, требование к заданию точности начальных данных оказываются в $e^{10}$ раз выше необходимой точности результата решения задачи. Это требование, скорее всего, окажется нереальным.

Решение оказывается очень чувствительным к заданию начальных данных. Такого рода задачи называются плохо обусловленными.

ПРИМЕР 4. Решением системы линейных алгебраических уравнений (СЛАУ):

left{ begin{array}{l} u + 10v = 11, 100u + 1001v = 1101; end{array} right.

является пара чисел .

Изменив правую часть системы на 0,01 , получим возмущенную систему:

left{ begin{array}{l} u + 10v = 11.01, 100u + 1001v = 1101; end{array} right.

с решением , сильно отличающимся от решения невозмущенной системы. Эта система также плохо обусловлена.

ПРИМЕР 5. Рассмотрим методический пример вычислений на модельном компьютере, обеспечивающем точность . Проанализируем причину происхождения ошибки, например, при вычитании двух чисел, взятых с точностью до третьей цифры после десятичной точки , разность которых составляет .

В памяти машины эти же числа представляются в виде:

u_M = u(1 + delta_M^u), quad v_M = v(1 + delta_M^v)

, причем

Тогда:

u_M - u approx udelta_M^u, quad v_M - v approx vdelta_M^v.

Относительная ошибка при вычислении разности будет равна:

$delta = frac{(u_M - v_M) - (u - v)}{(u - v)} = frac{(u_M - u) - (v_M - v)}{(u - v)} = frac{delta_M^u - delta_M^v}{(u - v)}.$

Очевидно, что $delta = left|{frac{delta_M^u - delta_M^v}{Delta }} right| le frac{2delta_M}{0,001} approx 2000delta_M = 1$ , т.е. все значащие цифры могут оказаться неверными.

ПРИМЕР 6. Рассмотрим рекуррентное соотношение $u_{i+1} = qu_i, quad i ge 0, quad u_0 = a,quad q > 0, quad u_i > 0.$

Пусть при выполнении реальных вычислений с конечной длиной мантиссы на -м шаге возникла погрешность округления, и вычисления проводятся с возмущенным значением , тогда вместо $u_{i+1}$ получим $u_{i + 1}^M = q(u_i + delta_i) = u_{i + 1} + qdelta_i$ , т.е. $delta_{i + 1} = qdelta_i,quad i = 0,1,ldots$ .

Следовательно, если |q| > 1 , то в процессе вычислений погрешность, связанная с возникшей ошибкой округления, будет возрастать (алгоритм неустойчив). В случае погрешность не возрастает и численный алгоритм устойчив.

Список литературы

А.А.Самарский, А.В.Гулин. Численные методы. Москва «Наука», 1989.
http://www.mgopu.ru/PVU/2.1/nummethods/Chapter1.htm
http://www.intuit.ru/department/calculate/calcmathbase/1/4.html

См. также

Практикум ММП ВМК, 4й курс, осень 2008

Среднее арифметическое, как известно, используется для получения обобщающей характеристики некоторого набора данных. Если данные более-менее однородны и в них нет аномальных наблюдений (выбросов), то среднее хорошо обобщает данные, сведя к минимуму влияние случайных факторов (они взаимопогашаются при сложении).

Когда анализируемые данные представляют собой выборку (которая состоит из случайных значений), то среднее арифметическое часто (но не всегда) выступает в роли приближенной оценки математического ожидания. Почему приближенной? Потому что среднее арифметическое – это величина, которая зависит от набора случайных чисел, и, следовательно, сама является случайной величиной. При повторных экспериментах (даже в одних и тех же условиях) средние будут отличаться друг от друга.

Для того, чтобы на основе статистического анализа данных делать корректные выводы, необходимо оценить возможный разброс полученного результата. Для этого рассчитываются различные показатели вариации. Но то исходные данные. И как мы только что установили, среднее арифметическое также обладает разбросом, который необходимо оценить и учитывать в дальнейшем (в выводах, в выборе метода анализа и т.д.).

Интуитивно понятно, что разброс средней должен быть как-то связан с разбросом исходных данных. Основной характеристикой разброса средней выступает та же дисперсия.

Дисперсия выборочных данных – это средний квадрат отклонения от средней, и рассчитать ее по исходным данным не составляет труда, например, в Excel предусмотрены специальные функции. Однако, как же рассчитать дисперсию средней, если в распоряжении есть только одна выборка и одно среднее арифметическое?

Расчет дисперсии и стандартной ошибки средней арифметической

Чтобы получить дисперсию средней арифметической нет необходимости проводить множество экспериментов, достаточно иметь только одну выборку. Это легко доказать. Для начала вспомним, что средняя арифметическая (простая) рассчитывается по формуле:

где x_i – значения переменной,
n – количество значений.

Теперь учтем два свойства дисперсии, согласно которым, 1) — постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат и 2) — дисперсия суммы независимых случайных величин равняется сумме соответствующих дисперсий. Предполагается, что каждое случайное значение x_i обладает одинаковым разбросом, поэтому несложно вывести формулу дисперсии средней арифметической:

Используя более привычные обозначения, формулу записывают как:

где σ² – это дисперсия, случайной величины, причем генеральная.

На практике же, генеральная дисперсия известна далеко не всегда, точнее совсем редко, поэтому в качестве оной используют выборочную дисперсию:

Стандартное отклонение средней арифметической называется стандартной ошибкой средней и рассчитывается, как квадратный корень из дисперсии.

Формула стандартной ошибки средней при использовании генеральной дисперсии

Формула стандартной ошибки средней при использовании выборочной дисперсии

Последняя формула на практике используется чаще всего, т.к. генеральная дисперсия обычно не известна. Чтобы не вводить новые обозначения, стандартную ошибку средней обычно записывают в виде соотношения стандартного отклонения выборки и корня объема выборки.

Назначение и свойство стандартной ошибки средней арифметической

Стандартная ошибка средней много, где используется. И очень полезно понимать ее свойства. Посмотрим еще раз на формулу стандартной ошибки средней:

Числитель – это стандартное отклонение выборки и здесь все понятно. Чем больше разброс данных, тем больше стандартная ошибка средней – прямо пропорциональная зависимость.

Посмотрим на знаменатель. Здесь находится квадратный корень из объема выборки. Соответственно, чем больше объем выборки, тем меньше стандартная ошибка средней. Для наглядности изобразим на одной диаграмме график нормально распределенной переменной со средней равной 10, сигмой – 3, и второй график – распределение средней арифметической этой же переменной, полученной по 16-ти наблюдениям (которое также будет нормальным).

Судя по формуле, разброс стандартной ошибки средней должен быть в 4 раза (корень из 16) меньше, чем разброс исходных данных, что и видно на рисунке выше. Чем больше наблюдений, тем меньше разброс средней.

Казалось бы, что для получения наиболее точной средней достаточно использовать максимально большую выборку и тогда стандартная ошибка средней будет стремиться к нулю, а сама средняя, соответственно, к математическому ожиданию. Однако квадратный корень объема выборки в знаменателе говорит о том, что связь между точностью выборочной средней и размером выборки не является линейной. Например, увеличение выборки с 20-ти до 50-ти наблюдений, то есть на 30 значений или в 2,5 раза, уменьшает стандартную ошибку средней только на 36%, а со 100-а до 130-ти наблюдений (на те же 30 значений), снижает разброс данных лишь на 12%.

Лучше всего изобразить эту мысль в виде графика зависимости стандартной ошибки средней от размера выборки. Пусть стандартное отклонение равно 10 (на форму графика это не влияет).

Видно, что примерно после 50-ти значений, уменьшение стандартной ошибки средней резко замедляется, после 100-а – наклон постепенно становится почти нулевым.

Таким образом, при достижении некоторого размера выборки ее дальнейшее увеличение уже почти не сказывается на точности средней. Этот факт имеет далеко идущие последствия. Например, при проведении выборочного обследования населения (опроса) чрезмерное увеличение выборки ведет к неоправданным затратам, т.к. точность почти не меняется. Именно поэтому количество опрошенных редко превышает 1,5 тысячи человек. Точность при таком размере выборки часто является достаточной, а дальнейшее увеличение выборки – нецелесообразным.

Подведем итог. Расчет дисперсии и стандартной ошибки средней имеет довольно простую формулу и обладает полезным свойством, связанным с тем, что относительно хорошая точность средней достигается уже при 100 наблюдениях (в этом случае стандартная ошибка средней становится в 10 раз меньше, чем стандартное отклонение выборки). Больше, конечно, лучше, но бесконечно увеличивать объем выборки не имеет практического смысла. Хотя, все зависит от поставленных задач и цены ошибки. В некоторых опросах участие принимают десятки тысяч людей.

Дисперсия и стандартная ошибка средней имеют большое практическое значение. Они используются в проверке гипотез и расчете доверительных интервалов.

Поделиться в социальных сетях:

Источник

Заметили ошибку в решении суда — ничего страшного, всё можно исправить.

Ошибки бывают разные. В зависимости от того, какая ошибка, закон предусматривает разные пути её исправления.

Имеет ли судья право на ошибку

Кто ничего не делает, тот и не ошибается — простое и понятное изречение.

Судья каждый день принимает решения и каждое решение несёт риск ошибки.

Можете возразить — судья представляет власть и не должен ошибаться.

Да, не должен, но иногда ошибается и с этим ничего не поделаешь.

Что такое описка в решении суда

Были времена, когда текст судебного решения печатали на механической машинке, иногда писали от руки.

Сегодня тексты набирают на компьютере: быстро, удобно, повышает производительность.

Однако ошибались всегда: в рукописном тексте допускали описку, в печатном — опечатку.

Отличие от судебной ошибки

Описка — это результат невнимательности: хотели написать одно, получилось другое.

Судья или помощник торопились при составлении текста решения, потом не проверили его, и вот результат.

Описка или опечатка — ошибка в букве, слове, предложении. Судебная ошибка — ошибка в мыслях.

Ошибка в арифметике: явная и неявная

У судей нет времени сидеть с калькулятором, делать или проверять сложные расчёты.

Особо сложные, например проверку бухгалтерского или налогового учёта, судьи поручают экспертам.

Расчёт предоставляют участники процесса. Судья либо соглашается с ним, либо делает свой.

Арифметическая ошибка — ошибка в математических расчётах.

Способы исправления

Исправление описки или арифметической ошибки в тексте решении суда — это НЕ изменение самого решения

При изменении решения меняется его смысловое содержание. Неважно, полностью или частично.

Суд не вправе изменить своё решение. Это запрещено законом и разрешено только вышестоящему суду.

А вот неумышленную описку и ошибку в расчётах исправляет суд, который её допустил.

Отсюда следующее правило:

Судья неумышленно в решении допустил описку (опечатку) или ошибся в математических расчётах — подаём заявление об исправлении
Судья ошибся в суждениях, оценке доказательств, выборе и применении закона (допустил осознанную судебную ошибку) — подаем апелляционную жалобу на решение суда

Когда нужно исправлять решение

«Исправить или оставить как есть» — зависит от конкретной ситуации, от обстоятельств дела.

Важно определить, какие последствия может повлечь такая описка. Лучше, если это сделает юрист.

Немаловажно в какой части решения описка.

Описка в резолютивной части (после «суд решил») — лучше исправить.

В мотивировочной части (где выводы суда) — на усмотрение, опять же в зависимости от возможных последствий.

Арифметические ошибки нужно исправлять, когда обсчёт существенен.

Не нужно тратить силы и время, если судья ошибся на несколько копеек или рублей.

Кто инициирует, кто исправляет, куда подавать

Исправление описки или арифметической ошибки инициирует тот, кто её обнаружил.

Не нужно ждать инициативы от суда — у судей много работы и нет времени на перепроверку своих же решений.

Просто помогите судье — подайте заявление об исправлении, не ждите что это сделает кто-то другой.

Заявление в суд об исправлении описки

Структура заявления проста и состоит из четырёх частей:

Обозначаем описку
Мотивируем, почему это описка
Ссылаемся на статьи 200 и 203.1 ГПК РФ (в арбитраже — статья 179 АПК РФ)
Просим исправить, предлагая свой вариант

Просительная часть заявления об исправлении описки будет выглядеть следующим образом:

изложив его в следующей редакции:

Когда лучше привлечь юриста

Заявление не всегда простенький текст на половину страницы. Иногда его нужно дополнить смысловой нагрузкой.

Другое дело, когда не совсем ясно, почему суд допустил описку и описка ли это вообще.

Почему меня не вызвали в суд

Раньше суд рассматривал заявление об исправлении описки в решении только в судебном заседании.

Рассмотрение вопроса об исправлении вне судебного заседания считалось процессуальным нарушением.

Сейчас у судьи два варианта:

Не проводить заседание, не извещать участников процесса
Провести заседание, предварительно сообщив участникам время и место проведения

Суд отказал в исправлении описки. Что дальше?

Рассмотрев заявление о исправлении, суд выносит определение — либо исправляет, либо отказывает в этом.

Если вопрос рассматривался в судебном заседании с вызовом, обычно копию определения вручают здесь же.

Если суд не проводил заседания, копию высылают в течение трёх дней по почте.

Почтовые отправления — всегда риск. Лучше отследить дело и получить определение в суде.

Судья отказал в исправлении, вы не согласны, позиции разошлись — можно подать частную жалобу

Здесь точно лучше обратиться к юристу.

Источник

Определяя
значение средней арифметической
величины, следует придерживаться
некоторых правил.

где
S — знак суммирования;

V
— полученные в исследовании значения
(варианты);

п
— число вариант.

Классы	Серединные варианты V_C	Число набл, р	V_CP	V_C-M=d	d²	d²P
0 – 1.9	1	28	28	-4.6	21.16	592.48
2 – 3.9	3	29	87	-2.6	6.76	196.04
4 – 5.9	5	22	110	-0.6	0.36	7.92
6 – 7.9	7	13	91	1.4	1.96	25.48
8 – 9.9	9	11	99	3.4	11.56	127.16
10 – 11.9	11	13	143	5.4	29.16	379.08
12 – 13.9	13	4	52	7.4	54.76	219.04
14 – 15.9	15	2	30	9.4	88.36	176.72
16 – 17.9	17	1	17	11.4	130.00	130.00
18 – 19.9	19	1	19	13.4	179.60	179.60
20 – 21.9	21	1	21	15.4	237.20	237.20
		125	697			2270.72

Очередность
числовых операций:

1)
вычислить сумму числа наблюдений (в
нашем примере она равна 125);

2)
вычислить произведение каждой срединной
варианты на ее частоту (например, 1*28 =
28);

3)
вычислить сумму произведений срединных
вариант на их частоты (в нашем примере
она равна 697);

4)
вычислить взвешенную среднюю арифметическую
величину по формуле:

Для
приведенного примера величина средней
ошибки среднего арифметического будет
равна:

Соседние файлы в предмете Ветеринарная генетика

Источник

В процессуальном праве действует правило неизменяемости судебного решения. Согласно этому правилу суд, принявший решение, не вправе самостоятельно изменять его*(986). В то же время из этого правила есть исключение, которое сводится к тому, что суду, принявшему решение, предоставлено право исправить допущенные ошибки, не затрагивая при этом существа принятого решения и не касаясь тех вопросов, которые не были предметом судебного разбирательства. К таким ошибкам относятся описки, опечатки и арифметические ошибки.
Под опиской в соответствии с общеупотребительной лексикой понимается ошибка в письменном тексте, сделанная по рассеянности или невнимательности*(987). Опечатка — это ошибка в печатном тексте, допущенная при наборе, печатании на машинке*(988) (компьютере). Арифметическая ошибка — это неправильность, допущенная в каком-либо вычислении.
Таким образом, все вышеуказанные типы ошибок не являются правовыми ошибками, т.е. ошибками в применении правовых норм. Исправлять собственные правовые ошибки третейский суд не компетентен. Это прерогатива государственного суда, проверяющего в установленных законом пределах на основании заявления заинтересованного лица законность решения третейского суда (в том случае, если третейское соглашение не предусматривает, что решение третейского суда является окончательным).
Не все арифметические ошибки могут быть исправлены третейским судом. Так, если арифметическая ошибка допущена вследствие неправильного применения норм, устанавливающих порядок исчисления цены иска, то такая ошибка не может быть исправлена третейским судом, принявшим решение, поскольку такая ошибка по своей сути является правовой. В этом случае исправление ошибки возможно только путем отмены соответствующего решения третейского суда либо отказа в принудительном его исполнении.
Федеральный закон «О третейских судах в Российской Федерации» не предусматривает, какова должна быть процедура исправления описок, опечаток, арифметических ошибок. В частности, неясно, является ли обязательным проведение в данном случае судебного заседания с обязательным уведомлением сторон. Представляется, что вопрос о внесении указанных изменений должен решаться в судебном заседании, если суд посчитает необходимым проведение такого заседания. При этом лица, участвующие в деле, должны быть извещены о времени и месте проведения заседания.
Действующий закон не урегулировал и вопрос о сроке, в течение которого заинтересованная сторона вправе обратиться с заявлением об исправлении ошибок, опечаток или арифметических ошибок. Законодатель, как представляется, в данном случае сделал шаг назад. Ранее действовавшее Временное положение о третейском суде для разрешения экономических споров содержало норму, которая устанавливала такой срок, составлявший 10 дней (ст. 22). Представляется, что возврат к указанной норме способствовал бы стабильности и предсказуемости третейского процесса, понуждая стороны к более ответственному отношению к своим правам и обязанностям.
Исправление описок, опечаток, арифметических ошибок оформляется определением, которое рассматривается в качестве составной части решения и, как следствие, может быть обжаловано в том порядке, который установлен для обжалования решения третейского суда.

Если в поступившем к вам счете-фактуре неверно (в том числе с арифметическими ошибками) указаны:

стоимость товаров, работ, услуг; и
сумма НДС,

не берите налог к вычету, а попросите продавца исправить ошибку. Если ее найдут налоговики, вычет снимут. Об этом напоминает Минфин (письмо от 19.04.2017 № 03-07-09/23491).

Алгоритм исправления арифметической ошибки такой же как при исправлении технических ошибок. Продавец создает новый счет-фактуру и вносит следующие данные:

в стр. 1 — номер и дату из строки 1 первичного экземпляра счета-фактуры. Эти данные менять нельзя;
в строке 1а — порядковый номер и дату исправления;
в графах 5, 8 и 9, в которых содержатся данные о стоимости поставки и суммы НДС, фиксирует правильные значения;
в остальных строках и графах — данные из первичного экземпляра с правильными значениями.

При необходимости также вносит новые данные (ранее не отраженные).
Исправленный счет-фактуру подписывают руководитель и главный бухгалтер или ИП либо иные уполномоченные лица (п. 6 ст. 169 НК РФ, п. 7 Правил заполнения счета-фактуры).

Образец исправлений см. ниже.

В каких случаях используется исправленный счет-фактура, узнайте .

См. также «Нюансы нумерации счетов-фактур не по порядку в 2017 г.».

Более полную информацию по теме вы можете найти в КонсультантПлюс.
Полный и бесплатный доступ к системе на 2 дня.

Источник

Представление результатов исследования

Ошибка среднего арифметического

Ошибка среднего арифметического обозначается как m или

Ошибка среднего арифметического рассчитывается по формуле:

Правила записи результатов исследования

В записи ошибки среднего арифметического оставляем две значащие цифры, если первые цифры в ошибке «1» или «2».
В остальных случаях в записи ошибки среднего арифметического оставляем одну значащую цифру.
В записи среднего арифметического положение последней значащей цифры должно соответствовать положению первой значащей цифры в записи ошибки среднего арифметического.

Представление результатов научных исследований

	Эффективный модуль упругости (Е), кПа	Эффективный модуль вязкости (V), Па с
Этап эксперимента	Рассл.	Напряж.	Рассл.	Напряж.
До ФН	7,0±0,3	17,1±1,4	29,7±1,7	46±4
После ФН	7,7±0,3	18,7±1,4	30,9±2,0	53±6

Литература

Высшая математика и математическая статистика: учебное пособие для вузов / Под общ. ред. Г. И. Попова. – М. Физическая культура, 2007.– 368 с.
Гласс Дж., Стэнли Дж. Статистические методы в педагогике и психологии. М.: Прогресс. 1976.- 495 с.
Зациорский В.М. Осторожно — статистика! // Теория и практика физической культуры, 1989.- №2.
Катранов А.Г. Компьютерная обработка данных экспериментальных исследований: Учебное пособие/ А. Г. Катранов, А. В. Самсонова; СПб ГУФК им. П.Ф. Лесгафта. – СПб.: изд-во СПб ГУФК им. П.Ф. Лесгафта, 2005. – 131 с.
Основы математической статистики: Учебное пособие для ин-тов физ. культ / Под ред. В.С. Иванова.– М.: Физкультура и спорт, 1990. 176 с.

Источник