Доверительная вероятность и доверительная погрешность
При
обработке результатов измерений любой
физической величины возникают две
задачи. Первая состоит в нахождении по
набору данных наилучшей оценки измеряемой
величины ,
которую с наибольшим основанием можно
принять за приближенное значение
величины .
Вторая – в определении точности
полученного результата.
Результат
измерения физической величины представляют
в виде
Приведенная
запись означает, что существует
определенная степень уверенности в
том, что значение измеряемой величины
находится в пределах рассчитанного по
результатам наблюдений интервала
,
называемогодоверительным.
Величина
называетсядоверительной
погрешностью.
Указание
значения доверительной
вероятности
означает, что при проведении большого
числа наблюдений вслучаев результаты наблюдений измеряемой
физической величины, выполненные с
одинаковой тщательностью и одними и
теми же измерительными приборами,
попадут внутрь доверительного интервала.
Значения доверительной
погрешности и доверительной вероятности
однозначно связаны друг с другом, а
именно: чем больше погрешность, тем
больше вероятность того, что результат
измерений находится в указанных пределах,
и наоборот.
Виды погрешностей
По
характеру, происхождению, а также по
способам оценки и исключения влияния
на результат измерений погрешности
делят на три основные группы: случайные,
систематические и грубые (промахи).
Систематические
и грубые погрешности
определяются факторами, чуждыми условиям
и проведению эксперимента. Погрешности
такого рода могут быть исключены путем
тщательных проверок. Систематические
погрешности связаны с ограниченной
точностью прибора и метода измерений,
а также округлением при считывании
значения со шкалы. Когда причины,
вызывающие эти погрешности, известны,
их можно исключить, уточняя метод
измерения и вводя поправки к показаниям
приборов. Систематические погрешности
не уменьшаются с увеличением числа
измерений.
Грубые
погрешности
(промахи) обычно связаны с отсутствием
достаточной квалификации экспериментатора,
неправильным отсчетом по прибору,
неправильной записью результата
наблюдения, невнимательностью и т.п.
Обычно грубые погрешности хорошо
заметны, т.к. при многократно проделанных
измерениях соответствующие промахам
результаты резко отличаются от остальных.
Такие погрешности могут возникать в
результате неустойчивой работы установки
или отдельного прибора. Они могут быть
устранены путем повторных измерений
или снятием показаний другим
экспериментатором.
Случайные
погрешности
обусловливаются большим количеством
трудноучитываемых факторов, влияющих
как на измерительные устройства,
исследуемый физический объект или
процесс, так и на самого экспериментатора.
Такими факторами могут быть, например,
колебания температуры элементов
установки, напряженностей электрического
и магнитного полей, движение воздуха,
вибрация зданий и приборов, трение в
движущихся элементах, погрешности при
отсчете делений шкалы и т.п. Исключить
случайные погрешности отдельных
измерений невозможно, но величину таких
погрешностей можно оценить, проводя
повторные (многократные) измерения.
Оценка величины случайных погрешностей
производится с помощью аппарата
математической статистики и теории
вероятностей.
Соседние файлы в предмете Физика
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Доверительная погрешность
Cтраница 1
Доверительная погрешность — верхняя и нижняя границы интервала погрешности результата измерений при данной доверительной вероятности.
[1]
Достоинство доверительной погрешности состоит в том, что ее значение может быть оценено по экспериментальным данным очень простым путем. Пусть проведена серия из п измерений. Из п погрешностей образуют вариационный ряд, расположив их в порядке возрастания. ЯЬ — ( — оо состоит из ( п 2) членов. Следовательно, значение Д; является оценкой 100 % — ной квантили.
[2]
Тем не менее очень часто доверительные погрешности рассчитывают, вводя ничем не обоснованное предположение о том, что вид закона распределения погрешностей будто бы точно известен.
[3]
Тем не менее очень часто доверительные погрешности рассчитывают, вводя ничем не обоснованное предположение о том, что вид закона распределения погрешностей будто бы точно известен. В частности, используют прием, заключающийся в вычислении по небольшой выборке в 20 — 30 отсчетов оценки среднего квадратического отклонения а, а затем указывают погрешность с доверительной вероятностью Рд 0 997, равную До э97 3ст на основании предположения о нормальности закона распределения.
[4]
Тем не менее очень часто доверительные погрешности рассчитывают, вводя ничем не обоснованное предположение о том, что вид закона распределения погрешностей будто бы точно известен.
[5]
Задаваясь определенными значениями доверительной вероятности, находят доверительную погрешность результата измерений и доверительный интервал для среднего квадратического отклонения.
[6]
Увеличивать число наблюдений целесообразно до тех пор, пока доверительная погрешность измерения не будет определяться только систематической погрешностью.
[7]
При необходимости представить полученную энтропийную оценку погрешности в форме доверительной погрешности по соотношению ( 2 — 4) можно рассчитать соответствующее ей значение доверительной вероятности.
[8]
Когда число уравнений в системе равно количеству искомых параметров, последние, а также доверительные погрешности измерения этих параметров, находят методами косвенных измерений. С увеличением размерности условных уравнений, когда они линейны или линеаризованы, а результаты измерений равноточны и некоррелированы, используют МНК. Если погрешности измерений представляют нестационарный случайный процесс с известными характеристиками, например, известна функция ае ( I), то обработку данных и результатов измерений выполняют методом максимального правдоподобия.
[9]
В интервале температур от 73 15 до 273 15 К существуют Образцовые медь-копелевые и медь-константановые термопары 2-го разряда, обеспечивающие доверительную погрешность.
[10]
Погрешности образцовых средств измерений характеризуются пределом допускаемой погрешности средств измерений ( А, До — абсолютная и относительная погрешности) или доверительной погрешностью средства измерений ( б, бо — абсолютная и относительная погрешности) при соответствующей доверительной вероятности. Для каждой поверочной схемы доверительная вероятность постоянна.
[11]
Если погрешности результатов измерений ограничиваются интервалами, верхняя и нижняя границы которых с заданной вероятностью включают погрешность результата измерений, то эти погрешности называются доверительными погрешностями. Доверительные погрешности характеризуются поставленными перед ними знаками или одним из этих знаков, если знаки распространяются только на одни положительные или отрицательные значения погрешностей.
[12]
Когда обнаружены действительно анормальные результаты наблюдений и они иключены из обрабатываемой выборки, то на основе оставшихся результатов наблюдений по ГОСТ 8.207 — 76 будут определены: среднее арифметическое X исправленных результатов наблюдений, выборочное среднее квадратическое отклонение Sx результата наблюдения и 5 — результата измерения, выборочная доверительная погрешность измерения Д -, другие характеристики.
[13]
Если погрешности результатов измерений ограничиваются интервалами, верхняя и нижняя границы которых с заданной вероятностью включают погрешность результата измерений, то эти погрешности называются доверительными погрешностями. Доверительные погрешности характеризуются поставленными перед ними знаками или одним из этих знаков, если знаки распространяются только на одни положительные или отрицательные значения погрешностей.
[14]
Qm) непрерывна вместе со своими производными первого и второго порядков в некоторой окрестности средних арифметических рядов измерений аргументов, и результаты прямых измерений аргументов распределены нормально, то по мере уменьшения их относительных средних квадратических отклонений закон распределения результата XQ косвенного измерения асимптотически приближается к нормальному. Поэтому для определения доверительной погрешности можно воспользоваться интегральной функцией нормированного нормального распределения, если число измерений велико.
[15]
Страницы:
1
2
Подобно основному вопросу философии «До какой степени познаваем мир?», метрология ставит вопрос «До какой степени измеряем мир?, т.е. на сколько точны наши оценки того или иного явления?». В приземленном, бытовом варианте это значит, что, используя какой-то измерительный прибор, мы хотим знать, до какой степени мы можем ему доверять.
Ближе к нашей термометрической тематике. Возьмем рабочий термометр сопротивления. Для рабочих термометров определен допуск, т.е. фактически допустимая погрешность Δ, равная отклонению показаний от стандартной зависимости НСХ. Поэтому критерий годности и разделение на классы не вызывает трудностей. Если термометр в допуске заявленного класса (с учетом неопределенности измерений), то он годен. Его можно подключать к вторичному прибору со стандартной НСХ и погрешность считываемых показаний будет в пределах допуска.
Сложнее обстоит дело с определением погрешности и сортировкой по разрядам образцовых термометров. Их градуировка индивидуальная. Номинальной характеристики для них нет. Чем же отличаются термометры например второго и третьего разряда? Согласно поверочной схеме – доверительной погрешностью.
Привожу выдержку из нового варианта текста поверочной схемы.
2.2.7 В качестве образцовых средств измерений 3-го разряда применяют меры температуры (аппаратуру для реализации реперных точек температурной шкалы, калибраторы температуры), платиновые термометры сопротивления, стеклянные, кварцевые, термоэлектрические термометры и другие, соответствующие по своим метрологическим характеристикам требованиям, предъявляемым к образцовым средствам измерений 3-го разряда.
2.2.8 Доверительные погрешности образцовых средств измерений 3 го разряда при доверительной вероятности 0,95 составляют от 0,02 до 17 °C при линейной зависимости от значения измеряемой величины. (красным здесь и далее выделена возможная опечатка, или ошибка, или вообще не понятная автору вещь)
2.2.9 Образцовые средства измерений 3-го разряда применяют для поверки рабочих средств измерений методом непосредственного сличения в термостате или методом прямых измерений в мерах температуры.
Дополним это информацией непосредственно из графической части схемы (часть 2)
Термометры (2разряд 0-1085 °С; δ = 0,01-0,1 °C) – (передача δм =0,003-0,4 °C) – (3 разряд 0-1085 °С; δ = 0,02-2,0 °C)
Меры температуры (2разряд 0-1085 °С; δ = 0,01-0,1 °C) – (передача δм =0,008-0,03 °C) – (3 разряд 0-1085 °С; δ = 0,05-0,5 °C)
Образцовые платинородий-платиновые термоэлектрические преобразователи (2разряд 300 ÷ 1200 °С; δ = 0,35-1 °C) – (передача δм =0,05-0,1 °C) – (3 разряд 0-1085 °С; δ =
0,35-1 °C)
Образцовые платинородиевые термоэлектрические преобразователи (2разряд 600 ÷ 1800 °С; δ = 0,8-4 °C) – (передача δм =0,05-0,1 °C) – (3 разряд 600-1800 °С; δ =
0,8-4 °C)
Итак, основной метрологической характеристикой образцовых СИ является доверительная погрешность. Что такое доверительная погрешность образцовых средств измерений при доверительной вероятности 0,95? Как она рассчитывается при поверке и может ли она быть достаточным критерием для классификации СИ по разрядам? Начнем с того, что в стандартах на образцовые термопары доверительная погрешность вообще не рассчитывается. Стандарт на образцовые термометры ГОСТ Р 8.571-98 вводит расчет доверительной погрешности как СКО среднего арифметического из трех измерений в реперной точке, приведенное к интервальной оценке с помощью коэффициента Стьюдента. В низкотемпературной области в формулу включена также инструментальная добавка от погрешности измерительной аппаратуры. Можно ли считать, что такая оценка точности характеризует сам термометр? Скорее она характеризует процесс измерения (в основном воспроизводимость температуры реперной точки). Без сомнения, если применить расчет расширенной неопределенности, включающий все возможные влияющие факторы, то мы получим более полную оценку точности результата измерения. Однако, что касается свойств термометра, то даже в такой оценке будет задействована только кратковременная стабильность сопротивления в течение трех измерительных циклов. А ведь она может быть достаточно хорошей как для образцовых, так и для рабочих ТС. Поэтому, следуя данной методике поверки практически из любого ТС можно сделать образцовый термометр, измеряя его сопротивление на прецизионной установке. Получается, что критерий доверительной погрешности не может применяться для разделения термометров и термопар на разряды.
Какая характеристика является определяющей и крайне желательной для образцового СИ при условии его индивидуальной градуировки? Если спросить специалистов поверочных центров то ответ будет: стабильность его индивидуальной градуировочной зависимости за межповерочный интервал в условиях ежедневного термоциклирования. Три цикла градуировки, выполняемые при поверке, не могут быть гарантией сохранения стабильности характеристики в течение года!
Все, что сказано выше кажется очевидным. Почему же никаких изменений в направлении нормирования характеристик образцовых СИ не происходит? Стандарты на технические требования и поверку образцовых СИ будут пересматриваться в ближайшее время. Хочется уже сейчас внести предварительные предложения для разработчиков новых редакций.
1) Нормировать в тех. требованиях стабильность термометра как минимум за 50 циклов охлаждение-нагрев рабочем диапазоне.
2) Нормировать долговременный дрейф характеристики как минимум за 100 ч. выдержки при верхнем пределе температур.
3) При поверке взять за основу расчет расширенной неопределенности результата с формированием полного бюджета входящих стандартных неопределенностей.
4) В бюджет включать стандартную неопределенность, характеризующую дрейф характеристики СИ за межповерочный интервал, определенный по данным предыдущей поверки.
В этом случае расширенная неопределенность будет характеризовать точность конкретного термометра и может быть выбрана как критерий классификации термометров по разрядам в поверочной схеме.
Я предвижу, что многие образцовые термометры сопротивления по этому критерию будут браковаться. Особенно ТС, изготовленные на основе рабочих ЧЭ. С одной стороны это удобно, иметь вибропрочный термометр повышенной точности для использования в термостатах для градуировки рабочих ТС. С другой стороны, конструкция ЧЭ (как правило, это спираль в каналах, заполненных оксидом алюминия) не выдерживает длительные тепловые циклы, и термометр сильно дрейфует. Производство образцовых ТС из рабочих ЧЭ не оптимальный вариант. Фирмы-производители таких СИ должны работать над новой конструкцией ЧЭ.
Недавно в каталоге одной иностранной фирмы я видела целую серию термометров повышенной точности на разные диапазоны температур и с разными защитными корпусами. Метрологические характеристики, нормируемые для таких ТС две: долговременная стабильность сопротивления (за 100 ч) и стабильность при циклическом изменении температуры (50 циклов). Фирма также приводит неопределенность поверки ТС, но уже не как характеристику термометра, а скорее как характеристику своего собственного конкретного оборудования. Для некоторых видов ТС приводится комбинированная оценка – стабильность плюс неопределенность поверки.
Образцовые термометры и термопары используются в каждой поверочной лаборатории для передачи размера единицы температуры рабочим СИ. Излишне говорить, что от их качества зависит точность измерения температуры в научных исследованиях, в быту, на энергетических узлах учета, на производстве, в том числе на особо важных объектах, атомных станциях, реакторах и т.д. Вопрос о точности образцовых СИ, их применении и поверке является важным для всех нас.
Приглашаю специалистов и всех посетителей сайта к дискуссии по поводу качества образцовых СИ и нормирования их характеристик. Все Ваши мнения, замечания, статьи по этой теме будут незамедлительно публиковаться на сайте.
Гл. редактор сайта Моисеева Наталия Павловна
Погрешность и доверительный интервал: в чем разница?
17 авг. 2022 г.
читать 2 мин
Часто в статистике мы используем доверительные интервалы для оценки значения параметра совокупности с определенным уровнем достоверности.
Каждый доверительный интервал принимает следующий вид:
Доверительный интервал = [нижняя граница, верхняя граница]
Погрешность равна половине ширины всего доверительного интервала.
Например, предположим, что у нас есть следующий доверительный интервал для среднего значения генеральной совокупности:
95% доверительный интервал = [12,5, 18,5]
Ширина доверительного интервала составляет 18,5 – 12,5 = 6. Допустимая погрешность равна половине ширины, которая будет равна 6/2 = 3 .
В следующих примерах показано, как рассчитать доверительный интервал вместе с погрешностью для нескольких различных сценариев.
Пример 1: Доверительный интервал и допустимая погрешность для среднего значения генеральной совокупности
Мы используем следующую формулу для расчета доверительного интервала для среднего значения генеральной совокупности:
Доверительный интервал = x +/- z*(s/ √n )
куда:
- x : выборочное среднее
- z: z-критическое значение
- s: стандартное отклонение выборки
- n: размер выборки
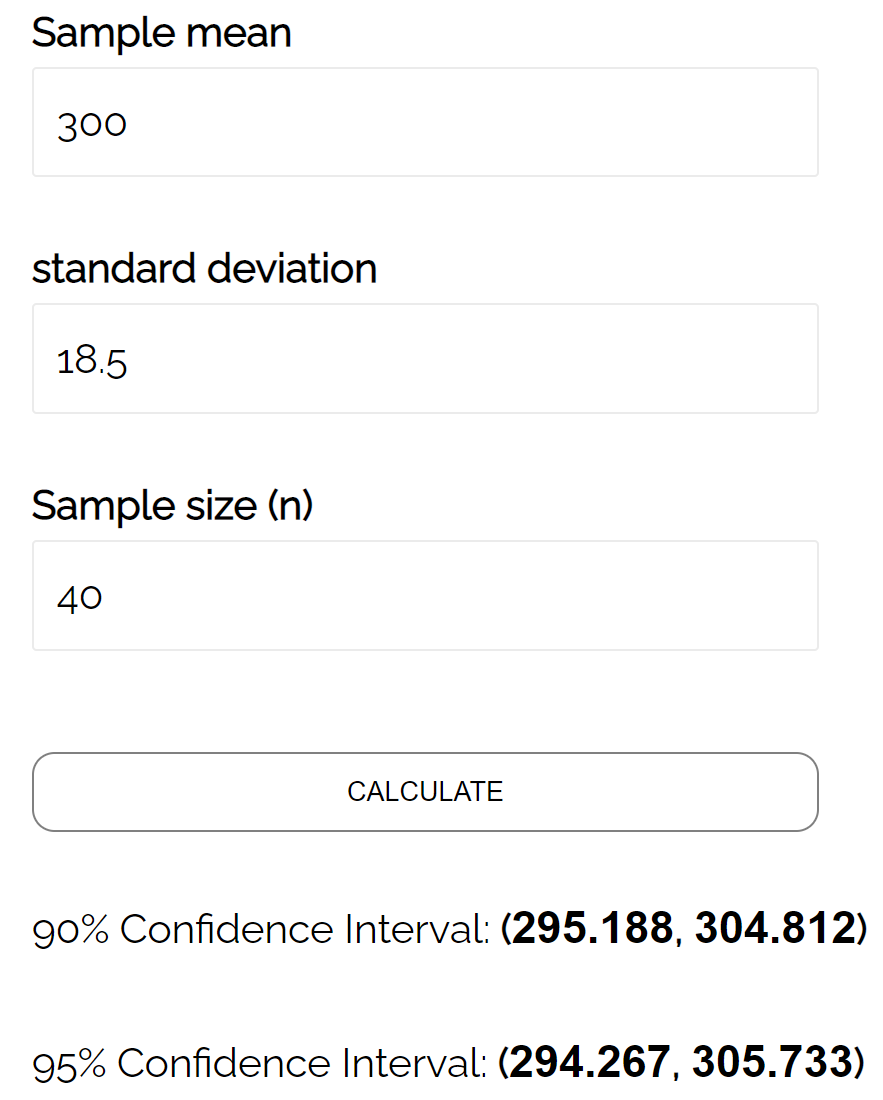
Пример: Предположим, мы собираем случайную выборку дельфинов со следующей информацией:
- Размер выборки n = 40
- Средний вес выборки x = 300
- Стандартное отклонение выборки s = 18,5
Мы можем подставить эти числа в калькулятор доверительного интервала , чтобы найти 95% доверительный интервал:
95% доверительный интервал для истинного среднего веса популяции черепах составляет [294,267, 305,733] .
Погрешность будет равна половине ширины доверительного интервала, который равен:
Погрешность: (305,733 – 294,267) / 2 = 5,733 .
Пример 2: Доверительный интервал и допустимая погрешность для доли населения
Мы используем следующую формулу для расчета доверительного интервала для доли населения:
Доверительный интервал = p +/- z * (√ p (1-p) / n )
куда:
- p: доля выборки
- z: выбранное значение z
- n: размер выборки
Пример: Предположим, мы хотим оценить долю жителей округа, поддерживающих определенный закон. Мы выбираем случайную выборку из 100 жителей и спрашиваем их об их отношении к закону. Вот результаты:
- Размер выборки n = 100
- Доля в пользу закона p = 0,56
Мы можем подставить эти числа в доверительный интервал для калькулятора пропорций , чтобы найти 95% доверительный интервал:
95% доверительный интервал для истинной доли населения составляет [0,4627, 0,6573] .
Погрешность будет равна половине ширины доверительного интервала, который равен:
Погрешность: (0,6573 – 0,4627) / 2 = 0,0973 .
Дополнительные ресурсы
Погрешность и стандартная ошибка: в чем разница?
Как найти погрешность в Excel
Как найти погрешность на калькуляторе TI-84