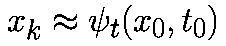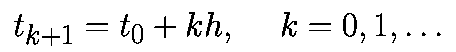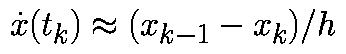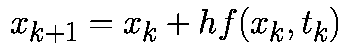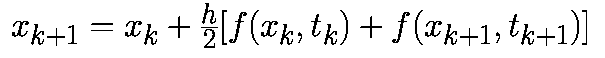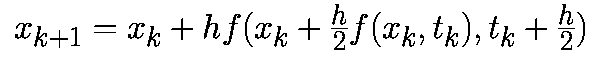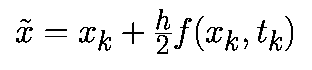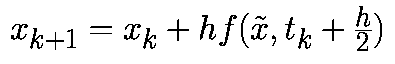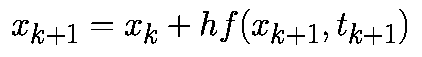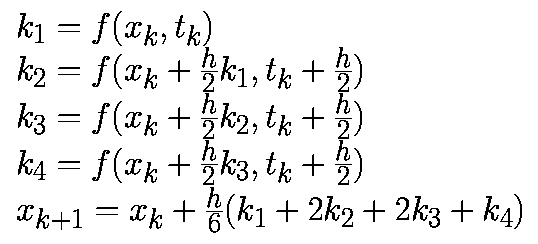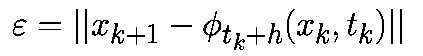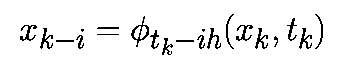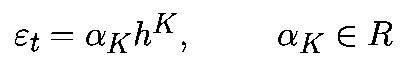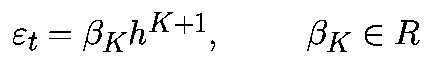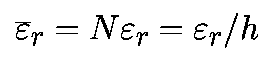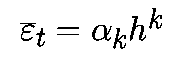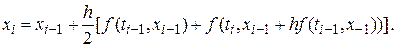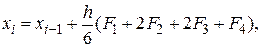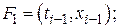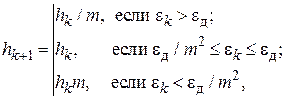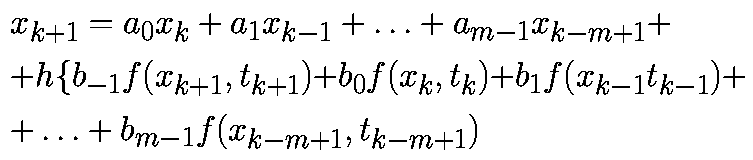Что такое ошибка дискретности

Обычно
в РВ при измерении частоты используют
метод «счёта нулей», который
заключается в подсчёте на определённом
отрезке времени числа импульсов,
формируемых из преобразованного сигнала
(см.подраздел 2.1). Будем определять число
импульсов на интервале Т_M,
поскольку преоб­разованный сигнал
повторяется с периодом модуляции. Пусть
на некото­рой высоте это число
импульсов равно n.
Тогда период разностной частоты

(8)

Предположим,
что дальность плавно увеличивается.
Число импуль­сов n
при этом будет изменяться дискретно,
увеличиваясь на один, затем ещё на один
и т.д. Величина дискрета при определении
числа импульсов n
= 1. В соответствии с формулой (8) это
приведёт к дискретным отсчётам разностной
частоты с величиной дискрета 
F_P
= n
F_M
= F_M
, что приведёт к дискретным отсчётам
дальности через интервал

(9)

Ошибку,
возникающую вследствие дискретного
характера отсчёта дальности (высоты),
называют дискретной или постоянной,
так как при полёте на постоянной высоте
эта ошибка имеет постоянную величину.
На рис. 7 изображена зависимость измеренной
дальности от истинной при наличии
дискретной ошибки.

Минимальное
число импульсов, которое может быть
определено на интервале
Т_M,
равно одному, т.е. минимальная измеряемая
разност­ная частота

F_Pmin
= F_M,
что соответствует минимальной измеряемой
дальности

(10)

Мы пояснили принцип
возникновения дискретной ошибки и
величину минимальной измеряемой
дальности на примере определения
разностной частоты по методу счёта
нулей. Однако природа этого явления
более глубокая — она связана с дискретной
структурой спектра преобразован­ного
сигнала. В случае дискретной структуры
спектра дискретная ошиб­ка имеет
место при любом методе измерения частоты.

В
практике радиовысотометрии разработаны
эффективные методы борьбы с дискретной
ошибкой, которые, в основном, сводятся
к разруше­нию дискретной структуры
спектра.

Вначале
рассмотрим случай, когда самолёт летит
над неровной местностью. Ранее мы пришли
к выводу, что в этом случае спектр
явля­ется сплошным, а преобразованный
сигнал — некогерентным. Число импульсов,
получаемых из преобразованного сигнала,
в каждом периоде мо­дуляции будет
изменяться случайным образом. При этом
дискретная ошиб­ка будет менять знак
и величину по случайному закону. Если
в измери­теле поставить сглаживающую
цепь с постоянной времени 
>> Т_M,
то ошибка станет усредняться. Результат
измерения будет близок к средней высоте
полёта.

Аналогичного
эффекта можно добиться при полёте над
гладкой местностью, если при каждом
новом периоде модуляции изменять
параметры модуляции f
или Т_M
. Тогда отдельные периоды колебаний
передатчика будут некогерентными,
спектры излучаемого и преобразованного
сигналов — сплошными, и дискретная ошибка
будет усредняться в сглаживающих цепях.
Такой метод применяется в РВ А-034, где
за счёт обратной связи в цепи слежения
изменяется длительность рабочего хода
модуляции. В некоторых РВ производят
модуляцию девиации частоты передатчика
по периодическому закону (дополнительную
модуляцию — рис. 8). Это позволяет изменять
величину R
и знак дискретной ошибки при полёте над
ровной местностью, что также приводит
к усреднению дискретной ошибки в
сглаживающих цепях измерителя.

Соседние файлы в папке Методички к лаб

• #
• #
• #
• #
• #
• #

В численном анализе , вычислительной физики и моделирования , ошибка дискретизации есть ошибка в результате того факта , что функция из непрерывной переменной представляется в компьютере с помощью конечного числа оценок, например, на решетке . Ошибка дискретизации обычно может быть уменьшена за счет использования решетки с более мелкими интервалами, что увеличивает вычислительные затраты .

Примеры

Ошибка дискретизации является основным источником ошибок в методах конечных разностей и псевдоспектральном методе вычислительной физики.

Когда мы определяем производную как или , где — конечно малое число, разница между первой формулой и этим приближением называется ошибкой дискретизации.

При обработке сигналов аналогом дискретизации является дискретизация , и она не приводит к потерям, если выполняются условия теоремы дискретизации , в противном случае результирующая ошибка называется наложением .

Ошибка дискретизации, которая возникает из-за конечного разрешения в области, не следует путать с ошибкой квантования , которая представляет собой конечное разрешение в диапазоне (значениях), ни с ошибкой округления, возникающей из арифметики с плавающей запятой . Ошибка дискретизации возникла бы, даже если бы можно было точно представить значения и использовать точную арифметику — это ошибка представления функции ее значениями в дискретном наборе точек, а не ошибка в этих значениях.

Ссылки

Смотрите также

• Дискретность
• Линейный многоступенчатый метод
• Ошибка квантования

Адаптивное построение сетки состоит в том, что после создания расчетной модели и задания граничных условий генерируется конечно-элементная сетка, затем выполняется анализ, оценивается ошибка дискретизации сетки, после чего меняется размер сетки. Процесс протекает до тех пор, пока значение погрешности не станет меньше заданного, или число итераций не достигнет допустимого значения.
 [c.67]

Ошибки дискретизации являются результатом замены реальной теплопроводящей среды дискретными электрическими ячейками. При этом следует иметь в виду, что ошибки в основном возникают в результате ири-менения сосредоточенных емкостей и индуктивностей. Ошибки, связанные с дискретизацией области, определяются шагом сетки и зависят от характера температурного поля. Это может быть легко продемонстрировано с помощью разложения в ряд Тейлора температуры в некоторой точке области. Ошибка дискретизации координат определяется зависимостью
 [c.359]

Шаг сетки Ах явно входит в выражение для ошибки. Если его уменьшить, то ошибка также уменьшится. При Дл —>»0 ошибка также стремится к нулю. Полагая, что члены, включающие производные выше четвертого порядка, пренебрежимо малы, определим ошибку дискретизации области  [c.359]

Эксперименты показывают, что для многих теплотехнических задач разбиение области в направлении одной координаты иа 8—10 элементарных слоев приводит к существенному уменьшению ошибки дискретизации. Это значит, что если (Д л /б) s O,l, то ошибка дискретизации оказывается настолько малой, что ее в ряде случаев можно не учитывать, так как она стремится к нулю.
 [c.359]

Ошибки дискретизации могут быть уменьшены использованием более мелких элементов или расположением криволинейных элементов около границ и, во всяком случае, стремятся к нулю по мере стремления к нулю размера элемента. Ошибки пробной функции не обязательно уменьшаются по мере уменьшения размера элементов и могут поэтому мешать сходимости к точному решению нли даже приводить к расходимости,
 [c.169]

Мы хотим предложить объяснение этого чуда, основанное на нашем наблюдении, что обычное измерение числа обусловленности для этих матриц неестественно. В вычислительных целях мы будем рассматривать эти матрицы как преобразования евклидова пространства (дискретного Ж°) в себя и потому возьмем одну и ту же норму для невязки уравнения и для результирующей ошибки в решении. Это целиком противоположно тому, что делается в дифференциальной задаче, или тому, что происходит при оценке ошибки дискретизации / измеряется в норме пространства Л1 и ее ошибка — в ш и ее ошибка — в Ж. (В вариационной задаче соответственно и Ж .) В самом деле, оператор I = с каким-либо обычным краевым условием вполне обусловлен как преобразование из Ж в Ж°. Ограниченность операторов I и была существенным моментом в разд. 1.2. Можно показать, что это верно и для разностного оператора б , а также для любого приемлемого аналога в методе конечных элементов, если только эти естественные нормы сохраняются. Следовательно, должен быть алгоритм решения уравнения КО, = Р, отражающий это свойство, и тогда чудо развеялось бы ошибки в Л1 и ш соответствовали бы их положению.
 [c.147]

Важный вывод ошибка округления не зависит сильно от степени полиномиального элемента. Главным образом она зависит от h, от порядка рассматриваемой задачи и от основного собственного значения непрерывной задачи. Поэтому при наличии ошибок округления достичь численную точность можно, увеличивая степень пробных функций. Число обусловленности для кубических элементов лишь немного хуже, чем для линейных, так что ошибки округления в этих случаях для заданного значения h сравнимы. Однако ошибка дискретизации для кубических элементов на порядок меньше. Поэтому в переходный момент, когда округления не позволяют получать более точные результаты за счет уменьшения h, с помощью кубического элемента этого можно достичь. Особенно это относится к вычислению напряжений, где дифференцирование (или взятие разностей) перемещений вводит в численную ошибку дополнительный множитель Л». Даже в задачах второго порядка ошибка округления становится значительной и наилучший выход из положения — увеличить степень пробных функций.
 [c.250]

Ошибки дискретизации возникают прн замене реальной конструкции ограниченны числом конечных элементов (с учетом их формы и размеров).
 [c.28]

В (15.3.1-8) не дается никаких оценок ошибки аппроксимации. Для неравномерной сетки (х. Фх , yj Фу 1) ошибка дискретизации уменьшается почти линейно с уменьшением шага. Некоторые идеи, касающиеся выбора подходящего шага с целью существенного ограничения этой ошибки, даются в п. 15.3.1.4. Кроме того, более полно этот вопрос рассмотрен в классической математической литературе [15.58, 15.47].
 [c.406]

Построение разностной сетки. Для того чтобы затраты времени счета и памяти ЭВМ оставались в разумных пределах, необходимо ограничить число узлов сетки. Соответствующий компромисс между точностью и стоимостью вычислительных ресурсов можно найти, оценив ошибки аппроксимации. В критических областях, с большими ошибками дискретизации, шаг сетки должен быть мелким, в то время как в областях, где ошибки невелики, его можно увеличить. Из этих соображений очевидно, что равномерная сетка непригодна, поскольку в этом случае шаг сетки должен был бы подстраиваться под критические области, и число узлов стало бы очень большим.
 [c.409]

Так как ошибки дискретизации зависят от распределения величин ф, п, р, то прием-
 [c.409]

Как уже обсуждалось ранее, скорость ионизации очень чувствительна к напряженности электрического поля. Следовательно, скорость генерации будет иметь в области отсечки канала сильный пик, который можно правильно рассчитать лишь используя очень мелкую сетку. Интеграл от генерационного члена по всей области дает ток через поверхность, и, следовательно, ошибка дискретизации пропорциональна ошибке в вычислении этого тока. Если мы рассмотрим лишь первую производную электрического поля
 [c.411]

Для снижения методической погрешности при использовании моделей средних значений важно осуществить рациональное условное деление конструкции ЭМУ на отдельные элементы, либо увеличить число таких разбиений. Но в последнем случае метод приближается к методу сеток и становится громоздким, в то время как практически важно получение высокой точности расчетов при ограниченной дискретизации. При умелом применении схем замещения методическая ошибка в сравнении с методом сеток составляет обычно не более 5 % даже при ограниченной степени дискретизации. По крайней мере, это заметно меньше, чем погрешности от неточности задания входной информации. При выборе числа разбиений важен и характер решаемой задачи. При грубой оценке показателей поля возможна упрощенная схема замещения с пятью-шестью укрупненными телами (ротора в целом, объединенных обмотки и пакета статора и т.д.). Если необходим анализ изменения осевой нагрузки на подшипники, то особо подробно должны быть представлены тела, входящие в замкнутую размерную цепь их установки, а остальные элементы могут рассматриваться укрупненно. При анализе относительных температурных деформаций требуется наиболее детальная дискретизация ЭМУ, особенно для элементов, имеющих различные коэффициенты линейного расширения. Здесь ТС, например, должна содержать не менее 15—20 тел.
 [c.127]

При получении совмеш,енных изображений в соответствии с уровнем обработки S остаточная среднеквадратическая ошибка регистрации не должна превышать 50% шага дискретизации. Значение этого параметра зависит главным образом от точности работы системы ориентации спутника.
 [c.98]

Поверхность тела представляется при помощи четырехугольных и треугольных элементов с квадратичным изменением формы и линейным, квадратичным или кубическим изменением перемещения и вектора напряжений относительно внутренней системы координат. Тело разбивается на подобласти производится дискретизация интегрального уравнения для каждой подобласти, и получается система уравнений ленточного типа. Для вычисления интегралов используется квадратурная формула Гаусса, число узлов в которой выбирается на основании верхней оценки для ошибки, определенной по значениям производных от подынтегральных выражений. Масштаб коэффициентов в уравнениях выбирается таким образом, чтобы получить устойчивую при счете систему, разрешимую методом исключения без итерации остатков. Поблочное решение уравнений позволяет рассматривать большие задачи. В программе используется большое число процедур, осуществляющих контроль и автоматическое формирование данных. Результаты решения задачи о фланце трубопровода и характеристики выполнения программы сравниваются с результатами, полученными методом конечных элементов, и экспериментальными результатами.
 [c.111]

Здесь штрихом обозначены измеряемые величины, символом 5 — ошибки измерений. Функции Wf t), Wh t) — импульсные переходные функции стационарных линейных фильтров, применяемых при формировании измерений СНС и гравиметра, — оператор свертки фильтра (указанные фильтры необходимы, в частности, для подавления сигнала вне интервала частот Найквиста, с целью исключения явления маскировки частот при дискретизации измерений). Заметим, что в общем случае измерения в (5) проводятся с разной частотой дискретизации.
 [c.136]

При этом следует соблюдать определенную осторожность. Если нестационарные конечно-разностные уравнения сходятся к устойчивому стационарному решению, то еше нельзя считать, что соответствующие дифференциальные уравнения в частных производных имеют устойчивое стационарное решение. Как мы уже видели, дискретизация иногда приводит к появлению схемной вязкости. Эта и другие ошибки аппроксимации могут привести к тому, что конечно-разностные уравнения окажутся более устойчивыми, чем дифференциальные уравнения в частных производных. Выяснение отличия гидродинамической устойчивости от завышенной численной устойчивости представляет трудную задачу (см. разд. 6.5).
 [c.165]

Заметим, что ошибка в г з, обусловленная дискретизацией, приводит к возникновению ошибки при вычислении толщины вытеснения б (Шлихтинг [1968]), если последнюю определять по формуле
 [c.236]

Вычислить локальную ошибку отсеченИя , или дискретизации, с помощью разложения в ряд Тейлора.
 [c.28]

Исследуем ошибки округления двумя способами. Рассмотрим свободно опертую балку с и и М, равными нулю на обоих концах. Тогда уравнения М» = / и гю» = М можно решить отдельно, сначала для М, а затем для ш, применяя для этого либо конечные разности, либо конечные элементы. Предположим, что приближенное решение задачи М» = / содержит ошибку округления еь обычно порядка для ЭВМ с длиной слова 1. Тогда приближенное решение задачи т» = —/ будет прежде всего содержать свою собственную ошибку округления е2 того же порядка и, кроме того, унаследованную ошибку ез. Последняя удовлетворяет равенству ез = Ъх, или, скорее, точно удовлетворяет используемой дискретизации этого уравнения, и потому порядок ошибки ез также равен Ошибки округления не объединяются в
 [c.146]

При втором способе получаются правильные величины скоростей, но в результате дискретизации вносится ошибка в величины г )1,/. Очевидно, что оба эти способа сходятся при Ау- 0. Поскольку наибольшее влияние на динамику течения оказывает и, а не г1), второй способ, заключающийся в задании во входном сечении потока профиля для и при допущении ошибок в величинах г , кажется предпочтительнее.
 [c.236]

Требования к отношению сигнал-помеха в канале передачи ИКМ сигнала (канала записи — воспроизведения) невысоки, поскольку необходимо передать лишь два уровня сигнала — О и 1. Нелинейные искажения, возникающие в этом канале, практически не оказывают существенного влияния на восстановленный сигнал. Точность передачи сигналов с ИКМ зависит от параметров аналого-цифрового преобразования (АЦП)— частоты дискретизации и шага квантования. Для неискаженной передачи частота дискретизации /д в соответствии с теоремой Котельникова должна по крайней мере вдвое превышать высшую частоту Fb передаваемого аналогового сигнала. Шаг квантования определяет максимальную погрешность восстановленного сигнала и характеризует ошибки квантования, которые проявляются как шум квантования . Шаг квантования связан с числом уровней
 [c.21]

Ошибки могут возникать на различных стадиях конечно-элементного анализа пр постановке задачи, дискретизации (построении модели), численном решении.
 [c.28]

Адаптивное построение сетки. Адаптивное построение сетки состоит в том, что после создания модели и задания граничных условий программа генерирует конечноэлементную сетку, выполняет расчет, оценивает ошибку за счет сеточной дискретизации и меняет размер сетки от решения к решению до тех пор, пока расчетная погрешность не станет меньше некоторой наперед заданной величины (или пока не будет достигнуто установленное число итераций).
 [c.92]

Для каналов первого класса принята частота дискретизации 21 1/3 кГц, второго класса — 14 2/9 кГц, высшего класса — 32 кГц. В каналах высшего класса применено 10-разрядное кодирование с мгновенным компандированием, в каналах первого и второго классов — 9-разрядное. Таким образом, скорость цифрового потока при организации канала высшего класса составляет 320 Кбит/с, первого класса — 192 Кбит/с и второго класса — 128 Кбит/с. В первичном цифровом потоке 2048 Кбит/с в системе Орбита-Рв передаются 10 каналов первого класса, либо 15 каналов второго класса, либо 6 каналов высшего класса. Всего для сигналов ЗВ выделяются два потока по 2048 Кбит/с. В системе использовано помехоустойчивое кодирование, обеспечивающее допустимую при цифровой передаче вероятность ошибки poш=10- .
 [c.314]

При применении прямых методов получение достаточно точных решений связано с решением больших систем уравнений, решение которых затруднено из-за ограниченных возможностей вычислительных машин (память, быстродействие, ошибки округления). Поэтому при составлении программ решения больших систем линейных алгебраических уравнений, полученных при дискретизации вариационных задач, стремятся учесть особый вид магриц таких систем например, их малую заполненность, ленточную структуру и т. д. Такие системы можно решать на ЭВМ точными методами (Гаусса, Жордана), если использовать внешние запоминающие устройства и применять специальные приемы, направленные на экономию памяти и времени счета, например блочный метод Гаусса.
 [c.180]

Штриховая кривая 1 на жс. 4.6 соответствует интегрированию уравнений продолжения модифицированным методом Эйлера с шагом АХ по параметру X, который на начальном участке деформирования при малых Р соответствовал приращению относительного прогиба w(0)/i = 0,005. Штрихпунктирная кривая 2 совтветствует тому же методу, но с шагом w(0)/R = 0/)( 5. Сплошная кривая 3 получена прт комбинировании двух шагов w 0)fR = 0,005 модифицированного метода Эйлера с одним шагом по неявной схеме дискретного продолжения, описанной в ЗА. Эта кривая практически соответствует точному решению задачи (4.3.2), (4.3.3) (конечно, в пределах принятой дискретизации). Как видно из жс. 4.6, модифицированный метод Эйлера дает накопление ошибки, особенно существенное в тех областях параметра, где решение претерпевает значительные изменения. В то же время расход машинного времени при получении кривых 2 и 3 практически одинаков (даже для кривой 5 он был несколько меньшим). Поэтому для всех дальнейших расчетов бьша использована именно такая комбинация непрерывного и дискретного продолжения.
 [c.120]

Для вычисления ДПФР, кроме матрицы bi k, I), определяющей комплексную амплитуду поля на объекте, необходимо еще задаться и величинами и и v, характеризующими относительные размеры объекта, наблюдаемого из воображаемой точки регистрации голограммы. При их выборе следует руководствоваться условиями (1.46) малости ошибки при дискретизации фазовых множителей.
 [c.21]

Численные эксперименты показали, что скорость сходимости итерационного процесса в смешанных задачах слабо зависит от степени дискретизации. Рассматривалась, например, следующа краевая задача [121] для единичного куба на центральной части граней куба, размером 0,8X0,8, задавались перемещения, а на остальной части куба — усилия, соответствующие гидростатическому сжатию. Граничная поверхность разбивалась на 96, 216 н 600 граничных элементов. Исследовался стационарный итерационный процесс (4,2) для дискретного уравнения (2,31) при р=1 и Р = 2, Для первой дискретизации при р=1 отклонение искомы поверхностных сил от точного решения на первой итерации составило 65%, на шестой — 7,5%, на одиннадцатой — 0,9%, Для остальных дискретизаций (216 и 600 граничных элементов) ошибка в 1 % была достигнута соответственно на тринадцатой и четырнадцатой итерациях. При р = 2 итерационный процесс (4,2) сходился значительно быстрее для первой дискретизации (96 гра ничных элементов) отклонение искомых поверхностных сил от точного решения на первой итерации составило 31, %, на второй-— 9%, на третьей —2,6 %, на четвертой — 0,86 % для остальньис дискретизаций (216 и 600 граничных элементов) ошибка в 1 % была достигнута соответственно на пятой и шестой итерациях.
 [c.239]

Базис Каруиепа — Лоэва не отвечает требованиям универсальности (т. е. применимости для достаточно широкого класса сигналов), устойчивости к ошибкам задания статистических характеристик сигнала и требует больших вычислительных затрат при реализации. Поэтому имеет смысл ставить задачу выбора не формально оптимального, а рационального базиса в (1.21), (1.22), удовлетворяющего указанным требованиям. Однако удовлетворить всем требованиям одновременно невозможно. На практике используются различные виды дискретизации [12]. Из них рассмотрим наиболее часто используемые при обработке сигналов аналитических приборов.
 [c.20]

Максимум ошибки всегда достигается на конце большой полуоси эллипса. Поэтому возникла гипотеза, что большая часть ошибки описывается геометрическими причинами — тем, что последовательность точек дискретизации, равномерная в стандартной координате на эллипсе, описывает эллипс неточно (с точки зрения вычислительного метода). Была найдена геометрическая характеристика, с которой ошибка хорошо коррел-лировала. Это отношение кривизны эллипса в вершине к кривизне окружности, проведенной через нее и еще две соседние точки дискретизации. Так, при отношении, близком к двум, ошибка достигала 16%, к трем — 19%. Наличие геометрического описания ошибок позволяет надеяться, что при более удачной расстановке точек на контуре трещины можно ожидать значительного уменьшения ошибок. Действительно, удалось найти геометрический критерий расстановки точек на контурах, позволяющий минимизировать ошибки вычислений (точнее максимум ошибки в точках контура трещины). Точнее, если расстановка точек удовлетворяла этому критерию, то соответствующая ошибка не более чем в 1,5 раза превышала минимально возможную. Опишем здесь результат оптимизации метода.
 [c.195]

Погрешности реконструкции в основном обусловлены неидеальностью используемых аппроксимаций алгоритма реконструкции. Среди наиболее существенных источников пофешностей реконструкции следует указать ошибки, возникающие из-за недостаточно малого интервала дискретизации по углу, пофешности неоптимальной интерполяции и двумерной дискретизации томофаммы, чрезмерный уровень низкочастотной фильтрации реконструированных структур из-за попытки компенсации отмеченных пофешностей снижением высокочастотных компонент ядра свертки или двумерной фильтрацией реконструированных томофамм.
 [c.150]

Общая идея постановки граничных условий, отвечающих бесконечности на наиболее удаленной границе разностной сетки, была предложена Ричардсоном [1910]. Кавагути [1965], Фридман [1970], а также Ли и Фын [1970] в выходном сечении брали, например, профиль Пуазейля. Заметим, что асимптотическое решение, используемое в качестве граничного условия, должно рассматриваться в переменных задачи-, например, если конечно-разностные уравнения записаны в переменных г]) и то и решение Пуазейля должно быть записано для ф и Если и задается по имеющемуся решению дифференциальных уравнений, а ф находится при помощи квадратур, то при этом возникает ошибка в результатах, обусловленная дискретизацией (аналогичная ситуация возникает и в случае постановки условий на входной границе потока см. предыдущий раздел). Для течений более общего вида, например таких, как асимптотическое течение в пограничном слое, решение дифференциальных уравнений будет отличаться от асимптотического конечно-разностного решения по всем переменным. На выходной границе предпочтительнее брать конечно-разностное решение асимптотического обыкновенного дифференциального уравнения (Кавагути [1965]).
 [c.237]

Заметим, что вычисление аппроксимации Ритца предполагалось непрерывньш по времени-, до сих пор лишь дискретизация заменяла все допустимое пространство его подпространством 5 . Это соответствует изложению задачи Коши в гл. 7, где ошибки метода» Ритца отделены от ошибок метода конечных. разностей (или другого метода) по временному направлению. Для нелинейной задачи большие дискуссии вызвал наилучший метод приращений , но мы полагаем, что все основные возможности сходятся в одном. Они просто вносят новую ошибку, пропорциональную степени приращения в случае разностного уравнения.
 [c.138]

В практических задачах времт тоже должно быть дискретизировано, что предполагает применение метода конечных разностей. Например, схема- Кранка — Николсона симметрична относительно п+1/2 при вычислении uf tn+ ) через и потому имеет точность порядка At . Таким образом, окончательно вычисленное приближение содержит эту ошибку, как и ошибку метода Галёркина, вызванную дискретизацией по х. Последнюю из них мы проанализируем подробно и покажем, что при к 2т ее оптимальный порядок для 5-й производной тоже р -вен Этот результат применяется к уравнениям параболического типа, например к уравнению теплопроводности Ь — эллиптический оператор того же типа, что и в стационарных задачах. В случае гиперболических уравнений, не содержащих диссипативных членов, возможности метода конечных элементов несколько меньше трудности в сравнении с явными разностными методами- могут оказаться слишком большими. Тем не менее даже в этом случае достигнуты значительные результаты исследование границ можно проводить почти автоматически в гл. 7 включен набросок теории метода конечных элементов для гиперболического случая.
 [c.139]

Естественно спросить почему конечные элементы не используются также и по временной переменной Конечно, можно было бы попытаться применить их, но это не даст особого успеха. С математической точки зрения вполне разумно изучить дискретизацию в два этапа сначала исследовать ошибку метода конечных элементов и(х, i) —u (x, t], а затем ошибку в возникающую при решении обыкновенных дифференциальных уравнений. По временной переменной геометрия области не вызывает трудностей, которые надо было бы преодолевать с помощью метода конечных элементов, и на самом деле непосредственное применение принципа Галёркина может связать все временные слои и уничтожить главное свойство распространения вперед по. времени. Мы не видим причин отказываться от этой дополнительной гибкости конечных разностей.
 [c.282]

Моделирование позволило отметить некоторые особенности аналогового вычисления суммарного изображения Это, прежде всего, отсутствие регистрации проекций, которое позволяет избежать погрешностей их съема и ввода в ЭВМ, т. е в этом случае восстанов тение искомого распределения осуществляется в отсутствие шумов При моделировании указанная особенность томографической Интерферометрии учитывалась Однако при реализации некоторых математических операций в оптических системах с преобразованием волнового фронта возможно их неточное выполнение из-за аберраций оптических элементов и погрешности юстировки. В томографическом интерферометре искажения, обусловленные аберрациями, устранялись голографической регистрацией волнового фронта. Возможная ошибка ( 30 ) из-за неточности согласования углов зондирования и поворота волнового фронта была равна погрешности из-за дискретизации проекций при цифровом вычислении суммарного изображения на сетке 51X51 отсчетов
 [c.138]

Форматы кодов у устройств разного назначения существенно различны, поскольку у них не совпадают законы кодирования, способы защиты от ощибок, число звуковых каналов, характер и объем дополнительной информации. Так, у студийной аппаратуры определяющими факторами являются высокое качество передачи и возможность введения дополнительной служебной информации (адресно-временного кода для монтажа программ, режиссерских комментариев и т. д.). Результирующая скорость цифрового потока больщой роли не играет, поскольку специфика работы студийной аппаратуры не связана с передачей этих потоков по каналам связи. Поэтому в таких устройствах применяют равномерное квантование с числом разрядов не менее 16 (в пультах и устройствах шумоподавления число разрядов на отсчет доходит до 24) и высокую частоту дискретизации (48 кГц). Избыточность, вводимая для борьбы с ошибками, достигает 33%, а управляющие сигналы, осуществляющие перестройку системы обработки сигнала, и адресно-временной код передаются совместно со звуковыми.
 [c.238]

---

Локальная и глобальная ошибки дискретизации при численном интегрировании дифференциальных уравнений

последовательностью точек x₀,x₁. в соответствующие моменты времени t₀,t₁. Значения точек должны удоволетворять приближенному равенству

Если специально не оговорено иное, то предполагается, что моменты времени выбираются через равные интервалы с величиной шага h>0, то есть

Аппроксимируем производную в момент времени t_k соотношением

При такой аппроксимации уравнение (1) примет вид:

Формула (2) известна как прямой метод Эйлера.

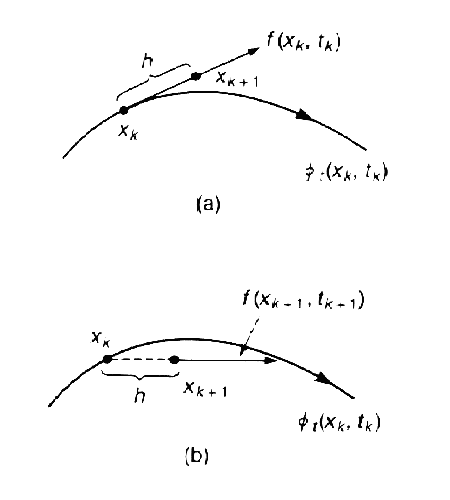
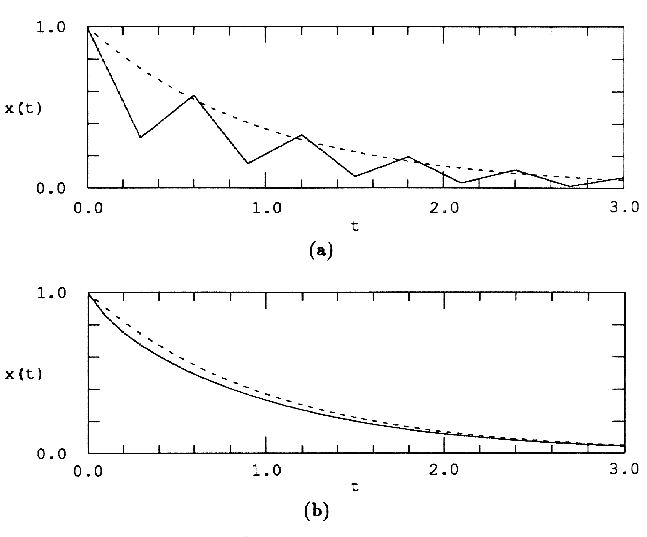
На рис.1(a) показана графическая интерпретация прямого метода Эйлера. На (k+1)-ом шаге векторное поле предполагается (локально) постоянным со значением f(x_k,t_k).

Рис.1 Иллюстрация алгоритмов (а) прямого метода Эйлера, (b) обратного метода Эйлера

Меньшее значение величины шага h в итоге дает точки аппроксимации чаще и, как демонстрирует рис.2, приводит к большей точности интегрирования, что приобретает математический смысл, поскольку (2) стремится к (1) при h->0.

Рис.2 Влияние величины шага. Уравнение dx/dt=-6x+5t -t интегрируется от x=1 прямым методом Эйлера при h=0.3 (а) и при h=0.1 (b). Точное решение показано штриховой линией.

Обратный метод Эйлера подобен прямому, но есть одно отличие в аппроксимации для производной

Такая аппроксимация дает формулу обратного метода Эйлера:

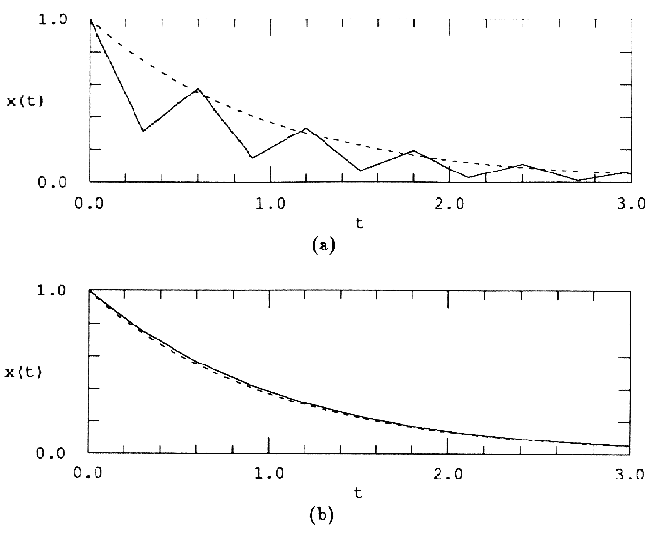
На рис.1(b) показана геометрическая интерпретация обратного метода Эйлера. На (k+1)-ом шаге векторное поле предполагается (локально) постоянным со значением f(x_k+1,t_k+1).

Обратный метод Эйлера — это пример неявного алгоритма интегрирования , где x_k+1 является функцией от самой себя. И напротив, прямой метод Эйлера представляет собой явный алгоритм. В неявных алгоритмах для определения x_k+1 требуются дополнительные вычисления, но они по сравнению с аналогичными прямыми алгоритмами более устойчивы и дают более высокую точность вычислений (см. рис.3). Возможно это обусловлено наличием члена x_k+1 в правой части формулы, что может рассматриваться как вид обратной связи.

Рис.3 Та же система, что и на рис.2 проинтегрирована от x₀=1.0 с h=0.3 (a) прямым методом Эйлера, (b) обратным методом Эйлера. Точное решение показано штриховой линией.

Трапецеидальный алгоритм имеет вид:

Имеется целое семейство уравнений Рунге-Кутта второго порядка. Мы рассмотрим модифицированный алгоритм Эйлера-Коши, заданный соотношением:

Из этой формулы следует, что модифицированный алгоритм Эйлера-Коши включает два этапа. На первом этапе с помощью прямого метода Эйлера происходит перемещение на пол шага вперед к моменту времени (t_k+h/2):

На втором этапе это промежуточное значение используется для аппроксимации векторного поля с помощью итераций Эйлера прямого типа:

Как и в случае алгоритма второго порядка метод Рунге-Кутта четвертого порядка относится к явным алгоритмам. Он использует промежуточные моменты времени для для вычисления состояния в момент времени t_k+1. Следующие формулы определяют алгоритм Рунге-Кутта четвертого порядка:

Для определенных выше алгоритмов на каждом шаге требуется только одна начальная точка x_k. Такие алгоритмы называются одношаговыми. Одношаговые алгоритмы высокого порядка имеют высокую точность, но они не эффективны, если велики затраты на вычисление f. Например, алгоритм Рунге-Кутта четвертого порядка требует на шаге четыре значения f. Кроме того, на текущем шаге не выполняются оценки функций с целью их использования на последующих шагах.
В отличие от одношаговых алгоритмов, многошаговые алгоритмы повторно используют предыдущую информацию о траектории. В m-шаговом алгоритме для определения x_k+1 используют m предыдущих точек x_k, x_k-1. x_k-m+1 и значения f в этих точках. Общая формула m-шагового алгоритма имеет вид

Локальная ошибка определяется как ошибка на шаге алгоритма:

Для m-шаговых алгоритмов предполагается, что предыдущие m точек x_k-i при i=0. m-1 являются точно заданными, т.е.

Ошибка усечения — это локальная ошибка, которая получилась бы в результате выполнения алгоритма на компьютере с бесконечной точностью.
Другими словами, подразумевается, что эта локальная ошибка возникает помимо ошибки округления. Также важно помнить, что для m-шаговых алгоритмов предыдущие m точек x_k. x_k-m+1 предполагаются точно заданными.
Ошибка усечения берет свое название от алгоритмов, основанных на рядах Тейлора (например, Рунге-Кутта). Эти алгоритмы были бы точными, если бы использовались полные (бесконечные) ряды. Ошибка возникает при усечении ряда до конечного числа членов.
Ошибка усечения зависит только от алгоритма. Она не зависит от используемого компьютера и, следовательно, может быть проанализирована. Для алгоритмов Рунге-Кутта K-го порядка, при подходящих условиях, локальная ошибка усечения представляет собой

где «альфа» зависит от K, f и x_k, но не зависит от h. Для многошагового алгоритма K-го порядка локальная ошибка усечения имеет вид

Глобальнае ошибка округления — это простое накопление локальных ошибок округления. Если локальная ошибка составляет «эпсилон», то ошибка округления на единичном интервале будет

Подобно ошибке округления, локальная ошибка усечения также накапливается с каждым шагом. Для одношаговых алгоритмов K-го порядка локальная ошибка усечения составляет

Если пренебречь зависимостью a_k от x_k, то на единичном интервале времени ошибка усечения будет:

Порядок метода интегрирования.

Дата добавления: 2015-06-12 ; просмотров: 3180 ; Нарушение авторских прав

Главный вопрос при использовании любого численного метода состоит в оценке точности приближенных вычислений 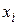. В разд. 3.2.1 уже отмечалось, что существуют два источника погрешности при выполнении шага интегрирования:

· ошибка дискретизации, возникающая в результате замены дифференциального уравнения (3.1) разностной аппроксимацией (3.2);

· ошибка округления, накопившаяся при выполнении арифметических операций.

При этом доминирующей является, как правило, ошибка дискретизации.

Будем считать, что все вычисления проводятся точно. Интуитивно ясно, что при 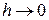ошибка дискретизации также должна стремиться к нулю и это действительно имеет место для любого метода. Однако взаимосвязь скорости уменьшения ошибки от скорости уменьшения для разных методов интегрирования различна.

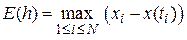
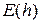
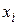
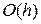
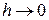
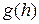
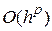
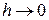
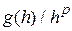
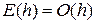
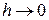
Введем величину , называемую глобальной ошибкой дискретизации. Отметим, что зависит от величины шага, поскольку предполагается, что значения вычисляются при определенном . Воспользуемся также стандартным обозначением для величины, стремящейся к нулю при с той же скоростью, что и . В общем случае будем говорить, что функция равна , если при величина ограничена. Проведя анализ можно показать [23], что для метода Эйлера . Это, обычно, выражают утверждением, что метод Эйлера имеет первый порядок. Практическим следствием этого факта является то, что при уменьшении приближенное решение будет все более точным, и при будет сходиться к точному решению с линейной скоростью по , т.е. при уменьшении шага вдвое ошибка дискретизации уменьшится примерно в 2 раза. Столь медленная сходимость служит препятствием использования простых методов первого порядка.

Очевидно, что повышение порядка метода позволяет повысить точность интегрирования при той же величине шага интегрирования . Способы повышения порядка могут быть различными.

Рассмотрим, например, явный одношаговый метод Хьюна (или метод Рунге – Кутты второго порядка). Он определяется формулой

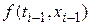
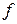
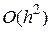
Сравнивая его с методом Эйлера легко заметить, что значение заменено на среднее значений функции , вычисленных в двух различных точках. Данный метод имеет ошибку дискретизации .

Наиболее знаменитым из методов Рунге – Кутты, а возможно и из всех методов численного интегрирования, является классический метод четвертого порядка, задаваемый формулой

где

;

;

.

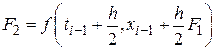
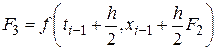
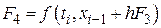
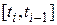
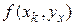
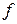
Суть метода в том, что вектор-функция правых частей системы ОДУ определяется не только в узлах сетки, но и в промежуточных точках интервала , а величина в методе Эйлера заменена на взвешенное среднее значений , вычисленных в четырех различных точках.

Как видно, повышение порядка метода связано с повышением затрат на вычисление значений функции 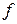. При нелинейной связи между ростом точности метода и объемом вычислений можно ожидать, что для каждой схемы интегрирования существует некоторый оптимальный порядок метода.

Для многошаговых методов порядок напрямую связан с объемом информации, используемой на каждом шаге. В частности, двух и трехшаговые методы Адамса – Бишфорта, задаваемые формулами (3.10) и (3.11) имеют второй и третий порядок, соответственно.

3.2.6. Процедуры численного моделирования
с автоматическим выбором шага

Данный раздел касается не выбора того или иного метода интегрирования, а реализации самой процедуры интегрирования на ЭВМ.

Выше уже отмечалось, что выбор шага интегрирования связан с динамическими свойствами моделируемого объекта. Для явных методов он должен быть меньше минимальной постоянной времени объекта, с тем, чтобы обеспечить устойчивость и позволить моделировать самые высокочастотные составляющие процесса. Неявные методы позволяют использовать больший шаг, но общий характер зависимости остается тем же самым. В то же время, на интервале моделирования характер моделируемых процессов может меняться. Например, в большинстве реальных систем высокочастотные составляющие переходного процесса затухают быстрее, чем низкочастотные, и процесс со временем приобретает более плавный характер. Это наводит на мысль организовать процедуру моделирования таким образом, чтобы шаг интегрирования менялся в процессе работы алгоритма. Там, где решение меняется плавно, можно вести интегрирование с относительно большим шагом. В областях же, где решение изменяется резко, необходимо считать с маленьким шагом. Проблема заключается в том, как определить величину шага, с которым следует начать следующий шаг интегрирования.

На выбор шага, как обычно влияют два фактора – точность и устойчивость. Шаг целесообразно поддерживать таким, чтобы погрешность интегрирования не превышала допустимого значения и величина шага при этом была максимально возможной.

Обычный подход состоит в оценке локальной ошибки дискретизации и, в зависимости от ее величины, уменьшении или увеличении текущего значения шага.

Два простых способа состоят либо в прохождении последнего шага интегрирования с половинным шагом и сравнении двух полученных результатов, либо в использовании двух методов интегрирования, имеющих разный порядок. Оба эти способа требуют дополнительных вычислений значений .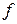

Первый способ реализует правило Рунге [29, 23], при котором ошибка дискретизации определяется по формуле

,

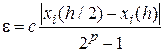
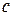
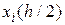
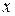
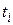
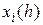
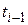
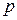
где – некоторая константа;

– значение фазовой переменной , полученной в точке тем же методом, что и , но только за два шага интегрирования от точки , каждый из которых в два раза меньше обычного шага ;

– порядок метода интегрирования.

Для метода Эйлера формула Рунге дает

,

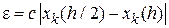
для метода Рунге – Кутты 4-го порядка

.

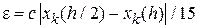
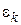
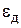
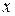
Величина погрешности аппроксимации на каждом шаге не должна превышать допускаемой погрешности . Обычно полагают, что она составляет от 0,01 до 0,001 от текущего значения определяемой фазовой координаты .

При автоматическом выборе шага наиболее популярным является алгоритм «трех зон» [29]:

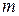
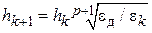
где – коэффициент изменения шага, обычно равный 2, позволяет дискретно менять шаг в процессе интегрирования. Другим вариантом является алгоритм плавного изменения шага интегрирования

,

где 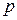– порядок метода интегрирования.

3.2.7. Особенности численного интегрирования
технических систем

Обширный набор методов численного интегрирования, которым обладают современные пакеты моделирования, позволяет эффективно решать самые различные задачи исследования технических систем, но при этом возникает проблема выбора наиболее подходящего метода
и правильного задания его параметров. Очень часто пользователь задает только интервал интегрирования и не обращает внимания на другие опции решателя. При решении простых задач с умеренной точностью такой подход вполне допустим, однако при решении сложных задач неудачный выбор метода либо неправильное задание его параметров может привести к неоправданно большим затратам машинного времени либо, вообще, к невозможности получить правильное решение.

Таким образом, для профессиональной работы с любым моделирующим программным обеспечением пользователь должен обладать некоторыми знаниями о реализованных в нем численных методах
и применимости их к требуемому кругу задач.

Практика показала, что наличие в технических системах объектов различной физической природы приводит к тому, что процессы в них характеризуются разнотемповостью, т.е. наличием быстрых и медленных составляющих движения. Кроме того, возможно одновременное присутствие как монотонных, так и медленно затухающих гармонических составляющих. Свойство системы содержать в своем переходном процессе существенно различные по своим спектральным характеристикам составляющие принято называть жесткостью[27].

Примером жесткой системы может служить робототехническая система, в которой быстрые составляющие связаны с включением тормозных устройств и демпферов, взятием или освобождением груза.

Жесткость часто является следствием избыточности модели, связанной с введением в нее малозначащих составляющих. Однако на этапе предварительных исследований такой избыточности трудно избежать. С другой стороны, часто жесткость имеет принципиальный характер и неучет быстрых движений может привести к неадекватности модели.

Жесткие системы требуют особого подхода к процедуре численного интегрирования, так как наличие быстрых и медленных составляющих в спектре движений предъявляет совершенно разные требования к методам интегрирования. Необходимо уметь оценивать характеристики жесткости и использовать эти оценки для выбора или настройки процедуры интегрирования.

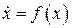
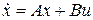
Пусть исследуемая система является линейной и может быть описана матричными уравнениями состояния

.

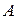
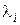
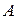
Матрица называется матрицей состояния или матрицей Якоби. Собственные значения матрицы определяют устойчивость и характер переходных процессов в исследуемой системе.

Составляющие движения (обычно называемые модами), связанные с собственными значениями 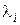, лежащими в левой полуплоскости далеко от мнимой оси, соответствуют быстро протекающим и, обычно, быстро затухающим процессам в системе. Собственные значения малые по модулю, лежащие близко к мнимой оси, определяют основное движение системы.

Исходя из распределения собственных значений матрицы Якоби на комплексной плоскости, можно назвать жесткой системой ОДУ такую систему, у которой матрица Якоби имеет различающиеся на несколько порядков максимальное и минимальное по модулю собственные значения.

Оценкой жесткости системы ОДУ обычно считается число обусловленности матрицы Якоби

,

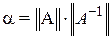
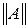
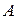
где – норма матрицы .

Для целей управления процессом моделирования под числом обусловленности чаще понимают отношение модулей максимального и минимального собственных значений матрицы

.

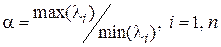
К жестким относят системы ОДУ, у которых 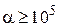. Их также называют плохо обусловленными, хотя, чаще, этот термин относится к системам алгебраических уравнений.

Для нелинейной системы матрицу Якоби можно определить после ее линеаризации в рабочей точке, как это описано в разд. 3.2.2.

Элементами матрицы Якоби являются частные производные от
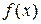
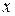
нелинейной вектор функции по переменным состояния системы . Для нелинейных систем жесткость, в общем случае, не является постоянной величиной и меняется в процессе интегрирования.

При умеренных значениях числа обусловленности 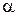(нежесткие задачи) интегрирование обычно выполняется традиционными явными методами и требует небольших вычислительных затрат. Трудности возникают при больших значениях , когда для получения правильного решения бывает необходимо выбирать очень малый шаг интегрирования.

При моделировании такой системы в начальный момент времени инициируются все, или большинство мод, как быстрых так и медленных. Однако через некоторое время быстрые моды затухают и решение сходится к медленному движению.

Исследователя могут интересовать и быстрые и медленные составляющие движения. В этом случае, целесообразно использование явных методов в сочетании с эффективной процедурой изменения величины шага интегрирования в зависимости от состояния моделируемой системы. Это позволит достаточно точно смоделировать быстрые движения и избежать чрезмерных затрат машинного времени, так как явные методы требуют минимальных временных затрат на каждый шаг интегрирования.

Если исследователя мало интересуют быстро затухающие движения, но отбросить их на этапе формирования модели у него нет достаточных оснований, предпочтительными являются неявные методы, которые в сумме способны дать меньшее время интегрирования при удовлетворительном качестве. Такие методы подавляют все составляющие решения, соответствующие большим по модулю собственным значениям (если только шаг не выбран очень малым).

Изложенные рекомендации по выбору методов интегрирования жестких систем предполагают, что исследователь хорошо знаком с особенностями объекта. Например, если речь идет о проектировании или оптимизации системы управления некоторого хорошо изученного объекта, то выбор метода интегрирования может быть проведен путем сравнения нескольких вариантов. Если же объект недостаточно исследован, то эффективными могут оказаться процедуры, обладающие элементами адаптации к особенностям объекта.

Некоторые современные моделирующие программные комплексы содержат наборы методов, расчетные формулы которых настраиваются на решаемую задачу, используя для этого оценки некоторых параметров, обычно, собственных значений якобиана. Особенно перспективными считаются явные адаптивные методы, не требующие при своей реализации вычисления матрицы Якоби и решения алгебраических уравнений [27]. Такие методы есть, в частности, среди решателей ОДУ программного комплекса «МВТУ».

3.3. Моделирование гибридных (событийно-управляемых)
технических систем

Технические системы, по определению, относятся к сложным техническим системам. Одной из особенностей этих систем является то, что поведение многих из них определяется событиями, происходящими как внутри этих систем, так и в окружающей среде. Соответственно, они обладают как непрерывной, так и дискретной динамикой, находящимися в сложном взаимодействии. Подобные системы часто называют гибридными системами [20, 21]. В отечественной литературе также используются синонимы – непрерывно-дискретные, системы с переменной структурой, реактивные, событийно-управляемые.

Примерами гибридных технических систем могут служить системы управления, используемые в промышленности (автоматизированные технологические процессы), в быту (сложные бытовые приборы), в военной области (высокотехнологичные виды вооружений), в сфере космонавтики, транспорта и связи.

Гибридное поведение может быть связано со следующими факторами:

· совместное функционирование непрерывных и дискретных объектов. Подобное поведение является типовым для непрерывных объектов (механических, гидравлических и т.д.) управляемых цифровыми регуляторами, например, для ИСЗ. Управление может формироваться как в фиксированные моменты времени, так и асинхронно, в зависимости от изменения фазовых координат объекта;

· гибридное поведение, связанное с особенностями физических процессов в непрерывных объектах. Например, учет в моделях механических систем таких эффектов как сухое трение или люфт может быть реализован в виде некоторых логических условий, меняющих модель системы;

· гибридное поведение, обусловленное изменением состава системы.

Все перечисленные факторы являются типичными для технических систем.

Учет дискретной динамики приводит к тому, что фазовое пространство гибридных систем разбивается на области с различным поведением, при этом фазовая траектория в зависимости от происходящих событий оказывается то в одной области фазового пространства, то в другой. Достижение фазовой траекторией границы областей является событием, приводящим к смене поведения.

События могут быть как внутренними, так и внешними. Например, при моделировании робота-манипулятора внутренние события могут быть связаны с типовыми нелинейностями механической части, а внешние – являться следствием взаимодействия со средой.

Очевидной и удобной моделью систем, управляемых событиями, является конечно-автоматная модель. Например, можно использовать конечный автомат, чтобы описать автоматическую передачу автомобиля. Передача имеет ряд состояний: парковка, нейтраль, движение, реверс и т.д. Система переходит из одного состояния в другое, когда водитель перемещает рычаг из одной позиции в другую, например, из позиции парковка в нейтральное положение.

При всей ее простоте и наглядности конечно-автоматная модель достаточно строга и формальна. Однако классическое графическое представление конечных автоматов обладает рядом недостатков. Главным недостатком является отсутствие понятия времени, что предполагает статичность состояний. Другие недостатки – отсутствие иерархии состояний, обобщения переходов, средств выражения прерываний
и продолжения нормальной работы после их обработки [11].

Для полноценного компьютерного моделирования физики процессов необходимо обеспечить сопряжение непрерывной составляющей поведения системы и логики работы управляющих ей устройств (дискретная компонента). Математический аппарат описания в данном случае – это система уравнений, но не дифференциальных, а дифференциально-алгебраическо-логических, для которых отсутствует стройная теория и единый подход.

В настоящее время для моделирования систем, управляемых событиями, широко используется предложенный Д. Харелом [7] визуальный формализм – Statechart (карты состояний и переходов). Карты состояния были разработаны применительно к моделированию дискретных систем, однако они могут служить хорошей основой и для моделирования гибридных систем, т.е. с их помощью можно описать поведение системы как в дискретном, так и в непрерывном времени [8]. Основные
неграфические компоненты таких диаграмм – это событие и действие, основные графические компоненты – состояние и переход.

Событие – нечто, происходящее вне рассматриваемой системы, возможно требующее некоторых ответных действий. События могут быть вызваны поступлением некоторых данных или некоторых задающих сигналов со стороны человека или некоторой другой части системы. События считаются мгновенными.

Действия –это реакции моделируемой системы на события. Подобно событиям, действия принято считать мгновенными.

Состояние –условия, в которых моделируемая система пребывает некоторое время, в течение которого она ведет себя одинаковым образом. В диаграмме переходов состояния представлены прямоугольными полями со скругленными углами.

Переход – изменение состояния, обычно вызываемое некоторым событием. Как правило, состояние соответствует промежутку времени между двумя такими событиями. Переходы показываются в диаграммах переходов линиями со стрелками, указывающими направление перехода. Каждому переходу могут быть сопоставлены условия, при выполнении которых переход осуществляется.

С каждым переходом и каждым состоянием могут быть соотнесены некоторые действия. Действия могут дополнительно обозначаться как действия, выполняемые однократно при входе в состояние; действия, выполняемые многократно внутри некоторого состояния; действия, выполняемые однократно при выходе из состояния.

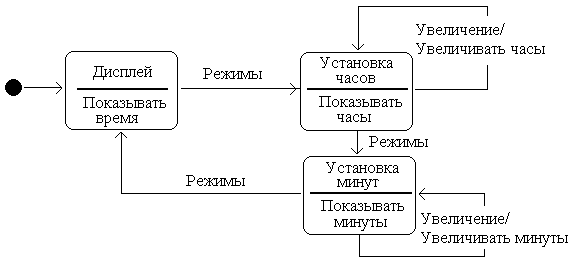
В [25] качестве примера простой дискретной системы (частного случая гибридной системы) рассмотрена диаграмма (карта) состояний и переходов цифровых часов, представленная на рис. 3.4.

Рис. 3.4. Диаграмма состояний и переходов цифровых часов

На часах имеется две кнопки: Кнопка Режима и Кнопка Увеличения. Нажатие любой из них генерирует событие, которое может вызывать переход из одного состояния в другое. Имеются три состояния: Дисплей, Установка Часов и Установка Минут. Состояние Дисплей – начальное состояние (что обозначается стрелкой, направленной от блока перехода по умолчанию в виде черного круга). Нажатие кнопки Режимы в состоянии Дисплей вызывает появление события Режимы и переход в состояние Установка часов. В состоянии Установка Часов, событие Режимы вызывает переход к состоянию Установка Минут, тогда как событие Увеличение увеличивает текущее время (число часов), которое отображается на экране, причем это происходит без изменения состояния. Каждому состоянию часов соответствует действие, записанное ниже горизонтальной линии. Оно начинает выполняться после того, как переход в это состояние произошел.

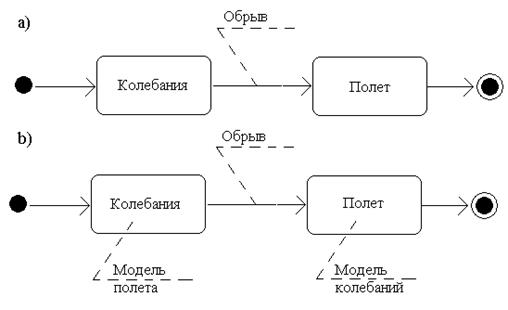
В [21] в качестве примера рассмотрена модель, которая описывает поведение маятника в виде шарика на нити, у которого в некоторый момент времени (событие «Обрыв») рвется нить. У этой модели два состояния – «Колебания» и «Полет». Оба описываются системами дифференциальных уравнений, каждая из которых является динамической системой. Карта поведений представляет собой совокупность состояний и переходов. В любой момент времени только одно состояние является текущим.

На рис. 3.5, а показана карта состояний обрывающегося маятника, на которой кроме двух обычных состояний помещены два особых состояния – начальное и конечное.

Рис. 3.5. Карта состояний и карта поведений обрывающегося маятника

В общем случае для состояния могут быть определены входные воздействия, выходные воздействия, а также локальная деятельность. Последовательность входных воздействий выполняется при каждом входе в состояние, последовательность выходных действий – при каждом выходе. Локальные действия выполняются все время, пока состояние является текущим.

Рис. 3.5, а отражает качественное поведение маятника. Для получения количественной картины необходимо связать с каждым состоянием локальное действие, в частности, интегрирование систем уравнений «Модель колебаний» и «Модель полета», как это сделано на рис. 3.5, b. Карта состояний, дополненная моделями состояний, названа в [20] картой поведения гибридной системы.

Одна из доступных реализаций концепции гибридного моделирования реализована в пакете StateFlow среды MATLAB, который кратко описан в главе 5. Также следует выделить отечественный пакет Model Vision Studium, ориентированный на моделирование сложных поведений [19].

Глава 4
Автоматизированное моделирование
технических объектов

Исторический экскурс. Необходимость автоматизации процессов моделирования технических объектов возникла практически одновременно с появлением вычислительных машин. Однако, исторически, разные этапы моделирования автоматизировались в разное время. Первым этапом следует считать создание библиотек численных методов исследования систем. Сами численные методы были разработаны задолго до появления ЭВМ и предназначались, прежде всего, для решения задач небесной механики. Так как первоначально расчеты велись вручную, алгоритмы методов были хорошо отлажены и оптимизированы. К концу 70-х годов прошлого столетия были созданы специализированные коллекции численных методов практически для всех областей численного анализа.

Дальнейшие шаги на пути автоматизации моделирования были связаны с разработкой систем автоматизированного проектирования (САПР) и систем автоматизации вычислительного эксперимента – пакетов прикладных программ. Автоматизации подлежали стандартные расчеты и оформление результатов экспериментов. Как правило, эти системы создавались под определенную предметную область, прежде всего, в наукоемких отраслях (космическая, авиация и т.д.). Для создания большинства пакетов прикладных программ для численных расчетов использовался язык Фортран, хорошо приспособленный именно для этих целей. Подобные пакеты создавались годами, их модификация и развитие требовали специальных знаний в предметной области, численных методах и программировании.

Наиболее трудно автоматизируемым этапом явился процесс построения модели. Ручная подготовка модели сложного технического объекта связана с большим объемом преобразований, в которых легко допустить ошибку. Использование систем автоматизации моделирования (САМ) позволило существенно повысить производительность труда, снизить число ошибок и, во многих случаях, исключить необходимость привлечение программистов к решению конкретных предметных задач. Опираясь на САМ, специалист в предметной (прикладной) области может самостоятельно создавать достаточно сложные модели.

При использовании системы автоматизированного моделирования исследователь формулирует математическую модель исследуемой системы на формальном входном языке моделирования. На ранних этапах развития САМ, когда отсутствовали возможности прямого изображения структуры модели на экране монитора, использовались методы кодирования структурной информации [1, 6]. Программа модели представляла собой последовательность вызовов процедур, каждая из которых являлась моделью структурного компонента. После связывания с модулями исполняющей системы пакета моделирования список компонентов преобразовывался в независимую исполняемую программу.

В современных системах автоматизированного моделирования, исходя из соображений удобства восприятия человеком, используются, как правило, графические средства задания исходной информации о модели. Переход к изображению структуры системы на экране монитора позволил исключить этап ручного кодирования схемы, однако потребовал разработки нового принципа организации самого процесса численных расчетов – принципа Data Flow, или принципа потока данных.

Можно отметить следующие факторы, способствующие внедрению систем автоматизированного моделирования:

· трудоемкость получения математической модели сложных технических объектов, связанная с опасностью совершить ошибку в многочисленных преобразованиях модельных выражений;

· необходимость многовариантного моделирования, при котором необходимо иметь для одного объекта несколько моделей, отличающихся по сложности;

· желание иметь дружественный интерфейс с программой и возможность оперативно вносить изменения в модель, что проще всего на основе использования графических языков задания исходной информации.

4.1. Особенности современных систем
автоматизированного моделирования

Современные профессиональные САМ имеют следующие отличительные черты [31]:

· поддержка иерархического проектирования как сверху – вниз, так и снизу – вверх, за счет реализации многоуровневого моделирования и метода локальной детализации модели;

· компонентное моделирование на основе использования библиотек, содержащих большое число графических и функциональных описаний компонентов, причем эти библиотеки открыты для добавления в них новых описаний, которые может сделать сам пользователь;

· графический пользовательский интерфейс, сочетающий графические средства формирования визуального образа исследуемого технического устройства с автоматической генерацией модели всей схемы по ее структурному описанию;

· наличие интерактивной рабочей среды проектирования (управляющей оболочки, монитора), т.е. специальной программы, из которой можно запускать все или большинство других программ пакета, не обращаясь к услугам штатной операционной системы;

· наличие в современных САПР и САМ постпроцессоров моделирования, что позволяет не только просматривать в удобной для пользователя форме результаты моделирования, но и обрабатывать эти результаты;

· наличие встроенных средств численного моделирования рабочего процесса в режиме реального времени или в режиме масштабирования модельного времени;

· реализация механизмов продвижения модельного времени, основанных как на принципе , так и на принципе ;

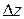
· интегрируемость с другими пакетами аналогичного назначения, которая обеспечивается соответствующими программами – конверторами, позволяющими импортировать и экспортировать данные из одной системы в другую;

· наличие средств, обеспечивающие формирование виртуальных аналогов измерительно-управляющей аппаратуры.

Если САМ предназначена для решения исследовательских задач, то к перечисленным качествам добавляются возможности активного вычислительного эксперимента [21]. В частности:

· визуализация результатов во время эксперимента;

· возможность интерактивного вмешательства в ход моделирования;

· возможность использования 2D и 3D анимации.

4.2. Иерархическое проектирование
и многоуровневое моделирование технических систем

С точки зрения инженера, основное назначение моделирования – поддержка процедур проектирования технических объектов и систем. Процедуры проектирования работают с моделями объектов реального мира и должны быть подстроены под их свойства.

Сложные системы имеют, как правило, иерархическую структуру. Естественные возможности человека позволяют оперативно обрабатывать не более 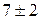единиц информации одновременно. В процессе проектирования исследователю удобно сосредотачиваться сначала на поведении отдельных компонентов системы, а затем на их взаимодействии [21]. При необходимости модели компонентов могут детализироваться или, наоборот, укрупняться.

Такой подход, известный как иерархическое проектирование [21, 31], является типовым при разработке сложных технических объектов и заключается в разбиении исходной задачи на подзадачи.

В процессе проектирования сложной системы формируются определенные представления о системе, отражающие ее существенные свойства с той или иной степенью подробности. В этих представлениях можно выделить составные части – уровни проектирования. В один уровень, как правило, включаются представления, имеющие общую физическую основу и допускающие для своего описания использование одного и того же математического аппарата. Уровни проектирования можно выделять по степени подробности, с какой отражаются свойства проектируемого объекта. Тогда их называют горизонтальными (иерархическими) уровнями проектирования.

В результате такого подхода объект проектирования декомпозируется на фрагменты (подсхемы) и проектирование каждого из них ведется в определенном смысле самостоятельно. На каждом уровне иерархии этот принцип применяется вновь, что позволяет заменить решение одной сложной задачи многократным решением задач меньшей размерности.

При иерархическом проектировании разработчику достаточно держать в поле зрения лишь один фрагмент объекта. Остальные части лишь имитируют внешнюю среду, т.е. взаимодействие проектируемого фрагмента с другими частями объекта.

Использование принципа иерархического проектирования позволяет ограничить текущую сложность проекта на приемлемом уровне, за счет того, что в каждый момент времени разработчик имеет дело только с двумя смежными уровнями декомпозиции объекта – структурным описанием проектируемого в данный момент фрагмента и функциональным описанием внешней среды.

Инструментальной поддержкой иерархического проектирования является многоуровневое моделирование.При многоуровневом моделировании различные фрагменты представляются на различных уровнях иерархии, т.е. с разной степенью детальности. Например, проектируемая в настоящий момент времени часть объекта раскрыта до уровня элементарных динамических компонентов и имитируется структурной моделью, а остальные фрагменты представлены на соседнем более высоком уровне в виде функциональных моделей.

Завершив проектирование одного фрагмента, разработчик может свернуть его в функциональный блок и перейти к детальной модели следующего фрагмента, с которым он собирается работать. Эта процедура повторяется многократно, на разных уровнях иерархии проектируемого объекта. Достоинством такого подхода является то, что в поле зрения разработчика находится в каждый момент времени минимум
необходимой информации, не перегруженной лишними деталями. Описанный метод проектирования называется методом локальной детализации объекта.

Программной поддержкой многоуровневого моделирования, реализованной в большинстве языков графического программирования, является процедура инкапсуляции, которая позволяет «свернуть» любой смысловой фрагмент графического представления в единичный блок. Кроме того, что инкапсуляция служит основой получения иерархически структурированных моделей, она так же позволяет расширить библиотеку базовых блоков блоками пользователя, которые, впоследствии, можно многократно использовать (например, типовые динамические звенья).

Такой возможностью обладает, в частности, пакет LabVIEW, пакет Simulink и основанные на нем пакеты SimMechanics и SimPower. Пакеты IDEF-моделирования (ERWIN, BPWIN) принципиально основаны на многоуровневом изображении объектов.

4.4. Архитектура программ
автоматизированного моделирования

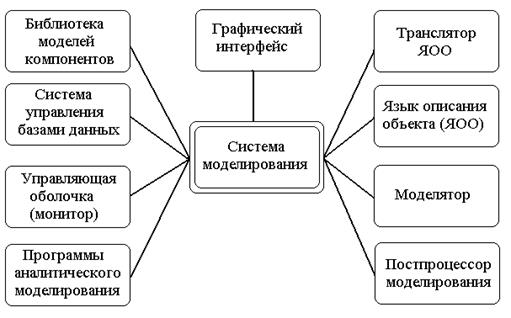
Существующие инструментальные средства автоматизированного моделирования могут относиться к разным предметным областям и существенно различаться по своим возможностям, но их модульные структуры мало отличаются друг от друга. На рис. 4.1 представлена типовая структура современного пакета визуального компонентного моделирования. Рассмотрим более детально назначение и особенности основных элементов этой структуры.

4.4.1. Графический интерфейс программ математического
моделирования динамических систем

Графический интерфейс является в настоящее время стандартным компонентом современной САМ. Он создает дружественный интерфейс между пользователем и программой, дает возможность оперировать с графическими образами вместо аналитических выражений. Это значительно облегчает работу в САМ и снижает вероятность ошибок при вводе информации о системе.

Рис. 4.1. Модульная структура
системы автоматизированного моделирования

Графический пользовательский интерфейс позволяет вводить информацию об исследуемой системе путем «рисования» на экране монитора проектируемой схемы в виде, понятном широкому кругу специалистов. Формой графического представления информации о моделируемой системе могут быть [16]:

· операторно-структурные схемы, принятые в ТАУ;

· функциональные и принципиальные схемы различных физических устройств;

· кинематические схемы механизмов;

· блок-схемы алгоритмов и другие графические модели.

Однако простым «рисованием» роль графического интерфейса не ограничивается. Задачами графического интерфейса, кроме того, могут быть [16]:

· контроль за соблюдением некоторых правил в процессе создания графического изображения на экране монитора (обычно накладываются ограничения на способы соединения компонентов и т.п.);

· преобразование информации о схеме в команды для моделирующей программы (моделятора);

· контроль за процессом моделирования, визуализация результатов моделирования.

П.5. Локальные и глобальные погрешности одношаговых методов решения ДУ

(метода Эйлера и методов Рунге-Кутта 2го, 4го порядка).

Теорема 6.1:

Если локальная погрешность метода , то глобальная .

как и при численном интегрировании, при переходе от локальной погрешности к глобальной, точность метода уменьшается на порядок. (6.8):

Методы	Локальная	Глобальная
Эйлер	const*h 2	const*h
Р.–К. 2го порядка по времени	const*h 3	const*h 2
Р.–К. 2го порядка по производной	const*h 3	const*h 2
Р.–К. 4го порядка	const*h 5	const*h 4

Как и при численном интегрировании, порядок метода – степень h в глобальной погрешности.

П.6. Многошаговые методы решения ДУ и СДУ.

Все рассмотренные ранее методы – одношаговые, т.к. для нахождения мы использовали только лишь значения с предыдущего шага. В многошаговых методах для нахождения используется не только лишь одно , но и предыдущие значения.

В k-шаговом методе используются значения с k предыдущих шагов.

Многошаговые методы, как правило, дают лучший результат, чем одношаговые, в силу того, что более устойчивы к вычислительным погрешностям. Многошаговых методов много, самый распространенный среди них – метод Милна.

Формулы метода Милна:

(6.9)

Метод Милна – 4х шаговый (т.к. использует 4 предыдущих значения) и имеет 4-ый порядок точности. Перед применением метода Милна нам надо знать 4y, следовательно, необходимо сделать хотя бы 3 шага каким-нибудь одношаговым методом.

П.7. Оценка погрешности решения ДУ и СДУ методом двойного пересчета. Коррекция решения.

Используя такую же идею, как и в численном интегрировании, находим решение ДУ на [a,b] дважды с шагом h и с шагом h/2. Получим следующую картину:

Сравниваем попарно, если расхождение между для метода 2го порядка, для метода 4го порядка, то в качестве точного решения берём . Если же точность не достигнута, то шаг h уменьшаем вдвое и т.д., пока она не будет достигнута.

Метод двойного пересчёта при решении ДУ и СДУ практически единственный имеет возможность для оценки погрешностей, так как иные формулы очень сложны и требуют оценок различных производных.

Как и при ЧИ, при решении ДУ и СДУ после 2го пересчёта в качестве точного решения выгодно брать не , а .

— для второго порядка

Метод двойного пересчёта применим не только лишь при ЧИ, при решении ДУ и СДУ, но и при решении других численных методов.

П.7. Краевые задачи для дифференциальных уравнений.

Выше рассматривалось решение ДУ и СДУ с начальными условиями, заданными в одной точке, так называемую задачу Коши, но для ДУ высших порядков часто бывает необходимо решить не з. Коши, а так называемую краевую задачу, т.е. начальные условия, которые заданы в разных точках.

Рассмотрим простейшую краевую задачу для ДУ 2го порядка:

(6.10)

А мы умеем решать:

(6.11),

В (6.11) нам известно , поэтому для решения задачи (6.10) мы будем подбирать в (6.11), с тем, чтобы у(b) = у₁

Метод стрельб

После пристрелки и определения интервала [a,b],

где идёт смена знака, запускаем МПД или МХ.

На практике это выглядит так, как будто мы

решаем уравнение , где возвращает

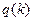
решение задачи Коши (6.11) в точке b при

П.9. Что делать, если ДУ не может быть разрешено относительно старшей производной?

Так как ДУ не может быть решено относительно старшей производной, то тогда на каждом шаге решаем нелинейное уравнение относительно y ( n) (все остальные неизвестные y,y’,y”,…, y ( n-1) -к этому моменту уже известны).

Решать уравнение относительно старшей производной любым методом(Хорд, МПД, Ньютона).

Замечание:

Таким образом, если ДУ не разрешается относительно старшей производной, то у нас возникает дополнительный цикл (самый внутренний) при написании программы.

Типы и классификация ошибок численного интегрирования

Современный численный метод одновременно с решением задачи Коши должен вычислять значение или оценку ошибки. Первый такой метод был предложен Мсрсоном в 1959 году (метод Рунгс-Кутта-Мсрсона). Теоретически таких методов описано достаточно много. Однако хороших практических реализаций в виде алгоритмов или прикладных программ мало. Рассмотрим причины возникновения ошибки при решении задачи Коши. Эта ошибка складывается из следующих компонент.

• 1. Неустранимая погрешность исходных данных. На нее повлиять нельзя, но учесть необходимо.
• 2. Локальная ошибка метода. Ее величина определяется порядком р используемого метода и зависит от шага: е,

()(h p *’). Эта ошибка связана с отбрасыванием остатка ряда при разложении точного решения в ряд по шагу при условии, что вес исходные данные заданы точно и вычисления проводятся без ошибок округления.

3. Ошибка переноса, которая возникает из-за того, что ошибка, сделанная на предыдущем шаге, переносится на следующий шаг с каким- то коэффициентом.

4. Ошибка округления, сопровождающая любые расчеты. Она возникает как при выполнении арифметических операций, так и при использовании алгоритмов вычисления значений многих элементарных функций (тригонометрических, показательных и других).

Если производить расчет на малом отрезке интегрирования, то ошибкой округления можно пренебречь, и преобладающей становится ошибка метода. Но когда количество шагов велико, ошибки округления накапливаются и становятся преобладающими. Экспериментально устаО а

количестве шагов взаимодействуют, в результате возникает общая ошибка, накопленная на веем отрезке интегрирования при применении данного метода. Эта общая ошибка ?_г называется глобальной ошибкой. Известно, что при интегрировании на отрезке |0; Т|

Здесь множитель Т)(Т) зависит только от вида функции f(x) и нс зависит от шага интегрирования. Соотношение (7.9) называют правилом Рунге.

Общая ошибка ?у, порожденная всеми составляющими, сеть их сумма (рис. 7.1). Существует оптимальное значение шага /Г, обеспечивающее наименьшую суммарную ошибку. В случае, изображенном на рис. 7.1, отклонение от этого оптимального значения нс вызывает силь-

„ _ , „ , ного изменения ошибки. Возможно, однако, си-

Рнс.7.1. Суммарная ошибка

численного интегрирования туация, когда график суммарной ошибки столь крут, что даже малое изменение шага вызывает резкий рост суммарной ошибки. Такая ситуация характеризует вычислительную неустойчивость процесса интегрирования.

Полученную в результате интегрирования ошибку нужно уметь оценивать. Кроме того, полезно иметь возможность сознательно так выбирать шаг интегрирования, чтобы влиять на величину ошибки.

Наиболее популярный метод вычисления локальной ошибки основан на разложении решения в ряд по шагу. Если используется метод порядка р. то остаток ряда начинается с члена, содержащего

Очевидно, именно этот член и характеризует величину ошибки. Значит, следует оценить значение величины R. Будем считать, что при малом /| на протяжении шага R = const. Пусть на некотором шаге с номером г выбрана точка t е [t_r‘,t_nl]. Тогда x(t’) — точное, а х*/, — вычисленное при интегрировании с шагом /; значение искомой функции. Можно считать, что на шаге

Теперь разобьем шаг на два, длины —. и вычислим то же значение,

выполнив два шага интегрирования. Будем считать, что величина R при этом нс изменилась. Получим:

Вычитая уравнения, можно получить

И можно считать, что при интегрировании с постоянным шагом И верно соотношение

Таким образом, схема выбора величины /г на шаге для достижения заданной точности Очакова:

1. при известном х, с шагом /г вычислить т_г+/;

Дискретность:

d (цена деления) — это наименьшее значение, на которое изменяется показание дисплея электронных весов.

Пример: Например, если дисплей весов показывает вес 1 кг, то при добавлении груза весом 3 г показания будут равны 1,005 кг, т.е. будут меняться с дискретностью d = 5 г. Многие ошибочно полагают, что эта величина d и является погрешностью измерения веса. Однако это не так.

Погрешность или цена поверочного деления

е — это условная величина, выраженная в единицах массы и предназначенная для расчета погрешности весов.  Значение е должно удовлетворять одному из следующих требований: — для весов специального (I) и высокого (II) класса точности е=2d, e=5d, e=10d — Для весов специального класса точности, у которых е не более 0,1 мг, допускаются следующие значения: е=20d, e=50d, e=100d е=200d, e=500d, e=1000d, где d — дискретность (цена деления). 

Наибольший предел взвешивания (НПВ)

НПВ это верхняя граница предела взвешивания. НПВ определяет самую большую массу при взвешивании на весах за один раз. 

Наименьший предел взвешивания (НмПВ)

НмПВ Очень важно знать, от какого наименьшего предела взвешивания производитель гарантирует указанную в руководстве по эксплуатации погрешность весов. Знать наименьший предел взвешивания принципиально важно, т.к. весы индицируют вес на дисплее даже в случае, если измеряемый вес меньше НмПВ, однако достоверными эти показания считать нельзя.

Класс точности

С 01.07.2001 г. вступил в действие новый ГОСТ 24104-2001 (взамен ГОСТ 24104-1988). Этот ГОСТ разработан на основе международных рекомендаций OIML и подразделяет весы на 3 класса точности:

• I специальный класс точности весов 
• II высокий класс точности
• III средний

Калибровка и поверка

Это процедура регулировки цены деления весов.

Часто путают калибровку с поверкой весов. Поверка осуществляется, как правило, раз в год независимыми метрологическим службами (ЦСМ). Поверку производят с целью определения и подтверждения соответствия весов установленным техническими требованиями (ГОСТов, ТУ )

Бывает так, что потребители «довольствуются» этим и не осуществляют калибровку весов, хотя процедура эта – ежедневная. Более того, чем выше класс точности весов, тем чаще придется их калибровать в течение дня. 

Калибровка бывает следующих видов:

• Внешняя калибровка — это калибровка с помощью калибровочной гири. Номинал гири того или иного класса должен быть близок, а еще лучше равен НПВ весов. Это коренным образом влияет на точность показаний. 
• Внутренняя — это калибровка с помощью встроенного в весы эталонного груза. Удобство внутренней калибровки очевидно. Достаточно нажать кнопку, и весы дальше сами выполняют все необходимые подстройки. Однако при прочих равных условиях такие весы дороже аналогичных с внешней калибровкой.
• Автоматическая — это разновидность внутренней калибровки, при которой калибровка весов происходит без участия оператора. Весы данного типа автоматически определяют необходимость и выполняют калибровку при изменении внешних условий (давление, влажность, температура). Кроме того, в некоторых моделях предусмотрена плановая калибровка по времени, задаваемым оператором. 

Классы гирь

Также как и весы, калибровочные гири делятся на несколько классов. Если подходить упрощенно, то чаще всего для типичных весов, находящихся в современных лабораториях, используются гири:

• класс Е2 (для калибровки весов Специального (I) класса точности – как правило, аналитические весы с дискретностью 0,1 мг);
• класс F1 (для калибровки весов Высокого (II) класса точности);
• класс F2 (для калибровки весов Среднего (III) класса точности).

Разумеется, допускается использование гирь более высокого класса для калибровки весов более низкого класса.

Повторяемость или среднеквадратическое отклонение (СКО)

СКО основано на рассмотрении отклонений значений признака отдельных единиц совокупности от средней арифметической. СКО показывает, насколько в среднем колеблется величина признака у единиц исследуемой совокупности, и выражается в тех же единицах измерения, что и варианты. 

Защита весов по IP

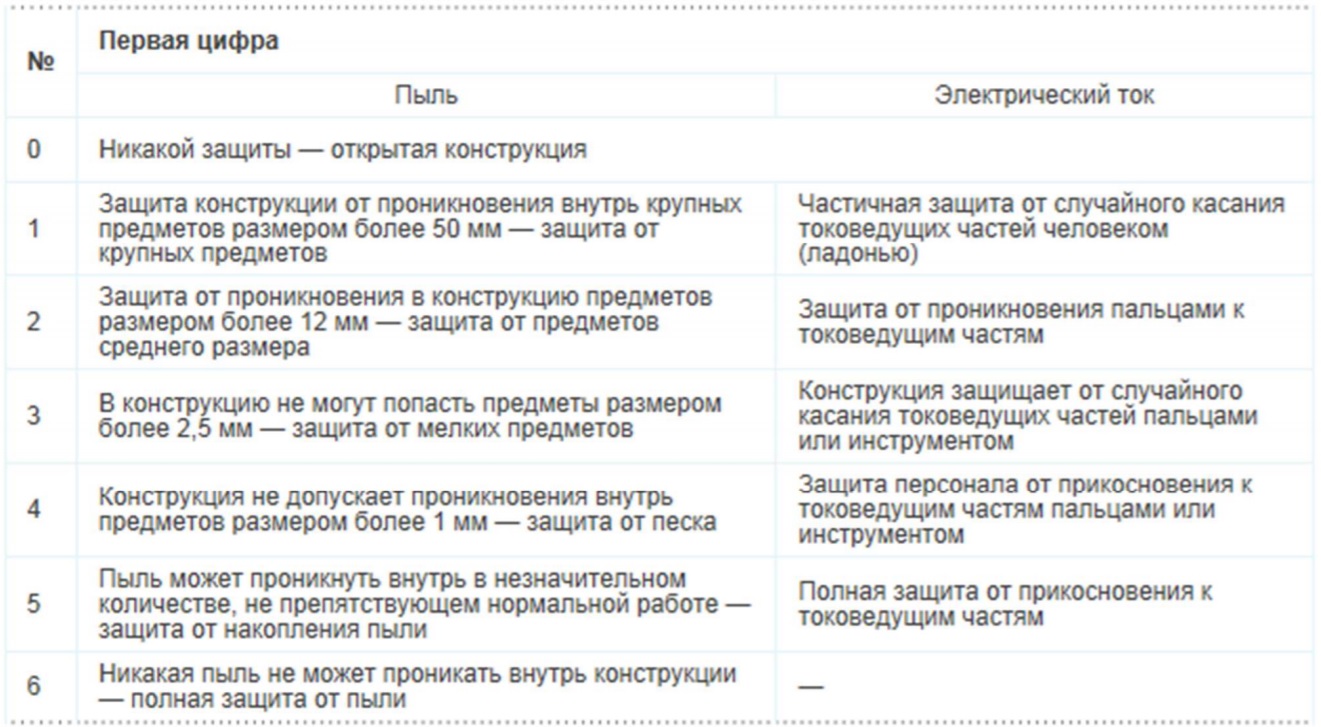
Чтобы охарактеризовать допустимые условия эксплуатации конкретного электротехнического оборудования, для него устанавливается т.н. класс защиты IP (International Protect). Он кодируется двухзначным (или трехзначным) числом, каждая из цифр которого указывает (по условленной шкале) степень допустимого внешнего воздействия на данное изделие. Название норматива имеет вид IP XY, где первая цифра X указывает степень защиты от пыли и поражения электрическим током, а вторая Y — от воды.

Научные статьи на тему «Погрешность дискретности»

Методы обработки данных и численные методы

с непрерывным аргументом на функции, обладающие дискретным аргументом….
При осуществлении перехода к дискретным моделям возникают погрешности аппроксимации изначальных функций…
операций при заданной погрешности….
Причём дискретную функцию тоже можно рассматривать как линейную комбинацию полиномов….
Чтобы оценить погрешности в расчётах могут использоваться следующие методики:

Оценка абсолютной погрешности

Статья от экспертов

Расчет погрешности дискретного уровнемера

Вычислительные методы в экономике

Во время перехода к дискретной модели может появиться погрешность аппроксимации, а в процессе реализации…
погрешности и устойчивости вычислительных алгоритмов….
аргумента на функции дискретного аргумента….
и критериев роста погрешности….
погрешности.

Статья от экспертов

Анализ погрешностей интерполяции случайных полей по дискретным отсчётам

Рассмотрены алгоритмы интерполяции случайных полей по неполным наблюдениям, позволяющие существенно снизить вычислительные затраты при незначительном снижении точности оценивания