Что такое ошибки ber - Не ошибается лишь тот, кто ничего не делает!

From Wikipedia, the free encyclopedia

In digital transmission, the number of bit errors is the numbers of received bits of a data stream over a communication channel that have been altered due to noise, interference, distortion or bit synchronization errors.

The bit error rate (BER) is the number of bit errors per unit time. The bit error ratio (also BER) is the number of bit errors divided by the total number of transferred bits during a studied time interval. Bit error ratio is a unitless performance measure, often expressed as a percentage.^[1]

The bit error probability p_e is the expected value of the bit error ratio. The bit error ratio can be considered as an approximate estimate of the bit error probability. This estimate is accurate for a long time interval and a high number of bit errors.

Example[edit]

As an example, assume this transmitted bit sequence:

1 1 0 0 0 1 0 1 1

and the following received bit sequence:

0 1 0 1 0 1 0 0 1,

The number of bit errors (the underlined bits) is, in this case, 3. The BER is 3 incorrect bits divided by 9 transferred bits, resulting in a BER of 0.333 or 33.3%.

Packet error ratio[edit]

The packet error ratio (PER) is the number of incorrectly received data packets divided by the total number of received packets. A packet is declared incorrect if at least one bit is erroneous. The expectation value of the PER is denoted packet error probability p_p, which for a data packet length of N bits can be expressed as

${displaystyle p_{p}=1-(1-p_{e})^{N}=1-e^{Nln(1-p_{e})}}$ ,

assuming that the bit errors are independent of each other. For small bit error probabilities and large data packets, this is approximately

$p_{p}approx p_{e}N.$

Similar measurements can be carried out for the transmission of frames, blocks, or symbols.

The above expression can be rearranged to express the corresponding BER (p_e) as a function of the PER (p_p) and the data packet length N in bits:

${displaystyle p_{e}=1-{sqrt[{N}]{(1-p_{p})}}}$

Factors affecting the BER[edit]

In a communication system, the receiver side BER may be affected by transmission channel noise, interference, distortion, bit synchronization problems, attenuation, wireless multipath fading, etc.

The BER may be improved by choosing a strong signal strength (unless this causes cross-talk and more bit errors), by choosing a slow and robust modulation scheme or line coding scheme, and by applying channel coding schemes such as redundant forward error correction codes.

The transmission BER is the number of detected bits that are incorrect before error correction, divided by the total number of transferred bits (including redundant error codes). The information BER, approximately equal to the decoding error probability, is the number of decoded bits that remain incorrect after the error correction, divided by the total number of decoded bits (the useful information). Normally the transmission BER is larger than the information BER. The information BER is affected by the strength of the forward error correction code.

Analysis of the BER[edit]

The BER may be evaluated using stochastic (Monte Carlo) computer simulations. If a simple transmission channel model and data source model is assumed, the BER may also be calculated analytically. An example of such a data source model is the Bernoulli source.

Examples of simple channel models used in information theory are:

Binary symmetric channel (used in analysis of decoding error probability in case of non-bursty bit errors on the transmission channel)
Additive white Gaussian noise (AWGN) channel without fading.

A worst-case scenario is a completely random channel, where noise totally dominates over the useful signal. This results in a transmission BER of 50% (provided that a Bernoulli binary data source and a binary symmetrical channel are assumed, see below).

Bit-error rate curves for BPSK, QPSK, 8-PSK and 16-PSK, AWGN channel.

In a noisy channel, the BER is often expressed as a function of the normalized carrier-to-noise ratio measure denoted Eb/N0, (energy per bit to noise power spectral density ratio), or Es/N0 (energy per modulation symbol to noise spectral density).

For example, in the case of QPSK modulation and AWGN channel, the BER as function of the Eb/N0 is given by:
$operatorname {BER}={frac {1}{2}}operatorname {erfc}({sqrt {E_{b}/N_{0}}})$ .^[2]

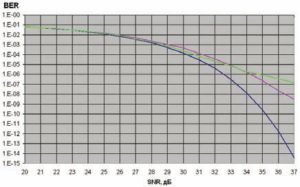
People usually plot the BER curves to describe the performance of a digital communication system. In optical communication, BER(dB) vs. Received Power(dBm) is usually used; while in wireless communication, BER(dB) vs. SNR(dB) is used.

Measuring the bit error ratio helps people choose the appropriate forward error correction codes. Since most such codes correct only bit-flips, but not bit-insertions or bit-deletions, the Hamming distance metric is the appropriate way to measure the number of bit errors. Many FEC coders also continuously measure the current BER.

A more general way of measuring the number of bit errors is the Levenshtein distance.
The Levenshtein distance measurement is more appropriate for measuring raw channel performance before frame synchronization, and when using error correction codes designed to correct bit-insertions and bit-deletions, such as Marker Codes and Watermark Codes.^[3]

Mathematical draft[edit]

The BER is the likelihood of a bit misinterpretation due to electrical noise w(t) . Considering a bipolar NRZ transmission, we have

$x_{1}(t)=A+w(t)$ for a «1» and $x_{0}(t)=-A+w(t)$ for a «0». Each of $x_{1}(t)$ and x_0(t) has a period of .

Knowing that the noise has a bilateral spectral density ${frac {N_{0}}{2}}$ ,

$x_{1}(t)$ is ${mathcal {N}}left(A,{frac {N_{0}}{2T}}right)$

and x_0(t) is ${mathcal {N}}left(-A,{frac {N_{0}}{2T}}right)$ .

Returning to BER, we have the likelihood of a bit misinterpretation $p_{e}=p(0|1)p_{1}+p(1|0)p_{0}$ .

$p(1|0)=0.5,operatorname {erfc}left({frac {A+lambda }{{sqrt {N_{o}/T}}}}right)$ and $p(0|1)=0.5,operatorname {erfc}left({frac {A-lambda }{{sqrt {N_{o}/T}}}}right)$

where lambda is the threshold of decision, set to 0 when $p_{1}=p_{0}=0.5$ .

We can use the average energy of the signal $E=A^{2}T$ to find the final expression :

$p_{e}=0.5,operatorname {erfc}left({sqrt {{frac {E}{N_{o}}}}}right).$
±§

Bit error rate test[edit]

BERT or bit error rate test is a testing method for digital communication circuits that uses predetermined stress patterns consisting of a sequence of logical ones and zeros generated by a test pattern generator.

A BERT typically consists of a test pattern generator and a receiver that can be set to the same pattern. They can be used in pairs, with one at either end of a transmission link, or singularly at one end with a loopback at the remote end. BERTs are typically stand-alone specialised instruments, but can be personal computer–based. In use, the number of errors, if any, are counted and presented as a ratio such as 1 in 1,000,000, or 1 in 1e06.

Common types of BERT stress patterns[edit]

PRBS (pseudorandom binary sequence) – A pseudorandom binary sequencer of N Bits. These pattern sequences are used to measure jitter and eye mask of TX-Data in electrical and optical data links.
QRSS (quasi random signal source) – A pseudorandom binary sequencer which generates every combination of a 20-bit word, repeats every 1,048,575 words, and suppresses consecutive zeros to no more than 14. It contains high-density sequences, low-density sequences, and sequences that change from low to high and vice versa. This pattern is also the standard pattern used to measure jitter.
3 in 24 – Pattern contains the longest string of consecutive zeros (15) with the lowest ones density (12.5%). This pattern simultaneously stresses minimum ones density and the maximum number of consecutive zeros. The D4 frame format of 3 in 24 may cause a D4 yellow alarm for frame circuits depending on the alignment of one bits to a frame.
1:7 – Also referred to as 1 in 8. It has only a single one in an eight-bit repeating sequence. This pattern stresses the minimum ones density of 12.5% and should be used when testing facilities set for B8ZS coding as the 3 in 24 pattern increases to 29.5% when converted to B8ZS.
Min/max – Pattern rapid sequence changes from low density to high density. Most useful when stressing the repeater’s ALBO feature.
All ones (or mark) – A pattern composed of ones only. This pattern causes the repeater to consume the maximum amount of power. If DC to the repeater is regulated properly, the repeater will have no trouble transmitting the long ones sequence. This pattern should be used when measuring span power regulation. An unframed all ones pattern is used to indicate an AIS (also known as a blue alarm).
All zeros – A pattern composed of zeros only. It is effective in finding equipment misoptioned for AMI, such as fiber/radio multiplex low-speed inputs.
Alternating 0s and 1s — A pattern composed of alternating ones and zeroes.
2 in 8 – Pattern contains a maximum of four consecutive zeros. It will not invoke a B8ZS sequence because eight consecutive zeros are required to cause a B8ZS substitution. The pattern is effective in finding equipment misoptioned for B8ZS.
Bridgetap — Bridge taps within a span can be detected by employing a number of test patterns with a variety of ones and zeros densities. This test generates 21 test patterns and runs for 15 minutes. If a signal error occurs, the span may have one or more bridge taps. This pattern is only effective for T1 spans that transmit the signal raw. Modulation used in HDSL spans negates the bridgetap patterns’ ability to uncover bridge taps.
Multipat — This test generates five commonly used test patterns to allow DS1 span testing without having to select each test pattern individually. Patterns are: all ones, 1:7, 2 in 8, 3 in 24, and QRSS.
T1-DALY and 55 OCTET — Each of these patterns contain fifty-five (55), eight bit octets of data in a sequence that changes rapidly between low and high density. These patterns are used primarily to stress the ALBO and equalizer circuitry but they will also stress timing recovery. 55 OCTET has fifteen (15) consecutive zeroes and can only be used unframed without violating one’s density requirements. For framed signals, the T1-DALY pattern should be used. Both patterns will force a B8ZS code in circuits optioned for B8ZS.

Bit error rate tester[edit]

A bit error rate tester (BERT), also known as a «bit error ratio tester»^[4] or bit error rate test solution (BERTs) is electronic test equipment used to test the quality of signal transmission of single components or complete systems.

The main building blocks of a BERT are:

Pattern generator, which transmits a defined test pattern to the DUT or test system
Error detector connected to the DUT or test system, to count the errors generated by the DUT or test system
Clock signal generator to synchronize the pattern generator and the error detector
Digital communication analyser is optional to display the transmitted or received signal
Electrical-optical converter and optical-electrical converter for testing optical communication signals

References[edit]

^ Jit Lim (14 December 2010). «Is BER the bit error ratio or the bit error rate?». EDN. Retrieved 2015-02-16.
^
Digital Communications, John Proakis, Massoud Salehi, McGraw-Hill Education, Nov 6, 2007
^
«Keyboards and Covert Channels»
by Gaurav Shah, Andres Molina, and Matt Blaze (2006?)
^ «Bit Error Rate Testing: BER Test BERT » Electronics Notes». www.electronics-notes.com. Retrieved 2020-04-11.

This article incorporates public domain material from Federal Standard 1037C. General Services Administration. (in support of MIL-STD-188).

External links[edit]

QPSK BER for AWGN channel – online experiment

Источник

Теоретические результаты

Общее обозначение

Следующее обозначение используется в этом Приложении:

Количество или операция	Обозначение
Размер созвездия модуляции	M
Количество битов на символ	k=log2M
Энергия на отношение спектральной плотности степени бита к шуму	EbN0
Энергия на отношение спектральной плотности степени символа к шуму	EsN0=kEbN0
Частота ошибок по битам (BER)	Pb
Коэффициент ошибок символа (SER)	Ps
Действительная часть	Re[⋅]
Самое большое целое число, меньшее, чем	⌊⋅⌋

Следующие математические функции используются:

Функция	Математическое выражение
Q функция	Q(x)=12π∫x∞exp(−t2/2)dt
Marcum Q функция	Q(a,b)=∫b∞texp(−t2+a22)I0(at)dt
Модифицированная функция Бесселя первого рода порядка ν	Iν(z)=∑k=0∞(z/2)υ+2kk!Γ(ν+k+1) где Γ(x)=∫0∞e−ttx−1dt гамма функция.
Вырожденная гипергеометрическая функция	F11(a,c;x)=∑k=0∞(a)k(c)kxkk! где символ Pochhammer, (λ)k, задан как (λ)0=1, (λ)k=λ(λ+1)(λ+2)⋯(λ+k−1).

Следующие акронимы используются:

Акроним	Определение
M-PSK	M-арное манипулирование сдвига фазы
DE-M-PSK	Дифференцированно закодированное M-арное манипулирование сдвига фазы
BPSK	Бинарное манипулирование сдвига фазы
DE-BPSK	Дифференцированно закодированное бинарное манипулирование сдвига фазы
QPSK	Четвертичное манипулирование сдвига фазы
DE-QPSK	Дифференцированно закодированное квадратурное манипулирование сдвига фазы
OQPSK	Возместите квадратурное манипулирование сдвига фазы
DE-OQPSK	Дифференцированно закодированное квадратурное манипулирование сдвига фазы смещения
M-DPSK	M-арное дифференциальное манипулирование сдвига фазы
M-PAM	M-арная импульсная амплитудная модуляция
M-QAM	M-арная квадратурная амплитудная модуляция
M-FSK	M-арное манипулирование сдвига частоты
MSK	Минимальное манипулирование сдвига
M-CPFSK	M-арное манипулирование сдвига частоты непрерывной фазы

Аналитические Выражения, Используемые в berawgn

M-PSK
DE-M-PSK
OQPSK
DE-OQPSK
M-DPSK
M-PAM
M-QAM
Ортогональный M-FSK с когерентным обнаружением
Неортогональный 2-FSK с когерентным обнаружением
Ортогональный M-FSK с некогерентным обнаружением
Неортогональный 2-FSK с некогерентным обнаружением
Предварительно закодированный MSK с когерентным обнаружением
Дифференцированно закодированный MSK с когерентным обнаружением
MSK с некогерентным обнаружением (оптимальный блок блоком)
CPFSK когерентное обнаружение (оптимальный блок блоком)

M-PSK. От уравнения 8.22 в [2]

Следующее выражение очень близко, но не строго равно к точному BER (от [4] и уравнение 8.29 от [2]):

где wi’=wi+wM−i, wM/2’=wM/2, wiвес Хэмминга битов, присвоенных символу i, и

Особый случай M=2, e.g., BPSK (уравнение 5.2-57 от [1]):

Особый случай M=4, e.g., QPSK (уравнения 5.2-59 и 5.2-62 от [1]):

DE-M-PSK. M=2, e.g., DE-BPSK (уравнение 8.36 от [2]):

M=4, e.g., DE-QPSK (уравнение 8.38 от [2]):

От уравнения 5 в [3]:

OQPSK. Тот же BER/SER как QPSK [2].

DE-OQPSK. Тот же BER/SER как DE-QPSK [3].

M-DPSK. От уравнения 8.84 в [2]:

Следующее выражение очень близко, но не строго равно к точному BER [4]:

где wi’=wi+wM−i, wM/2’=wM/2, wi вес Хэмминга битов, присвоенных символу i, и

Особый случай M=2 (уравнение 8.85 от [2]):

M-PAM. От уравнений 8.3 и 8.7 в [2] и уравнения 5.2-46 в [1]:

От [5]:

M-QAM. Для квадратного M-QAM, k=log2M является четным (уравнение 8.10 от [2] и уравнения 5.2-78 и 5.2-79 от [1]):

От [5]:

Для прямоугольного (неквадратного) M-QAM, k=log2M является нечетным, M=I×J, I=2k−12, и J=2k+12:

От [5]:

где

Ортогональный M-FSK с Когерентным Обнаружением. От уравнения 8.40 в [2] и уравнения 5.2-21 в [1]:

Неортогональный 2-FSK с когерентным обнаружением. Для M=2 (от уравнения 5.2-21 в [1] и уравнения 8.44 в [2]):

ρкомплексный коэффициент корреляции:

где s˜1(t) и s˜2(t) комплексные сигналы lowpass, и

Например:

где Δf=f1−f2.

(от уравнения 8.44 в [2], где h=ΔfTb)

Ортогональный M-FSK с Некогерентным Обнаружением. От уравнения 5.4-46 в [1] и уравнения 8.66 в [2]:

Неортогональный 2-FSK с некогерентным обнаружением. Для M=2 (от уравнения 5.4-53 в [1] и уравнения 8.69 в [2]):

где

Предварительно закодированный MSK с когерентным обнаружением. Тот же BER/SER как BPSK.

Дифференцированно закодированный MSK с когерентным обнаружением. Тот же BER/SER как DE-BPSK.

MSK с Некогерентным Обнаружением (Оптимальный Блок Блоком). Верхняя граница (от уравнений 10.166 и 10.164 в [6]):

где

CPFSK Когерентное Обнаружение (Оптимальный Блок Блоком). Нижняя граница (от уравнения 5.3-17 в [1]):

Верхняя граница:

где h является индексом модуляции, и Kδmin количество путей, имеющих минимальное расстояние.

Аналитические Выражения, Используемые в berfading

Обозначение
M-PSK с MRC
DE-M-PSK с MRC
M-PAM с MRC
M-QAM с MRC
M-DPSK с постобнаружением EGC
Ортогональный 2-FSK, когерентное обнаружение с MRC
Неортогональный 2-FSK, когерентное обнаружение с MRC
Ортогональный M-FSK, некогерентное обнаружение с EGC
Неортогональный 2-FSK, некогерентное обнаружение без разнообразия

Обозначение. Следующее обозначение используется для выражений, найденных в berfading.

Значение	Обозначение
Степень исчезающего амплитудного r	Ω=E[r2], где E[⋅] обозначает статистическое ожидание
Количество ветвей разнообразия	L
ОСШ на символ на ветвь	γ¯l=(ΩlEsN0)/L=(ΩlkEbN0)/L Для тождественно распределенных ветвей разнообразия: γ¯=(ΩkEbN0)/L
Производящие функции момента для каждой ветви разнообразия	Релеевское замирание: Mγl(s)=11−sγ¯l Исчезновение Rician: Mγl(s)=1+K1+K−sγ¯le[Ksγ¯l(1+K)−sγ¯l] где K является отношением энергии в зеркальном компоненте к энергии в рассеянном компоненте (линейная шкала). Для тождественно распределенных ветвей разнообразия:Mγl(s)=Mγ(s) для всего l.

Следующие акронимы используются:

Акроним	Определение
MRC	объединение максимального отношения
EGC	объединение равного усиления

M-PSK с MRC. От уравнения 9.15 в [2]:

От [4] и [2]:

где wi’=wi+wM−i, wM/2’=wM/2, wi вес Хэмминга битов, присвоенных символу i, и

Для особого случая Релеевского замирания с M=2 (от уравнений C-18, C-21 и Таблицы c-1 в [6]):

где

Если L=1:

DE-M-PSK с MRC. Для M=2 (от уравнений 8.37 и 9.8-9.11 в [2]):

M-PAM с MRC. От уравнения 9.19 в [2]:

От [5] и [2]:

M-QAM с MRC. Для квадратного M-QAM, k=log2M является четным (уравнение 9.21 в [2]):

От [5] и [2]:

Для прямоугольного (неквадратного) M-QAM, k=log2M является нечетным, M=I×J, I=2k−12, J=2k+12, γ¯l=Ωllog2(IJ)EbN0, и

От [5] и [2]:

M-DPSK с Постобнаружением EGC. От уравнения 8.165 в [2]:

От [4] и [2]:

где wi’=wi+wM−i, wM/2’=wM/2, wi вес Хэмминга битов, присвоенных символу i, и

Для особого случая Релеевского замирания с M=2, и L=1 (уравнение 8.173 от [2]):

Ортогональный 2-FSK, Когерентное Обнаружение с MRC. От уравнения 9.11 в [2]:

Для особого случая Релеевского замирания (уравнения 14.4-15 и 14.4-21 в [1]):

Неортогональный 2-FSK, когерентное обнаружение с MRC. Уравнения 9.11 и 8.44 в [2]:

Для особого случая Релеевского замирания с L=1 (уравнение 20 в [8] и уравнение 8.130 в [2]):

Ортогональный M-FSK, Некогерентное Обнаружение с EGC. Релеевское замирание (уравнение 14.4-47 в [1]):

Исчезновение Rician (уравнение 41 в [8]):

где

и I[a,b](i)=1 если a≤i≤b и 0 в противном случае.

Неортогональный 2-FSK, Некогерентное Обнаружение без Разнообразия. От уравнения 8.163 в [2]:

где

Аналитические Выражения, Используемые в bercoding и BERTool

Общее обозначение для этого раздела
Блочное кодирование
Сверточное кодирование

Общее обозначение для этого раздела

Описание	Обозначение
Отношение спектральной плотности степени бита к шуму энергии на информацию	γb=EbN0
Передайте длину	K
Разрядность кода	N
Уровень кода	Rc=KN

Блочное кодирование. Определенное обозначение для выражений блочного кодирования: dmin минимальное расстояние кода.

Мягкое решение

BPSK, QPSK, OQPSK, PAM-2, QAM-4 и предварительно закодированный MSK (уравнение 8.1-52 в [1]):

DE-BPSK, DE-QPSK, DE-OQPSK и DE-MSK:

BFSK, когерентное обнаружение (уравнения 8.1-50 и 8.1-58 в [1]):

BFSK, некогерентное квадратичное обнаружение (уравнения 8.1-65 и 8.1-64 в [1]):

DPSK:

Трудное решение

Общий линейный блочный код (уравнения 4.3, 4.4 в [9], и 12.136 в [6]):

Код Хемминга (уравнения 4.11, 4.12 в [9], и 6.72, 6.73 в [7]):

(24, 12), расширил код Golay (уравнение 4.17 в [9], и 12.139 в [6]):

где βm среднее количество ошибок символа канала, которые остаются в откорректированном N — кортеж, когда канал вызвал ошибки символа m (таблица 4.2 в [9]).

Код тростника-Solomon с N=Q−1=2q−1:

для FSK (уравнения 4.25, 4.27 в [9], 8.1-115, 8.1-116 в [1], 8.7, 8.8 в [7], и 12.142, 12.143 в [6]), и

в противном случае.

Если log2Q/log2M=q/k=h где h является целым числом (уравнение 1 в [10]):

где s является коэффициентом ошибок символа (SER) в незакодированном канале AWGN.

Например, для BPSK, M=2 и Ps=1−(1−s)q

В противном случае, Ps дан таблицей 1 и уравнением 2 в [10].

Сверточное Кодирование. Определенное обозначение для сверточных выражений кодирования: dfree свободное расстояние кода, и ad количество путей расстояния d от все-нулевого пути, которые объединяют со все-нулевым путем впервые.

Мягкое решение

От уравнений 8.2-26, 8.2-24, и 8.2-25 в [1], и уравнений 13.28 и 13.27 в [6]:

с передаточной функцией

где f(d) экспонента N как функция d.

Результаты для BPSK, QPSK, OQPSK, PAM-2, QAM-4, предварительно закодировали MSK, DE-BPSK, DE-QPSK, DE-OQPSK, DE-MSK, DPSK, и BFSK получен как:

где Pb BER в соответствующем незакодированном канале AWGN. Например, для BPSK (уравнение 8.2-20 в [1]):

Трудное решение

От уравнений 8.2-33, 8.2-28, и 8.2-29 в [1], и уравнений 13.28, 13.24, и 13.25 в [6]:

где

когда d является нечетным, и

когда d является четным (p является частотой ошибок по битам (BER) в незакодированном канале AWGN).

Результаты эффективности через Симуляцию

Разделите обзор
Используя симулированные данные, чтобы вычислить коэффициенты ошибок бита и символа
Пример: вычисление коэффициентов ошибок
Сравнение коэффициента ошибок символа и частоты ошибок по битам

Разделите обзор

Один способ вычислить частоту ошибок по битам или коэффициент ошибок символа для системы связи состоит в том, чтобы симулировать передачу сообщений данных и сравнить все сообщения до и после передачи. Симуляция компонентов системы связи с помощью Communications Toolbox™ покрыта другими частями этого руководства. В этом разделе описывается сравнить сообщения данных, которые вводят и оставляют симуляцию.

Другой пример вычислительных результатов эффективности через симуляцию находится в Curve Fitting для Графиков Коэффициента ошибок в обсуждении аппроксимирования кривыми.

Используя симулированные данные, чтобы вычислить коэффициенты ошибок бита и символа

biterr функция сравнивает два набора данных и вычисляет количество битовых ошибок и частоты ошибок по битам. symerr функция сравнивает два набора данных и вычисляет количество ошибок символа и коэффициента ошибок символа. Ошибка является несоответствием между соответствующими точками в двух наборах данных.

Из двух наборов данных обычно каждый представляет сообщения, вводящие передатчик, и другой представляет восстановленные сообщения, оставляя приемник. Вы можете также сравнить ввод данных и отъезд других частей вашей системы связи, например, данные, вводящие энкодер и данные, оставив декодер.

Если ваша система связи использует несколько битов, чтобы представлять один символ, подсчет битовых ошибок отличается от подсчета ошибок символа. Или в бите — или в считающем символ случае, коэффициент ошибок является количеством ошибок, разделенных на общее количество (битов или символов) переданный.

Примечание

Чтобы гарантировать точный коэффициент ошибок, необходимо обычно симулировать достаточно данных, чтобы произвести по крайней мере 100 ошибок.

Если коэффициент ошибок очень мал (например, ^10-6 или меньший), полуаналитический метод может вычислить результат более быстро, чем подход только для симуляции. Смотрите Результаты Эффективности через Полуаналитический Метод для получения дополнительной информации о том, как использовать этот метод.

Пример: вычисление коэффициентов ошибок

Скрипт ниже использует symerr функция, чтобы вычислить коэффициенты ошибок символа для шумного линейного блочного кода. После искусственного добавления шума к закодированному сообщению это сравнивает получившийся шумный код с оригинальным кодом. Затем это декодирует и сравнивает декодируемое сообщение с исходным.

m = 3; n = 2^m-1; k = n-m; % Prepare to use Hamming code.
msg = randi([0 1],k*200,1); % 200 messages of k bits each
code = encode(msg,n,k,'hamming');
codenoisy = rem(code+(rand(n*200,1)>.95),2); % Add noise.
% Decode and correct some errors.
newmsg = decode(codenoisy,n,k,'hamming');
% Compute and display symbol error rates.
noisyVec = step(comm.ErrorRate,code,codenoisy);
decodedVec = step(comm.ErrorRate,msg,newmsg);
disp(['Error rate in the received code: ',num2str(noisyVec(1))])
disp(['Error rate after decoding: ',num2str(decodedVec(1))])

Выход ниже. Уменьшения коэффициента ошибок после декодирования, потому что декодер Хэмминга корректирует некоторые ошибки. Ваши результаты могут варьироваться, потому что этот пример использует случайные числа.

Error rate in the received code: 0.054286
Error rate after decoding: 0.03

Сравнение коэффициента ошибок символа и частоты ошибок по битам

В примере выше, ошибки символа и битовые ошибки являются тем же самым, потому что каждый символ немного. Команды ниже иллюстрируют различие между ошибками символа и битовыми ошибками в других ситуациях.

a = [1 2 3]'; b = [1 4 4]';
format rat % Display fractions instead of decimals.
[snum,srate] = symerr(a,b)

[bnum,brate] = biterr(a,b)

Выход ниже.

snum =

      2      


srate =

     2/3     


bnum =

      5      


brate =

     5/9

bnum 5, потому что вторые записи отличаются по двум битам, и третьи записи отличаются по трем битам. brate 5/9, потому что общее количество битов равняется 9. Общее количество битов является, по определению, количеством записей в a или b времена максимальное количество битов среди всех записей a и b.

Результаты эффективности через Полуаналитический Метод

Метод, описанный в Результатах Эффективности через Моделирование хорошо для большого множества систем связи, но, может быть предельно длительным, если коэффициент ошибок системы очень мал (например, ^10-6 или меньше). В этом разделе описывается использовать полуаналитический метод в качестве альтернативного способа вычислить коэффициенты ошибок. Для определенных типов систем полуаналитический метод может привести к результатам намного более быстро, чем неаналитический метод, который использует только симулированные данные.

Полуаналитический метод использует комбинацию симуляции и анализа, чтобы определить коэффициент ошибок системы связи. semianalytic функция в Communications Toolbox помогает вам реализовать полуаналитический метод путем выполнения части анализа.

Когда использовать полуаналитический метод

Полуаналитический метод работает хорошо на определенные типы систем связи, но не на других. Полуаналитический метод применим, если система имеет все эти характеристики:

Любые эффекты многопутевого исчезновения, квантования и нелинейности усилителя должны предшествовать эффектам шума в фактическом смоделированном канале.
Приемник отлично синхронизируется с поставщиком услуг, и синхронизирующий дрожание незначительно. Поскольку шум фазы и синхронизирующий дрожание является медленными процессами, они уменьшают применимость полуаналитического метода к системе связи.
Бесшумная симуляция не имеет никаких ошибок в полученном сигнальном созвездии. Искажения из источников кроме шума должны быть достаточно умеренными, чтобы сохранить каждую точку сигнала в ее правильной области решения. Если дело обстоит не так, расчетный BER является слишком низким. Например, если смоделированная система имеет вращение фазы, которое помещает полученные очки сигнала за пределами их соответствующих областей решения, полуаналитический метод не подходит, чтобы предсказать производительность системы.

Кроме того, semianalytic функция принимает, что шум в фактическом смоделированном канале является Гауссовым. Для получения дополнительной информации о том, как адаптировать полуаналитический метод к негауссову шуму, смотрите обсуждение обобщенных экспоненциальных распределений в [11].

Процедура для полуаналитического метода

Процедура ниже описывает, как вы обычно реализовывали бы полуаналитический метод с помощью semianalytic функция:

Сгенерируйте сигнал сообщения, содержащий, по крайней мере, символы ^ML, где M является размером алфавита модуляции, и L является длиной импульсной характеристики канала в символах. Общий подход должен начать с увеличенного бинарного псевдошума (PN) последовательность общей длины _(log2M)ML. Увеличенная псевдошумовая последовательность является псевдошумовой последовательностью с дополнительным добавленным нулем, который делает распределение единиц и нулей равным.
Модулируйте поставщика услуг с сигналом сообщения использование полосовой модуляции. Поддерживаемые типы модуляции перечислены на странице с описанием для semianalytic. Сформируйте результирующий сигнал с формированием меандра, с помощью фактора сверхдискретизации, что вы будете дальнейшее использование, чтобы отфильтровать модулируемый сигнал. Сохраните результат этого шага как txsig для дальнейшего использования.
Отфильтруйте модулируемый сигнал с фильтром передачи. Этот фильтр часто является повышенным фильтром косинуса квадратного корня, но можно также использовать Баттерворта, функцию Бесселя, Чебышевский тип 1 или 2, эллиптического, или более общего КИХ или БИХ-фильтр. Если вы используете повышенный фильтр косинуса квадратного корня, используйте его на несверхдискретизированном модулируемом сигнале и укажите, что сверхдискретизация включает функцию фильтрации. Если вы используете другой тип фильтра, можно применить его к rectangularly сигналу импульсной формы.
Запустите пропущенный сигнал через бесшумный канал. Этот канал может включать многопутевые исчезающие эффекты, сдвиги фазы, нелинейность усилителя, квантование и дополнительную фильтрацию, но это не должно включать шум. Сохраните результат этого шага как rxsig для дальнейшего использования.
Вызовите semianalytic функция с помощью txsig и rxsig данные из более ранних шагов. Задайте получить фильтр как пару входных параметров, если вы не хотите использовать фильтр функции по умолчанию. Функция фильтрует rxsig и затем определяет вероятность появления ошибки каждого полученного очка сигнала путем аналитичного применения Гауссова шумового распределения к каждой точке. Функциональные средние значения вероятности появления ошибки по целому полученному сигналу определить полную вероятность появления ошибки. Если вероятность появления ошибки, вычисленная таким образом, является вероятностью появления ошибки символа, функция преобразует ее в небольшой коэффициент ошибок, обычно путем принятия Грэя, кодирующего. Функция возвращает частоту ошибок по битам (или, в случае модуляции DQPSK, верхней границы на частоте ошибок по битам).

Используя полуаналитический метод

Пример ниже иллюстрирует процедуру для полуаналитического метода, с помощью 16-QAM модуляции. Это также сравнивает коэффициенты ошибок, полученные из полуаналитического метода с теоретическими коэффициентами ошибок, полученными из опубликованных формул и вычисленного использования berawgn функция. Получившийся график показывает, что полученное использование коэффициентов ошибок этих двух методов почти идентично. Несоответствия между теоретическими и вычисленными коэффициентами ошибок происходят в основном из-за смещения фазы, вставленного через бесшумную модель канала.

Сгенерируйте сигнал сообщения длины> = M^L.

M = 16; % Alphabet size of modulation
L = 1; % Length of impulse response of channel
msg = [0:M-1 0]; % M-ary message sequence of length > M^L

Модулируйте сигнал сообщения использование полосовой модуляции.

modsig = qammod(msg',M); % Modulate data
Nsamp = 16;
modsig = rectpulse(modsig,Nsamp); % Use rectangular pulse shaping.

Примените фильтр передачи.

txsig = modsig; % No filter in this example

Запустите txsig через бесшумный канал.

rxsig = txsig*exp(1i*pi/180); % Static phase offset of 1 degree

Используйте semianalytic функция.

Задайте получить фильтр как пару входных параметров. В этом случае цифра и логово описывают идеальный интегратор.

num = ones(Nsamp,1)/Nsamp;
den = 1;
EbNo = 0:20; % Range of Eb/No values under study
ber = semianalytic(txsig,rxsig,'qam',M,Nsamp,num,den,EbNo);

% For comparison, calculate theoretical BER.
bertheory = berawgn(EbNo,'qam',M);

% Plot computed BER and theoretical BER.
figure; semilogy(EbNo,ber,'k*');
hold on; semilogy(EbNo,bertheory,'ro');
title('Semianalytic BER Compared with Theoretical BER');
legend('Semianalytic BER with Phase Offset',...
    'Theoretical BER Without Phase Offset','Location','SouthWest');
hold off;

Теоретические результаты эффективности

Вычисление теоретической ошибочной статистики
Графический вывод теоретических коэффициентов ошибок
Сравнение теоретических и эмпирических коэффициентов ошибок

Вычисление теоретической ошибочной статистики

В то время как biterr функция, обсужденная выше, может помочь вам собрать эмпирическую ошибочную статистику, вы можете также сравнить те результаты с теоретической ошибочной статистикой. Определенные типы систем связи сопоставлены с выражениями закрытой формы для частоты ошибок по битам или привязанного это. Функции, перечисленные в таблице ниже, вычисляют выражения закрытой формы для некоторых типов систем связи, где такие выражения существуют.

Тип системы связи	Функция
Незакодированный канал AWGN	`berawgn`
Закодированный канал AWGN	`bercoding`
Незакодированный Rayleigh и Rician, исчезающий канал	`berfading`
Незакодированные AWGN образовывают канал с несовершенной синхронизацией	`bersync`

Страница с описанием каждой функции перечисляет одну или несколько книг, содержащих выражения закрытой формы, которые реализует функция.

Графический вывод теоретических коэффициентов ошибок

Этот пример использует bercoding функция, чтобы вычислить верхние границы на частотах ошибок по битам для сверточного кодирования с декодером мягкого решения.

coderate = 1/4; % Code rate

Создайте структуру dspec с информацией о спектре расстояния. Задайте развертку EbNo, располагаются и генерируют теоретические связанные результаты.

dspec.dfree = 10; % Minimum free distance of code
dspec.weight = [1 0 4 0 12 0 32 0 80 0 192 0 448 0 1024 ...
    0 2304 0 5120 0]; % Distance spectrum of code
EbNo = 3:0.5:8;
berbound = bercoding(EbNo,'conv','soft',coderate,dspec);

Постройте теоретические связанные результаты.

semilogy(EbNo,berbound)
xlabel('E_b/N_0 (dB)'); 
ylabel('Upper Bound on BER');
title('Theoretical Bound on BER for Convolutional Coding');
grid on;

Ссылки

[1] Proakis, J. G. цифровая связь, 4-й Эд., McGraw-Hill, 2001.

[2] Frenger, Приятель, Приятель Ортен, и Тони Оттоссон, «Сверточные коды с Оптимальным Спектром Расстояния», Коммуникационные Буквы IEEE, Издание 3, № 11, ноябрь 1999, стр 317-319

Сравнение теоретических и эмпирических коэффициентов ошибок

Этот пример использует berawgn функция, чтобы вычислить коэффициенты ошибок символа для импульсной амплитудной модуляции (PAM) с серией значений Eb/N0. Для сравнения код симулирует 8-PAM с каналом AWGN и вычисляет эмпирические коэффициенты ошибок символа. Код также строит теоретические и эмпирические коэффициенты ошибок символа того же набора осей.

Вычислите и постройте теоретический коэффициент ошибок с помощью berawgn.

rng('default') % Set random number seed for repeatability
M = 8;
EbNo = 0:13;
[ber, ser] = berawgn(EbNo,'pam',M);

semilogy(EbNo,ser,'r');
xlabel('E_b/N_0 (dB)');
ylabel('Symbol Error Rate');
grid on;

Вычислите эмпирический коэффициент ошибок путем симуляции. Задайте параметры симуляции и предварительно выделите переменные, чтобы сэкономить время. Преобразуйте от EbNo до ОСШ. С тех пор No = 2*noiseVariance^2, мы должны добавить 3 дБ, чтобы получить ОСШ. Для получения дополнительной информации см. книгу Проукиса, перечисленную в «Выбранной Библиографии для Оценки результатов деятельности».

n = 10000; % Number of symbols to process
k = log2(M); % Number of bits per symbol
snr = EbNo+3+10*log10(k);
ynoisy = zeros(n,length(snr));
z = zeros(n,length(snr));
berVec = zeros(3,length(EbNo));

Создайте объекты для калькулятора коэффициента ошибок канала AWGN. Калькулятор коэффициента ошибок используется, чтобы сравнить декодируемые символы с исходными переданными символами.

awgnchan = comm.AWGNChannel('NoiseMethod', 'Signal to noise ratio (SNR)');
errcalc = comm.ErrorRate;

Сгенерируйте случайное сообщение данных и примените модуляцию PAM. Нормируйте канал, чтобы сигнализировать о степени. Симуляция цикла, чтобы сгенерировать BERs в области значений значений ОСШ.

x = randi([0 M-1],n,1); % Create message signal.
y = pammod(x,M); % Modulate.
awgnchan.SignalPower = (real(y)' * real(y))/ length(real(y));

for jj = 1:length(snr)
    reset(errcalc)
    awgnchan.SNR = snr(jj); % Assign Channel SNR
    ynoisy(:,jj) = awgnchan(real(y)); % Add AWGN
    z(:,jj) = pamdemod(complex(ynoisy(:,jj)),M); % Demodulate.
    
    % Compute symbol error rate from simulation.
    berVec(:,jj) = errcalc(x,z(:,jj));
end

Сравните теоретические и эмпирические результаты.

hold on;
semilogy(EbNo,berVec(1,:),'b.');
legend('Theoretical SER','Empirical SER');
title('Comparing Theoretical and Empirical Error Rates');
hold off;

Графики коэффициента ошибок

Разделите обзор
Создание коэффициента ошибок строит Используя semilogy
Curve Fitting для графиков коэффициента ошибок
Curve Fitting график коэффициента ошибок

Разделите обзор

Графики коэффициента ошибок обеспечивают визуальный способ исследовать эффективность системы связи, и они часто включаются в публикации. Этот раздел упоминает некоторые инструменты, которые можно использовать, чтобы создать графики коэффициента ошибок, изменить их, чтобы удовлетворить потребностям и сделать аппроксимирование кривыми на данных о коэффициенте ошибок. Это также обеспечивает пример аппроксимирования кривыми. Для более детальных обсуждений о более общих возможностях графического вывода в MATLAB^® смотрите набор документации MATLAB.

Создание коэффициента ошибок строит Используя `semilogy`

Во многих графиках коэффициента ошибок горизонтальная ось указывает на значения _Eb/N0 в дБ, и вертикальная ось указывает на коэффициент ошибок с помощью логарифмического (базируйтесь 10), шкала. Чтобы видеть пример такого графика, а также кода, который создает его, смотрите Сравнение Теоретических и Эмпирических Коэффициентов ошибок. Часть того примера, который создает использование графика semilogy функционируйте, чтобы произвести логарифмический масштаб на вертикальной оси и линейную шкалу на горизонтальной оси.

Другие примеры, которые иллюстрируют использование semilogy находятся в этих разделах:

Используя Полуаналитический Метод, который также иллюстрирует
- Графический вывод двух наборов данных по одной паре осей
- Добавление заголовка
- Добавление легенды
Графический вывод Теоретических Коэффициентов ошибок, который также иллюстрирует
- Добавление подписей по осям
- Добавление линий сетки

Curve Fitting для графиков коэффициента ошибок

Аппроксимирование кривыми полезно, когда вы имеете небольшой или несовершенный набор данных, но хотите построить плавную кривую в целях представления. berfit функция в Communications Toolbox предлагает возможности подбора кривых, которые хорошо подходят для ситуации, когда эмпирические данные описывают коэффициенты ошибок в различных значениях _Eb/N0. Эта функция позволяет

Настройте различные соответствующие аспекты процесса подбора кривых, такие как тип функции закрытой формы (из списка предварительно установленного выбора) раньше генерировал подгонку.
Отобразите эмпирические данные на графике наряду с кривой это berfit подгонки к данным.
Интерполируйте точки на кривой по экспериментальным точкам между значениями _Eb/N0 в вашем наборе эмпирических данных, чтобы сделать график более сглаженным взглядом.
Соберите релевантную информацию о подгонке, такой как численные значения точек вдоль кривой по экспериментальным точкам и коэффициентов подходящего выражения.

Примечание

berfit функция предназначается для аппроксимирования кривыми или интерполяции, не экстраполяции. Экстраполирование данных о BER вне порядка величины ниже наименьшего эмпирического значения BER по сути ненадежно.

Для полного списка вводов и выводов для berfit, смотрите его страницу с описанием.

Curve Fitting график коэффициента ошибок

Этот пример симулирует простую систему связи дифференциального бинарного манипулирования сдвига фазы (DBPSK) и отображает данные о коэффициенте ошибок на графике для серии значений Eb/N0. Это использует berfit функционируйте, чтобы соответствовать кривой к несколько грубому набору эмпирических коэффициентов ошибок.

Инициализируйте параметры симуляции

Задайте длину сообщения входного сигнала, порядок модуляции, область значений значений Eb/N0, чтобы рассмотреть, и минимальное количество ошибок, которые должны произойти, прежде чем симуляция вычислит коэффициент ошибок для этого значение Eb/N0. Предварительно выделите переменные для результатов и промежуточных результатов.

Для статистически точных результатов коэффициента ошибок минимальное количество ошибок должно быть на порядке 100, но эта симуляция использует небольшое количество ошибок сократить время выполнения и проиллюстрировать, как аппроксимирование кривыми может сгладить грубый набор данных.

siglen = 100000; % Number of bits in each trial
M = 2; % DBPSK is binary.
EbN0vec = 0:5; % Vector of EbN0 values
minnumerr = 5; % Compute BER only after 5 errors occur.
numEbN0 = length(EbN0vec); % Number of EbN0 values

ber = zeros(1,numEbN0); % final BER values
berVec = zeros(3,numEbN0); % Updated BER values
intv = cell(1,numEbN0); % Cell array of confidence intervals

Создайте Систему калькулятора коэффициента ошибок object™.

errorCalc = comm.ErrorRate;

Цикл симуляции

Симулируйте модулируемую систему связи DBPSK и вычислите BER с помощью for цикл, чтобы варьироваться значение Eb/N0. Внутренний while цикл гарантирует, что минимальное количество битовых ошибок происходит для каждого значения Eb/N0. Статистические данные коэффициента ошибок сохранены для каждого значения Eb/N0, чтобы использовать когда аппроксимирование кривыми и графический вывод.

% Loop over the vector of EbN0 values.
for jj = 1:numEbN0
    EbN0 = EbN0vec(jj);
    snr = EbN0; % Because of binary modulation
    reset(errorCalc)
    awgnChan.SNR = snr; % Assign Channel SNR
    
    while (berVec(2,jj) < minnumerr)
        msg = randi([0,M-1],siglen,1); % Generate message sequence
        %        txsig = step(hMod,msg); % Modulate
        txsig = dpskmod(msg,M); % Modulate
        awgnChan.SignalPower = (txsig'*txsig)/length(txsig); % Calculate and assign signal power
        %        rxsig = awgnChan(txsig); % Add noise.
        rxsig = awgn(txsig,snr,'measured'); % Add noise.
        %        decodmsg = step(hDemod, rxsig); % Demodulate.
        decodmsg = dpskdemod(rxsig,M); % Demodulate.
        berVec(:,jj) = errorCalc(msg,decodmsg); % Calculate BER
    end

Используйте berconfint вычислить коэффициент ошибок в 98%-м доверительном интервале для значения Eb/N0.

    [ber(jj), intv1] = berconfint(berVec(2,jj),berVec(3,jj),0.98);
    intv{jj} = intv1;
    disp(['EbN0 = ' num2str(EbN0) ' dB, ' num2str(berVec(2,jj)) ...
        ' errors, BER = ' num2str(ber(jj))])
end

EbN0 = 0 dB, 18392 errors, BER = 0.18392
EbN0 = 1 dB, 14307 errors, BER = 0.14307
EbN0 = 2 dB, 10190 errors, BER = 0.1019
EbN0 = 3 dB, 6940 errors, BER = 0.0694
EbN0 = 4 dB, 4151 errors, BER = 0.04151
EbN0 = 5 dB, 2098 errors, BER = 0.02098

Используйте berfit построить лучшую кривую по экспериментальным точкам, интерполируя, чтобы получить сглаженный график. Добавьте доверительные интервалы в график.

fitEbN0 = EbN0vec(1):0.25:EbN0vec(end); % Interpolation values
berfit(EbN0vec,ber,fitEbN0);
hold on;
for jj=1:numEbN0
    semilogy([EbN0vec(jj) EbN0vec(jj)],intv{jj},'g-+');
end
hold off;

BERTool

Команда bertool запускает Аналитический Инструмент Частоты ошибок по битам (BERTool) приложение.

Приложение позволяет вам анализировать эффективность частоты ошибок по битам (BER) систем связи. BERTool вычисляет BER как функцию отношения сигнал-шум. Это анализирует эффективность или с симуляциями Монте-Карло функций MATLAB и моделей Simulink^® или с теоретическими выражениями закрытой формы для выбранных типов систем связи.

Используя BERTool вы можете:

Сгенерируйте данные о BER для использования системы связи
- Выражения закрытой формы для теоретической эффективности BER выбранных типов систем связи.
- Полуаналитический метод.
- Симуляции содержатся в функциях симуляции MATLAB или моделях Simulink. После того, как вы создаете функцию или модель, которая симулирует систему, BERTool выполняет итерации по вашему выбору значений _Eb/N0 и собирает результаты.
Постройте один или несколько наборов данных BER на одном наборе осей. Например, можно графически сравнить данные моделирования с теоретическими результатами или данные моделирования от ряда подобных моделей системы связи.
Соответствуйте кривой к набору данных моделирования.
Отправьте данные о BER в рабочее пространство MATLAB, или в файл для дальнейшей обработки вас может хотеть выполнить.

Примечание

BERTool спроектирован для анализа частот ошибок по битам только, не коэффициентов ошибок символа, коэффициентов ошибок слова или других типов коэффициентов ошибок. Если, например, ваша симуляция вычисляет коэффициент ошибок символа (SER), преобразуйте SER в BER перед использованием симуляции с BERTool.

Следующие разделы описывают Аналитический Инструмент Частоты ошибок по битам (BERTool) и обеспечивают примеры, показывающие, как использовать его графический интерфейс пользователя.

Запустите BERTool
Среда BERTool
Вычисление теоретического BERs
Используя полуаналитический метод, чтобы вычислить BERs
Запустите симуляции MATLAB
Используйте функции симуляции с BERTool
Запустите симуляции Simulink
Используйте модели Simulink с BERTool
Управляйте данными о BER

Запустите BERTool

Чтобы открыть BERTool, ввести

Среда BERTool

Компоненты BERTool
Взаимодействие среди компонентов BERTool

Компоненты BERTool

Средство просмотра данных наверху. Это первоначально пусто.

После того, как вы дадите BERTool команду генерировать один или несколько наборов данных BER, они появляются в средстве просмотра данных. Пример, который показывает, как взгляд наборов данных в средстве просмотра данных находится в Примере: Используя Симуляцию MATLAB с BERTool.
Набор вкладок на нижней части. Пометил Theoretical, Semianalytic и Monte Carlo, вкладки соответствуют различным методам, которыми BERTool может сгенерировать данные о BER.

Примечание

При использовании BERTool, чтобы сравнить теоретические результаты и результаты Монте-Карло, предоставленная модель Simulink должна смоделировать точно систему, заданную параметрами на вкладке Theoretical.

Чтобы узнать больше о каждом из методов, смотрите
- Вычисление теоретического BERs
- Используя полуаналитический метод, чтобы вычислить BERs
- Запустите симуляции MATLAB или запущенные симуляции Simulink
Отдельное Окно рисунка BER, которое отображает некоторых или все наборы данных BER, которые перечислены в средстве просмотра данных. BERTool создает Окно фигуры BER после того, как это имеет по крайней мере один набор данных, чтобы отобразиться, таким образом, вы не видите Окно рисунка BER, когда вы открываете сначала BERTool. Для примера того, как Окно рисунка BER выглядит, смотрите Пример: Используя Теоретическую Вкладку в BERTool.

Взаимодействие Среди Компонентов BERTool. Компоненты BERTool действуют как один интегрированный инструмент. Эти поведения отражают свое интегрирование:

Если вы выбираете набор данных в средстве просмотра данных, BERTool реконфигурировал вкладки, чтобы отразить параметры, сопоставленные с тем набором данных, и также подсвечивает соответствующие данные в Окне рисунка BER. Это полезно, если средство просмотра данных отображает несколько наборов данных, и вы хотите вспомнить значение и источник каждого набора данных.
Если вы кликаете по данным, отображенным на графике в Окне рисунка BER, BERTool реконфигурировал вкладки, чтобы отразить параметры, сопоставленные с теми данными, и также подсвечивает соответствующий набор данных в средстве просмотра данных.

Примечание

Вы не можете нажать на точку данных, в то время как BERTool генерирует результаты симуляции Монте-Карло. Необходимо ожидать, пока инструмент не генерирует все точки данных прежде, чем щелкнуть для получения дополнительной информации.
Если вы конфигурируете вкладку Semianalytic или Theoretical способом, которая уже отражается в существующем наборе данных, BERTool подсвечивает что набор данных в средстве просмотра данных. Это препятствует тому, чтобы BERTool копировал свои расчеты и свои записи в средстве просмотра данных, все еще показывая вам результаты, которые вы запросили.
Если вы закрываете Окно рисунка BER, то можно вновь открыть его путем выбора из меню в BERTool.
Если вы выбираете опции в средстве просмотра данных, которые влияют на график BER, Окно рисунка BER сразу отражает ваши выборы. Такие опции относятся к именам набора данных, доверительным интервалам, аппроксимированию кривыми, и присутствию или отсутствию определенных наборов данных в графике BER.

Примечание

Если вы сохраняете Окно рисунка BER с помощью меню окна, получившийся файл содержит содержимое окна, но не данных BERTool, которые привели к графику. Чтобы сохранить целый сеанс BERTool, смотрите Сохранение Сеанса BERTool.

Вычисление теоретического BERs

Разделите обзор
Пример: Используя теоретическую вкладку в BERTool
Доступные наборы теоретических данных о BER

Разделите Обзор. Можно использовать BERTool, чтобы сгенерировать и анализировать теоретические данные о BER. Теоретические данные полезны для сравнения с вашими результатами симуляции. Однако выражения BER закрытой формы существуют только для определенных видов систем связи.

Чтобы получить доступ к возможностям BERTool, связанного с теоретическими данными о BER, используйте следующую процедуру:

Откройте BERTool и перейдите к вкладке Theoretical.
Установите параметры, чтобы отразить систему, эффективность которой вы хотите анализировать. Некоторые параметры отображаются и активны только, когда другие параметры имеют определенные значения. Смотрите Доступные Наборы Теоретических Данных о BER для деталей.
Нажмите Plot.

Для примера, который показывает, как сгенерировать и анализировать теоретические данные о BER через BERTool, смотрите Пример: Используя Теоретическую Вкладку в BERTool.

Кроме того, Доступные Наборы Теоретических Данных о BER указывает, какие комбинации параметров доступны на вкладке Theoretical и какие базовые функции выполняют расчеты.

Пример: Используя Теоретическую Вкладку в BERTool. Этот пример иллюстрирует, как использовать BERTool, чтобы сгенерировать и отобразить теоретические данные о BER на графике. В частности, пример сравнивает эффективность системы связи, которая использует канал AWGN и модуляцию QAM различных порядков.

Выполнение теоретического примера

Откройте BERTool и перейдите к вкладке Theoretical.
Установите параметры как показано в следующем рисунке.
Нажмите Plot.

BERTool создает запись в средстве просмотра данных и отображает данные на графике в Окне рисунка BER. Даже при том, что параметры запрашивают, чтобы _Eb/N0 подошли 18, BERTool строит только те значения BER, которые являются ^{по крайней мере 10-8}. Следующие фигуры иллюстрируют этот шаг.
Измените параметр Modulation order в 16, и нажмите Plot.

BERTool создает другую запись в средстве просмотра данных и отображает новые данные на графике в том же Окне рисунка BER (не изображенный).
Измените параметр Modulation order в 64, и нажмите Plot.

BERTool создает другую запись в средстве просмотра данных и отображает новые данные на графике в том же Окне рисунка BER, как показано на следующих рисунках.
Чтобы вспомнить, какое значение Modulation order соответствует данной кривой, кликните по кривой. BERTool отвечает путем корректировки параметров во вкладке Theoretical, чтобы отразить значения, которые соответствуют той кривой.
Чтобы удалить последнюю кривую из графика (но не из средства просмотра данных), снимите флажок в последней записи средства просмотра данных в столбце Plot. Чтобы восстановить кривую к графику, установите флажок снова.

Доступные Наборы Теоретических Данных о BER. BERTool может сгенерировать большой набор теоретических частот ошибок по битам, но не все комбинации параметров в настоящее время поддерживаются. Вкладка Theoretical настраивает себя к вашему выбору, так, чтобы комбинация параметров была всегда допустима. Можно установить параметр Modulation order путем выбора выбора из меню или путем ввода значения в поле. Normalized timing error должен быть между 0 и 0.5.

BERTool принимает, что Грэй, кодирующий, используется для всех модуляций.

Для QAM, когда log2M является нечетным (M, являющийся порядком модуляции), прямоугольное созвездие принято.

Комбинации параметров для систем канала AWGN

В следующей таблице перечислены доступные наборы теоретических данных о BER для систем, которые используют канал AWGN.

Модуляция	Порядок модуляции	Другой выбор
PSK	2, 4	Дифференциальное или недифференциальное кодирование.
8, 16, 32, 64, или более высокая степень 2
OQPSK	4	Дифференциальное или недифференциальное кодирование.
DPSK	2, 4, 8, 16, 32, 64, или более высокая степень 2
PAM	2, 4, 8, 16, 32, 64, или более высокая степень 2
QAM	4, 8, 16, 32, 64, 128, 256, 512, 1024, или более высокая степень 2
FSK	2	Ортогональный или неортогональный; `Coherent` или `Noncoherent` демодуляция.
4, 8, 16, 32, или более высокая степень 2	Ортогональный; `Coherent` демодуляция.
4, 8, 16, 32, или 64	Ортогональный; `Noncoherent` демодуляция.
MSK	2	`Coherent` обычный или предварительно закодированный MSK; `Noncoherent` предварительно закодированный MSK.
CPFSK	2, 4, 8, 16, или более высокая степень 2	`Modulation index` > 0.

Результаты BER также доступны для следующего:

блокируйтесь и сверточное кодирование с декодированием трудного решения для всех модуляций кроме CPFSK
блочное кодирование с декодированием мягкого решения для всех двоичных модуляций (включая 4-PSK и 4-QAM) кроме CPFSK, некогерентного неортогонального FSK и некогерентного MSK
сверточное кодирование с декодированием мягкого решения для всех двоичных модуляций (включая 4-PSK и 4-QAM) кроме CPFSK
незакодированный недифференцированно закодированный 2-PSK с ошибками синхронизации

Для получения дополнительной информации об определенных комбинациях параметров, включая библиографические ссылки, которые содержат выражения закрытой формы, смотрите страницы с описанием для следующих функций:

berawgn — Для систем без кодирования и совершенной синхронизации
bercoding — Для систем с кодированием канала
bersync — Для систем с модуляцией BPSK, никаким кодированием и несовершенной синхронизацией

Комбинации параметров для рэлеевского и систем канала Rician

В следующей таблице перечислены доступные наборы теоретических данных о BER для систем, которые используют канал Rayleigh или Rician.

Когда разнообразие используется, ОСШ на каждой ветви разнообразия выведен из ОСШ во входе канала (EbNo) разделенный на порядок разнообразия.

Модуляция	Порядок модуляции	Другой выбор
PSK	2	Дифференциальное или недифференциальное кодирование `Diversity order` ≧1 В случае недифференциального кодирования, порядок разнообразия, являющийся 1, и исчезновение Rician, может быть задано значение для шума фазы RMS (в радианах).
4, 8, 16, 32, 64, или более высокая степень 2	`Diversity order` ≧1
OQPSK	4	`Diversity order` ≧1
DPSK	2, 4, 8, 16, 32, 64, или более высокая степень 2	`Diversity order` ≧1
PAM	2, 4, 8, 16, 32, 64, или более высокая степень 2	`Diversity order` ≧1
QAM	4, 8, 16, 32, 64, 128, 256, 512, 1024, или более высокая степень 2	`Diversity order` ≧1
FSK	2	Коэффициент корреляции ∈[−1,1]. `Coherent` или `Noncoherent` демодуляция `Diversity order` ≧1 В случае ненулевого коэффициента корреляции и некогерентной демодуляции, порядок разнообразия равняется 1 только.
4, 8, 16, 32, или более высокая степень 2	`Noncoherent` демодуляция только. `Diversity order` ≧1

Для получения дополнительной информации об определенных комбинациях параметров, включая библиографические ссылки, которые содержат выражения закрытой формы, смотрите страницу с описанием для berfading функция.

Используя полуаналитический метод, чтобы вычислить BERs

Разделите обзор
Пример: Используя полуаналитическую вкладку в BERTool
Процедура для Использования полуаналитической вкладки в BERTool

Разделите Обзор. Можно использовать BERTool, чтобы сгенерировать и анализировать данные о BER через полуаналитический метод. Полуаналитический метод обсужден в Результатах Эффективности через Полуаналитический Метод, и Когда Использовать Полуаналитический Метод, особенно релевантно как справочный материал.

Чтобы получить доступ к полуаналитическим возможностям BERTool, откройте вкладку Semianalytic.

Для получения дальнейшей информации о том, как BERTool применяет полуаналитический метод, смотрите страницу с описанием для semianalytic функция, который использование BERTool выполнить расчеты.

Пример: Используя Полуаналитическую Вкладку в BERTool. Этот пример иллюстрирует, как BERTool применяет полуаналитический метод, с помощью 16-QAM модуляции. Этим примером является изменение на примере в Использовании Полуаналитического Метода, но это адаптируется, чтобы использовать BERTool вместо того, чтобы использовать semianalytic функционируйте непосредственно.

Выполнение полуаналитического примера

Настройте переданные и полученные сигналы. Сгенерируйте сигнал сообщения длины> = M ^L. Модулируйте сигнал сообщения использование полосовой модуляции. Примените формирование импульса без дальнейшей фильтрации передачи. Передайте сигнал передачи через бесшумный канал.
```
M = 16; % Alphabet size of modulation
L = 1; % Length of impulse response of channel
msg = [0:M-1 0]; % M-ary message sequence of length > M^L

modsig = qammod(msg,M); % Use 16-QAM.

Nsamp = 16;
modsig = rectpulse(modsig,Nsamp); % Use rectangular pulse shaping.
txsig = modsig; % No filter in this example

rxsig = txsig*exp(j*pi/180); % Static phase offset of 1 degree
```
Откройте BERTool и перейдите к вкладке Semianalytic.
Установите параметры как показано в следующем рисунке.
Нажмите Plot.

Видимые результаты полуаналитического примера

После того, как вы нажмете Plot, BERTool создает листинг для получившихся данных в средстве просмотра данных.

BERTool отображает данные на графике в Окне рисунка BER.

Процедура для Использования Полуаналитической Вкладки в BERTool. Процедура ниже описывает, как вы обычно реализуете полуаналитический метод с помощью BERTool:

Сгенерируйте сигнал сообщения, содержащий, по крайней мере, символы ^ML, где M является размером алфавита модуляции, и L является длиной импульсной характеристики канала в символах. Общий подход должен начать с увеличенного бинарного псевдошума (PN) последовательность общей длины _(log2M)ML. Увеличенная псевдошумовая последовательность является псевдошумовой последовательностью с дополнительным добавленным нулем, который делает распределение единиц и нулей равным.
Модулируйте поставщика услуг с сигналом сообщения использование полосовой модуляции. Поддерживаемые типы модуляции перечислены на странице с описанием для semianalytic. Сформируйте результирующий сигнал с формированием меандра, с помощью фактора сверхдискретизации, что вы будете дальнейшее использование, чтобы отфильтровать модулируемый сигнал. Сохраните результат этого шага как txsig для дальнейшего использования.
Отфильтруйте модулируемый сигнал с фильтром передачи. Этот фильтр часто является повышенным фильтром косинуса квадратного корня, но можно также использовать Баттерворта, функцию Бесселя, Чебышевский тип 1 или 2, эллиптического, или более общего КИХ или БИХ-фильтр. Если вы используете повышенный фильтр косинуса квадратного корня, используйте его на несверхдискретизированном модулируемом сигнале и укажите, что сверхдискретизация включает функцию фильтрации. Если вы используете другой тип фильтра, можно применить его к rectangularly сигналу импульсной формы.
Запустите пропущенный сигнал через бесшумный канал. Этот канал может включать многопутевые исчезающие эффекты, сдвиги фазы, нелинейность усилителя, квантование и дополнительную фильтрацию, но это не должно включать шум. Сохраните результат этого шага как rxsig для дальнейшего использования.

На вкладке Semianalytic BERTool введите параметры как в приведенную ниже таблицу.

‘ParameterName’	Значение
Eb/No range	Вектор, который перечисляет значения _Eb/N0, для которого вы хотите собрать данные о BER. Значение в этом поле может быть выражением MATLAB или именем переменной в рабочем пространстве MATLAB.
Modulation type	Эти параметры описывают схему модуляции, которую вы использовали ранее в этой процедуре.
Modulation order
Differential encoding	Этот флажок, который отображается и активен для MSK и модуляции PSK, позволяет вам выбрать между дифференциальным и недифференциальным кодированием.
Samples per symbol	Количество выборок на символ в переданном сигнале. Это значение является также частотой дискретизации переданных и полученных сигналов в Гц.
Transmitted signal	`txsig` сигнализируйте, что вы сгенерировали ранее в этой процедуре
Received signal	`rxsig` сигнализируйте, что вы сгенерировали ранее в этой процедуре
Numerator	Коэффициенты фильтра приемника, что BERTool применяется к полученному сигналу
Denominator

Примечание

Непротиворечивость среди значений в графический интерфейсе пользователя важна. Например, если сигнал, на который ссылаются в поле Transmitted signal, был сгенерирован с помощью DPSK, и вы устанавливаете Modulation type на MSK, результаты не могут быть значимыми.

Нажмите Plot.

Полуаналитические расчеты и результаты

После того, как вы нажмете Plot, BERTool выполняет эти задачи:

Фильтры rxsig и затем определяет вероятность появления ошибки каждого полученного очка сигнала путем аналитичного применения Гауссова шумового распределения к каждой точке. BERTool составляет в среднем вероятности появления ошибки по целому полученному сигналу определить полную вероятность появления ошибки. Если вероятность появления ошибки, вычисленная таким образом, является вероятностью появления ошибки символа, BERTool преобразует ее в небольшой коэффициент ошибок, обычно путем принятия Грэя, кодирующего. (Если тип модуляции является DQPSK или перекрестным QAM, результатом является верхняя граница на частоте ошибок по битам, а не самой частоте ошибок по битам.)
Вводит получившиеся данные о BER в средство просмотра данных окна BERTool.
Отображает получившиеся данные о BER на графике в Окне рисунка BER.

Запустите симуляции MATLAB

Разделите обзор
Пример: Используя симуляцию MATLAB с BERTool
Варьируясь критерий остановки
Графический вывод доверительных интервалов
Подходящий BER указывает на кривую

Разделите Обзор. Можно использовать BERTool в сочетании с собственными функциями симуляции MATLAB, чтобы сгенерировать и анализировать данные о BER. Функция MATLAB симулирует систему связи, эффективность которой вы хотите изучить. BERTool вызывает симуляцию для значений _Eb/N0, которые вы задаете, собирает данные о BER от симуляции и создает график. BERTool также позволяет вам легко изменить область значений _Eb/N0 и критерий остановки для симуляции.

Чтобы изучить, как сделать ваши собственные функции симуляции совместимыми с BERTool, смотрите Функции Симуляции Использования с BERTool.

Пример: Используя Симуляцию MATLAB с BERTool. Этот пример иллюстрирует, как BERTool может запустить функцию симуляции MATLAB. Функцией является viterbisim, один из демонстрационных файлов включен с программным обеспечением Communications Toolbox.

Чтобы запустить этот пример, выполните эти шаги:

Откройте BERTool и перейдите к вкладке Monte Carlo. (Параметры по умолчанию зависят от того, установили ли вам программное обеспечение Communications Toolbox. Также обратите внимание, что поле BER variable name применяется только к моделям Simulink.)
Установите параметры как показано в следующем рисунке.
Нажмите Run.

BERTool запускает функцию симуляции однажды для каждого заданного значения _Eb/N0 и собирает данные о BER. (В то время как BERTool занят этой задачей, он не может обработать определенные другие задачи, включая отображение на графике данных из других вкладок графический интерфейса пользователя.)

Затем BERTool создает листинг в средстве просмотра данных.

BERTool отображает данные на графике в Окне рисунка BER.
Чтобы изменить область значений _Eb/N0 при сокращении количества битов, обработанных в каждом случае, введите [5 5.2 5.3] в поле Eb/No range введите 1e5 в поле Number of bits, и нажимают Run.

BERTool запускает функцию симуляции снова для каждого нового значения _Eb/N0 и собирает новые данные о BER. Затем BERTool создает другой листинг в средстве просмотра данных.

BERTool отображает данные на графике в Окне рисунка BER, настраивая горизонтальную ось, чтобы хранить новые данные.

Две точки, соответствующие 5 дБ от этих двух наборов данных, отличаются, потому что меньшее значение Number of bits во второй симуляции заставило симуляцию заканчиваться прежде, чем наблюдать много ошибок. Чтобы узнать больше о критериях что использование BERTool для конечных симуляций, смотрите Варьирование Критерия остановки.

Для другого примера, который использует BERTool, чтобы запустить функцию симуляции MATLAB, смотрите Пример: Подготовьте Функцию Симуляции к Использованию с BERTool.

Варьируясь Критерий остановки. Когда вы создаете функцию симуляции MATLAB для использования с BERTool, необходимо управлять потоком так, чтобы симуляция закончилась, когда это или обнаруживает целевое количество ошибок или обрабатывает максимальное количество битов, какой бы ни происходит сначала. Чтобы узнать больше об этом требовании, смотрите Требования для Функций; для примера смотрите Пример: Подготовьте Функцию Симуляции к Использованию с BERTool.

После создания вашей функции, определенной целевой номер ошибок и максимальное количество битов во вкладке Monte Carlo BERTool.

Как правило, значение Number of errors, по крайней мере, 100 производит точный коэффициент ошибок. Значение Number of bits препятствует тому, чтобы симуляция запускалась слишком долго, особенно в больших значениях _Eb/N0. Однако, если значение Number of bits так мало, что симуляция собирает очень немного ошибок, коэффициент ошибок не может быть точным. Можно использовать доверительные интервалы, чтобы измерить точность коэффициентов ошибок, которые производит симуляция; чем больше доверительный интервал, тем менее точный вычисленный коэффициент ошибок.

Как пример, выполните процедуру, описанную в Примере: Используя Симуляцию MATLAB с BERTool и набором Confidence Level к 95 для каждого из этих двух наборов данных. Доверительные интервалы для второго набора данных больше, чем те для набора First Data. Это вызвано тем, что второй набор данных использует маленькое значение для Number of bits относительно свойств системы связи и значения в Eb/No range, приводящем к значениям BER только на основе небольшого количества наблюдаемых ошибок.

Примечание

Можно также использовать кнопку Stop в BERTool, чтобы остановить ряд симуляций преждевременно, пока функция настраивается, чтобы обнаружить и реагировать на нажатие кнопки.

Графический вывод Доверительных интервалов. После того, как вы запустите симуляцию с BERTool, получившийся набор данных в средстве просмотра данных имеет активное меню в столбце Confidence Level. Значением по умолчанию является off, так, чтобы данные моделирования в Окне рисунка BER не показывали доверительные интервалы.

Чтобы показать доверительные интервалы в Окне рисунка BER, установите Confidence Level на численное значение: 90%, 95%, или 99%.

График в Окне рисунка BER сразу отвечает на ваш выбор. Демонстрационный график ниже.

Для примера, который строит доверительные интервалы для симуляции Simulink, смотрите Пример: Используя Модель Simulink с BERTool.

Чтобы найти доверительные интервалы для уровней не перечисленными в меню Confidence Level, используйте berconfint функция.

Подходящие Точки BER к Кривой. После того, как вы запустите симуляцию с BERTool, Окно рисунка BER строит отдельные точки данных BER. Чтобы соответствовать кривой к набору данных, который содержит по крайней мере четыре точки, выберите поле в столбце Fit средства просмотра данных.

График в Окне рисунка BER сразу отвечает на ваш выбор. Демонстрационный график ниже.

Для примера, который выполняет аппроксимирование кривыми для данных из симуляции Simulink и генерирует график, показанный выше, смотрите Пример: Используя Модель Simulink с BERTool. Для примера, который выполняет аппроксимирование кривыми для данных из функции симуляции MATLAB, смотрите Пример: Подготовьте Функцию Симуляции к Использованию с BERTool.

Для большей гибкости в процессе подбора кривой кривой к данным о BER используйте berfit функция.

Используйте функции симуляции с BERTool

Требования для функций
Обработайте по шаблону для функции симуляции
Пример: подготовьте функцию симуляции к использованию с BERTool

Требования для Функций. Когда вы создаете функцию MATLAB для использования с BERTool, гарантируете, что функция взаимодействует правильно с графический интерфейсом пользователя. В этом разделе описываются входные параметры, выходные параметры и основную операцию BERTool-совместимой функции.

Входные параметры

BERTool оценивает ваши записи в областях графический интерфейса пользователя и передает данные функции как эти входные параметры в последовательности:

Одно значение от вектора Eb/No range каждый раз BERTool вызывает функцию симуляции
Значение Number of errors
Значение Number of bits

Выходные аргументы

Ваша функция симуляции должна вычислить и возвратить эти выходные аргументы в последовательности:

Частота ошибок по битам симуляции
Количество битов, обработанных при вычислении BER

BERTool использует эти выходные аргументы при создании отчетов и графическом выводе результатов.

Операция симуляции

Ваша функция симуляции должна выполнить эти задачи:

Симулируйте систему связи для значения _Eb/N0, заданного в первом входном параметре.
Прекратите симулировать, когда количество ошибок или количество обработанных битов будут равняться или будут превышать соответствующий порог, заданный во втором или третьем входном параметре, соответственно.
Обнаружьте, нажимаете ли вы Stop in BERTool и прерываете симуляцию в этом случае.

Обработайте по шаблону для Функции Симуляции. Используйте следующий шаблон при адаптации кода, чтобы работать с BERTool. Можно открыть его в редакторе путем ввода edit bertooltemplate в командном окне MATLAB. Понимание Шаблона объясняет ключевые разделы шаблона, в то время как Используя Шаблон указывает, как использовать шаблон с вашим собственным кодом симуляции. В качестве альтернативы можно разработать функцию симуляции, не используя шаблон, но быть уверены, что это удовлетворяет требованиям, описанным в Требованиях для Функций.

function [ber, numBits] = bertooltemplate(EbNo, maxNumErrs, maxNumBits)
% Import Java class for BERTool.
import com.mathworks.toolbox.comm.BERTool;

% Initialize variables related to exit criteria.
berVec = zeros(3,1); % Updated BER values

% --- Set up parameters. ---
% --- INSERT YOUR CODE HERE.
% Simulate until number of errors exceeds maxNumErrs
% or number of bits processed exceeds maxNumBits.
while((berVec(2) < maxNumErrs) && (berVec(3) < maxNumBits))

   % Check if the user clicked the Stop button of BERTool.
   if (BERTool.getSimulationStop)
      break;
   end

   % --- Proceed with simulation.
   % --- Be sure to update totErr and numBits.
   % --- INSERT YOUR CODE HERE.
end % End of loop

% Assign values to the output variables.
ber = berVec(1);
numBits = berVec(3);

Понимание шаблона.

От изучения кода в шаблоне функции наблюдайте, как функция или удовлетворяет требованиям, перечисленным в Требованиях для Функций, или указывает, где ваши собственные вставки кода должны сделать так. В частности,

Функция имеет соответствующие аргументы ввода и вывода.
Функция включает заполнителя для кода, который симулирует систему для данного значения E_b/N0.
Функция использует циклическую структуру, чтобы прекратить симулировать, когда количество ошибок превышает maxNumErrs или количество битов превышает maxNumBits, какой бы ни происходит сначала.

Примечание

Несмотря на то, что while оператор цикла описывает выходные критерии, ваш собственный код, введенный в раздел, отметил Proceed with simulation должен вычислить количество ошибок и количество битов. Если вы не выполняете эти расчеты в своем собственном коде, нажатие по Stop является единственным способом отключить цикл.
В каждой итерации цикла функция обнаруживает, когда пользователь нажимает Stop in BERTool.

Используя шаблон.

Вот процедура для использования шаблона с вашим собственным кодом симуляции:

Определите задачи настройки, которые необходимо выполнить. Например, вы можете хотеть инициализировать переменные, содержащие размер алфавита модуляции, коэффициенты фильтра, сверточную решетку кодирования или состояния сверточного interleaver. Поместите код для этих задач настройки в разделе шаблона отметил Set up parameters.
Определите базовые задачи симуляции, приняв, что вся настройка работает, был уже выполнен. Например, эти задачи могут включать кодирование контроля ошибок, модуляцию/демодуляцию и моделирование канала. Поместите код для этих базовых задач симуляции в разделе шаблона отметил Proceed with simulation.
Также в шаблоне раздел отметил Proceed with simulation, включайте код, который обновляет значения totErr и numBits. Количество totErr представляет количество ошибок, наблюдаемых до сих пор. Количество numBits представляет количество битов, обработанных до сих пор. Расчеты, чтобы обновить эти переменные зависят от того, как работают ваши базовые задачи симуляции.

Примечание

Обновление количеств ошибок и битов важно для обеспечения, что цикл завершает работу. Однако, если вы случайно создаете бесконечный цикл рано в вашей технической разработке с помощью шаблона функции, нажмите Stop in BERTool, чтобы прервать симуляцию.
Не используйте любой код настройки, который инициализирует EbNo, maxNumErrs, или maxNumBits, потому что BERTool передает эти количества функции как входные параметры после оценки данных, вводимых в графический интерфейс пользователя.
Настройте свой код или код шаблона по мере необходимости, чтобы использовать сопоставимые имена переменных и значения. Например, если ваш оригинальный код использует переменную под названием ebn0 и объявление функции шаблона (первая линия) использует имя переменной EbNo, необходимо поменять одно из имен, таким образом, они соответствуют. Как другой пример, если ваш оригинальный код использует ОСШ вместо E_b/N0, необходимо преобразовать количества соответственно.

Пример: Подготовьте Функцию Симуляции к Использованию с BERTool. Этот раздел адаптирует шаблон функции, данный в Шаблоне для Функции Симуляции.

Подготовка функции

Чтобы подготовить функцию к использованию с BERTool, выполните эти шаги:

Скопируйте шаблон с Шаблона для Функции Симуляции в новый файл MATLAB в редакторе MATLAB. Сохраните его в папке на своем пути MATLAB с помощью имени файла bertool_simfcn.
Из исходного примера следующие линии являются задачами настройки. Они изменяются из исходного примера, чтобы использовать входные параметры, которые BERTool предоставляет функции, вместо того, чтобы задать переменные, такие как EbNovec и numerrmin непосредственно.
```
% Set up initial parameters.
siglen = 1000; % Number of bits in each trial
M = 2; % DBPSK is binary.
snr = EbNo; % Because of binary modulation
% ErrorRate calculator System object to compare decoded symbols to the
% original transmitted symbols.
errorCalc = comm.ErrorRate;
```
Поместите эти строки кода в разделе шаблона отметили Set up parameters.

Из исходного примера следующие линии являются базовыми задачами симуляции, после того, как вся настройка работает, был выполнен.

msg = randi([0,M-1], siglen, 1); % Generate message sequence.
txsig = dpskmod(msg,M); % Modulate.
hChan.SignalPower = (txsig'*txsig)/length(txsig);  % Calculate and
                                                % assign signal power
rxsig = awgn(txsig,snr,'measured'); % Add noise.
decodmsg = dpskdemod(rxsig,M); % Demodulate.
berVec = errorCalc(msg,decodmsg); % Calculate BER

Поместите код для этих базовых задач симуляции в разделе шаблона отметил Proceed with simulation.

bertool_simfcn функция теперь совместима с BERTool. Обратите внимание на то, что различающийся исходный пример, функция здесь не инициализирует EbNovec, задайте EbNo как скаляр или использование numerrmin как целевое количество ошибок; это вызвано тем, что BERTool обеспечивает входные параметры для подобных количеств. bertool_simfcn функция также исключает код, связанный с графическим выводом, аппроксимированием кривыми и доверительными интервалами в исходном примере, потому что BERTool позволяет вам сделать подобные задачи в интерактивном режиме без написания кода.

Используя подготовленную функцию

Использовать bertool_simfcn в сочетании с BERTool продолжите пример путем выполнения этих шагов:

Откройте BERTool и перейдите к вкладке Monte Carlo.
Установите параметры на вкладке Monte Carlo как показано в следующем рисунке.
Нажмите Run.

BERTool тратит результаты вычисления некоторого времени и затем строит их. Они, кажется, не падают вдоль плавной кривой, потому что симуляция потребовала только пяти ошибок для каждого значения в EbNo.
Чтобы соответствовать кривой к серии точек в Окне рисунка BER, выберите поле рядом с Fit в средстве просмотра данных.

BERTool строит кривую как показано в следующем рисунке.

Запустите симуляции Simulink

Разделите обзор
Пример: Используя модель Simulink с BERTool
Варьируясь критерий остановки

Разделите Обзор. Можно использовать BERTool в сочетании с моделями Simulink, чтобы сгенерировать и анализировать данные о BER. Модель Simulink симулирует систему связи, эффективность которой вы хотите изучить, в то время как BERTool управляет рядом симуляций с помощью модели и собирает данные о BER.

Примечание

Чтобы использовать модели Simulink в BERTool, у вас должна быть лицензия Simulink. Программное обеспечение Communications Toolbox настоятельно рекомендовано. Остальная часть этого раздела принимает, что у вас есть лицензия и на Simulink и на приложения Communications Toolbox.

Чтобы получить доступ к возможностям BERTool, связанного с моделями Simulink, откройте вкладку Monte Carlo.

Для получения дальнейшей информации о доверительных интервалах и аппроксимировании кривыми для данных моделирования, смотрите Доверительные интервалы Графического вывода и Подходящие Точки BER к Кривой, соответственно.

Пример: Используя Модель Simulink с BERTool. Этот пример иллюстрирует, как BERTool может управлять рядом симуляций модели Simulink, и как можно варьироваться график. Моделью является commgraycode, одна из демонстрационных моделей включена с программным обеспечением Communications Toolbox. Пример принимает, что вам установили программное обеспечение Communications Toolbox.

Чтобы запустить этот пример, выполните эти шаги:

Откройте BERTool и перейдите к вкладке Monte Carlo. Имя файла модели, commgraycode.mdl, появляется как параметр Simulation MATLAB file or Simulink model. (Если viterbisim.m появляется там, выберите, чтобы указать, что программное обеспечение Communications Toolbox установлено.)
Нажмите Run.

BERTool загружает модель в память (который в свою очередь инициализирует несколько переменных в рабочем пространстве MATLAB), запускает симуляцию однажды для каждого значения _Eb/N0 и собирает данные о BER. BERTool создает листинг в средстве просмотра данных.

BERTool отображает данные на графике в Окне рисунка BER.
Чтобы соответствовать кривой к серии точек в Окне рисунка BER, выберите поле рядом с Fit в средстве просмотра данных.

BERTool строит кривую, как ниже.
Чтобы указать на 99%-й доверительный интервал вокруг каждой точки в данных моделирования, установите Confidence Level на 99% в средстве просмотра данных.

BERTool отображает значение погрешности, чтобы представлять доверительные интервалы, как ниже.

Другой пример, который использует BERTool, чтобы управлять рядом симуляций Simulink, находится в Примере: Подготовьте Модель к Использованию с BERTool.

Варьируясь Критерий остановки. Когда вы создаете модель Simulink для использования с BERTool, необходимо настроить его так, чтобы симуляция закончилась, когда это или обнаруживает целевое количество ошибок или обрабатывает максимальное количество битов, какой бы ни происходит сначала. Чтобы узнать больше об этом требовании, смотрите Требования для Моделей; для примера смотрите Пример: Подготовьте Модель к Использованию с BERTool.

После создания вашей модели Simulink, определенной целевой номер ошибок и максимальное количество битов во вкладке Monte Carlo BERTool.

Можно также нажать Stop in BERTool, чтобы остановить ряд симуляций преждевременно.

Используйте модели Simulink с BERTool

Требования для моделей
Советы для подготовки моделей
Пример: подготовьте модель к использованию с BERTool

Требования для Моделей. Модель Simulink должна удовлетворить этим требованиям, прежде чем можно будет использовать ее с BERTool, где чувствительные к регистру имена переменных нужно точно так же, как показать ниже:

Блок канала должен использовать переменную EbNo вместо трудно закодированного значения для _Eb/N0.
Симуляция должна остановиться, когда ошибочное количество достигает значения переменной maxNumErrs или когда количество обработанных битов достигает значения переменной maxNumBits, какой бы ни происходит сначала.

Можно сконфигурировать блок Error Rate Calculation в программном обеспечении Communications Toolbox, чтобы остановить симуляцию на основе таких критериев.
Симуляция должна отправить данные об уровне конечной погрешности в рабочее пространство MATLAB как переменная, имя которой вы вводите в поле BER variable name в BERTool. Переменная должна быть трехэлементным вектором, который перечисляет BER, количество битовых ошибок и количество обработанных битов.

Этот трехэлементный векторный формат поддерживается блоком Error Rate Calculation.

Советы для Подготовки Моделей. Вот некоторые советы для подготовки модели Simulink для использования с BERTool:

Чтобы избегать использования имени неопределенной переменной в диалоговом окне для блока Simulink на шагах, которые следуют, настройте переменные в рабочем пространстве MATLAB с помощью команды, такие как та ниже.
```
EbNo = 0; maxNumErrs = 100; maxNumBits = 1e8;
```
Вы можете также хотеть поместить ту же команду в коллбэк функции предварительной нагрузки модели, инициализировать переменные, если вы вновь открыли модель в будущем сеансе работы с MATLAB.

Когда вы используете BERTool, он вводит фактические значения на основе того, что вы вводите в графический интерфейс пользователя, таким образом, начальные значения выше несколько произвольны.
Чтобы смоделировать канал, используйте блок AWGN Channel в программном обеспечении Communications Toolbox этими параметрами:
- Mode = Signal to noise ratio (Eb/No)
- Eb/No = EbNo
Чтобы вычислить коэффициент ошибок, используйте блок Error Rate Calculation в программном обеспечении Communications Toolbox этими параметрами:
- Проверяйте Stop simulation.
- Target number of errors = maxNumErrs
- Maximum number of symbols = maxNumBits
Чтобы отправить данные от блока Error Rate Calculation до рабочего пространства MATLAB, установите Output data на Port, присоедините блок To Workspace (Simulink) и установите параметр Limit data points to last последнего блока на 1. Параметр Variable name в блоке To Workspace (Simulink) должен совпадать со значением, которое вы вводите в поле BER variable name BERTool.

Совет

Больше чем один блок To Workspace (Simulink) доступен. Обязательно выберите To Workspace (Simulink) из подбиблиотеки DSP System Toolbox™ / Sinks.
Если ваша модель вычисляет коэффициент ошибок символа вместо небольшого коэффициента ошибок, используйте блок Integer to Bit Converter в программном обеспечении Communications Toolbox, чтобы преобразовать символы вдребезги.
Обрабатываются основанные на системе координат симуляции, часто запускаемые быстрее, чем основанные на выборке симуляции для того же количества битов. Количество ошибок или количество обработанных битов могут превысить значения, которые вы вводите в BERTool, потому что симуляция всегда обрабатывает установленную сумму данных в каждой системе координат.
Если у вас есть существующая модель, которая использует блок AWGN Channel с помощью параметра Mode кроме Signal to noise ratio (Eb/No), можно адаптировать блок, чтобы использовать режим Eb/No вместо этого. Чтобы узнать о том, как различные режимы блока связаны друг с другом, нажмите кнопку Help блока AWGN Channel, чтобы просмотреть онлайновую страницу с описанием.
Если ваша модель использует функцию предварительной нагрузки или другой коллбэк, чтобы инициализировать переменные в рабочем пространстве MATLAB после загрузки, убедитесь, прежде чем вы будете использовать кнопку Run в BERTool, что одно из этих условий соблюдают:
- Модель не находится в настоящее время в памяти. В этом случае BERTool загружает модель в память и запускает функции обратного вызова.
- Модель находится в памяти (ли в окне или не), и переменные неповреждены.
Если вы очищаете или перезаписываете переменные модели и хотите восстановить их значения перед использованием кнопки Run в BERTool, можно использовать bdclose функция в командном окне MATLAB, чтобы очистить модель из памяти. Это заставляет BERTool перезагружать модель после того, как вы нажмете Run. Точно так же, если вы обновляете свою рабочую область путем издания clear all или clear variables команда, необходимо также очистить модель из памяти при помощи bdclose all.

Пример: Подготовьте Модель к Использованию с BERTool. Этот пример использует модель Simulink, которая настраивается для использования с BERTool. Пример также иллюстрирует, как сравнить эффективность BER симуляции Simulink теоретическими результатами BER. Пример принимает, что вам установили программное обеспечение Communications Toolbox.

Чтобы подготовить модель к использованию с BERTool, выполните эти шаги, с помощью точных чувствительных к регистру имен переменных как показано:

Откройте модель путем ввода следующей команды в командное окно MATLAB.
Чтобы инициализировать параметры в рабочем пространстве MATLAB и избегать использования неопределенных переменных как параметров блоков, введите следующую команду в командное окно MATLAB.
```
EbNo = 0; maxNumErrs = 100; maxNumBits = 1e8;
```
Чтобы гарантировать, что BERTool использует правильное количество шума каждый раз, это запускает симуляцию, откройте диалоговое окно для блока AWGN Channel путем двойного клика по блоку. Проверьте, что Es/No установлен в EbNo и нажмите OK. В этой конкретной модели _Es/N0 эквивалентен _Eb/N0, потому что тип модуляции является BPSK.
Гарантировать, что BERTool использует правильный критерий остановки для каждой итерации,
- Откройте диалоговое окно для блока Error Rate Calculation. Проверьте, что Target number of errors установлен в maxNumErrs, и что Maximum number of symbols установлен в maxNumBits. Нажмите OK.
- Время остановки симуляции должно быть установлено в Inf.
Позволять BERTool получить доступ к результатам BER, которые блок Error Rate Calculation вычисляет, блок To Workspace (Simulink), BER, соединяется с выходом блока Error Rate Calculation.

Совет

Больше чем один блок To Workspace (Simulink) доступен. Обязательно выберите To Workspace (Simulink) из подбиблиотеки DSP System Toolbox / Sinks.

Использовать doc_bpsk модель с BERTool, выполните эти шаги:

Откройте BERTool и перейдите к вкладке Monte Carlo.
Установите параметры на вкладке Monte Carlo как показано в следующем рисунке.
Нажмите Run.

BERTool тратит результаты вычисления некоторого времени и затем строит их.
Чтобы сравнить эти результаты симуляции с теоретическими результатами, перейдите к вкладке Theoretical в BERTool и установите параметры как показано ниже.
Нажмите Plot.

BERTool строит теоретическую кривую в Окне рисунка BER наряду с более ранними результатами симуляции.

Управляйте данными о BER

Экспорт наборов данных или сеансов BERTool
Импорт наборов данных или сеансов BERTool
Данные об управлении в средстве просмотра данных

Экспорт Наборов данных или Сеансов BERTool. BERTool позволяет вам экспортировать отдельные наборы данных в рабочее пространство MATLAB или в MAT-файлы. Одна опция для экспорта удобна для обработки данных вне BERTool. Например, чтобы создать очень индивидуально настраиваемый отображают данные об использовании на графике из BERTool, экспортируют набор данных BERTool в рабочее пространство MATLAB и используют любую из команд графического вывода в MATLAB. Другая опция для экспорта позволяет вам повторно импортировать данные в BERTool позже.

BERTool также позволяет вам сохранить целый сеанс, который полезен, если ваш сеанс содержит несколько наборов данных, к которым вы хотите возвратиться на более позднем сеансе.

В этом разделе описываются эти возможности:

Экспорт наборов данных

Чтобы экспортировать отдельный набор данных, выполните эти шаги:

В средстве просмотра данных выберите набор данных, который вы хотите экспортировать.
Выберите .
Установите Export to указывать на формат и место назначения данных.
1. Если вы хотите повторно импортировать данные в BERTool позже, необходимо выбрать Workspace structure или MAT-file structure создать структуру в рабочем пространстве MATLAB или MAT-файле, соответственно.
  
  Появляется новое поле под названием Structure name. Установите его на имя, которое вы хотите, чтобы BERTool использовал для структуры, которую это создает.
  
  Если вы выбрали Workspace structure и вы хотите, чтобы BERTool использовал ваше выбранное имя переменной, даже если переменная тем именем уже существует в рабочей области, выберите Overwrite variables.
2. Если вы не должны повторно импортировать данные в BERTool позже, удобный способ получить доступ к данным вне BERTool состоит в том, чтобы иметь BERTool, создают пару массивов в рабочем пространстве MATLAB. Один массив содержит значения _Eb/N0, в то время как другой массив содержит значения BER. Чтобы выбрать эту опцию, установите Export to на Workspace arrays.
  
  Затем введите два имен переменных в полях под Variable names.
  
  Если вы хотите, чтобы BERTool использовал ваши выбранные имена переменных, даже если переменные теми именами уже существуют в рабочей области, выберите Overwrite variables.
Нажмите OK. Если вы выбрали MAT-file structure, BERTool предлагает вам путь к MAT-файлу, который вы хотите создать.

Чтобы повторно импортировать структуру позже, смотрите Наборы данных Импорта.

Исследование экспортируемой структуры

Этот раздел кратко описывает содержимое структуры, которую BERTool экспортирует в рабочую область или в MAT-файл. Поля структуры обозначаются в приведенной ниже таблице. Полями, которые являются самыми важными для вас, когда это необходимо, чтобы управлять экспортированными данными, является paramsEvaled и data.

Имя поля	Значение
`params`	Значения параметров в БЕРТОЛЕ ГИ, некоторые из которых могут быть невидимыми и следовательно не важными для расчетов.
`paramsEvaled`	Значения параметров, которые BERTool использует при вычислении набора данных.
`data`	_Eb/N0, BER и количество битов обрабатываются.
`dataView`	Информация о внешнем виде в средстве просмотра данных. Используемый BERTool для переимпорта данных.
`cellEditabilities`	Указывает, имеет ли средство просмотра данных активный Confidence Level или запись Fit. Используемый BERTool для переимпорта данных.

Поля параметра

params и paramsEvaled поля похожи друг на друга, за исключением того, что params описывает точное состояние графический интерфейса пользователя тогда как paramsEvaled указывает на значения, которые на самом деле используются для расчетов. Как пример различия, для теоретической системы с каналом AWGN, params записи, но paramsEvaled не использует параметр порядка разнообразия. Порядок разнообразия не используется в расчетах, потому что это важно только для систем с каналами Рейли. Как другой пример, если вы вводите [0:3]+1 в графический интерфейсе пользователя как область значений значений _Eb/N0, params указывает на [0:3]+1 в то время как paramsEvaled указывает на 1 2 3 4.

Длина и точное содержимое paramsEvaled зависьте от набора данных, потому что только релевантная информация появляется. Если значение содержимого paramsEvaled не ясно после контроля, один способ узнать больше состоит в том, чтобы повторно импортировать набор данных в BERTool и смотреть значения параметров, которые появляются в графический интерфейсе пользователя. Чтобы повторно импортировать структуру, следуйте инструкциям в Импорте Наборов данных или Сеансов BERTool.

Поле данных

Если ваша экспортируемая переменная рабочей области называется ber0, поле ber0.data массив ячеек, который содержит числовые результаты в этих векторах:

ber0.data{1} перечисляет значения _Eb/N0.
ber0.data{2} перечисляет значения BER, соответствующие каждому из значений _Eb/N0.
ber0.data{3} указывает, для симуляции или полуаналитических результатов, сколько битов BERTool обработал при вычислении каждого из соответствующих значений BER.

Сохранение сеанса BERTool.

Чтобы сохранить целый сеанс BERTool, выполните эти шаги:

Выберите .
Когда BERTool предлагает вам, введите путь к файлу, который вы хотите создать.

BERTool создает текстовый файл, который записывает все наборы данных в настоящее время в средстве просмотра данных, наряду с параметрами графический интерфейса пользователя, сопоставленными с наборами данных.

Примечание

Если ваш сеанс BERTool требует конкретных переменных рабочей области (таких как txsig или rxsig для вкладки Semianalytic), сохраните тех отдельно в MAT-файле с помощью save команда в MATLAB.

Импорт Наборов данных или Сеансов BERTool. BERTool позволяет вам повторно импортировать отдельные наборы данных, которые вы ранее экспортировали в структуру, или перезагружать целые сеансы что вы ранее сохраненный. В этом разделе описываются эти возможности:

Чтобы узнать больше об экспорте наборов данных или сохранении сеансов от BERTool, смотрите Наборы данных Экспорта или Сеансы BERTool.

Импорт наборов данных.

Чтобы импортировать отдельный набор данных, который вы ранее экспортировали от BERTool до структуры, выполните эти шаги:

Выберите .
Установите Import from на любой Workspace structure или MAT-file structure. Если вы выбираете Workspace structure, введите имя переменной рабочей области в поле Structure name.
Нажмите OK. Если вы выбираете MAT-file, BERTool предлагает вам выбирать файл, который содержит структуру, которую вы хотите импортировать.

После того, как вы отклоняете диалоговое окно Data Import (и диалоговое окно выбора файла, в случае MAT-файла), средство просмотра данных показывает недавно импортированный набор данных, и Окно рисунка BER строит его.

Открытие предыдущего сеанса BERTool

Чтобы заменить наборы данных в средстве просмотра данных с наборами данных от предыдущего сеанса BERTool, выполните эти шаги:

Выберите .

Примечание

Если BERTool уже содержит наборы данных, он спрашивает вас, хотите ли вы сохранить текущий сеанс. Если вы отвечаете не и продолжаете процесс загрузки, BERTool отбрасывает текущий сеанс после открытия нового сеанса из файла.
Когда BERTool предлагает вам, введите путь к файлу, который вы хотите открыть. Это должен быть файл, что вы ранее создали использование опции в BERTool.

После того, как BERTool читает файл сеанса, средство просмотра данных показывает наборы данных из файла.

Если ваш сеанс BERTool требует конкретных переменных рабочей области (таких как txsig или rxsig для вкладки Semianalytic), что вы сохраненный отдельно в MAT-файле, можно получить их использующий load команда в MATLAB.

Данные об управлении в Средстве просмотра Данных. Средство просмотра данных дает вам гибкость, чтобы переименовать и удалить наборы данных и переупорядочить столбцы в средстве просмотра данных.

Чтобы переименовать набор данных в средстве просмотра данных, дважды кликните его имя в столбце BER Data Set и введите новое имя.
Чтобы удалить набор данных из средства просмотра данных, выберите его и выберите .

Примечание

Если набор данных произошел из вкладки Semianalytic или Theoretical, BERTool удаляет данные, не прося подтверждение. Вы не можете отменить эту операцию.
Чтобы переместить столбец в средство просмотра данных, перетащите заголовок столбца налево или направо с мышью. Например, изображение ниже показов мышь, перетаскивающая столбец BER слева от его положения по умолчанию. Когда вы отпускаете кнопку мыши, столбцы привязываются в место.

Источник

Качество сетей передачи данных. Транспорт

Время на прочтение
8 мин

Количество просмотров 28K

В предыдущей статье были затронуты базовые метрики качества сетей и систем передачи данных. Также было обещано написать про то, как все работает изнутри. И намеренно не было упомянуто про качество среды передачи данных и ее характеристиках. Надеюсь, что новая статья даст ответы на эти вопросы.

Среда передачи

Начну, пожалуй, с последнего пункта — качества среды передачи. Как уже написано выше, про нее ничего не говорилось в предыдущем повествовании, поскольку само по себе количество сред и их характеристики очень сильно различаются и зависят от просто колоссального множества факторов. Разбираться во всем этом многообразии задача соответствующих специалистов. Всем очевидно использование радио-эфира в качестве среды передачи данных. Я же помню в конце 90-х начале 00-х особой популярностью у операторов связи стали пользоваться такие экзотические способы передачи, как лазерные атмосферные передатчики. Выглядели они, в зависимости от производителя и конфигурации примерно как на картинке слева (да, почти такой себе светотелефон из радиолюбительского детства). Преимущество их было в том, что не надо было получать разрешение ГРКЧ, да и скорости, по сравнению с радиомостом были несколько больше, кроме того существовали модификации для организации каналов с временным разделением (E1 и т.п.), а подобное оборудование радио-доступа стоило непомерно дорого. Почему не оптический кабель? Потому что в те счастливые времена дикого провайдинга оптика еще была довольно дорогой, а за конвертер интерфейса или активное оборудование, способное принять оптический линк напрямую давали небольшой (а кто-то и большой) брусок золота. Были еще спутниковые каналы, но это вообще из области фантастики и позволить их себе могли разве что компании нефтяного сектора и прочего национального благосостояния. Но работа канала через спутник сводится к использованию радио-эфира, со всеми вытекающими и внесением огромной задержки.

Соответственно погружаясь в вопрос в результате будем иметь множество сред и ни одной обобщенной характеристики. Тем не менее для нас среда это всего лишь транспорт, передающий информацию из точки А в точку Б. А для транспорта (даже общественного) характеристикой отражающей его качество будет доставка всех битов (ну или пассажиров) без искажений и потерь (не хотелось бы лишиться части тела при перевозке, согласитесь). Т.е. мы приходим к такой обобщенной метрике качества транспорта как количество битовых ошибок, или BER (Bit error rate). В чисто пакетных сетях она практически не используется, поскольку ошибки передачи выявляются на уровне пакета, например подсчетом контрольных сумм: FCS (Frame check sequence) для L2 или сhecksum IP для L3. Если контрольная сумма не совпадает, то пакет целиком отбрасывается как невалидный. Если же рассмотреть гетерогенные сети, те в которых транспортом может служить непакетная сеть, а, например, один из вариантов описанных выше, либо вообще используется транзит через ATM, PDH, SDH и подобное без непосредственной (но с восстановлением) передачи пакета, то битовые ошибки транспорта могут значительно влиять, конечно в зависимости от технологии. Рассмотрим инкапсуляцию и передачу Ethernet-фрейма в HDLC. Другие технологии используют практически такую же технику.

Схема читается слева-направо (взята здесь).

Какой-то узел сети А отправляет пакет в сторону какого-то узла сети Б
Транспорт между сетями построен на сети PDH
Узел на границе выхода сети А вырезает из Ethernet-фрейма область полезной нагрузки (поля от DestinationAddress до FCS включительно), оборачивает в HDLC заголовки, и отправляет на граничный узел входа сети Б
Граничный узел входа сети Б выделяет область полезной нагрузки и восстанавливает Ethernet-фрейм
Фрейм с граничного узла отправляется получателю

Как можно видеть, в данном случае контрольная передается корректно и в случае повреждения битового потока в процессе передачи восстановленный пакет с неверной FCS будет отброшен получателем. В данном случае механизм обнаружения ошибки налицо.

Но не всегда используется надстройка инкапсуляции, либо передается вообще не полноценный фрейм, а лишь поле payload. Т.е. вырезается область, оборачивается во внутренний протокол, а на другой стороне восстанавливаются недостающие данные, включая отсутствующие заголовки L2. Соответственно пропадает и FCS — она просто рассчитывается заново. Таким образом получается, если данные были повреждены, а FCS рассчитан на основании “испорченных” данных, то получатель принимает совсем не тот пакет, который ему отправляли. Это довольно часто встречается в спутниковой связи, чтобы повысить полезную утилизацию канала, избегая передачи условно “лишней” информации. Резюмируя, получается что метрика BER может быть интересна в случаях когда:

необходимо проверить стабильность физического канала, например для оптики это 10E-12 (упоминается в IEEE802.3)
Ethernet-фреймы упаковывают в SDH(GFP), PDH, ATM и другие транспортные сети.
используются технологии xHSL, PPP протоколы в которые упаковывают IP пакеты

BER тест

Метрика известна — это отношение количество битовых ошибок к общему числу переданных битов. Методика измерения для сетей TDM известна как спецификация ITU-T G.821. Классически для проверки каналов используется BERT (BER Test) первого уровня, но с учетом специфики работы протоколов инкапсуляции пакетных сетей и самого принципа работы пакетных сетей необходимо иметь возможность проводить тесты на L1-L4. Немного далее будет рассмотрено подробнее. Ну а сейчас следует определиться что проверять и как проверять. На вопрос:” Что проверять?” Отвечает ITU-T 0.150. В его пункте 5 рассмотрены типы ПСП (псевдослучайных последовательностей), из которых просто берутся данные для формирования пакета. Т.е. нужно просто взять и заполнить соответствующий уровень пакета данными выбранной ПСП. У нас в приборах используются следующие ПСП:

ПСП 2е9 (ITU-T 0.150 пункт 5.1)
ПСП 2е11 (ITU-T 0.150 пункт 5.2)
ПСП 2е15 (ITU-T 0.150 пункт 5.3)
ПСП 2е23 (ITU-T 0.150 пункт 5.6)
ПСП 2е31 (ITU-T 0.150 пункт 5.8)
пользовательская последовательность (32 бита)
все нули
все единицы
альтернативная последовательность (01010101)

Пользовательская последовательность введена для совместимости с приборами, которые существуют на рынке, т.е можно задать любую последовательность и проводить совместный тест.

Вопрос как проверять пока что открыт, попробуем разобраться. Допустим мы умеем генерировать определенные пакеты. Если отправить такой пакет на другой конец транспорта, то как понять, что он не изменился (следует абстрагироваться от пакетного принципа, поскольку у нас может не быть FCS и других типов контроля, как описано ранее)? Самый простой вариант — завернуть пакет обратно (в TDM называется “сделать петлю”, в Ethernet — установить шлейф). Заворот, во многих случаях, можно сделать на выходе канала без изменения среды передачи, т.е. реально поставить петлю на выходе E1 и все будет работать. Но т.к. данные проделывают двойной путь, то вероятность возникновения ошибки также возрастает в 2 раза. Да и каналы могут быть асимметричными или однонаправленными. Соответственно идеальным было бы иметь возможность обладать информацией о корректном следовании и сравнивать приходящие пакеты с уже известной информацией. Первый, и наиболее простой вариант, применимый когда оба выхода канала располагаются рядом (например такое возможно при TDM коммутации, или тестировании оптического “кольца”) заключается в том, что один порт прибора генерирует тестовый трафик, а другой порт этого же прибора его получает и сравнивает, а т.к. сравнение происходит в том же узле, что и генерация, то проблем со сравнением данных последовательности не возникает. Второй вариант предполагает восстановление первоначальной последовательности и сравнение ее с приходящими данными. В случае с полностью случайной последовательностью реализовать такое не представляется возможным, а вот если последовательность псевдослучайная, то вполне. Какое-то время затрачивается на синхронизацию в самом начале теста, но затем сравнение не представляет сложности. Поскольку ПСП первого прибора и ПСП второго известны и одинаковы, синхронизация сводится к поиску места начала сравнения в ПСП второго прибора. Таким образом существуют следующие топологии:

«сам на себя» 1 — один прибор на одном порту, на другом конце транспорта стоит шлейф
«сам на себя» 2 — один прибор с одного порта своего порта на другой свой порт
с одного прибора на другой прибор, с синхронизацией

Еще раз стоит отметить, что тест BER не рекомендуется использовать на сетях лишь с пакетной коммутацией. Приведу пример. Допустим, уже идет тестовый поток и приборы синхронизированы (топология 3). В какой-то момент времени происходит следующее:

формируется Ethernet-фрейм, содержащий данные ПСП
для такого фрейма рассчитывается FCS и он укладывается в выходной буфер
фрейм отправляется по сети на другой прибор
по каким-то причинам происходит изменение всего одного бита внутри пакета
получатель принимает пакет
FCS принятого пакета не соответствует содержимому
пакет отбрасывается (если между отправителем и получателем есть, например, коммутатор, то “кривой” пакет вообще не дойдет до получателя, т.к. будет уничтожен до него)
отправитель формирует следующий пакет (все начинается с п.1)

В приведенном примере на шаге 8 произойдет срыв синхронизации на стороне получателя. Произойдет это потому, что отправитель возьмет следующий блок ПСП, а получатель будет сравнивать с тем блоком, который потерялся в предыдущем цикле (он ведь ничего не знает о потере). Срыв синхронизации приведет к необоснованно большому росту битовых ошибок, т.к. все вновь идущие блоки абсолютно не совпадают, что приведет к тому, что за один пакет число битовых ошибок будет увеличиваться на размер фрейма. Через какое-то время будет предпринята попытка восстановления синхронизации, но количество накопленных битовых ошибок будет сильно не соответствовать действительности.

А как в железе?

Как у других не знаю, но у наших приборов Беркут (ET, ETX, ETL, B100, а также модуль B5-GBE для MMT) дела обстоят следующим образом. Помня принцип о генерации и анализе трафика как можно ближе к физическому сегменту из первой статьи, все подобные задачи были возложены на FPGA. Упрощенная структурная схема выглядит так:

MAC ядро представлено двумя блоками: один на прием, другой на передачу. Это позволяет независимо принимать и отправлять пакеты, т.е. нет взаимовлияния очереди отправки на очередь приема и наоборот. Также с двух независимых блоков возможно вести общую статистику по полученному и отправленному трафику независимо от типа теста. Данные с блока передачи поступают на трансмиттер и отправляются в сеть, а входящие данные с трансивера поступают в блок приема.
Поскольку для некоторых топологий тестов необходим функционал шлейфа (loopback, петля), то он реализован отдельным блоком. Возможно установить шлейф уровня L1-L4:

L1 — просто заворачивает трафик обратно (происходит это еще в трансивере)
L2 — меняет DstMAC<->SrcMAC местами, пересчитывает FCS
L3 — меняет DstMAC<->SrcMAC и DstIP<->SrcIP местами, пересчитывает FCS
L4 — меняет DstMAC<->SrcMAC, DstIP<->SrcIP и DstPort<->SrcPort, пересчитывает FCS

Статистика по пакетам ведется и для режима шлейфа тоже, что позволяет грубо оценить соотношение отправленных и принятых пакетов.

Модуль генератора для каждого типа теста свой, для BERT он содержит генератор ПСП всех заявленных типов.
Работает это следующим образом. От генератора ПСП поступают данные на мультиплексор (проще говоря коммутатор), который, если не включен какой-то другой канал в данный момент, направляет поток в MAC tx модуль. MAC tx модуль, в соответствии с настройками теста (уровень BERT, размер пакета, данные полей) формирует из ПСП валидный Ethernet-фрейм и отправляет его в трансивер, который в свою очередь отправляет его в сеть. В зависимости от топологии теста фрейм либо заворачивается удаленной стороной, либо анализируется. В любом случае первичная обработка пакета не отличается. Фрейм попадает на MAC rx ядро, которое отправляет его на мультиплексор. Мультиплексор в зависимости от режима работы прибора направляет пакет либо в Loopback модуль, откуда после обработки он сразу же направляется в MAC tx для отправки, либо в модуль обработки и статистики теста, где, если потребуется, будет проведена попытка синхронизации ПСП и выполнено сравнение исходной последовательности с полученной. Результаты обработки отдаются в модуль вывода статистики.
Использование FPGA или ASIC позволяет все операции проводить параллельно, что не вносит какие либо задержки на обработку и исключает взаимовлияние модулей обработки.

Заключение

Несмотря на всю кажущуюся простоту алгоритмов и методик, за ними стоит много лет серьезных исследований. Огромное число факторов до сих пор влияет как на точность измерений, так и на стоимость приборов (прецизионные элементы, высокоскоростные ПЛИС). Например, приведенный выше BER тест не отличается значительной сложностью в общем алгоритмическом плане, но требует знаний в области математики, информатики и теории информации для разработки жизнеспособной модели. Модификация BER теста для пакетных сетей (поддержка уровней L2-L4) требует глубокого понимания принципов коммутации и маршрутизации. Надеюсь, что подобного рода статьи интересны и приносят пользу. В следующих публикациях планирую написать про сертифицированные тесты, генераторы трафика, фильтры и аналитические комплексы. Ведь как сказал Джон Фицджеральд Кеннеди на выступлении перед гражданами США перед стартом Лунной программы:

“И мы сделаем это. Не потому, что это легко, а потому что трудно.”

_{PS. Задавайте вопросы и предлагайте темы, в рамках нашей компетенции готовы на все}

Источник

Выполнил: Студент гр. СОД 3-15-1 Папсуев О.С.

Что такое BER?

Ber (Bit Error Rate) — отношение числа ошибочно принятых битов к общему числу принятых битов. Его величина статистически колеблется около значения среднего коэффициента ошибок за длительный промежуток времени. Разница между непосредственно измеренным коэффициентом ошибок и долговременным средним значением зависит от числа контролируемых бит и тем самым от длительности измерения.

Kош= Nош/N

где N – общее число символов, переданных за интервал измерения; Nош – число ошибочно принятых символов за интервал измерения

Например, если число ошибочно принятых бит оказалось равным 20, а заданное общее число принимаемых бит – 106, то коэффициент ошибок составит

20/106 = 20 x 10-6 = 2 x 10-5

Зачем измеряется BER

Измерения параметра ошибок – это самая важная часть практики эксплуатации цифровой системы связи. Так как информация передается в системе связи в цифровом виде, то единственной мерой качества работы системы связи является параметр ошибки. Эта мера является универсальной в том смысле, что она едина для любых цифровых систем передачи и коммутации. Действительно, вне зависимости от того, какие типы линейного кода используются в системе передачи, на каких принципах построена система коммутации и какие протоколы используются, единой мерой качества цифровой сети является уровень ошибок, который она привносит в передаваемый цифровой поток.

Все технические решения в области эксплуатации направлены на уменьшение параметра ошибок, все измерения соотносятся с параметром ошибок (например, исследуются вопросы о влиянии джиттера на параметр ошибок, кодовых ошибок на параметр ошибок и пр.). Таким образом, измерение параметра ошибок представляет собой ключ к эксплуатационным измерениям, и уже одного этого достаточно, чтобы посвятить раздел методам измерения ошибок.

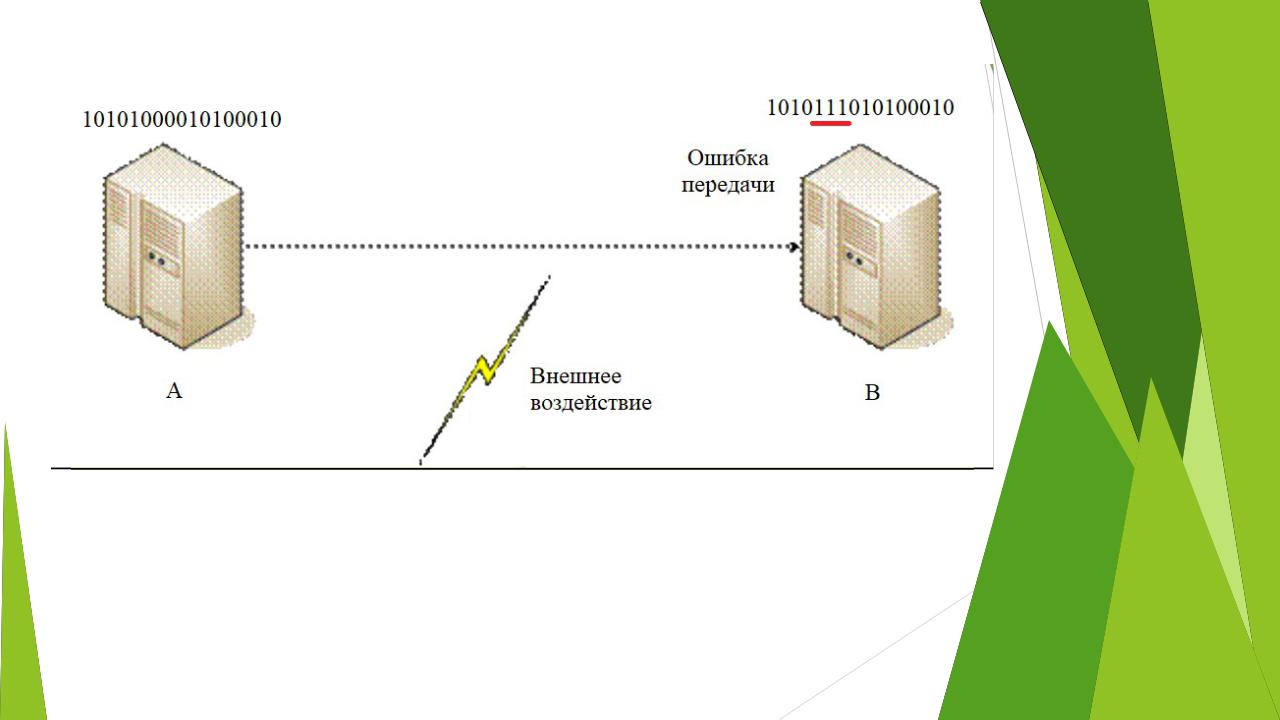
Модель возникновения ошибок в системе передачи

В самом общем виде модель возникновения ошибок выглядит следующим образом. Устройство А передает по рабочему каналу устройству В цифровой поток в виде единиц и нулей. Внешние воздействия на канал (шумы, интерференция, сбои в системе связи и т.д.) приводят к нарушению в интерпретации принимаемых символов на стороне В. В результате в некоторых случаях вместо 1 устройство В принимает 0 и наоборот.

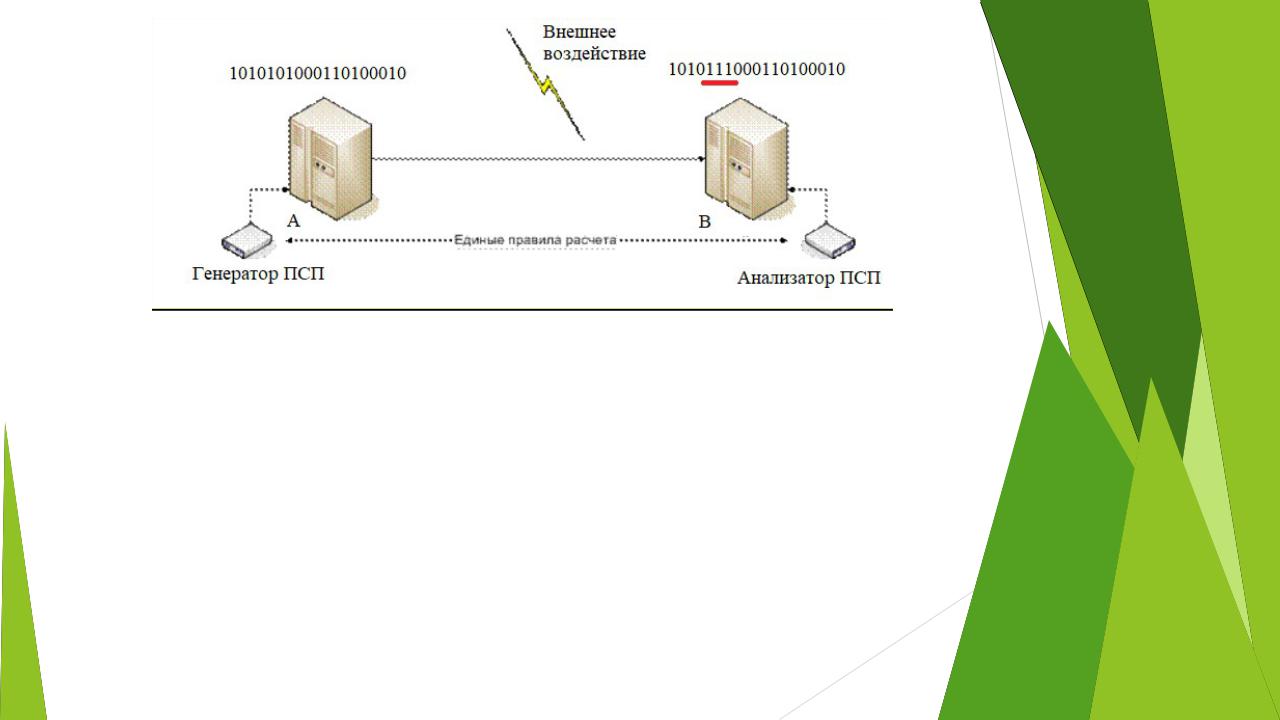
Измерение параметра ошибок с использованием тестовой последовательности

В методе использования тестовой последовательности очень важным является вопрос о том, каким образом передать на сторону В знание о структуре последовательности. Здесь существует два способа. Первый заключает в том, чтобы передавать одну и ту же последовательность циклично, например, одна единица, затем три нуля, тогда в канале будет передаваться информация

1000100010001000100010001000 … тестовая последовательность

Если на стороне В приемник понимает правило формирования этой тестовой последовательности, то он легко найдет все отклонения, например:

1000100010001010100000001000 … 2 битовые ошибки

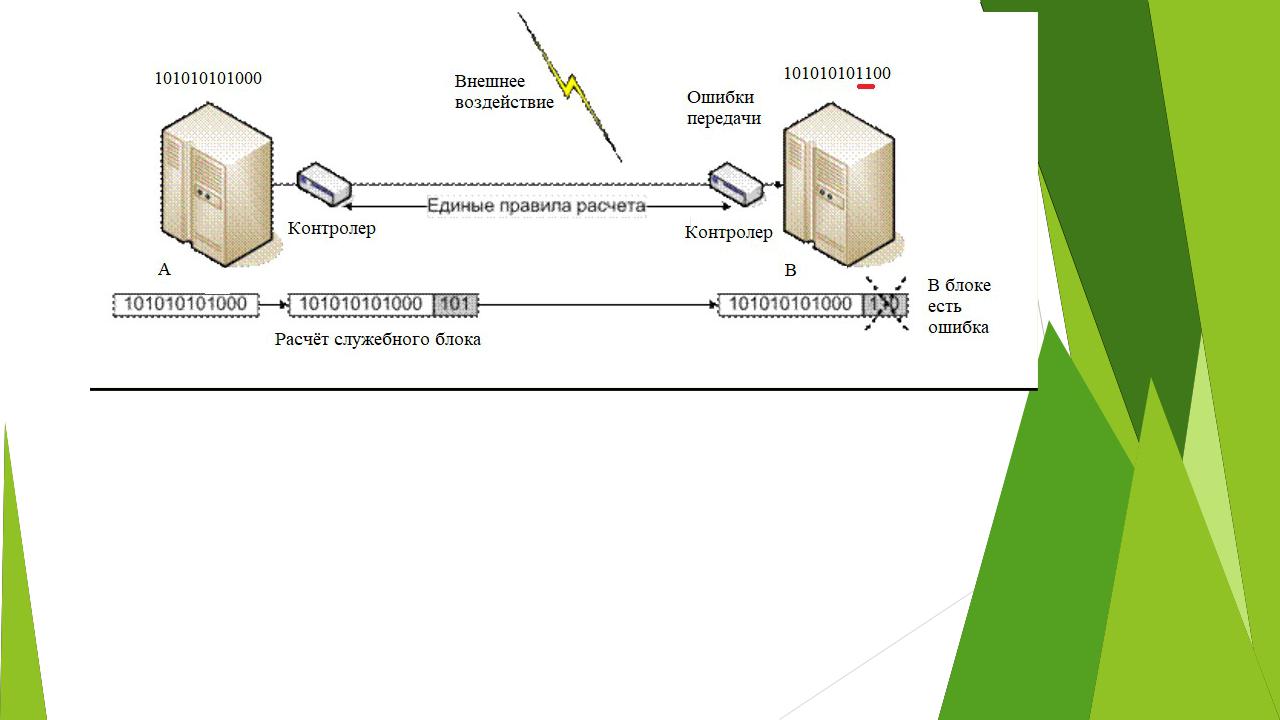
Метод измерения параметра ошибки без отключения канала

Суть метода состоит в том, что передаваемые данные реального трафика разделяются на блоки данных. Затем перед началом передачи данных в системе передачи над блоком совершается специальные вычисления, результат которых добавляется к блоку и передается на сторону В. На стороне приемника В над блоком производятся аналогичные вычисления, результат которых сравнивается с пересланным служебным полем от стороны А. Если результаты вычислений не совпадают, делается вывод о присутствии ошибки в блоке данных. Таким образом, можно проводить измерения на реальном трафике, без отключения канала. Единство методики определяется тем, что контроллеры, производящие вычисления, действуют по единым правилам расчета.

Принципы нормирования и измерения параметров ошибок

Выше уже было показано, что существует два метода измерений параметров соответственно BER и BLER. Рассмотрим теперь, каким образом эти методы накладываются на реальные методики измерений цифровых систем передачи.

Прежде всего, следует четко понять, что сами по себе параметры BER и BLER не могут быть использованы для нормирования качества в цифровых системах передачи. Возникает это потому, что оба параметра являются интегральными.

По определению, параметр BER представляет собой частное от деления количества ошибок на общее количество переданных битов:

BER=ErrB/BITS

Такое определение не учитывает природу возникновения ошибок и структуру их распределения. В то же время от структуры распределения битовых ошибок зависит окончательный вывод о том, качественный или некачественный канал системы передачи мы измеряем.

Для иллюстрации рассмотрим два случая возникновения ошибок в канале цифровой системы передачи

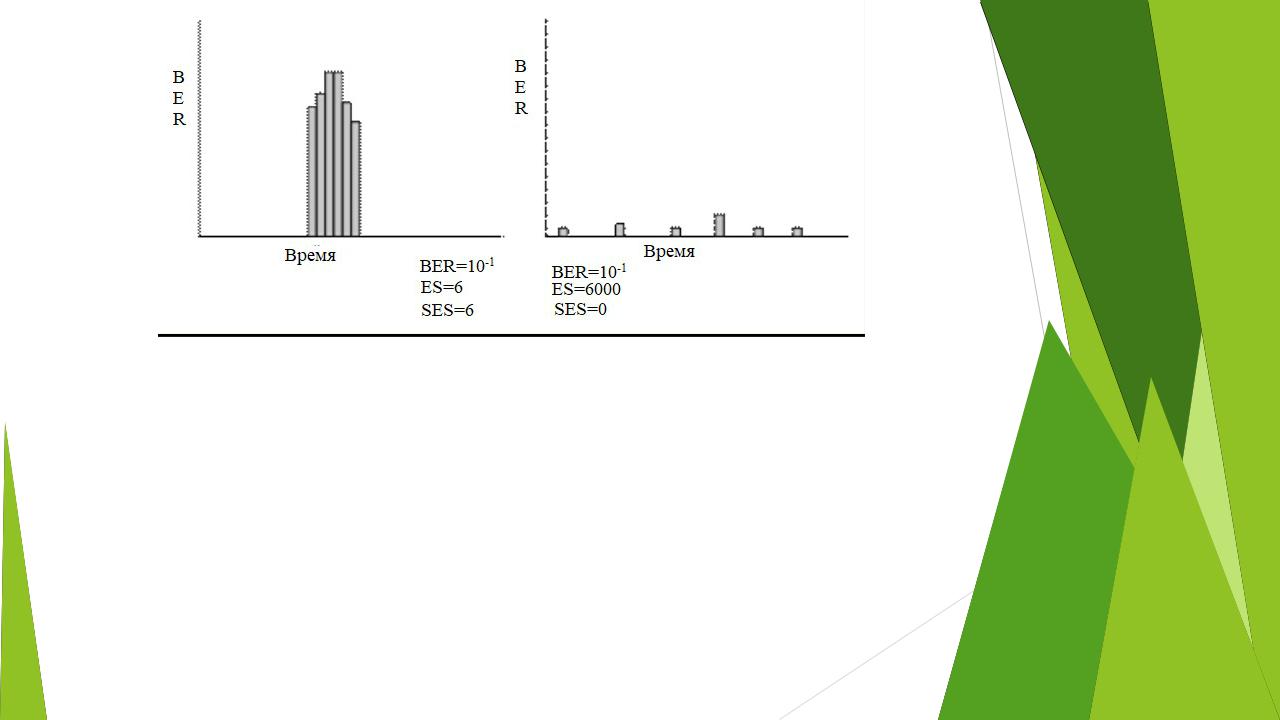
Слева представлен «пакет» ошибок, возникающий обычно вследствие наводок на кабель системы передачи.

Справа показан случай появления случайных ошибок, которые обусловлены самим качеством системы передачи и в большинстве случаев не связаны с какой-либо конкретной причиной.

В обоих случаях параметр BER оказывается очень высоким, например BER=10-5. Но сказать о практическом качестве цифровой системы передачи этот параметр не может. В рассмотренных примерах при одинаковом BER канал слева – это очень качественный канал. Все возникшие в нем ошибки помещаются в течение 6 сек, а других ошибок в канале нет. Если мы мысленно «вырежем» эти 6 секунд, то мы получим идеальный канал. В противоположность этому при BER=10-5 для канала справа мы имеем совершенно неприемлемое качество, т.к. появление единичных ошибок в таком канале – это слишком частое явление.

Эта иллюстрация показывает, что интегральная природа параметра BER (следовательно, и BLER) не позволяет использовать его в качестве корректного параметра нормирования и характеристики качества. Для полноты картины необходимо знать еще и характеристику распределения ошибок.

Для того, чтобы оценить распределение ошибок было предложено считать отдельно секунды с ошибками (ES) и секунды, пораженные ошибками (SES).

Секунды с ошибками ES – это все секунды в течении которых были ошибки, тогда как SES — это секунды, в течении которых BER был хуже, чем 10-3. Переход от анализа интегрированного параметра BER к дифференцированным значениям этого параметра в течении односекундных интервалов позволяет учесть распределение параметра ошибок. Например, на рисунке представлены значения не только параметра BER, но и соответствующие ситуации значения параметров ES и SES. По соотношению параметров ES и SES можно оценить кучность возникновения ошибок в измеряемом канале. Речь идет именно об оценке, а не о точном измерении параметров распределения ошибок, но для целей эксплуатации этого оказывается достаточно.

Следует отметить, что относительно измерений BER параметры ES, SES, а также другие параметры методики (AS, UAS и пр.) являются вторичными, т.к. непосредственно измеряется параметр BER в односекундных интервалах. Но именно эти параметры представляют интерес для отчетности по качеству в цифровом канале.

Измеритель коэффициента битовых ошибок Tektronix BERTScope BSA

Измерители коэффициента битовых ошибок Tektronix BERTScope серии BSA предлагают новый подход к измерению целостности сигнала в системах последовательных данных. Быстрое и точное определение коэффициента битовых ошибок (BER) за счет анализа диаграмм и генерации цифровых последовательностей с битовыми ошибками. Tektronix BERTScope серии BSA легко позволяет выделить проблемные биты или последовательности бит для дальнейшего анализа с помощью семи алгоритмов, обеспечивая непревзойденную глубину статистических измерений.

Источник

Как разработчика приборов для измерения параметров телевизионных сигналов меня часто спрашивают, как правильно интерпретировать результаты измерений. В настоящее время для специалистов, обслуживающих системы телеприема, доступно большое количество измерительных приборов, а значит, есть возможность количественно оценить качество телевизионных каналов, в том числе каналов с цифровой модуляцией. Однако при интерпретации измеренных величин до сих пор чувствуются неуверенность и сомнения. В этом материале я изложу свою точку зрения на значимость каждого из параметров, характеризующих качество телевизионного сигнала.

Mой взгляд на этот вопрос в основном формировался в процессе собственных разработок и производства телевизионных измерительных приборов. Но свою лепту внесли и консультации со специалистами всемирно известных компаний, производящих подобные приборы, и общение с операторами кабельных сетей.

Должен оговориться, что все нижеизложенное в первую очередь касается цифрового кабельного телевидения стандарта DVBC. Но в силу родственных связей между форматами DVB-вещания мои рассуждения с некоторыми оговорками можно отнести и к DVB-S, DVB-T, и др.

Содержание

Пять основных параметров
BER vs MER
Самый важный параметр
Время измерения BER
Преимущества MER
Констелляционная диаграмма
Особенности измерения уровня цифровых сигналов
Общие рекомендации по оценке качества цифровых каналов
Использованная литература

Пять основных параметров

Для начала рассмотрим набор измеряемых параметров цифровых каналов, доступных владельцам современных приборов. Как правило, эти приборы позволяют измерять пять параметров.

Первый из них — уровень сигнала в канале. Без сомнения, это один из важнейших параметров, характеризующих качество приема. Несмотря на то, что это самый понятный для специалистов параметр и его с достаточной точностью можно измерить даже приборами, предназначенными для аналоговых сигналов, при анализе результатов измерений иногда встречаются неправильные толкования и недопонимания.

Следующий параметр — MER (Modulation Error Ratio), или Коэффициент ошибок модуляции. По своей сути MER близок параметру SNR (сигнал/шум). В некоторых странах вместо параметра MER применяют EVM (Величина вектора ошибки), но по существу это одно и то же, выражаемое в разных единицах.

Третий параметр — BER (Bit Error Ratio), или Коэффициент битовых ошибок. Он характеризует частоту появления ошибочно восстановленных битов в демодулированном потоке данных и для стандарта DVB-C измеряется в двух точках: до декодера РидаСоломона и после него. Поэтому фактически это два параметра, которым часто присваивают названия preBER и postBER. Параметр postBER — та величина, которую пользователю иногда предъявляют как значение счетчика ошибочных пакетов за интервал наблюдения.

Последний параметр — констелляционная диаграмма, которая представляет собой график расположения символов на амплитуднофазовой плоскости, формируемый с накоплением за определенное время. Как правило, диаграмма рассматривается как некий качественный, а не количественный параметр, позволяющий оценить характер искажений входного радиосигнала.

Теперь можно приступить к более подробному анализу каждого из параметров на предмет их важности в оценке качества принимаемого цифрового сигнала.

BER vs MER

В специализированной литературе, журналах и на интернет-форумах часто разгораются дискуссии о значимости этих параметров; нередко можно встретить мнение, что самым важным и информативным параметром является MER. Сторонники этой точки зрения мотивируют ее тем, что зависимость величины MER от уровня шумов в полосе канала носит более пологий характер по сравнению с кривой BER, поэтому можно точнее оценить запас по устойчивому приему сигнала. В этом высказывании есть, конечно, большая доля истины. В самом деле, диапазон измерения MER, как правило, находится в пределах от 26-27 дБ до 38-42 дБ и выше (для модуляции QAM-256). Это позволяет оценить запас по качеству сигнала от порога синхронизации, когда демодулятор только-только начинает восстанавливать сигнал при значении preBER 1E-2…1E-3 . К тому же значение MER, как правило, более стабильно по сравнению с BER, особенно когда BER ниже 1E-7, что объясняется временем усреднения этих величин. К этому обстоятельству я вернусь немного позже.

Mux: MER-ы бывают пиковые и среднеквадратичные. Среднеквадратичные отражают усредненное значение за период измерения, а пиковые — максимальное. Если измеряется среднеквадратичное, то вполне возможны краткие развалы картинок принормальном MER-е, но переход на измерения пикового значения покажут эти сбои.

Mux: Достижимая точность измерения MER тем выше, чем ниже размерность модуляции измеряемого сигнала. Чем больше точек констелляции должен обрисовать ЦАП, тем меньше у него времени на каждую точку. Karlson2k: MER — хороший показатель, однако не единственный. Для приёмника

скорее важен BER или даже PER (BER после декодера Рида-Соломона). Иногда с одними тем же MER могут быть совсем разные BER.

В «обычных» условиях корреляция между MER и BER достаточно чёткая. Действительно, появление BER свидетельствует о подходе к границе (которая для цифры очень тонкая — здесь ещё есть, ещё чуть-чуть и уже совсем нет). Но как раз граница и важна. Тем не менее, в реальной жизни полно условий, когда чёткость корреляции начинает сбивается. Например — частотный сдвиг, из-за допплеровского эффекта (актуально для DVB-H) или по каким-то другим причинам. Иногда сбой может быть вызван «особенностями» передатчиков. Конечно, на BER сложно ориентироваться при измерениях, особенно «быстрых», и в большинстве случаев достаточно на MER. Но при любых важных измерениях без BER не обойтись.

А на практике для бытовых приёмников важен еще и уровень сигнала. К сожа- лению, разница в минимальном уровне, при котором бытовой приёмник цепляется за сигнал, доходит до 30-35 дБ у разных моделей даже от одного производителя. Штампуется же всё «подешевле». То есть на что ориентироваться при постройке

сети — вопрос ещё тот .

Самый важный параметр

Тем не менее, берусь утверждать, что самый важный параметр из всех измеряемых для цифрового сигнала — BER, а точнее — postBER. Ведь уверенно заявлять, что восстановление потока, полученного за определенный период, было абсолютным, можно только в случае, если postBER за это время оказался равным нулю. В реальности значение для postBER, равное 1E10…1E11, говорит о частоте появления ошибки в восстановленном потоке данных не более 2…20 бит в час. Такой прием можно характеризовать как безошибочный. В соответствии с научной терминологией соответствующий поток данных можно назвать «квазисвободным от ошибок».

У BER есть, правда, один недостаток — невозможность оценить запас сигнала по качеству, за счет которого можно уверенно принимать и восстанавливать цифровой поток в течение длительного времени. В пороговой ситуации уменьшение значения MER для одного канала всего на 1-2 дБ может изменить ситуацию от полного восстановления данных к полной невозможности приема сигнала на этом канале и скачкообразному изменению значения BER.

Но, тем не менее, важность этого параметра весьма высока. Особенно он может быть полезен сторонникам контроля телевизионного изображения. Параметр postBER полностью заменяет контроль картинки за исключением того случая, когда в структуре транспортного потока MPEG присутствуют ошибки, приводящие к артефактам изображения. Но они не всегда приводят к дефектам картинки, заметным на экране монитора, или же искажениям звукового сопровождения, да и вообще появляются достаточно редко.

Зато postBER по сравнению с контролем изображения имеет несколько преимуществ. Во-первых, он показывает общее количество ошибок в транспортном потоке, а не на одной программе, как при контроле картинки.

Во-вторых, вычислению postBER никак не препятствует шифровка потоков системами условного доступа. И для открытых, и для закрытых каналов он вычисляется одинаково.

И, в-третьих, postBER более чувствителен к ошибкам: счетчик невосстановленных пакетов будет неумолимо увеличиваться с каждой следующей ошибкой, хотя «битый» пакет может принадлежать другой программе или вообще не оказывать влияния на картинку или звук и, как результат, будет пропущен при визуальном контроле.

С точки зрения оценки запаса по качеству сигнала более информативен, конечно, preBER. Общеизвестно, что пороговое значение preBER, равное 2E-4, дает возможность восстанавливать данные до требуемых 1E-10…1E-11 значения postBER. Но это как раз тот случай, когда мы находимся на границе между уверенным приемом и отсутствием возможности восстановить сигнал при ухудшении значения MER. Если при измерении параметров мы получаем значение preBER, скажем, 1E-6, это уже указывает на наличие некоего запаса, позволяющего нам быть увереннее в будущем.

Время измерения BER

Большинство приборов для измерения параметров сигналов с цифровой модуляцией имеют нижнюю границу диапазона измерения параметра BER 1E-8 или 1E-9, реже — 1E-10, 1E-11. Совершенно естественно, что пользователи приборов хотят иметь границу как можно ниже, а результат измерения получать как можно быстрее. Давайте посчитаем: если мы используем модуляцию QAM-256 и символьную скорость 6,9 Мбод, то битовая скорость на входе декодера РидаСоломона будет составлять 6,9*8=55,2 Мбит/с. Если вероятность появления ошибки 1E-8, то для измерения этой величины нам надо накопить 10⁸ бит потока данных, из которых один бит будет ошибочным. А накапливать мы их будем в течение 10⁸/55,2×10⁶ = 1,8 с. То есть один неправильно декодированный бит будет появляться, в среднем, раз в две секунды.

Результат, измеренный за этот промежуток времени, будет, конечно, весьма неточным. Для уменьшения случайной погрешности необходимо его усреднить хотя бы за 10 периодов измерения, то есть за 18 секунд. Если мы захотим измерить BER с нижней границей 1E-9, то для этого нам потребуется в 10 раз больше времени: 180 секунд или 3 минуты, а для получения достоверного результата 1E-11 мы должны ждать пять часов! Если использовать модуляцию более низкого порядка или более низкую символьную скорость, время измерения увеличится еще больше

Преимущества MER

MER (Modulation Error Ratio) — это ошибка модуляции, характеризующая отклонение реального символа от местоположения символа идеального на констелляционной диаграмме¹.

По сравнению с BER параметр MER предоставляет более оперативную информацию о сигнале. Как я уже упоминал, MER является подобием параметра отношения сигнал/шум, хотя и учитывает большее число факторов, искажающих исходный радиосигнал. Значение параметра так же усредняется по времени, как и все величины, связанные с измерением мощности, но его измерение производится для каждого символа и, учитывая большие символьные скорости, накопление за одну секунду дает достаточно достоверный результат.

Вторым достоинством параметра MER является возможность его измерения с нормированной точностью. Большинство современных микросхем декодеров, на основе которых производятся приборы, позволяют вычислять MER аппаратно или на основе величин амплитуд векторов I и Q.

Под аппаратным вычислением я имею в виду возможность получения среднеквадратичного значения вектора ошибки из одного из внутренних регистров демодулятора. Во всяком случае производители микросхем утверждают, что это именно оно, и измерения, в принципе, это подтверждают. А зная среднеквадратичное значение вектора ошибки, вычислить MER уже несложно.

Использование значений амплитуд векторов квадратур для этих целей часто менее пригодно, потому что от микросхемы можно получить лишь 7 или 8 двоичных разрядов амплитуды QIвекторов. В результате динамический диапазон расчетного значения MER получается весьма низок. А разрядность регистра ошибки, напротив, часто бывает 10-, а то и 16-битная.

Погрешность измерения, связанную с неидеальными параметрами тюнера и демодулятора, можно скорректировать, имея источник сигнала с калиброванным параметром сигнал/шум. Калибровка производится для входного сигнала с добавлением только белого шума, но такой метод, тем не менее, дает весьма хороший результат.

Поэтому погрешность параметра MER для многих приборов является нормированной величиной в отличие от BER. Точность измерения BER зависит от качества приемника и демодулятора прибора, и корректировать ее невозможно. В результате измерение BER разными приборами дает близкие значения при плохом и заметно различающиеся при хорошем (при больших значениях MER).

То есть более качественный прибор показывает более низкие (более близкие к реальным) значения BER. Способность измерять низкие значения BER является хорошим индикатором качества измерительного прибора.

Если это так, возникает вопрос: «А не достаточно ли измерять один только MER для оценки качества принимаемого сигнала, ведь время измерения небольшое. Параметр предоставляет комплексную и точную информацию. С этим можно согласиться, но только в одном случае, когда к исходному сигналу примешивается только белый гауссовский шум. Как показывают практика и тестовое моделирование, при выполнении этого условия MER совпадает с SNR, и поэтому в данном случае для определения значений preBER и postBER можно воспользоваться кривыми зависимости BER от отношения SNR входного сигнала.

Констелляционная диаграмма

К сожалению, в реальной жизни все далеко не так идеально. На пути доставки телевизионного сигнала от источника до конечного пользователя существует великое множество факторов, приводящих к искажению сигнала. В результате для определения качества сигнала все-таки приходится использовать все возможные параметры, в том числе констелляционную диаграмму.

ассмотрим подробнее процесс демодуляции сигнала с цифровой модуляцией. После синхронизации с входным сигналом на выходе блока демодулятора для каждого символа появляются два значения векторов I и Q.² Пара векторов определяет точку на амплитуднофазовой плоскости, каждая из которых принадлежит одной клетке, определяющей конкретное значение символа. В идеальном случае точки ложатся точно в середины клеток.

В условиях воздействия шума точки получают некоторое смещение от ожидаемого положения, которое носит название вектора выходной ошибки. Если точка остается в пределах своей клетки, демодулятор принимает правильное решение, в противном случае символу присваивается значение соседней клетки, что к появлению ошибки во входном потоке данных. Добавление белого шума к входному сигналу приводит к «размазыванию» точки в пятно круглой формы (рис. 1). Наибольшая частота попадания точки — в центре, а к краю окружности она уменьшается. В этом случае все пятна имеют примерно одинаковый диаметр.

Теперь рассмотрим случай одновременного воздействия белого и фазового шумов на демодуляцию сигнала. На рис. 2 приведена констелляционная диаграмма для сигнала с добавлением паразитной фазовой модуляции (джиттер фазы), из которой видно, что фазовая модуляция приводит к большему отклонению точек от центра клетки с увеличением длины вектора. В результате вероятность возникновения ошибки при декодировании точек в углах констелляционной диаграммы резко увеличивается. При этом значение MER уменьшается не так сильно, потому как смещение для точек ближе к центру диаграммы незначительное.

Ситуация ухудшается еще сильнее в случае, если кроме фазовой модуляции присутствует компрессия сигнала, появившаяся при прохождении им активных устройств в зоне нелинейности их передаточной характеристики. Вершины длинных векторов смещаются к центру констелляционной диаграммы, в результате чего вероятность ошибок для этих векторов увеличивается еще значительнее. На значение MER такие искажения также не оказывают большого влияния.

Ниже приведены результаты моделирования трех перечисленных ситуаций: измерение сигнала QAM-256 в случае воздействия только белого шума, белого шума и фазовой модуляции и белого шума одновременно с компрессией амплитуды сигнала. Три соответствующие констелляционных диаграммы представлены на рис. 3.

На следующей диаграмме (рис. 4) представлены три кривые зависимости параметра BER при изменении отношения сигнал/шум во входном сигнале. Синяя линия соответствует первому случаю, когда во входном сигнале присутствует только белый шум, фиолетовая — белый шум и фазовая модуляция и, наконец, зеленая — белый шум и компрессия.

Рис. 4. Кривые зависимости параметра BER при изменении отношения сигнал/шум во входном сигнале

Видно, что при низких значениях сигнал/шум линии практически совпадают, но с увеличением параметра они начинают расходиться. Наконец, на последнем графике (рис. 5) приведена зависимость параметра MER при тех же условиях. Из графика видно: при соотношении сигнал/шум 36 дБ при добавления фазовой модуляции к входному сигналу MER уменьшается на 0,5 дБ, при этом значение BER ухудшается сразу на несколько порядков. Еще сильнее влияние компрессии, хотя она и едва различима на констелляционной диаграмме.

Это не единственные случаи искажения в исходном входном сигнале, которые приводят к сильному ухудшению BER при незначительном изменении значения MER. К аналогичным последствиям приводят фазовые искажения квадратур, амплитудный разбаланс векторов квадратур и т.д.

Правда, последние виды искажений возникают реже. Гораздо хуже ситуация с помехой импульсного характера. Такого рода искажения сигнала не редкость, поскольку существует большое количество устройств, излучающих радиосигнал, который может
выступать в роли импульсной помехи для cигнала телевизионного.

При достаточно низкой частоте повторения и короткой длительности такая помеха практически не влияет на значение MER, но при этом может приводить к полной деградации BER. Ситуация осложняется тем, что подобную помеху сложно обнаружить. Часто не помогает и анализатор спектра. К примеру, если мешающий сигнал находится в полосе канала и при этом меньше по мощности на 20-30 дБ, то он маскируется полезным сигналом.

Особенности измерения уровня цифровых сигналов

Пожалуй, самым понятным для цифровых ТВсигналов, как и для аналогового телевидения, является параметр, характеризующий мощность сигнала. Но, тем не менее, довольно часто возникают вопросы, связанные с определением уровня цифровых каналов, поэтому немного внимания уделим и этому параметру.

Для аналогового телевидения измеряется уровень напряжения радиосигнала несущей частоты изображения. Для цифрового ТВ — «мощность радиосигнала в полосе канала» (такое название часто применяется в зарубежной литературе) или «фактический уровень напряжения радиосигналов с цифровой модуляцией в полосе частот распределения радиосигналов», как он называется в российском ГОСТ Р 52023 — «Сети распределительных систем кабельного телевидения». В России параметр принято обычно измерять в дБ относительно 1 микровольта (дБмкВ) как для аналоговых, так и для цифровых каналов.

Мощность3 радиосигнала для цифровых каналов измеряется как уровень напряжения немодулированного сигнала, который на нагрузке 75 Ом рассеивает мощность, эквивалентную мощности сигнала измеряемого канала.

При измерении уровней сигналов с помощью специализированных телевизионных измерителей или универсальных анализаторов спектра следует учитывать, что в аналоговых каналах характер сигнала — узкополосный, то есть основная часть мощности канала сосредоточена в довольно узком частотном диапазоне, а цифровые каналы характеризуются равномерным распределением мощности в полосе канала. В основе работы измерителей уровня лежит принцип селективного вольтметра. То есть в спектре радиосигнала выделяется (отфильтровывается) определенная частотная полоса, а затем измеряется напряжение сигнала, попавшего в эту полосу.

Если при измерении уровня узкополосного сигнала ширина его спектра заведомо меньше полосы измерения4, уровень измеряемого сигнала будет постоянным при изменении полосы измерения в пределах канала. Ситуация меняется при измерении широкополосных сигналов, каковыми являются радиосигналы цифрового телевидения. В этом случае чем шире полоса измерения прибора, тем выше уровень измеряемого напряжения. На рис. 6 представлена спектрограмма частотного диапазона с несколькими телевизионными каналами с аналоговой и цифровой модуляциями.

Спектрограмма была снята с помощью прибора с полосой измерения 230 кГц. На первый взгляд, уровни цифровых каналов ниже аналоговых более чем на 10 дБ. Однако для аналогового канала S20 уровень (Uan) можно определить по спектру как 66 дБмкВ. А для определения мощности сигнала цифрового канала S23 необходимо применить следующую формулу:

U_цк = U_изм + 10lg(В_ц/В_из) + К,⁵

где U_цк — искомая мощность цифрового канала;

U_изм — уровень напряжения измеренный в центре полосы канала; В_ц — полоса частот, занимаемая цифровым каналом; В_из — полоса измерения прибора;

К — поправочный коэффициент, компенсирующий погрешности измерения⁶.

Подставив исходные данные в формулу, получим:

U_S23 = 53 + 10lg(7,5/0,23) + 1 = 69 дБмкВ.

Таким образом, на самом деле уровень мощности канала S23 на 3 дБ больше, чем S20.

В режиме измерения уровня специализированные телевизионные приборы автоматически производят такой пересчет цифровых каналов с учетом их полосы и отображают их мощность корректно. Но при работе в режиме анализатора спектра и при измерении приборами, не рассчитанными на работу с цифровыми каналами, надо помнить об этой особенности. Такой метод измерения мощности канала в одной частотной точке дает достаточно точный результат только в случае достаточной равномерности АЧХ в полосе канала.

Общие рекомендации по оценке качества цифровых каналов

Кабельные операторы, давно работающие с цифровым телевидением и имеющие большой опыт, советуют классифицировать состояние кабельной сети по трехбалльной шкале. Оценка три балла означает, что параметры каналов в сети соответствуют требованиям качественного приема и обладают достаточным запасом для стабильной, долговременной работы. От оператора при этом требуется только продолжение текущего контроля. Оценка два балла: параметры каналов также соответствуют требованиям качественного приема, но их значения не имеют достаточного запаса для обеспечения долговременной стабильной работы.

Такое состояние сети требует от оператора планового проведения работ для выявления источника проблем и принятия решения о методах восстановления состояния сети до трех баллов. И, наконец, третье состояние сети с оценкой один балл: параметры одного или нескольких каналов не отвечают требованиям качественного приема, что требует от оператора немедленных действий по ремонту или настраиванию сети для поднятия до второго или третьего уровня. Для оценки каждого канала необходимо измерить все параметры на абонентском отводе. Оценка присваивается в соответствии со следующими условиями.

Оценка 3 балла (выполняются все четыре условия): Уровень канала: соответствует расчетному уровню для данной точки сети с учетом неравномерности и принятой разницы между уровнями аналоговых и цифровых каналов.

MER: не меньше 36 дБ для модуляции QAM-256 и 28 дБ для модуляции QAM-64.

PreBER не превышает 1E7. PostBER: не превышает 1E9.

Оценка 2 балла (выполняются все четыре условия): Уровень канала: соответствует расчетному уровню для данной точки сети с учетом неравномерности и принятой разницы между уровнями аналоговых и цифровых каналов.

MER: находится в пределах от 34 до 36 дБ для модуляции QAM256 и от 26 до 28 дБ для модуляции QAM64.

PreBER: не превышает 1E6. PostBER: не превышает 1E9.

Оценка 1 балл (выполняется хотя бы одно условие):

Уровень канала: не соответствует расчетному уровню для данной точки сети с учетом неравномерности и принятой разницы между уровнями аналоговых и цифровых каналов.

MER: значение меньше 34 дБ для модуляции QAM-256 и меньше 26 дБ для модуляции QAM-64.

PreBER: значение выше 1E6. PostBER: значение выше 1E-9.

Если есть возможность контроля констелляционной диаграммы, необходимо добавить еще одно условие. Для оценки «3» форма констелляционной диаграммы не должна содержать ярко выраженных фазовых искажений, дисбаланса квадратур и искажений типа компрессии сигнала. При наличии подобных искажений измеряемому каналу должна быть присвоена оценка не выше двух баллов.

При указании значений параметров я исходил из предположения, что они измерены корректно, в пределах погрешности измерения прибора. Но при определенных условиях измеренные значения могут выпадать за пределы погрешности. В этом случае каналу может быть присвоена оценка, не соответствующая действительности.

Данная методика оценки качества не является, конечно, абсолютной и единственно верной. Каждый оператор может для себя выбрать границы значений параметров для оценки качества сигнала в соответствии с особенностями конкретной сети и отдельных каналов; при этом следует придерживаться общего подхода к методу проверки состояния сети.

——

¹ Физический смысл этого параметра и формула для вычисления его среднеквадратичного значения рассмотрены в статьях серии «Цифровое кабельное ТВ. Часть 2. Состав головной станции, расчет ретранслируемого потока», «ТелеСпутник», ноябрь 2007 и «Цифровое кабельное ТВ. Часть 4. Сигнал DVB в распределительной сети. Использование альтернативных стандартов», январь 2008 (прим. ред.).

² I= A cosφ, а Q = A sinφ где А – амплитуда QAM символа, а φ – фаза символа.

³ Имеется в виду мощностная характеристика, в качестве которой в телевидении принято использовать эквивалентное напряжение немодулированного сигнала, который по мощности равен сигналу телевизионному. Хотя в статье применяется термин «мощность цифрового канала», на самом деле подразумевается как раз напряжение этого эквивалентного сигнала (прим. автора).

⁴ Полоса измерения определяется полосой пропускания измерительного фильтра (прим. ред.).

⁵ Так эта формула выглядит в ГОСТ Р 52023 (прим. автора).

⁶ Коэффициент зависит в основном от параметров детектора (тип детектора и его постоянные времени) и прямоугольности измерительного фильтра. Определяется опытным путем и, как правило, составляет 13 дБ (прим. автора).

Андрей Конорев,

ведущий инженер ООО «Планар»

Использованная литература

Б.А. Локшин. Цифровое вещание: — от студии к телезрителю.
ГОСТ Р 52023-2003 «Сети распределительные систем кабельного телевидения».
ETSI TR 101 290 Measurement guidelines for DVB system.

Источник

Коэффициент битовых ошибок BER является ключевым параметром оценки качества цифровых систем передачи (ЦСП). Этот параметр незаменим при проверке цифровой аппаратуры (например, регенераторов) на этапе ее разработки и ремонта, когда оборудование выведено из эксплуатации. А что же делать, когда цифровые каналы и тракты требуется протестировать в процессе их нормальной эксплуатации?

У параметра BER есть и другой существенный недостаток: этот показатель практически невозможно использовать для оценки качества цифровой линии (скажем, для услуги IP телефонии). При заказе любой услуги связи пользователь и провайдер должны заключить соглашение о качестве обслуживания (Service Level Agreement, SLA), где четко оговариваются двусторонние обязательства. Для оценки качества сеанса связи в цифровом канале или тракте логично использовать относительное число ошибок передачи за фиксированные интервалы времени — за секунду или за период передачи фиксированной группы битов, которую называют блоком.

Именно эти показатели положены в основу двух базовых рекомендаций ITU-T — G.821 и G.826, о которых мы и поговорим ниже.

Прошло ужечетверть века с момента принятия рекомендации G.821 «Параметры ошибок международного цифрового соединения сети ISDN на скорости ниже первичной».

Первой сетью, где соединение между двумя пользователями было полностью цифровым, была сеть ISDN. Первичными скоростями ISDN являются скорости сигналов Т-1 и Е-1, равные 1544 и 2048 Кбит/c, соответственно. Ниже первичной стандартом предусматриваются скорости 64xN, где 64 Кбит/c представляет собой пропускную способность основного (или базового) цифрового канала (ОЦК), а N < 24 в случае Т-1 и N < 31 в случае Е-1.

В рекомендации G.821 в качестве параметра ошибок цифрового соединения выбраны два следующих.

Число секунд с ошибками (Errored Second, ES), к которым относится каждая секунда, в которой имеется по крайней мере одна ошибка. Как следует из определения, при таком подходе одиночная ошибка и пакет ошибок не различаются.
Число секунд с многочисленными ошибками (Severely Errored Second, SES), где SES означает секунду с коэффициентом ошибок >= 10^-3.

Поскольку оба параметра — и ES, и SES — зависят от времени измерения T, для практической оценки качества цифрового соединения применяют их относительные значения: Errored Second Ratio ESR =ES/T и Severely Errored Second Ratio SESR = SES/T.

Заметим, что наличие двух параметров оценки ошибок позволяет не только более точно определить качество цифрового соединения, но и во многих случаях оказывается полезным при локализации возможных повреждений.

По мере распространения широкополосных услуг связи рамки использования рекомендации G. 821 становились все более узкими. Попытки же приспособить ее для измерения широкополосных цифровых трактов оказались неудачными. Кроме того, определение параметров качества в G.821 основывается на оценке битовых ошибок, а те, в свою очередь, могут быть точно определены лишь тогда, когда достоверно известна измеряемая цифровая последовательность. Поэтому тестирование в соответствии с G.821 возможно только при выводе цифрового соединения из эксплуатации.

Таким образом, специалисты нуждались в новой рекомендации, где учитывались бы реалии цифровых сетей связи, включая потребность тестирования канала связи в рабочем режиме, в том числе и в цифровых соединениях с применением оборудования синхронной цифровой иерархии SDH и асинхронной передачи АТМ.

Всем этим требованиям отвечает рекомендация G.826 «Параметры и нормы ошибок международных цифровых соединений на скорости выше первичной», одобренная ITU-T в 1993 г. Она обеспечила решение трех главных задач по организации тестирования ошибок цифровых соединений:

во время нормальной эксплуатации;
на скоростях 1544 Кбит/c, 2048 Кбит/c и выше;
в сетях с использованием технологий SDH и АТМ.

Первая задача была решена путем перехода от тестирования ошибок по битам к тестированию ошибок по блокам. Напомним, блок представляет собой группу последовательных битов, которые относятся к исследуемому цифровому тракту. Каждый бит принадлежит к определенному блоку. Контроль блоков выполняется с помощью встроенных в системы передачи специальных устройств, применение которых гарантирует обнаружение ошибки с надежностью не ниже 90%.

Ошибки цифрового сигнала могут быть обнаружены множеством способов без перерыва связи. О недостатках двух из них — методах обнаружения ошибок кода передачи и циклового синхросигнала в цикле сигнала E-1 — мы уже упоминали. Их ограничения состоят, прежде всего, в частном характере и недостаточной точности. Между тем важнейшими требованиями к методам обнаружения ошибок цифрового сигнала являются универсальность, экономичность и точность. Универсальность означает применимость метода к любому цифровому сигналу, экономичность — эффективное использование дополнительной пропускной способности, ключевое же требование — несомненно, высокая точность.

Среди множества известных способов блочного контроля ошибок трем указанным требованиям наиболее полно удовлетворяет метод циклического контроля по избыточности (Cyclic Redundancy Code, CRC).

Метод CRC основан на делении и умножении многочленов. При этом делимый многочлен представляет собой последовательную запись блока данных в двоичной форме. Например, в системе Е-1 блок данных, для которого рассчитывается CRC, состоит из 256 байт. Поэтому делимое записывается как двоичное число длиной 2048 бит, которое по особому правилу делится на выбираемый так называемый порождающий многочлен. Полученный остаток используется в качестве контрольной информации и передается по каналу связи вместе с информационным сигналом.

Аналогичная обработка полученного блока данных выполняется на принимающей стороне, и остаток деления многочленов сравнивается с переданным остатком. Различие указанных остаточных многочленов является признаком ошибки в цифровом сигнале.

В рекомендации G.826 определены три типа блочных ошибок:

секунда с ошибками (Errored Second, ES), содержащая хотя бы один блок с ошибками или дефект;
секунда c многочисленными ошибками (Severely Errored Second, SES), содержащая >= 30% блоков с ошибками или, по крайней мере, один период с серьезными нарушениями соединения (Severely Disturbed Period, SDP);
блок с фоновой ошибкой (Background Block Error, BBE) — блок с ошибками вне отмеченных ошибками секунд (SES).

При измерениях во время нормальной эксплуатации SDP наблюдаются, если появляются так называемые дефекты, по-разному определяемые в плезиохронных (PDH) и синхронных (SDH) системах, а также при асинхронной передаче (АТМ). К этой категории принадлежат пропадание сигнала (Loss of Signal, LOS), потеря цикловой синхронизации (Loss of Frame, LOF) или прием сигнала индикации аварийного состояния (Alarm Indication Signal, AIS). При измерениях с выводом из эксплуатации опознается SDP, если частота ошибок в течение времени тестирования составляет >= 10^-2.

В рекомендации G.826, как и в G.821В, применяются три относительных параметра блочных ошибок:

коэффициент секунд с блочными ошибками (Errored Second Ratio, ESR), равный отношению секунд с блочными ошибками к общему числу секунд измерения;
коэффициент секунд с сильными блочными ошибками (Severely Errored Second Ratio, SESR), равный отношению секунд c сильными блочными ошибками к общему числу секунд измерения;
коэффициент блоков с фоновыми ошибками (Background Block Error Ratio, BBER), равный отношению блоков с ошибками к общему числу блоков в сеансе измерения, причем при расчете BBER все блоки из интервалов с сильными ошибками исключаются.

Нужно иметь в виду, что при расчете всех трех параметров учитывается только время, в течение которого система передачи находится в состоянии готовности.

Параметр готовности цифрового соединения обязательно включается в SLA.

Система считается неготовой с того момента времени, после которого имеют место 10 последовательных секунд с сильными ошибками SES. Согласно тому же определению, система передачи вновь возвращается в состояние готовности, если по крайней мере в течение 10 последовательных секунд ошибок не наблюдается или это ошибки SES.

Нормированный показатель готовности системы представляет собой отношение времени ее готовности к общему времени работы. Реальные значения показателя надежности системы составляют 99,5%. Если в аналоговых системах передачи (АСП) мощность помех в каналах пропорциональна длине соединения, то в ЦСП существует линейная зависимость числа ошибок от длины соеди-нения. Поэтому при расчете ошибок в ЦСП, как и при расчете шумов в АСП, используется принцип гипотетической эталонной цепи (Hypothetical Reference Path, HRP).

Эталонные цепи в соответствии с рекомендациями G.821 и G.826 имеют протяженность 27 500 км и описывают распределение показателей ошибок вдоль международного цифрового соединения. Обе цепи отражают особенности нормирования показателей ошибок, утвержденные в указанных рекомендациях.

Источник

В цифровой передаче , количество битовых ошибок является количеством принятых бит одного потока данных над каналом связи , которые были изменены из — за шум , помехи , искажений или битой синхронизацию ошибок.

Коэффициент битовых ошибок ( BER ) — это количество битовых ошибок в единицу времени. Коэффициент битовых ошибок (также BER ) — это количество битовых ошибок, деленное на общее количество переданных битов за исследуемый интервал времени. Коэффициент битовых ошибок — это безразмерная мера производительности, часто выражаемая в процентах .

Бита вероятность ошибка р _е является ожидаемым значением коэффициента ошибок по битам. Коэффициент битовых ошибок можно рассматривать как приблизительную оценку вероятности битовых ошибок. Эта оценка точна для длительного интервала времени и большого количества битовых ошибок.

Пример

В качестве примера предположим, что эта переданная битовая последовательность:

0 1 1 0 0 0 1 0 1 1

и следующая полученная битовая последовательность:

0 0 1 0 1 0 1 0 0 1,

Количество битовых ошибок (подчеркнутые биты) в этом случае равно 3. BER — это 3 неверных бита, разделенных на 10 переданных битов, в результате чего BER составляет 0,3 или 30%.

Коэффициент ошибок пакета

Коэффициент ошибок пакетов (PER) — это количество неправильно принятых пакетов данных, деленное на общее количество принятых пакетов. Пакет объявляется некорректным, если хотя бы один бит ошибочен. Ожидаемое значение PER обозначается вероятностью ошибки пакета p _p , которая для длины пакета данных N бит может быть выражена как

${ displaystyle p_ {p} = 1- (1-p_ {e}) ^ {N} = 1-e ^ {N ln (1-p_ {e})}}$

предполагая, что битовые ошибки не зависят друг от друга. Для малых вероятностей битовых ошибок и больших пакетов данных это примерно

$p_ {p} приблизительно p_ {e} N.$

Подобные измерения могут быть выполнены для передачи кадров , блоков или символов .

Факторы, влияющие на BER

В системе связи на BER на стороне приемника могут влиять шум канала передачи , помехи , искажения , проблемы битовой синхронизации , затухание , замирания из-за многолучевого распространения беспроводной связи и т. Д.

BER может быть улучшен путем выбора сильного уровня сигнала (если это не вызывает перекрестных помех и большего количества битовых ошибок), путем выбора медленной и надежной схемы модуляции или схемы линейного кодирования , а также путем применения схем канального кодирования , таких как избыточные коды прямого исправления ошибок. .

КОБ передачи является количество обнаруженных битов , которые являются неправильными до коррекции ошибок, разделенных на общее количество переданных битов ( в том числе избыточных кодов ошибок). Информация КОБ , примерно равна вероятности ошибки декодирования , это число декодированных битов , которые остаются неправильно после коррекции ошибок, деленное на общее число декодированных битов (полезная информация). Обычно BER передачи больше, чем BER информации. На информационный BER влияет сила кода прямого исправления ошибок.

Анализ BER

BER можно оценить с помощью стохастического ( Монте-Карло ) компьютерного моделирования. Если предполагается простая модель канала передачи и модель источника данных , BER также может быть вычислен аналитически. Примером такой модели источника данных является источник Бернулли .

Примеры простых моделей каналов, используемых в теории информации :

Двоичный симметричный канал (используется при анализе вероятности ошибки декодирования в случае непакетных битовых ошибок в канале передачи)
Канал аддитивного белого гауссова шума (AWGN) без замирания.

Наихудший сценарий — это полностью случайный канал, в котором шум полностью преобладает над полезным сигналом. Это приводит к BER передачи 50% (при условии, что предполагается источник двоичных данных Бернулли и двоичный симметричный канал, см. Ниже).

В канале с шумом BER часто выражается как функция нормированного показателя отношения несущей к шуму, обозначаемого Eb / N0 (отношение энергии на бит к спектральной плотности мощности шума) или Es / N0 (энергия на символ модуляции для спектральная плотность шума).

Например, в случае QPSK модуляции и канал АБГШ, КОБ в зависимости от Eb / N0 определяется по формуле:
.
$operatorname {BER} = { frac {1} {2}} operatorname {erfc} ({ sqrt {E_ {b} / N_ {0}}})$

Люди обычно строят кривые BER для описания производительности цифровой системы связи. В оптической связи обычно используется зависимость BER (дБ) от принимаемой мощности (дБм); в то время как в беспроводной связи используется BER (дБ) по сравнению с SNR (дБ).

Измерение коэффициента ошибок по битам помогает людям выбрать подходящие коды прямого исправления ошибок. Поскольку большинство таких кодов исправляют только перевороты битов, но не вставки или удаления битов, метрика расстояния Хэмминга является подходящим способом измерения количества битовых ошибок. Многие кодеры FEC также непрерывно измеряют текущий BER.

Более общий способ измерения количества битовых ошибок — это расстояние Левенштейна . Измерение расстояния Левенштейна больше подходит для измерения характеристик сырого канала перед кадровой синхронизацией , а также при использовании кодов коррекции ошибок, предназначенных для исправления вставки и удаления битов, таких как коды маркеров и коды водяных знаков.

Математический проект

BER — это вероятность неправильной интерпретации из-за электрического шума . Рассматривая биполярную передачу NRZ, мы имеем
ш (т)

$х_ {1} (t) = A + w (t)$ для «1» и для «0». Каждый из и имеет период .
$х_ {0} (t) = - A + w (t)$ $x_ {1} (т)$

Зная, что шум имеет двустороннюю спектральную плотность ,
${ frac {N_ {0}} {2}}$

$x_ {1} (т)$ является ${ mathcal {N}} left (A, { frac {N_ {0}} {2T}} right)$

и есть .
${ mathcal {N}} left (-A, { frac {N_ {0}} {2T}} right)$

Возвращаясь к BER, у нас есть вероятность неправильного толкования .
$p_ {e} = p (0 | 1) p_ {1} + p (1 | 0) p_ {0}$

$p (1 | 0) = 0,5 , operatorname {erfc} left ({ frac {A + lambda} {{ sqrt {N_ {o} / T}}}} right)$ и $p (0 | 1) = 0,5 , operatorname {erfc} left ({ frac {A- lambda} {{ sqrt {N_ {o} / T}}}} right)$

где — порог принятия решения, установленный в 0, когда .
lambda $p_ {1} = p_ {0} = 0,5$

Мы можем использовать среднюю энергию сигнала, чтобы найти окончательное выражение:
$E = A ^ {2} T$

$p_ {e} = 0,5 , operatorname {erfc} left ({ sqrt {{ frac {E} {N_ {o}}}}} right).$
± §

Проверка коэффициента битовых ошибок

BERT или тест на частоту ошибок по битам — это метод тестирования схем цифровой связи, в котором используются заранее определенные шаблоны нагрузки, состоящие из последовательности логических единиц и нулей, сгенерированных генератором тестовых шаблонов.

BERT обычно состоит из генератора тестовых шаблонов и приемника, который может быть настроен на один и тот же шаблон. Их можно использовать парами, по одному на любом конце линии передачи, или по отдельности на одном конце с кольцевой проверкой на удаленном конце. BERT обычно представляют собой автономные специализированные инструменты, но могут быть основаны на персональном компьютере . При использовании количество ошибок, если таковые имеются, подсчитывается и представляется в виде отношения, например 1 на 1 000 000 или 1 на 1e06.

Распространенные типы стресс-паттернов BERT

PRBS ( псевдослучайная двоичная последовательность ) — псевдослучайный двоичный секвенсор из N бит. Эти последовательности шаблонов используются для измерения джиттера и глаз-маски TX-данных в электрических и оптических каналах передачи данных.
QRSS (квазислучайный источник сигнала) — псевдослучайный двоичный секвенсор, который генерирует каждую комбинацию 20-битного слова, повторяет каждые 1048 575 слов и подавляет последовательные нули не более чем до 14. Он содержит последовательности с высокой плотностью, последовательности с низкой плотностью, и последовательности, которые меняются от низкого к высокому и наоборот. Этот шаблон также является стандартным шаблоном, используемым для измерения джиттера.
3 из 24 — шаблон содержит самую длинную строку последовательных нулей (15) с самой низкой плотностью (12,5%). Этот шаблон одновременно подчеркивает минимальную плотность единиц и максимальное количество последовательных нулей. Формат кадра D4 3 из 24 может вызвать желтый аварийный сигнал D4 для цепей кадра в зависимости от выравнивания одного бита с кадром.
1: 7 — Также упоминается как 1 из 8 . Он имеет только один в восьмибитной повторяющейся последовательности. Этот шаблон подчеркивает минимальную плотность 12,5% и должен использоваться при тестировании средств, установленных для кодирования B8ZS, поскольку шаблон 3 из 24 увеличивается до 29,5% при преобразовании в B8ZS.
Мин. / Макс. — последовательность быстрого перехода узора с низкой плотности на высокую. Наиболее полезно при усилении функции ALBO ретранслятора .
Все единицы (или отметка) — шаблон, состоящий только из единиц. Этот шаблон заставляет повторитель потреблять максимальное количество энергии. Если постоянный ток к ретранслятору отрегулирован должным образом, ретранслятор не будет иметь проблем с передачей длинной последовательности. Этот образец следует использовать при измерении регулирования мощности диапазона. Шаблон «все единицы без рамки» используется для обозначения AIS (также известного как синий сигнал тревоги ).
Все нули — шаблон, состоящий только из нулей. Это эффективно при поиске оборудования, неправильно настроенного для AMI , такого как низкоскоростные входы мультиплексного волокна / радио.
Чередование нулей и единиц — шаблон, состоящий из чередующихся единиц и нулей.
2 из 8 — шаблон содержит не более четырех последовательных нулей. Он не вызовет последовательность B8ZS, потому что для подстановки B8ZS требуется восемь последовательных нулей. Схема эффективна при поиске оборудования, не использованного для B8ZS.
Bridgetap — разветвления моста в пределах пролета можно обнаружить с помощью ряда тестовых шаблонов с различной плотностью единиц и нулей. Этот тест генерирует 21 тестовую таблицу и длится 15 минут. Если возникает ошибка сигнала, на участке может быть один или несколько ответвлений моста. Этот шаблон эффективен только для участков T1, которые передают необработанный сигнал. Модуляция, используемая в пролетах HDSL, сводит на нет способность шаблонов моста обнаруживать ответвления моста.
Multipat — этот тест генерирует пять часто используемых тестовых шаблонов, позволяющих проводить тестирование диапазона DS1 без необходимости выбирать каждый тестовый шаблон отдельно. Шаблоны: все единицы, 1: 7, 2 из 8, 3 из 24 и QRSS.
T1-DALY и 55 OCTET — Каждый из этих шаблонов содержит пятьдесят пять (55) восьмибитовых октетов данных в последовательности, которая быстро изменяется между низкой и высокой плотностью. Эти паттерны используются в основном для нагрузки на схему ALBO и эквалайзера, но они также усиливают восстановление синхронизации. 55 OCTET имеет пятнадцать (15) последовательных нулей и может использоваться только без рамки без нарушения требований к плотности. Для сигналов с фреймами следует использовать шаблон T1-DALY. Оба шаблона вызовут код B8ZS в схемах с опцией для B8ZS.

Тестер коэффициента битовых ошибок

Тестер коэффициента ошибок по битам (BERT), также известный как «тестер коэффициента ошибок по битам» или решение для тестирования коэффициента ошибок по битам (BERT), представляет собой электронное испытательное оборудование, используемое для проверки качества передачи сигнала отдельных компонентов или целых систем.

Основные строительные блоки BERT:

Генератор шаблонов , который передает определенный тестовый шаблон в ИУ или тестовую систему.
Детектор ошибок, подключенный к DUT или тестовой системе, для подсчета ошибок, генерируемых DUT или тестовой системой.
Генератор тактовых сигналов для синхронизации генератора шаблонов и детектора ошибок
Анализатор цифровой связи не является обязательным для отображения переданного или принятого сигнала.
Электрооптический преобразователь и оптико-электрический преобразователь для проверки сигналов оптической связи.

Смотрите также

Пакетная ошибка
Код исправления ошибок
Секунда с ошибкой
Частота ошибок Витерби

использованная литература

Эта статья включает материалы, являющиеся общественным достоянием, из документа Управления общих служб : «Федеральный стандарт 1037C» .(в поддержку MIL-STD-188 )

внешние ссылки

QPSK BER для канала AWGN — онлайн-эксперимент

Источник

Example[edit]

Packet error ratio[edit]

Factors affecting the BER[edit]

Analysis of the BER[edit]

Mathematical draft[edit]

Bit error rate test[edit]

Common types of BERT stress patterns[edit]

Bit error rate tester[edit]

See also[edit]

References[edit]

External links[edit]

Теоретические результаты

Общее обозначение

Аналитические Выражения, Используемые в berawgn

Аналитические Выражения, Используемые в berfading

Аналитические Выражения, Используемые в bercoding и BERTool

Результаты эффективности через Симуляцию

Разделите обзор

Используя симулированные данные, чтобы вычислить коэффициенты ошибок бита и символа

Пример: вычисление коэффициентов ошибок

Сравнение коэффициента ошибок символа и частоты ошибок по битам

Результаты эффективности через Полуаналитический Метод

Когда использовать полуаналитический метод

Процедура для полуаналитического метода

Используя полуаналитический метод

Теоретические результаты эффективности

Вычисление теоретической ошибочной статистики

Графический вывод теоретических коэффициентов ошибок

Ссылки

Сравнение теоретических и эмпирических коэффициентов ошибок

Графики коэффициента ошибок

Разделите обзор

Создание коэффициента ошибок строит Используя semilogy

Curve Fitting для графиков коэффициента ошибок

Curve Fitting график коэффициента ошибок

BERTool

Запустите BERTool

Среда BERTool

Вычисление теоретического BERs

Используя полуаналитический метод, чтобы вычислить BERs

Запустите симуляции MATLAB

Используйте функции симуляции с BERTool

Запустите симуляции Simulink

Используйте модели Simulink с BERTool

Управляйте данными о BER

Качество сетей передачи данных. Транспорт

Среда передачи

BER тест

А как в железе?

Заключение

Что такое BER?

Зачем измеряется BER

Модель возникновения ошибок в системе передачи

Измерение параметра ошибок с использованием тестовой последовательности

Метод измерения параметра ошибки без отключения канала

Принципы нормирования и измерения параметров ошибок

Слева представлен «пакет» ошибок, возникающий обычно вследствие наводок на кабель системы передачи.

Измеритель коэффициента битовых ошибок Tektronix BERTScope BSA

Пять основных параметров

BER vs MER

Самый важный параметр

Время измерения BER

Преимущества MER

Констелляционная диаграмма

Особенности измерения уровня цифровых сигналов

Общие рекомендации по оценке качества цифровых каналов

Использованная литература

Пример

Коэффициент ошибок пакета

Факторы, влияющие на BER

Анализ BER

Математический проект

Проверка коэффициента битовых ошибок

Распространенные типы стресс-паттернов BERT

Тестер коэффициента битовых ошибок

Смотрите также

использованная литература

внешние ссылки

Создание коэффициента ошибок строит Используя `semilogy`