Что такое ошибки измерений виды ошибок геодезия

Измерения
в геодезии рассматриваются с двух точек
зрения: количественной, выражающей
числовое значение измеренной величины,
и качественной, характеризующей ее
точность.

Из практики
известно, что даже при самой тщательной
и аккуратной работе многократные
(повторные) измерения не дают одинаковых
результатов. Это указывает на то, что
получаемые результаты не являются
точным значением измеряемой величины,
а несколько отклоняются от него. Значение
отклонения характеризует точность
измерений. Если обозначить истинное
значение измеряемой величины X, а
результат измерения l, то истинная ошибка
измерения ∆ определится из выражения

∆ = l — X(5.1)

Любая
ошибка результата измерения есть
следствие действия многих факторов,
каждый из которых порождает свою
погрешность.

Ошибки,
происходящие от отдельных факторов,
называют элементарными. Ошибки результата
измерения являются алгебраической
суммой элементарных ошибок.

Изучением
основных свойств и закономерностей
действия ошибок измерений, разработкой
методов получения наиболее точного
значения измеряемой величины и
характеристик ее точности занимается
теория ошибок измерений. Излагаемые в
ней методы решения задач позволяют
рассчитать необходимую точность
предстоящих измерений и на основании
этого расчета выбрать соответствующие
приборы и технологию измерений, а после
производства измерений получить
наилучшие их результаты и оценить их
точность. Математической основой теории
ошибок измерений являются теория
вероятностей и математическая статистика.

Ошибки
измерений разделяют по двум признакам:
характеру их действия и источнику
происхождения.

По характеру
действия ошибки бывают грубые,
систематические и случайные.

Грубыми
называют ошибки, превосходящие по
абсолютной величине некоторый,
установленный для данных условий
измерений, предел. Они происходят в
большинстве случаев в результате
промахов и просчетов исполнителя. Такие
ошибки обнаруживают повторными
измерениями, а результаты, содержащие
их, бракуют и заменяют новыми. Ошибки,
которые по знаку или величине однообразно
повторяются в многократных измерениях
(например в длине линии из-за неточного
знания длины мерного прибора, из-за
неточности уложения мерного прибора в
створе этой линии и т. п.), называют
систематическими. Влияние систематических
ошибок стремятся исключить из результатов
измерений или ослабить тщательной
проверкой измерительных приборов,
применением соответствующей методики
измерений, а также введением поправок
в результаты измерений.

Случайные
ошибки — это ошибки, размер и влияние
которых на каждый отдельный результат
измерения остается неизвестным. Величину
и знак случайной ошибки заранее установить
нельзя. Однако теоретические исследования
и многолетний опыт измерений показывают,
что случайные ошибки подчинены
определенным вероятностным закономерностям,
изучение которых дает возможность
получить наиболее надежный результат
и оценить его точность.

По источнику
происхождения различают ошибки приборов,
внешние и личные.

Ошибки
приборов обусловлены их несовершенством,
например, ошибка в угле, измеренном
теодолитом, ось вращения которого
неточно приведена в вертикальное
положение.

Внешние
ошибки происходят из-за влияния внешней
среды, в которой протекают измерения,
например, ошибка в отсчете по нивелирной
рейке из-за изменения температуры
воздуха на пути светового луча (рефракция)
или нагрева нивелира солнечными лучами.

Личные
ошибки связаны с особенностями
наблюдателя, например, разные наблюдатели
по-разному наводят зрительную трубу на
визирную цель.

Так
как грубые ошибки должны быть исключены
из результатов измерений, а систематические
исключены или ослаблены до минимально
допустимого предела, то проектирование
измерений с необходимой точностью,
оценку результатов выполненных измерений
производят, основываясь на свойствах
случайных ошибок.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Человеку свойственно ошибаться. Это касается не только общих вопросов и знаний жизни. Но и распространяется на любые сферы его деятельности, в том числе в области геодезии. В ней все проводимые измерения выполняются с ошибками. Значительная часть работ в геодезическом производстве основывается на измерениях. А измерения — своего рода сравнение с какой-то эталонной или истинной величиной. Если понимать, что истинного значения в идеале не существует, то все сравнения в измерениях сводятся к сравнению с конкретно полученным значением и принятому, как верное. Одним из наиболее приближенных к истинному значению, считается среднее арифметическое.

Понятие погрешности, её абсолютная и относительная величины

Если переходить на понятие погрешности, то отклонение отдельного замера от среднего арифметического из выполненных измерений и считается абсолютной его ошибкой. Числовая форма погрешности не дает представления о качестве произведенного измерения. Для этого существует понятие относительной погрешности. Под ним понимают отношение значения собственно ошибки к замеренной величине. Применяется этот параметр в определении точности работ при линейных замерах в полигонометрических и теодолитных ходах.

В нивелирных ходах для его оценки точности существует так называемая приведенная погрешность. Это тоже своего рода относительный показатель. Только он подразумевает под собой отношение абсолютного значения ошибки к конкретному принятому значению определяемой величины (для нивелировок на 1 км хода).

Погрешности по источникам возникновения

При производстве геодезических работ после окончания каждой выполненной операции в полевых условиях можно говорить об ошибках. Присутствуют они и при проведении камеральных работ. Так при установке приборов в рабочее положение возникают отклонения в центрировании инструмента над центром знака. Также возникают неточности при выставлении прибора в отвесное состояние, когда выводим его цилиндрический уровень в верхнее горизонтальное положение и круглый уровень на середину. Следующими причинами возникновения погрешностей считаются визирование и снятие отсчетов в момент исполнения наблюдений.  Влияние внешних условий окружающей среды: рефракция воздуха, дымка, туман, осадки, формирует еще одну группу ошибок. Помимо человеческого фактора и влияния внешней среды существуют конструктивные особенности приборов, с заложенными в них вероятностными составляющими точности измерений. Еще одной из причин возникновения погрешностей считается несовершенство методик их определений. Резюмируя выше сказанное, можно выделить следующий перечень ошибок по источникам их возникновения:

• инструментальные;
• индивидуальные;
• из-за условий окружающей среды;
• методические.

Погрешности по характеру действий

По данному признаку все ошибки можно разделить на следующие отклонения:

• грубые, то есть значительно превышающие ожидаемые ошибки, возникающие в результате просчетов, неверных действий и обнаруженные при дополнительном контроле;
• систематические отклонения, отличающиеся постоянством возникновения и закономерностями изменений при повторных операциях; к ним можно отнести периодические и функциональные погрешности;
• случайные, значения величин, которых не значительны, большая часть их мала, чем велика, встречаются как с положительными, так и с отрицательными значениями, в каждом конкретном случае они возникают отдельно случайным образом и в своей массе подчинены определенным вероятностным закономерностям;

Именно изучение случайных погрешностей в геодезии дает возможность производить оценки точности и получать наиболее надежные результаты.

Предельные и допустимые отклонения

При определенных факторах случайные ошибки по абсолютному значению своей величины не могут превышать определенного предела. Этот предел в геодезической и маркшейдерской практике имеет название предельной погрешности.

В строительном производстве нормативными документами введен термин предельного отклонения, который может иметь как положительное, так и отрицательное значения. Алгебраическая сумма этих параметров (предельных отклонений) имеет название допуска.

В геодезии крайние предельные значения отклонений, допускаемые нормативной документацией, называются допустимыми.

Средние, вероятные и средне квадратические погрешности

При различных оценках точности выполненных замеров применяются некоторые критерии случайных ошибок. К таким мерилам оценки относятся понятия:

• средне арифметического отклонения от всех случайных ошибок, имеющее название среднего уклонения;
• срединного отклонения, то есть находящегося в середине измеренного ряда по абсолютным значениям с учетом убывания и возрастания, именуемое вероятной ошибкой;
• средне квадратическое отклонение (СКО) – это параметр функции дисперсии (рассеивания) случайных величин результатов измерений. Он равен математическому ожиданию (среднему арифметическому значению) квадратов отклонений в измерениях от математического ожидания (среднего арифметического значения) результатов замеров.

Случайные погрешности подчиняются нормальному закону распределения и находятся в интервале от нуля до трех СКО. Большинство из них в пределах шестидесяти восьми процентов находятся в интервале до одного СКО. Девяносто пять процентов случайных величин попадает в интервал от нуля до двух СКО. Девяносто девять процентов случайных ошибок находится в интервале от нуля до трех СКО.

На основании этого в теоретических расчетах при предварительных оценках точности выполнения работ за предельные принимаются три средне квадратические ошибки. При геодезических и маркшейдерских работах на практике к расчетам принимаются двойные величины средне квадратических отклонений. 

Рассказываем о самых распространенных ошибках, с которыми встречается геодезист, выполняя измерения спутниковым оборудованием и как минимизировать их влияние на получаемый результат работы.

Ошибки исходных данных

Одним из видов ошибок, на которые геодезист не может повлиять своими действиями при проведении полевых измерений, являются ошибки исходных данных.

Следует помнить, что производимые измерения не могут быть точнее, чем произведены измерения исходных пунктов от которых работает геодезист.

Так, например, если геодезист работает от пунктов СГС-1, то к ошибке получаемых координат добавляется СКП, равное 3 мм + 1*10-7D для плановых координат и 5 мм + 2*10-7D по геодезической высоте (где D – расстояние между пунктами в км). Для СГС-1 оно составляет 15-25 км в обжитых районах и 25-50 км в необжитых.

Разберем пример, в котором расстояние между определенными пунктам СГС-1 составило 25 км.

Таким образом, при работе от этих пунктов получаемая точность определения координат изначально не может быть лучше, чем 5,5 мм СКП в плане и 10 мм СКП по высоте.

Ошибки наблюдателя

При производстве геодезических работ часто возникают ошибки, связанные с человеческим фактором. Поскольку источником данного типа ошибок является сам геодезист, особенно важно контролировать свои действия на каждом этапе работ. В первую очередь геодезист может столкнуться с ошибочно измеренной высотой используемой вехи. Ее обязательно необходимо проверить, принимая во внимание, что градуировка может иметь определенную специфику нанесения.

Встречается два типа геодезических вех с различной градуировкой:

• для работы с отражателем (высота указана с поправкой до центра отражателя). Как правило, эта поправка составляет 10 или 11,5 см и зависит от модели вехи/отражателя, связку которых следует проверять перед началом работ.
• для работы с ГНСС-приемником (высота указана до основания начала резьбового соединения). Следует учитывать, что соединение может иметь зазор по высоте, т.е. приемник не плотно прикручивается к основанию соединения.

Пример №1

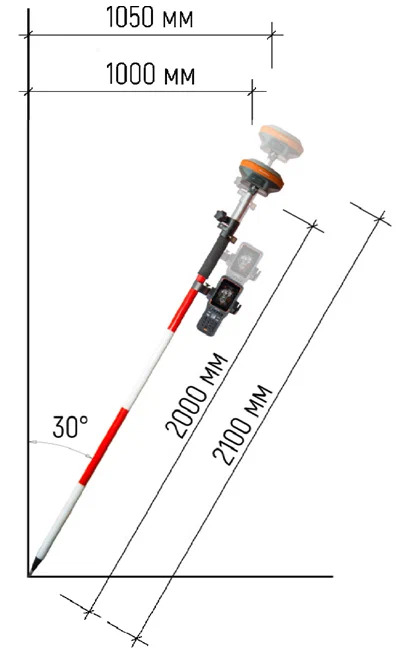
Рассмотрим ситуацию, когда геодезист принимает решение работать с ГНСС-приемником, используя веху для отражателя, и при этом не учитывать ошибку (допустим 10 см) по высоте, т.к. ему нужны только плановые координаты.

Давайте рассмотрим, как повлияет допущенная ошибка измерения высоты инструмента, равная 10 см, если приемник имеет функцию коррекции наклона?

Дано: наклон вехи равен 30°, высота правильно измеренной вехи = 2м, измеренная с учетом ошибки = 2,1 м.

В первом случае приращение будет равно 1 м, во втором 1,05 м.

Таким образом, ошибка определения высоты вехи (равная в рассмотренном случае 10 см) привела к ошибке определения планового положения равной 5 см.

Соответственно неверный ввод высоты, несет за собой ошибку расчетов корректировки наклона и впоследствии ошибки в координатах.

Пример №2

Следующая ошибка, влияние которой важно учитывать при работе, это наклон вехи или не поверенный уровень.

Давайте рассмотрим ситуацию, когда геодезист небрежно производит измерения с наклоном вехи 1 градус, используя приемник без компенсации наклона.

Задача решается с помощью прямоугольного треугольника. Дано: наклон вехи равен 1°, высота вехи (установки прибора) равна 2м.

Ошибка определения координат составит 3,5 см.

В случае если наклон будет составлять 5 градусов (у вехи разъюстирован уровень), ошибка определения координат составит уже 17,5 см!

Из примеров, описанных выше видно, что незначительные на первый взгляд ошибки достаточно серьезно влияют на общую погрешность измерений. В случае комбинации этих двух примеров, когда работы выполняется с вехой с не поверенным уровнем и с ошибочно измеренной высотой прибора, можно увидеть, насколько разительно будет отличаться итоговый результат от предполагаемого.

Ошибки аппаратуры

Спутниковые часы — Если работы выполняются в режиме РТК, данная ошибка исключается автоматически

Ошибки эфемерид — Одним из способов компенсации ошибок спутниковых орбит является загрузка точной эфемеридной информации из систем SBAS или PPP. Другой способ компенсации ошибок спутниковой орбиты — использование приемника в режиме дифференциальной коррекции или RTK, наш случай

Ионосферные и тропосферные задержки — Ионосферные и тропосферные условия очень похожи в пределах отдельной области, поэтому спутниковые сигналы, поступающие на приемники базовой станции и подвижные приемники, имеют очень похожую задержку. Это позволяет компенсировать ионосферную задержку дифференциальными методами ГНСС (работой от нескольких навигационных систем) и RTK

Многолучевость — Применительно к спутниковым измерениям под многолучевостью принято понимать такое распространение радиосигналов, при котором упомянутые сигналы достигают антенны спутникового приемника не только по прямому пути от спутника (псевдодальности), но и по ломаному. Образуется ломаный путь за счет отражений сигнала от различного рода объектов, окружающих приемник, например, зданий, разной этажности, крупных объектов и водоемов.

Именно поэтому в городской застройке геодезическую съемку следует проводить с особой аккуратностью. При желании получить действительно качественные измерения необходимо обязательно проверять снятые измерения, выполняя инициализацию на точке повторно и контролировать полученные измерения

Инструментальная ошибка — У любого ГНСС-приемника есть метрологическая характеристика «допустимая СКП измерений длины базиса», которая линейно влияет на измерения. На сложных объектах мы рекомендуем работать от ближайшей станции или устанавливать свою мобильную базовую станцию, максимально сокращая длину базовой линии

Геометрические факторы

Геометрическое расположение спутников в том виде, в котором они представлены приемнику в конкретном месте и в конкретное время, так же влияет на точность расчетов местоположения и времени. За качество геометрии спутников отвечает показатель PDOP.

PDOP – это коэффициент, показывающий снижение точности определения местоположения приемника относительно геометрии расположения спутников на небосводе. Оператор может увидеть его значение на экране контроллера и оценить возможность проведения съемки.

Чем меньше значение PDOP, тем точнее результат вычисления позиции.

PDOP считается очень высоким при значении 3 ед. В этом случае однозначно не рекомендуется проводить измерения в режиме RTK.

У геодезиста есть возможность попробовать снизить показатель PDOP, выключив ряд спутниковых группировок из общего решения и продолжить работу, либо окончательно принять решение о невозможности проведения качественных измерений.

Таким образом, показатель PDOP необходимо контролировать до и во время съемки.

GPS спуфинг

GPS спуфинг – это атака, которая пытается обмануть ГНСС-приемник, передавая в широком диапазоне вещания более мощный сигнал, чем полученный от спутников системы GPS, такой, чтобы быть похожим на ряд нормальных спутников GPS.

Где вероятнее всего можно встретиться с этим явлением?

• Спецобъекты
• Парковки дальнобойщиков/трассы

Что делать в ситуации, когда очевидно влияние GPS-спуфинга?

В таком случае не рекомендуется работать спутниковым приемником и лучшим вариантом является выполнение измерений другим методом, например традиционной тахеометрической съемкой.

Описанные выше примеры возможных ошибок, влияющих на качество измерений, это только верхушка айсберга. Несмотря на технологический прорыв в сфере спутникового оборудования и его доступность, специалисту необходимо иметь фундаментальные знания в области геодезии и всегда помнить одно из основных ее правил – обязательный контроль своих измерений.

Отдельно отметим, что при необходимости использования ГНСС-оборудования для создания съемочного обоснования на объекте, рекомендуется применять метод съемки (режим работы) «Статика», это позволит сократить влияние случайных ошибок и безусловно повысит качество данных относительно метода съемки RTK.

Рекомендуем своевременно проводить поверку/техническое обслуживание оборудования и следить за выходом обновлений программного обеспечения приборов.

Узнать актуальную прошивку для вашего ГНСС-оборудования EFT Вы можете обратившись в техническую поддержку удобным способом: support@eftgroup.ru, 8 (800) 500-97-72.

Теория ошибок измерений изучает свойства ошибок и законы их распределения, методы обработки измерений с учетом их ошибок, а также способы вычисления числовых характеристик точности измерений. При многократных измерениях одной и той же величины результаты измерений получаются неодинаковыми. Этот очевидный факт говорит о том, что измерения сопровождаются разными по величине и по знаку ошибками. Задача теории ошибок – нахождение наиболее надежного значения измеренной величины, оценка точности результатов измерений и их функций и установление допусков, ограничивающих использование результатов обработки измерений.

По своей природе ошибки бывают грубые, систематические и случайные.

Грубые ошибки являются результатом промахов и просчетов. Их можно избежать при внимательном и аккуратном отношении к работе и организации надежного полевого контроля измерений. В теории ошибок грубые ошибки не изучаются.

Систематические ошибки имеют определенный источник, направление и величину. Если источник систематической ошибки обнаружен и изучен, то можно получить формулу влияния этой ошибки на результат измерения и затем ввести в него поправку; это исключит влияние систематической ошибки. Пока источник какой-либо систематической ошибки не найден, приходится считать ее случайной ошибкой, ухудшающей качество измерений.

Случайные ошибки измерений обусловлены точностью способа измерений (строгостью теории), точностью измерительного прибора, квалификацией исполнителя и влиянием внешних условий. Закономерности случайных ошибок проявляются в массе, то-есть, при большом количестве измерений; такие закономерности называют статистическими. Освободить результат единичного измерения от случайных ошибок невозможно; невозможно также предсказать случайную ошибку единичного измерения. Теория ошибок занимается в основном изучением случайных ошибок.

Случайная истинная ошибка измерения Δ – это разность между измеренным значением величины l и ее истинным значением X:
(1.25)

Свойства случайных ошибок. Случайные ошибки подчиняются некоторым закономерностям:

1. при данных условиях измерений абсолютные значения случайных ошибок не превосходят некоторого предела; если какая-либо ошибка выходит за этот предел, она считается грубой,
2. положительные и отрицательные случайные ошибки равновозможны,
3. среднее арифметическое случайных ошибок стремится к нулю при неограниченном возрастании числа измерений. Третье свойство случайных ошибок записывается так:
(1.26)
4. малые по абсолютной величине случайные ошибки встречаются чаще, чем большие.

Кроме того, во всей массе случайных ошибок не должно быть явных закономерностей ни по знаку, ни по величине. Если закономерность обнаруживается, значит здесь сказывается влияние какой-то систематической ошибки.

Средняя квадратическая ошибка одного измерения. Для оценки точности измерений можно применять разные критерии; в геодезии таким критерием является средняя квадратическая ошибка. Это понятие было введено Гауссом; он же разработал основные положения теории ошибок. Средняя квадратическая ошибка одного измерения обозначается буквой m и вычисляется по формуле Гаусса:
(1.27)

где: ;
n – количество измерений одной величины.

Средняя квадратическая ошибка очень чувствительна к большим по абсолютной величине ошибкам, так как каждая ошибка возводится в квадрат. В то же время она является устойчивым критерием для оценки точности даже при небольшом количество измерений; начиная с некоторого n дальнейшее увеличение числа измерений почти не изменяет значения m; доказано, что уже при n = 8 значение m получается достаточно надежным.

Предельная ошибка ряда измерений обозначается Δпред; она обычно принимается равной 3*m при теоретических исследованиях и 2*m или 2.5*m при практических измерениях. Считается, что из тысячи измерений только три ошибки могут достигать или немного превосходить значение Δпред = 3*m.

Отношение mx/X называется средней квадратической относительной ошибкой; для некоторых видов измерений относительная ошибка более наглядна, чем m. Относительная ошибка выражается дробью с числителем, равным 1, например, mx/X = 1/10 000.

Средняя квадратическая ошибка функции измеренных величин. Выведем формулу средней квадратической ошибки функции нескольких аргументов произвольного вида:

F = f( X, Y, Z … ),                        (1.28)

здесь: X, Y, Z … – истинные значения аргументов,
F – истинное значение функции.

В результате измерений получены измеренные значения аргументов lX, lY, lZ, при этом:
(1.29)

где ΔX, ΔY, ΔZ – случайные истинные ошибки измерения аргументов.

Функцию F можно выразить через измеренные значения аргуметов и их истинные ошибки:

Разложим функцию F в ряд Тейлора, ограничившись первой степенью малых приращений ΔX, ΔY, ΔZ:
(1.30)

Разность является случайной истинной ошибкой функции с противоположным знаком, поэтому:
(1.31)

Если выполнить n измерений аргументов X, Y, Z, то можно записать n уравнений вида (1.31). Возведем все эти уравнения в квадрат и сложим их; суммарное уравнение разделим на n и получим

В силу третьего свойства случайных ошибок члены, содержащие произведения случайных ошибок, будут незначительными по величине, и их можно не учитывать; таким образом,
(1.32)

Как частные случаи формулы (1.32) можно написать выражения для средней квадратической ошибки некоторых функций:

Если функция имеет вид произведения нескольких аргументов,

F = x * y * z,

то для нее можно записать выражение относительной ошибки функции:
(1.33)

которое в некоторых случаях оказывается более удобным, чем формула (1.32).

Принцип равных влияний. В геодезии часто приходится определять средние квадратические ошибки аргументов по заданной средней квадратической ошибке функции. Если аргумент всего один, то решение задачи не представляет трудности. Если число аргументов t больше одного, то возникает задача нахождения t неизвестных из одного уравнения, которую можно решить, применяя принцип равных влияний. Согласно этому принципу все слагаемые правой части формулы (1.32) или (1.33) считаются равными между собой.

Арифметическая середина. Пусть имеется n измерений одной величины X, то-есть,
(1.34)

Сложим эти равенства, суммарное уравнение разделим на n и получим:
(1.35)

Величина   (1.36)

называется средним арифметическим или простой арифметической серединой. Запишем (1.35) в виде

по третьему свойству ошибок (1.26) можно написать:

что означает, что при неограниченном возрастании количества измерений простая арифметическая середина стремится к истинному значению измеряемой величины. При ограниченном количестве измерений арифметическая середина является наиболее надежным и достоверным значением измеряемой величины.

Запишем формулу (1.36) в виде

и подсчитаем среднюю квадратическую ошибку арифметической середины, которая обозначается буквой M. Согласно формуле (1.32) напишем:

или

Но ml1 = ml2 = … = mln= m по условию задачи, так как величина X измеряется при одних и тех же условиях. Тогда в квадратных скобках будет n * m2, одно n сократится и в итоге получим:

M2 = m2/n

или
(1.37)

то-есть, средняя квадратическая ошибка арифметической середины в корень из n раз меньше ошибки одного измерения.

Вычисление средней квадратической ошибки по уклонениям от арифметической середины. Формулу Гаусса (1.27) применяют лишь в теоретических выкладках и при исследованиях приборов и методов измерений, когда известно истинное значение измеряемой величины. На практике оно, как правило, неизвестно, и оценку точности выполняют по уклонениям от арифметической середины.

Пусть имеется ряд равноточных измерений величины X:

l1, l2 , …, ln .

Вычислим арифметическую середину X0 = [1]/n и образуем разности:
(1.38)

Сложим все разности и получим [l] – n * X0 = [V]. По определению арифметической середины n * X0 = [l], поэтому:

[V] = 0.                   (1.39)

Величины V называют вероятнейшими ошибками измерений; именно по их значениям и вычисляют на практике среднюю квадратическую ошибку одного измерения, используя для этого формулу Бесселя:
(1.40)

Приведем вывод этой формулы. Образуем разности случайных истинных ошибок измерений Δ и вероятнейших ошибок V:
(1.41)

Разность (X0 – X) равна истинной ошибке арифметической середины; обозначим ее Δ0 и перепишем уравнения (1.41):
(1.42)
Возведем все уравнения (1.42) в квадрат, сложим их и получим:
.

Второе слагаемое в правой части этого выражения равно нулю по свойству (1.39), следовательно,
.

Разделим это уравнение на n и учтя, что [Δ2]/n =m2, получим:
(1.43)

Заменим истинную ошибку арифметической середины Δ0 ее средней квадратической ошибкой ; такая замена практически не изменит правой части формулы (1.43). Итак,

,
откуда ;

после перенесения (n-1) в правую часть и извлечения квадратного корня получается формула Бесселя (1.40).

Для вычисления средней квадратической ошибки арифметической середины на основании (1.37) получается формула:
(1.44)

Веса измерений. Измерения бывают равноточные и неравноточные. Например, один и тот же угол можно измерить точным или техническим теодолитом, и результаты таких измерений будут неравноточными. Или один и тот же угол можно измерить разным количеством приемов; результаты тоже будут неравноточными. Понятно, что средние квадратические ошибки неравноточных измерений будут неодинаковы. Из опыта известно, что измерение, выполненное с большей точностью (с меньшей ошибкой), заслуживает большего доверия.

Вес измерения – это условное число, характеризующее надежность измерения, степень его доверия; вес обозначается буквой p. Значение веса измерения получают по формуле:

p = C/m2                  (1.45)

где C – в общем случае произвольное положительное число.

При неравноточных измерениях одной величины наиболее надежное ее значение получают по формуле средневесовой арифметической середины:
(1.46)
или              X0 = [l*p] / [p] .

Ошибку измерения, вес которого равен 1, называют средней квадратической ошибкой единицы веса; она обозначается буквой m. Из формулы (1.45) получаем

откуда  (1.47)

то-есть, за число C принимают квадрат ошибки единицы веса.

Подсчитаем вес P средневесовой арифметической середины. По определению веса имеем:
(1.48)

Согласно (1.46) и (1.32) напишем:

Подставим сюда вместо mli2 их выражения через вес m2 = C/p , тогда:

Подставим это выражение в формулу (1.48) и получим,

P = [p],                 (1.49)

то-есть, вес средневесовой арифметической середины равен сумме весов отдельных измерений.

В случае равноточных измерений, когда веса всех измерений одинаковы и равны единице, формула (1.49) принимает вид:

P = n.                  (1.50)

При обработке больших групп измерений (при уравнивании геодезических построений по МНК) вычисляются значение ошибки единицы веса, веса измерений и других элементов после уравнивания, а ошибка любого уравненного элемента подсчитывается по формуле:
(1.51)

где pi – вес i-того элемента.