Что такое пакет ошибок

Характерной
особенностью циклических кодов является
способность к распознаванию пакетов
ошибок. Под пакетом ошибок понимается
группирование ошибок в одной ограниченной
области кодового слова (рис. 3.16). Пакет
ошибок можно описать многочленом вида

.

(3.75)

Е
сли
длина пакета ошибок не превосходит
величины r
= п
— k,
то степень многочлена ошибок меньше r.
В этом случае е(Х)
не делится на
(Х)
без остатка и синдром принятого слова
всегда отличен от нулевого, следовательно,
пакет ошибок длины равной или меньшей
r
всегда распознается. Из теоремы 3.6.1
следует, что распознается также любой
циклический сдвиг многочлена В(Х)
степени, меньшей r,
т.е. и «концевой» пакет ошибок длины
меньшей или равной r
(рис. 3.17), всегда распознается.

Теорема 3.7.1.
Циклический (п,
k)-код
способен обнаруживать все пакеты ошибок
(в том числе концевые) длины r
= п
— k
и меньше.

Помимо распознавания
всех пакетов ошибок длины r
и меньше циклические коды обладают
способностью обнаруживать большую
часть пакетов ошибок, длина которых
превосходит r.

Рассмотрим пакет
ошибок длины r
+ 1, начинающийся в j-ой
компоненте. Так как первая и последняя
компоненты пакета оши­бок отличны от
нуля, всего имеется 2^r-1
возможных конфигураций ошибок.
Необнаружимой является только одна из
них, многочлен которой В(Х)
совпадает с
(Х),
то есть

.
(3.76)

Теорема 3.7.2.
Для циклического (п,
k)-кода
доля необнаружимых пакетов
ошибок длины
l
= r
+ 1 = п
— k+1
равна 2^-(r-1).

Рассмотрим пакет
ошибок длины l>r+1=n—k+1
начинающийся в j-ой
компоненте. Если соответствующий
многочлен В(Х)
делится на
(Х)
без остатка, то есть

,
(3.77)

то такой пакет не
может быть обнаружен.

Пусть коэффициенты
многочлена а(Х)
степени l
— r
— 1 имеют вид a₀,
a₁,
…, a_l—r1.
Так как пакет ошибок начинается и
заканчи­вается единицей, a₀
= a_l—r—1.
Следовательно, существует 2^l—r—2
наборов коэффициентов а(Х),
приводящих к необнаружимым ошиб­кам
в (3.77). С другой стороны, существует 2^l—2
различных пакетов ошибок длины l
и, таким образом, верно следующее
утверждение.

Теорема 3.7.3.
Для циклического (п,
k)-кода
доля необнаружимых пакетов ошибок длины
l>r
+ l = n
— k
+ 1 равна 2^—r.

Пример:
Распознавание ошибок циклическим
(7,4)-кодом Хэм­минга.

Рассмотрим
циклический (7,4)-код Хэмминга из предыдущих
при­меров с r
= п
— k
= 3. Так как минимальное кодовое расстояние
кода Хэмминга dmin
= 3, он способен обнаруживать все двойные
ошиб­ки или исправлять одиночные.
Рассматриваемый (7,4)-код Хэммин­га
является циклическим кодом и он способен
также обнаруживать все пакеты длины r
= 3. В частности, любые три следующие друг
за другом ошибки всегда обнаруживаются.

Доля необнаружимых
ошибок длины r
+ 1 = 4 равна 2^-(3-1)
= 1/4. При пакетах ошибок с длиной большей
4, не распознается только 2^-3
= 1/8 из них.

Замечание.
На практике,
как правило, используются циклические
коды с довольно большим числом проверочных
разрядов, например, r
= п — k
= 16. Доля необнаружимых пакетов ошибок
такими кодами достаточна мала. Так, при
r
= 16, обнаруживается более чем 99,9969 %
пакетов длины 17 и 99,9984 % пакетов длины
18 и выше.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Научные статьи на тему «Пакет ошибок»

LaTeX: возможности расширения и примеры верстки

Для коррекции найденных ошибок необходимо снова вернуться к редактированию исходного TeX -файла, а далее…
снова подвергнуть его компиляции и просмотру на предмет ошибок….
Имя пакета должно быть указано в фигурных скобках….
Пакеты должны состоять из команд TeX, но они не могут генерировать никаких печатных текстов….
Следует отметить, что один и тот же пакет может быть включён в различные тексты.

Статья от экспертов

Точная корректирующая способность кодов Гилберта при исправлении пакетов ошибок

Постановка проблемы: для решения задачи повышения скорости обмена информацией в системах передачи и хранения данных требуется разрабатывать эффективные методы борьбы с помехами, возникающими при передаче, хранении и обработке информации, при использовании как можно меньшей избыточности. Для этого необходимо строить схемы кодирования, ориентированные на ошибки, характерные для конкретного канала связи. Большинство реальных каналов связи являются каналами с группированием ошибок, и типичная помеха в таком канале может описываться как пакет ошибок. Коды Гилберта, обладающие простыми процедурами кодирования и декодирования, хотя и имеют малое минимальное расстояние и неэффективны для исправления независимых ошибок, тем не менее могут быть использованы для исправления пакетов ошибок. Однако корректирующая способность этих кодов при исправлении пакетов ошибок оценивается лишь с помощью не всегда точных границ. Цель: получение точных значений максимальных длин исправляемых пакетов для кодо…

Программные продукты в математическом моделировании

математическое описание модели в программные коды, существует достаточно большая вероятность появления ошибок…
Такие системы иногда именуются просто системами моделирования или пакетами моделирования….
(данный пакет принято называть интерпретирующим)….
Область использования универсальных пакетов значительно более широкая, так как они сориентированы на…
, которые в свою очередь делятся на математические пакеты и пакеты поэлементного моделирования.

Статья от экспертов

Подход к защите информации от пакетов ошибок в средствах радиосвязи декаметрового диапазона

Декаметровая связь, осуществляемая на дальности до сотни километров с помощью мобильных станций небольшой мощности, практически не уступает проводной или радиорелейной. Использование ее актуально не только в мирных, но и в военных целях. Для России связь играет немаловажную роль во многих сферах, а особенно в вопросах развития научного и военного сектора. Ведущие государства стремятся достичь превосходства в околоземном космическом пространстве для развертывания космических группировок способных выполнять широкий спектр задач, но главной из них остается организация связи. В статье проведен анализ особенностей функционирования средств в декаметровом диапазоне, а также рассмотрены способы защиты информации и предложен подход к ее защите от пакетов ошибок.

пакет ошибок

In coding theory, burst error-correcting codes employ methods of correcting burst errors, which are errors that occur in many consecutive bits rather than occurring in bits independently of each other.

Many codes have been designed to correct random errors. Sometimes, however, channels may introduce errors which are localized in a short interval. Such errors occur in a burst (called burst errors) because they occur in many consecutive bits. Examples of burst errors can be found extensively in storage mediums. These errors may be due to physical damage such as scratch on a disc or a stroke of lightning in case of wireless channels. They are not independent; they tend to be spatially concentrated. If one bit has an error, it is likely that the adjacent bits could also be corrupted. The methods used to correct random errors are inefficient to correct burst errors.

Definitions[edit]

A burst of length ℓ^[1]

Say a codeword is transmitted, and it is received as Then, the error vector is called a burst of length if the nonzero components of are confined to consecutive components. For example, is a burst of length

Although this definition is sufficient to describe what a burst error is, the majority of the tools developed for burst error correction rely on cyclic codes. This motivates our next definition.

A cyclic burst of length ℓ^[1]

An error vector is called a cyclic burst error of length if its nonzero components are confined to cyclically consecutive components. For example, the previously considered error vector , is a cyclic burst of length , since we consider the error starting at position and ending at position . Notice the indices are -based, that is, the first element is at position .

For the remainder of this article, we will use the term burst to refer to a cyclic burst, unless noted otherwise.

Burst description[edit]

It is often useful to have a compact definition of a burst error, that encompasses not only its length, but also the pattern, and location of such error. We define a burst description to be a tuple where is the pattern of the error (that is the string of symbols beginning with the first nonzero entry in the error pattern, and ending with the last nonzero symbol), and is the location, on the codeword, where the burst can be found.^[1]

For example, the burst description of the error pattern is . Notice that such description is not unique, because describes the same burst error. In general, if the number of nonzero components in is , then will have different burst descriptions each starting at a different nonzero entry of . To remedy the issues that arise by the ambiguity of burst descriptions with the theorem below, however before doing so we need a definition first.

Definition. The number of symbols in a given error pattern is denoted by

A corollary of the above theorem is that we cannot have two distinct burst descriptions for bursts of length

Cyclic codes for burst error correction[edit]

Cyclic codes are defined as follows: think of the symbols as elements in . Now, we can think of words as polynomials over where the individual symbols of a word correspond to the different coefficients of the polynomial. To define a cyclic code, we pick a fixed polynomial, called generator polynomial. The codewords of this cyclic code are all the polynomials that are divisible by this generator polynomial.

Codewords are polynomials of degree . Suppose that the generator polynomial has degree . Polynomials of degree that are divisible by result from multiplying by polynomials of degree . We have such polynomials. Each one of them corresponds to a codeword. Therefore, for cyclic codes.

Cyclic codes can detect all bursts of length up to . We will see later that the burst error detection ability of any code is bounded from above by . Cyclic codes are considered optimal for burst error detection since they meet this upper bound:

The above proof suggests a simple algorithm for burst error detection/correction in cyclic codes: given a transmitted word (i.e. a polynomial of degree ), compute the remainder of this word when divided by . If the remainder is zero (i.e. if the word is divisible by ), then it is a valid codeword. Otherwise, report an error. To correct this error, subtract this remainder from the transmitted word. The subtraction result is going to be divisible by (i.e. it is going to be a valid codeword).

By the upper bound on burst error detection (), we know that a cyclic code can not detect all bursts of length . However cyclic codes can indeed detect most bursts of length . The reason is that detection fails only when the burst is divisible by . Over binary alphabets, there exist bursts of length . Out of those, only are divisible by . Therefore, the detection failure probability is very small () assuming a uniform distribution over all bursts of length .

We now consider a fundamental theorem about cyclic codes that will aid in designing efficient burst-error correcting codes, by categorizing bursts into different cosets.

Burst error correction bounds[edit]

Upper bounds on burst error detection and correction[edit]

By upper bound, we mean a limit on our error detection ability that we can never go beyond. Suppose that we want to design an code that can detect all burst errors of length A natural question to ask is: given and , what is the maximum that we can never achieve beyond? In other words, what is the upper bound on the length of bursts that we can detect using any code? The following theorem provides an answer to this question.

Now, we repeat the same question but for error correction: given and , what is the upper bound on the length of bursts that we can correct using any code? The following theorem provides a preliminary answer to this question:

A stronger result is given by the Rieger bound:

Definition. A linear burst-error-correcting code achieving the above Rieger bound is called an optimal burst-error-correcting code.

Further bounds on burst error correction[edit]

There is more than one upper bound on the achievable code rate of linear block codes for multiple phased-burst correction (MPBC). One such bound is constrained to a maximum correctable cyclic burst length within every subblock, or equivalently a constraint on the minimum error free length or gap within every phased-burst. This bound, when reduced to the special case of a bound for single burst correction, is the Abramson bound (a corollary of the Hamming bound for burst-error correction) when the cyclic burst length is less than half the block length.^[3]

Remark. is called the redundancy of the code and in an alternative formulation for the Abramson’s bounds is

Fire codes^[3][4][5][edit]

While cyclic codes in general are powerful tools for detecting burst errors, we now consider a family of binary cyclic codes named Fire Codes, which possess good single burst error correction capabilities. By single burst, say of length , we mean that all errors that a received codeword possess lie within a fixed span of digits.

Let be an irreducible polynomial of degree over , and let be the period of . The period of , and indeed of any polynomial, is defined to be the least positive integer such that Let be a positive integer satisfying and not divisible by , where is the period of . Define the Fire Code by the following generator polynomial:

We will show that is an -burst-error correcting code.

Theorem — The Fire Code is -burst error correcting^[4][5]

If we can show that all bursts of length or less occur in different cosets, we can use them as coset leaders that form correctable error patterns. The reason is simple: we know that each coset has a unique syndrome decoding associated with it, and if all bursts of different lengths occur in different cosets, then all have unique syndromes, facilitating error correction.

Proof of Theorem[edit]

Let and be polynomials with degrees and , representing bursts of length and respectively with The integers represent the starting positions of the bursts, and are less than the block length of the code. For contradiction sake, assume that and are in the same coset. Then, is a valid codeword (since both terms are in the same coset). Without loss of generality, pick . By the division theorem we can write: for integers and . We rewrite the polynomial as follows:

Notice that at the second manipulation, we introduced the term . We are allowed to do so, since Fire Codes operate on . By our assumption, is a valid codeword, and thus, must be a multiple of . As mentioned earlier, since the factors of are relatively prime, has to be divisible by . Looking closely at the last expression derived for we notice that is divisible by (by the corollary of Lemma 2). Therefore, is either divisible by or is . Applying the division theorem again, we see that there exists a polynomial with degree such that:

Then we may write:

Equating the degree of both sides, gives us Since we can conclude which implies and . Notice that in the expansion:

The term appears, but since , the resulting expression does not contain , therefore and subsequently This requires that , and . We can further revise our division of by to reflect that is . Substituting back into gives us,

Since , we have . But is irreducible, therefore and must be relatively prime. Since is a codeword, must be divisible by , as it cannot be divisible by . Therefore, must be a multiple of . But it must also be a multiple of , which implies it must be a multiple of but that is precisely the block-length of the code. Therefore, cannot be a multiple of since they are both less than . Thus, our assumption of being a codeword is incorrect, and therefore and are in different cosets, with unique syndromes, and therefore correctable.

Example: 5-burst error correcting fire code[edit]

With the theory presented in the above section, consider the construction of a -burst error correcting Fire Code. Remember that to construct a Fire Code, we need an irreducible polynomial , an integer , representing the burst error correction capability of our code, and we need to satisfy the property that
is not divisible by the period of . With these requirements in mind, consider the irreducible polynomial , and let . Since is a primitive polynomial, its period is . We confirm that is not divisible by . Thus,

is a Fire Code generator. We can calculate the block-length of the code by evaluating the least common multiple of and . In other words, . Thus, the Fire Code above is a cyclic code capable of correcting any burst of length or less.

Binary Reed–Solomon codes[edit]

Certain families of codes, such as Reed–Solomon, operate on alphabet sizes larger than binary. This property awards such codes powerful burst error correction capabilities. Consider a code operating on . Each symbol of the alphabet can be represented by bits. If is an Reed–Solomon code over , we can think of as an code over .

The reason such codes are powerful for burst error correction is that each symbol is represented by bits, and in general, it is irrelevant how many of those bits are erroneous; whether a single bit, or all of the bits contain errors, from a decoding perspective it is still a single symbol error. In other words, since burst errors tend to occur in clusters, there is a strong possibility of several binary errors contributing to a single symbol error.

Notice that a burst of errors can affect at most symbols, and a burst of can affect at most symbols. Then, a burst of can affect at most symbols; this implies that a -symbols-error correcting code can correct a burst of length at most .

In general, a -error correcting Reed–Solomon code over can correct any combination of

or fewer bursts of length , on top of being able to correct -random worst case errors.

An example of a binary RS code[edit]

Let be a RS code over . This code was employed by NASA in their Cassini-Huygens spacecraft.^[6] It is capable of correcting symbol errors. We now construct a Binary RS Code from . Each symbol will be written using bits. Therefore, the Binary RS code will have as its parameters. It is capable of correcting any single burst of length .

Interleaved codes[edit]

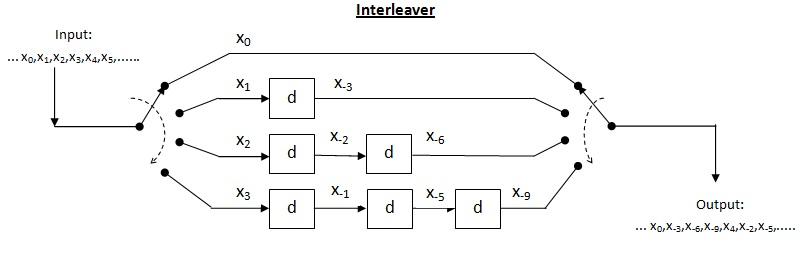
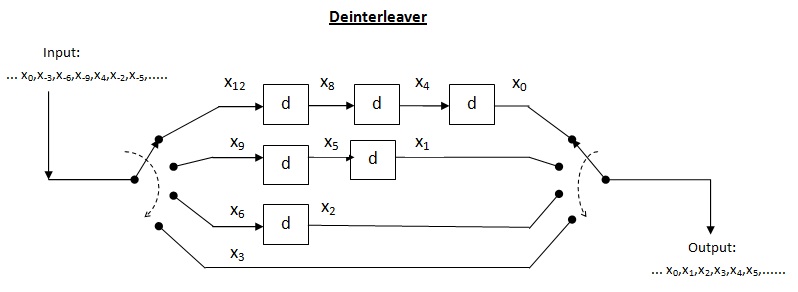
Interleaving is used to convert convolutional codes from random error correctors to burst error correctors. The basic idea behind the use of interleaved codes is to jumble symbols at the transmitter. This leads to randomization of bursts of received errors which are closely located and we can then apply the analysis for random channel. Thus, the main function performed by the interleaver at transmitter is to alter the input symbol sequence. At the receiver, the deinterleaver will alter the received sequence to get back the original unaltered sequence at the transmitter.

Burst error correcting capacity of interleaver[edit]

Block interleaver[edit]

The figure below shows a 4 by 3 interleaver.

The above interleaver is called as a block interleaver. Here, the input symbols are written sequentially in the rows and the output symbols are obtained by reading the columns sequentially. Thus, this is in the form of array. Generally, is length of the codeword.

Capacity of block interleaver: For an block interleaver and burst of length the upper limit on number of errors is This is obvious from the fact that we are reading the output column wise and the number of rows is . By the theorem above for error correction capacity up to the maximum burst length allowed is For burst length of , the decoder may fail.

Efficiency of block interleaver (): It is found by taking ratio of burst length where decoder may fail to the interleaver memory. Thus, we can formulate as

Drawbacks of block interleaver : As it is clear from the figure, the columns are read sequentially, the receiver can interpret single row only after it receives complete message and not before that. Also, the receiver requires a considerable amount of memory in order to store the received symbols and has to store the complete message. Thus, these factors give rise to two drawbacks, one is the latency and other is the storage (fairly large amount of memory). These drawbacks can be avoided by using the convolutional interleaver described below.

Convolutional interleaver[edit]

Cross interleaver is a kind of multiplexer-demultiplexer system. In this system, delay lines are used to progressively increase length. Delay line is basically an electronic circuit used to delay the signal by certain time duration. Let be the number of delay lines and be the number of symbols introduced by each delay line. Thus, the separation between consecutive inputs = symbols. Let the length of codeword Thus, each symbol in the input codeword will be on distinct delay line. Let a burst error of length occur. Since the separation between consecutive symbols is the number of errors that the deinterleaved output may contain is By the theorem above, for error correction capacity up to , maximum burst length allowed is For burst length of decoder may fail.

Efficiency of cross interleaver (): It is found by taking the ratio of burst length where decoder may fail to the interleaver memory. In this case, the memory of interleaver can be calculated as

Thus, we can formulate as follows:

Performance of cross interleaver : As shown in the above interleaver figure, the output is nothing but the diagonal symbols generated at the end of each delay line. In this case, when the input multiplexer switch completes around half switching, we can read first row at the receiver. Thus, we need to store maximum of around half message at receiver in order to read first row. This drastically brings down the storage requirement by half. Since just half message is now required to read first row, the latency is also reduced by half which is good improvement over the block interleaver. Thus, the total interleaver memory is split between transmitter and receiver.

Applications[edit]

Compact disc[edit]

Without error correcting codes, digital audio would not be technically feasible.^[7] The Reed–Solomon codes can correct a corrupted symbol with a single bit error just as easily as it can correct a symbol with all bits wrong. This makes the RS codes particularly suitable for correcting burst errors.^[5] By far, the most common application of RS codes is in compact discs. In addition to basic error correction provided by RS codes, protection against burst errors due to scratches on the disc is provided by a cross interleaver.^[3]

Current compact disc digital audio system was developed by N. V. Philips of The Netherlands and Sony Corporation of Japan (agreement signed in 1979).

A compact disc comprises a 120 mm aluminized disc coated with a clear plastic coating, with spiral track, approximately 5 km in length, which is optically scanned by a laser of wavelength ~0.8 μm, at a constant speed of ~1.25 m/s. For achieving this constant speed, rotation of the disc is varied from ~8 rev/s while scanning at the inner portion of the track to ~3.5 rev/s at the outer portion. Pits and lands are the depressions (0.12 μm deep) and flat segments constituting the binary data along the track (0.6 μm width).^[8]

The CD process can be abstracted as a sequence of the following sub-processes:

• Channel encoding of source of signals
• Mechanical sub-processes of preparing a master disc, producing user discs and sensing the signals embedded on user discs while playing – the channel
• Decoding the signals sensed from user discs

The process is subject to both burst errors and random errors.^[7] Burst errors include those due to disc material (defects of aluminum reflecting film, poor reflective index of transparent disc material), disc production (faults during disc forming and disc cutting etc.), disc handling (scratches – generally thin, radial and orthogonal to direction of recording) and variations in play-back mechanism. Random errors include those due to jitter of reconstructed signal wave and interference in signal. CIRC (Cross-Interleaved Reed–Solomon code) is the basis for error detection and correction in the CD process. It corrects error bursts up to 3,500 bits in sequence (2.4 mm in length as seen on CD surface) and compensates for error bursts up to 12,000 bits (8.5 mm) that may be caused by minor scratches.

Encoding: Sound-waves are sampled and converted to digital form by an A/D converter. The sound wave is sampled for amplitude (at 44.1 kHz or 44,100 pairs, one each for the left and right channels of the stereo sound). The amplitude at an instance is assigned a binary string of length 16. Thus, each sample produces two binary vectors from or 4 bytes of data. Every second of sound recorded results in 44,100 × 32 = 1,411,200 bits (176,400 bytes) of data.^[5] The 1.41 Mbit/s sampled data stream passes through the error correction system eventually getting converted to a stream of 1.88 Mbit/s.

Input for the encoder consists of input frames each of 24 8-bit symbols (12 16-bit samples from the A/D converter, 6 each from left and right data (sound) sources). A frame can be represented by where and are bytes from the left and right channels from the sample of the frame.

Initially, the bytes are permuted to form new frames represented by where represent -th left and right samples from the frame after 2 intervening frames.

Next, these 24 message symbols are encoded using C2 (28,24,5) Reed–Solomon code which is a shortened RS code over . This is two-error-correcting, being of minimum distance 5. This adds 4 bytes of redundancy, forming a new frame: . The resulting 28-symbol codeword is passed through a (28.4) cross interleaver leading to 28 interleaved symbols. These are then passed through C1 (32,28,5) RS code, resulting in codewords of 32 coded output symbols. Further regrouping of odd numbered symbols of a codeword with even numbered symbols of the next codeword is done to break up any short bursts that may still be present after the above 4-frame delay interleaving. Thus, for every 24 input symbols there will be 32 output symbols giving . Finally one byte of control and display information is added.^[5] Each of the 33 bytes is then converted to 17 bits through EFM (eight to fourteen modulation) and addition of 3 merge bits. Therefore, the frame of six samples results in 33 bytes × 17 bits (561 bits) to which are added 24 synchronization bits and 3 merging bits yielding a total of 588 bits.

Decoding: The CD player (CIRC decoder) receives the 32 output symbol data stream. This stream passes through the decoder D1 first. It is up to individual designers of CD systems to decide on decoding methods and optimize their product performance. Being of minimum distance 5 The D1, D2 decoders can each correct a combination of errors and erasures such that .^[5] In most decoding solutions, D1 is designed to correct single error. And in case of more than 1 error, this decoder outputs 28 erasures. The deinterleaver at the succeeding stage distributes these erasures across 28 D2 codewords. Again in most solutions, D2 is set to deal with erasures only (a simpler and less expensive solution). If more than 4 erasures were to be encountered, 24 erasures are output by D2. Thereafter, an error concealment system attempts to interpolate (from neighboring symbols) in case of uncorrectable symbols, failing which sounds corresponding to such erroneous symbols get muted.

Performance of CIRC:^[7] CIRC conceals long bust errors by simple linear interpolation. 2.5 mm of track length (4000 bits) is the maximum completely correctable burst length. 7.7 mm track length (12,300 bits) is the maximum burst length that can be interpolated. Sample interpolation rate is one every 10 hours at Bit Error Rate (BER) and 1000 samples per minute at BER = Undetectable error samples (clicks): less than one every 750 hours at BER = and negligible at BER = .

See also[edit]

• Error detection and correction
• Error-correcting codes with feedback
• Code rate
• Reed–Solomon error correction

References[edit]

Сразу хочу сказать, что здесь никакой воды про циклические коды исправляющие пакеты ошибок , и только нужная информация. Для того чтобы лучше понимать что такое
циклические коды исправляющие пакеты ошибок , настоятельно рекомендую прочитать все из категории Теория информации и кодирования.

Циклические коды, исправляющие пакеты ошибок.

В общем случае любой корректирующий код исправляющий t ошибок исправляет любую конфигурацию из t ошибок. Вместе с тем, если заранее известно, что ошибки расположены пакетом, то можно сконструировать коды более эффективно. Пакет ошибок описывается в виде e(x)=xⁱ*b(x)(mod xⁿ-1), где b(x) — многочлен, степень которого не выше чем t-1, xⁱ — локатор пакета, i — номер разряда.

Синдромные многочлены S(x) для исправляющего пакеты ошибок ЦК должны быть различны для любого пакета длины не более t.

Пример: g(x)=x⁶+ x³+ x²+ x+1, n=15 и корректирует пакеты из трех и менее ошибок.

e(x)=xⁱ,i=0,…,14

e(x)=xⁱ(1+x)(mod x¹⁵-1)

e(x)=xⁱ(1+x²)(mod x¹⁵-1)

e(x)=xⁱ(1+x+x²)(mod x¹⁵-1)

Непосредственным вычислением проявляется, что синдромы для всех 56 возможных пакетов различны . Об этом говорит сайт https://intellect.icu . Следовательно, g(x)=x⁶+ x³+ x²+ x+1 порождает код, исправляющий все пакеты длины 3.

Как правило, ЦК, исправляющие пакеты ошибок синтезируются с помощью ЭВМ.

Статью про циклические коды исправляющие пакеты ошибок я написал специально для тебя. Если ты хотел бы внести свой вклад в развии теории и практики,
ты можешь написать коммент или статью отправив на мою почту в разделе контакты.
Этим ты поможешь другим читателям, ведь ты хочешь это сделать? Надеюсь, что теперь ты понял что такое циклические коды исправляющие пакеты ошибок
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Теория информации и кодирования

Из статьи мы узнали кратко, но емко про циклические коды исправляющие пакеты ошибок

В последнее десятилетие мы успешно пользовались тем, что Go обрабатывает ошибки как значения. Хотя в стандартной библиотеке была минимальная поддержка ошибок: лишь функции errors.New и fmt.Errorf, которые генерируют ошибку, содержащую только сообщение — встроенный интерфейс позволяет Go-программистам добавлять любую информацию. Нужен лишь тип, реализующий метод Error:

type QueryError struct {
    Query string
    Err   error
}

func (e *QueryError) Error() string { return e.Query + ": " + e.Err.Error() }

Такие типы ошибок встречаются во всех языках и хранят самую разную информацию, от временных меток до названий файлов и адресов серверов. Часто упоминаются и низкоуровневые ошибки, предоставляющие дополнительный контекст.

Паттерн, когда одна ошибка содержит другую, встречается в Go столь часто, что после жаркой дискуссии в Go 1.13 была добавлена его явная поддержка. В этой статье мы рассмотрим дополнения к стандартной библиотеке, обеспечивающие упомянутую поддержку: три новые функции в пакете errors и новая форматирующая команда для fmt.Errorf.

Прежде чем подробно рассматривать изменения, давайте поговорим о том, как ошибки исследовались и конструировались в предыдущих версиях языка.

Ошибки до Go 1.13

Исследование ошибок

Ошибки в Go являются значениями. Программы принимают решения на основе этих значений разными способами. Чаще всего ошибка сравнивается с nil, чтобы понять, не было ли сбоя операции.

if err != nil {
    // something went wrong
}

Иногда мы сравниваем ошибку, чтобы узнать контрольное значение и понять, не возникла ли конкретная ошибка.

var ErrNotFound = errors.New("not found")

if err == ErrNotFound {
    // something wasn't found
}

Значение-ошибка может быть любого типа, который удовлетворяет определённому в языке интерфейсу ошибок. Программа может использовать утверждение типа или переключатель типа для просмотра значения-ошибки более специфического типа.

type NotFoundError struct {
    Name string
}

func (e *NotFoundError) Error() string { return e.Name + ": not found" }

if e, ok := err.(*NotFoundError); ok {
    // e.Name wasn't found
}

Добавление информации

Зачастую функция передаёт ошибку вверх по стеку вызовов, добавляя к ней информацию, например, короткое описание того, что происходило в момент возникновения ошибки. Это сделать просто, достаточно сконструировать новую ошибку, включающую в себя текст из предыдущей ошибки:

if err != nil {
    return fmt.Errorf("decompress %v: %v", name, err)
}

При создании новой ошибки с помощью fmt.Errorf мы выбрасываем из исходной ошибки всё, за исключением текста. Как мы видели в примере с QueryError, иногда нужно определять новый тип ошибки, который содержит исходную ошибку, чтобы сохранить её для анализа с помощью кода:

type QueryError struct {
    Query string
    Err   error
}

Программы могут заглянуть внутрь значения *QueryError и принять решение на основе исходной ошибки. Иногда это называется «распаковкой» (unwrapping) ошибки.

if e, ok := err.(*QueryError); ok && e.Err == ErrPermission {
    // query failed because of a permission problem
}

Тип os.PathError из стандартной библиотеки — ещё пример того, как одна ошибка содержит другую.

Ошибки в Go 1.13

Метод Unwrap

В Go 1.13 в пакетах стандартной библиотеки errors и fmt упрощена работа с ошибками, которые содержат другие ошибки. Самым важным является соглашение, а не изменение: ошибка, содержащая другую ошибку, может реализовать метод Unwrap, который возвращает исходную ошибку. Если e1.Unwrap() возвращает e2, то мы говорим, что e1 упаковывает e2 и можно распаковать e1 для получения e2.

Согласно этому соглашению, можно дать описанный выше тип QueryError методу Unwrap, который возвращает содержащуюся в нём ошибку:

func (e *QueryError) Unwrap() error { return e.Err }

Результат распаковки ошибки тоже может содержать метод Unwrap. Последовательность ошибок, полученных с помощью повторяющихся распаковок, мы называем цепочкой ошибок.

Исследование ошибок с помощью Is и As

В Go 1.13 пакет errors содержит две новые функции для исследования ошибок: Is и As.

Функция errors.Is сравнивает ошибку со значением.

// Similar to:
//   if err == ErrNotFound { … }
if errors.Is(err, ErrNotFound) {
    // something wasn't found
}

Функция As проверяет, относится ли ошибка к конкретному типу.

// Similar to:
//   if e, ok := err.(*QueryError); ok { … }
var e *QueryError
if errors.As(err, &e) {
    // err is a *QueryError, and e is set to the error's value
}

В простейшем случае функция errors.Is ведёт себя как сравнение с контрольной ошибкой, а функция errors.As ведёт себя как утверждение типа. Однако работая с упакованными ошибками, эти функции оценивают все ошибки в цепочке. Давайте посмотрим на вышеприведённый пример распаковки QueryError для исследования исходной ошибки:

if e, ok := err.(*QueryError); ok && e.Err == ErrPermission {
    // query failed because of a permission problem
}

С помощью функции errors.Is можно записать так:

if errors.Is(err, ErrPermission) {
    // err, or some error that it wraps, is a permission problem
}

Пакет errors также содержит новую функцию Unwrap, которая возвращает результат вызова метода Unwrap ошибки, или возвращает nil, если у ошибки нет метода Unwrap. Обычно лучше использовать errors.Is или errors.As, поскольку они позволяют исследовать всю цепочку одним вызовом.

Упаковка ошибок с помощью %w

Как я упоминал, нормальной практикой является использование функции fmt.Errorf для добавления к ошибке дополнительной информации.

if err != nil {
    return fmt.Errorf("decompress %v: %v", name, err)
}

В Go 1.13 функция fmt.Errorf поддерживает новая команда %w. Если она есть, то ошибка, возвращаемая fmt.Errorf, будет содержать метод Unwrap, возвращающий аргумент %w, который должен быть ошибкой. Во всех остальных случаях %w идентична %v.

if err != nil {
    // Return an error which unwraps to err.
    return fmt.Errorf("decompress %v: %w", name, err)
}

Упаковка ошибки с помощью %w делает её доступной для errors.Is и errors.As:

err := fmt.Errorf("access denied: %w", ErrPermission)
...
if errors.Is(err, ErrPermission) ...

Когда стоит упаковывать?

Когда вы добавляете к ошибке дополнительный контекст с помощью fmt.Errorf или реализации пользовательского типа вам нужно решить, будет ли новая ошибка содержать в себе исходную. На это нет однозначного ответа, всё зависит от контекста, в котором создана новая ошибка. Упакуйте, чтобы показать её вызывающим. Не упаковывайте ошибку, если это приведёт к раскрытию подробностей реализации.

Например, представьте функцию Parse, которая считывает из io.Reader сложную структуру данных. Если возникает ошибка, нам захочется узнать номер строки и столбца, где она произошла. Если ошибка возникла при чтении из io.Reader, нам нужно будет упаковать её, чтобы выяснить причину. Поскольку вызывающий был предоставлен функции io.Reader, имеет смысл показать сгенерированную им ошибку.

Другой случай: функция, которая делает несколько вызовов базы данных, вероятно, не должна возвращать ошибку, в которой упакован результат одного из этих вызовов. Если БД, которая использовалась этой функцией, является частью реализации, то раскрытие этих ошибок нарушит абстракцию. К примеру, если функция LookupUser из пакета pkg использует пакет Go database/sql, то она может столкнуться с ошибкой sql.ErrNoRows. Если вернуть ошибку с помощью fmt.Errorf("accessing DB: %v", err), тогда вызывающий не может заглянуть внутрь и найти sql.ErrNoRows. Но если функция вернёт fmt.Errorf("accessing DB: %w", err), тогда вызывающий мог бы написать:

err := pkg.LookupUser(...)
if errors.Is(err, sql.ErrNoRows) …

В таком случае функция должна всегда возвращать sql.ErrNoRows, если вы не хотите сломать клиенты, даже при переключении на пакет с другой базой данных. Иными словами, упаковка делает ошибку частью вашего API. Если не хотите в будущем коммитить поддержку этой ошибки как часть API, не упаковывайте её.

Важно помнить, что вне зависимости от того, упаковываете вы её или нет, ошибка останется неизменной. Человек, который будет в ней разбираться, будет иметь одну и ту же информацию. Принятие решения об упаковке зависит от того, нужно ли дать дополнительную информацию программам, чтобы они могли принимать более информированные решения; или если нужно скрыть эту информацию ради сохранения уровня абстракции.

Настройка тестирования ошибок с помощью методов Is и As

Функция errors.Is проверяет каждую ошибку в цепочке на соответствие целевому значению. По умолчанию ошибка соответствует этому значению, если они эквивалентны. Кроме того, ошибка в цепочке может объявлять о своём соответствии целевому значению с помощью реализации метода Is.

Рассмотрим ошибку, вызванную пакетом Upspin, которая сравнивает ошибку с шаблоном и оценивает только ненулевые поля:

type Error struct {
    Path string
    User string
}

func (e *Error) Is(target error) bool {
    t, ok := target.(*Error)
    if !ok {
        return false
    }
    return (e.Path == t.Path || t.Path == "") &&
           (e.User == t.User || t.User == "")
}

if errors.Is(err, &Error{User: "someuser"}) {
    // err's User field is "someuser".
}

Функция errors.As также консультирует метод As при его наличии.

Ошибки и API пакетов

Пакет, который возвращает ошибки (а это делают большинство пакетов), должен описать свойства этих ошибок, на которые может опираться программист. Хорошо спроектированный пакет также будет избегать возвращения ошибок со свойствами, на которые нельзя опираться.

Самое простое: говорить, была ли операция успешной, возвращая, соответственно, значение nil или не-nil. Во многих случаях другой информации не требуется.

Если вам нужно, чтобы функция возвращала индентифицируемое состояние ошибки, например, «элемент не найден», то можно возвращать ошибку, в которую упаковано сигнальное значение.

var ErrNotFound = errors.New("not found")

// FetchItem returns the named item.
//
// If no item with the name exists, FetchItem returns an error
// wrapping ErrNotFound.
func FetchItem(name string) (*Item, error) {
    if itemNotFound(name) {
        return nil, fmt.Errorf("%q: %w", name, ErrNotFound)
    }
    // ...
}

Есть и другие паттерны предоставления ошибок, которые вызывающий может семантически изучить. Например, напрямую возвращать контрольное значение, конкретный тип, или значение, которое можно проанализировать с помощью предикативной функции.

В любом случае, не раскрывайте пользователю внутренние подробности. Как упоминалось в главе «Когда стоит упаковывать?», если возвращаете ошибку из другого пакета, то преобразуйте её, чтобы не раскрывать исходную ошибку, если только не собираетесь брать на себя обязательство в будущем вернуть эту конкретную ошибку.

f, err := os.Open(filename)
if err != nil {
    // The *os.PathError returned by os.Open is an internal detail.
    // To avoid exposing it to the caller, repackage it as a new
    // error with the same text. We use the %v formatting verb, since
    // %w would permit the caller to unwrap the original *os.PathError.
    return fmt.Errorf("%v", err)
}

Если функция возвращает ошибку с упакованным сигнальным значением или типом, то не возвращайте напрямую исходную ошибку.

var ErrPermission = errors.New("permission denied")

// DoSomething returns an error wrapping ErrPermission if the user
// does not have permission to do something.
func DoSomething() {
    if !userHasPermission() {
        // If we return ErrPermission directly, callers might come
        // to depend on the exact error value, writing code like this:
        //
        //     if err := pkg.DoSomething(); err == pkg.ErrPermission { … }
        //
        // This will cause problems if we want to add additional
        // context to the error in the future. To avoid this, we
        // return an error wrapping the sentinel so that users must
        // always unwrap it:
        //
        //     if err := pkg.DoSomething(); errors.Is(err, pkg.ErrPermission) { ... }
        return fmt.Errorf("%w", ErrPermission)
    }
    // ...
}

Заключение

Хотя мы обсудили всего лишь три функции и форматирующую команду, надеемся, что они помогут сильно улучшить обработку ошибок в программах на Go. Мы надеемся, что упаковка ради предоставления дополнительного контекста станет нормальной практикой, помогающей программистам принимать более взвешенные решения и быстрее находить баги.

Как сказал Расс Кокс (Russ Cox) в своём выступлении на GopherCon 2019, на пути к Go 2 мы экспериментируем, упрощаем и отгружаем. И теперь, отгрузив эти изменения, мы принимаемся за новые эксперименты.