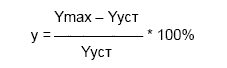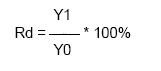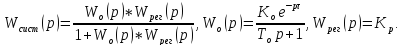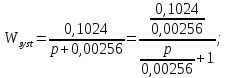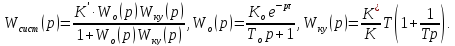Что такое статическая ошибка п регулятора - Не ошибается лишь тот, кто ничего не делает!

Максимальная
динамическая ошибка

– наибольшее
отклонение регулируемой переменной от
заданного значения У_зад:

.
(3.1)

В
устойчивой САР максимальным является
первое отклонение. Таким образом,
показатель

характеризует динамическую точность
регулирования [14].

Время
регулирования
t_p
–промежуток времени от момента нанесения
возмущающего воздействия до момента,
начиная с которого отклонение регулируемой
переменной от установившегося значения
становится и остается меньше наперед
заданного значения ].

Остаточное
отклонение (остаточная неравномерность)
—
абсолютная статическая ошибка
регулирования, определяемая как разность
между установившимся значением
регулируемой величины и ее заданным
значением:

=У_уст
– У_зад.
(3.2)

Показатель

характеризует точность регулирования
в статическом режиме [5].

Во
всех системах регулирования обязательно
имеется статическая ошибка. Ее можно
уменьшать путем увеличения общего
коэффициента усиления регулятора.
Однако она все равно остается, так как
увеличение коэффициента усиления
регулятора всегда ограничено.

Причиной
статической ошибки системы регулирования
является то, что в равновесном состоянии
регулятора положение регулирующего
органа жестко связано с величиной
регулируемой величины [6].

Система
регулирования, которая по принципу
своего действия обладает статической
ошибкой, называется статической
системой, а
регулятор в этом случае называется
статическим
регулятором.
Статический регулятор осуществляет
следующий закон регулирования:

y
= k_регх,

(3.3)

где
х
– отклонение регулируемой величины, у
– регулирующее воздействие регулятора
на объект.

Система
автоматического регулирования, не
обладающая статической ошибкой,
называется астатической
системой автоматического
регулирования,
а регулятор называется астатическим
регулятором [3].

3.2. Критерии устойчивости сар

Понятие
устойчивости САР связано с способностью
системы возвращаться в состояние
равновесия после исчезновения внешних
сил, которые вывели ее из этого состояния.

Устойчивость
систем автоматического управления
является одним из важнейших условий их
работоспособности, так как устойчивость
включает в себя требование затухания
переходных процессов во времени.
Очевидно, что система с расходящимся
процессом была бы неработоспособной.

Рассмотрим
дифференциальное уравнение движения
линеаризованной системы автоматического
регулирования, записанное для регулируемой
величины у(t)
при наличии управляющего воздействия
g(t)
и при равенстве нулю возмущающих
воздействий (см. формулу (2.4)):

.(3.4)

Процесс
регулирования определяется решением
дифференциального уравнения, как сумма
двух решений – частного решения
неоднородного уравнения (3.4)
с правой частью и общего решения уравнения
(3.4)
без правой части [1].

Характеристическое
уравнение САР имеет вид:

.
(3.5)

Корни
характеристического уравнения (3.5)
определяются только видом левой части
уравнения (3.4).
Постоянные интегрирования определяются
также и видом правой части. Поэтому
быстрота затухания и форма переходного
процесса определяются как левой, так и
правой частями исходного дифференциального
уравнения. Однако поскольку в понятие
устойчивости входит только факт наличия
или отсутствия затухания переходного
процесса (независимо от быстроты
затухания и формы переходного процесса),
то устойчивость линейной системы не
зависит от вида правой части
дифференциального уравнения (3.4)
и определяется только характеристическим
уравнением (3.5)
[13].

Так
как получающаяся при решении линейного
дифференциального уравнения (3.4) формула
переходного процесса содержит составляющие
в виде экспонент от вещественных частей
корней характеристического уравнения
САР (3.5) (см. главу 2), то для того, чтобы
САР была устойчивой и переходный процесс
затухал, необходимо, чтобы вещественные
части корней были отрицательными.

Следовательно,
для устойчивости линейной САР необходимо,
чтобы все корни лежали слева от мнимой
оси, в левой полуплоскости комплексных
чисел. Если хотя бы один корень окажется
справа от мнимой оси, то система будет
неустойчивой. Система будет находиться
на границе устойчивости при наличии:
нулевого корня

();
пары чисто мнимых корней
;
бесконечного корня

().
Во всех трех случаях предполагается,
что все остальные корни имеют отрицательные
вещественные части.

Необходимым
(но не достаточным) условием устойчивости
САР является положительность всех
коэффициентов характеристического
уравнения [7]. Это означает, что система
является неустойчивой, если хотя бы
один из коэффициентов характеристического
уравнения отрицателен. Если все
коэффициенты характеристического
уравнения положительны, то требуются
дополнительные исследования САР на
устойчивость с помощью критериев
устойчивости Гурвица, Михайлова или
Найквиста [3].

В
программе «SAU»
для определения устойчивости САР
используется критерий устойчивости
Гурвица, как наиболее удобный с точки
зрения компьютерной реализации. В методе
Гурвица для характеристического
уравнения (3.5) составляется квадратная
матрица коэффициентов, содержащая n
строк и n
столбцов:

.
(3.6)

Критерий
устойчивости сводится к тому, что при
а₀>0
должны быть больше нуля все n
определителей Гурвица, получаемых из
квадратной матрицы коэффициентов.

Определители
Гурвица составляются по следующему
правилу:

;
;

(3.7)

Последний
определитель включает в себя всю матрицу.
Но так как в последнем столбце матрицы
все элементы, кроме нижнего, равны нулю,
то последний определитель Гурвица
выражается через предпоследний следующим
образом:

.
(3.8)

Однако
в устойчивой системе предпоследний
определитель тоже должен быть
положительным. Поэтому условие
положительности последнего определителя
сводится к условию
,
т.е. к положительности свободного члена
характеристического уравнения [1].

Условия
нахождения системы на границе устойчивости
можно получить, приравнивая к нулю
последний определитель ()
при положительности всех остальных
определителей. Как следует из (3.8),
это условие распадается на два условия:

и
.
Первое
условие соответствует границе устойчивости
первого типа (апериодическая граница
устойчивости), а второе – границе
устойчивости второго типа (колебательная
граница устойчивости).

Для
уравнения второго порядка необходимым
и достаточным условием устойчивости
является положительность всех
коэффициентов характеристического
уравнения. Для уравнений более высокого
порядка необходимо исследование с
помощью составления определителей
Гурвица и проверки их на положительность.

Существенным
недостатком критерия Гурвица является
то, что для уравнений высоких порядков
в лучшем случае можно получить ответ о
том, устойчива или неустойчива система
автоматического регулирования. При
этом в случае неустойчивой системы
критерий не дает ответа на то, каким
образом надо изменять параметры системы,
чтобы сделать ее устойчивой. Это
обстоятельство привело к поискам других
критериев, которые более удобны в
инженерной практике.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Статическая ошибка — регулирование

Cтраница 1

Статическая ошибка регулирования может задаваться в абсолютной величине или в безразмерной: по отношению к номинальному значению регулируемого параметра или к диапазону шкалы вторичного прибора.
[1]

Статическая ошибка регулирования теоретически равна нулю, а практически определяется возможной точностью задания и измерения скорости.
[2]

Статическая ошибка регулирования указывает на величину остаточного отклонения параметра; она нежелательна в любом контуре регулирования.
[3]

Статическая ошибка регулирования получается тем меньше, чем больше коэффициент усиления регулятора.
[5]

Статическая ошибка регулирования системы гармонического компаундирования определяется различием воздействия поля реакции якоря по первой и высшим гармоникам. Снижение напряжения определяется воздействием продольной и поперечной составляющих тока якоря, компаундирующее же действие, то есть увеличение напряжения гармонической обмотки и соответственно тока возбуждения генератора, определяется только продольной составляющей тока якоря. Статическую ошибку регулирования возможно, по-видимому, свести к минимуму соответствующим выбором параметров xd и xq генератора.
[6]

Уменьшение статической ошибки регулирования ( ошибки в установившемся режиме) и увеличение быстродействия системы может быть достигнуто последовательным включением в контур системы автоматического регулирования ( в регулятор, осуществляющий основную обратную связь) безынерционного звена с большим коэффициентом усиления.
[8]

Для устранения статической ошибки регулирования ( остаточного отклонения регулируемой величины) напряжение небаланса, снимаемое с движка реостата Лр, подается на сетку левого триода лампы Лг, где усиливается по величине. Усиленное напряжение затем поступает на вход лампы Л3, в анодную цепь которой включена управляющая обмотка асинхронного конденсаторного двигателя Д-32. Скорость вращения двигателя пропорциональна величине сигнала небаланса. Перемещение движка сопротивления Л2 направлено в ту же сторону, что и движка реостата обратной связи RO. Частота импульсов может изменяться в пределах от 45 в минуту до 40 в час путем изменения положения движка переменного сопротивления Д4, изменяющего время разряда RC-цетш.
[9]

Для уменьшения статической ошибки регулирования иногда рекомендуется установка в приточной камере двух калориферов ( или двух рядов калориферов), соединенных последовательно по воздуху и параллельно по воде. Теплопроизводительность каждого калорифера составляет приблизительно 50 % от общей требуемой. Благодаря этому статическая ошибка выбранного регулятора может быть снижена вдвое, так как регулируется только половина нагрузки. Первый по ходу воздуха калорифер отключается двухпозиционным регулятором, датчик которого установлен на входе наружного воздуха, когда достигается температура, при которой требуется только половина нагрузки — теплопроизводительности. Для определения температуры настройки двухпозиционного регулятора требуется провести дополнительные несложные расчеты.
[10]

Говоря о статической ошибке регулирования, считают, что после каждого изменения нагрузки или после отклонения от заданного режима работы, которое вызывается другими причинами, снова устанавливается постоянная скорость вращения вала, пусть не та, что была раньше, но постоянная, и остается дальше неизменным положение всех элементов регулятора.
[11]

Что называется статической ошибкой регулирования.
[12]

При этом условии статическая ошибка регулирования может быть сведена до весьма малой величины.
[13]

Теоретически при kpoo статическая ошибка регулирования становится равной нулю.
[14]

Страницы:

Демьян Бондарь

Эксперт по предмету «Автоматизация технологических процессов»

преподавательский стаж — 5 лет

Задать вопрос автору статьи

Качество систем управления в переходном режиме

Определение 1

Качество системы управления – это комплексная оценка работы системы управления в зависимости от ее назначения.

Самыми распространенными показателями качества системы в переходном процессе являются:

Интегральные критерии.
Статическая ошибка регулирования.
Степень колебательности.
Динамическая ошибка регулирования.
Время регулирования.
Степень устойчивости.

Статическая ошибка регулирования представляет собой разность между установившемся значением регулируемого параметра и его заданным значением. Динамическая ошибка регулирования равняется наибольшему отклонению регулируемой величины от ее установившегося значения. Время регулирования определяется, как время, за которое разность между текущим значением регулируемого параметра и его заданным значением становится меньше допустимого отклонения. Степень устойчивости автоматической системы управления характеризует запас устойчивости в плоскости корней характеристического уравнения и равняется расстоянию до оси ближайшего корня. Данный критерий характеризует интенсивность затухания наиболее медленно затухающей неколебательной составляющей переходного процесса.

Подработка для студентов

Начни работу по профессии и зарабатывай первые деньги еще будучи студентом

Найти стажировку

Степень колебательности равняется минимальному модулю отношения действительной и мнимой частей корня, то есть:

Рисунок 1.

Если в плоскости корней характеристического уравнения устойчивой системы провести из начала координат два луча (как показано на рисунке ниже) таким образом, чтобы одна пара корней находилась на данных лучах, а остальные лежали слева от них, то тангенс угла, который заключен между лучами и мнимой осью, равный отношению действительной и мнимой частей корней, лежащих на лучах АОВ, является степенью колебательности системы.

Рисунок 2. График. Автор24 — интернет-биржа студенческих работ

«Качество систем управления в установившемся и переходном режимах» 👇

Степень затухания является количественной оценкой интенсивности затухания колебательного процесса:

Рисунок 3.

Между степенью затухания и степенью колебательности существует однозначная зависимость:

Рисунок 4.

Степень затухания может изменяться в пределах от 0,1 до 1, а степень колебательности от 0 до бесконечности. В отличии от прямых показателей интегральные критерии дают обобщенную оценку качества системы, они делятся на:

линейный интегральный критерий,
модульные интегральные критерии,
квадратичный интегральный критерий,
обобщенные интегральные критерии.

Качество системы управления в установившемся режиме

Определение 2

Установившийся режим – это режим, параметры которого не изменяются во времени или меняются в соответствии с периодическим законом.

Рассмотрим схему одноконтурной системы, которая представлена на рисунке ниже.

Рисунок 5. Схема одноконтурной системы. Автор24 — интернет-биржа студенческих работ

Рассматриваемая схема может быть упрощена следующим образом.

Рисунок 6. Упрощенная схема. Автор24 — интернет-биржа студенческих работ

Для того, чтобы согласовать сигналы u3(t) и uoc(t) надо подобрать одинаковые передаточные функции Wбз(р) и Wби(р), поэтому должно выполняться следующее равенство:

$Wбз(р) = Wби(р)$

С учетом представленного выше равенства схему рассматриваемой системы можно представить в следующем виде.

Рисунок 7. Схема системы. Автор24 — интернет-биржа студенческих работ

В этом случае ошибка регулирования входит в формулу для определения сигнала рассогласования:

$ΔU(р) = Δ(р) WБИ(р)$

Ошибка δ(t) зависит от величины параметров, задающего и возмущающего воздействия, таким образом ее значение может быть выражено как сумма ошибок данных воздействий:

$δ(t) =δy(t) + δf(t)$

Передаточные функции выражаются следующим образом:

Рисунок 8.

Рисунок 9.

Передаточная функция разомкнутого контура выражается следующим образом

$Wрк (р) =WБИ(р) WБУ (р) WОУ(р)$

Исходя из представленных выше выражений величина изображения ошибки определяется следующим образом:

Рисунок 10.

Существую типовые законы оценки установившегося режима, установленные условиями:

Возмущающее и задающее воздействия не изменяются во времени и постоянны, то есть — yз(t), f (t) = const.
Изменения в системе происходят с постоянной скоростью, то есть — yз (t) = a t и f (t) = const.
Изменения в системе происходят с постоянным ускорением, то есть — y(t) = b t2/2и f (t) = const.
Изменения в системе происходят по гармоническому закону, то есть — yз (t) = y0 sin(ω t) и f (t) = const.

Определение 3

Статическая ошибка – это значение ошибки регулирования при постоянной величине входного воздействия.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Глава 8. Типовые законы регулирования. Одноконтурные САР

8.1. Основные типы автоматических регуляторов

Регулятор на основе усилительного звена называется П-регулятором (пропорциональный). Его положительной характеристикой является высокое быстродействие: при отклонении регулируемой величины от заданного значения регулятор выдает регулирующее воздействие, пропорциональное величине отклонения x, что обеспечивает быструю компенсацию возмущения. Существенным недостатком П-регулятора является наличие статической ошибки в переходном процессе АСР с П-регулятором (рис. 37). Статическая ошибка возникает потому, что у П-регулятора между регулируемой величиной x и регулирующим воздействием xр существует зависимость, однозначно определяемая коэффициентом K. Поэтому генерировать регулирующее воздействие xр для компенсации возмущения xв П-регулятор может только путем изменения регулируемой величины x, что и создает статическую ошибку.
Регулятор на основе интегрирующего звена (48) называется И‑регулятором:

Если xвых усилительного звена (П-регулятор) однозначно определяется величиной правой части уравнения, что является причиной возникновения статической погрешности в АСР с П-регулятором, то правая часть уравнения (48) интегрирующего звена (И-регулятор) определяет не величину, а скорость изменения xвых. Величина xвых будет изменяться до тех пор, пока правая часть уравнения (48) не станет равна нулю, т. е. пока регулируемая величина x при наличии возмущения xв не вернется к заданному значению. Следовательно, в АСР с И-регулятором не возникает статическая погрешность.
Однако у И-регулятора имеется свой недостаток сравнительно с П-регулятором: в случае возникновения возмущения регулирующее воздействие П-регулятора меняется быстрее, чем у И-регулятора с его конечной скоростью, что замедляет процесс компенсации возмущения и ухудшает критерии качества регулирования (рис. 40).

Рис. 40. Переходные процессы в АСР с П- и И-регуляторами

Таким образом, П-регулятор обеспечивает высокое быстродействие (что уменьшает динамическую ошибку), но не может обеспечить при наличии возмущения заданное значение регулируемой величины (статическая ошибка). И-регулятор, наоборот, не создает статическую ошибку, но вследствие относительно медленного изменения xр имеет большую динамическую ошибку.
Сравнивая характеристики П- и И-регуляторов можно сделать вывод: если включить усилительное и интегрирующие звенья параллельно, то автоматический регулятор будет лишен указанных недостатков. Такой регулятор называется ПИ-регулятором (рис. 41).

Рис. 41. Принципиальная схема АСР с ПИ-регулятором

Действительно, быстродействие ПИ-регулятора обеспечивает усилительное звено, а статическую ошибку снимает интегрирующее звено. Для управления производственными процессами чаще всего используются ПИ-регуляторы.
Кривая разгона идеального ПИ-регулятора показана на рис. 42 .
Уравнение ПИ-регулятора при нулевых начальных условиях имеет вид:

Отношение коэффициентов Kp1/Kp определяет степень влияния интегрирующей части, и его обратная величина называется временем изодрома Tи.

Время изодрома – это время, в течение которого интегрирующее звено изменяет регулирующее воздействие xр ПИ-регулятора на величину Dxр, равную предварительному изменению Dxр усилительного звена (рис. 42). Поэтому иногда время изодрома называют временем удвоения.

Рис. 42. График кривой разгона идеального ПИ-регулятора:

а – скачкообразное изменение входного воздействия x;

б – реакция (кривая разгона) ПИ-регулятора xр

Уравнение ПИ-регулятора можно записать как

откуда передаточная функция

Амплитудно-фазовая характеристика:

В том случае, если рассмотренные регуляторы не обеспечивают требуемое качество регулирования, необходимо увеличить интенсивность процесса компенсации возмущения. Этого можно достигнуть увеличением регулирующего воздействия, которое в свою очередь определяется коэффициентом усиления автоматического регулятора Kp
. Однако ниже будет показано, что увеличение коэффициента усиления регулятора в АСР приводит к тому, что в системе начинают генерироваться незатухающие колебания.
В связи с этим представляет интерес рассмотреть алгоритм, который реализует дифференцирующее звено.
Входной величиной любого регулятора является кривая разгона регулируемой величины (рис. 27), которая определяется величиной возмущения и передаточной функцией объекта регулирования (9). В свою очередь, регулирующее воздействие xp (рис. 27) определяется кривой разгона x и передаточной функцией регулятора.
На рис. 43 показана реакция дифференцирующего звена (Д‑регулятора) на входное воздействие в виде кривой разгона в соответствии с уравнением (51).

Рис. 43. Реакция дифференцирующего звена на кривую разгона

а –изменение входного воздействия x в виде кривой разгона;

б – реакция xр дифференцирующего звена

Из рис. 43,а следует, что дифференцирующее звено обеспечивает большее регулирующее воздействие в начале переходного процесса. Это означает, что дифференцирующий регулятор активно компенсирует возмущение и исключает возникновение незатухающих колебаний.
Если включить дифференцирующее звено параллельно ПИ‑регулятору (рис. 44), то получим ПИД-регулятор, обеспечивающий интенсивную компенсацию возмущений. При этом недостаток дифференцирующего звена (при Хвх = const, Хвых = 0 ) компенсируется усилительным и интегрирующим звеньями.

Рис. 44. Принципиальная схема АСР с ПИД-регулятором

На рис. 45 показана кривая разгона ПИД-регулятора.

Рис. 45. Кривая разгона ПИД-регулятора

На рис. 46 показаны переходные процессы на с различными регуляторами. ПИД-регулятор уменьшает динамическую ошибку сравнительно с ПИ-регулятором на 25–30%. Также можно объединить дифференцирующее звено с усилительным звеном и улучшить показатели П-регулятора, получив ПД-регулятор.

Все пять типов рассмотренных автоматических регуляторов имеют общую особенность своего функционирования – обеспечивают стабилизацию регулируемой величины после окончания переходного процесса.

8.2. Критерии качества регулирования

Качество процесса регулирования в АСР характеризуют следующие показатели (критерии) (рис. 16):

Рис. 16. Показатели качества регулирования:

1 – переходной процесс без статической ошибки;

2 – переходной процесс со статической ошибкой

1. Максимальное отклонение в процессе регулирования от заданного значения (динамическая ошибка) ΔХдин.
2. Статическая ошибка ΔХст — возможные отклонения от заданного значения по окончании переходного процесса при использовании некоторых типов регуляторов (подробнее такие АСР рассмотрены ниже).
3. Длительность переходного процесса Тр – период времени с момента начала отклонения регулируемого параметра от задания до возвращения его к заданному значению с определенной степенью точности регулирования ±Δ.
Например, если ±Δ=±25%, это означает, что для заданного значения температуры в 100 °С процесс регулирования будет завершен при достижении диапазона (100 ± 2,5) °С.
4. Степень затухания показывает характер затухания переходного процесса регулирования:

Для того, чтобы переходный процесс затухал за 2 ¸ 3 периода колебаний, степень затухания должна быть равна

5. Степень колебательности процесса m определяет характер колебательности процесса и равна отношению действительной части корня характеристического уравнения к коэффициенту при его мнимой части. Степень колебательности связана со степенью затухания следующим соотношением:

6. Интегральный квадратичный критерий – критерий, определяющий площадь под кривой переходного процесса, возведенной в квадрат (рис. 17):

Уменьшение интегрального критерия соответствует ускорению процесса регулирования.

Рис. 17. Интегральный квадратичный критерий качества регулирования

Однако все приведенные шесть критериев качества не определяют величину потерь производства при отклонениях регулируемой величины от оптимального значения в переходных процессах регулирования. Для определения таких потерь можно использовать экономический критерий.
7. Экономический критерий рассмотрим на примере, регулирования температуры химического реактора θ, когда степень превращения Q в реакторе определяется температурой (рис. 18а).
Разделим переходной процесс на равные интервалы времени Δt и запишем значения θ
в этих точках по графику (18, б). На графике (18, а) для этих температур определим уменьшение степени превращения вследствие отклонения от оптимального режима, а затем сделаем расчет потерь исходных продуктов для каждого интервала Δθ, суммируем эти потери для всего переходного процесса и представим потери в денежном выражении.

Рис. 18. Экономический критерий качества регулирования:

а – зависимость степени превращения Q от температуры θ;

б – переходный процесс регулирования температуры

Совместно со специалистом по технологии или по его заданию необходимо определить, какой из указанных критериев для рассматриваемой АСР является превалирующим, и задать максимально допустимую величину этого критерия, т. е. определить, какое качество регулирования должна обеспечить проектируемая АСР.

8.3. Выбор закона регулирования

При выборе регулятора следует определиться с группой регулирующих устройств – непрерывного, релейного или импульсного действия. Такой выбор ориентировочно может быть сделан по величине отношения запаздывания к постоянной времени объекта τ/Tоб:
· при отношении τ/Tоб меньше 0.2 целесообразно использовать регулятор релейного действия;
· если отношение τ/Tоб от 0.2 до 1.0, то нужно использовать регулятор непрерывного действия;
· при отношении τ/Tоб больше единицы можно использовать регулятор импульсного действия, или специальные регуляторы, например, регулятор («предиктор») Смита.
Затем необходимо определиться с типом регулятора, т.е. выбрать определенный закон регулирования: П-, И-, ПИ-, ПД- или ПИД-закон

8.4. Методы расчета одноконтурных САР

Как указывалось выше, качество автоматического регулирования определяется свойствами системы в целом, т. е. суммарными свойствами объекта и регулятора. Поскольку объект обычно является неизменяемой частью системы, то обеспечить определенные свойства системы, а следовательно и заданное качество регулирования, можно соответствующим подбором свойств автоматического регулятора, что зависит от параметров его настройки. В свою очередь, параметры настройки являются коэффициентами передачи в уравнении автоматического регулятора.
Таким образом, параметры настройки автоматического регулятора определяются свойствами объекта регулирования, т. е. величинами τоб, Тоб, Коб.

8.4.1. Расчет по «приближенным» формулам

Приближенные формулы для расчета параметров настройки автоматических регуляторов (Kр – коэффициент усиления; Tи – время изодрома; Тд – время дифференцирования) сведены в следующую таблицу:

Таблица 8.1. Формулы для приближенного расчета

параметров настройки регуляторов

Формулы сгруппированы в столбцы в зависимости от характера переходного процесса, который желательно получить, используя рассчитанный таким образом регулятор: апериодический или с перерегулированием в 20 %. В формулы входят следующие свойства объекта регулирования: Коб – коэффициент усиления; Тоб – постоянная времени; τоб – время запаздывания (полного).

Рис. 53. Кривые разгона:

1 – фактическая кривая разгона промышленного объекта;

2 – аппроксимированная (приближенная) кривая разгона

Необходимо отметить, что для пневматических регуляторов требуется определять не Kp, а диапазон дросселирования:

Рассмотрим методику более точного определения параметров настройки на примере расчета наиболее «популярного» регулятора – ПИ-регулятора.

8.4.2. Метод незатухающих колебаний

(метод Циглера-Никольса)

При использовании метода незатухающих колебаний [6], который иногда также называется по именам авторов методом Циглера-Никольса, поиск оптимальных параметров настройки осуществляется по величине критического коэффициента усиления П-регулятора и величине периода автоколебательного процесса.

Рис. 54. К поиску параметров настройки методом Циглера-Никольса

Расчет параметров настройки регуляторов проводится в два этапа.
1. На исследуемом объекте устанавливается П-регулятор и, последовательно увеличивая коэффициент усиления (уменьшая диапазон дросселирования), АСР выводится в режим незатухающих колебаний (автоколебаний на границе устойчивости). При этом фиксируется величина коэффициента усиления П-регулятора Ккрр и период незатухающих автоколебаний Т (рис. 54).
2. На втором этапе по величинам Кркр и Т определяются параметры настройки П-, ПИ- и ПИД-регуляторов:

Метод незатухающих колебаний не требует сложных вычислений, но имеет свои характерные недостатки:
· получить Кркр и Т можно только на действующем объекте, оснащенном АСР с П-регулятором;
· не все объекты химической технологии допускают режим автоколебаний;
· практически трудно уловить момент начала автоколебаний.
Данные недостатки имеют место лишь при настройке регулятора методом Циглера-Никольса непосредственно на действующем объекте. Если заменить реальный объект его математической моделью, данный метод лишается указанных недостатков, кроме того, моделирование позволяет на порядок ускорить процесс поиска параметров настройки. Но для выполнения моделирования требуется достаточно точное математическое описание объекта регулирования, а получить его удается не всегда.

8.4.3. Метод расширенных частотных характеристик

Уравнение ПИ-регулятора (65) или (66):

Передаточная функция ПИ-регулятора:

Знак «минус» указывает, что действие регулятора направлено против возмущения.
Из передаточной функции получаем амплитудно-фазовую характеристику ПИ-регулятора путем замены p на iw:

Так как по формуле Эйлера

с затуханием за три периода

Заменив iw на комплексную переменную (-mw+iw), получаем расширенную амплитудно-фазовую характеристику (РАФХ)Ю

Расширенными такие характеристики называются потому, что они как бы «расширены» по отношению к обычной АФХ (рис. 56).
Предположим, что объект регулирования имеет передаточную функцию второго порядка следующего вида:

Для дальнейшего математического моделирования АСР передаточную функцию необходимо преобразовать:

Рис. 56. АФХ объекта регулирования с самовыравниванием:

1 – обычная; 2 – расширенная

Расширенная амплитудно-фазовая характеристика объекта регулирования при замене p на (-mw+iw) будет иметь вид:

Где Rоб(m,w) -расширенная амплитудно-частотная характеристика объекта; Fоб(m,w) -расширенная фазочастотная харктеристика объекта. Величина 40w в выражении для Fоб (m,w) опеделяет угол в радианах и для пересчета в градусы неоходимо 40w умножить на 57,3

Условием нахождения замкнутой АСР на границе устойчивости является уравнение:

Аналогично, исходным уравнением для получения заданной степени колебательности m, а следовательно, определенной степени затухания y, является соотношение:

Это соотношение двух комплексных чисел возможно в том случае, если произведение модулей РАФХ равно единице, а аргументы (фазы) равны между собой, т. е.

Решая эти уравнения относительно S0 и Kp, получаем:

Обычно принимают степень колебательности m = 0,221, что соответствует степени затухания ψ=0,75 и обеспечивает затухание процесса регулирования примерно за три периода. Тогда

Уравнения для определения параметров настройки ПИ-регулятора можно преобразовать:

Подставляя в приведенные уравнения численные значения частоты w от 0 до значения, когда S0 становится отрицательной величиной, строим на плоскости параметров настройки кривую равной степени колебательности

Пример кривых равной степени колебательности в плоскости параметров настройки ПИ-регулятора показан на рис. 57. Графики процессов регулирования с различными параметрами настройки ПИ-регулятора при m = 0,221 показаны на рис. 58. Все процессы регулирования, показанные на рис. 58, реализованы ПИ-регулятором с параметрами настройки, полученными по кривой равной степени колебательности в точках 1, 2, 3, 4 (рис. 57), и все имеют m = 0,221, т. е. затухают примерно за три периода, но обладают существенно различным характером.
В связи с этим возникает задача определения оптимальных параметров настройки на кривой равной степени колебательности.

Рис. 57. Кривые равной степени колебательности

В качестве критерия оптимальности выбираем продолжительность переходного процесса – время регулирования (т. е. быстродействие АСР) и отсутствие постоянной или врéменной статической ошибки. Это исключает из рассмотрения параметры настройки в точке 4 (параметры настройки П-регулятора) и в точке 3 (врéменная статическая ошибка) (рис. 58).

Рис. 58. Графики процессов регулирования для ПИ-регулятора

с различными параметрами настройки в точках 1, 2, 3 и 4

при степени колебательности m =0,221

Быстродействие автоматического регулятора прежде всего зависит от величины регулирующего воздействия, которое для ПИ-регулятора, как следует из уравнения (65), прямо пропорционально величине коэффициента усиления Kp и обратно пропорционально времени изодрома Tи. Расчеты показывают, что если двигаться по кривой равной степени колебательности вправо, то величина регулирующего воздействия при прочих равных условиях сначала возрастает и достигает максимального значения на кривой равной степени колебательности вблизи ее вершины, когда

а затем начинает уменьшаться в связи с резким увеличением Tи (рис. 57).

Рис. 59. Выбор оптимальных параметров настройки

Таким образом, оптимальные параметры настройки ПИ-регулятора находятся в точке 2 на кривой равной степени колебательности (рис. 59).

Источник
Плютто В. П., Дубровский И. И. Элементы теории управления химико-технологическими процессами и системами. Конспект лекций: Учеб. пособие – М.: РХТУ им. Д. И. Менделеева, 2003. – 127 с.

К системам автоматического регулирования (САР) предъявляются требования не только
устойчивости процессов регулирования. Для работоспособности системы не менее необходимо, чтобы процесс автоматического регулирования осуществлялся при обеспечении определенных показателей качества процесса управления.

Если исследуемая САР является устойчивой, возникает вопрос о том, насколько качественно происходит регулирование в этой системе и удовлетворяет ли оно технологическим требованиям обьекта управления.На практике качество регулирования определяется визуально по графику переходной характеристики. Однако, имеются точные но более сложные математические методы, дающие конкретные числовые значения (которые не рассматриваются в данной методике).

Классификация показателей качества состоит из нескольких групп:

прямые — определяемые непосредственно по переходной характеристике процесса,
корневые — определяемые по корням характеристического полинома,
частотные — по частотным характеристикам,
интегральные — получаемые путем интегрирования функций.

Прямыми показателями качества процесса управления, определяемые непосредственно по
переходной характеристике являются:

Установившееся значение выходной величины Yуст,
Степень затухания ?,
Время достижения первого максимума tmax,
Время регулирования tp,
Ошибка регулирования Ест (статистическая или среднеквадратическая составляющие),
Перерегулирование у,
Динамический коэффициент регулирования Rd,
Показатель колебательности М.

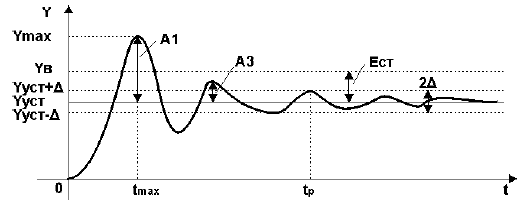
Например, переходная характеристика, снятая на объекте управления при отработке ступенчатого воздействия, имеет колебательный вид и представлена на рис.1.

Рисунок 1 — Определение показателей качества по переходной характеристике

Установившееся значение выходной величины Yуст

Установившееся значение выходной величины Yуст определяется по переходной характеристике,представленной на рис.1.

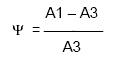
Степень затухания ?

Степень затухания ? определяется по формуле:

где А1 и А3 — соответственно 1-я и 3-я амплитуды переходной характеристики рис.1.

Время достижения первого максимума tmax

Время достижения первого максимума tmax определяется по переходной характеристике,представленной на рис.1.

Время регулирования tp

Время регулирования tp определяется согласно рис.1 следующим образом:Находится допустимое отклонение Д, например, задано Д = 5%Yуст и строится «зона» толщиной 2 Д(см. рис.1). Время tp соответствует последней точке пересечения Y(t) с данной границей. То есть время,когда колебания регулируемой величины перестают превышать 5 % от установившегося значения.
Настройки регулятора необходимо выбирать так, чтобы обеспечить минимально возможное значение общего времени регулирования, либо минимальное значение первой полуволны переходного процесса.

В непрерывных системах с типовыми регуляторами это время бывает минимальным при так называемых оптимальных апериодических переходных процессах. Дальнейшего уменьшения времени регулирования до абсолютного минимума можно достичь при использовании специальных оптимальных по быстродействию систем регулирования.

Ошибка регулирования Ест

Статическая ошибка регулирования Ест = Ув — Ууст, где Ув — входная величина (см. рис.1).В некоторых САР наблюдается ошибка, которая не исчезает даже по истечении длительногоинтервала времени — это статическая ошибка регулирования Ест. Данная ошибка не должна превышатьнекоторой наперед заданной величины. У регуляторов с интегральной составляющей ошибки в установившемся состоянии теоретическиравны нулю, но практически незначительные ошибки могут существовать из-за наличия зоннечувствительности в элементах системы.

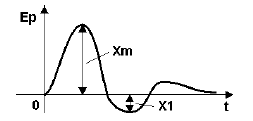
Перерегулирование у

Величина перерегулирования у зависит от вида отрабатываемого сигнала.При отработке ступенчатого воздействия (по сигналу задания) – см. рис.1 величина перерегулирования у определяется по формуле:

где значения величин Ymax и Yуст определяются согласно рис.1.

При отработке возмущающего воздействия, величина перерегулирования у определяется изсоотношения:

где значения величин Xm и X1 определяются согласно рис. 2.

Рисунок 2 — График переходного процесса при отработке возмущения

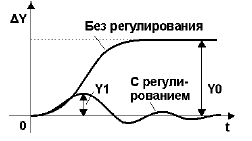
Динамический коэффициент регулирования Rd

Динамический коэффициент регулирования Rd определяется из формулы:

где значения величин Y1 и Y0 определяются согласно рис. 3.

Рисунок 3 — К понятию динамического коэффициента регулирования

Величина динамического коэффициента Rd характеризует степень воздействия регулятора напроцесс, т.е. степень понижения динамического отклонения в системе с регулятором и без него.

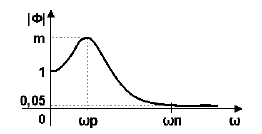
Показатель колебательности М

Показатель колебательности M характеризует величину максимума модуля частотной передаточной функции замкнутой системы (на частоте резонанса) и, тем самым, характеризует колебательные свойства системы. Показатель колебательности наглядно иллюстрируется на рисунке 4.

Рисунок 4 — График модуля частотной передаточной функции замкнутой системы

Условно считается, что значение М=1,5-1,6 является оптимальным для промышленных САР, т.к. вэтом случае у обеспечивается в районе от 20% до 40%. При увеличении значения M колебательность всистеме возрастает.

В некоторых случаях нормируется полоса пропускания системы щп, которая соответствует уровню усиления в замкнутой системе 0,05. Чем больше полоса пропускания, тем больше быстродействие замкнутой системы. Однако при этом повышается чувствительность системы к шумам в канале измерения и возрастает дисперсия ошибки регулирования.

Источник

Глава 8. Типовые законы регулирования. Одноконтурные САР

8.1. Основные типы автоматических регуляторов

Рис. 40. Переходные процессы в АСР с П- и И-регуляторами

Рис. 41. Принципиальная схема АСР с ПИ-регулятором

Рис. 42. График кривой разгона идеального ПИ-регулятора:

а – скачкообразное изменение входного воздействия x;

б – реакция (кривая разгона) ПИ-регулятора xр

Уравнение ПИ-регулятора можно записать как

откуда передаточная функция

Амплитудно-фазовая характеристика:

Рис. 43. Реакция дифференцирующего звена на кривую разгона

а –изменение входного воздействия x в виде кривой разгона;

б – реакция xр дифференцирующего звена

Рис. 44. Принципиальная схема АСР с ПИД-регулятором

На рис. 45 показана кривая разгона ПИД-регулятора.

Рис. 45. Кривая разгона ПИД-регулятора

8.2. Критерии качества регулирования

Качество процесса регулирования в АСР характеризуют следующие показатели (критерии) (рис. 16):

Рис. 16. Показатели качества регулирования:

1 – переходной процесс без статической ошибки;

2 – переходной процесс со статической ошибкой

Для того, чтобы переходный процесс затухал за 2 ¸ 3 периода колебаний, степень затухания должна быть равна

Уменьшение интегрального критерия соответствует ускорению процесса регулирования.

Рис. 17. Интегральный квадратичный критерий качества регулирования

Рис. 18. Экономический критерий качества регулирования:

а – зависимость степени превращения Q от температуры θ;

б – переходный процесс регулирования температуры

8.3. Выбор закона регулирования

8.4. Методы расчета одноконтурных САР

8.4.1. Расчет по «приближенным» формулам

Таблица 8.1. Формулы для приближенного расчета

параметров настройки регуляторов

Рис. 53. Кривые разгона:

1 – фактическая кривая разгона промышленного объекта;

2 – аппроксимированная (приближенная) кривая разгона

8.4.2. Метод незатухающих колебаний

(метод Циглера-Никольса)

Рис. 54. К поиску параметров настройки методом Циглера-Никольса

8.4.3. Метод расширенных частотных характеристик

Уравнение ПИ-регулятора (65) или (66):

Передаточная функция ПИ-регулятора:

Так как по формуле Эйлера

с затуханием за три периода

Заменив iw на комплексную переменную (-mw+iw), получаем расширенную амплитудно-фазовую характеристику (РАФХ)Ю

Для дальнейшего математического моделирования АСР передаточную функцию необходимо преобразовать:

Рис. 56. АФХ объекта регулирования с самовыравниванием:

1 – обычная; 2 – расширенная

Расширенная амплитудно-фазовая характеристика объекта регулирования при замене p на (-mw+iw) будет иметь вид:

Условием нахождения замкнутой АСР на границе устойчивости является уравнение:

Решая эти уравнения относительно S0 и Kp, получаем:

Уравнения для определения параметров настройки ПИ-регулятора можно преобразовать:

Рис. 57. Кривые равной степени колебательности

Рис. 58. Графики процессов регулирования для ПИ-регулятора

с различными параметрами настройки в точках 1, 2, 3 и 4

при степени колебательности m =0,221

а затем начинает уменьшаться в связи с резким увеличением Tи (рис. 57).

Рис. 59. Выбор оптимальных параметров настройки

Источник

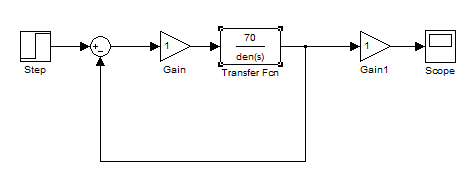
Рис.
11. Схема САР с П-регулятором.

Передаточная
функция:

Используя
найденную выше функцию корректирующего
устройства исследуем нашу систему для
П-регулятора.

Таким
образом в качестве корректирующего
устройства будем использовать:

Найдем
W_сист
используя функции Matlab:

W1=tf([70],[909.1
1]);

temp=70*feedback(W1*0.019,[1]);

Wsyst=minreal(temp);

Построим
графики переходной функции для эталонной
функции и для синтезированного нами
объекта.

We=tf([70],[666.7
1]);

hold
on

step(We,’-‘);

step(Wsyst,
‘—‘);

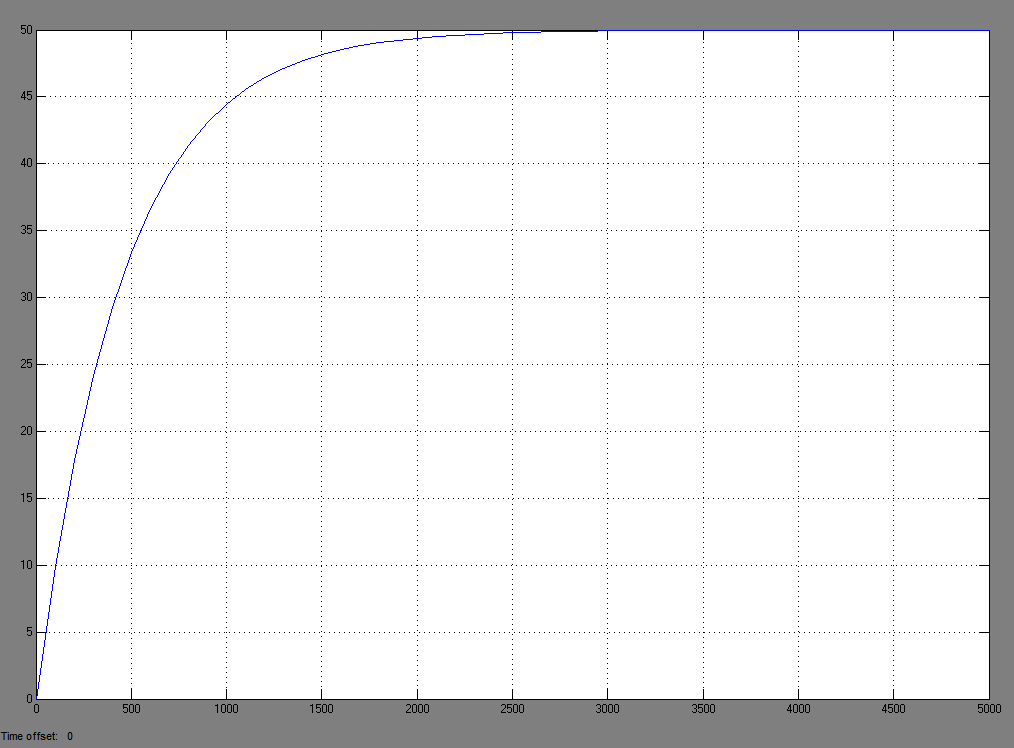
Рис.12.
График переходной функции САР с
П-регулятором и эталонного объекта.

Проведем
синтез объекта в Simulink:

Рис.
13. Синтез САР в Simulink.

Рис.14.
График переходной функции САР с
П-регулятором полученный при моделировании
в Simulink.

Путем
несложных преобразований получим:

Отсюда
следует, что:

Модель
динамики объекта:
подставим параметры и получим:

Вывод:
в результате проведенного синтеза САУ
мы получили объект автоматического
регулирования с пропорциональным
регулятором, ошибка полученного объекта
незначительна только при малых значениях
t.
При дальнейшем увеличении t,
статическая ошибка становится сравнимой
с величиной полученной функции.

Вывод:
были определены
параметры настройки системы автоматического
регулирования с пропорциональным (П-)
и пропорционально-интегральным (ПИ-)
регуляторами.

3.2. Система автоматического регулирования с пи-регулятором

Рис.
15. Схема САР с ПИ-регулятором.

Передаточная
функция:

Найдем
W_сист
используя функции Matlab:

Wo=tf([70],[909.1
1]);

temp=tf([0.0015],[1
0])/Wo;

Wky=minreal(temp);

temp=70*feedback(Wo*Wky,[1]);

Wsyst=minreal(temp);

Введем
задержку в 14 сек. для нашего объекта:

p=tf(‘p’);

p=exp(-p*14);

Построим
графики переходной функции для эталонной
функции и для синтезированного нами
объекта, для большей наглядности введем
задержку для синтезированного объекта.

We=tf([70],[666.7
1]);

Ws=Wsyst*p;

hold
on

step(We,’-‘);

step(Ws,
‘—‘);

Рис.16.
График переходной функции САР с
ПИ-регулятором и эталонного объекта.

Проведем
синтез этого объекта в Simulink:

Рис.
17. Синтез САР в Simulink.

Рис.18.
График переходной функции САР с
ПИ-регулятором полученный при моделировании
в Simulink.

Путем
несложных преобразований получим:

Отсюда
следует, что:
)

Модель
динамики объекта:
подставим параметры и получим:

Вывод:
в результате проведенного синтеза САУ
мы получили объект автоматического
регулирования с пропорционально-интегральным
регулятором полностью идентичный
заданной нами эталонной системе.

Анализ
показателей
качества: статическая ошибка ПИ-регулятора
меньше статической ошибки П-регулятора,
следовательно, использование ПИ-регулятора
даёт более точные результаты, однако
время регулирования П-регулятора меньше
времени регулирования ПИ-регулятора.

4.Исследование устойчивости сар

Устойчивость
– это способность системы, выведенной
из состояния равновесия под влиянием
возмущающих или управляющих воздействий
с течением времени прийти в равновесное
состояние под действием своих внутренних
сил.

Автоматическая
система управления называется устойчивой,
если она за счет своих внутренних сил
возвращается в состояние установившегося
равновесия после незапланированного
возмущения. Систему считают неустойчивой,
если при сколь угодно малых отклонениях
от состояния установившегося равновесия,
она не возвращается к этому состоянию,
а непрерывно удаляется от него или
совершает около него недопустимо большие
колебания.

Устойчивость
– это свойство, которым должна обладать
любая САР.

Рис.
19. Структурная схема САР с ПИ-регулятором.

Запишем
передаточную функцию САР в разомкнутом
состоянии:

где
— ПФ регулятора: ;

—
ПФ объекта: .

Исследуем
на устойчивость синтезированный объект,
охваченный единичной отрицательной
обратной связью.

Wo=tf([70],[909.1
1]);

Wky=tf([0.01948
2.14e-5],[1 0]);

Wz=70*feedback(Wo*Wky,[1]);

Найдем
критическую величину сдвига фазы, при
которой исследуемый объект теряет
устойчивость.

margin(Wz);

Рис.20.
Критическая величина сдвига фазы
объекта.

Найдем
критическую задержку, для нашего объекта:

Построим
АФЧХ объекта и объекта с запаздыванием
на величину τ.

p=tf(‘p’);

Wot=Wo*exp(-p*15);

Wraz=Wky*Wo;

Wrazt=Wky*Wot;

hold
on

nyquist(Wraz);

nyquist(Wrazt);

Рис.21.
АФЧХ разомкнутой системы.

Построим
АФЧХ замкнутой системы.

hold
on

Wz=feedback(Wraz,[1]);

Wzt=feedback(Wrazt,[1]);

Рис.21.
АФЧХ замкнутой
системы.

Рис.22.
АФЧХ замкнутой системы (увеличенный
фрагмент рис. 21.).

Устойчивость
системы определяем по критерию Найквиста.
Устойчивость определяется по АФЧХ
разомкнутой САР, для которой возможны
2 случая:

Разомкнутая
САР, устойчивая в разомкнутом состоянии,
будет устойчива и в замкнутом, если её
АФЧХ не охватывает точку (-1, j₀)
при изменении ω от 0 до ∞.
Разомкнутая
САР, неустойчивая в разомкнутом
состоянии, будет устойчива в замкнутом
состоянии, если её АФЧХ охватывается
точку (-1, j₀)
при изменении ω от 0 до ∞ q
раз (где q
– число корней характеристического
уравнения разомкнутой САР).

Вывод:
САР устойчива в разомкнутом состоянии,
так как её АФЧХ не охватывает точку (-1,
j₀)
при изменении ω от 0 до ∞, следовательно
по критерию Найквиста (1 случай) САР
будет устойчива и в замкнутом состоянии.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Статическая ошибка — регулирование

Cтраница 4

ПИ-регулятором, так же как и в системе с И-регулятором, статическая ошибка регулирования равна нулю.
[46]

Это отношение носит название степени или коэффициента неравномерности регулятора, или статической ошибки регулирования.
[47]

В прямой канал зачастую вводится также интегрирующее звено, позволяющее устранить статическую ошибку регулирования. Однако нужно иметь в виду, что включение интегрирующего звена, как правило, уменьшает запас устойчивости системы, но в сочетании с введением упреждающих звеньев позволяет получить систему с высокими качественными показателями регулирования. Корректирующие звенья, кроме того, ограничивают регулируемые параметры и их производные на заданном уровне.
[48]

Однако нужно иметь в виду, что со снижением коэффициента усиления возрастают статическая ошибка регулирования и неравномерность САР. Поэтому уменьшение коэффициента усиления часто влечет за собой понижение точности регулирования.
[49]

Однако нужно иметь в виду, что со снижением коэффициента усиления возрастают статическая ошибка регулирования и неравномерность системы. Поэтому уменьшение коэффициента усиления влечет за собой понижение точности регулирования; это следует всегда помнить.
[50]

Недостатком ПД-регулятора является наличие, как и у П — ре-гулятора, статической ошибки регулирования.
[52]

Сравнение переходных процессов на рис. 30.3.1, г и д показывает, что максимальная статическая ошибка регулирования давления пара снижается с 3 3 до 0 9 бар, а время установления переходного процесса уменьшается со 100 до 25 мин. Статическая ошибка регулирования температуры пара также снижается с 2 7 до — 2 4 К, а время установления уменьшается с 50 до 10 мин. Этот пример демонстрирует эффективность применения хорошо настроенного регулятора с прямой связью. Общее время расчета двух основных регуляторов в режиме on-line составляет около 230 мин. Из них 130 мин требуется для идентификации, 30 мин для выбора и расчета алгоритмов управления и 70 мин для проведения двух тестовых испытаний.
[53]

Стабилизация периодических процессов в пределах допустимой динамической ошибки или интегрального квадратичного критерия, а также ликвидация статической ошибки регулирования достигается путем использования одноконтурных или многоконтурных АСР с ПИ — или ПИД-регуляторами, подобных АСР непрерывных ХТП.
[55]

При этом, вне зависимости от значения а, числитель в выражении ( Х 18) и статическая ошибка регулирования равны нулю. Подобные системы автоматического регулирования являются астатическими относительно возмущений, приложенных к объекту.
[56]

Небольшие по величине силы трения, действующие между втулкой и плунжером при его возвратно-поступательном движении, практически устраняют статическую ошибку регулирования при отработке управляющего пневмосигнала.
[57]

Статизм при данном коэффициенте обратной связи уменьшается с возрастанием коэффициента усиления kn и теоретически при / г ckn — — со статическая ошибка регулирования стремится к нулю.
[59]

Страницы:

Источник

Классический ПИД-регулятор

Простейшая система автоматического регулирования с обратной связью показана на рисунке. В ней блок R называют регулятором (от слова Regulator), P — объектом регулирования (от слова Process), r — управляющим воздействием или уставкой (reference), e — сигналом рассогласования или ошибки (error), u — выходной величиной регулятора, y — регулируемой величиной.

Частный случай ПИД-регулятора — пропорциональный или П-регулятор: u(t)=K·e(t). С помощью П-регулятора можно управлять любым устойчивым объектом, однако он дает относительно медленные переходные процессы и ненулевую статическую ошибку (статическая ошибка e0 — постоянная ошибка в установившемся режиме системы; см. рис. ниже).

С увеличением пропорционального коэффициента K статическая ошибка e0 уменьшается, время нарастания переходного процесса tн уменьшается, перерегулирование σ увеличивается.

Чтобы убрать статическую ошибку в установившемся режиме, в регулятор вводят интегральный канал с коэффициентом усиления Ki, так что:

Такой регулятор называется пропорционально-интегральным или ПИ-регулятором. Интегратор выдает сигнал, пропорциональный накопленной ошибке, поэтому переходный процесс несколько замедляется.

Однако за счет интегрального канала обеспечивается нулевая ошибка e0 в установившемся состоянии при ступенчатом возмущении и ступенчатом изменении задающего сигнала-уставки.

С увеличением коэффициента интегральной составляющей ПИ-регулятора Ki время нарастания переходного процесса tн уменьшается, перерегулирование σ увеличивается, время регулирования tр увеличивается.

Для ускорения переходных процессов добавляют дифференциальный канал с коэффициентом усиления Kd:

(1.01)

Распространена также другая модификация выражения (1.01):

(1.02)

где t — время; K — пропорциональный коэффициент (безразмерный), Ti — постоянная интегрирования (размерность времени) и Td — постоянная дифференцирования (размерность времени) регулятора. Такой регулятор называют ПИД-регулятором.

Регуляторы этого типа очень хорошо зарекомендовали себя в практических задачах. Кроме того, иногда используются ПД-регуляторы (пропорционально-дифференциальные), у которых нет интегрального канала.

Управление по производной – это быстрый способ управления. Сигнал дифференциального канала наиболее важен при изменениях входов и исчезает в установившемся режиме. Он позволяет реагировать не на само увеличение ошибки, а на тенденцию ее изменения, и принять превентивные меры. Главный недостаток дифференциального канала – большое влияние высокочастотных помех, например, шумов измерений.

С увеличением коэффициента дифференциальной составляющей ПИД-регулятора Kd перерегулирование σ уменьшается, время регулирования tр уменьшается.

	При увеличении коэффициентов
	Kp	Ki	Kd
Время нарастания tн
Пере- регулирование σ
Время регулирования tр
Статическая ошибка e0

— Увеличивается. — Уменьшается. — Устраняется. — Нет определенной тенденции (No definite Trend). Незначительное изменение.

Для устойчивого объекта можно выбрать коэффициенты регулятора опытным путем, выполняя эксперименты с реальным объектом. Предложено несколько методов решения этой задачи, например, правила Зиглера-Никольса (Ziegler J. G. — Nichols N. B.), Коэна-Куна (Cohen O.H. – Coon O.A.) или CHR (Chien K. L. — Hrones J. A. — Reswick J. B.).

Список используемой литературы

Поляков К.Ю., Теория автоматического управления для чайников, Санкт-Петербург, 2008 г.
Востриков А.С., Французова Г.А., Теория автоматического регулирования. 2003 г.
Глушков В.М., Амосов Н.М., Артеменко И.А. Энциклопедия кибернетики. Том 2. Киев, 1974 г.
Теория автоматического управления: Учеб. для вузов по спец. Автоматика и телемеханика. В 2-х ч. Ч. I. Теория линейных систем автоматического управления / Н. А. Бабаков, А. А. Воронов, А. А. Воронова и др.; Под ред. А. А. Воронова.—2-е изд., перераб. и доп. — М.: Высш. шк., 1986. — 367 с.
Денисенко В.В., Энциклопедия АСУ ТП, bookasutp.ru
Dew Toochinda, Scilab Ninja. Control Engineering with Scilab, Scilab Control Engineering Basics, scilab.ninja/study-modules/scilab-control-engineering-basics/

У нас на сайте Вы можете приобрести качественные частотные преобразователи. Подробности тут

Источник