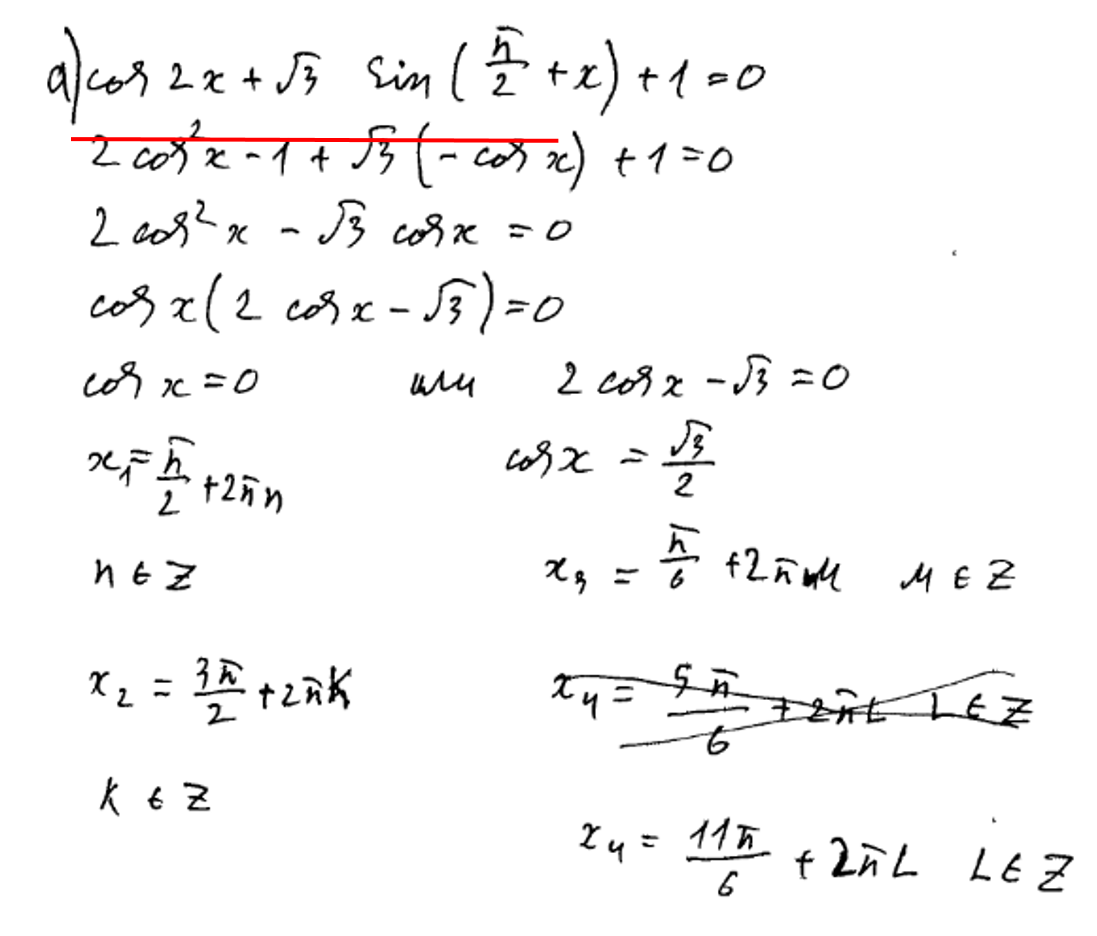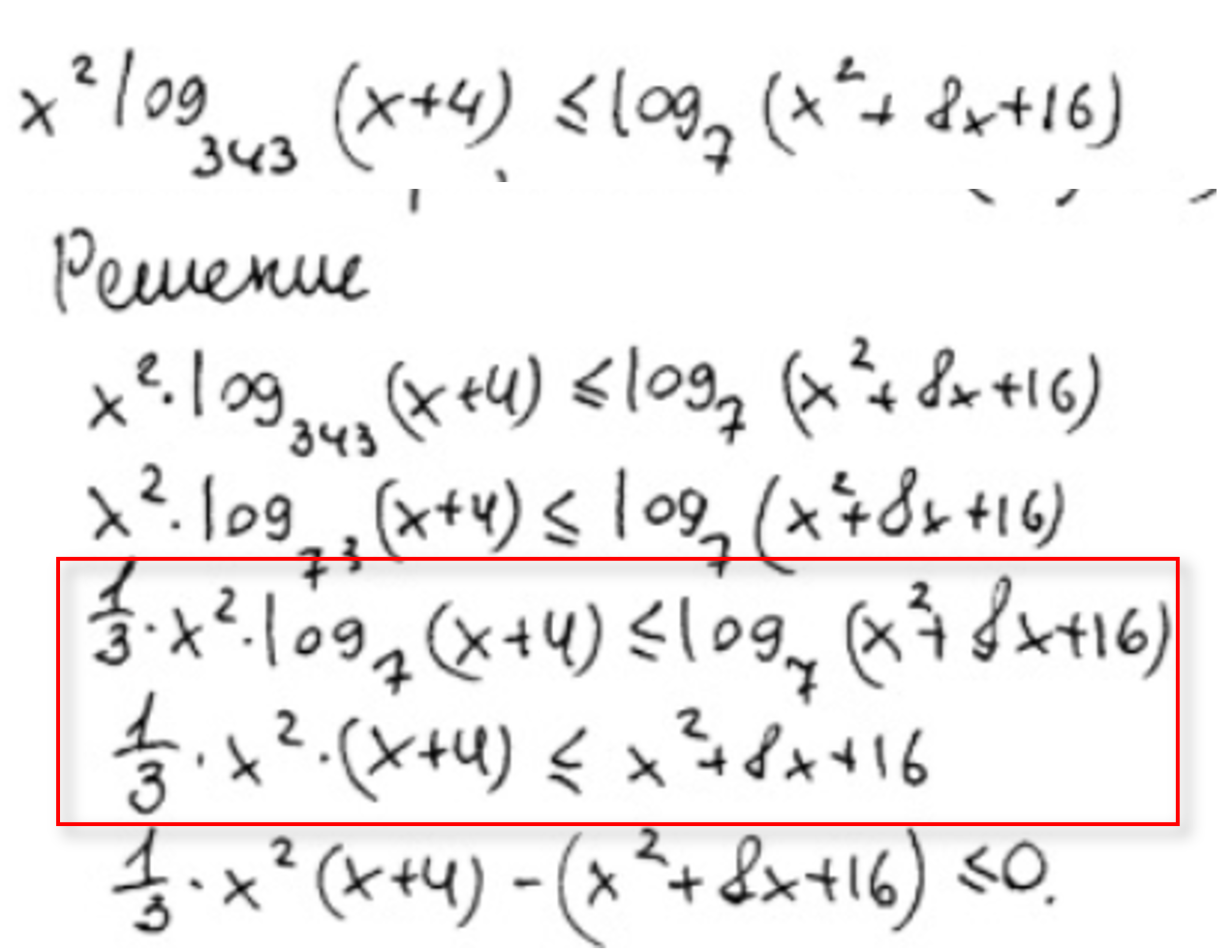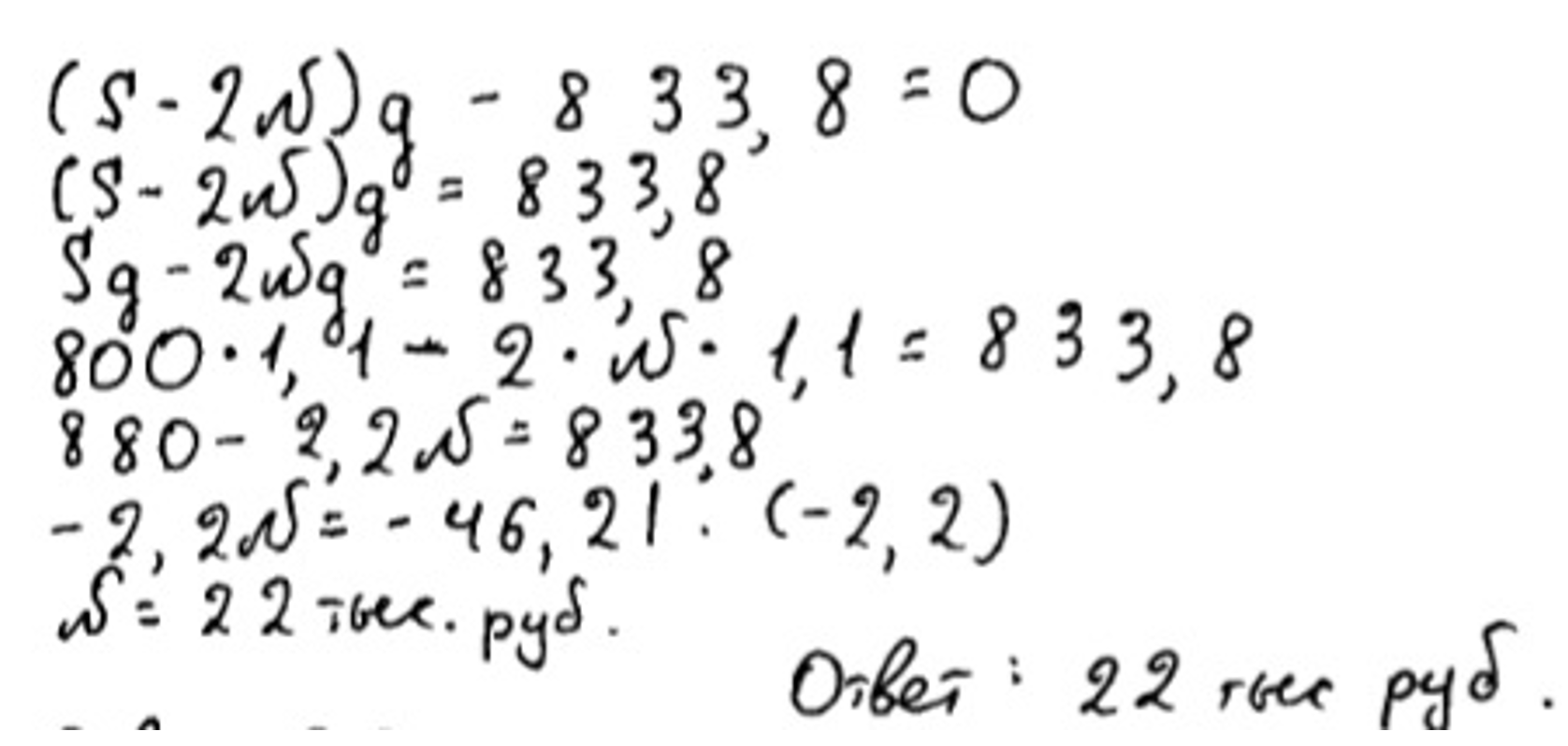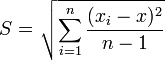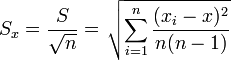Что значит вычислительная ошибка - Не ошибается лишь тот, кто ничего не делает!

Что считается вычислительной ошибкой на егэ по математике

Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!

—>

Задание 12 № 485973

А) Решите уравнение

Б) Укажите корни уравнения, принадлежащие отрезку

А) Преобразуем уравнение:

Б) С помощью числовой окружности отберем корни на отрезке Получим числа:

Почему в ответе сохранили минус под знаком арккосинуса? в этом случае задание считается решенным не до конца. (см. критерии для экспертов по проверке заданий ЕГЭ)

Честно говоря, я ничего подобного в критериях для экспертах не помню. Собственно, в критериях написано именно то, что написано в критериях выше. Форма записи ответа не является ошибкой.

Симметрию я ещё могу понять, но КАК вы без калькулятора поняли что arccos (1/4) находится именно там??

Я, например, располагал их симметрично в I и IV четвертях.

Косинусы положительны в первой и четвертой четвертях, отрицательны — во второй и третьей.

Задание 12 № 485973

—>

Почему в ответе сохранили минус под знаком арккосинуса.

Ege. sdamgia. ru

04.01.2019 13:42:49

2019-01-04 13:42:49

Источники:

Https://ege. sdamgia. ru/problem? id=485973

МГУ ВМК | Вступительные экзамены на различные специальности » /> » /> .keyword { color: red; } Что считается вычислительной ошибкой на егэ по математике

МГУ ВМК: вступительные испытания

Факультет вычислительной математики и кибернетики МГУ является лучшим в области подготовки по прикладной математике, вычислительной математике, теории информации и программированию. Именно поэтому большинство абитуриентов выбирают именно этот факультет. Ещё одно преимущество факультета ВМК — это сотрудничество со многими зарубежными университетами для обучения по обмену, что дает молодым специалистам хороший старт в карьере. Ввиду этого с этим крупные IT-компании постоянно ищут новые таланты именно с факультета Вычислительной математики и кибернетики, предлагая студентам курсы с последующим трудоустройством. Помимо всего на факультете располагаются лаборатории таких известных компаний, как Intel и Microsoft, региональная академия CISCO, а также факультет ВМК принимает участие в программе Microsoft IT-Academy.

Чему учат студентов факультета ВМК?

6-летняя программа подготовки специалистов в области прикладной математики и теории информации позволяет получить квалификацию математика и системного программиста. Математика как наука представляет собой совокупность отраслей. Учебные программы включают следующие математические дисциплины:

Также студенты глубоко изучают курс английского, ведь без него стать хорошим специалистом невозможно. Особое внимание уделяется практической работе, освоению студентами нескольких операционных систем и не менее трех языков программирования на высоком уровне.

Первый и второй семестр факультет дает базовую подготовку по математике и теоретическому и прикладному программированию, потом студенты должны выбрать специализацию. Математика — это наука, которая учит составлять алгоритмы разной сложности. В программировании – математика играет ключевую роль, на ее основе решаются многие задачи.

Также студенты могут заниматься научно-исследовательской работой для этого в их распоряжении лаборатории математики и физики.
Выпускники факультета востребованы различными компаниями и учреждениями в которых применяются IT-технологии, в том числе научно-исследовательскими институтами РАН, высшими учебными заведениями, государственными организациями, банками, страховыми компаниями, финансово-консалтинговыми компаниями, различными и зарубежными предприятиями и др. Около трети выпускников продолжают обучение в аспирантуре на одной из 18-ти кафедр:

Как стать студентом ВМК?

Вот какие требования нужны для поступления в МГУ ВМК: экзамены ЕГЭ по математике, физике и русскому языку и ДВИ по математике. Каждый год большое количество абитуриентов подают заявление на факультет ВМК, поэтому, чтобы поступить, результаты ЕГЭ должны быть внушительными. Для этого тебе надо узнать в МГУ (ВМК) вступительные экзамены и проходные баллы за прошлый год, чтобы примерно знать на какой уровень тебе надо готовиться. Эти данные о факультете ты можешь найти в нашей статье ниже.

Что такое ДВИ?

Для того чтобы поступить на ВМК надо сдать дополнительные вступительные испытания или сокращенно ДВИ по математике. Поступить можно только когда у тебя есть результаты ЕГЭ по трем предметам и ДВИ по математике. То есть на ВМК вступительные испытания по математике являются обязательными. То есть это еще один дополнительный экзамен. Экзамен состоит из 8 заданий повышенной сложности. За все 8 правильно решенных заданий можно получить 100 баллов. Для того чтобы стать студентом факультета ВМК надо набрать 75-100 баллов.

Поступление на бюджет

Как поступить в ВМК на бюджет? Задача это непростая, так как в среднем конкурс на место составляет 5-7 человек. Поэтому тебе нужны превосходные знания, а для этого надо много работать. Даже если у тебя хорошие оценки в школе, это не дает гарантии того, что ты наберешь нужные баллы для поступления в МГУ ВМК на бюджет. Обычная подготовка здесь не подойдет, так как набрать нужно высокий балл. Стоит записаться на курсы при МГУ, а лучше всего найти хорошего репетитора.

План поступления на факультет ВМК

Начинать подготовку в университет нужно заранее за 2 года до поступления, так как проходные баллы на факультет достаточно высокие. Пути подготовки ты можешь выбрать сам:

олимпиады; школы и курсы от МГУ репетиторы; самостоятельная подготовка;

Олимпиады

Олимпиады – хорошая возможность поступить на факультет ВМК. Принимать участие в олимпиадах могут школьники 9 и 10 классов. Подготовка к олимпиаде сложный процесс, так как обучение нужно начинать за год, за два до участия. Задачи там требуют хороших и нестандартных подходов. Всероссийская олимпиада для школьников – это хороший шанс набрать максимальный балл по выбранному предмету, но для этого тебе надо взять победу на региональных олимпиадах. Призёры олимпиад, кроме всероссийской олимпиады, могут поступать без экзаменов, однако ваш результат по ЕГЭ должен быть не менее 75 баллов по данному предмету. Участие в олимпиаде это шаг в будущее, который требует от тебя терпения, силы воли, времени, упорства на протяжении многих лет обучения. Первое место на региональном уровне не даёт тебе права выставления высшего экзаменационного балла на вступительных испытаниях.

Школы и курсы от МГУ

Школьники 9 и 10 классов имеют право поступать на курсы СУНЦ. СУНЦ — это специализированный учебно-научный центр, точнее школа, дающая аттестат о среднем образовании. Поступить в нее можно, если сдать внутренний экзамен.

Самостоятельная подготовка

Сосредоточенно подойди к своей цели, ведь поступить хочет каждый. Поэтому все свободное время планируй правильно: решай тесты по ЕГЭ, заполни пробелы в знаниях, повторяй пройденные темы. Результаты ЕГЭ по математике нужны для поступления в МГУ ВМК по специальностям:

прикладная математика и информатика. фундаментальная информатика и информационные технологии.

Курсы по математике от Альфа-школы хороший вариант подготовки к ЕГЭ по математике. У тебя будет личный репетитор, который будет постоянно направлять тебя. Подготовка и поступление в университет — очень важный шаг, поэтому к обучению следует подойти серьезно. Правильно планируй время занимайся каждую неделю и не отходи от плана, так как будет весьма обидно, если тебе не хватит пару баллов, чтобы поступить на мехмат. Наиболее действенный и проверенный способ — онлайн-репетитор по математике. У тебя будут большие преимущества: репетитор уделяет время только тебе и ты не тратишь время на дорогу, которого у тебя и так мало. Профессионалы своего дела — репетиторы Альфа-школы знают как лучше подготовить тебя к такому сложному экзамену как математика. Система тестирования Альфа-школы помогает определить твои слабые стороны, поэтому результаты наших учеников высокие при регулярных и действенный занятиях. Также в Альфа-школе есть специальная программа подготовки к ЕГЭ и ДВИ по математике — решаются задания за прошлый и предыдущие года, подробно объясняется решение.

Приём документов

Подавать документы можно одновременно в 5 вузов, на 3 направления в каждом университете. Также можно приносить результаты ЕГЭ за 2013, 2014, 2015, 2016 и 2017 год. Начало приема документов в МГУ факультета ВМК идет после вступительных экзаменов по ЕГЭ и проходит в две волны, подача документов начинается с 20 июня по 26. 26 июля последний день подачи документов по результатам ЕГЭ. Узнать результаты ты уже можешь 3-8 августа. Зачисление происходит по результатам набранных баллов по ЕГЭ абитуриенты, набравшие наибольшее количество баллов поступают первые. Проходной балл за прошлый год ты узнаешь ниже. Каждый год количество баллов разное, в зависимости от количества поданных заявлений абитуриентов.

Документы, которые нужны для поступления:

Льготы

Льгота первой степени – олимпиады. Всероссийская олимпиада и олимпиада «Ломоносов». Победителям всероссийской олимпиады выставляется максимальный балл по предмету. Победители олимпиады «Ломоносов» получают возможность максимального балла по экзамену, при условии, что они наберут не менее 75 баллов по тому же предмету на ЕГЭ. Льготы имеют категория граждан:

Для получения льгот необходимо предоставить документы, доказывающие данное положение.
Выпускники школы СУНЦ не имеют право льготы при поступлении.

Абитуриентам, окончившим школу с золотой или серебряной медалью, дается льгота: плюс 5 баллов. Также льгота за спортивные достижения – 2 балла. Школьное сочинение -3 балла;

Если же льгот у тебя нет, то не стоит расстраиваться, с репетиторами Альфа школы ты сможешь хорошо подготовиться как к экзамену ЕГЭ так и к ДВИ по математике и набрать высокий балл для поступления в МГУ ВМК. Также ты сможешь бесплатно пройти первое занятие и протестировать свои знания. Удачи тебе!

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

МГУ ВМК: вступительные испытания

Также в Альфа-школе есть специальная программа подготовки к ЕГЭ и ДВИ по математике — решаются задания за прошлый и предыдущие года, подробно объясняется решение.

Myalfaschool. ru

19.02.2019 2:05:46

2020-07-20 11:37:14

Источники:

Https://myalfaschool. ru/articles/mgu-vmk-vstupitelnye-ispytaniya

Вторая часть ЕГЭ по профильной математике: лайфхаки решения заданий » /> » /> .keyword { color: red; } Что считается вычислительной ошибкой на егэ по математике

Вторая часть ЕГЭ по профильной математике: лайфхаки решения заданий

Профильная математика — один из самых сложных экзаменов для большинства выпускников, от которого зависит аттестат. Именно стоит узнать, как решается вторая часть профильной математики ЕГЭ, так как именно за нее даются баллы, необходимые для результата 85+.

Что из себя представляет вторая часть в 2021

В 2021 году вторая часть профильной математики ЕГЭ состоит из одиннадцати номеров (четыре с кратким ответом, семь — с развернутым). Для их решения необходимо приобрести определенные знания и навыки:

умение решать задачи (текстовые, прикладные, экономические, олимпиадные), умение анализировать функции, умение составлять и решать выражения, умение решать уравнения, умение решать неравенства, умение работать с параметром, знание стереометрии, знание планиметрии.

Критерии оценивания

Вторая часть профильной математики ЕГЭ весит 24 первичных балла из 32 возможных:

№ 9-12 — 1б, № 13-15 — 2б, № 16-17 — 3б, № 18-19 — 4б.

Для получения балла за № 9-12 необходимо записать правильный ответ в бланк, решение номера не рассматривается, однако по сложности это все же вторая часть профильной математики ЕГЭ.

В №13 балл могут дать за написание верного ответа или верного хода решения при неверном ответе.

В №14 балл дадут за решение одного из двух пунктов.

В №15 балл дадут за вычислительную ошибку или неверное исключение точки.

В №16 можно получить баллы за решение одного из пунктов: более сложного (2 балла) или более простого (1 балл).

В №17 баллы дают за верную математическую модель: два — за доведенное до конца решение с вычислительной ошибкой или недостаточным обоснованием, один — за не доведенное до конца решение.

В №18 три балла можно получить, если назвать два верных решения (и два неверных или недостаточно их обосновать), два балла за одно верное решение и один балл за верный ход мысли.

В №19 три балла дадут за три верных ответа, два — за два, один — за один (с обоснованием, если решение легкое).

Как решать вторую часть ЕГЭ по профильной математике

Вторая часть профильной математики ЕГЭ требует углубленных знаний в области дисциплины. При этом, каждый номер направлен на отработку каких-то конкретных знаний и навыков. Поэтому готовиться стоит к каждому номеру отдельно.

Задание 9

Задание №9 — это проверка простейших вычислений, для которых необходимо знать свойства логарифмов, тригонометрических функций, корней и степеней. Чтобы решить этот номер, можно воспользоваться приложенным к КИМ списком формул. Заранее стоит научиться выводить из них другие полезные формулы, это избавит от лишнего заучивания и поможет подготовиться к решению более сложных задач.

Задание 10

Вторая часть профильной математики ЕГЭ включает также задачу прикладного характера с формулой для ее решения. Нужно проследить, чтобы все значения измерялись однотипно (все время в секундах, например), а переменные представлялись в общем виде. Также лучше попробовать сократить выражение, если это возможно: так можно исключить вычислительную ошибку при подставлении.

Обязательно следует перепроверять свое решение.

Задание 11

В №11 может встретиться задача на один из шести типов. Решение любой из этих типов задач начинается с составления уравнения: искомая величина — Х. Оно чаще всего выходит линейным или квадратным. Для составления уравнения стоит пользоваться основными формулами: пути, работы и концентрации.

Задание 12

Для подготовки к заданию на точки экстремумов необходимо изучить таблицу основных производных и их графики, а также их свойства. Помимо этого, стоит попрактиковаться в нахождении нулей производных. Они помогут определить все точки экстремумов, из которых можно будет найти наибольшее и наименьшее значения функций.

Задание 13

Задание № 13, с которого начинается настоящая (с проверкой решения) вторая часть профильной математики ЕГЭ, проверяет умение выпускников ориентироваться в тригонометрии. Чтобы выполнить этот номер на максимум, необходимо, во-первых, найти ОДЗ, а во-вторых, с ее учетом решить полученное уравнение. Для этого может пригодится огромное количество формул и свойств, запомнить которые поможет мнемотехника. Так, одним из полезный упражнений на запоминание будет правило лошади: если она качает головой по вертикали, получается кивок — «да», поэтому вдоль оси ординат функция меняется; а вот качание головой по горизонтали, это «нет», функция не меняется.

Задание 14

№14 содержит два задания: на доказательство и вычисление. С первым могут помочь теорема Фалеса и подобие треугольников, а в последнем очень выручают теоремы синусов и косинусов, Пифагора, о трех перпендикулярах и тригонометрические функции в частности.

Задание 15

Неравенства задания №15 решаются благодаря постоянности логарифмической функции. От изменчивого основания можно избавиться, если перейти к новому постоянному основанию. Отдельное внимание стоит уделить ОДЗ, которое может меняться.

При решении важно помнить про методы интервалов и рационализации, правила замены тригонометрических функций.

Задание 16

Лучше запомнить все теоремы, свойства и аксиомы, связанные с треугольниками, так как они содержатся в любой фигуре и, соответственно, будут полезны при решении любого номера, который содержит вторая часть профильной математики ЕГЭ. Также особое внимание в №16 следует уделить рисунку: он должен быть наглядным, содержать необходимые пометки. Это поможет в решении любой задачи по планиметрии.

Задание 17

Вторая часть профильной математики ЕГЭ под видом №17 может предложить три типа задач:

Для их решения следует постепенно преобразовывать каждое условие задачи в уравнение или его часть. При подготовке следует заранее ознакомиться со схемами кредитования (дифференцированные и аннуитетные платежи), к задаче на оптимизацию нужно будет попрактиковаться в работе с целевыми функциями с точками экстремумов.

Задание 18

Этот номер проверяет умение мыслить логически и составлять схему рассуждений. Каждая из задач под этим номером нестандартна, поэтому помочь в их решении может только регулярная практика по вариантам прошлых лет. Однако стоит отметить, что в задании допустимо и графическое решение: так, в уравнениях с двумя переменными часто прячутся фигуры, которые могут оказаться ответом на задание.

Задание 19

№19 — последний, который включает вторая часть профильной математики ЕГЭ. Это задание олимпиадного уровня, поэтому оно требует нестандартного мышления. Для подготовки к нему можно изучить признаки делимости чисел (четное окончание как признак деления на «2» — это недостаточно для экзамена), а также формулы арифметической и геометрической прогрессий. Отлично помогут также решение заданий из вариантов прошлых лет, разборы олимпиадных заданий похожего типа.

Таким образом, видно, что вторая часть профильной математики ЕГЭ — это действительно сложные задачи, решить которые под силу не каждому выпускнику. Поэтому для того, чтобы сдать экзамен на 85+ баллов, необходимо усердно готовиться.

Таким образом, видно, что вторая часть профильной математики ЕГЭ это действительно сложные задачи, решить которые под силу не каждому выпускнику.

Umschool. net

24.07.2019 19:03:07

2020-12-23 04:34:34

Источники:

Https://umschool. net/journal/ege/vtoraya-chast-ege-po-profilnoj-matematike-lajfhaki-resheniya-zadanij/

Математику базового уровня часто недооценивают, пренебрегая подготовкой к ней. Однако от нее зависит судьба аттестата: без «отлично» за математику отличник не получит красный аттестат, а без порогового балла выпускники в принципе рискуют уйти из школы со справкой! Типичные ошибки на ЕГЭ по математике помогут избежать этой участи.

Типичные ошибки ЕГЭ по математике в задачах на проценты

Проблемы возникают из-за неумения рассчитывать процент от суммы. Так, стоит обратить внимание, что процент повышения или понижения стоимости вычисляется от старой, а не новой цены, поэтому принимать новую цену за 100% и исходить из нее станет причиной ошибки на ЕГЭ по математике. Новая цена — это 100% ± процент повышения (+) или понижения (-).

Частые ошибки в вычислениях

Вычислительные ошибки на ЕГЭ по математике не редкость, но от этого они не перестают быть опасными и обидными. Стоит следить за наличием минуса (и его сокращением), а также помнить правила преобразования выражений, действий с дробями. Не стоит полагаться исключительно на умение считать в уме: лучше выполнять свои вычисления на бумаге и обязательно производить проверку (подставляя значение на место неизвестной в уравнениях и производя смежные действия (сложение-вычитание, деление-умножение) в простых примерах).

Основные ошибки теоретического характера

Ошибки на ЕГЭ по математике часто возникают из-за неумение работать с чертежами и терминологией. Большинство выпускников пытается найти заданную в номере величину с помощью инструментов или на глаз, часть из них не знает терминологии и находит не ту величину. Чтобы не допустить этого, стоит научиться работать с объемными фигурами: находить площадь их поверхности (всей или боковой), объемы и их части.

Также стоит обратить внимание на важные аспекты теории: основные теоремы, аксиомы, свойства.

Распространенные ошибки в алгоритмах и методах решения

Последовательность выполнения действий проходится еще во втором классе, однако даже такие ошибки на ЕГЭ по математике встречаются. Стоит помнить как простейшие алгоритмы решения примеров: сначала действия в скобках, а потом остальные; первыми идут умножение и деление, потом сложение и вычитание, — так и более сложные. Так, в дробях ни в коем случае нельзя забывать про знаменатель, а сокращаться из числителя и знаменателя могут только множители (простые числа и выражения в скобках).

Ошибки при чтении и построении чертежа

Ошибки на ЕГЭ по математике, касающиеся чертежа, возникают при работе как с объемными фигурами, так и с расположенными в одной плоскости. Они связаны с отсутствием пространственного представления и невнимательностью, вызванной неправильным прочтением буквенной записи (угол АВС — это не то же самое, что углы АСВ и САВ). Также сложности могут возникнуть при неумении ориентироваться в основных обозначениях на чертеже (равные стороны, равные углы, прямые углы).

Типовые ошибки в заданиях по тригонометрии

Раздел тригонометрии построен на знании тригонометрических тождеств и свойств тригонометрических функций, поэтому ошибки на ЕГЭ по математике могут быть допущены из-за недостаточного владения теорией. В КИМ-е базовой математике даны основные формулы, которые могут быть полезны выпускникам, однако стоит также научиться выводить из них остальные.

Ошибки математического моделирования

Трудности, связанные с математическими моделями, вызваны неумением решать практические текстовые задачи. Для их решения необходимо понимать принцип работы действия (чаще всего, один из видов движения). Сложности возникают с подстановкой в формулу неверных данных, из-за чего искажается ответ.

Таким образом, базовая математика не так проста, как может показаться на первый взгляд. Она не займет так много времени, как профильная, но все равно требует подготовки.

Прочтите статью об ошибках на ЕГЭ, подготовленную по моей просьбе репетитором по математике из подмосковного Зеленограда Ермаковой Дианой. Я приложил к статье свою руку в качестве редактора — консультанта.

Почему ребята допускают те или иные ошибки на ЕГЭ по математике? Почему за безошибочные работы снимают баллы?

Сразу после обнародования результатов экзамена я проанализировала сканеры учеников, которых, будучи репетитором по математике, готовила к ЕГЭ длительное время. Были сделаны определенные выводам. Я не буду рассматривать здесь случаи, когда ученик вообще не умеет решать характерные типы задач, не берется за них или берется, но пишет откровенную ерунду. Рассмотрю лишь ошибки в заданиях, которые школьники обычно решают более-менее уверенно.

Причины ошибок на ЕГЭ по математике — часть «В».

Здесь я остановлюсь подробно только на вычислительных ошибках, поскольку в сканах работ не отражается сам ход решения и проверить его невозможно.

Первая причина

То, что многие ребята плохо считают без калькулятора — не секрет. Но и те, которые считают хорошо, тоже допускают вычислительные ошибки. Причина видится не только в банальной невнимательности, но и в том, что порой учащимся не хватает умения и/или желания заниматься проверками полученные результатов. Ошибки некоторых заданий «В» всплывают на поверхность сами, проявляя явные числовые или житейские коллизии. Например, получив в задаче об оплате за свет в текущем месяце сумму в 300 тысяч рублей, ученик не задумываясь, переносит ее в бланк. Но разве она может равняться полугодовой зарплате среднестатистического работника? Ответ в В5 и В12 можно всегда проверить подстановкой полученного ответа в исходное уравнение и т.д.

Нужно ли репетитору по математике обучать проверке ответа?

Не только можно, но и нужно. Вопрос только в том, какие задания давать для реализации этого замысла. В обязательном порядке включаются примеры серии «найди ошибку в решении», «проверь полученный ответ подстановкой в уравнение (систему)» и т.д. Вместе с репетитором по математике проводится анализ сканеров работ с реального ЕГЭ, которые в большом количестве есть в пособиях для подготовки экспертов на сайте ФИПИ.

Вторая причина

Часто человек, который дружит с математикой не первый год, часто может решить одну и ту же задачу разными способам. Соответствующий опыт решения позволяет не только искать, но и реалозывать тот или иной план. В силу возрастных особенностей детей школьники выдают репетитору по математике далеко не всегда рациональные решения. Громоздкий пути — рассадник целого спектра ошибок, с которым нужно бороться.

Математические ошибки в части С

Кроме уже описанных выше вычислительных ошибок, здесь ученики допускают промахи еще и логическо — смыслового характера.

В задании С1 ошибки встречаются реже всего. В основном, они связаны не с тригонометрией, а с алгебраическими преобразованиями (потеря знака, неверное извлечение корня при решении простейшего квадратного уравнения и т.д).

Ошибки в тригонометрии связаны обычно или с нетвердым знанием значений функций табличных углов (или непонимании, как решаются простейшие тригонометрические уравнения), или с тем, что ребята путаются в расположении корней на тригонометрическом круге. Для тех, кто отбирает корни с помощью двойного неравенства, наиболее типична ошибка в преобразованиях или при верных преобразованиях потеря значений параметра N. Ребята не замечают, что в интервал входит целое значение N или, наоборот, считают, что в интервал попадает значение, которого там нет. Здесь я рекомендую всегда рисовать ось действительных чисел, сначала расставив на ней целые значения, обозначив их жирными точками, а потом полученные интервалы.

Тригонометрический круг — важнейший инструмент репетитора по математике для механики объяснений. С первых же уроков на синусы и косинусы репетитору необходимо нагружать ученика заданиями на отображение углов на круге, а в перспективе учить отбору корней, удовлетворяющих условию (через представление об оси, как о спирали). Своевременные объяснения и четкие инструкции репетитора по математике, направленные на тренировку отбора позволяет разобраться в оборотах, четвертях, положительном и отрицательном направлении обхода, в расположении корней на круге.

Встречались работы, в которых снимали баллы за оформление. Например, за то, что не обоснован отбор корней, или за то, что необоснованно деление на cosX обеих частей уравнения. Плох тот репетитор по математике, кто в процессе подготовки к ЕГЭ не уделяет вермя на отработку грамотного оформления решений. Это приводит к обидной потере баллов в реальных работах даже при полностью верном ответе.

В задании С2 чаще всего встречается недостаточно полное обоснование решения. Геометрия для ребят традиционно сложнее алгебры, так как связана с тем, что на чертеже не только надо уметь видеть расположение объектов, но и доказывать это расположение. Необходимо учиться доказывать каждый шаг в решении, не пропуская ни одного важного перехода. Это не значит, что надо углубляться в дебри доказательств, доходя до аксиом 7 класса, но важные моменты, например, перпендикулярность диагоналей дельтоида, которое используется при нахождении его площади, обосновать необходимо. Именно на этой перпендикулярности или на том, что сечение построено, но никак не описано его построение, ребята теряли балл.

В сканах своих учеников в двух работах я обнаружила в решении системы неравенств С3 абсолютную чепуху, которую и решением-то назвать нельзя. При этом ребята на уроках решали эти задания почти уверенно, но на экзамене не справились даже с дробно-рациональным уравнением, в котором не нужно ни проверять ОДЗ, ни знать равносильность переходов. Причина проста: ни один из них не принес мне ни одного домашнего задания по С3, хотя я предупреждала, что решать на уроках с репетитором, который поможет, подскажет, направит, исправит ошибки — одно, а решать дома, когда остаешься с заданием один на один — совсем другое. В итоге выявилось, что они вообще не понимают, что надо делать в неравенствах, хотя при объяснении я всегда стараюсь дать суть решения, а не научить механическим действиям. Например, наиболее распространены ошибки в ОДЗ логарифмических неравенств. Ребята не понимают, что логарифм — это показатель степени. Почему основание логарифма должно быть не равно единице? Да потому, что единица в любой СТЕПЕНИ даст единицу, поставив которую в основание мы изменим функцию до «неузнаваемости». Ее область определения превратится в вырожденную точку, сама функция получится неоднозначной, а если считать ее многозначной, то графиком уравнения , вместо привычного логарифмического, окажется прямая линия, перпендикулярная оси абсцисс. Почему основание положительно? Да потому, что отрицательные числа можно возводить только в целую степень. При таком раскладе график логарифмической функции превратится во множество вырожденных точек и потеряет непрерывность. Почему подлогарифмическое выражение положительно? Да потому, что положительное число при возведении в любую степень даст только положительное число. Непонимание сути выполняемых действий, попытки решить «по шаблону», которого нет и не может быть в заданиях С3, приводит к ахинее в решении неравенств.

Еще одна распространенная ошибка в С3 как под копирку встречается в большинстве работ, хотя в течение года очень много времени я уделяю сути метода интервалов. Дробно — рациональное неравенство путают с уравнением, отбрасывая знаменатель и не учитывая знаки знаменателя. Опять непонимание сути выполняемых действий: при решении уравнения мы ищем корни, точки пересечения с осями, поэтому приравниваем к нулю числитель, проверив неравенство нулю знаменателя, а при решении уравнения мы ищем интервалы, в которых функция принимает нужный знак. Отбросив знаменатель, мы получим ДРУГУЮ ФУНКЦИЮ с другими знаками. В течение года я строила ребятам графики исходной функции и той функции, которая получается в результате избавления от знаменателя, показывая, что они имеют разный вид и разные знаки на промежутках.

Ошибки в С3 могут быть очень разнообразны, начиная от вычислительных и заканчивая системными, поэтому рассмотреть их все в рамках одной статьи, конечно, не представляется возможным. Единственный момент, на который я в итоге хочу обратить внимание — С3 нельзя решать по шаблону, без понимания выполняемых действий. Также при решении этого задания необходимо быть максимально внимательным и сосредоточенным, поскольку задание имеет большую смысловую нагрузку и объем вычислений, и сделать ошибку легко может даже очень хороший ученик.

Наконец, в одной из работ моей довольно толковой ученицы я встретила очень обидную вещь, объяснить которую я могу только паникой и испугом, потому что она никогда не делала подобных ошибок. Кстати, еще одна причина ошибок — страх перед экзаменом, который упорно культивируют в детях весь период обучения и учителя, и родители, и даже, к сожалению, некоторые репетиторы. Это в принципе нельзя допускать, так как психика у детей еще не сформирована, у них решается судьба поступления в ВУЗы, огромна нагрузка по всем предметам, а их тут еще и ЕГЭ пугают.

Девочка решила дробно-рациональное неравенство, правильно расставила знаки на осях. Осталось списать с оси ответ. И тут она начинает вычислять какое-то несуществующее ОДЗ (числитель больше нуля, знаменатель больше нуля…) Сказала, что растерялась и запаниковала. Перепутала дробно-рациональное неравенство с логарифмическим. Ну, что тут скажешь? Перед этим бессилен даже профессиональный репетитор по математике с немалым сажем. Разве что применять методику специального запутывания и отвлекания ученика на уроках, но она подходит только сильным ученикам с устойчивой психикой. Слабого она только испугает и вызовет лишнюю панику.

В задачах С4 я встретила только незнание функции половинного угла, в результате чего решение не было доведено до конца. Причем именно на тригонометрию в геометрии я обычно делала особый упор. От углов можно было легко уйти к вычислению площади через высоту и основание, но ребята то ли не увидели этого, то ли зациклились на формуле площади треугольника через синус, потому что углы были даны в задаче. Были также и случаи, когда ученик не увидел или не захотел рассматривать второй вариант чертежа.

Особо хотелось бы поговорить о задании С5. Ребята, которые умеют решать С5, обладают высоким уровнем математической культуры, поэтому редко допускают вычислительные ошибки. Но критерии проверки этого задания традиционно очень строгие. При обучении графическим методам решения этого вида заданий репетитор по математике должен обратить внимание на следующие вещи:

1. Нужно расписывать решение как можно более подробно и обоснованно. Не обязательно писать дискриминант квадратного уравнения, но все важные переходы должны быть описаны и разъяснены.

2. Необходимо задавать функции обеих частей уравнения (неравенства).

3. Если функция элементарная, достаточно ее построить так, как учили в школе и назвать вид полученного графика.

4. Если функция не является элементарной, необходимо ее ПОЛНОСТЬЮ исследовать на монотонность, экстремумы и пересечение с осями координат. В этом году многие не увидели полуокружность и строили «по точкам», что недопустимо и грозило потерей 2-3 баллов.

5. Все положения графика с параметром должны быть обязательно описаны (даже те, которые не используются). Таким образом доказывается, что при других значениях параметра нужных нам решений не будет.

При соблюдении указанных выше условий и отсутствии вычислительных ошибок велика вероятность получить за задание максимальный балл. Ребята ленятся расписывать решение подробно и упускают важные переходы, за что получают меньше максимального на 1 — 2 — 3 балла.

Полное избавление ребят от ошибок для репетитора по математике — неподъемная задача, но нужно стремиться уменьшать вероятность оплошностей. Выделять время не только на решение задач, но и предлагать специальные задания для самоконтроля. Важно научить внимательно и просто вести записи. Время на ЕГЭ ограничено и поэтому внимание репетитора в конце года должно быть сосредоточено на скорости решения. Кроме этого также правильному распределению времени в зависимости от того, на какой балл ученик претендует.

Ермакова Диана Владимировна, репетитор по математике, г. Зеленоград.

Метки:
ЕГЭ по математике,
Ошибки,
Репетиторам по математике

И снова здравствуйте, уважаемые одиннадцатиклассники! Полагаю, что Вы хорошо отдохнули и готовы к работе для достижения своих высоких целей.

В этом году июнь месяц выдался очень продуктивным. Моя работа не закончилась 6 июня, когда мои ученики написали ЕГЭ по физике. После публикации результатов ЕГЭ (сначала по математике, а потом и по физике) стало поступать множество сообщений от учеников, даже тех, с кем я не занималась, с просьбой помочь разобраться, за что сняли баллы. А в некоторых случаях даже была необходима помощь с составлением апелляции. Бесценный опыт, если честно…..Только вот от этого опыта седых волос становится больше. И желание сжечь критерии не отпускает меня.

Сразу замечу, что апелляция возможна только по заданиям второй части. По первой части апелляция производится только тогда, когда компьютер неверно считал знак, записанный Вами в бланке ответов.

Уважаемые одиннадцатиклассники, вы должны понимать, что недостаточно просто получить верный ответ, недостаточно записать решение в стиле «я художник, я так вижу». Ваше решение будут оценивать по вполне определенным критериям. И даже абсолютно верный ответ не гарантирует полный балл за выполненное задание.

Анализ ошибок мы начнем с разбора сканов работ по профильной математике. Эти сканы я собирала не один год. К сожалению, в математике, просто за идею решения, за набор формул, не дадут ни одного балла. А снимают баллы за наличие вычислительных ошибок, недостаточную обоснованность, наличие лишних записей. Не указали необходимые признаки, свойства, теоремы – все, полный балл Вам не дадут.

Основной упор будет сделан на задачи 12, 14, 15 (уравнения, неравенства, задачи с экономическим содержанием). Это так называемый джентельменский набор, который старается выполнить большая часть выпускников. Погнали…

Для удобства статья представлена в двух форматах. Текст и видео. Вот ролик:

Уравнения

Основные ошибки:

1) неправильное использование формул приведения.

При преобразовании допущена ошибка. Минуса перед косинусом быть не должно. Задание оценивается в 0 баллов.

2) незнание свойств четных и нечетных функций. Также ребята забывают, что косинус функция честная, а вот синус, тангенс и котангенс нечетные.

Классическая ошибка! – нечетная функция, следовательно знак минус выносится вперед, а не пропадает. Если бы функция была четная, то мы смело могли бы убрать знак минус. Задание оценивается в 0 баллов.

3) неправильное или некорректное использование тригонометрических формул.

Пару лет назад мне написал ученик, которому на экзамене досталось уравнение вида .

Скан он мне не отправил, но в процессе обсуждений выяснилось, что в первой скобке для он использовал не формулу синуса суммы, а формулы приведения. Чего делать категорически нельзя! Как Вы понимаете, задание оценили в 0 баллов.

4) Самое банальное. Неверное решение простейших тригонометрических уравнений.

При решении простейшего тригонометрического уравнения допущена ошибка. Третий и четвертый корень записаны неверно. Задание оценивается в 0 баллов.

Неравенства

С неравенствами у ребят дела идут посложнее, чем с уравнениями. Тут ваша фантазия разыгрывается по полной. Какие только ошибки не встречались(( Постараюсь выделить основные.

1)Пожалуй, самая распространенная ошибка – ошибка в расстановке знаков на координатной прямой. В идеале, если выпускник умеет определять – перед ним корень четного или нечетного порядка, меняется знак или дублируется.

Нули найдены верно. Но при расстановке знаков на координатной прямой допущена ошибка. Мы видим, что единица – нуль числителя второго порядка, следовательно знак сохраняется, и в крайнем левом интервале должен быть плюс. Эта ошибка уже позволяет эксперту поставить за данное задание 0 баллов.

2)Отбрасывание знаменателя и, как следствие, потеря части корней. В примере, приведенном ниже, выпускник отбросил знаменатель и находил нули только числителя.

Это привело к тому, что на координатной прямой не хватает нулей двух скобок: .

Такая грубая ошибка на экзамене не прощается.

Оценка эксперта – 0 баллов.

3) Неравносильный переход от неравенства к системе неравенств.

Я думаю, эта ошибка даже не нуждается в комментариях. Даже несмотря на то, что ученик верно нашел нули, верно расставил знаки на координатной прямой, это задание оценили в 0 баллов. Если бы системы с тремя неравенствами не было, ученик имел бы возможность взять полный балл.

4) Ошибки при использовании свойств логарифмов.

Стоит заметить, что для снятия логарифмов в правой и левой части, необходимо, чтобы перед логарифмом не было никаких цифр или букв. Выпускник снял логарифмы, хотя по задумке нужно было в правой части свернуть в полный квадрат подлогарифмическое выражение и вынести общий множитель. Как Вы понимаете, эксперт оценил это задание в 0 баллов.

Из моего текста у Вас, возможно, сложилось впечатление, что эксперты по всем поводам снимают сразу два балла. К счастью, это не так. Один балл Вам могут поставить, если Вы допустили ошибку в скобке (вместо круглой написали квадратную или наоборот) или допустили вычислительную ошибку, но при этом присутствует верная последовательность всех шагов решения.

Экономические задачи

В решении задач с экономическим содержанием ребятам в первую очередь нужно определить, какая форма кредитования – с дифференцированными платежами, аннуитентными или иная форма кредитования.

Могу выделить несколько основных ошибок.

1)Неверное построение математической модели, связанное с неверным определением формы кредитования.

Для лучшего понимания начну с условия задачи.

В июле 2026 года будет взят кредит на три года в размере 800 тыс рублей. Условия возврата таковы:

– каждый январь долг возрастает на 10 процентов по сравнению с концом прошлого года

– размер платежей в 2027 и 2028 годах одинаковый

– к июлю 2029 года долг выплачивается полностью.

Также известно, что в 2029 году платеж составит 833,8 тыс рублей. Сколько рублей будет составлять платеж в 2027 году?

Согласно записям таблицы, ученик решил, что перед ним дифференцированная форма кредитования и остаток уменьшается у него равномерно, ровно на N рублей каждый год. Но это совсем не так. Из условия задачи, мы видим, что выплаты одинаковые первые два года. Но при этом остаток не будет уменьшаться равномерно. Правильная запись остатка во второй строчке должна выглядеть так: .

Основываясь на критериях оценивания данного задания, математическая модель построена неверно, задание оценивается в 0 баллов.

Идем дальше. Наверняка Вы встречали задачи вида:

15 января 2020 года был выдан кредит на сумму 900 тыс. рублей на 31 месяц. Условия возврата таковы:

– 1 -го числа каждого месяца долг увеличивается на 2 по сравнению с концом предыдущего месяца.

– со 2 по 14 число необходимо выплатить часть долга;

– 15 -го числа каждого месяца с 1-го по 30-й долг должен быть на одну и ту же величину меньше долго на 15 число предыдущего месяца;

– 15 июля 2027 года долг составит 300 тыс рублей.

– 15 августа 2027 года долг должен быть выплачен полностью.

Найдите общую сумму выплат после полного погашения кредита.

В этой таблице полностью неправильно записаны столбцы с остатками и выплатами. Согласно условию задачи, первые 30 месяцев долг уменьшается равномерно, на меньше чем, прошлом месяце. Но не забываем, что первоначальный долг – это S, а не Sk рублей. То есть остаток в первые 30 месяцев должен выглядеть так: . Как Вы понимаете, и выплаты будет принимать совсем другой вид, так как они получаются путем вычитания из долга после начисления процентов самого остатка. Для примера запишем первую выплату: .

С учетом полностью неправильно построенной математической модели, задание оценивается в 0 баллов.

2)Ошибки при применении формул арифметической прогрессии и расчета общей суммы выплат.

Год назад ребятам на экзамене попалась задача, где в процессе кредитования менялась процентная ставка. Приведу пример:

25 августа 2020 года был дан кредит на 12 лет в размере 300 тыс рублей.

— 25 января с 2021 по 2026 года долг возрастает на 10 процентов;

— 25 января с 2027 по 2032 года долг возрастает на 15 процентов;

– с февраля по июль необходимо выплатить часть долга;

– в августе каждого года долг должен быть на одну и туже величину меньше по сравнению с августом прошлого года;

– к августу 2032 года кредит должен быть полностью погашен.

Найдите общую сумму выплат после полного погашения кредита.

Я уверена, что для многих ребят покажется очевидным, что нельзя складывать первую и последнюю (двенадцатую) выплату. Но я все же поясню.

Действительно, это задача на дифференцированные платежи. И можно заметить, что выплаты подчиняются арифметической прогрессии. Но так как у вас меняется процентная ставка, у Вас меняется и так называемый коэффициент или разность арифметической прогрессии. Поэтому правильно будет сначала просуммировать по формуле арифметической прогрессии первые шесть выплат, потом вторые шесть и полученные выражения сложить. Таким образом Вы получите верный ответ.

В каком же случае Вы можете получить 1 балл – если Вы верно построили математическую модель, но допустили вычислительную ошибку при получении численного значения.

PS: в подавляющем большинстве работ, которые поступали на проверку, ребята просили пояснить, почему за параметр (17 задание) и за задание на числа и их свойства так сильно срезали баллы. В большинстве случаев ребята получали по одному баллу за параметр, а в задаче на числа им засчитывали только пункт а), который также дает только один балл. Ребята, эти задачи считаются олимпиадными, не зря за их полное выполнение дается целых 4 балла. Критерии оценивания данных номеров очень жесткие. Должно быть и максимальное подробное объяснение, и разбор всех случаев и вариантов. В 17 задании это и правильно построенный график (если это необходимо), и рассчитаные все точки, и правильно раскрытый модуль, и расписанные все значения параметра и т.д и т.д.

В погоне за «легкими «баллами ребята даже не трогают планиметрию и стереометрию. А они, напомню, оцениваются в три балла каждый. Даже если Вы испытываете трудности в геометрии, пункт а (доказательство) не пропускайте мимо, как правило он значительно легче пункта б), где нужно найти численное значение той или иной величины. Но по одному первичному баллу за каждый номер Вы спокойно можете получить.

На этом мой краткий обзор подошел к концу. Я желаю удачи и сил всем одиннадцатиклассникам в этом году. Не бойтесь ЕГЭ, настраивайтесь на работу, идите к своей цели. У Вас все получится!

Все, что не убивает, делает нас сильнее!

P.S.: Вот моя группа ВКонтакте, где я выкладываю подобные тексты, ролики и полезности для ЕГЭ по физике и математике: https://vk.com/public185877660 Подписывайтесь!

Источник

Материал из MachineLearning.

Перейти к: навигация, поиск

Содержание

1 Введение
- 1.1 Постановка вопроса. Виды погрешностей
2 Виды мер точности
3 Предельные погрешности
4 Погрешности округлений при представлении чисел в компьютере
5 Погрешности арифметических операций
6 Погрешности вычисления функций
7 Числовые примеры
8 Список литературы
9 См. также

Введение

Постановка вопроса. Виды погрешностей

Процесс исследования исходного объекта методом математического моделирования и вычислительного эксперимента неизбежно носит приближенный характер, так как на каждом этапе вносятся погрешности. Построение математической модели связано с упрощением исходного явления, недостаточно точным заданием коэффициентов уравнения и других входных данных. По отношению к численному методу, реализующему данную математическую модель, указанные погрешности являются неустранимыми, поскольку они неизбежны в рамках данной модели.

При переходе от математической модели к численному методу возникают погрешности, называемые погрешностями метода. Они связаны с тем, что всякий численный метод воспроизводит исходную математическую модель приближенно. Наиболее типичными погрешностями метода являются погрешность дискретизации и погрешность округления.
При построении численного метода в качестве аналога исходной математической задачи обычно рассматривается её дискретная модель. Разность решений дискретизированной задачи и исходной называется погрешностью дискретизации. Обычно дискретная модель зависит от некоторого параметра (или их множества) дискретизации, при стремлении которого к нулю должна стремиться к нулю и погрешность дискретизации.
Дискретная модель представляет собой систему большого числа алгебраических уравнений. Для её решения используется тот или иной численный алгоритм. Входные данные этой системы, а именно коэффициенты и правые части, задаются в ЭВМ не точно, а с округлением. В процессе работы алгоритма погрешности округления обычно накапливаются, и в результате, решение, полученное на ЭВМ, будет отличаться от точного решения дискретизированной задачи. Результирующая погрешность называется погрешностью округления (вычислительной погрешностью). Величина этой погрешности определяется двумя факторами: точностью представления вещественных чисел в ЭВМ и чувствительностью данного алгоритма к погрешностям округления.

Итак, следует различать погрешности модели, дискретизации и округления. В вопросе преобладания какой-либо погрешности ответ неоднозначен. В общем случае нужно стремиться, чтобы все погрешности имели один и тот же порядок. Например, нецелесообразно пользоваться разностными схемами, имеющими точность 10⁻⁶, если коэффициенты исходных уравнений задаются с точностью 10⁻².

Виды мер точности

Мерой точности вычислений являются абсолютные и относительные погрешности. Абсолютная погрешность определяется формулой

где tilde a – приближение к точному значению .
Относительная погрешность определяется формулой

$delta(tilde a)=frac{|tilde a-a|}{a}.$

Относительная погрешность часто выражается в процентах. Абсолютная и относительная погрешности тесно связаны с понятием верных значащих цифр. Значащими цифрами числа называют все цифры в его записи, начиная с первой ненулевой цифры слева. Например, число 0,000129 имеет три значащих цифры. Значащая цифра называется верной, если абсолютная погрешность числа не превышает половины веса разряда, соответствующего этой цифре. Например, , абсолютная погрешность . Записывая число в виде

имеем , следовательно, число имеет две верных значащих цифр (9 и 3).

В общем случае абсолютная погрешность должна удовлетворять следующему неравенству:

$Delta(tilde a)<0,5cdot10^{m-n+1} ,$

где — порядок (вес) старшей цифры, — количество верных значащих цифр.
В рассматриваемом примере $Delta(tilde a)le0,5cdot10^{3-2+1}le0,5cdot10^2=50$ .

Относительная погрешность связана с количеством верных цифр приближенного числа соотношением:

$delta(tilde a)lefrac{Delta(tilde a)}{alpha_m}10^mlefrac{10^{m-n+1}}{alpha_m10^m}lefrac{1}{alpha_m10^{n-1}},$

где alpha_m — старшая значащая цифра числа.

Для двоичного представления чисел имеем $delta(tilde a)le2^{-n}$ .

Тот факт, что число tilde a является приближенным значением числа с абсолютной погрешностью , записывают в виде

причем числа tilde a и записываются с одинаковым количеством знаков после запятой, например, или $a=2,347pm2cdot10^{-3}$ .

Запись вида

означает, что число tilde a является приближенным значение числа с относительной погрешностью .

Так как точное решение задачи как правило неизвестно, то погрешности приходится оценивать через исходные данные и особенности алгоритма. Если оценка может быть вычислена до решения задачи, то она называется априорной. Если оценка вычисляется после получения приближенного решения задачи, то она называется апостериорной.

Очень часто степень точности решения задачи характеризуется некоторыми косвенными вспомогательными величинами. Например точность решения системы алгебраических уравнений

AX=F

характеризуется невязкой

где tilde X — приближенное решение системы.
Причём невязка достаточно сложным образом связана с погрешностью решения , причём если невязка мала, то погрешность может быть значительной.

Предельные погрешности

Пусть искомая величина является функцией параметров — приближенное значение . Тогда предельной абсолютной погрешностью называется величина

$D(a^*) = suplimits_{(t_1, ldots ,t_n) in Omega } left|{a(t_1, ldots ,t_n) - a^*}right| ,$

Предельной относительной погрешностью называется величина .

Пусть $left|{t_j - t_j^*}right| le Delta (t_j^* ), qquad j = 1 div n$ — приближенное значение . Предполагаем, что — непрерывно дифференцируемая функция своих аргументов. Тогда, по формуле Лагранжа,

$a(t_1, ldots ,t_n) - a^* = sumlimits_{j = 1}^n gamma_j (alpha )(t_j - t_j^*),$

где $gamma_j (alpha ) = a^{prime}_{t_j}(t_1^* + alpha (t_1 - t_1^*), ldots ,t_n^* + alpha (t_n - t_n^*)), qquad 0 le alpha le 1$ .

Отсюда

$left|{a(t_1, ldots ,t_n) - a^*}right| le D_1 (a^*) = sumlimits_{j = 1}^n b_j Delta (t_j^*),$

где $b_j = suplimits_Omega left|{a^{prime}_{t_j}(t_1, ldots ,t_n)}right|$ .

Можно показать, что при малых $rho = sqrt{{(Delta (t_1^* ))}^2 + ldots + {(Delta (t_n^* ))}^2 }$ эта оценка не может быть существенно улучшена. На практике иногда пользуются грубой (линейной) оценкой

$left|{a(t_1, ldots ,t_n) - a^*}right| le D_2 (a^*),$

где $D_2 (a^*) = sumlimits_{j = 1} left|{gamma_j (0)}right| Delta (t^*)$ .

Несложно показать, что:

— предельная погрешность суммы или разности равна сумме предельных погрешностей.
$delta (t_1^* cdots t_m^* cdot d_1^{* - 1} cdots d_m^{* - 1} ) = delta (t_1^* ) + ldots + delta (t_m^*) + delta (d_1^*) + ldots + delta (d_n^*)$ — предельная относительная погрешность произведения или частного приближенного равна сумме предельных относительных погрешностей.

Погрешности округлений при представлении чисел в компьютере

Одним из основных источников вычислительных погрешностей является приближенное представление чисел в компьютере, обусловленное конечностью разрядной сетки (см. Международный стандарт представления чисел с плавающей точкой в ЭВМ). Число , не представимое в компьютере, подвергается округлению, т. е. заменяется близким числом tilde a , представимым в компьютере точно.
Найдем границу относительной погрешности представления числа с плавающей точкой. Допустим, что применяется простейшее округление – отбрасывание всех разрядов числа, выходящих за пределы разрядной сетки. Система счисления – двоичная. Пусть надо записать число, представляющее бесконечную двоичную дробь

$a=underbrace{pm2^p}_{order}underbrace{left(frac{a_1}{2}+frac{a_2}{2^2}+dots+frac{a_t}{2^t}+frac{a_{t+1}}{2^{t+1}}+dotsright)}_{mantissa},$

где $a_j={0\1$ , — цифры мантиссы.
Пусть под запись мантиссы отводится t двоичных разрядов. Отбрасывая лишние разряды, получим округлённое число

$tilde a=pm2^pleft(frac{a_1}{2}+frac{a_2}{2^2}+dots+frac{a_t}{2^t}right).$

Абсолютная погрешность округления в этом случае равна

$a-tilde a=pm2^pleft(frac{a_{t+1}}{2^{t+1}}+frac{a_{t+2}}{2^{t+2}}+dotsright).$

Наибольшая погрешность будет в случае $a_{t+1}=1, qquad a_{t+2}=1,$ , тогда

$|a-tilde a|lepm2^pfrac{1}{2^{t+1}}underbrace{left(1+frac{1}{2}+frac{1}{2^2}+dotsright)}_{=2}=2^{p-t}.$

Т.к. , где — мантисса числа , то всегда a_1=1 . Тогда $|a|ge2^pcdot2^{-1}=2^{p-1}$ и относительная погрешность равна $frac{|a-tilde a|}{|a|}le2^{-t+1}$ . Практически применяют более точные методы округления и погрешность представления чисел равна

( 1 )

$frac{|a-tilde a|}{|a|}le2^{-t},$

т.е. точность представления чисел определяется разрядностью мантиссы .
Тогда приближенно представленное в компьютере число можно записать в виде , где $|epsilon|le2^{-t}$ – «машинный эпсилон» – относительная погрешность представления чисел.

Погрешности арифметических операций

При вычислениях с плавающей точкой операция округления может потребоваться после выполнения любой из арифметических операций. Так умножение или деление двух чисел сводится к умножению или делению мантисс. Так как в общем случае количество разрядов мантисс произведений и частных больше допустимой разрядности мантиссы, то требуется округление мантиссы результатов. При сложении или вычитании чисел с плавающей точкой операнды должны быть предварительно приведены к одному порядку, что осуществляется сдвигом вправо мантиссы числа, имеющего меньший порядок, и увеличением в соответствующее число раз порядка этого числа. Сдвиг мантиссы вправо может привести к потере младших разрядов мантиссы, т.е. появляется погрешность округления.

Округленное в системе с плавающей точкой число, соответствующее точному числу , обозначается через fl(x) (от англ. floating – плавающий). Выполнение каждой арифметической операции вносит относительную погрешность, не большую, чем погрешность представления чисел с плавающей точкой (1). Верна следующая запись:

где box — любая из арифметических операций, $|epsilon|le2^{-t}$ .

Рассмотрим трансформированные погрешности арифметических операций. Арифметические операции проводятся над приближенными числами, ошибка арифметических операций не учитывается (эту ошибку легко учесть, прибавив ошибку округления соответствующей операции к вычисленной ошибке).

Рассмотрим сложение и вычитание приближенных чисел. Абсолютная погрешность алгебраической суммы нескольких приближенных чисел равна сумме абсолютных погрешностей слагаемых.

Если сумма точных чисел равна

сумма приближенных чисел равна

где — абсолютные погрешности представления чисел.

Тогда абсолютная погрешность суммы равна

Относительная погрешность суммы нескольких чисел равна

( 2 )

$delta(S)=frac{Delta(S)}{S}=frac{a_1}{S}left(frac{Delta(a_1)}{a_1}right)+frac{a_2}{S}left(frac{Delta(a_2)}{a_2}right)+dots=frac{a_1delta(a_1)+a_2delta(a_2)+dots}{S},$

где — относительные погрешности представления чисел.

Из (2) следует, что относительная погрешность суммы нескольких чисел одного и того же знака заключена между наименьшей и наибольшей из относительных погрешностей слагаемых:

При сложении чисел разного знака или вычитании чисел одного знака относительная погрешность может быть очень большой (если числа близки между собой). Так как даже при малых величина может быть очень малой. Поэтому вычислительные алгоритмы необходимо строить таким образом, чтобы избегать вычитания близких чисел.

Необходимо отметить, что погрешности вычислений зависят от порядка вычислений. Далее будет рассмотрен пример сложения трех чисел.

( 3 )

tilde S=(tilde S_1+x_3)(1+delta_2)=(x_1+x_2)(1+delta_1)(1+delta_2)+x_3(1+delta_2).

При другой последовательности действий погрешность будет другой:

tilde S=(x_3+x_2)(1+delta_1)(1+delta_2)+x_1(1+delta_2).

Из (3) видно, что результат выполнения некоторого алгоритма, искаженный погрешностями округлений, совпадает с результатом выполнения того же алгоритма, но с неточными исходными данными. Т.е. можно применять обратный анализ: свести влияние погрешностей округления к возмущению исходных данных. Тогда вместо (3) будет следующая запись:

где

При умножении и делении приближенных чисел складываются и вычитаются их относительные погрешности.

tilde S=a_1cdot a_2(1+delta(a_1))(1+delta(a_2))

≅

с точностью величин второго порядка малости относительно delta .

Тогда .

Если $S=frac{a_1}{a_2}$ , то $Delta(S)=frac{a_1(1+delta_1)}{a_2(1+delta_2)}-frac{a_1}{a_2}=frac{a_1(delta_1-delta_2)}{a_2(1+delta_2)}approx frac{a_1}{a_2}(delta_1-delta_2), qquad delta(S)$ ≅

При большом числе n арифметических операций можно пользоваться приближенной статистической оценкой погрешности арифметических операций, учитывающей частичную компенсацию погрешностей разных знаков:

$delta_Sigma approx delta_{fl} quad sqrt{n},$

где – суммарная погрешность, $|delta_{fl}|leepsilon$ – погрешность выполнения операций с плавающей точкой, epsilon – погрешность представления чисел с плавающей точкой.

Погрешности вычисления функций

Рассмотрим трансформированную погрешность вычисления значений функций.

Абсолютная трансформированная погрешность дифференцируемой функции y=f(x) , вызываемая достаточно малой погрешностью аргумента , оценивается величиной .

Если f(x)>0 , то $delta(y)=frac{|f'(x)|}{f(x)}Delta(x)=left|(ln(f(x)))'right|cdotDelta(x)$ .

Абсолютная погрешность дифференцируемой функции многих аргументов , вызываемая достаточно малыми погрешностями аргументов оценивается величиной:

$Delta(y)=sumlimits_{i=1}^nleft|frac{partial f}{partial x_i}right|Delta(x_i)$

Если , то $delta(y)=sumlimits_{i=1}^nfrac{1}{f}cdotleft|frac{partial f}{partial x_i}right|cdotDelta(x_i)=sumlimits_{i=1}^{n}left|frac{partial l_n(f)}{partial x_i}right|Delta(x_i)$ .

Практически важно определить допустимую погрешность аргументов и допустимую погрешность функции (обратная задача). Эта задача имеет однозначное решение только для функций одной переменной y=f(x) , если f(x) дифференцируема и :

$Delta(x)=frac{1}{|f'(x)|}Delta(y)$ .

Для функций многих переменных задача не имеет однозначного решения, необходимо ввести дополнительные ограничения. Например, если функция наиболее критична к погрешности , то:

$Delta(x_i)=frac{Delta(y)}{left|frac{partial f}{partial x_i}right|}qquad$

(погрешностью других аргументов пренебрегаем).

Если вклад погрешностей всех аргументов примерно одинаков, то применяют принцип равных влияний:

$Delta(x_i)=frac{Delta(y)}{nleft|frac{partial f}{partial x_i}right|},qquad i=overline{1,n}.$

Числовые примеры

Специфику машинных вычислений можно пояснить на нескольких элементарных примерах.

ПРИМЕР 1. Вычислить все корни уравнения

$x^4 - 4x^3 + 8x^2 - 16x + 15.underbrace{99999999}_8 = {(x - 2)}^4 - 10^{- 8} = 0.$

Точное решение задачи легко найти:

$(x - 2)^2 = pm 10^{- 4},$

$x_1= 2,01; x_2= 1,99; x_{3,4}= 2 pm 0,01i.$

Если компьютер работает при $delta _M > 10^{ - 8}$ , то свободный член в исходном уравнении будет округлен до 16,0 и, с точки зрения представления чисел с плавающей точкой, будет решаться уравнение , т.е. $x_{1,2,3,4} = 2$ , что, очевидно, неверно. В данном случае малые погрешности в задании свободного члена $approx10^{-8}$ привели, независимо от метода решения, к погрешности в решении $approx10^{-2}$ .

ПРИМЕР 2. Решается задача Коши для обыкновенного дифференциального уравнения 2-го порядка:

u''(t) = u(t), qquad u(0) = 1, qquad u'(0) = - 1.

Общее решение имеет вид:

$u(t) = 0,5[u(0) + u'(0)]e^t + 0,5[u(0) - u'(0)]e^{- t}.$

При заданных начальных данных точное решение задачи: $u(x) = e^{-t}$ , однако малая погрешность delta в их задании приведет к появлению члена , который при больших значениях аргумента может существенно исказить решение.

ПРИМЕР 3. Пусть необходимо найти решение обыкновенного дифференциального уравнения:

$stackrel{cdot}{u} = 10u,qquad u = u(t),\ u(t_0) = u_0,qquad t in [0,1].$

Его решение: $u(t) = u_0e^{10(t - t_0 )}$ , однако значение u(t_0) известно лишь приближенно: , и на самом деле $u^*(t) = u_0^*e^{10(t - t_0)}$ .

Соответственно, разность u* - u будет:

$u^* - u = (u_0^* - u_0)e^{10(t - t_0)}.$

Предположим, что необходимо гарантировать некоторую заданную точность вычислений всюду на отрезке . Тогда должно выполняться условие:

$|{u^*(t) - u(t)}| le varepsilon.$

Очевидно, что:

$maxlimits_{t in [0,1]} |{u^*(t) - u(t)}| = |{u*(1) - u(1)}| = |{u_0^* - u_0}|e^{10(1 - t_0)}.$

Отсюда можно получить требования к точности задания начальных данных $delta: qquad|u_0^* - u_0| < delta, qquad delta le varepsilon e^{ - 10}$ при t_0= 0 .

Таким образом, требование к заданию точности начальных данных оказываются в $e^{10}$ раз выше необходимой точности результата решения задачи. Это требование, скорее всего, окажется нереальным.

Решение оказывается очень чувствительным к заданию начальных данных. Такого рода задачи называются плохо обусловленными.

ПРИМЕР 4. Решением системы линейных алгебраических уравнений (СЛАУ):

$left{ begin{array}{l} u + 10v = 11, \ 100u + 1001v = 1101; \ end{array} right.$

является пара чисел .

Изменив правую часть системы на 0,01 , получим возмущенную систему:

$left{ begin{array}{l} u + 10v = 11.01, \ 100u + 1001v = 1101; \ end{array} right.$

с решением , сильно отличающимся от решения невозмущенной системы. Эта система также плохо обусловлена.

ПРИМЕР 5. Рассмотрим методический пример вычислений на модельном компьютере, обеспечивающем точность . Проанализируем причину происхождения ошибки, например, при вычитании двух чисел, взятых с точностью до третьей цифры после десятичной точки , разность которых составляет .

В памяти машины эти же числа представляются в виде:

u_M = u(1 + delta_M^u), quad v_M = v(1 + delta_M^v)

, причем

Тогда:

u_M - u approx udelta_M^u, quad v_M - v approx vdelta_M^v.

Относительная ошибка при вычислении разности будет равна:

$delta = frac{(u_M - v_M) - (u - v)}{(u - v)} = frac{(u_M - u) - (v_M - v)}{(u - v)} = frac{delta_M^u - delta_M^v}{(u - v)}.$

Очевидно, что $delta = left|{frac{delta_M^u - delta_M^v}{Delta }} right| le frac{2delta_M}{0,001} approx 2000delta_M = 1$ , т.е. все значащие цифры могут оказаться неверными.

ПРИМЕР 6. Рассмотрим рекуррентное соотношение $u_{i+1} = qu_i, quad i ge 0, quad u_0 = a,quad q > 0, quad u_i > 0.$

Пусть при выполнении реальных вычислений с конечной длиной мантиссы на -м шаге возникла погрешность округления, и вычисления проводятся с возмущенным значением , тогда вместо $u_{i+1}$ получим $u_{i + 1}^M = q(u_i + delta_i) = u_{i + 1} + qdelta_i$ , т.е. $delta_{i + 1} = qdelta_i,quad i = 0,1,ldots$ .

Следовательно, если |q| > 1 , то в процессе вычислений погрешность, связанная с возникшей ошибкой округления, будет возрастать (алгоритм неустойчив). В случае погрешность не возрастает и численный алгоритм устойчив.

Список литературы

А.А.Самарский, А.В.Гулин. Численные методы. Москва «Наука», 1989.
http://www.mgopu.ru/PVU/2.1/nummethods/Chapter1.htm
http://www.intuit.ru/department/calculate/calcmathbase/1/4.html

См. также

Практикум ММП ВМК, 4й курс, осень 2008

Источник

Системы оценивания письменных работ по
математике

При проверке
усвоения материала необходимо выявлять полноту, прочность усвоения
учащимися теории и
умения применять ее на практике в знакомых и незнакомых ситуациях.

Формами контроля качества освоения содержания
учебной программы учащимися являются:

·
Письменная
проверка предполагает письменный
ответ учащегося на один или систему вопросов (заданий). К письменным ответам
относятся: домашние, проверочные, практические, контрольные, творческие работы,
письменные ответы на вопросы теста, рефераты и пр.

·
Устная проверка предполагает устный ответ учащегося на один
или систему вопросов в форме рассказа, беседы, собеседования и другое.

·
Комбинированная проверка
предполагает сочетание устных и письменных форм работы.

Рассмотрим оценивание письменной проверки.

Оценка ответа
учащегося при письменном опросе проводится по пятибалльной системе, т.
е. за ответ выставляется одна из отметок:5 (отлично), 4
(хорошо), 3 (удовлетворительно), 2 (неудовлетворительно), 1 (плохо) на
практике такую оценку практически не используют.

Учителю
важно знать, как соотнести фактические знания ученика и оценку, отражающую эти
знания.

В
зависимости от поставленных целей по-разному строится программа контроля,
подбираются различные типы вопросов и заданий. Но применение примерных норм
оценки знаний должно внести единообразие в оценку знаний и умений учащихся и
сделать ее более объективной. Примерные нормы представляют основу, исходя из
которой, учитель оценивает знания и умения учащихся.

Содержание и объем материала, подлежащего проверке и оценке, определяются программой по математике
для средней школы. В задания для проверки включаются основные, типичные и
притом различной сложности вопросы, соответствующие проверяемому разделу
программы.

При
проверке знаний и умений, учащихся учитель выявляет не только степень усвоения
учащимися теории и умения применять ее на практике, но также умение
самостоятельно мыслить.

Основными формами проверки знаний и умений учащихся по математике в средней школе являются устный
опрос и письменная контрольная работа, наряду с которыми применяются и другие
формы проверки. Письменная контрольная работа позволяет оценить умение учащихся
излагать свои мысли на бумаге; навыки грамотного и фактически грамотного
оформления выполняемых ими заданий.

При оценке письменных контрольных работ учитель в первую очередь учитывает имеющиеся у
учащегося фактические знания и умения, их полноту, прочность, умение применять
на практике в различных ситуациях. Результат оценки зависит также от наличия и
характера погрешностей, допущенных при письменной контрольной работе.

Среди
погрешностей выделяются ошибки, недочеты и мелкие погрешности.

Погрешность
считается ошибкой, если она свидетельствует о том, что ученик не овладел
основными знаниями, умениями и их применением.

К
недочетам относятся погрешности, свидетельствующие о недостаточно полном
или недостаточно прочном усвоении основных знаний и умений или об отсутствии
знаний, не считающихся в соответствии с программой основными. К недочетам относятся
погрешности, объясняющиеся рассеянностью или недосмотром, но которые не привели
к искажению смысла полученного учеником задания или способа его выполнения.
Грамматическая ошибка, допущенная в написании известного учащемуся
математического термина, небрежная запись, небрежное выполнение чертежа
считаются недочетом.

К
мелким погрешностям относятся погрешности в письменной речи, не
искажающие смысла ответа или решения, случайные описки и т. п.

Граница между ошибками и недочетами является в некоторой степени условной. В одно время
при одних обстоятельствах допущенная учащимися погрешность может
рассматриваться как ошибка, в другое время и при других обстоятельствах она
может рассматриваться как недочет.

Решение
задачи считается безупречным, если получен верный ответ при правильном ходе
решения, выбран соответствующий задаче способ решения, правильно выполнены
необходимые вычисления и преобразования, последовательно и аккуратно оформлено
решение.

Оценивание письменных контрольных работ.

Ответ оценивается отметкой «5»,
если:

·
работа выполнена
полностью;

·
в логических рассуждениях
и обосновании решения нет пробелов и ошибок;

·
в решении нет
математических ошибок (возможна одна неточность, описка, которая не является
следствием незнания или непонимания учебного материала).

Отметка «4» ставится в следующих случаях:

·
работа выполнена
полностью, но обоснования шагов решения недостаточны (если умение обосновывать
рассуждения не являлось специальным объектом проверки);

·
допущены одна ошибка или
есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти
виды работ не являлись специальным объектом проверки).

Отметка «3» ставится, если:

·
допущено более одной
ошибки или более двух – трех недочетов в выкладках, чертежах или графиках, но
учащийся обладает обязательными умениями по проверяемой теме.

Отметка «2» ставится, если:

·
допущены существенные
ошибки, показавшие, что учащийся не обладает обязательными умениями по данной
теме в полной мере.

Отметка «1» ставится в случае:

·
полного незнания
изученного материала, отсутствия элементарных умений и навыков.

Общая классификация ошибок

При оценке знаний, умений и навыков учащихся
следует учитывать все ошибки (грубые и негрубые) и недочёты.

Грубыми считаются ошибки:

·
незнание определения
основных понятий, законов, правил, основных положений теории, незнание формул,
общепринятых символов обозначений величин, единиц их измерения;

·
незнание наименований
единиц измерения;

·
неумение выделить в ответе
главное;

·
неумение применять знания,
алгоритмы для решения задач;

·
неумение делать выводы и
обобщения;

·
неумение читать и строить
графики;

·
неумение пользоваться
первоисточниками, учебником и справочниками;

·
потеря корня или
сохранение постороннего корня;

·
отбрасывание без
объяснений одного из них;

·
равнозначные им ошибки;

·
вычислительные ошибки,
если они не являются опиской;

·
логические ошибки

·
вычислительные ошибки в
примерах и задачах;

·
-ошибки на незнание
порядка выполнения арифметических действий;

·
-неправильное решение
задачи (пропуск действий, неправильный выбор действий, лишнее действие);

·
-недоведение до конца
решения задачи или примера;

·
-невыполненное задание

·
-неправильный выбор
порядка выполнения действий в выражении;

·
-пропуск нуля в частном
при делении натуральных чисел или десятичных дробей;

·
-неправильный выбор знака
в результате выполнения действий над положительными и отрицательными числами; а
так же при раскрытии скобок и при переносе слагаемых из одной части уравнения в
другую;

·
— неправильный выбор
действий при решении текстовых задач;

·
-неправильное измерение
или построение угла с помощью транспортира, связанное с отсутствием умения
выбирать нужную шкалу;

·
-неправильное проведение
перпендикуляра к прямой или высот в тупоугольном треугольнике;

·
-умножение показателей при
умножении степеней с одинаковыми основаниями;

·
-“сокращение” дроби на
слагаемое;

·
-замена частного
десятичных дробей частным целых чисел в том случае, когда в делителе после
запятой меньше цифр, чем в делимом;

·
-сохранение знака
неравенства при делении обеих его частей на одно и тоже отрицательное число;

·
-неверное нахождение
значения функции по значению аргумента и ее графику;

·
-потеря корней при решении
тригонометрических уравнений;

·
-непонимание смысла
решения системы двух уравнений с двумя переменными как пары чисел;

·
-незнание определенных
программой формул (формулы корней квадратного уравнения, формул производной
частного и произведения, формул приведения, основных тригонометрических
тождеств и др.);

·
-приобретение посторонних
корней при решении иррациональных, показательных и логарифмических уравнений;

·
-погрешность в нахождении
координат вектора;

·
-погрешность в разложении
вектора по трем неколлинеарным векторам, отложенным от разных точек;

·
-неумение сформулировать
предложение, обратное данной теореме;

·
-ссылка при доказательстве
или обосновании решения на обратное утверждение, вместо прямого;

·
— использование вместо
коэффициента подобия обратного ему числа.

К негрубым ошибкам следует
отнести:

·
неточность формулировок,
определений, понятий, теорий, вызванная неполнотой охвата основных признаков
определяемого понятия или заменой одного — двух из этих признаков
второстепенными;

·
неточность графика;

·
нерациональный метод
решения задачи или недостаточно продуманный план ответа (нарушение логики,
подмена отдельных основных вопросов второстепенными);

·
нерациональные методы
работы со справочной и другой литературой;

неумение решать задачи, выполнять задания в
общем виде

·
неправильная постановка
вопроса к действию при решении задачи;

·
неверно сформулированный
ответ задачи;

·
неправильное списывание
данных чисел, знаков;

·
недоведение до конца
преобразований.

·
неправильная ссылка на
сочетательный и распределительный законы при вычислениях;

·
неправильное использование
в отдельных случаях наименований, например, обозначение единиц длины для единиц
площади и объема;

·
сохранение в окончательном
результате при вычислениях или преобразованиях выражений неправильной дроби или
сократимой дроби;

·
приведение алгебраических
дробей не к наиболее простому общему знаменателю;

·
случайные погрешности в
вычислениях при решении геометрических задач и выполнении тождественных
преобразований.

Недочетами являются:

·
нерациональные приемы
вычислений и преобразований; небрежное выполнение записей, чертежей, схем,
графиков.

Оценивание решения одной задачи, одного примера, ответа на один вопрос.

Это
необходимо, т. к. у доски, да часто и самостоятельно в классе учащиеся решают
одну задачу. К тому же умение оценивать решение одной задачи облегчает оценку
комплексного задания.

Решение
задачи обычно состоит из нескольких этапов:

а)
осмысление условия и цели задачи;

б)
возникновение плана решения;

в)
осуществление намеченного плана;

г)
проверка полученного результата.

Оценивая
выполненную работу, естественно учитывать результаты деятельности учащегося на
каждом этапе; правильность высказанной идеи, плана решения, а так же степень
осуществления этого плана при выставлении оценки нужно считать решающими. Т.о.,
при оценке решения задачи необходимо учитывать, насколько правильно учащийся
понял ее, высказал ли он плодотворную идею и как осуществил намеченный план
решения, какие навыки и умения показал, какие использовал знания.

Приведем пример.

Ученик
решает задачу, где важнейшим является составление системы уравнений. Если он
получил систему, но не довел решение до конца, то можно выставить “4”. Если же
основная задача состоит в решении полученной системы, то за ее составление
можно выставить “3”.

Оценка письменной работы по выполнению
вычислительных заданий и алгебраических преобразований

Оценка «5» ставится за безукоризненное выполнение письменной
работы, т.е.:

а) если решение всех примеров верное;

б) если все действия и преобразования
выполнены правильно, без ошибок; все записи хода решения расположены
последовательно, а также сделана проверка решения в тех случаях, когда это
требуется.

Оценка «4» ставится за работу, в которой допущена одна (негрубая)
ошибка или два-три недочета.

Оценка «3» ставится в следующих случаях:

а) если в работе имеется одна грубая ошибка и
не более одной негрубой ошибки;

б) при наличии одной грубой ошибки и
одного-двух недочетов;

в) при отсутствии грубых ошибок, но при
наличии от двух до четырех (негрубых) ошибок;

г) при наличии двух негрубых ошибок и не более
трех недочетов;

д) при отсутствии ошибок, но при наличии
четырех и более недочетов;

е) если неверно выполнено не более половины
объема всей работы.

Оценка «2» ставится, когда число ошибок превосходит норму, при
которой может быть выставлена положительная оценка, или если правильно
выполнено менее половины всей работы.

Оценка «1» ставится, если ученик совсем не выполнил работу.

Примечание. Оценка «5» может быть поставлена,
несмотря на наличие одного-двух недочетов, если ученик дал оригинальное решение
заданий, свидетельствующее о его хорошем математическом развитии.

Оценка письменной работы на решение текстовых
задач

Оценка «5» ставится в том случае, когда задача решена правильно:
ход решения задачи верен, все действия и преобразования выполнены верно и
рационально; в задаче, решаемой с вопросами или пояснениями к действиям, даны
точные и правильные формулировки; в задаче, решаемой с помощью уравнения, даны необходимые
пояснения; записи правильны, расположены последовательно, дан верный и
исчерпывающий ответ на вопросы задачи; сделана проверка решения (в тех случаях,
когда это требуется).

Оценка «4» ставится в том случае, если при правильном ходе
решения задачи допущена одна негрубая ошибка или два-три недочета.

Оценка «3» ставится в том случае, если ход решения правилен, но
допущены:

а) одна грубая ошибка и не более одной
негрубой;

б) одна грубая ошибка и не более двух
недочетов;

в) три-четыре негрубые ошибки при отсутствии
недочетов;

г) допущено не более двух негрубых ошибок и
трех недочетов;

д) более трех недочетов при отсутствии ошибок.

Оценка «2» ставится в том случае, когда число ошибок превосходит
норму, при которой может быть выставлена положительная оценка.

Оценка «1» ставится в том случае, если ученик не выполнил ни одного
задания работы.

Примечания:

1. Оценка «5» может быть поставлена
несмотря на наличие описки или недочета, если ученик дал оригинальное решение, свидетельствующее
о его хорошем математическом развитии.

2. Положительная оценка «3» может быть
выставлена ученику, выполнившему работу не полностью, если он безошибочно выполнил
более половины объема всей работы.

Оценка комбинированных письменных работ по
математике

Письменная работа по математике, подлежащая
оцениванию, может состоять из задач и примеров (комбинированная работа). В таком
случае преподаватель сначала дает предварительную оценку каждой части работы, а
затем общую, руководствуясь следующим:

а) если обе части работы оценены одинаково, то
эта оценка должна быть общей для всей работы в целом;

б) если оценки частей разнятся на один балл,
например, даны оценки «5» и «4» или «4» и «3» и т. п., то за работу в целом,
как правило, ставится балл, оценивающий основную часть работы;

в) если одна часть работы оценена баллом «5»,
а другая — баллом «3», то преподаватель может оценить такую работу в целом баллом
«4» при условии, что оценка «5» поставлена за основную часть работы;

г) если одна из частей работы оценена баллом
«5» или «4», а другая — баллом «2» или «1», то преподаватель может оценить всю
работу баллом «3» при условии, что высшая из двух данных оценок поставлена за
основную часть работы.

Примечание. Основной считается та часть работы, которая включает
больший по объему или наиболее важный по значению материал по изучаемым темам
программы.

Оценка текущих письменных работ

При оценке повседневных обучающих работ по
математике учитель руководствуется указанными нормами оценок, но учитывает
степень самостоятельности выполнения работ учащимися.

Обучающие письменные работы, выполненные
учащимися вполне самостоятельно с применением ранее изученных и хорошо закрепленных
знаний, оцениваются так же, как и контрольные работы.

Обучающие письменные работы, выполненные
вполне самостоятельно, на только что изученные и недостаточно закрепленные правила,
могут оцениваться менее строго.

Письменные работы, выполненные в классе с предварительным
разбором их под руководством учителя, оцениваются более строго.

Домашние письменные работы оцениваются так же,
как классная работа обучающего характера.

В соответствии с особенностями математики как
учебного предмета оценки за письменные работы имеют большее значение, чем
оценки за устные ответы и другие виды работ.

Источник

Содержание

Приложение А. Погрешности вычислений
Абсолютная и относительная погрешности
Источники погрешностей
Математическая модель задачи является неточной
Ошибки в исходных данных
Вычислительные ошибки (ошибки округления)
Вычислительные ошибки
Представление чисел с плавающей точкой
Погрешность округления
Погрешность арифметических действий над приближенными числами
Относительная погрешность
Содержание
Определение погрешности
Классификация погрешностей
По форме представления
По причине возникновения

Приложение А. Погрешности вычислений

Абсолютная и относительная погрешности

Точность полученного в результате вычисления результата определяется погрешностью вычислений. Различают два вида погрешностей – абсолютную и относительную.

Абсолютная погрешность некоторого числа равна разности между его истинным значением и приближенным значением, полученным в результате вычисления или измерения:

(А.1)

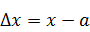
где а – приближенное значение числа х.

Относительная погрешность – это отношение абсолютной погрешности к приближенному значению числа:

(А.2)

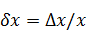
Истинное значение величины х обычно неизвестно. Имеется лишь приближенное значение а и нужно найти его предельную погрешность . В дальнейшем значение принимается в качестве абсолютной погрешности приближенного числа а. Тогда истинное значение х находится в интервале .

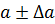
Источники погрешностей

Рассмотрим различные причины возникновения погрешностей.

Математическая модель задачи является неточной

Погрешность возникает из-за того, что сам численный метод или математическая модель является лишь приближением к точному методу (например, дифференцирование). Кроме того, любая математическая модель или метод могут внести существенные погрешности, если в ней не учтены какие-то особенности рассматриваемой задачи. Модель может прекрасно работать в одних условиях и быть совершенно неприемлемой в других. Такую погрешность называют также методической. Она всегда имеет место, даже при абсолютно точных данных и абсолютно точных вычислениях. В большинстве случаев погрешность численного метода можно уменьшить до требуемого значения за счет изменения параметров метода (например, уменьшением шага дискретизации, или увеличением количества итераций).

Ошибки в исходных данных

Исходные данные задачи часто являются основным источником погрешностей. Ошибки такого типа неизбежны и проявляются в любых реальных задачах, поскольку любое измерение может быть проведено с только какой-то предельной точностью. Вместе с погрешностями, вносимыми математической моделью, их называют неустранимыми погрешностями, поскольку они не могут быть уменьшены ни до начала решения задачи, ни в процессе ее решения.

Следует стремиться к тому, чтобы все исходные данные были примерно одинаковой точности. Сильное уточнение одних исходных данных при наличии больших погрешностей в других не приводит к повышению точности конечных результатов. Если какие-то отдельные точки данных (измерения) явно ошибочные, их можно исключить из вычислений.

Вычислительные ошибки (ошибки округления)

Ошибки этого типа проявляются из-за дискретной (а не непрерывной) формы представления величин в компьютере. Вычислительные ошибки можно свести к минимуму продуманно организовывая алгоритмы.

Вычислительные ошибки

Рассмотрим подробнее вычислительные ошибки. Допустим, исходные данные не имеют погрешности, но поскольку место в памяти компьютера, отведенное на хранение чисел, ограничено, и соответственно ограничена точность представления чисел, возникновение вычислительных ошибок неизбежно.

Представление чисел с плавающей точкой

Для хранения целых чисел (int, long, unsigned int и т.д.) обычно отводится 4 байта памяти, что позволяет представлять целые числа, находящиеся примерно в диапазоне от .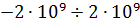

В вычислениях чаще используются вещественные числа (float, double). Такие числа представляются в компьютере в форме с плавающей точкой, и хранятся в логарифмическом виде – мантисса и порядок:

(А.3)

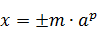
где m – мантисса, p – порядок, а – основание степени.

Мантисса записывается в нормализованной форме – с фиксированной точкой, подразумеваемой после первой значащей цифры. Нормализованной формой числа с плавающей точкой называется такая форма, в которой мантисса десятичного числа (без учёта знака) принимает значения , а мантисса двоичного числа принимает значения от .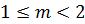

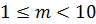
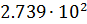
Например, число 273.9 можно представить в виде или в компьютерном представлении 2.739E+02.

В таблице А.1 приводится диапазон допустимых значений и другие параметры для чисел с плавающей точкой одинарной (float) и двойной (double) точности.

Точность	Одинарная	Двойная
Размер (байты)	4	8
Наименьшее значение	1.2·10 −38	2.3·10 −308
Наибольшее значение	3.4×10 +38	1.7×10 +308
Размеры степени и мантиссы (биты)	8-23	11-52

Таблица A.1. Диапазон чисел, представимых в формате с плавающей точкой

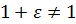
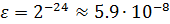
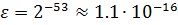
Для чисел с плавающей точкой существует понятие машинного эпсилон – наименьшего положительного число ε такого, что . Например, для числа с одинарной точностью 1 + 0.00000001 = 1. Для одинарной точности , а для двойной точности .

Погрешность округления

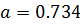
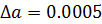
При вычислениях с помощью компьютера неизбежны погрешности округлений, связанные с ограниченностью хранимых разрядов мантиссы. Для приближенного числа, полученного в результате округления, абсолютная погрешность принимается равной половине единицы последнего разряда числа. Например, значение могло быть получено округлением чисел 0.73441, 0.73353 и др. При этом . При простом отбрасывании лишних разрядов эта погрешность увеличивается вдвое.

Перевод чисел из одной системы счисления в другую также может быть источником погрешности из-за того, что основание одной системы счисления не является степенью основания другой (например, 10 и 2). Это может привести к тому, что в новой системе счисления число невозможно представить абсолютно точно, например:

Погрешность арифметических действий над приближенными числами

При выполнении операций над приближенными числами можно оценить предельную погрешность результата в зависимости от выполняемой операции. При умножении или делении чисел друг на друга их относительные погрешности складываются:

, (А.4)

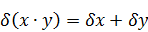
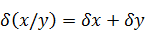
При возведении в степень приближенного числа его относительная погрешность умножается на показатель степени:

(А.5)

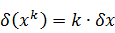
При сложении или вычитании чисел их абсолютные погрешности складываются:

(А.6)

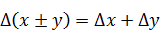
Относительная погрешность суммы положительных слагаемых вычисляется как:

. (А.7)

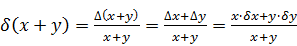
Отсюда следует, что относительная погрешность суммы нескольких чисел одного и того же знака, заключена между наименьшей и наибольшей из относительных погрешностей слагаемых:

. (А.8)

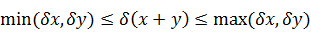
На практике для оценки погрешности при сложении чисел обычно используют максимальную погрешность .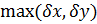

При сложении погрешность будет сильно завесить от абсолютных величин складываемых чисел. Рассмотрим пример сложения двух чисел с одинаковым количеством значащих цифр, но разных по абсолютному значению:

1234 + 0.005678 = 1234.00005678

или в компьютерном представлении:

1.234Е+03 + 5.678Е-03 = 1.234005678Е+03

После сложения количество значащих цифр равно 10. Число с одинарной точностью (float) позволяет хранить только 8 значащих цифр, то есть на самом деле число будет равно 1.2340056Е+03. Две значащие цифры потерялись в процессе сложения. Потеря точности здесь возникает из-за того, что при прибавлении к большому числу малых чисел результат сложения выходит за пределы точности при округлении. Для того чтобы уменьшить погрешность вычислений, нужно складывать числа в порядке возрастания их абсолютной величины. Таким образом можно минимизировать абсолютную величину промежуточной погрешности при каждом сложении.

Рассмотрим теперь вычитание чисел (сложение чисел разного знака, или вычитание чисел одного знака). В соответствии с выражением (А.7) относительная погрешность может быть очень большой в случае, если числа близки между собой, так как даже при малых погрешностях 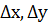результат их сложения в знаменателе может быть очень малым. Чтобы уменьшить погрешность при вычитании, необходимо строить вычислительные алгоритмы таким образом, чтобы избегать вычитания близких чисел.

Таким образом, можно сделать вывод, что сложение и вычисление являются плохо обусловленными (неустойчивыми) операторами, так как при некоторых данных даже небольшая погрешность в исходных данных может привести к большой погрешности результата. Уменьшить погрешность можно за счет правильной последовательности операций. Из-за погрешности округления в машинной арифметике важен порядок выполнения операций, и известные из алгебры законы коммутативности (и дистрибутивности) здесь не всегда выполняются.

Источник

Относительная погрешность

Погре́шность измере́ния — оценка отклонения величины измеренного значения величины от её истинного значения. Погрешность измерения является характеристикой (мерой) точности измерения.

Поскольку выяснить с абсолютной точностью истинное значение любой величины невозможно, то невозможно и указать величину отклонения измеренного значения от истинного. (Это отклонение принято называть ошибкой измерения. В ряде источников, например, в БСЭ, термины ошибка измерения и погрешность измерения используются как синонимы.) Возможно лишь оценить величину этого отклонения, например, при помощи статистических методов. При этом за истинное значение принимается среднестатистическое значение, полученное при статистической обработке результатов серии измерений. Это полученное значение не является точным, а лишь наиболее вероятным. Поэтому в измерениях необходимо указывать, какова их точность. Для этого вместе с полученным результатом указывается погрешность измерений. Например, запись T=2.8±0.1 c. означает, что истинное значение величины T лежит в интервале от 2.7 с. до 2.9 с. некоторой оговоренной вероятностью (см. доверительный интервал, доверительная вероятность, стандартная ошибка).

В 2006 году на международном уровне был принят новый документ, диктующий условия проведения измерений и установивший новые правила сличения государственных эталонов. Понятие «погрешность» стало устаревать, вместо него было введено понятие «неопределенность измерений».

Содержание

Определение погрешности

В зависимости от характеристик измеряемой величины для определения погрешности измерений используют различные методы.

Метод Корнфельда, заключается в выборе доверительного интервала в пределах от минимального до максимального результата измерений, и погрешность как половина разности между максимальным и минимальным результатом измерения:

Средняя квадратическая погрешность:

Средняя квадратическая погрешность среднего арифметического:

Классификация погрешностей

По форме представления

Абсолютная погрешность — ΔX является оценкой абсолютной ошибки измерения. Величина этой погрешности зависит от способа её вычисления, который, в свою очередь, определяется распределением случайной величины X_meas . При этом равенство:

где X_true — истинное значение, а X_meas — измеренное значение, должно выполняться с некоторой вероятностью близкой к 1. Если случайная величина X_meas распределена по нормальному закону, то, обычно, за абсолютную погрешность принимают её среднеквадратичное отклонение. Абсолютная погрешность измеряется в тех же единицах измерения, что и сама величина.

Относительная погрешность — отношение абсолютной погрешности к тому значению, которое принимается за истинное:

Относительная погрешность является безразмерной величиной, либо измеряется в процентах.

Приведенная погрешность — относительная погрешность, выраженная отношением абсолютной погрешности средства измерений к условно принятому значению величины, постоянному во всем диапазоне измерений или в части диапазона. Вычисляется по формуле

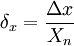
где X_n — нормирующее значение, которое зависит от типа шкалы измерительного прибора и определяется по его градуировке:

— если шкала прибора односторонняя, т.е. нижний предел измерений равен нулю, то X_n определяется равным верхнему пределу измерений;
— если шкала прибора двухсторонняя, то нормирующее значение равно ширине диапазона измерений прибора.

Приведенная погрешность — безразмерная величина (может измеряться в процентах).

По причине возникновения

Инструментальные / приборные погрешности — погрешности, которые определяются погрешностями применяемых средств измерений и вызываются несовершенством принципа действия, неточностью градуировки шкалы, ненаглядностью прибора.
Методические погрешности — погрешности, обусловленные несовершенством метода, а также упрощениями, положенными в основу методики.
Субъективные / операторные / личные погрешности — погрешности, обусловленные степенью внимательности, сосредоточенности, подготовленности и другими качествами оператора.

В технике применяют приборы для измерения лишь с определенной заранее заданной точностью – основной погрешностью, допускаемой нормали в нормальных условиях эксплуатации для данного прибора.

Если прибор работает в условиях, отличных от нормальных, то возникает дополнительная погрешность, увеличивающая общую погрешность прибора. К дополнительным погрешностям относятся: температурная, вызванная отклонением температуры окружающей среды от нормальной, установочная, обусловленная отклонением положения прибора от нормального рабочего положения, и т.п. За нормальную температуру окружающего воздуха принимают 20°С, за нормальное атмосферное давление 01,325 кПа.

Обобщенной характеристикой средств измерения является класс точности, определяемый предельными значениями допускаемых основной и дополнительной погрешностей, а также другими параметрами, влияющими на точность средств измерения; значение параметров установлено стандартами на отдельные виды средств измерений. Класс точности средств измерений характеризует их точностные свойства, но не является непосредственным показателем точности измерений, выполняемых с помощью этих средств, так как точность зависит также от метода измерений и условий их выполнения. Измерительным приборам, пределы допускаемой основной погрешности которых заданы в виде приведенных основных (относительных) погрешностей, присваивают классы точности, выбираемые из ряда следующих чисел: (1; 1,5; 2,0; 2,5; 3,0; 4,0; 5,0; 6,0)*10n, где n = 1; 0; -1; -2 и т.д.

Источник

Точность цифрового моделирования

В реальности мы будем иметь:

Моделирование сопровождается
алгоритмической и вычислительной
ошибками:

1) Алгоритмическая ошибка – это
методическая ошибка. Связана с заменой
ДУ на разностные уравнения (дискретизация).

2) Вычислительная ошибка: связана с
округлением величин, с неточным заданием
коэффициентов.

Алгоритмическая ошибка

Для любого типа цифрового фильтра
ограничивается сверху значением:

;

— максимальная частота в спектре сигнала

Т – шаг
дискретизации.

и R
определяются сигналом и устройством.

Значит: для уменьшения алгоритмической
ошибки надо уменьшать шаг дискретизации
Т.

Вычислительная ошибка

Если задано время реализации

,
то при увеличении Т
количество математических операций
уменьшается, а, значит, уменьшается
вычислительная ошибка.

Для нахождения

необходимо исследовать суммарную
погрешность на экстремум, что не всегда
удобно.

Практически делается следующее.

Исследуется выходная решетчатая функция

при различных Т. При этом шаг дискретизации
то увеличивают, то уменьшают. Далее
выбирают шаги дискретизации, при
которых функции

в определенные моменты времени совпадают.
Из этих двух шагов выбирают больший.

Цифровое моделирование нелинейных узлов р/устройств

Нелинейные узлы делятся на 4 части:

Безынерционные
нелинейные звенья (БНЗ).

Цифровое моделирование таких узлов
связано с преобразованием входного
сигнала

в выходной

в соответствии с характеристикой
нелинейности:

Если

задана аналитически, моделирование
осуществляется путем вычисления по
формуле; если

задана графически или таблицей, то
моделирование осуществляется с помощью
таблиц.

Нелинейные
инерционные функциональные разомкнутые
звенья.

Это звенья, в которых можно выделить
развязанные относительно друг друга
линейные инерционные и безынерционные
звенья.

— передаточные функции линейных
инерционных звеньев.

Нелинейные
инерционные функциональные замкнутые
звенья.

К таким замкнутым звеньям сводятся
большинство следящих устройств.

Нелинейные
инерционные нефункциональные звенья.

Способ моделирования – с помощью
нелинейных ДУ.

Рассмотрим моделирование нелинейных
инерционных функциональных замкнутых
звеньев.

Пусть звено с

— это фильтр первого порядка с постоянными
коэффициентами

Пусть

.

Тогда:

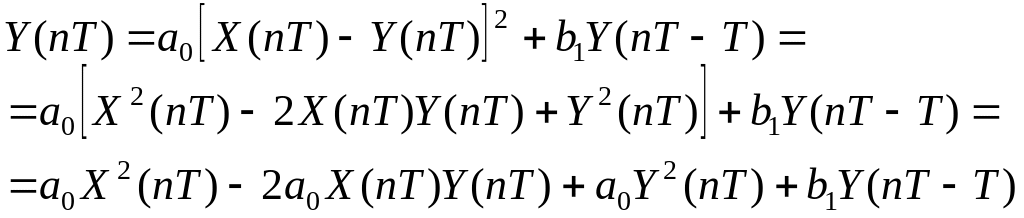
В каждом такте моделирования надо решать
нелинейное относительно

уравнение. Это всегда имеет место при
моделировании замкнутых функциональных
нелинейных узлов.

Для упрощения вычислений используют
вычисленные в предыдущем такте значения
Y.
Получим:

В модель вводится блок

.
Введение этого блока приводит к
дополнительной ошибке, которую можно
сделать сколь угодно малой, уменьшая
Т. Получаем:

Одно и то же устройство может принадлежать
к любому из 4-ех классов.

Р
ассмотрим
амплитудный детектор.

1. Как устройство первого класса АД
моделируется, если моделируются его
функциональные преобразования (формально
описывается преобразование сигнала).

Недостаток данной цифровой модели:
необходимость помнить всю реализацию
входного сигнала от

до

.

2. Если надо проанализировать возможные
искажения огибающей сигнала, вызванные,
допустим, неправильным выбором постоянной
времени фильтра, то детектор моделируется
как устройство 2-ого класса. В этом случае
добавляется фильтр с передаточной
функцией

и этот фильтр – цифровая модель RC-цепи.

3. Если при моделировании надо учесть
реакцию нагрузки на диод, то детектор
моделируется как устройство 3-его класса.

— температурный потенциал

—
тепловая энергия

—
заряд

;

Переход от тока диода к выходному
напряжению осуществляется с помощью
линейного инерционного звена, имеющего
передаточную функцию, определяемую
нагрузкой детектора:

4. Если требуется учесть инерционные
свойства диода, то АД моделируется как
4-ый класс. Решение – решение нелинейного
дифференциального уравнения.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник