Crc ошибки сети

Introduction

This document describes details surrounding Cyclic Redundancy Check (CRC) errors observed on interface counters and statistics of Cisco Nexus switches.

Prerequisites

Requirements

Cisco recommends that you understand the basics of Ethernet switching and the Cisco NX-OS Command Line Interface (CLI). For more information, refer to one of these applicable documents:

• Cisco Nexus 9000 NX-OS Fundamentals Configuration Guide, Release 10.2(x)
• Cisco Nexus 9000 Series NX-OS Fundamentals Configuration Guide, Release 9.3(x)
• Cisco Nexus 9000 Series NX-OS Fundamentals Configuration Guide, Release 9.2(x)
• Cisco Nexus 9000 Series NX-OS Fundamentals Configuration Guide, Release 7.x

• Troubleshooting Ethernet

Components Used

The information in this document is based on these software and hardware versions: 

• Nexus 9000 series switches starting from NX-OS software release 9.3(8) 

• Nexus 3000 series switches starting from NX-OS software release 9.3(8) 

The information in this document was created from devices in a specific lab environment. All of the devices used in this document started with a cleared (default) configuration. If your network is live, ensure that you understand the potential impact of any command.

The information in this document was created from the devices in a specific lab environment. All of the devices used in this document started with a cleared (default) configuration. If your network is live, ensure that you understand the potential impact of any command.

Background Information

This document describes details surrounding Cyclic Redundancy Check (CRC) errors observed on interface counters on Cisco Nexus series switches. This document describes what a CRC is, how it is used in the Frame Check Sequence (FCS) field of Ethernet frames, how CRC errors manifest on Nexus switches, how CRC errors interact in Store-and-Forward switching and Cut-Through switching scenarios, the most likely root causes of CRC errors, and how to troubleshoot and resolve CRC errors. 

Applicable Hardware

The information in this document is applicable to all Cisco Nexus Series switches. Some of the information in this document can also be applicable to other Cisco routing and switching platforms, such as Cisco Catalyst routers and switches.

CRC Definition

A CRC is an error detection mechanism commonly used in computer and storage networks to identify data changed or corrupted during transmission. When a device connected to the network needs to transmit data, the device runs a computation algorithm based on cyclic codes against the data that results in a fixed-length number. This fixed-length number is called the CRC value, but colloquially, it is often called the CRC for short. This CRC value is appended to the data and transmitted through the network towards another device. This remote device runs the same cyclic code algorithm against the data and compares the resulting value with the CRC appended to the data. If both values match, then the remote device assumes the data was transmitted across the network without being corrupted. If the values do not match, then the remote device assumes the data was corrupted during transmission across the network. This corrupted data cannot be trusted and is discarded.

CRCs are used for error detection across multiple computer networking technologies, such as Ethernet (both wired and wireless variants), Token Ring, Asynchronous Transfer Mode (ATM), and Frame Relay. Ethernet frames have a 32-bit Frame Check Sequence (FCS) field at the end of the frame (immediately after the payload of the frame) where a 32-bit CRC value is inserted. 

For example, consider a scenario where two hosts named Host-A and Host-B are directly connected to each other through their Network Interface Cards (NICs). Host-A needs to send the sentence “This is an example” to Host-B over the network. Host-A crafts an Ethernet frame destined to Host-B with a payload of “This is an example” and calculates that the CRC value of the frame is a hexadecimal value of 0xABCD. Host-A inserts the CRC value of 0xABCD into the FCS field of the Ethernet frame, then transmits the Ethernet frame out of Host-A’s NIC towards Host-B.

When Host-B receives this frame, it will calculate the CRC value of the frame with the use of the exact same algorithm as Host-A. Host-B calculates that the CRC value of the frame is a hexadecimal value of 0xABCD, which indicates to Host-B that the Ethernet frame was not corrupted while the frame was transmitted to Host-B. 

CRC Error Definition

A CRC error occurs when a device (either a network device or a host connected to the network) receives an Ethernet frame with a CRC value in the FCS field of the frame that does not match the CRC value calculated by the device for the frame. 

This concept is best demonstrated through an example. Consider a scenario where two hosts named Host-A and Host-B are directly connected to each other through their Network Interface Cards (NICs). Host-A needs to send the sentence “This is an example” to Host-B over the network. Host-A crafts an Ethernet frame destined to Host-B with a payload of “This is an example” and calculates that the CRC value of the frame is the hexadecimal value 0xABCD. Host-A inserts the CRC value of 0xABCD into the FCS field of the Ethernet frame, then transmits the Ethernet frame out of Host-A’s NIC towards Host-B.

However, damage on the physical media connecting Host-A to Host-B corrupts the contents of the frame such that the sentence within the frame changes to “This was an example” instead of the desired payload of “This is an example”. 

When Host-B receives this frame, it will calculate the CRC value of the frame including the corrupted payload. Host-B calculates that the CRC value of the frame is a hexadecimal value of 0xDEAD, which is different from the 0xABCD CRC value within the FCS field of the Ethernet frame. This difference in CRC values tells Host-B that the Ethernet frame was corrupted while the frame was transmitted to Host-B. As a result, Host-B cannot trust the contents of this Ethernet frame, so it will drop it. Host-B will usually increment some sort of error counter on its Network Interface Card (NIC) as well, such as the “input errors”, “CRC errors”, or “RX errors” counters. 

Common Symptoms of CRC Errors

CRC errors typically manifest themselves in one of two ways: 

1. Incrementing or non-zero error counters on interfaces of network-connected devices.
2. Packet/Frame loss for traffic traversing the network due to network-connected devices dropping corrupted frames.

These errors manifest themselves in slightly different ways depending on the device you are working with. These sub-sections go into detail for each type of device. 

Received Errors on Windows Hosts

CRC errors on Windows hosts typically manifest as a non-zero Received Errors counter displayed in the output of the netstat -e command from the Command Prompt. An example of a non-zero Received Errors counter from the Command Prompt of a Windows host is here: 

>netstat -e
Interface Statistics 
                           Received            Sent 
Bytes                    1116139893      3374201234 
Unicast packets           101276400        49751195 
Non-unicast packets               0               0 
Discards                          0               0 
Errors                        47294               0 
Unknown protocols                 0 

The NIC and its respective driver must support accounting of CRC errors received by the NIC in order for the number of Received Errors reported by the netstat -e command to be accurate. Most modern NICs and their respective drivers support accurate accounting of CRC errors received by the NIC.

RX Errors on Linux Hosts 

CRC errors on Linux hosts typically manifest as a non-zero “RX errors” counter displayed in the output of the ifconfig command. An example of a non-zero RX errors counter from a Linux host is here: 

$ ifconfig eth0
eth0: flags=4163<UP,BROADCAST,RUNNING,MULTICAST>  mtu 1500 
        inet 192.0.2.10  netmask 255.255.255.128  broadcast 192.0.2.255 
        inet6 fe80::10  prefixlen 64  scopeid 0x20<link> 
        ether 08:62:66:be:48:9b  txqueuelen 1000  (Ethernet) 
        RX packets 591511682  bytes 214790684016 (200.0 GiB) 
        RX errors 478920  dropped 0  overruns 0  frame 0 
        TX packets 85495109  bytes 288004112030 (268.2 GiB) 
        TX errors 0  dropped 0 overruns 0  carrier 0  collisions 0 

CRC errors on Linux hosts can also manifest as a non-zero “RX errors” counter displayed in the output of ip -s link show command. An example of a non-zero RX errors counter from a Linux host is here: 

$ ip -s link show eth0
2: eth0: <BROADCAST,MULTICAST,UP,LOWER_UP> mtu 1500 qdisc mq state UP mode DEFAULT group default qlen 1000 
    link/ether 08:62:66:84:8f:6d brd ff:ff:ff:ff:ff:ff 
    RX: bytes  packets  errors  dropped overrun mcast 
    32246366102 444908978 478920       647     0       419445867 
    TX: bytes  packets  errors  dropped carrier collsns 
    3352693923 30185715 0       0       0       0 
    altname enp11s0 

The NIC and its respective driver must support accounting of CRC errors received by the NIC in order for the number of RX Errors reported by the ifconfig or ip -s link show commands to be accurate. Most modern NICs and their respective drivers support accurate accounting of CRC errors received by the NIC.

CRC Errors on Network Devices

Network devices operate in one of two forwarding modes — Store-and-Forward forwarding mode, and Cut-Through forwarding mode. The way a network device handles a received CRC error differs depending on its forwarding modes. The subsections here will describe the specific behavior for each forwarding mode.

Input Errors on Store-and-Forward Network Devices

When a network device operating in a Store-and-Forward forwarding mode receives a frame, the network device will buffer the entire frame (“Store”) before you validate the frame’s CRC value, make a forwarding decision on the frame, and transmit the frame out of an interface (“Forward”). Therefore, when a network device operating in a Store-and-Forward forwarding mode receives a corrupted frame with an incorrect CRC value on a specific interface, it will drop the frame and increment the “Input Errors” counter on the interface.

In other words, corrupt Ethernet frames are not forwarded by network devices operating in a Store-and-Forward forwarding mode; they are dropped on ingress.

Cisco Nexus 7000 and 7700 Series switches operate in a Store-and-Forward forwarding mode. An example of a non-zero Input Errors counter and a non-zero CRC/FCS counter from a Nexus 7000 or 7700 Series switch is here: 

switch# show interface
<snip> 
Ethernet1/1 is up 
  RX 
    241052345 unicast packets  5236252 multicast packets  5 broadcast packets 
    245794858 input packets  17901276787 bytes 
    0 jumbo packets  0 storm suppression packets 
    0 runts  0 giants  579204 CRC/FCS  0 no buffer 
    579204 input error  0 short frame  0 overrun   0 underrun  0 ignored 
    0 watchdog  0 bad etype drop  0 bad proto drop  0 if down drop 
    0 input with dribble  0 input discard 
    0 Rx pause 

CRC errors can also manifest themselves as a non-zero “FCS-Err” counter in the output of show interface counters errors. The «Rcv-Err» counter in the output of this command will also have a non-zero value, which is the sum of all input errors (CRC or otherwise) received by the interface. An example of this is shown here: 

switch# show interface counters errors
<snip> 
-------------------------------------------------------------------------------- 
Port          Align-Err    FCS-Err   Xmit-Err    Rcv-Err  UnderSize OutDiscards 
-------------------------------------------------------------------------------- 
Eth1/1                0     579204          0     579204          0           0 

Input and Output Errors on Cut-Through Network Devices

When a network device operating in a Cut-Through forwarding mode starts to receive a frame, the network device will make a forwarding decision on the frame’s header and begin transmitting the frame out of an interface as soon as it receives enough of the frame to make a valid forwarding decision. As frame and packet headers are at the beginning of the frame, this forwarding decision is usually made before the payload of the frame is received. 

The FCS field of an Ethernet frame is at the end of the frame, immediately after the frame’s payload. Therefore, a network device operating in a Cut-Through forwarding mode will already have started transmitting the frame out of another interface by the time it can calculate the CRC of the frame. If the CRC calculated by the network device for the frame does not match the CRC value present in the FCS field, that means the network device forwarded a corrupted frame into the network. When this happens, the network device will increment two counters: 

1. The “Input Errors” counter on the interface where the corrupted frame was originally received. 
2. The “Output Errors” counter on all interfaces where the corrupted frame was transmitted. For unicast traffic, this will typically be a single interface – however, for broadcast, multicast, or unknown unicast traffic, this could be one or more interfaces.

An example of this is shown here, where the output of the show interface command indicates multiple corrupted frames were received on Ethernet1/1 of the network device and transmitted out of Ethernet1/2 due to the Cut-Through forwarding mode of the network device: 

switch# show interface
<snip> 
Ethernet1/1 is up 
  RX 
    46739903 unicast packets  29596632 multicast packets  0 broadcast packets 
    76336535 input packets  6743810714 bytes 
    15 jumbo packets  0 storm suppression bytes 
    0 runts  0 giants  47294 CRC  0 no buffer 
    47294 input error  0 short frame  0 overrun   0 underrun  0 ignored 
    0 watchdog  0 bad etype drop  0 bad proto drop  0 if down drop 
    0 input with dribble  0 input discard 
    0 Rx pause 
  Ethernet1/2 is up 
  TX 
    46091721 unicast packets  2852390 multicast packets  102619 broadcast packets 
    49046730 output packets  3859955290 bytes 
    50230 jumbo packets 
    47294 output error  0 collision  0 deferred  0 late collision 
    0 lost carrier  0 no carrier  0 babble  0 output discard 
    0 Tx pause 

CRC errors can also manifest themselves as a non-zero “FCS-Err” counter on the ingress interface and non-zero «Xmit-Err» counters on egress interfaces in the output of show interface counters errors. The «Rcv-Err» counter on the ingress interface in the output of this command will also have a non-zero value, which is the sum of all input errors (CRC or otherwise) received by the interface. An example of this is shown here: 

switch# show interface counters errors 
<snip> 
-------------------------------------------------------------------------------- 
Port          Align-Err    FCS-Err   Xmit-Err    Rcv-Err  UnderSize OutDiscards 
-------------------------------------------------------------------------------- 
Eth1/1                0      47294          0      47294          0           0 
Eth1/2                0          0      47294          0          0           0  

The network device will also modify the CRC value in the frame’s FCS field in a specific manner that signifies to upstream network devices that this frame is corrupt. This behavior is known as “stomping” the CRC. The precise manner in which the CRC is modified varies from one platform to another, but generally, it involves inverting the current CRC value present in the frame’s FCS field. An example of this is here: 

Original CRC: 0xABCD (1010101111001101) 
Stomped CRC:  0x5432 (0101010000110010) 

As a result of this behavior, network devices operating in a Cut-Through forwarding mode can propagate a corrupt frame throughout a network. If a network consists of multiple network devices operating in a Cut-Through forwarding mode, a single corrupt frame can cause input error and output error counters to increment on multiple network devices within your network. 

Trace and Isolate CRC Errors

The first step in order to identify and resolve the root cause of CRC errors is isolating the source of the CRC errors to a specific link between two devices within your network. One device connected to this link will have an interface output errors counter with a value of zero or is not incrementing, while the other device connected to this link will have a non-zero or incrementing interface input errors counter. This suggests that traffic egresses the interface of one device intact is corrupted at the time of the transmission to the remote device, and is counted as an input error by the ingress interface of the other device on the link.

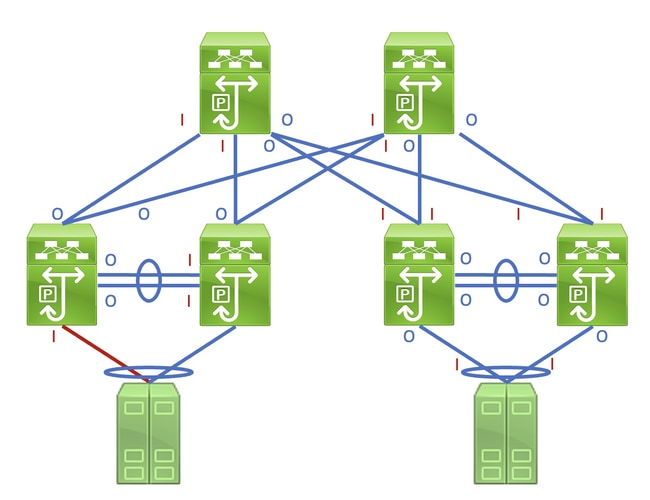
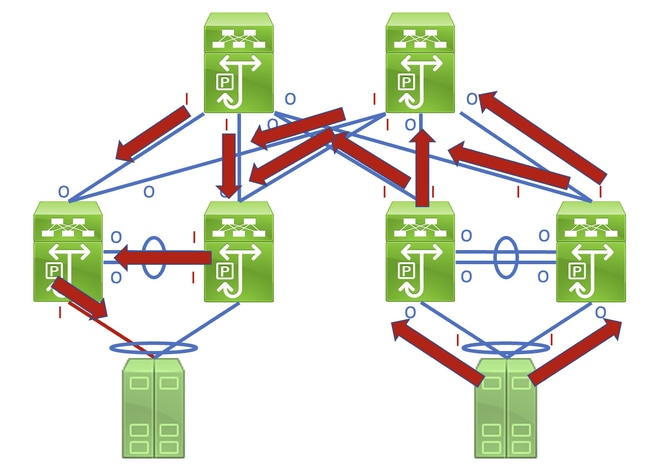
Identifying this link in a network consisting of network devices operating in a Store-and-Forward forwarding mode is a straightforward task. However, identifying this link in a network consisting of network devices operating in a Cut-Through forwarding mode is more difficult, as many network devices will have non-zero input and output error counters. An example of this phenomenon can be seen in the topology here, where the link highlighted in red is damaged such that traffic traversing the link is corrupted. Interfaces labeled with a red «I» indicate interfaces that could have non-zero input errors, while interfaces labeled with a blue «O» indicate interfaces that could have non-zero output errors.

Identifying the faulty link requires you to recursively trace the «path» corrupted frames follow in the network through non-zero input and output error counters, with non-zero input errors pointing upstream towards the damaged link in the network. This is demonstrated in the diagram here.

A detailed process for tracing and identifying a damaged link is best demonstrated through an example. Consider the topology here:

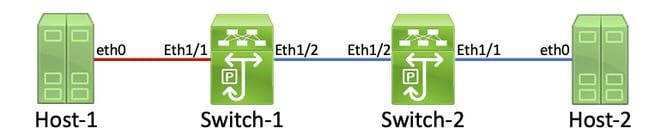
In this topology, interface Ethernet1/1 of a Nexus switch named Switch-1 is connected to a host named Host-1 through Host-1’s Network Interface Card (NIC) eth0. Interface Ethernet1/2 of Switch-1 is connected to a second Nexus switch, named Switch-2, through Switch-2’s interface Ethernet1/2. Interface Ethernet1/1 of Switch-2 is connected to a host named Host-2 through Host-2’s NIC eth0.

The link between Host-1 and Switch-1 through Switch-1’s Ethernet1/1 interface is damaged, causing traffic that traverses the link to be intermittently corrupted. However, we do not yet know that this link is damaged. We must trace the path the corrupted frames leave in the network through non-zero or incrementing input and output error counters to locate the damaged link in this network.

In this example, Host-2’s NIC reports that it is receiving CRC errors.

Host-2$ ip -s link show eth0
2: eth0: <BROADCAST,MULTICAST,UP,LOWER_UP> mtu 1500 qdisc mq state UP mode DEFAULT group default qlen 1000 
    link/ether 00:50:56:84:8f:6d brd ff:ff:ff:ff:ff:ff 
    RX: bytes  packets  errors  dropped overrun mcast 
    32246366102 444908978 478920       647     0       419445867 
    TX: bytes  packets  errors  dropped carrier collsns 
    3352693923 30185715 0       0       0       0 
    altname enp11s0 

You know that Host-2’s NIC connects to Switch-2 via interface Ethernet1/1. You can confirm that interface Ethernet1/1 has a non-zero output errors counter with the show interface command.

Switch-2# show interface
<snip>
Ethernet1/1 is up
admin state is up, Dedicated Interface
    RX
      30184570 unicast packets  872 multicast packets  273 broadcast packets
      30185715 input packets  3352693923 bytes
      0 jumbo packets  0 storm suppression bytes
      0 runts  0 giants 0 CRC  0 no buffer
      0 input error  0 short frame  0 overrun   0 underrun  0 ignored
      0 watchdog  0 bad etype drop  0 bad proto drop  0 if down drop
      0 input with dribble  0 input discard
      0 Rx pause
    TX
      444907944 unicast packets  932 multicast packets  102 broadcast packets
      444908978 output packets  32246366102 bytes
      0 jumbo packets
      478920 output error  0 collision  0 deferred  0 late collision
      0 lost carrier  0 no carrier  0 babble  0 output discard
      0 Tx pause

Since the output errors counter of interface Ethernet1/1 is non-zero, there is most likely another interface of Switch-2 that has a non-zero input errors counter. You can use the show interface counters errors non-zero command in order to identify if any interfaces of Switch-2 have a non-zero input errors counter.

Switch-2# show interface counters errors non-zero
<snip>
--------------------------------------------------------------------------------
Port          Align-Err    FCS-Err   Xmit-Err    Rcv-Err  UnderSize OutDiscards
--------------------------------------------------------------------------------
Eth1/1                0          0     478920          0          0           0
Eth1/2                0     478920          0     478920          0           0

--------------------------------------------------------------------------------
Port         Single-Col  Multi-Col   Late-Col  Exces-Col  Carri-Sen       Runts
--------------------------------------------------------------------------------

--------------------------------------------------------------------------------
Port          Giants SQETest-Err Deferred-Tx IntMacTx-Er IntMacRx-Er Symbol-Err
--------------------------------------------------------------------------------

--------------------------------------------------------------------------------
Port         InDiscards
--------------------------------------------------------------------------------

You can see that Ethernet1/2 of Switch-2 has a non-zero input errors counter. This suggests that Switch-2 receives corrupted traffic on this interface. You can confirm which device is connected to Ethernet1/2 of Switch-2 through the Cisco Discovery Protocol (CDP) or Link Local Discovery Protocol (LLDP) features. An example of this is shown here with the show cdp neighbors command.

Switch-2# show cdp neighbors
<snip>
    Capability Codes: R - Router, T - Trans-Bridge, B - Source-Route-Bridge
    S - Switch, H - Host, I - IGMP, r - Repeater,
    V - VoIP-Phone, D - Remotely-Managed-Device,
    s - Supports-STP-Dispute

Device-ID          Local Intrfce  Hldtme Capability  Platform      Port ID
Switch-1(FDO12345678)
                    Eth1/2         125    R S I s   N9K-C93180YC- Eth1/2        

You can confirm Switch-1’s Ethernet1/2 interface has a non-zero output errors counter with the show interfaces command.

Switch-1# show interface
<snip>
Ethernet1/2 is up
admin state is up, Dedicated Interface
    RX
      30581666 unicast packets  178 multicast packets  931 broadcast packets
      30582775 input packets  3352693923 bytes
      0 jumbo packets  0 storm suppression bytes
      0 runts  0 giants 0 CRC  0 no buffer
      0 input error  0 short frame  0 overrun   0 underrun  0 ignored
      0 watchdog  0 bad etype drop  0 bad proto drop  0 if down drop
      0 input with dribble  0 input discard
      0 Rx pause
    TX
      454301132 unicast packets  734 multicast packets  72 broadcast packets
      454301938 output packets  32246366102 bytes
      0 jumbo packets
      478920 output error  0 collision  0 deferred  0 late collision
      0 lost carrier  0 no carrier  0 babble  0 output discard
      0 Tx pause

You can see that Ethernet1/2 of Switch-1 has a non-zero output errors counter. This suggests that the link between Switch-1’s Ethernet1/2 and Switch-2’s Ethernet1/2 is not damaged — instead, Switch-1 is a cut-through switch forwarding corrupted traffic it receives on some other interface. As previously demonstrated with Switch-2, you can use the show interface counters errors non-zero command in order to identify if any interfaces of Switch-1 have a non-zero input errors counter.

Switch-1# show interface counters errors non-zero
<snip>
--------------------------------------------------------------------------------
Port          Align-Err    FCS-Err   Xmit-Err    Rcv-Err  UnderSize OutDiscards
--------------------------------------------------------------------------------
Eth1/1                0     478920          0     478920          0           0
Eth1/2                0          0     478920          0          0           0

--------------------------------------------------------------------------------
Port         Single-Col  Multi-Col   Late-Col  Exces-Col  Carri-Sen       Runts
--------------------------------------------------------------------------------

--------------------------------------------------------------------------------
Port          Giants SQETest-Err Deferred-Tx IntMacTx-Er IntMacRx-Er Symbol-Err
--------------------------------------------------------------------------------

--------------------------------------------------------------------------------
Port         InDiscards
--------------------------------------------------------------------------------

You can see that Ethernet1/1 of Switch-1 has a non-zero input errors counter. This suggests that Switch-1 is receiving corrupted traffic on this interface. We know that this interface connects to Host-1’s eth0 NIC. We can review Host-1’s eth0 NIC interface statistics to confirm whether Host-1 sends corrupted frames out of this interface.

Host-1$ ip -s link show eth0
2: eth0: <BROADCAST,MULTICAST,UP,LOWER_UP> mtu 1500 qdisc mq state UP mode DEFAULT group default qlen 1000 
    link/ether 00:50:56:84:8f:6d brd ff:ff:ff:ff:ff:ff 
    RX: bytes  packets  errors  dropped overrun mcast 
    73146816142 423112898 0       0     0       437368817 
    TX: bytes  packets  errors  dropped carrier collsns 
    3312398924 37942624 0       0       0       0 
    altname enp11s0 

The eth0 NIC statistics of Host-1 suggest the host is not transmitting corrupted traffic. This suggests that the link between Host-1’s eth0 and Switch-1’s Ethernet1/1 is damaged and is the source of this traffic corruption. Further troubleshooting will need to be performed on this link to identify the faulty component causing this corruption and replace it.

Root Causes of CRC Errors

The most common root cause of CRC errors is a damaged or malfunctioning component of a physical link between two devices. Examples include:

• Failing or damaged physical medium (copper or fiber) or Direct Attach Cables (DACs).
• Failing or damaged transceivers/optics.
• Failing or damaged patch panel ports.
• Faulty network device hardware (including specific ports, line card Application-Specific Integrated Circuits [ASICs], Media Access Controls [MACs], fabric modules, etc.),

• Malfunctioning network interface card inserted in a host.

It is also possible for one or more misconfigured devices to inadvertently causes CRC errors within a network. One example of this is a Maximum Transmission Unit (MTU) configuration mismatch between two or more devices within the network causing large packets to be incorrectly truncated. Identifying and resolving this configuration issue can correct CRC errors within a network as well.

Resolve CRC Errors

You can identify the specific malfunctioning component through a process of elimination:

1. Replace the physical medium (either copper or fiber) or DAC with a known-good physical medium of the same type.
2. Replace the transceiver inserted in one device’s interface with a known-good transceiver of the same model. If this does not resolve the CRC errors, replace the transceiver inserted in the other device’s interface with a known-good transceiver of the same model.
3. If any patch panels are used as part of the damaged link, move the link to a known-good port on the patch panel. Alternatively, eliminate the patch panel as a potential root cause by connecting the link without using the patch panel if possible.
4. Move the damaged link to a different, known-good port on each device. You will need to test multiple different ports to isolate a MAC, ASIC, or line card failure.
5. If the damaged link involves a host, move the link to a different NIC on the host. Alternatively, connect the damaged link to a known-good host to isolate a failure of the host’s NIC.

If the malfunctioning component is a Cisco product (such as a Cisco network device or transceiver) that is covered by an active support contract, you can open a support case with Cisco TAC detailing your troubleshooting to have the malfunctioning component replaced through a Return Material Authorization (RMA).

Related Information

• Nexus 9000 Cloud Scale ASIC CRC Identification & Tracing Procedure
• Technical Support & Documentation — Cisco Systems

A cyclic redundancy check (CRC) is an error-detecting code commonly used in digital networks and storage devices to detect accidental changes to digital data. Blocks of data entering these systems get a short check value attached, based on the remainder of a polynomial division of their contents. On retrieval, the calculation is repeated and, in the event the check values do not match, corrective action can be taken against data corruption. CRCs can be used for error correction (see bitfilters).^[1]

CRCs are so called because the check (data verification) value is a redundancy (it expands the message without adding information) and the algorithm is based on cyclic codes. CRCs are popular because they are simple to implement in binary hardware, easy to analyze mathematically, and particularly good at detecting common errors caused by noise in transmission channels. Because the check value has a fixed length, the function that generates it is occasionally used as a hash function.

Introduction[edit]

CRCs are based on the theory of cyclic error-correcting codes. The use of systematic cyclic codes, which encode messages by adding a fixed-length check value, for the purpose of error detection in communication networks, was first proposed by W. Wesley Peterson in 1961.^[2]
Cyclic codes are not only simple to implement but have the benefit of being particularly well suited for the detection of burst errors: contiguous sequences of erroneous data symbols in messages. This is important because burst errors are common transmission errors in many communication channels, including magnetic and optical storage devices. Typically an n-bit CRC applied to a data block of arbitrary length will detect any single error burst not longer than n bits, and the fraction of all longer error bursts that it will detect is approximately (1 − 2⁻ⁿ).

Specification of a CRC code requires definition of a so-called generator polynomial. This polynomial becomes the divisor in a polynomial long division, which takes the message as the dividend and in which the quotient is discarded and the remainder becomes the result. The important caveat is that the polynomial coefficients are calculated according to the arithmetic of a finite field, so the addition operation can always be performed bitwise-parallel (there is no carry between digits).

In practice, all commonly used CRCs employ the finite field of two elements, GF(2). The two elements are usually called 0 and 1, comfortably matching computer architecture.

A CRC is called an n-bit CRC when its check value is n bits long. For a given n, multiple CRCs are possible, each with a different polynomial. Such a polynomial has highest degree n, which means it has n + 1 terms. In other words, the polynomial has a length of n + 1; its encoding requires n + 1 bits. Note that most polynomial specifications either drop the MSB or LSB, since they are always 1. The CRC and associated polynomial typically have a name of the form CRC-n-XXX as in the table below.

The simplest error-detection system, the parity bit, is in fact a 1-bit CRC: it uses the generator polynomial x + 1 (two terms),^[3] and has the name CRC-1.

Application[edit]

A CRC-enabled device calculates a short, fixed-length binary sequence, known as the check value or CRC, for each block of data to be sent or stored and appends it to the data, forming a codeword.

When a codeword is received or read, the device either compares its check value with one freshly calculated from the data block, or equivalently, performs a CRC on the whole codeword and compares the resulting check value with an expected residue constant.

If the CRC values do not match, then the block contains a data error.

The device may take corrective action, such as rereading the block or requesting that it be sent again. Otherwise, the data is assumed to be error-free (though, with some small probability, it may contain undetected errors; this is inherent in the nature of error-checking).^[4]

Data integrity[edit]

CRCs are specifically designed to protect against common types of errors on communication channels, where they can provide quick and reasonable assurance of the integrity of messages delivered. However, they are not suitable for protecting against intentional alteration of data.

Firstly, as there is no authentication, an attacker can edit a message and recompute the CRC without the substitution being detected. When stored alongside the data, CRCs and cryptographic hash functions by themselves do not protect against intentional modification of data. Any application that requires protection against such attacks must use cryptographic authentication mechanisms, such as message authentication codes or digital signatures (which are commonly based on cryptographic hash functions).

Secondly, unlike cryptographic hash functions, CRC is an easily reversible function, which makes it unsuitable for use in digital signatures.^[5]

Thirdly, CRC satisfies a relation similar to that of a linear function (or more accurately, an affine function):^[6]

where depends on the length of and . This can be also stated as follows, where , and have the same length

as a result, even if the CRC is encrypted with a stream cipher that uses XOR as its combining operation (or mode of block cipher which effectively turns it into a stream cipher, such as OFB or CFB), both the message and the associated CRC can be manipulated without knowledge of the encryption key; this was one of the well-known design flaws of the Wired Equivalent Privacy (WEP) protocol.^[7]

Computation[edit]

To compute an n-bit binary CRC, line the bits representing the input in a row, and position the (n + 1)-bit pattern representing the CRC’s divisor (called a «polynomial») underneath the left end of the row.

In this example, we shall encode 14 bits of message with a 3-bit CRC, with a polynomial x³ + x + 1. The polynomial is written in binary as the coefficients; a 3rd-degree polynomial has 4 coefficients (1x³ + 0x² + 1x + 1). In this case, the coefficients are 1, 0, 1 and 1. The result of the calculation is 3 bits long, which is why it is called a 3-bit CRC. However, you need 4 bits to explicitly state the polynomial.

Start with the message to be encoded:

11010011101100

This is first padded with zeros corresponding to the bit length n of the CRC. This is done so that the resulting code word is in systematic form. Here is the first calculation for computing a 3-bit CRC:

11010011101100 000 <--- input right padded by 3 bits
1011               <--- divisor (4 bits) = x³ + x + 1
------------------
01100011101100 000 <--- result

The algorithm acts on the bits directly above the divisor in each step. The result for that iteration is the bitwise XOR of the polynomial divisor with the bits above it. The bits not above the divisor are simply copied directly below for that step. The divisor is then shifted right to align with the highest remaining 1 bit in the input, and the process is repeated until the divisor reaches the right-hand end of the input row. Here is the entire calculation:

11010011101100 000 <--- input right padded by 3 bits
1011               <--- divisor
01100011101100 000 <--- result (note the first four bits are the XOR with the divisor beneath, the rest of the bits are unchanged)
 1011              <--- divisor ...
00111011101100 000
  1011
00010111101100 000
   1011
00000001101100 000 <--- note that the divisor moves over to align with the next 1 in the dividend (since quotient for that step was zero)
       1011             (in other words, it doesn't necessarily move one bit per iteration)
00000000110100 000
        1011
00000000011000 000
         1011
00000000001110 000
          1011
00000000000101 000
           101 1
-----------------
00000000000000 100 <--- remainder (3 bits).  Division algorithm stops here as dividend is equal to zero.

Since the leftmost divisor bit zeroed every input bit it touched, when this process ends the only bits in the input row that can be nonzero are the n bits at the right-hand end of the row. These n bits are the remainder of the division step, and will also be the value of the CRC function (unless the chosen CRC specification calls for some postprocessing).

The validity of a received message can easily be verified by performing the above calculation again, this time with the check value added instead of zeroes. The remainder should equal zero if there are no detectable errors.

11010011101100 100 <--- input with check value
1011               <--- divisor
01100011101100 100 <--- result
 1011              <--- divisor ...
00111011101100 100

......

00000000001110 100
          1011
00000000000101 100
           101 1
------------------
00000000000000 000 <--- remainder

The following Python code outlines a function which will return the initial CRC remainder for a chosen input and polynomial, with either 1 or 0 as the initial padding. Note that this code works with string inputs rather than raw numbers:

def crc_remainder(input_bitstring, polynomial_bitstring, initial_filler):
    """Calculate the CRC remainder of a string of bits using a chosen polynomial.
    initial_filler should be '1' or '0'.
    """
    polynomial_bitstring = polynomial_bitstring.lstrip('0')
    len_input = len(input_bitstring)
    initial_padding = (len(polynomial_bitstring) - 1) * initial_filler
    input_padded_array = list(input_bitstring + initial_padding)
    while '1' in input_padded_array[:len_input]:
        cur_shift = input_padded_array.index('1')
        for i in range(len(polynomial_bitstring)):
            input_padded_array[cur_shift + i] 
            = str(int(polynomial_bitstring[i] != input_padded_array[cur_shift + i]))
    return ''.join(input_padded_array)[len_input:]

def crc_check(input_bitstring, polynomial_bitstring, check_value):
    """Calculate the CRC check of a string of bits using a chosen polynomial."""
    polynomial_bitstring = polynomial_bitstring.lstrip('0')
    len_input = len(input_bitstring)
    initial_padding = check_value
    input_padded_array = list(input_bitstring + initial_padding)
    while '1' in input_padded_array[:len_input]:
        cur_shift = input_padded_array.index('1')
        for i in range(len(polynomial_bitstring)):
            input_padded_array[cur_shift + i] 
            = str(int(polynomial_bitstring[i] != input_padded_array[cur_shift + i]))
    return ('1' not in ''.join(input_padded_array)[len_input:])

>>> crc_remainder('11010011101100', '1011', '0')
'100'
>>> crc_check('11010011101100', '1011', '100')
True

Mathematics[edit]

Mathematical analysis of this division-like process reveals how to select a divisor that guarantees good error-detection properties. In this analysis, the digits of the bit strings are taken as the coefficients of a polynomial in some variable x—coefficients that are elements of the finite field GF(2) (the integers modulo 2, i.e. either a zero or a one), instead of more familiar numbers. The set of binary polynomials is a mathematical ring.

Designing polynomials[edit]

The selection of the generator polynomial is the most important part of implementing the CRC algorithm. The polynomial must be chosen to maximize the error-detecting capabilities while minimizing overall collision probabilities.

The most important attribute of the polynomial is its length (largest degree(exponent) +1 of any one term in the polynomial), because of its direct influence on the length of the computed check value.

The most commonly used polynomial lengths are 9 bits (CRC-8), 17 bits (CRC-16), 33 bits (CRC-32), and 65 bits (CRC-64).^[3]

A CRC is called an n-bit CRC when its check value is n-bits. For a given n, multiple CRCs are possible, each with a different polynomial. Such a polynomial has highest degree n, and hence n + 1 terms (the polynomial has a length of n + 1). The remainder has length n. The CRC has a name of the form CRC-n-XXX.

The design of the CRC polynomial depends on the maximum total length of the block to be protected (data + CRC bits), the desired error protection features, and the type of resources for implementing the CRC, as well as the desired performance. A common misconception is that the «best» CRC polynomials are derived from either irreducible polynomials or irreducible polynomials times the factor 1 + x, which adds to the code the ability to detect all errors affecting an odd number of bits.^[8] In reality, all the factors described above should enter into the selection of the polynomial and may lead to a reducible polynomial. However, choosing a reducible polynomial will result in a certain proportion of missed errors, due to the quotient ring having zero divisors.

The advantage of choosing a primitive polynomial as the generator for a CRC code is that the resulting code has maximal total block length in the sense that all 1-bit errors within that block length have different remainders (also called syndromes) and therefore, since the remainder is a linear function of the block, the code can detect all 2-bit errors within that block length. If is the degree of the primitive generator polynomial, then the maximal total block length is , and the associated code is able to detect any single-bit or double-bit errors.^[9] We can improve this situation. If we use the generator polynomial , where is a primitive polynomial of degree , then the maximal total block length is , and the code is able to detect single, double, triple and any odd number of errors.

A polynomial that admits other factorizations may be chosen then so as to balance the maximal total blocklength with a desired error detection power. The BCH codes are a powerful class of such polynomials. They subsume the two examples above. Regardless of the reducibility properties of a generator polynomial of degree r, if it includes the «+1» term, the code will be able to detect error patterns that are confined to a window of r contiguous bits. These patterns are called «error bursts».

Specification[edit]

The concept of the CRC as an error-detecting code gets complicated when an implementer or standards committee uses it to design a practical system. Here are some of the complications:

• Sometimes an implementation prefixes a fixed bit pattern to the bitstream to be checked. This is useful when clocking errors might insert 0-bits in front of a message, an alteration that would otherwise leave the check value unchanged.
• Usually, but not always, an implementation appends n 0-bits (n being the size of the CRC) to the bitstream to be checked before the polynomial division occurs. Such appending is explicitly demonstrated in the Computation of CRC article. This has the convenience that the remainder of the original bitstream with the check value appended is exactly zero, so the CRC can be checked simply by performing the polynomial division on the received bitstream and comparing the remainder with zero. Due to the associative and commutative properties of the exclusive-or operation, practical table driven implementations can obtain a result numerically equivalent to zero-appending without explicitly appending any zeroes, by using an equivalent,^[8] faster algorithm that combines the message bitstream with the stream being shifted out of the CRC register.
• Sometimes an implementation exclusive-ORs a fixed bit pattern into the remainder of the polynomial division.
• Bit order: Some schemes view the low-order bit of each byte as «first», which then during polynomial division means «leftmost», which is contrary to our customary understanding of «low-order». This convention makes sense when serial-port transmissions are CRC-checked in hardware, because some widespread serial-port transmission conventions transmit bytes least-significant bit first.
• Byte order: With multi-byte CRCs, there can be confusion over whether the byte transmitted first (or stored in the lowest-addressed byte of memory) is the least-significant byte (LSB) or the most-significant byte (MSB). For example, some 16-bit CRC schemes swap the bytes of the check value.
• Omission of the high-order bit of the divisor polynomial: Since the high-order bit is always 1, and since an n-bit CRC must be defined by an (n + 1)-bit divisor which overflows an n-bit register, some writers assume that it is unnecessary to mention the divisor’s high-order bit.
• Omission of the low-order bit of the divisor polynomial: Since the low-order bit is always 1, authors such as Philip Koopman represent polynomials with their high-order bit intact, but without the low-order bit (the or 1 term). This convention encodes the polynomial complete with its degree in one integer.

These complications mean that there are three common ways to express a polynomial as an integer: the first two, which are mirror images in binary, are the constants found in code; the third is the number found in Koopman’s papers. In each case, one term is omitted. So the polynomial may be transcribed as:

In the table below they are shown as:

Obfuscation[edit]

CRCs in proprietary protocols might be obfuscated by using a non-trivial initial value and a final XOR, but these techniques do not add cryptographic strength to the algorithm and can be reverse engineered using straightforward methods.^[10]

Standards and common use[edit]

Numerous varieties of cyclic redundancy checks have been incorporated into technical standards. By no means does one algorithm, or one of each degree, suit every purpose; Koopman and Chakravarty recommend selecting a polynomial according to the application requirements and the expected distribution of message lengths.^[11] The number of distinct CRCs in use has confused developers, a situation which authors have sought to address.^[8] There are three polynomials reported for CRC-12,^[11] twenty-two conflicting definitions of CRC-16, and seven of CRC-32.^[12]

The polynomials commonly applied are not the most efficient ones possible. Since 1993, Koopman, Castagnoli and others have surveyed the space of polynomials between 3 and 64 bits in size,^{[11][13][14][15]} finding examples that have much better performance (in terms of Hamming distance for a given message size) than the polynomials of earlier protocols, and publishing the best of these with the aim of improving the error detection capacity of future standards.^[14] In particular, iSCSI and SCTP have adopted one of the findings of this research, the CRC-32C (Castagnoli) polynomial.

The design of the 32-bit polynomial most commonly used by standards bodies, CRC-32-IEEE, was the result of a joint effort for the Rome Laboratory and the Air Force Electronic Systems Division by Joseph Hammond, James Brown and Shyan-Shiang Liu of the Georgia Institute of Technology and Kenneth Brayer of the Mitre Corporation. The earliest known appearances of the 32-bit polynomial were in their 1975 publications: Technical Report 2956 by Brayer for Mitre, published in January and released for public dissemination through DTIC in August,^[16] and Hammond, Brown and Liu’s report for the Rome Laboratory, published in May.^[17] Both reports contained contributions from the other team. During December 1975, Brayer and Hammond presented their work in a paper at the IEEE National Telecommunications Conference: the IEEE CRC-32 polynomial is the generating polynomial of a Hamming code and was selected for its error detection performance.^[18] Even so, the Castagnoli CRC-32C polynomial used in iSCSI or SCTP matches its performance on messages from 58 bits to 131 kbits, and outperforms it in several size ranges including the two most common sizes of Internet packet.^[14] The ITU-T G.hn standard also uses CRC-32C to detect errors in the payload (although it uses CRC-16-CCITT for PHY headers).

CRC-32C computation is implemented in hardware as an operation (CRC32) of SSE4.2 instruction set, first introduced in Intel processors’ Nehalem microarchitecture. ARM AArch64 architecture also provides hardware acceleration for both CRC-32 and CRC-32C operations.

Polynomial representations of cyclic redundancy checks[edit]

The table below lists only the polynomials of the various algorithms in use. Variations of a particular protocol can impose pre-inversion, post-inversion and reversed bit ordering as described above. For example, the CRC32 used in Gzip and Bzip2 use the same polynomial, but Gzip employs reversed bit ordering, while Bzip2 does not.^[12]
Note that even parity polynomials in GF(2) with degree greater than 1 are never primitive. Even parity polynomial marked as primitive in this table represent a primitive polynomial multiplied by . The most significant bit of a polynomial is always 1, and is not shown in the hex representations.

Name	Uses	Polynomial representations	Parity[19]	Primitive[20]	Maximum bits of payload by Hamming distance[21][14][20]
Normal	Reversed	Reciprocal	Reversed reciprocal	≥ 16	15	14	13	12	11	10	9	8	7	6	5	4	3	2[22]
CRC-1	most hardware; also known as parity bit	0x1	0x1	0x1	0x1	even
CRC-3-GSM	mobile networks[23]	0x3	0x6	0x5	0x5	odd	yes [24]	–	–	–	–	–	–	–	–	–	–	–	–	–	4	∞
CRC-4-ITU	ITU-T G.704, p. 12	0x3	0xC	0x9	0x9	odd
CRC-5-EPC	Gen 2 RFID[25]	0x09	0x12	0x05	0x14	odd
CRC-5-ITU	ITU-T G.704, p. 9	0x15	0x15	0x0B	0x1A	even
CRC-5-USB	USB token packets	0x05	0x14	0x09	0x12	odd
CRC-6-CDMA2000-A	mobile networks[26]	0x27	0x39	0x33	0x33	odd
CRC-6-CDMA2000-B	mobile networks[26]	0x07	0x38	0x31	0x23	even
CRC-6-DARC	Data Radio Channel[27]	0x19	0x26	0x0D	0x2C	even
CRC-6-GSM	mobile networks[23]	0x2F	0x3D	0x3B	0x37	even	yes [28]	–	–	–	–	–	–	–	–	–	–	1	1	25	25	∞
CRC-6-ITU	ITU-T G.704, p. 3	0x03	0x30	0x21	0x21	odd
CRC-7	telecom systems, ITU-T G.707, ITU-T G.832, MMC, SD	0x09	0x48	0x11	0x44	odd
CRC-7-MVB	Train Communication Network, IEC 60870-5[29]	0x65	0x53	0x27	0x72	odd
CRC-8	DVB-S2[30]	0xD5	0xAB	0x57	0xEA[11]	even	no [31]	–	–	–	–	–	–	–	–	–	–	2	2	85	85	∞
CRC-8-AUTOSAR	automotive integration,[32] OpenSafety[33]	0x2F	0xF4	0xE9	0x97[11]	even	yes [31]	–	–	–	–	–	–	–	–	–	–	3	3	119	119	∞
CRC-8-Bluetooth	wireless connectivity[34]	0xA7	0xE5	0xCB	0xD3	even
CRC-8-CCITT	ITU-T I.432.1 (02/99); ATM HEC, ISDN HEC and cell delineation, SMBus PEC	0x07	0xE0	0xC1	0x83	even
CRC-8-Dallas/Maxim	1-Wire bus[35]	0x31	0x8C	0x19	0x98	even
CRC-8-DARC	Data Radio Channel[27]	0x39	0x9C	0x39	0x9C	odd
CRC-8-GSM-B	mobile networks[23]	0x49	0x92	0x25	0xA4	even
CRC-8-SAE J1850	AES3; OBD	0x1D	0xB8	0x71	0x8E	odd
CRC-8-WCDMA	mobile networks[26][36]	0x9B	0xD9	0xB3	0xCD[11]	even
CRC-10	ATM; ITU-T I.610	0x233	0x331	0x263	0x319	even
CRC-10-CDMA2000	mobile networks[26]	0x3D9	0x26F	0x0DF	0x3EC	even
CRC-10-GSM	mobile networks[23]	0x175	0x2BA	0x175	0x2BA	odd
CRC-11	FlexRay[37]	0x385	0x50E	0x21D	0x5C2	even
CRC-12	telecom systems[38][39]	0x80F	0xF01	0xE03	0xC07[11]	even
CRC-12-CDMA2000	mobile networks[26]	0xF13	0xC8F	0x91F	0xF89	even
CRC-12-GSM	mobile networks[23]	0xD31	0x8CB	0x197	0xE98	odd
CRC-13-BBC	Time signal, Radio teleswitch[40][41]	0x1CF5	0x15E7	0x0BCF	0x1E7A	even
CRC-14-DARC	Data Radio Channel[27]	0x0805	0x2804	0x1009	0x2402	even
CRC-14-GSM	mobile networks[23]	0x202D	0x2D01	0x1A03	0x3016	even
CRC-15-CAN		0x4599[42][43]	0x4CD1	0x19A3	0x62CC	even
CRC-15-MPT1327	[44]	0x6815	0x540B	0x2817	0x740A	odd
CRC-16-Chakravarty	Optimal for payloads ≤64 bits[29]	0x2F15	0xA8F4	0x51E9	0x978A	odd
CRC-16-ARINC	ACARS applications[45]	0xA02B	0xD405	0xA80B	0xD015	odd
CRC-16-CCITT	X.25, V.41, HDLC FCS, XMODEM, Bluetooth, PACTOR, SD, DigRF, many others; known as CRC-CCITT	0x1021	0x8408	0x811	0x8810[11]	even
CRC-16-CDMA2000	mobile networks[26]	0xC867	0xE613	0xCC27	0xE433	odd
CRC-16-DECT	cordless telephones[46]	0x0589	0x91A0	0x2341	0x82C4	even
CRC-16-T10-DIF	SCSI DIF	0x8BB7[47]	0xEDD1	0xDBA3	0xC5DB	odd
CRC-16-DNP	DNP, IEC 870, M-Bus	0x3D65	0xA6BC	0x4D79	0x9EB2	even
CRC-16-IBM	Bisync, Modbus, USB, ANSI X3.28, SIA DC-07, many others; also known as CRC-16 and CRC-16-ANSI	0x8005	0xA001	0x4003	0xC002	even
CRC-16-OpenSafety-A	safety fieldbus[33]	0x5935	0xAC9A	0x5935	0xAC9A[11]	odd
CRC-16-OpenSafety-B	safety fieldbus[33]	0x755B	0xDAAE	0xB55D	0xBAAD[11]	odd
CRC-16-Profibus	fieldbus networks[48]	0x1DCF	0xF3B8	0xE771	0x8EE7	odd
Fletcher-16	Used in Adler-32 A & B Checksums	Often confused to be a CRC, but actually a checksum; see Fletcher’s checksum
CRC-17-CAN	CAN FD[49]	0x1685B	0x1B42D	0x1685B	0x1B42D	even
CRC-21-CAN	CAN FD[49]	0x102899	0x132281	0x064503	0x18144C	even
CRC-24	FlexRay[37]	0x5D6DCB	0xD3B6BA	0xA76D75	0xAEB6E5	even
CRC-24-Radix-64	OpenPGP, RTCM104v3	0x864CFB	0xDF3261	0xBE64C3	0xC3267D	even
CRC-24-WCDMA	Used in OS-9 RTOS. Residue = 0x800FE3.[50]	0x800063	0xC60001	0x8C0003	0xC00031	even	yes[51]	–	–	–	–	–	–	–	–	–	–	4	4	8388583	8388583	∞
CRC-30	CDMA	0x2030B9C7	0x38E74301	0x31CE8603	0x30185CE3	even
CRC-32	ISO 3309 (HDLC), ANSI X3.66 (ADCCP), FIPS PUB 71, FED-STD-1003, ITU-T V.42, ISO/IEC/IEEE 802-3 (Ethernet), SATA, MPEG-2, PKZIP, Gzip, Bzip2, POSIX cksum,[52] PNG,[53] ZMODEM, many others	0x04C11DB7	0xEDB88320	0xDB710641	0x82608EDB[14]	odd	yes	–	10	–	–	12	21	34	57	91	171	268	2974	91607	4294967263	∞
CRC-32C (Castagnoli)	iSCSI, SCTP, G.hn payload, SSE4.2, Btrfs, ext4, Ceph	0x1EDC6F41	0x82F63B78	0x05EC76F1	0x8F6E37A0[14]	even	yes	6	–	8	–	20	–	47	–	177	–	5243	–	2147483615	–	∞
CRC-32K (Koopman {1,3,28})	Excellent at Ethernet frame length, poor performance with long files	0x741B8CD7	0xEB31D82E	0xD663B05D	0xBA0DC66B[14]	even	no	2	–	4	–	16	–	18	–	152	–	16360	–	114663	–	∞
CRC-32K2 (Koopman {1,1,30})	Excellent at Ethernet frame length, poor performance with long files	0x32583499	0x992C1A4C	0x32583499	0x992C1A4C[14]	even	no	–	–	3	–	16	–	26	–	134	–	32738	–	65506	–	∞
CRC-32Q	aviation; AIXM[54]	0x814141AB	0xD5828281	0xAB050503	0xC0A0A0D5	even
Adler-32		Often confused to be a CRC, but actually a checksum; see Adler-32
CRC-40-GSM	GSM control channel[55][56][57]	0x0004820009	0x9000412000	0x2000824001	0x8002410004	even
CRC-64-ECMA	ECMA-182 p. 51, XZ Utils	0x42F0E1EBA9EA3693	0xC96C5795D7870F42	0x92D8AF2BAF0E1E85	0xA17870F5D4F51B49	even
CRC-64-ISO	ISO 3309 (HDLC), Swiss-Prot/TrEMBL; considered weak for hashing[58]	0x000000000000001B	0xD800000000000000	0xB000000000000001	0x800000000000000D	odd

Implementations[edit]

• Implementation of CRC32 in GNU Radio up to 3.6.1 (ca. 2012)
• C class code for CRC checksum calculation with many different CRCs to choose from

CRC catalogues[edit]

• Catalogue of parametrised CRC algorithms
• CRC Polynomial Zoo

See also[edit]

• Checksum
• Mathematics of cyclic redundancy checks
• Computation of cyclic redundancy checks
• List of hash functions
• List of checksum algorithms
• Information security
• Simple file verification
• LRC

References[edit]

Further reading[edit]

• Warren Jr., Henry S. (2013). Hacker’s Delight (2 ed.). Addison Wesley. ISBN 978-0-321-84268-8.

External links[edit]

• ISO/IEC 13239:2002: Information technology — Telecommunications and information exchange between systems — High-level data link control (HDLC) procedures
• CRC32-Castagnoli Linux Library

Время на прочтение
4 мин

Количество просмотров 12K

Нередко на сети хранения данных возникают такие неприятные вещи, как рост числа ошибок на портах и увеличение уровня затухания сигнала на sfp модулях. Принимая во внимание высокий уровень надежности SAN инфраструктуры, состоящей из двух и более фабрик, вероятность возникновения аварийной ситуации не так велика, но наложение негативных факторов может привести к потере данных или деградации производительности. К примеру, представьте себе ситуацию: на одной из фабрик проводится обновление FOS, все работает через вторую фабрику, а на ней между коммутатором к которому подключен дисковый массив и коммутатором к которому подключены серверы начинают быстро расти CRC ошибки на одном из транковых портов. Или еще хуже, пропадает линк из-за понижения уровня сигнала, вызванного повышением температуры SFP модуля, которая в свою очередь возросла из-за повысившейся утилизации данного канала. В таких случаях обычно говорят: «Ну кто же знал» или «100% надежных систем не бывает» и тд.

Грамотная архитектура + правильный мониторинг = отказоустойчивость

Итак проблема обозначена, необходимо разработать комплекс мер по повышению отказоустойчивости сети хранения данных, его можно разделить на два этапа:

• приведение архитектуры сети хранения данных в соответствие с «SAN best practices»
• развертывание системы мониторинга

Если про SAN best practices есть много литературы и курсов обучения, и можно пригласить крутых специалистов из интегратора для проведения экспертизы, то выбрать верный способ создать хорошую систему мониторинга SAN сети не так легко. Это можно объяснить жесткой привязкой: разработчик ПО — изготовитель коммутаторов. Я конечно не хочу сказать, что Cisco Fabric Manager или Brocade Network Advisor плохи, но они не позволяют делать все то, что необходимо на мой взгляд для повышения отказоустойчивости SAN сети.

Что делать

И так, задача поставлена, необходимо найти путь решения, часто это может осложняться отсутствием денег в бюджете на этот год, или неосведомленностью интегратора о существовании подходящего ПО, но это не проблема т.к. все необходимые компоненты есть в свободном доступе и требуется лишь заставить это все работать.
Разберем реализацию мониторинга CRC ошибок на портах SAN свичей brocade, большинство остальных параметров можно мониторить аналогичным образом.

Шаг первый, протокол сбора данных

Информацию о числе CRC ошибок можно получать с коммутаторов разными способами (snmp, https, telnet и ssh) мой выбор пал на последний т.к. telnet не безопасен и его лучше отключать, https сложен для извлечения конкретных значений, а snmp дерево может значительно меняться как на разных свичах, так и при переходе на новый FOS.

Шаг второй, метод сбора данных

Для работы с ssh лучше всего адаптирован linux в связке bash+expect, этим методом можно подключаться по ssh с диалоговым вводом команд.

Шаг третий, где хранить

Тут большой разницы нет, можно хранить хоть в текстовых файлах, но мы рассмотрим пример с mysql. Весь мониторинг реализован в двух скриптах:

porterrshow.sh — сбор информации и поиск инкремента значений CRC ошибок
expect.tcl — подключение по ssh

и трех txt файлах:
temp.txt — буфер данных
switches.txt — список san свичей в формате имя логин пароль на каждой строке
crc.txt — отчет о найденных CRC ошибках

Select запрос ищет инкремент роста CRC ошибок по сравнению с данными полученными один час назад, соответственно запуск скрипта необходимо производить один раз в час, причем начать и закончить свою работу скрипт должен в одном и том же часу. Данное ограничение можно легко обойти, если ввести поле порядкового номера запуска скрипта, либо потерять в производительности и задать более сложное условие выборки значений времени. На сервере должны быть установлены пакеты expect, mysql и ssh клиент. В базе данных dbname должен присутствовать пользователь user с правами на чтение и запись в таблицу tablename. В таблице tablename получаем данные аналогичные выводу команды porterrshow на свиче + дата и время.

porterrshow.sh

#!/bin/bash

rm /var/scripts/temp.txt        #Удаляем ранее созданный temp.txt
while read line                 #Читаем строку из файла switches.txt
do read sw user pass <<< $line  #Разбиваем строку на переменные

n=0                                                               #Обнуляем счетчик
while read line;                                                  #Читаем строку из вывода expect.tcl
do array[n]="$line"; n=$[n+1];                                    #Заполняем массив строками из вывода expect.tcl
done < <(/var/scripts/expect.tcl $sw $user $pass porterrshow)     #Отправляем данные в цикл

if echo ${array[4]} | grep -q '=';             #Проверяем с какой строки начинается вывод полезной информации
then k=5;
else k=4;
fi;

for i in `seq $k $[n-1]`;                                                                                                                            #В последней строке данных нет
do read a1 a2 a3 a4 a5 a6 a7 a8 a9 a10 a11 a12 a13 a14 a15 a16 a17 a18 a19 <<<  ${array[i]};      #Разбиваем строку на значения
(echo $sw,${a1%:},`date +%F`,`date +%T`,$a2,$a3,$a4,$a5,$a6,$a7,$a8,$a9,$a10,$a11,$a12,$a13,$a14,$a15,$a16,$a17) >> temp.txt		#Формируем подгрузочный файл
done;

done < /var/scripts/switches.txt          #Читаем файл со списком свичей

mysql -uuser -ppass dbname << EOF;
LOAD DATA LOCAL INFILE "temp.txt" INTO TABLE tablename FIELDS TERMINATED BY ',';
EOF
#Загружаем данные в БД

(mysql -uuser -ppass dbname << EOF
select new.switch, new.port, new.crcerr-old.crcerr from tablename new, tablename old where new.switch=old.switch and new.port=old.port and new.date=old.date and new.crcerr!=old.crcerr and new.crcerr!=0 and new.date=curdate() and hour(new.time)=hour(now()) and hour(old.time)=hour(now())-1;
EOF
) > /var/scripts/crc.txt           #Проверяем инкремент CRC по портам и пишем отчет в файл

if grep -q 'switch' /var/scripts/crc.txt
then
cat /var/scripts/crc.txt | mailx -r SAN_Switch_CRC_Tester -s "CRC errors is increased" sanadmin1@mywork.com
fi
#Отправляем информацию администратору

expect.tcl

#!/usr/bin/expect

#Устанавливаем таймаут соединения 10 сек 
set timeout 10

#Проверям число параметров передаваемых скрипту
if {$argc != 4} {
    puts "Usage $argv0 host user pass command"
    exit 1}

#Назначаем параметры переменным
set host    [lindex $argv 0]
set user    [lindex $argv 1]
set pass    [lindex $argv 2]
set command [lindex $argv 3]

#Производим подключение по SSH
spawn ssh -oStrictHostKeyChecking=no -oCheckHostIP=no $user@$host $command
expect *assword:
send "$passr"
expect eof