Простой расчет контрольной суммы
Время на прочтение
12 мин
Количество просмотров 198K
При передачи данных по линиям связи, используется контрольная сумма, рассчитанная по некоторому алгоритму. Алгоритм часто сложный, конечно, он обоснован математически, но очень уж неудобен при дефиците ресурсов, например при программировании микроконтроллеров.
Чтобы упростить алгоритм, без потери качества, нужно немного «битовой магии», что интересная тема сама по себе.
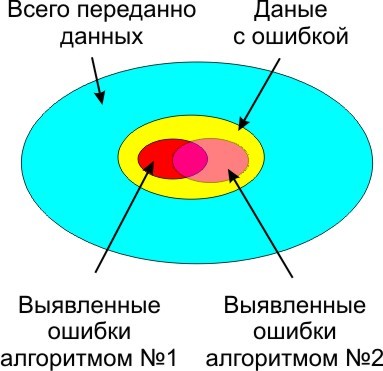
Без контрольной суммы, передавать данные опасно, так как помехи присутствуют везде и всегда, весь вопрос только в их вероятности возникновения и вызываемых ими побочных эффектах. В зависимости от условий и выбирается алгоритм выявления ошибок и количество данных в контрольной сумме. Сложнее алгоритм, и больше контрольная сумма, меньше не распознанных ошибок.
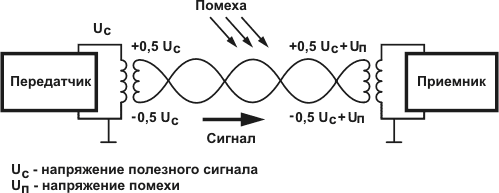
Причина помех на физическом уровне, при передаче данных.
Вот пример самого типичного алгоритма для микроконтроллера, ставшего, фактически, промышленным стандартом с 1979 года.
Расчет контрольной суммы для протокола Modbus
void crc_calculating(unsigned char puchMsg, unsigned short usDataLen) /*##Расчёт контрольной суммы##*/
{
{
unsigned char uchCRCHi = 0xFF ; /* Инициализация последнего байта CRC */
unsigned char uchCRCLo = 0xFF ; /* Инициализация первого байта CRC */
unsigned uIndex ; /* will index into CRC lookup table */
while (usDataLen--) /* pass through message buffer */
{
uIndex = uchCRCHi ^ *puchMsg++ ; /* Расчёт CRC */
uchCRCLo = uchCRCLo ^ auchCRCHi[uIndex] ;
uchCRCHi = auchCRCLo[uIndex] ;
}
return (uchCRCHi << 8 | uchCRCLo) ;
/* Table of CRC values for high–order byte */
static unsigned char auchCRCHi[] = {
0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81,
0x40, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0,
0x80, 0x41, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x00, 0xC1, 0x81, 0x40, 0x01,
0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x01, 0xC0, 0x80, 0x41,
0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x00, 0xC1, 0x81,
0x40, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x01, 0xC0,
0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x01,
0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40,
0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81,
0x40, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0,
0x80, 0x41, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x00, 0xC1, 0x81, 0x40, 0x01,
0xC0, 0x80, 0x41, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41,
0x00, 0xC1, 0x81, 0x40, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81,
0x40, 0x01, 0xC0, 0x80, 0x41, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0,
0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x01,
0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81, 0x40, 0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41,
0x00, 0xC1, 0x81, 0x40, 0x01, 0xC0, 0x80, 0x41, 0x01, 0xC0, 0x80, 0x41, 0x00, 0xC1, 0x81,
0x40
};
/* Table of CRC values for low–order byte */
static char auchCRCLo[] = {
0x00, 0xC0, 0xC1, 0x01, 0xC3, 0x03, 0x02, 0xC2, 0xC6, 0x06, 0x07, 0xC7, 0x05, 0xC5, 0xC4,
0x04, 0xCC, 0x0C, 0x0D, 0xCD, 0x0F, 0xCF, 0xCE, 0x0E, 0x0A, 0xCA, 0xCB, 0x0B, 0xC9, 0x09,
0x08, 0xC8, 0xD8, 0x18, 0x19, 0xD9, 0x1B, 0xDB, 0xDA, 0x1A, 0x1E, 0xDE, 0xDF, 0x1F, 0xDD,
0x1D, 0x1C, 0xDC, 0x14, 0xD4, 0xD5, 0x15, 0xD7, 0x17, 0x16, 0xD6, 0xD2, 0x12, 0x13, 0xD3,
0x11, 0xD1, 0xD0, 0x10, 0xF0, 0x30, 0x31, 0xF1, 0x33, 0xF3, 0xF2, 0x32, 0x36, 0xF6, 0xF7,
0x37, 0xF5, 0x35, 0x34, 0xF4, 0x3C, 0xFC, 0xFD, 0x3D, 0xFF, 0x3F, 0x3E, 0xFE, 0xFA, 0x3A,
0x3B, 0xFB, 0x39, 0xF9, 0xF8, 0x38, 0x28, 0xE8, 0xE9, 0x29, 0xEB, 0x2B, 0x2A, 0xEA, 0xEE,
0x2E, 0x2F, 0xEF, 0x2D, 0xED, 0xEC, 0x2C, 0xE4, 0x24, 0x25, 0xE5, 0x27, 0xE7, 0xE6, 0x26,
0x22, 0xE2, 0xE3, 0x23, 0xE1, 0x21, 0x20, 0xE0, 0xA0, 0x60, 0x61, 0xA1, 0x63, 0xA3, 0xA2,
0x62, 0x66, 0xA6, 0xA7, 0x67, 0xA5, 0x65, 0x64, 0xA4, 0x6C, 0xAC, 0xAD, 0x6D, 0xAF, 0x6F,
0x6E, 0xAE, 0xAA, 0x6A, 0x6B, 0xAB, 0x69, 0xA9, 0xA8, 0x68, 0x78, 0xB8, 0xB9, 0x79, 0xBB,
0x7B, 0x7A, 0xBA, 0xBE, 0x7E, 0x7F, 0xBF, 0x7D, 0xBD, 0xBC, 0x7C, 0xB4, 0x74, 0x75, 0xB5,
0x77, 0xB7, 0xB6, 0x76, 0x72, 0xB2, 0xB3, 0x73, 0xB1, 0x71, 0x70, 0xB0, 0x50, 0x90, 0x91,
0x51, 0x93, 0x53, 0x52, 0x92, 0x96, 0x56, 0x57, 0x97, 0x55, 0x95, 0x94, 0x54, 0x9C, 0x5C,
0x5D, 0x9D, 0x5F, 0x9F, 0x9E, 0x5E, 0x5A, 0x9A, 0x9B, 0x5B, 0x99, 0x59, 0x58, 0x98, 0x88,
0x48, 0x49, 0x89, 0x4B, 0x8B, 0x8A, 0x4A, 0x4E, 0x8E, 0x8F, 0x4F, 0x8D, 0x4D, 0x4C, 0x8C,
0x44, 0x84, 0x85, 0x45, 0x87, 0x47, 0x46, 0x86, 0x82, 0x42, 0x43, 0x83, 0x41, 0x81, 0x80,
0x40
};
}
}
Не слабый такой код, есть вариант без таблицы, но более медленный (необходима побитовая обработка данных), в любом случае способный вынести мозг как программисту, так и микроконтроллеру. Не во всякий микроконтроллер алгоритм с таблицей влезет вообще.
Давайте разберем алгоритмы, которые вообще могут подтвердить целостность данных невысокой ценой.
Бит четности (1-битная контрольная сумма)
На первом месте простой бит четности. При необходимости формируется аппаратно, принцип простейший, и подробно расписан в википедии. Недостаток только один, пропускает двойные ошибки (и вообще четное число ошибок), когда четность всех бит не меняется. Можно использовать для сбора статистики о наличии ошибок в потоке передаваемых данных, но целостность данных не гарантирует, хотя и снижает вероятность пропущенной ошибки на 50% (зависит, конечно, от типа помех на линии, в данном случае подразумевается что число четных и нечетных сбоев равновероятно).
Для включения бита четности, часто и код никакой не нужен, просто указываем что UART должен задействовать бит четности. Типично, просто указываем:
включение бита четности на микроконтроллере
void setup(){
Serial.begin(9600,SERIAL_8N1); // по умолчанию, бит четности выключен;
Serial1.begin(38400,SERIAL_8E1); // бит четности включен
Serial.println("Hello Computer");
Serial1.println("Hello Serial 1");
}
Часто разработчики забывают даже, что UART имеет на борту возможность проверки бита четности. Кроме целостности передаваемых данных, это позволяет избежать устойчивого срыва синхронизации (например при передаче данных по радиоканалу), когда полезные данные могу случайно имитировать старт и стоп биты, а вместо данных на выходе буфера старт и стоп биты в случайном порядке.
8-битная контрольная сумма
Если контроля четности мало (а этого обычно мало), добавляется дополнительная контрольная сумма. Рассчитать контрольную сумму, можно как сумму ранее переданных байт, просто и логично
Естественно биты переполнения не учитываем, результат укладываем в выделенные под контрольную сумму 8 бит. Можно пропустить ошибку, если при случайном сбое один байт увеличится на некоторое значение, а другой байт уменьшится на то же значение. Контрольная сумма не изменится. Проведем эксперимент по передаче данных. Исходные данные такие:
- Блок данных 8 байт.
- Заполненность псевдослучайными данными Random($FF+1)
- Случайным образом меняем 1 бит в блоке данных операцией XOR со специально подготовленным байтом, у которого один единичный бит на случайной позиции.
- Повторяем предыдущий пункт 10 раз, при этом может получится от 0 до 10 сбойных бит (2 ошибки могут накладываться друг на друга восстанавливая данные), вариант с 0 сбойных бит игнорируем в дальнейшем как бесполезный для нас.
Передаем виртуальную телеграмму N раз. Идеальная контрольная сумма выявит ошибку по количеству доступной ей информации о сообщении, больше информации, выше вероятность выявления сбойной телеграммы. Вероятность пропустить ошибку, для 1 бита контрольной суммы:
.
Для 8 бит:
,
на 256 отправленных телеграмм с ошибкой, одна пройдет проверку контрольной суммы. Смотрим статистику от виртуальной передачи данных, с помощью простой тестовой программы:
Статистика
1: 144 (тут и далее — вероятность прохождения ошибки)
1: 143
1: 144
1: 145
1: 144
1: 142
1: 143
1: 143
1: 142
1: 140
Общее число ошибок 69892 из 10 млн. итераций, или 1: 143.078
Или условный КПД=55%, от возможностей «идеальной» контрольной суммы. Такова плата за простоту алгоритма и скорость обработки данных. В целом, для многих применений, алгоритм работоспособен. Используется одна операция сложения и одна переменная 8-битовая. Нет возможности не корректной реализации. Поэтому алгоритм и применяется в контроллерах ADAMS, ICP, в составе протокола DCON (там дополнительно может быть включен бит четности, символы только ASCI, что так же способствует повышению надежности передачи данных и итоговая надежность несколько выше, так как часть ошибок выявляется по другим, дополнительным признакам, не связанных с контрольной суммой).
Не смотря на вероятность прохождения ошибки 1:143, вероятность обнаружения ошибки лучше, чем 1:256 невозможна теоретически. Потери в качестве работы есть, но не всегда это существенно. Если нужна надежность выше, нужно использовать контрольную сумму с большим числом бит. Или, иначе говоря, простая контрольная сумма, недостаточно эффективно использует примерно 0.75 бита из 8 имеющихся бит информации в контрольной сумме.
Для сравнения применим, вместо суммы, побитовое сложение XOR. Стало существенно хуже, вероятность обнаружения ошибки 1:67 или 26% от теоретического предела. Упрощенно, это можно объяснить тем, что XOR меняет при возникновении ошибке еще меньше бит в контрольной сумме, ниже отклик на единичный битовый сбой, и повторной ошибке более вероятно вернуть контрольную сумму в исходное состояние.
Так же можно утверждать, что контрольная сумма по XOR представляет из себя 8 независимых контрольных сумм из 1 бита. Вероятность того, что ошибка придется на один из 8 бит равна 1:8, вероятность двойного сбоя 1:64, что мы и наблюдаем, теоретическая величина совпала с экспериментальными данными.
Нам же нужен такой алгоритм, чтобы заменял при единичной ошибке максимальное количество бит в контрольной сумме. Но мы, в общей сложности, ограниченны сложностью алгоритма, и ресурсами в нашем распоряжении. Не во всех микроконтроллерах есть аппаратный блок расчета CRC. Но, практически везде, есть блок умножения. Рассчитаем контрольную сумму как произведение последовательности байт, на некоторую «магическую» константу:
CRC=CRC + byte*211
Константа должна быть простой, и быть достаточно большой, для изменения большего числа бит после каждой операции, 211 вполне подходит, проверяем:
Статистика
1: 185
1: 186
1: 185
1: 185
1: 193
1: 188
1: 187
1: 194
1: 190
1: 200
Всего 72% от теоретического предела, небольшое улучшение перед простой суммой. Алгоритм в таком виде не имеет смысла. В данном случае теряется важная информация из отбрасываемых старших 8..16 бит, а их необходимо учитывать. Проще всего, смешать функцией XOR с младшими битами 1..8. Приходим к еще более интенсивной модификации контрольной суммы, желательно с минимальным затратами ресурсов. Добавляем фокус из криптографических алгоритмов
CRC=CRC + byte*211
CRC= CRC XOR (CRC SHR 8); // "миксер" битовый, далее его применяем везде
CRC=CRC AND $FF; //или просто возвращаем результат как 8, а не 16 бит
- Промежуточная CRC для первого действия 16-битная (после вычислений обрезается до 8 бит) и в дальнейшем работаем как с 8-битной, если у нас 8-битный микроконтроллер это ускорит обработку данных.
- Возвращаем старшие биты и перемешиваем с младшими.
Проверяем:
Статистика
1: 237
1: 234
1: 241
1: 234
1: 227
1: 238
1: 235
1: 233
1: 231
1: 236
Результат 91% от теоретического предела. Вполне годится для применения.
Если в микроконтроллере нет блока умножения, можно имитировать умножение операций сложения, смещения и XOR. Суть процесса такая же, модифицированный ошибкой бит, равномерно «распределяется» по остальным битам контрольной суммы.
CRC := (CRC shl 3) + byte;
CRC := (CRC shl 3) + byte;
CRC:=(CRC XOR (CRC SHR 8)) ; // как и в предыдущем алгоритме
Результат:
Статистика
1: 255
1: 257
1: 255
1: 255
1: 254
1: 255
1: 250
1: 254
1: 256
1: 254
На удивление хороший результат. Среднее значение 254,5 или 99% от теоретического предела, операций немного больше, но все они простые и не используется умножение.
Если для внутреннего хранения промежуточных значений контрольной суммы отдать 16 бит переменную (но передавать по линии связи будем только младшие 8 бит), что не проблема даже для самого слабого микроконтроллера, получим некоторое улучшение работы алгоритма. В целом экономить 8 бит нет особого смысла, и 8-битовая промежуточная переменная использовалась ранее просто для упрощения понимания работы алгоритма.
Статистика
1: 260
1: 250
1: 252
1: 258
1: 261
1: 255
1: 254
1: 261
1: 264
1: 262
Что соответствует 100.6% от теоретического предела, вполне хороший результат для такого простого алгоритма из одной строчки:
CRC:=CRC + byte*44111; // все переменные 16-битные
Используется полноценное 16-битное умножение. Опять же не обошлось без магического числа 44111 (выбрано из общих соображений без перебора всего подмножества чисел). Более точно, константу имеет смысл подбирать, только определившись с предполагаемым типом ошибок в линии передачи данных.
Столь высокий результат объясняется тем, что 2 цикла умножения подряд, полностью перемешивают биты, что нам и требовалось. Исключением, похоже, является последний байт телеграммы, особенно его старшие биты, они не полностью замешиваются в контрольную сумму, но и вероятность того, что ошибка придется на них невелика, примерно 4%. Эта особенность практически ни как не проявляется статистически, по крайней мере на моем наборе тестовых данных и ошибке ограниченной 10 сбойными битами. Для исключения этой особенности можно делать N+1 итераций, добавив виртуальный байт в дополнение к имеющимся в тестовом блоке данных (но это усложнение алгоритма).
Вариант без умножения с аналогичным результатом. Переменная CRC 16-битная, данные 8-битные, результат работы алгоритма — младшие 8 бит найденной контрольной суммы:
CRC := (CRC shl 2) + CRC + byte;
CRC := (CRC shl 2) + CRC + byte;
CRC:=(CRC XOR (CRC SHR 8));
Результат 100.6% от теоретического предела.
Вариант без умножения более простой, оставлен самый минимум функций, всего 3 математических операции:
CRC:=byte + CRC;
CRC:=CRC xor (CRC shr 2);
Результат 86% от теоретического предела.
В этом случае потери старших бит нет, они возвращаются в младшую часть переменной через функцию XOR (битовый миксер).
Небольшое улучшение в некоторых случаях дает так же:
- Двойной проход по обрабатываемым данным. Но ценой усложнения алгоритма (внешний цикл нужно указать), ценой удвоения времени обработки данных.
- Обработка дополнительного, виртуального байта в конце обрабатываемых данных, усложнения алгоритма и времени работы алгоритма практически нет.
- Использование переменной для хранения контрольной суммы большей по разрядности, чем итоговая контрольная сумма и перемешивание младших бит со старшими.
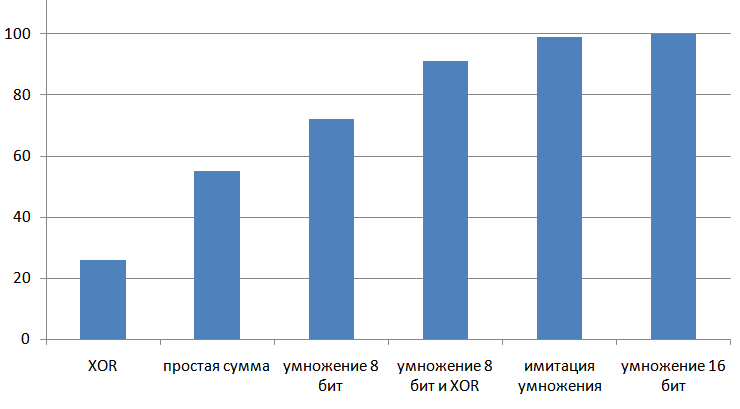
Результат работы рассмотренных алгоритмов, от простых и слабых, к сложным и качественным:
16-битная контрольная сумма
Далее, предположим что нам мало 8 бит для формирования контрольной суммы.
Следующий вариант 16 бит, и теоретическая вероятность ошибки переданных данных 1:65536, что намного лучше. Надежность растет по экспоненте. Но, как побочный эффект, растет количество вспомогательных данных, на примере нашей телеграммы, к 8 байтам полезной информации добавляется 2 байта контрольной суммы.
Простые алгоритмы суммы и XOR, применительно к 16-битной и последующим CRC не рассматриваем вообще, они практически не улучают качество работы, по сравнению с 8-битным вариантов.
Модифицируем алгоритм для обработки контрольной суммы разрядностью 16 бит, надо отметить, что тут так же есть магическое число 8 и 44111, значительное и необоснованное их изменение ухудшает работу алгоритма в разы.
CRC:=CRC + byte16*44111; //все данные 16-битные
CRC:=CRC XOR (CRC SHR 8);
Результат:
Статистика
1: 43478
1: 76923
1: 83333
1: 50000
1: 83333
1: 100000
1: 90909
1: 47619
1: 50000
1: 90909
Что соответствует 109% от теоретического предела. Присутствует ошибка измерений, но это простительно для 10 млн. итераций. Так же сказывается алгоритм создания, и вообще тип ошибок. Для более точного анализа, в любом случае нужно подстраивать условия под ошибки в конкретной линии передачи данных.
Дополнительно отмечу, что можно использовать 32-битные промежуточные переменные для накопления результата, а итоговую контрольную сумму использовать как младшие 16 бит. Во многих случаях, при любой разрядности контрольной суммы, так несколько улучшается качество работы алгоритма.
32-битная контрольная сумма
Перейдем к варианту 32-битной контрольной суммы. Появляется проблема со временем отводимым для анализа статистических данных, так как число переданных телеграмм уже сравнимо с 2^32. Алгоритм такой же, магические числа меняются в сторону увеличения
CRC:=CRC+byte32*$990C9AB5;
CRC:=CRC XOR (CRC SHR 16);
За 10 млн. итераций ошибка не обнаружена. Чтобы ускорить сбор статистики обрезал CRC до 24 бит:
CRC = CRC AND $FFFFFF;
Результат, из 10 млн. итераций ошибка обнаружена 3 раза
Статистика
1: 1000000
1: no
1: no
1: no
1: 1000000
1: no
1: 1000000
1: no
1: no
1: no
Вполне хороший результат и в целом близок к теоретическому пределу для 24 бит контрольной суммы (1:16777216). Тут надо отметить что функция контроля целостности данных равномерно распределена по всем битам CRC, и вполне возможно их отбрасывание с любой стороны, если есть ограничение на размер передаваемой CRC.
Для полноценных 32 бит, достаточно долго ждать результата, ошибок просто нет, за приемлемое время ожидания.
Вариант без умножения:
CRC := (CRC shl 5) + CRC + byte;
CRC := (CRC shl 5) + CRC;
CRC:=CRC xor (CRC shr 16);
Сбоя для полноценной контрольной суммы дождаться не получилось. Контрольная сумма урезанная до 24 бит показывает примерно такие же результаты, 8 ошибок на 100 млн. итераций. Промежуточная переменная CRC 64-битная.
64-битная контрольная сумма
Ну и напоследок 64-битная контрольная сумма, максимальная контрольная сумма, которая имеет смысл при передачи данных на нижнем уровне:
CRC:=CRC+byte64*$5FB7D03C81AE5243;
CRC:=CRC XOR (CRC SHR 8); // магическое число 1..20
Дождаться ошибки передачи данных, до конца существования вселенной, наверное не получится 
Метод аналогичный тому, какой применили для CRC32 показал аналогичные результаты. Больше бит оставляем, выше надежность в полном соответствии с теоретическим пределом. Проверял на младших 20 и 24 битах, этого кажется вполне достаточным, для оценки качества работы алгоритма.
Так же можно применить для 128-битных чисел (и еще больших), главное подобрать корректно 128-битные магические константы. Но это уже явно не для микроконтроллеров, такие числа и компилятор не поддерживает.
Комментарии
В целом метод умножения похож на генерацию псевдослучайной последовательности, только с учетом полезных данных участвующих в процессе.
Рекомендую к использованию в микроконтроллерах, или для проверки целостности любых переданных данных. Вполне рабочий метод, уже как есть, не смотря на простоту алгоритма.
Мой проект по исследованию CRC на гитхаб.
Далее интересно было бы оптимизировать алгоритм на более реальных данных (не псевдослучайные числа по стандартному алгоритму), подобрать более подходящие магические числа под ряд задач и начальных условий, думаю можно еще выиграть доли процента по качеству работы алгоритма. Оптимизировать алгоритм по скорости, читаемости кода (простоте алгоритма), качеству работы. В идеале получить и протестировать образцы кода для всех типов микроконтроллеров, для этого как-раз и нужны примеры с использованием умножения 8, 16, 32 битных данных, и без умножения вообще.
$begingroup$
I have a table which stores all serial numbers of devices in my system:
|------------------------|--------------------------|
| # | Serial number (4 bytes) |
|------------------------|--------------------------|
| 1 | 0x???????? |
|------------------------|--------------------------|
| 2 | 0x???????? |
|------------------------|--------------------------|
| ... | ... |
|------------------------|--------------------------|
| 31 | 0x???????? |
|------------------------|--------------------------|
If I add a device to the system the position in the table is not predictable. If something in the system changes (e.g. add one or more devices, remove one or more devices, replace a device) I want to detect with a «high» propability that the system change. Therefor I want to use a CRC-32. In my system I have at least always 2 devices but max. 31 devcies. Meaning that the input of the CRC can vary between $2^{64}$ to $2^{992}$ different input streams.
As far as I understand:
- The minimum input should be at least 32 bits
- The most important is to use the right generator polynom. E.g.:
- CRC-32
- CRC-32-IEEE
- CRC-32C
- The selection of generator polynom depends on:
- Input stream length
- Error-detection-feasability
- Collision probablility
- Detection of a single bit error: All CRC’s can do this
- Detection of burst errors: All $n$-bit CRC’s can detect burst errors up to $n$ consecutive bits. Also meaning appending new $n$-bit to the end of the input stream.
My concerns are the collision probability of the CRC32 is to high and due to that I don’t detect a change in the configuration. Therefor I want to calcualte this probabilities and my questions are:
-
Is CRC the right method to use for my use case? If not what would be the best?
-
What is the «best» generator polynom for my use case?
-
How to cacluate the error-detection-feasability or collision probability if more then 32 consecutive bits change?
-
How to cacluate the error-detection-feasability or collision probability if $x$ not consecutive (different locations in the complete input stream) bits change?
Raphael♦
71.7k27 gold badges175 silver badges382 bronze badges
asked Jan 10, 2018 at 17:52
$endgroup$
$begingroup$
There’s nothing in your requirements that forces you to use a CRC32. You could use any checksum. If the collision probability for a CRC32seems too high, use a different checksum.
For instance, if you use SHA256, you will never have to worry about collisions — for all engineering purposes, you can treat them as impossible (something that will never happen in your lifetime). And then you won’t need to worry about selecting generator polynomials or anything like that; someone else has done all that work for you. You just use the standard SHA256 algorithm.
P.S. Using a basic checksum algorithm will require you to recompute the checksum on the entire table any time you insert or delete one row. If that’s too slow, there are a number of schemes to speed that up, such as a Merkle hash tree.
answered Jan 10, 2018 at 22:16
D.W.♦D.W.
152k19 gold badges214 silver badges440 bronze badges
$endgroup$
2
2004 г.
2.7. Обнаружение ошибок
Семёнов Ю.А. (ГНЦ ИТЭФ), book.itep.ru
Каналы передачи данных ненадежны, да и само оборудование обработки информации работает со сбоями. По этой причине важную роль приобретают механизмы детектирования ошибок. Ведь если ошибка обнаружена, можно осуществить повторную передачу данных и решить проблему. Если исходный код по своей длине равен полученному коду, обнаружить ошибку передачи не предоставляется возможным.
Простейшим способом обнаружения ошибок является контроль по четности. Обычно контролируется передача блока данных (М бит). Этому блоку ставится в соответствие кодовое слово длиной N бит, причем N>M. Избыточность кода характеризуется величиной 1-M/N. Вероятность обнаружения ошибки определяется отношением M/N (чем меньше это отношение, тем выше вероятность обнаружения ошибки, но и выше избыточность).
При передаче информации она кодируется таким образом, чтобы с одной стороны характеризовать ее минимальным числом символов, а с другой – минимизировать вероятность ошибки при декодировании получателем. Для выбора типа кодирования важную роль играет так называемое расстояние Хэмминга.
Пусть А и Б две двоичные кодовые последовательности равной длины. Расстояние Хэмминга между двумя этими кодовыми последовательностями равно числу символов, которыми они отличаются. Например, расстояние Хэмминга между кодами 00111 и 10101 равно 2.
Можно показать, что для детектирования ошибок в n битах, схема кодирования требует применения кодовых слов с расстоянием Хэмминга не менее N+1. Можно также показать, что для исправления ошибок в N битах необходима схема кодирования с расстоянием Хэмминга между кодами не менее 2N+1. Таким образом, конструируя код, мы пытаемся обеспечить расстояние Хэмминга между возможными кодовыми последовательностями больше, чем оно может возникнуть из-за ошибок.
Широко распространены коды с одиночным битом четности. В этих кодах к каждым М бит добавляется 1 бит, значение которого определяется четностью (или нечетностью) суммы этих М бит. Так, например, для двухбитовых кодов 00, 01, 10, 11 кодами с контролем четности будут 000, 011, 101 и 110. Если в процессе передачи один бит будет передан неверно, четность кода из М+1 бита изменится.
Предположим, что частота ошибок (BER) равна р=10-4. В этом случае вероятность передачи 8 бит с ошибкой составит 1-(1-p)8=7,9х10-4. Добавление бита четности позволяет детектировать любую ошибку в одном из переданных битах. Здесь вероятность ошибки в одном из 9 бит равна 9p(1-p)8. Вероятность же реализации необнаруженной ошибки составит 1-(1-p)9 – 9p(1-p)8 = 3,6×10-7. Таким образом, добавление бита четности уменьшает вероятность необнаруженной ошибки почти в 1000 раз. Использование одного бита четности типично для асинхронного метода передачи. В синхронных каналах чаще используется вычисление и передача битов четности как для строк, так и для столбцов передаваемого массива данных. Такая схема позволяет не только регистрировать но и исправлять ошибки в одном из битов переданного блока.
Контроль по четности достаточно эффективен для выявления одиночных и множественных ошибок в условиях, когда они являются независимыми. При возникновении ошибок в кластерах бит метод контроля четности неэффективен и тогда предпочтительнее метод вычисления циклических сумм (CRC). В этом методе передаваемый кадр делится на специально подобранный образующий полином. Дополнение остатка от деления и является контрольной суммой.
В Ethernet Вычисление crc производится аппаратно (см. также ethernet). На рис. 2.7.1. показан пример реализации аппаратного расчета CRC для образующего полинома B(x)= 1 + x2 + x3 +x5 + x7. В этой схеме входной код приходит слева.
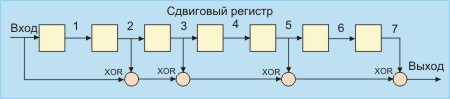
Рис. 2.7.1. Схема реализации расчета CRC
Эффективность CRC для обнаружения ошибок на многие порядки выше простого контроля четности. В настоящее время стандартизовано несколько типов образующих полиномов. Для оценочных целей можно считать, что вероятность невыявления ошибки в случае использования CRC, если ошибка на самом деле имеет место, равна (1/2)r, где r — степень образующего полинома.
| CRC-12 | x12 + x11 + x3 + x2 + x1 + 1 |
| CRC-16 | x16 + x15 + x2 + 1 |
| CRC-CCITT | x16 + x12 + x5 + 1 |
Назад: 2.6.5. Статический алгоритм Хафмана
Оглавление: Телекоммуникационные технологии
Вперёд: 2.8. Коррекция ошибок
Почему часто многие испытывают проблемы с CRC, и как это исправить (перевод [1]).
Насколько много разных способов, какими можно реализовать алгоритм проверки контрольной суммы (Cyclic Redundancy Check, CRC)? В частности, что такое вычисление CRC по 32-битному полиному, также известное как CRC32?
Давайте рассмотрим варианты вычисления CRC32. В общем случае алгоритм CRC может быть реализован одним из двух основных методов:
• На основе формулы.
• На основе таблицы.
Для каждого из этих методов существуют различные опции, которые можно выбрать. Во-первых, для каждого вычисления CRC мы можем использовать один из двух полиномов, отличаются они обратным порядком бит в полиноме:
• «Прямую» константу полинома.
• «Обратную» константу полинома.
Во-вторых, когда мы инициализируем таблицу, инициализацию можно делать сдвигом бит влево или вправо.
В третьих, когда мы вычисляем значение CRC, биты можно сдвигать влево или вправо. Об этих моментах Ross Williams рассказывает в своем руководстве «A PAINLESS GUIDE TO CRC ERROR DETECTION ALGORITHMS» (Безболезненное руководство по алгоритмам обнаружения ошибок):
«В сущности есть только 2 формы вычисления CRC: нормальная (normal) и отраженная (reflected). Нормальная форма со сдвигом влево охватывает случай алгоритмов с Refin=FALSE и Refot=FALSE. Отраженная делает сдвиг вправо, и относится к алгоритмам, у которых оба этих параметра true.»
Это дает 2 формулы, показанные ниже.
// Нормальная форма: crc = table[ ((crc>>24) ^ *data++) & 0xFF ] ^ (crc << 8);
// Отраженная форма: crc = table[ (crc ^ *data++) & 0xFF ] ^ (crc >> 8);
Примечание: в то время как последняя «отраженная» формула верна, первая «нормальная» формула неверна — необходимо обратить вспять обе формулы, т. е. биты данных и конечное значение CRC.
В результате получается 4 и 5 опций соответственно.
В четвертых — когда мы считываем каждый байт данных, мы не обязательно при вычислении CRC можем делать реверс бит в алгоритме CRC. В пятых — мы опционально можем делать реверс бит конечного значения CRC.
Таким образом, в зависимости от формы (нормальная или отраженная) и от константы полинома (прямая или обратная), наивный пользователь может получить как минимум 4 разных значения вычисления CRC! Два из них будут корректны, а два других нет.
• Нормальная форма (сдвиг влево) с прямым полиномом (корректна).
• Отраженная форма (сдвиг вправо) с прямым полиномом.
• Нормальная форма (сдвиг влево) с обратным полиномом.
• Отраженная форма (сдвиг вправо) с обратным полиномом (корректна).
[Контрольная сумма]
Ross также упоминает контрольную сумму, называя её «CHECK»:
«CHECK: … поле, содержащее контрольную сумму, полученную их строки ASCII «123456789». Эта строка прогоняется через указанный алгоритм, например 313233… (hex-форма).
Для CRC32 популярен прямой полином 0x04C11DB7. Реверсированием бит мы получаем полином 0xEDB88320.
| Полином | Двоичное представление полинома |
| 0x04C11DB7 | 00000100_11000001_00011101_10110111 |
| 0xEDB88320 | 11101101_10111000_10000011_00100000 |
Примечание: см. далее «CRC32 или CRC33?».
Эти полиномы (при корректном использовании) генерируют одинаковую контрольную сумму:
| Форма | Полином | CRC32 по контрольным данным ASCII «123456789» |
| Нормальная | 0x04C11DB7 | 0xCBF43926 |
| Отраженная | 0xEDB88320 | 0xCBF43926 |
Обратите внимание, что значение этих двух контрольных сумм одинаковое, несмотря на то, что их полиномы разные! Ниже будет показано, почему так происходит независимо от любого из 4 используемых методов вычисления CRC:
• По формуле.
• С помощью таблицы.
• То и другое с нормальным полиномом.
• То и другое с отраженным полиномом.
В реальной жизни используют не только полиномы CRC32. В Википедии есть таблица популярных полиномов CRC. См. также ссылки [2, 3, 4]. И конечно, разные алгоритмы вычислят CRC по-разному.
123456789 зашифрованное CRC32A, даст значение 181989fc
123456789 зашифрованное CRC32B, даст значение cbf43926
Первым CRC32A является алгоритм ITU I.363.5, популяризированный утилитой BZIP2. Следующий CRC32B это алгоритм ITU V.42, используемый в Ethernet, и он популяризирован PKZip.
Почему на одинаковом полиноме 0x04C11DB7, при одинаковых входных данных получается разные значения CRC32? Забегая вперед, обобщим вычисленные значения:
| Полином | Сдвиг | Реверс данных | Реверс CRC | CRC | Имя |
| 0x04C11DB7 | Влево | Нет | Нет | 0xFC891918 | crc32a |
| Да | Да | 0xCBF43926 | crc32b | ||
| 0xEDB88320 | Вправо | Нет | Нет | 0xCBF43926 | crc32b |
| Да | Да | 0xFC891918 | crc32a |
Подробности можно узнать в enum_crc32.cpp [1]. В этом документе основное внимание уделено CRC32B. На *nix машинах можно использовать штатную утилиту cksum. Например, команды:
echo -n "123456789" > crctest.txt cksum -o 3 crctest.txt
дадут результат
Путем преобразования в hex с помощью Basic Calculator [5]:
echo "obase=16; 3421780262;" | bc CBF43926
Это соответствует ожидаемому значению контрольной суммы.
[Реализация CRC32]
Как мы можем действительно реализовать подсчет CRC32?
• Инициализируем значение CRC, часто нулем, но по соглашению обычно инвертируем эти биты, т. е. берем -1.
• Проходим через все байты, по которым хотим вычислить CRC. Для каждого байта делается операция исключающего ИЛИ (exclusive-or, XOR) с текущим CRC по одному биту за раз.
• По соглашению для конечной CRC мы инвертируем её биты.
Звучит просто, не так ли?
Необходимо учесть и другие не такие важные, но все-таки имеющие значения детали реализации:
• Когда мы делаем операцию XOR над байтом данных и текущим CRC, то начинаем с верхних или нижних бит?
• В каком направлении сдвигаем биты CRC?
• Как мы преобразуем эту формулу в таблицу, чтобы обрабатывать сразу 8 бит?
Начнем с версии, вычисляющей CRC по формуле.
[Вычисление CRC по формуле]
Если используется метод с формулой, то мы можем обобщить 4 варианта реализаций двумя алгоритмами:
a) «Нормальная» CRC32, вычисляемая по формуле:
uint32_t crc32_formula_normal( size_t len, const void *data, const uint32_t POLY = 0x04C11DB7 ) { const unsigned char *buffer = (const unsigned char*) data; uint32_t crc = -1;
while( len-- ) { crc = crc ^ (reverse[ *buffer++ ] << 24); for( int bit = 0; bit < 8; bit++ ) { if( crc & (1L << 31)) crc = (crc << 1) ^ POLY; else crc = (crc << 1); } } return reflect32( ~crc ); }
Замечания:
• Здесь reverse это таблица байт, у которых значения бит реверсированы.
• Подобным образом reflect32() реверсирует 32-разрядное значение.
uint8_t reverse (uint8_t val8)
{
uint8_t result = 0;
uint8_t maskSRC = 0x01;
uint8_t maskDST = 0x80;
for (int i=0; i < 8; i++) { if (val8 & maskSRC) result |= maskDST; maskSRC << = 1; maskDST >> = 1; } return result; }
uint32_t reflect32 (uint32_t val32)
{
uint32_t result = 0;
uint32_t maskSRC = 0x00000001;
uint32_t maskDST = 0x80000000;
for (int i=0; i < 32; i++) { if (val32 & maskSRC) result |= maskDST; maskSRC << = 1; maskDST >> = 1; } return result; }
Здесь важны несколько ключевых моментов:
• «Нормальная» означает сдвиг влево.
• Мы реверсируем байты буфере перед их операцией XOR со значением CRC.
• Байты данных поступают в верхние 8 бит значения CRC.
• Мы проверяем верхний бит значения CRC.
• Мы инвертируем конечное значение CRC.
• Мы реверсируем конечное значение CRC.
Что произойдет, если не делать реверсирование никаких бит?
uint32_t crc32_formula_normal_noreverse( size_t len, const void *data, const uint32_t POLY = 0x04C11DB7 ) { const unsigned char *buffer = (const unsigned char*) data; uint32_t crc = -1;
while( len-- ) { crc = crc ^ (*buffer++ << 24); for( int bit = 0; bit < 8; bit++ ) { if( crc & (1L << 31)) crc = (crc << 1) ^ POLY; else crc = (crc << 1); } } return ~crc; }
Если прогнать этот алгоритм по строке «123456789», то получим значение CRC32 0xFC891918. Обратите внимание, что это little endian форма значения big endian 0x181989FC, упомянутая выше! Т. е. здесь у нас получился вариант CRC32A.
b) «Отраженная» CRC32, вычисляемая по формуле. Если мы хотим убрать все эти реверсирования бит, то получим упрощенную версию алгоритма:
uint32_t crc32_formula_reflect( size_t len, const void *data, const uint32_t POLY = 0xEDB88320 ) { const unsigned char *buffer = (const unsigned char*) data; uint32_t crc = -1;
while( len-- ) { crc = crc ^ *buffer++; for( int bit = 0; bit < 8; bit++ ) { if( crc & 1 ) crc = (crc >> 1) ^ POLY; else crc = (crc >> 1); } } return ~crc; }
Замечания:
• «Отраженная» (reflected) означает сдвиг вправо.
• Байты данных поступают в нижние 8 бит значения CRC.
• Мы проверяем нижний бит значения CRC.
• Мы инвертируем конечное значение CRC.
Что произойдет, если у нас будет несоответствие между формой (нормальная/отраженная) и полиномом (0x04C11DB7/0xEDB88320)? На проверочной строке «123456789» получатся следующие результаты:
Нормальная форма (0x04C11DB7): 0xCBF43926
Отраженная форма (0x04C11DB7): 0xFC4F2BE9, что неправильно!
Нормальная форма (0xEDB88320): 0xFC4F2BE9, что неправильно!
Отраженная форма (0xEDB88320): 0xCBF43926
Теперь понятно, почему многие пользователи просят помощи в Интернете, когда используют значение 0x04C11DB7 (прямой полином) и получают некорректное вычисление CRC. Типовое решение проблемы, которое часто советуют — использовать другой (обратный) полином 0x0xEDB88320, и при этом обе стороны часто не понимают, что оба полинома правильные!
Реальная проблема заключается в НЕСООТВЕТСТВИИ между битовым сдвигом, используемым при инициализации таблицы CRC32, и вычислением CRC32.
[Вычисление CRC на основе таблицы]
У «формульного» алгоритма есть один большой, раздражающий недостаток: нам нужно проверять значение CRC по одному биту в цикле. Конечно, это занимает много процессорного времени.
Можно ли сразу проверять не один, а 8 бит? Да, это реально с помощью заранее подготовленной таблицы. Табличный алгоритм вычисления CRC разбивается на 2 шага:
• Инициализация таблицы.
• Вычисление CRC с использованием этой таблицы.
Как уже упоминалось в обсуждении «формульного» алгоритма, существует 4 разные варианта (пермутации) алгоритма вычисления CRC, два правильных и 2 неправильных:
• Нормальная форма (сдвиг влево) с прямым полиномом (корректна).
• Отраженная форма (сдвиг вправо) с прямым полиномом.
• Нормальная форма (сдвиг влево) с обратным полиномом.
• Отраженная форма (сдвиг вправо) с обратным полиномом (корректна).
Фаза вычисления по таблице добавляет 8 дополнительных пермутаций алгоритма.
| Фаза | Сколько вариаций (пермутаций) алгоритма |
| Инициализация | 22 = 4 |
| Вычисление CRC | 23 = 8 |
Итого получается 22 * 23 = 4 * 8 = 32 пермутации. Из этих 32 только 4 пермутации корректны, или можно так сказать, стандартизированы. Остальные 28 неправильные, и они встречаются иногда из-за того, что кто-то не понимает теорию и неправильно применяет её. Так что не удивляйтесь, что многие люди путаются с CRC32. Слишком просто здесь сделать ошибку.
Итак, как можно реализовать таблицу для вычисления CRC32 четырьмя разными способами?
| Форма | Проверяемый бит | Сдвиг | Полином | Правильно? | Функция |
| Нормальная | Старший | Влево | 0x04C11DB7 | Да | crc32_init_normal ( прямой полином ) |
| Отраженная | Младший | Вправо | Нет! | crc32_init_reflect ( прямой полином ) | |
| Нормальная | Старший | Влево | 0xEDB88320 | Нет! | crc32_init_normal ( обратный полином ) |
| Отраженная | Младший | Вправо | Да | crc32_init_reflect ( обратный полином ) |
Нормальная форма с полиномом 0x04C11DB7: & << 31 [1] = poly, [16] = poly << 8, правильная таблица.
00000000, 04C11DB7, 09823B6E, 0D4326D9, 130476DC, 17C56B6B, 1A864DB2, 1E475005, // 0 [0x00 .. 0x07] 2608EDB8, 22C9F00F, 2F8AD6D6, 2B4BCB61, 350C9B64, 31CD86D3, 3C8EA00A, 384FBDBD, // 8 [0x08 .. 0x0F] 4C11DB70, 48D0C6C7, 4593E01E, 4152FDA9, 5F15ADAC, 5BD4B01B, 569796C2, 52568B75, // 16 [0x10 .. 0x17] 6A1936C8, 6ED82B7F, 639B0DA6, 675A1011, 791D4014, 7DDC5DA3, 709F7B7A, 745E66CD, // 24 [0x18 .. 0x1F] 9823B6E0, 9CE2AB57, 91A18D8E, 95609039, 8B27C03C, 8FE6DD8B, 82A5FB52, 8664E6E5, // 32 [0x20 .. 0x27] BE2B5B58, BAEA46EF, B7A96036, B3687D81, AD2F2D84, A9EE3033, A4AD16EA, A06C0B5D, // 40 [0x28 .. 0x2F] D4326D90, D0F37027, DDB056FE, D9714B49, C7361B4C, C3F706FB, CEB42022, CA753D95, // 48 [0x30 .. 0x37] F23A8028, F6FB9D9F, FBB8BB46, FF79A6F1, E13EF6F4, E5FFEB43, E8BCCD9A, EC7DD02D, // 56 [0x38 .. 0x3F] 34867077, 30476DC0, 3D044B19, 39C556AE, 278206AB, 23431B1C, 2E003DC5, 2AC12072, // 64 [0x40 .. 0x47] 128E9DCF, 164F8078, 1B0CA6A1, 1FCDBB16, 018AEB13, 054BF6A4, 0808D07D, 0CC9CDCA, // 72 [0x48 .. 0x4F] 7897AB07, 7C56B6B0, 71159069, 75D48DDE, 6B93DDDB, 6F52C06C, 6211E6B5, 66D0FB02, // 80 [0x50 .. 0x57] 5E9F46BF, 5A5E5B08, 571D7DD1, 53DC6066, 4D9B3063, 495A2DD4, 44190B0D, 40D816BA, // 88 [0x58 .. 0x5F] ACA5C697, A864DB20, A527FDF9, A1E6E04E, BFA1B04B, BB60ADFC, B6238B25, B2E29692, // 96 [0x60 .. 0x67] 8AAD2B2F, 8E6C3698, 832F1041, 87EE0DF6, 99A95DF3, 9D684044, 902B669D, 94EA7B2A, // 104 [0x68 .. 0x6F] E0B41DE7, E4750050, E9362689, EDF73B3E, F3B06B3B, F771768C, FA325055, FEF34DE2, // 112 [0x70 .. 0x77] C6BCF05F, C27DEDE8, CF3ECB31, CBFFD686, D5B88683, D1799B34, DC3ABDED, D8FBA05A, // 120 [0x78 .. 0x7F] 690CE0EE, 6DCDFD59, 608EDB80, 644FC637, 7A089632, 7EC98B85, 738AAD5C, 774BB0EB, // 128 [0x80 .. 0x87] 4F040D56, 4BC510E1, 46863638, 42472B8F, 5C007B8A, 58C1663D, 558240E4, 51435D53, // 136 [0x88 .. 0x8F] 251D3B9E, 21DC2629, 2C9F00F0, 285E1D47, 36194D42, 32D850F5, 3F9B762C, 3B5A6B9B, // 144 [0x90 .. 0x97] 0315D626, 07D4CB91, 0A97ED48, 0E56F0FF, 1011A0FA, 14D0BD4D, 19939B94, 1D528623, // 152 [0x98 .. 0x9F] F12F560E, F5EE4BB9, F8AD6D60, FC6C70D7, E22B20D2, E6EA3D65, EBA91BBC, EF68060B, // 160 [0xA0 .. 0xA7] D727BBB6, D3E6A601, DEA580D8, DA649D6F, C423CD6A, C0E2D0DD, CDA1F604, C960EBB3, // 168 [0xA8 .. 0xAF] BD3E8D7E, B9FF90C9, B4BCB610, B07DABA7, AE3AFBA2, AAFBE615, A7B8C0CC, A379DD7B, // 176 [0xB0 .. 0xB7] 9B3660C6, 9FF77D71, 92B45BA8, 9675461F, 8832161A, 8CF30BAD, 81B02D74, 857130C3, // 184 [0xB8 .. 0xBF] 5D8A9099, 594B8D2E, 5408ABF7, 50C9B640, 4E8EE645, 4A4FFBF2, 470CDD2B, 43CDC09C, // 192 [0xC0 .. 0xC7] 7B827D21, 7F436096, 7200464F, 76C15BF8, 68860BFD, 6C47164A, 61043093, 65C52D24, // 200 [0xC8 .. 0xCF] 119B4BE9, 155A565E, 18197087, 1CD86D30, 029F3D35, 065E2082, 0B1D065B, 0FDC1BEC, // 208 [0xD0 .. 0xD7] 3793A651, 3352BBE6, 3E119D3F, 3AD08088, 2497D08D, 2056CD3A, 2D15EBE3, 29D4F654, // 216 [0xD8 .. 0xDF] C5A92679, C1683BCE, CC2B1D17, C8EA00A0, D6AD50A5, D26C4D12, DF2F6BCB, DBEE767C, // 224 [0xE0 .. 0xE7] E3A1CBC1, E760D676, EA23F0AF, EEE2ED18, F0A5BD1D, F464A0AA, F9278673, FDE69BC4, // 232 [0xE8 .. 0xEF] 89B8FD09, 8D79E0BE, 803AC667, 84FBDBD0, 9ABC8BD5, 9E7D9662, 933EB0BB, 97FFAD0C, // 240 [0xF0 .. 0xF7] AFB010B1, AB710D06, A6322BDF, A2F33668, BCB4666D, B8757BDA, B5365D03, B1F740B4, // 248 [0xF8 .. 0xFF]
Отраженная форма с полиномом 0x04C11DB7: &1 >> [1] = rev. poly, [30] = rev.poly << 8, неправильная таблица.
00000000, 06233697, 05C45641, 03E760D6, 020A97ED, 0429A17A, 07CEC1AC, 01EDF73B, // 0 [0x00 .. 0x07] 04152FDA, 0236194D, 01D1799B, 07F24F0C, 061FB837, 003C8EA0, 03DBEE76, 05F8D8E1, // 8 [0x08 .. 0x0F] 01A864DB, 078B524C, 046C329A, 024F040D, 03A2F336, 0581C5A1, 0666A577, 004593E0, // 16 [0x10 .. 0x17] 05BD4B01, 039E7D96, 00791D40, 065A2BD7, 07B7DCEC, 0194EA7B, 02738AAD, 0450BC3A, // 24 [0x18 .. 0x1F] 0350C9B6, 0573FF21, 06949FF7, 00B7A960, 015A5E5B, 077968CC, 049E081A, 02BD3E8D, // 32 [0x20 .. 0x27] 0745E66C, 0166D0FB, 0281B02D, 04A286BA, 054F7181, 036C4716, 008B27C0, 06A81157, // 40 [0x28 .. 0x2F] 02F8AD6D, 04DB9BFA, 073CFB2C, 011FCDBB, 00F23A80, 06D10C17, 05366CC1, 03155A56, // 48 [0x30 .. 0x37] 06ED82B7, 00CEB420, 0329D4F6, 050AE261, 04E7155A, 02C423CD, 0123431B, 0700758C, // 56 [0x38 .. 0x3F] 06A1936C, 0082A5FB, 0365C52D, 0546F3BA, 04AB0481, 02883216, 016F52C0, 074C6457, // 64 [0x40 .. 0x47] 02B4BCB6, 04978A21, 0770EAF7, 0153DC60, 00BE2B5B, 069D1DCC, 057A7D1A, 03594B8D, // 72 [0x48 .. 0x4F] 0709F7B7, 012AC120, 02CDA1F6, 04EE9761, 0503605A, 032056CD, 00C7361B, 06E4008C, // 80 [0x50 .. 0x57] 031CD86D, 053FEEFA, 06D88E2C, 00FBB8BB, 01164F80, 07357917, 04D219C1, 02F12F56, // 88 [0x58 .. 0x5F] 05F15ADA, 03D26C4D, 00350C9B, 06163A0C, 07FBCD37, 01D8FBA0, 023F9B76, 041CADE1, // 96 [0x60 .. 0x67] 01E47500, 07C74397, 04202341, 020315D6, 03EEE2ED, 05CDD47A, 062AB4AC, 0009823B, // 104 [0x68 .. 0x6F] 04593E01, 027A0896, 019D6840, 07BE5ED7, 0653A9EC, 00709F7B, 0397FFAD, 05B4C93A, // 112 [0x70 .. 0x77] 004C11DB, 066F274C, 0588479A, 03AB710D, 02468636, 0465B0A1, 0782D077, 01A1E6E0, // 120 [0x78 .. 0x7F] 04C11DB7, 02E22B20, 01054BF6, 07267D61, 06CB8A5A, 00E8BCCD, 030FDC1B, 052CEA8C, // 128 [0x80 .. 0x87] 00D4326D, 06F704FA, 0510642C, 033352BB, 02DEA580, 04FD9317, 071AF3C1, 0139C556, // 136 [0x88 .. 0x8F] 0569796C, 034A4FFB, 00AD2F2D, 068E19BA, 0763EE81, 0140D816, 02A7B8C0, 04848E57, // 144 [0x90 .. 0x97] 017C56B6, 075F6021, 04B800F7, 029B3660, 0376C15B, 0555F7CC, 06B2971A, 0091A18D, // 152 [0x98 .. 0x9F] 0791D401, 01B2E296, 02558240, 0476B4D7, 059B43EC, 03B8757B, 005F15AD, 067C233A, // 160 [0xA0 .. 0xA7] 0384FBDB, 05A7CD4C, 0640AD9A, 00639B0D, 018E6C36, 07AD5AA1, 044A3A77, 02690CE0, // 168 [0xA8 .. 0xAF] 0639B0DA, 001A864D, 03FDE69B, 05DED00C, 04332737, 021011A0, 01F77176, 07D447E1, // 176 [0xB0 .. 0xB7] 022C9F00, 040FA997, 07E8C941, 01CBFFD6, 002608ED, 06053E7A, 05E25EAC, 03C1683B, // 184 [0xB8 .. 0xBF] 02608EDB, 0443B84C, 07A4D89A, 0187EE0D, 006A1936, 06492FA1, 05AE4F77, 038D79E0, // 192 [0xC0 .. 0xC7] 0675A101, 00569796, 03B1F740, 0592C1D7, 047F36EC, 025C007B, 01BB60AD, 0798563A, // 200 [0xC8 .. 0xCF] 03C8EA00, 05EBDC97, 060CBC41, 002F8AD6, 01C27DED, 07E14B7A, 04062BAC, 02251D3B, // 208 [0xD0 .. 0xD7] 07DDC5DA, 01FEF34D, 0219939B, 043AA50C, 05D75237, 03F464A0, 00130476, 063032E1, // 216 [0xD8 .. 0xDF] 0130476D, 071371FA, 04F4112C, 02D727BB, 033AD080, 0519E617, 06FE86C1, 00DDB056, // 224 [0xE0 .. 0xE7] 052568B7, 03065E20, 00E13EF6, 06C20861, 072FFF5A, 010CC9CD, 02EBA91B, 04C89F8C, // 232 [0xE8 .. 0xEF] 009823B6, 06BB1521, 055C75F7, 037F4360, 0292B45B, 04B182CC, 0756E21A, 0175D48D, // 240 [0xF0 .. 0xF7] 048D0C6C, 02AE3AFB, 01495A2D, 076A6CBA, 06879B81, 00A4AD16, 0343CDC0, 0560FB57, // 248 [0xF8 .. 0xFF]
Нормальная форма с полиномом 0xEDB88320: & << 31 [128] = rev. poly, [120] = rev.poly >> 8, неправильная таблица.
00000000, EDB88320, 36C98560, DB710640, 6D930AC0, 802B89E0, 5B5A8FA0, B6E20C80, // 0 [0x00 .. 0x07] DB261580, 369E96A0, EDEF90E0, 005713C0, B6B51F40, 5B0D9C60, 807C9A20, 6DC41900, // 8 [0x08 .. 0x0F] 5BF4A820, B64C2B00, 6D3D2D40, 8085AE60, 3667A2E0, DBDF21C0, 00AE2780, ED16A4A0, // 16 [0x10 .. 0x17] 80D2BDA0, 6D6A3E80, B61B38C0, 5BA3BBE0, ED41B760, 00F93440, DB883200, 3630B120, // 24 [0x18 .. 0x1F] B7E95040, 5A51D360, 8120D520, 6C985600, DA7A5A80, 37C2D9A0, ECB3DFE0, 010B5CC0, // 32 [0x20 .. 0x27] 6CCF45C0, 8177C6E0, 5A06C0A0, B7BE4380, 015C4F00, ECE4CC20, 3795CA60, DA2D4940, // 40 [0x28 .. 0x2F] EC1DF860, 01A57B40, DAD47D00, 376CFE20, 818EF2A0, 6C367180, B74777C0, 5AFFF4E0, // 48 [0x30 .. 0x37] 373BEDE0, DA836EC0, 01F26880, EC4AEBA0, 5AA8E720, B7106400, 6C616240, 81D9E160, // 56 [0x38 .. 0x3F] 826A23A0, 6FD2A080, B4A3A6C0, 591B25E0, EFF92960, 0241AA40, D930AC00, 34882F20, // 64 [0x40 .. 0x47] 594C3620, B4F4B500, 6F85B340, 823D3060, 34DF3CE0, D967BFC0, 0216B980, EFAE3AA0, // 72 [0x48 .. 0x4F] D99E8B80, 342608A0, EF570EE0, 02EF8DC0, B40D8140, 59B50260, 82C40420, 6F7C8700, // 80 [0x50 .. 0x57] 02B89E00, EF001D20, 34711B60, D9C99840, 6F2B94C0, 829317E0, 59E211A0, B45A9280, // 88 [0x58 .. 0x5F] 358373E0, D83BF0C0, 034AF680, EEF275A0, 58107920, B5A8FA00, 6ED9FC40, 83617F60, // 96 [0x60 .. 0x67] EEA56660, 031DE540, D86CE300, 35D46020, 83366CA0, 6E8EEF80, B5FFE9C0, 58476AE0, // 104 [0x68 .. 0x6F] 6E77DBC0, 83CF58E0, 58BE5EA0, B506DD80, 03E4D100, EE5C5220, 352D5460, D895D740, // 112 [0x70 .. 0x77] B551CE40, 58E94D60, 83984B20, 6E20C800, D8C2C480, 357A47A0, EE0B41E0, 03B3C2C0, // 120 [0x78 .. 0x7F] E96CC460, 04D44740, DFA54100, 321DC220, 84FFCEA0, 69474D80, B2364BC0, 5F8EC8E0, // 128 [0x80 .. 0x87] 324AD1E0, DFF252C0, 04835480, E93BD7A0, 5FD9DB20, B2615800, 69105E40, 84A8DD60, // 136 [0x88 .. 0x8F] B2986C40, 5F20EF60, 8451E920, 69E96A00, DF0B6680, 32B3E5A0, E9C2E3E0, 047A60C0, // 144 [0x90 .. 0x97] 69BE79C0, 8406FAE0, 5F77FCA0, B2CF7F80, 042D7300, E995F020, 32E4F660, DF5C7540, // 152 [0x98 .. 0x9F] 5E859420, B33D1700, 684C1140, 85F49260, 33169EE0, DEAE1DC0, 05DF1B80, E86798A0, // 160 [0xA0 .. 0xA7] 85A381A0, 681B0280, B36A04C0, 5ED287E0, E8308B60, 05880840, DEF90E00, 33418D20, // 168 [0xA8 .. 0xAF] 05713C00, E8C9BF20, 33B8B960, DE003A40, 68E236C0, 855AB5E0, 5E2BB3A0, B3933080, // 176 [0xB0 .. 0xB7] DE572980, 33EFAAA0, E89EACE0, 05262FC0, B3C42340, 5E7CA060, 850DA620, 68B52500, // 184 [0xB8 .. 0xBF] 6B06E7C0, 86BE64E0, 5DCF62A0, B077E180, 0695ED00, EB2D6E20, 305C6860, DDE4EB40, // 192 [0xC0 .. 0xC7] B020F240, 5D987160, 86E97720, 6B51F400, DDB3F880, 300B7BA0, EB7A7DE0, 06C2FEC0, // 200 [0xC8 .. 0xCF] 30F24FE0, DD4ACCC0, 063BCA80, EB8349A0, 5D614520, B0D9C600, 6BA8C040, 86104360, // 208 [0xD0 .. 0xD7] EBD45A60, 066CD940, DD1DDF00, 30A55C20, 864750A0, 6BFFD380, B08ED5C0, 5D3656E0, // 216 [0xD8 .. 0xDF] DCEFB780, 315734A0, EA2632E0, 079EB1C0, B17CBD40, 5CC43E60, 87B53820, 6A0DBB00, // 224 [0xE0 .. 0xE7] 07C9A200, EA712120, 31002760, DCB8A440, 6A5AA8C0, 87E22BE0, 5C932DA0, B12BAE80, // 232 [0xE8 .. 0xEF] 871B1FA0, 6AA39C80, B1D29AC0, 5C6A19E0, EA881560, 07309640, DC419000, 31F91320, // 240 [0xF0 .. 0xF7] 5C3D0A20, B1858900, 6AF48F40, 874C0C60, 31AE00E0, DC1683C0, 07678580, EADF06A0, // 248 [0xF8 .. 0xFF]
Отраженная форма с полиномом 0xEDB88320: &1 >> [128] = poly, [8] = poly >> 8, правильная таблица.
00000000, 77073096, EE0E612C, 990951BA, 076DC419, 706AF48F, E963A535, 9E6495A3, // 0 [0x00 .. 0x07] 0EDB8832, 79DCB8A4, E0D5E91E, 97D2D988, 09B64C2B, 7EB17CBD, E7B82D07, 90BF1D91, // 8 [0x08 .. 0x0F] 1DB71064, 6AB020F2, F3B97148, 84BE41DE, 1ADAD47D, 6DDDE4EB, F4D4B551, 83D385C7, // 16 [0x10 .. 0x17] 136C9856, 646BA8C0, FD62F97A, 8A65C9EC, 14015C4F, 63066CD9, FA0F3D63, 8D080DF5, // 24 [0x18 .. 0x1F] 3B6E20C8, 4C69105E, D56041E4, A2677172, 3C03E4D1, 4B04D447, D20D85FD, A50AB56B, // 32 [0x20 .. 0x27] 35B5A8FA, 42B2986C, DBBBC9D6, ACBCF940, 32D86CE3, 45DF5C75, DCD60DCF, ABD13D59, // 40 [0x28 .. 0x2F] 26D930AC, 51DE003A, C8D75180, BFD06116, 21B4F4B5, 56B3C423, CFBA9599, B8BDA50F, // 48 [0x30 .. 0x37] 2802B89E, 5F058808, C60CD9B2, B10BE924, 2F6F7C87, 58684C11, C1611DAB, B6662D3D, // 56 [0x38 .. 0x3F] 76DC4190, 01DB7106, 98D220BC, EFD5102A, 71B18589, 06B6B51F, 9FBFE4A5, E8B8D433, // 64 [0x40 .. 0x47] 7807C9A2, 0F00F934, 9609A88E, E10E9818, 7F6A0DBB, 086D3D2D, 91646C97, E6635C01, // 72 [0x48 .. 0x4F] 6B6B51F4, 1C6C6162, 856530D8, F262004E, 6C0695ED, 1B01A57B, 8208F4C1, F50FC457, // 80 [0x50 .. 0x57] 65B0D9C6, 12B7E950, 8BBEB8EA, FCB9887C, 62DD1DDF, 15DA2D49, 8CD37CF3, FBD44C65, // 88 [0x58 .. 0x5F] 4DB26158, 3AB551CE, A3BC0074, D4BB30E2, 4ADFA541, 3DD895D7, A4D1C46D, D3D6F4FB, // 96 [0x60 .. 0x67] 4369E96A, 346ED9FC, AD678846, DA60B8D0, 44042D73, 33031DE5, AA0A4C5F, DD0D7CC9, // 104 [0x68 .. 0x6F] 5005713C, 270241AA, BE0B1010, C90C2086, 5768B525, 206F85B3, B966D409, CE61E49F, // 112 [0x70 .. 0x77] 5EDEF90E, 29D9C998, B0D09822, C7D7A8B4, 59B33D17, 2EB40D81, B7BD5C3B, C0BA6CAD, // 120 [0x78 .. 0x7F] EDB88320, 9ABFB3B6, 03B6E20C, 74B1D29A, EAD54739, 9DD277AF, 04DB2615, 73DC1683, // 128 [0x80 .. 0x87] E3630B12, 94643B84, 0D6D6A3E, 7A6A5AA8, E40ECF0B, 9309FF9D, 0A00AE27, 7D079EB1, // 136 [0x88 .. 0x8F] F00F9344, 8708A3D2, 1E01F268, 6906C2FE, F762575D, 806567CB, 196C3671, 6E6B06E7, // 144 [0x90 .. 0x97] FED41B76, 89D32BE0, 10DA7A5A, 67DD4ACC, F9B9DF6F, 8EBEEFF9, 17B7BE43, 60B08ED5, // 152 [0x98 .. 0x9F] D6D6A3E8, A1D1937E, 38D8C2C4, 4FDFF252, D1BB67F1, A6BC5767, 3FB506DD, 48B2364B, // 160 [0xA0 .. 0xA7] D80D2BDA, AF0A1B4C, 36034AF6, 41047A60, DF60EFC3, A867DF55, 316E8EEF, 4669BE79, // 168 [0xA8 .. 0xAF] CB61B38C, BC66831A, 256FD2A0, 5268E236, CC0C7795, BB0B4703, 220216B9, 5505262F, // 176 [0xB0 .. 0xB7] C5BA3BBE, B2BD0B28, 2BB45A92, 5CB36A04, C2D7FFA7, B5D0CF31, 2CD99E8B, 5BDEAE1D, // 184 [0xB8 .. 0xBF] 9B64C2B0, EC63F226, 756AA39C, 026D930A, 9C0906A9, EB0E363F, 72076785, 05005713, // 192 [0xC0 .. 0xC7] 95BF4A82, E2B87A14, 7BB12BAE, 0CB61B38, 92D28E9B, E5D5BE0D, 7CDCEFB7, 0BDBDF21, // 200 [0xC8 .. 0xCF] 86D3D2D4, F1D4E242, 68DDB3F8, 1FDA836E, 81BE16CD, F6B9265B, 6FB077E1, 18B74777, // 208 [0xD0 .. 0xD7] 88085AE6, FF0F6A70, 66063BCA, 11010B5C, 8F659EFF, F862AE69, 616BFFD3, 166CCF45, // 216 [0xD8 .. 0xDF] A00AE278, D70DD2EE, 4E048354, 3903B3C2, A7672661, D06016F7, 4969474D, 3E6E77DB, // 224 [0xE0 .. 0xE7] AED16A4A, D9D65ADC, 40DF0B66, 37D83BF0, A9BCAE53, DEBB9EC5, 47B2CF7F, 30B5FFE9, // 232 [0xE8 .. 0xEF] BDBDF21C, CABAC28A, 53B39330, 24B4A3A6, BAD03605, CDD70693, 54DE5729, 23D967BF, // 240 [0xF0 .. 0xF7] B3667A2E, C4614AB8, 5D681B02, 2A6F2B94, B40BBE37, C30C8EA1, 5A05DF1B, 2D02EF8D, // 248 [0xF8 .. 0xFF]
Проверкой элементов table[1] и table[128] мы можем определить:
• Какая используется форма алгоритма (нормальная или отраженная).
• Какой используется полином.
• Какое направление сдвига следует использовать.
Как можно реализовать вычисление CRC восемью разными способами?
| Сдвиг CRC | Биты данных реверсированы | Конечная CRC реверсирована |
| Влево | Нет | Нет |
| Вправо | Да | Да |
Биты данных реверсируются в зависимости от используемой формы:
| Форма | Биты данных |
| Нормальная |
crc32 = table[ (crc32 >> 24) ^ reverse[ *data ] ^ (crc << 8); |
| Отраженная |
crc32 = table[ (crc32 ) ^ *data ] ^ (crc >> 8); |
Конечное значение CRC реверсируется в зависимости от используемой формы:
| Форма | Биты данных |
| Нормальная | |
| Отраженная |
crc32 = reflect32( ~crc32 ); |
Перечислим 8 пермутаций для вычислений:
| Сдвиг вправо | Реверс данных | Реверс CRC | Функция |
| 0 | 0 | 0 | crc32_000() |
| 0 | 0 | 1 | crc32_001() |
| 0 | 1 | 0 | crc32_010() |
| 0 | 1 | 1 | crc32_011() |
| 1 | 0 | 0 | crc32_100() |
| 1 | 0 | 1 | crc32_101() |
| 1 | 1 | 0 | crc32_110() |
| 1 | 1 | 1 | crc32_111() |
См. enum_crc32.cpp [1].
| Полином | Bit | Init | Shift CRC | Реверс данных | Реверс CRC | Функция | Допустимо |
| 0x04C11DB7 | 31 | crc32_init_normal |
Влево | 0 | 0 | crc32_000() | crc32a |
| 31 | 0 | 1 | crc32_001() | нет | |||
| 31 | 1 | 0 | crc32_010() | нет | |||
| 31 | 1 | 1 | crc32_011() | crc32b | |||
| 31 | Вправо | 0 | 0 | crc32_100() | нет | ||
| 31 | 0 | 1 | crc32_101() | нет | |||
| 31 | 1 | 0 | crc32_110() | нет | |||
| 31 | 1 | 1 | crc32_111() | нет | |||
| 1 | crc32_init_reflect |
Влево | 0 | 0 | crc32_000() | нет | |
| 1 | 0 | 1 | crc32_001() | нет | |||
| 1 | 1 | 0 | crc32_010() | нет | |||
| 1 | 1 | 1 | crc32_011() | нет | |||
| 1 | Вправо | 0 | 0 | crc32_100() | нет | ||
| 1 | 0 | 1 | crc32_101() | нет | |||
| 1 | 1 | 0 | crc32_110() | нет | |||
| 1 | 1 | 1 | crc32_111() | нет | |||
| 0xEDB88320 | 31 | crc32_init_normal |
Влево | 0 | 0 | crc32_000() | нет |
| 31 | 0 | 1 | crc32_001() | нет | |||
| 31 | 1 | 0 | crc32_010() | нет | |||
| 31 | 1 | 1 | crc32_011() | нет | |||
| 31 | Вправо | 0 | 0 | crc32_100() | нет | ||
| 31 | 0 | 1 | crc32_101() | нет | |||
| 31 | 1 | 0 | crc32_110() | нет | |||
| 31 | 1 | 1 | crc32_111() | нет | |||
| 1 | crc32_init_reflect |
Влево | 0 | 0 | crc32_000() | нет | |
| 1 | 0 | 1 | crc32_001() | нет | |||
| 1 | 1 | 0 | crc32_010() | нет | |||
| 1 | 1 | 1 | crc32_011() | нет | |||
| 1 | Вправо | 0 | 0 | crc32_000() | crc32b | ||
| 1 | 0 | 1 | crc32_001() | нет | |||
| 1 | 1 | 0 | crc32_010() | нет | |||
| 1 | 1 | 1 | crc32_011() | crc32a |
Легенда таблицы:
Bit: какой бит проверяется при инициализации таблицы.
Shift CRC: какое направление сдвига CRC во время вычисления. Обратите внимание, что это не зависит от того, в каком направлении используется сдвиг во время инициализации!
[CRC32, общие выводы]
В следующей таблице суммарно показаны 2 формы CRC32:
| Описание | Нормальная | Отраженная |
| Биты полинома реверсированы? | Нет | Да |
| Значение полинома | 0x04C11DB7 | 0xEDB88320 |
| Полиномиальная номенклатура | Прямая | Обратная |
| Инициализируемый бит таблицы | Старший | Младший |
| Проверяемый бит таблицы | 31 | 1 |
| Сдвиг бит таблицы инициализации | Влево | Вправо |
| Биты данных реверсированы? | Да | Нет |
| Сдвиг при вычислении CRC | Влево | Вправо |
| Конечная CRC реверсируется? | Да | Нет |
| Корректная функция инициализации | crc32_init_normal | crc32_init_reflect |
| Корректная функция вычисления CRC | crc32_011() | crc32_100() |
| CRC32 от строки «123456789» | 0xCBF43926 |
Из-за того, что кто-то один совсем не понял CRC32, другие люди начинают думать, что CRC32 это плохой вариант вычисления хеша.
CRC32 никогда не предназначалась для использования в хеш-таблице. На самом деле нет никаких веских причин использовать CRC32 для этой цели, и автор [1] рекомендует избегать этого. Если Вы решите использовать CRC32, то важно использовать хеш-биты со стороны конца противоположного тому, в который подаются октеты ключа. Какой именно конец — зависит от специфической реализации CRC32. Не рассматривайте CRC32 как хеш-функцию «черного ящика», и не используйте её как хеш общего назначения. Обязательно проверяйте каждое приложение на пригодность к определенной ситуации.
Примечательно, что Bret Mulvey реализовал неправильную версию CRC32! Вот оригинальный код:
public class CRC32 : HashFunction
{
uint[] tab;
public CRC32() { Init(0x04c11db7); }
public CRC32(uint poly)
{
Init(poly);
}
void Init(uint poly) { tab = new uint[256]; for (uint i=0; i < 256; i++) { uint t = i; for (int j=0; j < 8; j++) if ((t & 1) == 0) t >>= 1; else t = (t >> 1) ^ poly; tab[i] = t; } }
public override uint ComputeHash(byte[] data) { uint hash = 0xFFFFFFFF; foreach (byte b in data) hash = (hash << 8) ^ tab[b ^ (hash >> 24)]; return ~hash; } }
Оригинальная страничка Bret-а мертва (http://home.comcast.net/~bretm/hash/8.html), но к счастью есть зеркала (https://web.archive.org/web/20130420172816/http://home.comcast.net/~bretm/hash/8.html).
Замечание: у Bret-а есть новая страничка, но он ловко опускает CRC32 из-за своего непонимания CRC32 (http://papa.bretmulvey.com/post/124027987928/hash-functions).
Вот вопрос на Stack Overflow:
http://stackoverflow.com/questions/10953958/can-crc32-be-used-as-a-hash-function
Видно, что Bret не реализовал правильно CRC32, но никто на самом деле не говорит, в чем заключается его ошибка! Можно посмотреть соответствующий код и данные, что определить, где Bret допустил ошибки.
[Неправильный код]
1. Bret взял инициализацию таблицы, не совпадающую с вычислением CRC.
Напомню, что для CRC32 существует 2 полинома: прямой 0x04C11DB7 и реверсный 0xEDB88320. У реверсного порядок следования бит обратный. Алгоритм CRC существует в 2 формах: нормальная форма проверяет старший бит и делает сдвиг влево, отраженная форма проверяет младший бит и сдвигает вправо. Bret в функции Init() использует прямой полином, не соответствующий «отраженной» форме инициализации младшего бита.
2. Неправильное вычисление CRC. Bret в функции ComputeHash() делает сдвиг влево, но не делает реверсирование бит в как в данных, так и конечном значении CRC!
Если мы рассмотрим возможные способы, которыми кто-то мог бы инициализировать таблицу с прямым полиномом 0x04C11DB7, то обнаружем 8 значений CRC для текста «123456789». НИ ОДНО из них не будет корректным!
Reflected 0x04C11DB7: &1 >> [ 1] = rev. poly, [ 30] = rev.poly << 8 broken Shift: Left , Rev. Data: 0, Rev. CRC: 0, 0xC9A0B7E5 no Shift: Left , Rev. Data: 0, Rev. CRC: 1, 0xA7ED0593 no Shift: Left , Rev. Data: 1, Rev. CRC: 0, 0x9D594C04 no Shift: Left , Rev. Data: 1, Rev. CRC: 1, 0x20329AB9 no Shift: Right, Rev. Data: 0, Rev. CRC: 0, 0xFC4F2BE9 no Shift: Right, Rev. Data: 0, Rev. CRC: 1, 0x97D4F23F no Shift: Right, Rev. Data: 1, Rev. CRC: 0, 0xFDEFB72E no Shift: Right, Rev. Data: 1, Rev. CRC: 1, 0x74EDF7BF no
Почему так?
[Почему существуют 2 формы?]
Возможно Вам будет интересно, почему вообще существую 2 формы алгоритма. Давным-давно, когда CRC был только что разработан и реализован, разработчики аппаратуры сдвигали биты справа налево, используя так называемый barrel shifter (см. Википедию). Впоследствии, когда CRC был реализован программно, кое-кто заметил, что все эти реверсирования бит не нужны, если:
• Использовать реверсный полином.
• В обратном порядке опрашивать биты у байт.
• Реверсировать конечное значение CRC.
Если вывести трассировку, как вычисляется CRC32 при помощи таблиц (см. выше во врезке правильную таблицу для 0x04C11DB7 и правильную таблицу для 0xEDB88320), то получим:
========== Байт: 9 ==========
[ 31, 32, 33, 34, 35, 36, 37, 38, 39, ]
---------- Нормальная форма ----------
crc32=FFFFFFFF
^buf[0000]: 31 -> 8C биты реверсированы
= crc32[ 73 ]: 07BE5ED7 ^ FFFFFF__
crc32=1208C43E
^buf[0001]: 32 -> 4C биты реверсированы
= crc32[ 5E ]: 04D219C1 ^ 08C43E__
crc32=4CDD350D
^buf[0002]: 33 -> CC биты реверсированы
= crc32[ 80 ]: 04C11DB7 ^ DD350D__
crc32=B439EDEE
^buf[0003]: 34 -> 2C биты реверсированы
= crc32[ 98 ]: 017C56B6 ^ 39EDEE__
crc32=3AF83826
^buf[0004]: 35 -> AC биты реверсированы
= crc32[ 96 ]: 02A7B8C0 ^ F83826__
crc32=C7A3502C
^buf[0005]: 36 -> 6C биты реверсированы
= crc32[ AB ]: 00639B0D ^ A3502C__
crc32=7934B16F
^buf[0006]: 37 -> EC биты реверсированы
= crc32[ 95 ]: 0140D816 ^ 34B16F__
crc32=06693FF5
^buf[0007]: 38 -> 1C биты реверсированы
= crc32[ 1A ]: 00791D40 ^ 693FF5__
crc32=0AA4F8A6
^buf[0008]: 39 -> 9C биты реверсированы
= crc32[ 96 ]: 02A7B8C0 ^ A4F8A6__
crc32=9B63D02C
~=649C2FD3
=CBF43926 биты реверсированы
OK
---------- Отраженная форма ----------
crc32=FFFFFFFF
^buf[0000]: 31
= crc32[ CE ]: 61043093 ^ __FFFFFF
crc32=7C231048
^buf[0001]: 32
= crc32[ 7A ]: CF3ECB31 ^ __7C2310
crc32=B0ACBB32
^buf[0002]: 33
= crc32[ 01 ]: 04C11DB7 ^ __B0ACBB
crc32=77B79C2D
^buf[0003]: 34
= crc32[ 19 ]: 6ED82B7F ^ __77B79C
crc32=641C1F5C
^buf[0004]: 35
= crc32[ 69 ]: 8E6C3698 ^ __641C1F
crc32=340AC5E3
^buf[0005]: 36
= crc32[ D5 ]: 065E2082 ^ __340AC5
crc32=F68D2C9E
^buf[0006]: 37
= crc32[ A9 ]: D3E6A601 ^ __F68D2C
crc32=AFFC9660
^buf[0007]: 38
= crc32[ 58 ]: 5E9F46BF ^ __AFFC96
crc32=651F2550
^buf[0008]: 39
= crc32[ 69 ]: 8E6C3698 ^ __651F25
crc32=340BC6D9
~=CBF43926
OK
[Неправильные данные]
Код Bret-а генерирует неправильную таблицу CRC:
00000000, 06233697, 05C45641, 03E760D6, 020A97ED, 0429A17A, 07CEC1AC, 01EDF73B, 04152FDA, 0236194D, 01D1799B, 07F24F0C, 061FB837, 003C8EA0, 03DBEE76, 05F8D8E1, 01A864DB, 078B524C, 046C329A, 024F040D, 03A2F336, 0581C5A1, 0666A577, 004593E0, .. 052568B7, 03065E20, 00E13EF6, 06C20861, 072FFF5A, 010CC9CD, 02EBA91B, 04C89F8C, 009823B6, 06BB1521, 055C75F7, 037F4360, 0292B45B, 04B182CC, 0756E21A, 0175D48D, 048D0C6C, 02AE3AFB, 01495A2D, 076A6CBA, 06879B81, 00A4AD16, 0343CDC0, 0560FB57,
В результате по этой неправильной таблице вычисляется неправильная контрольная сумма:
------- Не соответствующие друг другу полином и вычисление CRC -------
crc32=FFFFFFFF
^buf[0000]: 31
= crc32[ 73 ]: 07BE5ED7 ^ FFFFFF__
crc32=FE449FAD
^buf[0001]: 32
= crc32[ B2 ]: 03FDE69B ^ 449FAD__
crc32=40E09BEC
^buf[0002]: 33
= crc32[ 8C ]: 02DEA580 ^ E09BEC__
crc32=E725B2D7
^buf[0003]: 34
= crc32[ CB ]: 0592C1D7 ^ 25B2D7__
crc32=259D5DD6
^buf[0004]: 35
= crc32[ 89 ]: 06F704FA ^ 9D5DD6__
crc32=9CF5B2DB
^buf[0005]: 36
= crc32[ F0 ]: 009823B6 ^ F5B2DB__
crc32=F3F2769A
^buf[0006]: 37
= crc32[ 1F ]: 0450BC3A ^ F2769A__
crc32=F21C8336
^buf[0007]: 38
= crc32[ EE ]: 02EBA91B ^ 1C8336__
crc32=1F32C140
^buf[0008]: 39
= crc32[ 83 ]: 07267D61 ^ 32C140__
crc32=365F481A
~=C9A0B7E5
ОШИБКА!
[Исправление кода Bret-а]
Можно исправить эту реализацию двумя способами, в зависимости от того, какой полином хотим использовать.
1. Исправление с обратным полиномом.
a) Инициализация таблицы должна использовать обратный полином:
b) При вычислении CRC поменяйте неправильный левый сдвиг сдвиг на правильный правый сдвиг:
hash = tab[ (b ^ hash) & 0xFF ] ^ ((hash >> 8) & 0xFFFFFF); // Clamp 'hash >> 8' to 24-bit
2. Исправление с прямым полиномом.
a) Инициализация таблицы. Здесь нужно установить начальное значение CRC. Если старший бит установлен, то выполняется левый сдвиг и XOR с полиномом.
for( int bite = 0; bite < 256; bite++ ) { int crc = bite << 24;
for( int bit = 0; bit < 8; bit++ ) { // Оптимизировано if (crc & (1 << 31)) if (crc < 0) { crc <<= 1; crc ^= POLY; } else { crc <<= 1; } }
tab[ bite ] = crc;
}
b) Вычисление CRC. У байт данных должны быть реверсированы биты. Изначальный код:
hash = (hash << 8) ^ tab[ b ^ (hash >> 24)];
… надо исправить так:
hash = tab[ (reverse8[ b ] ^ (hash >> 24)) & 0xFF ] ^ (hash << 8);
Итого: не принимайте ничего на веру, проверяйте свой код и данные.
[CRC32 или CRC33?]
Технически 32-разрядная константа 0x04C11DB7 это на самом деле 33-разрядная константа 0x104C11DB7, которая классифицируется как IEEE-802 CRC (см. RFC 3385 [6]).
| Полином | Двоичное значение полинома |
| 0x04C11DB7 | 00000100_11000001_00011101_10110111 |
| 0x104C11DB7 | 1_00000100_11000001_00011101_10110111 |
Поскольку когда-то 64-разрядные вычисления были неоправданно дорогими, полином CRC33 был усечен до 32 бит без каких-либо значимых потерь, даже если вычисление дает несколько другие результаты, чем чистая 33-разрядная реализация:
| Полином | 64-bit reversed | 33-bit reversed |
| 0x104C11DB7 | 0xEDB8832080000000 | 0x1DB710641 |
[Ссылки]
1. CRC32 Demystified site:github.com.
2. Enter the passphrase to be encrypted site:decryptpassword.com.
3. What are the different hash algorithm outputs for 123,456,789 site:integers.co.
4. hash_file — Generate a hash value using the contents of a given file site:php.net.
5. Bc (programming language) site:wikipedia.org.
6. Request for Comments: 3385 site:tools.ietf.org.
7. Reversing CRC – Theory and Practice site:stigge.org.
8. Calculating 32-bit CRCs (CRC-32) site:mdfs.net.
9. Which hashing algorithm is best for uniqueness and speed? site:softwareengineering.stackexchange.com.
10. Calculate a 32-bit CRC lookup table in C/C++ site:stackoverflow.com.
11. Can CRC32 be used as a hash function? site:stackoverflow.com.
12. CRC32 site:wiki.osdev.org.
13. Программная реализация CRC-алгоритма STM32.
Вы что смеётесь? Вероятность пропуска ошибки CRC16 1 к 2^16, CRC32 1 к 2^32, а для простой суммы на ПОРЯДКИ больше!!!
Вы что ещё до сих пор верите в благотворительность? То что просто заXORить массив намного менее затратно чем посчитать CRC я не спорю, но что-то мне подсказывает, что и вероятность пропуска ошибки примерно (прюс-минус трамвайная остановка, конечно):) во столько же раз больше.
За всё надо платить — закон сохранения энергии, однако!
Вы полагаете, это аргумент — все так делают, поэтому так делать — правильно?
Закон сохранения энергия вроде не гласит — чем больше энергии затрачено, тем лучше вещь получается…
Вероятность пропуска ошибки CRC16 1 к 2^16, CRC32 1 к 2^32 — знаете, как считается?
Всего разных значений у 16 битного числа 2^16, если ошибка равновероятно порождает одно из значений, то вероятность, что она
породит нужное, равна 1 к 2^16.
Это справедливо для многобитной ошибки ( например, от мощной импульсной помехи ), но справедливо как для CRC, так и для прямой суммы.
Исторически CRC появилась по простой причине — в механических телетайпах основной ошибкой были сбои в одном из реле, что порождало
многократные ошибки в одном из разрядов. СRC тут намного лучше прямой суммы.
Но времена те ушли, а CRC осталось…
Кстати, прямая сумма чуть лучше побитового XOR — пропускает в два раза меньше двойных ошибок в одном разряде.