Вычисление синдрома и исправление ошибок в циклических кодах
Вычисление
синдрома для циклических кодов является
довольно простой процедурой.
Пусть
U(x)
и r(х) ‑
полиномы, соответствующие переданному
кодовому слову и принятой последовательности.
Разделив
r(x)
на g(x),
получим
r(x)
= q(x)
g(x) + s(x),
(22)
где
— q(x) — частное от деления, s(x)
— остаток от деления.
Если
r(x)
является кодовым полиномом, то он делится
на g(x)
без остатка, то есть s(x)
= 0.
Следовательно,
s(x)
0 является
условием наличия ошибки в принятой
последовательности, то есть синдромом
принятой последовательности.
Синдром
s(x)
имеет в общем случае вид
S(x)
= S0
+ S1
x + … + Sn- k-1
xn-k-1
. (23)
При
наличии в принятой последовательности
r
хотя бы одной ошибки вектор синдрома S
будет иметь, по крайней мере, один
нулевой элемент, при этом факт наличия
ошибки легко обнаружить
Покажем,
что синдромный многочлен S(x)
однозначно связан с многочленом ошибки
e(x), а
значит, с его помощью можно не только
обнаруживать, но и локализовать ошибку
в принятой последовательности.
Пусть
e(x)
= e0 + e1
x
+ e2
x2 + … + en-1
x
n-1
(24)
—
полином
вектора ошибки.
Тогда
полином принятой последовательности
r(x)
= U(x) + e(x).
(25)
Прибавим
в этом выражении слева и справа U(x),
а также учтем, что
r(x)
= q(x)
g(x) + S(x), U(x) = m(x)
g(x), (26)
тогда
,
(27)
то
есть синдромный полином S(x)
есть остаток от деления полинома
ошибки e(x) на порождающий
полином g(x).
Отсюда
следует, что по синдрому S(x)
можно однозначно определить вектор
ошибки e(x),
а
следовательно, исправить эту ошибку.
Список
заданий
1
По
кодирующему многочлену x7
+ x5
+ x + 1 построить полиномиальные коды для
двоичных сообщений 0100, 10001101, 11110.
2
Принадлежат
ли коду Голея кодовые слова
10000101011111010011111 и 11000111011110010011111?
3
Получено
сообщение циклическим кодом
.
Проверить декодированием наличие ошибок
в принятой комбинации, если образующий
полином
.
4
Получена
комбинация
,
закодированная циклическим кодом.
Образующий полином
.
Проверить наличие ошибок в кодовой
комбинации.
Лабораторная
работа № 11
Коды Боуза- Чоудхури – Хоккенгема
1. Порядок выполнения работы
1.1.Ознакомится
с методическими указаниями, изложенными
в п.3;
1.2.Выполнить
задания (по указанию преподавателя)
2. Содержание отчета:
2.1.Тема
и цель работы
2.2.Условия
заданий
2.3.Подробное
решение
2.4.Выводы
по работе.
3.Общие сведения
Французский
ученый А. Хоквингем (1959 г.) и американцы
Р. К. Боуз и Д. К. Рой-Чоудхури (1960 г.) нашли
большой класс кодов, обеспечивающий
произвольное минимальное кодовое
расстояние dmin ≥ 5. Они получили название
БЧХ (Боуза-Чоудхури-Хоквингема).
Порождающие полиномы для таких кодов
в зависимости от предъявляемых к ним
требований, можно найти в таблице
Где
n — общее число элементов, m — число
информационных элементов, k — число
избыточных элементов (n = m + k).
Процедура
построения кода БЧХ по заданным M и dmin:
-
по
dmin
найти значение, при котором обеспечивается
необходимое число информационных
элементов m при минимальной избыточности
kmin; -
найти
в таблице соответствующий порождающий
полином; -
если
dmin
четное, умножить найденный полином на
(x + 1); -
если
mтабл
>> mзадан,
то можно перейти к укороченному
циклическому коду, вычеркивая в
порождающей матрице исходного кода с
параметрами mтабл,
kmin
(mтабл
− mзадан)
столбцов слева и столько же строк
сверху.
Методика
построения БЧХ.
Методика построения кодов БЧХ аналогична
общей методике построения ц. к. и
отличается в основном выбором
образующего многочлена.
Последовательность
построения P(x)
для кодов БЧХ тоже, что и для обычных
ц.к., однако образующий полином является
произведением t
неприводимых полиномов,
G(x)
= M1(x)*M2(x)…Mt(x),
где t
– кратность ошибки.
Методика
выбора (построения) образующего полинома
основана на понятии корня двоичного
многочлена и теоремы
БЧХ.
Понятие
корня двоичного многочлена.
-
Элемент
является
корнем двоичного полинома f(x),
если f()=0. -
Количество
корней многочлена равно степени
полинома.
Если
f(x)=q0+q1x+q2x2+…+qnxn;
qn0;
тогда ,
n
при которых
f(i)=0,
i=1,2,n.
Пример
1: f(x)=(x+1)
– количество корней – 1;
f(1)=
f()=0.
Пример
2: Пусть
требуется определить все корни бинома
x15+1.
-
Количество
корней ,
15. -
Представление
x15+1
в виде произведения неприводимых
сомножителей:
f1
f2
f3
f4
f5
x15+1
= (x+1)(x2+x+1)(x4+x+1)(x4+x3+1)(x4+x3+x2+x+1).
Корни
полинома получены Питерсеном и сведены
в специальную таблицу.
Фрагмент
таблицы:
|
Бином |
Неприводимые |
Корни |
|
x15+1 |
f1(x): |
|
|
f2(x): |
, |
|
|
f3(x):
f4(x): f5(x): |
,
, , |
Т.е.
каждый корень i
является
корнем fj(x)
и корнем порождающего бинома x15+1
и имеет свой порядковый номер.
Для
построения полинома кодов БЧХ используется
теорема БЧХ: (без доказательств)
Если
образующий полином содержит непрерывную
цепь из m
корней, то данный порождающий полином
обладает корректирующими свойствами
кода с dmin=m+1.
При
этом ц.к., исправляющие одиночные ошибки
являются частным случаем (m=2)
из общей теоремы БЧХ.
Пример:
1). Если взять в качестве порождающего

,
,
m=2
dmin3.
f
,
,
m=2
2). F=f3(x)*f5(x)
,
4,
,
7,
10,
3
m=4
dmin5.
Поскольку
(как уже было отмечено выше) методика
этапов кодирования и декодирования
кодов БЧХ отличается от кодов, исправляющих
одиночные ошибки, только выбором
образующего многочлена, рассмотрим
методику выбора P(x)
для БЧХ.
Методика
выбора порождающего полинома для кодов
БЧХ.
-
Определение
количества информационных разрядов:
k
= [log2N].
-
Определение
количества проверочных разрядов:
n
= k + r = k + t *
h
2h
– 1;
t
– кратность
ошибки.
Длины
кодовой комбинации n
= k
+ r
и степени бинома xn
+ 1.
3.
Разложение (представление) xn
+ 1
в виде произведения неприводимых
сомножителей (по таблице Питерсона).
4.
Выбор неприводимых многочленов в
качестве сомножителей образующего
полинома т.о., чтобы
набор
корней содержал непрерывную цепь корней
длиной не менее чем m=dmin-1=2t;
-
Представление
в виде произведения неприводимых
сомножителей.
Этап
декодирования аналогичен ц.к. При этом
l>1.
Пример.
Построить
ц.к. для передачи различных символов,
исправляющий одну или две ошибки:
-
k
= [log2N]
= [log2100]
= 7, dmin5. -
n
= k + r = 7 + 2*h
2n
– 1; h = 4; r = l*h = 2*4 = 8 n
= 15.
f1
f2
f3
f4
f5
x15+1
= (x+1)(x2+x+1)(x4+x+1)(x4+x3+1)(x4+x3+x2+x+1).
,
,
,
,
,
,
,
F1(x)
4
f3*f5
= (x4+x+1)(x4+x3+x2+x+1)
В
качестве
F(x) ,
4,,
7,
910,13
F2(x)
f4*f5
= (x4+x3+1)(x4+x3+x2+x+1)
4,
78,10,
12,
1314,15
m=4
При
выборе в качестве порождающего F1(x)
или F2(x)
– корректирующие возможности полученного
ц.к. будут равны.
-
Степень
образующего многочлена F(x)
= 8;
F(x)
= F1(x)
= (x4+x+1)(x4+x3+x2+x+1)
= x8
+ x7
+ x6
+ x4
+ 1.
7
разр.
8 разр.
C
=
0000001 11010001 W(Ei)
dmin
=
5;
0000010
01110011 W(R(x2)
4.
0000100
11100110
0001000
00011101
0010000
00111010
0100000
01110100
1000000
11101000

111010001
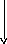
R1(x)
1101,00010
1110,10001
R2(x)
011,10011,0
R3(x)
11,10011,00
11,10100,01
R4(x)
0,00111,01
R5(x)
0,01110,10
R6(x)
0,11101,00
R7(x)
1,11010,00
Необходимо
закодировать и передать:
Н=1000011
*
* ~
* *
1
01001101
Ex)
= 1101011|01001101,
k
r
1).
R1(x)
= 01101110
W(R1(x))
> 2.
2).
Циклический сдвиг на 4 позиции
* *
E2(x)
= 0110100|11011101
R2(x)
= 01110101
W(R2(x))
> 2;
3).
Ц.к. влево на 2 позиции
~
* *
E3(x)
= 1010011|01110101;
R3(x)
= 00000101
W(R3(x))
= 2;
~
E3(x)
= E3(x)
+ R3(x).
4).
Циклический сдвиг вправо на 4 + 2 = 6
позиций.
После
этого получаем направленную кодовую
комбинацию.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
In coding theory, burst error-correcting codes employ methods of correcting burst errors, which are errors that occur in many consecutive bits rather than occurring in bits independently of each other.
Many codes have been designed to correct random errors. Sometimes, however, channels may introduce errors which are localized in a short interval. Such errors occur in a burst (called burst errors) because they occur in many consecutive bits. Examples of burst errors can be found extensively in storage mediums. These errors may be due to physical damage such as scratch on a disc or a stroke of lightning in case of wireless channels. They are not independent; they tend to be spatially concentrated. If one bit has an error, it is likely that the adjacent bits could also be corrupted. The methods used to correct random errors are inefficient to correct burst errors.
Definitions[edit]
A burst of length ℓ[1]
Say a codeword 







Although this definition is sufficient to describe what a burst error is, the majority of the tools developed for burst error correction rely on cyclic codes. This motivates our next definition.
A cyclic burst of length ℓ[1]
An error vector 








For the remainder of this article, we will use the term burst to refer to a cyclic burst, unless noted otherwise.
Burst description[edit]
It is often useful to have a compact definition of a burst error, that encompasses not only its length, but also the pattern, and location of such error. We define a burst description to be a tuple 


For example, the burst description of the error pattern 







Definition. The number of symbols in a given error pattern 

A corollary of the above theorem is that we cannot have two distinct burst descriptions for bursts of length 
Cyclic codes for burst error correction[edit]
Cyclic codes are defined as follows: think of the 


Codewords are polynomials of degree 








Cyclic codes can detect all bursts of length up to 


Theorem (Cyclic burst correction capability) — Every cyclic code with generator polynomial of degree 

The above proof suggests a simple algorithm for burst error detection/correction in cyclic codes: given a transmitted word (i.e. a polynomial of degree 



By the upper bound on burst error detection (









We now consider a fundamental theorem about cyclic codes that will aid in designing efficient burst-error correcting codes, by categorizing bursts into different cosets.
Burst error correction bounds[edit]
Upper bounds on burst error detection and correction[edit]
By upper bound, we mean a limit on our error detection ability that we can never go beyond. Suppose that we want to design an 






Theorem (Burst error detection ability) — The burst error detection ability of any 

Now, we repeat the same question but for error correction: given 



Theorem (Burst error correction ability) — The burst error correction ability of any 

A stronger result is given by the Rieger bound:
Definition. A linear burst-error-correcting code achieving the above Rieger bound is called an optimal burst-error-correcting code.
Further bounds on burst error correction[edit]
There is more than one upper bound on the achievable code rate of linear block codes for multiple phased-burst correction (MPBC). One such bound is constrained to a maximum correctable cyclic burst length within every subblock, or equivalently a constraint on the minimum error free length or gap within every phased-burst. This bound, when reduced to the special case of a bound for single burst correction, is the Abramson bound (a corollary of the Hamming bound for burst-error correction) when the cyclic burst length is less than half the block length.[3]
Theorem (Abramson’s bounds) — If 

Proof
For a linear 

Isolating 




Remark. 

Fire codes[3][4][5][edit]
While cyclic codes in general are powerful tools for detecting burst errors, we now consider a family of binary cyclic codes named Fire Codes, which possess good single burst error correction capabilities. By single burst, say of length 

Let 














We will show that 

Lemma 1 — 
Lemma 2 — If 



Proof
If 


Now suppose 








But 








A corollary to Lemma 2 is that since 




Theorem — The Fire Code is 
If we can show that all bursts of length 
Proof of Theorem[edit]
Let 















Notice that at the second manipulation, we introduced the term 














Then we may write:
Equating the degree of both sides, gives us 




The term 












Since 


















Example: 5-burst error correcting fire code[edit]
With the theory presented in the above section, consider the construction of a 










is a Fire Code generator. We can calculate the block-length of the code by evaluating the least common multiple of 



Binary Reed–Solomon codes[edit]
Certain families of codes, such as Reed–Solomon, operate on alphabet sizes larger than binary. This property awards such codes powerful burst error correction capabilities. Consider a code operating on 





![{displaystyle [mn,mk]_{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/479cc66e2a601a8f28c80c0d3136e9d45f84728d)

The reason such codes are powerful for burst error correction is that each symbol is represented by 


Notice that a burst of 







In general, a 

or fewer bursts of length 

An example of a binary RS code[edit]
Let 
![{displaystyle [255,223,33]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc05fee57b496252bf9064f1e35606fae8d805dc)





![{displaystyle [2040,1784,33]_{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0de5be730230c649eac90e01bb084dbcd81319a)

Interleaved codes[edit]
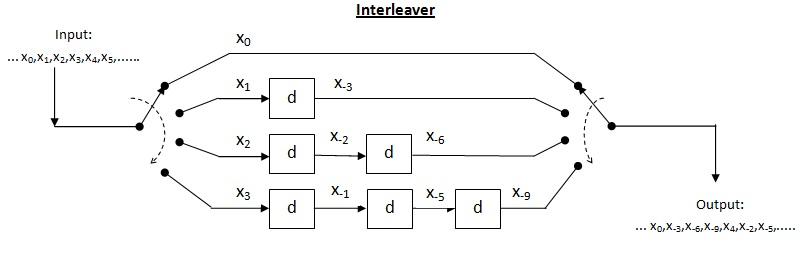
Interleaving is used to convert convolutional codes from random error correctors to burst error correctors. The basic idea behind the use of interleaved codes is to jumble symbols at the transmitter. This leads to randomization of bursts of received errors which are closely located and we can then apply the analysis for random channel. Thus, the main function performed by the interleaver at transmitter is to alter the input symbol sequence. At the receiver, the deinterleaver will alter the received sequence to get back the original unaltered sequence at the transmitter.
Burst error correcting capacity of interleaver[edit]
Illustration of row- and column-major order
Block interleaver[edit]
The figure below shows a 4 by 3 interleaver.
An example of a block interleaver
The above interleaver is called as a block interleaver. Here, the input symbols are written sequentially in the rows and the output symbols are obtained by reading the columns sequentially. Thus, this is in the form of 

Capacity of block interleaver: For an 






Efficiency of block interleaver (

Drawbacks of block interleaver : As it is clear from the figure, the columns are read sequentially, the receiver can interpret single row only after it receives complete message and not before that. Also, the receiver requires a considerable amount of memory in order to store the received symbols and has to store the complete message. Thus, these factors give rise to two drawbacks, one is the latency and other is the storage (fairly large amount of memory). These drawbacks can be avoided by using the convolutional interleaver described below.
Convolutional interleaver[edit]
Cross interleaver is a kind of multiplexer-demultiplexer system. In this system, delay lines are used to progressively increase length. Delay line is basically an electronic circuit used to delay the signal by certain time duration. Let 









An example of a convolutional interleaver
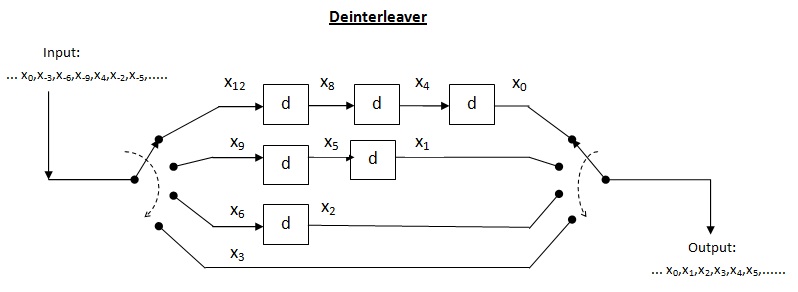
An example of a deinterleaver
Efficiency of cross interleaver (
Thus, we can formulate 
Performance of cross interleaver : As shown in the above interleaver figure, the output is nothing but the diagonal symbols generated at the end of each delay line. In this case, when the input multiplexer switch completes around half switching, we can read first row at the receiver. Thus, we need to store maximum of around half message at receiver in order to read first row. This drastically brings down the storage requirement by half. Since just half message is now required to read first row, the latency is also reduced by half which is good improvement over the block interleaver. Thus, the total interleaver memory is split between transmitter and receiver.
Applications[edit]
Compact disc[edit]
Without error correcting codes, digital audio would not be technically feasible.[7] The Reed–Solomon codes can correct a corrupted symbol with a single bit error just as easily as it can correct a symbol with all bits wrong. This makes the RS codes particularly suitable for correcting burst errors.[5] By far, the most common application of RS codes is in compact discs. In addition to basic error correction provided by RS codes, protection against burst errors due to scratches on the disc is provided by a cross interleaver.[3]
Current compact disc digital audio system was developed by N. V. Philips of The Netherlands and Sony Corporation of Japan (agreement signed in 1979).
A compact disc comprises a 120 mm aluminized disc coated with a clear plastic coating, with spiral track, approximately 5 km in length, which is optically scanned by a laser of wavelength ~0.8 μm, at a constant speed of ~1.25 m/s. For achieving this constant speed, rotation of the disc is varied from ~8 rev/s while scanning at the inner portion of the track to ~3.5 rev/s at the outer portion. Pits and lands are the depressions (0.12 μm deep) and flat segments constituting the binary data along the track (0.6 μm width).[8]
The CD process can be abstracted as a sequence of the following sub-processes:
- Channel encoding of source of signals
- Mechanical sub-processes of preparing a master disc, producing user discs and sensing the signals embedded on user discs while playing – the channel
- Decoding the signals sensed from user discs
The process is subject to both burst errors and random errors.[7] Burst errors include those due to disc material (defects of aluminum reflecting film, poor reflective index of transparent disc material), disc production (faults during disc forming and disc cutting etc.), disc handling (scratches – generally thin, radial and orthogonal to direction of recording) and variations in play-back mechanism. Random errors include those due to jitter of reconstructed signal wave and interference in signal. CIRC (Cross-Interleaved Reed–Solomon code) is the basis for error detection and correction in the CD process. It corrects error bursts up to 3,500 bits in sequence (2.4 mm in length as seen on CD surface) and compensates for error bursts up to 12,000 bits (8.5 mm) that may be caused by minor scratches.
Encoding: Sound-waves are sampled and converted to digital form by an A/D converter. The sound wave is sampled for amplitude (at 44.1 kHz or 44,100 pairs, one each for the left and right channels of the stereo sound). The amplitude at an instance is assigned a binary string of length 16. Thus, each sample produces two binary vectors from 

Input for the encoder consists of input frames each of 24 8-bit symbols (12 16-bit samples from the A/D converter, 6 each from left and right data (sound) sources). A frame can be represented by 



Initially, the bytes are permuted to form new frames represented by 


Next, these 24 message symbols are encoded using C2 (28,24,5) Reed–Solomon code which is a shortened RS code over 



Decoding: The CD player (CIRC decoder) receives the 32 output symbol data stream. This stream passes through the decoder D1 first. It is up to individual designers of CD systems to decide on decoding methods and optimize their product performance. Being of minimum distance 5 The D1, D2 decoders can each correct a combination of 


Performance of CIRC:[7] CIRC conceals long bust errors by simple linear interpolation. 2.5 mm of track length (4000 bits) is the maximum completely correctable burst length. 7.7 mm track length (12,300 bits) is the maximum burst length that can be interpolated. Sample interpolation rate is one every 10 hours at Bit Error Rate (BER) 



See also[edit]
- Error detection and correction
- Error-correcting codes with feedback
- Code rate
- Reed–Solomon error correction
References[edit]
- ^ a b c d Coding Bounds for Multiple Phased-Burst Correction and Single Burst Correction Codes
- ^ The Theory of Information and Coding: Student Edition, by R. J. McEliece
- ^ a b c Ling, San, and Chaoping Xing. Coding Theory: A First Course. Cambridge, UK: Cambridge UP, 2004. Print
- ^ a b Moon, Todd K. Error Correction Coding: Mathematical Methods and Algorithms. Hoboken, NJ: Wiley-Interscience, 2005. Print
- ^ a b c d e f Lin, Shu, and Daniel J. Costello. Error Control Coding: Fundamentals and Applications. Upper Saddle River, NJ: Pearson-Prentice Hall, 2004. Print
- ^ quest.arc.nasa.gov https://web.archive.org/web/20120627022807/http://quest.arc.nasa.gov/saturn/qa/cassini/Error_correction.txt. Archived from the original on 2012-06-27.
- ^ a b c Algebraic Error Control Codes (Autumn 2012) – Handouts from Stanford University
- ^ McEliece, Robert J. The Theory of Information and Coding: A Mathematical Framework for Communication. Reading, MA: Addison-Wesley Pub., Advanced Book Program, 1977. Print
Содержание
Раздел разработан в 2010 г. при поддержке компании RAIDIX
Циклические коды
Рассмотрим линейное пространство $ mathbb V^n $ двоичных кодов, т.е. упорядоченных наборов (строк) $ (x_1,dots,x_{n}) $ из $ n_{} $ чисел $ {x_1,dots,x_n}subset {0,1} $.
Рассмотрим непустое подмножество $ mathbb U $ пространства $ mathbb V^n $, обладающее следующим свойством: если строка $ (u_1,u_2,dots,u_n) $ принадлежит $ mathbb U $, то этому подмножеству принадлежит и строка, полученная из этой в результате циклического сдвига вправо:
$$ (u_n,u_1,u_2,dots,u_{n-1}) in mathbb U $$
т.е. все компоненты (разряды) вектора сдвигаются вправо на одну позицию, тот элемент, что при этом сдвиге «вываливается» за пределы строки, переставляется в ее начало.
Очевидно, что:
$$ (u_{n-1},u_n,u_1dots,u_{n-2}) in mathbb U , dots , (u_2,u_3,dots,u_{n-1},u_{1}) in mathbb U , $$
т.е. множество $ mathbb U $ должно содержать, по крайней мере, $ n_{} $ строк (которые, впрочем, не обязательно будут различными). Если, вдобавок, множество $ mathbb U $ является подпространством пространства $ mathbb V^n $, т.е. замкнуто относительно операции сложения строк по модулю $ 2_{} $, то такое множество называется циклическим кодом. Будем обозначать его буквой $ C_{} $.
Заметим, что циклический код можно определить и на основе циклического сдвига влево:
$$
begin{array}{c}
rightarrow \
begin{array}{c}
(u_1,u_2,u_3, u_4, u_5) \
(u_5,u_1, u_2, u_3, u_4) \
(u_4,u_5, u_1, u_2, u_3) \
(u_3,u_4, u_5, u_1, u_2) \
(u_2,u_3, u_4, u_5, u_1)
end{array}
end{array} qquad qquad
begin{array}{c}
leftarrow \
begin{array}{c}
(u_1,u_2, u_3, u_4, u_5) \
(u_2, u_3, u_4, u_5, u_1) \
(u_3, u_4, u_5, u_1, u_2) \
(u_4,u_5, u_1, u_2, u_3) \
(u_5,u_1, u_2, u_3, u_4)
end{array}
end{array}
$$
В самом деле, правый набор строк получается в результате перестановки строк левого набора.
Структура кода
Для прояснения идейных основ использования циклических кодов в зашумленных каналах связи рассмотрим сначала их прототип в $ mathbb Z^n $, т.е. в пространстве строк с целочисленными элементами.
С точки зрения традиционного для линейной алгебры определения, $ mathbb Z^n $ не является линейным пространством. Тем не менее если рассмотреть его как множество строк с целочисленными компонентами
$$ mathbb Z^n = left{ (x_1,dots,x_n) mid {x_j}_{j=1}^n subset mathbb Z right} $$
относительно операций покомпонентного сложения и умножения на целочисленные скаляры, то все аксиомы
1
—
8
линейного векторного пространства будут выполнены.
Рассмотрим строку $ (a_{0},a_{1},dots,a_{n-1}) in mathbb Z^n $. Она порождает следующую циклическую матрицу
$$
mathfrak C=left(begin{array}{lllll}
a_{0} & a_{1} & a_2 & dots & a_{n-1} \
a_{n-1} & a_{0} & a_{1} & dots & a_{n-2} \
a_{n-2} & a_{n-1} & a_{0} & dots & a_{n-3} \
vdots & & & & vdots \
a_{1} & a_{2} & a_{3} & dots & a_{0}
end{array}
right) .
$$
Тогда линейная оболочка строк этой матрицы
$$ mathcal L (mathfrak C^{[1]},mathfrak C^{[2]},dots, mathfrak C^{[n]}) $$
образует циклический код $ C_{} $. Чему равна размерность $ dim C $ этого подпространства ? Очевидно, это будет зависеть от вида строки
$ (a_{0},a_{1},dots,a_{n-1}) $. Так,
$$ . mbox{ при выборе } quad a_0=1,a_{1}=0,a_{2}=0,dots,a_{n-1}=0, quad mbox{ получим } dim C = n , $$
$$ . mbox{ при выборе } quad a_{0}=1,a_{1}=1,dots,a_{n-1}=1 quad mbox{ получим } dim C = 1 . $$
В общем же случае, вопрос можно переформулировать в терминах ранга матрицы $ {mathfrak C} $. Вычисление этого ранга проведем с использованием соображений из пункта
☞
ЦИКЛИЧЕСКАЯ МАТРИЦА.
Рассмотрим полином $ g(x)= a_{0}+ a_{1}x+ dots +a_{n-2}x^{n-2}+ a_{n-1}x^{n-1} $. Вычислим остаток $ g_1(x) $ от деления произведения $ xcdot g(x) $ на полином $ x^{n}-1 $:
$$ xcdot g(x) equiv a_{0}x+ a_{1}x^2+ dots + a_{n-2}x^{n-1}+ a_{n-1}x^{n} equiv
$$
$$
equiv a_{0}x+ a_{1}x^2+ dots + a_{n-2}x^{n-1}+a_{n-1}(x^{n}-1+1) equiv
$$
$$
equiv underbrace{a_{n-1}+a_{0}x+ a_{1}x^2+ dots + a_{n-2}x^{n-1}}_{g_{_1}(x)} + a_{n-1}(x^{n}-1) .
$$
Оказывается, что коэффициенты остатка даются второй строкой матрицы $ mathfrak C $. Далее по аналогии остаток от деления произведения $ x^2cdot g(x) $ на полином $ x^{n}-1 $ совпадает с остатком от деления $ xcdot g_1(x) $ на $ x^{n}-1 $ и коэффициенты этого остатка даются третьей строкой матрицы $ mathfrak C $.
Вывод: матрица $ mathfrak C_{} $ состоит из коэффициентов остатков деления полиномов $ {x^jg(x)}_{j=0}^{n-1} $
на $ x^{n}-1 $. Будем говорить, что полином $ g_{} (x) $ порождает циклический код $ C_{} $.
Оказывается, ранг матрицы $ mathfrak C_{} $ связан с наибольшим общим делителем полиномов $ g_{}(x) $ и $ x^{n}-1 $.
Т
Теорема 1. Если полином $ g_{}(x) $ порождает циклический код $ C_{} $, то
$$ operatorname{rank} ({mathfrak C} ) = n — deg operatorname{HOD}(g(x), x^n-1) ; $$
$$ det mathfrak C_{} = mathcal R(g(x), x^n-1) , $$
где в правой части последней формулы стоит результант.
Доказательство
☞
ЗДЕСЬ.
Как выяснить принадлежность заданной строки $ B= (b_{0},b_{1},dots,b_{n-1}) in mathbb Z^n $ циклическому коду $ C_{} $? В общем случае, для ответа на этот вопрос приходится вычислять ранг расширенной матрицы, полученной присоединением к матрице $ mathfrak C_{} $ данной строки1):
$$ tilde {mathfrak C} = left(begin{array}{c} mathfrak C \ B end{array} right) . $$
Т
Теорема 2. Имеем:
$$ B in C qquad iff qquad operatorname{rank} ({mathfrak C} ) = operatorname{rank} ( tilde {mathfrak C} ) . $$
П
Пример. Пусть $ n_{}=4 $ и циклический код $ C_{} $ порождается полиномом $ g(x)=-2+2,x-x^2+x^3 $. Имеем:
$$
mathfrak C=left(begin{array}{rrrr}
-2&2&-1&1\
1&-2&2&-1\
-1&1&-2&2\
2&-1&1&-2
end{array}
right)
$$
и $ operatorname{rank} ({mathfrak C} ) = 3 $ поскольку $ det {mathfrak C} =0 $, а
$$
left|
begin{array}{rrr}
-2&2&-1\
1&-2&2\
-1&1&-2
end{array}
right| ne 0 .
$$
Пусть теперь требуется установить значения параметра $ {color{Red} alpha } $, при которых строка
$ B= (-3,1,{color{Red} alpha },2) $ принадлежит циклическому коду $ C_{} $. Имеем, согласно теореме 2:
$$
B in C quad iff quad
operatorname{rank} left(begin{array}{rrrr}
-2&2&-1&1\
1&-2&2&-1\
-1&1&-2&2\
2&-1&1&-2 \
-3&1&{color{Red} alpha }& 2
end{array}
right)=3 quad iff
$$
$$
iff quad
left|begin{array}{rrrr}
-2&2&-1&1\
1&-2&2&-1\
-1&1&-2&2\
-3&1&{color{Red} alpha } & 2
end{array}
right|=0 quad iff quad {color{Red} alpha }=0 .
$$
♦
!
Попробуем теперь выбрать порождающий циклический код полином $ g(x) $ среди делителей полинома $ x^{n}-1 $.
Т
Теорема 3. Пусть порождающий полином
$$ g(x)=a_0+a_1x+dots+a_rx^rin mathbb Z[x], (0< r<n, a_rne 0) $$
кода $ C_{} $ является делителем полинома $ x^{n}-1 $. Тогда $ operatorname{rank} (mathfrak C_{} ) = n — r $. Строка $ (b_0,b_1,dots,b_{n-1}) $ принадлежит коду $ C_{} $ тогда и только тогда, когда полином $ b_0+b_1x+dots+b_{n-1}x^{n-1} $ делится на $ g(x) $.
Доказательство. Циклическая матрица имеет следующую структуру2):
$$
begin{array}{rl}
mathfrak C=
left(begin{array}{llllllll}
a_0 & a_1 & dots & a_r & 0 & dots & 0 & 0 \
& a_0 & dots & a_{r-1} & a_r & dots & 0 & 0 \
& & ddots & & & ddots & & \
& & & a_0 & a_1& dots & & a_r \
hline
a_r & 0 & dots & & a_0 & dots & & a_{r-1} \
a_{r-1} & a_r & dots & & & & & a_{r-2} \
vdots & & ddots & & & & ddots & vdots \
a_1 & a_2 & dots & a_r & & dots & & a_0
end{array}
right) &
begin{array}{l}
left.begin{array}{l}
\ \ \ \
end{array}right} n-r
\
begin{array}{l}
\ \ \ \
end{array}
end{array}
end{array}
$$
Поскольку $ operatorname{HOD}(g(x),x^n-1)equiv g(x) $, то, в соответствии с теоремой 1, $ operatorname{rank} ({mathfrak C} ) = n — r $. Легко видеть, что линейно независимыми строками матрицы являются первые $ n-r $ строк (над горизонтальной чертой). Строка $ B= (b_0,b_1,dots,b_{n-1}) $, принадлежащая коду $ C_{} $, должна линейно выражаться через эти строки:
$$ B=gamma_0 (a_0,a_1,dots,a_r,0,dots,0)+gamma_1 (0,a_0,a_1,dots,a_r,dots,0)+dots+gamma_{n-r-1}
(0,dots,0,a_0,dots,a_r) , $$
и это равенство может быть переписано как полиномиальное тождество:
$$b_0+b_1x+dots+b_{n-1}x^{n-1}equiv $$
$$
equiv gamma_0(a_0+a_1x+dots+a_rx^{r})+gamma_1(a_0x+a_1x^2+dots+a_rx^{r+1})+
$$
$$
+dots+gamma_{n-r-1}(a_0x^{n-r-1}+a_1x^{n-r}+dots+a_rx^{n-1}) equiv
$$
$$
equiv (gamma_0+gamma_1x+dots+gamma_{n-r-1}x^{n-r-1})(a_0+a_1x+dots+a_rx^{r}) .
$$
♦
=>
Обозначим через $ h_{}(x) $ частное от деления $ x^n-1 $ на $ g_{}(x) $. Строка $ (b_0,b_1,dots,b_{n-1}) $ принадлежит коду $ C_{} $ тогда и только тогда, когда
$$ (b_0+b_1x+dots+b_{n-1}x^{n-1})h(x) equiv 0 pmod{x^n-1} . $$
Доказательство. Если $ (b_0,b_1,dots,b_{n-1}) in C_{} $, то, в соответствии с теоремой,
полином $ G(x)= b_0+b_1x+dots+b_{n-1}x^{n-1} $ может быть представлен в виде произведения $ Q(x) g(x) $; тогда $ Q(x) g(x)h(x) equiv Q(x)(x^n-1) equiv 0 pmod{x^n-1} $.
С другой стороны, если $ G(x)h(x) equiv 0 pmod{x^n-1} $, то $ G(x)h(x) equiv tilde Q(x) (x^n-1) $ при $ tilde Q(x) in mathbb Z[x] $ и, следовательно, $ G(x) equiv tilde Q(x) g(x) $. Применение теоремы завершает доказательство.
♦
Полином $ h_{}(x) $, связанный с порождающим циклический код $ C_{} $ полиномом $ g_{}(x) $ тождеством
$$ h(x) g(x) equiv x^n-1 $$
называется проверочным полиномом циклического кода.
П
Пример. Пусть $ n_{}=6 $ и циклический код порождается полиномом $ g(x)=1+2,x+2,x^2+x^3 $.
Проверить принадлежность строки $ B=(-1,-1,1,3,3,1) $ данному коду.
Решение. Имеем:
$$ x^6-1equiv overbrace{(x^3+2,x^2+2,x+1)}^{=g(x)}overbrace{(x^3-2,x^2+2,x-1)}^{=h(x)} . $$
1.
Можно действовать по аналогии с предыдущим примером и вычислить $ operatorname{rank} (tilde {mathfrak C}) $.
2.
Можно, в соответствии с теоремой 3, составить полином $ G(x)=-1-x+x^2+3,x^3+3,x^4+x^5 $ и проверить его на делимость с порождающим код полиномом $ g_{}(x) $:
$$ G(x)equiv (x^2+x-1) g(x) . $$
3.
Можно проверить выполнение условия следствия к теореме 3:
$$ G(x)h(x) equiv x^8+x^7-x^6-x^2-x+1 equiv x^2+x-1-x^2-x+1 pmod{x^6-1} . $$
4.
Наконец, можно рассмотреть корни $ lambda_1=-1, lambda_2=-frac{1}{2}+mathbf i frac{sqrt{3}}{2}, lambda_3=-frac{1}{2}-mathbf i frac{sqrt{3}}{2} $ полинома $ g_{} (x) $ и проверить, что в каждом из них полином $ G_{}(x) $ обращается в нуль.
Последний способ кажется неконструктивным. В самом деле, он является очевидным следствием способа
2
и основной теоремы высшей алгебры. Я привожу его как «заготовку на будущее», которое грядёт
☟
НИЖЕ.
♦
Кодирование
В предыдущем пункте было проведено описание циклического кода $ C_{} $ как подмножества (линейного подпространства) пространства $ mathbb Z^n $. Теперь надо описать способы кодирования, т.е. сопоставления вектору информационных разрядов $ (x_1,dots,x_k) $ конкретного кодового слова
$ (b_0,b_1,dots,b_{n-1}) $ из $ C_{} $.
На практике используются два способа кодирования. Оба используют циклические коды с порождающим полиномом $ g(x)=a_0+a_1x+dots+a_{r-1}x^{r-1}+x^r $, который удовлетворяет двум условиям3):
1.
$ g_{}(x) $ является нетривиальным делителем полинома $ x^n-1 $;
2.
его степень $ r_{} $ связана с числом информационных разрядов $ k_{} $ равенством: $ k=n-r $.
Несистематическое кодирование заключается в сопоставлении информационному вектору $ (x_1,dots,x_k) $ кодового слова $ (b_0,b_1,dots,b_{n-1}) $ по правилу, которое описывается на языке полиномов:
$$ b_0+b_1x+dots+b_{n-1}x^{n-1}equiv (x_1+x_2x+dots+x_kx^{k-1}) g(x) , $$
т.е. заключается в умножении «информационного» полинома на полином, порождающий код.
Систематическое кодирование заключается в сопоставлении информационному вектору $ (x_1,dots,x_k) $ кодового слова $ (c_0,c_1,dots,c_{n-1}) $ по правилу:
$$ c_0+c_1x+dots+c_{n-1}x^{n-1}equiv (x_1+x_2x+dots+x_kx^{k-1}) x^{n-k} — R(x) , $$
где $ R(x) $ — остаток от деления полинома $ (x_1+x_2x+dots+x_kx^{k-1}) x^{n-k} $ на порождающий код полином $ g_{}(x) $.
На основании теоремы 3 из предыдущего ПУНКТА, можно утверждать, что оба способа кодирования корректны: полиномы $ b_0+b_1x+dots+b_{n-1}x^{n-1} $ и $ c_0+c_1x+dots+c_{n-1}x^{n-1} $ делятся на порождающий код полином $ g_{}(x) $, а значит, наборы их коэффициентов являются кодовыми словами.
Теперь проиллюстрируем оба этих способа на примере.
П
Пример. Пусть $ n_{}=6 $ и циклический код порождается полиномом $ g(x)=1+2,x+2,x^2+x^3 $. Найти кодовые слова, соответствующие информационному вектору $ (x_1,x_2,x_3) $.
Решение. Составляем полином $ M(x)= x_1+x_2x+x_3x^2 $.
В случае несистематического кодирования
$$ M(x)g(x)equiv x_1+(2,x_1+x_2)x+(2,x_1+2,x_2+x_3)x^2+(x_1+2,x_2+2,x_3)x^3+
(x_2+2,x_3)x^4+x_3x^5 , $$
т.е. кодовое слово имеет вид
$$ (x_1, 2,x_1+x_2, 2,x_1+2,x_2+x_3, x_1+2,x_2+2,x_3, x_2+2,x_3, x_3) . $$
Легко убедиться, что это слово является результатом умножения информационного вектора на верхнюю часть циклической матрицы $ mathfrak C $:
$$
(x_1,x_2,x_3)
left(begin{array}{cccccc}
1 & 2 & 2 & 1 & 0 & 0 \
0 & 1 & 2 & 2 & 1 & 0 \
0 & 0 & 1 & 2 & 2 & 1
end{array}
right) ;
$$
что, впрочем, вполне ожидаемо, если посмотреть доказательство теоремы 3 из предыдущего ПУНКТА: кодовое слово обязано быть линейной комбинацией строк циклической матрицы.
Для систематического кодирования вычисляем сначала остаток от деления $ M(x)x^3 $ на $ g_{}(x) $:
$$ R(x) equiv (-x_1+2,x_2-2,x_3)+(-2,x_1+3,x_2-2,x_3)x+(-2,x_1+2,x_2-x_3)x^2 ; $$
и кодовое слово имеет вид
$$ (x_1-2,x_2+2,x_3, 2,x_1-3,x_2+2,x_3, 2,x_1-2,x_2+x_3, x_1, x_2, x_3) . $$
Здесь тоже можно выписать матричное представление:
$$
(x_1,x_2,x_3)
left(begin{array}{rrrrrr}
1 & 2 & 2 & 1 & 0 & 0 \
-2 & -3 & -2 & 0 & 1 & 0 \
2 & 2 & 1 & 0 & 0 & 1
end{array}
right) .
$$
Матрица систематического кодирования может быть получена из матрицы несистематического кодирования с помощью элементарных преобразований над строками:
$$
left(begin{array}{cccccc}
1 & 2 & 2 & 1 & 0 & 0 \
0 & 1 & 2 & 2 & 1 & 0 \
0 & 0 & 1 & 2 & 2 & 1
end{array}
right)quad
rightarrow quad
left(begin{array}{rrrrrr}
1 & 2 & 2 & 1 & 0 & 0 \
-2 & -3 & -2 & 0 & 1 & 0 \
0 & 0 & 1 & 2 & 2 & 1
end{array}
right)
quad
rightarrow quad
left(begin{array}{rrrrrr}
1 & 2 & 2 & 1 & 0 & 0 \
-2 & -3 & -2 & 0 & 1 & 0 \
-2 & -4 & -3 & 0 & 2 & 1
end{array}
right)
quad
rightarrow
$$
$$
rightarrow quad
left(begin{array}{rrrrrr}
1 & 2 & 2 & 1 & 0 & 0 \
-2 & -3 & -2 & 0 & 1 & 0 \
2 & 2 & 1 & 0 & 0 & 1
end{array}
right) ;
$$
и этот факт достаточно ожидаем, поскольку два способа кодирования соответствуют разным выборам кодовых слов (базисных строк) в одном и том же линейном подпространстве пространства $ mathbb Z^n $ — циклическом коде $ C_{} $. Какую информацию содержат строки этой матрицы — какие полиномы они порождают? — Оказывается, эти строки состоят из коэффициентов полиномов вида
$$ x^{j}-(b_{j,r-1}x^{r-1}+b_{j,r-2}x^{r-2}+dots+b_{j1}x^1+b_{j0}) quad npu quad jin{r,dots,n-1} , $$
где полином в скобках является остатком от деления $ x^{j} $ на порождающий код полином $ g_{}(x) $.
$$ x^3 equiv -1-2,x-2,x^2, x^4 equiv 2+3,x+2,x^2, x^5 equiv -2-2,x-x^2 pmod{1+2,x+2,x^2+x^3} . $$
♦
Вывод. Несистематический способ кодирования проще в реализации; систематический — удобнее с точки зрения расположения в кодовом слове информационных и проверочных разрядов — они объединены в блоки.
В одном из последующих ПУНКТОВ будет сменена на противоположную нумерация разрядов кодового слова; в сравнении с используемой до сих пор, мы будем записывать коэффициенты полиномов по убыванию степеней $ x_{} $. Тогда при систематическом способе кодирования информационные разряды займут привычные для теории кодирования места в начале кодового слова.
Свёртка
Исследование операции умножения полиномов по модулю $ x^{n}-1 $, использованной в
☝
ВЫШЕ требует отдельного пункта. Впрочем, при первом чтении этот материал можно пропустить.
Предположим, что заданы два полинома
$$ f(x)=a_0+a_1x+dots+a_{n-1}x^{n-1} qquad mbox{ и } qquad g(x)=b_0+b_1x+dots+b_{n-1}x^{n-1} $$
с целыми коэффициентами. Организуем их умножение по модулю полинома $ x^n-1 $, действуя по схеме, которую проиллюстрируем для случая $ n_{}=5 $:
$$ (a_0+a_1x+a_2x^2+a_3x^3+a_4x^4)(b_0+b_1x+b_2x^2+b_3x^3+b_4x^4) = $$
$$
=
begin{array}{l|rrrrr|rrrr}
b_0times & a_0&+a_1x&+a_2x^2 &+a_3x^3 &+a_4x^4 & + & & &\
b_1times & & a_0x&+a_1x^2 &+a_2x^3 &+a_3x^4 &+a_4x^5 &+ & &\
b_2times & & & a_0x^2 & +a_1x^3 & +a_2x^4& +a_3x^5&+a_4x^6 & + &\
b_3times & & & & a_0x^3 & +a_1x^4 & +a_2x^5&+a_3x^6&+a_4x^7& + \
b_4times & & & & & a_0x^4 & +a_1x^5& +a_2x^6&+a_3x^7&+a_4x^8
end{array}
$$
Использование соотношений $ x^5 equiv 1, x^6 equiv x, x^7 equiv x^2, x^8 equiv x^3 pmod{x^5-1} $ позволяет циклически перебросить слагаемые, стоящие справа от правой черты влево от нее:
$$
equiv
begin{array}{l|lllll}
b_0times & a_0&+a_1x&+a_2x^2 &+a_3x^3 &+a_4x^4 + \
b_1times & a_4&+ a_0x&+a_1x^2 &+a_2x^3 &+a_3x^4 + \
b_2times & a_3&+ a_4x& +a_0x^2 & +a_1x^3 & +a_2x^4+ \
b_3times & a_2&+ a_3x& +a_4x^2 &+a_0x^3 & +a_1x^4 + \
b_4times & a_1&+ a_2x&+a_3x^2&+a_4x^3 & +a_0x^4
end{array} pmod{x^5-1} .
$$
Дальше остается только собрать подобные члены. Результатом такого умножения полиномов будет полином
$ c_0+c_1x+c_2x^2+c_3x^3+c_4x^4 $ с коэффициентами, задаваемыми соотношениями:
$$
begin{array}{llllll}
c_0=&a_0b_0&+a_1b_4&+a_2b_3&+a_3b_2&+a_4b_1 \
c_1=&a_0b_1&+a_1b_0&+a_2b_4&+a_3b_3&+a_4b_2 \
c_2=&a_0b_2&+a_1b_1&+a_2b_0&+a_3b_4&+a_4b_3 \
c_3=&a_0b_3&+a_1b_2&+a_2b_1&+a_3b_0&+a_4b_4 \
c_4=&a_0b_4&+a_1b_3&+a_2b_2&+a_3b_1&+a_4b_0
end{array}
$$
Здесь коэффициенты $ a_0,a_1,a_2,a_3,a_4 $ расположены в «естественном» порядке, а их сомножители — коэффициенты $ b_4,b_3,b_2,b_1,b_0 $ — при подъеме с последней формулы вверх циклически сдвигаются влево. Эту цикличность можно «заложить» в индексы если воспользоваться модулярным формализмом:
$$ c_0=sum_{j=0}^4 a_jb_{5-j pmod{5}}, c_1=sum_{j=0}^4 a_jb_{6-j pmod{5}},
c_2=sum_{j=0}^4 a_jb_{7-j pmod{5}}, c_3=sum_{j=0}^4 a_jb_{8-j pmod{5}}, c_4=sum_{j=0}^4 a_jb_{9-j pmod{5}} ;
$$
как принято
☞
ЗДЕСЬ, $ n pmod{5} $ означает остаток от деления натурального числа $ n_{} $ на $ 5_{} $.
Циклическая свёртка
Для произвольных векторов-строк $ X=(x_{1},dots,x_n) $ и $ Y=(y_{1},dots,y_n) $ вектор $ Z=(z_{1},dots,z_n) $,
с элементами, определяемыми формулами
$$ z_k=sum_{j=1}^n x_jy_{n+k-j pmod{n}}= $$
$$
begin{array}{lcl}
=x_1y_k+x_2y_{k-1}+dots+x_ky_1 & + & \
& + & x_{k+1}y_n+x_{k+2}y_{n-1}+dots+x_ny_{k+1}
end{array}
$$
при $ k in {1,dots,n} $, называется циклической свёрткой векторов $ X_{} $ и $ Y_{} $, сама операция нахождения свертки обозначается $ ast $:
$$ Z=Xast Y .$$
Аналогичное определение используется и для полиномов. Если $ f(x)=a_0+a_{1}x+dots+a_{n-1}x^{n-1} $ и $ g(x)=b_0+b_1x+dots+b_{n-1}x^{n-1} $, то
$$ c_0+c_1x+dots+c_{n-1}x^{n-1}=f(x)cdot g(x) pmod{x^n-1} qquad iff $$
$$ iff qquad (c_0,c_1,dots,c_{n-1})= (a_0,a_1,dots,a_{n-1})ast (b_0,b_1,dots,b_{n-1}) . $$
Мы не вводили формальных ограничений на то, чтобы старшие коэффициенты полиномов $ f_{} $ и $ g_{} $ были отличны от нуля. Если применить определение к полиномам, степени которых удовлетворяют неравенству $ deg f+ deg g < n $, то результатом циклической свертки оказывается произведение полиномов $ f_{}(x) $ и $ g_{}(x) $ — в традиционном смысле, а не по какому-либо модулю!
Задача. Организовать экономное вычисление циклической свёртки.
Решение этой задачи см. в разделе
☞
УМНОЖЕНИЕ ПОЛИНОМОВ.
Исправление ошибок…
Снова рассматриваем циклические коды в $ mathbb Z^n $. В соответствии с определением, принадлежность кодового слова $ (b_0,b_1,dots,b_{n-1}) $ циклическому коду $ C_{} $, порождаемому полиномом $ g(x)=a_0+a_1x+a_2x^2+dots+a_{r}x^{r}, (r<n,a_{r}ne 0) $, равносильна тому, что полином $ G(x)=b_0+b_1x+b_2x^2+dots+b_{n-1}x^{n-1} $ делится на $ g_{}(x) $. Предположим теперь, что при передаче по зашумленному каналу связи кодовое слово исказилось и на выходе мы получили вектор
$ (tilde b_0,tilde b_1,dots,tilde b_{n-1}) $. Этот вектор задает некоторый полином $ tilde G(x)= tilde b_0+ tilde b_1x+ tilde b_2x^2+dots+ tilde b_{n-1}x^{n-1} $.
В дальнейшем, для простоты, будем говорить о передаваемых по каналу полиномах, имея в виду строки их коэффициентов; кроме того, будем нумеровать разряды строк $ (tilde b_0,tilde b_1,dots,tilde b_{n-1}) $, начиная с нулевого.
…анализом остатков
Полином $ s_{}(x) $, равный остатку от деления полинома $ tilde G(x) $ на порождающий циклический код полином $ g_{}(x) $, называется синдромом полинома $ tilde G(x) $ в данном коде:
$$ s(x)={bf mbox{СИНДРОМ }}(tilde G(x)) = tilde G(x) pmod{g(x)} . $$
Если синдром $ s_{}(x) $ полученного на выходе из канала полинома $ tilde G(x) $ тождественно равен $ 0_{} $, то будем считать, что ошибка передачи не обнаружена.
П
Пример. Пусть $ n=6 $ и циклический код порождается полиномом
$$ g(x)=1+2,x+2,x^2+x^3 , . $$
Пусть при передаче по каналу кодового полинома $ G(x)=-1-x+x^2+3,x^3+3,x^4+x^5 $ произошла ошибка ровно в одном из коэффициентов. Вычислим синдромы получающихся полиномов $ tilde G(x) $.
Пусть сначала «испортился» старший коэффициент и мы получили на выходе полином
$$ tilde G(x)=-1-x+x^2+3,x^3+3,x^4+alpha, x^5 qquad npu quad alpha in mathbb Z . $$
Имеем:
$$ {bf mbox{СИНДРОМ }}(tilde G(x))equiv (2-2,alpha)+(2-2,alpha),x+(1-alpha),x^2 ; $$
т.е. получился полином $ 2_{} $-й степени, в котором пока трудно увидеть намек на какую-то идею. Вычислим теперь синдром от полинома $ xtilde G(x) $:
$$ {bf mbox{СИНДРОМ }}(xtilde G(x))equiv alpha — 1 ; $$
и вот этот полином — вместо ожидаемой $ 2_{} $-й степени — имеет нулевую степень, т.е. равен константе. Более того, эта константа обращается в нуль как раз при том единственном значении параметра $ alpha_{} $, которое обеспечивает совпадение полинома $ tilde G(x) $ с кодовым полиномом $ G_{}(x) $!
Пойдем дальше:
$$ {bf mbox{СИНДРОМ }}(x^2tilde G(x))equiv (alpha — 1)x ; $$
т.е. синдром получается домножением предыдущего на $ x_{} $. Аналогично:
$$ {bf mbox{СИНДРОМ }}(x^3tilde G(x))equiv (alpha — 1)x^2 , $$
и т.д.
Попробуем теперь испортить в кодовом полиноме $ G_{}(x) $ коэффициент при $ x^{4} $:
$$ tilde G(x)=-1-x+x^2+3,x^3+beta,x^4+x^5 qquad npu quad beta in mathbb Z . $$
Снова последовательно вычисляем синдромы для последовательности $ G_{}(x),xG_{}(x),x^2G_{}(x),dots $:
$$
begin{array}{lcl}
{bf mbox{СИНДРОМ }}(tilde G(x))&equiv& (2,beta-6) +(3beta-9)x+(2beta-6)x^2, \
{bf mbox{СИНДРОМ }}(xtilde G(x))&equiv& (6-2beta)+(6-2beta)x+ (3-beta)x^2,\
{bf mbox{СИНДРОМ }}(x^2tilde G(x))&equiv&beta- 3, \
{bf mbox{СИНДРОМ }}(x^3tilde G(x))&equiv&(beta- 3)x,\
{bf mbox{СИНДРОМ }}(x^4tilde G(x))&equiv&(beta- 3)x^2,\
dots & & dots \
end{array}
$$
Видим проявление того же эффекта, что и в предыдущем случае: при каком-то показателе $ j_{} $ синдром полинома $ x^j tilde G(x) $ становится равным константе, причем эта константа обращается в нуль только при значении параметра, обеспечивающем выполнение тождества $ tilde G(x)equiv G(x) $.
Проверим наблюдение для случая «порчи» других коэффициентов. Оформим результаты в виде таблицы:
верхняя ее строка показывает при каком мономе полинома
$$ G(x)=-1-x+x^2+3,x^3+3,x^4+x^5 $$
портится коэффициент, а сама таблица содержит степени синдромов полиномов $ x^j tilde G(x) $
$$
begin{array}{r|cccccc}
& x^5 & x^4 & x^3 & x^2 & x & x^{0} \
hline
\
tilde G & 2 & 2 & 2 & 2 & 1 & 0 \
xtilde G & 0 & 2 & 2 & 2 & 2 & 1 \
x^2tilde G & 1 & 0 & 2 & 2 & 2 & 2 \
x^3tilde G & 2 & 1 & 0 & 2 & 2 & 2 \
x^4tilde G & 2 & 2 & 1 & 0 & 2 & 2 \
x^5tilde G & 2 & 2 & 2 & 1 & 0 & 2 \
x^6tilde G & 2 & 2 & 2 & 2 & 1 & 0
end{array}
$$
Видим, что в последовательности синдромов обязательно встречается константа и встречается она при значении показателя $ j_{} $, устойчиво связанного с номером разряда кодового слова (или индекса коэффициента полинома), в котором происходит ошибка. Более того, подтверждается и другое наблюдение: эта константа обращается в нуль только при условии когда ошибки при передаче кодового слова по каналу не происходит.
♦
Т
Теорема 1. Пусть порождающий циклический код полином $ g_{}(x) $ является нетривиальным делителем полинома $ x^{n}-1 $. Если при передаче кодового полинома $ G_{}(x) $ по каналу связи произошла ровно одна ошибка в $ j_{} $-м коэффициенте и получен полином $ tilde G(x)=G(x)+E x^j $, то
$$ {bf mbox{СИНДРОМ }}(x^{n-j}tilde G(x))equiv E . $$
Доказательство. Имеем:
$$ x^{n-j}tilde G(x) equiv x^{n-j} G(x)+E x^n equiv E pmod{g(x)} , $$
поскольку $ G_{}(x) $ делится на $ g_{}(x) $ и $ x^n-1 $ делится на $ g_{}(x) $.
Итак, ошибка обнаружена. Теперь осталось показать, что остальные синдромы — «нормальные», т.е. отличные от константы, и, следовательно, ошибка обнаружена однозначно. В общем случае это утверждение неверно. Так, к примеру, при
$$ n=12, g=x^6-1, tilde G(x)=underbrace{1+x-x^3+x^4-x^5-x^6-x^7+x^9-x^{10}+x^{11}}_{=G(x)}+E,x^5 $$
получим, что
$$ {bf mbox{СИНДРОМ }}(xtilde G(x))equiv {bf mbox{СИНДРОМ }}(x^7tilde G(x))equiv E , $$
т.е. наряду с возможностью декодирования в истинный полином $ G_{}(x) $ , обнаруживается еще и «фантом» — полином
$$ G_{E}(x)= 1+x-x^3+x^4+(E-1)x^5-x^6-x^7+x^9-x^{10}+(1-E)x^{11} , $$
являющийся кодовым при любом значении $ E in mathbb Z $.
Тем не менее, можно утверждать, что, как правило, такой ситуации не возникнет. Не будем пока строго обосновывать этот вывод, а покажем, что всегда возможно выбрать порождающий полином $ g_{}(x) $ так, чтобы не возникло указанного в предыдущем абзаце эффекта. Итак, фактически надо гарантировать, чтобы сравнение
$$
x^{ell} equiv gamma pmod{g(x)}
$$
при $ gamma in mathbb Z $ не выполнялось ни при одном показателе $ ellin {1,2,dots,n-1} $.
С этой целью, выберем в качестве $ g_{}(x) $ полином $ g(x)equiv (x-1)X_{n}(x) $, где $ X_n(x) $ — полином из пункта
☞
УРАВНЕНИЕ ДЕЛЕНИЯ КРУГА, корнями которого являются все первообразные корни $ n_{} $-й степени из единицы (и только такие корни). Таким образом, $ r=deg g=phi(n)+1 $, где $ phi $ — функция Эйлера. Обозначим $ lambda_1=1,lambda_2,dots,lambda_r $ — корни $ g_{}(x) $. Тогда требуемое сравнение эквивалентно полиномиальному тождеству
$$ iff x^{ell} equiv g(x)Q_k(x)+ gamma quad npu quad Q_k(x)in mathbb Z[x] . $$
При подстановке в него корней $ lambda_{j} $ получаем:
$$ 1=gamma, lambda_2^{ell}=gamma,dots,lambda_r^{ell}=gamma , $$
откуда $ lambda_2^{ell}=1 $ и это равенство невозможно при $ ellin {1,2,dots,n-1} $ поскольку его выполнение противоречило бы первообразности корня $ lambda_{2} $.
♦
Мы пока умышленно не касаемся реальных способов выбора порождающего полинома кода, а только постепенно сужаем область его выбора формулированием естественных ограничений, возникающих из практики его использования.
Алгоритм. Последовательно строим синдромы полиномов $ tilde G, xtilde G,x^2 tilde G,dots, x^{n-1} tilde G $ до тех пор, пока не встретим полином нулевой степени (константу): $ {bf mbox{СИНДРОМ }}(x^{n-j}tilde G(x))=E $; заключаем, что в соответствующем моному $ x^{j} $ разряде кодового слова произошла ошибка; вычитаем эту константу из соответствующего разряда полученного слова:
$$ (b_0,b_1,dots,b_{j-1},tilde b_j-E,dots,b_{n-1}) $$
и получим истинное кодовое слово.
Последовательное вычисление синдромов организуется достаточно просто с учетом следующего утверждения.
Т
Теорема 2. Если
$$ s(x)=s_0+s_1x+dots+s_{r-1}x^{r-1} $$
— синдром полинома $ F(x) in mathbb Z[x] $, а $ tilde s(x)=tilde s_0+tilde s_1x+dots+ tilde s_{r-1}x^{r-1} $ — синдром полинома $ xF(x) $, то коэффициенты $ tilde s_j $ вычисляются по правилу:
$$ tilde s_0=-s_{r-1}a_0, tilde s_1=s_0-s_{r-1}a_1, tilde s_2=s_1-s_{r-1}a_2,dots,
tilde s_{r-1}=s_{r-2}-s_{r-1}a_{r-1} .
$$
Для исправления единичной ошибки можно также использовать проверочный полином $ h_{}(x) $ кода. В самом деле, факт ошибки устанавливается проверкой $ tilde G(x) h(x) notequiv 0 pmod{x^n-1} $.
Т
Теорема 3. Если $ tilde G(x)equiv G(x)+E x^j $, то
$$ tilde G(x) h(x) equiv E, x^j h(x) pmod{x^n-1} , $$
т.е. место ошибки устанавливается по совпадению остатка от деления $ tilde G(x) h(x) $ на $ x^n-1 $ с циклическим сдвигом строки коэффициентов полинома $ h_{}(x) $.
Можно развить предложенный подход к коррекции ошибок, основанный на проверке степеней синдромов последовательности $ {x^{ell} tilde G(x) }_{ell=0}^{n-1} $, на случай появления нескольких ошибок.
П
Пример. Пусть $ n=12 $ и циклический код порождается полиномом $ g(x)= 1-x+2,x^2-x^3+x^4 $. Пусть при передаче по каналу кодового полинома
$$ G(x)=1-4,x+4,x^2-x^3-5,x^4+11,x^5-13,x^6+14,x^7-10,x^8+9,x^9-
$$
$$ -5,x^{10}+3,x^{11} $$
произошли ошибки в двух коэффициентах. Вычислим синдромы получающихся полиномов $ tilde G(x) $.
Пусть сначала испорчены два старших коэффициента:
$$ tilde G(x)=1-4,x+4,x^2-x^3-5,x^4+11,x^5-13,x^6+14,x^7-10,x^8+9,x^9+
$$
$$
+beta x^{10}+alpha x^{11} quad npu quad {alpha,beta} subset mathbb Z .
$$
Получаем:
$$
{bf mbox{СИНДРОМ }}(tilde G(x))equiv (alpha-beta-8)+(1-2alpha-beta)x+(alpha-3)x^2+(-2-beta-alpha)x^3 ;
$$
и степень синдрома «не внушает подозрений» — она равна ожидаемой степени остатка от деления произвольного полинома на $ g_{}(x) $. Далее,
$$
{bf mbox{СИНДРОМ }}(xtilde G(x))equiv (alpha+beta+2)+(-2beta-10)x+(beta+5)x^2+(-beta-5)x^3 ,
$$
и снова не подозрений нет. Но вот следующий синдром
$$
{bf mbox{СИНДРОМ }}(x^2tilde G(x))equiv (beta+5)+(alpha-3)x
$$
имеет степень меньшую $ 3_{} $, более того, обращение в нуль его коэффициентов позволяет установить исходный (кодовый) полином $ G_{}(x) $. Формально:
$$ G(x) equiv tilde G(x) — x^{12-2}times {bf mbox{СИНДРОМ }}(x^2tilde G(x)) .$$
Проверим гипотезу на другом примере. Пусть
$$ tilde G(x)=1-4,x+4,x^2-x^3-5,x^4+11,x^5+delta,x^6+gamma,x^7-10,x^8+9,x^9-5,x^{10}+3,x^{11}
quad npu quad {gamma,delta} subset mathbb Z .
$$
Опустим вычисления, приведя только оценки степеней синдромов
$$
begin{array}{c|c|c|c|c|c|c|c}
j & 0 & 1 & 2 & 3 & 4 & 5 & 6 \
hline
&&&&&&& \
deg {bf mbox{СИНДРОМ }}(x^jtilde G(x)) & 3 & 3 & 3 & 3 & 3 & 3 & 1
end{array}
$$
при
$$
{bf mbox{СИНДРОМ }}(x^6tilde G(x))equiv (delta+13)+(gamma-14),x .
$$
Снова понижение степени синдрома свидетельствует об обнаружении ошибки, снова коэффициенты подсказывают величины этих ошибок:
$$ G(x) equiv tilde G(x) — x^{12-6}times {bf mbox{СИНДРОМ }}(x^6tilde G(x)) .$$
Испортим теперь два коэффициента «вразбивку»:
$$ tilde G(x)=1-4,x+4,x^2-x^3+zeta x^4+11,x^5+eta,x^6+14,x^7-10,x^8+9,x^9-5,x^{10}+3,x^{11}
quad npu quad {zeta,eta} subset mathbb Z .
$$
$$
begin{array}{c|c|c|c|c|c|c|c|c|c}
j & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \
hline
&&&&&&&& \
deg {bf mbox{СИНДРОМ }}(x^jtilde G(x)) & 3 & 3 & 3 & 3 & 3 & 3 & 3 & 3 & 2
end{array}
$$
при
$$
{bf mbox{СИНДРОМ }}(x^8tilde G(x))equiv (zeta+5)+(eta+13)x^2 .
$$
Исправление возможно:
$$ G(x) equiv tilde G(x) — x^{12-8}times {bf mbox{СИНДРОМ }}(x^8tilde G(x)) .$$
Однако если ошибочные коэффициенты оказываются разнесенными по полиному $ tilde G $ немного больше, как, к примеру, в
$$ tilde G(x)=1-4,x+4,x^2-x^3-5,x^4+theta x^5-13,x^6+14,x^7+xi,x^8+9,x^9-5,x^{10}+3,x^{11} ,
$$
то оценки степеней синдромов последовательности $ {x^{ell} tilde G(x) }_{ell=0}^{11} $ не позволят определить местоположение ошибок, поскольку все они имеют степень $ 3_{} $. Хотя наблюдательный читатель — с помощью интуиции — выделит в последовательности этих синдромов один, отличающийся по внешнему виду от остальных, именно —
$$
{bf mbox{СИНДРОМ }}(x^7tilde G(x))equiv (theta-11)+(10+xi),x^3 ,
$$
и убедится, что кодовый полином получится по формуле, которую вывели выше:
$$ G(x) equiv tilde G(x) — x^{12-7}times {bf mbox{СИНДРОМ }}(x^7tilde G(x)) ;$$
но эту человеческую бдительность трудно реализовать программно…
♦
Возникает подозрение, что обнаруженный эффект понижения степени синдрома сработает и в общем случае:
$$ tilde G(x)=G(x)+x^j E(x) $$
при $ deg E< r=deg g $, т.е. в случае, когда при передаче по каналу ошибки происходят серией4) в (не более чем) $ deg E(x) $ подряд идущих разрядах. Действительно, при таком ограничении на степень полинома $ E(x) $ имеем:
$$ {bf mbox{СИНДРОМ }}(x^{n-j} tilde G(x)) equiv E(x) , $$
т.е. «поврежденный кусок» при проверке не пропустим. Если же, вдобавок, $ deg E(x) $ много меньше $ r_{} $, то «место повреждения» — число $ j_{} $ — будем производить по принципу максимального правдоподобия, полагая
$$ j=min_{ellin{0,1,dots,n-1}} deg {bf mbox{СИНДРОМ }}(x^{n-ell} tilde G(x)) ; $$
иными словами, выбирая из последовательности синдромов те, что имеют минимальную степень.
Можно сходу придумать контрпример к предлагаемой схеме.
П
Пример. Пусть
$$ n=18, g(x)= 1+x+x^2-x^3-x^4-x^5+x^6+x^7+x^8 ,$$
и полученный полином имеет вид:
$$ tilde G(x)= 10+4,x+8,x^2-15,x^3-9,x^4-12,x^5+12,x^6+13,x^7+18,x^8+8,x^9
$$
$$
-8,x^{11}-11,x^{12}-5,x^{13}+4,x^{14}+9,x^{15}+9,x^{16}+2,x^{17} . $$
Подобрать кодовый полином $ G_{}(x) $, «породивший» $ tilde G(x) $.
Решение. Последовательным вычислением синдромов полиномов $ x^{n-ell} tilde G(x) $ обнаружим полиномы минимальной степени
$$ x^6tilde G(x)equiv 2-x^3 qquad u qquad x^{12}tilde G(x)equiv -1+2,x^3 . $$
Таким образом, кодовыми полиномами, выбираемыми по критерию минимализации степени синдрома оказываются два:
$$
G_1(x)equiv tilde G(x) — (-2,x^{12}+x^{15}) qquad u qquad G_2(x)equiv tilde G(x)-(x^6-2,x^9) .
$$
♦
Однако нельзя слишком уж сильно портить линейный код: понятие кодового расстояния не зря вводилось…
…анализом с помощью корней порождающего полинома
Вернемся к случаю одиночной ошибки, описанному в теореме $ 1_{} $ предыдущего пункта. Пусть
$ tilde G(x) equiv G(x)+E x^j $, где $ Ein mathbb Z $ и $ G_{}(x) $ — кодовый полином. Последнее означает, что $ G_{}(x) $ делится нацело на полином $ g_{}(x) $, порождающий циклический код: $ G_{}(x) equiv Q(x)g(x) $ при $ Q(x)in mathbb Z[x] $.
Рассмотрим какой-то из корней полинома $ g_{}(x) $; поскольку $ g_{}(x) $ договорились выбирать среди делителей полинома $ x^n -1 $, то этот корень — это корень $ n_{} $-й степени из $ 1_{} $ и, в общем случае, комплексное число. Обозначим его $ varepsilon_{} $. Подстановка $ x=varepsilon_{} $ в кодовый полином $ G_{}(x) $ даст $ 0_{} $, а в полином $ tilde G(x) $ — величину
$$ tilde G(varepsilon_{}) = G(varepsilon)+E varepsilon_{}^j = E varepsilon_{}^j . $$
Можно было бы назвать эту величину синдромом полинома $ tilde G(x) $ поскольку ее отличие от нуля свидетельствует о наличии ошибки при передаче по каналу связи, но мы пока не будем вводить новых определений.
Таким образом, место ошибки (т.е. поврежденного коэффициента = разряда кодового слова) обнаруживается по совпадению числа
$ tilde G(varepsilon_{}) $ с элементом последовательности
$$ E varepsilon_{}^0, E varepsilon_{}^1, E varepsilon_{}^2,dots, E varepsilon_{}^{n-1} . $$
При дополнительном условии, что в этой последовательности не будет одинаковых элементов (или коллизий).
Последнее замечание накладывает дополнительное ограничение на выбор полинома $ g_{} $. Выберем его так, чтобы среди его корней находился хотя бы один первообразный корень степени n из единицы. Для определенности, пусть это будет корень
$$ varepsilon_1= cos frac{2 pi}{n} + mathbf i sin frac{2 pi}{n} . $$
Тогда, по теореме из пункта
☞
КОРНИ ИЗ ЕДИНИЦЫ, все элементы последовательности $ { varepsilon_1^k }_{k=0}^{n-1} $ будут различными и представление комплексного числа $ tilde G(varepsilon_1) $ в тригонометрической форме:
$$ tilde G(varepsilon_1) = rho left( cos varphi + mathbf i sin varphi right) quad npu quad
varphiin [0,2, pi [ ,
$$
позволит однозначно определить место ошибки $ j_{} $ и ее величину $ E_{} $ по формулам:
$$ E= rho,quad 2pi k/n= varphi . $$
В предложенной схеме есть один изъян, который проиллюстрируем на примере.
П
Пример. Пусть
$$ n=6, g(x)=-1+2,x-2,x^2+x^3 , ;. $$
Корнем $ g_{}(x) $ является
$ varepsilon_1=frac{1}{2}+ mathbf i frac{sqrt{3}}{2} $ — первообразный корень $ 6_{} $-й степени из единицы.
Пусть при передаче кодового полинома $ G(x)=3-5,x+2,x^2+3,x^3-5,x^4+2,x^5 $ произошла одна ошибка и на выходе из канала получен полином $ tilde G(x)equiv G(x)-3,x^2 $. Подставляем в него $ x=varepsilon_1 $:
$$ tilde G(varepsilon_1)=frac{3}{2}(1-mathbf i sqrt{3}) $$
и начинаем сравнивать полученное выражение со степенями $ varepsilon_1^k $:
$$ { varepsilon_1^k }_{k=0}^{5}=1, frac{1}{2}(1+mathbf i sqrt{3}), frac{1}{2}(-1+mathbf i sqrt{3}), -1, frac{1}{2}(-1-mathbf i sqrt{3}), frac{1}{2}(1-mathbf i sqrt{3}) .
$$
Видим, что возможны два варианта:
$$ tilde G(varepsilon_1)=- 3 varepsilon_1^2=3 varepsilon_1^5 . $$
Эта неоднозначность возникла вследствие того, что в предложенной выше схеме мы ошибочно предположили величину $ E_{} $ положительной.
♦
Для ликвидации изъяна схемы, будем выбирать $ n_{} $ нечетным. Тогда множество $ { varepsilon_1^k }_{k=0}^{n-1} $ теряет симметрию относительно начала координат и ошибку будем обнаруживать проверкой условия ee вещественности5):
$$ tilde G(varepsilon_1)/varepsilon_1^k in mathbb R quad iff quad tilde G(varepsilon_1)varepsilon_1^{n-k} in mathbb R . $$
(Последнее соотношение следует из равенства $ varepsilon_1^k varepsilon_1^{n-k}= varepsilon_1^{n}=1 $.)
П
Пример. Пусть
$$ n=15, g(x)=1-x+x^3-x^4+x^5-x^7+x^8 $$
Корнем $ g_{}(x) $ является
$$ varepsilon_1= frac{1}{8}left(1+sqrt{5}+sqrt{30-6sqrt{5}}+mathbf ileft[-sqrt{10-2,sqrt{5}}+sqrt{3}+sqrt{15}right]right)approx 0.913545+ 0.406737 , mathbf i $$
— первообразный корень $ 15_{} $-й степени из единицы.
Пусть при передаче кодового полинома
$$
G(x)=-2+6,x-5,x^2+x^3+x^4-5,x^5+10,x^6-6,x^7-2,x^8+5,x^9-6,x^{10}+7,x^{11}-2,x^{12}-3,x^{13}+2,x^{14}
$$
произошла одна ошибка и на выходе из канала получен полином $ tilde G(x)equiv G(x)-2,x^4 $. Домножаем $ tilde G(varepsilon_1) $ на степени $ varepsilon_1 $ и проверяем полученные выражения на вещественность6):
$$ tilde G(varepsilon_1)approx 0.209057-1.989044, mathbf i, tilde G(varepsilon_1)varepsilon_1= 1- sqrt{3} , mathbf i, tilde G(varepsilon_1)varepsilon_1^2approx 1.956295+0.415823 , mathbf i, dots, tilde G(varepsilon_1)varepsilon_1^{11}=-2, dots $$
Здесь ошибка обнаруживается однозначно.
♦
Можно ли развить этот подход до метода исправления двух (и более) ошибок? Попробуем это сделать для случая ошибок, возникших в двух соседних коэффициентах. Если это — младшие коэффициенты полинома:
$$ tilde G(x)equiv G(x)+E_0+E_1x , $$
то при $ r=deg g>2 $ линейный полином $ E_0+E_1x $ представляет собой остаток от деления $ tilde G(x) $ на порождащий код полином $ g_{}(x) $: поскольку $ G_{}(x) $ — кодовый полином, то
$ G(x) equiv Q(x) g(x) $ при $ Q(x)in mathbb Z $, но тогда тождество
$$ tilde G(x)equiv Q(x) g(x)+E_0+E_1x $$
фактически является определением остатка и частного от деления $ tilde G(x) $ на $ g_{}(x) $.
Если мы знаем выражения для хотя бы двух корней $ lambda_{1} $ и $ lambda_{2} $ полинома $ g_{}(x) $, то мы сможем установить коэффициенты $ E_0+E_1x $ из системы линейных уравнений:
$$ tilde G(lambda_1)=E_0+E_1 lambda_1, tilde G(lambda_2)=E_0+E_1 lambda_2 . $$
Схема понятна, и очевидным образом обобщается на случай, если полином $ tilde G(x) $ содержит больше двух ошибок, но они сконцентрированы в младших $ r-1 $ коэффициентах этого полинома — в этом случае, фактически, задача превращается в задачу полиномиальной интерполяции. Но вот общую ситуацию, когда расположение двух подряд идущих ошибок, т.е. число $ j_{} $ в
$$ tilde G(x)equiv G(x)+E_jx^j+E_{j+1}x^{j+1} $$
неизвестно, предложенный подход не покроет — например, в случае $ j+1 ge r $. Альтернативой может служить следующий алгоритм, который мы изложим в слегка упрощенном варианте, выбрав в качестве порождающего полинома $ g_{}(x) $ полином, имеющий корнем наряду с $ varepsilon_1 $ (первообразным корнем степени $ n_{} $ из единицы) еще и $ 1_{} $. Подстановка этих двух корней в последнее тождество даст систему уравнений:
$$ tilde G(1)=E_j+E_{j+1},quad tilde G(varepsilon_1)=varepsilon_1^j(E_j+E_{j+1}varepsilon_1) . $$
Домножим второе равенство на $ varepsilon_1^{n-j} $:
$$ tilde G(1)=E_j+E_{j+1},quad varepsilon_1^{n-j}tilde G(varepsilon_1)=E_j+E_{j+1}varepsilon_1 . $$
Из этих уравнений получим выражения для $ E_j $ и $ E_{j+1} $:
$$ E_j=-varepsilon_1frac{varepsilon_1^{n-j-1}tilde G(varepsilon_1)-tilde G(1)}{varepsilon_1-1},quad
E_{j+1}=frac{varepsilon_1^{n-j}tilde G(varepsilon_1)-tilde G(1)}{varepsilon_1-1}
.
$$
Ключевым обстоятельством является вещественность обоих чисел. Именно на этом построим критерий поиска «места ошибки», т.е. величины $ j_{} $: будем последовательно по $ kin {0,1,2,dots,n-2} $ вычислять величины
$$
-varepsilon_1frac{varepsilon_1^{k-1}tilde G(varepsilon_1)-tilde G(1)}{varepsilon_1-1}quad u quad
frac{varepsilon_1^{k}tilde G(varepsilon_1)-tilde G(1)}{varepsilon_1-1}
$$
до тех пор, пока оба числа не станут вещественными.
П
Пример. Пусть
$$ n=15, g(x)=(1-x+x^3-x^4+x^5-x^7+x^8)(x-1) , ,$$
т.е. полином $ g(x) $ получается домножением полинома из предыдущего примера на $ x_{}-1 $.
Пусть при передаче кодового полинома
$$
G(x)=2-8,x+11,x^2-6,x^3+8,x^5-17,x^6+14,x^7-9,x^9+11,x^{10}-11,x^{11}+5,x^{12}+3,x^{13}-3,x^{14}
$$
произошли две ошибки подряд и на выходе из канала получен полином $ tilde G(x)equiv G(x)-2,x^5+x^6 $.
Подстановка $ x_{}=1 $ в полученный полином дает $ tilde G(1)=-1 ne 0 $, т.е. наличие ошибки подтверждено. Далее, начинаем параллельное вычисление двух последовательностей:
$$ tilde G(varepsilon_1), tilde G(varepsilon_1)varepsilon_1,
tilde G(varepsilon_1)varepsilon_1^2,dots
$$
и
$$
frac{tilde G(varepsilon_1)-tilde G(1)}{varepsilon_1-1}, frac{varepsilon_1tilde G(varepsilon_1)-tilde G(1)}{varepsilon_1-1}, frac{varepsilon_1^{2}tilde G(varepsilon_1)-tilde G(1)}{varepsilon_1-1}, dots ,
$$
где величина $ varepsilon_{1} $ — такая же, как и в предыдущем примере. Первая из этих последовательностей была рассмотрена в предыдущем случае — одиночной ошибки передачи. Вещественность какого-то элемента этой последовательности означает наличие ошибки в соответствующем коэффициенте полученного полинома. Таким образом, алгоритм содержит в себе еще и проверку гипотезы на одиночность ошибки. Если очередной элемент этой последовательности не является вещественным числом, произведем — с его помощью — вычисление соответствующего элемента второй последовательности. Если этот элемент — вещественное число, — а так и происходит в рассматриваемом примере на $ 10_{} $-м шаге:
$$
frac{varepsilon_1^{10}tilde G(varepsilon_1)-tilde G(1)}{varepsilon_1-1} approx 1 ,
$$
то для контроля вычисляем еще и величину7)
$$
-varepsilon_1frac{varepsilon_1^{9}tilde G(varepsilon_1)-tilde G(1)}{varepsilon_1-1} approx -2 ,
$$
которая также оказывается вещественным числом. Место двух подряд идущих ошибок обнаружено. Их исправление производится по формуле $ tilde G(x)+ x^{15-10}(-2+x) $.
♦
Остался нерассмотренным общий случай — когда две ошибки не обязательно соседствуют:
$$ tilde G(x)equiv G(x)+E_jx^j+E_{k}x^{k} mbox{ при } j<k , . $$
Рассмотрение этого случая
☞
ЗДЕСЬ, но для понимания последующего материала настоящего раздела вполне достаточно уже разобранных выше случаев.
Двоичные коды
По ходу изложения существенно используются материалы из разделов
☞
ПОЛЯ ГАЛУА и
☞
КОД ХЭММИНГА.
Наша задача состоит в том, чтобы развитые в предыдущих пунктах идеи перевести на язык двоичных кодов — перейти к арифметике по модулю $ 2_{} $.
Циклический код образует линейное подпространство пространства $ mathbb V^n $ и, следовательно, является частным случаем линейного кода. Но тогда можно установить соответствие между способами их определения.
С целью состыковки обозначений принятым в литературе, изменим порядок записи разрядов циклического кода. Будем считать, что строке $ (b_{n-1},b_{n-2},dots,b_1,b_0) in mathbb V^n $ соответствует полином $ b_{n-1}x^{n-1}+b_{n-2}x^{n-2}+dots+b_1x+b_0 $, т.е. младшие разряды строки соответствуют старшим коэффициентам полинома.
Пусть
$$ g(x)=x^r+a_{r-1}x^{r-1}+dots+a_0 quad npu quad {a_0,dots,a_{r-1}} subset {0,1} ,$$
— порождающий полином кода; мы выбираем его среди нетривиальных делителей по модулю $ 2_{} $ полинома $ x^n — 1 $. Проверочный полином $ h_{}(x) $ удовлетворяет теперь сравнению
$$ g(x)h(x) equiv 1 pmod{2} . $$
Циклический код $ C_{} $, порожденный полиномом $ g_{}(x) $, имеет базисными строки, составленные из коэффициентов полиномов $ x^{k-1}g(x),x^{k-2}g(x), dots,g(x) $. Иными словами, порождающей матрицей кода $ C_{} $ будет матрица
$$
begin{array}{rl}
& x^{n-1} x^{n-2} x^{n-3} dots x^k x^{k-1} dots 1 \
& downarrow downarrow downarrow quad quad quad downarrow downarrow qquad qquad downarrow \
mathbf G_{ktimes n}=&left(
begin{array}{ccccccccc}
1 & a_{r-1} & a_{r-2} & dots & a_1 & a_0 & 0 & dots & 0 \
& 1 & a_{r-1} & dots & a_2 & a_1 & a_0 & & 0 \
mathbb O & & ddots & & & & & ddots & vdots \
& & & 1 & dots & & & & a_0
end{array}
right)
end{array} .
$$
Эта матрица соответствует несистематическому способу кодирования.
В теории кодирования матрицу именно такого вида называют циклической — она представляет собой «верхнюю часть» квадратной циклической матрицы $ mathfrak C $ из
☝
ПУНКТА.
Базисные строки кода, а, значит, и порождающую матрицу, можно выбрать не единственным способом; так, систематическому способу кодирования соответствует порождающая матрица
$$mathbf G=left(
begin{array}{ccccc|lll}
1 & 0 & 0 & dots & 0 & b_{n-1,r-1} & dots & b_{n-1,0} \
& 1 & 0 & dots & 0 & b_{n-2,r-1} & dots & b_{n-2,0} \
mathbb O & & ddots & & vdots & vdots & & vdots \
& & & & 1 & b_{r,r-1} & dots & b_{r0}
end{array}
right) ,
$$
которая уже не является циклической. Справа от черты стоят коэффициенты остатков от деления мономов $ x^{n-1},x^{n-2},dots,x^r $ на $ g_{}(x) $:
$$ x^jequiv b_{j,r-1}x^{r-1}+b_{j,r-2}x^{r-2}+dots+b_{j0} equiv — (b_{j,r-1}x^{r-1}+b_{j,r-2}x^{r-2}+dots+b_{j0}) quad (operatorname{modd} 2,g(x)) . $$
Посмотрим что представляют собой проверочные матрицы соответствующие двум видам порождающей матрицы. Для последней матрицы она строится просто — поскольку она имеет блочную структуру вида
$ mathbf G = left[ E_k mid P right] $ при $ E_{k} $ — единичной матрице $ k_{} $-го порядка, то, в соответствии со следствием к теореме 1 из
☝
ПУНКТА, — проверочная матрица имеет вид $ mathbf H=left[ P^{top} mid E_{r} right] $
П
Пример. Пусть $ n=7, g(x)=x^3+x^2+1 $. Тогда для систематического кодирования
$$
mathbf G=
left(begin{array}{cccc|ccc}
1 & 0 & 0 & 0 & 1 & 1 & 0 \
0 & 1 & 0 & 0 & 0 & 1 & 1 \
0 & 0 & 1 & 0 & 1 & 1 & 1 \
0 & 0 & 0 & 1 & 1 & 0 & 1
end{array}
right) quad Rightarrow quad
mathbf H=
left(begin{array}{cccc|ccc}
1 & 0 & 1 & 1 & 1 & 0 & 0 \
1 & 1 & 1 & 0 & 0 & 1 & 0 \
0 & 1 & 1 & 1 & 0 & 0 & 1
end{array}
right) .
$$
Что представляют собой строки проверочной матрицы $ mathbf H $? — Оказывается, они содержат коэффициенты проверочного полинома $ h_{}(x) $ кода $ C_{} $. Действительно, в данном примере
$ h(x)=x^4+x^3+x^2+1 $ и
$$
begin{array}{ll}
begin{array}{c}
1 x x^2 x^3 x^4 x^5 x^6
end{array} & \
begin{array}{cccccccc}
downarrow & downarrow & downarrow & downarrow & downarrow & downarrow & downarrow &
end{array} & \
left(begin{array}{ccccccc}
1 & 0 & 1 & 1 & 1 & 0 & 0 \
1 & 1 & 1 & 0 & 0 & 1 & 0 \
0 & 1 & 1 & 1 & 0 & 0 & 1
end{array}
right)
&
begin{array}{l}
leftarrow h(x) \
leftarrow x^5+x^2+x+1equiv h(x)x^5 pmod{x^7-1} \
leftarrow x^6+x^3+x^2+xequiv h(x)x^6 pmod{x^7-1}
end{array}
end{array}
$$
Для несистематического кодирования структура проверочной матрицы оказывается еще более простой:
$$
mathbf G=
left(begin{array}{ccccccc}
1 & 1 & 0 & 1 & 0 & 0 & 0 \
0 & 1 & 1 & 0 & 1 & 0 & 0 \
0 & 0 & 1 & 1 & 0 & 1 & 0 \
0 & 0 & 0 & 1 & 1 & 0 & 1
end{array}
right) Rightarrow
$$
$$
Rightarrow
mathbf H=
left(
begin{array}{ccccccc}
0 & 0 & 1 & 0 & 1 & 1 & 1 \
0 & 1 & 0 & 1 & 1 & 1 & 0 \
1 & 0 & 1 & 1 & 1 & 0 & 0
end{array}
right)
begin{array}{l}
leftarrow h(x) \
leftarrow h(x)x \
leftarrow h(x)x^2
end{array}
,
$$
т.е. можно сказать, что $ mathbf H $ тоже является циклической матрицей с порождающим полиномом $ h_{}(x) $ — если записать этот полином «в обратном порядке» (т.е. формально рассмотреть полином $ h^{*}(x)equiv x^4h(1/x) $) и циклически переставить строки.
♦
Теперь обсудим разобранные в предыдущих пунктах способы обнаружения и исправления ошибок.
П
Пример. Рассмотрим циклический код из предыдущего примера: $ n=7, g(x)=x^3+x^2+1 $. Пусть при передаче кодового полинома $ G(x)=x^6+x^3+x+1 $ по каналу связи произошла ровно одна ошибка и на выходе получили полином $ tilde G(x)=x^6+x^4+x^3+x+1 $.
1-й cпособ.
Вычисление синдромов $ x^jtilde G(x) $ как остатков от деления на полином $ g_{}(x) $ — только теперь все вычисления идут по модулю $ 2_{} $:
$$ {bf mbox{СИНДРОМ }} (tilde G(x))equiv x^2+x+1 , $$
и, поскольку синдром ненулевой, то ошибка при передаче действительно произошла. Далее, последовательно вычисляем остатки от деления полиномов $ {bf mbox{СИНДРОМ }}(x^jtilde G(x)) $ при $ jin {1,2,dots } $
и при этих вычислениях можем воспользоваться теоремой 2 из
☝
ПУНКТА:
$$ {bf mbox{СИНДРОМ }}(xtilde G(x))equiv x+1 , {bf mbox{СИНДРОМ }}(x^2tilde G(x))equiv x(x+1)=x^2+1,
$$
$$ {bf mbox{СИНДРОМ }}(x^3tilde G(x))equiv x(x^2+1) pmod{g(x)} equiv 1 . $$
Остаток оказался равным константе, следовательно ошибочный коэффициент найден, и $ G(x) equiv tilde G(x) + x^{7-3} pmod{2} $.
2-й cпособ.
Домножение $ tilde G(x) $ на проверочный полином — использование теоремы 3 из
☝
ПУНКТА. Здесь $ h(x)=x^4+x^3+x^2+1 $ и
$$ tilde G(x) h(x) equiv x^6+x^4+x+1 equiv x^4h(x) equiv x quad (operatorname{modd} 2,x^7-1) . $$
Снова ошибочный коэффициент обнаружен.
3-й cпособ.
Подстановка в $ tilde G(x) $ корня порождающего полинома. А какого, собственно, корня? Если в случае предыдущего
☝
ПУНКТА, когда мы рассматривали коды в $ mathbb Z^n $, мы спокойно подставляли корень $ n_{} $-й степени из единицы, то для данного примера этот прием не пройдет — полином $ g_{}(x) $ не является делителем полинома $ x^7-1 $ во множестве $ mathbb Z_{} $, а только по модулю $ 2_{} $. Комплексные корни у полинома $ g_{} (x) $, разумеется, имеются, но они не являются корнями полинома $ x^7-1 $!
Рассматриваем поле Галуа $ mathbf{GF}(2^3) $. Поле содержит $ 8_{} $ элементов — полиномов вида
$ A_2x^2+A_1x+A_0 $ с коэффициентами из $ {0,1} $. Полином $ g(x)=x^3+x^2+1 $ является неприводимым по модулю $ 2_{} $ полиномом и, следовательно, операция умножения полиномов из поля по двойному модулю $ 2, g(x) $ удовлетворяет всем аксиомам поля. Полиномы $ x_{}, x^2, x^4 $ удовлетворяют уравнению $ g(mathfrak x)=0 quad (operatorname{modd} 2,g(x)) $ и являются примитивными элементами поля.
Последнее означает, что любой ненулевой элемент поля совпадает с какой-то степенью любого из этих полиномов, например:
$$
begin{array}{l|rrr||}
x^0 & & & 1 \
x^1 & & x & \
x^2 & x^2 & & \
x^3 & x^2 & &+1 \
x^4 & x^2 &+x &+1 \
x^5 & & x &+1 \
x^6 & x^2 &+x &
end{array}
qquad
begin{array}{|l|rrr}
(x^2)^0 & & & 1 \
(x^2)^1 & x^2 & & \
(x^2)^2 & x^2 & +x &+1 \
(x^2)^3 & x^2 &+x & \
(x^2)^4 & &x & \
(x^2)^5 & x^2 & &+1 \
(x^2)^6 & &x &+1
end{array}
$$
Эти полиномы и будут аналогами первообразных корней из
☝
ПУНКТА. Подставим любой из них в полином $ tilde G(mathfrak x) $ и проведем вычисления по двойному модулю. Например,
$$ tilde G(x) = x^6+x^4+x^3+x+1 equiv x^2+x+1 quad (operatorname{modd} 2,g(x)) $$
В приведенной выше таблице полином $ x^2+x+1 $ соответствует элементу $ x^4 quad (operatorname{modd} 2,g(x)) $. Это и есть моном полинома, в котором допущена ошибка.
Проверим, на всякий случай, наше заключение: не изменится ли оно если возьмем в качестве примитивного элемента полином $ x^{2} $?
$$ tilde G(x^2) = x^{12}+x^8+x^6+x^2+1 equiv x equiv (x^2)^4 quad (operatorname{modd} 2,g(x)) , $$
т.е. снова имеем $ 4 $-ю степень примитивного элемента поля.
♦
Итак, для целей корректировки ошибок порождающий циклический код полином $ g_{}(x) $ имеет смысл выбрать среди примитивных — тогда любой его корень можно использовать для исправления одной ошибки.
Теперь сделаем выжимку из всего предшествующего материала, оформив последовательно накладываемые на порождающий код полином ограничения в виде схемы:

Надо оправдать последний вывод. Циклический код является линейным кодом, у него имеется проверочная матрица $ mathbf H $. В предыдущем примере эта матрица как раз строилась для случая, когда степень полинома $ g_{}(x) $ равнялась $ 7=2^3-1 $. Столбцами этой $ 3times 7 $-матрицы были все трехбитные ненулевые столбцы — но тогда, с точностью до их перестановки, эта матрица совпадает с
проверочной матрицей (7,4)-кода Хэмминга.
Покажем теперь справедливость этого утверждения для общего случая $ n=2^M-1 $. Выбираем в качестве порождающего код полинома произвольный примитивный полином $ g_{}(x) $ степени $ M_{} $. Если $ mathfrak A in mathbf{GF}(2^M) $ — его корень, то этот корень будет примитивным элементом поля $ mathbf{GF}(2^M) $, построенного на основе операции умножения по двойному модулю $ 2,g(x) $. Примитивность корня означает, что все его степени
$$ mathfrak A^{n-1}, mathfrak A^{n-2},dots ,mathfrak A, mathfrak A^0=1 $$
будут различными элементами этого поля. Любой кодовый полином $ G(x)=b_0x^{n-1}+b_1x^{n-2}+dots+b_{n-1} in C $ делится на $ g_{}(x) $, и, следовательно (см. начало
☞
ПУНКТА ):
$$ G(mathfrak A)= b_0mathfrak A^{n-1}+b_1mathfrak A^{n-2}+dots+b_{n-1} =mathfrak o .$$
Любую степень $ mathfrak A^k $ элемента поля можно линейно выразить через первые $ M-1 $ степеней посредством соотношения $ g(mathfrak A)= mathfrak o $. Так, для приведенного выше примера:
$$
begin{array}{c}
n=7, g(x)=x^3+x^2+1 \
hline \
begin{array}{l|rrr|r}
mathfrak A^0 & & & 1 & 001\
mathfrak A^1 & & mathfrak A & & 010 \
mathfrak A^2 & mathfrak A^2 & & & 100 \
mathfrak A^3 & mathfrak A^2 & &+1 & 101 \
mathfrak A^4 & mathfrak A^2 &+mathfrak A &+1 & 111 \
mathfrak A^5 & & mathfrak A &+1 & 011 \
mathfrak A^6 & mathfrak A^2 &+mathfrak A & & 110
end{array}
end{array}
$$
и
$$
begin{array}{rrrrl}
G(mathfrak A)= b_0 (& mathfrak A^2 & +mathfrak A & )+ \
+ b_1 (& & mathfrak A &+1 ) + \
+ b_2 (& mathfrak A^2 &+mathfrak A &+1 ) + \
+ b_3 (& mathfrak A^2 & &+1 ) + \
+b_4 (& mathfrak A^2 & & ) + \
+b_5 (& &mathfrak A & ) + \
+b_6 (& & & +1 )= \
= mathfrak o .
end{array}
$$
Это равенство можно рассматривать как полиномиальное тождество относительно величины $ mathfrak A $.
Приравниваем нулю коэффициенты при $ mathfrak A^2, mathfrak A, 1 $ и получаем систему линейных уравнений, которой должны удовлетворять величины $ {b_j}_{j=0}^6 $:
$$
b_0 left(begin{array}{c} 1 \ 1 \ 0 end{array}right) + b_1 left(begin{array}{c} 0 \ 1 \ 1 end{array}right)+ b_2 left(begin{array}{c} 1 \ 1 \ 1 end{array}right)+ b_3 left(begin{array}{c} 1 \ 0 \ 1 end{array}right)+ b_4 left(begin{array}{c} 1 \ 0 \ 0 end{array}right)+b_5 left(begin{array}{c} 0 \ 1 \ 0 end{array}right)+
b_6 left(begin{array}{c} 0 \ 0 \ 1 end{array}right)= left(begin{array}{c} 0 \ 0 \ 0 end{array}right) .
$$
Все столбцы в левой части равенства различны, поскольку они соответствуют различным элементам поля $ mathbf{GF}(8) $. Именно в этом моменте существенно проявляется свойство примитивности элемента поля $ mathfrak A $: множество $ {mathfrak A^j}_{j=0}^6 $ совпадает со множеством
$$ {a_2 mathfrak A^2+a_1 mathfrak A+a_0 mid {a_0,a_1,a_2} subset {0,1}, (a_0,a_1,a_2) ne (0,0,0) }
$$
различных ненулевых полиномов над $ mathbf{GF}(2) $ степеней $ le 2 $.
Аналогичное утверждение справедливо и в общем случае поля $ mathbf{GF}(2^m) $.
Переписав эти соотношения в матричной форме, мы получим равенство вида
$$ mathbf H cdot left(begin{array}{l} b_0\ b_1\ vdots \ b_{n-1}end{array}right) = mathbb O $$
и столбцы матрицы $ mathbf H_{Mtimes (2^M-1)} $ — это все ненулевые $ M_{} $-разрядные двоичные столбцы. Но тогда матрица $ mathbf H $ — с точностью до перестановки — является проверочной матрицей кода Хэмминга.
.
Источники
[1]. Питерсон У., Уэлдон Э. Коды, исправляющие ошибки. М.Мир. 1976.
Сразу хочу сказать, что здесь никакой воды про циклические коды исправляющие пакеты ошибок , и только нужная информация. Для того чтобы лучше понимать что такое
циклические коды исправляющие пакеты ошибок , настоятельно рекомендую прочитать все из категории Теория информации и кодирования.
Циклические коды, исправляющие пакеты ошибок.
В общем случае любой корректирующий код исправляющий t ошибок исправляет любую конфигурацию из t ошибок. Вместе с тем, если заранее известно, что ошибки расположены пакетом, то можно сконструировать коды более эффективно. Пакет ошибок описывается в виде e(x)=xi*b(x)(mod xn-1), где b(x) — многочлен, степень которого не выше чем t-1, xi — локатор пакета, i — номер разряда.
Синдромные многочлены S(x) для исправляющего пакеты ошибок ЦК должны быть различны для любого пакета длины не более t.
Пример: g(x)=x6+ x3+ x2+ x+1, n=15 и корректирует пакеты из трех и менее ошибок.
e(x)=xi,i=0,…,14
e(x)=xi(1+x)(mod x15-1)
e(x)=xi(1+x2)(mod x15-1)
e(x)=xi(1+x+x2)(mod x15-1)
Непосредственным вычислением проявляется, что синдромы для всех 56 возможных пакетов различны . Об этом говорит сайт https://intellect.icu . Следовательно, g(x)=x6+ x3+ x2+ x+1 порождает код, исправляющий все пакеты длины 3.
Как правило, ЦК, исправляющие пакеты ошибок синтезируются с помощью ЭВМ.
Статью про циклические коды исправляющие пакеты ошибок я написал специально для тебя. Если ты хотел бы внести свой вклад в развии теории и практики,
ты можешь написать коммент или статью отправив на мою почту в разделе контакты.
Этим ты поможешь другим читателям, ведь ты хочешь это сделать? Надеюсь, что теперь ты понял что такое циклические коды исправляющие пакеты ошибок
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Теория информации и кодирования
Из статьи мы узнали кратко, но емко про циклические коды исправляющие пакеты ошибок