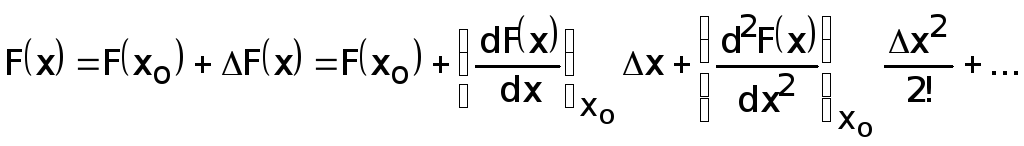Максимальная
динамическая ошибка
– наибольшее
отклонение регулируемой переменной от
заданного значения Узад:
.
(3.1)
В
устойчивой САР максимальным является
первое отклонение. Таким образом,
показатель
характеризует динамическую точность
регулирования [14].
Время
регулирования
tp
–промежуток времени от момента нанесения
возмущающего воздействия до момента,
начиная с которого отклонение регулируемой
переменной от установившегося значения
становится и остается меньше наперед
заданного значения ].
Остаточное
отклонение (остаточная неравномерность)
—
абсолютная статическая ошибка
регулирования, определяемая как разность
между установившимся значением
регулируемой величины и ее заданным
значением:
=Ууст
– Узад.
(3.2)
Показатель
характеризует точность регулирования
в статическом режиме [5].
Во
всех системах регулирования обязательно
имеется статическая ошибка. Ее можно
уменьшать путем увеличения общего
коэффициента усиления регулятора.
Однако она все равно остается, так как
увеличение коэффициента усиления
регулятора всегда ограничено.
Причиной
статической ошибки системы регулирования
является то, что в равновесном состоянии
регулятора положение регулирующего
органа жестко связано с величиной
регулируемой величины [6].
Система
регулирования, которая по принципу
своего действия обладает статической
ошибкой, называется статической
системой, а
регулятор в этом случае называется
статическим
регулятором.
Статический регулятор осуществляет
следующий закон регулирования:
y
= kрегх,
(3.3)
где
х
– отклонение регулируемой величины, у
– регулирующее воздействие регулятора
на объект.
Система
автоматического регулирования, не
обладающая статической ошибкой,
называется астатической
системой автоматического
регулирования,
а регулятор называется астатическим
регулятором [3].
3.2. Критерии устойчивости сар
Понятие
устойчивости САР связано с способностью
системы возвращаться в состояние
равновесия после исчезновения внешних
сил, которые вывели ее из этого состояния.
Устойчивость
систем автоматического управления
является одним из важнейших условий их
работоспособности, так как устойчивость
включает в себя требование затухания
переходных процессов во времени.
Очевидно, что система с расходящимся
процессом была бы неработоспособной.
Рассмотрим
дифференциальное уравнение движения
линеаризованной системы автоматического
регулирования, записанное для регулируемой
величины у(t)
при наличии управляющего воздействия
g(t)
и при равенстве нулю возмущающих
воздействий (см. формулу (2.4)):
.(3.4)
Процесс
регулирования определяется решением
дифференциального уравнения, как сумма
двух решений – частного решения
неоднородного уравнения (3.4)
с правой частью и общего решения уравнения
(3.4)
без правой части [1].
Характеристическое
уравнение САР имеет вид:
.
(3.5)
Корни
характеристического уравнения (3.5)
определяются только видом левой части
уравнения (3.4).
Постоянные интегрирования определяются
также и видом правой части. Поэтому
быстрота затухания и форма переходного
процесса определяются как левой, так и
правой частями исходного дифференциального
уравнения. Однако поскольку в понятие
устойчивости входит только факт наличия
или отсутствия затухания переходного
процесса (независимо от быстроты
затухания и формы переходного процесса),
то устойчивость линейной системы не
зависит от вида правой части
дифференциального уравнения (3.4)
и определяется только характеристическим
уравнением (3.5)
[13].
Так
как получающаяся при решении линейного
дифференциального уравнения (3.4) формула
переходного процесса содержит составляющие
в виде экспонент от вещественных частей
корней характеристического уравнения
САР (3.5) (см. главу 2), то для того, чтобы
САР была устойчивой и переходный процесс
затухал, необходимо, чтобы вещественные
части корней были отрицательными.
Следовательно,
для устойчивости линейной САР необходимо,
чтобы все корни лежали слева от мнимой
оси, в левой полуплоскости комплексных
чисел. Если хотя бы один корень окажется
справа от мнимой оси, то система будет
неустойчивой. Система будет находиться
на границе устойчивости при наличии:
нулевого корня
();
пары чисто мнимых корней
;
бесконечного корня
().
Во всех трех случаях предполагается,
что все остальные корни имеют отрицательные
вещественные части.
Необходимым
(но не достаточным) условием устойчивости
САР является положительность всех
коэффициентов характеристического
уравнения [7]. Это означает, что система
является неустойчивой, если хотя бы
один из коэффициентов характеристического
уравнения отрицателен. Если все
коэффициенты характеристического
уравнения положительны, то требуются
дополнительные исследования САР на
устойчивость с помощью критериев
устойчивости Гурвица, Михайлова или
Найквиста [3].
В
программе «SAU»
для определения устойчивости САР
используется критерий устойчивости
Гурвица, как наиболее удобный с точки
зрения компьютерной реализации. В методе
Гурвица для характеристического
уравнения (3.5) составляется квадратная
матрица коэффициентов, содержащая n
строк и n
столбцов:

(3.6)
Критерий
устойчивости сводится к тому, что при
а0>0
должны быть больше нуля все n
определителей Гурвица, получаемых из
квадратной матрицы коэффициентов.
Определители
Гурвица составляются по следующему
правилу:
;
;
(3.7)
Последний
определитель включает в себя всю матрицу.
Но так как в последнем столбце матрицы
все элементы, кроме нижнего, равны нулю,
то последний определитель Гурвица
выражается через предпоследний следующим
образом:
.
(3.8)
Однако
в устойчивой системе предпоследний
определитель тоже должен быть
положительным. Поэтому условие
положительности последнего определителя
сводится к условию
,
т.е. к положительности свободного члена
характеристического уравнения [1].
Условия
нахождения системы на границе устойчивости
можно получить, приравнивая к нулю
последний определитель ()
при положительности всех остальных
определителей. Как следует из (3.8),
это условие распадается на два условия:
и
.
Первое
условие соответствует границе устойчивости
первого типа (апериодическая граница
устойчивости), а второе – границе
устойчивости второго типа (колебательная
граница устойчивости).
Для
уравнения второго порядка необходимым
и достаточным условием устойчивости
является положительность всех
коэффициентов характеристического
уравнения. Для уравнений более высокого
порядка необходимо исследование с
помощью составления определителей
Гурвица и проверки их на положительность.
Существенным
недостатком критерия Гурвица является
то, что для уравнений высоких порядков
в лучшем случае можно получить ответ о
том, устойчива или неустойчива система
автоматического регулирования. При
этом в случае неустойчивой системы
критерий не дает ответа на то, каким
образом надо изменять параметры системы,
чтобы сделать ее устойчивой. Это
обстоятельство привело к поискам других
критериев, которые более удобны в
инженерной практике.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
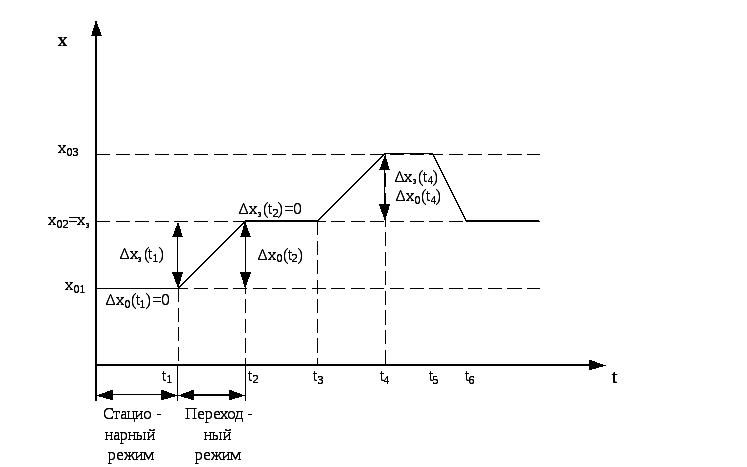
Действительные
значения регулируемой величины в
реальных САР отличаются от предписанных.
Разность между предписанным и
действительным значениями регулируемой
величины называется ошибкой
регулирования.
∆xз(t)
= xз
– x(t)
– ошибка регулирования
хз
– предписанное (заданное) значение
управляемой величины;
x(t)
– ее текущее значение
В
процессе функционирования САР может
переходить от одного состояния,
принимаемого за исходное, в другое.
Разность между текущими значениями
регулируемой величины и значением,
соответствующим исходному состоянию,
принято называть отклонением регулируемой
величины
∆x0(t)
= x(t)
– x0(t) (1.3)
где
xo
– значение регулируемой величины в
исходном состоянии.
x0(t)
– исходное значение регулируемой
величины.
|
|
|
Рис. |
1.4. Статическое и астатическое регулирование
В
зависимости от того, является или нет
ошибка регулирования функцией возмущающего
воздействия в установившемся режиме,
различают статическое
и астатическое
регулирование.
При
статическом регулировании ошибка
регулирования возрастает с увеличением
значения возмущающего воздействия.
Пример статического регулирования
приведен на рис. 1.4, а).
|
|
|
а) |
|
|
|
б) |
|
|
|
в) |
|
Рис. |
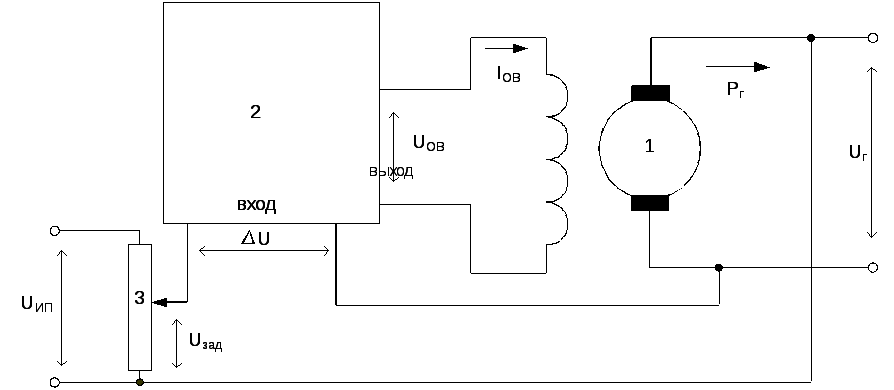
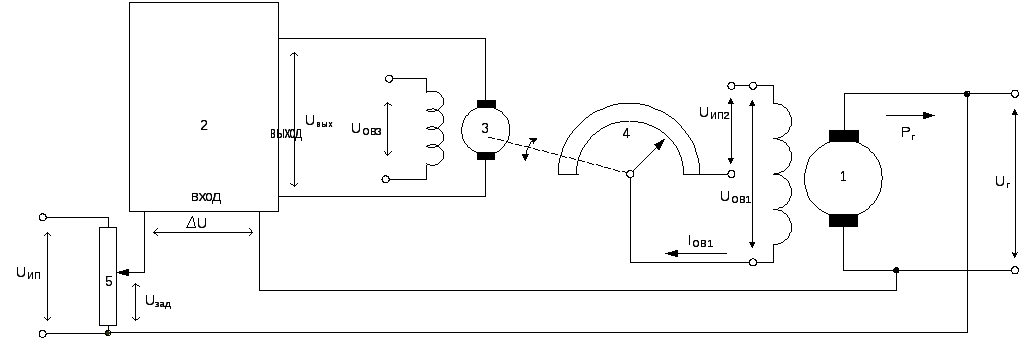
Принцип
действия этого регулятора достаточно
ясно виден из рассмотрения схемы и
особых пояснений не требует. Заметим
лишь, что требуемого возбуждение
генератора 1 осуществляется путем
изменения входного сигнала (ΔU)
электронного усилителя 2. В свою очередь
этот сигнал пропорционален отклонению
регулируемого параметра Uг
от заданного значения Uзад
(ΔU=Uг–Uзад).
Поэтому такое отклонение, т.е. наличие
ΔU,
является неизбежным и должно быть тем
больше, чем больше изменяется величина
внешнего возмущения Pг.
Очевидно, что это отклонение регулируемого
параметра от заданного значения
сохраняется также и в установившемся
режиме.
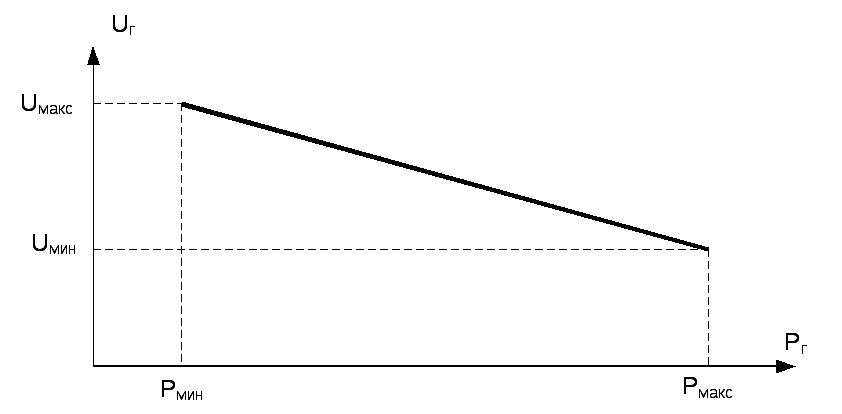
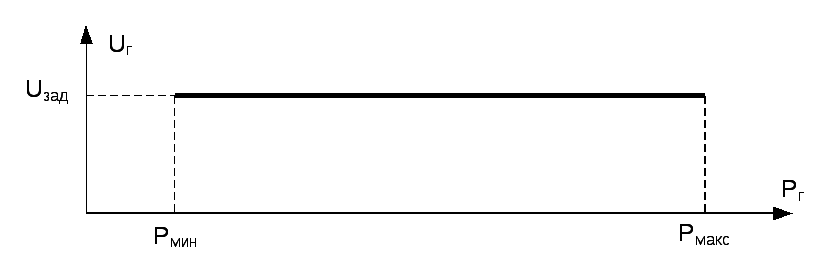
Рабочая
характеристика (зависимость напряжения
генератора от нагрузки – активной
мощности Pг)
статического регулятора приведена на
рис. 1.4, б).
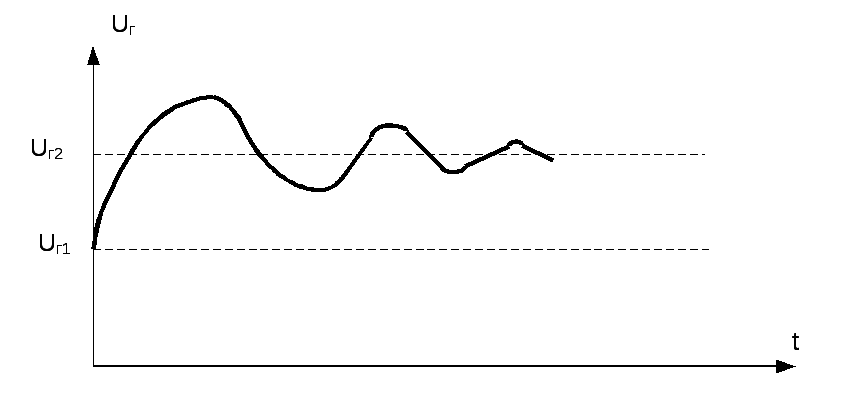
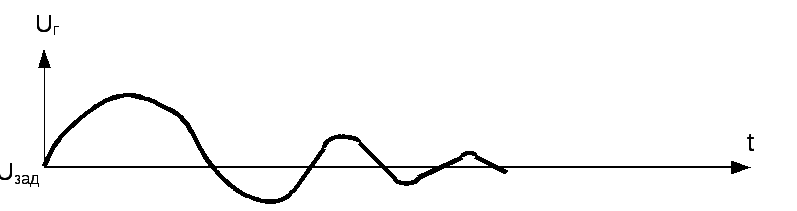
На
рис. 1.4, в)
показан переходный процесс в системе
при уменьшении нагрузки генератора.
Регулированием
с астатической
характеристикой
называется такое регулирование, при
котором в установившемся состоянии
системы отклонение регулируемого
параметра от заданного значения равно
нулю при любой величине внешнего
возмущения. Равновесие системы имеет
место всегда при заданном значении
регулируемого параметра.
Пример
астатического регулирования приведен
на рис. 1.5, а).
|
|
|
а) |
|
|
|
б) |
|
|
|
в) |
|
Рис. |
Характеристика
астатического регулятора приведена на
рис. 1.5, б),
а кривая переходного процесса – на рис.
1.5, в).
При
увеличении нагрузки на генераторе, т.е.
увеличении активной мощности генератора
Pг,
уменьшается напряжение на его выводах
Uг,
что приводит к появлению отклонения
регулируемого параметра Uг
от заданного значения Uзад
(ΔU=Uг–Uзад).
Параметр Uзад
задается
регулировочным реостатом 5. При этом
появляется напряжение на якоре двигателя
постоянного тока Uвых,
и двигатель начинает перемещать контакт
регулировочного реостата 4 по часовой
стрелке, что приводит к увеличению тока
возбуждения генератора IОВ1,
а значит, и напряжения на его выводах
Uг.
Параметр Uг
будет увеличиваться до тех пор, пока
ошибка регулирования ΔU
не станет равной 0.
Астатические
САР обеспечивают высокую точность
регулирования. Однако по сравнению со
статическими они являются более сложными
и инерционными, т.е. процессы регулирования
в них являются замедленными.
1.5.
Линейные и нелинейные системы. Линеаризация
уравнений
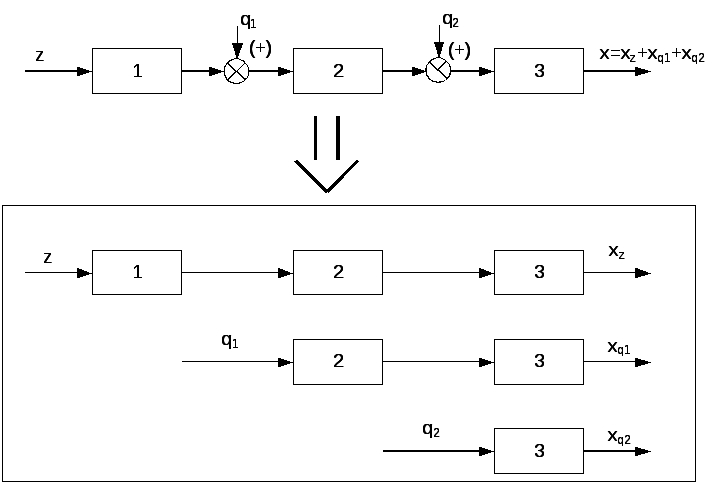
Системы,
процессы в которых могут быть описаны
линейными дифференциальными уравнениями
с постоянными коэффициентами, называются
линейными.
Для линейных систем применим принцип
суперпозиции, позволяющий рассматривать
независимое прохождение воздействий,
что дает существенное упрощение (рис.
1.6).
|
|
|
Рис. |
Нелинейной
называется система, для описания
процессов в которой приходится применять
одно или несколько нелинейных уравнений.
К нелинейным относятся уравнения,
коэффициенты которых зависят от значений
переменных величин или их производных,
а также уравнения, содержащие произведения
или степени (выше первой) этих величин.
Строго
говоря, линейных САУ в технике практически
нет или очень мало. Однако большинство
систем при определенных условиях могут
рассматриваться как линейные. Так, если
оценивать поведение системы при малых
отклонениях величин от исходных значений,
то в большинстве случаев имеющей место
нелинейностью можно пренебречь. Такая
возможность имеет математическое
обоснование.
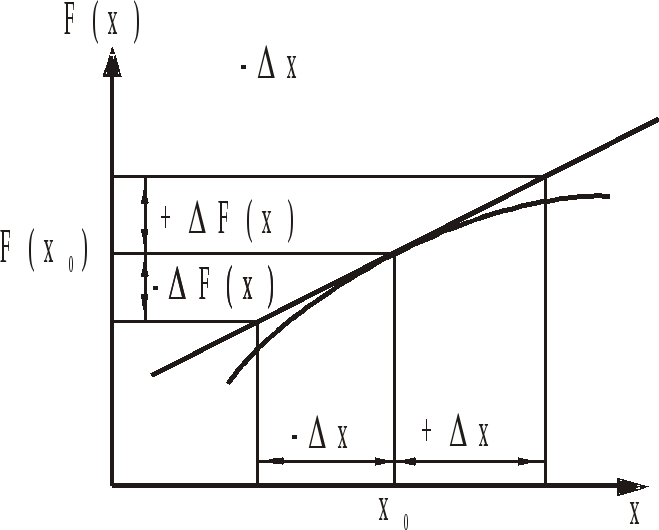
Пусть
имеем некоторую непрерывную функцию
F(x)
(рис. 1.7).
Если
аргумент X
получил приращение ΔX
от исходного значения Xo,
то функция получит приращение ΔF(X).
Новое значение функции F(X)
можно разложить в ряд Тейлора:
Рис.
1.7. Пример линеаризации нелинейной
функции
При
малых значениях Δx
можно ограничиться только первыми двумя
членами разложения, т.к. остальные имеют
более высокий порядок малости, т.е. можно
считать
,
где
.
Теоретически
это означает, что на интервале ±Δx
(рис. 1.6) кривая F(x)
заменяется прямой линией, являющейся
касательной при x=xo.
Таким
образом, если составлять уравнение
системы не для полных значений величин,
а только для отклонений, то эти уравнения
будут линейными. Такая операция называется
линеаризацией
уравнений.
Следует, однако, отметить, что это
справедливо только для тех случаев,
когда нелинейные функции являются
непрерывными и имеют непрерывные
производные при x=xo.
Пример
линеаризации нелинейного элемента
системы.
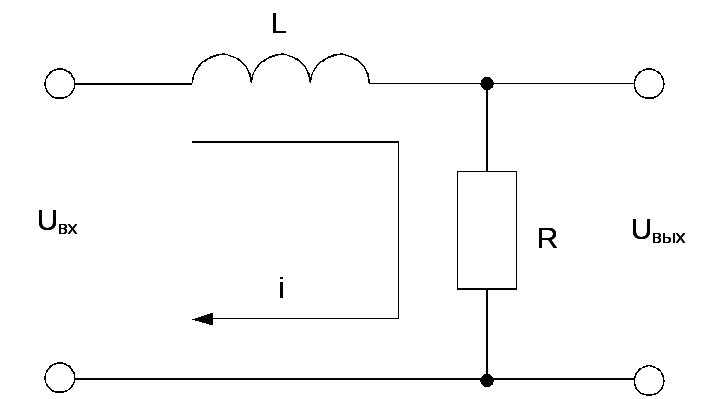
В
качестве типового элемента, уравнение
которого подлежит линеаризации, возьмем
RL-элемент,
часто встречающийся в электрических
системах регулирования и изображенный
на рис. 1.8, а). Пусть входной и выходной
величинами такого элемента являются
напряжения.
|
|
|
|
а) |
б) |
|
Рис. |
Предположим
сначала, что активные сопротивления и
индуктивность не зависят от протекающего
через них тока, т.е. будем считать, что
элемент является линейным.
Тогда
дифференциальное уравнение элемента
в случае, если потокосцепление
катушки
элементазависит от тока линейно, т.е.
если индуктивность L=/i
не зависит от тока и является величиной
постоянной, имеет вид:
Обозначив
и
,
учитывая, что
,
и пользуясь операторной (символической)
формой записи, в которой принято
,
получим:
|
|
(1.3) |
Предположим
теперь, что в рассматриваемом примере
индуктивность зависит от тока и,
следовательно, элемент является
нелинейным. Тогда уравнение (1.3) для
такого элемента неправомерно, ибо
потокосцепление
зависит от тока нелинейно и, следовательно,
L=/i
есть величина переменная. Для
усатновившегося режима элемента при
входном постоянном напряжении uвх
потокосцепление 0
тоже постоянно во времени и, следовательно,
.
Тогда можно написать:
.
Изменение
входного напряжения повлечет за собой
изменение тока и выходного напряжения.
Текущие
значения uвх
и uвых
и i
можно представить так:
;
;
,
где
Δuвх,
Δuвых
и Δi
– отклонения
соответствующих величин от их
установившихся значений.
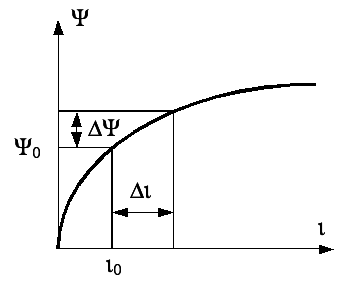
Пусть
потокосцепление является нелинейной
функцией тока, как это показано на рис.
1.8, б).
Эту функцию можно разложить в ряд:
|
|
(1.4) |
При
достаточно малых отклонения тока можно
ограничиться первыми двумя членами
ряда. Величина
определяется тангенсом угла наклона
касательной к кривой, приведенной на
рис. 1.8,б), в
точке с абсциссой i0.
Обозначив
динамическую индуктивность элемента
для тока i0
через Lд,
т. е.
,
можем написать:
.
Так
как
,
то будем иметь:
.
Исходное
уравнение запишется теперь так:
,
или,
подставляя ранее найденное выражение
для uвых0,
получим:
.
Последнее
выражение является линейным дифференциальным
уравнением с постоянными коэффициентами,
которое можно записать в операторной
форме так:
|
|
(1.5) |
где
и k=1.
Оно
справедливо только для малых отклонений
входной и выходной величины относительно
начального значения uвх0.
Глава 8. Типовые законы регулирования. Одноконтурные САР
8.1. Основные типы автоматических регуляторов
Регулятор на основе усилительного звена называется П-регулятором (пропорциональный). Его положительной характеристикой является высокое быстродействие: при отклонении регулируемой величины от заданного значения регулятор выдает регулирующее воздействие, пропорциональное величине отклонения x, что обеспечивает быструю компенсацию возмущения. Существенным недостатком П-регулятора является наличие статической ошибки в переходном процессе АСР с П-регулятором (рис. 37). Статическая ошибка возникает потому, что у П-регулятора между регулируемой величиной x и регулирующим воздействием xр существует зависимость, однозначно определяемая коэффициентом K. Поэтому генерировать регулирующее воздействие xр для компенсации возмущения xв П-регулятор может только путем изменения регулируемой величины x, что и создает статическую ошибку.
Регулятор на основе интегрирующего звена (48) называется И‑регулятором:
Если xвых усилительного звена (П-регулятор) однозначно определяется величиной правой части уравнения, что является причиной возникновения статической погрешности в АСР с П-регулятором, то правая часть уравнения (48) интегрирующего звена (И-регулятор) определяет не величину, а скорость изменения xвых. Величина xвых будет изменяться до тех пор, пока правая часть уравнения (48) не станет равна нулю, т. е. пока регулируемая величина x при наличии возмущения xв не вернется к заданному значению. Следовательно, в АСР с И-регулятором не возникает статическая погрешность.
Однако у И-регулятора имеется свой недостаток сравнительно с П-регулятором: в случае возникновения возмущения регулирующее воздействие П-регулятора меняется быстрее, чем у И-регулятора с его конечной скоростью, что замедляет процесс компенсации возмущения и ухудшает критерии качества регулирования (рис. 40).
Рис. 40. Переходные процессы в АСР с П- и И-регуляторами
Таким образом, П-регулятор обеспечивает высокое быстродействие (что уменьшает динамическую ошибку), но не может обеспечить при наличии возмущения заданное значение регулируемой величины (статическая ошибка). И-регулятор, наоборот, не создает статическую ошибку, но вследствие относительно медленного изменения xр имеет большую динамическую ошибку.
Сравнивая характеристики П- и И-регуляторов можно сделать вывод: если включить усилительное и интегрирующие звенья параллельно, то автоматический регулятор будет лишен указанных недостатков. Такой регулятор называется ПИ-регулятором (рис. 41).
Рис. 41. Принципиальная схема АСР с ПИ-регулятором
Действительно, быстродействие ПИ-регулятора обеспечивает усилительное звено, а статическую ошибку снимает интегрирующее звено. Для управления производственными процессами чаще всего используются ПИ-регуляторы.
Кривая разгона идеального ПИ-регулятора показана на рис. 42 .
Уравнение ПИ-регулятора при нулевых начальных условиях имеет вид:

Отношение коэффициентов Kp1/Kp определяет степень влияния интегрирующей части, и его обратная величина называется временем изодрома Tи.

Время изодрома – это время, в течение которого интегрирующее звено изменяет регулирующее воздействие xр ПИ-регулятора на величину Dxр, равную предварительному изменению Dxр усилительного звена (рис. 42). Поэтому иногда время изодрома называют временем удвоения.
Рис. 42. График кривой разгона идеального ПИ-регулятора:
а – скачкообразное изменение входного воздействия x;
б – реакция (кривая разгона) ПИ-регулятора xр
Уравнение ПИ-регулятора можно записать как
откуда передаточная функция
Амплитудно-фазовая характеристика:

В том случае, если рассмотренные регуляторы не обеспечивают требуемое качество регулирования, необходимо увеличить интенсивность процесса компенсации возмущения. Этого можно достигнуть увеличением регулирующего воздействия, которое в свою очередь определяется коэффициентом усиления автоматического регулятора Kp
. Однако ниже будет показано, что увеличение коэффициента усиления регулятора в АСР приводит к тому, что в системе начинают генерироваться незатухающие колебания.
В связи с этим представляет интерес рассмотреть алгоритм, который реализует дифференцирующее звено.
Входной величиной любого регулятора является кривая разгона регулируемой величины (рис. 27), которая определяется величиной возмущения и передаточной функцией объекта регулирования (9). В свою очередь, регулирующее воздействие xp (рис. 27) определяется кривой разгона x и передаточной функцией регулятора.
На рис. 43 показана реакция дифференцирующего звена (Д‑регулятора) на входное воздействие в виде кривой разгона в соответствии с уравнением (51).
Рис. 43. Реакция дифференцирующего звена на кривую разгона
а –изменение входного воздействия x в виде кривой разгона;
б – реакция xр дифференцирующего звена
Из рис. 43,а следует, что дифференцирующее звено обеспечивает большее регулирующее воздействие в начале переходного процесса. Это означает, что дифференцирующий регулятор активно компенсирует возмущение и исключает возникновение незатухающих колебаний.
Если включить дифференцирующее звено параллельно ПИ‑регулятору (рис. 44), то получим ПИД-регулятор, обеспечивающий интенсивную компенсацию возмущений. При этом недостаток дифференцирующего звена (при Хвх = const, Хвых = 0 ) компенсируется усилительным и интегрирующим звеньями.
Рис. 44. Принципиальная схема АСР с ПИД-регулятором
На рис. 45 показана кривая разгона ПИД-регулятора.
Рис. 45. Кривая разгона ПИД-регулятора
На рис. 46 показаны переходные процессы на с различными регуляторами. ПИД-регулятор уменьшает динамическую ошибку сравнительно с ПИ-регулятором на 25–30%. Также можно объединить дифференцирующее звено с усилительным звеном и улучшить показатели П-регулятора, получив ПД-регулятор.

Все пять типов рассмотренных автоматических регуляторов имеют общую особенность своего функционирования – обеспечивают стабилизацию регулируемой величины после окончания переходного процесса.
8.2. Критерии качества регулирования
Качество процесса регулирования в АСР характеризуют следующие показатели (критерии) (рис. 16):
Рис. 16. Показатели качества регулирования:
1 – переходной процесс без статической ошибки;
2 – переходной процесс со статической ошибкой
1. Максимальное отклонение в процессе регулирования от заданного значения (динамическая ошибка) ΔХдин.
2. Статическая ошибка ΔХст — возможные отклонения от заданного значения по окончании переходного процесса при использовании некоторых типов регуляторов (подробнее такие АСР рассмотрены ниже).
3. Длительность переходного процесса Тр – период времени с момента начала отклонения регулируемого параметра от задания до возвращения его к заданному значению с определенной степенью точности регулирования ±Δ.
Например, если ±Δ=±25%, это означает, что для заданного значения температуры в 100 °С процесс регулирования будет завершен при достижении диапазона (100 ± 2,5) °С.
4. Степень затухания показывает характер затухания переходного процесса регулирования:
Для того, чтобы переходный процесс затухал за 2 ¸ 3 периода колебаний, степень затухания должна быть равна

5. Степень колебательности процесса m определяет характер колебательности процесса и равна отношению действительной части корня характеристического уравнения к коэффициенту при его мнимой части. Степень колебательности связана со степенью затухания следующим соотношением:
6. Интегральный квадратичный критерий – критерий, определяющий площадь под кривой переходного процесса, возведенной в квадрат (рис. 17):
Уменьшение интегрального критерия соответствует ускорению процесса регулирования.
Рис. 17. Интегральный квадратичный критерий качества регулирования
Однако все приведенные шесть критериев качества не определяют величину потерь производства при отклонениях регулируемой величины от оптимального значения в переходных процессах регулирования. Для определения таких потерь можно использовать экономический критерий.
7. Экономический критерий рассмотрим на примере, регулирования температуры химического реактора θ, когда степень превращения Q в реакторе определяется температурой (рис. 18а).
Разделим переходной процесс на равные интервалы времени Δt и запишем значения θ
в этих точках по графику (18, б). На графике (18, а) для этих температур определим уменьшение степени превращения вследствие отклонения от оптимального режима, а затем сделаем расчет потерь исходных продуктов для каждого интервала Δθ, суммируем эти потери для всего переходного процесса и представим потери в денежном выражении.
Рис. 18. Экономический критерий качества регулирования:
а – зависимость степени превращения Q от температуры θ;
б – переходный процесс регулирования температуры
Совместно со специалистом по технологии или по его заданию необходимо определить, какой из указанных критериев для рассматриваемой АСР является превалирующим, и задать максимально допустимую величину этого критерия, т. е. определить, какое качество регулирования должна обеспечить проектируемая АСР.
8.3. Выбор закона регулирования
При выборе регулятора следует определиться с группой регулирующих устройств – непрерывного, релейного или импульсного действия. Такой выбор ориентировочно может быть сделан по величине отношения запаздывания к постоянной времени объекта τ/Tоб:
· при отношении τ/Tоб меньше 0.2 целесообразно использовать регулятор релейного действия;
· если отношение τ/Tоб от 0.2 до 1.0, то нужно использовать регулятор непрерывного действия;
· при отношении τ/Tоб больше единицы можно использовать регулятор импульсного действия, или специальные регуляторы, например, регулятор («предиктор») Смита.
Затем необходимо определиться с типом регулятора, т.е. выбрать определенный закон регулирования: П-, И-, ПИ-, ПД- или ПИД-закон
8.4. Методы расчета одноконтурных САР
Как указывалось выше, качество автоматического регулирования определяется свойствами системы в целом, т. е. суммарными свойствами объекта и регулятора. Поскольку объект обычно является неизменяемой частью системы, то обеспечить определенные свойства системы, а следовательно и заданное качество регулирования, можно соответствующим подбором свойств автоматического регулятора, что зависит от параметров его настройки. В свою очередь, параметры настройки являются коэффициентами передачи в уравнении автоматического регулятора.
Таким образом, параметры настройки автоматического регулятора определяются свойствами объекта регулирования, т. е. величинами τоб, Тоб, Коб.
8.4.1. Расчет по «приближенным» формулам
Приближенные формулы для расчета параметров настройки автоматических регуляторов (Kр – коэффициент усиления; Tи – время изодрома; Тд – время дифференцирования) сведены в следующую таблицу:
Таблица 8.1. Формулы для приближенного расчета
параметров настройки регуляторов

Формулы сгруппированы в столбцы в зависимости от характера переходного процесса, который желательно получить, используя рассчитанный таким образом регулятор: апериодический или с перерегулированием в 20 %. В формулы входят следующие свойства объекта регулирования: Коб – коэффициент усиления; Тоб – постоянная времени; τоб – время запаздывания (полного).
Рис. 53. Кривые разгона:
1 – фактическая кривая разгона промышленного объекта;
2 – аппроксимированная (приближенная) кривая разгона
Необходимо отметить, что для пневматических регуляторов требуется определять не Kp, а диапазон дросселирования:
Рассмотрим методику более точного определения параметров настройки на примере расчета наиболее «популярного» регулятора – ПИ-регулятора.
8.4.2. Метод незатухающих колебаний
(метод Циглера-Никольса)
При использовании метода незатухающих колебаний [6], который иногда также называется по именам авторов методом Циглера-Никольса, поиск оптимальных параметров настройки осуществляется по величине критического коэффициента усиления П-регулятора и величине периода автоколебательного процесса.
Рис. 54. К поиску параметров настройки методом Циглера-Никольса
Расчет параметров настройки регуляторов проводится в два этапа.
1. На исследуемом объекте устанавливается П-регулятор и, последовательно увеличивая коэффициент усиления (уменьшая диапазон дросселирования), АСР выводится в режим незатухающих колебаний (автоколебаний на границе устойчивости). При этом фиксируется величина коэффициента усиления П-регулятора Ккрр и период незатухающих автоколебаний Т (рис. 54).
2. На втором этапе по величинам Кркр и Т определяются параметры настройки П-, ПИ- и ПИД-регуляторов:
Метод незатухающих колебаний не требует сложных вычислений, но имеет свои характерные недостатки:
· получить Кркр и Т можно только на действующем объекте, оснащенном АСР с П-регулятором;
· не все объекты химической технологии допускают режим автоколебаний;
· практически трудно уловить момент начала автоколебаний.
Данные недостатки имеют место лишь при настройке регулятора методом Циглера-Никольса непосредственно на действующем объекте. Если заменить реальный объект его математической моделью, данный метод лишается указанных недостатков, кроме того, моделирование позволяет на порядок ускорить процесс поиска параметров настройки. Но для выполнения моделирования требуется достаточно точное математическое описание объекта регулирования, а получить его удается не всегда.
8.4.3. Метод расширенных частотных характеристик
Уравнение ПИ-регулятора (65) или (66):
Передаточная функция ПИ-регулятора:

Знак «минус» указывает, что действие регулятора направлено против возмущения.
Из передаточной функции получаем амплитудно-фазовую характеристику ПИ-регулятора путем замены p на iw:

Так как по формуле Эйлера


с затуханием за три периода
Заменив iw на комплексную переменную (-mw+iw), получаем расширенную амплитудно-фазовую характеристику (РАФХ)Ю

Расширенными такие характеристики называются потому, что они как бы «расширены» по отношению к обычной АФХ (рис. 56).
Предположим, что объект регулирования имеет передаточную функцию второго порядка следующего вида:

Для дальнейшего математического моделирования АСР передаточную функцию необходимо преобразовать:

Рис. 56. АФХ объекта регулирования с самовыравниванием:
1 – обычная; 2 – расширенная
Расширенная амплитудно-фазовая характеристика объекта регулирования при замене p на (-mw+iw) будет иметь вид:



Где Rоб(m,w) -расширенная амплитудно-частотная характеристика объекта; Fоб(m,w) -расширенная фазочастотная харктеристика объекта. Величина 40w в выражении для Fоб (m,w) опеделяет угол в радианах и для пересчета в градусы неоходимо 40w умножить на 57,3
Условием нахождения замкнутой АСР на границе устойчивости является уравнение:

Аналогично, исходным уравнением для получения заданной степени колебательности m, а следовательно, определенной степени затухания y, является соотношение:
Это соотношение двух комплексных чисел возможно в том случае, если произведение модулей РАФХ равно единице, а аргументы (фазы) равны между собой, т. е.

Решая эти уравнения относительно S0 и Kp, получаем:


Обычно принимают степень колебательности m = 0,221, что соответствует степени затухания ψ=0,75 и обеспечивает затухание процесса регулирования примерно за три периода. Тогда

Уравнения для определения параметров настройки ПИ-регулятора можно преобразовать:


Подставляя в приведенные уравнения численные значения частоты w от 0 до значения, когда S0 становится отрицательной величиной, строим на плоскости параметров настройки кривую равной степени колебательности


Пример кривых равной степени колебательности в плоскости параметров настройки ПИ-регулятора показан на рис. 57. Графики процессов регулирования с различными параметрами настройки ПИ-регулятора при m = 0,221 показаны на рис. 58. Все процессы регулирования, показанные на рис. 58, реализованы ПИ-регулятором с параметрами настройки, полученными по кривой равной степени колебательности в точках 1, 2, 3, 4 (рис. 57), и все имеют m = 0,221, т. е. затухают примерно за три периода, но обладают существенно различным характером.
В связи с этим возникает задача определения оптимальных параметров настройки на кривой равной степени колебательности.
Рис. 57. Кривые равной степени колебательности
В качестве критерия оптимальности выбираем продолжительность переходного процесса – время регулирования (т. е. быстродействие АСР) и отсутствие постоянной или врéменной статической ошибки. Это исключает из рассмотрения параметры настройки в точке 4 (параметры настройки П-регулятора) и в точке 3 (врéменная статическая ошибка) (рис. 58).
Рис. 58. Графики процессов регулирования для ПИ-регулятора
с различными параметрами настройки в точках 1, 2, 3 и 4
при степени колебательности m =0,221
Быстродействие автоматического регулятора прежде всего зависит от величины регулирующего воздействия, которое для ПИ-регулятора, как следует из уравнения (65), прямо пропорционально величине коэффициента усиления Kp и обратно пропорционально времени изодрома Tи. Расчеты показывают, что если двигаться по кривой равной степени колебательности вправо, то величина регулирующего воздействия при прочих равных условиях сначала возрастает и достигает максимального значения на кривой равной степени колебательности вблизи ее вершины, когда
а затем начинает уменьшаться в связи с резким увеличением Tи (рис. 57).
Рис. 59. Выбор оптимальных параметров настройки
Таким образом, оптимальные параметры настройки ПИ-регулятора находятся в точке 2 на кривой равной степени колебательности (рис. 59).
Источник
Плютто В. П., Дубровский И. И. Элементы теории управления химико-технологическими процессами и системами. Конспект лекций: Учеб. пособие – М.: РХТУ им. Д. И. Менделеева, 2003. – 127 с.