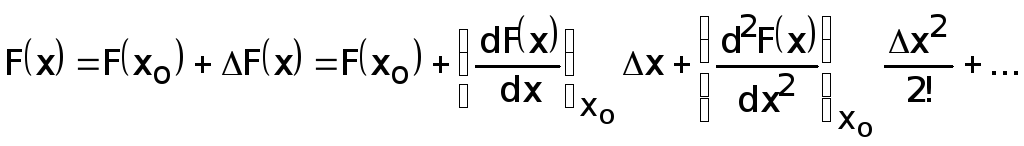Динамическая ошибка регулятора - Не ошибается лишь тот, кто ничего не делает!

Максимальная
динамическая ошибка

– наибольшее
отклонение регулируемой переменной от
заданного значения У_зад:

.
(3.1)

В
устойчивой САР максимальным является
первое отклонение. Таким образом,
показатель

характеризует динамическую точность
регулирования [14].

Время
регулирования
t_p
–промежуток времени от момента нанесения
возмущающего воздействия до момента,
начиная с которого отклонение регулируемой
переменной от установившегося значения
становится и остается меньше наперед
заданного значения ].

Остаточное
отклонение (остаточная неравномерность)
—
абсолютная статическая ошибка
регулирования, определяемая как разность
между установившимся значением
регулируемой величины и ее заданным
значением:

=У_уст
– У_зад.
(3.2)

Показатель

характеризует точность регулирования
в статическом режиме [5].

Во
всех системах регулирования обязательно
имеется статическая ошибка. Ее можно
уменьшать путем увеличения общего
коэффициента усиления регулятора.
Однако она все равно остается, так как
увеличение коэффициента усиления
регулятора всегда ограничено.

Причиной
статической ошибки системы регулирования
является то, что в равновесном состоянии
регулятора положение регулирующего
органа жестко связано с величиной
регулируемой величины [6].

Система
регулирования, которая по принципу
своего действия обладает статической
ошибкой, называется статической
системой, а
регулятор в этом случае называется
статическим
регулятором.
Статический регулятор осуществляет
следующий закон регулирования:

y
= k_регх,

(3.3)

где
х
– отклонение регулируемой величины, у
– регулирующее воздействие регулятора
на объект.

Система
автоматического регулирования, не
обладающая статической ошибкой,
называется астатической
системой автоматического
регулирования,
а регулятор называется астатическим
регулятором [3].

3.2. Критерии устойчивости сар

Понятие
устойчивости САР связано с способностью
системы возвращаться в состояние
равновесия после исчезновения внешних
сил, которые вывели ее из этого состояния.

Устойчивость
систем автоматического управления
является одним из важнейших условий их
работоспособности, так как устойчивость
включает в себя требование затухания
переходных процессов во времени.
Очевидно, что система с расходящимся
процессом была бы неработоспособной.

Рассмотрим
дифференциальное уравнение движения
линеаризованной системы автоматического
регулирования, записанное для регулируемой
величины у(t)
при наличии управляющего воздействия
g(t)
и при равенстве нулю возмущающих
воздействий (см. формулу (2.4)):

.(3.4)

Процесс
регулирования определяется решением
дифференциального уравнения, как сумма
двух решений – частного решения
неоднородного уравнения (3.4)
с правой частью и общего решения уравнения
(3.4)
без правой части [1].

Характеристическое
уравнение САР имеет вид:

.
(3.5)

Корни
характеристического уравнения (3.5)
определяются только видом левой части
уравнения (3.4).
Постоянные интегрирования определяются
также и видом правой части. Поэтому
быстрота затухания и форма переходного
процесса определяются как левой, так и
правой частями исходного дифференциального
уравнения. Однако поскольку в понятие
устойчивости входит только факт наличия
или отсутствия затухания переходного
процесса (независимо от быстроты
затухания и формы переходного процесса),
то устойчивость линейной системы не
зависит от вида правой части
дифференциального уравнения (3.4)
и определяется только характеристическим
уравнением (3.5)
[13].

Так
как получающаяся при решении линейного
дифференциального уравнения (3.4) формула
переходного процесса содержит составляющие
в виде экспонент от вещественных частей
корней характеристического уравнения
САР (3.5) (см. главу 2), то для того, чтобы
САР была устойчивой и переходный процесс
затухал, необходимо, чтобы вещественные
части корней были отрицательными.

Следовательно,
для устойчивости линейной САР необходимо,
чтобы все корни лежали слева от мнимой
оси, в левой полуплоскости комплексных
чисел. Если хотя бы один корень окажется
справа от мнимой оси, то система будет
неустойчивой. Система будет находиться
на границе устойчивости при наличии:
нулевого корня

();
пары чисто мнимых корней
;
бесконечного корня

().
Во всех трех случаях предполагается,
что все остальные корни имеют отрицательные
вещественные части.

Необходимым
(но не достаточным) условием устойчивости
САР является положительность всех
коэффициентов характеристического
уравнения [7]. Это означает, что система
является неустойчивой, если хотя бы
один из коэффициентов характеристического
уравнения отрицателен. Если все
коэффициенты характеристического
уравнения положительны, то требуются
дополнительные исследования САР на
устойчивость с помощью критериев
устойчивости Гурвица, Михайлова или
Найквиста [3].

В
программе «SAU»
для определения устойчивости САР
используется критерий устойчивости
Гурвица, как наиболее удобный с точки
зрения компьютерной реализации. В методе
Гурвица для характеристического
уравнения (3.5) составляется квадратная
матрица коэффициентов, содержащая n
строк и n
столбцов:

.
(3.6)

Критерий
устойчивости сводится к тому, что при
а₀>0
должны быть больше нуля все n
определителей Гурвица, получаемых из
квадратной матрицы коэффициентов.

Определители
Гурвица составляются по следующему
правилу:

;
;

(3.7)

Последний
определитель включает в себя всю матрицу.
Но так как в последнем столбце матрицы
все элементы, кроме нижнего, равны нулю,
то последний определитель Гурвица
выражается через предпоследний следующим
образом:

.
(3.8)

Однако
в устойчивой системе предпоследний
определитель тоже должен быть
положительным. Поэтому условие
положительности последнего определителя
сводится к условию
,
т.е. к положительности свободного члена
характеристического уравнения [1].

Условия
нахождения системы на границе устойчивости
можно получить, приравнивая к нулю
последний определитель ()
при положительности всех остальных
определителей. Как следует из (3.8),
это условие распадается на два условия:

и
.
Первое
условие соответствует границе устойчивости
первого типа (апериодическая граница
устойчивости), а второе – границе
устойчивости второго типа (колебательная
граница устойчивости).

Для
уравнения второго порядка необходимым
и достаточным условием устойчивости
является положительность всех
коэффициентов характеристического
уравнения. Для уравнений более высокого
порядка необходимо исследование с
помощью составления определителей
Гурвица и проверки их на положительность.

Существенным
недостатком критерия Гурвица является
то, что для уравнений высоких порядков
в лучшем случае можно получить ответ о
том, устойчива или неустойчива система
автоматического регулирования. При
этом в случае неустойчивой системы
критерий не дает ответа на то, каким
образом надо изменять параметры системы,
чтобы сделать ее устойчивой. Это
обстоятельство привело к поискам других
критериев, которые более удобны в
инженерной практике.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

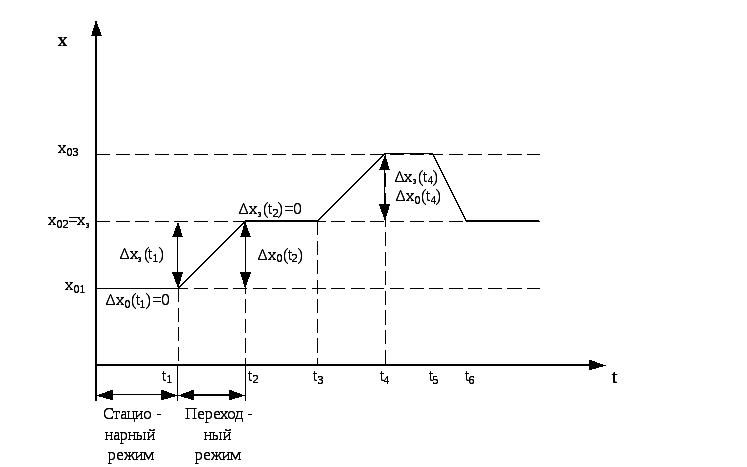
Действительные
значения регулируемой величины в
реальных САР отличаются от предписанных.
Разность между предписанным и
действительным значениями регулируемой
величины называется ошибкой
регулирования.

∆x_з(t)
= x_з
– x(t)
– ошибка регулирования

х_з
– предписанное (заданное) значение
управляемой величины;

x(t)
– ее текущее значение

В
процессе функционирования САР может
переходить от одного состояния,
принимаемого за исходное, в другое.
Разность между текущими значениями
регулируемой величины и значением,
соответствующим исходному состоянию,
принято называть отклонением регулируемой
величины

∆x₀(t)
= x(t)
– x₀(t) (1.3)

где
x_o
– значение регулируемой величины в
исходном состоянии.

x₀(t)
– исходное значение регулируемой
величины.

Рис.
1.3. Изменение значения регулируемой
величины в процессе регулирования

1.4. Статическое и астатическое регулирование

В
зависимости от того, является или нет
ошибка регулирования функцией возмущающего
воздействия в установившемся режиме,
различают статическое
и астатическое
регулирование.

При
статическом регулировании ошибка
регулирования возрастает с увеличением
значения возмущающего воздействия.
Пример статического регулирования
приведен на рис. 1.4, а).

а)

б)

в)

Рис.
1.4. Пример статического регулятора и
его характеристика (1 – генератор; 2 –
электронный усилитель, 3 – регулировочный
реостат, U_г
– напряжение генератора (регулируемый
параметр);U_зад
– задающее воздействие, которое равно
заданному (предписанному) значению
напряжения генератора; P_г
– активная мощность генератора
(возмущающее воздействие); U_ИП
– напряжение источника питания; U_ОВ
– напряжения обмотки возбуждения; ΔU
– входное напряжения электронного
усилителя)

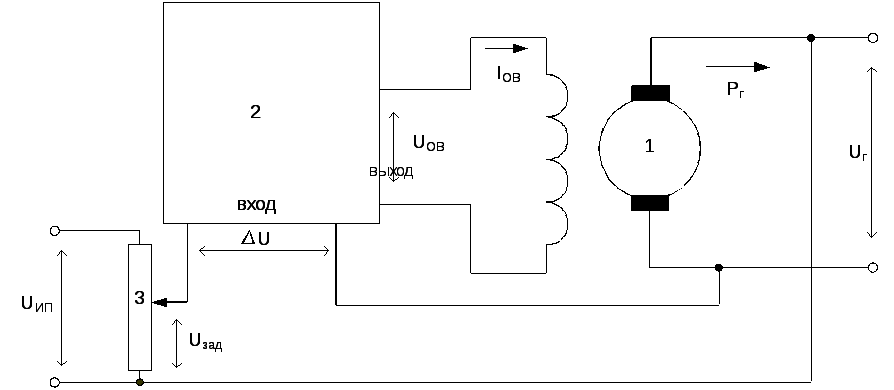
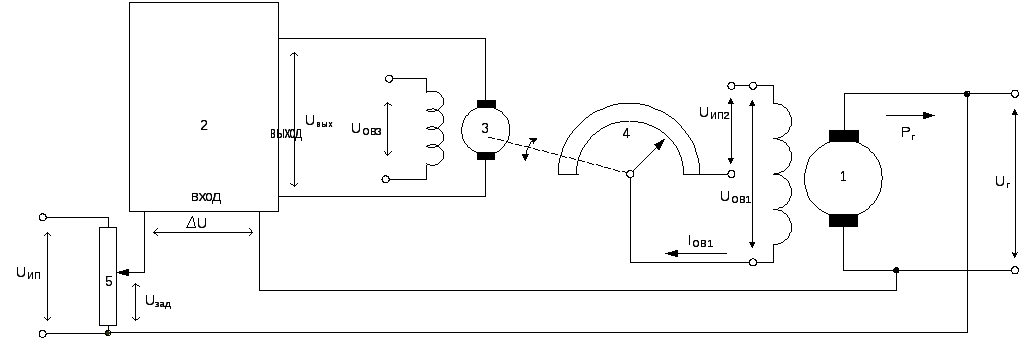
Принцип
действия этого регулятора достаточно
ясно виден из рассмотрения схемы и
особых пояснений не требует. Заметим
лишь, что требуемого возбуждение
генератора 1 осуществляется путем
изменения входного сигнала (ΔU)
электронного усилителя 2. В свою очередь
этот сигнал пропорционален отклонению
регулируемого параметра U_г
от заданного значения U_зад
(ΔU=U_г–U_зад).
Поэтому такое отклонение, т.е. наличие
ΔU,
является неизбежным и должно быть тем
больше, чем больше изменяется величина
внешнего возмущения P_г.
Очевидно, что это отклонение регулируемого
параметра от заданного значения
сохраняется также и в установившемся
режиме.

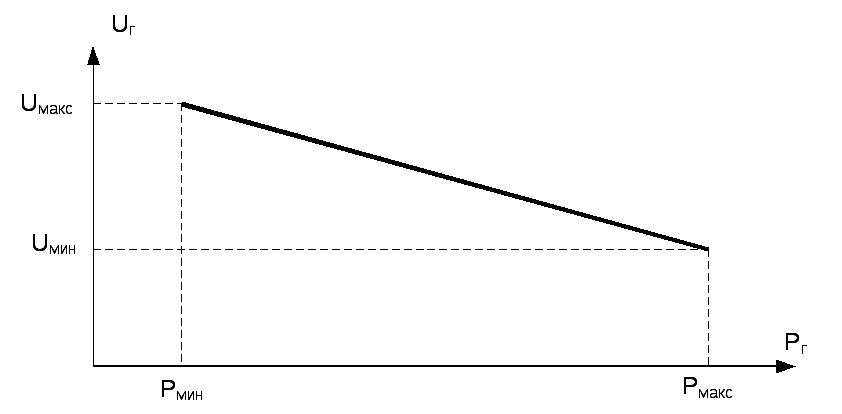
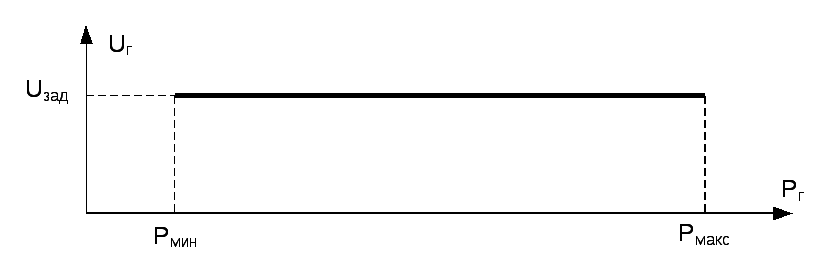
Рабочая
характеристика (зависимость напряжения
генератора от нагрузки – активной
мощности Pг)
статического регулятора приведена на
рис. 1.4, б).

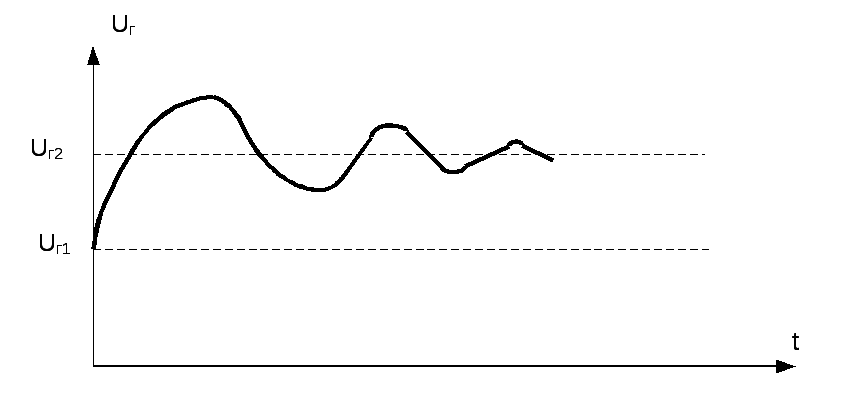
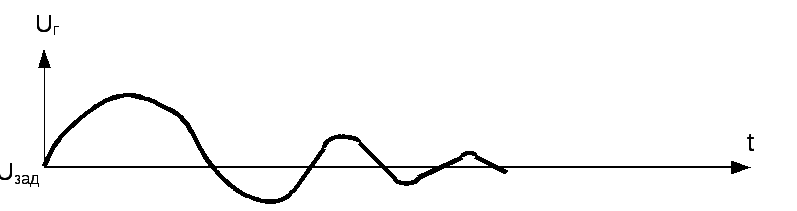
На
рис. 1.4, в)
показан переходный процесс в системе
при уменьшении нагрузки генератора.

Регулированием
с астатической
характеристикой
называется такое регулирование, при
котором в установившемся состоянии
системы отклонение регулируемого
параметра от заданного значения равно
нулю при любой величине внешнего
возмущения. Равновесие системы имеет
место всегда при заданном значении
регулируемого параметра.

Пример
астатического регулирования приведен
на рис. 1.5, а).

а)

б)

в)

Рис.
1.5. Пример астатического регулятора
и его характеристика (1 – генератор;
2 – электронный усилитель; 3 – якорь
двигателя постоянного тока; 4, 5 –
регулировочные реостаты, U_г
– напряжение генератора (регулируемый
параметр); U_зад
– задающее воздействие, которое равно
заданному (предписанному) значению
напряжения генератора; P_г
– активная мощность генератора
(возмущающее воздействие); U_ИП1,
U_ИП2
– напряжения источников питания №1
и №2; U_ОВ1и U_ОВ3
– напряжения обмоток возбуждений
генератора и двигателя; ΔU
– входное напряжения электронного
усилителя; U_вых
–напряжение на выходе электронного
усилителя)

Характеристика
астатического регулятора приведена на
рис. 1.5, б),
а кривая переходного процесса – на рис.
1.5, в).

При
увеличении нагрузки на генераторе, т.е.
увеличении активной мощности генератора
P_г,
уменьшается напряжение на его выводах
U_г,
что приводит к появлению отклонения
регулируемого параметра U_г
от заданного значения U_зад
(ΔU=U_г–U_зад).
Параметр U_задзадается
регулировочным реостатом 5. При этом
появляется напряжение на якоре двигателя
постоянного тока U_вых,
и двигатель начинает перемещать контакт
регулировочного реостата 4 по часовой
стрелке, что приводит к увеличению тока
возбуждения генератора I_ОВ1,
а значит, и напряжения на его выводах
U_г.
Параметр U_г
будет увеличиваться до тех пор, пока
ошибка регулирования ΔU
не станет равной 0.

Астатические
САР обеспечивают высокую точность
регулирования. Однако по сравнению со
статическими они являются более сложными
и инерционными, т.е. процессы регулирования
в них являются замедленными.

1.5.
Линейные и нелинейные системы. Линеаризация
уравнений

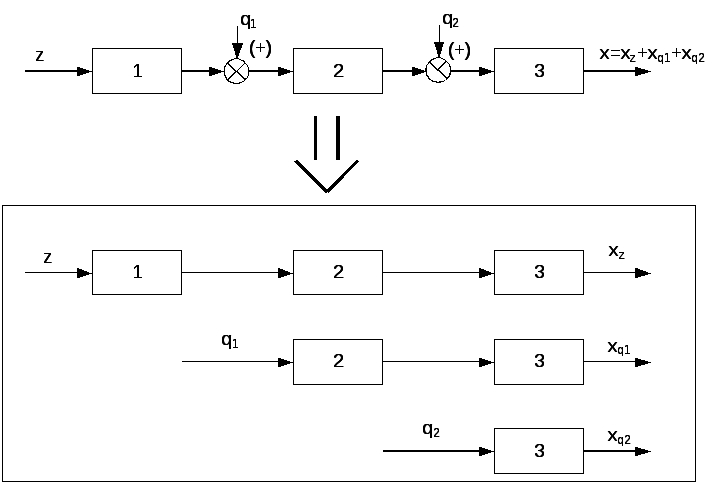
Системы,
процессы в которых могут быть описаны
линейными дифференциальными уравнениями
с постоянными коэффициентами, называются
линейными.
Для линейных систем применим принцип
суперпозиции, позволяющий рассматривать
независимое прохождение воздействий,
что дает существенное упрощение (рис.
1.6).

Рис.
1.6. Принцип суперпозиции

Нелинейной
называется система, для описания
процессов в которой приходится применять
одно или несколько нелинейных уравнений.
К нелинейным относятся уравнения,
коэффициенты которых зависят от значений
переменных величин или их производных,
а также уравнения, содержащие произведения
или степени (выше первой) этих величин.

Строго
говоря, линейных САУ в технике практически
нет или очень мало. Однако большинство
систем при определенных условиях могут
рассматриваться как линейные. Так, если
оценивать поведение системы при малых
отклонениях величин от исходных значений,
то в большинстве случаев имеющей место
нелинейностью можно пренебречь. Такая
возможность имеет математическое
обоснование.

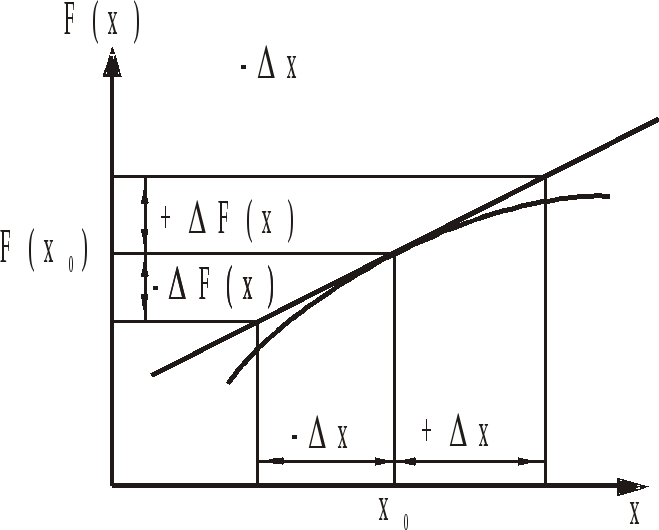
Пусть
имеем некоторую непрерывную функцию
F(x)
(рис. 1.7).

Если
аргумент X
получил приращение ΔX
от исходного значения X_o,
то функция получит приращение ΔF(X).
Новое значение функции F(X)
можно разложить в ряд Тейлора:

Рис.
1.7. Пример линеаризации нелинейной
функции

При
малых значениях Δx
можно ограничиться только первыми двумя
членами разложения, т.к. остальные имеют
более высокий порядок малости, т.е. можно
считать

где
.

Теоретически
это означает, что на интервале ±Δx
(рис. 1.6) кривая F(x)
заменяется прямой линией, являющейся
касательной при x=x_o.

Таким
образом, если составлять уравнение
системы не для полных значений величин,
а только для отклонений, то эти уравнения
будут линейными. Такая операция называется
линеаризацией
уравнений.
Следует, однако, отметить, что это
справедливо только для тех случаев,
когда нелинейные функции являются
непрерывными и имеют непрерывные
производные при x=x_o.

Пример
линеаризации нелинейного элемента
системы.

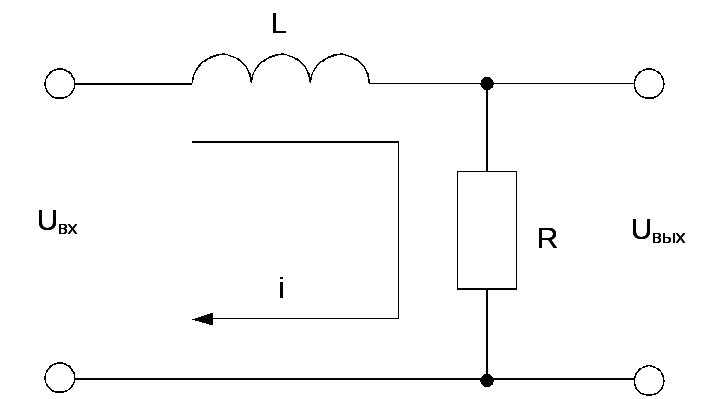
В
качестве типового элемента, уравнение
которого подлежит линеаризации, возьмем
RL-элемент,
часто встречающийся в электрических
системах регулирования и изображенный
на рис. 1.8, а). Пусть входной и выходной
величинами такого элемента являются
напряжения.


а)	б)
Рис. 1.8. Линеаризация нелинейного элемента системы

Предположим
сначала, что активные сопротивления и
индуктивность не зависят от протекающего
через них тока, т.е. будем считать, что
элемент является линейным.

Тогда
дифференциальное уравнение элемента
в случае, если потокосцепление 
катушки
элементазависит от тока линейно, т.е.
если индуктивность L=/i
не зависит от тока и является величиной
постоянной, имеет вид:

Обозначив

и
,
учитывая, что
,
и пользуясь операторной (символической)
формой записи, в которой принято
,
получим:

(1.3)

Предположим
теперь, что в рассматриваемом примере
индуктивность зависит от тока и,
следовательно, элемент является
нелинейным. Тогда уравнение (1.3) для
такого элемента неправомерно, ибо
потокосцепление 
зависит от тока нелинейно и, следовательно,
L=/i
есть величина переменная. Для
усатновившегося режима элемента при
входном постоянном напряжении u_вх
потокосцепление ₀
тоже постоянно во времени и, следовательно,
.
Тогда можно написать:

Изменение
входного напряжения повлечет за собой
изменение тока и выходного напряжения.

Текущие
значения u_вх
и u_вых
и i
можно представить так:

;

где
Δu_вх,
Δu_вых
и Δi
– отклонения
соответствующих величин от их
установившихся значений.

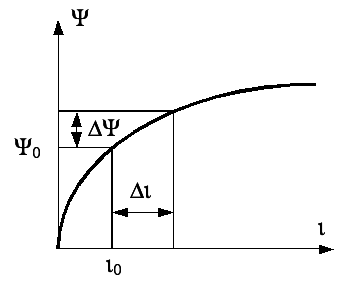
Пусть
потокосцепление является нелинейной
функцией тока, как это показано на рис.
1.8, б).
Эту функцию можно разложить в ряд:

(1.4)

При
достаточно малых отклонения тока можно
ограничиться первыми двумя членами
ряда. Величина

определяется тангенсом угла наклона
касательной к кривой, приведенной на
рис. 1.8,б), в
точке с абсциссой i₀.

Обозначив
динамическую индуктивность элемента
для тока i₀
через L_д,
т. е.
,
можем написать:

Так
как
,
то будем иметь:

Исходное
уравнение запишется теперь так:

или,
подставляя ранее найденное выражение
для u_вых0,
получим:

Последнее
выражение является линейным дифференциальным
уравнением с постоянными коэффициентами,
которое можно записать в операторной
форме так:

(1.5)

где

и k=1.

Оно
справедливо только для малых отклонений
входной и выходной величины относительно
начального значения u_вх0.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Часть 1. От практики к теории.

Часть 2. Реализация регулятора – от простого к настоящему.

Часть 3. Реализация регулятора – вот теперь регулятор.

Часть 4. Мир развивается, а «велосипед» остается.

Реализация регулятора в ПЛК

Лирика

Все, что будет написано ниже про реализацию ПИД-регулятора в ПЛК, не является чем-то новым и революционным. Практически всю эту информацию можно найти в документации на ПЛК серьезных производителей. Если вы инженер АСУТП со стажем и добросовестно изучали документацию на ПЛК, то все это вам известно. Но в текущей реалии есть каста молодых инженеров и студентов, которая все знания черпает из роликов на ютубе. Заставив себя посмотреть несколько самых популярных роликов про реализацию ПИД-регулятора, я был огорчен качеством излагаемого материала: объяснение работы ПИД-регулятора уж очень «колхозное», а реализация сводится к 15 строкам кода на С++, что порождает
упрощенное и ошибочное понимание предмета. Вот для касты ютуб специалистов в
первую очередь и предназначено это описание.

Теперь необходимо определиться с терминологией

Для более наглядного изложения перейдем от теоретического описания к «инженерному», которое используется в повседневной практике, пусть это и не совсем корректно, т.е. регулируем уровень в колонне посредством изменения положения регулирующего клапана:

ПИД – функция (функциональный или программный блок) реализующая алгоритм регулирования, включает три составляющих: П – пропорциональная составляющая, И – интегральная составляющая, Д – дифференциальная составляющая;
переменная процесса PV – значение текущего уровня, полученное с уровнемера, может измеряться как в инженерных единицах (мм), так и в относительных (%);
уставка SP (задание регулятору) – значение уровня, которое должен поддерживать регулятор в автоматическом режиме, единицы измерения как у PV;
выход регулятора OP – значение, которое формирует регулятор и которое определяет положение клапана, в нашем примере будет 0-100%;
E – ошибка или рассогласование, разница между уставкой и фактическим значением переменной процесса, ошибка подается на вход ПИД-функции;
tс – время цикла, периодичность с которой в ПЛК выполняется ПИД-функция (можно конечно поместить ПИД-функцию в циклическую задачу, и она будет выполняться каждый цикл ПЛК, но тогда время цикла предсказать невозможно и для расчета интегральной и дифференциальной составляющей определять время придется внутри ПИД-функции, проще всю ПИД-функцию выполнять периодически с фиксированным временем цикла);
прямое/обратное направление действия регулятора – режим формирования регулятором выходного значения, прямое действие — при увеличении значения переменной процесса PV регулятор увеличивает значение выхода OP, обратном действие — при увеличении значения переменной процесса PV регулятор уменьшает значение выхода OP.

Реализуется направление действия регулятора методом вычисления ошибки, для прямого действия E=PV-SP, для обратного E=SP-PV. На рисунке показаны два варианта установки клапана для регулирования уровня в емкости. Первый вариант – клапан LV1 установлен на отводящем трубопроводе, т.е при увеличении уровня (PV) клапан должен открываться, это прямое действие регулятора E=PV-SP. Второй вариант – клапан LV2 установлен на подающем трубопроводе, т.е. при повышении уровня клапан должен закрываться, это будет обратное действие регулятора E=SP-PV.

ПЛК является дискретным устройством, поэтому ПИД-функция выполняется периодически с заданным временем цикла tc и формула ПИД-регулятора трансформируется из непрерывной формы в дискретную:

OP – выход ПИД-функции, E – ошибка (рассогласование), n – текущий цикл, n-1 – предыдущий цикл, tc – время цикла ПИД-функции, kP,kI,kD – коэффициенты П,И,Д-составляющих. Для дискретной формы вместо времени используется номер отсчета (цикла). В таком виде ПИД-функция и реализуется в ПЛК.

Рассмотрим работу регулятора только с П-составляющей (пропорциональное регулирование) для исходного примера — поддержание уровня в емкости клапаном на отводящем трубопроводе. Регулятор получается прямого действия E=PV-SP. Время цикла для выполнения ПИД-функции примем 0,3 секунды, коэффициент kP=2, диапазон уровнемера 0-100%, диапазон открытия регулирующего клапана 0-100%, расход на отводящем трубопроводе линейно зависит от положения клапана, 10% открытия клапана соответствует расходу 10м3/час.

В начальный момент жидкость в емкости отсутствует (уровень равен нулю), расхода в подающем трубопроводе нет. В регуляторе задана уставка 30%. При таких условиях ошибка (рассогласование) на входе в П-функцию E=PV-SP=0-30=-30 (отрицательная). Выход П-функции OP=kP*E также получается отрицательным, но положение клапана не может быть меньше «0», поэтому клапан просто полностью закрыт.

Подаем жидкость в емкость с фиксированным расходом (условно 10м3/ч), емкость наполняется, значение уровня увеличивается, достигает значения уставки 30% и продолжает постепенно увеличивается. Ошибка E=PV-SP становится положительной и также увеличивается, соответственно значение выхода П-функции OP=kP*E становится положительным клапан начинает открываться. Чем выше уровень в емкости, тем больше значение ошибки на входе П-функции и больше открытие клапана. При значении уровня в 35% значение ошибки будет E=PV-SP=35-30=5, открытие клапана будет OP=kP*E=5*2=10%, что обеспечивает расход в отходящем трубопроводе 10м3/час. Расход в отводящем трубопроводе равен расходу в подающем трубопроводе, следовательно изменение уровня в емкости прекратилось, система пришла в равновесие, т.е. при kP=2 равновесие (стабилизация, окончание процесса регулирования) наступает при ошибке E=5%.

В П-регуляторе значение ошибки не может быть равным «0». Чтобы обеспечивать требуемый расход в отходящем трубопроводе, на входе П-регулятора должна быть ошибка, соответствующая необходимому положению клапана, а при E=0 выход OP также будет равен «0», клапан будет закрыт.

Чтобы уменьшить ошибку П-регулятора, нужно увеличивать коэффициент kP. При kP=5 ошибка будет E=2, так как OP=kP*E=5*2=10, что соответствует требуемому положению клапана.

В идеальной системе, в которой отсутствует запаздывание, коэффициент kP можно увеличивать до бесконечности, тем самым уменьшая ошибку в установившимся режиме. В реальных системах запаздывание присутствует всегда. В нашем примере, изменение уровня в емкости будет отставать от изменения положения клапана, а показания уровнемера будут отставать от фактического значения уровня. На следующем рисунке показано поведение системы при наличии запаздывания между показаниями уровнемера и фактическим уровнем на 10 циклов. При том же kP=2 в системе появилось перерегулирование, «перебег» клапана и затухающие колебания.

Теперь, при наличии запаздывания в системе, если увеличить коэффициент усиления kP=3, колебания в системе становятся незатухающими, система теряет устойчивость.

Это означает, что в реальной системе коэффициент kP имеет предельное максимальное значение, выше которого система теряет устойчивость. Максимальному kP соответствует минимальная ошибка, которую можно обеспечить без потери устойчивости. Дальнейшее уменьшение ошибки одной П-функцией невозможно.

Эксперименты с П-функцией на этом можно закончить, возвращаемся к реализации регулятора в ПЛК.

По наличию статической ошибки — регуляторы статические и астатические. [c.35]

Интегральное регулирование допускает, большие изменения нагрузки и исключает возможность появления статической ошибки. Поэтому такая комбинация дает хорошие результаты почти во всех случаях, за исключением процессов с очень резкими возмущающими воздействиями или очень большими запаздываниями. Регуляторы такого типа иногда называют регуляторами с автоматической обратной перестановкой, так как они автоматически сводят к нулю статическую ошибку, возникающую при пропорциональном регулировании. [c.460]

Введение интеграла (использование ПИ-регулятора) устраняет статическую ошибку, но мало улучшает динамику процесса. Добавление импульса по производной (применение ПИД-регуля-тора) существенно повышает быстродействие системы, но при большом коэффициенте усиления возникает значительное перерегулирование и САР становится более чувствительной к внешним возмущениям. Для устранения этих недостатков возможны два пути усложнение САР (создание многоконтурной системы с дополнительными перекрещивающимися обратными связями) или создание регулятора со специальной характеристикой. При этом передаточная функция регулятора должна иметь вид [21] [c.711]

Величины Xyi, Phi, Ху, и р, — координаты узловых точек реальной статической характеристики регулятора (см. рис. 4.8, б). В качестве примера на рис. 4.10 изображена характеристика статической точности регулирования насоса при Dj, = 6,33, рв = 0,05, Ху1 = 0,555, Рн1 = 0,315, Ху2 = 0,86 и рна = 0.56. В шести точках характеристики относительная ошибка регулирования равна нулю, максимальное вначение ее не превышает 6,2%. [c.297]

Полезно заметить, что при астатическом объекте (vj ф 0), но статическом регуляторе (vj = 0), как показывает формула (5.85), постоянное возмущающее воздействие создает в системе статическую ошибку, которая не возникает, если объект статический (vx = 0), а регулятор астатический (vj Ф 0). [c.158]

Изодромные, или пропорционально-инте-тральные, регуляторы (сокращенно ПИ-регуляторы) объединяют в себе положительные свойства пропорциональных и интегральных регуляторов. Как следует из сказанного выше, наличие отрицательной обратной связи благотворно влияет на переходный процесс регулирования, но приводит к остаточному отклонению. В пропорционально-интегральных регуляторах применяется особая обратная связь — упругая, действие которой постепенно исчезает после осуществления пропорционального воздействия. Благодаря этому возникают дополнительные перемещения регулирующего органа, ликвидирующие статическую ошибку. Устройство упругой обратной связи носит название изодрома, откуда и происходит наименование самого регулятора. [c.42]

Величина отклонения параметра в конце процесса регулирования от заданного значения называется остаточной неравномерностью, или статической ошибкой. Она представляет собой отклонение регулируемого параметра в процентах от заданного значения, вызывающее полный ход исполнительного механизма. Например, если степень неравномерности регулятора равна 10%, то это значит, что изменение параметра на I % от шкалы регулятора вызовет перемещение регулирующего органа на Vio его полного хода из одного крайнего положения в другое. Неравномерность, или статическая ошибка, регулирующего органа с чувствительным элементом определяется жесткостью связи. Чем жестче связь, тем большее изменение задания регулируемого параметра вызывает перемещение регулирующего органа на единицу его полного хода. В данном примере жесткость связи определяется положением точки 4 на рычаге 1. Чем больше расстояние между точками 2 я 4, тем жестче связь и больше статическая ошибка. [c.262]

У астатических регуляторов (рис. 18, д) малейшее отклонение входного параметра X вызывает непрерывное движение РО с определенной скоростью до предельного значения К акс- Регулирующий орган остановится только при X = Хо. Если при этом окажется МрФ Мн,, то снова возникнет рассогласование X — Хо и РО дополнительно переместится, пока не остановится в положении, при котором Мр == Мн. и X = Хо, т. е. когда статическая ошибка равна нулю. Именно поэтому их и называют астатическими. [c.36]

Диапазон пропорциональности и соответственно коэффициент усиления (чувствительность прибора) зависит от жесткости пружины, площади мембраны и обычно не регулируется. В схеме на рис. 19, а коэффициент усиления зависит также от соотношения плеч рычага ОА и ОБ. Перемещая винтом 2 центр О вправо, можно повысить чувствительность прибора. Характеристика 1 — 2 станет круче. Это уменьшит ДП, а следовательно, и статическую ошибку. Однако в реальных регуляторах увеличение чувствительности ухудшает переходные характеристики. [c.39]

Устраняя статическую ошибку, И-регуляторы, однако, ухудшают качество переходного процесса в системе. При малой скорости перемещения РО изменение нагрузки вызывает слишком большие отклонения регулируемого параметра, а при большой скорости РО возникают долго незатухающие колебания. Эти особенности И-регуляторов станут понятнее, когда будет рассмотрена совместная работа регуляторов с объектом (см. рис. 25). [c.41]

С увеличением тепловой нагрузки установившийся режим может наступить только при условии большей подачи жидкости через ТРВ. Из статической характеристики видно, что это возможно лишь при большем перегреве, т. е. испаритель будет заполнен меньше (точка Б на рис. 75, а). С увеличением давления на входе в ТРВ (р ) пропускная способность его увеличивается и требуемая производительность его будет обеспечена при меньшем перегреве (точка Б» на рис. 75,а). Таким образом, ТРВ, как всякий пропорциональный регулятор, неизбежно дает статическую ошибку, однако ошибка эта невелика и практически не ухудшает работу испарителя (см. гл. IV). [c.155]

Более экономичен способ регулирования р водорегулирующим вентилем. При снижении р давление на мембрану регулятора падает и под действием пружины ВРВ уменьшает подачу воды. В пределах статической ошибки ( 1,5 кгс/см ) ВРВ поддерживает р постоянным. [c.220]

Пропорциональные регуляторы неизбежно дают статическую ошибку, поэтому их относят к классу статических регуляторов. Действительно, при больших нагрузках должно возрасти и регулирующее воздействие, т. е. открытие клапана К должно быть больше среднего значения Уц- А, значение Х ст при этом как видно из статической характеристики, должно быть больше, чем Хо, т. е. устанавливается статическая ошибка, равная Ху т — Хц. [c.130]

У статических регуляторов (рис. 18, а) установившееся значение выходного параметра У однозначно ( жестко ) определяется значением входного параметра X. При регулировании они неизбежно дают статическую ошибку (см. рис. 7,б и в). [c.39]

Статическая ошибка регулятора прямого действия существенно зависит от силы, возникающей со стороны регулирующего органа насоса, в частности, наклонной шайбы. Сила трения на регулирующем органе насоса приводит к петлевой статической характеристике регулятора прямого действия. Снизить влияние нагрузки на регулятор можно, увеличив эффективную плоы адь плунжера и соответственно жесткость пружинного блока. Однако из-за этого во многих случаях габаритные размеры регулятора мощности прямого действия значительно увеличиваются. [c.284]

Сиглске [21], анализируя полученные динамические характеристики колпачковой абсорбционной колонны, предположил, что необходимо поддерживать постоянным состав выходящего газа. В результате показано, что по динамике лучше всего воздействовать на состав входящей жидкости (канал состав входящей жидкости—состав выходящего газа является наименее инерционным). Однако из практических соображений удобнее воздействовать на подачу входящей жидкости некоторое ухудшение динамических свойств при этом компенсируется техническими преимуществами. При использовании в этом случае П-регулятора САР устойчива, но передемпфирована она имеет статическую ошибку, и процесс регулирования проходит медленно. [c.711]

На рис. 4.5 показан аксиально-поршневой насос / с валом 2 и регулятором мощности прямого действия. Через отверстия А Б камеру с плунжером 5 поступа<т рабочая жидкость под давлением Рн- Плунжер 5 через промежуточный толкатель 4 поворачивает наклонную шайбу 6, пока сила со стороны пружинного блока 3 не уравновесит силу давления жидкости. Перемещение Ху и поворот шайбы приводят к изменению удельного рабочего объема i7n насоса. Пружинный блок составлен из двух цилиндрических пружин различной длины, поэтому статическая характеристика данного регулятора имеет вид ломаной линии (см. на рис. 4.4, б линию 2). Отклоиеиие ломаной линии 2 от идеальной статической характеристики (линии 1) приводит к появлению статической ошибки регулирования. (Изготовление специальной пружины с заданной нелинейной характеристикой сопряжено со значительными трудностями). [c.283]

Рассматриваемый регулятор имеет дополнительный подвод энергии в виде рабочей жидкости, поступающей от вспомогательного насоса в исполнительный механизм через отверстие Б и уходящей на слив через В. Благодаря вспомогательному следящему приводу, называемому иногда гидроусилителем, нагрузка со стороны регулирующего органа насоса несущественно влияет на статическую характеристику регулятора мощности. Использование в пружинном блоке трех пружин различной жесткости уменьшает статическую ошибку по сравнению с двухпружинным блоком. Демпфирующий поршень снижает колебания регулятора при переходном процессе. [c.285]

Соотношение (5.88) показывает, что при отсутствии в системе интегрирующих звеньев (разомкнутая система — статическая) постоянные воздействия и /о вызывают постоянную установив-щуюся ошибку (,, которую называют статической. Эта ошибка будет тем меньше, чем больше коэффициент-усиления К. системы, причем для уменьшения статической ошибки, вызываемой возмущающим воздействием, следует для увеличения К увеличивать коэффициент /Са регулятора, а не К объекта. [c.158]

Критерий статической ошибки. При использовании статических, регуляторов каждому значению величины статичеокого отклонения возмущающего воздействия соответствует определенное отклонение выходного пара-M Tipa объекта. [c.109]

Отклонение выходного параметра от требуемого значения есть величина статической ошибкй, которая тем меньше, чем меньше коэффициент усиления по дйн-ному каналу, т. е. чем выше коэфф ицие Нт усиления uetiH регулированиями ниже так называемая степень нерав- номерности самого регулятора. [c.109]

Пропорциональные регуляторы не могут поддерживать постоянное значение регулируемой величины, так как перемещение регулирующего органа в таких системах однозначно связано с изменением входной величины, следовательно, всякому новому его положению, необходимому при изменениях нагрузки, отвечает некоторое новое значение регулируемого параметра. Это неизбежное отклонение называют остаточной неравномерностью регулирования или статической ошибкой. Величина остаточной неравномерности тем менЫне, чем больше коэффициент передачи регулятора по прямому тракту. [c.41]

У астатических регуляторов регулирующий орган перемещается со-скоростью, пропорциональной отклонению регулируемого параметра. Преимуществом регуляторов этого типа является то, что установившееся значение регулируемой величины не зависит от нагруз-ки, и статическая ошибка равна нулю. Однако астатические регуляторы можно применять лишь для управления объектами, обладающими самовыравни-ванием в противном случае система будет неустойчивой. [c.543]

У статических регуляторов (рис. 18,г) установившееся значение вырдного параметра У однозначно ( жестко ) определяется величиной входного параметра X. При регулировании они дают статическую ошибку (см рис. 7, в). [c.35]

Сопоставляя переходные характеристики П-регулятора и ПД-регулятора видим, что у ПД-регулятора отклонения регулируемого параметра меньше (более быстрое затухание процесса). Поэтому если колебания параметра в переходном процессе у П-регулятора выходят за допустимые пределы, то следует выбрать ПД-регулятор. Для уменьшения статической ошибки применяют интегральные регуляторы (рис. 25, е). Однако при большой скорости РО они дают долгр не затухающий переходный процесс. При малой скорости РО возникают слишком большие отклонения регулируемого параметра в переходном процессе (показаны пунктиром). Поэтому И-регуляторы целесообразно применять в случаях, когда нагрузка меняется очень редко и решающую роль играет не переходный процесс, а установившееся состояние. [c.51]

Статическая характеристика регуляторов. По установившемуся значению регулируемого параметра различают регуляторы статические (пропорциопальные) и астатические (простые и изодромные). У статич. регулятора имеется монотонная связь между воспринимаемым им установившимся значением регулируемого параметра и положением регулирующего органа. Напр., в регуляторе уровня жидкости (в резервуаре) воспринимающий элемент (поплавок) связан системой рычагов с золотником задвижки на линии подачи жидкости в резервуар. Если изменится нагрузка объекта (расход жидкости из резервуара), то для приведения его к новому установившемуся состоянию нужно в том же направлении и на столько же изменить подачу в резервуар, т. е. нужно соответственно передвинуть золотник задвижки. Когда последний займет новое положение, при к-ром поступление и расход жидкости уравняются, поплавок, связанный рычажной системой с золотником задвижки, окажется уже в новом положении, отличающемся от исходного. Соответственно этому изменится и уровень жидкости в резервуаре. Следовательно, статич. регулятор не может обеспечить постоянства регулируемого параметра на заданном уровне при переменной нагрузке объекта (при этом возникает статич. ошибка регулирования). У астатич. регулятора нет непосредственной постоянной связи между установившимися значениями регулируемого параметра и положением регулирующего органа. Поэтому при изменении нагрузки не возникает статич. ошибка регулирования, и равновесие подобного регулятора имеет место лишь в случае, когда действительное значение [c.285]

Статическая ошибка регулирования (отклонение регулируемого параметра от заданного значения последостижения САР нового установившегося состояния). Возмущающие воздействия могут быть приложены к любому звену САР, но важнейшими являются возмущения, приложенные к входу объекта (изменения нагрузки) или к входу регулятора (его перенастройка). Возмущающее воздействие, приложенное к объекту регулирования, считается положительным, если приводит к увеличению регулируемого параметра. Увеличение нагрузки объекта уменьшает регулируемый параметр и является поэтому отрицательным возмущением снижение нагрузки приводит к увеличению качественного показателя и является положительным возмущением. Если возмущение скачком приложено к входу объекта, то при установке астатич. регулятора статич. ошибка равна пулю (для любых объектов регулирования). Подобная САР наз. астатической относительно возмущения, приложенного к объекту (т.е. по нагрузке). При установке статич. регулятора и возмущениях, приложенных к входу объекта, всегда имеется статич. ошибка. Подобная ( АР наз. статической относительно возмущения, приложенного к объекту. Величина статич. ошибки равна ири статич. объекте регулирования [c.290]

О качестве системы удобно судить по переходному процессу, т. е. по процессу регулирования, вызванному стуиенчатым изые-нениег.1 нагрузки (рис. 69). Примером ступенчатого изменения нагрузки может служить включение лампочек в холодильной камере. Если нагрузки от М о резко возросла до Л4 ь то ДХ начинает увеличиваться. Регулятор увеличивает Мр, причем мол<ет оказаться Мр > М 1. Тогда X станет уменьшаться. Возникает колебательный процесс. При затухании колебаний X принимает новое установившееся значение Хуст- Отклонение этого значения от начального называют статической ошибкой [c.124]

Из статической характеристики И-регулятора (рис. 76, б) видно, что клапан может занять одно из промежуточных значений только при X = Хо. Так, при X > Хо клапан полностью открыт, а при X < Хо полностью закрыт. Отсюда видно, что в установившемся состоянии статическая ошибка АХст = X — Хо равна нулю, т. е. интегральные регуляторы относятся к классу астатических регуляторов. [c.131]

Для улучшения качества регулирования применяют регуляторы с более сложными законами регулирования пропорциональноинтегральные, которые в первый момент времени работают как П-регуляторы, но затем сводят к нулю статическую ошибку пропорционально-дифференциальные, которые реагируют не только на б 131 [c.131]

С увеличением тепловой нагрузки подача жидкости через ТРВ должна быть больше. А это возможно лишь при большем перегреве (точка Б ), т. е. испаритель немного недозаполнен. А с увеличением давления Рк пропускная способность ТРВ увеличивается, и требуемая производительность будет обеспечена при меньшем перегреве (точка Б»). Таким образом, ТРВ, как всякий П-регулятор, дает некоторую статическую ошибку. [c.149]

У регуляторов с высокой чувствительностью (например, с мягкой пружиной) статическая ошибка значительно меньше, но в переходном процессе возникают долго не затухаюш,ие колебания с большими отклонениями параметров в начале процесса. [c.131]

Устройство, монтаж и ремонт холодильных установок Издание 4 (1985) — [

c.129

c.130

c.131

c.132

]

Устройство, монтаж и ремонт холодильных установок Издание 4 (1986) — [

c.129

c.130

c.131

c.132

]

Содержание

Что такое ПИД регулятор?
Как работают значения PID, их изменение
Усиление P
Усиление I
Усиление D
Назначение ПИД регулятора
Пример схемы регулирования температуры
Три коэффициента ПИД регулятора и принцип работы
Не все проблемы из-за плохих настроек PID
Вибрация
Центр тяжести (CG)
Настраивание ПИД-регулятора общего вида
Регулятор пропорционального типа
Регулятор интегрального типа
Регулятор дифференциального типа
ПИД-регулятор
Пример
Формула ПИД-регулятора
Настройка ПИД регулятора
Как настроить PID по шагам
Составляющие сигнала ПИД-регулятора
Настройки ПИД-регулятора
Пример применения ПИД-регулятора в частотно-регулируемом приводе насоса
Вопрос: «Какие у тебя ПИДы?» — неправильный вопрос!
Примечания и советы
Death Rolls (крен смерти)
Дополнительная информация для версии BetaFlight 3 (3.0 и 3.1)
Формула ПИД-регулятора
Когда нужно перенастраивать PID?

Что такое ПИД регулятор?

ПИД-регулятор – это устройство, интегрированное в схему управления с обязательной обратной связью. Он предназначен для поддержания заданных уровней заданных значений, например температуры воздуха.

Устройство подает управляющий или выходной сигнал на управляющее устройство на основе данных, полученных от датчиков или датчиков. Контроллеры обладают высокими показателями точности переходных процессов и качества выполнения задачи.

Как работают значения PID, их изменение

Обычно изменение значений PID (усиления) влияет на поведение квадрокоптера:

Усиление P

P определяет, насколько сильно полетный контроллер исправляет ошибки для достижения желаемой траектории полета. Этот параметр регулирует чувствительность и реакцию на изменение положения стика. Чем выше число, тем выше чувствительность и отзывчивость.

Более высокое значение P означает более резкое обращение, а более низкое значение P означает более плавное и плавное обращение. Но если это значение будет слишком высоким, дрон станет слишком чувствительным и начнет корректировать себя, а значения положения стика также начнут колебаться.

Вы можете снизить P, чтобы уменьшить колебание, но дрон не будет четко следовать вашим командам, поэтому вам придется поиграть с I и D, чтобы это компенсировать.

Усиление I

Значение I определяет, сколько квадрокоптер выдержит при воздействии внешних факторов, например, ветра и смещения центра тяжести.

Это настройка жесткости при повороте коптера.

Обычно настройки по умолчанию работают с этим довольно хорошо, но если вы заметили некоторый дрейф в дроне без вашей команды, немного увеличьте значение I. Если значение слишком низкое, вам часто потребуется скорректировать траекторию полета дрона, особенно если вы часто меняете уровень газа.

Если значение I слишком велико, квадрокоптер будет вести себя «деревянным», он плохо отреагирует на ваши изменения положения стика на пульте дистанционного управления. Нет регулятора, двигателя и пропеллера, каждый по отдельности, но он работает по-своему, поэтому, когда вы резко дросселируете, а затем резко опускаете ручку газа, один двигатель останавливается быстрее, чем другой, и наоборот, все из которых вызывает сбой в положении квадрокоптера в воздухе, один двигатель все еще имеет тягу, а другой нет.

Итак, я привык решать эти мелкие проблемы.

Усиление D

D действует как демпфер (глушитель, демпфер) и снижает чрезмерную коррекцию и регулировку усиления P. Увеличение значения D смягчает эффект P, как будто добавляя «пружину», а также минимизирует вибрацию гребного винта.

Если D слишком мало, дрон будет “отскакивать” назад в конце переворотов и кувырков, а также будет сильная вибрация, вызванная вертикальным спуском.

Слишком большое значение также приводит к вибрациям. Пытаясь стабилизировать квадрокоптер, полетный контроллер будет давать команду контроллерам скорости увеличить скорость двигателей, а затем уменьшить их до такой скорости (в смысле более медленной), что двигатели будут перегреваться и перегорать. Вибрация также повлияет на полетный контроллер, и со временем ситуация ухудшится.

Еще один побочный эффект D – квадрокоптер становится «мягким», то есть реакция на команды слишком медленная.

Назначение ПИД регулятора

ПИД-регулятор предназначен для поддержания определенного значения на требуемом уровне: температуры, давления, уровня в резервуаре, расхода в трубопроводе, концентрации чего-либо и так далее, путем изменения управляющего воздействия на исполнительные механизмы, такие как автоматический клапан управление с помощью пропорционального интеграла, дифференцирующего значения для его регулирования.

Целью использования является получение точного управляющего сигнала, который может управлять крупными производствами и даже реакторами электростанций.

Пример схемы регулирования температуры

Часто ПИД-регуляторы используются при регулировании температуры, давайте рассмотрим этот автоматический процесс на простом примере нагрева воды в резервуаре.

В емкость наливается жидкость, которую необходимо нагреть до нужной температуры и поддерживать на определенном уровне. Внутри емкости установлен датчик измерения температуры – термопара или термометр сопротивления и подключается непосредственно к ПИД-регулятору.

Чтобы нагреть жидкость, мы подадим пар, как показано на рисунке ниже, с автоматическим регулирующим клапаном. Сам клапан получает сигнал от регулятора. Оператор вводит значение уставки температуры в ПИД-регулятор, которое должно поддерживаться в резервуаре.

При неправильной настройке коэффициентов регулятора будут скачки температуры воды, при этом клапан будет полностью открыт, а затем полностью закрыт. В этом случае необходимо рассчитать коэффициенты ПИД-регулятора и ввести их заново. Если все было сделано правильно, через короткий промежуток времени система выровняет процесс, и температура в резервуаре будет поддерживаться на заданном уровне, а степень открытия регулирующего клапана будет в центральном положении.

Три коэффициента ПИД регулятора и принцип работы

Задача ПИД-регулятора – обеспечить выходной сигнал о мощности, необходимой для поддержания регулируемого параметра на заданном уровне. Для расчета показателя используется сложная математическая формула, в которую входят 3 коэффициента: пропорциональный, интегральный, дифференциальный.

Возьмем за объект регулирования емкость с водой, в которой необходимо поддерживать температуру на заданном уровне, регулируя степень открытия клапана паром.

Пропорциональная составляющая появляется в момент несоответствия входным данным. Проще говоря, это звучит так: берется разница между фактической температурой и желаемой температурой, умножается на регулируемый коэффициент, и получается выходной сигнал, который следует отправить на клапан. Те, как только градусы упали, начинается процесс нагрева, поднимается выше нужной отметки – отключение или даже охлаждение.

Далее идет интегральный компонент, предназначенный для компенсации влияния окружающей среды или других мешающих воздействий на поддержание нашей температуры на определенном уровне. Поскольку всегда есть дополнительные факторы, влияющие на управляемые устройства, к моменту поступления данных для расчета пропорциональной составляющей данные уже меняются. И чем больше внешнее влияние, тем сильнее происходят колебания показателя. Возникают всплески тока.

Интегральный компонент пытается на основе прошлых значений температуры вернуть свое значение, если оно изменилось. Более подробно процесс описан в видео ниже.

А затем выдается выходной сигнал регулятора, в зависимости от коэффициента, на повышение или понижение температуры. Со временем выбирается величина, компенсирующая внешние факторы, и скачки исчезают.

Интеграл используется для устранения ошибок путем вычисления статической ошибки. Главное в этом процессе – правильно выбрать коэффициент, иначе погрешность (несовпадение) затронет и интегральную составляющую.

Третий компонент PID – дифференциация. Он предназначен для компенсации влияния задержек, возникающих между воздействием на систему и обратной связью. Пропорциональный контроллер подает питание до тех пор, пока температура не достигнет желаемого уровня, но при передаче информации на устройство, особенно при высоких значениях, всегда возникают ошибки. Это может привести к перегреву. Дифференциал предсказывает отклонения, вызванные задержками или влиянием окружающей среды, и заранее снижает мощность, подаваемую на него.

Не все проблемы из-за плохих настроек PID

Перед изменением PID следует также посмотреть другие данные:

Вибрация

Не все вибрации вызваны высоким значением P. Перед настройкой PID следует максимально устранить источники вибрации на дроне. Например, баланс двигателя и стойки, жесткость рамы и т.д.

Центр тяжести (CG)

Центр тяжести должен быть точно посередине между всеми 4 двигателями. Плохая центровка приведет к тому, что некоторые двигатели будут работать сильнее, чем другие, что приведет к перегреву двигателя и плохой устойчивости полета. Например, аккумулятор находится сзади, а не в центре, поэтому задние двигатели будут работать на 100%, а передние двигатели – на 80%. Вся масса на дроне должна быть отцентрирована и равномерно распределена. По этой причине X-образные оправы являются наиболее популярными.

Настраивание ПИД-регулятора общего вида

Для поддержания этого давления есть устройство, называемое эталонным регулятором. Давление в трубопроводах к датчику сравнивается с заданным параметром давления. Регулятор сравнивает давление в системе с эталонным давлением и определяет целевую скорость двигателя, чтобы изменить ошибку. В контроллере простого типа применяется план действий ПИД-регулирования. Он использует три составляющих типа регуляторов для устранения ошибок: дифференциальный, интегральный и пропорциональный регулятор.

Регулятор пропорционального типа

Такой регулятор является основным, скорость выставляется прямо пропорционально погрешности. При использовании пропорционального регулятора в системе будет ошибка. Малые значения коэффициента пропорционального регулятора приводят к замедлению работы системы, а высокие параметры приводят к колебаниям и нестабильности системы.

Регулятор интегрального типа

Этот регулятор используется для устранения ошибки. Скорость будет увеличиваться, пока ошибка не будет устранена (при отрицательной ошибке она будет уменьшаться). Небольшие значения суммирующей составляющей слишком сильно влияют на деятельность регулятора в целом. Когда устанавливаются большие значения, система перескакивает, работает с перерегулированием.

Регулятор дифференциального типа

Этот регулятор измеряет скорость исправления ошибок, использует ее для увеличения скорости системы и увеличивает скорость регулирования в целом. При увеличении скорости регулятора перерегулирование увеличивается. Это приводит к системной нестабильности. Во многих случаях производная становится равной нулю или приближается к наименьшему значению, чтобы избежать этого условия. Это полезно в системе позиционирования.

ПИД-регулятор

С помощью настройки ПИД-регулятора мы можем настроить переходный процесс, необходимый для решения нашей проблемы.

Hzad – указанное (желаемое) значение выходной переменной
Xmax – допустимый верхний предел выходной переменной
Xmin – допустимый нижний предел выходной переменной
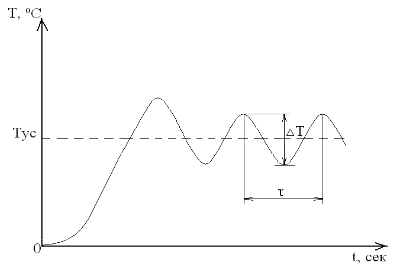
Т – период колебания
Н – время нарастания
Tr – переходное время (последняя точка пересечения кривой с Xmin или Xmax)
A1 – первый промах
A2 – второй перерегулирование
d = A1 / A2 – степень (уменьшение) сглаживания переходного процесса (отношение первого перебега ко второму)

Несовпадение, перерегулирование, время нарастания, время переходного процесса, коэффициент затухания характеризуют качество регулирования.

Пример

ПИД-регулятор открывает и закрывает регулирующий клапан на горячей трубе, чтобы вода с температурой + 40 ° C текла из крана с погрешностью плюс-минус 2 градуса. Контроллер вычисляет несоответствие (погрешность) – отклонение фактической температуры (например, + 20 ° C) от заданного значения (+ 40 ° C) и решает, когда и на сколько необходимо открыть горячий клапан, чтобы температура увеличивается на 20 ° C. Контроллер распознает реальную (фактическую) температуру через датчик температуры (обратная связь), и оператор сообщает ему установленную температуру (заданное значение), например, путем набора номера «40» на своем ПК.

Для настройки ПИД-регулятора нужно правильно подобрать комбинацию из трех коэффициентов:

Пропорциональный – Kp
Интегральный – Ki
Дифференциал – Kd

Также можно использовать более простые П- и ПИ-регуляторы.

Формула ПИД-регулятора

где e (t) – ошибка (рассогласование), u (t) – выходной сигнал регулятора (управляющее воздействие).

Чем выше коэффициент пропорциональности, тем выше производительность, но меньше запас устойчивости. Но! простой P-контроллер не может полностью справиться с несоответствием, т.е всегда выходит из строя.

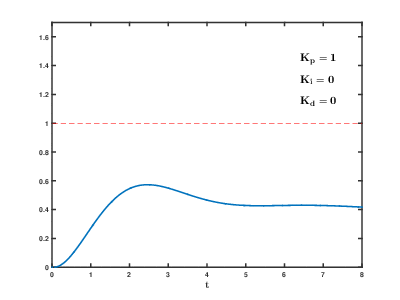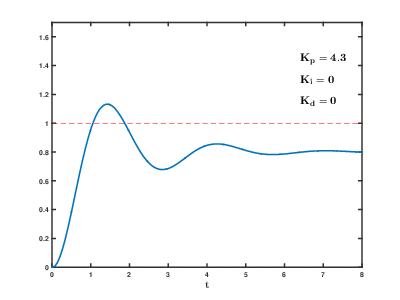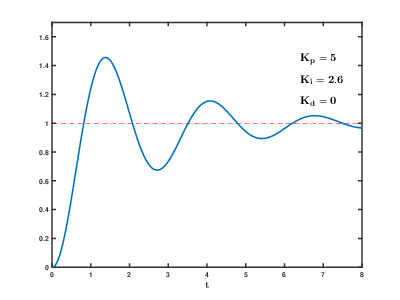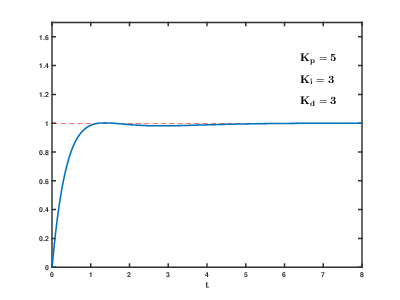
ПИ-регулятор устраняет статическую ошибку (установившееся состояние), но чем выше интегральный коэффициент, тем больше перерегулирование (динамическая ошибка).

ПИД-регулятор позволяет уменьшить перерегулирование, но чем больше коэффициент дифференциала, тем больше ошибка из-за влияния шума.

Если шум проходит через канал обратной связи, мы можем отфильтровать его с помощью низкочастотного фильтра, но чем выше постоянная этого фильтра, тем медленнее регулятор будет устранять шум.

Настройка ПИД регулятора

Настройка ПИД-регулятора осуществляется двумя способами:

Синтез включает расчет параметров на основе модели системы. Этот параметр точен, но требует глубокого понимания теории автоматического управления. Это подвластно только инженерам и ученым. Так как необходимо снять характеристики потока и произвести ряд расчетов.
Ручной метод основан на пробах и ошибках. Для этого за основу берутся данные готовой системы, вносятся изменения в один или несколько коэффициентов регулятора. После включения и наблюдения за конечным результатом параметры меняются в желаемом направлении. И так до тех пор, пока не будет достигнут желаемый уровень производительности.

Теоретический метод анализа и настройки на практике используется очень редко, что связано с незнанием характеристик объекта управления и массой возможных мешающих воздействий. Чаще встречаются экспериментальные методы, основанные на наблюдении за системой.

Современные автоматизированные процессы реализованы в виде специализированных модулей под управлением программ настройки коэффициентов регулятора.

Как настроить PID по шагам

Убедитесь, что двигатели сбалансированы и самолет максимально свободен от вибраций. Попытка настроить PID без «чистого» гироскопа (балансировка и подавление вибрации выполняются, чтобы гироскоп работал без помех), все равно что построить дом без хорошего фундамента. В этом видео вы узнаете, как легко контролировать вибрацию. При необходимости отрегулируйте настройки фильтра нижних частот, чтобы получить чистый «гироскопический сигнал.
важно, чтобы этот шаг выполнялся в режиме Acro, даже если вы всегда летаете в режиме стабилизации / горизонта. Режимы «Угол Горизонт» имеют собственное значение и влияют на ПИД-регулирование. Пример параметра PID ниже соответствует Rewrite PID (PID Controller # 1). При выполнении этой начальной настройки установите значение APT на 0. При необходимости вы можете добавить APT позже.
Начните с внесения небольших изменений в настройки по умолчанию и начните с фактора P. Хорошей отправной точкой будет P для Pitch and Roll 4.0. Кроме того, уменьшите I и D для Pitch and Roll, чтобы отрегулировать P с минимальным шумом. Поэтому рекомендуется установить I равным 20 и D равным 5. Для рыскания рекомендуется взять значение по умолчанию, разделить на 2 и немного уменьшить значение I, чтобы исключить эту ось как источник колебаний. Рыскание настраивается последним.
Во время тестовых полетов увеличивайте параметр P на оси крена до тех пор, пока вы не заметите колебание по мере приближения к максимуму и не услышите видимое и слышимое колебание. Затем установите параметр P примерно на 70% от значения, вызвавшего колебания. Теперь я думаю, понятно, почему, не имея опыта полетов на конкретном квадрокоптере, вы не сможете настроить его PID?
Повторите шаг 4 для оси наклона.
Проверьте, сохраняет ли квадрокоптер необходимый угол крена и не двигается ли он во время крена, затем несколько раз резко дайте газу и резко отпустите его до 0. Обратите внимание: угол крена, который вы делали до того, как поиграть с дросселем, не должен существенно измениться. Если угол отклонения кажется вам очень отклоненным (дрон начал дрейфовать), увеличьте параметр I. Если все в порядке и дрейфа нет, не меняйте I. Вы можете изменить “ощущение” подъема дрона или понижение параметра I после достижения хороших настроек PID, поскольку I не влияет на окончательные значения P и D.
Повторите шаг 6 для оси наклона.
Параметр D следует увеличивать на каждой оси ТОЛЬКО до такой степени, чтобы это помогало уменьшить отдачу после переворота и крена (переворот – переворот вбок, кувырок – перевернутый вверх ногами), а также после колебаний после свободного падения при ускорении до 0 и дрон падает, значит, вы включаете двигатели на газе, и они начинают, так сказать, падать в воздухе, и в этот момент дрон начинает раскачиваться из стороны в сторону. Когда эти проблемы исчезнут при увеличении параметра D, уменьшите этот параметр до 80-90% от этого уровня.

Примечание: слишком высокое значение параметра D может привести к перегреву двигателей. Для контроля прогрева нужно 20-30 секунд лететь, приземляться и управлять моторами руками. Если вы можете держать моторы пальцами, они не сильно нагреваются.
Часто установка рыскания не нужна или будет минимальной, так как она все равно может вызывать колебания, если ничего не предпринимать.
Начните с Yaw P и проверьте вибрацию дрона, как в первом шаге, а также убедитесь, что нет вибрации, если вы даете сильный и длинный газ или быстро двигаетесь вперед
Начинайте увеличивать рыскание P с шагом 5, пока не увидите на видео камеры вибрации при полете вперед или на полном газу. Затем немного уменьшите значение.
Теперь нам нужно взглянуть на данные в черном ящике. Yaw P, скорее всего, будет немного раскачиваться, поэтому попробуйте увеличить гироскоп Yaw, чтобы увидеть, действительно ли колебания достигают гироскопа. Если гироскоп по рысканью выглядит более-менее ровно, значит, все в порядке.

Примечание. Поскольку рыскание по своей сути имеет меньший контроль по тангажу и крену, для этой оси существует широкий диапазон значений. P и я могли быть высокими, а D – низкими, это нормально.
Теперь необходимо отрегулировать соотношение P к I, то есть будет ли квадрокоптер сопротивляться в крутых поворотах или, наоборот, отказывать в этих поворотах. Очень низкие значения I со временем приводят к осевым смещениям. Низкие значения I на оси также позволяют вам свободно менять положение, но при этом сохранять это положение. Более высокие значения оси будут держать дрон в хорошем состоянии, но могут иметь тенденцию сопротивляться движению + добавляется небольшой накат. Очень высокие значения означают «роботизированные» движения и колебания дрона.
После завершения настройки в режиме Acro вы можете перейти к настройкам других режимов, например Horizon).

Помните, что вам не нужно слишком глубоко копаться в журналах Blackbox, чтобы точно настроить идеальные PID. Если квадрокоптер хорошо летает и вас все устраивает, летите и летайте

Составляющие сигнала ПИД-регулятора

Управляющий сигнал, генерируемый ПИД-регулятором, представляет собой сумму трех компонентов:

Пропорционально.
Интеграл.
Дифференциальный.

Пропорциональная составляющая формируется исходя из разницы между заданным значением параметра и его фактическим значением. Чем больше отклонение характеристики, тем выше уровень пропорционального сигнала. Устройства, управляющие системой, называются П-регуляторами только по пропорциональному закону.

Основным недостатком такой настройки является статическая погрешность, указывающая на величину остаточного отклонения параметра. Пропорциональные регуляторы имеют ограниченную точность.

Для его устранения был введен интегральный компонент. Он пропорционален интегралу по времени отклонения значения контролируемой характеристики.

Если параметр отклоняется, пропорциональная составляющая возвращает его к предыдущему значению. Уровень выходного сигнала стремится к нулю, однако из-за статической ошибки регулируемый параметр не достигает заданного значения. Интегральный компонент обеспечивает компенсацию ошибок и позволяет характеристике вернуться к заданным значениям.

Пропорционально-интегральное управление имеет низкую скорость и не подходит для регулирования динамических систем. Накопление и сумма ошибок приводит к увеличению управляющего сигнала. Система может «сойти с ума».

Для увеличения быстродействия в конструкцию регулятора введена дифференциальная составляющая. Он увеличивается и уменьшается пропорционально скорости изменения контролируемого параметра.

Следовательно, результирующий сигнал на выходе ПИД-регулятора можно определить по выражению:

где Kp, Ki, Kd – пропорциональные, интегральные, дифференциальные коэффициенты соответственно, а (t) – ошибка рассогласования.

Настройки ПИД-регулятора

Настройка ПИД-регулятора сводится к определению коэффициентов Kp, Ki, Kd. Компоненты определяются по формуле:

Они используются для определения передаточных функций системы автоматического управления и расчета их параметров:

Точность.
Скорость регулировки.
Форма графиков переходных процессов.
Инерция.
Прочие количества и функции.

Математическая модель АТС не может дать полной картины функционирования системы. Расчеты выполнены для «идеального регулятора». Нелинейность контролируемых параметров, внешние возмущения, шумы на объекте управления не позволяют применять расчетные данные для построения системы автоматического управления на практике. Результаты математических расчетов используются в качестве вспомогательных данных.

При разработке контроллеров ПИД и СКУД используется оборудование, моделирующее изменение контролируемых характеристик, средства измерений и ПК. Устройства позволяют определять и анализировать реакцию системы на удары и с большей точностью выбирать коэффициенты.

На практике используется экспертный подбор коэффициентов. ПИД-регуляторы устанавливаются на месте, вводят коэффициенты, полученные в результате расчетов или стендовых испытаний, и регулируют параметры на месте.

Пример применения ПИД-регулятора в частотно-регулируемом приводе насоса

Цепи преобразователя частоты содержат контроллеры управления, которые могут обеспечивать работу устройства в режиме ПИ- или ПИД-регулятора. Пользователи частоты часто уже имеют предустановленные настройки, которые изменяются после установки оборудования.

На рисунке показана простейшая схема регулирования давления ПИД-насоса. Аналоговые входы подключены к датчику, установленному на напорном трубопроводе, и к внешнему приводу. Требуемое значение давления также можно установить в настройках контроллера. Когда регулируемый параметр изменяется на контроллере, который сравнивает сигнал обратной связи с установленным значением, генерируется управляющий сигнал.

Преобразователь изменяет производительность насоса, увеличивая или уменьшая частоту напряжения питания электродвигателя до тех пор, пока давление в системе не достигнет установленного значения. Следовательно, давление в системе не зависит от расхода.

Приведенная выше диаграмма значительно упрощена. Преобразователи частоты с ПИД-регулятором могут управлять производительностью несколькими способами. Например, насосы в системах отопления можно регулировать по температуре теплоносителя, а также по тепловому режиму и давлению снаружи и внутри помещения.

Преобразователи частоты с функциями ПИД-регулирования также используются в сложных системах управления для систем наддува и других систем управления технологическими процессами.

Вопрос: «Какие у тебя ПИДы?» — неправильный вопрос!

Использовать чужие PID на своем квадрокоптере совершенно бесполезно. Каждый дрон уникален, его оборудование и даже ветер и климат влияют на регулирование PID.

Примечания и советы

В журналах черного ящика высокие колебания P не проявляются в виде резких пиков или больших волн. Эти колебания сначала появляются в верхней части газового диапазона и выглядят как узкие синусоидальные волны. Когда они появляются в журналах, они еще не видны визуально или на слух, поэтому во время начальной настройки (визуальной и на слух) рекомендуется сначала достичь точки визуальных и слуховых колебаний, а затем уменьшить значения. До 70%. Когда все колебания видны визуально или на слух, они также будут четко отображаться в журналах.

Death Rolls (крен смерти)

Самая распространенная причина, по которой квадрокоптер переворачивается и не выключает свои двигатели, заключается в том, что дроссельная заслонка слишком низкая. Регулятор не может запустить двигатель после команды с низким значением газа (газ был на 0 в течение некоторого времени). В журнале черного ящика двигатель работает на полном газу, но дрон продолжает вращаться. Первое, что нужно сделать, это увеличить настройку min_throttle (значение параметра Idle% при работе протокола DSHOT).

Вторая причина – неисправный мотор, или плохой ESC, или даже ослабленное крепление шасси. В этом случае в журналах Blackbox вы увидите, что двигатель работает на полную мощность, но радиус шасси уменьшается (если включен акселерометр), что указывает на то, что двигатель не имеет тяги. Для проверки замените двигатель или регулятор.

Третья причина – неудачная комбинация ESC мотор. Некоторые регуляторы просто не могут работать с современными двигателями. Здесь поможет только замена ESC на другой.

Дополнительная информация для версии BetaFlight 3 (3.0 и 3.1)

Настройки PID по умолчанию очень хорошо настроены и работают на большинстве дронов и требуют лишь незначительных корректировок.
Параметр P Roll и Pitch может быть довольно высоким без дальнейших колебаний, поэтому их можно увеличивать до тех пор, пока те же колебания не исчезнут, когда они присутствуют. Этот параметр можно поднять до максимального предела, если у вас D минимум, и вы не получите новых колебаний при резком управлении стиками.
Регулировка скорости рыскания может потребовать регулировки нижнего предела yaw_accel_limit и yaw_p_limit, особенно для двигателей большой мощности и высоких значений KV.
Некоторые мощные системы и сборки не работают с PID по умолчанию и требуют настройки с нуля, как описано в предыдущих шагах, например, DJI Snail System:

Еще у нас есть старая статья, может быть, вы тоже найдете что-нибудь полезное для себя: что такое PID, на что он влияет и как его настроить.

Формула ПИД-регулятора

Как и обещал, формул тут не будет . ну почти нет. И этот раздел будет просто формулой. Обещаю, формул больше не будет! Так что наберитесь терпения!
Итак, формула для ПИД-регулятора:
(по мотивам Википедии)
Здесь у нас есть следующие буквы (мы объясним немного ниже):

u (t) – наша функция;
П – пропорциональная составляющая;
I – составной компонент;
D – дифференциальная составляющая;
e (t) – текущая ошибка;
Kp – коэффициент пропорциональности;
Ki – интегральный коэффициент;
Kd – дифференциальный коэффициент;

Все, расслабьтесь – эта формула нам больше не понадобится в работе, она для уточнения сути.
И суть в следующем.
У нас есть влияние, наша Функция (u (t)). Он состоит из трех компонентов: пропорционального, интегрального и дифференциального (отсюда и ПИД-регулятор).
Формула в приведенном выше виде хороша для изучения, но неудобна для расчетов (хотя бы потому, что в расчетах необходимо переходить на численные методы). В программной реализации, согласно этой статье, переходят к дискретной реализации:
u (t) = P (t) + I (t) + D (t);
P (t) = Kp * e (t);
I (t) = I (t – 1) + Ki * e (t);
D (t) = Kd * {e (t) – e (t – 1)};
Это уже кажется намного более реальным и понятным! Давайте посчитаем сумму трех составляющих. Каждый из них определяется своими коэффициентами. Если этот коэффициент равен нулю, компонент не участвует в расчетах. Мы будем дальше работать с этой формулой, и я буду ее реализовывать.
Однако есть и другая повторяющаяся реализация:
u (t) = u (t – 1) + P (t) + I (t) + D (t);
P (t) = Kp * {e (t) – e (t – 1)};
I (t) = I * e (t);
D (t) = Kd * {e (t) – 2 * e (t – 1) + e (t – 2)};
Что лучше / правильно? Математика в основном такая же. Даже шансы. Говорят, что при реализации будет несколько подводных камешков.
Примечание! Коэффициенты здесь обязательно дробные! В языке программирования C – хотя бы одно число с плавающей запятой, а лучше бы double.
В этих коэффициентах заключается вся магия ПИД-регуляторов. Как их выбрать – увидим в конце. А теперь давайте отвлечемся от математики и пойдем изучать поведение этой формулы.
Все расчеты и моделирование я сделал на модели в Excel. Это – файл – прикреплен ниже, вы можете воспроизвести его сами. Модель чисто для ознакомления с идеей! То есть не нужно пытаться воплотить его в какой-то реальный процесс, искать в нем научный смысл и т.д. Там все цифры слегка «от лампы». Но зато файл простой и незамысловатый. И он быстро моделируется. И это дает возможность понять суть ПИД-регулятора. Напоследок несколько слов о файле.

Когда нужно перенастраивать PID?

Почти все компоненты в квадрокоптере влияют на PID, поэтому, когда вы меняете компонент, также настраивайте PID. Если вы изменили время цикла в Betaflight и Cleanflight, вам также потребуется настроить PID.

Источник

Динамическая ошибка

Cтраница 3

Динамическая ошибка переходного процесса зависит только от KOQ и всегда остается постоянной независимо от настройки регулятора. Если при наладке системы регулятор настроен на переходный процесс, соответствующий границе апериодичности, и необходимо перенастроить систему на колебательный переходный процесс, достаточно увеличить ер в восемь раз.
[31]

Динамическая ошибка инерционного звена первого порядка уменьшается по экспоненциальному закону.
[33]

Динамической ошибкой в процессе регулирования называется разность между теоретическим установившимся значением выходной величины по окончании переходного процесса и действительным ее значением в данный момент времени.
[35]

Динамическими ошибками механизма называется разность сил реакций в действительном и идеальном механизмах при одинаковых положениях ведущих звеньев. Эти ошибки получаются в виде отклонений сил реакций или реактивных импульсов.
[36]

Динамической ошибкой контрольно-измерительного прибора называют разность показаний при переходном ( неустановившемся) и статическом режимах его эксплуатации при одной и той же измеряемой величине.
[37]

Поскольку динамическая ошибка является характеристикой установившегося режима, то выходная функция определяется частным решением дифференциального уравнения. Коэффициенты 1Н определяются только параметрами системы и не зависят от формы входного сигнала, поэтому целесообразно выбрать вид входного сигнала ф — ф ( 1 таким, чтобы определение аь было наиболее простым.
[38]

Рассмотрим динамические ошибки, неизбежно сопровождающие измерения переменных во времени расходов, и дадим им определение.
[39]

Чем больше динамическая ошибка, тем постоянная времени оптимальной модели меньше.
[40]

Уменьшение динамических ошибок достигается не бесплатно; оно может, во-первых, приводить к ухудшению некоторых других динамических критериев качества. Так, например, стабилизация угловой скорости машины в установившемся режиме с помощью дополнительной маховой массы сопровождается в общем случае увеличением динамических нагрузок в передаточном механизме. Во-вторых, введение системы управления движением приводит к усложнению структуры машины, а зачастую и к увеличению потребляемой мощности. Факторы такого рода могут быть условно названы расходами на управление. Все это показывает, что качество системы управления движением должно характеризоваться комбинированными критериями, учитывающими как уровень динамических ошибок, так и уровни динамических нагрузок и расходов на управление. Рассмотрим некоторые критерии качества управления, учитывающие отмеченные выше обстоятельства.
[41]

Величина динамической ошибки при изменении скорости подач незначительна и практически может считаться равной нулю. Погрешность обработки деталей с учетом всех технологических факторов ( отжатие инструмента, биение фрезы и неточности программирования) не превышает 0 05 мм для деталей, имеющих контур в виде окружности.
[43]

Появление динамических ошибок связано с изменением аналоговой величины в течение цикла преобразования. Циклические преобразователи чаще всего выполняют с промежуточным преобразованием исходной величины во временной интервал, в частоту или фазу напряжения.
[44]

Страницы:

Источник

Данная статья посвящена исследованию методов настройки непрерывных ПИД-регуляторов на примере объектов первого и второго порядка и второго порядка с запаздыванием, а также выбору оптимальной настройки регулятора путем сравнения полученных результатов.

Сразу оговорюсь, что это не статья, а скорее реферат, то есть информация, собранная из разных источников с некой оценкой полезности и эффективности/применимости каждого метода.

Начнем с того, что с настройкой ПИД регулятора можно столкнуться где угодно, например, на преобразователе частоты, и хорошо, если это будет регулятор давления, они настраиваются достаточно просто, если не считать особенностей настройки ПИД, чтобы ПЧ гарантировано «уходил в сон», то есть если отсутствует расход воды, частоник может снизить обороты до указанных минимальных, а дальше просто остановить двигатель и ждать, когда ошибка регулирования не превысит какую-то тоже настроенную величину. В термоконтроллерах чаще всего есть автонастройка, но не всегда она дает приемлемые показатели работы. На сервоприводах контур положения часто тоже имеет ПИ регулятор, он хоть и представляет из себя только часть от ПИД-регулятора, но общие принципы настройки тоже присутствуют, тк имеются основные канал пропорциональный и интегральный.
А что если регулятор не имеет автонастройки и регулируемый объект достаточно сложен, например, чтобы вывести в автонастройку агрегат мощностью 100кВт требуется ее прогрев и работа, а это может составить десятки минут (а иногда и часы, а время- деньги, особенно если это время работы энергоемкого прибора) не говоря уже о себестоимости материала. Тут стоит для начала разобраться в особенностях самого ПИД, чтобы подобрать во-первых подходящий метод, а во-вторых, понять где и как стоит добиваться устойчивости в первую очередь, а где и как можно и потом делать тонкую настройку.

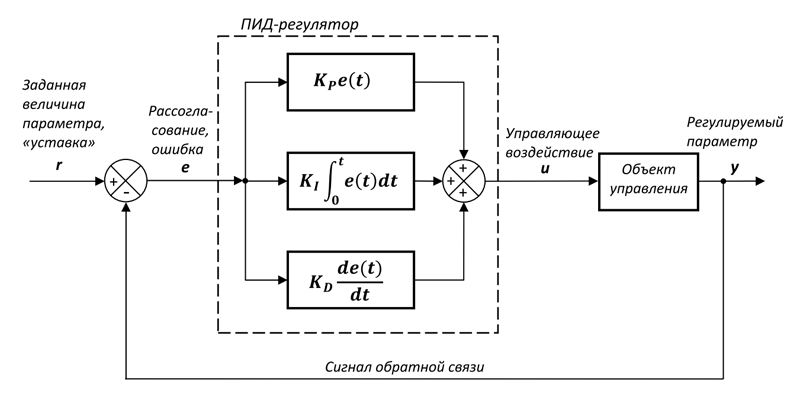
Структура регулятора по классике приведена на картинке, хотя существуют варианты, когда коэффициенты объединяются, это конечно усложняет работу, но общий принцип остается один, главное вовремя заметить, что изменение коэффициента пропорционального влияет например на интегральный канал.

Пропорциональный канал выдает величину выходного сигнала, который рассчитывается как ошибка (разница, рассогласование) e(t) сигнала обратной связи (ОС) и сигнала задания r, умноженная на коэффициент Kp, который опять же может быть выражен и как 1/Tp — постоянная времени пропорционального канала регулятора. Если убрать (обнулив коэффициенты) остальные составляющий ПИД-регулятора, то результат такого регулятора будет иметь статическую ошибку, тк пропорциональный канал может только компенсировать часть рассогласования. Дальнейшее увеличение значение коэффициента в попытках увеличить эффективность, приведет к перерегулированию (превышению величины над уставкой, иногда многократному и повторяющемуся, в худшем случае в виде автоколебаний) при появлении большого рассогласования (например пуск или резкое изменение параметра). Данный канал отвечает за быстродействие регулятора в целом и наибольшую часть работы (компенсация большей части рассогласования).
Интегральный канал в общем тоже берет за основу ошибку регулирования, но при этом выход интегрирует эту ошибку, умноженную на коэффициент Ki (1/Ti). Это дает возможность компенсации статической ошибки, если система не испытывает внешних возмущений (со временем конечно, если процесс не устойчивый, это событие может и не наступить), но не избавляет от динамической. Попытки уменьшить динамическую ошибку или как-то уменьшить время, за которое регулятор компенсирует ошибку, приведут к тому, что тоже появится перерегулирование и почти гарантировано автоколебания (ну как минимум несколько затухающих даже на фоне отсутствия перерегулирования в целом, если пропорциональный канал имеет слабое значение).
Дифференциальный канал подает на выход скорость изменения ошибки de/dt, умноженную на коэффициент Kd (1/Td), что дает возможность как бы предугадать описанное выше резкое изменение рассогласования (пуск или резкое изменение параметра) и тем самым помочь своим более медленным братьям компенсировать величину ошибки. В дальнейшем, когда вступят в дело каналы пропорциональный и интегральный, роль дифференциального канала должна затухать. Конечно отыграют и электрические составляющие, и задержка расчета, и механика с инерцией, которая часто является самой долгой в перечне задержек, но что-то все же можно получить и от этого канала. Дифференциальный канал чувствителен к ВЧ-помехам. Поэтому, при построении системы регулирования, необходимо принять меры для защиты от помех. Кстати в теории дифференциальный канал может уменьшить значение перерегулирования, полученного при настройки пропорционального и интегрального канала за счет более быстрого уменьшения ошибки регулирования до вмешательства других каналов.

Итак теперь перейдем непосредственно к методам настройки

Ручная настройка или метод настройки «по графикам».

Часто можно услышать о простейшем подходе к настройке (сейчас говорим о ручной), когда вручную настраивают сперва Kp, предварительно обнулив остальные каналы, потом Ki, а последним Kd, оценивая результат работы чисто по графикам процессе (так называемый эмпирический и эвристический методы), либо пользуясь ТАУ (нахождение частоты устойчивости и отступ от нее на 2-4 лога), такая инструкция встречается практически для всех ПЧ и даже сервоприводов, возможно это оправдано тем, что процесс быстрый и графики можно получить без особых затрат просто перебирая коэффициенты по логарифмической шкале, но для температуры так будет настраивать неудобно. Да-да если коэффициент равный двум слишком мал, а введение в коэффициент цифры 4 не дало необходимого изменения, нет смысла вводить K=6, нужно вводить 8, а потом 16, смысл в том, что мы тем самым ищем нужную нам частоту среза, а она как многие помнят из ТАУ у нас на логарифмической шкале выложена, и если она далеко, то перебор по обычной шкале сильно удлинит время поиска.

Важное замечание: даже для одного и того же объекта процедуру настройки ПИД регулятора следует повторять, если изменились параметры объекта (например, загрузка печи) или значительно изменилась рабочая температура (остывание и соответственно отток мощности зависит от градиента температур).

Второй вариант больше подходит для долгих процессов (температура) — предварительно нужно вывести систему на границу устойчивости. Для этого нужно вывести регуляторы И и Д (записать нули), оставив только П (пропорциональный), устойчивость необходимо проверять на той температуре, которая близка к рабочей, то есть эксперименты с большим Кр нужно проводить уже после выхода на установившийся процесс, до этого лучше постараться выбрать коэффициент поменьше, либо уменьшить его уже когда перескочили уставку. На установившемся процессе добиваемся увеличением Кп коэффициента появления заметных колебаний, либо если колебания уже есть, то уменьшаем Кр до их исчезновения, полученный коэффициент Кркр запомним. Что делать с полученной частотой среза (частота, на которой настройка теряет устойчивость)? Переведем ее в период колебаний τ (хотя можно сразу измерить именно период колебаний τ). Далее для термоконтроллеров Термодат предлагает следующую таблицу.

Тип регулирования	Пропорциональный коэффициент Kp	Интегральный коэффициент Ki	Дифференциальный коэффициент Kd
Только P	2*Кркр	Выключено	Выключено
P+I	2.2*Кркр	0.8* τ	Выключено
P+I+D	1.7*Кркр	0.5*τ	0.12*τ

Для других применений думаю лучше пользоваться методом «по графикам» для ручной настройки.

Тангенциальный метод настройки ПИД-регулятора (первый метод Зиглера-Никольса).

Следующий метод, который предлагается опять же для настройки ПИД регулировки температуры, это Тангенциальный метод.
В тангенциальном методе для нахождения ПИД коэффициентов используется переходная характеристика объекта, в случае терморегулирования кривая разогрева объекта.

Для начала опишу метод, который предлагается производителем приборов Термодат (коэффициенты соответственно могут отличаться у разных производителей).

В режиме ручного управления контроллера задается некоторое значение мощности на нагрузке. Значение мощности должно быть таким, чтобы установившаяся температура не превысила допустимого значения. Нужно дождаться установления температуры Т1, в этом режиме и в некоторый момент времени скачком изменить значение мощности (например: на 5%). Записать процесс изменения температуры (на компьютере, на самописце или по точкам, вручную) до установления нового устоявшегося значения температуры Т2.

Провести касательную к полученной кривой в точке, где наклон касательной будет максимален.
Определить «мёртвое» время процесса как промежуток времени, прошедший с момента изменения мощности до момента времени, определяемого точкой пересечения касательной и средней линии температуры первого устойчивого состояния Т1 (до изменения мощности нагрева).
Определить величину относительного наклона касательной по формуле:
К = (∆T/∆t)/∆N.
∆T — изменение температуры в °С,
∆t — соответствующее изменение времени в секундах,
∆N — изменение мощности в %.

Установите значения коэффициентов Kp, Ki, Kd в соответствии с таблицей.

Тип регулирования	Пропорциональный коэффициент Kp	Интегральный коэффициент Ki	Дифференциальный коэффициент Kd
Только P	100τмК	Выключено	Выключено
P+I	111τмК	3.3*τм	Выключено
P+I+D	83τмК	2*τм	0.25*τм

К сожалению данный метод имеет еще пару трактовок, посему приведу обе, а решать какая лучше подойдет вам. Оба используют только два параметра для описания объекта, проводится линия по участку, соответствующему максимальному наклону графика переходной характеристики.

Первый вариант основан на поиске мертвого времени и длительности переходного процесса.

В первом случае ищется пересечение с осью времени и с мнимой линией максимального задания, значения параметров L и T, используются в расчете, формулы приведены в таблице:

Тип регулирования	Пропорциональный коэффициент Kp	Интегральный коэффициент Ti=Kp/Ki	Дифференциальный коэффициент Td=Kd/Kp
Только P	T/L	Выключено	Выключено
P+I	0.9*T/L	L/0.3	Выключено
P+I+D	1.2*T/L	2*L	0.5*L

Второй вариант использует: a и L, которые определяются по графику переходной характеристике объекта управления так:

Формулы для расчета коэффициентов сведены в следующую таблицу:

Тип регулирования	Пропорциональный коэффициент Kp	Интегральный коэффициент Ti	Дифференциальный коэффициент Td
Только P	1/a	Выключено	Выключено
P+I	0,9/a	3*L/Kp	Выключено
P+I+D	1,2/a	0,9*L/Kp	0.5*L/Kp

Замечание: метод Зиглера-Никольса даёт параметры, далёкие от оптимальных. Это объясняется не только упрощённостью самого метода (он использует только 2 параметра для описания объекта), но и тем, что параметры регулятора в этом методе определялись Зиглером и Никольсом, исходя из требования к декременту затухания, равному 4, что и даёт медленное затухание процесса колебаний.

Метод Зиглера-Никольса никак не учитывает требования к запасу устойчивости системы, что является вторым его недостатком. Судя по медленному затуханию переходного процесса в системе, этот метод даёт слишком малый запас устойчивости. Но все же для начальной настройки вполне пойдет.

Метод колебаний (или второй частотный метод Зиглера-Никольса)

Данный метод основан на поиске частоты устойчивости, на которой сдвиг по фазе в разомкнутом контуре равен 180°.

Назначить уставку Тус, равной температуре регулирования (или 0.7Тус, если перегрев во время настройки нежелателен, а он может быть значительным).

Тоже существует два варианта, первый упрощенный от Термодата:

Включить позиционный (пороговый) режим регулирования.

В установившемся режиме колебаний температуры измерить период τ колебаний температуры (время между соседними максимальными или минимальными значениями температуры). Измерить также полный размах колебаний температуры ΔТ=Тmax-Тmin (разность максимального и минимального значений температуры).

Установите значения коэффициентов Kp, Ki, Kd в соответствии с таблицей. Параметр «Ограничение ПИД» или «Зона» (если он есть в приборе) сделать равным Kp.

Тип регулирования	Пропорциональный коэффициент Kp	Интегральный коэффициент Ki	Дифференциальный коэффициент Kd
Только P	1.4*∆Т	Выключено	Выключено
P+I	1.6*∆Т	2.4*τ	Выключено
P+I+D	1.2*∆Т	1.5*τ	0.2*τ

Второй вариант такой:
Настройка пропорциональной компоненты (Kp)
1.Перед настройкой зоны пропорциональности интегральная и дифференциальная компоненты отключаются (Kи =0, Kд = 0) и задаем некоторое целевое значение регулируемого параметра (например, температуры):

Тο — начальная температура в системе;
Тsp — заданная температура (уставка);
∆T — размах колебаний температуры (в расчетах не участвует);
∆t — период колебаний температуры.
2.Меняем значение пропорциональной составляющей Kp от минимума (можно от 0) до момента, пока не появятся устойчивые колебания системы с периодом ∆t. Фиксируем это значение как Kуст, а также период колебаний системы ∆t. Система должна находится в постоянном колебательном процессе, притом колебательный процесс незатухающий, колебания должны быть одинаковы относительно Тsp.
После получения данной кривой на нашем объекте, засекаем время периода колебаний ∆t – полный период. Данное время есть характеристика системы, оборудования.
3.На этом практическая часть метода заканчивается. Из полученных значений рассчитываем коэффициенты ПИД:
Kp=0.6⋅Kуст
Ki=(2⋅Kp)/∆t
Kd=(Kp⋅∆t)/8
Здесь Kуст – тот самый коэффициент пропорциональной составляющей, при котором возникли колебания, а ∆t – период этих колебаний.

Второй вариант, когда надо найти постоянные времени Ti и Td

Используя полученные параметры рассчитываем Ти и Тд по таблице.

	Пропорциональный коэффициент Kp	Интегральный коэффициент Ti	Дифференциальный коэффициент Td
П-регулятор	0.5*Kуст
ПИ-регулятор	0.4*Kуст	0.8*∆t/Kp
ПИД-регулятор	0.6*Kуст	0.5*∆t/Kp	0.125*∆t/Kp

Хочется сказать, что данный метод не несет за собой никаких улучшений, просто он построен на другом способе поиска, недостатки те же, что и у метода Зиглера-Никольса первого.

Метод CHR (Chien, Hrones и Reswick) или Чина-Хронеса-Ресвика, если по-русски

Этот метод предполагает предварительное определение времени задержки L и времени выравнивания T по переходной характеристике объекта. Ну это мы делали и для Зиглера-Никольса, но в отличие от Зиглера и Никольса, которые использовали в качестве критерия качества настройки декремент затухания, равный 4, Chien, Hrones и Reswick (CHR) использовали критерий максимальной скорости нарастания при отсутствии перерегулирования или при наличии не более чем 20 процентного перерегулирования. Такой критерий позволяет получить больший запас устойчивости, чем в методе Зиглера-Никольса. Метод CHR даёт две разные системы параметров регулятора. Одна из них получена при наблюдении отклика на изменение уставки (таблица), вторая – при наблюдении отклика на внешние возмущения (не представлена). Какую систему параметров выбирать, зависит от того, что важнее для конкретного регулятора: качество регулирования при изменении уставки или ослабление внешних воздействий (в жизни изменение уставки вызывает намного более существенные процессы в регулятора, потому лучше настраивать по этой таблице, будет настройка не «в малом», а «в большом»). Если же важно и то и другое, то необходимо использовать регуляторы с двумя степенями свободы. Метод CHR использует аппроксимацию объекта моделью первого порядка с задержкой. В CHR используются те же исходные параметры a и L, что и в методе Зиглера-Никольса. Обратим внимание, что пропорциональный коэффициент в методе CHR меньше, чем в методе Зиглера-Никольса.

Формулы для определения коэффициентов приведены в таблице:

	Без перерегулирования	С 20% перерегулированием
Пропорциональный коэффициент Kp	Интегральный коэффициент Ti	Дифференциальный коэффициент Td	Пропорциональный коэффициент Kp	Интегральный коэффициент Ti	Дифференциальный коэффициент Td
П-регулятор	0.3/a			0.7/a
ПИ-регулятор	0.35/a	1.2*L/Kp		0.6/a	L/Kp
ПИД-регулятор	0.6/a	L/Kp	0.5*L/Kp	0.95/a	1.4*L/Kp	0.47*L/Kp

Остальные методы, а именно Спектральный метод, метод Куна, метод Стогестада, метод Шеделя требуют уже больших знаний ТАУ и самое главное требуют либо реальной переходной характеристики, которую придется искать методом интерполяции и аппроксимации, либо вовсе моделирования объекта управления. Если вкратце, то суть методов можно описать парой предложений.

Спектральный метод

Спектральный метод предполагает компенсацию нулями регулятора нежелательных полюсов объекта.

На основе полюсов объекта {p1, p2} определяются компенсирующие значения постоянных времени интегрального и дифференцирующего каналов:
Tи = |1/p1|, Tд = |1/p2|.

и коэффициенты регулятора Kp и Kd в виде:
Kp = Ki(Tи + Tд), Kd = Ki*Tи*Tд/(Tи + Tд).

Метод Куна

Параметром, характеризующим быстродействие любых рассматриваемых объектов, является суммарная постоянная времени. Метод настройки Куна (или метод «Т-правило») основан на аппроксимации объекта звеном третьего порядка. Параметры ПИД-регулятора Ti и Td выбирают, таким образом, чтобы компенсировать два полюса. Расчетные значения для регулятора даны в таблице, но я здесь ее приводить не стану.

Метод Стогестада

По идентифицированным параметрам модели ОУ находят необходимые параметры настройки регулятора. Принцип синтеза ПИД-регулятора с использованием метода Стогестада заключается в следующем: задание желаемого вида переходной характеристики замкнутой САУ (желаемый вид описывается инерционным звеном первого порядка) путем выбора постоянной времени.

Для апериодического звена второго порядка с транспортным запаздыванием параметры ПИД-регулятора могут быть найдены по следующим формулам:
kp = T1/k*(Tc+τ), Ti=min[T1;c(Tc+τ)],Td=T2.
где T1, T2, k и τ–параметры объекта; с–параметр, который рекомендуют принимать равным 4, для обеспечения апериодического вида переходного процесса на выходе системы управления (например пароперегревателем котла).

Метод Шеделя

Метод Шеделя основан на принципе каскадного коэффициента демпфирования. В методе обобщается понятие коэффициента демпфирования на случай системы 3-го порядка. Параметры ПИД-регулятора должны быть выбраны таким образом, чтобы коэффициенты демпфирования системы принимали определенные значения. Их если будет интересно лучше поискать в справочниках.

Источник

3.2. Критерии устойчивости сар

1.4. Статическое и астатическое регулирование

Реализация регулятора в ПЛК

Теперь необходимо определиться с терминологией

Что такое ПИД регулятор?

Как работают значения PID, их изменение

Усиление P

Усиление I

Усиление D

Назначение ПИД регулятора

Пример схемы регулирования температуры

Три коэффициента ПИД регулятора и принцип работы

Не все проблемы из-за плохих настроек PID

Вибрация

Центр тяжести (CG)

Настраивание ПИД-регулятора общего вида

Регулятор пропорционального типа

Регулятор интегрального типа

Регулятор дифференциального типа

ПИД-регулятор

Пример

Формула ПИД-регулятора

Настройка ПИД регулятора

Как настроить PID по шагам

Составляющие сигнала ПИД-регулятора

Настройки ПИД-регулятора

Пример применения ПИД-регулятора в частотно-регулируемом приводе насоса

Вопрос: «Какие у тебя ПИДы?» — неправильный вопрос!

Примечания и советы

Death Rolls (крен смерти)

Дополнительная информация для версии BetaFlight 3 (3.0 и 3.1)

Формула ПИД-регулятора

Когда нужно перенастраивать PID?

Динамическая ошибка

Ручная настройка или метод настройки «по графикам».

Тангенциальный метод настройки ПИД-регулятора (первый метод Зиглера-Никольса).

Метод колебаний (или второй частотный метод Зиглера-Никольса)

Метод CHR (Chien, Hrones и Reswick) или Чина-Хронеса-Ресвика, если по-русски

Спектральный метод

Метод Куна

Метод Стогестада

Метод Шеделя

Не пропустите эти материалы по теме: