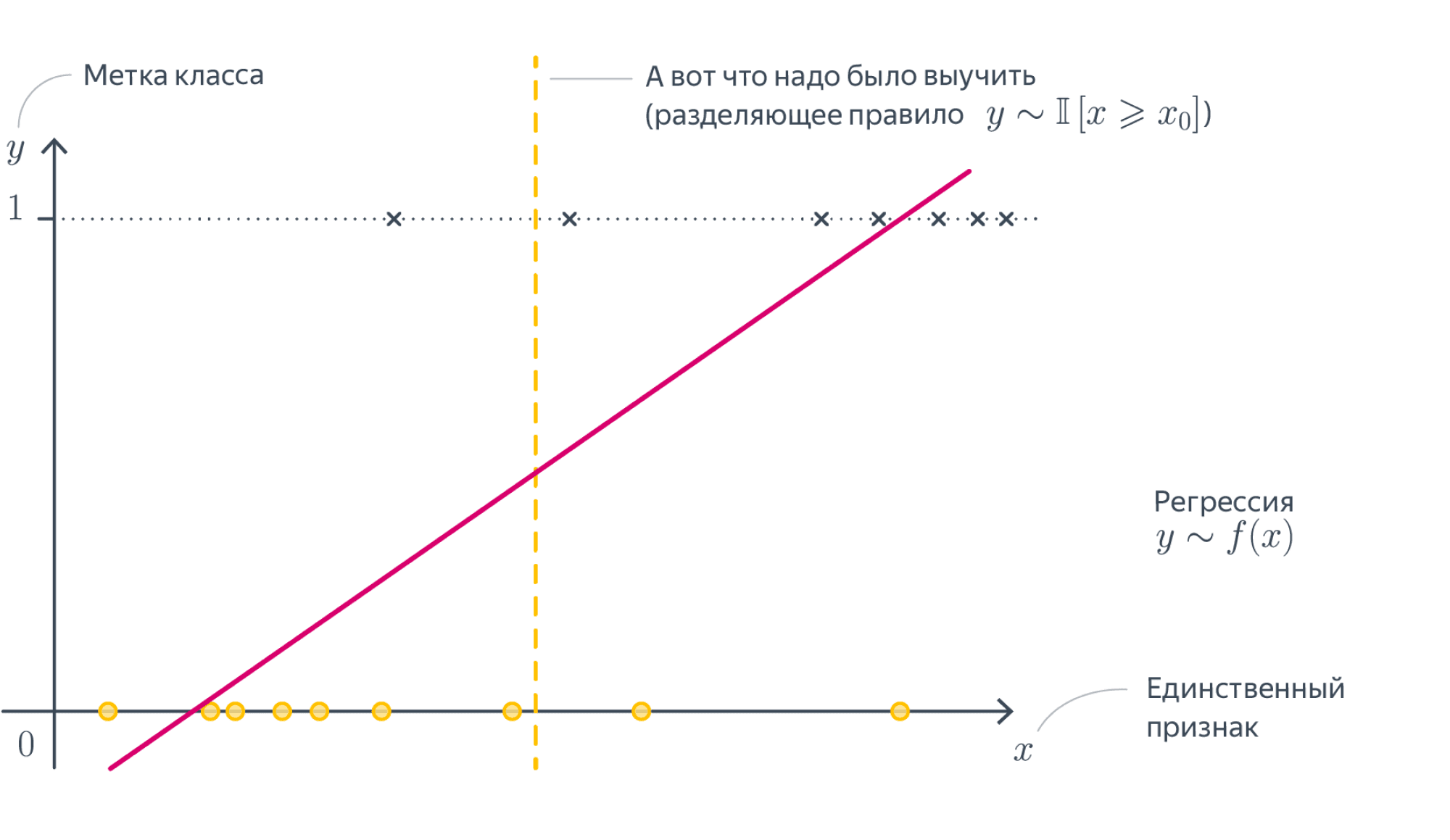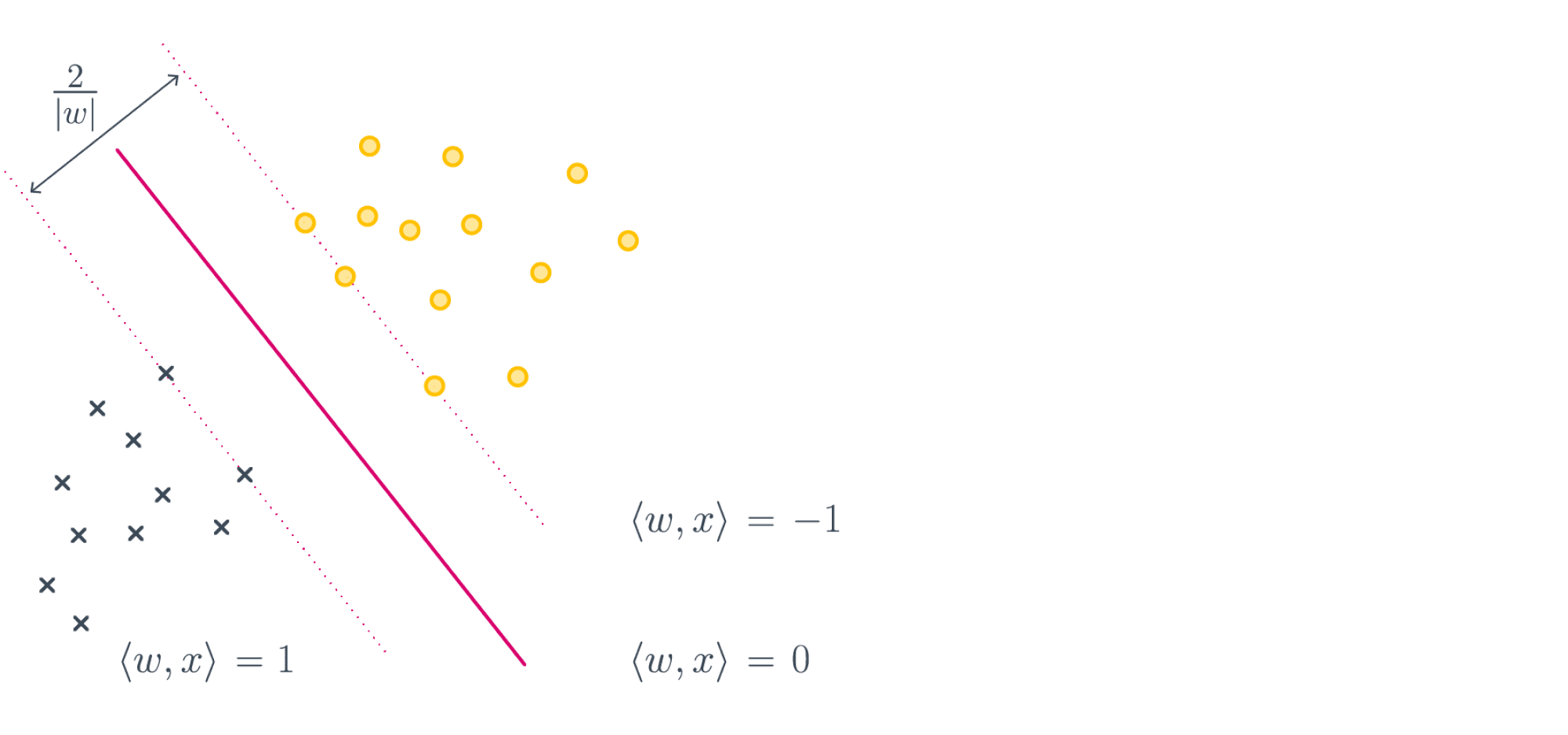1. Что такое объект, целевая переменная, признак, модель, функционал ошибки и обучение?
Объект – некая абстрактная сущность, с которой мы хотим работать и для которой хотим делать предсказания.
Пространство объектов – множество всех возможных объектов в данной задаче.
Целевая переменная – некая характеристика объекта, которую мы хотим научиться предсказывать с помощью методов машинного обучения. Обычно объект обозначается (x), пространство объектов — (mathbb{X}). Целевая переменная обозначается — (y), пространство ответов — (mathbb{Y}).
Объекты описываются с помощью своих характеристик, называемых признаками (т.е. признак – некая характеристика объекта), вектор признаков является признаковым описанием объекта. Мы будем отождествлять объект и его признаковое описание.
Модель – некоторый алгоритм, позволяющий предсказывать целевую переменную по признаковому описанию объекта. По сути, это функция (a: mathbb{X} to mathbb{Y}).
Функционал качества позволяет оценить качество работы такого алгоритма, при этом, если функционал устроен так, что его нужно минимизировать, будем называть его функционалом ошибки. Функционал обозначается (Q(a, X)) и чаще всего представляет собой сумму ошибок на отдельных объектах, а функция, измеряющая ошибку на одном объекте, называется функцией потерь.
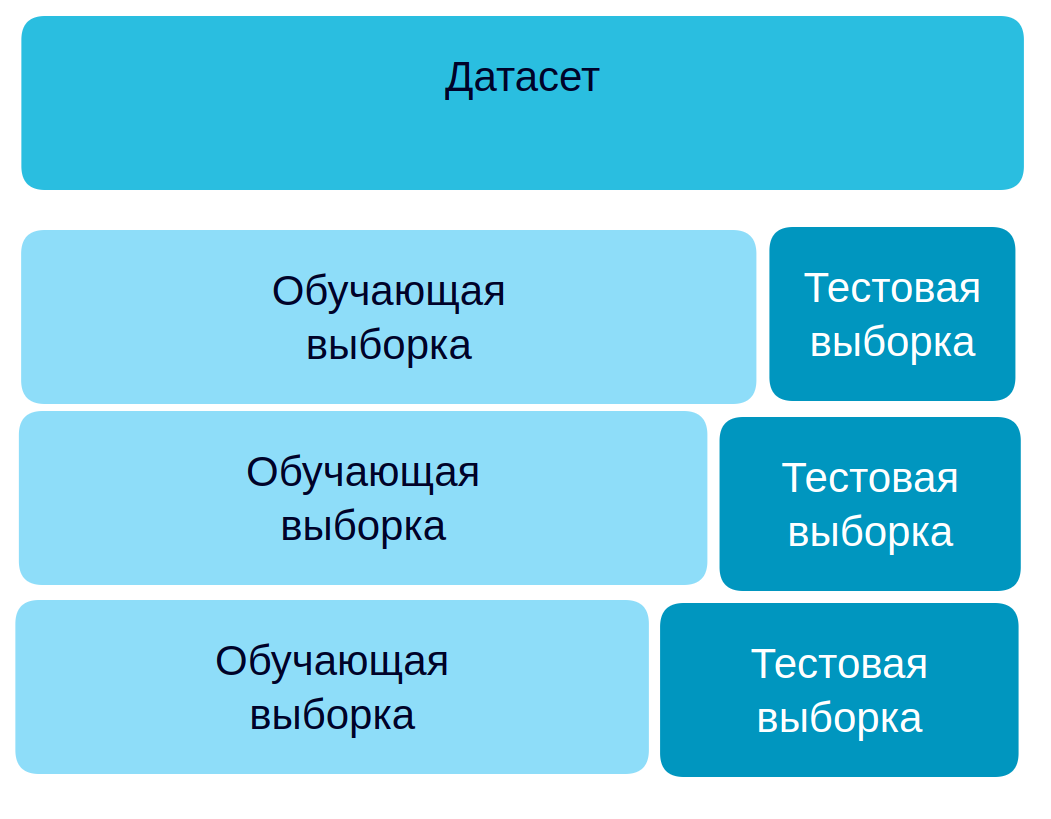
Пусть нам дано множество объектов (mathbb{X}) — матрица объекты-признаки — с известными ответами (mathbb{Y}). Назовем совокупность ((mathbb{X}), (mathbb{Y})) обучающей выборкой. Обучением будем называть процесс построения оптимального с точки зрения функционала ошибки на обучающей выборке алгоритма (a).
2. Запишите формулы для линейной модели регрессии и для среднеквадратичной ошибки. Запишите среднеквадратичную ошибку в матричном виде.
Линейная модель:
[
mathbb{A}
=
{
a(x) = w_0 + w_1 x_1 + dots + w_d x_d|w_0, w_1, dots, w_d in mathbb{R}
}
], где через (x_i) обозначается значение (i) -го признака у объекта (x), a (d) – количество объектов, (w_{i}) – вес для $i$-го признака.
MSE:
В общем виде
[
Q(a,X)=frac{1}{ell}sum_{i=1}^{ell}(a(x_{i})-y_{i})^{2}
], где (a(x)) – модель, (l) – количество объектов.
Для некой модели (a(x)) описанной выше
[
frac{1}{ell}sum_{i = 1}^{ell} left(w_0+sum_{j = 1}^{d}w_j x_{ij}-y_iright)^2tomin_{w_0, w_1,dots, w_d}.
]
В матричном виде
[
frac{1}{ell}||Xw-y||^{2}_{2}to min_{w}
]
[
Q(w)=(y-Xw)^{T}(y-Xw)
]
где (X) — матрица объекты-признаки, (w) — вектор весов, (y) — вектор целевых значений,(||x||^{2}_{2}) — L2 норма (квадратный корень из суммы квадратов значений вектора)
3. Что такое коэффициент детерминации? Как интерпретировать его значения?
[
R^{2}(a,X)=1-frac{sum_{i=1}^{l}(a(x_{i}-y_{i})^{2})}{sum_{i=1}^{l}(y_{i}-hat{y})^{2}}
]
Коэффициент детерминации измеряет долю дисперсии, объяснённую моделью, в общей дисперсии целевой переменной. Фактически, данная мера качества это нормированная среднеквадратичная ошибка. Если она близка к единице, то модель хорошо объясняет данные, если же она близка к нулю, то прогнозы сопоставимы по качеству с константным предсказанием.
4. Чем отличаются функционалы MSE и MAE?
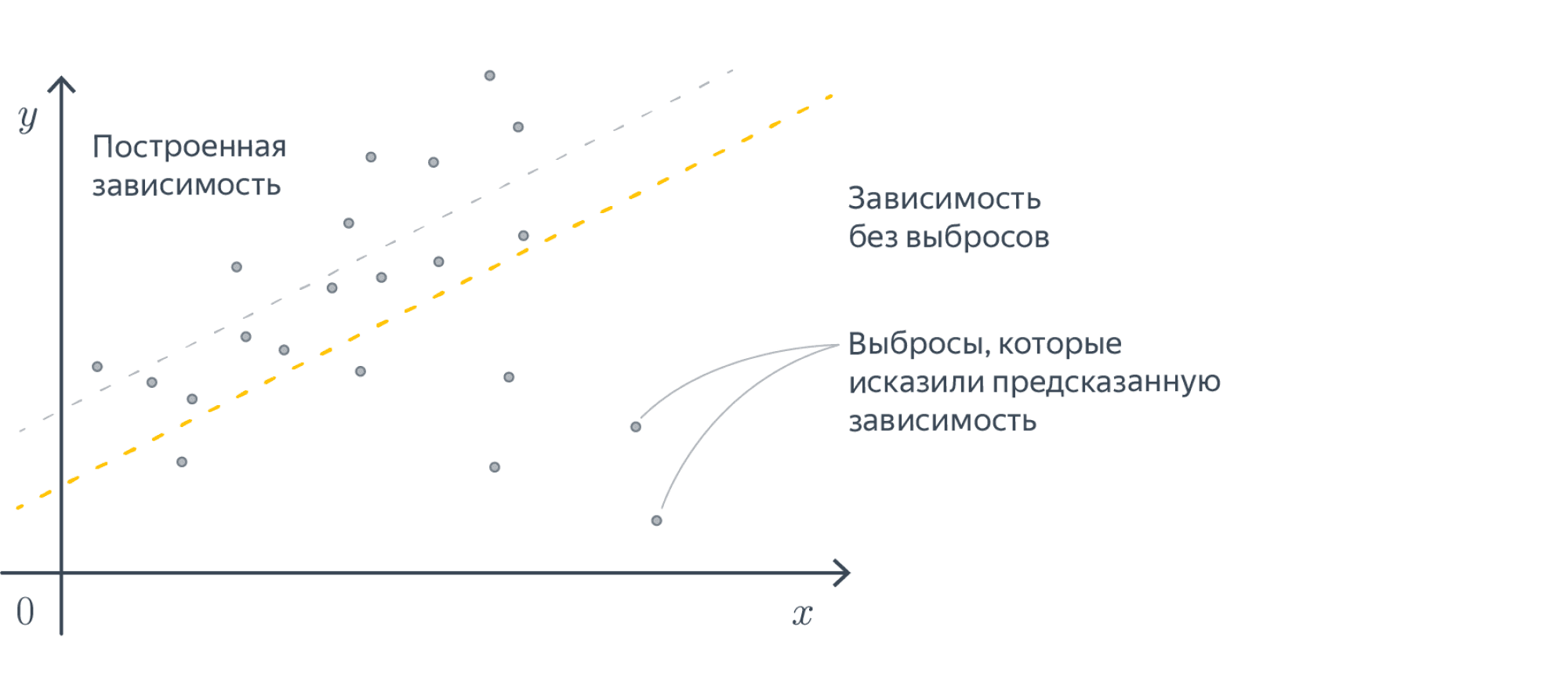
- MAE более устойчива к выбросам (но гораздо менее точна при приближении к минимуму (произв не содержит инф о близости к экстремуму (в 0 вообще ее нет)) и большим значениям
- MSE увеличит ошибку из-за возведения в квадрат из-за чего появится некоторое искажение реальной ошибки. Если выбросов больше чем нормальных объектов, то устойчивость MAE пропадает.
5. Как устроены робастные функции потерь (Huber loss, log-cosh)? Чем log-cosh лучше функции потерь Хубера?
Huber loss
Huber Loss объединяет в себе MSE и MAE с параметром дельта, этот параметр определяет, что мы считаем за выброс. При (deltarightarrow0) функция потерь Хубера вырождается в абсолютную функцию (MAE) потерь, а при (deltarightarrowinfty) — в квадратичную (MSE). Не имеет вторую производную
[
L_delta(y, a)=
left{begin{aligned}
½ (y — a)^2, quad |y — a| < delta \
&delta left(|y — a| — frac12 delta
right), quad |y — a| geq delta
end{aligned}
right.
]
Log Cosh
Log Cosh (логарифм от гиперболического косинуса) имеет вторую производную. Как и в случае с функцией потерь Хубера, для маленьких отклонений здесь имеет место квадратичное поведение, а для больших — линейное.
[
L(y,a)=log(cosh(a-y))
]
Сравнение
Log Cosh > Huber Loss т.к. Вторая производная в Хубере имеет разрывы, Log Cosh же без разрывов, не нужно подбирать параметр дельта.
6. Что такое градиент? Какое его свойство используется при минимизации функций?
Градиент — направление наискорейшего роста функции, а антиградиент (т.е. (−nabla f) ) направлением наискорейшего убывания функции. Это ключевое свойство градиента, обосновывающее его использование в методах оптимизации.
7. Как устроен градиентный спуск?
Пусть (w^0) начальный набор параметров (например, нулевой или сгенерированный из некоторого случайного распределения). Тогда градиентный спуск состоит в повторении следующих шагов до сходимости:
[
w^{(k)}=w^{(k — 1)}-eta_knabla Q(w^{(k — 1)})
]
Здесь под (Q(w)) понимается значение функционала ошибки для набора параметров (w).
Через (eta_k) обозначается длина шага, которая нужна для контроля скорости движения.
Можно делать её константной: (eta_k = c). При этом если длина шага слишком большая, то есть риск постоянно <перепрыгивать> через точку минимума, а если шаг слишком маленький, то движение к минимуму может занять слишком много итераций. Иногда длину шага монотонно уменьшают по мере движения — например, по простой формуле ((frac{1}{k})).
8. Почему не всегда можно использовать полный градиентный спуск? Какие способы оценивания градиента вы знаете? Почему в стохастическом градиентном спуске важно менять длину шага по мере итераций? Какие стратегии изменения шага вы знаете?
Использование полного градиентного спуска может быть очень трудоёмко при больших размерах выборки. В то же время точное вычисление градиента может быть не так уж необходимо — как правило, мы делаем не очень большие шаги в сторону антиградиента, и наличие в нём неточностей не должно сильно сказаться на общей траектории. Опишем несколько способов оценивания полного градиента.
SGD
[
w^{(k)}=w^{(k — 1)}-eta_knabla q_{ik}(w^{(k — 1)})
] где (i_k) – случайно выбранный номер слагаемого из функционала.
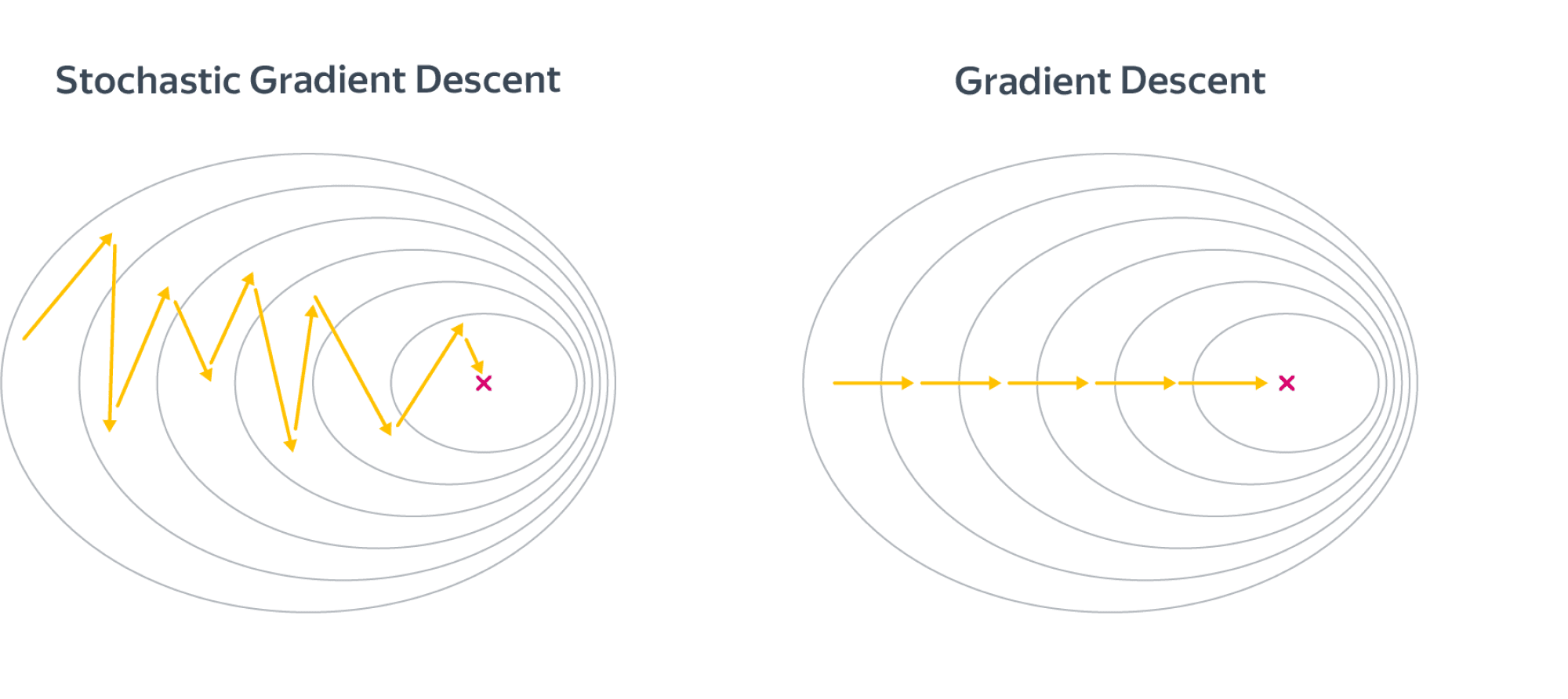
Параметры, оптимальные для средней ошибки на всей выборке, не обязаны являться оптимальными для ошибки на одном из объектов. Поэтому SGD метод запросто может отдаляться от минимума, даже оказавшись рядом с ним. Чтобы исправить эту проблему, важно в SGD делать длину шага убывающей – тогда в окрестности оптимума мы уже не сможем делать длинные шаги и, как следствие, не сможем из этой окрестности выйти. Разумеется, потребуется выбирать формулу для длины шага аккуратно, чтобы не остановиться слишком рано и не уйти от минимума. В частности, сходимость для выпуклых дифференцируемых функций гарантируется (с вероятностью 1), если функционал удовлетворяет ряду условий (как правило, это выпуклость, дифференцируемость и липшицевость градиента) и длина шага удовлетворяет условиям Роббинса-Монро:
[
sum_{k = 1}^{infty} eta_k = infty; quad
sum_{k = 1}^{infty} eta_k^2 < infty.
]
Этим условиям, например, удовлетворяет шаг (eta_k = frac{1}{k}).
Примеры использования
(eta_{k}=frac{1}{k})
(eta_{k}=lambda(frac{s_{0}}{s_{0}+k})^{p})
SAG
На (k) -й итерации выбирается случайное слагаемое (i_{k}) и обновляются вспомогательные переменные:
[
z_i^{(k)}
=
begin{cases}
nabla q_i(w^{(k — 1)}),
quad
&text{если} i = i_k;\
z_i^{(k — 1)}
quad
&text{иначе}.
end{cases}]
[
w^{(k)}=w^{(k — 1)}-eta_kfrac{1}{ell}sum_{i = 1}^{ell}z_i^{(k)}
]
9. В чём заключаются метод инерции и AdaGrad/RMSProp?
Adagrad
В методе AdaGrad предлагается сделать свою длину шага для каждой компоненты вектора параметров. При этом шаг будет тем меньше, чем более длинные шаги мы делали на предыдущих итерациях
[
G_{kj} = G_{k-1,j} + (nabla_w Q(w^{(k-1)}))_j^2
]
[
w_j^{(k)} = w_j^{(k-1)} — frac{eta_t}{sqrt{G_{kj} + varepsilon}} (nabla_w Q(w^{(k-1)}))_j
]
недостаток: переменная (G_{kj}) монотонно растёт, из-за чего шаги становятся всё медленнее и могут остановиться ещё до того, как достигнут минимум функционала
RMSprop
Улучшение над AdaGrad. В этом случае размер шага по координате зависит в основном от того, насколько быстро мы двигались по ней на последних итерациях
[G_{kj} = alpha G_{k-1,j} + (1 — alpha) (nabla_w Q(w^{(k-1)}))_j^2.]
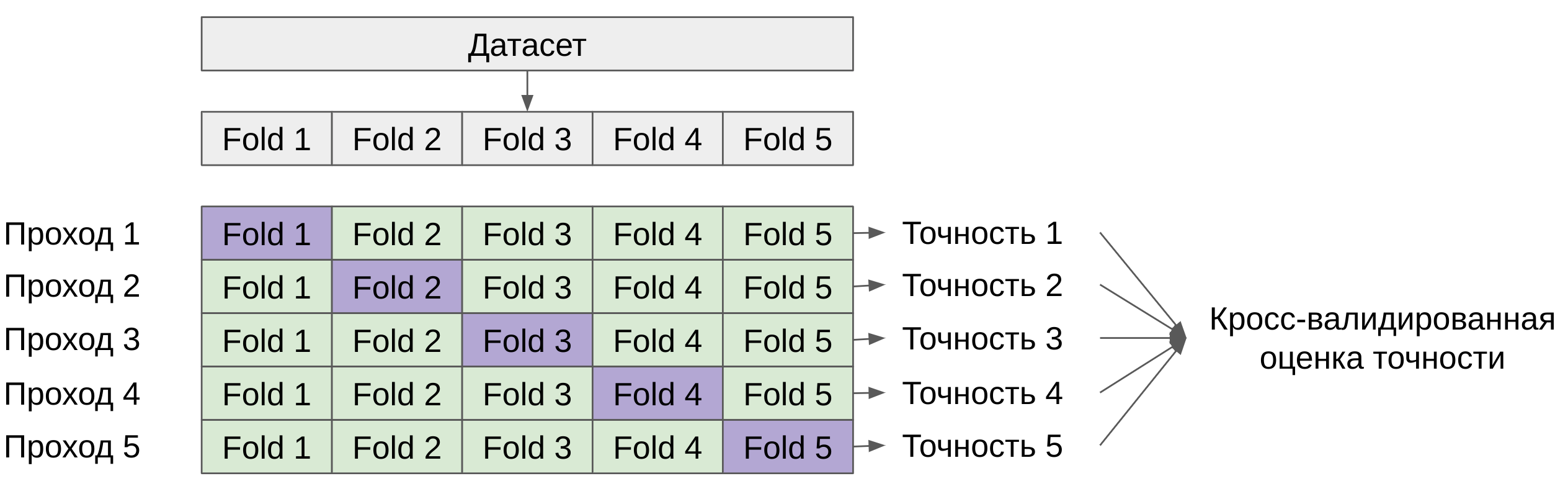
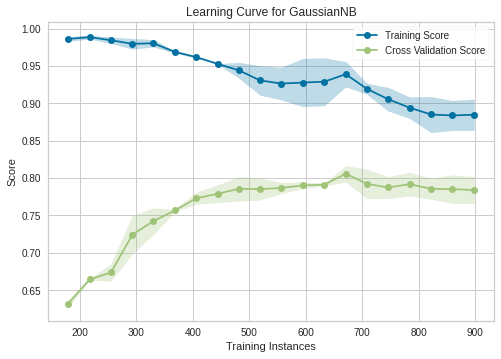
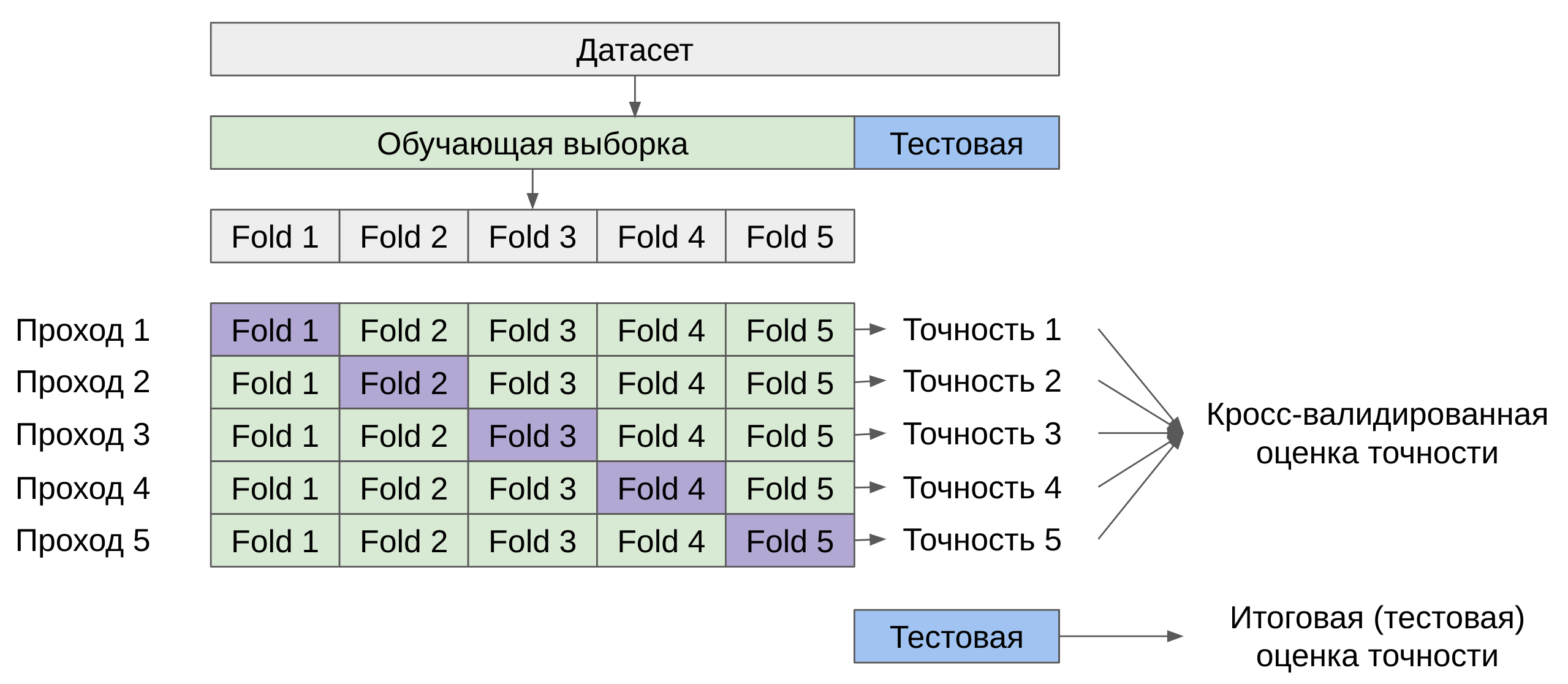
10. Что такое кросс-валидация? На что влияет количество блоков в кросс-валидации? Как построить итоговую модель после того, как по кросс-валидации подобраны оптимальные гиперпараметры?
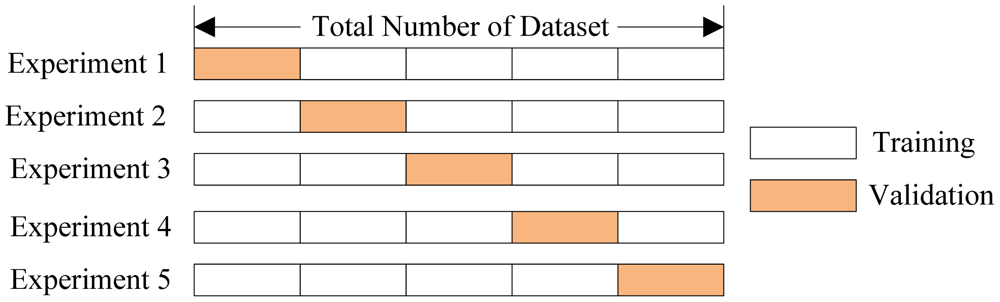
- CV – размеченные данные разбиваются на (k) блоков примерно одинакового размера. Затем обучается (k) моделей (a_1(x), dots, a_k(x)) причём (i) -я модель обучается на объектах из всех блоков, кроме блока (i).
После этого качество каждой модели оценивается по тому блоку, который не участвовал в её обучении, и результаты усредняются:
[text{CV}
=
frac{1}{k}
sum_{i = 1}^{k}
Qleft( a_i(x), X_i right).] - можно построить композицию из моделей (a_1(x), dots, a_k(x)), полученных в процессе кросс-валидации. Под композицией может пониматься, например, усреднение прогнозов этих моделей, если мы решаем задачу регрессии.
11. Чем гиперпараметры отличаются от параметров? Что является параметрами и гиперпараметрами в линейных моделях и в решающих деревьях?
- Параметры — величины, которые настраиваются по обучающей выборке
- Гиперпараметры — относят величины, которые контролируют сам процесс обучения и не могут быть подобраны по обучающей выборке
- Параметры для линейных моделей:
- Веса
- Гиперпараметр для линейных моделей:
- Коэффициент регуляризации
- Размер шага градиента
- Параметр для деревьев:
- Разбиение
- Гиперпараметр для деревьев:
- Глубина дерева
- Минимальное количество элементов в листьях
- Минимальное количество элементов для разбиения
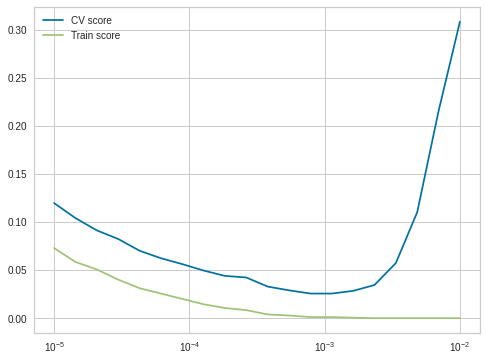
12. Что такое регуляризация? Запишите L1- и L2-регуляризаторы.
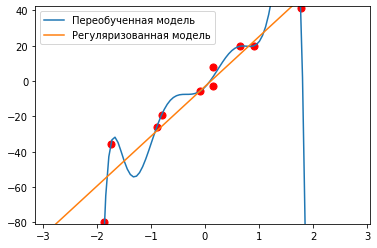
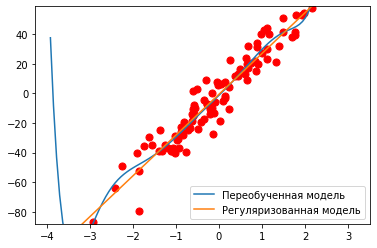
Регуляризация – способ штрафовать модель за высокую норму весов с помощью коэффициента регуляризации для предотвращения переобучения.
Наиболее распространенными являются (L_2) и (L_1) -регуляризаторы:
[
R(w) = |w|_2 = sum_{i = 1}^d w_i^2,
]
[
R(w) = |w|_1 = sum_{i = 1}^d |w_i|.
]
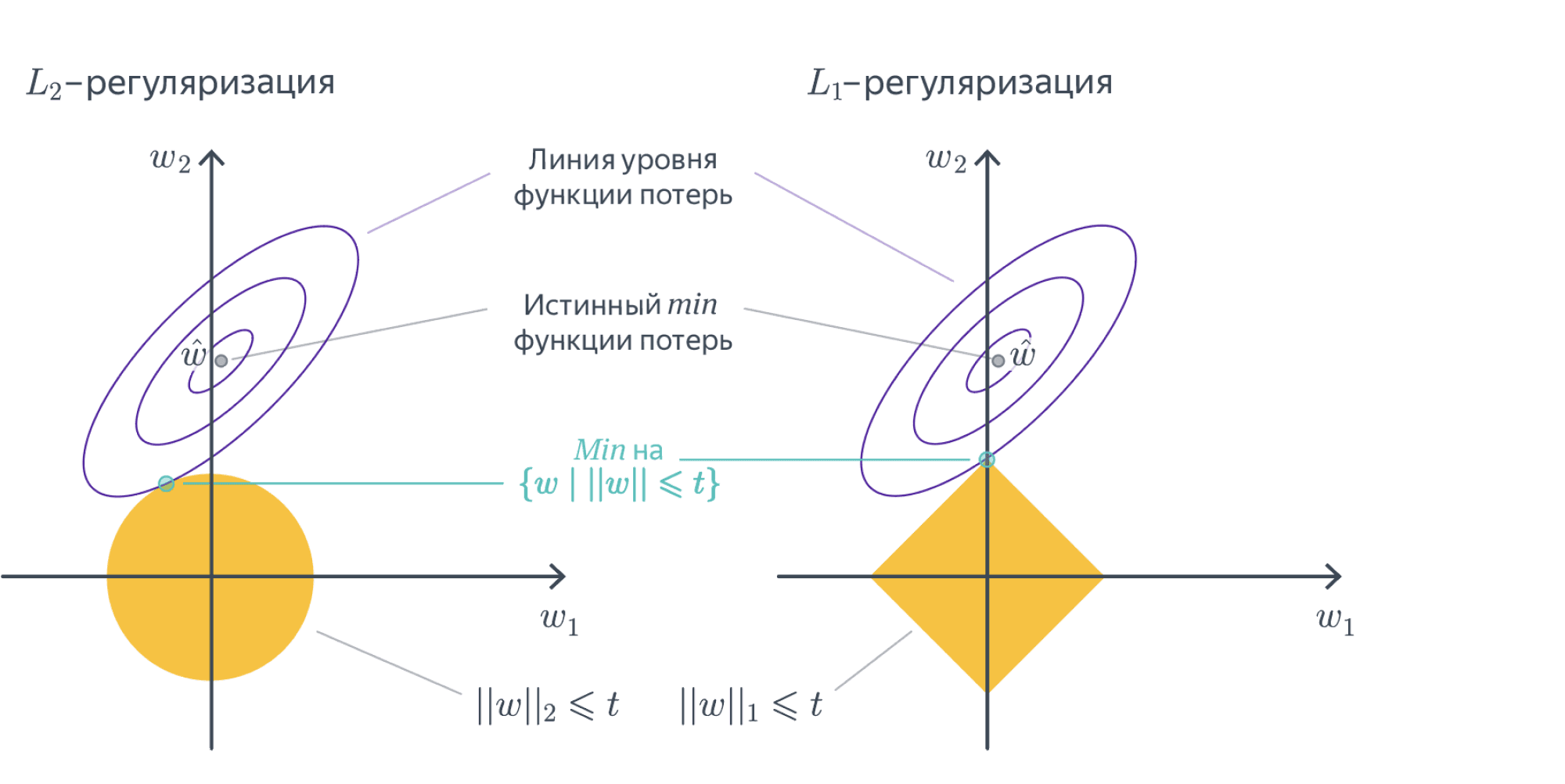
13. Почему L1-регуляризация отбирает признаки?
Зануление весов
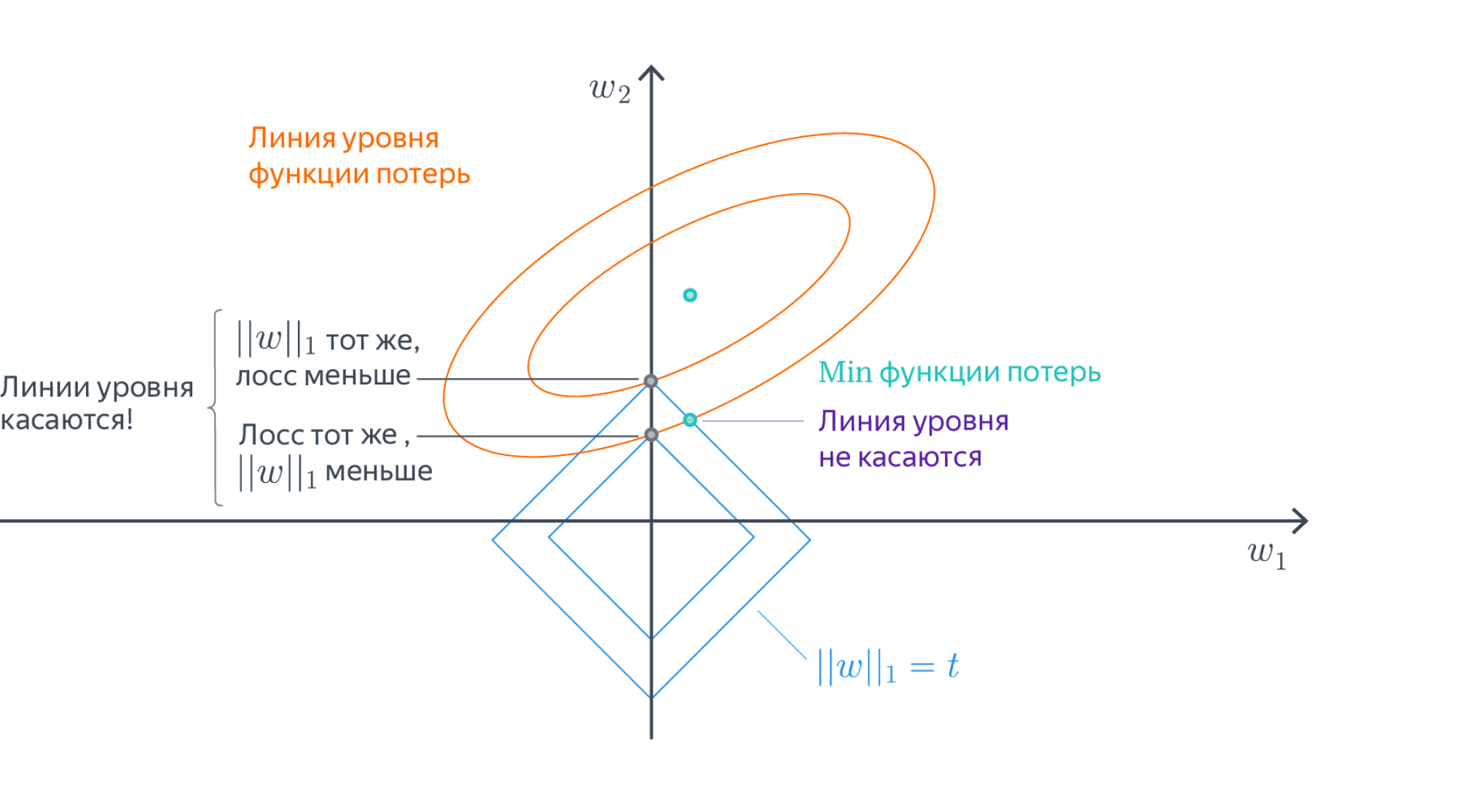
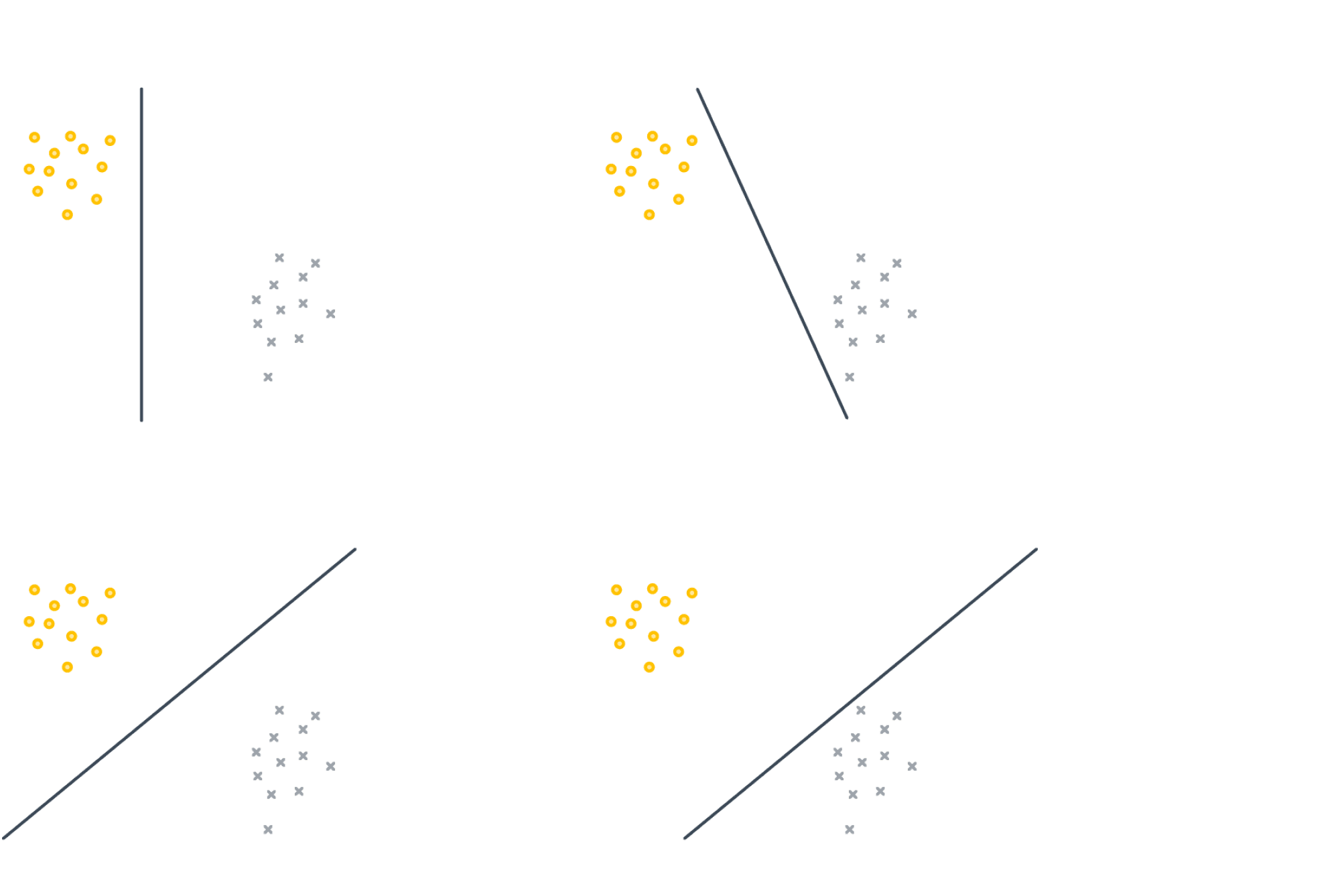
Можно показать, что если функционал (Q(w)) является выпуклым, то задача безусловной минимизации функции (Q(w) + alpha |w|_1) эквивалентна задаче условной оптимизации [Q(w) to min_{w}] [|w|_1 leq C] для некоторого (C). Изображены линии уровня функционала (Q(w)), а также множество, определяемое ограничением (|w|_1 leq C). Решение определяется точкой пересечения допустимого множества с линией уровня, ближайшей к безусловному минимуму. Из изображения можно предположить, что в большинстве случаев эта точка будет лежать на одной из вершин ромба, что соответствует решению с одной зануленной компонентой.
Штрафы при малых весах
Предположим, что текущий вектор весов состоит из двух элементов (w = (1, varepsilon)), где (varepsilon) близко к нулю, и мы хотим немного изменить данный вектор по одной из координат. Найдём изменение (L_2) — и (L_1) -норм вектора при уменьшении первой компоненты на некоторое положительное число (delta < varepsilon):
[|w — (delta, 0)|_2^2=1 — 2 delta + delta^2 + varepsilon^2]
[|w — (delta, 0)|_1=1 — delta + varepsilon]
Вычислим то же самое для изменения второй компоненты:
[|w — (0, delta)|_2^2=1 — 2 varepsilon delta + delta^2 + varepsilon^2]
[|w — (0, delta)|_1 =1 — delta + varepsilon]
Видно, что с точки зрения (L_2) -нормы выгоднее уменьшать первую компоненту, а для (L_1) -нормы оба изменения равноценны. Таким образом, при выборе (L_2) -регуляризации гораздо меньше шансов, что маленькие веса будут окончательно обнулены.
Проксимальный шаг
Проксимальные методы – это класс методов оптимизации, которые хорошо подходят для функционалов с негладкими слагаемыми. Формула для шага проксимального метода в применении к линейной регрессии с квадратичным функционалом ошибки и (L_1) -регуляризатором:
[w^{(k)}=S_{eta alpha} left(w^{(k — 1)}-etanabla_w F(w^{(k — 1)})right),]
где (F(w) = |Xw — y|^2) – функционал ошибки без регуляризатора, (eta) – длина шага, (alpha) – коэффициент регуляризации, а функция (S_{eta alpha}(w)) применяется к вектору весов покомпонентно, и для одного элемента выглядит как
[S_{eta alpha} (w_i)=
begin{cases}
w_i — eta alpha, quad &w_i > eta alpha\
0, qquad &|w_i| < eta alpha\
w_i + eta alpha, quad &w_i < -eta alpha
end{cases}]
Из формулы видно, что если на данном шаге значение некоторого веса не очень большое, то на следующем шаге этот вес будет обнулён, причём чем больше коэффициент регуляризации, тем больше весов будут обнуляться.
14. Почему плохо накладывать регуляризацию на свободный коэффициент? Почему регуляризация может странно работать на немасштабированных данных?
-
Отметим, что свободный коэффициент (w_0) нет смысла регуляризовывать — если мы будем штрафовать за его величину, то получится, что мы учитываем некие априорные представления о близости целевой переменной к нулю и отсутствии необходимости в учёте её смещения. Такое предположение является достаточно странным. Особенно об этом следует помнить, если в выборке есть константный признак и коэффициент (w_0) обучается наряду с остальными весами; в этом случае следует исключить слагаемое, соответствующее константному признаку, из регуляризатора.
-
Может быть большой разброс порядков весов.
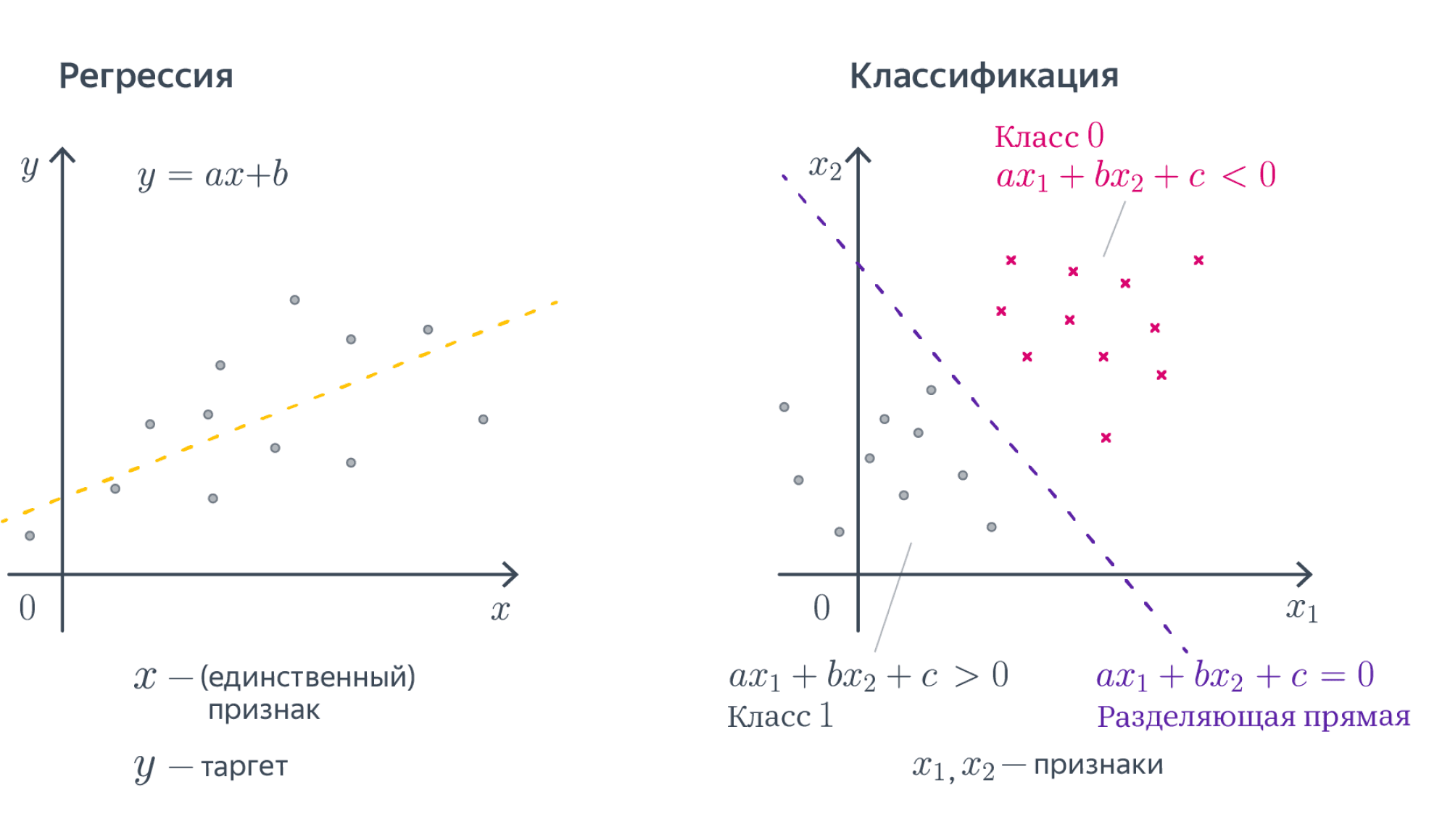
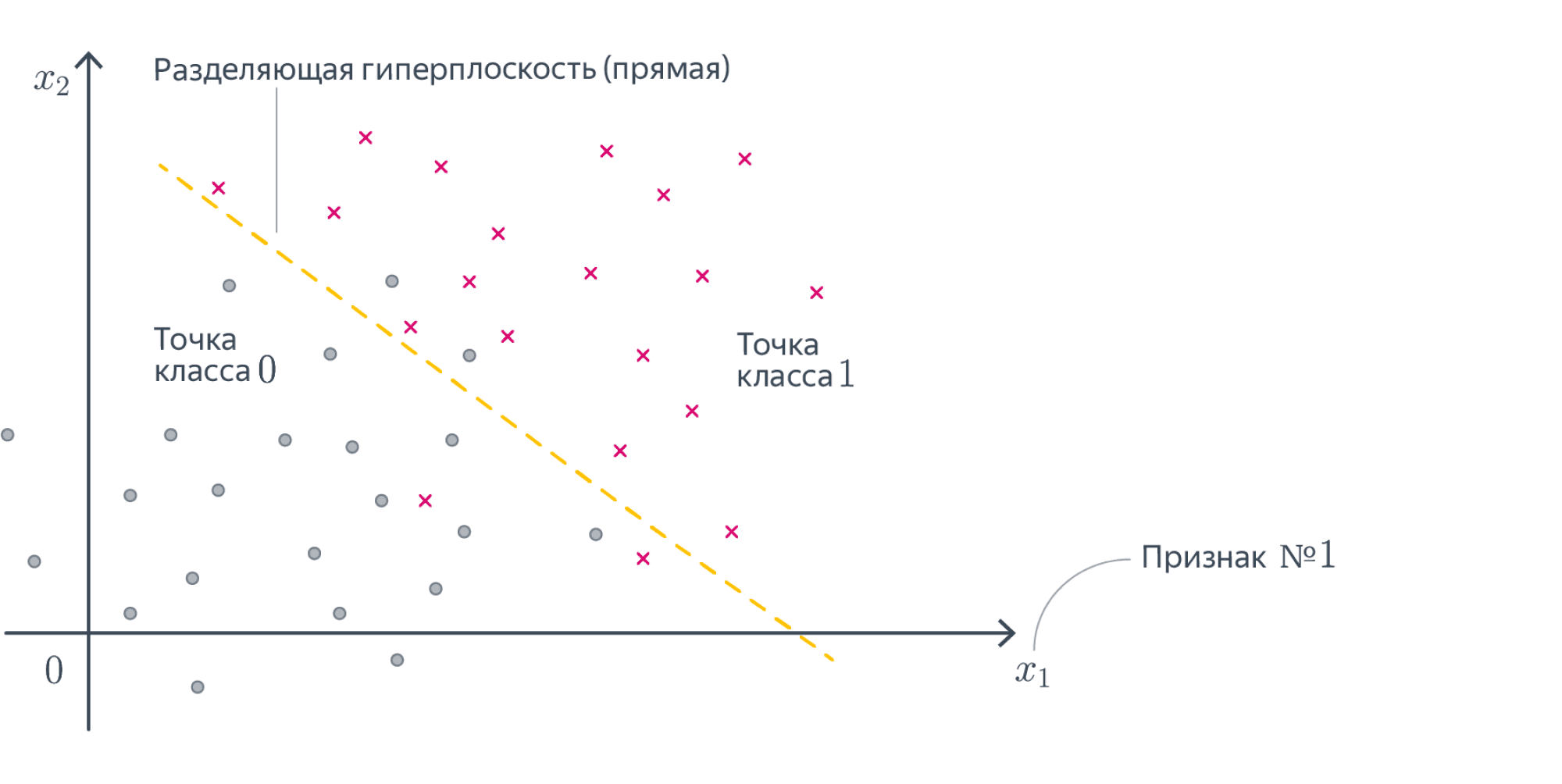
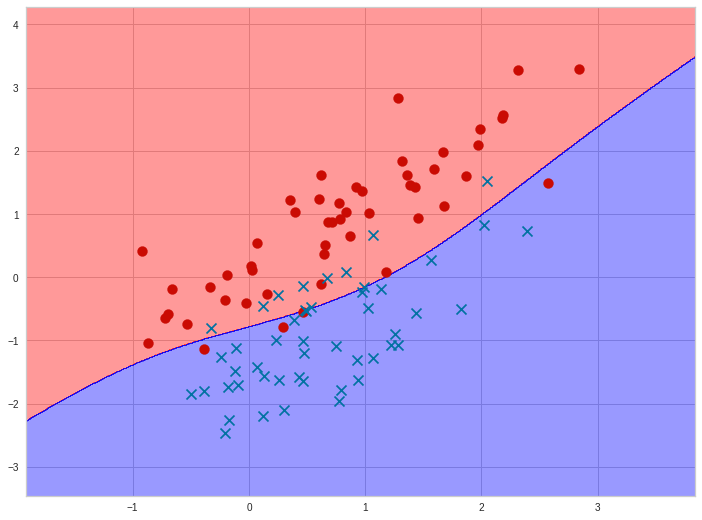
15. Запишите формулу для линейной модели классификации. Что такое отступ? Как обучаются линейные классификаторы и для чего нужны верхние оценки пороговой функции потерь?
Формула
[
a(x) = text{sign}left(
langle w, x rangle + w_0
right)
=
text{sign} left(
sum_{j = 1}^{d} w_j x_j + w_0
right)
]
Отступ
[
M_i = y<w,x_i>
]
Знак отступа говорит о корректности ответа классификатора (положительный отступ соответствует правильному ответу, отрицательный неправильному), а его абсолютная величина характеризует степень уверенности классификатора в своём ответе. Напомним, что скалярное произведение (<w,x_i>) пропорционально расстоянию от разделяющей гиперплоскости до объекта; соответственно, чем ближе отступ к нулю, тем ближе объект к границе классов, тем ниже уверенность в его принадлежности.
Обучение линейных классификаторов
Нам будет удобнее решать задачу минимизации, поэтому будем вместо этого использовать долю неправильных ответов
[
Q(a, X)=
frac{1}{ell}
sum_{i = 1}^{ell}
[a(x_i) neq y_i]
=
frac{1}{ell}
sum_{i = 1}^{ell}
[mathop{rm sign}limits langle w, x_i rangle neq y_i]
to
min_w
]
Этот функционал является дискретным относительно весов, и поэтому искать его минимум с помощью градиентных методов мы не сможем. Более того, у данного функционала может быть много глобальных минимумов вполне может оказаться, что существует много способов добиться оптимального количества ошибок. Чтобы не пытаться решать все эти проблемы, попытаемся свести задачу к минимизации гладкого функционала (верхней оценки).
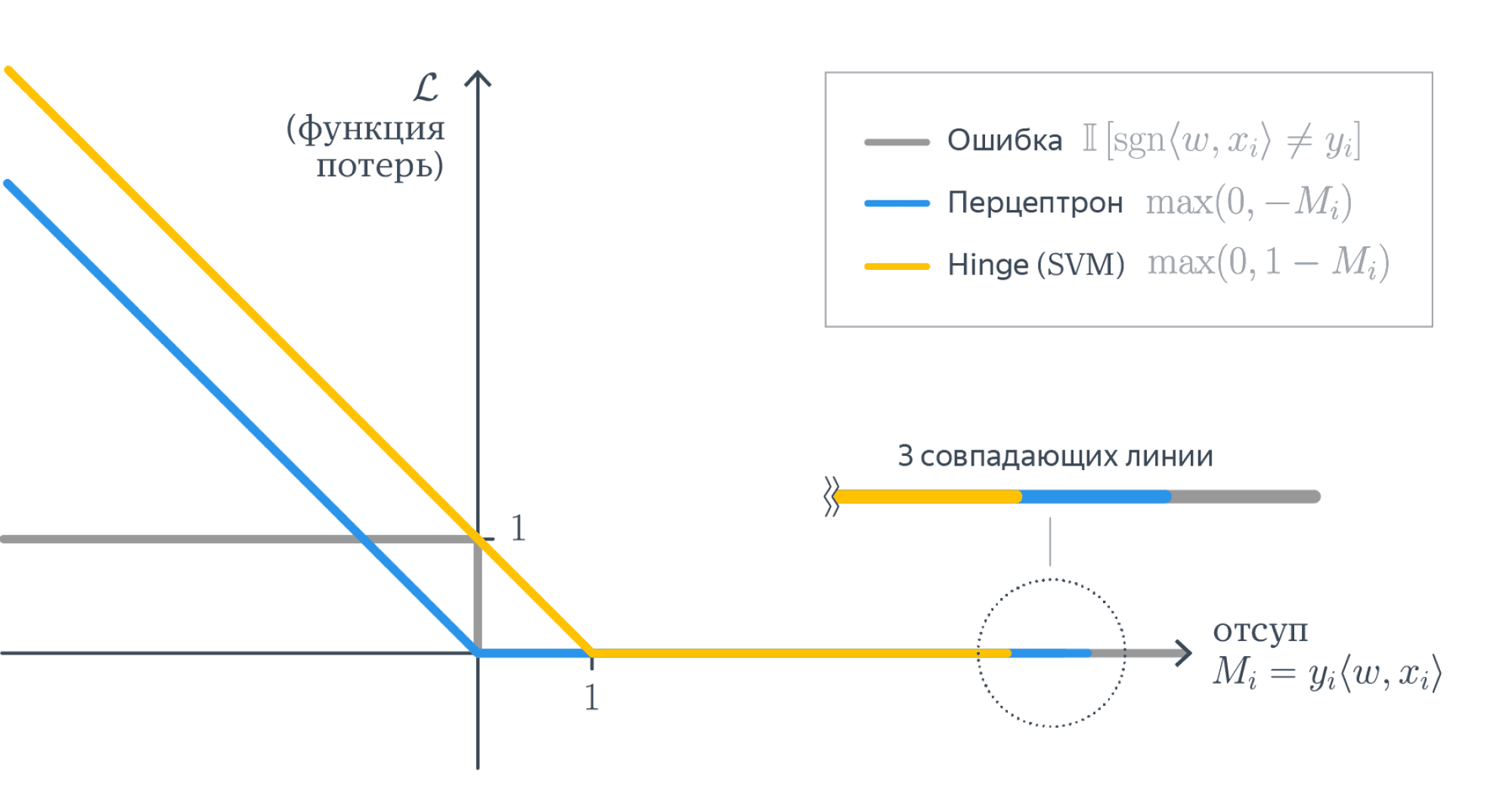
Верхние оценки
Функционал оценивает ошибку алгоритма на объекте (x) с помощью пороговой функции потерь (L(M) = [M < 0]),
где аргументом функции является отступ (M = y langle w, x rangle). Оценим эту функцию сверху во всех точках (M) кроме, может быть, небольшой полуокрестности левее нуля:[
L(M) leq tilde L(M).
]
После этого можно получить верхнюю оценку на функционал:
[
Q(a, X)
leq
frac{1}{ell}
sum_{i = 1}^{ell}
tilde L(y_i langle w, x_i rangle)
to
min_w
]
Если верхняя оценка (tilde L(M)) является гладкой, то и данная верхняя оценка будет гладкой. В этом случае её можно будет минимизировать с помощью, например, градиентного спуска. Если верхнюю оценку удастся приблизить к нулю, то и доля неправильных ответов тоже будет близка к нулю.
Приведём несколько примеров верхних оценок:
- (tilde L(M) = log left(1 + e^{-M} right)) – логистическая функция потерь
- (tilde L(M) = (1 — M)_+ = max(0, 1 — M)) – кусочно-линейная функция потерь (используется в методе опорных векторов)
- (tilde L(M) = (-M)_+ = max(0, -M)) – кусочно-линейная функция потерь (соответствует персептрону Розенблатта)
- (tilde L(M) = e^{-M}) – экспоненциальная функция потерь
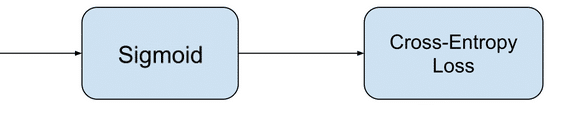
- (tilde L(M) = 2/(1 + e^M)) – сигмоидная функция потерь
Любая из них подойдёт для обучения линейного классификатора.
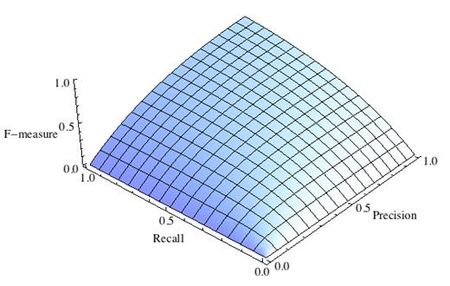
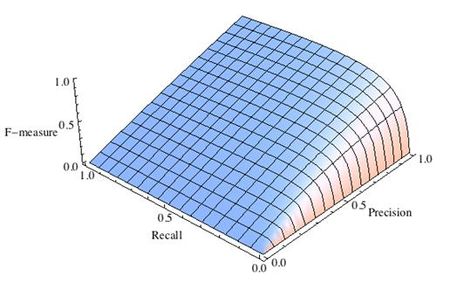
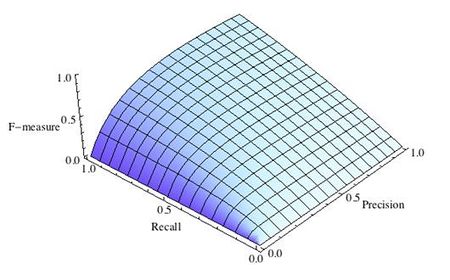
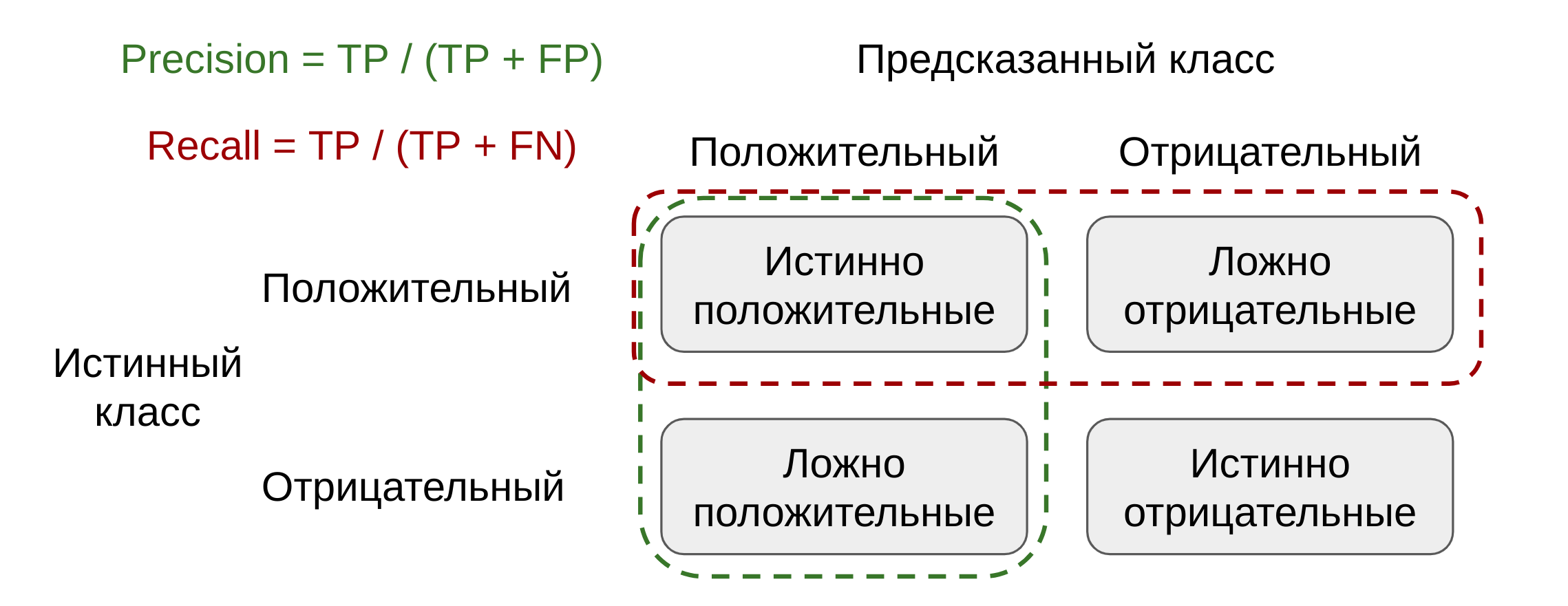
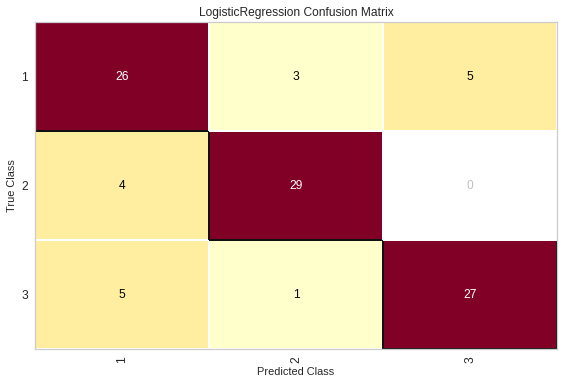
16. Что такое точность, полнота и F-мера? Почему F-мера лучше арифметического среднего и минимума?
| y=1 | y=-1 | |
|---|---|---|
| a(x)=1 | True Positive (TP) | False Positive (FP) |
| a(x)=-1 | False Negative (FN) | True Negative (TN) |
Точность
Точность (которая не accuracy (которой точный перевод — доля верных ответов), а precision) — метрика того, насколько можно доверять модели если она сказала что объект относится к положительному классу.
[
text{precision}=frac{text{TP}}{text{TP} + text{FP}}
]
Полнота
Полнота (recall) — метрика того, насколько хорошо модель покрыла положительный класс
[
text{recall}=frac{text{TP}}{text{TP} + text{FN}}
]
F-мера
F — мера — гармоническое среднее точности и полноты, (сохраняет хорошее от ариф. минимума, но более гладкая. Близко к 0 если хотя бы 1 из аргументов близок к нулю). В отличие от геометрического среднего — гармоническое среднее гораздо устойчивее к выбросам.
[
F=frac{2 * text{precision} * text{recall}}{text{precision} + text{recall}}
]
17. Для чего нужен порог в линейном классификаторе? Из каких соображений он может выбираться?
- Для определения класса объекта
- Может выбираться:
- из цен ошибок
- из требуемого количества
- из требований к recall и precision
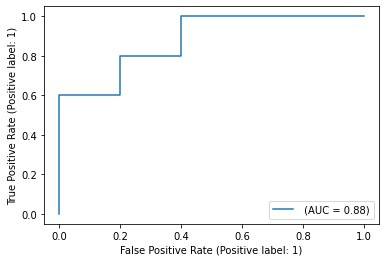
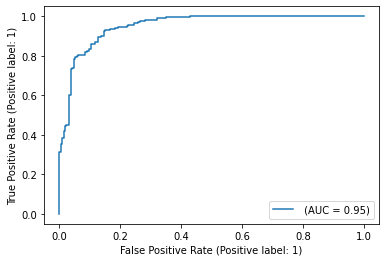
18. Что такое AUC-ROC? Опишите алгоритм построения ROC-кривой.
AUC ROC-area under ROC (receiving operating characteristic) curve, — площадь под ROC-кривой.
Сортируем объекты (b(x)), по размеру порога; размер шага для объектов с ([y = 0] =frac{1}{L_{-}}) отрицательных (шаги по FPR (горизонт ось)), шаги для ([y = 1] =frac{1}{L_+}) положительных (шаги по TPR (верт ось) )
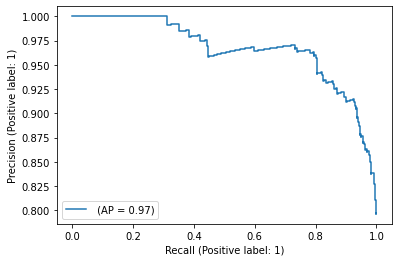
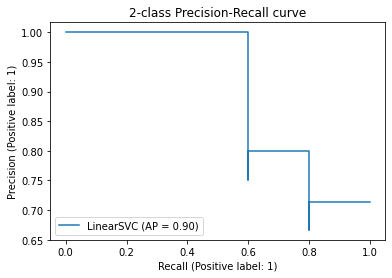
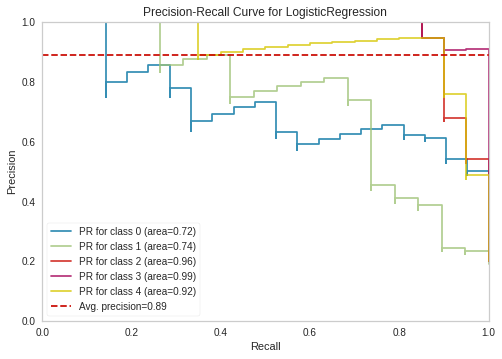
19. Что такое AUC-PRC? Опишите алгоритм построения PR-кривой.
Она определяется аналогично ROC-кривой, только по осям откладываются не FPR и TPR, а полнота (по оси абсцисс) и точность (по оси ординат). Критерием качества семейства алгоритмов выступает площадь под PR-кривой (AUC-PR).
Описание алгоритма
Стартуем из точки (0, 1). Будем идти по ранжированной выборке, начиная с первого объекта; пусть текущий объект находится на позиции (k). Если он относится к классу −1, то полнота не меняется, точность падает соответственно, кривая опускается строго вниз на (frac{1}{l_{-}}). Если же объект относится к классу 1, то полнота увеличивается на (frac{1}{l_+}), точность растет, и кривая поднимается вправо и вверх. Площадь под этим участком можно аппроксимировать площадью прямоугольника с высотой, равной precision@k и шириной (frac{1}{l_{+}}).
20. Что означает “модель оценивает вероятность положительного класса”? Как можно внедрить это требование в процедуру обучения модели?
Рассмотрим точку (x) пространства объектов. Как мы договорились, в ней имеется распределение на ответах (p(y = +1 | x)). Допустим, алгоритм (b(x)) возвращает числа из отрезка ([0, 1]). Наша задача – выбрать для него такую процедуру обучения, что в точке (x) ему будет оптимально выдавать число (p(y = +1 | x)).
Если в выборке объект (x) встречается (n) раз с ответами ({y_1, dots, y_n}), то получаем следующее требование:
[
mathop{rm arg,min}limits_{b in mathbb{R}}
frac{1}{n}
sum_{i = 1}^{n}
L(y_i, b)
approx
p(y = +1 | x)
]
При стремлении (n) к бесконечности получим, что функционал стремится к матожиданию ошибки:
[
mathop{rm arg,min}limits_{b in mathbb{R}}mathbb{E} left[L(y, b)|xright]
=
p(y = +1 | x)
]
На семинаре будет показано, что этим свойством обладает, например, квадратичная функция потерь (L(y, z) = (y — z)^2), если в ней для положительных объектов использовать истинную метку (y = 1), а для отрицательных брать (y = 0). Если функция потерь (L) удовлетворяет второй формуле, то (b(x)approx p(y=+1|x))
21. Что такое калибровочная кривая? Какие методы калибровки вероятности вы знаете? Почему важно проводить калибровку не на обучающей выборке?
Калибровка вероятностей нужна для того, чтобы заставить модель выдавать корректные вероятности принадлежности к классам. В задаче бинарной классификации откалиброванным алгоритмом называют такой алгоритм, для которого доля положительных примеров (на основе реальных меток классов) для предсказаний в окрестности произвольной вероятности (p) совпадает с этим значением (p).
На этой кривой абсцисса точки соответствуют значению (p) (предсказаний алгоритма), а ордината соответствует доле положительных примеров, для которых алгоритм предсказал вероятность, близкую к (p). В идеальном случае эта кривая совпадает с прямой (y = x).
Есть два подхода к калибровке.
- Масштабирование Платта. Он заключается к подгонке всех предсказаний к логистической кривой (по сути, логистическая регрессия на ответах классификатора) [P(y = 1 | x) = frac{1}{1+exp (af(x) + b)},] где (a, b) – скалярные параметры. Эти параметры настраиваются методом максимума правдоподобия (минимизируя логистическую функцию потерь) на отложенной выборке или с помощью кросс валидации. Также Платт предложил настраивать параметры на обучающей выборке базовой модели, а для избежания переобучения изменить метки объектов на следующие значения:
- [t_{+} = frac{N_{+} + 1}{N_{-} + 2}] для положительных примеров
- [t_{-} = frac{1}{N_{-} + 2}] для отрицательных.
- Изотоническая регрессия. В этом методе также строится отображение из предсказаний модели в откалиброванные вероятности. Для этого используем изотоническую функцию (неубывающая кусочно-постоянная функция), в которой (x) – выходы нашего алгоритма, а (y) – целевая переменная. Мы хотим найти такую функцию (m(t)): (P(y = 1 | x) = m(f(x))). Она настраивается под квадратичную ошибку:
[m = mathop{rm arg,min}limits_{z} sum (y_i — z(f(x_i))^2,] с помощью специального алгоритма (Pool-Adjacent-Violators Algorithm). В результате калибровки получаем надстройку над нашей моделью, которая применяется поверх предсказаний базовой модели.
22. Запишите функционал логистической регрессии. Как он связан с методом максимума правдоподобия?
Модель: [
p(y = 1| x)
=
frac{1}{1 + exp(-langle w, x rangle)}.
]
Подставим трансформированный ответ линейной модели в логарифмическую функцию потерь:
[
-sum_{i = 1}^{ell}left([y_i = +1]
log frac{1}{1 + exp(-langle w, x_i rangle)}
+[y_i = -1]log frac{exp(-langle w, x_i rangle)}{1 + exp(-langle w, x_i rangle)}
right)
=
-sum_{i = 1}^{ell} left(
[y_i = +1]log frac{1}{1 + exp(-langle w, x_i rangle)}
+[y_i = -1]log frac{1}{1 + exp(langle w, x_i rangle)}
right)
=
sum_{i = 1}^{ell}
log left(
1 + exp(-y_i langle w, x_i rangle)
right).
]
Попробуем сконструировать функцию потерь из других соображений. Если алгоритм (b(x) in [0, 1]) действительно выдает вероятности, то они должны согласовываться с выборкой. С точки зрения алгоритма вероятность того, что в выборке встретится объект (x_i) с классом (y_i), равна (b(x_i)^{[y_i = +1]} (1 — b(x_i))^{[y_i = -1]}).
Исходя из этого, можно записать правдоподобие выборки (т.е. вероятность получить такую выборку с точки зрения алгоритма):
[
Q(a, X)=
prod_{i = 1}^{ell}
b(x_i)^{[y_i = +1]} (1 — b(x_i))^{[y_i = -1]}.
]
Данное правдоподобие можно использовать как функционал для обучения алгоритма – с той лишь оговоркой, что удобнее оптимизировать его логарифм:[-sum_{i = 1}^{ell} left([y_i = +1] log b(x_i) + [y_i = -1] log (1 — b(x_i))right)
tomin
]
23. Запишите задачу метода опорных векторов для линейно неразделимого случая. Как функционал этой задачи связан с отступом классификатора? Как выглядит задача безусловной оптимизации в SVM?
Условный
[
left{begin{aligned}
& frac{1}{2} |w|^2 + C sum_{i = 1}^{ell} xi_i to min_{w, b, xi} \
& y_i left(
langle w, x_i rangle + b
right) geq 1 — xi_i, quad i = 1, dots, ell, \
& xi_i geq 0, quad i = 1, dots, ell.
end{aligned}
right.
]
Безусловный
[
frac12 |w|^2+
C
sum_{i = 1}^{ell}
max(0,
1 — y_i (langle w, x_i rangle + b))
to
min_{w, b}
]
Величина (frac{1}{|w|}) в данном случае называется мягким отступом (soft margin). С одной стороны, мы хотим максимизировать отступ, с другой – минимизировать штраф за неидеальное разделение выборки (sum_{i = 1}^{ell} xi_i).
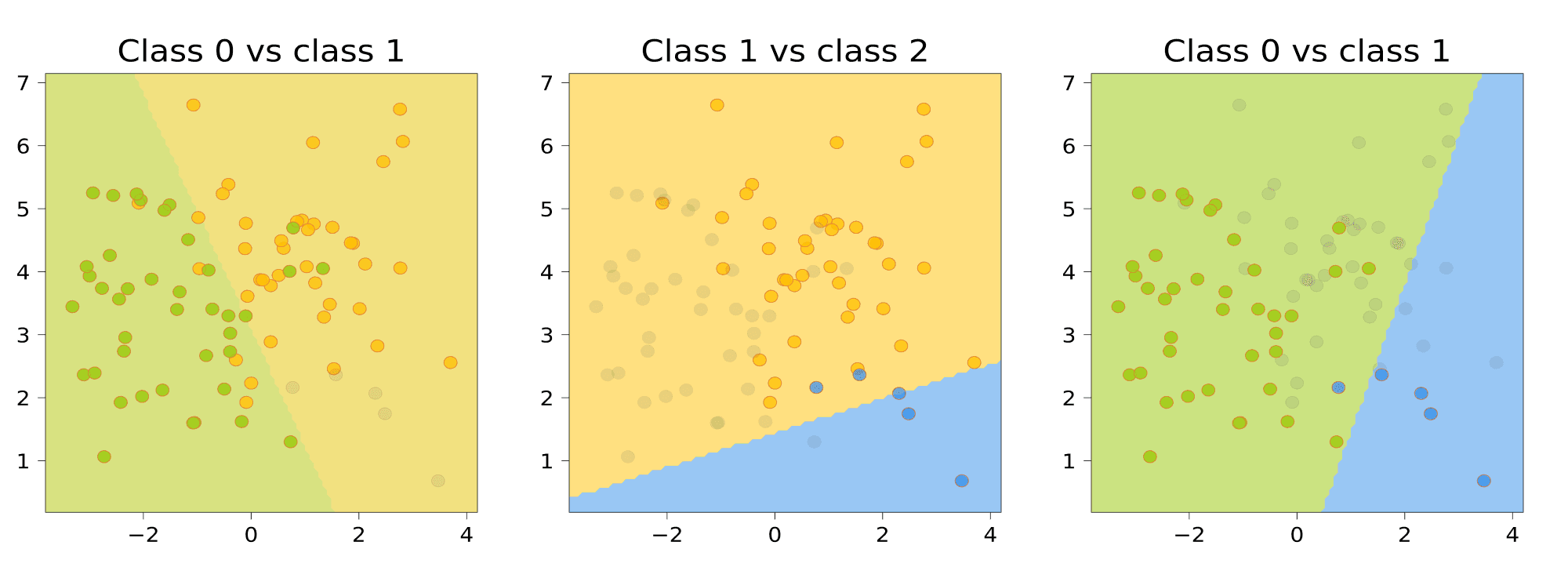
24. В чём заключаются one-vs-all и all-vs-all подходы в многоклассовой классификации?
One-vs-all
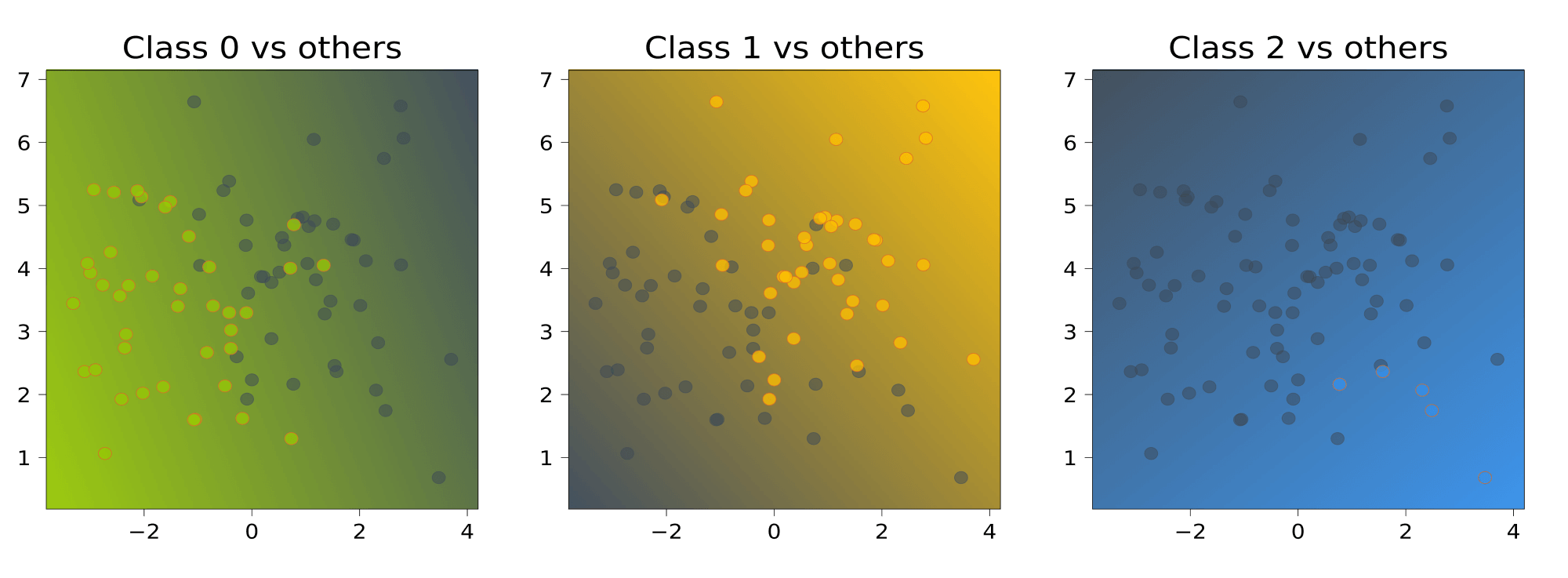
Обучим (K) линейных классификаторов (b_1(x), dots, b_K(x)), выдающих оценки принадлежности классам (1, dots, K) соответственно. Например, в случае с линейными моделями эти модели будут иметь вид (b_k(x) = langle w_k, x rangle + w_{0k}). Классификатор с номером (k) будем обучать по выборке (left(x_i, 2 [y_i = k] — 1right)_{i = 1}^{ell}); иными словами, мы учим классификатор отличать (k) -й класс от всех остальных.
Итоговый классификатор будет выдавать класс, соответствующий самому уверенному из бинарных алгоритмов:
[
a(x)
=
mathop{rm arg,max}limits_{k in {1, dots, K}}
b_k(x).
]
Проблема данного подхода заключается в том, что каждый из классификаторов (b_1(x), dots, b_K(x)) обучается на своей выборке, и выходы этих классификаторов могут иметь разные масштабы, из-за чего сравнивать их будет неправильно. Нормировать вектора весов, чтобы они выдавали ответы в одной и той же шкале, не всегда может быть разумным решением – так, в случае с SVM веса перестанут являться решением задачи, поскольку нормировка изменит норму весов.
All-vs-all
Обучим (C_K^2) классификаторов (a_{ij}(x)), (i, j = 1, dots, K), (i neq j).
Например, в случае с линейными моделями эти модели будут иметь вид
[
b_k(x) = mathop{rm sign}limits(langle w_k, x rangle + w_{0k} ).
]
Классификатор (a_{ij}(x)) будем настраивать по подвыборк (X_{ij} subset X), содержащей только объекты классов (i) и (j):
[
X_{ij} = {(x_n, y_n) in X | [y_n = i] = 1 text{или} [y_n = j] = 1 }.
]
Соответственно, классификатор (a_{ij}(x)) будет выдавать для любого объекта либо класс (i), либо класс (j).
Чтобы классифицировать новый объект, подадим его на вход каждого из построенных бинарных классификаторов. Каждый из них проголосует за своей класс; в качестве ответа выберем тот класс, за который наберется больше всего голосов:
[
a(x) = mathop{rm arg,max}limits_{k in {1, dots, K}}
sum_{i = 1}^{K} sum_{j neq i}
[a_{ij}(x) = k].
]
25. Как измеряется качество в задаче многоклассовой классификации? Что такое микро- и макро-усреднение?
В многоклассовых задачах, как правило, стараются свести подсчет качества к вычислению одной из двухклассовых метрик. Выделяют два подхода к такому сведению: микро- и макро-усреднение.
Пусть выборка состоит из (K) классов. Рассмотрим (K) двухклассовых задач, каждая из которых заключается в отделении своего класса от остальных, то есть целевые значения для (k) -й задаче вычисляются как (y_i^k = [y_i = k]). Для каждой из них можно вычислить различные характеристики (TP, FP, и т.д.) алгоритма (a^k(x) = [a(x) = k]); будем обозначать эти величины как (text{TP}_k, text{FP}_k, text{FN}_k, text{TN}_k). Заметим, что в двухклассовом случае все метрики качества, которые мы изучали, выражались через эти элементы матрицы ошибок.
Микро-усренднение
При микро-усреднении сначала эти характеристики усредняются по всем классам, а затем вычисляется итоговая двухклассовая метрика – например, точность, полнота или F-мера. Например, точность будет вычисляться по формуле
[
text{precision}(a, X)
=
frac{overline{text{TP}}}{overline{text{TP}}+overline{text{FP}}},
] где, например, (overline{text{TP}}) вычисляется по формуле [
overline{text{TP}}
=
frac{1}{K}
sum_{k = 1}^{K}
text{TP}_k.
]
Макро-усреднение
При макро-усреднении сначала вычисляется итоговая метрика для каждого класса, а затем результаты усредняются по всем классам. Например, точность будет вычислена как [text{precision}(a, X)=frac{1}{K}sum_{k = 1}^{K}text{precision}_k(a, X);qquad]
[
text{precision}_k(a, X)=frac{text{TP}_k}{text{TP}_k+text{FP}_k}.
]
Сравнение
Если какой-то класс имеет очень маленькую мощность, то при микро-усреднении он практически никак не будет влиять на результат, поскольку его вклад в средние TP, FP, FN и TN будет незначителен. В случае же с макро-вариантом усреднение проводится для величин, которые уже не чувствительны к соотношению размеров классов (если мы используем, например, точность или полноту), и поэтому каждый класс внесет равный вклад в итоговую метрику.
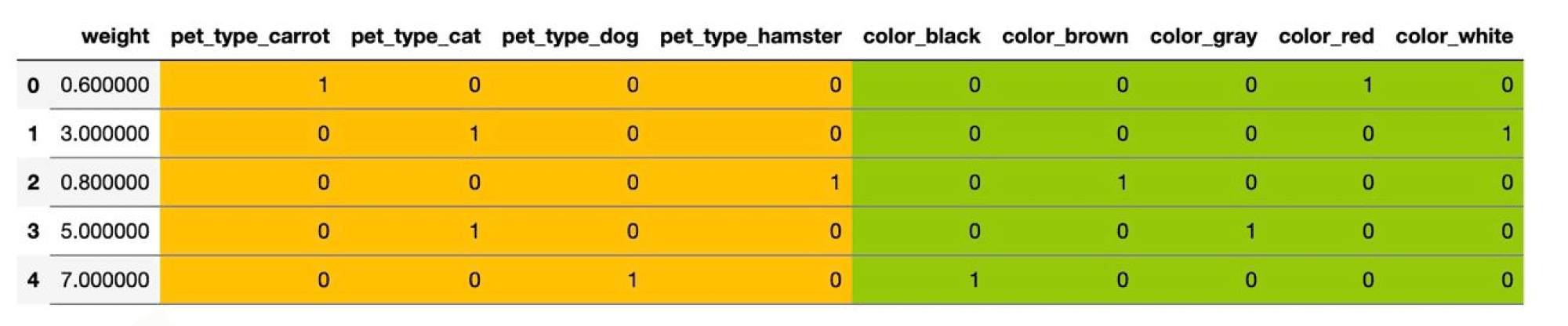
26. В чём заключается преобразование категориальных признаков в вещественные с помощью mean-target encoding? Почему использование этого способа кодирования может привести к переобучению? Какие методы борьбы с этой проблемой вам известны?
Mean target encoding
Более сложный метод кодирования категориальных признаков – через целевую переменную. Идея в том, что алгоритму для предсказания цены необходимо знать не конкретный цвет автомобиля, а то, как этот цвет сказывается на цене. Разберём сначала базовый подход – mean target encoding (иногда его называют ).
Заменим каждую категорию на среднее значение целевой переменной по всем объектам этой категории. Пусть (j) -й признак является категориальным. Для бинарной классификации новый признак будет выглядеть следующим образом:
[
g_j(x, X)
=
frac{
sum_{i=1}^{ell}
[f_j(x) = f_j(x_i)][y_i = +1]
}{
sum_{i=1}^{ell}
[f_j(x) = f_j(x_i)]
},
]
где (f_j(x_i)) – (j) -й признак (i) -го объекта, (y_i) – класс (i) -го объекта.
Отметим, что эту формулу легко перенести как на случай многоклассовой классификации (в этом случае будем считать (K) признаков, по одному для каждого класса, и в числителе будет подсчитывать долю объектов с заданной категорией и с заданным классом), так и на случай регрессии (будем вычислять среднее значение целевой переменной среди объектов данной категории).
Вернёмся к бинарной классификации. Можно заметить, что для редких категорий мы получим некорректные средние значения целевой переменной. Например, в выборке было только три золотистых автомобиля, которые оказались старыми и дешёвыми. Из-за этого наш алгоритм начнёт считать золотистый цвет дешёвым. Для исправления этой проблемы можно регуляризировать признак средним значением целевой переменной по всем категориям так, чтобы у редких категорий значение было близко к среднему по всей выборке, а для популярных к среднему значению по категории.
Формально для задачи бинарной классификации это выражается так:
[
g_j(x, X)
=
frac{
sum_{i=1}^{ell}[f_j(x) = f_j(x_i)][y_i = +1]+
frac{C}{ell}sum_{i=1}^{ell}[y_i = +1]
}{
sum_{i=1}^{ell}
[f_j(x) = f_j(x_i)] + C
},
]
где (C) – коэффициент, отвечающий за баланс между средним значением по категории и глобальным средним значением.
Однако если мы вычислим значения (g_j(x, X)) по всей выборке, то столкнёмся с переобучением, так как мы внесли информацию о целевой переменной в признаки (новый признак слабая, но модель, предсказывающая целевое значение). Поэтому вычисление таких признаков следует производить по блокам, то есть вычислять средние значения на основе одних фолдов для заполнения на другом блоке (аналогично процессу кросс-валидации). Если же ещё планируется оценка качества модели с помощью кросс-валидации по блокам, то придётся применить для подсчёта признаков. Этот подход заключается в кодировании категориальных признаков по блокам внутри блоков, по которым оценивается качество модели.
Разберём этот процесс. Представим, что хотим посчитать качество модели на 3-м блоке. Для этого:
- Разбиваем все внешние блоки, кроме 3-го, на внутренние блоки. Количество внутренних блоков может не совпадать с количеством внешних.
- Рассмотрим конкретный внешний
Для каждого из его внутренних блоков считаем значение (g(x, X)) на основе средних значений целевой переменной по блокам, исключая текущий. Для 3-го внешнего блока (который сейчас играет роль тестовой выборки) вычисляем (g(x, X)) как среднее вычисленных признаков по каждому из внутренних фолдов. - Обучаем модель на всех блоках, кроме 3-го, делаем предсказание на 3-м и считаем на нём качество.
Существуют альтернативы кодированию категориальных признаков по блокам.
Зашумление
Можно посчитать новые признаки по базовой формуле, а затем просто добавить к каждому значению случайный шум (например, нормальный). Это действительно снизит уровень корреляции счётчиков с целевой переменной. Проблема в том, что это делается за счёт снижения силы такого признака, а значит, мы ухудшаем итоговое качество модели. Поэтому важно подбирать дисперсию шума, чтобы соблюсти баланс между борьбой с переобучением и предсказательной силой счётчиков.
Сглаживание
Можно немного модифицировать формулу, чтобы сила регуляризации зависела от объёма данных по конкретной категории:
[
g_j(x, X)
=
lambda left( n(f_j(x)) right)
frac{
sum_{i=1}^{ell}[f_j(x) = f_j(x_i)][y_i = +1]
}{
sum_{i=1}^{ell}[f_j(x) = f_j(x_i)]
}
+left( 1 — lambda left( n(f_j(x)) right) right)
frac{1}{ell}
sum_{i = 1}^{ell}
[y_i = +1]
,
]
где (n(z) = sum_{i = 1}^{ell} [f_j(x_i) = z]) – число объектов категории (z), (lambda(n)) – некоторая монотонно возрастающая функция, дающая значения из отрезка ([0, 1]).
Примером может служить (lambda(n) = frac{1}{1 + exp(-n)}). Если грамотно подобрать эту функцию, то она будет вычищать значение целевой переменной из редких категорий и мешать переобучению.
Кодирование по времени.
Можно отсортировать выборку некоторым образом и для (i) -го объекта вычислять статистики только по предыдущим объектам:
[
g_j(x_k, X)
=
frac{
sum_{i=1}^{k — 1}
[f_j(x) = f_j(x_i)][y_i = +1]
}{
sum_{i=1}^{k — 1}
[f_j(x) = f_j(x_i)]
}.
]
Для хорошего качества имеет смысл отсортировать выборку случайным образом несколько раз, и для каждого такого порядка посчитать свои счётчики.
Это даёт улучшение качества, например, потому что для объектов, находящихся в начале выборки, признаки будут считаться по очень небольшой подвыборке, и поэтому вряд ли будут хорошо предсказывать целевую переменную. При наличии нескольких перестановок хотя бы один из новых признаков будет вычислен по подвыборке достаточного размера. Такой подход, например, используется в библиотеке CatBoost.
Weight of Evidence
Существует альтернативный способ кодирования категориальных признаков, основанный на подсчёте соотношения положительных и отрицательных объектов среди объектов данной категории. Этот подход, в отличие от других, сложнее обобщить на многоклассовый случай или для регрессии.
Введём обозначение для доли объектов класса (b) внутри заданной категории (c) среди всех объектов данного класса в выборке:
[
P(c | y = b)=
frac{
sum_{i = 1}^{ell}[y_i = b] [f_j(x_i) = c]+alpha
}{
sum_{i = 1}^{ell}[y_i = b]+2 alpha
},
]
где (alpha) – параметр сглаживания.
Вычислим новое значение признака как
[
g_j(x, X)
=
logleft(
frac{
P(f_j(x) | y = +1)
}{
P(f_j(x) | y = -1)
}
right).
]
Если (g_j(x, X)) близко к нулю, то данная категория примерно с одинаковой вероятностью встречается в обоих классах, и поэтому вряд ли будет хорошо предсказывать значение целевой переменной. Чем сильнее отличие от нуля, тем сильнее категория характеризует один из классов.
Разумеется, в конкретной задаче лучше всего может себя проявлять любой из этих подходов, поэтому имеет смысл сравнивать их и выбирать лучший – или использовать все сразу.
27. Как определить для линейной модели, какие признаки являются самыми важными?
- наибольшим модулем соответствующего параметра линейной модели
- (t) -статистика
[
t(j) = frac{|mu_+ — mu_-|}{sqrt{frac{n_+ sigma^2_+ + n_- sigma^2_-}{n_+ + n_-}}}
] - исключаем по очереди один из признаков и смотрим, как это влияет на качество. Удаляем признаки таким жадным способом, пока не окажется выполненным некоторое условие (количество признаков или ухудшение качества).
- Можно использовать L1-регуляризацию, которая занулит веса на самых бесполезных признаках.
- Можно, в конце концов, посчитать корреляцию таргета и признака.
28. Опишите жадный алгоритм обучения решающего дерева.
Опишем базовый жадный алгоритм построения бинарного решающего дерева. Начнем со всей обучающей выборки (X) и найдем наилучшее ее разбиение на две части (R_1(j, t) = {x | x_j < t}) и (R_2(j, t) = {x | x_j geq t})
с точки зрения заранее заданного функционала качества (Q(X, j, t)). Найдя наилучшие значения (j) и (t), создадим корневую вершину дерева, поставив ей в соответствие предикат ([x_j < t]).
Объекты разобьются на две части – одни попадут в левое поддерево, другие в правое. Для каждой из этих подвыборок рекурсивно повторим процедуру, построив дочерние вершины для корневой, и так далее. В каждой вершине мы проверяем, не выполнилось ли некоторое условие останова – и если выполнилось, то прекращаем рекурсию и объявляем эту вершину листом. Когда дерево построено, каждому листу ставится в соответствие ответ. В случае с классификацией это может быть класс, к которому относится больше всего объектов в листе, или вектор вероятностей (скажем, вероятность класса может быть равна доле его объектов в листе). Для регрессии это может быть среднее значение, медиана или другая функция от целевых переменных объектов в листе. Выбор конкретной функции зависит от функционала качества в исходной задаче.
29. Почему с помощью бинарного решающего дерева можно достичь нулевой ошибки на обучающей выборке без повторяющихся объектов?
Для выборки без повторяющихся объектов мы можем построить такое дерево, что количество листов в нем будет равно количеству объектов в выборке, и в каждом листе будет стоять отдельный объект. У каждого объекта будет уникальное признаковое описание, а значит, мы можем построить дерево предикатов так, чтобы оно делило выборку идеально. Само собой, обобщающая способность такого дерева будет не очень хорошей.
30. Как в общем случае выглядит критерий хаотичности? Как он используется для выбора предиката во внутренней вершине решающего дерева? Как вывести критерий Джини и энтропийный критерий?
Общий случай
[
H( R)
=
min_{c in mathbb{Y}}
frac{1}{|R|}
sum_{(x_i, y_i) in R}
L(y_i, c),
]
Т.е. критерий показывает, насколько хорошо целевая переменная в данном множестве приближается константой.
Чем менее разнообразно значение целевой переменной среди объектов, тем меньше значение критерия — поэтому мы пытаемся его минимизировать. При этом в процессе разбиения мы пытаемся максимизировать такой функционал:
[
Q(R_m, j, s)=H(R_m)-frac{|R_ell|}{|R_m|}H(R_ell)-frac{|R_r|}{|R_m|}H(R_r)
]
Джини
Рассмотрим ситуацию, в которой мы выдаём в вершине не один класс, а распределение на всех классах (c = (c_1, dots, c_K)), (sum_{k = 1}^{K} c_k = 1). Качество такого распределения можно измерять, например, с помощью критерия Бриера (Brier score):
[
H( R)
=
min_{sum_k c_k = 1}
frac{1}{|R|}
sum_{(x_i, y_i) in R}
sum_{k = 1}^{K}
(c_k — [y_i = k])^2.
]
Легко заметить, что здесь мы, по сути, ищем каждый (c_k) как оптимальную с точки зрения MSE константу, приближающую индикаторы попадания объектов выборки в класс (k). Это означает, что оптимальный вектор вероятностей состоит из долей классов (p_k): [c_* = (p_1, dots, p_K)]
Если подставить эти вероятности в исходный критерий информативности и провести ряд преобразований, то мы получим критерий Джини: [H( R)=sum_{k = 1}^{K}p_k (1 — p_k).]
Энтропийный
Мы уже знакомы с более популярным способом оценивания качества вероятностей – логарифмическими потерями, или логарифмом правдоподобия:
[
H( R)=min_{sum_k c_k = 1} left(-frac{1}{|R|}sum_{(x_i, y_i) in R}sum_{k = 1}^{K}[y_i = k]log c_kright)
]
Для вывода оптимальных значений (c_k) вспомним, что все значения (c_k) должны суммироваться в единицу.
Как известного из методов оптимизации, для учёта этого ограничения необходимо искать минимум лагранжиана:
[
L(c, lambda)=-frac{1}{|R|}sum_{(x_i, y_i) in R}sum_{k = 1}^{K}[y_i = k]log c_k+lambdasum_{k = 1}^{K}c_ktomin_{c_k}
]
Дифференцируя, получаем:
[
frac{partial}{partial c_k}L(c, lambda)=-frac{1}{|R|}sum_{(x_i, y_i) in R}[y_i = k]frac{1}{c_k}+lambda=-frac{p_k}{c_k}+lambda=0
]
откуда выражаем (c_k = p_k / lambda).
Суммируя эти равенства по (k), получим
[
1 = sum_{k = 1}^{K} c_k = frac{1}{lambda} sum_{k = 1}^{K} p_k = frac{1}{lambda},
] откуда (lambda = 1).
Значит, минимум достигается при (c_k = p_k), как и в предыдущем случае. Подставляя эти выражения в критерий, получим, что он будет представлять собой энтропию распределения классов:
[H( R)=-sum_{k = 1}^{K}p_klog p_k.]
Из теории вероятностей известно, что энтропия ограничена снизу нулем, причем минимум достигается на вырожденных распределениях ((p_i = 1), (p_j = 0) для (i neq j)). Максимальное же значение энтропия принимает для равномерного распределения. Отсюда видно, что энтропийный критерий отдает предпочтение более распределениям классов в вершине.
31. Для какой ошибки строится разложение на шум, смещение и разброс? Запишите формулу этой ошибки.
Разложение ошибки на три компоненты, которое мы только что вывели, верно только для квадратичной функции потерь. Существуют более общие формы этого разложения, которые состоят из трёх компонент с аналогичным смыслом, поэтому можно утверждать, что для большинства распространённых функций потерь ошибка метода обучения складывается из шума, смещения и разброса; значит, и дальнейшие рассуждения про изменение этих компонент в композициях также можно обобщить на другие функции потерь (например, на индикатор ошибки классификации).
BVD для среднеквадратичного риска метода (mu) (обученного на выборке (X)), усредненного по всем возможным выборкам.
[
L(mu)=
mathbb{E}_{X} Bigl[
mathbb{E}_{x, y} Bigl[
bigl(
y — mu(X)(x)
bigr)^2
Bigr]
Bigr]
]
[
L(mu)=
underbrace{mathbb{E}_{x, y}Bigl[bigl(y — mathbb{E}[y | x]bigr)^2Bigr]}_{text{шум}}+
underbrace{mathbb{E}_{x} Bigl[bigl(mathbb{E}_{X} bigl[ mu(X) bigr]-mathbb{E}[y | x]bigr)^2Bigr]}_{text{смещение}}
+underbrace{mathbb{E}_{x} Bigl[mathbb{E}_{X} Bigl[bigl(mu(X)-mathbb{E}_{X} bigl[ mu(X) bigr]bigr)^2Bigr]Bigr]}_{text{разброс}}.
]
32. Запишите формулы для шума, смещения и разброса метода обучения для случая квадратичной функции потерь.
[
L(mu)=
underbrace{mathbb{E}_{x, y}Bigl[bigl(y — mathbb{E}[y | x]bigr)^2Bigr]}_{text{шум}}+
underbrace{mathbb{E}_{x} Bigl[bigl(mathbb{E}_{X} bigl[ mu(X) bigr]-mathbb{E}[y | x]bigr)^2Bigr]}_{text{смещение}}
+underbrace{mathbb{E}_{x} Bigl[mathbb{E}_{X} Bigl[bigl(mu(X)-mathbb{E}_{X} bigl[ mu(X) bigr]bigr)^2Bigr]Bigr]}_{text{разброс}}.
]
33. Приведите пример семейства алгоритмов с низким смещением и большим разбросом; семейства алгоритмов с большим смещением и низким разбросом. Поясните примеры.
Смещение показывает, насколько хорошо с помощью данных метода обучения и семейства алгоритмов можно приблизить оптимальный алгоритм. Как правило, смещение маленькое у сложных (precision) семейств (например, у деревьев) и большое у простых семейств (например, линейных классификаторов). Дисперсия показывает, насколько сильно может изменяться ответ обученного алгоритма в зависимости от выборки иными словами, она характеризует чувствительность метода обучения к изменениям в выборке. Как правило, простые семейства имеют маленькую дисперсию (variance), а сложные семейства большую дисперсию.
34. Что такое бэггинг? Как его смещение и разброс связаны со смещением и разбросом базовых моделей?
Для начала, бутстрап – способ ресэмплинга. По имеющейся выборке (X) создадим (N) новых выборок путем взятия элементов из (X) с повторениями.
Пусть имеется некоторый метод обучения (mu(X)). Построим на его основе метод (tilde mu(X)), который генерирует случайную подвыборку (tilde X) с помощью бутстрапа и подает ее на вход метода (mu): (tilde mu(X) = mu(tilde X)). Напомним, что бутстрап представляет собой сэмплирование (ell) объектов из выборки с возвращением, в результате чего некоторые объекты выбираются несколько раз, а некоторые – ни разу.
Помещение нескольких копий одного объекта в бутстрапированную выборку соответствует выставлению веса при данном объекте – соответствующее ему слагаемое несколько раз войдет в функционал, и поэтому штраф за ошибку на нем будет больше.
В бэггинге (bagging, bootstrap aggregation) предлагается обучить некоторое число алгоритмов (b_n(x)) с помощью метода (tilde mu), и построить итоговую композицию как среднее данных базовых алгоритмов:
[
a_N(x)
=
frac{1}{N}
sum_{n = 1}^{N}
b_n(x)
=
frac{1}{N}
sum_{n = 1}^{N}
tilde mu(X)(x).
]
Такая композиция и называется бэггингом. Он позволяет объединить базовые алгоритмы с низким смещением, но высоким разбросом, в композицию с низким смещением и разбросом, причем, в идеальном случае (модели совсем не коррелируют) разброс падает в N раз. Если же корреляция имеет место, то уменьшение дисперсии может быть гораздо менее существенным.
Помещение нескольких копий одного объекта в бутстрапированную выборку соответствует выставлению веса при данном объекте соответствующее ему слагаемое несколько раз войдет в функционал, и поэтому штраф за ошибку на нем будет больше.
35. Что такое случайный лес? Чем он отличается от бэггинга над решающими деревьями?
Случайный лес — метод построения композиции, основанный на бэггинге над деревьями. Т.к. Бэггинг сильнее понижает разброс при слабой корреляции моделей, в RF предлагается специально ее понижать с помощью
- рандомизации по признакам (для каждого базового алгоритма используется некое подмножество признаков вместо всех) (это отличие от бэггинга над деревьями)
- рандомизации по объектам (для каждого базового алгоритма в бутстрапе используется не вся выборка X, а какая-то подвыборка)
36. Что такое out-of-bag оценка в бэггинге?
Мы можем для каждого объекта (x_{i}) найти деревья, которые были обучены без него, и вычислить по их ответам out-of-bag-ошибку
Каждое дерево в случайном лесе обучается по подмножеству объектов. Это значит, что те объекты, которые не вошли в бутстрапированную выборку (X_n) дерева (b_n), по сути являются контрольными для данного дерева.
Значит, мы можем для каждого объекта (x_i) найти деревья, которые были обучены без него, и вычислить по их ответам out-of-bag-ошибку:
[
text{OOB}
=
sum_{i = 1}^{ell}
L left(
y_i,
frac{1}{sum_{n = 1}^{N} [x_i notin X_n]}
sum_{n = 1}^{N}
[x_i notin X_n] b_n(x_i)
right),
] где (L(y, z)) – функция потерь.
Можно показать, что по мере увеличения числа деревьев (N) данная оценка стремится к leave-one-out-оценке, но при этом существенно проще для вычисления.
37. Запишите вид композиции, которая обучается в градиентном бустинге. Как выбирают количество базовых алгоритмов в ней?
(a_{N}(x)=sumlimits_{n=0}^{N}gamma_{n}b_{n}(x))
В такой композиции каждый следующий базовый алгоритм исправляет ошибки предыдущего.
При большом их числе мы начинаем переобучаться — можем использовать валидационную выборку для подбора (это просто гиперпараметр).
38. Что такое сдвиги в градиентном бустинге? Как они вычисляются и для чего используются?
Сдвиг (остаток) — расстояния от ответа нашего алгоритма до истинного ответа.
[
s_i^{(N)}=y_i — sum_{n = 1}^{N — 1} b_n(x_i)=y_i- a_{N — 1}(x_i),qquad i = 1, dots, ell
]
Или
[
s_i=-left.frac{partial L}{partial z}right|_{z = a_{N — 1}(x_i)}
]
С помощью сдвига мы настраиваем очередной базовой алгоритм:
[
b_N(x)
:=
mathop{rm arg,min}limits_{b in mathbb{A}}
frac12
sum_{i = 1}^{ell}
(b(x_i) — s_i^{(N)})^2
]
39. Как обучается очередной базовый алгоритм в градиентном бустинге? Что такое сокращение шага?
Пусть мы построили композицию (a_{N-1}(x)) из (N-1) базовых алгоритмов. Хотим выбрать такой алгоритм следующим, чтобы как можно сильнее уменьшить ошибку
Допустим, мы построили композицию (a_{N — 1}(x)) из (N — 1) алгоритма, и хотим выбрать следующий базовый алгоритм (b_N(x)) так, чтобы как можно сильнее уменьшить ошибку:
[
sum_{i = 1}^{ell}L(y_i, a_{N — 1}(x_i) + gamma_N b_N(x_i))tomin_{b_N, gamma_N}
]
Ответим в первую очередь на следующий вопрос: если бы в качестве алгоритма (b_{N}(x)) мы могли выбрать совершенно любую функцию, то какие значения ей следовало бы принимать на объектах обучающей выборки? Иными словами, нам нужно понять, какие числа (s_1, dots, s_ell) надо выбрать для решения следующей задачи:
[
sum_{i = 1}^{ell}L(y_i, a_{N — 1}(x_i) + s_i)tomin_{s_1, dots, s_ell}
]
Понятно, что можно требовать (s_i = y_i — a_{N — 1}(x_i)), но такой подход никак не учитывает особенностей функции потерь (L(y, z)) и требует лишь точного совпадения предсказаний и истинных ответов. Более разумно потребовать, чтобы сдвиг (s_i) был противоположен производной функции потерь в точке (z = a_{N — 1}(x_i)):
[
s_i=-left.frac{partial L}{partial z}right|_{z = a_{N — 1}(x_i)}
]
В этом случае мы сдвинемся в сторону скорейшего убывания функции потерь. Заметим, что вектор сдвигов (s = (s_1, dots, s_ell)) совпадает с антиградиентом:
[
left(-left.frac{partial L}{partial z}right|_{z = a_{N — 1}(x_i)}right)_{i = 1}^{ell}=-nabla_zsum_{i = 1}^{ell}L(y_i, z_i)big|_{z_i = a_{N — 1}(x_i)}
]
При таком выборе сдвигов (s_i) мы, по сути, сделаем один шаг градиентного спуска, двигаясь в сторону наискорейшего убывания ошибки на обучающей выборке. Отметим, что речь идет о градиентном спуске в (ell) -мерном пространстве предсказаний алгоритма на объектах обучающей выборки. Поскольку вектор сдвига будет свой на каждой итерации, правильнее обозначать его как (s_i^{(N)}), но для простоты будем иногда опускать верхний индекс. Итак, мы поняли, какие значения новый алгоритм должен принимать на объектах обучающей выборки. По данным значениям в конечном числе точек необходимо построить функцию, заданную на всем пространстве объектов. Это классическая задача обучения с учителем, которую мы уже хорошо умеем решать. Один из самых простых функционалов – среднеквадратичная ошибка. Воспользуемся им для поиска базового алгоритма, приближающего градиент функции потерь на обучающей выборке:
[
b_N(x)=mathop{rm arg,min}limits_{b in mathbb{A}}sum_{i = 1}^{ell}left(b(x_i) — s_iright)^2
]
Отметим, что здесь мы оптимизируем квадратичную функцию потерь независимо от функционала исходной задачи – вся информация о функции потерь (L) находится в антиградиенте (s_i), а на данном шаге лишь решается задача аппроксимации функции по (ell) точкам. Разумеется, можно использовать и другие функционалы, но среднеквадратичной ошибки, как правило, оказывается достаточно.
Ещё одна причина для использования среднеквадратичной ошибки состоит в том, что от алгоритма требуется как можно точнее приблизить направление наискорейшего убывания функционала (то есть направление ((s_i)_i)); совпадение направлений вполне логично оценивать через косинус угла между ними, который напрямую связан со среднеквадратичной ошибкой.
После того, как новый базовый алгоритм найден, можно подобрать коэффициент при нем по аналогии с наискорейшим градиентным спуском:
[
gamma_N=mathop{rm arg,min}limits_{gamma in mathbb{R}}sum_{i = 1}^{ell}L(y_i, a_{N — 1}(x_i) + gamma b_N(x_i))
]
Описанный подход с аппроксимацией антиградиента базовыми алгоритмами и называется градиентным бустингом. Данный метод представляет собой поиск лучшей функции, восстанавливающей истинную зависимость ответов от объектов, в пространстве всех возможных функций. Ищем мы данную функцию с помощью спуска – каждый шаг делается вдоль направления, задаваемого некоторым базовым алгоритмом. При этом сам базовый алгоритм выбирается так, чтобы как можно лучше приближать антиградиент ошибки на обучающей выборке.
Сокращение шага — вместо перехода в оптимальную точку делаем укороченный шаг. По сути, мы снижаем доверие к каждому базовому алгоритму. (eta in (0, 1]) (a_{N}(x)=a_{N-1}(x)+etagamma_{N}b_{N}(x))
40. В чём заключается переподбор прогнозов в листьях решающих деревьев в градиентном бустинге?
Вспомним, что решающее дерево разбивает все пространство на непересекающиеся области,в каждой из которых его ответ равен константе:
[
b_n(x)=sum_{j = 1}^{J_n}b_{nj}[x in R_j],
]
где (j = 1, dots, J_n) – индексы листьев, (R_j) – соответствующие области разбиения, (b_{nj}) – значения в листьях.
Значит, на (N) -й итерации бустинга композиция обновляется как
[
a_N(x)=a_{N — 1}(x)+gamma_Nsum_{j = 1}^{J_N}b_{Nj}[x in R_j]=a_{N — 1}(x)+sum_{j = 1}^{J_N}gamma_Nb_{Nj}[x in R_j].
]
Видно, что добавление в композицию одного дерева с (J_N) листьями равносильно добавлению (J_N) базовых алгоритмов, представляющих собой предикаты вида ([x in R_j]). Если бы вместо общего коэффициента (gamma_N) был свой коэффициент (gamma_{Nj}) при каждом предикате, то мы могли бы его подобрать так, чтобы повысить качество композиции. Если подбирать свой коэффициент (gamma_{Nj}) при каждом слагаемом, то потребность в (b_{Nj}) отпадает, его можно просто убрать:
[
sum_{i = 1}^{ell}Lleft(y_i,a_{N — 1}(x_i)+sum_{j = 1}^{J_N}gamma_{Nj}[x in R_j]right)tomin_{{gamma_{Nj}}_{j = 1}^{J_N}}.
]
Поскольку области разбиения (R_j) не пересекаются, данная задача распадается на (J_N) независимых подзадач:
[
gamma_{Nj}=mathop{rm arg,min}limits_gammasum_{x_i in R_j}L(y_i, a_{N — 1}(x_i) + gamma),qquad j = 1, dots, J_N.
]
41. Как в xgboost выводится функционал ошибки с помощью разложения в ряд Тейлора?
Мы хотим найти алгоритм (b(x)), решающий следующую задачу:
[
sum_{i = 1}^{ell}
L(y_i, a_{N — 1}(x_i) + b(x_i))
to
min_{b}
]
Разложим функцию (L) в каждом слагаемом в ряд Тейлора до второго члена с центром в ответе композиции (a_{N — 1}(x_i)):
[
sum_{i = 1}^{ell}L(y_i, a_{N — 1}(x_i) + b(x_i))approx
sum_{i = 1}^{ell} left(L(y_i, a_{N — 1}(x_i))-s_i b(x_i)+frac12h_i b^2(x_i)right),
]
где через (h_i) обозначены вторые производные по сдвигам:
[
h_i
=
left.
frac{partial^2}{partial z^2}
L(y_i, z)
right|_{a_{N — 1}(x_i)}
]
Первое слагаемое не зависит от нового базового алгоритма, и поэтому его можно выкинуть. Получаем функционал:
[
sum_{i = 1}^{ell} left(-s_i b(x_i)+frac{1}{2}h_i b^2(x_i)right)tomin_{b}
]
Покажем, что он очень похож на среднеквадратичный из формулы. Преобразуем его:
[
sum_{i = 1}^{ell}left(b(x_i) — s_iright)^2\
=
sum_{i = 1}^{ell} left(b^2(x_i)-2 s_i b(x_i)+s_i^2right) = {text{последнее слагаемое не зависит от $b$}} \
=
sum_{i = 1}^{ell} left(b^2(x_i)-2 s_i b(x_i)right)\
=
2sum_{i = 1}^{ell}left(-s_ib(x_i)+frac{1}{2}b^2(x_i)right)
tomin_{b}
]
Видно, что последняя формула совпадает с точностью до константы, если положить (h_i = 1). Таким образом, в обычном градиентном бустинге мы используем аппроксимацию второго порядка при обучении очередного базового алгоритма, и при этом отбрасываем информацию о вторых производных (то есть считаем, что функция имеет одинаковую кривизну по всем направлениям).
42. Какие регуляризации используются в xgboost?
Будем далее работать с функционалом. Он измеряет лишь ошибку композиции после добавления нового алгоритма, никак при этом не штрафуя за излишнюю сложность этого алгоритма. Ранее мы решали проблему переобучения путем ограничения глубины деревьев, но можно подойти к вопросу и более гибко. Мы выясняли, что дерево (b(x)) можно описать формулой
[
b(x)
=
sum_{j = 1}^{J}
b_{j}
[x in R_{j}]
]
Его сложность зависит от двух показателей:
- Число листьев (J). Чем больше листьев имеет дерево, тем сложнее его разделяющая поверхность, тем больше у него параметров и тем выше риск переобучения.
- Норма коэффициентов в листьях (|b|_2^2 = sum_{j = 1}^{J} b_j^2). Чем сильнее коэффициенты отличаются от нуля, тем сильнее данный базовый алгоритм будет влиять на итоговый ответ композиции.
Добавляя регуляризаторы, штрафующие за оба этих вида сложности, получаем следующую задачу:
[
sum_{i = 1}^{ell} left(-s_i b(x_i)+frac{1}{2}h_i b^2(x_i)right)
+gamma J
+frac{lambda}{2}sum_{j = 1}^{J}b_j^2
tomin_{b}
]
Если вспомнить, что дерево (b(x)) дает одинаковые ответы на объектах, попадающих в один лист, то можно упростить функционал:
[
sum_{j = 1}^{J} Biggl{
underbrace{
Biggl(-sum_{i in R_j} s_iBiggr)
}_{=-S_j}
b_j+frac12
Biggl(lambda+
underbrace{sum_{i in R_j} h_i}_{=H_j}
Biggr)
b_j^2+gamma
Biggr}
to
min_{b}
]
Каждое слагаемое здесь можно минимизировать по (b_j) независимо. Заметим, что отдельное слагаемое представляет собой параболу относительно (b_j), благодаря чему можно аналитически найти оптимальные коэффициенты в листьях:
[
b_j
=
frac{S_j}{H_j + lambda}
]
Подставляя данное выражение обратно в функционал, получаем, что ошибка дерева с оптимальными коэффициентами в листьях вычисляется по формуле
[
H(b)=
-frac12sum_{j = 1}^{J}
frac{S_j^2}{H_j + lambda}+gamma J
]
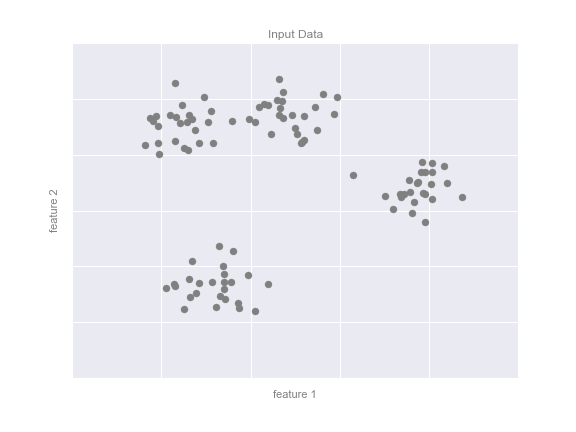
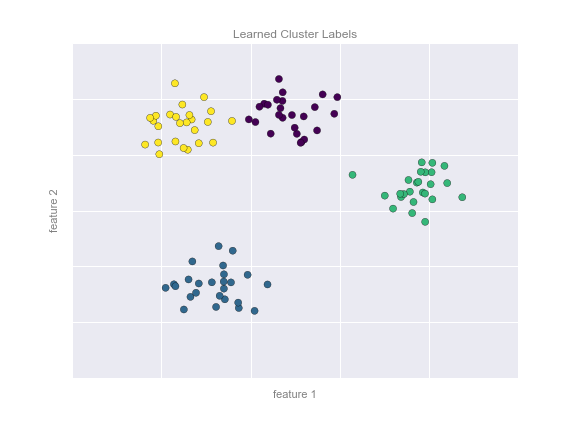
43. Задача кластеризации. Метрики качества.
Приведём несколько примеров внутренних метрик качества. Будем считать, что каждый кластер характеризуется своим центром (c_k).
Внутрикластерное расстояние
[
sum_{k = 1}^{K}sum_{i = 1}^{ell}[a(x_i) = k]rho(x_i, c_k),
]
где (rho(x, z)) – некоторая функция расстояния. Данный функционал требуется минимизировать, поскольку в идеале все объекты кластера должны быть одинаковыми.
Межкластерное расстояние
[
sum_{i, j = 1}^{ell}[a(x_i) neq a(x_j)]rho(x_i, x_j).
]
Данный функционал нужно максимизировать, поскольку объекты из разных кластеров должны быть как можно менее похожими друг на друга.
Индекс Данна (Dunn Index)
[
frac{
min_{1 leq k < k^prime leq K}d(k, k^prime)
}{
max_{1 leq k leq K}d(k)
},
]
где (d(k, k^prime)) – расстояние между кластерами (k) и (k^prime) (например, евклидово расстояние между их центрами), а (d(k)) – внутрикластерное расстояние для (k) -го кластера (например, сумма расстояний от всех объектов этого кластера до его центра). Данный индекс необходимо максимизировать.
44. Метод K-Means, вывод его шагов.
Одним из наиболее популярных методов кластеризации является, который оптимизирует внутрикластерное расстояние, в котором используется квадрат евклидовой метрики.
Заметим, что в данном функционале имеется две степени свободы: центры кластеров (c_k) и распределение объектов по кластерам (a(x_i)). Выберем для этих величин произвольные начальные приближения, а затем будем оптимизировать их по очереди:
- Зафиксируем центры кластеров.
В этом случае внутрикластерное расстояние будет минимальным, если каждый объект будет относиться к тому кластеру, чей центр является ближайшим:
[
a(x_i)=mathop{rm arg,min}limits_{1 leq k leq K}rho(x_i, c_k).
] - Зафиксируем распределение объектов по кластерам. В этом случае внутрикластерное расстояние с квадратом евклидовой метрики можно продифференцировать по центрам кластеров и вывести аналитические формулы для них:
[
c_k=frac{1}{sum_{i = 1}^{ell} [a(x_i) = k]}sum_{i = 1}^{ell}[a(x_i) = k] x_i.
]
Повторяя эти шаги до сходимости, мы получим некоторое распределение объектов по кластерам. Новый объект относится к тому кластеру, чей центр является ближайшим.
Результат работы метода K-Means существенно зависит от начального приблжения. Существует большое количество подходов к инициализации; одним из наиболее успешных считается k-means++.
Регрессия как задача машинного обучения
38 мин на чтение
(55.116 символов)
Постановка задачи регрессии
Источник: Analytics Vidhya.
Задача регрессии — это одна из основных задач машинного обучения. И хотя, большинство задач на практике относятся к другому типу — классификации, мы начнем знакомство с машинным обучением именно с регрессии. Регрессионные модели были известны задолго до появления машинного обучения как отрасли и активно применяются в статистике, эконометрике, математическом моделировании. Машинное обучение предлагает новый взгляд на уже известные модели. И этот новый взгляд позволит строить более сложные и мощные модели, чем классические математические дисциплины.
Задача регрессии относится к категории задач обучения с учителем. Это значит, что набор данных, который используется для обучения, должен иметь определенную структуру. Обычно, наборы данных для машинного обучения представляют собой таблицу, в которой по строкам перечислены разные объекты наблюдений или измерений. В столбцах — различные характеристики, или атрибуты, объектов. А на пересечении строк и столбцов — значение данной характеристики у данного объекта. Обычно один атрибут (или переменная) имеет особый характер — именно ее значение мы и хотим научиться предсказывать с помощью модели машинного обучения. Эта характеристика объекта называется целевая переменная. И если эта целевая переменная выражена числом (а точнее, некоторой непрерывной величиной) — то мы говорим о задаче регрессии.
Задачи регрессии на практике встречаются довольно часто. Например, предсказание цены объекта недвижимости — классическая регрессионная задача. В таких проблемах атрибутами выступают разные характеристики квартир или домов — площадь, этажность, расположение, расстояние до центра города, количество комнат, год постройки. В разных наборах данных собрана разная информация И, соответственно, модели тоже должны быть разные. Другой пример — предсказание цены акций или других финансовых активов. Или предсказание температуры завтрашним днем.
Во всех таких задачах нам нужно иметь данные, которые позволят осуществить такое предсказание. Да, “предсказание” — это условный термин, не всегда мы говорим о будущих событиях. Регрессионные модели используют информацию об объектах в обучающем наборе данных, чтобы сделать вывод о возможном значении целевой переменной. И для этого нужно, чтобы ее значение имело какую-то зависимость от имеющихся у нас атрибутов. Если построить модель предсказания цены акции, но на вход подать информацию о футбольных матчах — ничего не получится. Мы предполагаем, что в наборе данных собраны именно те атрибуты объектов, которые имеют влияние на на значение целевой переменной. И чем больше это предположение выполняется, тем точнее будет потенциально наша модель.
Немного поговорим о терминах. Набор данных который мы используем для обучения модели называют датасетом (dataset) или обучающей выборкой (training set). Объекты, которые описываются в датасете еще называют точками данных (data points). Целевую переменную еще называют на статистический манер зависимой переменной (dependent variable) или результативной, выходной (output), а остальные атрибуты — независимыми переменными (dependent variables), или признаками (features), или факторами, или входными переменными (input). Значения одного конкретного атрибута для всех объектов обучающей выборки часто представляют как вектор этого признака (feature vector). А всю таблицу всех атрибутов называют матрицей атрибутов (feature matrix). Соответственно, еще есть вектор целевой переменной, он не входит в матрицу атрибутов.
С точки зрения информатики, регрессионная модель — это функция, которая принимает на вход значения атрибутов какого-то конкретного объекта и выдает на выходе предполагаемое значение целевой переменной. В большинстве случаев мы предполагаем, что целевая переменная у нас одна. Если стоит задача предсказания нескольких характеристик, то их чаще воспринимают как несколько независимых задач регрессии на одних и тех же атрибутах.
Мы пока ничего не говорили о том, как изнутри устроена регрессионная модель. Это потому, что она может быть какой угодно. Это может быть математическое выражение, условный алгоритм, сложная программа со множеством ветвлений и циклов, нейронная сеть — все это можно представить регрессионной моделью. Единственное требование к модели машинного обучения — она должна быть параметрической. То есть иметь какие-то внутренние параметры, от которых тоже зависит результат вычисления. В простых случаях, чаще всего в качестве регрессионной модели используют аналитические функции. Таких функций бесконечное количество, но чаще всего используется самая простая функция, с которой мы и начнем изучение регрессии — линейная функция.
Так же надо сказать, что иногда регрессионные модели подразделяют на парную и множественную регрессии. Парная регрессия — это когда у нас всего один атрибут. Множественная — когда больше одного. Конечно, на практике парная регрессия почти не встречается, но на примере такой простой модели мы поймем основные концепции машинного обучения. Плюс, парную регрессию очень удобно и наглядно можно изобразить на графике. Когда у нас больше двух переменных, графики уже не особо построишь, и модели приходится визуализировать иначе, более косвенно.
Выводы:
- Регрессия — это задача машинного обучения с учителем, которая заключается в предсказании некоторой непрерывной величины.
- Для использования регрессионных моделей нужно, чтобы в датасете были характеристики объектов и “правильные” значения целевой переменной.
- Примеры регрессионных задач — предсказание цены акции, оценка цены объекта недвижимости.
- Задача регрессии основывается на предположении, что значение целевой переменной зависит от значения признаков.
- Регрессионная модель принимает набор значений и выдает предсказание значения целевой переменной.
- В качестве регрессионных моделей часто берут аналитические функции, например, линейную.
Линейная регрессия с одной переменной
Функция гипотезы
Напомним, что в задачах регрессии мы принимаем входные переменные и пытаемся получить более-менее достоверное значение целевой переменной. Любая функция, даже самая простая линейная может выдавать совершенно разные значения для одних и тех же входных данных, если в функции будут разные параметры. Поэтому, любая регрессионная модель — это не какая-то конкретная математическая функция, а целое семейство функций. И задача алгоритма обучения — подобрать значения параметров таким образом, чтобы для объектов обучающей выборки, для которых мы уже знаем правильные ответы, предсказанные (или теоретические, вычисленные из модели) значения были как можно ближе к тем, которые есть в датасете (эмпирические, истинные значения).
Парная, или одномерная (univariate) регрессия используется, когда вы хотите предсказать одно выходное значение (чаще всего обозначаемое $y$), зависящее от одного входного значения (обычно обозначается $x$). Сама функция называется функцией гипотезы или моделью. В качестве функции гипотезы для парной регрессии можно выбрать любую функцию, но мы пока потренируемся с самой простой функцией одной переменной — линейной функцией. Тогда нашу модель можно назвать парной линейной регрессией.
В случае парной линейной регрессии функция гипотезы имеет следующий общий вид:
[hat{y} = h_b (x) = b_0 + b_1 x]
Обратите внимание, что это похоже на уравнение прямой. Эта модель соответствует множеству всех возможных прямых на плоскости. Когда мы конкретизируем модель значениями параметров (в данном случае — $b_0$ и $b_1$), мы получаем конкретную прямую. И наша задача состоит в том, чтобы выбрать такую прямую, которая бы лучше всего “легла” в точки из нашей обучающей выборки.
В данном случае, мы пытаемся подобрать функцию h(x) таким образом, чтобы отобразить данные нам значения x в данные значения y.
Допустим, мы имеем следующий обучающий набор данных:
| входная переменная x | выходная переменная y |
| 0 | 4 |
| 1 | 7 |
| 2 | 7 |
| 3 | 8 |
Мы можем составить случайную гипотезу с параметрами $ b_0 = 2, b_1 = 2 $. Тогда для входного значения $ x=1 $ модель выдаст предсказание, что $ y=4 $, что на 3 меньше данного. Значение $y$б которое посчитала модель будем называть теоретическим или предсказанным (predicted), а значение, которое дано в наборе данных — эмпирическим или истинным (true). Задача регрессии состоит в нахождении таких параметров функции гипотезы, чтобы она отображала входные значения в выходные как можно более точно, или, другими словами, описывала линию, наиболее точно ложащуюся в данные точки на плоскости $(x, y)$.
Выводы:
- Модель машинного обучения — это параметрическая функция.
- Задача обучения состоит в том, чтобы подобрать параметры модели таким образом, чтобы она лучше всего описывала обучающие данные.
- Парная линейная регрессия работает, если есть всего одна входящая переменная.
- Парная линейная регрессия — одна из самых простых моделей машинного обучения.
- Парная линейная регрессия соответствует множеству всех прямых на плоскости. Из них мы выбираем одну, наиболее подходящую.
Функция ошибки
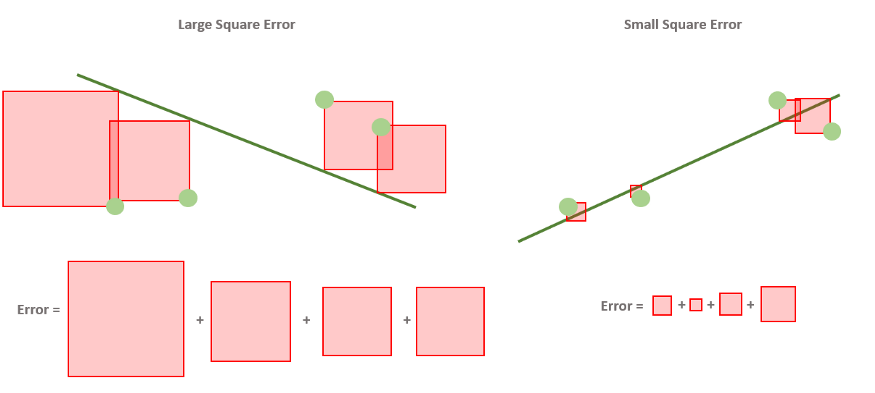
Как мы уже говорили, разные значения параметров дают разные модели. Для того, чтобы подобрать наилучшую модель, нам нужно средство измерения “точности” модели, некоторая функция, которая показывает, насколько модель хорошо или плохо соответствует имеющимся данным.
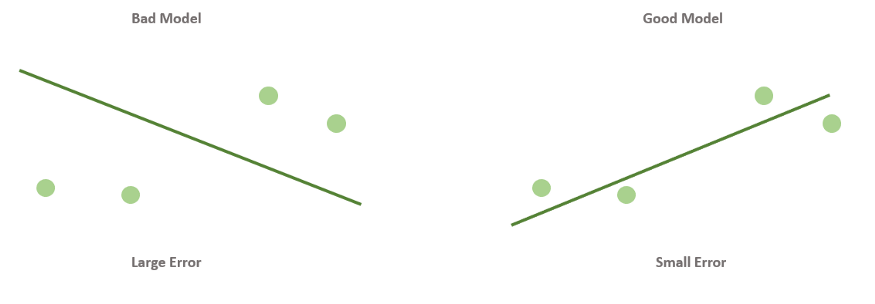
В простых случаях мы можем отличить хорошие модели от плохих, только взглянув на график. Но это затруднительно, если количество признаков очень велико, если модели лишь немного отличаются друг от друга. Да и для автоматизации процесса нужен способ формализовать наше общее представление о том, что модель “ложится” в точки данных.
Такая функция называется функцией ошибки (cost function). Она измеряет отклонения теоретических значений (то есть тех, которые предсказывает модель) от эмпирических (то есть тех, которые есть в данных). Чем выше значение функции ошибки, тем хуже модель соответствует имеющимся данным, хуже описывает их. Если модель полностью соответствует данным, то значение функции ошибки будет нулевым.
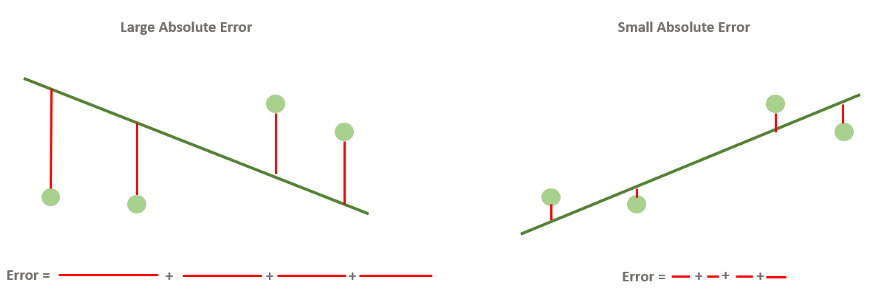
В задачах регрессии в качестве функции ошибки чаще всего берут среднеквадратичное отклонение теоретических значений от эмпирических. То есть сумму квадратов отклонений, деленную на удвоенное количество измерений.
[J(b_0, b_1)
= frac{1}{2m} sum_{i=1}^{m} (hat{y_i} — y_i)^2
= frac{1}{2m} sum_{i=1}^{m} (h_b(x_i) — y_i)^2]
Эту функцию называют «функцией квадрата ошибки» или «среднеквадратичной ошибкой» (mean squared error, MSE). Среднее значение уменьшено вдвое для удобства вычисления градиентного спуска, так как производная квадратичной функции будет отменять множитель 1/2. Вообще, функцию ошибки можно свободно домножить или разделить на любое число (положительное), ведь нам не важна конкретная величина этой функции. Нам важно, что какие-то модели (то есть наборы значений параметров модели) имеют низкую ошибку, они нам подходят больше, а какие-то — высокую ошибку, они подходят нам меньше.
Возведение в квадрат в этой формуле нужно для того, чтобы положительные отклонения не компенсировали отрицательные. Можно было бы для этого брать, например, абсолютное значение, но эта функция не везде дифференцируема, а это станет нам важно позднее.
Обратите внимание, что в качестве аргументов у функции ошибки выступают параметры нашей функции гипотезы. Ведь функция ошибки оценивает отклонение конкретной функции гипотезы (то есть набора значений параметров этой функции) от эмпирических значений, то есть ставит в соответствие каждому набору параметров модели число, характеризующее ошибку этого набора.
Давайте проследим формирование функции ошибки на еще более простом примере. Возьмем упрощенную форму линейной модели — прямую пропорциональность. Она выражается формулой:
[hat{y} = h_b (x) = b_1 x]
Эта модель поможет нам, так как у нее всего один параметр. И функцию ошибки можно будет изобразить на плоскости. Возьмем фиксированный набор точек и попробуем несколько значений параметра для вычисления функции ошибки. Слева на графике изображены точки данных и текущая функция гипотезы, а на правом графике бы будем отмечать значение использованного параметра (по горизонтали) и получившуюся величину функции ошибки (по вертикали):
При значении $b_1 = -1$ линия существенно отклоняется от точек. Отметим уровень ошибки (примерно 10) на правом графике.
Если взять значение $b_1 = 0$ линия гораздо ближе к точкам, но ошибка все еще есть. Отметим новое значение на правом графике в точке 0.
При значении $b_1 = 1$ график точно ложится в точки, таким образом ошибка становится равной нулю. Отмечаем ее так же.
При дальнейшем увеличении $b_1$ линия становится выше точек. Но функция ошибки все равно будет положительной. Теперь она опять станет расти.
На этом примере мы видим еще одно преимущество возведения в квадрат — это то, что такая функция в простых случаях имеет один глобальный минимум. На правом графике формируется точка за точкой некоторая функция, которая похожа очертаниями на параболу. Но мы не знаем аналитического вида этой параболы, мы можем лишь строить ее точка за точкой.
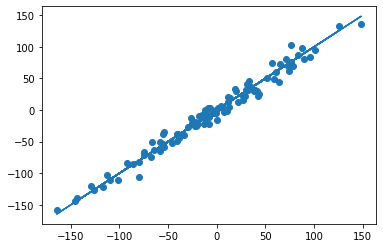
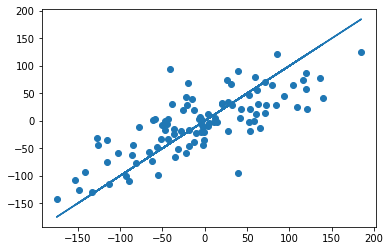
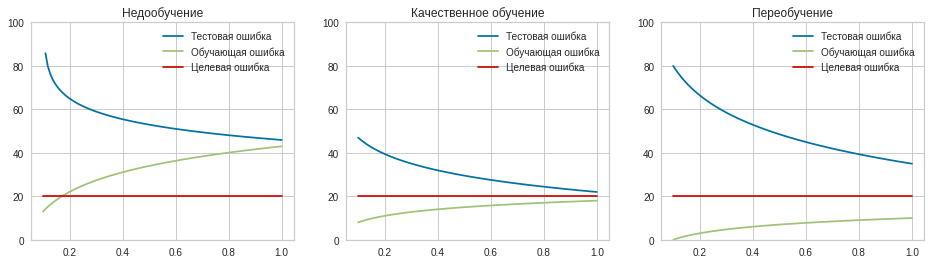
В нашем примере, в определенной точке функция ошибки обращается в ноль. Это соответствует “идеальной” функции гипотезы. То есть такой, когда она проходит четко через все точки. В нашем примере это стало возможно благодаря тому, что точки данных и так располагаются на одной прямой. В общем случае это не выполняется и функция ошибки, вообще говоря, не обязана иметь нули. Но она должна иметь глобальный минимум. Рассмотрим такой неидеальный случай:
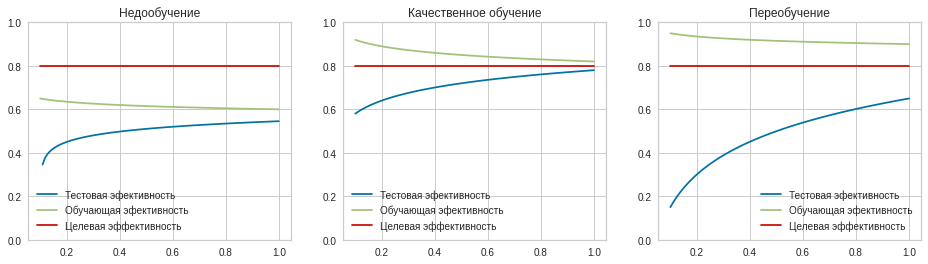
Какое бы значение параметра мы не использовали, линейная функция неспособна идеально пройти через такие три точки, которые не лежат на одной прямой. Эта ситуация называется “недообучение”, об этом мы еще будем говорить дальше. Это значит, что наша модель слишком простая, чтобы идеально описать данные. Но зачастую, идеальная модель и не требуется. Важно лишь найти наилучшую модель из данного класса (например, линейных функций).
Выше мы рассмотрели упрощенный пример с функцией гипотезы с одним параметром. Но у парной линейной регрессии же два параметра. В таком случае, функция ошибки будет описывать не параболу, а параболоид:
Теперь мы можем конкретно измерить точность нашей предсказывающей функции по сравнению с правильными результатами, которые мы имеем, чтобы мы могли предсказать новые результаты, которых у нас нет.
Если мы попытаемся представить это наглядно, наш набор данных обучения будет разбросан по плоскости x-y. Мы пытаемся подобрать прямую линию, которая проходит через этот разбросанный набор данных. Наша цель — получить наилучшую возможную линию. Лучшая линия будет такой, чтобы средние квадраты вертикальных расстояний точек от линии были наименьшими. В лучшем случае линия должна проходить через все точки нашего набора данных обучения. В таком случае значение J будет равно 0.
В более сложных моделях параметров может быть еще больше, но это не важно, ведь нам не нужно строить функцию ошибки, нам нужно лишь оптимизировать ее.
Выводы:
- Функция ошибки нужна для того, чтобы отличать хорошие модели от плохих.
- Функция ошибки показывает численно, насколько модель хорошо описывает данные.
- Аргументами функции ошибки являются параметры модели, ошибка зависит от них.
- Само значение функции ошибки не несет никакого смысла, оно используется только в сравнении.
- Цель алгоритма машинного обучения — минимизировать функцию ошибки, то есть найти такой набор параметров модели, при которых ошибка минимальна.
- Чаще всего используется так называемая L2-ошибка — средний квадрат отклонений теоретических значений от эмпирических (метрика MSE).
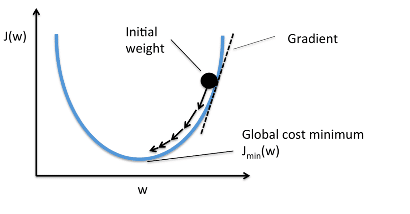
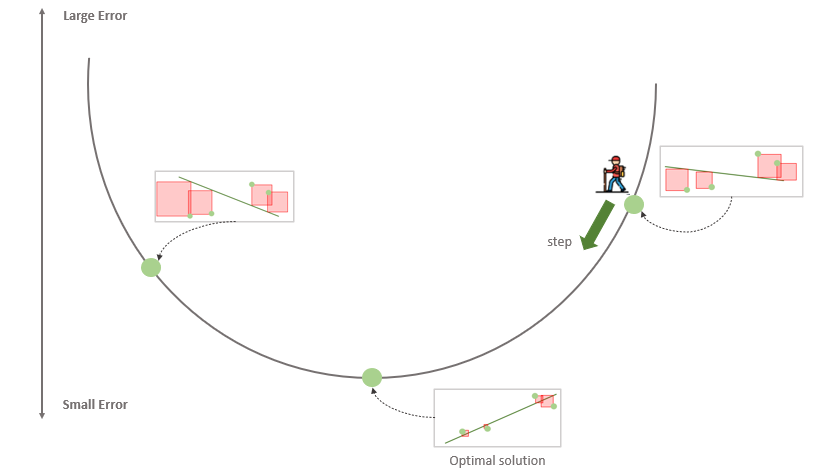
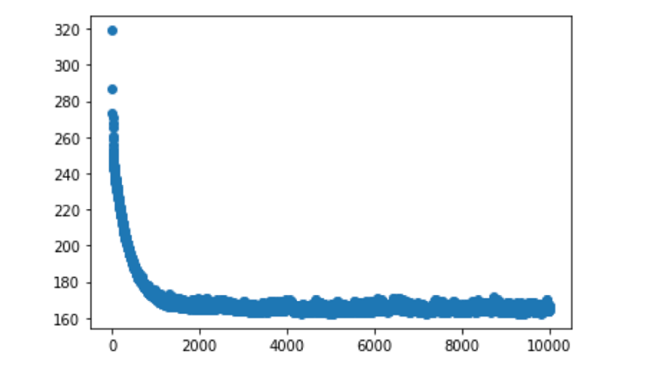
Метод градиентного спуска
Таким образом, у нас есть функция гипотезы, и способ оценить, насколько хорошо конкретная гипотеза вписывается в данные. Теперь нам нужно подобрать параметры функции гипотезы. Вот где приходит на помощь метод градиентного спуска.
Это происходит при помощи производной функции ошибки. Необходимое условие минимума функции — обращение в ноль ее производной. А так как мы знаем, что квадратичная функция имеет один глобальный экстремум — минимум, то наша задача очень проста — вычислить производную функции ошибки и найти, где она равна нулю.
Давайте найдем производную среднеквадратической функции ошибки:
[J(b_0, b_1) = frac{1}{2m} sum_{i=1}^{m} (h_b(x_i) — y_i)^2]
[J(b_0, b_1) = frac{1}{2m} sum_{i=1}^{m} (h_b(x_i) — y_i)^2]
[frac{partial}{partial b_i} J =
frac{1}{m} sum_{i=1}^{m} (h_b(x_i) — y^{(i)}) cdot frac{partial}{partial b_i} h_b(x_i)]
[J(b_0, b_1) = frac{1}{2m} sum_{i=1}^{m} (b_0 + b_1 x_i — y_i)^2]
[frac{partial J}{partial b_0} =
frac{1}{m} sum (b_0 + b_1 x_i — y_i) =
frac{1}{m} sum (h_b(x_i) — y_i)]
[frac{partial J}{partial b_1} =
frac{1}{m} sum (b_0 + b_1 x_i — y_i) cdot x_i =
frac{1}{m} sum (h_b(x_i) — y_i) cdot x_i]
Проблема в том, что мы не можем просто решить эти уравнения аналитически. Ведь мы не знаем общий вид функции ошибки, не то, что ее производной. Ведь он зависит, от всех точек данных. Но мы можем вычислить эту функцию (и ее производную) в любой точке. А точка на этой функции — это конкретный набор значений параметров модели. Поэтому пришлось изобрести численный алгоритм. Он работает следующим образом.
Сначала, мы выбираем произвольное значение параметров модели. То есть, произвольную точку в области определения функции. Мы не знаем, является ли эта точка оптимальной (скорее нет), не знаем, насколько она далека от оптимума. Но мы можем вычислить направление к оптимуму. Ведь мы знаем наклон касательной к графику функции ошибки.
Наклон касательной является производной в этой точке, и это даст нам направление движения в сторону самого крутого уменьшения значения функции. Если представить себе функцию одной переменной (параболу), то там все очень просто. Если производная в точке отрицательна, значит функция убывает, значит, что оптимум находится справа от данной точки. То есть, чтобы приблизиться к оптимуму надо увеличить аргумент функции. Если же производная положительна, то все наоборот — функция возрастает, оптимум находится слева и нам нужно уменьшить значение аргумента. Причем, чем дальше от оптимума, тем быстрее возрастает или убывает функция. То есть значение производной дает нам не только направление, но и величину нужного шага. Сделав шаг, пропорциональный величине производной и в направлении, противоположном ей, можно повторить процесс и еще больше приблизиться к оптимуму. С каждой итерацией мы будем приближаться к минимуму ошибки и математически доказано, что мы можем приблизиться к ней произвольно близко. То есть, данный метод сходится в пределе.
В случае с функцией нескольких переменных все немного сложнее, но принцип остается прежним. Только мы оперируем не полной производной функции, а вектором частных производных по каждому параметру. Он задает нам направление максимального увеличения функции. Чтобы получить направление максимального спада функции нужно просто домножить этот вектор на -1. После этого нужно обновить значения каждого компонента вектора параметров модели на величину, пропорциональную соответствующему компоненту вектора градиента. Таким образом мы делаем шаги вниз по функции ошибки в направлении с самым крутым спуском, а размер каждого шага пропорционален определяется параметром $alpha$, который называется скоростью обучения.
Алгоритм градиентного спуска:
повторяйте до сходимости:
[b_j := b_j — alpha frac{partial}{partial b_j} J(b_0, b_1)]
где j=0,1 — представляет собой индекс номера признака.
Это общий алгоритм градиентного спуска. Она работает для любых моделей и для любых функций ошибки. Это итеративный алгоритм, который сходится в пределе. То есть, мы никогда не придем в сам оптимум, но можем приблизиться к нему сколь угодно близко. На практике нам не так уж важно получить точное решение, достаточно решения с определенной точностью.
Алгоритм градиентного спуска имеет один параметр — скорость обучения. Он влияет на то, как быстро мы будем приближаться к оптимуму. Кажется, что чем быстрее, тем лучше, но оказывается, что если значение данного параметра слишком велико, то мы буем постоянно промахиваться и алгоритм будет расходиться.
Алгоритм градиентного спуска для парной линейной регрессии:
повторяйте до сходимости:
[b_0 := b_0 — alpha frac{1}{m} sum_{i=1}^{m} (h_b(x^{(i)} )- y^{(i)})]
[b_1 := b_1 — alpha frac{1}{m} sum_{i=1}^{m} (h_b(x^{(i)}) — y^{(i)}) cdot x^{(i)}]
На практике “повторяйте до сходимости” означает, что мы повторяем алгоритм градиентного спуска до тех пор, пока значение функции ошибки не перестанет значимо изменяться. Это будет означать, что мы уже достаточно близко к минимуму и дальнейшие шаги градиентного спуска слишком малы, чтобы быть целесообразными. Конечно, это оценочное суждение, но на практике обычно, нескольких значащих цифр достаточно для практического применения моделей машинного обучения.
Алгоритм градиентного спуска имеет одну особенность, про которую нужно помнить. Он в состоянии находить только локальный минимум функции. Он в принципе, по своей природе, локален. Поэтому, если функция ошибки будет очень сложна и иметь несколько локальных оптимумов, то результат работы градиентного спуска будет зависеть от выбора начальной точки:
На практике эту проблему решают методом семплирования — запускают градиентный спуск из множества случайных точек и выбирают то минимум, который оказался меньше по значению функции ошибки. Но этот подход понадобится нам при рассмотрении более сложных и глубоких моделей машинного обучения. Для простых линейных, полиномиальных и других моделей метод градиентного спуска работает прекрасно. В настоящее время этот алгоритм — это основная рабочая лошадка классических моделей машинного обучения.
Выводы:
- Метод градиентного спуска нужен, чтобы найти минимум функции, если мы не можем ее вычислить аналитически.
- Это численный итеративный алгоритм локальной оптимизации.
- Для запуска градиентного спуска нужно знать частную производную функции ошибки.
- Для начала мы берем произвольные значения параметров, затем обновляем их по данной формуле.
- Доказано, что этот метод сходится к локальному минимуму.
- Если функция ошибки достаточно сложная, то разные начальные точки дадут разный результат.
- Метод градиентного спуска имеет свой параметр — скорость обучения. Обычно его подстаивают автоматически.
- Метод градиентного спуска повторяют много раз до тех пор, пока функция ошибки не перестанет значимо изменяться.
Регрессия с несколькими переменными
Множественная линейная регрессия
Парная регрессия, как мы увидели выше, имеет дело с объектами, которые характеризуются одним числовым признаком ($x$). На практике, конечно, объекты характеризуются несколькими признаками, а значит в модели должна быть не одна входящая переменная, а несколько (или, что то же самое, вектор). Линейная регрессия с несколькими переменными также известна как «множественная линейная регрессия». Введем обозначения для уравнений, где мы можем иметь любое количество входных переменных:
$ x^{(i)} $- вектор-столбец всех значений признаков i-го обучающего примера;
$ x_j^{(i)} $ — значение j-го признака i-го обучающего примера;
$ x_j $ — вектор j-го признака всех обучающих примеров;
m — количество примеров в обучающей выборке;
n — количество признаков;
X — матрица признаков;
b — вектор параметров регрессии.
Задачи множественной регрессии уже очень сложно представить на графике, ведь количество параметров каждого объекта обучающей выборки соответствует измерению, в котором находятся точки данных. Плюс нужно еще одно измерение для целевой переменной. И вместо того, чтобы подбирать оптимальную прямую, мы будем подбирать оптимальную гиперплоскость. Но в целом идея линейной регрессии остается неизменной.
Для удобства примем, что $ x_0^{(i)} = 1 $ для всех $i$. Другими словами, мы ведем некий суррогатный признак, для всех объектов равный единице. Это никак не сказывается на самой функции гипотезы, это лишь условность обозначения, но это сильно упростит математические выкладки, особенно в матричной форме.
Теперь определим множественную форму функции гипотезы следующим образом, используя несколько признаков. Она очень похожа на парную, но имеет больше входных переменных и, как следствие, больше параметров.
Общий вид модели множественной линейной регрессии:
[h_b(x) = b_0 + b_1 x_1 + b_2 x_2 + … + b_n x_n]
Или в матричной форме:
[h_b(x) = X cdot vec{b}]
Используя определение матричного умножения, наша многопараметрическая функция гипотезы может быть кратко представлена в виде: $h(x) = B X$.
Обратите внимание, что в любой модели линейной регрессии количество параметров на единицу больше количества входных переменных. Это верно для любой линейной модели машинного обучения. Вообще, всегда чем больше признаков, тем больше параметров. Это будет важно для нас позже, когда мы будем говорить о сложности моделей.
Теперь, когда мы знаем виды функции гипотезы, то есть нашей модели, мы можем переходить к следующему шагу: функции ошибки. Мы построим ее по аналогии с функцией ошибки для парной модели. Для множественной регрессии функция ошибки от вектора параметров b выглядит следующим образом:
Функция ошибки для множественной линейной регрессии:
[J(b) = frac{1}{2m} sum_{i=1}^{m} (h_b(x^{(i)}) — y^{(i)})^2]
Или в матричной форме:
[J(b) = frac{1}{2m} (X b — vec{y})^T (X b — vec{y})]
Обратите внимание, что мы специально не раскрываем выражение (h_b(x^{(i)})). Это нужно, чтобы подчеркнуть, что форма функции ошибки не зависит от функции гипотезы, она выражается через нее.
Теперь нам нужно взять производную этой функции ошибки. Здесь уже нужно знать производную самой функции гипотезы, так как:
[frac{partial}{partial b_i} J =
frac{1}{m} sum_{i=1}^{m} (h_b(x^{(i)}) — y^{(i)}) cdot frac{partial}{partial b_i} h_b(x^{(i)})]
В такой формулировке мы представляем частные производные функции ошибки (градиент) через частную производную функции гипотезы. Это так называемое моделенезависимое представление градиента. Ведь для этой формулы совершенно неважно, какой функцией будет наша гипотеза. Пока она является дифференцируемой, мы можем использовать градиент ее функции ошибки. Именно поэтому метод градиентного спуска работает с любыми аналитическими моделями, и нам не нужно каждый раз заново “переизобретать” математику градиентного спуска, адаптировать ее к каждой конкретной модели машинного обучения. Достаточно изучить этот метод один раз, в общей форме.
Метод градиентного спуска для множественной регрессии определяется следующими уравнениями:
повторять до сходимости:
[b_0 := b_0 — alpha frac{1}{m} sum_{i=1}^{m} (h_b(x^{(i)}) — y^{(i)}) cdot x_0^{(i)}]
[b_1 := b_1 — alpha frac{1}{m} sum_{i=1}^{m} (h_b(x^{(i)}) — y^{(i)}) cdot x_1^{(i)}]
[b_2 := b_2 — alpha frac{1}{m} sum_{i=1}^{m} (h_b(x^{(i)}) — y^{(i)}) cdot x_2^{(i)}]
[…]
Или в матричной форме:
[b := b — frac{alpha}{m} X^T (X b — vec{y})]
Выводы:
- Множественная регрессия очень похожа на парную, но с большим количеством признаков.
- Для удобства и однообразия, почти всегда обозначают $x_0 = 1$.
- Признаки образуют матрицу, поэтому уравнения множественной регрессии часто приводят в матричной форме, так короче.
- Алгоритм градиентного спуска для множественной регрессии точно такой же, как и для парной.
Нормализация признаков
Мы можем ускорить сходимость метода градиентного спуска, преобразовав входные данные таким образом, чтобы все атрибуты имели значения примерно в том же диапазоне. Это называется нормализация данных — приведение всех признаков к одной шкале. Это ускоряет сходимость градиентного спуска за счет эффекта масштаба. Дело в том, что зачастую значения разных признаков измеряются по шкалам с очень разным порядком величины. Например, $x_1$ измеряется в миллионах, а $x_2$ — в долях единицы.
В таком случае форма функции ошибки будет очень вытянутой. Это не проблема для математической формализации градиентного спуска — при достаточно малых $alpha$ метод все равно рано или поздно сходится. Проблема в практической реализации. Получается, что если выбрать скорость обучения выше определенного предела по самому компактному признаку, спуск разойдется. Значит, скорость обучения надо делать меньше. Но тогда в направлении второго признака спуск будет проходить слишком медленно. И получается, что градиентный спуск потребует гораздо больше итераций для завершения.
Эту проблему можно решить если изменить диапазоны входных данных, чтобы они выражались величинами примерно одного порядка. Это не позволит одному измерению численно доминировать над другим. На практике применяют несколько алгоритмов нормализации, самые распространенные из которых — минимаксная нормализация и стандартизация или z-оценки.
Минимаксная нормализация — это изменение входных данных по следующей формуле:
[x’ = frac{x — x_{min}}{x_{max} — x_{min}}]
После преобразования все значения будут лежать в диапазоне $x in [0; 1]$.
Z-оценки или стандартизация производится по формуле:
[x’ = frac{x — M[x]}{sigma_x}]
В таком случае данный признак приводится к стандартному распределению, то есть такому, у которого среднее 0, а дисперсия — 1.
У каждого из этих двух методов нормализации есть по два параметра. У минимаксной — минимальное и максимальное значение признака. У стандартизации — выборочные среднее и дисперсия. Параметры нормализации, конечно, вычисляются по каждому признаку (столбцу данных) отдельно. Причем, эти параметры надо запомнить, чтобы при использовании модели для предсказании использовать именно их (вычисленные по обучающей выборке). Даже если вы используете тестовую выборку, ее надо нормировать с использованием параметров, вычисленных по обучающей. Да, при этом может получиться, что при применении модели на данных, которых не было в обучающей выборке, могут получиться значения, например, меньше нуля или больше единицы (при использовании минимаксной нормализации). Это не страшно, главное, что будет соблюдена последовательность вычисления нормированных значений.
Целевая переменная не нормируется.
При использовании библиотечных моделей машинного обучения беспокоиться о нормализации входных данных вручную, как правило, не нужно. Большинство готовых реализаций моделей уже включают нормализацию как неотъемлемый этап подготовки данных. Более того, некоторые типы моделей обучения с учителем вовсе не нуждаются в нормализации. Но об этом пойдет речь в следующих главах.
Выводы:
- Нормализация нужна для ускорения метода градиентного спуска.
- Есть два основных метода нормализации — минимаксная и стандартизация.
- Параметры нормализации высчитываются по обучающей выборке.
- Нормализация встроена в большинство библиотечных методов.
- Некоторые методы более чувствительны к нормализации, чем другие.
- Нормализацию лучше сделать, чем не делать.
Полиномиальная регрессия
Функция гипотезы не обязательно должна быть линейной, если это не соответствует данным. На практике вы не всегда будете иметь данные, которые можно хорошо аппроксимировать линейной функцией. Наглядный пример вы видите на иллюстрации. Вполне очевидно, что в среднем увеличение целевой переменной замедляется с ростом входной переменной. Это значит, что данные демонстрируют нелинейную динамику. И это так же значит, что мы никак не сможем их хорошо приблизить линейной моделью.
Надо подчеркнуть, что это не свидетельствует о несовершенстве наших методов оптимизации. Мы действительно можем найти самую лучшую линейную функцию для данных точек, но проблема в том, что мы всегда выбираем лучшую функцию из некоторого класса функций, в данном случае — линейных. То есть проблема не в алгоритмах оптимизации, а в ограничении самого вида модели.
вполне логично предположить, что для описания таких нелинейных наборов данных следует использовать нелинейные же функции моделей. Но очень бы не хотелось, для каждого нового класса функций изобретать собственный метод оптимизации, поэтому мы постараемся максимально “переиспользовать” те подходы, которые описали выше. И механизм множественной регрессии в этом сильно поможет.
Мы можем изменить поведение или кривую нашей функции гипотезы, сделав ее квадратичной, кубической или любой другой формой.
Например, если наша функция гипотезы
$ hat{y} = h_b (x) = b_0 + b_1 x $,
то мы можем добавить еще один признак, основанный на $ x_1 $, получив квадратичную функцию
[hat{y} = h_b (x) = b_0 + b_1 x + b_2 x^2]
или кубическую функцию
[hat{y} = h_b (x) = b_0 + b_1 x + b_2 x^2 + b_3 x^3]
В кубической функции мы по сути ввели два новых признака:
$ x_2 = x^2, x_3 = x^3 $.
Точно таким же образом, мы можем создать, например, такую функцию:
[hat{y} = h_b (x) = b_0 + b_1 x + b_2 sqrt{x}]
В любом случае, мы из парной линейной функции сделали какую-то другую функцию. И к этой нелинейной функции можно относиться по разному. С одной стороны, это другой класс функций, который обладает нелинейным поведением, а следовательно, может описывать более сложные зависимости в данных. С другой стороны, это линейна функция от нескольких переменных. Только сами эти переменные оказываются в функциональной зависимости друг от друга. Но никто не говорил, что признаки должны быть независимы.
И вот такое представление нелинейной функции как множественной линейной позволяет нам без изменений воспользоваться алгоритмом градиентного спуска для множественной линейной регрессии. Только вместо $ x_2, x_3, … , x_n $ нам нужно будет подставить соответствующие функции от $ x_1 $.
Источник: Wikimedia.
Очевидно, что нелинейных функций можно придумать бесконечное количество. Поэтому встает вопрос, как выбрать нужный класс функций для решения конкретной задачи. В случае парной регрессии мы можем взглянув на график точек обучающей выборки сделать предположение о том, какой вид нелинейной зависимости связывает входную и целевую переменные. Но если у нас множество признаков, просто так проанализировать график нам не удастся. Поэтому по умолчанию используют полиномиальную регрессию, когда в модель добавляют входные переменные второго, третьего, четвертого и так далее порядков.
Порядок полиномиальной регрессии подбирается в качестве компромисса между качеством получаемой регрессии, и вычислительной сложностью. Ведь чем выше порядок полинома, тем более сложные зависимости он может аппроксимировать. И вообще, чем выше степень полинома, тем меньше будет ошибка при прочих равных. Если степень полинома на единицу меньше количества точек — ошибка будет нулевая. Но одновременно с этим, чем выше степень полинома, тем больше в модели параметров, тем она сложнее и занимает больше времени на обучение. Есть еще вопросы переобучения, но про это мы поговорим позднее.
А что делать, если изначально в модели было несколько признаков? Тогда обычно для определенной степени полинома берутся все возможные комбинации признаком соответствующей степени и ниже. Например:
Для регрессии с двумя признаками.
Линейная модель (полином степени 1):
[h_b (x) = b_0 + b_1 x_1 + b_2 x_2]
Квадратичная модель (полином степени 2):
[h_b (x) = b_0 + b_1 x + b_2 x_2 + b_3 x_1^2 + b_4 x_2^2 + b_5 x_1 x_2]
Кубическая модель (полином степени 3):
[hat{y} = h_b (x) = b_0 + b_1 x_1 + b_2 x_2 + b_3 x_1^2 + b_4 x_2^2 + b_5 x_1 x_2 + b_6 x_1^3 + b_7 x_2^3 + b_7 x_1^2 x_2 + b_8 x_1 x_2^2]
При этом количество признаков и, соответственно, количество параметров растет экспоненциально с ростом степени полинома. Поэтому полиномиальные модели обычно очень затратные в обучении при больших степенях. Но полиномы высоких степеней более универсальны и могут аппроксимировать более сложные данные лучше и точнее.
Выводы:
- Данные в датасете не всегда располагаются так, что их хорошо может описывать линейная функция.
- Для описания нелинейных зависимостей нужна более сложная, нелинейная модель.
- Чтобы не изобретать алгоритм обучения заново, можно просто ввести в модель суррогатные признаки.
- Суррогатный признак — это новый признак, который считается из существующих атрибутов.
- Чаще всего используют полиномиальную регрессию — это когда в модель вводят полиномиальные признаки — степени существующих атрибутов.
- Обычно берут все комбинации факторов до какой-то определенной степени полинома.
- Полиномиальная регрессия может аппроксимировать любую функцию, нужно только подобрать степень полинома.
- Чем больше степень полиномиальной регрессии, тем она сложнее и универсальнее, но вычислительно сложнее (экспоненциально).
Практическое построение регрессии
В данном разделе мы посмотрим, как можно реализовать методы линейной регрессии на практике. Сначала мы попробуем создать алгоритм регрессии с нуля, а затем воспользуемся библиотечной функцией. Это поможет нам более полно понять, как работают модели машинного обучения в целом и в библиотеке sckikit-learn (самом популярном инструменте для создания и обучения моделей на языке программирования Python) в частности.
Для понимания данного раздела предполагаем, что читатель знаком с основами языка программирования Python. Нам понадобится знание его базового синтаксиса, немного — объектно-ориентированного программирования, немного — использования стандартных библиотек и модулей. Никаких продвинутых возможностей языка (типа метапрограммирования или декораторов) мы использовать не будем.
Как должны быть представлены данные для машинного обучения?
Применение любых моделей машинного обучения начинается с подготовки данных в необходимом формате. Для этого очень удобными для нас будут библиотеки numpy и pandas. Они практически всегда используются совместно с библиотекой sckikit-learn и другими инструментами машинного обучения. В первую очередь мы будем использовать numpy для создания массивов и операций с векторами и матрицами. Pandas нам понадобится для работы с табличными структурами — датасетами.
Если вы хотите самостоятельно задать в явном виде данные обучающей выборки, то нет ничего лучше использования обычных массивов ndarray. Обычно в одном массиве хранятся значения атрибутов — x, а в другом — значения целевой переменной — y.
1
2
3
4
5
6
7
8
9
10
11
import numpy as np
x = np.array([1.46, 1.13, -2.30, 1.74, 0.04,
-0.61, 0.32, -0.76, 0.58, -1.10,
0.87, 1.62, -0.53, -0.25, -1.07,
-0.38, -0.17, -0.32, -2.06, -0.88, ])
y = np.array([101.16, 78.44, -159.24, 120.72, 2.92,
-42.33, 22.07, -52.67, 40.32, -76.10,
59.88, 112.38, -36.54, -17.25, -74.24,
-26.57, -11.93, -22.31, -142.54, -60.74,])
Если мы имеем дело с задачей множественной регрессии, то в массиве атрибутов будет уже двумерный массив, состоящий из нескольких векторов атрибутов, вот так:
1
2
3
4
5
x = np.array([
[0, 1, 2, 3, 4],
[5, 4, 9, 6, 3],
[7.8, -0.1, 0.0, -2.14, 10.7],
])
Важно следить за тем, чтобы в массиве атрибутов в каждом вложенном массиве количество элементов было одинаковым и в свою очередь совпадало с количеством элементов в массиве целевой переменной. Это называется соблюдение размерности задачи. Если размерность не соблюдается, то модели машинного обучения будут работать неправильно. А библиотечные функции чаще всего будут выдавать ошибку, связанную с формой массива (shape).
Но чаще всего вы не будете задавать исходные данные явно. Практически всегда их приходится читать из каких-либо входных файлов. Удобнее всего это сделать при помощи библиотеки pandas вот так:
1
2
3
4
import pandas as pd
x = pd.read_csv('x.csv', index_col=0)
y = pd.read_csv('y.csv', index_col=0)
Или, если данные лежат в одном файле в общей таблице (что происходит чаще всего), тогда его читают в один датафрейм, а затем выделяют целевую переменную, и факторные переменные:
1
2
3
4
5
6
7
8
import pandas as pd
data = pd.read_csv('data.csv', index_col=0)
y = data.Y
y = data["Y"]
x = data.drop(["Y"])
Обратите внимание, что матрицу атрибутов проще всего сформировать, удалив из полной таблицы целевую переменную. Но, если вы хотите выбрать только конкретные столбцы, тогда можно использовать более явный вид, через перечисление выбранных колонок.
Если вы используете pandas или numpy для формирования массивов данных, то получившиеся переменные будут разных типов — DataFrame или ndarray, соответственно. Но на дальнейшую работу это не повлияет, так как интерфейс работы с этими структурами данных очень похож. Например, неважно, какие именно массивы мы используем, их можно изобразить на графике вот так:
1
2
3
4
5
import maiplotlib.pyplot as plt
plt.figure()
plt.scatter(x, y)
plt.show()
Конечно, такая визуализация будет работать только в случае задачи парной регрессии. Если x многомерно, то простой график использовать не получится.
Давайте соберем весь наш код вместе:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
import numpy as np
import pandas as pd
import maiplotlib.pyplot as plt
# x = pd.read_csv('x.csv', index_col=0)
x = np.array([1.46, 1.13, -2.30, 1.74, 0.04,
-0.61, 0.32, -0.76, 0.58, -1.10,
0.87, 1.62, -0.53, -0.25, -1.07,
-0.38, -0.17, -0.32, -2.06, -0.88, ])
# y = pd.read_csv('y.csv', index_col=0)
y = np.array([101.16, 78.44, -159.24, 120.72, 2.92,
-42.33, 22.07, -52.67, 40.32, -76.10,
59.88, 112.38, -36.54, -17.25, -74.24,
-26.57, -11.93, -22.31, -142.54, -60.74,])
plt.figure()
plt.scatter(x, y)
plt.show()
Это код генерирует вот такой вот график:
Как работает метод машинного обучения “на пальцах”?
Для того, чтобы более полно понимать, как работает метод градиентного спуска для линейной регрессии, давайте реализуем его самостоятельно, не обращаясь к библиотечным методам. На этом примере мы проследим все шаги обучения модели.
Мы будем использовать объектно-ориентированный подход, так как именно он используется в современных библиотеках. Начнем строить класс, который будет реализовывать метод парной линейной регрессии:
1
2
3
4
5
class hypothesis(object):
"""Модель парной линейной регрессии"""
def __init__(self):
self.b0 = 0
self.b1 = 0
Здесь мы определили конструктор класса, который запоминает в полях экземпляра параметры регрессии. Начальные значения этих параметров не очень важны, так как градиентный спуск сойдется из любой точки. В данном случае мы выбрали нулевые, но можно задать любые другие начальные значения.
Реализуем метод, который принимает значение входной переменной и возвращает теоретическое значение выходной — это прямое действие нашей регрессии — метод предсказания результата по факторам (в случае парной регрессии — по одному фактору):
1
2
def predict(self, x):
return self.b0 + self.b1 * x
Название выбрано не случайно, именно так этот метод называется и работает в большинстве библиотечных классов.
Теперь зададим функцию ошибки:
1
2
def error(self, X, Y):
return sum((self.predict(X) - Y)**2) / (2 * len(X))
В данном случае мы используем простую функцию ошибки — среднеквадратическое отклонение (mean squared error, MSE). Можно использовать и другие функции ошибки. Именно вид функции ошибки будет определять то, какой вид регрессии мы реализуем. Существует много разных вариаций простого алгоритма регрессии. О большинстве распространенных методах регрессии можно почитать в официальной документации sklearn.
Теперь реализуем метод градиентного спуска. Он должен принимать массив X и массив Y и обновлять параметры регрессии в соответствии в формулами градиентного спуска:
1
2
3
4
5
6
def BGD(self, X, Y):
alpha = 0.5
dJ0 = sum(self.predict(X) - Y) /len(X)
dJ1 = sum((self.predict(X) - Y) * X) /len(X)
self.b0 -= alpha * dJ0
self.b1 -= alpha * dJ1
О выборе конкретного значения alpha мы говорить пока не будем,на практике его довольно просто подбирают, мы же возьмем нейтральное значение.
Давайте создадим объект регрессии и проверим начальное значение ошибки. В примерах приведены значения на модельном наборе данных, но этот метод можно использовать на любых данных, которые подходят по формату — x и y должны быть одномерными массивами чисел.
1
2
3
4
5
6
7
8
hyp = hypothesis()
print(hyp.predict(0))
print(hyp.predict(100))
J = hyp.error(x, y)
print("initial error:", J)
0
0
initial error: 36271.58344889084
Как мы видим, для начала оба параметра регрессии равны нулю. Конечно, такая модель не дает надежных предсказаний, но в этом и состоит суть метода градиентного спуска: начиная с любого решения мы постепенно его улучшаем и приходим к оптимальному решению.
Теперь все готово к запуску градиентного спуска.
1
2
3
4
5
6
7
8
9
10
hyp.BGD(x, y)
J = hyp.error(x, y)
print("error after gradient descent:", J)
error after gradient descent: 6734.135540194945
X0 = np.linspace(60, 180, 100)
Y0 = hyp.predict(X0)
plt.figure()
plt.scatter(x, y)
plt.plot(X0, Y0, 'r')
plt.show()
Как мы видим, численное значение ошибки значительно уменьшилось. Да и линия на графике существенно приблизилась к точкам. Конечно, наша модель еще далека от совершенства. Мы прошли всего лишь одну итерацию градиентного спуска. Модифицируем метод так, чтобы он запускался в цикле пока ошибка не перестанет меняться существенно:
1
2
3
4
5
6
7
8
9
10
11
12
13
def BGD(self, X, Y, alpha=0.5, accuracy=0.01, max_steps=5000):
step = 0
old_err = hyp.error(X, Y)
new_err = hyp.error(X, Y)
dJ = 1
while (dJ > accuracy) and (step < max_steps):
dJ0 = sum(self.predict(X) - Y) /len(X)
dJ1 = sum((self.predict(X) - Y) * X) /len(X)
self.b0 -= alpha * dJ0
self.b1 -= alpha * dJ1
old_err = new_err
new_err = hyp.error(X, Y)
dJ = abs(old_err - new_err)
Заодно мы проверяем, насколько изменилось значение функции ошибки. Если оно изменилось на величину, меньшую, чем заранее заданная точность, мы завершаем спуск. Таким образом, мы реализовали два стоп-механизма — по количеству итераций и по стабилизации ошибки. Вы можете выбрать любой или использовать оба в связке.
Запустим наш градиентный спуск:
1
2
3
4
5
hyp = hypothesis()
hyp.BGD(x, y)
J = hyp.error(x, y)
print("error after gradient descent:", J)
error after gradient descent: 298.76881676471504
Как мы видим, теперь ошибка снизилась гораздо больше. Однако, она все еще не достигла нуля. Заметим, что нулевая ошибка не всегда возможна в принципе из-за того, что точки данных не всегда будут располагаться на одной линии. Нужно стремиться не к нулевой, а к минимально возможной ошибке.
Посмотрим, как теперь наша регрессия выглядит на графике:
1
2
3
4
5
6
X0 = np.linspace(60, 180, 100)
Y0 = hyp.predict(X0)
plt.figure()
plt.scatter(x, y)
plt.plot(X0, Y0, 'r')
plt.show()
Уже значительно лучше. Линия регрессии довольно похожа на оптимальную. Так ли это на самом деле, глядя на график, сказать сложно, для этого нужно проанализировать, как ошибка регрессии менялась со временем:
Как оценить качество регрессионной модели?
В простых случаях качество модели можно оценить визуально на графике. Но если у вас многомерная задача, это уже не представляется возможным. Кроме того, если ошибка и сама модель меняется незначительно, то очень сложно определить, стало хуже или лучше. Поэтому для диагностики моделей машинного обучения используют кривые.
Самая простая кривая обучения — зависимость ошибки от времени (итерации градиентного спуска). Для того, чтобы построить эту кривую, нам нужно немного модифицировать наш метод обучения так, чтобы он возвращал нужную нам информацию:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
def BGD(self, X, Y, alpha=0.1, accuracy=0.01, max_steps=1000):
steps, errors = [], []
step = 0
old_err = hyp.error(X, Y)
new_err = hyp.error(X, Y) - 1
dJ = 1
while (dJ > accuracy) and (step < max_steps):
dJ0 = sum(self.predict(X) - Y) /len(X)
dJ1 = sum((self.predict(X) - Y) * X) /len(X)
self.b0 -= alpha * dJ0
self.b1 -= alpha * dJ1
old_err = new_err
new_err = hyp.error(X, Y)
dJ = abs(old_err - new_err)
step += 1
steps.append(step)
errors.append(new_err)
return steps, errors
Мы просто запоминаем в массивах на номер шаа и ошибку на каждом шаге. Получив эти данные можно легко построить их на графике:
1
2
3
4
5
6
hyp = hypothesis()
steps, errors = hyp.BGD(x, y)
plt.figure()
plt.plot(steps, errors, 'g')
plt.show()
На этом графике наглядно видно, что в начале обучения ошибка падала быстро, но в ходе градиентного спуска она вышла на плато. Учитывая, что мы используем гладкую функцию ошибки второго порядка, это свидетельствует о том, что мы достигли локального оптимума и дальнейшее повторение алгоритма не принесет улучшения модели.
Если бы мы наблюдали на графике обучения ситуацию, когда по достижении конца обучения ошибка все еще заметно снижалась, это значит, что мы рано прекратили обучение, и нужно продолжить его еще на какое-то количество итераций.
При анализе графиков с библиотечными моделями не получится таких гладких графиков, они больше напоминают случайные колебания. Это из-за того, что в готовых реализациях используется очень оптимизированный вариант метода градиентного спуска. А он может работать с произвольными флуктуациями. В любом случае, нас интересует общий вид этой кривой.
Как подбирать скорость обучения?
В нашей реализации метода градиентного спуска есть один параметр — скорость обучения — который нам приходится так же подбирать руками. Какой смысл автоматизировать подбор параметров линейной регрессии, если все равно приходится вручную подбирать какой-то другой параметр?
На самом деле подобрать скорость обучения гораздо легче. Нужно использовать тот факт, что при превышении определенного порогового значения ошибка начинает возрастать. Кроме того, мы знаем, что скорость обучения должна быть положительна, но меньше единицы. Вся проблема в этом пороговом значении, которое сильно зависит от размерности задачи. При одних данных хорошо работает $ alpha = 0.5 $, а при каких-то приходится уменьшать ее на несколько порядков, например, $ alpha = 0.00000001 $.
Мы еще не говорили о нормализации данных, которая тоже практически всегда применяется при обучении. Она “благотворно” влияет на возможный диапазон значений скорости обучения. При использовании нормализации меньше вероятность, что скорость обучения нужно будет уменьшать очень сильно.
Подбирать скорость обучения можно по следующему алгоритму. Сначала мы выбираем $ alpha $ близкое к 1, скажем, $ alpha = 0.7 $. Производим одну итерацию градиентного спуска и оцениваем, как изменилась ошибка. Если она уменьшилась, то ничего не надо менять, продолжаем спуск как обычно. Если же ошибка увеличилась, то скорость обучения нужно уменьшить. Например, раа в два. После чего мы повторяем первый шаг градиентного спуска. Таким образом мы не начинаем спуск, пока скорость обучения не снизится настолько, чтобы он начал сходиться.
Как применять регрессию с использованием scikit-learn?
Для серьезной работы, все-таки рекомендуется использовать готовые библиотечные решения. Они работаю гораздо быстрее, надежнее и гораздо проще, чем написанные самостоятельно. Мы будем использовать библиотеку scikit-learn для языка программирования Python как наш основной инструмент реализации простых моделей. Сегодня это одна их самых популярных библиотек для машинного обучения. Мы не будем повторять официальную документацию этой библиотеки, которая на редкость подробная и понятная. Наша задача — на примере этих инструментов понять, как работают и как применяются модели машинного обучения.
В библиотеке scikit-learn существует огромное количество моделей машинного обучения и других функций, которые могут понадобиться для их работы. Поэтому внутри самой библиотеки есть много разных пакетов. Все простые модели, например, модель линейной регрессии, собраны в пакете linear_models. Подключить его можно так:
1
from sklearn import linear_model
Надо помнить, что все модели машинного обучения из это библиотеки имеют одинаковый интерфейс. Это очень удобно и универсально. Но это значит, в частности, что все модели предполагают, что массив входных переменных — двумерный, а массивы целевых переменных — одномерный. Отдельного класса для парной регрессии не существует. Поэтому надо убедиться, что наш массив имеет нужную форму. Проще всего для преобразования формы массива использовать метод reshape, например, вот так:
Если вы используете DataFrame, то они обычно всегда настроены правильно, поэтому этого шага может не потребоваться. Важно запомнить, что все методы библиотечных моделей машинного обучения предполагают, что в x будет двумерный массив или DataFrame, а в y, соответственно, одномерный массив или Series.
Эта строка преобразует любой массив в вектор-столбец. Это если у вас один признак, то есть парная регрессия. Если признаков несколько, то вместо 1 следует указать число признаков. -1 на первой позиции означает, что по нулевому измерению будет столько элементов, сколько останется в массиве.
Само использование модели машинного обучения в этой библиотеке очень просто и сводится к трем действиям: создание экземпляра модели, обучение модели методом fit(), получение предсказаний методом predict(). Это общее поведение для любых моделей библиотеки. Для модели парной линейной регрессии нам понадобится класс LinearRegression.
1
2
3
4
5
6
reg = linear_model.LinearRegression()
reg.fit(x, y)
y_pred = reg.predict(x)
print(reg.score(x, y))
print("Коэффициенты: n", reg.coef_)
В этом классе кроме уже упомянутых методов fit() и predict(), которые есть в любой модели, есть большое количество методов и полей для получения дополнительной информации о моделях. Так, практически в каждой модели есть встроенный метод score(), который оценивает качество полученной модели. А поле coef_ содержит коэффициенты модели.
Обратите внимание, что в большинстве моделей коэффициентами считаются именно параметры при входящих переменных, то есть $ b_1, b_2, …, b_n $. Коэффициент $b_0$ считается особым и хранится отдельно в поле intercept_
Так как мы работаем с парной линейной регрессией, результат можно нарисовать на графике:
1
2
3
4
plt.figure(figsize=(12, 9))
plt.scatter(x, y, color="black")
plt.plot(x, y_pred, color="blue", linewidth=3)
plt.show()
Как мы видим, результат ничем не отличается от модели, которую мы обучили сами, вручную:
Соберем код вместе и получим пример довольно реалистичного фрагмента работы с моделью машинного обучение. Примерно такой код можно встретить и в промышленных проектах по интеллектуальному анализу данных:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
from sklearn.linear_model import LinearRegression
x = x.reshape((-1, 1))
reg = LinearRegression()
reg.fit(x, y)
print(reg.score(x, y))
from sklearn.metrics import mean_squared_error, r2_score
y_pred = reg.predict(x)
print("Коэффициенты: n", reg.coef_)
print("Среднеквадратичная ошибка: %.2f" % mean_squared_error(y, y_pred))
print("Коэффициент детерминации: %.2f" % r2_score(y, y_pred))
plt.figure(figsize=(12, 9))
plt.scatter(x, y, color="black")
plt.plot(x, y_pred, color="blue", linewidth=3)
plt.show()
| Error function | |
|---|---|

Plot of the error function |
|
| General information | |
| General definition |  |
| Fields of application | Probability, thermodynamics |
| Domain, Codomain and Image | |
| Domain |  |
| Image |  |
| Basic features | |
| Parity | Odd |
| Specific features | |
| Root | 0 |
| Derivative |  |
| Antiderivative |  |
| Series definition | |
| Taylor series |  |
In mathematics, the error function (also called the Gauss error function), often denoted by erf, is a complex function of a complex variable defined as:[1]
This integral is a special (non-elementary) sigmoid function that occurs often in probability, statistics, and partial differential equations. In many of these applications, the function argument is a real number. If the function argument is real, then the function value is also real.
In statistics, for non-negative values of x, the error function has the following interpretation: for a random variable Y that is normally distributed with mean 0 and standard deviation 1/√2, erf x is the probability that Y falls in the range [−x, x].
Two closely related functions are the complementary error function (erfc) defined as
and the imaginary error function (erfi) defined as
where i is the imaginary unit
Name[edit]
The name «error function» and its abbreviation erf were proposed by J. W. L. Glaisher in 1871 on account of its connection with «the theory of Probability, and notably the theory of Errors.»[2] The error function complement was also discussed by Glaisher in a separate publication in the same year.[3]
For the «law of facility» of errors whose density is given by
(the normal distribution), Glaisher calculates the probability of an error lying between p and q as:
Plot of the error function Erf(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D
Applications[edit]
When the results of a series of measurements are described by a normal distribution with standard deviation σ and expected value 0, then erf (a/σ √2) is the probability that the error of a single measurement lies between −a and +a, for positive a. This is useful, for example, in determining the bit error rate of a digital communication system.
The error and complementary error functions occur, for example, in solutions of the heat equation when boundary conditions are given by the Heaviside step function.
The error function and its approximations can be used to estimate results that hold with high probability or with low probability. Given a random variable X ~ Norm[μ,σ] (a normal distribution with mean μ and standard deviation σ) and a constant L < μ:
where A and B are certain numeric constants. If L is sufficiently far from the mean, specifically μ − L ≥ σ√ln k, then:
so the probability goes to 0 as k → ∞.
The probability for X being in the interval [La, Lb] can be derived as
Properties[edit]
Integrand exp(−z2)
erf z
The property erf (−z) = −erf z means that the error function is an odd function. This directly results from the fact that the integrand e−t2 is an even function (the antiderivative of an even function which is zero at the origin is an odd function and vice versa).
Since the error function is an entire function which takes real numbers to real numbers, for any complex number z:
where z is the complex conjugate of z.
The integrand f = exp(−z2) and f = erf z are shown in the complex z-plane in the figures at right with domain coloring.
The error function at +∞ is exactly 1 (see Gaussian integral). At the real axis, erf z approaches unity at z → +∞ and −1 at z → −∞. At the imaginary axis, it tends to ±i∞.
Taylor series[edit]
The error function is an entire function; it has no singularities (except that at infinity) and its Taylor expansion always converges, but is famously known «[…] for its bad convergence if x > 1.»[4]
The defining integral cannot be evaluated in closed form in terms of elementary functions, but by expanding the integrand e−z2 into its Maclaurin series and integrating term by term, one obtains the error function’s Maclaurin series as:
which holds for every complex number z. The denominator terms are sequence A007680 in the OEIS.
For iterative calculation of the above series, the following alternative formulation may be useful:
because −(2k − 1)z2/k(2k + 1) expresses the multiplier to turn the kth term into the (k + 1)th term (considering z as the first term).
The imaginary error function has a very similar Maclaurin series, which is:
which holds for every complex number z.
Derivative and integral[edit]
The derivative of the error function follows immediately from its definition:
From this, the derivative of the imaginary error function is also immediate:
An antiderivative of the error function, obtainable by integration by parts, is
An antiderivative of the imaginary error function, also obtainable by integration by parts, is
Higher order derivatives are given by
where H are the physicists’ Hermite polynomials.[5]
Bürmann series[edit]
An expansion,[6] which converges more rapidly for all real values of x than a Taylor expansion, is obtained by using Hans Heinrich Bürmann’s theorem:[7]
where sgn is the sign function. By keeping only the first two coefficients and choosing c1 = 31/200 and c2 = −341/8000, the resulting approximation shows its largest relative error at x = ±1.3796, where it is less than 0.0036127:
Inverse functions[edit]
Given a complex number z, there is not a unique complex number w satisfying erf w = z, so a true inverse function would be multivalued. However, for −1 < x < 1, there is a unique real number denoted erf−1 x satisfying
The inverse error function is usually defined with domain (−1,1), and it is restricted to this domain in many computer algebra systems. However, it can be extended to the disk |z| < 1 of the complex plane, using the Maclaurin series
where c0 = 1 and
So we have the series expansion (common factors have been canceled from numerators and denominators):
(After cancellation the numerator/denominator fractions are entries OEIS: A092676/OEIS: A092677 in the OEIS; without cancellation the numerator terms are given in entry OEIS: A002067.) The error function’s value at ±∞ is equal to ±1.
For |z| < 1, we have erf(erf−1 z) = z.
The inverse complementary error function is defined as
For real x, there is a unique real number erfi−1 x satisfying erfi(erfi−1 x) = x. The inverse imaginary error function is defined as erfi−1 x.[8]
For any real x, Newton’s method can be used to compute erfi−1 x, and for −1 ≤ x ≤ 1, the following Maclaurin series converges:
where ck is defined as above.
Asymptotic expansion[edit]
A useful asymptotic expansion of the complementary error function (and therefore also of the error function) for large real x is
where (2n − 1)!! is the double factorial of (2n − 1), which is the product of all odd numbers up to (2n − 1). This series diverges for every finite x, and its meaning as asymptotic expansion is that for any integer N ≥ 1 one has
where the remainder, in Landau notation, is
as x → ∞.
Indeed, the exact value of the remainder is
which follows easily by induction, writing
and integrating by parts.
For large enough values of x, only the first few terms of this asymptotic expansion are needed to obtain a good approximation of erfc x (while for not too large values of x, the above Taylor expansion at 0 provides a very fast convergence).
Continued fraction expansion[edit]
A continued fraction expansion of the complementary error function is:[9]
Integral of error function with Gaussian density function[edit]
which appears related to Ng and Geller, formula 13 in section 4.3[10] with a change of variables.
Factorial series[edit]
The inverse factorial series:
converges for Re(z2) > 0. Here
zn denotes the rising factorial, and s(n,k) denotes a signed Stirling number of the first kind.[11][12]
There also exists a representation by an infinite sum containing the double factorial:
Numerical approximations[edit]
Approximation with elementary functions[edit]
- Abramowitz and Stegun give several approximations of varying accuracy (equations 7.1.25–28). This allows one to choose the fastest approximation suitable for a given application. In order of increasing accuracy, they are:
(maximum error: 5×10−4)
where a1 = 0.278393, a2 = 0.230389, a3 = 0.000972, a4 = 0.078108
(maximum error: 2.5×10−5)
where p = 0.47047, a1 = 0.3480242, a2 = −0.0958798, a3 = 0.7478556
(maximum error: 3×10−7)
where a1 = 0.0705230784, a2 = 0.0422820123, a3 = 0.0092705272, a4 = 0.0001520143, a5 = 0.0002765672, a6 = 0.0000430638
(maximum error: 1.5×10−7)
where p = 0.3275911, a1 = 0.254829592, a2 = −0.284496736, a3 = 1.421413741, a4 = −1.453152027, a5 = 1.061405429
All of these approximations are valid for x ≥ 0. To use these approximations for negative x, use the fact that erf x is an odd function, so erf x = −erf(−x).
- Exponential bounds and a pure exponential approximation for the complementary error function are given by[13]
- The above have been generalized to sums of N exponentials[14] with increasing accuracy in terms of N so that erfc x can be accurately approximated or bounded by 2Q̃(√2x), where
In particular, there is a systematic methodology to solve the numerical coefficients {(an,bn)}N
n = 1 that yield a minimax approximation or bound for the closely related Q-function: Q(x) ≈ Q̃(x), Q(x) ≤ Q̃(x), or Q(x) ≥ Q̃(x) for x ≥ 0. The coefficients {(an,bn)}N
n = 1 for many variations of the exponential approximations and bounds up to N = 25 have been released to open access as a comprehensive dataset.[15] - A tight approximation of the complementary error function for x ∈ [0,∞) is given by Karagiannidis & Lioumpas (2007)[16] who showed for the appropriate choice of parameters {A,B} that
They determined {A,B} = {1.98,1.135}, which gave a good approximation for all x ≥ 0. Alternative coefficients are also available for tailoring accuracy for a specific application or transforming the expression into a tight bound.[17]
- A single-term lower bound is[18]
where the parameter β can be picked to minimize error on the desired interval of approximation.
-
- Another approximation is given by Sergei Winitzki using his «global Padé approximations»:[19][20]: 2–3
where
This is designed to be very accurate in a neighborhood of 0 and a neighborhood of infinity, and the relative error is less than 0.00035 for all real x. Using the alternate value a ≈ 0.147 reduces the maximum relative error to about 0.00013.[21]
This approximation can be inverted to obtain an approximation for the inverse error function:
- An approximation with a maximal error of 1.2×10−7 for any real argument is:[22]
with
and
Table of values[edit]
| x | erf x | 1 − erf x |
|---|---|---|
| 0 | 0 | 1 |
| 0.02 | 0.022564575 | 0.977435425 |
| 0.04 | 0.045111106 | 0.954888894 |
| 0.06 | 0.067621594 | 0.932378406 |
| 0.08 | 0.090078126 | 0.909921874 |
| 0.1 | 0.112462916 | 0.887537084 |
| 0.2 | 0.222702589 | 0.777297411 |
| 0.3 | 0.328626759 | 0.671373241 |
| 0.4 | 0.428392355 | 0.571607645 |
| 0.5 | 0.520499878 | 0.479500122 |
| 0.6 | 0.603856091 | 0.396143909 |
| 0.7 | 0.677801194 | 0.322198806 |
| 0.8 | 0.742100965 | 0.257899035 |
| 0.9 | 0.796908212 | 0.203091788 |
| 1 | 0.842700793 | 0.157299207 |
| 1.1 | 0.880205070 | 0.119794930 |
| 1.2 | 0.910313978 | 0.089686022 |
| 1.3 | 0.934007945 | 0.065992055 |
| 1.4 | 0.952285120 | 0.047714880 |
| 1.5 | 0.966105146 | 0.033894854 |
| 1.6 | 0.976348383 | 0.023651617 |
| 1.7 | 0.983790459 | 0.016209541 |
| 1.8 | 0.989090502 | 0.010909498 |
| 1.9 | 0.992790429 | 0.007209571 |
| 2 | 0.995322265 | 0.004677735 |
| 2.1 | 0.997020533 | 0.002979467 |
| 2.2 | 0.998137154 | 0.001862846 |
| 2.3 | 0.998856823 | 0.001143177 |
| 2.4 | 0.999311486 | 0.000688514 |
| 2.5 | 0.999593048 | 0.000406952 |
| 3 | 0.999977910 | 0.000022090 |
| 3.5 | 0.999999257 | 0.000000743 |
[edit]
Complementary error function[edit]
The complementary error function, denoted erfc, is defined as
-
Plot of the complementary error function Erfc(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D
which also defines erfcx, the scaled complementary error function[23] (which can be used instead of erfc to avoid arithmetic underflow[23][24]). Another form of erfc x for x ≥ 0 is known as Craig’s formula, after its discoverer:[25]
This expression is valid only for positive values of x, but it can be used in conjunction with erfc x = 2 − erfc(−x) to obtain erfc(x) for negative values. This form is advantageous in that the range of integration is fixed and finite. An extension of this expression for the erfc of the sum of two non-negative variables is as follows:[26]
Imaginary error function[edit]
The imaginary error function, denoted erfi, is defined as
Plot of the imaginary error function Erfi(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D
where D(x) is the Dawson function (which can be used instead of erfi to avoid arithmetic overflow[23]).
Despite the name «imaginary error function», erfi x is real when x is real.
When the error function is evaluated for arbitrary complex arguments z, the resulting complex error function is usually discussed in scaled form as the Faddeeva function:
Cumulative distribution function[edit]
The error function is essentially identical to the standard normal cumulative distribution function, denoted Φ, also named norm(x) by some software languages[citation needed], as they differ only by scaling and translation. Indeed,
-
the normal cumulative distribution function plotted in the complex plane
or rearranged for erf and erfc:
Consequently, the error function is also closely related to the Q-function, which is the tail probability of the standard normal distribution. The Q-function can be expressed in terms of the error function as
The inverse of Φ is known as the normal quantile function, or probit function and may be expressed in terms of the inverse error function as
The standard normal cdf is used more often in probability and statistics, and the error function is used more often in other branches of mathematics.
The error function is a special case of the Mittag-Leffler function, and can also be expressed as a confluent hypergeometric function (Kummer’s function):
It has a simple expression in terms of the Fresnel integral.[further explanation needed]
In terms of the regularized gamma function P and the incomplete gamma function,
sgn x is the sign function.
Generalized error functions[edit]
Graph of generalised error functions En(x):
grey curve: E1(x) = 1 − e−x/√π
red curve: E2(x) = erf(x)
green curve: E3(x)
blue curve: E4(x)
gold curve: E5(x).
Some authors discuss the more general functions:[citation needed]
Notable cases are:
- E0(x) is a straight line through the origin: E0(x) = x/e√π
- E2(x) is the error function, erf x.
After division by n!, all the En for odd n look similar (but not identical) to each other. Similarly, the En for even n look similar (but not identical) to each other after a simple division by n!. All generalised error functions for n > 0 look similar on the positive x side of the graph.
These generalised functions can equivalently be expressed for x > 0 using the gamma function and incomplete gamma function:
Therefore, we can define the error function in terms of the incomplete gamma function:
Iterated integrals of the complementary error function[edit]
The iterated integrals of the complementary error function are defined by[27]
The general recurrence formula is
They have the power series
from which follow the symmetry properties
and
Implementations[edit]
As real function of a real argument[edit]
- In Posix-compliant operating systems, the header
math.hshall declare and the mathematical librarylibmshall provide the functionserfanderfc(double precision) as well as their single precision and extended precision counterpartserff,erflanderfcf,erfcl.[28] - The GNU Scientific Library provides
erf,erfc,log(erf), and scaled error functions.[29]
As complex function of a complex argument[edit]
libcerf, numeric C library for complex error functions, provides the complex functionscerf,cerfc,cerfcxand the real functionserfi,erfcxwith approximately 13–14 digits precision, based on the Faddeeva function as implemented in the MIT Faddeeva Package
See also[edit]
[edit]
- Gaussian integral, over the whole real line
- Gaussian function, derivative
- Dawson function, renormalized imaginary error function
- Goodwin–Staton integral
In probability[edit]
- Normal distribution
- Normal cumulative distribution function, a scaled and shifted form of error function
- Probit, the inverse or quantile function of the normal CDF
- Q-function, the tail probability of the normal distribution
References[edit]
- ^ Andrews, Larry C. (1998). Special functions of mathematics for engineers. SPIE Press. p. 110. ISBN 9780819426161.
- ^ Glaisher, James Whitbread Lee (July 1871). «On a class of definite integrals». London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 4. 42 (277): 294–302. doi:10.1080/14786447108640568. Retrieved 6 December 2017.
- ^ Glaisher, James Whitbread Lee (September 1871). «On a class of definite integrals. Part II». London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 4. 42 (279): 421–436. doi:10.1080/14786447108640600. Retrieved 6 December 2017.
- ^ «A007680 – OEIS». oeis.org. Retrieved 2 April 2020.
- ^ Weisstein, Eric W. «Erf». MathWorld.
- ^ Schöpf, H. M.; Supancic, P. H. (2014). «On Bürmann’s Theorem and Its Application to Problems of Linear and Nonlinear Heat Transfer and Diffusion». The Mathematica Journal. 16. doi:10.3888/tmj.16-11.
- ^ Weisstein, Eric W. «Bürmann’s Theorem». MathWorld.
- ^ Bergsma, Wicher (2006). «On a new correlation coefficient, its orthogonal decomposition and associated tests of independence». arXiv:math/0604627.
- ^ Cuyt, Annie A. M.; Petersen, Vigdis B.; Verdonk, Brigitte; Waadeland, Haakon; Jones, William B. (2008). Handbook of Continued Fractions for Special Functions. Springer-Verlag. ISBN 978-1-4020-6948-2.
- ^ Ng, Edward W.; Geller, Murray (January 1969). «A table of integrals of the Error functions». Journal of Research of the National Bureau of Standards Section B. 73B (1): 1. doi:10.6028/jres.073B.001.
- ^ Schlömilch, Oskar Xavier (1859). «Ueber facultätenreihen». Zeitschrift für Mathematik und Physik (in German). 4: 390–415. Retrieved 4 December 2017.
- ^ Nielson, Niels (1906). Handbuch der Theorie der Gammafunktion (in German). Leipzig: B. G. Teubner. p. 283 Eq. 3. Retrieved 4 December 2017.
- ^ Chiani, M.; Dardari, D.; Simon, M.K. (2003). «New Exponential Bounds and Approximations for the Computation of Error Probability in Fading Channels» (PDF). IEEE Transactions on Wireless Communications. 2 (4): 840–845. CiteSeerX 10.1.1.190.6761. doi:10.1109/TWC.2003.814350.
- ^ Tanash, I.M.; Riihonen, T. (2020). «Global minimax approximations and bounds for the Gaussian Q-function by sums of exponentials». IEEE Transactions on Communications. 68 (10): 6514–6524. arXiv:2007.06939. doi:10.1109/TCOMM.2020.3006902. S2CID 220514754.
- ^ Tanash, I.M.; Riihonen, T. (2020). «Coefficients for Global Minimax Approximations and Bounds for the Gaussian Q-Function by Sums of Exponentials [Data set]». Zenodo. doi:10.5281/zenodo.4112978.
- ^ Karagiannidis, G. K.; Lioumpas, A. S. (2007). «An improved approximation for the Gaussian Q-function» (PDF). IEEE Communications Letters. 11 (8): 644–646. doi:10.1109/LCOMM.2007.070470. S2CID 4043576.
- ^ Tanash, I.M.; Riihonen, T. (2021). «Improved coefficients for the Karagiannidis–Lioumpas approximations and bounds to the Gaussian Q-function». IEEE Communications Letters. 25 (5): 1468–1471. arXiv:2101.07631. doi:10.1109/LCOMM.2021.3052257. S2CID 231639206.
- ^ Chang, Seok-Ho; Cosman, Pamela C.; Milstein, Laurence B. (November 2011). «Chernoff-Type Bounds for the Gaussian Error Function». IEEE Transactions on Communications. 59 (11): 2939–2944. doi:10.1109/TCOMM.2011.072011.100049. S2CID 13636638.
- ^ Winitzki, Sergei (2003). «Uniform approximations for transcendental functions». Computational Science and Its Applications – ICCSA 2003. Lecture Notes in Computer Science. Vol. 2667. Springer, Berlin. pp. 780–789. doi:10.1007/3-540-44839-X_82. ISBN 978-3-540-40155-1.
- ^ Zeng, Caibin; Chen, Yang Cuan (2015). «Global Padé approximations of the generalized Mittag-Leffler function and its inverse». Fractional Calculus and Applied Analysis. 18 (6): 1492–1506. arXiv:1310.5592. doi:10.1515/fca-2015-0086. S2CID 118148950.
Indeed, Winitzki [32] provided the so-called global Padé approximation
- ^ Winitzki, Sergei (6 February 2008). «A handy approximation for the error function and its inverse».
- ^ Numerical Recipes in Fortran 77: The Art of Scientific Computing (ISBN 0-521-43064-X), 1992, page 214, Cambridge University Press.
- ^ a b c Cody, W. J. (March 1993), «Algorithm 715: SPECFUN—A portable FORTRAN package of special function routines and test drivers» (PDF), ACM Trans. Math. Softw., 19 (1): 22–32, CiteSeerX 10.1.1.643.4394, doi:10.1145/151271.151273, S2CID 5621105
- ^ Zaghloul, M. R. (1 March 2007), «On the calculation of the Voigt line profile: a single proper integral with a damped sine integrand», Monthly Notices of the Royal Astronomical Society, 375 (3): 1043–1048, Bibcode:2007MNRAS.375.1043Z, doi:10.1111/j.1365-2966.2006.11377.x
- ^ John W. Craig, A new, simple and exact result for calculating the probability of error for two-dimensional signal constellations Archived 3 April 2012 at the Wayback Machine, Proceedings of the 1991 IEEE Military Communication Conference, vol. 2, pp. 571–575.
- ^ Behnad, Aydin (2020). «A Novel Extension to Craig’s Q-Function Formula and Its Application in Dual-Branch EGC Performance Analysis». IEEE Transactions on Communications. 68 (7): 4117–4125. doi:10.1109/TCOMM.2020.2986209. S2CID 216500014.
- ^ Carslaw, H. S.; Jaeger, J. C. (1959), Conduction of Heat in Solids (2nd ed.), Oxford University Press, ISBN 978-0-19-853368-9, p 484
- ^ https://pubs.opengroup.org/onlinepubs/9699919799/basedefs/math.h.html
- ^ «Special Functions – GSL 2.7 documentation».
Further reading[edit]
- Abramowitz, Milton; Stegun, Irene Ann, eds. (1983) [June 1964]. «Chapter 7». Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Applied Mathematics Series. Vol. 55 (Ninth reprint with additional corrections of tenth original printing with corrections (December 1972); first ed.). Washington D.C.; New York: United States Department of Commerce, National Bureau of Standards; Dover Publications. p. 297. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253.
- Press, William H.; Teukolsky, Saul A.; Vetterling, William T.; Flannery, Brian P. (2007), «Section 6.2. Incomplete Gamma Function and Error Function», Numerical Recipes: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8
- Temme, Nico M. (2010), «Error Functions, Dawson’s and Fresnel Integrals», in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248
External links[edit]
- A Table of Integrals of the Error Functions
| Error function | |
|---|---|

Plot of the error function |
|
| General information | |
| General definition |  |
| Fields of application | Probability, thermodynamics |
| Domain, Codomain and Image | |
| Domain |  |
| Image |  |
| Basic features | |
| Parity | Odd |
| Specific features | |
| Root | 0 |
| Derivative |  |
| Antiderivative |  |
| Series definition | |
| Taylor series |  |
In mathematics, the error function (also called the Gauss error function), often denoted by erf, is a complex function of a complex variable defined as:[1]
This integral is a special (non-elementary) sigmoid function that occurs often in probability, statistics, and partial differential equations. In many of these applications, the function argument is a real number. If the function argument is real, then the function value is also real.
In statistics, for non-negative values of x, the error function has the following interpretation: for a random variable Y that is normally distributed with mean 0 and standard deviation 1/√2, erf x is the probability that Y falls in the range [−x, x].
Two closely related functions are the complementary error function (erfc) defined as
and the imaginary error function (erfi) defined as
where i is the imaginary unit
Name[edit]
The name «error function» and its abbreviation erf were proposed by J. W. L. Glaisher in 1871 on account of its connection with «the theory of Probability, and notably the theory of Errors.»[2] The error function complement was also discussed by Glaisher in a separate publication in the same year.[3]
For the «law of facility» of errors whose density is given by
(the normal distribution), Glaisher calculates the probability of an error lying between p and q as:
Plot of the error function Erf(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D
Applications[edit]
When the results of a series of measurements are described by a normal distribution with standard deviation σ and expected value 0, then erf (a/σ √2) is the probability that the error of a single measurement lies between −a and +a, for positive a. This is useful, for example, in determining the bit error rate of a digital communication system.
The error and complementary error functions occur, for example, in solutions of the heat equation when boundary conditions are given by the Heaviside step function.
The error function and its approximations can be used to estimate results that hold with high probability or with low probability. Given a random variable X ~ Norm[μ,σ] (a normal distribution with mean μ and standard deviation σ) and a constant L < μ:
where A and B are certain numeric constants. If L is sufficiently far from the mean, specifically μ − L ≥ σ√ln k, then:
so the probability goes to 0 as k → ∞.
The probability for X being in the interval [La, Lb] can be derived as
Properties[edit]
Integrand exp(−z2)
erf z
The property erf (−z) = −erf z means that the error function is an odd function. This directly results from the fact that the integrand e−t2 is an even function (the antiderivative of an even function which is zero at the origin is an odd function and vice versa).
Since the error function is an entire function which takes real numbers to real numbers, for any complex number z:
where z is the complex conjugate of z.
The integrand f = exp(−z2) and f = erf z are shown in the complex z-plane in the figures at right with domain coloring.
The error function at +∞ is exactly 1 (see Gaussian integral). At the real axis, erf z approaches unity at z → +∞ and −1 at z → −∞. At the imaginary axis, it tends to ±i∞.
Taylor series[edit]
The error function is an entire function; it has no singularities (except that at infinity) and its Taylor expansion always converges, but is famously known «[…] for its bad convergence if x > 1.»[4]
The defining integral cannot be evaluated in closed form in terms of elementary functions, but by expanding the integrand e−z2 into its Maclaurin series and integrating term by term, one obtains the error function’s Maclaurin series as:
which holds for every complex number z. The denominator terms are sequence A007680 in the OEIS.
For iterative calculation of the above series, the following alternative formulation may be useful:
because −(2k − 1)z2/k(2k + 1) expresses the multiplier to turn the kth term into the (k + 1)th term (considering z as the first term).
The imaginary error function has a very similar Maclaurin series, which is:
which holds for every complex number z.
Derivative and integral[edit]
The derivative of the error function follows immediately from its definition:
From this, the derivative of the imaginary error function is also immediate:
An antiderivative of the error function, obtainable by integration by parts, is
An antiderivative of the imaginary error function, also obtainable by integration by parts, is
Higher order derivatives are given by
where H are the physicists’ Hermite polynomials.[5]
Bürmann series[edit]
An expansion,[6] which converges more rapidly for all real values of x than a Taylor expansion, is obtained by using Hans Heinrich Bürmann’s theorem:[7]
where sgn is the sign function. By keeping only the first two coefficients and choosing c1 = 31/200 and c2 = −341/8000, the resulting approximation shows its largest relative error at x = ±1.3796, where it is less than 0.0036127:
Inverse functions[edit]
Given a complex number z, there is not a unique complex number w satisfying erf w = z, so a true inverse function would be multivalued. However, for −1 < x < 1, there is a unique real number denoted erf−1 x satisfying
The inverse error function is usually defined with domain (−1,1), and it is restricted to this domain in many computer algebra systems. However, it can be extended to the disk |z| < 1 of the complex plane, using the Maclaurin series
where c0 = 1 and
So we have the series expansion (common factors have been canceled from numerators and denominators):
(After cancellation the numerator/denominator fractions are entries OEIS: A092676/OEIS: A092677 in the OEIS; without cancellation the numerator terms are given in entry OEIS: A002067.) The error function’s value at ±∞ is equal to ±1.
For |z| < 1, we have erf(erf−1 z) = z.
The inverse complementary error function is defined as
For real x, there is a unique real number erfi−1 x satisfying erfi(erfi−1 x) = x. The inverse imaginary error function is defined as erfi−1 x.[8]
For any real x, Newton’s method can be used to compute erfi−1 x, and for −1 ≤ x ≤ 1, the following Maclaurin series converges:
where ck is defined as above.
Asymptotic expansion[edit]
A useful asymptotic expansion of the complementary error function (and therefore also of the error function) for large real x is
where (2n − 1)!! is the double factorial of (2n − 1), which is the product of all odd numbers up to (2n − 1). This series diverges for every finite x, and its meaning as asymptotic expansion is that for any integer N ≥ 1 one has
where the remainder, in Landau notation, is
as x → ∞.
Indeed, the exact value of the remainder is
which follows easily by induction, writing
and integrating by parts.
For large enough values of x, only the first few terms of this asymptotic expansion are needed to obtain a good approximation of erfc x (while for not too large values of x, the above Taylor expansion at 0 provides a very fast convergence).
Continued fraction expansion[edit]
A continued fraction expansion of the complementary error function is:[9]
Integral of error function with Gaussian density function[edit]
which appears related to Ng and Geller, formula 13 in section 4.3[10] with a change of variables.
Factorial series[edit]
The inverse factorial series:
converges for Re(z2) > 0. Here
zn denotes the rising factorial, and s(n,k) denotes a signed Stirling number of the first kind.[11][12]
There also exists a representation by an infinite sum containing the double factorial:
Numerical approximations[edit]
Approximation with elementary functions[edit]
- Abramowitz and Stegun give several approximations of varying accuracy (equations 7.1.25–28). This allows one to choose the fastest approximation suitable for a given application. In order of increasing accuracy, they are:
(maximum error: 5×10−4)
where a1 = 0.278393, a2 = 0.230389, a3 = 0.000972, a4 = 0.078108
(maximum error: 2.5×10−5)
where p = 0.47047, a1 = 0.3480242, a2 = −0.0958798, a3 = 0.7478556
(maximum error: 3×10−7)
where a1 = 0.0705230784, a2 = 0.0422820123, a3 = 0.0092705272, a4 = 0.0001520143, a5 = 0.0002765672, a6 = 0.0000430638
(maximum error: 1.5×10−7)
where p = 0.3275911, a1 = 0.254829592, a2 = −0.284496736, a3 = 1.421413741, a4 = −1.453152027, a5 = 1.061405429
All of these approximations are valid for x ≥ 0. To use these approximations for negative x, use the fact that erf x is an odd function, so erf x = −erf(−x).
- Exponential bounds and a pure exponential approximation for the complementary error function are given by[13]
- The above have been generalized to sums of N exponentials[14] with increasing accuracy in terms of N so that erfc x can be accurately approximated or bounded by 2Q̃(√2x), where
In particular, there is a systematic methodology to solve the numerical coefficients {(an,bn)}N
n = 1 that yield a minimax approximation or bound for the closely related Q-function: Q(x) ≈ Q̃(x), Q(x) ≤ Q̃(x), or Q(x) ≥ Q̃(x) for x ≥ 0. The coefficients {(an,bn)}N
n = 1 for many variations of the exponential approximations and bounds up to N = 25 have been released to open access as a comprehensive dataset.[15] - A tight approximation of the complementary error function for x ∈ [0,∞) is given by Karagiannidis & Lioumpas (2007)[16] who showed for the appropriate choice of parameters {A,B} that
They determined {A,B} = {1.98,1.135}, which gave a good approximation for all x ≥ 0. Alternative coefficients are also available for tailoring accuracy for a specific application or transforming the expression into a tight bound.[17]
- A single-term lower bound is[18]
where the parameter β can be picked to minimize error on the desired interval of approximation.
-
- Another approximation is given by Sergei Winitzki using his «global Padé approximations»:[19][20]: 2–3
where
This is designed to be very accurate in a neighborhood of 0 and a neighborhood of infinity, and the relative error is less than 0.00035 for all real x. Using the alternate value a ≈ 0.147 reduces the maximum relative error to about 0.00013.[21]
This approximation can be inverted to obtain an approximation for the inverse error function:
- An approximation with a maximal error of 1.2×10−7 for any real argument is:[22]
with
and
Table of values[edit]
| x | erf x | 1 − erf x |
|---|---|---|
| 0 | 0 | 1 |
| 0.02 | 0.022564575 | 0.977435425 |
| 0.04 | 0.045111106 | 0.954888894 |
| 0.06 | 0.067621594 | 0.932378406 |
| 0.08 | 0.090078126 | 0.909921874 |
| 0.1 | 0.112462916 | 0.887537084 |
| 0.2 | 0.222702589 | 0.777297411 |
| 0.3 | 0.328626759 | 0.671373241 |
| 0.4 | 0.428392355 | 0.571607645 |
| 0.5 | 0.520499878 | 0.479500122 |
| 0.6 | 0.603856091 | 0.396143909 |
| 0.7 | 0.677801194 | 0.322198806 |
| 0.8 | 0.742100965 | 0.257899035 |
| 0.9 | 0.796908212 | 0.203091788 |
| 1 | 0.842700793 | 0.157299207 |
| 1.1 | 0.880205070 | 0.119794930 |
| 1.2 | 0.910313978 | 0.089686022 |
| 1.3 | 0.934007945 | 0.065992055 |
| 1.4 | 0.952285120 | 0.047714880 |
| 1.5 | 0.966105146 | 0.033894854 |
| 1.6 | 0.976348383 | 0.023651617 |
| 1.7 | 0.983790459 | 0.016209541 |
| 1.8 | 0.989090502 | 0.010909498 |
| 1.9 | 0.992790429 | 0.007209571 |
| 2 | 0.995322265 | 0.004677735 |
| 2.1 | 0.997020533 | 0.002979467 |
| 2.2 | 0.998137154 | 0.001862846 |
| 2.3 | 0.998856823 | 0.001143177 |
| 2.4 | 0.999311486 | 0.000688514 |
| 2.5 | 0.999593048 | 0.000406952 |
| 3 | 0.999977910 | 0.000022090 |
| 3.5 | 0.999999257 | 0.000000743 |
[edit]
Complementary error function[edit]
The complementary error function, denoted erfc, is defined as
-
Plot of the complementary error function Erfc(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D
which also defines erfcx, the scaled complementary error function[23] (which can be used instead of erfc to avoid arithmetic underflow[23][24]). Another form of erfc x for x ≥ 0 is known as Craig’s formula, after its discoverer:[25]
This expression is valid only for positive values of x, but it can be used in conjunction with erfc x = 2 − erfc(−x) to obtain erfc(x) for negative values. This form is advantageous in that the range of integration is fixed and finite. An extension of this expression for the erfc of the sum of two non-negative variables is as follows:[26]
Imaginary error function[edit]
The imaginary error function, denoted erfi, is defined as
Plot of the imaginary error function Erfi(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D
where D(x) is the Dawson function (which can be used instead of erfi to avoid arithmetic overflow[23]).
Despite the name «imaginary error function», erfi x is real when x is real.
When the error function is evaluated for arbitrary complex arguments z, the resulting complex error function is usually discussed in scaled form as the Faddeeva function:
Cumulative distribution function[edit]
The error function is essentially identical to the standard normal cumulative distribution function, denoted Φ, also named norm(x) by some software languages[citation needed], as they differ only by scaling and translation. Indeed,
-
the normal cumulative distribution function plotted in the complex plane
or rearranged for erf and erfc:
Consequently, the error function is also closely related to the Q-function, which is the tail probability of the standard normal distribution. The Q-function can be expressed in terms of the error function as
The inverse of Φ is known as the normal quantile function, or probit function and may be expressed in terms of the inverse error function as
The standard normal cdf is used more often in probability and statistics, and the error function is used more often in other branches of mathematics.
The error function is a special case of the Mittag-Leffler function, and can also be expressed as a confluent hypergeometric function (Kummer’s function):
It has a simple expression in terms of the Fresnel integral.[further explanation needed]
In terms of the regularized gamma function P and the incomplete gamma function,
sgn x is the sign function.
Generalized error functions[edit]
Graph of generalised error functions En(x):
grey curve: E1(x) = 1 − e−x/√π
red curve: E2(x) = erf(x)
green curve: E3(x)
blue curve: E4(x)
gold curve: E5(x).
Some authors discuss the more general functions:[citation needed]
Notable cases are:
- E0(x) is a straight line through the origin: E0(x) = x/e√π
- E2(x) is the error function, erf x.
After division by n!, all the En for odd n look similar (but not identical) to each other. Similarly, the En for even n look similar (but not identical) to each other after a simple division by n!. All generalised error functions for n > 0 look similar on the positive x side of the graph.
These generalised functions can equivalently be expressed for x > 0 using the gamma function and incomplete gamma function:
Therefore, we can define the error function in terms of the incomplete gamma function:
Iterated integrals of the complementary error function[edit]
The iterated integrals of the complementary error function are defined by[27]
The general recurrence formula is
They have the power series
from which follow the symmetry properties
and
Implementations[edit]
As real function of a real argument[edit]
- In Posix-compliant operating systems, the header
math.hshall declare and the mathematical librarylibmshall provide the functionserfanderfc(double precision) as well as their single precision and extended precision counterpartserff,erflanderfcf,erfcl.[28] - The GNU Scientific Library provides
erf,erfc,log(erf), and scaled error functions.[29]
As complex function of a complex argument[edit]
libcerf, numeric C library for complex error functions, provides the complex functionscerf,cerfc,cerfcxand the real functionserfi,erfcxwith approximately 13–14 digits precision, based on the Faddeeva function as implemented in the MIT Faddeeva Package
See also[edit]
[edit]
- Gaussian integral, over the whole real line
- Gaussian function, derivative
- Dawson function, renormalized imaginary error function
- Goodwin–Staton integral
In probability[edit]
- Normal distribution
- Normal cumulative distribution function, a scaled and shifted form of error function
- Probit, the inverse or quantile function of the normal CDF
- Q-function, the tail probability of the normal distribution
References[edit]
- ^ Andrews, Larry C. (1998). Special functions of mathematics for engineers. SPIE Press. p. 110. ISBN 9780819426161.
- ^ Glaisher, James Whitbread Lee (July 1871). «On a class of definite integrals». London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 4. 42 (277): 294–302. doi:10.1080/14786447108640568. Retrieved 6 December 2017.
- ^ Glaisher, James Whitbread Lee (September 1871). «On a class of definite integrals. Part II». London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 4. 42 (279): 421–436. doi:10.1080/14786447108640600. Retrieved 6 December 2017.
- ^ «A007680 – OEIS». oeis.org. Retrieved 2 April 2020.
- ^ Weisstein, Eric W. «Erf». MathWorld.
- ^ Schöpf, H. M.; Supancic, P. H. (2014). «On Bürmann’s Theorem and Its Application to Problems of Linear and Nonlinear Heat Transfer and Diffusion». The Mathematica Journal. 16. doi:10.3888/tmj.16-11.
- ^ Weisstein, Eric W. «Bürmann’s Theorem». MathWorld.
- ^ Bergsma, Wicher (2006). «On a new correlation coefficient, its orthogonal decomposition and associated tests of independence». arXiv:math/0604627.
- ^ Cuyt, Annie A. M.; Petersen, Vigdis B.; Verdonk, Brigitte; Waadeland, Haakon; Jones, William B. (2008). Handbook of Continued Fractions for Special Functions. Springer-Verlag. ISBN 978-1-4020-6948-2.
- ^ Ng, Edward W.; Geller, Murray (January 1969). «A table of integrals of the Error functions». Journal of Research of the National Bureau of Standards Section B. 73B (1): 1. doi:10.6028/jres.073B.001.
- ^ Schlömilch, Oskar Xavier (1859). «Ueber facultätenreihen». Zeitschrift für Mathematik und Physik (in German). 4: 390–415. Retrieved 4 December 2017.
- ^ Nielson, Niels (1906). Handbuch der Theorie der Gammafunktion (in German). Leipzig: B. G. Teubner. p. 283 Eq. 3. Retrieved 4 December 2017.
- ^ Chiani, M.; Dardari, D.; Simon, M.K. (2003). «New Exponential Bounds and Approximations for the Computation of Error Probability in Fading Channels» (PDF). IEEE Transactions on Wireless Communications. 2 (4): 840–845. CiteSeerX 10.1.1.190.6761. doi:10.1109/TWC.2003.814350.
- ^ Tanash, I.M.; Riihonen, T. (2020). «Global minimax approximations and bounds for the Gaussian Q-function by sums of exponentials». IEEE Transactions on Communications. 68 (10): 6514–6524. arXiv:2007.06939. doi:10.1109/TCOMM.2020.3006902. S2CID 220514754.
- ^ Tanash, I.M.; Riihonen, T. (2020). «Coefficients for Global Minimax Approximations and Bounds for the Gaussian Q-Function by Sums of Exponentials [Data set]». Zenodo. doi:10.5281/zenodo.4112978.
- ^ Karagiannidis, G. K.; Lioumpas, A. S. (2007). «An improved approximation for the Gaussian Q-function» (PDF). IEEE Communications Letters. 11 (8): 644–646. doi:10.1109/LCOMM.2007.070470. S2CID 4043576.
- ^ Tanash, I.M.; Riihonen, T. (2021). «Improved coefficients for the Karagiannidis–Lioumpas approximations and bounds to the Gaussian Q-function». IEEE Communications Letters. 25 (5): 1468–1471. arXiv:2101.07631. doi:10.1109/LCOMM.2021.3052257. S2CID 231639206.
- ^ Chang, Seok-Ho; Cosman, Pamela C.; Milstein, Laurence B. (November 2011). «Chernoff-Type Bounds for the Gaussian Error Function». IEEE Transactions on Communications. 59 (11): 2939–2944. doi:10.1109/TCOMM.2011.072011.100049. S2CID 13636638.
- ^ Winitzki, Sergei (2003). «Uniform approximations for transcendental functions». Computational Science and Its Applications – ICCSA 2003. Lecture Notes in Computer Science. Vol. 2667. Springer, Berlin. pp. 780–789. doi:10.1007/3-540-44839-X_82. ISBN 978-3-540-40155-1.
- ^ Zeng, Caibin; Chen, Yang Cuan (2015). «Global Padé approximations of the generalized Mittag-Leffler function and its inverse». Fractional Calculus and Applied Analysis. 18 (6): 1492–1506. arXiv:1310.5592. doi:10.1515/fca-2015-0086. S2CID 118148950.
Indeed, Winitzki [32] provided the so-called global Padé approximation
- ^ Winitzki, Sergei (6 February 2008). «A handy approximation for the error function and its inverse».
- ^ Numerical Recipes in Fortran 77: The Art of Scientific Computing (ISBN 0-521-43064-X), 1992, page 214, Cambridge University Press.
- ^ a b c Cody, W. J. (March 1993), «Algorithm 715: SPECFUN—A portable FORTRAN package of special function routines and test drivers» (PDF), ACM Trans. Math. Softw., 19 (1): 22–32, CiteSeerX 10.1.1.643.4394, doi:10.1145/151271.151273, S2CID 5621105
- ^ Zaghloul, M. R. (1 March 2007), «On the calculation of the Voigt line profile: a single proper integral with a damped sine integrand», Monthly Notices of the Royal Astronomical Society, 375 (3): 1043–1048, Bibcode:2007MNRAS.375.1043Z, doi:10.1111/j.1365-2966.2006.11377.x
- ^ John W. Craig, A new, simple and exact result for calculating the probability of error for two-dimensional signal constellations Archived 3 April 2012 at the Wayback Machine, Proceedings of the 1991 IEEE Military Communication Conference, vol. 2, pp. 571–575.
- ^ Behnad, Aydin (2020). «A Novel Extension to Craig’s Q-Function Formula and Its Application in Dual-Branch EGC Performance Analysis». IEEE Transactions on Communications. 68 (7): 4117–4125. doi:10.1109/TCOMM.2020.2986209. S2CID 216500014.
- ^ Carslaw, H. S.; Jaeger, J. C. (1959), Conduction of Heat in Solids (2nd ed.), Oxford University Press, ISBN 978-0-19-853368-9, p 484
- ^ https://pubs.opengroup.org/onlinepubs/9699919799/basedefs/math.h.html
- ^ «Special Functions – GSL 2.7 documentation».
Further reading[edit]
- Abramowitz, Milton; Stegun, Irene Ann, eds. (1983) [June 1964]. «Chapter 7». Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Applied Mathematics Series. Vol. 55 (Ninth reprint with additional corrections of tenth original printing with corrections (December 1972); first ed.). Washington D.C.; New York: United States Department of Commerce, National Bureau of Standards; Dover Publications. p. 297. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253.
- Press, William H.; Teukolsky, Saul A.; Vetterling, William T.; Flannery, Brian P. (2007), «Section 6.2. Incomplete Gamma Function and Error Function», Numerical Recipes: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8
- Temme, Nico M. (2010), «Error Functions, Dawson’s and Fresnel Integrals», in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248
External links[edit]
- A Table of Integrals of the Error Functions
Сегодня будет сделанный с любовью обзор функций ошибок и функционалов качества в задачах регрессии.
Выкладываю часть главы «Метрики качества» из своей вечно недописанной книги. Она полностью сделана по материалам моего курса в МГУ. Краткое содержание:
- Качество работы алгоритма
- Функции ошибки в задачах регрессии
- Средний модуль отклонения (MAE – Mean Absolute Error или MAD – Mean Absolute Deviation)
- Средний квадрат отклонения (MSE – Mean Squared Error), корень из этой ошибки: RMSE – Root Mean Squared Error, коэффициент детерминации (R2)
- функция ошибки Хьюбера (Huber loss) и logcosh
- Обобщения MAE и RMSE
- Средний процент отклонения (MAPE – Mean Absolute Percent Error)
- Симметричный средний процент отклонения (SMAPE – Symmetric Mean Absolute Percentage Error)
- MRAE – Mean Relative Absolute Error, REL_MAE, Percent Better
- MASE (Mean Absolute Scaled Error)
- eB – процент случаев, когда ответ алгоритма верен с некоторой заранее заданной точностью
- Несимметричные функции ошибки
- Реализация функций ошибок в scikit-learn
Материал ещё сырой, поэтому все замечания, предложения, найденные неточности и ошибки пишите в комментарии.
Предыдущие посты из этой серии:
- Логистическая функция ошибки
- AUC ROC (площадь под кривой ошибок)
- Задачки про AUC (ROC)
И побуду «заядлым блогером»: если пост наберёт больше 2000 просмотров, то опубликую продолжение главы;)
Адаптированный перевод прекрасной статьи энтузиаста технологий машинного обучения Javaid Nabi.
Чтобы понимать как алгоритм машинного обучения учится предсказывать результаты на основе данных, важно разобраться в основных концепциях и понятиях, используемых при обучении алгоритма.
Функции оценки
В контексте технологии машинного обучения, оценка – это
статистический термин для нахождения некоторого приближения неизвестного
параметра на основе некоторых данных. Точечная
оценка – это попытка найти единственное лучшее приближение некоторого
количества интересующих нас параметров. Или на более формальном языке математической статистики — точечная оценка это число, оцениваемое на основе наблюдений,
предположительно близкое к оцениваемому параметру.
Под количеством
интересующих параметров обычно подразумевается:
• Один параметр
• Вектор параметров – например, веса в линейной
регрессии
• Целая функция
Точечная оценка
Чтобы отличать оценки параметров от их истинного значения, представим точечную оценку параметра θ как θˆ. Пусть {x(1), x(2), .. x(m)} будут m независимыми и одинаково распределенными величинами. Тогда точечная оценка может быть записана как некоторая функция этих величин:
Такое определение точечной оценки является очень общим и предоставляет разработчику большую свободу действий. Почти любая функция, таким образом, может рассматриваться как оценщик, но хороший оценщик – это функция, значения которой близки к истинному базовому значению θ, которое сгенерированно обучающими данными.
Точечная оценка также может относиться к оценке взаимосвязи между
входными и целевыми переменными, в этом случае чаще называемой функцией оценки.
Функция оценки
Задача, решаемая машинным обучением, заключается в попытке
предсказать переменную y по
заданному входному вектору x. Мы
предполагаем, что существует функция f(x), которая описывает приблизительную
связь между y и x. Например, можно предположить, что y = f(x) + ε, где ε обозначает
часть y, которая явно не
предсказывается входным вектором x.
При оценке функций нас интересует приближение f с помощью модели или оценки fˆ.
Функция оценки в действительности это тоже самое, что оценка параметра θ; функция оценки f это просто точечная
оценка в функциональном пространстве. Пример: в полиномиальной регрессии мы
либо оцениваем параметр w, либо оцениваем функцию отображения из x в y.
Смещение и дисперсия
Смещение и дисперсия измеряют два разных источника ошибки функции оценки.
Смещение измеряет ожидаемое отклонение от истинного значения функции или
параметра. Дисперсия, с другой стороны, показывает меру отклонения от
ожидаемого значения оценки, которую может вызвать любая конкретная выборка
данных.
Смещение
Смещение определяется следующим
образом:
где ожидаемое значение E(θˆm) для данных (рассматриваемых как выборки из случайной величины) и
θ является истинным базовым значением, используемым для определения
распределения, генерирующего данные.
Оценщик θˆm называется несмещенным, если bias(θˆm)=0, что подразумевает что E(θˆm) = θ.
Дисперсия и Стандартная ошибка
Дисперсия оценки обозначается как Var(θˆ), где случайная величина
является обучающим множеством. Альтернативно, квадратный корень дисперсии
называется стандартной ошибкой, обозначаемой как SE(θˆ). Дисперсия или стандартная ошибка
оценщика показывает меру ожидания того, как оценка, которую мы вычисляем, будет
изменяться по мере того, как мы меняем выборки из базового набора данных,
генерирующих процесс.
Точно так же, как мы хотели бы, чтобы функция оценки имела малое
смещение, мы также стремимся, чтобы у нее была относительно низкая дисперсия.
Давайте теперь рассмотрим некоторые обычно используемые функции оценки.
Оценка Максимального Правдоподобия (MLE)
Оценка максимального правдоподобия может быть определена как метод
оценки параметров (таких как среднее значение или дисперсия) из выборки данных,
так что вероятность получения наблюдаемых данных максимальна.
Рассмотрим набор из m примеров X={x(1),… , x(m)} взятых независимо из неизвестного набора данных,
генерирующих распределение Pdata(x). Пусть Pmodel(x;θ) –
параметрическое семейство распределений вероятностей над тем же пространством,
индексированное параметром θ.
Другими словами, Pmodel(x;θ) отображает любую конфигурацию x в значение, оценивающее истинную
вероятность Pdata(x).
Оценка максимального правдоподобия для θ определяется как:
Поскольку мы предположили, что примеры являются независимыми выборками, приведенное выше
уравнение можно записать в виде:
Эта произведение многих вероятностей может быть неудобным по ряду
причин. В частности, оно склонно к числовой недооценке. Кроме того, чтобы найти
максимумы/минимумы этой функции, мы должны взять производную этой функции от θ и приравнять ее к 0. Поскольку это
произведение членов, нам нужно применить правило цепочки, которое довольно
громоздко. Чтобы получить более удобную, но эквивалентную задачу оптимизации,
можно использовать логарифм вероятности, который не меняет его argmax, но
удобно превращает произведение в сумму, и поскольку логарифм – строго
возрастающая функция (функция натурального логарифма – монотонное
преобразование), это не повлияет на итоговое значение θ.
В итоге, получаем:
Два важных свойства: сходимость и
эффективность
Сходимость. По мере того, как число обучающих выборок приближается к
бесконечности, оценка максимального правдоподобия сходится к истинному значению
параметра.
Эффективность. Способ измерения того, насколько мы близки к истинному
параметру, – это ожидаемая средняя квадратичная ошибка, вычисление квадратичной
разницы между оценочными и истинными значениями параметров, где математическое
ожидание вычисляется над m обучающими выборками из данных, генерирующих
распределение. Эта параметрическая среднеквадратичная ошибка уменьшается с
увеличением m, и для
больших m нижняя
граница неравенства Крамера-Рао показывает, что ни у одной сходящейся функции оценки нет
среднеквадратичной ошибки меньше, чем у оценки максимального правдоподобия.
Именно по причине
сходимости и эффективности, оценка максимального правдоподобия часто считается
предпочтительным оценщиком для машинного обучения.
Когда количество примеров достаточно мало, чтобы привести к
переобучению, стратегии регуляризации, такие как понижающие веса, могут
использоваться для получения смещенной версии оценки максимального
правдоподобия, которая имеет меньшую дисперсию, когда данные обучения
ограничены.
Максимальная апостериорная (MAP) оценка
Согласно байесовскому подходу, можно учесть влияние предварительных
данных на выбор точечной оценки. MAP может использоваться для получения
точечной оценки ненаблюдаемой величины на основе эмпирических данных. Оценка
MAP выбирает точку максимальной апостериорной вероятности (или максимальной
плотности вероятности в более распространенном случае непрерывного θ):
где с правой стороны, log(p(x|θ)) – стандартный член
логарифмической вероятности и log(p(θ)) соответствует изначальному
распределению.
Как и при полном байесовском методе, байесовский MAP имеет преимущество
использования изначальной информации, которой нет
в обучающих данных. Эта дополнительная информация помогает уменьшить дисперсию
для точечной оценки MAP (по сравнению с оценкой MLE). Однако, это происходит ценой повышенного смещения.
Функции потерь
В большинстве обучающих сетей ошибка рассчитывается как разница
между фактическим выходным значением y и прогнозируемым выходным значением ŷ.
Функция, используемая для вычисления этой ошибки, известна как функция потерь,
также часто называемая функцией ошибки или затрат.
До сих пор наше основное внимание уделялось оценке параметров с
помощью MLE или MAP. Причина, по которой мы обсуждали это раньше, заключается в
том, что и MLE, и MAP предоставляют механизм для получения функции потерь.
Давайте рассмотрим некоторые часто используемые функции потерь.
Средняя
квадратичная ошибка (MSE): средняя
квадратичная ошибка является наиболее распространенной функцией потерь. Функция
потерь MSE широко используется в линейной регрессии в качестве показателя
эффективности. Чтобы рассчитать MSE, надо взять разницу между предсказанными
значениями и истинными, возвести ее в квадрат и усреднить по всему набору
данных.
где y(i) – фактический ожидаемый результат, а ŷ(i) – прогноз модели.
Многие функции потерь (затрат), используемые в машинном обучении,
включая MSE, могут быть получены из метода максимального правдоподобия.
Чтобы увидеть, как мы можем вывести функции потерь из MLE или MAP,
требуется некоторая математика. Вы можете пропустить ее и перейти к следующему
разделу.
Получение MSE из MLE
Алгоритм линейной регрессии учится принимать входные данные x и получать выходные значения ŷ. Отображение x в ŷ делается так,
чтобы минимизировать среднеквадратичную ошибку. Но как мы выбрали MSE в
качестве критерия для линейной регрессии? Придем к этому решению с точки зрения
оценки максимального правдоподобия. Вместо того, чтобы производить одно
предсказание ŷ , давайте рассмотрим
модель условного распределения p(y|x).
Можно смоделировать модель
линейной регрессии следующим образом:
мы предполагаем, что у имеет
нормальное распределение с ŷ в качестве
среднего значения распределения и некоторой постоянной σ² в качестве дисперсии, выбранной пользователем. Нормальное
распределения являются разумным выбором во многих случаях. В отсутствие
предварительных данных о том, какое распределение в действительности
соответствует рассматриваемым данным, нормальное распределение является хорошим
выбором по умолчанию.
Вернемся к логарифмической вероятности, определенной ранее:
где ŷ(i) – результат
линейной регрессии на i-м входе, а m – количество обучающих примеров. Мы видим,
что две первые величины являются постоянными, поэтому максимизация
логарифмической вероятности сводится к минимизации MSE:
Таким образом, максимизация логарифмического правдоподобия
относительно θ дает такую же оценку параметров θ, что и минимизация
среднеквадратичной ошибки. Два критерия имеют разные значения, но одинаковое
расположение оптимума. Это оправдывает использование MSE в качестве функции
оценки максимального правдоподобия.
Кросс-энтропия
(или логарифмическая функция потерь – log loss): Кросс-энтропия измеряет расхождение между двумя вероятностными
распределениями. Если кросс-энтропия велика, это означает, что разница между
двумя распределениями велика, а если кросс-энтропия мала, то распределения
похожи друг на друга.
Кросс-энтропия определяется как:
где P – распределение истинных ответов, а Q – распределение
вероятностей прогнозов модели. Можно
показать, что функция кросс-энтропии также получается из MLE, но я не буду
утомлять вас большим количеством математики.
Давайте еще
упростим это для нашей модели с:
• N – количество наблюдений
• M – количество возможных меток класса (собака,
кошка, рыба)
• y – двоичный индикатор (0 или 1) того, является
ли метка класса C правильной классификацией для наблюдения O
• p – прогнозируемая вероятность модели
Бинарная классификация
В случае бинарной классификации (M=2),
формула имеет вид:
При двоичной классификации каждая предсказанная вероятность
сравнивается с фактическим значением класса (0 или 1), и вычисляется оценка,
которая штрафует вероятность на основе расстояния от ожидаемого значения.
Визуализация
На приведенном ниже графике показан диапазон возможных значений
логистической функции потерь с учетом истинного наблюдения (y = 1). Когда
прогнозируемая вероятность приближается к 1, логистическая функция потерь
медленно уменьшается. Однако при уменьшении прогнозируемой вероятности она быстро возрастает.
Логистическая функция потерь наказывает оба типа ошибок, но
особенно те прогнозы, которые являются достоверными и ошибочными!
Мульти-классовая классификация
В случае мульти-классовой классификации (M>2) мы берем сумму значений логарифмических функций потерь для
каждого прогноза наблюдаемых классов.
Кросс-энтропия для бинарной или двух-классовой задачи
прогнозирования фактически рассчитывается как средняя кросс-энтропия среди всех
примеров. Log loss использует отрицательные
значения логарифма, чтобы обеспечить удобную метрику для сравнения. Этот подход
основан на том, что логарифм чисел <1 возвращает отрицательные значения, что
затрудняет работу при сравнении производительности двух моделей. Вы можете
почитать эту статью, где детально обсуждается функция кросс-энтропии потерь.
Задачи ML и соответствующие функции потерь
Давайте посмотрим, какие обычно используются выходные слои и
функции потерь в задачах машинного обучения:
Задача регрессии
Задача, когда
вы прогнозируете вещественное число.
• Конфигурация выходного уровня: один
узел с линейной единицей активации.
• Функция
потерь: средняя квадратическая ошибка (MSE).
Задача бинарной классификации
Задача состоит в том, чтобы классифицировать пример как
принадлежащий одному из двух классов. Или более точно, задача сформулирована
как предсказание вероятности того, что пример принадлежит первому классу,
например, классу, которому вы присваиваете целочисленное значение 1, тогда как
другому классу присваивается значение 0.
• Конфигурация выходного
уровня: один узел с сигмовидной активационной функцией.
• Функция
потерь: кросс-энтропия, также называемая логарифмической функцией потерь.
Задача мульти-классовой классификации
Эта задача состоит в том, чтобы классифицировать пример как
принадлежащий одному из нескольких классов. Задача сформулирована как
предсказание вероятности того, что пример принадлежит каждому классу.
• Конфигурация выходного уровня: один
узел для каждого класса, использующий функцию активации softmax.
• Функция потерь: кросс-энтропия, также называемая логарифмической функцией потерь.
Рассмотрев оценку и различные функции потерь, давайте перейдем к
роли оптимизаторов в алгоритмах ML.
Оптимизаторы
Чтобы свести к минимуму ошибку или потерю в прогнозировании,
модель, используя примеры из обучающей выборки, обновляет параметры модели W. Расчеты
ошибок строятся в зависимости от W и также описываются графиком функции затрат
J(w), поскольку она определяет затраты/наказание модели. Таким образом, минимизация
ошибки также часто называется минимизацией функции затрат.
Но как именно это делается? Используя оптимизаторы.
Оптимизаторы используются для обновления весов и смещений, то есть
внутренних параметров модели, чтобы уменьшить ошибку.
Самым важным методом и основой того, как мы обучаем и оптимизируем
нашу модель, является метод Градиентного Спуска.
Градиентный Спуск
Когда мы строим функцию затрат J(w), это можно представить следующим
образом:
Как видно из кривой, существует значение параметров W, которое
имеет минимальное значение Jmin. Нам нужно найти способ достичь
этого минимального значения.
В алгоритме градиентного спуска мы начинаем со случайных
параметров модели и вычисляем ошибку для каждой итерации обучения, продолжая
обновлять параметры, чтобы приблизиться к минимальным значениям.
Повторяем до достижения минимума:
{
}
В приведенном выше уравнении мы обновляем параметры модели после
каждой итерации. Второй член уравнения вычисляет наклон или градиент кривой на
каждой итерации.
Градиент функции затрат вычисляется как частная производная
функции затрат J по каждому параметру модели Wj, где j принимает
значение числа признаков [1, n]. α – альфа, это скорость обучения, определяющий
как быстро мы хотим двигаться к минимуму. Если α слишком велико, мы можем
проскочить минимум. Если α слишком мало, это приведет к небольшим этапам обучения,
поэтому общее время, затрачиваемое моделью для достижения минимума, будет
больше.
Есть три способа сделать градиентный спуск:
Пакетный
градиентный спуск: использует
все обучающие данные для обновления параметров модели в каждой итерации.
Мини-пакетный градиентный спуск: вместо использования всех данных, мини-пакетный градиентный спуск делит тренировочный набор на меньший размер, называемый партией, и обозначаемый буквой «b». Таким образом, мини-пакет «b» используется для обновления параметров модели на каждой итерации.
Вот некоторые другие часто
используемые Оптимизаторы:
Стохастический
Градиентный Спуск (SGD): обновляет
параметры, используя только один обучающий параметр на каждой итерации. Такой
параметр обычно выбирается случайным образом. Стохастический градиентный спуск
часто предпочтителен для оптимизации функций затрат, когда есть сотни тысяч
обучающих или более параметров, поскольку он будет сходиться быстрее, чем
пакетный градиентный спуск.
Адаград
Адаград адаптирует скорость обучения конкретно к индивидуальным
особенностям: это означает, что некоторые веса в вашем наборе данных будут
отличаться от других. Это работает очень хорошо для разреженных наборов данных,
где пропущено много входных значений. Однако, у Адаграда есть одна серьезная
проблема: адаптивная скорость обучения со временем становится очень маленькой.
Некоторые другие оптимизаторы, описанные ниже, пытаются справиться
с этой проблемой.
RMSprop
RMSprop – это специальная версия Adagrad,
разработанная профессором Джеффри Хинтоном в его
классе нейронных сетей. Вместо того,
чтобы вычислять все градиенты, он вычисляет градиенты только в фиксированном
окне. RMSprop похож на Adaprop, это еще один оптимизатор, который пытается
решить некоторые проблемы, которые Адаград оставляет открытыми.
Адам
Адам означает адаптивную оценку момента и является еще одним способом использования
предыдущих градиентов для вычисления текущих градиентов. Адам также использует
концепцию импульса,
добавляя доли предыдущих градиентов к текущему. Этот оптимизатор получил
довольно широкое распространение и практически принят для использования в
обучающих нейронных сетях.
Вы только что ознакомились с кратким обзором
оптимизаторов. Более подробно об этом можно прочитать здесь.
Я надеюсь,
что после прочтения этой статьи, вы будете лучше понимать что происходит, когда
Вы пишите следующий код:
# loss function: Binary Cross-entropy and optimizer: Adam
model.compile(loss='binary_crossentropy', optimizer='adam')или
# loss function: MSE and optimizer: stochastic gradient descent
model.compile(loss='mean_squared_error', optimizer='sgd')Спасибо за проявленный интерес!
Ссылки:
[1] https://www.deeplearningbook.org/contents/ml.html
[2] https://machinelearningmastery.com/loss-and-loss-functions-for-training-deep-learning-neural-networks/
[3] https://blog.algorithmia.com/introduction-to-optimizers/
[4] https://jhui.github.io/2017/01/05/Deep-learning-Information-theory/
[5] https://blog.algorithmia.com/introduction-to-loss-functions/
[6] https://gombru.github.io/2018/05/23/cross_entropy_loss/
[7] https://www.kdnuggets.com/2018/04/right-metric-evaluating-machine-learning-models-1.html
[8] https://rohanvarma.me/Loss-Functions/
[9] http://blog.christianperone.com/2019/01/mle/
Содержание
- Общая постановка задачи обучения по прецедентам
- Основные типы задач
- Обучение с учителем и без учителя
- Пример
- Метрики качества
- Основные подходы
- Пример задачи Классификации
- k-NN
- Плюсы и минусы метода ближайших соседей
- Класс KNeighborsClassifier в Scikit-learn
- Первый пример: Ирисы Фишера
- Знакомство с данными
- Набор данных про ирисы (dataset)
- Измерение качества: обучающая и контрольная выборки
- Предобработка данных (preconditioning)
- Мой первый классификатор: k-Nearest Neighbors
- Предсказание
- Оценка качества модели
- Итого
- Выбор параметров модели и кросс-валидация
- Задание:
Онлайн-лекция: https://youtu.be/IKaxaE0fKNc
ссылка jupyter notebook
Машинное обучение (Machine Learning) — обширный подраздел искусственного
интеллекта, изучающий методы построения алгоритмов, способных обучаться.
Общая постановка задачи обучения по прецедентам
Дано конечное множество прецедентов (объектов, ситуаций), по каждому из
которых собраны (измерены) некоторые данные. Данные о прецеденте
называют также его описанием. Совокупность всех имеющихся описаний
прецедентов называется обучающей выборкой. Требуется по этим частным
данным выявить общие зависимости, закономерности, взаимосвязи, присущие
не только этой конкретной выборке, но вообще всем прецедентам, в том
числе тем, которые ещё не наблюдались. Говорят также о восстановлении
зависимостей по эмпирическим данным — этот термин был введён в работах
Вапника и Червоненкиса.
Наиболее распространённым способом описания прецедентов является
признаковое описание. Фиксируется совокупность n показателей, измеряемых
у всех прецедентов. Если все n показателей числовые, то признаковые
описания представляют собой числовые векторы размерности n. Возможны и
более сложные случаи, когда прецеденты описываются временными рядами или
сигналами, изображениями, видеорядами, текстами, попарными отношениями
сходства или интенсивности взаимодействия, и т. д.
Для решения задачи обучения по прецедентам в первую очередь фиксируется
модель восстанавливаемой зависимости. Затем вводится функционал
качества, значение которого показывает, насколько хорошо модель
описывает наблюдаемые данные. Алгоритм обучения (learning algorithm)
ищет такой набор параметров модели, при котором функционал качества на
заданной обучающей выборке принимает оптимальное значение. Процесс
настройки (fitting) модели по выборке данных в большинстве случаев
сводится к применению численных методов оптимизации.
Основные типы задач
-
- Обучение с учителем (Supervised Machine Learning): наиболее распространённый случай. Каждый прецедент представляет собой пару «объект, ответ». Требуется найти функциональную зависимость ответов от описаний объектов и построить алгоритм, принимающий на входе описание объекта и выдающий на выходе ответ. Функционал качества обычно определяется как средняя ошибка ответов, выданных алгоритмом, по всем объектам выборки. Задачи обучения с учителем делятся на следующие типы :
- Ранжирование (ranking) и прогнозирование (forecasting) — другие примеры задач , сводящихся к классификации и регрессии.
-
- Ранжирование отличается тем, что ответы надо получить сразу на множестве объектов, после чего отсортировать их по значениям ответов.
- Прогнозирование отличается тем, что объектами являются отрезки временных рядов, обрывающиеся в тот момент, когда требуется сделать прогноз на будущее.
-
- Обучение без учителя (Unsupervised Machine Learning): В этом случае ответы не задаются, и требуется искать зависимости между объектами. Пример: банк хочет разделить клиентов на группы собразно их поведению.
-
-
кластеризация (clustering) заключается в том, чтобы сгруппировать объекты в кластеры, используя данные о попарном сходстве объектов. Функционалы качества могут определяться по-разному, например, как отношение средних межкластерных и внутрикластерных расстояний.
-
поиск ассоциативных правил (association rules learning). Исходные данные представляются в виде признаковых описаний. Требуется найти такие наборы признаков, и такие значения этих признаков, которые особенно часто (неслучайно часто) встречаются в признаковых описаниях объектов.
-
снижение размерности (dimensionality reduction) заключается в том, чтобы по исходным признакам с помощью некоторых функций преобразования перейти к наименьшему числу новых признаков, не потеряв при этом никакой существенной информации об объектах выборки. В классе линейных преобразований наиболее известным примером является метод главных компонент .
-
-
Обучение с подкреплением (Reinforcement Learning): считается основной надеждой «истинного» искусственного интеллекта. Считается, что потенциал этого подхода огромен. Хотя это на данный момент самая сложная часть теории анализа данных. Роль объектов играют пары «ситуация, принятое решение», ответами являются значения функционала качества, характеризующего правильность принятых решений (реакцию среды). Как и в задачах прогнозирования, здесь существенную роль играет фактор времени. Примеры прикладных задач: формирование инвестиционных стратегий, автоматическое управление технологическими процессами, самообучение роботов.
- Картинка с сайта https://courses.analyticsvidhya.com/courses/Machine-Learning-Certification-Course-for-Beginners?utm_source=blog_navbar&utm_medium=start_here_button
В эту красивую схему укладываются все или почти все задачи машинного обучения. Другие типы представляют собой комбинации и модификации перечисленных. Примеры:
- Частичное обучение (semi-supervised learning) занимает промежуточное положение между обучением с учителем и без учителя. Каждый прецедент представляет собой пару «объект, ответ», но ответы известны только на части прецедентов. Пример прикладной задачи — автоматическая рубрикация большого количества текстов при условии, что некоторые из них уже отнесены к каким-то рубрикам. К частичному обучению сводится также трансдуктивное обучение (transductive learning) — когда дана конечная обучающая выборка прецедентов и требуется по этим частным данным сделать предсказания отностительно других частных данных.
- Метаобучение (meta-learning или learning-to-learn) — когда прецедентами являются ранее решённые задачи обучения. Требуется определить, какие из используемых в них эвристик работают более эффективно. Конечная цель — обеспечить постоянное автоматическое совершенствование алгоритма обучения с течением времени.
Обучение с учителем и без учителя
В зависимости от данных алгоритмы машинного обучения могут быть поделены
на те, что обучаются с учителем и без учителя (supervised & unsupervised
learning). В задачах обучения без учителя имеется выборка, состоящая из
объектов, описываемых набором признаков. В задачах обучения с учителем
вдобавок к этому для каждого объекта некоторой выборки, называемой
обучающей, известен целевой признак – по сути это то, что хотелось бы
прогнозировать для прочих объектов, не из обучающей выборки. Т.е в
задачах МО с учителем на обучающей выборке у нас есть “правильные”
ответы, а когда задача без учителя — то нет
Пример
Задачи классификации и регрессии – это задачи обучения с учителем. В
качестве примера будем представлять задачу кредитного скоринга: на
основе накопленных кредитной организацией данных о своих клиентах
хочется прогнозировать невозврат кредита. Здесь для алгоритма данные –
это имеющаяся обучающая выборка: набор объектов (людей), каждый из
которых характеризуется набором признаков (таких как возраст, зарплата,
тип кредита, невозвраты в прошлом и т.д.), а также целевым признаком.
Если этот целевой признак – просто факт невозврата кредита (1 или 0,
т.е. банк знает о своих клиентах, кто вернул кредит, а кто – нет), то
это задача (бинарной) классификации. Если известно, на сколько по
времени клиент затянул с возвратом кредита и хочется то же самое
прогнозировать для новых клиентов, то это будет задачей регрессии.
Метрики качества
Наконец, третья абстракция в машинном обучении – это метрика оценки
производительности алгоритмов. Такие метрики различаются для разных
задач и алгоритмов. Пока скажем, что самая простая метрика качества
алгоритма, решающего задачу классификации – это доля правильных ответов
(accuracy, не называйте ее точностью, этот перевод зарезервирован под
другую метрику, precision) – то есть попросту доля верных прогнозов
алгоритма на тестовой выборке.
Пример задачи Классификации
Начнем с задач Классификации, хотя зачастую эти задачи можно свести к
задаче регрессии
k-NN
Заметим одно житейское наблюдение: обычно схожие объекты лежат гораздо
чаще лежат в одном классе, чем в разных. Это свойство называется
гипотезой компактности и все метрические методы опираются на нее.
Более строго Гипотеза компактности формулируется так: если мера сходства
объектов введена достаточно удачно, то схожие объекты гораздо чаще лежат
в одном классе, чем в разных. В этом случае граница между классами имеет
достаточно простую форму, а классы образуют компактно локализованные
области в пространстве объектов.
Пусть мы каким то образом можем измерять расстояние между объектами, т.е
у нас задана функция расстояний (метрика, не путайте с метрикой
качества!) на пространстве признаков.
Метод ближайшего соседа является, пожалуй, самым простым алгоритмом
классификации. Классифицируемый объект x относится к тому классу
yi, которому принадлежит ближайший объект обучающей выборки
xi.
Метод k ближайших соседей. Для повышения надёжности классификации
объект относится к тому классу, которому принадлежит большинство из его
соседей — k ближайших к нему объектов обучающей выборки
xi. В задачах с двумя классами число соседей берут нечётным,
чтобы не возникало ситуаций неоднозначности, когда одинаковое число
соседей принадлежат разным классам.
Метод взвешенных ближайших соседей. В задачах с числом классов 3 и
более нечётность уже не помогает, и ситуации неоднозначности всё равно
могут возникать. Тогда i-му соседу приписывается вес wi, как
правило, убывающий с ростом ранга соседа i. Объект относится к тому
классу, который набирает больший суммарный вес среди k ближайших
соседей.
В чистом виде kNN может послужить хорошим стартом (baseline) в решении
какой-либо задачи; В соревнованиях Kaggle kNN часто используется для
построения мета-признаков (прогноз kNN подается на вход прочим моделям)
или в стекинге/блендинге; Идея ближайшего соседа расширяется и на другие
задачи, например, в рекомендательных системах простым начальным решением
может быть рекомендация какого-то товара (или услуги), популярного среди
ближайших соседей человека, которому хотим сделать рекомендацию;
Плюсы и минусы метода ближайших соседей
Плюсы:
- Простая реализация;
- Неплохо изучен теоретически;
-
- Как правило, метод хорош для первого решения задачи, причем не только
- классификации или регрессии, но и, например, рекомендации;
-
- Можно адаптировать под нужную задачу выбором метрики или ядра (в двух
- словах: ядро может задавать операцию сходства для сложных объектов
типа графов, а сам подход kNN остается тем же). Кстати, профессор ВМК
МГУ и опытный участник соревнований по анализу данных Александр
Дьяконов любит самый простой kNN, но с настроенной метрикой сходства
объектов.
-
- Неплохая интерпретация, можно объяснить, почему тестовый пример был
- классифицирован именно так. Хотя этот аргумент можно атаковать: если
число соседей большое, то интерпретация ухудшается (условно: “мы не
дали ему кредит, потому что он похож на 350 клиентов, из которых 70 –
плохие, что на 12% больше, чем в среднем по выборке”).
Минусы:
-
- Метод считается быстрым в сравнении, например, с композициями
- алгоритмов, но в реальных задачах, как правило, число соседей,
используемых для классификации, будет большим (100-150), и в таком
случае алгоритм будет работать не так быстро, как дерево решений;
-
- Если в наборе данных много признаков, то трудно подобрать подходящие
- веса и определить, какие признаки не важны для
классификации/регрессии;
-
- Зависимость от выбранной метрики расстояния между примерами. Выбор по
- умолчанию евклидового расстояния чаще всего ничем не обоснован. Можно
отыскать хорошее решение перебором параметров, но для большого набора
данных это отнимает много времени;
-
- Нет теоретических оснований выбора определенного числа соседей —
- только перебор (впрочем, чаще всего это верно для всех
гиперпараметров всех моделей). В случае малого числа соседей метод
чувствителен к выбросам, то есть склонен переобучаться;
-
- Как правило, плохо работает, когда признаков много, из-за “прояклятия
- размерности”. Про это хорошо рассказывает известный в ML-сообществе
профессор Pedro Domingos – тут в популярной статье “A Few Useful
Things to Know about Machine Learning”, также “the curse of
dimensionality” описывается в книге Deep Learning в главе “Machine
Learning basics”.
Класс KNeighborsClassifier в Scikit-learn
sklearn.neighbors.KNeighborsClassifier: * weights: “uniform” (все веса
равны), “distance” (вес обратно пропорционален расстоянию до тестового
примера) или другая определенная пользователем функция
-
- algorithm (опционально): “brute”, “ball_tree”, “KD_tree”, или “auto”.
- В первом случае ближайшие соседи для каждого тестового примера
считаются перебором обучающей выборки. Во втором и третьем —
расстояние между примерами хранятся в дереве, что ускоряет нахождение
ближайших соседей. В случае указания параметра “auto” подходящий
способ нахождения соседей будет выбран автоматически на основе
обучающей выборки.
-
- leaf_size (опционально): порог переключения на полный перебор в
- случае выбора BallTree или KDTree для нахождения соседей
- metric: “minkowski”, “manhattan”, “euclidean”, “chebyshev” и другие
Первый пример: Ирисы Фишера
Знакомство с данными
Хранятся как стандартный набор внутри библиотеки Scikit-learn
from sklearn.datasets import load_iris iris_dataset = load_iris()
print("Keys of iris_dataset:n", iris_dataset.keys())
Keys of iris_dataset: dict_keys(['data', 'target', 'frame', 'target_names', 'DESCR', 'feature_names', 'filename'])
print(iris_dataset['DESCR'][:193] + "n...")
Набор данных про ирисы (dataset)
Характеристики набора данных:
Всего прецедентов: 150 (по 50 в каждом из 3 классов) всего признаков: 4 числовых
Названия классов
print("Target names:", iris_dataset['target_names'])
Target names: ['setosa' 'versicolor' 'virginica']
Названия признаков
print("Feature names:n", iris_dataset['feature_names'])
Feature names: ['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']
print("Type of data:", type(iris_dataset['data']))
Type of data: <class 'numpy.ndarray'>
print("Shape of data:", iris_dataset['data'].shape)
Shape of data: (150, 4)
Пример из набора данных
print("First five rows of data:n", iris_dataset['data'][:5])
First five rows of data: [[5.1 3.5 1.4 0.2] [4.9 3. 1.4 0.2] [4.7 3.2 1.3 0.2] [4.6 3.1 1.5 0.2] [5. 3.6 1.4 0.2]]
print("Type of target:", type(iris_dataset['target']))
Type of target: <class 'numpy.ndarray'>
print("Shape of target:", iris_dataset['target'].shape)
Shape of target: (150,)
Известные ответы для прецедентов (классы, к которым они принадлежат).
print("Target:n", iris_dataset['target'])
Target: [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2]
Измерение качества: обучающая и контрольная выборки
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(
iris_dataset['data'], iris_dataset['target'], random_state=0)
print("X_train shape:", X_train.shape)
print("y_train shape:", y_train.shape)
X_train shape: (112, 4) y_train shape: (112,)
print("X_test shape:", X_test.shape)
print("y_test shape:", y_test.shape)
X_test shape: (38, 4) y_test shape: (38,)
Предобработка данных (preconditioning)
# create dataframe from data in X_train
# label the columns using the strings in iris_dataset.feature_names
iris_dataframe = pd.DataFrame(X_train, columns=iris_dataset.feature_names)
# create a scatter matrix from the dataframe, color by y_train
pd.plotting.scatter_matrix(iris_dataframe, c=y_train, figsize=(15, 15),
marker='o', hist_kwds={'bins': 20}, s=60,
alpha=.8, cmap=mglearn.cm3)
array([[<matplotlib.axes._subplots.AxesSubplot object at 0x000001BE868F9C88>,
<matplotlib.axes._subplots.AxesSubplot object at 0x000001BE869714C8>,
<matplotlib.axes._subplots.AxesSubplot object at 0x000001BE869A5D48>,
<matplotlib.axes._subplots.AxesSubplot object at 0x000001BE869DFE08>],
[<matplotlib.axes._subplots.AxesSubplot object at 0x000001BE86A18E48>,
<matplotlib.axes._subplots.AxesSubplot object at 0x000001BE86A4FEC8>,
<matplotlib.axes._subplots.AxesSubplot object at 0x000001BE86A88F88>,
<matplotlib.axes._subplots.AxesSubplot object at 0x000001BE86AC8088>],
[<matplotlib.axes._subplots.AxesSubplot object at 0x000001BE86ACEC48>,
<matplotlib.axes._subplots.AxesSubplot object at 0x000001BE86B06D88>,
<matplotlib.axes._subplots.AxesSubplot object at 0x000001BE86B71188>,
<matplotlib.axes._subplots.AxesSubplot object at 0x000001BE86BAA208>],
[<matplotlib.axes._subplots.AxesSubplot object at 0x000001BE86BE22C8>,
<matplotlib.axes._subplots.AxesSubplot object at 0x000001BE86C1A388>,
<matplotlib.axes._subplots.AxesSubplot object at 0x000001BE86C54408>,
<matplotlib.axes._subplots.AxesSubplot object at 0x000001BE86C8C3C8>]],
dtype=object)
Мой первый классификатор: k-Nearest Neighbors
Создаём классификатор по 1 ближайшему соседу
from sklearn.neighbors import KNeighborsClassifier knn = KNeighborsClassifier(n_neighbors=1)
Обучаем его, вызывая функцию fit
knn.fit(X_train, y_train)
Предсказание
Создаём искусственный прецедент для классификации
X_new = np.array([[5, 2.9, 1, 0.2]])
print("X_new.shape:", X_new.shape)
X_new.shape: (1, 4)
Узнаём прежссказанное значение для него. которое даёт наш обученный классификатор
prediction = knn.predict(X_new)
print("Prediction:", prediction)
print("Predicted target name:",
iris_dataset['target_names'][prediction])
Prediction: [0] Predicted target name: ['setosa']
Оценка качества модели
Узнаем ответ обученного классификатора на контрольной выборке
y_pred = knn.predict(X_test)
print("Test set predictions:n", y_pred)
Test set predictions: [2 1 0 2 0 2 0 1 1 1 2 1 1 1 1 0 1 1 0 0 2 1 0 0 2 0 0 1 1 0 2 1 0 2 2 1 0 2]
print("Test set score: {:.2f}".format(np.mean(y_pred == y_test)))
Test set score: 0.97
print("Test set score: {:.2f}".format(knn.score(X_test, y_test)))
Test set score: 0.97
Итого
Делим выборку на обучающую и контрольную, обучаем классификатор по 1 ближайшему соседу на обучающей, сравниваем предсказанные значения на контрольной выборке с известными.
X_train, X_test, y_train, y_test = train_test_split(
iris_dataset['data'], iris_dataset['target'], random_state=0)
knn = KNeighborsClassifier(n_neighbors=1)
knn.fit(X_train, y_train)
print("Test set score: {:.2f}".format(knn.score(X_test, y_test)))
Выводим результат в виде качества нашего классификатора (функционал эмпирического риска)
Test set score: 0.97
Выбор параметров модели и кросс-валидация
Главная задача обучаемых алгоритмов – их способность обобщаться, то есть
хорошо работать на новых данных. Поскольку на новых данных мы сразу не
можем проверить качество построенной модели (нам ведь надо для них
сделать прогноз, то есть истинных значений целевого признака мы для них
не знаем), то надо пожертвовать небольшой порцией данных, чтоб на ней
проверить качество модели.
Чаще всего это делается одним из 2 способов: * отложенная выборка
(held-out/hold-out set). При таком подходе мы оставляем какую-то долю
обучающей выборки (как правило от 20% до 40%), обучаем модель на
остальных данных (60-80% исходной выборки) и считаем некоторую метрику
качества модели (например, самое простое – долю правильных ответов в
задаче классификации) на отложенной выборке. * кросс-валидация
(cross-validation, на русский еще переводят как скользящий или
перекрестный контроль). Тут самый частый случай – K-fold
кросс-валидация.
Тут модель обучается K раз на разных (K-1) подвыборках исходной выборки
(белый цвет), а проверяется на одной подвыборке (каждый раз на разной,
оранжевый цвет). Получаются K оценок качества модели, которые обычно
усредняются, выдавая среднюю оценку качества классификации/регрессии на
кросс-валидации.
Кросс-валидация дает лучшую по сравнению с отложенной выборкой оценку
качества модели на новых данных. Но кросс-валидация вычислительно
дорогостоящая, если данных много.
Кросс-валидация – очень важная техника в машинном обучении (применяемая
также в статистике и эконометрике), с ее помощью выбираются
гиперпараметры моделей, сравниваются модели между собой, оценивается
полезность новых признаков в задаче и т.д.
Задание:
Оценить работу kNN классификатора для Ирисов (или любого другого набора данных) с помощью Перекрестного контроля с разными параметрами разбиения выборки на обучающую и контрольную.
Функция потерь (Loss Function, Cost Function, Error Function; J) – фрагмент программного кода, который используется для оптимизации Алгоритма (Algorithm) Машинного обучения (ML). Значение, вычисленное такой функцией, называется «потерей».
Функция (Function) потерь может дать бо́льшую практическую гибкость вашим Нейронным сетям (Neural Network) и будет определять, как именно выходные данные связаны с исходными.
Нейронные сети могут выполнять несколько задач: от прогнозирования непрерывных значений, таких как ежемесячные расходы, до Бинарной классификации (Binary Classification) на кошек и собак. Для каждой отдельной задачи потребуются разные типы функций, поскольку выходной формат индивидуален.
С очень упрощенной точки зрения Loss Function может быть определена как функция, которая принимает два параметра:
- Прогнозируемые выходные данные
- Истинные выходные данные
Эта функция, по сути, вычислит, насколько хорошо работает наша модель, сравнив то, что модель прогнозирует, с фактическим значением, которое она должна выдает. Если Ypred очень далеко от Yi, значение потерь будет очень высоким. Однако, если оба значения почти одинаковы, значение потерь будет очень низким. Следовательно, нам нужно сохранить функцию потерь, которая может эффективно наказывать модель, пока та обучается на Тренировочных данных (Train Data).
Этот сценарий в чем-то аналогичен подготовке к экзаменам. Если кто-то плохо сдает экзамен, мы можем сказать, что потеря очень высока, и этому человеку придется многое изменить внутри себя, чтобы в следующий раз получить лучшую оценку. Однако, если экзамен пройдет хорошо, студент может вести себя подобным образом и в следующий раз.
Теперь давайте рассмотрим классификацию как задачу и поймем, как в этом случае работает функция потерь.
Классификационные потери
Когда нейронная сеть пытается предсказать дискретное значение, мы рассматриваем это как модель классификации. Это может быть сеть, пытающаяся предсказать, какое животное присутствует на изображении, или является ли электронное письмо спамом. Сначала давайте посмотрим, как представлены выходные данные классификационной нейронной сети.
Количество узлов выходного слоя будет зависеть от количества классов, присутствующих в данных. Каждый узел будет представлять один класс. Значение каждого выходного узла по существу представляет вероятность того, что этот класс является правильным.
Как только мы получим вероятности всех различных классов, рассмотрим тот, что имеет наибольшую вероятность. Посмотрим, как выполняется двоичная классификация.
Бинарная классификация
В двоичной классификации на выходном слое будет только один узел. Чтобы получить результат в формате вероятности, нам нужно применить Функцию активации (Activation Function). Поскольку для вероятности требуется значение от 0 до 1, мы будем использовать Сигмоид (Sigmoid), которая приведет любое реальное значение к диапазону значений от 0 до 1.
По мере того, как входные реальные данные становятся больше и стремятся к плюс бесконечности, выходные данные сигмоида будут стремиться к единице. А когда на входе значения становятся меньше и стремятся к отрицательной бесконечности, на выходе числа будут стремиться к нулю. Теперь мы гарантированно получаем значение от 0 до 1, и это именно то, что нам нужно, поскольку нам нужны вероятности.
Если выход выше 0,5 (вероятность 50%), мы будем считать, что он попадает в положительный класс, а если он ниже 0,5, мы будем считать, что он попадает в отрицательный класс. Например, если мы обучаем нейросеть для классификации кошек и собак, мы можем назначить собакам положительный класс, и выходное значение в наборе данных для собак будет равно 1, аналогично кошкам будет назначен отрицательный класс, а выходное значение для кошек будет быть 0.
Функция потерь, которую мы используем для двоичной классификации, называется Двоичной перекрестной энтропией (BCE). Эта функция эффективно наказывает нейронную сеть за Ошибки (Error) двоичной классификации. Давайте посмотрим, как она выглядит.
Как видите, есть две отдельные функции, по одной для каждого значения Y. Когда нам нужно предсказать положительный класс (Y = 1), мы будем использовать следующую формулу:
$$Потеря = -log(Y_{pred})space{,}space{где}$$
$$Jspace{}{–}space{Потеря,}$$
$$Y_predspace{}{–}space{Предсказанные}space{значения}$$
И когда нам нужно предсказать отрицательный класс (Y = 0), мы будем использовать немного трансформированный аналог:
$$Потеря = -log(1 — Y_{pred})space{,}space{где}$$
$$Jspace{}{–}space{Потеря,}$$
$$Y_predspace{}{–}space{Предсказанные}space{значения}$$
Для первой функции, когда Ypred равно 1, потеря равна 0, что имеет смысл, потому что Ypred точно такое же, как Y. Когда значение Ypred становится ближе к 0, мы можем наблюдать, как значение потери сильно увеличивается. Когда же Ypred становится равным 0, потеря стремится к бесконечности. Это происходит, потому что с точки зрения классификации, 0 и 1 – полярные противоположности: каждый из них представляет совершенно разные классы. Поэтому, когда Ypred равно 0, а Y равно 1, потери должны быть очень высокими, чтобы сеть могла более эффективно распознавать свои ошибки.
Полиномиальная классификация
Полиномиальная классификация (Multiclass Classification) подходит, когда нам нужно, чтобы наша модель каждый раз предсказывала один возможный класс. Теперь, поскольку мы все еще имеем дело с вероятностями, имеет смысл просто применить сигмоид ко всем выходным узлам, чтобы мы получали значения от 0 до 1 для всех выходных значений, но здесь кроется проблема. Когда мы рассматриваем вероятности для нескольких классов, нам необходимо убедиться, что сумма всех индивидуальных вероятностей равна единице, поскольку именно так определяется вероятность. Применение сигмоида не гарантирует, что сумма всегда равна единице, поэтому нам нужно использовать другую функцию активации.
В данном случае мы используем функцию активации Softmax. Эта функция гарантирует, что все выходные узлы имеют значения от 0 до 1, а сумма всех значений выходных узлов всегда равна 1. Вычисляется с помощью формулы:
$$Softmax(y_i) = frac{e^{y_i}}{sum_{i = 0}^n e^{y_i}}space{,}space{где}$$
$$y_ispace{}{–}space{i-e}space{наблюдение}$$
Пример:
Как видите, мы просто передаем все значения в экспоненциальную функцию. После этого, чтобы убедиться, что все они находятся в диапазоне от 0 до 1 и сумма всех выходных значений равна 1, мы просто делим каждую экспоненту на сумму экспонент.
Итак, почему мы должны передавать каждое значение через экспоненту перед их нормализацией? Почему мы не можем просто нормализовать сами значения? Это связано с тем, что цель Softmax – убедиться, что одно значение очень высокое (близко к 1), а все остальные значения очень низкие (близко к 0). Softmax использует экспоненту, чтобы убедиться, что это произойдет. А затем мы нормализуем результат, потому что нам нужны вероятности.
Теперь, когда наши выходные данные имеют правильный формат, давайте посмотрим, как мы настраиваем для этого функцию потерь. Хорошо то, что функция потерь по сути такая же, как у двоичной классификации. Мы просто применим Логарифмическую потерю (Log Loss) к каждому выходному узлу по отношению к его соответствующему целевому значению, а затем найдем сумму этих значений по всем выходным узлам.
Эта потеря называется категориальной Кросс-энтропией (Cross Entropy). Теперь перейдем к частному случаю классификации, называемому многозначной классификацией.
Классификация по нескольким меткам
Классификация по нескольким меткам (MLC) выполняется, когда нашей модели необходимо предсказать несколько классов в качестве выходных данных. Например, мы тренируем нейронную сеть, чтобы предсказывать ингредиенты, присутствующие на изображении какой-то еды. Нам нужно будет предсказать несколько ингредиентов, поэтому в Y будет несколько единиц.
Для этого мы не можем использовать Softmax, потому что он всегда заставляет только один класс «становиться единицей», а другие классы приводит к нулю. Вместо этого мы можем просто сохранить сигмоид на всех значениях выходных узлов, поскольку пытаемся предсказать индивидуальную вероятность каждого класса.
Что касается потерь, мы можем напрямую использовать логарифмические потери на каждом узле и суммировать их, аналогично тому, что мы делали в мультиклассовой классификации.
Теперь, когда мы рассмотрели классификацию, перейдем к регрессии.
Потеря регрессии
В Регрессии (Regression) наша модель пытается предсказать непрерывное значение, например, цены на жилье или возраст человека. Наша нейронная сеть будет иметь один выходной узел для каждого непрерывного значения, которое мы пытаемся предсказать. Потери регрессии рассчитываются путем прямого сравнения выходного и истинного значения.
Самая популярная функция потерь, которую мы используем для регрессионных моделей, – это Среднеквадратическая ошибка (MSE). Здесь мы просто вычисляем квадрат разницы между Y и YPred и усредняем полученное значение.
Автор оригинальной статьи: deeplearningdemystified.com
Фото: @leni_eleni
В машинном обучении различают оценки качества для задачи классификации и регрессии. Причем оценка задачи классификации часто значительно сложнее, чем оценка регрессии.
Содержание
- 1 Оценки качества классификации
- 1.1 Матрица ошибок (англ. Сonfusion matrix)
- 1.2 Аккуратность (англ. Accuracy)
- 1.3 Точность (англ. Precision)
- 1.4 Полнота (англ. Recall)
- 1.5 F-мера (англ. F-score)
- 1.6 ROC-кривая
- 1.7 Precison-recall кривая
- 2 Оценки качества регрессии
- 2.1 Средняя квадратичная ошибка (англ. Mean Squared Error, MSE)
- 2.2 Cредняя абсолютная ошибка (англ. Mean Absolute Error, MAE)
- 2.3 Коэффициент детерминации
- 2.4 Средняя абсолютная процентная ошибка (англ. Mean Absolute Percentage Error, MAPE)
- 2.5 Корень из средней квадратичной ошибки (англ. Root Mean Squared Error, RMSE)
- 2.6 Cимметричная MAPE (англ. Symmetric MAPE, SMAPE)
- 2.7 Средняя абсолютная масштабированная ошибка (англ. Mean absolute scaled error, MASE)
- 3 Кросс-валидация
- 4 Примечания
- 5 См. также
- 6 Источники информации
Оценки качества классификации
Матрица ошибок (англ. Сonfusion matrix)
Перед переходом к самим метрикам необходимо ввести важную концепцию для описания этих метрик в терминах ошибок классификации — confusion matrix (матрица ошибок).
Допустим, что у нас есть два класса и алгоритм, предсказывающий принадлежность каждого объекта одному из классов.
Рассмотрим пример. Пусть банк использует систему классификации заёмщиков на кредитоспособных и некредитоспособных. При этом первым кредит выдаётся, а вторые получат отказ. Таким образом, обнаружение некредитоспособного заёмщика () можно рассматривать как «сигнал тревоги», сообщающий о возможных рисках.
Любой реальный классификатор совершает ошибки. В нашем случае таких ошибок может быть две:
- Кредитоспособный заёмщик распознается моделью как некредитоспособный и ему отказывается в кредите. Данный случай можно трактовать как «ложную тревогу».
- Некредитоспособный заёмщик распознаётся как кредитоспособный и ему ошибочно выдаётся кредит. Данный случай можно рассматривать как «пропуск цели».
Несложно увидеть, что эти ошибки неравноценны по связанным с ними проблемам. В случае «ложной тревоги» потери банка составят только проценты по невыданному кредиту (только упущенная выгода). В случае «пропуска цели» можно потерять всю сумму выданного кредита. Поэтому системе важнее не допустить «пропуск цели», чем «ложную тревогу».
Поскольку с точки зрения логики задачи нам важнее правильно распознать некредитоспособного заёмщика с меткой , чем ошибиться в распознавании кредитоспособного, будем называть соответствующий исход классификации положительным (заёмщик некредитоспособен), а противоположный — отрицательным (заемщик кредитоспособен ). Тогда возможны следующие исходы классификации:
- Некредитоспособный заёмщик классифицирован как некредитоспособный, т.е. положительный класс распознан как положительный. Наблюдения, для которых это имеет место называются истинно-положительными (True Positive — TP).
- Кредитоспособный заёмщик классифицирован как кредитоспособный, т.е. отрицательный класс распознан как отрицательный. Наблюдения, которых это имеет место, называются истинно отрицательными (True Negative — TN).
- Кредитоспособный заёмщик классифицирован как некредитоспособный, т.е. имела место ошибка, в результате которой отрицательный класс был распознан как положительный. Наблюдения, для которых был получен такой исход классификации, называются ложно-положительными (False Positive — FP), а ошибка классификации называется ошибкой I рода.
- Некредитоспособный заёмщик распознан как кредитоспособный, т.е. имела место ошибка, в результате которой положительный класс был распознан как отрицательный. Наблюдения, для которых был получен такой исход классификации, называются ложно-отрицательными (False Negative — FN), а ошибка классификации называется ошибкой II рода.
Таким образом, ошибка I рода, или ложно-положительный исход классификации, имеет место, когда отрицательное наблюдение распознано моделью как положительное. Ошибкой II рода, или ложно-отрицательным исходом классификации, называют случай, когда положительное наблюдение распознано как отрицательное. Поясним это с помощью матрицы ошибок классификации:
-
Истинно-положительный (True Positive — TP) Ложно-положительный (False Positive — FP) Ложно-отрицательный (False Negative — FN) Истинно-отрицательный (True Negative — TN)
Здесь — это ответ алгоритма на объекте, а — истинная метка класса на этом объекте.
Таким образом, ошибки классификации бывают двух видов: False Negative (FN) и False Positive (FP).
P означает что классификатор определяет класс объекта как положительный (N — отрицательный). T значит что класс предсказан правильно (соответственно F — неправильно). Каждая строка в матрице ошибок представляет спрогнозированный класс, а каждый столбец — фактический класс.
# код для матрицы ошибок # Пример классификатора, способного проводить различие между всего лишь двумя # классами, "пятерка" и "не пятерка" из набора рукописных цифр MNIST import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.metrics import confusion_matrix from sklearn.linear_model import SGDClassifier mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (англ. Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе # Для расчета матрицы ошибок сначала понадобится иметь набор прогнозов, чтобы их можно было сравнивать с фактическими целями y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) print(confusion_matrix(y_train_5, y_train_pred)) # array([[53892, 687], # [ 1891, 3530]])
Безупречный классификатор имел бы только истинно-положительные и истинно отрицательные классификации, так что его матрица ошибок содержала бы ненулевые значения только на своей главной диагонали (от левого верхнего до правого нижнего угла):
import numpy as np
from sklearn.datasets import fetch_openml
from sklearn.metrics import confusion_matrix
mnist = fetch_openml('mnist_784', version=1)
X, y = mnist["data"], mnist["target"]
y = y.astype(np.uint8)
X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:]
y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки
y_test_5 = (y_test == 5)
y_train_perfect_predictions = y_train_5 # притворись, что мы достигли совершенства
print(confusion_matrix(y_train_5, y_train_perfect_predictions))
# array([[54579, 0],
# [ 0, 5421]])
Аккуратность (англ. Accuracy)
Интуитивно понятной, очевидной и почти неиспользуемой метрикой является accuracy — доля правильных ответов алгоритма:
Эта метрика бесполезна в задачах с неравными классами, что как вариант можно исправить с помощью алгоритмов сэмплирования и это легко показать на примере.
Допустим, мы хотим оценить работу спам-фильтра почты. У нас есть 100 не-спам писем, 90 из которых наш классификатор определил верно (True Negative = 90, False Positive = 10), и 10 спам-писем, 5 из которых классификатор также определил верно (True Positive = 5, False Negative = 5).
Тогда accuracy:
Однако если мы просто будем предсказывать все письма как не-спам, то получим более высокую аккуратность:
При этом, наша модель совершенно не обладает никакой предсказательной силой, так как изначально мы хотели определять письма со спамом. Преодолеть это нам поможет переход с общей для всех классов метрики к отдельным показателям качества классов.
# код для для подсчета аккуратности: # Пример классификатора, способного проводить различие между всего лишь двумя # классами, "пятерка" и "не пятерка" из набора рукописных цифр MNIST import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.metrics import accuracy_score from sklearn.linear_model import SGDClassifier mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) # print(confusion_matrix(y_train_5, y_train_pred)) # array([[53892, 687] # [ 1891, 3530]]) print(accuracy_score(y_train_5, y_train_pred)) # == (53892 + 3530) / (53892 + 3530 + 1891 +687) # 0.9570333333333333
Точность (англ. Precision)
Точностью (precision) называется доля правильных ответов модели в пределах класса — это доля объектов действительно принадлежащих данному классу относительно всех объектов которые система отнесла к этому классу.
Именно введение precision не позволяет нам записывать все объекты в один класс, так как в этом случае мы получаем рост уровня False Positive.
Полнота (англ. Recall)
Полнота — это доля истинно положительных классификаций. Полнота показывает, какую долю объектов, реально относящихся к положительному классу, мы предсказали верно.
Полнота (recall) демонстрирует способность алгоритма обнаруживать данный класс вообще.
Имея матрицу ошибок, очень просто можно вычислить точность и полноту для каждого класса. Точность (precision) равняется отношению соответствующего диагонального элемента матрицы и суммы всей строки класса. Полнота (recall) — отношению диагонального элемента матрицы и суммы всего столбца класса. Формально:
Результирующая точность классификатора рассчитывается как арифметическое среднее его точности по всем классам. То же самое с полнотой. Технически этот подход называется macro-averaging.
# код для для подсчета точности и полноты: # Пример классификатора, способного проводить различие между всего лишь двумя # классами, "пятерка" и "не пятерка" из набора рукописных цифр MNIST import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.metrics import precision_score, recall_score from sklearn.linear_model import SGDClassifier mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) # print(confusion_matrix(y_train_5, y_train_pred)) # array([[53892, 687] # [ 1891, 3530]]) print(precision_score(y_train_5, y_train_pred)) # == 3530 / (3530 + 687) print(recall_score(y_train_5, y_train_pred)) # == 3530 / (3530 + 1891) # 0.8370879772350012 # 0.6511713705958311
F-мера (англ. F-score)
Precision и recall не зависят, в отличие от accuracy, от соотношения классов и потому применимы в условиях несбалансированных выборок.
Часто в реальной практике стоит задача найти оптимальный (для заказчика) баланс между этими двумя метриками. Понятно что чем выше точность и полнота, тем лучше. Но в реальной жизни максимальная точность и полнота не достижимы одновременно и приходится искать некий баланс. Поэтому, хотелось бы иметь некую метрику которая объединяла бы в себе информацию о точности и полноте нашего алгоритма. В этом случае нам будет проще принимать решение о том какую реализацию запускать в производство (у кого больше тот и круче). Именно такой метрикой является F-мера.
F-мера представляет собой гармоническое среднее между точностью и полнотой. Она стремится к нулю, если точность или полнота стремится к нулю.
Данная формула придает одинаковый вес точности и полноте, поэтому F-мера будет падать одинаково при уменьшении и точности и полноты. Возможно рассчитать F-меру придав различный вес точности и полноте, если вы осознанно отдаете приоритет одной из этих метрик при разработке алгоритма:
где принимает значения в диапазоне если вы хотите отдать приоритет точности, а при приоритет отдается полноте. При формула сводится к предыдущей и вы получаете сбалансированную F-меру (также ее называют ).
-
Рис.1 Сбалансированная F-мера,
-
Рис.2 F-мера c приоритетом точности,
-
Рис.3 F-мера c приоритетом полноты,
F-мера достигает максимума при максимальной полноте и точности, и близка к нулю, если один из аргументов близок к нулю.
F-мера является хорошим кандидатом на формальную метрику оценки качества классификатора. Она сводит к одному числу две других основополагающих метрики: точность и полноту. Имея «F-меру» гораздо проще ответить на вопрос: «поменялся алгоритм в лучшую сторону или нет?»
# код для подсчета метрики F-mera: # Пример классификатора, способного проводить различие между всего лишь двумя # классами, "пятерка" и "не пятерка" из набора рукописных цифр MNIST import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.linear_model import SGDClassifier from sklearn.metrics import f1_score mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распознавать пятерки на целом обучающем наборе y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) print(f1_score(y_train_5, y_train_pred)) # 0.7325171197343846
ROC-кривая
Кривая рабочих характеристик (англ. Receiver Operating Characteristics curve).
Используется для анализа поведения классификаторов при различных пороговых значениях.
Позволяет рассмотреть все пороговые значения для данного классификатора.
Показывает долю ложно положительных примеров (англ. false positive rate, FPR) в сравнении с долей истинно положительных примеров (англ. true positive rate, TPR).
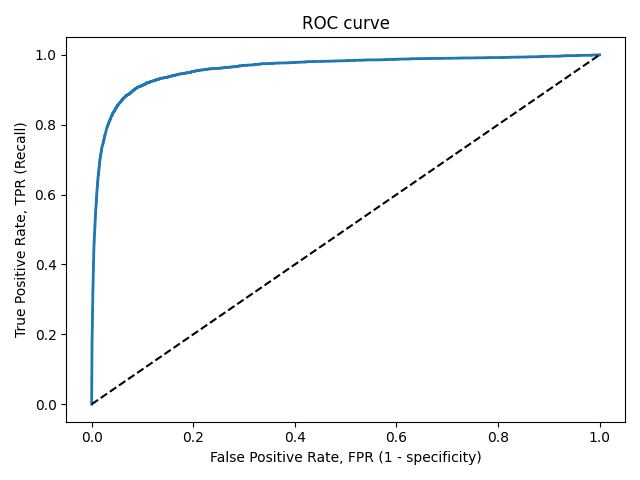
Доля FPR — это пропорция отрицательных образцов, которые были некорректно классифицированы как положительные.
- ,
где TNR — доля истинно отрицательных классификаций (англ. Тrие Negative Rate), представляющая собой пропорцию отрицательных образцов, которые были корректно классифицированы как отрицательные.
Доля TNR также называется специфичностью (англ. specificity). Следовательно, ROC-кривая изображает чувствительность (англ. seпsitivity), т.е. полноту, в сравнении с разностью 1 — specificity.
Прямая линия по диагонали представляет ROC-кривую чисто случайного классификатора. Хороший классификатор держится от указанной линии настолько далеко, насколько это
возможно (стремясь к левому верхнему углу).
Один из способов сравнения классификаторов предусматривает измерение площади под кривой (англ. Area Under the Curve — AUC). Безупречный классификатор будет иметь площадь под ROC-кривой (ROC-AUC), равную 1, тогда как чисто случайный классификатор — площадь 0.5.
# Код отрисовки ROC-кривой # На примере классификатора, способного проводить различие между всего лишь двумя классами # "пятерка" и "не пятерка" из набора рукописных цифр MNIST from sklearn.metrics import roc_curve import matplotlib.pyplot as plt import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.linear_model import SGDClassifier mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) y_scores = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3, method="decision_function") fpr, tpr, thresholds = roc_curve(y_train_5, y_scores) def plot_roc_curve(fpr, tpr, label=None): plt.plot(fpr, tpr, linewidth=2, label=label) plt.plot([0, 1], [0, 1], 'k--') # dashed diagonal plt.xlabel('False Positive Rate, FPR (1 - specificity)') plt.ylabel('True Positive Rate, TPR (Recall)') plt.title('ROC curve') plt.savefig("ROC.png") plot_roc_curve(fpr, tpr) plt.show()
Precison-recall кривая
Чувствительность к соотношению классов.
Рассмотрим задачу выделения математических статей из множества научных статей. Допустим, что всего имеется 1.000.100 статей, из которых лишь 100 относятся к математике. Если нам удастся построить алгоритм , идеально решающий задачу, то его TPR будет равен единице, а FPR — нулю. Рассмотрим теперь плохой алгоритм, дающий положительный ответ на 95 математических и 50.000 нематематических статьях. Такой алгоритм совершенно бесполезен, но при этом имеет TPR = 0.95 и FPR = 0.05, что крайне близко к показателям идеального алгоритма.
Таким образом, если положительный класс существенно меньше по размеру, то AUC-ROC может давать неадекватную оценку качества работы алгоритма, поскольку измеряет долю неверно принятых объектов относительно общего числа отрицательных. Так, алгоритм , помещающий 100 релевантных документов на позиции с 50.001-й по 50.101-ю, будет иметь AUC-ROC 0.95.
Precison-recall (PR) кривая. Избавиться от указанной проблемы с несбалансированными классами можно, перейдя от ROC-кривой к PR-кривой. Она определяется аналогично ROC-кривой, только по осям откладываются не FPR и TPR, а полнота (по оси абсцисс) и точность (по оси ординат). Критерием качества семейства алгоритмов выступает площадь под PR-кривой (англ. Area Under the Curve — AUC-PR)
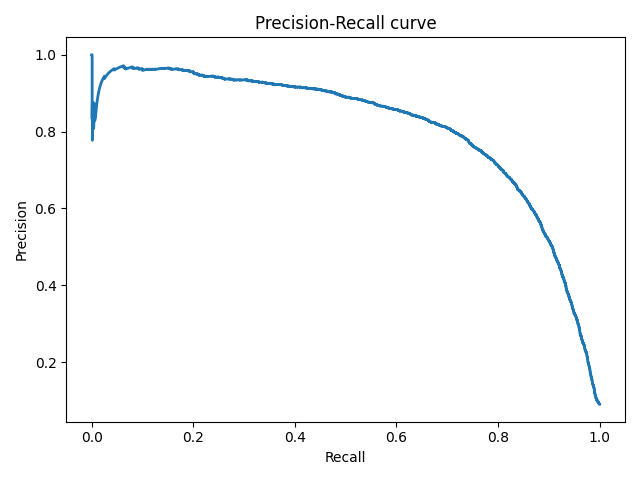
# Код отрисовки Precison-recall кривой # На примере классификатора, способного проводить различие между всего лишь двумя классами # "пятерка" и "не пятерка" из набора рукописных цифр MNIST from sklearn.metrics import precision_recall_curve import matplotlib.pyplot as plt import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.linear_model import SGDClassifier mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) y_scores = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3, method="decision_function") precisions, recalls, thresholds = precision_recall_curve(y_train_5, y_scores) def plot_precision_recall_vs_threshold(precisions, recalls, thresholds): plt.plot(recalls, precisions, linewidth=2) plt.xlabel('Recall') plt.ylabel('Precision') plt.title('Precision-Recall curve') plt.savefig("Precision_Recall_curve.png") plot_precision_recall_vs_threshold(precisions, recalls, thresholds) plt.show()
Оценки качества регрессии
Наиболее типичными мерами качества в задачах регрессии являются
Средняя квадратичная ошибка (англ. Mean Squared Error, MSE)
MSE применяется в ситуациях, когда нам надо подчеркнуть большие ошибки и выбрать модель, которая дает меньше больших ошибок прогноза. Грубые ошибки становятся заметнее за счет того, что ошибку прогноза мы возводим в квадрат. И модель, которая дает нам меньшее значение среднеквадратической ошибки, можно сказать, что что у этой модели меньше грубых ошибок.
- и
Cредняя абсолютная ошибка (англ. Mean Absolute Error, MAE)
Среднеквадратичный функционал сильнее штрафует за большие отклонения по сравнению со среднеабсолютным, и поэтому более чувствителен к выбросам. При использовании любого из этих двух функционалов может быть полезно проанализировать, какие объекты вносят наибольший вклад в общую ошибку — не исключено, что на этих объектах была допущена ошибка при вычислении признаков или целевой величины.
Среднеквадратичная ошибка подходит для сравнения двух моделей или для контроля качества во время обучения, но не позволяет сделать выводов о том, на сколько хорошо данная модель решает задачу. Например, MSE = 10 является очень плохим показателем, если целевая переменная принимает значения от 0 до 1, и очень хорошим, если целевая переменная лежит в интервале (10000, 100000). В таких ситуациях вместо среднеквадратичной ошибки полезно использовать коэффициент детерминации —
Коэффициент детерминации
Коэффициент детерминации измеряет долю дисперсии, объясненную моделью, в общей дисперсии целевой переменной. Фактически, данная мера качества — это нормированная среднеквадратичная ошибка. Если она близка к единице, то модель хорошо объясняет данные, если же она близка к нулю, то прогнозы сопоставимы по качеству с константным предсказанием.
Средняя абсолютная процентная ошибка (англ. Mean Absolute Percentage Error, MAPE)
Это коэффициент, не имеющий размерности, с очень простой интерпретацией. Его можно измерять в долях или процентах. Если у вас получилось, например, что MAPE=11.4%, то это говорит о том, что ошибка составила 11,4% от фактических значений.
Основная проблема данной ошибки — нестабильность.
Корень из средней квадратичной ошибки (англ. Root Mean Squared Error, RMSE)
Примерно такая же проблема, как и в MAPE: так как каждое отклонение возводится в квадрат, любое небольшое отклонение может значительно повлиять на показатель ошибки. Стоит отметить, что существует также ошибка MSE, из которой RMSE как раз и получается путем извлечения корня.
Cимметричная MAPE (англ. Symmetric MAPE, SMAPE)
Средняя абсолютная масштабированная ошибка (англ. Mean absolute scaled error, MASE)
MASE является очень хорошим вариантом для расчета точности, так как сама ошибка не зависит от масштабов данных и является симметричной: то есть положительные и отрицательные отклонения от факта рассматриваются в равной степени.
Обратите внимание, что в MASE мы имеем дело с двумя суммами: та, что в числителе, соответствует тестовой выборке, та, что в знаменателе — обучающей. Вторая фактически представляет собой среднюю абсолютную ошибку прогноза. Она же соответствует среднему абсолютному отклонению ряда в первых разностях. Эта величина, по сути, показывает, насколько обучающая выборка предсказуема. Она может быть равна нулю только в том случае, когда все значения в обучающей выборке равны друг другу, что соответствует отсутствию каких-либо изменений в ряде данных, ситуации на практике почти невозможной. Кроме того, если ряд имеет тенденцию к росту либо снижению, его первые разности будут колебаться около некоторого фиксированного уровня. В результате этого по разным рядам с разной структурой, знаменатели будут более-менее сопоставимыми. Всё это, конечно же, является очевидными плюсами MASE, так как позволяет складывать разные значения по разным рядам и получать несмещённые оценки.
Недостаток MASE в том, что её тяжело интерпретировать. Например, MASE=1.21 ни о чём, по сути, не говорит. Это просто означает, что ошибка прогноза оказалась в 1.21 раза выше среднего абсолютного отклонения ряда в первых разностях, и ничего более.
Кросс-валидация
Хороший способ оценки модели предусматривает применение кросс-валидации (cкользящего контроля или перекрестной проверки).
В этом случае фиксируется некоторое множество разбиений исходной выборки на две подвыборки: обучающую и контрольную. Для каждого разбиения выполняется настройка алгоритма по обучающей подвыборке, затем оценивается его средняя ошибка на объектах контрольной подвыборки. Оценкой скользящего контроля называется средняя по всем разбиениям величина ошибки на контрольных подвыборках.
Примечания
- [1] Лекция «Оценивание качества» на www.coursera.org
- [2] Лекция на www.stepik.org о кросвалидации
- [3] Лекция на www.stepik.org о метриках качества, Precison и Recall
- [4] Лекция на www.stepik.org о метриках качества, F-мера
- [5] Лекция на www.stepik.org о метриках качества, примеры
См. также
- Оценка качества в задаче кластеризации
- Кросс-валидация
Источники информации
- [6] Соколов Е.А. Лекция линейная регрессия
- [7] — Дьяконов А. Функции ошибки / функционалы качества
- [8] — Оценка качества прогнозных моделей
- [9] — HeinzBr Ошибка прогнозирования: виды, формулы, примеры
- [10] — egor_labintcev Метрики в задачах машинного обучения
- [11] — grossu Методы оценки качества прогноза
- [12] — К.В.Воронцов, Классификация
- [13] — К.В.Воронцов, Скользящий контроль
Линейная регрессия
Сегодня пойдет речь о регрессии, как обучать и какие проблемы могут вам попасться при использовании таких моделей.
Для начала давайте введем удобные обозначения.
$mathbb{X} — text{пространство объектов}$
$mathbb{Y} — text{пространство ответов}$
$ x = (x^1, … x^n) — text{признаковое описание объекта}$
$ X = (x_i,y_i)^l_{i=1} — text{обучающая выборка} $
$ a(x) — text{алгоритм, модель} $
$ Q(a,X) — text{функция ошибки алгоритма a на выборке X} $
$ text{Обучение} — a(x) = text{argmin}_{a in mathbb{A}} Q(a,X)$
Но этого мало, давайте разберем, что такое функционал ошибки, семейство алгоритмов, метод обучения.
- Функционал ошибки Q: способ измерения того, хорошо или плохо работает алгоритм на конкретной выборке
- Семейство алгоритмов $mathbb{A}$: как выглядит множество алгоритмов, из которых выбирается лучший
- Метод обучения: как именно выбирается лучший алгоритм из семейства алгоритмов.
Пример задачи регрессии: предсказание количества заказов магазина
Пусть известен один признак — расстояние кафе от метро, а предсказать необходимо количество заказов. Поскольку количество заказов — вещественное число $mathbb{R}$, здесь идет речь о задаче регрессии.
По графику можно сделать вывод о существование зависимости между расстоянием от метро и количеством заказов. Можно предположить, что зависимость линейна, ее можно представить в видео прямой на графике. По этой прямой и можно будет предсказывать количество заказов, если известно расстояние от метро.
В целом такая модель угадывает тенденцию, то есть описывает зависимость между ответом и признаком.
При этом, разумеется ,она делает это не идеально, с некоторой ошибкой. Истинный ответ на каждом объекте несколько отклоняется от прогноза.
Один признак — это несерьезно. Гораздо сложнее и интереснее работать с многомерными выборками, которые описываются большим количеством признаков. В этом случае отобразить выборку и понять, подходит ли модель или нет, нельзя. Можно лишь оценить ее качество и по нему уже понять, подходит ли эта модель.
Описание линейной модели
Давайте обсудим, как выглядит семейство алгоритмов в случае с линейными моделями. Линейный алгоритм в задачах регрессии выглядит следующим образом
$$ a(x)=w_0 + sumlimits_{j=1}^d w_j x^j $$
где $w_0$ — свободный коэффициент, $x^j$ — признаки, а $w_j$ — их веса.
Если у нашего набора данных есть только один признак, то алгоритм выглядит так
$$ a(x)=w_0 + w x $$
Ничего не напоминает? Да, действительно это обычная линейная функция, известная с 7 класса.
$$ y = kx+b $$
В качестве меры ошибки мы не может быть выбрано отклонение от прогноза $Q(a,y)=a(x)-y$, так как в этом случае минимум функционала не будет достигаться при правильном ответе $a(x)=y$. Самый простой способ — считать модуль отклонения.
$$ |a(x)-y| $$
Но функция модуля не является гладкой функцией, и для оптимизации такого функционала неудобно использовать градиентные методы. Поэтому в качестве меры ошибки часто используют квадрат отклонения:
$$ (a(x)-y)^2 $$
Функционал ошибки, именуемый среднеквадратичной ошибкой алгоритма, задается следующим образом:
$$ Q(a,x) = frac{1}{l} sumlimits_{i=1}^l (a(x_i)- y_i)^2 $$
В случае линейной модели его можно переписать в виде функции (поскольку теперь Q зависит от вектора, а не от функции) ошибок:
$$ Q(omega,x) = frac{1}{l} sumlimits_{i=1}^l ( langle w_i,x_irangle- y_i) ^2 $$
Обучение модели линейной регрессии
Разберем том, как обучать модель линейной регрессии, то есть как настраивать ее параметры.
$$ Q(w,x) = frac{1}{l} sumlimits_{i=1}^l ( langle w_i,x_irangle- y_i) ^2 to min_{w}$$
То есть нам необходимо подобрать $w$, что бы линия могла описать наши данные. Или же задача состоит в нахождение таких $w$, что бы была минимальна ошибка $ Q(w,x)$
Матричная форма записи
Прежде, чем рассмотрим задачу о оптимизации этой функции, имеет смысл используемые соотношения в матричной форме. Матрица «объекты-признаки» $X$ составлена из признаков описаний все объектов выборки
$$ X = begin{pmatrix} x_{11} & … & x_{1d} … & … & … x_{l1} & … & x_{ld} end{pmatrix} $$
Таким образом, в $ij$ элементе матрицы $X$ записано значение $j$-го признака на i объекте обучающей выборки. Или короче говоря, каждая строчка — это объект, а каждый столбец — это признак.Так же понадобится вектор ответов y, который составлен из истинных ответов для всех объектов.
$$ y = begin{pmatrix} y_{1} … y_{l} end{pmatrix} $$
В этом случае среднеквадратичная шибка может быть переписана в матричном виде:
$$ Q(w,X) = frac{1}{l} || Xw-y ||^2 to min_{w}$$
Оптимизационный метод решения
Самый лучший метод — это численный метод оптимизации.
Не сложно показать, что среднеквадратичная ошибка — это выпуклая и гладкая функция. Выпуклость гарантирует существование лишь одного минимумам, а гладкость — существование вектора градиента в каждой точке. Это позволяет использовать метод градиентного спуска.
При использовании метода градиентного спуска необходимо указать начальное приближение. Есть много
подходов к тому, как это сделать, в том числе инициализировать случайными числами (не очень большими). Самый простой способ это сделать — инициализировать значения всех весов равными нулю:
$$ w^0=0 $$
На каждой следующей итерации, $t = 1, 2, 3, …,$ из приближения, полученного в предыдущей итерации $w^{t−1}$, вычитается вектор градиента в соответствующей точке $w^{t−1}$, умноженный на некоторый коэффициент $eta_t$, называемый шагом:
$$ w^t = w^{t-1} — eta_t Delta Q(w^{t-1},X) $$
Остановить итерации следует , когда наступает сходимость. Сходимость можно определять по-разному .В данном случае разумно определить сходимость следующим образом: итерации следует завершить, если разница
двух последовательных приближений не слишком велика:
$$ ||w^t — w^{t-1} ||<epsilon $$
Случай парной регрессии
В случае парной регрессии признак всего один, а линейная модель выглядит следующим образом:
$$ a(x)=w_0 + w x $$
где $w_1$ и $w_0$ — два параметра.
Среднеквадратичная ошибка принимает вид:
$$ Q(w_0,w_1,X) = frac{1}{l} sumlimits_{i=1}^l (w_1x_i+w_0 -y_i) ^2$$
Для нахождения оптимальных параметров будет применяться метод градиентного спуска, про который уже было сказано ранее. Чтобы это сделать, необходимо сначала вычислить частные производные функции ошибки:
$$frac{partial Q}{partial w_1} = frac{2}{l} sumlimits_{i=1}^l (w_1x_i+w_0-y_i)x_i$$
$$frac{partial Q}{partial w_0} = frac{2}{l} sumlimits_{i=1}^l (w_1x_i+w_0-y_i)$$
Следующие два графика демонстрируют применение метода градиентного спуска в случае парной регрессии. Справа изображены точки выборки, а слева — пространство параметров. Точка в этом пространстве обозначает конкретную модель (кафе)
График зависимости функции ошибки от числа произведенных операции выглядит следующим образом:
Выбор размера шага в методе градиентного спуска
Очень важно при использовании метода градиентного спуска правильно подбирать шаг. Каких-либо концерт- иных правил подбора шага не существует, выбор шага — это искусство, но существует несколько полезных закономерностей.
Если длина шага слишком мала, то метод будет неспешна, но верно шагать в сторону минимума. Если же
взять размер шага очень большим, появляется риск, что метод будет перепрыгивать через минимум. Более
того, есть риск того, что градиентный спуск не сойдется.
Имеет смысл использовать переменный размер шага: сначала, когда точка минимума находится еще да-
легко, двигаться быстро, а позже, спустя некоторое количество итерации — делать более аккуратные шаги.
Один из способов задать размер шага следующий:
$$ eta_t = frac{k}{t} $$
где $k$-константа, которую необходимо подобрать, а $t$ — номер шага.
import matplotlib.pyplot as plt # библиотека для отрисовки графиков import numpy as np # импортируем numpy для создания своего датасета from sklearn import linear_model, model_selection # импортируем линейную модель для обучения и библиотеку для разделения нашей выборки X = np.random.randint(100,size=(500, 1)) # создаем вектор признаков, вектора так как у нас один признак y = np.random.normal(np.random.randint(300,360,size=(500, 1))-X) # создаем вектор ответом plt.scatter(X, y) # рисуем график точек plt.xlabel('Расстояние до кафе в метрах') # добавляем описание для оси x plt.ylabel('Количество заказов')# добавляем описание для оси y plt.show()
# Делим созданную нами выборку на тестовую и обучающую X_train, X_test, y_train, y_test = model_selection.train_test_split(X, y)
Давайте посмотрим какие параметры принимает LinearRegression.
fit_intercept — подбирать ли значения для свободного член $w_0$. True или False. Если ваши данные центрированны, то можете указать False. По умолчанию — True
normalize— нормализация данных перед обучением. Если fit_intercept=False то параметр будет проигнорирован. Если True — то данные перед обучением будут нормализованы при помощи L^2-Norm нормализации. По умолчанию — False
copy_X — True — копировать матрицу признаков. False — не копировать. **По умолчанию — **True
n_jobs — количество ядер используемых для сборки. Скорость будет существенно выше n_targets>1. По умолчанию — None
Параметры которые можно у модели:
coef_ — коэффициенты $w$, количество возвращаемых коэффициентов зависит от количества признаков. смотри пункт Описание линейной модели
intercept_ — свободный член $w_0$
Что бы предсказать значения необходимо вызвать функцию:
predict и передать массив из признаков.
Example: regr.predict([[40]])
regr = linear_model.LinearRegression() # создаем линейную регрессию #Обучаем модель regr.fit(X_train, y_train)
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
После выполнения кода, вам вернется ответ с установленными параметрами
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
# Посмотрим какие коэффициенты установила модель print('Коэфициент: n', regr.coef_) # Средний квадрат ошибки print("Средний квадрат ошибки: %.2f" % np.mean((regr.predict(X_test) - y_test) ** 2)) # Оценка дисперсии: 1 - идеальное предсказание. Качество предсказания. print('Оценка дисперсии:: %.2f' % regr.score(X_test, y_test))
Коэфициент:
[[-1.03950324]]
Средний квадрат ошибки: 325.63
Оценка дисперсии:: 0.70
# Посмотрим на получившуюся функцию print ("y = {:.2f}*x + {:.2f}".format(regr.coef_[0][0], regr.intercept_[0]))
# Посмотрим, как предскажет наша модель тестовые данные. plt.scatter(X_test, y_test, color='black')# рисуем график точек plt.plot(X_test, regr.predict(X_test), color='blue') # рисуем график линейной регрессии plt.show() # Покажем график
Давайте предскажем количество заказов, для нашего потенциального магазина. Скажем, что мы планируем построить магазин в 40 метрах от метро
290 заказов мы получим если построим магазин в 40 метрах от метро, но при этом качество предсказания всего лишь 71%, думаю не стоит доверять.
А что если, мы увеличим количество признаков?
Для этого воспользуемся встроенным датасетом make_regression из sklearn.
n_features — отвечает за количество признаков один нормальный другой избыточный
n_informative — отвечает за количество информативных признаков
n_targets — отвечает за размер ответов
noise — шум накладываемый на признаки
соef — возвращать ли коэффициенты
random_state — определяет генерацию случайных чисел для создания набора данных.
# Импортируем библиотеки для валидация, создания датасетов, и метрик качества from sklearn import cross_validation, datasets, metrics # Создаем датасет с избыточной информацией X, y, coef = datasets.make_regression(n_features = 2, n_informative = 1, n_targets = 1, noise = 5., coef = True, random_state = 2)
# Поскольку у нас есть два признака,для отрисовки надо их разделить на две части data_1, data_2 = [],[] for x in X: data_1.append(x[0]) data_2.append(x[1]) plt.scatter(data_1, y, color = 'r') plt.scatter(data_2, y, color = 'b')
<matplotlib.collections.PathCollection at 0x1134a6e10>
Можно заметить, что признак отмеченный красным цветом имеет явную линейную зависимость, а признак отмеченный синим, никакой информативность нам не дает.
# Разделение выборку для обучения и тестирования # test_size - отвечает за размер тестовой выборки X_train, X_test, y_train, y_test = cross_validation.train_test_split(X, y, test_size = 0.3)
# Создаем линейную регрессию linear_regressor = linear_model.LinearRegression() # Тренируем ее linear_regressor.fit(X_train, y_train) # Делаем предсказания predictions = linear_regressor.predict(X_test)
# Выводим массив для просмотра наших ответов (меток) print (y_test)
[ 28.15553021 38.36241814 -24.77820218 -61.47026695 13.02656201
23.87701013 12.74038341 -70.11132234 27.83791274 -14.97110322
-80.80239408 24.82763821 58.26281761 -45.27502383 10.33267887
-48.28700118 -21.48288019 -32.71074998 -21.47606913 -15.01435792
78.24817537 19.66406455 5.86887774 -42.44469577 -12.0017312
14.76930132 -16.65927231 -13.99339669 4.45578287 22.13032804]
# Смотрим и сравниваем предсказания print (predictions)
[ 22.32670386 40.26305989 -27.69502682 -56.5548183 18.47241345
31.86585663 6.08896992 -66.15105402 22.99937016 -12.65174022
-78.50894588 30.90311195 56.21877707 -47.81097232 8.98196478
-56.41188567 -24.46096716 -43.55445698 -17.99670898 -9.09225523
65.49657633 26.50900527 4.74114126 -39.28939851 -6.80665816
8.30372903 -15.27594937 -15.15598987 8.34469779 19.45159738]
# Средняя ошибка предсказания metrics.mean_absolute_error(y_test, predictions)
Для валидации можем выполнить перекрестную проверкую cross_val_score.
http://scikit-learn.org/stable/modules/generated/sklearn.model_selection.cross_val_score.html
Передадим, нашу линейную модель, признаки, ответы, количество разделений кросс-валидация
linear_scoring = cross_validation.cross_val_score(linear_regressor, X, y, cv=10) print ('Средняя ошибка: {}, Отклонение: {}'.format(linear_scoring.mean(), linear_scoring.std()))
Средняя ошибка: 0.9792410447209384, Отклонение: 0.020331171766276405
# Создаем свое тестирование на основе абсолютной средней ошибкой scorer = metrics.make_scorer(metrics.mean_absolute_error)
linear_scoring = cross_validation.cross_val_score(linear_regressor, X, y, scoring=scorer, cv=10) print ('Средняя ошибка: {}, Отклонение: {}'.format(linear_scoring.mean(), linear_scoring.std()))
Средняя ошибка: 4.0700714987797, Отклонение: 1.0737104492890193
# Коэффициенты который дал обучающий датасет coef
array([38.07925837, 0. ])
# Коэффициент полученный при обучении linear_regressor.coef_
array([38.18191713, 0.81751244])
# обученная модель так же дает свободный член linear_regressor.intercept_
print ("y = {:.2f}*x1 + {:.2f}*x2".format(coef[0], coef[1]))
print ("y = {:.2f}*x1 + {:.2f}*x2 + {:.2f}".format(linear_regressor.coef_[0], linear_regressor.coef_[1], linear_regressor.intercept_))
y = 37.76*x1 + 0.17*x2 + -0.86
# Посмотрим качество обучения print('Оценка дисперсии:: %.2f' % linear_regressor.score(X_test, y_test))
Домашнее задание
Вы уже знаете как создать модель линейной регрессии, можете создать датасет.
Давайте посмотрим как влияет количество признаков на качество обучения линейной модели.
Скачайте этот файл, можете редактировать этот ноутбук, да бы уменьшить/увеличить количество признаков.
Будут вопросы пишите нам в Slack канал #machine_learning
Мы начнем с самых простых и понятных моделей машинного обучения: линейных. В этой главе мы разберёмся, что это такое, почему они работают и в каких случаях их стоит использовать. Так как это первый класс моделей, с которым вы столкнётесь, мы постараемся подробно проговорить все важные моменты. Заодно объясним, как работает машинное обучение, на сравнительно простых примерах.
Почему модели линейные?
Представьте, что у вас есть множество объектов $mathbb{X}$, а вы хотели бы каждому объекту сопоставить какое-то значение. К примеру, у вас есть набор операций по банковской карте, а вы бы хотели, понять, какие из этих операций сделали мошенники. Если вы разделите все операции на два класса и нулём обозначите законные действия, а единицей мошеннические, то у вас получится простейшая задача классификации. Представьте другую ситуацию: у вас есть данные геологоразведки, по которым вы хотели бы оценить перспективы разных месторождений. В данном случае по набору геологических данных ваша модель будет, к примеру, оценивать потенциальную годовую доходность шахты. Это пример задачи регрессии. Числа, которым мы хотим сопоставить объекты из нашего множества иногда называют таргетами (от английского target).
Таким образом, задачи классификации и регрессии можно сформулировать как поиск отображения из множества объектов $mathbb{X}$ в множество возможных таргетов.
Математически задачи можно описать так:
- классификация: $mathbb{X} to {0,1,ldots,K}$, где $0, ldots, K$ – номера классов,
- регрессия: $mathbb{X} to mathbb{R}$.
Очевидно, что просто сопоставить какие-то объекты каким-то числам — дело довольно бессмысленное. Мы же хотим быстро обнаруживать мошенников или принимать решение, где строить шахту. Значит нам нужен какой-то критерий качества. Мы бы хотели найти такое отображение, которое лучше всего приближает истинное соответствие между объектами и таргетами. Что значит «лучше всего» – вопрос сложный. Мы к нему будем много раз возвращаться. Однако, есть более простой вопрос: среди каких отображений мы будем искать самое лучшее? Возможных отображений может быть много, но мы можем упростить себе задачу и договориться, что хотим искать решение только в каком-то заранее заданном параметризированном семействе функций. Вся эта глава будет посвящена самому простому такому семейству — линейным функциям вида
$$
y = w_1 x_1 + ldots + w_D x_D + w_0,
$$
где $y$ – целевая переменная (таргет), $(x_1, ldots, x_D)$ – вектор, соответствующий объекту выборки (вектор признаков), а $w_1, ldots, w_D, w_0$ – параметры модели. Признаки ещё называют фичами (от английского features). Вектор $w = (w_1,ldots,w_D)$ часто называют вектором весов, так как на предсказание модели можно смотреть как на взвешенную сумму признаков объекта, а число $w_0$ – свободным коэффициентом, или сдвигом (bias). Более компактно линейную модель можно записать в виде
$$y = langle x, wrangle + w_0$$
Теперь, когда мы выбрали семейство функций, в котором будем искать решение, задача стала существенно проще. Мы теперь ищем не какое-то абстрактное отображение, а конкретный вектор $(w_0,w_1,ldots,w_D)inmathbb{R}^{D+1}$.
Замечание. Чтобы применять линейную модель, нужно, чтобы каждый объект уже был представлен вектором численных признаков $x_1,ldots,x_D$. Конечно, просто текст или граф в линейную модель не положить, придётся сначала придумать для него численные фичи. Модель называют линейной, если она является линейной по этим численным признакам.
Разберёмся, как будет работать такая модель в случае, если $D = 1$. То есть у наших объектов есть ровно один численный признак, по которому они отличаются. Теперь наша линейная модель будет выглядеть совсем просто: $y = w_1 x_1 + w_0$. Для задачи регрессии мы теперь пытаемся приблизить значение игрек какой-то линейной функцией от переменной икс. А что будет значить линейность для задачи классификации? Давайте вспомним про пример с поиском мошеннических транзакций по картам. Допустим, нам известна ровно одна численная переменная — объём транзакции. Для бинарной классификации транзакций на законные и потенциально мошеннические мы будем искать так называемое разделяющее правило: там, где значение функции положительно, мы будем предсказывать один класс, где отрицательно – другой. В нашем примере простейшим правилом будет какое-то пороговое значение объёма транзакций, после которого есть смысл пометить транзакцию как подозрительную.
В случае более высоких размерностей вместо прямой будет гиперплоскость с аналогичным смыслом.
Вопрос на подумать. Если вы посмотрите содержание учебника, то не найдёте в нём ни «полиномиальных» моделей, ни каких-нибудь «логарифмических», хотя, казалось бы, зависимости бывают довольно сложными. Почему так?
Ответ (не открывайте сразу; сначала подумайте сами!)Линейные зависимости не так просты, как кажется. Пусть мы решаем задачу регрессии. Если мы подозреваем, что целевая переменная $y$ не выражается через $x_1, x_2$ как линейная функция, а зависит ещё от логарифма $x_1$ и ещё как-нибудь от того, разные ли знаки у признаков, то мы можем ввести дополнительные слагаемые в нашу линейную зависимость, просто объявим эти слагаемые новыми переменными и добавив перед ними соответствующие регрессионные коэффициенты
$$y approx w_1 x_1 + w_2 x_2 + w_3log{x_1} + w_4text{sgn}(x_1x_2) + w_0,$$
и в итоге из двумерной нелинейной задачи мы получили четырёхмерную линейную регрессию.
Вопрос на подумать. А как быть, если одна из фичей является категориальной, то есть принимает значения из (обычно конечного числа) значений, не являющихся числами? Например, это может быть время года, уровень образования, марка машины и так далее. Как правило, с такими значениями невозможно производить арифметические операции или же результаты их применения не имеют смысла.
Ответ (не открывайте сразу; сначала подумайте сами!)В линейную модель можно подать только численные признаки, так что категориальную фичу придётся как-то закодировать. Рассмотрим для примера вот такой датасет
Здесь два категориальных признака – pet_type и color. Первый принимает четыре различных значения, второй – пять.
Самый простой способ – использовать one-hot кодирование (one-hot encoding). Пусть исходный признак мог принимать $M$ значений $c_1,ldots, c_M$. Давайте заменим категориальный признак на $M$ признаков, которые принимают значения $0$ и $1$: $i$-й будет отвечать на вопрос «принимает ли признак значение $c_i$?». Иными словами, вместо ячейки со значением $c_i$ у объекта появляется строка нулей и единиц, в которой единица стоит только на $i$-м месте.
В нашем примере получится вот такая табличка:
Можно было бы на этом остановиться, но добавленные признаки обладают одним неприятным свойством: в каждом из них ровно одна единица, так что сумма соответствующих столбцов равна столбцу из единиц. А это уже плохо. Представьте, что у нас есть линейная модель
$$y sim w_1x_1 + ldots + w_{D-1}x_{d-1} + w_{c_1}x_{c_1} + ldots + w_{c_M}x_{c_M} + w_0$$
Преобразуем немного правую часть:
$$ysim w_1x_1 + ldots + w_{D-1}x_{d-1} + underbrace{(w_{c_1} — w_{c_M})}_{=:w’_{c_1}}x_{c_1} + ldots + underbrace{(w_{c_{M-1}} — w_{c_M})}_{=:w’_{C_{M-1}}}x_{c_{M-1}} + w_{c_M}underbrace{(x_{c_1} + ldots + x_{c_M})}_{=1} + w_0 = $$
$$ = w_1x_1 + ldots + w_{D-1}x_{d-1} + w’_{c_1}x_{c_1} + ldots + w’_{c_{M-1}}x_{c_{M-1}} + underbrace{(w_{c_M} + w_0)}_{=w’_{0}}$$
Как видим, от одного из новых признаков можно избавиться, не меняя модель. Больше того, это стоит сделать, потому что наличие «лишних» признаков ведёт к переобучению или вовсе ломает модель – подробнее об этом мы поговорим в разделе про регуляризацию. Поэтому при использовании one-hot-encoding обычно выкидывают признак, соответствующий одному из значений. Например, в нашем примере итоговая матрица объекты-признаки будет иметь вид:
Конечно, one-hot кодирование – это самый наивный способ работы с категориальными признаками, и для более сложных фичей или фичей с большим количеством значений оно плохо подходит. С рядом более продвинутых техник вы познакомитесь в разделе про обучение представлений.
Помимо простоты, у линейных моделей есть несколько других достоинств. К примеру, мы можем достаточно легко судить, как влияют на результат те или иные признаки. Скажем, если вес $w_i$ положителен, то с ростом $i$-го признака таргет в случае регрессии будет увеличиваться, а в случае классификации наш выбор будет сдвигаться в пользу одного из классов. Значение весов тоже имеет прозрачную интерпретацию: чем вес $w_i$ больше, тем «важнее» $i$-й признак для итогового предсказания. То есть, если вы построили линейную модель, вы неплохо можете объяснить заказчику те или иные её результаты. Это качество моделей называют интерпретируемостью. Оно особенно ценится в индустриальных задачах, цена ошибки в которых высока. Если от работы вашей модели может зависеть жизнь человека, то очень важно понимать, как модель принимает те или иные решения и какими принципами руководствуется. При этом не все методы машинного обучения хорошо интерпретируемы, к примеру, поведение искусственных нейронных сетей или градиентного бустинга интерпретировать довольно сложно.
В то же время слепо доверять весам линейных моделей тоже не стоит по целому ряду причин:
- Линейные модели всё-таки довольно узкий класс функций, они неплохо работают для небольших датасетов и простых задач. Однако, если вы решаете линейной моделью более сложную задачу, то вам, скорее всего, придётся выдумывать дополнительные признаки, являющиеся сложными функциями от исходных. Поиск таких дополнительных признаков называется feature engineering, технически он устроен примерно так, как мы описали в вопросе про «полиномиальные модели». Вот только поиском таких искусственных фичей можно сильно увлечься, так что осмысленность интерпретации будет сильно зависеть от здравого смысла эксперта, строившего модель.
- Если между признаками есть приближённая линейная зависимость, коэффициенты в линейной модели могут совершенно потерять физический смысл (об этой проблеме и о том, как с ней бороться, мы поговорим дальше, когда будем обсуждать регуляризацию).
- Особенно осторожно стоит верить в утверждения вида «этот коэффициент маленький, значит, этот признак не важен». Во-первых, всё зависит от масштаба признака: вдруг коэффициент мал, чтобы скомпенсировать его. Во-вторых, зависимость действительно может быть слабой, но кто знает, в какой ситуации она окажется важна. Такие решения принимаются на основе данных, например, путём проверки статистического критерия (об этом мы коротко упомянем в разделе про вероятностные модели).
- Конкретные значения весов могут меняться в зависимости от обучающей выборки, хотя с ростом её размера они будут потихоньку сходиться к весам «наилучшей» линейной модели, которую можно было бы построить по всем-всем-всем данным на свете.
Обсудив немного общие свойства линейных моделей, перейдём к тому, как их всё-таки обучать. Сначала разберёмся с регрессией, а затем настанет черёд классификации.
Линейная регрессия и метод наименьших квадратов (МНК)
Мы начнём с использования линейных моделей для решения задачи регрессии. Простейшим примером постановки задачи линейной регрессии является метод наименьших квадратов (Ordinary least squares).
Пусть у нас задан датасет $(X, y)$, где $y=(y_i)_{i=1}^N in mathbb{R}^N$ – вектор значений целевой переменной, а $X=(x_i)_{i = 1}^N in mathbb{R}^{N times D}, x_i in mathbb{R}^D$ – матрица объекты-признаки, в которой $i$-я строка – это вектор признаков $i$-го объекта выборки. Мы хотим моделировать зависимость $y_i$ от $x_i$ как линейную функцию со свободным членом. Общий вид такой функции из $mathbb{R}^D$ в $mathbb{R}$ выглядит следующим образом:
$$color{#348FEA}{f_w(x_i) = langle w, x_i rangle + w_0}$$
Свободный член $w_0$ часто опускают, потому что такого же результата можно добиться, добавив ко всем $x_i$ признак, тождественно равный единице; тогда роль свободного члена будет играть соответствующий ему вес:
$$begin{pmatrix}x_{i1} & ldots & x_{iD} end{pmatrix}cdotbegin{pmatrix}w_1\ vdots \ w_Dend{pmatrix} + w_0 =
begin{pmatrix}1 & x_{i1} & ldots & x_{iD} end{pmatrix}cdotbegin{pmatrix}w_0 \ w_1\ vdots \ w_D end{pmatrix}$$
Поскольку это сильно упрощает запись, в дальнейшем мы будем считать, что это уже сделано и зависимость имеет вид просто $f_w(x_i) = langle w, x_i rangle$.
Сведение к задаче оптимизации
Мы хотим, чтобы на нашем датасете (то есть на парах $(x_i, y_i)$ из обучающей выборки) функция $f_w$ как можно лучше приближала нашу зависимость.
Для того, чтобы чётко сформулировать задачу, нам осталось только одно: на математическом языке выразить желание «приблизить $f_w(x)$ к $y$». Говоря простым языком, мы должны научиться измерять качество модели и минимизировать её ошибку, как-то меняя обучаемые параметры. В нашем примере обучаемые параметры — это веса $w$. Функция, оценивающая то, как часто модель ошибается, традиционно называется функцией потерь, функционалом качества или просто лоссом (loss function). Важно, чтобы её было легко оптимизировать: скажем, гладкая функция потерь – это хорошо, а кусочно постоянная – просто ужасно.
Функции потерь бывают разными. От их выбора зависит то, насколько задачу в дальнейшем легко решать, и то, в каком смысле у нас получится приблизить предсказание модели к целевым значениям. Интуитивно понятно, что для нашей текущей задачи нам нужно взять вектор $y$ и вектор предсказаний модели и как-то сравнить, насколько они похожи. Так как эти вектора «живут» в одном векторном пространстве, расстояние между ними вполне может быть функцией потерь. Более того, положительная непрерывная функция от этого расстояния тоже подойдёт в качестве функции потерь. При этом способов задать расстояние между векторами тоже довольно много. От всего этого разнообразия глаза разбегаются, но мы обязательно поговорим про это позже. Сейчас давайте в качестве лосса возьмём квадрат $L^2$-нормы вектора разницы предсказаний модели и $y$. Во-первых, как мы увидим дальше, так задачу будет нетрудно решить, а во-вторых, у этого лосса есть ещё несколько дополнительных свойств:
-
$L^2$-норма разницы – это евклидово расстояние $|y — f_w(x)|_2$ между вектором таргетов и вектором ответов модели, то есть мы их приближаем в смысле самого простого и понятного «расстояния».
-
Как мы увидим в разделе про вероятностные модели, с точки зрения статистики это соответствует гипотезе о том, что наши данные состоят из линейного «сигнала» и нормально распределенного «шума».
Так вот, наша функция потерь выглядит так:
$$L(f, X, y) = |y — f(X)|_2^2 = $$
$$= |y — Xw|_2^2 = sum_{i=1}^N(y_i — langle x_i, w rangle)^2$$
Такой функционал ошибки не очень хорош для сравнения поведения моделей на выборках разного размера. Представьте, что вы хотите понять, насколько качество модели на тестовой выборке из $2500$ объектов хуже, чем на обучающей из $5000$ объектов. Вы измерили $L^2$-норму ошибки и получили в одном случае $300$, а в другом $500$. Эти числа не очень интерпретируемы. Гораздо лучше посмотреть на среднеквадратичное отклонение
$$L(f, X, y) = frac1Nsum_{i=1}^N(y_i — langle x_i, w rangle)^2$$
По этой метрике на тестовой выборке получаем $0,12$, а на обучающей $0,1$.
Функция потерь $frac1Nsum_{i=1}^N(y_i — langle x_i, w rangle)^2$ называется Mean Squared Error, MSE или среднеквадратическим отклонением. Разница с $L^2$-нормой чисто косметическая, на алгоритм решения задачи она не влияет:
$$color{#348FEA}{text{MSE}(f, X, y) = frac{1}{N}|y — X w|_2^2}$$
В самом широком смысле, функции работают с объектами множеств: берут какой-то входящий объект из одного множества и выдают на выходе соответствующий ему объект из другого. Если мы имеем дело с отображением, которое на вход принимает функции, а на выходе выдаёт число, то такое отображение называют функционалом. Если вы посмотрите на нашу функцию потерь, то увидите, что это именно функционал. Для каждой конкретной линейной функции, которую задают веса $w_i$, мы получаем число, которое оценивает, насколько точно эта функция приближает наши значения $y$. Чем меньше это число, тем точнее наше решение, значит для того, чтобы найти лучшую модель, этот функционал нам надо минимизировать по $w$:
$$color{#348FEA}{|y — Xw|_2^2 longrightarrow min_w}$$
Эту задачу можно решать разными способами. В этой главе мы сначала решим эту задачу аналитически, а потом приближенно. Сравнение двух этих решений позволит нам проиллюстрировать преимущества того подхода, которому посвящена эта книга. На наш взгляд, это самый простой способ «на пальцах» показать суть машинного обучения.
МНК: точный аналитический метод
Точку минимума можно найти разными способами. Если вам интересно аналитическое решение, вы можете найти его в главе про матричные дифференцирования (раздел «Примеры вычисления производных сложных функций»). Здесь же мы воспользуемся геометрическим подходом.
Пусть $x^{(1)},ldots,x^{(D)}$ – столбцы матрицы $X$, то есть столбцы признаков. Тогда
$$Xw = w_1x^{(1)}+ldots+w_Dx^{(D)},$$
и задачу регрессии можно сформулировать следующим образом: найти линейную комбинацию столбцов $x^{(1)},ldots,x^{(D)}$, которая наилучшим способом приближает столбец $y$ по евклидовой норме – то есть найти проекцию вектора $y$ на подпространство, образованное векторами $x^{(1)},ldots,x^{(D)}$.
Разложим $y = y_{parallel} + y_{perp}$, где $y_{parallel} = Xw$ – та самая проекция, а $y_{perp}$ – ортогональная составляющая, то есть $y_{perp} = y — Xwperp x^{(1)},ldots,x^{(D)}$. Как это можно выразить в матричном виде? Оказывается, очень просто:
$$X^T(y — Xw) = 0$$
В самом деле, каждый элемент столбца $X^T(y — Xw)$ – это скалярное произведение строки $X^T$ (=столбца $X$ = одного из $x^{(i)}$) на $y — Xw$. Из уравнения $X^T(y — Xw) = 0$ уже очень легко выразить $w$:
$$w = (X^TX)^{-1}X^Ty$$
Вопрос на подумать Для вычисления $w_{ast}$ нам приходится обращать (квадратную) матрицу $X^TX$, что возможно, только если она невырожденна. Что это значит с точки зрения анализа данных? Почему мы верим, что это выполняется во всех разумных ситуациях?
Ответ (не открывайте сразу; сначала подумайте сами!)Как известно из линейной алгебры, для вещественной матрицы $X$ ранги матриц $X$ и $X^TX$ совпадают. Матрица $X^TX$ невырожденна тогда и только тогда, когда её ранг равен числу её столбцов, что равно числу столбцов матрицы $X$. Иными словами, формула регрессии поломается, только если столбцы матрицы $X$ линейно зависимы. Столбцы матрицы $X$ – это признаки. А если наши признаки линейно зависимы, то, наверное, что-то идёт не так и мы должны выкинуть часть из них, чтобы остались только линейно независимые.
Другое дело, что зачастую признаки могут быть приближённо линейно зависимы, особенно если их много. Тогда матрица $X^TX$ будет близка к вырожденной, и это, как мы дальше увидим, будет вести к разным, в том числе вычислительным проблемам.
Вычислительная сложность аналитического решения — $O(N^2D + D^3)$, где $N$ — длина выборки, $D$ — число признаков у одного объекта. Слагаемое $N^2D$ отвечает за сложность перемножения матриц $X^T$ и $X$, а слагаемое $D^3$ — за сложность обращения их произведения. Перемножать матрицы $(X^TX)^{-1}$ и $X^T$ не стоит. Гораздо лучше сначала умножить $y$ на $X^T$, а затем полученный вектор на $(X^TX)^{-1}$: так будет быстрее и, кроме того, не нужно будет хранить матрицу $(X^TX)^{-1}X^T$.
Вычисление можно ускорить, используя продвинутые алгоритмы перемножения матриц или итерационные методы поиска обратной матрицы.
Проблемы «точного» решения
Заметим, что для получения ответа нам нужно обратить матрицу $X^TX$. Это создает множество проблем:
- Основная проблема в обращении матрицы — это то, что вычислительно обращать большие матрицы дело сложное, а мы бы хотели работать с датасетами, в которых у нас могут быть миллионы точек,
- Матрица $X^TX$, хотя почти всегда обратима в разумных задачах машинного обучения, зачастую плохо обусловлена. Особенно если признаков много, между ними может появляться приближённая линейная зависимость, которую мы можем упустить на этапе формулировки задачи. В подобных случаях погрешность нахождения $w$ будет зависеть от квадрата числа обусловленности матрицы $X$, что очень плохо. Это делает полученное таким образом решение численно неустойчивым: малые возмущения $y$ могут приводить к катастрофическим изменениям $w$.
Пара слов про число обусловленности.Пожертвовав математической строгостью, мы можем считать, что число обусловленности матрицы $X$ – это корень из отношения наибольшего и наименьшего из собственных чисел матрицы $X^TX$. Грубо говоря, оно показывает, насколько разного масштаба бывают собственные значения $X^TX$. Если рассмотреть $L^2$-норму ошибки предсказания, как функцию от $w$, то её линии уровня будут эллипсоидами, форма которых определяется квадратичной формой с матрицей $X^TX$ (проверьте это!). Таким образом, число обусловленности говорит о том, насколько вытянутыми являются эти эллипсоиды.ПодробнееДанные проблемы не являются поводом выбросить решение на помойку. Существует как минимум два способа улучшить его численные свойства, однако если вы не знаете про сингулярное разложение, то лучше вернитесь сюда, когда узнаете.
-
Построим $QR$-разложение матрицы $X$. Напомним, что это разложение, в котором матрица $Q$ ортогональна по столбцам (то есть её столбцы ортогональны и имеют длину 1; в частности, $Q^TQ=E$), а $R$ квадратная и верхнетреугольная. Подставив его в формулу, получим
$$w = ((QR)^TQR)^{-1}(QR)^T y = (R^Tunderbrace{Q^TQ}_{=E}R)^{-1}R^TQ^Ty = R^{-1}R^{-T}R^TQ^Ty = R^{-1}Q^Ty$$
Отметим, что написать $(R^TR)^{-1} = R^{-1}R^{-T}$ мы имеем право благодаря тому, что $R$ квадратная. Полученная формула намного проще, обращение верхнетреугольной матрицы (=решение системы с верхнетреугольной левой частью) производится быстро и хорошо, погрешность вычисления $w$ будет зависеть просто от числа обусловленности матрицы $X$, а поскольку нахождение $QR$-разложения является достаточно стабильной операцией, мы получаем решение с более хорошими, чем у исходной формулы, численными свойствами.
-
Также можно использовать псевдообратную матрицу, построенную с помощью сингулярного разложения, о котором подробно написано в разделе про матричные разложения. А именно, пусть
$$A = Uunderbrace{mathrm{diag}(sigma_1,ldots,sigma_r)}_{=Sigma}V^T$$
– это усечённое сингулярное разложение, где $r$ – это ранг $A$. В таком случае диагональная матрица посередине является квадратной, $U$ и $V$ ортогональны по столбцам: $U^TU = E$, $V^TV = E$. Тогда
$$w = (VSigma underbrace{U^TU}_{=E}Sigma V^T)^{-1}VSigma U^Ty$$
Заметим, что $VSigma^{-2}V^Tcdot VSigma^2V^T = E = VSigma^2V^Tcdot VSigma^{-2}V^T$, так что $(VSigma^2 V^T)^{-1} = VSigma^{-2}V^T$, откуда
$$w = VSigma^{-2}underbrace{V^TV}_{=E}Sigma U^Ty = VSigma^{-1}Uy$$
Хорошие численные свойства сингулярного разложения позволяют утверждать, что и это решение ведёт себя довольно неплохо.
Тем не менее, вычисление всё равно остаётся довольно долгим и будет по-прежнему страдать (хоть и не так сильно) в случае плохой обусловленности матрицы $X$.
Полностью вылечить проблемы мы не сможем, но никто и не обязывает нас останавливаться на «точном» решении (которое всё равно никогда не будет вполне точным). Поэтому ниже мы познакомим вас с совершенно другим методом.
МНК: приближенный численный метод
Минимизируемый функционал является гладким и выпуклым, а это значит, что можно эффективно искать точку его минимума с помощью итеративных градиентных методов. Более подробно вы можете прочитать о них в разделе про методы оптимизации, а здесь мы лишь коротко расскажем об одном самом базовом подходе.
Как известно, градиент функции в точке направлен в сторону её наискорейшего роста, а антиградиент (противоположный градиенту вектор) в сторону наискорейшего убывания. То есть имея какое-то приближение оптимального значения параметра $w$, мы можем его улучшить, посчитав градиент функции потерь в точке и немного сдвинув вектор весов в направлении антиградиента:
$$w_j mapsto w_j — alpha frac{d}{d{w_j}} L(f_w, X, y) $$
где $alpha$ – это параметр алгоритма («темп обучения»), который контролирует величину шага в направлении антиградиента. Описанный алгоритм называется градиентным спуском.
Посмотрим, как будет выглядеть градиентный спуск для функции потерь $L(f_w, X, y) = frac1Nvertvert Xw — yvertvert^2$. Градиент квадрата евклидовой нормы мы уже считали; соответственно,
$$
nabla_wL = frac2{N} X^T (Xw — y)
$$
Следовательно, стартовав из какого-то начального приближения, мы можем итеративно уменьшать значение функции, пока не сойдёмся (по крайней мере в теории) к минимуму (вообще говоря, локальному, но в данном случае глобальному).
Алгоритм градиентного спуска
w = random_normal() # можно пробовать и другие виды инициализации
repeat S times: # другой вариант: while abs(err) > tolerance
f = X.dot(w) # посчитать предсказание
err = f - y # посчитать ошибку
grad = 2 * X.T.dot(err) / N # посчитать градиент
w -= alpha * grad # обновить веса
С теоретическими результатами о скорости и гарантиях сходимости градиентного спуска вы можете познакомиться в главе про методы оптимизации. Мы позволим себе лишь несколько общих замечаний:
- Поскольку задача выпуклая, выбор начальной точки влияет на скорость сходимости, но не настолько сильно, чтобы на практике нельзя было стартовать всегда из нуля или из любой другой приятной вам точки;
- Число обусловленности матрицы $X$ существенно влияет на скорость сходимости градиентного спуска: чем более вытянуты эллипсоиды уровня функции потерь, тем хуже;
- Темп обучения $alpha$ тоже сильно влияет на поведение градиентного спуска; вообще говоря, он является гиперпараметром алгоритма, и его, возможно, придётся подбирать отдельно. Другими гиперпараметрами являются максимальное число итераций $S$ и/или порог tolerance.
Иллюстрация.Рассмотрим три задачи регрессии, для которых матрица $X$ имеет соответственно маленькое, среднее и большое числа обусловленности. Будем строить для них модели вида $y=w_1x_1 + w_2x_2$. Раскрасим плоскость $(w_1, w_2)$ в соответствии со значениями $|X_{text{train}}w — y_{text{train}}|^2$. Тёмная область содержит минимум этой функции – оптимальное значение $w_{ast}$. Также запустим из из двух точек градиентный спуск с разными значениями темпа обучения $alpha$ и посмотрим, что получится:
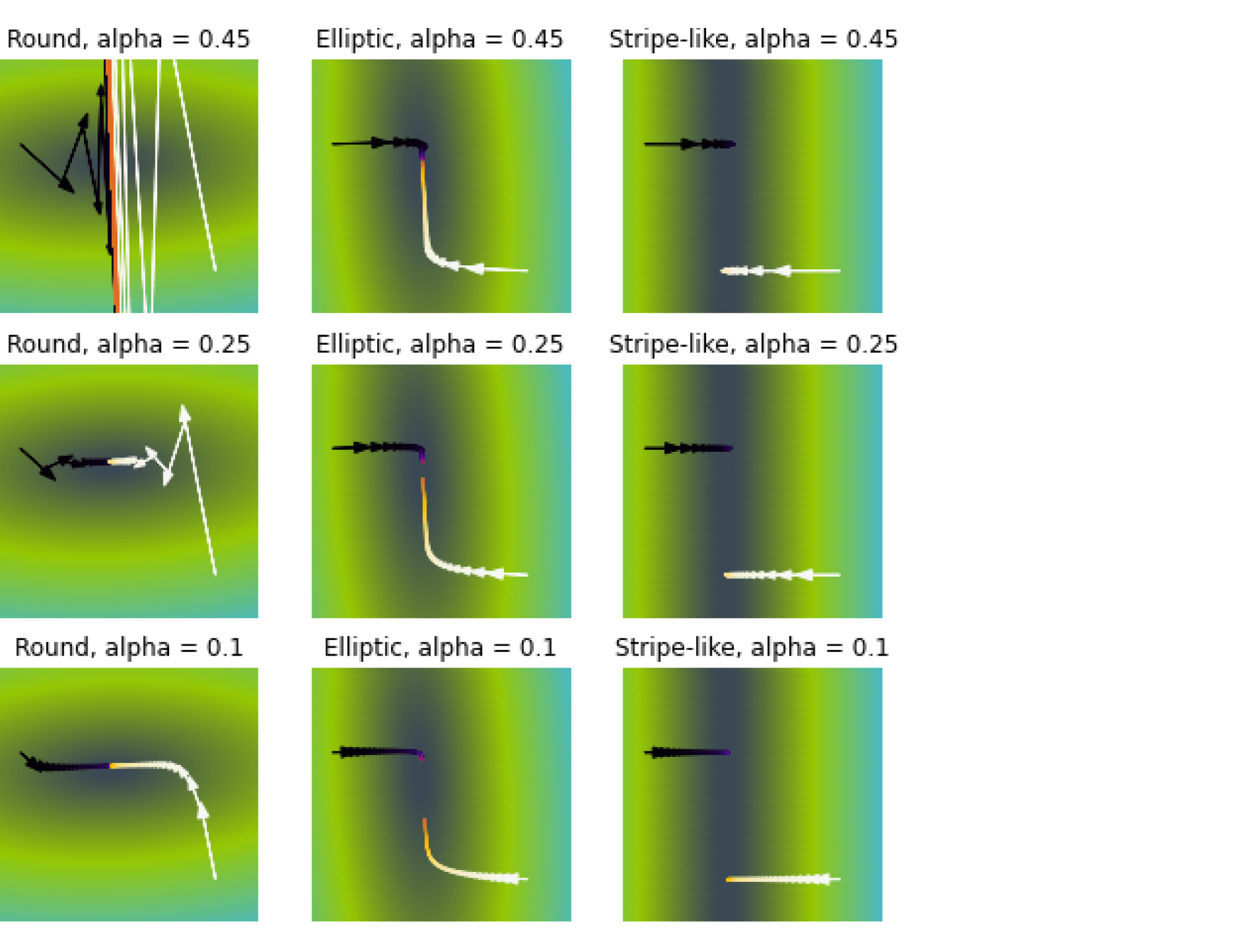
Итог: при неудачном выборе $alpha$ алгоритм не сходится или идёт вразнос, а для плохо обусловленной задачи он сходится абы куда.
Вычислительная сложность градиентного спуска – $O(NDS)$, где, как и выше, $N$ – длина выборки, $D$ – число признаков у одного объекта. Сравните с оценкой $O(N^2D + D^3)$ для «наивного» вычисления аналитического решения.
Сложность по памяти – $O(ND)$ на хранение выборки. В памяти мы держим и выборку, и градиент, но в большинстве реалистичных сценариев доминирует выборка.
Стохастический градиентный спуск
На каждом шаге градиентного спуска нам требуется выполнить потенциально дорогую операцию вычисления градиента по всей выборке (сложность $O(ND)$). Возникает идея заменить градиент его оценкой на подвыборке (в английской литературе такую подвыборку обычно именуют batch или mini-batch; в русской разговорной терминологии тоже часто встречается слово батч или мини-батч).
А именно, если функция потерь имеет вид суммы по отдельным парам объект-таргет
$$L(w, X, y) = frac1Nsum_{i=1}^NL(w, x_i, y_i),$$
а градиент, соответственно, записывается в виде
$$nabla_wL(w, X, y) = frac1Nsum_{i=1}^Nnabla_wL(w, x_i, y_i),$$
то предлагается брать оценку
$$nabla_wL(w, X, y) approx frac1Bsum_{t=1}^Bnabla_wL(w, x_{i_t}, y_{i_t})$$
для некоторого подмножества этих пар $(x_{i_t}, y_{i_t})_{t=1}^B$. Обратите внимание на множители $frac1N$ и $frac1B$ перед суммами. Почему они нужны? Полный градиент $nabla_wL(w, X, y)$ можно воспринимать как среднее градиентов по всем объектам, то есть как оценку матожидания $mathbb{E}nabla_wL(w, x, y)$; тогда, конечно, оценка матожидания по меньшей подвыборке тоже будет иметь вид среднего градиентов по объектам этой подвыборки.
Как делить выборку на батчи? Ясно, что можно было бы случайным образом сэмплировать их из полного датасета, но даже если использовать быстрый алгоритм вроде резервуарного сэмплирования, сложность этой операции не самая оптимальная. Поэтому используют линейный проход по выборке (которую перед этим лучше всё-таки случайным образом перемешать). Давайте введём ещё один параметр нашего алгоритма: размер батча, который мы обозначим $B$. Теперь на $B$ очередных примерах вычислим градиент и обновим веса модели. При этом вместо количества шагов алгоритма обычно задают количество эпох $E$. Это ещё один гиперпараметр. Одна эпоха – это один полный проход нашего сэмплера по выборке. Заметим, что если выборка очень большая, а модель компактная, то даже первый проход бывает можно не заканчивать.
Алгоритм:
w = normal(0, 1)
repeat E times:
for i = B, i <= n, i += B
X_batch = X[i-B : i]
y_batch = y[i-B : i]
f = X_batch.dot(w) # посчитать предсказание
err = f - y_batch # посчитать ошибку
grad = 2 * X_batch.T.dot(err) / B # посчитать градиент
w -= alpha * grad
Сложность по времени – $O(NDE)$. На первый взгляд, она такая же, как и у обычного градиентного спуска, но заметим, что мы сделали в $N / B$ раз больше шагов, то есть веса модели претерпели намного больше обновлений.
Сложность по памяти можно довести до $O(BD)$: ведь теперь всю выборку не надо держать в памяти, а достаточно загружать лишь текущий батч (а остальная выборка может лежать на диске, что удобно, так как в реальности задачи, в которых выборка целиком не влезает в оперативную память, встречаются сплошь и рядом). Заметим, впрочем, что при этом лучше бы $B$ взять побольше: ведь чтение с диска – намного более затратная по времени операция, чем чтение из оперативной памяти.
В целом, разницу между алгоритмами можно представлять как-то так:
Шаги стохастического градиентного спуска заметно более шумные, но считать их получается значительно быстрее. В итоге они тоже сходятся к оптимальному значению из-за того, что матожидание оценки градиента на батче равно самому градиенту. По крайней мере, сходимость можно получить при хорошо подобранных коэффициентах темпа обучения в случае выпуклого функционала качества. Подробнее мы об этом поговорим в главе про оптимизацию. Для сложных моделей и лоссов стохастический градиентный спуск может сходиться плохо или застревать в локальных минимумах, поэтому придумано множество его улучшений. О некоторых из них также рассказано в главе про оптимизацию.
Существует определённая терминологическая путаница, иногда стохастическим градиентным спуском называют версию алгоритма, в которой размер батча равен единице (то есть максимально шумная и быстрая версия алгоритма), а версии с бОльшим размером батча называют batch gradient descent. В книгах, которые, возможно, старше вас, такая процедура иногда ещё называется incremental gradient descent. Это не очень принципиально, но вы будьте готовы, если что.
Вопрос на подумать. Вообще говоря, если объём данных не слишком велик и позволяет это сделать, объекты лучше случайным образом перемешивать перед тем, как подавать их в алгоритм стохастического градиентного спуска. Как вам кажется, почему?
Также можно использовать различные стратегии отбора объектов. Например, чаще брать объекты, на которых ошибка больше. Какие ещё стратегии вы могли бы придумать?
Ответ (не открывайте сразу; сначала подумайте сами!)Легко представить себе ситуацию, в которой объекты как-нибудь неудачно упорядочены, скажем, по возрастанию таргета. Тогда модель будет попеременно то запоминать, что все таргеты маленькие, то – что все таргеты большие. Это может и не повлиять на качество итоговой модели, но может привести и к довольно печальным последствиям. И вообще, чем более разнообразные батчи модель увидит в процессе обучения, тем лучше.
Стратегий можно придумать много. Например, не брать объекты, на которых ошибка слишком большая (возможно, это выбросы – зачем на них учиться), или вообще не брать те, на которых ошибка достаточно мала (они «ничему не учат»). Рекомендуем, впрочем, прибегать к этим эвристикам, только если вы понимаете, зачем они вам нужны и почему есть надежда, что они помогут.
Неградиентные методы
После прочтения этой главы у вас может сложиться ощущение, что приближённые способы решения ML задач и градиентные методы – это одно и тоже, но вы будете правы в этом только на 98%. В принципе, существуют и другие способы численно решать эти задачи, но в общем случае они работают гораздо хуже, чем градиентный спуск, и не обладают таким хорошим теоретическим обоснованием. Мы не будем рассказывать про них подробно, но можете на досуге почитать, скажем, про Stepwise regression, Orthogonal matching pursuit или LARS. У LARS, кстати, есть довольно интересное свойство: он может эффективно работать на выборках, в которых число признаков больше числа примеров. С алгоритмом LARS вы можете познакомиться в главе про оптимизацию.
Регуляризация
Всегда ли решение задачи регрессии единственно? Вообще говоря, нет. Так, если в выборке два признака будут линейно зависимы (и следовательно, ранг матрицы будет меньше $D$), то гарантировано найдётся такой вектор весов $nu$ что $langlenu, x_irangle = 0 forall x_i$. В этом случае, если какой-то $w$ является решением оптимизационной задачи, то и $w + alpha nu $ тоже является решением для любого $alpha$. То есть решение не только не обязано быть уникальным, так ещё может быть сколь угодно большим по модулю. Это создаёт вычислительные трудности. Малые погрешности признаков сильно возрастают при предсказании ответа, а в градиентном спуске накапливается погрешность из-за операций со слишком большими числами.
Конечно, в жизни редко бывает так, что признаки строго линейно зависимы, а вот быть приближённо линейно зависимыми они вполне могут быть. Такая ситуация называется мультиколлинеарностью. В этом случае у нас, всё равно, возникают проблемы, близкие к описанным выше. Дело в том, что $Xnusim 0$ для вектора $nu$, состоящего из коэффициентов приближённой линейной зависимости, и, соответственно, $X^TXnuapprox 0$, то есть матрица $X^TX$ снова будет близка к вырожденной. Как и любая симметричная матрица, она диагонализуется в некотором ортонормированном базисе, и некоторые из собственных значений $lambda_i$ близки к нулю. Если вектор $X^Ty$ в выражении $(X^TX)^{-1}X^Ty$ будет близким к соответствующему собственному вектору, то он будет умножаться на $1 /{lambda_i}$, что опять же приведёт к появлению у $w$ очень больших по модулю компонент (при этом $w$ ещё и будет вычислен с большой погрешностью из-за деления на маленькое число). И, конечно же, все ошибки и весь шум, которые имелись в матрице $X$, при вычислении $ysim Xw$ будут умножаться на эти большие и неточные числа и возрастать во много-много раз, что приведёт к проблемам, от которых нас не спасёт никакое сингулярное разложение.
Важно ещё отметить, что в случае, когда несколько признаков линейно зависимы, веса $w_i$ при них теряют физический смысл. Может даже оказаться, что вес признака, с ростом которого таргет, казалось бы, должен увеличиваться, станет отрицательным. Это делает модель не только неточной, но и принципиально не интерпретируемой. Вообще, неадекватность знаков или величины весов – хорошее указание на мультиколлинеарность.
Для того, чтобы справиться с этой проблемой, задачу обычно регуляризуют, то есть добавляют к ней дополнительное ограничение на вектор весов. Это ограничение можно, как и исходный лосс, задавать по-разному, но, как правило, ничего сложнее, чем $L^1$- и $L^2$-нормы, не требуется.
Вместо исходной задачи теперь предлагается решить такую:
$$color{#348FEA}{min_w L(f, X, y) = min_w(|X w — y|_2^2 + lambda |w|^k_k )}$$
$lambda$ – это очередной параметр, а $|w|^k_k $ – это один из двух вариантов:
$$color{#348FEA}{|w|^2_2 = w^2_1 + ldots + w^2_D}$$
или
$$color{#348FEA}{|w|_1^1 = vert w_1 vert + ldots + vert w_D vert}$$
Добавка $lambda|w|^k_k$ называется регуляризационным членом или регуляризатором, а число $lambda$ – коэффициентом регуляризации.
Коэффициент $lambda$ является гиперпараметром модели и достаточно сильно влияет на качество итогового решения. Его подбирают по логарифмической шкале (скажем, от 1e-2 до 1e+2), используя для сравнения моделей с разными значениями $lambda$ дополнительную валидационную выборку. При этом качество модели с подобранным коэффициентом регуляризации уже проверяют на тестовой выборке, чтобы исключить переобучение. Более подробно о том, как нужно подбирать гиперпараметры, вы можете почитать в соответствующей главе.
Отдельно надо договориться о том, что вес $w_0$, соответствующий отступу от начала координат (то есть признаку из всех единичек), мы регуляризовать не будем, потому что это не имеет смысла: если даже все значения $y$ равномерно велики, это не должно портить качество обучения. Обычно это не отображают в формулах, но если придираться к деталям, то стоило бы написать сумму по всем весам, кроме $w_0$:
$$|w|^2_2 = sum_{color{red}{j=1}}^{D}w_j^2,$$
$$|w|_1 = sum_{color{red}{j=1}}^{D} vert w_j vert$$
В случае $L^2$-регуляризации решение задачи изменяется не очень сильно. Например, продифференцировав новый лосс по $w$, легко получить, что «точное» решение имеет вид:
$$w = (X^TX + lambda I)^{-1}X^Ty$$
Отметим, что за этой формулой стоит и понятная численная интуиция: раз матрица $X^TX$ близка к вырожденной, то обращать её сродни самоубийству. Мы лучше слегка исказим её добавкой $lambda I$, которая увеличит все собственные значения на $lambda$, отодвинув их от нуля. Да, аналитическое решение перестаёт быть «точным», но за счёт снижения численных проблем мы получим более качественное решение, чем при использовании «точной» формулы.
В свою очередь, градиент функции потерь
$$L(f_w, X, y) = |Xw — y|^2 + lambda|w|^2$$
по весам теперь выглядит так:
$$
nabla_wL(f_w, X, y) = 2X^T(Xw — y) + 2lambda w
$$
Подставив этот градиент в алгоритм стохастического градиентного спуска, мы получаем обновлённую версию приближенного алгоритма, отличающуюся от старой только наличием дополнительного слагаемого.
Вопрос на подумать. Рассмотрим стохастический градиентный спуск для $L^2$-регуляризованной линейной регрессии с батчами размера $1$. Выберите правильный вариант шага SGD:
(а) $w_imapsto w_i — 2alpha(langle w, x_jrangle — y_j)x_{ji} — frac{2alphalambda}N w_i,quad i=1,ldots,D$;
(б) $w_imapsto w_i — 2alpha(langle w, x_jrangle — y_j)x_{ji} — 2alphalambda w_i,quad i=1,ldots,D$;
(в) $w_imapsto w_i — 2alpha(langle w, x_jrangle — y_j)x_{ji} — 2lambda N w_i,quad i=1,ldots D$.
Ответ (не открывайте сразу; сначала подумайте сами!)Не регуляризованная функция потерь имеет вид $mathcal{L}(X, y, w) = frac1Nsum_{i=1}^Nmathcal{L}(x_i, y_i, w)$, и её можно воспринимать, как оценку по выборке $(x_i, y_i)_{i=1}^N$ идеальной функции потерь
$$mathcal{L}(w) = mathbb{E}_{x, y}mathcal{L}(x, y, w)$$
Регуляризационный член не зависит от выборки и добавляется отдельно:
$$mathcal{L}_{text{reg}}(w) = mathbb{E}_{x, y}mathcal{L}(x, y, w) + lambda|w|^2$$
Соответственно, идеальный градиент регуляризованной функции потерь имеет вид
$$nabla_wmathcal{L}_{text{reg}}(w) = mathbb{E}_{x, y}nabla_wmathcal{L}(x, y, w) + 2lambda w,$$
Градиент по батчу – это тоже оценка градиента идеальной функции потерь, только не на выборке $(X, y)$, а на батче $(x_{t_i}, y_{t_i})_{i=1}^B$ размера $B$. Он будет выглядеть так:
$$nabla_wmathcal{L}_{text{reg}}(w) = frac1Bsum_{i=1}^Bnabla_wmathcal{L}(x_{t_i}, y_{t_i}, w) + 2lambda w.$$
Как видите, коэффициентов, связанных с числом объектов в батче или в исходной выборке, во втором слагаемом нет. Так что верным является второй вариант. Кстати, обратите внимание, что в третьем ещё и нет коэффициента $alpha$ перед производной регуляризационного слагаемого, это тоже ошибка.
Вопрос на подумать. Распишите процедуру стохастического градиентного спуска для $L^1$-регуляризованной линейной регрессии. Как вам кажется, почему никого не волнует, что функция потерь, строго говоря, не дифференцируема?
Ответ (не открывайте сразу; сначала подумайте сами!)Распишем для случая батча размера 1:
$$w_imapsto w_i — alpha(langle w, x_jrangle — y_j)x_{ji} — frac{lambda}alpha text{sign}(w_i),quad i=1,ldots,D$$
Функция потерь не дифференцируема лишь в одной точке. Так как в машинном обучении чаще всего мы имеем дело с данными вероятностного характера, это не влечёт каких-то особых проблем. Дело в том, что попадание прямо в ноль очень маловероятно из-за численных погрешностей в данных, так что мы можем просто доопределить производную в одной точке, а если даже пару раз попадём в неё за время обучения, это не приведёт к каким-то значительным изменениям результатов.
Отметим, что $L^1$- и $L^2$-регуляризацию можно определять для любой функции потерь $L(w, X, y)$ (и не только в задаче регрессии, а и, например, в задаче классификации тоже). Новая функция потерь будет соответственно равна
$$widetilde{L}(w, X, y) = L(w, X, y) + lambda|w|_1$$
или
$$widetilde{L}(w, X, y) = L(w, X, y) + lambda|w|_2^2$$
Разреживание весов в $L^1$-регуляризации
$L^2$-регуляризация работает прекрасно и используется в большинстве случаев, но есть одна полезная особенность $L^1$-регуляризации: её применение приводит к тому, что у признаков, которые не оказывают большого влияния на ответ, вес в результате оптимизации получается равным $0$. Это позволяет удобным образом удалять признаки, слабо влияющие на таргет. Кроме того, это даёт возможность автоматически избавляться от признаков, которые участвуют в соотношениях приближённой линейной зависимости, соответственно, спасает от проблем, связанных с мультиколлинеарностью, о которых мы писали выше.
Не очень строгим, но довольно интуитивным образом это можно объяснить так:
- В точке оптимума линии уровня регуляризационного члена касаются линий уровня основного лосса, потому что, во-первых, и те, и другие выпуклые, а во-вторых, если они пересекаются трансверсально, то существует более оптимальная точка:
- Линии уровня $L^1$-нормы – это $N$-мерные октаэдры. Точки их касания с линиями уровня лосса, скорее всего, лежат на грани размерности, меньшей $N-1$, то есть как раз в области, где часть координат равна нулю:
Заметим, что данное построение говорит о том, как выглядит оптимальное решение задачи, но ничего не говорит о способе, которым это решение можно найти. На самом деле, найти такой оптимум непросто: у $L^1$ меры довольно плохая производная. Однако, способы есть. Можете на досуге прочитать, например, вот эту статью о том, как работало предсказание CTR в google в 2012 году. Там этой теме посвящается довольно много места. Кроме того, рекомендуем посмотреть про проксимальные методы в разделе этой книги про оптимизацию в ML.
Заметим также, что вообще-то оптимизация любой нормы $L_x, 0 < x leq 1$, приведёт к появлению разреженных векторов весов, просто если c $L^1$ ещё хоть как-то можно работать, то с остальными всё будет ещё сложнее.
Другие лоссы
Стохастический градиентный спуск можно очевидным образом обобщить для решения задачи линейной регрессии с любой другой функцией потерь, не только квадратичной: ведь всё, что нам нужно от неё, – это чтобы у функции потерь был градиент. На практике это делают редко, но тем не менее рассмотрим ещё пару вариантов.
MAE
Mean absolute error, абсолютная ошибка, появляется при замене $L^2$ нормы в MSE на $L^1$:
$$color{#348FEA}{MAE(y, widehat{y}) = frac1Nsum_{i=1}^N vert y_i — widehat{y}_ivert}$$
Можно заметить, что в MAE по сравнению с MSE существенно меньший вклад в ошибку будут вносить примеры, сильно удалённые от ответов модели. Дело тут в том, что в MAE мы считаем модуль расстояния, а не квадрат, соответственно, вклад больших ошибок в MSE получается существенно больше. Такая функция потерь уместна в случаях, когда вы пытаетесь обучить регрессию на данных с большим количеством выбросов в таргете.
Иначе на эту разницу можно посмотреть так: MSE приближает матожидание условного распределения $y mid x$, а MAE – медиану.
MAPE
Mean absolute percentage error, относительная ошибка.
$$MAPE(y, widehat{y}) = frac1Nsum_{i=1}^N left|frac{widehat{y}_i-y_i}{y_i}right|$$
Часто используется в задачах прогнозирования (например, погоды, загруженности дорог, кассовых сборов фильмов, цен), когда ответы могут быть различными по порядку величины, и при этом мы бы хотели верно угадать порядок, то есть мы не хотим штрафовать модель за предсказание 2000 вместо 1000 в разы сильней, чем за предсказание 2 вместо 1.
Вопрос на подумать. Кроме описанных выше в задаче линейной регрессии можно использовать и другие функции потерь, например, Huber loss:
$$mathcal{L}(f, X, y) = sum_{i=1}^Nh_{delta}(y_i — langle w_i, xrangle),mbox{ где }h_{delta}(z) = begin{cases}
frac12z^2, |z|leqslantdelta,\
delta(|z| — frac12delta), |z| > delta
end{cases}$$
Число $delta$ является гиперпараметром. Сложная формула при $vert zvert > delta$ нужна, чтобы функция $h_{delta}(z)$ была непрерывной. Попробуйте объяснить, зачем может быть нужна такая функция потерь.
Ответ (не открывайте сразу; сначала подумайте сами!)Часто требования формулируют в духе «функция потерь должна слабее штрафовать то-то и сильней штрафовать вот это». Например, $L^2$-регуляризованный лосс штрафует за большие по модулю веса. В данном случае можно заметить, что при небольших значениях ошибки берётся просто MSE, а при больших мы начинаем штрафовать нашу модель менее сурово. Например, это может быть полезно для того, чтобы выбросы не так сильно влияли на результат обучения.
Линейная классификация
Теперь давайте поговорим про задачу классификации. Для начала будем говорить про бинарную классификацию на два класса. Обобщить эту задачу до задачи классификации на $K$ классов не составит большого труда. Пусть теперь наши таргеты $y$ кодируют принадлежность к положительному или отрицательному классу, то есть принадлежность множеству ${-1,1}$ (в этой главе договоримся именно так обозначать классы, хотя в жизни вам будут нередко встречаться и метки ${0,1}$), а $x$ – по-прежнему векторы из $mathbb{R}^D$. Мы хотим обучить линейную модель так, чтобы плоскость, которую она задаёт, как можно лучше отделяла объекты одного класса от другого.
В идеальной ситуации найдётся плоскость, которая разделит классы: положительный окажется с одной стороны от неё, а отрицательный с другой. Выборка, для которой это возможно, называется линейно разделимой. Увы, в реальной жизни такое встречается крайне редко.
Как обучить линейную модель классификации, нам ещё предстоит понять, но уже ясно, что итоговое предсказание можно будет вычислить по формуле
$$y = text{sign} langle w, x_irangle$$
Почему бы не решать, как задачу регрессии?Мы можем попробовать предсказывать числа $-1$ и $1$, минимизируя для этого, например, MSE с последующим взятием знака, но ничего хорошего не получится. Во-первых, регрессия почти не штрафует за ошибки на объектах, которые лежат близко к *разделяющей плоскости*, но не с той стороны. Во вторых, ошибкой будет считаться предсказание, например, $5$ вместо $1$, хотя нам-то на самом деле не важно, какой у числа модуль, лишь бы знак был правильным. Если визуализировать такое решение, то проблемы тоже вполне заметны:
Нам нужна прямая, которая разделяет эти точки, а не проходит через них!
Сконструируем теперь функционал ошибки так, чтобы он вышеперечисленными проблемами не обладал. Мы хотим минимизировать число ошибок классификатора, то есть
$$sum_i mathbb{I}[y_i neq sign langle w, x_irangle]longrightarrow min_w$$
Домножим обе части на $$y_i$$ и немного упростим
$$sum_i mathbb{I}[y_i langle w, x_irangle < 0]longrightarrow min_w$$
Величина $M = y_i langle w, x_irangle$ называется отступом (margin) классификатора. Такая фунция потерь называется misclassification loss. Легко видеть, что
-
отступ положителен, когда $sign(y_i) = sign(langle w, x_irangle)$, то есть класс угадан верно; при этом чем больше отступ, тем больше расстояние от $x_i$ до разделяющей гиперплоскости, то есть «уверенность классификатора»;
-
отступ отрицателен, когда $sign(y_i) ne sign(langle w, x_irangle)$, то есть класс угадан неверно; при этом чем больше по модулю отступ, тем более сокрушительно ошибается классификатор.
От каждого из отступов мы вычисляем функцию
$$F(M) = mathbb{I}[M < 0] = begin{cases}1, M < 0,\ 0, Mgeqslant 0end{cases}$$
Она кусочно-постоянная, и из-за этого всю сумму невозможно оптимизировать градиентными методами: ведь её производная равна нулю во всех точках, где она существует. Но мы можем мажорировать её какой-нибудь более гладкой функцией, и тогда задачу можно будет решить. Функции можно использовать разные, у них свои достоинства и недостатки, давайте рассмотрим несколько примеров:
Вопрос на подумать. Допустим, мы как-то обучили классификатор, и подавляющее большинство отступов оказались отрицательными. Правда ли нас постигла катастрофа?
Ответ (не открывайте сразу; сначала подумайте сами!)Наверное, мы что-то сделали не так, но ситуацию можно локально выправить, если предсказывать классы, противоположные тем, которые выдаёт наша модель.
Вопрос на подумать. Предположим, что у нас есть два классификатора с примерно одинаковыми и достаточно приемлемыми значениями интересующей нас метрики. При этом одна почти всегда выдаёт предсказания с большими по модулю отступами, а вторая – с относительно маленькими. Верно ли, что первая модель лучше, чем вторая?
Ответ (не открывайте сразу; сначала подумайте сами!)На первый взгляд кажется, что первая модель действительно лучше: ведь она предсказывает «увереннее», но на самом деле всё не так однозначно: во многих случаях модель, которая умеет «честно признать, что не очень уверена в ответе», может быть предпочтительней модели, которая врёт с той же непотопляемой уверенностью, что и говорит правду. В некоторых случаях лучше может оказаться модель, которая, по сути, просто отказывается от классификации на каких-то объектах.
Ошибка перцептрона
Реализуем простейшую идею: давайте считать отступы только на неправильно классифицированных объектах и учитывать их не бинарно, а линейно, пропорционально их размеру. Получается такая функция:
$$F(M) = max(0, -M)$$
Давайте запишем такой лосс с $L^2$-регуляризацией:
$$L(w, x, y) = lambdavertvert wvertvert^2_2 + sum_i max(0, -y_i langle w, x_irangle)$$
Найдём градиент:
$$
nabla_w L(w, x, y) = 2 lambda w + sum_i
begin{cases}
0, & y_i langle w, x_i rangle > 0 \
— y_i x_i, & y_i langle w, x_i rangle leq 0
end{cases}
$$
Имея аналитическую формулу для градиента, мы теперь можем так же, как и раньше, применить стохастический градиентный спуск, и задача будет решена.
Данная функция потерь впервые была предложена для перцептрона Розенблатта, первой вычислительной модели нейросети, которая в итоге привела к появлению глубокого обучения.
Она решает задачу линейной классификации, но у неё есть одна особенность: её решение не единственно и сильно зависит от начальных параметров. Например, все изображённые ниже классификаторы имеют одинаковый нулевой лосс:
Hinge loss, SVM
Для таких случаев, как на картинке выше, возникает логичное желание не только найти разделяющую прямую, но и постараться провести её на одинаковом удалении от обоих классов, то есть максимизировать минимальный отступ:
Это можно сделать, слегка поменяв функцию ошибки, а именно положив её равной:
$$F(M) = max(0, 1-M)$$
$$L(w, x, y) = lambda||w||^2_2 + sum_i max(0, 1-y_i langle w, x_irangle)$$
$$
nabla_w L(w, x, y) = 2 lambda w + sum_i
begin{cases}
0, & 1 — y_i langle w, x_i rangle leq 0 \
— y_i x_i, & 1 — y_i langle w, x_i rangle > 0
end{cases}
$$
Почему же добавленная единичка приводит к желаемому результату?
Интуитивно это можно объяснить так: объекты, которые проклассифицированы правильно, но не очень «уверенно» (то есть $0 leq y_i langle w, x_irangle < 1$), продолжают вносить свой вклад в градиент и пытаются «отодвинуть» от себя разделяющую плоскость как можно дальше.
К данному выводу можно прийти и чуть более строго; для этого надо совершенно по-другому взглянуть на выражение, которое мы минимизируем. Поможет вот эта картинка:
Если мы максимизируем минимальный отступ, то надо максимизировать $frac{2}{|w|_2}$, то есть ширину полосы при условии того, что большинство объектов лежат с правильной стороны, что эквивалентно решению нашей исходной задачи:
$$lambda|w|^2_2 + sum_i max(0, 1-y_i langle w, x_irangle) longrightarrowminlimits_{w}$$
Отметим, что первое слагаемое у нас обратно пропорционально ширине полосы, но мы и максимизацию заменили на минимизацию, так что тут всё в порядке. Второе слагаемое – это штраф за то, что некоторые объекты неправильно расположены относительно разделительной полосы. В конце концов, никто нам не обещал, что классы наши линейно разделимы и можно провести оптимальную плоскость вообще без ошибок.
Итоговое положение плоскости задаётся всего несколькими обучающими примерами. Это ближайшие к плоскости правильно классифицированные объекты, которые называют опорными векторами или support vectors. Весь метод, соответственно, зовётся методом опорных векторов, или support vector machine, или сокращённо SVM. Начиная с шестидесятых годов это был сильнейший из известных методов машинного обучения. В девяностые его сменили методы, основанные на деревьях решений, которые, в свою очередь, недавно передали «пальму первенства» нейросетям.
Почему же SVM был столь популярен? Из-за небольшого количества параметров и доказуемой оптимальности. Сейчас для нас нормально выбирать специальный алгоритм под задачу и подбирать оптимальные гиперпараметры для этого алгоритма перебором, а когда-то трава была зеленее, а компьютеры медленнее, и такой роскоши у людей не было. Поэтому им нужны были модели, которые гарантированно неплохо работали бы в любой ситуации. Такой моделью и был SVM.
Другие замечательные свойства SVM: существование уникального решения и доказуемо минимальная склонность к переобучению среди всех популярных классов линейных классификаторов. Кроме того, несложная модификация алгоритма, ядровый SVM, позволяет проводить нелинейные разделяющие поверхности.
Строгий вывод постановки задачи SVM можно прочитать тут или в лекции К.В. Воронцова.
Логистическая регрессия
В этом параграфе мы будем обозначать классы нулём и единицей.
Ещё один интересный метод появляется из желания посмотреть на классификацию как на задачу предсказания вероятностей. Хороший пример – предсказание кликов в интернете (например, в рекламе и поиске). Наличие клика в обучающем логе не означает, что, если повторить полностью условия эксперимента, пользователь обязательно кликнет по объекту опять. Скорее у объектов есть какая-то «кликабельность», то есть истинная вероятность клика по данному объекту. Клик на каждом обучающем примере является реализацией этой случайной величины, и мы считаем, что в пределе в каждой точке отношение положительных и отрицательных примеров должно сходиться к этой вероятности.
Проблема состоит в том, что вероятность, по определению, величина от 0 до 1, а простого способа обучить линейную модель так, чтобы это ограничение соблюдалось, нет. Из этой ситуации можно выйти так: научить линейную модель правильно предсказывать какой-то объект, связанный с вероятностью, но с диапазоном значений $(-infty,infty)$, и преобразовать ответы модели в вероятность. Таким объектом является logit или log odds – логарифм отношения вероятности положительного события к отрицательному $logleft(frac{p}{1-p}right)$.
Если ответом нашей модели является $logleft(frac{p}{1-p}right)$, то искомую вероятность посчитать не трудно:
$$langle w, x_irangle = logleft(frac{p}{1-p}right)$$
$$e^{langle w, x_irangle} = frac{p}{1-p}$$
$$p=frac{1}{1 + e^{-langle w, x_irangle}}$$
Функция в правой части называется сигмоидой и обозначается
$$color{#348FEA}{sigma(z) = frac1{1 + e^{-z}}}$$
Таким образом, $p = sigma(langle w, x_irangle)$
Как теперь научиться оптимизировать $w$ так, чтобы модель как можно лучше предсказывала логиты? Нужно применить метод максимума правдоподобия для распределения Бернулли. Это самое простое распределение, которое возникает, к примеру, при бросках монетки, которая орлом выпадает с вероятностью $p$. У нас только событием будет не орёл, а то, что пользователь кликнул на объект с такой вероятностью. Если хотите больше подробностей, почитайте про распределение Бернулли в теоретическом минимуме.
Правдоподобие позволяет понять, насколько вероятно получить данные значения таргета $y$ при данных $X$ и весах $w$. Оно имеет вид
$$ p(ymid X, w) =prod_i p(y_imid x_i, w) $$
и для распределения Бернулли его можно выписать следующим образом:
$$ p(ymid X, w) =prod_i p_i^{y_i} (1-p_i)^{1-y_i} $$
где $p_i$ – это вероятность, посчитанная из ответов модели. Оптимизировать произведение неудобно, хочется иметь дело с суммой, так что мы перейдём к логарифмическому правдоподобию и подставим формулу для вероятности, которую мы получили выше:
$$ ell(w, X, y) = sum_i big( y_i log(p_i) + (1-y_i)log(1-p_i) big) =$$
$$ =sum_i big( y_i log(sigma(langle w, x_i rangle)) + (1-y_i)log(1 — sigma(langle w, x_i rangle)) big) $$
Если заметить, что
$$
sigma(-z) = frac{1}{1 + e^z} = frac{e^{-z}}{e^{-z} + 1} = 1 — sigma(z),
$$
то выражение можно переписать проще:
$$
ell(w, X, y)=sum_i big( y_i log(sigma(langle w, x_i rangle)) + (1 — y_i) log(sigma(-langle w, x_i rangle)) big)
$$
Нас интересует $w$, для которого правдоподобие максимально. Чтобы получить функцию потерь, которую мы будем минимизировать, умножим его на минус один:
$$color{#348FEA}{L(w, X, y) = -sum_i big( y_i log(sigma(langle w, x_i rangle)) + (1 — y_i) log(sigma(-langle w, x_i rangle)) big)}$$
В отличие от линейной регрессии, для логистической нет явной формулы решения. Деваться некуда, будем использовать градиентный спуск. К счастью, градиент устроен очень просто:
$$
nabla_w L(y, X, w) = -sum_i x_i big( y_i — sigma(langle w, x_i rangle)) big)
$$
Вывод формулы градиентаНам окажется полезным ещё одно свойство сигмоиды:
$$
frac{d log sigma(z)}{d z} = left( log left( frac{1}{1 + e^{-z}} right) right)’ = frac{e^{-z}}{1 + e^{-z}} = sigma(-z)
$$ $$
frac{d log sigma(-z)}{d z} = -sigma(z)
$$
Отсюда:
$$
nabla_w log sigma(langle w, x_i rangle) = sigma(-langle w, x_i rangle) x_i
$$ $$
nabla_w log sigma(-langle w, x_i rangle) = -sigma(langle w, x_i rangle) x_i
$$
и градиент оказывается равным
$$
nabla_w L(y, X, w) = -sum_i big( y_i x_i sigma(-langle w, x_i rangle) — (1 — y_i) x_i sigma(langle w, x_i rangle)) big) =
$$ $$
= -sum_i big( y_i x_i (1 — sigma(langle w, x_i rangle)) — (1 — y_i) x_i sigma(langle w, x_i rangle)) big) =
$$ $$
= -sum_i big( y_i x_i — y_i x_i sigma(langle w, x_i rangle) — x_i sigma(langle w, x_i rangle) + y_i x_i sigma(langle w, x_i rangle)) big) =
$$ $$
= -sum_i big( y_i x_i — x_i sigma(langle w, x_i rangle)) big)
$$
Предсказание модели будет вычисляться, как мы договаривались, следующим образом:
$$p=sigma(langle w, x_irangle)$$
Это вероятность положительного класса, а как от неё перейти к предсказанию самого класса? В других методах нам достаточно было посчитать знак предсказания, но теперь все наши предсказания положительные и находятся в диапазоне от 0 до 1. Что же делать? Интуитивным и не совсем (и даже совсем не) правильным является ответ «взять порог 0.5». Более корректным будет подобрать этот порог отдельно, для уже построенной регрессии минимизируя нужную вам метрику на отложенной тестовой выборке. Например, сделать так, чтобы доля положительных и отрицательных классов примерно совпадала с реальной.
Отдельно заметим, что метод называется логистической регрессией, а не логистической классификацией именно потому, что предсказываем мы не классы, а вещественные числа – логиты.
Вопрос на подумать. Проверьте, что, если метки классов – это $pm1$, а не $0$ и $1$, то функцию потерь для логистической регрессии можно записать в более компактном виде:
$$mathcal{L}(w, X, y) = sum_{i=1}^Nlog(1 + e^{-y_ilangle w, x_irangle})$$
Вопрос на подумать. Правда ли разделяющая поверхность модели логистической регрессии является гиперплоскостью?
Ответ (не открывайте сразу; сначала подумайте сами!)Разделяющая поверхность отделяет множество точек, которым мы присваиваем класс $0$ (или $-1$), и множество точек, которым мы присваиваем класс $1$. Представляется логичным провести отсечку по какому-либо значению предсказанной вероятности. Однако, выбор этого значения — дело не очевидное. Как мы увидим в главе про калибровку классификаторов, это может быть не настоящая вероятность. Допустим, мы решили провести границу по значению $frac12$. Тогда разделяющая поверхность как раз задаётся равенством $p = frac12$, что равносильно $langle w, xrangle = 0$. А это гиперплоскость.
Вопрос на подумать. Допустим, что матрица объекты-признаки $X$ имеет полный ранг по столбцам (то есть все её столбцы линейно независимы). Верно ли, что решение задачи восстановления логистической регрессии единственно?
Ответ (не открывайте сразу; сначала подумайте сами!)В этот раз хорошего геометрического доказательства, как было для линейной регрессии, пожалуй, нет; нам придётся честно посчитать вторую производную и доказать, что она является положительно определённой. Сделаем это для случая, когда метки классов – это $pm1$. Формулы так получатся немного попроще. Напомним, что в этом случае
$$L(w, X, y) = -sum_{i=1}^Nlog(1 + e^{-y_ilangle w, x_irangle})$$
Следовательно,
$$frac{partial}{partial w_{j}}L(w, X, y) = sum_{i=1}^Nfrac{y_ix_{ij}e^{-y_ilangle w, x_irangle}}{1 + e^{-y_ilangle w, x_irangle}} = sum_{i=1}^Ny_ix_{ij}left(1 — frac1{1 + e^{-y_ilangle w, x_irangle}}right)$$
$$frac{partial^2L}{partial w_jpartial w_k}(w, X, y) = sum_{i=1}^Ny^2_ix_{ij}x_{ik}frac{e^{-y_ilangle w, x_irangle}}{(1 + e^{-y_ilangle w, x_irangle})^2} =$$
$$ = sum_{i=1}^Ny^2_ix_{ij}x_{ik}sigma(y_ilangle w, x_irangle)(1 — sigma(y_ilangle w, x_irangle))$$
Теперь заметим, что $y_i^2 = 1$ и что, если обозначить через $D$ диагональную матрицу с элементами $sigma(y_ilangle w, x_irangle)(1 — sigma(y_ilangle w, x_irangle))$ на диагонали, матрицу вторых производных можно представить в виде:
$$nabla^2L = left(frac{partial^2mathcal{L}}{partial w_jpartial w_k}right) = X^TDX$$
Так как $0 < sigma(y_ilangle w, x_irangle) < 1$, у матрицы $D$ на диагонали стоят положительные числа, из которых можно извлечь квадратные корни, представив $D$ в виде $D = D^{1/2}D^{1/2}$. В свою очередь, матрица $X$ имеет полный ранг по столбцам. Стало быть, для любого вектора приращения $une 0$ имеем
$$u^TX^TDXu = u^TX^T(D^{1/2})^TD^{1/2}Xu = vert D^{1/2}Xu vert^2 > 0$$
Таким образом, функция $L$ выпукла вниз как функция от $w$, и, соответственно, точка её экстремума непременно будет точкой минимума.
А теперь – почему это не совсем правда. Дело в том, что, говоря «точка её экстремума непременно будет точкой минимума», мы уже подразумеваем существование этой самой точки экстремума. Только вот существует этот экстремум не всегда. Можно показать, что для линейно разделимой выборки функция потерь логистической регрессии не ограничена снизу, и, соответственно, никакого экстремума нет. Доказательство мы оставляем читателю.
Вопрос на подумать. На картинке ниже представлены результаты работы на одном и том же датасете трёх моделей логистической регрессии с разными коэффициентами $L^2$-регуляризации:
Наверху показаны предсказанные вероятности положительного класса, внизу – вид разделяющей поверхности.
Как вам кажется, какие картинки соответствуют самому большому коэффициенту регуляризации, а какие – самому маленькому? Почему?
Ответ (не открывайте сразу; сначала подумайте сами!)Коэффициент регуляризации максимален у левой модели. На это нас могут натолкнуть два соображения. Во-первых, разделяющая прямая проведена достаточно странно, то есть можно заподозрить, что регуляризационный член в лосс-функции перевесил функцию потерь исходной задачи. Во-вторых, модель предсказывает довольно близкие к $frac12$ вероятности – это значит, что значения $langle w, xrangle$ близки к нулю, то есть сам вектор $w$ близок к нулевому. Это также свидетельствует о том, что регуляризационный член играет слишком важную роль при оптимизации.
Наименьший коэффициент регуляризации у правой модели. Её предсказания достаточно «уверенные» (цвета на верхнем графике сочные, то есть вероятности быстро приближаются к $0$ или $1$). Это может свидетельствовать о том, что числа $langle w, xrangle$ достаточно велики по модулю, то есть $vertvert w vertvert$ достаточно велик.
Многоклассовая классификация
В этом разделе мы будем следовать изложению из лекций Евгения Соколова.
Пусть каждый объект нашей выборки относится к одному из $K$ классов: $mathbb{Y} = {1, ldots, K}$. Чтобы предсказывать эти классы с помощью линейных моделей, нам придётся свести задачу многоклассовой классификации к набору бинарных, которые мы уже хорошо умеем решать. Мы разберём два самых популярных способа это сделать – one-vs-all и all-vs-all, а проиллюстрировать их нам поможет вот такой игрушечный датасет
Один против всех (one-versus-all)
Обучим $K$ линейных классификаторов $b_1(x), ldots, b_K(x)$, выдающих оценки принадлежности классам $1, ldots, K$ соответственно. В случае с линейными моделями эти классификаторы будут иметь вид
$$b_k(x) = text{sgn}left(langle w_k, x rangle + w_{0k}right)$$
Классификатор с номером $k$ будем обучать по выборке $left(x_i, 2mathbb{I}[y_i = k] — 1right)_{i = 1}^{N}$; иными словами, мы учим классификатор отличать $k$-й класс от всех остальных.
Логично, чтобы итоговый классификатор выдавал класс, соответствующий самому уверенному из бинарных алгоритмов. Уверенность можно в каком-то смысле измерить с помощью значений линейных функций:
$$a(x) = text{argmax}_k left(langle w_k, x rangle + w_{0k}right) $$
Давайте посмотрим, что даст этот подход применительно к нашему датасету. Обучим три линейных модели, отличающих один класс от остальных:
Теперь сравним значения линейных функций
и для каждой точки выберем тот класс, которому соответствует большее значение, то есть самый «уверенный» классификатор:
Хочется сказать, что самый маленький класс «обидели».
Проблема данного подхода заключается в том, что каждый из классификаторов $b_1(x), dots, b_K(x)$ обучается на своей выборке, и значения линейных функций $langle w_k, x rangle + w_{0k}$ или, проще говоря, «выходы» классификаторов могут иметь разные масштабы. Из-за этого сравнивать их будет неправильно. Нормировать вектора весов, чтобы они выдавали ответы в одной и той же шкале, не всегда может быть разумным решением: так, в случае с SVM веса перестанут являться решением задачи, поскольку нормировка изменит норму весов.
Все против всех (all-versus-all)
Обучим $C_K^2$ классификаторов $a_{ij}(x)$, $i, j = 1, dots, K$, $i neq j$. Например, в случае с линейными моделями эти модели будут иметь вид
$$b_{ij}(x) = text{sgn}left( langle w_{ij}, x rangle + w_{0,ij} right)$$
Классификатор $a_{ij}(x)$ будем настраивать по подвыборке $X_{ij} subset X$, содержащей только объекты классов $i$ и $j$. Соответственно, классификатор $a_{ij}(x)$ будет выдавать для любого объекта либо класс $i$, либо класс $j$. Проиллюстрируем это для нашей выборки:
Чтобы классифицировать новый объект, подадим его на вход каждого из построенных бинарных классификаторов. Каждый из них проголосует за своей класс; в качестве ответа выберем тот класс, за который наберется больше всего голосов:
$$a(x) = text{argmax}_ksum_{i = 1}^{K} sum_{j neq i}mathbb{I}[a_{ij}(x) = k]$$
Для нашего датасета получается следующая картинка:
Обратите внимание на серый треугольник на стыке областей. Это точки, для которых голоса разделились (в данном случае каждый классификатор выдал какой-то свой класс, то есть у каждого класса было по одному голосу). Для этих точек нет явного способа выдать обоснованное предсказание.
Многоклассовая логистическая регрессия
Некоторые методы бинарной классификации можно напрямую обобщить на случай многих классов. Выясним, как это можно проделать с логистической регрессией.
В логистической регрессии для двух классов мы строили линейную модель
$$b(x) = langle w, x rangle + w_0,$$
а затем переводили её прогноз в вероятность с помощью сигмоидной функции $sigma(z) = frac{1}{1 + exp(-z)}$. Допустим, что мы теперь решаем многоклассовую задачу и построили $K$ линейных моделей
$$b_k(x) = langle w_k, x rangle + w_{0k},$$
каждая из которых даёт оценку принадлежности объекта одному из классов. Как преобразовать вектор оценок $(b_1(x), ldots, b_K(x))$ в вероятности? Для этого можно воспользоваться оператором $text{softmax}(z_1, ldots, z_K)$, который производит «нормировку» вектора:
$$text{softmax}(z_1, ldots, z_K) = left(frac{exp(z_1)}{sum_{k = 1}^{K} exp(z_k)},
dots, frac{exp(z_K)}{sum_{k = 1}^{K} exp(z_k)}right).$$
В этом случае вероятность $k$-го класса будет выражаться как
$$P(y = k vert x, w) = frac{
exp{(langle w_k, x rangle + w_{0k})}}{ sum_{j = 1}^{K} exp{(langle w_j, x rangle + w_{0j})}}.$$
Обучать эти веса предлагается с помощью метода максимального правдоподобия: так же, как и в случае с двухклассовой логистической регрессией:
$$sum_{i = 1}^{N} log P(y = y_i vert x_i, w) to max_{w_1, dots, w_K}$$
Масштабируемость линейных моделей
Мы уже обсуждали, что SGD позволяет обучению хорошо масштабироваться по числу объектов, так как мы можем не загружать их целиком в оперативную память. А что делать, если признаков очень много, или мы не знаем заранее, сколько их будет? Такое может быть актуально, например, в следующих ситуациях:
- Классификация текстов: мы можем представить текст в формате «мешка слов», то есть неупорядоченного набора слов, встретившихся в данном тексте, и обучить на нём, например, определение тональности отзыва в интернете. Наличие каждого слова из языка в тексте у нас будет кодироваться отдельной фичой. Тогда размерность каждого элемента обучающей выборки будет порядка нескольких сотен тысяч.
- В задаче предсказания кликов по рекламе можно получить выборку любой размерности, например, так: в качестве фичи закодируем индикатор того, что пользователь X побывал на веб-странице Y. Суммарная размерность тогда будет порядка $10^9 cdot 10^7 = 10^{16}$. Кроме того, всё время появляются новые пользователи и веб-страницы, так что на этапе применения нас ждут сюрпризы.
Есть несколько хаков, которые позволяют бороться с такими проблемами:
- Несмотря на то, что полная размерность объекта в выборке огромна, количество ненулевых элементов в нём невелико. Значит, можно использовать разреженное кодирование, то есть вместо плотного вектора хранить словарь, в котором будут перечислены индексы и значения ненулевых элементов вектора.
- Даже хранить все веса не обязательно! Можно хранить их в хэш-таблице и вычислять индекс по формуле
hash(feature) % tablesize. Хэш может вычисляться прямо от слова или id пользователя. Таким образом, несколько фичей будут иметь общий вес, который тем не менее обучится оптимальным образом. Такой подход называется hashing trick. Ясно, что сжатие вектора весов приводит к потерям в качестве, но, как правило, ценой совсем небольших потерь можно сжать этот вектор на много порядков.
Примером открытой библиотеки, в которой реализованы эти возможности, является vowpal wabbit.
Parameter server
Если при решении задачи ставки столь высоки, что мы не можем разменивать качество на сжатие вектора весов, а признаков всё-таки очень много, то задачу можно решать распределённо, храня все признаки в шардированной хеш-таблице
Кружки здесь означают отдельные сервера. Жёлтые загружают данные, а серые хранят части модели. Для обучения жёлтый кружок запрашивает у серого нужные ему для предсказания веса, считает градиент и отправляет его обратно, где тот потом применяется. Схема обладает бесконечной масштабируемостью, но задач, где это оправдано, не очень много.
Подытожим
На линейную модель можно смотреть как на однослойную нейросеть, поэтому многие методы, которые были изначально разработаны для них, сейчас переиспользуются в задачах глубокого обучения, а базовые подходы к регрессии, классификации и оптимизации вообще выглядят абсолютно так же. Так что несмотря на то, что в целом линейные модели на сегодня применяются редко, то, из чего они состоят и как строятся, знать очень и очень полезно.
Надеемся также, что главным итогом прочтения этой главы для вас будет осознание того, что решение любой ML-задачи состоит из выбора функции потерь, параметризованного класса моделей и способа оптимизации. В следующих главах мы познакомимся с другими моделями и оптимизаторами, но эти базовые принципы не изменятся.
Второй
из способов построения итерационного
метода решения системы линейных
алгебраических уравнений
(
)
состоит из построения последовательности
приближений
такой, что
,
т.е. строгого убывания на каждом шаге
функционала ошибки
.
|
Теорема. |
Если ( и (оператор шага для ошибки: |
|
Док–во. |
Т.к. Предположим, Т.к. Т.к. , Тогда,
получим |
Обычно
используют нормы, порождаемые симметричной
положительно определенной матрицей:
.
|
Доказать: |
– скалярное – норма в . |
Метод полной релаксации
для решения
системы
с матрицей
– очередное приближение
определяется по известному приближению
за
шагов:

где
параметр
выбирается из условия минимума
.
|
Теорема. |
и . |
|
Док–во. |
Т.к. ,
Очевидно, будет максимальное уменьшение ошибки
если (в Итак, Найдем имеем
или – метод Зейделя – непрерывный по теореме о |
Метод неполной релаксации
для решения
системы
с матрицей
– очередное приближение
определяется по известному приближению
за
шагов:
где
параметр
,
т.е. ошибка уменьшается меньше, чем в
методе полной релаксации (
):
Расчетные
формулы имеют вид (проверить!):

или

|
Теорема. |
Если , |
|
Док–во |
практически |
Оценка сходимости методов релаксации
Итак,
ошибка
монотонно убывает в норме
.
Оценим
.
Т. к.
,
где
,
то
,
если
.
.
Т.к.
,
то


где
.
Пусть
.
Т.к.
,
то
.
|
Теорема. |
где и таковы, что ( |
|
Док–во |
очевидно. |
Доказать:
.
Доказать:
.
Пример
,
,
т.к.
,
то
и
,
тогда
(проверить):
|
верхняя релаксация |
|
|
полная релаксация |
|
т.е. метод
верхней релаксации в
раз дешевле.
Лекция 8.
Градиент, метод наискорейшего спуска
Как
выбирать вектор
при построении итерационного метода
из условия минимизации ошибки:
?
Если
,
то

Следовательно,
.
|
Теорема. |
Метод сходится |
|
|
Док–во. |
Очевидно, : непрерывен |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Адаптированный перевод прекрасной статьи энтузиаста технологий машинного обучения Javaid Nabi.
Чтобы понимать как алгоритм машинного обучения учится предсказывать результаты на основе данных, важно разобраться в основных концепциях и понятиях, используемых при обучении алгоритма.
Функции оценки
В контексте технологии машинного обучения, оценка – это
статистический термин для нахождения некоторого приближения неизвестного
параметра на основе некоторых данных. Точечная
оценка – это попытка найти единственное лучшее приближение некоторого
количества интересующих нас параметров. Или на более формальном языке математической статистики — точечная оценка это число, оцениваемое на основе наблюдений,
предположительно близкое к оцениваемому параметру.
Под количеством
интересующих параметров обычно подразумевается:
• Один параметр
• Вектор параметров – например, веса в линейной
регрессии
• Целая функция
Точечная оценка
Чтобы отличать оценки параметров от их истинного значения, представим точечную оценку параметра θ как θˆ. Пусть {x(1), x(2), .. x(m)} будут m независимыми и одинаково распределенными величинами. Тогда точечная оценка может быть записана как некоторая функция этих величин:
Такое определение точечной оценки является очень общим и предоставляет разработчику большую свободу действий. Почти любая функция, таким образом, может рассматриваться как оценщик, но хороший оценщик – это функция, значения которой близки к истинному базовому значению θ, которое сгенерированно обучающими данными.
Точечная оценка также может относиться к оценке взаимосвязи между
входными и целевыми переменными, в этом случае чаще называемой функцией оценки.
Функция оценки
Задача, решаемая машинным обучением, заключается в попытке
предсказать переменную y по
заданному входному вектору x. Мы
предполагаем, что существует функция f(x), которая описывает приблизительную
связь между y и x. Например, можно предположить, что y = f(x) + ε, где ε обозначает
часть y, которая явно не
предсказывается входным вектором x.
При оценке функций нас интересует приближение f с помощью модели или оценки fˆ.
Функция оценки в действительности это тоже самое, что оценка параметра θ; функция оценки f это просто точечная
оценка в функциональном пространстве. Пример: в полиномиальной регрессии мы
либо оцениваем параметр w, либо оцениваем функцию отображения из x в y.
Смещение и дисперсия
Смещение и дисперсия измеряют два разных источника ошибки функции оценки.
Смещение измеряет ожидаемое отклонение от истинного значения функции или
параметра. Дисперсия, с другой стороны, показывает меру отклонения от
ожидаемого значения оценки, которую может вызвать любая конкретная выборка
данных.
Смещение
Смещение определяется следующим
образом:
где ожидаемое значение E(θˆm) для данных (рассматриваемых как выборки из случайной величины) и
θ является истинным базовым значением, используемым для определения
распределения, генерирующего данные.
Оценщик θˆm называется несмещенным, если bias(θˆm)=0, что подразумевает что E(θˆm) = θ.
Дисперсия и Стандартная ошибка
Дисперсия оценки обозначается как Var(θˆ), где случайная величина
является обучающим множеством. Альтернативно, квадратный корень дисперсии
называется стандартной ошибкой, обозначаемой как SE(θˆ). Дисперсия или стандартная ошибка
оценщика показывает меру ожидания того, как оценка, которую мы вычисляем, будет
изменяться по мере того, как мы меняем выборки из базового набора данных,
генерирующих процесс.
Точно так же, как мы хотели бы, чтобы функция оценки имела малое
смещение, мы также стремимся, чтобы у нее была относительно низкая дисперсия.
Давайте теперь рассмотрим некоторые обычно используемые функции оценки.
Оценка Максимального Правдоподобия (MLE)
Оценка максимального правдоподобия может быть определена как метод
оценки параметров (таких как среднее значение или дисперсия) из выборки данных,
так что вероятность получения наблюдаемых данных максимальна.
Рассмотрим набор из m примеров X={x(1),… , x(m)} взятых независимо из неизвестного набора данных,
генерирующих распределение Pdata(x). Пусть Pmodel(x;θ) –
параметрическое семейство распределений вероятностей над тем же пространством,
индексированное параметром θ.
Другими словами, Pmodel(x;θ) отображает любую конфигурацию x в значение, оценивающее истинную
вероятность Pdata(x).
Оценка максимального правдоподобия для θ определяется как:
Поскольку мы предположили, что примеры являются независимыми выборками, приведенное выше
уравнение можно записать в виде:
Эта произведение многих вероятностей может быть неудобным по ряду
причин. В частности, оно склонно к числовой недооценке. Кроме того, чтобы найти
максимумы/минимумы этой функции, мы должны взять производную этой функции от θ и приравнять ее к 0. Поскольку это
произведение членов, нам нужно применить правило цепочки, которое довольно
громоздко. Чтобы получить более удобную, но эквивалентную задачу оптимизации,
можно использовать логарифм вероятности, который не меняет его argmax, но
удобно превращает произведение в сумму, и поскольку логарифм – строго
возрастающая функция (функция натурального логарифма – монотонное
преобразование), это не повлияет на итоговое значение θ.
В итоге, получаем:
Два важных свойства: сходимость и
эффективность
Сходимость. По мере того, как число обучающих выборок приближается к
бесконечности, оценка максимального правдоподобия сходится к истинному значению
параметра.
Эффективность. Способ измерения того, насколько мы близки к истинному
параметру, – это ожидаемая средняя квадратичная ошибка, вычисление квадратичной
разницы между оценочными и истинными значениями параметров, где математическое
ожидание вычисляется над m обучающими выборками из данных, генерирующих
распределение. Эта параметрическая среднеквадратичная ошибка уменьшается с
увеличением m, и для
больших m нижняя
граница неравенства Крамера-Рао показывает, что ни у одной сходящейся функции оценки нет
среднеквадратичной ошибки меньше, чем у оценки максимального правдоподобия.
Именно по причине
сходимости и эффективности, оценка максимального правдоподобия часто считается
предпочтительным оценщиком для машинного обучения.
Когда количество примеров достаточно мало, чтобы привести к
переобучению, стратегии регуляризации, такие как понижающие веса, могут
использоваться для получения смещенной версии оценки максимального
правдоподобия, которая имеет меньшую дисперсию, когда данные обучения
ограничены.
Максимальная апостериорная (MAP) оценка
Согласно байесовскому подходу, можно учесть влияние предварительных
данных на выбор точечной оценки. MAP может использоваться для получения
точечной оценки ненаблюдаемой величины на основе эмпирических данных. Оценка
MAP выбирает точку максимальной апостериорной вероятности (или максимальной
плотности вероятности в более распространенном случае непрерывного θ):
где с правой стороны, log(p(x|θ)) – стандартный член
логарифмической вероятности и log(p(θ)) соответствует изначальному
распределению.
Как и при полном байесовском методе, байесовский MAP имеет преимущество
использования изначальной информации, которой нет
в обучающих данных. Эта дополнительная информация помогает уменьшить дисперсию
для точечной оценки MAP (по сравнению с оценкой MLE). Однако, это происходит ценой повышенного смещения.
Функции потерь
В большинстве обучающих сетей ошибка рассчитывается как разница
между фактическим выходным значением y и прогнозируемым выходным значением ŷ.
Функция, используемая для вычисления этой ошибки, известна как функция потерь,
также часто называемая функцией ошибки или затрат.
До сих пор наше основное внимание уделялось оценке параметров с
помощью MLE или MAP. Причина, по которой мы обсуждали это раньше, заключается в
том, что и MLE, и MAP предоставляют механизм для получения функции потерь.
Давайте рассмотрим некоторые часто используемые функции потерь.
Средняя
квадратичная ошибка (MSE): средняя
квадратичная ошибка является наиболее распространенной функцией потерь. Функция
потерь MSE широко используется в линейной регрессии в качестве показателя
эффективности. Чтобы рассчитать MSE, надо взять разницу между предсказанными
значениями и истинными, возвести ее в квадрат и усреднить по всему набору
данных.
где y(i) – фактический ожидаемый результат, а ŷ(i) – прогноз модели.
Многие функции потерь (затрат), используемые в машинном обучении,
включая MSE, могут быть получены из метода максимального правдоподобия.
Чтобы увидеть, как мы можем вывести функции потерь из MLE или MAP,
требуется некоторая математика. Вы можете пропустить ее и перейти к следующему
разделу.
Получение MSE из MLE
Алгоритм линейной регрессии учится принимать входные данные x и получать выходные значения ŷ. Отображение x в ŷ делается так,
чтобы минимизировать среднеквадратичную ошибку. Но как мы выбрали MSE в
качестве критерия для линейной регрессии? Придем к этому решению с точки зрения
оценки максимального правдоподобия. Вместо того, чтобы производить одно
предсказание ŷ , давайте рассмотрим
модель условного распределения p(y|x).
Можно смоделировать модель
линейной регрессии следующим образом:
мы предполагаем, что у имеет
нормальное распределение с ŷ в качестве
среднего значения распределения и некоторой постоянной σ² в качестве дисперсии, выбранной пользователем. Нормальное
распределения являются разумным выбором во многих случаях. В отсутствие
предварительных данных о том, какое распределение в действительности
соответствует рассматриваемым данным, нормальное распределение является хорошим
выбором по умолчанию.
Вернемся к логарифмической вероятности, определенной ранее:
где ŷ(i) – результат
линейной регрессии на i-м входе, а m – количество обучающих примеров. Мы видим,
что две первые величины являются постоянными, поэтому максимизация
логарифмической вероятности сводится к минимизации MSE:
Таким образом, максимизация логарифмического правдоподобия
относительно θ дает такую же оценку параметров θ, что и минимизация
среднеквадратичной ошибки. Два критерия имеют разные значения, но одинаковое
расположение оптимума. Это оправдывает использование MSE в качестве функции
оценки максимального правдоподобия.
Кросс-энтропия
(или логарифмическая функция потерь – log loss): Кросс-энтропия измеряет расхождение между двумя вероятностными
распределениями. Если кросс-энтропия велика, это означает, что разница между
двумя распределениями велика, а если кросс-энтропия мала, то распределения
похожи друг на друга.
Кросс-энтропия определяется как:
где P – распределение истинных ответов, а Q – распределение
вероятностей прогнозов модели. Можно
показать, что функция кросс-энтропии также получается из MLE, но я не буду
утомлять вас большим количеством математики.
Давайте еще
упростим это для нашей модели с:
• N – количество наблюдений
• M – количество возможных меток класса (собака,
кошка, рыба)
• y – двоичный индикатор (0 или 1) того, является
ли метка класса C правильной классификацией для наблюдения O
• p – прогнозируемая вероятность модели
Бинарная классификация
В случае бинарной классификации (M=2),
формула имеет вид:
При двоичной классификации каждая предсказанная вероятность
сравнивается с фактическим значением класса (0 или 1), и вычисляется оценка,
которая штрафует вероятность на основе расстояния от ожидаемого значения.
Визуализация
На приведенном ниже графике показан диапазон возможных значений
логистической функции потерь с учетом истинного наблюдения (y = 1). Когда
прогнозируемая вероятность приближается к 1, логистическая функция потерь
медленно уменьшается. Однако при уменьшении прогнозируемой вероятности она быстро возрастает.
Логистическая функция потерь наказывает оба типа ошибок, но
особенно те прогнозы, которые являются достоверными и ошибочными!
Мульти-классовая классификация
В случае мульти-классовой классификации (M>2) мы берем сумму значений логарифмических функций потерь для
каждого прогноза наблюдаемых классов.
Кросс-энтропия для бинарной или двух-классовой задачи
прогнозирования фактически рассчитывается как средняя кросс-энтропия среди всех
примеров. Log loss использует отрицательные
значения логарифма, чтобы обеспечить удобную метрику для сравнения. Этот подход
основан на том, что логарифм чисел <1 возвращает отрицательные значения, что
затрудняет работу при сравнении производительности двух моделей. Вы можете
почитать эту статью, где детально обсуждается функция кросс-энтропии потерь.
Задачи ML и соответствующие функции потерь
Давайте посмотрим, какие обычно используются выходные слои и
функции потерь в задачах машинного обучения:
Задача регрессии
Задача, когда
вы прогнозируете вещественное число.
• Конфигурация выходного уровня: один
узел с линейной единицей активации.
• Функция
потерь: средняя квадратическая ошибка (MSE).
Задача бинарной классификации
Задача состоит в том, чтобы классифицировать пример как
принадлежащий одному из двух классов. Или более точно, задача сформулирована
как предсказание вероятности того, что пример принадлежит первому классу,
например, классу, которому вы присваиваете целочисленное значение 1, тогда как
другому классу присваивается значение 0.
• Конфигурация выходного
уровня: один узел с сигмовидной активационной функцией.
• Функция
потерь: кросс-энтропия, также называемая логарифмической функцией потерь.
Задача мульти-классовой классификации
Эта задача состоит в том, чтобы классифицировать пример как
принадлежащий одному из нескольких классов. Задача сформулирована как
предсказание вероятности того, что пример принадлежит каждому классу.
• Конфигурация выходного уровня: один
узел для каждого класса, использующий функцию активации softmax.
• Функция потерь: кросс-энтропия, также называемая логарифмической функцией потерь.
Рассмотрев оценку и различные функции потерь, давайте перейдем к
роли оптимизаторов в алгоритмах ML.
Оптимизаторы
Чтобы свести к минимуму ошибку или потерю в прогнозировании,
модель, используя примеры из обучающей выборки, обновляет параметры модели W. Расчеты
ошибок строятся в зависимости от W и также описываются графиком функции затрат
J(w), поскольку она определяет затраты/наказание модели. Таким образом, минимизация
ошибки также часто называется минимизацией функции затрат.
Но как именно это делается? Используя оптимизаторы.
Оптимизаторы используются для обновления весов и смещений, то есть
внутренних параметров модели, чтобы уменьшить ошибку.
Самым важным методом и основой того, как мы обучаем и оптимизируем
нашу модель, является метод Градиентного Спуска.
Градиентный Спуск
Когда мы строим функцию затрат J(w), это можно представить следующим
образом:
Как видно из кривой, существует значение параметров W, которое
имеет минимальное значение Jmin. Нам нужно найти способ достичь
этого минимального значения.
В алгоритме градиентного спуска мы начинаем со случайных
параметров модели и вычисляем ошибку для каждой итерации обучения, продолжая
обновлять параметры, чтобы приблизиться к минимальным значениям.
Повторяем до достижения минимума:
{
}
В приведенном выше уравнении мы обновляем параметры модели после
каждой итерации. Второй член уравнения вычисляет наклон или градиент кривой на
каждой итерации.
Градиент функции затрат вычисляется как частная производная
функции затрат J по каждому параметру модели Wj, где j принимает
значение числа признаков [1, n]. α – альфа, это скорость обучения, определяющий
как быстро мы хотим двигаться к минимуму. Если α слишком велико, мы можем
проскочить минимум. Если α слишком мало, это приведет к небольшим этапам обучения,
поэтому общее время, затрачиваемое моделью для достижения минимума, будет
больше.
Есть три способа сделать градиентный спуск:
Пакетный
градиентный спуск: использует
все обучающие данные для обновления параметров модели в каждой итерации.
Мини-пакетный градиентный спуск: вместо использования всех данных, мини-пакетный градиентный спуск делит тренировочный набор на меньший размер, называемый партией, и обозначаемый буквой «b». Таким образом, мини-пакет «b» используется для обновления параметров модели на каждой итерации.
Вот некоторые другие часто
используемые Оптимизаторы:
Стохастический
Градиентный Спуск (SGD): обновляет
параметры, используя только один обучающий параметр на каждой итерации. Такой
параметр обычно выбирается случайным образом. Стохастический градиентный спуск
часто предпочтителен для оптимизации функций затрат, когда есть сотни тысяч
обучающих или более параметров, поскольку он будет сходиться быстрее, чем
пакетный градиентный спуск.
Адаград
Адаград адаптирует скорость обучения конкретно к индивидуальным
особенностям: это означает, что некоторые веса в вашем наборе данных будут
отличаться от других. Это работает очень хорошо для разреженных наборов данных,
где пропущено много входных значений. Однако, у Адаграда есть одна серьезная
проблема: адаптивная скорость обучения со временем становится очень маленькой.
Некоторые другие оптимизаторы, описанные ниже, пытаются справиться
с этой проблемой.
RMSprop
RMSprop – это специальная версия Adagrad,
разработанная профессором Джеффри Хинтоном в его
классе нейронных сетей. Вместо того,
чтобы вычислять все градиенты, он вычисляет градиенты только в фиксированном
окне. RMSprop похож на Adaprop, это еще один оптимизатор, который пытается
решить некоторые проблемы, которые Адаград оставляет открытыми.
Адам
Адам означает адаптивную оценку момента и является еще одним способом использования
предыдущих градиентов для вычисления текущих градиентов. Адам также использует
концепцию импульса,
добавляя доли предыдущих градиентов к текущему. Этот оптимизатор получил
довольно широкое распространение и практически принят для использования в
обучающих нейронных сетях.
Вы только что ознакомились с кратким обзором
оптимизаторов. Более подробно об этом можно прочитать здесь.
Я надеюсь,
что после прочтения этой статьи, вы будете лучше понимать что происходит, когда
Вы пишите следующий код:
# loss function: Binary Cross-entropy and optimizer: Adam
model.compile(loss='binary_crossentropy', optimizer='adam')или
# loss function: MSE and optimizer: stochastic gradient descent
model.compile(loss='mean_squared_error', optimizer='sgd')Спасибо за проявленный интерес!
Ссылки:
[1] https://www.deeplearningbook.org/contents/ml.html
[2] https://machinelearningmastery.com/loss-and-loss-functions-for-training-deep-learning-neural-networks/
[3] https://blog.algorithmia.com/introduction-to-optimizers/
[4] https://jhui.github.io/2017/01/05/Deep-learning-Information-theory/
[5] https://blog.algorithmia.com/introduction-to-loss-functions/
[6] https://gombru.github.io/2018/05/23/cross_entropy_loss/
[7] https://www.kdnuggets.com/2018/04/right-metric-evaluating-machine-learning-models-1.html
[8] https://rohanvarma.me/Loss-Functions/
[9] http://blog.christianperone.com/2019/01/mle/
“Мир полон волшебных вещей, терпеливо ожидающих того момента, когда наши чувства станут острее”. — У.Б. Йейтс
Что стоит за #(хэштегом)?
Совсем недавно я начала новую серию статей, смысл которых выражен хэштегом: #TheNotSoToughML (#НисколькоНеСложноеМО).
Предыдущие части: Часть 1, Часть 2.
Мне хотелось бы дать вам упрощенные решения некоторых проблем, возникающих в связи с алгоритмами/концепциями. Вместо того, чтобы сразу вдаваться в математику, я обращаюсь к вашей интуиции. Поверьте: машинное обучение вовсе не сложно. Оно больше похоже на интуитивное постижение, проверяемое алгоритмически.
Концепция 1: Функция ошибки. Измерение результатов
Когда вы смотрите на две модели выше и сравниваете их, приходите ли вы к тому же выводу, что и я? Как по-вашему, является ли плохая модель действительно “плохой” по сравнению с моделью справа? Если да, это значит, что вы сконцентрировали внимание на “зазоре” или расстоянии линии от каждой точки данных; таким образом, в среднем (или по совокупности признаков) вам показалось, что модель слева имеет большее расстояние между точками и линией по сравнению с моделью справа.
Функция ошибки помогает нам понять то же самое! Это метрика, показывающая то, как работает наша модель.
Функция ошибки будет присваивать большее значение модели слева и меньшее — модели справа. В специальной литературе такие функции также называют функциями потерь или функциями затрат.
Теперь перейдем к более важному вопросу.
Как определить, насколько точно работает функция ошибки для моделей линейной регрессии?
Сейчас мы поговорим об абсолютной ошибке и квадратичной ошибке.
Абсолютная ошибка — метрика, которая складывает расстояния и показывает, насколько хороша наша модель.
Это самый простой для понимания и интерпретации показатель.
Это просто суммирование расстояний между точками данных и линией. Оно называется “абсолютным”, потому что расстояние может быть положительным или отрицательным в зависимости от расположения точек данных по отношению к линии. Следовательно, чтобы не упустить ни одного нюанса в поведении модели, мы принимаем абсолютное значение ошибок.
Итак, мы знаем, что хорошая модель линейной регрессии — это та модель, в которой линия близка к точкам данных.
Но что значит “близка”?
Выбираем ли мы линию, которая близка к некоторым точкам и далека от других? Или мы выбираем линию, которая близка ко всем точкам?
Вот тут-то и пригодится функция абсолютной ошибки. Мы выбираем линию, которая минимизирует абсолютную ошибку, т.е. ту, для которой сумма вертикальных расстояний от каждой точки до линии минимальна.
На рисунке ниже показаны разные абсолютные ошибки.
Теперь перейдем к следующему приему, связанному с ошибками.
Квадратичная ошибка — метрика, которая складывает квадраты расстояний и показывает, насколько хороша наша модель.
Квадратичная ошибка очень похожа на абсолютную ошибку. Но теперь, вместо того, чтобы брать абсолютное значение разницы между меткой и прогнозированной меткой, мы используем квадрат, что снова превращает число в положительное.
Давайте попробуем представить это так же, как мы это делали для абсолютной ошибки!
Квадратичная ошибка используется на практике чаще, чем абсолютная. Почему? Одна из причин заключается в том, что у квадрата гораздо более наглядная производная, чем у абсолютного значения, что очень удобно в процессе обучения.
Мы убедимся в этом чуть ниже.
Средняя абсолютная ошибка и (корневая) средняя квадратичная ошибка — самые распространенные и наиболее полезные ошибки для нашей модели
Абсолютная и квадратичная ошибки, показанные выше, служили простыми примерами того, что такое ошибки и как они могут выглядеть. Однако наиболее часто используемыми ошибками в проектах машинного обучения, особенно когда мы имеем дело с регрессионными моделями, являются средняя абсолютная ошибка (MAE) и средняя квадратичная ошибка (MSE).
Они определяются практически так же, только вместо вычисления сумм мы вычисляем средние значения.
Итак, MAE — это среднее значение вертикальных расстояний от точек до линии, а MSE — среднее значение квадратов этих же расстояний.
Эти ошибки более полезны, чем абсолютная и квадратичная ошибка, которые мы вычисляли в предыдущем разделе, и вот почему. Допустим, мы пытаемся подогнать одну и ту же модель к двум разным наборам данных, в одном из которых всего 10 точек данных, а в другом — миллион. Если ошибка является суммой величин (как в случае абсолютной или квадратичной ошибки), то она, вероятно, будет намного выше в наборе данных, состоящем из миллиона точек, потому что мы будем складывать гораздо больше чисел. Но эта проблема решается с помощью средних значений.
Еще один полезный показатель — среднеквадратичная ошибка (RMSE). Как следует из названия, это корень из средней квадратичной ошибки. Этот показатель используется для сопоставления единиц в задаче, а также для того, чтобы дать нам лучшее представление о том, насколько сильно модель ошибается при прогнозировании.
Концепция 2: Градиентный спуск. Уменьшение функции ошибки путем медленного “спуска с горы”
Теперь поговорим о перемещении линий на некоторое расстояние в контексте МО.
Поскольку цель этого цикла — объяснить интуитивный подход, а математические понятия использовать только там, где это абсолютно необходимо, мы воздержимся от того, чтобы углубляться в технические аспекты в этом разделе. Но если вы хотите разобраться в расчетах, которые проводятся при градиентном спуске, можете зайти на этот сайт и ознакомиться с ними.
Пока же мы попробуем понять, как градиентный спуск помогает нам уменьшить ошибку модели. При этом постараемся не погружаться в высшую математику. Скромная попытка, но все же.
Давайте решим вышеуказанную задачу в следующем порядке:
- Кратко разберем, как работает градиентный спуск.
- Расскажем, как он может решить задачу уменьшения ошибки
- Выясним, как с помощью полученных знаний мы узнаем, когда нужно останавливать работу алгоритма.
Как работает градиентный спуск
Представьте, что вы находитесь на вершине высокой горы — скажем, горы “Эррорест”.
Вы хотите спуститься с нее, но стоит очень туманная погода и вы видите только на расстоянии около 1 метра от себя. Что же делать? Вот вам дельный совет — оглянитесь вокруг себя и определите, в каком направлении можно сделать один единственный шаг так, чтобы спуститься максимально низко.
Нашли это направление? Теперь сделайте маленький шаг. Поскольку этот шаг был сделан в направлении максимального спуска, то, скорее всего, вы спуститесь на небольшое расстояние.
Теперь вам нужно повторять это действие много раз до тех пор, пока вы не достигнете подножия горы (хотелось бы надеяться на это).
Я написал “хотелось бы надеяться”, потому что в этом примере слишком много нюансов, которые мы разбирать не будем, чтобы не вдаваться в сложные математические понятия. Вы можете достичь подножия горы, а можете очутиться в долине, и вам больше некуда будет идти. Сейчас мы не станем разбирать все эти варианты.
Суть в том, что при градиентном спуске мы делаем один шаг за раз в направлении самой низкой точки (в нашем примере — подножия горы).
Как градиентный спуск помогает решить задачу уменьшения ошибки
Напомню, что мы определяем алгоритм линейной регрессии по следующей схеме:
- Начинаем с любой линии.
- Находим наилучшее направление, в котором можно немного сдвинуть нашу линию, используя прием из сферы абсолютных или квадратичных значений.
- Перемещаем линию в этом направлении.
- Повторяем эти шаги 2, 3 и более раз.
В предыдущем разделе мы говорили о градиентном спуске. Чтобы закрепить принцип его работы с помощью примера с горой, пройдем описанные этапы еще раз:
- Мы находимся на вершине горы.
- Находим оптимальное направление для первого маленького шага.
- Делаем маленький шаг в этом направлении.
- Повторяем эти шаги 2, 3 и более раз.
Знакомая схема, не так ли? Посмотрим на рисунок ниже.
Единственное отличие от нашего прежнего понимания линейной регрессии заключается в том, что эта функция ошибки больше напоминает долину, чем гору. Наша цель — спуститься в самую низкую точку. Каждая точка в этой долине соответствует некоторой модели (линии), которая пытается подогнать наши данные. Высота точки — это ошибка, которую выдает данная модель. Таким образом, плохие модели располагаются сверху, а хорошие — снизу. Мы стараемся опуститься как можно ниже. Каждый шаг ведет нас от худшей модели к чуть лучшей. Если мы будем делать такие шаги много раз, то в конце концов дойдем до лучшей модели (или, по крайней мере, довольно хорошей!).
Подытожим: что же нам нужно делать?
Мы хотим найти линию, которая лучше всего соответствует нашим данным. У нас есть метрика “функция ошибки”, которая показывает, насколько линия далека от данных. Таким образом, если мы сможем уменьшить это число как можно больше, мы найдем наиболее подходящую линию.
Этот процесс часто используется во многих областях математики и называется минимизацией функций (т.е. нахождение наименьшего возможного значения, которое может вернуть функция). В данном случае функция, которую мы пытаемся минимизировать, — это ошибка (абсолютная или квадратичная) нашей модели. Для минимизации этой функции мы используем градиентный спуск.
Как узнать, когда нужно останавливать работу алгоритма?
Давайте рассчитаем RMSE для любого набора данных, где мы пытаемся предсказать неизвестные значения (“метки”) и получить новые метки после запуска нашей модели (“прогнозы”):
def rmse(labels, predictions):
n = len(labels)
differences = np.subtract(labels, predictions)
return np.sqrt(1.0/n * (np.dot(differences, differences)))
Теперь построим график, отобразив на нем, помимо прочего, количество эпох (итераций), в течение которых работает ваша модель. В итоге вы получите результат, похожий на тот, который вышел у меня, когда я тестировал таким образом свой образец набора данных:
Мы видим стремительное падение примерно после 1000 итераций, и после этого изменений на графике практически не наблюдается. Это говорит нам о том, что для данной конкретной модели мы можем запустить алгоритм обучения не на 10 000, а всего на 1000 или 2000 итераций. Тем не менее, мы все равно получим схожие результаты.
В целом, функция ошибки предоставляет надежную информацию, помогающую определиться с тем, когда следует прекращать выполнение алгоритма. Очень часто такое решение основывается на доступном нам времени и вычислительной мощности. Однако есть и другие полезные факторы, на которые часто ориентируются специалисты в сфере данных. Выполнение алгоритма также прекращают в следующих случаях:
- когда функция потерь достигает определенного значения, которое мы заранее установили;
- когда функция потерь не уменьшается в течение нескольких эпох.
Что дальше?
Это был краткий обзор работы функции ошибки и того, как градиентный спуск помогает нам уменьшить ее. Но, думаю, вы уже поняли, что есть масса других моментов, которые я не стал затрагивать в этой статье, чтобы не перегружать вас. Если у вас возникли дополнительные вопросы, можете заняться самообразованием и продолжать “копать” в этом направлении дальше.
Тем не менее, представленный в этой статье материал должен дать вам базовое представление о том, как работает большинство моделей. Наверняка вы убедились в том, что вам не нужны глубинные познания в математике, чтобы понять принципы машинного обучения!
В следующей статье мы рассмотрим другую форму подгонки, а именно полиномиальную подгонку к данным (а не линейную) и будем использовать ее в дальнейшем, чтобы понять, как можно спасти наши модели от “недо/переподгонки”.
Самое главное, мы поймем, как функции ошибок и концепция градиентного спуска помогают регулировать веса, находить лучшее решение при оптимальном завершении процесса, и узнаем, как определить, что наша модель действительно работает!
Эта статья, как и многие другие, была написана под впечатлением от книги, которую я сейчас читаю — “Grokking Machine Learning” Луиса Серрано. Книга еще не вышла, но я приобрела ранний доступ к ней и думаю, что поступила правильно. Я считаю, что книги/материалы этого автора определенно заслуживают того, чтобы их прочитал каждый, кто хочет получить полное представление об алгоритмах и о том, как работают модели МО.
Читайте также:
- Создание модели машинного обучения с помощью Google Colab без дополнительных настроек
- 6 концептов книги Эндрю Ына «Жажда машинного обучения»
- Самая лучшая идея в науке о данных
Читайте нас в Telegram, VK и Яндекс.Дзен
Перевод статьи Anushree Chatterjee, #03TheNotSoToughML | Regression: Errors → Descending from a Mountain Top
В машинном обучении различают оценки качества для задачи классификации и регрессии. Причем оценка задачи классификации часто значительно сложнее, чем оценка регрессии.
Содержание
- 1 Оценки качества классификации
- 1.1 Матрица ошибок (англ. Сonfusion matrix)
- 1.2 Аккуратность (англ. Accuracy)
- 1.3 Точность (англ. Precision)
- 1.4 Полнота (англ. Recall)
- 1.5 F-мера (англ. F-score)
- 1.6 ROC-кривая
- 1.7 Precison-recall кривая
- 2 Оценки качества регрессии
- 2.1 Средняя квадратичная ошибка (англ. Mean Squared Error, MSE)
- 2.2 Cредняя абсолютная ошибка (англ. Mean Absolute Error, MAE)
- 2.3 Коэффициент детерминации
- 2.4 Средняя абсолютная процентная ошибка (англ. Mean Absolute Percentage Error, MAPE)
- 2.5 Корень из средней квадратичной ошибки (англ. Root Mean Squared Error, RMSE)
- 2.6 Cимметричная MAPE (англ. Symmetric MAPE, SMAPE)
- 2.7 Средняя абсолютная масштабированная ошибка (англ. Mean absolute scaled error, MASE)
- 3 Кросс-валидация
- 4 Примечания
- 5 См. также
- 6 Источники информации
Оценки качества классификации
Матрица ошибок (англ. Сonfusion matrix)
Перед переходом к самим метрикам необходимо ввести важную концепцию для описания этих метрик в терминах ошибок классификации — confusion matrix (матрица ошибок).
Допустим, что у нас есть два класса и алгоритм, предсказывающий принадлежность каждого объекта одному из классов.
Рассмотрим пример. Пусть банк использует систему классификации заёмщиков на кредитоспособных и некредитоспособных. При этом первым кредит выдаётся, а вторые получат отказ. Таким образом, обнаружение некредитоспособного заёмщика () можно рассматривать как «сигнал тревоги», сообщающий о возможных рисках.
Любой реальный классификатор совершает ошибки. В нашем случае таких ошибок может быть две:
- Кредитоспособный заёмщик распознается моделью как некредитоспособный и ему отказывается в кредите. Данный случай можно трактовать как «ложную тревогу».
- Некредитоспособный заёмщик распознаётся как кредитоспособный и ему ошибочно выдаётся кредит. Данный случай можно рассматривать как «пропуск цели».
Несложно увидеть, что эти ошибки неравноценны по связанным с ними проблемам. В случае «ложной тревоги» потери банка составят только проценты по невыданному кредиту (только упущенная выгода). В случае «пропуска цели» можно потерять всю сумму выданного кредита. Поэтому системе важнее не допустить «пропуск цели», чем «ложную тревогу».
Поскольку с точки зрения логики задачи нам важнее правильно распознать некредитоспособного заёмщика с меткой , чем ошибиться в распознавании кредитоспособного, будем называть соответствующий исход классификации положительным (заёмщик некредитоспособен), а противоположный — отрицательным (заемщик кредитоспособен ). Тогда возможны следующие исходы классификации:
- Некредитоспособный заёмщик классифицирован как некредитоспособный, т.е. положительный класс распознан как положительный. Наблюдения, для которых это имеет место называются истинно-положительными (True Positive — TP).
- Кредитоспособный заёмщик классифицирован как кредитоспособный, т.е. отрицательный класс распознан как отрицательный. Наблюдения, которых это имеет место, называются истинно отрицательными (True Negative — TN).
- Кредитоспособный заёмщик классифицирован как некредитоспособный, т.е. имела место ошибка, в результате которой отрицательный класс был распознан как положительный. Наблюдения, для которых был получен такой исход классификации, называются ложно-положительными (False Positive — FP), а ошибка классификации называется ошибкой I рода.
- Некредитоспособный заёмщик распознан как кредитоспособный, т.е. имела место ошибка, в результате которой положительный класс был распознан как отрицательный. Наблюдения, для которых был получен такой исход классификации, называются ложно-отрицательными (False Negative — FN), а ошибка классификации называется ошибкой II рода.
Таким образом, ошибка I рода, или ложно-положительный исход классификации, имеет место, когда отрицательное наблюдение распознано моделью как положительное. Ошибкой II рода, или ложно-отрицательным исходом классификации, называют случай, когда положительное наблюдение распознано как отрицательное. Поясним это с помощью матрицы ошибок классификации:
-
Истинно-положительный (True Positive — TP) Ложно-положительный (False Positive — FP) Ложно-отрицательный (False Negative — FN) Истинно-отрицательный (True Negative — TN)
Здесь — это ответ алгоритма на объекте, а — истинная метка класса на этом объекте.
Таким образом, ошибки классификации бывают двух видов: False Negative (FN) и False Positive (FP).
P означает что классификатор определяет класс объекта как положительный (N — отрицательный). T значит что класс предсказан правильно (соответственно F — неправильно). Каждая строка в матрице ошибок представляет спрогнозированный класс, а каждый столбец — фактический класс.
# код для матрицы ошибок # Пример классификатора, способного проводить различие между всего лишь двумя # классами, "пятерка" и "не пятерка" из набора рукописных цифр MNIST import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.metrics import confusion_matrix from sklearn.linear_model import SGDClassifier mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (англ. Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе # Для расчета матрицы ошибок сначала понадобится иметь набор прогнозов, чтобы их можно было сравнивать с фактическими целями y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) print(confusion_matrix(y_train_5, y_train_pred)) # array([[53892, 687], # [ 1891, 3530]])
Безупречный классификатор имел бы только истинно-положительные и истинно отрицательные классификации, так что его матрица ошибок содержала бы ненулевые значения только на своей главной диагонали (от левого верхнего до правого нижнего угла):
import numpy as np
from sklearn.datasets import fetch_openml
from sklearn.metrics import confusion_matrix
mnist = fetch_openml('mnist_784', version=1)
X, y = mnist["data"], mnist["target"]
y = y.astype(np.uint8)
X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:]
y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки
y_test_5 = (y_test == 5)
y_train_perfect_predictions = y_train_5 # притворись, что мы достигли совершенства
print(confusion_matrix(y_train_5, y_train_perfect_predictions))
# array([[54579, 0],
# [ 0, 5421]])
Аккуратность (англ. Accuracy)
Интуитивно понятной, очевидной и почти неиспользуемой метрикой является accuracy — доля правильных ответов алгоритма:
Эта метрика бесполезна в задачах с неравными классами, что как вариант можно исправить с помощью алгоритмов сэмплирования и это легко показать на примере.
Допустим, мы хотим оценить работу спам-фильтра почты. У нас есть 100 не-спам писем, 90 из которых наш классификатор определил верно (True Negative = 90, False Positive = 10), и 10 спам-писем, 5 из которых классификатор также определил верно (True Positive = 5, False Negative = 5).
Тогда accuracy:
Однако если мы просто будем предсказывать все письма как не-спам, то получим более высокую аккуратность:
При этом, наша модель совершенно не обладает никакой предсказательной силой, так как изначально мы хотели определять письма со спамом. Преодолеть это нам поможет переход с общей для всех классов метрики к отдельным показателям качества классов.
# код для для подсчета аккуратности: # Пример классификатора, способного проводить различие между всего лишь двумя # классами, "пятерка" и "не пятерка" из набора рукописных цифр MNIST import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.metrics import accuracy_score from sklearn.linear_model import SGDClassifier mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) # print(confusion_matrix(y_train_5, y_train_pred)) # array([[53892, 687] # [ 1891, 3530]]) print(accuracy_score(y_train_5, y_train_pred)) # == (53892 + 3530) / (53892 + 3530 + 1891 +687) # 0.9570333333333333
Точность (англ. Precision)
Точностью (precision) называется доля правильных ответов модели в пределах класса — это доля объектов действительно принадлежащих данному классу относительно всех объектов которые система отнесла к этому классу.
Именно введение precision не позволяет нам записывать все объекты в один класс, так как в этом случае мы получаем рост уровня False Positive.
Полнота (англ. Recall)
Полнота — это доля истинно положительных классификаций. Полнота показывает, какую долю объектов, реально относящихся к положительному классу, мы предсказали верно.
Полнота (recall) демонстрирует способность алгоритма обнаруживать данный класс вообще.
Имея матрицу ошибок, очень просто можно вычислить точность и полноту для каждого класса. Точность (precision) равняется отношению соответствующего диагонального элемента матрицы и суммы всей строки класса. Полнота (recall) — отношению диагонального элемента матрицы и суммы всего столбца класса. Формально:
Результирующая точность классификатора рассчитывается как арифметическое среднее его точности по всем классам. То же самое с полнотой. Технически этот подход называется macro-averaging.
# код для для подсчета точности и полноты: # Пример классификатора, способного проводить различие между всего лишь двумя # классами, "пятерка" и "не пятерка" из набора рукописных цифр MNIST import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.metrics import precision_score, recall_score from sklearn.linear_model import SGDClassifier mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) # print(confusion_matrix(y_train_5, y_train_pred)) # array([[53892, 687] # [ 1891, 3530]]) print(precision_score(y_train_5, y_train_pred)) # == 3530 / (3530 + 687) print(recall_score(y_train_5, y_train_pred)) # == 3530 / (3530 + 1891) # 0.8370879772350012 # 0.6511713705958311
F-мера (англ. F-score)
Precision и recall не зависят, в отличие от accuracy, от соотношения классов и потому применимы в условиях несбалансированных выборок.
Часто в реальной практике стоит задача найти оптимальный (для заказчика) баланс между этими двумя метриками. Понятно что чем выше точность и полнота, тем лучше. Но в реальной жизни максимальная точность и полнота не достижимы одновременно и приходится искать некий баланс. Поэтому, хотелось бы иметь некую метрику которая объединяла бы в себе информацию о точности и полноте нашего алгоритма. В этом случае нам будет проще принимать решение о том какую реализацию запускать в производство (у кого больше тот и круче). Именно такой метрикой является F-мера.
F-мера представляет собой гармоническое среднее между точностью и полнотой. Она стремится к нулю, если точность или полнота стремится к нулю.
Данная формула придает одинаковый вес точности и полноте, поэтому F-мера будет падать одинаково при уменьшении и точности и полноты. Возможно рассчитать F-меру придав различный вес точности и полноте, если вы осознанно отдаете приоритет одной из этих метрик при разработке алгоритма:
где принимает значения в диапазоне если вы хотите отдать приоритет точности, а при приоритет отдается полноте. При формула сводится к предыдущей и вы получаете сбалансированную F-меру (также ее называют ).
-
Рис.1 Сбалансированная F-мера,
-
Рис.2 F-мера c приоритетом точности,
-
Рис.3 F-мера c приоритетом полноты,
F-мера достигает максимума при максимальной полноте и точности, и близка к нулю, если один из аргументов близок к нулю.
F-мера является хорошим кандидатом на формальную метрику оценки качества классификатора. Она сводит к одному числу две других основополагающих метрики: точность и полноту. Имея «F-меру» гораздо проще ответить на вопрос: «поменялся алгоритм в лучшую сторону или нет?»
# код для подсчета метрики F-mera: # Пример классификатора, способного проводить различие между всего лишь двумя # классами, "пятерка" и "не пятерка" из набора рукописных цифр MNIST import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.linear_model import SGDClassifier from sklearn.metrics import f1_score mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распознавать пятерки на целом обучающем наборе y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) print(f1_score(y_train_5, y_train_pred)) # 0.7325171197343846
ROC-кривая
Кривая рабочих характеристик (англ. Receiver Operating Characteristics curve).
Используется для анализа поведения классификаторов при различных пороговых значениях.
Позволяет рассмотреть все пороговые значения для данного классификатора.
Показывает долю ложно положительных примеров (англ. false positive rate, FPR) в сравнении с долей истинно положительных примеров (англ. true positive rate, TPR).

Доля FPR — это пропорция отрицательных образцов, которые были некорректно классифицированы как положительные.
- ,
где TNR — доля истинно отрицательных классификаций (англ. Тrие Negative Rate), представляющая собой пропорцию отрицательных образцов, которые были корректно классифицированы как отрицательные.
Доля TNR также называется специфичностью (англ. specificity). Следовательно, ROC-кривая изображает чувствительность (англ. seпsitivity), т.е. полноту, в сравнении с разностью 1 — specificity.
Прямая линия по диагонали представляет ROC-кривую чисто случайного классификатора. Хороший классификатор держится от указанной линии настолько далеко, насколько это
возможно (стремясь к левому верхнему углу).
Один из способов сравнения классификаторов предусматривает измерение площади под кривой (англ. Area Under the Curve — AUC). Безупречный классификатор будет иметь площадь под ROC-кривой (ROC-AUC), равную 1, тогда как чисто случайный классификатор — площадь 0.5.
# Код отрисовки ROC-кривой # На примере классификатора, способного проводить различие между всего лишь двумя классами # "пятерка" и "не пятерка" из набора рукописных цифр MNIST from sklearn.metrics import roc_curve import matplotlib.pyplot as plt import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.linear_model import SGDClassifier mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) y_scores = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3, method="decision_function") fpr, tpr, thresholds = roc_curve(y_train_5, y_scores) def plot_roc_curve(fpr, tpr, label=None): plt.plot(fpr, tpr, linewidth=2, label=label) plt.plot([0, 1], [0, 1], 'k--') # dashed diagonal plt.xlabel('False Positive Rate, FPR (1 - specificity)') plt.ylabel('True Positive Rate, TPR (Recall)') plt.title('ROC curve') plt.savefig("ROC.png") plot_roc_curve(fpr, tpr) plt.show()
Precison-recall кривая
Чувствительность к соотношению классов.
Рассмотрим задачу выделения математических статей из множества научных статей. Допустим, что всего имеется 1.000.100 статей, из которых лишь 100 относятся к математике. Если нам удастся построить алгоритм , идеально решающий задачу, то его TPR будет равен единице, а FPR — нулю. Рассмотрим теперь плохой алгоритм, дающий положительный ответ на 95 математических и 50.000 нематематических статьях. Такой алгоритм совершенно бесполезен, но при этом имеет TPR = 0.95 и FPR = 0.05, что крайне близко к показателям идеального алгоритма.
Таким образом, если положительный класс существенно меньше по размеру, то AUC-ROC может давать неадекватную оценку качества работы алгоритма, поскольку измеряет долю неверно принятых объектов относительно общего числа отрицательных. Так, алгоритм , помещающий 100 релевантных документов на позиции с 50.001-й по 50.101-ю, будет иметь AUC-ROC 0.95.
Precison-recall (PR) кривая. Избавиться от указанной проблемы с несбалансированными классами можно, перейдя от ROC-кривой к PR-кривой. Она определяется аналогично ROC-кривой, только по осям откладываются не FPR и TPR, а полнота (по оси абсцисс) и точность (по оси ординат). Критерием качества семейства алгоритмов выступает площадь под PR-кривой (англ. Area Under the Curve — AUC-PR)

# Код отрисовки Precison-recall кривой # На примере классификатора, способного проводить различие между всего лишь двумя классами # "пятерка" и "не пятерка" из набора рукописных цифр MNIST from sklearn.metrics import precision_recall_curve import matplotlib.pyplot as plt import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.linear_model import SGDClassifier mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) y_scores = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3, method="decision_function") precisions, recalls, thresholds = precision_recall_curve(y_train_5, y_scores) def plot_precision_recall_vs_threshold(precisions, recalls, thresholds): plt.plot(recalls, precisions, linewidth=2) plt.xlabel('Recall') plt.ylabel('Precision') plt.title('Precision-Recall curve') plt.savefig("Precision_Recall_curve.png") plot_precision_recall_vs_threshold(precisions, recalls, thresholds) plt.show()
Оценки качества регрессии
Наиболее типичными мерами качества в задачах регрессии являются
Средняя квадратичная ошибка (англ. Mean Squared Error, MSE)
MSE применяется в ситуациях, когда нам надо подчеркнуть большие ошибки и выбрать модель, которая дает меньше больших ошибок прогноза. Грубые ошибки становятся заметнее за счет того, что ошибку прогноза мы возводим в квадрат. И модель, которая дает нам меньшее значение среднеквадратической ошибки, можно сказать, что что у этой модели меньше грубых ошибок.
- и
Cредняя абсолютная ошибка (англ. Mean Absolute Error, MAE)
Среднеквадратичный функционал сильнее штрафует за большие отклонения по сравнению со среднеабсолютным, и поэтому более чувствителен к выбросам. При использовании любого из этих двух функционалов может быть полезно проанализировать, какие объекты вносят наибольший вклад в общую ошибку — не исключено, что на этих объектах была допущена ошибка при вычислении признаков или целевой величины.
Среднеквадратичная ошибка подходит для сравнения двух моделей или для контроля качества во время обучения, но не позволяет сделать выводов о том, на сколько хорошо данная модель решает задачу. Например, MSE = 10 является очень плохим показателем, если целевая переменная принимает значения от 0 до 1, и очень хорошим, если целевая переменная лежит в интервале (10000, 100000). В таких ситуациях вместо среднеквадратичной ошибки полезно использовать коэффициент детерминации —
Коэффициент детерминации
Коэффициент детерминации измеряет долю дисперсии, объясненную моделью, в общей дисперсии целевой переменной. Фактически, данная мера качества — это нормированная среднеквадратичная ошибка. Если она близка к единице, то модель хорошо объясняет данные, если же она близка к нулю, то прогнозы сопоставимы по качеству с константным предсказанием.
Средняя абсолютная процентная ошибка (англ. Mean Absolute Percentage Error, MAPE)
Это коэффициент, не имеющий размерности, с очень простой интерпретацией. Его можно измерять в долях или процентах. Если у вас получилось, например, что MAPE=11.4%, то это говорит о том, что ошибка составила 11,4% от фактических значений.
Основная проблема данной ошибки — нестабильность.
Корень из средней квадратичной ошибки (англ. Root Mean Squared Error, RMSE)
Примерно такая же проблема, как и в MAPE: так как каждое отклонение возводится в квадрат, любое небольшое отклонение может значительно повлиять на показатель ошибки. Стоит отметить, что существует также ошибка MSE, из которой RMSE как раз и получается путем извлечения корня.
Cимметричная MAPE (англ. Symmetric MAPE, SMAPE)
Средняя абсолютная масштабированная ошибка (англ. Mean absolute scaled error, MASE)
MASE является очень хорошим вариантом для расчета точности, так как сама ошибка не зависит от масштабов данных и является симметричной: то есть положительные и отрицательные отклонения от факта рассматриваются в равной степени.
Обратите внимание, что в MASE мы имеем дело с двумя суммами: та, что в числителе, соответствует тестовой выборке, та, что в знаменателе — обучающей. Вторая фактически представляет собой среднюю абсолютную ошибку прогноза. Она же соответствует среднему абсолютному отклонению ряда в первых разностях. Эта величина, по сути, показывает, насколько обучающая выборка предсказуема. Она может быть равна нулю только в том случае, когда все значения в обучающей выборке равны друг другу, что соответствует отсутствию каких-либо изменений в ряде данных, ситуации на практике почти невозможной. Кроме того, если ряд имеет тенденцию к росту либо снижению, его первые разности будут колебаться около некоторого фиксированного уровня. В результате этого по разным рядам с разной структурой, знаменатели будут более-менее сопоставимыми. Всё это, конечно же, является очевидными плюсами MASE, так как позволяет складывать разные значения по разным рядам и получать несмещённые оценки.
Недостаток MASE в том, что её тяжело интерпретировать. Например, MASE=1.21 ни о чём, по сути, не говорит. Это просто означает, что ошибка прогноза оказалась в 1.21 раза выше среднего абсолютного отклонения ряда в первых разностях, и ничего более.
Кросс-валидация
Хороший способ оценки модели предусматривает применение кросс-валидации (cкользящего контроля или перекрестной проверки).
В этом случае фиксируется некоторое множество разбиений исходной выборки на две подвыборки: обучающую и контрольную. Для каждого разбиения выполняется настройка алгоритма по обучающей подвыборке, затем оценивается его средняя ошибка на объектах контрольной подвыборки. Оценкой скользящего контроля называется средняя по всем разбиениям величина ошибки на контрольных подвыборках.
Примечания
- [1] Лекция «Оценивание качества» на www.coursera.org
- [2] Лекция на www.stepik.org о кросвалидации
- [3] Лекция на www.stepik.org о метриках качества, Precison и Recall
- [4] Лекция на www.stepik.org о метриках качества, F-мера
- [5] Лекция на www.stepik.org о метриках качества, примеры
См. также
- Оценка качества в задаче кластеризации
- Кросс-валидация
Источники информации
- [6] Соколов Е.А. Лекция линейная регрессия
- [7] — Дьяконов А. Функции ошибки / функционалы качества
- [8] — Оценка качества прогнозных моделей
- [9] — HeinzBr Ошибка прогнозирования: виды, формулы, примеры
- [10] — egor_labintcev Метрики в задачах машинного обучения
- [11] — grossu Методы оценки качества прогноза
- [12] — К.В.Воронцов, Классификация
- [13] — К.В.Воронцов, Скользящий контроль
Что такое метрики эффективности?
Для того, чтобы эффективно проводить обучение моделей необходимо иметь способ оценки, насколько хорошо та или иная модель выполняет свою работу — предсказывает значение целевой переменной. Кажется, мы уже что-то подобное изучали. У каждой модели есть функция ошибки, которая показывает, на сколько модель соответствует эмпирическим значениям. Однако, использование функции ошибки не очень удобно для оценки именно “качества” уже построенных моделей. Ведь эта функция специально создается для единственной цели — организации процесса обучения. Поэтому для оценки уже построенных моделей используется не функция ошибки, а так называемые метрики эффективности — специальные функции, которые показывают, насколько эффективна уже готовая, обученная модель.
Метрики эффективности на первый взгляд очень похожи на функции ошибки, ведь у них одна цель — отличать хорошие модели от плохих. Но делают они это по-разному, по-разному и применяются. К метрикам эффективности предъявляются совершенно другие требования, нежели к функциям ошибки. Поэтому давайте рассмотрим, для чего нужны и те и другие.
Функция ошибки нужна в первую очередь для формализации процесса обучения модели. То есть для того, чтобы подбирать параметры модели именно такими, чтобы модель как можно больше соответствовала реальным данным в обучающей выборке. Да, значение этой функции можно использовать как некоторую оценку качества модели уже после того, как она обучена, но это не удобно.
Функция ошибки нужна, чтобы формализовать отклонения предсказанных моделью значений от реальных. Например, в методе линейной регрессии функция ошибки (среднеквадратическое отклонение) используется для метода градиентного спуска. Поэтому функция ошибки обязательно должна быть везде дифференцируемой, мы это отдельно отмечали, когда говорили про метод градиентного спуска. Это требование — дифференцируемость — нужно исключительно для метода оптимизации, то есть для обучения модели.
Зато функция, которая используется для оценки качества модели совершенно не должна быть аналитической и гладкой. Ведь мы не будем вычислять ее производную, мы только вычислим ее один раз для того, чтобы понять, насколько хорошая модель получилась. Так что не любую метрику эффективности вообще физически возможно использовать как функцию ошибки — метод обучения может просто не сработать.
Кроме того, функция ошибки должна быть вычислительно простой, ведь ее придется считать много раз в процессе обучения — тысячи или миллионы раз. Это еще одно требование, которое совершенно необязательно для метрики эффективности. Она как раз может считаться довольно сложно, ведь вычислять ее приходится всего несколько раз.
Зато метрика эффективности должна быть понятной и интерпретируемой, в отличие от функции ошибки. Раньше мы подчеркивали, что само абсолютное значение функции ошибки ничего не показывает. Важно лишь, снижается ли оно в процессе обучения. И разные значения функции ошибки имеет смысл сравнивать только на одних и тех же данных. Что значит, если значение функции ошибки модели равно 35 000? Да ничего, только то, что эта модель хуже, чем та, у которой ошибка 32 000.
Для того, чтобы значение было более понятно, метрики эффективности зачастую выражаются в каких-то определенных единицах измерения — чеще всего в натуральных или в процентах. Натуральные единицы — это единицы измерения целевой переменной. Допустим, целевая переменная выражается в рублях. То есть, мы предсказываем некоторую стоимость. В таком случае будет вполне понятно, если качество этой модели мы тоже выразим в рублях. Например, так: модель в среднем ошибается на 500 рублей. И сразу становится ясно, насколько эта модель применима на практике.
Еще одно важное отличие. Как мы сказали, требования к функции ошибки определяются алгоритмом оптимизации. Который, в свою очередь зависит от типа модели. У линейной регрессии будет один алгоритм (и одна функция ошибки), а у, например, решающего дерева — другой алгоритм и совершенно другая функция ошибки. Это в частности значит, что функцию ошибки невозможно применять для сравнения нескольких разных моделей, обученных на одной и той же задаче.
И вот для этого как раз и нужны метрики эффективности. Они не зависят от типа модели, а выбираются исходя из задачи и тех вопросов, ответы на которые мы хотим получить. Например, в одной задаче качество модели лучше измерять через среднеквадратическую логарифмическую ошибку, а в другой — через медианную ошибку. Как раз в этой главе мы посмотрим на примеры разных метрик эффективности, на их особенности и сферы применения.
Кстати, это еще означает, что в каждой конкретной задаче вы можете применять сразу несколько метрик эффективности, для более глубокого понимания работы модели. Зачастую так и поступают, ведь одна метрика не может дать полной информации о сильных и слабых сторонах модели. Тут исследователи ничем не ограничены. А вот функция ошибки обязательно должна быть только одна, ведь нельзя одновременно находить минимум сразу нескольких разных функций (на самом деле можно, но многокритериальная оптимизация — это гораздо сложнее и не используется для обучения моделей).
| Функция ошибки | Метрика эффективности |
|---|---|
| Используется для организации процесса обучения | Используется для оценки качества полученной модели |
| Используется для нахождения оптимума | Используется для сравнения моделей между собой |
| Должна быть быстро вычислимой | Должна быть понятной |
| Должна конструироваться исходя их типа модели | Должна выбираться исходя из задачи |
| Может быть только одна | Может быть несколько |
Еще раз определим, эффективность — это свойство модели машинного обучения давать предсказания значения целевой переменной, как можно ближе к реальным данным. Это самая главная характеристика модели. Но надо помнить, что исходя из задачи и ее условий, к моделям могут предъявляться и другие требования, как сказали бы в программной инженерии — нефункциональные. Типичный пример — скорость работы. Иногда маленький выигрыш в эффективности не стоит того, что модель стала работать в десять раз меньше. Другой пример — интерпретируемость модели. В некоторых областях важно не только сделать точное предсказание, но и иметь возможность обосновать его, провести анализ, выработать рекомендации по улучшению ситуации и так далее. Все эти нефункциональные требования — скорость обучения, скорость предсказания, надежность, робастность, федеративность, интерпретируемость — выходят за рамки данного пособия. Здесь мы сконцентрируемся на измерении именно эффективности модели.
Обратите внимание, что мы старательно избегаем употребления слова “точность” при описании качества работы модели. Хотя казалось бы, оно подходит как нельзя лучше. Дело в том, что “точностью” называют одну из метрик эффективности моделей классификации. Поэтому мы не хотим внести путаницу в термины.
Как мы говорили, метрики эффективности не зависят от самого типа модели. Для их вычисления обычно используется два вектора — вектор эмпирических значений целевой переменной (то есть тех, которые даны в датасете) и вектор теоретических значений (то есть тех, которые выдала модель). Естественно, эти вектора должны быть сопоставимы — на соответствующих местах должны быть значения целевой переменной, соответствующие одном у и тому же объекту. И, конечно, у них должна быть одинаковая длина. То есть метрика зависит от самих предсказаний, но не от модели, которая их выдала. Причем, большинство метрик устроены симметрично — если поменять местами эти два вектора, результат не изменится.
При рассмотрении метрик надо помнить следующее — чем выше эффективность модели, тем лучше. Но некоторые метрики устроены как измерение ошибки модели. В таком случае, конечно, тем ниже, тем лучше. Так что эффективность и ошибка модели — это по сути противоположные понятия. Так сложилось, что метрики регрессии чаще устроены именно как ошибки, а метрики классификации — как метрики именно эффективности. При использовании конкретной метрики на это надо обращать внимание.
Выводы:
- Метрики эффективности — это способ показать, насколько точно модель отражает реальный мир.
- Метрики эффективность должны выбираться исходя из задачи, которую решает модель.
- Функция ошибки и метрика эффективности — это разные вещи, к ним предъявляются разные требования.
- В задаче можно (и, зачастую, нужно) применять несколько метрик эффективности.
- Наряду с метриками эффективности есть и другие характеристики моделей — скорость обучения, скорость работы, надежность, робастность, интерпретируемость.
- Метрики эффективности вычисляются как правило из двух векторов — предсказанных (теоретических) значений целевой переменной и эмпирических (реальных) значений.
- Обычно метрики устроены таким образом, что чем выше значение, тем модель лучше.
Метрики эффективности для регрессии
Как мы говорили в предыдущей главе, метрики зависят от конкретной задачи. А все задачи обучения с учителем разделяются на регрессию и классификацию. Совершенно естественно, что метрики для регрессии и для классификации будут разными.
Метрики эффективности для регрессии оценивают отклонение (расстояние) между предсказанными значениями и реальными. Кажется, что это очевидно, но метрики эффективности классификации устроены по-другому. Предполагается, что чем меньше каждое конкретное отклонение, тем лучше. Разница между разными метриками в том, как учитывать индивидуальные отклонения в общей метрике и в том, как агрегировать ряд значений в один интегральный показатель.
Все метрики эффективности моделей регрессии покажутся вам знакомыми, если вы изучали математическую статистику, ведь именно статистические методы легли в основу измерения эффективности моделей машинного обучения. Причем, метрики эффективности — это лишь самые простые статистические показатели, которые можно использовать для анализа качества модели. При желании можно и нужно задействовать более мощные статистические методы исследования данных. Например, можно проанализировать вид распределения отклонений, и сделать из этого вывод о необходимость корректировки моделей. Но в 99% случаев можно обойтись простым вычислением одной или двух рассматриваемых ниже метрик.
Так как метрики эффективности позволяют интерпретировать оценку качества модели, они зачастую неявно сравнивают данную модель с некоторой тривиальной. Тривиальна модель — это очень простая, даже примитивная модель, которая выдает предсказания оценки целевой переменной абсолютно без оглядки на эффективность и вообще соответствие реальным данным. Тривиальной моделью может выступать, например, предсказание для любого объекта среднего значения целевой переменной из обучающей выборки. Такие тривиальные модели нужны, чтобы оценить, насколько данная модель лучше или хуже них.
Естественно, мы хотим получить модель, которая лучше тривиальной. Причем, у нас есть некоторый идеал — модель, которая никогда не ошибается, то есть чьи предсказания всегда совпадают с реальными значениями. Поэтому реальная модель может быть лучше тривиальной только до этого предела. У такой идеальной модели, говорят, 100% эффективность или нулевая ошибка.
Но надо помнить, что в задачах регрессии модель предсказывает непрерывное значение. Это значит, что величина отклонения может быть неограниченно большой. Так что не бывает нижнего предела качества модели. Модель регрессии может быть бесконечно далекой от идеала, бесконечно хуже даже тривиальной модели. Поэтому ошибки моделей регрессии не ограничиваются сверху (или, что то же самое, эффективность моделей регрессии не ограничивается снизу).
Поэтому в задачах регрессии
Выводы:
- Метрики эффективности для регрессий обычно анализируют отклонения предсказанных значений от реальных.
- Большинство метрик пришло в машинное обучение из математической статистики.
- Результаты работы модели можно исследовать более продвинутыми статистическими методами.
- Обычно метрики сравнивают данную модель с тривиальной — моделью, которая всегда предсказывает среднее реальное значение целевой переменной.
- Модель могут быть точны на 100%, но плохи они могут быть без ограничений.
Коэффициент детерминации (r-квадрат)
Те, кто раньше хотя бы немного изучал математическую статистику, без труда узнают первую метрику эффективности моделей регрессии. Это так называемый коэффициент детерминации. Это доля дисперсии (вариации) целевой переменной, объясненная данной моделью. Данная метрика вычисляется по такой формуле:
[R^2(y, hat{y}) = 1 — frac
{sum_{i=1}^n (y_i — hat{y_i})^2}
{sum_{i=1}^n (y_i — bar{y_i})^2}]
где
$y$ — вектор эмпирических (истинных) значений целевой переменной,
$hat{y}$ — вектор теоретических (предсказанных) значений целевой переменной,
$y_i$ — эмпирическое значение целевой переменной для $i$-го объекта,
$hat{y_i}$ — теоретическое значение целевой переменной для $i$-го объекта,
$bar{y_i}$ — среднее из эмпирических значений целевой переменной для $i$-го объекта.
Если модель всегда предсказывает идеально (то есть ее предсказания всегда совпадают с реальностью, другими словами, теоретические значения — с эмпирическими), то числитель дроби в формуле будет равен 0, а значит, вся метрика будет равна 1. Если же мы рассмотрим тривиальную модель, которая всегда предсказывает среднее значение, то числитель будет равен знаменателю, дробь будет равна 1, а метрика — 0. Если модель хуже идеальной, но лучше тривиальной, то метрика будет в диапазоне от 0 до 1, причем чем ближе к 1 — тем лучше.
Если же модель предсказывает такие значения, что отклонения их от теоретических получаются больше, чем от среднего значения, то числитель будет больше знаменателя, а значит, что метрика будет принимать отрицательные значения. Запомните, что отрицательные значения коэффициента детерминации означают, что модель хуже, чем тривиальная.
В целом эта метрика показывает силу линейной связи между двумя случайными величинами. В нашем случае этими величинами выступают теоретические и эмпирические значения целевой переменной (то есть предсказанные и реальные). Если модель дает точные предсказания, то будет наблюдаться сильная связь (зависимость) между теоретическим значением и реальным, то есть высокая детерминация, близкая к 1. Если эе модель дает случайные предсказания, никак не связанные с реальными значениями, то связь будет отсутствовать.
Причем так как нас интересует, насколько значения совпадают, нам достаточно использовать именно линейную связь. Ведь когда мы оцениваем связь, например, одного из факторов в целевой переменной, то связь может быть нелинейной, и линейный коэффициент детерминации ее не покажет, то есть пропустит. Но в данному случае это не важно, так как наличие нелинейной связи означает, что предсказанные значения все-таки отклоняются от реальных. Такую линейную связь можно увидеть на графике, если построить диаграмму рассеяния между теоретическими и эмпирическими значениями, вот так:
1
2
3
4
5
6
from sklearn.linear_model import LinearRegression
reg = LinearRegression().fit(X, Y)
Y_ = reg.predict(X)
plt.scatter(Y, Y_)
plt.plot(Y, Y)
Здесь мы еще строим прямую $y = y$. Она нужна только для удобства. Вот как может выглядеть этот график:
Здесь мы видим, что точки немного отклоняются от центральной линии, но в целом ей следуют. Такая картина характерна для высокого коэффициента детерминации. А вот как может выглядеть менее точная модель:
И в целом, чем точки ближе к центральной линии, тем лучше модель и тем ближе коэффициент детерминации к 1.
В англоязычной литература эта метрика называется $R^2$, так как в определенных случаях она равна квадрату коэффициента корреляции. Пусть это название не вводит вас в заблуждение. Некоторые думаю, что раз метрика в квадрате, то она не может быть отрицательной. Это лишь условное название.
Пару слов об использовании метрик эффективности в библиотеке sklearn. Именно коэффициент детерминации чаще всего используется как метрика по умолчанию, которую можно посмотреть при помощи метода score() у модели регрессии. Обратите внимание, что этот метод принимает на вход саму обучающую выборку. Это сделано для единообразия с методами наподобие fit().
Но более универсально будет использовать эту метрику независимо от модели. Все метрики эффективности собраны в отдельный пакет metrics. Данная метрика называется r2_score. Обратите внимание, что при использовании этой функции ей надо передавать два вектора целевой переменной — сначала эмпирический, а вторым аргументом — теоретический.
1
2
3
4
5
6
7
8
from sklearn.metrics import r2_score
def r2(y, y_):
return 1 - ((y - y_)**2).sum() / ((y - y.mean())**2).sum()
print(reg.score(X, Y))
print(r2_score(Y, Y_))
print(r2(Y, Y_))
В данном коде мы еще реализовали самостоятельный расчет данной метрики, чтобы пояснить применение формулы выше. Можете самостоятельно убедиться, что три этих вызова напечатают одинаковые значения.
Коэффициент детерминации, или $R^2$ — это одна из немногих метрик эффективности для моделей регрессии, значение которой чем больше, тем лучше. Почти все остальные измеряют именно ошибку, что мы и увидим ниже. Еще это одна из немногих несимметричных метрик. Ведь если в формуле поменять теоретические и эмпирические значения, ее смысл и значение могут поменяться. Поэтому при использовании этой метрики нужно обязательно следить за порядком передачи аргументов.
При использовании этой метрики есть один небольшой подводный камень. Так как в знаменатели у этой формулы стоит вариация реального значения целевой переменной, важно следить, чтобы эта вариация присутствовала. Ведь если реальное значение целевой переменной будет одинаковым для всех объектов выборки, то вариация этой переменной будет равна 0. А значит, метрика будет не определена. Причем это единственная причина, почему эта метрика может быть неопределена. Надо понимать, что отсутствие вариации целевой переменной ставит под сомнение вообще целесообразность машинного обучения и моделирования в целом. Ведь что нам предсказывать если $y$ всегда один и тот же? С другой стороны, такая ситуация может случиться, например, при случайном разбиении выборки на обучающую и тестовую. Но об этом мы поговорим дальше.
Выводы:
- Коэффициент детерминации показывает силу связи между двумя случайными величинами.
- Если модель всегда предсказывает точно, метрика равна 1. Для тривиальной модели — 0.
- Значение метрики может быть отрицательно, если модель предсказывает хуже, чем тривиальная.
- Это одна из немногих несимметричных метрик эффективности.
- Эта метрика не определена, если $y=const$. Надо следить, чтобы в выборке присутствовали разные значения целевой переменной.
Средняя абсолютная ошибка (MAE)
Коэффициент детерминации — не единственная возможная характеристика эффективности моделей регрессии. Иногда полезно оценить отклонения предсказаний от истинных значений более явно. Как раз для этого служат сразу несколько метрик ошибок моделей регрессии. Самая простая из них — средняя абсолютная ошибка (mean absolute error, MAE). Она вычисляется по формуле:
[MAE(y, _hat{y}) = frac{1}{n} sum_{i=0}^{n-1} |y_i — hat{y_i}|]
Данная метрика действительно очень проста: это средняя величина разницы между предсказанными и реальными значениями целевой переменной. Причем эта разница берется по модулю, чтобы компенсировать возможные отрицательные отклонения. Мы уже рассматривали похожую функцию, когда говорили о конструировании функции ошибки для градиентного спуска. Но тогда мы отмели использование абсолютного значения, так как эта функция не везде дифференцируема. Но вот для метрики эффективности такого требования нет и MAE вполне можно использовать.
Если модель предсказывает идеально, то, естественно, все отклонения равны 0 и MAE в целом равна нулю. Но эта метрика не учитывает явно сравнение с тривиальной моделью — она просто тем хуже, чем больше. Ниже нуля она быть, конечно, не может.
Данная метрика выражается в натуральных единицах и имеет очень простой и понятный смысл — средняя ошибка модели. Степень применимости модели в таком случае можно очень просто понять исходя из предметной области. Например, наша модель ошибается в среднем на 500 рублей. Хорошо это или плохо? Зависит от размерности исходных данных. Если мы предсказываем цены на недвижимость — то модель прекрасно справляется с задачей. Если же мы моделируем цены на спички — то такая модель скорее всего очень неэффективна.
Использование данной метрики в пакете sklearn очень похоже на любую другую метрику, меняется только название:
1
2
3
4
5
>>> from sklearn.metrics import mean_absolute_error
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> mean_absolute_error(y_true, y_pred)
0.5
Выводы:
- MAE показывает среднее абсолютное отклонение предсказанных значений от реальных.
- Чем выше значение MAE, тем модель хуже. У идеальной модели $MAE=0$
- MAE очень легко интерпретировать — на сколько в среднем ошибается модель.
Средний квадрат ошибки (MSE)
Средний квадрат ошибки (mean squared error, MSE) очень похож на предыдущую метрику, но вместо абсолютного значения (модуля) используется квадрат:
[MSE(y, _hat{y}) = frac{1}{n} sum_{i=0}^{n-1} (y_i — hat{y_i})^2]
Граничные случаи у этой метрики такие же, как у предыдущей — 0 у идеальной модели, а в остальном — чем больше, тем хуже. MSE у тривиальной модели будет равна дисперсии целевой переменной. Но это не то, чтобы очень полезно на практике.
Эта метрика используется во многих моделях регрессии как функция ошибки. Но вот как метрику эффективности ее применяют довольно редко. Дело в ее интерпретируемости. Ведь она измеряется в квадратах натуральной величины. А какой физический смысл имеют, например, рубли в квадрате? На самом деле никакого. Поэтому несмотря на то, что математически MAE и MSE в общем-то эквивалентны, первая более проста и понятна, и используется гораздо чаще.
Единственное существенное отличие данной метрики от предыдущей состоит в том, что она чуть больший “вес” в общей ошибке придает большим значениям отклонений. То есть чем больше значение отклонения, тем сильнее оно будет вкладываться в значение MSE. Это иногда бывает полезно, когда исходя из задачи стоит штрафовать сильные отклонения предсказанных значений от реальных. Но с другой стороны это свойство делает эту метрику чувствительной к аномалиям.
Пример расчета метрики MSE:
1
2
3
4
5
>>> from sklearn.metrics import mean_squared_error
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> mean_squared_error(y_true, y_pred, squared=False)
0.612...
Выводы:
- MAE показывает средний квадрат отклонений предсказанных значений от реальных.
- Чем выше значение MSE, тем модель хуже. У идеальной модели $MSE=0$
- MSE больше учитывает сильные отклонения, но хуже интерпретируется, чем MAE.
Среднеквадратичная ошибка (RMSE)
Если главная проблема метрики MSE в том, что она измеряется в квадратах натуральных величин, что что будет, если мы возьмем от нее квадратный корень? Тогда мы получим среднеквадратичную ошибку (root mean squared error, RMSE):
[RMSE(y, _hat{y}) = sqrt{frac{1}{n} sum_{i=0}^{n-1} (y_i — hat{y_i})^2}]
Использование данной метрики достаточно привычно при статистическом анализе данных. Однако, для интерпретации результатов машинного обучения она имеет те же недостатки, что и MSE. Главный из них — чувствительность к аномалиям. Поэтому при интерпретации эффективности моделей регрессии чаще рекомендуется применять метрику MAE.
Пример использования:
1
2
3
4
5
>>> from sklearn.metrics import mean_squared_error
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> mean_squared_error(y_true, y_pred)
0.375
Выводы:
- RMSE — это по сути корень из MSE. Выражается в тех же единицах, что и целевая переменная.
- Чаще применяется при статистическом анализа данных.
- Данная метрика очень чувствительна к аномалиям и выбросам.
Среднеквадратичная логарифмическая ошибка (MSLE)
Еще одна довольно редкая метрика — среднеквадратическая логарифмическая ошибка (mean squared logarithmic error, MSLE). Она очень похожа на MSE, но квадрат вычисляется не от самих отклонений, а от разницы логарифмов (про то, зачем там +1 поговорим позднее):
[MSLE(y, _hat{y}) = frac{1}{n} sum_{i=0}^{n-1} (
ln(1 + y_i) — ln(1 + hat{y_i})
)^2]
Данная материка имеет специфическую, но довольно полезную сферу применения. Она применяется в тех случаях, когда значения целевой переменной простираются на несколько порядков величины. Например, если мы анализируем доходы физических лиц, они могут измеряться от тысяч до сотен миллионов. Понятно, что при использовании более привычных метрик, таких как MSE, RMSE и даже MAE, отклонения в больших значениях, даже небольшие относительно, будут полностью доминировать над отклонениями в малых значениях.
Это приведет к тому, что оценка моделей в подобных задачах классическими метриками будет давать преимущество моделям, которые более точны в одной части выборки, но почти не будут учитывать ошибки в других частях выборки. Это может привести к несправедливой оценке моделей. А вот использование логарифма поможет сгладить это противоречие.
Чаще всего, величины с таким больших размахом, что имеет смысл использовать логарифмическую ошибку, возникают в тех задачах, которые моделируют некоторые естественные процессы, характеризующиеся экспоненциальным ростом. Например, моделирование популяций, эпидемий, финансов. Такие процессы часто порождают величины, распределенные по экспоненциальному закону. А они чаще всего имеют область значений от нуля до плюс бесконечности, то есть иногда могут обращаться в ноль.
Проблема в том, что логарифм от нуля не определен. Именно поэтому в формуле данной метрики присутствует +1. Это искусственный способ избежать неопределенности. Конечно, если вы имеете дело с величиной, которая может принимать значение -1, то у вас опять будут проблемы. Но на практике такие особые распределения не встречаются почти никогда.
Использование данной метрике в коде полностью аналогично другим:
1
2
3
4
5
>>> from sklearn.metrics import mean_squared_log_error
>>> y_true = [3, 5, 2.5, 7]
>>> y_pred = [2.5, 5, 4, 8]
>>> mean_squared_log_error(y_true, y_pred)
0.039...
Выводы:
- MSLE это среднее отклонение логарифмов реальных и предсказанных данных.
- Так же, идеальная модель имеет $MSLE = 0$.
- Данная метрика используется, когда целевая переменная простирается на несколько порядков величины.
- Еще эта метрика может быть полезна, если моделируется процесс в экспоненциальным ростом.
Среднее процентное отклонение (MAPE)
Все метрики, которые мы рассматривали до этого рассчитывали абсолютную величину отклонения. Но ведь отклонение в 5 единиц при истинном значении 5 и при значении в 100 — разные вещи. В первом случае мы имеем ошибку в 100%, а во втором — только в 5%. Очевидно, что первый и второй случай должны по-разному учитываться в ошибке. Для этого придумана средняя абсолютная процентная ошибка (mean absolute percentage error, MAPE). В ней каждое отклонение оценивается в процентах от истинного значения целевой переменной:
[MAPE(y, _hat{y}) = frac{1}{n} sum_{i=0}^{n-1}
frac{|y_i — hat{y_i}|}{max(epsilon, |y_i|)}]
Эта метрика имеет одно критическое преимущество над остальными — с ее помощью можно сравнивать эффективность моделей на разных обучающих выборках. Ведь если мы возьмем классические метрики (например, MAE), то размер отклонений будет очевидно зависеть от самих данных. А в двух разных выборках и средняя величина скорее всего будет разная. Поэтому метрики MAE, MSE, RMSE, MSLE не сопоставимы при сравнении предсказаний, сделанных на разных выборках.
А вот по метрике MAPE можно сравнивать разные модели, которые были обучены на разных данных. Это очень полезно, например, в научных публикациях, где метрика MAPE (и ее вариации) практически обязательны для описания эффективности моделей регрессии.Ведь если одна модель ошибается в среднем на 3,9%, а другая — на 3,5%, очевидно, что вторая более точна. А вот если оперировать той же MAE, так сказать нельзя. Ведь если одна модель ошибается в среднем на 500 рублей, а вторая — на 490, очевидно ли, что вторая лучше? Может, она даже хуже, просто в исходных данных величина целевой переменной во втором случае была чуть меньше.
При этом у метрики MAPE есть пара недостатков. Во-первых, она не определена, если истинное значение целевой переменной равно 0. Именно для преодоления этого в знаменателе формулы этой метрики присутствует $max(epsilon, |y_i|)$. $epsilon$ — это некоторое очень маленькое значение. Оно нужно только для того, чтобы избежать деления на ноль. Это, конечно, настоящий математический костыль, но позволяет без опаски применять эту метрику на практике.
Во-вторых, данная метрика дает преимущество более низким предсказаниям. Ведь если предсказание ниже, чем реальное значение, процентное отклонение может быть от 0% до 100%. В это же время если предсказание выше реального, то верхней границы нет, предсказание может быть больше и на 200%, и на 1000%.
В-третьих, эта метрика несимметрична. Ведь в этой формуле $y$ и $hat{y}$ не взаимозаменяемы. Это не большая проблема и может быть исправлена использованием симметричного варианта этой метрики, который называется SMAPE (symmetric mean absolute percentage error):
[MAPE(y, _hat{y}) = frac{1}{n} sum_{i=0}^{n-1}
frac{|y_i — hat{y_i}|}{max(epsilon, (|hat{y_i}|, |y_i|) / 2)}]
В русскоязычной литературе данная метрика часто называется относительной ошибкой, так как она учитывает отклонение относительно целевого значения. В английском названии метрики она называется абсолютной. Тут нет никакого противоречия, так как “абсолютный” здесь значит просто взятие по модулю.
С точки зрения использования в коде, все полностью аналогично:
1
2
3
4
5
>>> from sklearn.metrics import mean_absolute_percentage_error
>>> y_true = [1, 10, 1e6]
>>> y_pred = [0.9, 15, 1.2e6]
>>> mean_absolute_percentage_error(y_true, y_pred)
0.2666...
Выводы:
- Идея этой метрики — это чувствительность к относительным отклонениям.
- Данная модель выражается в процентах и имеет хорошую интерпретируемость.
- Идеальная модель имеет $MAPE = 0$. Верхний предел — не ограничен.
- Данная метрика отдает предпочтение предсказанию меньших значений.
Абсолютная медианная ошибка
Практически во всех ранее рассмотренных метриках используется среднее арифметическое для агрегации частных отклонений в общую величину ошибки. Иногда это может быть не очень уместно, если в выборке присутствует очень неравномерное распределение по целевой переменной. В таких случаях может быть целесообразно использование медианной ошибки:
[MedAE(y, _hat{y}) = frac{1}{n} median_{i=0}^{n-1}
|y_i — hat{y_i}|]
Эта метрика полностью аналогична MAE за одним исключением: вместо среднего арифметического подсчитывается медианное значение. Медиана — это такое значение в выборке, больше которого и меньше которого примерно половина объектов выборки (с точностью до одного объекта).
Эта метрика чаще всего применяется при анализе демографических и экономических данных. Ее особенность в том, что она не так чувствительна к выбросам и аномальным значениям, ведь они практически не влияют на медианное значение выборки, что делает эту метрику более надежной и робастной, чем абсолютная ошибка.
Пример использования:
1
2
3
4
5
>>> from sklearn.metrics import median_absolute_error
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> median_absolute_error(y_true, y_pred)
0.5
Выводы:
- Медианная абсолютная ошибка похожа на среднюю абсолютную, но более устойчива к аномалиям.
- Применяется в задачах, когда известно, что в данных присутствуют выбросы, аномальные , непоказательные значения.
- Эта метрика более робастная, нежели MAE.
Максимальная ошибка
Еще одна достаточно экзотическая, но очень простая метрика эффективности регрессии — максимальная ошибка:
[ME(y, _hat{y}) = max_{i=0}^{n-1}
|y_i — hat{y_i}|]
Как следует из названия, это просто величина максимального абсолютного отклонения предсказанных значений от теоретических. Особенность этой метрики в том, что она вообще не характеризует распределение отклонений в целом. Поэтому она практически никогда не применяется самостоятельно, в качестве единственной метрики.
Эта метрика именно вспомогательная. В сочетании с другими метриками, она может дополнительно охарактеризовать, насколько сильно модель может ошибаться в самом худшем случае. Опять же, в зависимости от задачи, это может быть важно. В некоторых задачах модель, которая в среднем ошибается пусть чуть больше, но при этом не допускает очень больших “промахов”, может быть предпочтительнее, чем более точная модель в среднем, но у которой встречаются сильные отклонения.
Применение этой метрики та же просто, как и других:
1
2
3
4
5
>>> from sklearn.metrics import max_error
>>> y_true = [3, 2, 7, 1]
>>> y_pred = [9, 2, 7, 1]
>>> max_error(y_true, y_pred)
6
Выводы:
- Максимальная ошибка показывает наихудший случай предсказания модели.
- В некоторых задачах важно, чтобы модель не ошибалась сильно, а небольшие отклонения не критичны.
- Зачастую эта метрика используется как вспомогательная совместно с другими.
Метрики эффективности для классификации
Приступим к рассмотрению метрик эффективности, которые применяются для оценки моделей классификации. Для начала ответим на вопрос, почему для них нельзя использовать те метрики, которые мы уже рассмотрели в предыдущей части? Дело в том, что метрики эффективности регрессии так или иначе оценивают расстояние от предсказанного значения до реального. Это подразумевает, что в значениях целевой переменной существует определенный порядок. Формально говоря, предполагается, что целевая переменная измеряется по относительной шкале. Это значит, что разница между значениями имеет какой-то смысл. Например, если мы ошиблись в предполагаемой цене товара на 10 рублей, это лучше, чем ошибка на 20 рублей. Причем, можно сказать, что это в два раза лучше.
Но вот целевые переменные, которые существуют в задачах классификации обычно не обладают таким свойством. Да, метки классов часто обозначают числами (класс 0, класс 1, класс 5 и так далее). И мы используем эти числа в качестве значения переменных в программе. Но это ничего не значит. Представим объект, принадлежащий 0 классу, что бы этот класс не значил. Допустим, мы предсказали 1 класс. Было бы хуже, если бы мы предсказали 2 класс. Можно ли сказать, что во втором случае модель ошиблась в два раза сильнее? В общем случае, нельзя. Что в первом, что во втором случае модель просто ошиблась. Имеет значение только разница между правильным предсказанием и неправильным. Отклонение в задачах классификации не играет роли.
Поэтому метрики эффективности для классификации оценивают количество правильно и неправильно классифицированных (иногда еще говорят, распознанных) объектов. При этом разные метрики, как мы увидим, концентрируются на разных соотношениях этих количеств, особенно в случае, когда классов больше двух, то есть имеет место задача множественной классификации.
Причем метрики эффективности классификации тоже нельзя применять для оценки регрессионных моделей. Дело в том, что в задачах регрессии почти никогда не встречается полное совпадение предсказанного и реального значения. Так как мы работам с непрерывным континуумом значений, вероятность такого совпадения равна, буквально, нулю. Поэтому по метрикам для классификации практически любая регрессионная модель будет иметь нулевую эффективность, даже очень хорошая и точная модель. Именно потому, что для метрик классификации даже самая небольшая ошибка уже считается как промах.
Как мы говорили ранее,для оценки конкретной модели можно использовать несколько метрик одновременно. Это хорошая практика для задач регрессии, но для классификации — это практически необходимость. Дело в том, что метрики классификации гораздо легче “обмануть” с помощью тривиальных моделей, особенно в случае несбалансированных классов (об этом мы поговорим чуть позже). Тривиальной моделью в задачах классификации может выступать модель, которая предсказывает случайный класс (такая используется чаще всего), либо которая предсказывает всегда какой-то определенный класс.
Надо обратить внимание, что по многим метрикам, ожидаемая эффективность моделей классификации сильно зависит от количества классов в задаче. Чем больше классов, тем на меньшую эффективность в среднем можно рассчитывать.Поэтому метрики эффективности классификации не позволяют сопоставить задачи, состоящие из разного количества классов. Это следует помнить при анализе моделей. Если точность бинарной классификации составляет 50%, это значит, что модель работает не лучше случайного угадывания. Но в модели множественной классификации из, допустим, 10 000 классов, точность 50% — это существенно лучше случайного гадания.
Еще обратим внимание, что некоторые метрики учитывают только само предсказание, в то время, как другие — степень уверенности модели в предсказании. Вообще, все модели классификации разделяются на логические и метрические. Логические методы классификации выдают конкретное значение класса, без дополнительной информации. Типичные примеры — дерево решений, метод ближайших соседей. Метрические же методы выдают степень уверенности (принадлежности) объекта к одному или, чаще, ко всем классам. Так, например, работает метод логистической регрессии в сочетании с алгоритмом “один против всех”. Так вот, в зависимости, от того, какую модель классификации вы используете, вам могут быть доступны разные метрики. Те метрики, которые оценивают эффективность классификации в зависимости от выбранной величины порога не могут работать с логическими методами. Поэтому, например, нет смысла строить PR-кривую для метода ближайших соседей. Остальные метрики, которые не используют порог, могут работать с любыми методами классификации.
Выводы:
- Метрики эффективности классификации подсчитывают количество правильно распознанных объектов.
- В задачах классификации почти всегда надо применять несколько метрик одновременно.
- Тривиальной моделью в задачах классификации считается та, которая предсказывает случайный класс, либо самый популярный класс.
- Качество бинарной классификации при прочих равных почти всегда будет сильно выше, чем для множественной.
- Вообще, чем больше в задаче классов, тем ниже ожидаемые значения эффективности.
- Некоторые метрики работают с метрическими методами, другие — со всеми.
Доля правильных ответов (accuracy)
Если попробовать самостоятельно придумать способ оценить качество модели классификации, ничего не зная о существующих метриках, скорее всего получится именно метрика точности (accuracy). Это самая простая и естественная метрика эффективности классификации. Она подсчитывается как количество объектов в выборке, которые были классифицированы правильно (то есть, для которых теоретическое и эмпирическое значение метки класса — целевой переменной — совпадает), разделенное на общее количество объектов выборки. Вот формула для вычисления точности классификации:
[acc(y, hat{y}) = frac{1}{n} sum_{i=0}^{n} 1(hat{y_i} = y_i)]
В этой формуле используется так называемая индикаторная функция $1()$. Эта функция равна 1 тогда, когда ее аргумент — истинное выражение, и 0 — если ложное. В данном случае она равна единице для всех объектов, у которых предсказанное значение равно реальному ($hat{y_i} = y_i$). Суммируя по всем объектам мы получим количество объектов, классифицированных верно. Перед суммой стоит множитель $frac{1}{n}$, где $n$ — количество объектов в выборке. То есть в итоге мы получаем долю правильных ответов исследуемой модели.
Значение данной метрики может быть выражено в долях единицы, либо в процентах, домножив значение на 100%. Чем выше значение accuracy, тем лучше модель классифицирует выборку, то есть тем лучше ответы модели соответствуют значениям целевой переменной, присутствующим в выборке. Если модель всегда дает правильные предсказания, то ее accuracy будет равн 1 (или 100%). Худшая модель, которая всегда предсказывает неверно будет иметь accuracy, равную нулю, причем это нижняя граница, хуже быть не может.
В дальнейшем, для обозначения названий метрик эффективности я буду использовать именно английские названия — accuracy, precision, recall. У каждого из этих слов есть перевод на русский, но так случилось, что в русскоязычных терминах существует путаница. Дело в том, что и accuracy и precision чаще всего переводятся словом “точность”. А это разные метрики, имеющие разный смысл и разные формулы. Accuracy еще называют “правильность”, precision — “прецизионность”. Причем у последнего термина есть несколько другое значение в метрологии. Поэтому, пока будем обозначать эти метрики изначальными названиями.
А вот accuracy тривиальной модели будет как раз зависеть от количества классов. Если мы имеем дело с бинарной классификацией, то модель будет ошибаться примерно в половине случаев. То есть ее accuracy будет 0,5. В общем же случае, если есть $m$ классов, то тривиальная модель, которая предсказывает случайный класс будет иметь accuracy в среднем около $frac{1}{m}$.
Но это в случае, если в выборке объекты разных классов встречаются примерно поровну. В реальности же часто встречаются несбалансированные выборки, в которых распределение объектов по классам очень неравномерно. Например, может быть такое, что объектов одного класса в десять раз больше, чем другого. В таком случае, accuracy тривиальной модели может быть как выше, так и ниже $1/m$. Вообще, метрика accuracy очень чувствительна к соотношению классов в выборке. И именно поэтому мы рассматриваем другие способы оценки качества моделей классификации.
Использование метрики accuracy в библиотеке sklearn ничем принципиальным не отличается от использования других численных метрик эффективности:
1
2
3
4
5
6
>>> import numpy as np
>>> from sklearn.metrics import accuracy_score
>>> y_pred = [0, 2, 1, 3]
>>> y_true = [0, 1, 2, 3]
>>> accuracy_score(y_true, y_pred)
0.5
В данном примере в задаче 4 класса (0, 1, 2, 3) и столько же объектов, по одному на каждый класс. Модель правильно классифицировала первый и третий объект, то есть половину. Поэтому ее accuracy составляет 0,5 или 50%.
Выводы:
- Точность (accuracy) — самая простая метрика качества классификации, доля правильных ответов.
- Может быть выражена в процентах и в долях единицы.
- Идеальная модель дает точность 1.0, тривиальная — 0.5, самая худшая — 0.0.
- Тривиальная модель в множественной сбалансированной задаче классификации дает точность 1/m.
- Метрика точности очень чувствительная к несбалансированности классов.
Метрики классификации для неравных классов (precision, recall, F1)
Как мы говорили ранее, метрика accuracy может быть чувствительна к несбалансированности классов. Рассмотрим типичный пример — диагностика заболевания. Допустим, в случайной выборке людей заболевание встречается один раз на 100 человек. То есть в выборке у нас может быть всего 1% объектов, принадлежащих положительному классу и 99% — отрицательному, то есть почти в 100 раз больше. Какая accuracy будет у абсолютно тривиальной модели, которая всегда предсказывает отрицательный класс? Такая модель будет права в 99% случаев и ошибаться только в 1%. То есть иметь accuracy 0,99. Естественно, ценность такой модели минимальна, несмотря на высокий показатель метрики. Поэтому в случае с сильно несбалансированными классами метрика accuracy не то, чтобы неверна, она непоказательна, то есть не дает хорошего представления о качественных характеристиках модели.
Для более полного описания модели используется ряд других метрик. Для того, чтобы понять, как они устроены и что показывают нужно разобраться с понятием ошибок первого и второго рода. Пока будем рассматривать случай бинарной классификации, а о том, как эти метрики обобщаются на множественные задачи, поговорим позднее. Итак, у нас есть задача бинарной классификации, объекты положительного и отрицательного класса. Идеальным примером для этого будет все та же медицинская диагностика.
По отношению к модели бинарной классификации все объекты выборки можно разделить на четыре непересекающихся множества. Истинноположительные (true positive, TP) — это те объекты, которые отнесены моделью к положительному классу и действительно ему принадлежат. Истинноотрицательные (true negative, TN) — соответственно те, которые правильно распознаны моделью как принадлежащие отрицательному классу. Ложноположительные объекты (FP, false positive) — это те, которые модель распознала как положительные, хотя на самом деле они отрицательные. В математической статистике такая ситуация называется ошибкой первого рода. И, наконец, ложноотрицательные значения (false negative, FN) — это те, которые ошибочно отнесены моделью к отрицательному классу, хотя на самом деле они принадлежат положительному.
В примере с медицинско диагностикой, ложноположительные объекты или ошибки первого рода — это здоровые пациенты, которых при диагностике ошибочно назвали больными. Ложноотрицательные, или ошибки второго рода, — это больные пациенты, которых диагностическая модель “пропустила”, ошибочно приняв за здоровых. Очевидно, что в этой задаче, как и во многих других, ошибки первого и второго рода не равнозначны. В медицинской диагностике, например, гораздо важнее распознать всех здоровых пациентов, то есть не допустить ложноотрицательных объектов или ошибок второго рода. Ошибки же первого рода, или ложноположительные предсказания, тоже нежелательны, но значительно меньше, чем ложноотрицательные.
Так вот, метрика accuracy учитывает и те и другие ошибки одинаково, абсолютно симметрично. В терминах наших четырех классов она может выражаться такой формулой:
[A = frac{TP + TN}{TP + TN + FP + FN}]
Обратите внимание, что если в модели переименовать положительный класс в отрицательный и наоборот, то это никак не повлияет на accuracy. Так вот, в зависимости от решаемой задачи, нам может быть необходимо воспользоваться другими метриками. Вообще, их существует большое количество, но на практике чаще других применяются метрики precision и recall.
Precision (чаще переводится как “точность”, “прецизионность”) — это доля объектов, плавильно распознанных как положительные из всех, распознанных как положительные. Считается этот показатель по следующей формуле: $P = frac{TP}{TP + FP}$. Как можно видеть, precision будет равен 1, если модель не делает ошибок первого рода, то есть не дает ложноположительных предсказаний. Причем ошибки второго рода (ложноотрицательные) вообще не влияют на величину precision, так как эта метрика рассматривает только объекты, отнесенные моделью к положительным.
Precision характеризует способность модели отличать положительный класс от отрицательного, не делать ложноположительных предсказаний. Ведь если мы будем всегда предсказывать отрицательный класс, precision будет не определен. А вот если модель будет всегда предсказывать положительный класс, то precision будет равен доли объектов этого класса в выборке. В нашем примере с медицинской диагностикой, модель, всех пациентов записывающая в больные даст precision всего 0,01.
Метрика recall (обычно переводится как “полнота” или “правильность”) — это доля положительных объектов выборки, распознанных моделью. То есть это отношение все тех же истинноположительных объектов к числу всех положительных объектов выборки: $R = frac{TP}{TP + FN}$. Recall будет равен 1 только в том случае, если модель не делает ошибок второго рода, то есть не дает ложноотрицательных предсказаний. А вот ошибки первого рода (ложноположительные) не влияют на эту метрику, так как она рассматривает только объекты, которые на самом деле принадлежат положительному классу.
Recall характеризует способность модели обнаруживать все объекты положительного класса. Если мы будем всегда предсказывать отрицательный класс, то данная метрика будет равна 0, а если всегда положительный — то 1. Метрика Recall еще называется полнотой, так как она характеризует полноту распознавания положительного класса моделью.
В примере с медицинской диагностикой нам гораздо важнее, как мы говорили, не делать ложноотрицательных предсказаний. Поэтому метрика recall будет для нас важнее, чем precision и даже accuracy. Однако, как видно из примеров, каждый из этих метрик легко можно максимизировать довольно тривиальной моделью. Если мы будет ориентироваться на recall, то наилучшей моделью будет считаться та, которая всегда предсказывает положительный класс. Если только на precision — то “выиграет” модель, которая всегда предсказывает наоборот, положительный. А если брать в расчет только accuracy, то при сильно несбалансированных классах модель, предсказывающая самый популярный класс. Поэтому эти метрики нелья использовать по отдельности, только сразу как минимум две из них.
Так как метрики precision и recall почти всегда используются совместно, часто возникает ситуация, когда есть две модели, у одной из которых выше precision, а у второй — recall. Возникает вопрос, как выбрать лучшую? Для такого случая можно посчитать среднее значение. Но для этих метрик больше подойдет среднее не арифметическое, а гармоническое, ведь оно равно 0, если хотя бы одно число равно 0. Эта метрика называется $F_1$:
[F_1 = frac{2 P R}{P + R} = frac{2 TP}{2 TP + FP + FN}]
Эта метрика полезна, если нужно одно число, которое в себе объединяет и precision и recall. Но эта формула подразумевает, что нам одинаково важны и то и другое. А как мы заметили раньше, часто одна из этих метрик важнее. Поэтому иногда используют обобщение метрики $F_1$, так называемое семейство F-метрик:
[F_{beta} = (1 + beta^2) frac{P R}{beta^2 P + R}]
Эта метрика имеет параметр $beta > 0$, который определяет, во сколько раз recall важнее precision. Если этот параметр больше единицы, то метрика будет полагать recall более важным. А если меньше — то важнее будет precision. Если же $beta = 1$, то мы получим уже известную нам метрику $F_1$. Все метрики из F-семейства измеряются от 0 до 1, причем чем значение больше, тем модель лучше.
1
2
3
4
5
6
7
8
9
>>> from sklearn import metrics
>>> y_pred = [0, 1, 0, 0]
>>> y_true = [0, 1, 0, 1]
>>> metrics.precision_score(y_true, y_pred)
1.0
>>> metrics.recall_score(y_true, y_pred)
0.5
>>> metrics.f1_score(y_true, y_pred)
0.66...
Выводы:
- Если классы в задаче не сбалансированы, то метрика точности не дает полного представления о качестве работы моделей.
- Для бинарной классификации подсчитывается количество истинно положительных, истинно отрицательных, ложно положительных и ложно отрицательных объектов.
- Precision — доля истинно положительных объектов во всех, распознанных как положительные.
- Precision характеризует способность модели не помечать положительные объекты как отрицательные (не делать ложно положительных прогнозов).
- Recall — для истинно положительных объектов во всех положительных.
- Recall характеризует способность модели выявлять все положительные объекты (не делать ложно отрицательных прогнозов).
- F1 — среднее гармоническое между этими двумя метриками. F1 — это частный случай. Вообще, семейство F-метрик — это взвешенное среднее гармоническое.
- Часто используют все вместе для более полной характеристики модели.
Матрица классификации
Матрица классификации — это не метрика сама по себе, но очень удобный способ “заглянуть” внутрь модели и посмотреть, насколько хорошо она классифицирует какую-то выборку объектов. Особенно удобна эта матрица в задачах множественной классификации, когда из-за большого количества классов численные метрики не всегда наглядно показывают, какие объекты к каким классам относятся.
С использованием библиотеки sklearn матрица классификации может быть сформирована всего одной строчкой кода:
1
2
3
4
5
6
7
>>> from sklearn.metrics import confusion_matrix
>>> y_true = [2, 0, 2, 2, 0, 1]
>>> y_pred = [0, 0, 2, 2, 0, 2]
>>> confusion_matrix(y_true, y_pred)
array([[2, 0, 0],
[0, 0, 1],
[1, 0, 2]])
В этой матрице по строкам располагаются истинные значения целевой переменной, то есть действительные значения классов. По столбцам же отмечены предсказанные классы. В самой матрице на пересечении строки и столбца отмечается число объектов, которые принадлежат данному действительному классу, но моделью были распознаны как объекты данного предсказанного класса.
Естественно, элементы, располагающиеся на главной диагонали, показывают объекты, которые были правильно распознаны моделью. Элементы же вне этой диагонали — это ошибки классификации. Поэтому чем лучше модель, тем выше должны быть значения по диагонали и тем меньше — вне ее. В идеале все элементы вне главной диагонали должны быть нулевыми.
Но гораздо удобнее представлять ее в графическом виде:
В таком виде матрица представляется в виде тепловой карты, в которой чем выше значение, тем насыщеннее оттенок цвета. Это позволяет при первом взгляде на матрицу понять, как часто она ошибается и в каких именно классах. В отличие от простых численных метрик, матрица классификации может дать информацию о паттернах распространенных ошибок, которые допускает данная модель.
Практически любое аномальное или тривиальное поведение модели будет иметь отражение в матрице классификации. Например, если модель чаще чем нужно предсказывает один класс, это сразу подсветит отдельный столбец в ней. Если же модель путает два класса, то есть не различает объекты этих классов, то в матрице будут подсвечены четыре элемента, располагающиеся в углах прямоугольника. Еще одно распространенное поведение модель — когда она распознает объекты одного класса, как объекты другого — подсветит один элемент вне главной диагонали.
Эта матрица очень наглядно показывает, как часто и в каких конкретно классах ошибается модель. Поэтому анализ этой матрицы может дать ценную информацию о путях увеличения эффективности моделей. Например, можно провести анализ ошибок на основе показаний данной матрицы — проанализировать объекты, на которых модель чаще всего ошибается. Может, будет выявлена какая-то закономерность, либо общая характеристика. Добавление информации о таких параметрах объектов к матрице атрибутов обычно очень сильно улучшает эффективность моделей.
Выводы:
- Матрица классификации, или матрица ошибок представляет собой количество объектов по двум осям — истинный класс и предсказанный класс.
- Обычно, истинный класс располагается по строкам, а предсказанный — по столбцам.
- Для идеальной модели матрица должна содержать ненулевые элементы только на главной диагонали.
- Матрица позволяет наглядно представить результаты классификации и увидеть, в каких случаях модель делает ошибки.
- Матрица незаменима при анализе ошибок, когда исследуется, какие объекты были неправильно классифицированы.
Метрики множественной классификации
Все метрики, о которых мы говорили выше рассчитываются в случае бинарной классификации, так как определяются через понятия ложноположительных, ложноотрицательных прогнозов. Но на практике чаще встречаются задачи множественной классификации. В них не определяется один положительный и один отрицательный класс, поэтому все рассуждения о precision и recall, казалось бы, не имеют смысла.
На самом деле, все рассмотренные метрики прекрасно обобщаются на случай множественных классов. Рассмотрим простой пример. У нас есть три класса — 0, 1 и 2. Есть пять объектов, каждый их которых принадлежит одному их этих трех классов. Истинные значения целевой переменной такие: $y = lbrace 0, 1, 2, 2, 0 rbrace$. Имеется модель, которая предсказывает классы этих объектов, соответственно так: $hat{y} = lbrace 0, 0, 2, 1, 0 rbrace$. Давайте рассчитаем известные нам метрики качества классификации.
С метрикой accuracy все просто. Модель правильно предсказала класс в трех случаях из пяти — первом, третьем и пятом. А в двух случаях — ошиблась. Поэтому метрика рассчитывается так: $A = 3 / 5 = 0.6$. То есть точность модели — 60%.
А вот precision и recall рассчитываются более сложно. В моделях множественной классификации эти метрики могут быть рассчитаны отдельно по каждому классу. Подход в этом случае очень похож на алгоритм “один против всех” — для каждого класса он предполагается положительным, а все остальные классы — отрицательными. Давайте рассчитаем эти метрики на нашем примере.
Возьмем нулевой класс. Его обозначим за 1, а все остальные — за 0. Тогда вектора эмпирических и теоретических значений целевой пременной станут выглядеть так:
$y = lbrace 1, 0, 0, 0, 1 rbrace$,
$hat{y} = lbrace 1, 1, 0, 0, 1 rbrace$.
Тогда $P = frac{TP}{TP + FP} = frac{2}{3} approx 0.67$, ведь у нас получается 2 истинноположительных предсказания (первый и пятый объекты) и одно ложноположительное (второй). $R = frac{TP}{TP + FN} = frac{2}{2} = 1$, ведь в модели нет ложноотрицательных прогнозов.
$F_1 = frac{2 P R}{P + R} = frac{2 TP}{2 TP + FP + FN} = frac{2 cdot 2}{2 cdot 2 + 1 + 0} = frac{4}{5} = 0.8$.
Аналогично рассчитываются метрики и по остальным классам. Например, для первого класса вектора целевой переменной будут такими:
$y = lbrace 0, 1, 0, 0, 0 rbrace$,
$hat{y} = lbrace 0, 0, 0, 1, 0 rbrace$. Обратите внимание, что в данном случае получается, что модель ни разу не угадала. Такое тоже бывает, и в таком случае, метрики будут нулевые. Для третьего класса попробуйте рассчитать метрики самостоятельно, а чуть ниже можно увидеть правильный ответ.
Конечно, при использовании библиотечный функций не придется рассчитывать все эти метрики вручную. В библиотеке sklearn для этого есть очень удобная функция — classification_report, отчет о классификации, которая как раз вычисляет все необходимые метрики и представляет результат в виде наглядной таблицы. Вот как будет выглядеть рассмотренный нами пример:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
>>> from sklearn.metrics import classification_report
>>> y_true = [0, 1, 2, 2, 0]
>>> y_pred = [0, 0, 2, 1, 0]
>>> target_names = ['class 0', 'class 1', 'class 2']
>>> print(classification_report(y_true, y_pred, target_names=target_names))
precision recall f1-score support
class 0 0.67 1.00 0.80 2
class 1 0.00 0.00 0.00 1
class 2 1.00 0.50 0.67 2
accuracy 0.60 5
macro avg 0.56 0.50 0.49 5
weighted avg 0.67 0.60 0.59 5
Здесь мы видим несколько строк, соответствующих классам в нашей задаче. По каждому классу рассчитаны метрики precision, recall и $F_1$. Последний столбец называется support — это количество объектов данного класса в используемой выборке. Это тоже важный показатель, так как чем меньше объектов какого-то класса, тем хуже он обычно распознается.
Ниже приведены интегральные, то есть общие метрики эффективности модели. Это три последние строки таблицы. В первую очередь это accuracy — она всегда рассчитывается один раз. Обратите внимание, что в столбце support здесь везде стоит 5 — это общее число объектов выборки. Ниже приведены средние значения по метрикам precision, recall и $F_1$. Почему же строк две? Дело в том, что усреднять эти метрики можно по-разному.
Во-первых, можно взять обычное среднее арифметическое из метрик всех классов. Это называется macro average. Это самый простой способ, но у него есть одна проблема. Почему метрики очень малочисленных классов должны давать тот же вклад в итоговый результат, что и метрики очень многочисленных? Можно усреднить метрики используя в качестве весов долю каждого класса в выборке. Такое усреднение называется weighted average. Обратите внимание, что при усреднении метрика $F_1$ может получиться не между precision и recall.
Отчет о классификации — очень полезная функция, использование которой практически обязательно при анализе эффективности моделей классификации. Особенно для задач множественной классификации. Эта таблица может дать важную информацию о том, какие классы распознаются моделью лучше, какие — хуже, как это связано в численностью классов в выборке. Анализ этой таблицы может навести на необходимость определенных действий по повышению эффективности модели. Например, можно понять, какие данные полезно будет добавить в модель.
Выводы:
- Метрики для каждого класса рассчитываются, полагая данный класс положительным, а все остальные — отрицательными.
- Каждую метрику можно усреднить арифметически или взвешенно по классам. Весами выступают объемы классов.
- В модуле sklearn реализовано несколько алгоритмов усреднения они выбираются исходя их задачи.
- В случае средневзвешенного, F1-метрика может получиться не между P и R.
- Отчет о классификации содержит всю необходимую информацию в стандартной форме.
- Отчет показывает метрики для каждого класса, а так же объем каждого класса.
- Также отчет показывает средние и средневзвешенные метрики для всей модели.
- Отчет о классификации — обязательный элемент представления результатов моделирования.
- По отчету можно понять сбалансированность задачи, какие классы определяются лучше, какие — хуже.
PR-AUC
При рассмотрении разных моделей классификации мы упоминали о том, что они подразделяются на метрические и логические методы. Логические методы (дерево решений, k ближайших соседей) выдают конкретную метку класса,без какой-либо дополнительной информации. Метрические методы (логистическая регрессия, перцептрон, SVM) выдают принадлежность данного объекта к разным классам, присутствующим в задаче. При рассмотрении модели логистической регрессии мы говорили, что предсказывается положительный класс, если значение логистической функции больше 0,5.
Но это пороговое значение можно поменять. Что будет, если мы измени его на 0,6? Тогда мы для некоторых объектовы выборки изменим предсказание с положительного класса на отрицательный. То есть без изменения модели можно менять ее предсказания. Это значит, что изменятся и метрики модели, то есть ее эффективность.
Чем больше мы установим порог, тем чаще будем предсказывать отрицательный класс. Это значит, что в среднем, у модели будет меньше ложноположительных предсказаний, но может стать больше ложноотрицательных. Значит, у модели может увеличится precision, то упадет recall. В крайнем случае, если мы возьмем порог равный 1, мы всегда будем предсказывать отрицательный класс. Тогда у модели будет $P = 1, R = 0$. Если же, наоборот, возьмем в качестве порога 0, то мы всегда будем предсказывать отрицательный класс, а значит у модели будет $P = 0, R = 1$, так как она не будет давать ложноположительных прогнозов, но будут встречаться ложноотрицательные.
Это означает, что эффективность моделей метрической классификации зависит не только от того, как модель соотносится с данными, но и от значения порога. Из этого следует, кстати, что было бы не совсем правильно вообще сравнивать метрики двух разных моделей между собой. Ведь значение этих метрик будет зависеть не только от самих моделей, но и от порогов, которые они используют. Может, первая модель будет лучше, если немного изменить ее пороговое значение? Может, одна из метрик второй модели станет выше, если изменить ее порог.
Это все сильно затрудняет анализ метрических моделей классификации. Для сравнения разных моделей необходим способ “убрать” влияние порога, сравнить модели вне зависимости от его значения. И такой способ есть. Достаточно просто взять все возможные значения порога, посчитать метрики в каждом из них и затем усреднить. Для этого служит PR-кривая или кривая “precision-recall”:
Каждая точка на этом графике представляет собой значение precision и recall для конкретного значения порога. Для построения этого графика выбирают все возможные значение порога и отмечают на графике. Давайте рассмотрим простой пример из 10 точек. Истинные значения классов этих точек равны, соответственно, $y = lbrace 0, 0, 0, 0, 0, 1, 1, 1, 1, 1 rbrace$. Модель (сейчас совершенно неважно, какая) выдает следующие предсказания для этих объектов: $h(x) = lbrace 0.1, 0.2, 0.3, 0.45, 0.6, 0.4, 0.55, 0.7, 0.8, 0.9 rbrace$. Заметим, что модель немного ошибается для средних объектов, то есть она не будет достигать стопроцентной точности. Построим таблицу, в которой переберем некоторые значения порога и вычислим, к какому классу будет относиться объект при каждом значении порога:
| y | h(x) | 0,1 | 0,15 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0,1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0,2 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0,3 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0,45 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0,6 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0,4 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0,55 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0,7 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| 1 | 0,8 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
| 1 | 0,9 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
Можно сразу заметить, что чем выше порог, тем чаще предсказывается отрицательный класс. В крайних случаях модель всегда предсказывает либо положительный класс (при малых значениях порога), либо отрицательный (при больших).
Далее, для каждого значения порога рассчитаем количество истинно положительных, истинно отрицательных, ложноположительных и ложноотрицательных предсказаний. На основе этих данных легко рассчитать и метрики precision и recall. Запишем это в таблицу:
| y | h(x) | 0,1 | 0,15 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| TP | 5 | 5 | 5 | 5 | 5 | 4 | 3 | 3 | 2 | 1 | 0 | |
| TN | 0 | 0 | 1 | 2 | 3 | 4 | 4 | 5 | 5 | 5 | 5 | |
| FP | 5 | 5 | 4 | 3 | 2 | 1 | 1 | 0 | 0 | 0 | 0 | |
| FN | 0 | 0 | 0 | 0 | 0 | 1 | 2 | 2 | 3 | 4 | 5 | |
| P | 0,50 | 0,50 | 0,56 | 0,63 | 0,71 | 0,80 | 0,75 | 1,00 | 1,00 | 1,00 | 1,00 | |
| R | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 0,80 | 0,60 | 0,60 | 0,40 | 0,20 | 0,00 |
При самом низком значении порога модель всегда предсказывает отрицательный класс, метрика recall равна 1, а метрика precision равна доли отрицательного класса в выборке. Причем ниже этого значения precision уже не опускается. Можно заметить, что в целом при повышении порога precision повышается, а recall понижается. В другом крайнем случае, когда порог равен 1, модель всегда предсказывает отрицательный класс, метрика recall равна 0, а precision — 1 (на самом деле эта метрика не определена, но считается равной именно 1, так как ее значение стремится к этому при повышении порога). За счет чего это происходит?
При повышении порога может произойти один из трех случаев. Первый заключается в том, что данное изменение может не влияет ни на одно предсказание. Так происходит, например, при повышении порога с 0,1 до 0,15. Оценка ни одного объекта не попадает в данный диапазон, поэтому ни одно предсказание не меняется. И, соответственно, не изменится ни одна метрика.
Если же повышение порога все-таки затрагивает один или несколько объектов, то изменение предсказания может произойти только с положительного на отрицательное. Допустим, для простоты, что повышение порога затрагивает только один объект. То есть мы изменяем предсказание по одному объекту с 1 на 0. Второй случай заключается в том, что это изменение правильное. То есть объект в действительности принадлежит отрицательному классу. Так происходит, например, при изменении порога с 0,15 до 0,2. В данном случае первый объект из ложноположительного стал истинно отрицательным. Такое изменение не влияет на recall, но повышает precision.
Третий случай заключается в том, что изменение предсказаные было неверным. То есть объект из истинно положительного стал ложноотрицательным. Это происходит, например, при изменении порога с 0,4 до 0,5 — в данном случае шестой объект становится классифицированным ошибочно. Уменьшение количества истинно положительных объектов снижает обе метрики — и precision и recall.
Таким образом можно заключить, что recall при повышении порога может оставаться неизменным или снижаться, а precision может как повышаться, так и понижаться, но в среднем будет повышаться за счет уменьшения доли ложноположительных предсказаний. Если изобразить рассмотренный пример на графике можно получить такую кривую:
PR-кривая не всегда монотонна, обе метрики могут изменяться как однонаправленно, так и разнонаправленно при изменении порогового значения. Но главный смысл этой кривой не в этом. При таком анализе очень просто обобщить эффективность модели вне зависимости от значения порога. Для этого нужно всего лишь найти площадь под графиком этой кривой. Эта метрика называется PR-AUC (area under the curve) или average precision (AP). Чем она выше, тем качественнее модель.
Давайте порассуждаем, ка будет вести себя идеальная модель. Крайние случаи, когда порога равны 0 и 1, значения метрик будут такими же, как и всегда. Но вот при любом другом значении порога модель будет классифицировать все объекты правильно. И обе метрики у нее будут равны 1. Таким образом, PR-кривая выродится в два отрезка, один из которых проходит из точки (0, 1) в точку (1, 1). и площадь под графиком будет равна 1. У самой худшей же модели метрики будут равны 0, так как она всегда будет предсказывать неверно. И площадь тоже будет равна 0.
У случайной модели, как можно догадаться, площадь под графиком будет равна 0,5. Поэтому метрика PR-AUC может использоваться для сравнения разных моделей метрической классификации вне зависимости от значения порога. Также эта метрика показывает соотношение данной модели и случайной. Если PR-AUC модели меньше 0,5, значит она хуже предсказывает класс, чем простое угадывание.
Выводы:
- Кривая precision-recall используется для методов метрической классификации, которые выдают вероятность принадлежности объекта данному классу.
- Дискретная классификации производится при помощи порогового значения.
- Чем больше порог, тем больше объектов модель будет относить к отрицательному классу.
- Повышение порога в среднем увеличивает precision модели, но понижает recall.
- PR-кривая используется чтобы выбрать оптимальное значение порога.
- PR-кривая нужна для того, чтобы сравнивать и оценивать модели вне зависимости от выбранного уровня порога.
- PR-AUC — площадь под PR-кривой, у лучшей модели — 1.0, у тривиальной — 0.5, у худшей — 0.0.
ROC_AUC
Помимо кривой PR есть еще один довольно популярный метод оценки эффективности метрических моделей классификации. Он использует тот же подход, что и PR-кривая, но немного другие координаты. ROC-кривая (receiver operating characteristic) — это график показывающий соотношение доли истинно положительных предсказаний и ложноположительных предсказаний в модели метрической классификации для разных значений порога.
В этой кривой используются два новых термина — доля истинно положительных и доля ложноположительных предсказаний. Доля истинно положительных предсказаний (TPR, true positive rate), как можно догадаться, это отношение количества объектов выборки, правильно распознанных как положительные, ко всем положительным объектам. Другими словами, это всего лишь иное название метрики recall.
А вот доля ложноположительных предсказаний (FPR, false positive rate) считается как отношение количества отрицательных объектов, неправильно распознанных как положительные, в общем количестве отрицательных объектов выборки:
[TPR = frac{TP}{TP + FN} = R \
FRP = frac{FP}{TN + FP} = 1 — S]
Обратите внимание, что FPR — мера ошибки модели. То есть, чем больше — тем хуже. У идеальной модели $FRP=0$, а у наихудшей — $FPR=1$. Для иллюстрации давайте рассчитаем эти метрики для нашего примера, который мы использовали выше (для дополнительной информации еще приведена метрика accuracy для каждого значения порога):
| y | h(x) | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| TPR | 1,00 | 1,00 | 1,00 | 1,00 | 0,80 | 0,60 | 0,60 | 0,40 | 0,20 | 0,00 | |
| FPR | 1,00 | 0,80 | 0,60 | 0,40 | 0,20 | 0,20 | 0,00 | 0,00 | 0,00 | 0,00 | |
| A | 0,50 | 0,60 | 0,70 | 0,80 | 0,80 | 0,70 | 0,80 | 0,70 | 0,60 | 0,50 |
Можно заметить, что при увеличении порога обе эти метрики увеличиваются, начиная со значения 1 до нуля. Причем, движения этих двух показателей всегда однонаправленно. Давайте опять же разберемся, почему так. Если увеличение порога приводит к правильному изменению классификации, то есть изменению ложноположительного значения на истинно отрицательное, то это уменьшит FRP, но не затронет TRP. Если же изменение будет неверным, то есть истинно положительное значение поменялось на ложноотрицательное, это однозначно уменьшит TPR, при этом FRP либо уменьшится так же, либо останется неименным.
В итоге, кривая получается монотонной, причем она всегда проходит через центр координат и через точку (1, 1). В нашем примере кривая будет выглядеть так:
Более сложные данные могут выглядеть с большим количеством деталей, но общая форма и монотонность сохраняются:
Также, как и с кривой PR, важное значение имеет площадь под графиком. Эта метрика называется ROC-AUC и является одной из самых популярных метрик качества метрических моделей классификации. Ее главное преимущество перед другими метриками состоит в том, что она позволяет объективно сопоставить уровень качества разных моделей классификации, решающих одну и ту же задачу, но обученных на разных данных. Это приводит к частому использованию ROC-AUC, например, в научной литературе для представления результатов моделирования.
Существует множество споров, какая диагностическая кривая более адекватно измеряет качество классификации — ROC или PR. Считается, что PR-кривая больше ориентирована на задачи, в которых присутствует дисбаланс классов. Это задачи в которых объектов одного класса значительно больше чем другого, классы имеют разное толкование и, как следствие, ошибки первого и второго рода не равнозначны. Зачастую это модели бинарной классификации. ROC же дает более адекватную картину в задачах, где классов примерно поровну в выборке. Но для полного анализа модели все равно рекомендуется использовать оба метода.
В случае с множественной классификацией построение диагностических кривых происходит отдельно по каждому классу. Так же, как и при расчете метрик precision и recall, каждый класс поочередно полагается положительным, а остальные — отрицательными. Каждая такая частная кривая показывает качество распознавания конкретного класса. Поэтому кривые могут выглядеть примерно так:
На данном графике мы видим PR-кривую модели множественной классификации из 3 классов. Кроме отдельных значений precision и recall в каждой точке рассчитываются и усредненные значения. Так формируется кривая средних значений. Интегральная метрика качества модели классификации считается как площадь под кривой средних значений. Алгоритм построения ROC-кривой полностью аналогичен.
Выводы:
- ROC-кривая показывает качество бинарной классификации при разных значениях порога.
- В отличие от PR-кривой, ROC-кривая монотонна.
- Площадь под графиком ROC-кривой, ROC_AUC — одна из основных метрик качества классификационных моделей.
- ROC_AUC можно использовать для сравнения качества разных моделей, обученных на разных данных.
- ROC чаще используют для сбалансированных и множественных задач, PR — для несбалансированных.
- Кривые для множественной классификации строятся отдельно для каждого класса.
- Метрика AUC считается по кривой средних значений.
Топ k классов
Все метрики, которые мы обсуждали выше оперируют точным совпадением предсказанного класса с истинным. В некоторых особых задачах может быть полезно немного смягчить это условие. Как мы говорили, метрические методы классификации выдают больше информации — степень принадлежности объекта выборки каждому классу. Обычно, мы выбираем из них тот класс, который имеет наибольшую принадлежность. Но можно выбрать не один класс, а несколько. Таким образом можно рассматривать не единственный вариант класса для конкретного объекта, а 3, 5, 10 и так далее.
Другими словами можно говорить о том, находится ли истинный класс объекта среди 3, 5 или 10 классов, которые выбрала для него модель. Количество классов, которые мы рассматриваем, можно брать любым. В данной метрике оно обозначается k. Таким образом, можно построить метрику, которая оценивает долю объектов выборки, для которых истинный класс находится среди k лучших предсказаний модели:
[tka(y, hat{f}) = frac{1}{n} sum_{i=0}^{n-1}
sum_{j=1}^{k} 1(hat{f_{ij}} = y_i)]
где $hat{f_{ij}}$ — это j-й в порядке убывания уверенности модели класс i-го объекта.
Рассмотрим такой пример. Пусть у нас есть задача классификации из 3 классов. Мы оцениваем 4 объекта, которые имеют на самом деле такие классы:
$y = lbrace 0, 1, 2, 2 rbrace$.
1
2
3
>>> import numpy as np
>>> from sklearn.metrics import top_k_accuracy_score
>>> y_true = np.array([0, 1, 2, 2])
Модель предсказывает следующие вероятности для каждого объекта:
1
2
3
4
>>> y_score = np.array([[0.5, 0.2, 0.2],
... [0.4, 0.3, 0.2],
... [0.2, 0.4, 0.3],
... [0.7, 0.2, 0.1]])
То есть для первого объекта она выбирает первый класс, но немного предполагает и второй. А вот, например, последний, четвертый объект она уверенно относит тоже к первому классу. Давайте посчитаем метрику топ-2 для этой модели. Для этого для каждого объекта рассмотрим, какие 2 класса модель называет наиболее вероятными. Для первого — это 0 и 1, для второго — также 0 и 1, причем модель отдает предпочтение 0 классу, хотя на самом деле объект относится к 1 классу. Для третьего — уже 2 и 2 класс, причем класс 1 кажется модели более вероятным, для четвертого — так же наиболее вероятными модели кажутся 0 и 1 класс.
Если бы мы говорили об обычной accuracy, то для такой модели она была бы равна 0,25. Ведь только для первого объекта модель дала правильное предсказание наиболее вероятного класса. Но по метрике топ-2, для целых трех объектов истинный класс находится среди двух наиболее вероятных. Модель полностью ошибается только в последнем случае. Так что эта метрика равна 0,75. Это же подтверждают и автоматические расчеты:
1
2
>>> top_k_accuracy_score(y_true, y_score, k=2)
0.75
Как мы говорили, количество классов k можно взять любым. В частном случае $k=1$ эта метрика превращается в классическую accuracy. Чем больше возьмем k, тем выше будет значение данной метрики, но слабее условие. Так что брать очень большие k нет никакого смысла. В другом крайнем случае, когда k равно количеству классов, метрика будет равна 1 для любой модели.
Эта метрика имеет не очень много практического смысла. Ведь при прикладном применении моделей машинного обучения важен все-таки итоговый результат классификации. И если модель ошиблась, то модель ошиблась. Но эта метрика может пролить свет на внутреннее устройство модели, показать, насколько сильно она ошибается. Ведь одно дело, если модель иногда называет правильный ответ может и не наиболее вероятным, но в топ, скажем, 3. Совсем другое дело, если модель не находит правильный ответ и среди топ-10. Так что эта метрика может использоваться для диагностики моделей классификации и для поиска путей их совершенствования. Еще она бывает полезна, если две модели имеют равные значения метрики accuracy, но нужно понять, какая их них адекватнее имеющимся данным.
Такие проблемы часто возникают в задачах, где классов очень много. Например, в распознавании объектов на изображениях количество объектов может быть несколько тысяч. А в задачах обработки текста количество классов может определяться количеством слов в языке — сотни тысяч и миллионы (если учитывать разные формы слов). Естественно, что эффективность моделей классификации в таких задачах, измеренная обычными способами будет очень низкой. А данная метрика позволяет эффективно сравнивать и оценивать такие модели.
Выводы:
- Эта метрика — обобщение точности для случая, когда модель выдает вероятности отнесения к каждому классу.
- Вычисляется как доля объектов, для которых правильный класс попадает в список k лучших предсказанных классов.
- Чем больше k, тем выше метрика, но бесполезнее результат.
- Эта метрика часто применяется в задачах с большим количеством классов.
- Применимость этой метрики сильно зависит от характера задачи.
Проблема пере- и недообучения
Проблема Bias/Variance
При решении задачи методами машинного обучения всегда встает задача выбора вида модели. Как мы обсуждали в предыдущих главах, существует большое количество классов модели — достаточно вспомнить линейные модели, метод опорных векторов, перцептрон и другие. Каждая их этих моделей, будучи обученной на одном и том же наборе данных может давать разные результаты. Важно понимать, что мы не говорим о степени подстройки модели к данным. Даже если обучение прошло до конца, найдены оптимальные значения параметров, все равно модели могут и, скорее всего, будут различаться.
Причем многие классы моделей представляют собой не одно, а целое множество семейств функций. Например, та же логарифмическая регрессия — это не одна функция, а бесконечное количество — квадратичные, кубические, четвертой степени и так далее. Множество функций или моделей, имеющих единую форму, но различающуюся значениями параметров составляет так называемое параметрическое семейство функций. Так, все возможные линейные функции — это одно параметрическое семейство, все возможные квадратические — другое, а, например, множество всех возможных однослойных перцептронов с 5 нейронами во входном, 3 нейронами в скрытом и одном нейроне в выходном слое — третье семейство.
Таким образом можно говорить, что перед аналитиком стоит задача выбора параметрического семейства модели, которую он будет обучать на имеющихся данных. Причем разные семейства дадут модели разного уровня качества после обучения. К сожалению, очень сложно заранее предугадать, какое семейство моделей после завершения обучения даст наилучшее качество предсказания по данной выборке.
Что является главным фактором выбора этого семейства? Как показывает практика, самое существенное влияние на эффективность оказывает уровень сложности модели. Любое параметрическое семейство моделей имеет определенное количество степеней свободы, которое определяет то, насколько сложное и изменчивое поведение может демонстрировать получившаяся функция.
Сложность модели можно определять разными способами, но в контексте нашего рассуждения сложность однозначно ассоциируется с количеством параметров в модели. Чем больше параметров, тем больше у модели степеней свободы, возможности изменять свое поведение при разных значениях входных признаков. Конечно, это не означает полной эквивалентности разных типов моделей с одинаковым количеством параметров. Например, никто не говорит, что модель, скажем, регрессии по методу опорных векторов эквивалентна модели нейронной сети с тем же самым количеством весов. Главное, что модели со сходным уровнем сложности демонстрируют сходное поведение по отношению к конкретному набору данных.
Влияние уровня сложности на поведение модели относительно данных наиболее наглядно можно проследить на примере модели полиномиальной модели. Степень полинома — это очень показательная характеристика уровня сложности модели. Давайте рассмотрим три модели регрессии — линейную (которую можно рассматривать как полином первой степени), полином второй и восьмой степени. Мы обучили эти модели на одном и том же датасете и вот что получилось:
Следует отдельно заметить, что в каждом из представленных случаев модель обучалась до конца, то есть до схождения метода численной оптимизации параметров. То есть для каждой модели на графике представлены оптимальные значения параметров. Гладя на эти три графика и то, как эти линии ложатся в имеющиеся точки, можно заметить некоторое противоречие. Естественно предположить, что модель, изображенная на втором графике показывает наилучшее описание точек данных. Но по любой метрике качества третья модель будет показывать более высокий результат.
Человек, глядя на график третьей модели, сразу сделает вывод, что она “слишком” хорошо подстроилась под имеющиеся данные. Сравните это поведение с первым графиком, который демонстрирует самую низкую эффективность на имеющихся данных. Можно проследить, как именно сложность модели влияет на ее применимость. Если модель слишком простая, то она может не выявить имеющиеся сложные зависимости между признаками и целевой переменной. Говорят, что у простых моделей низкая вариативность (variance). Слишком же сложная модель имеет слишком высокую вариативность, что тоже не очень хорошо.
Те же самые рассуждения можно применить и к моделям классификации. Можно взглянуть на форму границы принятия решения для трех моделей разного уровня сложности, обученных на одних и тех же данных:
В данном случае мы видим ту же картину — слишком простая модель не может распознать сложную форму зависимости между факторами и целевой переменной. Такая ситуация называется недообучение. Обратите внимание, что недообучение не говорит о том, что модель не обучилась не до конца. Просто недостаток сложности, вариативности модели не дает ни одной возможной функции их этого параметрического семейства хорошо описывать данные.
Слишком сложные модели избыточно подстраиваются под малейшие выбросы в данных. Это увеличивает значение метрик эффективности, но снижает пригодность модели на практике, так как очевидно, что модель будет делать большие ошибки на новых данных из той же выборки. Такая ситуация называется переобучением. Переобучение — это очень коварная проблема моделей машинного обучения, ведь на “бумаге” все метрики показывают отличный результат.
Конечно, в общем случае не получится так наглядно увидеть то, как модель подстраивается под данные. Ведь в случае, когда данные имеют большую размерность, строить графики в проекции не даст представления об общей картине. Поэтому ситуацию пере- и недообучения довольно сложно обнаружить. Для этого нужно проводить отдельную диагностику.
Это происходит потому, что в практически любой выборке данных конкретное положение точек, их совместное распределение определяется как существенной зависимостью между признаками и целевой переменной, так и случайными отклонениями. Эти случайные отклонения, выбросы, аномалии не позволяют сделать однозначный вывод, что модель, которая лучше описывает имеющиеся данные, является лучшей в глобальном смысле.
Выводы:
- Прежде чем обучать модель, нужно выбрать ее вид (параметрическое семейство функций).
- Разные модели при своих оптимальных параметрах будут давать разный результат.
- Чем сложнее и вариативнее модель, тем больше у нее параметров.
- Простые модели быстрые, но им недостает вариативности, изменчивости, у них высокое смещение (bias).
- Сложные модели могут описывать больше зависимостей, но вычислительно более трудоемкие и имеют большую дисперсию (variance).
- Слишком вариативные (сложные) модели алгоритм может подстраиваться под случайный шум в данных — переобучение.
- Слишком смещенные (простые) модели алгоритм может пропустить связь признака и целевой переменной — недообучение.
- Не всегда модель, которая лучше подстраивается под данные (имеет более высокие метрики эффективности) лучше.
Обобщающая способность модели, тестовый набор
Как было показано выше, не всякая модель, которая показывает высокую эффективность на тех данных, на которых она обучалась, полезна на практике. Нужно всегда помнить, что модели машинного обучения строят не для того, чтобы точно описывать объекты из обучающего набора. На то он и обучающий набор, что мы уже знаем правильные ответы. Цель моделирования — создать модель, которая на примере этих данных формализует некоторые внутренние зависимости в данных для того, чтобы адекватно описывать новые объекты, которые модель не учитывала при обучении.
Полезность модели машинного обучения определяется именно способность описывать новые данные. Это называется обобщающей способностью модели. И как мы показали в предыдущей главе, эффективность модели на тех данных, на которых она обучается, не дает адекватного понимания этой самой обобщающей способности модели. Вместе с тем, обобщающая способность — это главный показатель качества модели машинного обучения и у нас должен быть способ ее измерять.
Конечно, мы не можем измерить эффективность модели на тех данных, которых у нас нет. Поэтому для того, чтобы иметь адекватное представление об уровне качества модели применяется следующий трюк: до начала обучения весь имеющийся датасет разбивают на две части. Первая часть носит название обучающая выборка (training set) и используется для подбора оптимальных параметров модели, то есть для ее обучения. Вторая часть — тестовый набор (test set) — используется только для оценки эффективности модели.
Такая эффективность, измеренная на “новых” данных — объектах, которые модель не видела при своем обучении — дает более объективную оценку обобщающей силы модели, то есть эффективности, которую модель будет показывать на неизвестных данных. В машинном обучении часто действует такое правило — никогда не оценивать эффективность модели на тех данных, на которых она обучалась. Не то, чтобы этого нельзя делать категорически (и в следующих главах мы это часто будем применять), просто нужно осознавать, что эффективность модели на обучающей выборки всегда будет завышенной, ведь модель подстроилась именно к этим данным, включая все их случайные колебания.
Надо помнить, что все рассуждения и выводы в этой и последующих главах носят чисто вероятностный характер. Так что в конкретном случае, тестовая эффективность вполне может оказаться даже выше, чем эффективность на обучающей выборке. Когда мы говорим о наборах данных и случайных процессах, все возможно. Но смысл в том, что распределение оценки эффективности модели, измеренное на обучающих данных имеет значимо более высокое математическое ожидание, чем “истинная” эффективность этой модели.
Для практического применения этого приема надо ответить на два вопроса: как делить выборку и сколько данных оставлять на тестовый датасет. Что касается способа деления, здесь чуть проще — практически всегда делят случайным образом. Случайное разбиение выгодно тем, что у каждого объекта датасета равная вероятность оказаться в обучающей или в тестовой выборке. Причем, эта вероятность независима для всех объектов выборки. Это делает все случайные ошибки выборки нормально распределенными, то есть их математическое ожидание равно нулю. Об этом мы еще поговорим в следующей главе.
Алгоритм случайного разбиения, который используется чаще всего лежит в основе встроенной функции sklearn train_test_split(), которая как раз и разбивает выборку на две части в соответствии с заданной пропорцией. Так как этот алгоритм использует генератор случайных чисел, он будет давать разные результаты при разных запусках. То есть вы можете запустить один и тот же код два раза, и он покажет разные результаты. То есть модели будут обучаться на немного разных данных, а значит и метрики могут немного “плавать”.
Если по каким-то причинам вам важно обеспечить идентичную работу алгоритма при разных запусках, то для этого используют специальный аргумент random_state. Они присутствует в разных функциях sklearn, использующих случайность. Значение этого аргумента используется для инициализации встроенного генератора случайных чисел. После инициализации определенным числом он будет генерировать определенную последовательность случайных (точнее псевдослучайных) чисел. Это значит, что все случайные процессы будут протекать полностью идентично. Если изменить значение random_state, последовательность уже будет другой и результаты будут отличаться. Этот параметр нужен для обеспечения воспроизводимости результатов выполнения кода.
Но этот способ не работает в случае со специальными наборами данных. Например с временными рядами. Ведь при разбиении выборки важно, чтобы сами объекты в тестовой выборке были независимы от объектов обучающей. В случае, если мы анализируем какое-то неупорядоченное множество объектов, это почти всегда выполняется. Но для временных рядов это не так. Объекты более позднего времени могут зависеть от предыдущих объектов. Так цена актива за текущий период однозначно зависит от цены актива за предыдущий. Поэтому нельзя допустить, чтобы в обучающей выборке оказались объекты более ранние, чем в обучающей. Поэтому такие временные ряды делят строго хронологически — в тестовую выборку попадает определенное количество последних по времени объектов. Но анализ временных рядов сам по себе довольно специфичен как статистическая дисциплина, и как раздел машинного обучения.
Что касается пропорции деления, то, опять же, как правило, выборку разделяют в соотношении 80/20. То есть если в исходном датасете, например, 1000 объектов, то случайно выбранные 800 из них образуют обучающую выборку, а оставшиеся 200 — тестовую. Но это соотношение “по умолчанию” в общем-то ничем не обосновано. Его можно изменять в любую сторону исходя из обстоятельств. Но для этого надо понимать, как вообще формируется эта пропорция и что на нее влияет.
Что будет, если на тестовую выборку оставить слишком много данных, скажем, 50% всего датасета? Очевидно, у нас останется мало данных для обучения. То есть модель будет обучена на всего лишь небольшой части объектов, которых может не хватить для того, чтобы модель “распознала” зависимости в данных. Вообще, чем больше данных для обучения, тем в целом лучше, так как на маленьком объеме большую роль играют те самые случайные колебания. Поэтому модель может переобучаться. И чем меньше данных, тем переобученнее и “случайнее” будет получившаяся модель. И это не проблема модели, это именно проблема нехватки данных. А чем больше точек данных, тем больше все эти случайные колебания будут усредняться и это сильно повысит качество обученной модели.
А что будет, если наоборот, слишком мало данных оставить на тестовую выборку? Скажем, всего 1% от имеющихся данных. Мы же сказали, что чем больше данных для обучения, тем лучше. Значит, но обучающую выборку надо оставить как можно большую часть датасета? Не совсем так. Да, обучение модели пройдет более полно. Но вот оценка ее эффективности будет не такой надежной. Ведь такие же случайные колебания будут присутствовать и в тестовой выборке. И если мы оценим эффективность модели на слишком маленьком количестве точек, случайные колебания этой оценки будут слишком большими. Другими словами мы получим оценку, в которой будет сильно не уверены. Истинная оценка эффективности может быть как сильно больше, так и сильно меньше получившегося уровня. То есть даже если модель обучается хорошо, мы этого никогда не узнаем с точностью.
То есть пропорция деления выборки на обучающуюся и тестовую является следствием компромисса между полнотой обучения и надежность оценки эффективности. Соотношение 80/20 является хорошим балансом — не сильно много, но и не сильно мало. Но это оптимально для среднего размера датасетов. Если у вас очень мало данных, то его можно немного увеличить в пользу тестовой выборки. Если же данных слишком много — то в пользу обучающей. Кроме того, при использовании кросс-валидации размер тестовой выборки тоже можно уменьшить.Но на практике очень редько используются соотношения больше, чем 70/30 или меньше чем 90/10 — такое значения уже считаются экстремальными.
Выводы:
- Цель разработки моделей машинного обучения — не описывать обучающий набор, а на его примере описывать другие объекты реального мира.
- Главное качество модели — описывать объекты, которых она не видела при обучении — обобщающая способность.
- Для того, чтобы оценить обобщающую способность модели нужно вычислить метрики эффективности на новых данных.
- Для этого исходный датасет разбивают на обучающую и тестовую выборки. Делить можно в любой пропорции, обычно 80-20.
- Чаще всего выборку делят случайным образом, но временные ряды — только в хронологической последовательности.
- Обучающая выборки используется для подбора параметров модели (обучения), а тестовая — для оценки ее эффективности.
- Никогда не оценивайте эффективность модели на тех же данных, на которых она училась — оценка получится слишком оптимистичная.
Кросс-валидация
Как мы говорили ранее, маленькая тестовая выборка проблемна тем, что большое влияние на результат оценки эффективности модели имеют случайные отклонения. Это становится меньше заметно при росте объема выборки, но полностью проблема не исчезает. Эта проблема состоит в том, что каждый раз разбивая датасет на две выборки, мы вносим случайные ошибки выборки. Эта случайная ошибка обоснована тем, что две получившиеся подвыборки наверняка будут демонстрировать немного разное распределение. Даже если взять простой пример. Возьмем группу людей и разделим ее случайным образом на две половины. В каждой половине посчитаем какую-нибудь статистику, например, средний рост. Будут ли в двух группах выборочные средние точно совпадать? Наверняка нет. Обосновано ли чем-то существенным такое различие? Тоже нет, это случайные отклонения, которые возникают при выборке объектов из какого-то множества.
Поэтому разбиение выборки на тестовую и обучающую вносит такие случайные колебания, из-за которых мы не можем быть полностью уверены в получившейся оценке эффективности модели. Допустим, мы получили тестовую эффективность 95% (непример, измеренную по метрике accuracy, но вообще это не важно). Можем ли мы быть уверены, что это абсолютно точный уровень эффективности? Нет, ведь как любая выборочная оценка, то есть статистика, рассчитанная на определенной выборке метрика эффективности представляет собой случайную величину с некоторым распределением. А у этого распределения есть математическое ожидание и дисперсия. Как мы говорили в предыдущей главе, случайное разделение выборки на тестовую и обучающую приводит к тому, что распределение этой величины имеет математическое ожидание, совпадающее с истинным уровнем эффективности модели. Но это именно математическое ожидание. И у этой случайной величины есть какая-то ненулевая дисперсия. Это значит, что при каждом измерении, выборочная оценка может отклоняться от матожидания, то есть быть произвольно больше или меньше.
Есть ли способ уменьшить эту дисперсию, то есть неопределенность при измерении эффективности модели? Да, очень простой. Нужно всего лишь повторить измерение несколько раз, а затем усреднить полученные значения. Так как математическое ожидание случайных отклонений всегда предполагается равным нулю, чем больше независимых оценок эффективности мы получим, тем ближе среднее этих оценок будет к математическом ожиданию распределения, то есть к истинному значению эффективности.
Проблема в том, что эти измерения должны быть независимы, то есть производиться на разных данных. Но кратное увеличение тестовой выборки имеет существенные недостатки — соответствующее уменьшение обучающей выборки. Поэтому так никогда не делают. Гораздо лучше повторить случайное разбиение датасета на обучающую и тестовую выборки еще раз и измерить метрику эффективности на другой тестовой выборки из того же изначального датасета.
К сожалению, это означает, что и обучающая выборка будет другая. То есть нам необходимо будет повторить обучение. Но зато после обучения мы получим новую, независимую оценку эффективности модели. Если мы повторим этот процесс несколько раз, мы сможем усреднить эти значения и получить гораздо более точную оценку эффективности модели.
Имейте в виду, что все, что мы говорим в этой части применимо к любой метрике эффективности или метрике ошибки модели. Чаще всего, на практике измеряют метрики accuracy для моделей классификации и $R^2$ для регрессии. Но вы можете использовать эти методики для оценки любых метрик качества моделей машинного обучения. Напомним, что они должны выбираться исходя из задачи.
Конечно, можно реализовать это случайное разбиение руками и повторить процедуру оценивания несколько раз, но на практике используют готовую схему, которая называется кросс-валидация или перекрестная проверка. Она заключается в том, что датасет заранее делят на несколько равных частей случайным образом. Затем каждая из этих частей выступает как тестовый набор, а остальные вместе взятые — как обучающий:
На схеме части датасета изображены для наглядности непрерывными блоками, но на самом деле это именно случайные разбиения. Так что они буду в датасете “вперемешку”. Количество блоков, на которые делится выборка задает количество проходов или оценок. Это количество называется k. Обычно его берут равным 5 или трем. Это называется, 5-fold cross-validation. То есть на первом проходе блоки 1,2,3 и 4 в совокупность составляют обучающую выборку. Модель обучается на них, а затем ее эффективность измеряется на блоке 5. Во втором проходе та же модель заново обучается на данных их блоков 1,2,3 и 5, и ее эффективность измеряется на блоке 4. И таким образом мы получаем 5 независимых оценок эффективности модели. Они могут различаться из-за тех самых случайных оценок выборки. Но если посчитать их среднее, оно будет значительно ближе к истинному значению эффективности. Поэтому что статистика.
Количество проходов k еще определяет то, сколько раз будет повторяться обучение модели. Чем больше выбрать k, тем более надежными будут оценки, но вся процедура займет больше машинного времени. Это особенно актуально для моделей, которые сами по себе обучаются долго — например, глубокие нейронные сети. Надо помнить, что использование кросс-валидации сильно замедляет процесс обучения. Если же выбрать k слишком маленьким, то не будет главного эффекта кросс-валидации — усреднения индивидуальных оценок эффективности. Кроме того, чем больше k, тем меньшая часть выборки будет отводиться на тестовый набор. Поэтому k не стоит брать больше, скажем, 10, даже если у вас достаточно вычислительных мощностей.
Кросс-валидация никак не влияет на эффективность модели. Многие думают, что валидированные модели получаются более эффективными. Это не так, просто использование перекрестной проверки позволяет более точно и надежно измерить уже имеющуюся эффективность данной модели. И уж тем более кросс-валидация не может ускорить процесс обучения, совсем наоборот. Но несмотря на это, использование кросс-валидации с k равным 5 или, в крайнем случае, 3, совершенно обязательно в любом серьезном проекте по машинному обучению, ведь оценки, полученные без использования этой методики совершенно ненадежны.
В библиотеке sklearn, естественно, кросс-валидация реализована в виде готовых функций. Поэтому ее применение очень просто. В примере ниже используется кросс-валидация с количеством проходов по умолчанию для получения робастных оценок заранее выбранных метрик (precision и recall):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
>>> from sklearn.model_selection import cross_validate
>>> from sklearn.metrics import recall_score
>>> scoring = ['precision_macro','recall_macro']
>>> clf =
svm.SVC(kernel='linear', C=1, random_state=0)
>>> scores =
cross_validate(clf, X, y, scoring=scoring)
>>> sorted(scores.keys())
['fit_time', 'score_time',
'test_precision_macro', 'test_recall_macro']
>>> scores['test_recall_macro']
array([0.96..., 1. ..., 0.96..., 0.96..., 1. ])
Такой код просто оценивает значение метрик. Но обратите внимание, что он возвращает не просто одно значение метрики, но целый вектор. Это именно те индивидуальные оценки. Из них очень легко получить средние и выборочную дисперсию. Эта выборочная дисперсия как раз и показывает степень уверенности в данной оценке — чем она ниже, тем уверенность больше, как доверенный интервал в статистике. Кроме такого явного использования кросс-валидации для оценки метрик, она зачастую встроена в большое количество функций, которые используют ее неявно. О некоторых таких функциях, осуществляющих оптимизацию гиперпараметров модели, пойдет речь чуть позже.
Выводы:
- Разбиение выборки на обучающую и тестовую может внести случайные ошибки.
- Нужно повторить разбиение несколько раз, посчитать метрики и усреднить.
- Кросс-валидация разбивает выборку на $k$ блоков, каждый из которых используется по очереди как тестовый.
- Сколько задать $k$, столько и будет проходов. Обычно берут 3 или 5.
- Чем больше $k$ тем надежнее оценка, но дольше ее получение, так как модель каждый раз заново обучается.
- Использование кросс-валидации обязательно для получения робастных оценок.
- В библиотеке sklearn кросс-валидация (CV) встроена во многие функции.
Кривые обучения
Как мы говорили раньше, не следует ориентироваться на эффективность модели, измеренную на обучающей выборке, ведь она получается слишком оптимистичной. Но эта обучающая эффективность все равно может дать интересную информацию о работе модели. А именно с ее помощью можно оценить, переобучается модель или недообучается. В этой главе мы расскажем об одном из самых наглядных способов диагностики моделей машинного обучения — кривых обучения.
Построение кривых обучения может быть проведено после разделения датасета на обучающую и тестовую выборки. Происходит это следующим образом. Тестовый набор фиксируется и каждый раз используется один и тот же. Из обучающего набора же сначала берут малую часть, скажем 10% от общего количества точек в нем. Обучают модель на этой малой части, а затем измеряют ее эффективность на этой части и на постоянной тестовой выборке. Первая оценка называется обучающая эффективность (training score), а вторая — тестовая эффективность (test score). Затем повторяют процесс с чуть большей частью обучающей выборки, например, 20%, затем еще с большей и так, пока мы не дойдем до полной обучающей выборки.
На каждом этапе мы измеряем обучающую эффективность (измеренную именно на той части данных, на которых модель училась, не на полной обучающей выборке) и тестовую эффективность. Таким образом мы получаем зависимость эффективности модели от размера обучающей выборки. Эти данные можно построить на графике. Это график и называется кривой обучения (learning curve). Такой график может выглядеть, например, так:
В данном случае, на графике мы видим всего пять точек на каждой кривой. Верхняя кривая показывает обучающую эффективность, нижняя — тестовую. Значит, мы использовали всего пять делений обучающей выборки на подвыборки разного размера. Это размер как раз и отложен на горизонтальной оси. Сколько таких разбиений брать? Если взять слишком мало, то не будет понятна форма графика, а именно она нам важна для диагностики. Если же взять слишком много — то построение кривой обучения займет много времени, так как каждая точка на графике — это заново обученная модель.
Давайте объясним форму этого графика. Слева, когда обучающая выборка мала, обучающая эффективность довольно высока. Это вполне понятно, ведь чем меньше данных, тем проще модели к ним подстроиться. Помните, что через любые две точки можно провести линию (то есть линейную регрессию)? Это, конечно, крайний случай, но в общем, чем меньше обучающая выборка, тем большую эффективность одной и той же модели (параметрического семейства функций) можно на ней ожидать. А вот тестовая эффективность довольно маленькая. Это тоже понятно. Ведь на маленькой выборке модель не смогла обнаружить зависимости в данных так, чтобы эффективно предсказывать значение целевой переменной в новых данных. То есть она подстроилась под конкретные точки без какой-либо обобщающей способности.
Сперва отметим, что обычно кривые обучения демонстрируют некоторые общие тенденции. Например, при малых объемах обучающей выборки, обучающая эффективность модели может быть очень большой. Ведь чем меньше данных, тем проще подобрать параметры любой, пусть даже простой модели, так, чтобы эта модель ошибалась меньше. В самом предельном случае, вспомните, что через любые две точки можно провести прямую. Это значит, что линейная регрессия, обученная на двух точках, всегда будет давать нулевую ошибку или полную, 100%-ю эффективность. То же можно сказать и про квадратичную функцию, обученную на трех точках. Но и в целом, чем меньше данных, тем меньше можно ожидать суммарную ошибку любого рассматриваемого класса моделей на этих данных.
Тестовая же эффективность модели, обученной на малом объеме выборки, скорее всего будет очень невысокой. Это тоже естественно. Ведь модель видела всего малую часть примеров и не может подстроиться под какие-то глобальные зависимости в данных. Поэтому в левой части кривых обучения почти всегда будет большой зазор.
При повышении объема обучающей выборки обучающая же эффективность будет падать. Это связано в тем, что чем больше данных, тем больше пространства для ошибки для конкретной модели. Поэтому чем больше точек описывает модель, тем хуже она это делает в среднем. Это неизбежно и не страшно. Важно то, что тестовая эффективность наоборот, растет. Это происходит потому, что чем больше данных, тем больше вероятность того, что модель подстроится под существенные связи между признаками и целевой переменной, и таким образом, повысит обобщающую способность, свою предсказательную силу.
В итоге, кривая обучения показывает, как изменяется эффективность модели по сравнению к конкретному набору данных. В частности, именно с помощью кривых обучения можно предположить пере- и недообучение модели, что является главной целью диагностики моделей машинного обучения. Например, взглянув на график кривой обучения, приведенный выше, можно ответить на вопрос, хватает ли модели данных для обучения. Для этого можно спросить, улучшится ли тестовая эффективность модели, если добавить в датасет больше точек. Для этого можно мысленно продолжить кривую обучения вправо.
При построении кривых обучения обращайте внимание на деления вертикальной оси. Если вы строите графики с использованием библиотечных инструментов, то они автоматически масштабируются по осям. Имейте в виду, что одна и та же кривая обучения может выглядеть при разном масштабе совершенно по-разному. А навык сопоставления разных кривых очень важен при диагностике моделей. Лучше всего вручную задавать масштаб вертикальной оси и использовать один и тот же для всех графиков в одной задаче.
Обратите внимание, что на графике помимо самих кривых обучения присутствуют еще какие-то полосы. Что они значат? Дело в том, что при построении кривых обучения очень часто применяется кросс-валидация, о которой мы говорили в предыдущей главе. Ведь разбиение выборки на тестовую и обучающую вносит случайные ошибки. Поэтому для построения на кривых обучения более надежных оценок всех измеряемых оценок эффективности процесс повторяют несколько раз и усредняют полученные оценки. Каждая точка на графике — это не просто оценка эффективности, это среднее из всех кросс-валидированных оценок. Именно поэтому, кстати, в легенде нижняя линяя называется не test score, а cross-validation score. А ширина полосы вокруг точки определяется величиной дисперсии этих оценок. Чем шире полоса, тем больше разброс оценки на разных проходах кросс-валидации и тем меньше мы уверены в значении этой оценки. При построении кривых обучения эта неопределенность почти всегда выше при малых объемах обучающей выборки (слева на графике) и меньше — справа.
Выводы:
- Кривая обучения — это зависимость эффективности модели от размера обучающей выборки.
- Для построения кривых обучения модель обучают много раз, каждый раз с другим размером обучающей выборки (от одного элемента до всех, что есть).
- При малых объемах обучающая эффективность будет очень большой, а тестовая — очень маленькой.
- При увеличении объема обучающей выборки они будут сходиться, но обычно тестовая эффективность всегда ниже обучающей.
- Кривые обучения позволяют увидеть, как быстро модель учится, хватает ли ей данных, а также обнаруживать пере- и недообучение.
- Кривые обучения часто используют кросс-валидацию.
Обнаружение пере- и недообучения
Как мы говорили, построение кривых обучения — это исключительно диагностическая процедура. Именно они позволяют нам предполагать, к чему более склонна модель, обученная на конкретном наборе данных — к переобучению или к недообучению. Это важно, так как подходы у повышению эффективности в этих двух случаях будут совершенно противоположными. Давайте предположим, как будут вести себя на кривых обучения переобученные и недообученные модели.
Что будет, если модель слишком проста для имеющихся данных? При увеличении количества объектов в обучающей выборке, эффективность, измеренная на ней же будет вначале заметно падать по причинам, описанным выше. Но постепенно она будет выходить на плато и больше не будет уменьшаться. Это связано с тем, что начиная с какого-то объема выборки в ней будут превалировать нелинейные зависимости, слишком сложные для данной модели. С ростом объема обучающей выборки неизбежно растет тестовая эффективность, но так как модель слишком проста и не может ухватить этих сложных зависимостей в данных, то ее тестовая эффективность не будет повышаться сильно. Причем при достаточном объеме обучающей выборки тестовая и обучающая эффективности будут достаточно близкими. Другими словами, простые модели одинаково работают как на старых, так и на новых данных, но одинаково плохо.
А что будет происходить со слишком сложной моделью для существующих данных? Ее показатели в левой части графика будут аналогичны — высокая обучающая и низкая тестовая эффективности. Причины все те же. Но вот с ростом объема обучающей выборки, разрыв между этими двумя показателями не будет сокращаться так сильно. Модель, обученная на полном датасете покажет высокую эффективность на обучающей выборке, но гораздо более низкую — на тестовой. Это же практически определение переобучения — низкая ошибка, но отсутствие обобщающей способности. Это происходит, как мы уже обсуждали, за счет того, что слишком сложная модель имеет достаточный запас вариативности, чтобы подстроиться под случайные отклонения в данных.
Таким образом, недообученные и переобученные модели демонстрируют совершенно разное поведение на кривых обучения. А значит, недообучение и переобучения можно выявить, проанализировав поведение модели на графике. Типичное переобучение характеризуется большим разрывом между тестовой и обучающей эффективность. Признак типичного недообучения — низкая эффективность как на тестовой, так и на обучающей выборке. Но на практике, конечно, диагностика моделей машинного обучения не такая простая.
На данном графике представлены абстрактные картины, наиболее характерные для недообучения, переобучения, и ситуации, когда сложность модели оптимальна — мы назовем ее качественное обучение. Именно анализируя схожесть кривой обучения исследуемой модели с этими “идеальными” случаями, можно сделать обоснованный вывод о наличии недо- или переобучения модели.
Как вы могли заметить, мы нигде не говорим о четких критериях. Недо- и переобученность моделей — это вообще относительные понятия. И кривые обучения измеряют их только косвенно. Поэтому диагностика не сводится к оценке какой-либо метрики или статистики. Нам нужно оценить общую форму графика кривых обучения, что не является точной наукой. Возникает множество вопросов. Например, мы говорили, что большой зазор между тестовой и обучающей эффективностью — это признак переобучения. Но какой зазор считать большим? Это вопрос интерпретации. Точно так же, что считать низким уровнем эффективности? 50%? Может, 75%? Вообще это очень зависит от самой задачи. В некоторых задачах 80% accuracy — это выдающийся результат, а в других — даже 99% считается недостаточной точностью.
Поэтому рассматривая один график кривой обучения очень сложно понять, особенно без опыта анализа моделей машинного обучения, на что мы смотрим — на слишком простую недообученную модель, или на слишком сложную — переобученную. Вообще, строго говоря, большой зазор между эффективностями модели указывает на присутствующую в модели вариативность (variance), а низкий,не 100%-й уровень обучающей эффективности — на наличие в модели смещения (bias). А любые модели в той или иной степени обладают этими характеристиками. Вопрос в их соотношении друг к другу и к конкретному набору данных.
Чтобы облегчить задачу диагностики модели очень часто эффективность данной модели рассматривают не абстрактно, а сравнивают с аналогами. Практически всегда выбор моделей осуществляется от простого к сложному — сначала строят очень простые модели. Их тестовая эффективность может задать некоторых базовый уровень, планку, по сравнению к которой уже можно готовить об улучшении эффективности у данной, более сложной модели, насколько это улучшение существенно и так далее. Кроме того, строя кривые обучения нескольких моделей можно получить сравнительное представление о том, как эти модели соотносятся между собой, какие из них более недообученные, какие — наоборот.
Ситуация еще очень осложняется тем, что на практике вы никогда не получите таких красивых и однозначных кривых обучения, как в учебнике. Положение точек на кривых обучения зависит, в том числе и от тех самых случайных отклонений в данных, которые так портят нам жизнь. Поэтому в реальности графики могут произвольно искривляться, быть немонотонными. Тестовая эффективность вообще может быть выше обучающей. Что это начит для диагностики? Да в общем-то, ничего, это лишь свидетельствует об особом характере имеющихся данных. И, естественно, чем меньше данных, тем более явно проявляются эти случайности и тем менее показательными будут графики.
Достаточно сильно от этих случайных колебаний помогает применение кросс-валидации. Так как усреднение случайности — это и есть цель перекрестной проверки, она может быть полезна и для “сглаживания” кривых обучения. Еще надо помнить, что во многих библиотеках по умолчанию кривые обучения строятся на основе всего нескольких точек, то есть всего пяти-десяти вариантов размера обучающей выборки. Если такой график не дает достаточной информации, можно попробовать построить кривую по большему количеству точек. Но при этом и случайные колебания тоже могут проявиться сильнее.
Вообще, все факторы, которые улучшают “читаемость” кривых обучения, одновременно сильно замедляют их построение — кросс-валидация, использование большей выборки, построение большего количества точек. Помните, что это приводит к кратному увеличению количества циклов обучения модели.
Как мы говорили, поведение модели в целом не зависит от выбранной метрики, которую вы используете для построения кривых обучения. Поэтому зачастую используют не метрики эффективности, а метрики ошибок. Поэтому графики кривых обучения выглядят “перевернутыми” — тестовая ошибка больше, чем обучающая и так далее. Следует помнить, что все сказанное выше остается справедливым в этом случае, только следует помнить, где у модели высокая эффективность и малая ошибка.
На этом графике вы видите тоже идеальные случаи, но выраженные в терминах величины ошибки, а не эффективности. Можно проследить те же тенденции, но как бы “отраженные” по вертикальной оси.
Как мы говорили, реальные наборы данных, имеющие случайные колебания, ненадежные зависимости, случайные ошибки выборки могут существенно искажать кривые обучения. Рассмотри пример, приближенный к реальности. Возьмем датасет, содержащий рукописные цифры и обучим на нем классификатор по методу опорных векторов с гауссовым ядром. Для примера возьмем значение параметра “гамма”, который задает масштабирование функции расстояния в ядре, равным 0,008. Построив кривые обучения для этой модели мы получаем следующий график:
Данный график, несмотря на свою сложную форму достаточно легко интерпретируется. Мы видим, что обучающая эффективность равна 1 при любых объемах обучающей выборки. То есть модель разделяет классы полностью идеально. Но вот тестовая эффективность всегда остается гораздо ниже. И хотя она растет при увеличении объема обучающей выборки, все равно, даже при использовании полного набора данных, остается большой разрыв между тестовой и обучающей эффективностями модели. Налицо явное и типичное переобучение.
Теперь давайте уменьшим параметр “гамма” в четыре раза. В методе опорных векторов это может ограничить вариативность модели. Получаем следующий график кривых обучения:
Видно, что общее поведение модели значительно улучшилось. Обратите внимание на масштаб вертикальной оси. На первом графике мы говорили о разнице между тестовой и обучающей эффективностью в примерно 0,3. На этом же графике разница сократилась до примерно 0,025 — больше, чем в 10 раз. Это говорит о том, что модель очень сильно увеличила свою обобщающую способность. Давайте теперь уменьшим параметр еще в сто раз и посмотрим на кривую обучения:
Поведение модели явно не улучшилось. Хотя, итоговая эффективность тоже получается достаточно высокой (около 0,9), она все равно значительно меньше, чем в предыдущем случае. Другими словами, дальнейшее сокращение “гаммы” не пошло модели на пользу. Низкая тестовая эффективность и небольшая разница между тестовой и обучающей эффективностью — типичные признаки недообучения.
Обратите внимание, что интерпретация графика кривых обучения и, соответственно, диагностика модели, приобретает гораздо больше смысла к контексте сравнения нескольких моделей. Третья модель дает относительно неплохой результат с тестовой эффективностью в 0,9. Эту модель вполне можно признать валидной и качественно обученной, если бы мы не знали, что мы можем достичь точности в 0,975 (вторая модель).
Для сравнения рассмотрим результаты анализа еще одной модели на тех же самых данных — наивного байесовского классификатора с гауссовым распределением:
Хотя график сильно отличается от любого из трех предыдущих, самое главное, на что следует обратить внимание — низкое значение обучающей эффективности на полном наборе данных. Это показывает, что даже если мы продолжим добавлять данные в обучающую выборку, максимум, на который мы можем рассчитывать — это что тестовая эффективность приблизится к обучающей, которая все равно недостаточная (в данном примере меньше 0,9). Это свидетельствует о недообученности модели.
Как мы говорили, недообучение и переобучение — это условные понятия, которые называют распространенные ситуации при использовании моделей машинного обучения. Недообучение — это когда у модели низкая вариация и высокое смещение. Переобучение — это наоборот, когда низкое смещение и высокая вариация. На самом деле эти свойства в моделях присутствуют всегда. Более тщательный анализ может сделать вывод, что последняя модель имеет как высокую вариацию (что выражается в сильной разнице между эффективностями), так и высокое смещение (об этом говорит низкое значение обучающей эффективности).
Выводы:
- При недообучении тестовая и обучающая эффективности будут достаточно близкими, но недостаточными.
- При переобучении тестовая и обучающая эффективности будут сильно различаться — тестовая будет значительно ниже.
- Пере- и недообучение — это относительные понятия.
- Более простые модели склонны к недообучению, более сложные — к переобучению.
- Диагностика пере- и недообучения очень важна, так как для повышения эффективности предпринимаются противоположные меры.
- Для построения можно использовать функцию ошибки, метрику эффективности или метрику ошибки, важна только динамика этих показателей.
- Диагностика моделей машинного обучения — это не точная наука, здесь нужно принимать в расчет и задачу, и выбор признаков и многие другие факторы.
Методы повышения эффективности моделей
Регуляризация
Как мы говорили, диагностика моделей нужна для поиска путей повышения ее эффективности. И мы выяснили, что пере- и недообучение моделей напрямую связаны с уровнем сложности моделей. Можно рассмотреть гипотетический график, на котором показан уровень ошибок моделей на конкретном наборе данных в зависимости от уровня сложности этой модели. Пока мы не сталкивались с тем, как можно плавно менять уровень сложности модели в рамках одного параметрического класса. Но представим, что речь идет о полиномиальной модели, а по горизонтали отложена степень этого полинома.
Если модель слишком проста, то уровень тестовых и обучающих ошибок будет высок и достаточно близок друг к другу. Мы говорили об этом (правда другими словами, в терминах эффективности) в предыдущей главе. По мере увеличения сложности разрыв между этими уровнями ошибок будет в среднем увеличиваться. Это происходит за счет более глубокой подстройки модели именно к обучающей выборке. Причем уровень ошибок на обучающей выборке будет в среднем падать за счет повышения вариативности модели. Но уровень ошибок не может опуститься ниже нуля. Поэтому либо с какого-то момента он стабилизируется, либо будет асимптотически приближаться к 0. А это значит, что уровень тестовой ошибки неизбежно рано или поздно начнет повышаться с ростом сложности модели. Таким образом, у уровня тестовой ошибки есть некоторое оптимальное значение.
Другими словами, для любого конкретного датасета существует некоторый оптимальный уровень сложности модели, который дает наименьшую ошибку на тестовой выборке. Модели, имеющие более низкую сложность будут недообучаться, а более высокую — переобучаться. Поэтому существует задача нахождения этого оптимального уровня сложности. К сожалению, это не получится сделать методом обучения, или любой другой численной оптимизации, так как изменение уровня сложности модели требует запуска ее обучения заново. Мы не можем непрерывно менять уровень сложности, как какой-то дополнительный параметр модели.
Изучив несколько видов моделей обучения с учителем легко сделать вывод, что сложность модели — это некоторое “встроенное” свойство, которое определяется видом самой модели, то есть параметрическим классом функций, которые аппроксимируются этой моделью. Некоторые модели просто сложнее чем другие. Например, многослойный перцептрон гораздо сложнее линейной регрессии, а глубокое дерево решений сложнее более мелкого.
Выше мы определяли уровень сложности модели через количество ее параметров. Но стоит сказать, что численное значение этих параметров тоже имеет значение. Рассмотрим для примера две модели — линейную ($y = b_0 + b_1 x$) и квадратичную ($y = b_0 + b_1 x + b_2 x^2$). Очевидно, вторая модель сложнее, так как у нее больше параметров. Квадратичная функция имеет больше степеней свободы и демонстрирует нелинейное поведение — рост функции на разных участках может сильно отличаться.
Но что, если параметр $b_2$ у квадратичной модели будет очень маленьким, скажем, $b_2 = 0.0001$. Если у нас есть функция, например, $y = -8 + 15 x + 0.0001 x^2$, то взглянув на ее график мы не отличим ее от линейной. Да, формально она будет относиться к классу квадратичных функций, но на практике она будет почти прямой линией. Рост функции на разных участках будет отличаться, но очень незначительно. Тем более, что нас интересует поведение функции не на всей числовой прямой а в окрестностях имеющихся точек данных. Если на этом участке функция ведет себя как линейная, то для прикладной задачи она и эквивалентна линейной.
То есть чем ближе параметр $b_2$ к нулю, тем эффективно ближе квадратичная модель к линейной. Так можно сказать про любой параметр любой модели обучения с учителем. Только в более сложных моделях связь между конкретным параметром и уровнем сложности не так очевидна, так в случае с полиномиальными функциями. Но в любом случае, чем меньше в модели параметров, существенно отклоняющихся от нуля, тем она проще. Причем, это обычно не распространяется на свободный коэффициент $b_0$, у него особая роль — его значение смещает все предсказания модели (поэтому он часто называется параметром смещения). Его отличие от нуля несущественно. На этом эффекте основан один очень полезный и распространенный на практике математический прием, который позволяет гибко и очень удобно управлять сложностью параметрических моделей машинного обучения. Этот прием называется регуляризация.
Допустим, у нас есть набор данных и мы не знаем, модель какого вида подойдет к нему лучше — линейная или квадратичная. При прочих равных, квадратичная модель всегда даст меньшую величину ошибки и поэтому будет предпочтительнее. Но мы уже видели, что малая ошибка — не всегда показатель качества модели. Если обычная функция ошибки, основанная на суммарном отклонении значений данных от модели (которую мы рассматривали до этого), не дает адекватной оценки качества модели, может стоит ее как-нибудь изменить?
Функция ошибки — это по сути система штрафов. Каждый раз, когда модель ошибается, к значению ошибки прибавляется величина, пропорциональная отклонению. Это — штраф за ошибку модели. Но может быть, мы можем штрафовать что-нибудь еще? Например, уровень сложности модели. Представьте, что мы добавляем к ошибке некоторые штрафы за высокие значения параметров модели. Тогда алгоритм обучения, который минимизирует именно функцию ошибки будет не так сильно отдавать сложным переобученным моделям. Небольшие ошибки модели могут быть скомпенсированы тем, что модель становится более простой.
Причем эти штрафы очень легко выражаются математически. Если штраф за ошибки модели — это некоторое математическое выражение, основанное на отклонениях предсказанных значений от эмпирических, то штрафы за сложность модели — это выражение, основанное на отклонениях параметров самой модели от нуля. Существует несколько конкретных реализаций регуляризации и о них мы поговорим чуть далее. Кстати, регуляризация обычно не затрагивает свободный коэффициент. Причины этого мы только что обсуждали — он не влияет на сложность модели.
В этом и состоит идея регуляризации — модификация функции ошибки таким образом, чтобы штрафовать сложные модели в пользу более простых. Да, достаточно странно складывать отклонения целевой переменной (которые могут быть выражены в натуральных единицах) и безразмерные параметры модели. Это может выглядеть, как сложение метров с красным. Регуляризация — это именно математический трюк. У нее нет физического значения, какой-то внятной интерпретации в терминах предметной области.Это лишь способ отдавать предпочтение моделям с низкими значениями параметров, ведь такие модели ведут себя как более простые и поэтому менее склонны к переобучению.
Можно заметить, что регуляризация — это способ искусственно понизить сложность модели. То есть при использовании регуляризации берут модель более сложную, которая в “чистом” виде будет явно переобучаться на имеющихся данных. Но за счет этих дополнительных штрафов, ее сложность принижают. Причем, самое удобное в регуляризации то, что она параметрическая. То есть соотношением “силы” штрафа за ошибки и штрафа за сложность легко управлять, введя множитель — так называемый параметр регуляризации. Чем он больше, тем сильнее штрафуются сложные модели, то есть даже большие ошибки модели могут быть скомпенсированы небольшим понижением сложности. Таким образом, возвращаясь к графику в начале главы, именно параметр регуляризации может быть отложен на нем по горизонтали.
Регуляризация настолько удобна и универсальна, что большинство библиотечных реализаций тех моделей, которые мы проходили раньше, уже реализуют встроенную регуляризацию. Причем это относится равно как к моделям классификации, так и к моделям регрессии, это прием не зависит от типа задачи обучения с учителем. За счет способности уменьшить сложность любой модели регуляризация является одним их основных способов борьбы с переобучением.
Обратите внимание, что мы в основном говорим именно о борьбе с переобучением. Борьба с недообучением в основном сводится к использованию более сложной модели. В настоящее время разработаны настолько сложные модели, что узким местом современного машинного обучения становятся вычислительные мощности и доступность данных.
Выводы:
- Регуляризация — это способ искусственно ограничить вариативность моделей.
- При использовании регуляризации можно применять более сложные модели и снижать склонность к переобучению.
- Регуляризация модифицирует функцию ошибки модели, добавляя в нее штрафы за повышение сложности.
- Основная идея регуляризации — отдавать предпочтение низким значениям параметров в модели.
- Регуляризация обычно не затрагивает свободный коэффициент $b_0$.
- Регуляризация обычно параметрическая, можно управлять ее степенью.
Ridge
Зачастую переобучение модели, которое является следствием большого количества параметров в модели, появляется потому, что в наборе данных присутствует много “лишних” атрибутов. Количество параметров любой модели обучения с учителем зависит от количества признаков в данных. Для борьбы с этим явлением используется регуляризация. Как мы говорили, регуляризация “штрафует” отклонения параметров модели (за исключением свободного) от нуля. Совершенно естественно формализовать это отклонение так же, как и в самой функции ошибки — как сумму квадратов этих значений. Такая модель называется гребневой регрессией (ridge regression). В ней функция ошибки принимает такой вид:
[J(vec{b}) = frac{1}{2m} sum_{i=1}^{m} (h_b(x_i) — y_i)^2 + lambda sum_{j=1}^{n} b_j^2]
Как мы можем видеть, что функция ошибки аналогична обычной модели регрессии, но имеет одно дополнительное слагаемое — регуляризационный член. Это сумма квадратов значений параметров модели (начиная с первого). Эта сумма умножается на специальный параметр — параметр регуляризации $lambda$. Он как раз отвечает за “силу” регуляризации модели. В передельном случае, когда $lambda = 0$, мы имеем обычную нерегуляризованную регрессию. Чем больше этот параметр, тем сравнительно больший вклад в ошибку дают отклонения параметров модели. То есть, чем больше этот параметр, тем более простые модели мы будем получать после обучения, при достижении минимума этой функции. Естественно, параметр регуляризации не может быть отрицательным, так как в таком случае мы наоборот, будем отдавать предпочтение более сложным моделям. А сложность, как и ошибка могут возрастать неограниченно.
Но если мы модифицируем функцию ошибки, то это влечет изменение и метода градиентного спуска. На самом деле он меняется незначительно. Вспомним, что градиентный спуск основан на вычислении частной производной функции ошибки по параметрам модели. Если взять свободный параметр, то вообще ничего не меняется, так как регуляризационный член от него не зависит:
[frac{partial}{partial b_0} J =
frac{1}{m} sum_{i=1}^{m} (h_b(x_i) — y^{(i)}) cdot frac{partial}{partial b_0} h_b(x_i)]
Если же рассматривать другие параметры модели, то в выражение производной добавится всего одно небольшое слагаемое:
[frac{partial}{partial b_i} J =
frac{1}{m} sum_{i=1}^{m} (h_b(x_i) — y^{(i)}) cdot frac{partial}{partial b_i} h_b(x_i) + 2 lambda b_i]
Это слагаемое $2 lambda b_i$ как раз и будет учитывать значения параметров при выполнении шагов градиентного спуска в регуляризованной модели регрессии. В остальном метод обучения никак не меняется. Если мы рассматриваем линейную модель, то получается почти знакомое нам по предыдущим главам выражение:
[frac{partial}{partial b_i} J =
frac{1}{m} sum_{i=1}^{m} (h_b(x_i) — y^{(i)}) cdot x_i + 2 lambda b_i]
Как мы уже говорили, этот прием может быть применен как к задачам классификации, так и к задачам регрессии. Но применяя регуляризованные модели на практике стоит быть внимательнее. Дело в том, что в некоторых моделях (например, в методе опорных векторов) регуляризация задается чуть иначе:
[J(vec{b}) = С frac{1}{m} sum_{i=1}^{m} cost(h_b(x_i) , y^{(i)}) + sum_{j=1}^{n} b_j^2]
Где $C$ — это тоже параметр регуляризации. Обратили внимание, что этот множитель стоит перед другим слагаемым — самой функцией ошибки? Численно, это эквивалентно предыдущей формализации, если полагать, что $C = frac{1}{lambda}$. Но стоит помнить, что в такой форме чем больше $C$, тем меньше регуляризации присутствует в модели.
Гребневую регрессию еще называют регрессией по L2-норме (L2 означает норма Лагранжа второго порядка) или регуляризацией Тихонова. Простыми словами это означает, что мы считаем сумму квадратов параметров.Гребневая регрессия полезна тем, что она может помочь повысить эффективность модели, если в данных присутствует большое количество мультиколлинеарных факторов, то есть атрибутов, которые очень сильно зависят друг от друга. Вообще, мультиколлинеарность в статистике — это в принципе не очень хорошее явление. В машинном обучении она опасна тем, что оптимальные параметры модели становятся гораздо менее устойчивыми, а значит обучение будет не очень надежным. Ну и вдобавок, большое количество признаков, как мы уже говорили, увеличивает количество параметров и порядок сложности модели, что приводит к переобучению. На практике мультиколлинеарные признаки можно обнаруживать и удалять из датасета руками, но гребневая регрессия может это делать автоматически.
Рассмотрим работу гребневой регрессии на примере. Для лучшего понимания того, как регуляризация влияет на получаемую модель, мы возьмем одни и те же данные и построим одну и ту же модель классификации с L2 регуляризацией, но с разными значениями параметра регуляризации. В качестве базовой модели мы используем полином пятой степени. Для начала классификация без регуляризации ($lambda=0$):
Мы видим достаточно сложную границу принятия решения и высокую точность модели — на этих данных эта модель показывает 0,91 accuracy. Давайте возьмем $lambda=2$:
За счет использования регуляризации точность модели немного снизилась и составила 0,89. Граница принятия решения тоже стала более гладкой и простой.
Обратите внимание, что расположение границы принятия решения полностью изменилось по сравнению с первой моделью. Ведь параметр регуляризации — это не то же самое, что и обычный параметр модели, коэффициент в функции. Один и тот же алгоритм, обученный с разными значениями параметра регуляризации даст две совершенно разные модели, не имеющие ничего общего. Поэтому нельзя, например, плавно менять параметр регуляризации и смотреть, как изменится граница принятия решения. И физического смысла параметр регуляризации никакого не несет. Это лишь численная переменная в алгоритме обучения, которая влияет на то, какая модель из определенного параметрического класса будет считаться оптимальной для данной задаче. В дальнейшем такие “сложные” параметры мы будем называть гиперпараметрами.
Увеличим регуляризацию еще больше и получим такую модель:
Точность снизилась еще больше — до 0,85. Очевидно, что точность регуляризованных моделей будет меньше, так как функция ошибки может “променять” точность на упрощение модели. Но в метриках эффективности сложность модели не учитывается, поэтому они падают. Ну и граница принятия решения тоже становится все более плоской.
Рассмотрим влияние регуляризации на модель регрессии. Для этого также возьмем один и тот же набор данных и будем строить на нем разные модели. Также будем использовать полиномиальные признаки пятой степени. Но на этот раз обратим внимание и на сами коэффициенты модели. Для начала посмотрим на модель практически без регуляризации ($lambda=0.1$):
Эта модель имеет точность 0,714 (по метрике r-квадрат) и следующие коэффициенты — 0, -2.84, -4.49, 8.03, -2.92, 0.34. Как видно, все полиномиальные признаки имеют влияние на модель, коэффициенты при них отличаются от нуля существенн. Теперь добавим регуляризацию ($lambda=1$):
Точность модели немного упала — до 0,712. Теперь взглянем на коэффициенты: 0, -2.51, -0.97, 4.48, -1.76, 0.22. Заметно, что все они сильно уменьшились (в абсолютном выражении), особенно третий и четвертый. Это как раз и есть влияние регуляризации — она стремится держать коэффициенты как можно более близкими к нулю, даже за счет понижения точности. А параметр регуляризации — это своего рода “обменный курс” между коэффициентами и точностью. Давайте поднимем его еще сильнее (до $lambda=100$):
Точность модели понизилась более существенно — до 0,698. А вот ее коэффициенты: 0, 0.13, 0.37, 0.49, -0.04, 0.01. По мере увеличения регуляризации ни один из коэффициентов не удалялся от нуля. А некоторые вплотную к нему приблизились. При этом заметим, что ни один коэффициент не стал нулем — гребневая регрессия даже с запредельным уровнем регуляризации стремится оставить в модели все имеющиеся признаки.
Выводы:
- $lambda > 0$ — параметр регуляризации.
- Чем он больше, тем сильнее штрафуются сложные модели.
- Этот прием может применяться как к классификации, так и к регрессии.
- Ridge еще называют регуляризацией по L2-норме. Она же — гребневая регрессия.
- Такая регуляризация делает параметры более робастными к мультиколлинеарности признаков.
Lasso
У гребневой регрессии есть один недостаток, проявляющий себя при работе с данным, в которых есть много “лишних” признаков — она всегда включает в модель все признаки. Но параметры у них могут быть близки к нулю, что затрудняет интерпретацию модели и не сокращает размерность задачи. На практике в данных могут присутствовать не просто мультиколлинеарные атрибуты, но и такие, которые имеют очень маленькое влияние на целевую переменную или не имеют его вообще. Включать их в модель не имеет никакого смысла.
Для решения этой проблемы существует так называемая лассо-регрессия. Она по своей формализации очень похожа на гребневую, но чуть по-другому учитывает значения параметров модели:
[J(vec{b}) = sum_{i=1}^{m} (h_b(x_i) — y_i)^2 + lambda sum_{j=1}^{n} mid b_j mid]
В данном случае говорят о регуляризации по L1-норме. За счет того, что функция абсолютного значения, которая используется здесь не везде дифференцируема, для обучения такой модели используется специальный метод координатного спуска (coordinate descent), а не градиентного. Но рассмотрение всех вариантов алгоритмов обучения выходит за рамки данного пособия. В остальном же использование лассо на практике абсолютно идентично другим моделям обучения с учителем.
Из-за своей специфической формализации, модель лассо стремиться обратить в ноль как можно больше параметров модели. Это значит, что если какой-то признак не оказывает сильного влияния на целевую переменную, то модель с L1-регуляризацией с большой долей вероятности “занулит” этот признак. Это бывает очень полезно в задачах, где в данных присутствует больше количество ненужной информации. Такие задачи еще часто называют разреженными. К ним часто относятся, например, задачи анализа текстов.
В таких задачах регрессия по методу лассо может использоваться для отбора признаков. Часто эта модель потом вообще не используется, а на оставшихся признаках строится какая-то другая модель обучения с учителем. Так лассо-регрессия может играть вспомогательную роль. Регрессию лассо поэтому часто называют методом понижения размерности — после ее применения в модели остаются (ненулевыми) только те признаки, которые действительно влияют на значение целевой переменной. Хотя это не совсем то, что называют понижением размерности в задачах обучения без учителя.
Также как и любая регуляризация, лассо управляет компромиссом между bias и variance модели за счет введения параметра регуляризации. Он имеет точно такой же смысл, как и в гребневой регрессии — чем он больше численно, тем более простые модели будет предпочитать этот алгоритм. Можно построить график зависимость обучающей и тестовой эффективностей модели от значения параметра регуляризации:
Здесь мы видим, что при малых значениях этого параметра наблюдается большая разница между эффективностями. ПО мере увеличения значения параметра регуляризации сложность, а следовательно и обучающая эффективность модели падают, а разница между ними сокращается. Тестовая же эффективность поначалу растет, но начиная в определенного значения параметра регуляризации (в районе $10^{-1}$) снова начинает снижаться. В левой части этого графика мы наблюдаем ситуацию переобучения, а в правой — недообучения. А примерно $10^{-1}$ — это оптимальное значение параметра регуляризации, при котором получается наиболее качественная модель линейной регрессии.
Давайте построим регрессию по методу лассо на тех же данных, на которых строили в предыдущей главе гребневую регрессию. На этот раз ограничимся одной моделью со средним уровнем регуляризации ($lambda=1$):
Обратим внимание на коэффициенты модели: 0, 0, 0, 0.55, 0, 0. Даже при таком небольшом значении параметра регуляризации модель оставила только один признак — признак третьей степени (что мы и видим на графике — это кубическая парабола, только масштабированная по вертикали). В этом и проявляется действие алгоритма лассо — он стремится как можно больше коэффициентов обратить в ноль.
Lasso, кстати, расшифровывается как least absolute shrinkage and selection operator, оператор наименьшего абсолютного сокращения и выбора.
В данном примере можно сделать вывод, что среди полиномиальных признаков только признак третьей степени оказывал сколь-нибудь существенное влияние на целевую переменную. Таким образом, регрессия по методу лассо работает как алгоритм отбора признаков. В дальнейшем можно используя только этот один признак строить и другие модели машинного обучения на данной задаче, или просто ввести его в датасет, таким образом лассо станет основой для инжиниринга признаков.
Выводы:
- Lasso еще называют регуляризацией по L1-норме.
- Lasso заставляет модель использовать меньше ненулевых коэффициентов.
- Фактически, эта регуляризация уменьшает количество признаков, от которых зависит модель.
- Может использоваться для отбора признаков.
- Полезна в задачах с разреженной матрицей признаков.
Elastic net
После прочтения двух предыдущих разделов может появиться вопрос: какой метод регуляризации лучше? Как всегда не существует универсального ответа. Это целиком зависит от данных. С разреженностью признаков лучше справляется лассо, а с мультиколлинеарностью — гребневая модель. Как всегда, когда есть два подхода, каждый со своими преимуществами, есть способ их скомбинировать. Рассмотрим модель, которая обычно называется elastic net или “эластичная сеть”:
[J(vec{b}) = frac{1}{2m} sum_{i=1}^{m} (h_b(x_i) — y_i)^2 +
lambda_1 sum_{j=1}^{n} | b_j | + lambda_2 sum_{j=1}^{n} b_j^2]
Как мы видим, функция ошибки такой модели комбинирует подходы гребневой и лассо-регрессии. То есть включает в себя регуляризацию и по L1 и по L2 нормам. Поэтому в этой модели присутствует целых два параметра регуляризации, причем они независимы друг от друга и задают не только соотношение регуляризации того или иного типа и классической функции ошибки, но и соотношение силы двух типов регуляризации между собой.
А между тем мы еще не говорили о том, как подбирать оптимальные значение параметров регуляризации. А ведь это достаточно серьезная проблема. Их не подберешь обычным методом обучения — это не просто параметры модели. Чуть позже мы назовем их гиперпараметрами. Но подбирать их можно только непосредственной проверкой, то есть подбором в классическом смысле. И это достаточно трудоемкий процесс, так как надо проверить потенциально бесконечное количество значений, причем еще хорошо бы использовать кросс-валидацию для надежности результатов.
А как быть с двумя гиперпараметрами. Обычно их значения подбираются “наивным” способом, в два прохода. Сначала находится оптимальный параметр $lambda_2$ для гребневой регрессии, а потом он фиксируется и подбирается наилучший параметр $lambda_1$ для лассо. Понятно, что они могут зависеть еще и друг от друга. И чуть позже мы изучим более вычислительно емкий, но правильный способ искать оптимальные значения гиперпараметров.
Давайте построим регрессию методом эластичной сети по уже известным нам данным из двух предыдущих глав. В данном случае используем $lambda_1 = lambda_2 = 10$:
Коэффициенты у модели следующие: 0, 0, 0, 0, 0.202, -0.016. Очень заметно совместное влияние двух регуляризаций. L1 выбирает только самые значимые признаки, оставляя у других коэффициенты равными нулю, а L2 еще приближает к нулю оставшиеся коэффициенты. В результате получается очень компактная модель, которая имеет только очень обоснованные коэффициенты.
Конечно, приведенные в данных главах модели не являются обязательно лучшими или оптимальными для решения данной задачи регрессии. Их цель — проиллюстрировать работу алгоритмов и для этого зачастую приходилось на максимум “выкручивать” регуляризацию. В реальности надо искать оптимальный уровень регуляризации, но об этом речь пойдет в следующих главах.
Выводы:
- По сути, это комбинация регуляризации по L1 и L2 нормам.
- Имеет два параметра, которые определяют соотношение соответствующих норм.
- Комбинирует достоинства предыдущих двух методов.
- Недостаток в необходимости задавать сразу два параметра регуляризации.
Методы борьбы с недообучением
В этой главе мы говорим о диагностике моделей машинного обучения в контексте диагностики недо- и переобучения. И мы много говорили о том, как обнаружить эти состояния модели. Так что же делать, если мы обнаружили, что наша модель недообучается. Сейчас поговорим о типичных путях повышения эффективности моделей. И начнем с более простого случая — недообучения.
В первую очередь напомним себе, что такое недообучение. Это ситуация, когда модель демонстрирует слишком большой bias по отношению к имеющимся данным. Модели не хватает вариативности, чтобы “ухватить” зависимости между признаками и целевой переменной. С точки зрения модели, их вообще нет. Простыми словами можно сказать, что модель слишком проста, примитивна для решения поставленной задачи. При этом может быть такое, что имеющиеся данные действительно не содержат необходимой информации, позволяющей надежно предсказать значение целевой переменной.
Поэтому при недообучении первое о чем нужно подумать: есть ли в датасете информация (признак или комбинация признаков), которые бы определяли значение целевой переменной. Если таких нет, то неважно, сколько точек данных, примеров мы соберем, модель всегда будет недообучаться. Неважно, насколько сложную модель мы будем использовать, она покажет случайных шум. Наиболее эффективный способ борьбы с недообучением — инжиниринг признаков. Необходимо ввести в модель признаки (или атрибуты, неважно, важно чтобы была нужная информация), которые позволят модели предсказать значение целевой переменной.
Помните, как мы решали задачу с полиномиальными признаками, как они превращали нерешаемую задачу классификации в линейно разделимую? Так может произойти в любой задаче. Может, одного свойства объекта нам и не хватает, чтобы превратить случайный перемешанный набор точек в многомерном пространстве в четкую и очевидную зависимость.
К сожалению, нет универсального алгоритма инжиниринга признаков. Это всегда творческая деятельность, которая требует, причем, глубокого знания предметной области. Иногда нужно просто вернуться на этап сбора данных и найти (или сгенерировать) больше информации. Иногда помогает вдумчивое и осмысленное преобразование имеющихся атрибутов. Главный вопрос, который надо себе задать: что в реальности влияет на целевую переменную? Затем собирать как можно больше информации об этом, добавлять ее в модель в виде признаков и надеяться, что это повысит эффективность моделей.
Если такой возможности нет, то очевидно, имеет смысл уменьшить степень регуляризации модели. Конечно, этот способ подходит только, если вы используете регуляризованные модели. Но как мы уже обсуждали выше, очень многие модели используют регуляризацию автоматически. А если она применяется, то можно легко манипулировать ее степенью. Понижение регуляризации приведет к тому, что после обучения мы получим более сложную и вариативную модель, что может исправить ситуацию с недообучением.
Другой очевидный способ — использование более сложных моделей в целом. Имеется в виду смена класса моделей. Если недообучается, например, модель линейной регрессии, стоит попробовать дерево решений. Если недообучилась логистическая — попробуйте многослойный перцептрон. Хотя, регуляризация обычно работает более эффективно, чем использование более сложной модели, она ограничена рамками одного параметрического класса функций.
Возможно стоит попытаться повторить обучение или увеличить количество итераций обучения. Возможна ситуация, когда существующего количества итераций недостаточно для схождения метода обучения к локальному минимуму функции ошибки. Это опять же может происходить вследствие того, что задача слишком сложна. В особо сложных случаях можно использовать предобученные модели. Это так называемое трансферное обучение — когда используют уже обученную модель на каком-то одном наборе данных для решения подобной задачи на другом датасете. Например, существуют так называемые глубокие языковые модели — огромные нейросети с миллиардами параметров, которые обучаются на гигантских корпусах текстов. Они используются для разнообразных задач текстовой аналитики. Конечно, каждый раз нецелесообразно обучать такую огромную модель с нуля — можно воспользоваться уже обученной и дообучить ее (или обучить, например, только последний слой нейронной сети) под собственную задачу. Трансферное обучение — отдельная и очень интересная дисциплина машинного обучения, но ее подробное рассмотрение выходит за рамки этого пособия.
Отдельно стоит сказать, что не поможет при недообучении. Вам вряд ли поможет увеличение объема выборки. Многие думают, что собрать больше данных — это универсальный рецепт эффективности. Это тоже не так. Хотя, большая по объему выборка особенно и не помешает, то есть не уменьшит эффективность модели, она увеличит вычислительную емкость. Другими словами, модель будет обучаться значительно дольше, но без видимого положительного эффекта по эффективности.
Обратите внимание, что мы здесь всегда имеем в виду эффективность, измеренную на тестовой выборке. А еще лучше — с использованием кросс-валидации. Эффективность на обучающей выборке нужна только для диагностики и анализа моделей.
Стоит помнить, что машинное обучение — это всегда итеративный процесс. Построив первую модель нужно ее исследовать и пытаться улучшить, увеличить эффективность. При этом возможно стоит попробовать множество разных видов моделей и способов обработки данных.
Выводы:
- Ввести в модель новые данные об объектах (атрибуты).
- Уменьшение степени регуляризации модели.
- Введение полиномиальных и других суррогатных признаков.
- В целом, инжиниринг признаков.
- Использование более сложных моделей.
- Увеличение количества итераций.
- Трансферное обучение.
Методы борьбы с переобучением
Переобучение на практике более частая и более коварная проблема потому, что несложно взять для решение конкретной задачи более сложную модель. Гораздо труднее заставить ее работать хорошо на новых данных. Проблему переобучения обнаружить сложнее и потому, что при этой ситуации модель работает вроде бы хорошо — дает низкую ошибку на данных. Но на других точках модель почему-то начинает ошибаться гораздо сильнее.
Опять же вспомним, что суть ситуации переобучения состоит в том, что модель оказывается слишком сложной для имеющихся данных и зависимостей в них. Поэтому вместо общих тенденций модель начинает обращать внимание на конкретное расположение точек в обучающей выборке, на случайные флуктуации, которые не несут смысловой нагрузки и не будут повторяться в новых данных.
Чем меньше данных присутствует в обучающей выборке, тем больше в них “шума” по отношению к полезному “сигналу” — информации о случайных колебаниях значений признаков по сравнению с информацией о тенденциях и реальных зависимостях. Поэтому неудивительно, что на малых объемах данных при прочих равных модели склонны к переобучению. Взгляните на график выше — даже человеку неочевидно, что точки выборки образуют линейную тенденцию — их просто слишком мало, чтобы показать эту тенденцию.
Самый действенный способ борьбы с переобучением — собрать больше обучающих примеров.
Если мы добавим больше точек, принадлежащих тому же распределению, мы неизбежно более четко увидим имеющуюся тенденцию. Все дело в том, что основное свойство случайных колебаний — их математическое ожидание равно нулю. То есть значение показателя может под воздействием неизвестных или неучтенных факторов отклоняться от “правильного” значения как в сторону увеличения, так и в сторону уменьшения. Причем вероятность этого примерно равна. И если мы рассматриваем одну точку данных, то сложно сказать, чем обосновано ее конкретное значение — существенными факторами или случайностью. Но если рассмотреть большое множество точек, можно увидеть, что они группируются вокруг некоторого среднего.
Другими словами, при увеличении количества точек обучающей выборки все случайные колебания будут усредняться — на каждое положительное отклонение найдется примерно равное отрицательное. А тенденция же будет, наоборот, усиливаться. В итоге и человеку и модели будет значительно легче эту тенденцию “ухватить”. Посмотрите, например, что будет, если к выборке, изображенной на рисунке выше добавить еще в 10 раз больше точек из того же распределения:
Теперь довольно очевидно, что на лицо линейная тенденция. И даже более сложная полиномиальная функция работает гораздо более эффективно на этих данных. Именно так добавление данных борется с переобучением моделей.
Причем необходимое количество данных зависит от вида тенденции и величины случайных отклонений. Чем более сложная, нелинейная тенденция в данных существует, чем тоньше зависимость целевой переменной от значения атрибутов, тем больше данных нужно для адекватной работы моделей. И чем больше по величине случайные отклонения, чем “сильнее” они размывают эту тенденцию, тем больше данных понадобится. Поэтому не существует какого-то оптимального объема данных, все зависит от конкретной задачи.
Как мы видели на примерах ранее, переобучение зачастую возникает вследствие того, что в модели присутствует большое количество параметров за счет большого количества лишних признаков в датасете. Именно для борьбы с этим используется регуляризация и в целом отбор признаков. Незначимые атрибуты лучше убирать из данных еще на этапе предварительного анализа и очистки данных. Чем меньше в данных будет лишних признаков, тем более четко и ясно будет прослеживаться та самая заветная тенденция.
Однако следует помнить, что регуляризация на практике работает лучше, чем ручное удаление признаков, так как подбор коэффициентов модели происходит автоматически. При этом регуляризация имеет свои недостатки — необходимость подбора параметра регуляризации. Поэтому стоит комбинировать эти способы — если какие-то признаки явно не влияют на целевую переменную — их стоит убрать при обработке данных, а если есть сомнения — то лучше оставить на усмотрение регуляризации.
Кроме того, следует помнить, что в других классах моделей могут применяться и иные способы управления сложностью модели, которые эффективно в чем-то похожи на регуляризацию. Например, в деревьях решений — это ограничение глубины дерева. Мы уже говорили об этом: чем больше слоев в дереве, тем сложнее получается модель. В нейронных сетях для подобного же используются Dropout-слои. Подробно мы не сможем рассказать про все эти способы, тем более что они специфичны для разных классов моделей. Но на практике они применяются примерно также, как и обычная регуляризация.
Как мы видим на втором графике даже после добавления большого количества точек более простая модель все равно описывает выборку лучше, так как полиномиальная модель имеет не очень понятные “хвосты” на концах распределения. Поэтому при обнаружении переобучения стоит задуматься об использовании более простого параметрического класса функций. Этот способ работает лучше в совокупности с увеличением объема выборки. Вообще, комбинация нескольких способов может быть более эффективной, чем применение только одного.
В глубоком обучении есть эмпирическое правило, которое гласит, что количество параметров модели должно быть в 2-3 раза меньше, чем количество примеров в обучающей выборке. Это ни в коем случае не универсальное правило и не гарантия от переобучения. Помните, вся зависит от задачи. Но можно помнить об этом ориентире. Если количество параметров больше, чем рекомендует это правило, вы практически точно получите переобученную модель.
Кроме того, не стоит забывать о ложных корреляциях в данных, которые тоже могут стать причиной переобучения. Хотя, ложные зависимости данных в силу их ограниченности — это явление несколько другой природы, на практике оно проявляет себя точно как переобучение — снижает обобщающую способность модели. Для устранения ложных корреляций необходимо хорошо разбираться в предметной области или привлекать для анализа данных экспертов.
Еще устраняют или сильно снижают переобучение так называемые ансамблевые модели, особенно основанные на методе бустинга. Ансамблевые модели это отдельная большая тема, которую мы не сможем рассмотреть в этой главе, про них можно написать отдельную книгу. Но если вкратце, ансамбль — это набор моделей, обученных на одном и том же наборе данных. Метод бустинга заключается в том, что каждая следующая модель в ансамбле исправляет или компенсирует ошибки предыдущей. В итоге мы получаем такую метамодель, которая может работать более эффективно, чем каждая модель ансамбля по отдельности.
Еще один способ избежать переобучения моделей — ранняя остановка обучения. Раньше мы говорили, что процесс обучения всегда продолжается до полной сходимости, то есть до нахождения оптимальных значений параметров по заданной функции ошибки. Но это не всегда так. В процессе обучения можно контролировать ту самую тестовую эффективность и остановить обучение тогда, когда она начнет падать. Этот способ часто применяется в обучении нейронных сетей, так как оно начинается с малых случайных значений весов (параметров) сети. Поэтому само обучение, то есть подбор весов, немного имеет эффект повышения значения коэффициентов, который противоположен регуляризации, то есть повышение степени сложности модели. Поэтому ранняя остановка обучения эффективно похожа на введение регуляризации в модель. Важно остановить обучение именно в тот момент, когда сложность модели начнет превышать оптимальное значение, после которого начинается переобучение. Это простой, но не очень универсальный способ.
Каждый способ борьбы с переобучением (впрочем как и с недообучением) имеет свои достоинства и недостатки. Не существует универсального алгоритма действий. Поэтому всегда надо исходить из поставленной задачи, а также руководствоваться всеми факторами: характер модели, нефункциональные требования, особенности набора данных, возможность собрать больше точек или атрибутов. При возможности стоит попробовать несколько разных способов увеличения эффективности моделей.
Выводы:
- Ввести в модель данные о новых объектах, использовать выборку большего объема.
- Убрать признаки из модели, использовать отбор признаков, устранить ложные корреляции.
- Увеличить степень регуляризации модели.
- Использовать более простые модели.
- Регуляризация обычно работает лучше уменьшения количества параметров.
- Можно использовать ансамблевые модели.
- Ранняя остановка обучения.
Анализ ошибок
Рассматривая алгоритмические и математические способы повышения эффективности работы моделей машинного обучения не стоит забывать и о самом простом, но в тоже время одном из самых эффективных — ручном анализе ошибок модели. После обучения модели, если она не достигает желаемого уровня эффективности стоит просто обратить внимание на те объекты, на которых она делает ошибки. Этот подход называется анализ ошибок и может дать достаточно неожиданную информацию о модели, данных и самой задаче.
В отдельных случаях анализ ошибок приводит к выводу, что модель работает хорошо. Например, очень известна задача по распознаванию рукописных цифр по картинке. Даже относительно простые модели справляются с ней очень хорошо, но могут не достигать стопроцентной эффективности. Вот пример картинки, которую простая модель может классифицировать неправильно:
Свидетельствует ли эта ошибка о том, что модель обучилась неправильно? Скорее нет, это свидетельствует о низком разрешении картинок и наличии некоторых двусмысленных объектов в обучающей выборке. Такую рукописную цифру и человек бы не распознал.
Кроме того, в данных могут присутствовать просто ошибки. Особенно это касается датасетов, размеченных вручную. Человек мог просто опечататься или ошибиться и в наборе данных появился объект с неправильным значением целевой переменной. На практике все случается и именно ручной анализ ошибок может выявить такую ситуацию.
Ручная проверка индивидуальных объектов, на которых модель работает неправильно часто подсказывает, какие общие характеристики имеют такие объекты или чем они отличаются от остальной выборки. Поняв эти особенности можно найти способы модифицировать признаки таким образом, чтобы лучше учитывать эти особенности. Например, анализируя модель распознавания человека по лицу можно придти к выводу о том, что такая модель значительно чаще ошибается на лицах с растительностью или на людях в очках. Это вполне объяснимо с логической точки зрения. Так что же делать в таком случае? Можно просто собрать больше точек данных, лиц с растительностью или очками. Это не только просто повысит эффективность модели, но и сделает ее более устойчивой к подобным особенностям в принципе.
При проведении анализа ошибок следует ориентироваться на ошибки, которые модель делает именно в тестовой выборке. В задачах классификации в первую очередь следует проанализировать ошибки в тех классах, в которых модель делает больше всего ошибок. Это очень заметно в отчете о классификации и в марице классификации. Обычно бывает, что модель постоянно относит объекты одного класса к какому-то другому. А в задачах регрессии очень логично обратить внимание на объекты, на которых модель ошибается сильнее всего в численном выражении.
Выводы:
- Анализ ошибок — это ручная проверка объектов, на которых модель делает ошибки.
- Анализ характеристик таких объектов может подсказать направление инжиниринга признаков.
- Можно сравнить эти объекты с остальной выборкой. Может, это аномалии.
- В задачах регрессии в первую очередь обращать внимание на объекты с самым высоким отклонением.
Выбор модели
При решении конкретной задачи машинного обучения нельзя сказать заранее, какой вид модели будет наиболее эффективен. Разные типы моделей могут давать кардинально разный результат и показывать очень разную эффективность на одних и тех же данных. В одних задачах хорошо себя показывают линейные модели, а в других они совершенно непригодны. Какие-то данные прекрасно моделируются деревом решений, а другой набор данных лучше всего описывается методом ближайших соседей. Другими словами, на практике стоит проблема выбора модели для решения имеющейся задачи. И здесь имеются некоторые неочевидные нюансы, про которые и поговорим в этой главе.
Проблему выбора модели чаще всего решают перебором — нужно попробовать разные типы моделей и выбрать те, которые показывают наибольшую эффективность. При этом стоит учитывать те ограничения и характерные черты разных моделей, которые мы обсуждали в предыдущей главе. Особенно это касается нефункциональных требований к информационной системе. Всегда следует помнить, что модели машинного обучения часто создаются не только для научного и исследовательского интереса, но и для работы в реальных программных системах. И к этим системам могут предъявляться специфические требования. Например, по скорости работы, по объему используемой памяти. К работе самих алгоритмов тоже могут существовать особые требования, например, по интерпретируемости.
Характер данных тоже может подсказать, какие модели будут эффективны с большей вероятностью. Еще до начала моделирования, по результатам предварительного анализа данных, или по истории решения подобных задач можно прикинуть порядок сложности решаемой проблемы. Например, известно, что задача генерации осмысленного текста на естественном языке относится к разряду очень сложных. Такую задачу скорее всего не решить простыми линейными классификаторами. Здесь понадобится тяжелая артиллерия — глубокие нейронные сети. В глубоком обучении есть специализированные модели, которые “заточены” на анализ определенного типа информации. Например сверточные сети хорошо работают с графическими изображениями, а рекуррентные — с последовательностями. За исключением этого аналитику приходится в выборе типа моделей полагаться на свою интуицию, сравнение как можно большего количества моделей.
Если решается известная задача, то обязательно надо проводить анализ литературы и прошлой истории решения подобных проблем. Во многих известных задачах есть известные алгоритмы, которые решают задачу лучше всего. Они часто известны под названием state-of-the-art. В таких задачах целесообразно использовать именно их как базу сравнения. Если у вас получилось создать модель, которая превзошла state-of-the-art — это уже огромный успех и несомненный повод опубликовать свое исследование. Для более последовательного сравнения разных моделей, которые решают одну и ту же или сходные задачи существуют специальные модельные датасеты — наборы данных, которые служат эталоном, по которым сравнивают разные модели и подходы к решению задачи.
Если же никакой информации о предпочтительных видах моделей у исследователя нет, то самым естественным первым шагом будет построение самых простых моделей. Здесь имеются в виду простые как по классу сложности, так и по вычислительным затратам. Логичным выбором будет использование линейной или логистической регрессии (в зависимости от поставленной задачи) и дерева решения (иногда используют его ансамблевый вариант — случайный лес). Эти модели хороши тем, что довольно быстро работают, даже на относительно больших массивах данных. Кроме того, их результаты интерпретируемы — внутреннее устройство этих моделей можно проанализировать вручную и сделать какие-то значимые выводы о данных.
В любом случае, результат работы таких простых моделей дает нам оценку начального уровня эффективности модели, с которым можно сравнивать качество более сложных моделей, если придется такие строить. База сравнения — это очень полезная вещь в машинном обучении, особенно если вы решаете новую задачу, по которой нет научной литературы и не с чем сравнивать (либо известную задачу, но на принципиально других данных). Эта базовая эффективность станет нижним порогом для других моделей. То есть будет очевидно, что если более сложная модель показывает уровень качества ниже, чем такая базовая, то это совершенно неудовлетворительный результат.
После построения базовой модели обязательно надо провести диагностику для поиска путей повышения ее эффективности. Про это мы подробно говорили в предыдущих главах. Здесь первоочередная задача — детектировать пере- или недообучение. Стоит сказать, что такой анализ целесообразно проводить только в том случае, если эффективность базовой модели является неудовлетворительной. Довольно часто на практике бывает так, что даже самая простая модель уже достигает желаемого уровня точности. Ведь в прикладной области иногда не нужно стремиться к максимальной точности, достаточно достигнуть какого-то заранее определенного уровня.
Часто при начале моделирования строят большое количество самых разных моделей на одних и тех же данных для определения наиболее потенциальных. Можно определить пул из 15 — 20 различных алгоритмов машинного обучения и их вариаций, построить их на одинаковых данных и сравнить их эффективность. Например, для задачи классификации такой пул может выглядеть, например так:
- Логистическая регрессия
- Полиномиальная регрессия 3 степени
- Полиномиальная регрессия 7 степени
- Классификатор на опорных векторах без ядра
- Классификатор на опорных векторах с гауссовым ядром
- Классификатор на опорных векторах с сигмоидальным ядром
- Наивный байесовский классификатор
- Однослойный перцептрон
- Многослойный перцептрон с 1 скрытым слоем с количеством нейронов, равным количеству признаков
- Многослойный перцептрон с 3 слоями, на каждом из которых количество нейронов уменьшается вдвое
- Дерево решений
- Случайный лес
- К ближайших соседей
- Пассивно-агрессивный классификатор
- Классификатор на гауссовых процессах
- Экстремально рандомизированные деревья
- AdaBoost
- Градиентный бустинг
- XGBoost
- CatBoost
По сути это все модели, реализованные в sklearn за исключением моделей специального назначения (типа пассивно-агрессивного классификатора), плюс несколько сторонних моделей, реализованных в других библиотеках. Такой пул даст неплохой охват разных типов моделей. На практике после оценки эффективности модели всего несколько из этого списка показывают относительно неплохую эффективность, остальные же сильно отстают. Такой поиск перебором помогает определить один-два класса моделей, на которых можно сосредоточиться более подробно в своем анализе, а остальные — без сожаления отбросить. Кроме того такой способ даст более полную картину базового уровня сложности задачи и эффективности простых моделей.
Как мы понимаем, такой перебор может занимать достаточно много времени, особенно при большом объеме данных. Некоторые модели их списка могут обучаться на порядки дольше остальных. Если поиск занимает слишком большое время, можно взять для перебора не весь датасет а случайную часть, например, 10% (для этого можно использовать тот же_train_test_split_). По результатам анализа можно отобрать 5-6 наиболее перспективных моделей и повторить обучение на более полном наборе данных. Часто это сильно быстрее, чем обучать все на всем.
Вообще, выбор модели в машинном обучении, как и многие другие задачи — творческий и непредсказуемый процесс. В нем надо руководствоваться многими факторами — требованиями к моделям, интуицией, анализом данных, результатами диагностики. При этом приходится повторять одни и те же действия по многу раз. Конечно, существуют попытки автоматизировать эту задачу. Существуют специальные библиотеки (типа auto-sklearn), которые производят некоторые операции алгоритмически. Эта сфера в машинном обучении называется AutoML — автоматизированное построение и поиск моделей. Но на сегодняшний день эти алгоритмы пока недалеко ушли от примитивного перебора. И следует помнить, что применение этих подходов по-прежнему на порядки увеличивает время, необходимое на подбор и обучение модели.
Выводы:
- Очень сложно сказать априори какой класс моделей будет работать лучше на конкретных данных.
- Следует учитывать нефункциональные требования к задаче.
- Обычно начинают с самых простых моделей — они быстро считаются и дают базовый уровень эффективности.
- В исследовательских задачах модели сравниваются со state-of-the-art.
- По результатам диагностики простых моделей принимают решение о дальнейших действиях.
- Можно провести поиск по разным классам моделей для определения самых перспективных.
- Выбор модели — это творческий и исследовательский процесс.
- Есть подходы автоматизации выбора модели (AutoML), но они пока несовершенны.
Гиперпараметры модели
Усложняет задачу выбора модели тот факт, что у многих типов моделей существуют разные вариации, особые параметры. Например, при использовании полиномиальной регрессии мы должны указать степень полинома. При этом полиномиальные модели с разной степенью — это по сути дела разные классы. Поэтому в списке выше некоторые модели повторяются несколько раз, но с разными значениями этих “параметров”. В кавычках потому, что они ведут себя не как обычные параметры модели. Оптимальные значения обычных параметров мы подбираем в процессе обучения, в этом он, собственно, и заключается. Оптимальную степень полинома не подберешь в процессе градиентного спуска — если посередине алгоритма ее поменять, то мы окажемся о совершенно другом семействе функций, что нарушит связность алгоритма.
Эти особенные значения называются гиперпараметрами моделей. Гиперпараметры не подбираются при обучении — они задаются при определении модели и должны оставаться неизменными до схождения алгоритма обучения. Если мы хотим изменить значение гиперпараметра, мы должны заново запустить процесс обучения. В этом их основное отличие от параметров модели. Схожесть же в том, что гиперпараметры — это тоже численные значения, которые влияют на работу модели. Более конкретно они влияют на то, какая конкретная модель из всего класса моделей получится в результате обучения. То есть их действие более косвенное.
На самом деле мы знаем уже много примеров гиперпараметров — практически в каждом типе модели они есть. В методе k ближайших соседей то самое k, количество соседей, которое алгоритм учитывает, тоже является гиперпараметром. В дереве решений максимальная глубина дерева — тоже гиперпараметр. В моделях, использующих регуляризацию, коэффициент этой самой регуляризации (или два коэффициента, как в эластичной сети) — тоже является гиперпараметром. Вообще, у каждой модели может быть довольно много гиперпараметров. В библиотеке sklearn значения гиперпараметров задаются при создании объекта модели. Раньше мы использовали конструктор по умолчанию, но стоит посмотреть в документации, какие аргументы принимает конструктор того или иного объекта модели — некоторые их этих аргументов и есть гиперпараметры.
Рассмотрим, например, конструктор объекта KNeighborsClassifier. Он принимает семь необязательных аргументов:
- n_neighbors — количество ближайших соседей (то самое k);
- weights — метод взвешивания соседей по расстоянию (чтобы более близкие соседи влияли на значение больше чем далекие), причем по умолчанию используется метод без весов, то есть отсутствие взвешивания;
- algorithm — алгоритм вычисления матрицы ближайших соседей (кроме брут-форса есть более оптимизированные на некоторых данных способы);
- leaf_size — размер ячейки для одного из алгоритмов вычисления матрицы (для других алгоритмов этот аргумент бесполезен);
- metric — метрика вычисления расстояния (по умолчанию используется метрика Минковского);
- p — степень метрики (метрика Минковского использует это значение, при $p=2$ получается обычное Евклидово расстояние);
- n_jobs — количество потоков, которые используются для параллельных вычислений для ускорения работы алгоритма;
Итого из 7 аргументов конструктора 4 являются гиперпараметрами (n_neighbors, weights, metric, p). И это алгоритм ближайших соседей, который считается одним из самых простых. В других видах моделей гиперпараметров еще больше. Конкретный набор гиперпараметров зависит от деталей программной реализации самой модели, поэтому для определения, какие гиперпараметры существуют у данной модели необходимо обратиться к документации соответствующего класса. При этом все аргументы конструктора имеют значения по умолчанию. То есть даже если вы не задаете их значения, они все равно присутствуют в модели. Для гиперпараметров это важно — они всегда имеют какое-то значение. Модель нельзя не является строго определенной, если у хотя бы одного используемого гиперпараметра не определено значение.
При этом обратите внимание, что не все аргументы конструктора являются гиперпараметрами. Например, для рассмотренного выше класса, аргумент algorithm не влияет на то, какая конкретная модель получится в результате обучения. Да, алгоритм расчета матрицы может оказать влияние на скорость подсчета, но результат расчета или обучения модели от него на зависит. Поэтому этот аргумент нельзя считать гиперпараметром.
Рассматривая различные гиперпараметры можно заметить, что они бывают категориальные и численные. Например, вид метрики в методе ближайших соседей — это категориальный гиперпараметр. Он может принимать одно из конечного множества заранее известных значений. При разных значениях в модели используются разные формулы расчета расстояний между точками. А вот, для примера, параметр регуляризации — это численный гиперпараметр. Он может принимать любые значения больше нуля. Поэтому в отличие от обычных параметров моделей, которые бывают только численные, гиперпараметры могут быть категориальные.
Очевидно, что при разных значениях гиперпараметров будут получаться различные оптимальные модели, которые покажут разный уровень эффективности. Поэтому стоит задача нахождения оптимальных значений гиперпараметров. Но мы не можем подбирать их в процессе обучения. Задав до начала обучения значения всех гиперпараметров модели, мы не можем менять их. Поэтому мы можем только говорить о нахождении оптимальной модели при определенных значениях гиперпараметров.
Обычные параметры модели мы можем подбирать в процессе обучения потому, что сами модели сконструированы таким образом, чтобы существовал математический способ оптимизировать набор их значений. Этот способ может быть аналитический (как метод нормальный уравнений, который используется в самых простых случаях линейной регрессии), численный (как метод градиентного спуска) или алгоритмический (как методы построения оптимальных деревьев решений). Но в случае с гиперпараметрами таких алгоритмов в общем случае не существует. То есть мы не имеем представления о виде зависимости эффективности получающейся оптимальной модели от значения гиперпараметров — в общем случае она слишком сложная, неочевидная, может быть имеющая разрывы, в общем ведет себя полностью непредсказуемо. В каких-то частных случаях мы можем предполагать гладкость и выпуклость такой зависимости. Например, мы рассуждали о наличии оптимального значения параметра регуляризации. Это значит, что этот гиперпараметр всегда имеет один глобальный оптимум. Но в других случаях мы не можем утверждать даже этого наверняка.
Поэтому единственный применимый на практике способ нахождения оптимальных значений гиперпараметров — перебор. То есть нам нужно построить несколько моделей одного класса с разными значениями гиперпараметров и сравнить их эффективность на тестовой выборке. Конечно это подразумевает многократное повторение процесса обучения модели. Поэтому оптимизация гиперпараметров — это очень вычислительно емкий процесс. Это, наверное, самая вычислительно трудная и тяжелая часть машинного обучения. И конечно на практике невозможно проверить все возможные комбинации значений гиперпараметров. Для организации поиска существуют две главные стратегии, о которых мы поговорим в следующих главах.
Может быть вы обратили внимание на то, что в предыдущей главе мы похожим образом описывали процесс выбора наилучшей модели. Это не совпадение. Давайте рассмотрим степень полинома в полиномиальных моделях. Можно считать, что, например, квадратичная и кубические функции — это два разных параметрических класса моделей (у которых просто используются похожие алгоритмы обучения). А можно считать степень полинома гиперпараметром, тогда эти две модели будут считаться одним классом. Или, например, метод опорных векторов с разными ядерными функциями, что это — разные модели или просто разные значения гиперпараметра? В многослойном перцептроне можно рассматривать количество скрытых слоев тоже как особый гиперпараметр.
Формально, модели считаются разными, если у них разный набор обычных параметров. Но на практике различие между двумя моделями можно представить как гиперпараметр. Доводя это рассуждение до предела можно сказать, что сам вид модели тоже можно рассматривать как такой особый категориальный гиперпарамер. Важно, что как разные значения гиперпараметров приводят к различным моделям после обучения, так и разные классы моделей тоже порождают разные модели в результате. Поэтому задача оптимизации гиперпараметров и задача выбора модели — это принципиально одна и та же проблема. Именно поэтому мы начали говорить о гиперпараметрах моделей именно в этой главе. Методологические подходы к решению этих двух задач одинаковы.
Выводы:
- Гиперпараметр модели — это численное значение, которое влияет на работу модели, но не подбирается в процессе обучения.
- Гиперпараметры модели нужно задавать до начала обучения.
- Если значение гиперпараметра изменилось, то обучение надо начинать заново.
- Примеры гиперпараметров — k в kNN, параметр регуляризации, степень полиномиальной регрессии, глубина дерева решения.
- У каждой модели множество гиперпараметров, которые можно посмотреть в документации.
- Гиперпараметры бывают дискретные и непрерывные.
- Оптимизация гиперпараметров осуществляется перебором.
- Оптимизация гиперпараметров и задача выбора модели — одно и то же.
Поиск по сетке
В предыдущей главе мы говорили, что единственный применимый на практике способ нахождения оптимальных значений гиперпараметров модели — полный перебор. Однако, есть две трудности в организации такого процесса. Во-первых, если у модели несколько гиперпараметров, то их оптимум надо искать в совокупности. Не получится сначала оптимизировать один из них, а потом следующий. Дело в том, что значения гиперпараметров могут сложным способом взаимодействовать в модели и оптимальное значение по одному из них может измениться при изменении значения другого.
Например, в уже рассмотренной модели ближайших соседей. Допустим, мы нашли, что наилучшая модель получается при рассмотрении 10 соседей (при всех остальных гиперпараметрах имеющих значения по умолчанию). Теперь мы хотим понять наилучший алгоритм взвешивания соседей и начинаем изменять его. Но оптимальное количество соседей мы нашли для метода взвешивания по умолчанию (в данном примере — без взвешивания). А если мы будем строить взвешенные модели, то оптимальное количество соседей может быть совершенно другим. Поэтому два этих гиперпараметра надо изменять вместе — то есть проверять все комбинации значений количества соседей и алгоритмов взвешивания. И так для всех гиперпараметров модели.
Конечно, это означает огромный рост количества циклов обучения модели, так как для проверки каждой комбинации значений нужно заново проводить обучение до сходимости. Поэтому на практике бывает возможно проверить только определенное количество значений. И это вторая проблема оптимизации гиперпараметров: невозможно проверить все возможные комбинации значений. А значит, невозможно найти абсолютно оптимальные значения гиперпараметров модели. Тем более, что у всех моделей присутствуют и численные гиперпараметры, у которых может быть бесконечное количество значений. Типичный пример — праметр регуляризации — только по нему одному нельзя проверить все возможные значения.
Все это заставляет искать метод, который позволяет максимизировать вероятность нахождения более-менее оптимальной модели в условиях ограниченных ресурсов. И один из популярных методов — поиск по сетке. Его идея довольно проста. Для начала рассмотрим один непрерывный гиперпараметр. Допустим, область его допустимых значений лежит в некотором диапазоне. И где-то внутри этого диапазона есть оптимальное значение. Вряд ли мы найдем его точно, но мы можем приблизиться к нему, насколько это возможно. Для этого разделим диапазон на некоторое количество равных интервалов и проверим значения гиперпараметра на концах этих интервалов. То есть если мы проверяем диапазон, например, от 0 до 100, то мы можем поделить его на, допустим, 10 равных интервалов и проверить 11 разных значений — 0, 10, 20 и так далее. Или можно поделить на 2 интервала и проверить всего три разных значения — 0, 50 и 100.
Если добавить сюда еще один численный гиперпараметр, то по второму можно провести точно такое же разбиение. Причем здесь может быть совершенно другое количество проверяемых значений. Теперь мы должны проверить все комбинации значений первого параметра и второго. То есть если у нас 10 значений первого параметра и, допустим, 5 значений второго, то всего получается 50 комбинаций. Заметьте, как быстро растет количество комбинаций при росте количества гиперпараметров. Поиск по сетке демонстрирует экспоненциальный рост сложности — это очень неэффективный алгоритм.
Как сюда вписываются категориальные гиперпараметры? Очень просто, мы всего лишь должны определить список значений, которые будем проверять. А дальше работает та же логика — составляются все возможные комбинации значений и на каждой их них обучается модель. Заметьте, что если для какого-то параметра мы будем проверять только одно значение, это не добавит сложности. Поэтому можно проверять не все гиперпараметры, а только часть — по остальным будут использоваться значения по умолчанию.
Но что делать, если гиперпараметр измеряется по полуоткрытой шкале? Например тот же параметр регуляризации имеет область допустимых значений от нуля до плюс бесконечности. Как делить такой диапазон? В таком случае чаще всего применяют логарифмическую шкалу. Поэтому в качестве опорных значений берут, например, 0.01, 0.1, 1, 10, 100 и так далее. Такое разбиение более равномерно покрывает все возможные значения. Тем более, что для таких параметров решающее значение имеет именно порядок величины, использование для них логарифмической шкалы очень логично.
Ту же самую логику можно применить и для построения, например, диагностических кривых. Например, при построении графика зависимости между уровнем регуляризации и точностью модели. Не пытайтесь воспользоваться равномерным диапазоном значений. Для таких параметров разница между, например, уровнем 3 и 4 не так существенна, как между 0.1 и 0.01. Возьмите за правило — если переменная измеряется на полуоткрытом диапазоне и покрывает несколько порядков величины — ее надо рассматривать на логарифмической шкале.
Очевидно, что чем больше значений мы проверяем, тем больше вероятность получить модель, близкую к оптимальной — мы проходим более частой сеткой. Но чем подробнее наш поиск, тем больше времени он занимает. Так что количество проверяемых значений это результат компромисса между доступными вычислительными ресурсами и желанием получить более оптимальные значения, то есть модель с наибольшей эффективностью. Для хоть какого-то ускорения работы поиска его часто проводят только на части обучающей выборки, особенно если она очень большая.
Логика поиска по сетке уже реализована в библиотеке sklearn в соответствующих методах. Чтобы ими воспользоваться нужно определить перебираемые гиперпараметры и их значения. Для этого используют вспомогательный словарь. Рассмотрим для примера метод опорных векторов. Допустим, мы хотим проверить две разных функции ядра и несколько значений параметра регуляризации. Для этого создадим такой словарь:
1
2
3
4
tuned_parameters = {
"kernel": ["rbf"], ["linear"]
"C": [1, 10, 100, 1000]
}
Такой словарь называется пространство поиска. Здесь важно, чтобы ключи в этом словаре совпадали с названиями соответствующих аргументов конструктора модели. Иначе метод не сработает. После этого можно создать объект поиска по сетке. Ему передается сам объект модели и созданный словарь значений гиперпараметров:
1
2
3
4
from sklearn.model_selection import GridSearchCV
from sklearn.svm import SVC
grid_search = GridSearchCV(SVC(), tuned_parameters).fit(X_train, y_train)
Обратите внимание, что у данного объекта есть метод fit(), как у любого объекта модели. В этом опять проявляется единообразие библиотеки sklearn в построении интерфейсов. Здесь обучение будет проходить много раз, используя каждую комбинацию значений гиперпараметров. После завершения обучения в этом объекте будут доступны ссылка на лучшую модель, лучший набор значений гиперпараметров, максимально достигнутая эффективность и еще много внутренней информации (все результаты всех обучений в том числе). Например лучшую модель можно получить вот так (причем по умолчанию, она будет уже обучена на переданных в поиск данных):
1
best_model = grid_search.best_estimator_
Обратите внимание, что в названии этого метода есть CV. Это означает, что он внутри себя использует кросс-валидацию. По умолчанию используется пятипроходная кросс-валидация, но это можно изменить специальным аргументом (cv). Поэтому давайте посчитаем, сколько раз будет проходить обучение в данном примере? Мы проверяем два значения функции ядра и четыре значения параметра регуляризации. Итого получается 8 комбинаций, причем каждая их них обучается пять раз из-за кросс-валидации, то есть всего данный код запустит обучение 40 раз. Таким образом, если модель обучается за полторы минуты, то подбор гиперпараметров займет ровно час. А мы даже не рассматривали все гиперпараметры модели. Оптимизация гиперпараметров — очень вычислительно сложный и долгий процесс.
Несмотря на то, что кросс-валидация кратно увеличивает время поиска, ее все равно крайне желательно использовать. Ведь значения метрик, измеренные без нее могут существенно отклоняться от истинных. Так что мы можем получить не оптимальные значения гиперпараметров. Да. обучение пройдет быстрее, но результат будет гораздо менее надежным. Гораздо лучше использовать перекрестную проверку, а сэкономить время, например, используя только часть обучающей выборки.
Также можно вручную задать метрики, которые используются для оценки моделей. По умолчанию используется оценка модели, встроенная в сам объект модели через метод score, то есть точность (accuracy) для классификации и коэффициент детерминации (r-квадрат) для регрессии. Метод поиска по сетке подбирает модель, которая показывает наилучшее значение именно этой метрики. Но в разных задачах для нас могут быть важны разные метрики. Поэтому часто необходимо указать, что выбирать модель стоит по другой метрике. Для этого у метода поиска по сетке есть аргумент scoring, которому можно передать одну или несколько метрик в массиве, по которым и будет проводиться поиск:
1
2
3
scores = ["precision", "recall"]
grid_search = GridSearchCV(SVC(), tuned_parameters,
scoring=scores).fit(X_train, y_train)
Зачем может понадобится указывать сразу несколько метрик? Это может быть полезно, если два алгоритма показывают одинаковый результат по одной метрике, но разную эффективность по другой. Например, две модели (или два разных набора значений гиперпараметров, что сейчас для нас одно и то же) показывают precision 0.92, но у первой recall составляет 0.85, а у второй — 0.7. В таком случае если мы укажем только precision как критерий оптимизации, то алгоритм может назвать лучшей любую из этих моделей, в зависимости от того, какая попадется позже. А если мы указываем две метрики, то при равенстве первой из них будет учитываться вторая. То есть поиск точно назовет лучшей первую модель. При этом решающее значение будет все-таки иметь первая метрика.
А что делать, если нужно значения одних гиперпараметров зависят от других? Например, в методе опорных векторов с гауссовым ядром есть гиперпараметр gamma, который влияет на параметры ядерной функции. Его тоже можно оптимизировать. Проблема в том, что для метода опорных векторов без ядра этого гиперпараметра не существует. Поэтому мы не можем просто написать:
1
2
3
4
5
tuned_parameters = {
"kernel": ["rbf", "linear"],
"gamma": [1e-3, 1e-4],
"C": [1, 10, 100, 1000]
}
Это приведет к ошибке, когда метод поиска по сетке попытается составить все комбинации значений гиперпараметров. Именно в таких случаях можно задавать несколько разных комбинаций гиперпараметров:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
from sklearn.model_selection import GridSearchCV
from sklearn.svm import SVC
tuned_parameters = [
{"kernel": ["rbf"],
"gamma": [1e-3, 1e-4],
"C": [1, 10, 100, 1000]},
{"kernel": ["linear"],
"C": [1, 10, 100, 1000]},
]
scores = ["precision", "recall"]
grid_search = GridSearchCV(SVC(), tuned_parameters,
scoring=scores).fit(X_train, y_train)
В данном примере мы определяем разные наборы гиперпараметров для разных значений ядерной функции. То есть получается такой условный набор. Сколько же в итоге комбинаций проверит этот код? Для гауссовой функции — восемь, для линейного ядра — четыре. Итого получается 12 комбинаций.
Как вы могли заметить, экспоненциальный рост сложности поиска по сетке существенно ограничивает количество комбинаций, которые мы можем проверить за разумное время. Если мы хотим перебрать, например, всего шесть гиперпараметров по десять значений в каждом, это нам даст миллион возможных комбинаций. Даже если одна модель обучается всего секунду, такой поиск займет 11 дней. И это без использования кросс-валидации. Для того, чтобы хоть как-то уменьшить количество проверяемых комбинаций можно использовать иерархический подход: сначала пройтись по пространству возможных значений крупной сеткой, а потом по окрестностях оптимальных значений более мелкой. Либо можно использовать более сложные стратегии поиска, например двоичный поиск (HalvingGridSearchCV).
Выводы:
- Поиск по сетке — полный перебор всех комбинаций значений гиперпараметров для поиска оптимальных значений.
- Для его организации надо задать список гиперпараметров и их конкретных значений.
- Непрерывные гиперпараметры надо дискретизировать.
- Для непрерывных гиперпараметров часто используется логарифмическая шкала.
- Поиск по сетке имеет экспоненциальную сложность.
- Чем больше параметров и значений задать, тем лучше получится модель, но дольше поиск.
- Можно задать критерии поиска — целевые метрики.
- Рекомендуется использовать кросс-валидацию.
Случайный поиск
Хуже всего поиск по сетке работает с непрерывными гиперпараметрами. Мало того, что невозможно проверить все возможные их значения, интересующие нас значения еще очень часто неравномерно распределены по числовой оси. Метод случайного поиска реализует совсем другую стратегию проверки разных комбинаций. Поиск по сетке просто проверяет все возможные комбинации по порядку. Это дает гарантированный результат (то есть мы всегда найдем наилучшую комбинацию из представленных), но работает очень долго.
Случайный поиск, как следует из названия, проверяет разные комбинации значений гиперпараметров в случайном порядке. Для его организации мы также должны сначала задать, какие гиперпараметры мы будем проверять, и какие их значения нас интересуют. Но на каждой итерации поиска данный алгоритм будет просто случайно выбирать значение каждого гиперпараметра из приведенного списка. Казалось бы, что эта стратегия строго хуже полного перебора, так как она теперь вообще ничего не гарантирует. Но у нее есть несколько особенностей, из-за которых на практике к ней стоит присмотреться.
Самое главное отличие случайного поиска от поиска по сетке состоит в том, мы можем не просто явно перечислять возможные значения каждого гиперпараметра. Мы можем задать вид его распределения. Давайте рассмотрим такой код:
1
2
3
4
5
6
7
8
clf = SGDClassifier(loss="hinge", penalty="elasticnet", fit_intercept=True)
param_dist = {
"average": [True, False],
"l1_ratio": stats.uniform(0, 1),
"alpha": loguniform(1e-2, 1e0),
}
Здесь мы задаем пространство поиска из трех параметров. Значения первого мы будем выбирать их списка. Именно так мы задавали значения в поиске по сетке. Значения второго будем генерировать случайно из равномерного распределения от 0 до 1. То есть каждую новую итерацию для второго гиперпараметра будет просто браться новое случайное число от 0 до 1. А значения третьего параметра будем генерировать из логравномерного. Это распределение очень подходит для таких гиперпараметров, как, например, параметр регуляризации, для которых значим именно порядок величины. Таких параметров достаточно много. Они обычно измеряются от 0 до бесконечности, а “среднее значение” у них — 1. То есть “равномерное” распределение таких параметров, например — 0.01, 0.1, 1, 10, 100 и так далее.
Так как на каждой итерации мы заново генерируем случайно все значения параметров, мы можем это делать произвольное количество раз. То есть мы можем задать явно количество итераций поиска, не оглядываясь на число используемых гиперпараметров и количество их потенциальных значений. Вот как запускается случайный поиск:
1
2
3
4
n_iter_search = 15
random_search = RandomizedSearchCV(
clf, param_distributions=param_dist, n_iter=n_iter_search
).fit(X, y)
Здесь мы явно указываем, что хотим произвести 15 случайных генераций значений гиперпараметров. То есть такой код будет искать наилучшую модель среди 15, значения гиперпараметров которых сгенерированы по заданному описанию случайно. Это даст нам 75 циклов обучения моделей (не забывайте про кросс-валидацию). С теми же значениями мы могли бы задать 5, 10 или 100 итераций.
Естественно, что чем больше итераций мы пройдем, тем более оптимальную модель мы найдем (скорее всего). Также как и в поиске по сетке, чем “мельче” сетка, чем больше комбинаций мы проверим, тем больше вероятность, что мы найдем хорошую (то есть более эффективную) модель. Различие лишь в том, что в случайном поиске количество итераций не фиксировано, а может задаваться произвольно.
Кстати, это означает, что мы можем добавлять в поиск новые гиперпараметры без опасений экспоненциального роста вычислительной сложности. Можно добавить еще один гиперпараметр и оставить количество итераций прежним. В таком случае поиск станет более разреженным. Или можно увеличить количество проходов вдвое, втрое или насколько позволяют вычислительные мощности. Случайный поиск позволяет ориентироваться именно на имеющиеся мощности и желаемое время поиска, а не на количество гиперпараметров. Он в каком-то смысле даже более предсказуемый, чем поиск по сетке, ведь он будет идти именно столько времени, сколько вы ему отвели.
Еще одно существенной отличие случайного поиска в том, что он именно случаен. То есть запустив два раза поиск с теми же самыми исходными данными, совершенно не факт, что мы получим одинаковый результат. Так как значения генерируются случайно, скорее всего, наоборот, мы получим, разные значения. Особенно, если количество итераций сильно меньше, чем потенциальное пространство поиска. И получаемые лучшие модели могут очень сильно отличаться. Чем больше итераций проводить, тем вероятнее, что модели будут более схожи. Но об этой особенности случайного поиска нужно помнить: он не гарантирует результат. Даже можно получить модель, которая хуже, чем “дефолтная” (со значениями гиперпараметров по умолчанию). Хотя на практике почти всегда случайный поиск находит более эффективный набор параметров.
Если необходимо обеспечить воспроизводимость результатов случайного поиска, то есть, чтобы при последующих запусках генерировались одни и те же значения, то можно использовать аргумент random_state, также, как и в train_test_split(). Этот параметр устанавливает значение инициализации генератора случайных чисел и он генерирует одну и ту же последовательность. Это бывает полено в демонстрационных и учебных целях.
В многих технических моментах, разные алгоритмы оптимизации гиперпараметров имеют общие черты. Так же, как и в поиске по сетке можно задавать другие метрики поиска, можно запускать поиск параллельно в многопоточном режиме, можно задавать свой алгоритм кросс-валидации и использовать другие возможности библиотеки, описанные в документации. Отдельно заметим, что использование кросс-валидации в случайном поиске не менее актуально, чем с поиске по сетке и в любых других алгоритмах оптимизации гиперпараметров.
Выводы:
- Случайный поиск позволяет задать распределение гиперпараметра, в котором будет вестись поиск.
- Случайный поиск генерирует набор значений гиперпараметров из указанных распределений.
- Можно задать количество итераций поиска независимо от количества гиперпараметров.
- Добавление параметров не влияет на продолжительность поиска.
- Результат не гарантируется. Воспроизводимость можно настроить.
- Также рекомендуется использовать кросс-валидацию.
Сравнение эффективности моделей (валидационный набор)
При сравнении эффективности нескольких моделей, либо при оптимизации гиперпараметров модели возникает еще одна незаметная, но значимая проблема. Когда мы сравниваем несколько моделей по какой-то метрике эффективности, мы выбираем среди них наилучшую. Допустим, у нас есть три модели, которые показали значение метрики, например, accuracy 0.91, 0.93 и 0.95. Эти метрики были измерены методом кросс-валидации, но есть в их надежности можно не сомневаться. Соответственно, мы делаем вывод, что третья модель лучше всего описывает данные и поэтому именно ее мы будем использовать. Неожиданный вопрос: а какая у этой модели будет эффективность на новых данных? Казалось бы, очевидно, 0.95, ведь это валидированная оценка качества этой модели. Но не все так просто.
Дело в том, что мы специально выбрали эту модель за ее высокое значение точности. А в этом значении, как мы знаем, всегда какую-то долю составляют случайные составляющие, даже при использовании кросс-валидации. Получается, что полученная оценка 0.95 может быть слишком оптимистичной. Здесь работает та же логика, что и с оптимизацией обычных параметров. Так как мы специально подбираем значения параметров под данные обучающей выборки, модель под них подстраивается и на новых данных может показывать чуть худшую эффективность. Также и при оптимизации гиперпараметров модель немного подстраивается именно под используемую выборку (и обучающую и тестовую вместе).
Поэтому при выборе модели для итоговой оценки ее эффективности опять нужно использовать новые данные, которые мы не использовали ни при обучении модели, ни при оптимизации гиперпараметров. Причем, так как оптимизация гиперпараметров и выбор модели — по сути одно и то же, точно такое же рассуждение можно применить и к нашему примеру выше. Можно думать об этом так: когда мы выбираем модель, дающую наилучший показатель эффективности, мы выбираем модель, лучше приспособленную под этот показатель эффективности. Получается, что как только мы выбрали лучшую модель по значению какой-то метрики, само это значение становится ненадежным и его надо заново измерить на новых данных. Это очень неочевидный момент и даже многие серьезные исследователи пропускают его в крупных научных публикациях.
Приведем еще одно объяснение этого феномена. Как мы сказали, при любом измерении возникают некоторые случайные факторы, которые обусловлены как минимум ограниченностью имеющихся данных, случайными ошибками выборки, недостаточностью признаков датасета для детерминированного предсказания целевой переменной, и вообще неучтенными факторами. Поэтому мы не можем быть уверенны ни в каком измерении на 100%, втом числе в оценке значения метрик эффективности. Если мы получили, ка в примере выше, 0.95, то “в реальности” модель может иметь эффективность как чуть выше, так и чуть ниже. То есть измеренное значение может иметь отрицательный или положительный случайный компонент.
Так как математическое ожидание случайной ошибки равно нулю, то в разных измерениях эти случайные компоненты встречаются как и положительные, так и отрицательные с равной вероятностью. Но, когда мы выбираем наилучшую модель, то с большей вероятностью выберем такую, в значении оценки качества которой этот самый случайный компонент именно положительный, то есть работает на рост этой оценки. Поэтому после выбора оптимальной модели мы получаем в среднем оптимистическую, то есть завышенную оценку ее качества.
Единственный способ оценить более близкое к реальному значению ее эффективности — измерить его на новом, еще не использованном наборе данных. Причем может получиться парадоксальная ситуация. В примере выше мы выбрали модель с эффективностью 95%. Но когда мы измерили ту же метрику, но на новых данных, модель показала, скажем всего 92%. Получается, что эта “самая лучшая” модель показала эффективность ниже, чем другая. Значит ли это, что мы выбрали неправильно? Нет, так как в оценке каждой из трех моделей сидит этот случайный, неизвестный нам компонент.
Такая схема выбора модели, как любое вероятностное рассуждение, не дает гарантированного результата, но обеспечивает наилучшую стратегию в среднем. То есть пользуясь таким способом мы чаще будем получать оптимальные модели и более надежные оценки их точности. Поэтому использование третьего набора данных для оценки эффективности при сравнении нескольких моделей является обязательной частью хорошей методики проведения машинного обучения.
При использовании этой методики все имеющиеся данные разделяют на три непересекающиеся части. Первая — обучающий набор — используется для подбора параметров модели (или моделей). Вторая — ее в таком случае чаще всего называют валидационным набором — используется для оценки эффективности разных моделей, их сравнения и выбора наилучшей, а также для оптимизации гиперпараметров. А третья — тестовый набор — используется только для итоговой оценки эффективности наилучшей модели. Обратите внимание, что тестовый набор используется только один раз.
Но как мы говорили, на практике всегда необходимо использовать кросс-валидацию. Перекрестная проверка по сути разбивает выборку на обучающий и валидационный наборы. Поэтому при начале машинного обучения исходный датасет разбивают всего на две части. Меньшая становится тестовым набором, она понадобится только на последнем этапе. Поэтому эти данные еще часто называют отложенным набором (holdout set). Оставшиеся данные (которые часто называют обучающей выборкой, что вносит определенную путаницу в термины) используют для кросс-валидированного выбора моделей.
Надо сказать, что вся эта сложная схема нужна только для наиболее точного и надежного выбора наилучшей модели и оценки ее эффективности, в которой мы можем быть максимально уверенными. То есть в итоге мы получаем модель (то есть параметрический класс функций, с определенными значениями гиперпараметров), про которую знаем с уверенностью, что она во-первых, лучше всех других моделей решает конкретную задачу, и, во-вторых, будет показывать на новых данных вот такую эффективность. После этого мы можем взять эту модель и обучить на всех имеющихся данных для запуска в реальную эксплуатацию. То есть не нужно использовать разбиение выборки для реального применения моделей машинного обучения, скажем, в пользовательских приложениях. Если мы уже выбрали наилучшую модель, для максимальной эффективности стоит использовать для обучения все данные, которые имеются в наличии.
Выводы:
- При сравнении нескольких моделей между собой возникает проблема оптимистичной оценки эффективности.
- Поэтому для исследования выбранной модели нужно использовать третью часть выборки.
- Это также надо использовать при оптимизации гиперпараметров.
- Во многих случаях использование кросс-валидации автоматически разбивает выборку.
- На практике после выбора модели и оценки ее эффективности ее обучают на всех имеющихся данных для реального использования.
Линейная регрессия
Сегодня пойдет речь о регрессии, как обучать и какие проблемы могут вам попасться при использовании таких моделей.
Для начала давайте введем удобные обозначения.
$mathbb{X} — text{пространство объектов}$
$mathbb{Y} — text{пространство ответов}$
$ x = (x^1, … x^n) — text{признаковое описание объекта}$
$ X = (x_i,y_i)^l_{i=1} — text{обучающая выборка} $
$ a(x) — text{алгоритм, модель} $
$ Q(a,X) — text{функция ошибки алгоритма a на выборке X} $
$ text{Обучение} — a(x) = text{argmin}_{a in mathbb{A}} Q(a,X)$
Но этого мало, давайте разберем, что такое функционал ошибки, семейство алгоритмов, метод обучения.
- Функционал ошибки Q: способ измерения того, хорошо или плохо работает алгоритм на конкретной выборке
- Семейство алгоритмов $mathbb{A}$: как выглядит множество алгоритмов, из которых выбирается лучший
- Метод обучения: как именно выбирается лучший алгоритм из семейства алгоритмов.
Пример задачи регрессии: предсказание количества заказов магазина
Пусть известен один признак — расстояние кафе от метро, а предсказать необходимо количество заказов. Поскольку количество заказов — вещественное число $mathbb{R}$, здесь идет речь о задаче регрессии.
По графику можно сделать вывод о существование зависимости между расстоянием от метро и количеством заказов. Можно предположить, что зависимость линейна, ее можно представить в видео прямой на графике. По этой прямой и можно будет предсказывать количество заказов, если известно расстояние от метро.
В целом такая модель угадывает тенденцию, то есть описывает зависимость между ответом и признаком.
При этом, разумеется ,она делает это не идеально, с некоторой ошибкой. Истинный ответ на каждом объекте несколько отклоняется от прогноза.
Один признак — это несерьезно. Гораздо сложнее и интереснее работать с многомерными выборками, которые описываются большим количеством признаков. В этом случае отобразить выборку и понять, подходит ли модель или нет, нельзя. Можно лишь оценить ее качество и по нему уже понять, подходит ли эта модель.
Описание линейной модели
Давайте обсудим, как выглядит семейство алгоритмов в случае с линейными моделями. Линейный алгоритм в задачах регрессии выглядит следующим образом
$$ a(x)=w_0 + sumlimits_{j=1}^d w_j x^j $$
где $w_0$ — свободный коэффициент, $x^j$ — признаки, а $w_j$ — их веса.
Если у нашего набора данных есть только один признак, то алгоритм выглядит так
$$ a(x)=w_0 + w x $$
Ничего не напоминает? Да, действительно это обычная линейная функция, известная с 7 класса.
$$ y = kx+b $$
В качестве меры ошибки мы не может быть выбрано отклонение от прогноза $Q(a,y)=a(x)-y$, так как в этом случае минимум функционала не будет достигаться при правильном ответе $a(x)=y$. Самый простой способ — считать модуль отклонения.
$$ |a(x)-y| $$
Но функция модуля не является гладкой функцией, и для оптимизации такого функционала неудобно использовать градиентные методы. Поэтому в качестве меры ошибки часто используют квадрат отклонения:
$$ (a(x)-y)^2 $$
Функционал ошибки, именуемый среднеквадратичной ошибкой алгоритма, задается следующим образом:
$$ Q(a,x) = frac{1}{l} sumlimits_{i=1}^l (a(x_i)- y_i)^2 $$
В случае линейной модели его можно переписать в виде функции (поскольку теперь Q зависит от вектора, а не от функции) ошибок:
$$ Q(omega,x) = frac{1}{l} sumlimits_{i=1}^l ( langle w_i,x_irangle- y_i) ^2 $$
Обучение модели линейной регрессии
Разберем том, как обучать модель линейной регрессии, то есть как настраивать ее параметры.
$$ Q(w,x) = frac{1}{l} sumlimits_{i=1}^l ( langle w_i,x_irangle- y_i) ^2 to min_{w}$$
То есть нам необходимо подобрать $w$, что бы линия могла описать наши данные. Или же задача состоит в нахождение таких $w$, что бы была минимальна ошибка $ Q(w,x)$
Матричная форма записи
Прежде, чем рассмотрим задачу о оптимизации этой функции, имеет смысл используемые соотношения в матричной форме. Матрица «объекты-признаки» $X$ составлена из признаков описаний все объектов выборки
$$ X = begin{pmatrix} x_{11} & … & x_{1d} … & … & … x_{l1} & … & x_{ld} end{pmatrix} $$
Таким образом, в $ij$ элементе матрицы $X$ записано значение $j$-го признака на i объекте обучающей выборки. Или короче говоря, каждая строчка — это объект, а каждый столбец — это признак.Так же понадобится вектор ответов y, который составлен из истинных ответов для всех объектов.
$$ y = begin{pmatrix} y_{1} … y_{l} end{pmatrix} $$
В этом случае среднеквадратичная шибка может быть переписана в матричном виде:
$$ Q(w,X) = frac{1}{l} || Xw-y ||^2 to min_{w}$$
Оптимизационный метод решения
Самый лучший метод — это численный метод оптимизации.
Не сложно показать, что среднеквадратичная ошибка — это выпуклая и гладкая функция. Выпуклость гарантирует существование лишь одного минимумам, а гладкость — существование вектора градиента в каждой точке. Это позволяет использовать метод градиентного спуска.
При использовании метода градиентного спуска необходимо указать начальное приближение. Есть много
подходов к тому, как это сделать, в том числе инициализировать случайными числами (не очень большими). Самый простой способ это сделать — инициализировать значения всех весов равными нулю:
$$ w^0=0 $$
На каждой следующей итерации, $t = 1, 2, 3, …,$ из приближения, полученного в предыдущей итерации $w^{t−1}$, вычитается вектор градиента в соответствующей точке $w^{t−1}$, умноженный на некоторый коэффициент $eta_t$, называемый шагом:
$$ w^t = w^{t-1} — eta_t Delta Q(w^{t-1},X) $$
Остановить итерации следует , когда наступает сходимость. Сходимость можно определять по-разному .В данном случае разумно определить сходимость следующим образом: итерации следует завершить, если разница
двух последовательных приближений не слишком велика:
$$ ||w^t — w^{t-1} ||<epsilon $$
Случай парной регрессии
В случае парной регрессии признак всего один, а линейная модель выглядит следующим образом:
$$ a(x)=w_0 + w x $$
где $w_1$ и $w_0$ — два параметра.
Среднеквадратичная ошибка принимает вид:
$$ Q(w_0,w_1,X) = frac{1}{l} sumlimits_{i=1}^l (w_1x_i+w_0 -y_i) ^2$$
Для нахождения оптимальных параметров будет применяться метод градиентного спуска, про который уже было сказано ранее. Чтобы это сделать, необходимо сначала вычислить частные производные функции ошибки:
$$frac{partial Q}{partial w_1} = frac{2}{l} sumlimits_{i=1}^l (w_1x_i+w_0-y_i)x_i$$
$$frac{partial Q}{partial w_0} = frac{2}{l} sumlimits_{i=1}^l (w_1x_i+w_0-y_i)$$
Следующие два графика демонстрируют применение метода градиентного спуска в случае парной регрессии. Справа изображены точки выборки, а слева — пространство параметров. Точка в этом пространстве обозначает конкретную модель (кафе)
График зависимости функции ошибки от числа произведенных операции выглядит следующим образом:
Выбор размера шага в методе градиентного спуска
Очень важно при использовании метода градиентного спуска правильно подбирать шаг. Каких-либо концерт- иных правил подбора шага не существует, выбор шага — это искусство, но существует несколько полезных закономерностей.
Если длина шага слишком мала, то метод будет неспешна, но верно шагать в сторону минимума. Если же
взять размер шага очень большим, появляется риск, что метод будет перепрыгивать через минимум. Более
того, есть риск того, что градиентный спуск не сойдется.
Имеет смысл использовать переменный размер шага: сначала, когда точка минимума находится еще да-
легко, двигаться быстро, а позже, спустя некоторое количество итерации — делать более аккуратные шаги.
Один из способов задать размер шага следующий:
$$ eta_t = frac{k}{t} $$
где $k$-константа, которую необходимо подобрать, а $t$ — номер шага.
import matplotlib.pyplot as plt # библиотека для отрисовки графиков import numpy as np # импортируем numpy для создания своего датасета from sklearn import linear_model, model_selection # импортируем линейную модель для обучения и библиотеку для разделения нашей выборки X = np.random.randint(100,size=(500, 1)) # создаем вектор признаков, вектора так как у нас один признак y = np.random.normal(np.random.randint(300,360,size=(500, 1))-X) # создаем вектор ответом plt.scatter(X, y) # рисуем график точек plt.xlabel('Расстояние до кафе в метрах') # добавляем описание для оси x plt.ylabel('Количество заказов')# добавляем описание для оси y plt.show()
# Делим созданную нами выборку на тестовую и обучающую X_train, X_test, y_train, y_test = model_selection.train_test_split(X, y)
Давайте посмотрим какие параметры принимает LinearRegression.
fit_intercept — подбирать ли значения для свободного член $w_0$. True или False. Если ваши данные центрированны, то можете указать False. По умолчанию — True
normalize— нормализация данных перед обучением. Если fit_intercept=False то параметр будет проигнорирован. Если True — то данные перед обучением будут нормализованы при помощи L^2-Norm нормализации. По умолчанию — False
copy_X — True — копировать матрицу признаков. False — не копировать. **По умолчанию — **True
n_jobs — количество ядер используемых для сборки. Скорость будет существенно выше n_targets>1. По умолчанию — None
Параметры которые можно у модели:
coef_ — коэффициенты $w$, количество возвращаемых коэффициентов зависит от количества признаков. смотри пункт Описание линейной модели
intercept_ — свободный член $w_0$
Что бы предсказать значения необходимо вызвать функцию:
predict и передать массив из признаков.
Example: regr.predict([[40]])
regr = linear_model.LinearRegression() # создаем линейную регрессию #Обучаем модель regr.fit(X_train, y_train)
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
После выполнения кода, вам вернется ответ с установленными параметрами
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
# Посмотрим какие коэффициенты установила модель print('Коэфициент: n', regr.coef_) # Средний квадрат ошибки print("Средний квадрат ошибки: %.2f" % np.mean((regr.predict(X_test) - y_test) ** 2)) # Оценка дисперсии: 1 - идеальное предсказание. Качество предсказания. print('Оценка дисперсии:: %.2f' % regr.score(X_test, y_test))
Коэфициент:
[[-1.03950324]]
Средний квадрат ошибки: 325.63
Оценка дисперсии:: 0.70
# Посмотрим на получившуюся функцию print ("y = {:.2f}*x + {:.2f}".format(regr.coef_[0][0], regr.intercept_[0]))
# Посмотрим, как предскажет наша модель тестовые данные. plt.scatter(X_test, y_test, color='black')# рисуем график точек plt.plot(X_test, regr.predict(X_test), color='blue') # рисуем график линейной регрессии plt.show() # Покажем график
Давайте предскажем количество заказов, для нашего потенциального магазина. Скажем, что мы планируем построить магазин в 40 метрах от метро
290 заказов мы получим если построим магазин в 40 метрах от метро, но при этом качество предсказания всего лишь 71%, думаю не стоит доверять.
А что если, мы увеличим количество признаков?
Для этого воспользуемся встроенным датасетом make_regression из sklearn.
n_features — отвечает за количество признаков один нормальный другой избыточный
n_informative — отвечает за количество информативных признаков
n_targets — отвечает за размер ответов
noise — шум накладываемый на признаки
соef — возвращать ли коэффициенты
random_state — определяет генерацию случайных чисел для создания набора данных.
# Импортируем библиотеки для валидация, создания датасетов, и метрик качества from sklearn import cross_validation, datasets, metrics # Создаем датасет с избыточной информацией X, y, coef = datasets.make_regression(n_features = 2, n_informative = 1, n_targets = 1, noise = 5., coef = True, random_state = 2)
# Поскольку у нас есть два признака,для отрисовки надо их разделить на две части data_1, data_2 = [],[] for x in X: data_1.append(x[0]) data_2.append(x[1]) plt.scatter(data_1, y, color = 'r') plt.scatter(data_2, y, color = 'b')
<matplotlib.collections.PathCollection at 0x1134a6e10>
Можно заметить, что признак отмеченный красным цветом имеет явную линейную зависимость, а признак отмеченный синим, никакой информативность нам не дает.
# Разделение выборку для обучения и тестирования # test_size - отвечает за размер тестовой выборки X_train, X_test, y_train, y_test = cross_validation.train_test_split(X, y, test_size = 0.3)
# Создаем линейную регрессию linear_regressor = linear_model.LinearRegression() # Тренируем ее linear_regressor.fit(X_train, y_train) # Делаем предсказания predictions = linear_regressor.predict(X_test)
# Выводим массив для просмотра наших ответов (меток) print (y_test)
[ 28.15553021 38.36241814 -24.77820218 -61.47026695 13.02656201
23.87701013 12.74038341 -70.11132234 27.83791274 -14.97110322
-80.80239408 24.82763821 58.26281761 -45.27502383 10.33267887
-48.28700118 -21.48288019 -32.71074998 -21.47606913 -15.01435792
78.24817537 19.66406455 5.86887774 -42.44469577 -12.0017312
14.76930132 -16.65927231 -13.99339669 4.45578287 22.13032804]
# Смотрим и сравниваем предсказания print (predictions)
[ 22.32670386 40.26305989 -27.69502682 -56.5548183 18.47241345
31.86585663 6.08896992 -66.15105402 22.99937016 -12.65174022
-78.50894588 30.90311195 56.21877707 -47.81097232 8.98196478
-56.41188567 -24.46096716 -43.55445698 -17.99670898 -9.09225523
65.49657633 26.50900527 4.74114126 -39.28939851 -6.80665816
8.30372903 -15.27594937 -15.15598987 8.34469779 19.45159738]
# Средняя ошибка предсказания metrics.mean_absolute_error(y_test, predictions)
Для валидации можем выполнить перекрестную проверкую cross_val_score.
http://scikit-learn.org/stable/modules/generated/sklearn.model_selection.cross_val_score.html
Передадим, нашу линейную модель, признаки, ответы, количество разделений кросс-валидация
linear_scoring = cross_validation.cross_val_score(linear_regressor, X, y, cv=10) print ('Средняя ошибка: {}, Отклонение: {}'.format(linear_scoring.mean(), linear_scoring.std()))
Средняя ошибка: 0.9792410447209384, Отклонение: 0.020331171766276405
# Создаем свое тестирование на основе абсолютной средней ошибкой scorer = metrics.make_scorer(metrics.mean_absolute_error)
linear_scoring = cross_validation.cross_val_score(linear_regressor, X, y, scoring=scorer, cv=10) print ('Средняя ошибка: {}, Отклонение: {}'.format(linear_scoring.mean(), linear_scoring.std()))
Средняя ошибка: 4.0700714987797, Отклонение: 1.0737104492890193
# Коэффициенты который дал обучающий датасет coef
array([38.07925837, 0. ])
# Коэффициент полученный при обучении linear_regressor.coef_
array([38.18191713, 0.81751244])
# обученная модель так же дает свободный член linear_regressor.intercept_
print ("y = {:.2f}*x1 + {:.2f}*x2".format(coef[0], coef[1]))
print ("y = {:.2f}*x1 + {:.2f}*x2 + {:.2f}".format(linear_regressor.coef_[0], linear_regressor.coef_[1], linear_regressor.intercept_))
y = 37.76*x1 + 0.17*x2 + -0.86
# Посмотрим качество обучения print('Оценка дисперсии:: %.2f' % linear_regressor.score(X_test, y_test))
Домашнее задание
Вы уже знаете как создать модель линейной регрессии, можете создать датасет.
Давайте посмотрим как влияет количество признаков на качество обучения линейной модели.
Скачайте этот файл, можете редактировать этот ноутбук, да бы уменьшить/увеличить количество признаков.
Будут вопросы пишите нам в Slack канал #machine_learning

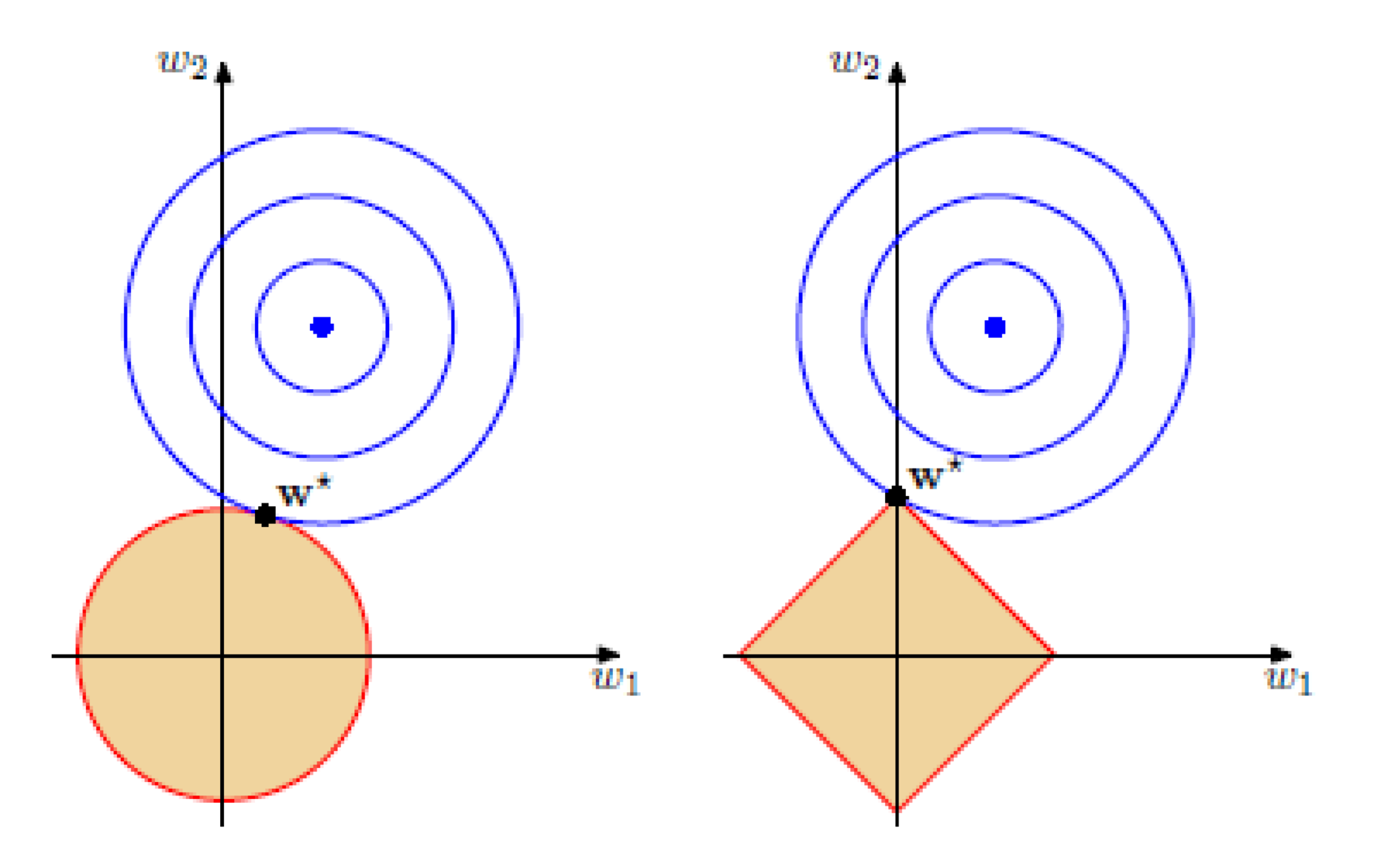
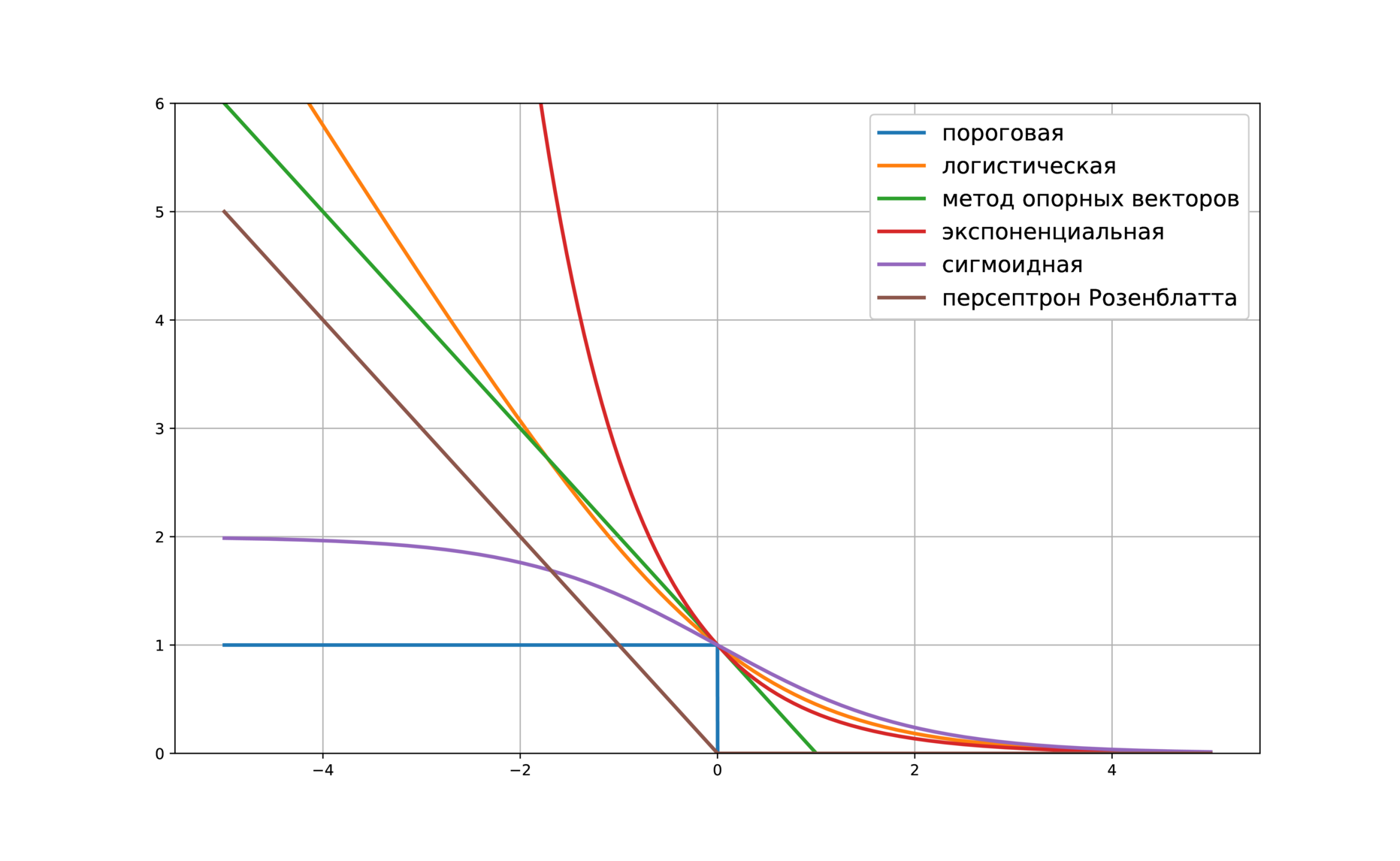
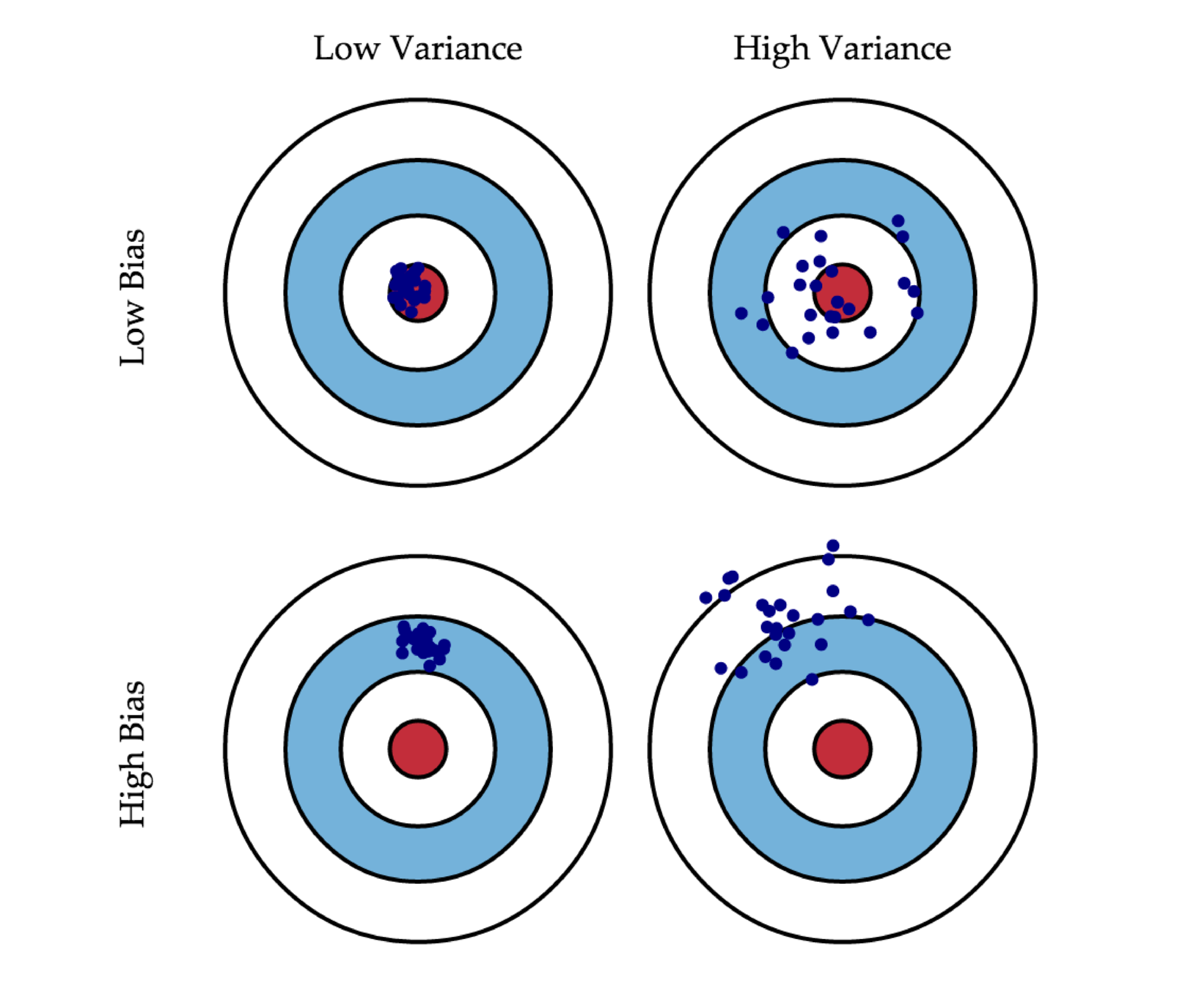
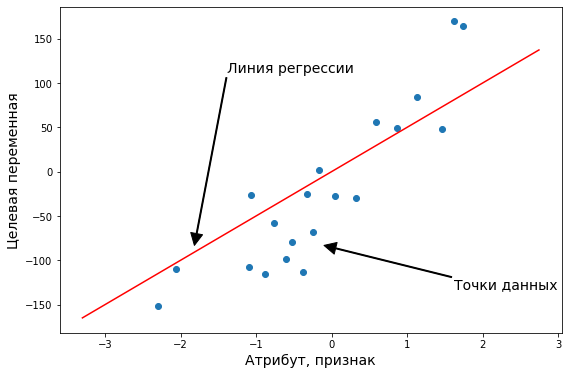
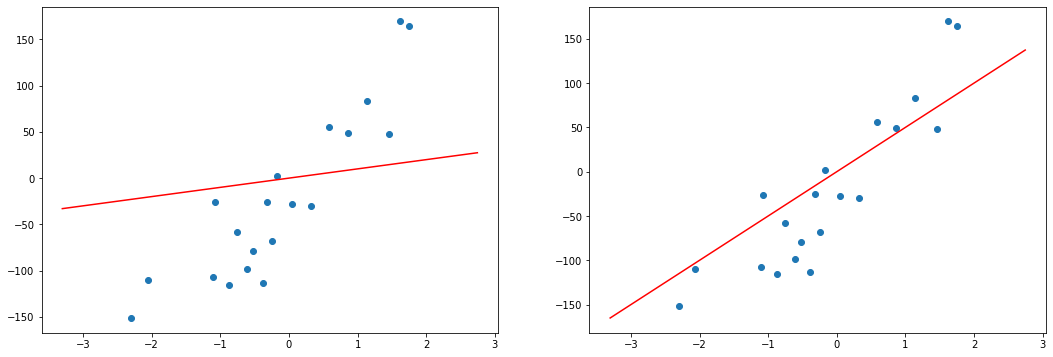
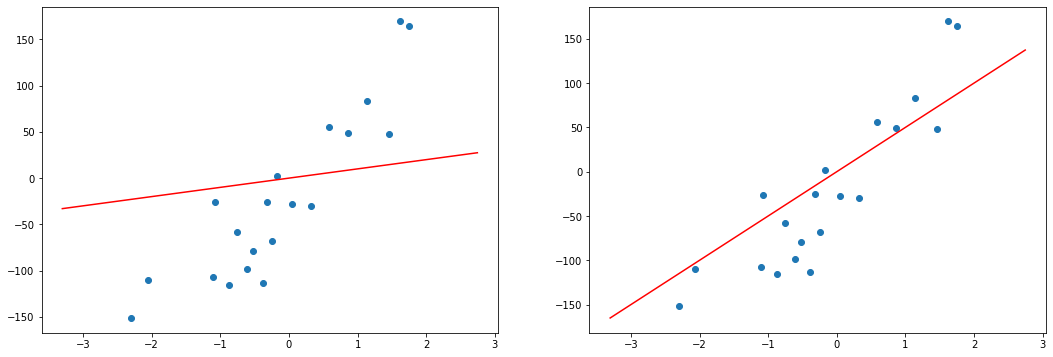
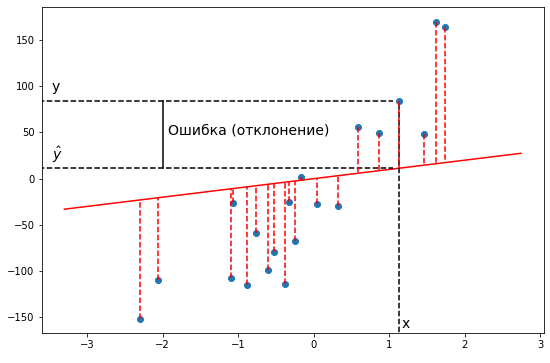
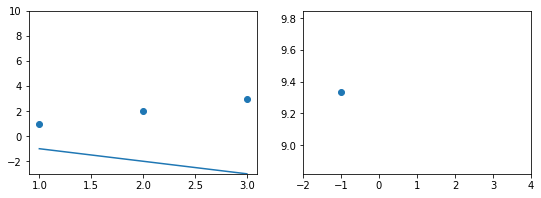
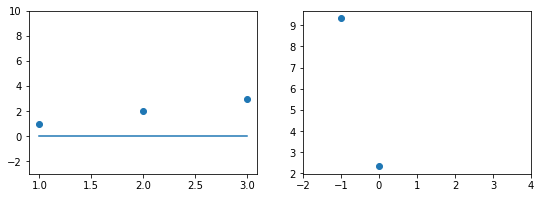
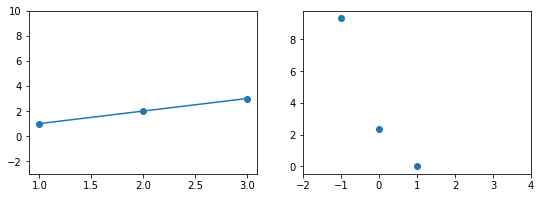
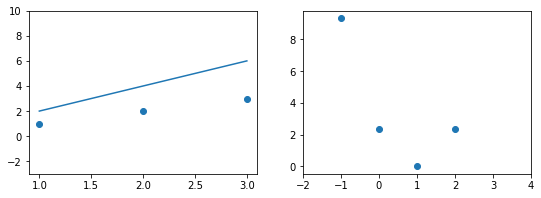
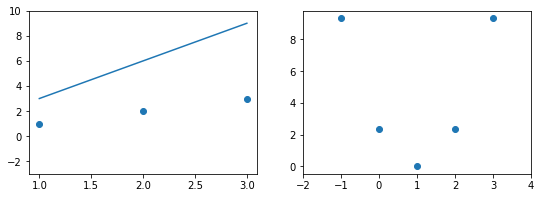
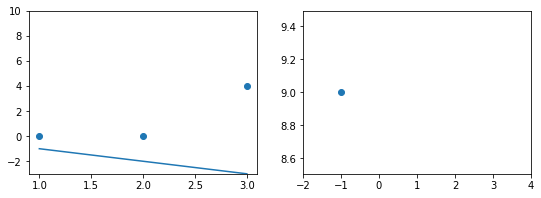
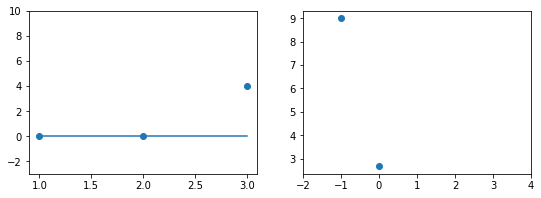
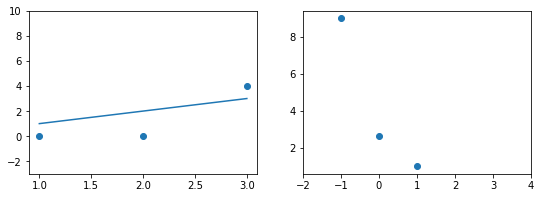
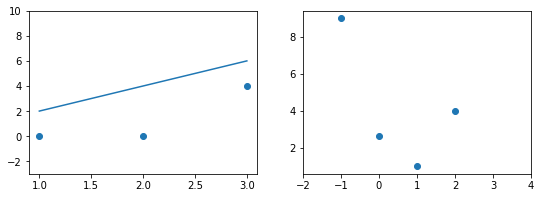
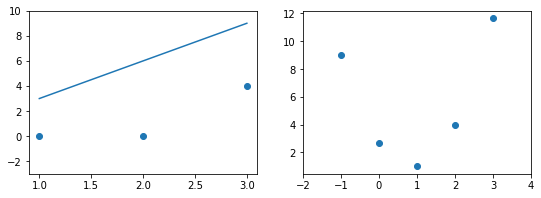
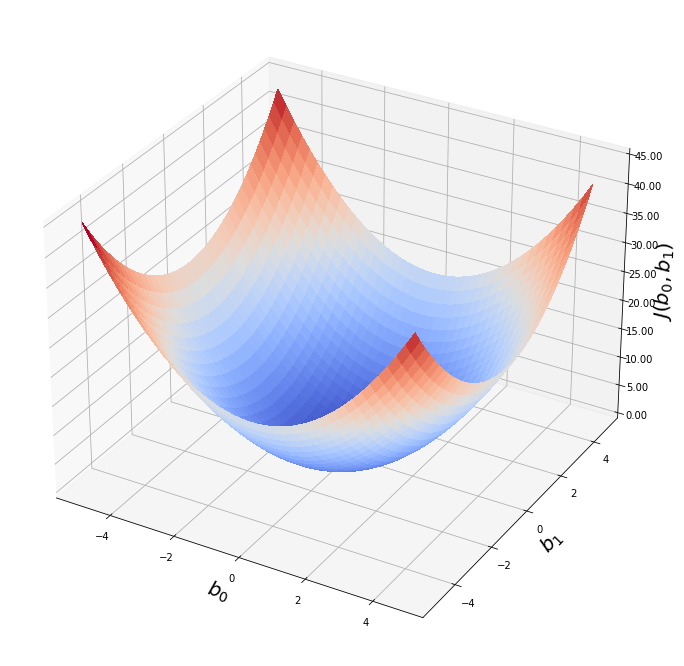
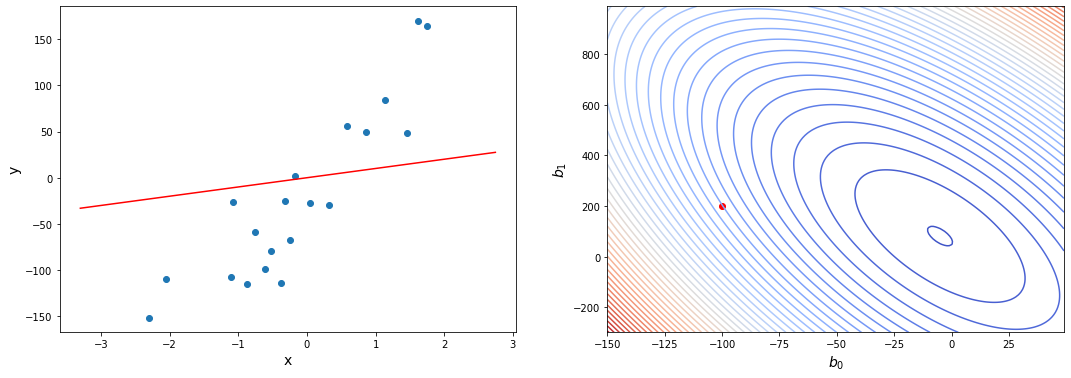
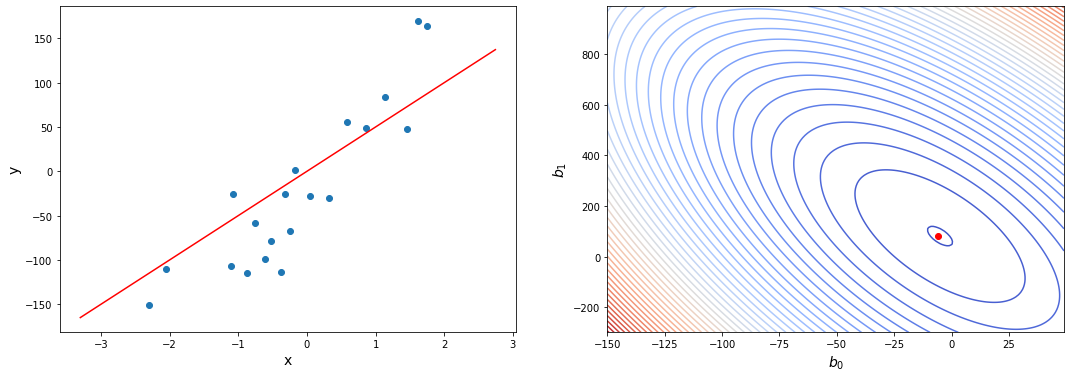
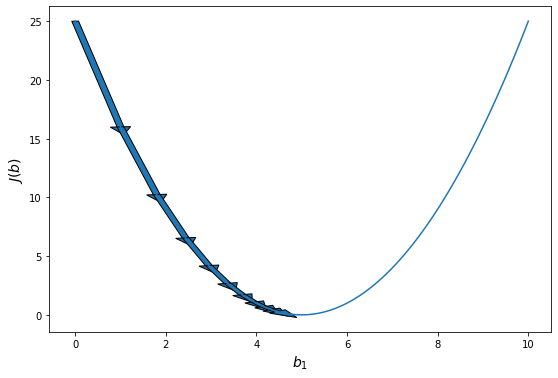

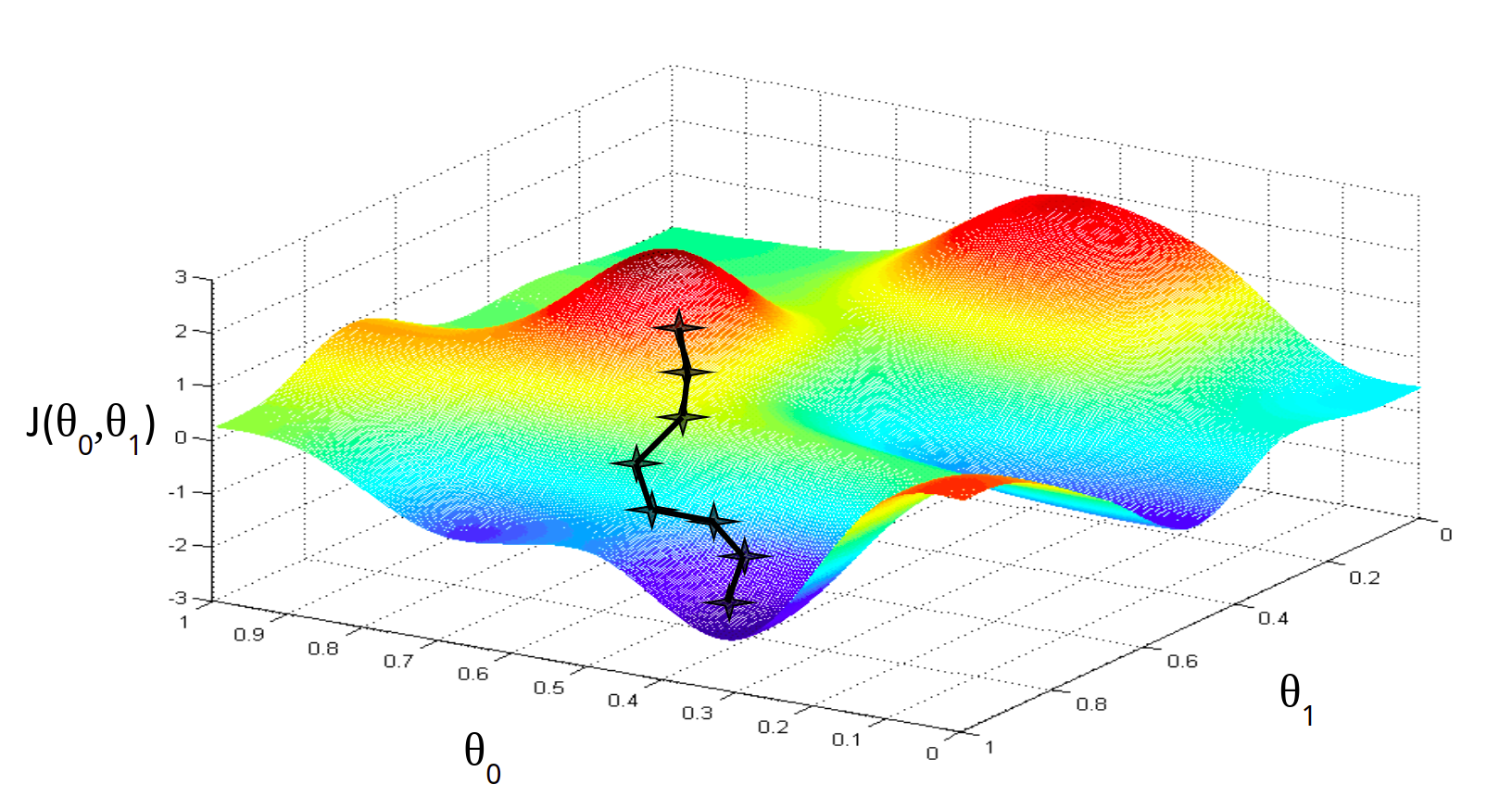
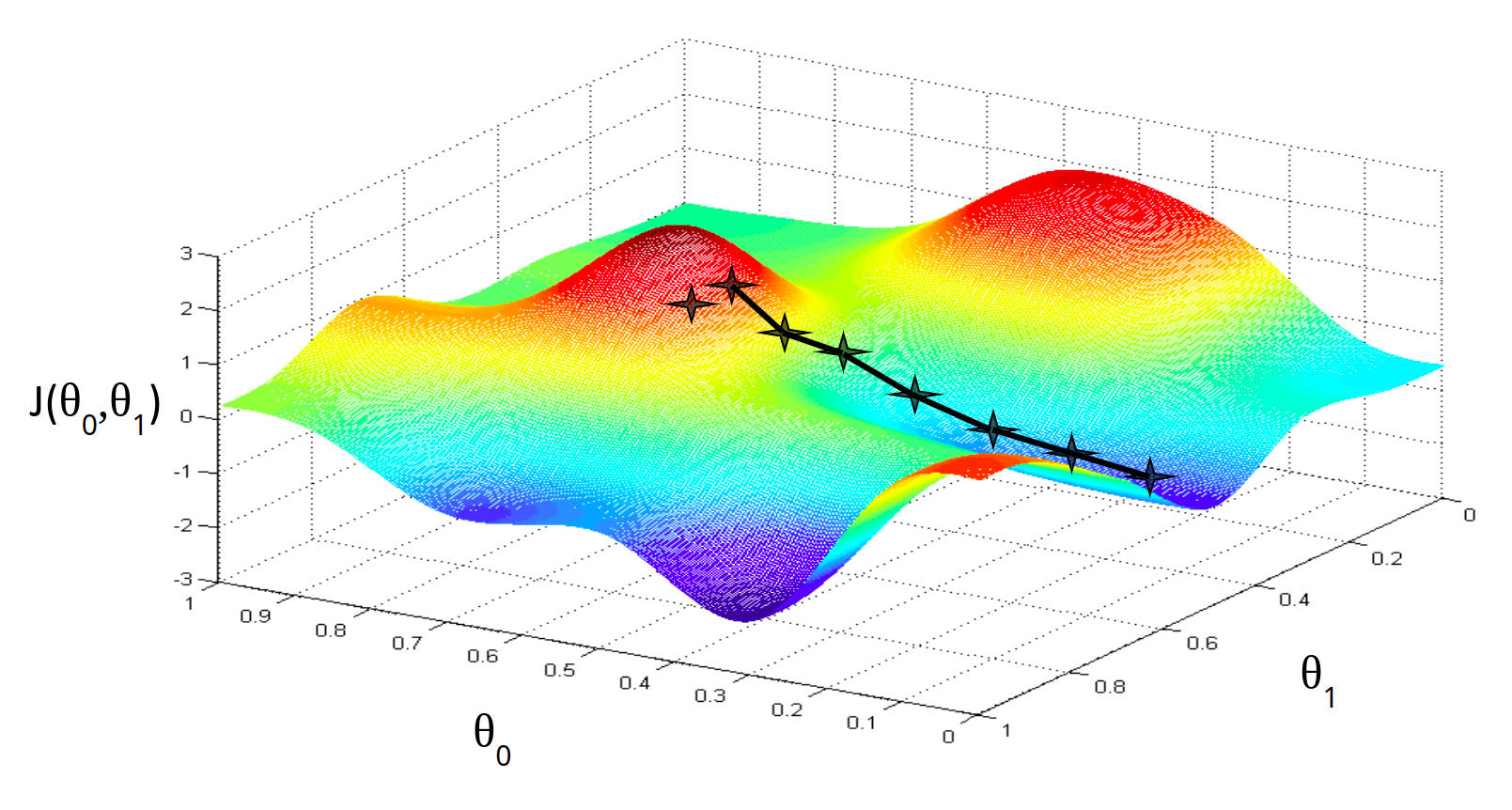
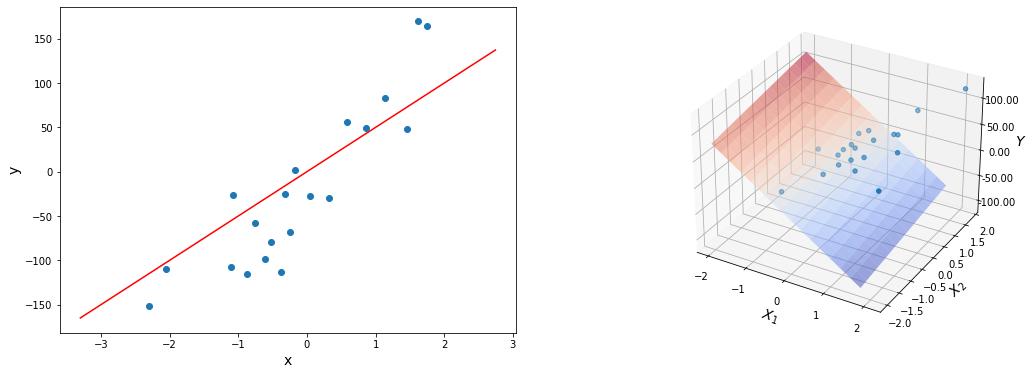
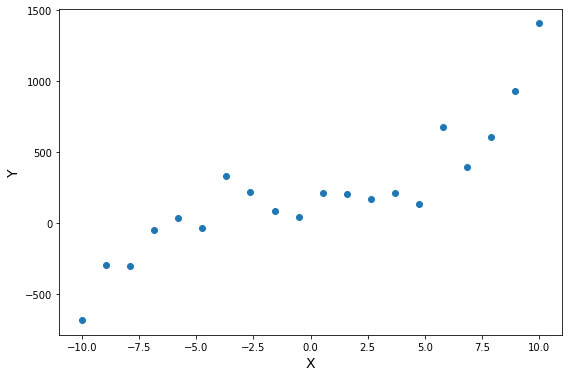

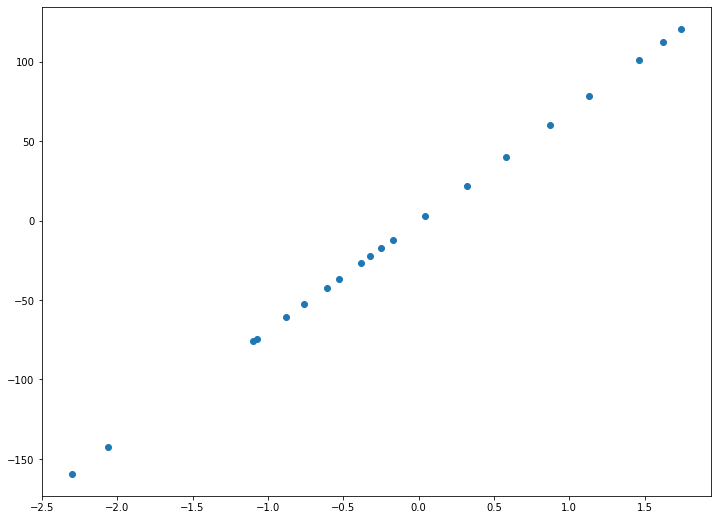
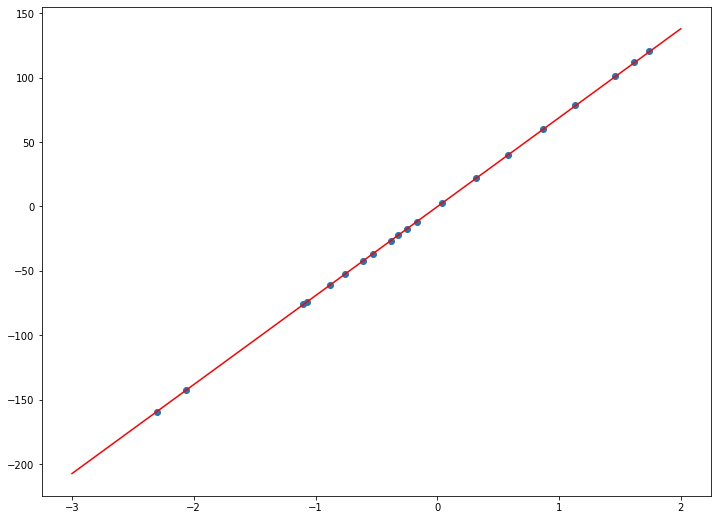

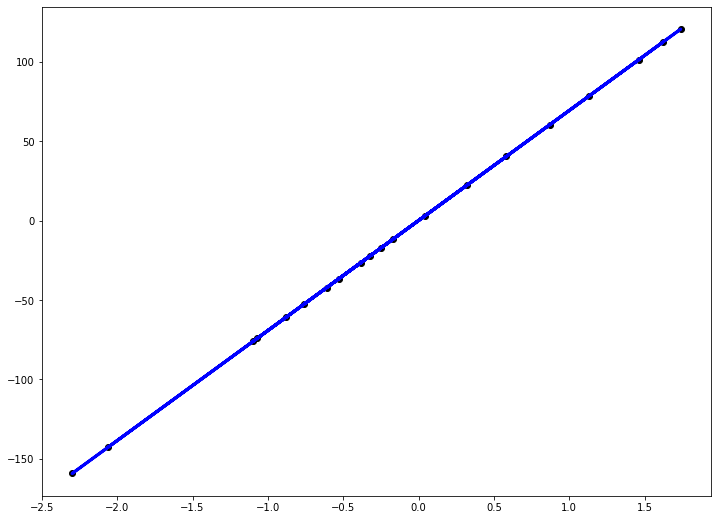





![{displaystyle {begin{aligned}Pr[Xleq L]&={frac {1}{2}}+{frac {1}{2}}operatorname {erf} {frac {L-mu }{{sqrt {2}}sigma }}&approx Aexp left(-Bleft({frac {L-mu }{sigma }}right)^{2}right)end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f3cb760eaf336393db9fd0bb12c4465655a27de8)
![{displaystyle Pr[Xleq L]leq Aexp(-Bln {k})={frac {A}{k^{B}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2baadea015e20a45d1034fd88eed861e7fcce178)
![{displaystyle {begin{aligned}Pr[L_{a}leq Xleq L_{b}]&=int _{L_{a}}^{L_{b}}{frac {1}{{sqrt {2pi }}sigma }}exp left(-{frac {(x-mu )^{2}}{2sigma ^{2}}}right),mathrm {d} x&={frac {1}{2}}left(operatorname {erf} {frac {L_{b}-mu }{{sqrt {2}}sigma }}-operatorname {erf} {frac {L_{a}-mu }{{sqrt {2}}sigma }}right).end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd2214f0db2c1d36075815825b616501175c6283)


![{displaystyle {begin{aligned}operatorname {erf} z&={frac {2}{sqrt {pi }}}sum _{n=0}^{infty }{frac {(-1)^{n}z^{2n+1}}{n!(2n+1)}}[6pt]&={frac {2}{sqrt {pi }}}left(z-{frac {z^{3}}{3}}+{frac {z^{5}}{10}}-{frac {z^{7}}{42}}+{frac {z^{9}}{216}}-cdots right)end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c80541f305af070bb0510625c584fe1559a0cd2c)
![{displaystyle {begin{aligned}operatorname {erf} z&={frac {2}{sqrt {pi }}}sum _{n=0}^{infty }left(zprod _{k=1}^{n}{frac {-(2k-1)z^{2}}{k(2k+1)}}right)[6pt]&={frac {2}{sqrt {pi }}}sum _{n=0}^{infty }{frac {z}{2n+1}}prod _{k=1}^{n}{frac {-z^{2}}{k}}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dca22e8e7dee0297e87a455249c282c6b92fedcb)
![{displaystyle {begin{aligned}operatorname {erfi} z&={frac {2}{sqrt {pi }}}sum _{n=0}^{infty }{frac {z^{2n+1}}{n!(2n+1)}}[6pt]&={frac {2}{sqrt {pi }}}left(z+{frac {z^{3}}{3}}+{frac {z^{5}}{10}}+{frac {z^{7}}{42}}+{frac {z^{9}}{216}}+cdots right)end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ff91095cd6825137cc951ec0a786db0b7f68fac)





![{displaystyle {begin{aligned}operatorname {erf} x&={frac {2}{sqrt {pi }}}operatorname {sgn} xcdot {sqrt {1-e^{-x^{2}}}}left(1-{frac {1}{12}}left(1-e^{-x^{2}}right)-{frac {7}{480}}left(1-e^{-x^{2}}right)^{2}-{frac {5}{896}}left(1-e^{-x^{2}}right)^{3}-{frac {787}{276480}}left(1-e^{-x^{2}}right)^{4}-cdots right)[10pt]&={frac {2}{sqrt {pi }}}operatorname {sgn} xcdot {sqrt {1-e^{-x^{2}}}}left({frac {sqrt {pi }}{2}}+sum _{k=1}^{infty }c_{k}e^{-kx^{2}}right).end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/164e7f029977edb47c83845b04abfe5b2d28b837)








![{displaystyle {begin{aligned}operatorname {erfc} x&={frac {e^{-x^{2}}}{x{sqrt {pi }}}}left(1+sum _{n=1}^{infty }(-1)^{n}{frac {1cdot 3cdot 5cdots (2n-1)}{left(2x^{2}right)^{n}}}right)[6pt]&={frac {e^{-x^{2}}}{x{sqrt {pi }}}}sum _{n=0}^{infty }(-1)^{n}{frac {(2n-1)!!}{left(2x^{2}right)^{n}}},end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/35a11e2e5b22ca898c74f2e913d276c9ac11124a)























![{displaystyle {begin{aligned}operatorname {erfc} x&=1-operatorname {erf} x[5pt]&={frac {2}{sqrt {pi }}}int _{x}^{infty }e^{-t^{2}},mathrm {d} t[5pt]&=e^{-x^{2}}operatorname {erfcx} x,end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4acd0062271e2a19c209a02c8cc33d44a28af7cc)



![{displaystyle {begin{aligned}operatorname {erfi} x&=-ioperatorname {erf} ix[5pt]&={frac {2}{sqrt {pi }}}int _{0}^{x}e^{t^{2}},mathrm {d} t[5pt]&={frac {2}{sqrt {pi }}}e^{x^{2}}D(x),end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bfd2dd94cd6d0325224d412f6b5e5ed63ca81d4a)

![{displaystyle {begin{aligned}Phi (x)&={frac {1}{sqrt {2pi }}}int _{-infty }^{x}e^{tfrac {-t^{2}}{2}},mathrm {d} t[6pt]&={frac {1}{2}}left(1+operatorname {erf} {frac {x}{sqrt {2}}}right)[6pt]&={frac {1}{2}}operatorname {erfc} left(-{frac {x}{sqrt {2}}}right)end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/89a9e9eaaddcd7a91ade15a41b8d1e272d437559)
![{displaystyle {begin{aligned}operatorname {erf} (x)&=2Phi left(x{sqrt {2}}right)-1[6pt]operatorname {erfc} (x)&=2Phi left(-x{sqrt {2}}right)&=2left(1-Phi left(x{sqrt {2}}right)right).end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86c84a4d2d79631fe9996e30f1d6c0da3089bfe2)








![{displaystyle {begin{aligned}operatorname {i} ^{n}!operatorname {erfc} z&=int _{z}^{infty }operatorname {i} ^{n-1}!operatorname {erfc} zeta ,mathrm {d} zeta [6pt]operatorname {i} ^{0}!operatorname {erfc} z&=operatorname {erfc} zoperatorname {i} ^{1}!operatorname {erfc} z&=operatorname {ierfc} z={frac {1}{sqrt {pi }}}e^{-z^{2}}-zoperatorname {erfc} zoperatorname {i} ^{2}!operatorname {erfc} z&={tfrac {1}{4}}left(operatorname {erfc} z-2zoperatorname {ierfc} zright)end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c3e7b953efaa4d730a5479bd61a2c378c8f761dc)