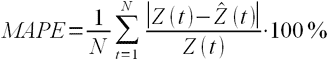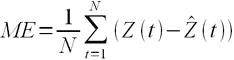Для оценки точности модели используют среднюю ошибку аппроксимации

Для
оценки точности полученной модели будем
использовать показатель относительной
ошибки аппроксимации, который вычисляется
по формуле:

,
где

Расчет
относительной ошибки аппроксимации

Таблица
4.4

	t	Y	Предсказанное Y
	1	5	4,58	0,42	0,08
	2	7	7,21	-0,21	0,03
	3	10	9,84	0,16	0,02
	4	12	12,48	-0,48	0,04
	5	15	15,11	-0,11	0,01
	6	18	17,74	0,26	0,01
	7	20	20,38	-0,38	0,02
	8	23	23,01	-0,01	0,00
	9	26	25,64	0,36	0,01
Сумма	45	136		0,00	0,23
Среднее	5	15,11

Если
ошибка, вычисленная по формуле, не
превосходит 15%, точность модели считается
приемлемой.

5)
По построенной модели
осуществить прогноз спроса на следующие
две недели (доверительный интервал
прогноза рассчитать при доверительной
вероятности р = 70%).

Воспользуемся
функцией Excel
СТЬЮДРАСПОБР. (рис. 4.10)

t
= 1,12

Рис.
4.6

Для
построения интервального прогноза
рассчитаем доверительный интервал.
Примем значение уровня значимости
,
следовательно, доверительная вероятность
равна 70 %, а критерий Стьюдента приравен 1,12.

Ширину
доверительного интервала вычислим по
формуле:

,
где

(находим
из таблицы 4.1)

,

.

Вычисляем
верхнюю и нижнюю границы прогноза (таб.
4.11).

Таблица
4.5

Таблица
прогноза

n +k	U (k)	Прогноз	Формула	Верхняя граница	Нижняя граница
10	U(1) =0.84	28.24	Прогноз + U(1)	29.сен	27.40
11	U(2) =1.02	30.87	Прогноз — U(2)	31.89	29.85

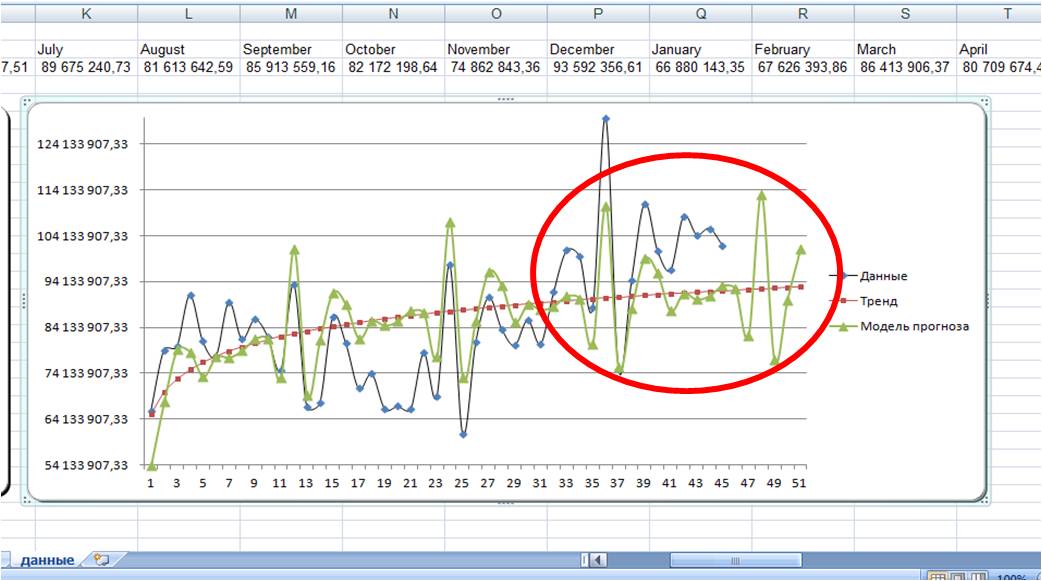
6) Фактические значения показателя, результаты моделирования и прогнозирования представить графически.

Преобразуем
график подбора (рис. 4.5), дополнив его
данными прогноза.

Рис.
4.7

Соседние файлы в предмете Методы оптимизации

• #
• #

18 Янв Ошибка прогнозирования: как рассчитать и применять.

Posted at 11:37h
in Статьи

Основной задачей при управлении запасами является определение объема пополнения, то есть, сколько необходимо заказать поставщику. При расчете этого объема используется несколько параметров — сколько будет продано в будущем, за какое время происходит пополнение, какие остатки у нас на складе и какое количество уже заказано у поставщика. То, насколько правильно мы определим эти параметры, будет влиять на то, будет ли достаточно товара на складе или его будет слишком много. Но наибольшее влияние на эффективность управления запасами влияет то, насколько точен будет прогноз. Многие считают, что это вообще основной вопрос в управлении запасами. Действительно, точность прогнозирования очень важный параметр. Поэтому важно понимать, как его оценивать. Это важно и для выявления причин дефицитов или неликвидов, и при выборе  программных продуктов для прогнозирования продаж и управления запасами.

В данной статье я представила несколько формул для расчета точности прогноза и ошибки прогнозирования. Кроме этого, вы сможете скачать файлы с примерами расчетов этого показателя.

Статистические методы

Для оценки прогноза продаж используются статистические оценки Оценка ошибки прогнозирования временного ряда. Самый простой показатель – отклонение факта от прогноза в количественном выражении.

В практике рассчитывают ошибку прогнозирования по каждой отдельной позиции, а также рассчитывают среднюю ошибку прогнозирования. Следующие распространенные показатели ошибки относятся именно  к показателям средних ошибок прогнозирования.

К ним относятся:

MAPE – средняя абсолютная ошибка в процентах

где Z(t) – фактическое значение временного ряда, а   – прогнозное.

Данная оценка применяется для временных рядов, фактические значения которых значительно больше 1. Например, оценки ошибки прогнозирования энергопотребления почти во всех статьях приводятся как значения MAPE.

Если же фактические значения временного ряда близки к 0, то в знаменателе окажется очень маленькое число, что сделает значение MAPE близким к бесконечности – это не совсем корректно. Например, фактическая цена РСВ = 0.01 руб/МВт.ч, a прогнозная = 10 руб/МВт.ч, тогда MAPE = (0.01 – 10)/0.01 = 999%, хотя в действительности мы не так уж сильно ошиблись, всего на 10 руб/МВт.ч. Для рядов, содержащих значения близкие к нулю, применяют следующую оценку ошибки прогноза.

MAE – средняя абсолютная ошибка

.

Для оценки ошибки прогнозирования цен РСВ и индикатора БР корректнее использовать MAE.

После того, как получены значения для MAPE и/или MAE, то в работах обычно пишут: «Прогнозирование временного ряда энергопотребления с часовым разрешение проводилось на интервале с 01.01.2001 до 31.12.2001 (общее количество отсчетов N ~ 8500). Для данного прогноза значение MAPE = 1.5%». При этом, просматривая статьи, можно сложить общее впечатление об ошибки прогнозирования энергопотребления, для которого MAPE обычно колеблется от 1 до 5%; или ошибки прогнозирования цен на электроэнергию, для которого MAPE колеблется от 5 до 15% в зависимости от периода и рынка. Получив значение MAPE для собственного прогноза, вы можете оценить, насколько здорово у вас получается прогнозировать.

Кроме указанных методов иногда используют другие оценки ошибки, менее популярные, но также применимые. Подробнее об этих оценках ошибки прогноза читайте указанные статьи в Википедии.

ME – средняя ошибка

Встречается еще другое название этого показателя — Bias (англ. – смещение) демонстрирует величину отклонения, а также — в какую сторону прогноз продаж отклоняется от фактической потребности. Этот индикатор показывает, был ли прогноз оптимистичным или пессимистичным. То есть, отрицательное значение Bias говорит о том, что прогноз был завышен (реальная потребность оказалась ниже), и, наоборот, положительное значение о том, что прогноз был занижен. Цифровое значение показателя определяет величину отклонения (смещения).

MSE – среднеквадратичная ошибка

.

RMSE – квадратный корень из среднеквадратичной ошибки

.

.

SD – стандартное отклонение

где ME – есть средняя ошибка, определенная по формуле выше.

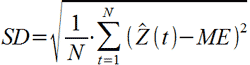
Примечание. Примеры расчетов данных показателей представлены в файле Excel, который можно скачать, оставив электронный адрес в форме ниже.

Связь точности и ошибки прогнозирования

В начале этого обсуждения разберемся с определениями.

Ошибка прогноза — апостериорная величина отклонения прогноза от действительного состояния объекта. Если говорить о прогнозе продаж, то это показатель отклонения фактических продаж от прогноза.

Точность прогнозирования есть понятие прямо противоположное ошибке прогнозирования. Если ошибка прогнозирования велика, то точность мала и наоборот, если ошибка прогнозирования мала, то точность велика. По сути дела оценка ошибки прогноза MAPE есть обратная величина для точности прогнозирования — зависимость здесь простая.

Точность прогноза в % = 100% – MAPE, встречается еще название этого показателя Forecast Accuracy. Вы практически не найдете материалов о прогнозировании, в которых приведены оценки именно точности прогноза, хотя с точки зрения здравого маркетинга корректней говорить именно о высокой точности. В рекламных статьях всегда будет написано о высокой точности. Показатель точности прогноза выражается в процентах:

• Если точность прогноза равна 100%, то выбранная модель описывает фактические значения на 100%, т.е. очень точно. Нужно сразу оговориться, что такого показателя никогда не будет, основное свойство прогноза в том, что он всегда ошибочен.
• Если 0% или отрицательное число, то совсем не описывает, и данной модели доверять не стоит.

Выбрать подходящую модель прогноза можно с помощью расчета показателя точность прогноза. Модель прогноза, у которой показатель точность прогноза будет ближе к 100%, с большей вероятностью сделает более точный прогноз. Такую модель можно назвать оптимальной для выбранного временного ряда.  Говоря о высокой точности, мы говорим о низкой ошибки прогноза и в этой области недопонимания быть не должно. Не имеет значения, что именно вы будете отслеживать, но важно, чтобы вы сравнивали модели прогнозирования или целевые показатели по одному показателю – ошибка прогноза или точность прогнозирования.

Ранее я использовала оценку MAPE, до тех пор пока не встретила формулу, которую рекомендует Валерий Разгуляев.

Примечание. Примеры расчетов данных показателей представлены в файле Excel, который можно скачать, оставив электронный адрес в форме ниже.

Оценка ошибки прогноза – формула Валерия Разгуляева (сайт http://upravlenie-zapasami.ru/)

Одной из самых используемых формул оценки ошибки прогнозирования является следующая формула:

где: P – это прогноз, а S – факт за тот же месяц. Однако у этой формулы есть серьезное ограничение — как оценить ошибку, если факт равен нулю? Возможный ответ, что в таком случае D = 100% – который означает, что мы полностью ошиблись. Однако простой пример показывает, что такой ответ — не верен:

вариант	прогноз	факт	ошибка прогноза
№1	4	0	100%
№2	4	1	300%
№3	1	4	75%

Оказывается, что в варианте развития событий №2, когда мы лучше угадали спрос, чем в варианте №1, ошибка по данной формуле оказалась – больше. То есть ошиблась уже сама формула. Есть и другая проблема, если мы посмотрим на варианты №2 и №3, то увидим, что имеем дело с зеркальной ситуацией в прогнозе и факте, а ошибка при этом отличается – в разы!.. То есть при такой оценке ошибки прогноза нам лучше его заведомо делать менее точным, занижая показатель – тогда ошибка будет меньше!.. Хотя понятно, что чем точнее будет прогноз – тем лучше будет и закупка. Поэтому для расчёта ошибки Валерий Разгуляев рекомендует использовать следующую формулу:

В таком случае для тех же примеров ошибка рассчитается иначе:

вариант	прогноз	факт	ошибка прогноза
№1	4	0	100%
№2	4	1	75%
№3	1	4	75%

Как мы видим, в варианте №1 ошибка становится равной 100%, причём это уже – не наше предположение, а чистый расчёт, который можно доверить машине. Зеркальные же варианты №2 и №3 – имеют и одинаковую ошибку, причём эта ошибка меньше ошибки самого плохого варианта №1. Единственная ситуация, когда данная формула не сможет дать однозначный ответ – это равенство знаменателя нулю. Но максимум из прогноза и факта равен нулю, только когда они оба равны нулю. В таком случае получается, что мы спрогнозировали отсутствие спроса, и его, действительно, не было – то есть ошибка тоже равна нулю – мы сделали совершенно точное предсказание.

Визуальный метод – графический

Визуальный метод состоит в том, что мы на график выводим значение прогнозной модели и факта продаж по тем моделям, которые хотим сравнить. Далее  сравниваем визуально, насколько прогнозная модель близка к фактическим продажам. Давайте рассмотрим на примере. В таблице представлены две прогнозные модели, а также фактические продажи по этому товару за тот же период. Для наглядности мы также рассчитали ошибку прогнозирования по обеим моделям.

По графикам очевидно, что модель 2 описывает лучше продажи этого товара. Оценка ошибки прогнозирования тоже это показывает – 65% и 31% ошибка прогнозирования по модели 1 и модели 2 соответственно.

Недостатком данного метода является то, что небольшую разницу между моделями сложно выявить — разницу в несколько процентов сложно оценить по диаграмме. Однако эти несколько процентов могут существенно улучшить качество прогнозирования и планирования пополнения запасов в целом.

Использование формул ошибки прогнозирования на практике

Практический аспект оценки ошибки прогнозирования я вывела отдельным пунктом. Это связано с тем, что все статистические методы расчета показателя ошибки прогнозирования рассчитывают то, насколько мы ошиблись в прогнозе в количественных показателях. Давайте теперь обсудим, насколько такой показатель будет полезен в вопросах управления запасами. Дело в том, что основная цель управления запасами  — обеспечить продажи, спрос наших клиентов. И, в конечном счете, максимизировать доход и прибыль компании. А эти показатели оцениваются как раз  в стоимостном выражении. Таким образом, нам важно при оценке ошибки прогнозирования понимать какой вклад каждая позиция внесла в объем продаж в стоимостном выражении. Когда мы оцениваем ошибку прогнозирования в количественном выражении мы предполагаем, что каждый товар имеет одинаковый вес в общем объеме продаж, но на самом деле это не так – есть очень дорогие товары, есть товары, которые продаются в большом количестве, наша группа А, а есть не очень дорогие товары, есть товары которые вносят небольшой вклад в объем продаж. Другими словами большая ошибка прогнозирования по товарам группы А будет нам «стоить» дороже, чем низкая ошибка прогнозирования по товарам группы С, например. Для того, чтобы наша оценка ошибки прогнозирования была корректной, релевантной целям управления запасами, нам необходимо оценивать ошибку прогнозирования по всем товарам или по отдельной группе не по средними показателями, а средневзвешенными с учетом прогноза и факта в стоимостном выражении.

Пример расчета такой оценки Вы сможете увидеть в файле Excel.

Примечание. Примеры расчетов данных показателей представлены в файле Excel, который можно скачать, оставив электронный адрес в форме ниже.

При этом нужно помнить, что для оценки ошибки прогнозирования по отдельным позициям мы рассчитываем по количеству, но вот если нам важно понять в целом ошибку прогнозирования по компании, например, для оценки модели, которую используем, то нам нужно рассчитывать не среднюю оценку по всем товарам, а средневзвешенную с учетом стоимостной оценки. Оценку можно брать по ценам себестоимости или ценам продажи, это не играет большой роли, главное, эти же цены (тип цен) использовать при всех расчетах.

Для чего используется ошибка прогнозирования

В первую очередь, оценка ошибки прогнозирования нам необходима для оценки того, насколько мы ошибаемся при планировании продаж, а значит при планировании поставок товаров. Если мы все время прогнозируем продажи значительно больше, чем потом фактически продаем, то вероятнее всего у нас будет излишки товаров, и это невыгодно компании. В случае, когда мы ошибаемся в обратную сторону – прогнозируем продажи меньше чем фактические продажи, с большой вероятностью у нас будут дефициты и компания не дополучит прибыль. В этом случае ошибка прогнозирования служит индикатором качества планирования и качества управления запасами.

Индикатором того, что повышение эффективности возможно за счет улучшения качества прогнозирования. За счет чего можно улучшить качество прогнозирования мы не будем здесь рассматривать, но одним из вариантов является поиск другой модели прогнозирования, изменения параметров расчета, но вот насколько новая модель будет лучше, как раз поможет показатель ошибки прогнозирования или точности прогноза. Сравнение этих показателей по нескольким моделям поможет определить ту модель, которая дает лучше результат.

В идеальном случае, мы можем так подбирать модель для каждой отдельной позиции. В этом случае мы будем рассчитывать прогноз по разным товарам по разным моделям, по тем, которые дают наилучший вариант именно для конкретного товара.

Также этот показатель можно использовать при выборе автоматизированного инструмента для прогнозирования спроса и управления запасами. Вы можете сделать тестовые расчеты прогноза в предлагаемой программе и сравнить ошибку прогнозирования полученного прогноза с той, которая есть у вашей существующей модели. Если у предлагаемого инструмента ошибка прогнозирования меньше. Значит, этот инструмент можно рассматривать для применения в компании. Кроме этого, показатель точности прогноза или ошибки прогнозирования можно использовать как KPI сотрудников, которые отвечают за подготовку прогноза продаж или менеджеров по закупкам, в том случае, если они рассчитывают прогноз будущих продаж при расчете заказа.

Примечание. Примеры расчетов данных показателей представлены в файле Excel, который можно скачать, оставив электронный адрес в форме ниже.

Если вы хотите повысить эффективность управления запасами и увеличить оборачиваемость товарных запасов, предлагаю изучить мастер-класс «Как увеличить оборачиваемость товарных запасов».

Копирование статьи возможно только вместе с этим текстом, с обязательным указанием автора, и ссылки на первоисточник: https://uppravuk.net/

Существует множество моделей прогноза, но как выбрать среди них ту, которая наиболее точно сделает прогноз?

Из данной статьи вы узнаете:

1. Какие способы оценки прогноза вы можете использовать?
2. Как выбрать оптимальную модель, которая поможет вам сделать максимально точный прогноз?
3. Как рассчитать показатель «Точность прогноза»?

Какие способы оценки прогнозной модели вы можете использовать:

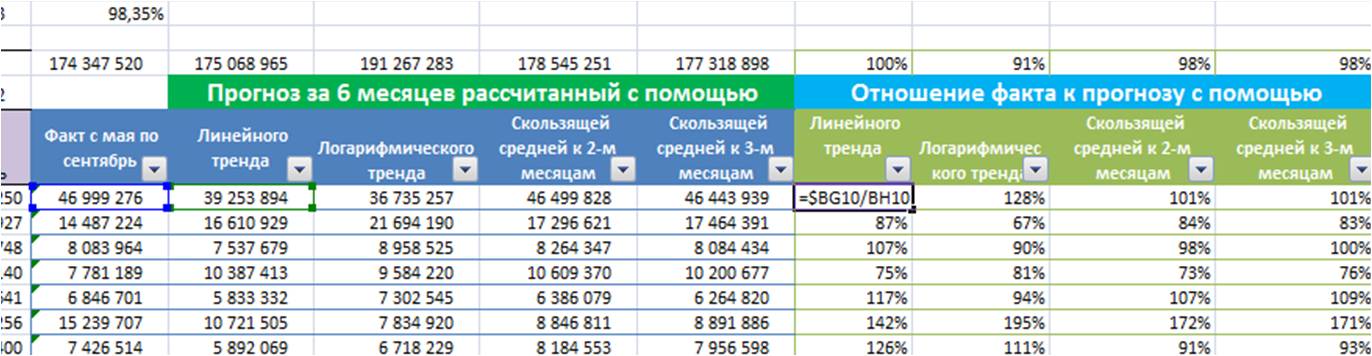
1.  Оценить отношение фактических продаж к прогнозу;

2. Расчет показателя точность прогноза — оценка на сколько точно выбранная модель описывает анализируемые данные;

3. Графический анализ — строим график и визуально оцениваем адекватность модели прогноза относительно фактических продаж за последний период ;
 

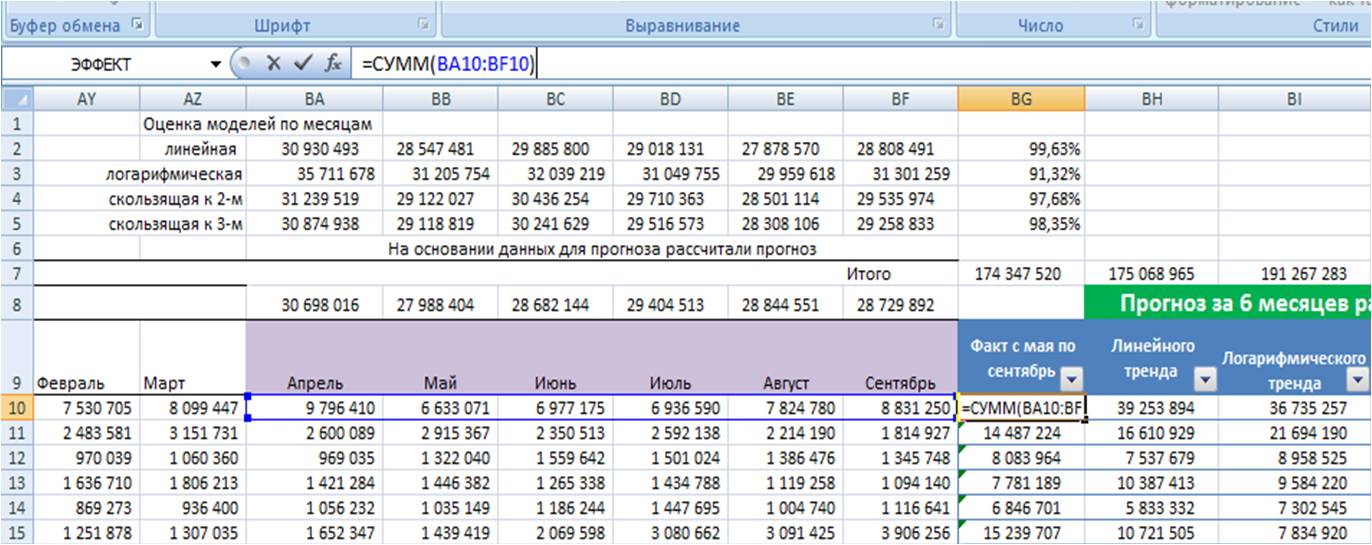
1-й способ — Расчет отношения фактических продаж к прогнозу.

Сначала рассчитываем прогноз разными способами и оцениваем отношение фактических продаж к прогнозу. ВАЖНО протестировать модели не по одному товару или направлению продаж, а сразу взять 10 и более товарных позиций или направлений продаж и рассчитать прогноз по ним на минимум на 3 периода вперед (количество периодов и направления прогноза зависят от ваших задач. Если задача — сделать точный прогноз на 6 месяцев, то рассчитываем прогноз на 6 месяцев несколькими вариантами и оцениваем отношение факта к прогнозу по сумме полугода).

Рассчитаем прогноз 4 способами на полгода. Протестируем следующие модели:

1. Линейный тренд + сезонность — лист «Линейный» в приложенном файле (см. статью «Как рассчитать прогноз с учетом роста и сезонности в Excel»)

2. Логарифмический тренд + сезонность — лист «Логарифмический» в приложенном файле (см. статью «5 способов расчета значений логарифмического тренда»)

3. Скользящая средняя с сезонностью к 2-м месяцам — лист «Скользящая к 2-м» (см. статью «Как рассчитать прогноз по методу скользящей средней»);

4. Скользящяя средняя с сезонностью к 3-м месяцам — лист «Скользящая к 3-м»;

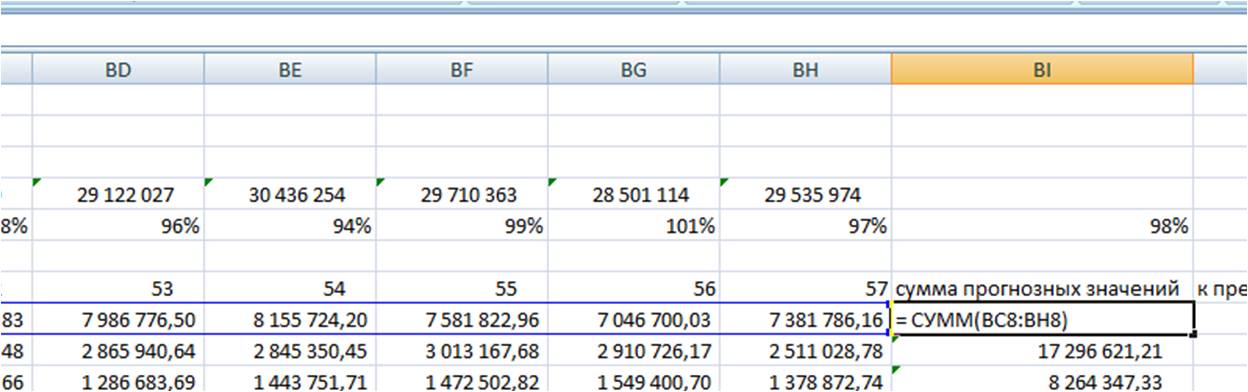
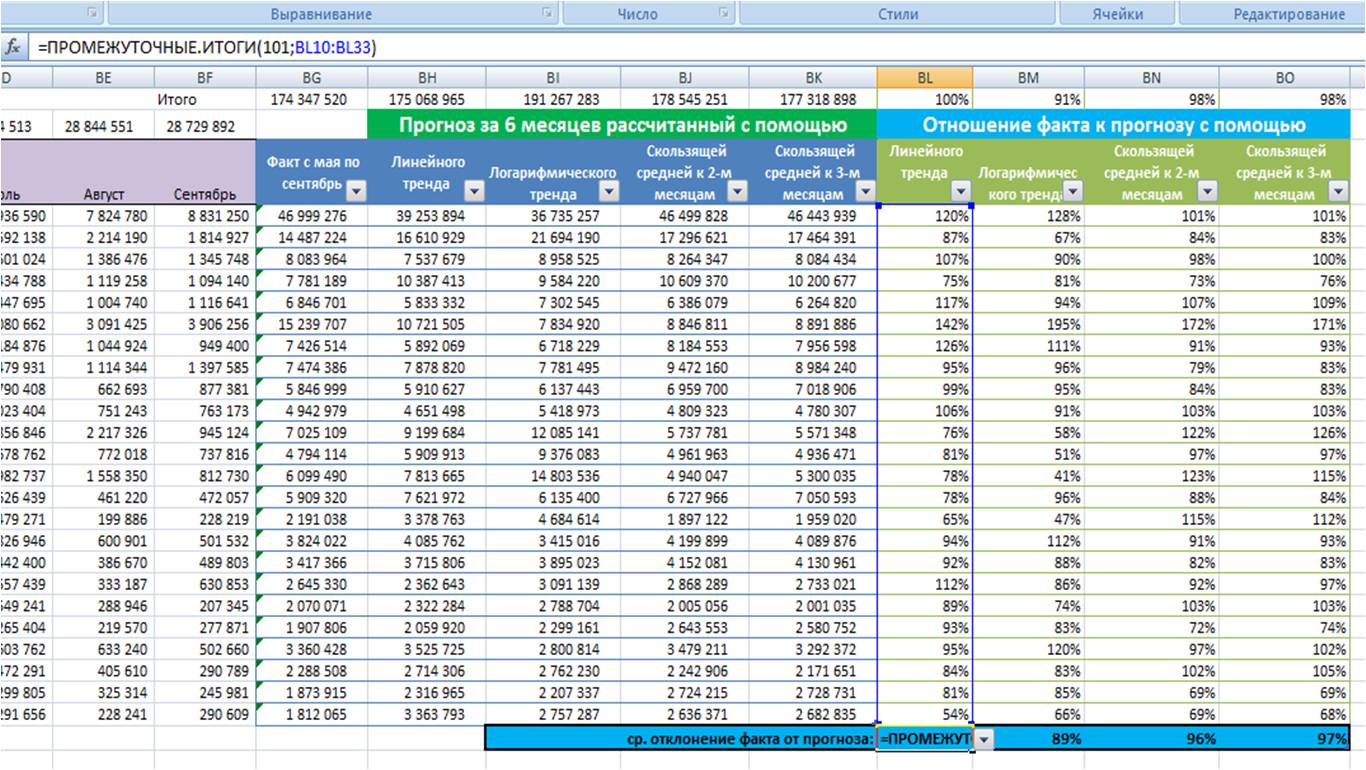
Для каждой из 4-х прогнозных моделей в листе «Оценка моделей»:

• Суммируем прогноз по каждой модели за 6 месяцев;

• Суммируем фактические продажи, которые мы будем сравнивать с прогнозом;

• Рассчитываем отношение факта к прогнозу по каждой позиции для каждой модели;

 

• Рассчитываем по каждой модели среднее отношение факта к прогнозу;

 

• Выбираем модель прогноза, которая по показателю «среднее отношение факта к прогнозу» оказалась максимально приближена к 100%;

 

Для наших данных самой точной моделью оказалась скользящая средняя к 3-м месяцам с сезонностью, среднее отклонение факта от прогноза 97%.

Мы протестировали каждую модель прогноза на реальных данных и выбрали для себя оптимальную, которая в среднем показала минимальное отклонение от факлических продаж.

2-й способ оценки модели прогноза — расчет показателя точность прогноза.

Показатель точность прогноза показывает, на сколько точно выбранная модель прогноза описывает данные. Идея в том, чем точнее выбранная модель описывает фактические данные, тем точнее она сделает прогноз.

Как рассчитать точность прогноза? Рассмотрим на примере расчета для модели прогноза с линейным трендом и сезонностью.

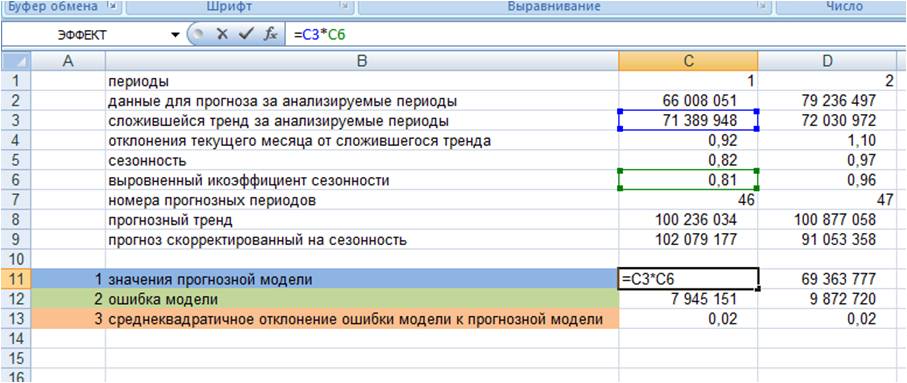
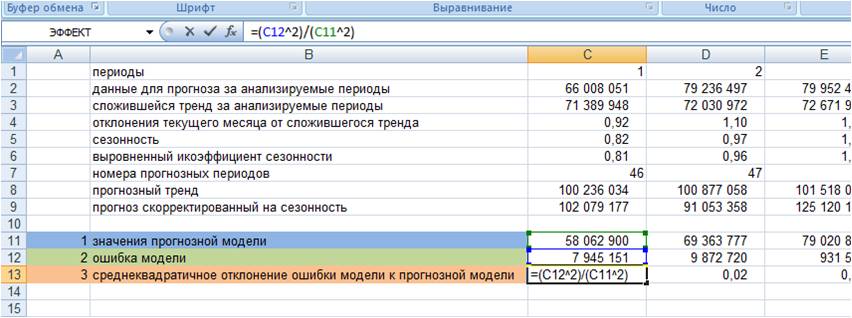
1. Рассчитываем значения прогнозной модели для каждого анализируемого момента времени в прошлом.

Для этого значения тренда для анализируемых периодов умножаем на выровненные коэффициенты сезонности (см. файл с примером)

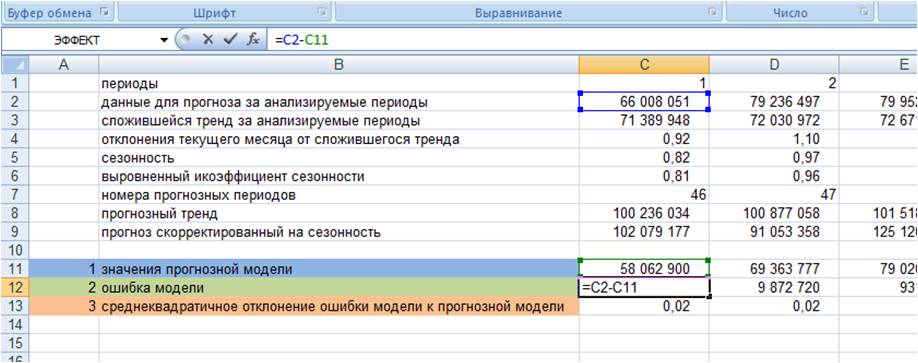
2. Рассчитываем ошибку прогнозной модели. Для этого за каждый период от фактических значений вычитаем значения прогнозной модели.

3. Рассчитываем квадратическое отклонение ошибки от значений прогнозной модели (см. файл с примером);

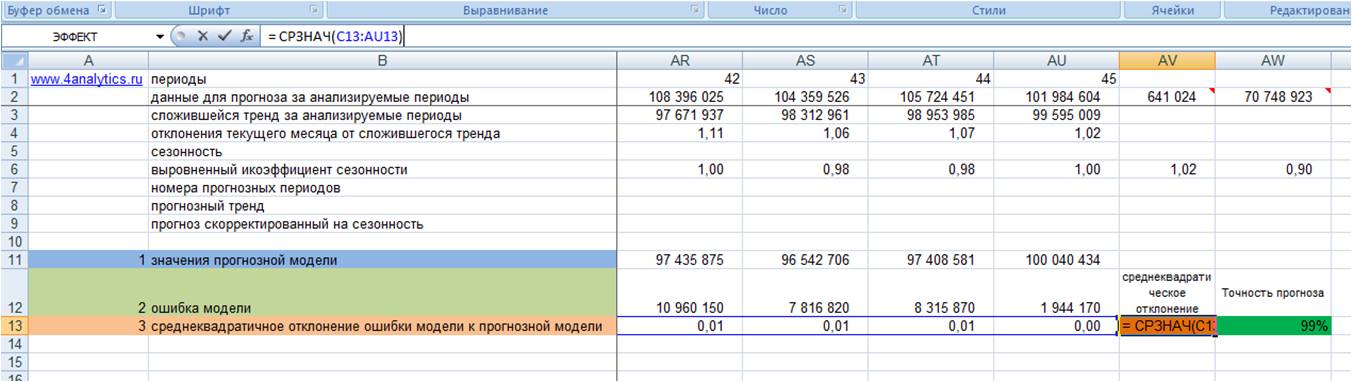
4. Рассчитываем среднее значение квадратического отклонения, т.е. среднеквадратическое отклонение

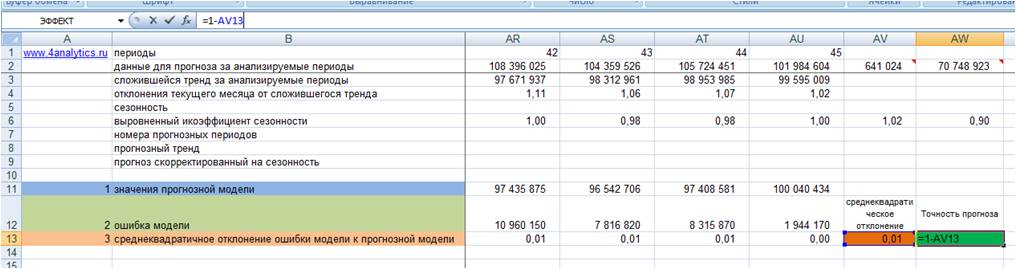
5. Точность прогноза = (1- среднеквадратическое отклонение ошибки прогнозной модели)*100 (см. файл с примером).

Показатель точности прогноза выражается в процентах:

• Если точность прогноза равна 100%, то выбранная модель описывает фактические значения на 100%, т.е. очень точно.

• Если 0% или отрицательное число, то совсем не описывает, и данной модели доверять не стоит.

 Выбрать подходящую модель прогноза можно с помощью расчета показателя точность прогноза. Модель прогноза, у которой показатель точность прогноза будет ближе к 100%, с большей вероятностью сделает более точный прогноз. Такую модель можно назвать оптимальной для выбранного временного ряда.

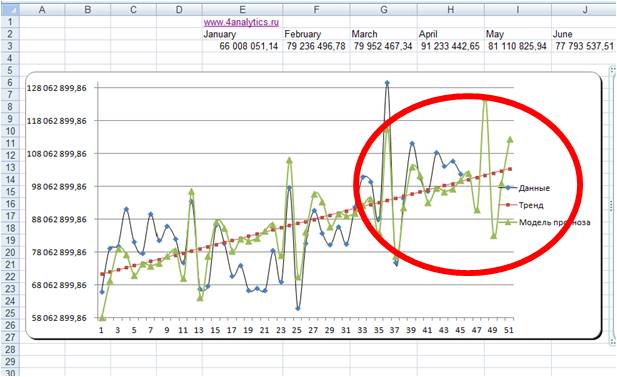
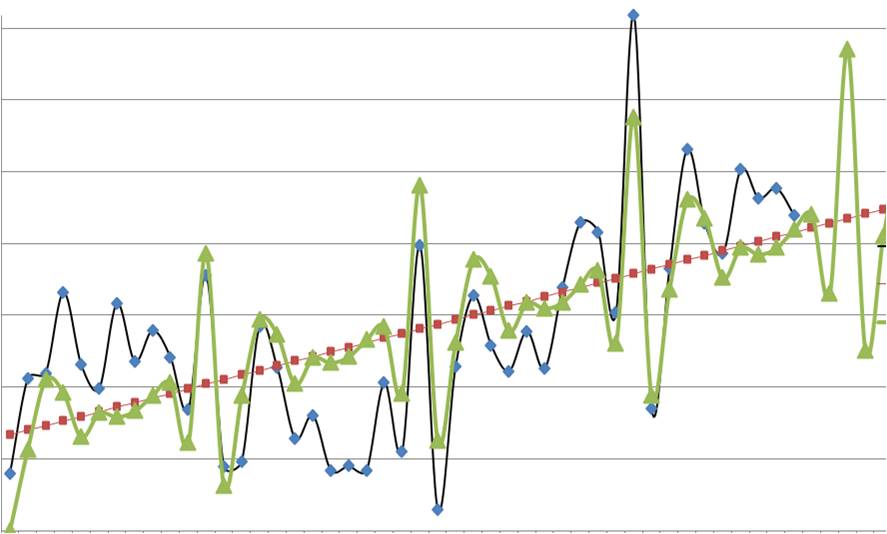
3. Способ оценки прогнозной модели — визуальный.

На график выводим анализируемые данные, тренд, значение модели и прогноз (см. вложенный файл). Обычно визуально видно, какая модель адекватнее строит прогноз . 3-й способ по своей сути схож с 1-м и вторым, только мы верим не цифрам, а тому что мы видим на графике.

Линейная модель:

 

Логарифмическая модель:

 

По последним периодам видно, что линейная модель более точно описывает данные за последние месяцы, и она, вероятнее всего, сделает более точный прогноз.

Какую модель прогноза выбрать?

1. Которая на основании тестирования на реальных данных для выбранного промежутка времени (месяца, 3-х месяцев, полугода, года) будет делать максимально точный прогноз, т.е. отношение факта к прогнозу будет близко к 1 или 100%.

2. Модель, которая будет максимально точно описывать фактические данные, т.е. показатель точность прогноза будет приближаться к 1, но не всегда модели точно описывающие данные делают адекватные прогнозы (это надо понимать и оценивать графически).

3. Модель, которой визуально вы больше доверяете с точки зрения описания входящих данных и продления прогнозной модели в будущее.

Для повышения точности прогноза я в своей практике стараюсь использовать 3 этих способа параллельно:

• По завершении прогнозного периода и в промежутках всегда оцениваю отношение фактических продаж к прогнозу.

• При построении прогноза анализирую показатель «среднеквадратическое отклонение» и рассчитываю показатель «точность прогноза» для оценки данных и модели.

• А также на график вывожу анализируемые данные и прогнозную модель, для визуального контроля.

Оценивая прогноз по факту или в промежуточные периоды в случае значительных отклонений фактических продаж от прогнозных, разбираю ситуацию и выясняю причины, в случае необходимости вношу корректировки в прогнозную модель.

С помощью программы Forecast4AC PRO вы можете рассчитать показатель точность прогноза автоматически.

Также Forecast4AC умеет автоматически выбирать оптимальную модель прогноза для каждого временного ряда.

+ одним нажатием строить график «Анализируемые данные + модель прогноза», на котором вы можете оценить, как соотносятся между собой:

• анализируемые данные;

• выбранный тренд;

• модель прогноза;

как в анализируемом периоде, так и в будущем. 

Точных прогнозов!

Статья полезная? Поделитесь с друзьями

Показатели качества модели парной регрессии

Основным показателем качества модели является коэффициент детерминации

.

Он показывает долю изменений результата Y, обусловленную изменениями фактора X. R² принимает значения от 0 до 1. Чем ближе R² к единице, тем лучше модель объясняет формирование Y. Для линейной парной регрессии коэффициент детерминации равен квадрату коэффициента корреляции: .

Точность модели, т. е. близость расчетных значений к фактическим, характеризует стандартная ошибка регрессии

.

Для оценки относительной точности модели используется средняя относительная ошибка аппроксимации

.

Если , то точность модели высокая, при — хорошая, при — удовлетворительная, а при — неудовлетворительная.

Продолжение примера 1. Коэффициент детерминации был определен с помощью функции «КВПИРСОН»: R²0,869. Он показывает, что 86,9 % изменений выручки от продаж Y обусловлено изменением стоимости активов X.

Стандартная ошибка регрессии была определена с помощью функции «СТОШYX»: S_рег3,92 млн. руб.

Средняя относительная ошибка аппроксимации

%.

Рассчитанные по уравнению регрессии значения выручки от продаж Y отклоняются от фактических в среднем на 3,92 млн. руб. или на 7,1%. Модель имеет хорошую точность.

Средняя ошибка аппроксимации

По семи территориям Уральского района за 199Х г. известны значения двух признаков.

Район	Расходы на покупку продовольственных товаров в общих расходах, %, у	Среднедневная заработная плата одного работающего, руб., х
Удмуртская респ.	68,8	45,1
Свердловская обл.	61,2	59,0
Башкортостан	59,9	57,2
Челябинская обл.	56,7	61,8
Пермская обл.	55,0	58,8
Курганская обл.	54,3	47,2
Оренбургская обл.	49,3	55,2

Требуется:
1. Для характеристики зависимости у от х рассчитать параметры следующих функций:
а) линейной;
б) степенной;
в) показательной;
г) равносторонней гиперболы (так же нужно придумать как предварительно линеаризовать данную модель).
2. Оценить каждую модель через среднюю ошибку аппроксимации А_ср и F-критерий Фишера.

Решение проводим при помощь онлайн калькулятора Линейное уравнение регрессии.
а) линейное уравнение регрессии;
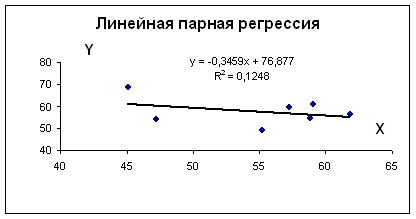
Использование графического метода.
Этот метод применяют для наглядного изображения формы связи между изучаемыми экономическими показателями. Для этого в прямоугольной системе координат строят график, по оси ординат откладывают индивидуальные значения результативного признака Y, а по оси абсцисс — индивидуальные значения факторного признака X.
Совокупность точек результативного и факторного признаков называется полем корреляции.

Для наших данных система уравнений имеет вид

Из первого уравнения выражаем а и подставим во второе уравнение
Получаем b = -0.35, a = 76.88
Уравнение регрессии: y = -0.35 x + 76.88

x	y	x 2	y 2	x • y	y(x)	(y i -y cp ) 2	(y-y(x)) 2	|y — y x |:y
45,1	68,8	2034,01	4733,44	3102,88	61,28	119,12	56,61	0,1094
59	61,2	3481	3745,44	3610,8	56,47	10,98	22,4	0,0773
57,2	59,9	3271,84	3588,01	3426,28	57,09	4,06	7,9	0,0469
61,8	56,7	3819,24	3214,89	3504,06	55,5	1,41	1,44	0,0212
58,8	55	3457,44	3025	3234	56,54	8,33	2,36	0,0279
47,2	54,3	2227,84	2948,49	2562,96	60,55	12,86	39,05	0,1151
55,2	49,3	3047,04	2430,49	2721,36	57,78	73,71	71,94	0,172
384,3	405,2	21338,41	23685,76	22162,34	405,2	230,47	201,71	0,5699

Примечание: значения y(x) находятся из полученного уравнения регрессии:
y(45.1) = -0.35*45.1 + 76.88 = 61.28
y(59) = -0.35*59 + 76.88 = 56.47
. . .

Ошибка аппроксимации
Оценим качество уравнения регрессии с помощью ошибки абсолютной аппроксимации. Средняя ошибка аппроксимации — среднее отклонение расчетных значений от фактических:

F-статистики. Критерий Фишера.
Проверка значимости модели регрессии проводится с использованием F-критерия Фишера, расчетное значение которого находится как отношение дисперсии исходного ряда наблюдений изучаемого показателя и несмещенной оценки дисперсии остаточной последовательности для данной модели.
Если расчетное значение с k1=(m) и k2=(n-m-1) степенями свободы больше табличного при заданном уровне значимости, то модель считается значимой.

где m – число факторов в модели.
Оценка статистической значимости парной линейной регрессии производится по следующему алгоритму:
1. Выдвигается нулевая гипотеза о том, что уравнение в целом статистически незначимо: H₀: R 2 =0 на уровне значимости α.
2. Далее определяют фактическое значение F-критерия:

где m=1 для парной регрессии.
3. Табличное значение определяется по таблицам распределения Фишера для заданного уровня значимости, принимая во внимание, что число степеней свободы для общей суммы квадратов (большей дисперсии) равно 1 и число степеней свободы остаточной суммы квадратов (меньшей дисперсии) при линейной регрессии равно n-2.
4. Если фактическое значение F-критерия меньше табличного, то говорят, что нет основания отклонять нулевую гипотезу.
В противном случае, нулевая гипотеза отклоняется и с вероятностью (1-α) принимается альтернативная гипотеза о статистической значимости уравнения в целом.
Табличное значение критерия со степенями свободы k1=1 и k2=5, Fkp = 6.61
Поскольку фактическое значение F b
в) показательная регрессия;
г) модель равносторонней гиперболы.
Система нормальных уравнений.

Для наших данных система уравнений имеет вид
7a + 0.1291b = 405.2
0.1291a + 0.0024b = 7.51
Из первого уравнения выражаем а и подставим во второе уравнение
Получаем b = 1054.67, a = 38.44
Уравнение регрессии:
y = 1054.67 / x + 38.44
Ошибка аппроксимации.
Оценим качество уравнения регрессии с помощью ошибки абсолютной аппроксимации.

Задача №3. Расчёт параметров регрессии и корреляции с помощью Excel

По территориям региона приводятся данные за 200Х г.

Номер региона	Среднедушевой прожиточный минимум в день одного трудоспособного, руб., х	Среднедневная заработная плата, руб., у
1	78	133
2	82	148
3	87	134
4	79	154
5	89	162
6	106	195
7	67	139
8	88	158
9	73	152
10	87	162
11	76	159
12	115	173

Задание:

1. Постройте поле корреляции и сформулируйте гипотезу о форме связи.

2. Рассчитайте параметры уравнения линейной регрессии

.

3. Оцените тесноту связи с помощью показателей корреляции и детерминации.

4. Дайте с помощью среднего (общего) коэффициента эластичности сравнительную оценку силы связи фактора с результатом.

5. Оцените с помощью средней ошибки аппроксимации качество уравнений.

6. Оцените с помощью F-критерия Фишера статистическую надёжность результатов регрессионного моделирования.

7. Рассчитайте прогнозное значение результата, если прогнозное значение фактора увеличится на 10% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости .

8. Оцените полученные результаты, выводы оформите в аналитической записке.

Решение:

Решим данную задачу с помощью Excel.

1. Сопоставив имеющиеся данные х и у, например, ранжировав их в порядке возрастания фактора х, можно наблюдать наличие прямой зависимости между признаками, когда увеличение среднедушевого прожиточного минимума увеличивает среднедневную заработную плату. Исходя из этого, можно сделать предположение, что связь между признаками прямая и её можно описать уравнением прямой. Этот же вывод подтверждается и на основе графического анализа.

Чтобы построить поле корреляции можно воспользоваться ППП Excel. Введите исходные данные в последовательности: сначала х, затем у.

Выделите область ячеек, содержащую данные.

Затем выберете: Вставка / Точечная диаграмма / Точечная с маркерами как показано на рисунке 1.

Рисунок 1 Построение поля корреляции

Анализ поля корреляции показывает наличие близкой к прямолинейной зависимости, так как точки расположены практически по прямой линии.

2. Для расчёта параметров уравнения линейной регрессии
воспользуемся встроенной статистической функцией ЛИНЕЙН.

1) Откройте существующий файл, содержащий анализируемые данные;
2) Выделите область пустых ячеек 5×2 (5 строк, 2 столбца) для вывода результатов регрессионной статистики.
3) Активизируйте Мастер функций: в главном меню выберете Формулы / Вставить функцию.
4) В окне Категория выберете Статистические, в окне функция – ЛИНЕЙН. Щёлкните по кнопке ОК как показано на Рисунке 2;

Рисунок 2 Диалоговое окно «Мастер функций»

5) Заполните аргументы функции:

Известные значения у – диапазон, содержащий данные результативного признака;

Известные значения х – диапазон, содержащий данные факторного признака;

Константа – логическое значение, которое указывает на наличие или на отсутствие свободного члена в уравнении; если Константа = 1, то свободный член рассчитывается обычным образом, если Константа = 0, то свободный член равен 0;

Статистика – логическое значение, которое указывает, выводить дополнительную информацию по регрессионному анализу или нет. Если Статистика = 1, то дополнительная информация выводится, если Статистика = 0, то выводятся только оценки параметров уравнения.

Щёлкните по кнопке ОК;

Рисунок 3 Диалоговое окно аргументов функции ЛИНЕЙН

6) В левой верхней ячейке выделенной области появится первый элемент итоговой таблицы. Чтобы раскрыть всю таблицу, нажмите на клавишу , а затем на комбинацию клавиш + + .

Дополнительная регрессионная статистика будет выводиться в порядке, указанном в следующей схеме:

Значение коэффициента b	Значение коэффициента a
Стандартная ошибка b	Стандартная ошибка a
Коэффициент детерминации R 2	Стандартная ошибка y
F-статистика	Число степеней свободы df
Регрессионная сумма квадратов

Остаточная сумма квадратов

Рисунок 4 Результат вычисления функции ЛИНЕЙН

Получили уровнение регрессии:

Делаем вывод: С увеличением среднедушевого прожиточного минимума на 1 руб. среднедневная заработная плата возрастает в среднем на 0,92 руб.

3. Коэффициент детерминации означает, что 52% вариации заработной платы (у) объясняется вариацией фактора х – среднедушевого прожиточного минимума, а 48% — действием других факторов, не включённых в модель.

По вычисленному коэффициенту детерминации можно рассчитать коэффициент корреляции: .

Связь оценивается как тесная.

4. С помощью среднего (общего) коэффициента эластичности определим силу влияния фактора на результат.

Для уравнения прямой средний (общий) коэффициент эластичности определим по формуле:

Средние значения найдём, выделив область ячеек со значениями х, и выберем Формулы / Автосумма / Среднее, и то же самое произведём со значениями у.

Рисунок 5 Расчёт средних значений функции и аргумент

Таким образом, при изменении среднедушевого прожиточного минимума на 1% от своего среднего значения среднедневная заработная плата изменится в среднем на 0,51%.

С помощью инструмента анализа данных Регрессия можно получить:
— результаты регрессионной статистики,
— результаты дисперсионного анализа,
— результаты доверительных интервалов,
— остатки и графики подбора линии регрессии,
— остатки и нормальную вероятность.

Порядок действий следующий:

1) проверьте доступ к Пакету анализа. В главном меню последовательно выберите: Файл/Параметры/Надстройки.

2) В раскрывающемся списке Управление выберите пункт Надстройки Excel и нажмите кнопку Перейти.

3) В окне Надстройки установите флажок Пакет анализа, а затем нажмите кнопку ОК.

• Если Пакет анализа отсутствует в списке поля Доступные надстройки, нажмите кнопку Обзор, чтобы выполнить поиск.

• Если выводится сообщение о том, что пакет анализа не установлен на компьютере, нажмите кнопку Да, чтобы установить его.

4) В главном меню последовательно выберите: Данные / Анализ данных / Инструменты анализа / Регрессия, а затем нажмите кнопку ОК.

5) Заполните диалоговое окно ввода данных и параметров вывода:

Входной интервал Y – диапазон, содержащий данные результативного признака;

Входной интервал X – диапазон, содержащий данные факторного признака;

Метки – флажок, который указывает, содержит ли первая строка названия столбцов или нет;

Константа – ноль – флажок, указывающий на наличие или отсутствие свободного члена в уравнении;

Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона;

6) Новый рабочий лист – можно задать произвольное имя нового листа.

Затем нажмите кнопку ОК.

Рисунок 6 Диалоговое окно ввода параметров инструмента Регрессия

Результаты регрессионного анализа для данных задачи представлены на рисунке 7.

Рисунок 7 Результат применения инструмента регрессия

5. Оценим с помощью средней ошибки аппроксимации качество уравнений. Воспользуемся результатами регрессионного анализа представленного на Рисунке 8.

Рисунок 8 Результат применения инструмента регрессия «Вывод остатка»

Составим новую таблицу как показано на рисунке 9. В графе С рассчитаем относительную ошибку аппроксимации по формуле:

Рисунок 9 Расчёт средней ошибки аппроксимации

Средняя ошибка аппроксимации рассчитывается по формуле:

Качество построенной модели оценивается как хорошее, так как не превышает 8 – 10%.

6. Из таблицы с регрессионной статистикой (Рисунок 4) выпишем фактическое значение F-критерия Фишера:

Поскольку при 5%-ном уровне значимости, то можно сделать вывод о значимости уравнения регрессии (связь доказана).

8. Оценку статистической значимости параметров регрессии проведём с помощью t-статистики Стьюдента и путём расчёта доверительного интервала каждого из показателей.

Выдвигаем гипотезу Н₀ о статистически незначимом отличии показателей от нуля:

.

для числа степеней свободы

На рисунке 7 имеются фактические значения t-статистики:

t-критерий для коэффициента корреляции можно рассчитать двумя способами:

I способ:

где – случайная ошибка коэффициента корреляции.

Данные для расчёта возьмём из таблицы на Рисунке 7.

II способ:

Фактические значения t-статистики превосходят табличные значения:

Поэтому гипотеза Н₀ отклоняется, то есть параметры регрессии и коэффициент корреляции не случайно отличаются от нуля, а статистически значимы.

Доверительный интервал для параметра a определяется как

Для параметра a 95%-ные границы как показано на рисунке 7 составили:

Доверительный интервал для коэффициента регрессии определяется как

Для коэффициента регрессии b 95%-ные границы как показано на рисунке 7 составили:

Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью параметры a и b, находясь в указанных границах, не принимают нулевых значений, т.е. не являются статистически незначимыми и существенно отличны от нуля.

7. Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение прожиточного минимума составит:

Тогда прогнозное значение прожиточного минимума составит:

Ошибку прогноза рассчитаем по формуле:

где

Дисперсию посчитаем также с помощью ППП Excel. Для этого:

1) Активизируйте Мастер функций: в главном меню выберете Формулы / Вставить функцию.

2) В окне Категория выберете Статистические, в окне функция – ДИСП.Г. Щёлкните по кнопке ОК.

3) Заполните диапазон, содержащий числовые данные факторного признака. Нажмите ОК.

Рисунок 10 Расчёт дисперсии

Получили значение дисперсии

Для подсчёта остаточной дисперсии на одну степень свободы воспользуемся результатами дисперсионного анализа как показано на Рисунке 7.

Доверительные интервалы прогноза индивидуальных значений у при с вероятностью 0,95 определяются выражением:

Интервал достаточно широк, прежде всего, за счёт малого объёма наблюдений. В целом выполненный прогноз среднемесячной заработной платы оказался надёжным.

Условие задачи взято из: Практикум по эконометрике: Учеб. пособие / И.И. Елисеева, С.В. Курышева, Н.М. Гордеенко и др.; Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2003. – 192 с.: ил.

Средней ошибки аппроксимации качество уравнений

Оценка этой формы связи по коэффициенту множественной корреляции и средней ошибке аппроксимации показывает, что адекватность данной модели не подтверждается. Действительно, хотя значение коэффициента достаточно высокое (0,92), средняя ошибка аппроксимации составляет более 10% (I = 14,5%). Поэтому данная форма должна быть исключена из перебора известных уравнений регрессии. [c.29]

Анализ полученной формы связи по той же причине, что и в первом случае, позволяет сделать вывод о непригодности и этой модели. Коэффициент множественной корреляции хотя и имеет более высокое значение, чем в линейной зависимости (0,93), но по величине средней ошибки аппроксимации (б = 12,4%) это уравнение регрессии подлежит исключению из дальнейшего перебора. [c.29]

Последняя модель себестоимости добычи нефти, как показывает оценка ее по известным критериям, удовлетворяет условиям адекватности. Коэффициент множественной корреляции R составляет 0,98, что свидетельствует о том, что колеблемость исследуемого показателя более чем на 96 % определяется факторами, включенными в эту модель. При оценке по f-критерию (t R = 30,5) можно утверждать, что с вероятностью 0,99 факторы, включенные в модель, имеют существенную связь с исследуемым показателем (t a n = 2,58). Средняя ошибка аппроксимации составляет всего лишь 2,9 %, а F-критерий, характеризующий уровень остаточной дисперсии, превышает критическое (табличное) значение в четыре раза. К этому следует добавить, что полученная модель себестоимости добычи нефти представляет собой достаточно простую форму связи, легко решается и поддается экономической интерпретации. [c.30]

Оценка полученной модели по статистическим характеристикам показывает, что колеблемость затрат исследуемой подсистемы на 85 % обусловлена колеблемостью факторов, включенных в модель, коэффициент множественной корреляции высокий (/ = 0,92) и существенный (f = = 39,8), модель является адекватной, средняя ошибка аппроксимации (ё = 5,7%) меньше 10%. [c.39]

Статистический анализ показывает, что уравнение значимо Рф = 5,054 при /»табл = 3,01, корреляционное отношение равно 0,9959, ее»стандартная ошибка равна 0,0015. Среднее квадратическое отклонение расчетной себестоимости от фактической равно 0,018. Средняя ошибка аппроксимации 1,1%. [c.90]

Средняя ошибка аппроксимации [c.94]

Средняя ошибка аппроксимации. [c.95]

В случаях, когда трудно обосновать форму зависимости, решение задачи можно провести по разным моделям и сравнить полученные результаты. Адекватность разных моделей фактическим зависимостям проверяется по критерию Фишера, показателю средней ошибки аппроксимации и величине множественного коэффициента детерминации, о которых речь пойдет несколько позже (см. 7.4). [c.144]

Эти сведения вводятся в ПЭВМ и рассчитываются матрицы парных и частных коэффициентов корреляции, уравнение множественной регрессии, а также показатели, с помощью которых оценивается надежность коэффициентов корреляции и уравнения связи критерий Стьюдента, критерий Фишера, средняя ошибка аппроксимации, множественные коэффициенты корреляции и детерминации. [c.145]

Для того чтобы убедиться в надежности уравнения связи и правомерности его использования для практической цели, необходимо дать статистическую оценку надежности показателей связи. Для этого используются критерий Фишера (F-отношение), средняя ошибка аппроксимации ( ), коэффициенты множественной корреляции (/ ) и детерминации (D). [c.151]

Для статистической оценки точности уравнения связи используется также средняя ошибка аппроксимации [c.152]

Чем меньше теоретическая линия регрессии (рассчитанная по уравнению) отклоняется от фактической (эмпиричной), тем меньше средняя ошибка аппроксимации. В нашем примере она составляет 0,0364, или 3,64 %. Учитывая, что в экономических расчетах допускается погрешность 5-8 %, можно сделать вывод, что исследуемое уравнение связи довольно точно описывает изучаемые зависимости. [c.152]

После построения уравнения регрессии необходимо сделать проверку его значимости с помощью специальных критериев установить, не является ли полученная зависимость, выраженная уравнением регрессии, случайной, т.е. можно ли ее использовать в прогнозных целях и для факторного анализа. В статистике разработаны методики строгой проверки значимости коэффициентов регрессии с помощью дисперсионного анализа и расчета специальных критериев (например, F-критерия). Нестрогая проверка может быть выполнена путем расчета среднего относительного линейного отклонения (ё), называемого средней ошибкой аппроксимации [c.123]

Модель считается адекватной, т.е. пригодной для практического использования, если средняя ошибка аппроксимации не превосходит 15%. [c.123]

Оценку качества построенной модели даст коэффициент (индекс) детерминации, а также средняя ошибка аппроксимации. [c.6]

Средняя ошибка аппроксимации — среднее отклонение расчетных значений от фактических [c.6]

Подставляя в данное уравнение фактические значения х, получаем теоретические значения результата ух. По ним рассчитаем показатели тесноты связи — индекс корреляции рху и среднюю ошибку аппроксимации 7, [c.13]

Рассчитать линейный коэффициент парной корреляции и среднюю ошибку аппроксимации. [c.16]

Это означает, что 52% вариации заработной латы (у) объясняется вариацией фактора х — среднедушевого прожиточного минимума. Качество модели определяет средняя ошибка аппроксимации [c.18]

Оцените с помощью средней ошибки аппроксимации качество уравнений. [c.38]

Оцените качество уравнений с помощью средней ошибки аппроксимации. [c.42]

Оцените качество уравнения через среднюю ошибку аппроксимации. [c.92]

Оцените качество каждого тренда через среднюю ошибку аппроксимации, линейный коэффициент автокорреляции отклонений. [c.166]

СРЕДНЯЯ ОШИБКА АППРОКСИМАЦИИ [c.87]

Представим расчет средней ошибки аппроксимации для уравнения ух = 9,876 + 5,129 hue в табл. 2.7. А = — 7,3 = 1,2%, что [c.88]

Расчет средней ошибки аппроксимации [c.88]

В стандартных программах чаще используется первая формула для расчета Средней ошибки аппроксимации. [c.88]

В чем смысл средней ошибки аппроксимации и как она определяется [c.89]

Средняя ошибка аппроксимации [c.10]

Выбор вида модели основан на логическом анализе изучаемых показателей, сравнении статистических характеристик (средняя ошибка аппроксимации, критерий Фишера, коэффициенты множественной корреляции и детерминации), рассчитанных для различных функций по одним и тем же первичным данным. [c.31]

Проверка приведенной в формуле (154) себестоимости по фактическим данным 103 СМУ показала, что средняя ошибка аппроксимации, определяющая степень соответствия расчетных значений фактическим, составила всего 1,5%, что вполне допустимо. [c.227]

Исчисляемый коэффициент детерминации получился равным 0,869. Это говорит о том, что размер заработной платы водителей на 86,9% зависит от Р и Л ри на 13,1% — от неучтенных в модели факторов. Средняя ошибка аппроксимации составила всего лишь 0,17%. Модель была получена на основе конкретных показателей ряда автотранспортных предприятий Владимирского транспортного управления, поэтому она может -быть использована в практической работе только на этих предприятиях. Предлагаемая же методика может быть использована в любом транспортном управлении, министерстве при планировании и анализе себестоимости автомобильных перевозок и установлении нормативов по заработной плате водителей за время работы на линии. [c.36]