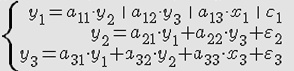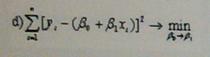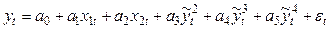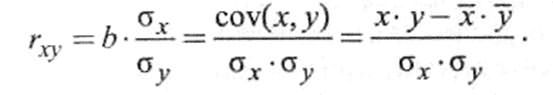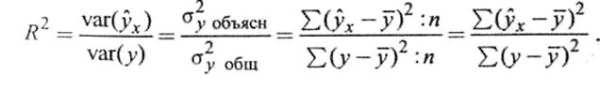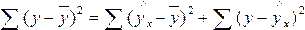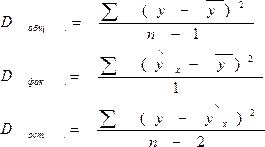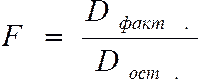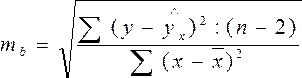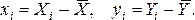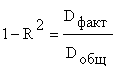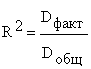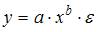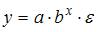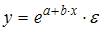уравнения ошибочная

уравнения ошибочная
…, которая
характеризует результат функционирования
анализируемой аналитической системы
наз-ся Эндогенной
ARIMA
(0, C, 1) является: моделью
скользящей средней
DS-процесс
это … процесс имеющий статестический
тренд и приводной …
F-статистика
Фишера используется: определения
статистической значимости модели в
целом.
F-тест
применяется для…выбора лучшей модели
RESET-тест
применяется для…. ошибки линейной
спецификации регрессии
ti —
расчетное значение критерия Стьюдента
для коэффициента В,. Критическое значение
критерия Стьюдента t,5=1.96 для уровня
значимости 0,05 и числа степеней свобод»
более 200…если t1=2.5. то коэффициент S1
значим с уровнем доверия 0.95 . если t1=
-2,5, то коэффициент S1 значим с уровнем
доверия 0.95
TS-процесс
— это… процесс, приводимый к стационарному
путем выделения тренда
t-статистика
Стьюдента используется: для определения
статистической значимости коэффициентов
регрессионного уравнения;
Автокореляция
в остатках –это…кореляция зависимости
между состакомрегриссионного во времени
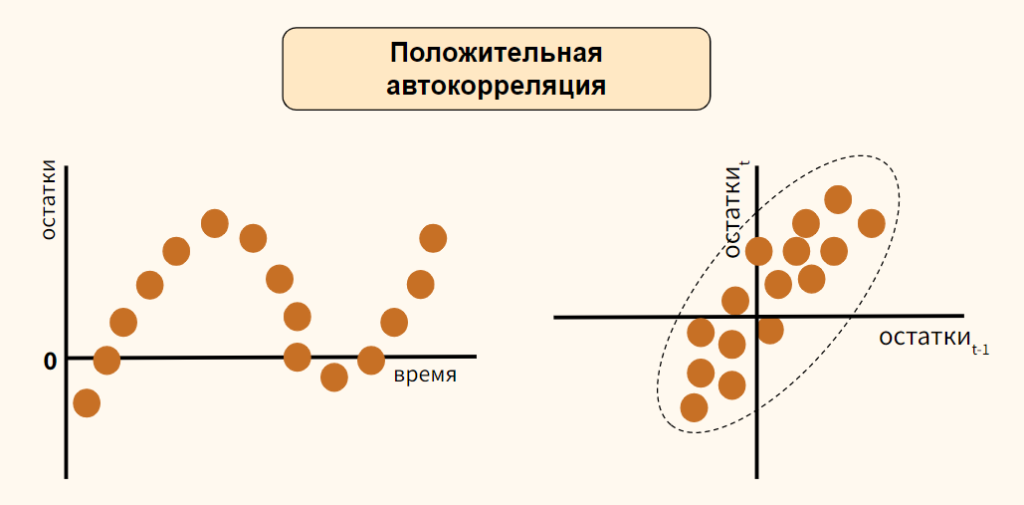
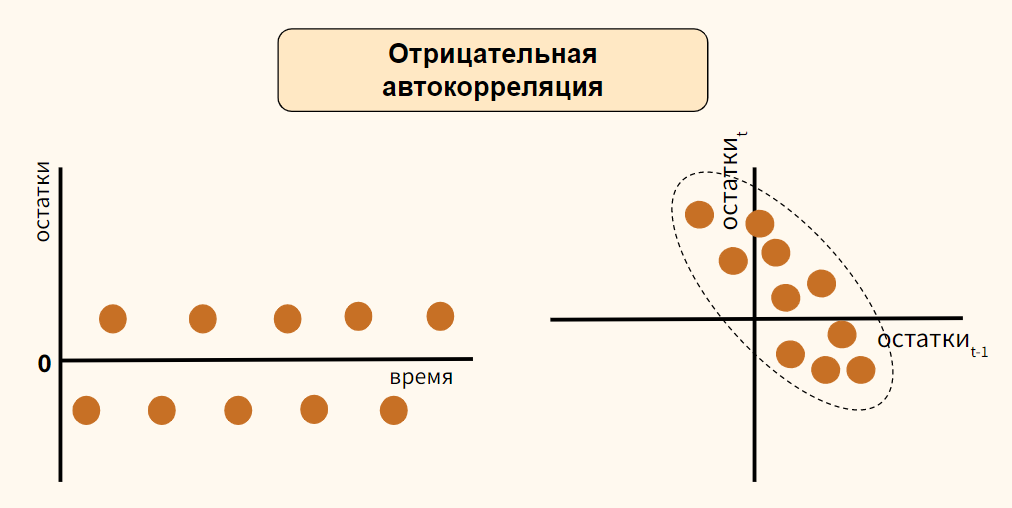
Автокорреляция
остатков бывает следующих видов:
отрицательная положительная
Автокорреляция
ошибок – это линейная связь между
более чем двумя объясняющими переменными
Автокорреляция
ошибок- это — корреляция ошибок
регрессии для разных наблюдений
Авторегрессионными
моделями порядка p являются
модели вида:
Была
исследована зависимость рентабельности
предприятия (у) от оборачиваемости
оборотных активов (х), фондоотдачи [к)
и производительности труда [/) за 24
квартала. По выборочным данным построены
несколько типов зависимостей и рассчитаны
значения F-статистики для них. Какая из
представленных регрессий является
значимой, если критическое значение
F-статистики равно 3.1 при уровне значимости
5%?ОТВЕТ: 3 1)у=4.12+0.15 F=2,9 2) у-0.75.x
F=l.7 3) у=е^****
F=4.6 4) y=ln F =3,09
В каких
случаях значение коэффициента
детерминации R² может выйти за
пределы[0;1]? —если в уравнении регрессии
отсутствует константа β0
В командной
строке EViews введена следующая
последовательность команд: genr y=3+4*@rnd
genr z=@var(y)
Что появится в рабочем файле после
выполнения этих команд? — будет
создан ряд У , значения которого будут
распределены по равномерному закону
распределения на интервалеот 3 до 7.
Затем будет создан ряд Z, значения
которого будут равны дисперсии ряда У
В
оцениваемо» модели у = хВ +Zу +е присутствуют
несущественные независимые переменные
у. тогда оценка & . полученная в данной
регрессии…дисперсия оценки
увеличивается от включения в модель
несущественных переменных, несмещенная
В
оцениваемой модели y=XB+е отсутствует
часть существенных независимых
переменных тогда оценка B полученная
в данной регрессии в общем случае…смешанная
В
оцениваемой модели у=ХВ+е отсутствует
часть существенных независимых
переменных, тогда оценка В^, полученная
в данной регрессии, в общем случае
смещенная
В результате
оценки параметров регрессии y = β0
+ β1x + ε были получены следующие
результаты: 4,7 β 10,4; β 1 0 = = ˆ ˆ .
Доверительный интервал для 1 βˆ
на 10%ном уровне значимости составил
(4,3; 5,1). Что показывает полученный
доверительный интервал на указанном
уровне значимости? истинное значение
коэффициента β1 находится
в указанном интервале с
вероятностью 90 %;
В результате
оценки параметров регрессии у=α+βх+
ɛ были получены следующие результаты:
ᾶ= 10, ᵬ=4,7. Доверительный интервал для
ᵬ с уровнем доверия 95% составил [3,9;5,5].
Что показывает полученный доверительный
интервал с указанным уровнем доверия?
— истинное значение коэффициента β
находится в указанном интервале с
вероятностью 0,95
В результате
оценки параметров регрессии у=α+βх+
ɛ были получены следующие результаты:
ᾶ= 10, 4, ᵬ=4,7. Доверительный интервал для
ᵬ с уровнем доверия 90% составил [4.3;5,1].
Что показывает полученный доверительный
интервал с указанным уровнем доверия?
— истинное значение коэффициента В
находится в указанном интервале с
вероятностью 0,90
В системе
одновременных уравнений значения
экзогенных переменных… формируются
вне системы и не должны коррелировать
с остатками
В системе
рекурсивных эконометрических уравнений…
матрица коэффициентов при эндогенных
переменных треугольная
В
стационарном временном ряду трендовая
компонента: отсутствует
В чем
суть гетероскедастичности?- дисперсии
случайных отклонений изменяются
В
эконометрической модели линейного
уравнения регрессии у=a+b1x1+b2x2…+bkxk+
ɛ коэффициетом регрессии, характеризующим
среднее изменение зависимой переменной
при изменении независимой переменной
на 1 единицу измерения, является…-bj
В
экономической модели линейного уравнения
регрессии у=a+b1x1+b2x2…+bkxk+
ɛ параметром является…— a,bj
Величина
коэффициента апатичности показывает
… на сколько процентов изменится в
среденем результат при изменении
фактора на 1%
Величина
коэффициента множественное линейной
регрессии при объясняющей переменной
показывает…среднее изменения
результата при изменения фактора на
одну единицу.
Выберите
верные утверждения о производственной
функции Кобба-Дугласа- записывается
степенным уравнением, является нелинейной
зависимостью
Выберите
ответ, который наиболее точно описывает
сущность эконометрики. Эконометрика
– это наука, которая, используя методы
экономической теории, математической
статистики и математического
моделирования, позволяет: количественно
оценивать качественные экономические
закономерности;
Выберите
показатели качества уравнения регрессии
в цепом?1. R^2.2 Скорректированный R^2.
Значения 1-статистик. 4. Значение
F-статистики. Ответ :2,4
Выбирите
показатели качества уравнения регрессии
в целом ? R^2
,скорректированный R^2 , значения F
статистики.
Выражение
вида

суммой квадратов отклонений, объясненных
регрессией
Гетероскедастичность
— это:- зависимость дисперсии случайных
ошибок от номера наблюдения
Гомоскедастичность
– это: независимость дисперсии
случайных ошибок от номера наблюдения;
Дана
приведенная форма системы одновременных
уравнений:
эндогенная переменная системы
Дана
приведенная форма системы одновременных
уравнений…Wt-эндогенная переменная
система , Сt-эксанное переменная системы
Дана
система одновременных эконометрических
уравнений :
Данная система является : неидентифицируемой
Дана
система одновременных эконометрических
уравнений. Определите, является ли она
идентифицируемой , неидентифицируемой
или сверхидентифицируемой: идентифицируемой
Дана
система одновременных эконометрических
уравнений:
Данная система является: сверхидентифицируемой
Даны
структурная и приведенная формы модели
системы одновременных уравнений:
переменная модели , случайная компонента
Для
выбора лучше модели применяется…РЕ-тест,
J-тест
Для выбора
лучшей спецификации модели применяется:
PE-тест, J-тест
Для
выявления ошибки линейной спецификации
регрессии применяется- RESET-тест
Для
гиперболического уравнена
y=B0+B1/X1+..+BN/XN+e
коэффициент B1 имеет
следующий экономический смысл… Нет
простой интерпретации коэффициента
Для
гиперболической зависимости
коэффициент имеет следующую
интерпретацию:–нет простой интерпретации
данного коэффициента регрессии
Для двух
случайных величин x и y было
получено значение парного коэффициента
корреляции rxy = –0,9. Какой вывод
можно сделать о тесноте линейной
зависимости между x и y? связь
тесная и отрицательная;
Для двух
случайных величин х и у было получено
значение парного коэффициента корреляции
r=0,9. Какой вывод можно сделать о тесноте
линейной связи между х и у?- связь
тесная и прямая
Для
изучения зависимости спроса и предложения
на товары повседневного спроса от цены
и дохода строится: система одновременных
уравнений
Для
какого типа данных в окне создания
рабочего файла EViews необходимо указать
только размер выборки (число
наблюдений)?…Пространственные данные
Для
логарифмического уравнения
y=B0+B1*Ln..коэффициент В имеет следующий
экономический смысл…Для увеличения
У на единицу необходимо увеличить Х1
примерно на {100/В1) %
Для
нелинейной регрессионной модели
зависимости рассчитано значение индекса
детерминации R^2= 0,9. Тогда значение
индекса корреляции составит…Корень
квадратный из 0,9
Для
обнаружения автокорреляции в остатках
используется: статистика Дарбина-Уотсона
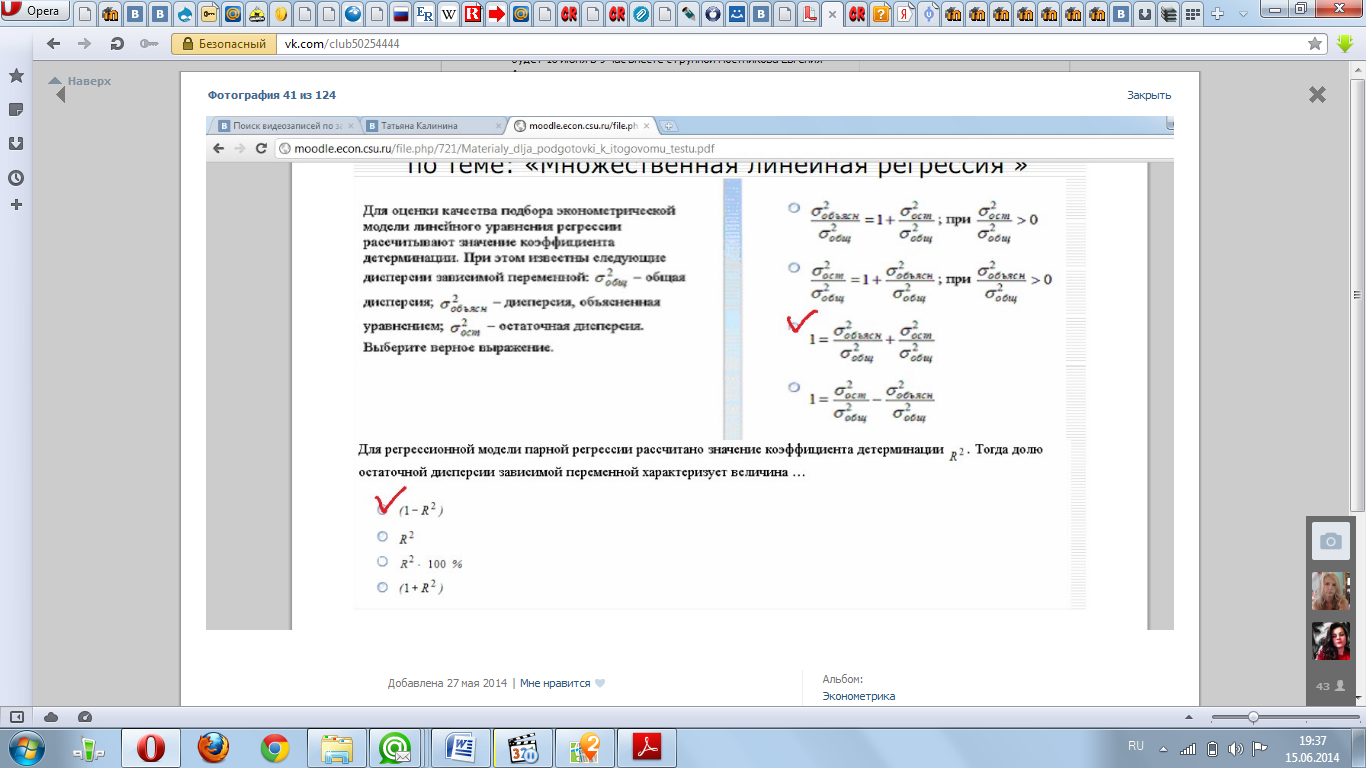
Для оценки
качества подбора эконометрической
модели линейного уравнения регрессии
рассчитывают значение коэффициента
детерминации. При этом известны следующие
дисперсии зависимой переменной
Для оценки
параметров регрессионной модели с
гетероскедастичными остатками
используется ___________ метод наименьших
квадратов.- обобщенный
Для оценки
параметров регрессионной модели с
коррелированными остатками используется____
метод наименьших квадратов- обобщенный
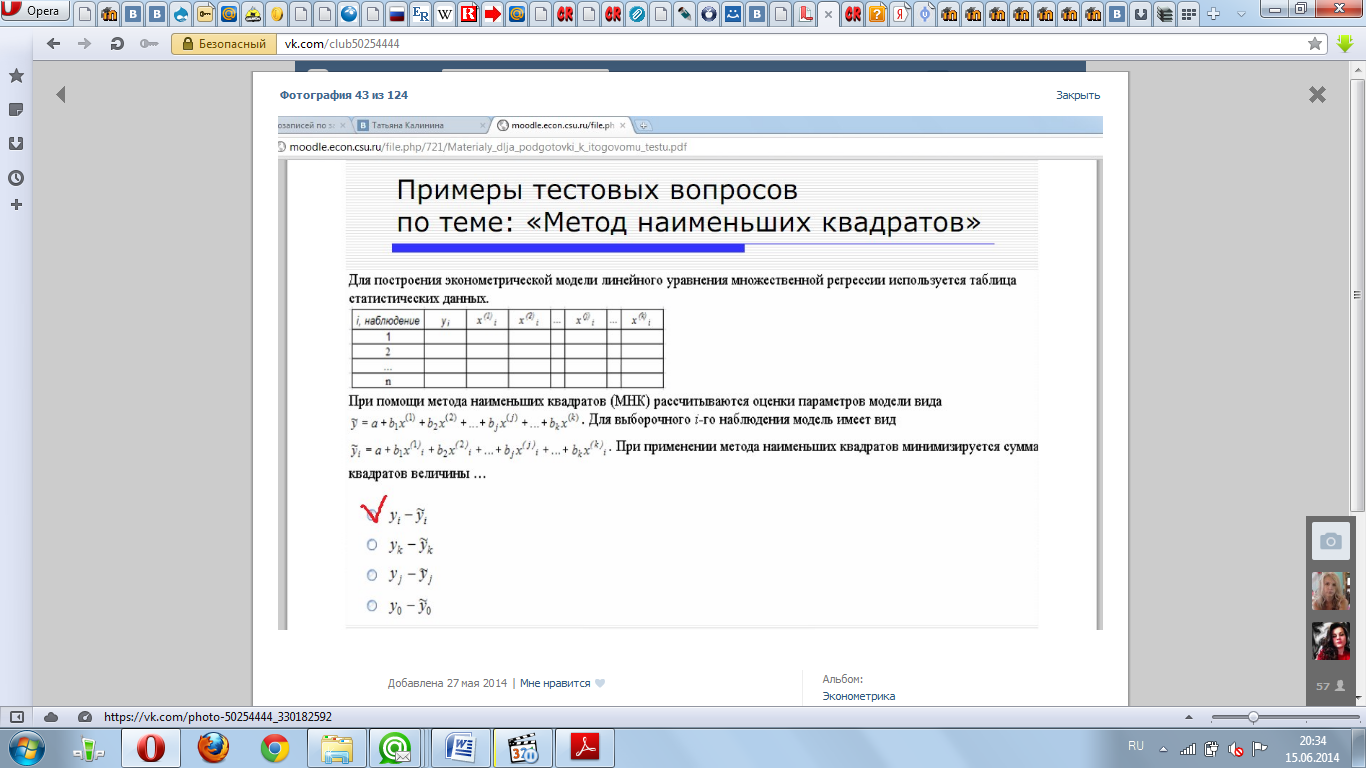
Для
построения эконометрической модели
линейного уравнения множественной
регрессии используется таблица
статистических данных.
Для
проверки гипотез равенства коэффициентов
какому-либо значению или соотношения
коэффициентов между собой применяется…Тест
Вальда
Для
производной функции Кобба-Дугласа
Q=B0*K^B1*L^B2?
Известно, что B1+b2<1. Выберите верные
утверждения:-отдача от увеличения
масштаба уменьшается, В2-коэффициент
эластичности выпуска по труду,
В1-коэффициент эластичности выпуска
по капиталу
Для
производной функции Кобба-Дугласа
Q=B0*K^B1*L^B2?
Известно, что B1+b2<1. Выберите верные
утверждения- отдача от увеличения
масштаба уменьшается; коэффициент В2
показывает ,на сколько процентов в
среднем изменится объем выпуска ,если
затраты труда увеличить на 1 %
Для
производственной функции Кобба-Дугласа
Q=B0*KB1*LB2 известно что B1 и B2= 1 тогда
увеличения затрат труда и капитала в
несколько раз приведёт к …увеличению
выпуска производства в такой же число
раз.
Для
производственной функции Кобба-Дугласа
отдача от
увеличения масштаба убывает; в2
коэффициент эластичности выпуска по
труду; в1 коэффициент эластичности
выпуска по капиталу
Для
регрессионной модели вида y=a+bx+ɛ
построена на координатной плоскости
совокупность точек с координатами
(у,х), данное графическое отображение
зависимости называется:- полем
корреляции
Для
регрессионной модели вида показателем
тесноты связи является коэффициент
множественной корреляции
Для
регрессионной модели зависимости
потребления материала на единицу
продукции от объема выпуска построено
нелинейное уравнение Объёмом
выпуска продукции объяснено 90,4% дисперсии
потребления материалов на единицу
продукции
Для
регрессионной модели известны следующие
величины дисперсий:
Для указанных дисперсий справедливо
равенство…-
Для
регрессионной модели несмещенность
оценки параметра означает, что ее
выборочное математическое ожидание
равно…- оцениваемому параметру,
рассчитанному по генеральной совокупности
Для
регрессионной модели парной линейной
модели рассчитано значение коэффициента
детерминации R²=0,831 На дисперсию
зависимой переменной, объясненную
построенным уравнением приходится______________
общей дисперсии зависимой переменной-
16,9%
Для
регрессионной модели парной линейной
регрессии
Для совокупности из n
единиц наблюдений рассчитывают
общую дисперсию на одну степень свободы,
при этом величину дисперсии относят к
значению…n-1
Для совокупности из n единиц наблюдений
построена модель линейного уравнения
множественной регрессии с количеством
параметров при независимых переменных,
равным k. Тогда при расчете остаточной
дисперсии на одну степень свободы
величину дисперсии относят к значению…n—k-1
Для
стационарных временных рядов Y1
, Y2, Yt,
Yn, Y
(t=1, … , n)
автоковариация зависит только от
величины: лага
Для
степенной зависимости:
увеличении переменной х1 на 1% переменная
у в среднем увел-ся на 81%
Для
эконометрической модели линейного
уравнения множественной регрессии
вида
Для
экспоненциальной зависимости у=…
коэффициент В1 имеет следующую
интерпретацию:— при увеличении
переменной х1 на единицу переменная у
в среднем увеличится примерно на
(100В1)%; при увеличении переменной х1 на
единицу переменная у в среднем увеличится
в ехр(В1) раз
Долю
объясненной с помощью регрессии
дисперсии в общей дисперсии зависимой
переменной характеризует коэффициент
детерминации
Ежегодные
денные об уровне инфляции за последний
15 лет во всех странах Европы относятся
к…панельным данным
Ежеквартальные
данные по инфляции за 15 лет в РФ относят
к Временным рядам
Если
коэффициент β1 уравнения регрессии
ˆyt = βˆ 0 + βˆ
1x1t + βˆ 2 x2t статистически
значим, то: β1 ≠ 0;
Если
параметр эконометрической модели не
является статистически значимым,
то его значение признается…-равным
0
Если
параметр эконометрической модели не
является статистически значимым
, то соответствующая независимая
переменная на определенном уровне
доверия…- не оказывает влияния на
моделируемый показатель (зависимую
переменную)
Если
параметр эконометрической модели
ЯВЛЯЕТСЯ статистически значимым,
то его значение признается…-отличным
от 0
Зависимость
объема выпускаемой продукции Q от объема
трудовых L и материальных затрат
дописываемая функцией…Q=B0*K^B1*L^B2 ,где
В0 ,В1 и В2- параметры регрессии
….производственной функцией
Кобба-Дугласа
Замещающая
переменная – это… переменная,
коррелирующая с отсутствующей переменной
уравнения регрессии, выполняя функции
этой отсутствующей переменной
Значение
коэффициента множественной корреляции
рассчитывается по формуле R=корень
квадратный из R^2…. Тогда
значение коэффициента множественной
корреляции будет находиться в интервале…
[0;1]
Изменение
объема продаж молока объясняется
переменными 93%
Имеется
матрица парных коэффициентов корреляции.
Мультиколлинеэрность наблюдается
между величинами: ОТВЕТ X1 и X2
Информационные
критики (AIC) и(SBIC
) принимаются для …сравнивая модели
по качеству подгонки …
Исследуется
влияние качества определенного вида
продукции и сервисного обслуживания
ее покупателей на стоимость этой
продукции. Предполагается следующий
вид зависимости: у = β1 ⋅
x1 + β2 ⋅
22 x + ε. В данном уравнении β1,
β2 называются:коэффициентами
регрессии;
Исследуется
влияние качества определенного вида
продукции и сервисного обслуживания
ее покупателей на стоимость этой
продукции. Предполагается следующий
вид зависимости: у = β1 ⋅
x1 + β2 ⋅
22 x + ε. В данном уравнении ε
называется: ошибкой регрессии.
Исследуется
зависимость выпуска продукции Y от
затрат на труд L и капитал K на
основе имеющихся статистических данных
для 40 металлургических предприятий
уральского экономического региона.
Экономическая теория рекомендует
следующий вид модели: ln Yt = ln А + α ln
Кt + β ln Lt + εt, t = 1…40. Что
представляют собой коэффициенты α, β?
коэффициенты эластичности;
Исследуется
зависимость объема продаж от цены
одного галлона и расходов на рекламу
Исследуется
зависимость урожайности зерновых
культур y (ц/га) от ряда факторов x1,
x2, x3, x4, x5. В результате моделирования
были получены большие стандартные
ошибки и малая значимость оценок, в то
время как модель в целом оказалась
значима. Также некоторые коэффициенты
имели неправильные с экономической
точки зрения знаки. Эти признаки
указывают на возможное наличие:
мультиколлинеарности;
Исследуется
регрессия y = β0 + β1×1 + β2×2 +
β3×3 + ε. Известно, что 4,3 + 10×1 –
3,5×2 = x3. В этом случае говорят о наличии:
мультиколлинеарности;
Исследуется
регрессия y=B0+B1X1+B2X2+B3X3+e известно, что
D(e) =/= o^2 В этом случае говорят о
наличии…мультиколлинеарности
Исследуется
регрессия у= β₀+ β ₁х₁+ β₂х₂+ β₃х₃+
ɛ. Известно, что 4,3-10х₁/3.5х₂=х₃. В
этом случае говорят о наличии:—
гетероскедаститчности
Исследуется
регрессия у= β₀+ β ₁х₁+ β₂х₂+ β₃х₃+
ɛ. Известно, что дисперсия ошибок
регрессии D(ɛt)=q^2
для любого t. В этом случае
говорят о наличии —гомоскедастичности
Как влияет
исключение переменной из уравнения
множественной регрессии на значение
F-критерия и коэффициент детерминации?-
F-критерий может
как уменьшиться, так и увеличиться, R2
уменьшится
Как
называется вид графика, по которому
визуально можно сделать предположение
о законе распределения исследуемых
величин?…Гистограмма
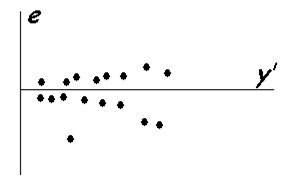
Как
проявляется гетероскедастичность на
графике остатков? Разброс остатков
увеличивается или уменьшается с ростом
номера наблюдений
Как
проявляется гомоскедастичность на
графике остатков?… Разброс остатков
не изменяется с ростом наблюдений
Какая
характеристика определяет среднее
значение случайной величины?…Математическое
ожидание
Какие
виды уравнений в системах одновременных
уравнений с точки зрения идентифицируемости
параметров Вы знаете: неидентифицируемые
уравнения , точно идентифицируемые
уравнения , сверхидентифицируемые
уравнения
Каким
будет объём продаж, если цена одного
галлона молока составит 2 доллара 6
Какими
свойствами обладают оценки, полученные
при решении уравнения парной линейной
регрессии у=α+β+ɛ методом наименьших
квадратов, если выполнены условия
Гаусса-Маркова и случайные остатки ɛ
имеют нормальное распределение:-
состоятельностью, несмещенностью,
эффективностью
Какими
свойствами обладают оценки, полученные
при решении уравнения парной линейной
регрессии у-=а,—&-1; методом наименьших
квадратов, если выполнены условия
Гаусса-Маркова и случайные остатки е
имеют нормальное распределение…
Состоятельностью, несмещенностью и
эффективностью
Какими
свойствами обладают оценки, полученные
при решении уравнения парной линейной
регрессии Yt= axt+B+et
методом наименьших квадратов, если
выполнены условия Гаусса-Маркова и
случайные остатки е имеют нормальное
распределение:Состоятельностью,
несмещенностью и эффективностью
Каковы
показатели качества уравнения регрессии
в целом:- значения F-статистики для
уравнения регрессии -скорректированный
коэффициент детерминации
Какое
из уравнении является
показательным?…y=B0*B1^x1..
Какое
из уравнении является экспоненциальным?…y=e^***
Какой
вывод можно сделать по результату
проведения теста Рамсея?
спецификация уравнения ошибочная
Корреляция
ошибок – это: корреляция ошибок для
разных наблюдений.
Когда
целесообразно добавление новой
объясняющей переменной в модель при
росте скорректированного коэффициента
детерминации после ее включения
Коллинеарность
факторов эконометрической модели
y=a+b1x1+b2x2+…+bkxk+ɛ проверяется
на основе матрицы парных коэффициентов
линейной…КОРРЕЛЯЦИИ
Оценка
а^ значения параметра а модели У= aX + B
+ е является эффективной, если 1.
математическое а^ ожидание равно а
2.a^=a3. a^ обладает наименьшей дисперсией
по сравнению с другими оценками
4.a^->a… ОТВЕТ : . a^ обладает наименьшей
дисперсией по сравнению с другими
оценками
Оценка
альфа значения параметра альфа является
несмещенной, если: Мат ожидание альфа
равно альфа
Оценка
альфа со скоб значения параметра альфа
является состоятельной, если: а^->а
при стремлении числа наблюдений к
бесконечности
Оценка
параметров модели – это Сбор необх
стат информации
Оценки
параметров идентифицируемой системы
независимых (внешне не связанных)
эконометрических уравнений могут быть
найдены с помощью…обычного МНК
Параметр
экономической модели не является
статистически значимым, то соответствующая
независимая переменная на определенном
уровне доверия не
оказывает влияния на моделируемый
показатель
Парный
коэффициент линейной корреляции rxy
между случайными переменными x и
y показывает: уровень линейной
зависимости между x и y.
Если rxy > 0, то
x и y связаны
положительной линейной зависимостью.
Если rxy < 0, то x
и y связаны отрицательной
зависимостью;
Переменные
задаваемые извне автономно от модели
называются …экзогенными
Переменные,
которые хар-т результат функцион-я
экспонируемой эконометрической системы,
наз Лаговой
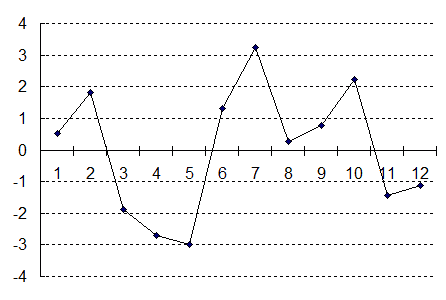
По
графику можно сделать вывод о том, что
представленный на рисунке ряд : ряд
не является стационарным
По типу
функциональной зависимости между
переменными эконометрической модели
различают___ уравнения регрессии-линейные
и нелинейные
Под
верификацией модели понимается:- оценка
качества модели
Под
спецификацией модели понимается…
выбор регрессорое и вида модели
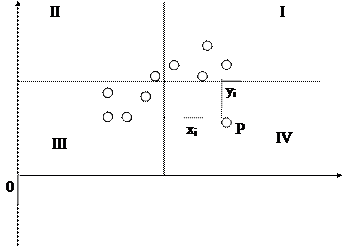
Покажите
на рисунке отклонение фактического
значения от расчетного:
Последствием
гетероскедастичности является то, что
Дисперсии оценок коэф регрессии
остаются несмещенной
Последствием
гетероскедастичности является то, что:
стандартные ошибки коэффициентов
становятся заниженными, а вычисленные
t-статистики – завышенными;
Последствия
включения в уравнение регрессии
несущественных переменных:-Оценки
параметров будут несмещенными,
эффективность оценок снизится
Последствия
мультиколлинеарности:- оценки
становятся очень чувствительными к
изменению отдельных наблюдений, оценки
коэффициентов остаются несмещенными
Последствия
невключения в уравнение регрессии
существенной переменной в общем случае:-
оценки параметров будут смещенными
Построено
несколько типов зависимостей и рассчитаны
значения F-статистики для них. Какая из
представленных регрессий является
значимой, если ____________критическое
значение F-статистики равно 2,56 при
уровне значимости 5 %? y=583⋅k
−0,29 ⋅r
−8,6 ⋅s0,69
, F = 2,75;
Предположения
теоремы Гаусса-Маркова включают в себя
ошибки регрессии
должны быть независимы друг от друга;
дисперсия ошибок регрессии постоянна
для всех наблюдений
Представленная
на рисунке модель будет описываться
уравнением:
При
вводе в командной строке Eviews
команды « plot X
Y » появятся: один график,
на котором будут изображены и значения
ряда X, и значения
ряда Y
При
возникновении мультиколлинеарности:
стандартные ошибки коэффициентов
увеличиваются, вычисленные t-статистики
становятся заниженными;
При
выполнении команды «genr
Z+@cor(X,Y)
в ивьюс будет создана переменная Z,
в которую будет записано Значение
коэф-та кореляции между рядами
При
выполнении команды «plot
X Z» в EViews
,будет построен график, на котором:- по
оси абсцисс будут расположены значения
ряда Z, а по оси ординат- ряда Х.
При
выполнении команды «scat
X Z» в ивьюс
будет построен график Зависимости
ряда Z на разных
плоскостях
При
выполнении команды agenr Z=@cor{X.Y)o в Eviews
будет создана переменная Z. в которую
будет записано….значение коэффициента
корреляции между рядами X и Y.
При
выполнении предпосылок метода наименьших
квадратов оценки параметров регрессионной
модели, рассчитанные с помощью МНК,
обладают свойствами…
— состоятельности, несмещенности
и эффективности
При
добавлении в линейной регрессионной
модели новых регрессоров, коэф детерм
R2 Увеличивается
При
добавлении в линейной регрессионной
модели новых регрессоров коэф-т
детерминации R2^ Уменьшается
При
изучении зависимости зарплаты в
Казахстане от возраста и пола была
получена следующая регрессия…W*1500+735’AGE
*1746’S где W-зарплата (тенге/месяц) AGE —
возраст (лет).Какойвывод можно сделать
о зависимости зарплаты от пола?…мужчины
получают в среднем зарплату больше
женщин на 1746 тенге/месяц
При
изучении зависимости зарплаты в
Казахстане от возраста и пола была
получена следующая регрессия
получают в среднем зарплату меньше чем
мужчины на 1678
При
изучении зависимости издержек
производства y (тыс. р.) от основных
производственных фондов x (тыс. р.)
была построена модель: y = 10 + 0,75x. Это
означает, что: 4) при увеличении основных
производственных фондов на 1 тыс.
р. издержки производства в среднем
увеличиваются на 750 р.
При
изучении зависимости издержек
производства y (тыс. р.) от основных
производственных фондов x (тыс. р.)
была построена модель: y = α + βx + ε.
В результате исследования были
получены следующие оценки параметров
регрессии: 0,45 β 7,5; α = = ˆ ˆ .
Доверительный интервал для βˆ на
5%-ном уровне значимости составил
(0,42; 0,48). Какой вывод можно сделать
о точности полученной оценки коэффициента
β? оценка β получена
с достаточно высокой точностью;
При
изучении зависимости издержек
производства y (тыс. р.) от основных
производственных фондов x (тыс. р.)
была построена модель: y = β0 +
β1x + ε . В результате исследования
были получены следующие оценки параметров
регрессии: 10,5 β 7,5; β 1 0 = = ˆ ˆ .
Доверительный интервал для 1 βˆ
на 5%-ном уровне значимости составил
[9,4; 11,6]. Какой вывод можно сделать о
точности полученной оценки коэффициента
β? оценка β
получена с достаточно высокой
точностью;
При
изучении зависимости издержек
производства y (тыс.руб)
от основных производственных фондов
x (тыс.руб) была построена
модель: y=10+0,75x . Это
означает, что: при увеличении основных
производственных фондов на 1 тыс.руб.
издержки производства в среднем
увеличиваются на 750 руб.
При
изучении зависимости издержек
производства у (тыс. руб.) от основных
производственных фондов х (тыс. руб.)
была построена модель: у=а+Bх+£ в результате
исследования были получены следующие
оценки параметров регрессии: a = 7.5B=0.45
.доверительныйинтервал для B на 5%-м
уровне значимости составил [0,42; 0,48].
Какой вывод можно сделать о точности
полученной оценки коэффициентаB?1)
оценка B получена с достаточно высокой
точностью;
При
изучении зависимости издержек
производства у (тыс.руб.) от инвестиций
в совершенствование технологий х
(тыс.руб.)была построена модель у=10-0,15х.
Это означает, что:- при увеличении
инвестиций в совершенствование
технологий на 1 тыс.руб. издержки
производства в среднем снижаются на
150 руб.
При
изучении зависимости между показ безраб
и инфл в Болгарии х=2,1 Не можем, поскольку
абсол значение т-статистики для
показателя безраб меньше крит
При
изучении зависимости между показателями
безработицы (x) и инфляции (y) в
Болгарии была построена модель и
получены оценки коэффициентов для этой
модели: y = 4,23 –2,41x. Расчетное значение
t-статистики для показателя безработицы
x получилось равным 2,1. Можем ли мы
принять гипотезу о значимости показателя
безработицы в модели с уровнем значимости
0,05, если критическое значение t-статистики,
найденное из таблиц распределения
Стьюдента, равно –2,57? не можем,
поскольку абсолютное значение
t-статистики для показателя
безработицы меньше критического
значения;
При
изучении зависимости между показателями
Безработицы (х ) и инфляции ( у ) в Болгарии
была построена модель и получены оценки
коэффициентов для этой модели:
у=4.23-2,41х. Расчетное значение t-статистики
для показателя безработицы х получилось
равным: 2,1. Можем ли мы принять гипотезу
о значимости показателя безработицы
в модели с уровнем значимости 0,06, если
критическое значение t-статистики,
наиденное из таблиц распределения
Стьюдента, равно 2,57?…Не можем, поскольку
абсолютное значение t-статистики для
показателя безработицы меньше
критического значения
При
изучении зависимости между показателями
безработицы (х ) и инфляции (у ) в Чехии
была построена модель и получены оценки
коэффициентов для этой модели: у=3,
22*1,75х. Расчетное значение t-стетистики
для показателя безработицы х получилось
равным: 1.65, Можем ли мы принять гипотезу
о значимости показателя безработицы
в модели с уровнем значимости 0.1. если
критическое значение t-статистики,
наиденное из таблиц распределения
Стьюдента.равно 1.75?…Не можем* поскольку
абсолютное значение t-статистики для
показателя безработицы меньше
критического значения
При
изучении зависимости между показателями
безработицы {х) и инфляции {у ) в Швеции
была построена модель и получены оценки
коэффициентов для этой модели:
у=2,4б-0.б9х. Расчетное значение t-статистики
для показателя безработицы х получилось
равным: 5.2. Можем пи мы принять гипотезу
о значимости показателя безработицы
в модели с уровнем значимости 0,05. если
критическое значение t-статистики,
найденное из таблиц распределения
Стьюдента, равно 2.57?…Можем, поскольку
абсолютное значение t-статистики для
показателя безработицы больше
критического значения t-статистики
При
изучении зависимости между показателями
безработицы и инфляции в Швеции Можем,
поскольку абсол значение т-статистики
для показателя безраб больше крит
При
исследовании выбора обнаружено
«аномальное» значения фактора Y для
одного наблюдения. При каких условиях
корректно будет провести исключение
соответствующего наблюден из выбора
… В случае если «аномальное» значение
Y соответствует действительности, но
это отличие невозможно объяснить в
рамках проводимого исследования
При
исследовании зависимости сумм» активов
банка (у) от собственного капитала {к),
привлеченных ресурсов [г) и объема
вложений в государственные ценные
бумаги (s) было построено несколько
типов зависимостей и рассчитаны значения
F-статистики для них. Какая из представленных
регрессий является значимой, если
критическое значение F-статистики равно
2,56 при уровне значимости 5%?…у=583*К…
При
исследовании зависимости суммы активов
банка (y) от собственного капитала
(k), привлеченных ресурсов (r) и
объема вложений в государственные
ценные бумаги (s) было
При
исследовании зависимости суммы активов
банка (у) от собственного капитала (к).
у=у85-0,46к-19r+0,48s,
F=4,75
При
исследовании зависимости суммы активов
банка (у) от собственного капитала [If),
привлеченных ресурсов [г) и объема
вложений в государственные ценные
бумаги Is) было построено несколько
типов зависимостей и рассчитаны значения
F-статистики для них. Какая из представленных
регрессий является значимой, если
критическое значение F-статистики равно
3,74 при уровне значимости 1%?ОТВЕТ : 4
1)F=2.67 2) F=2.75 3). F=3.6S 4) у=е^*** F=4.75
При
исследовании зависимости суммы активов
банка (у) от собственного капитала(к),
привлеченных ресурсов (r) и объема
вложений в гос цен бумаги (s) было
построено несколько типов зависимостей
и рассчитаны значения F-статистики для
них. Какая из представленных регрессий
является значимой, если критическое
значение F-статистики равно 2,56 при
уровне значимости 5%- у=583к^-029 *r^-8,6
*s^0,69, F=2,75
При
отсутствии свободного члена регрессии
В0 в уравнении… нарушается предпосылка
теоремы Гаусса-Маркова: E(£i)=0
При оценке
качества уравнения регрессии был
рассчитан коэффициент детерминации
R^2=0.91. Это означает, что…- построенная
модель достаточно хорошо подогнана к
выборочным данным
При оценке
качества уравнения регрессии был
рассчитан коэффициент детерминации
R^2=0.18. Это означает, что…-построенная
модель довольно плохо подогнана к
выборочным данным
При
оценке модели вида y=
a0+a1yt-1+a2
yt-2
+ εt необходимо
написать в командной строке: Is
y с ar(1)
ar(2)
При
переходе к линейному виду для …
зависимости вводится замена Х=лп(х),
У=лн(у) Логарифмический
При
переходе к линейному виду для____
зависимости зависимая переменная
преобразуется по формуле Y=ln(y) —
степенной, экспоненциальной
При
переходе обратно от построенного
вспомогательного линейного уравнения
у=в0+в1х к нелинейному виду, для парной
степенной зависимости в0=ев0,
в1=в1
При
переходе обратно от построенного
вспомогательного линейного уравнения
Y=B0-B1X к нелинейному виду, для парной
гиперболической зависимости Y=B0+B1 1/X
надо найти искомое значение коэффициентов
по формуле:B0=BOB1=B1
При
переходе обратно от построенного
линейного уравнения
к нелинейному виду, для парной степенной
зависимости
надо найти значение коэффициентов по
формуле
При
перходе к линейному виду для______зависимости
замена X=ln(x),Y=ln(y)— степенной
При
построении какого уравнения в EVews
вводится команда Is у с 1/х1 1/х2 1/хЗ…
Гиперболического
При
построении какого уравнения в EViews
вводится команда Is
log(y)
c x1
x2 x3
— Экспоненциального
При
построении какого уравнения в EViews
вводится команда Is log( у) с log(x1) lоg(х2)
lоg(хЗ)…
степенного
При
построении уравнения множественной
регрессии проверку тесноты связи между
независимыми переменными (объясняющими
переменными, регрессорами, факторами)
модели осуществляют на основе…-матрицы
парных коэффициентов линейной корреляции
При
проведении RESET-теста в EViews линейная
спецификация регрессии является
ошибочной с уровнем доверия 0.9, если
Р-знаиение = Prob. F…меньше 0.1
При
проведении RESET-теста в EViews линейная
спецификация регрессии является
ошибочной с уровнем доверия 0.95. если
Р-значение = Prob. F….меньше 0.05
Применение
обычного МНК непосредственно к системе
одновременных уравнений в структурной
форме приводит в общем случае к…
смещенным и несостоятельным оценкам
коэффициентов
Примера
фиктивны переменных в эконометрической
модели зависимости 1м2 жилья являются
площадь жилья;
величина прожиточного минимума в
регионе
Примерами
фиктивных переменных в эконометрической
модели зависимости стоимости 1м^2 жилья
НЕ ЯВЛЯЮТСЯ… — площадь жилья; величина
прожиточного минимума в регионе
Проверка
наличия коллинеарных факторов в
эконометрической модели х1
и х2
Процесс
является: нестационарным , случайным
блужданием , авторегрессионным процессом
1-го порядка
Процесс
является: процессом белого шума ,
стационарным
Процесс
является: процессом скользящего
среднего 1-го порядка , стационарным
Процесс
ARMA (p,q)
называется : авторегрессионным
процессом скользящего среднего
Пусть
в уравнении Н эндогенных переменных и
D экзогенных переменных, которые в этом
уравнение (в его структурной форме)
отсутствуют Тогда в случае, если 0=3.
н-2. уравнение является:…сверхидентифицируемым
Пусть
качественный признак принимает 4
значения, сколько фиктивных переменных
надо ввести в уравнение 3
Пусть
оцененное уравнение регрессии имеет
вид: у=-2,3+0,4х1-3,7х2+1,2х3. Что можно
сказать об интерпретации значения
коэффициента при переменной х1?—
при увеличении переменной х1 на единицу
ее измерения при неизменных значениях
других переменных у увеличится в среднем
на 0,4 единиц своего измерения.
Рассматривается
зависимость объема выпускаемой продукции
Q от объема трудовых L и материальных
затрат К. Результатом оценки параметров
производственной функции Кобба-Дугласа
стала модель Q=12.8*K^0.4*L^0,3. Это означает,
что…средние издержки, рассчитанные
на единицу продукции, растут по мере
расширения масштабов производства
Расширенный
тест Дики Фуллера показывает, что : ряд
не является стационарным относительно
первой разности , ряд на разностей
исходного ряда содержит единичный
корень
Расширенный
тест Дики-Фуллера показывает, что : ряд
содержит единичный корень , ряд не
является стационарным
Расширенный
тест Дики-Фуллера показывает, что: ряд
не является стационарным , ряд не
является стационарным относительно
линейного тренда
Регрессионная
модель вида y=a+bx1+c(x2^2)+ɛ является
нелинейной относительно…- переменной
Х2
Связь
между объёмом продаж и переменными
«Цена одного галлона» и «Расходы на
рекламу» являются тесной
Слабая
стационарность временного ряда
означает…самый большой
Среднегодовые
цены на бензин во всех субъектах
Российской Федерации за 2011 год относятся
… к пространственным данным .
Стандартное
нормальное распределение имеет параметры
математическое ожидание=0, дисперсия=1
Стационарность
временного ряда означает отсутствие
…тренда
Степенная
зависимость записана уравнением-
Стоится
эконометрическая модель уравнения
множественной регрессии для зависимости
у от пяти факторов у=f(x1,x2,x3,x4)+E
Строгая
стационарность временного ряда означает:
независимость распределений уровней
ряда от сдвига по времени
Структура
сдвига временного ряда …характерезует
разные внезапные ….
Суть
коэффициента детерминации состоит в
следующем:- коэффициент определяет
долю общего разброса значений,
объясненного уравнением регрессии
Сформулируйте
необходимое условие идентифицируемости
структурного уравнения (порядковое)….число
отсутствующих экзогенных переменных
в уравнении больше числа эндогенных
переменных входящих в уравнение без
единицы
Сформулируйте
необходимое условие идентифицируемости
структурного уравнения (порядковое):…
число отсутствующих экзогенных
переменных в уравнении равно числу
эндогенных переменных, входящих ответ.
уравнение, плюс единица
Тест
Вэльдэ применяется для… проверки
гипотез равенства коэффициентов
какому-либо значению или соотношения
коэффициентов между собой
Тест Чоу
применяется для выявления структурных
сдвигов
Тип данных
«Alpha» в ивьюс соответствует
ряду, содержащему Текстовую информацию
Удаление
из выборки наблюдений, значения факторов
для которых существенно больше или
меньше средних по выборке позволяет
добиться…однородности выборки
Укажите
тест, который используется для выявления
гетероскедастичности? Уайта
Укажите
тест, который не используется для
выявления гетероскедастичности-
Дарбина-Уотсона
Уравнение
множественной регрессии имеет вид
у=-27,16+1,37 х₁-0,29 х₂. Параметр при
переменной х2 означает следующее:-
при увеличении х2 на единицу своего
измерения и при фиксированном значении
фактора х1, переменная у уменьшится на
0,29 единиц своего измерения
Уравнение
множественной регрессии имеет вид:
у=-27,16+1,37 х₁-0,29 х₂. Параметр а₁=1.37
означает следующее:-при увеличении
х₁ на одну единицу своего измерения и
при фиксированном значении фактора
х₂, переменная у увеличится на 1,37 единиц
своего измерения
Уравнение
регрессии называется значимым в целом,
если- есть достаточно высокая
вероятность того, что существует хотя
бы один коэффициент, отличный от нуля
Уравнение
регрессии называется незначимым в
целом, если- есть достаточно высокая
вероятность того, что все коэффициенты
равны 0
Установите
соответствие 1)команда для созд ряда
Х, 2) ком для созд графика ряда Х, 3) ком
для созд группы гр1 и рядов Х и У, 4) ком
для созд гр зависимости А. скат Х У, Б.
Сериес Х, В. Груп, Д. лайн 1-Б, 2-Д, 3-В,
4-А
Фиктивные
переменные заменяют ….качественные
переменные
Фиктивные
переменные эконометрической модели…-
используются в случае совокупностей
данных; отражают качественные признаки
исследуемого объекта наблюдения
Фиктивными
переменными в уравнении множественной
регресси являются… качественные
переменные, преобразованные в
количественные
Фильтрацию
данных (удаление сильно отличающихся
наблюдений) можно проводить, если…определена
причина такого отклонения
Функционал
метода наименьших квадратов для случая
парной линейной регрессии выглядит
следующим образом:
Функционал
метода наименьших квадратов для случая
парной регрессии выглядит следующим
образом:
Циклические
колебание могут связаны с…сезонность
некоторых видов …
Чем на
ваш взгляд более оправдано использование
скорректированного коэффициента
детерминации R^2adj,
чем R^2 для сравнения двух 1) Попыткой
устранить эффект, связанный с увеличением
значения R2 при добавлении регрессоров.
Чем, на
ваш взгляд, более оправдано использование
скорректированного коэффициента
детерминации R2 adj, чем R2 100
для сравнения двух линейных регрессионных
моделей, одна из которых отличается от
другой добавленными новыми регрессорами?
попыткой устранить эффект, связанный
с увеличением значения R2 при
добавлении регрессоров;
Что бы
оценить модель ARIMA (1.1.0)в командной
строке рабочего окна Eviews необходимо
ввести …isd(y) car(1)
Что не
является целью исследований
эконометрических явлений и процессов?
Разработка теоретико-экон моделей,
поиск зависимостей между признаками…
Что
обозначает команда genr X=2+9*nrnd?… Создание
ряда чисел X, имеющего нормальное
распределение с математическим ожиданием
2 и дисперсией 81
Что
обозначает команда genr Y=10-t-20*rnd?… Создание
ряда чисел Y. представляющего собой
равномерно распределенные на интервале
(10;30) случайные числа
Что
означает «правильно специфицированное
уравнение регрессии» правильная
функциональная зависимость
Что
означает команда genr
Y=10+20*rnd?
Создание ряда чисел У, представляющего
собой равномерно распред-е на интервале
(10;20) случ
Эконометрика
— это… наука, которая дает количественное
выражение взаимосвязей экономических
явлений и процессов
Эконометрическое
моделирование зависимости по неоднородной
совокупности данных может осуществляться
на основе…-разделения неоднородной
совокупности данных на однородные;
использования фиктивных переменных
Экспоненциальная
зависимость записана уравнением
у=ув0+в1*х1+….+вн*хн+Е
Экспоненциальная
зависимость записана уравнением…

верные утверждения — коэфф Z значим,
а С не значим на уровне значимости 0,05
Эндогенные
переменные в системах одновременных
уравнений в общем случае… коррелируют
со случайными ошибками уравнений

уравнения ошибочная

уравнения ошибочная
…, которая
характеризует результат функционирования
анализируемой аналитической системы
наз-ся Эндогенной
ARIMA
(0, C, 1) является: моделью
скользящей средней
DS-процесс
это … процесс имеющий статестический
тренд и приводной …
F-статистика
Фишера используется: определения
статистической значимости модели в
целом.
F-тест
применяется для…выбора лучшей модели
RESET-тест
применяется для…. ошибки линейной
спецификации регрессии
ti —
расчетное значение критерия Стьюдента
для коэффициента В,. Критическое значение
критерия Стьюдента t,5=1.96 для уровня
значимости 0,05 и числа степеней свобод»
более 200…если t1=2.5. то коэффициент S1
значим с уровнем доверия 0.95 . если t1=
-2,5, то коэффициент S1 значим с уровнем
доверия 0.95
TS-процесс
— это… процесс, приводимый к стационарному
путем выделения тренда
t-статистика
Стьюдента используется: для определения
статистической значимости коэффициентов
регрессионного уравнения;
Автокореляция
в остатках –это…кореляция зависимости
между состакомрегриссионного во времени
Автокорреляция
остатков бывает следующих видов:
отрицательная положительная
Автокорреляция
ошибок – это линейная связь между
более чем двумя объясняющими переменными
Автокорреляция
ошибок- это — корреляция ошибок
регрессии для разных наблюдений
Авторегрессионными
моделями порядка p являются
модели вида:
Была
исследована зависимость рентабельности
предприятия (у) от оборачиваемости
оборотных активов (х), фондоотдачи [к)
и производительности труда [/) за 24
квартала. По выборочным данным построены
несколько типов зависимостей и рассчитаны
значения F-статистики для них. Какая из
представленных регрессий является
значимой, если критическое значение
F-статистики равно 3.1 при уровне значимости
5%?ОТВЕТ: 3 1)у=4.12+0.15 F=2,9 2) у-0.75.x
F=l.7 3) у=е^****
F=4.6 4) y=ln F =3,09
В каких
случаях значение коэффициента
детерминации R² может выйти за
пределы[0;1]? —если в уравнении регрессии
отсутствует константа β0
В командной
строке EViews введена следующая
последовательность команд: genr y=3+4*@rnd
genr z=@var(y)
Что появится в рабочем файле после
выполнения этих команд? — будет
создан ряд У , значения которого будут
распределены по равномерному закону
распределения на интервалеот 3 до 7.
Затем будет создан ряд Z, значения
которого будут равны дисперсии ряда У
В
оцениваемо» модели у = хВ +Zу +е присутствуют
несущественные независимые переменные
у. тогда оценка & . полученная в данной
регрессии…дисперсия оценки
увеличивается от включения в модель
несущественных переменных, несмещенная
В
оцениваемой модели y=XB+е отсутствует
часть существенных независимых
переменных тогда оценка B полученная
в данной регрессии в общем случае…смешанная
В
оцениваемой модели у=ХВ+е отсутствует
часть существенных независимых
переменных, тогда оценка В^, полученная
в данной регрессии, в общем случае
смещенная
В результате
оценки параметров регрессии y = β0
+ β1x + ε были получены следующие
результаты: 4,7 β 10,4; β 1 0 = = ˆ ˆ .
Доверительный интервал для 1 βˆ
на 10%ном уровне значимости составил
(4,3; 5,1). Что показывает полученный
доверительный интервал на указанном
уровне значимости? истинное значение
коэффициента β1 находится
в указанном интервале с
вероятностью 90 %;
В результате
оценки параметров регрессии у=α+βх+
ɛ были получены следующие результаты:
ᾶ= 10, ᵬ=4,7. Доверительный интервал для
ᵬ с уровнем доверия 95% составил [3,9;5,5].
Что показывает полученный доверительный
интервал с указанным уровнем доверия?
— истинное значение коэффициента β
находится в указанном интервале с
вероятностью 0,95
В результате
оценки параметров регрессии у=α+βх+
ɛ были получены следующие результаты:
ᾶ= 10, 4, ᵬ=4,7. Доверительный интервал для
ᵬ с уровнем доверия 90% составил [4.3;5,1].
Что показывает полученный доверительный
интервал с указанным уровнем доверия?
— истинное значение коэффициента В
находится в указанном интервале с
вероятностью 0,90
В системе
одновременных уравнений значения
экзогенных переменных… формируются
вне системы и не должны коррелировать
с остатками
В системе
рекурсивных эконометрических уравнений…
матрица коэффициентов при эндогенных
переменных треугольная
В
стационарном временном ряду трендовая
компонента: отсутствует
В чем
суть гетероскедастичности?- дисперсии
случайных отклонений изменяются
В
эконометрической модели линейного
уравнения регрессии у=a+b1x1+b2x2…+bkxk+
ɛ коэффициетом регрессии, характеризующим
среднее изменение зависимой переменной
при изменении независимой переменной
на 1 единицу измерения, является…-bj
В
экономической модели линейного уравнения
регрессии у=a+b1x1+b2x2…+bkxk+
ɛ параметром является…— a,bj
Величина
коэффициента апатичности показывает
… на сколько процентов изменится в
среденем результат при изменении
фактора на 1%
Величина
коэффициента множественное линейной
регрессии при объясняющей переменной
показывает…среднее изменения
результата при изменения фактора на
одну единицу.
Выберите
верные утверждения о производственной
функции Кобба-Дугласа- записывается
степенным уравнением, является нелинейной
зависимостью
Выберите
ответ, который наиболее точно описывает
сущность эконометрики. Эконометрика
– это наука, которая, используя методы
экономической теории, математической
статистики и математического
моделирования, позволяет: количественно
оценивать качественные экономические
закономерности;
Выберите
показатели качества уравнения регрессии
в цепом?1. R^2.2 Скорректированный R^2.
Значения 1-статистик. 4. Значение
F-статистики. Ответ :2,4
Выбирите
показатели качества уравнения регрессии
в целом ? R^2
,скорректированный R^2 , значения F
статистики.
Выражение
вида

суммой квадратов отклонений, объясненных
регрессией
Гетероскедастичность
— это:- зависимость дисперсии случайных
ошибок от номера наблюдения
Гомоскедастичность
– это: независимость дисперсии
случайных ошибок от номера наблюдения;
Дана
приведенная форма системы одновременных
уравнений:
эндогенная переменная системы
Дана
приведенная форма системы одновременных
уравнений…Wt-эндогенная переменная
система , Сt-эксанное переменная системы
Дана
система одновременных эконометрических
уравнений :
Данная система является : неидентифицируемой
Дана
система одновременных эконометрических
уравнений. Определите, является ли она
идентифицируемой , неидентифицируемой
или сверхидентифицируемой: идентифицируемой
Дана
система одновременных эконометрических
уравнений:
Данная система является: сверхидентифицируемой
Даны
структурная и приведенная формы модели
системы одновременных уравнений:
переменная модели , случайная компонента
Для
выбора лучше модели применяется…РЕ-тест,
J-тест
Для выбора
лучшей спецификации модели применяется:
PE-тест, J-тест
Для
выявления ошибки линейной спецификации
регрессии применяется- RESET-тест
Для
гиперболического уравнена
y=B0+B1/X1+..+BN/XN+e
коэффициент B1 имеет
следующий экономический смысл… Нет
простой интерпретации коэффициента
Для
гиперболической зависимости
коэффициент имеет следующую
интерпретацию:–нет простой интерпретации
данного коэффициента регрессии
Для двух
случайных величин x и y было
получено значение парного коэффициента
корреляции rxy = –0,9. Какой вывод
можно сделать о тесноте линейной
зависимости между x и y? связь
тесная и отрицательная;
Для двух
случайных величин х и у было получено
значение парного коэффициента корреляции
r=0,9. Какой вывод можно сделать о тесноте
линейной связи между х и у?- связь
тесная и прямая
Для
изучения зависимости спроса и предложения
на товары повседневного спроса от цены
и дохода строится: система одновременных
уравнений
Для
какого типа данных в окне создания
рабочего файла EViews необходимо указать
только размер выборки (число
наблюдений)?…Пространственные данные
Для
логарифмического уравнения
y=B0+B1*Ln..коэффициент В имеет следующий
экономический смысл…Для увеличения
У на единицу необходимо увеличить Х1
примерно на {100/В1) %
Для
нелинейной регрессионной модели
зависимости рассчитано значение индекса
детерминации R^2= 0,9. Тогда значение
индекса корреляции составит…Корень
квадратный из 0,9
Для
обнаружения автокорреляции в остатках
используется: статистика Дарбина-Уотсона
Для оценки
качества подбора эконометрической
модели линейного уравнения регрессии
рассчитывают значение коэффициента
детерминации. При этом известны следующие
дисперсии зависимой переменной
Для оценки
параметров регрессионной модели с
гетероскедастичными остатками
используется ___________ метод наименьших
квадратов.- обобщенный
Для оценки
параметров регрессионной модели с
коррелированными остатками используется____
метод наименьших квадратов- обобщенный
Для
построения эконометрической модели
линейного уравнения множественной
регрессии используется таблица
статистических данных.
Для
проверки гипотез равенства коэффициентов
какому-либо значению или соотношения
коэффициентов между собой применяется…Тест
Вальда
Для
производной функции Кобба-Дугласа
Q=B0*K^B1*L^B2?
Известно, что B1+b2<1. Выберите верные
утверждения:-отдача от увеличения
масштаба уменьшается, В2-коэффициент
эластичности выпуска по труду,
В1-коэффициент эластичности выпуска
по капиталу
Для
производной функции Кобба-Дугласа
Q=B0*K^B1*L^B2?
Известно, что B1+b2<1. Выберите верные
утверждения- отдача от увеличения
масштаба уменьшается; коэффициент В2
показывает ,на сколько процентов в
среднем изменится объем выпуска ,если
затраты труда увеличить на 1 %
Для
производственной функции Кобба-Дугласа
Q=B0*KB1*LB2 известно что B1 и B2= 1 тогда
увеличения затрат труда и капитала в
несколько раз приведёт к …увеличению
выпуска производства в такой же число
раз.
Для
производственной функции Кобба-Дугласа
отдача от
увеличения масштаба убывает; в2
коэффициент эластичности выпуска по
труду; в1 коэффициент эластичности
выпуска по капиталу
Для
регрессионной модели вида y=a+bx+ɛ
построена на координатной плоскости
совокупность точек с координатами
(у,х), данное графическое отображение
зависимости называется:- полем
корреляции
Для
регрессионной модели вида показателем
тесноты связи является коэффициент
множественной корреляции
Для
регрессионной модели зависимости
потребления материала на единицу
продукции от объема выпуска построено
нелинейное уравнение Объёмом
выпуска продукции объяснено 90,4% дисперсии
потребления материалов на единицу
продукции
Для
регрессионной модели известны следующие
величины дисперсий:
Для указанных дисперсий справедливо
равенство…-
Для
регрессионной модели несмещенность
оценки параметра означает, что ее
выборочное математическое ожидание
равно…- оцениваемому параметру,
рассчитанному по генеральной совокупности
Для
регрессионной модели парной линейной
модели рассчитано значение коэффициента
детерминации R²=0,831 На дисперсию
зависимой переменной, объясненную
построенным уравнением приходится______________
общей дисперсии зависимой переменной-
16,9%
Для
регрессионной модели парной линейной
регрессии
Для совокупности из n
единиц наблюдений рассчитывают
общую дисперсию на одну степень свободы,
при этом величину дисперсии относят к
значению…n-1
Для совокупности из n единиц наблюдений
построена модель линейного уравнения
множественной регрессии с количеством
параметров при независимых переменных,
равным k. Тогда при расчете остаточной
дисперсии на одну степень свободы
величину дисперсии относят к значению…n—k-1
Для
стационарных временных рядов Y1
, Y2, Yt,
Yn, Y
(t=1, … , n)
автоковариация зависит только от
величины: лага
Для
степенной зависимости:
увеличении переменной х1 на 1% переменная
у в среднем увел-ся на 81%
Для
эконометрической модели линейного
уравнения множественной регрессии
вида
Для
экспоненциальной зависимости у=…
коэффициент В1 имеет следующую
интерпретацию:— при увеличении
переменной х1 на единицу переменная у
в среднем увеличится примерно на
(100В1)%; при увеличении переменной х1 на
единицу переменная у в среднем увеличится
в ехр(В1) раз
Долю
объясненной с помощью регрессии
дисперсии в общей дисперсии зависимой
переменной характеризует коэффициент
детерминации
Ежегодные
денные об уровне инфляции за последний
15 лет во всех странах Европы относятся
к…панельным данным
Ежеквартальные
данные по инфляции за 15 лет в РФ относят
к Временным рядам
Если
коэффициент β1 уравнения регрессии
ˆyt = βˆ 0 + βˆ
1x1t + βˆ 2 x2t статистически
значим, то: β1 ≠ 0;
Если
параметр эконометрической модели не
является статистически значимым,
то его значение признается…-равным
0
Если
параметр эконометрической модели не
является статистически значимым
, то соответствующая независимая
переменная на определенном уровне
доверия…- не оказывает влияния на
моделируемый показатель (зависимую
переменную)
Если
параметр эконометрической модели
ЯВЛЯЕТСЯ статистически значимым,
то его значение признается…-отличным
от 0
Зависимость
объема выпускаемой продукции Q от объема
трудовых L и материальных затрат
дописываемая функцией…Q=B0*K^B1*L^B2 ,где
В0 ,В1 и В2- параметры регрессии
….производственной функцией
Кобба-Дугласа
Замещающая
переменная – это… переменная,
коррелирующая с отсутствующей переменной
уравнения регрессии, выполняя функции
этой отсутствующей переменной
Значение
коэффициента множественной корреляции
рассчитывается по формуле R=корень
квадратный из R^2…. Тогда
значение коэффициента множественной
корреляции будет находиться в интервале…
[0;1]
Изменение
объема продаж молока объясняется
переменными 93%
Имеется
матрица парных коэффициентов корреляции.
Мультиколлинеэрность наблюдается
между величинами: ОТВЕТ X1 и X2
Информационные
критики (AIC) и(SBIC
) принимаются для …сравнивая модели
по качеству подгонки …
Исследуется
влияние качества определенного вида
продукции и сервисного обслуживания
ее покупателей на стоимость этой
продукции. Предполагается следующий
вид зависимости: у = β1 ⋅
x1 + β2 ⋅
22 x + ε. В данном уравнении β1,
β2 называются:коэффициентами
регрессии;
Исследуется
влияние качества определенного вида
продукции и сервисного обслуживания
ее покупателей на стоимость этой
продукции. Предполагается следующий
вид зависимости: у = β1 ⋅
x1 + β2 ⋅
22 x + ε. В данном уравнении ε
называется: ошибкой регрессии.
Исследуется
зависимость выпуска продукции Y от
затрат на труд L и капитал K на
основе имеющихся статистических данных
для 40 металлургических предприятий
уральского экономического региона.
Экономическая теория рекомендует
следующий вид модели: ln Yt = ln А + α ln
Кt + β ln Lt + εt, t = 1…40. Что
представляют собой коэффициенты α, β?
коэффициенты эластичности;
Исследуется
зависимость объема продаж от цены
одного галлона и расходов на рекламу
Исследуется
зависимость урожайности зерновых
культур y (ц/га) от ряда факторов x1,
x2, x3, x4, x5. В результате моделирования
были получены большие стандартные
ошибки и малая значимость оценок, в то
время как модель в целом оказалась
значима. Также некоторые коэффициенты
имели неправильные с экономической
точки зрения знаки. Эти признаки
указывают на возможное наличие:
мультиколлинеарности;
Исследуется
регрессия y = β0 + β1×1 + β2×2 +
β3×3 + ε. Известно, что 4,3 + 10×1 –
3,5×2 = x3. В этом случае говорят о наличии:
мультиколлинеарности;
Исследуется
регрессия y=B0+B1X1+B2X2+B3X3+e известно, что
D(e) =/= o^2 В этом случае говорят о
наличии…мультиколлинеарности
Исследуется
регрессия у= β₀+ β ₁х₁+ β₂х₂+ β₃х₃+
ɛ. Известно, что 4,3-10х₁/3.5х₂=х₃. В
этом случае говорят о наличии:—
гетероскедаститчности
Исследуется
регрессия у= β₀+ β ₁х₁+ β₂х₂+ β₃х₃+
ɛ. Известно, что дисперсия ошибок
регрессии D(ɛt)=q^2
для любого t. В этом случае
говорят о наличии —гомоскедастичности
Как влияет
исключение переменной из уравнения
множественной регрессии на значение
F-критерия и коэффициент детерминации?-
F-критерий может
как уменьшиться, так и увеличиться, R2
уменьшится
Как
называется вид графика, по которому
визуально можно сделать предположение
о законе распределения исследуемых
величин?…Гистограмма
Как
проявляется гетероскедастичность на
графике остатков? Разброс остатков
увеличивается или уменьшается с ростом
номера наблюдений
Как
проявляется гомоскедастичность на
графике остатков?… Разброс остатков
не изменяется с ростом наблюдений
Какая
характеристика определяет среднее
значение случайной величины?…Математическое
ожидание
Какие
виды уравнений в системах одновременных
уравнений с точки зрения идентифицируемости
параметров Вы знаете: неидентифицируемые
уравнения , точно идентифицируемые
уравнения , сверхидентифицируемые
уравнения
Каким
будет объём продаж, если цена одного
галлона молока составит 2 доллара 6
Какими
свойствами обладают оценки, полученные
при решении уравнения парной линейной
регрессии у=α+β+ɛ методом наименьших
квадратов, если выполнены условия
Гаусса-Маркова и случайные остатки ɛ
имеют нормальное распределение:-
состоятельностью, несмещенностью,
эффективностью
Какими
свойствами обладают оценки, полученные
при решении уравнения парной линейной
регрессии у-=а,—&-1; методом наименьших
квадратов, если выполнены условия
Гаусса-Маркова и случайные остатки е
имеют нормальное распределение…
Состоятельностью, несмещенностью и
эффективностью
Какими
свойствами обладают оценки, полученные
при решении уравнения парной линейной
регрессии Yt= axt+B+et
методом наименьших квадратов, если
выполнены условия Гаусса-Маркова и
случайные остатки е имеют нормальное
распределение:Состоятельностью,
несмещенностью и эффективностью
Каковы
показатели качества уравнения регрессии
в целом:- значения F-статистики для
уравнения регрессии -скорректированный
коэффициент детерминации
Какое
из уравнении является
показательным?…y=B0*B1^x1..
Какое
из уравнении является экспоненциальным?…y=e^***
Какой
вывод можно сделать по результату
проведения теста Рамсея?
спецификация уравнения ошибочная
Корреляция
ошибок – это: корреляция ошибок для
разных наблюдений.
Когда
целесообразно добавление новой
объясняющей переменной в модель при
росте скорректированного коэффициента
детерминации после ее включения
Коллинеарность
факторов эконометрической модели
y=a+b1x1+b2x2+…+bkxk+ɛ проверяется
на основе матрицы парных коэффициентов
линейной…КОРРЕЛЯЦИИ
Оценка
а^ значения параметра а модели У= aX + B
+ е является эффективной, если 1.
математическое а^ ожидание равно а
2.a^=a3. a^ обладает наименьшей дисперсией
по сравнению с другими оценками
4.a^->a… ОТВЕТ : . a^ обладает наименьшей
дисперсией по сравнению с другими
оценками
Оценка
альфа значения параметра альфа является
несмещенной, если: Мат ожидание альфа
равно альфа
Оценка
альфа со скоб значения параметра альфа
является состоятельной, если: а^->а
при стремлении числа наблюдений к
бесконечности
Оценка
параметров модели – это Сбор необх
стат информации
Оценки
параметров идентифицируемой системы
независимых (внешне не связанных)
эконометрических уравнений могут быть
найдены с помощью…обычного МНК
Параметр
экономической модели не является
статистически значимым, то соответствующая
независимая переменная на определенном
уровне доверия не
оказывает влияния на моделируемый
показатель
Парный
коэффициент линейной корреляции rxy
между случайными переменными x и
y показывает: уровень линейной
зависимости между x и y.
Если rxy > 0, то
x и y связаны
положительной линейной зависимостью.
Если rxy < 0, то x
и y связаны отрицательной
зависимостью;
Переменные
задаваемые извне автономно от модели
называются …экзогенными
Переменные,
которые хар-т результат функцион-я
экспонируемой эконометрической системы,
наз Лаговой
По
графику можно сделать вывод о том, что
представленный на рисунке ряд : ряд
не является стационарным
По типу
функциональной зависимости между
переменными эконометрической модели
различают___ уравнения регрессии-линейные
и нелинейные
Под
верификацией модели понимается:- оценка
качества модели
Под
спецификацией модели понимается…
выбор регрессорое и вида модели
Покажите
на рисунке отклонение фактического
значения от расчетного:
Последствием
гетероскедастичности является то, что
Дисперсии оценок коэф регрессии
остаются несмещенной
Последствием
гетероскедастичности является то, что:
стандартные ошибки коэффициентов
становятся заниженными, а вычисленные
t-статистики – завышенными;
Последствия
включения в уравнение регрессии
несущественных переменных:-Оценки
параметров будут несмещенными,
эффективность оценок снизится
Последствия
мультиколлинеарности:- оценки
становятся очень чувствительными к
изменению отдельных наблюдений, оценки
коэффициентов остаются несмещенными
Последствия
невключения в уравнение регрессии
существенной переменной в общем случае:-
оценки параметров будут смещенными
Построено
несколько типов зависимостей и рассчитаны
значения F-статистики для них. Какая из
представленных регрессий является
значимой, если ____________критическое
значение F-статистики равно 2,56 при
уровне значимости 5 %? y=583⋅k
−0,29 ⋅r
−8,6 ⋅s0,69
, F = 2,75;
Предположения
теоремы Гаусса-Маркова включают в себя
ошибки регрессии
должны быть независимы друг от друга;
дисперсия ошибок регрессии постоянна
для всех наблюдений
Представленная
на рисунке модель будет описываться
уравнением:
При
вводе в командной строке Eviews
команды « plot X
Y » появятся: один график,
на котором будут изображены и значения
ряда X, и значения
ряда Y
При
возникновении мультиколлинеарности:
стандартные ошибки коэффициентов
увеличиваются, вычисленные t-статистики
становятся заниженными;
При
выполнении команды «genr
Z+@cor(X,Y)
в ивьюс будет создана переменная Z,
в которую будет записано Значение
коэф-та кореляции между рядами
При
выполнении команды «plot
X Z» в EViews
,будет построен график, на котором:- по
оси абсцисс будут расположены значения
ряда Z, а по оси ординат- ряда Х.
При
выполнении команды «scat
X Z» в ивьюс
будет построен график Зависимости
ряда Z на разных
плоскостях
При
выполнении команды agenr Z=@cor{X.Y)o в Eviews
будет создана переменная Z. в которую
будет записано….значение коэффициента
корреляции между рядами X и Y.
При
выполнении предпосылок метода наименьших
квадратов оценки параметров регрессионной
модели, рассчитанные с помощью МНК,
обладают свойствами…
— состоятельности, несмещенности
и эффективности
При
добавлении в линейной регрессионной
модели новых регрессоров, коэф детерм
R2 Увеличивается
При
добавлении в линейной регрессионной
модели новых регрессоров коэф-т
детерминации R2^ Уменьшается
При
изучении зависимости зарплаты в
Казахстане от возраста и пола была
получена следующая регрессия…W*1500+735’AGE
*1746’S где W-зарплата (тенге/месяц) AGE —
возраст (лет).Какойвывод можно сделать
о зависимости зарплаты от пола?…мужчины
получают в среднем зарплату больше
женщин на 1746 тенге/месяц
При
изучении зависимости зарплаты в
Казахстане от возраста и пола была
получена следующая регрессия

получают в среднем зарплату меньше чем
мужчины на 1678
При
изучении зависимости издержек
производства y (тыс. р.) от основных
производственных фондов x (тыс. р.)
была построена модель: y = 10 + 0,75x. Это
означает, что: 4) при увеличении основных
производственных фондов на 1 тыс.
р. издержки производства в среднем
увеличиваются на 750 р.
При
изучении зависимости издержек
производства y (тыс. р.) от основных
производственных фондов x (тыс. р.)
была построена модель: y = α + βx + ε.
В результате исследования были
получены следующие оценки параметров
регрессии: 0,45 β 7,5; α = = ˆ ˆ .
Доверительный интервал для βˆ на
5%-ном уровне значимости составил
(0,42; 0,48). Какой вывод можно сделать
о точности полученной оценки коэффициента
β? оценка β получена
с достаточно высокой точностью;
При
изучении зависимости издержек
производства y (тыс. р.) от основных
производственных фондов x (тыс. р.)
была построена модель: y = β0 +
β1x + ε . В результате исследования
были получены следующие оценки параметров
регрессии: 10,5 β 7,5; β 1 0 = = ˆ ˆ .
Доверительный интервал для 1 βˆ
на 5%-ном уровне значимости составил
[9,4; 11,6]. Какой вывод можно сделать о
точности полученной оценки коэффициента
β? оценка β
получена с достаточно высокой
точностью;
При
изучении зависимости издержек
производства y (тыс.руб)
от основных производственных фондов
x (тыс.руб) была построена
модель: y=10+0,75x . Это
означает, что: при увеличении основных
производственных фондов на 1 тыс.руб.
издержки производства в среднем
увеличиваются на 750 руб.
При
изучении зависимости издержек
производства у (тыс. руб.) от основных
производственных фондов х (тыс. руб.)
была построена модель: у=а+Bх+£ в результате
исследования были получены следующие
оценки параметров регрессии: a = 7.5B=0.45
.доверительныйинтервал для B на 5%-м
уровне значимости составил [0,42; 0,48].
Какой вывод можно сделать о точности
полученной оценки коэффициентаB?1)
оценка B получена с достаточно высокой
точностью;
При
изучении зависимости издержек
производства у (тыс.руб.) от инвестиций
в совершенствование технологий х
(тыс.руб.)была построена модель у=10-0,15х.
Это означает, что:- при увеличении
инвестиций в совершенствование
технологий на 1 тыс.руб. издержки
производства в среднем снижаются на
150 руб.
При
изучении зависимости между показ безраб
и инфл в Болгарии х=2,1 Не можем, поскольку
абсол значение т-статистики для
показателя безраб меньше крит
При
изучении зависимости между показателями
безработицы (x) и инфляции (y) в
Болгарии была построена модель и
получены оценки коэффициентов для этой
модели: y = 4,23 –2,41x. Расчетное значение
t-статистики для показателя безработицы
x получилось равным 2,1. Можем ли мы
принять гипотезу о значимости показателя
безработицы в модели с уровнем значимости
0,05, если критическое значение t-статистики,
найденное из таблиц распределения
Стьюдента, равно –2,57? не можем,
поскольку абсолютное значение
t-статистики для показателя
безработицы меньше критического
значения;
При
изучении зависимости между показателями
Безработицы (х ) и инфляции ( у ) в Болгарии
была построена модель и получены оценки
коэффициентов для этой модели:
у=4.23-2,41х. Расчетное значение t-статистики
для показателя безработицы х получилось
равным: 2,1. Можем ли мы принять гипотезу
о значимости показателя безработицы
в модели с уровнем значимости 0,06, если
критическое значение t-статистики,
наиденное из таблиц распределения
Стьюдента, равно 2,57?…Не можем, поскольку
абсолютное значение t-статистики для
показателя безработицы меньше
критического значения
При
изучении зависимости между показателями
безработицы (х ) и инфляции (у ) в Чехии
была построена модель и получены оценки
коэффициентов для этой модели: у=3,
22*1,75х. Расчетное значение t-стетистики
для показателя безработицы х получилось
равным: 1.65, Можем ли мы принять гипотезу
о значимости показателя безработицы
в модели с уровнем значимости 0.1. если
критическое значение t-статистики,
наиденное из таблиц распределения
Стьюдента.равно 1.75?…Не можем* поскольку
абсолютное значение t-статистики для
показателя безработицы меньше
критического значения
При
изучении зависимости между показателями
безработицы {х) и инфляции {у ) в Швеции
была построена модель и получены оценки
коэффициентов для этой модели:
у=2,4б-0.б9х. Расчетное значение t-статистики
для показателя безработицы х получилось
равным: 5.2. Можем пи мы принять гипотезу
о значимости показателя безработицы
в модели с уровнем значимости 0,05. если
критическое значение t-статистики,
найденное из таблиц распределения
Стьюдента, равно 2.57?…Можем, поскольку
абсолютное значение t-статистики для
показателя безработицы больше
критического значения t-статистики
При
изучении зависимости между показателями
безработицы и инфляции в Швеции Можем,
поскольку абсол значение т-статистики
для показателя безраб больше крит
При
исследовании выбора обнаружено
«аномальное» значения фактора Y для
одного наблюдения. При каких условиях
корректно будет провести исключение
соответствующего наблюден из выбора
… В случае если «аномальное» значение
Y соответствует действительности, но
это отличие невозможно объяснить в
рамках проводимого исследования
При
исследовании зависимости сумм» активов
банка (у) от собственного капитала {к),
привлеченных ресурсов [г) и объема
вложений в государственные ценные
бумаги (s) было построено несколько
типов зависимостей и рассчитаны значения
F-статистики для них. Какая из представленных
регрессий является значимой, если
критическое значение F-статистики равно
2,56 при уровне значимости 5%?…у=583*К…
При
исследовании зависимости суммы активов
банка (y) от собственного капитала
(k), привлеченных ресурсов (r) и
объема вложений в государственные
ценные бумаги (s) было
При
исследовании зависимости суммы активов
банка (у) от собственного капитала (к).
у=у85-0,46к-19r+0,48s,
F=4,75
При
исследовании зависимости суммы активов
банка (у) от собственного капитала [If),
привлеченных ресурсов [г) и объема
вложений в государственные ценные
бумаги Is) было построено несколько
типов зависимостей и рассчитаны значения
F-статистики для них. Какая из представленных
регрессий является значимой, если
критическое значение F-статистики равно
3,74 при уровне значимости 1%?ОТВЕТ : 4
1)F=2.67 2) F=2.75 3). F=3.6S 4) у=е^*** F=4.75
При
исследовании зависимости суммы активов
банка (у) от собственного капитала(к),
привлеченных ресурсов (r) и объема
вложений в гос цен бумаги (s) было
построено несколько типов зависимостей
и рассчитаны значения F-статистики для
них. Какая из представленных регрессий
является значимой, если критическое
значение F-статистики равно 2,56 при
уровне значимости 5%- у=583к^-029 *r^-8,6
*s^0,69, F=2,75
При
отсутствии свободного члена регрессии
В0 в уравнении… нарушается предпосылка
теоремы Гаусса-Маркова: E(£i)=0
При оценке
качества уравнения регрессии был
рассчитан коэффициент детерминации
R^2=0.91. Это означает, что…- построенная
модель достаточно хорошо подогнана к
выборочным данным
При оценке
качества уравнения регрессии был
рассчитан коэффициент детерминации
R^2=0.18. Это означает, что…-построенная
модель довольно плохо подогнана к
выборочным данным
При
оценке модели вида y=
a0+a1yt-1+a2
yt-2
+ εt необходимо
написать в командной строке: Is
y с ar(1)
ar(2)
При
переходе к линейному виду для …
зависимости вводится замена Х=лп(х),
У=лн(у) Логарифмический
При
переходе к линейному виду для____
зависимости зависимая переменная
преобразуется по формуле Y=ln(y) —
степенной, экспоненциальной
При
переходе обратно от построенного
вспомогательного линейного уравнения
у=в0+в1х к нелинейному виду, для парной
степенной зависимости в0=ев0,
в1=в1
При
переходе обратно от построенного
вспомогательного линейного уравнения
Y=B0-B1X к нелинейному виду, для парной
гиперболической зависимости Y=B0+B1 1/X
надо найти искомое значение коэффициентов
по формуле:B0=BOB1=B1
При
переходе обратно от построенного
линейного уравнения
к нелинейному виду, для парной степенной
зависимости
надо найти значение коэффициентов по
формуле
При
перходе к линейному виду для______зависимости
замена X=ln(x),Y=ln(y)— степенной
При
построении какого уравнения в EVews
вводится команда Is у с 1/х1 1/х2 1/хЗ…
Гиперболического
При
построении какого уравнения в EViews
вводится команда Is
log(y)
c x1
x2 x3
— Экспоненциального
При
построении какого уравнения в EViews
вводится команда Is log( у) с log(x1) lоg(х2)
lоg(хЗ)…
степенного
При
построении уравнения множественной
регрессии проверку тесноты связи между
независимыми переменными (объясняющими
переменными, регрессорами, факторами)
модели осуществляют на основе…-матрицы
парных коэффициентов линейной корреляции
При
проведении RESET-теста в EViews линейная
спецификация регрессии является
ошибочной с уровнем доверия 0.9, если
Р-знаиение = Prob. F…меньше 0.1
При
проведении RESET-теста в EViews линейная
спецификация регрессии является
ошибочной с уровнем доверия 0.95. если
Р-значение = Prob. F….меньше 0.05
Применение
обычного МНК непосредственно к системе
одновременных уравнений в структурной
форме приводит в общем случае к…
смещенным и несостоятельным оценкам
коэффициентов
Примера
фиктивны переменных в эконометрической
модели зависимости 1м2 жилья являются
площадь жилья;
величина прожиточного минимума в
регионе
Примерами
фиктивных переменных в эконометрической
модели зависимости стоимости 1м^2 жилья
НЕ ЯВЛЯЮТСЯ… — площадь жилья; величина
прожиточного минимума в регионе
Проверка
наличия коллинеарных факторов в
эконометрической модели х1
и х2
Процесс
является: нестационарным , случайным
блужданием , авторегрессионным процессом
1-го порядка
Процесс
является: процессом белого шума ,
стационарным
Процесс
является: процессом скользящего
среднего 1-го порядка , стационарным
Процесс
ARMA (p,q)
называется : авторегрессионным
процессом скользящего среднего
Пусть
в уравнении Н эндогенных переменных и
D экзогенных переменных, которые в этом
уравнение (в его структурной форме)
отсутствуют Тогда в случае, если 0=3.
н-2. уравнение является:…сверхидентифицируемым
Пусть
качественный признак принимает 4
значения, сколько фиктивных переменных
надо ввести в уравнение 3
Пусть
оцененное уравнение регрессии имеет
вид: у=-2,3+0,4х1-3,7х2+1,2х3. Что можно
сказать об интерпретации значения
коэффициента при переменной х1?—
при увеличении переменной х1 на единицу
ее измерения при неизменных значениях
других переменных у увеличится в среднем
на 0,4 единиц своего измерения.
Рассматривается
зависимость объема выпускаемой продукции
Q от объема трудовых L и материальных
затрат К. Результатом оценки параметров
производственной функции Кобба-Дугласа
стала модель Q=12.8*K^0.4*L^0,3. Это означает,
что…средние издержки, рассчитанные
на единицу продукции, растут по мере
расширения масштабов производства
Расширенный
тест Дики Фуллера показывает, что : ряд
не является стационарным относительно
первой разности , ряд на разностей
исходного ряда содержит единичный
корень
Расширенный
тест Дики-Фуллера показывает, что : ряд
содержит единичный корень , ряд не
является стационарным
Расширенный
тест Дики-Фуллера показывает, что: ряд
не является стационарным , ряд не
является стационарным относительно
линейного тренда
Регрессионная
модель вида y=a+bx1+c(x2^2)+ɛ является
нелинейной относительно…- переменной
Х2
Связь
между объёмом продаж и переменными
«Цена одного галлона» и «Расходы на
рекламу» являются тесной
Слабая
стационарность временного ряда
означает…самый большой
Среднегодовые
цены на бензин во всех субъектах
Российской Федерации за 2011 год относятся
… к пространственным данным .
Стандартное
нормальное распределение имеет параметры
математическое ожидание=0, дисперсия=1
Стационарность
временного ряда означает отсутствие
…тренда
Степенная
зависимость записана уравнением-
Стоится
эконометрическая модель уравнения
множественной регрессии для зависимости
у от пяти факторов у=f(x1,x2,x3,x4)+E
Строгая
стационарность временного ряда означает:
независимость распределений уровней
ряда от сдвига по времени
Структура
сдвига временного ряда …характерезует
разные внезапные ….
Суть
коэффициента детерминации состоит в
следующем:- коэффициент определяет
долю общего разброса значений,
объясненного уравнением регрессии
Сформулируйте
необходимое условие идентифицируемости
структурного уравнения (порядковое)….число
отсутствующих экзогенных переменных
в уравнении больше числа эндогенных
переменных входящих в уравнение без
единицы
Сформулируйте
необходимое условие идентифицируемости
структурного уравнения (порядковое):…
число отсутствующих экзогенных
переменных в уравнении равно числу
эндогенных переменных, входящих ответ.
уравнение, плюс единица
Тест
Вэльдэ применяется для… проверки
гипотез равенства коэффициентов
какому-либо значению или соотношения
коэффициентов между собой
Тест Чоу
применяется для выявления структурных
сдвигов
Тип данных
«Alpha» в ивьюс соответствует
ряду, содержащему Текстовую информацию
Удаление
из выборки наблюдений, значения факторов
для которых существенно больше или
меньше средних по выборке позволяет
добиться…однородности выборки
Укажите
тест, который используется для выявления
гетероскедастичности? Уайта
Укажите
тест, который не используется для
выявления гетероскедастичности-
Дарбина-Уотсона
Уравнение
множественной регрессии имеет вид
у=-27,16+1,37 х₁-0,29 х₂. Параметр при
переменной х2 означает следующее:-
при увеличении х2 на единицу своего
измерения и при фиксированном значении
фактора х1, переменная у уменьшится на
0,29 единиц своего измерения
Уравнение
множественной регрессии имеет вид:
у=-27,16+1,37 х₁-0,29 х₂. Параметр а₁=1.37
означает следующее:-при увеличении
х₁ на одну единицу своего измерения и
при фиксированном значении фактора
х₂, переменная у увеличится на 1,37 единиц
своего измерения
Уравнение
регрессии называется значимым в целом,
если- есть достаточно высокая
вероятность того, что существует хотя
бы один коэффициент, отличный от нуля
Уравнение
регрессии называется незначимым в
целом, если- есть достаточно высокая
вероятность того, что все коэффициенты
равны 0
Установите
соответствие 1)команда для созд ряда
Х, 2) ком для созд графика ряда Х, 3) ком
для созд группы гр1 и рядов Х и У, 4) ком
для созд гр зависимости А. скат Х У, Б.
Сериес Х, В. Груп, Д. лайн 1-Б, 2-Д, 3-В,
4-А
Фиктивные
переменные заменяют ….качественные
переменные
Фиктивные
переменные эконометрической модели…-
используются в случае совокупностей
данных; отражают качественные признаки
исследуемого объекта наблюдения
Фиктивными
переменными в уравнении множественной
регресси являются… качественные
переменные, преобразованные в
количественные
Фильтрацию
данных (удаление сильно отличающихся
наблюдений) можно проводить, если…определена
причина такого отклонения
Функционал
метода наименьших квадратов для случая
парной линейной регрессии выглядит
следующим образом:
Функционал
метода наименьших квадратов для случая
парной регрессии выглядит следующим
образом:
Циклические
колебание могут связаны с…сезонность
некоторых видов …
Чем на
ваш взгляд более оправдано использование
скорректированного коэффициента
детерминации R^2adj,
чем R^2 для сравнения двух 1) Попыткой
устранить эффект, связанный с увеличением
значения R2 при добавлении регрессоров.
Чем, на
ваш взгляд, более оправдано использование
скорректированного коэффициента
детерминации R2 adj, чем R2 100
для сравнения двух линейных регрессионных
моделей, одна из которых отличается от
другой добавленными новыми регрессорами?
попыткой устранить эффект, связанный
с увеличением значения R2 при
добавлении регрессоров;
Что бы
оценить модель ARIMA (1.1.0)в командной
строке рабочего окна Eviews необходимо
ввести …isd(y) car(1)
Что не
является целью исследований
эконометрических явлений и процессов?
Разработка теоретико-экон моделей,
поиск зависимостей между признаками…
Что
обозначает команда genr X=2+9*nrnd?… Создание
ряда чисел X, имеющего нормальное
распределение с математическим ожиданием
2 и дисперсией 81
Что
обозначает команда genr Y=10-t-20*rnd?… Создание
ряда чисел Y. представляющего собой
равномерно распределенные на интервале
(10;30) случайные числа
Что
означает «правильно специфицированное
уравнение регрессии» правильная
функциональная зависимость
Что
означает команда genr
Y=10+20*rnd?
Создание ряда чисел У, представляющего
собой равномерно распред-е на интервале
(10;20) случ
Эконометрика
— это… наука, которая дает количественное
выражение взаимосвязей экономических
явлений и процессов
Эконометрическое
моделирование зависимости по неоднородной
совокупности данных может осуществляться
на основе…-разделения неоднородной
совокупности данных на однородные;
использования фиктивных переменных
Экспоненциальная
зависимость записана уравнением
у=ув0+в1*х1+….+вн*хн+Е
Экспоненциальная
зависимость записана уравнением…

верные утверждения — коэфф Z значим,
а С не значим на уровне значимости 0,05
Эндогенные
переменные в системах одновременных
уравнений в общем случае… коррелируют
со случайными ошибками уравнений
Спецификация эконометрической модели: способы и диагностика отбора экзогенных переменных. Тесты Рамсея и Амемья.
Спецификация модели множественной линейной регрессии включает проверку:
1. правильного выбора экзогенных переменных.
2. корректного выбора формы зависимости мду эндо- и экзогенной переменными.
Для решения 1 задачи различают пропущенные и избыточные экзогенные переменные
Пропущенные переменные – существенные факторы, которые не были включены в эконометрическую модель по ошибке. Опасность наличия пропущенных переменных заключается в смещении оценок параметров при включенных переменных. Признак, по которому определяют пропущенную переменную: Знак “+” у произведения оценки параметра при подозреваемой пропущенной переменной и коэффициента корреляции этой переменной с другими переменными, включенными в модель.
Выбранная модель с пропуском переменной 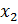

Тогда, применяя МНК для оценки усеченной модели получаем формулу смещения оценки 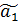
Экзогенную переменную относят к избыточным, если она по ошибке включена в эконометрическую модель. Включение избыточной переменной оказывает влияние на уменьшение точности (увеличение дисперсии) оценок параметров модели, что, в свою очередь, вызывает уменьшение t-статистик и коэффициента детерминации.
Если 

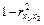

Замещающие переменные – обычно бывает полезно вместо пропущенной переменной, которую трудно измерить, использовать некоторый её заменитель.
4 основных качественных правила спецификации экономической модели:
1. Опираясь на эконометрическую теорию, следует ответить на вопрос: «Является ли переменная существенной в модели зависимости с эндогенной переменной?».
2. Осуществить проверку значимого отличия от нуля t-статистик.
3. Осуществить проверку, насколько значимо изменяется коэффициент детерминации при добавлении некоторой переменной в модель.
4. Существенно ли изменяются оценки других переменных после добавления новой переменной в модель.
Кроме отмеченных правил спецификации модели, наиболее из-вестны два следующих количественных критерия спецификации:
Критерий Рамсея (Ramsey):
RESET-тест Рамсея — это обобщенный тест на наличие следующих ошибок спецификации модели линейной регрессии:
- наличие пропущенных переменных. Регрессия содержит не все объясняющие переменные;
- неверная функциональная форма. Некоторые или все переменные должны быть преобразованы с помощью логарифмической, степенной, обратной или какой-либо другой функции;
- корреляция между фактором Х и случайной составляющей модели, которая может быть вызвана ошибками измерения факторов, рассмотрением систем уравнений или другими причинами.
Тест Рамсея позволяет проверить, стоит ли начинать поиск дополнительной переменной для включения в уравнение
1. Оценивается уравнение регрессии
2. Вычисляются степени оценок зависимой переменной
3. Оценивается уравнение регрессии с этими степенями
4. Проводится оценка улучшения по F-критерию
Ошибки такого рода приводят к смещению среднего остатков регрессионной модели.
1. Оценивают зависимость в соответствии с выбранной моделью по МНК:
2. Анализируют вид функциональной зависимости остатков 
3. Например, с учетом 2) вычисляют величины 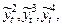
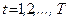
и применяют для ее оценивания по МНК.
4) Сравнивают качество модели по отношению к модели с помощью F-критерия:
Если 

Недостаток: он указывает только на наличие ошибочной спец-ции модели, но не выявляет, сколько и какого рода переменную нужно добавить в модель.
Критерий Амемья (Amemiya):
Решающей функцией F-критерия служит:
Модель, для которой значение AF меньше, является лучше специфицированной.
Этот критерий минимизирует число экзогенных переменных.
F-тест качества спецификации парной линейной регрессионной модели
F-тест — оценивание качества уравнения регрессии — состоит в проверке гипотезы Н0 о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического Fвыч и критического (табличного) Fкрит значений F-критерия Фишера. Fвыч определяется из соотношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы.
Коэффициент детерминации является случайной величиной (так как вычисляется по выборочным данным), и для оценки его статистической
значимости, в соответствии со стандартной процедурой, следовало бы
сравнить его вычисленное значение с табличным (критическим). Однако
таблиц распределения коэффициента детерминации не существует, поэтому для проверки статистической гипотезы о значимости R 2 используется косвенный метод: вычисляется некоторая вспомогательная статистика с известным распределением; проверяется гипотеза ее статистической значимости; устанавливается взаимосвязь между вспомогательной статисткой и коэффициентом детерминации; на основании этой взаимосвязи делается вывод о статистической значимости коэффициента детерминации. Для составления вспомогательной статистики рассмотрим две случайные величины U и V. Статистика U имеет распределение х 2 (хи-квадрат)
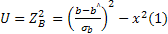
так как случайная величина 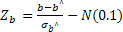
В качестве второй вспомогательной статистики, имеющей распределение х 2 с параметром, равным числу степеней свободы n — 2, используется статистика вида:
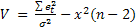
Статистика F, как легко проверить, совпадает с квадратом f-статистики для параметра b:
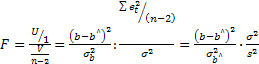
и имеет распределение Фишера с параметрами v1=1,v2=n-2 (n— объем выборки):
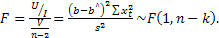
Для проверки гипотезы Н0:b = 0 статистика (3) принимает вид:
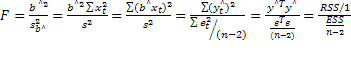
Связь между статистиками F и R 2 для случая парной регрессии
(k=2) имеет вид:
F= 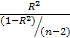
Справедливость (4) проверяется непосредственно:
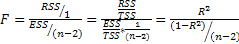
Таким образом, как следует из формулы (5), F = 0 в том случае, если R 2 =0. Поэтому, проверяя значимость F статистики (сравнивая ее вычисленное по выборочным данным значение с табличным), мы можем проверить статистическую значимость коэффициента детерминации. ЕслиFвыч
Дата добавления: 2015-01-10 ; просмотров: 5107 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
F-тест качества спецификации множественной регрессионной модели
Цель этой статьи — рассказать о роли степеней свободы в статистическом анализе, вывести формулу F-теста для отбора модели при множественной регрессии.
1. Роль степеней свободы (degree of freedom) в статистике
Имея выборочную совокупность, мы можем лишь оценивать числовые характеристики совокупности, параметры выбранной модели. Так не имеет смысла говорить о среднеквадратическом отклонении при наличии лишь одного наблюдения. Представим линейную регрессионную модель в виде:
Сколько нужно наблюдений, чтобы построить линейную регрессионную модель? В случае двух наблюдений можем получить идеальную модель (рис.1), однако есть в этом недостаток. Причина в том, что сумма квадратов ошибки (MSE) равна нулю и не можем оценить оценить неопределенность коэффициентов . Например не можем построить доверительный интервал для коэффициента наклона по формуле:
А значит не можем сказать ничего о целесообразности использования коэффициента в данной регрессионной модели. Необходимо по крайней мере 3 точки. А что же, если все три точки могут поместиться на одну линию? Такое может быть. Но при большом количестве наблюдений маловероятна идеальная линейная зависимость между зависимой и независимыми переменными (рис. 1).

Количество степеней свободы — количество значений, используемых при расчете статистической характеристики, которые могут свободно изменяться. С помощью количества степеней свободы оцениваются коэффициенты модели и стандартные ошибки. Так, если имеется n наблюдений и нужно вычислить дисперсию выборки, то имеем n-1 степеней свободы.
Мы не знаем среднее генеральной совокупности, поэтому оцениваем его средним значением по выборке. Это стоит нам одну степень свободы.
Представим теперь что имеется 4 выборочных совокупностей (рис.3).

Каждая выборочная совокупность имеет свое среднее значение, определяемое по формуле . И каждое выборочное среднее может быть оценено
. Для оценки мы используем 2 параметра
, а значит теряем 2 степени свободы (нужно знать 2 точки). То есть количество степеней свобод
Заметим, что при 2 наблюдениях получаем 0 степеней свободы, а значит не можем оценить коэффициенты модели и стандартные ошибки.
Таким образом сумма квадратов ошибок имеет (SSE, SSE — standard error of estimate) вид:
Стоит упомянуть, что в знаменателе стоит n-2, а не n-1 в связи с тем, что среднее значение оценивается по формуле . Квадратные корень формулы (4) — ошибка стандартного отклонения.
В общем случае количество степеней свободы для линейной регрессии рассчитывается по формуле:
где n — число наблюдений, k — число независимых переменных.
2. Анализ дисперсии, F-тест
При выполнении основных предположений линейной регрессии имеет место формула:
где ,
,
В случае, если имеем модель по формуле (1), то из предыдущего раздела знаем, что количество степеней свободы у SSTO равно n-1. Количество степеней свободы у SSE равно n-2. Таким образом количество степеней свободы у SSR равно 1. Только в таком случае получаем равенство .
Масштабируем SSE и SSR с учетом их степеней свободы:
Получены хи-квадрат распределения. F-статистика вычисляется по формуле:
Формула (9) используется при проверке нулевой гипотезы при альтернативной гипотезе
в случае линейной регрессионной модели вида (1).
3. Выбор линейной регрессионной модели
Известно, что с увеличением количества предикторов (независимых переменных в регрессионной модели) исправленный коэффициент детерминации увеличивается. Однако с ростом количества используемых предикторов растет стоимость модели (под стоимостью подразумевается количество данных которые нужно собрать). Однако возникает вопрос: “Какие предикторы разумно использовать в регрессионной модели?”. Критерий Фишера или по-другому F-тест позволяет ответить на данный вопрос.
Определим “полную” модель: (10)
Определим “укороченную” модель: (11)
Вычисляем сумму квадратов ошибок для каждой модели:
(12)
(13)
Определяем количество степеней свобод
(14)
Нулевая гипотеза — “укороченная” модель мало отличается от “полной (удлиненной) модели”. Поэтому выбираем “укороченную” модель. Альтернативная гипотеза — “полная (удлиненная)” модель объясняет значимо большую долю дисперсии в данных по сравнению с “укороченной” моделью.
Коэффициент детерминации из формулы (6):
Из формулы (15) выразим SSE(F):
SSTO одинаково как для “укороченной”, так и для “длинной” модели. Тогда (14) примет вид:
Поделим числитель и знаменатель (14a) на SSTO, после чего прибавим и вычтем единицу в числителе.
Используя формулу (15) в конечном счете получим F-статистику, выраженную через коэффициенты детерминации.
3 Проверка значимости линейной регрессии
Данный тест очень важен в регрессионном анализе и по существу является частным случаем проверки ограничений. Рассмотрим ситуацию. У линейной регрессионной модели всего k параметров (Сейчас среди этих k параметров также учитываем ).Рассмотрим нулевую гипотеза — об одновременном равенстве нулю всех коэффициентов при предикторах регрессионной модели (то есть всего ограничений k-1). Тогда “короткая модель” имеет вид
. Следовательно
. Используя формулу (14.в), получим
Заключение
Показан смысл числа степеней свободы в статистическом анализе. Выведена формула F-теста в простом случае(9). Представлены шаги выбора лучшей модели. Выведена формула F-критерия Фишера и его запись через коэффициенты детерминации.
Можно посчитать F-статистику самому, а можно передать две обученные модели функции aov, реализующей ANOVA в RStudio. Для автоматического отбора лучшего набора предикторов удобна функция step.
Надеюсь вам было интересно, спасибо за внимание.
При выводе формул очень помогли некоторые главы из курса по статистике STAT 501
источники:
http://helpiks.org/2-3401.html
http://habr.com/ru/post/592677/
Расчет коэффициента корреляции и детерминации
Уравнение регрессии всегда дополняется показателем тесноты связи. При использовании линейной регрессии таким показателем является линейный коэффициент корреляции rxy . Существует несколько видов формулы линейного коэффициента корреляции, приведем основные из них:
Линейный коэффициент корреляции, как известно, всегда находится в следующих пределах: -1 < rxy < 1. Знак коэффициента регрессии определяет знак коэффициента корреляции. Если b < 0, тогда — 1 < rxy < 0 , и наоборот, если Ь > 0, тогда 0 < rxy < 1. Чем ближе значение коэффициента корреляции по модулю | rxy|, к единице, тем теснее связь между признаками в линейной форме. Однако, если абсолютная величина коэффициента корреляции близка к нулю, то это означает, что между рассматриваемыми признаками отсутствует линейная связь. При другом виде уравнения регрессии связь может оказаться достаточно тесной. В приведенном выше примере коэффициент корреляции равен 0,97, следовательно, в данном случае имеет место достаточно тесная связь между результатом и фактором.
Для оценки качества подбора линейного уравнения регрессии находят также квадрат коэффициента корреляции, называемый коэффициентом детерминации R = (rxy)2 . Он отражает долю вариации результативного признака, объясненную с помощью уравнения регрессии, или, иными словами, долю дисперсии результата, объясненную регрессией, в общей дисперсии у:
Следовательно, величина (1— R2) характеризует долю вариации, или долю дисперсии результата у, вызванную влиянием всех остальных, не учтенных в модели факторов. Значения коэффициента детерминации могут изменяться от нуля до единицы (0 < R2 < 1) • Для рассмотренного примера R2=0,94 это означает, что уравнением регрессии объясняется 94% дисперсии результативного признака, а прочими, не учтенными в модели факторами — 6%. Чем ближе коэффициент детерминации к единице, тем меньше роль других факторов и линейное уравнение регрессии описывает лучше исходные данные.
7. Критерий Фишера.
После выбора уравнения линейной регрессии и оценки его параметров проводится оценка значимости как уравнения в целом, так и отдельных его параметров.
Оценка значимости уравнения регрессии в целом осуществляется с помощью критерия Фишера,который называют также F-критерием. При этом выдвигается нулевая гипотез (Н0): коэффициент регрессии равен нулю (b = 0), следовательно, фактор хне оказывает влияния на результат у и линия регрессии параллельна оси абсцисс.
Перед тем как приступить к расчету критерия Фишер; проведем анализ дисперсии. Общую сумму квадратов отклонений уот 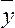
Где:
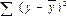
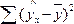
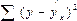
Общая сумма квадратов отклонений результативного признака у от среднего значения определяется влиянием различных причин. Условно всю совокупность последних можно разделить на две группы: изучаемый фактор х и прочие, случайные и не включаемые в модель факторы.
Определение дисперсии на одну степень свободы
Так как эти дисперсии рассчитаны на одну степень свободы, их можно сравнивать между собой.
Критерий Фишера позволяет проверить нулевую гипотезу Hо том, что факторная и остаточная дисперсии на одну степень свободы равны между собой (Dфак.=Dост.). Критерий Фишера рассчитывается по следующей формуле:
Если (Fфак.>Fтабл..), тогда гипотеза H0 отклоняется и делается вывод, что связь между у и х существенна и уравнение регрессии статистически значимо. Если (Fфак.≤Fтабл.), тогда гипотеза H0 принимается и делается вывод, что уравнение регрессии статистически незначимо, так как существует риск (при заданном уровне надежности) сделать неправильный вывод о наличии связи между х и у.
8. Стандартные ошибки параметров.В
9. линейной регрессии часто оценивается не только значимость уравнения регрессии в целом, но и значимость его отдельных параметров, а также коэффициента корреляции.
Для того чтобы осуществить такую оценку, необходимо для всех параметров рассчитывать стандартные ошибки(ma, mb, mr)
обозначив остаточную дисперсию на одну степень свободы через S2, получим
Величины стандартных ошибок применяются не только для проверки значимости параметров, но и для расчета доверительных интервалов.
studopedia.ru
/ эконометрика 1
-
Автокорелляция ошибок –это:корреляция ошибок регрессии для разных наблюдений
-
Автокорреляция остатков бывает следующих видов – отрицательная, положительная
-
В каких случаях значение коэффициента детерминации R^2 может выйти за пределы 0:1:если в уравнении регрессии отсутствует константа Во
-
В оцениваемой модели у=хВ+Eотсутствует часть существенных независимых переменных , тогда оценкаB, полученная в данной регрессии в общем случаесмещенная
-
В результате оценки параметров регрессии у=а+В*Х+Eбыли получены следующие результаты =10,4 В=4,7 Доверительный интервал для В с уравнением доверия 95% составил (3,9,5,5)Что показывает полученный доверительный интервал с указанным уровнем доверия?Истинное значение коэффициента В находится в указанном интервале с вероятностью 0,95
-
В чем суть гетероскедастичности: дисперсии случайных отклонений изменяются
-
В эконометрической модели линейного уравнения регрессии у=а+в1х1+в2х2+…вkхk+Eпараметрами являютсяа ,bj
-
В эконометрической модели линейного уравнения регрессии у=а+в1х1+в2х2+…вkхk+Eкоэффициентом регрессии ,характеризующим среднее изменение зависимой перменной …..bj
-
Выберите верные утверждения о производственной функции Кобба-Дугласса: записывается степенным уравнением, является нелинейной зависимостью.
-
Гетероскедастичность – это зависимость дисперсии случайных ошибок от номера наблюдения
-
Для выбора лучшей спецификации модели применяется РЕ-тест, J-тест
-
Для выявления ошибки линейной спецификации регрессии применяется RESET-тест
-
Для двух случайных величин х и у было получено значение парного коэффициента корреляции r-0.9 вывод:связь тесная и прямая
-
Для нелинейной регрессионной модели зависимости рассчитано значение индекса детерминации R^2=0,9.Тогда значение индекса корреляции составиткорень из 0.9
-
Для оценки параметров регрессионной модели с гетероскедастичным остатками используется обобщенныйметод наименьших квадратов
-
Для регрессионной модели вида у= а+в1*х1+в2*х2…..показателем тесноты связи является коэффициент множественной корреляции
-
Для регрессионной модели вида у=а+в*х+Eпостроена на координатной плоскости совокупность точек с координатами уiхi..данное графическое отображение зависимости называетсяполем корреляции
-
Для регрессионной модели зависимости потребления материала на единицу продукции от объема выпуска продукции построено нелинейное уравнение..см рисунок R2=0,904.Следовательно объемом выпуска продукции объяснено 90,4 дисперсии потребления материалов на единицу продукции
-
Для регрессионной модели известны следующие величины дисперсий …….сумм(у-у)^2=сумм(у-у)^2+сумм(у-у)^2
-
Для регрессионной модели несмещенность оценки параметра означает, что ее выборочное математическое ожидание равно оцениваемому параметру, рассчитанному по генеральной совокупности.
-
Для регрессионной модели парной регрессии рассчитано значение коэфф.детерминации R=0,831 ……16,9%
-
Для регрессионной модели парной регрессии рассчитано значение коэффициента детерминации R2.Тогда долю остаточной дисперсии зависимой переменной характеризует величина(1-R)^2
-
Для совокупности из nединиц наблюдений построена модель линейного уравнения множеств регрессии с количеством параметров при независимых переменных равнымkТогда при расчете остаточной дисперсии на одну степень свободы величину дисперсии относят к значениюn—k-1
-
Для совокупности из nединиц наблюдений рассчитывают общую дисперсию на одну степень свободы , при этом величину дисперсии относят к значениюn-1
-
Долю объясненной с помощью регрессии дисперсии в общей дисперсии зависимой переменной характеризует коэффициент детерминации
-
Если параметр эконометрической модели не является статистически значимым, то соответствующая независимая переменная на определенном уровне доверия: не оказывает влияния на моделируемы показатель (зависимую переменную)
-
Если параметр эконометрической модели не является статистически значимым , то его значение признается равным 0
-
Если параметр эконометрической модели не является статистически значимым , то соответствующая независимая переменная не оказывает влияния на моделируемый показатель (зависимую переменную)
-
Если параметр эконометрической модели является статистически значимым , то его значение признается отличным от 0
-
Исследуется регрессия у=В0+В11+В22+В33+E…известно что 4,3+10х1-3,5=х3. В этом случае говорят о наличиигетероскедастичности
-
Как влияет исключение переменной из уравнения множественной регрессии на занчение F-критерия и коэффициент детерминации?F– критерий может как умен так и увел , R2 уменьшится
-
Какими свойствами обладают оценки , полученные при решении ур-ия парной линейной регрессии у1=ах+в+Eметодом наименьших квадратов , если выполнены условия Гаусса-Маркова и случайные остатки имеют нормальное распределение ..Состоятельность, несмещенностью и эффективностью
-
Каковы показатели качества уравнения регрессии в целом? Значение F-статистики для уравнения регрессии , скорректированный коэффициент детерминации
-
Каковы показатели качества уравнения регрессии в целом? Скорректированный коэффициент детерминации, значение Fстатистики для уравнения регрессии.
-
Какой вывод можно сделать по результату проведения теста Рамсея? Спецификация уравнения ошибочная
-
Когда целесообразно добавление новой объясняющей переменной в модель? При росте скорректированного коэффициента детерминации после ее включения
-
Коллинеарность факторов эконометрической модели у=а+в1х1+в2х2+…+вjхj+…вkxk+Eпроверяется на основе матрицы парных коэффициентов линейнойкорреляции
-
Коэффициент при экзогенной переменной в уравнении линейной регрессии показывает:на сколько ед изменится эндогенная переменная при изменении экзогенной перменной на 1 ед
-
Коэффициент регрессии называется значимым, если есть достаточная высокая вероятность того , что его истинное значение отлично от 0
-
Коэффициент регрессии называется незначимым если: есть достаточно высокая вероятность того, что его истинное значение равно0
-
Метод наименьших квадратов может применятся для оценки параметров исходной регрессионной модели в линейнойформе
-
Нелинейным уравнением парной регрессии является у=а+в*х+с*х2+E
-
Одной из предпосылок МНК является то , что в остатках регрессионной модели автокорреляция должна отсутствовать
-
Особенность эконометрики как прикладной науки заключается в количественном измерении существующих взаимосвязей социально-экономических показателей и систем.
-
Оценка А значения параметра а явлеется состоятельной если: при стремлении числа наблюдений к бесконечности
-
Оценка А значения параметра а является несмещенной если : математическое ожидание а равно а
-
Оценка А значения параметра а является состоятельной если …….при стремлении числа наблюдений к бесконечности
-
По типу функциональной зависимости между переменными эконометрической модели различают линейные и нелинейные ур-ия регрессии
-
Под верификацией модели понимается оценка качества модели
-
Последствия включения в ур-ие регрессии несущественной переменной : оценки параметров будут несмещенными ,эффективность оценок снизится
-
Последствия мультиколлинеарности : ОЦЕНКИ ОЦЕНКИ
-
Последствия мультиколлинеарности : оценки становятся очень чувствительными …..оценки коэффициентов остаются не смещенными
-
Последствия невключения в уравнение регрессии существенной переменной в общем случае Оценки параметров будут смещенными
-
Предположения теоремы Гаусса-Маркова включают в себя: Ошибки регрессии должны быть независимы друг от друга , дисперсия ошибок регрессии постоянна для всех наблюдений.
-
При возникновении мультиколлинеарности :стандартные ошибки коэффициента увеличиваются, вычисленные t-статистики становятся занижены
-
При выполнении предпосылок МНК оценки параметров регрессионной модели , рассчитанные с помощью МНК обладают свойствами состоятельности несмещенности эффективности
-
При изучении зависимости зарплаты в Казахстане от возраста и пола была получена следующая регрессия W=1489 +747+AGE-1678*S, гдеW-зарплата …..женщины получают в среднем зарплату меньше минимума 1678
-
При изучении зависимости издержек производства ….была построена модель у= 10 -0,15х,это означает что при увеличении инвестиций в совершенствование технологий на 1 тыс руб издержки производства в среднем снижаются на 150 р.
-
При изучении зависимости издержек производства у от основных производственных фондов х была построена модель у=10+0,75 х, это означает, что при увеличении основных производственных фондов на 1 тыс руб издержки производства в среднем увел на 750р
-
При изучении зависимости между показателями безработицы х и инфляции у…у=4,23-2,41х…расчетное значение -2.1Можем ли принять гипотезу …0.05, если критическое значение tстатистики = 2.57НЕ можем поскольку абсолютное значение tстатистики для показателя безработицы меньше критического значения
-
При исследовании выборки обнаружено аномальное значения фактора Yдля одного наблюдения .При каких условиях корректно будет провести исключение соответствующего наблюдения из выборки:в случае если аномальное значение Yневозможно объяснить и вы как исследователь не знаете, соответствует оно действительности или нет.: в случае если аномальное значение Yсоответствует действительности , но это отличие не возможно объяснить в рамках проводимого исследования
-
При исследовании зависимости суммы активов банка у от собственного капитала k.привлеченных ресурсовr….=3,74 при уровне значимости 1% у=e85-0,46к-19r+0,48sF=4,75
-
При оценки качества уравнения регрессии был рассчитан коэффициент детерминации R^2=0,91.Это означает что построенная модель достаточно хорошо подогнана к выборочным данным
-
При оценки качества ур-ия регрессии был рассчитан коэффициент детреминации R=0.18,это означает что построенная модель довольно плохо подогнана к выборочным данным
-
При переходе к линейному виду для степеннойзависимости вводится замена Х=ln(х),Y=ln(y)
-
При переходе к линейному виду для степенной, экспоненциальнойзависимости зависимая переменная преобразуется по формулеY=ln(y)
-
При переходе обратно от построенного вспомогательного линейного уравнения У=В0+В1Х к нелинейному виду для парной степенной зависимоти у= В0*XВ1 надо найти искомое значение коэффициентов по формулеВ0=Е^Во, В1=В1
-
При построении какого уравнения в EViewsвводится командаlslog(у) с х1 х2 х3Экспоненциального
-
При построении уравнения множественной регрессии проверку тесноты связи между независимыми переменными модели осуществляют на основе :матрицы парных коэффициентов линейной корреляции
-
При проведении RESET-теста..линейная спецификация регрессии является ошибочной с уравнением доверия 0,95, если Р-значениеменьше 0,05
-
Примерами фиктивных переменных в эконометрич модели зависимости стоимости 1м^2 жилья не являются :площадь жилья, величина прожитого минимума в регионе.
-
Проверка наличия коллинеарных факторов в эконометрической модели у=а+в1х1+в2х2+Eоснована на рассмотрении коэффициента корреляции между х1 и х2
-
Пусть качественный признак принимает 4 значения, сколько фиктивных переменных надо ввести в у равнение (при условии наличия в ур-ии константы) ТРИ
-
Регрессионная модель вида у=а+в*х1+с*(х2)^2+Eявляется нелинейной относительнопеременной х2
-
Стандартное нормальное распределение имеет параметры : мат ожидание =0,дисперсия=1
-
Строится эконометрическая модель уравнения множественной регрессии для зависимости Уот пяти факторов…….у=х(1),х(2),х(4))+E
-
Суть коэффициента детерминации состоит в следующем :коэффициент определяет долю общего разброса значений, объясненного ур-ием регрессии
-
Укажите тест, который не используется для выявления гетероскедастичности ДАРБИНА-УОТСОНА
-
Уравнение множественной регрессии имеет вид у= — 27,16 +1,37х-0,29х2 Параметр а1=1,37 означает следующее при увеличении х1 на одну единицу своего измерения и при фиксированном значении фактора Х2 переменная увеличивается на 1,37 единиц своего измерения.
-
Уравнение регрессии называется незначимым в целом, если есть достаточно высокая вероятность того , что все коэффициенты равны 0
-
Фиктивные переменные эконометрической модели : используются в случае неоднородных совокупностей данных, отражают качественные признаки исследуемого объекта наблюдения
-
Что означает правильно специфицировано уравнение регрессии :правильная функциональная зависимость
-
Эконометрическое моделирование зависимости по неоднородной совокупности данных может осуществляется на основе разделения неоднородной совокупности данных на однородные
-
Эконометрическое моделирование зависимости по неоднородной совокупности данных может осуществляться на основе: использования фиктивных переменных, разделения неоднородной совокупности данных на однородные
-
Экспоненциальная зависимость записана уравнением: у=e^В0+В1*х1….+Вn*хn+E
Основные задачи эконометрики:
-
Количественная оценка экономических связей
-
Проверка на реальных данных теоритических моделей
-
Статистическое тестирование гипотез
-
Экономическое прогнозирование
-
Имитация возможных сценариев социально-экономического развития
Стохастическиминазываются связи, при которых допускается случайное изменение зависимых переменных даже при сохранении значений всех остальных переменных, от которых они зависят.
Зависимая(эндогенная, результирующая, объясняемая) переменная характеризует результат функционирования анализируемой экономической системы.
Независимые(экзогенные, объясняющие) переменные или регрессоры являются «причиной» изменения зависимой переменной.
Уравнение регрессии:y=f(x, β) +ε, у-зависимая переменная, х-независимая, β-параметры регрессии, ε-случайная компонента(ошибка регрессии)
Системы эконометрических уравнений– это эконометрические модели, описывающиеся системой уравнений, в которые входят как регрессионные уравнения, так и тождества.
Каждое из регрессионных уравнений может включать в себя как независимые переменные, так и зависимые из других уравнений.
В моделях временных рядоврассматриваются зависимость эндогенной переменнойот времени или от ее значений в прошлые периоды времени.
Типы моделей временных рядов:
-
Модели тренда
-
Модели сезонности
-
Модели тренда и сезонности
-
Адаптивные модели
-
Модели авторегрессии и скользящего среднего
Пространственные данныепредставляют собой данные о совокупности объектов в определенный момент времени
Временные данные (временной ряд) есть серия наблюдений об одном и том же объекте в последовательные моменты времени
Панельные данные представляютсобой совокупность наблюдений о нескольких объектах в разные моменты времени в течении некоторого периода
Этапы эконометрического исследования:
-
Постановка задачи. На этом этапе определяются цели моделирования, набор факторов и показателей.
-
Анализ предметной области. Проводится предварительный анализ сущности изучаемого явления, изучаются теоретические результаты и опят проведения подобных исследований.
-
Формулировка моделей (выбор спецификации). Определяется вид модели и вид зависимости, а также уточняется набор переменных.
-
Сбор данных и анализ их качества
-
Определение (оценка) параметров модели. По имеющимся данным рассчитываются параметры выбранной модели, проводится ее статистический анализ, проверка гипотез относительно тех закономерностей, на изучение которых направлено данное исследование.
-
Верификация (оценка качества модели). Сопоставление реальных и рассчитанных по построенной модели данных и оценка их точности, т.е. проверка адекватности модели исследуемому явлению или процессу.
-
Интерпретация результатов. Формулировка качественных и количественных выводов об изучаемом объекте и сопоставление их с теоритическими результатами.
StudFiles.ru
Коэффициент корреляции, коэффициент детерминации, корреляционное отношение
Таблица 2.1
Индивидуальное потребление и личные доходы (США, 1954-1965 гг.)
| Год | Индивидуальное потребление, млрд. долл. | Личные доходы, млрд. долл. |
Заметим, что исходные данные должны быть выражены величинами примерно одного порядка. Вычисления удобно организовать, как показано в таблице 2.2. Сначала рассчитываются 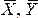

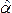
Оцененное уравнение регрессии запишется в виде 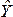
Следующая важная проблема состоит в том, чтобы определить, насколько «хороши» полученные оценки и уравнение регрессии. Этот вопрос рассматривается по следующим стадиям исследования: квалифицирование (выяснение условий применимости результатов), определение качества оценок, проверка выполнения допущений метода наименьших квадратов.
Относительно квалифицирования уравнения 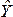
Таблица 2.2
Рабочая таблица расчетов (по данным табл. 2.1)
| Год | X | Y | x | y | x2 | xy | 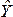 |
ei |
| -93 | -85,75 | 7974,75 | 235,48 | 0,52 | ||||
| -75 | -67,75 | 5081,25 | 252,18 | 1,82 | ||||
| -57 | -54,75 | 3120,75 | 268,88 | -1,88 | ||||
| -41 | -40,75 | 1670,75 | 283,72 | -2,72 | ||||
| -31 | -31,75 | 984,25 | 292,99 | -2,99 | ||||
| -13 | -10,75 | 139,75 | 309,69 | 1,31 | ||||
| 3,25 | 321,75 | 3,25 | ||||||
| 13,25 | 185,5 | 334,74 | 0,26 | |||||
| 33,25 | 1163,75 | 354,22 | 0,78 | |||||
| 53,25 | 2928,75 | 372,77 | 2,23 | |||||
| 79,25 | 6894,75 | 402,45 | -1,45 | |||||
| 109,25 | 13000,75 | 432,13 | -1,13 | |||||
| å | 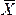 =350,00 =350,00 |
 =321,75 =321,75 |
0,00 |  =321,75 =321,75 |
0,00 |
Полученное уравнение 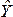
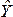
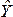
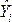
Заметим, что ошибка прогноза ei фактически является оценкой значений ui. График ошибки ei представлен на рис. 2.2. Следует отметить факт равенства нулю суммы Sei=0, что согласуется с первым ограничением модели парной регрессии — Eui=0, i=1,…,n. Ñ
Рис. 2.2. График ошибки прогноза
В модели (2.2) функция f может быть и нелинейной. Причем выделяют два класса нелинейных регрессий:
q регрессии, нелинейные относительно включенной объясняющей переменной, но линейные по параметрам, например полиномы разных степеней — Yi =a0 + a1Xi + a2Xi2+ ui, i=1,…,n или гипербола — Yi =a0 + a1/Xi + ui, i=1,…,n;
q регрессии нелинейные по оцениваемым параметрам, например степенная функция — Yi =a0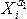
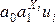
В первом случае МНК применяется так же, как и в линейной регрессии, поскольку после замены, например, в квадратичной параболе Yi =a0 + a1Xi + a2Xi2+ ui переменной Xi2 на X1i: Xi2=X1i, получаем линейное уравнение регрессии Yi =a0 + a1Xi + a2X1i+ ui, i=1,…,n.
Во втором случае в зависимости от вида функции возможно применение линеаризующих преобразований, приводящих функцию к виду линейной. Например, для степенной функции Yi =a0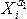
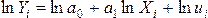
Однако для, например, модели Yi =a0+a2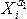
Для трактовки линейной связи между двумя переменными акцентируют внимание на коэффициенте корреляции.
Пусть имеется выборка наблюдений (Xi, Yi), i=1,…,n, которая представлена на диаграмме рассеяния, именуемой также полем корреляции (рис. 2.3).
Y
X
Рис. 2.3. Диаграмма рассеяния
Разобьем диаграмму на четыре квадранта так, что для любой точки P(Xi, Yi) будут определены отклонения
Ясно, что для всех точек I квадранта xiyi>0; для всех точек II квадранта xiyixiyi>0; для всех точек IV квадранта xiyixiyi может служить мерой зависимости между переменными X и Y. Если большая часть точек лежит в первом и третьем квадрантах, то åxiyi>0 и зависимость положительная, если большая часть точек лежит во втором и четвертом квадрантах, то åxiyixiyi близка к нулю и между X и Y связи нет.
Указанная мера зависимости изменяется при выборе единиц измерения переменных X и Y. Выразив åxiyi в единицах среднеквадратических отклонений, получим после усреднения выборочный коэффициент корреляции:
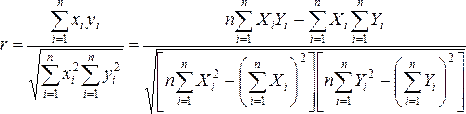
Из последнего выражения можно после преобразований получить следующую формулу для квадрата коэффициента корреляции:

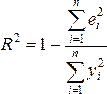
Квадрат коэффициента корреляции называется коэффициентом детерминации. Согласно (2.10) значение коэффициента детерминации не может быть больше единицы, причем это максимальное значение будет достигнуто при 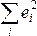
Кроме того, из (2.10) следует, что коэффициент детерминации равен доле дисперсии Y (знаменатель формулы), объясненной линейной зависимостью от X (числитель формулы). Это обстоятельство позволяет использовать R2 как обобщенную меру «качества» статистического подбора модели (2.6). Чем лучше регрессия соответствует наблюдениям, тем меньше 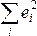
Поскольку коэффициент корреляции симметричен относительно X и Y, то есть rXY=rYX, то можно говорить о корреляции как о мере взаимозависимости переменных. Однако из того, что значения этого коэффициента близки по модулю к единице, нельзя сделать ни один из следующих выводов: Y является причиной X; X является причиной Y; X и Y совместно зависят от какой-то третьей переменной. Величина r ничего не говорит о причинно-следственных связях. Эти вопросы должны решаться, исходя из содержательного анализа задачи. Следует избегать и так называемых ложных корреляций, т.е. нельзя пытаться связать явления, между которыми отсутствуют реальные причинно-следственные связи. Например, корреляция между успехами местной футбольной команды и индексом Доу-Джонса. Классическим является пример ложной корреляции, приведенный в начале ХХ века известным российским статистиком А.А. Чупровым: если в качестве независимой переменной взять число пожарных команд в городе, а в качестве зависимой переменной – сумму убытков от пожаров за год, то между ними есть прямая корреляционная зависимость, т.е. чем больше пожарных команд, тем больше сумма убытков. На самом деле здесь нет причинно-следственной связи, а есть лишь следствия общей причины – величины города.
Проверка гипотезы о значимости выборочного коэффициента корреляции эквивалентна проверке гипотезы о b=0 (см. ниже) и, следовательно, равносильна проверке основной гипотезы об отсутствии линейной связи между Y и X. Вычисляя значение t-статистики
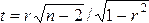
вывод о значимости r делается при |t|>te, где te — соответствующее табличное значение t-распределения с (n-2) степенями свободы и уровнем значимости e.
Пример. Вычислим коэффициент корреляции и проверим его значимость для нашего примера табл. 2.1.
По (2.9) r=43145/(46510×40068,25)0,5=0,9994. R2=0,998. Значение t-статистики t=0,9994×[10/(1-0,998)]0,5=70,67. Поскольку t0,05;10=2,228, то t>t0,05;10 и коэффициент корреляции значим. Следовательно, можно считать, что линейная связь между переменными Y и X в примере существует. Ñ
Если между переменными имеет место нелинейная зависимость, то коэффициент корреляции теряет смысл как характеристика степени тесноты связи. В этом случае используется наряду с расчетом коэффициента детерминации расчет корреляционного отношения.
Предположим, что выборочные данные могут быть сгруппированы по оси объясняющей переменной X. Обозначим s – число интервалов группирования, 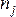

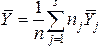

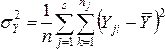
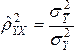
Величину 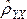
Величина 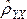
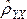
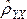
Можно показать, что 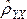
Это позволяет использовать величину разности 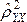
studopedia.ru
/ test
На рисунке представлена реализация процесса, нестационарного по дисперсии
εi это:Вклад случайных мелких незначительных факторов*
Аддитивная модель содержит компоненты в виде …слагаемых
Было замечено, что при увеличении количества вносимых удобрений урожайность также возрастает, однако, по достижении определённого значения фактора моделируемый показатель начинает убывать. Для исследования данной зависимости можно использовать спецификацию уравнения регрессии …
В зависимости от количества регрессоров, модели подразделяются напарные и множественные
В качестве показателя тесноты связи для линейного уравнения парной регрессии используется… линейный коэффициент корреляции
В линейной эконометрической модели наблюдаемое значение результирующей переменной, зависящей от факторов модели, и случайной составляющей равно …сумме
В линейном уравнении множественной регрессии коэффициентами регрессии являются … (несколько правильных ответов)b2 b1
В линейном уравнении парной регрессии параметрами не являютсяyx
В модель множественной регрессии необходимо включать факторы, которыеуменьшают величину остаточной дисперсии; увеличивают величину объяснения
В правой части системы независимых уравнений находится…Совокупность переменных случайных факторов
В системах рекурсивных уравнений количество переменных в правой части каждого уравнения определяется как количества зависимых переменных уравнений и количества независимых факторов суммапредыдущих
В системе независимых уравнений каждое уравнение представлено изолированным уравнением регрессии*
В системе независимых уравнений определён набор экзогенных переменных, при этом в каждом уравнении набор существенных экзогенных переменных…может быть различным
В стандартизированном уравнении множественной регрессии стандартизированными переменными не являются
В таблице представлены результаты дисперсионного анализа. Значение остаточной дисперсии на одну степень свободы равно отношению чисел, определенных на пересечении строки «Остаток» и столбцов «SS» и «df»
В таблице представлены результаты дисперсионного анализа. Значения суммы квадратов можно определить по соответствующей строке в столбцеSS
В таблице представлены результаты дисперсионного анализа. По строке «Остаток» можно определить информацию относительно числа степеней свободы для ___ дисперсии. остаточной
В таблице представлены результаты дисперсионного анализа. Число степеней свободы объясненной (факторной) дисперсии равно отношению чисел, определенных на пересечении строки «регрессия» и столбцов *SS* и *MS*
В таблице представлены результаты дисперсного анализа. Значение суммы квадратов можно определить по соответствующей строке в столбце SS
В эконометрике для проверки статистической значимости уравнения в целом используют…сумма квадратов*
В эконометрических моделях присвоение численных значений признакам качественного характера проводится на основании включения в модель…стандартизированных переменных
В эконометрической практике стационарность временного ряда означает отсутствие тренда
В эконометрическую модель линейным образом включены параметр с, параметр b
В эконометрическую модель нелинейным образом включены переменная x1 переменная x2
В экономической практике стационарность временного ряда означает…. отсутствие систематических изменений дисперсии
Верификация модели заключается в:сопоставлении модельных и реальных данных
Взаимодействие коллинеарных факторов эконометрической модели означает, что …дублируют влияние друг друга на результат; теснота связи между ними превышает по абсолютной величине 0,7
Вид уравнения регрессии выбирают исходя из…существующей природы взаимосвязи исследуемых показателей
Влияние фиктивной переменной наклона на регрессивную модель состоит в …изменении величины свободного слагаемого
Временной ряд, отличающийся от стационарного на неслучайную составляющую (трендовую или периодическую компоненту), называется… регрессионным
Временный ряд называется стационарным, если он является реализацией стационарного стохастическогопроцесса.
Выберете верные утверждения по поводу приведенной формы эконометрических уравнений (несколько правильных ответов): представлена в виде системы независимых уравнений; параметры приведенной формы могут быть выражены как нелинейные функции от параметров структурной формы
Выберите верные утверждения по поводу модели нелинейная, линейная относительно параметров регрессии
Выберите верные утверждения по поводу приведенной формы системы эконометрических уравнений: система независимых уравнений; получается в результате преобразования структурной формы модели
Выберите верные утверждения по поводу экзогенных переменных (несколько правильных ответов):значения экзогенных переменных определяются вне модели; предопределенные переменные
Выберите верные утверждения по поводу экзогенных переменных: не зависят от эндогенных переменных; оказывают влияние на эндогенные переменные
Выберите верные утверждения по поводу эндогенных переменных (несколько правильных ответов):значения эндогенных переменных определяются внутри модели; зависимые переменные
Выберите правильные варианты ответа: гомоскедастичность остатков, отсутствует автокорреляции в остатках
Выбор списка переменных модели и типа взаимосвязи между ними выполняется на этапеспецификация модели
Выделяют три класса систем эконометрических уравнений…системы независимых уравнений, системы взаимозависимых уравнений и системы рекурсивных уравнений
Выражение позволяет вычислить значение коэффициента эластичности*
Гетероскедастичность это:непостоянство дисперсий возмущаюших воздействий*
Гипотеза о мультипликативной структурной схеме взаимодействия факторов. формирующих уровни временного ряда означает… уровень временного ряда = тренд конъюнктурная компонента сезонный фактор случайная компонента
Гипотеза об аддитивной структурной схеме взаимодействия факторов, формирующих уровни временного ряда, означает правомерность следующего представления… уровень временного ряда = тренд + конъюнктурная компонента + сезонный фактор + случайная компонента
Дано уравнение регрессии . Определите спецификацию модели:линейное уравнение множественной регрессии; линейное уравнение множественной регрессии
Даны 2 СВ X и Y. Известны стандартные отклонения и коэффициент корреляции
. Чему равна выборочная ковариация:1,489581
Двухшаговый метод наименьших квадратов применяется для оценки параметров…систем экономических уравнений
Двухшаговый метод наименьших квадратов является частным случаем …косвенного метода наименьших квадратов
Детерминированная компонента уровней временного ряда, описывающая периодические колебания значений характеристики экономического процесса, называется… циклической
Дисперсия — это отношение:среднего квадратичного отклонения к средней арифметической величине
Дисперсия значений временного ряда зависит от времени и неограниченно возрастает с течением времени. Это характерно для… нестационарных рядов
Для временного ряда рассматривается авторегрессионный прогресс первого порядка Y1=α0+α1·Yt-1+εt. Известно, α1=1. Временной ряд является…. описанием взрывного процесса
Для линейного уравнения множественной регрессии проблема спецификации модели связана…с отбором факторов, включаемых в модель
Для множественного коэффициента корреляции модели в естественном масштабе переменных (R1)и множественного коэффициента корреляции для модели в стандартизированном масштабе переменных (R2)справедливо соотношение …R1=R2
Для некоторой выборки известно среднеквадратическое отклонение . Дисперсия для этой выборки равна: (0,21)2*
Для общей (Dобщ), факторной (Dфакт) и остаточной (Dост) дисперсий зависимой переменной и коэффициента детерминации R2 выполняется ….
Для описания тесноты (силы) связи между зависимой переменной и фактором (факторами) проводят расчет…коэффициент корреляции
Для получения системы нормальных уравнений в методе наименьших квадратов следует…взять частные производные первого порядка*
Для проверки значимости коэффициента детерминации используется статистика с распределением Фишера
Для проверки наличия гетероскедастичности остатков служат: графический метод, тест Голдфелда — Квандта
Для расчета доверительных интервалов коэффициента регрессии служат следующие параметрыстандартная ошибка коэффициента регрессии;критическое значение распределения Стьюдента (табличное значение)
Для системы рекурсивных уравнений матрица параметров при эндогенных переменных имеет структуру.треугольную
Для стационарного временного ряда среднее значение по множеству реализаций для заданных моментов времени равно среднему по времени, вычисленному по одной реализации. Такой ряд называют… эргодическим
Для стационарного процесса второго порядка y1 на любых двух временных интервалах должны выполняться условия будут равны между собой пары показателей: _____, рассчитанные на этих интервалах. математическое ожидание, дисперсия, коэффициент автокорреляции второго порядка
Для точно идентифицируемой структурной формы системы одновременных уравнений при оценке параметров применяется _____ метод наименьших квадратов. косвенный*
Для уравнения зависимости предложения на некоторый товар от цены за единицу товара получено значение коэффициента детерминации, равное 0,64. Следовательно, отношение____ дисперсии предложения к его общей дисперсии равно____факторной…0,64;остаточной….0,36
Для успешного применения МНК необходимо, чтобы математическое ожидание случайного отклонения ei равнялось нулю. Это означает, что равны математические ожидания случайного отклонения для каждого наблюдени
Если большие серии соседних остатков имеют одинаковые знаки, то статистика Дарбина-Уотсона приближенно равна: 0
Если доверительный интервал для коэффициента регрессии содержит 0, то справедливы следующие утверждения:фактическое значение статистики Стьюдента для этого коэффициента по модулю меньше критического (табличного);регрессии статистически незначим
Если зависимость между СВ близка к линейной, то статистика Дарбина-Уотсона приближенно равна: 2
Если значение индекса корреляции для нелинейного уравнения регрессии стремится к 1, следовательно нелинейная связь …очень тесная
Если качественный признак имеет k атрибутивных значений, то количество фиктивных переменных в модели должно быть равно…k -2
Если коэффициент регрессии является несущественным, то для него выполняются условия ….стандартная ошибка превышает половину значения параметров;расчетное значение t- критерия Стьюдента меньше табличного
Если коэффициент регрессии является несущественным, то для него выполняются условия …доверительный интервал одновременно содержит положительные и отрицательные величины, расчетное значение t-критерия меньше табличного
Если коэффициент регрессии является существенным, то для него выполняются условия ….стандартная ошибка не превышает половины значения параметра*;значение t- критерия Стьюдента больше табличного*
Если предпосылки метода наименьших квадратов (МНК) не выполняются, то остатки могут характеризоваться …высокой степенью автокорреляции, гетероскедастичностью
Если предпосылки метода наименьших квадратов (МНК) не выполняются, то остатки могут характеризоваться …гетероскедастичностью, высокой степенью автокорреляции
Если справедлива гипотеза H0: a1 =0 относительно коэффициента a1 модели множественной регрессии
Если статистическая оценка θ*n параметра θ содержит всю информацию об оцениваемом параметре, она называется…достаточной
Если структурная форма модели системы эконометрических уравнений точно идентифицируема, то с помощью косвенного МНК получают единственную оценку параметров модели
Если факторы входят в модуль как сумма, то модель называется… аддитивной
Зависимость дисперсии возмущения от номера наблюдения называется гетероскедастичностью*
Зависимость прибыли Y от расходов на рекламу X характеризуется полиномиальной эконометрической моделью второй степени вида
Закон изменения нестационарного временного ряда yt близок к линейному. Этот ряд приводится к стационарному процессу xt c помощью расчеты первых разностей
Значение коэффициента детерминации составило 0,9 следовательно …уравнение регрессии объяснено 90% дисперсии результативного признака;доля остаточной дисперсии зависимой переменной y в ее общей дисперсии составила 10%
Значение коэффициента детерминации составило 0,9 следовательно отношение длины __ дисперсии к общей дисперсии равно ____ Остаточный…0,1, Факторный…0,9
Значение множественного коэффициента линейной корреляции близко к 1. Это означает, что результирующая переменная является линейной функцией от набора факторных переменных
Из теоремы Гаусса-Маркова следует, что оценки являются эффективными, несмещенными, состоятельными
Изображение корреляционного поля для парной регрессионной модели относится к статическим графикам, характеризующим …тесноту и форму зависимости между признаками
Использование в эконометрическом моделировании парной регрессии вместо множественной является ошибкой…спецификации
Использование полинома третьего порядка в качестве регрессионной зависимости для однофакторной модели обусловлено …неоднородностью выборки
Использование фиктивных переменных является оперативным при исследовании…однородных массивов данных
К достоинствам метода наименьших квадратов можно отнести … типовой характер расчётов, интерпретируемость полученных результатов*
К методам обнаружения автокорреляции относятся: критерий Дарбина-Уотсона
К методам устранения гетероскедастичности остатков относятся: метод Кохрана-Оркатта, взвешенный метод наименьших квадратов
К методам устранения мультиколлинеарности факторных переменных относятся добавление фиктивных переменных, изменение спецификации модели, исключение переменных
К ошибкам спецификации относится …неправильный выбор той или иной математической функции
Какие веса используются в сглаживании временных рядов Методом скользящего среднего при m=2-3/35, 12/35, 17/35, 12/35, -3/35
Какие методы используются для сглаживания временного ряда: Аналитические, алгоритмические
Какие основные понятия связаны с временными рядами: Тренд, фильтрация, сглаживание, автоковариация, спектральная плотность, модели генерации значений
Какое из этих значений может принимать линейный коэффициент корреляции при прямой связи?0,6
Какое из этих уравнений является выборочным уравнением регрессии:
Какое из этих уравнений является модельным уравнением регрессии
Какой показатель характеризует значимость коэффициента регрессии? t-статистика Стьюдента этогокоэффициента регрессии
Какому коэффициенту корреляции соответствует возрастающая линейно-функциональная регрессионная зависимость?1
Компонента уровней временного ряда, отражающая влияние неподдающихся учету и регистрации случайных факторов на изучаемый экономический процесс, называетсяслучайной
Коррелированность возмущений с различными номерами называется автокорреляцией*
Коррелограмма — это … график автокорреляционной функции
Корреляция подразумевает наличие связи между …переменными
Коэффициент детерминации в парной регрессии применяется для проверкиадекватности модели; общего качества регрессии
Коэффициент детерминации является величинойдетерминированной
Коэффициент корреляции представляет собой …Число
Коэффициент корреляции это:относительная мера взаимосвязи переменных
Коэффициент парной линейной корреляции между признаками Y и X равен 0,9. Следовательно, доля дисперсии результативного признака Y, не объяснённая линейной парной регрессией Y по фактору X, будет равно …10%*
Коэффициент парной линейной корреляции равен нулю. Это значит, чтомежду признаками нет линейной корреляционной зависимости
Коэффициент эластичности является постоянной величиной и не зависит от значения факторного признака для …степенной функции регрессии
Коэффициенты регрессионных моделей с фиктивными переменными оцениваются _______ методом наименьших квадратов.традиционным
Критерий Стьюдента используется для проверки гипотезы о: Значимости коэффициента корреляции
Критерий Фишера в эконометрических моделях служит показателем преимущества выбранной модели пред другими; для проверки статистической значимости уравнения регрессии
Критерий Фишера используется для оценки значимости …построенного уравнения
Лаговые переменные – это эндогенные переменные в предшествовавшие моменты времени
Левая часть системы взаимозависимых уравнений представлена вектором… зависимых переменных
Линейный коэффициент корреляции — это отношение …ковариации к произведению средних квадратичных отклонений двух показателей
Линейный коэффициент корреляции изменяется в пределах[-1, 1]*
Линейный коэффициент корреляциипоказывает меру тесноты связи между двумя показателями
Математическое выраж-е линейной модели переменного ряда имеет вид Yt= a1Yt-1+a2Yt-2+…+anYt—n
Математическое выражение линейной модели временного ряда имеет вид.
Метод инструментальных переменных применяется в случае корреляции регрессора со случайным возмущением*
Метод наименьших квадратов может применяться для оценки параметров нелинейных регрессионных моделей, если эти модели …имеют автокорреляцию в остатках; характеризуются гетероскедастичностью случайных отклонений;являются нелинейными по параметрам, но внутренние линейными;являются нелинейными по параметрам и внутренние нелинейными
Метод скользящего среднего — это: Алгоритмический метод сглаживания временного ряда
Минимальная дисперсия остатков характерна для оценок, обладающих свойством эффективности*
МНК — оценки параметров обобщенной регрессионной модели несмещенные*
МНК для оценки параметров уравнений регрессии дает хорошие результаты при выполнении определенных предпосылок*
МНК используется для оценивания …параметров линейной регрессии*
Множественный коэффициент линейной корреляции близок к единице. Это означает, что …рассматриваются факторы, значимо влияющие на результат*
Моделирование тенденции осуществляется на основе построения уравнения регрессии зависимости трендовойкомпоненты от времени.
Модель, содержащая фиктивную переменную, относится к ____ модели.регрессионной
На первом этапе применения косвенного метода наименьших квадратов…структурную форму преобразуют в приведенную
Наиболее часто используемый порог вероятности безошибочности выводов при проверке статистических гипотез в эконометрике.. 0,95
Найти коэффициент корреляции, если известен коэффициент детерминации R2=0.992016
Найти среднее квадратичное отклонение, если дисперсия совокупности равна 12,253,5
Найти среднюю урожайность пшеницы с 1 га за три года: 60ц, 49ц, 41ц.50
Наличие возмущения зависимой переменной, вызванное неоднородностью данных в исходной статистической совокупности, является учетомошибки выборки
Невязки это: Отклонение наблюдаемого значения от значения, вычисленного по теоретической функции регрессии
Независимые переменные в регрессионных моделях называютсярегрессорами*
Независимые переменные системы одновременных уравнений, определяемые вне модели, называются экзогенными переменными
Неидентифицируемая система совместных эконометрических уравнений решается не может решаться
Несмещенность оценки на практике означает … что при большом числе выборочных оцениваний остатки не будут накапливать; невозможность перехода от точечного оценивания к интервалу
Обобщенный метод наименьших квадратов может использоваться для корректировки __ остатков гетероскедастичности*
Обобщенный метод наименьших квадратов подразумевает …Введение в выражение для дисперсии остатков коэффициента пропорциональности;Преобразование переменных
Объем выборки должен превышать число рассчитываемых параметров при исследуемых факторах в 5-6 раз*
Один из этапов построения экономической модели, на котором проверяются статистические свойства построенной модели, называется…верификацией модели
Одним из методов присвоения числовых значений фиктивными переменными является…ранжирование
Одним из нарушений предпосылок метода наименьших квадратов для системы одновременных уравнений является …корреляция случайных отклонений с результативными переменными;гетероскедастичность остатков
Остаток регрессионной модели представляет собой оценку:случайной ошибки
от теоретических значений зависимости переменной уУкажите выводы, которые соответствуют графику зависимости остатков имеет место гетероскедастичность остатков;нарушена предпосылка МНК и равенство дисперсий случайных отклонений
Отбор факторов в модель множественной регрессии с использованием метода включения может 83.быть основан на сравнении …величины объясненной дисперсии до и после включения фактора в модель; величины остаточной дисперсии до и после включения фактора в модель
Отношение факторной дисперсии к общей дисперсии равно 0,93, следовательно величина:разности (1 — R2), где R2 — коэффициент детерминации равна 0,07;коэффициент детерминации R2 равна 0,93
Оценки коэффициентов по МНК являются __ оценками теоретических коэффициентов регрессии точечными*
Оценки параметров неидентифицируемой системы эконометрических уравнений… не могут быть найдены обычным МНК
Оценки параметров сверхидентифицируемой системы эконометрических уравнений могут быть найдены с помощью __ метода наименьших квадратов двухшагового*
Оценку существенности (значимости) отдельного параметра уравнения регрессии можно проводить на основании показателей …t-критерия Стьюдента;доверительного интервала
Параметры управления тренда определяются обычным*методом наименьших квадратов.
Первый шаг двухшагового метода наименьших квадратов состоит в нахождении теоретических значений…эндогенных переменных из приведенной формы модели традиционным методом наименьших квадратов
Переменные системы одновременных уравнений, известные к расчетному моменту времени, называются предопределенными переменными*
Переход от точечного оценивая к интервальному возможен, если оценки являются…Эффективными и несмещенными*
По мере удаления индивидуального значения эндогенной переменной от среднего по выборке длина доверительного интервала Увеличивается
По отношению к выбранной спецификации модели, все экономические переменные объекта подразделяются наэндогенные и экзогенные
StudFiles.ru
Читайте также
В этой главе мы сконцентрируемся на том, как при помощи эконометрики получать корректные ответы на вопросы о причинно-следственных связях. Чтобы это сделать, нужно верно специфицировать вашу модель. Под верной спецификацией будем понимать такую, которая позволяет получить состоятельные оценки коэффициентов при интересующих вас переменных. А также получить состоятельные стандартные ошибки для тестирования гипотез.
Глава будет устроена так: мы будем перечислять типичные ловушки, которые приводят к неверной спецификации. Далее для каждой такой ловушки мы будем указывать возможные способы избежать её и устранить проблему.
В каких-то случаях мы будем опираться на уже знакомые вам концепции и понятия. В некоторых же ситуациях мы будем, наоборот, ссылаться на более продвинутые методы и модели, с которыми нам ещё предстоит разобраться в следующих главах учебника (надеемся, это станет для вас дополнительной мотивацией все-таки дочитать его до конца).
Напомним, что в предыдущей главе мы сформулировали два важных определения:
- Эндогенный регрессор — регрессор, который коррелирован со случайными ошибками модели.
- Экзогенный регрессор — регрессор, который не коррелирован со случайными ошибками модели.
Кроме того, в той же главе мы выяснили, что для состоятельности оценки коэффициента при переменной необходимо, чтобы эта переменная была экзогенной (точнее, необходимо выполнение предпосылки №4 линейной регрессионной модели со стохастическими регрессорами из главы 6). Если же регрессор эндогенный, результаты вашего моделирования нельзя интерпретировать в терминах причинно-следственных связей. Нарушение предпосылки №4 об экзогенности регрессора — это самая частая проблема при проведении прикладных исследований на пространственных и панельных данных. Поэтому важно понимать, в каких случаях вам следует опасаться её возникновения. Есть следующие типичные ситуации:
- Эндогенность регрессора из-за пропуска существенной переменной. В качестве важного частного случая тут также следует указать проблему эндогенности из-за самоотбора.
- Эндогенность регрессора из-за выбора неверной функциональной формы связи.
- Эндогенность регрессора из-за двусторонней причинно-следственной связи.
- Эндогенность регрессора из-за ошибок измерения.
В последующих четырех параграфах главы мы подробно обсудим каждый из этих пунктов. В пятом параграфе мы поговорим о других (помимо эндогенности) проблемах, которые могут делать выводы эконометрических исследований необоснованными. В каждом случае мы также укажем основные возможные пути преодоления перечисленных трудностей.
-
7.1. Эндогенность из-за пропуска существенной переменной
-
7.2. Эндогенность из-за выбора неверной функциональной формы связи
-
7.3. Эндогенность из-за двусторонней причинно-следственной связи
-
7.4. Эндогенность из-за ошибок измерения
-
7.5. Другие (помимо эндогенности) потенциальные угрозы обоснованности выводов эконометрического исследования
-
7.6. Чек-лист эконометриста
-
Задания для самостоятельного решения
Расчет коэффициента корреляции и детерминации
Уравнение регрессии всегда дополняется показателем тесноты связи. При использовании линейной регрессии таким показателем является линейный коэффициент корреляции rxy . Существует несколько видов формулы линейного коэффициента корреляции, приведем основные из них:
Линейный коэффициент корреляции, как известно, всегда находится в следующих пределах: -1 < rxy < 1. Знак коэффициента регрессии определяет знак коэффициента корреляции. Если b < 0, тогда — 1 < rxy < 0 , и наоборот, если Ь > 0, тогда 0 < rxy < 1. Чем ближе значение коэффициента корреляции по модулю | rxy|, к единице, тем теснее связь между признаками в линейной форме. Однако, если абсолютная величина коэффициента корреляции близка к нулю, то это означает, что между рассматриваемыми признаками отсутствует линейная связь. При другом виде уравнения регрессии связь может оказаться достаточно тесной. В приведенном выше примере коэффициент корреляции равен 0,97, следовательно, в данном случае имеет место достаточно тесная связь между результатом и фактором.
Для оценки качества подбора линейного уравнения регрессии находят также квадрат коэффициента корреляции, называемый коэффициентом детерминации R = (rxy)2 . Он отражает долю вариации результативного признака, объясненную с помощью уравнения регрессии, или, иными словами, долю дисперсии результата, объясненную регрессией, в общей дисперсии у:
Следовательно, величина (1— R2) характеризует долю вариации, или долю дисперсии результата у, вызванную влиянием всех остальных, не учтенных в модели факторов. Значения коэффициента детерминации могут изменяться от нуля до единицы (0 < R2 < 1) • Для рассмотренного примера R2=0,94 это означает, что уравнением регрессии объясняется 94% дисперсии результативного признака, а прочими, не учтенными в модели факторами — 6%. Чем ближе коэффициент детерминации к единице, тем меньше роль других факторов и линейное уравнение регрессии описывает лучше исходные данные.
7. Критерий Фишера.
После выбора уравнения линейной регрессии и оценки его параметров проводится оценка значимости как уравнения в целом, так и отдельных его параметров.
Оценка значимости уравнения регрессии в целом осуществляется с помощью критерия Фишера,который называют также F-критерием. При этом выдвигается нулевая гипотез (Н0): коэффициент регрессии равен нулю (b = 0), следовательно, фактор хне оказывает влияния на результат у и линия регрессии параллельна оси абсцисс.
Перед тем как приступить к расчету критерия Фишер; проведем анализ дисперсии. Общую сумму квадратов отклонений уот 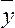
Где:
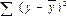
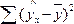
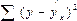
Общая сумма квадратов отклонений результативного признака у от среднего значения определяется влиянием различных причин. Условно всю совокупность последних можно разделить на две группы: изучаемый фактор х и прочие, случайные и не включаемые в модель факторы.
Определение дисперсии на одну степень свободы
Так как эти дисперсии рассчитаны на одну степень свободы, их можно сравнивать между собой.
Критерий Фишера позволяет проверить нулевую гипотезу Hо том, что факторная и остаточная дисперсии на одну степень свободы равны между собой (Dфак.=Dост.). Критерий Фишера рассчитывается по следующей формуле:
Если (Fфак.>Fтабл..), тогда гипотеза H0 отклоняется и делается вывод, что связь между у и х существенна и уравнение регрессии статистически значимо. Если (Fфак.≤Fтабл.), тогда гипотеза H0 принимается и делается вывод, что уравнение регрессии статистически незначимо, так как существует риск (при заданном уровне надежности) сделать неправильный вывод о наличии связи между х и у.
8. Стандартные ошибки параметров.В
9. линейной регрессии часто оценивается не только значимость уравнения регрессии в целом, но и значимость его отдельных параметров, а также коэффициента корреляции.
Для того чтобы осуществить такую оценку, необходимо для всех параметров рассчитывать стандартные ошибки(ma, mb, mr)
обозначив остаточную дисперсию на одну степень свободы через S2, получим
Величины стандартных ошибок применяются не только для проверки значимости параметров, но и для расчета доверительных интервалов.
studopedia.ru
/ эконометрика 1
-
Автокорелляция ошибок –это:корреляция ошибок регрессии для разных наблюдений
-
Автокорреляция остатков бывает следующих видов – отрицательная, положительная
-
В каких случаях значение коэффициента детерминации R^2 может выйти за пределы 0:1:если в уравнении регрессии отсутствует константа Во
-
В оцениваемой модели у=хВ+Eотсутствует часть существенных независимых переменных , тогда оценкаB, полученная в данной регрессии в общем случаесмещенная
-
В результате оценки параметров регрессии у=а+В*Х+Eбыли получены следующие результаты =10,4 В=4,7 Доверительный интервал для В с уравнением доверия 95% составил (3,9,5,5)Что показывает полученный доверительный интервал с указанным уровнем доверия?Истинное значение коэффициента В находится в указанном интервале с вероятностью 0,95
-
В чем суть гетероскедастичности: дисперсии случайных отклонений изменяются
-
В эконометрической модели линейного уравнения регрессии у=а+в1х1+в2х2+…вkхk+Eпараметрами являютсяа ,bj
-
В эконометрической модели линейного уравнения регрессии у=а+в1х1+в2х2+…вkхk+Eкоэффициентом регрессии ,характеризующим среднее изменение зависимой перменной …..bj
-
Выберите верные утверждения о производственной функции Кобба-Дугласса: записывается степенным уравнением, является нелинейной зависимостью.
-
Гетероскедастичность – это зависимость дисперсии случайных ошибок от номера наблюдения
-
Для выбора лучшей спецификации модели применяется РЕ-тест, J-тест
-
Для выявления ошибки линейной спецификации регрессии применяется RESET-тест
-
Для двух случайных величин х и у было получено значение парного коэффициента корреляции r-0.9 вывод:связь тесная и прямая
-
Для нелинейной регрессионной модели зависимости рассчитано значение индекса детерминации R^2=0,9.Тогда значение индекса корреляции составиткорень из 0.9
-
Для оценки параметров регрессионной модели с гетероскедастичным остатками используется обобщенныйметод наименьших квадратов
-
Для регрессионной модели вида у= а+в1*х1+в2*х2…..показателем тесноты связи является коэффициент множественной корреляции
-
Для регрессионной модели вида у=а+в*х+Eпостроена на координатной плоскости совокупность точек с координатами уiхi..данное графическое отображение зависимости называетсяполем корреляции
-
Для регрессионной модели зависимости потребления материала на единицу продукции от объема выпуска продукции построено нелинейное уравнение..см рисунок R2=0,904.Следовательно объемом выпуска продукции объяснено 90,4 дисперсии потребления материалов на единицу продукции
-
Для регрессионной модели известны следующие величины дисперсий …….сумм(у-у)^2=сумм(у-у)^2+сумм(у-у)^2
-
Для регрессионной модели несмещенность оценки параметра означает, что ее выборочное математическое ожидание равно оцениваемому параметру, рассчитанному по генеральной совокупности.
-
Для регрессионной модели парной регрессии рассчитано значение коэфф.детерминации R=0,831 ……16,9%
-
Для регрессионной модели парной регрессии рассчитано значение коэффициента детерминации R2.Тогда долю остаточной дисперсии зависимой переменной характеризует величина(1-R)^2
-
Для совокупности из nединиц наблюдений построена модель линейного уравнения множеств регрессии с количеством параметров при независимых переменных равнымkТогда при расчете остаточной дисперсии на одну степень свободы величину дисперсии относят к значениюn—k-1
-
Для совокупности из nединиц наблюдений рассчитывают общую дисперсию на одну степень свободы , при этом величину дисперсии относят к значениюn-1
-
Долю объясненной с помощью регрессии дисперсии в общей дисперсии зависимой переменной характеризует коэффициент детерминации
-
Если параметр эконометрической модели не является статистически значимым, то соответствующая независимая переменная на определенном уровне доверия: не оказывает влияния на моделируемы показатель (зависимую переменную)
-
Если параметр эконометрической модели не является статистически значимым , то его значение признается равным 0
-
Если параметр эконометрической модели не является статистически значимым , то соответствующая независимая переменная не оказывает влияния на моделируемый показатель (зависимую переменную)
-
Если параметр эконометрической модели является статистически значимым , то его значение признается отличным от 0
-
Исследуется регрессия у=В0+В11+В22+В33+E…известно что 4,3+10х1-3,5=х3. В этом случае говорят о наличиигетероскедастичности
-
Как влияет исключение переменной из уравнения множественной регрессии на занчение F-критерия и коэффициент детерминации?F– критерий может как умен так и увел , R2 уменьшится
-
Какими свойствами обладают оценки , полученные при решении ур-ия парной линейной регрессии у1=ах+в+Eметодом наименьших квадратов , если выполнены условия Гаусса-Маркова и случайные остатки имеют нормальное распределение ..Состоятельность, несмещенностью и эффективностью
-
Каковы показатели качества уравнения регрессии в целом? Значение F-статистики для уравнения регрессии , скорректированный коэффициент детерминации
-
Каковы показатели качества уравнения регрессии в целом? Скорректированный коэффициент детерминации, значение Fстатистики для уравнения регрессии.
-
Какой вывод можно сделать по результату проведения теста Рамсея? Спецификация уравнения ошибочная
-
Когда целесообразно добавление новой объясняющей переменной в модель? При росте скорректированного коэффициента детерминации после ее включения
-
Коллинеарность факторов эконометрической модели у=а+в1х1+в2х2+…+вjхj+…вkxk+Eпроверяется на основе матрицы парных коэффициентов линейнойкорреляции
-
Коэффициент при экзогенной переменной в уравнении линейной регрессии показывает:на сколько ед изменится эндогенная переменная при изменении экзогенной перменной на 1 ед
-
Коэффициент регрессии называется значимым, если есть достаточная высокая вероятность того , что его истинное значение отлично от 0
-
Коэффициент регрессии называется незначимым если: есть достаточно высокая вероятность того, что его истинное значение равно0
-
Метод наименьших квадратов может применятся для оценки параметров исходной регрессионной модели в линейнойформе
-
Нелинейным уравнением парной регрессии является у=а+в*х+с*х2+E
-
Одной из предпосылок МНК является то , что в остатках регрессионной модели автокорреляция должна отсутствовать
-
Особенность эконометрики как прикладной науки заключается в количественном измерении существующих взаимосвязей социально-экономических показателей и систем.
-
Оценка А значения параметра а явлеется состоятельной если: при стремлении числа наблюдений к бесконечности
-
Оценка А значения параметра а является несмещенной если : математическое ожидание а равно а
-
Оценка А значения параметра а является состоятельной если …….при стремлении числа наблюдений к бесконечности
-
По типу функциональной зависимости между переменными эконометрической модели различают линейные и нелинейные ур-ия регрессии
-
Под верификацией модели понимается оценка качества модели
-
Последствия включения в ур-ие регрессии несущественной переменной : оценки параметров будут несмещенными ,эффективность оценок снизится
-
Последствия мультиколлинеарности : ОЦЕНКИ ОЦЕНКИ
-
Последствия мультиколлинеарности : оценки становятся очень чувствительными …..оценки коэффициентов остаются не смещенными
-
Последствия невключения в уравнение регрессии существенной переменной в общем случае Оценки параметров будут смещенными
-
Предположения теоремы Гаусса-Маркова включают в себя: Ошибки регрессии должны быть независимы друг от друга , дисперсия ошибок регрессии постоянна для всех наблюдений.
-
При возникновении мультиколлинеарности :стандартные ошибки коэффициента увеличиваются, вычисленные t-статистики становятся занижены
-
При выполнении предпосылок МНК оценки параметров регрессионной модели , рассчитанные с помощью МНК обладают свойствами состоятельности несмещенности эффективности
-
При изучении зависимости зарплаты в Казахстане от возраста и пола была получена следующая регрессия W=1489 +747+AGE-1678*S, гдеW-зарплата …..женщины получают в среднем зарплату меньше минимума 1678
-
При изучении зависимости издержек производства ….была построена модель у= 10 -0,15х,это означает что при увеличении инвестиций в совершенствование технологий на 1 тыс руб издержки производства в среднем снижаются на 150 р.
-
При изучении зависимости издержек производства у от основных производственных фондов х была построена модель у=10+0,75 х, это означает, что при увеличении основных производственных фондов на 1 тыс руб издержки производства в среднем увел на 750р
-
При изучении зависимости между показателями безработицы х и инфляции у…у=4,23-2,41х…расчетное значение -2.1Можем ли принять гипотезу …0.05, если критическое значение tстатистики = 2.57НЕ можем поскольку абсолютное значение tстатистики для показателя безработицы меньше критического значения
-
При исследовании выборки обнаружено аномальное значения фактора Yдля одного наблюдения .При каких условиях корректно будет провести исключение соответствующего наблюдения из выборки:в случае если аномальное значение Yневозможно объяснить и вы как исследователь не знаете, соответствует оно действительности или нет.: в случае если аномальное значение Yсоответствует действительности , но это отличие не возможно объяснить в рамках проводимого исследования
-
При исследовании зависимости суммы активов банка у от собственного капитала k.привлеченных ресурсовr….=3,74 при уровне значимости 1% у=e85-0,46к-19r+0,48sF=4,75
-
При оценки качества уравнения регрессии был рассчитан коэффициент детерминации R^2=0,91.Это означает что построенная модель достаточно хорошо подогнана к выборочным данным
-
При оценки качества ур-ия регрессии был рассчитан коэффициент детреминации R=0.18,это означает что построенная модель довольно плохо подогнана к выборочным данным
-
При переходе к линейному виду для степеннойзависимости вводится замена Х=ln(х),Y=ln(y)
-
При переходе к линейному виду для степенной, экспоненциальнойзависимости зависимая переменная преобразуется по формулеY=ln(y)
-
При переходе обратно от построенного вспомогательного линейного уравнения У=В0+В1Х к нелинейному виду для парной степенной зависимоти у= В0*XВ1 надо найти искомое значение коэффициентов по формулеВ0=Е^Во, В1=В1
-
При построении какого уравнения в EViewsвводится командаlslog(у) с х1 х2 х3Экспоненциального
-
При построении уравнения множественной регрессии проверку тесноты связи между независимыми переменными модели осуществляют на основе :матрицы парных коэффициентов линейной корреляции
-
При проведении RESET-теста..линейная спецификация регрессии является ошибочной с уравнением доверия 0,95, если Р-значениеменьше 0,05
-
Примерами фиктивных переменных в эконометрич модели зависимости стоимости 1м^2 жилья не являются :площадь жилья, величина прожитого минимума в регионе.
-
Проверка наличия коллинеарных факторов в эконометрической модели у=а+в1х1+в2х2+Eоснована на рассмотрении коэффициента корреляции между х1 и х2
-
Пусть качественный признак принимает 4 значения, сколько фиктивных переменных надо ввести в у равнение (при условии наличия в ур-ии константы) ТРИ
-
Регрессионная модель вида у=а+в*х1+с*(х2)^2+Eявляется нелинейной относительнопеременной х2
-
Стандартное нормальное распределение имеет параметры : мат ожидание =0,дисперсия=1
-
Строится эконометрическая модель уравнения множественной регрессии для зависимости Уот пяти факторов…….у=х(1),х(2),х(4))+E
-
Суть коэффициента детерминации состоит в следующем :коэффициент определяет долю общего разброса значений, объясненного ур-ием регрессии
-
Укажите тест, который не используется для выявления гетероскедастичности ДАРБИНА-УОТСОНА
-
Уравнение множественной регрессии имеет вид у= — 27,16 +1,37х-0,29х2 Параметр а1=1,37 означает следующее при увеличении х1 на одну единицу своего измерения и при фиксированном значении фактора Х2 переменная увеличивается на 1,37 единиц своего измерения.
-
Уравнение регрессии называется незначимым в целом, если есть достаточно высокая вероятность того , что все коэффициенты равны 0
-
Фиктивные переменные эконометрической модели : используются в случае неоднородных совокупностей данных, отражают качественные признаки исследуемого объекта наблюдения
-
Что означает правильно специфицировано уравнение регрессии :правильная функциональная зависимость
-
Эконометрическое моделирование зависимости по неоднородной совокупности данных может осуществляется на основе разделения неоднородной совокупности данных на однородные
-
Эконометрическое моделирование зависимости по неоднородной совокупности данных может осуществляться на основе: использования фиктивных переменных, разделения неоднородной совокупности данных на однородные
-
Экспоненциальная зависимость записана уравнением: у=e^В0+В1*х1….+Вn*хn+E
Основные задачи эконометрики:
-
Количественная оценка экономических связей
-
Проверка на реальных данных теоритических моделей
-
Статистическое тестирование гипотез
-
Экономическое прогнозирование
-
Имитация возможных сценариев социально-экономического развития
Стохастическиминазываются связи, при которых допускается случайное изменение зависимых переменных даже при сохранении значений всех остальных переменных, от которых они зависят.
Зависимая(эндогенная, результирующая, объясняемая) переменная характеризует результат функционирования анализируемой экономической системы.
Независимые(экзогенные, объясняющие) переменные или регрессоры являются «причиной» изменения зависимой переменной.
Уравнение регрессии:y=f(x, β) +ε, у-зависимая переменная, х-независимая, β-параметры регрессии, ε-случайная компонента(ошибка регрессии)
Системы эконометрических уравнений– это эконометрические модели, описывающиеся системой уравнений, в которые входят как регрессионные уравнения, так и тождества.
Каждое из регрессионных уравнений может включать в себя как независимые переменные, так и зависимые из других уравнений.
В моделях временных рядоврассматриваются зависимость эндогенной переменнойот времени или от ее значений в прошлые периоды времени.
Типы моделей временных рядов:
-
Модели тренда
-
Модели сезонности
-
Модели тренда и сезонности
-
Адаптивные модели
-
Модели авторегрессии и скользящего среднего
Пространственные данныепредставляют собой данные о совокупности объектов в определенный момент времени
Временные данные (временной ряд) есть серия наблюдений об одном и том же объекте в последовательные моменты времени
Панельные данные представляютсобой совокупность наблюдений о нескольких объектах в разные моменты времени в течении некоторого периода
Этапы эконометрического исследования:
-
Постановка задачи. На этом этапе определяются цели моделирования, набор факторов и показателей.
-
Анализ предметной области. Проводится предварительный анализ сущности изучаемого явления, изучаются теоретические результаты и опят проведения подобных исследований.
-
Формулировка моделей (выбор спецификации). Определяется вид модели и вид зависимости, а также уточняется набор переменных.
-
Сбор данных и анализ их качества
-
Определение (оценка) параметров модели. По имеющимся данным рассчитываются параметры выбранной модели, проводится ее статистический анализ, проверка гипотез относительно тех закономерностей, на изучение которых направлено данное исследование.
-
Верификация (оценка качества модели). Сопоставление реальных и рассчитанных по построенной модели данных и оценка их точности, т.е. проверка адекватности модели исследуемому явлению или процессу.
-
Интерпретация результатов. Формулировка качественных и количественных выводов об изучаемом объекте и сопоставление их с теоритическими результатами.
StudFiles.ru
Коэффициент корреляции, коэффициент детерминации, корреляционное отношение
Таблица 2.1
Индивидуальное потребление и личные доходы (США, 1954-1965 гг.)
| Год | Индивидуальное потребление, млрд. долл. | Личные доходы, млрд. долл. |
Заметим, что исходные данные должны быть выражены величинами примерно одного порядка. Вычисления удобно организовать, как показано в таблице 2.2. Сначала рассчитываются 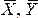

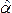
Оцененное уравнение регрессии запишется в виде 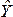
Следующая важная проблема состоит в том, чтобы определить, насколько «хороши» полученные оценки и уравнение регрессии. Этот вопрос рассматривается по следующим стадиям исследования: квалифицирование (выяснение условий применимости результатов), определение качества оценок, проверка выполнения допущений метода наименьших квадратов.
Относительно квалифицирования уравнения 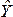
Таблица 2.2
Рабочая таблица расчетов (по данным табл. 2.1)
| Год | X | Y | x | y | x2 | xy | 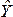 |
ei |
| -93 | -85,75 | 7974,75 | 235,48 | 0,52 | ||||
| -75 | -67,75 | 5081,25 | 252,18 | 1,82 | ||||
| -57 | -54,75 | 3120,75 | 268,88 | -1,88 | ||||
| -41 | -40,75 | 1670,75 | 283,72 | -2,72 | ||||
| -31 | -31,75 | 984,25 | 292,99 | -2,99 | ||||
| -13 | -10,75 | 139,75 | 309,69 | 1,31 | ||||
| 3,25 | 321,75 | 3,25 | ||||||
| 13,25 | 185,5 | 334,74 | 0,26 | |||||
| 33,25 | 1163,75 | 354,22 | 0,78 | |||||
| 53,25 | 2928,75 | 372,77 | 2,23 | |||||
| 79,25 | 6894,75 | 402,45 | -1,45 | |||||
| 109,25 | 13000,75 | 432,13 | -1,13 | |||||
| å | 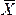 =350,00 =350,00 |
 =321,75 =321,75 |
0,00 |  =321,75 =321,75 |
0,00 |
Полученное уравнение 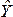
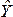
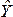
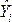
Заметим, что ошибка прогноза ei фактически является оценкой значений ui. График ошибки ei представлен на рис. 2.2. Следует отметить факт равенства нулю суммы Sei=0, что согласуется с первым ограничением модели парной регрессии — Eui=0, i=1,…,n. Ñ
Рис. 2.2. График ошибки прогноза
В модели (2.2) функция f может быть и нелинейной. Причем выделяют два класса нелинейных регрессий:
q регрессии, нелинейные относительно включенной объясняющей переменной, но линейные по параметрам, например полиномы разных степеней — Yi =a0 + a1Xi + a2Xi2+ ui, i=1,…,n или гипербола — Yi =a0 + a1/Xi + ui, i=1,…,n;
q регрессии нелинейные по оцениваемым параметрам, например степенная функция — Yi =a0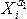
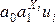
В первом случае МНК применяется так же, как и в линейной регрессии, поскольку после замены, например, в квадратичной параболе Yi =a0 + a1Xi + a2Xi2+ ui переменной Xi2 на X1i: Xi2=X1i, получаем линейное уравнение регрессии Yi =a0 + a1Xi + a2X1i+ ui, i=1,…,n.
Во втором случае в зависимости от вида функции возможно применение линеаризующих преобразований, приводящих функцию к виду линейной. Например, для степенной функции Yi =a0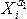
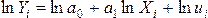
Однако для, например, модели Yi =a0+a2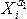
Для трактовки линейной связи между двумя переменными акцентируют внимание на коэффициенте корреляции.
Пусть имеется выборка наблюдений (Xi, Yi), i=1,…,n, которая представлена на диаграмме рассеяния, именуемой также полем корреляции (рис. 2.3).
Y
X
Рис. 2.3. Диаграмма рассеяния
Разобьем диаграмму на четыре квадранта так, что для любой точки P(Xi, Yi) будут определены отклонения
Ясно, что для всех точек I квадранта xiyi>0; для всех точек II квадранта xiyixiyi>0; для всех точек IV квадранта xiyixiyi может служить мерой зависимости между переменными X и Y. Если большая часть точек лежит в первом и третьем квадрантах, то åxiyi>0 и зависимость положительная, если большая часть точек лежит во втором и четвертом квадрантах, то åxiyixiyi близка к нулю и между X и Y связи нет.
Указанная мера зависимости изменяется при выборе единиц измерения переменных X и Y. Выразив åxiyi в единицах среднеквадратических отклонений, получим после усреднения выборочный коэффициент корреляции:
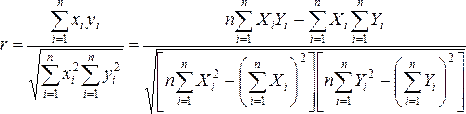
Из последнего выражения можно после преобразований получить следующую формулу для квадрата коэффициента корреляции:


Квадрат коэффициента корреляции называется коэффициентом детерминации. Согласно (2.10) значение коэффициента детерминации не может быть больше единицы, причем это максимальное значение будет достигнуто при 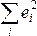
Кроме того, из (2.10) следует, что коэффициент детерминации равен доле дисперсии Y (знаменатель формулы), объясненной линейной зависимостью от X (числитель формулы). Это обстоятельство позволяет использовать R2 как обобщенную меру «качества» статистического подбора модели (2.6). Чем лучше регрессия соответствует наблюдениям, тем меньше 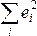
Поскольку коэффициент корреляции симметричен относительно X и Y, то есть rXY=rYX, то можно говорить о корреляции как о мере взаимозависимости переменных. Однако из того, что значения этого коэффициента близки по модулю к единице, нельзя сделать ни один из следующих выводов: Y является причиной X; X является причиной Y; X и Y совместно зависят от какой-то третьей переменной. Величина r ничего не говорит о причинно-следственных связях. Эти вопросы должны решаться, исходя из содержательного анализа задачи. Следует избегать и так называемых ложных корреляций, т.е. нельзя пытаться связать явления, между которыми отсутствуют реальные причинно-следственные связи. Например, корреляция между успехами местной футбольной команды и индексом Доу-Джонса. Классическим является пример ложной корреляции, приведенный в начале ХХ века известным российским статистиком А.А. Чупровым: если в качестве независимой переменной взять число пожарных команд в городе, а в качестве зависимой переменной – сумму убытков от пожаров за год, то между ними есть прямая корреляционная зависимость, т.е. чем больше пожарных команд, тем больше сумма убытков. На самом деле здесь нет причинно-следственной связи, а есть лишь следствия общей причины – величины города.
Проверка гипотезы о значимости выборочного коэффициента корреляции эквивалентна проверке гипотезы о b=0 (см. ниже) и, следовательно, равносильна проверке основной гипотезы об отсутствии линейной связи между Y и X. Вычисляя значение t-статистики
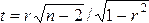
вывод о значимости r делается при |t|>te, где te — соответствующее табличное значение t-распределения с (n-2) степенями свободы и уровнем значимости e.
Пример. Вычислим коэффициент корреляции и проверим его значимость для нашего примера табл. 2.1.
По (2.9) r=43145/(46510×40068,25)0,5=0,9994. R2=0,998. Значение t-статистики t=0,9994×[10/(1-0,998)]0,5=70,67. Поскольку t0,05;10=2,228, то t>t0,05;10 и коэффициент корреляции значим. Следовательно, можно считать, что линейная связь между переменными Y и X в примере существует. Ñ
Если между переменными имеет место нелинейная зависимость, то коэффициент корреляции теряет смысл как характеристика степени тесноты связи. В этом случае используется наряду с расчетом коэффициента детерминации расчет корреляционного отношения.
Предположим, что выборочные данные могут быть сгруппированы по оси объясняющей переменной X. Обозначим s – число интервалов группирования, 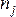

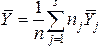

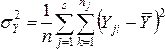
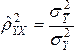
Величину 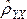
Величина 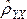
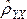
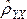
Можно показать, что 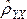
Это позволяет использовать величину разности 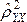
studopedia.ru
/ test
На рисунке представлена реализация процесса, нестационарного по дисперсии
εi это:Вклад случайных мелких незначительных факторов*
Аддитивная модель содержит компоненты в виде …слагаемых
Было замечено, что при увеличении количества вносимых удобрений урожайность также возрастает, однако, по достижении определённого значения фактора моделируемый показатель начинает убывать. Для исследования данной зависимости можно использовать спецификацию уравнения регрессии …
В зависимости от количества регрессоров, модели подразделяются напарные и множественные
В качестве показателя тесноты связи для линейного уравнения парной регрессии используется… линейный коэффициент корреляции
В линейной эконометрической модели наблюдаемое значение результирующей переменной, зависящей от факторов модели, и случайной составляющей равно …сумме
В линейном уравнении множественной регрессии коэффициентами регрессии являются … (несколько правильных ответов)b2 b1
В линейном уравнении парной регрессии параметрами не являютсяyx
В модель множественной регрессии необходимо включать факторы, которыеуменьшают величину остаточной дисперсии; увеличивают величину объяснения
В правой части системы независимых уравнений находится…Совокупность переменных случайных факторов
В системах рекурсивных уравнений количество переменных в правой части каждого уравнения определяется как количества зависимых переменных уравнений и количества независимых факторов суммапредыдущих
В системе независимых уравнений каждое уравнение представлено изолированным уравнением регрессии*
В системе независимых уравнений определён набор экзогенных переменных, при этом в каждом уравнении набор существенных экзогенных переменных…может быть различным
В стандартизированном уравнении множественной регрессии стандартизированными переменными не являются
В таблице представлены результаты дисперсионного анализа. Значение остаточной дисперсии на одну степень свободы равно отношению чисел, определенных на пересечении строки «Остаток» и столбцов «SS» и «df»
В таблице представлены результаты дисперсионного анализа. Значения суммы квадратов можно определить по соответствующей строке в столбцеSS
В таблице представлены результаты дисперсионного анализа. По строке «Остаток» можно определить информацию относительно числа степеней свободы для ___ дисперсии. остаточной
В таблице представлены результаты дисперсионного анализа. Число степеней свободы объясненной (факторной) дисперсии равно отношению чисел, определенных на пересечении строки «регрессия» и столбцов *SS* и *MS*
В таблице представлены результаты дисперсного анализа. Значение суммы квадратов можно определить по соответствующей строке в столбце SS
В эконометрике для проверки статистической значимости уравнения в целом используют…сумма квадратов*
В эконометрических моделях присвоение численных значений признакам качественного характера проводится на основании включения в модель…стандартизированных переменных
В эконометрической практике стационарность временного ряда означает отсутствие тренда
В эконометрическую модель линейным образом включены параметр с, параметр b
В эконометрическую модель нелинейным образом включены переменная x1 переменная x2
В экономической практике стационарность временного ряда означает…. отсутствие систематических изменений дисперсии
Верификация модели заключается в:сопоставлении модельных и реальных данных
Взаимодействие коллинеарных факторов эконометрической модели означает, что …дублируют влияние друг друга на результат; теснота связи между ними превышает по абсолютной величине 0,7
Вид уравнения регрессии выбирают исходя из…существующей природы взаимосвязи исследуемых показателей
Влияние фиктивной переменной наклона на регрессивную модель состоит в …изменении величины свободного слагаемого
Временной ряд, отличающийся от стационарного на неслучайную составляющую (трендовую или периодическую компоненту), называется… регрессионным
Временный ряд называется стационарным, если он является реализацией стационарного стохастическогопроцесса.
Выберете верные утверждения по поводу приведенной формы эконометрических уравнений (несколько правильных ответов): представлена в виде системы независимых уравнений; параметры приведенной формы могут быть выражены как нелинейные функции от параметров структурной формы
Выберите верные утверждения по поводу модели нелинейная, линейная относительно параметров регрессии
Выберите верные утверждения по поводу приведенной формы системы эконометрических уравнений: система независимых уравнений; получается в результате преобразования структурной формы модели
Выберите верные утверждения по поводу экзогенных переменных (несколько правильных ответов):значения экзогенных переменных определяются вне модели; предопределенные переменные
Выберите верные утверждения по поводу экзогенных переменных: не зависят от эндогенных переменных; оказывают влияние на эндогенные переменные
Выберите верные утверждения по поводу эндогенных переменных (несколько правильных ответов):значения эндогенных переменных определяются внутри модели; зависимые переменные
Выберите правильные варианты ответа: гомоскедастичность остатков, отсутствует автокорреляции в остатках
Выбор списка переменных модели и типа взаимосвязи между ними выполняется на этапеспецификация модели
Выделяют три класса систем эконометрических уравнений…системы независимых уравнений, системы взаимозависимых уравнений и системы рекурсивных уравнений
Выражение позволяет вычислить значение коэффициента эластичности*
Гетероскедастичность это:непостоянство дисперсий возмущаюших воздействий*
Гипотеза о мультипликативной структурной схеме взаимодействия факторов. формирующих уровни временного ряда означает… уровень временного ряда = тренд конъюнктурная компонента сезонный фактор случайная компонента
Гипотеза об аддитивной структурной схеме взаимодействия факторов, формирующих уровни временного ряда, означает правомерность следующего представления… уровень временного ряда = тренд + конъюнктурная компонента + сезонный фактор + случайная компонента
Дано уравнение регрессии . Определите спецификацию модели:линейное уравнение множественной регрессии; линейное уравнение множественной регрессии
Даны 2 СВ X и Y. Известны стандартные отклонения и коэффициент корреляции
. Чему равна выборочная ковариация:1,489581
Двухшаговый метод наименьших квадратов применяется для оценки параметров…систем экономических уравнений
Двухшаговый метод наименьших квадратов является частным случаем …косвенного метода наименьших квадратов
Детерминированная компонента уровней временного ряда, описывающая периодические колебания значений характеристики экономического процесса, называется… циклической
Дисперсия — это отношение:среднего квадратичного отклонения к средней арифметической величине
Дисперсия значений временного ряда зависит от времени и неограниченно возрастает с течением времени. Это характерно для… нестационарных рядов
Для временного ряда рассматривается авторегрессионный прогресс первого порядка Y1=α0+α1·Yt-1+εt. Известно, α1=1. Временной ряд является…. описанием взрывного процесса
Для линейного уравнения множественной регрессии проблема спецификации модели связана…с отбором факторов, включаемых в модель
Для множественного коэффициента корреляции модели в естественном масштабе переменных (R1)и множественного коэффициента корреляции для модели в стандартизированном масштабе переменных (R2)справедливо соотношение …R1=R2
Для некоторой выборки известно среднеквадратическое отклонение . Дисперсия для этой выборки равна: (0,21)2*
Для общей (Dобщ), факторной (Dфакт) и остаточной (Dост) дисперсий зависимой переменной и коэффициента детерминации R2 выполняется ….
Для описания тесноты (силы) связи между зависимой переменной и фактором (факторами) проводят расчет…коэффициент корреляции
Для получения системы нормальных уравнений в методе наименьших квадратов следует…взять частные производные первого порядка*
Для проверки значимости коэффициента детерминации используется статистика с распределением Фишера
Для проверки наличия гетероскедастичности остатков служат: графический метод, тест Голдфелда — Квандта
Для расчета доверительных интервалов коэффициента регрессии служат следующие параметрыстандартная ошибка коэффициента регрессии;критическое значение распределения Стьюдента (табличное значение)
Для системы рекурсивных уравнений матрица параметров при эндогенных переменных имеет структуру.треугольную
Для стационарного временного ряда среднее значение по множеству реализаций для заданных моментов времени равно среднему по времени, вычисленному по одной реализации. Такой ряд называют… эргодическим
Для стационарного процесса второго порядка y1 на любых двух временных интервалах должны выполняться условия будут равны между собой пары показателей: _____, рассчитанные на этих интервалах. математическое ожидание, дисперсия, коэффициент автокорреляции второго порядка
Для точно идентифицируемой структурной формы системы одновременных уравнений при оценке параметров применяется _____ метод наименьших квадратов. косвенный*
Для уравнения зависимости предложения на некоторый товар от цены за единицу товара получено значение коэффициента детерминации, равное 0,64. Следовательно, отношение____ дисперсии предложения к его общей дисперсии равно____факторной…0,64;остаточной….0,36
Для успешного применения МНК необходимо, чтобы математическое ожидание случайного отклонения ei равнялось нулю. Это означает, что равны математические ожидания случайного отклонения для каждого наблюдени
Если большие серии соседних остатков имеют одинаковые знаки, то статистика Дарбина-Уотсона приближенно равна: 0
Если доверительный интервал для коэффициента регрессии содержит 0, то справедливы следующие утверждения:фактическое значение статистики Стьюдента для этого коэффициента по модулю меньше критического (табличного);регрессии статистически незначим
Если зависимость между СВ близка к линейной, то статистика Дарбина-Уотсона приближенно равна: 2
Если значение индекса корреляции для нелинейного уравнения регрессии стремится к 1, следовательно нелинейная связь …очень тесная
Если качественный признак имеет k атрибутивных значений, то количество фиктивных переменных в модели должно быть равно…k -2
Если коэффициент регрессии является несущественным, то для него выполняются условия ….стандартная ошибка превышает половину значения параметров;расчетное значение t- критерия Стьюдента меньше табличного
Если коэффициент регрессии является несущественным, то для него выполняются условия …доверительный интервал одновременно содержит положительные и отрицательные величины, расчетное значение t-критерия меньше табличного
Если коэффициент регрессии является существенным, то для него выполняются условия ….стандартная ошибка не превышает половины значения параметра*;значение t- критерия Стьюдента больше табличного*
Если предпосылки метода наименьших квадратов (МНК) не выполняются, то остатки могут характеризоваться …высокой степенью автокорреляции, гетероскедастичностью
Если предпосылки метода наименьших квадратов (МНК) не выполняются, то остатки могут характеризоваться …гетероскедастичностью, высокой степенью автокорреляции
Если справедлива гипотеза H0: a1 =0 относительно коэффициента a1 модели множественной регрессии
Если статистическая оценка θ*n параметра θ содержит всю информацию об оцениваемом параметре, она называется…достаточной
Если структурная форма модели системы эконометрических уравнений точно идентифицируема, то с помощью косвенного МНК получают единственную оценку параметров модели
Если факторы входят в модуль как сумма, то модель называется… аддитивной
Зависимость дисперсии возмущения от номера наблюдения называется гетероскедастичностью*
Зависимость прибыли Y от расходов на рекламу X характеризуется полиномиальной эконометрической моделью второй степени вида
Закон изменения нестационарного временного ряда yt близок к линейному. Этот ряд приводится к стационарному процессу xt c помощью расчеты первых разностей
Значение коэффициента детерминации составило 0,9 следовательно …уравнение регрессии объяснено 90% дисперсии результативного признака;доля остаточной дисперсии зависимой переменной y в ее общей дисперсии составила 10%
Значение коэффициента детерминации составило 0,9 следовательно отношение длины __ дисперсии к общей дисперсии равно ____ Остаточный…0,1, Факторный…0,9
Значение множественного коэффициента линейной корреляции близко к 1. Это означает, что результирующая переменная является линейной функцией от набора факторных переменных
Из теоремы Гаусса-Маркова следует, что оценки являются эффективными, несмещенными, состоятельными
Изображение корреляционного поля для парной регрессионной модели относится к статическим графикам, характеризующим …тесноту и форму зависимости между признаками
Использование в эконометрическом моделировании парной регрессии вместо множественной является ошибкой…спецификации
Использование полинома третьего порядка в качестве регрессионной зависимости для однофакторной модели обусловлено …неоднородностью выборки
Использование фиктивных переменных является оперативным при исследовании…однородных массивов данных
К достоинствам метода наименьших квадратов можно отнести … типовой характер расчётов, интерпретируемость полученных результатов*
К методам обнаружения автокорреляции относятся: критерий Дарбина-Уотсона
К методам устранения гетероскедастичности остатков относятся: метод Кохрана-Оркатта, взвешенный метод наименьших квадратов
К методам устранения мультиколлинеарности факторных переменных относятся добавление фиктивных переменных, изменение спецификации модели, исключение переменных
К ошибкам спецификации относится …неправильный выбор той или иной математической функции
Какие веса используются в сглаживании временных рядов Методом скользящего среднего при m=2-3/35, 12/35, 17/35, 12/35, -3/35
Какие методы используются для сглаживания временного ряда: Аналитические, алгоритмические
Какие основные понятия связаны с временными рядами: Тренд, фильтрация, сглаживание, автоковариация, спектральная плотность, модели генерации значений
Какое из этих значений может принимать линейный коэффициент корреляции при прямой связи?0,6
Какое из этих уравнений является выборочным уравнением регрессии:
Какое из этих уравнений является модельным уравнением регрессии
Какой показатель характеризует значимость коэффициента регрессии? t-статистика Стьюдента этогокоэффициента регрессии
Какому коэффициенту корреляции соответствует возрастающая линейно-функциональная регрессионная зависимость?1
Компонента уровней временного ряда, отражающая влияние неподдающихся учету и регистрации случайных факторов на изучаемый экономический процесс, называетсяслучайной
Коррелированность возмущений с различными номерами называется автокорреляцией*
Коррелограмма — это … график автокорреляционной функции
Корреляция подразумевает наличие связи между …переменными
Коэффициент детерминации в парной регрессии применяется для проверкиадекватности модели; общего качества регрессии
Коэффициент детерминации является величинойдетерминированной
Коэффициент корреляции представляет собой …Число
Коэффициент корреляции это:относительная мера взаимосвязи переменных
Коэффициент парной линейной корреляции между признаками Y и X равен 0,9. Следовательно, доля дисперсии результативного признака Y, не объяснённая линейной парной регрессией Y по фактору X, будет равно …10%*
Коэффициент парной линейной корреляции равен нулю. Это значит, чтомежду признаками нет линейной корреляционной зависимости
Коэффициент эластичности является постоянной величиной и не зависит от значения факторного признака для …степенной функции регрессии
Коэффициенты регрессионных моделей с фиктивными переменными оцениваются _______ методом наименьших квадратов.традиционным
Критерий Стьюдента используется для проверки гипотезы о: Значимости коэффициента корреляции
Критерий Фишера в эконометрических моделях служит показателем преимущества выбранной модели пред другими; для проверки статистической значимости уравнения регрессии
Критерий Фишера используется для оценки значимости …построенного уравнения
Лаговые переменные – это эндогенные переменные в предшествовавшие моменты времени
Левая часть системы взаимозависимых уравнений представлена вектором… зависимых переменных
Линейный коэффициент корреляции — это отношение …ковариации к произведению средних квадратичных отклонений двух показателей
Линейный коэффициент корреляции изменяется в пределах[-1, 1]*
Линейный коэффициент корреляциипоказывает меру тесноты связи между двумя показателями
Математическое выраж-е линейной модели переменного ряда имеет вид Yt= a1Yt-1+a2Yt-2+…+anYt—n
Математическое выражение линейной модели временного ряда имеет вид.
Метод инструментальных переменных применяется в случае корреляции регрессора со случайным возмущением*
Метод наименьших квадратов может применяться для оценки параметров нелинейных регрессионных моделей, если эти модели …имеют автокорреляцию в остатках; характеризуются гетероскедастичностью случайных отклонений;являются нелинейными по параметрам, но внутренние линейными;являются нелинейными по параметрам и внутренние нелинейными
Метод скользящего среднего — это: Алгоритмический метод сглаживания временного ряда
Минимальная дисперсия остатков характерна для оценок, обладающих свойством эффективности*
МНК — оценки параметров обобщенной регрессионной модели несмещенные*
МНК для оценки параметров уравнений регрессии дает хорошие результаты при выполнении определенных предпосылок*
МНК используется для оценивания …параметров линейной регрессии*
Множественный коэффициент линейной корреляции близок к единице. Это означает, что …рассматриваются факторы, значимо влияющие на результат*
Моделирование тенденции осуществляется на основе построения уравнения регрессии зависимости трендовойкомпоненты от времени.
Модель, содержащая фиктивную переменную, относится к ____ модели.регрессионной
На первом этапе применения косвенного метода наименьших квадратов…структурную форму преобразуют в приведенную
Наиболее часто используемый порог вероятности безошибочности выводов при проверке статистических гипотез в эконометрике.. 0,95
Найти коэффициент корреляции, если известен коэффициент детерминации R2=0.992016
Найти среднее квадратичное отклонение, если дисперсия совокупности равна 12,253,5
Найти среднюю урожайность пшеницы с 1 га за три года: 60ц, 49ц, 41ц.50
Наличие возмущения зависимой переменной, вызванное неоднородностью данных в исходной статистической совокупности, является учетомошибки выборки
Невязки это: Отклонение наблюдаемого значения от значения, вычисленного по теоретической функции регрессии
Независимые переменные в регрессионных моделях называютсярегрессорами*
Независимые переменные системы одновременных уравнений, определяемые вне модели, называются экзогенными переменными
Неидентифицируемая система совместных эконометрических уравнений решается не может решаться
Несмещенность оценки на практике означает … что при большом числе выборочных оцениваний остатки не будут накапливать; невозможность перехода от точечного оценивания к интервалу
Обобщенный метод наименьших квадратов может использоваться для корректировки __ остатков гетероскедастичности*
Обобщенный метод наименьших квадратов подразумевает …Введение в выражение для дисперсии остатков коэффициента пропорциональности;Преобразование переменных
Объем выборки должен превышать число рассчитываемых параметров при исследуемых факторах в 5-6 раз*
Один из этапов построения экономической модели, на котором проверяются статистические свойства построенной модели, называется…верификацией модели
Одним из методов присвоения числовых значений фиктивными переменными является…ранжирование
Одним из нарушений предпосылок метода наименьших квадратов для системы одновременных уравнений является …корреляция случайных отклонений с результативными переменными;гетероскедастичность остатков
Остаток регрессионной модели представляет собой оценку:случайной ошибки
от теоретических значений зависимости переменной уУкажите выводы, которые соответствуют графику зависимости остатков имеет место гетероскедастичность остатков;нарушена предпосылка МНК и равенство дисперсий случайных отклонений
Отбор факторов в модель множественной регрессии с использованием метода включения может 83.быть основан на сравнении …величины объясненной дисперсии до и после включения фактора в модель; величины остаточной дисперсии до и после включения фактора в модель
Отношение факторной дисперсии к общей дисперсии равно 0,93, следовательно величина:разности (1 — R2), где R2 — коэффициент детерминации равна 0,07;коэффициент детерминации R2 равна 0,93
Оценки коэффициентов по МНК являются __ оценками теоретических коэффициентов регрессии точечными*
Оценки параметров неидентифицируемой системы эконометрических уравнений… не могут быть найдены обычным МНК
Оценки параметров сверхидентифицируемой системы эконометрических уравнений могут быть найдены с помощью __ метода наименьших квадратов двухшагового*
Оценку существенности (значимости) отдельного параметра уравнения регрессии можно проводить на основании показателей …t-критерия Стьюдента;доверительного интервала
Параметры управления тренда определяются обычным*методом наименьших квадратов.
Первый шаг двухшагового метода наименьших квадратов состоит в нахождении теоретических значений…эндогенных переменных из приведенной формы модели традиционным методом наименьших квадратов
Переменные системы одновременных уравнений, известные к расчетному моменту времени, называются предопределенными переменными*
Переход от точечного оценивая к интервальному возможен, если оценки являются…Эффективными и несмещенными*
По мере удаления индивидуального значения эндогенной переменной от среднего по выборке длина доверительного интервала Увеличивается
По отношению к выбранной спецификации модели, все экономические переменные объекта подразделяются наэндогенные и экзогенные
StudFiles.ru
Читайте также
Тема 2: Отбор факторов, включаемых в модель множественной регрессии
Тема 1: Спецификация эконометрической модели
1. Ошибки спецификации эконометрической модели имеют место вследствие …
неправильного выбора математической функции или недоучета в уравнении регрессии какого-то существенного фактора
недостоверности или недостаточности исходной информации
неоднородности данных в исходной статистической совокупности
недостаточного количества данных
Решение:
Спецификацией модели называется отбор факторов, включаемых в модель, и выбор математической функции для 

2. Для регрессионной модели вида 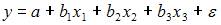
Решение:
Считается, на каждый оцениваемый коэффициент регрессии необходимо не менее 5–7 объектов статистических наблюдений. Так как представленная модель содержит 3 независимые переменные, то на каждый из параметров регрессии при независимой переменной необходимо по 5–7 наблюдений, то есть в совокупности не менее 15–21 наблюдения. Берем нижнюю границу интервала, тогда правильный вариант ответа – «15».
3. Нелинейным по объясняющим переменным, но линейным по параметрам уравнением регрессии является …
Решение:
Из приведенных функций только в функции 
4. В модели вида 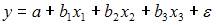
Решение:
Эконометрическая модель уравнения регрессии может быть представлена линейным уравнением множественной регрессии в виде выражения 

5. При идентификации модели множественной регрессии 
Решение:
При оценке модели множественной регрессии 
Тема 2: Отбор факторов, включаемых в модель множественной регрессии
1. В модели множественной регрессии 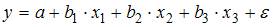






Решение:
Для оценки мультиколлинеарности факторов может использоваться определитель матрицы парных коэффициентов корреляции между факторами. Если факторы не коррелированы между собой, то матрица парных коэффициентов корреляции между факторами была бы единичной. Поскольку все недиагональные элементы 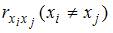

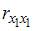
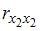
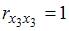
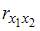
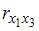
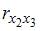
Если между факторами существует полная линейная зависимость и все коэффициенты парной корреляции равны единице, то определитель такой матрицы равен нулю.
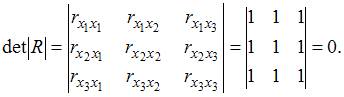
Чем ближе к нулю определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И, наоборот, чем ближе к единице определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов.
2. При моделировании линейного уравнения множественной регрессии вида 
Решение:
Эконометрическая модель уравнения регрессии может быть представлена линейным уравнением множественной регрессии в виде выражения 

Ошибка спецификации эконометрической модели уравнения регрессии
Ошибка спецификации
К ошибкам спецификации будут относиться не только неправильный выбор той или иной математической функции для ух, но и недоучет в уравнении регрессии какого-либо существенного фактора, т. е. использование парной регрессии вместо множественной. Так, спрос на конкретный товар может определяться не только ценой, но и доходом на душу населения. [c.36]
Наряду с ошибками спецификации могут иметь место ошибки выборки, поскольку исследователь чаще всего имеет дело с выборочными данными при установлении закономерной связи между признаками. Ошибки выборки имеют место и в силу неоднородности данных в исходной статистической совокупности, что, как правило, бывает при изучении экономических процессов. Если совокупность неоднородна, то уравнение регрессии не имеет практического смысла. Для получения хорошего результата обычно исключают из совокупности единицы с аномальными значениями исследуемых признаков. И в этом случае результаты регрессии представляют собой выборочные характеристики. [c.36]
Наибольшую опасность в практическом использовании методов регрессии представляют ошибки измерения. Если ошибки спецификации можно уменьшить, изменяя форму модели (вид математической формулы), а ошибки выборки — увеличивая объем исходных данных, то ошибки измерения практически сводят на нет все усилия по количественной оценке связи между признаками. Особенно велика роль ошибок измерения при ис- [c.36]
Предполагая, что ошибки измерения сведены к минимуму, основное внимание в эконометрических исследованиях уделяется ошибкам спецификации модели. [c.37]
В чем состоят ошибки спецификации модели [c.88]
Под системой эконометрических уравнений обычно понимается система одновременных, совместных уравнений. Ее применение имеет ряд сложностей, которые связаны с ошибками спецификации модели. Ввиду большого числа факторов, влияющих на экономические переменные, исследователь, как правило, не уверен в точности предлагаемой модели для описания экономических процессов. Набор эндогенных и экзогенных переменных модели соответствует теоретическому представлению исследователя о [c.204]
Иллюстрация возможного появления ошибки спецификации приводится на рис. 5.4. [c.239]
| Рис. 5.4. Ошибка спецификации при выборе уравнения тренда |  |
Ошибкой спецификации называются неправильный выбор типа связей и соотношений между элементами модели, а также выбор в качестве существенных таких переменных и параметров, которые на самом деле таковыми не являются, и наконец, отсутствие в модели некоторых существенных переменных. [c.338]
Следовательно, шаг 4 заключается в вычислении (50), (53), (59) — (60). Таким образом, для регрессионных уравнений первого порядка с запаздывающей переменной продолжение итеративного процесса от первичных обобщенных оценок наименьших квадратов приводит к асимптотическим оценкам наибольшего правдоподобия, а последующее применение техники оценки ошибки спецификации дает возможность получить оценки и доверительные интервалы прогноза также и при наличии ошибок в переменных. [c.80]
Даже если бы удалось получить программы, свободные от ошибок, то возникает необходимость учитывать некоторый переходный период, в течение которого структура системы не должна основываться на предположении об отсутствии ошибок в отдельных модулях, но должна допускать возможность неправильного функционирования компонентов ПО вследствие внутренней ошибки. Спецификации модуля должны закреплять за каждым из них функцию выполнения определенных проверок модулей, с которыми последний взаимодействует. Кроме того, если даже ПО было написано корректно, более ранние ошибки оборудования могли сделать его некорректным. [c.15]
Оценки с ограниченной информацией оказываются более устойчивыми к ошибкам спецификации модели. Наоборот, оценки с полной информацией весьма чувствительно реагируют на изменения структуры. [c.424]
Какие ошибки спецификации встречаются, и каковы последствия данных ошибок [c.190]
Как обнаружить ошибку спецификации [c.190]
Каким образом можно исправить ошибку спецификации и перейти к лучшей (качественной) модели [c.190]
Неправильный выбор функциональной формы или набора объясняющих переменных называется ошибками спецификации. Рассмотрим основные типы ошибок спецификации. [c.192]
При построении уравнений регрессии, особенно на начальных этапах, ошибки спецификации весьма нередки. Они допускаются обычно из-за поверхностных знаний об исследуемых экономических процессах, либо из-за недостаточно глубоко проработанной теории, или из-за погрешностей при сборе и обработке статистических данных при построении эмпирического уравнения регрессии. Важно уметь [c.195]
Как можно обнаружить ошибки спецификации [c.202]
Можно ли обнаружить ошибки спецификации с помощью исследования остаточного члена [c.202]
Совершается ли при этом ошибка спецификации Если да, то каковы ее последствия Что можно сказать, если указанные модели поменять ролями [c.203]
Совершается ли при этом ошибка спецификации и каковы ее последствия [c.203]
Среди основных причин, вызывающих появление автокорреляции, можно выделить ошибки спецификации, инерцию в изменении экономических показателей, эффект паутины, сглаживание данных. [c.228]
Ошибки спецификации. Неучет в модели какой-либо важной объясняющей переменной либо неправильный выбор формы зависимости обычно приводит к системным отклонениям точек наблюдений от линии регрессии, что может привести к автокорреляции. [c.228]
PiQ + выбрать линейную модель МС = ро + PiQ + s, то совершается ошибка спецификации. Ее можно рассматривать как неправильный выбор формы модели или как отбрасывание значимой переменной при линеаризации указанных моделей. Последствия данной ошибки выразятся в системном отклонении точек наблюдений от прямой регрессии (рис. 9.3) и существенном преобладании последовательных отклонений одинакового знака над соседними отклонениями противоположных знаков. Налицо типичная картина, характерная для положительной автокорреляции. [c.228]
Однако необходима определенная осмотрительность при применении данного метода. В этой ситуации возможны ошибки спецификации. Например, при исследовании спроса на некоторое благо в качестве объясняющих переменных можно использовать цену данного блага и цены заменителей данного блага, которые зачастую коррелируют друг с другом. Исключив из модели цены заменителей, мы, скорее всего, допустим ошибку спецификации. Вследствие этого возможно получение смещенных оценок и осуществление необоснованных выводов. Таким образом, в прикладных эконометрических моделях желательно не исключать объясняющие переменные до тех пор, пока коллинеарность не станет серьезной проблемой. [c.252]
Выбор правильной формы модели регрессии является в данной ситуации достаточно серьезной проблемой, т. к. в этом случае вполне вероятны ошибки спецификации. Наиболее рациональной практической стратегией выбора модели является следующая схема. [c.267]
Однако применение этого метода весьма ограничено в силу постоянно уменьшающегося числа степеней свободы, сопровождающегося увеличением стандартных ошибок и ухудшением качества оценок, а также возможности мультиколлинеарности. Кроме этого, при неправильном определении количества лагов возможны ошибки спецификации. [c.279]
Мы видим, что квадраты остатков регрессии е2, которыми оперируют тесты на гетероскедастичность, зависят от значения переменной xt, и, соответственно, тесты отвергают гипотезу гомоскедастичности, что в данном случае является следствием ошибки спецификации модели. [c.181]
Теперь оба коэффициента значимо отличаются от нуля и имеют правильные знаки . Тест Уайта показывает отсутствие гетероскедастичности. Из последнего уравнения можно также получить, что возраст, при котором достигается максимальная зарплата, равен примерно 54 годам, что согласуется со здравым смыслом. По-видимому следует заключить, что в первом уравнении результат теста указывал на ошибку спецификации. Пример показывает, что при эконометрическом анализе полезна любая дополнительная информация (в нашем случае — механизм формирования зарплаты). [c.183]
Следовательно, влияние ошибочной спецификации на смещение и среднеквадратичное отклонение оценки ш /З проявляется через величину с /ф2 72> которая, конечно, неизвестна. Заметим, что абсолютная величина смещения оценки и ее среднеквадратичное отклонение в результате ошибки спецификации могут как возрасти, так и уменьшиться. [c.430]
Другой важный вопрос связан с устойчивостью оценок по отношению к ошибкам спецификации, т. е. к неправильно выбранной форме связи, автокоррелированности или гетеро-скедастичности отклонений, нарушениям гипотезы о нормальности возмущений и т. д. [c.423]
Совершается ли ошибка спецификации при использовании следующей ре грессии [c.203]
Из таблицы видно, что коэффициенты при интересующих нас переменных AGE и AGE2 не значимы. Тест Уайта показывает наличие гетероскедастичности. Прежде чем начать коррекцию гетероскедастичности, вспомним, что тест может давать такой результат при ошибке спецификации функциональной формы. В самом деле, поскольку, как правило, все надбавки к зарплате формулируются в мультипликативной форме ( увеличение на 5% ), то более естественно взять в качестве зависимой переменной логарифм зарплаты InW. Результаты регрессии In W на остальные переменные приведены в таблице 6.4. [c.183]
Этот разрыв между теорией и практикой имеет довольно интересные последствия. Одно из них то, что прикладные эконо-метристы чувствуют необходимость проверки гипотез, потому что они проходили курс Теория эконометрики и хотят использовать свои знания. Однако они редко могут объяснить, почему они тестируют конкретную гипотезу, скажем, однородность или выпуклость. Если гипотеза отклоняется, как и происходит в большинстве случаев, они видят в этом свидетельство ошибки спецификации. Зачем же тогда проводить тестирование, если его логические следствия игнорируются Размышление о последствиях тестирования перед его выполнением было бы разумным, но редко встречается в эконометрической практике. [c.477]
В этой книге мы будем различать понятия спецификация ошибки i ошибка спецификации. Первое понятие относится к выбору неко-горого типа ошибок при спецификацииУмодели, подлежащей оцени-занию, а второе понятие означает, властности, ошибку спецификации матрицы X1. Предположим, как обычно, что истинная модель шеет вид [c.168]
Рассмотрим оценку Ъг параметра 32, полученную простой регрес сией у на xz на основе таблицы, построенной в результате классифи кации данных по переменной Xz, и оценку Ь3 параметра р3, получен ную в результате простой регрессии у на ха на основе таблицы, соот ветствующей классификации по Xs. Обе оценки окажутся смещенными поскольку в каждом случае допущена ошибка спецификации из-з исключения из регрессии существенной переменной. Поэтому [c.234]
Любое ранжирование остальных четырех методов должно рассматриваться как пробное. Первым рассмотрим наименее противоречивый случай. В экспериментах, содержащих ошибку спецификации, двухшаговый метод наименьших квадратов показывает заметно худшие результаты по сравнению с остальными тремя методами, если предопределенные переменные не сильно коррелированы друг с другом, и его качества становятся относительно лучшими, когда такая корреляция присутствует. В итоге представляется правильным присвоение этому методу наименьшего рангового значения. Неожиданно метод максимального правдоподобия с полной информацией оказался лучше других. Можно было ожидать, что он более других методов пострадает от ошибочной спецификации. Конечно, для достаточно больших значений у21 это вполне может произойти. Также неожиданным оказалось и то, что метод наименьших квадратов, без ограничений не проявил себя в этих экспериментах. Это произошло потому, что при работе с малыми выборками использование априорной информации «о модели, которое достигается с помощью метода максимального правдоподобия с полной информацией и метода ограниченной информации для отдельного урав нения, дает больший вклад в качество оценок, чем уменьшение ошибок спецификации этой модели. Метод наименьших квадратов без ограничений не введен нас в заблуждение из-за неправильных ограничений на элементы матрицы П, не в то же время он не способен воспринять верные ограничения. В результате ov. не выдерживает конкуренции с двумя методами, использующими априорнук информацию, когда степень неточности ограничений не очень велика. [c.422]
Смотреть страницы где упоминается термин Ошибка спецификации
Экономико-математический словарь Изд.5 (2003) — [ c.338 ]
Тема 1 Спецификация эконометрической модели Ошибки спецификации эконометрической модели имеют место вследствие
| Название | Тема 1 Спецификация эконометрической модели Ошибки спецификации эконометрической модели имеют место вследствие |
| Дата | 02.02.2019 |
| Размер | 1.2 Mb. |
| Формат файла | |
| Имя файла | Baza_po_ekonometrike.doc |
| Тип | Документы #66133 |
| страница | 1 из 4 |
1. Ошибки спецификации эконометрической модели имеют место вследствие …
неправильного выбора математической функции или недоучета в уравнении регрессии какого-то существенного фактора
2. Для регрессионной модели вида необходим минимальный объем наблюдений, содержащий _____ объектов наблюдения.
3. Нелинейным по объясняющим переменным, но линейным по параметрам уравнением регрессии является …
4. В модели вида количество объясняющих переменных равно …
5. При идентификации модели множественной регрессии количество оцениваемых параметров равно …
Тема 2: Отбор факторов, включаемых в модель множественной регрессии
1. В модели множественной регрессии определитель матрицы парных коэффициентов корреляции между факторами , и близок к единице. Это означает, что факторы , и …
2. При моделировании линейного уравнения множественной регрессии вида необходимо, чтобы выполнялось требование отсутствия взаимосвязи между …
3. Дана матрица парных коэффициентов корреляции.
Коллинеарными являются факторы …
и
4. В модели множественной регрессии определитель матрицы парных коэффициентов корреляции между факторами , и близок к нулю. Это означает, что факторы , и …
5. Для эконометрической модели линейного уравнения множественной регрессии вида построена матрица парных коэффициентов линейной корреляции (y – зависимая переменная; х (1) , х (2) , х (3) , x (4) – независимые переменные):
Коллинеарными (тесно связанными) независимыми (объясняющими) переменными не являются …
Тема 3: Фиктивные переменные
1. Дана таблица исходных данных для построения эконометрической регрессионной модели:
Фиктивными переменными не являются …
2. При исследовании зависимости потребления мяса от уровня дохода и пола потребителя можно рекомендовать …
использовать фиктивную переменную – пол потребителя
разделить совокупность на две: для потребителей женского пола и для потребителей мужского пола
3. Изучается зависимость цены квартиры (у) от ее жилой площади (х) и типа дома. В модель включены фиктивные переменные, отражающие рассматриваемые типы домов: монолитный, панельный, кирпичный. Получено уравнение регрессии: ,
где ,
Частными уравнениями регрессии для кирпичного и монолитного являются …
для типа дома кирпичный
для типа дома монолитный
для типа дома кирпичный
для типа дома монолитный
Требуется узнать частное уравнение регрессии для кирпичного и монолитного домов. Для кирпичного дома значения фиктивных переменных следующие , . Уравнение примет вид: или для типа дома кирпичный.
Для монолитного дома значения фиктивных переменных следующие , . Уравнение примет вид
или для типа дома монолитный.
4. При анализе промышленных предприятий в трех регионах (Республика Марий Эл, Республика Чувашия, Республика Татарстан) были построены три частных уравнения регрессии:
для Республики Марий Эл;
для Республики Чувашия;
для Республики Татарстан.
Укажите вид фиктивных переменных и уравнение с фиктивными переменными, обобщающее три частных уравнения регрессии.
Итоговое уравнение будет
5. В эконометрике фиктивной переменной принято считать …
переменную, принимающую значения 0 и 1
Тема 4: Линейное уравнение множественной регрессии
1. Для регрессионной модели зависимости среднедушевого денежного дохода населения (руб., у) от объема валового регионального продукта (тыс. р., х1) и уровня безработицы в субъекте (%, х2) получено уравнение . Величина коэффициента регрессии при переменной х2 свидетельствует о том, что при изменении уровня безработицы на 1% среднедушевой денежный доход ______ рубля при неизменной величине валового регионального продукта.
2. В уравнении линейной множественной регрессии: , где – стоимость основных фондов (тыс. руб.); – численность занятых (тыс. чел.); y – объем промышленного производства (тыс. руб.) параметр при переменной х1, равный 10,8, означает, что при увеличении объема основных фондов на _____ объем промышленного производства _____ при постоянной численности занятых.
на 1 тыс. руб. … увеличится на 10,8 тыс. руб.
3. Известно, что доля остаточной дисперсии зависимой переменной в ее общей дисперсии равна 0,2. Тогда значение коэффициента детерминации составляет …
4. Построена эконометрическая модель для зависимости прибыли от реализации единицы продукции (руб., у) от величины оборотных средств предприятия (тыс. р., х1): . Следовательно, средний размер прибыли от реализации, не зависящий от объема оборотных средств предприятия, составляет _____ рубля.
5. F-статистика рассчитывается как отношение ______ дисперсии к ________ дисперсии, рассчитанных на одну степень свободы.
Тема 5: Оценка параметров линейных уравнений регрессии
1. Для эконометрической модели уравнения регрессии ошибка модели определяется как ______ между фактическим значением зависимой переменной и ее расчетным значением.
3. В эконометрической модели уравнения регрессии величина отклонения фактического значения зависимой переменной от ее расчетного значения характеризует …
4. Известно, что доля объясненной дисперсии в общей дисперсии равна 0,2. Тогда значение коэффициента детерминации составляет …
0,2
5. При методе наименьших квадратов параметры уравнения парной линейной регрессии определяются из условия ______ остатков .
минимизации суммы квадратов
1. Для обнаружения автокорреляции в остатках используется …
статистика Дарбина – Уотсона
критерий Гольдфельда – Квандта
2. Известно, что коэффициент автокорреляции остатков первого порядка равен –0,3. Также даны критические значения статистики Дарбина – Уотсона для заданного количества параметров при неизвестном и количестве наблюдений , . По данным характеристикам можно сделать вывод о том, что …
автокорреляция остатков отсутствует
3. Значение критерия Дарбина – Уотсона можно приблизительно рассчитать по формуле , где – значение коэффициента автокорреляции остатков модели. Минимальная величина значения будет наблюдаться при ________ автокорреляции остатков.
4. Из перечисленного условием выполнения предпосылок метода наименьших квадратов не является ____ остатков.
5. Значение критерия Дарбина – Уотсона можно приблизительно рассчитать по формуле , где – значение коэффициента автокорреляции остатков модели. Максимальная величина значения будет наблюдаться при ________ автокорреляции остатков.
Тема 7: Свойства оценок параметров эконометрической модели, получаемых при помощи МНК
1. Пусть – оценка параметра регрессионной модели, полученная с помощью метода наименьших квадратов; – математическое ожидание оценки . В том случае если , то оценка обладает свойством …
2. Из несмещенности оценки параметра следует, что среднее значение остатков равно …
3. Несмещенность оценок параметров регрессии означает, что …
математическое ожидание остатков равно нулю
4. Если оценка параметра является смещенной, то нарушается предпосылка метода наименьших квадратов о _________ остатков.
нулевой средней величине
5. Состоятельность оценок параметров регрессии означает, что …
точность оценок выборки увеличивается с увеличением объема выборки
Тема 8: Обобщенный метод наименьших квадратов (ОМНК)
1. В случае нарушений предпосылок метода наименьших квадратов применяют обобщенный метод наименьших квадратов, который используется для оценки параметров линейных регрессионных моделей с __________ остатками.
автокоррелированными и/или гетероскедастичными
2. При нарушении гомоскедастичности остатков и наличии автокорреляции остатков рекомендуется применять _____________ метод наименьших квадратов.
3. Пусть y – издержки производства, – объем продукции, – основные производственные фонды, – численность работников. Известно, что в уравнении дисперсии остатков пропорциональны квадрату численности работников .После применения обобщенного метода наименьших квадратов новая модель приняла вид . Тогда параметр в новом уравнении характеризует среднее изменение затрат …
на работника при увеличении производительности труда на единицу при неизменном уровне фондовооруженности труда
4. Обобщенный метод наименьших квадратов не может применяться для оценки параметров линейных регрессионных моделей в случае, если …
средняя величина остатков не равна нулю
5. Пусть y – издержки производства, – объем продукции, – основные производственные фонды, – численность работников. Известно, что в уравнении дисперсии остатков пропорциональны квадрату объема продукции .Применим обобщенный метод наименьших квадратов, поделив обе части уравнения на После применения обобщенного метода наименьших квадратов новая модель приняла вид . Тогда параметр в новом уравнении характеризует среднее изменение затрат на единицу продукции при увеличении …
1. Для эконометрической модели вида показателем тесноты связи между переменными и является парный коэффициент линейной …
2. Самым коротким интервалом изменения коэффициента корреляции для уравнения парной линейной регрессии является …
3. Самым коротким интервалом изменения показателя множественной корреляции для уравнения множественной линейной регрессии , если известны парные коэффициенты корреляции , является интервал …
4. Для регрессионной модели вида получена диаграмма
Такое графическое отображение называется …
Тема 10: Оценка качества подбора уравнения
1. Известно, что доля остаточной регрессии в общей составила 0,19. Тогда значение коэффициента корреляции равно …
0,9
2. Известно, что общая сумма квадратов отклонений , а остаточная сумма квадратов отклонений, . Тогда значение коэффициента детерминации равно …
3. Для регрессионной модели вида , где рассчитаны дисперсии: ; ; . Тогда величина характеризует долю …
остаточной дисперсии
4. Если общая сумма квадратов отклонений , и остаточная сумма квадратов отклонений , то сумма квадратов отклонений, объясненная регрессией, равна …
http://economy-ru.info/info/15273/
http://topuch.ru/tema-1-specifikaciya-ekonometricheskoj-modeli-oshibki-specifik-v2/index.html
Все курсы > Оптимизация > Занятие 4 (часть 1)
Прежде чем обратиться к теме множественной линейной регрессии, давайте вспомним, что было сделано до сих пор. Возможно, будет полезно посмотреть эти уроки, чтобы освежить знания.
- В рамках вводного курса мы узнали про моделирование взаимосвязи переменных и минимизацию ошибки при обучении алгоритма, а также научились строить несложные модели линейной регрессии с помощью библиотеки sklearn.
- При изучении объектно-ориентированного программирования мы создали класс простой линейной регрессии. Сегодня эти знания пригодятся при создании классов более сложных моделей.
- Также рекомендую вспомнить умножение векторов и матриц.
- Кроме того, в рамках текущего курса по оптимизации мы познакомились с понятием производной и методом градиентного спуска, а также построили модель простой линейной регрессии (использовав метод наименьших квадратов и градиент).
- Наконец, на прошлом занятии мы вновь поговорили про взаимосвязь переменных.
В рамках сегодняшнего занятия мы с нуля построим несколько алгоритмов множественной линейной регрессии.
Регрессионный анализ
Прежде чем обратиться к практике, обсудим некоторые теоретические вопросы регрессионного анализа.
Генеральная совокупность и выборка
Как мы уже знаем, множество всех имеющихся наблюдений принято считать генеральной совокупностью (population). И эти наблюдения, если в них есть взаимосвязи, можно теоретически аппроксимировать, например, линией регрессии. При этом важно понимать, что это некоторая идеальная модель, которую мы никогда не сможем построить.
Единственное, что мы можем сделать, взять выборку (sample) и на ней построить нашу модель, предполагая, что если выборка достаточно велика, она сможет достоверно описать генсовокупность.
Отклонение прогнозного значения от фактического для «идеальной» линии принято называть ошибкой (error или true error).
$$ varepsilon = y-hat{y} $$
Отклонение прогноза от факта для выборочной модели (которую мы и строим) называют остатками (residuals или residual error).
$$ varepsilon = y-f(x) $$
В этом смысле среднеквадратическую ошибку (mean squared error, MSE) корректнее называть средними квадратичными остатками (mean squared residuals).
На практике ошибку и остатки нередко используют как взаимозаменяемые термины.
Уравнение множественной линейной регрессии
Посмотрим на уравнение множественной линейной регрессии.
$$ y = theta_0 + theta_1x_1 + theta_2x_2 + … + theta_jx_j + varepsilon $$
В отличие от простой линейной регрессии в данном случае у нас несколько признаков x (независимых переменных) и несколько коэффициентов $ theta $ («тета»).
Интерпретация результатов модели
Коэффициент $ theta_0 $ задает некоторый базовый уровень (baseline) при условии, что остальные коэффициенты равны нулю и зачастую не имеет смысла с точки зрения интерпретации модели (нужен лишь для того, что поднять линию на нужный уровень).
Параметры $ theta_1, theta_2, …, theta_n $ показывают изменение зависимой переменной при условии «неподвижности» остальных коэффициентов. Например, каждая дополнительная комната может увеличивать цену дома в 1.3 раза.
Переменная $ varepsilon $ (ошибка) представляет собой отклонение фактических данных от прогнозных. В этой переменной могут быть заложены две составляющие. Во-первых, она может включать вариативность целевой переменной, описанную другими (не включенными в нашу модель) признаками. Во-вторых, «улавливать» случайный шум, случайные колебания.
Категориальные признаки
Модель линейной регрессии может включать категориальные признаки. Продолжая пример с квартирой, предположим, что мы строим модель, в которой цена зависит от того, находится ли квартира в центре города или в спальном районе.
Перед этим переменную необходимо закодировать, создав, например, через Label Encoder признак «центр», который примет значение 1, если квартира в центре, и 0, если она находится в спальном районе.
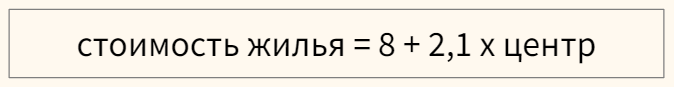
В модели, представленной выше, если квартира находится в центре (переменная «центр» равна единице), ее стоимость составит 10,1 миллиона рублей, если на окраине (переменная «центр» равна нулю) — лишь восемь.
Для категориального признака с множеством классов можно использовать one-hot encoding, если между классами признака отсутствует иерархия,
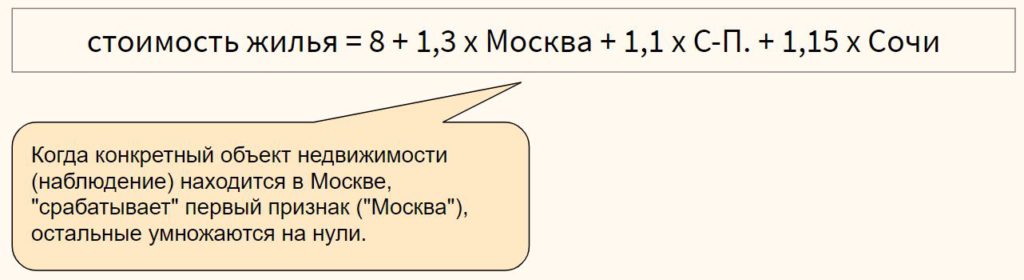
или, например, ordinal encoding в случае наличия иерархии классов в признаке

Выбросы в линейной регрессии
Как и коэффициент корреляции Пирсона, модель линейной регрессии чувствительна к выбросам (outliers), то есть наблюдениям, серьезно выпадающим из общей совокупности. Сравните рисунки ниже.
При наличии выброса (слева), линия регрессии имеет наклон и может использоваться для построения прогноза. Удалив это наблюдение (справа), линия регрессии становится горизонтальной и построение прогноза теряет смысл.
При этом различают два типа выбросов:
- горизонтальные выбросы или влиятельные точки (leverage points) — они сильно отклоняются от среднего по оси x; и
- вертикальные выбросы или просто выбросы (influential points) — отклоняются от среднего по оси y
Ключевое отличие заключается в том, что вертикальные выбросы влияют на наклон модели (изменяют ее коэффициенты), а горизонтальные — нет.
Сравним два графика.
На левом графике черная точка (leverage point) сильно отличается от остальных наблюдений, но наклон прямой линии регрессии с ее появлением не изменился. На правом графике, напротив, появление выброса (influential point) существенно изменяет наклон прямой.
На практике нас конечно больше интересуют influential points, потому что именно они существенно влияют на качество модели.
Если в простой линейной регрессии мы можем оценить leverage и influence наблюдения графически⧉, в многомерной модели это сделать сложнее. Можно использовать график остатков (об этом ниже) или применить один из уже известных нам методов выявления выбросов.
Про выявление leverage и infuential points можно почитать здесь⧉.
Допущения модели регрессии
Применение алгоритма линейной регрессии предполагает несколько допущений (assumptions) или условий, при выполнении которых мы можем говорить о качественно построенной модели.
1. Правильный выбор модели
Вначале важно убедиться, что данные можно аппроксимировать с помощью линейной модели (correct model specification).
Оценить распределение данных можно через график остатков (residuals plot), где по оси x отложен прогноз модели, а на оси y — сами остатки.
В отличие от простой линейной регрессии мы не используем точечную диаграмму X vs. y, потому что хотим оценить зависимость целевой переменной от всех признаков сразу.
Остатки модели относительно ее прогнозных значений должны быть распределены случайным образом без систематической составляющей (residuals do not follow a pattern).
- Если вы попробовали применить линейную модель с коэффициентами первой степени ($x_n^1$) и выявили некоторый паттерн в данных, можно попробовать полиномиальную или какую-либо еще функцию (об этом ниже).
- Кроме того, количественные признаки можно попробовать преобразовать таким образом, чтобы их можно было аппроксимировать прямой линией.
- Если ни то, ни другое не помогло, вероятно данные не стоит моделировать линейной регрессией.
Также замечу, что график остатков показывает выбросы в данных.
2. Нормальность распределения остатков
Среднее значение остатков должно быть равно нулю. Если это не так, и среднее значение меньше нуля (скажем –5), то это значит, что модель регулярно недооценивает (underestimates) фактические значения. В противном случае, если среднее больше нуля, переоценивает (overestimated).
Кроме того, предполагается, что остатки следуют нормальному распределению.
$$ varepsilon sim N(0, sigma) $$
Проверить нормальность остатков можно визуально с помощью гистограммы или рассмотренных ранее критериев нормальности распределения.
Если остатки не распределены нормально, мы не сможем провести статистические тесты на значимость коэффициентов или построить доверительные интервалы. Иначе говоря, мы не сможем сделать статистически значимый вывод о надежности нашей модели.
Причинами могут быть (1) выбросы в данных или (2) неверный выбор модели. Решением может быть, соответственно, исследование выбросов, выбор новой модели и преобразование как признаков, так и целевой переменной.
3. Гомоскедастичность остатков
Гомоскедастичность (homoscedasticity) или одинаковая изменчивость остатков предполагают, что дисперсия остатков не изменяется для различных наблюдений. Противоположное и нежелательное явление называется гетероскедастичностью (heteroscedasticity) или разной изменчивостью.
Гетероскедастичность остатков показывает, что модель ошибается сильнее при более высоких или более низких значениях признаков. Как следствие, если для разных прогнозов у нас разная погрешность, модель нельзя назвать надежной (robust).
Как правило, гетероскедастичность бывает изначально заложена в данные. Ее можно попробовать исправить через преобразование целевой переменной (например, логарифмирование)
4. Отсутствие мультиколлинеарности
Еще одним важным допущением является отсутствие мультиколлинеарности. Мультиколлинеарность (multicollinearity) — это корреляция между зависимыми переменными. Например, если мы предсказываем стоимость жилья по квадратным метрам и количеству комнат, то метры и комнаты логичным образом также будут коррелировать между собой.
Почему плохо, если такая корреляция существует? Базовое предположение линейной регрессии — каждый коэффициент $theta$ оказывает влияние на конечный результат при условии, что остальные коэффициенты постоянны. При мультиколлинеарности на целевую переменную оказывают эффект сразу несколько признаков, и мы не можем с точностью интерпретировать каждый из них.
Также говорят о том, что нужно стремиться к экономной (parsimonious) модели то есть такой модели, которая при наименьшем количестве признаков в наибольшей степени объясняет поведение целевой переменной.
Variance inflation factor
Расчет коэффициента
Variance inflation factor (VIF) или коэффициент увеличения дисперсии позволяет выявить корреляцию между признаками модели.
Принцип расчета VIF заключается в том, чтобы поочередно делать каждый из признаков целевой переменной и строить модель линейной регрессии на основе оставшихся независимых переменных. Например, если у нас есть три признака $x_1, x_2, x_3$, мы поочередно построим три модели линейной регрессии: $x_1 sim x_2 + x_3, x_2 sim x_1 + x_3$ и $x_3 sim x_1 + x_3$.
Обратите внимание на новый для нас формат записи целевой и зависимых переменных модели через символ $sim$.
Затем для каждой модели (то есть для каждого признака $x_1, x_2, x_3$) мы рассчитаем коэффициент детерминации $R^2$. Если он велик, значит данный признак можно объяснить с помощью других независимых переменных и имеется мультиколлинеарность. Если $R^2$ мал, то нельзя и мультиколлинеарность отсутствует.
Теперь рассчитаем VIF на основе $R^2$:
$$ VIF = frac{1}{1-R^2} $$
При таком способе расчета большой (близкий к единице) $R^2$ уменьшит знаменатель и существенно увеличит VIF, при небольшом коэффициенте детерминации коэффициент увеличения дисперсии наоборот уменьшится.
Замечу, что $1-R^2$ принято называть tolerance.
Другие способы выявления мультиколлинеарности
Для выявления корреляции между независимыми переменными можно использовать точечные диаграммы или корреляционные матрицы. При этом важно понимать, что в данном случае мы выявляем зависимость лишь между двумя признаками. Корреляцию множества признаков выявляет только коэффициент увеличения дисперсии.
Интерпретация VIF
VIF находится в диапазон от единицы до плюс бесконечности. Как правило, при интерпретации показателей variance inflation factor придерживаются следующих принципов:
- VIF = 1, между признаками отсутствует корреляция
- 1 < VIF $leq$ 5 — умеренная корреляция
- 5 < VIF $leq$ 10 — высокая корреляция
- Более 10 — очень высокая
После расчета VIF можно по одному удалять признаки с наибольшей корреляцией и смотреть как изменится этот показатель для оставшихся независимых переменных.
5. Отсутствие автокорреляции остатков
На занятии по временным рядам (time series), мы сказали, что автокорреляция (autocorrelation) — это корреляция между значениями одной и той же переменной в разные моменты времени.
Применительно к модели линейной регрессии автокорреляция целевой переменной (для простой линейной регрессии) и автокорреляция остатков, residuals autocorrelation (для модели множественной регрессии) означает, что результат или прогноз зависят не от признаков, а от самой этой целевой переменной. В такой ситуации признаки теряют свою значимость и применение модели регрессии становится нецелесообразным.
Причины автокорреляции остатков
Существует несколько возможных причин:
- Прогнозирование целевой переменной с высокой автокорреляцией (например, если мы моделируем цену акций с помощью других переменных, то можем ожидать высокую автокорреляцию остатков, поскольку цена акций как правило сильно зависит от времени)
- Удаление значимых признаков
- Другие причины
Автокорреляция первого порядка
Дадим формальное определение автокорреляции первого порядка (first order correlation), то есть автокорреляции с лагом 1.
$$ varepsilon_t = pvarepsilon_{t-1} + u_t $$
где $u_t$ — некоррелированная при различных t одинаково распределенная случайная величина (independent and identically distributed (i.i.d.) random variable), а $p$ — коэффициент автокорреляции, который находится в диапазоне $-1 < p < 1$. Чем он ближе к нулю, тем меньше зависимость остатка $varepsilon_t$ от остатка предыдущего периода $varepsilon_{t-1}$.
Такое уравнение также называется схемой Маркова первого порядка (Markov first-order scheme).
Обратите внимание, что для модели автокорреляции первого порядка коэффициент автокорреляции $p$ совпадает с коэффициентом авторегрессии AR(1) $varphi$.
$$ y_t = c + varphi cdot y_{t-1} $$
Разумеется, мы можем построить модель автокорреляции, например, третьего порядка.
$$ varepsilon_t = p_1varepsilon_{t-1} + p_2varepsilon_{t-2} + p_3varepsilon_{t-3} + u_t $$
Выявление автокорреляции остатков
Для выявления автокорреляции остатков можно использовать график последовательности и график остатков с лагом 1, график автокорреляционной функции или критерий Дарбина-Уотсона.
График последовательности и график остатков с лагом 1
На графике последовательности (sequence plot) по оси x откладывается время (или порядковый номер наблюдения), а по оси y — остатки модели. Кроме того, на графике остатков с лагом 1 (lag-1 plot) остатки (ось y) можно сравнить с этими же значениями, взятыми с лагом 1 (ось x).
Рассмотрим вариант положительной автокорреляции (positive autocorrelation) на графиках остатков типа (а) и (б).
Как вы видите, при положительной автокорреляции в большинстве случаев, если одно наблюдение демонстрирует рост по отношению к предыдущему значению, то и последующее будет демонстрировать рост, и наоборот.
Теперь обратимся к отрицательной автокорреляции (negative autocorrelation).
Здесь наоборот, если одно наблюдение демонстрирует рост показателя по отношению к предыдущему значению, то последующее наблюдение будет наоборот снижением. Опять же справедливо и обратное утверждение.
В случае отсутствия автокорреляции мы не должны увидеть на графиках какого-либо паттерна.
График автокорреляционной функции
Еще один способ выявить автокорреляцию — построить график автокорреляционной функции (autocorrelation function, ACF).
Напомню, такой график показывает автокорреляцию данных с этими же данными, взятыми с первым, вторым и последующими лагами.
Критерий Дарбина-Уотсона
Количественным выражением автокорреляции является критерий Дарбина-Уотсона (Durbin-Watson test). Этот критерий выявляет только автокорреляцию первого порядка.
- Нулевая гипотеза утверждает, что такая автокорреляция отсутствует ($p=0$),
- Альтернативная гипотеза соответственно утверждает, что присутствует
- Положительная ($p approx -1$) или
- Отрицательная ($p approx 1$) автокорреляция
Значение теста находится в диапазоне от 0 до 4.
- При показателе близком к двум можно говорить об отсутствии автокорреляции
- Приближение к четырем говорит о положительной автокорреляции
- К нулю, об отрицательной
Как избавиться от автокорреляции
Автокорреляцию можно преодолеть, добавив значимый признак в модель, выбрав иной тип модели (например, полиномиальную регрессию) или в целом перейдя к моделированию и прогнозированию временного ряда.
Рассмотрение этих методов находится за рамками сегодняшнего занятия. Перейдем к практике.