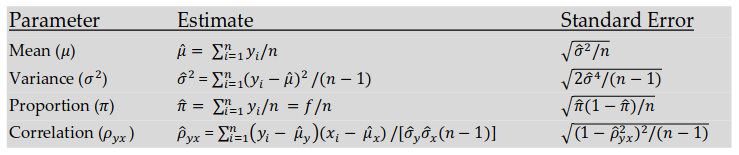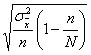Доверительный интервал ошибка выборки - Не ошибается лишь тот, кто ничего не делает!

Один из первых шагов при планировании количественного маркетингового исследования – определение объема выборки.

Калькулятор для расчета достаточного объема выборки
Калькулятор ошибки выборки для доли признака
Калькулятор ошибки выборки для среднего значения
Калькулятор значимости различий долей
Калькулятор значимости различий средних

1. Формула (даже две)

Бытует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с размером генеральной совокупности. Например, при опросах организаций (B2B).

Если речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная.

На рис.1. пример выборки 15000 человек (!) при опросе в муниципальном районе. Возможно, от численности населения взяли 10%?
Размер выборки никогда не рассчитывается как процент от генеральной совокупности!

Рис.1. Размер выборки 15000 человек, как реальный пример некомпетентности (или хуже).

В таких случаях для расчета объема выборки используется следующая формула:

где

n – объем выборки,
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня,
p – доля респондентов с наличием исследуемого признака,
q = 1 – p – доля респондентов, у которых исследуемый признак отсутствует,
∆ – предельная ошибка выборки.

Доверительный уровень – это вероятность того, что реальная доля лежит в границах полученного доверительного интервала: выборочная доля (p) ± ошибка выборки (Δ). Доверительный уровень устанавливает сам исследователь в соответствии со своими требованиями к надежности полученных результатов. Чаще всего применяются доверительные уровни, равные 0,95 или 0,99. В маркетинговых исследованиях, как правило, выбирается доверительный уровень, равный 0,95. При этом уровне коэффициент Z равен 1,96.

Значения p и q чаще всего неизвестны до проведения исследования и принимаются за 0,5. При этом значении размер ошибки выборки максимален.

Допустимая предельная ошибка выборки выбирается исследователем в зависимости от целей исследования. Считается, что для принятия бизнес-решений ошибка выборки должна быть не больше 4%. Этому значению соответствует объем выборки 500-600 респондентов. Для важных стратегических решений целесообразно минимизировать ошибку выборки.

Рассмотрим кривую зависимости ошибки выборки от ее объема (Рис.2).

Рис.2. Зависимость ошибки выборки от ее объема при 95% доверительном уровне

Как видно из диаграммы, с ростом объема выборки значение ошибки уменьшается все медленнее. Так, при объеме выборки 1500 человек предельная ошибка выборки составит ±2,5%, а при объеме 2000 человек – ±2,2%. То есть, при определенном объеме выборки дальнейшее его увеличение не дает значительного выигрыша в ее точности.

ШПАРГАЛКА (скопируйте ссылку или текст)

Подходы к решению проблемы:

Случай 1. Генеральная совокупность значительно больше выборки:

Случай 2. Генеральная совокупность сопоставима с объемом выборки: (см. раздел исследований B2B)

где
n – объем выборки,

N – объем генеральной совокупности,

Z – коэффициент, зависящий от выбранного исследователем доверительного уровня,

p – доля респондентов с наличием исследуемого признака,

q = 1 – p – доля респондентов, у которых исследуемый признак отсутствует, (значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования)

∆ – предельная ошибка выборки.

Например,

рассчитаем ошибку выборки объемом 1000 человек при 95% доверительном уровне, если генеральная совокупность значительно больше объема выборки:

Ошибка выборки = 1,96 * КОРЕНЬ(0,5*0,5/1000) = 0,031 = ±3,1%

При расчете объема выборки следует также учитывать стоимость проведения исследования. Например, при цене за 1 анкету 200 рублей стоимость опроса 1000 человек составит 200 000 рублей, а опрос 1500 человек будет стоить 300 000 рублей. Увеличение затрат в полтора раза сократит ошибку выборки всего на 0,6%, что обычно неоправданно экономически.

2. Причины «раздувать» выборку

Анализ полученных данных обычно включает в себя и анализ подвыборок, объемы которых меньше основной выборки. Поэтому ошибка для выводов по подвыборкам больше, чем ошибка по выборке в целом. Если планируется анализ подгрупп / сегментов, объем выборки должен быть увеличен (в разумных пределах).

Рис.3 демонстрирует данную ситуацию. Если для исследования авиапассажиров используется выборка численностью 500 человек, то для выводов по выборке в целом ошибка составляет 4,4%, что вполне приемлемо для принятия бизнес-решений. Но при делении выборки на подгруппы в зависимости от цели поездки, выводы по каждой подгруппе уже недостаточно точны. Если мы захотим узнать какие-либо количественные характеристики группы пассажиров, совершающих бизнес-поездку и покупавших билет самостоятельно, ошибка полученных показателей будет достаточно велика. Даже увеличение выборки до 2000 человек не обеспечит приемлемой точности выводов по этой подвыборке.

Рис.3. Проектирование объема выборки с учетом необходимости анализа подвыборок

Другой пример – анализ подгрупп потребителей услуг торгово-развлекательного центра (Рис.4).

Рис.4. Потенциальный спрос на услуги торгово-развлекательного центра

При объеме выборки в 1000 человек выводы по каждой отдельной услуге (например, социально-демографический профиль, частота пользования, средний чек и др.) будут недостаточно точными для использования в бизнес планировании. Особенно это касается наименее популярных услуг (Таблица 1).

Таблица 1. Ошибка по подвыборкам потенциальных потребителей услуг торгово-развлекательного центра при выборке 1000 чел.

Чтобы ошибка в самой малочисленной подвыборке «Ночной клуб» составила меньше 5%, объем выборки исследования должен составлять около 4000 человек. Но это будет означать 4-кратное удорожание проекта. В таких случаях возможно компромиссное решение:

увеличение выборки до 1800 человек, что даст достаточную точность для 6 самых популярных видов услуг (от кинотеатра до парка аттракционов);
добор 200-300 пользователей менее популярных услуг с опросом по укороченной анкете (см. Таблицу 2).

Таблица 2. Разница в ошибке выборки по подвыборкам при разных объемах выборки.

При обсуждении с исследовательским агентством точности результатов планируемого исследования рекомендуется принимать во внимание бюджет, требования к точности результатов в целом по выборке и в разрезе подгрупп. Если бюджет не позволяет получить информацию с приемлемой ошибкой, лучше пока отложить проект (или поторговаться).

КАЛЬКУЛЯТОРЫ ДЛЯ РАСЧЕТА СТАТИСТИЧЕСКИХ ПОКАЗАТЕЛЕЙ И ОПРЕДЕЛЕНИЯ ЗНАЧИМОСТИ РАЗЛИЧИЙ:

КАЛЬКУЛЯТОР ДЛЯ РАСЧЕТА
ДОСТАТОЧНОГО ОБЪЁМА ВЫБОРКИ

Доверительный уровень:

Ошибка выборки (?):
%

Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)

РЕЗУЛЬТАТ

Один из важных вопросов, на которые нужно ответить при планировании исследования, — это оптимальный объем выборки. Слишком маленькая выборка не сможет обеспечить приемлемую точность результатов опроса, а слишком большая приведет к лишним расходам.

Онлайн-калькулятор объема выборки поможет рассчитать оптимальный размер выборки, исходя из максимально приемлемого для исследователя размера ошибки выборки.

Все дальнейшие формулы и расчеты относятся только к простой случайной выборке!
Формулы для других типов выборки отличаются.

Объем выборки рассчитывается по следующим формулам

1) если объем выборки значительно меньше генеральной совокупности:

(в данной формуле не используется показатель объема генеральной совокупности N)

2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:

Z – коэффициент, зависящий от выбранного исследователем доверительного уровня. Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Ему соответствует значение Z = 1,96.

N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели соков и нектаров, постоянно проживающие в Москве и Московской области). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).

p – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.

q = 1 — p – доля респондентов, у которых исследуемый признак отсутствует. Значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования. При этом значении размер ошибки выборки максимален. В данном калькуляторе значения p и q по умолчанию равны 0,5.

Δ– предельная ошибка выборки (для доли признака), приемлемая для исследователя. Считается, что для принятия бизнес-решений ошибка выборки не должна превышать 4%.

n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании.

ПРИМЕР РАСЧЕТА ОБЪЕМА ВЫБОРКИ:

Допустим, мы хотим рассчитать объем выборки, предельная ошибка которой составит 4%. Мы принимаем доверительный уровень, равный 95%. Генеральная совокупность значительно больше выборки. Тогда объем выборки составит:

n = 1,96 * 1,96 * 0,5 * 0,5 / (0,04 * 0,04) = 600,25 ≈ 600 человек

Таким образом, если мы хотим получить результаты с предельной ошибкой 4%, нам нужно опросить 600 человек.

КАЛЬКУЛЯТОР ОШИБКИ ВЫБОРКИ ДЛЯ ДОЛИ ПРИЗНАКА

Доверительный уровень:

Объём выборки (n):

Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)

Доля признака (p):
%

РЕЗУЛЬТАТ

Зная объем выборки исследования, можно рассчитать значение ошибки выборки (или, другими словами, погрешность выборки).

Если бы в ходе исследования мы могли опросить абсолютно всех интересующих нас людей, мы могли бы быть на 100% уверены в полученном результате. Но ввиду экономической нецелесообразности сплошного опроса применяют выборочный подход, когда опрашивается только часть генеральной совокупности. Выборочный метод не гарантирует 100%-й точности измерения, но, тем не менее, вероятность ошибки может быть сведена к приемлемому минимуму.

Все дальнейшие формулы и расчеты относятся только к простой случайной выборке! Формулы для других типов выборки отличаются.

Ошибка выборки для доли признака рассчитывается по следующим формулам.

1) если объем выборки значительно меньше генеральной совокупности:

(в данной формуле не используется показатель объема генеральной совокупности N)

2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:

N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели шоколада, постоянно проживающие в Москве). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).

n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании. Существует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть и объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с объемом генеральной совокупности. Например, при опросах организаций (B2B). Если же речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная. ВАЖНО: если предполагается сравнивать какие-то группы внутри города, например, жителей разных районов, то выборку следует рассчитывать для каждой такой группы.

Δ– предельная ошибка выборки.

Таким образом, зная объем выборки исследования, мы можем заранее оценить показатель ее ошибки.
А получив значение p, мы можем рассчитать доверительный интервал для доли признака: (p — ∆; p + ∆)

ПРИМЕР РАСЧЕТА ОШИБКИ ВЫБОРКИ ДЛЯ ДОЛИ ПРИЗНАКА:

Например, в ходе исследования были опрошены 1000 человек (n=1000). 20% из них заинтересовались новым продуктом (p=0,2). Рассчитаем показатель ошибки выборки по формуле 1 (выберем доверительный уровень, равный 95%):

∆ = 1,96 * КОРЕНЬ (0,2*0,8/1000) = 0,0248 = ±2,48%

Рассчитаем доверительный интервал:

(p — ∆; p + ∆) = (20% — 2,48%; 20% + 2,48%) = (17,52%; 22,48%)

Таким образом, с вероятностью 95% мы можем быть уверены, что реальная доля заинтересованных в новом продукте (среди всей генеральной совокупности) находится в пределах полученного диапазона (17,52%; 22,48%).

Если бы мы выбрали доверительный уровень, равный 99%, то для тех же значений p и n ошибка выборки была бы больше, а доверительный интервал – шире. Это логично, поскольку, если мы хотим быть более уверены в том, что наш доверительный интервал «накроет» реальное значение признака, то интервал должен быть более широким.

КАЛЬКУЛЯТОР ОШИБКИ ВЫБОРКИ ДЛЯ СРЕДНЕГО ЗНАЧЕНИЯ

Доверительный уровень:

Объём выборки (n):

Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)

Среднее значение (x̄):

Стандартное отклонение (s):

РЕЗУЛЬТАТ

Ошибка выборки для среднего значения рассчитывается по следующим формулам.

1) если объем выборки значительно меньше генеральной совокупности:

(в данной формуле не используется показатель объема генеральной совокупности N)

2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:

N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели мороженого, постоянно проживающие в Москве). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).

s — выборочное стандартное отклонение измеряемого показателя. В идеале на месте этого аргумента должно быть стандартное отклонение показателя в генеральной совокупности (σ), но так как обычно оно неизвестно, используется выборочное стандартное отклонение, рассчитываемое по следующей формуле:

где, x ̅ – среднее арифметическое показателя, x_i– значение i-го показателя, n – объем выборки

Δ– предельная ошибка выборки.

Зная среднее значение показателя x ̅ и ошибку ∆, мы можем рассчитать доверительный интервал для среднего значения:(x ̅ — ∆; x ̅ + ∆)

ПРИМЕР РАСЧЕТА ОШИБКИ ВЫБОРКИ ДЛЯ СРЕДНЕГО ЗНАЧЕНИЯ:

Например, в ходе исследования были опрошены 1000 человек (n=1000). Каждого из них попросили указать их примерную среднюю сумму покупки (средний чек) в известной сети магазинов. Среднее арифметическое всех ответов составило 500 руб. (x ̅=500), а стандартное отклонение составило 120 руб. (s=120). Рассчитаем показатель ошибки выборки по формуле 1 (выберем доверительный уровень, равный 95%):

∆ = 1,96 * 120 / КОРЕНЬ (1000) = 7,44

Рассчитаем доверительный интервал:

(x ̅ — ∆; x ̅ + ∆) = (500 – 7,44; 500 + 7,44) = (492,56; 507,44)

Таким образом, с вероятностью 95% мы можем быть уверены, что значение среднего чека по всей генеральной совокупности находится в границах полученного диапазона: от 492,56 руб. до 507,44 руб.

КАЛЬКУЛЯТОР ЗНАЧИМОСТИ РАЗЛИЧИЙ ДОЛЕЙ

Доверительный уровень:

	Измерение 1	Измерение 2
Доля признака (p):	%	%
Объём выборки (n):

РЕЗУЛЬТАТ

Если в прошлогоднем исследовании вашу марку вспомнили 10% респондентов, а в исследовании текущего года – 15%, не спешите открывать шампанское, пока не воспользуетесь нашим онлайн-калькулятором для оценки статистической значимости различий.

Сравнивая два разных значения, полученные на двух независимых выборках, исследователь должен убедиться, что различия статистически значимы, прежде чем делать выводы.

Как известно, выборочные исследования не обеспечивают 100%-й точности измерения (для этого пришлось бы опрашивать всю целевую аудиторию поголовно, что слишком дорого). Тем не менее, благодаря методам математической статистики, мы можем оценить точность результатов любого количественного исследования и учесть ее в выводах.

В приведенном здесь калькуляторе используется двухвыборочный z-тест для долей. Для его применения должны соблюдаться следующие условия:

Обе выборки – простые случайные
Выборки независимы (между значениями двух выборок нет закономерной связи)
Генеральные совокупности значительно больше выборок
Произведения n*p и n*(1-p), где n=размер выборки а p=доля признака, – не меньше 5.

В калькуляторе используются следующие вводные данные:

Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень.

Доля признака (p) – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.

Объем выборки (n) – это количество людей, которые опрашиваются в исследовании.

Результат расчетов – вывод о статистической значимости или незначимости различий двух измерений.

КАЛЬКУЛЯТОР ЗНАЧИМОСТИ РАЗЛИЧИЙ СРЕДНИХ

Доверительный уровень:

	Измерение 1	Измерение 2
Среднее значение (x̄):
Стандартное отклонение (s):
Объём выборки (n):

РЕЗУЛЬТАТ

Допустим, выборочный опрос посетителей двух разных ТРЦ показал, что средний чек в одном из них равен 1000 рублей, а в другом – 1200 рублей. Следует ли отсюда вывод, что суммы среднего чека в двух этих ТРЦ действительно отличаются?

В приведенном здесь калькуляторе используется двухвыборочный z-тест для средних значений. Для его применения должны соблюдаться следующие условия:

Обе выборки – простые случайные
Выборки независимы (между значениями двух выборок нет закономерной связи)
Генеральные совокупности значительно больше выборок
Распределения значений в выборках близки к нормальному распределению.

В калькуляторе используются следующие вводные данные:

Среднее значение ( ̅x) – среднее арифметическое показателя.

Стандартное отклонение (s) – выборочное стандартное отклонение измеряемого показателя. В идеале на месте этого аргумента должно быть стандартное отклонение показателя в генеральной совокупности (σ), но так как обычно оно неизвестно, используется выборочное стандартное отклонение, рассчитываемое по следующей формуле:

где, x ̅ – среднее арифметическое показателя, x_i– значение i-го показателя, n – объем выборки

Объем выборки (n) – это количество людей, которые опрашиваются в исследовании.

Результат расчетов – вывод о статистической значимости или незначимости различий двух измерений.

Вы можете подписаться на уведомления о новых материалах СканМаркет

Источник

Как определить размер выборки?

Время на прочтение
4 мин

Количество просмотров 56K

Статистика знает все. И Ильф и Е. Петров, «12 Стульев»

Представьте себе, что вы строите крупный торговый центр и желаете оценить автомобильный поток въезда на территорию парковки. Нет, давайте другой пример… они все равно этого никогда не будут делать. Вам необходимо оценить вкусовые предпочтения посетителей вашего портала, для чего необходимо провести среди них опрос. Как увязать количество данных и возможную погрешность? Ничего сложного — чем больше ваша выборка, тем меньше погрешность. Однако и здесь есть нюансы.

Теоретический минимум

Не будет лишним освежить память, эти термины нам пригодятся далее.

Популяция – Множество всех объектов, среди которых проводится исследования.
Выборка – Подмножество, часть объектов из всей популяции, которая непосредственно участвует в исследовании.
Ошибка первого рода — (α) Вероятность отвергнуть нулевую гипотезу, в то время как она верна.
Ошибка второго рода — (β) Вероятность не отвергнуть нулевую гипотезу, в то время как она ложна.
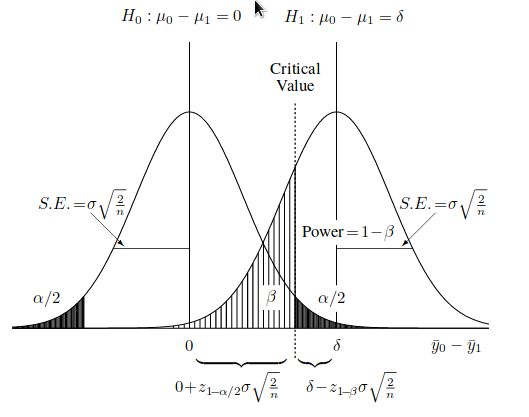
1 — β — Статистическая мощность критерия.
μ₀ и μ₁ — Средние значения при нулевой и альтернативной гипотезе.

Уже в самих определениях ошибки первого и второго рода имеется простор для дебатов и толкований. Как с ними определиться и какую выбрать в качестве нулевой? Если вы исследуете уровень загрязнения почвы или вод, то как сформулируете нулевую гипотезу: загрязнение присутствует, или нет загрязнения? А ведь от этого зависит объем выборки из общей популяции объектов.

Исходная популяция, также как и выборка может иметь любое распределение, однако среднее значение имеет нормальное или гауссово распределение благодаря Центральной Предельной Теореме.

Относительно параметров распределения и среднего значения в частности возможно несколько типов умозаключений. Первое из них называется доверительным интервалом. Он указывает на интервал возможных значений параметра, с указанным коэффициентом доверия. Так например 100(1-α)% доверительный интервал для μ будет таким (Ур. 1).

$hat{mu} pm t_{{alpha/2};df}sqrt{frac{hatsigma^2}{n}}$

df — Степень свободы = n — 1, от английского «degrees of freedom».
$t_{{alpha/2};df}$ — Двусторонняя критическая величина, t-критерий Стьюдента.

Второе из умозаключений — проверка гипотезы. Оно может быть примерно таким.

H₀: μ = h
H₁: μ > h
H₂: μ < h

С доверительным интервалом 100(1-α) для μ можно сделать выбор в пользу H₁ и H₂ :

Если нижний предел доверительного интервала 100(1-α) < h, то тогда отвергаем H₀ в пользу H₂.
Если верхний предел доверительного интервала 100(1-α) > h, то тогда отвергаем H₀ в пользу H₁.
Если доверительного интервала 100(1-α) включает в себя h, то тогда мы не может отвергнуть H₀ и такой результат считается неопределенным.

Если нам нужно проверить значение μ для одной выборки из общей совокупности, то критерий обретет вид.

Где $t = (hat{mu} - h)/sqrtfrac{hatsigma^2}{n}$ .

Доверительный интервал, погрешность и размер выборки

Возьмем самое первое уравнение и выразим оттуда ширину доверительного интервала (Ур. 2).

$w = 2t_{{alpha/2};df}sqrt{frac{hatsigma^2}{n}}$

В некоторых случаях мы можем заменить t-статистику Стьюдента на z стандартного нормального распределения. Еще одним упрощением заменим половину от w на погрешность измерения E. Тогда наше уравнения примет вид (Ур. 3).

$E = z_{alpha/2}sqrt{frac{hatsigma^2}{n}}$

Как видим погрешность действительно уменьшается вместе с ростом количества входных данных. Откуда легко вывести искомое (Ур. 4).

$n = left[frac{z_{alpha/2}*sigma}{E}right]^2$

Практика — считаем с R

Проверим гипотезу о том, что среднее значение данной выборки количества насекомых в ловушке равно 1.

H₀: μ = 1
H₁: μ > 1

Насекомые	0	1	2	3	4	5	6
Ловушки	10	9	5	5	1	2	1

> x <- read.table("/tmp/tcounts.txt")
> y = unlist(x, use.names="false")
> mean(z);sd(z)
[1] 1.636364
[1] 1.654883

Обратите внимание, что среднее и стандартное отклонение практически равны, что естественно для распределения Пуассона. Доверительный интервал 95% для t-статистики Стьюдента и df=32.

> qt(.975, 32)
[1] 2.036933

и наконец получаем критический интервал для среднего значения: 1.05 — 2.22.

> μ=mean(z)
> st = qt(.975, 32)
> μ + st * sd(z)/sqrt(33)
[1] 2.223159
> μ - st * sd(z)/sqrt(33)
[1] 1.049568

В итоге, следует отбраковать H₀ и принять H₁ так как с вероятностью 95%, μ > 1.

В том же самом примере, если принять, что нам известно действительное стандартное отклонение — σ, а не ее оценка полученная с помощью случайной выборки, можно рассчитать необходимое n для данной погрешности. Посчитаем для E=0.5.

> za2 = qnorm(.975)
> (za2*sd(z)/.5)^2
[1] 42.08144

Поправка на ветер

На самом деле нет никаких причин, полагать, что нам будет известна σ (дисперсия), в то время как μ (среднее) нам еще только предстоит оценить. Из-за этого уравнение 4 имеет мало практической пользы, кроме особо рафинированных примеров из области комбинаторики, а реалистичное уравнение для n несколько сложнее при неизвестной σ (Ур. 5).

$n = 4tildesigma^2 (z_{alpha/2}/w)^2 + z^2_{alpha/2}/2$

Обратите внимание, что σ в последнем уравнении не с шапкой (^), а тильдой (~). Это следствие того, что в самом начале у нас нет даже оценочного стандартного отклонения случайной выборки — , и вместо нее мы используем запланированное — . Откуда же мы берем последнее? Можно сказать, что с потолка: экспертная оценка, грубые прикидки, прошлый опыт и т. д.

А что на счет второго слагаемого правой стороны 5-го уравнения, откуда оно взялось? Так как $z_{alpha/2} < t_{{alpha/2};df}$ , необходима поправка Гюнтера.

Помимо уравнений 4 и 5 есть еще несколько приблизительно-оценочных формул, но это уже заслуживает отдельного поста.

Использованные материалы

Sample sizes
Hypothesis testing

Источник

Ошибки выборки
бывают систематические и случайные.

Систематические
— в том
случае, когда нарушен основной принцип
выборки — случайности.
Случайные
— возникают обычно ввиду того, что
структура выборочной совокупности
всегда отличается от структуры
генеральной совокупности, как бы
правильно ни был произведен отбор, то
есть, несмотря на принцип случайности
отбора единиц совокупности, все же
имеются расхождения между характеристиками
выборочной и генеральной совокупности.
Изучение и измерение случайных ошибок
репрезентативности и является основной
задачей выборочного метода.

Как правило,
чаще всего рассчитывают ошибку средней
и ошибку доли. При расчетах используются
следующие условные обозначения:

—средняя, рассчитанная
в пределах генеральной совокупности;

— средняя,
рассчитанная в пределах выборочной
совокупности;

p — доля данной
группы в генеральной совокупности;

w — доля данной
группы в выборочной совокупности.

Используя условные
обозначения, ошибки выборки для средней
и для доли можно записать следующим
образом:

В этих формулах
дисперсия признака является характеристикой
генеральной совокупности, которые при
выборочном наблюдении неизвестны. На
практике их заменяют аналогичными
характеристиками выборочной совокупности
на основании закона больших чисел, по
которому выборочная совокупность при
большом объеме точно воспроизводит
характеристики генеральной совокупности.

Формулы определения
средней ошибки для различных способов
отбора:

Повторный

Бесповторный

Способ
отбора

ошибка
средней

ошибка
доли

ошибка
средней

ошибка
доли

Собственно-случайный

и
механический

Типический

Серийный

D — предельная
ошибка;

m — средняя ошибка;

n — численность
выборки;

N — численность
генеральной совокупности;

—
общая дисперсия;

w — доля данной
категории в общей численности выборки;

—
средняя из внутригрупповых дисперсий;

d2 — межгрупповая
дисперсия;

r — число серий в
выборке;

R — общее число
серий.

Предельная ошибка
для всех способов отбора связана со
средней ошибкой выборки следующим
образом:

D = tm,

где t — коэффициент
доверия, функционально связанный с
вероятностью, с которой обеспечивается
величина предельной ошибки. В зависимости
от вероятности коэффициент доверия t
принимает следующие значения:

t P

1 0,683

1,5 0,866

2 0,954

2,5 0,988

3 0,997

4 0,9999

Величина предельной
ошибки зависит от следующих величин:

колеблемости
признака (прямая связь), которую
характеризует величина дисперсии;
численности
выборки (обратная связь);
доверительной
вероятности (прямая связь);
метода отбора.

Помимо прямой
задачи (определение величины ошибки)
формула предельной ошибки позволяет
решать еще две задачи.

Определить
необходимую численность выборки, при
которой пределы возможной ошибки не
превышают некоторой заданной величины.

Определить
вероятность того, что в проведенной
выборке ошибка будет заключаться в
заданных пределах.

Решение этих
задач зависит от способа отбора. Например,
необходимая численность выборки для
повторного отбора:

при без повторной:

Построение
доверительных интервалов.

При выборке малого объема точечная
оценка может значительно отличаться
от оцениваемого параметра, что приводит
к грубым ошибкам. Поэтому в таком случае
лучше пользоваться интервальными
оценками, то есть указывать интервал,
в который с заданной вероятностью
попадает истинное значение оцениваемого
параметра. Разумеется, чем меньше длина
этого интервала, тем точнее оценка
параметра. Поэтому, если для оценки Θ*
некоторого параметра Θ справедливо
неравенство | Θ* — Θ | < δ, число δ > 0
характеризуетточность оценки ( чем
меньше δ, тем точнее оценка). Но
статистические методы позволяют говорить
только о том, что это неравенство
выполняется с некоторой вероятностью.

Определение 18.1. Надежностью
(доверительной вероятностью)оценки
Θ* параметра Θ называется вероятность
γ того, что выполняется неравенство |
Θ* — Θ | < δ. Если заменить это неравенство
двойным неравенством – δ < Θ* — Θ < δ,
то получим:

p(Θ* -δ<Θ<Θ* +δ) =γ.

Таким образом, γ есть вероятность того,
что Θ попадает в интервал ( Θ* — δ, Θ* + δ).

Определение 18.2. Доверительным
называется интервал, в который попадает
неизвестный параметр с заданной
надежностью γ.

Построение доверительных
интервалов.

1. Доверительный интервал для оценки
математического ожидания нормального
распределения при известной дисперсии.

Пример. Найдем доверительный интервал
для математического ожидания нормально
распреде-ленной случайной величины,
если объем выборки п= 49,σ
= 1,4, а доверительная вероятность γ = 0,9.

Определим t, при котором
Ф(t) = 0,9:2 = 0,45:t= 1,645. Тогда

, или 2,471 < a<
3,129. Найден доверительный интервал, в
который попадаетас надежностью
0,9.

2. Доверительный интервал для оценки
математического ожидания нормального
распределения при неизвестной дисперсии.

Пример. Пусть объем выборки п= 25,= 3,s= 1,5. Найдем доверительный интервал дляапри γ = 0,99. Из таблицы находим, чтоt_γ(п= 25, γ = 0,99) = 2,797. Тогда, или 2,161<a< 3,839 – доверительный интервал, в
который попадаетас вероятностью
0,99.

3. Доверительные интервалы для оценки
среднего квадратического отклонения
нормального распределения.

Будем искать для среднего квадратического
отклонения нормально распределенной
случайной величины доверительный
интервал вида (s –
δ, s +δ), гдеs– исправленное выборочное среднее
квадратическое отклонение, а для δ
выполняется условие:p( |σ –s| < δ ) = γ.

. Тогда Существуют таблицы для
распределения «хи-квадрат», из которых
можно найти qпо
заданнымпи γ, не решая этого
уравнения. Таким образом, вычислив по
выборке значениеsи
определив по таблице значение q,
можно найти доверительный интервал
(18.4), в который значение σ попадает с
заданной вероятностью γ.

Замечание.Еслиq> 1, то с учетом условия σ > 0 доверительный
интервал для σ будет иметь границы

Пример.

Пусть п= 20,s= 1,3.
Найдем доверительный интервал для σ
при заданной надежности γ = 0,95. Из
соответствующей таблицы находимq(n= 20,γ= 0,95 ) = 0,37. Следовательно, границы
доверительного интервала: 1,3(1-0,37) = 0,819
и 1,3(1+0,37) = 1,781. Итак, 0,819< σ <
1,781 с вероятностью 0,95.

Виды
выборок.

В зависимости от методики формирования
выборочной совокупности различают
следующие основные виды выборки:

собственно случайную;

механическую;

типическую (стратифицированную,
районированную);

серийную (гнездовую);

комбинированную;

многоступенчатую;

многофазную;

взаимопроникающую.

Собственно случайная выборка формируется
в строгом соответствии с научными
принципами и правилами случайного
отбора. Для получения собственно
случайной выборки генеральная совокупность
строго подразделяется на единицы отбора,
и затем в случайном повторном или
бесповторном порядке отбирается
достаточное число единиц.

Случайный порядок подобен жеребьевке.
На практике он чаще всего применяется
при использовании специальных таблиц
случайных чисел. Если, например, из
совокупности, содержащей 1587 единиц,
следует отобрать 40 единиц, то из таблицы
отбирают 40 четырехзначных чисел, которые
меньше 1587.

В том случае, когда собственно случайная
выборка организуется как повторная,
расчет стандартной ошибки производится
в соответствии с формулой (6.2). При
бесповторном способе отбора формула
для расчета стандартной ошибки будет:

где 1 – n / N – доля единиц генеральной
совокупности, не попавших в выборку.
Так как эта доля всегда меньше единицы,
то ошибка при бесповторном отборе при
прочих равных условиях всегда меньше,
чем при повторном. Бесповторный отбор
организовать легче, чем повторный, и он
применяется намного чаще. Однако величину
стандартной ошибки при бесповторном
отборе можно определять по более простой
формуле (5.1). Такая замена возможна, если
доля единиц генеральной совокупности,
не попавших в выборку, большая и,
следовательно, величина близка к единице.

Формировать выборку в строгом соответствии
с правилами случайного отбора практически
очень сложно, а иногда невозможно, так
как при использовании таблиц случайных
чисел необходимо пронумеровать все
единицы генеральной совокупности.
Довольно часто генеральная совокупность
такая большая, что провести подобную
предварительную работу чрезвычайно
сложно и нецелесообразно, поэтому на
практике применяют другие виды выборок,
каждая из которых не является строго
случайной. Однако организуются они так,
чтобы было обеспечено максимальное
приближение к условиям случайного
отбора.

При чисто механической выборке вся
генеральная совокупность единиц должна
быть прежде всего представлена в виде
списка единиц отбора, составленного в
каком-то нейтральном по отношению к
изучаемому признаку порядке, например
по алфавиту. Затем список единиц отбора
разбивается на столько равных частей,
сколько необходимо отобрать единиц.
Далее по заранее установленному правилу,
не связанному с вариацией исследуемого
признака, из каждой части списка
отбирается одна единица. Этот вид выборки
не всегда может обеспечить случайный
характер отбора, и полученная выборка
может оказаться смещенной. Объясняется
это тем, что, во-первых, упорядочение
единиц генеральной совокупности может
иметь элемент неслучайного характера.
Во-вторых, отбор из каждой части
генеральной совокупности при неправильном
установлении начала отсчета может также
привести к ошибке смещения. Однако
практически легче организовать
механическую выборку, чем собственно
случайную, и при проведении выборочных
обследований чаще всего пользуются
этим видом выборки. Стандартную ошибку
при механической выборке определяют
по формуле собственно случайной
бесповторной выборки (6.2).

Типическая (районированная,
стратифицированная) выборка преследует
две цели:

• обеспечить представительство в
выборке соответствующих типических
групп генеральной совокупности по
интересующим исследователя признакам;

• увеличить точность результатов
выборочного обследования.

При типической выборке до начала ее
формирования генеральная совокупность
единиц разбивается на типические группы.
При этом очень важным моментом является
правильный выбор группировочного
признака. Выделенные типические группы
могут содержать одинаковое или различное
число единиц отбора. В первом случае
выборочная совокупность формируется
с одинаковой долей отбора из каждой
группы, во втором – с долей, пропорциональной
ее доле в генеральной совокупности.
Если выборка формируется с равной долей
отбора, по существу она равносильна
ряду собственно случайных выборок из
меньших генеральных совокупностей,
каждая из которых и есть типическая
группа. Отбор из каждой группы
осуществляется в случайном (повторном
или бесповторном) либо механическом
порядке. При типической выборке, как с
равной, так и неравной долей отбора,
удается устранить влияние межгрупповой
вариации изучаемого признака на точность
ее результатов, так как обеспечивается
обязательное представительство в
выборочной совокупности каждой из
типических групп. Стандартная ошибка
выборки будет зависеть не от величины
общей дисперсии ?2, а от величины средней
из групповых дисперсий ?i2. Поскольку
средняя из групповых дисперсий всегда
меньше общей дисперсии, постольку при
прочих равных условиях стандартная
ошибка типической выборки будет меньше
стандартной ошибки собственно случайной
выборки.

При определении стандартных ошибок
типической выборки применяются следующие
формулы:

• при повторном способе отбора

• при бесповторном способе отбора:

– средняя из групповых дисперсий в
выборочной совокупности.

Серийная (гнездовая) выборка – это такой
вид формирования выборочной совокупности,
когда в случайном порядке отбираются
не единицы, подлежащие обследованию, а
группы единиц (серии, гнезда). Внутри
отобранных серий (гнезд) обследованию
подвергаются все единицы. Серийную
выборку практически организовать и
провести легче, чем отбор отдельных
единиц. Однако при этом виде выборки,
во-первых, не обеспечивается
представительство каждой из серий и,
во-вторых, не устраняется влияние
межсерийной вариации изучаемого признака
на результаты обследования. В том случае,
когда эта вариация значительна, она
приведет к увеличению случайной ошибки
репрезентативности. При выборе вида
выборки исследователю необходимо
учитывать это обстоятельство. Стандартная
ошибка серийной выборки определяется
по формулам:

• при повторном способе отбора —

где ?– межсерийная дисперсия выборочной
совокупности; r – число отобранных
серий;

• при бесповторном способе отбора —

где R – число серий в генеральной
совокупности.

В практике те или иные способы и виды
выборок применяются в зависимости от
цели и задач выборочных обследований,
а также возможностей их организации и
проведения. Чаще всего применяется
комбинирование способов отбора и видов
выборки. Такие выборки получили название
комбинированные. Комбинирование возможно
в разных сочетаниях: механической и
серийной выборки, типической и
механической, серийной и собственно
случайной и т. д. К комбинированной
выборке прибегают для обеспечения
наибольшей репрезентативности с
наименьшими трудовыми и денежными
затратами на организацию и проведение
обследования.

При комбинированной выборке величина
стандартной ошибки выборки состоит из
ошибок на каждой ее ступени и может быть
определена как корень квадратный из
суммы квадратов ошибок соответствующих
выборок. Так, если при комбинированной
выборке в сочетании использовались
механическая и типическая выборки, то
стандартную ошибку можно определить
по формуле

где ?1 и ?2 – стандартные ошибки
соответственно механической и типической
выборок.

Особенность многоступенчатой выгборки
состоит в том, что выборочная совокупность
формируется постепенно, по ступеням
отбора. На первой ступени с помощью
заранее определенного способа и вида
отбора отбираются единицы первой
ступени. На второй ступени из каждой
единицы первой ступени, попавшей в
выборку, отбираются единицы второй
ступени и т. д. Число ступеней может быть
и больше двух. На последней ступени
формируется выборочная совокупность,
единицы которой подлежат обследованию.
Так, например, для выборочного обследования
бюджетов домашних хозяйств на первой
ступени отбираются территориальные
субъекты страны, на второй – районы в
отобранных регионах, на третьей – в
каждом муниципальном образовании
отбираются предприятия или организации
и, наконец, на четвертой ступени – в
отобранных предприятиях отбираются
семьи.

Таким образом, выборочная совокупность
формируется на последней ступени.
Многоступенчатая выборка более гибкая,
чем другие виды, хотя в общем она дает
менее точные результаты, чем выборка
того же объема, но сформированная в одну
ступень. Однако при этом она имеет одно
важное преимущество, которое заключается
в том, что основу выборки при многоступенчатом
отборе нужно строить на каждой из
ступеней только для тех единиц, которые
попали в выборку, а это очень важно, так
как нередко готовой основы выборки нет.

Стандартную ошибку выборки при
многоступенчатом отборе при группах
разных объемов определяют по формуле

где ?1, ?2, ?3, … – стандартные ошибки на
разных ступенях;

n1, n2, n3, … – численность выборок на
соответствующих ступенях отбора.

В том случае, если группы неодинаковы
по объему, то теоретически этой формулой
пользоваться нельзя. Но если общая доля
отбора на всех ступенях постоянна, то
практически расчет по этой формуле не
приведет к искажению величины ошибки.

Сущность многофазной выгборки состоит
в том, что на основе первоначально
сформированной выборочной совокупности
образуют подвыборку, из этой подвыборки
– следующую подвыборку и т. д. Первоначальная
выборочная совокупность представляет
собой первую фазу, подвыборка из нее –
вторую и т. д. Многофазную выборку
целесообразно применять в случаях,
если:

для изучения различных признаков
требуется неодинаковый объем выборки;

колеблемость изучаемых признаков
неодинакова и требуемая точность
различна;

в отношении всех единиц первоначальной
выборочной совокупности (первая фаза)
необходимо собрать менее подробные
сведения, а в отношении единиц каждой
последующей фазы – более подробные.

Одним из несомненных достоинств
многофазной выборки является то
обстоятельство, что сведениями,
полученными на первой фазе, можно
пользоваться как дополнительной
информацией на последующих фазах,
информацией второй фазы – как
дополнительной информацией на следующих
фазах и т. д. Такое использование сведений
повышает точность результатов выборочного
обследования.

При организации многофазной выборки
можно применять сочетание различных
способов и видов отбора (типическую
выборку с механической и т. д.). Многофазный
отбор можно сочетать с многоступенчатым.
На каждой ступени выборка может быть
многофазной.

Стандартная ошибка при многофазной
выборке рассчитывается на каждой фазе
в отдельности в соответствии с формулами
того способа отбора и вида выборки, при
помощи которых формировалась ее
выборочная совокупность.

Взаимопроникающие выгборки – это две
или более независимые выборки из одной
и той же генеральной совокупности,
образованные одним и тем же способом и
видом. К взаимопроникающим выборкам
целесообразно прибегать, если необходимо
за короткий срок получить предварительные
итоги выборочных обследований.
Взаимопроникающие выборки эффективны
для оценки результатов обследования.
Если в независимых выборках результаты
одинаковы, то это свидетельствует о
надежности данных выборочного
обследования. Взаимопроникающие выборки
иногда можно применять для проверки
работы различных исследователей, поручив
каждому из них провести обследование
разных выборок.

Стандартная ошибка при взаимопроникающих
выборках определяется по той же формуле,
что и типическая пропорциональная
выборка (5.3). Взаимопроникающие выборки
по сравнению с другими видами требуют
больших трудовых затрат и денежных
расходов, поэтому исследователь должен
учитывать это обстоятельство при
проектировании выборочного обследования.

Предельные ошибки при различных способах
отбора и видах выборки определяются по
формуле ? = t?, где ? – соответствующая
стандартная ошибка.

Малые
выборки.

Таблицы интеграла вероятностей
используются для выборок большого
объема из бесконечно большой генеральной
совокупности. Но уже при п < 00 получается
несоответствие между табличными данными
и вероятностью предела; при п < 100
погрешность становится значительной.
Несоответствие вызывается главным
образом характером распределения единиц
генеральной совокупности. При большом
объеме выборки особенность распределения
в генеральной совокупности не имеет
значения, так как распределение отклонений
выборочного показателя от генеральной
характеристики при большой выборке
всегда оказывается нормальным.

В выборках небольшого объема п ≤ 30
характер распределения генеральной
совокупности сказывается на распределении
ошибок выборки. Поэтому для расчета
ошибки выборки при небольшом объеме
наблюдения (уже менее 100 единиц) отбор
должен проводиться из совокупности,
имеющей нормальное распределение.

Теория малых выборок разработана
английским статистиком В. Госсетом
(писавшим под псевдонимом Стьюдент) в
начале XX в. В 1908 г. им построено специальное
распределение, которое позволяет и при
малых выборках соотносить t и доверительную
вероятность F(t). При п > 100 таблицы
распределения Стьюдента дают те же
результаты, что и таблицы интеграла
вероятностей Лапласа, при 30 ≤ п ≤ 100
различия незначительны. Поэтому
практически к малым выборкам относят
выборки объемом менее 30 единиц (безусловно,
большой считается выборка с объемом
более 100 единиц).

Использование малых выборок в ряде
случаев обусловлено характером
обследуемой совокупности. Так, в
селекционной работе «чистого» опыта
легче добиться на небольшом числе
делянок. Производственный и экономический
эксперимент, связанный с экономическими
затратами, также проводится на небольшом
числе испытаний.

Как уже отмечалось, в случае малой
выборки только для нормально распределенной
генеральной совокупности могут быть
рассчитаны и доверительные вероятности,
и доверительные пределы генеральной
средней.

Плотность вероятностей распределения
Стьюдента описывается функцией

где t — текущая переменная;

п — объем выборки;

В — величина, зависящая лишь от п.

Распределение Стьюдента имеет только
один параметр: d.f. -число степеней свободы
(иногда обозначается k).

Это распределение, как и нормальное,
симметрично относительно точки t = 0, но
оно более пологое. При увеличении объема
выборки, а следовательно, и числа степеней
свободы распределение Стьюдента быстро
приближается к нормальному. Число
степеней свободы равно числу тех
индивидуальных значений признаков,
которыми нужно располагать для определения
искомой характеристики.

Так, для расчета дисперсии должна быть
известна средняя величина. Поэтому при
расчете дисперсии d.f. = п — 1

Таблицы распределения Стьюдента
публикуются в двух вариантах:

1) аналогично таблицам интеграла
вероятностей приводятся значения t и
соответствующие вероятности F(t) при
разном числе степеней свободы;

2) значения t приводятся для наиболее
употребимых доверительных вероятностей
0,90; 0,95 и 0,99 или для 1 — 0,9 = 0,1, 1 — 0,95 = = 0,05 и
1 — 0,99 == 0,01 при разном числе степеней
свободы. Такого рода таблица приведена
в приложении (табл. 2), а также значение
t-критерия Стьюдента при уровне значимости
0,10; 0,05; 0,01.

При малых выборках расчет средней
возможной ошибки основан на выборочных
дисперсиях, поэтому

Приведенная формула используется для
определения предела возможной ошибки
выборочного показателя:

Порядок расчетов тот же, что и при больших
выборках.

Пример. Для изучения интенсивности
труда было организовано наблюдение за
10 отобранными рабочими. Доля работавших
все время оказалась равной 0,40, дисперсия
0,4•0,6 = 0,24. По табл. 2 приложения находим
для F(t) = 0,95 и d.f. = n — 1 = 9, t = 2,26. Рассчитаем
среднюю ошибку выборки доли работавших
все время:

Тогда предельная ошибка выборки ?p =
2,26•0,16 = ± 0,36. Таким образом, с вероятностью
0,95 доля рабочих, работавших без простоев,
в данном цехе предприятия находится в
пределах

39,64% ≤ ? ≤ 40,36%

или

39,6% ≤ ? ≤ 40,4%.

Если бы мы использовали для расчета
доверительных границ генерального
параметра таблицу интеграла вероятностей,
то t было бы равно 1,96 и ?p — ± 0,31, т. е.
доверительный интервал был бы несколько
уже.

Малые выборки широко используются для
решения задач, связанных с испытанием
статистических гипотез, особенно гипотез
о средних величинах.

Индексный
анализ финансовых показателей.

Индексный метод позволяет определить
влияние факторов на обобщающий показатель
в динамике. Метод основывается на
использовании относительных показателей,
выражающих отношение уровня данного
явления к его уровню, принятому в качестве
базы. Различают индивидуальные и
групповые индексы. Кроме того, в анализе
хозяйственной деятельности используются
индексы базисные, показывающие изменение
явления относительно базисного периода,
и цепные, характеризующие изменение
явления относительно предыдущего
периода.

Например, анализируется изменение
объема товарной продукции (Т) за четыре
месяца – Т1, Т2, Т3,

Принимая в качестве базисного периода
один месяц, получаем для каждого 1-го
месяца базисный

Iбаз = Тi /Т1 и цепной индекс Iцеп = Тi /Тi–1:

Iбаз5/1 = Iцеп1/1 • Iцеп2/1 • Iцеп3/2 • Iцеп4/3.

Индексный метод может быть использован
для факторного анализа какого-либо
показателя.

Например, необходимо определить изменение
по сравнению с прошлым годом объема
товарной продукции ?Т под влиянием
переменной численности рабочих (а) и
производительности их труда (в). Для
решения строится система взаимосвязанных
индексов:

Iобщ = (в1• а1)/(в0• а0) = Т1/ Т0,

где Iобщ – общий групповой индекс
изменения объема выпуска продукции;
в1, в0 – среднегодовая выработка товарной
продукции на одного рабочего соответственно
в анализируемом и базисном периодах;
а1, а0 – среднегодовая выработка товарной
продукции на одного рабочего соответственно
в анализируемом и базисном периодах;
Т1, Т0 – объем товарной продукции
соответственно в анализируемом и прошлом
базисном периодах.

При построении факторных индексов для
определения влияния количественного
показателя качественный фиксируется
на базисном уровне в0, а при установлении
влияния качественного показателя
количественный фиксируется на уровне
а1. Тогда:

Iобщ = Iа • Iв,

где Iа – факторный индивидуальный индекс
изменения численности рабочих;

Iв– факторный индивидуальный индекс
изменения средней годовой выработки
одного рабочего.

При этой величине отклонение товарной
продукции под действием обоих факторов
равна:

?Т = (в0а1 – в0а0) + (в1а1 – в0а1) = в1а1 – в0а0.

Виды
статистических индексов.

Статистический
индекс — это относительная величина
сравнения сложных совокупностей и
отдельных их единиц. При этом под сложной
понимается такая статистическая
совокупность, отдельные элементы которой
непосредственно не подлежат суммированию.

Основой
индексного метода при определении
изменений в производстве и обращении
товаров является переход от
натурально-вещественной формы выражения
товарных масс к стоимостным (денежным)
измерителям. Именно посредством денежного
выражения стоимости отдельных товаров
устраняется их несравнимость и достигается
единство.

Виды
индексов различают по следующим факторам:

по
степени охвата элементов совокупности:

индивидуальные
– характеризуют изменение только
одного элемента совокупности;

сводные
(общие) – отражают изменения по всей
совокупности элементов сложного
явления. Их разновидностью являются
групповые индексы.

в
зависимости от содержания и характера
индексируемой величины:

индексы
количественных показателей (например,
индекс физического объема);

индексы
качественных показателей (например,
индекс цен, себестоимости, производительности
труда).

в
зависимости от методологии расчета:

агрегатные
– могут быть рассчитаны как индексы
переменного и постоянного состава;

средние
из индивидуальных – получаются путем
нахождения общих индексов с использованием
индивидуальных.

Для
удобства восприятия индексов в теории
статистики разработана символика:

—
q – количество единиц какого-либо вида
продукции;

—
p – цена единицы какого-либо вида
продукции;

—
z – себестоимость единицы какого-либо
вида продукции;

—
t – трудоемкость единицы какого-либо
вида продукции

Индивидуальные
индексы. Правила построения и анализа.

индивидуальные
индексы
— это индексы, которые характеризуют
изменение только одного элемента
совокупности.

Различают
следующие индивидуальные индексы:

индекс
физического объема
– показывает во сколько раз увеличился
(уменьшился) объем в натуральных единицах
в отчетном периоде по сравнению с
базисным

где
q1 и q0 — количество продукции данного
вида в натуральном выражении в текущем
и базисном периодах.

Аналогично
рассчитывается индекс затрат на выпуск
продукции (ЗВП), который отражает
изменение затрат на производство и
может быть как индивидуальным, так и
агрегатным.

индекс
цен
– показывает во сколько раз увеличилась
(уменьшилась) цена единицы продукции в
отчетном периоде по сравнению с базисным;

где
p1 и p0 — цена за единицу продукции в текущем
и базисном периодах.

индекс
себестоимости
– показывает во сколько раз увеличилась
(уменьшилась) себестоимость единицы
продукции в отчетном периоде по сравнению
с базисным.

где
p1 и p0 — цена единицы продукции данного
вида в текущем и базисном периодах; q1
p1 и q0 p0 — стоимость продукции данного
вида в текущем и базисном периодах.

15.
Агрегатная
форма сводного индекса. Правила
построения и анализа.

Основной формой общих индексов являются
агрегатные индексы.

Расчет индексов по агрегатным формулам
возможен, если есть полные данные о
физическом объеме продукции и о ценах
как на уровне отчетного так и базисного
периодов. В реальной действительности
полные данные имеются не всегда. В таких
случаях приходится исчислять индексы
как среднюю взвешенную величину из
индивидуальных индексов. Средний из
индивидуальных индексов будет тогда
правильным, когда он тождественен
агрегатному индексу. Это означает, что
средние из индивидуальных индексов не
самостоятельные индексы, а преобразованная
форма агрегатного индекса. При исчислении
средних индексов могут быть использованы
только две формы средних: средняя
арифметическая и средняя гармоническая:

Источник

См. начало:

CFA — Выборочный метод и простая случайная выборка
CFA — Стратифицированная случайная выборка
CFA — Временные ряды и перекрестные данные
CFA — Центральная предельная теорема и распределение выборочного среднего
CFA — Точечные оценки среднего значения совокупности

Когда нам нужно получить одно число в качестве оценки параметра совокупности, мы используем точечную оценку. Тем не менее, из-за ошибки выборки, точечная оценка не будет в точности равняться параметру совокупности при любом размере данной выборки.

Часто, вместо точечной оценки, более полезным подходом будет найти диапазон значений, в рамках которого, как мы ожидаем, может находится значение искомого параметра с заданным уровнем вероятности.

Этот подход называется интервальной оценкой параметра (англ. ‘interval estimate of parameter’), а доверительный интервал выполняет роль этого диапазона значений.

Определение доверительного интервала.

Доверительный интервал (англ. ‘confidence interval’) представляет собой диапазон, для которого можно утверждать, с заданной вероятностью (1 — alpha ), называемой степенью доверия (или степенью уверенности, англ. ‘degree of confidence’), что он будет содержать оцениваемый параметр.

Этот интервал часто упоминается как (100 (1 — alpha)% ) доверительный интервал для параметра.

Конечные значения доверительного интервала называются нижним и верхним доверительными пределами (или доверительными границами или предельной погрешностью, англ. ‘lower/upper confidence limits’).

В этом чтении, мы имеем дело только с двусторонними доверительными интервалами — доверительные интервалами, для которых мы вычисляем и нижние и верхние пределы.

Кроме того, можно определить два типа односторонних доверительных интервалов для параметра совокупности.

Нижний односторонний доверительный интервал устанавливает только нижний предел. Это означает допущение, что с определенной степенью доверия параметр совокупности равен или превышает нижний предел.

Верхний односторонний доверительный интервал устанавливает только верхний предел. Это означает допущение, что с определенной степенью доверия параметр совокупности меньше или равен верхнему пределу.

Инвестиционные аналитики редко используют односторонние доверительные интервалы.

Доверительные интервалы часто дают либо вероятностную интерпретацию, либо практическую интерпретацию.

При вероятностной интерпретации, мы интерпретируем 95%-ный доверительный интервал для среднего значения совокупности следующим образом.

При повторяющейся выборке, 95% таких доверительных интервалов будут, в конечном счете, включать в себя среднее значение совокупности.

Например, предположим, что мы делаем выборку из совокупности 1000 раз, и на основании каждой выборки мы построим 95%-ный доверительный интервал, используя вычисленное выборочное среднее.

Из-за случайного характера выборок, эти доверительные интервалы отличаются друг от друга, но мы ожидаем, что 95% (или 950) этих интервалов включают неизвестное значение среднего по совокупности.

На практике мы обычно не делаем такие повторяющиеся выборки. Поэтому в практической интерпретации, мы утверждаем, что мы 95% уверены в том, что один 95%-ный доверительный интервал содержит среднее по совокупности.

Мы вправе сделать это заявление, потому что мы знаем, что 95% всех возможных доверительных интервалов, построенных аналогичным образом, будут содержать среднее по совокупности.

Доверительные интервалы, которые мы обсудим в этом чтении, имеют структуры, подобные описанной ниже базовой структуре.

Построение доверительных интервалов.

Доверительный интервал (100 (1 — alpha)% ) для параметра имеет следующую структуру.

Точечная оценка (pm) Фактор надежности (times) Стандартная ошибка

где

Точечная оценка = точечная оценка параметра (значение выборочной статистики).
Фактор надежности (англ. ‘reliability factor’) = коэффициент, основанный на предполагаемом распределении точечной оценки и степени доверия ((1 — alpha)) для доверительного интервала.
Стандартная ошибка = стандартная ошибка выборочной статистики, значение которой получено с помощью точечной оценки.

Величину (Фактор надежности) (times) (Cтандартная ошибка) иногда называют точностью оценки (англ. ‘precision of estimator’). Большие значения этой величины подразумевают более низкую точность оценки параметра совокупности.

Самый базовый доверительный интервал для среднего значения по совокупности появляется тогда, когда мы делаем выборку из нормального распределения с известной дисперсией. Фактор надежности в данном случае на основан стандартном нормальном распределении, которое имеет среднее значение, равное 0 и дисперсию 1.

Стандартная нормальная случайная величина обычно обозначается как (Z). Обозначение (z_alpha ) обозначает такую точку стандартного нормального распределения, в которой (alpha) вероятности остается в правом хвосте.

Например, 0.05 или 5% возможных значений стандартной нормальной случайной величины больше, чем ( z_{0.05} = 1.65 ).

Предположим, что мы хотим построить 95%-ный доверительный интервал для среднего по совокупности, и для этой цели, мы сделали выборку размером 100 из нормально распределенной совокупности с известной дисперсией (sigma^2) = 400 (значит, (sigma) = 20).

Мы рассчитываем выборочное среднее как ( overline X = 25 ). Наша точечная оценка среднего по совокупности, таким образом, 25.

Если мы перемещаем 1.96 стандартных отклонений выше среднего значения нормального распределения, то 0.025 или 2.5% вероятности остается в правом хвосте. В силу симметрии нормального распределения, если мы перемещаем 1.96 стандартных отклонений ниже среднего, то 0.025 или 2.5% вероятности остается в левом хвосте.

В общей сложности, 0.05 или 5% вероятности лежит в двух хвостах и 0.95 или 95% вероятности лежит между ними.

Таким образом, ( z_{0.025} = 1.96) является фактором надежности для этого 95%-ного доверительного интервала. Обратите внимание на связь (100 (1 — alpha)% ) для доверительного интервала и (z_{alpha/2}) для фактора надежности.

Стандартная ошибка среднего значения выборки, заданная Формулой 1, равна:

( sigma_{overline X} = 20 Big / sqrt{100} = 2 )

Доверительный интервал, таким образом, имеет нижний предел:

( overline X — 1.96 sigma_{overline X} ) = 25 — 1.96(2) = 25 — 3.92 = 21.08.

Верхний предел доверительного интервала равен:

( overline X + 1.96sigma_{overline X} ) = 25 + 1.96(2) = 25 + 3.92 = 28.92

95%-ный доверительный интервал для среднего по совокупности охватывает значения от 21.08 до 28.92.

Доверительные интервалы для среднего по совокупности (нормально распределенная совокупность с известной дисперсией).

Доверительный интервал (100 (1 — alpha)% ) для среднего по совокупности ( mu ), когда мы делаем выборку из нормального распределения с известной дисперсией ( sigma^2 ) задается формулой:

( Large dst overline X pm z_{alpha /2}{sigma over sqrt n} ) (Формула 4)

Факторы надежности для наиболее часто используемых доверительных интервалов приведены ниже.

Факторы надежности для доверительных интервалов на основе стандартного нормального распределения.

Мы используем следующие факторы надежности при построении доверительных интервалов на основе стандартного нормального распределения:

90%-ные доверительные интервалы: используется (z_{0.05}) = 1.65
95%-ные доверительные интервалы: используется (z_{0.025}) = 1.96
99%-ные доверительные интервалы: используется (z_{0.005}) = 2.58

На практике, большинство финансовых аналитиков используют значения для (z_{0.05}) и (z_{0.005}), округленные до двух знаков после запятой.

Для справки, более точными значениями для (z_{0.05}) и (z_{0.005}) являются 1.645 и 2.575, соответственно.

Для быстрого расчета 95%-ного доверительного интервала (z_{0.025}) иногда округляют 1.96 до 2.

Эти факторы надежности подчеркивают важный факт о всех доверительных интервалах. По мере того, как мы повышаем степень доверия, доверительный интервал становится все шире и дает нам менее точную информацию о величине, которую мы хотим оценить.

«Чем уверенней мы хотим быть, тем меньше мы должны быть уверены»

см. Freund и Williams (1977), стр. 266.

На практике, допущение о том, что выборочное распределение выборочного среднего, по меньшей мере, приблизительно нормальное, часто является обоснованным, либо потому, что исходное распределение приблизительно нормальное, либо потому что мы имеем большую выборку и поэтому к ней применима центральная предельная теорема.

Однако, на практике, мы редко знаем дисперсию совокупности. Когда дисперсия генеральной совокупности неизвестна, но выборочное среднее, по меньшей мере, приблизительно нормально распределено, у нас есть два приемлемых пути чтобы вычислить доверительные интервалы для среднего значения совокупности.

Вскоре мы обсудим более консервативный подход, который основан на t-распределении Стьюдента (t-распределение, для краткости).

Распределение статистики (t) называется t-распределением Стьюдента (англ. «Student’s t-distribution») из-за псевдонима «Студент» (Student), использованного британским математиком Уильямом Сили Госсеттом, который опубликовал свою работу в 1908 году.

В финансовой литературе, это наиболее часто используемый подход для статистической оценки и проверки статистических гипотез, касающихся среднего значения, когда дисперсия генеральной совокупности не известна, как для малого, так и для большого размер выборки.

Второй подход к доверительным интервалам для среднего по совокупности, основанного на стандартном нормальном распределении, — это z-альтернатива (англ. ‘z-alternative’). Он может быть использован только тогда, когда размер выборки является большим (в общем случае, размер выборки 30 или больше, можно считать большим).

В отличии от доверительного интервала, приведенного в Формуле 4, этот доверительный интервал использует стандартное отклонение выборки (s) при вычислении стандартной ошибки выборочного среднего (по Формуле 2).

Доверительные интервалы для среднего по совокупности — z-альтернатива (большая выборка, дисперсия совокупности неизвестна).

Доверительный интервал (100 (1 — alpha)% ) для среднего по совокупности ( mu ) при выборке из любого распределения с неизвестной дисперсией, когда размер выборки большой, задается формулой:

( Large dst overline X pm z_{alpha /2}{s over sqrt n} ) (Формула 5)

Поскольку этот тип доверительного интервала применяется довольно часто, мы проиллюстрируем его вычисление в Примере 4.

Пример (4) расчета доверительного интервала для среднего по совокупности коэффициентов Шарпа с использованием z-статистики.

Предположим, что инвестиционный аналитик делает случайную выборку акций взаимных фондов США и рассчитывает средний коэффициент Шарпа.

[см. также: CFA — Коэффициент Шарпа]

Размер выборки равен 100, а средний коэффициент Шарпа составляет 0.45. Выборка имеет стандартное отклонение 0.30.

Рассчитайте и интерпретируйте 90-процентный доверительный интервал для среднего по совокупности всех акций взаимных фондов США с использованием фактора надежности на основе стандартного нормального распределения.

Фактор надежности для 90-процентного доверительного интервала, как указано ранее, составляет ( z_{0.05} = 1.65 ).

Доверительный интервал будет равен:

( begin{aligned} & overline X pm z_{0.05}{s over sqrt n } \ &= 0.45 pm 1.65{0.30 over sqrt {100}} \ &= 0.45 pm 1.65(0.03) = 0.45 pm 0.0495 end{aligned} )

Доверительный интервал охватывает значения 0.4005 до 0.4995, или от 0.40 до 0.50, с округлением до двух знаков после запятой. Аналитик может сказать с 90-процентной уверенностью, что интервал включает среднее по совокупности.

В этом примере аналитик не делает никаких конкретных предположений о распределении вероятностей, характеризующем совокупность. Скорее всего, аналитик опирается на центральную предельную теорему для получения приближенного нормального распределения для выборочного среднего.

Как показывает Пример 4, даже если мы не уверены в характере распределения совокупности, мы все еще можем построить доверительные интервалы для среднего по совокупности, если размер выборки достаточно большой, поскольку можем применить центральную предельную теорему.

Концепция степеней свободы.

Обратимся теперь к консервативной альтернативе и используем t-распределение Стьюдента, чтобы построить доверительные интервалы для среднего по совокупности, когда дисперсия генеральной совокупности не известна.

Для доверительных интервалов на основе выборок из нормально распределенных совокупностей с неизвестной дисперсией, теоретически правильный фактор надежности основан на t-распределении. Использование фактора надежности, основанного на t-распределении, имеет важное значение для выборок небольшого размера.

Применение фактора надежности (t) уместно, когда дисперсия генеральной совокупности неизвестна, даже если у нас есть большая выборка и мы можем использовать центральную предельную теорему для обоснования использования фактора надежности (z). В этом случае большой выборки, t-распределение обеспечивает более консервативные (широкие) доверительные интервалы.

t-распределение является симметричным распределением вероятностей и определяется одним параметром, известным как степени свободы (DF, от англ. ‘degrees of freedom’). Каждое значение для числа степеней свободы определяет одно распределение в этом семействе распределений.

Далее мы сравним t-распределения со стандартным нормальным распределением, но сначала мы должны понять концепцию степеней свободы. Мы можем сделать это путем изучения расчета выборочной дисперсии.

Формула 3 дает несмещенную оценку выборочной дисперсии, которую мы используем. Выражение в знаменателе, ( n — 1 ), означающее размер выборки минус 1, это число степеней свободы при расчете дисперсии совокупности с использованием Формулы 3.

Мы также используем ( n — 1 ) как число степеней свободы для определения факторов надежности на основе распределения Стьюдента. Термин «степени свободы» используются, так как мы предполагаем, что в случайной выборке наблюдения отобраны независимо друг от друга. Числитель выборочной дисперсии, однако, использует выборочное среднее.

Каким образом использование выборочного среднего влияет на количество наблюдений, отобранных независимо, для формулы выборочной дисперсии?

При выборке размера 10 и среднем значении в 10%, к примеру, мы можем свободно отобрать только 9 наблюдений. Независимо от отобранных 9 наблюдений, мы всегда можем найти значение для 10-го наблюдения, которое дает среднее значение, равное 10%. С точки зрения формулы выборочной дисперсии, здесь есть 9 степеней свободы.

Учитывая, что мы должны сначала вычислить выборочное среднее от общего числа (n) независимых наблюдений, только (n — 1) наблюдений могут быть отобраны независимо друг от друга для расчета выборочной дисперсии.

Концепция степеней свободы часто применяется в финансовой статистике, и вы встретите ее в последующих чтениях.

t-распределение Стьюдента.

Предположим, что мы делаем выборку из нормального распределения.

Коэффициент (z = (overline X — mu) Big / (sigma big / sqrt n) ) нормально распределен со средним значением 0 и стандартным отклонением 1, однако, коэффициент (t = (overline X — mu) Big / (s big / sqrt n) ) следует t-распределению со средним 0 и (n — 1) степеней свободы.

Коэффициент (t) не является нормальным, поскольку представляет собой отношение двух случайных величин, выборочного среднего и стандартного отклонения выборки.

Определение стандартной нормальной случайной величины включает в себя только одну случайную величину, выборочное среднее. По мере увеличения степеней свободы, однако, t-распределение приближается к стандартному нормальному распределению.

На Рисунке 1 показано стандартное нормальное распределение и два t-распределения, одно с DF = 2 и одно с DF = 8.

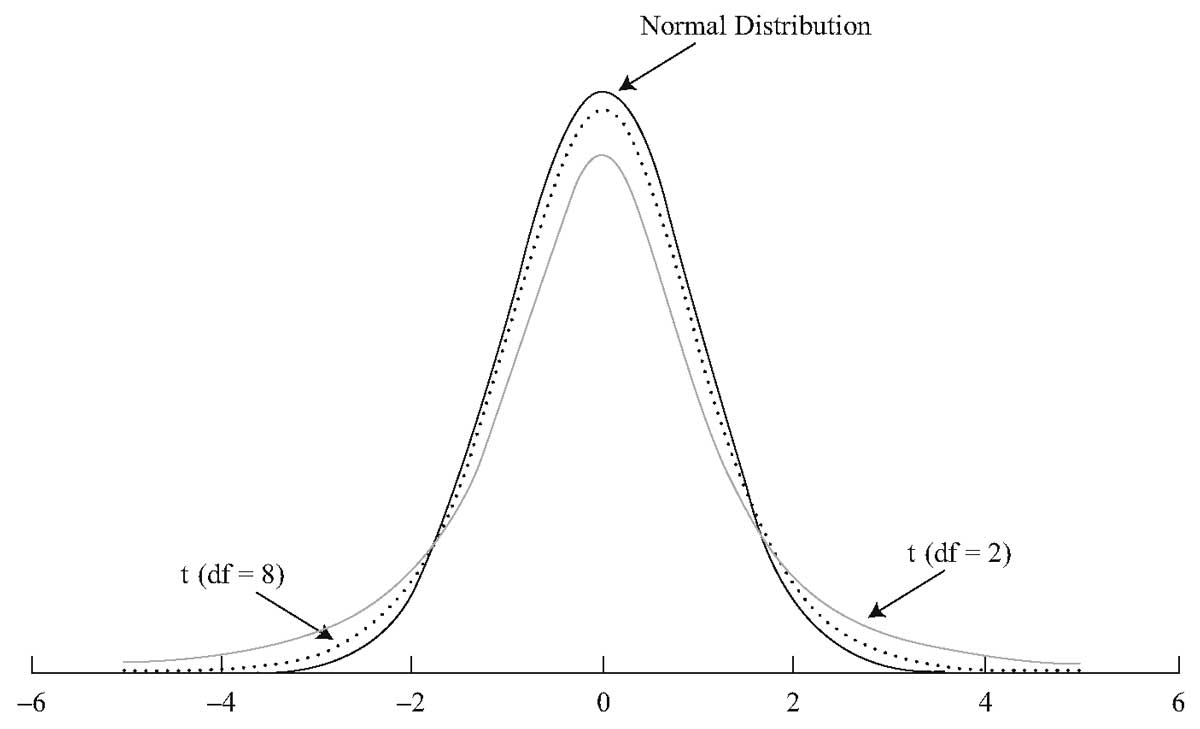
Рисунок (1) t-распределение Стьюдента по сравнению со стандартным нормальным распределением.

Из трех распределений, показанных на Рисунке 1, стандартное нормальное распределение имеет хвосты, которые стремятся к нулю быстрее, чем хвосты двух t-распределений. t-распределение симметрично распределено вокруг среднего нулевого значения, так же как и нормальное распределение.

По мере увеличения степеней свободы, t-распределение приближается к стандартному нормальному распределению. t-распределение с DF = 8 ближе к стандартному нормальному, чем t-распределение с DF = 2.

Помимо области плюс и минус четырех стандартных отклонений от среднего значения, остальная область под стандартным нормальным распределением, как представляется, близка к 0. Однако, оба t-распределения содержать некоторую площадь под каждой кривой за пределом четырех стандартных отклонений.

t-распределения имеют более толстые хвосты, но хвосты t-распределения Стьюдента с DF = 8 сильнее напоминают хвосты нормального распределения. По мере увеличения степеней свободы, хвосты распределения Стьюдента становятся менее толстыми.

Для часто используемых значений распределения Стьюдента составлены таблицы. Например, для каждой степени свободы (t_{0.10}), (t_{0.05}), (t_{0.025}), (t_{0.01}) и (t_{0.005}) значения будут такими, что соответственно, 0.10, 0.05, 0.025, 0.01 и 0.005 вероятности останется в правом хвосте для заданного числа степеней свободы.

Значения (t_{0.10}), (t_{0.05}), (t_{0.025}), (t_{0.01}) и (t_{0.005}) также называют односторонними критическими значениями t на значимых уровнях 0.10, 0.05, 0.025, 0.01 и 0.005, для указанного числа степеней свободы.

Например,

для DF = 30,

(t_{0.10}) = 1.310,
(t_{0.05}) = 1.697,
(t_{0.025}) = 2.042,
(t_{0.01}) = 2.457,
(t_{0.005}) = 2.750.

Приведем форму доверительных интервалов для среднего по совокупности, используя распределение Стьюдента.

Доверительные интервалы для среднего по совокупности (дисперсия совокупности неизвестна) — t-распределение.

Если мы делаем выборку из генеральной совокупности с неизвестной дисперсией и соблюдается одно из перечисленных ниже условий:

выборка является большой, или
выборка небольшая, но совокупность имеет нормальное распределение, или приблизительно нормально распределена,

то доверительный интервал (100 (1 — alpha)% ) для среднего совокупности ( mu ) задается формулой:

( Large dst overline X pm t_{alpha /2}{s over sqrt n} ) (Формула 6)

где число степеней свободы для ( t_{alpha /2}) равно ( n-1 ), а ( n ) — это размер выборки.

Пример 5 использует данные Примера 4, но применяет t-статистику, а не z-статистику, чтобы рассчитать доверительный интервал для среднего значения совокупности коэффициентов Шарпа.

Пример (5) расчета доверительного интервала для среднего по совокупности коэффициентов Шарпа с использованием t-статистики.

Как и в Примере 4, инвестиционный аналитик стремится вычислить 90-процентный доверительный интервал для среднего по совокупности коэффициентов Шарпа, основанных на случайной выборке из 100 взаимных фондов США.

Выборочное среднее коэффициентов Шарпа составляет 0.45, а выборочное стандартное отклонение — 0.30.

Теперь, признав, что дисперсия генеральной совокупности распределения коэффициентов Шарпа неизвестна, аналитик решает вычислить доверительный интервал, используя теоретически правильную t-статистику.

Поскольку размер выборки равен 100, DF = 99. Используя таблицу степеней свободы, мы находим, что (t_{0.05}) = 1.66.

Этот фактор надежности немного больше, чем фактор надежности (z_{0.05}) = 1.65, который был использован в Примере 4.

Доверительный интервал будет:

( begin{aligned} & overline X pm t_{0.05}{s over sqrt n } \ &= 0.45 pm 1.66{0.30 over sqrt {100}} \ &= 0.45 pm 1.66(0.03) = 0.45 pm 0.0498 end{aligned} )

Доверительный интервал охватывает значения 0.4002 до 0.4998, или 0.40 до 0.50, с двумя знаками после запятой. При округлении до двух знаков после запятой, доверительный интервал не изменился по сравнению с Примером 4.

В Таблице 3 приведены различные факторы надежности, которые мы использовали.

Таблица 3. Основы для расчета факторов надежности.

Выборка из:	Статистика для выборки малого размера	Статистика для выборки большого размера
Нормальное распределение с известной дисперсией	(z)	(z)
Нормальное распределение с неизвестной дисперсией	(t)	(t)*
Ненормальное распределение с известной дисперсией	недоступно	(z)
Ненормальное распределение с неизвестной дисперсией	недоступно	(t)*

* Использование (z) также приемлемо.

Источник

Выборочная совокупность (выборка)

При проведении исследования в подавляющем большинстве случаев не представляется возможным опросить
генеральную совокупность, т.е. общую численность объектов наблюдения (например, всех жителей
столицы). Чтобы решить данную проблему и иметь возможность дать заключение обо всей генеральной
совокупности, используется отбор выборочной совокупности.

Выборочная совокупность – часть объектов генеральной совокупности, характеристики которой корректно
отражают характеристики генеральной совокупности (репрезентируют ее).

Приведем пример:
Выборка, состоящая из студентов московских вузов, не репрезентирует всю московскую молодежь (т.к.
как минимум не включает неучащуюся молодежь) и тем более не репрезентирует население Москвы.
Как бы мы ни увеличивали число опрошенных студентов московских вузов, данная выборка не будет
отражать характеристики населения города Москвы. В этом случае понимание того, что «мы опросили
МНОГО», не имеет никакой ценности. Важно знать, КАК отобрать корректную выборку.

Типы выборок

В зависимости от целей исследования используются различные типы выборок:

вероятностные
невероятностные

1. Использование вероятностной выборки предполагает, что все члены генеральной совокупности имеют
равные шансы попасть в выборку.

1.1. Простая случайная выборка

Основной вид вероятностной выборки. Респонденты выбираются СЛУЧАЙНЫМ ОБРАЗОМ из ПОЛНОГО списка
единиц генеральной совокупности. На практике сформировать данный список достаточно трудно. Например,
список всех мобильных телефонов не включает жителей, которые его не имеют, и т.д. Случайный отбор
осуществляет компьютер (генератор случайных чисел), или используется таблица случайных чисел.

Только для данного типа выборки возможно использование:

1.1.1. Калькулятор размера выборки

Доверительная вероятность

«Точность» – вероятность того, что случайный ответ попадет в доверительный интервал.

90%

95%

99%

Наиболее
распространенный

Ошибка выборки или доверительный интервал

«Погрешность» – отклонение средних характеристик выборочной совокупности от средних характеристик генеральной совокупности

5%
Наиболее
распространенный

Размер генеральной совокупности

человек

1.1.2. Калькулятор ошибки выборки

1.2. Случайная систематическая выборка

Генеральная совокупность упорядочивается (например, по алфавитному порядку, по номеру телефона и
т.д.), случайным образом выбирается первый элемент выборки, каждый последующий выбирается с равным
шагом (например, каждый 5-й, 20-й, 100-й респондент).

1.3. Стратифицированная случайная выборка

Генеральная совокупность разделяется на группы (страты). Внутри каждой страты совершается простой
случайный или систематический отбор. При этом выборка должна отражать структуру генеральной
совокупности, т.е. в выборке должны быть сохранены пропорции.

1.4. Кластерная выборка

Используется тогда, когда единицами отбора выступают кластеры (группы). Например, при исследовании
сотрудников медицинских учреждений целесообразно отобрать сначала сами учреждения. Внутри кластера
производится сплошной опрос (опрашиваются все его представители).

2. Использование невероятностных выборок обусловлено невозможностью случайного отбора. Отбор
происходит по субъективным критериям – доступности, типичности и т.д.

2.1. Квотная выборка

Генеральная структура в данном случае воспроизводится за счет квот (пропорций), которые обычно
отражают социально-демографические критерии. Например, заранее известно только число женщин и мужчин
в генеральной совокупности. В этом случае в той же пропорции они отбираются и для выборочной
совокупности. Внутри групп единицы отбора выбираются произвольно.

2.2. Метод «снежного» кома

Используется в том случае, если опросу принадлежат «труднодоступные» респонденты (например, люди с
очень высоким доходом). У всех респондентов (начиная с первого) спрашивают контакты их знакомых,
родственников, друзей, которые подходят для опроса.

2.3. Стихийная выборка

Выборка так называемого «первого встречного». Ее размер и состав достоверно не известен, он
определяется лишь активностью самих респондентов. Используется, например, в телеопросах.

2.4. Выборка типичных случаев

Выбирается типичный признак, на основании которого отбираются и другие участники исследования. Выбор
признака и его типичное значение производятся исследователем самостоятельно.

Новости отдела

Источник