From Wikipedia, the free encyclopedia
In statistics and optimization, errors and residuals are two closely related and easily confused measures of the deviation of an observed value of an element of a statistical sample from its «true value» (not necessarily observable). The error of an observation is the deviation of the observed value from the true value of a quantity of interest (for example, a population mean). The residual is the difference between the observed value and the estimated value of the quantity of interest (for example, a sample mean). The distinction is most important in regression analysis, where the concepts are sometimes called the regression errors and regression residuals and where they lead to the concept of studentized residuals.
In econometrics, «errors» are also called disturbances.[1][2][3]
Introduction[edit]
Suppose there is a series of observations from a univariate distribution and we want to estimate the mean of that distribution (the so-called location model). In this case, the errors are the deviations of the observations from the population mean, while the residuals are the deviations of the observations from the sample mean.
A statistical error (or disturbance) is the amount by which an observation differs from its expected value, the latter being based on the whole population from which the statistical unit was chosen randomly. For example, if the mean height in a population of 21-year-old men is 1.75 meters, and one randomly chosen man is 1.80 meters tall, then the «error» is 0.05 meters; if the randomly chosen man is 1.70 meters tall, then the «error» is −0.05 meters. The expected value, being the mean of the entire population, is typically unobservable, and hence the statistical error cannot be observed either.
A residual (or fitting deviation), on the other hand, is an observable estimate of the unobservable statistical error. Consider the previous example with men’s heights and suppose we have a random sample of n people. The sample mean could serve as a good estimator of the population mean. Then we have:
- The difference between the height of each man in the sample and the unobservable population mean is a statistical error, whereas
- The difference between the height of each man in the sample and the observable sample mean is a residual.
Note that, because of the definition of the sample mean, the sum of the residuals within a random sample is necessarily zero, and thus the residuals are necessarily not independent. The statistical errors, on the other hand, are independent, and their sum within the random sample is almost surely not zero.
One can standardize statistical errors (especially of a normal distribution) in a z-score (or «standard score»), and standardize residuals in a t-statistic, or more generally studentized residuals.
In univariate distributions[edit]
If we assume a normally distributed population with mean μ and standard deviation σ, and choose individuals independently, then we have
and the sample mean
is a random variable distributed such that:
The statistical errors are then
with expected values of zero,[4] whereas the residuals are
The sum of squares of the statistical errors, divided by σ2, has a chi-squared distribution with n degrees of freedom:
However, this quantity is not observable as the population mean is unknown. The sum of squares of the residuals, on the other hand, is observable. The quotient of that sum by σ2 has a chi-squared distribution with only n − 1 degrees of freedom:
This difference between n and n − 1 degrees of freedom results in Bessel’s correction for the estimation of sample variance of a population with unknown mean and unknown variance. No correction is necessary if the population mean is known.
[edit]
It is remarkable that the sum of squares of the residuals and the sample mean can be shown to be independent of each other, using, e.g. Basu’s theorem. That fact, and the normal and chi-squared distributions given above form the basis of calculations involving the t-statistic:
where 


The probability distributions of the numerator and the denominator separately depend on the value of the unobservable population standard deviation σ, but σ appears in both the numerator and the denominator and cancels. That is fortunate because it means that even though we do not know σ, we know the probability distribution of this quotient: it has a Student’s t-distribution with n − 1 degrees of freedom. We can therefore use this quotient to find a confidence interval for μ. This t-statistic can be interpreted as «the number of standard errors away from the regression line.»[6]
Regressions[edit]
In regression analysis, the distinction between errors and residuals is subtle and important, and leads to the concept of studentized residuals. Given an unobservable function that relates the independent variable to the dependent variable – say, a line – the deviations of the dependent variable observations from this function are the unobservable errors. If one runs a regression on some data, then the deviations of the dependent variable observations from the fitted function are the residuals. If the linear model is applicable, a scatterplot of residuals plotted against the independent variable should be random about zero with no trend to the residuals.[5] If the data exhibit a trend, the regression model is likely incorrect; for example, the true function may be a quadratic or higher order polynomial. If they are random, or have no trend, but «fan out» — they exhibit a phenomenon called heteroscedasticity. If all of the residuals are equal, or do not fan out, they exhibit homoscedasticity.
However, a terminological difference arises in the expression mean squared error (MSE). The mean squared error of a regression is a number computed from the sum of squares of the computed residuals, and not of the unobservable errors. If that sum of squares is divided by n, the number of observations, the result is the mean of the squared residuals. Since this is a biased estimate of the variance of the unobserved errors, the bias is removed by dividing the sum of the squared residuals by df = n − p − 1, instead of n, where df is the number of degrees of freedom (n minus the number of parameters (excluding the intercept) p being estimated — 1). This forms an unbiased estimate of the variance of the unobserved errors, and is called the mean squared error.[7]
Another method to calculate the mean square of error when analyzing the variance of linear regression using a technique like that used in ANOVA (they are the same because ANOVA is a type of regression), the sum of squares of the residuals (aka sum of squares of the error) is divided by the degrees of freedom (where the degrees of freedom equal n − p − 1, where p is the number of parameters estimated in the model (one for each variable in the regression equation, not including the intercept)). One can then also calculate the mean square of the model by dividing the sum of squares of the model minus the degrees of freedom, which is just the number of parameters. Then the F value can be calculated by dividing the mean square of the model by the mean square of the error, and we can then determine significance (which is why you want the mean squares to begin with.).[8]
However, because of the behavior of the process of regression, the distributions of residuals at different data points (of the input variable) may vary even if the errors themselves are identically distributed. Concretely, in a linear regression where the errors are identically distributed, the variability of residuals of inputs in the middle of the domain will be higher than the variability of residuals at the ends of the domain:[9] linear regressions fit endpoints better than the middle. This is also reflected in the influence functions of various data points on the regression coefficients: endpoints have more influence.
Thus to compare residuals at different inputs, one needs to adjust the residuals by the expected variability of residuals, which is called studentizing. This is particularly important in the case of detecting outliers, where the case in question is somehow different from the others in a dataset. For example, a large residual may be expected in the middle of the domain, but considered an outlier at the end of the domain.
Other uses of the word «error» in statistics[edit]
The use of the term «error» as discussed in the sections above is in the sense of a deviation of a value from a hypothetical unobserved value. At least two other uses also occur in statistics, both referring to observable prediction errors:
The mean squared error (MSE) refers to the amount by which the values predicted by an estimator differ from the quantities being estimated (typically outside the sample from which the model was estimated).
The root mean square error (RMSE) is the square-root of MSE.
The sum of squares of errors (SSE) is the MSE multiplied by the sample size.
Sum of squares of residuals (SSR) is the sum of the squares of the deviations of the actual values from the predicted values, within the sample used for estimation. This is the basis for the least squares estimate, where the regression coefficients are chosen such that the SSR is minimal (i.e. its derivative is zero).
Likewise, the sum of absolute errors (SAE) is the sum of the absolute values of the residuals, which is minimized in the least absolute deviations approach to regression.
The mean error (ME) is the bias.
The mean residual (MR) is always zero for least-squares estimators.
See also[edit]
- Absolute deviation
- Consensus forecasts
- Error detection and correction
- Explained sum of squares
- Innovation (signal processing)
- Lack-of-fit sum of squares
- Margin of error
- Mean absolute error
- Observational error
- Propagation of error
- Probable error
- Random and systematic errors
- Reduced chi-squared statistic
- Regression dilution
- Root mean square deviation
- Sampling error
- Standard error
- Studentized residual
- Type I and type II errors
References[edit]
- ^ Kennedy, P. (2008). A Guide to Econometrics. Wiley. p. 576. ISBN 978-1-4051-8257-7. Retrieved 2022-05-13.
- ^ Wooldridge, J.M. (2019). Introductory Econometrics: A Modern Approach. Cengage Learning. p. 57. ISBN 978-1-337-67133-0. Retrieved 2022-05-13.
- ^ Das, P. (2019). Econometrics in Theory and Practice: Analysis of Cross Section, Time Series and Panel Data with Stata 15.1. Springer Singapore. p. 7. ISBN 978-981-329-019-8. Retrieved 2022-05-13.
- ^ Wetherill, G. Barrie. (1981). Intermediate statistical methods. London: Chapman and Hall. ISBN 0-412-16440-X. OCLC 7779780.
- ^ a b Frederik Michel Dekking; Cornelis Kraaikamp; Hendrik Paul Lopuhaä; Ludolf Erwin Meester (2005-06-15). A modern introduction to probability and statistics : understanding why and how. London: Springer London. ISBN 978-1-85233-896-1. OCLC 262680588.
- ^ Peter Bruce; Andrew Bruce (2017-05-10). Practical statistics for data scientists : 50 essential concepts (First ed.). Sebastopol, CA: O’Reilly Media Inc. ISBN 978-1-4919-5296-2. OCLC 987251007.
- ^ Steel, Robert G. D.; Torrie, James H. (1960). Principles and Procedures of Statistics, with Special Reference to Biological Sciences. McGraw-Hill. p. 288.
- ^ Zelterman, Daniel (2010). Applied linear models with SAS ([Online-Ausg.]. ed.). Cambridge: Cambridge University Press. ISBN 9780521761598.
- ^ «7.3: Types of Outliers in Linear Regression». Statistics LibreTexts. 2013-11-21. Retrieved 2019-11-22.
- Cook, R. Dennis; Weisberg, Sanford (1982). Residuals and Influence in Regression (Repr. ed.). New York: Chapman and Hall. ISBN 041224280X. Retrieved 23 February 2013.
- Cox, David R.; Snell, E. Joyce (1968). «A general definition of residuals». Journal of the Royal Statistical Society, Series B. 30 (2): 248–275. JSTOR 2984505.
- Weisberg, Sanford (1985). Applied Linear Regression (2nd ed.). New York: Wiley. ISBN 9780471879572. Retrieved 23 February 2013.
- «Errors, theory of», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
External links[edit]
Media related to Errors and residuals at Wikimedia Commons
Различие между остатками регрессии и ошибками
1)
,
здесь
— ошибки.
2)
,
e
– остатки.
В
силу случайности
и
,
e
является случайным вектором. Обычно
говорят, что e
является оценкой
.
При этом, ошибки являются ненаблюдаемой
величиной, а остатки – наблюдаемой.
Мультиколлинеарность
Рассмотрим
модель регрессии:
X
– матрица данных, Y
– столбец,
— вектор случайных значений. Тогда оценка
коэффициентов регрессии:
,
точность
оценки рассчитывается по формуле:
.
При
описании модели различают два вида
мультиколлинеарности:
-
чистая
или полная мультиколлинеарность: ранг
матрицы X
не полный по столбцам, т.е. меньше k,
или
.
В этом случае по свойству определителей
имеем чистую линейную зависимость
между строками или столбцами. -
Частичная
или практическая мультиколлинеарность,
т.е. матрица слабо обусловлена, т.е.
,
таким образом, определитель соизмерим
с ошибкой измерения.
Возможны
домодельные и постмодельные признаки
мультиколлинераности:
|
домодельные |
(i) |
|
(ii) |
|
|
(iii) |
|
|
(i4) |
|
|
постмодельные |
(i5) |
Например,
если модель имеет вид:
,
и
,
между переменными почти линейная связь.
Тогда модель можно записать в одном из
видов:
,
.
Итак,
эти три модели одинаковы («неустойчивость»).
По
этой модели возможно прогнозирование,
но точность оценки «расползается». А в
структурном плане, т.е. экономической
интерпретации доверять нельзя.
Одно
из направлений борьбы с мультиколлинеарностью
— переход к смещенному оцениванию
(регуляризация).
Примером
могут служить ridge-оценки
(гребневые оценки). Т.е. оценку параметра
регрессии заменяем оценкой вида:
Идея
отказа от несмещенности состоит в
следующем:
Если
между факторами существует высокая
корреляция, то нельзя определить их
изолированное влияние на результативный
показатель и параметры уравнения
регрессии оказываются не интерпретируемыми.
Пример.
Рассмотрим регрессию себестоимости
единицы продукции (руб., y)
от заработной платы работника (руб., x)
и производительности его труда (единиц
в час, z):
.
Коэффициент
регрессии при переменной z
показывает, что с ростом производительности
труда на 1 ед. себестоимость единицы
продукции снижается в среднем на 10 руб.
при постоянном уровне оплаты труда.
Вместе с тем параметр при x
нельзя интерпретировать как снижение
себестоимости единицы продукции за
счет роста заработной платы. Отрицательное
значение коэффициента регрессии при
переменной x
в данном случае обусловлено высокой
корреляцией между x
и z
().
Поэтому роста заработной платы при
неизменности производительности труда
не может быть (если не учитывать инфляцию).
Насыщение
модели лишними факторами не только не
снижает величину остаточной дисперсии
и не увеличивает величину остаточной
дисперсии и не увеличивает показатель
детерминации, но и приводит к статистической
незначимости параметров регрессии по
t-критерию
Стьюдента.
Таким
образом, хотя теоретически регрессионная
модель позволяет учесть любое число
факторов, практически в этом нет
необходимости. Отбор факторов обычно
осуществляется в две стадии: на первой
подбираются факторы исходя из сущности
проблемы; на второй – на основе матрицы
показателей корреляции определяют
t—статистики
для параметров регрессии.
Коэффициенты
интеркорреляции (т.е. корреляции между
объясняющими переменными) позволяют
исключать из модели дублирующие факторы.
Считается, что две переменные явно
коллинеарны, т.е. находятся между собой
в линейной зависимости, если
.
По
величине парных коэффициентов корреляции
обнаруживается лишь явная коллинеарность
факторов. Наибольшие трудности в
использовании аппарата множественной
регрессии возникают при наличии
мультиколлинеарности факторов, когда
более чем два фактора связаны между
собой линейной зависимостью, т.е. имеет
место совокупное воздействие факторов
друг на друга. В этом случае вариация в
исходных данных перестает быть полностью
независимой, и нельзя оценить воздействие
каждого фактора в отдельности. Чем
сильнее мультиколлинеарность факторов,
тем менее надежна оценка распределения
суммы объясненной вариации по отдельным
факторам с помощью метода наименьших
квадратов.
Включение
в модель мультиколлинеарных факторов
нежелательно в силу следующих причин:
-
затрудняется
интерпретация параметров множественной
регрессии как характеристик действия
факторов в чистом виде, ибо факторы
коррелированны; параметры линейной
регрессии теряют экономический смысл; -
оценки
параметров ненадежны, обнаруживают
большие стандартные ошибки и меняются
с изменением объема наблюдений (не
только по величине, но и по знаку), что
делает модель непригодной для анализа
и прогнозирования.
Мультиколлинеарность
может возникать в силу различных причин.
Например, несколько независимых
переменных могут иметь общий временной
тренд, относительно которого они
совершают малые колебания.
Выделим
некоторые наиболее характерные признаки
мультиколлинеарности:
-
Небольшое
изменение исходных данных (например,
добавление новых наблюдений) приводит
к существенному изменению оценок
коэффициентов модели. -
Оценки
имеют большие стандартные ошибки, малую
значимость, в то время как модель в
целом является значимой (высокой
значение коэффициента детерминации и
соответствующей статистики Фишера). -
Оценки
коэффициентов имеют неправильные с
точки зрения теории знаки или неоправданно
большие значения.
При
столкновении с проблемой мультиколлинеарности
возникает желание отбросить «лишние»
независимые переменные, которые,
возможно, служат ее причиной. Однако,
во-первых, далеко не всегда ясно, какие
переменные являются лишними в указанном
смысле. Во-вторых, во многих ситуациях
удаление какой-либо независимой
переменной может значительно отразится
на содержательном смысле модели.
В-третьих, отбрасывание существенных
переменных, которые реально влияют на
изучаемую зависимую переменную, приводит
к смещенности оценок.
По
такой модели удобно прогнозировать, но
точность прогнозов невысокая.
Итак,
рассмотрим классическую модель в тех
же предположения, что и для парной
регрессии.
.
Если
,
то
— константа.
Все
условия, налагаемее на
— те же, что и для парной регрессии. Для
вычисления оценок удобно перейти к
матрицам. Будем считать, что в задаче
имеется k
регрессоров.
Направления
борьбы с мультиколлинеарностью:
(а)
переход к смещенному оцениванию
(регуляризация). Например, ridge
– оценки (гребневые оценки). Происходит
замена исходной оценки на следующую:
.
Идея,
на которой основан
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В статистике и оптимизации ошибки и остатки тесно связаны и легко запутанные меры отклонения наблюдаемого значения элемента статистической выборки от его «теоретического значения». ошибка (или возмущение ) наблюдаемого значения — это отклонение наблюдаемого значения от (ненаблюдаемого) истинного значения интересующей величины (например, среднего генерального значения), и остаток наблюдаемого значения представляет собой разность между наблюдаемым значением и оценочным значением представляющей интерес величины (например, выборочное среднее). Это различие наиболее важно в регрессионном анализе, где концепции иногда называют ошибками регрессии и остатками регрессии, и где они приводят к концепции студентизированных остатков.
Содержание
- 1 Введение
- 2 В одномерных распределениях
- 2.1 Замечание
- 3 Регрессии
- 4 Другие варианты использования слова «ошибка» в статистике
- 5 См. Также
- 6 Ссылки
- 7 Внешние ссылки
Введение
Предположим, есть серия наблюдений из одномерного распределения, и мы хотим оценить среднее этого распределения. (так называемая локационная модель ). В этом случае ошибки — это отклонения наблюдений от среднего по совокупности, а остатки — это отклонения наблюдений от среднего по выборке.
A статистическая ошибка (или нарушение ) — это величина, на которую наблюдение отличается от его ожидаемого значения, последнее основано на всей генеральной совокупности из которого статистическая единица была выбрана случайным образом. Например, если средний рост среди 21-летних мужчин составляет 1,75 метра, а рост одного случайно выбранного мужчины — 1,80 метра, то «ошибка» составляет 0,05 метра; если рост случайно выбранного мужчины составляет 1,70 метра, то «ошибка» составляет -0,05 метра. Ожидаемое значение, являющееся средним для всей генеральной совокупности, обычно ненаблюдаемо, и, следовательно, статистическая ошибка также не может быть обнаружена.
A невязка (или аппроксимирующее отклонение), с другой стороны, представляет собой наблюдаемую оценку ненаблюдаемой статистической ошибки. Рассмотрим предыдущий пример с ростом мужчин и предположим, что у нас есть случайная выборка из n человек. среднее значение выборки может служить хорошей оценкой среднего значения генеральной совокупности. Тогда у нас есть:
- Разница между ростом каждого человека в выборке и ненаблюдаемым средним по совокупности является статистической ошибкой, тогда как
- разница между ростом каждого человека в выборке и наблюдаемой выборкой среднее — это остаток.
Обратите внимание, что из-за определения выборочного среднего, сумма остатков в случайной выборке обязательно равна нулю, и, таким образом, остатки не обязательно независимы. Статистические ошибки, с другой стороны, независимы, и их сумма в случайной выборке почти наверняка не равна нулю.
Можно стандартизировать статистические ошибки (особенно нормального распределения ) в z-балле (или «стандартном балле») и стандартизировать остатки в t-статистика или, в более общем смысле, стьюдентизированные остатки.
в одномерном распределении
Если мы предположим нормально распределенную совокупность со средним μ и стандартным отклонением σ и независимо выбираем людей, тогда мы имеем
- X 1,…, X n ∼ N (μ, σ 2) { displaystyle X_ {1}, dots, X_ {n} sim N ( mu, sigma ^ {2}) ,}
и выборочное среднее
- X ¯ = X 1 + ⋯ + X nn { displaystyle { overline {X}} = {X_ { 1} + cdots + X_ {n} over n}}
— случайная величина, распределенная так, что:
- X ¯ ∼ N (μ, σ 2 n). { displaystyle { overline {X}} sim N left ( mu, { frac { sigma ^ {2}} {n}} right).}
Тогда статистические ошибки
- ei = X i — μ, { displaystyle e_ {i} = X_ {i} — mu, ,}
с ожидаемыми значениями нуля, тогда как остатки равны
- ri = X i — X ¯. { displaystyle r_ {i} = X_ {i} — { overline {X}}.}
Сумма квадратов статистических ошибок, деленная на σ, имеет хи -квадратное распределение с n степенями свободы :
- 1 σ 2 ∑ i = 1 nei 2 ∼ χ n 2. { displaystyle { frac {1} { sigma ^ {2}}} sum _ {i = 1} ^ {n} e_ {i} ^ {2} sim chi _ {n} ^ {2}.}
Однако это количество не наблюдается, так как среднее значение для генеральной совокупности неизвестно. Сумма квадратов остатков, с другой стороны, является наблюдаемой. Частное этой суммы по σ имеет распределение хи-квадрат только с n — 1 степенями свободы:
- 1 σ 2 ∑ i = 1 n r i 2 ∼ χ n — 1 2. { displaystyle { frac {1} { sigma ^ {2}}} sum _ {i = 1} ^ {n} r_ {i} ^ {2} sim chi _ {n-1} ^ { 2}.}
Эта разница между n и n — 1 степенями свободы приводит к поправке Бесселя для оценки выборочной дисперсии генеральной совокупности с неизвестным средним и неизвестной дисперсией. Коррекция не требуется, если известно среднее значение для генеральной совокупности.
Замечание
Примечательно, что сумма квадратов остатков и выборочного среднего могут быть показаны как независимые друг от друга, используя, например, Теорема Басу. Этот факт, а также приведенные выше нормальное распределение и распределение хи-квадрат составляют основу вычислений с использованием t-статистики :
- T = X ¯ n — μ 0 S n / n, { displaystyle T = { frac {{ overline {X}} _ {n} — mu _ {0}} {S_ {n} / { sqrt {n}}}},}
где X ¯ n — μ 0 { displaystyle { overline {X}} _ {n} — mu _ {0}}


- Var (X ¯ n) = σ 2 n { displaystyle operatorname {Var} ({ overline {X}} _ {n}) = { frac { sigma ^ {2}} {n}}}
Распределения вероятностей числителя и знаменателя по отдельности зависят от значения ненаблюдаемого стандартного отклонения генеральной совокупности σ, но σ появляется как в числителе, так и в знаменателе и отменяет. Это удачно, потому что это означает, что, хотя мы не знаем σ, мы знаем распределение вероятностей этого частного: оно имеет t-распределение Стьюдента с n — 1 степенями свободы. Таким образом, мы можем использовать это частное, чтобы найти доверительный интервал для μ. Эту t-статистику можно интерпретировать как «количество стандартных ошибок от линии регрессии».
Регрессии
В регрессионном анализе различие между ошибками и остатками является тонким и важным, и приводит к концепции стьюдентизированных остатков. Для ненаблюдаемой функции, которая связывает независимую переменную с зависимой переменной — скажем, линии — отклонения наблюдений зависимой переменной от этой функции являются ненаблюдаемыми ошибками. Если запустить регрессию на некоторых данных, то отклонения наблюдений зависимой переменной от подобранной функции являются остатками. Если линейная модель применима, диаграмма рассеяния остатков, построенная против независимой переменной, должна быть случайной около нуля без тенденции к остаткам. Если данные демонстрируют тенденцию, регрессионная модель, вероятно, неверна; например, истинная функция может быть квадратичным полиномом или полиномом более высокого порядка. Если они случайны или не имеют тенденции, но «разветвляются» — они демонстрируют явление, называемое гетероскедастичностью. Если все остатки равны или не разветвляются, они проявляют гомоскедастичность.
Однако терминологическое различие возникает в выражении среднеквадратическая ошибка (MSE). Среднеквадратичная ошибка регрессии — это число, вычисляемое из суммы квадратов вычисленных остатков, а не ненаблюдаемых ошибок. Если эту сумму квадратов разделить на n, количество наблюдений, результатом будет среднее квадратов остатков. Поскольку это смещенная оценка дисперсии ненаблюдаемых ошибок, смещение устраняется путем деления суммы квадратов остатков на df = n — p — 1 вместо n, где df — число степеней свободы (n минус количество оцениваемых параметров (без учета точки пересечения) p — 1). Это формирует объективную оценку дисперсии ненаблюдаемых ошибок и называется среднеквадратической ошибкой.
Другой метод вычисления среднего квадрата ошибки при анализе дисперсии линейной регрессии с использованием техники, подобной той, что использовалась в ANOVA (они одинаковы, потому что ANOVA — это тип регрессии), сумма квадратов остатков (иначе говоря, сумма квадратов ошибки) делится на степени свободы (где степени свободы равно n — p — 1, где p — количество параметров, оцениваемых в модели (по одному для каждой переменной в уравнении регрессии, не включая точку пересечения). Затем можно также вычислить средний квадрат модели, разделив сумму квадратов модели за вычетом степеней свободы, которые представляют собой просто количество параметров. Затем значение F можно рассчитать путем деления среднего квадрата модели на средний квадрат ошибки, и затем мы можем определить значимость (вот почему вы хотите, чтобы средние квадраты начинались с.).
Однако из-за поведения процесса регрессии распределения остатков в разных точках данных (входной переменной) могут различаться, даже если сами ошибки распределены одинаково. Конкретно, в линейной регрессии , где ошибки одинаково распределены, изменчивость остатков входных данных в середине области будет выше, чем изменчивость остатков на концах области: линейные регрессии соответствуют конечным точкам лучше среднего. Это также отражено в функциях влияния различных точек данных на коэффициенты регрессии : конечные точки имеют большее влияние.
Таким образом, чтобы сравнить остатки на разных входах, нужно скорректировать остатки на ожидаемую изменчивость остатков, что называется стьюдентизацией. Это особенно важно в случае обнаружения выбросов, когда рассматриваемый случай каким-то образом отличается от другого в наборе данных. Например, можно ожидать большой остаток в середине домена, но он будет считаться выбросом в конце домена.
Другое использование слова «ошибка» в статистике
Использование термина «ошибка», как обсуждалось в разделах выше, означает отклонение значения от гипотетического ненаблюдаемого значение. По крайней мере, два других использования также встречаются в статистике, оба относятся к наблюдаемым ошибкам прогнозирования:
Среднеквадратичная ошибка или Среднеквадратичная ошибка (MSE) и Среднеквадратичная ошибка (RMSE) относятся к величине, на которую значения, предсказанные оценщиком, отличаются от оцениваемых количеств (обычно за пределами выборки, на основе которой была оценена модель).
Сумма квадратов ошибок (SSE или SSe), обычно сокращенно SSE или SS e, относится к остаточной сумме квадратов (сумма квадратов остатков) регрессии; это сумма квадратов отклонений фактических значений от прогнозируемых значений в пределах выборки, используемой для оценки. Это также называется оценкой методом наименьших квадратов, где коэффициенты регрессии выбираются так, чтобы сумма квадратов минимально (т.е. его производная равна нулю).
Аналогично, сумма абсолютных ошибок (SAE) является суммой абсолютных значений остатков, которая минимизирована в наименьшие абсолютные отклонения подход к регрессии.
См. также
Портал математики
- Абсолютное отклонение
- Консенсус-прогнозы
- Обнаружение и исправление ошибок
- Объясненная сумма квадраты
- Инновация (обработка сигналов)
- Неподходящая сумма квадратов
- Погрешность
- Средняя абсолютная погрешность
- Погрешность наблюдения
- Распространение ошибки
- Вероятная ошибка
- Случайные и систематические ошибки
- Разбавление регрессии
- Среднеквадратичное отклонение
- Ошибка выборки
- Стандартная ошибка
- Стьюдентизированная невязка
- Ошибки типа I и типа II
Ссылки
- Кук, Р. Деннис; Вайсберг, Сэнфорд (1982). Остатки и влияние на регресс (Отредактированный ред.). Нью-Йорк: Чепмен и Холл. ISBN 041224280X . Проверено 23 февраля 2013 г.
- Кокс, Дэвид Р. ; Снелл, Э. Джойс (1968). «Общее определение остатков». Журнал Королевского статистического общества, серия B. 30(2): 248–275. JSTOR 2984505.
- Вайсберг, Сэнфорд (1985). Прикладная линейная регрессия (2-е изд.). Нью-Йорк: Вили. ISBN 9780471879572 . Проверено 23 февраля 2013 г.
- , Энциклопедия математики, EMS Press, 2001 [1994]
Внешние ссылки
СМИ, связанные с ошибками и остатками на Викимедиа Commons
В статистике и оптимизации , ошибка и остатки два тесно связанные и легко спутать меры по отклонению от наблюдаемого значения элемента в статистическую выборке из его «теоретического значения». Ошибки (или нарушения ) от наблюдаемого значения является отклонение наблюдаемого значения от (ненаблюдаемой) истинного значения величины , представляющего интерес (например, среднее население ), а также остаточного наблюдаемого значения представляет собой разность между наблюдаемое значение и оценочное значение интересующей величины (например, выборочное среднее ). Различие является наиболее важным в регрессионном анализе , где понятия иногда называют ошибку регрессии и регрессией остатки и где они приводят к понятию стьюдентизированных остатков .
Вступление
Предположим, есть серия наблюдений из одномерного распределения, и мы хотим оценить среднее значение этого распределения (так называемая модель местоположения ). В этом случае ошибки — это отклонения наблюдений от среднего по генеральной совокупности, а остатки — это отклонения наблюдений от среднего по выборке.
Статистическая погрешность (или нарушение ) представляет собой количество , с помощью которого наблюдение отличается от своего ожидаемого значения , причем последнего на основе всей популяции , из которой была выбрана случайным образом статистической единица. Например, если средний рост среди 21-летних мужчин составляет 1,75 метра, а рост одного случайно выбранного мужчины — 1,80 метра, то «ошибка» составляет 0,05 метра; если случайно выбранный мужчина имеет рост 1,70 метра, то «ошибка» составляет -0,05 метра. Ожидаемое значение, являющееся средним для всей генеральной совокупности, обычно ненаблюдаемо, и, следовательно, статистическая ошибка также не может быть обнаружена.
С другой стороны, невязка (или аппроксимирующее отклонение) — это наблюдаемая оценка ненаблюдаемой статистической ошибки. Рассмотрим предыдущий пример с ростом мужчин и предположим, что у нас есть случайная выборка из n человек. Выборочное среднее может служить хорошей оценкой в популяции среднего значения. Тогда у нас есть:
- Разница между ростом каждого мужчины в выборке и ненаблюдаемым средним по совокупности является статистической ошибкой , тогда как
- Разница между ростом каждого человека в выборке и наблюдаемым средним по выборке является невязкой .
Обратите внимание, что из-за определения выборочного среднего сумма остатков в случайной выборке обязательно равна нулю, и, таким образом, остатки обязательно не являются независимыми . С другой стороны, статистические ошибки независимы, и их сумма в пределах случайной выборки почти наверняка не равна нулю.
Можно стандартизировать статистические ошибки (особенно нормального распределения ) в z-балле (или «стандартном балле») и стандартизировать остатки в t- статистике или, в более общем смысле, студентизированных остатках .
В одномерных распределениях
Если мы предположим, что популяция нормально распределена со средним значением μ и стандартным отклонением σ, и выберем индивидуумов независимо, то мы имеем
и выборочное среднее
случайная величина, распределенная таким образом, что:
В статистических ошибках затем
с ожидаемыми значениями нуля, тогда как остатки равны
Сумма квадратов статистических ошибок , деленная на σ 2 , имеет распределение хи-квадрат с n степенями свободы :
Однако это количество не наблюдается, так как среднее значение по совокупности неизвестно. Сумма квадратов остатков , с другой стороны, наблюдаема. Частное этой суммы по σ 2 имеет распределение хи-квадрат только с n — 1 степенями свободы:
Эта разница между n и n — 1 степенью свободы приводит к поправке Бесселя для оценки выборочной дисперсии совокупности с неизвестным средним и неизвестной дисперсией. Коррекция не требуется, если известно среднее значение для генеральной совокупности.
Примечательно, что можно показать, что сумма квадратов остатков и выборочное среднее не зависят друг от друга, используя, например , теорему Басу . Этот факт, а также приведенные выше нормальное распределение и распределение хи-квадрат составляют основу вычислений с использованием t-статистики :
где представляет ошибки, представляет стандартное отклонение выборки для выборки размера n и неизвестного σ , а член знаменателя учитывает стандартное отклонение ошибок в соответствии с:

Распределения вероятностей числителя и знаменателя по отдельности зависят от значения ненаблюдаемого стандартного отклонения совокупности σ , но σ появляется как в числителе, так и в знаменателе и сокращается. Это удачно, потому что это означает, что, хотя мы не знаем σ , мы знаем распределение вероятностей этого частного: оно имеет t-распределение Стьюдента с n — 1 степенями свободы. Таким образом, мы можем использовать это частное, чтобы найти доверительный интервал для μ . Эту t-статистику можно интерпретировать как «количество стандартных ошибок от линии регрессии».
Регрессии
В регрессионном анализе различие между ошибками и остатками является тонким и важным, что приводит к концепции студентизированных остатков . Учитывая ненаблюдаемую функцию, которая связывает независимую переменную с зависимой переменной — скажем, линию — отклонения наблюдений зависимой переменной от этой функции являются ненаблюдаемыми ошибками. Если запустить регрессию на некоторых данных, то отклонения наблюдений зависимой переменной от подобранной функции являются остатками. Если линейная модель применима, диаграмма рассеяния остатков, построенная против независимой переменной, должна быть случайной около нуля без тенденции к остаткам. Если данные демонстрируют тенденцию, регрессионная модель, вероятно, неверна; например, истинная функция может быть квадратичным полиномом или полиномом более высокого порядка. Если они случайны или не имеют тенденции, но «разветвляются» — они демонстрируют явление, называемое гетероскедастичностью . Если все остатки равны или не разветвляются, они проявляют гомоскедастичность .
Однако возникает терминологическая разница в выражении среднеквадратичной ошибки (MSE). Среднеквадратичная ошибка регрессии — это число, вычисленное из суммы квадратов вычисленных остатков , а не ненаблюдаемых ошибок . Если эту сумму квадратов разделить на n , количество наблюдений, результатом будет среднее значение квадратов остатков. Поскольку это смещенная оценка дисперсии ненаблюдаемых ошибок, смещение устраняется путем деления суммы квадратов остатков на df = n — p — 1 вместо n , где df — количество степеней свободы ( n минус количество оцениваемых параметров (без учета точки пересечения) p — 1). Это формирует объективную оценку дисперсии ненаблюдаемых ошибок и называется среднеквадратичной ошибкой.
Другой метод вычисления среднего квадрата ошибки при анализе дисперсии линейной регрессии с использованием техники, подобной той, что используется в ANOVA (они такие же, потому что ANOVA — это тип регрессии), сумма квадратов остатков (также известная как сумма квадратов ошибки) делится на степени свободы (где степени свободы равны n — p — 1, где p — количество параметров, оцениваемых в модели (по одному для каждой переменной в уравнении регрессии, не включая точку пересечения) ). Затем можно также вычислить средний квадрат модели, разделив сумму квадратов модели за вычетом степеней свободы, которые представляют собой просто количество параметров. Затем значение F можно рассчитать путем деления среднего квадрата модели на средний квадрат ошибки, и затем мы можем определить значимость (вот почему вы хотите, чтобы средние квадраты начинались с).
Однако из-за поведения процесса регрессии распределения остатков в разных точках данных (входной переменной) могут различаться, даже если сами ошибки распределены одинаково. Конкретно, в линейной регрессии, где ошибки одинаково распределены, изменчивость остатков входных данных в середине области будет выше, чем изменчивость остатков на концах области: линейные регрессии подходят конечным точкам лучше, чем середина. Это также отражается в функциях влияния различных точек данных на коэффициенты регрессии : конечные точки имеют большее влияние.
Таким образом, чтобы сравнить остатки на разных входах, необходимо скорректировать остатки на ожидаемую изменчивость остатков, что называется студентизацией . Это особенно важно в случае обнаружения выбросов , когда рассматриваемый случай каким-то образом отличается от другого в наборе данных. Например, можно ожидать большой остаток в середине домена, но он будет считаться выбросом в конце домена.
Другие варианты использования слова «ошибка» в статистике
Использование термина «ошибка», как обсуждалось в разделах выше, означает отклонение значения от гипотетического ненаблюдаемого значения. По крайней мере, два других использования также встречаются в статистике, оба относятся к наблюдаемым ошибкам прогнозирования:
Среднеквадратичная ошибка (СКО) относится к количеству , по которому значение , предсказанное с помощью оценки отличается от количества оцениваемого ( как правило , вне образца , из которого была оценена модель). Корень средний квадрат ошибки (СКО) является квадратным корнем из MSE. Сумма квадратов ошибок (SSE) является СКО , умноженное на размер выборки.
Сумма квадратов остатков (SSR) — это сумма квадратов отклонений фактических значений от прогнозируемых значений в пределах выборки, используемой для оценки. Это основа дляоценки наименьших квадратов , где коэффициенты регрессии выбираются так, чтобы SSR был минимальным (т. Е. Его производная равна нулю).
Аналогичным образом, сумма абсолютных ошибок (SAE) — это сумма абсолютных значений остатков, которая минимизируется в подходе к регрессии с наименьшими абсолютными отклонениями .
Средняя ошибка (ME) является смещение . Среднее остаточное (МР) всегда равна нулю для оценок наименьших квадратов.
Смотрите также
- Абсолютное отклонение
- Прогнозы консенсуса
- Обнаружение и исправление ошибок
- Объясненная сумма квадратов
- Инновации (обработка сигналов)
- Неподходящая сумма квадратов
- Допустимая погрешность
- Средняя абсолютная ошибка
- Ошибка наблюдения
- Распространение ошибки
- Вероятная ошибка
- Случайные и систематические ошибки
- Уменьшенная статистика хи-квадрат
- Разбавление регрессии
- Среднеквадратичное отклонение
- Ошибка выборки
- Стандартная ошибка
- Студентизованный остаток
- Ошибки типа I и типа II
использованная литература
- Кук, Р. Деннис; Вайсберг, Сэнфорд (1982). Остатки и влияние в регрессии (Repr. Ed.). Нью-Йорк: Чепмен и Холл . ISBN 041224280X. Проверено 23 февраля 2013 года .
- Кокс, Дэвид Р .; Снелл, Э. Джойс (1968). «Общее определение остатков». Журнал Королевского статистического общества, Series B . 30 (2): 248–275. JSTOR 2984505 .
- Вайсберг, Сэнфорд (1985). Прикладная линейная регрессия (2-е изд.). Нью-Йорк: Вили. ISBN 9780471879572. Проверено 23 февраля 2013 года .
- «Ошибки, теория» , Математическая энциклопедия , EMS Press , 2001 [1994]
внешние ссылки
-
СМИ, связанные с ошибками и остатками на Викискладе?
Все курсы > Оптимизация > Занятие 4 (часть 1)
Прежде чем обратиться к теме множественной линейной регрессии, давайте вспомним, что было сделано до сих пор. Возможно, будет полезно посмотреть эти уроки, чтобы освежить знания.
- В рамках вводного курса мы узнали про моделирование взаимосвязи переменных и минимизацию ошибки при обучении алгоритма, а также научились строить несложные модели линейной регрессии с помощью библиотеки sklearn.
- При изучении объектно-ориентированного программирования мы создали класс простой линейной регрессии. Сегодня эти знания пригодятся при создании классов более сложных моделей.
- Также рекомендую вспомнить умножение векторов и матриц.
- Кроме того, в рамках текущего курса по оптимизации мы познакомились с понятием производной и методом градиентного спуска, а также построили модель простой линейной регрессии (использовав метод наименьших квадратов и градиент).
- Наконец, на прошлом занятии мы вновь поговорили про взаимосвязь переменных.
В рамках сегодняшнего занятия мы с нуля построим несколько алгоритмов множественной линейной регрессии.
Регрессионный анализ
Прежде чем обратиться к практике, обсудим некоторые теоретические вопросы регрессионного анализа.
Генеральная совокупность и выборка
Как мы уже знаем, множество всех имеющихся наблюдений принято считать генеральной совокупностью (population). И эти наблюдения, если в них есть взаимосвязи, можно теоретически аппроксимировать, например, линией регрессии. При этом важно понимать, что это некоторая идеальная модель, которую мы никогда не сможем построить.
Единственное, что мы можем сделать, взять выборку (sample) и на ней построить нашу модель, предполагая, что если выборка достаточно велика, она сможет достоверно описать генсовокупность.
Отклонение прогнозного значения от фактического для «идеальной» линии принято называть ошибкой (error или true error).
$$ varepsilon = y-hat{y} $$
Отклонение прогноза от факта для выборочной модели (которую мы и строим) называют остатками (residuals или residual error).
$$ varepsilon = y-f(x) $$
В этом смысле среднеквадратическую ошибку (mean squared error, MSE) корректнее называть средними квадратичными остатками (mean squared residuals).
На практике ошибку и остатки нередко используют как взаимозаменяемые термины.
Уравнение множественной линейной регрессии
Посмотрим на уравнение множественной линейной регрессии.
$$ y = theta_0 + theta_1x_1 + theta_2x_2 + … + theta_jx_j + varepsilon $$
В отличие от простой линейной регрессии в данном случае у нас несколько признаков x (независимых переменных) и несколько коэффициентов $ theta $ («тета»).
Интерпретация результатов модели
Коэффициент $ theta_0 $ задает некоторый базовый уровень (baseline) при условии, что остальные коэффициенты равны нулю и зачастую не имеет смысла с точки зрения интерпретации модели (нужен лишь для того, что поднять линию на нужный уровень).
Параметры $ theta_1, theta_2, …, theta_n $ показывают изменение зависимой переменной при условии «неподвижности» остальных коэффициентов. Например, каждая дополнительная комната может увеличивать цену дома в 1.3 раза.
Переменная $ varepsilon $ (ошибка) представляет собой отклонение фактических данных от прогнозных. В этой переменной могут быть заложены две составляющие. Во-первых, она может включать вариативность целевой переменной, описанную другими (не включенными в нашу модель) признаками. Во-вторых, «улавливать» случайный шум, случайные колебания.
Категориальные признаки
Модель линейной регрессии может включать категориальные признаки. Продолжая пример с квартирой, предположим, что мы строим модель, в которой цена зависит от того, находится ли квартира в центре города или в спальном районе.
Перед этим переменную необходимо закодировать, создав, например, через Label Encoder признак «центр», который примет значение 1, если квартира в центре, и 0, если она находится в спальном районе.
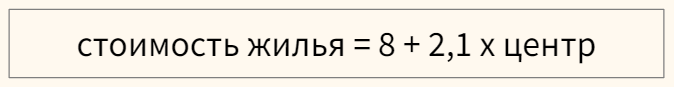
В модели, представленной выше, если квартира находится в центре (переменная «центр» равна единице), ее стоимость составит 10,1 миллиона рублей, если на окраине (переменная «центр» равна нулю) — лишь восемь.
Для категориального признака с множеством классов можно использовать one-hot encoding, если между классами признака отсутствует иерархия,
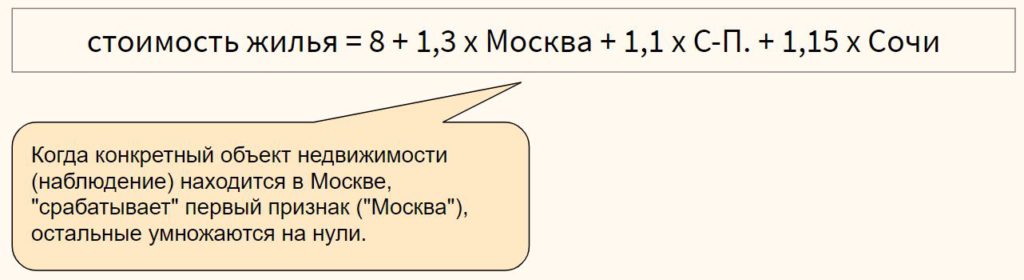
или, например, ordinal encoding в случае наличия иерархии классов в признаке

Выбросы в линейной регрессии
Как и коэффициент корреляции Пирсона, модель линейной регрессии чувствительна к выбросам (outliers), то есть наблюдениям, серьезно выпадающим из общей совокупности. Сравните рисунки ниже.
При наличии выброса (слева), линия регрессии имеет наклон и может использоваться для построения прогноза. Удалив это наблюдение (справа), линия регрессии становится горизонтальной и построение прогноза теряет смысл.
При этом различают два типа выбросов:
- горизонтальные выбросы или влиятельные точки (leverage points) — они сильно отклоняются от среднего по оси x; и
- вертикальные выбросы или просто выбросы (influential points) — отклоняются от среднего по оси y
Ключевое отличие заключается в том, что вертикальные выбросы влияют на наклон модели (изменяют ее коэффициенты), а горизонтальные — нет.
Сравним два графика.
На левом графике черная точка (leverage point) сильно отличается от остальных наблюдений, но наклон прямой линии регрессии с ее появлением не изменился. На правом графике, напротив, появление выброса (influential point) существенно изменяет наклон прямой.
На практике нас конечно больше интересуют influential points, потому что именно они существенно влияют на качество модели.
Если в простой линейной регрессии мы можем оценить leverage и influence наблюдения графически⧉, в многомерной модели это сделать сложнее. Можно использовать график остатков (об этом ниже) или применить один из уже известных нам методов выявления выбросов.
Про выявление leverage и infuential points можно почитать здесь⧉.
Допущения модели регрессии
Применение алгоритма линейной регрессии предполагает несколько допущений (assumptions) или условий, при выполнении которых мы можем говорить о качественно построенной модели.
1. Правильный выбор модели
Вначале важно убедиться, что данные можно аппроксимировать с помощью линейной модели (correct model specification).
Оценить распределение данных можно через график остатков (residuals plot), где по оси x отложен прогноз модели, а на оси y — сами остатки.
В отличие от простой линейной регрессии мы не используем точечную диаграмму X vs. y, потому что хотим оценить зависимость целевой переменной от всех признаков сразу.
Остатки модели относительно ее прогнозных значений должны быть распределены случайным образом без систематической составляющей (residuals do not follow a pattern).
- Если вы попробовали применить линейную модель с коэффициентами первой степени ($x_n^1$) и выявили некоторый паттерн в данных, можно попробовать полиномиальную или какую-либо еще функцию (об этом ниже).
- Кроме того, количественные признаки можно попробовать преобразовать таким образом, чтобы их можно было аппроксимировать прямой линией.
- Если ни то, ни другое не помогло, вероятно данные не стоит моделировать линейной регрессией.
Также замечу, что график остатков показывает выбросы в данных.
2. Нормальность распределения остатков
Среднее значение остатков должно быть равно нулю. Если это не так, и среднее значение меньше нуля (скажем –5), то это значит, что модель регулярно недооценивает (underestimates) фактические значения. В противном случае, если среднее больше нуля, переоценивает (overestimated).
Кроме того, предполагается, что остатки следуют нормальному распределению.
$$ varepsilon sim N(0, sigma) $$
Проверить нормальность остатков можно визуально с помощью гистограммы или рассмотренных ранее критериев нормальности распределения.
Если остатки не распределены нормально, мы не сможем провести статистические тесты на значимость коэффициентов или построить доверительные интервалы. Иначе говоря, мы не сможем сделать статистически значимый вывод о надежности нашей модели.
Причинами могут быть (1) выбросы в данных или (2) неверный выбор модели. Решением может быть, соответственно, исследование выбросов, выбор новой модели и преобразование как признаков, так и целевой переменной.
3. Гомоскедастичность остатков
Гомоскедастичность (homoscedasticity) или одинаковая изменчивость остатков предполагают, что дисперсия остатков не изменяется для различных наблюдений. Противоположное и нежелательное явление называется гетероскедастичностью (heteroscedasticity) или разной изменчивостью.
Гетероскедастичность остатков показывает, что модель ошибается сильнее при более высоких или более низких значениях признаков. Как следствие, если для разных прогнозов у нас разная погрешность, модель нельзя назвать надежной (robust).
Как правило, гетероскедастичность бывает изначально заложена в данные. Ее можно попробовать исправить через преобразование целевой переменной (например, логарифмирование)
4. Отсутствие мультиколлинеарности
Еще одним важным допущением является отсутствие мультиколлинеарности. Мультиколлинеарность (multicollinearity) — это корреляция между зависимыми переменными. Например, если мы предсказываем стоимость жилья по квадратным метрам и количеству комнат, то метры и комнаты логичным образом также будут коррелировать между собой.
Почему плохо, если такая корреляция существует? Базовое предположение линейной регрессии — каждый коэффициент $theta$ оказывает влияние на конечный результат при условии, что остальные коэффициенты постоянны. При мультиколлинеарности на целевую переменную оказывают эффект сразу несколько признаков, и мы не можем с точностью интерпретировать каждый из них.
Также говорят о том, что нужно стремиться к экономной (parsimonious) модели то есть такой модели, которая при наименьшем количестве признаков в наибольшей степени объясняет поведение целевой переменной.
Variance inflation factor
Расчет коэффициента
Variance inflation factor (VIF) или коэффициент увеличения дисперсии позволяет выявить корреляцию между признаками модели.
Принцип расчета VIF заключается в том, чтобы поочередно делать каждый из признаков целевой переменной и строить модель линейной регрессии на основе оставшихся независимых переменных. Например, если у нас есть три признака $x_1, x_2, x_3$, мы поочередно построим три модели линейной регрессии: $x_1 sim x_2 + x_3, x_2 sim x_1 + x_3$ и $x_3 sim x_1 + x_3$.
Обратите внимание на новый для нас формат записи целевой и зависимых переменных модели через символ $sim$.
Затем для каждой модели (то есть для каждого признака $x_1, x_2, x_3$) мы рассчитаем коэффициент детерминации $R^2$. Если он велик, значит данный признак можно объяснить с помощью других независимых переменных и имеется мультиколлинеарность. Если $R^2$ мал, то нельзя и мультиколлинеарность отсутствует.
Теперь рассчитаем VIF на основе $R^2$:
$$ VIF = frac{1}{1-R^2} $$
При таком способе расчета большой (близкий к единице) $R^2$ уменьшит знаменатель и существенно увеличит VIF, при небольшом коэффициенте детерминации коэффициент увеличения дисперсии наоборот уменьшится.
Замечу, что $1-R^2$ принято называть tolerance.
Другие способы выявления мультиколлинеарности
Для выявления корреляции между независимыми переменными можно использовать точечные диаграммы или корреляционные матрицы. При этом важно понимать, что в данном случае мы выявляем зависимость лишь между двумя признаками. Корреляцию множества признаков выявляет только коэффициент увеличения дисперсии.
Интерпретация VIF
VIF находится в диапазон от единицы до плюс бесконечности. Как правило, при интерпретации показателей variance inflation factor придерживаются следующих принципов:
- VIF = 1, между признаками отсутствует корреляция
- 1 < VIF $leq$ 5 — умеренная корреляция
- 5 < VIF $leq$ 10 — высокая корреляция
- Более 10 — очень высокая
После расчета VIF можно по одному удалять признаки с наибольшей корреляцией и смотреть как изменится этот показатель для оставшихся независимых переменных.
5. Отсутствие автокорреляции остатков
На занятии по временным рядам (time series), мы сказали, что автокорреляция (autocorrelation) — это корреляция между значениями одной и той же переменной в разные моменты времени.
Применительно к модели линейной регрессии автокорреляция целевой переменной (для простой линейной регрессии) и автокорреляция остатков, residuals autocorrelation (для модели множественной регрессии) означает, что результат или прогноз зависят не от признаков, а от самой этой целевой переменной. В такой ситуации признаки теряют свою значимость и применение модели регрессии становится нецелесообразным.
Причины автокорреляции остатков
Существует несколько возможных причин:
- Прогнозирование целевой переменной с высокой автокорреляцией (например, если мы моделируем цену акций с помощью других переменных, то можем ожидать высокую автокорреляцию остатков, поскольку цена акций как правило сильно зависит от времени)
- Удаление значимых признаков
- Другие причины
Автокорреляция первого порядка
Дадим формальное определение автокорреляции первого порядка (first order correlation), то есть автокорреляции с лагом 1.
$$ varepsilon_t = pvarepsilon_{t-1} + u_t $$
где $u_t$ — некоррелированная при различных t одинаково распределенная случайная величина (independent and identically distributed (i.i.d.) random variable), а $p$ — коэффициент автокорреляции, который находится в диапазоне $-1 < p < 1$. Чем он ближе к нулю, тем меньше зависимость остатка $varepsilon_t$ от остатка предыдущего периода $varepsilon_{t-1}$.
Такое уравнение также называется схемой Маркова первого порядка (Markov first-order scheme).
Обратите внимание, что для модели автокорреляции первого порядка коэффициент автокорреляции $p$ совпадает с коэффициентом авторегрессии AR(1) $varphi$.
$$ y_t = c + varphi cdot y_{t-1} $$
Разумеется, мы можем построить модель автокорреляции, например, третьего порядка.
$$ varepsilon_t = p_1varepsilon_{t-1} + p_2varepsilon_{t-2} + p_3varepsilon_{t-3} + u_t $$
Выявление автокорреляции остатков
Для выявления автокорреляции остатков можно использовать график последовательности и график остатков с лагом 1, график автокорреляционной функции или критерий Дарбина-Уотсона.
График последовательности и график остатков с лагом 1
На графике последовательности (sequence plot) по оси x откладывается время (или порядковый номер наблюдения), а по оси y — остатки модели. Кроме того, на графике остатков с лагом 1 (lag-1 plot) остатки (ось y) можно сравнить с этими же значениями, взятыми с лагом 1 (ось x).
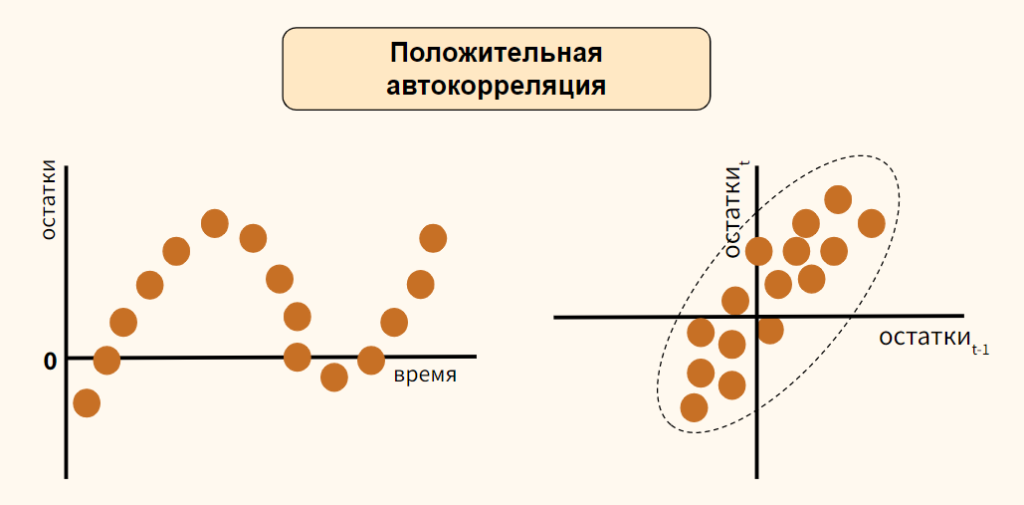
Рассмотрим вариант положительной автокорреляции (positive autocorrelation) на графиках остатков типа (а) и (б).
Как вы видите, при положительной автокорреляции в большинстве случаев, если одно наблюдение демонстрирует рост по отношению к предыдущему значению, то и последующее будет демонстрировать рост, и наоборот.
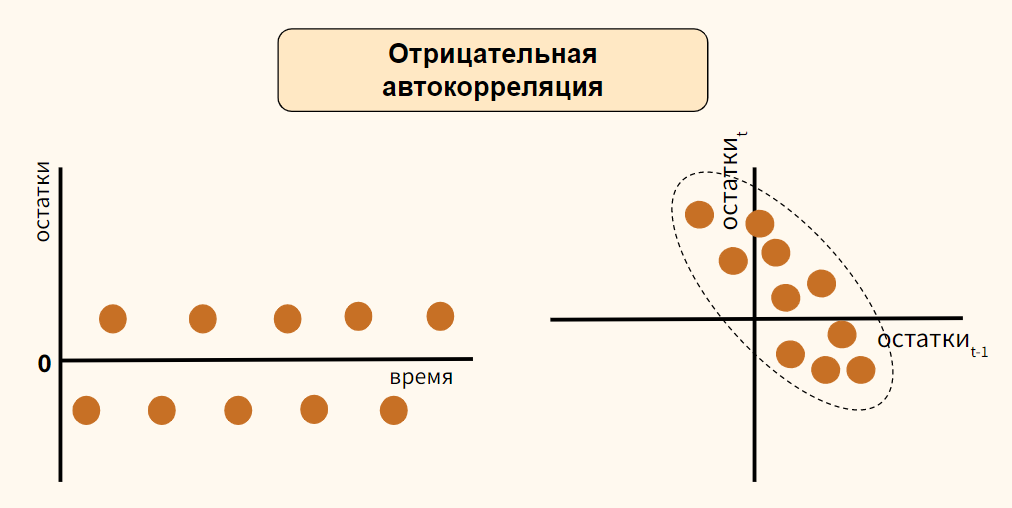
Теперь обратимся к отрицательной автокорреляции (negative autocorrelation).
Здесь наоборот, если одно наблюдение демонстрирует рост показателя по отношению к предыдущему значению, то последующее наблюдение будет наоборот снижением. Опять же справедливо и обратное утверждение.
В случае отсутствия автокорреляции мы не должны увидеть на графиках какого-либо паттерна.
График автокорреляционной функции
Еще один способ выявить автокорреляцию — построить график автокорреляционной функции (autocorrelation function, ACF).
Напомню, такой график показывает автокорреляцию данных с этими же данными, взятыми с первым, вторым и последующими лагами.
Критерий Дарбина-Уотсона
Количественным выражением автокорреляции является критерий Дарбина-Уотсона (Durbin-Watson test). Этот критерий выявляет только автокорреляцию первого порядка.
- Нулевая гипотеза утверждает, что такая автокорреляция отсутствует ($p=0$),
- Альтернативная гипотеза соответственно утверждает, что присутствует
- Положительная ($p approx -1$) или
- Отрицательная ($p approx 1$) автокорреляция
Значение теста находится в диапазоне от 0 до 4.
- При показателе близком к двум можно говорить об отсутствии автокорреляции
- Приближение к четырем говорит о положительной автокорреляции
- К нулю, об отрицательной
Как избавиться от автокорреляции
Автокорреляцию можно преодолеть, добавив значимый признак в модель, выбрав иной тип модели (например, полиномиальную регрессию) или в целом перейдя к моделированию и прогнозированию временного ряда.
Рассмотрение этих методов находится за рамками сегодняшнего занятия. Перейдем к практике.