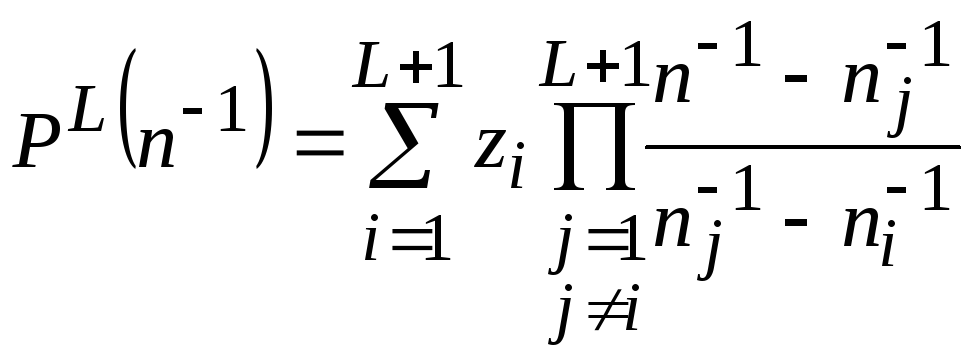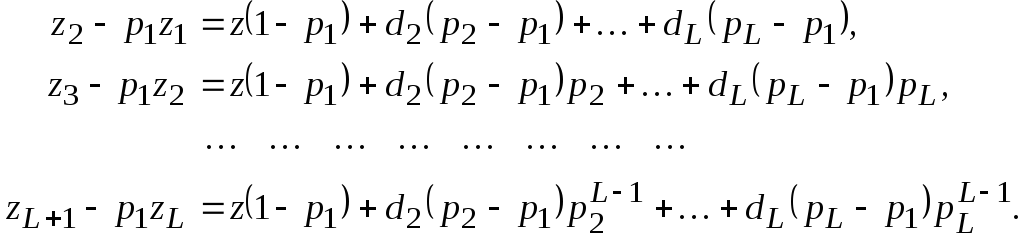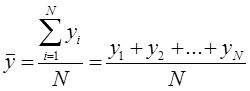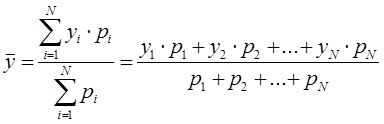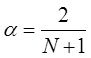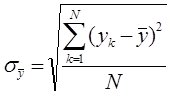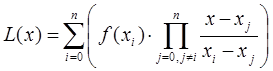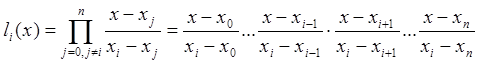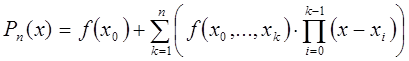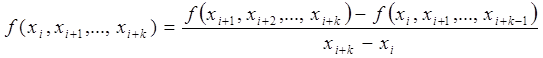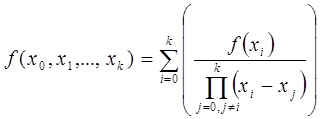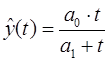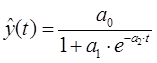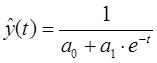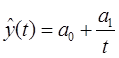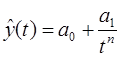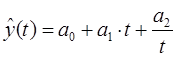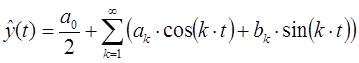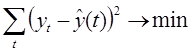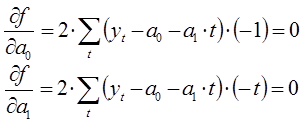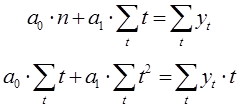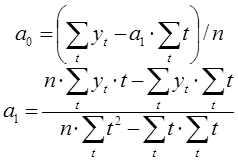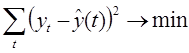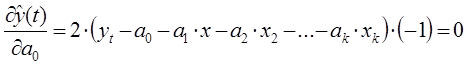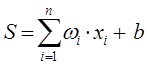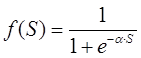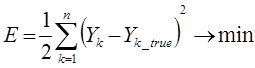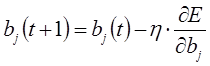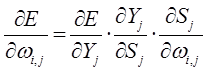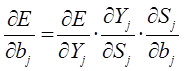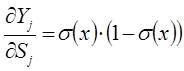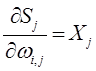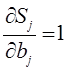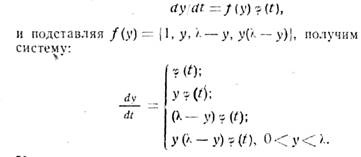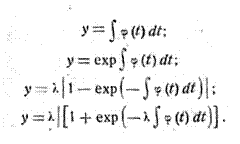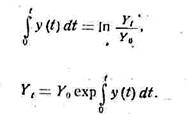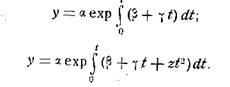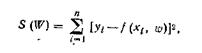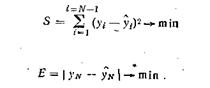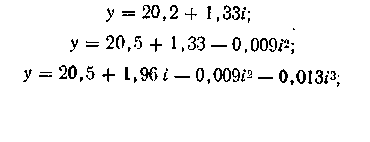В качестве исходного
положения будем считать, что известно
некоторое число членов последовательности
zn.
Например, оценка
по правилу Рунге основана на предположении,
что известен порядок точности численного
метода (или порядок аппроксимации), т.е.
znможно
представить в виде
, (2.4)
где
z– точное значение;zn–
приближенный результат, полученный при
числе узловых точек (или числе слагаемых
суммы) равномn;c1–
коэффициент, который предполагается
не зависящим отn;k–порядок точности
метода (или порядок аппроксимации);(n)
– величина, полагаемая малой по сравнению
сc1n—kпри тех значенияхn,
которые использовались в данных
конкретных расчетах.1
Правила
Рунге и Ричардсона. Одним из наиболее
распространенных способов оценки
погрешности численных методов с помощью
экстраполяции, является правило Рунге
[1].
В этом случае,
уменьшив nвQраз (предполагается, чтоQ>1
иn/Q— целое), отбросив малые, приходим к
системе двух уравнений
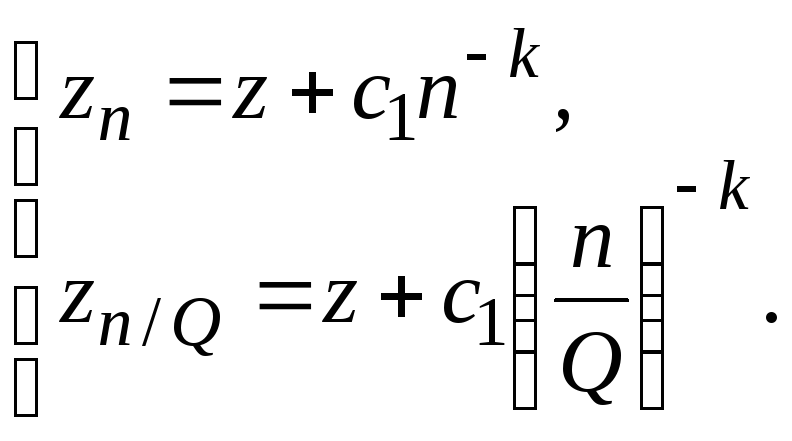
Вычитая первое
уравнение из второго, найдем
,
откуда
нетрудно найти c1, а, тем самым иz:
, (2.6)
С помощью (2.6)
определяется экстраполированное (по
правилу Ричардсона) значение искомого
параметраz, а с его помощью оценивается
погрешностьzn‑zприближенного значения zn.
Этот способ оценки погрешности называетсяправилом Рунге.
Метод
Ромберга. В некоторых случаях можно
построить более подробную математическую
модель погрешности, представив
приближенный результат в виде суммы
. (2.7)
Тогда, чтобы найти
неизвестные z,c1,…,cLнужно использоватьL+1
значениеziи записать задачу в виде системы линейных
уравнений, пренебрегая малыми величинами:
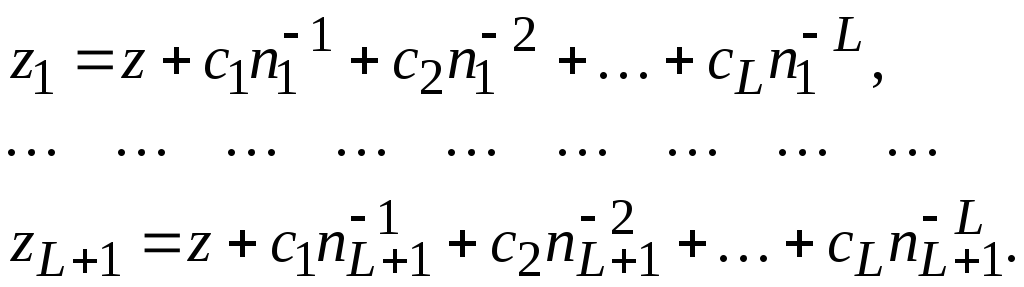
Эта задачу можно
решить путем построения интерполяционного
многочлена Лагранжа [1,2] L-й
степени
и
экстраполяцией его до n
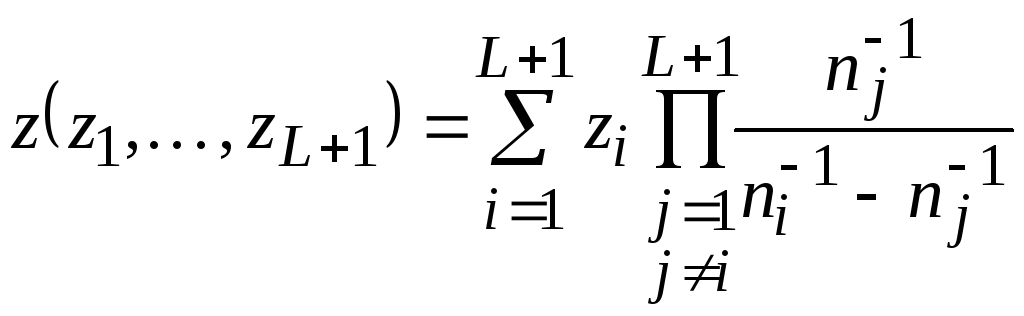
(в
скобках перечислены числа zi,
которые использованы для получения
экстраполированного значенияz).
Интерполяционная
формула обладает весьма полезным для
практического применения свойством.
Значение z, которое
получается по формуле (2.9), может быть
найдено путем последовательного
применения рекуррентного соотношения
Эйткена

то
есть для получения экстраполированного
значения L+1-го порядка
можно использовать два значенияL-го
порядка, вычисленные для двух наборов
данныхzi,
причем номер первой точки одного набора
сдвинут на единицу относительно другого.
В случае если
nj=n1Qj1,
выражение (2.10) принимает вид
, (2.11)
что
при L=1 совпадает с
(2.6), а приL>1 представляет
собой аналогичное выражение, в котором
вместо вычисленных участвуют
экстраполированные значения.
Повторное применение
правила Рунге для оценки погрешности
результата вычислений znпри последовательном увеличении номераnвQраз называютметодом Ромберга [1].
Аналогичный подход
имеет место и в случае, когда номер члена
последовательности увеличивается на
единицу (т.е. nj+1=nj+1).
Для последовательности {zn}
строитсятаблица Нэвилла [7,8],
представляющая собой матрицуzjL(,
),
в которой нулевой столбец – исходная
последовательность, а все остальные
столбцы находятся по правилу
. (2.12)
В более общем
случае приближенный результат
представляется в виде
, (2.13)
где
k1,…, kL– произвольные действительные числа.
Тем не менее, приnj=n1Qj1задача определения коэффициентовciи экстраполированного значенияzрешается аналитически. Подставив в
(2.8)nj=n1Qj1преобразуем систему уравнений:
Введя обозначения
,
получим
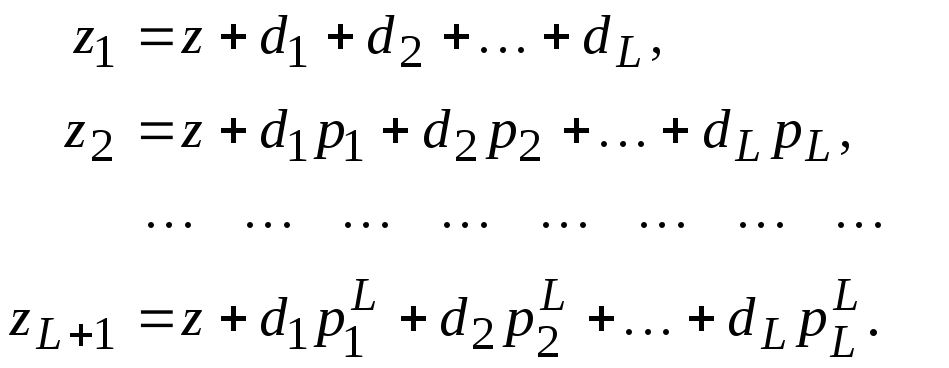
Вычитая в (2.14)
предыдущее уравнение, умноженное на
p1, из последующего, будем иметь
Разделив все
уравнения на 1p1и обозначив,
,
приходим к новой системе

которая
по виду аналогична (2.14), но имеет на одно
неизвестное меньше. Повторяя этот
процесс Lраз, можно
найтиz. Отметим, чтопредставляют собой Ричардсоновские
экстраполяции (2.6).
Таким образом,
определение искомого значения zи в случае произвольных (в общем случае
не целых) показателяхki(но только приnj=n1Qj1)
сводится к повторному использованию
уточнения (2.6), то есть, к методу Ромберга.
В случае njn1Qj1задача экстраполяции сводится к решению
системыL+1 линейных
уравнений типа (2.13) численным методом.
Главным ограничением
для применения рассмотренных методов,
основанных на разложении по степеням
n, является то, что
показатели степенейkjдолжны быть известны заранее.
Определение формулы экстраполяции
Формула экстраполяции — это формула, используемая для оценки значения зависимой переменной относительно независимой переменной, которая должна лежать в диапазоне за пределами данного набора данных. Например, точно известен расчет линейного исследования с использованием двух конечных точек (x1, y1) и (x2, y2) на линейном графике, когда значение экстраполируемой точки равно «x», формула, которую можно использовать представляется как y1+ [(x−x1) / (x2−x1)] *(у2-у1).
Оглавление
- Определение формулы экстраполяции
- Расчет линейной экстраполяции (шаг за шагом)
- Примеры
- Пример №1
- Пример #2
- Пример №3
- Актуальность и использование
- Рекомендуемые статьи
Y(x) = Y(1)+ (x-x(1)/x(2)-x(1)) * (Y(2) — Y(1))
Формулу линейной экстраполяции можно разделить на следующие шаги:
- Во-первых, необходимо проанализировать данные, чтобы определить, следуют ли данные за тенденцией и можно ли прогнозировать то же самое.
- Должно быть две переменные: одна должна быть зависимой переменной, а вторая должна быть независимой переменной.
- Числитель формулы начинается с предыдущего значения зависимой переменной. Затем нужно добавить долю независимой переменной при расчете среднего значения для интервалов классов.
- Наконец, умножьте значение, полученное на шаге 3, на разницу непосредственно заданных зависимых значений. Добавление шага 4 к значению зависимой переменной даст экстраполированное значение.
Примеры
.free_excel_div{фон:#d9d9d9;размер шрифта:16px;радиус границы:7px;позиция:относительная;margin:30px;padding:25px 25px 25px 45px}.free_excel_div:before{content:»»;фон:url(центр центр без повтора #207245;ширина:70px;высота:70px;позиция:абсолютная;верх:50%;margin-top:-35px;слева:-35px;граница:5px сплошная #fff;граница-радиус:50%} Вы можете скачать этот шаблон формулы экстраполяции Excel здесь — Формула экстраполяции Шаблон Excel
Пример №1
Предположим, что значение некоторых переменных приведено ниже в виде (X, Y):
- (4, 5)
- (5, 6)
Основываясь на приведенной выше информации, вы должны найти значение Y(6), используя метод экстраполяции.
Решение
Используйте приведенные ниже данные для расчета.
- Х1: 4,00
- Y2: 6.00
- Y1: 5,00
- Х2: 5,00
Расчет Y(6) по формуле экстраполяции выглядит следующим образом:
Экстраполяция Y(x) = Y(1) + (x) – (x1) / (x2) – (x1) x {Y(2) – Y(1)}
Y(6) = 5 + 6 – 4 / 5 – 4 х (6 – 5)
Ответ будет —
- Y3 = 7
Следовательно, значение для Y, когда значение X равно 6, будет равно 7.
Пример #2
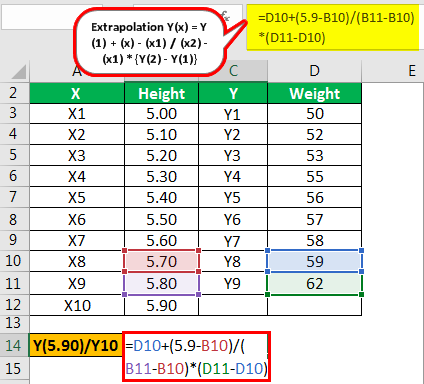
Г-н М и г-н Н являются учащимися 5-го стандарта, и в настоящее время они анализируют данные, предоставленные им их учителем математики. Учитель попросил их вычислить вес учеников, чей рост будет 5,90, и сообщил им, что приведенный ниже набор данных следует линейной экстраполяции.
ИксВысотаДМассаX15.00Y150X25.10Y252X35.20Y353X45.30Y455X55.40Y556X65.50Y657X75.60Y758X85.70Y859X95.80Y962
Предполагая, что эти данные следуют линейному ряду, вы должны рассчитать вес, который будет зависимой переменной Y в этом примере, когда независимая переменная x (рост) равна 5,90.
Решение
В этом примере нам теперь нужно узнать значение, или, другими словами, нам нужно спрогнозировать значение учащихся, чей рост равен 5,90, на основе тенденции, указанной в примере. Затем мы можем использовать приведенную ниже формулу экстраполяции в Excel для расчета веса, который является зависимой переменной для заданного роста и независимой переменной.
Расчет Y (5,90) выглядит следующим образом:
- Экстраполяция Y(5.90) = Y(8) + (x) – (x8) /(x9) – (x8) x [Y(9) – Y(8)]
- Y(5,90) = 59 + 5,90 – 5,70 / 5,80 – 5,70 х (62 – 59)
Ответ будет —
- = 65
Следовательно, значение Y, когда значение X равно 5,90, будет равно 65.
Пример №3
Г-н В. является исполнительным директором компании ABC. Он был обеспокоен продажами компании после тенденции к снижению. Поэтому он попросил свой исследовательский отдел произвести новый продукт, который будет соответствовать растущему спросу по мере увеличения производства. Через 2 года они разработали продукт, спрос на который рос.
Ниже приведены подробности за последние несколько месяцев:
Х (Производство)Произведено (единиц)Y (спрос)Спрос (единиц)X110.0Y120.00X220.00Y230.00X330.00Y340.00X440.00Y450.00X550.00Y560.00X660.00Y670.00X770.00Y780.00X880.00Y890.00X990.00Y9100.00
Они заметили, что, поскольку изначально это был новый и дешевый продукт, спрос на него будет линейным до определенного момента.
Следовательно, продвигаясь вперед, они сначала прогнозируют спрос, а затем сравнивают его с фактическим и производят соответственно, поскольку это потребовало от них огромных затрат.
Менеджер по маркетингу хочет знать, что будет требоваться, если они произведут 100 единиц. Основываясь на приведенной выше информации, вы должны рассчитать спрос в единицах, когда они производят 100 единиц.
Решение
Мы можем использовать приведенную ниже формулу для расчета потребности в единицах, которая является зависимой переменной для данных произведенных единиц, которая является независимой переменной.
Расчет Y(100) выглядит следующим образом:
- Экстраполяция Y(100) = Y(8) + (x) — (x8) / (x9) — (x8) x [ Y(9) – Y(8)]
- Y(100) = 90 + 100 – 80 / 90 – 80 х (100 – 90)
Ответ будет —
- = 110
Следовательно, значение для Y, когда значение X равно 100, будет равно 110.
Актуальность и использование
В основном используется для прогнозирования данных, выходящих за пределы текущего диапазона данных. В этом случае предполагается, что тенденция будет продолжаться для данных данных и даже за пределами этого диапазона, что не всегда так. Следовательно, следует осторожно использовать экстраполяцию. Вместо этого interpolationInterpolationInterpolation представляет собой математическую процедуру, применяемую для получения значения между двумя точками, имеющими заданное значение. Он аппроксимирует значение данной функции в заданном наборе дискретных точек. Его можно применять для оценки различных концепций стоимости, математики, статистики. Этот метод лучше подходит для того, чтобы сделать то же самое.
Рекомендуемые статьи
Эта статья была руководством по формуле экстраполяции. Здесь мы обсуждаем формулу для расчета значения зависимой переменной для независимой переменной, а также практические примеры и загружаемый шаблон Excel. Вы можете узнать больше об экономике из следующих статей:
- Revenue Run RateRevenue Run RateКомпании используют показатель выручки для прогнозирования годовой выручки на основе текущих уровней выручки, темпов роста, рыночного спроса и других соответствующих факторов, предполагая, что текущие доходы свободны от какой-либо сезонности или эффекта выбросов, а рыночные условия останутся неизменными. постоянный.Подробнее
- Формула скорости обращения денег
- Линия тренда ExcelЛиния тренда ExcelЛиния тренда, часто называемая линией наилучшего соответствия, отображает тренд данных. Он показывает общую тенденцию, закономерность или направление на основе доступных точек данных.Подробнее
- Формула множественной регрессииФормула множественной регрессииФормула множественной регрессии используется при анализе связи между зависимыми и многочисленными независимыми переменными. Формула = y = mx1 + mx2+ mx3+ хлеб больше
- Эффективная годовая ставкаЭффективная годовая ставкаЭффективная годовая ставка (EAR) — это ставка, фактически полученная от инвестиций или выплаченная по кредиту после начисления сложных процентов за определенный период времени, и используется для сравнения финансовых продуктов с различными периодами начисления сложных процентов, т. е. еженедельно, ежемесячно, ежегодно и т. д. По мере увеличения периодов начисления EAR увеличивается. Эффективная годовая ставка = (1 + i/n)n – 1Подробнее
2.4 Методы прогнозной экстраполяции
При формировании прогнозов с помощью экстраполяции обычно исходят из статистически складывающихся тенденций изменения тех или иных количественных характеристик объекта. Экстраполируются оценочные функциональные системные и структурные характеристики. Экстраполяционные методы являются одними из самых распространенных и наиболее разработанных среди всей совокупности методов прогнозирования.
С помощью этих методов экстраполируются количественные параметры больших систем, количественные характеристики экономического, научного, производственного потенциала, данные о результативности научно-технического прогресса, характеристики соотношения отдельных подсистем, блоков, элементов в системе показателей сложных систем и др.
Однако степень реальности такого рода прогнозов и соответственно мера доверия к ним в значительной мере обусловливаются аргументированностью выбора пределов экстраполяции и стабильностью соответствия «измерителей» по отношению к сущности рассматриваемого явления. Следует обратить внимание на то, что сложные объекты, как правило, не могут быть охарактеризованы одним параметром. В связи с этим можно сделать некоторое представление о последовательности действий при статистическом анализе тенденций и экстраполировании, которое состоит в следующем:
— во-первых, должно быть четкое определение задачи, выдвижение гипотез о возможном развитии прогнозируемого объекта, обсуждение факторов, стимулирующих и препятствующих развитию данного объекта, определение необходимой экстраполяции и её допустимой дальности;
— во-вторых, выбор системы параметров, унификация различных единиц измерения, относящихся к каждому параметру в отдельности;
— в-третьих, сбор и систематизация данных. Перед сведением их в соответствующие таблицы еще раз проверяется однородность данных и их сопоставимость: одни данные относятся к серийным изделиям, а другие могут характеризовать лишь конструируемые объекты;
— в-четвертых, когда вышеперечисленные требования выполнены, задача состоит в том, чтобы в ходе статистического анализа и непосредственной экстраполяции данных выявить тенденции или симптомы изменения изучаемых величин. В экстраполяционных прогнозах особо важным является не столько предсказание конкретных значений изучаемого объекта или параметра в таком-то году, сколько своевременное фиксирование объективно намечающихся сдвигов, лежащих в зародыше назревающих тенденций.
Для повышения точности экстраполяции используются различные приемы. Один из них состоит, например, в том, чтобы экстраполируемую часть общей кривой развития (тренда) корректировать с учетом реального опыта развития отрасли-аналога исследований или объекта, опережающих в своем развитии прогнозируемый объект.
Под трендом понимается характеристика основной закономерности движения во времени, в некоторой мере свободной от случайных воздействий. Тренд — это длительная тенденция изменения экономических показателей. При разработке моделей прогнозирования тренд оказывается основной составляющей прогнозируемого временного ряда, на которую уже накладываются другие составляющие. Результат при этом связывается исключительно с ходом времени. Предполагается, что через время можно выразить влияние всех основных факторов.
Под тенденцией развития понимают некоторое его общее направление, долговременную эволюцию. Обычно тенденцию стремятся представить в виде более или менее гладкой траектории.
Анализ показывает, что ни один из существующих методов не может дать достаточной точности прогнозов на 20-25 лет. Применяемый в прогнозировании метод экстраполяции не дает точных результатов на длительный срок прогноза, потому что данный метод исходит из прошлого и настоящего, и тем самым погрешность накапливается. Этот метод дает положительные результаты на ближайшую перспективу прогнозирования тех или иных объектов не более 5 лет.
Для нахождения параметров приближенных зависимостей между двумя или несколькими прогнозируемыми величинами по их эмпирическим значениям применяется метод наименьших квадратов. Его сущность состоит в минимизации суммы квадратов отклонений между наблюдаемыми (фактическими) величинами и соответствующими оценками (расчетными величинами), вычисленными по подобранному уравнению связи.
Этот метод лучше других соответствует идее усреднения как единичного влияния учтенных факторов, так и общего влияния неучтенных.
Рассмотрим простейшие приемы экстраполяции. Операцию экстраполяции в общем виде можно представить в виде определения значения функции:
, (2.7)
где — экстраполируемое значение уровня; L – период упреждения; Уt – уровень, принятый за базу экстраполяции.
Под периодом упреждения при прогнозировании понимается отрезок времени от момента, для которого имеются последние статистические данные об изучаемом объекте, до момента, к которому относится прогноз.
Экстраполяция на основе среднего значения временного ряда. В самом простом случае при предположении о том, что средний уровень ряда не имеет тенденции к изменению или если это изменение незначительно, можно принятьт.е. прогнозируемый уровень равен среднему значению уровней в прошлом.
Доверительные границы для средней при небольшом числе наблюдений определяются следующим образом:
(2.8)
где ta – табличное значение t – статистики Стьюдента с n-1 степенями и уровнем вероятности p;— средняя квадратическая ошибка средней величины. Значение ее определяется по формуле . В свою очередь, среднее квадратическое отклонение для выборки равно:
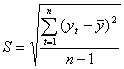
где yt – фактические значения показателя.
Доверительный интервал, полученный как ta, учитывает неопределенность, которая связана с оценкой средней величины.
Общая дисперсия, связанная как с колеблемостью выборочной средней, так и с варьированием ндивидуальных значений вокруг средней, составит величину S2+S2/n. Таким образом, доверительные интервалы для прогностической оценки равны:
(2.10)
Экстраполяция по скользящей и экспоненциальной средней. Для краткосрочного прогнозирования наряду с другими приемами могут быть применены адаптивная или экспоненциальная скользящие средние. Если прогнозирование ведется на один шаг вперед, то или
, где Мt — адаптивная скользящая средняя; Nt — экспоненциальная средняя. Здесь доверительный интервал для скользящей средней можно определить по формуле (2.10), в которой число наблюдений обозначено символом n. Поскольку при расчете скользящей средней через m обозначалось число членов ряда, участвующих в расчете средней, то заменим в этой формуле n на m, равным нечетным числам.
При экспоненциальном сглаживании дисперсия экспоненциальной средней равна , где S -среднее квадратическое отклонение, вместо величины
в формуле (2.10) при исчислении доверительного интервала прогноза следует взять величину
или
. Здесь a— коэффициент экспоненциального сглаживания, изменяется от 0 до 1. Если 0<a<0,5, то при расчете прогноза учитываются прошлые значения временного ряда, а при 0,5<a<1 – значения, близкие к периоду упреждения. Примерное значение коэффициента сглаживания определяют по формуле Р.Брауна:
(2.11)
где m – число уровней временного ряда, входящих в интервал сглаживания.
Экстраполяция на основе среднего темпа. Если в основу прогностического расчета положен средний темп роста, то экстраполируемое значение уровня можно получить с помощью формулы: ,
где — средний темп роста, Уt — уровень, принятый за базу для экстраполяции. Здесь принят только один путь развития — развитие по геометрической прогрессии, или по экспонентной кривой. Во многих же случаях фактическое развитие явления следует иному закону, и экстраполяция по среднему темпу нарушает основное допущение, принимаемое при экстраполяции, — допущение о том, что развитие будет следовать основной тенденции — тренду, наблюдавшемуся в прошлом. Чем больше фактический тренд отличается от экспоненты, тем больше данные, получаемые при экстраполяции тренда, будут отличаться от экстраполяции на основе среднего темпа.
Средний темп или определяется на основе изучения прошлого, или оценивается каким-либо другим путем (например, подбор вариантов для различных ситуаций). В качестве исходного (базового) уровня для экстраполяции представляется естественным взять последний уровень ряда, поскольку будущее развитие начинается именно с этого уровня.
Статистическая надежность вышеприведенных методов оценивается с помощью коэффициента вариации:
(2.12)
где— среднее квадратическое отклонение;
— среднее значение временного ряда.
Метод считается статистически надежным и может быть использован для прогнозирования, если значение коэффициента вариации не превышает 10%.
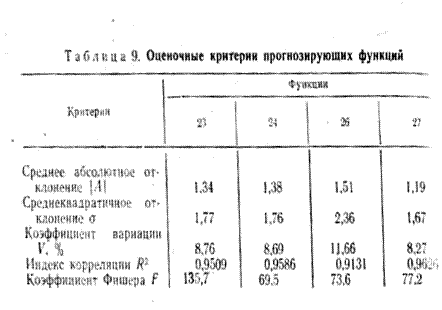
Однофакторные прогнозирующие функции
Это такие функции, в которых прогнозируемый показатель зависит только от одного факториального признака.
В научно-техническом и экономическом прогнозировании в качестве главного фактора аргумента обычно используют время. Вполне очевидно, что не ход времени определяет величины прогнозируемого показателя, а действие многочисленных влияющих на него факторов. Однако каждому моменту времени соответствуют определенные характеристики всех этих факториальных признаков, которые со временем в той или иной мере изменяются. Таким образом, время можно рассматривать как интегральный показатель суммарного воздействия всех факториальных признаков.
В качестве фактора-аргумента в однофакторной прогнозирующей функции можно использовать не только время, но и другие факторы, если известна их количественная оценка на перспективу.
Наиболее простым из методов прогнозирования является экстраполяция тренда явления (процесса) за истекший период. Тренд (или вековая тенденция) характеризует процесс изменения показателя за длительное время, исключая случайные колебания. Тренд явления находят путем аппроксимации фактических уровней временного ряда на основе выбранной функции. Наиболее часто применяемые при прогнозировании функции показаны в табл. 2.3. В них фактор-аргумент обозначен символом t.
Таблица 2.3 Однофакторные прогнозирующие функции
|
Наименования функции |
Вид функции |
|
Степенной полином |
y = a0 + a1t + a2t2 +…antn |
|
Парабола |
y=a0+a1t+a2t2 |
|
Линейная функция |
у = а0+а1t |
|
Экспоненциальная (показательная) |
|
|
Степенная |
|
|
Логарифмическая |
у = а0+а1lnt |
|
Комбинация линейной и логарифмической функций |
у = а0+a1t+а2lnt |
|
Функция Конюса |
|
|
Функция Торнквиста |
|
|
Логистическая (сигмоидальная) |
|
|
Частный случай логистической функции |
|
|
Гипербола |
|
|
Комбинация линейной функции и гиперболы |
у = а0+а1t + |
При прогнозировании колебательных (циклических) процессов применяют тригонометрические функции, ряды Фурье.
Степенной полином может описать любые процессы изменения показателя y в зависимости от значений t. Корреляционное отношение для степенного полинома, служащее мерой тесноты корреляционной связи в нелинейных моделях, приближается к единице по мере увеличения числа степеней полинома до числа уровней временного ряда. Одновременно линия регрессии приближается к фактическим уровням показателя за прошедшее время, что не позволяет установить его тренд и экстраполировать его на перспективу. Поэтому для прогнозирования обычно не применяют полином выше третьей степени. Таким образом, в качестве прогнозирующей функции целесообразно использовать лишь три частных случая степенного полинома: линейную модель, параболу и полином третьего порядка.
Однофакторная линейная модель отражает постоянный ежегодный абсолютный прирост в размере a1, т.е. арифметическую прогрессию. Парабола (степенной полином) второго порядка описывает случаи увеличения абсолютного ежегодного прироста на постоянную величину 2a2, а третьего порядка – S – образную кривую с двумя точками изгибов.
Экспонента первого порядка (показательная функция) предусматривает постоянный ежегодный темп роста, равный процентов (т.е. геометрическую прогрессию), а второго порядка – постоянное увеличение ежегодных темпов роста в
раз. Степенная функция соответствует случаю ускоряющегося при а1>1 или замедляющегося при а1<1 роста абсолютного ежегодного прироста. Логарифмическая функция выражает случай сокращения абсолютного ежегодного прироста, а функции Торнквиста и Конюса, комбинация линейной функции с логарифмической – затухающий рост абсолютного ежегодного прироста. Логистическая (сигмоидальная) кривая представляет собой модифицированную геометрическую прогрессию, в которой возрастание затухает по мере приближения к определенному пределу. Наконец, гиперболы характерны для тех случаев, когда в начальной стадии абсолютные уровни показателя резко сокращаются, а на последующих этапах этот процесс сокращения постепенно затухает
Коэффициенты в однофакторных прогнозирующих функциях а0 и а1 определяются с помощью метода наименьших квадратов, сущность которого заключается в минимизации суммы квадратов отклонений фактических значений от расчетных:
(2.13)
где— вид исследуемой функции (см. табл.2.3)
Пусть временной ряд может быть описан линейной функцией:
.
Подставим это выражение в формулу (2.13), получим:
.
Возьмем частные производные по а0 и а1:
,
.
В результате алгебраических преобразований данной системы: (сокращений, раскрытия скобок, переноса известных величин вправо, а неизвестных влево) — получим систему нормальных уравнений:
Из первого уравнения найдем а0, из второго – а1.
Формулы расчета а0 и а1 имею вид:
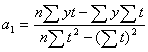
или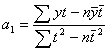
Прогнозируемые значения показателя у определяется по формуле:
=а0+а1(t+L), где L=1,2,…,(2.15)
если фактором-аргументом является время t. В случае, когда фактор-аргумент – независимая переменная (любой показатель х) то необходимо найти его прогнозируемые значения. Тогда:
=а0+а1хt+L, где L=1,2,… (2.16)
Для оценки качества и надежности анализа регрессии используются следующие показатели: корреляционное отношение (η), коэффициент парной корреляции (r), коэффициент детерминации (r2), средняя ошибка предвидения (Sс), средняя ошибка коэффициента регрессии (Sаj, j=0, 1,2, …).
Корреляционное отношение (η) указывает на степень взаимозависимости между у и х. Принимает значения между 0 и 1:
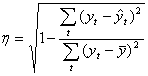
Коэффициент парной корреляции может быть определен по формуле:
(2.18)
где S11, S22, S12 – соответственно остаточные дисперсии для функции, фактора-аргумента и их произведения: определяются по формулам:
;
;
.
Коэффициент корреляции, рассчитывается по формуле (2.18) и принимает значения от -1 до +1. Чем ближе значения коэффициента к единице, тем большая связь существует между функцией и аргументом.
Для проверки гипотезы о наличии связи определим критерий Стьюдента:
(2.19)
Если tr>tтабл, то принимаем гипотезу о наличии связи, в противном случае – она отсутствует.
Коэффициент детерминации (r2) показывает, насколько уравнение регрессии подходит к значениям временного ряда или какой процент составляют учтенные факторы в уравнении регрессии.
Точность регрессионной модели определяется с помощью средней ошибки предвидения или среднего отклонения по формуле:
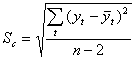
Средняя ошибка коэффициентов регрессии определяется по формуле:
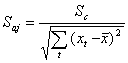
или 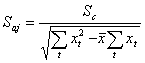
где j=1, 2, … , m; m – число факторов;
t=1, 2, … , n; n – число данных.
Оценка Стьюдента (tаj) показывает удельный вес фактора-аргумента х при объяснении у. Она вычисляется делением коэффициентов aj на их средние ошибки Saj:
(2.22)
Оценка Стьюдента показывает, во сколько раз значения j-го коэффициента превосходят его среднюю ошибку. Любое значение taj больше 2 или меньше -2 считается приемлемым. Чем больше величина taj, тем больше значимость коэффициентов регрессии, тем надежнее уравнение регрессии.
Статистическая надежность аппроксимирующей функции или коэффициента парной корреляции устанавливается также с помощью критерия Стьюдента (2.19).
С вероятностью ошибки р и с (n-2) степенями свободы выбранная функция признается статистически надежной, если рассчитанное значение критерия tr превышает табличное.
Ошибкой прогноза называется отклонение предсказанного значения от наблюдаемого (фактического). Для оценки совокупной ошибки прогноза используются два показателя: средняя абсолютная ошибка ( ) и средняя относительная ошибка (
), которые определяются по формулам:
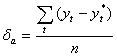
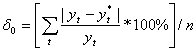
С помощью метода наименьших квадратов могут быть определены а0 и а1 во всех однофакторных прогнозирующих функциях, если эти функции предварительно линеаризовать, т.е. преобразовать в линейную модель. Линеаризация достигается логарифмированием или получением обратных значений функции, а также заменой переменных, представляющих собой преобразованные значения показателей у и t.
Многофакторные прогнозирующие функции
Каждый прогнозируемый показатель уt (t=1,2…,n) можно рассматривать не только как функцию одного фактора-аргумента, но и от нескольких:
— в виде линейной многофакторной модели:
уt=а0+а1х1t+а2х2t+…+аjхjt+…+аmхmt(2.25)
где а0, аj – коэффициенты модели при j=1, 2, … , k;
хjt – факторы-аргументы, влияющие на прогнозируемый показатель уt, при j=1, 2, … , m; t=1,2,…, n;
— в виде нелинейной многофакторной модели (степенного типа):
(2.26)
которая путем логарифмирования преобразуется в линейную. Более сложные виды нелинейных многофакторных моделей редко используются в практике прогнозирования и планирования.
Коэффициенты а0, аj в моделях типа (2.25) и (2.26) определяются с помощью метода наименьших квадратов (2.13) из системы нормальных уравнений, представляющих собой частные производные по а0, аj равные нулю:
В результате решения данной системы уравнений находятся такие а0 и аj, при которых (2.13) стремится к нулю.
Факторы-аргументы должны отвечать следующим условиям: во-первых, иметь количественное измерение и отражаться в отчетах или, по крайней мере, определяться на основе специального анализа отчетных данных; во-вторых, иметь перспективные оценки значений на прогнозируемый период; в-третьих, число включаемых в модель факторов должно быть меньше числа данных ряда в три раза; в-четвертых, быть линейно независимыми.
Факторы считаются зависимыми (мультиколлинеарными), если линейный (парный) коэффициент корреляции (см. формулу 2.18) двух факторов более 0,8. Из них в модели оставляют тот, который имеет больший коэффициент корреляции с функцией у.
Оптимальное количество факторов-аргументов можно установить с помощью так называемого метода исключений. Сущность его заключается в следующем.
В модель типа (2.25) включают все возможные факторы, удовлетворяющие указанным выше условиям и строят эту модель. Для каждого j-го фактора-аргумента по формуле (2.22) находят оценки Стьюдента. Выбирают наименьшую величину оценки min ta1 и сравнивают с табличным значением – tp при (n-k-1) – степенях свободы и выбранном уровне значимости р (обычно принимают р=0,05 или 5%). Если минимальная из рассчитанных оценок ta>tp, то модель оставляют в полученном виде. Если же tap, то фактор а1 исключается из модели как незначимый. Затем с оставшимися факторами строят новую модель, определяют новое значение оценок Стьюдента, находят минимальную из них и т.д. до тех пор, пока в модели останутся все значимые факторы.
Тесноту связей между функцией и факторами-аргументами можно установить с помощью квадрата коэффициента множественной корреляции:
(2.27)
где
Квадрат коэффициента множественной корреляции показывает, какая часть общего рассеяния зависимой переменной может быть объяснена функцией вида (2.25) или вида (2.26).
Статистическая надежность многофакторной регрессионной модели (или коэффициента детерминации) устанавливается с помощью критерия Фишера:
(2.28)
где n – число данных;
m – число факторов-аргументов в модели;
R2 – квадрат коэффициента множественной корреляции.
Если расчетное значение критерия Фишера превышает табличное при (n-m) и (m-1) степенях свободы и принятом р – уровне значимости то модель признается статистически надежной и значимой. Многофакторная регрессионная модель может быть использована для прогнозирования не более трехлетнего периода упреждения. Ошибки прогноза определяются по формулам (2.23-2.24).
Метод экспоненциального сглаживания
Сущность этого метода заключается в том, что прогноз ожидаемых величин (объемов, продаж и т.д.) определяется путем взвешенных средних величин текущего периода и сглаженных значений, сделанных в предшествующий. Такой процесс продолжается назад к началу временного ряда и представляет собой простую экспоненциальную модель для временных рядов с устойчивым трендом и малыми (независимыми) периодическими колебаниями.
Для многих временных рядов (показателей) наблюдается очевидная картина периодичности и случайности. Поэтому простая экспоненциальная модель расширяется с включением в нее двух последних компонент.
а) С устойчивым трендом
Пусть глаженное значение в момент времени t определяется по рекуррентной формуле:
(2.29)
где уt – фактическое значение в момент времени t; ;
а – параметр сглаживания, определяется по формуле (2.11)
Тогда сглаженное значение в момент времени (t-1) равно:
(2.30)
Подставив в выражение (2.29), получим:
(2.31)
Продолжая этот процесс, прогноз может быть выражен в величинах прошлых значений временного ряда, т.е.:
, (2.32)
где L – период предсказания, но не более трех-пяти лет.
При t=1,2,…, n сглаженные значения в момент времени t определяются по формуле (2.29). Для этого же периода времени определяется среднее квадратическое отклонение (см. формулу 2.9) и коэффициент вариации (см. формулу 2.12), чтобы оценить точность выбранного параметра сглаживания. При t=1
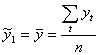
В случае если коэффициент вариации превышает 10%, то необходимо изменить интервал сглаживания, а следовательно, и параметр сглаживания .
При ,…, n прогнозы в момент времени t определяются по формуле (2.32) для оценки точности предсказания по среднему квадратическому отклонению и коэффициенту вариации.
При t=n+1, n+2, … определяются соответственно прогнозы данного показателя, в предположении, что текущее значение в момент времени t=n+1 совпадает с прогнозным в момент времени t=n.
б) С периодической компонентой
Пусть — сглаженное значение в момент времени t с учетом периодической компоненты. Периодичность совпадает с периодом предсказания. На практике обычно рассматриваются годовые или месячные изменения. Тогда оценка сглаженного значения запишется так:
(2.33)
.
где ft—T – оценка периодической компоненты в предшествующем периоде; Т – длина периода.
В момент времени t периодическая компонента определяется по формуле:
(2.34)
.
Весовые параметры α и β подбираются либо с учетом текущих значений , либо с учетом прошлых значений
. Оптимальные их значения устанавливаются по минимуму среднего квадратического отклонения.
Прогноз ожидаемых значений для оценки выбранных параметров α и β может быть определен мультипликативным образом по формуле:
(2.35)
где .
При t=n+1, n+2,…, N определяются собственно прогнозы по формуле:
(2.36)
где — прогноз сглаженного значения определяемый по формуле (2.32).
в) С периодической и случайной компонентами
Пусть оценка сглаженного значения с учетом периодической и случайной компоненты имеет вид:
(2.37)
где εt-1 – оценка случайной компоненты в момент времени (t-1), текущее значение εt определяется по формуле:
(2.38)
где γ – параметр сглаживания для случайной компоненты, .
Прогноз ожидаемых значений для оценки выбранных параметров α, β и γ может быть получен по формуле:
(2.39)
где Т – период предсказания, Т=1, 2, …, 5;
,…, n.
При t=n+1, n+2, …, N определяются собственно прогнозы по формуле:
(2.40)
где — прогноз сглаженного значения, определяется по формуле (2.32).
Метод авторегрессионного преобразования
Сущность его заключается в построении модели по отклонениям значений временного ряда от выравненных по тренду значений. Пусть эти отклонения представляют собой случайные колебания временного ряда в каждый момент времени t:
(2.41)
Тогда для случайной величины εt можно построить модель авторегрессии, т.е. регрессионную модель линейного вида для остатков значений временного ряда. Эти случайные переменные распределены со средним значением 0 и конечным рассеиванием (дисперсией) и подчиняются закону стохастического линейного разностного уровня 1-го порядка с постоянными коэффициентами (процесс Маркова), то есть:
(2.42)
где εt-1 – временной ряд случайной компоненты, сдвинутый на один шаг, t=1, 2, …, n.
По формулам вида (2.14) определим b0 и b1, получим:
;
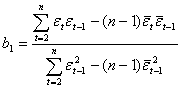
гдеи
— соответственно средние значения по данному временному ряду и сдвинутому на один шаг.
Прогнозируемые значения случайной компоненты определяются по формуле:
(2.44)
где L=1, 2, …
При L=1 , при L=2, 3, … справедлива формула (2.44).
Определяем коэффициент автокорреляции r2 по формуле парного коэффициента корреляции (см. формулу 2.18). Тогда коэффициент автокорреляции для авторегрессионной модели 1-го порядка равен:
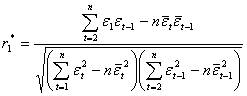
Затем строим авторегрессионную модель 2-го порядка:
(2.46)
где εt-2 – временный ряд случайной компоненты, сдвинутой на два шага, при t=1, 2, …, n.
Коэффициенты b0, b1, b2 находятся с помощью метода наименьших квадратов из системы нормальных уравнений.
Находим:
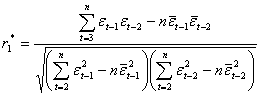
Если , то случайная компонента следует закону линейного разностного уравнения 1-го порядка (2.42), а прогнозы определяются по формуле (2.44). Если же
, то строится линейное разностное уравнение 3-го порядка рассчитывается
и т.д. Эти расчеты продолжаются до тех пор, пока
, при τ=1,2,…, n/2. Выбирается авторегрессионная модель (τ-1) порядка. Оценка точности и надежности авторегрессионной модели определяется по среднему квадратическому отклонению (см. формулу 2.9) и коэффициенту вариации (см. формулу 2.12).
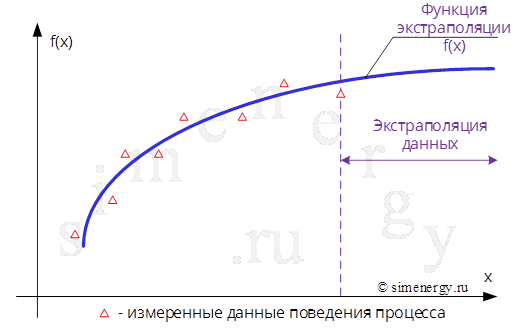
Экстраполяция – это способ предсказания поведения процесса (зависимость изменения данных) в будущем используя известные данные из прошлого. Другими словами, с помощью экстраполяции обобщают заведомо известные данные из прошлого и делают вывод об изменении этих данных в будущем.
Рис.1. Экстраполяция по данным измерений
Экстраполяция – это операция построения функции за пределами интервалов, на которых эта функция определена.
При использовании метода экстраполяции учитываются следующие допущения:
.- период времени, для которого построена функция, должен быть достаточным для выявлении тенденции развития;
.- анализируемый процесс является устойчиво динамическим и обладает инерционностью, т.е. для значительных изменений характеристик процесса требуется время;
.- не ожидается сильных внешних воздействий на изучаемый процесс, которые могут серьезно повлиять на тенденцию развития.
Методы экстраполяции являются одними из самых распространенных методов прогнозирования. С помощью этих методов экстраполируются количественные параметры больших систем, количественные характеристики экономического, научного, производственного потенциала, данные о результативности научно-технического прогресса, характеристики соотношения отдельных подсистем, блоков, элементов в системе показателей сложных систем и др. Следует заметить, что метод экстраполяции позволяет предсказать поведение процесса в будущем, но степень истинности такого прогноза в значительной мере обусловливается аргументированностью выбора пределов экстраполяции и стабильностью измерений. Так же следует обратить внимание на то, что сложные объекты, как правило, не могут быть охарактеризованы одним параметром.
Основные этапы действий при статистическом анализе тенденций и экстраполяции:
.- во-первых, сбор и систематизация данных. Сбор исходной информации о значении исследуемой характеристики. Проверка однородности данных и их сопоставимость. При необходимости предварительная обработка исходной информации: усреднение значений временного ряда (сглаживание данных). Построение временной характеристики;
.- во-вторых, выбор функции экстраполяции и расчет параметров выбранной функции. В зависимости от того, какая функция будет выбрана, будет зависеть точность выполненного прогноза.
.- в-третьих, расчет границ доверительного интервала прогноза.
Использование экстраполяции имеет в своей основе предположение о том, что рассматриваемый процесс представляет собой сочетание двух составляющих: регулярной составляющей
и случайной переменной
. Временной ряд может условно представлен в виде:
Регулярная составляющая называется трендом (или тенденцией) и характеризует существующую динамику развития процесса в целом. Случайная составляющая отражает случайные колебания (шумы процесса).
При разработке моделей прогнозирования тренд является основной составляющей прогнозируемого временного ряда, на которую уже накладываются другие составляющие. Результат при этом связывается исключительно с ходом времени. Предполагается, что через время можно выразить влияние всех основных факторов.
Выделение тенденции в массиве данных сводится к определению среднего значения за выбранный период. При этом среднее значение может определяться в виде:
— Среднее арифметическое значение
— Взвешенное среднее арифметическое значение
— Среднее экспоненциальное значение
Средние скользящие значения обычно используются для сглаживания краткосрочных колебаний и выделения основных тенденций или циклов, тем самым позволяя увидеть скрытые тренды в рассматриваемых данных. Тренд характеризует процесс изменения показателя за длительное время, исключая случайные колебания.
Среднее арифметическое значение (Simple Moving Average, SMA) определяется как сумма чисел за рассматриваемый период, которую разделили на количество этих чисел за период.
— значение функции (значение случайной величины) в i-точке;
— период расчета (целое положительное число);
— среднее арифметическое значение за рассматриваемый период N.
Взвешенное среднее арифметическое значение (Weighted Moving Average, WMA) применяется, когда к каждому известному значению можно присвоить отдельные значения веса
.
— значение функции (значение случайной величины) в i-точке;
— вес известного значения;
— период расчета (целое положительное число);
— взвешенное среднее арифметическое значение за рассматриваемый период N.
Экспоненциальное среднее значение (Exponential Moving Average, EMA) является частным случаем взвешенного скользящего среднего, когда значение веса убывает экспоненциально и никогда не равно нулю. Среднее экспоненциальное значение определяется следующей формулой:
— среднее экспоненциальное значение в i-точке
— значение функции (значение случайной величины) в i-точке
— сглаживающая константа, коэффициент характеризующий скорость уменьшения весов, принимает значение от 0 и до 1, чем меньше его значение тем больше влияние предыдущих значений на текущую величину среднего.
При этом, в качестве первого значения берется простое скользящее среднее (Simple Moving Average) с тем же самым интервалом сглаживания. экспоненциального скользящего среднего.
Коэффициент , может быть выбран произвольным образом, в пределах от 0 до 1. Однако в практике технического анализа на реальном рынке такой подход не применим, поскольку статистический ряд постоянно дополняется новыми значениями цен. Это делает невозможным одновременно зафиксировать α коэффициент и соблюсти критерий минимизации среднеквадратической ошибки. С этой целью для расчета α коэффициента используется следующая формула:
— период расчета (целое положительное число) или интервал сглаживания.
Измеренные значения находятся в диапазоне (интервале) относительно рассчитанного среднего значения. Диапазон измерений обозначается буквой греческого алфавита — сигма
.
— среднее значение за рассматриваемый период N;
— отклонение от среднего значения.
Аналитический расчет диапазона (интервала) измерений может быть выполнен по формуле определения среднеквадратичного отклонения.
Среднеквадратичное (стандартное) отклонение — показывает среднее значение разброса измеренной величины относительно среднего значения. Оценка среднеквадратичного (стандартного) отклонения может быть выполнена по формуле:
— период расчета (целое положительное число);
— среднее арифметическое значение за рассматриваемый период N;
Cреднеквадратическое отклонение позволяет оценить, насколько значения из множества могут отличаться от среднего значения. Следует заметить, что с вероятностью 0,9973 (99,73%) значение нормально распределённой случайной величины лежит в интервале ., другими словами значения распределённой случайной величины лежат в диапазоне:
Методы экстраполяции
Далее в статье рассмотрены основные методы экстраполяции данных. Следует отметить, что ни один из существующих методов не может обеспечить достаточной точности прогнозов. Применяемый в прогнозировании метод экстраполяции не дает точных результатов на длительный срок прогноза, потому что данный метод исходит из прошлого и настоящего, и тем самым погрешность накапливается. Этот метод дает положительные результаты на ближайшую (краткосрочную) перспективу прогнозирования тех или иных объектов.
Ниже представленные методы экстраполяции, которые позволяют определить параметры функции на основе ранее полученных данных (точки из заданной выборки). Вначале рассматривается способ построения интерполяционного полинома через (непосредственно) точки заданной выборки. В последствии в статье рассматривается способ построения интерполяционного полинома (однофакторные и многофакторные функции) в непосредственной близости от точек из заданной выборки.
П1. Экстраполяция на основе интерполяционного полиномома n-степени.
Интерполяционный полином n-степени – это математическая функция позволяющая записать полином n-степени, который будет соединять все заданные точки из набора значений, полученных опытным путём или методом случайной выборки в различные моменты времени с непостоянным временным шагом измерений.
В общем виде интерполяционный многочлен записывается следующим образом:
Для получения интерполяционного многочлена, который будет соединять все заданные точки из набора значений, используют либо построение через форму Лагранжа, либо построение через форму Ньютона.
Интерполяционный многочлен в форме Лагранжа – это математическая функция позволяющая записать полином n-степени, который будет соединять все заданные точки из набора значений, полученных опытным путём или методом случайной выборки в различные моменты времени с непостоянным временным шагом измерений.
В общем виде интерполяционный многочлен в форме Лагранжа записывается в следующем виде:
где ˗ степень полинома
;
˗ значение значения интерполирующей функции
в точке
;
˗ базисные полиномы (множитель Лагранжа), которые определяются по формуле:
Интерполяционный многочлен в форме Ньютона – это математическая функция позволяющая записать полином n-степени, который будет соединять все заданные точки из набора значений, полученных опытным путём или методом случайной выборки с постоянным временным шагом измерений.
В общем виде интерполяционный многочлен в форме Ньютона записывается в следующем виде:
где n – вещественное число, которое указывает степень полинома;
– переменная, которая представляет собой разделенную разность k-го порядка, которая вычисляется по следующей формуле:
Разделённая разность является симметричной функцией своих аргументов, то есть при любой их перестановке её значение не меняется. Следует отметить, что для разделённой разности k-го порядка справедлива следующая формула:
Недостатки метода интерполяции данных на основе интерполяционного полиномома n-степени:
П1. С ростом числа точек порядок многочлена возрастает, а вместе с ним возрастает число операций, которое нужно выполнить для вычисления точки на кривой.
П2. С ростом числа точек у интерполяционной кривой могут возникнуть осцилляции, когда построенный интерполяционный многочлен в промежуточных точках кривой будет очень сильно (нехарактерно) раскачиваться и далеко уходить от заданных точек.
П3. С ростом числа точек плохо подходит для экстраполяции, так как значение многочлена степени n>0 вне отрезка интерполяции всегда расходится к бесконечности (тем быстрее, чем больше n) вне зависимости от сходимости экстраполируемой функции.
П2. Экстраполяция на основе однофакторной функции
Однофакторные функции — это такие функции, в которых прогнозируемый показатель зависит только от одной переменной (одного признака). В научно-техническом и экономическом прогнозировании в качестве главного фактора аргумента обычно используют время. Однако вполне очевидно, что не ход времени определяет величины прогнозируемого показателя, а действие многочисленных влияющих на него факторов, которые сложно выделить и определить.
В качестве однофакторных функций используются следующие функции, в которых временная переменная обозначена символом t (фактор-аргумент).
П.1. Степенной полином
Степенной полином может описать любые процессы изменения показателя в зависимости от значений времени. Корреляционное отношение для степенного полинома, служащее мерой тесноты корреляционной связи в нелинейных моделях, приближается к единице по мере увеличения числа степеней полинома до числа уровней временного ряда. Одновременно линия регрессии приближается к фактическим уровням показателя за прошедшее время, что не позволяет установить его тренд и экстраполировать его на перспективу. Поэтому для прогнозирования обычно не применяют полином выше третьей степени. Таким образом, в качестве прогнозирующей функции целесообразно использовать лишь три частных случая степенного полинома: линейную модель, параболу и полином третьего порядка.
П.1.1. Линейная функция (частный случай полинома)
Однофакторная линейная модель отражает постоянный ежегодный абсолютный прирост, т.е. арифметическую прогрессию.
П.1.2. Парабола (частный случай полинома)
Парабола (степенной полином) второго порядка описывает случаи увеличения абсолютного ежегодного прироста на постоянную величину, а третьего порядка – кривую с двумя точками изгибов.
П.2. Экспоненциальная (показательная) функция
Экспонента первого порядка (показательная функция) предусматривает постоянный ежегодный темп роста, равный процентов (т.е. геометрическую прогрессию), а второго порядка – постоянное увеличение ежегодных темпов роста в
раз.
П.3. Степенная функция
Степенная функция соответствует случаю ускоряющегося при а1>1 или замедляющегося при а1<1 роста абсолютного ежегодного прироста.
П.4. Логарифмическая функция
Логарифмическая функция выражает случай сокращения абсолютного ежегодного прироста, а функции Торнквиста и Конюса, комбинация линейной функции с логарифмической – затухающий рост абсолютного ежегодного прироста. Логистическая (сигмоидальная) кривая представляет собой модифицированную геометрическую прогрессию, в которой возрастание затухает по мере приближения к определенному пределу.
П.4.1. Комбинация линейной и логарифмической функций
П.4.2. Функция Конюса
П.4.3. Функция Торнквиста
П.4.4. Функция логистическая (сигмоидальная)
П.5. Гиперболическая функция (Гипербола)
Гиперболическая функция характерна для тех случаев, когда в начальной стадии абсолютные уровни показателя резко сокращаются, а на последующих этапах этот процесс сокращения постепенно затухает
П.5.1. Комбинация линейной функции и гиперболы
П.6. При прогнозировании колебательных (циклических) процессов применяют тригонометрические функции, ряды Фурье.
k – количество учитываемых гармоник в сигнале.
Прогнозирование данных в будущем обеспечивают с помощью выбора функции, которая наилучшем образом описывает изменение наблюдаемой величины в прошлом. Для выбранной функции определяют значения коэффициентов выбранной функции. Для нахождения параметров приближенных зависимостей между двумя или несколькими прогнозируемыми величинами по их эмпирическим значениям применяется метод наименьших квадратов. Его сущность состоит в минимизации суммы квадратов отклонений между наблюдаемыми (фактическими) величинами и соответствующими оценками (расчетными величинами), вычисленными по подобранному уравнению связи.
где – значение выбранной однофакторной функции в заданной точке,
— исследуемый временной ряд в заданной точке
Полученное выражение носит название целевой функции. Целевая функция – эта функция нескольких переменных, подлежащая оптимизации (минимизации или максимизации) в целях решения некоторой оптимизационной задачи.
С помощью метода наименьших квадратов могут быть определены неизвестные коэффициенты во всех однофакторных прогнозирующих функциях.
В качестве примера, рассмотрим однофакторную функцию вида «линейная функция», с помощью которой будем моделировать заданный временной ряд.
Поиск неизвестных коэффициентов осуществляется с помощью метода наименьших квадратов. В соответствии с методом наименьших квадратов запишем целевую функцию:
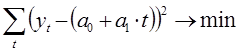
Целевая функция имеет минимум там, где частная производная по неизвестным коэффициентам равна нулю. В результате у нас выражение перепишется в следующую систему уравнений:
Преобразуем полученную систему уравнений: для системы уравнений проведены сокращения, раскрытие скобок, перенос известных величин вправо, а неизвестных влево. В результате получим следующую систему уравнений:
n – количество используемых измерений в заданном временном ряду.
Из полученной системы уравнений определим неизвестные коэффициенты следующим образом:
Таким образом, определив неизвестные коэффициенты можно построить однофакторную функцию на заданном отрезке времени и сделать прогноз изменения функции в будущем.
П3. Экстраполяция на основе многофакторных прогнозирующих функций
Многофакторные зависимости определяются поведением не одного параметра, а многих факторов одновременно. Чтобы построить такую модель, вначале необходимо определить факторы, которые оказывают наибольшее влияние на исходные данные.
Многофакторные модели могут быть как линейными, так и нелинейными.
П.1. в виде линейной многофакторной модели:
где – неизвестные коэффициенты модели,
– аргументы, влияющие на прогнозируемый показатель
П.2. в виде нелинейной многофакторной модели (степенного типа), которая может быть преобразована в линейную модель с помощью логарифмирования:
Более сложные виды нелинейных многофакторных моделей редко используются в практике прогнозирования и планирования.
Неизвестные коэффициенты выражений определяются с помощью метода наименьших квадратов из системы нормальных уравнений. Его сущность состоит в минимизации суммы квадратов отклонений между наблюдаемыми (фактическими) величинами и соответствующими оценками (расчетными величинами), вычисленными по подобранному уравнению связи.
Целевая функция имеет минимум там, где частная производная по неизвестным коэффициентам равна нулю. В результате у нас выражение перепишется в следующую систему уравнений:
В результате решения данной системы уравнений определяются неизвестные коэффициентам при которых полученная система уравнений стремится к нулю.
Факторы-аргументы должны отвечать следующим условиям:
во-первых, иметь количественное измерение и отражаться в отчетах или, по крайней мере, определяться на основе специального анализа отчетных данных;
во-вторых, иметь перспективные оценки значений на прогнозируемый период;
в-третьих, число включаемых в модель факторов должно быть меньше числа данных ряда в три раза;
в-четвертых, быть линейно независимыми.
П4. Экстраполяция на основе нейронной сети
Искусственные нейронные сети широко используются в задачах экстраполяции данных, когда неизвестен точный вид связи (функции) между входными и выходными значениями. Нейронная сеть является сложной нелинейной системой с огромным числом степеней свободы, что позволяет ей подстраивается под любые начальные данные.
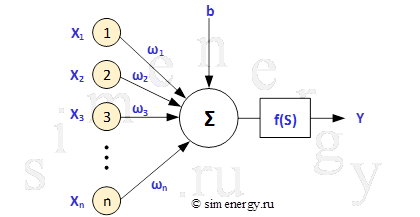
Искусственная нейронная сеть состоит из искусственных нейронов. Структурная схема искусственного нейрона приведена ниже.
Рис.2. Структурная схема искусственного нейрона
Искусственный нейрон имеет несколько входных сигналов (несколько входов) и только один выходной (единственный выход). Каждый вход имеет некоторый вес, на который умножается значение, поступившее по данному входу. В теле (ячейке) нейрона происходит суммирование взвешенных входов в соответствии с формулой:
n — размерность входного вектора
— вес i-го входа нейрон
— значение, поступающее на i-й вход нейрона
Как уже было написано, в теле нейрона происходит суммирование взвешенных входов, а полученная сумма преобразуется с помощью активационной (передаточной) функции нейрона (обычно нелинейной) в выходное значение нейрона. Полученная сумма поступает в качестве аргумента S на функцию активации , результат которой является выходным значением нейрона.
Активационная функция (передаточная функция) может иметь различный вид: бинарный, пороговый, линейный, сигмоидальный. Одной из наиболее распространенных видов активационной функции является нелинейная функция с насыщением, так называемая логистическая функция или сигмоид (т.е. функция S-образного вида):
При уменьшении α сигмоид становится более пологим, в пределе при α=0 вырождаясь в горизонтальную линию на уровне 0.5, при увеличении α сигмоид приближается по внешнему виду к функции единичного скачка с порогом T в точке x=0. Следует отметить, что сигмоидная функция дифференцируема на всей оси абсцисс, что используется в некоторых алгоритмах обучения. Из выражения для сигмоида очевидно, что выходное значение нейрона лежит в диапазоне [0,1].
Нейроны соединены между собой с помощью синапсов — упрощенных аналогов синаптических контактов нервных клеток, обладающих способностью изменять и сохранять свой вес (величину). Целенаправленная перестройка весов синапсов (т.е. коэффициентов, на которые умножаются входные сигналы, или подстроечных параметров) позволяет нейрону избирательно реагировать на сигналы других нейронов, обеспечивая на выходе наиболее “полезные” сигналы.
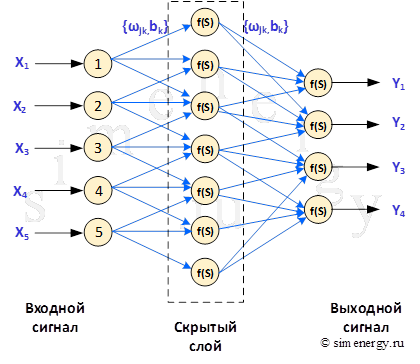
Если нейронная сеть имеет дополнительные слои между входным и выходным слоем, то они называются скрытыми, а обучение такой сети — глубоким. Дополнительные скрытые слои могут помочь нейросети определить более сложные закономерности между входными и желаемыми выходными данными.
Рис.3. Структурная схема нейронной сети
После создания структуры нейронной сети выполняется процесс обучения нейронной сети. В процессе обучения происходит подбор коэффициентов нейронной сети тем самым выстраивается зависимость между заранее известными входными и выходными данными. Обучение нейронной сети означает, что для заданного набора заранее известных входных и выходных данных, необходимо подобрать оптимальные коэффициенты
нейросети так, что квадратичная ошибка между точным выходным значением и выходным значением, полученным посредством распространения входных значений через нейронную сеть, стремилась к минимуму:
Поиск оптимальных коэффициентов производится методом градиентного спуска с использованием метода обратного распространения ошибки.
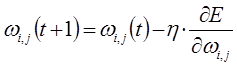
Производные функции минимизации определяются по следующим формулам:
В представленной системе уравнений частные производные имеют следующий вид:
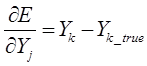
В настоящее время для создания и обучения нейронных сетей используют программные комплексы с готовыми библиотеками, например, на базе языка программирования Python.
Таким образом, экстраполяцию можно использовать в качестве средства для определения будущих, ожидаемых значений величин, на основе имеющихся данных о тенденциях их изменений в прошлые периоды. С оптимальным выбором метода экстраполяции возможно получить максимально точный результат, который будет правильно отражать будущие значения.
Прогнозирование путём прямой экстраполяции. Ошибки прогнозирования
Министерство образования и науки РФ
ГОУ ВПО
Саратовский государственный технический
университет
Кафедра: организация перевозок и
управления на транспорте
Реферат
по дисциплине на тему
«Прогнозирование путём прямой
экстраполяции
Выполнил:
студент АМФ гр.ОПТ41
Никитин Р.В.
Саратов 2006
Содержание
Введение
3
Прогнозирование путём прямой экстраполяции
4
Ошибки
прогнозирования 16
Заключение
18
Список используемых
источников 19
Введение
Процесс прогнозирования
достаточно актуален в настоящее время. Широка сфера его применения.
Прогнозирование широко используется в экономике, а именно в управлении. В
менеджменте понятие «планирование» и «прогнозирование» тесно переплетены. Они
не идентичны и не подменяют друг друга. Планы и прогнозы различаются между
собой временными границами, степенью детализации содержащихся в них
показателей, степенью точности и вероятности их достижения, адресностью и,
наконец, правовой основой. Прогнозы, как правило, носят индикативный характер,
а планы обладают силой директивного характера. Не подмена и противопоставление
плана и прогноза, а их правильное сочетание – таков путь планомерного регулирования
экономики в условиях рыночной экономики и перехода к ней.
Для того чтобы управлять
будущим, человечество создало определенные механизмы, которые в экономической
науке называются прогнозирование, макроэкономическое планирование и
экономическое программирование.[2]
Прогнозирование – это
предвидение, получение информации о будущем, которое базируется на специальном
научном исследовании.
Прогнозирование имеет два конкретных
аспекта: предсказывать и предвидеть. В зависимости от того, какой результат
необходимо получить или, что необходимо спрогнозировать, преимущество
предоставляется то одному, то другому аспекту.
Прогнозирование
необходимо, потому что будущее необычно и эффект многих решений, принимаемых
сегодня, на протяжении определённого времени не ощущаются. Поэтому точное
предвидение будущего повышает эффективность процесса принятия решения.
Прогнозирование путём прямой
экстраполяции.
Многие социальные
процессы, теоретически поддающиеся управлению, на практике развиваются
стихийно, что дает основание применять к ним методы естествоведческих
прогнозов. При этом следует иметь в виду, что стихийность протекания анализируемого
процесса может смениться строго контролируемым целенаправленным развитием
(например, давно назрела необходимость таких перемен в сферах расселения,
градостроительства, демографии и многих других). Такие изменения могут
осуществляться как волевым порядком, так и с учетом научного анализа, диагноза
и прогноза исследуемого явления. Из этого следует, что в отличие от
естественнонаучных социальный прогноз должен быть ориентирован не на
безусловное предсказание, а на содействие оптимизации принимаемых решений.
Реализуется эта задача
путем использования исследовательской техники поискового и нормативного
прогнозирования, дающего достаточно обоснованные материалы при выработке
рекомендаций для целеполагания, планирования, проектирования и управления в
целом.
Основная задача
поискового прогноза при этом — выявление перспективных проблем, подлежащих
решению средствами управления. Предсказание в данном случае носит сугубо
условный характер, базирующийся на абстрагировании от возможного и даже необходимого
вмешательства со стороны сферы управления. Методологически недопустимо сводить
социальный прогноз к поиску, но столь же недопустимо переходить сразу к
нормативной разработке данной модели, не имея представления о проблемной
ситуации, в условиях которой и для преодоления которой будет функционировать
предложенный оптимум.
В наиболее общем виде поисковый
(изыскательский, исследовательский, трендовый, генетический, эксплоративный)
прогноз выглядит как условное продолжение в будущее тенденций развития
изучаемых явлений, закономерности развития которых в прошлом и настоящем
достаточно хорошо известны. При этом заведомо абстрагируются от возможных и
даже необходимых, неизбежных плановых, программных проектных и организационных
решений, способных существенно изменить наметившиеся тенденции. Суть и цель
прогнозного поиска не в адекватном предвосхищении будущего реального состояния
прогнозируемого объекта, а в выяснении того, что реально произойдет при
сохранении существующих тенденций развития, т.е. при условии, что сфера влияния
не выработает поисковых решений, способных изменить неблагоприятные тенденции.
Исследовательская техника
разработки поискового прогноза базируется на принципе экстраполяции в будущее
(или интерполяции отсутствующих значений) динамических и на данных, закономерности
развития которых в прошлом известны. Собственно экстраполяция (интерполяция)
может быть довольно сложной, учитывающей разнообразные факторы и делающей
прогноз более информативным. При этом на практике поисковый прогноз дает не
одно, а целый ряд возможных значений, позволяющих точнее ориентироваться в
складывающейся ситуации.
Наиболее простой является
так называемая прямая (механическая, наивная) экстраполяция, которая
продолжает начатый динамический ряд со времени основания до времени упреждения
прогноза, реализуясь по принципу: если имеется 1, 2, 3, 4 (период основания),
то при условии невмешательства извне и сохранения наметившейся тенденции
динамический ряд будет выглядеть как 5, 6, 7, 8 и т.д. по периоду упреждения
(или в случае интерполяции: если 1, 2, 3, 6, 7, 8, то в середине окажется 4, 5)
Не следует недооценивать эффективность такой логики: во многих случаях жизни
важные социальные процессы развиваются именно подобным образом и прогноз на
этой основе оказывается в высокой степени достоверным.
Правда, на практике
социальные прогнозы часто развертываются гораздо более сложным образом — не обязательно
линейно, а, допустим, в геометрической прогрессии, экспоненциально, гиперболически,
логистически и т.д. Однако на каждый такой случай существует или может быть
введена соответствующая математическая формула, позволяющая усложнять
экстраполяцию до любой требуемой степени. Поэтому 1, 2, 3, 4 не обязательно
должны означать в экстраполяции 5, 6, 7, 8. Экстраполяция может выглядеть и
как 6, 9, 15, 24, и как 16, 32, 64, 128, и даже как 5, 4, 3, 2, 1 (в
зависимости от используемой формулы). Она может быть не только количественной
(статистической), но и качественной (логической), например при экстраполяции
какого-нибудь явления на более широкий круг других явлений во времени или
пространстве (либо в том и другом сразу) с использованием метода аналогии.
Такая техника широко
используется в естествоведческих прогнозах в тех случаях, когда исследуемые
процессы развиваются сообразно выявленным закономерностям устойчиво, без
отклонений и колебаний. В социальной сфере такие процессы встречаются редко.
Как правило, в своем развитии они претерпевают изменения, математическая
формализация которых требует использования дополнительных приемов минимизации
недочетов прямой экстраполяции.
Один из них — вычленение
крайних возможных значений экстраполируемого динамического ряда по заранее
заданным критериям, т.е. определение верхней и нижней экстрем. Причем предполагается,
что за верхней экстремой простирается область абсолютно нереального,
фантастического, а за нижней — абсолютной невозможности функционирования прогнозируемого
объекта, область катастрофического. Сложность в использовании этого приема —
определение и основание критериев построения экстрем.
Другой прием (дополняющий
первый) — определение наиболее вероятного значения с учетом данных прогнозного
фона (научно-технического, демографического, экономического, социологического,
социокультурного, политического и международного). Необходимо выявить по
каждой группе наиболее информативные в каждом конкретном случае показатели и
соотнести их со значениями прямой экстраполяции, а если понадобится, — и со
значениями верхней и нижней экстрем. В результате операции будет определено
значение наиболее вероятного тренда — экстраполированной в будущее тенденции.
Таким образом, поисковый
прогноз содержит четыре основные компоненты:
1) данные прямой экстраполяции
динамических рядов исходной модели, служащие первоначальным ориентиром
дальнейших прогнозных построений;
2) верхняя экстрема прогнозного
поиска: результат сопоставления данных первой поисковой модели с данными
прогнозного фона. Позволяет определить максимальное отклонение тренда в сторону
области нереального;
3) нижняя экстрема прогнозного
поиска: вычисляется теми же способами, что и верхняя. Определяют максимально
возможное отклонение тренда до предела, за которым начинается область катастрофического;
4) наиболее вероятный тренд
(экстраполированная в будущее тенденция) между верхней и нижней экстремами с
учетом данных прогнозного фона.[3]
В процессе
прогностического исследования недопустимо принижение значения ни одного из
перечисленных компонентов. Первые три (прямая экстраполяция, верхняя и нижняя
экстремы) служат как бы ограничителями наиболее вероятного тренда, очерчивающими
границы реального в возможных его изменениях. Прямая экстраполяция здесь играет
роль исходного момента, сдерживающего фактора при чрезмерном разбросе оценок
противоречащих данных прогнозного фона.
Вместе же взятые, все
четыре компоненты расширяют познавательные возможности лиц, принимающих
решения, показывают недопустимость решений, выводящих объект на уровень утопии
или катастрофы, стимулируют эвристичность мышления, дают возможность более
основательно взвешивать возможные последствия принимаемых решений, а все это
вместе обеспечивает высокую степень объективности и, следовательно,
эффективность этих решений.[6]
Необходимо также
отметить, что при разработке целевых, плановых, программных, проектных,
организационных прогнозов специфические особенности поискового прогноза будут
проявляться сообразно особенностям процессов разработки целей, планов, программ,
проектов, организационных решений. Результатом прогнозного поиска будет не
реально ожидаемое состояние, к которому следует приспособиться, а комплекс
проблем, которые необходимо решить. Сама по себе цель поискового прогноза —
выявление ожидаемого проблемного состояния, перспективных проблем, каждая из
которых является составляющим звеном своеобразной ситуации — проблемной.
Прогнозирование размеров перевозок
основывается на анализе развития экономики за прошедший период, причем этот
анализ должен давать точную количественную формулировку исследуемому
процессу перевозки грузов путем использования математико-статистических методов.
Предвидение будущего состояния размеров перевозок базируется на результатах
анализа прошлого и, следовательно, описывает перспективу в той мере, в какой
она определяется объективно сложившимися явлениями и процессами. При этом
используются главным образом методы и модели экстраполяционного характера.
Методы экстраполирования опираются на принцип детерминизма, согласно которому
будущее вытекает из настоящего, т. е. на преемственность связи между прошлым,
настоящим и Экстраполяция является научным методом прогнозирования, так как ее
применение основано на учете объективно существующей инерционности больших
систем, что подтверждается всем опытом социалистического строительства. Для
экономической системы этот закон выражается в невозможности ограниченными
средствами в короткие сроки изменить поведение системы.
Существует много способов, приемов прогнозирования, основанных
на экстраполяции тенденций. Однако большинство из них не учитывает специфику
объекта прогнозирования. Поэтому рассмотрим методы и способы, повышающие
надежность и точность экстраполяционных прогнозов размеров перевозок грузов
на уровне АТП, объединений и управлении.
Под точностью прогнозирования
размеров перевозок грузов (ошибкой прогноза) будем понимать величину отклонения
фактического значения прогнозируемого показателя от ее истинного значения.
Прогнозу присуща та или иная степень неопределенности, поэтому прогнозируемая
величина определяется с допуски разной вероятностью. Поэтому оценка только
точности показателя является недостаточной. Эту оценку надо дополнить
показателем, определяющим надежность самой оценки
точности. Под надежностью прогнозирования размеров перевозок дует
понимать вероятность наступления предсказываемого бытия при заданном комплексе условий
и в пределах установленных допусков. Оценки точность и надежность
взаимосвязаны.
Чем шире установлен предел точности,
тем с. большей вероятностью он будет соблюдаться. Чем жестче допуск на величину
показателя, тем меньше шансов на его такое соблюдение.
Поставленная задача решается в трех
направлениях: исследование новых форм связи, разработка новых критериев оценки
моделей и разработка новых методов прогноза.[6]
Объектом прогнозирования служили
показатели размеров перевозок Владимирского транспортного управления за
1967—1975 гг.
Развитие транспорта характеризуется ростом объемов перевозок
грузов, который зависит от уровня развития- экономики региона, сложившейся
системы внутренних и внешних связей. Высокие темпы развития общественного
производства обусловливают быстрый рост перевозочной работы «транспорта.
Пропорциональное развитие транспорта и всего народного хозяйства :в целом
достигается тогда, когда транспорт полностью удовлетворяет потребности
экономики и населения в перевозках.
Анализируя содержание таблице можно видеть, что рост объемов
перевозок грузов полностью определяется ростом валовой продукции
промышленности и сельского хозяйства Владимирской области, т. е. объем
перевозок грузов автомобильным транспортом общего пользования как бы ‘
синтезирует в себе размеры производства промышленной и сельскохозяйственной
продукции, развитие непроизводственной сферы и т. д. Таким образом, объем
перевозок грузов автомобильным транспортом
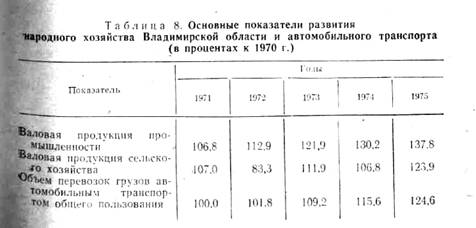
общего
пользования, являясь важнейшим отраслевым показателем, в то же время отражает и
динамику развития экономики региона.
Следовательно, прогнозирование размера перевозок грузов на основании данных за
прошлые периоды приобретает исключительно важное значение, так как от точности
прогнозирования размеров перевозок зависят реальность планов и их
согласованность с планами развития других отраслей.
Полная и систематизированная информация об объекте прогнозирования
необходима для повышения достоверности и надежности прогноза. Ведь
практическая деятельность по составлению прогноза в том и состоит, что
обработанная определенным образом информация о состоянии объекта на текущий момент,
о его тенденциях превращается в информацию о будущем состоянии объекта.
Наиболее ответственная часть работы по составлению краткосрочного
прогноза заключается в выборе математической функции, которая отражает общую
тенденцию. Здесь очень важным становится правильный выбор вида кривой, потому
что если уравнение хорошо подобрано к исходным данным, то оно точнее выражает
общую тенденцию, что в конечном счете сказывается на результатах прогноза. Выбор
кривой, которая наилучшим образом описывает закономерности изменения данного
эмпирического ряда, одна из важнейших проблем экстраполяционного прогноза.
Вид моделей тенденций развития определяется внутренними свойствами
исследуемого процесса. Анализируя динамику размеров перевозок для обоснования
формы моделей, воспользуемся методами теории экономического роста.
Процесс роста размеров перевозок на автомобильном транспорте можно
описать дифференциальным уравнением вида:
которое показывает, что изменение зависимой переменной (в нашем
случае размер перевозок) зависит как от времени, так и от величины самих
размеров перевозок.
Рассматривая частный случай уравнения
Эти уравнения показывают различные
варианты изменения размеров перевозок. Если ввести логарифмическую
производную(относительную скорость роста, пропорциональное увеличение в единицу
времени) то уравнение примет вид:
Эти уравнения содержат постоянную интегрирования, которую
можно определить по заданному значению I, у
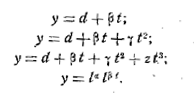
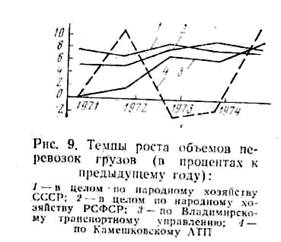
размеров перевозок, описывающая траекторию экономического роста. Эти функции
могут применяться и применяются для прогнозирования размеров перевозок на
макроуровне, где присутствует большая инерционность и темпы прироста примерно
одинаковы. Это показано в работе, а также подтверждается нашими расчетами.
Инерционность развития в наибольшей мере присуща тем
параметрам, которые характеризуют макроструктуру народного хозяйства и в
меньшей мере проявляются на уровне отраслей, предприятий, отдельных участков
производства. В свою очередь, инерционность параметров, принадлежащих одному
уровню, но различным отраслям, предприятиям тоже различна.
транспортной системы — министерство, автоуправление, автотранспортное
предприятие (объединение)- различна. Модели полиномиального вида, полученные
методом прямой экстраполяции, достаточно хорошо работающие на высшем уровне,
могут быть не применимы для прогнозирования показателей низшего уровня.
Анализ
рис. 9 показывает, что на уровне автотранспортного предприятия
инерционность намного меньше, а основная тенденция часто искажена
случайной составляющей, поэтому для прогнозирования на уровне АТП
(объединения) необходимо применять функции специального ви-1а,
учитывающие неравномерность темпа прироста в каждый момент времени, т. е.
Таким образом, рекомендуемый нами набор функций для
краткосрочного прогнозирования на уровне АТП и управлений включает не только
широко распространенные в практике экономического прогнозирования полиномы до
третьей степени включительно и экспоненциальную функцию, но и две еще не
применявшиеся формы связи (обобщенно-экспоненциальные функции). Параметры
прогнозирующих функций рассчитываются методом наименьших квадратов.
Согласно
методу наименьших квадратов находится разность y—f, а сумма квадратов этих разностей S=будет
функцией неизвестных «параметров. Так,
Определяют такую оценку параметров №, которая минимизирует
5(1Г), для чего определяется й81с!№ и приравнивается нулю, что дает систему
т нормальных уравнений, которая должна быть решена относительно W
После нахождения неизвестных параметров
прогнозных кривых необходимо оценить их близость к эмпирическим
данным и выбрать наилучшую функцию. Критериями выбора являются:
среднее абсолютное отклонение (|Л|); среднеквадратичное отклонение —
о; коэффициент вариации — V; индекc корреляции Я.2; коэффициент
Фишера Р. Все эти критерии предназначены для оценки качества
аппроксимации, поэтому использование их выбора наилучшей прогнозирующей
функции может привести к большим погрешностям. В работе применяется новый
критерий — критерий минимума отклонения в последней точке (МОПТ).
Рассмотрим этот метод более подробно. Применение этого критерия
основывается на следующем: качество прогнозов путем прямой экстраполяции
тенденций улучшается, если за прогнозирующую функцию выбирается та,
которая дает наименьшее отклонение в последней точке исследуемого
временного ряда, т. е. задача определения неизвестных параметров принимает вид
Для отыскания наилучшей функции применялась следующая
процедура. Исходный временной ряд уменьшался на единицу, т. е. отбрасывалось последнее
значение ряда, которое служило для проверки условия минимальности. По
укороченному временному ряду находились параметры прогнозирующих функций и
выбиралась та, которая обеспечивала минимальное отклонение в последней точке.
Полученная форма связи применялась для экстраполяции уже по полному временному
ряду.
С целью проверки изложенного метода прогнозирования на
конкретном цифровом материале были проведены экспериментальные расчеты по
определению перспективных величин размеров перевозок для предприятий Владимирского
транспортного управления.
Методику выбора лучшей функции проследим на примере
определения перспективной величины
выработки в тонно-километрах на одну списочную автомобиле-тонну по АТП
г. Суздаля (предпрогнозный период 9 лет). Для определения неизвестных
параметров и оценочных критериев функций использовалась специально
разработанная авторами программа РРОС—1.
После расчета на ЭВМ были получены
следующие зависимости:
Поочерёдно все критерии, при
этом получены следующие средние ошибки прогноза
Критерий
выбора /А/ F МОПТ
Ошибка прогноза 7,9 7,8 5,3 4,8
Анализируя результаты, приходим к
выводу о том, что критерий минимума отклонения в последней точке является
наиболее целесообразным при краткосрочном прогнозе на уровне
автотранспортных предприятий (объединений).[1]
Основными источниками могут быть
названы:
1. Простое перенесение (экстраполяция) данных из прошлого в будущие (например, отсутствие
у фирмы иных вариантов прогноза, кроме 10% роста продаж).
2. Невозможность точно определить вероятность события и его воздействия на исследуемый
объект.
3. Непредвиденные трудности (разрушительные события), влияющие на
осуществление плана, например внезапное увольнение начальника отдела сбыта, ошибки
первой категории могут быть сужены путем применения методов регрессионного
анализа, криволинейного сглаживания и других техник.
Ошибки второй категории
частично могут быть преодолены при помощи метода Дельфи, сценариев, моделей, анализа
модели жизненного цикла.
В целом точность
прогнозирования повышается по мере накопления опыта прогнозирования и отработки
его методов.[4]
ПУТИ ПОВЫШЕНИЯ
ЭФФЕКТИВНОСТИ И ОБОСНОВАННОСТИ ПРОГНОЗОВ
В наибольшей степени,
эффективность прогноза зависит от того, на сколько они полезны для
планирования и осуществления деловых операций. Прогнозы полезны в тех случаях,
когда его компоненты тщательно продуманы и ограничения, содержащиеся в прогнозе
откровенно названы. Существует несколько способов сделать это. Спросите себя,
для чего нужен прогноз, какие решения будут на нем основаны.
Этим определяется потребная точность прогноза. Некоторые решения принимать
опасно, даже если возможная погрешность прогноза—менее 10%. Другие решения
можно принимать безбоязненно даже при значительно более высокой допустимой
ошибке. Определите изменения, которые должны произойти, чтобы прогноз оказался
достоверным. Затем с осмотрительностью оцените вероятность соответствующих
событий. Определите компоненты прогноза. Подумайте об источниках данных, определите,
насколько ценен опыт прошлого в составлении прогноза. Не настолько ли быстры
изменения, что основанный на опыте прогноз будет бесполезным? Дают ли данные
по подобным продуктам (или вариантам развития) основания для составления прогноза
о судьбе вашего продукта? Насколько просто или недорого можно будет
получить надежную информацию об опыте прошлого? Определите, насколько структурированным
должен быть прогноз. При прогнозировании сбыта может быть целесообразно
выделить отдельные части рынка (развивающиеся потребители, стабильные потребители,
крупные и мелкие потребители, вероятность появления новых потребителей и
т.п.).
Также путем повышения эффективности прогнозов является применение анализа безубыточности.
Этот анализ определяет точку, в которой общий доход уравнивается с суммарными
издержками, то есть точку, в которой предприятие становится прибыльным. Точка
безубыточности обозначает ситуацию, при которой общий доход становится
равным суммарным издержкам. Для определения точки безубыточности необходимо учесть
три основных фактора: продажную цену единицы продукции, переменные издержки на
единицу продукции и общие постоянные издержки на единицу продукции.[5]
Из всего вышесказанного
можно сделать вывод, что при современных условиях функционирования рыночной
экономики, невозможно успешно управлять коммерческой фирмой, без эффективного
прогнозирования её деятельности. От того, на сколько прогнозирование будет
точным и своевременным, а также соответствовать поставленным
проблемам, будут зависеть, в конечном счете, прибыли, получаемые предприятием.
Для того, чтобы эффект прогноза был максимально полезен, необходимо создание на
средних и крупных предприятиях так называемых прогнозных отделов (для малых предприятий
создание этих отделов будет нерентабельным). Но даже без таких отделов обойтись
без прогнозирования невозможно. В этом случае прогноз должен быть получен
силами менеджеров и задействованными в этом процессе специалистами.
Что касается самих прогнозов, то они должны быть реалистичными, то есть их вероятность
должна быть достаточно высока и соответствовать ресурсам предприятия. Для
улучшения качества прогноза необходимо улучшить качество информации, необходимой
при его разработке. Эта информация, в первую очередь, должна обладать такими
свойствами, как достоверность, полнота, своевременность и точность. Так как
прогнозирование является отдельной наукой, то целесообразно (по мере возможности)
использование нескольких методов прогнозирования при решении какой-
либо проблемы. Это повысит качество прогноза и позволит определить «подводные камни»,
которые могут быть незамечены при использовании только одного метода. Также
необходимо соотносить полученный прогноз с прецедентами в решении данной проблемы,
если такие имели место при похожих условиях функционирования аналогичной
организации (конкурента). И при определенной корректировке, в
соответствии с этим прецедентом, принимать решения.
Список используемых источников
1. Мандрица В.М., Краев В.Н. прогнозирование перевозок грузов
на автомобильном транспорте, М. Транспорт., 1981, 152с.
2. www.referatov.net
3. www.5ballov.ru
4. Поисковое социальное прогнозирование. М.: Наука, 1994.
5. Нормативное социальное прогнозирование. М.: Наука, 1997
6. Основы экономического и социального прогнозирования / Под
ред. В.Н. Мосина, Д.М. Крука. М.: Высшая школа, 1985.