Время на прочтение
6 мин
Количество просмотров 18K
Вчера мне в очередной раз пришлось объяснять почему DataScientist-ы не используют ошибки первого и второго рода и зачем же ввели полноту и точность. Вот прямо заняться нам нечем, лишь бы новые критерии вводить.
И если ошибка второго рода выражается просто:
где Π — это полнота;
то вот ошибка первого рода весьма нетривиально выражается через полноту и точность (см.ниже).
Но это лирика. Самый важный вопрос:
Почему в DataScience используют полноту и точность и почти никогда не говорят об ошибках первого и второго рода?
Кто не знает или забыл — прошу под кат.
Бизнес-задача
Так как Хабр — это блог IT-шников, постараюсь по минимуму использовать мат.абстракции и рассказывать сразу на примере. Предположим, что мы решаем задачу Fraud-мониторинга в ДБО условного банка Roga & Copyta, сокращённо R&C.
Предположим, что у мы разработали некую автоматизированную экспертную систему (ЭС), определяющую для каждой платёжной транзакции: является ли данная транзакция мошеннической (fraud, F) или легитимной (genuine, G).
Необходимо определить «хорошие» критерии оценки качества системы и дать формулы расчета этих критериев.
Так как Roga & Copyta — это хоть и маленький, но всё же банк, то в нём работают люди меркантильные и ничего кроме денег их не интересует. Поэтому разрабатываемые критерии должны максимально прозрачно показывать: насколько выгодно им использовать нашу ЭС? Может быть выгодно установить ЭС конкурентов?
События и вероятности
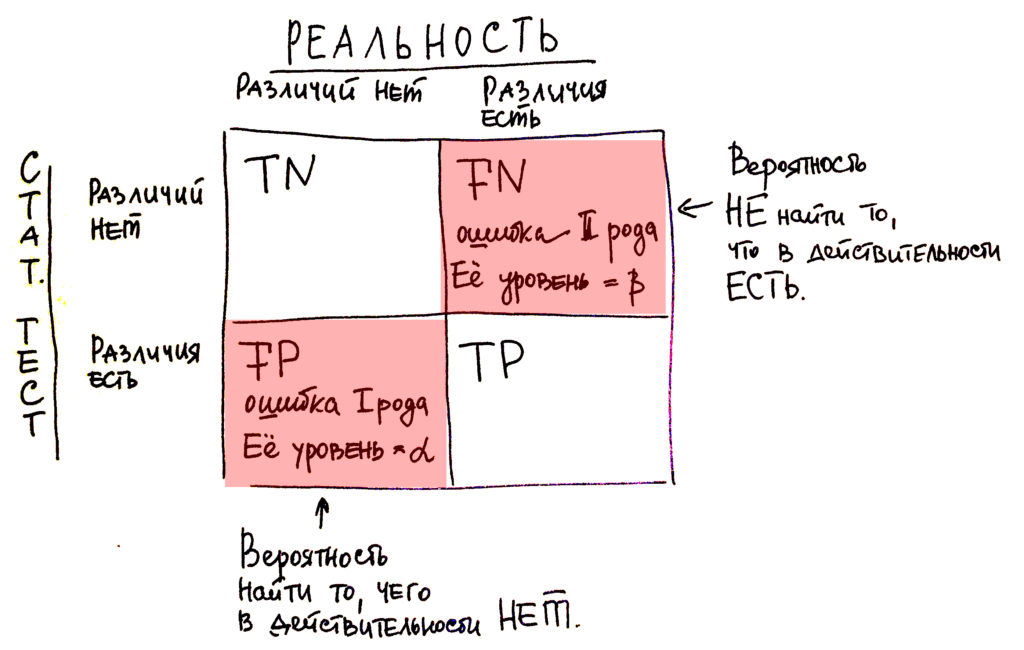
Для каждой транзакции могут быть определены четыре события:
- Fr (fraud real) — событие того, что транзакция в действительности окажется мошеннической;
- Gr (genuine real) — событие того, что транзакция в действительности окажется легитимной;
- F — событие того, что ЭС «определит» транзакцию как мошенническую;
- G — событие того, что ЭС «определит» транзакцию как легитимную
Очевидно, что Fr и Gr — несовместные события; аналогично F и G — несовместные. По этой причине разумно рассматривать четыре вероятности:
Аббревиатуры читаются так:
- tn — true negative
- fn — false negative
- fp — false positive
- tp — true positive
Мы можем рассматривать условные вероятности:
Так же нам будут интересны и «обратные» условные вероятности:
Например вероятность означает следующее:
Какова вероятность того, что транзакция действительно окажется мошеннической, если ЭС «определила» это событие как мошенническое.
Не следует путать с
, которое можно определить словами:
Какова вероятность того, что ЭС «назовёт» транзакцию мошеннической, если данная транзакция действительно мошенническая.
Аналогично можно определить словами и другие условные вероятности.
Вспомним определения
В статистике любят говорить о нулевой гипотезе (H0) и альтернативной (H1) гипотезе. Обычно под нулевой гипотезой определяют «естественное» состояние. В случае фрод-мониторинга «естественным» состоянием является то, что транзакция легитимная. Это действительно разумно, хотя бы по той причине, что количество мошеннических транзакций гораздо меньше количества легитимных.
Поэтому за нулевую гипотезу примем Gr, а за альтернативную Fr.
Ошибки первого (O1) и второго (O2) рода определяются так:
Словами
Ошибка первого рода (O1) — это вероятность того, что ЭС «определит» транзакцию как мошенническую, при условии, что она легитимная.
Ошибка второго рода (O2) — это вероятность того, что ЭС «определит» транзакцию как легитимную, при условии, что она мошенническая.
Замечание: часто ошибку первого рода называют false positives а ошибку второго рода как false negatives. В том числе, таковы определения в википедии. Это верно по сути. Но
и
. Очень многие новички в DataScience делают такую ошибку и путаются.
Полнота (П) и точность (Т) по определению:
Т.е. полнота — это вероятность того, что ЭС «определит» транзакцию мошеннической, при условии, что она действительно мошенническая. А точность — это вероятность того, что транзакция действительно мошенническая, при условии, что ЭС «определила» транзакцию как мошенническую.
Полноту и точность можно выразить через tp, fp, fn следующим образом:
Вывод формул
Выводим тупо в лоб.
Для полноты:
Для точности:
Следует заметить, что именно эти формулы очень частно приводят в качестве определения полноты и точности. Тут вопрос во вкусе. Можно сказать, что квадрат — это прямоугольник, у которого все стороны равны и доказать, что ромб с прямым углом — это квадрат. А можно наоборот. Например, когда я учился в школе, у меня квадрат определяли как ромб с прямым углом и доказывали, что прямоугольник с равными сторонами — это квадрат.
Но все же определение полноты как и точности как T
мне кажется более правильным. Сразу понятно в чем физический смысл этих величин. Понятно, зачем они нужны.
Бизнес-смысл полноты и точности
Предположим, что для Roga & Copyta мы создали систему с полнотой в 80% и точностью в 10%.
Предположим, что без ЭС банк теряет на мошенничестве 1 миллиард тугриков (₮) в год. Это значит, что благодаря ЭС они смогут предотвратить хищение на сумму в 800 миллионов ₮. Останется еще 200 миллионов ₮ — это ущерб банку (или клиентам банка), который не смогла предотвратить ЭС.
А что на счет точности в 10%? Данная величина значит, что из 100 сработок ЭС только 10 будут попадать по цели, а в остальных случаях мы приостановим легитимные транзакции. Хорошо это или плохо?
Во-первых при остановки транзакции банк совершает какие-либо действия. Например звонит клиентам с просьбой подтвердить операции.
Во-вторых заблокировать легитимные транзакции тоже не всегда хорошая идея. Представьте, что вы сидите с девушкой в ресторане, просите счёт, оплачиваете картой… А тут бах… ЭС ошибочно подсчитала что вы — мошенник… Наверное не очень удобно будет перед барышней… Но мы, чтобы не усложнять, пока опустим эту проблему.
Итак, предположим один звонок стоит 1000 ₮. Так же предположим что средний чек хакера у нас составляет 100 тысяч ₮.
Так как мы предотвращаем мошенничества на 800 миллионов ₮, то в среднем у нас будет 8000 правильных мошеннических сработок. Но 8000 — это, судя по точности, лишь 10%; следовательно всего мы позвоним 80000 раз. Умножаем эту цифру на стоимость одного звонка (1000 ₮) и получаем аж 80 миллионов ₮!
Итоговый ущерб в год для банка R&C равен: 200 + 80 = 280 миллионов ₮. Но без ЭС банк терял бы один один миллиард. Следовательно выгода R&C составляет 720 миллионов тугриков.
нюанс
Следует различать полноту и точность по количеству транзакций и по суммам. Это четыре разные величины. Здесь я «смешал все в кучу», что, конечно не верно! ;)) Будем считать что полнота и точность 80% и 10% как по количеству транзакций, так и по денежным суммам.
Бизнес-смысл ошибок первого и второго рода
Ошибка второго рода элементарно выводится через полноту:
Вывод формулы элементарен (см. следующий параграф)
Поэтому что считать — полноту или упущенный фрод (ошибка второго рода) особой разницы не представляет.
А что на счет ошибки первого рода?
Это вероятность того, что ЭС назовёт мошеннической операцией транзакцию, при условии что она легитимная. Проблема в том, что легитимных транзакций существенно больше мошеннических. Есть банки, в которых более 50 платёжных транзакций в секунду… И это совсем не предел.
R&C — банк небольшой, там всего пять платёжных транзакций в секунду. Давайте посчитаем, сколько это в сутки:
В прошлом параграфе мы узнали, что в R&C 80000 сработок в год, это значит что в сутки в среднем 80000 / 365 = 219,17 сработок. Из них только 10% попали в цель (такова точность), то есть 22. Значит остальные — подлинные: 432000 — 22 = 431978.
Так как полнота 80%, то из этих 22 мы только 4.4 будем упускать.
Значит ошибка первого рода:
Слишком маленькая величина! Бизнес не любит такие числа. Так же сложнее, чем для точности высчитать пользу и ущерб для бизнеса. И есть еще одна проблема:
через ошибку первого рода, можно косвенно понять об объемах платёжных операций в банке!
Что касается точности, то такой проблемы нет. Специалисты из отдела безопасности R&C знают об объемах мошенничества. Они узнают о допустимой нагрузке на контактный центр у самой главной девочки + спрашивают руководство банка о желаемой полноте. Зная абсолютную нагрузку, желаемую полноту и объем фрода можно без труда вычислить приемлемую точность. Эти две цифры вписываются в техническое задание (или тендер).
Разработчику выдают выборку из мошеннических транзакций и легитимных. Если выборка репрезентативна, этих данных достаточно.
«Неправильность» точности с точки зрения чистой математики
Если объем транзакций увеличится в два раза, то точность уменьшится. Если объем мошенничества увеличится в два раза, то точность так же будет больше… С ошибкой первого рода такой проблемы нет, поэтому с точки зрения «чистой математики», эта величина гораздо более «правильная»…
Но на практике, если и резко увеличивается объем мошенничества, то как правило это фрод нового типа и ЭС просто не обучена его ловить… Точность останется той же (а вот полнота уменьшиться, т.к. появится фрод, который мы не умеем ловить). Что касается увеличения количества легитимных транзакций — то это увеличение постепенное и никаких «рывков» не будет.
Поэтому на практике точность — замечательный, понятный для бизнеса критерий оценки качества ЭС.
Вывод ошибок первого рода и второго рода из полноты и точности
Но может быть существует изящная формула вывода ошибки первого рода через точность?
Вот с ошибкой второго рода как все красиво:
Вывод формулы
К сожалению с O1 так изящно не получится. Вот отношение через точность (Т) и полноту (П):
Вывод формулы
Эй! Ты что такой ленивый! А ну давай сам попробуй!
Я сегодня плохо спал, Павел! Ну покажи!
Из и
можно составить выражение:
Откуда следует:
Уже из этого отношения легко получить формулу для O1
Заключение
Точность и полнота «не хуже» и «не лучше» чем ошибки первого и второго рода. Всё зависит от задачи. Мы же не едим столовой ложкой торт, а чайной борщ? Хотя это возможно.
Точность и полнота более понятные критерии качества. Ими легче оперировать. С помощью них просто вычислить предотвращённый ущерб в задаче фрод-мониторинга.
Если вы обнаружили описку или грамматическую ошибку — прошу написать в личку.
Вчера мне в очередной раз пришлось объяснять почему DataScientist-ы не используют ошибки первого и второго рода и зачем же ввели полноту и точность. Вот прямо заняться нам нечем, лишь бы новые критерии вводить.
И если ошибка второго рода выражается просто:
где Π — это полнота;
то вот ошибка первого рода весьма нетривиально выражается через полноту и точность (см.ниже).
Но это лирика. Самый важный вопрос:
Почему в DataScience используют полноту и точность и почти никогда не говорят об ошибках первого и второго рода?
Кто не знает или забыл — прошу под кат.
Бизнес-задача
Так как Хабр — это блог IT-шников, постараюсь по минимуму использовать мат.абстракции и рассказывать сразу на примере. Предположим, что мы решаем задачу Fraud-мониторинга в ДБО условного банка Roga & Copyta, сокращённо R&C.
Предположим, что у мы разработали некую автоматизированную экспертную систему (ЭС), определяющую для каждой платёжной транзакции: является ли данная транзакция мошеннической (fraud, F) или легитимной (genuine, G).
Необходимо определить «хорошие» критерии оценки качества системы и дать формулы расчета этих критериев.
Так как Roga & Copyta — это хоть и маленький, но всё же банк, то в нём работают люди меркантильные и ничего кроме денег их не интересует. Поэтому разрабатываемые критерии должны максимально прозрачно показывать: насколько выгодно им использовать нашу ЭС? Может быть выгодно установить ЭС конкурентов?
События и вероятности
Для каждой транзакции могут быть определены четыре события:
- Fr (fraud real) — событие того, что транзакция в действительности окажется мошеннической;
- Gr (genuine real) — событие того, что транзакция в действительности окажется легитимной;
- F — событие того, что ЭС «определит» транзакцию как мошенническую;
- G — событие того, что ЭС «определит» транзакцию как легитимную
Очевидно, что Fr и Gr — несовместные события; аналогично F и G — несовместные. По этой причине разумно рассматривать четыре вероятности:
Аббревиатуры читаются так:
- tn — true negative
- fn — false negative
- fp — false positive
- tp — true positive
Мы можем рассматривать условные вероятности:
Так же нам будут интересны и «обратные» условные вероятности:
Например вероятность означает следующее:
Какова вероятность того, что транзакция действительно окажется мошеннической, если ЭС «определила» это событие как мошенническое.
Не следует путать с
, которое можно определить словами:
Какова вероятность того, что ЭС «назовёт» транзакцию мошеннической, если данная транзакция действительно мошенническая.
Аналогично можно определить словами и другие условные вероятности.
Вспомним определения
В статистике любят говорить о нулевой гипотезе (H0) и альтернативной (H1) гипотезе. Обычно под нулевой гипотезой определяют «естественное» состояние. В случае фрод-мониторинга «естественным» состоянием является то, что транзакция легитимная. Это действительно разумно, хотя бы по той причине, что количество мошеннических транзакций гораздо меньше количества легитимных.
Поэтому за нулевую гипотезу примем Gr, а за альтернативную Fr.
Ошибки первого (O1) и второго (O2) рода определяются так:
Словами
Ошибка первого рода (O1) — это вероятность того, что ЭС «определит» транзакцию как мошенническую, при условии, что она легитимная.
Ошибка второго рода (O2) — это вероятность того, что ЭС «определит» транзакцию как легитимную, при условии, что она мошенническая.
Замечание: часто ошибку первого рода называют false positives а ошибку второго рода как false negatives. В том числе, таковы определения в википедии. Это верно по сути. Но
и
. Очень многие новички в DataScience делают такую ошибку и путаются.
Полнота (П) и точность (Т) по определению:
Т.е. полнота — это вероятность того, что ЭС «определит» транзакцию мошеннической, при условии, что она действительно мошенническая. А точность — это вероятность того, что транзакция действительно мошенническая, при условии, что ЭС «определила» транзакцию как мошенническую.
Полноту и точность можно выразить через tp, fp, fn следующим образом:
Вывод формул
Выводим тупо в лоб.
Для полноты:
Для точности:
Следует заметить, что именно эти формулы очень частно приводят в качестве определения полноты и точности. Тут вопрос во вкусе. Можно сказать, что квадрат — это прямоугольник, у которого все стороны равны и доказать, что ромб с прямым углом — это квадрат. А можно наоборот. Например, когда я учился в школе, у меня квадрат определяли как ромб с прямым углом и доказывали, что прямоугольник с равными сторонами — это квадрат.
Но все же определение полноты как и точности как T
мне кажется более правильным. Сразу понятно в чем физический смысл этих величин. Понятно, зачем они нужны.
Бизнес-смысл полноты и точности
Предположим, что для Roga & Copyta мы создали систему с полнотой в 80% и точностью в 10%.
Предположим, что без ЭС банк теряет на мошенничестве 1 миллиард тугриков (₮) в год. Это значит, что благодаря ЭС они смогут предотвратить хищение на сумму в 800 миллионов ₮. Останется еще 200 миллионов ₮ — это ущерб банку (или клиентам банка), который не смогла предотвратить ЭС.
А что на счет точности в 10%? Данная величина значит, что из 100 сработок ЭС только 10 будут попадать по цели, а в остальных случаях мы приостановим легитимные транзакции. Хорошо это или плохо?
Во-первых при остановки транзакции банк совершает какие-либо действия. Например звонит клиентам с просьбой подтвердить операции.
Во-вторых заблокировать легитимные транзакции тоже не всегда хорошая идея. Представьте, что вы сидите с девушкой в ресторане, просите счёт, оплачиваете картой… А тут бах… ЭС ошибочно подсчитала что вы — мошенник… Наверное не очень удобно будет перед барышней… Но мы, чтобы не усложнять, пока опустим эту проблему.
Итак, предположим один звонок стоит 1000 ₮. Так же предположим что средний чек хакера у нас составляет 100 тысяч ₮.
Так как мы предотвращаем мошенничества на 800 миллионов ₮, то в среднем у нас будет 8000 правильных мошеннических сработок. Но 8000 — это, судя по точности, лишь 10%; следовательно всего мы позвоним 80000 раз. Умножаем эту цифру на стоимость одного звонка (1000 ₮) и получаем аж 80 миллионов ₮!
Итоговый ущерб в год для банка R&C равен: 200 + 80 = 280 миллионов ₮. Но без ЭС банк терял бы один один миллиард. Следовательно выгода R&C составляет 720 миллионов тугриков.
нюанс
Следует различать полноту и точность по количеству транзакций и по суммам. Это четыре разные величины. Здесь я «смешал все в кучу», что, конечно не верно! ;)) Будем считать что полнота и точность 80% и 10% как по количеству транзакций, так и по денежным суммам.
Бизнес-смысл ошибок первого и второго рода
Ошибка второго рода элементарно выводится через полноту:
Вывод формулы элементарен (см. следующий параграф)
Поэтому что считать — полноту или упущенный фрод (ошибка второго рода) особой разницы не представляет.
А что на счет ошибки первого рода?
Это вероятность того, что ЭС назовёт мошеннической операцией транзакцию, при условии что она легитимная. Проблема в том, что легитимных транзакций существенно больше мошеннических. Есть банки, в которых более 50 платёжных транзакций в секунду… И это совсем не предел.
R&C — банк небольшой, там всего пять платёжных транзакций в секунду. Давайте посчитаем, сколько это в сутки:
В прошлом параграфе мы узнали, что в R&C 80000 сработок в год, это значит что в сутки в среднем 80000 / 365 = 219,17 сработок. Из них только 10% попали в цель (такова точность), то есть 22. Значит остальные — подлинные: 432000 — 22 = 431978.
Так как полнота 80%, то из этих 22 мы только 4.4 будем упускать.
Значит ошибка первого рода:
Слишком маленькая величина! Бизнес не любит такие числа. Так же сложнее, чем для точности высчитать пользу и ущерб для бизнеса. И есть еще одна проблема:
через ошибку первого рода, можно косвенно понять об объемах платёжных операций в банке!
Что касается точности, то такой проблемы нет. Специалисты из отдела безопасности R&C знают об объемах мошенничества. Они узнают о допустимой нагрузке на контактный центр у самой главной девочки + спрашивают руководство банка о желаемой полноте. Зная абсолютную нагрузку, желаемую полноту и объем фрода можно без труда вычислить приемлемую точность. Эти две цифры вписываются в техническое задание (или тендер).
Разработчику выдают выборку из мошеннических транзакций и легитимных. Если выборка репрезентативна, этих данных достаточно.
«Неправильность» точности с точки зрения чистой математики
Если объем транзакций увеличится в два раза, то точность уменьшится. Если объем мошенничества увеличится в два раза, то точность так же будет больше… С ошибкой первого рода такой проблемы нет, поэтому с точки зрения «чистой математики», эта величина гораздо более «правильная»…
Но на практике, если и резко увеличивается объем мошенничества, то как правило это фрод нового типа и ЭС просто не обучена его ловить… Точность останется той же (а вот полнота уменьшиться, т.к. появится фрод, который мы не умеем ловить). Что касается увеличения количества легитимных транзакций — то это увеличение постепенное и никаких «рывков» не будет.
Поэтому на практике точность — замечательный, понятный для бизнеса критерий оценки качества ЭС.
Вывод ошибок первого рода и второго рода из полноты и точности
Но может быть существует изящная формула вывода ошибки первого рода через точность?
Вот с ошибкой второго рода как все красиво:
Вывод формулы
К сожалению с O1 так изящно не получится. Вот отношение через точность (Т) и полноту (П):
Вывод формулы
Эй! Ты что такой ленивый! А ну давай сам попробуй!
Я сегодня плохо спал, Павел! Ну покажи!
Из и
можно составить выражение:
Откуда следует:
Уже из этого отношения легко получить формулу для O1
Заключение
Точность и полнота «не хуже» и «не лучше» чем ошибки первого и второго рода. Всё зависит от задачи. Мы же не едим столовой ложкой торт, а чайной борщ? Хотя это возможно.
Точность и полнота более понятные критерии качества. Ими легче оперировать. С помощью них просто вычислить предотвращённый ущерб в задаче фрод-мониторинга.
Если вы обнаружили описку или грамматическую ошибку — прошу написать в личку.
В машинном обучении различают оценки качества для задачи классификации и регрессии. Причем оценка задачи классификации часто значительно сложнее, чем оценка регрессии.
Содержание
- 1 Оценки качества классификации
- 1.1 Матрица ошибок (англ. Сonfusion matrix)
- 1.2 Аккуратность (англ. Accuracy)
- 1.3 Точность (англ. Precision)
- 1.4 Полнота (англ. Recall)
- 1.5 F-мера (англ. F-score)
- 1.6 ROC-кривая
- 1.7 Precison-recall кривая
- 2 Оценки качества регрессии
- 2.1 Средняя квадратичная ошибка (англ. Mean Squared Error, MSE)
- 2.2 Cредняя абсолютная ошибка (англ. Mean Absolute Error, MAE)
- 2.3 Коэффициент детерминации
- 2.4 Средняя абсолютная процентная ошибка (англ. Mean Absolute Percentage Error, MAPE)
- 2.5 Корень из средней квадратичной ошибки (англ. Root Mean Squared Error, RMSE)
- 2.6 Cимметричная MAPE (англ. Symmetric MAPE, SMAPE)
- 2.7 Средняя абсолютная масштабированная ошибка (англ. Mean absolute scaled error, MASE)
- 3 Кросс-валидация
- 4 Примечания
- 5 См. также
- 6 Источники информации
Оценки качества классификации
Матрица ошибок (англ. Сonfusion matrix)
Перед переходом к самим метрикам необходимо ввести важную концепцию для описания этих метрик в терминах ошибок классификации — confusion matrix (матрица ошибок).
Допустим, что у нас есть два класса и алгоритм, предсказывающий принадлежность каждого объекта одному из классов.
Рассмотрим пример. Пусть банк использует систему классификации заёмщиков на кредитоспособных и некредитоспособных. При этом первым кредит выдаётся, а вторые получат отказ. Таким образом, обнаружение некредитоспособного заёмщика () можно рассматривать как «сигнал тревоги», сообщающий о возможных рисках.
Любой реальный классификатор совершает ошибки. В нашем случае таких ошибок может быть две:
- Кредитоспособный заёмщик распознается моделью как некредитоспособный и ему отказывается в кредите. Данный случай можно трактовать как «ложную тревогу».
- Некредитоспособный заёмщик распознаётся как кредитоспособный и ему ошибочно выдаётся кредит. Данный случай можно рассматривать как «пропуск цели».
Несложно увидеть, что эти ошибки неравноценны по связанным с ними проблемам. В случае «ложной тревоги» потери банка составят только проценты по невыданному кредиту (только упущенная выгода). В случае «пропуска цели» можно потерять всю сумму выданного кредита. Поэтому системе важнее не допустить «пропуск цели», чем «ложную тревогу».
Поскольку с точки зрения логики задачи нам важнее правильно распознать некредитоспособного заёмщика с меткой , чем ошибиться в распознавании кредитоспособного, будем называть соответствующий исход классификации положительным (заёмщик некредитоспособен), а противоположный — отрицательным (заемщик кредитоспособен ). Тогда возможны следующие исходы классификации:
- Некредитоспособный заёмщик классифицирован как некредитоспособный, т.е. положительный класс распознан как положительный. Наблюдения, для которых это имеет место называются истинно-положительными (True Positive — TP).
- Кредитоспособный заёмщик классифицирован как кредитоспособный, т.е. отрицательный класс распознан как отрицательный. Наблюдения, которых это имеет место, называются истинно отрицательными (True Negative — TN).
- Кредитоспособный заёмщик классифицирован как некредитоспособный, т.е. имела место ошибка, в результате которой отрицательный класс был распознан как положительный. Наблюдения, для которых был получен такой исход классификации, называются ложно-положительными (False Positive — FP), а ошибка классификации называется ошибкой I рода.
- Некредитоспособный заёмщик распознан как кредитоспособный, т.е. имела место ошибка, в результате которой положительный класс был распознан как отрицательный. Наблюдения, для которых был получен такой исход классификации, называются ложно-отрицательными (False Negative — FN), а ошибка классификации называется ошибкой II рода.
Таким образом, ошибка I рода, или ложно-положительный исход классификации, имеет место, когда отрицательное наблюдение распознано моделью как положительное. Ошибкой II рода, или ложно-отрицательным исходом классификации, называют случай, когда положительное наблюдение распознано как отрицательное. Поясним это с помощью матрицы ошибок классификации:
-
Истинно-положительный (True Positive — TP) Ложно-положительный (False Positive — FP) Ложно-отрицательный (False Negative — FN) Истинно-отрицательный (True Negative — TN)
Здесь — это ответ алгоритма на объекте, а — истинная метка класса на этом объекте.
Таким образом, ошибки классификации бывают двух видов: False Negative (FN) и False Positive (FP).
P означает что классификатор определяет класс объекта как положительный (N — отрицательный). T значит что класс предсказан правильно (соответственно F — неправильно). Каждая строка в матрице ошибок представляет спрогнозированный класс, а каждый столбец — фактический класс.
# код для матрицы ошибок # Пример классификатора, способного проводить различие между всего лишь двумя # классами, "пятерка" и "не пятерка" из набора рукописных цифр MNIST import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.metrics import confusion_matrix from sklearn.linear_model import SGDClassifier mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (англ. Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе # Для расчета матрицы ошибок сначала понадобится иметь набор прогнозов, чтобы их можно было сравнивать с фактическими целями y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) print(confusion_matrix(y_train_5, y_train_pred)) # array([[53892, 687], # [ 1891, 3530]])
Безупречный классификатор имел бы только истинно-положительные и истинно отрицательные классификации, так что его матрица ошибок содержала бы ненулевые значения только на своей главной диагонали (от левого верхнего до правого нижнего угла):
import numpy as np
from sklearn.datasets import fetch_openml
from sklearn.metrics import confusion_matrix
mnist = fetch_openml('mnist_784', version=1)
X, y = mnist["data"], mnist["target"]
y = y.astype(np.uint8)
X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:]
y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки
y_test_5 = (y_test == 5)
y_train_perfect_predictions = y_train_5 # притворись, что мы достигли совершенства
print(confusion_matrix(y_train_5, y_train_perfect_predictions))
# array([[54579, 0],
# [ 0, 5421]])
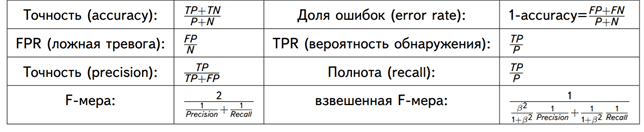
Аккуратность (англ. Accuracy)
Интуитивно понятной, очевидной и почти неиспользуемой метрикой является accuracy — доля правильных ответов алгоритма:
Эта метрика бесполезна в задачах с неравными классами, что как вариант можно исправить с помощью алгоритмов сэмплирования и это легко показать на примере.
Допустим, мы хотим оценить работу спам-фильтра почты. У нас есть 100 не-спам писем, 90 из которых наш классификатор определил верно (True Negative = 90, False Positive = 10), и 10 спам-писем, 5 из которых классификатор также определил верно (True Positive = 5, False Negative = 5).
Тогда accuracy:
Однако если мы просто будем предсказывать все письма как не-спам, то получим более высокую аккуратность:
При этом, наша модель совершенно не обладает никакой предсказательной силой, так как изначально мы хотели определять письма со спамом. Преодолеть это нам поможет переход с общей для всех классов метрики к отдельным показателям качества классов.
# код для для подсчета аккуратности: # Пример классификатора, способного проводить различие между всего лишь двумя # классами, "пятерка" и "не пятерка" из набора рукописных цифр MNIST import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.metrics import accuracy_score from sklearn.linear_model import SGDClassifier mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) # print(confusion_matrix(y_train_5, y_train_pred)) # array([[53892, 687] # [ 1891, 3530]]) print(accuracy_score(y_train_5, y_train_pred)) # == (53892 + 3530) / (53892 + 3530 + 1891 +687) # 0.9570333333333333
Точность (англ. Precision)
Точностью (precision) называется доля правильных ответов модели в пределах класса — это доля объектов действительно принадлежащих данному классу относительно всех объектов которые система отнесла к этому классу.
Именно введение precision не позволяет нам записывать все объекты в один класс, так как в этом случае мы получаем рост уровня False Positive.
Полнота (англ. Recall)
Полнота — это доля истинно положительных классификаций. Полнота показывает, какую долю объектов, реально относящихся к положительному классу, мы предсказали верно.
Полнота (recall) демонстрирует способность алгоритма обнаруживать данный класс вообще.
Имея матрицу ошибок, очень просто можно вычислить точность и полноту для каждого класса. Точность (precision) равняется отношению соответствующего диагонального элемента матрицы и суммы всей строки класса. Полнота (recall) — отношению диагонального элемента матрицы и суммы всего столбца класса. Формально:
Результирующая точность классификатора рассчитывается как арифметическое среднее его точности по всем классам. То же самое с полнотой. Технически этот подход называется macro-averaging.
# код для для подсчета точности и полноты: # Пример классификатора, способного проводить различие между всего лишь двумя # классами, "пятерка" и "не пятерка" из набора рукописных цифр MNIST import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.metrics import precision_score, recall_score from sklearn.linear_model import SGDClassifier mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) # print(confusion_matrix(y_train_5, y_train_pred)) # array([[53892, 687] # [ 1891, 3530]]) print(precision_score(y_train_5, y_train_pred)) # == 3530 / (3530 + 687) print(recall_score(y_train_5, y_train_pred)) # == 3530 / (3530 + 1891) # 0.8370879772350012 # 0.6511713705958311
F-мера (англ. F-score)
Precision и recall не зависят, в отличие от accuracy, от соотношения классов и потому применимы в условиях несбалансированных выборок.
Часто в реальной практике стоит задача найти оптимальный (для заказчика) баланс между этими двумя метриками. Понятно что чем выше точность и полнота, тем лучше. Но в реальной жизни максимальная точность и полнота не достижимы одновременно и приходится искать некий баланс. Поэтому, хотелось бы иметь некую метрику которая объединяла бы в себе информацию о точности и полноте нашего алгоритма. В этом случае нам будет проще принимать решение о том какую реализацию запускать в производство (у кого больше тот и круче). Именно такой метрикой является F-мера.
F-мера представляет собой гармоническое среднее между точностью и полнотой. Она стремится к нулю, если точность или полнота стремится к нулю.
Данная формула придает одинаковый вес точности и полноте, поэтому F-мера будет падать одинаково при уменьшении и точности и полноты. Возможно рассчитать F-меру придав различный вес точности и полноте, если вы осознанно отдаете приоритет одной из этих метрик при разработке алгоритма:
где принимает значения в диапазоне если вы хотите отдать приоритет точности, а при приоритет отдается полноте. При формула сводится к предыдущей и вы получаете сбалансированную F-меру (также ее называют ).
-
Рис.1 Сбалансированная F-мера,
-
Рис.2 F-мера c приоритетом точности,
-
Рис.3 F-мера c приоритетом полноты,
F-мера достигает максимума при максимальной полноте и точности, и близка к нулю, если один из аргументов близок к нулю.
F-мера является хорошим кандидатом на формальную метрику оценки качества классификатора. Она сводит к одному числу две других основополагающих метрики: точность и полноту. Имея «F-меру» гораздо проще ответить на вопрос: «поменялся алгоритм в лучшую сторону или нет?»
# код для подсчета метрики F-mera: # Пример классификатора, способного проводить различие между всего лишь двумя # классами, "пятерка" и "не пятерка" из набора рукописных цифр MNIST import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.linear_model import SGDClassifier from sklearn.metrics import f1_score mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распознавать пятерки на целом обучающем наборе y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) print(f1_score(y_train_5, y_train_pred)) # 0.7325171197343846
ROC-кривая
Кривая рабочих характеристик (англ. Receiver Operating Characteristics curve).
Используется для анализа поведения классификаторов при различных пороговых значениях.
Позволяет рассмотреть все пороговые значения для данного классификатора.
Показывает долю ложно положительных примеров (англ. false positive rate, FPR) в сравнении с долей истинно положительных примеров (англ. true positive rate, TPR).
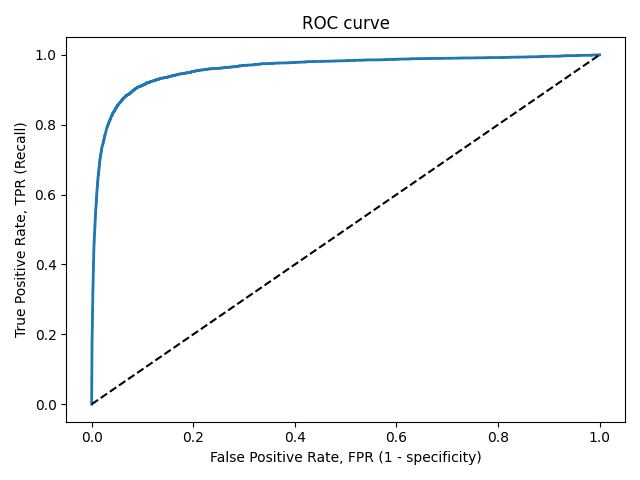
Доля FPR — это пропорция отрицательных образцов, которые были некорректно классифицированы как положительные.
- ,
где TNR — доля истинно отрицательных классификаций (англ. Тrие Negative Rate), представляющая собой пропорцию отрицательных образцов, которые были корректно классифицированы как отрицательные.
Доля TNR также называется специфичностью (англ. specificity). Следовательно, ROC-кривая изображает чувствительность (англ. seпsitivity), т.е. полноту, в сравнении с разностью 1 — specificity.
Прямая линия по диагонали представляет ROC-кривую чисто случайного классификатора. Хороший классификатор держится от указанной линии настолько далеко, насколько это
возможно (стремясь к левому верхнему углу).
Один из способов сравнения классификаторов предусматривает измерение площади под кривой (англ. Area Under the Curve — AUC). Безупречный классификатор будет иметь площадь под ROC-кривой (ROC-AUC), равную 1, тогда как чисто случайный классификатор — площадь 0.5.
# Код отрисовки ROC-кривой # На примере классификатора, способного проводить различие между всего лишь двумя классами # "пятерка" и "не пятерка" из набора рукописных цифр MNIST from sklearn.metrics import roc_curve import matplotlib.pyplot as plt import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.linear_model import SGDClassifier mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) y_scores = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3, method="decision_function") fpr, tpr, thresholds = roc_curve(y_train_5, y_scores) def plot_roc_curve(fpr, tpr, label=None): plt.plot(fpr, tpr, linewidth=2, label=label) plt.plot([0, 1], [0, 1], 'k--') # dashed diagonal plt.xlabel('False Positive Rate, FPR (1 - specificity)') plt.ylabel('True Positive Rate, TPR (Recall)') plt.title('ROC curve') plt.savefig("ROC.png") plot_roc_curve(fpr, tpr) plt.show()
Precison-recall кривая
Чувствительность к соотношению классов.
Рассмотрим задачу выделения математических статей из множества научных статей. Допустим, что всего имеется 1.000.100 статей, из которых лишь 100 относятся к математике. Если нам удастся построить алгоритм , идеально решающий задачу, то его TPR будет равен единице, а FPR — нулю. Рассмотрим теперь плохой алгоритм, дающий положительный ответ на 95 математических и 50.000 нематематических статьях. Такой алгоритм совершенно бесполезен, но при этом имеет TPR = 0.95 и FPR = 0.05, что крайне близко к показателям идеального алгоритма.
Таким образом, если положительный класс существенно меньше по размеру, то AUC-ROC может давать неадекватную оценку качества работы алгоритма, поскольку измеряет долю неверно принятых объектов относительно общего числа отрицательных. Так, алгоритм , помещающий 100 релевантных документов на позиции с 50.001-й по 50.101-ю, будет иметь AUC-ROC 0.95.
Precison-recall (PR) кривая. Избавиться от указанной проблемы с несбалансированными классами можно, перейдя от ROC-кривой к PR-кривой. Она определяется аналогично ROC-кривой, только по осям откладываются не FPR и TPR, а полнота (по оси абсцисс) и точность (по оси ординат). Критерием качества семейства алгоритмов выступает площадь под PR-кривой (англ. Area Under the Curve — AUC-PR)
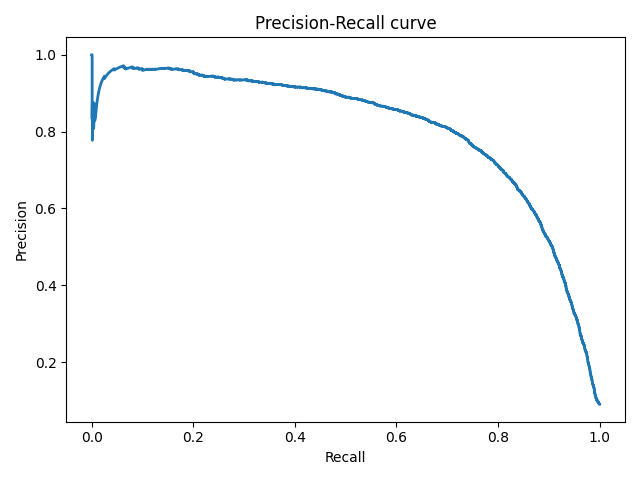
# Код отрисовки Precison-recall кривой # На примере классификатора, способного проводить различие между всего лишь двумя классами # "пятерка" и "не пятерка" из набора рукописных цифр MNIST from sklearn.metrics import precision_recall_curve import matplotlib.pyplot as plt import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.linear_model import SGDClassifier mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) y_scores = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3, method="decision_function") precisions, recalls, thresholds = precision_recall_curve(y_train_5, y_scores) def plot_precision_recall_vs_threshold(precisions, recalls, thresholds): plt.plot(recalls, precisions, linewidth=2) plt.xlabel('Recall') plt.ylabel('Precision') plt.title('Precision-Recall curve') plt.savefig("Precision_Recall_curve.png") plot_precision_recall_vs_threshold(precisions, recalls, thresholds) plt.show()
Оценки качества регрессии
Наиболее типичными мерами качества в задачах регрессии являются
Средняя квадратичная ошибка (англ. Mean Squared Error, MSE)
MSE применяется в ситуациях, когда нам надо подчеркнуть большие ошибки и выбрать модель, которая дает меньше больших ошибок прогноза. Грубые ошибки становятся заметнее за счет того, что ошибку прогноза мы возводим в квадрат. И модель, которая дает нам меньшее значение среднеквадратической ошибки, можно сказать, что что у этой модели меньше грубых ошибок.
- и
Cредняя абсолютная ошибка (англ. Mean Absolute Error, MAE)
Среднеквадратичный функционал сильнее штрафует за большие отклонения по сравнению со среднеабсолютным, и поэтому более чувствителен к выбросам. При использовании любого из этих двух функционалов может быть полезно проанализировать, какие объекты вносят наибольший вклад в общую ошибку — не исключено, что на этих объектах была допущена ошибка при вычислении признаков или целевой величины.
Среднеквадратичная ошибка подходит для сравнения двух моделей или для контроля качества во время обучения, но не позволяет сделать выводов о том, на сколько хорошо данная модель решает задачу. Например, MSE = 10 является очень плохим показателем, если целевая переменная принимает значения от 0 до 1, и очень хорошим, если целевая переменная лежит в интервале (10000, 100000). В таких ситуациях вместо среднеквадратичной ошибки полезно использовать коэффициент детерминации —
Коэффициент детерминации
Коэффициент детерминации измеряет долю дисперсии, объясненную моделью, в общей дисперсии целевой переменной. Фактически, данная мера качества — это нормированная среднеквадратичная ошибка. Если она близка к единице, то модель хорошо объясняет данные, если же она близка к нулю, то прогнозы сопоставимы по качеству с константным предсказанием.
Средняя абсолютная процентная ошибка (англ. Mean Absolute Percentage Error, MAPE)
Это коэффициент, не имеющий размерности, с очень простой интерпретацией. Его можно измерять в долях или процентах. Если у вас получилось, например, что MAPE=11.4%, то это говорит о том, что ошибка составила 11,4% от фактических значений.
Основная проблема данной ошибки — нестабильность.
Корень из средней квадратичной ошибки (англ. Root Mean Squared Error, RMSE)
Примерно такая же проблема, как и в MAPE: так как каждое отклонение возводится в квадрат, любое небольшое отклонение может значительно повлиять на показатель ошибки. Стоит отметить, что существует также ошибка MSE, из которой RMSE как раз и получается путем извлечения корня.
Cимметричная MAPE (англ. Symmetric MAPE, SMAPE)
Средняя абсолютная масштабированная ошибка (англ. Mean absolute scaled error, MASE)
MASE является очень хорошим вариантом для расчета точности, так как сама ошибка не зависит от масштабов данных и является симметричной: то есть положительные и отрицательные отклонения от факта рассматриваются в равной степени.
Обратите внимание, что в MASE мы имеем дело с двумя суммами: та, что в числителе, соответствует тестовой выборке, та, что в знаменателе — обучающей. Вторая фактически представляет собой среднюю абсолютную ошибку прогноза. Она же соответствует среднему абсолютному отклонению ряда в первых разностях. Эта величина, по сути, показывает, насколько обучающая выборка предсказуема. Она может быть равна нулю только в том случае, когда все значения в обучающей выборке равны друг другу, что соответствует отсутствию каких-либо изменений в ряде данных, ситуации на практике почти невозможной. Кроме того, если ряд имеет тенденцию к росту либо снижению, его первые разности будут колебаться около некоторого фиксированного уровня. В результате этого по разным рядам с разной структурой, знаменатели будут более-менее сопоставимыми. Всё это, конечно же, является очевидными плюсами MASE, так как позволяет складывать разные значения по разным рядам и получать несмещённые оценки.
Недостаток MASE в том, что её тяжело интерпретировать. Например, MASE=1.21 ни о чём, по сути, не говорит. Это просто означает, что ошибка прогноза оказалась в 1.21 раза выше среднего абсолютного отклонения ряда в первых разностях, и ничего более.
Кросс-валидация
Хороший способ оценки модели предусматривает применение кросс-валидации (cкользящего контроля или перекрестной проверки).
В этом случае фиксируется некоторое множество разбиений исходной выборки на две подвыборки: обучающую и контрольную. Для каждого разбиения выполняется настройка алгоритма по обучающей подвыборке, затем оценивается его средняя ошибка на объектах контрольной подвыборки. Оценкой скользящего контроля называется средняя по всем разбиениям величина ошибки на контрольных подвыборках.
Примечания
- [1] Лекция «Оценивание качества» на www.coursera.org
- [2] Лекция на www.stepik.org о кросвалидации
- [3] Лекция на www.stepik.org о метриках качества, Precison и Recall
- [4] Лекция на www.stepik.org о метриках качества, F-мера
- [5] Лекция на www.stepik.org о метриках качества, примеры
См. также
- Оценка качества в задаче кластеризации
- Кросс-валидация
Источники информации
- [6] Соколов Е.А. Лекция линейная регрессия
- [7] — Дьяконов А. Функции ошибки / функционалы качества
- [8] — Оценка качества прогнозных моделей
- [9] — HeinzBr Ошибка прогнозирования: виды, формулы, примеры
- [10] — egor_labintcev Метрики в задачах машинного обучения
- [11] — grossu Методы оценки качества прогноза
- [12] — К.В.Воронцов, Классификация
- [13] — К.В.Воронцов, Скользящий контроль
Ошибки первого рода (англ. type I errors, α errors, false positives) и ошибки второго рода (англ. type II errors, β errors, false negatives) в математической статистике — это ключевые понятия задач проверки статистических гипотез. Тем не менее, данные понятия часто используются и в других областях, когда речь идёт о принятии «бинарного» решения (да/нет) на основе некоего критерия (теста, проверки, измерения), который с некоторой вероятностью может давать ложный результат.
Содержание
- 1 Определения
- 2 О смысле ошибок первого и второго рода
- 3 Вероятности ошибок (уровень значимости и мощность)
- 4 Примеры использования
- 4.1 Радиолокация
- 4.2 Компьютеры
- 4.2.1 Компьютерная безопасность
- 4.2.2 Фильтрация спама
- 4.2.3 Вредоносное программное обеспечение
- 4.2.4 Поиск в компьютерных базах данных
- 4.2.5 Оптическое распознавание текстов (OCR)
- 4.2.6 Досмотр пассажиров и багажа
- 4.2.7 Биометрия
- 4.3 Массовая медицинская диагностика (скрининг)
- 4.4 Медицинское тестирование
- 4.5 Исследования сверхъестественных явлений
- 5 См. также
- 6 Примечания
Определения
Пусть дана выборка 

где 

,
сопоставляющий каждой реализации выборки 
- Распределение
выборки
соответствует гипотезе
, и она точно определена статистическим критерием, то есть
.
- Распределение
выборки
соответствует гипотезе
, но она неверно отвергнута статистическим критерием, то есть
.
- Распределение
выборки
соответствует гипотезе
, и она точно определена статистическим критерием, то есть
.
- Распределение
выборки
соответствует гипотезе
, но она неверно отвергнута статистическим критерием, то есть
.
Во втором и четвертом случае говорят, что произошла статистическая ошибка, и её называют ошибкой первого и второго рода соответственно. [1][2]
| Верная гипотеза | |||
|---|---|---|---|
 |
 |
||
| Результат применения критерия |
 |
 верно принята верно принята |
 неверно принята неверно принята (Ошибка второго рода) |
 |
 неверно отвергнута неверно отвергнута (Ошибка первого рода) |
 верно отвергнута верно отвергнута |
О смысле ошибок первого и второго рода
Как видно из вышеприведённого определения, ошибки первого и второго рода являются взаимно-симметричными, то есть если поменять местами гипотезы 



С учётом этого ошибку первого рода часто называют ложной тревогой, ложным срабатыванием или ложноположительным срабатыванием — например, анализ крови показал наличие заболевания, хотя на самом деле человек здоров, или металлодетектор выдал сигнал тревоги, сработав на металлическую пряжку ремня. Слово «положительный» в данном случае не имеет отношения к желательности или нежелательности самого события.
Термин широко используется в медицине. Например, тесты, предназначенные для диагностики заболеваний, иногда дают положительный результат (т.е. показывают наличие заболевания у пациента), когда на самом деле пациент этим заболеванием не страдает. Такой результат называется ложноположительным.
В других областях обычно используют словосочетания со схожим смыслом, например, «ложное срабатывание», «ложная тревога» и т.п. В информационных технологиях часто используют английский термин false positive без перевода.
Из-за возможности ложных срабатываний не удаётся полностью автоматизировать борьбу со многими видами угроз. Как правило, вероятность ложного срабатывания коррелирует с вероятностью пропуска события (ошибки второго рода). То есть: чем более чувствительна система, тем больше опасных событий она детектирует и, следовательно, предотвращает. Но при повышении чувствительности неизбежно вырастает и вероятность ложных срабатываний. Поэтому чересчур чувствительно (параноидально) настроенная система защиты может выродиться в свою противоположность и привести к тому, что побочный вред от неё будет превышать пользу.
Соответственно, ошибку второго рода иногда называют пропуском события или ложноотрицательным срабатыванием — человек болен, но анализ крови этого не показал, или у пассажира имеется холодное оружие, но рамка металлодетектора его не обнаружила (например, из-за того, что чувствительность рамки отрегулирована на обнаружение только очень массивных металлических предметов).
Слово «отрицательный» в данном случае не имеет отношения к желательности или нежелательности самого события.
Термин широко используется в медицине. Например, тесты, предназначенные для диагностики заболеваний, иногда дают отрицательный результат (т.е. показывают отсутствие заболевания у пациента), когда на самом деле пациент страдает этим заболеванием. Такой результат называется ложноотрицательным.
В других областях обычно используют словосочетания со схожим смыслом, например, «пропуск события», и т.п. В информационных технологиях часто используют английский термин false negative без перевода.
Степень чувствительности системы защиты должна представлять собой компромисс между вероятностью ошибок первого и второго рода. Где именно находится точка баланса, зависит от оценки рисков обоих видов ошибок.
Вероятности ошибок (уровень значимости и мощность)
Вероятность ошибки первого рода при проверке статистических гипотез называют уровнем значимости и обычно обозначают греческой буквой 

Вероятность ошибки второго рода не имеет какого-то особого общепринятого названия, на письме обозначается греческой буквой 


Обе эти характеристики обычно вычисляются с помощью так называемой функции мощности критерия. В частности, вероятность ошибки первого рода есть функция мощности, вычисленная при нулевой гипотезе. Для критериев, основанных на выборке фиксированного объема, вероятность ошибки второго рода есть единица минус функция мощности, вычисленная в предположении, что распределение наблюдений соответствует альтернативной гипотезе. Для последовательных критериев это также верно, если критерий останавливается с вероятностью единица (при данном распределении из альтернативы).
В статистических тестах обычно приходится идти на компромисс между приемлемым уровнем ошибок первого и второго рода. Зачастую для принятия решения используется пороговое значение, которое может варьироваться с целью сделать тест более строгим или, наоборот, более мягким. Этим пороговым значением является уровень значимости, которым задаются при проверке статистических гипотез. Например, в случае металлодетектора повышение чувствительности прибора приведёт к увеличению риска ошибки первого рода (ложная тревога), а понижение чувствительности — к увеличению риска ошибки второго рода (пропуск запрещённого предмета).
Примеры использования
Радиолокация
В задаче радиолокационного обнаружения воздушных целей, прежде всего, в системе ПВО ошибки первого и второго рода, с формулировкой «ложная тревога» и «пропуск цели» являются одним из основных элементов как теории, так и практики построения радиолокационных станций. Вероятно, это первый пример последовательного применения статистических методов в целой технической области.
Компьютеры
Понятия ошибок первого и второго рода широко используются в области компьютеров и программного обеспечения.
Компьютерная безопасность
Наличие уязвимостей в вычислительных системах приводит к тому, что приходится, с одной стороны, решать задачу сохранения целостности компьютерных данных, а с другой стороны — обеспечивать нормальный доступ легальных пользователей к этим данным (см. компьютерная безопасность). Moulton (1983, с.125) отмечает, что в данном контексте возможны следующие нежелательные ситуации:
- когда нарушители классифицируются как авторизованные пользователи (ошибки первого рода)
- когда авторизованные пользователи классифицируются как нарушители (ошибки второго рода)
Фильтрация спама
Ошибка первого рода происходит, когда механизм блокировки/фильтрации спама ошибочно классифицирует легитимное email-сообщение как спам и препятствует его нормальной доставке. В то время как большинство «антиспам»-алгоритмов способны блокировать/фильтровать большой процент нежелательных email-сообщений, гораздо более важной задачей является минимизировать число «ложных тревог» (ошибочных блокировок нужных сообщений).
Ошибка второго рода происходит, когда антиспам-система ошибочно пропускает нежелательное сообщение, классифицируя его как «не спам». Низкий уровень таких ошибок является индикатором эффективности антиспам-алгоритма.
Пока не удалось создать антиспамовую систему без корреляции между вероятностью ошибок первого и второго рода. Вероятность пропустить спам у современных систем колеблется в пределах от 1% до 30%. Вероятность ошибочно отвергнуть валидное сообщение — от 0,001 % до 3 %. Выбор системы и её настроек зависит от условий конкретного получателя: для одних получателей риск потерять 1% хорошей почты оценивается как незначительный, для других же потеря даже 0,1% является недопустимой.
Вредоносное программное обеспечение
Понятие ошибки первого рода также используется, когда антивирусное программное обеспечение ошибочно классифицирует безвредный файл как вирус. Неверное обнаружение может быть вызвано особенностями эвристики, либо неправильной сигнатурой вируса в базе данных. Подобные проблемы могут происходить также и с антитроянскими и антишпионскими программами.
Поиск в компьютерных базах данных
При поиске в базе данных к ошибкам первого рода можно отнести документы, которые выдаются поиском, несмотря на их иррелевантность (несоответствие) поисковому запросу. Ошибочные срабатывания характерны для полнотекстового поиска, когда поисковый алгоритм анализирует полные тексты всех хранимых в базе данных документов и пытается найти соответствия одному или нескольким терминам, заданным пользователем в запросе.
Большинство ложных срабатываний обусловлены сложностью естественных языков, многозначностью слов: например, «home» может обозначать как «место проживания человека», так и «корневую страницу веб-сайта». Число подобных ошибок может быть снижено за счёт использования специального словаря. Однако это решение относительно дорогое, поскольку подобный словарь и разметка документов (индексирование) должны создаваться экспертом.
Оптическое распознавание текстов (OCR)
Разнообразные детектирующие алгоритмы нередко выдают ошибки первого рода. Программное обеспечение оптического распознавания текстов может распознать букву «a» в ситуации, когда на самом деле изображены несколько точек, которые используемый алгоритм расценил как «a».
Досмотр пассажиров и багажа
Ошибки первого рода регулярно встречаются каждый день в компьютерных системах предварительного досмотра пассажиров в аэропортах. Установленные в них детекторы предназначены для предотвращения проноса оружия на борт самолёта; тем не менее, уровень чувствительности в них зачастую настраивается настолько высоко, что много раз за день они срабатывают на незначительные предметы, такие как ключи, пряжки ремней, монеты, мобильные телефоны, гвозди в подошвах обуви и т.п. (см. обнаружение взрывчатых веществ, металлодетекторы).
Таким образом, соотношение числа ложных тревог (идентифицикация благопристойного пассажира как правонарушителя) к числу правильных срабатываний (обнаружение действительно запрещённых предметов) очень велико.
Биометрия
Ошибки первого и второго рода являются большой проблемой в системах биометрического сканирования, использующих распознавание радужной оболочки или сетчатки глаза, черт лица и т.д. Такие сканирующие системы могут ошибочно отождествить кого-то с другим, «известным» системе человеком, информация о котором хранится в базе данных (к примеру, это может быть лицо, имеющее право входа в систему, или подозреваемый преступник и т.п.). Противоположной ошибкой будет неспособность системы распознать легитимного зарегистрированного пользователя, или опознать подозреваемого в преступлении.[3]
Массовая медицинская диагностика (скрининг)
В медицинской практике есть существенное различие между скринингом и тестированием:
- Скрининг включает в себя относительно дешёвые тесты, которые проводятся для большой группы людей при отсутствии каких-либо клинических признаков болезни (например, мазок Папаниколау).
- Тестирование подразумевает гораздо более дорогие, зачастую инвазивные, процедуры, которые проводятся только для тех, у кого проявляются клинические признаки заболевания, и которые, в основном, применяются для подтверждения предполагаемого диагноза.
К примеру, в большинстве штатов в США обязательно прохождение новорожденными процедуры скрининга на оксифенилкетонурию и гипотиреоз, помимо других врождённых аномалий. Несмотря на высокий уровень ошибок первого рода, эти процедуры скрининга считаются целесообразными, поскольку они существенно увеличивают вероятность обнаружения этих расстройств на самой ранней стадии.[4]
Простые анализы крови, используемые для скрининга потенциальных доноров на ВИЧ и гепатит, имеют существенный уровень ошибок первого рода; однако в арсенале врачей есть гораздо более точные (и, соответственно, дорогие) тесты для проверки, действительно ли человек инфицирован каким-либо из этих вирусов.
Возможно, наиболее широкие дискуссии вызывают ошибки первого рода в процедурах скрининга на рак груди (маммография). В США уровень ошибок первого рода в маммограммах достигает 15%, это самый высокий показатель в мире.[5] Самый низкий уровень наблюдается в Нидерландах, 1%.[6]
Медицинское тестирование
Ошибки второго рода являются существенной проблемой в медицинском тестировании. Они дают пациенту и врачу ложное убеждение, что заболевание отсутствует, в то время как в действительности оно есть. Это зачастую приводит к неуместному или неадекватному лечению. Типичным примером является доверие результатам кардиотестирования при выявлении коронарного атеросклероза, хотя известно, что кардиотестирование выявляет только те затруднения кровотока в коронарной артерии, которые вызваны стенозом.
Ошибки второго рода вызывают серьёзные и трудные для понимания проблемы, особенно когда искомое условие является широкораспространённым. Если тест с 10%-ным уровнем ошибок второго рода используется для обследования группы, где вероятность «истинно-положительных» случаев составляет 70%, то многие отрицательные результаты теста окажутся ложными. (См. Теорему Байеса).
Ошибки первого рода также могут вызывать серьёзные и трудные для понимания проблемы. Это происходит, когда искомое условие является редким. Если уровень ошибок первого рода у теста составляет один случай на десять тысяч, но в тестируемой группе образцов (или людей) вероятность «истинно-положительных» случаев составляет в среднем один случай на миллион, то большинство положительных результатов этого теста будут ложными.[7]
Исследования сверхъестественных явлений
Термин ошибка первого рода был взят на вооружение исследователями в области паранормальных явлений и привидений для описания фотографии или записи или какого-либо другого свидетельства, которое ошибочно трактуется как имеющее паранормальное происхождение — в данном контексте ошибка первого рода — это какое-либо несостоятельное «медиасвидетельство» (изображение, видеозапись, аудиозапись и т.д.), которое имеет обычное объяснение.[8]
См. также
- Статистическая значимость
- Ложноположительный
- Атака второго рода
- Случаи ложного срабатывания систем предупреждения о ракетном нападении
- Receiver_operating_characteristic
Примечания
- ↑ ГОСТ Р 50779.10-2000. «Статистические методы. Вероятность и основы статистики. Термины и определения.». Стр. 26
- ↑ Valerie J. Easton, John H. McColl. Statistics Glossary: Hypothesis Testing.
- ↑ Данный пример как раз характеризует случай, когда классификация ошибок будет зависеть от назначения системы: если биометрическое сканирование используется для допуска сотрудников (нулевая гипотеза: «проходящий сканирование человек действительно является сотрудником»), то ошибочное отождествление будет ошибкой второго рода, а «неузнавание» — ошибкой первого рода; если же сканирование используется для опознания преступников (нулевая гипотеза: «проходящий сканирование человек не является преступником»), то ошибочное отождествление будет ошибкой первого рода, а «неузнавание» — ошибкой второго рода.
- ↑ Относительно скрининга новорожденных, последние исследования показали, что количество ошибок первого рода в 12 раз больше, чем количество верных обнаружений (Gambrill, 2006. [1])
- ↑ Одним из последствий такого высокого уровня ошибок первого рода в США является то, что за произвольный 10-летний период половина обследуемых американских женщин получают как минимум одну ложноположительную маммограмму. Такие ошибочные маммограммы обходятся дорого, приводя к ежегодным расходам в 100 миллионов долларов на последующее (ненужное) лечение. Кроме того, они вызывают излишнюю тревогу у женщин. В результате высокого уровня подобных ошибок первого рода в США, примерно у 90-95% женщин, получивших хотя бы раз в жизни положительную маммограмму, на самом деле заболевание отсутствует.
- ↑ Наиболее низкие уровни этих ошибок наблюдаются в северной Европе, где маммографические плёнки считываются дважды, и для дополнительного тестирования устанавливается повышенное пороговое значение (высокий порог снижает статистическую эффективность теста).
- ↑ Вероятность того, что выдаваемый тестом результат окажется ошибкой первого рода, может быть вычислена при помощи Теоремы Байеса.
- ↑ На некоторых сайтах приведены примеры ошибок первого рода, например: Атлантическое Сообщество Паранормальных явлений (The Atlantic Paranormal Society, TAPS) и Морстаунская организация по Исследованию Привидений (Moorestown Ghost Research).
Оши́бка пе́рвого ро́да (α-ошибка, ложноположительное заключение) — ситуация, когда отвергнута верная нулевая гипотеза (b) (об отсутствии связи между явлениями или искомого эффекта).
Оши́бка второ́го ро́да (β-ошибка, ложноотрицательное заключение) — ситуация, когда принята неверная нулевая гипотеза.
В математической статистике (b) это ключевые понятия задач проверки статистических гипотез (b) . Данные понятия часто используются и в других областях, когда речь идёт о принятии «бинарного» решения (да/нет) на основе некоего критерия (теста, проверки, измерения), который с некоторой вероятностью может давать ложный результат.
Определения
Пусть дана выборка из неизвестного совместного распределения , и поставлена бинарная задача проверки статистических гипотез:
где — нулевая гипотеза (b) , а — альтернативная гипотеза (b) . Предположим, что задан статистический критерий
- ,
сопоставляющий каждой реализации выборки одну из имеющихся гипотез. Тогда возможны следующие четыре ситуации:
- Распределение выборки соответствует гипотезе , и она точно определена статистическим критерием, то есть .
- Распределение выборки соответствует гипотезе , но она неверно отвергнута статистическим критерием, то есть .
- Распределение выборки соответствует гипотезе , и она точно определена статистическим критерием, то есть .
- Распределение выборки соответствует гипотезе , но она неверно отвергнута статистическим критерием, то есть .
Во втором и четвёртом случае говорят, что произошла статистическая ошибка, и её называют ошибкой первого и второго рода соответственно[1][2].
| Верная гипотеза | |||
|---|---|---|---|
| Результат применения критерия |
верно принята | неверно принята (Ошибка второго рода) |
|
| неверно отвергнута (Ошибка первого рода) |
верно отвергнута |
О смысле ошибок первого и второго рода
Из определения выше видно, что ошибки первого и второго рода являются взаимно-симметричными, то есть если поменять местами гипотезы и , то ошибки первого рода превратятся в ошибки второго рода и наоборот. Тем не менее, в большинстве практических ситуаций путаницы не происходит, поскольку принято считать, что нулевая гипотеза соответствует состоянию «по умолчанию» (естественному, наиболее ожидаемому положению вещей) — например, что обследуемый человек здоров, или что проходящий через рамку металлодетектора пассажир не имеет запрещённых металлических предметов. Соответственно, альтернативная гипотеза обозначает противоположную ситуацию, которая обычно трактуется как менее вероятная, неординарная, требующая какой-либо реакции.
С учётом вышесказанного, ошибку первого рода часто называют ложной тревогой, ложным срабатыванием или ложноположительным срабатыванием. Если, например, анализ крови показал наличие заболевания, хотя на самом деле человек здоров, или металлодетектор выдал сигнал тревоги, сработав на металлическую пряжку ремня, то принятая гипотеза не верна, а следовательно совершена ошибка первого рода. Слово «ложноположительный» в данном случае не имеет отношения к желательности или нежелательности самого события.
Термин широко используется в медицине. Например, тесты, предназначенные для диагностики заболеваний, иногда дают положительный результат (то есть показывают наличие заболевания у пациента), когда на самом деле пациент этим заболеванием не страдает. Такой результат называется ложноположительным.
В других областях обычно используют словосочетания со схожим смыслом, например, «ложное срабатывание», «ложная тревога» и т. п. В информационных технологиях часто используют английский термин false positive без перевода.
Из-за возможности ложных срабатываний не удаётся полностью автоматизировать борьбу со многими видами угроз. Как правило, вероятность ложного срабатывания коррелирует с вероятностью пропуска события (ошибки второго рода). То есть: чем более чувствительна система, тем больше опасных событий она детектирует и, следовательно, предотвращает. Но при повышении чувствительности неизбежно вырастает и вероятность ложных срабатываний. Поэтому чересчур чувствительно (параноидально) настроенная система защиты может выродиться в свою противоположность и привести к тому, что побочный вред от неё будет превышать пользу.
Соответственно, ошибку второго рода иногда называют пропуском события или ложноотрицательным срабатыванием. Человек болен, но анализ крови этого не показал, или у пассажира имеется холодное оружие, но рамка металлодетектора его не обнаружила (например, из-за того, что чувствительность рамки отрегулирована на обнаружение только очень массивных металлических предметов). Данные примеры указывают на совершение ошибки второго рода. Слово «ложноотрицательный» в данном случае не имеет отношения к желательности или нежелательности самого события.
Термин широко используется в медицине. Например, тесты, предназначенные для диагностики заболеваний, иногда дают отрицательный результат (то есть показывают отсутствие заболевания у пациента), когда на самом деле пациент страдает этим заболеванием. Такой результат называется ложноотрицательным.
В других областях обычно используют словосочетания со схожим смыслом, например, «пропуск события», и т. п.
Так как с ростом вероятности ошибки первого рода обычно уменьшается вероятность ошибки второго рода, и наоборот, настройка принимающей решение системы должна представлять собой компромисс. Где именно находится точка получаемого такой настройкой баланса, зависит от оценки последствий при совершении обоих видов ошибок.
Вероятности ошибок (уровень значимости и мощность)
Вероятность ошибки первого рода при проверке статистических гипотез (b) называют уровнем значимости (b) и обычно обозначают греческой буквой (отсюда название -ошибка).
Вероятность ошибки второго рода не имеет какого-то особого общепринятого названия, она обозначается греческой буквой (отсюда название -ошибка). Однако с этой величиной тесно связана другая, имеющая большое статистическое значение — мощность критерия. Она вычисляется по формуле Таким образом, чем выше мощность критерия, тем меньше вероятность совершить ошибку второго рода.
Обе эти характеристики обычно вычисляются с помощью так называемой функции мощности (b) критерия. В частности, вероятность ошибки первого рода есть функция мощности, вычисленная при нулевой гипотезе. Для критериев, основанных на выборке фиксированного объёма, вероятность ошибки второго рода есть единица минус функция мощности, вычисленная в предположении, что распределение наблюдений соответствует альтернативной гипотезе. Для последовательных критериев (b) это также верно, если критерий останавливается с вероятностью единица (при данном распределении из альтернативы).
В статистических тестах обычно приходится идти на компромисс между приемлемым уровнем ошибок первого и второго рода. Зачастую для принятия решения используется пороговое значение, которое может варьироваться с целью сделать тест более строгим или, наоборот, более мягким. Этим пороговым значением является уровень значимости (b) , которым задаются при проверке статистических гипотез (b) . Например, в случае металлодетектора повышение чувствительности прибора приведёт к увеличению риска ошибки первого рода (ложная тревога), а понижение чувствительности — к увеличению риска ошибки второго рода (пропуск запрещённого предмета).
Примеры использования
Радиолокация (b)
В задаче радиолокационного обнаружения воздушных целей, прежде всего, в системе ПВО ошибки первого и второго рода, с формулировкой «ложная тревога» и «пропуск цели» являются одним из основных элементов как теории, так и практики построения радиолокационных станций (b) . Вероятно, это первый пример последовательного применения статистических методов в целой технической области.
Компьютеры
Понятия ошибок первого и второго рода широко используются в области компьютеров и программного обеспечения.
Компьютерная безопасность
Наличие уязвимостей в вычислительных системах приводит к тому, что приходится, с одной стороны, решать задачу сохранения целостности компьютерных данных, а с другой стороны — обеспечивать нормальный доступ легальных пользователей к этим данным (см. компьютерная безопасность (b) ). В данном контексте возможны следующие нежелательные ситуации[3]:
- когда авторизованные пользователи классифицируются как нарушители (ошибки первого рода);
- когда нарушители классифицируются как авторизованные пользователи (ошибки второго рода).
Фильтрация спама
Ошибка первого рода происходит, когда механизм блокировки/фильтрации спама (b) ошибочно классифицирует легитимное email (b) -сообщение как спам и препятствует его нормальной доставке. В то время как большинство «антиспам»-алгоритмов способны блокировать/фильтровать большой процент нежелательных email-сообщений, гораздо более важной задачей является минимизировать число «ложных тревог» (ошибочных блокировок нужных сообщений).
Ошибка второго рода происходит, когда антиспам-система ошибочно пропускает нежелательное сообщение, классифицируя его как «не спам». Низкий уровень таких ошибок является индикатором эффективности антиспам-алгоритма.
Пока не удалось создать антиспамовую систему без корреляции между вероятностью ошибок первого и второго рода. Вероятность пропустить спам у современных систем колеблется в пределах от 1 % до 30 %. Вероятность ошибочно отвергнуть валидное сообщение — от 0,001 % до 3 %. Выбор системы и её настроек зависит от условий конкретного получателя: для одних получателей риск потерять 1 % хорошей почты оценивается как незначительный, для других же потеря даже 0,1 % является недопустимой.
Вредоносное программное обеспечение
Понятие ошибки первого рода также используется, когда антивирусное (b) программное обеспечение ошибочно классифицирует безвредный файл как вирус (b) . Неверное обнаружение может быть вызвано особенностями эвристики (b) , либо неправильной сигнатурой вируса (b) в базе данных. Подобные проблемы могут происходить также и с антитроянскими (b) и антишпионскими (b) программами.
Поиск в компьютерных базах данных
При поиске в базе данных к ошибкам первого рода можно отнести документы, которые выдаются поиском, несмотря на их иррелевантность (b) (несоответствие) поисковому запросу. Ошибочные срабатывания характерны для полнотекстового поиска (b) , когда поисковый алгоритм (b) анализирует полные тексты всех хранимых в базе данных документов и пытается найти соответствия одному или нескольким терминам, заданным пользователем в запросе.
Большинство ложных срабатываний обусловлены сложностью естественных языков (b) , многозначностью слов: например, «home» может обозначать как «место проживания человека», так и «корневую страницу веб-сайта». Число подобных ошибок может быть снижено за счёт использования специального словаря (b) . Однако это решение относительно дорогое, поскольку подобный словарь и разметка документов (индексирование (b) ) должны создаваться экспертом.
Оптическое распознавание текстов (OCR)
Разнообразные детектирующие алгоритмы нередко выдают ошибки первого рода. Программное обеспечение оптического распознавания текстов (b) может распознать букву «a» в ситуации, когда на самом деле изображены несколько точек.
Досмотр пассажиров и багажа
Ошибки первого рода регулярно встречаются каждый день в компьютерных системах предварительного досмотра пассажиров в аэропортах. Установленные в них детекторы предназначены для предотвращения проноса оружия на борт самолёта; тем не менее, уровень чувствительности (b) в них зачастую настраивается настолько высоко, что много раз за день они срабатывают на незначительные предметы, такие как ключи, пряжки ремней, монеты, мобильные телефоны, гвозди в подошвах обуви и т. п. (см. обнаружение взрывчатых веществ (англ.) (рус. (b) , металлодетекторы (b) ).
Таким образом, соотношение числа ложных тревог (идентифицикация благопристойного пассажира как правонарушителя) к числу правильных срабатываний (обнаружение действительно запрещённых предметов) очень велико.
Биометрия
Ошибки первого и второго рода являются большой проблемой в системах биометрического (b) сканирования, использующих распознавание радужной оболочки (b) или сетчатки (b) глаза, черт лица (b) и т. д. Такие сканирующие системы могут ошибочно отождествить кого-то с другим, «известным» системе человеком, информация о котором хранится в базе данных (к примеру, это может быть лицо, имеющее право входа в систему, или подозреваемый преступник и т. п.). Противоположной ошибкой будет неспособность системы распознать легитимного зарегистрированного пользователя, или опознать подозреваемого в преступлении[4].
Массовая медицинская диагностика (скрининг)
В медицинской практике есть существенное различие между скринингом (b) и тестированием (b) :
- Скрининг включает в себя относительно дешёвые тесты, которые проводятся для большой группы людей при отсутствии каких-либо клинических признаков болезни (например, мазок Папаниколау (b) ).
- Тестирование подразумевает гораздо более дорогие, зачастую инвазивные, процедуры, которые проводятся только для тех, у кого проявляются клинические признаки заболевания, и которые, в основном, применяются для подтверждения предполагаемого диагноза.
К примеру, в большинстве штатов в США обязательно прохождение новорожденными процедуры скрининга на оксифенилкетонурию (b) и гипотиреоз (b) , помимо других врождённых аномалий (b) . Несмотря на высокий уровень ошибок первого рода, эти процедуры скрининга считаются целесообразными, поскольку они существенно увеличивают вероятность обнаружения этих расстройств на самой ранней стадии[5].
Простые анализы крови, используемые для скрининга потенциальных доноров (b) на ВИЧ (b) и гепатит (b) , имеют существенный уровень ошибок первого рода; однако в арсенале врачей есть гораздо более точные (и, соответственно, дорогие) тесты для проверки, действительно ли человек инфицирован каким-либо из этих вирусов.
Возможно, наиболее широкие дискуссии вызывают ошибки первого рода в процедурах скрининга на рак груди (маммография (b) ). В США уровень ошибок первого рода в маммограммах достигает 15 %, это самый высокий показатель в мире[6]. Самый низкий уровень наблюдается в Нидерландах (b) , 1 %[7].
Медицинское тестирование
Ошибки второго рода являются существенной проблемой в медицинском тестировании (b) . Они дают пациенту и врачу ложное убеждение, что заболевание отсутствует, в то время как в действительности оно есть. Это зачастую приводит к неуместному или неадекватному лечению. Типичным примером является доверие результатам велоэргометрии (b) при выявлении коронарного атеросклероза (b) , хотя известно, что велоэргометрия выявляет только те затруднения кровотока в коронарной артерии (b) , которые вызваны стенозом (b) .
Ошибки второго рода вызывают серьёзные и трудные для понимания проблемы, особенно когда искомое условие является широкораспространённым. Если тест с 10%-ным уровнем ошибок второго рода используется для обследования группы, где вероятность «истинно-положительных» случаев составляет 70 %, то многие отрицательные результаты теста окажутся ложными. (См. теорему Байеса).
Ошибки первого рода также могут вызывать серьёзные и трудные для понимания проблемы. Это происходит, когда искомое условие является редким. Если уровень ошибок первого рода у теста составляет один случай на десять тысяч, но в тестируемой группе образцов (или людей) вероятность «истинно-положительных» случаев составляет в среднем один случай на миллион, то большинство положительных результатов этого теста будут ложными[8].
Исследования сверхъестественных явлений
Термин ошибка первого рода был взят на вооружение исследователями в области паранормальных явлений (b) и привидений (b) для описания фотографии или записи или какого-либо другого свидетельства, которое ошибочно трактуется как имеющее паранормальное происхождение — в данном контексте ошибка первого рода — это какое-либо несостоятельное «медиасвидетельство» (изображение, видеозапись, аудиозапись и т. д.), которое имеет обычное объяснение.[9]
См. также
- Статистическая значимость (b)
- Атака второго рода (b)
- Случаи ложного срабатывания систем предупреждения о ракетном нападении (b)
- ROC-кривая (b)
- Коррекция на множественное тестирование (b)
Примечания
- ↑ ГОСТ Р 50779.10-2000. «Статистические методы. Вероятность и основы статистики. Термины и определения». — С. 26Архивная копия от 9 ноября 2018 на Wayback Machine (b)
- ↑ Easton V. J., McColl J. H.Statistics Glossary: Hypothesis Testing.Архивная копия от 24 сентября 2011 на Wayback Machine (b)
- ↑ Moulton R. T. Network Security (англ.) // Datamation. — 1983. — Vol. 29, iss. 7. — P. 121—127.
- ↑ Данный пример как раз характеризует случай, когда классификация ошибок будет зависеть от назначения системы: если биометрическое сканирование используется для допуска сотрудников (нулевая гипотеза: «проходящий сканирование человек действительно является сотрудником»), то ошибочное отождествление будет ошибкой второго рода, а «неузнавание» — ошибкой первого рода; если же сканирование используется для опознания преступников (нулевая гипотеза: «проходящий сканирование человек не является преступником»), то ошибочное отождествление будет ошибкой первого рода, а «неузнавание» — ошибкой второго рода.
- ↑ Относительно скрининга новорожденных, последние исследования показали, что количество ошибок первого рода в 12 раз больше, чем количество верных обнаружений (Gambrill, 2006. )
- ↑ Одним из последствий такого высокого уровня ошибок первого рода в США является то, что за произвольный 10-летний период половина обследуемых американских женщин получают как минимум одну ложноположительную (b) маммограмму. Такие ошибочные маммограммы обходятся дорого, приводя к ежегодным расходам в 100 миллионов долларов на последующее (ненужное) лечение. Кроме того, они вызывают излишнюю тревогу у женщин. В результате высокого уровня подобных ошибок первого рода в США, примерно у 90—95 % женщин, получивших хотя бы раз в жизни положительную маммограмму, на самом деле заболевание отсутствует.
- ↑ Наиболее низкие уровни этих ошибок наблюдаются в северной Европе, где маммографические плёнки считываются дважды, и для дополнительного тестирования устанавливается повышенное пороговое значение (b) (высокий порог снижает статистическую эффективность (b) теста).
- ↑ Вероятность того, что выдаваемый тестом результат окажется ошибкой первого рода, может быть вычислена при помощи теоремы Байеса.
- ↑ На некоторых сайтах приведены примеры ошибок первого рода, например: Атлантическое Сообщество Паранормальных явлений (The Atlantic Paranormal Society, TAPS)Архивировано 28 марта 2005 года. (недоступная ссылка с 13-05-2013 [3546 дней]) и Морстаунская организация по Исследованию Привидений (Moorestown Ghost Research)Архивировано 14 июня 2006 года. (недоступная ссылка с 13-05-2013 [3546 дней] — история).
This article is about erroneous outcomes of statistical tests. For closely related concepts in binary classification and testing generally, see false positives and false negatives.
In statistical hypothesis testing, a type I error is the mistaken rejection of an actually true null hypothesis (also known as a «false positive» finding or conclusion; example: «an innocent person is convicted»), while a type II error is the failure to reject a null hypothesis that is actually false (also known as a «false negative» finding or conclusion; example: «a guilty person is not convicted»).[1] Much of statistical theory revolves around the minimization of one or both of these errors, though the complete elimination of either is a statistical impossibility if the outcome is not determined by a known, observable causal process.
By selecting a low threshold (cut-off) value and modifying the alpha (α) level, the quality of the hypothesis test can be increased.[2] The knowledge of type I errors and type II errors is widely used in medical science, biometrics and computer science.[clarification needed]
Intuitively, type I errors can be thought of as errors of commission, i.e. the researcher unluckily concludes that something is the fact. For instance, consider a study where researchers compare a drug with a placebo. If the patients who are given the drug get better than the patients given the placebo by chance, it may appear that the drug is effective, but in fact the conclusion is incorrect.
In reverse, type II errors are errors of omission. In the example above, if the patients who got the drug did not get better at a higher rate than the ones who got the placebo, but this was a random fluke, that would be a type II error. The consequence of a type II error depends on the size and direction of the missed determination and the circumstances. An expensive cure for one in a million patients may be inconsequential even if it truly is a cure.
Definition[edit]
Statistical background[edit]
In statistical test theory, the notion of a statistical error is an integral part of hypothesis testing. The test goes about choosing about two competing propositions called null hypothesis, denoted by H0 and alternative hypothesis, denoted by H1. This is conceptually similar to the judgement in a court trial. The null hypothesis corresponds to the position of the defendant: just as he is presumed to be innocent until proven guilty, so is the null hypothesis presumed to be true until the data provide convincing evidence against it. The alternative hypothesis corresponds to the position against the defendant. Specifically, the null hypothesis also involves the absence of a difference or the absence of an association. Thus, the null hypothesis can never be that there is a difference or an association.
If the result of the test corresponds with reality, then a correct decision has been made. However, if the result of the test does not correspond with reality, then an error has occurred. There are two situations in which the decision is wrong. The null hypothesis may be true, whereas we reject H0. On the other hand, the alternative hypothesis H1 may be true, whereas we do not reject H0. Two types of error are distinguished: type I error and type II error.[3]
Type I error[edit]
The first kind of error is the mistaken rejection of a null hypothesis as the result of a test procedure. This kind of error is called a type I error (false positive) and is sometimes called an error of the first kind. In terms of the courtroom example, a type I error corresponds to convicting an innocent defendant.
Type II error[edit]
The second kind of error is the mistaken failure to reject the null hypothesis as the result of a test procedure. This sort of error is called a type II error (false negative) and is also referred to as an error of the second kind. In terms of the courtroom example, a type II error corresponds to acquitting a criminal.[4]
Crossover error rate[edit]
The crossover error rate (CER) is the point at which type I errors and type II errors are equal. A system with a lower CER value provides more accuracy than a system with a higher CER value.
False positive and false negative[edit]
In terms of false positives and false negatives, a positive result corresponds to rejecting the null hypothesis, while a negative result corresponds to failing to reject the null hypothesis; «false» means the conclusion drawn is incorrect. Thus, a type I error is equivalent to a false positive, and a type II error is equivalent to a false negative.
Table of error types[edit]
Tabularised relations between truth/falseness of the null hypothesis and outcomes of the test:[5]
| Table of error types | Null hypothesis (H0) is |
||
|---|---|---|---|
| True | False | ||
| Decision about null hypothesis (H0) |
Don’t reject |
Correct inference (true negative) (probability = 1−α) |
Type II error (false negative) (probability = β) |
| Reject | Type I error (false positive) (probability = α) |
Correct inference (true positive) (probability = 1−β) |
Error rate[edit]
The results obtained from negative sample (left curve) overlap with the results obtained from positive samples (right curve). By moving the result cutoff value (vertical bar), the rate of false positives (FP) can be decreased, at the cost of raising the number of false negatives (FN), or vice versa (TP = True Positives, TPR = True Positive Rate, FPR = False Positive Rate, TN = True Negatives).
A perfect test would have zero false positives and zero false negatives. However, statistical methods are probabilistic, and it cannot be known for certain whether statistical conclusions are correct. Whenever there is uncertainty, there is the possibility of making an error. Considering this nature of statistics science, all statistical hypothesis tests have a probability of making type I and type II errors.[6]
- The type I error rate is the probability of rejecting the null hypothesis given that it is true. The test is designed to keep the type I error rate below a prespecified bound called the significance level, usually denoted by the Greek letter α (alpha) and is also called the alpha level. Usually, the significance level is set to 0.05 (5%), implying that it is acceptable to have a 5% probability of incorrectly rejecting the true null hypothesis.[7]
- The rate of the type II error is denoted by the Greek letter β (beta) and related to the power of a test, which equals 1−β.[8]
These two types of error rates are traded off against each other: for any given sample set, the effort to reduce one type of error generally results in increasing the other type of error.[9]
The quality of hypothesis test[edit]
The same idea can be expressed in terms of the rate of correct results and therefore used to minimize error rates and improve the quality of hypothesis test. To reduce the probability of committing a type I error, making the alpha value more stringent is quite simple and efficient. To decrease the probability of committing a type II error, which is closely associated with analyses’ power, either increasing the test’s sample size or relaxing the alpha level could increase the analyses’ power.[10] A test statistic is robust if the type I error rate is controlled.
Varying different threshold (cut-off) value could also be used to make the test either more specific or more sensitive, which in turn elevates the test quality. For example, imagine a medical test, in which an experimenter might measure the concentration of a certain protein in the blood sample. The experimenter could adjust the threshold (black vertical line in the figure) and people would be diagnosed as having diseases if any number is detected above this certain threshold. According to the image, changing the threshold would result in changes in false positives and false negatives, corresponding to movement on the curve.[11]
Example[edit]
Since in a real experiment it is impossible to avoid all type I and type II errors, it is important to consider the amount of risk one is willing to take to falsely reject H0 or accept H0. The solution to this question would be to report the p-value or significance level α of the statistic. For example, if the p-value of a test statistic result is estimated at 0.0596, then there is a probability of 5.96% that we falsely reject H0. Or, if we say, the statistic is performed at level α, like 0.05, then we allow to falsely reject H0 at 5%. A significance level α of 0.05 is relatively common, but there is no general rule that fits all scenarios.
Vehicle speed measuring[edit]
The speed limit of a freeway in the United States is 120 kilometers per hour. A device is set to measure the speed of passing vehicles. Suppose that the device will conduct three measurements of the speed of a passing vehicle, recording as a random sample X1, X2, X3. The traffic police will or will not fine the drivers depending on the average speed 

In addition, we suppose that the measurements X1, X2, X3 are modeled as normal distribution N(μ,4). Then, T should follow N(μ,4/3) and the parameter μ represents the true speed of passing vehicle. In this experiment, the null hypothesis H0 and the alternative hypothesis H1 should be
H0: μ=120 against H1: μ1>120.
If we perform the statistic level at α=0.05, then a critical value c should be calculated to solve

According to change-of-units rule for the normal distribution. Referring to Z-table, we can get

Here, the critical region. That is to say, if the recorded speed of a vehicle is greater than critical value 121.9, the driver will be fined. However, there are still 5% of the drivers are falsely fined since the recorded average speed is greater than 121.9 but the true speed does not pass 120, which we say, a type I error.
The type II error corresponds to the case that the true speed of a vehicle is over 120 kilometers per hour but the driver is not fined. For example, if the true speed of a vehicle μ=125, the probability that the driver is not fined can be calculated as

which means, if the true speed of a vehicle is 125, the driver has the probability of 0.36% to avoid the fine when the statistic is performed at level 125 since the recorded average speed is lower than 121.9. If the true speed is closer to 121.9 than 125, then the probability of avoiding the fine will also be higher.
The tradeoffs between type I error and type II error should also be considered. That is, in this case, if the traffic police do not want to falsely fine innocent drivers, the level α can be set to a smaller value, like 0.01. However, if that is the case, more drivers whose true speed is over 120 kilometers per hour, like 125, would be more likely to avoid the fine.
Etymology[edit]
In 1928, Jerzy Neyman (1894–1981) and Egon Pearson (1895–1980), both eminent statisticians, discussed the problems associated with «deciding whether or not a particular sample may be judged as likely to have been randomly drawn from a certain population»:[12] and, as Florence Nightingale David remarked, «it is necessary to remember the adjective ‘random’ [in the term ‘random sample’] should apply to the method of drawing the sample and not to the sample itself».[13]
They identified «two sources of error», namely:
- (a) the error of rejecting a hypothesis that should have not been rejected, and
- (b) the error of failing to reject a hypothesis that should have been rejected.
In 1930, they elaborated on these two sources of error, remarking that:
…in testing hypotheses two considerations must be kept in view, we must be able to reduce the chance of rejecting a true hypothesis to as low a value as desired; the test must be so devised that it will reject the hypothesis tested when it is likely to be false.
In 1933, they observed that these «problems are rarely presented in such a form that we can discriminate with certainty between the true and false hypothesis» . They also noted that, in deciding whether to fail to reject, or reject a particular hypothesis amongst a «set of alternative hypotheses», H1, H2…, it was easy to make an error:
…[and] these errors will be of two kinds:
- (I) we reject H0 [i.e., the hypothesis to be tested] when it is true,[14]
- (II) we fail to reject H0 when some alternative hypothesis HA or H1 is true. (There are various notations for the alternative).
In all of the papers co-written by Neyman and Pearson the expression H0 always signifies «the hypothesis to be tested».
In the same paper they call these two sources of error, errors of type I and errors of type II respectively.[15]
[edit]
Null hypothesis[edit]
It is standard practice for statisticians to conduct tests in order to determine whether or not a «speculative hypothesis» concerning the observed phenomena of the world (or its inhabitants) can be supported. The results of such testing determine whether a particular set of results agrees reasonably (or does not agree) with the speculated hypothesis.
On the basis that it is always assumed, by statistical convention, that the speculated hypothesis is wrong, and the so-called «null hypothesis» that the observed phenomena simply occur by chance (and that, as a consequence, the speculated agent has no effect) – the test will determine whether this hypothesis is right or wrong. This is why the hypothesis under test is often called the null hypothesis (most likely, coined by Fisher (1935, p. 19)), because it is this hypothesis that is to be either nullified or not nullified by the test. When the null hypothesis is nullified, it is possible to conclude that data support the «alternative hypothesis» (which is the original speculated one).
The consistent application by statisticians of Neyman and Pearson’s convention of representing «the hypothesis to be tested» (or «the hypothesis to be nullified») with the expression H0 has led to circumstances where many understand the term «the null hypothesis» as meaning «the nil hypothesis» – a statement that the results in question have arisen through chance. This is not necessarily the case – the key restriction, as per Fisher (1966), is that «the null hypothesis must be exact, that is free from vagueness and ambiguity, because it must supply the basis of the ‘problem of distribution,’ of which the test of significance is the solution.»[16] As a consequence of this, in experimental science the null hypothesis is generally a statement that a particular treatment has no effect; in observational science, it is that there is no difference between the value of a particular measured variable, and that of an experimental prediction.[citation needed]
Statistical significance[edit]
If the probability of obtaining a result as extreme as the one obtained, supposing that the null hypothesis were true, is lower than a pre-specified cut-off probability (for example, 5%), then the result is said to be statistically significant and the null hypothesis is rejected.
British statistician Sir Ronald Aylmer Fisher (1890–1962) stressed that the «null hypothesis»:
… is never proved or established, but is possibly disproved, in the course of experimentation. Every experiment may be said to exist only in order to give the facts a chance of disproving the null hypothesis.
— Fisher, 1935, p.19
Application domains[edit]
Medicine[edit]
In the practice of medicine, the differences between the applications of screening and testing are considerable.
Medical screening[edit]
Screening involves relatively cheap tests that are given to large populations, none of whom manifest any clinical indication of disease (e.g., Pap smears).
Testing involves far more expensive, often invasive, procedures that are given only to those who manifest some clinical indication of disease, and are most often applied to confirm a suspected diagnosis.
For example, most states in the USA require newborns to be screened for phenylketonuria and hypothyroidism, among other congenital disorders.
Hypothesis: «The newborns have phenylketonuria and hypothyroidism»
Null Hypothesis (H0): «The newborns do not have phenylketonuria and hypothyroidism»,
Type I error (false positive): The true fact is that the newborns do not have phenylketonuria and hypothyroidism but we consider they have the disorders according to the data.
Type II error (false negative): The true fact is that the newborns have phenylketonuria and hypothyroidism but we consider they do not have the disorders according to the data.
Although they display a high rate of false positives, the screening tests are considered valuable because they greatly increase the likelihood of detecting these disorders at a far earlier stage.
The simple blood tests used to screen possible blood donors for HIV and hepatitis have a significant rate of false positives; however, physicians use much more expensive and far more precise tests to determine whether a person is actually infected with either of these viruses.
Perhaps the most widely discussed false positives in medical screening come from the breast cancer screening procedure mammography. The US rate of false positive mammograms is up to 15%, the highest in world. One consequence of the high false positive rate in the US is that, in any 10-year period, half of the American women screened receive a false positive mammogram. False positive mammograms are costly, with over $100 million spent annually in the U.S. on follow-up testing and treatment. They also cause women unneeded anxiety. As a result of the high false positive rate in the US, as many as 90–95% of women who get a positive mammogram do not have the condition. The lowest rate in the world is in the Netherlands, 1%. The lowest rates are generally in Northern Europe where mammography films are read twice and a high threshold for additional testing is set (the high threshold decreases the power of the test).
The ideal population screening test would be cheap, easy to administer, and produce zero false-negatives, if possible. Such tests usually produce more false-positives, which can subsequently be sorted out by more sophisticated (and expensive) testing.
Medical testing[edit]
False negatives and false positives are significant issues in medical testing.
Hypothesis: «The patients have the specific disease».
Null hypothesis (H0): «The patients do not have the specific disease».
Type I error (false positive): «The true fact is that the patients do not have a specific disease but the physicians judges the patients was ill according to the test reports».
False positives can also produce serious and counter-intuitive problems when the condition being searched for is rare, as in screening. If a test has a false positive rate of one in ten thousand, but only one in a million samples (or people) is a true positive, most of the positives detected by that test will be false. The probability that an observed positive result is a false positive may be calculated using Bayes’ theorem.
Type II error (false negative): «The true fact is that the disease is actually present but the test reports provide a falsely reassuring message to patients and physicians that the disease is absent».
False negatives produce serious and counter-intuitive problems, especially when the condition being searched for is common. If a test with a false negative rate of only 10% is used to test a population with a true occurrence rate of 70%, many of the negatives detected by the test will be false.
This sometimes leads to inappropriate or inadequate treatment of both the patient and their disease. A common example is relying on cardiac stress tests to detect coronary atherosclerosis, even though cardiac stress tests are known to only detect limitations of coronary artery blood flow due to advanced stenosis.
Biometrics[edit]
Biometric matching, such as for fingerprint recognition, facial recognition or iris recognition, is susceptible to type I and type II errors.
Hypothesis: «The input does not identify someone in the searched list of people»
Null hypothesis: «The input does identify someone in the searched list of people»
Type I error (false reject rate): «The true fact is that the person is someone in the searched list but the system concludes that the person is not according to the data».
Type II error (false match rate): «The true fact is that the person is not someone in the searched list but the system concludes that the person is someone whom we are looking for according to the data».
The probability of type I errors is called the «false reject rate» (FRR) or false non-match rate (FNMR), while the probability of type II errors is called the «false accept rate» (FAR) or false match rate (FMR).
If the system is designed to rarely match suspects then the probability of type II errors can be called the «false alarm rate». On the other hand, if the system is used for validation (and acceptance is the norm) then the FAR is a measure of system security, while the FRR measures user inconvenience level.
Security screening[edit]
False positives are routinely found every day in airport security screening, which are ultimately visual inspection systems. The installed security alarms are intended to prevent weapons being brought onto aircraft; yet they are often set to such high sensitivity that they alarm many times a day for minor items, such as keys, belt buckles, loose change, mobile phones, and tacks in shoes.
Here, the null hypothesis is that the item is not a weapon, while the alternative hypothesis is that the item is a weapon.
A type I error (false positive): «The true fact is that the item is not a weapon but the system still alarms».
Type II error (false negative) «The true fact is that the item is a weapon but the system keeps silent at this time».
The ratio of false positives (identifying an innocent traveler as a terrorist) to true positives (detecting a would-be terrorist) is, therefore, very high; and because almost every alarm is a false positive, the positive predictive value of these screening tests is very low.
The relative cost of false results determines the likelihood that test creators allow these events to occur. As the cost of a false negative in this scenario is extremely high (not detecting a bomb being brought onto a plane could result in hundreds of deaths) whilst the cost of a false positive is relatively low (a reasonably simple further inspection) the most appropriate test is one with a low statistical specificity but high statistical sensitivity (one that allows a high rate of false positives in return for minimal false negatives).
Computers[edit]
The notions of false positives and false negatives have a wide currency in the realm of computers and computer applications, including computer security, spam filtering, Malware, Optical character recognition and many others.
For example, in the case of spam filtering the hypothesis here is that the message is a spam.
Thus, null hypothesis: «The message is not a spam».
Type I error (false positive): «Spam filtering or spam blocking techniques wrongly classify a legitimate email message as spam and, as a result, interferes with its delivery».
While most anti-spam tactics can block or filter a high percentage of unwanted emails, doing so without creating significant false-positive results is a much more demanding task.
Type II error (false negative): «Spam email is not detected as spam, but is classified as non-spam». A low number of false negatives is an indicator of the efficiency of spam filtering.
See also[edit]
- Binary classification
- Detection theory
- Egon Pearson
- Ethics in mathematics
- False positive paradox
- False discovery rate
- Family-wise error rate
- Information retrieval performance measures
- Neyman–Pearson lemma
- Null hypothesis
- Probability of a hypothesis for Bayesian inference
- Precision and recall
- Prosecutor’s fallacy
- Prozone phenomenon
- Receiver operating characteristic
- Sensitivity and specificity
- Statisticians’ and engineers’ cross-reference of statistical terms
- Testing hypotheses suggested by the data
- Type III error
References[edit]
- ^ «Type I Error and Type II Error». explorable.com. Retrieved 14 December 2019.
- ^ Chow, Y. W.; Pietranico, R.; Mukerji, A. (27 October 1975). «Studies of oxygen binding energy to hemoglobin molecule». Biochemical and Biophysical Research Communications. 66 (4): 1424–1431. doi:10.1016/0006-291x(75)90518-5. ISSN 0006-291X. PMID 6.
- ^ A modern introduction to probability and statistics : understanding why and how. Dekking, Michel, 1946-. London: Springer. 2005. ISBN 978-1-85233-896-1. OCLC 262680588.
{{cite book}}: CS1 maint: others (link) - ^ A modern introduction to probability and statistics : understanding why and how. Dekking, Michel, 1946-. London: Springer. 2005. ISBN 978-1-85233-896-1. OCLC 262680588.
{{cite book}}: CS1 maint: others (link) - ^ Sheskin, David (2004). Handbook of Parametric and Nonparametric Statistical Procedures. CRC Press. p. 54. ISBN 1584884401.
- ^ Smith, R. J.; Bryant, R. G. (27 October 1975). «Metal substitutions incarbonic anhydrase: a halide ion probe study». Biochemical and Biophysical Research Communications. 66 (4): 1281–1286. doi:10.1016/0006-291x(75)90498-2. ISSN 0006-291X. PMC 9650581. PMID 3.
- ^ Lindenmayer, David. (2005). Practical conservation biology. Burgman, Mark A. Collingwood, Vic.: CSIRO Pub. ISBN 0-643-09310-9. OCLC 65216357.
- ^ Chow, Y. W.; Pietranico, R.; Mukerji, A. (27 October 1975). «Studies of oxygen binding energy to hemoglobin molecule». Biochemical and Biophysical Research Communications. 66 (4): 1424–1431. doi:10.1016/0006-291x(75)90518-5. ISSN 0006-291X. PMID 6.
- ^ Smith, R. J.; Bryant, R. G. (27 October 1975). «Metal substitutions incarbonic anhydrase: a halide ion probe study». Biochemical and Biophysical Research Communications. 66 (4): 1281–1286. doi:10.1016/0006-291x(75)90498-2. ISSN 0006-291X. PMC 9650581. PMID 3.
- ^ Smith, R. J.; Bryant, R. G. (27 October 1975). «Metal substitutions incarbonic anhydrase: a halide ion probe study». Biochemical and Biophysical Research Communications. 66 (4): 1281–1286. doi:10.1016/0006-291x(75)90498-2. ISSN 0006-291X. PMC 9650581. PMID 3.
- ^ Moroi, K.; Sato, T. (15 August 1975). «Comparison between procaine and isocarboxazid metabolism in vitro by a liver microsomal amidase-esterase». Biochemical Pharmacology. 24 (16): 1517–1521. doi:10.1016/0006-2952(75)90029-5. ISSN 1873-2968. PMID 8.
- ^ NEYMAN, J.; PEARSON, E. S. (1928). «On the Use and Interpretation of Certain Test Criteria for Purposes of Statistical Inference Part I». Biometrika. 20A (1–2): 175–240. doi:10.1093/biomet/20a.1-2.175. ISSN 0006-3444.
- ^ C.I.K.F. (July 1951). «Probability Theory for Statistical Methods. By F. N. David. [Pp. ix + 230. Cambridge University Press. 1949. Price 155.]». Journal of the Staple Inn Actuarial Society. 10 (3): 243–244. doi:10.1017/s0020269x00004564. ISSN 0020-269X.
- ^ Note that the subscript in the expression H0 is a zero (indicating null), and is not an «O» (indicating original).
- ^ Neyman, J.; Pearson, E. S. (30 October 1933). «The testing of statistical hypotheses in relation to probabilities a priori». Mathematical Proceedings of the Cambridge Philosophical Society. 29 (4): 492–510. Bibcode:1933PCPS…29..492N. doi:10.1017/s030500410001152x. ISSN 0305-0041. S2CID 119855116.
- ^ Fisher, R.A. (1966). The design of experiments. 8th edition. Hafner:Edinburgh.
Bibliography[edit]
- Betz, M.A. & Gabriel, K.R., «Type IV Errors and Analysis of Simple Effects», Journal of Educational Statistics, Vol.3, No.2, (Summer 1978), pp. 121–144.
- David, F.N., «A Power Function for Tests of Randomness in a Sequence of Alternatives», Biometrika, Vol.34, Nos.3/4, (December 1947), pp. 335–339.
- Fisher, R.A., The Design of Experiments, Oliver & Boyd (Edinburgh), 1935.
- Gambrill, W., «False Positives on Newborns’ Disease Tests Worry Parents», Health Day, (5 June 2006). [1] Archived 17 May 2018 at the Wayback Machine
- Kaiser, H.F., «Directional Statistical Decisions», Psychological Review, Vol.67, No.3, (May 1960), pp. 160–167.
- Kimball, A.W., «Errors of the Third Kind in Statistical Consulting», Journal of the American Statistical Association, Vol.52, No.278, (June 1957), pp. 133–142.
- Lubin, A., «The Interpretation of Significant Interaction», Educational and Psychological Measurement, Vol.21, No.4, (Winter 1961), pp. 807–817.
- Marascuilo, L.A. & Levin, J.R., «Appropriate Post Hoc Comparisons for Interaction and nested Hypotheses in Analysis of Variance Designs: The Elimination of Type-IV Errors», American Educational Research Journal, Vol.7., No.3, (May 1970), pp. 397–421.
- Mitroff, I.I. & Featheringham, T.R., «On Systemic Problem Solving and the Error of the Third Kind», Behavioral Science, Vol.19, No.6, (November 1974), pp. 383–393.
- Mosteller, F., «A k-Sample Slippage Test for an Extreme Population», The Annals of Mathematical Statistics, Vol.19, No.1, (March 1948), pp. 58–65.
- Moulton, R.T., «Network Security», Datamation, Vol.29, No.7, (July 1983), pp. 121–127.
- Raiffa, H., Decision Analysis: Introductory Lectures on Choices Under Uncertainty, Addison–Wesley, (Reading), 1968.
External links[edit]
- Bias and Confounding – presentation by Nigel Paneth, Graduate School of Public Health, University of Pittsburgh
This article is about erroneous outcomes of statistical tests. For closely related concepts in binary classification and testing generally, see false positives and false negatives.
In statistical hypothesis testing, a type I error is the mistaken rejection of an actually true null hypothesis (also known as a «false positive» finding or conclusion; example: «an innocent person is convicted»), while a type II error is the failure to reject a null hypothesis that is actually false (also known as a «false negative» finding or conclusion; example: «a guilty person is not convicted»).[1] Much of statistical theory revolves around the minimization of one or both of these errors, though the complete elimination of either is a statistical impossibility if the outcome is not determined by a known, observable causal process.
By selecting a low threshold (cut-off) value and modifying the alpha (α) level, the quality of the hypothesis test can be increased.[2] The knowledge of type I errors and type II errors is widely used in medical science, biometrics and computer science.[clarification needed]
Intuitively, type I errors can be thought of as errors of commission, i.e. the researcher unluckily concludes that something is the fact. For instance, consider a study where researchers compare a drug with a placebo. If the patients who are given the drug get better than the patients given the placebo by chance, it may appear that the drug is effective, but in fact the conclusion is incorrect.
In reverse, type II errors are errors of omission. In the example above, if the patients who got the drug did not get better at a higher rate than the ones who got the placebo, but this was a random fluke, that would be a type II error. The consequence of a type II error depends on the size and direction of the missed determination and the circumstances. An expensive cure for one in a million patients may be inconsequential even if it truly is a cure.
Definition[edit]
Statistical background[edit]
In statistical test theory, the notion of a statistical error is an integral part of hypothesis testing. The test goes about choosing about two competing propositions called null hypothesis, denoted by H0 and alternative hypothesis, denoted by H1. This is conceptually similar to the judgement in a court trial. The null hypothesis corresponds to the position of the defendant: just as he is presumed to be innocent until proven guilty, so is the null hypothesis presumed to be true until the data provide convincing evidence against it. The alternative hypothesis corresponds to the position against the defendant. Specifically, the null hypothesis also involves the absence of a difference or the absence of an association. Thus, the null hypothesis can never be that there is a difference or an association.
If the result of the test corresponds with reality, then a correct decision has been made. However, if the result of the test does not correspond with reality, then an error has occurred. There are two situations in which the decision is wrong. The null hypothesis may be true, whereas we reject H0. On the other hand, the alternative hypothesis H1 may be true, whereas we do not reject H0. Two types of error are distinguished: type I error and type II error.[3]
Type I error[edit]
The first kind of error is the mistaken rejection of a null hypothesis as the result of a test procedure. This kind of error is called a type I error (false positive) and is sometimes called an error of the first kind. In terms of the courtroom example, a type I error corresponds to convicting an innocent defendant.
Type II error[edit]
The second kind of error is the mistaken failure to reject the null hypothesis as the result of a test procedure. This sort of error is called a type II error (false negative) and is also referred to as an error of the second kind. In terms of the courtroom example, a type II error corresponds to acquitting a criminal.[4]
Crossover error rate[edit]
The crossover error rate (CER) is the point at which type I errors and type II errors are equal. A system with a lower CER value provides more accuracy than a system with a higher CER value.
False positive and false negative[edit]
In terms of false positives and false negatives, a positive result corresponds to rejecting the null hypothesis, while a negative result corresponds to failing to reject the null hypothesis; «false» means the conclusion drawn is incorrect. Thus, a type I error is equivalent to a false positive, and a type II error is equivalent to a false negative.
Table of error types[edit]
Tabularised relations between truth/falseness of the null hypothesis and outcomes of the test:[5]
| Table of error types | Null hypothesis (H0) is |
||
|---|---|---|---|
| True | False | ||
| Decision about null hypothesis (H0) |
Don’t reject |
Correct inference (true negative) (probability = 1−α) |
Type II error (false negative) (probability = β) |
| Reject | Type I error (false positive) (probability = α) |
Correct inference (true positive) (probability = 1−β) |
Error rate[edit]
The results obtained from negative sample (left curve) overlap with the results obtained from positive samples (right curve). By moving the result cutoff value (vertical bar), the rate of false positives (FP) can be decreased, at the cost of raising the number of false negatives (FN), or vice versa (TP = True Positives, TPR = True Positive Rate, FPR = False Positive Rate, TN = True Negatives).
A perfect test would have zero false positives and zero false negatives. However, statistical methods are probabilistic, and it cannot be known for certain whether statistical conclusions are correct. Whenever there is uncertainty, there is the possibility of making an error. Considering this nature of statistics science, all statistical hypothesis tests have a probability of making type I and type II errors.[6]
- The type I error rate is the probability of rejecting the null hypothesis given that it is true. The test is designed to keep the type I error rate below a prespecified bound called the significance level, usually denoted by the Greek letter α (alpha) and is also called the alpha level. Usually, the significance level is set to 0.05 (5%), implying that it is acceptable to have a 5% probability of incorrectly rejecting the true null hypothesis.[7]
- The rate of the type II error is denoted by the Greek letter β (beta) and related to the power of a test, which equals 1−β.[8]
These two types of error rates are traded off against each other: for any given sample set, the effort to reduce one type of error generally results in increasing the other type of error.[9]
The quality of hypothesis test[edit]
The same idea can be expressed in terms of the rate of correct results and therefore used to minimize error rates and improve the quality of hypothesis test. To reduce the probability of committing a type I error, making the alpha value more stringent is quite simple and efficient. To decrease the probability of committing a type II error, which is closely associated with analyses’ power, either increasing the test’s sample size or relaxing the alpha level could increase the analyses’ power.[10] A test statistic is robust if the type I error rate is controlled.
Varying different threshold (cut-off) value could also be used to make the test either more specific or more sensitive, which in turn elevates the test quality. For example, imagine a medical test, in which an experimenter might measure the concentration of a certain protein in the blood sample. The experimenter could adjust the threshold (black vertical line in the figure) and people would be diagnosed as having diseases if any number is detected above this certain threshold. According to the image, changing the threshold would result in changes in false positives and false negatives, corresponding to movement on the curve.[11]
Example[edit]
Since in a real experiment it is impossible to avoid all type I and type II errors, it is important to consider the amount of risk one is willing to take to falsely reject H0 or accept H0. The solution to this question would be to report the p-value or significance level α of the statistic. For example, if the p-value of a test statistic result is estimated at 0.0596, then there is a probability of 5.96% that we falsely reject H0. Or, if we say, the statistic is performed at level α, like 0.05, then we allow to falsely reject H0 at 5%. A significance level α of 0.05 is relatively common, but there is no general rule that fits all scenarios.
Vehicle speed measuring[edit]
The speed limit of a freeway in the United States is 120 kilometers per hour. A device is set to measure the speed of passing vehicles. Suppose that the device will conduct three measurements of the speed of a passing vehicle, recording as a random sample X1, X2, X3. The traffic police will or will not fine the drivers depending on the average speed 

In addition, we suppose that the measurements X1, X2, X3 are modeled as normal distribution N(μ,4). Then, T should follow N(μ,4/3) and the parameter μ represents the true speed of passing vehicle. In this experiment, the null hypothesis H0 and the alternative hypothesis H1 should be
H0: μ=120 against H1: μ1>120.
If we perform the statistic level at α=0.05, then a critical value c should be calculated to solve

According to change-of-units rule for the normal distribution. Referring to Z-table, we can get

Here, the critical region. That is to say, if the recorded speed of a vehicle is greater than critical value 121.9, the driver will be fined. However, there are still 5% of the drivers are falsely fined since the recorded average speed is greater than 121.9 but the true speed does not pass 120, which we say, a type I error.
The type II error corresponds to the case that the true speed of a vehicle is over 120 kilometers per hour but the driver is not fined. For example, if the true speed of a vehicle μ=125, the probability that the driver is not fined can be calculated as

which means, if the true speed of a vehicle is 125, the driver has the probability of 0.36% to avoid the fine when the statistic is performed at level 125 since the recorded average speed is lower than 121.9. If the true speed is closer to 121.9 than 125, then the probability of avoiding the fine will also be higher.
The tradeoffs between type I error and type II error should also be considered. That is, in this case, if the traffic police do not want to falsely fine innocent drivers, the level α can be set to a smaller value, like 0.01. However, if that is the case, more drivers whose true speed is over 120 kilometers per hour, like 125, would be more likely to avoid the fine.
Etymology[edit]
In 1928, Jerzy Neyman (1894–1981) and Egon Pearson (1895–1980), both eminent statisticians, discussed the problems associated with «deciding whether or not a particular sample may be judged as likely to have been randomly drawn from a certain population»:[12] and, as Florence Nightingale David remarked, «it is necessary to remember the adjective ‘random’ [in the term ‘random sample’] should apply to the method of drawing the sample and not to the sample itself».[13]
They identified «two sources of error», namely:
- (a) the error of rejecting a hypothesis that should have not been rejected, and
- (b) the error of failing to reject a hypothesis that should have been rejected.
In 1930, they elaborated on these two sources of error, remarking that:
…in testing hypotheses two considerations must be kept in view, we must be able to reduce the chance of rejecting a true hypothesis to as low a value as desired; the test must be so devised that it will reject the hypothesis tested when it is likely to be false.
In 1933, they observed that these «problems are rarely presented in such a form that we can discriminate with certainty between the true and false hypothesis» . They also noted that, in deciding whether to fail to reject, or reject a particular hypothesis amongst a «set of alternative hypotheses», H1, H2…, it was easy to make an error:
…[and] these errors will be of two kinds:
- (I) we reject H0 [i.e., the hypothesis to be tested] when it is true,[14]
- (II) we fail to reject H0 when some alternative hypothesis HA or H1 is true. (There are various notations for the alternative).
In all of the papers co-written by Neyman and Pearson the expression H0 always signifies «the hypothesis to be tested».
In the same paper they call these two sources of error, errors of type I and errors of type II respectively.[15]
[edit]
Null hypothesis[edit]
It is standard practice for statisticians to conduct tests in order to determine whether or not a «speculative hypothesis» concerning the observed phenomena of the world (or its inhabitants) can be supported. The results of such testing determine whether a particular set of results agrees reasonably (or does not agree) with the speculated hypothesis.
On the basis that it is always assumed, by statistical convention, that the speculated hypothesis is wrong, and the so-called «null hypothesis» that the observed phenomena simply occur by chance (and that, as a consequence, the speculated agent has no effect) – the test will determine whether this hypothesis is right or wrong. This is why the hypothesis under test is often called the null hypothesis (most likely, coined by Fisher (1935, p. 19)), because it is this hypothesis that is to be either nullified or not nullified by the test. When the null hypothesis is nullified, it is possible to conclude that data support the «alternative hypothesis» (which is the original speculated one).
The consistent application by statisticians of Neyman and Pearson’s convention of representing «the hypothesis to be tested» (or «the hypothesis to be nullified») with the expression H0 has led to circumstances where many understand the term «the null hypothesis» as meaning «the nil hypothesis» – a statement that the results in question have arisen through chance. This is not necessarily the case – the key restriction, as per Fisher (1966), is that «the null hypothesis must be exact, that is free from vagueness and ambiguity, because it must supply the basis of the ‘problem of distribution,’ of which the test of significance is the solution.»[16] As a consequence of this, in experimental science the null hypothesis is generally a statement that a particular treatment has no effect; in observational science, it is that there is no difference between the value of a particular measured variable, and that of an experimental prediction.[citation needed]
Statistical significance[edit]
If the probability of obtaining a result as extreme as the one obtained, supposing that the null hypothesis were true, is lower than a pre-specified cut-off probability (for example, 5%), then the result is said to be statistically significant and the null hypothesis is rejected.
British statistician Sir Ronald Aylmer Fisher (1890–1962) stressed that the «null hypothesis»:
… is never proved or established, but is possibly disproved, in the course of experimentation. Every experiment may be said to exist only in order to give the facts a chance of disproving the null hypothesis.
— Fisher, 1935, p.19
Application domains[edit]
Medicine[edit]
In the practice of medicine, the differences between the applications of screening and testing are considerable.
Medical screening[edit]
Screening involves relatively cheap tests that are given to large populations, none of whom manifest any clinical indication of disease (e.g., Pap smears).
Testing involves far more expensive, often invasive, procedures that are given only to those who manifest some clinical indication of disease, and are most often applied to confirm a suspected diagnosis.
For example, most states in the USA require newborns to be screened for phenylketonuria and hypothyroidism, among other congenital disorders.
Hypothesis: «The newborns have phenylketonuria and hypothyroidism»
Null Hypothesis (H0): «The newborns do not have phenylketonuria and hypothyroidism»,
Type I error (false positive): The true fact is that the newborns do not have phenylketonuria and hypothyroidism but we consider they have the disorders according to the data.
Type II error (false negative): The true fact is that the newborns have phenylketonuria and hypothyroidism but we consider they do not have the disorders according to the data.
Although they display a high rate of false positives, the screening tests are considered valuable because they greatly increase the likelihood of detecting these disorders at a far earlier stage.
The simple blood tests used to screen possible blood donors for HIV and hepatitis have a significant rate of false positives; however, physicians use much more expensive and far more precise tests to determine whether a person is actually infected with either of these viruses.
Perhaps the most widely discussed false positives in medical screening come from the breast cancer screening procedure mammography. The US rate of false positive mammograms is up to 15%, the highest in world. One consequence of the high false positive rate in the US is that, in any 10-year period, half of the American women screened receive a false positive mammogram. False positive mammograms are costly, with over $100 million spent annually in the U.S. on follow-up testing and treatment. They also cause women unneeded anxiety. As a result of the high false positive rate in the US, as many as 90–95% of women who get a positive mammogram do not have the condition. The lowest rate in the world is in the Netherlands, 1%. The lowest rates are generally in Northern Europe where mammography films are read twice and a high threshold for additional testing is set (the high threshold decreases the power of the test).
The ideal population screening test would be cheap, easy to administer, and produce zero false-negatives, if possible. Such tests usually produce more false-positives, which can subsequently be sorted out by more sophisticated (and expensive) testing.
Medical testing[edit]
False negatives and false positives are significant issues in medical testing.
Hypothesis: «The patients have the specific disease».
Null hypothesis (H0): «The patients do not have the specific disease».
Type I error (false positive): «The true fact is that the patients do not have a specific disease but the physicians judges the patients was ill according to the test reports».
False positives can also produce serious and counter-intuitive problems when the condition being searched for is rare, as in screening. If a test has a false positive rate of one in ten thousand, but only one in a million samples (or people) is a true positive, most of the positives detected by that test will be false. The probability that an observed positive result is a false positive may be calculated using Bayes’ theorem.
Type II error (false negative): «The true fact is that the disease is actually present but the test reports provide a falsely reassuring message to patients and physicians that the disease is absent».
False negatives produce serious and counter-intuitive problems, especially when the condition being searched for is common. If a test with a false negative rate of only 10% is used to test a population with a true occurrence rate of 70%, many of the negatives detected by the test will be false.
This sometimes leads to inappropriate or inadequate treatment of both the patient and their disease. A common example is relying on cardiac stress tests to detect coronary atherosclerosis, even though cardiac stress tests are known to only detect limitations of coronary artery blood flow due to advanced stenosis.
Biometrics[edit]
Biometric matching, such as for fingerprint recognition, facial recognition or iris recognition, is susceptible to type I and type II errors.
Hypothesis: «The input does not identify someone in the searched list of people»
Null hypothesis: «The input does identify someone in the searched list of people»
Type I error (false reject rate): «The true fact is that the person is someone in the searched list but the system concludes that the person is not according to the data».
Type II error (false match rate): «The true fact is that the person is not someone in the searched list but the system concludes that the person is someone whom we are looking for according to the data».
The probability of type I errors is called the «false reject rate» (FRR) or false non-match rate (FNMR), while the probability of type II errors is called the «false accept rate» (FAR) or false match rate (FMR).
If the system is designed to rarely match suspects then the probability of type II errors can be called the «false alarm rate». On the other hand, if the system is used for validation (and acceptance is the norm) then the FAR is a measure of system security, while the FRR measures user inconvenience level.
Security screening[edit]
False positives are routinely found every day in airport security screening, which are ultimately visual inspection systems. The installed security alarms are intended to prevent weapons being brought onto aircraft; yet they are often set to such high sensitivity that they alarm many times a day for minor items, such as keys, belt buckles, loose change, mobile phones, and tacks in shoes.
Here, the null hypothesis is that the item is not a weapon, while the alternative hypothesis is that the item is a weapon.
A type I error (false positive): «The true fact is that the item is not a weapon but the system still alarms».
Type II error (false negative) «The true fact is that the item is a weapon but the system keeps silent at this time».
The ratio of false positives (identifying an innocent traveler as a terrorist) to true positives (detecting a would-be terrorist) is, therefore, very high; and because almost every alarm is a false positive, the positive predictive value of these screening tests is very low.
The relative cost of false results determines the likelihood that test creators allow these events to occur. As the cost of a false negative in this scenario is extremely high (not detecting a bomb being brought onto a plane could result in hundreds of deaths) whilst the cost of a false positive is relatively low (a reasonably simple further inspection) the most appropriate test is one with a low statistical specificity but high statistical sensitivity (one that allows a high rate of false positives in return for minimal false negatives).
Computers[edit]
The notions of false positives and false negatives have a wide currency in the realm of computers and computer applications, including computer security, spam filtering, Malware, Optical character recognition and many others.
For example, in the case of spam filtering the hypothesis here is that the message is a spam.
Thus, null hypothesis: «The message is not a spam».
Type I error (false positive): «Spam filtering or spam blocking techniques wrongly classify a legitimate email message as spam and, as a result, interferes with its delivery».
While most anti-spam tactics can block or filter a high percentage of unwanted emails, doing so without creating significant false-positive results is a much more demanding task.
Type II error (false negative): «Spam email is not detected as spam, but is classified as non-spam». A low number of false negatives is an indicator of the efficiency of spam filtering.
See also[edit]
- Binary classification
- Detection theory
- Egon Pearson
- Ethics in mathematics
- False positive paradox
- False discovery rate
- Family-wise error rate
- Information retrieval performance measures
- Neyman–Pearson lemma
- Null hypothesis
- Probability of a hypothesis for Bayesian inference
- Precision and recall
- Prosecutor’s fallacy
- Prozone phenomenon
- Receiver operating characteristic
- Sensitivity and specificity
- Statisticians’ and engineers’ cross-reference of statistical terms
- Testing hypotheses suggested by the data
- Type III error
References[edit]
- ^ «Type I Error and Type II Error». explorable.com. Retrieved 14 December 2019.
- ^ Chow, Y. W.; Pietranico, R.; Mukerji, A. (27 October 1975). «Studies of oxygen binding energy to hemoglobin molecule». Biochemical and Biophysical Research Communications. 66 (4): 1424–1431. doi:10.1016/0006-291x(75)90518-5. ISSN 0006-291X. PMID 6.
- ^ A modern introduction to probability and statistics : understanding why and how. Dekking, Michel, 1946-. London: Springer. 2005. ISBN 978-1-85233-896-1. OCLC 262680588.
{{cite book}}: CS1 maint: others (link) - ^ A modern introduction to probability and statistics : understanding why and how. Dekking, Michel, 1946-. London: Springer. 2005. ISBN 978-1-85233-896-1. OCLC 262680588.
{{cite book}}: CS1 maint: others (link) - ^ Sheskin, David (2004). Handbook of Parametric and Nonparametric Statistical Procedures. CRC Press. p. 54. ISBN 1584884401.
- ^ Smith, R. J.; Bryant, R. G. (27 October 1975). «Metal substitutions incarbonic anhydrase: a halide ion probe study». Biochemical and Biophysical Research Communications. 66 (4): 1281–1286. doi:10.1016/0006-291x(75)90498-2. ISSN 0006-291X. PMC 9650581. PMID 3.
- ^ Lindenmayer, David. (2005). Practical conservation biology. Burgman, Mark A. Collingwood, Vic.: CSIRO Pub. ISBN 0-643-09310-9. OCLC 65216357.
- ^ Chow, Y. W.; Pietranico, R.; Mukerji, A. (27 October 1975). «Studies of oxygen binding energy to hemoglobin molecule». Biochemical and Biophysical Research Communications. 66 (4): 1424–1431. doi:10.1016/0006-291x(75)90518-5. ISSN 0006-291X. PMID 6.
- ^ Smith, R. J.; Bryant, R. G. (27 October 1975). «Metal substitutions incarbonic anhydrase: a halide ion probe study». Biochemical and Biophysical Research Communications. 66 (4): 1281–1286. doi:10.1016/0006-291x(75)90498-2. ISSN 0006-291X. PMC 9650581. PMID 3.
- ^ Smith, R. J.; Bryant, R. G. (27 October 1975). «Metal substitutions incarbonic anhydrase: a halide ion probe study». Biochemical and Biophysical Research Communications. 66 (4): 1281–1286. doi:10.1016/0006-291x(75)90498-2. ISSN 0006-291X. PMC 9650581. PMID 3.
- ^ Moroi, K.; Sato, T. (15 August 1975). «Comparison between procaine and isocarboxazid metabolism in vitro by a liver microsomal amidase-esterase». Biochemical Pharmacology. 24 (16): 1517–1521. doi:10.1016/0006-2952(75)90029-5. ISSN 1873-2968. PMID 8.
- ^ NEYMAN, J.; PEARSON, E. S. (1928). «On the Use and Interpretation of Certain Test Criteria for Purposes of Statistical Inference Part I». Biometrika. 20A (1–2): 175–240. doi:10.1093/biomet/20a.1-2.175. ISSN 0006-3444.
- ^ C.I.K.F. (July 1951). «Probability Theory for Statistical Methods. By F. N. David. [Pp. ix + 230. Cambridge University Press. 1949. Price 155.]». Journal of the Staple Inn Actuarial Society. 10 (3): 243–244. doi:10.1017/s0020269x00004564. ISSN 0020-269X.
- ^ Note that the subscript in the expression H0 is a zero (indicating null), and is not an «O» (indicating original).
- ^ Neyman, J.; Pearson, E. S. (30 October 1933). «The testing of statistical hypotheses in relation to probabilities a priori». Mathematical Proceedings of the Cambridge Philosophical Society. 29 (4): 492–510. Bibcode:1933PCPS…29..492N. doi:10.1017/s030500410001152x. ISSN 0305-0041. S2CID 119855116.
- ^ Fisher, R.A. (1966). The design of experiments. 8th edition. Hafner:Edinburgh.
Bibliography[edit]
- Betz, M.A. & Gabriel, K.R., «Type IV Errors and Analysis of Simple Effects», Journal of Educational Statistics, Vol.3, No.2, (Summer 1978), pp. 121–144.
- David, F.N., «A Power Function for Tests of Randomness in a Sequence of Alternatives», Biometrika, Vol.34, Nos.3/4, (December 1947), pp. 335–339.
- Fisher, R.A., The Design of Experiments, Oliver & Boyd (Edinburgh), 1935.
- Gambrill, W., «False Positives on Newborns’ Disease Tests Worry Parents», Health Day, (5 June 2006). [1] Archived 17 May 2018 at the Wayback Machine
- Kaiser, H.F., «Directional Statistical Decisions», Psychological Review, Vol.67, No.3, (May 1960), pp. 160–167.
- Kimball, A.W., «Errors of the Third Kind in Statistical Consulting», Journal of the American Statistical Association, Vol.52, No.278, (June 1957), pp. 133–142.
- Lubin, A., «The Interpretation of Significant Interaction», Educational and Psychological Measurement, Vol.21, No.4, (Winter 1961), pp. 807–817.
- Marascuilo, L.A. & Levin, J.R., «Appropriate Post Hoc Comparisons for Interaction and nested Hypotheses in Analysis of Variance Designs: The Elimination of Type-IV Errors», American Educational Research Journal, Vol.7., No.3, (May 1970), pp. 397–421.
- Mitroff, I.I. & Featheringham, T.R., «On Systemic Problem Solving and the Error of the Third Kind», Behavioral Science, Vol.19, No.6, (November 1974), pp. 383–393.
- Mosteller, F., «A k-Sample Slippage Test for an Extreme Population», The Annals of Mathematical Statistics, Vol.19, No.1, (March 1948), pp. 58–65.
- Moulton, R.T., «Network Security», Datamation, Vol.29, No.7, (July 1983), pp. 121–127.
- Raiffa, H., Decision Analysis: Introductory Lectures on Choices Under Uncertainty, Addison–Wesley, (Reading), 1968.
External links[edit]
- Bias and Confounding – presentation by Nigel Paneth, Graduate School of Public Health, University of Pittsburgh
Ошибки первого и второго рода
Ошибки первого рода (false positives) и ошибки второго рода (false negatives) — ключевые понятия задач проверки статистических гипотез. Они используются также и в других областях, когда речь идёт о принятии «бинарного» решения (да/нет).
Ошибку первого рода часто называют ложной тревогой, ложным срабатыванием или ложноположительным результатом — например, анализ крови показал наличие заболевания, хотя на самом деле человек здоров, или металлодетектор выдал сигнал тревоги, сработав на металлическую пряжку ремня. В информационных технологиях часто используют английский термин false positive без перевода.
Из-за возможности ложных срабатываний не удаётся полностью автоматизировать борьбу со многими видами угроз. Как правило, вероятность ложного срабатывания коррелирует с вероятностью пропуска события (ошибки второго рода). То есть: чем более чувствительна система, тем больше опасных событий она детектирует и, следовательно, предотвращает. Но при повышении чувствительности неизбежно вырастает и вероятность ложных срабатываний. Поэтому чересчур чувствительно (параноидально) настроенная система защиты может выродиться в свою противоположность и привести к тому, что побочный вред от неё будет превышать пользу.
Соответственно, ошибку второго рода иногда называют пропуском события или ложноотрицательным срабатыванием — человек болен, но анализ крови этого не показал, или у пассажира имеется холодное оружие, но рамка металлодетектора его не обнаружила (например, из-за того, что чувствительность рамки отрегулирована на обнаружение только очень массивных металлических предметов).
Степень чувствительности системы защиты должна представлять собой компромисс между вероятностью ошибок первого и второго рода. Где именно находится точка баланса, зависит от оценки рисков обоих видов ошибок.
Радиолокация
В задаче радиолокационного обнаружения воздушных целей, прежде всего, в системе ПВО ошибки первого и второго рода, с формулировкой «ложная тревога» и «пропуск цели» являются одним из основных элементов как теории, так и практики построения радиолокационных станций. Вероятно, это первый пример последовательного применения статистических методов в целой технической области.
Компьютерная безопасность
Наличие уязвимостей в вычислительных системах приводит к тому, что приходится, с одной стороны, решать задачу сохранности данных, а с другой стороны — обеспечивать доступ пользователей к этим данным. В этом контексте возможны следующие нежелательные ситуации:
когда авторизованные пользователи классифицируются как нарушители (ошибки первого рода)
когда нарушители классифицируются как авторизованные пользователи (ошибки второго рода)
Вредоносное программное обеспечение
Понятие ошибки первого рода также используется, когда антивирусное программное обеспечение ошибочно классифицирует безвредный файл как вирус.
Неверное обнаружение может быть вызвано особенностями эвристики, либо неправильной сигнатурой вируса в базе данных. Подобные проблемы могут происходить также и с антитроянскими и антишпионскими программами.
Досмотр пассажиров и багажа
Ошибки первого рода регулярно встречаются каждый день в компьютерных системах предварительного досмотра пассажиров в аэропортах. Установленные в них детекторы предназначены для предотвращения проноса оружия на борт самолёта; тем не менее, уровень чувствительности в них зачастую настраивается настолько высоко, что много раз за день они срабатывают на незначительные предметы, такие как ключи, пряжки ремней, монеты, мобильные телефоны, гвозди в подошвах обуви и т.п.
Таким образом, соотношение числа ложных тревог (идентифицикация благопристойного пассажира как правонарушителя) к числу правильных срабатываний (обнаружение действительно запрещённых предметов) очень велико.
Медицинское тестирование
Ошибки второго рода являются существенной проблемой в медицинском тестировании. Они дают пациенту и врачу ложное убеждение, что заболевание отсутствует, в то время как в действительности оно есть. Это зачастую приводит к неуместному или неадекватному лечению. Типичным примером является доверие результатам кардиотестирования при выявлении коронарного атеросклероза, хотя известно, что кардиотестирование выявляет только те затруднения кровотока в коронарной артерии, которые вызваны стенозом.
Ошибки второго рода вызывают серьёзные и трудные для понимания проблемы, особенно когда искомое условие является широкораспространённым. Если тест с 10%-ным уровнем ошибок второго рода используется для обследования группы, где вероятность «истинно-положительных» случаев составляет 70%, то многие отрицательные результаты теста окажутся ложными. (См. Теорему Байеса).
Ошибки первого рода также могут вызывать серьёзные и трудные для понимания проблемы. Это происходит, когда искомое условие является редким. Если уровень ошибок первого рода у теста составляет один случай на десять тысяч, но в тестируемой группе образцов (или людей) вероятность «истинно-положительных» случаев составляет в среднем один случай на миллион, то большинство положительных результатов этого теста будут ложными.
Исследования сверхъестественных явлений
Термин ошибка первого рода был взят на вооружение исследователями в области паранормальных явлений и привидений для описания фотографии или записи или какого-либо другого свидетельства, которое ошибочно трактуется как имеющее паранормальное происхождение — в данном контексте ошибка первого рода — это какое-либо несостоятельное «медиасвидетельство» (изображение, видеозапись, аудиозапись и т.д.), которое имеет обычное объяснение
Источник: https://ru.wikipedia.org/wiki/Ошибки_первого_и_второго_рода
18
766
-
Ошибки первого и второго рода при проверке гипотез.
шибки первого рода (англ. type
I
errors,
α
errors,
false
positives)
и ошибки
второго рода (англ. type
II
errors,
β
errors,
false
negatives)
в математической
статистике —
это ключевые понятия задач проверки
статистических гипотез. Тем не менее,
данные понятия часто используются и в
других областях, когда речь идёт о
принятии «бинарного» решения (да/нет)
на основе некоего критерия (теста,
проверки, измерения), который с некоторой
вероятностью может давать ложный
результат.
[Править]Определения
Пусть дана выборка
из
неизвестного совместного распределения
,
и поставлена бинарная задача проверки
статистических гипотез:
где
— нулевая
гипотеза,
а
— альтернативная
гипотеза.
Предположим, что задан статистический
критерий
,
сопоставляющий каждой
реализации выборки
одну
из имеющихся гипотез. Тогда возможны
следующие четыре ситуации:
-
Распределение
выборки
соответствует
гипотезе
,
и она точно определена статистическим
критерием, то есть
. -
Распределение
выборки
соответствует
гипотезе
,
но она неверно отвергнута статистическим
критерием, то есть
. -
Распределение
выборки
соответствует
гипотезе
,
и она точно определена статистическим
критерием, то есть
. -
Распределение
выборки
соответствует
гипотезе
,
но она неверно отвергнута статистическим
критерием, то есть
.
Во втором и четвертом случае
говорят, что произошла статистическая
ошибка, и её называют ошибкой
первого и второго рода соответственно. [1][2]
|
Верная гипотеза |
|||
|
Результат
применения
критерия |
верно |
(Ошибка второго рода) |
|
|
(Ошибка первого рода) |
верно |
[Править]о смысле ошибок первого и второго рода
Как видно из вышеприведённого
определения, ошибки
первого и второго рода являются
взаимно-симметричными, то есть если
поменять местами гипотезы
и
,
то ошибки
первого рода превратятся
в ошибки
второго рода и
наоборот. Тем не менее, в большинстве
практических ситуаций путаницы не
происходит, поскольку принято считать,
что нулевая
гипотеза
соответствует
состоянию «по умолчанию» (естественному,
наиболее ожидаемому положению вещей) —
например, что обследумый человек здоров,
или что проходящий через рамку
металлодетектора пассажир не имеет
запрещённых металлических предметов.
Соответственно, альтернативная
гипотеза
обозначает
противоположную ситуацию, которая
обычно трактуется как менее вероятная,
неординарная, требующая какой-либо
реакции.
С учётом этого ошибку
первого рода часто
называют ложной
тревогой, ложным
срабатыванием илиложноположительным срабатыванием —
например, анализ крови показал наличие
заболевания, хотя на самом деле человек
здоров, или металлодетектор выдал сигнал
тревоги, сработав на металлическую
пряжку ремня. Слово «положительный» в
данном случае не имеет отношения к
желательности или нежелательности
самого события.
Термин широко используется в медицине.
Например, тесты, предназначенные для
диагностики заболеваний, иногда дают
положительный результат (т. е. показывают
наличие заболевания у пациента), когда,
на самом деле пациент этим заболеванием
не страдает. Такой результат называется
ложноположительным.
В других областях, обычно, используют
словосочетания со схожим смыслом,
например, «ложное срабатывание», «ложная
тревога» и т. п. В информационных
технологиях часто используют английский
термин false positive без перевода.
Из-за возможности ложных срабатываний
не удаётся полностью автоматизировать
борьбу со многими видами угроз. Как
правило, вероятность ложного срабатывания
коррелирует с вероятностью пропуска
события (ошибки второго рода). То есть,
чем более чувствительна система, тем
больше опасных событий она детектирует
и, следовательно, предотвращает. Но при
повышении чувствительности неизбежно
вырастает и вероятность ложных
срабатываний. Поэтому чересчур
чувствительно (параноидально) настроенная
система защиты может выродиться в свою
противоположность и привести к тому,
что побочный вред от неё будет превышать
пользу.
Соответственно, ошибку
второго рода иногда
называют пропуском
события или ложноотрицательным срабатыванием —
человек болен, но анализ крови этого не
показал, или у пассажира имеется холодное
оружие, но рамка металлодетектора его
не обнаружила (например, из-за того, что
чувствительность рамки отрегулирована
на обнаружение только очень массивных
металлических предметов).
Слово «отрицательный» в данном случае
не имеет отношения к желательности или
нежелательности самого события.
Термин широко используется в медицине.
Например, тесты, предназначенные для
диагностики заболеваний иногда дают
отрицательный результат (т. е. показывают
отсутствие заболевания у пациента),
когда, на самом деле пациент страдает
этим заболеванием. Такой результат
называется ложноотрицательным.
В других областях, обычно, используют
словосочетания со схожим смыслом,
например, «пропуск события», и т. п. В
информационных технологиях часто
используют английский термин false negative
без перевода.
Степень чувствительности системы защиты
должна представлять собой компромисс
между вероятностью ошибок первого и
второго рода. Где именно находится точка
баланса, зависит от оценки рисков обоих
видов ошибок.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
При работе со статистическим отчетом, научной статьей или диссертацией Вы постоянно сталкиваетесь таким термином, как уровень значимости или альфа (ошибка первого рода), чаще всего этот уровень задается относительно 5% или вероятности р=о,05. Решение о достоверности различий или «статистически значимых различиях» принимается относительно этого порогового значения. В данной статье мы предлагаем читателю разобраться в том, почему так важен этот уровень и что он значит в практическом смысле.
Определение (словарь Дж. М. Ласта):
ОШИБКА ТИПА I (ERROR TYPE I; син. alpha-error — ошибка альфа)
ошибочное отклонение нулевой гипотезы, т.е. утверждение о том, что различия существуют, тогда как их нет.
Немного о смысле уровня значимости и достовернности различий
Для понимания темы статистических ошибок мы перейдем к простейшей матрице соотношения статистики (что она нам говорит по результатам статистических тестов) и реальности. Так вот, предположим, что статистика нам говорит о существовании связей, о существовании различий. В реальности же они также существуют, тогда мы считаем этот результат правильным положительным или truth positive (ТР). Например, статистика нам говорит об отсутствии связей, об отсутствии различий, а в реальности же они действительно существуют. Такая ситуация называется ложноотрицательной или false-negative (FN). Соответственно существуют ситуации, когда статистика нам говорит о существовании каких-то определенных взаимосвязей или о существовании различий, которые в реальности не существуют. Тогда это называется ложноположительной или false-positive (FP). И последний случай касается отсутствия по данным статистических тестов того, чего в действительности не существует, различий в действительности нет. И эта ситуация именуется как truth negative (TN) или ложноотрицательный результат.
Рисунок 1. Матрица соотношения реальность-результаты статистического теста. TN (true negative) — верноотрицательный, FN (false negative) — ложноотрицательный, FP (false positive) — ложноположительный, TP (true positive) — верно позитивный.
Так вот, как видно из этой матрицы, у нас существуют 2 ситуации, в которых мы можем ошибаться: это false-positive и truth negative. Это как раз два типа ошибок, о которых я говорил в начале этого блока: о ложноотрицательной ошибке и ложноположительной. Что на самом деле это значит?
Что в какой-то ситуации мы можем пересмотреть, а в какой-то – недосмотреть.
Пересмотреть, то есть найти то, чего в действительности нет, это является false-positive – это ошибка первого рода.
Или недосмотреть, то есть упустить то, что в действительности существует в реальности, но по данным статистических тестов мы чего-то не находим – это ложноотрицательный результат или ошибка второго рода.
Давайте нанесем те термины, которые, возможно, вы уже слышали – «уровень достоверности», «достоверные различия». Что это за слово такое «достоверность»? Оно относится как раз к ошибке первого рода и обозначается буквой α. Вы наверняка знаете обозначение уровня в р=0,05. Уровень достоверности в 0,05 как раз является критическим значением для результатов большинства статистических тестов ( 5 %). Мы делаем вывод относительно этих 5 %. Что в практическом смысле это значит? Что в 95 % мы находим различия, которые действительно существуют, и в 5 % даем себе возможность переобнаружить то, чего в действительности не существует в реальности.
Что касается ошибки второго рода, то здесь это уже не 5 %. И мы задаем либо 20, либо 10 %, что-то в этом диапазоне, это ошибка в 0,2; в 0,1. И как раз мы подходим к следующему чрезвычайно важному статистическому понятию как «мощность исследования». Мощность исследования это: (1 – β), где β это ошибка второго рода. Если стандартный уровень ошибки это 0,2 и 0,1, то мы получаем, что мощность исследования в норме составляет 0,8 или 0,9 (чаще, конечно, 0,8).
NB! по уровню значимости
Уровень значимости, то есть ошибки первого рода составляет чаще всего относительно уровня в 5 %, это уровень той ошибки, при которой мы даем возможность себе «перенайти» то, что в действительности не существует. В ошибке второго рода мы даем себе определенный люфт до 20 % не обнаружить того, что в действительности существует, то есть когда статистические тесты нам скажут, что чего-то нет, а в реальности эти различия существуют.
Автор: Кирилл Мильчаков
-
Ошибки первого и второго рода при проверке гипотез.
шибки первого рода (англ. type
I
errors,
α
errors,
false
positives)
и ошибки
второго рода (англ. type
II
errors,
β
errors,
false
negatives)
в математической
статистике —
это ключевые понятия задач проверки
статистических гипотез. Тем не менее,
данные понятия часто используются и в
других областях, когда речь идёт о
принятии «бинарного» решения (да/нет)
на основе некоего критерия (теста,
проверки, измерения), который с некоторой
вероятностью может давать ложный
результат.
[Править]Определения
Пусть дана выборка
из
неизвестного совместного распределения
,
и поставлена бинарная задача проверки
статистических гипотез:
где
— нулевая
гипотеза,
а
— альтернативная
гипотеза.
Предположим, что задан статистический
критерий
,
сопоставляющий каждой
реализации выборки
одну
из имеющихся гипотез. Тогда возможны
следующие четыре ситуации:
-
Распределение
выборки
соответствует
гипотезе
,
и она точно определена статистическим
критерием, то есть
. -
Распределение
выборки
соответствует
гипотезе
,
но она неверно отвергнута статистическим
критерием, то есть
. -
Распределение
выборки
соответствует
гипотезе
,
и она точно определена статистическим
критерием, то есть
. -
Распределение
выборки
соответствует
гипотезе
,
но она неверно отвергнута статистическим
критерием, то есть
.
Во втором и четвертом случае
говорят, что произошла статистическая
ошибка, и её называют ошибкой
первого и второго рода соответственно. [1][2]
|
Верная гипотеза |
|||
|
Результат применения критерия |
верно |
(Ошибка второго рода) |
|
|
(Ошибка первого рода) |
верно |
[Править]о смысле ошибок первого и второго рода
Как видно из вышеприведённого
определения, ошибки
первого и второго рода являются
взаимно-симметричными, то есть если
поменять местами гипотезы
и
,
то ошибки
первого рода превратятся
в ошибки
второго рода и
наоборот. Тем не менее, в большинстве
практических ситуаций путаницы не
происходит, поскольку принято считать,
что нулевая
гипотеза
соответствует
состоянию «по умолчанию» (естественному,
наиболее ожидаемому положению вещей) —
например, что обследумый человек здоров,
или что проходящий через рамку
металлодетектора пассажир не имеет
запрещённых металлических предметов.
Соответственно, альтернативная
гипотеза
обозначает
противоположную ситуацию, которая
обычно трактуется как менее вероятная,
неординарная, требующая какой-либо
реакции.
С учётом этого ошибку
первого рода часто
называют ложной
тревогой, ложным
срабатыванием илиложноположительным срабатыванием —
например, анализ крови показал наличие
заболевания, хотя на самом деле человек
здоров, или металлодетектор выдал сигнал
тревоги, сработав на металлическую
пряжку ремня. Слово «положительный» в
данном случае не имеет отношения к
желательности или нежелательности
самого события.
Термин широко используется в медицине.
Например, тесты, предназначенные для
диагностики заболеваний, иногда дают
положительный результат (т. е. показывают
наличие заболевания у пациента), когда,
на самом деле пациент этим заболеванием
не страдает. Такой результат называется
ложноположительным.
В других областях, обычно, используют
словосочетания со схожим смыслом,
например, «ложное срабатывание», «ложная
тревога» и т. п. В информационных
технологиях часто используют английский
термин false positive без перевода.
Из-за возможности ложных срабатываний
не удаётся полностью автоматизировать
борьбу со многими видами угроз. Как
правило, вероятность ложного срабатывания
коррелирует с вероятностью пропуска
события (ошибки второго рода). То есть,
чем более чувствительна система, тем
больше опасных событий она детектирует
и, следовательно, предотвращает. Но при
повышении чувствительности неизбежно
вырастает и вероятность ложных
срабатываний. Поэтому чересчур
чувствительно (параноидально) настроенная
система защиты может выродиться в свою
противоположность и привести к тому,
что побочный вред от неё будет превышать
пользу.
Соответственно, ошибку
второго рода иногда
называют пропуском
события или ложноотрицательным срабатыванием —
человек болен, но анализ крови этого не
показал, или у пассажира имеется холодное
оружие, но рамка металлодетектора его
не обнаружила (например, из-за того, что
чувствительность рамки отрегулирована
на обнаружение только очень массивных
металлических предметов).
Слово «отрицательный» в данном случае
не имеет отношения к желательности или
нежелательности самого события.
Термин широко используется в медицине.
Например, тесты, предназначенные для
диагностики заболеваний иногда дают
отрицательный результат (т. е. показывают
отсутствие заболевания у пациента),
когда, на самом деле пациент страдает
этим заболеванием. Такой результат
называется ложноотрицательным.
В других областях, обычно, используют
словосочетания со схожим смыслом,
например, «пропуск события», и т. п. В
информационных технологиях часто
используют английский термин false negative
без перевода.
Степень чувствительности системы защиты
должна представлять собой компромисс
между вероятностью ошибок первого и
второго рода. Где именно находится точка
баланса, зависит от оценки рисков обоих
видов ошибок.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Ошибки первого рода (англ. type I errors, α errors, false positives) и ошибки второго рода (англ. type II errors, β errors, false negatives) в математической статистике — это ключевые понятия задач проверки статистических гипотез. Тем не менее, данные понятия часто используются и в других областях, когда речь идёт о принятии «бинарного» решения (да/нет) на основе некоего критерия (теста, проверки, измерения), который с некоторой вероятностью может давать ложный результат.
Определения
Пусть дана выборка из неизвестного совместного распределения
, и поставлена бинарная задача проверки статистических гипотез:
где — нулевая гипотеза, а
— альтернативная гипотеза. Предположим, что задан статистический критерий
,
сопоставляющий каждой реализации выборки одну из имеющихся гипотез. Тогда возможны следующие четыре ситуации:
-
Распределение
выборки
соответствует гипотезе
, и она точно определена статистическим критерием, то есть
.
-
Распределение
выборки
соответствует гипотезе
, но она неверно отвергнута статистическим критерием, то есть
.
-
Распределение
выборки
соответствует гипотезе
, и она точно определена статистическим критерием, то есть
.
-
Распределение
выборки
соответствует гипотезе
, но она неверно отвергнута статистическим критерием, то есть
.
Во втором и четвертом случае говорят, что произошла статистическая ошибка, и её называют ошибкой первого и второго рода соответственно. 1)2)
| Верная гипотеза | |||
|---|---|---|---|
|
|
|
||
|
Результат
применения критерия |
|
|
(Ошибка второго рода) |
|
|
(Ошибка первого рода) |
|
О смысле ошибок первого и второго рода
Из определения выше видно, что ошибки первого и второго рода являются взаимно-симметричными, то есть если поменять местами гипотезы и
, то ошибки первого рода превратятся в ошибки второго рода и наоборот. Тем не менее, в большинстве практических ситуаций путаницы не происходит, поскольку принято считать, что нулевая гипотеза
соответствует состоянию «по умолчанию» (естественному, наиболее ожидаемому положению вещей) — например, что обследуемый человек здоров, или что проходящий через рамку металлодетектора пассажир не имеет запрещённых металлических предметов. Соответственно, альтернативная гипотеза
обозначает противоположную ситуацию, которая обычно трактуется как менее вероятная, неординарная, требующая какой-либо реакции.
С учётом этого ошибку первого рода часто называют ложной тревогой, ложным срабатыванием или ложноположительным срабатыванием — например, анализ крови показал наличие заболевания, хотя на самом деле человек здоров, или металлодетектор выдал сигнал тревоги, сработав на металлическую пряжку ремня. Слово «положительный» в данном случае не имеет отношения к желательности или нежелательности самого события.
Термин широко используется в медицине. Например, тесты, предназначенные для диагностики заболеваний, иногда дают положительный результат (т.е. показывают наличие заболевания у пациента), когда на самом деле пациент этим заболеванием не страдает. Такой результат называется ложноположительным.
В других областях обычно используют словосочетания со схожим смыслом, например, «ложное срабатывание», «ложная тревога» и т.п. В информационных технологиях часто используют английский термин false positive без перевода.
Из-за возможности ложных срабатываний не удаётся полностью автоматизировать борьбу со многими видами угроз. Как правило, вероятность ложного срабатывания коррелирует с вероятностью пропуска события (ошибки второго рода). То есть: чем более чувствительна система, тем больше опасных событий она детектирует и, следовательно, предотвращает. Но при повышении чувствительности неизбежно вырастает и вероятность ложных срабатываний. Поэтому чересчур чувствительно (параноидально) настроенная система защиты может выродиться в свою противоположность и привести к тому, что побочный вред от неё будет превышать пользу.
Соответственно, ошибку второго рода иногда называют пропуском события или ложноотрицательным срабатыванием — человек болен, но анализ крови этого не показал, или у пассажира имеется холодное оружие, но рамка металлодетектора его не обнаружила (например, из-за того, что чувствительность рамки отрегулирована на обнаружение только очень массивных металлических предметов).
Слово «отрицательный» в данном случае не имеет отношения к желательности или нежелательности самого события.
Термин широко используется в медицине. Например, тесты, предназначенные для диагностики заболеваний, иногда дают отрицательный результат (т.е. показывают отсутствие заболевания у пациента), когда на самом деле пациент страдает этим заболеванием. Такой результат называется ложноотрицательным.
В других областях обычно используют словосочетания со схожим смыслом, например, «пропуск события», и т.п. В информационных технологиях часто используют английский термин false negative без перевода.
Степень чувствительности системы защиты должна представлять собой компромисс между вероятностью ошибок первого и второго рода. Где именно находится точка баланса, зависит от оценки рисков обоих видов ошибок.
Вероятности ошибок (уровень значимости и мощность)
Вероятность ошибки первого рода при проверке статистических гипотез называют уровнем значимости и обычно обозначают греческой буквой (отсюда название
-errors).
Вероятность ошибки второго рода не имеет какого-то особого общепринятого названия, на письме обозначается греческой буквой (отсюда
-errors). Однако с этой величиной тесно связана другая, имеющая большое статистическое значение — мощность критерия. Она вычисляется по формуле
. Таким образом, чем выше мощность, тем меньше вероятность совершить ошибку второго рода.
Обе эти характеристики обычно вычисляются с помощью так называемой функции мощности критерия. В частности, вероятность ошибки первого рода есть функция мощности, вычисленная при нулевой гипотезе. Для критериев, основанных на выборке фиксированного объема, вероятность ошибки второго рода есть единица минус функция мощности, вычисленная в предположении, что распределение наблюдений соответствует альтернативной гипотезе. Для последовательных критериев это также верно, если критерий останавливается с вероятностью единица (при данном распределении из альтернативы).
В статистических тестах обычно приходится идти на компромисс между приемлемым уровнем ошибок первого и второго рода. Зачастую для принятия решения используется пороговое значение, которое может варьироваться с целью сделать тест более строгим или, наоборот, более мягким. Этим пороговым значением является уровень значимости, которым задаются при проверке статистических гипотез. Например, в случае металлодетектора повышение чувствительности прибора приведёт к увеличению риска ошибки первого рода (ложная тревога), а понижение чувствительности — к увеличению риска ошибки второго рода (пропуск запрещённого предмета).
Примеры использования
Радиолокация
В задаче радиолокационного обнаружения воздушных целей, прежде всего, в системе ПВО ошибки первого и второго рода, с формулировкой «ложная тревога» и «пропуск цели» являются одним из основных элементов как теории, так и практики построения радиолокационных станций. Вероятно, это первый пример последовательного применения статистических методов в целой технической области.
Компьютеры
Понятия ошибок первого и второго рода широко используются в области компьютеров и программного обеспечения.
Компьютерная безопасность
Наличие уязвимостей в вычислительных системах приводит к тому, что приходится, с одной стороны, решать задачу сохранения целостности компьютерных данных, а с другой стороны — обеспечивать нормальный доступ легальных пользователей к этим данным (см. компьютерная безопасность). Moulton (1983, с.125) отмечает, что в данном контексте возможны следующие нежелательные ситуации:
-
когда авторизованные пользователи классифицируются как нарушители (ошибки первого рода)
-
когда нарушители классифицируются как авторизованные пользователи (ошибки второго рода)
Фильтрация спама
Ошибка первого рода происходит, когда механизм блокировки/фильтрации спама ошибочно классифицирует легитимное email-сообщение как спам и препятствует его нормальной доставке. В то время как большинство «антиспам»-алгоритмов способны блокировать/фильтровать большой процент нежелательных email-сообщений, гораздо более важной задачей является минимизировать число «ложных тревог» (ошибочных блокировок нужных сообщений).
Ошибка второго рода происходит, когда антиспам-система ошибочно пропускает нежелательное сообщение, классифицируя его как «не спам». Низкий уровень таких ошибок является индикатором эффективности антиспам-алгоритма.
Пока не удалось создать антиспамовую систему без корреляции между вероятностью ошибок первого и второго рода. Вероятность пропустить спам у современных систем колеблется в пределах от 1% до 30%. Вероятность ошибочно отвергнуть валидное сообщение — от 0,001 % до 3 %. Выбор системы и её настроек зависит от условий конкретного получателя: для одних получателей риск потерять 1% хорошей почты оценивается как незначительный, для других же потеря даже 0,1% является недопустимой.
Вредоносное программное обеспечение
Понятие ошибки первого рода также используется, когда антивирусное программное обеспечение ошибочно классифицирует безвредный файл как вирус. Неверное обнаружение может быть вызвано особенностями эвристики, либо неправильной сигнатурой вируса в базе данных. Подобные проблемы могут происходить также и с антитроянскими и антишпионскими программами.
Поиск в компьютерных базах данных
При поиске в базе данных к ошибкам первого рода можно отнести документы, которые выдаются поиском, несмотря на их иррелевантность (несоответствие) поисковому запросу. Ошибочные срабатывания характерны для полнотекстового поиска, когда поисковый алгоритм анализирует полные тексты всех хранимых в базе данных документов и пытается найти соответствия одному или нескольким терминам, заданным пользователем в запросе.
Большинство ложных срабатываний обусловлены сложностью естественных языков, многозначностью слов: например, «home» может обозначать как «место проживания человека», так и «корневую страницу веб-сайта». Число подобных ошибок может быть снижено за счёт использования специального словаря. Однако это решение относительно дорогое, поскольку подобный словарь и разметка документов (индексирование) должны создаваться экспертом.
Оптическое распознавание текстов (OCR)
Разнообразные детектирующие алгоритмы нередко выдают ошибки первого рода. Программное обеспечение оптического распознавания текстов может распознать букву «a» в ситуации, когда на самом деле изображены несколько точек.
Досмотр пассажиров и багажа
Ошибки первого рода регулярно встречаются каждый день в компьютерных системах предварительного досмотра пассажиров в аэропортах. Установленные в них детекторы предназначены для предотвращения проноса оружия на борт самолёта; тем не менее, уровень чувствительности в них зачастую настраивается настолько высоко, что много раз за день они срабатывают на незначительные предметы, такие как ключи, пряжки ремней, монеты, мобильные телефоны, гвозди в подошвах обуви и т.п. (см. обнаружение взрывчатых веществ, металлодетекторы).
Таким образом, соотношение числа ложных тревог (идентифицикация благопристойного пассажира как правонарушителя) к числу правильных срабатываний (обнаружение действительно запрещённых предметов) очень велико.
Биометрия
Ошибки первого и второго рода являются большой проблемой в системах биометрического сканирования, использующих распознавание радужной оболочки или сетчатки глаза, черт лица и т.д. Такие сканирующие системы могут ошибочно отождествить кого-то с другим, «известным» системе человеком, информация о котором хранится в базе данных (к примеру, это может быть лицо, имеющее право входа в систему, или подозреваемый преступник и т.п.). Противоположной ошибкой будет неспособность системы распознать легитимного зарегистрированного пользователя, или опознать подозреваемого в преступлении.3)
Массовая медицинская диагностика (скрининг)
В медицинской практике есть существенное различие между скринингом и тестированием:
-
Скрининг включает в себя относительно дешёвые тесты, которые проводятся для большой группы людей при отсутствии каких-либо клинических признаков болезни (например, мазок Папаниколау).
-
Тестирование подразумевает гораздо более дорогие, зачастую инвазивные, процедуры, которые проводятся только для тех, у кого проявляются клинические признаки заболевания, и которые, в основном, применяются для подтверждения предполагаемого диагноза.
К примеру, в большинстве штатов в США обязательно прохождение новорожденными процедуры скрининга на оксифенилкетонурию и гипотиреоз, помимо других врождённых аномалий. Несмотря на высокий уровень ошибок первого рода, эти процедуры скрининга считаются целесообразными, поскольку они существенно увеличивают вероятность обнаружения этих расстройств на самой ранней стадии.4))
Простые анализы крови, используемые для скрининга потенциальных доноров на ВИЧ и гепатит, имеют существенный уровень ошибок первого рода; однако в арсенале врачей есть гораздо более точные (и, соответственно, дорогие) тесты для проверки, действительно ли человек инфицирован каким-либо из этих вирусов.
Возможно, наиболее широкие дискуссии вызывают ошибки первого рода в процедурах скрининга на рак груди (маммография). В США уровень ошибок первого рода в маммограммах достигает 15%, это самый высокий показатель в мире.5) Самый низкий уровень наблюдается в Нидерландах, 1%.6)
Медицинское тестирование
Ошибки второго рода являются существенной проблемой в медицинском тестировании. Они дают пациенту и врачу ложное убеждение, что заболевание отсутствует, в то время как в действительности оно есть. Это зачастую приводит к неуместному или неадекватному лечению. Типичным примером является доверие результатам кардиотестирования при выявлении коронарного атеросклероза, хотя известно, что кардиотестирование выявляет только те затруднения кровотока в коронарной артерии, которые вызваны стенозом.
Ошибки второго рода вызывают серьёзные и трудные для понимания проблемы, особенно когда искомое условие является широкораспространённым. Если тест с 10%-ным уровнем ошибок второго рода используется для обследования группы, где вероятность «истинно-положительных» случаев составляет 70%, то многие отрицательные результаты теста окажутся ложными. (См. Теорему Байеса).
Ошибки первого рода также могут вызывать серьёзные и трудные для понимания проблемы. Это происходит, когда искомое условие является редким. Если уровень ошибок первого рода у теста составляет один случай на десять тысяч, но в тестируемой группе образцов (или людей) вероятность «истинно-положительных» случаев составляет в среднем один случай на миллион, то большинство положительных результатов этого теста будут ложными.7)
Исследования сверхъестественных явлений
Термин ошибка первого рода был взят на вооружение исследователями в области паранормальных явлений и привидений для описания фотографии или записи или какого-либо другого свидетельства, которое ошибочно трактуется как имеющее паранормальное происхождение — в данном контексте ошибка первого рода — это какое-либо несостоятельное «медиасвидетельство» (изображение, видеозапись, аудиозапись и т.д.), которое имеет обычное объяснение. 
См. также
Проблема множественного тестирования гипотез
Ваш исследовательский вопрос может быть таким, что вам интересно оценить воздействия разных типов тритмента, то есть у вас есть несколько экспериментальных групп и одна контрольная. При такой постановке мы хотим проверить не одну, а сразу много статистических гипотез о различии в группах. При проверке любой гипотезы существует вероятность совершить ошибку первого рода (отклонить нулевую гипотезу, если она верна = обнаружить эффект, которого нет). Особенность множественного тестирования гипотез состоит в том, что чем больше гипотез мы проверяем на одних и тех же данных, тем больше будет вероятность допустить как минимум одну ошибку первого рода – эффект множественных сравнений (multiple comparisons/testing).
Источниками множественного тестирования могут быть:
-
Несколько типов воздействия (Multiple treatment arms)
-
Гетерогенное воздействие (Heterogeneous treatment effects)
-
Несколько способов оценки (Multiple estimators)
-
Несколько зависимых переменных (Multiple outcomes), эффект на которые мы хотим оценить
Рассмотрим это на примере. Предположим, что у нас есть 3 группы (A, B и С), в которых мы хотим сравнить среднее значение переменной интереса. Как и ранее, мы будем использовать t-тест Стьюдента. Если мы получили достаточно большое значение t-статистики такое, что p-value < 0.05, то мы отклоняем нулевую гипотезу и заключаем, что группы статистически различаются по переменной интереса. Отсечка p-value < 0.05 значит, что вероятность ошибочного вывода о различии между групповыми средними не превышает 0.05. Это будет работать именно так, когда у нас всего две группы, но в случае множественного тестирования вероятность будет больше 5%.
Выполняя тест Стьюдента, исследователь проверяет нулевую гипотезу об отсутствии разницы между двумя группами. Сравнивая группы A и В, он может ошибиться с вероятностью 5%, В и С – 5%, А и С – тоже 5%. Соответственно, вероятность ошибиться хотя бы в одном из этих трех сравнений составит:
(P = 1 — left(1-alpha right)^n = 1 — 0.95^3 approx 0.14 > 0.05) – такая ошибка называется family-wise error rate
Если бы групп было бы 5:
(P = 1 — left(1-alpha right)^n = 1 — 0.95^{10} approx 0.4 > 0.05)
К счастью, существует несколько методов, позволяющих преодолеть эту сложность:
-
Корректировка p-value (p-value adjustments)
-
Планирование эксперимента и фиксирование его условий (pre-analysis plans)
-
Повтороное проведение эксперимента (replication)
В рамках курса мы будем обсуждать первый способ борьбы с ошибками, возникающими при множественном тестировании гипотез.
Предположим, что мы проверяем (n) гипотез. Для каждой гипотезы мы будем проводить тест Стьюдента. Результаты наших тестов можно обобщить следующим образом:
| Число принятых нулевых гипотез ((p-value > alpha) Rightarrow hat{tau}=0) | Число отвергнутых нулевых гипотез ((p-value < alpha) Rightarrow hat{tau}neq 0) | Всего гипотез | |
|---|---|---|---|
| Число верных нулевых гипотез (hat{tau}=0) | Число безошибочно принятых нулевых гипотез (TN, true negatives) | Число ошибочно отвергнутых нулевых гипотез (FP, false positives) – ошибка первого рода | (m_0) – Число верных нулевых гипотез (true null hypotheses) |
| Число неверных нулевых гипотез (hat{tau}neq 0) | Число ошибочно принятых нулевых гипотез (FN, false negatives) – ошибка второго рода) | Число безошибочно отвергнутых нулевых гипотез (TP, true positives) | (m-m_0) – Число истинных альтернативных гипотез (true alternative hypotheses) |
| Всего гипотез | (m-R) – Общее число принятых гипотез | (R) – Общее число отвергнутых гипотез | (m) – всего гипотез |
В теории всего существует (m_0) верных нулевых гипотез. В результате наших тестов мы ошибочно отвергаем (FP) гипотез и верно принимаем остальные (TN) гипотез. Также существует (m−m_0) альтернативных гипотез, из которых (TP) гипотез безошибочно отвергаются, а (FN) гипотез – ошибочно принимаются. Важно, что общие количества отвергнутых и принятых гипотез ((R) и (m-R)), а следовательно, и суммарное число гипотез (n) нам известны, тогда как остальные величины ((m_0), (TN), (FP), (FN) и (TP)) мы не наблюдаем.
Групповая вероятность ошибки первого рода (family-wise error rate)
При одновременной проверке семейства статистических гипотез мы хотим, чтобы количество наших ошибок ((FP) и (FN)) было минимальным. Традиционно исследователи пытаются минимизировать величину ошибочно отвергнутых гипотез (FP). Это вполне логично, поскольку ложно отвергнутая нулевая гипотеза грозит нам ложноположительным найденным эффектом, которого реально может не быть.
Если (FP geq 1), мы совершаем как минимум одну ошибку первого рода. Вероятность допущения такой ошибки при множественной проверке гипотез называют групповой вероятностью ошибки (familywise error rate, FWER или experiment-wise error rate). По определению, (FWER = P(FP geq 1)) – вероятность ошибочно отклонить хотя бы одну нулевую гипотезу во всех тестах. Соответственно, когда мы говорим, что хотим контролировать групповую вероятность ошибки на определенном уровне значимости (alpha), мы подразумеваем, что должно выполняться неравенство (FWER leq alpha).
Ниже мы обсудим методы, которые позволяют это делать.
Коррекция Бонферрони
Вернемся к нашему примеру, когда мы сравнили 3 группы A, B и C с помощью t-теста. Предположим, что мы получили следующие Р-значения: 0.001, 0.01 и 0.04.
Как было сказано выше, мы хотим, чтобы групповая вероятность ошибки была не больше уровня значимости (FWER leq alpha). Согласно методу Бонферрони, мы должны сравнить каждое из полученных p-значений не с (alpha), а с (frac{alpha}{n}), где (n) – число проверяемых гипотез. Деление исходного уровня значимости (alpha) на (n) – это и есть поправка Бонферрони. В рассматриваемом примере каждое из полученных p-значений необходимо было бы сравнить с (frac{alpha}{n}), например, с (frac{0.01}{3}approx 0.017).
- (p-value_1=0.001 < alpha_{adjusted}=0.017) – гипотеза отклонена
- (p-value_2=0.01 < alpha_{adjusted}=0.017) – гипотеза отклонена
- (p-value_3=0.04 > alpha_{adjusted}=0.017) – гипотеза принята
Вместо деления уровня значимости на число гипотез, мы могли бы умножить каждое p-значение на это число и получить точно такие же выводы (эта эквивалентная процедура реалирована в R):
- (p-value_{1,adjusted} = 0.001 cdot 3 = 0.003 < alpha = 0.05) – гипотеза отклонена
- (p-value_{2,adjusted} = 0.01 cdot 3 = 0.03 < alpha = 0.05) – гипотеза отклонена
- (p-value_{3,adjusted} = 0.04 cdot 3 = 0.12 > alpha = 0.05) – гипотеза принята
Иногда при домножении p-значений результат может получиться больше единицы. Из теории вероятностей мы знаем, что вероятность не может быть больше одного, поэтому в таких случаях p-значение принимают равным за единицу.
Различные виды коррекций p-значений представлены в функции p.adjust(), выбрать тип коррекции можно с помощью аргумента method. В этой функции используется домножение исходных p-значений на количество тестируемых гипотез, а не корректировка уровня значимости.
Проверим наши рассчеты:
p.adjust(c(0.001, 0.01, 0.04), method = "bonferroni")Можно на выходе сразу получить выводы относительно гипотез при (alpha = 5%):
alpha <- 0.05
p.adjust(c(0.001, 0.01, 0.04), method = "bonferroni") < alpha # отклоняем H_0 (есть эффект)? Важно помнить об уязвимости коррекции Бонферрони – с ростом числа гипотез мощность метода уменьшается. Чем больше гипотез мы хотим проверить, тем сложнее нам будет их отвергать (даже если они реально должны быть отвергнуты). Например, для 5 групп (10 гипотез), применение поправки Бонферрони привело бы к снижению исходного уровня значимости до 0.01/10 = 0.001. Соответственно, для отклонения гипотез, соответствующие p-значения должны быть меньше 0.001, а это довольно жесткая отсечка. Из этого делаем вывод, что при большом числе гипотез коррекцию Бонферрони лучше не использовать.
Низходящая процедура Хольма (Хольма-Бонферрони)
Метод Хольма позволяет побороть недостатки метода Бонферрони. Он устроен следующим образом:
- Сначала p-значения сортируются по возрастанию (displaystyle{p-value_1 leq p-value_2 leq … leq p-value_n}).
- Затем проверяется условие для первого из p-значений: (displaystyle{p-value_1 geq frac{alpha}{n-i+1}=frac{alpha}{n}}), если условие выполнено, то все нулевые гипотезы принимаются, и процедура останавливается, иначе первая из гипотез отвергается, и начинается следующий шаг.
- На следующем шаге проверяется условие (displaystyle{p-value_2 geq frac{alpha}{n-i+1}=frac{alpha}{n-1}}), если условние выполнено, то все гипотезы, начиная со второй, принимаются, иначе первые две гипотезы отклоняются и начинается следующий шаг.
- На последнем шаге проверяется условие вида (displaystyle{p-value_n geq frac{alpha}{n-n+1}}), если оно выполнено, то последняя гипотеза принимается, если нет – отклоняется, на этом процедура заканчивается.
Метод Хольма называют нисходящей (step-down) процедурой. Он начинается с наименьшего p-значения в упорядоченном ряду и последовательно “спускается” вниз к более высоким значениям. На каждом шаге соответствующее значение (p-value_i) сравнивается со скорректированным уровнем значимости (displaystyle{alpha_{adjusted}=frac{alpha}{n+i-1}}). Аналогично коррекции Бонферрони можно вместо корректировки уровня значимости корректировать p-значения (displaystyle{p-value_{i,adjusted}=p-value_{i}cdot(n-i+1)}) (эта эквивалентная процедура реалирована в R). Возвращаясь к нашему примеру:
- (p-value_{1,adjusted} = 0.001 cdot (3-1+1) = 0.003 < alpha = 0.01) – гипотеза отклонена
- (p-value_{2,adjusted} = 0.01 cdot (3-2+1) = 0.02 > alpha = 0.01) – гипотеза принята
- (p-value_{3,adjusted} = 0.04 cdot (3-3+1) = 0.04 > alpha = 0.01) – гипотеза принята
А теперь проверим себя с помощью R:
p.adjust(c(0.001, 0.01, 0.04), method = "holm")И результаты проверки гипотез при (alpha =5%):
alpha <- 0.05
p.adjust(c(0.001, 0.01, 0.04), method = "holm") < alpha # отклоняем H_0 (есть эффект)? Средняя доля ложных отклонений (false discovery rate)
Рассмотренные выше FWER методы обеспечивают контроль над групповой вероятностью ошибки первого рода. Как мы выяснили, эти методы чересчур жестко работают, когда нужно одновременно проверить слишком много гипотез (падает статистическая мощность).Под “недостаточной мощностью” понимается сохранение многих нулевых гипотез, которые потенциально могут представлять исследовательский интерес и которые, соответственно, следовало бы отклонить. Недостаточная мощность традиционных процедур множественной проверки гипотез привела к разработке новых методов, например, метода Бенджамини-Хохберга.
Для преодоления недостаточной мощности FWER методов был предложен новый подход к проблеме множественных проверок статистических гипотез. Суть подхода заключается в том, что вместо контроля над групповой вероятностью ошибки первого рода выполняется контроль над ожидаемой долей ложных отклонений (false discovery rate, FDR) среди всех отклоненных гипотез.
В терминах таблицы выше эта ожидаемая доля может быть записана следующим образом: (displaystyle{FDR=left(frac{FP}{R}right)}) (считают, что если (R=0), то и (FDR=0)). Часто можно встретить запись через мат. ожидание (displaystyle{FDR=mathbb{E}left(frac{FP}{R}right)}). FDR – ожидаемая доля ложных отклоненийсреди всех отклоненных гипотез.
В отличие от уровня значимости (alpha), каких-либо общепринятых значений FDR не существует. Многие исследователи по аналогии контролируют FDR на уровне 5%. Интерпретация порогового значения FDR очень проста: например, если в ходе анализа данных отклонено 1000 гипотез, то при q=0.10 ожидаемая доля ложно отклоненных гипотез не превысит 100.
Восходящая процедура Бенджамини — Хохберга
В статье (Benjamini, Hochberg, 1995) описание процедуры контроля над FDR выглядит так:
- Сначала p-значения сортируются по возрастанию (displaystyle{p-value_1 leq p-value_2 leq … leq p-value_n}).
- Находят максимальное значение (k) среди всех индексов (i=1,…,n), для которого (p-value_i leq frac{i}{n}q) выполняется неравенство
- Отклоняют все гипотезы (H_i) с индексами (i=1,…,k)
Эквивалентная процедура, реалированая в R отличается тем, что вместо нахождения максимального индекса (k), исходные p-значения корректируются следующим образом: (q_i=frac{p_in}{i}).
В качестве примера рассмотрим следующий ряд из 15 упорядоченных по возрастанию p-значений (из оригинальной статьи Benjamini and Hochberg 1995):
p.adjust(c(0.0001, 0.0004, 0.0019, 0.0095, 0.0201, 0.0278, 0.0298, 0.0344, 0.0459, 0.3240, 0.4262, 0.5719, 0.6528, 0.7590, 1.000), method = "BH") [1] 0.00150000 0.00300000 0.00950000 0.03562500 0.06030000 0.06385714
[7] 0.06385714 0.06450000 0.07650000 0.48600000 0.58118182 0.71487500
[13] 0.75323077 0.81321429 1.00000000И результаты проверки гипотез при (alpha =5 %):
alpha <- 0.05
p.adjust(c(0.0001, 0.0004, 0.0019, 0.0095, 0.0201, 0.0278, 0.0298, 0.0344, 0.0459, 0.3240, 0.4262, 0.5719, 0.6528, 0.7590, 1.000), method = "BH") < alpha # отклоняем H_0 (есть эффект)? [1] TRUE TRUE TRUE TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
[13] FALSE FALSE FALSEИнтерпретация этих Р-значений с поправкой (в большинстве литературных источников их называют q-значениями) такова:
- Допустим, что мы хотим контролировать долю ложно отклоненных гипотез на уровне FDR = 0.05
- Все гипотезы, q-значения которых (q-value leq 0.05), отклоняются
- Среди всех этих отклоненных гипотез доля отклоненных по ошибке не превышает 5%
Коррекция Р-значений по методу Беньямини-Хохберга работает особенно хорошо в ситуациях, когда необходимо принять общее решение по какому-либо вопросу при наличии информации (=проверенных гипотез) по многим параметрам.
Следует помнить, что описанный здесь метод контроля над ожидаемой долей ложных отклонений предполагает, что все тесты, при помощи которых получают p-значения, независимы. На практике в большинстве случаев это условие выполняться не будет.
Восходящая процедура Бенджамини-Йекутили
Для преодоления ограничения независимости тестов при проверке гипотез в работе (Benjamini and Yekutieli 2001) был предложен усовершенствованный метод, учитывающий наличие корреляции между проверяемыми гипотезами.
Процедура Бенджамини-Йекутили очень похожа на процедуру Бенджамини-Хохберга. Основное отличие заключается во введении поправочной константы (displaystyle{c_n=sum limits_{i=1}^{n}frac{1}{i}}), далее аналогично:
- Сначала p-значения сортируются по возрастанию (displaystyle{p-value_1 leq p-value_2 leq … leq p-value_n}).
- Находят максимальное значение (k) среди всех индексов (i=1,…,n), для которого (p-value_i leq frac{i}{n} frac{q}{c_n}) выполняется неравенство
- Отклоняют все гипотезы (H_i) с индексами (i=1,…,k)
В R реализуется эквивалентная процедура:
Эквивалентная процедура, реалированая в R отличается тем, что вместо нахождения максимального индекса (k), исходные p-значения корректируются следующим образом: (displaystyle{q_i=frac{p_icdot ncdot c_n}{i}}).
p.adjust(c(0.0001, 0.0004, 0.0019, 0.0095, 0.0201, 0.0278, 0.0298, 0.0344, 0.0459, 0.3240, 0.4262, 0.5719, 0.6528, 0.7590, 1.000), method = "BY") [1] 0.004977343 0.009954687 0.031523175 0.118211908 0.200089208 0.211892623
[7] 0.211892623 0.214025770 0.253844518 1.000000000 1.000000000 1.000000000
[13] 1.000000000 1.000000000 1.000000000И результаты проверки гипотез при (alpha = 5%):
alpha <- 0.05
p.adjust(c(0.0001, 0.0004, 0.0019, 0.0095, 0.0201, 0.0278, 0.0298, 0.0344, 0.0459, 0.3240, 0.4262, 0.5719, 0.6528, 0.7590, 1.000), method = "BY") < alpha # отклоняем H_0 (есть эффект)? [1] TRUE TRUE TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
[13] FALSE FALSE FALSEОбобщающий алгоритм для разных процедур
Источник – мне не очень нравится сам текст, но схема хорошая.
Симуляция и сравнение результатов работы разных коррекций p-value
Сравним как работают разные методы:
alpha <- 0.05
n <- 50
set.seed(123)
x <- rnorm(n, mean = c(rep(0, n/2), rep(3, n/2))) # генерим вектор t статистик
pval <- round(2*pnorm(sort(-abs(x))), 3) # переводим статистики в p-value
default_bool <- pval < alpha # вектор с исходными выводами о принятии гипотез без коррекции
bonferroni_pval <- p.adjust(pval, method = "bonferroni")
bonferroni_bool <- p.adjust(pval, method = "bonferroni") < alpha # отклоняем H_0 (есть эффект)?
holm_pval <- p.adjust(pval, method = "holm")
holm_bool <- p.adjust(pval, method = "holm") < alpha # отклоняем H_0 (есть эффект)?
bh_pval <- p.adjust(pval, method = "BH")
bh_bool <- p.adjust(pval, method = "BH") < alpha # отклоняем H_0 (есть эффект)?
by_pval <- p.adjust(pval, method = "BY")
by_bool <- p.adjust(pval, method = "BY") < alpha # отклоняем H_0 (есть эффект)?
methods <- cbind(default_bool, bonferroni_bool, holm_bool, bh_bool, by_bool) # склеиваем столбики с выводами о принятии гипотез для разных корректировок; если бы вдруг хотели склеить строчки, то есть аналогичная функция rbind()
colnames(methods) <- c('Без коррекции', 'Бонферрони', 'Хольм', 'Бенджамини-Хохберг', 'Бенджамини-Йекутили') # добавляем шапку таблицы
rownames(methods) <- c(1:n) # добавляем номера строчкам
methods Без коррекции Бонферрони Хольм Бенджамини-Хохберг Бенджамини-Йекутили
1 TRUE TRUE TRUE TRUE TRUE
2 TRUE TRUE TRUE TRUE TRUE
3 TRUE TRUE TRUE TRUE TRUE
4 TRUE TRUE TRUE TRUE TRUE
5 TRUE TRUE TRUE TRUE TRUE
6 TRUE TRUE TRUE TRUE TRUE
7 TRUE TRUE TRUE TRUE TRUE
8 TRUE TRUE TRUE TRUE TRUE
9 TRUE TRUE TRUE TRUE TRUE
10 TRUE TRUE TRUE TRUE TRUE
11 TRUE FALSE TRUE TRUE TRUE
12 TRUE FALSE FALSE TRUE TRUE
13 TRUE FALSE FALSE TRUE FALSE
14 TRUE FALSE FALSE TRUE FALSE
15 TRUE FALSE FALSE TRUE FALSE
16 TRUE FALSE FALSE TRUE FALSE
17 TRUE FALSE FALSE TRUE FALSE
18 TRUE FALSE FALSE TRUE FALSE
19 TRUE FALSE FALSE TRUE FALSE
20 TRUE FALSE FALSE TRUE FALSE
21 TRUE FALSE FALSE FALSE FALSE
22 TRUE FALSE FALSE FALSE FALSE
23 FALSE FALSE FALSE FALSE FALSE
24 FALSE FALSE FALSE FALSE FALSE
25 FALSE FALSE FALSE FALSE FALSE
26 FALSE FALSE FALSE FALSE FALSE
27 FALSE FALSE FALSE FALSE FALSE
28 FALSE FALSE FALSE FALSE FALSE
29 FALSE FALSE FALSE FALSE FALSE
30 FALSE FALSE FALSE FALSE FALSE
31 FALSE FALSE FALSE FALSE FALSE
32 FALSE FALSE FALSE FALSE FALSE
33 FALSE FALSE FALSE FALSE FALSE
34 FALSE FALSE FALSE FALSE FALSE
35 FALSE FALSE FALSE FALSE FALSE
36 FALSE FALSE FALSE FALSE FALSE
37 FALSE FALSE FALSE FALSE FALSE
38 FALSE FALSE FALSE FALSE FALSE
39 FALSE FALSE FALSE FALSE FALSE
40 FALSE FALSE FALSE FALSE FALSE
41 FALSE FALSE FALSE FALSE FALSE
42 FALSE FALSE FALSE FALSE FALSE
43 FALSE FALSE FALSE FALSE FALSE
44 FALSE FALSE FALSE FALSE FALSE
45 FALSE FALSE FALSE FALSE FALSE
46 FALSE FALSE FALSE FALSE FALSE
47 FALSE FALSE FALSE FALSE FALSE
48 FALSE FALSE FALSE FALSE FALSE
49 FALSE FALSE FALSE FALSE FALSE
50 FALSE FALSE FALSE FALSE FALSEplot(pval, bonferroni_pval, col = "orange", type="p", pch=1)
lines(pval, holm_pval, col="green", type="p", pch=1)
lines(pval, bh_pval, col="blue", type="p", pch=1)
lines(pval, by_pval, col="violet", type="p", pch=1)
abline(h=alpha, col="red")
abline(v=alpha, col="red")
legend(x=0.6, y=0.5, # координаты верхнего левого угла легенды
legend=c('Бонферрони', 'Хольм', 'Бенджамини-Хохберг', 'Бенджамини-Йекутили', 'Уровень значимости'), # категории легенды
col=c("orange", "green", "blue", "violet", "red"), # цвета категорий
bty = "n", # чтобы не было рамочки вокруг легенды
pch=1) # форма маркераЗанырнем глубже в механику классического A/B тестирования, познакомимся с понятием “статистическая значимость” и разберемся, что может угрожать достоверности результатов ваших тестов.
Автор английской версии: Идан Михаэли, директор по Data Science в Hippo Insurance
(Если вы здесь впервые, то лучше начните сначала)
A/B тестирование — это одна из самых популярных техник оптимизации веб-страниц. Техника позволяет маркетологам, владельцам сайтов принимать более взвешенные и обоснованные решения относительно целесообразности внедрения их творческих идей. Другими словами, когда кто-то предлагает что-то на сайте поменять, мы можем оценить эти изменения не интуитивно и не с высоты чьего-то опыта, а объективно, отталкиваясь от конкретных целей: как ближних (например, CTR кнопки), так и долгосрочных (например, конверсия в покупатели). В то же время, тесты страхуют нас от серьезных ошибок, которые могут подорвать вовлеченность.
Давайте же занырнем глубже в механику классического A/B тестирования, познакомимся с понятием статистическая значимость (statistical significance) и разберемся, что может угрожать достоверности результатов ваших тестов. В конце статьи я приведу пару альтернатив классическому A/B тестированию от Dynamic Yield.
На первый взгляд, процедура тестирования предельно проста. Во-первых, мы создаем вариацию некой оригинальной веб-страницы (базы). Далее, мы случайным образом делим трафик между двумя версиями страницы (распределение посетителей проходит случайно, согласно некой вероятности). Наконец, мы собираем данные, как отработала каждая версия страницы (метрики). После этого мы анализируем данные, выбираем версию с наилучшими результатами и отключаем ту, что отработала хуже. Вроде бы все очевидно и просто? Нет.
Важно помнить, что когда мы выбираем одну из версий, то фактически масштабируем показатели, полученные в результате тестирования, на всю аудиторию потенциальных пользователей, а это — серьезный прыжок веры. Поэтому тестирование должно быть достоверным; иначе есть риск принять неверное решение, которое в долгосрочной перспективе негативно скажется на показателях сайта. Процесс достижения нужной достоверности мы называем тестированием гипотезы (hypothesis testing), а саму искомую достоверность — статистической значимостью (statistical significance).
Тестирование гипотезы начинается с того, что мы формулируем нулевую гипотезу (Null hypothesis) — некое утверждение, которое закрепляет статус кво, например “оригинальная страница (база) дает тот же CTR, что и вариация с новым дизайном”. Далее мы смотрим, можно ли отклонить это утверждение как крайне маловероятное.
Как мы это делаем?
Во-первых, нужно понять, где нас подстерегают ошибки. Вариантов тут два: во-первых, мы можем ошибочно опровергнуть нулевую гипотезу. Мельком взглянув на данные, мы можем прийти к выводу, что разница в показателях двух страниц имеется.
Ошибки первого рода. На деле же, этой разницы может не быть, а различия в результатах, на которые мы опираемся — это воля случая. Такой тип ошибок называется ошибки первого рода (type I error) или ложноположительные результаты (false positive).
Ошибки второго рода. Второй тип ошибок наблюдается, когда мы не наблюдаем значительной разницы между вариациями страницы, в то время как разница на самом деле есть, а ее отсутствие в тестировании — это случайность. Такие ошибки называют ошибками второго рода (type II error) или ложноотрицательными результатами (false negative).
Как избежать ошибок первого и второго рода?
Краткий ответ такой: устанавливайте правильный размер выборки. Чтобы определить нужный размер выборки, необходимо задать несколько параметров для нашего теста. Чтобы избежать ложноположительных результатов, нужно установить уровень достоверности (confidence level) или, другими словами, статистическую значимость. Это должно быть небольшое положительное число. Как правило, уровень значимости принимают равным 0,05: это означает, что на действующей модели лишь в 5% случаев есть вероятность выявить ложную разницу между двумя вариациями (то есть пятипроцентная вероятность ошибки). Про эту общепринятую константу обычно говорят “достоверность более 95%”.
Большинство специалистов по проведению тестирований (как и большинство инструментов, доступных на сегодняшний день) довольствуются этим первым параметром. Но, если мы хотим также застраховаться от ложноотрицательных результатов (false negative), нужно определить еще два параметра.
- Первый — это минимальная разница в результатах, которую мы хотим отслеживать (при условии, что разница была выявлена). Второй — это вероятность выявить эту разницу (при условии, что она существует).
- Второй параметр называют статистической мощностью (statistical power) и часто по умолчанию принимают его за 80%. Далее нужный размер выборки рассчитывается на основании этих трёх значений (можно воспользоваться онлайн-калькулятором).
Хотя этот процесс может показаться достаточно сложным, а рассчитанный таким образом размер выборки часто кажется слишком большим, стандартный подход к тестированию диктует именно такую процедуру — иначе о достоверности говорить не приходится. Горькая правда в том, что даже при условии чёткого следования вышеописанному алгоритму, вы всё равно можете получить некорректные результаты. Давайте разберемся почему.
Я провел все вычисления; теперь можно полностью доверять результатам?
Хотя метод проверки гипотез выглядит многообещающе, на практике он совершенно не застрахован от ошибок, потому что при тестировании мы опираемся на определенные скрытые предположения, которые часто не имеют места в реальных жизненных сценариях.
Первое предположение обычно не вызывает сомнений: мы предполагаем, что “образцы” нашей выборки — то есть посетители сайта, которым мы показываем вариации страницы — никак не связаны друг с другом, и их поступки не созависимы. Обычно это предположение достоверно, если конечно мы не показываем наши вариации одному и тому же посетителю по несколько раз, считая каждый раз как отдельный показ.
Второе предположение состоит в том, что элементы каждой выборки распределены одинаково (identically distributed). Проще говоря, это означает, что вероятность конверсии равна для всех посетителей. Конечно, это не так. Вероятность конверсии зависит от времени, местоположения, предпочтений посетителя, источников трафика и многих других факторов. К примеру, если во время проведения эксперимента, на сайте крутится какая-то рекламная кампания, мы можем наблюдать прилив трафика с Facebook. Это может привести к резким изменениям в CTR (click-through rates) — ведь люди, привлеченные рекламой, отличаются от ваших обычных посетителей. Такие колебания влияют не только на A/B тесты, но и на более продвинутые техники оптимизации, которые мы применяем в Dynamic Yield.
Третье предположение заключается в том, что измеряемые нами показатели (например, CTR или конверсия) имеют нормальное распределение. Возможно для вас это звучит как абстрактный математический термин, но правда в том, что все “магические” формулы расчета уровня достоверности основаны на этом предположении, которое, кстати, очень шаткое и соблюдается далеко не всегда. В целом можно выделить такую зависимость: чем больше размер выборки и чем больше мы наблюдаем конверсий, тем сильнее соблюдается это предположение — согласно центральной предельной теореме.
Окей, понятно, что математика не застрахована от ошибок, но на какие подводные камни стоит обратить внимание?
Таких подводных камней два.
Во-первых, платформы для проведения A/B тестов часто предлагают наблюдать за результатами тестирования в реальном времени. С одной стороны, это дает чувство контроля над ситуацией и позволяет специалисту следить за прозрачностью тестирования. Однако, наблюдая за показателями “в прямом эфире”, мы рискуем приступить к активным действиям раньше времени, отталкиваясь от сырых данных. Кто-то останавливает тестирование, получив первые результаты — даже если нужный размер выборки еще не достигнут, кто-то тормозит, как только достигнута статистическая значимость; оба сценария — прямой путь к ошибкам. Это вызывает статистическую погрешность (statistical bias) в сторону выявления разницы, которой на самом деле нет; более того, эту погрешность мы не можем заранее рассчитать и скорректировать (например, установив более высокий уровень значимости). Больше на тему: Как не надо анализировать A/B тесты. Проблема подглядывания →
Второй подводный камень — это завышенные ожидания от вариации-победителя после проведения тестирования. В результате проявления статистического эффекта известного как регрессия к среднему (regression toward the mean), долговременные результаты вариации-победителя могут быть не такими высокими, как в процессе тестирования. Проще говоря, есть вероятность, что вариация-победитель на самом деле была не объективно лучшей, а просто более “везучей”. Это везение со временем заканчивается и сглаживается, в результате чего возникает ощущение, что результаты падают.
Есть ли альтернативы A/B тестированию?
Конечно. Есть множество разных кейсов оптимизации страниц, и A/B тестирование подходит лишь в ряде случаев. Допустим, мы хотим провести тест на странице, которая давно работает и по показателям которой у нас уже собрана определенная история. Изменение, которое мы хотим внести, будет внедрено на страницу надолго и для всей совокупности посетителей сайта. Конечно, в этом случае нужно глубоко и точно измерить все результаты и принять обоснованное решение относительно данного изменения. Однако, на практике часто встречаются другие кейсы.
К примеру, нам нужно узнать, какой из трёх заголовков статей сработает лучше. При этом сайт, на котором будет размещена статья, относительно новый, а сама статья будет висеть на главной странице лишь несколько часов. Это означает, что нам нужно быстро выявить самый эффективный заголовок и применить это знание в рамках нескольких часов. В этом нам поможет метод “многорукого бандита”.
Если кратко, многорукий бандит постоянно делит трафик между вариациями в зависимости от результатов и уровня достоверности, зафиксированных на каждом этапе пути. При таком подходе мы немного теряем в плане уверенности, что вариация-побелитель действительно лучшая вариация, но получаем более быструю конвергенцию. Это первый уровень оптимизации, который мы предлагаем в Dynamic Yield.
Более глубокий уровень оптимизации делает ставку на полную персонализацию. Это можно делать вручную или автоматически. Суть в том, что мы показываем определенным пользователям определенные вариации. Рассмотрим пример персонализации вручную. Допустим мы хотим на День Королевы показывать всем посетителям из Нидерландов оранжевый фон страницы. Очень часто такие ручные изменения приносят свои результаты. Минус в том, что они плохо масштабируются. Допустим, у нас на сайте действует рекламная акция для посетителей с Facebook. Что делать, если с Facebook приходит голландец? По мере появления новых групп посетителей, количество вариаций будет расти, а правила оптимизации — усложняться. Кроме того, здесь в игру вступает метод научного тыка — вроде бы эксперименты должны принести какие-то результаты, но никто не знает какие.
Поэтому в подобных случаях может лучше сработать подход автоматической персонализации. Допустим, у нас кулинарный сайт, на котором есть секция с рекомендованными рецептами. С помощью механизма персонализации мы можем настроить сайт так, чтобы рекомендовать каждому посетителю персональный рецепт, на основании истории его взаимодействия со страницами, разделами и тегами на сайте.
Заключение
A/B тесты — эффективный инструмент, но если проводить их неправильно, можно прийти к ложным выводам. Достижение нужного уровня статистической значимости — это обязательное условие для получения надежных результатов тестирования. Чтобы этого добиться, нужно правильно установить ряд параметров, а также определить необходимый размер выборки и придерживаться его в процессе тестирования.
Классическая ошибка, которая ведет к потере достоверности — это сбор результатов до момента достижения нужного размера выборки. Если вас интересуют быстрые способ оптимизации, присмотритесь к методам из второй части статьи: многорукий бандит и персонализация на базе машинного обучения.
В машинном обучении различают оценки качества для задачи классификации и регрессии. Причем оценка задачи классификации часто значительно сложнее, чем оценка регрессии.
Содержание
- 1 Оценки качества классификации
- 1.1 Матрица ошибок (англ. Сonfusion matrix)
- 1.2 Аккуратность (англ. Accuracy)
- 1.3 Точность (англ. Precision)
- 1.4 Полнота (англ. Recall)
- 1.5 F-мера (англ. F-score)
- 1.6 ROC-кривая
- 1.7 Precison-recall кривая
- 2 Оценки качества регрессии
- 2.1 Средняя квадратичная ошибка (англ. Mean Squared Error, MSE)
- 2.2 Cредняя абсолютная ошибка (англ. Mean Absolute Error, MAE)
- 2.3 Коэффициент детерминации
- 2.4 Средняя абсолютная процентная ошибка (англ. Mean Absolute Percentage Error, MAPE)
- 2.5 Корень из средней квадратичной ошибки (англ. Root Mean Squared Error, RMSE)
- 2.6 Cимметричная MAPE (англ. Symmetric MAPE, SMAPE)
- 2.7 Средняя абсолютная масштабированная ошибка (англ. Mean absolute scaled error, MASE)
- 3 Кросс-валидация
- 4 Примечания
- 5 См. также
- 6 Источники информации
Оценки качества классификации
Матрица ошибок (англ. Сonfusion matrix)
Перед переходом к самим метрикам необходимо ввести важную концепцию для описания этих метрик в терминах ошибок классификации — confusion matrix (матрица ошибок).
Допустим, что у нас есть два класса и алгоритм, предсказывающий принадлежность каждого объекта одному из классов.
Рассмотрим пример. Пусть банк использует систему классификации заёмщиков на кредитоспособных и некредитоспособных. При этом первым кредит выдаётся, а вторые получат отказ. Таким образом, обнаружение некредитоспособного заёмщика () можно рассматривать как «сигнал тревоги», сообщающий о возможных рисках.
Любой реальный классификатор совершает ошибки. В нашем случае таких ошибок может быть две:
- Кредитоспособный заёмщик распознается моделью как некредитоспособный и ему отказывается в кредите. Данный случай можно трактовать как «ложную тревогу».
- Некредитоспособный заёмщик распознаётся как кредитоспособный и ему ошибочно выдаётся кредит. Данный случай можно рассматривать как «пропуск цели».
Несложно увидеть, что эти ошибки неравноценны по связанным с ними проблемам. В случае «ложной тревоги» потери банка составят только проценты по невыданному кредиту (только упущенная выгода). В случае «пропуска цели» можно потерять всю сумму выданного кредита. Поэтому системе важнее не допустить «пропуск цели», чем «ложную тревогу».
Поскольку с точки зрения логики задачи нам важнее правильно распознать некредитоспособного заёмщика с меткой , чем ошибиться в распознавании кредитоспособного, будем называть соответствующий исход классификации положительным (заёмщик некредитоспособен), а противоположный — отрицательным (заемщик кредитоспособен ). Тогда возможны следующие исходы классификации:
- Некредитоспособный заёмщик классифицирован как некредитоспособный, т.е. положительный класс распознан как положительный. Наблюдения, для которых это имеет место называются истинно-положительными (True Positive — TP).
- Кредитоспособный заёмщик классифицирован как кредитоспособный, т.е. отрицательный класс распознан как отрицательный. Наблюдения, которых это имеет место, называются истинно отрицательными (True Negative — TN).
- Кредитоспособный заёмщик классифицирован как некредитоспособный, т.е. имела место ошибка, в результате которой отрицательный класс был распознан как положительный. Наблюдения, для которых был получен такой исход классификации, называются ложно-положительными (False Positive — FP), а ошибка классификации называется ошибкой I рода.
- Некредитоспособный заёмщик распознан как кредитоспособный, т.е. имела место ошибка, в результате которой положительный класс был распознан как отрицательный. Наблюдения, для которых был получен такой исход классификации, называются ложно-отрицательными (False Negative — FN), а ошибка классификации называется ошибкой II рода.
Таким образом, ошибка I рода, или ложно-положительный исход классификации, имеет место, когда отрицательное наблюдение распознано моделью как положительное. Ошибкой II рода, или ложно-отрицательным исходом классификации, называют случай, когда положительное наблюдение распознано как отрицательное. Поясним это с помощью матрицы ошибок классификации:
-
Истинно-положительный (True Positive — TP) Ложно-положительный (False Positive — FP) Ложно-отрицательный (False Negative — FN) Истинно-отрицательный (True Negative — TN)
Здесь — это ответ алгоритма на объекте, а — истинная метка класса на этом объекте.
Таким образом, ошибки классификации бывают двух видов: False Negative (FN) и False Positive (FP).
P означает что классификатор определяет класс объекта как положительный (N — отрицательный). T значит что класс предсказан правильно (соответственно F — неправильно). Каждая строка в матрице ошибок представляет спрогнозированный класс, а каждый столбец — фактический класс.
# код для матрицы ошибок # Пример классификатора, способного проводить различие между всего лишь двумя # классами, "пятерка" и "не пятерка" из набора рукописных цифр MNIST import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.metrics import confusion_matrix from sklearn.linear_model import SGDClassifier mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (англ. Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе # Для расчета матрицы ошибок сначала понадобится иметь набор прогнозов, чтобы их можно было сравнивать с фактическими целями y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) print(confusion_matrix(y_train_5, y_train_pred)) # array([[53892, 687], # [ 1891, 3530]])
Безупречный классификатор имел бы только истинно-положительные и истинно отрицательные классификации, так что его матрица ошибок содержала бы ненулевые значения только на своей главной диагонали (от левого верхнего до правого нижнего угла):
import numpy as np
from sklearn.datasets import fetch_openml
from sklearn.metrics import confusion_matrix
mnist = fetch_openml('mnist_784', version=1)
X, y = mnist["data"], mnist["target"]
y = y.astype(np.uint8)
X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:]
y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки
y_test_5 = (y_test == 5)
y_train_perfect_predictions = y_train_5 # притворись, что мы достигли совершенства
print(confusion_matrix(y_train_5, y_train_perfect_predictions))
# array([[54579, 0],
# [ 0, 5421]])
Аккуратность (англ. Accuracy)
Интуитивно понятной, очевидной и почти неиспользуемой метрикой является accuracy — доля правильных ответов алгоритма:
Эта метрика бесполезна в задачах с неравными классами, что как вариант можно исправить с помощью алгоритмов сэмплирования и это легко показать на примере.
Допустим, мы хотим оценить работу спам-фильтра почты. У нас есть 100 не-спам писем, 90 из которых наш классификатор определил верно (True Negative = 90, False Positive = 10), и 10 спам-писем, 5 из которых классификатор также определил верно (True Positive = 5, False Negative = 5).
Тогда accuracy:
Однако если мы просто будем предсказывать все письма как не-спам, то получим более высокую аккуратность:
При этом, наша модель совершенно не обладает никакой предсказательной силой, так как изначально мы хотели определять письма со спамом. Преодолеть это нам поможет переход с общей для всех классов метрики к отдельным показателям качества классов.
# код для для подсчета аккуратности: # Пример классификатора, способного проводить различие между всего лишь двумя # классами, "пятерка" и "не пятерка" из набора рукописных цифр MNIST import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.metrics import accuracy_score from sklearn.linear_model import SGDClassifier mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) # print(confusion_matrix(y_train_5, y_train_pred)) # array([[53892, 687] # [ 1891, 3530]]) print(accuracy_score(y_train_5, y_train_pred)) # == (53892 + 3530) / (53892 + 3530 + 1891 +687) # 0.9570333333333333
Точность (англ. Precision)
Точностью (precision) называется доля правильных ответов модели в пределах класса — это доля объектов действительно принадлежащих данному классу относительно всех объектов которые система отнесла к этому классу.
Именно введение precision не позволяет нам записывать все объекты в один класс, так как в этом случае мы получаем рост уровня False Positive.
Полнота (англ. Recall)
Полнота — это доля истинно положительных классификаций. Полнота показывает, какую долю объектов, реально относящихся к положительному классу, мы предсказали верно.
Полнота (recall) демонстрирует способность алгоритма обнаруживать данный класс вообще.
Имея матрицу ошибок, очень просто можно вычислить точность и полноту для каждого класса. Точность (precision) равняется отношению соответствующего диагонального элемента матрицы и суммы всей строки класса. Полнота (recall) — отношению диагонального элемента матрицы и суммы всего столбца класса. Формально:
Результирующая точность классификатора рассчитывается как арифметическое среднее его точности по всем классам. То же самое с полнотой. Технически этот подход называется macro-averaging.
# код для для подсчета точности и полноты: # Пример классификатора, способного проводить различие между всего лишь двумя # классами, "пятерка" и "не пятерка" из набора рукописных цифр MNIST import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.metrics import precision_score, recall_score from sklearn.linear_model import SGDClassifier mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) # print(confusion_matrix(y_train_5, y_train_pred)) # array([[53892, 687] # [ 1891, 3530]]) print(precision_score(y_train_5, y_train_pred)) # == 3530 / (3530 + 687) print(recall_score(y_train_5, y_train_pred)) # == 3530 / (3530 + 1891) # 0.8370879772350012 # 0.6511713705958311
F-мера (англ. F-score)
Precision и recall не зависят, в отличие от accuracy, от соотношения классов и потому применимы в условиях несбалансированных выборок.
Часто в реальной практике стоит задача найти оптимальный (для заказчика) баланс между этими двумя метриками. Понятно что чем выше точность и полнота, тем лучше. Но в реальной жизни максимальная точность и полнота не достижимы одновременно и приходится искать некий баланс. Поэтому, хотелось бы иметь некую метрику которая объединяла бы в себе информацию о точности и полноте нашего алгоритма. В этом случае нам будет проще принимать решение о том какую реализацию запускать в производство (у кого больше тот и круче). Именно такой метрикой является F-мера.
F-мера представляет собой гармоническое среднее между точностью и полнотой. Она стремится к нулю, если точность или полнота стремится к нулю.
Данная формула придает одинаковый вес точности и полноте, поэтому F-мера будет падать одинаково при уменьшении и точности и полноты. Возможно рассчитать F-меру придав различный вес точности и полноте, если вы осознанно отдаете приоритет одной из этих метрик при разработке алгоритма:
где принимает значения в диапазоне если вы хотите отдать приоритет точности, а при приоритет отдается полноте. При формула сводится к предыдущей и вы получаете сбалансированную F-меру (также ее называют ).
-
Рис.1 Сбалансированная F-мера,
-
Рис.2 F-мера c приоритетом точности,
-
Рис.3 F-мера c приоритетом полноты,
F-мера достигает максимума при максимальной полноте и точности, и близка к нулю, если один из аргументов близок к нулю.
F-мера является хорошим кандидатом на формальную метрику оценки качества классификатора. Она сводит к одному числу две других основополагающих метрики: точность и полноту. Имея «F-меру» гораздо проще ответить на вопрос: «поменялся алгоритм в лучшую сторону или нет?»
# код для подсчета метрики F-mera: # Пример классификатора, способного проводить различие между всего лишь двумя # классами, "пятерка" и "не пятерка" из набора рукописных цифр MNIST import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.linear_model import SGDClassifier from sklearn.metrics import f1_score mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распознавать пятерки на целом обучающем наборе y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) print(f1_score(y_train_5, y_train_pred)) # 0.7325171197343846
ROC-кривая
Кривая рабочих характеристик (англ. Receiver Operating Characteristics curve).
Используется для анализа поведения классификаторов при различных пороговых значениях.
Позволяет рассмотреть все пороговые значения для данного классификатора.
Показывает долю ложно положительных примеров (англ. false positive rate, FPR) в сравнении с долей истинно положительных примеров (англ. true positive rate, TPR).

Доля FPR — это пропорция отрицательных образцов, которые были некорректно классифицированы как положительные.
- ,
где TNR — доля истинно отрицательных классификаций (англ. Тrие Negative Rate), представляющая собой пропорцию отрицательных образцов, которые были корректно классифицированы как отрицательные.
Доля TNR также называется специфичностью (англ. specificity). Следовательно, ROC-кривая изображает чувствительность (англ. seпsitivity), т.е. полноту, в сравнении с разностью 1 — specificity.
Прямая линия по диагонали представляет ROC-кривую чисто случайного классификатора. Хороший классификатор держится от указанной линии настолько далеко, насколько это
возможно (стремясь к левому верхнему углу).
Один из способов сравнения классификаторов предусматривает измерение площади под кривой (англ. Area Under the Curve — AUC). Безупречный классификатор будет иметь площадь под ROC-кривой (ROC-AUC), равную 1, тогда как чисто случайный классификатор — площадь 0.5.
# Код отрисовки ROC-кривой # На примере классификатора, способного проводить различие между всего лишь двумя классами # "пятерка" и "не пятерка" из набора рукописных цифр MNIST from sklearn.metrics import roc_curve import matplotlib.pyplot as plt import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.linear_model import SGDClassifier mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) y_scores = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3, method="decision_function") fpr, tpr, thresholds = roc_curve(y_train_5, y_scores) def plot_roc_curve(fpr, tpr, label=None): plt.plot(fpr, tpr, linewidth=2, label=label) plt.plot([0, 1], [0, 1], 'k--') # dashed diagonal plt.xlabel('False Positive Rate, FPR (1 - specificity)') plt.ylabel('True Positive Rate, TPR (Recall)') plt.title('ROC curve') plt.savefig("ROC.png") plot_roc_curve(fpr, tpr) plt.show()
Precison-recall кривая
Чувствительность к соотношению классов.
Рассмотрим задачу выделения математических статей из множества научных статей. Допустим, что всего имеется 1.000.100 статей, из которых лишь 100 относятся к математике. Если нам удастся построить алгоритм , идеально решающий задачу, то его TPR будет равен единице, а FPR — нулю. Рассмотрим теперь плохой алгоритм, дающий положительный ответ на 95 математических и 50.000 нематематических статьях. Такой алгоритм совершенно бесполезен, но при этом имеет TPR = 0.95 и FPR = 0.05, что крайне близко к показателям идеального алгоритма.
Таким образом, если положительный класс существенно меньше по размеру, то AUC-ROC может давать неадекватную оценку качества работы алгоритма, поскольку измеряет долю неверно принятых объектов относительно общего числа отрицательных. Так, алгоритм , помещающий 100 релевантных документов на позиции с 50.001-й по 50.101-ю, будет иметь AUC-ROC 0.95.
Precison-recall (PR) кривая. Избавиться от указанной проблемы с несбалансированными классами можно, перейдя от ROC-кривой к PR-кривой. Она определяется аналогично ROC-кривой, только по осям откладываются не FPR и TPR, а полнота (по оси абсцисс) и точность (по оси ординат). Критерием качества семейства алгоритмов выступает площадь под PR-кривой (англ. Area Under the Curve — AUC-PR)

# Код отрисовки Precison-recall кривой # На примере классификатора, способного проводить различие между всего лишь двумя классами # "пятерка" и "не пятерка" из набора рукописных цифр MNIST from sklearn.metrics import precision_recall_curve import matplotlib.pyplot as plt import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.linear_model import SGDClassifier mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) y_scores = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3, method="decision_function") precisions, recalls, thresholds = precision_recall_curve(y_train_5, y_scores) def plot_precision_recall_vs_threshold(precisions, recalls, thresholds): plt.plot(recalls, precisions, linewidth=2) plt.xlabel('Recall') plt.ylabel('Precision') plt.title('Precision-Recall curve') plt.savefig("Precision_Recall_curve.png") plot_precision_recall_vs_threshold(precisions, recalls, thresholds) plt.show()
Оценки качества регрессии
Наиболее типичными мерами качества в задачах регрессии являются
Средняя квадратичная ошибка (англ. Mean Squared Error, MSE)
MSE применяется в ситуациях, когда нам надо подчеркнуть большие ошибки и выбрать модель, которая дает меньше больших ошибок прогноза. Грубые ошибки становятся заметнее за счет того, что ошибку прогноза мы возводим в квадрат. И модель, которая дает нам меньшее значение среднеквадратической ошибки, можно сказать, что что у этой модели меньше грубых ошибок.
- и
Cредняя абсолютная ошибка (англ. Mean Absolute Error, MAE)
Среднеквадратичный функционал сильнее штрафует за большие отклонения по сравнению со среднеабсолютным, и поэтому более чувствителен к выбросам. При использовании любого из этих двух функционалов может быть полезно проанализировать, какие объекты вносят наибольший вклад в общую ошибку — не исключено, что на этих объектах была допущена ошибка при вычислении признаков или целевой величины.
Среднеквадратичная ошибка подходит для сравнения двух моделей или для контроля качества во время обучения, но не позволяет сделать выводов о том, на сколько хорошо данная модель решает задачу. Например, MSE = 10 является очень плохим показателем, если целевая переменная принимает значения от 0 до 1, и очень хорошим, если целевая переменная лежит в интервале (10000, 100000). В таких ситуациях вместо среднеквадратичной ошибки полезно использовать коэффициент детерминации —
Коэффициент детерминации
Коэффициент детерминации измеряет долю дисперсии, объясненную моделью, в общей дисперсии целевой переменной. Фактически, данная мера качества — это нормированная среднеквадратичная ошибка. Если она близка к единице, то модель хорошо объясняет данные, если же она близка к нулю, то прогнозы сопоставимы по качеству с константным предсказанием.
Средняя абсолютная процентная ошибка (англ. Mean Absolute Percentage Error, MAPE)
Это коэффициент, не имеющий размерности, с очень простой интерпретацией. Его можно измерять в долях или процентах. Если у вас получилось, например, что MAPE=11.4%, то это говорит о том, что ошибка составила 11,4% от фактических значений.
Основная проблема данной ошибки — нестабильность.
Корень из средней квадратичной ошибки (англ. Root Mean Squared Error, RMSE)
Примерно такая же проблема, как и в MAPE: так как каждое отклонение возводится в квадрат, любое небольшое отклонение может значительно повлиять на показатель ошибки. Стоит отметить, что существует также ошибка MSE, из которой RMSE как раз и получается путем извлечения корня.
Cимметричная MAPE (англ. Symmetric MAPE, SMAPE)
Средняя абсолютная масштабированная ошибка (англ. Mean absolute scaled error, MASE)
MASE является очень хорошим вариантом для расчета точности, так как сама ошибка не зависит от масштабов данных и является симметричной: то есть положительные и отрицательные отклонения от факта рассматриваются в равной степени.
Обратите внимание, что в MASE мы имеем дело с двумя суммами: та, что в числителе, соответствует тестовой выборке, та, что в знаменателе — обучающей. Вторая фактически представляет собой среднюю абсолютную ошибку прогноза. Она же соответствует среднему абсолютному отклонению ряда в первых разностях. Эта величина, по сути, показывает, насколько обучающая выборка предсказуема. Она может быть равна нулю только в том случае, когда все значения в обучающей выборке равны друг другу, что соответствует отсутствию каких-либо изменений в ряде данных, ситуации на практике почти невозможной. Кроме того, если ряд имеет тенденцию к росту либо снижению, его первые разности будут колебаться около некоторого фиксированного уровня. В результате этого по разным рядам с разной структурой, знаменатели будут более-менее сопоставимыми. Всё это, конечно же, является очевидными плюсами MASE, так как позволяет складывать разные значения по разным рядам и получать несмещённые оценки.
Недостаток MASE в том, что её тяжело интерпретировать. Например, MASE=1.21 ни о чём, по сути, не говорит. Это просто означает, что ошибка прогноза оказалась в 1.21 раза выше среднего абсолютного отклонения ряда в первых разностях, и ничего более.
Кросс-валидация
Хороший способ оценки модели предусматривает применение кросс-валидации (cкользящего контроля или перекрестной проверки).
В этом случае фиксируется некоторое множество разбиений исходной выборки на две подвыборки: обучающую и контрольную. Для каждого разбиения выполняется настройка алгоритма по обучающей подвыборке, затем оценивается его средняя ошибка на объектах контрольной подвыборки. Оценкой скользящего контроля называется средняя по всем разбиениям величина ошибки на контрольных подвыборках.
Примечания
- [1] Лекция «Оценивание качества» на www.coursera.org
- [2] Лекция на www.stepik.org о кросвалидации
- [3] Лекция на www.stepik.org о метриках качества, Precison и Recall
- [4] Лекция на www.stepik.org о метриках качества, F-мера
- [5] Лекция на www.stepik.org о метриках качества, примеры
См. также
- Оценка качества в задаче кластеризации
- Кросс-валидация
Источники информации
- [6] Соколов Е.А. Лекция линейная регрессия
- [7] — Дьяконов А. Функции ошибки / функционалы качества
- [8] — Оценка качества прогнозных моделей
- [9] — HeinzBr Ошибка прогнозирования: виды, формулы, примеры
- [10] — egor_labintcev Метрики в задачах машинного обучения
- [11] — grossu Методы оценки качества прогноза
- [12] — К.В.Воронцов, Классификация
- [13] — К.В.Воронцов, Скользящий контроль
Мы уже рассказывали, как машинное обучение применяется для прогнозирования будущих событий в финансовом секторе, нефтегазовой промышленности, логистике, HR-менеджменте, девелопменте, страховании, муниципальном управлении, маркетинге, ритейле и других отраслях экономики. Сегодня рассмотрим еще несколько практических примеров такого приложения Machine Learning и в этом контексте разберем одно из ключевых понятий Data Science по оценке моделей. Читайте в нашей статье, что такое матрица ошибок (confusion matrix) и как она помогает измерить эффективность используемых ML-алгоритмов и других инструментов бизнес-аналитики, оценив потенциальные убытки и выгоды от возможных сценариев будущего в задаче прогнозирования спроса.
От ритейла до банка: 5 примеров применения Big Data и Machine Learning в задачах прогнозирования спроса и предложения
Вообще сегодня задача прогнозирования спроса стала довольно обыденным приложением методов Machine Learning (ML) в реальном бизнесе. В частности, в декабре 2019 года сервис объявлений «Юла» ускорил публикацию объявлений по продаже товаров с помощью функции их распознавания по фотографии. Помимо собственно распознавания того, что сфотографировано, нейросетевые модели предлагают пользователю уточнить характеристики продукта и оценивают его стоимость в среднем по рынку. При этом пользователю выдается прогноз, насколько быстро он продаст товар при различных ценах [1].
Другой пример, московский сервис приготовления и доставки еды навынос «Кухня на районе» с помощью нейросетей и ежедневной статистики продаж рассчитывает, сколько продуктов нужно привезти на каждую точку, чтобы минимизировать количество остатков. Анализируя данные по проданным позициям в разных локациях, нейросеть из 3 500 вариантов отбирает сотню блюд, которые будут максимально востребованы, чтобы готовить именно их на районных кухнях в течение следующей недели [2].
Подобным образом, на основе постоянного анализа продаж, машинное обучение позволяет эффективно решить задачу ценообразования, установив наиболее оптимальную стоимость на отдельные продукты и целые товарные категории. Например, именно это было сделано в отечественном интернет-магазине детских игрушек Babadu.ru, когда методы Machine Learning помогли разработать несколько маркетинговых стратегий, наиболее выгодных для ритейлера [3]. Аналогично строятся ML-модели эластичного спроса в другом российском гиганте интернет-торговли, Ozon.ru. Разработанный алгоритм анализирует значения более 150 признаков в истории продаж, чтобы на выходе предоставить точный прогноз по будущим заказам. При этом в модели заложена функция минимизации денежных потерь на покупку и хранение лишних товаров на складе или отток клиента (Churn Rate) из-за отсутствия нужного продукта [4].
Похожая задача прогнозирования спроса актуальна и для банков, которые стремятся оптимизировать процессы работы с наличными деньгами в своих банкоматах. Финансовые корпорации хотят, с одной стороны, чтобы средства не лежали в банкоматах «без дела»: гораздо выгоднее, например, разместить их на краткосрочном депозите. Но, клиенты будут недовольны, когда столкнутся с отказом из-за недостаточного количества денег в банкомате. Это грозит репутационными потерями, поэтому банк стремится решить данную проблему с помощью точного предсказания спроса на наличность в каждой точке расположения банкоматов. При этом нужно учитывать, что спрос на наличные зависит от множества параметров: макроэкономические факторы, политические новости, социальные события, расположение банкомата, прогноз погоды, время года, день недели и т.д. Чтобы предсказать завтрашнюю потребность в наличных для конкретного банкомата, Сбербанк, например, с 2016 года использует адаптивные алгоритмы машинного обучения вместе с классическими методами анализа временных рядов. Такие модели обеспечивают динамическое перестроение всех анализируемых параметров, предоставляя на выходе эффективный план оптимального распределения и перемещения наличных между банкоматами [5].
Машинное обучение на Python
Код курса
PYML
Ближайшая дата курса
19 июня, 2023
Длительность обучения
24 ак.часов
Стоимость обучения
49 500 руб.
Что такое матрица ошибок и зачем она нужна: пример расчета стоимости ошибки прогнозирования
Поскольку в бизнесе поиск баланса между спросом и предложением напрямую конвертируется в деньги, возникает вопрос, насколько выгодно применение методов Machine Learning для решения этой задачи. С целью сопоставления предсказаний и реальности в Data Science используется матрица ошибок (confusion matrix) – таблица с 4 различными комбинациями прогнозируемых и фактических значений. Прогнозируемые значения описываются как положительные и отрицательные, а фактические – как истинные и ложные [6]. Вообще матрица ошибок используется для оценки точности моделей в задачах классификации. Но прогнозирование и распознавание образов можно рассматривать как частный случай этой проблемы, поэтому confusion matrix актуальна и для измерения точности предсказаний. Важно, что матрица ошибок позволяет оценить эффективность прогноза не только в качественном, но и в количественном выражении, т.е. измерить стоимость ошибки в деньгах. Например, каковы будут расходы на удержание пользователя, если машинное обучение предсказало, что он перестанет приносить компании пользу [7]? Аналогичный вопрос по предсказанию оттока (Churn Rate) актуален и в HR-сфере для удержания ключевых сотрудников, мотивация которых снижается. Впрочем, матрица ошибок может использоваться не только в рамках применения Machine Learning. По сути, этот метод оценки стоимости прогноза является универсальным аналитическим инструментом.
|
Прогноз |
Реальность |
|
|
+ |
— |
|
|
+ |
True Positive (истинно-положительное решение): прогноз совпал с реальностью, результат положительный произошел, как и было предсказано ML-моделью |
False Positive (ложноположительное решение): ошибка 1-го рода, ML-модель предсказала положительный результат, а на самом деле он отрицательный |
|
— |
False Negative (ложноотрицательное решение): ошибка 2-го рода – ML-модель предсказала отрицательный результат, но на самом деле он положительный |
True Negative (истинно-отрицательное решение): результат отрицательный, ML-прогноз совпал с реальностью |
С математической точки зрения оценить точность ML-модели можно с помощью следующих метрик [8]:
- Точность – сколько всего результатов было предсказано верно;
- Доля ошибок;
- Полнота – сколько истинных результатов было предсказано верно;
- F-мера, которая позволяет сравнить 2 модели, одновременно оценив полноту и точность. Здесь используется среднее гармоническое вместо среднего арифметического, сглаживая расчеты за счет исключения экстремальных значений.
В количественном выражении это будет выглядеть так:
- P – число истинных результатов, P = TP + FN;
- N – число ложных результатов, N = TN + FP.
Рассмотрим матрицу ошибок на практическом примере для задачи прогнозирования спроса на скоропортящуюся продукцию, которая должна быть продана конечному пользователю в течение суток. Например, букеты цветов, продающиеся по цене k рублей при закупочной стоимости в p рублей. Предположим, с помощью Machine Learning было предложена 2 варианта:
- Положительный прогноз (+), что по цене k будут полностью раскуплены все цветы в количестве n букетов.
- Отрицательный прогноз (+), что по цене k будут полностью раскуплены не все цветы, останется m не проданных букетов.
Соответственно, матрица ошибок для этого случая будет выглядеть следующим образом:
|
Прогноз |
Реальность |
|
|
Проданы все букеты цветов |
Остались не проданные m букетов |
|
|
+: Проданы все n букетов по k рублей c ценой закупки p |
True Positive: прогноз совпал с реальностью, все закупленные n букетов проданы Выручка = n*k Затраты = n*p Прибыль = n*(k-p) Стоимость ошибки = 0 |
False Positive: ошибка 1-го рода, ML-модель предсказала, что будет n продаж, а на самом деле их было (n-m), осталось m не проданных букетов, которые пропали и не вернули затраты на их покупку Выручка = (n-m)*k Затраты = n*p Прибыль = n*(k-p) – m*k Стоимость ошибки = m*p |
|
—: Остались не проданные m букетов c ценой закупки p |
False Negative: ошибка 2-го рода – ML-модель предсказала, что n букетов не будет продано, поэтому закупили (n-m) букетов, но спрос был на n букетов. Эффект недополученной прибыли Выручка = (n-m)*k Затраты = (n-m)*p Прибыль = (n-m)*(k-p) Стоимость ошибки = m*k |
True Negative: ML-прогноз совпал с реальностью, было раскуплено (n-m) букетов по цене k, сколько и было изначально закуплено по цене p Выручка = (n-m)*k Затраты = (n-m)*p Прибыль = (n-m)*(k-p) Стоимость ошибки = 0 |
Аналитика больших данных для руководителей
Код курса
BDAM
Ближайшая дата курса
28 июня, 2023
Длительность обучения
24 ак.часов
Стоимость обучения
66 000 руб.
Таким образом, с помощью confusion matrix можно измерить эффективность прогноза в денежном выражении, что весьма актуально для практического бизнес-приложения Machine Learning. Впрочем, отметим еще раз, что данный метод предварительной оценки будущих сценариев можно использовать и вне сферы Data Science, оценивая риски и перспективы в рамках классического бизнес-анализа.
Другие практические вопросы системного и бизнес-анализа рассматриваются в рамках нашей Школы прикладного бизнес-анализа. А особенности практического применения больших данных и машинного обучения разбираются на наших образовательных курсах в лицензированном учебном центре обучения и повышения квалификации ИТ-специалистов (менеджеров, архитекторов, инженеров, администраторов, Data Scientist’ов и аналитиков Big Data) в Москве:
- Аналитика больших данных для руководителей
- Машинное обучение на Python
Источники
- https://www.the-village.ru/village/city/news-city/371179-tseny
- https://www.the-village.ru/village/business/businessmen/371631-kuhnya-na-rayone
- https://chernobrovov.ru/articles/kak-mashinnoe-obuchenie-pomogaet-pravilno-ustanavlivat-pravilnye-ceny.html
- https://habr.com/ru/company/ozontech/blog/431950/
- http://futurebanking.ru/post/3213
- https://hranalytic.ru/kak-ponyat-matrica-nesootvetstvij-confusion-matrix/
- https://chernobrovov.ru/articles/kak-izmerit-effektivnost-machine-learning-schitaem-metriki-i-dengi-na-primere-prognozirovaniya-ottoka-polzovatelej.html
- http://www.machinelearning.ru/wiki/images/archive/5/54/20151001162720!Kitov-ML-05-Model_evaluation.pdf

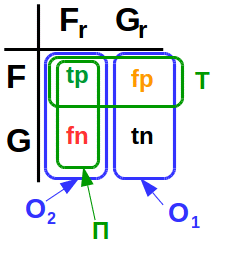
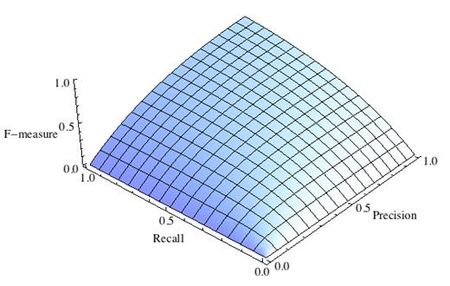
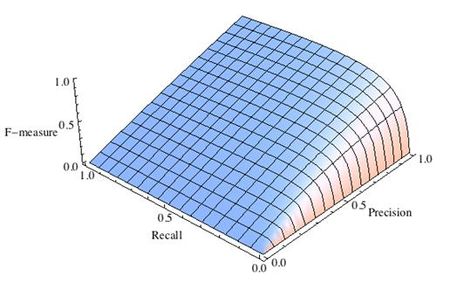
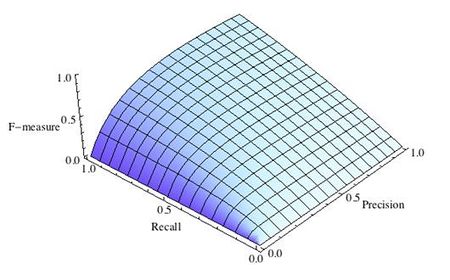

 ,
, соответствует гипотезе
соответствует гипотезе  .
. .
.