From Wikipedia, the free encyclopedia
In signal processing, the Wiener filter is a filter used to produce an estimate of a desired or target random process by linear time-invariant (LTI) filtering of an observed noisy process, assuming known stationary signal and noise spectra, and additive noise. The Wiener filter minimizes the mean square error between the estimated random process and the desired process.
Description[edit]
The goal of the Wiener filter is to compute a statistical estimate of an unknown signal using a related signal as an input and filtering that known signal to produce the estimate as an output. For example, the known signal might consist of an unknown signal of interest that has been corrupted by additive noise. The Wiener filter can be used to filter out the noise from the corrupted signal to provide an estimate of the underlying signal of interest. The Wiener filter is based on a statistical approach, and a more statistical account of the theory is given in the minimum mean square error (MMSE) estimator article.
Typical deterministic filters are designed for a desired frequency response. However, the design of the Wiener filter takes a different approach. One is assumed to have knowledge of the spectral properties of the original signal and the noise, and one seeks the linear time-invariant filter whose output would come as close to the original signal as possible. Wiener filters are characterized by the following:[1]
- Assumption: signal and (additive) noise are stationary linear stochastic processes with known spectral characteristics or known autocorrelation and cross-correlation
- Requirement: the filter must be physically realizable/causal (this requirement can be dropped, resulting in a non-causal solution)
- Performance criterion: minimum mean-square error (MMSE)
This filter is frequently used in the process of deconvolution; for this application, see Wiener deconvolution.
Wiener filter solutions[edit]
Let 




The Wiener filter problem has solutions for three possible cases: one where a noncausal filter is acceptable (requiring an infinite amount of both past and future data), the case where a causal filter is desired (using an infinite amount of past data), and the finite impulse response (FIR) case where only input data is used (i.e. the result or output is not fed back into the filter as in the IIR case). The first case is simple to solve but is not suited for real-time applications. Wiener’s main accomplishment was solving the case where the causality requirement is in effect; Norman Levinson gave the FIR solution in an appendix of Wiener’s book.
Noncausal solution[edit]
where 

and the solution 

Causal solution[edit]
where
This general formula is complicated and deserves a more detailed explanation. To write down the solution 
- Start with the spectrum
in rational form and factor it into causal and anti-causal components:
where
contains all the zeros and poles in the left half plane (LHP) and
contains the zeroes and poles in the right half plane (RHP). This is called the Wiener–Hopf factorization.
- Divide
by
and write out the result as a partial fraction expansion.
- Select only those terms in this expansion having poles in the LHP. Call these terms
.
- Divide
by
. The result is the desired filter transfer function
.
Finite impulse response Wiener filter for discrete series[edit]
Block diagram view of the FIR Wiener filter for discrete series. An input signal w[n] is convolved with the Wiener filter g[n] and the result is compared to a reference signal s[n] to obtain the filtering error e[n].
The causal finite impulse response (FIR) Wiener filter, instead of using some given data matrix X and output vector Y, finds optimal tap weights by using the statistics of the input and output signals. It populates the input matrix X with estimates of the auto-correlation of the input signal (T) and populates the output vector Y with estimates of the cross-correlation between the output and input signals (V).
In order to derive the coefficients of the Wiener filter, consider the signal w[n] being fed to a Wiener filter of order (number of past taps) N and with coefficients 
The residual error is denoted e[n] and is defined as e[n] = x[n] − s[n] (see the corresponding block diagram). The Wiener filter is designed so as to minimize the mean square error (MMSE criteria) which can be stated concisely as follows:
where ![E[cdot ]](https://wikimedia.org/api/rest_v1/media/math/render/svg/57d488a22bc9f41e976d3afb6036190bcbb36b2e)

To find the vector ![[a_{0},,ldots ,,a_{N}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/23b15c3b4639ed827b254c60c133606cec814d33)

Assuming that w[n] and s[n] are each stationary and jointly stationary, the sequences ![R_{w}[m]](https://wikimedia.org/api/rest_v1/media/math/render/svg/6fd433a0ac1fe24b6b95d7bad92cea453be5c7f2)
![{displaystyle R_{ws}[m]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e7790e74796ce594e25ef54c65a4af6ea895803)
The derivative of the MSE may therefore be rewritten as:
Note that for real ![w[n]](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a4e3e5afc2a8c6da9020b8c6b21450959101a18)
Letting the derivative be equal to zero results in:
which can be rewritten (using the above symmetric property) in matrix form
These equations are known as the Wiener–Hopf equations. The matrix T appearing in the equation is a symmetric Toeplitz matrix. Under suitable conditions on 

In some articles, the cross correlation function is defined in the opposite way:
Then, the 
![{displaystyle R_{sw}[0]ldots R_{sw}[N]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c74f1a47c80f31bc0f228f14d5efc080ecfb440e)
Whichever notation is used, note that for real ![{displaystyle w[n],s[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/47e41c9959e941c5694db0af5c0634c4537c574c)
Relationship to the least squares filter[edit]
The realization of the causal Wiener filter looks a lot like the solution to the least squares estimate, except in the signal processing domain. The least squares solution, for input matrix 

The FIR Wiener filter is related to the least mean squares filter, but minimizing the error criterion of the latter does not rely on cross-correlations or auto-correlations. Its solution converges to the Wiener filter solution.
Complex signals[edit]
For complex signals, the derivation of the complex Wiener filter is performed by minimizing ![{displaystyle Eleft[|e[n]|^{2}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff9d46fcdf6b205655f7182df44cc92ec004ce5d)
![{displaystyle Eleft[e[n]e^{*}[n]right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/660e20966e374f35618b457d09451af5d0b1d7b1)

The resulting Wiener-Hopf equations are:
which can be rewritten in matrix form:
Note here that:
The Wiener coefficient vector is then computed as:
Applications[edit]
The Wiener filter has a variety of applications in signal processing, image processing,[3] control systems, and digital communications. These applications generally fall into one of four main categories:
- System identification
- Deconvolution
- Noise reduction
- Signal detection
Noisy image of an astronaut
The image after a Wiener filter is applied (full-view recommended)
For example, the Wiener filter can be used in image processing to remove noise from a picture. For example, using the Mathematica function:
WienerFilter[image,2] on the first image on the right, produces the filtered image below it.
It is commonly used to denoise audio signals, especially speech, as a preprocessor before speech recognition.
History[edit]
The filter was proposed by Norbert Wiener during the 1940s and published in 1949.[4][5] The discrete-time equivalent of Wiener’s work was derived independently by Andrey Kolmogorov and published in 1941.[6] Hence the theory is often called the Wiener–Kolmogorov filtering theory (cf. Kriging). The Wiener filter was the first statistically designed filter to be proposed and subsequently gave rise to many others including the Kalman filter.
See also[edit]
- Wiener deconvolution
- least mean squares filter
- similarities between Wiener and LMS
- linear prediction
- MMSE estimator
- Kalman filter
- generalized Wiener filter
- matched filter
- Information field theory
References[edit]
- ^ a b Brown, Robert Grover; Hwang, Patrick Y.C. (1996). Introduction to Random Signals and Applied Kalman Filtering (3 ed.). New York: John Wiley & Sons. ISBN 978-0-471-12839-7.
- ^ Welch, Lloyd R. «Wiener–Hopf Theory» (PDF). Archived from the original (PDF) on 2006-09-20. Retrieved 2006-11-25.
- ^ Boulfelfel, D.; Rangayyan, R. M.; Hahn, L. J.; Kloiber, R. (1994). «Three-dimensional restoration of single photon emission computed tomography images». IEEE Transactions on Nuclear Science. 41 (5): 1746–1754. Bibcode:1994ITNS…41.1746B. doi:10.1109/23.317385. S2CID 33708058.
- ^ Wiener N: The interpolation, extrapolation and smoothing of stationary time series’, Report of the Services 19, Research Project DIC-6037 MIT, February 1942
- ^ Wiener, Norbert (1949). Extrapolation, Interpolation, and Smoothing of Stationary Time Series. New York: Wiley. ISBN 978-0-262-73005-1.
- ^ Kolmogorov A.N: ‘Stationary sequences in Hilbert space’, (In Russian) Bull. Moscow Univ. 1941 vol.2 no.6 1-40. English translation in Kailath T. (ed.) Linear least squares estimation Dowden, Hutchinson & Ross 1977 ISBN 0-87933-098-8
Further reading[edit]
- Thomas Kailath, Ali H. Sayed, and Babak Hassibi, Linear Estimation, Prentice-Hall, NJ, 2000, ISBN 978-0-13-022464-4.
External links[edit]
- Mathematica WienerFilter function
Вариант
1 Стат.теория, Студент;
________________________гр__________
<br>1Линейные
фильтры, обеспечивающие минимум
среднеквадратичной ошибки, полезны в
том случае, если:
Требуется
наилучшее воспроизведение всего
колебания.
Требуется
наилучшее воспроизведение сообщения.
Решается
задача распознавания двух ненулевых
сигналов.
Решается
задача, бинарного приема сигнала.
<br>2.Сообщение
передается в виде одиночного видеоимпульса
с прямоугольной огибающей. Как он будет
выглядеть на выходе оптимального фильтра
рис
7
<br>3.При
получении выводов для линейного фильтра,
обеспечивающего максимальное отношение
сигнал/шум, полагают что входной процесс
это:
аддитивная
смесь сигнала и белого шума.
мультипликативная
смесь сигнала и шума
аддитивная
смесь сигнал и помехи с произвольным
спектром
мультипликативная
смесь сигнала и помехи с произвольным
спектром
<br>4.
Коэффициент
в формуле 4 это:
весовой
коэффициент, определяемый из условия
нормировки
автокорреляционная
функция
взаимокорреляционная
функция
плотность
шума
<br>5.Кто
впервые сформулировал задачу
квазиоптимальной фильтрации за счет
оптимизации полосы пропускания фильтра
с П-образной АЧХ:
Тихонов
Котельников
Сифоров
Гудкин
<br>6.
При постановке задачи о линейном фильтре
Виннера считается, что:
помеха
и сигнал являются стационарными
случайными процессами с нулевым средним
значением и известной корреляционной
функцией;
помеха
и сигнал являются заранее известным
процессом с нулевым средним значением
и функцией корреляции, постоянной во
времени и равной единице;
функция
взаимной корреляции линейно зависит
от точки отсчета, а помеха и сигнал на
входе являются стационарным процессом;
помеха
и сигнал на входе фильтра являются
заранее известным процессом с ненулевым
средним значением и неизвестной функцией
корреляции;
<br>7.
По какой формуле определяется функция
корреляции ε при распознавании двух
ненулевых сигналов:
25
<br>8.
Системы с пассивной паузой с точки
зрения потребления мощности оказывается:
менее
выгодной по сравнению с системой с
активной паузой.
более
выгодной по сравнению с системой с
активной паузой.
такой,
что средняя энергия больше, чем у других
систем.
не
отличается от других систем.
<br>9.В
каких цепях обычно осуществляется
первичная обработка сигналов?
в
цепях до детектора сигналов,
в
цепях после детектора сигналов
в
усилителе звуковой частоты
в
усилителе видеочастоты
<br>10.
Передающая функция оптимального фильтра,
максимизирующего отношение сигнал /
шум — соответствует комплексному спектру
сигнала
соответствует
спектру шума
является
комплексно-сопряжением величиной к
спектру сигнала.
имеет
прямоугольную форму
<br>11.
Какая длительность выходного импульса
оптимального фильтра при воздействии
на входе прямоугольного импульса
длительности T
T
2T
3T
0,5T
<br>12.
Какое из приведенных ниже выражений
правильно описывает вероятность ошибки
при бинарном обнаружении?
48
<br>13.
В каком случае ЧМ модуляция обеспечивает
более высокую помехоустойчивость по
сравнению с амплитудной модуляцией?
при
любых отношениях сигнал/шум
при
произвольном значении T
при
T1
и больших отношениях сигнал/шум
при
T1
и малых отношениях сигнал/шум
Вариант
2 Стат.теория. , Студент;
________________________гр__________
<br>1.
Линейные фильтры, обеспечивающие
максимальное отношение сигнал/шум,
полезны в том случае, если:
Требуется
наилучшее воспроизведение всего
колебания.
Требуется
фильтрация сигнала после детектора.
Требуется
снизить величину пульсаций питающего
напряжения.
Решается
задача фильтрации радиосигнала.
<br>2.Приемник
может воспроизвести сообщение Х абсолютно
точно если:
имеет
фильтр с минимальной среднеквадратичной
ошибкой
имеет
фильтр с максимальным отношением
сигнал/шум
имеет
в своем составе коррелятор
только
при отсутствии шумов
<br>3.
«Белый» шумом являются шумовые флуктуации
с
равномерным спектром и равномерным
распределением
с
равномерным спектром и гауссовым
распределением
с
равномерным спектром и рэлеевским
распределением
с
гауссовым спектром и гауссовым
распределением
<br>4.В
формуле 80 что такое К2?
весовой
коэффициент, определяемый из условия
нормировки
автокорреляционная
функция
взаимокорреляционная
функция
плотность
шума
<br>5.
Квазиоптимальный фильтр — это фильтр,
у которого
АЧХ
согласована со спектром полезного
сигнала
АЧХ
согласована со спектром помехи
АЧХ
имеет вид гауссовой кривой
оптимальной
является только полоса пропускания
<br>6.
В каком случае приемник должен дать
ответ «да» при бинарном обнаружении
сигналов:
17
<br>7.
При распознавании двух не нулевых
сигналов коэффициент «а», определяемый
по формуле:
<br>8.
Возможные ошибки при бинарном обнаружении
сигнала:
ложная
тревога; обнаружение сигнала;
ложная
тревога; пропуск сигнала;
ложное
сравнение сигналов; пропуск сигнала;
ложное
сравнение сигналов; ложная тревога;
<br>9.В
каких цепях обычно осуществляется
вторичная обработка сигналов?
в
цепях до детектора сигналов,
в
цепях после детектора сигналов
в
усилителе звуковой частоты
в
усилителе видеочастоты
<br>10.
Зависит ли величина отношения сигнал/шум
на выходе согласованного линейного
фильтра от формы сигнала?
да
нет
затрудняюсь
ответить
<br>11.
За счет чего достигается максимум
отношения сигнал/шум в квазиоптимальном
линейном фильтре
за
счет выбора формы частотной характеристики;
за
счет выбора ширины полосы пропускания
при заданной форме амплитудно-частотной
характеристики;
за
счет выбора способа кодирования;
за
счет выбора способа модуляции;
<br>12.
В каком случае достигаются минимальные
ошибки при распознавании двух ненулевых
сигналов?
55
<br>13.
Какое из приведенных выражений
соответствует критерию минимальной
полной вероятности ошибки:
56
Вариант
3 Стат.теория. , Студент;
________________________гр__________
<br>1.Сообщение
передается в виде серии видеоимпульсов
с прямоугольной огибающей. Как он будет
выглядеть на выходе оптимального фильтра
Рис
3
<br>2.Приемник
оптимальный в том смысле, как он был
принят Котельниковым, определяет по
входному процессу У(t)
обратную
вероятность для всех значений Х.
априорную
вероятность присутствия сигнала
вероятность
ошибки
вероятность
правильного обнаружения
<br>3.В
каком из нижеперечисленных выражений
указана аддитивная смесь сигнала и
помехи:
68
<br>4.В
формуле 80 что такое N0?
весовой
коэффициент, определяемый из условия
нормировки
автокорреляционная
функция;
взаимокорреляционная
функция;
плотность
шума;
<br>5.
Оптимальный фильтр — это фильтр у
которого
АЧХ
согласована со спектром полезного
сигнала
АЧХ
согласована со спектром помехи
АЧХ
имеет вид гауссовой кривой
оптимальной
является только полоса пропускания
<br>6.В
каком случае приемник должен дать ответ
«да» при бинарном обнаружении сигналов:
17
<br>7.В
случае если два сигнала ортогональны,
и имеют равные энергии и выполняется
условие U1=-U2
коэффициент «а»:
34
<br>8.Различие
общей теории связи и теории оптимальных
методов приема заключается в том, что
в теории оптимальных методов приема
оптимум
ищется по всем возможным видам сигналов
и способов обработки смеси сигнала и
шума;
по
всевозможным способам обработки смеси
сигнала при заданном типе сигнала;
по
всевозможным способам кодирования
сообщения;
по
всевозможным способам передачи сигналов;
<br>9.По
какому критерию работает оптимальный
линейный фильтр Винера?
по
критерию минимума среднеквадратичной
ошибки.
по
критерию максимального отношения сигнал
шум
по
критерию максимума среднеквадратичной
ошибки.
по
критерию минимального отношения сигнал
шум
<br>10.
Укажите условия физической реализуемости
согласованного линейного фильтра
37
<br>11.
При выборе какой полосы пропуска
достигается максимальное отношение
сигнала к шуму при приеме одиночного
радиоимпульса с прямоугольной огибающей
с длительностью Т0
43
<br>12.
Какое выражение соответствует
фазоманипулированному сигналу
52
<br>13.
Какое из приведенных выражений
соответствует критерию минимального
среднего риска
58
Вариант
4 Стат.теория. , Студент;
<br>1.Сообщение
передается в виде серии радиоимпульсов
с прямоугольной огибающей. Как он будет
выглядеть на выходе оптимального фильтра
рис.
5
<br>2.ЧМ
дает существенный выигрыш по сравнению
с АМ:
никогда
всегда
если
произведение Ω*T>>1
если
произведение Ω*T<<1
<br>3.Что
можно вычислить, если приемник не может
произвести сообщение абсолютно точно?
априорную
вероятность
обратную
вероятность того или иного значения х
математическое
ожидание
дисперсию
<br>4.Кто
разработал теорию потенциальной
помехоустойчивости
Тихонов
Котельников
Сифоров
Гудкин
<br>5.Оптимальным
считается такой фильтр, у которого
функция взаимной корреляции:
максимальна
минимальна
равна
среднеквадратичной погрешности
меньше
среднеквадратичной погрешности
<br>6.Пороговое
значение напряжения U0
при бинарном обнаружении сигналов:
23
<br>7.В
случае если два сигнала имеют равные
энергии, но условие U1=-U2
не выполняется, то коэффициент «а»:
33
<br>8.Относится
ли поиск различных критериев оптимальности
к основным задачам, решаемым в теории
оптимальных методов приема.
да
нет.
только
для радиосвязи
только
для радиолокации
<br>9.По
какому критерию работает согласованный
линейный фильтр?
по
критерию минимума среднеквадратичной
ошибки.
по
критерию максимального отношения сигнал
шум
по
критерию максимума среднеквадратичной
ошибки.
по
критерию минимального отношения сигнал
шум
<br>10.
Форма выходного импульса на выходе
согласованного линейного фильтра
прямоугольная
с длительностью T
треугольная
с длительностью 2T
треугольная
с длительностью T
прямоугольная
с длительностью 2T
<br>11.
Укажите величину проигрыша в отношении
сигнал/шум на выходе квазиоптимального
фильтра с П- образной амплитудно-частотной
характеристикой при приеме одиночного
радиоимпульса
0,82
0,9
0,707
0.5
<br>12.
При частотном манипулировании, какое
из приведенных условий должно выполняться?
53
<br>13.
Какое из приведенных выражений
соответствует критерию минимальной
взвешенности вероятности ошибки:
57
Вариант
5 Стат.теория. , Студент;
________________________гр__________
<br>1.Сообщение
передается в виде одиночного радиоимпульса
с прямоугольной огибающей. Как он будет
выглядеть на выходе оптимального фильтра
Рис.
4
<br>2.При
бинарном обнаружении сигнала, надежность
обнаружения (вероятность ошибки) зависит
от:
формы
сигнала
частоты
сигнала
энергии
сигнала
фазы
сигнала
<br>3.Какая
величина в формуле 80
является неизвестной:
84
<br>4.В
формуле 80 что такое Qx?
весовой
коэффициент, определяемый из условия
нормировки
энергия
сигнала
взаимокорреляционная
функция
плотность
шума
<br>5.
Оптимальным считается тот фильтр, у
которого значение коэффициента r:
наибольшее
наименьшее
равно
0
равно
1
<br>6.
По какой формуле определяется функция
корреляции ε при бинарном обнаружении
сигнала:
<br>7.В
случае бинарного обнаружения сигнала
с пассивной паузой коэффициент «а»
определяется:
34
<br>8.Относится
ли оценка потенциальной помехоустойчивости
приемного устройства к основным задачам,
решаемым в теории оптимальных методов
приема.
да
нет.
только
для радиосвязи
только
для радиолокации
<br>9.
В каком случае используется согласованный
линейный фильтр?
при
фильтрации модулированного сигнала.
фильтрация
всего сигнала (после детектора, устройства
автоматики и телемеханики).
при
фильтрации сигнала в усилителе звуковой
частоты
при
фильтрации сигнала в усилителе
видеочастоты
<br>10.
Форма огибающей радиоимпульса на выходе
согласованного линейного фильтра
прямоугольная
с длительностью T;
треугольная
с длительностью 2T;
треугольная
с длительностью T;
прямоугольная
с длительностью 2T;
<br>11.
Какой параметр определяет оптимальный
приемник при приеме сигнала известного
типа по Котельникову? На входе оптимального
приемника действует смесь сигнала и
шума.
45
<br>12.
В системах с активной паузой, какой вид
манипуляции обладает максимальной
помехоустойчивостью
фазовая
частотная
амплитудная
<br>13.
Какое из приведенных выражений
соответствует критерию Неймана- Пирсона
59
5
В обработке сигналов фильтр Винера является фильтром используется для получения оценки желаемого или целевого случайного процесса посредством линейной не зависящей от времени (LTI ) фильтрации наблюдаемого зашумленного процесса, предполагая известные стационарные спектры сигнала и шума, а также аддитивные шум. Фильтр Винера минимизирует среднеквадратичную ошибку между оцененным случайным процессом и желаемым процессом.
Содержание
- 1 Описание
- 2 Решения с фильтром Винера
- 2.1 Непричинное решение
- 2.2 Причинное решение
- 3 Фильтр Винера с конечной импульсной характеристикой для дискретных серий
- 3.1 Связь с фильтром наименьших квадратов
- 3.2 Сложные сигналы
- 4 Приложения
- 5 История
- 6 См. Также
- 7 Ссылки
- 8 Внешние ссылки
Описание
Цель фильтра Винера — для вычисления статистической оценки неизвестного сигнала с использованием связанного сигнала в качестве входа и фильтрации этого известного сигнала для получения оценки в качестве выхода. Например, известный сигнал может состоять из интересующего неизвестного сигнала, который был искажен аддитивным шумом. Фильтр Винера может использоваться для фильтрации шума из искаженного сигнала, чтобы обеспечить оценку основного сигнала, представляющего интерес. Фильтр Винера основан на статистическом подходе, и более статистическое изложение теории дается в статье оценщика минимальной среднеквадратичной ошибки (MMSE).
Типичные детерминированные фильтры разработаны для желаемой частотной характеристики. Однако конструкция фильтра Винера использует другой подход. Предполагается, что кто-то знает спектральные свойства исходного сигнала и шума, а другой ищет линейный не зависящий от времени фильтр, выходной сигнал которого будет максимально приближен к исходному сигналу. Фильтры Винера характеризуются следующим:
- Допущение: сигнал и (аддитивный) шум являются стационарными линейными случайными процессами с известными спектральными характеристиками или известной автокорреляцией и взаимной корреляцией.
- Требование: фильтр должен быть физически реализуемым / причинным (это требование можно отбросить, что приведет к непричинному решению)
- Критерий эффективности: минимальный среднеквадратичный ошибка (MMSE)
Этот фильтр часто используется в процессе деконволюции ; для этого приложения см. деконволюция Винера.
Решения винеровского фильтра
Пусть s (t) { displaystyle s (t)}

Непричинное решение
- G (s) = S x, s (s) S x (s) e α s, { displaystyle G (s) = { frac {S_ {x, s}) (s)} {S_ {x} (s)}} e ^ { alpha s},}
где S { displaystyle S}

- E (e 2) Знак равно р s (0) — ∫ — ∞ ∞ г (τ) р Икс, s (τ + α) d τ, { displaystyle E (e ^ {2}) = R_ {s} (0) — int _ {- infty} ^ { infty} g ( tau) R_ {x, s} ( tau + alpha) , d tau,}
и решение g (t) { displaystyle g (t)}

Причинное решение
- G (s) = H (s) S Икс + (s), { Displaystyle G (s) = { frac {H (s)} {S_ {x} ^ {+} (s)}},}
где
Эта общая формула сложна и заслуживает более подробного объяснения. Чтобы записать решение G (s) { displaystyle G (s)}
- Начать со спектра S x ( s) { displaystyle S_ {x} (s)}
в рациональной форме и разложите его на причинные и антипричинные компоненты: S x (s) = S x + (s) S x — (s) { displaystyle S_ {x} (s) = S_ {x} ^ {+} (s) S_ {x} ^ {-} (s)}
где S + { displaystyle S ^ {+}}
содержит все нули и полюсы в левой полуплоскости (LHP), а S — { displaystyle S ^ {-}}
содержит нули и полюсы в правой полуплоскости (RHP). Это называется факторизацией Винера – Хопфа.
- Divide S x, s (s) e α s { displaystyle S_ {x, s} (s) e ^ { alpha s}}
на S x — (s) { displaystyle S_ {x} ^ {-} (s)}
и запишите результат в виде разложения частичной дроби.
- Выберите в этом расширении только те термины, у которых есть полюсы в LHP. Назовите эти термины H (s) { displaystyle H (s)}
.
- Разделите H (s) { displaystyle H (s)}
на S x + (s) { displaystyle S_ {x} ^ {+} (s)}
. Результатом является желаемая передаточная функция фильтра G (s) { displaystyle G (s)}
.
Фильтр Винера с конечной импульсной характеристикой для дискретных серий

Причинный конечный импульс response (FIR) Фильтр Винера вместо использования некоторой заданной матрицы данных X и выходного вектора Y находит оптимальные веса отводов, используя статистику входных и выходных сигналов. Он заполняет входную матрицу X оценками автокорреляции входного сигнала (T) и заполняет выходной вектор Y оценками взаимной корреляции между выходным и входным сигналами (V).
Чтобы вывести коэффициенты фильтра Винера, рассмотрим сигнал w [n], подаваемый на фильтр Винера порядка (количества прошедших отводов) N и с коэффициентами {a 0, ⋯, а N} { displaystyle {a_ {0}, cdots, a_ {N} }}
- x [n] = ∑ i = 0 N a i w [n — i]. { displaystyle x [n] = sum _ {i = 0} ^ {N} a_ {i} w [ni].}
Остаточная ошибка обозначается e [n] и определяется как e [n] = x [n] — s [n] (см. соответствующую блок-схему). Фильтр Винера разработан таким образом, чтобы минимизировать среднеквадратичную ошибку (критерии MMSE ), которую можно кратко сформулировать следующим образом:
- ai = arg min E [e 2 [n]], { displaystyle a_ {i} = arg min E left [e ^ {2} [n] right],}
где E [⋅] { displaystyle E [ cdot]}![E [ cdot]](https://wikimedia.org/api/rest_v1/media/math/render/svg/57d488a22bc9f41e976d3afb6036190bcbb36b2e)

- E [e 2 [n]] = E [(x [n] — s [n]) 2] = E [x 2 [n]] + E [s 2 [n]] — 2 E [x [n] s [n]] = E [(∑ i = 0 N aiw [n — i]) 2] + E [s 2 [n]] — 2 E [∑ я знак равно 0 N aiw [n — я] s [n]] { displaystyle { begin {выровнено} E left [e ^ {2} [n] right] = E left [(x [ n] -s [n]) ^ {2} right] \ = E left [x ^ {2} [n] right] + E left [s ^ {2} [n] right] -2E [x [n] s [n]] \ = E left [ left ( sum _ {i = 0} ^ {N} a_ {i} w [ni] right) ^ {2} right] + E left [s ^ {2} [n] right] -2E left [ sum _ {i = 0} ^ {N} a_ {i} w [ni] s [n] right ] end {align}}}
Найти вектор [a 0,…, a N] { displaystyle [a_ {0}, , ldots, , a_ {N}]}![[a_ {0}, , ldots, , a_ {N}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/23b15c3b4639ed827b254c60c133606cec814d33)
- ∂ ∂ ai E [e 2 [n]] = ∂ ∂ ai {E [(∑ i = 0 N aiw [n — i]) 2] + E [s 2 [n]] — 2 E [∑ i = 0 N aiw [n — i] s [n]]} = 2 E [ (∑ j = 0 N ajw [n — j]) w [n — i]] — 2 E [w [n — i] s [n]] = 2 (∑ J = 0 NE [вес [N — J] вес [N — I]] aj) — 2 E [вес [N — I] s [N]] { Displaystyle { begin {align} { frac { partial} { partial a_ {i}}} E left [e ^ {2} [n] right] = { frac { partial} { partial a_ {i}}} left {E left [ left ( sum _ {i = 0} ^ {N} a_ {i} w [ni] right) ^ {2} right] + E left [s ^ {2} [n] right] -2E left [ sum _ {i = 0} ^ {N} a_ {i} w [ni] s [n] right] right } \ = 2E left [ left ( sum _ {j = 0} ^ {N} a_ {j} w [nj] right) w [ni] right] -2E [w [ni] s [n]] \ = 2 left ( sum _ {j = 0} ^ {N} E [w [nj] w [ni]] a_ {j} right) -2E [w [ni] s [n]] end {align}}}
Предполагая, что каждый из w [n] и s [n] является стационарным и вместе стационарным, последовательности R w [m] { displaystyle R_ {w} [m]}![R_ {w} [m]](https://wikimedia.org/api/rest_v1/media/math/render/svg/6fd433a0ac1fe24b6b95d7bad92cea453be5c7f2)
![{ displaystyle R_ {ws} [m]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e7790e74796ce594e25ef54c65a4af6ea895803)
- R w [m] = E {w [n] w [n + m]} R ws [m] = E {w [n] s [n + m]} { displaystyle { begin {выровнено} R_ {w} [m] = E {w [n] w [n + m] } \ R_ {ws} [m] = E {w [n] s [n + m ]}конец {выравнивается}}}
Следовательно, производная MSE может быть переписана как:
- ∂ ∂ ai E [e 2 [n]] = 2 (∑ j = 0 NR w [j — i] aj) — 2 R ws [i] i = 0, ⋯, N. { displaystyle { frac { partial} { partial a_ {i}}} E left [e ^ {2} [n] right] = 2 left ( sum _ {j = 0} ^ {N } R_ {w} [ji] a_ {j} right) -2R_ {ws} [i] qquad i = 0, cdots, N.}
Обратите внимание, что для реального w [n] { displaystyle w [n]}![w [n]](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a4e3e5afc2a8c6da9020b8c6b21450959101a18)
R w [j — i] = R w [i — j] { displaystyle R_ {w} [ji] = R_ { w} [ij]}
![{ displaystyle R_ {w} [ji] = R_ {w} [ij]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a7c44b249eb0d5faa8fd08516814ecedbebc451)
- ∑ j = 0 NR w [j — i] aj = R ws [i] i = 0, ⋯, N. { displaystyle sum _ {j = 0} ^ {N} R_ {w} [ji] a_ {j} = R_ {ws} [i] qquad i = 0, cdots, N.}
который можно переписать (используя указанное выше свойство симметрии) в матричной форме
- [R w [0] R w [1] ⋯ R w [N] R w [1] R w [0] ⋯ R w [N — 1] ] ⋮ ⋮ ⋱ ⋮ R w [N] R w [N — 1] ⋯ R w [0]] ⏟ T [a 0 a 1 ⋮ a N] ⏟ a = [R ws [0] R ws [1] ⋮ R ws [N]] ⏟ v { displaystyle underbrace { begin {bmatrix} R_ {w} [0] R_ {w} [1] cdots R_ {w} [N] \ R_ {w} [ 1] R_ {w} [0] cdots R_ {w} [N-1] \ vdots vdots ddots vdots \ R_ {w} [N] R_ {w} [N- 1] cdots R_ {w} [0] end {bmatrix}} _ { mathbf {T}} underbrace { begin {bmatrix} a_ {0} \ a_ {1} \ vdots \ a_ {N} end {bmatrix}} _ { mathbf {a}} = underbrace { begin {bmatrix} R_ {ws} [0] \ R_ {ws} [1] \ vdots \ R_ {ws} [N] end {bmatrix}} _ { mathbf {v}}}
Эти уравнения известны как уравнения Винера – Хопфа. Матрица T, встречающаяся в уравнении, является симметричной матрицей Теплица. При подходящих условиях на R { displaystyle R}

В некоторых статьях функция взаимной корреляции определяется противоположным образом:
R sw [m] = E {w [n] s [n + m]} { displaystyle R_ {sw} [m] = E {w [n] s [n + m] }}
![{ displaystyle R_ {sw} [m] = E {w [n] s [n + m] }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/674ae192cf58157ffa143e5a78c60150f9e0ec96)
v { displaystyle mathbf {v}}

R sw [0]… R sw [N] { displaystyle R_ {sw} [0] ldots R_ {sw} [N]}
![{ displaystyle R_ {sw } [0] ldots R_ {sw} [N]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c74f1a47c80f31bc0f228f14d5efc080ecfb440e)
Какое бы обозначение ни использовалось, обратите внимание, что для вещественного w [n], s [n] { displaystyle w [n], s [n]}![{ displaystyle w [n], s [n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/47e41c9959e941c5694db0af5c0634c4537c574c)
R sw [k] = R ws [- k] { displaystyle R_ {sw} [k] = R_ {ws} [- k]}
Отношение к фильтру наименьших квадратов
Реализация причинного фильтра Винера очень похожа на решение к оценке наименьших квадратов, за исключением области обработки сигналов. Решение методом наименьших квадратов для входной матрицы X { displaystyle mathbf {X}}

- β ^ = (XTX) — 1 XT y. { displaystyle { boldsymbol { hat { beta}}} = ( mathbf {X} ^ { mathbf {T}} mathbf {X}) ^ {- 1} mathbf {X} ^ { mathbf {T}} { boldsymbol {y}}.}
КИХ-фильтр Винера связан с фильтром наименьших средних квадратов, но минимизация критерия ошибки последнего не зависит от взаимной корреляции или автокорреляции. Его решение сходится к решению фильтра Винера.
Сложные сигналы
Для сложных сигналов вывод комплексного винеровского фильтра выполняется путем минимизации E [| e [n] | 2] { displaystyle E left [| e [n] | ^ {2} right]}![{ displaystyle E left [| e [n] | ^ {2} right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff9d46fcdf6b205655f7182df44cc92ec004ce5d)
![{ displaystyle E left [e [n] e ^ {*} [n] справа]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/660e20966e374f35618b457d09451af5d0b1d7b1)

Результирующие уравнения Винера-Хопфа:
- ∑ j = 0 N R w [j — i] a j ∗ = R w s [i] i = 0, ⋯, N. { displaystyle sum _ {j = 0} ^ {N} R_ {w} [ji] a_ {j} ^ {*} = R_ {ws} [i] qquad i = 0, cdots, N.}
, который можно переписать в матричном виде:
- [R w [0] R w ∗ [1] ⋯ R w ∗ [N — 1] R w ∗ [N] R w [1] R w [0 ] ⋯ R w ∗ [N — 2] R w ∗ [N — 1] ⋮ ⋮ ⋱ ⋮ ⋮ R w [N — 1] R w [N — 2] ⋯ R w [0] R w ∗ [1] R w [N] R w [N — 1] ⋯ R w [1] R w [0]] ⏟ T [a 0 ∗ a 1 ∗ ⋮ a N — 1 ∗ a N ∗] ⏟ a ∗ = [R ws [ 0] R WS [1] ⋮ R WS [N — 1] R WS [N]] ⏟ v { displaystyle underbrace { begin {bmatrix} R_ {w} [0] R_ {w} ^ {*} [ 1] cdots R_ {w} ^ {*} [N-1] R_ {w} ^ {*} [N] \ R_ {w} [1] R_ {w} [0] cdots R_ { w} ^ {*} [N-2] R_ {w} ^ {*} [N-1] \ vdots vdots ddots vdots vdots \ R_ {w} [N-1 ] R_ {w} [N-2] cdots R_ {w} [0] R_ {w} ^ {*} [1] \ R_ {w} [N] R_ {w} [N-1] cdots R_ {w} [1] R_ {w} [0] end {bmatrix}} _ { mathbf {T}} underbrace { begin {bmatrix} a_ {0} ^ {*} \ a_ { 1} ^ {*} \ vdots \ a_ {N-1} ^ {*} \ a_ {N} ^ {*} end {bmatrix}} _ { mathbf {a ^ {*}}} = underbrace { begin {bmatrix} R_ {ws} [0] \ R_ {ws} [1] \ vdots \ R_ {ws} [N-1] \ R_ {ws} [N] конец {bmatrix}} _ { mathbf {v}}}
Обратите внимание, что:
R w [- k] = R w ∗ [k] R sw [k] = R ws ∗ [- k] { displaystyle { begin {выровнено } R_ {w} [- k] = R_ {w} ^ {*} [k] \ R_ {sw} [k] = R_ {ws} ^ {*} [- k] end {выровнено} }}
Затем вектор коэффициентов Винера вычисляется как:
a = (T — 1 v) ∗ { displaystyle mathbf {a} = {( mathbf {T} ^ {- 1} mathbf { v})} ^ {*}}
Приложения
Фильтр Винера имеет множество применений в обработке сигналов, обработке изображений, системах управления и цифровой связи. Эти приложения обычно относятся к одной из четырех основных категорий:
- Идентификация системы
- Деконволюция
- Подавление шума
- Обнаружение сигнала
Например, фильтр Винера может использоваться при обработке изображений для удаления шума из картина. Например, использование функции Mathematica: WienerFilter [image, 2]на первом изображении справа, создает отфильтрованное изображение под ним.


Обычно используется для подавления звуковых сигналов, особенно речи, в качестве препроцессора перед распознаванием речи.
История
Фильтр был предложен Норбертом Винером в 1940-х годах и опубликован в 1949 году. Дискретный эквивалент работы Винера был независимо выведен Андреем Колмогоровым и опубликован в 1941 году. Поэтому эту теорию часто называют теорией фильтрации Винера – Колмогорова (см. Кригинг ). Фильтр Винера был первым предложенным статистически разработанным фильтром, впоследствии породившим множество других, включая фильтр Калмана.
См. Также
- Норберт Винер
- Эберхард Хопф
- Винер деконволюция
- минимум фильтр средних квадратов
- сходства между Винером и LMS
- линейное прогнозирование
- оценка MMSE
- фильтр Калмана
- обобщенный фильтр Винера
- согласованный фильтр
- Теория информационного поля
Ссылки
- Томас Кайлат, Али Х. Сайед и Бабак Хассиби, Линейная оценка, Прентис-Холл, Нью-Джерси, 2000, ISBN 978-0-13-022464-4 .
- Винер Н.: Интерполяция, экстраполяция и сглаживание стационарных временных рядов », Отчет Службы 19, Исследовательский проект DIC-6037 MIT, февраль 1942 г.
- Колмогоров АН: Стационарные последовательности в гильбертовом пространстве, Бюл. Московский унив. 1941 том 2 номер 6 1-40. Английский перевод в Kailath T. (ред.) Оценка линейных наименьших квадратов Dowden, Hutchinson Ross 1977
Внешние ссылки
- Mathematica WienerFilter function
Обзор адаптивных фильтров и приложения
Адаптивные фильтры являются цифровыми фильтрами чье содействующее изменение с целью заставить фильтр сходиться к оптимальному состоянию. Критерий оптимизации является функцией стоимости, которая является обычно средним квадратичным сигнала ошибки между выходом адаптивного фильтра и желаемым сигналом. Когда фильтр адаптирует свои коэффициенты, среднеквадратичная погрешность (MSE) сходится к своему минимальному значению. В этом состоянии адаптируется фильтр, и коэффициенты сходились к решению. Фильтр вывел, y(k), как затем говорят, соответствует очень тесно к желаемому сигналу, d(k). Когда вы изменяете характеристики входных данных, иногда названные средой фильтра, фильтр адаптируется к новой среде путем генерации нового набора коэффициентов для новых данных.
Общий адаптивный алгоритм фильтра
Адаптивные фильтры в DSP System Toolbox
Основанный на Наименьшее количество средних квадратичных (LMS) КИХ адаптивные фильтры
|
Адаптивный объект фильтра |
Адаптация алгоритма |
|---|---|
|
|
Блокируйте КИХ LMS адаптивный алгоритм фильтра |
|
|
Фильтрованный-x КИХ LMS адаптивный алгоритм фильтра |
|
|
КИХ LMS адаптивный алгоритм фильтра Нормированный КИХ LMS адаптивный алгоритм фильтра КИХ Sign-data LMS адаптивный алгоритм фильтра КИХ Sign-error LMS адаптивный алгоритм фильтра КИХ Sign-sign LMS адаптивный алгоритм фильтра |
|
Адаптивный блок фильтра |
Адаптация алгоритма |
|---|---|
|
Block LMS Filter |
Блокируйте КИХ LMS адаптивный алгоритм фильтра |
|
Fast Block LMS Filter |
Блокируйте КИХ LMS адаптивный алгоритм фильтра в частотном диапазоне |
|
LMS Filter |
КИХ LMS адаптивный алгоритм фильтра Нормированный КИХ LMS адаптивный алгоритм фильтра КИХ Sign-data LMS адаптивный алгоритм фильтра КИХ Sign-error LMS адаптивный алгоритм фильтра КИХ Sign-sign LMS адаптивный алгоритм фильтра |
| LMS Update |
КИХ-вес LMS обновляет алгоритм Нормированный КИХ-вес LMS обновляет алгоритм КИХ-вес Sign-data LMS обновляет алгоритм КИХ-вес Sign-error LMS обновляет алгоритм КИХ-вес Sign-sign LMS обновляет алгоритм |
Основанный на Рекурсивных наименьших квадратах (RLS) КИХ адаптивные фильтры
|
Адаптивный объект фильтра |
Адаптация алгоритма |
|---|---|
|
|
Быстро трансверсальный алгоритм адаптации наименьших квадратов Раздвижное окно алгоритм адаптации FTF |
|
|
Алгоритм адаптации QR-decomposition RLS Домовладелец алгоритм адаптации RLS Домовладелец алгоритм адаптации SWRLS Алгоритм адаптации рекурсивных наименьших квадратов (RLS) Раздвижное окно (SW) алгоритм адаптации RLS |
|
Адаптивный блок фильтра |
Адаптация алгоритма |
|---|---|
|
RLS Filter |
Экспоненциально взвешенный алгоритм рекурсивных наименьших квадратов (RLS) |
КИХ Аффинной проекции (AP) адаптивные фильтры
|
Адаптивный объект фильтра |
Адаптация алгоритма |
|---|---|
|
|
Аффинный алгоритм проекции, который использует прямую матричную инверсию Аффинный алгоритм проекции, который использует рекурсивное матричное обновление Блокируйте аффинный алгоритм адаптации проекции |
КИХ адаптивные фильтры в частотном диапазоне (FD)
|
Адаптивный объект фильтра |
Адаптация алгоритма |
|---|---|
|
|
Ограниченный алгоритм адаптации частотного диапазона Неограниченный алгоритм адаптации частотного диапазона Разделенный и ограниченный алгоритм адаптации частотного диапазона Разделенный и неограниченный алгоритм адаптации частотного диапазона |
|
Адаптивный блок фильтра |
Адаптация алгоритма |
|---|---|
|
Frequency-Domain Adaptive Filter |
Ограниченный алгоритм адаптации частотного диапазона Неограниченный алгоритм адаптации частотного диапазона Разделенный и ограниченный алгоритм адаптации частотного диапазона Разделенный и неограниченный алгоритм адаптации частотного диапазона |
Основанный на решетке (L) КИХ адаптивные фильтры
|
Адаптивный объект фильтра |
Адаптация алгоритма |
|---|---|
|
|
Градиент адаптивный алгоритм адаптации фильтра решетки Наименьшие квадраты образовывают решетку алгоритм адаптации Разложение QR алгоритм адаптации RLS |
Для получения дополнительной информации об этих алгоритмах обратитесь к разделу алгоритма соответствующих страниц с описанием. Полные описания теории появляются в адаптивных ссылках фильтра [1] и [2].
Выбор адаптивного фильтра
В устойчивом состоянии, когда фильтр адаптировался, ошибка между фильтром, выход и желаемый сигнал минимальны, не нуль. Эта ошибка известна как установившуюся ошибку. Скорость, с которой фильтр сходится к оптимальному состоянию, известному как быстроту сходимости, зависит от нескольких факторов такая природа входного сигнала, выбор адаптивного алгоритма фильтра и размер шага алгоритма. Выбор алгоритма фильтра обычно зависит факторы, такие как производительность сходимости, требуемая для приложения, вычислительной сложности алгоритма, устойчивости фильтра в среде и любых других ограничений.
LMS-алгоритм прост реализовать, но имеет проблемы устойчивости. Нормированная версия LMS-алгоритма идет с улучшенной быстротой сходимости, большей устойчивостью, но увеличила вычислительную сложность. Для примера, который сравнивает эти два, смотрите, Сравнивают Производительность Сходимости Между LMS-алгоритмом и Нормированным LMS-алгоритмом. Алгоритмы RLS очень устойчивы, сделайте очень хорошо в изменяющихся во времени средах, но являются в вычислительном отношении более комплексными, чем LMS-алгоритмы. Для сравнения смотрите, Сравнивают RLS и Адаптивные Алгоритмы Фильтра LMS. Аффинные фильтры проекции преуспевают, когда вход окрашен, и имейте очень хорошую производительность сходимости. Адаптивные фильтры решетки обеспечивают хорошую сходимость, но идут с увеличенной вычислительной стоимостью. Выбор алгоритма зависит от среды и специфических особенностей приложения.
Производительность среднеквадратической ошибки
Минимизация среднего квадратичного сигнала ошибки между выходом адаптивного фильтра и желаемым сигналом является наиболее распространенным критерием оптимизации адаптивных фильтров. Фактический MSE (MSESIM) адаптивного фильтра, который вы реализуете, может быть определен с помощью msesim функция. Траектория этого MSE, как ожидают, будет следовать за тем из предсказанных MSE (MSEPred), который вычисляется с помощью msepred функция. Минимальная среднеквадратичная погрешность (MMSE) оценивается msepred функция с помощью Винеровского фильтра. Фильтр Вайнера минимизирует среднеквадратическую ошибку между желаемым сигналом и входным сигналом, отфильтрованным Винеровским фильтром. Большое значение среднеквадратической ошибки указывает, что адаптивный фильтр не может точно отследить желаемый сигнал. Минимальное значение среднеквадратической ошибки гарантирует, что адаптивный фильтр оптимален. Избыточная среднеквадратичная погрешность (EMSE), определенная msepred функционируйте, различие между MSE, введенным адаптивными фильтрами и MMSE, произведенным соответствующим Винеровским фильтром. Итоговый MSE, показанный ниже, является суммой EMSE и MMSE, и равняется предсказанному MSE после сходимости.
Распространенные приложения
System Identification – Используя адаптивный фильтр, чтобы идентифицировать неизвестную систему
Одно общее адаптивное приложение фильтра должно использовать адаптивные фильтры, чтобы идентифицировать неизвестную систему, такую как ответ неизвестного коммуникационного канала или частотная характеристика аудитории, выбрать довольно расходящиеся приложения. Другие приложения включают отмену эха и идентификацию канала.
В фигуре неизвестная система помещается параллельно с адаптивным фильтром. Это размещение представляет только одну из многих возможных структур. Заштрихованная область содержит адаптивную систему фильтра.
Безусловно, когда e (k) очень мал, адаптивный ответ фильтра близко к ответу неизвестной системы. В этом случае тот же вход питает и адаптивный фильтр и неизвестное. Если, например, неизвестная система является модемом, вход часто представляет белый шум и является частью звука, вы получаете известие от своего модема, когда вы входите в систему своего поставщика интернет-услуг.
Обратный System Identification – определение обратного ответа на неизвестную систему
Путем размещения неизвестной системы последовательно с адаптивным фильтром фильтр адаптируется, чтобы стать инверсией неизвестной системы, когда e (k) становится очень маленьким. Как показано в фигуре, процесс требует, чтобы задержка, вставленная в желаемый путь к сигналу d (k), сохранила данные при суммировании синхронизируемыми. Добавление задержки сохраняет систему причинной.
Включая задержку, чтобы составлять задержку, вызванную неизвестной системой, предотвращает это условие.
Простые телефонные сети (POTS) обычно используют обратную систему идентификации, чтобы компенсировать медный носитель передачи. Когда вы отправляете данные или речь по телефонным линиям, медные провода ведут себя как фильтр, имея ответ, который прокручивается прочь на более высоких частотах (или скорости передачи данных) и наличие других аномалий также.
Добавление адаптивного фильтра, который имеет ответ, который является инверсией проводного ответа и конфигурирования фильтра, чтобы адаптироваться в режиме реального времени, позволяет фильтру компенсировать спад и аномалии, увеличивая доступную область значений частотного вывода и скорость передачи данных для телефонной сети.
Шумовая или интерференционная отмена – Используя адаптивный фильтр, чтобы удалить шум из неизвестной системы
В подавлении помех адаптивные фильтры позволяют вам удалить шум из сигнала в режиме реального времени. Здесь, желаемый сигнал, тот, чтобы вымыться, комбинирует шум и желаемую информацию. Чтобы удалить шум, накормите сигналом n’ (k) адаптивный фильтр, который коррелируется к шуму, который будет удален из желаемого сигнала.
Пока входной шум к фильтру остается коррелированым к нежелательному шуму, сопровождающему желаемый сигнал, адаптивный фильтр настраивает свои коэффициенты, чтобы уменьшать значение различия между y (k) и d (k), удаляя шум и приводя к чистому сигналу в e (k). Заметьте, что в этом приложении, сигнал ошибки на самом деле сходится к сигналу входных данных, вместо того, чтобы сходиться, чтобы обнулить.
Предсказание – предсказание будущих значений периодического сигнала
Предсказание сигналов требует, чтобы вы сделали некоторые ключевые предположения. Примите, что сигнал является или устойчивым или медленно различным в зависимости от времени и периодическим в зависимости от времени также.
Принимая эти предположения, адаптивный фильтр должен предсказать будущие значения желаемого сигнала на основе прошлых значений. Когда s (k) является периодическим, и фильтр достаточно длинен, чтобы помнить, что предыдущие значения, эта структура с задержкой входного сигнала, могут выполнить предсказание. Вы можете использовать эту структуру, чтобы удалить периодический сигнал из стохастических шумовых сигналов.
Наконец, заметьте, что большинство систем интереса содержит элементы больше чем одной из четырех адаптивных структур фильтра. Тщательно рассмотрение действительной структуры может потребоваться, чтобы определять то, к чему адаптируется адаптивный фильтр.
Кроме того, для ясности в фигурах не появляются аналого-цифровое (A/D) и цифро-аналоговые компоненты (D/A). Поскольку адаптивные фильтры приняты, чтобы быть цифровыми по своей природе, и многие проблемы производят аналоговые данные, преобразование входных сигналов к и от аналоговой области, вероятно, необходимо.
Ссылки
[1] Hayes, Монсон Х., Статистическая Цифровая обработка сигналов и Моделирование. Хобокен, NJ: John Wiley & Sons, 1996, pp.493–552.
[2] Haykin, Саймон, адаптивная теория фильтра. Верхний Сэддл-Ривер, NJ: Prentice-Hall, Inc., 1996.
Алгоритмы наименьших средних квадратов ( LMS ) представляют собой класс адаптивных фильтров, используемых для имитации желаемого фильтра путем нахождения коэффициентов фильтра, которые относятся к получению наименьшего среднего квадрата сигнала ошибки (разницы между желаемым и фактическим сигналами). Это метод стохастического градиентного спуска, в котором фильтр адаптируется только на основе ошибки в текущий момент времени. Он был изобретен в 1960 году профессором Стэнфордского университета Бернардом Видроу и его первым доктором философии. студент, Тед Хофф .
Постановка проблемы

Связь с фильтром Винера
Реализация причинного фильтра Винера очень похожа на решение оценки наименьших квадратов, за исключением области обработки сигналов. Решение методом наименьших квадратов для входной матрицы и выходного вектора
:

КИХ-фильтр наименьших средних квадратов связан с фильтром Винера, но минимизация критерия ошибки первого не зависит от взаимной корреляции или автокорреляции. Его решение сходится к решению фильтра Винера. Большинство задач линейной адаптивной фильтрации можно сформулировать с помощью приведенной выше блок-схемы. То есть должна быть идентифицирована неизвестная система, и адаптивный фильтр пытается адаптировать фильтр, чтобы сделать его как можно ближе к нему , используя только наблюдаемые сигналы , и ; но , и не наблюдаются напрямую. Его решение тесно связано с фильтром Винера .
Определение символов
-
номер текущего входного отсчета
-
количество отводов фильтра
-
( Эрмитовское транспонирование или сопряженное транспонирование )
-
оценочный фильтр; интерпретировать как оценку коэффициентов фильтра после n выборок
Идея
Основная идея фильтра LMS состоит в том, чтобы приблизиться к оптимальным весам фильтра , обновляя веса фильтра таким образом, чтобы они сходились к оптимальному весу фильтра. Это основано на алгоритме градиентного спуска. Алгоритм начинается с предположения малых весов (в большинстве случаев равных нулю), и на каждом шаге путем нахождения градиента среднеквадратичной ошибки веса обновляются. То есть, если MSE-градиент положительный, это означает, что ошибка будет продолжать увеличиваться в положительном направлении, если тот же вес используется для дальнейших итераций, что означает, что нам нужно уменьшить веса. Таким же образом, если градиент отрицательный, нам нужно увеличить веса. Уравнение обновления веса:
![W_ {n + 1} = W_n - mu nabla varepsilon [n]](https://wikimedia.org/api/rest_v1/media/math/render/svg/3408cbbe737f93c5eda40cefdc1af3feb0411f9c)
где
представляет собой среднеквадратичную ошибку, а — коэффициент сходимости.
Отрицательный знак показывает, что мы спускаемся по наклону ошибки, чтобы найти веса фильтра , которые минимизируют ошибку.
Среднеквадратичная ошибка как функция весов фильтра является квадратичной функцией, что означает, что она имеет только один экстремум, который минимизирует среднеквадратичную ошибку, которая является оптимальным весом. Таким образом, LMS приближается к этим оптимальным весам, поднимаясь / опускаясь вниз по кривой зависимости среднеквадратичной ошибки от веса фильтра.
Вывод
Идея фильтров LMS заключается в использовании наискорейшего спуска для нахождения весов фильтров, которые минимизируют функцию стоимости . Начнем с определения функции стоимости как
где — ошибка в текущей выборке n и обозначает ожидаемое значение .
Эта функция стоимости ( ) представляет собой среднеквадратическую ошибку, которая минимизируется LMS. Отсюда LMS получила свое название. Применение наискорейшего спуска означает получение частных производных по отдельным элементам вектора коэффициента (веса) фильтра.
где — оператор
градиента
Теперь это вектор, который указывает на самый крутой подъем функции стоимости. Чтобы найти минимум функции стоимости, нам нужно сделать шаг в противоположном направлении . Чтобы выразить это в математических терминах
где — размер шага (постоянная адаптации). Это означает, что мы нашли алгоритм последовательного обновления, который минимизирует функцию стоимости. К сожалению, этот алгоритм невозможно реализовать, пока мы не узнаем об этом .
Как правило, вышеприведенное ожидание не вычисляется. Вместо этого, чтобы запустить LMS в онлайн-среде (обновление после получения каждого нового образца), мы используем мгновенную оценку этого ожидания. См. ниже.
Упрощения
Для большинства систем функция ожидания должна быть аппроксимирована. Это можно сделать с помощью следующей объективной оценки
где указывает количество образцов, которые мы используем для этой оценки. Самый простой случай — это
Для этого простого случая алгоритм обновления выглядит следующим образом:
Фактически, это составляет алгоритм обновления для фильтра LMS.
Сводка алгоритма LMS
Алгоритм LMS для фильтра-го порядка можно резюмировать как
| Параметры: |
 порядок фильтров порядок фильтров
|
 размер шага размер шага
|
|
| Инициализация: |

|
| Расчет: | Для 
|
|
|
|

|
|

|
Сходимость и стабильность в среднем
Поскольку алгоритм LMS не использует точные значения ожиданий, веса никогда не достигнут оптимальных весов в абсолютном смысле, но в среднем возможна сходимость. То есть, даже если веса могут изменяться на небольшие значения, они меняются примерно на оптимальные веса. Однако, если дисперсия, с которой изменяются веса, велика, сходимость средних значений может ввести в заблуждение. Эта проблема может возникнуть, если значение шага выбрано неправильно.
Если выбран большой, величина, с которой изменяются веса, сильно зависит от оценки градиента, и поэтому веса могут измениться на большое значение, так что градиент, который был отрицательным в первый момент, теперь может стать положительным. А во второй момент вес может сильно измениться в противоположном направлении из-за отрицательного градиента и, таким образом, будет продолжать колебаться с большим отклонением от оптимального веса. С другой стороны, если выбран слишком маленький, время для достижения оптимальных весов будет слишком большим.
Таким образом, требуется верхняя граница , которая задается как

где — наибольшее собственное значение автокорреляционной матрицы . Если это условие не выполняется, алгоритм становится нестабильным и расходится.
Максимальная скорость схождения достигается, когда
где — наименьшее собственное значение . При условии, что это значение меньше или равно этому оптимуму, скорость сходимости определяется , причем большее значение обеспечивает более быструю сходимость. Это означает , что более быстрое сближение может быть достигнуто , когда близко к , то есть максимально достижимая скорость сходимости зависит от разброса собственных значений от .
Сигнал белого шума имеет матрицу автокорреляции, где — дисперсия сигнала. В этом случае все собственные значения равны, а разброс собственных значений является минимальным по всем возможным матрицам. Таким образом, общая интерпретация этого результата состоит в том, что LMS сходится быстро для белых входных сигналов и медленно для цветных входных сигналов, таких как процессы с характеристиками нижних или верхних частот.
Важно отметить, что вышеупомянутая верхняя граница только обеспечивает стабильность в среднем, но коэффициенты все еще могут расти бесконечно большими, т.е. расхождение коэффициентов все еще возможно. Более практическая оценка
где обозначает след из . Эта граница гарантирует, что коэффициенты не расходятся (на практике значение не следует выбирать близко к этой верхней границе, поскольку это несколько оптимистично из-за приближений и предположений, сделанных при выводе оценки).
Нормализованный фильтр наименьших средних квадратов (NLMS)
Главный недостаток «чистого» алгоритма LMS заключается в том, что он чувствителен к масштабированию входных данных . Это делает очень трудным (если не невозможным) выбор скорости обучения , гарантирующей стабильность алгоритма (Хайкин, 2002). Фильтр Нормализованного минимум среднего квадратов (NLMS) представляет собой вариант LMS алгоритм , который решает эту проблему путем нормализации с силой входного сигнала. Алгоритм NLMS можно резюмировать как:

| Параметры: |
 порядок фильтров порядок фильтров
|
 размер шага размер шага
|
|
| Инициализация: |

|
| Расчет: | Для 
|
|
|
|

|
|

|
Оптимальная скорость обучения
Можно показать, что при отсутствии помех ( ) оптимальная скорость обучения для алгоритма NLMS равна
и не зависит от входа и реальной (неизвестной) импульсной характеристики . В общем случае с помехой ( ) оптимальная скорость обучения равна
Приведенные выше результаты предполагают, что сигналы и не коррелируют друг с другом, что обычно и имеет место на практике.
Доказательство
Пусть рассогласование фильтра определяется как , мы можем получить ожидаемое рассогласование для следующего образца как:
Пусть и
Предполагая независимость, мы имеем:
Оптимальная скорость обучения найдена при , что приводит к:
Смотрите также
- Рекурсивный метод наименьших квадратов
- Для статистических методов, относящихся к фильтру LMS, см. Наименьшие квадраты .
- Сходства между Wiener и LMS
- Адаптивный фильтр с блоком с несколькими задержками в частотной области
- Эквалайзер с нулевым форсированием
- Адаптивный фильтр ядра
- согласованный фильтр
- Винеровский фильтр
Рекомендации
- Монсон Х. Хейс: Статистическая обработка и моделирование цифровых сигналов, Wiley, 1996,
ISBN 0-471-59431-8 - Саймон Хайкин: теория адаптивного фильтра, Prentice Hall, 2002, ISBN 0-13-048434-2
- Саймон С. Хайкин, Бернард Видроу (редактор): Адаптивные фильтры наименьшего среднего квадрата, Wiley, 2003, ISBN 0-471-21570-8
- Бернард Видроу, Сэмюэл Д. Стернс: адаптивная обработка сигналов, Прентис-Холл, 1985, ISBN 0-13-004029-0
- Вайфенг Лю, Хосе Принсипи и Саймон Хайкин: Адаптивная фильтрация ядра: всестороннее введение, Джон Вили, 2010, ISBN 0-470-44753-2
- Пауло С.Р. Диниц: Адаптивная фильтрация: алгоритмы и практическая реализация, Kluwer Academic Publishers, 1997, ISBN 0-7923-9912-9
Внешние ссылки
- Алгоритм LMS в адаптивных антенных решетках www.antenna-theory.com
- Демонстрация шумоподавления LMS www.advsolned.com
Алгоритм, который оценивает неизвестные из серии измерений во времени

x ^ k ∣ k — 1 { displaystyle { hat {x}} _ status {k mid k-1}}

P k ∣ k — 1 { displaystyle P_ {k mid k-1}}

В статистике и теории управления, Фильтрация Калмана, также известная как линейно-квадратичная оценка (LQE ), представляет собой алгоритм, который использует серию измерений наблюдаемый с течением времени, статистический шум и другие неточности, и дает оценку неизвестных чисел, которые имеют тенденцию быть более точными, чем оценки, основанные только на одном измерении, путем оценки совместного распределения вероятностей по переменным для каждого таймфрейма. Фильтр назван в честь Рудольфа Э. Кальмана, одного основного из разработчиков его теории.
Фильтр Калмана находит множество применений в технике. Распространенным приложением наведение, навигация и управление транспортными средствами, особенно самолетами, космическими кораблями и динамически позиционируемыми кораблями. Кроме того, фильтр Калмана — широко применяемая концепция в анализах временных рядов, используемом в таких областях, как обработка сигналов и эконометрика. Фильтры Калмана также являются одной из основных в области роботизированного планирования движения и управления и управления в оптимизации траектории. Фильтр Калмана также работает для моделирования управления движением центральной нервной системы. Из-за временной задержки между выдачей команд двигателя и получением сенсорной обратной связи использование фильтра Калмана поддерживает реалистичную модель для текущего состояния моторной системы и выдачи обновленных команд.
Алгоритм состоит из двух этапов. На этапе прогнозирования фильтр Калмана производит текущие данные состояния вместе с их неопределенностями. Как наблюдается результат следующего измерения (включая случайный шум), эти оценки обновляются с использованием средневзвешенного, при этом больший вес присваивается оценкам с большей достоверностью. Алгоритм рекурсивный. Он может работать в реального времени, используя только текущие входные измерения и ранее вычисленное состояние и его матрицу неопределенности; никакой дополнительной прошлой информации не требуется.
Оптимальность фильтра Калмана предполагает, что ошибки гауссовского. По словам Рудольфа Э. Кальмана : «Итак, в отношении случайных процессов делаются следующие предположения: физические явления можно рассматривать как следствие первичных случайных источников, возбуждающих случайные динамические системы. быть независимыми гауссовскими случайными процессами с нулевым средним; динамические системы будут линейными ». Несмотря на то, что независимо от гауссовости, если известны ковариации процесса и измерения, фильтр Калмана наилучшей возможной линейной оценкой в смысле минимальной средней квадратичной ошибки.
Расширения и обобщения способы также были разработаны, например, расширенный фильтр Калмана и фильтр Калмана без запаха, которые работают с нелинейными системами. Базовая модель — это , где пространство состояний для латентных чисел равно непрерывно, все скрытые и наблюдаемые переменные имеют гауссовский раздачи. Кроме того, фильтр Калмана успешно использовался в слиянии нескольких датчиков и в распределенных сетях датчиков для разработки распределенного или консенсусного фильтра Калмана.
Содержание
- 1 История
- 2 Обзор расчета
- 3 Пример приложения
- 4 Техническое описание и контекст
- 5 Базовая модель динамической системы
- 6 Подробности
- 6.1 Прогноз
- 6.2 Обновление
- 6.3 Инварианты
- 6.4 Оценка ковариаций шума Q k и R k
- 6.5 Оптимизация и производительность
- 7 Пример применения, технический
- 8 Асимптотическая форма
- 9 Выведение
- 9.1 Выведение ковариационной матрицы апостериорной оценки
- 9.2 Выведение коэффициента усиления Калмана
- 9.3 Упрощение формулы ковариации апостериорной ошибки
- 10 Анализ чувствительности
- 11 Форма квадратного корня
- 12 Связь с рекурсивной байесовской оценкой
- 13 Предельное правдоподобие
- 14 Информационный фильтр
- 15 Сглаживатель с фиксированным запаздыванием
- 16 Сглаживатель с фиксированным интервалом
- 16.1 Раух — Тунг –Striebel
- 16.2 Модифицированный сглаживание Брайсона — Фрейзера
- 16.3 Сглаживание сглаживания минимальной дисперсией
- 17 Частотно-взвешенные фильтры Калмана
- 18 Нелинейные фильтры
- 18.1 Расширенный фильтр Калмана
- 18.2 Безцентированный фильтр Калмана
- 18.2.1 Сигма-точки
- 18.2.2 Прогноз
- 18.2.3 Обновление
- 19 Фильтр Калмана — Бьюси
- 20 Гибридный фильтр Калмана
- 20.1 Инициализация
- 20.2 Прогноз
- 20.3 Обновление
- 21 Варианты восстановления разреженных сигналов
- 22 Приложения
- 23 См.
- 24 Ссылки
- 25 Дополнительная литература
- 26 Также Внешние ссылки
История
Фильтр назван в честь венгерского émigré Рудольфа Э. Кальмана, хотя Торвальд Николай Тиле и Питер Сверлинг разработали аналогичный алгоритм ранее. Ричард С. Бьюси из Лаборатории прикладной физики Джона Хопкинса внес вклад в теорию, в результате чего ее иногда называют фильтром Калмана — Бьюси. Стэнли Ф. Шмидту обычно приписывают первую реализацию фильтра Калмана. Он понял, что фильтр можно разделить на две части, одна часть для периодов времени между выходами датчиков, другая часть для включения измерений. Во время визита Кальмана в Исследовательский центр Эймса НАСА, Шмидт увидел применимость идей Кальмана к нелинейной задаче оценки траектории для программы Аполлон, что привело к ее достижению в Навигационный компьютер Apollo. Этот фильтр Калмана был впервые описан и частично разработан в технических статьях Сверлинга (1958 г.), Калмана (1960 г.) и Калмана и Бьюси (1961 г.).
Компьютер Apollo использовал 2k ОЗУ магнитного сердечника и трос 36k […]. ЦП был построен из микросхем […]. Тактовая частота была ниже 100 кГц […]. Тот факт, что инженеры института Массачусетского технологического института смогли упаковать такое хорошее программное обеспечение (одно из самых первых применений фильтра Калмана) в такой крошечный компьютер, поистине замечателен.
— Интервью Мэтью Рида с Джеком Креншоу, TRS-80. org (2009) [1]
Фильтр сыграли роль в реализации навигационных систем США. ВМС ядерные подводные лодки с баллистическими ракетами, а также системы наведения и навигации крылатых ракет, таких как ракета Томагавк ВМС США и США. Крылатая ракета воздушного базирования ВВС. Они также используются в системах наведения и навигации многоразовых ракет-носителей и управления ориентацией, а также в навигационных системах космических кораблей, которые состыкованы с Международной космической станцией.
Эта цифровая цифровая система. Фильтр иногда называют фильтром Стратоновича — Калмана — Бьюси, потому что это частный случай более общего нелинейного фильтра, разработанного несколько ранее советским математиком Русланом Стратоновичем. Фактически, некоторые частные уравнения линейных фильтров появились в этих статьях Стратоновича, которые были опубликованы до лета 1960 г., когда Калман встретился со Стратоновичем во время конференции в Москве.
Обзор вычислений
использует
Фильтр Калмана динамическую модель системы (например, физические законы движения), известные входные данные для этой системы и несколько последовательных измерений (например, чтобы от датчиков), сформировать оценку различных величин системы (ее состояние ), что лучше, чем оценка, полученная с использованием только одного измерения. Таким образом, это обычный алгоритм объединения датчиков и объединения данных.
Зашумленные данные датчика, приближения в уравнениях эволюции системы, и внешние факторы, которые не учитываются для всех, ограничения ограничения на то, насколько хорошо можно определить состояние системы. Фильтр Калмана эффективно справляется с неопределенностью из-за зашумленных данных датчика и, в некоторой степени, случайных факторов внешних факторов. Фильтр Калмана оценки состояния системы как среднее значение прогнозируемого состояния системы и измерения нового с использованием средневзвешенного значения. Назначение весов состоит в том, чтобы значения с лучшим (есть меньшим) оценочной неопределенности больше доверяли. Веса вычисляются на основе ковариации , оценочной неопределенности прогноза состояния системы. Результатом средневзвешенного значения является новая оценка состояния, которая находится между прогнозируемым и измеренным состояниями и имеет более точную оценку неопределенности, чем любой другой. Этот процесс повторяется на каждом временном шаге, при этом новая оценка и ее ковариация определяет прогноз, используется в следующей итерации. Это означает, что фильтр Калмана работает рекурсивно и требует только последнего «предположения», а не всего истории состояния системы для вычислений нового состояния.
Относительная достоверность измерений и оценки состояния обычно представляют собой важные особенности, и обсуждают отклик фильтра в терминах фильтра Калмана. Коэффициент Калмана — это относительный вес, придаваемый измерениям и оценка текущего состояния, и его можно «настроить» для достижения производительности. При высоком усилении фильтр придает больший вес самым последним измерением и, следовательно, более оперативно отслеживает их. При низком усилении фильтр более точно следует прогнозам модели. В крайних случаях высокое усиление, близкое к единице, к более скачкообразной расчетной траектории, в то время как низкое усиление, близкое к нулю, сгладит шум, но снизит отзывчивость.
При выполнении фактических вычислений для фильтра (как обсуждается ниже) оценка состояния и ковариации кодируются в матрицы для обработки нескольких измерений, задействованных в единственном наборе вычислений. Это позволяет представить линейные отношения между различными переменными состояниями (такими положениями, скоростью и ускорением) в любом из переходных моделей или ковариаций.
Пример приложения
В качестве приложения рассмотрим задачу определения точного местоположения грузовика. Грузовик может быть оснащен системой GPS, обеспечивающей определение местоположения в пределах нескольких метров. Оценка GPS, вероятно, будет зашумленной; показания быстро «прыгают», но остаются в пределах нескольких метров от реального положения. Кроме того, это должно быть интегрировано в систему управления движением колес и угла поворота рулевого колеса. Это метод, известный как расплата. Как правило, точный расчет обеспечивает очень плавную оценку положения грузовика, но он будет дрейфовать со временем по мере накопления небольших ошибок.
В этом примере фильтр Калмана можно представить как работающий в двух различных фазах: прогнозирование и обновление. На этапе прогнозирования старшего положения грузовика будет изменено в соответствии с физическими законами движения (динамическая модель или модель «перехода состояний»). Будет рассчитана не только новая оценка местоположения, но и новая ковариация. Определения скорости точного определения местоположения. Затем на этапе обновления данные о грузовика снимаются с устройства GPS. Наряду с этим измерением некоторая степень неопределенности, и ее степень ковариации прогноза из предыдущей фазы определяет, насколько новое измерение повлияет на обновленный прогноз. В идеале, поскольку оценка точного исчисления определяет отклонение от реального положения, измерения GPS подтягивает определение местоположения к реальному положению, но не мешает ей до такой степени, что она становится шумной и быстро прыгает.
Техническое описание и контекст
Фильтр Калмана — это эффективный рекурсивный фильтр, который оценивает внутреннее состояние линейной динамической системы из серии зашумленных измерений. Он используется в широком диапазоне инженерных и эконометрических приложений от радара и компьютерного зрения до структурных макроэкономических моделей, и важная тема в теории управления и разработка систем управления. Вместе с линейно-квадратичным регулятором (LQR) фильтр Калмана решает задачу линейно-квадратично-гауссовского управления (LQG). Фильтр Калмана, линейно-квадратичный регулятор и линейно-квадратично-гауссовский регулятор являются решениями, возможно, наиболее фундаментальных проблем теории управления.
В большинстве приложений внутреннее состояние намного больше (больше степеней свободы ), чем несколько «наблюдаемых» параметров, которые измеряются. Однако, объединив серию измерений, фильтр Калмана может оценить все внутреннее состояние.
В теории Демпстера — Шейфера уравнение состояния или рассмотрение как частный случай линейной функции доверия, а фильтр Калмана представляет собой частный случай объединения линейные функции доверия на дереве соединения или дереве Маркова. Дополнительные подходы включают байесовских или доказательных обновлений использования состояний.
На основе первичной формулировки Калмана было разработано большое количество фильтров Калмана, теперь называемых «общий» фильтром Калмана, фильтром Калмана — Бьюси, «расширенным» фильтром Шмидта, информационный фильтр и различные фильтры «квадратного корня», разработанные Бирманом, Торнтоном и другими. Калмана является контуром фазовой автоподстройки с частотой, который теперь повсеместно используется в радио, особенно с частотной модуляцией (FM) радио, телевизоры, <275.>приемники спутниковой связи, системы космической связи и почти любое другое электронное оборудование связи.
Базовая модель динамической системы
Фильтры Калмана основаны на линейных динамических систем, дискретизированных во временной области. Они моделируются на основе цепи Маркова, построенной на линейных операторов, возмущенных ошибками, которые могут включать гауссовский шум. Состояние системы как вектор из вещественных чисел. При каждом приращении дискретного времени к состоянию применяемого линейного оператора для генерации нового состояния с добавлением некоторого шума и, необязательно, некоторой информации от элементов управления в системе, если они известны. Затем другой линейный оператор, смешанный с большим количеством шума, генерирует наблюдаемые выходные данные из истинного («скрытого») состояния. Фильтр Калмана можно рассматривать как аналог скрытой модели Маркова с тем ключевыми отличием, что скрытые переменные состояния принимают значения в непрерывном пространстве (в отличие от дискретного пространства состояний, как в скрытой марковской модели). Существует сильная аналогия между уравнениями фильтра Калмана и уравнениями скрытой марковской модели. Обзор этой и других моделей дан в Roweis и Ghahramani (1999) и Hamilton (1994), глава 13.
Чтобы использовать фильтр Калмана для оценки состояния внутреннего процесса, учитывая только последовательность зашумленных наблюдений, необходимо моделировать процесс в соответствии с рамками фильтра Калмана. Это означает следующие матриц:
- Fk, модель перехода между состояниями;
- Hk, модель наблюдения;
- Qk, ковариация шумового процесса;
- Rk, ковариация наблюдения за шумом;
- и иногда Bk, модель управляющего входа, для каждого временного шага k, как описано ниже.

Модель фильтра Калмана предполагает истинное состояние в момент изменения k. из состояния в (k — 1) согласно
- xk = F kxk — 1 + B kuk + wk { displaystyle mathbf {x} _ {k} = mathbf {F} _ {k} mathbf { x} _ {k-1} + mathbf {B} _ {k} mathbf {u} _ {k} + mathbf {w} _ {k}}
где
В момент времени k наблюдение (или измерение) zkистинное состояние xkсоздается согласно
- zk = H kxk + vk { displaystyle mathbf {z} _ {k} = mathbf {H} _ {k} mathbf {x} _ {k} + mathbf {v} _ {k}}
где
- Hk- модель наблюдения, которая отображает истинное пространство состояний в наблюдаемое пространство, а
- vk- шум наблюдения, который предполагается равным нулевому среднему гауссову белый шум с ковариацией Rk: vk ∼ N (0, р К) { Displaystyle mathbf {v} _ {k} sim { mathcal {N}} left (0, mathbf {R} _ {k} right)}
.
Предполагается, что начальное состояние и векторы шума на каждом шаге {x0, w1,…, wk, v1… vk} взаимно независимы.
Многие реальные динамические системы не точно подходят этой модели. Фактически, немоделированная динамика может серьезно ухудшить характеристики фильтра, даже если он должен был работать с неизвестными стохастическими сигналами в качестве входных данных. Причина этого в том, что эффект немоделированной динамики зависит от входа и, следовательно, может привести алгоритм оценки к нестабильности (он расходится). С другой стороны, независимые сигналы белого шума не заставят алгоритм расходиться. Проблема различения между шумом измерения и немоделированной динамикой является сложной и рассматривается в теории управления в рамках робастного управления.
Подробности
Фильтр Калмана является рекурсивным оценщик. Это означает, что для вычисления оценки текущего состояния необходимы только оценочное состояние из предыдущего временного шага и текущее измерение. В отличие от методов пакетной оценки, история наблюдений и / или оценок не требуется. Далее обозначение x ^ n ∣ m { displaystyle { hat { mathbf {x}}} _ {n mid m}}

Состояние фильтра представлено двумя переменными:
Фильтр Калмана может быть записан в одном виде уравнения, однако он чаще всего концептуализируется как две фазы: «Прогнозирование» и «Обновление». Фаза прогноза использует оценку состояния из предыдущего временного шага, чтобы оценки состояния на текущем временном шаге. Эта прогнозируемая оценка состояния также известна как априорная оценка состояния, потому что, хотя это оценка состояния на текущем временном шаге, она не включает в себя информацию наблюдения из текущего временного шага. На этапе обновления текущего априорного предсказания объединяется с текущим наблюдением для уточнения оценки состояния. Эта улучшенная оценка называется апостериорной оценкой состояния.
Обычно две фазы чередуются, при этом прогнозировании продвигает состояние до следующего запланированного наблюдения, а обновление включает наблюдение. Однако в этом нет необходимости; если наблюдение недоступно по какой-либо причине, обновление может быть пропущено и выполнено несколько шагов прогнозирования. Прогнозируемая (априорная) оценка состоянияx ^ k ∣ k — 1 = F kx ^ k, может быть выполнено несколько шагов обновления (обычно с разными матрицами наблюдений Hk).
Прогноз
Обновить
| Инновация или остаток предварительной подгонки измерения | y ~ k = zk — H kx ^ k ∣ k — 1 { displaystyle { tilde { mathbf {y}}} _ {k} = mathbf {z} _ { k} — mathbf {H} _ {k} { hat { mathbf {x}}} _ {k mid k-1}} |
| Новаторская (или предварительная подгонка остаточная) ковариация | S К знак равно ЧАС К П К ∣ К — 1 ЧАС К T + Р К { Displaystyle mathbf {S} _ {k} = mathbf {H} _ {k} mathbf {P } _ {k mid k-1} mathbf {H} _ {k} ^ { textf {T}} + mathbf {R} _ {k}} |
| Оптимальное усиление Калмана | K k = П К ∣ К — 1 ЧАС К ТС К — 1 { Displaystyle mathbf {K} _ {k} = mathbf {P} _ {k mid k-1} mathbf {H} _ {k} ^ { textf {T}} mathbf {S} _ {k} ^ {- 1}} |
| Обновленная (апостериорная) оценка состояния | x ^ k ∣ k = x ^ k ∣ k — 1 + K ky ~ к { displaystyle { hat { mathbf {x}}} _ {k mid k} = { hat { mathbf {x}}} _ {k mid k-1} + mathbf {K} _ {k} { tilde { mathbf {y}}} _ {k}} |
| Обновленная (апостериорная) ковариация оценки | P k | k = (I — K k H k) P k | к — 1 { displaystyle mathbf {P} _ {k | k} = left ( mathbf {I} — mathbf {K} _ {k} mathbf {H} _ {k} right) mathbf {P} _ {k | k-1}} |
| Измерение после подгонки остаток | y ~ k ∣ k = zk — H kx ^ k ∣ k { displaystyle { tilde { mathbf {y}}} _ {k mid k} = mathbf {z} _ {k} — mathbf {H} _ {k} { hat { mathbf {x}}} _ {k mid k}} |
Формула для обновленной (апостериорной) ковариации оценки, приведенная выше, действительна для оптимального Kkкоэффициента усиления, который минимизирует остаточную ошибку, в какой форме она наиболее широко используется в приложениих. Доказательства формул можно найти в разделе производные, где также оказать формула, действующая для любого Kk.
Инварианты
Если модель точна и значения для x ^ 0 ∣ 0 { displaystyle { hat { mathbf {x}}} _ {0 mid 0}}

- E [xk — x ^ k ∣ k] = E [xk — x ^ k ∣ k — 1] = 0 E [y ~ k] = 0 { displaystyle { начало {выровнено} operatorname {E} [ mathbf {x} _ {k} — { hat { mathbf {x}}} _ {k mid k}] = operatorname {E} [ mathbf {x} _ {k} — { шляпа { mathbf {x}}} _ {k mid k-1}] = 0 \ имя оператора {E} [{ tilde { mathbf {y}}} _ {k}] = 0 end {align}}}
где E [ξ] { displaystyle operatorname {E} [ xi]}![{displaystyle operatorname {E} [xi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/261957bffe5d89e65e9d27dfa34c5f86f6017baa)

Также:
- P k ∣ k = cov (xk — x ^ k ∣ k) P k ∣ k — 1 = cov (xk — x ^ k ∣ k — 1) S k = cov (Y ~ К) { Displaystyle { begin {align} mathbf {P} _ {k mid k} = operatorname {cov} left ( mathbf {x} _ {k} — { шляпа { mathbf {x}}} _ {k mid k} right) \ mathbf {P} _ {k mid k-1} = operatorname {cov} left ( mathbf {x} _ {k} — { hat { mathbf {x}}} _ {k mid k-1} right) \ mathbf {S} _ {k} = operatorname {cov} left ({ tilde { mathbf {y}}} _ {k} right) end {align}}}
, поэтому ковариационные матрицы точно отражают ковариацию оценок.
Оценка ковариаций шума Q k и R k
Практическая реализация фильтра Калмана часто затруднена из-за получения хорошей оценки ковариационных матриц шума Qkи Rk. Системные исследования для оценки этих ковариаций на основе данных. Одним из практических подходов является этот метод наименьших квадратов автоковариации (ALS), в котором для оценки ковариаций используются запаздывающие по времени автоковариации стандартных рабочих данных. Код GNU Octave и Matlab, использование для вычисления ковариационных матриц шума с использованием техники ALS, доступно в Интернете под Стандартной общественной лицензией GNU. Полевой фильтр Калмана (FKF), байесовский алгоритм, который позволяет одновременно оценивать состояние, параметры и ковариацию шума, был предложен в. Алгоритм FKF имеет рекурсивную формулировку, хорошую наблюдаемую сходимость и относительно низкую сложность. Это дает возможность того, что алгоритм FKF может быть альтернативой методам наименьших квадратов автоковариации.
Оптимизация и производительность
Из теории следует, что фильтр Калмана является оптимальным линейным фильтром в случаях, когда а) модель идеально соответствует реальной системе, б) входящий шум белый (некоррелированный) и в) ковариации шума точно известны. В течение последних десятилетий было предложено несколько методов оценки ковариации шума, включая упомянутый в разделе выше. После оценки ковариаций оценить производительность фильтра; то есть можно ли улучшить качество оценки состояния. Если фильтр Калмана работает оптимально, представляет собой белый шум, поэтому качество данных нововведений измеряет эффективность фильтра. Для этого можно использовать несколько различных методов. Если шумовые составляющие распределены не по Гауссу, в литературе известны методы оценки эффективности фильтра, используются вероятностные неравенства или теория большой выборки.
Пример применения, технический

Представьте грузовик, движущийся по прямому рельсам без трения. Первоначально грузовик неподвижен в позиции 0, но он подвергается тому или иному воздействию случайных неконтролируемых сил. Мы измеряем положение грузовика каждые Δt секунд, но эти измерения неточны; мы хотим сохранить модель положения грузовика и скорости. Мы покажем здесь, как мы выводим модель, из которой мы создаем наш фильтр Калмана.
Начало с F, H, R, Q { displaystyle mathbf {F}, mathbf {H}, mathbf {R}, mathbf {Q}}
Положение и скорость грузовика описываются линейным пространством состояния
- xk = [xx ˙] { displaystyle mathbf {x} _ {k} = { begin {bmatrix} x { dot {x }} end {bmatrix}}}
где x ˙ { displaystyle { dot {x}}}
Мы предполагаем, что между (k — 1) и k временным шагом неконтролируемые силы вызывают постоянное ускорение k, которое нормально распределено, со средним 0 и стандартным отклонением σ а. Из корон движения мы заключаем, что
- xk = F xk — 1 + G ak { displaystyle mathbf {x} _ {k} = mathbf {F} mathbf {x} _ { k-1} + mathbf {G} a_ {k}}
(термин B u { displaystyle mathbf {B} u}

- F = [ 1 Δ t 0 1] G знак равно [1 2 Δ t 2 Δ t] { displaystyle { begin {align} mathbf {F} = { begin {bmatrix} 1 Delta t \ 0 1 end {bmatrix}} \ [4pt] mathbf {G} = { begin {bmatrix} { frac {1} {2}} { Delta t} ^ {2} \ [6pt] Дельта t end {bmatrix}} end {align}}}
так, чтобы
- xk = F xk — 1 + wk { displaystyle mathbf {x} _ {k} = mathbf {F} mathbf {x} _ {k-1} + mathbf {w} _ {k}}
где
- wk ∼ N (0, Q) Q = GGT σ a 2 = [1 4 Δ t 4 1 2 Δ T 3 1 2 Δ T 3 Δ T 2] σ a 2. { displaystyle { begin {align} mathbf {w} _ {k } sim N (0, mathbf {Q}) \ mathbf {Q} = mathbf {G} mathbf {G} ^ { textf {T}} sigma _ {a} ^ {2 } = { begin {bmatrix} { frac {1} {4}} { Delta t} ^ {4} { frac {1} {2}} { Delta t} ^ {3} \ [ 6pt] { frac {1} {2}} { Delta t} ^ {3} { Delta t} ^ {2} end {bmatrix}} sigma _ {a} ^ {2}. end {align}}}
Матрица Q { displaystyle mathbf {Q}}


- w k ∼ G ⋅ N (0, σ a 2). { displaystyle mathbf {w} _ {k} sim mathbf {G} cdot N left (0, sigma _ {a} ^ {2} right).}
На каждом временном шаге произведено измерение истинного положения грузовика с шумом. Предположим, что шум измерения v k также нормально распределен со средним отклонением 0 и стандартным отклонением σ z.
- zk = H xk + vk { displaystyle mathbf {z} _ {k} = mathbf {Hx } _ {k} + mathbf {v} _ {k}}
где
- H = [1 0] { displaystyle mathbf {H} = { begin {bmatrix} 1 0 end { bmatrix}}}
и
- R = E [vkvk T] = [σ z 2] { displaystyle mathbf {R} = mathrm {E} left [ mathbf {v} _ {k} mathbf {v} _ {k} ^ { textf {T}} right] = { begin {bmatrix} sigma _ {z} ^ {2} end {bmatrix}}}
Мы знаем начальное начальное состояние грузовика с идеальной точностью, поэтому мы инициализируем
- x ^ 0 ∣ 0 = [0 0] { displaystyle { hat { mathbf {x}}} _ {0 mid 0} = { begin {bmatrix } 0 \ 0 end {bmatrix}}}
и чтобы сообщить фильтру, что мы знаем точное положение и скорость, мы даем ему матрицу нулевой ковариации:
- P 0 ∣ 0 = [0 0 0 0] { displaystyle mathbf {P} _ {0 mid 0} = { begin {bmatrix} 0 0 \ 0 0 end {bmatrix}}}
Если начальное положение и скорость неизвестны точно, ковариационная матрица rix должна быть инициализирована с подходящей дисперсией на ее диагонали:
- P 0 ∣ 0 = [σ x 2 0 0 σ x ˙ 2] { displaystyle mathbf {P} _ {0 mid 0} = { begin {bmatrix} sigma _ {x} ^ {2} 0 \ 0 sigma _ { dot {x}} ^ {2} end {bmatrix}}}
Тогда фильтр предпочтет информацию из первых измерений информации, уже содержащейся в модели.
Асимптотическая форма
Для простоты предположим, что управляющий вход uk = 0 { displaystyle mathbf {u} _ {k} = mathbf {0}}
- x ^ k ∣ k = F k x ^ k — 1 ∣ k — 1 + K k [z k — H k F k x ^ k — 1 ∣ k — 1]. { displaystyle { hat { mathbf {x}}} _ {k mid k} = mathbf {F} _ {k} { hat { mathbf {x}}} _ {k-1 mid k -1} + mathbf {K} _ {k} [ mathbf {z} _ {k} — mathbf {H} _ {k} mathbf {F} _ {k} { hat { mathbf {x }}} _ {k-1 mid k-1}].}
Аналогичное уравнение выполняется, если мы включаем ненулевой управляющий вход. Матрицы усиления K k { displaystyle mathbf {K} _ {k}}

- P k ∣ k — 1 = F k P k — 1 ∣ k — 1 F k T + Q k, { displaystyle mathbf {P } _ {k mid k-1} = mathbf {F} _ {k} mathbf {P} _ {k-1 mid k-1} mathbf {F} _ {k} ^ {textf { T}} + mathbf {Q} _ {k},}
- S k = R k + H k P k ∣ k — 1 H k T, { displaystyle mathbf {S} _ {k} = mathbf {R} _ {k} + mathbf {H} _ {k} mathbf {P} _ {k mid k-1} mathbf {H} _ {k} ^ {textf {T}}, }
- К К = П К ∣ К — 1 ЧАС К ТС К — 1, { Displaystyle mathbf {K} _ {k} = mathbf {P} _ {k mid k-1} mathbf { H} _ {k} ^ {textf {T}} mathbf {S} _ {k} ^ {- 1},}
- P k | k = (I — K k H k) P k | к — 1. { Displaystyle mathbf {P} _ {k | k} = left ( mathbf {I} — mathbf {K} _ {k} mathbf {H} _ {k} right) mathbf {P} _ {k | k-1}.}
Поскольку матрицы усиления зависят только от модели, а не от измерений, их можно вычислить в автономном режиме. Сходимость матриц усиления K k { displaystyle mathbf {K} _ {k}}




Используя асимптотическое усиление и предполагая H k { displaystyle mathbf {H} _ {k}}


- x ^ k = F x ^ k — 1 + K ∞ [zk — HF x ^ к — 1]. { displaystyle { hat { mathbf {x}}} _ {k} = mathbf {F} { hat { mathbf {x}}} _ {k-1} + mathbf {K} _ { infty} [ mathbf {z} _ {k} — mathbf {H} mathbf {F} { hat { mathbf {x}}} _ {k-1}].}
Асимптотическое усиление K ∞ { displaystyle mathbf {K} _ { infty}}

- P ∞ = F (P ∞ — P ∞ HT (HP ∞ HT + R) — 1 HP ∞) FT + Q. { displaystyle mathbf {P} _ { infty} = mathbf {F} left ( mathbf {P} _ { infty} — mathbf {P} _ { infty} mathbf {H} ^ { textf {T}} left ( mathbf {H} mathbf {P} _ { infty} mathbf {H} ^ { textf {T}} + mathbf {R} right) ^ {- 1} mathbf {H} mathbf {P } _ { infty} right) mathbf {F} ^ { textf {T}} + mathbf {Q}.}
Затем асимптотическое усиление вычисляется как перед.
- К ∞ = P ∞ HT (HP ∞ HT + R) — 1. { Displaystyle mathbf {K} _ { infty} = mathbf {P} _ { infty} mathbf {H} ^ { textf {T}} left ( mathbf {H} mathbf {P} _ { infty} mathbf {H} ^ { textf {T}} + mathbf {R} right) ^ {- 1 }.}
Выводы
Вывод ковариационной матрицы апостериорной оценки
Начало с нашей инварианта ковариации ошибок Pk | к как указано выше
- п К ∣ к = cov (xk — x ^ k ∣ k) { displaystyle mathbf {P} _ {k mid k} = operatorname {cov} left ( mathbf {x} _ {k} — { hat { mathbf {x}}} _ {k mid k} right)}
заменить в определении x ^ К ∣ К { Displaystyle { Шляпа { mathbf {x}}} _ {k mid k}}
- P k ∣ k = cov [xk — (x ^ k ∣ k — 1 + K ky ~ k)] { displaystyle mathbf {P} _ {k mid k} = operatorname {cov} left [ mathbf {x} _ {k} — left ({ hat { mathbf {x})}} _ {k mid k -1} + mathbf {K} _ {k} { tilde { mathbf {y}}} _ {k} right) right]}
и замените Y ~ К { Displaystyle { тильда { mathbf {y}}} _ {k}}
- P k ∣ k = cov (xk — [x ^ k ∣ k — 1 + K k (zk — ЧАС КХ ^ К ∣ К — 1)]) { Displaystyle mathbf {P} _ {k mid k} = operatorname {cov} left ( mathbf {x} _ {k} — left [{ шляпа { mathbf {x} }} _ {k mid k-1} + mathbf {K} _ {k} left ( mathbf {z} _ {k} — mathbf {H} _ {k} { hat { mathbf { x}}} _ {k mid k-1} right) right] right)}
и zk { displaystyle mathbf {z} _ {k}}
- п К ∣ К знак равно cov (xk — [x ^ k ∣ k — 1 + K k (ЧАС kxk + vk — H kx ^ к ∣ к — 1)]) { displaystyle mathbf {P} _ {k mid k} = operatorname {co v} left ( mathbf {x} _ {k } — left [{ hat { mathbf {x}}} _ {k mid k-1} + mathbf {K} _ {k} left ( mathbf {H} _ {k} mathbf { x} _ {k} + mathbf {v} _ {k} — mathbf {H} _ {k} { hat { mathbf {x}}} _ {k mid k-1} right) right] right)}
и, собрав возник ошибок, мы получаем
- P k ∣ k = cov [(I — K k H k) (хк — х ^ К ∣ К — 1) — K kvk ] { displaystyle mathbf {P} _ {k mid k} = operatorname {cov} left [ left ( mathbf {I} — mathbf {K} _ {k} mathbf {H} _ { k} right) left ( mathbf {x} _ {k} — { hat { mathbf {x}}} _ {k mid k-1} right) — mathbf {K} _ {k } mathbf {v} _ {k} right]}
«Регистрация» vkне коррелирует с другими членами, это становится
- P К ∣ К равно COV [(I — К К ЧАС К) (XK — Икс ^ К ∣ К — 1)] + C OV [К KVK] { Displaystyle mathbf {P} _ {к середине k} = operatorname {cov} left [ left ( mathbf {I} — mathbf {K} _ {k} mathbf {H} _ {k} right) left ( mathbf {x} _ {k} — { hat { mathbf {x}}} _ {k mid k-1} right) right] + operatorname {cov} left [ mathbf {K} _ {k} mathbf {v} _ {k} right]}
по свойствам ковариации вектора это становится
- P к ∣ К знак равно (I — К К ЧАС к) cov (xk — x ^ k ∣ k — 1) (I — K k ЧАС К) T + К К К ков (vk) К К T { Displaystyle mathbf {P} _ {k mid k} = left ( mathbf {I} — mathbf {K} _ {k} mathbf {H} _ {k} right) operatorname {cov} left ( mathbf {x} _ {k} — { hat { mathbf {x}}} _ {k mid k-1} справа) слева ( mathbf {I} — mathbf {K} _ { k} mathbf {H} _ {k} right) ^ { textf {T}} + mathbf {K} _ {k} operatorname {cov} left ( mathbf {v} _ {k} справа) mathbf {K} _ {k} ^ { textf {T}}}
который, используя наш инвариант на Pk | k — 1 и определение Rkстановится
- P k ∣ k = (I — K k H k) P k ∣ k — 1 (I — K k H k) T + K k R k К К T { displaystyle mathbf {P} _ {k mid k} = left ( mathbf {I} — mathbf {K} _ {k} mathbf {H} _ {k} right) mathbf { P} _ {k mid k-1} left ( mathbf {I} — mathbf {K} _ {k} mathbf {H} _ {k} right) ^ { textf {T}} + mathbf {K} _ {k} mathbf {R} _ {k} mathbf {K} _ {k} ^ { textf {T}}}
Эта формула (иногда известная как Форма Джозефа уравнения обновления ковариации) действительна для любого значения Kk. Оказывается, что если Kkявляется оптимальным усилением Калмана, это можно упростить, как показано ниже.
Выведение коэффициента усиления Калмана
Фильтр Калмана представляет собой средство оценки минимальной среднеквадратичной ошибки. Ошибка в апостериальной оценке состояния составляет
- xk — x ^ k ∣ k { displaystyle mathbf {x} _ {k} — { hat { mathbf {x}}} _ {k mid k}}
Мы стремимся минимизировать математическое ожидание квадрата величины этого события, E [‖ xk — x ^ k | к ‖ 2] { Displaystyle OperatorName {E} left [ left | mathbf {x} _ {k} — { hat { mathbf {x}}} _ {k | k} right | ^ {2} right]}![{ displaystyle operatorname {E} left [ left | mathbf {x} _ {k} - { hat { mathbf {x}}} _ {k | k} right | ^ { 2} right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9980afd591249f61711d6020cb30a0bcd54ec641)

- P k ∣ k = P k ∣ k — 1 — K k H k P k ∣ k — 1 — P k ∣ k — 1 H k TK k T + K k (H k P k ∣ k — 1 H k T + R k) K k T = P k ∣ k — 1 — K k H k P k ∣ k — 1 — P k ∣ k — 1 H К ТК К Т + К К S К К К Т { Displaystyle { begin {выровнено} mathbf {P} _ {k mid k} = mathbf {P} _ {k mid k-1} — mathbf { K} _ {k} mathbf {H} _ {k} mathbf {P} _ {k mid k-1} — mathbf {P} _ {k mid k-1} mathbf {H} _ {k} ^ { textf {T}} mathbf {K} _ {k} ^ { textf {T}} + mathbf {K} _ {k} left ( mathbf {H} _ {k} mathbf {P} _ {k mid k-1} mathbf {H} _ {k} ^ { textf {T}} + mathbf {R} _ {k} right) mathbf {K} _ {k} ^ { textf {T}} \ [6pt] = mathbf {P} _ {k mid k-1} — mathbf {K} _ {k} mathbf {H} _ {k } mathbf {P} _ {k mid k-1} — mathbf {P} _ {k mid k-1} mathbf {H} _ {k} ^ { textf {T}} mathbf { K} _ {k} ^ { textf {T}} + mathbf {K} _ {k} mathbf {S} _ {k} mathbf {K} _ {k} ^ { textf {T}} end {ali gn}}}
Трасса минимизируется, когда ее производная матрица по матрице усиления равна нулю. Используя правила градиентных матриц и симметрию задействованных матриц, мы находим, что
- ∂ tr (P k ∣ k) ∂ K k = — 2 (H k P k ∣ k — 1) T + 2 К К S К знак равно 0. { Displaystyle { frac { partial ; operatorname {tr} ( mathbf {P} _ {k mid k})} { partial ; mathbf {K} _ {k}}} = — 2 left ( mathbf {H} _ {k} mathbf {P} _ {k mid k-1} right) ^ { textf {T} } + 2 mathbf {K} _ {k} mathbf {S} _ {k} = 0.}
Решение этого для Kkдает усиление Калмана:
- K k S k = (H k P k ∣ k — 1) Т знак равно п К ∣ К — 1 ЧАС К T ⇒ К К = П К ∣ К — 1 ЧАС К ТС к — 1 { Displaystyle { begin {выровнено} mathbf {K} _ { k} mathbf {S} _ {k} = left ( mathbf {H} _ {k} mathbf {P} _ {k mid k-1} right) ^ { textf {T}} = mathbf {P} _ {k mid k-1} mathbf {H} _ {k} ^ { textf {T}} \ Rightarrow mathbf {K} _ {k} = mathbf { P} _ {k mid k-1} mathbf {H} _ {k} ^ { textf {T}} mathbf {S} _ {k} ^ {- 1} end {align}}}
Это усиление, которое известно как оптимальное усиление Калмана, при использовании эффективности MMSE.
Упрощение формулы ковариации апостериорной ошибки
Формулу, используемую для вычислений ковариации апостериорной ошибки, можно упростить, если коэффициент Калмана равен оптимальному значению, полученному выше. Умножая обе части нашей формулы усиления справа на SkKk, получаем, что
- K k S k K k T = P k ∣ k — 1 H k TK k T { displaystyle mathbf {K} _ {k} mathbf {S} _ {k} mathbf {K} _ {k} ^ { textf {T}} = mathbf {P} _ {k mid k-1} mathbf {H} _ {k} ^ { textf {T}} mathbf {K} _ {k} ^ { textf {T}}}
Возвращаясь к нашей расширенной формуле для ошибок ковариации апостериорной,
- P k ∣ К знак равно п К ∣ К — 1 — К К ЧАС К П К ∣ К — 1 — П К ∣ К — 1 Н К ТК К Т + К К S К К К К Т { Displaystyle mathbf {P} _ {k mid k } = mathbf {P} _ {k mid k-1} — mathbf {K} _ {k} mathbf {H} _ {k} mathbf {P} _ {k mid k -1} — mathbf {P} _ {k mid k-1} mathbf {H} _ {k} ^ { textf {T}} mathbf {K} _ {k} ^ { textf {T}} + mathbf {K} _ {k} mathbf {S} _ {k} mathbf {K} _ {k} ^ { textf {T}}}
мы обнаруживаем, что последние два члена сокращаются, что дает
- п К ∣ К знак равно п К ∣ К — 1 — К К Ч К П К ∣ К — 1 = (I — К К Н К) П К ∣ К — 1. { Displaystyle mathbf {P} _ { k mid k} = mathbf {P} _ {k mid k-1} — mathbf {K} _ {k} mathbf {H} _ {k} mathbf {P} _ {k mid k- 1} = ( mathbf {I} — mathbf {K} _ {k} mathbf {H} _ {k}) mathbf {P} _ {k mid k-1}.}
формула Этала дешевле в вычислительном отношении и поэтому почти всегда используется на практике, но верна для оптимального усиления. , если неоптимальное усиление Калмана используется намеренно, это упрощение не может использоваться; должна быть номинала ковари апостериорной ошибки, полученная выше (форма Джозефа).
Анализ чувствительности
Уравнения фильтрации Калмана наступления состояния x ^ k ∣ k { displaystyle { hat { mathbf {x}}} _ {k mid k}}



- P k ∣ k = (I — K k H k) P k ∣ k — 1 (I — K k H k) T + K k Р К К К К T { Displaystyle mathbf {P} _ {k mid k} = left ( mathbf {I} — mathbf {K} _ {k} mathbf {H} _ {k} right) mathbf { P} _ {k mid k-1} left ( mathbf {I} — mathbf {K} _ {k} mathbf {H} _ {k} right) ^ { textf {T}} + mathbf {K} _ {k} mathbf {R} _ {k} mathbf {K} _ {k} ^ { textf {T}}}
больше не обеспечивает фактическую ковариацию ошибок. Другими словами, P k ∣ k ≠ E [(xk — x ^ k ∣ k) (xk — x ^ k ∣ k) T] { displaystyle mathbf {P} _ {k mid k} neq E left [ left ( mathbf {x} _ {k} — { hat { mathbf {x}}} _ {k mid k} right) left ( mathbf {x} _ {k} — { hat { mathbf {x}}} _ {k mid k} right) ^ { textf {T}} right]}![{displaystyle mathbf {P} _{kmid k}neq Eleft[left(mathbf {x} _{k}-{hat {mathbf {x} }}_{kmid k}right)left(mathbf {x} _{k}-{hat {mathbf {x} }}_{kmid k}right)^{textsf {T}}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/14f468d3696299953a87882fe8987d019be46f87)


Это обсуждение ограничивается анализом чувствительности к ошибкам для случая статистических неопределенностей. Здесь фактические ковариации шума обозначаются Q ka { displaystyle mathbf {Q} _ {k} ^ {a}}








![{displaystyle mathbf {P} _{kmid k}^{a}=Eleft[left(mathbf {x} _{k}-{hat {mathbf {x} }}_{kmid k}right)left(mathbf {x} _{k}-{hat {mathbf {x} }}_{kmid k}right)^{textsf {T}}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b8bfa69cc3749d0b62c6d50dc98080b54b24ea12)

![{displaystyle Eleft[mathbf {w} _{k}mathbf {w} _{k}^{textsf {T}}right]=mathbf {Q} _{k}^{a}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d683b5e826696f9302ad471107d89cbd574a2861)
![{displaystyle Eleft[mathbf {v} _{k}mathbf {v} _{k}^{textsf {T}}right]=mathbf {R} _{k}^{a}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d89dca74f5288b67fbe0fa2855a370545ddb4006)

- П К ∣ К — 1 а = F К П К — 1 ∣ К — 1 а F К Т + Q ка { Displaystyle mathbf {P} _ { k mid k-1} ^ {a} = mathbf {F} _ {k} mathbf {P} _ {k-1 mid k-1} ^ {a} mathbf {F} _ {k} ^ { textf {T}} + mathbf {Q} _ {k} ^ {a}}
и
- P k ∣ ka = (I — K k H k) P k ∣ k — 1 a (I — К К ЧАС К) T + К К К р ка К К T { Displaystyle mathbf {P} _ {k mid k} ^ {a} = left ( mathbf {I} — mathbf {K} _ {k} mathbf {H} _ {k} right) mathbf {P} _ {k mid k-1} ^ {a} left ( mathbf {I} — mathbf {K} _ {k } mathbf {H} _ {k} right) ^ { textf {T}} + mathbf {K} _ {k} mathbf {R} _ {k} ^ {a} mathbf {K} _ {k} ^ { textf {T}}}
При вычислении P k ∣ k { displaystyle mathbf {P} _ {k mid k}}
![{displaystyle Eleft[mathbf {w} _{k}mathbf {w} _{k}^{textsf {T}}right]=mathbf {Q} _{k}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e913b662d3d03c3b59ce4a86767ae6c4a57c311)
![{displaystyle Eleft[mathbf {v} _{k}mathbf {v} _{k}^{textsf {T}}right]=mathbf {R} _{k}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/819ee3b84d0b2613dc716ed09927696fda25baf5)






Форма квадратного корня
Одной из проблем с фильтром Калмана является его числовая стабильность. Если ковариация шума процесса Qkмала, ошибка округления часто приводит к тому, что небольшое положительное собственное значение вычисляется как отрицательное число. Это отображает числовое представление ковариационной матрицы состояния Pнеопределенной, в то время как ее истинная форма — положительно-воспроизвод.
Положительно воспроизводящие матрицы обладают тем своим качеством, что они имеют треугольную матрицу квадратный корень P= S·S. Это может быть эффективно вычислено с использованием алгоритма факторизации Холецкого, но, что более важно, если ковариация сохраняется в этой форме, она никогда не может иметь отрицательную диагональ или стать асимметричной. Эквивалентная форма, которая позволяет избежать многих операций извлечения квадратного корня, требуемых для квадратного корня матрицы, но сохраняет желаемые числовые свойства, является формой разложения UD, P= U·D·U, где U — это единичная треугольная матрица (с единичной диагональю), а D — диагональная матрица.
Между этим двумя факторизациями U-D использует тот же объем памяти и несколько меньшее количество вычислений и является наиболее часто используемой формой квадратного корня. (Ранняя литература об относительной эффективности несколько вводит в заблуждение, поскольку предполагалось, что извлечение квадратного корня занимает больше времени, чем деление, в то время как на компьютере 21-го века они намного больше времени.)
Эффективные алгоритмы для шагов прогнозирования Калмана и обновления в форме квадратного корня были разработаны GJ Bierman и CL Thornton.
L·D·Lразложение ковариационной матрицы инноваций Skиспользуется для другого типа численный эффективный и надежный фильтр квадратного корня. Алгоритм начинается с разложения LU, как это реализовано в ПАКЕТЕ линейной алгебры (LAPACK ). Эти результаты матрицы вводятся в структуру L·D·Lс помощью методов, данных Голубом и Ван Лоаном (алгоритм 4.1.2) для симметричной невырожденной. Любая сингулярная ковариационная матрица повернута на так, чтобы первое диагональное разбиение было невырожденным и хорошо обусловленным. Алгоритм поворота должен любую часть ковариационной матрицы нововведений непосредственно, соответствующего наблюдаемым переменным состоянием Hk·xk | k-1, которые связаны со вспомогательными наблюдениями в yk. Фильтр квадратного корня l·d·lтребует ортогонализации Вектор наблюдения. Это может быть сделано с помощью обратного квадратного корня из ковариационной матрицы для вспомогательных чисел, используя метод 2 в Higham (2002, стр. 263).
Связь с рекурсивным байесовским оцениванием
Кальман фильтр можно представить как одну из простейших динамических байесовских сетей. Фильтр Калмана вычисляет истинных состояний рекурсивно с течением времени, используя входящие измерения и математическую модель процесса. Аналогично, рекурсивная байесовская оценка вычисляет оценки неизвестной функции плотности вероятности (PDF) рекурсивно с течением времени с использованием измерений и математической модели процесса.
В рекурсивной байесовской оценке истинного состояния ненаблюдаемым состоянием марковским процессом, наблюдаемыхми скрытой марковской модели (HMM).
из-за марковского предположения, истинное состояние условно не зависит от всех предыдущих состояний, непосредственно предыдущее состояние.
- п (xk ∣ x 0,…, xk — 1) = p (xk ∣ xk — 1) { displaystyle p ( mathbf {x} _ {k} mid mathbf {x} _ {0}, dots, mathbf {x} _ {k-1}) = p ( mathbf {x} _ {k} mid mathbf {x} _ {k-1})}
Аналогично, измерение на k-м временном шаге зависит только от текущего состояния и условно не зависит от всех других состояний с учетом текущего состояния.
- п (zk ∣ Икс 0,…, xk) = p (zk ∣ xk) { displaystyle p ( mathbf {z} _ {k} mid mathbf {x} _ {0}, dots, mathbf {x} _ {k}) = p ( mathbf {z} _ {k} mid mathbf {x} _ {k})}
Используя эти предположения, распределение вероятностей по всем состояниям скрытого Марковскую модель можно записать просто так:
- p (x 0,…, xk, z 1,…, zk) = p (x 0) ∏ i = 1 kp (zi ∣ xi) p (xi ∣ xi — 1) { displaystyle p left ( mathbf {x} _ {0}, dots, mathbf {x} _ {k}, mathbf {z} _ {1}, dots, mathbf {z} _ {k} right) = p left ( mathbf {x} _ {0} right) prod _ {i = 1} ^ {k} p left ( mathbf {z} _ {i} mid mathbf { x} _ {i} right) p left ( mathbf {x} _ {i} mid mathbf {x} _ {i-1} right)}
Однако, когда Кальман Фильтр используется для оценки состояния x, интересное распределение вероятностей связано с текущими состояниями, обусловленными измерениями, вплоть до текущего временного шага. Это достигается за счет исключения предыдущих состояний и деления на вероятность набора измерений.
Это приводит к тому, что шаги прогнозирования и обновления фильтра Калмана записываются вероятностно. Распределение вероятностей, связанное с предсказанным состоянием, представляет собой сумму (интеграл) произведений распределения вероятностей, связанных с переходом от (k — 1) -го временного шага к k-му, и распределения вероятностей, связанного с предыдущим состоянием, по всем возможным хк — 1 { displaystyle x_ {k-1}}
- p (xk ∣ Z k — 1) = ∫ p (xk ∣ xk — 1) p (xk — 1 ∣ Z k — 1) dxk — 1 { displaystyle p left ( mathbf {x} _ {k} mid mathbf {Z} _ {k-1} right) = int p left ( mathbf {x} _ {k} mid mathbf {x} _ {k-1} right) p left ( mathbf {x} _ {k-1} mid mathbf {Z} _ {k-1} right) , d mathbf {x} _ {k-1}}
Измерение, установленное на время t, равно
- Z t = {z 1,…, zt} { displaystyle mathbf {Z} _ {t} = left { mathbf {z} _ {1}, dots, mathbf {z} _ {t} right }}
Распределение вероятностей обновлений пропорционально произведению вероятности измерения и прогнозируемого состояния.
- п (xk ∣ Z К) знак равно п (zk ∣ xk) p (xk ∣ ZK — 1) p (zk ∣ Z k — 1) { displaystyle p left ( mathbf {x} _ {k } mid mathbf {Z} _ {k} right) = { frac {p left ( mathbf {z} _ {k} mid mathbf {x} _ {k} right) p left ( mathbf {x} _ {k} mid mathbf {Z} _ {k-1} right)} {p left ( mathbf {z} _ {k} mid mathbf {Z} _ { k-1} right)}}}
Знаменатель
- p (zk ∣ Z k — 1) = ∫ p (zk ∣ xk) p (xk ∣ Z k — 1) dxk { displaystyle p left ( mathbf {z} _ {k} mid mathbf {Z} _ {k-1} right) = int p left ( mathbf {z} _ {k} mid mathbf {x} _ {k} right) p left ( mathbf {x} _ {k} mid mathbf {Z} _ {k-1} right) , d mathbf {x} _ {k}}
— это нормализация.
Остальные функции плотности вероятности:
- p (xk ∣ xk — 1) = N (F kxk — 1, Q k) p (zk ∣ xk) = N (H kxk, R k) p ( Икс — 1 ∣ Z К — 1) знак равно N (Икс ^ К — 1, П К — 1) { Displaystyle { begin {align} p left ( mathbf {x} _ {k} mid mathbf {x} _ {k-1} right) = { mathcal {N}} left ( mathbf {F} _ {k} mathbf {x} _ {k-1}, mathbf {Q} _ {k} right) \ p left ( mathbf {z} _ {k} mid mathbf {x} _ {k} right) = { mathcal {N}} left ( mathbf {H} _ {k} mathbf {x} _ {k}, mathbf {R} _ {k} right) \ p left ( mathbf {x} _ {k-1} mid mathbf {Z} _ {k-1} right) = { mathcal {N}} left ({ hat { mathbf {x}}} _ {k-1}, mathbf {P} _ {k -1} right) end {align}}}
Индуктивно предполагается, что PDF на предыдущем временном шаге является оценочным состоянием и ковариацией. Это оправдано, поскольку в качестве оптимального средства оценки фильтр Калмана наилучшим образом использует измерения, поэтому PDF для xk { displaystyle mathbf {x} _ {k}}

Предельное правдоподобие
В отношении рекурсивной байесовской интерпретации, описанной выше, фильтр Калмана можно рассматривать как генеративную модель, т. Е. Процесс генерации потока случайных наблюдения z = (z0, z1, z2,…). В частности, процесс
- Выборка скрытого состояния x 0 { displaystyle mathbf {x} _ {0}}
из априорного распределения Гаусса p (x 0) = N (Икс ^ 0 ∣ 0, п 0 ∣ 0) { displaystyle p left ( mathbf {x} _ {0} right) = { mathcal {N}} left ({ hat { mathbf { x}}} _ {0 mid 0}, mathbf {P} _ {0 mid 0} right)}
.
- Пример наблюдения z 0 { displaystyle mathbf {z} _ {0 }}
из модели наблюдения p (z 0 ∣ x 0) = N (H 0 x 0, R 0) { displaystyle p left ( mathbf {z} _ {0} mid mathbf {x} _ {0} right) = { mathcal {N}} left ( mathbf {H} _ {0} mathbf {x} _ {0}, mathbf {R} _ {0} right)}
.
- Для k = 1, 2, 3,… { displaystyle k = 1,2,3, ldots}
, выполните
- Пример следующего скрытого состояния xk { displaystyle mathbf {x} _ {k}}
из модели перехода p (xk ∣ xk — 1) = N (F kxk — 1 + Б кук, Q к). { displaystyle p left ( mathbf {x} _ {k} mid mathbf {x} _ {k-1} right) = { mathcal {N}} left ( mathbf {F} _ { k} mathbf {x} _ {k-1} + mathbf {B} _ {k} mathbf {u} _ {k}, mathbf {Q} _ {k} right).}
- Выберите наблюдение zk { displaystyle mathbf {z} _ {k}}
из модели наблюдения p (zk ∣ xk) = N (H kxk, R k). { displaystyle p left ( mathbf {z} _ {k} mid mathbf {x} _ {k} right) = { mathcal {N}} left ( mathbf {H} _ {k} mathbf {x} _ {k}, mathbf {R} _ {k} right).}
- Пример следующего скрытого состояния xk { displaystyle mathbf {x} _ {k}}
Этот процесс имеет структуру, идентичную скрытой марковской модели, за исключением того, что дискретное состояние и наблюдения заменяются непрерывными переменными, выбранными из гауссовых распределений.
В некоторых приложениях полезно вычислить вероятность того, что фильтр Калмана с заданным набором параметров (предварительное распределение, модели перехода и наблюдения, а также управляющие входные данные) сгенерирует конкретный наблюдаемый сигнал. Эта вероятность известна как предельное правдоподобие, потому что она интегрирует («маргинализирует»)значения скрытых переменных состояния, поэтому ее можно вычислить, используя только наблюдаемый сигнал. Предельное правдоподобие может быть полезно для оценки выбора различных параметров или сравнения фильтра Калмана с другими моделями с использованием сравнения байесовских моделей.
Легко вычислить предельное правдоподобие как побочный эффект вычисления рекурсивной фильтрации. Согласно правилу цепочки , вероятность может быть разложена на множители как произведение вероятности каждого наблюдения с учетом предыдущих наблюдений,
- p (z) = ∏ k = 0 T p (zk ∣ zk — 1, …, Z 0) { displaystyle p ( mathbf {z}) = prod _ {k = 0} ^ {T} p left ( mathbf {z} _ {k} mid mathbf {z} _ {k-1}, ldots, mathbf {z} _ {0} right)}
,
и поскольку фильтр Калмана описывает марковский процесс, вся соответствующая информация из предыдущих наблюдений содержится в оценке текущего состояния х ^ k ∣ k — 1, P k ∣ k — 1. { displaystyle { hat { mathbf {x}}} _ {k mid k-1}, mathbf {P} _ {k mid k-1}.}
- p (z) = ∏ k = 0 T ∫ p (zk ∣ xk) p (xk ∣ zk — 1,…, z 0) dxk = ∏ k = 0 T ∫ N (zk; H kxk, R k) N (xk; x ^ k ∣ k — 1, P k ∣ k — 1) dxk = ∏ k = 0 TN (zk; H kx ^ k ∣ k — 1, R k + H k P k ∣ К — 1 ЧАС К T) знак равно ∏ К знак равно 0 TN (ZK; ЧАС КХ ^ К ∣ К — 1, S К), { Displaystyle { begin {выровнено} p ( mathbf {z}) = prod _ {k = 0} ^ {T} int p left ( mathbf {z} _ {k} mid mathbf {x} _ {k} right) p left ( mathbf {x} _ { k} mid mathbf {z} _ {k-1}, ldots, mathbf {z} _ {0} right) d mathbf {x} _ {k} \ = prod _ {k = 0} ^ {T} int { mathcal {N}} left ( mathbf {z} _ {k}; mathbf {H} _ {k} mathbf {x} _ {k}, mathbf {R} _ {k} right) { mathcal {N}} left ( mathbf {x} _ {k}; { hat { mathbf {x}}} _ {k mid k-1}, mathbf {P} _ {k mid k-1} right) d mathbf {x} _ {k} \ = prod _ {k = 0} ^ {T} { mathcal {N} } left ( mathbf {z} _ {k}; mathbf {H} _ {k} { hat { mathbf {x}}} _ {k mid k-1}, mathbf {R} _ {k} + mathbf { H} _ {k} mathbf {P} _ {k mid k-1} mathbf {H} _ {k} ^ {textf {T}} right) \ = prod _ {k = 0} ^ {T} { mathcal {N}} left ( mathbf {z} _ {k}; mathbf {H} _ {k} { hat { mathbf {x}}} _ {k mid k-1}, mathbf {S} _ {k} right), end {align}}}
то есть, произведение гауссовых плотностей, каждая из которых соответствует плотности одного наблюдения zkпод текущее распределение фильтрации H kx ^ k ∣ k — 1, S k { displaystyle mathbf {H} _ {k} { hat { mathbf {x}}} _ {k mid k-1}, mathbf {S} _ {k}}


- ℓ (k) знак равно ℓ (К — 1) — 1 2 (Y ~ К ТС К — 1 Y ~ К + журнал | S К | + dy журнал 2 π), { Displaystyle ell ^ {(k)} = ell ^ {(k-1)} — { frac {1} {2}} left ({ tilde { mathbf {y}}} _ {k} ^ {textf {T}} mathbf {S } _ {k} ^ {- 1} { tilde { mathbf {y}}} _ {k} + log left | mathbf {S} _ {k} right | + d_ {y} log 2 pi right),}
где dy { displaystyle d_ {y}}
Важное приложение, в котором такой (log) вероятность наблюдений (с учетом параметров фильтра) используется для отслеживания нескольких целей. Например, рассмотрим сценарий отслеживания объекта, в котором поток наблюдений является входом, однако неизвестно, сколько объектов находится в сцене (или количество объектов известно, но больше единицы). В таком сценарии может быть неизвестно априори, какие наблюдения / измерения были произведены каким объектом. Устройство отслеживания множественных гипотез (MHT) обычно формирует различные гипотезы ассоциации треков, где каждую гипотезу можно рассматривать как фильтр Калмана (в линейном гауссовском случае) с определенным набором параметров, связанных с гипотетическим объектом. Таким образом, важно вычислить вероятность наблюдений для различных рассматриваемых гипотез, чтобы можно было найти наиболее вероятную.
Информационный фильтр
В информационном фильтре или фильтре обратной ковариации оцененная ковариация и оценочное состояние заменяются информационной матрицей и информацией вектор соответственно. Они определяются как:
- Y k ∣ k = P k ∣ k — 1 y ^ k ∣ k = P k ∣ k — 1 x ^ k ∣ k { displaystyle { begin {align} mathbf {Y} _ {k mid k} = mathbf {P} _ {k mid k} ^ {- 1} \ { hat { mathbf {y}}} _ {k mid k} = mathbf {P} _ {k mid k} ^ {- 1} { hat { mathbf {x}}} _ {k mid k} end {align}}}
Аналогично предсказанная ковариация и состояние эквивалентные информационные формы, определяемые как:
- Y k ∣ k — 1 = P k ∣ k — 1 — 1 y ^ k ∣ k — 1 = P k ∣ k — 1 — 1 x ^ k ∣ k — 1 { displaystyle { begin {выровненный} mathbf {Y} _ {k mid k-1} = mathbf {P} _ {k mid k-1} ^ {- 1} \ { hat { mathbf {y}}} _ {k mid k-1} = mathbf {P} _ {k mid k-1} ^ {- 1} { hat { mathbf {x}}} _ {k mid k-1} end {align}}}
, а также ковариация измерения и вектор измерения, которые определены как:
- I k = H k TR k — 1 H kik = H k TR k — 1 zk { displaystyle { begin {align} mathbf {I} _ {k} = mathbf {H} _ {k} ^ {textf {T}} mathbf {R} _ {k} ^ {- 1} mathbf {H} _ {k} \ mathbf {i} _ {k} = mathbf {H} _ {k} ^ {textf {T}} mathbf {R} _ {k} ^ {- 1} mathbf {z} _ {k} end {align}}}
Обновление информации теперь становится тривиальной суммой.
- Y k ∣ k = Y k ∣ k — 1 + I ky ^ k ∣ k = y ^ k ∣ k — 1 + ik { Displaystyle { begin {align} mathbf {Y} _ {k mid k} = mathbf {Y} _ {k mid k-1} + mathbf {I} _ {k} \ { шляпа { mathbf {y}}} _ {k mid k} = { hat { mathbf {y}}} _ {k mid k-1} + mathbf {i} _ {k} end {align}}}
Основное преимущество информационного фильтра состоит в том, что N измерений можно фильтровать на каждом временном шаге, просто суммируя их информационные матрицы и векторы.
- Y К ∣ К знак равно Y К ∣ К — 1 + ∑ J = 1 NI K, jy ^ K ∣ K = Y ^ K ∣ K — 1 + ∑ J = 1 N ik, j { Displaystyle { begin {выровнено} mathbf {Y} _ {k mid k} = mathbf {Y} _ {k mid k-1} + sum _ {j = 1} ^ {N} mathbf {I} _ {k, j} \ { hat { mathbf {y}}} _ {k mid k} = { hat { mathbf {y}}} _ {k mid k-1} + sum _ {j = 1} ^ {N} mathbf {i} _ {k, j} end {align}}}
Для прогнозирования информационного фильтра информационная матрица и вектор могут быть преобразованы обратно в их эквиваленты в пространстве состояний, или, альтернативно, может использоваться прогнозирование информационного пространства.
- M k = [F k — 1] TY k — 1 ∣ k — 1 F k — 1 C k = M k [M k + Q k — 1] — 1 L k = I — C k Y k ∣ k — 1 = L k M k L k T + C k Q k — 1 C k T y ^ k ∣ k — 1 = L k [F k — 1] T y ^ К — 1 ∣ К — 1 { Displaystyle { begin {align} mathbf {M} _ {k} = left [ mathbf {F} _ {k} ^ {- 1} right] ^ { textf {T}} mathbf {Y} _ {k-1 mid k-1} mathbf {F} _ {k} ^ {- 1} \ mathbf {C} _ {k} = mathbf {M} _ {k} left [ mathbf {M} _ {k} + mathbf {Q} _ {k} ^ {- 1} right] ^ {- 1} \ mathbf {L} _ {k} = mathbf {I} — mathbf {C} _ {k} \ mathbf {Y} _ {k mid k-1} = mathbf {L} _ {k} mathbf {M} _ {k} mathbf {L} _ {k} ^ {textf {T} } + mathbf {C} _ {k} mathbf {Q} _ {k} ^ {- 1} mathbf {C} _ {k} ^ {textf {T}} \ { hat { mathbf {y}}} _ {k mid k-1} = mathbf {L} _ {k} left [ mathbf {F} _ {k} ^ {- 1} right] ^ {textf { T}} { hat { mathbf {y}}} _ {k-1 mid k-1} end {align}}}
Если F и Q не зависят от времени, эти значения можно кэшировать, а F и Q должны быт ь обратимыми.
Сглаживание с фиксированной задержкой
Оптимальное сглаживание с фиксированной задержкой обеспечивает оптимальную оценку x ^ k — N ∣ k { displaystyle { hat { mathbf {x}} } _ {kN mid k}}



- [x ^ t ∣ tx ^ t — 1 ∣ t ⋮ x ^ t — N + 1 ∣ t] = [ I 0 ⋮ 0 ] x ^ t ∣ t − 1 + [ 0 … 0 I 0 ⋮ ⋮ ⋱ ⋮ 0 … I ] [ x ^ t − 1 ∣ t − 1 x ^ t − 2 ∣ t − 1 ⋮ x ^ t − N + 1 ∣ t − 1 ] + [ K ( 0) K ( 1) ⋮ K ( N − 1) ] yt ∣ t − 1 {displaystyle {begin{bmatrix}{hat {mathbf { x} }}_{tmid t}\{hat {mathbf {x} }}_{t-1mid t}\vdots \{hat {mathbf {x} }} _{t-N+1mid t}\end{bmatrix}}={begin{bmatrix}mathbf {I} \0\vdots \0\end{bmatrix}}{ hat {mathbf {x} }}_{tmid t-1}+{begin{bmatrix}0ldots 0\mathbf {I} 0vdots \vdots ddots vdots \0ldots mathbf {I} \end{bmatrix}}{begin{bmatrix}{hat {mathbf {x}}} _ {t-1 mid t-1} \ { hat { mathbf {x}}} _ {t-2 mid t-1} \ vdots \ { hat { mathbf {x}}} _ {t-N + 1 mid t-1} \ end {bmatrix}} + { begin {bmatrix} mathbf {K} ^ {(0)} \ mathbf {K} ^ {(1)} \ vdots \ mathbf {K} ^ {(N-1)} \ end {bmatrix}} mathbf {y} _ {t mid t-1} }
где:
- и
- P (i) = P [(F — KH) T] я { displaystyle mathbf {P} ^ {(i)} = mathbf {P} left [ left ( mathbf {F} — mathbf {K} mathbf {H} right) ^ { textf {T}} right] ^ {i}}
- P (i) = P [(F — KH) T] я { displaystyle mathbf {P} ^ {(i)} = mathbf {P} left [ left ( mathbf {F} — mathbf {K} mathbf {H} right) ^ { textf {T}} right] ^ {i}}
- где P { displaystyle mathbf {P}}
и K { displaystyle mathbf {K} }
— ковариация ошибки прогнозирования и коэффициенты усиления стандартного фильтра Калмана (т. Е. P t ∣ t — 1 { displaystyle mathbf {P} _ {t mid t-1}}
).
Если ковариация ошибки оценки определена так, что
- P i: = E [(xt — i — x ^ t — i ∣ t) ∗ (xt — i — x ^ t — i ∣ t) ∣ z 1… zt], { displaystyle mathbf {P} _ {i}: = E left [ left ( mathbf {x} _ {ti} — { hat { mathbf {x}}} _ {ti м id t} right) ^ {*} left ( mathbf {x} _ {ti} — { hat { mathbf {x}}} _ {ti mid t} right) mid z_ {1} ldots z_ {t} right],}
тогда мы видим, что улучшение оценки xt — i { displaystyle mathbf {x} _ {ti}}
- P — P я знак равно ∑ j = 0 я [P (j) HT (HPHT + R) — 1 H (P (i)) T] { displaystyle mathbf {P} — mathbf { P} _ {i} = sum _ {j = 0} ^ {i} left [ mathbf {P} ^ {(j)} mathbf {H} ^ {textf {T}} left ( mathbf {H} mathbf {P} mathbf {H} ^ {textf {T}} + mathbf {R} right) ^ {- 1} mathbf {H} left ( mathbf {P} ^ {(i)} right) ^ { textf {T}} right]}
Сглаживающие устройства с фиксированным интервалом
Оптимальный сглаживание с фиксированным интервалом обеспечивает оптимальную оценку x ^ k ∣ N { displaystyle { hat { mathbf {x}}} _ {k mid n}}



Rauch – Tung – Striebel
Сглаживатель Rauch – Tung – Striebel (RTS) — это эффективный двухпроходный алгоритм для сглаживания фиксированного интервала.
Прямой проход — это то же, что и обычный алгоритм фильтра Калмана. Эти отфильтрованные априорные и апостериорные оценки состояния x ^ k ∣ k — 1 { displaystyle { hat { mathbf {x}}} _ {k mid k-1}}



При обратном проходе мы вычисляем сглаженные оценки состояния x ^ k ∣ n { displaystyle { hat { mathbf {x}}} _ {k mid n}}

- x ^ k ∣ n = x ^ k ∣ k + C k (x ^ k + 1 ∣ n — x ^ k + 1 ∣ к) п К ∣ N знак равно п К ∣ К + С К (П К + 1 ∣ N — П К + 1 ∣ К) С К T { Displaystyle { begin {выровнено} { hat { mathbf {x} }} _ {k mid n} = { hat { mathbf {x}}} _ {k mid k} + mathbf {C} _ {k} left ({ hat { mathbf {x }}} _ {k + 1 mid n} — { hat { mathbf {x}}} _ {k + 1 mid k} right) \ mathbf {P} _ {k mid n} = mathbf {P} _ {k mid k} + mathbf {C} _ {k} left ( mathbf {P} _ {k + 1 mid n} — mathbf {P} _ {k + 1 mid k} right) mathbf {C} _ {k} ^ { textf {T}} end {align}}}
где
- C k = P k ∣ k F k + 1 TP К + 1 ∣ К — 1. { Displaystyle mathbf {C} _ {k} = mathbf {P} _ {k mid k} mathbf {F} _ {k + 1} ^ { textf {T}} mathbf {P} _ {k + 1 mid k} ^ {- 1}.}
xk ∣ k { displaystyle mathbf {x} _ {k mid k}}



Модифицированный сглаживание Брайсона — Фрейзера
Альтернативной алгоритму RTS является модифицированным сглаживанием с фиксированным интервалом Брайсона — Фрейзера (MBF), вашим Бирманом. При этом также используется обратный проход, который обрабатывает данные, сохраненные из прямого прохода фильтра Калмана. Уравнения для обратного прохода включает рекурсивное вычисление данных, используются в каждый момент наблюдения для выполнения сглаженного состояния и ковариации.
Рекурсивные уравнения:
- Λ ~ k = H k TS k — 1 H k + C ^ k T Λ ^ k C ^ k Λ ^ k — 1 = F k T Λ ~ k F k Λ ^ N знак равно 0 λ ~ К = — ЧАС К TS К — 1 YK + C ^ KT λ ^ K λ ^ K — 1 = F К T λ ~ к λ ^ N = 0 { Displaystyle { begin {выровнено} { tilde { Lambda}} _ {k} = mathbf {H} _ {k} ^ { textf {T}} mathbf {S} _ {k} ^ {- 1} mathbf {H} _ {k} + { hat { mathbf {C}}} _ {k} ^ { textf {T}} { hat { Lambda}} _ {k} { hat { mathbf {C}} } _ {k} \ { hat { Lambda}} _ {k-1} = mathbf {F} _ {k} ^ { textf {T}} { tilde { Lambda}} _ { k} mathbf {F} _ {k} \ { hat { Lambda}} _ {n} = 0 \ { tilde { lambda}} _ {k} = — mathbf {H} _ {k} ^ { textf {T}} mathbf {S} _ {k} ^ {- 1} mathbf {y} _ {k} + { hat { mathbf {C}}} _ {k } ^ { textf {T}} { hat { lambda}} _ {k} \ { hat { lambda}} _ {k-1} = mathbf {F} _ {k} ^ { textf {T}} { tilde { lambda}} _ {k} \ { hat { lambda}} _ {n} = 0 end {align}}}
где S К { displaystyle mathbf {S} _ {k}}

- P k ∣ n = P k ∣ k — P k ∣ k Λ ^ k P k ∣ kxk ∣ n = xk ∣ k — P k ∣ k λ ^ к { Displaystyle { begin {выровнено} mathbf {P} _ {k mid n} = mathbf {P} _ {k mid k} — mathbf {P} _ {k mid k} { hat { Lambda}} _ {k} mathbf {P} _ {k mid k} \ mathbf {x} _ {k mid n} = mathbf {x} _ {k mid k} — mathbf {P} _ {k mid k} { hat { lambda}} _ {k} end {align}}}
или
- P k ∣ n = P k ∣ k — 1 — P k ∣ k — 1 Λ ~ k P k ∣ k — 1 xk ∣ n знак равно xk ∣ k — 1 — P k ∣ k — 1 λ ~ k. { displaystyle { begin {align} mathbf {P} _ {k mid n} = mathbf {P} _ {k mid k-1} — mathbf {P} _ {k mid k- 1} { tilde { Lambda}} _ {k} mathbf {P} _ {k mid k-1} \ mathbf {x} _ {k mid n} = mathbf {x} _ {k mid k-1} — mathbf {P} _ {k mid k-1} { tilde { lambda}} _ {k}. end {align}}}
Важное преимущество MBF в том, что он не требует нахождения обратной матрицы ковариационной матрицы.
Сглаживатель с минимальной дисперсией
Сглаживатель с минимальной дисперсией может обеспечить наилучшие характеристики ошибок при условии, что модели являются линейными, их параметры и статистика шума известны точно. Этот сглаживающий фильтр является изменяющимся во времени оптимального непричинного фильтра Винера.
в пространстве состояний. Более сглаженные вычисления выполняются за два прохода. Прямые вычисления включают предсказатель на один шаг вперед и задаются следующим образом:
- x ^ k + 1 ∣ k = (F k — K k H k) x ^ k ∣ k — 1 + K kzk α k = — S к — 1 2 ЧАС кх ^ К ∣ К — 1 + S К — 1 2 zk { displaystyle { begin {align} { hat { mathbf {x}}} _ {k + 1 mid k} = ( mathbf {F} _ {k} — mathbf {K} _ {k} mathbf {H} _ {k}) { hat { mathbf {x}}} _ {k mid k-1} + mathbf {K} _ {k} mathbf {z} _ {k} \ alpha _ {k} = — mathbf {S} _ {k} ^ {- { frac {1} {2}} } mathbf {H} _ {k} { hat { mathbf {x}}} _ {k mid k-1} + mathbf {S} _ {k} ^ {- { frac {1} { 2}}} mathbf {z} _ {k} end {align}}}
Вышеупомянутая система известна как обратный фактор Винера-Хопфа. Обратная рекурсия является дополнением к вышеупомянутому прямому. Результат обратного прохода β k { displaystyle beta _ {k}}

- y ^ k ∣ N = zk — R k β k { displaystyle { hat { mathbf {y}}} _ {k mid N} = mathbf { z} _ {k} — mathbf {R} _ {k} beta _ {k}}
Взятие причинной части этого сглаживания с минимальной дисперсией дает
- y ^ k ∣ k = zk — Р К S К — 1 2 α К { Displaystyle { Hat { mathbf {y}}} _ {к mid k} = mathbf {z} _ {k} — mathbf {R} _ {k} mathbf {S } _ {k} ^ {- { frac {1} {2}}} alpha _ {k}}
, идентичен фильтру Калмана с минимальной дисперсией. Приведенные выше решения минимизируют дисперсию оценки ошибки выхода. Обратите внимание, что более гладкий вывод Рауха — Тунга — Штрибеля предполагает, что лежащие в основе распределения гауссовскими, тогда как решения с минимальной дисперсией — нет. Аналогичным образом могут быть созданы оптимальные сглаживающие устройства для оценки состояния и оценки входных данных.
Версия вышеупомянутого устройства сглаживания для непрерывного времени описана в.
Алгоритмы максимизации ожидания Нагрузка для достижения приблизительных оценок максимального правдоподобия неизвестных параметров в пространстве состояний в фильтрах с минимальной дисперсией и сглаживателях. Часто неуверенность остается в пределах проблемных предположений. Более сглаживающее устройство, учитывающее неопределенность, может быть разработано путем добавления положительно определенного члена к уравнению Риккати.
В случаях, когда модели имеют нелинейные, пошаговаялинеаризация может находиться в пределах фильтра минимальной дисперсии и более плавных рекурсий (расширенная фильтрация Калмана ).
Частотно-взвешенные фильтры Калмана
Новаторские исследования восприятия звуков на разных частотах были проведены Флетчером и Мансоном в 1930-х годах. Их работа привела к стандартному способу взвешивания измеренных уровней звука в исследованиях промышленного шума и слуха. С тех пор частотные весовые коэффициенты используются в конструкциях фильтров и контроллеров для управления производительностью в пределах интересующих диапазонов.
Обычно функция формирования частот используется для взвешивания средней мощности спектральной плотности ошибки в заданной полосе частот. Пусть y — y ^ { displaystyle mathbf {y} — { hat { mathbf {y}}}}



Дизайн W { displaystyle mathbf {W}}

Нелинейные фильтры
Базовый фильтр Калмана ограничен линейным предположением. Однако более сложные системы могут быть нелинейными. Нелинейность может быть связана с моделью процесса, либо с моделью наблюдения, либо с обоими.
Наиболее распространенными вариантами фильтров Калмана для нелинейных систем расширенный фильтр Калмана и фильтр Калмана без запаха. Пригодность того, какой фильтр использовать, зависит от нелинейности процесса и модели наблюдения.
Расширенный фильтр Калмана
В расширенном фильтре Калмана (EKF) переходные состояния и наблюдение модели не обязательно должны быть линейными функциями, но вместо могут быть нелинейными функциями. Эти функции безопасности к дифференцируемому типу.
- xk = f (xk — 1, uk) + wkzk = h (xk) + vk { displaystyle { begin {align} mathbf {x} _ {k} = f ( mathbf {x} _ {k-1}, mathbf {u} _ {k}) + mathbf {w} _ {k} \ mathbf {z} _ {k} = h ( mathbf {x} _ {k}) + mathbf {v} _ {k} end {align}}}
Функция f может выполнить расчет прогнозируемого состояния на основе предыдущей оценки, аналогично функция h может использоваться для вычисления прогнозируемого измерения на основе прогнозируемого состояния. Однако f и h не могут быть применены к ковариации напрямую. Вместо этого вычисляется матрица частных производных (якобиан ).
На каждом временном шаге якобианвается с текущими прогнозируемыми состояниями. Эти люди мать в Нагорстве фильтра Калмана. Этот процесс проходит через текущую оценку.
Фильтр Калмана без запаха
При моделях перехода состояний и наблюдений, то есть функции прогнозирования и обновления f { displaystyle f}

Сигма-точки
Для случайного вектора x = (x 1,…, x L) { displaystyle mathbf {x} = (x_ {1}, dots, x_ {L})}
- {s 0,…, s N} = {(s 0, 1 s 0, 2… s 0, L),…, (SN, 1 s N, 2… s N, L)} { displaystyle { mathbf {s} _ {0}, dots, mathbf {s} _ {N} } = { bigl {} { begin {pmatrix} s_ {0,1} s_ {0,2} ldots s_ {0, L} end {pmatrix}}, dots, { begin {pmatrix} s_ {N, 1} s_ {N, 2} ldots s_ {N, L} end {pmatrix}} { bigr }}}
с атрибутами
- весами первого порядка W 0 a,…, WN a { displaystyle W_ {0} ^ {a}, dots, W_ {N} ^ {a}}
, которые удовлетворяют
- ∑ j = 0 NW ja = 1 { displaystyle sum _ {j = 0} ^ {N} W_ {j} ^ {a} = 1}
- для всех i = 1,…, L { displaystyle i = 1, точек, L}
: E [xi] = ∑ j = 0 NW jasj, i { displaystyle E [x_ {i}] = sum _ {j = 0} ^ {N} W_ {j} ^ {a } s_ {j, i}}
- веса второго порядка W 0 c,…, WN c { displaystyle W_ {0} ^ {c}, dots, W_ {N} ^ {c}}
, которые удовлетворяют
- ∑ j = 0 NW jc = 1 { displayst yle sum _ {j = 0} ^ {N} W_ {j} ^ {c} = 1}
- для всех пар (i, l) ∈ {1,…, L} 2: E [xixl] = ∑ j = 0 NW jcsj, isj, l { displaystyle (i, l) in {1, dots, L } ^ {2}: E [x_ {i} x_ {l}] = sum _ {j = 0} ^ { N} W_ {j} ^ {c} s_ {j, i} s_ {j, l}}
.
Простой выбор сигма-точек и весов для xk — 1 ∣ k — 1 { displaystyle mathbf { x} _ {k-1 mid k-1}}
- s 0 = x ^ k — 1 ∣ k — 1-1 < W 0 a = W 0 c < 1 s j = x ^ k − 1 ∣ k − 1 + L 1 − W 0 A j, j = 1, …, L s L + j = x ^ k − 1 ∣ k − 1 − L 1 − W 0 A j, j = 1, …, L W j a = W j c = 1 − W 0 2 L, j = 1, …, 2 L {displaystyle {begin{aligned}mathbf {s} _{0}={hat {mathbf {x} }}_{k-1mid k-1}\-1
где x ^ k — 1 ∣ k — 1 { displaystyle { hat { mathbf {x}}} _ {k-1 mid k-1}}






Другой популярной параметризацией (которая обобщает вышеизложенное) является
- s 0 = x ^ k — 1 ∣ k — 1 W 0 a = α 2 κ — L α 2 κ W 0 c = W 0 a + 1 — α 2 + β sj = x ^ k — 1 ∣ k — 1 + α κ A j, j = 1,…, L s L + j = x ^ k — 1 ∣ k — 1 — α κ A j, j = 1,…, LW ja = W jc = 1 2 α 2 κ, j = 1,…, 2 L. { displaystyle { begin {align} mathbf {s} _ {0} = { hat { mathbf {x}}} _ {k-1 mid k-1} \ W_ {0} ^ {a} = { frac { alpha ^ {2} kappa -L} { alpha ^ {2} kappa}} \ W_ {0} ^ {c} = W_ {0} ^ {a} + 1- alpha ^ {2} + beta \ mathbf {s} _ {j} = { hat { mathbf {x}}} _ {k-1 mid k-1} + alpha { sqrt { kappa}} mathbf {A} _ {j}, quad j = 1, точки, L \ mathbf {s} _ {L + j} = { hat { mathbf {x}}} _ {k-1 mid k-1} — alpha { sqrt { каппа}} mathbf {A} _ {j}, quad j = 1, dots, L \ W_ {j} ^ {a} = W_ {j} ^ {c} = { frac {1} {2 alpha ^ {2} kappa}}, quad j = 1, dots, 2L. end {выровнено}}}
α { displaystyle alpha}



Соответствующие значения зависят от решаемой проблемы, но типичная рекомендация — α = 10 — 3 { Displaystyle альфа = 10 ^ {- 3}}






Predict
Как и в случае с EKF, прогноз UKF может самостоятельно от обновления UKF, в объединении с линейным (или действительно EKF) обновлением, или наоборот.
Учитывая оценки среднего и ковариации, x ^ k — 1 ∣ k — 1 { displaystyle { hat { mathbf {x}}} _ {k-1 mid k-1}}


- xj = f (sj) j = 0,…, 2 L { displaystyle mathbf {x} _ {j} = f left ( mathbf {s} _ {j} right) quad j = 0, dots, 2L}
.
Распространенные сигма-взвешивания точки применяются для получения прогнозируемого среднего значения и ковариации.
- x ^ k ∣ k — 1 = ∑ j = 0 2 LW jaxj P k ∣ k — 1 = ∑ j = 0 2 LW jc (xj — x ^ k ∣ k — 1) (xj — x ^ k ∣ к — 1) T + Q К { Displaystyle { begin {align} { hat { mathbf {x}}} _ {k mid k-1} = sum _ {j = 0} ^ {2L } W_ {j} ^ {a} mathbf {x} _ {j} \ mathbf {P} _ {k mid k-1} = sum _ {j = 0} ^ {2L} W_ { j} ^ {c} left ( mathbf {x} _ {j} — { hat { mathbf {x}}} _ {k mid k-1} right) left ( mathbf {x} _ {j} — { hat { mathbf {x}}} _ {k mid k-1} right) ^ { textf {T}} + mathbf {Q} _ {k} end {выровнено }}}
где W ja { displaystyle W_ {j} ^ {a}}



Обновление
Данные прогнозов x ^ k ∣ k — 1 { displaystyle { hat { mathbf {x}}} _ {k mid k-1}}






- zj = h (sj), j = 0, 1,…, 2 L { displaystyle mathbf {z} _ {j} = h ( mathbf {s} _ {j}), , , j = 0,1, dots, 2L}
.
Затем вычисляются эмпирическое среднее значение и ковариация преобразованных точек.
- z ^ = ∑ j знак равно 0 2 LW jazj S ^ k = ∑ j = 0 2 LW jc (zj — z ^) (zj — z ^) T + R k { displaystyle { begin {align} { hat { mathbf {z}}} = sum _ {j = 0} ^ {2L} W_ {j} ^ {a} mathbf {z} _ {j} \ [6pt] { hat { mathbf {S}}} _ {k} = sum _ {j = 0} ^ {2L} W_ {j} ^ {c} ( mathbf {z} _ {j} — { hat { mathbf {z}}}) ( mathbf {z} _ {j} — { hat { mathbf {z}}}) ^ { textf {T}} + mathbf {R} _ {k} end {выровненный}}}
где R k { displaystyle mathbf {R} _ {k}}

- C sz = ∑ j = 0 2 LW jc (sj — x ^ k | k — 1) (zj — z ^) T { displaystyle { begin {align} mathbf {C_ {sz}} = sum _ {j = 0} ^ {2L} W_ {j} ^ {c} ( mathbf {s} _ {j} — { hat { mathbf {x}} } _ {k | k-1}) ( mathbf {z} _ {j} — { hat { mathbf {z}}}) ^ { textf {T}} end {align}}}
где sj { displaystyle mathbf {s} _ {j}}


Коэффициент Калмана составляет
- K k = C sz S ^ k — 1. { displaystyle { begin {align} mathbf {K} _ {k} = mathbf {C_ {sz}} { hat { mathbf {S}}} _ {k} ^ {- 1}. end {выровнено}}}
Обновленные оценки среднего и ковариации:
- x ^ k ∣ k = x ^ k | К — 1 + К К (Z К — Z ^) П К ∣ К знак равно П К ∣ К — 1 — К К S ^ К К К Т. { displaystyle { begin {align} { hat { mathbf {x}}} _ {k mid k} = { hat { mathbf {x}}} _ {k | k-1} + mathbf {K} _ {k} ( mathbf {z} _ {k} — { hat { mathbf {z}}}) \ mathbf {P} _ {k mid k} = mathbf { P} _ {k mid k-1} — mathbf {K} _ {k} { hat { mathbf {S}}} _ {k} mathbf {K} _ {k} ^ {textf { T}}. End {align}}}
Фильтр Калмана – Бьюси
Фильтр Калмана – Бьюси (названный в честь Ричарда Сноудена Бьюси) — это версия фильтра Калмана с непрерывным временем.
Он основан на модели пространства состояний
- ddtx (t) = F (t) x (t) + B (t) u (t) + w (t) z (t) = H (t) x (т) + v (t) { displaystyle { begin {align} { frac {d} {dt}} mathbf {x} (t) = mathbf {F} (t) mathbf {x} (t) + mathbf {B} (t) mathbf {u} (t) + mathbf {w} (t) \ mathbf {z} (t) = mathbf {H} (t) mathbf {x} (t) + mathbf {v} (t) end {align}}}
где Q (t) { displaystyle mathbf {Q} (t)}



Фильтр состоит из двух дифференциальных уравнений, одного для оценки состояния и одного для ковариации:
- ddtx ^ (t) = F (t) x ^ (t) + B (t) u ( t) + K (t) (z (t) — H (t) x ^ (t)) ddt P (t) = F (t) P (t) + P (t) FT (t) + Q (t) — К (t) р (t) KT (t) { displaystyle { begin {align} { frac {d} {dt}} { hat { mathbf {x}}} (t) = mathbf {F} (t) { hat { mathbf {x}}} (t) + mathbf {B} (t) mathbf {u} (t) + mathbf {K} (t) left ( mathbf {z} (t) — mathbf {H} (t) { hat { mathbf {x}}} (t) right) \ { frac {d} {dt}} mathbf {P } (t) = mathbf {F} (t) mathbf {P} (t) + mathbf {P} (t) mathbf {F} ^ {textf {T}} (t) + mathbf {Q} (t) — mathbf {K} (t) mathbf {R} (t) mathbf {K} ^ {textf {T}} (t) end {align}}}
где коэффициент Калмана определяется выражением
- K (t) = P (t) HT (t) R — 1 (t) { displaystyle mathbf {K} (t) = mathbf {P} (t) mathbf {H} ^ {textf {T}} (t) mathbf {R} ^ {- 1} (t)}
Обратите внимание, что в этом выражении для K (t) { displaystyle mathbf { K} (t)}


Различия между этапами прогнозирования и обновления фильтрации Калмана в дискретном времени не существует в непрерывном времени.
Второе дифференциальное уравнение для ковариации является примером уравнения Риккати. Нелинейные обобщения фильтров Калмана – Бьюси включают расширенный фильтр Калмана с непрерывным временем и кубический фильтр Калмана.
Гибридный фильтр Калмана
Большинство физических систем представлены в виде моделей с непрерывным временем, в то время как измерения с дискретным временем часто проводятся взяты для оценки состояния с помощью цифрового процессора. Следовательно, модель системы и модель измерения задаются следующим образом:
- x ˙ (t) = F (t) x (t) + B (t) u (t) + w (t), w (t) ∼ N ( 0, Q (t)) zk = ЧАС kxk + vk, vk ∼ N (0, R k) { displaystyle { begin {align} { dot { mathbf {x}}} (t) = mathbf {F} (t) mathbf {x} (t) + mathbf {B} (t) mathbf {u} (t) + mathbf {w} (t), mathbf {w} (t) sim N left ( mathbf {0}, mathbf {Q} (t) right) \ mathbf {z} _ {k} = mathbf {H} _ {k} mathbf {x } _ {k} + mathbf {v} _ {k}, mathbf {v} _ {k} sim N ( mathbf {0}, mathbf {R} _ {k}) end { выровнено}}}
где
- xk = x (tk) { displaystyle mathbf {x} _ {k} = mathbf {x} (t_ {k})}
.
Инициализировать
- x ^ 0 ∣ 0 знак равно Е [Икс (T 0)], П 0 ∣ 0 = Вар [Икс (T 0)] { Displaystyle { Hat { mathbf {x}}} _ {0 mid 0} = E left [ mathbf {x} (t_ {0}) right], mathbf {P} _ {0 mid 0} = operatorname {Var} left [ mathbf {x} left (t_ { 0} right) right]}
Прогноз
- x ^ ˙ (t) = F (t) x ^ (t) + B (t) u (t), где x ^ (tk — 1) = x ^ k — 1 ∣ k — 1 ⇒ x ^ k ∣ k — 1 = x ^ (tk) P ˙ (t) = F (t) P (t) + P (t) F (t) T + Q (t), причем P (tk — 1) = P k — 1 ∣ к — 1 ⇒ п К ∣ К — 1 знак равно п (тк) { Displaystyle { begin {выровнено} { точка { шляпа { mathbf {x}}}} (т) = mathbf {F} ( t) { hat { mathbf {x}}} (t) + mathbf {B} (t) mathbf {u} (t) { text {, с}} { hat { mathbf {x} }} left (t_ {k-1} right) = { hat { mathbf {x}}} _ {k-1 mid k-1} \ Rightarrow { hat { mathbf {x} }} _ {k mid k-1} = { hat { mathbf {x}}} left (t_ {k} right) \ { dot { mathbf {P}}} (t) = mathbf {F} (t) mathbf {P} (t) + mathbf {P} (t) mathbf {F} (t) ^ {textf {T}} + mathbf {Q} ( t) { text {, with}} mathbf {P} left (t_ {k-1} right) = mathbf {P} _ {k-1 mid k-1} \ Rightarrow mathbf {P} _ {k mid k-1} = mathbf {P} left (t_ {k} right) end {align}}}
Уравнения прогнозирования получены из уравнений непрерывного времени Фильтр Ка лмана без обновления по результатам измерений, т. Е. K (t) = 0 { displaystyle mathbf {K} (t) = 0}
В случае линейно-инвариантных во времени систем, динамика непрерывного времени может быть точно дискретизирована в систему с дискретным временем, используя матричные экспоненты.
Обновить
- К k = P k ∣ k — 1 H k T (H k P k ∣ k — 1 H k T + R k) — 1 x ^ k ∣ k = x ^ k ∣ k — 1 + K k ( ZK — ЧАС КХ ^ К ∣ К — 1) П К ∣ К знак равно (I — К К К ЧАС) П К ∣ К — 1 { Displaystyle { begin {align} mathbf {K} _ {k} = mathbf {P} _ {k mid k-1} mathbf {H} _ {k} ^ {textf {T}} left ( mathbf {H} _ {k} mathbf {P} _ { k mid k-1} mathbf {H} _ {k} ^ {textf {T}} + mathbf {R} _ {k} right) ^ {- 1} \ { hat { mathbf {x}}} _ {k mid k} = { hat { mathbf {x}}} _ {k mid k-1} + mathbf {K} _ {k} left ( mathbf { z} _ {k} — mathbf {H} _ {k} { hat { mathbf {x}}} _ {k mid k-1} right) \ mathbf {P} _ {k mid k} = left ( mathbf {I} — mathbf {K} _ {k} mathbf {H} _ {k} right) mathbf {P} _ {k mid k-1} end {align}}}
У равнения обновления идентичны уравнениям дискретного фильтра Калмана.
Варианты восстановления разреженных сигналов
Традиционный фильтр Калмана также использовался для восстановления, возможно, динамических сигналов из зашумленных наблюдений. В недавних работах используются понятия теории сжатого зондирования / выборки, такие как свойство ограниченной изометрии и соответствующие аргументы вероятностного восстановления, для последовательной оценки разреженного состояния в изначально низкоразмерных системах.
Приложения
См. Также
Ссылки
Дополнительная литература
Внешние ссылки
- Новый подход к Проблемы линейной фильтрации и прогнозирования, Р.Э. Калман, 1960
- Калман и байесовские фильтры в Python. Учебник по фильтрации Калмана с открытым исходным кодом.
- Как работает фильтр Калмана, на рисунках. Освещает фильтр Калмана изображениями и цветами
- Фильтр Калмана – Бьюси, производный от фильтра Калмана – Бьюси
- Видео-лекция Массачусетского технологического института по фильтру Калмана на YouTube
- фильтр Калмана в Javascript. Библиотека фильтров Калмана с открытым исходным кодом для node.js и веб-браузера.
- Введение в фильтр Калмана, курс SIGGRAPH 2001, веб-страница Грега Велча и Гэри Бишопа
- Фильтр Калмана со множеством ссылок
- «Фильтры Калмана, используемые в погодных моделях» (PDF). Новости СИАМ. 36 (8). Октябрь 2003 г. Архивировано из оригинального (PDF) 17 мая 2011 г. Проверено 27 января 2007 г.
- Haseltine, Eric L.; Роулингс, Джеймс Б. (2005). «Критическая оценка расширенной фильтрации Калмана и оценки движущегося горизонта». Промышленные и инженерные химические исследования. 44 (8): 2451. doi : 10.1021 / ie034308l.
- Библиотека подпрограмм оценки Джеральда Дж. Бирмана : соответствует коду в исследовательской монографии » Методы факторизации для дискретного последовательного оценивания », первоначально опубликованные Academic Press в 1977 году. Переиздано Dover.
- Matlab Toolbox, реализующий части библиотеки подпрограмм оценки Джеральда Дж. Бирмана : факторизация UD / UDU ‘и LD / LDL’ с соответствующими обновления времени и измерений, составляющие фильтр Калмана.
- Набор инструментов Matlab для фильтрации Калмана, применяемый для одновременной локализации и отображения : Транспортное средство, движущееся в 1D, 2D и 3D
- Фильтр Калмана в воспроизведении гильбертовых пространств ядра Подробное введение.
- Код Matlab для оценки модели процентных ставок Кокса – Ингерсолла – Росса с фильтром Калмана : Соответствует статье «Оценка и тестирование экспоненциально-аффинных моделей временной структуры с помощью фильтра Калмана», опубликованной Review of Quantitative Finance и бухгалтерский учет в 1999 году.
- Онлайн-демонстрация фильтра Калмана. Демонстрация фильтра Калмана (и других методов ассимиляции данных) с использованием двойных экспериментов
- Ботелла, Гильермо; Мартин Х., Хосе Антонио; Сантос, Матильда; Мейер-Бейз, Уве (2011). «Мультимодальная встроенная сенсорная система на основе ПЛИС, интегрирующая зрение низкого и среднего уровня». Датчики. 11 (12): 1251–1259. doi : 10.3390 / s110808164. PMC 3231703. PMID 22164069.
- Примеры и инструкции по использованию фильтров Калмана с MATLAB Учебное пособие по фильтрации и оценке
- Объяснение фильтрации (оценки) за один час, десять минут, один Минуты и одно предложение Ю-Чи Хо












![x[n]=sum _{{i=0}}^{N}a_{i}w[n-i].](https://wikimedia.org/api/rest_v1/media/math/render/svg/b52e807887e91ea452fcc1d5c0b8037593336d05)
![{displaystyle a_{i}=arg min Eleft[e^{2}[n]right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c1479360ebceaf703b055388dcd8a3f1d251ca6)
![{displaystyle {begin{aligned}Eleft[e^{2}[n]right]&=Eleft[(x[n]-s[n])^{2}right]\&=Eleft[x^{2}[n]right]+Eleft[s^{2}[n]right]-2E[x[n]s[n]]\&=Eleft[left(sum _{i=0}^{N}a_{i}w[n-i]right)^{2}right]+Eleft[s^{2}[n]right]-2Eleft[sum _{i=0}^{N}a_{i}w[n-i]s[n]right]end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93fade3732a89c3c06d14e7532d4e5ac8e8ba5e0)
![{displaystyle {begin{aligned}{frac {partial }{partial a_{i}}}Eleft[e^{2}[n]right]&={frac {partial }{partial a_{i}}}left{Eleft[left(sum _{j=0}^{N}a_{j}w[n-j]right)^{2}right]+Eleft[s^{2}[n]right]-2Eleft[sum _{j=0}^{N}a_{j}w[n-j]s[n]right]right}\&=2Eleft[left(sum _{j=0}^{N}a_{j}w[n-j]right)w[n-i]right]-2E[w[n-i]s[n]]\&=2left(sum _{j=0}^{N}E[w[n-j]w[n-i]]a_{j}right)-2E[w[n-i]s[n]]end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32d0c093c419d914a8d0b81eb7b53aec3d2e77bf)
![{displaystyle {begin{aligned}R_{w}[m]&=E{w[n]w[n+m]}\R_{ws}[m]&=E{w[n]s[n+m]}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/013fa6d6fbd4e75c4c4ffefdc98dde2ba69d0aeb)
![{displaystyle {frac {partial }{partial a_{i}}}Eleft[e^{2}[n]right]=2left(sum _{j=0}^{N}R_{w}[j-i]a_{j}right)-2R_{ws}[i]qquad i=0,cdots ,N.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b838dec6ea00072ce0d8b4ec7e69c4c24768811)
![{displaystyle sum _{j=0}^{N}R_{w}[j-i]a_{j}=R_{ws}[i]qquad i=0,cdots ,N.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a9984c26d8ebeb301f22cbeeaa797ee44ef7632)
![{displaystyle underbrace {begin{bmatrix}R_{w}[0]&R_{w}[1]&cdots &R_{w}[N]\R_{w}[1]&R_{w}[0]&cdots &R_{w}[N-1]\vdots &vdots &ddots &vdots \R_{w}[N]&R_{w}[N-1]&cdots &R_{w}[0]end{bmatrix}} _{mathbf {T} }underbrace {begin{bmatrix}a_{0}\a_{1}\vdots \a_{N}end{bmatrix}} _{mathbf {a} }=underbrace {begin{bmatrix}R_{ws}[0]\R_{ws}[1]\vdots \R_{ws}[N]end{bmatrix}} _{mathbf {v} }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/22ca4ea294dd47b8d634cb78e5be93073547626f)
![{displaystyle R_{sw}[k]=R_{ws}[-k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/185aafdce950ee0f36925021ae3c93f5c5023d5b)
![{displaystyle sum _{j=0}^{N}R_{w}[j-i]a_{j}^{*}=R_{ws}[i]qquad i=0,cdots ,N.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a382076f2533f0688f1875d8f3a133be3d531f1)
![{displaystyle underbrace {begin{bmatrix}R_{w}[0]&R_{w}^{*}[1]&cdots &R_{w}^{*}[N-1]&R_{w}^{*}[N]\R_{w}[1]&R_{w}[0]&cdots &R_{w}^{*}[N-2]&R_{w}^{*}[N-1]\vdots &vdots &ddots &vdots &vdots \R_{w}[N-1]&R_{w}[N-2]&cdots &R_{w}[0]&R_{w}^{*}[1]\R_{w}[N]&R_{w}[N-1]&cdots &R_{w}[1]&R_{w}[0]end{bmatrix}} _{mathbf {T} }underbrace {begin{bmatrix}a_{0}^{*}\a_{1}^{*}\vdots \a_{N-1}^{*}\a_{N}^{*}end{bmatrix}} _{mathbf {a^{*}} }=underbrace {begin{bmatrix}R_{ws}[0]\R_{ws}[1]\vdots \R_{ws}[N-1]\R_{ws}[N]end{bmatrix}} _{mathbf {v} }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5189a3cd5eb8558934169b1ed63016fa0f5b14a7)
![{displaystyle {begin{aligned}R_{w}[-k]&=R_{w}^{*}[k]\R_{sw}[k]&=R_{ws}^{*}[-k]end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b747272d7edd8e56a4fa0ae17bc829245cefd5c2)



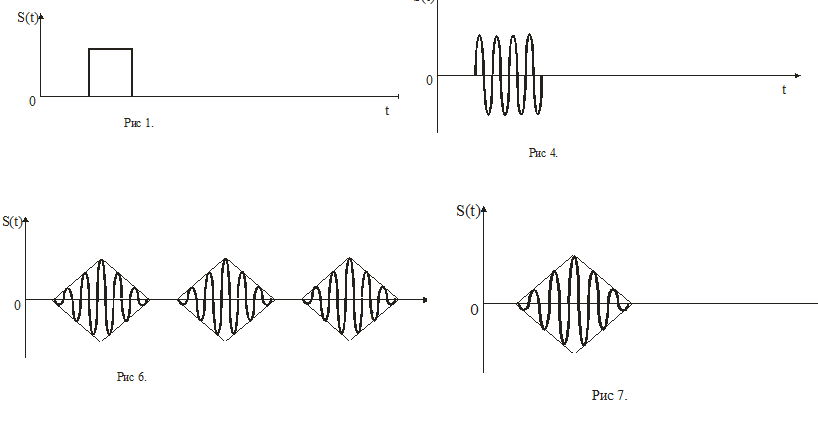
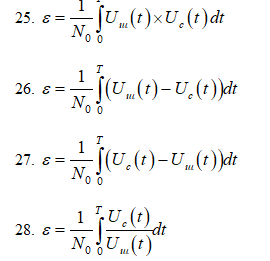
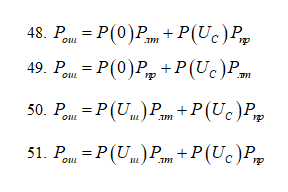
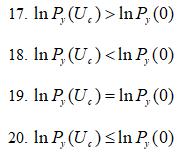


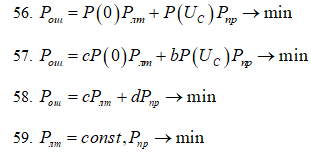

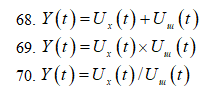
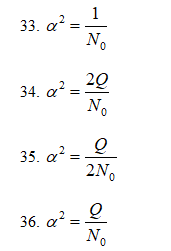



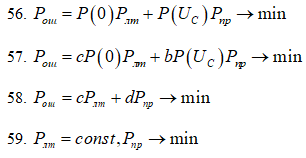



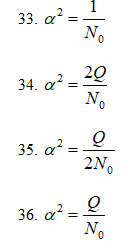
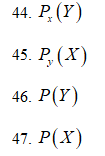
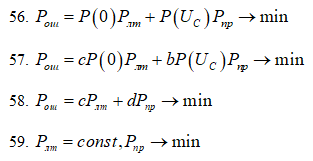
![{ displaystyle { begin {выровнено} { frac { partial} { partial a_ {i}}} E left [e ^ {2} [n] right] = { frac { partial} { partial a_ {i}}} left {E left [ left ( sum _ {i = 0} ^ {N} a_ {i} w [ni] right) ^ {2} right] + E left [s ^ {2} [n] right] -2E left [ sum _ {i = 0} ^ {N } a_ {i} w [ni] s [n] right] right } \ = 2E left [ left ( sum _ {j = 0} ^ {N} a_ {j} w [nj ] right) w [ni] right] -2E [w [ni] s [n]] \ = 2 left ( sum _ {j = 0} ^ {N} E [w [nj] w [ni]] a_ {j} right) -2E [w [ni] s [n]] end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d6d976673c02272293e722d361805d16cc612ee)
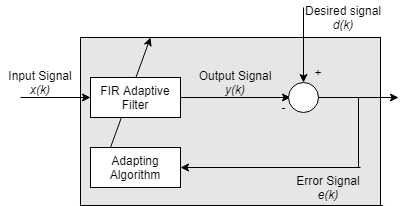
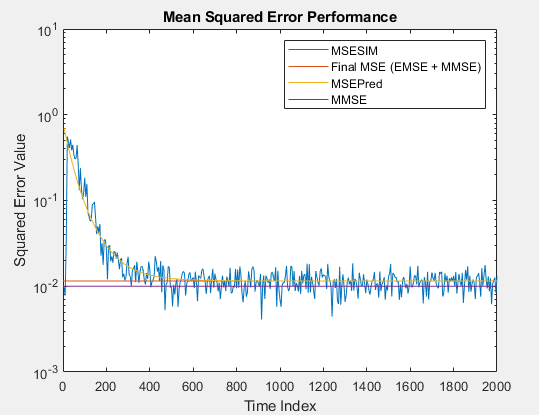
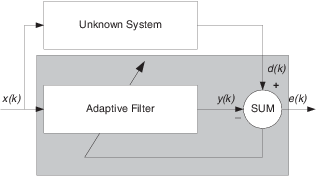
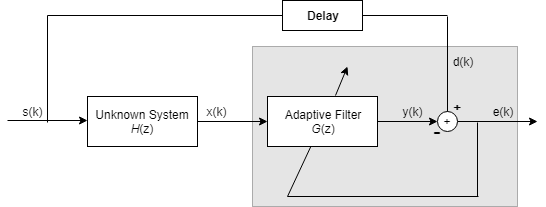
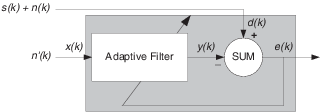
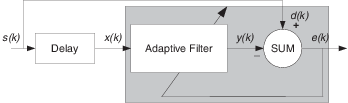











![mathbf {x} (n) = left [x (n), x (n-1), dots, x (n-p + 1) right] ^ T](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a9144713e4baa446220f201d7892010076e6e9e)
![mathbf {h} (n) = left [h_0 (n), h_1 (n), dots, h_ {p-1} (n) right] ^ T, quad mathbf {h} (n) in mathbb {C} ^ p](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c1220711a49789eabbf8ad814d71e7c3ea8155c)





























![0 < mu < frac {2} { mathrm {tr} left [{ mathbf {R}} right]},](https://wikimedia.org/api/rest_v1/media/math/render/svg/102db2818ad8d2df326f4197ed70b89401e1e47f)
![mathrm {tr} [{ mathbf {R}}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/54b47cb3e505af7348e68f1ca37094f8d4686215)



![mu_ {opt} = frac {E left [ left | y (n) - hat {y} (n) right | ^ 2 right]} {E left [| e (n) | ^ 2 right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/529e6acfc5f4e29be90cbf88167fad783860dce6)

![E left [ Lambda (n + 1) right] = E left [ left | hat { mathbf {h}} (n) + frac { mu , e ^ {*} (n) mathbf {x} (n)} { mathbf {x} ^ H (n) mathbf {x} (n)} - mathbf {h} (n) right | ^ 2 right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/18705eafd7fc2a82e519f9cefd9caa5ac6219c73)
![E left [ Lambda (n + 1) right] = E left [ left | hat { mathbf {h}} (n) + frac { mu , left (v ^ * (n) + y ^ * (n) - hat {y} ^ * (n) right) mathbf {x} (n)} { mathbf {x} ^ H (n) mathbf {x} (n)} - mathbf {h} (n) right | ^ 2 right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/a548832404c6ae83e0cf2ca977652c6f942a8060)

![E left [ Lambda (n + 1) right] = E left [ left | mathbf { delta} (n) - frac { mu , left (v (n) + r (n) right) mathbf {x} (n)} { mathbf {x} ^ H ( n) mathbf {x} (n)} right | ^ 2 right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/6401070ffb4f3da143810178301b7c1b271f1927)
![E left [ Lambda (n + 1) right] = E left [ left ( mathbf { delta} (n) - frac { mu , left (v (n) + r (n) ) right) mathbf {x} (n)} { mathbf {x} ^ H (n) mathbf {x} (n)} right) ^ H left ( mathbf { delta} (n) - frac { mu , left (v (n) + r (n) right) mathbf {x} (n)} { mathbf {x} ^ H (n) mathbf {x} (n )} верно-верно]](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a54266b1c94d17951480c419fc4352a75602f99)
![{ Displaystyle E left [ Lambda (n + 1) right] = Lambda (n) + E left [ left ({ frac { mu , left (v (n) + r (n) ) right) mathbf {x} (n)} { mathbf {x} ^ {H} (n) mathbf {x} (n)}} right) ^ {H} left ({ frac { mu , left (v (n) + r (n) right) mathbf {x} (n)} { mathbf {x} ^ {H} (n) mathbf {x} (n)} } right) right] -2E left [{ frac { mu | r (n) | ^ {2}} { mathbf {x} ^ {H} (n) mathbf {x} (n) }}верно]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/baf215570166652b34f43718c2c15de196336a7f)
![E left [ Lambda (n + 1) right] = Lambda (n) + frac { mu ^ 2 E left [| e (n) | ^ 2 right]} { mathbf {x} ^ H (n) mathbf {x} (n)} - frac {2 mu E left [| r (n) | ^ 2 right]} { mathbf {x} ^ H (n) mathbf {x} (n)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f15422607283d5574f28261726f3b68b69fb2fd7)
![frac {dE left [ Lambda (n + 1) right]} {d mu} = 0](https://wikimedia.org/api/rest_v1/media/math/render/svg/0bfdd63603bd46d57b17a745a4951fc35d4d4a9f)
![2 mu E left [| e (n) | ^ 2 right] - 2 E left [| r (n) | ^ 2 right] = 0](https://wikimedia.org/api/rest_v1/media/math/render/svg/8cd365f334fb1d99808f740d1255b8b893d7eb44)
![mu = frac {E left [| r (n) | ^ 2 right]} {E left [| e (n) | ^ 2 right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d03f34c36b43063aa4a98659f6c1fa9e8a3c9f7)


 .
.![{displaystyle {begin{aligned}operatorname {E} [mathbf {x} _{k}-{hat {mathbf {x} }}_{kmid k}]=operatorname {E} [mathbf {x} _{k}-{hat {mathbf {x} }}_{kmid k-1}]=0\operatorname {E} [{tilde {mathbf {y} }}_{k}]=0end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b8f5d60c0c6af2a77e632b6b4140752357d1d908)



![{displaystyle {begin{aligned}mathbf {F} ={begin{bmatrix}1Delta t\01end{bmatrix}}\[4pt]mathbf {G} ={begin{bmatrix}{frac {1}{2}}{Delta t}^{2}\[6pt]Delta tend{bmatrix}}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/03f9aa60ead12f434f4197b8c91ddad8c1b08ac6)

![{displaystyle {begin{aligned}mathbf {w} _{k}sim N(0,mathbf {Q})\mathbf {Q} =mathbf {G} mathbf {G} ^{textsf {T}}sigma _{a}^{2}={begin{bmatrix}{frac {1}{4}}{Delta t}^{4}{frac {1}{2}}{Delta t}^{3}\[6pt]{frac {1}{2}}{Delta t}^{3}{Delta t}^{2}end{bmatrix}}sigma _{a}^{2}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ec09cb336ca77b3ef6203ebc27d13a302cf62cc)



![{displaystyle mathbf {R} =mathrm {E} left[mathbf {v} _{k}mathbf {v} _{k}^{textsf {T}}right]={begin{bmatrix}sigma _{z}^{2}end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dbbc9b31d008d00147cf59b62a0a92d78297ca0b)



![{displaystyle {hat {mathbf {x} }}_{kmid k}=mathbf {F} _{k}{hat {mathbf {x} }}_{k-1mid k-1}+mathbf {K} _{k}[mathbf {z} _{k}-mathbf {H} _{k}mathbf {F} _{k}{hat {mathbf {x} }}_{k-1mid k-1}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0fcfb5a306bbf523000da1394518cf482488fd1d)




![{displaystyle {hat {mathbf {x} }}_{k}=mathbf {F} {hat {mathbf {x} }}_{k-1}+mathbf {K} _{infty }[mathbf {z} _{k}-mathbf {H} mathbf {F} {hat {mathbf {x} }}_{k-1}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/76b977e658b713bf9847f509957c98319d73cacb)



![{displaystyle mathbf {P} _{kmid k}=operatorname {cov} left[mathbf {x} _{k}-left({hat {mathbf {x} }}_{kmid k-1}+mathbf {K} _{k}{tilde {mathbf {y} }}_{k}right)right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b31ed7985490d3d6803ac08a7965ad1b250c4554)

![{displaystyle mathbf {P} _{kmid k}=operatorname {cov} left(mathbf {x} _{k}-left[{hat {mathbf {x} }}_{kmid k-1}+mathbf {K} _{k}left(mathbf {z} _{k}-mathbf {H} _{k}{hat {mathbf {x} }}_{kmid k-1}right)right]right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3fc500651c69cafbe9f07a93541cb3166d787126)
![{displaystyle mathbf {P} _{kmid k}=operatorname {cov} left(mathbf {x} _{k}-left[{hat {mathbf {x} }}_{kmid k-1}+mathbf {K} _{k}left(mathbf {H} _{k}mathbf {x} _{k}+mathbf {v} _{k}-mathbf {H} _{k}{hat {mathbf {x} }}_{kmid k-1}right)right]right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f9076bf807d7ed72fbd6246635cf2b7da91ee7c)
![{displaystyle mathbf {P} _{kmid k}=operatorname {cov} left[left(mathbf {I} -mathbf {K} _{k}mathbf {H} _{k}right)left(mathbf {x} _{k}-{hat {mathbf {x} }}_{kmid k-1}right)-mathbf {K} _{k}mathbf {v} _{k}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1df4494c4e4fbff6fccdac6368485af96dac9b82)
![{displaystyle mathbf {P} _{kmid k}=operatorname {cov} left[left(mathbf {I} -mathbf {K} _{k}mathbf {H} _{k}right)left(mathbf {x} _{k}-{hat {mathbf {x} }}_{kmid k-1}right)right]+operatorname {cov} left[mathbf {K} _{k}mathbf {v} _{k}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4591ba7c762680cfc0eb090f2c358df87b4d1e4c)



![{displaystyle {begin{aligned}mathbf {P} _{kmid k}=mathbf {P} _{kmid k-1}-mathbf {K} _{k}mathbf {H} _{k}mathbf {P} _{kmid k-1}-mathbf {P} _{kmid k-1}mathbf {H} _{k}^{textsf {T}}mathbf {K} _{k}^{textsf {T}}+mathbf {K} _{k}left(mathbf {H} _{k}mathbf {P} _{kmid k-1}mathbf {H} _{k}^{textsf {T}}+mathbf {R} _{k}right)mathbf {K} _{k}^{textsf {T}}\[6pt]=mathbf {P} _{kmid k-1}-mathbf {K} _{k}mathbf {H} _{k}mathbf {P} _{kmid k-1}-mathbf {P} _{kmid k-1}mathbf {H} _{k}^{textsf {T}}mathbf {K} _{k}^{textsf {T}}+mathbf {K} _{k}mathbf {S} _{k}mathbf {K} _{k}^{textsf {T}}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/be6f9e0fc4bee39b78b2b9d62ecafaf0954143af)
















 из априорного распределения Гаусса p (x 0) = N (Икс ^ 0 ∣ 0, п 0 ∣ 0) { displaystyle p left ( mathbf {x} _ {0} right) = { mathcal {N}} left ({ hat { mathbf { x}}} _ {0 mid 0}, mathbf {P} _ {0 mid 0} right)}
из априорного распределения Гаусса p (x 0) = N (Икс ^ 0 ∣ 0, п 0 ∣ 0) { displaystyle p left ( mathbf {x} _ {0} right) = { mathcal {N}} left ({ hat { mathbf { x}}} _ {0 mid 0}, mathbf {P} _ {0 mid 0} right)} .
. из модели наблюдения p (z 0 ∣ x 0) = N (H 0 x 0, R 0) { displaystyle p left ( mathbf {z} _ {0} mid mathbf {x} _ {0} right) = { mathcal {N}} left ( mathbf {H} _ {0} mathbf {x} _ {0}, mathbf {R} _ {0} right)}
из модели наблюдения p (z 0 ∣ x 0) = N (H 0 x 0, R 0) { displaystyle p left ( mathbf {z} _ {0} mid mathbf {x} _ {0} right) = { mathcal {N}} left ( mathbf {H} _ {0} mathbf {x} _ {0}, mathbf {R} _ {0} right)} .
. , выполните
, выполните


 ,
,






![{displaystyle {begin{aligned}mathbf {M} _{k}=left[mathbf {F} _{k}^{-1}right]^{textsf {T}}mathbf {Y} _{k-1mid k-1}mathbf {F} _{k}^{-1}\mathbf {C} _{k}=mathbf {M} _{k}left[mathbf {M} _{k}+mathbf {Q} _{k}^{-1}right]^{-1}\mathbf {L} _{k}=mathbf {I} -mathbf {C} _{k}\mathbf {Y} _{kmid k-1}=mathbf {L} _{k}mathbf {M} _{k}mathbf {L} _{k}^{textsf {T}}+mathbf {C} _{k}mathbf {Q} _{k}^{-1}mathbf {C} _{k}^{textsf {T}}\{hat {mathbf {y} }}_{kmid k-1}=mathbf {L} _{k}left[mathbf { F} _{k}^{-1}right]^{textsf {T}}{hat {mathbf {y} }}_{k-1mid k-1}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/160c07d9b85fcb57249512dc02c8c657e0bb986c)

![{displaystyle mathbf {P} ^{(i)}=mathbf {P} left[left(mathbf {F} -mathbf {K} mathbf {H} right)^{textsf {T}}right]^{i}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3f062727421b3b0781655e42ca094d1d950fb93)
 и K { displaystyle mathbf {K} }
и K { displaystyle mathbf {K} } — ковариация ошибки прогнозирования и коэффициенты усиления стандартного фильтра Калмана (т. Е. P t ∣ t — 1 { displaystyle mathbf {P} _ {t mid t-1}}
— ковариация ошибки прогнозирования и коэффициенты усиления стандартного фильтра Калмана (т. Е. P t ∣ t — 1 { displaystyle mathbf {P} _ {t mid t-1}} ).
).![{displaystyle mathbf {P} _{i}:=Eleft[left(mathbf {x} _{t-i}-{hat {mathbf {x} }}_{t-imid t}right)^{*}left(mathbf {x} _{t-i}-{hat {mathbf {x} }}_{t-imid t}right)mid z_{1}ldots z_{t}right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8780d91a9b0e63eced8dd27ec2f8ed0b45c1de89)
![{displaystyle mathbf {P} -mathbf {P} _{i}=sum _{j=0}^{i}left[mathbf {P} ^{(j)}mathbf {H} ^{textsf {T}}left(mathbf {H} mathbf {P} mathbf {H} ^{textsf {T}}+mathbf {R} right)^{-1}mathbf {H} left(mathbf {P} ^{(i)}right)^{textsf {T}}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b0f8a12ef0ba8f26d287adc97353160f6cb9af36)










 , которые удовлетворяют
, которые удовлетворяют
 : E [xi] = ∑ j = 0 NW jasj, i { displaystyle E [x_ {i}] = sum _ {j = 0} ^ {N} W_ {j} ^ {a } s_ {j, i}}
: E [xi] = ∑ j = 0 NW jasj, i { displaystyle E [x_ {i}] = sum _ {j = 0} ^ {N} W_ {j} ^ {a } s_ {j, i}}![{displaystyle E[x_{i}]=sum _{j=0}^{N}W_{j}^{a}s_{j,i}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/675007e4cd61311f7ca86cfa1e7182c2a18d2fa1)
 , которые удовлетворяют
, которые удовлетворяют
![{displaystyle (i,l)in {1,dots,L}^{2}:E[x_{i}x_{l}]=sum _{j=0}^{N}W_{j}^{c}s_{j,i}s_{j,l}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4568b4d145d78fcd8e7e109df907af1021ef13cd) .
.

 .
.
 .
.![{displaystyle {begin{aligned}{hat {mathbf {z} }}=sum _{j=0}^{2L}W_{j}^{a}mathbf {z} _{j}\[6pt]{hat {mathbf {S} }}_{k}=sum _{j=0}^{2L}W_{j}^{c}(mathbf {z} _{j}-{hat {mathbf {z} }})(mathbf {z} _{j}-{hat {mathbf {z} }})^{textsf {T}}+mathbf {R} _{k}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4cbfafad41274db6e909b41006299ad5ba6400c)







 .
.![{displaystyle {hat {mathbf {x} }}_{0mid 0}=Eleft[mathbf {x} (t_{0})right],mathbf {P} _{0mid 0}=operatorname {Var} left[mathbf {x} left(t_{0}right)right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/22f8d1d2c5bc4283dd4032d5de0b9dff4da51f0d)

