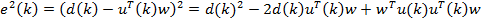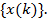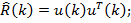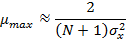ГЛАВА 9
6
4
2
0
|
0 |
0.5 |
1 |
1.5 |
2 |
2.5 |
3 |
3.5 |
4 |
Адаптивные фильтры
При поиске оптимальных алгоритмов обработки сигнала неизбежно приходится опираться на некоторые статистические модели сигналов и шумов. Чаще всего при формировании этих моделей используются концепции линейности, стационарности и нормальности (гауссовости). Однако перечисленные принципы далеко не всегда выполняются на практике, а от адекватности выбранной модели в значительной мере зависит качество приема сигнала. Адаптивные фильтры позволяют системе подстраиваться под статистические параметры входного сигнала, не требуя при этом задания каких-либо моделей.
Появившись в конце 1950-х гг., адаптивные фильтры прошли большой путь, превратившись из экзотической технологии, применявшейся преимущественно в военных целях, в «ширпотреб», без которого сейчас была бы немыслима работа модемов, сотовых телефонов и многого другого.
Существует большое количество адаптивных алгоритмов, различающихся вычислительной сложностью, особенностями поведения, используемыми исходными данными и структурами самих адаптирующихся систем. В данной главе будут рассмотрены лишь несколько основных алгоритмов, но сначала следует остановиться на классификации адаптивных систем.
ЗАМЕЧАНИЕ
К сожалению, число книг на русском языке, посвященных адаптивной фильтрации, крайне ограничено. В списке литературы приведены книги [13] и [14], некоторая информация имеется также в классическом труде по цифровой связи [35]. Однако эти публикации не затрагивают целого ряда важных вопросов. В качестве дополнительных, но, к сожалению, менее доступных источников информации можно рекомендовать замечательную книгу Саймона Хайкина (S. Haykin. Adaptive Filter Theory. Prentice Hall, четыре издания вышли в 1986, 1991, 1996 и 2002 гг.), а также обзорную статью, содержащую сведения о большом числе адаптивных алгоритмов (Glentis G.-O., Berberidis K., Theodoridis S. Efficient Least Squares Adaptive Algorithms for FIR Transversal Filtering // IEEE Signal Processing Magazine, 1999, Vol. 16, No. 4, pp. 13–41).
Основные понятия адаптивной обработки сигналов
Важнейшим признаком классификации является наличие или отсутствие образцового, или опорного сигнала (desired signal, reference signal). При наличии образцового сигнала процесс адаптации называется обучением с учителем (supervised learning). В данном случае адаптивный фильтр стремится сделать свой выходной сигнал максимально близким к образцовому сигналу. О том, что именно подразумевается под близостью сигналов, сказано далее при описании конкретных алгоритмов. Адаптация без использования образцового сигнала называется слепой адаптацией (blind adaptation) или обучением без учителя (unsupervised learning). Разумеется, в этом случае требуется некоторая информация о структуре полезного входного сигнала (например, знание типа и параметров используемой модуляции). Очевидно, что слепая адаптация является более сложной вычислительной задачей, чем адаптация с использованием образцового сигнала.
ЗАМЕЧАНИЕ
У внимательного читателя должен возникнуть вопрос — какой практический смысл могут иметь алгоритмы с использованием образцового сигнала, если при этом выходной сигнал должен быть заранее известен? Однако есть целый ряд практических задач, при решении которых образцовый сигнал оказывается доступен. Подробнее об этом далее в разд. «Применение адаптивных фильтров» этой главы. Забегая вперед, заметим, что в ряде случаев при этом полезным сигналом является не выходной сигнал фильтра, а сигнал ошибки, т. е. разность между образцовым сигналом и выходным сигналом адаптивного фильтра.
Следующим признаком классификации является тип системы, осуществляющей обработку сигнала. Различают линейные и нелинейные адаптивные системы, при этом имеется в виду линейность по отношению не ко входному сигналу, а к параметрам системы, настраиваемым в процессе адаптации.
Наиболее распространены линейные адаптивные системы, в которых обработка сигнала производится нерекурсивным дискретным фильтром. Одним из главных достоинств такого варианта является то, что нерекурсивный фильтр является устойчивым при любых значениях его коэффициентов. Однако следует отметить, что алгоритм адаптации в любом случае вносит в систему обратную связь, вследствие чего адаптивная система в целом может стать неустойчивой.
К нелинейным адаптивным системам относятся, в частности, нейронные сети (neural networks), в определенной степени моделирующие работу нервной системы живых организмов. Рассмотрение таких систем выходит за рамки тематики данной книги. За дополнительной информацией можно обратиться, например, к книгам [43, 44].
Еще одна разновидность нелинейных адаптивных систем — рекурсивные адаптивные фильтры. Однако их создание связано с серьезными проблемами, прежде всего связанными с устойчивостью, поэтому такие фильтры не получили широкого распространения. Некоторые теоретические сведения на эту тему содержатся в [13].

Итак, в данной главе речь пойдет об адаптивных фильтрах, использующих образцовый сигнал. Общая структура такой адаптивной системы показана на рис. 9.1.
Рис. 9.1. Общая структура адаптивного фильтра
Входной дискретный сигнал x(k) обрабатывается дискретным фильтром, в результате чего получается выходной сигнал y(k). Этот выходной сигнал сравнивается с образцовым сигналом d(k), разность между ними образует сигнал ошибки e(k). Задача адаптивного фильтра — минимизировать ошибку воспроизведения образцового сигнала. С этой целью блок адаптации после обработки каждого отсчета анализирует сигнал ошибки и дополнительные данные, поступающие из фильтра, используя результаты этого анализа для подстройки параметров (коэффициентов) фильтра.
В данной главе рассмотрены два адаптивных алгоритма, часто применяемых на практике в различных радиотехнических системах. Это алгоритмы LMS (Least Mean Square, метод наименьшего квадрата, в отечественных источниках иногда используется аббревиатура МНК), и RLS (Recursive Least Squares, рекурсивный метод наименьших квадратов, в отечественных источниках иногда используется аббревиатура РНК).
Вывод формул, описывающих данные алгоритмы, производится на основе уравнений оптимальной фильтрации сигнала. Возможны различные подходы к решению задачи оптимальной фильтрации. Статистический подход в сочетании с методом градиентной оптимизации дает алгоритм LMS, а детерминированный подход приводит к алгоритму RLS.
Далее мы рассмотрим перечисленные подходы к решению задачи оптимальной фильтрации и идеи, лежащие в основе адаптивных алгоритмов.
Все перечисленное относится к алгоритмам, использующим образцовый сигнал (т. е. к обучению с учителем).
Оптимальный фильтр Винера
Говоря об оптимальной фильтрации сигнала, следует помнить, что данная задача становится осмысленной лишь после задания двух вещей — математической модели входного сигнала и оптимизируемого критерия качества. Тогда задача оптимальной фильтрации сводится к математической оптимизационной задаче, которая может быть решена аналитически либо численно.
Итак, пусть входной дискретный случайный сигнал {x(k)} обрабатывается дискретным фильтром порядка N с коэффициентами {wn} , n = 0, 1, …, N (рис. 9.2).

|
594 |
Глава 9 |
|||||||||||||||||||||||||||||||||||||||
|
x(k) |
z–1 |
z–1 |
z–1 |
|||||||||||||||||||||||||||||||||||||
|
w0 |
w1 |
w2 |
wN–1 |
wN |
||||||||||||||||||||||||||||||||||||
|
d(k) |
||||||||||||||||||||||||||||||||||||||||
|
y(k) |
–1 |
e(k) |
||||||||||||||||||||||||||||||||||||||
|
Рис. 9.2. Формирование сигнала ошибки |
||||||||||||||||||||||||||||||||||||||||
|
Выходной сигнал фильтра равен |
||||||||||||||||||||||||||||||||||||||||
|
N |
||||||||||||||||||||||||||||||||||||||||
|
y(k) = ∑wn x(k − n) . |
(9.1) |
n=0
Кроме того, имеется образцовый (также случайный) сигнал d(k). Ошибка воспроизведения образцового сигнала равна
|
N |
|
|
e(k) = d(k) − y(k) = d(k) − ∑wn x(k − n) . |
(9.2) |
n=0
Наша задача — найти такие коэффициенты фильтра {wn} , которые обеспечивают максимальную близость выходного сигнала фильтра к образцовому, т. е. минимизируют ошибку e(k). Но поскольку e(k) также является случайным процессом, в качестве меры ее величины разумно принять средний квадрат. Таким образом, оптимизируемая функция выглядит так:
J ({wn}) = e2 (k) → min .
Для решения поставленной задачи прежде всего перепишем (9.2) в матричном виде. Для этого обозначим вектор-столбец коэффициентов фильтра как w, а векторстолбец содержимого линии задержки фильтра на k-м шаге как x(k):
|
x(k) |
||
|
x(k −1) |
||
|
x(k) = |
. |
|
x(k − N)
С учетом этих обозначений (9.2) принимает следующий вид:
|
e(k) = d (k) − xT (k)w . |
(9.3) |
Квадрат ошибки будет равен
e2 (k) = (d (k) − xT (k)w)2 = d 2 (k) − 2d (k)xT (k)w + (xT (k)w)2 = = d 2 (k) − 2d (k)xT (k)w + wTx(k)xT (k)w.

|
Адаптивные фильтры |
595 |
|||||||||
|
Статистически усредняя это выражение, получаем следующее: |
||||||||||
|
− 2( |
)T w + wT |
w . |
||||||||
|
e2 (k) |
d 2 (k) |
x(k)xT (k) |
(9.4) |
|||||||
|
J (w) = |
= |
d (k)x(k) |
Рассмотрим подробнее входящие в полученную формулу усредненные величины:
d 2 (k) — это средний квадрат образцового сигнала. Он представляет собой отдельное слагаемое, которое не зависит от коэффициентов фильтра и потому может быть отброшено (однако оно влияет на величину среднего квадрата ошибки, получаемую при оптимальных значениях коэффициентов фильтра). Обозначим данную величину как σ2d ;
d (k)x(k) — это вектор-столбец взаимных корреляций между k-м отсчетом образцового сигнала и содержимым линии задержки фильтра на k-м шаге. Будем считать случайные процессы x(k) и d(k) совместно стационарными, тогда вектор взаимных корреляций не зависит от номера шага k. В дальнейших выкладках этот вектор будет обозначен как p:
|
d(k)x(k) |
|||||
|
p = d(k)x(k −1) |
. |
||||
d(k)x(k − N )
x(k)xT (k) — это квадратная матрица размером (N + 1) × (N + 1), являющаяся корреляционной матрицей сигнала (см. разд. «Дискретные случайные процессы» главы 3). Как отмечалось в указанном разделе, для стационарного случайного процесса корреляционная матрица имеет вид матрицы Теплица, вдоль диагоналей которой стоят значения корреляционной функции:
|
Rx (0) |
|||||
|
Rx (1) |
|||||
|
R = |
Rx (2) |
||||
|
R |
x ( |
N |
) |
||
|
Rx (1) |
Rx (2) |
|
Rx (0) |
Rx (1) |
|
Rx (1) |
Rx (0) |
Rx (N −1) Rx (N − 2)
…Rx (N)
…R (N −1)
…Rx(N − 2) ,
|
… |
R |
(0) |
|
|
x |
где Rx ( k) = x(k)x(k − k) — КФ входного сигнала.
С учетом введенных обозначений (9.4) принимает следующий вид:
|
J (w) = σd2 − 2pTw + wT R w . |
(9.5) |
Данное выражение представляет собой квадратичную форму относительно w и потому при невырожденной матрице R имеет единственный минимум, для нахождения которого необходимо приравнять к нулю вектор градиента:
|
J (w) = −2p + 2R w = 0 . |
(9.6) |

Отсюда получаем равенство, называемое уравнением Винера — Хопфа (Wiener — Hopf equation):
Умножив слева обе части равенства на обратную корреляционную матрицу R−1 , получаем искомое решение для оптимальных коэффициентов фильтра:
Такой фильтр называется фильтром Винера (Wiener filter). Подстановка (9.8) в (9.5) дает минимально достижимую дисперсию сигнала ошибки:
|
e2 (k)min = σd2 |
− pT R−1p . |
(9.9) |
|||
|
Несложно также показать, что e(k) y(k) = 0 |
и e(k)x(k) = 0 , т. е. что сигнал ошибки |
для фильтра Винера некоррелирован с входным и выходным сигналами фильтра.
В качестве примера с помощью MATLAB рассчитаем оптимальный фильтр для коррекции искажений, вносимых в передаваемый сигнал x0 (k) каналом связи, имеющим четырехэлементную импульсную характеристику следующего вида:
{hk } = {−2, − 4, 6, 3}, k = 0, 1, 2, 3.
Отсчеты передаваемого сигнала будем считать независимыми случайными величинами с нулевым средним значением и единичной дисперсией. В этом случае корреляционная функция сигнала, прошедшего через канал связи, будет совпадать с корреляционной функцией импульсной характеристики канала:
|
{R( k)} = ∑hk hk − k = {65, 2, –24, –6}, |
k = 0, 1, 2, 3. |
|
|
k |
Корреляционная матрица входного сигнала строится как матрица Теплица на основе данной корреляционной функции:
|
65 |
2 |
−24 −6 0 |
… 0 |
|||||
|
2 |
65 |
2 |
−24 −6 |
… 0 |
||||
|
−24 2 |
65 |
2 |
−24 |
… |
0 |
|||
|
R = |
−6 |
−24 2 |
65 |
2 |
… |
0 |
. |
|
|
0 |
−6 −24 2 |
65 … 0 |
||||||
|
… |
||||||||
|
0 |
0 |
0 |
0 |
0 |
65 |
Восстановление переданного сигнала неизбежно требует внесения некоторой временной задержки, поэтому образцовый сигнал должен представлять собой задержанную копию переданного:
d (k) = x0 (k − k) .

В линии задержки фильтра на k-м шаге находятся отсчеты искаженного сигнала с номерами k, k – 1, k – 2, …, k – N, где N — порядок фильтра. Каждый из этих отсчетов представляет собой линейную комбинацию отсчетов переданного сигнала:
|
∞ |
|
|
x(k − n) = ∑ x0 (m)hk −n−m . |
(9.10) |
m=−∞
Поскольку отсчеты исходного сигнала считаются статистически независимыми, при вычислении n-го элемента вектора p результат усреднения будет отличен от нуля только для одного слагаемого (9.10). Сразу же учтем тот факт, что средний квадрат сигнала x0 (k) равен единице:
∞
pn = x(k − n)d(k) = ∑ x0 (m) hk−n−m x0 (k − k) =
m=−∞
∞
= ∑ hk−n−m x0 (m) x0 (k − k) = h k−m.
m=−∞
Таким образом, вектор p содержит перевернутую импульсную характеристику канала, при необходимости обрезанную или дополненную нулями с одной или двух сторон:
h k
k−1
|
p = |
h1 |
. |
|
h |
||
|
0 |
||
|
0 |
||
|
0 |
||
Далее приводится код MATLAB-программы, реализующей расчет оптимального фильтра. Код составлен так, чтобы можно было легко варьировать вид импульсной характеристики канала и порядок рассчитываемого фильтра (единственное ограничение — предполагается, что импульсная характеристика канала связи целиком укладывается в пределах вектора p):
h = [-2 -4 6 3]; % импульсная характеристика канала связи N = 32; % порядок рассчитываемого фильтра
r = xcorr(h, N); % двусторонняя КФ импульсной характеристики канала r = r(N+1:end); % односторонняя КФ импульсной характеристики канала R = toeplitz(r); % корреляционная матрица искаженного сигнала
p = zeros(N+1, 1);
delay = 16; % задержка фильтрации
p(delay-length(h)+2:delay+1) = fliplr(h); % вектор взаимных корреляций w = Rp; % коэффициенты оптимального фильтра
subplot(1,2,1)

|
598 |
Глава 9 |
|||||||||||||
|
impz(w) |
% график имп. х-ки рассчитанного фильтра |
|||||||||||||
|
subplot(1,2,2) |
||||||||||||||
|
impz(conv(h, w)) % график имп. х-ки скорректированного канала |
||||||||||||||
|
Impulse Response |
Impulse Response |
|||||||||||||
|
0.14 |
1.2 |
|||||||||||||
|
0.12 |
||||||||||||||
|
1 |
||||||||||||||
|
0.1 |
||||||||||||||
|
0.08 |
0.8 |
|||||||||||||
|
0.06 |
0.6 |
|||||||||||||
|
0.04 |
||||||||||||||
|
0.02 |
0.4 |
|||||||||||||
|
0 |
0.2 |
|||||||||||||
|
-0.02 |
||||||||||||||
|
0 |
||||||||||||||
|
-0.04 |
||||||||||||||
|
-0.06 |
-0.2 |
|||||||||||||
|
0 |
5 |
10 |
15 |
20 |
25 |
30 |
0 |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
|
n (samples) |
n (samples) |
Рис. 9.3. Импульсные характеристики корректирующего фильтра (слева) и скорректированного канала связи (справа)
ЗАМЕЧАНИЕ
В приведенном коде следует обратить внимание на использование оператора матричного деления () для решения системы линейных уравнений (9.7).
На рис. 9.3 приведены графики импульсной характеристики корректирующего фильтра и сквозной импульсной характеристики скорректированного канала связи. Видно, что сквозная характеристика близка к единичному импульсу, что говорит о хорошем качестве коррекции. Столь качественная коррекция оказалась возможна потому, что частотная характеристика канала не имеет глубоких провалов (с помощью функции freqz легко убедиться в том, что неравномерность АЧХ канала составляет около 11 дБ).
Градиентный поиск оптимального решения
Один из наиболее распространенных адаптивных алгоритмов основан на поиске минимума целевой функции (9.4) методом наискорейшего спуска. При использовании данного способа оптимизации вектор коэффициентов фильтра зависит от номера итерации k: w(k). На каждой итерации вектор коэффициентов смещается на величину, пропорциональную градиенту целевой функции в данной точке (см. формулу (9.6)):
|
w(k +1) = w(k) − |
μ |
J (w(k)) = w(k) + μp − μR w(k) , |
(9.11) |
2
где μ — положительный коэффициент, называемый размером шага.

Анализ сходимости данного процесса приведен, например, в [13]. Показано, что алгоритм сходится, если
где λmax — максимальное собственное число корреляционной матрицы R. Скорость сходимости при этом зависит от разброса собственных чисел корреляционной матрицы R — чем меньше отношение λmax/λmin, тем быстрее сходится итерационный процесс.
Адаптивный алгоритм LMS
При реализации наискорейшего спуска по формуле (9.11) нужно вычислять значения градиента, а для их расчета, в свою очередь, необходимо знать значения матрицы R и вектора p. На практике могут быть доступны лишь оценки этих параметров, получаемые по входным данным. Простейшими такими оценками являются мгновенные значения корреляционной матрицы и вектора взаимных корреляций, получаемые без какого-либо усреднения:
pˆ (k) = d (k) x(k) .
При использовании данных оценок формула (9.11) принимает следующий вид:
w(k +1) = w(k) + µ d (k)x(k) − µ x(k)xT (k) w(k) =
(9.13)
= w(k) + µ x(k)(d (k) − xT (k) w(k)).
Выражение, стоящее в скобках, согласно (9.3), представляет собой разность между образцовым сигналом и выходным сигналом фильтра на k-м шаге, т. е. ошибку фильтрации e(k). С учетом этого выражение для рекурсивного обновления коэффициентов фильтра оказывается очень простым:
|
w(k +1) = w(k) + μ e(k) x(k) . |
(9.14) |
Алгоритм адаптивной фильтрации, основанный на формуле (9.14), получил название LMS (Least Mean Square, метод наименьшего квадрата). Можно получить ту же формулу и несколько иным образом: использовав вместо градиента статисти-
чески усредненного квадрата ошибки e2 (k) градиент его мгновенного значения e2 (k) .
Несмотря на простоту алгоритма LMS, анализ его поведения оказывается чрезвычайно сложной задачей, для которой не существует точного аналитического решения. Частные результаты, полученные при использовании различных приближений, можно найти в большом количестве книг и статей. Достаточно подробный анализ выполнен в упоминавшейся в начале главы книге С. Хайкина, при этом получены следующие результаты. Алгоритм LMS сходится в среднем (converges in the mean values; это означает, что математические ожидания коэффициентов фильтра при

k → ∞ стремятся к оптимальному решению (9.8)), если коэффициент μ удовлетворяет тому же условию (9.12), которое требуется для сходимости детерминированного градиентного спуска. Однако это еще не гарантирует того, что средние квадраты коэффициентов будут стремиться к фиксированным значениям. Алгоритм
сходится в среднем квадрате (converges in the mean square) в более узком диапазоне значений μ:
|
2 |
2 |
2 |
|||||
|
μmax ≈ |
= |
= |
, |
(9.15) |
|||
|
N |
trace(R) |
2 |
|||||
|
∑λn |
(N +1) σx |
||||||
n=0
где λk — собственные числа корреляционной матрицы R, а σ2x — средний квадрат входного сигнала фильтра.
На формуле (9.15) основан нормированный (normalized) LMS-алгоритм, в котором коэффициент μ на каждом шаге рассчитывается исходя из энергии сигнала, содержащегося в линии задержки:
|
μ(k) = |
μ0 |
, |
(9.16) |
|
T |
|||
|
x x + ε |
где μ0 — нормированное значение μ, лежащее в диапазоне от 0 до 2, а ε — малая
положительная константа, назначение которой — ограничить рост μ при нулевом сигнале на входе фильтра (из формулы (9.16) видно, что максимально возможное значение μ составляет μ0 
Даже если LMS-алгоритм сходится, дисперсии коэффициентов фильтра при k → ∞ не стремятся к нулю — коэффициенты флуктуируют вокруг оптимальных значений. Из-за этого ошибка фильтрации в установившемся режиме оказывается боль-
ше, чем ошибка для винеровского фильтра e2 (k)min (см. ранее формулу (9.9)):
e2 (k)LMS = e2 (k)min + Eex ,
где Eex — средний квадрат избыточной ошибки (excess error) алгоритма LMS. В той же книге С. Хайкина приводится следующая приближенная формула для так называемого коэффициента расстройки (misalignment), равного отношению средних квадратов избыточной и винеровской ошибок:
|
N |
|||||||||||||||||
|
μ∑λn |
|||||||||||||||||
|
2 |
(k) |
2 |
|||||||||||||||
|
Μ = |
e |
LMS |
−1 = |
Eex |
≈ |
n=0 |
= |
μ(N +1)σвх |
= |
μ |
. (9.17) |
||||||
|
N |
2 |
||||||||||||||||
|
e2 (k)min |
e2 (k)min |
μmax − μ |
|||||||||||||||
|
2 − μ∑λn |
2 |
− μ(N +1)σвх |
n=0
Значение коэффициента μ влияет на два главных параметра LMS-фильтра — скорость сходимости и коэффициент расстройки. Чем больше μ, тем быстрее сходится алгоритм, но тем больше, согласно (9.17), становится коэффициент расстройки, и наоборот.
Основным достоинством алгоритма LMS является предельная вычислительная простота — для подстройки коэффициентов фильтра на каждом шаге нужно выполнить N + 1 пар операций «умножение-сложение». Платой за простоту являются медленная сходимость и повышенная (по сравнению с минимально достижимым значением (9.9)) дисперсия ошибки в установившемся режиме.
Существует большое число модификаций алгоритма LMS (см., например, обзорную статью, упомянутую в начале этой главы), направленных на ускорение сходимости либо на уменьшение числа арифметических операций. Ускорение сходимости может быть достигнуто за счет улучшения используемой оценки градиента, а также за счет преобразования входного сигнала с целью сделать его отсчеты некоррелированными. Уменьшение вычислительной сложности может быть достигнуто, в частности, за счет использования в (9.14) не самих сигнала ошибки и содержимого линии задержки фильтра, а лишь их знаков. Это позволяет полностью избавиться от операций умножения при обновлении коэффициентов фильтра. В целом следует отметить, что требования ускорения сходимости и сокращения вычислительных затрат являются взаимоисключающими.
Детерминированная задача оптимальной фильтрации
Рассматривая статистическую задачу оптимизации, мы считали входной сигнал случайным процессом и минимизировали дисперсию ошибки воспроизведения образцового сигнала. Однако возможен и иной подход, не использующий статистические методы.
Итак, пусть обработке подвергается последовательность отсчетов {x(k)}, коэффициенты нерекурсивного фильтра порядка N образуют набор {wn} , n = 0, 1, …, N, а отсчеты образцового сигнала равны {d(k)}. Выходной сигнал фильтра определяется формулой (9.1), а ошибка воспроизведения образцового сигнала — формулой (9.2) или, в векторном виде, (9.3).
Теперь сформулируем детерминированную оптимизационную задачу: мы хотим отыскать такие коэффициенты фильтра {wn} , чтобы суммарная квадратичная ошибка воспроизведения образцового сигнала была минимальной:
|
K −1 |
|
|
J ({wn}) = ∑| e(k) |2 → min . |
(9.18) |
k =0
Для решения задачи необходимо перейти в формуле (9.3) к матричной записи, так сказать, вдоль координаты k, получив формулы для векторов-столбцов выходного сигнала y и ошибки воспроизведения входного сигнала e:
|
y = XTw , e = d − XT w . |
(9.19) |
Здесь d — вектор-столбец отсчетов образцового сигнала, а X — матрица, столбцы которой представляют собой содержимое линии задержки фильтра на разных тактах:
|
602 |
Глава 9 |
||
|
d(0) |
|||
|
d(1) |
|||
|
d = |
, X = [x(0) x(1) … x(N – 1)]. |
||
|
d(K − |
1) |
Выражение (9.18) для суммарной квадратичной ошибки в матричном виде можно записать следующим образом:
|
T |
(9.20) |
|
J (w) = e e → min . |
Подставив (9.19) в (9.20), имеем
J (w) = (d − XT w)T (d − XTw) =
=dTd − (XTw)T d − dT (XTw) + (XTw)T (XTw) =
=dTd − wT Xd − dT XTw + wT XXTw.
Для нахождения минимума необходимо вычислить градиент данного функционала и приравнять его к нулю:
J (w) = −2Xd + 2XXTw = 0.
Отсюда легко получается искомое оптимальное решение:
В формуле (9.21) прослеживается близкое родство с формулой (9.8), описывающей оптимальный в статистическом смысле фильтр Винера. Действительно, если
учесть, что (XXT )−1 
Адаптивный алгоритм RLS
В принципе, в процессе приема сигнала можно на каждом очередном шаге пересчитывать коэффициенты фильтра непосредственно по формуле (9.21), однако это связано с неоправданно большими вычислительными затратами. Действительно, на каждом шаге увеличивается размер матрицы X; кроме того, необходимо каждый
раз заново вычислять обратную матрицу (X XT )−1 .
Сократить вычислительные затраты можно, если заметить, что на каждом шаге к матрице X добавляется лишь один новый столбец, а к вектору d — один новый элемент. Это дает возможность организовать вычисления рекурсивно. Соответствующий алгоритм получил название рекурсивного метода наименьших квадратов (Recursive Least Squares, RLS).
На k-м шаге оптимальный вектор коэффициентов фильтра, согласно (9.21), равен
w(k) = (X(k)XT (k))−1 X(k)d(k) . (9.22)
Посмотрим, какие новые данные добавляются к X(k) и d(k) на следующем шаге и как мы можем использовать их для обновления рассчитанного ранее решения — ведь именно в таком постоянном обновлении состоит суть работы адаптивного фильтра.
К матрице X на каждом шаге добавляется новый столбец x(k + 1), а к вектору d — новый элемент d(k + 1):
|
d(k) |
||||||||||||||||
|
X(k +1) = [X(k) |
x(k +1)] , |
d(k + 1) = |
. |
(9.23) |
||||||||||||
|
d (k + 1) |
В алгоритме RLS производится рекурсивное обновление оценки обратной корреляционной матрицы
P(k) = (X(k)XT (k))−1 .
При переходе к следующему шагу мы имеем
|
( |
T |
) |
−1 |
XT (k) |
−1 |
|||||||||||||||
|
[ |
] |
T |
||||||||||||||||||
|
P(k +1) = |
X(k +1)X |
(k +1) |
= |
X(k) |
x(k +1) |
x |
(k +1) |
= |
||||||||||||
|
(9.24) |
||||||||||||||||||||
|
= (X(k)XT (k) + x(k +1)xT (k +1))−1 . |
||||||||||||||||||||
|
Теперь воспользуемся матричным тождеством |
||||||||||||||||||||
|
(A + BCD)−1 = A−1 − A−1B(C−1 + DA−1B)−1 DA−1 , |
(9.25) |
которое является справедливым для произвольных квадратных невырожденных матриц A и C и произвольных матриц B и D совместимых размеров.
Установим между (9.24) и (9.25) следующее соответствие:
A = X(k)XT (k) = P−1(k) , A−1 = P(k) (квадратная матрица);
B = x(k + 1) (вектор-столбец);
C = 1 (скаляр);
D = xT (k +1) (вектор-строка).
В результате равенство (9.24) можно записать следующим образом:
P(k +1) = P(k) − P(k)x(k +1) (1 + xT (k +1)P(k)x(k +1))−1 xT (k +1)P(k) . (9.26)
Здесь следует заметить, что фрагмент выражения в круглых скобках, возводимый в минус первую степень, представляет собой скаляр. Далее используем (9.23) и (9.26) в выражении (9.22) для коэффициентов фильтра:

|
604 |
Глава 9 |
|||||||||||||||
|
d(k) |
||||||||||||||||
|
w(k +1) = P(k +1)X(k +1)d(k +1) = P(k +1)[X(k) |
x(k +1)] |
= |
||||||||||||||
|
d(k +1) |
= P(k +1) ( X(k)d(k) + x(k +1)d(k +1)) =
|
P(k)x(k +1)xT (k +1)P(k) |
|||||
|
= P(k) − |
( X(k)d(k) + x(k +1)d(k +1)). |
||||
|
1 + x |
T |
(k +1)P(k)x(k +1) |
|||
Раскроем скобки в этом выражении:
w(k +1) = P(k)X(k)d(k) − P(k)x(k +1)xT (k +1)P(k) X(k)d(k) + 1 + xT (k +1)P(k)x(k +1)
+ P(k)x(k +1)d (k +1) − P(k)x(k +1)xT (k +1)P(k) x(k +1)d(k +1). 1 + xT (k +1)P(k)x(k +1)
Первое слагаемое в полученной формуле, согласно (9.22), представляет собой коэффициенты оптимального фильтра для k-го шага — w(k). Этот же вектор можно выделить в качестве множителя во втором слагаемом. Что касается третьего и четвертого слагаемых, в них можно выделить общий множитель P(k) x(k + 1) d(k + 1):
|
w(k +1) = w(k) − |
P(k)x(k +1)xT (k +1) |
w(k) + |
||||
|
1 |
+ xT (k +1)P(k)x(k +1) |
|||||
|
xT (k +1)P(k)x(k +1) |
||||||
|
+P(k)x(k +1)d (k +1) 1 |
− |
. |
||||
|
+ xT (k +1)P(k)x(k +1) |
||||||
|
1 |
Выполнив вычитание в круглых скобках, получаем
|
w(k +1) = w(k) − |
P(k)x(k +1)xT (k +1) |
w(k) + |
P(k)x(k +1)d(k +1) |
. |
|
1 + xT (k +1)P(k)x(k +1) |
1 + xT (k +1)P(k)x(k +1) |
Теперь видно, что второе и третье слагаемые имеют общий множитель, который можно вынести за скобки:
|
w(k +1) = w(k) + |
P(k)x(k +1) |
(d (k +1) − xT (k +1)w(k)) . |
||
|
T |
(k +1)P(k)x(k +1) |
|||
|
1 + x |
Далее заметим, что произведение xT (k +1) w(k) есть результат обработки нового (поступившего на (k + 1)-м шаге) входного сигнала фильтром со старыми (т. е. имеющимися на данный момент) коэффициентами w(k). Иными словами, это произведение представляет собой выходной сигнал адаптивного фильтра y(k + 1). Соответственно, получается, что разность, стоящая в скобках, — не что иное, как ошибка фильтрации e(k + 1):
|
P(k)x(k +1) |
||
|
w(k +1) = w(k) + |
e(k +1) . |
|
|
1 + xT (k +1)P(k)x(k +1) |
Наконец, в качестве последнего штриха введем обозначение для вынесенного за скобки векторного множителя:
|
K(k +1) = |
P(k)x(k +1) |
. |
|
|
1 + xT (k +1)P(k)x(k +1) |
|||
С учетом этого формула для коэффициентов фильтра примет вид
|
w(k + 1) = w(k) + K(k + 1) e(k + 1). |
(9.27) |
Вектор K(k + 1) называют вектором коэффициентов усиления.
ЗАМЕЧАНИЕ
Структура формулы (9.27) совпадает со структурой формулы (9.14), описывающей обновление коэффициентов фильтра для LMS-алгоритма — к текущему вектору коэффициентов фильтра добавляется слагаемое, рассчитываемое как произведение сигнала ошибки на некий вектор коэффициентов усиления. Различие состоит лишь в способе получения этого вектора — в алгоритме LMS он пропорционален содержимому линии задержки фильтра, а в алгоритме RLS рассчитывается более сложным образом.
Итак, при использовании адаптивного алгоритма RLS необходимо на каждом временном такте выполнить следующие шаги:
1.При поступлении новых входных данных x(k) производится фильтрация сигнала с использованием текущих коэффициентов фильтра w(k – 1) и вычисление величины ошибки воспроизведения образцового сигнала:
y(k) = x(k)T w(k −1) , e(k) = d (k) − y(k) .
2.Рассчитывается вектор-столбец коэффициентов усиления (обратите внимание на то, что при вычислениях не используются предыдущие значения — вектор K всякий раз рассчитывается заново, т. е. вычисления не являются рекурсивными; кроме того, еще раз отметим, что знаменатель дроби в следующих двух формулах является скаляром, а не матрицей):
|
K(k) = |
P(k −1)x(k ) |
. |
(9.28) |
|
|
1 + xT (k)P(k −1)x(k) |
||||
3. Выполняется обновление оценки обратной корреляционной матрицы сигнала:
|
P(k) = P(k −1) − |
P(k −1)x(k)x(k)T P(k −1) |
. |
(9.29) |
|
1+ x(k)T P(k −1)x(k) |
4. Наконец, производится обновление коэффициентов фильтра: w(k) = w(k −1) + K(k)e(k) .
Осталось разобраться с начальными значениями рекурсивно обновляемых матрицы P и вектора w. Вектор коэффициентов фильтра w перед началом работы алгоритма обычно заполняется нулями. Что касается матрицы P, то строгий анализ показыва-

606 Глава 9
ет, что после заполнения линии задержки фильтра отсчетами сигнала результат вычислений не будет зависеть от начальных условий, если
|
∞ |
0 |
0 |
… |
0 |
||||
|
0 |
∞ |
0 |
… |
0 |
||||
|
P(−1) = |
∞ … |
|||||||
|
0 |
0 |
0 |
. |
|||||
|
0 |
0 |
0 |
… ∞ |
|||||
На практике диагональ матрицы заполняется большими положительными значениями. Например, в [13] рекомендуется величина 100
По сравнению с LMS-алгоритмом алгоритм RLS требует значительно большего числа вычислительных операций. При оптимальной организации вычислений для
обновления коэффициентов фильтра необходимо 2,5N2 + 4N пар операций «ум- ножение—сложение» [13]. Под оптимальной организацией здесь, в частности, подразумевается учет симметрии матрицы P. Таким образом, число операций в алгоритме RLS квадратично возрастает с увеличением порядка фильтра.
Зато алгоритм RLS сходится значительно быстрее, чем алгоритм LMS. Строго говоря, само понятие сходимости применимо здесь лишь условно, поскольку данный алгоритм не является алгоритмом последовательного приближения. Алгоритм RLS на каждом шаге дает оптимальные коэффициенты фильтра, соответствующие формуле (9.21), и переходный процесс в начале работы связан лишь с рекурсивным расчетом оценки матрицы P и постепенным заполнением линии задержки фильтра отсчетами входного сигнала.
Экспоненциальное забывание
В формулах (9.18) и (9.20) значениям ошибки на всех временных тактах придается одинаковый вес. В результате, если статистические свойства входного сигнала со временем изменяются, это приведет к ухудшению качества фильтрации. Чтобы дать фильтру возможность отслеживать нестационарный входной сигнал, можно применить в (9.18) экспоненциальное забывание (exponential forgetting), при котором вес прошлых значений сигнала ошибки экспоненциально уменьшается:
K −1
J (w) = ∑λK −1−k | e(k) |2 ,
k=0
где λ — коэффициент забывания (forgetting factor), 0 <λ ≤ 1.
При использовании экспоненциального забывания формулы (9.28) и (9.29) принимают следующий вид:
|
K(k) = |
P(k −1)x(k) |
, |
||
|
λ + xT (k) P(k −1) x(n) |
||||
|
P(k) = |
1 |
(P(k −1) − K(k) xT (k)P(k −1)) . |
||
|
λ |
||||

Применение адаптивных фильтров
Адаптивные фильтры в настоящее время нашли применение во многих системах обработки сигналов. В данном разделе мы рассмотрим лишь некоторые из возможных областей их использования.
Идентификация систем
Все способы применения адаптивных фильтров так или иначе сводятся к решению задачи идентификации, т. е. определения характеристик, некоторой системы. Возможны два варианта идентификации — прямая и обратная. В первом случае адаптивный фильтр включается параллельно с исследуемой системой (рис. 9.4, а).
|
Исследуемая |
Исследуемая |
Вход |
Адаптивный |
|||||||||||
|
система |
система |
фильтр |
||||||||||||
|
Образец |
||||||||||||||
|
Адаптивный |
||||||||||||||
|
Вход |
фильтр |
Образец |
||||||||||||
|
а |
б |
Рис. 9.4. Идентификация систем с помощью адаптивного фильтра: а — прямая, б — обратная
Входной сигнал является общим для исследуемой системы и адаптивного фильтра, а выходной сигнал системы служит для адаптивного фильтра образцовым сигналом. В процессе адаптации временные и частотные характеристики фильтра будут стремиться к соответствующим характеристикам исследуемой системы.
При обратной идентификации адаптивный фильтр включается последовательно с исследуемой системой (см. рис. 9.4, б). Выходной сигнал системы поступает на вход адаптивного фильтра, а входной сигнал системы является для адаптивного фильтра образцом. Таким образом, фильтр стремится компенсировать влияние системы и восстановить исходный сигнал, устранив внесенные системой искажения.
Теперь перейдем от этих обобщенных схем к рассмотрению более конкретных вариантов.
Линейное предсказание
Согласно определению, данному в разд. «Авторегрессионная модель» главы 5 для предсказывающего фильтра, он минимизирует средний квадрат ошибки предсказания сигнала по его предыдущим отсчетам. Однако такую же задачу будет решать и рассмотренный в этой главе ранее фильтр Винера, если в качестве образца использовать текущий отсчет сигнала, а на вход фильтра подать сигнал, задержанный на один такт. Адаптивные алгоритмы в процессе работы сходятся к оптимальному винеровскому решению, поэтому для решения задачи линейного предсказания можно использовать адаптивный фильтр, включенный по схеме, показанной на рис. 9.5.

|
608 |
Глава 9 |
||||||||
Рис. 9.5. Линейное предсказание с помощью адаптивного фильтра
В процессе адаптации коэффициенты фильтра будут стремиться к коэффициентам авторегрессионной модели (см. рис. 5.16 в главе 5), а сигнал ошибки дает оценку белого шума, возбуждающего эту модель.
Подавление шума
Пусть нам необходимо обеспечить системой речевой связи пилота самолета или, скажем, водителя трактора. При этом воспринимаемый микрофоном речевой сигнал неизбежно окажется сильно зашумленным звуками работающего двигателя и т. п. Мы не можем избавиться от этих шумов, но можем получить образец шумового сигнала, установив второй микрофон в непосредственной близости от двигателя или иного источника шумов. Разумеется, этот шум нельзя просто вычесть из речевого сигнала, поскольку по дороге до двух микрофонов шум следует разными путями и, следовательно, претерпевает разные искажения (рис. 9.6). Однако шумовые случайные процессы, воспринимаемые двумя микрофонами, будут коррелированными, т. к. они происходят из общего источника. В то же время, очевидно, что шумовой сигнал не коррелирован с полезным речевым сигналом.
|
Источник |
||||
|
сигнала |
||||
|
Датчик |
Образец |
|||
|
Путь 1 |
сигнала |
|||
|
Сигнал |
||||
|
Источник |
Вход Адаптивный ошибки |
Очищенный от шумов |
||
|
шума |
Путь 2 |
фильтр |
речевой сигнал |
|
|
Датчик |
||||
|
шума |
Рис. 9.6. Подавление шума с помощью адаптивного фильтра
С помощью адаптивного фильтра в данном случае решается задача прямой идентификации преобразований шума на пути к сигнальному микрофону. Входным сигналом адаптивного фильтра является шумовой сигнал от дополнительного микрофона (на рис. 9.6 он обозначен как датчик шума), а в качестве образцового сигнала используется сигнально-шумовая смесь, воспринимаемая основным микрофоном (на рис. 9.6 — датчик сигнала).
Адаптивный фильтр стремится преобразовать входной сигнал так, чтобы сделать его как можно ближе (в смысле среднеквадратической ошибки) к образцовому. Поскольку с входным сигналом фильтра коррелирована лишь шумовая составляющая образцового сигнала, после завершения процесса адаптации на выходе фильтра будет получена оценка шума, присутствующего в образцовом сигнале. Сигнал ошиб-

ки, рассчитываемый как разность между образцовым сигналом и выходным сигналом адаптивного фильтра, будет в этом случае представлять собой очищенный от шума речевой сигнал.
Система речевой связи не является единственно возможным объектом применения рассматриваемой системы шумоподавления. Возможны и иные области использования данной идеи.
Выравнивание частотной характеристики канала связи
При передаче по каналу связи информационный сигнал неизбежно претерпевает некоторые искажения. В системах цифровой связи эти искажения могут привести к возникновению ошибок при приеме данных. Для устранения этих ошибок (или, во всяком случае, уменьшения их числа) необходимо компенсировать влияние канала связи, т. е. решить задачу обратной идентификации (см. рис. 9.4, б). В частотной области компенсация вносимых каналом искажений означает выравнивание (equalization) его частотной характеристики, поэтому фильтры, выполняющие такое выравнивание, получили название эквалайзеров (equalizer).
При использовании адаптивного фильтра в качестве эквалайзера возникает проблема получения образцового сигнала. Эта проблема решается путем передачи специального настроечного сигнала перед началом передачи данных. В качестве такого настроечного сигнала обычно используется псевдослучайная последовательность символов. Алгоритм формирования этого сигнала известен приемной стороне, поэтому образцовый сигнал может быть сгенерирован автономно и использован для обучения адаптивного фильтра. Этот режим работы называется режимом обучения (training mode) (рис. 9.7).
|
Выбор |
|||||||||||||
|
Вход |
Адаптивный |
Выход |
ближайшей |
||||||||||
|
фильтр |
точки |
||||||||||||
|
созвездия |
|||||||||||||
|
Образец |
|||||||||||||
|
Режим |
Режим |
||||||||||||
|
обучения |
оценивания |
||||||||||||
|
Генератор |
|||||||||||||
|
настроечного |
|||||||||||||
|
сигнала |
Рис. 9.7. Выравнивание частотной характеристики канала связи с помощью адаптивного фильтра
После окончания настроечного сигнала начинается собственно передача данных. Приемник при этом переключается в другой режим, называемый режимом оценивания (decision-directed mode). В этом режиме для получения образцового сигнала используется тот факт, что множество возможных значений сигнала в системе цифровой связи является конечным. После приема очередного отсчета (или целого фрагмента сигнала) ищется ближайшее к принятому сигналу допустимое значение.

Оно используется в качестве образцового сигнала, а разность между этим значением и принятым сигналом дает сигнал ошибки, используемый для адаптации. На рис. 9.8 это иллюстрируется применительно к 16-позиционной квадратурной модуляции.
Im
Принятый сигнал
Сигнал ошибки
Re
Ближайшее допустимое значение выбирается в качестве образцового сигнала
Рис. 9.8. Формирование образцового сигнала и сигнала ошибки в режиме оценивания
Если после настройки эквалайзера, произведенной в режиме обучения, уровень шумов на выходе фильтра оказывается таким, что ближайшая допустимая точка в большинстве случаев оказывается правильной (т. е. если вероятность ошибки мала), адаптивный алгоритм сохраняет стабильность.
ЗАМЕЧАНИЕ
В некоторых, в частности многопользовательских, системах связи передавать настроечный сигнал не представляется возможным. В этом случае может использоваться слепая (blind) адаптация, рассмотрение которой выходит за рамки данной книги. Некоторые алгоритмы слепой адаптации приведены в [35].
Эхоподавление
Данная технология, так же как и выравнивание канала связи, широко используется в современных модемах. Скоростные модемы для телефонных линий связи работают в дуплексном режиме, т. е. передают и принимают данные одновременно, при этом для передачи и приема используется одна и та же полоса частот. Однако сигнал собственного передатчика в данном случае неизбежно просачивается в приемник, мешая работе последнего. Просачивающийся сигнал может распространяться разными путями, приобретая при этом не известные заранее искажения (рис. 9.9).
Подавить эхо-сигнал можно с помощью адаптивного фильтра. При этом решается задача прямой идентификации тракта распространения эхо. На вход адаптивного фильтра поступает сигнал передатчика модема, а в качестве образцового сигнала используется принимаемый сигнал, содержащий эхо (рис. 9.10). Адаптивный фильтр формирует оценку эхо-сигнала, а сигнал ошибки представляет собой принимаемый сигнал, очищенный от эха.
Для правильной работы системы эхоподавления необходимо, чтобы передаваемый и принимаемый сигналы были некоррелированы. Для обеспечения некоррелиро-

ванности входные данные, поступающие в модем для передачи, прежде всего подвергаются скремблированию (scrambling), т. е. преобразуются в псевдослучайный битовый поток. При этом два взаимодействующих модема используют разные скремблеры, что и обеспечивает некоррелированность передаваемых ими сигналов.
Эхоподавление, осуществляемое согласно схеме рис. 9.10, используется во всех современных модемах.
|
Абонентская линия Цифровой канал связи Абонентская линия |
||||||||||||||||||||||||||||||||||
|
между АТС |
||||||||||||||||||||||||||||||||||
|
Передатчик |
Передатчик |
|||||||||||||||||||||||||||||||||
|
Приемник |
Приемник |
|||||||||||||||||||||||||||||||||
|
Пути прохождения эхо-сигнала |
Удаленный модем |
|||||||||||||||||||||||||||||||||
|
Рис. 9.9. Формирование эхо-сигнала |
||||||||||||||||||||||||||||||||||
|
Передатчик |
||||||||||||||||||||||||||||||||||
|
Вход |
Адаптивный |
Образец |
Линия |
|||||||||||||||||||||||||||||||
|
фильтр |
связи |
|||||||||||||||||||||||||||||||||
|
Приемник |
Сигнал ошибки |
Сигнал + эхо |
||||||||||||||||||||||||||||||||
Рис. 9.10. Эхоподавление, осуществляемое с помощью адаптивного фильтра
Объекты адаптивной фильтрации пакета Filter Design
В версии 4.7 пакета Filter Design (R2010a) адаптивные фильтры реализованы только в виде объектов MATLAB, а существовавшие ранее функции адаптивной фильтрации не только объявлены устаревшими, но и удалены.
Общие сведения об использовании объектов в MATLAB были приведены в главе 4. Для создания объекта адаптивного фильтра служит функция adaptfilt. При ее вызове необходимо указать требуемый алгоритм адаптивной фильтрации — для этого после имени функции ставится точка и указывается соответствующий идентификатор метода (конструктора):
ha = adaptfilt.algorithm(…)
В настоящее время в пакете Filter Design реализовано около тридцати разновидностей алгоритмов адаптивной фильтрации. К сожалению, автору неизвестен источник на русском языке, который содержал бы обзор этих алгоритмов. При наличии доступа к зарубежным книгам и журналам можно рекомендовать статьи, ссылки на
которые имеются в справочной системе MATLAB, а также литературу, упомянутую в начале этой главы.
Полный список реализованных алгоритмов адаптивной фильтрации и имена соответствующих конструкторов объектов adaptfilt приведены в табл. 9.1.
|
Таблица 9.1. Свойства объектов адаптивных фильтров |
|
|
Конструктор |
Алгоритм |
|
Семейство алгоритмов LMS |
|
|
adaptfilt.adjlms |
Сопряженный (adjoint) LMS-алгоритм |
|
adaptfilt.blms |
Блоковый LMS-алгоритм |
|
adaptfilt.blmsfft |
Блоковый LMS-алгоритм, реализованный в частотной области |
|
с применением БПФ |
|
|
adaptfilt.dlms |
LMS-алгоритм с задержкой обновления коэффициентов фильтра |
|
adaptfilt.filtxlms |
LMS-алгоритм с дополнительной фильтрацией выходного сигнала |
|
фильтра перед формированием сигнала ошибки (filtered-x LMS) |
|
|
adaptfilt.lms |
«Классический» LMS-алгоритм (см. формулу (9.14)) |
|
adaptfilt.nlms |
Нормированный LMS-алгоритм (расчет шага μ на каждом такте осу- |
|
ществляется автоматически по формуле (9.16) исходя из энергии |
|
|
фрагмента сигнала, содержащегося в линии задержки фильтра) |
|
|
adaptfilt.sd |
LMS-алгоритм с использованием для адаптации только знака дан- |
|
ных, содержащихся в линии задержки фильтра (sign-data; вместо x(k) |
|
|
в формуле (9.14) используется sign(x(k))) |
|
|
adaptfilt.se |
LMS-алгоритм с использованием для адаптации только знака сигнала |
|
ошибки (sign-error; вместо e(k) в формуле (9.14) используется |
|
|
sign(e(k))) |
|
|
adaptfilt.ss |
LMS-алгоритм с использованием для адаптации только знаков сиг- |
|
нала ошибки и данных, содержащихся в линии задержки фильтра |
|
|
(sign-sign; комбинация двух предыдущих вариантов) |
|
|
Семейство алгоритмов RLS |
|
|
adaptfilt.ftf |
Быстрый RLS-алгоритм |
|
adaptfilt.hrls |
RLS-алгоритм с использованием преобразования Хаусхолдера |
|
adaptfilt.hswrls |
RLS-алгоритм со скользящим окном и использованием преобразова- |
|
ния Хаусхолдера |
|
|
adaptfilt.qrdrls |
RLS-алгоритм с использованием QR-разложения матрицы |
|
adaptfilt.rls |
«Классический» RLS-алгоритм, в том числе с экспоненциальным |
|
забыванием данных |
|
|
adaptfilt.swftf |
Быстрый RLS-алгоритм со скользящим окном |
|
adaptfilt.swrls |
RLS-алгоритм со скользящим окном |
|
Адаптивные фильтры |
613 |
|
|
Таблица 9.1 (окончание) |
||
|
Конструктор |
Алгоритм |
|
|
Алгоритмы, основанные на методе аффинных проекций |
||
|
adaptfilt.ap |
Метод аффинных проекций с прямым обращением матрицы |
|
|
adaptfilt.apru |
Метод аффинных проекций с рекурсивным обновлением обратной |
|
|
матрицы |
||
|
adaptfilt.bap |
Блоковый алгоритм аффинных проекций |
|
|
Алгоритмы адаптации, работающие в частотной области |
||
|
adaptfilt.fdaf |
LMS-алгоритм в частотной области с индивидуальной нормировкой |
|
|
размера шага в каждом частотном канале (frequency domain adaptive |
||
|
filter, FDAF) |
||
|
adaptfilt.pbfdaf |
Нормированный LMS-алгоритм в частотной области, использующий |
|
|
деление сигнала на блоки малого размера во временной области |
||
|
(partitioned block frequency domain adaptive filter, PBFDAF) |
||
|
adaptfilt.pbufdaf |
Нормированный LMS-алгоритм в частотной области, использующий |
|
|
деление сигнала на блоки малого размера во временной области, без |
||
|
ограничения длины эквивалентной импульсной характеристики |
||
|
(partitioned block unconstrained frequency domain adaptive filter, |
||
|
PBUFDAF) |
||
|
adaptfilt.tdafdct |
Адаптивный фильтр, использующий LMS-алгоритм после предвари- |
|
|
тельного применения к входному сигналу дискретного косинусного |
||
|
преобразования |
||
|
adaptfilt.tdafdft |
Адаптивный фильтр, использующий LMS-алгоритм после предвари- |
|
|
тельного применения к входному сигналу дискретного преобразова- |
||
|
ния Фурье |
||
|
adaptfilt.ufdaf |
Нормированный LMS-алгоритм в частотной области без ограничения |
|
|
длины эквивалентной импульсной характеристики (unconstrained |
||
|
frequency domain adaptive filter, UFDAF) |
||
|
Адаптивные алгоритмы для решетчатых фильтров |
||
|
adaptfilt.gal |
Алгоритм адаптации для решетчатого фильтра, основанный |
|
|
на градиентном спуске (gradient-adaptive lattice, GAL) |
||
|
adaptfilt.lsl |
Алгоритм адаптации для решетчатого фильтра, основанный на |
|
|
рекурсивном методе наименьших квадратов (least squares lattice, LSL) |
||
|
adaptfilt.qrdlsl |
Вариант алгоритма LSL, использующий QR-разложение матрицы |
|
Набор входных параметров конструктора зависит от реализуемого алгоритма. Рассмотрим более подробно использование объектов адаптивных фильтров для тех алгоритмов, которые были ранее описаны в этой главе. Вызов конструкторов для них имеет следующий вид:

ha = adaptfilt.lms(L, step, leakage, coeffs, states)
ha = adaptfilt.nlms(L, step, leakage, offset, coeffs, states) ha = adaptfilt.sd(L, step, leakage, coeffs, states)
ha = adaptfilt.se(L, step, leakage, coeffs, states) ha = adaptfilt.ss(L, step, leakage, coeffs, states) ha = adaptfilt.rls(L, lambda, invcov, coeffs, states)
Назначение входных параметров расшифровано в табл. 9.2. Там же приведены и значения по умолчанию, которые имеются для всех параметров конструкторов.
Таблица 9.2. Параметры конструкторов рассматриваемых адаптивных фильтров
|
Параметр |
Назначение |
Имеет смысл |
|
|
для |
|||
|
L |
Длина фильтра (напомним, что это значение на единицу |
всех алгоритмов |
|
|
превышает порядок фильтра). По умолчанию L = 10 |
|||
|
coeffs |
Вектор (строка длиной L) начальных значений коэффици- |
всех алгоритмов |
|
|
ентов фильтра. По умолчанию этот вектор заполняется |
|||
|
нулями |
|||
|
states |
Вектор (столбец высотой L-1) начального содержимого |
всех алгоритмов |
|
|
линии задержки фильтра. По умолчанию этот вектор за- |
|||
|
полняется нулями |
|||
|
step |
Размер шага μ. По умолчанию step = 0.1 (в случае норми- |
всех разновид- |
|
|
рованного LMS step = 1) |
ностей LMS |
||
|
leakage |
Коэффициент утечки (в диапазоне 0…1). По умолчанию |
всех разновид- |
|
|
leakage = 1 |
ностей LMS |
||
|
offset |
Константа ε (см. формулу (9.16)). По умолчанию |
нормированного |
|
|
offset = 0 |
LMS |
||
|
lambda |
Коэффициент экспоненциального забывания λ (в диапазоне |
RLS |
|
|
0…1). По умолчанию lambda = 1 |
|||
|
invcov |
Начальное значение оценки обратной корреляционной мат- |
RLS |
|
|
рицы входного сигнала. По умолчанию используется мат- |
|||
|
рица, главная диагональ которой заполнена значением, рав- |
|||
|
ным 1000: invcov = 1000*eye(L) |
|||
ЗАМЕЧАНИЕ
В табл. 9.2 и далее в табл. 9.3 упоминается не рассматривавшийся в теоретической части главы параметр LMS-алгоритма — коэффициент утечки (leakage). Это коэффициент, лежащий в диапазоне от 0 до 1, на который может умножаться старый вектор коэффициентов w(k) в формуле (9.14) для улучшения стабильности алгоритма.
Список свойств объектов адаптивных фильтров для рассматриваемых алгоритмов приведен в табл. 9.3. Считывать и задавать значения этих свойств можно с помощью функций get и set соответственно (см. разд. «Общая информация об объектах MATLAB» главы 4).
|
Адаптивные фильтры |
615 |
|
|
Таблица 9.3. Свойства объектов адаптивных фильтров |
||
|
Имя свойства |
Описание |
|
|
Algorithm |
Строка, содержащая название используемого алгоритма |
|
|
адаптации (только для чтения) |
||
|
FilterLength |
Длина вектора коэффициентов фильтра (напомним, что это |
|
|
значение на единицу превышает порядок фильтра) |
||
|
Coefficients |
Вектор коэффициентов фильтра |
|
|
States |
Содержимое линии задержки фильтра |
|
|
PersistentMemory |
Данное свойство может принимать логические значения true |
|
|
(включено) и false (выключено). При включении данного |
||
|
режима (принято по умолчанию) перед каждой операцией |
||
|
фильтрации (метод filter) производится сброс фильтра |
||
|
в исходное состояние. При выключении данного режима |
||
|
текущее состояние фильтра сохраняется, что позволяет орга- |
||
|
низовать блоковую обработку сигнала |
||
|
NumSamplesProcessed |
Число обработанных отсчетов сигнала (только для чтения) |
|
|
StepSize (для всех вариантов |
Размер шага μ |
|
|
алгоритма LMS) |
||
|
Leakage (для всех вариантов |
Коэффициент утечки (в диапазоне 0…1, по умолчанию |
|
|
алгоритма LMS) |
равен 1) |
|
|
Offset (для алгоритма nlms) |
Константа ε (см. формулу (9.16)) |
|
|
ForgettingFactor |
Коэффициент забывания λ (в диапазоне 0…1, по умолча- |
|
|
(для алгоритма RLS) |
нию 1) |
|
|
KalmanGain |
Вектор коэффициентов усиления K (см. формулу (9.28); |
|
|
(для алгоритма RLS) |
только для чтения) |
|
|
InvCov (для алгоритма RLS) |
Оценка обратной корреляционной матрицы P |
|
Обработка сигнала адаптивным фильтром осуществляется с помощью функции
filter:
[y, e] = filter(ha, x, d)
Здесь ha — объект адаптивного фильтра, x — вектор отсчетов входного сигнала, d — вектор отсчетов образцового сигнала. Результатами работы функции являются векторы отсчетов выходного сигнала y и сигнала ошибки фильтрации e.
Как показывает синтаксис вызова функции фильтрации, образцовый сигнал должен быть известен заранее, что делает невозможным применение данных функций в режиме адаптации по оценке сигнала (decision-directed mode). Кроме того, реализация данной функции подразумевает на каждом временном такте сдвиг данных
влинии задержки фильтра на один отсчет. Это затрудняет применение объектов
втех ситуациях, когда данные обновляются иным образом (это имеет место, например, в так называемых дробных (fractionally-spaced equalizer) эквалайзерах).
Требуемое обновление можно реализовать путем осуществления поотсчетной обработки с ручной коррекцией состояния линии задержки, но такой код будет громоздким, медленным и надуманным.
ЗАМЕЧАНИЕ
Возможность адаптации по оценке сигнала реализована в пакете расширения Communications Toolbox, где для этого имеются специальные объекты эквалайзеров.
С объектами адаптивных фильтров можно использовать многие методы, описанные в главе 4 применительно к объектам класса dfilt. Поскольку адаптивный фильтр является системой с переменными параметрами, эти методы дают результаты, соответствующие текущему состоянию фильтра.
Аналогичным образом объекты адаптивных фильтров поддерживаются и визуализатором фильтров FVTool:
fvtool(ha)
К методам, специфическим именно для адаптивных фильтров, относятся три функции, перечисленные далее:
[mumax, mumaxmse] = maxstep(ha, x) — данная функция производит оценку максимально допустимой величины размера шага µ для объекта адаптивного фильтра ha (функция применима для следующих вариантов алгоритма LMS: lms, nlms, blms, blmsfft, se). Входной параметр x — пример возможного входного сигнала фильтра (для алгоритма nlms задавать этот параметр не нужно). Этот параметр может быть матрицей, тогда ее столбцы рассматриваются как различные реализации входного случайного сигнала. Выходной параметр mumax — предельная величина µ, при которой обеспечивается сходимость алгоритма в среднем (см. формулу (9.12)), выходной параметр mumaxmse — предельная величина µ, при которой обеспечивается сходимость алгоритма в среднем квадрате (см. формулу (9.15));
[mmse, emse, meanw, mse, tracek] = msepred(ha, x, d, m) — данная функция
производит оценку среднего квадрата ошибки фильтрации для объекта адаптивного фильтра ha (функция применима для следующих вариантов алгоритма LMS: lms, nlms, blms, blmsfft, se). Входные параметры x и d — векторы отсчетов входного и образцового сигнала соответственно. Выходные параметры: mmse — средний квадрат ошибки фильтрации в установившемся режиме, emse — избыточная ошибка фильтрации (см. формулу (9.17)), meanw — матрица предсказанных математических ожиданий коэффициентов фильтра для всех моментов времени, mse — вектор зависимости среднего квадрата ошибки от времени, tracek — вектор зависимости от времени для суммарного квадратичного отклонения коэффициентов фильтра от оптимальных. При расчете трех последних выходных параметров может производиться прореживание по времени с коэффициентом m (по умолчанию m = 1);
[mse, meanw, w, tracek] = msesim(ha, x, d, m) — данная функция по назначе-
нию аналогична предыдущей, но измерение среднего квадрата ошибки производится путем моделирования, без использования теоретических оценок. Поэтому
функция применима к любым объектам адаптивных фильтров, работающих во временной области, независимо от используемых ими алгоритмов адаптации. Производимое моделирование предполагает усреднение по ансамблю реализаций, поэтому входные параметры x и d должны быть матрицами, столбцы которых содержат отдельные реализации входного и образцового сигналов соответственно. Выходной параметр w представляет собой вектор финальных значений коэффициентов фильтра. Остальные входные и выходные параметры совпадают по назначению с одноименными параметрами функции msepred.
Примеры реализации адаптивной фильтрации
Приведем несколько примеров, показывающих, как различные задачи, рассмотренные ранее в разд. «Применение адаптивных фильтров» этой главы, могут быть смоделированы с использованием объектов адаптивных фильтров из пакета Filter Design.
Идентификация системы
В данном примере мы реализуем решение задачи прямой идентификации системы согласно рис. 9.4, а. Входным сигналом системы будет служить дискретный белый гауссов шум, а сама система будет представлять собой нерекурсивный фильтр 31-го порядка с импульсной характеристикой в виде экспоненциально затухающей синусоиды, на период колебаний которой приходится 4 отсчета. Кроме того, после обработки половины входного сигнала параметры системы скачкообразно изменятся — у ее импульсной характеристики поменяется знак. Это позволит нам посмотреть на то, как реагируют алгоритмы LMS и RLS на резкое изменение статистических свойств обрабатываемого сигнала. Итак, формируем входной и выходной сигналы идентифицируемой системы:
>>x = randn(2000, 1); % дискретный белый гауссов шум
>>t = 0:31;
>>b = exp(-t/5) .* cos(t*pi/2); % импульсная характеристика системы
>>% генерируем первую половину выходного сигнала
>>[y(1:1000), state] = filter(b, 1, x(1:1000));
>>% генерируем вторую половину выходного сигнала
>>y(1001:2000) = filter(-b, 1, x(1001:2000), state);
Далее создадим объекты LMS- и RLS-адаптивных фильтров с помощью соответствующих конструкторов. Для LMS-алгоритма предварительно рассчитаем значение коэффициента µ, выбрав его в два раза меньшим предельного значения, определяемого формулой (9.15), для всех остальных параметров используем значения по умолчанию:
|
>> N = 16; |
% длина фильтров |
>>mu = 1/N/var(y); % расчет размера шага для алгоритма LMS
>>ha_lms = adaptfilt.lms(N, mu); % создание объекта LMS-фильтра
|
>> ha_rls = adaptfilt.rls(N); |
% создание объекта RLS-фильтра |

Теперь реализуем собственно фильтрацию, воспользовавшись функцией filter. В соответствии с рис. 9.4, а входной сигнал адаптивного фильтра совпадает с входным сигналом исследуемой системы (x), а образцовый сигнал — это выходной сигнал системы (y):
>>[y_lms, e_lms] = filter(ha_lms, x, y); % фильтрация LMS-фильтром
>>[y_rls, e_rls] = filter(ha_rls, x, y); % фильтрация RLS-фильтром
Построим для обоих фильтров графики зависимости сигнала ошибки от времени, а также выведем на экран их импульсные характеристики, полученные на момент завершения обработки сигнала (рис. 9.11):
>>subplot(2,2,1)
>>plot(e_lms)
>>title(‘LMS error’)
>>subplot(2,2,2)
>>impz(ha_lms.coefficients)
>>title(‘LMS impulse response’)
>>subplot(2,2,3)
>>plot(e_rls)
>>title(‘RLS error’)
>>subplot(2,2,4)
>>impz(ha_rls.coefficients)
>>title(‘RLS impulse response’)
|
LMS error |
|||||||||||
|
4 |
1 |
||||||||||
|
2 |
0.5 |
||||||||||
|
0 |
|||||||||||
|
0 |
|||||||||||
|
-2 |
|||||||||||
|
-4 |
-0.5 |
||||||||||
|
-6 |
-1 |
||||||||||
|
0 |
200 |
400 |
600 |
800 |
1000 |
1200 |
1400 |
1600 |
1800 |
2000 |
0 |
|
RLS error |
|||||||||||
|
10 |
0.04 |
||||||||||
|
5 |
0.02 |
||||||||||
|
0 |
0 |
||||||||||
|
-5 |
-0.02 |
||||||||||
|
-10 |
-0.04 |
||||||||||
|
0 |
200 |
400 |
600 |
800 |
1000 |
1200 |
1400 |
1600 |
1800 |
2000 |
0 |
LMS impulse response
n (samples) RLS impulse response
Рис. 9.11. Результаты идентификации системы с помощью адаптивных алгоритмов LMS (сверху) и RLS (снизу): слева — зависимость ошибки от времени,
справа — итоговые импульсные характеристики фильтров
Полученные результаты наглядно демонстрируют основные особенности LMS- и RLS-алгоритмов. На начальном этапе RLS-алгоритм показал отсутствие скольконибудь заметного переходного процесса и меньшую (по сравнению с LMSалгоритмом) ошибку в установившемся режиме. Однако после скачкообразного изменения характеристик системы RLS-алгоритм так и не смог приспособиться
к новым условиям, тогда как LMS-фильтр после некоторого переходного процесса свел ошибку фильтрации к тому же уровню, который она имела раньше.
Сказанному соответствуют и итоговые импульсные характеристики фильтров (см. рис. 9.11, справа) — характеристика LMS-фильтра хорошо совпадает с экспоненциально затухающими колебаниями импульсной характеристики анализируемой системы, а характеристика RLS-фильтра выглядит абсолютно случайным набором значений.
ЗАМЕЧАНИЕ
В данном примере не использовалось экспоненциальное забывание, дающее RLSалгоритму возможность отслеживать изменения статистических свойств обрабатываемого сигнала. Чтобы использовать забывание, полю ForgettingFactor объекта RLS-фильтра в данном примере необходимо присвоить значение, меньшее единицы.
Линейное предсказание
Реализуем с помощью RLS-фильтра линейное предсказание сигнала, сформированного с помощью авторегрессионной модели. В качестве коэффициентов модели используем знаменатель фильтра Баттерворта 8-го порядка с частотой среза, равной 0,3 от частоты Найквиста:
|
>> [b, a] = butter(8, 0.3); |
% фильтр Баттерворта |
|
>> b = 1; |
% оставляем только знаменатель |
|
>> x = randn(1000, 1); |
% входной сигнал АР-модели |
|
>> y = filter(b, a, x); |
% формирование сигнала |
>>ha = adaptfilt.rls(16); % создание RLS-фильтра
>>% линейное предсказание с помощью адаптивного фильтра
>>[y1, e] = filter(ha, y(1:end-1), y(2:end));
>>subplot(2, 2, 1)
|
>> impz(a) |
% коэффициенты АР-модели |
|
>> subplot(2, 2, 2) |
|
|
>> impz(ha.coefficients) |
% имп. х-ка адаптивного фильтра |
|
>> subplot(2, 1, 2) |
|
|
>> plot(e) |
% ошибка фильтрации |
Результаты работы программы показаны на рис. 9.12. Видно, что коэффициенты адаптивного фильтра совпадают с коэффициентами использованной авторегрессионной модели (при сравнении верхних графиков на рис. 9.12 следует учесть, что первый элемент вектора a, равный единице, не входит в число коэффициентов модели; кроме того, коэффициенты модели и коэффициенты предсказывающего фильтра имеют разные знаки (см. рис. 5.13 в главе 5)). На нижнем графике рис. 9.12, демонстрирующем поведение ошибки фильтрации во времени, хорошо видно, что после начального переходного процесса устанавливается стационарный режим работы. Согласно идее линейного предсказания (см. разд. «Авторегрессионная модель» главы 5), сигнал ошибки фильтрации при этом является оценкой белого шума, возбуждающего авторегрессионную модель.

|
620 |
Глава 9 |
|||||||||||||
|
Impulse Response |
Impulse Response |
|||||||||||||
|
10 |
10 |
|||||||||||||
|
5 |
5 |
|||||||||||||
|
0 |
0 |
|||||||||||||
|
-5 |
-5 |
|||||||||||||
|
-10 |
-10 |
|||||||||||||
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
0 |
5 |
10 |
15 |
||
|
n (samples) |
n (samples) |
|||||||||||||
|
20 |
||||||||||||||
|
10 |
||||||||||||||
|
0 |
||||||||||||||
|
-10 |
||||||||||||||
|
-20 |
||||||||||||||
|
0 |
100 |
200 |
300 |
400 |
500 |
600 |
700 |
800 |
900 |
1000 |
||||
|
Рис. 9.12. Линейное предсказание с помощью адаптивного фильтра: |
||||||||||||||
|
сверху — коэффициенты авторегрессионной модели (слева) и итоговая импульсная |
||||||||||||||
|
характеристика адаптивного фильтра (справа), |
||||||||||||||
|
снизу — зависимость ошибки фильтрации от времени |
Шумоподавление
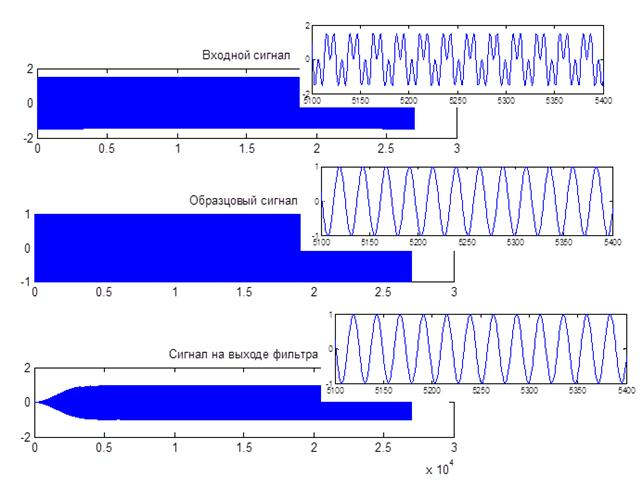
Для демонстрации шумоподавления используем входящий в состав поставки MATLAB файл mtlb.mat, в котором содержатся запись произнесенного слова «MATLAB» (переменная mtlb) и частота дискретизации данного сигнала (переменная Fs). Речевой сигнал является очень коротким, поэтому повторим его 10 раз с помощью функции repmat (график одного периода исходного речевого сигнала показан на рис. 9.13, сверху):
|
>> load mtlb |
% загрузка данных |
>>s = repmat(mtlb, 10, 1); % 10-кратное повторение сигнала
>>subplot(3, 1, 1)
>>plot(s(1:length(mtlb))) % график сигнала
Можно также прослушать исходный звук с помощью функции soundsc:
>> soundsc(s, Fs)
Теперь сформируем дискретный белый шум и пропустим его через два фильтра, чтобы получить коррелированные случайные сигналы. В данном эксперименте мы используем нерекурсивные фильтры первого порядка, один из которых будет вычислять сумму, а другой — разность пары соседних отсчетов. Эти фильтры являются простейшими ФНЧ и ФВЧ соответственно:
|
>> noise = randn(length(s), 1); |
% дискретный белый шум |
>>noise1 = filter([1 1], 1, noise); % шум, пропущенный через ФНЧ
>>noise2 = filter([1 -1], 1, noise); % шум, пропущенный через ФВЧ
Шум noise1 мы добавим к речевому сигналу. На графике (см. рис. 9.13, в центре) видно, что полезный сигнал визуально не выделяется над шумом:

>>sn = s + noise1; % добавляем шум к сигналу
>>subplot(3, 1, 2)
>>plot(sn(1:length(mtlb))) % график зашумленного сигнала
Воспроизведение зашумленного звука показывает, что и на слух полезный сигнал разобрать нельзя:
>> soundsc(sn, Fs)
Теперь создадим объект адаптивного фильтра длины 16, использующего алгоритм RLS, и в соответствии с рис. 9.6 подадим на вход фильтра шумовой сигнал noise2, использовав в качестве образцового зашумленный полезный сигнал sn:
>>ha1 = adaptfilt.rls(16);
>>[y, e] = filter(ha1, noise2, sn);
Полученный сигнал ошибки e представляет собой очищенный от шума полезный сигнал (график одного его периода показан на рис. 9.13, снизу):
>>subplot(3, 1, 3)
>>plot(e(1:length(mtlb)))
>>ylim([-5 5])
На рисунке хорошо видно, что сигнал ошибки визуально весьма близок к полезному сигналу, показанному на верхнем графике. Воспроизведем получившийся звук:
>> soundsc(e, Fs)
|
Прослушивание показывает, что остаточный шум все равно присутствует, но слова |
|||||||||
|
разбираются без труда. |
|||||||||
|
5 |
|||||||||
|
0 |
|||||||||
|
-5 |
|||||||||
|
0 |
500 |
1000 |
1500 |
2000 |
2500 |
3000 |
3500 |
4000 |
4500 |
|
10 |
|||||||||
|
0 |
|||||||||
|
-10 |
|||||||||
|
0 |
500 |
1000 |
1500 |
2000 |
2500 |
3000 |
3500 |
4000 |
4500 |
|
5 |
|||||||||
|
0 |
|||||||||
|
-5 |
|||||||||
|
0 |
500 |
1000 |
1500 |
2000 |
2500 |
3000 |
3500 |
4000 |
4500 |
Рис. 9.13. Исходный сигнал (сверху), зашумленный сигнал (в центре) и сигнал, очищенный от шума с помощью адаптивного фильтра (снизу)
Завершая рассмотрение данного примера, следует отметить, что сигнал был более чем в четыре раза (более чем на 6 дБ) слабее по мощности, чем шум:
>> 10*log10(var(s)/var(noise1)) % отношение С/Ш в децибелах ans =
-6.6026
Компенсация искажений, вносимых каналом связи
В качестве примера реализуем адаптивную коррекцию искажений, вносимых в сигнал тем же каналом связи, что использовался в примере расчета фильтра Винера. При этом сравним качество работы четырех версий алгоритма LMS — классического варианта и трех вариантов с использованием знаковых преобразований. Чтобы более наглядно показать результат компенсации, в качестве входного используем четырехуровневый цифровой сигнал, равновероятно и независимо принимающий значения –3, –1, 1 и 3. Код соответствующей MATLAB-программы приведен далее.
h = [-2 -4 6 3]; % импульсная характеристика канала связи
|
% генерация сигнала |
||
|
NX = 4000; |
% число отсчетов |
|
|
levels = [-3 -1 1 3]; |
% возможные уровни исходного сигнала |
|
|
x = randsrc(NX, 1, levels); |
% случайный сигнал |
|
|
y = conv(x, h); |
% искаженный сигнал |
|
|
N = 32; |
% длина адаптивного фильтра |
|
|
mu = 1/var(levels, 1)/sum(h.^2)/N; % размер шага для LMS |
||
|
% создание объектов |
||
|
ha_lms |
= adaptfilt.lms(N, mu); |
ha_lms_se = adaptfilt.se(N, mu/10);
ha_lms_sd = adaptfilt.sd(N, mu); ha_lms_ss = adaptfilt.ss(N, mu);
y = y(round(N/2)+1:end); % задержка фильтрации
[x, y] = eqtflength(x, y); % выравнивание длин векторов x и y % адаптивная фильтрация
[x1_lms, e_lms] = filter(ha_lms, y(1:1000), x(1:1000)); [x1_lms_se, e_lms_se] = filter(ha_lms_se, y, x); [x1_lms_sd, e_lms_sd] = filter(ha_lms_sd, y, x); [x1_lms_ss, e_lms_ss] = filter(ha_lms_ss, y, x);
% вывод графиков
subplot(4,2,1), plot(e_lms), title(‘LMS’) subplot(4,2,2), plot(x1_lms,’.’)
subplot(4,2,3), plot(e_lms_se), title(‘LMS — sign error’) subplot(4,2,4), plot(x1_lms_se,’.’)
subplot(4,2,5), plot(e_lms_sd), title(‘LMS — sign data’) subplot(4,2,6), plot(x1_lms_sd,’.’)
subplot(4,2,7), plot(e_lms_ss), title(‘LMS — sign sign’) subplot(4,2,8), plot(x1_lms_ss,’.’)
На рис. 9.14 показаны результаты работы программы. В левом столбце — зависимость сигнала ошибки от номера шага, в правом — график выходного сигнала

фильтра. Видно, что использование знаковых преобразований замедляет сходимость LMS-алгоритма (пришлось даже увеличить число отображаемых итераций с 1000 до 4000). В наименьшей степени сходимость замедляется при знаковом преобразовании сигнала ошибки (sign error), в наибольшей — при одновременном знаковом преобразовании сигнала ошибки и содержимого линии задержки фильтра (sign sign). Вариант со знаковым преобразованием только содержимого линии задержки (sign data) занимает промежуточное положение. Кроме того, предельное значение µ для знаковых вариантов сильно зависит от масштаба уровней образцового и входного сигналов. Так, в данном примере пришлось в 10 раз уменьшить значение µ для варианта со знаковым преобразованием сигнала ошибки.
|
LMS |
||||||||||
|
5 |
||||||||||
|
0 |
||||||||||
|
-5 |
||||||||||
|
0 |
100 |
200 |
300 |
400 |
500 |
600 |
700 |
800 |
900 |
1000 |
|
LMS — sign error |
|
4 |
||||||||
|
2 |
||||||||
|
0 |
||||||||
|
-2 |
||||||||
|
-4 |
||||||||
|
0 |
500 |
1000 |
1500 |
2000 |
2500 |
3000 |
3500 |
4000 |
|
LMS — sign data |
|
4 |
||||||||
|
2 |
||||||||
|
0 |
||||||||
|
-2 |
||||||||
|
-4 |
||||||||
|
0 |
500 |
1000 |
1500 |
2000 |
2500 |
3000 |
3500 |
4000 |
|
LMS — sign sign |
|
4 |
||||||||
|
2 |
||||||||
|
0 |
||||||||
|
-2 |
||||||||
|
-4 |
||||||||
|
0 |
500 |
1000 |
1500 |
2000 |
2500 |
3000 |
3500 |
4000 |
|
4 |
||||||||||||
|
2 |
||||||||||||
|
0 |
||||||||||||
|
-2 |
||||||||||||
|
-4 |
||||||||||||
|
0 |
100 |
200 |
300 |
400 |
500 |
600 |
700 |
800 |
900 |
1000 |
||
|
4 |
||||||||||||
|
2 |
||||||||||||
|
0 |
||||||||||||
|
-2 |
||||||||||||
|
-4 |
||||||||||||
|
0 |
500 |
1000 |
1500 |
2000 |
2500 |
3000 |
3500 |
4000 |
||||
|
4 |
||||||||||||
|
2 |
||||||||||||
|
0 |
||||||||||||
|
-2 |
||||||||||||
|
-4 |
||||||||||||
|
0 |
500 |
1000 |
1500 |
2000 |
2500 |
3000 |
3500 |
4000 |
||||
|
4 |
||||||||||||
|
2 |
||||||||||||
|
0 |
||||||||||||
|
-2 |
||||||||||||
|
-4 |
||||||||||||
|
0 |
500 |
1000 |
1500 |
2000 |
2500 |
3000 |
3500 |
4000 |
Рис. 9.14. Компенсация искажений, вносимых каналом связи, с помощью различных вариантов LMS-алгоритма: слева — ошибка фильтрации, справа — выходной сигнал
Шум при измерениях
Шум можно условно разделить на два типа: постоянный шум датчика с одинаковым отклонением (скриншот 1), и случайный шум, который возникает при различных случайных (чаще всего внешних) обстоятельствах (скриншот 2). 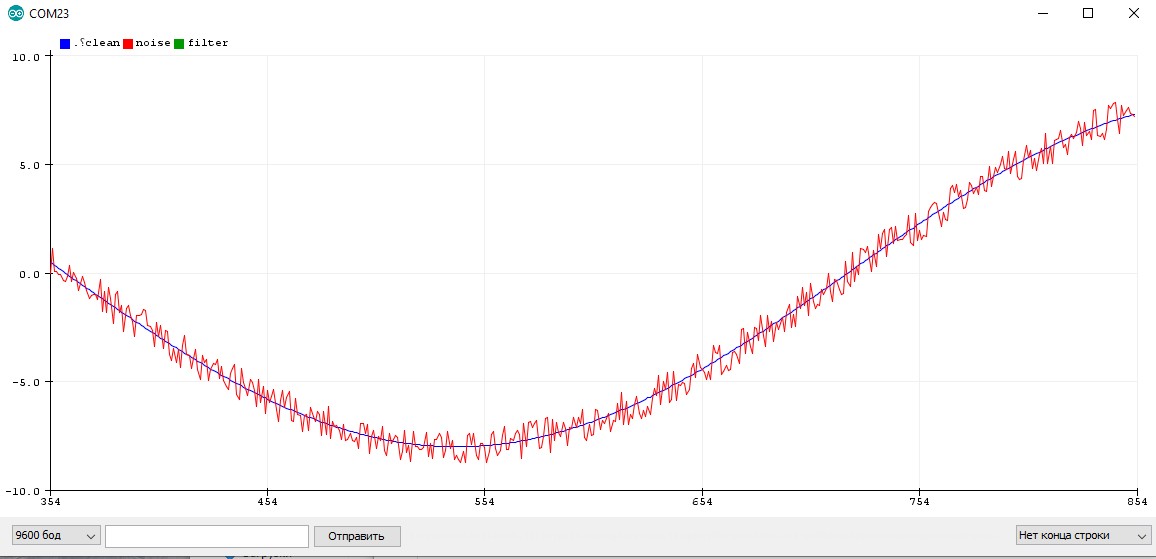
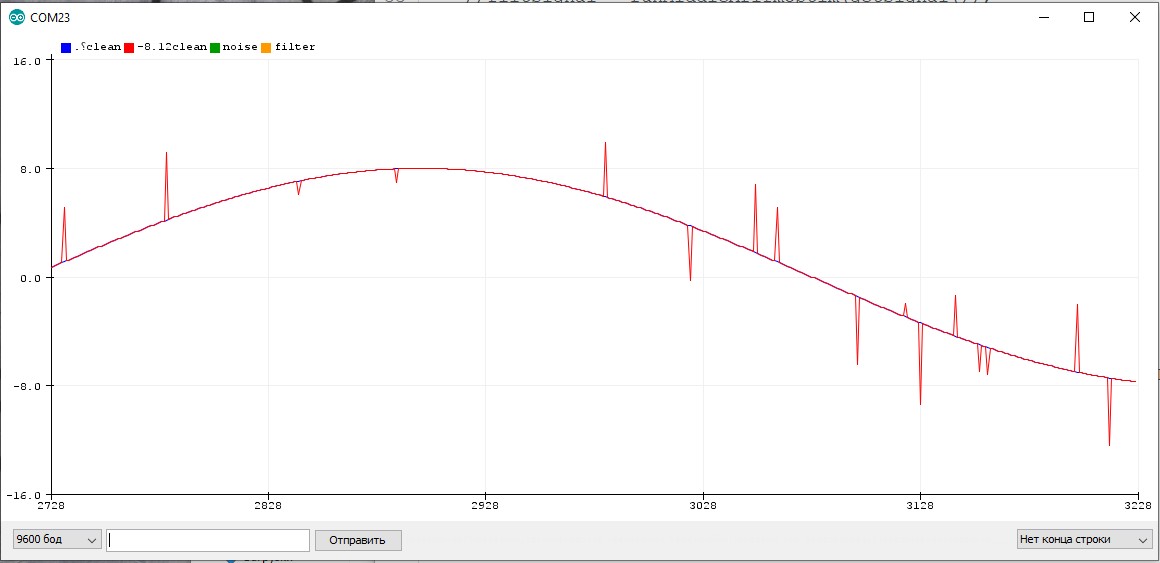
Измерение значений
Давайте посмотрим, как измеряется сигнал в реальном устройстве. Естественно это происходит не каждую итерацию loop, а например по какому то таймеру. Представим что синий график отражает реальный процесс, а красный – измеренное значение с некоторым периодом. 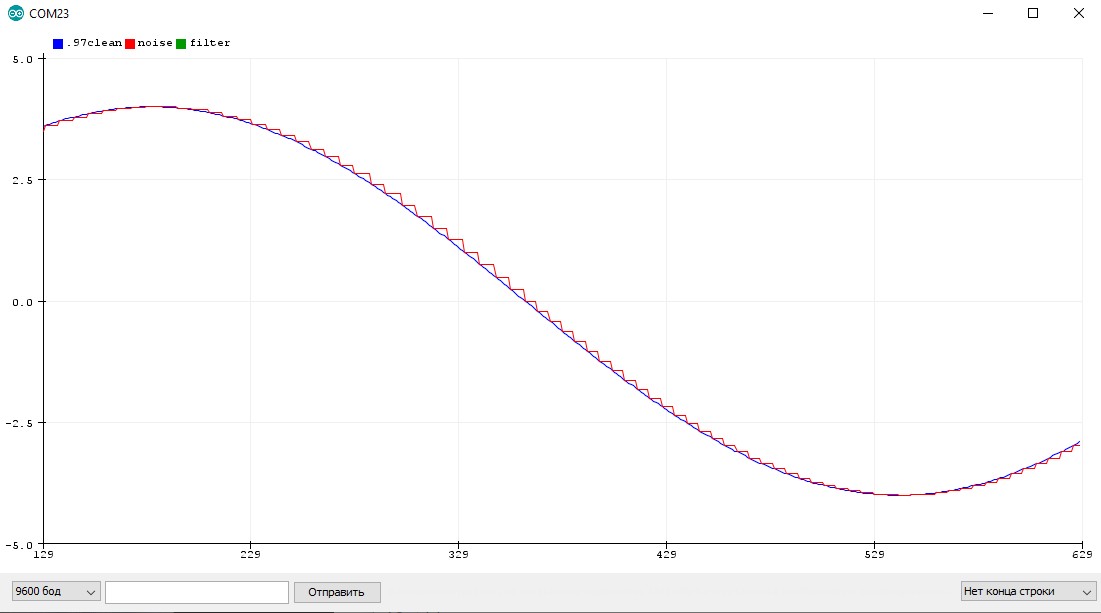
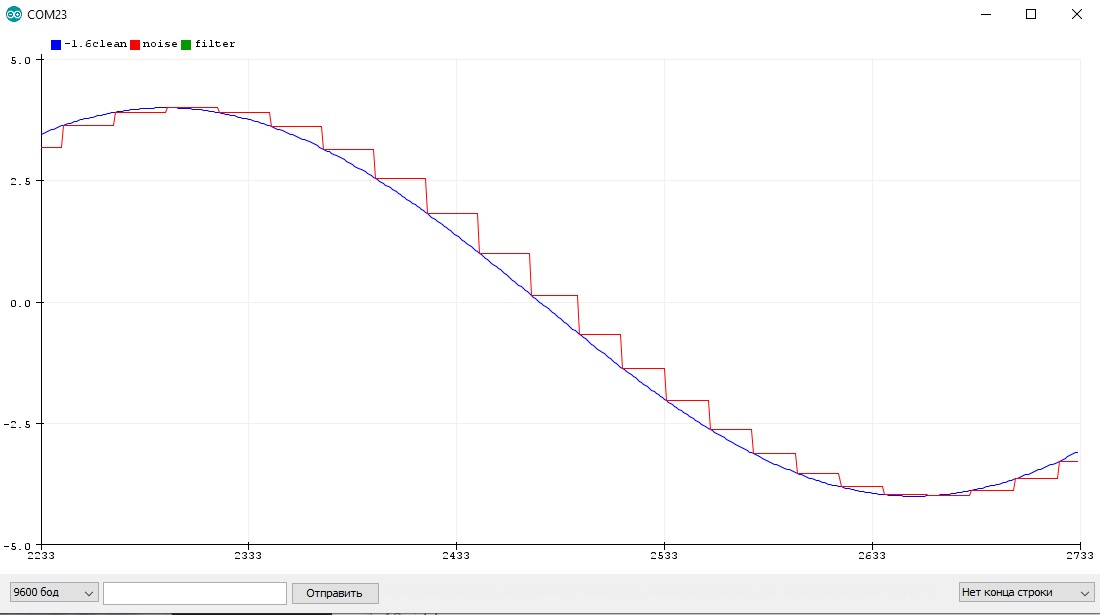
Фильтры
Цифровые (программные) фильтры позволяют отфильтровать различные шумы. В следующих примерах будут показаны некоторые популярные фильтры. Все примеры оформлены как фильтрующая функция, которой в качестве параметра передаётся новое значение, и функция возвращает фильтрованную величину. Некоторым функциям нужны дополнительные настройки, которые вынесены как переменные. Важно: практически каждый фильтр можно настроить лучше, чем показано на примерах с графиками. На примерах фильтр специально настроен не идеально, чтобы можно было оценить особенность работы алгоритма каждого из фильтров.
Среднее арифметическое
Однократная выборка
Среднее арифметическое вычисляется как сумма значений, делённая на их количество. Первый алгоритм именно так и работает: в цикле суммируем всё в какую-нибудь переменную, потом делим на количество измерений. Вуаля!
const int NUM_READ = 30; // количество усреднений для средних арифм. фильтров
// обычное среднее арифметическое для float
float midArifm() {
float sum = 0; // локальная переменная sum
for (int i = 0; i < NUM_READ; i++) // согласно количеству усреднений
sum += значение; // суммируем значения с любого датчика в переменную sum
return (sum / NUM_READ);
}
// обычное среднее арифметическое для int
int midArifm() {
long sum = 0; // локальная переменная sum
for (int i = 0; i < NUM_READ; i++) // согласно количеству усреднений
sum += значение; // суммируем значения с любого датчика в переменную sum
return ((float)sum / NUM_READ);
}
Особенности использования
- Отлично усредняет шум любого характера и величины
- Для целочисленных значений количество измерений есть смысл брать из степеней двойки (2, 4, 8, 16, 32…) тогда компилятор оптимизирует деление в сдвиг, который выполняется в сотню раз быстрее. Это если вы совсем гонитесь за оптимизацией выполнения кода
- “Сила” фильтра настраивается размером выборки (NUM_READS)
- Делает несколько измерений за один раз, что может приводить к большим затратам времени!
- Рекомендуется использовать там, где время одного измерения ничтожно мало, или измерения в принципе делаются редко
Растянутая выборка
Отличается от предыдущего тем, что суммирует несколько измерений, и только после этого выдаёт результат. Между расчётами выдаёт предыдущий результат:
const int NUM_READ = 10; // количество усреднений для средних арифм. фильтров
// растянутое среднее арифметическое
float midArifm2(float newVal) {
static byte counter = 0; // счётчик
static float prevResult = 0; // хранит предыдущее готовое значение
static float sum = 0; // сумма
sum += newVal; // суммируем новое значение
counter++; // счётчик++
if (counter == NUM_READ) { // достигли кол-ва измерений
prevResult = sum / NUM_READ; // считаем среднее
sum = 0; // обнуляем сумму
counter = 0; // сброс счётчика
}
return prevResult;
}
Примечание: это просто пример, функция статически хранит предыдущие данные “в себе”. Реализация в реальном коде может отличаться.
Особенности использования
- Отлично усредняет шум любого характера и величины
- “Сила” фильтра настраивается размером выборки (NUM_READS)
- Для целочисленных значений количество измерений есть смысл брать из степеней двойки (2, 4, 8, 16, 32…) тогда компилятор оптимизирует деление в сдвиг, который выполняется в сотню раз быстрее. Это если вы совсем гонитесь за оптимизацией выполнения кода
- Делает только одно измерение за раз, не блокирует код на длительный период
- Рекомендуется использовать там, где сам сигнал изменяется медленно, потому что за счёт растянутой по времени выборки сигнал может успеть измениться
Бегущее среднее арифметическое
Данный алгоритм работает по принципу буфера, в котором хранятся несколько последних измерений для усреднения. При каждом вызове фильтра буфер сдвигается, в него добавляется новое значение и убирается самое старое, далее буфер усредняется по среднему арифметическому. Есть два варианта исполнения: понятный и оптимальный:
const int NUM_READ = 10; // количество усреднений для средних арифм. фильтров
// бегущее среднее арифметическое
float runMiddleArifm(float newVal) { // принимает новое значение
static byte idx = 0; // индекс
static float valArray[NUM_READ]; // массив
valArray[idx] = newVal; // пишем каждый раз в новую ячейку
if (++idx >= NUM_READ) idx = 0; // перезаписывая самое старое значение
float average = 0; // обнуляем среднее
for (int i = 0; i < NUM_READ; i++) {
average += valArray[i]; // суммируем
}
return (float)average / NUM_READ; // возвращаем
}
// оптимальное бегущее среднее арифметическое
float runMiddleArifmOptim(float newVal) {
static int t = 0;
static float vals[NUM_READ];
static float average = 0;
if (++t >= NUM_READ) t = 0; // перемотка t
average -= vals[t]; // вычитаем старое
average += newVal; // прибавляем новое
vals[t] = newVal; // запоминаем в массив
return ((float)average / NUM_READ);
}
Примечание: это просто пример, функция статически хранит предыдущие данные “в себе”. Реализация в реальном коде может отличаться.
Особенности использования
- Усредняет последние N измерений, за счёт чего значение запаздывает. Нуждается в тонкой настройке частоты опроса и размера выборки
- Для целочисленных значений количество измерений есть смысл брать из степеней двойки (2, 4, 8, 16, 32…) тогда компилятор оптимизирует деление в сдвиг, который выполняется в сотню раз быстрее. Это если вы совсем гонитесь за оптимизацией выполнения кода
- “Сила” фильтра настраивается размером выборки (NUM_READS)
- Делает только одно измерение за раз, не блокирует код на длительный период
- Данный фильтр показываю чисто для ознакомления, в реальных проектах лучше использовать бегущее среднее. О нём ниже
Экспоненциальное бегущее среднее
Бегущее среднее (Running Average) – самый простой и эффективный фильтр значений, по эффекту аналогичен предыдущему, но гораздо оптимальнее в плане реализации фильтрованное += (новое - фильтрованное) * коэффициент:
float k = 0.1; // коэффициент фильтрации, 0.0-1.0
// бегущее среднее
float expRunningAverage(float newVal) {
static float filVal = 0;
filVal += (newVal - filVal) * k;
return filVal;
}
Примечание: это просто пример, функция статически хранит предыдущие данные “в себе”. Реализация в реальном коде может отличаться.
Особенности использования
- Самый лёгкий, быстрый и простой для вычисления алгоритм! В то же время очень эффективный
- “Сила” фильтра настраивается коэффициентом (0.0 – 1.0). Чем он меньше, тем плавнее фильтр
- Делает только одно измерение за раз, не блокирует код на длительный период
- Чем чаще измерения, тем лучше работает
- При маленьких значениях коэффициента работает очень плавно, что также можно использовать в своих целях
Вот так бегущее среднее справляется с равномерно растущим сигналом + случайные выбросы. Синий график – реальное значение, красный – фильтрованное с коэффициентом 0.1, зелёное – коэффициент 0.5.
Пример с шумящим синусом
Пример с шумным квадратным сигналом, на котором видно запаздывание фильтра:
Адаптивный коэффициент
Чтобы бегущее среднее корректно работало с резко изменяющимися сигналами, коэффициент можно сделать адаптивным, чтобы он подстраивался под резкие изменения значения, например так: если фильтрованное значение “далеко” от реального – коэффициент резко увеличивается, позволяя быстро сократить “разрыв” между величинами. Если значение “близко” – коэффициент ставится маленьким, чтобы хорошо фильтровать шум:
// бегущее среднее с адаптивным коэффициентом
float expRunningAverageAdaptive(float newVal) {
static float filVal = 0;
float k;
// резкость фильтра зависит от модуля разности значений
if (abs(newVal - filVal) > 1.5) k = 0.9;
else k = 0.03;
filVal += (newVal - filVal) * k;
return filVal;
}
Таким образом даже простейший фильтр можно “программировать” и делать более умным. В этом и заключается прелесть программирования!
Простой пример
Покажу отдельный простой пример реальной работы фильтра бегущее среднее, как самого часто используемого. Остальные фильтры – по аналогии. Фильтровать будем сигнал с аналогового пина А0:
void setup() {
Serial.begin(9600);
Serial.println("raw , filter");
}
float filtVal = 0;
void loop() {
int newVal = analogRead(0);
filtVal += (newVal - filtVal) * 0.1;
Serial.print(newVal);
Serial.print(',');
Serial.println(filtVal);
delay(10);
}
Код выводит в порт реальное и фильтрованное значение. Можно подключить к А0 потенциометр и покрутить его, наблюдая за графиком.
Целочисленная реализация
Для экономии ресурсов МК (поддержка дробных чисел требует пару килобайт Flash) можно отказаться от float и сделать фильтр целочисленным, для этого все переменные будут целого типа, а вместо умножения на дробный коэффициент будем делить на целое число, например fil += (val - fil) / 10 – получим фильтр с коэффициентом 0.1. Если вы читали урок по оптимизации кода, то знаете, что умножение на float быстрее деления на целое число! Не беда, всегда можно заменить деление сдвигом. Например фильтр с коэффициентом 1/16 можно записать так: fil += (val - fil) >> 4. Оптимизировать получится коэффициенты, кратные “степени двойки”, то есть 1/2, 1/4, 1/8 и так далее.
Но есть один неприятный момент: в реализации с float у нас в распоряжении огромная точность вычислений и максимальная плавность фильтра, фильтрованное значение со временем полностью совпадёт с текущим. В целочисленной же реализации точность будет ограничена коэффициентом: если разность в скобках (фильтрованное – текущее) будет меньше делителя – переменная фильтра не изменится, так как к ней будет прибавляться 0! Простой пример: float и целочисленный фильтры “фильтруют” величину от значения 1000 к значению 100 с коэффициентом 0.1 (используем число 10 для наглядности):
fu += (val - fu) / 10; ff += (val - ff) * 0.1;
Посмотрим графики:
Где синий график – целочисленный фильтр, красный – float. Из графика видно, что фильтры работают +- одинаково, но вот целочисленный резко остановился на значении 109, как и ожидалось: в уравнении фильтра получается (100 – 109) / 10, что даёт 0 и переменная фильтра больше не меняется. Таким образом точность фильтра определяется делителем коэффициента. Поэтому при использовании целочисленной реализации нужно подумать о двух вещах:
- Либо порядок фильтруемых величин у нас такой, что точность +- делитель не критична
- Либо искусственно повышаем разрядность фильтра следующим образом: переменная фильтра хранит увеличенное значение, и текущее значение мы для вычислений тоже домножаем, а при получении результата – делим, например:
fu += (val * 16 - fu) / 10; Serial.print(fu / 16);
Или на сдвигах:
fu += ((val << 4) - fu) / 10; Serial.print(fu >> 4);
Таким образом переменная фильтра хранит наше число с 16 кратной точностью, что позволяет в 16 раз увеличить плавность фильтра на критическом участке.
Не забываем, что сдвиг может переполнить два байта и вычисление будет неправильным. Можно заранее прикинуть и подбирать коэффициенты так, чтобы не превышать 2 байта в вычислениях, либо приводить к uint32_t.
fu += (uint32_t)(((uint32_t)val << 4) - fu) >> 5; Serial.print(fu >> 4);
Ещё целочисленные варианты
На сайте easyelectronics есть отличная статья по целочисленным реализациям, давайте коротко их рассмотрим.
Вариант 1
Фильтр не имеет настроек, состоит из сложения и двух сдвигов, выполняется моментально. По сути это среднее арифметическое, или же рассмотренный выше фильтр с коэффициентом 1/2.
filt = (filt >> 1) + (signal >> 1);
Вариант 2
filt = (A * filt + B * signal) >> k;
Коэффициенты у этого фильтра выбираются следующим образом:
- k = 1, 2, 3…
- A + B = 2^k
- Чем больше А, тем плавнее фильтр (отношение A/B)
- Чем больше k, тем более плавным можно сделать фильтр. Но больше 5 уже нет смысла, т.к. A=31, B=1 уже очень плавно, а при увеличении может переполниться int и придётся использовать 32-х битные типы данных.
- Результат умножения не должен выходить за int, иначе придётся преобразовывать к long
- Более подробно о выборе коэффициентов читайте в статье, ссылка выше
- Особенность: если “ошибка” сигнала (signal – filter) меньше 2^k – фильтрованное значение меняться не будет. Для повышения “разрешения” фильтра можно домножить (или сдвинуть) переменную фильтра, то есть фильтровать в бОльших величинах
Например k = 4, значит A+B = 16. Хотим плавный фильтр, принимаем A=14, B=16: filt = (14 * filt + 2 * signal) >> 4;
Вариант 3
Третий алгоритм вытекает из второго: коэффициент B принимаем равным 1 и экономим одно умножение: filt = (A * filt + signal) >> k;
Тогда коэффициенты выбираются так:
- k = 1, 2, 3…
- A = (2^k) – 1
- [k=2 A=3], [k=3 A=7], [k=4 A=15], [k=5 A=31]…
- Чем больше k, тем плавнее фильтр
Медианный фильтр
Медианный фильтр тоже находит среднее значение, но не усредняя, а выбирая его из представленных. Алгоритм для медианы 3-го порядка (выбор из трёх значений) выглядит так:
int middle;
if ((a <= b) && (a <= c)) middle = (b <= c) ? b : c;
else {
if ((b <= a) && (b <= c)) middle = (a <= c) ? a : c;
else middle = (a <= b) ? a : b;
}
// тут middle - ваша медиана
Мой постоянный читатель Андрей Степанов предложил сокращённую версию этого алгоритма, которая занимает одну строку кода и выполняется чуть быстрее за счёт меньшего количества сравнений:
middle = (a < b) ? ((b < c) ? b : ((c < a) ? a : c)) : ((a < c) ? a : ((c < b) ? b : c));
Можно ещё визуально сократить за счёт использования функций min() и max():
middle = (max(a,b) == max(b, c)) ? max(a, c) : max(b, min(a, c));
Для удобства использования можно сделать функцию, которая будет хранить в себе буфер на последние три значения и автоматически добавлять в него новые:
// медиана на 3 значения со своим буфером
int median(int newVal) {
static int buf[3];
static byte count = 0;
buf[count] = newVal;
if (++count >= 3) count = 0;
return (max(buf[0], buf[1]) == max(buf[1], buf[2])) ? max(buf[0], buf[2]) : max(buf[1], min(buf[0], buf[2]));
}
Большое преимущество медианного фильтра заключается в том, что он ничего не вычислят, а просто сравнивает числа. Это делает его быстрее фильтров других типов!
Медиана для большего окна значений описывается весьма внушительным алгоритмом, но я предлагаю пару более оптимальных вариантов:
Медиана для N значений лёгкая
// облегчённый вариант медианы для N значений
// предложен Виталием Емельяновым, доработан AlexGyver
// фильтр лёгкий с точки зрения кода и памяти, но выполняется долго
// возвращает медиану по последним NUM_READ вызовам
#define NUM_READ 10
int findMedianN(int newVal) {
static int buffer[NUM_READ]; // статический буфер
static byte count = 0; // счётчик
buffer[count] = newVal;
if (++count >= NUM_READ) count = 0; // перемотка буфера
int buf[NUM_READ]; // локальный буфер для медианы
for (byte i = 0; i < NUM_READ; i++) buf[i] = buffer[i];
for (int i = 0; i <= (int) ((NUM_READ / 2) + 1); i++) { // пузырьковая сортировка массива (можно использовать любую)
for (int m = 0; m < NUM_READ - i - 1; m++) {
if (buf[m] > buf[m + 1]) {
int buff = buf[m];
buf[m] = buf[m + 1];
buf[m + 1] = buff;
}
}
}
int ans = 0;
if (NUM_READ % 2 == 0) { // кол-во элементов в массиве четное (NUM_READ - последний индекс массива)
ans = buf[(int) (NUM_READ / 2)]; // берем центральное
} else {
ans = (buf[(int) (NUM_READ / 2)] + buf[((int) (NUM_READ / 2)) + 1]) / 2; // берем среднее от двух центральных
}
return ans;
}
Медиана для N значений лёгкая оптимальная
// облегчённый вариант медианы для N значений
// предложен Виталием Емельяновым, доработан AlexGyver
// возвращает медиану по последним NUM_READ вызовам
// НАВЕРНОЕ ЛУЧШИЙ ВАРИАНТ!
#define NUM_READ 10 // порядок медианы
// медиана на N значений со своим буфером, ускоренный вариант
float findMedianN_optim(float newVal) {
static float buffer[NUM_READ]; // статический буфер
static byte count = 0;
buffer[count] = newVal;
if ((count < NUM_READ - 1) and (buffer[count] > buffer[count + 1])) {
for (int i = count; i < NUM_READ - 1; i++) {
if (buffer[i] > buffer[i + 1]) {
float buff = buffer[i];
buffer[i] = buffer[i + 1];
buffer[i + 1] = buff;
}
}
} else {
if ((count > 0) and (buffer[count - 1] > buffer[count])) {
for (int i = count; i > 0; i--) {
if (buffer[i] < buffer[i - 1]) {
float buff = buffer[i];
buffer[i] = buffer[i - 1];
buffer[i - 1] = buff;
}
}
}
}
if (++count >= NUM_READ) count = 0;
return buffer[(int)NUM_READ / 2];
}
Особенности использования
- Медиана отлично фильтрует резкие изменения значения
- Делает только одно измерение за раз, не блокирует код на длительный период
- Алгоритм “больше трёх” весьма громоздкий
- Запаздывает на половину размерности фильтра

Простой “Калман”
Данный алгоритм я нашёл на просторах Интернета, источник потерял. В фильтре настраивается разброс измерения (ожидаемый шум измерения), разброс оценки (подстраивается сам в процессе работы фильтра, можно поставить таким же как разброс измерения), скорость изменения значений (0.001-1, варьировать самому).
float _err_measure = 0.8; // примерный шум измерений
float _q = 0.1; // скорость изменения значений 0.001-1, варьировать самому
float simpleKalman(float newVal) {
float _kalman_gain, _current_estimate;
static float _err_estimate = _err_measure;
static float _last_estimate;
_kalman_gain = (float)_err_estimate / (_err_estimate + _err_measure);
_current_estimate = _last_estimate + (float)_kalman_gain * (newVal - _last_estimate);
_err_estimate = (1.0 - _kalman_gain) * _err_estimate + fabs(_last_estimate - _current_estimate) * _q;
_last_estimate = _current_estimate;
return _current_estimate;
}
Особенности использования
- Хорошо фильтрует и постоянный шум, и резкие выбросы
- Делает только одно измерение за раз, не блокирует код на длительный период
- Слегка запаздывает, как бегущее среднее
- Подстраивается в процессе работы
- Чем чаще измерения, тем лучше работает
- Алгоритм весьма тяжёлый, вычисление длится ~90 мкс при системной частоте 16 МГц
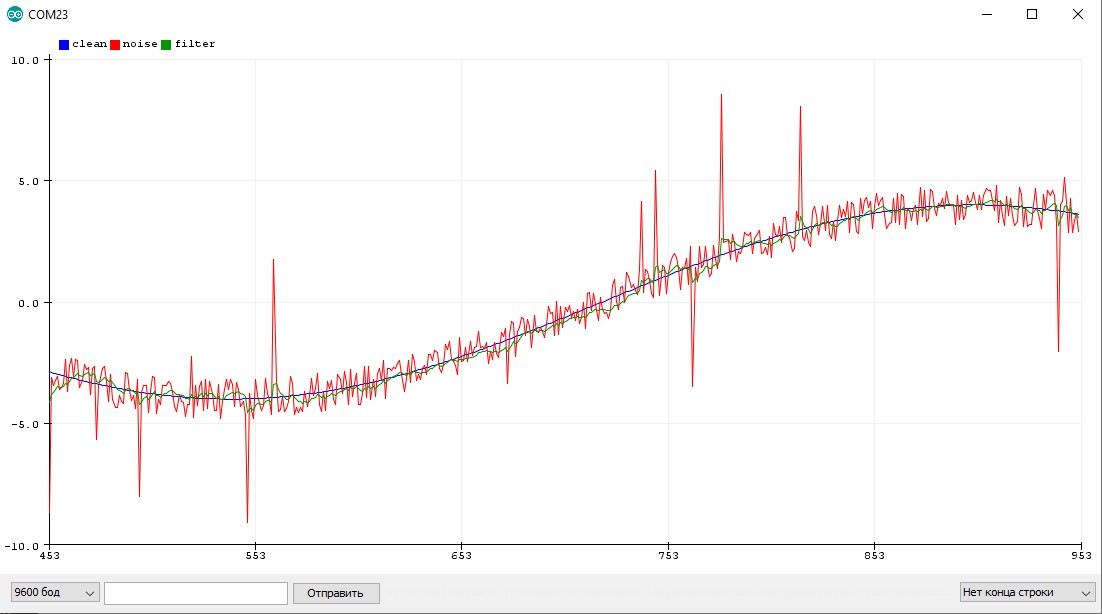
Альфа-Бета фильтр
AB фильтр тоже является одним из видов фильтра Калмана, подробнее можно почитать можно на Википедии.
// период дискретизации (измерений), process variation, noise variation
float dt = 0.02;
float sigma_process = 3.0;
float sigma_noise = 0.7;
float ABfilter(float newVal) {
static float xk_1, vk_1, a, b;
static float xk, vk, rk;
static float xm;
float lambda = (float)sigma_process * dt * dt / sigma_noise;
float r = (4 + lambda - (float)sqrt(8 * lambda + lambda * lambda)) / 4;
a = (float)1 - r * r;
b = (float)2 * (2 - a) - 4 * (float)sqrt(1 - a);
xm = newVal;
xk = xk_1 + ((float) vk_1 * dt );
vk = vk_1;
rk = xm - xk;
xk += (float)a * rk;
vk += (float)( b * rk ) / dt;
xk_1 = xk;
vk_1 = vk;
return xk_1;
}
Особенности использования
- Хороший фильтр, если правильно настроить
- Но очень тяжёлый!
Метод наименьших квадратов
Следующий фильтр позволяет наблюдать за шумным процессом и предсказывать его поведение, называется он метод наименьших квадратов, теорию читаем тут. Чисто графическое объяснение здесь такое: у нас есть набор данных в виде несколько точек. Мы видим, что общее направление идёт на увеличение, но шум не позволяет сделать точный вывод или прогноз. Предположим, что существует линия, сумма квадратов расстояний от каждой точки до которой – минимальна. Такая линия наиболее точно будет показывать реальное изменение среди шумного значения. В какой то статье я нашел алгоритм, который позволяет найти параметры этой линии, опять же портировал на с++ и готов вам показать. Этот алгоритм выдает параметры прямой линии, которая равноудалена от всех точек.
float a, b, delta; // переменные, которые получат значения после вызова minQuad
void minQuad(int *x_array, int *y_array, int arrSize) {
int32_t sumX = 0, sumY = 0, sumX2 = 0, sumXY = 0;
arrSize /= sizeof(int);
for (int i = 0; i < arrSize; i++) { // для всех элементов массива
sumX += x_array[i];
sumY += (long)y_array[i];
sumX2 += x_array[i] * x_array[i];
sumXY += (long)y_array[i] * x_array[i];
}
a = (long)arrSize * sumXY; // расчёт коэффициента наклона прямой
a = a - (long)sumX * sumY;
a = (float)a / (arrSize * sumX2 - sumX * sumX);
b = (float)(sumY - (float)a * sumX) / arrSize;
delta = a * (x_array[arrSize-1] - x_array[0]); // расчёт изменения
}
Особенности использования
- В моей реализации принимает два массива и рассчитывает параметры линии, равноудалённой от всех точек
Какой фильтр выбрать?
Выбор фильтра зависит от типа сигнала и ограничений по времени фильтрации. Среднее арифметическое – хорошо подходит, если фильтрации производятся редко и время одного измерения значения мало. Для большинства ситуаций подходит бегущее среднее, он довольно быстрый и даёт хороший результат на правильной настройке. Медианный фильтр 3-го порядка тоже очень быстрый, но он может только отсеить выбросы, сам сигнал он не сгладит. Медиана большего порядка является довольно более громоздким и долгим алгоритмом, но работает уже лучше. Очень хорошо работает медиана 3 порядка + бегущее среднее, получается сглаженный сигнал с отфильтрованными выбросами (сначала фильтровать медианой, потом бегущим). AB фильтр и фильтр Калмана – отличные фильтры, справляются с шумным сигналом не хуже связки медиана + бегущее среднее, но нуждаются в тонкой настройке, также они довольно громоздкие с точки зрения кода. Линейная аппроксимация – инструмент специального назначения, позволяющий буквально предсказывать поведение значения за период – ведь мы получаем уравнение прямой. Если нужно максимальное быстродействие – работаем только с целыми числами и используем целочисленные фильтры.
Библиотека GyverFilters
Библиотека содержит все описанные выше фильтры в виде удобного инструмента для Arduino. Документацию и примеры к библиотеке можно посмотреть здесь.
- GFilterRA – компактная альтернатива фильтра экспоненциальное бегущее среднее (Running Average)
- GMedian3 – быстрый медианный фильтр 3-го порядка (отсекает выбросы)
- GMedian – медианный фильтр N-го порядка. Порядок настраивается в GyverFilters.h – MEDIAN_FILTER_SIZE
- GABfilter – альфа-бета фильтр (разновидность Калмана для одномерного случая)
- GKalman – упрощённый Калман для одномерного случая (на мой взгляд лучший из фильтров)
- GLinear – линейная аппроксимация методом наименьших квадратов для двух массивов
Видео
Полезные страницы
- Набор GyverKIT – большой стартовый набор Arduino моей разработки, продаётся в России
- Каталог ссылок на дешёвые Ардуины, датчики, модули и прочие железки с AliExpress у проверенных продавцов
- Подборка библиотек для Arduino, самых интересных и полезных, официальных и не очень
- Полная документация по языку Ардуино, все встроенные функции и макросы, все доступные типы данных
- Сборник полезных алгоритмов для написания скетчей: структура кода, таймеры, фильтры, парсинг данных
- Видео уроки по программированию Arduino с канала “Заметки Ардуинщика” – одни из самых подробных в рунете
- Поддержать автора за работу над уроками
- Обратная связь – сообщить об ошибке в уроке или предложить дополнение по тексту ([email protected])
From Wikipedia, the free encyclopedia
An adaptive filter is a system with a linear filter that has a transfer function controlled by variable parameters and a means to adjust those parameters according to an optimization algorithm. Because of the complexity of the optimization algorithms, almost all adaptive filters are digital filters. Adaptive filters are required for some applications because some parameters of the desired processing operation (for instance, the locations of reflective surfaces in a reverberant space) are not known in advance or are changing. The closed loop adaptive filter uses feedback in the form of an error signal to refine its transfer function.
Generally speaking, the closed loop adaptive process involves the use of a cost function, which is a criterion for optimum performance of the filter, to feed an algorithm, which determines how to modify filter transfer function to minimize the cost on the next iteration. The most common cost function is the mean square of the error signal.
As the power of digital signal processors has increased, adaptive filters have become much more common and are now routinely used in devices such as mobile phones and other communication devices, camcorders and digital cameras, and medical monitoring equipment.
Example application[edit]
The recording of a heart beat (an ECG), may be corrupted by noise from the AC mains. The exact frequency of the power and its harmonics may vary from moment to moment.
One way to remove the noise is to filter the signal with a notch filter at the mains frequency and its vicinity, but this could excessively degrade the quality of the ECG since the heart beat would also likely have frequency components in the rejected range.
To circumvent this potential loss of information, an adaptive filter could be used. The adaptive filter would take input both from the patient and from the mains and would thus be able to track the actual frequency of the noise as it fluctuates and subtract the noise from the recording. Such an adaptive technique generally allows for a filter with a smaller rejection range, which means, in this case, that the quality of the output signal is more accurate for medical purposes.[1][2]
Block diagram[edit]
The idea behind a closed loop adaptive filter is that a variable filter is adjusted until the error (the difference between the filter output and the desired signal) is minimized. The Least Mean Squares (LMS) filter and the Recursive Least Squares (RLS) filter are types of adaptive filter.
-
Adaptive Filter. k = sample number, x = reference input, X = set of recent values of x, d = desired input, W = set of filter coefficients, ε = error output, f = filter impulse response, * = convolution, Σ = summation, upper box=linear filter, lower box=adaption algorithm
Adaptive Filter, compact representation. k = sample number, x = reference input, d = desired input, ε = error output, f = filter impulse response, Σ = summation, box=linear filter and adaption algorithm.
There are two input signals to the adaptive filter: 



which includes the desired signal plus undesired interference and
which includes the signals that are correlated to some of the undesired interference in
.
- k represents the discrete sample number.
The filter is controlled by a set of L+1 coefficients or weights.
represents the set or vector of weights, which control the filter at sample time k.
- where
refers to the
‘th weight at k’th time.
- where
represents the change in the weights that occurs as a result of adjustments computed at sample time k.
- These changes will be applied after sample time k and before they are used at sample time k+1.
The output is usually 

The input signals are defined as follows:
- where:
- g = the desired signal,
- g‘ = a signal that is correlated with the desired signal g ,
- u = an undesired signal that is added to g , but not correlated with g or g‘
- u‘ = a signal that is correlated with the undesired signal u, but not correlated with g or g‘,
- v = an undesired signal (typically random noise) not correlated with g, g‘, u, u‘ or v‘,
- v‘ = an undesired signal (typically random noise) not correlated with g, g‘, u, u‘ or v.
The output signals are defined as follows:
.
- where:
= the output of the filter if the input was only g‘,
= the output of the filter if the input was only u‘,
= the output of the filter if the input was only v‘.
Tapped delay line FIR filter[edit]
If the variable filter has a tapped delay line Finite Impulse Response (FIR) structure, then the impulse response is equal to the filter coefficients. The output of the filter is given by
- where
refers to the
‘th weight at k’th time.
- where
Ideal case[edit]
In the ideal case 




The output of the variable filter in the ideal case is
.
The error signal or cost function is the difference between 

. The desired signal gk passes through without being changed.
The error signal 
![[u_{k}-{hat {u}}_{k}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/cbc75695df122bd9dc20a1832864efec904c1446)





Signal components in the reference input[edit]
In some situations, the reference input 
Perfect cancelation of the undesired interference is not possible in the case, but improvement of the signal to interference ratio is possible. The output will be
. The desired signal will be modified (usually decreased).
The output signal to interference ratio has a simple formula referred to as power inversion.
.
- where
= output signal to interference ratio.
= reference signal to interference ratio.
= frequency in the z-domain.
- where
This formula means that the output signal to interference ratio at a particular frequency is the reciprocal of the reference signal to interference ratio.[5]
Example: A fast food restaurant has a drive-up window. Before getting to the window, customers place their order by speaking into a microphone. The microphone also picks up noise from the engine and the environment. This microphone provides the primary signal. The signal power from the customer’s voice and the noise power from the engine are equal. It is difficult for the employees in the restaurant to understand the customer. To reduce the amount of interference in the primary microphone, a second microphone is located where it is intended to pick up sounds from the engine. It also picks up the customer’s voice. This microphone is the source of the reference signal. In this case, the engine noise is 50 times more powerful than the customer’s voice. Once the canceler has converged, the primary signal to interference ratio will be improved from 1:1 to 50:1.
Adaptive Linear Combiner[edit]
-
Adaptive linear combiner showing the combiner and the adaption process. k = sample number, n=input variable index, x = reference inputs, d = desired input, W = set of filter coefficients, ε = error output, Σ = summation, upper box=linear combiner, lower box=adaption algorithm.
Adaptive linear combiner, compact representation. k = sample number, n=input variable index, x = reference inputs, d = desired input, ε = error output, Σ = summation.
The adaptive linear combiner (ALC) resembles the adaptive tapped delay line FIR filter except that there is no assumed relationship between the X values. If the X values were from the outputs of a tapped delay line, then the combination of tapped delay line and ALC would comprise an adaptive filter. However, the X values could be the values of an array of pixels. Or they could be the outputs of multiple tapped delay lines. The ALC finds use as an adaptive beam former for arrays of hydrophones or antennas.
- where
refers to the
‘th weight at k’th time.
- where
LMS algorithm[edit]
If the variable filter has a tapped delay line FIR structure, then the LMS update algorithm is especially simple. Typically, after each sample, the coefficients of the FIR filter are adjusted as follows:[6](Widrow)
- for
-
- μ is called the convergence factor.
-
The LMS algorithm does not require that the X values have any particular relationship; therefore it can be used to adapt a linear combiner as well as an FIR filter. In this case the update formula is written as:
The effect of the LMS algorithm is at each time, k, to make a small change in each weight. The direction of the change is such that it would decrease the error if it had been applied at time k. The magnitude of the change in each weight depends on μ, the associated X value and the error at time k. The weights making the largest contribution to the output, 
Convergence[edit]
μ controls how fast and how well the algorithm converges to the optimum filter coefficients. If μ is too large, the algorithm will not converge. If μ is too small the algorithm converges slowly and may not be able to track changing conditions. If μ is large but not too large to prevent convergence, the algorithm reaches steady state rapidly but continuously overshoots the optimum weight vector. Sometimes, μ is made large at first for rapid convergence and then decreased to minimize overshoot.
Widrow and Stearns state in 1985 that they have no knowledge of a proof that the LMS algorithm will converge in all cases.[7]
However under certain assumptions about stationarity and independence it can be shown that the algorithm will converge if
-
- where
= sum of all input power
- where
-
-
is the RMS value of the
‘th input
-
In the case of the tapped delay line filter, each input has the same RMS value because they are simply the same values delayed. In this case the total power is
-
- where
is the RMS value of
, the input stream.[7]
- where
This leads to a normalized LMS algorithm:
in which case the convergence criteria becomes:
.
Nonlinear Adaptive Filters[edit]
The goal of nonlinear filters is to overcome limitation of linear models. There are some commonly used approaches: Volterra LMS, Kernel adaptive filter, Spline Adaptive Filter [8] and Urysohn Adaptive Filter.[9][10] Many authors [11] include also Neural networks into this list. The general idea behind Volterra LMS and Kernel LMS is to replace data samples by different nonlinear algebraic expressions. For Volterra LMS this expression is Volterra series. In Spline Adaptive Filter the model is a cascade of linear dynamic block and static non-linearity, which is approximated by splines.
In Urysohn Adaptive Filter the linear terms in a model
are replaced by piecewise linear functions
which are identified from data samples.
Applications of adaptive filters[edit]
- Adaptive Noise Cancelling
- Acoustic Noise Control
- Signal prediction
- Adaptive feedback cancellation
- Echo cancellation
Filter implementations[edit]
- Least mean squares filter
- Recursive least squares filter
- Multidelay block frequency domain adaptive filter
See also[edit]
- 2D adaptive filters
- Filter (signal processing)
- Kalman filter
- Kernel adaptive filter
- Linear prediction
- MMSE estimator
- Wiener filter
- Wiener-Hopf equation
References[edit]
- ^ Thakor, N.V.; Zhu, Yi-Sheng (1991-08-01). «Applications of adaptive filtering to ECG analysis: noise cancellation and arrhythmia detection». IEEE Transactions on Biomedical Engineering. 38 (8): 785–794. doi:10.1109/10.83591. ISSN 0018-9294. PMID 1937512. S2CID 11271450.
- ^ Widrow, Bernard; Stearns, Samuel D. (1985). Adaptive Signal Processing (1st ed.). Prentice-Hall. p. 329. ISBN 978-0130040299.
- ^ Widrow p 304
- ^ Widrow p 212
- ^ Widrow p 313
- ^ Widrow p 100
- ^ a b Widrow p 103
- ^ Danilo Comminiello; José C. Príncipe (2018). Adaptive Learning Methods for Nonlinear System Modeling. Elsevier Inc. ISBN 978-0-12-812976-0.
- ^ M.Poluektov and A.Polar. Urysohn Adaptive Filter. 2019.
- ^ «Nonlinear Adaptive Filtering». ezcodesample.com.
- ^ Weifeng Liu; José C. Principe; Simon Haykin (March 2010). Kernel Adaptive Filtering: A Comprehensive Introduction (PDF). Wiley. pp. 12–20. ISBN 978-0-470-44753-6.
Sources[edit]
- Hayes, Monson H. (1996). Statistical Digital Signal Processing and Modeling. Wiley. ISBN 978-0-471-59431-4.
- Haykin, Simon (2002). Adaptive Filter Theory. Prentice Hall. ISBN 978-0-13-048434-5.
- Widrow, Bernard; Stearns, Samuel D. (1985). Adaptive Signal Processing. Englewood Cliffs, NJ: Prentice Hall. ISBN 978-0-13-004029-9.
Библиографическое описание:
Калыгина, Л. А. Применение адаптивных фильтров для анализа сигналов / Л. А. Калыгина, В. В. Савенкова. — Текст : непосредственный // Молодой ученый. — 2013. — № 12 (59). — С. 128-134. — URL: https://moluch.ru/archive/59/8307/ (дата обращения: 07.06.2023).
Статья посвящена цифровым адаптивным фильтрам, параметры которых автоматически подстраиваются под статистические свойства обрабатываемого сигнала. Это позволяет создавать системы обработки сигналов, успешно функционирующие в присутствии помех. Рассмотрим сигнал, представляющий собой сумму гармонических составляющих с неизвестными амплитудами и фазами. Задан набор частот возможных гармонических составляющих. Требуется определить:
1. Наличие определенной составляющей в исходном сигнале;
2. При наличии составляющей — определить ее амплитуду и начальную фазу.
Для решения задачи предлагается использовать адаптивные фильтры.
Пусть входной дискретный случайный сигнал 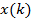
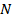
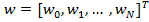
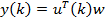
где 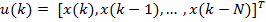
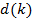
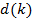
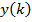
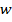
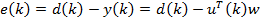
Необходимо найти такие коэффициенты фильтра 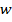
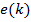
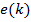
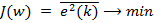
Квадрат ошибки равен:
Статистически усредняя это выражение, получаем следующее:
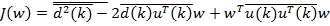
Входящие в полученную формулу усредненные величины имеют следующий смысл:
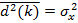
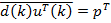
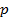
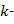
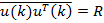
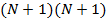
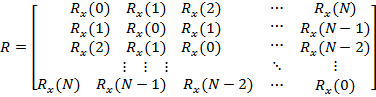
где 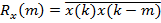
С учетом введенных обозначений целевая функция принимает следующий вид:
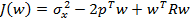
Данное выражение представляет собой квадратичную форму относительно 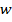
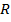
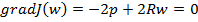
Отсюда получаем искомое решение для оптимальных коэффициентов фильтра:
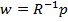
Подстановка этого выражения в конечную формулу целевой функции даёт минимально достижимую дисперсию сигнала ошибки:
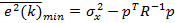
Для нахождения минимума целевой функции можно использовать метод наискорейшего спуска. При использовании данного способа оптимизации вектор коэффициентов фильтра 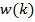
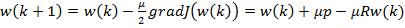
где 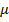
Алгоритм сходится, если 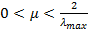
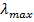
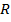
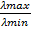
Однако для расчета градиента необходимо знать значения матрицы 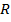
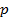
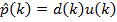
При использовании данных оценок формула вычисления 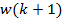
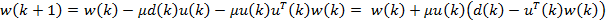
Выражение, стоящее в скобках, представляет собой разность между образцовым сигналом и выходным сигналом фильтра на k-м шаге, то есть ошибку фильтрации 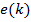
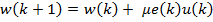
Алгоритм адаптивной фильтрации, основанный на этой формуле, получил название МНК (метод наименьших квадратов или LMS — LeastMeanSquare,).
Анализ сходимости алгоритма МНК показывает, что верхняя граница для размера шага 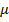
где 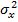
Исследования сигналов с использованием алгоритма МНК проводились на модели, реализованной в пакете в Matlab.
Далее приводятся результаты работы программы для фильтра 12000 порядка. Частота дискретизации анализируемого сигнала равна 6/3600=1,(6)*10–3Гц. Полоса пропускания фильтра по уровню 3 дБ составляет 2,3*10–7 Гц или 1,4*10–4 частоты дискретизации. Графики на рисунках 1–2 соответствуют двум гармоническим составляющим, одна из которых входит в полосу пропускания фильтра, а вторая не входит; сигнал на выходе адаптивного фильтра после 4000-го отсчета совпадает с тестовым. На рисунке 3 показана ошибка фильтрации в случае, когда тестовый сигнал не совпадает ни с одной частотой. Таким образом, адаптивный фильтр можно использовать для определения факта наличия или отсутствия заданной гармонической составляющей во входном сигнале.
Рис. 1. Ошибка фильтрации (образцовый сигнал соответствует частоте одного сигнала)
Рис. 2. Входной сигнал, образцовый сигнал и сигнал на выходе фильтра (образцовый сигнал соответствует частоте одного сигнала)
Рис. 3. Ошибка фильтрации (образцовый сигнал не соответствует частотам входного сигнала)
На рисунках 4–5 показаны ошибка фильтрации и сигналы для случая, когда оба сигнала находятся в полосе пропускания фильтра (разница частот составляет 10–7). Очевидно, что адаптивный фильтр позволяет определить наличие сигнала заданной частоты и в случае присутствия сигнала близкой частоты; при этом увеличивается время установления выходного сигнала (переходного процесса).
Рис. 4. Ошибка фильтрации (двухчастотный входной сигнал с частотами в полосе фильтра)
Рис. 5. Входной сигнал, образцовый сигнал и сигнал выходе фильтра (двухчастотный входной сигнал с частотами в полосе фильтра)
В рассмотренных выше экспериментах начальная фаза и амплитуда тестовых сигналов равна фазе и амплитуде образцового сигнала. При изменении начальной фазы или амплитуды тестовых сигналов выходной сигнал фильтра совпадает с тестовым, т. е. действительно выполняется минимизация ошибки выходного сигнала фильтра и образцового сигнала. Очевидно, что для определения амплитуды и начальной фазы сигнала необходимо проанализировать АЧХ и ФЧХ фильтров.
Для установления степени влияния на результаты фильтрации начальной фазы входного сигнала сравниваются частотные характеристики фильтров при подаче входного сигнала сначальной фазой, совпадающей с начальной фазой образцового сигнала, и со сдвигом фазы 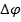
Образцовый сигнал: 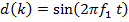
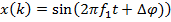
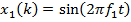
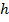
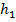
На рисунке 6 показаны ФЧХ фильтров. Видно, что ФЧХ фильтра, полученная для сигнала со сдвигом фазы, сдвинута относительно ФЧХ базового фильтра.
Рис. 6. Фазовые характеристики фильтра для сигнала со сдвигом фаз и без него
Сдвиг фазы сигнала можно вычислить усреднением разности ФЧХ в диапазоне определения ФЧХ: 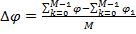
где 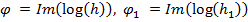
Зависимость ошибки определения начальной фазы сигнала от величины сдвига показана на рисунке 7.
Рис. 7. Ошибка определения начальной фазы
На рисунке 8 показана зависимость ошибки определения фазы для случая суммы двух гармонических сигналов, входящих в полосу фильтра.
Рис. 8. Ошибка определения начальной фазы для суммы двух частот
Путем последовательной коррекции начальной фазы образцового сигнала можно точно определить начальную фазу тестируемого сигнала; нулевая ошибка соответствует сдвигу π/5.
Для определения амплитуды входного сигнала необходимо рассчитать:
— реакцию фильтра 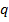
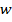
— реакцию фильтра 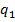
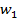
Тогда амплитуда сигнала 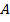
На рисунке 9 показаны графики изменения заданной амплитуды и рассчитанной амплитуды. Таким образом, можно сделать вывод о корректности описанного алгоритма расчета амплитуды сигнала и возможности определения амплитуды исследуемой гармонической составляющей с помощью адаптивного фильтра.
Рис. 9. Входная и рассчитанная амплитуда
Проведенные исследования показали, что адаптивные фильтры могут быть использованы для анализа параметров составляющих суммы гармонических сигналов. Сначала надо определить наличие сигнала заданной частоты в исходном сигнале. Затем определяется сдвиг начальной фазы исследуемого сигнала относительно образцового сигнала, в результате изменяется начальная фаза образцового сигнала. По модифицированному образцовому сигналу определяется амплитуда исследуемого сигнала.
Литература:
1. Адаптивные фильтры: Пер. с англ. Под ред. К.Ф. Н. Коуэна и П. М. Гранта. — М.:Мир, 1988. — 392 с.
2. Haykin S. Adaptive Filter Theory, 5th edition. / Prentice Hall, 2012. — 936 p.
3. Прокис Дж. Цифровая связь: Пер. с англ. / Под ред.Д. Д. Кловского.— М.: Радио и связь, 2000.— 800 с.
Основные термины (генерируются автоматически): образцовый сигнал, входной сигнал, начальная фаза, ошибка фильтрации, выходной сигнал фильтра, сигнал, адаптивный фильтр, корреляционная матрица, целевая функция, выход фильтра.
Подборка по базе: Презентация красная книга России.pptx, Проект Книга или компьютер.docx, 07-Ежемесячная книга за Июль 2022г. г.Шымкент .doc, ГО и МобП Тема №3 зан.1 Организационная структура гражданской об, 4 Книга ВШК факультативы.doc, Электронная кНИГА.pptx, Учебник сержанта артиллерии. Книга 1 — 1944. Part 2.djvu, ГО и МобП Тема №3 зан.1 Организационная структура гражданской об, 3.5 Книга ВШК календ. и поур. планы.docx, Красная книга Республики Казахстан 9 (1).pdf
7.6.1. Решетчатый фильтр сигнала ошибки предсказания
В процедуре вычисления коэффициентов предсказания Левинсона –
Дарбина в качестве промежуточных величин используются коэффициенты
k m , которые называются коэффициентами отражения. Их физический смысл заключается в следующем. Голосовой тракт человека представляет собой трубу, состоящую из секций, соединенных последовательно и имею- щих разный диаметр. При прохождении звуковой волны через такую сис- тему возникают отражения на стыках секций, так как каждый стык являет- ся неоднородностью. Коэффициент отражения характеризует величину проходимости стыка двух секций (сред) и равен
136 1
;
1 1;
0 1
s
s
m
m
r
r
s
m
m
i
s
s
m
m
−
+
=
− ≤
≤
⇐
≥
+
+
Поясним его смысл на рис. 7.5: жирной линией показана m-я – секция голосового тракта.
Рис. 7.5. Коэффициент отражения
Если
1
rm = −
, то произойдет обрыв в цепи передачи сигнала (обрыв прямой ветви). Такого быть не должно.
Модель акустических труб может быть представлена в виде фильтра, имеющего решетчатую (или лестничную) структуру. Основные параметры такого фильтра – коэффициенты отражения [40, 42].
Система акустических труб – резонансная система, поэтому если фильтр без потерь, то на его амплитудно-частотной характеристике (АЧХ) будут наблюдаться разрывы (всплески в бесконечность). В действительно- сти на месте этих всплесков будут резонансные пики. Частоты таких пиков называются формантными. Обычно в голосовых трактах человека фор- мантных частот (или формант) не более трех.
Так как коэффициенты отражения и коэффициенты предсказания вы- числяются в рамках одной и той же процедуры алгоритма Левинсона –
Дарбина, то они могут быть выражены друг через друга. Рассмотрим эти алгоритмы.
Прямая рекурсия. Коэффициенты предсказания находят по коэффици- ентам отражения
( )
устанавливается,
1,
( )
(
1)
(
1),
1,
1,
( ),
1,
m
a
r
m
m
m
M
m
m
m
a
a
r a
j
m
j
j
m m
j
M
a
a
j
M
j
j
⎫
= −
−
⎪
=
⎬
−
−
⎪
=
+
=
−
−
⎭
=
=
Обратная рекурсия. Коэффициенты отражения находят по коэффици- ентам предсказания
1
rm = −
1
rm =
S m
0 1
S m
=
+
S m
1
S m
→∞
+
m m
137
( )
,
1, ,
( ) устанавливается,
( )
( )
( )
,
, 1.
(
1)
,
1,
1.
2 1
M
a
a
j
M
j
j
m
r
a
m
m
m
m
m
m M
a
a
a
j
m
m
j
m
a
j
m
j
rm
=
=
⎫
= −
−
⎪
⎪
=
⎬
+
−
−
⎪
=
=
−
⎪
−
⎭
Как уже было сказано, фильтры сигнала ошибки представляют собой
КИХ-фильтры, или нерекурсивные фильтры, что означает отсутствие вет- вей обратной связи. Системы с КИХ также могут обладать строго линей- ной фазо-частотной характеристикой (ФЧХ). Линейность ФЧХ – очень важное свойство применительно к речевому сигналу в тех случаях, когда требуется сохранить взаимное расположение элементов сигнала. Это су- щественно облегчает задачу проектирования фильтров и позволяет уделять внимание лишь аппроксимации их АЧХ. За это достоинство приходится расплачиваться необходимостью аппроксимации протяженной импульсной реакции в случае фильтров с крутыми АЧХ [39, 40].
Изобразим граф фильтра, имеющего решетчатую структуру 3-го по- рядка (рис. 7.6).
Рис. 7.6. Граф решетчатого фильтра
В отличие от формирующего фильтра этот фильтр имеет один вход и два выхода:
ei – последовательность отсчетов сигнала ошибки прямого линейного предсказания;
bi – последовательность отсчетов сигнала ошибки обратного линей- ного предсказания, где
1 1
1
b
x
x
n
n
n
=
−
−
−
− .
Важность bi определяется тем, что по ним совместно с сигналом ошибки ei могут быть оценены коэффициенты отражения:
(0)
n
e
1 1
(1)
n
e
1 1
(2)
n
e
1 1
(3)
n
e
n
e
n
x
1
r
2
r
3
r
1
r
2
r
3
r
1
z
−
1 1
z
−
1 1
z
−
1
(0)
n
b
(0)
1
n
b
−
(1)
n
b
(1)
1
n
b
−
(2)
n
b
(2)
1
n
b
−
(3)
n
b
n
b
138
(
)
(
)
(
1) (
1)
1 2
2
(
1)
(
1)
1 1
N
m
m
e
b
n
n
n
rm
N
N
m
m
e
b
n
n
n
n
−
−
∑
=
= −
−
−
∑
∑
=
=
, (7.9) где N – количество отсчетов в сегменте.
Полученная формула для расчета коэффициентов отражения имеет также другой физический смысл – расчет коэффициентов корреляции ме- жду последовательностью отсчетов сигнала ошибки прямого и обратного линейных предсказаний.
Приведем также рекуррентные разностные уравнения решетчатого фильтра сигнала ошибки:
(
1),
( )
(
1)
1 1,
,
(
1)
( )
(
1),
1
m
m
m
e
e
r b
n
n
m n
m
M
m
m
m
b
b
r e
n
m n
n
−
−
⎧
⎫
=
+
⎪
⎪
−
=
⎨
⎬
−
−
⎪
⎪
=
+
−
⎩
⎭
где
( )
( )
;
M
M
e
e
b
b
n
n
n
n
=
=
– выход фильтра, а начальные условия для ре- куррентной процедуры – (0)
(0)
;
e
x
b
x
n
n
n
n
=
=
7.6.2. Реализация ДИКМ
Зная метод определения коэффициентов предсказания, рассмотрим блок-схему практической системы ДИКМ, показанную на рис. 7.7 [39, 40].
В этой схеме предсказатель стоит в цепи обратной связи, охватываю- щей квантователь (К). Вход предсказателя обозначен xn. Он представляет собой сигнальный отсчет
xn
, искаженный в результате квантования сигна- ла ошибки. Выход предсказателя (П)
ˆ
1
M
x
a x
n
k n k
k
= ∑
−
=
(7.10)
Рис. 7.7. Блок-схема практической системы ДИКМ
( )
x t
{ }
n
x
{ }
n
e
{ }
n
e
к модему
+ _
{ }
ˆ
n
x
{ }
n
x
АЦП
К
П
139
Разность
ˆ
e
x
x
n
n
n
=
−
– вход квантователя, а en – его выход. Величи- на квантованной ошибки предсказания
en
кодируется последовательно- стью двоичных символов и передается через канал в пункт приема.
Квантованную ошибку en также суммируют с предсказанной величи- ной ˆxn, чтобы получить xn.
В месте приема используют такой же предсказатель, как и на передаче.
Выход речевого сигнала ˆxn суммируют с en, чтобы получить xn (рис. 7.8).
Рис. 7.8. Схема предсказателя на приеме и передаче
Сигналы
xn
являются входными для предсказателя. По ним с помо- щью ЦАП восстанавливается сигнал
( )
x t . Ошибка в xn становится ошиб- кой квантования
q
e
e
n
n
n
=
−
. Использование обратной связи вокруг кван- тователя позволяет избежать накопления предыдущих ошибок квантова- ния при декодировании
ˆ
(
)
q
e
e
e
x
x
x
x
n
n
n
n
n
n
n
n
=
−
=
−
−
=
−
Следовательно,
x
x
q
n
n
n
=
+
, что означает, что квантованный отсчет
xn отличается от входа xn ошибкой квантования qn независимо от исполь- зования предсказателя. Значит, ошибки квантования не накапливаются.
В рассмотренной выше системе ДИКМ оценка, или предсказанная ве- личина ˆxn отсчета сигнала, получается посредством линейной комбинации предыдущих значений
xn k
−
, k = 1, 2, …, M. Улучшенное качество оценки можно получить включением в неё линейно отфильтрованных последних значений квантованной ошибки.
Оценку ˆxn можно выразить так:
?
1 1
m
l
x
a x
b e
n
k n k
k n k
k
k
=
+
∑
∑
−
−
=
=
,
{ }
n
e
{ }
n
x
к ЦАП
{ }
ˆ
n
x
{ }
k
a
П
140
где
{ }
bk – коэффициенты фильтра для квантованной последовательности ошибок en. Блок-схемы кодера на передаче и декодера на приеме приведе- ны ниже (рис. 7.9, 7.10).
Рис. 7.9. Блок-схема кодера на передаче
Рис. 7.10. Блок-схема декодера на приеме
Здесь два ряда коэффициентов
{ }
ak и
{ }
bk выбираются так, чтобы минимизировать некоторую функцию ошибки
ˆ
e
x
x
n
n
n
=
−
, например среднеквадратическую ошибку.
7.7. Способы кодирования речи на основе анализа
временных параметров
При цифровом кодировании стремятся по возможности к наиболее точному представлению речевого сигнала для того, чтобы по этому циф- ровому представлению восстановить исходный акустический сигнал. Дру- гая задача – представление речевого сигнала совокупностью свойств или
( )
x t
{ }
n
x
{ }
n
e
{ }
n
e
к модему
+ _
{ }
ˆ
n
x
{ }
n
e
{ }
n
x
АЦП
К
Лин. фильтр
{ }
k
b
Лин. фильтр
{ }
k
a
{ }
n
e
{ }
n
x
к ЦАП
{ }
ˆ
n
x
{ }
k
b
{ }
k
a
Лин. фильтр
Лин. фильтр
141
параметров модели. Ряд сравнительно простых и полезных характеристик можно определить путем непосредственных измерений параметров самого сигнала, а именно по его ИКМ-представлению.
Ключ ко всем параметрическим представлениям – процедура кратко- временного анализа [46].
7.7.1. Измерение энергии
Одна из характеристик сигнала – его энергия. Энергия вещественно- го дискретного во времени сигнала
( )
x n
( )
2
E
x n
n
∞
= ∑
= −∞
. (7.11)
Для нестационарных сигналов, например, речевого, более удобно вычислять изменяющуюся во времени энергию в виде:
( )
( ) (
)
N 1
m 0
2
E n
w m x n m
−
=
⎡
⎤
=
−
∑ ⎣
⎦ , (7.12) где ( )
w m – весовая последовательность, или окно, которое выделяет уча- сток ( )
x n , a N – количество отсчетов в окне. Таким образом, один из спо- собов измерения энергии (7.12) основывается на сглаживании последова- тельности ( )
x n фильтром с импульсной реакцией ( )
W n .
Как и следовало ожидать, функция ( )
E n отображает изменяющиеся во времени амплитудные свойства речевого сигнала. Однако формула
(7.12) нуждается в тщательной интерпретации. Во-первых, это касается выбора окна, задача которого состоит в приписывании меньших весов бо- лее старым отсчетам речи, поэтому с увеличением m ( )
w m , как правило, монотонно стремится к нулю. Если на всем интервале отсчеты должны иметь одинаковый вес, используют прямоугольное окно.
Во-вторых, трудность заключается в выборе интервала измерения
N . При слишком малом N , когда его величина меньше периода основного тона, величина энергии Е(n), определяемой выражением (7.12), подверже- на быстрым флуктуациям, зависящим от тонкой структуры сигнала. Если
N слишком велико и равно нескольким периодам основного тона, величи- на ( )
E n изменяется незначительно и поэтому не может отразить изменяю- щиеся свойства речевого сигнала. Практически наиболее подходящее зна- чение N при частоте дискретизации 10 кГц составляет величину порядка
100 – 200 отсчетов (10 – 20 мс речи).
142
Основное значение характеристики ( )
E n состоит в том, что она мо- жет служить хорошим критерием разделения вокализованных и невокали- зованных участков речи. На невокализованных участках величина ( )
E n намного меньше, чем на вокализованных. Кроме того, чем меньше N , тем меньше ошибка определения точного положения границ, где невокализи- рованная речь переходит в вокализированную и обратно. Более того, при- менительно к высококачественной речи энергию можно использовать для отделения невокализированных участков речи от паузы.
Процедура измерения энергии осложняется тем обстоятельством, что величина уровня возводится в квадрат, тем самым в ( )
E n появляются большие перепады. Один из сравнительно простых способов преодоления этой трудности – использование для оценки энергии функции, в которой вместо суммы квадратов вычисляется сумма абсолютных величин
( ) (
)
1 0
ˆ
N
m
E
w n x n m
−
=
=
−
∑
(7.13)
7.7.2. Измерение числа переходов через нуль
Еще один весьма простой способ анализа временных параметров сигнала основан на измерении числа переходов через нуль. Имея в виду цифровое представление сигнала, можно утверждать, что между момента- ми взятия n -го и (
1
n
− )-го отсчетов произошло пересечение нулевого уровня, если
[
]
[
]
sign ( )
sign (
1)
x n
x n
≠
− . (7.14)
Это измерение несложно в реализации и часто используется для гру- бой оценки частотного содержания речевого сигнала. Возможность его применения объясняется тем, что для синусоидального сигнала с частотой
0
f среднее число пересечений нулевого уровня за 1 с
2 0
m
f
=
. (7.15)
Однако соотношение (7.15) нельзя без оговорок распространить на речевой сигнал, поскольку большая часть звуков речи имеет широкий спектр частот. Тем не менее иногда достаточно даже такой грубой оценки.
Например, хорошо известно, что энергия вокализованной речи обычно концентрируется в диапазоне ниже 3 кГц, тогда как энергия фри- кативных звуков в основном сосредоточена выше 3 кГц. На этом основа- нии результаты измерений числа переходов через нуль (наряду с информа- цией об энергии) часто используются для принятия решения о том, вокали- зованный или не вокализованный характер имеет данный участок речи.
Если частота пересечений высока, то это свидетельствует о не вокализо-
143
ванном характере речи, если же она мала, то весьма вероятно, что анализи- руется вокализованный участок. Число переходов через нуль в сочетании с измерением основного тона речи используется при оценке параметров воз- буждения, а также при распознавании речи [43].
При цифровой реализации измерений числа переходов через нуль следует учитывать ряд важных обстоятельств. Хотя в соответствии с ос- новным алгоритмом требуется произвести лишь сравнение знаков двух следующих друг за другом отсчетов, необходимо также весьма тщательно выполнять и саму процедуру дискретизации. Большие искажения в резуль- таты измерений числа переходов через нуль вносят наличие шума, смеще- ние уровня постоянного тока и напряжение фона с частотой питающей се- ти 50 Гц, поэтому для ослабления мешающего влияния указанных факто- ров перед устройством дискретизации вместо фильтра нижних частот ста- вится полосовой фильтр. Кроме того, поскольку временное разрешение при измерении числа переходов через нуль определяется периодом дис- кретизации Т, его повышение сопряжено с увеличением частоты дискрети- зации. Для измерения числа переходов через нуль можно применять двух- уровневое квантование.
7.7.3. Кратковременный автокорреляционный анализ
Функция автокорреляции дискретного во времени сигнала ( )
x n оп- ределяется как
( )
( ) (
)
N
N
n
N
1
m
lim
x n x n m
2N 1
ϕ
→∞
=−
=
+
∑
+
. (7.16)
Автокорреляционная функция весьма полезна для выявления струк- туры любого сигнала, и в этом смысле речь не составляет исключения [46].
Если, например, некоторый сигнал имеет структуру с периодом T :
(
)
( )
x n T
x n
+
=
для всех n , то
( )
(
)
m
m T
ϕ
ϕ
=
+
. (7.17)
Таким образом, периодичность автокорреляционной функции указы- вает на периодичность исходного сигнала. Если автокорреляционная функция в окрестности точки
0
m
= имеет острый пик и с возрастанием m быстро падает к нулю, то это указывает на отсутствие в сигнале предска- зуемой структуры.
Как уже отмечалось, речь является нестационарным сигналом. Одна- ко на коротких интервалах времени свойства речевого сигнала сохраняют- ся неизменными. Как мы уже видели, это свойство служит основой крат- ковременного анализа.
144
Рассмотрим для примера отрезок сигнала из N отсчетов:
( )
(
),
0 1
x n
x n l
n N
l
=
+
≤ ≤ − , (7.18) где l – начало этого отрезка. В этом случае кратковременная автокорреля- ционная функция может быть определена как
( )
( ) (
)
1 1
, 0 1
0 0
p
m
x n x n m
m M
l
l
l
N n
ϕ
−
=
+
≤ ≤
−
∑
=
, (7.19) где 0
M – максимально требуемая задержка. Так, например, для выявления периодичности сигнала необходимо выполнить условие M T
> . Значение целого числа p оговорено ниже.
Выражение (7.19) можно трактовать как автокорреляцию отрезка ре- чевого сигнала протяженностью N отсчетов, начиная с отсчета l . Если
p N
= , то для вычисления используются отсчеты, находящиеся вне отрезка
1
l n N l
< < + − ; если p N m
= − , то – отсчеты только внутри интервала. В последнем случае исследуемый отрезок часто взвешивается с помощью функции окна, которая плавно сводит к нулю величины отсчетов на концах отрезка.
Обычно предполагается, что для хранения существенных признаков речевого сигнала при его кодировании с помощью ИКМ может потребо- ваться частота дискретизации от 6 до 20 кГц, однако кодирование медлен- но изменяющихся параметров модели возможно со значительно меньшей частотой (от 50 до 100 Гц). Предположим для примера, что частота дис- кретизации речевого сигнала равна 10 кГц, а кратковременная автокорре- ляция должна вычисляться 100 раз в секунду. Оценка величины автокор- реляции обычно производится на отрезках речевого сигнала длительно- стью 20 – 40 мс (для оценки периодичности сигнала длительность окна должна быть достаточной для перекрытия как минимум двух периодов ре- чевого сигнала). Таким образом, при частоте дискретизации 10 кГц коли- чество отсчетов находится в интервале 200 400
N
< <
, а требуемые оценки величины автокорреляции должны вычисляться для приращения, равного
100 отсчетам [46].
При использовании кратковременной автокорреляционной функции для оценки периода основного тона желательно, чтобы эта функция имела острые пики с интервалом, кратным периоду T . Корреляционная функция речи не имеет острых пиков, поскольку структуру каждого периода рече- вого сигнала в значительной степени можно предсказать заранее.
145
7.8. Кодирование речи на основе адаптивного
mel-кепстрального анализа
Mel-кепстральные коэффициенты – популярные характеристики при исследовании речи и распознавании спикера.
Достаточно часто системы кодирования речи используют авторег- рессионное (AR – autoregressive) спектральное представление для кратко- временного предсказания. Однако в некоторых случаях кепстральные ко- эффициенты позволяют достичь лучших результатов [4].
Кепстр – спектр, полученный преобразованием Фурье логарифма сигнала. Спектр, представленный mel-кепстральными коэффициентами, должен иметь разрешающую способность, по частоте подобную человече- скому слуху, который имеет более высокую разрешающую способность на низких частотах. Поэтому ожидается, что использование mel-кепстра мо- жет быть эффективным для спектрального моделирования в кодерах речи вместо AR-моделирования.
Чтобы продемонстрировать эффективность mel-кепстрального пред- ставления в кодировании речи, рассмотрим кодер АДИКМ, который ис- пользует кратковременный адаптивный предсказатель, основанный на mel- кепстральном представлении спектра речи. При этом mel-кепстральные коэффициенты будут обработаны алгоритмом для адаптивного mel- кепстрального анализа. Так как передаточная функция шумового форми- рования и постфильтрования также определена через mel-кепстральные коэффициенты, эффекты шумового формирования и постфильтрования должны соответствовать особенностям человеческого слухового ощуще- ния.
Качество речи кодера оценивается объективными и субъективными исследованиями. Показано, что высококачественная речь, соответствую- щая CCITT G.721 ADPCM-кодеру на скорости 32 кбит/с, может быть вос- произведена кодером на основе mel-кепстра на скорости 16 кбит/с без ал- горитмической задержки.
7.8.1. Адаптивный mel-кепстральный анализ
Модель спектра речи
(
)
j
D e
ω
, использующая М-й порядок mel-кепстральных коэффициентов ( )
C m , имеет вид
( )
( )
M
m
D z
exp
C m z
m 0
−
=
∑
=
, (7.20) где
1 1
1
,
1 1
z
z
z
α α
α
−
−
−
−
=
<
−
. (7.21)
146
Например, когда частота дискретизации равна 8 кГц, фазовая харак- теристика
ω
и передаточная функция при
0,31
α
=
будут приближенными к масштабу me1-частоты, основанному на субъективных оценках основно- го тона [4].
В mel-кепстральном анализе коэффициент усиления ( )
D z предпола- гается равным единице. При этом условии коэффициенты( )
C m однознач- но минимизированы:
2
( )
E e n
ε
⎡
⎤
= ⎣
⎦ ,
где ( )
e n – выход обратного фильтра
( )
1 D z , как показано на рис. 7.11.
Адаптивный mel- кепстральный анализ решает проблему минимизации ошиб- ки с использованием оценки для градиента
ε
. Исследования показывают, что адаптивный алгоритм имеет достаточно быструю сходимость при ана- лизе речи.
Сигнал ( )
e n может рассматриваться как ошибка линейного предска- зания, поэтому адаптивный mel-кепстральный анализ может использо- ваться для кратковременного адаптивного предсказания вместо метода ли- нейного предсказания.
7.8.2. Структура кодера
Базовая структура кодера, основанного на адаптивном mel-кепстральном анализе, приведена на рис. 7.12.
Рис. 7.12. Базовая структура кодера
Z-преобразование декодированной речи ˆ( )
x n будет иметь вид:
ˆ ( )
( )
( )
X z
X z
Q z
=
+
, (7.22)
( )
x n
Кодировщик
Q
( )
1
D z
−
( )
ˆe n
Цифровой канал
Декодер
( )
D z
( )
ˆx n
( )
x n
( )
1 D z
( )
e n
Рис. 7.11. Схема адаптивного mel-кепстрального анализа
147
где ( )
X z и
( )
Q z – это Z-преобразования от
( )
x n и ( )
q n соответственно,
( )
q n – квантованный шум, создаваемый квантователем Q . Передаточная функция ( )
D z реализуется при использовании MLSA-фильтров.
MLSA (Mel Logarithmic Spectral Approximation) – mel-лога- рифмический спектральный фильтр приближения, коэффициенты которого определяются mel-кепстральными коэффициентами согласно информации о высоте тона [10].
Ограничение шума и постфильтрация
Передаточные функции ( )
D z и
( )
D z
реализуются при использова- нии MLSA-фильтров. Мы можем также реализовать
( )
D
z
γ
и
( z )
D
β
тем же способом, что и ( )
D z и ( )
D z : умножением ( )
C m на
γ
и
β
соответст- венно. Чтобы избежать изменения усиления на выходе постфильтра, до- бавляем регулятор выходного усиления, который поддерживает выходной сигнал постфильтра таким образом, чтобы он имел приблизительно ту же самую мощность (энергию), что и нефильтрованная речь [4].
Передаточная функция ( )
D z
аналогична ( )
D z за исключением того, что (1)
C
γ
должно быть равно нулю, чтобы уравновешивать глобальный спектральный наклон. Настраиваемые параметры
γ
и
β
регулируют вели- чину ограничения шума и постфильтрования соответственно.
Рис. 7.13 показывает структуру кодера, основанного на mel-кепстральном анализе с ограничением шума и постфильтрованием.
Рис. 7.13. Структура кодера, основанного на адаптивном mel-кепстральном анализе
Z-преобразование от декодированной речи ˆ( )
x n будет иметь вид:
{
}
ˆ ( )
( )
( )
( )
( )
X z
X z
D
z
Q z D
z
β
γ
=
+
+
. (7.23)
Передаточная функция
( )
D
z
γ
ограничивает спектр шумов и
( )
D
z
β
– постфильтрование.
( )
x n
Кодировщик
Q
( )
1
D
z
γ
−
( )
1
D z
−
( )
ˆe n
Цифровой канал
( )
D z
( )
D
z
β
( )
ˆx n
Декодер
148
Структура с предсказателем основного тона
Рис. 7.14 показывает структуру кодера с предсказателем основного тона.
Рис. 7.14. Структура кодера с предсказателем основного тона
Z-преобразование от декодированной речи
ˆ ( )
x n
будет иметь вид:
( )
ˆ ( )
( )
( )
( )
( )
( )
D z
X z
X z
Q z A z D
z
p
A z
n
γ
β
⎧
⎫
⎪
⎪
=
+
+
⎨
⎬
⎪
⎪
⎩
⎭
. (7.24)
Передаточную функцию фильтра предсказания основного тона нахо- дят по формуле
1
( ) 1
( )
1
p
k
A z
a k z
k
p
+
−
= +
∑
= −
. (7.25)
Период основного тона p и коэффициенты предсказателя основного тона ( )
a k вычисляют на основе корреляции
ˆ( )
e n
,
получающейся при ис- пользовании экспоненциального окна [4].
Передаточные функции
( z )
An
и
( z )
A p
определяют по формулам:
1
( ) 1
( )
1
p
k
z
a k
A
z
n
n
k
p
ε
+
−
= +
∑
= −
, (7.26)
( )
x n
Кодер
Q
( )
p
ˆ
e
z
Цифровой канал
e( n )
Декодер
( )
1 A z
( )
D z
( )
p
A z
( )
D
z
β
( )
ˆx n
( )
1
n
A z
−
( )
1
D
z
γ
−
( )
1
A z
−
D(z)–1
e( n )
149 1
1 1
( )
1
( )
1
( )
1 1
p
p
z
a k
a k
A
z
p
p
p
k
p
k
p
ε
ε
⎛
⎞
⎛
⎞
+
+
−
⎜
⎟
⎜
⎟
= −
−
∑
∑
⎜
⎟
⎜
⎟
= −
= −
⎝
⎠
⎝
⎠
. (7.27)
Настраиваемые параметры n
ε
и
p
ε
регулируют величину ограниче- ния шума и постфильтрования соответственно. В декодере p и ( )
a k всегда вычисляют по квантованным значениям ˆ( )
e n .
7.9. Кодирование речи в стандарте GSM
GSM – это цифровая система, следовательно, аналоговая речь долж- на быть оцифрована на входе и восстановлена на выходе.
Кодер речи – первый элемент собственно цифрового участка пере- дающего тракта АЦП. Основная задача кодера – предельно возможное сжатие сигнала речи, т.е. предельно возможное устранение избыточности речевого сигнала но при сохранении приемлемого качества. Компромисс между степенью сжатия и сохранением качества отыскивается экспери- ментально, а проблема получения высокой степени сжатия без чрезмерно- го снижения качества составляет основную трудность при разработке ко- дера. В приемном тракте перед ЦАП размещен декодер речи; задача деко- дера – восстановление цифрового сигнала речи по принятому кодирован- ному сигналу (с присущей ему естественной избыточностью). Сочетание кодера и декодера называют кодеком.
Кодирование сигнала источника первоначально основывалось на данных о механизмах речеобразования. Этот метод использовал модель голосового тракта и приводил к системам типа анализ-синтез, получившим название вокодеров (кодер голоса, или кодер речи). Ранние вокодеры по- зволяли получать весьма низкую скорость передачи информации при ха- рактерном «синтетическом» качестве речи на выходе, поэтому вокодерные методы долгое время оставались в основном областью приложения усилий исследователей и энтузиастов и не находили широкого практического применения.
Ситуация существенно изменилась с появлением метода линейного предсказания, предложенного в 1960-х гг. и получившего мощное развитие в 1980-х гг. на основе достижений микроэлектроники.
В настоящее время в системах подвижной связи получили распро- странение вокодерные методы на базе метода линейного предсказания.
Суть кодирования речи методом линейного предсказания (Linear
Predictive Coding – LРС) заключается в том, что по линии связи переда-
150
ются не параметры речевого сигнала, а параметры фильтра, в определен- ном смысле эквивалентного голосовому тракту, и параметры сигнала воз- буждения этого фильтра, в качестве которого используется фильтр ли- нейного предсказания. Задача кодирования на передающем конце линии связи состоит в оценке параметров фильтра и параметров сигнала возбу- ждения, а задача декодирования на приемном конце – в пропускании сиг- нала возбуждения через фильтр, на выходе которого получается восста- новленный сигнал речи.
Значения коэффициентов предсказания, постоянные на интервале кодируемого сегмента речи (на практике длительность сегмента составляет
20 мс), находят из условия минимизации среднеквадратического значения остатка предсказания на интервале сегмента.
Таким образом, процедура кодирования речи в методе линейного предсказания сводится к следующему:
−
оцифрованный сигнал речи нарезается на сегменты длительностью по 20 мс;
−
для каждого сегмента оцениваются параметры фильтра линейного предсказания и параметры сигнала возбуждения; в качестве сигнала воз- буждения в простейшем случае может выступать остаток предсказания, получаемый при пропускании сегмента речи через фильтр с параметрами, найденными из оценки для данного сегмента;
−
параметры фильтра и параметры сигнала возбуждения кодируются по определенному закону и передаются в канал связи.
Процедура декодирования речи заключается в пропускании принято- го сигнала возбуждения через синтезирующий фильтр известной структу- ры, параметры которого переданы одновременно с сигналом возбуждения.
Линейное предсказание является кратковременным (STP – Short-
Term Prediction) и не обеспечивает достаточной степени устранения из- быточности речи, поэтому в дополнение к кратковременному предсказа- нию используется еще долговременное (LTP – Long-Term Prediction), в значительной мере устраняющее остаточную избыточность и прибли- жающее остаток предсказания по своим статистическим характеристи- кам к белому шуму.
В стандарте GSM применяется метод полноскоростного (13,6 кбит/с) кодирования речи RPE-LTP (Regular Pulse Excited Long-Term Predictor – линейное предсказание с возбуждением регулярной последовательностью импульсов и долговременным предсказателем) – стандарт GSM 06.10. Уп- рощенная блок-схема кодека приведена на рис. 7.15, 7.16 [15].
151
Рис. 7.15. Блок-схема кодера кодека в стандарте GSM 06.10
Кодирование
1. Непрерывный речевой сигнал дискретизуется с частотой 8 кГц, и оцифровывается с равномерным законом квантования и разрядно- стью 13 бит/отсчет: число уровней квантования
13 4096 2
M
= ±
=
, уровень шумов квантования
2 10 lg1 12 2 90дБ
,дБ
R
Dq
−
= ⋅
⋅
≈ −
2.
Для повышения разборчивости речи осуществляют предыска- жение входного сигнала при помощи цифрового фильтра, подчеркивающе- го верхние частоты.
Рис. 7.16. Блок-схема декодера кодека в стандарте GSM 06.10 3.
Непрерывная последовательность отсчетов разбивается на сег- менты по 160 отсчетов (длительностью 160·1/8 кГц = 20 мс).
ДЕКОДЕР
От кодера
fn′
en′
Sn′
Формирование сигнала возбужде- ния
Фильтр-анализатор долговрем. пред- сказания
( )
R Z
Фильтр-синтезатор кратковрем. пред- сказания
( )
H z
Постфильтрация
КОДЕР
Sn
fn
en
На декодер
Предварит. обработка
Оценка параметров фильтра кратковрем. предсказания
Фильтр-анализатор кратковрем. пред- сказания
( )
A Z
Оценка параметров фильтра долговрем. предсказания
Фильтр-анализатор кратковрем. пред- сказания
( )
P z
Оценка параметров сигнала возбужде- ния
152 4.
Проводят «взвешивание» каждого сегмента окном Хэмминга –
«косинус на пьедестале», при этом амплитуда сигнала внутри сегмента плавно падает от центра окна к краям. Это делается для того, чтобы не бы- ло резких разрывов сигнала на краях сегментов.
5.
Для каждого 20-миллисекундного сегмента (160 «взвешенных» отсчетов сигнала) оценивают параметры фильтра кратковременного ли- нейного предсказания. Оптимальные коэффициенты фильтра кратковре- менного линейного предсказания ak находят путем решения системы ли- нейных уравнений Юла – Волкера:
(
)
( ),
1, 2, 3, ,
,
8
M
a R k l
R l
l
M
M
k
k l
…
− =
=
=
∑
=
, которая в матричной форме записывается следующим образом:
(0)
(1)
(2)
(
1)
(1)
1
(1)
(0)
(1)
(
2)
(2)
2
(2)
(1)
(0)
(
3)
(3)
3
(
1)
(
2)
(
3)
(
0)
( )
a
R
R
R
R M
R
a
R
R
R
R M
R
a
R
R
R
R M
R
R M
R M
R M
R M
R M
aM
−
−
⋅
=
−
−
−
−
−
…
…
…
…
…
…
…
…
…
…
Здесь (0)
( )
R
R M
…
– значения кратковременной автокорреляцион- ной функции речевого сигнала, вычисленные по его отсчетам на текущем сегменте
1
( )
( ) (
), 0 1, 0
,
160,
8 0
N
R k
x i x i k
i N
k M N
M
i
−
=
−
≤ ≤ −
≤ ≤
=
=
∑
=
6.
На основе полученных коэффициентов фильтра кратковременно- го предсказания проводят фильтрацию текущего речевого сегмента
(160 отсчетов) фильтром-анализатором кратковременного предсказания
(инверсным фильтром) с передаточной характеристикой
( ) 1 1
M
k
A z
a z
k
k
−
= − ∑
=
На выходе получается остаток (ошибка) кратковременного предска- зания en (160 отсчетов ошибки кратковременного предсказания). При этом из-за наличия в речевом сигнале долговременной повторяемости (перио- дичности), обусловленной гласными звуками, в ошибке кратковременного предсказания остаются периодические всплески достаточно большой ам- плитуды. Для их устранения (уменьшения) используется долговременное линейное предсказание.
153 7.
Вычисляют параметры фильтра долговременного линейного предсказания с передаточной характеристикой
( ) 1
D i
P z
G z
i
i
− −
= − ∑
Сегмент остатка кратковременного линейного предсказания
(160 отсчетов) разбивается на четыре подсегмента размером по 40 отсче- тов. Параметры долговременного предсказания – коэффициент предска- зания G и задержка D – оценивают для каждого подсегмента в отдель- ности. Укорочение интервала анализа долговременного предсказания обусловлено тем, что параметры сигнала возбуждения (с которыми связа- на его периодичность) изменяются гораздо быстрее, чем параметры голо- сового тракта (которые вошли в коэффициенты кратковременного линей- ного предсказания ak ).
В каждом подсегменте находят параметр задержки D (период ос- новного тона, определяемый как среднее расстояние между периодиче- скими всплесками автокорреляционной функции остатка кратковременно- го предсказания) и коэффициент предсказания G (определяемый как на- клон огибающей автокорреляционной функции остатка кратковременного предсказания). При этом параметр задержки D для текущего подсегмента вычисляют путем сглаживания (усреднения) текущего значения D и трех предшествующих ему значений (определенных на трех предыдущих под- сегментах).
8.
Сигнал остатка кратковременного линейного предсказания (под- сегмент длительностью в 40 отсчетов) en обрабатывается фильтром- анализатором долговременного линейного предсказания с параметрами G и D , найденными для этого подсегмента, и на его выходе получается оста- ток долговременного и кратковременного предсказания fn . Далее по это- му сигналу будут находиться параметры сигнала возбуждения (в отдельно- сти для каждого из подсегментов).
9.
Сигнал возбуждения одного подсегмента состоит из 13 импуль- сов, следующих через равные промежутки времени (втрое реже, чем ин- тервал дискретизации исходного сигнала) и имеющих различные амплиту- ды. Для формирования сигнала возбуждения 40 отсчетов подсегмент ос- татка
fn обрабатывают следующим образом.
Последний (40-й) отсчет отбрасывают, а первые 39 отсчетов проре- живают и разбивают на три подпоследовательности: в первую включаются
1, 4, … 37-й отсчеты, во вторую – отсчеты с номерами 2, 5, … 38, в тре- тью – отсчеты с номерами 3, 6, … 39. В качестве сигнала возбуждения вы- бирают ту подпоследовательность, энергия которой больше. Амплитуды
154
импульсов нормируют по отношению к импульсу с наибольшей амплиту- дой. Нормированные амплитуды кодируют тремя битами каждую (с ли- нейным законом квантования). Абсолютное значение наибольшей ампли- туды кодируют шестью битами в логарифмическом масштабе. Положение первого импульса 13-элементной последовательности кодируют двумя би- тами, т.е. фактически кодируют номер последовательности, выбранной в качестве сигнала возбуждения для данного подсегмента.
Таким образом, выходная информация кодера для одного
20-миллисекундного сегмента речи включает:
−
параметры фильтра кратковременного линейного предсказания – во- семь коэффициентов на сегмент, кодируют 36 битами;
−
параметры фильтра долговременного линейного предсказания – ко- эффициент предсказания G и задержка D – для каждого из четырех под- сегментов, также кодируют 36 битами;
−
параметры сигнала возбуждения – номер подпоследовательности n , максимальная амплитуда v , нормированные амплитуды импульсов после- довательности
,
1 13
b i
i
=
…
– для каждого из четырех подсегментов. Все вместе кодируют 188 битами.
Итого на 20 -миллисекундный сегмент речи (160 отсчетов) получает- ся 260 бит. При этом коэффициент сжатия сегмента (по сравнению с ИКМ, использующей логарифмическую шкалу квантования 160 отсчетов по
8 бит/отсчет) составляет 1280/260 = 4,92
≈ 5.
Декодирование
Последовательность выполняемых при декодировании функций представлена на рис. 7.16. Блок формирования сигнала возбуждения, ис- пользуя полученные параметры сигнала возбуждения, восстанавливает 13- импульсную последовательность сигнала возбуждения для каждого из подсегментов, включая амплитуды импульсов и их расположение во вре- мени. Сформированный таким образом сигнал возбуждения обрабатывает- ся фильтром-синтезатором долговременного предсказания, на выходе ко- торого получается восстановленный остаток кратковременного предсказа- ния. Последний обрабатывается фильтром-синтезатором кратковременного предсказания. Выходной сигнал фильтра-синтезатора кратковременного предсказания (а это уже почти синтезированный речевой сигнал) фильтру- ется цифровым фильтром низких частот, компенсирующим предыскаже- ние, внесенное входным фильтром блока предварительной обработки ко- дера. Сигнал с выхода низкочастотного постфильтра является восстанов- ленным цифровым сигналом речи.
Все перечисленные процедуры несмотря на их сложность выполня- ются в реальном масштабе времени процессором обработки речи, реализо- ванным аппаратно-программно в мобильном телефоне стандарта GSM.
155
Контрольные вопросы
1.
Что дает кодирование речи?
2.
Изложите методы кодирования речевой информации.
3.
Каковы особенности ИКМ?
4.
Каковы особенности законов
μ
и
A
, применяемых в кодирова- нии речи?
5.
Каковы особенности ДИКМ на основе ЛП?
6.
Чем характеризуется алгоритм Левинсона – Дарбина?
7.
Что такое решетчатый фильтр. Какова его граф-структура?
8.
Каковы особенности практической системы ДИКМ?
9.
Что такое кратковременный анализ речевого сигнала?
10.
Как определяется энергия речевого сигнала?
11.
Как определяется число переходов через нуль при анализе рече- вого сигнала?
12.
Каковы особенности автокорреляционного анализа?
13.
Каковы особенности кодирования на основе линейного предсказания?
14.
Что такое постфильтрация и для чего она применяется?
15.
Какова структура предсказателя основного тона?
16.
Как происходят процессы кодирования и декодирования в стан- дарте GSM?


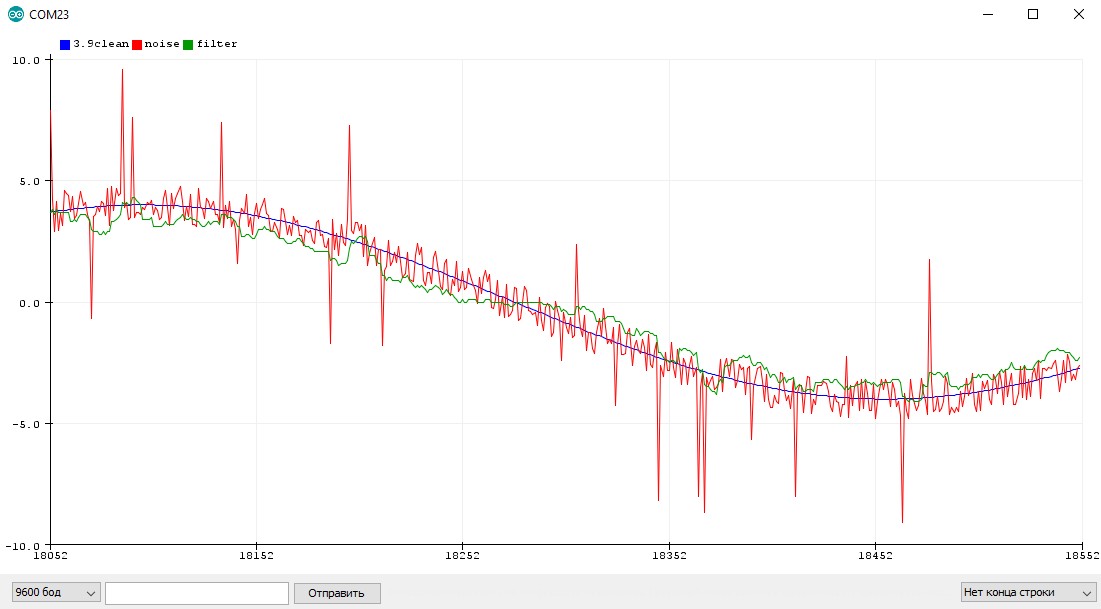
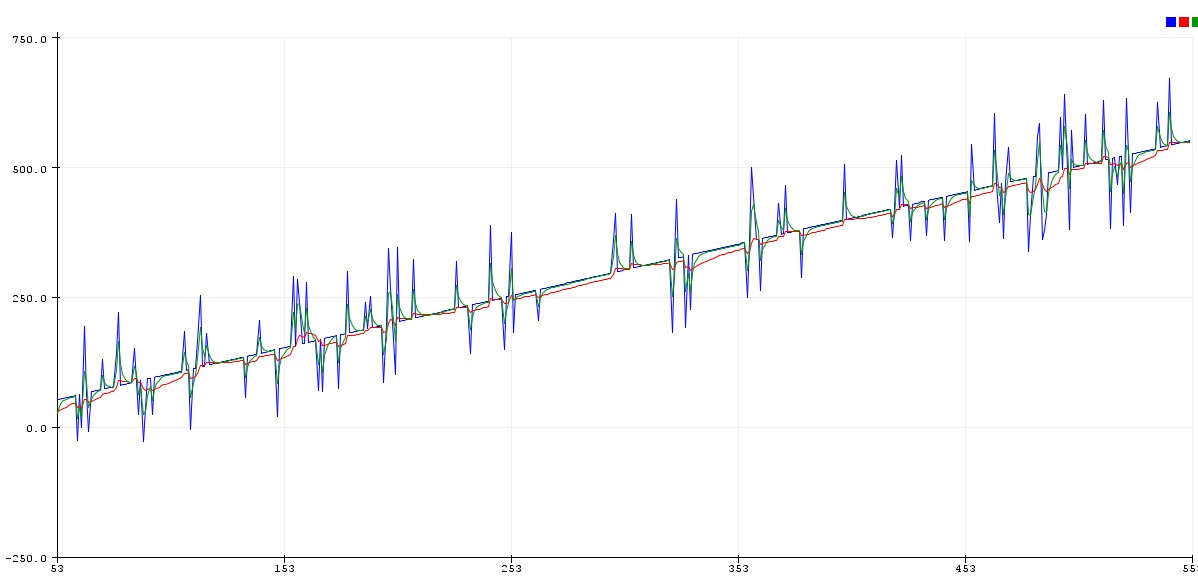
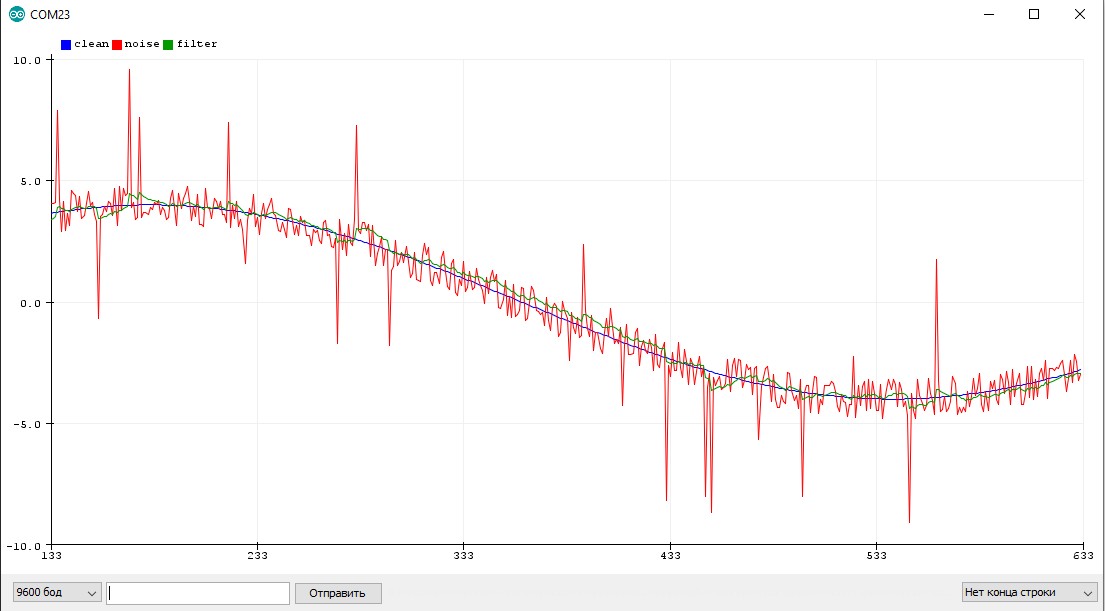

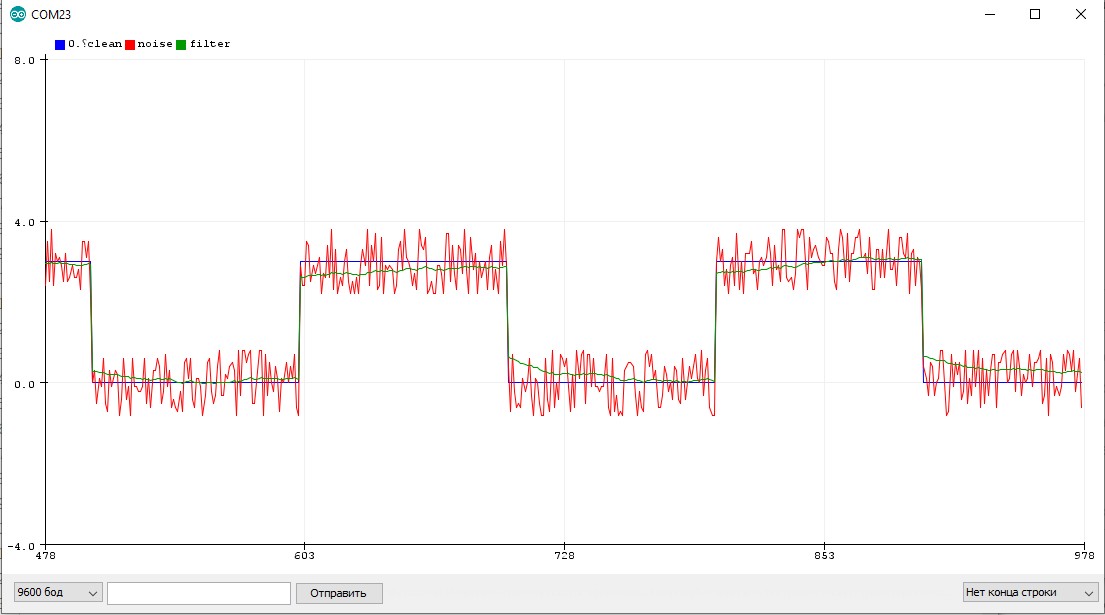
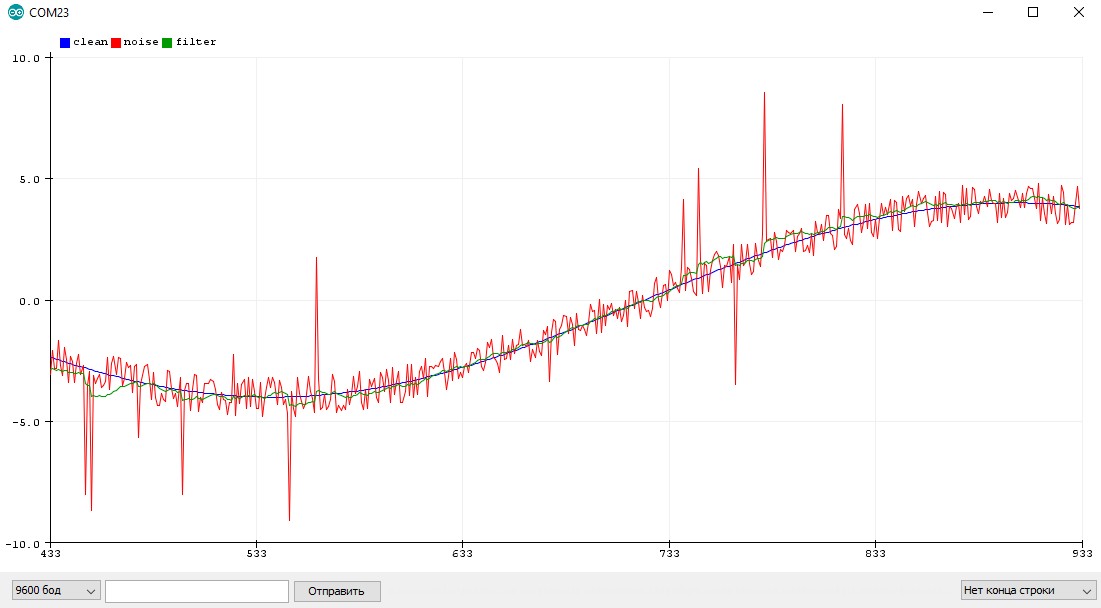
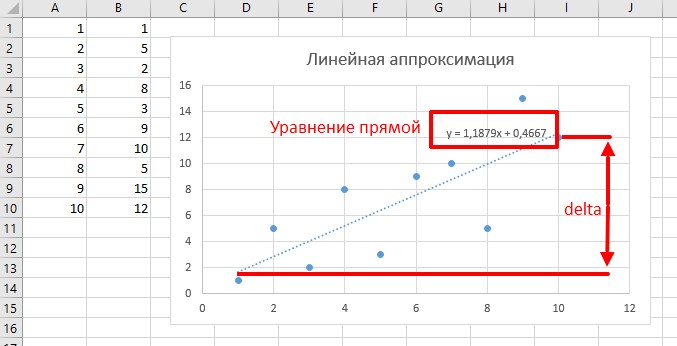
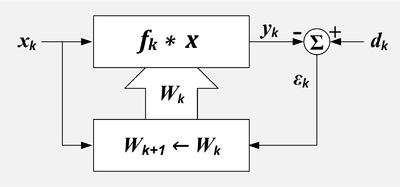

![{mathbf {W}}_{{k}}=left[w_{{0k}},,w_{{1k}},,...,,w_{{Lk}}right]^{{T}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/927bf9a780012f1a80bb6608a3ff410221a7b43e)