Формула вычисления случайной ошибки - Не ошибается лишь тот, кто ничего не делает!

Случайные погрешности в лабораторных работах по физике можно оценивать только с использованием калькулятора

О теории случайных погрешностей

Теория случайных погрешностей была создана К.Ф.Гауссом в первой половине XIX в. в связи с его занятиями астрономией и геодезией.

Напомним, что случайные погрешности δ_i = x_i — a проявляются при проведении серии измерений одной и той же физической величины в неизменных условиях одним и тем же методом.

Одним из фундаментальных положений теории Гаусса является «принцип арифметической середины». В соответствии с этим принципом за истинное значение величины а принимается среднее значение

при n → ∞, если метод не сопровождается систематическими погрешностями.

Для случайных погрешностей характерны следующие свойства:

Положительные и отрицательные случайные погрешности встречаются с одинаковой вероятностью, т. е. одинаково часто.
Среднее арифметическое из алгебраической суммы случайных погрешностей при неограниченном возрастании числа наблюдений стремится к нулю, т. е.
Малые по абсолютной величине случайные погрешности встречаются с большей вероятностью, чем большие.

Основная идея теории Гаусса может быть выражена следующим образом

Возможные конкретные значения случайной погрешности, как и сам результат измерения, предсказать невозможно. Однако после того как экспериментатор определил измеряемый параметр и метод его измерения, сразу «возник» объективный закон, неизвестный исследователю. Этот закон определяет совокупность случайных погрешностей, которые возникают в процессе измерений.

Всегда можно эмпирически (на конкретных опытах) выявить закон распределения случайных погрешностей, который обычно выражается в виде так называемой функции распределения f(δ). Этот закон позволяет определить вероятность, с которой погрешность может оказаться в интервале от δ₁ до δ₂. Вероятность эта равна площади заштрихованной криволинейной трапеции, представленной на графике функции распределения.

Гауссу удалось определить универсальный закон распределения, которому подчиняется огромный класс случайных погрешностей измерений самых разных величин различными методами.

Этот закон носит название нормального закона распределения. Конечно, существуют измерения, погрешность которых не распределена по нормальному закону. Однако всегда можно определить степень их отклонения от нормального закона.

Функция распределения φ(δ), открытая Гауссом, имеет следующие свойства:

1) Функция δ(φ) четная, т. е. δ-(φ-)δ(φ), и в силу этого симметрична относительно оси координат.

2) Функция δ(φ) имеет максимум при значениях случайной погрешности, равных нулю.

3) Функция δ(φ) имеет две точки перегиба, расположенные симметрично относительно оси координат. Координаты точек перегиба равны ±σ.

4) Касательные к кривой δ(φ) в точках перегиба отсекают на оси абcцисс отрезки, равные ±2σ.

5) Максимальное значение функции δ(φ) равно

6) Площадь под всей кривой δ(φ) стремится к 1. Площадь криволинейной трапеции, ограниченной прямыми, проходящими через точки δ_1,2= ±σ, составляет 0,68 от всей площади; если прямые проходят через точки δ_3,4= ±2σ, то площадь составляет 0,95; площадь криволинейной трапеции, ограниченной прямыми δ_5,6= ±3σ, равна 0,99.

Параметр σ, определяющий все фундаментальные свойства нормального закона, называется средним квадратическим отклонением. Этот параметр может быть определен после получения достаточно большой серии результатов измерений x₁, х₂, х₃, …, х_n. Тогда

Важность параметра σ состоит в том, что он позволяет определить границы случайных погрешностей. Действительно, вероятность получения случайных погрешностей, превосходящих по абсолютной величине 3σ, равна 1%.

При обычной организации измерений не представляется возможности провести не только бесконечно большое число измерений, но и провести просто большое их число.

Специальные исследования показали, что такая граница может быть определена при небольшом числе опытов в серии.

В такой серии из k измерений находят так называемую среднюю квадратичную погрешность

Затем Δх_кв увеличивают в S раз.

Число S называется коэффициентом Стьюдента (коэффициент был предложен в 1908 г. английским математиком В. С. Госсетом, публиковавшим свои работы под псевдонимом Стьюдент — студент). Коэффициент Стьюдента позволяет определить границу случайной погрешности серии: Δх_случ= S Δх_кв.

Таблица коэффициентов S для различного числа опытов в серии

Погрешность среднего арифметического

После проведения серии равноточных измерений и нахождения х_ср и σ легко определяется интервал, к которому с вероятностью 99% принадлежит результат любого следующего измерения. Этот интервал равен [х_ср± 3σ], если в серии достаточно много измерений, и имеет вид [х_ср± S Δх_кв] при небольшом числе опытов. Это означает, что 3σ (или S Δх_кв) характеризует погрешность каждого опыта серии. Итак, среднее квадратичное отклонение серии опытов есть погрешность каждого опыта серии. Именно поэтому вводится обозначение σ_х или ΔS_кв.х. Однако среднее арифметическое есть разумная комбинация всех измерений, и поэтому следует ожидать, что истинное значение находится в более узком интервале около х_ср, чем [x_cp± 3σ_х].

Понять, почему должно быть именно так, помогут следующие рассуждения

Выполняется N серий по n опытов в каждой. В каждой серии из n опытов определяется среднее значение х_ср. Таких средних значений получается N: х_ср1, х_ср2, …, x_cpN. Для этой совокупности средних определяется среднее квадратичное отклонение

Величина σ_{х ср} характеризует предельное распределение средних значений, это и есть величина, которая позволяет найти интервал, в котором находится истинное значение измеряемой в опыте величины [х_ср± 3σ_{х ср}]. На практике такая процедура никогда не реализуется не только потому, что это очень трудоемко, но и потому, что теория погрешностей позволяет по результатам одной серии определить погрешность среднего. Это делается на основе фундаментального результата теории погрешностей:

стандартное отклонение среднего σ_{х ср} в раз меньше стандартного отклонения каждого опыта серии σ_х, т.е.

Итак, если в серии с достаточно большим числом опытов определено х_ср, то граница случайной погрешности среднего равна

Если в серии небольшое число опытов, то граница случайной погрешности среднего находится по формуле:

Все расчеты случайных погрешностей возможны только с использованием режима статистических расчетов (см. раздел «Статистические расчеты»), следуя методическим рекомендациям, приведенным ниже.

Использование калькулятора CASIO fx-82EX СLASSWIZ для оценки случайных погрешностей

Включаем калькулятор, клавиша [ON]
Нажимаем клавишу [SHIFT](SETUP)
Входим в режим статистики. Нажимаем клавишу [2]
Выбираем режим 1-Variable. Нажимаем клавишу [1]
Заполняем таблицу
Нажимаем клавишу [OPTN]
Выбираем режим 1-Variable. Нажимаем клавишу [3]
На дисплее получаем ряд характеристик
8.1. Первая сверху — значение среднего значения
8.2. Вторая снизу — случайная погрешность каждого опыта серии σ_х
Вычисляем погрешность среднего
Находим границу случайной погрешности среднего

Пример

Измерялась скорость тела, брошенного горизонтально. В десяти опытах были получены следующие значения дальности полета L (в мм): 250, 245, 250, 262, 245, 248, 262, 260, 260, 248. Дальность полета тела измерялась линейкой с основной погрешностью Δ₁= 1мм. Высота, с которой брошено тело, в опыте равнялась Н = 1 м и измерялась мерной лентой с основной погрешностью Δ₂= 1 см и ценой деления С₂=1 см.

Решение

Сначала определим среднее значение дальности полета тела и вычислим его начальную скорость. Для этого сведем все данные в таблицу и проведем их первичную обработку.

Так как

Легко определить среднее значение скорости по результатам серии опытов:

Граница относительной погрешности измерения скорости:

В этой формуле ΔL — граница абсолютной погрешности измерения дальности полета, Δg — погрешность округления g, ΔН — погрешность прямого однократного измерения высоты.

ΔН = 1 см + 0,5 см = 1,5 см

ΔL складывается из погрешности линейки Δ₁ и случайной погрешности ΔL_случ.:

ΔL = Δ₁ + ΔL_случ.

Так как ΔL_кв = 7мм, то при оценке ΔL_случ. нет смысла учитывать погрешность линейки Δ₁ = 1мм.

Определим погрешность измерения скорости в любом однократном опыте, который можно провести на данной установке. В этом случае в формулу для ε_v следует вместо ∆L подставить его границу ∆L = S ∆L_кв. Здесь S = 3,2 (см. таблицу коэффициентов S для различного числа опытов в серии).

Имеем:

Первое слагаемое в этой сумме равно 0,09; слагаемое в скобках (0,01 + 0,0075) = 0,0175. Следовательно, ε_v= 0,09. Граница абсолютной погрешности каждого опыта серии не превосходит

ε_v = ε₀= 0,565 ∙ 0,09 = 0,05 м/с

Это значит, если на данной установке провести еще один опыт, то гарантировать можно, что значение скорости, рассчитанное по его результатам, будет принадлежать интервалу [(0,56 — 0,05)м/с; (0,56 + 0,05)м/с].

Найдем границу случайной погрешности среднего значения скорости тела, брошенного горизонтально. Для этого в формулу для ε_vследует вместо ∆L подставить границу случайной погрешности среднего:

Таким образом,

Относительная погрешность среднего равна

0,027 + 0,01 + 0,0075

Последним слагаемым в этой сумме можно пренебречь. Итак, ср = 0,04 = 4%. Мы видим, что погрешность среднего в два раза меньше погрешности каждого опыта. Граница абсолютной погрешности среднего равна:

Таким образом, из серии 10 опытов по измерению скорости можно сделать вывод о том, что в любой другой такой серии из 10 опытов на данной установке среднее значение скорости будет находиться в интервале [(0,56 — 0,02)м/с; (0,56 + 0,02)м/с]. Этому же интервалу принадлежит неизвестное значение скорости, которое получится, если проделать серию с очень большим числом опытов, т. е. такое значение, которое можно назвать истинным значением.

Источник

Если
повторять несколько раз измерения одной
и той же физической величины (например,
веса или, скажем, времени падения
грузика), стараясь при этом сохранить
все условия опыта постоянными, то, тем
не менее, полученные результаты будут
обязательно несколько отличаться друг
от друга (если, конечно, для результатов
каждого измерения записать достаточное
количество значащих цифр). Тому существует
множество разных причин, которые
практически невозможно учесть. Как
пример: неточности в фиксации времени
включения и выключения секундомера,
которые, кстати, важны для точного
определения интервалов времени не
только при физических измерениях, но и
во многих других случаях, в частности,
на спортивных соревнованиях. Как уже
указывалось ранее, соответствующие
ошибки называют случайными
ошибками.

Со
случайными изменениями некоторых
величин мы встречаемся и в повседневной
жизни, например, многократно отмечая
время, которое требуется, чтобы доехать
до нужного пункта. Случайные величины
важны для многих разделов естествознания,
например, для молекулярной физики при
измерениях скорости теплового движения
молекул газа или в ядерной физике при
изучении закономерностей радиоактивности.
Для количественного описания всех таких
случайно изменяющихся величин используют
хорошо разработанные методы теории
вероятностей. Эти методы позволяют
строго определить не только средние и
наиболее вероятные значения величин,
но и вероятности отклонений от этих
значений.

Среднее
значение любой случайной величины х,
а в данном случае результатов нескольких
последовательных её измерений (x₁,
x₂,
x_3…x_n),
определяют как среднее
арифметическое значение x
по формуле:

,
(5)

где
n
– число
измерений.

Далее
необходимо установить тот интервал
значений (—x
≤ x
≤
+x),
так называемый доверительный
интервал, в
пределах которого с обусловленной
доверительной
вероятностью
P(Δx)
(определяющей коэффициент надежности
полученных результатов измерения)
должны находиться значения x.

Доверительная
вероятность P(Δx)
в случае непрерывного распределения
значений x
определяется как:

,
(6)

где ρ(x)
– плотность вероятности реализации
значений x
в диапазоне от x
до x + dx,
причем знаменатель в этом выражении
обычно принимается равным 1 (условие
нормировки).

Еще
важнее, что эти две величины (доверительный
интервал и доверительная вероятность)
однозначно определяют отличие измеренного
значения x
от истинного значения той же физической
величины a.
Именно в их определении и состоит
основная задача математической обработки
результатов измерений.

Для
решения этой задачи необходимо, помимо
,
найтисреднюю
квадратичную ошибку измерений
в
данной серии опытов, которая определяется
по следующей формуле:

.
(7)

Вычисление
средней квадратичной, а не, как часто
делается, средней арифметической ошибки
измерений:

, (8)

позволяет
более корректно и просто определить
затем доверительный интервал и
доверительную вероятность, как это
будет показано в дальнейшем.

При
большом числе измерений (n
> 30) можно воспользоваться и более
простым расчётом средней арифметической
ошибки, так как в этом случае: ()_ср≈0,8.

Таким
образом, при n
,
0
и случайную ошибку измерения можно в
принципе сделать столь угодно малой
величиной, что однако потребует бесконечно
долгого процесса измерения.

Определение
доверительного интервала для случайной
ошибки и, соответственно, отличие
среднего значения
от истинного значения этой величиныа
для заданного значения доверительной
вероятности P(x)
очевидно требует знания конкретного
вида функции распределения ρ_i(x_i),
т.е. функции реализации определенных
значений x_i.

Рассмотрим
вначале наиболее простой для математической
обработки, но сложный для практического
осуществления случай достаточно большого
числа измерений. Строго говоря, для
этого необходимо, чтобы n
и дискретная функция распределения
ρ_i(x_i)
переходила в непрерывную функцию
плотности вероятности ρ(x).
Однако, как будет показано далее, для
этого достаточно n100
или даже n30.
При этом обычно реализуется функция
нормального распределения или функция
Гаусса, названная так в честь великого
немецкого математика, впервые установившего
вид этой функции:

.
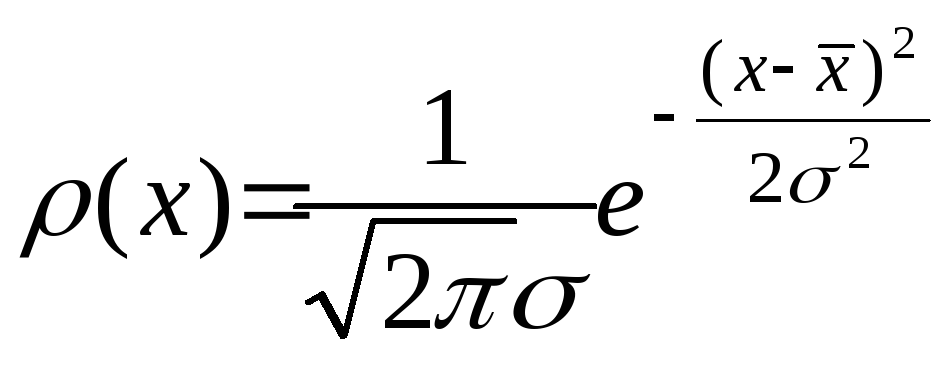
(9)

Здесь
использована новая величина 
– среднестатистический предел средней
квадратичной ошибки одного измерения
при очень большом количестве измерений.
Квадрат этой величины ²,
однозначно определяющей ширину функции
распределения для ошибок измерения и
вообще распределения случайных величин,
называют нормой или дисперсией
распределения.

Для
обоснования применимости формулы Гаусса
необходимо выполнение трех положений,
а именно:

— ошибки
измерений могут принимать непрерывный
ряд значений,

— при
достаточно большом числе измерений
ошибки одинаковой абсолютной величины,
но разного знака, встречаются одинаково
часто

— большие
ошибки наблюдается реже, чем меньшие.

Тогда
измеренные значения величины x,
будут находиться внутри доверительного
интервала (-x
≤ x
≤
+x)
с доверительной вероятностью P(x),
определяемой по формуле:

.
(10)

При
этом, чем больше требуется доверительная
вероятность P(x)
и, соответственно, надежность того, что
измеренные значения x
отличаются
от истинного значения этой величины а
не более, чем на x,
тем шире по отношению к 
становится доверительный интервал.
Так, если, например, требуется, чтобы
P(x)
= 0,7; 0,95; 0,98 или 0,999, то соответствующие
доверительные интервалы будут равны
;
2;
2,3
или 3,3.
В учебных лабораториях достаточно
выбирать доверительный интервал не
более 2σ, то есть брать доверительную
вероятность не более 0,95.

Для
выбора конкретного значения доверительной
вероятности P(x),
определяющей значения доверительного
интервала x,
необходимо понимать, насколько опасен
выход за пределы этого интервала,
вероятность которого, очевидно, равна
1 – P(x).
Такие задачи возникают на практике,
например, при отбраковке изделий,
выпускаемых в машиностроительной
промышленности, по их габаритам или
другим параметрам.

Реально
очень трудно осуществить (по причинам
большой длительности и малой продуктивности)
вышеуказанный идеализированный случай,
требующий, чтобы число измерений было,
по крайней мере, больше тридцати. Поэтому
необходимо рассмотреть реальный, но
более сложный для анализа случай
относительно небольшого числа измерений
(3
n
10).
Интуитивно понятно, что в этом случае
возникают повышенные требования к
доверительному интервалу (-x
;
+x)
при заданном значении P(x),
то есть он становится шире. Увеличение
числа измерений, наоборот, сужает этот
интервал.

На
опыте часто измеряют физические величины,
которые могут принимать лишь дискретные
значения, а число этих измерений конечно.
В ряде случаев вероятность реализации
определенных значений таких величин
хорошо описывается распределением
Пуассона (знаменитый французский
математик и физик).

Коэффициенты
Стьюдента .
Таблица №1.

(число измерений)

Доверительная вероятность
P

0,1

0,2

0,3

0,4

0,5

0,6

0,7

0,8

0,9

0,95

0,98

0,99

0,999

21-24

26-27

120

0,16

0,14

0,13

0,33

0,29

0,28

0,27

0,26

0,25

0,51

0,45

0,42

0,41

0,40

0,39

0,73

0,62

0,58

0,57

0,56

0,55

0,54

0,53

0,52

1,00

0,82

0,77

0,74

0,73

0,72

0,71

0,70

0,69

0,68

0,67

1,38

1,06

0,98

0,94

0,92

0,90

0,88

0,87

0,86

0,85

0,84

2,0

1,3

1,2

1,1

1,0

3,1

1,9

1,6

1,5

1,4

1,3

6,3

2,9

2,4

2,1

2,0

1,9

1,8

1,7

1,6

12,7

4,3

3,2

2,8

2,6

2,4

2,3

2,2

2,1

2,0

31,8

7,0

4,5

3,7

3,4

3,1

3,0

2,9

2,8

2,7

2,6

2,5

2,4

2,3

63,7

9,9

5,8

4,6

4,0

3,7

3,5

3,4

3,3

3,2

3,1

3,0

2,9

2,8

2,7

2,6

636,6

31,6

12,9

8,6

6,9

6,0

5,4

5,0

4,8

4,6

4,5

4,3

4,2

4,1

4,0

3,9

3,8

3,7

3,6

3,5

3,4

3,3

Для
многих лабораторных работ, когда число
измерений не велико, распределение
погрешностей описывается еще более
сложными, специальными гамма–функциями
(распределение Стьюдента или “t”–
распределение. “Стьюдент” – это
псевдоним английского математика
Уильяма Сита Госсета.). Для такого
распределения с высокой точностью
вычислены и затабулированы так называемые
коэффициенты Стьюдента 
(таблица №1). Они определяют отношение
доверительного интервала x
к средней квадратичной ошибке
для данной серии измерений и определенных
значенийn
и P(x),
то есть:

.
(11)

Из
таблицы 1 следует, что при доверительной
вероятности P(x)
0,7 доверительный интервал x
всегда несколько превышает значение
,
но дляP(x)=0,7
по мере увеличения числа измерений n
стремится
к этому значению, причем их различие
становится незначительным (меньше 10%)
уже при n 
7. Аналогичное, но более медленное
уменьшение 
наблюдается и для более высоких значений
P(x)=
0,95; 0,98; 0,999. Для этих значений P,
чтобы достаточно приблизиться к
предельным значениям 
(2; 2,3; 3,3), соответствующим функции Гаусса,
необходимо значительно большее число
измерений (n
15,
20 и 40). В большинстве лабораторных работ
число измерений (3 
n 
10), а доверительная вероятность P(x)
принимается равной 0,95, так что
соответствующие коэффициенты Стьюдента
изменяются от 4,3 до 2,3. Если значения
доверительной вероятности не указаны,
то её обычно выбирают равной 0,7.

Таким
образом, окончательный результат
измерений с указанием доверительной
вероятности P
в лабораторных практикумах следует
представлять в виде:

,
(12)

где за
скобкой указывают единицу измерения
данной величины в общепринятой
международной системе единиц (СИ).

При
этом необходимо, чтобы среднее значение
и доверительный интервалx
были записаны в одних и тех же единицах
и с одинаковой точностью. Доверительный
интервал x
обычно
записывают в виде двух (реже одной)
значащих цифр, округляя последующие
цифры. Если число n
измерений невелико (менее 5 – 6), что
имеет место в большинстве лабораторных
работ, то достаточно округления
доверительного интервала до первой
значащей цифры, и только если она является
единицей – до двух значащих цифр. При
большем числе измерений (n
> 10) одна значащая цифра в доверительном
интервале оставляется только, когда
она больше трёх. При ещё большем числе
измерений (n

30 и более) оставляются две значащие
цифры. Предварительные вычисления
иследует
проводить, разумеется, с несколько более
высокой точностью.

Таким
же образом округляются и приборные
абсолютная x_пр
и относительная
_пр
ошибки: с точностью до двух значащих
цифр, если первая значащая цифра равна
1, и до одной значащей цифры, если она
больше единицы.

При
округлении последняя из оставляемых
цифр в доверительном интервале x
всегда увеличивается на 1 (округление
с избытком).

Среднее
значение измеряемой величины

округляется до того же порядка величины,
что и значение x,
при этом
и xдолжны быть
выражены в одинаковых единицах измерения.
Если в значении

первая отбрасываемая цифра, следующая
за последней оставляемой, больше или
равна 5 (но только, если за этой пятёркой
есть ещё цифры), то последняя из оставляемых
цифр увеличивается на 1 (округление с
избытком). Если же первая отбрасываемая
цифра меньше 5, то последняя из оставляемых
цифр не изменяется (округление с
недостатком).

Так,
если полученные при вычислении значения
∆x
составляют,
например, в одном случае: 1,255, а в другом
случае: 2,455, то, округляя их, в первом
случае следует записать: x
= 1,3 (округление с избытком до двух
значащих цифр, т.к. первая значащая цифра
— единица), а во втором – x= 3
(округление с избытком до одной значащей
цифры, т.к. она – больше единицы). Если
при этом результат измерения составил,
скажем,

= 40,71 , то окончательно правильная запись:

в
первом случае x
= 40,7 
1,3,

во
втором случае x
= 41

3.

Если
же в полученном результате измерения

первая
отбрасываемая цифра равна 5, а других
цифр после неё нет, то можно как оставить
предыдущую цифру неизменной, так и
увеличить её на 1. Часто для удобства
расчётов делают эту последнюю из
оставленных цифр чётной. Если, скажем,
получено значение тока 2,375 А, а погрешность
0,125 А, то результат удобнее записать
так:

I
= (2,38 
0,13) A.

В
случае приборных погрешностей допустима
запись, когда в самой величине и
погрешности не совпадают разряды, в
которых стоят последние оставленные
цифры, например:

I
= (2,38 ± 0,005) А.

Если
случайная ошибка x_сл
заметно превосходит приборную x_np
(приблизительно, раза в три и более), то
последней можно пренебречь, и, наоборот.
Если случайные и приборные ошибки
сравнимы, то они складываются по общему
закону сложения всех случайных величин,
а именно:

Рассмотрим
как пример расчёта случайных ошибок, а
также учета приборных ошибок и правильной
записи окончательного результата,
измерение величины тока I
через фотоэлемент, возникающего при
его освещении. Опыт повторялся пять раз
(n
= 5) при одинаковых условиях освещения
и были зафиксированы следующие результаты:
I₁= 0,292 мА; I₂
= 0,284 мА; I₃
= 0,305 мА; I₄
= 0,293 мА; I₅
= 0,290 мА. Измерения проводились цифровым
миллиамперметром, приборная ошибка
которого составляет единицу последнего
разряда цифрового табло индикатора
миллиамперметра: ∆I_пр
= 0,001 мА

Среднее
значение
= 0,2928 мА. Для доверительной вероятности
P
= 0,95 в таблице находится коэффициент
Стьюдента α = 2,8. Тогда доверительный
интервал: ∆I
= 2,8·

·=0,009594 мА.

Так
как ∆I
>> ∆I_пр,
то окончательный результат с учётом
округления: I
= 0,293±0,010 мА.

Всё
вышесказанное справедливо, прежде
всего, для прямых измерений, когда на
опыте непосредственно измеряется
интересующая нас физическая величина.
При косвенных
измерениях,
когда эта величина определяется по
известной формуле, в которую входят
несколько других измеряемых на опыте
независимых величин, необходимо провести
дополнительный анализ общей ошибки
измерения. Если искомая величина y
= (x₁,
x₂….x_k),
то есть является известной функцией
нескольких непосредственно измеряемых
величин x_i,
то её среднее значение определяется,
как.
Если в данном опыте преобладают приборные
ошибки, то
оценку
абсолютной y
ошибки
измерения следует производить по
формуле:

,
(13)

Если,
наоборот, в измерениях преобладают
случайные ошибки, то расчет общей ошибки
производят по формуле:

.
(14)

Вопрос
о том, какими формулами пользоваться,
решают при анализе результатов измерений.
Если отклонения большинства из результатов
измерений от среднего арифметического
значения не превышает абсолютную ошибку
используемых приборов, то расчет
производят по формуле (13), а в противоположном
случае, по формуле (14).

В
общем случае случайные x_сл
и приборные ошибки x_np
складываются по общему закону сложения
всех случайных величин, а именно:

(15)

и расчёт
абсолютной ошибки ∆y
косвенных измерений производят по
формуле (14).

Поэтому,
если одна из этих ошибок в три и более
раз превышает другую ошибку, то последняя
из этих ошибок будет очень слабо влиять
на общую точность измерения. Исходя из
этих соображений, обычно и выбирается
необходимое число измерений n,
поскольку нет никакого смысла стремиться
получить случайную ошибку значительно
меньше приборной ошибки.

Наглядной
иллюстрацией систематических и случайных
ошибок могут служить результаты стрельбы
из различных видов оружия, в том числе
на спортивных соревнованиях. Так, если
имеется только систематическая ошибка
(сбит прицел, неправильное прицеливание
или расчеты), то все пули (снаряды, стрелы,
бомбы и т.д.) попадут в одно и то же место,
но смещенное от центра мишени или цели.
Наоборот, если существуют только
случайные ошибки, то будет значительный
разброс в местах попадания («плохая
кучность»), но усредненное отклонение
от центра мишени (или цели) будет
стремиться к нулю. Реально, конечно,
наблюдаются оба вида ошибок, но один из
них обычно существенно преобладает над
другим.

Разберём
пример нахождения плотности ρ материала
шара по измерениям его массы m
и объёма V
(объём шара находится через его диаметр
D:
V
= πD³/6):
ρ = 6m/πD³.

Если
масса шара была измерена на отъюстированных
рычажных весах с точностью 0,02 г и
составила m
= 11,20 г, то результат измерения запишется:
m
= 11,20 ± 0,02 г.

Диаметр
шара измерялся штангенциркулем, имеющем
погрешность ∆D_пр
= 0,05 мм. Десятикратное (n
= 10) повторение измерений диаметра даёт
среднее значение диаметра
=
13,615 мм.При
этом для случайных ошибок измерений
доверительный интервал ∆D
находится по формуле (11):
=,
гдеn
= 10, и для доверительной вероятности P
= 0,95 по таблице №1 коэффициент Стьюдента
α = 2,3.

Произведённый
подсчёт показывает, что ∆D
= 0,1676 мм, то есть случайная ошибка более
чем в три раза превосходит приборную
ошибку ∆D_пр
= 0,05 мм, и последнюю можно не учитывать:
D
= 13,62 ± 0,17 мм.

Среднее
значение плотности находится из:
= 6m/π=
8,480 г/см³.
А ошибка в определении плотности
находится по формуле (14):=.

Подставляя
полученные ранее значения
,,,
∆m,
∆D,
находится ∆ρ = 0,1069 г/см³.
Округляя результаты, окончательный
результат записывается: ρ = 8,48 ± 0,11 г/см³.

При
сложении (вычитании) неточных значений
величин в окончательной записи полученной
суммы следует оставлять только те
разряды, которые имеются во всех
складываемых величинах, проводя
соответствующее округление. При умножении
(делении) неточных значений величин в
результате оставляется только то число
значащих цифр, которое имеется в
перемножаемой величине с наименьшим
их количеством.

Как
пример: нужно записать результат
вычислений с неточно полученными
величинами x
= 8,232 + 0,31π = 8,232 + 0,97 = 9,20.

Теория
вероятностей полезна и для правильного
построения
графиков на
основе полученных экспериментальных
данных. Недопустимо рисовать изломанную
кривую, точно проходящую через
экспериментальные точки: следует
провести такую плавную линию, чтобы
отклонение экспериментальных точек от
нее в разные стороны приблизительно
компенсировали друг друга. По методу
наименьших квадратов построение графика
экспериментальной зависимости y=(x)
следует проводить таким образом, чтобы
свести к минимуму сумму квадратичных
отклонений

экспериментальных точек y_i от
проводимой кривой f(x_i),
где i
— номер
экспериментальной точки, n
– число
экспериментальных точек.

Для
построения графика кривой по
экспериментальным точкам вначале
подбирается функциональная зависимость
определённого вида (линейная: y=a+bx,
квадратичная: y=a+bx+cx²,
экспоненциальная: y
= a+be^x
и т.д.),
которая предположительно наилучшим
образом соответствует экспериментальным
данным, и определяются значения её
параметров a,b,c.
При этих значениях функция S
должна быть минимальна, то есть её
частные производные по этим параметрам
должны быть равны нулю:.
Решая полученную систему уравнений,
сначала находят значения этих параметров,
а затем и значениеS.
Сравнивая значения S,
полученные таким образом для разного
вида функций f(x),
выбирают функцию, для которой S
будет
минимальна – этой функцией и
аппроксимируются полученные
экспериментальные данные.

Следует
отметить, что разработаны способы, с
помощью которых можно достаточно просто
оценить наиболее подходящую функцию y
= f(x)
для описания известных экспериментальных
данных. Кроме того, существует компьютерная
программа Grapher,
которая даёт возможность подбирать
необходимые функции с соответствующими
параметрами для приближения экспериментально
полученных точек x_i
и y_i.
Добавим, что удобно использовать для
построения графиков такие координаты,
при которых график функции представляет
собой прямую (эти координаты следует
выбирать на основании подобранной
функции y=f(x)).

Методы
теории вероятностей успешно используют
и для планирования различных экспериментов,
например по разработке технологии
синтеза многокомпонентных материалов
с оптимальными свойствами (электрическими,
оптическими, механическими и др.),
требующимися для их практических
применений.

Прогресс
физики и других разделов естествознания
во многом определяется точностью
экспериментов. В настоящее время
достигнута поразительная точность при
измерении ряда физических величин
(расстояние, время и др.). Так, с помощью
молекулярных генераторов и стандартов
частоты удается осуществить такие
молекулярные часы, что их ошибка
составляет всего одну секунду за 10⁶
лет, т.е. относительная погрешность
равна 10^-12%.

С
очень высокой точностью измерена и
такая важнейшая физическая величина
как скорость распространения света в
вакууме с = (299792458,0 
1,2) м/с. Это позволяет производить очень
точные измерения больших расстояний:
до Луны, планет Солнечной системы и
других космических объектов.

На
смену общеизвестного эталона метра в
виде стержня, изготовленного из
платиноиридиевого сплава и хранящегося
в международной Палате мер и весов
вблизи Парижа, пришел «оптический
эталон». Он равен 1650763,73 длин волн
оранжевой линии излучения атомов
криптона, то есть на одном метре должно
укладываться ровно столько длин волн
этого излучения. Такой эталон примерно
в 100 раз точнее прежнего и может быть
легче воспроизведен в научных лабораториях.
При обычных измерениях, например в
физическом практикуме, конечно, не
удается достичь таких прецизионных
точностей измерений, которые во многом
определяются погрешностью используемых
приборов. Вместе с тем при работе в
практикуме нужно стремиться к уменьшению
ошибок измерения, правильно производить
их оценки и грамотно оформлять
промежуточные и окончательные результаты
измерений.

Статья обновлена 10.07.2022

Что такое погрешность измерения

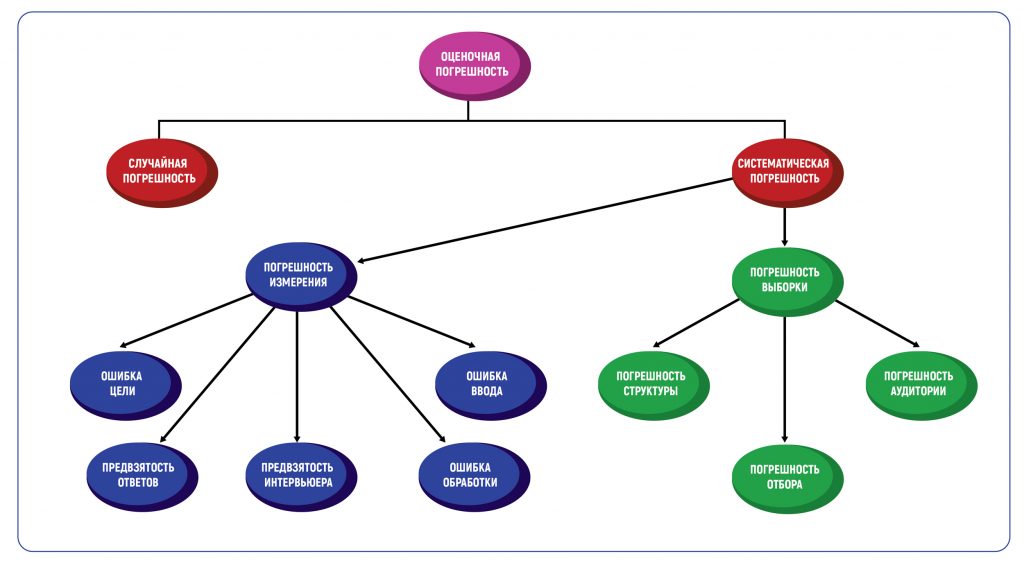
Любой расчет состоит из истинного и вычисляемого значения. При этом всегда должны учитываться значения ошибки или погрешности. Погрешность — это расхождение между истинным значением и вычисляемым. В маркетинге выделяют следующие виды погрешностей.

Математическая погрешность. Она описывается алгебраической формулой и бывает абсолютной, относительной и приведенной. Абсолютная погрешность измерения — это разница между вычисляемым и истинным значением. Относительная погрешность вычисляется в процентном соотношении истинного значения и полученного. Вычисление погрешности приведенной схоже с относительной, указывается она также в процентах, но дает разницу между нормирующей шкалой и полученными данными, то есть между эталонными и полученными значениями.
Оценочная погрешность. В маркетинге она бывает случайной и систематической. Случайная погрешность возникает из-за любых факторов, которые случайным образом влияют на измерение переменной в выборке. Систематическая погрешность вызывается факторами, которые систематически влияют на измерение переменной в выборке.

Математическая погрешность: формула для каждого типа

Если определение погрешности можно провести точным путем, она считается математической. Зачем нужно вычисление этого значения в маркетинге?

Погрешности возникают настолько часто, что популярной практикой в исследованиях является включение значения погрешности в окончательные результаты. Для этого используются формулы. Математическая погрешность — это значение, которое отражает разницу между выборкой и фактическим результатом. Если при расчетах учитывалась погрешность, в тексте исследования указывается что-то вроде: «Абсолютная погрешность для этих данных составляет 3,25%». Погрешность можно вычислить с любыми цифрами: количество человек, участвующих в опросе, погрешность суммы, затраченной на маркетинговый бюджет, и так далее.

Формулы погрешностей вычисляются следующим образом.

Абсолютная погрешность измерений: формула

Формула дает разницу между измеренным и реальным значением.

Формула абсолютной погрешности

Относительная погрешность: формула

Формула использует значение абсолютной погрешности и вычисляется в процентах по отношению к фактическому значению.

Формула относительной погрешности

Приведенная погрешность: формула

Формула также использует значение абсолютной погрешности. В чем измеряется приведенная погрешность? Тоже в процентах, но в качестве «эталона» используется не реальное значение, а единица измерения любой нормирующей шкалы. Например, для обычной линейки это значение равно 1 мм.

Формула приведенной погрешности

Классификация оценочной погрешности

Определение погрешности в оценках — это всегда методическая погрешность, то есть допустимое значение ошибки, основанное на методах проведения исследования. Погрешность метода вызывает два типа погрешностей — случайные и систематические. Таблица погрешностей в графической форме покажет все возможные типы.

Классификация оценочной погрешности

Что такое случайная погрешность

Случайная погрешность бывает статической и динамической. Динамическая погрешность возникает, когда мы имеем дело с меняющимися значениями — например, количество человек в выборке при маркетинговом исследовании. Статическая погрешность описывает ошибки при вычислении неизменных величин — вроде количества вопросов в вопроснике. Все они относятся к случайным погрешностям.

Типичный пример возникновения случайной погрешности — настроение участников маркетингового опроса. Как известно, эмоциональный настрой человека всегда влияет на его производительность. В ходе тестирования одни люди могут быть в хорошем расположении духа, а другие — в «миноре». Если настроение влияет на их ответы по заданному критерию выборки, это может искусственно завышать или занижать наблюдаемые оценки. Например, в случае с истинным значением 1 случайная погрешность может дать как -0,8, так и +0,5 к этому числу. Очень часто это случается при оценке времени ответа, например.

Случайная погрешность добавляет изменчивости данным, но не оказывает постоянного влияния на всю выборку. Вместо этого она произвольно изменяет измеряемые значения в диапазоне. В маркетинговой практике считается, что все случайные погрешности в распределении перекрывают друг друга и практически не влияют на конечный результат. Поэтому случайная погрешность считается «шумом» и в расчет не принимается. Эту погрешность нельзя устранить совсем, но можно уменьшить, просто увеличив размер выборки.

Что такое систематическая погрешность

Систематическая погрешность существует в результатах исследования, если эти результаты показывают устойчивую тенденцию к отклонению от истинных значений. Иными словами, если полученные цифры постоянно выше или ниже расчетных, речь идет о том, что в данных имеется систематическая погрешность.

В маркетинговых исследованиях есть два основных типа систематической погрешности: погрешность выборки и погрешность измерения.

Погрешность выборки

Погрешность выборки возникает, когда выборка, используемая в исследовании, не репрезентативна для всей совокупности данных. Типы такой погрешности включают погрешность структуры, погрешность аудитории и погрешность отбора.

Погрешность структуры

Погрешность структуры возникает из-за использования неполной или неточной основы для выборки. Распространенным источником такой погрешности в рамках маркетинговых исследований является проведение какого-либо опроса по телефону на основе существующего телефонного справочника или базы данных абонентов. Многие данные там указаны неполно или неточно — например, если люди недавно переехали или изменили свой номер телефона. Также такие данные часто указывают неполную или неверную демографию.

Если в качестве основы для исследования взят телефонный справочник, оно подвержено погрешности структуры, так как не учитывает всех возможных респондентов.

Погрешность аудитории

Погрешность аудитории возникает, если исследователь не знает, как определить аудиторию для исследования. Пример — оценка результатов исследования, проведенного среди клиентов крупного банка. Доля ответов на анкету составила чуть менее 1%. Анализ профессий всех опрошенных показал, что процент пенсионеров среди них в 20 раз выше, чем в целом по городу. Если эта группа значительно различается по интересующим переменным, то результаты будут неверными из-за погрешности аудитории.

Погрешность отбора

Даже если маркетологи правильно определили структуру и аудиторию, они не застрахованы от погрешности отбора. Она возникает, когда процедуры отбора являются неполными, неправильными или не соблюдаются должным образом. Например, интервьюеры при полевом исследовании могут избегать людей, которые живут в муниципальных домах. Потому что, по их мнению, жители вряд ли согласятся пройти такой опрос. Если жители муниципальных домов отличаются от тех, кто проживает в домах бизнес-класса, в результаты опроса будет внесена погрешность отбора.

Как минимизировать погрешность выборки

Знайте свою аудиторию.
Знайте, кто покупает ваш продукт, использует его, работает с вами и так далее. Имея базовую социально-экономическую информацию, можно составить стабильную выборку целевой аудитории. Маркетинговые исследования часто касаются одной конкретной группы населения — например, пользователей Facebook или молодых мам.
Разделите аудиторию на группы.
Вместо случайной выборки разбейте аудиторию на группы в соответствии с их численностью в общей совокупности данных. Например, если люди с определенной демографией составляют 35% населения, убедитесь, что 35% респондентов исследования отвечают этому условию.
Увеличьте размер выборки.
Больший размер выборки приводит к более точному результату.

Погрешность измерения

Погрешность измерения представляет собой серьезную угрозу точности исследования. Она возникает, когда существует разница между искомой информацией — то есть истинным значением, и информацией, фактически полученной в процессе измерения. К таким погрешностям приводят различные недостатки процесса исследования. Погрешность измерения, в основном, вызывается человеческим фактором — например, формулировкой вопросника, ошибками ввода данных и необъективными выводами.

К погрешностям измерения приводят следующие виды ошибок.

Ошибка цели

Ошибка цели возникает, когда существует несоответствие между информацией, фактически необходимой для решения проблемы, и данными , которые собирает исследование. Например, компания Kellogg впустую потратила миллионы на разработку завтраков для снижения уровня холестерина. Реальный вопрос, который нужно было бы задать в исследовании, заключался в том, купят ли люди овсяные хлопья для решения своей проблемы. Ответ «Нет» обошелся бы компании дешевле.

Предвзятость ответов

Некоторые люди склонны отвечать на конкретный вопрос определенным образом. Тогда возникает предвзятость ответа. Предвзятость ответа может быть результатом умышленной фальсификации или неосознанного искажения фактов.

Умышленная фальсификация происходит, когда респонденты целенаправленно дают неверные ответы на вопросы. Есть много причин, по которым люди могут сознательно искажать информацию. Например, они хотят скрыть или хотят казаться лучше, чем есть на самом деле.

Бессознательное искажение информации происходит, когда респондент пытается быть правдивым, но дает неточный ответ. Этот тип предвзятости может возникать из-за формата вопроса, его содержания или по другим причинам.

Предвзятость интервьюера

Интервьюер оказывает влияние на респондента — сознательно или бессознательно. Одежда, возраст, пол, выражение лица, язык тела или тон голоса могут повлиять на ответы некоторых или всех респондентов.

Ошибка обработки

Примеры включают наводящие вопросы или элементы дизайна анкеты, которые затрудняют запись ответов или приводят к ошибкам в них.

Ошибка ввода

Это ошибки, возникающие при вводе информации. Например, документ может быть отсканирован неправильно, и его данные по ошибке перенесутся неверно. Или люди, заполняющие опросы на смартфоне или ноутбуке, могут нажимать не те клавиши.

Виды проводимых маркетинговых исследований различны, поэтому универсальных рецептов не существует. Мы дадим несколько общих советов, используемых для минимизации систематических погрешностей разного типа.

Как минимизировать погрешность измерения

Предварительно протестируйте.
Погрешностей обработки и предвзятости можно избежать, если проводить предварительные тесты вопросника до начала основных интервью.
Проводите выборку случайным образом.
Чтобы устранить предвзятость, при выборке респондентов можно включать каждого четвертого человека из общего списка.
Тренируйте команду интервьюеров и наблюдателей.
Отбор и обучение тех, кто проводит исследования, должен быть тщательным. Особое внимание нужно уделять соблюдению инструкций в ходе каждого исследования.
Всегда выполняйте проверку сделанных записей.
Чтобы исключить ошибки ввода, все данные, вводимые для компьютерного анализа, должны быть перепроверены как минимум дважды.

Мир без ошибок не может существовать. Но понимание факторов, влияющих на маркетинговые исследования и измеряемые погрешности, имеет важное значение для сбора качественных данных.

Случайная погрешность — это ошибка в измерениях, которая носит неконтролируемый характер и очень труднопредсказуема. Так происходит из-за того, что существует огромное количество параметров, находящихся вне контроля экспериментатора, которые влияют на итоговые показатели. Случайные погрешности с абсолютной точностью вычислить невозможно. Они вызваны не сразу очевидными источниками и требуют много времени на выяснение причины их возникновения.

Как определить наличие случайной погрешности

Непредсказуемые ошибки присутствует не во всех измерениях. Но для того чтобы полностью исключить ее возможное влияние на результаты измерений, необходимо повторить эту процедуру несколько раз. Если итог не меняется от эксперимента к эксперименту либо изменяется, но на определенное относительное число — величина этой случайной погрешности равна нулю, и о ней можно не думать. И, наоборот, если полученный результат измерений каждый раз другой (близкий к какому-то среднему значению, но отличный), и отличия носят неопределенный характер, следовательно, на него влияет непредсказуемая ошибка.

Пример возникновения

Случайная составляющая погрешности возникает вследствие действия различных факторов. Например, при измерении сопротивления проводника, необходимо собрать электрическую цепь, состоящую из вольтметра, амперметра и источника тока, которым служит выпрямитель, подключенный в осветительную сеть. Первым делом нужно измерить напряжение, записав показания с вольтметра. Затем перенести взгляд на амперметр, чтобы зафиксировать его данные о силе тока. После использовать формулу, где R = U / I.

Но может случиться так, что в момент снятия показаний с вольтметра в соседней комнате включили кондиционер. Это довольно мощный прибор. В результате этого напряжение сети немного уменьшилось. Если бы не пришлось отводить взгляд на амперметр, можно было заметить, что показания вольтметра изменились. Поэтому данные первого прибора уже не соответствуют записанным ранее значениям. Из-за непредсказуемого включения кондиционера в соседней комнате получается результат уже со случайной погрешностью. Сквозняки, трения в осях измерительных приборов — потенциальные источники ошибок в измерениях.

Как проявляется

Допустим, необходимо рассчитать сопротивление круглого проводника. Для этого нужно знать его длину и диаметр. Помимо этого, учитывается удельное сопротивление материала, из которого он изготовлен. При измерении длины проводника случайная погрешность себя проявлять не будет. Ведь этот параметр всегда один и тот же. Но вот при измерении диаметра штангенциркулем или микрометром окажется, что данные разняться. Так происходит потому, что идеально круглый проводник невозможно изготовить в принципе. Поэтому, если измерить диаметр в нескольких местах изделия, то он может оказаться разным вследствие действия непредсказуемых факторов в момент его изготовления. Это случайная погрешность.

Иногда она также называется статистической погрешностью, поскольку эту величину можно уменьшить, увеличив количество экспериментов при одинаковых условиях их проведения.

Природа возникновения

В отличие от систематической ошибки, простое усреднение нескольких итоговых показателей одной и той же величины компенсирует случайные погрешности результатов измерений. Природа их возникновения определяется очень редко, и поэтому никогда не фиксируется, как постоянная величина. Случайная погрешность — это отсутствие каких-либо природных закономерностей. Например, она не пропорциональна измеряемой величине или никогда не остается постоянной при проведении нескольких измерений.

Может существовать ряд возможных источников случайных ошибок в экспериментах, и он полностью зависит от типа эксперимента и используемых приборов.

Например, биолог, изучающий размножение конкретного штамма бактерии, может столкнуться с непредсказуемой ошибкой из-за небольшого изменения температуры или освещения в помещении. Однако когда эксперимент будет повторяться в течение определенного периода времени, он избавится от этих различий в результатах путем их усреднения.

Формула случайной погрешности

Допустим, нужно определить какую-то физическую величину x. Чтобы исключить случайную погрешность необходимо провести несколько измерений, итогом которых будет серия результатов N количества измерений — x_1,x_2,…,x_n.

Чтобы обработать эти данные следует:

За результат измерений х₀принять среднее арифметическое х̅. Иными словами, х₀= (x₁ +x₂ +… +x_n)/ N_.
Найти стандартное отклонение. Обозначается оно греческой буквой σ и вычисляется следующим образом: σ = √((х₁— х̅ )²+ (х₂-х̅ )²+ … + (х_n— х̅ )²/ N — 1). Физический смысл σ состоит в том, что если провести еще одно измерение (N+1), то оно с вероятностью 997 шансов из 1000 ляжет в интервал х̅ -3σ < х_n+1< с + 3σ.
Найти границу абсолютной погрешности среднего арифметического х̅. Находится она по следующей формуле: Δх = 3σ / √N.
Ответ: х = х̅ + (-Δх).

Относительная погрешность будет равна ε = Δх /х̅.

Пример вычисления

Формулы расчета случайной погрешности достаточно громоздкие, поэтому, чтобы не запутаться в вычислениях, лучше использовать табличный способ.

Пример:

При измерении длины l, были получены следующие значения: 250 см, 245 см, 262 см, 248 см, 260 см. Количество измерений N = 5.

N п/п	l, см	I _{ср. арифм.,}см	\|l-l _{ср. арифм.}\|	(l-l _{ср. арифм.})²	σ, см	Δ l, см
1	250	253,0	3	9	7,55	10,13
2	245	8	64
3	262	9	81
4	248	5	25
5	260	7	49
	Σ = 1265			Σ = 228

Относительная погрешность равна ε = 10,13 см / 253,0 см = 0,0400 см.

Ответ: l = (253 + (-10)) см, ε = 4 %.

Практическая польза высокой точности измерений

Следует учитывать, что достоверность результатов тем выше, чем большее количество измерений проводится. Чтобы повысить точность в 10 раз, необходимо провести в 100 раз больше измерений. Это достаточно трудоемкое занятие. Однако оно может привести к очень важным результатам. Иногда приходится иметь дело со слабыми сигналами.

Например, в астрономических наблюдениях. Допустим, необходимо изучить звезду, блеск которой изменяется периодически. Но это небесное тело настолько далеко, что шум электронной аппаратуры или датчиков, принимающих излучения, может быть во много раз больше, чем сигнал, который необходимо обработать. Что же делать? Оказывается, если проводить миллионы измерений, то возможно среди этого шума выделить необходимый сигнал с очень большой достоверностью. Однако для этого потребуется совершать огромное количество измерений. Такая методика используется, чтобы различать слабые сигналы, которые едва заметны на фоне различных шумов.

Причина, по которой случайные погрешности могут быть решены путем усреднения, заключается в том, что они имеют нулевое ожидаемое значение. Они действительно непредсказуемы и разбросаны по среднему значению. Исходя из этого, среднее арифметическое ошибок ожидается равным нулю.

Случайная погрешность присутствуют в большинстве экспериментов. Поэтому исследователь должен быть подготовлен к ним. В отличие от систематических, случайные погрешности не предсказуемы. Это затрудняет их обнаружение, но от них легче избавиться, поскольку они являются статистическими и удаляются математическим методом, таким как усреднение.

Источник

Как определить наличие случайной погрешности

Пример возникновения

Как проявляется

Природа возникновения

Формула случайной погрешности

Чтобы обработать эти данные следует:

За результат измерений х₀принять среднее арифметическое х̅. Иными словами, х₀= (x₁ +x₂ +… +x_n)/ N_.
Найти стандартное отклонение. Обозначается оно греческой буквой σ и вычисляется следующим образом: σ = √((х₁— х̅ )²+ (х₂-х̅ )²+ … + (х_n— х̅ )²/ N — 1). Физический смысл σ состоит в том, что если провести еще одно измерение (N+1), то оно с вероятностью 997 шансов из 1000 ляжет в интервал х̅ -3σ < х_n+1< с + 3σ.
Найти границу абсолютной погрешности среднего арифметического х̅. Находится она по следующей формуле: Δх = 3σ / √N.
Ответ: х = х̅ + (-Δх).

Относительная погрешность будет равна ε = Δх /х̅.

Пример вычисления

Пример:

При измерении длины l, были получены следующие значения: 250 см, 245 см, 262 см, 248 см, 260 см. Количество измерений N = 5.

N п/п	l, см	I _{ср. арифм.,}см	\|l-l _{ср. арифм.}\|	(l-l _{ср. арифм.})²	σ, см	Δ l, см
1	250	253,0	3	9	7,55	10,13
2	245	8	64
3	262	9	81
4	248	5	25
5	260	7	49
	Σ = 1265			Σ = 228

Относительная погрешность равна ε = 10,13 см / 253,0 см = 0,0400 см.

Ответ: l = (253 + (-10)) см, ε = 4 %.

Практическая польза высокой точности измерений

Источник