Нейронные сети обучаются с помощью тех или иных модификаций градиентного спуска, а чтобы применять его, нужно уметь эффективно вычислять градиенты функции потерь по всем обучающим параметрам. Казалось бы, для какого-нибудь запутанного вычислительного графа это может быть очень сложной задачей, но на помощь спешит метод обратного распространения ошибки.
Открытие метода обратного распространения ошибки стало одним из наиболее значимых событий в области искусственного интеллекта. В актуальном виде он был предложен в 1986 году Дэвидом Э. Румельхартом, Джеффри Э. Хинтоном и Рональдом Дж. Вильямсом и независимо и одновременно красноярскими математиками С. И. Барцевым и В. А. Охониным. С тех пор для нахождения градиентов параметров нейронной сети используется метод вычисления производной сложной функции, и оценка градиентов параметров сети стала хоть сложной инженерной задачей, но уже не искусством. Несмотря на простоту используемого математического аппарата, появление этого метода привело к значительному скачку в развитии искусственных нейронных сетей.
Суть метода можно записать одной формулой, тривиально следующей из формулы производной сложной функции: если $f(x) = g_m(g_{m-1}(ldots (g_1(x)) ldots))$, то $frac{partial f}{partial x} = frac{partial g_m}{partial g_{m-1}}frac{partial g_{m-1}}{partial g_{m-2}}ldots frac{partial g_2}{partial g_1}frac{partial g_1}{partial x}$. Уже сейчас мы видим, что градиенты можно вычислять последовательно, в ходе одного обратного прохода, начиная с $frac{partial g_m}{partial g_{m-1}}$ и умножая каждый раз на частные производные предыдущего слоя.
Backpropagation в одномерном случае
В одномерном случае всё выглядит особенно просто. Пусть $w_0$ — переменная, по которой мы хотим продифференцировать, причём сложная функция имеет вид
$$f(w_0) = g_m(g_{m-1}(ldots g_1(w_0)ldots)),$$
где все $g_i$ скалярные. Тогда
$$f'(w_0) = g_m'(g_{m-1}(ldots g_1(w_0)ldots))cdot g’_{m-1}(g_{m-2}(ldots g_1(w_0)ldots))cdotldots cdot g’_1(w_0)$$
Суть этой формулы такова. Если мы уже совершили forward pass, то есть уже знаем
$$g_1(w_0), g_2(g_1(w_0)),ldots,g_{m-1}(ldots g_1(w_0)ldots),$$
то мы действуем следующим образом:
-
берём производную $g_m$ в точке $g_{m-1}(ldots g_1(w_0)ldots)$;
-
умножаем на производную $g_{m-1}$ в точке $g_{m-2}(ldots g_1(w_0)ldots)$;
-
и так далее, пока не дойдём до производной $g_1$ в точке $w_0$.
Проиллюстрируем это на картинке, расписав по шагам дифференцирование по весам $w_i$ функции потерь логистической регрессии на одном объекте (то есть для батча размера 1):
Собирая все множители вместе, получаем:
$$frac{partial f}{partial w_0} = (-y)cdot e^{-y(w_0 + w_1x_1 + w_2x_2)}cdotfrac{-1}{1 + e^{-y(w_0 + w_1x_1 + w_2x_2)}}$$
$$frac{partial f}{partial w_1} = x_1cdot(-y)cdot e^{-y(w_0 + w_1x_1 + w_2x_2)}cdotfrac{-1}{1 + e^{-y(w_0 + w_1x_1 + w_2x_2)}}$$
$$frac{partial f}{partial w_2} = x_2cdot(-y)cdot e^{-y(w_0 + w_1x_1 + w_2x_2)}cdotfrac{-1}{1 + e^{-y(w_0 + w_1x_1 + w_2x_2)}}$$
Таким образом, мы видим, что сперва совершается forward pass для вычисления всех промежуточных значений (и да, все промежуточные представления нужно будет хранить в памяти), а потом запускается backward pass, на котором в один проход вычисляются все градиенты.
Почему же нельзя просто пойти и начать везде вычислять производные?
В главе, посвящённой матричным дифференцированиям, мы поднимаем вопрос о том, что вычислять частные производные по отдельности — это зло, лучше пользоваться матричными вычислениями. Но есть и ещё одна причина: даже и с матричной производной в принципе не всегда хочется иметь дело. Рассмотрим простой пример. Допустим, что $X^r$ и $X^{r+1}$ — два последовательных промежуточных представления $Ntimes M$ и $Ntimes K$, связанных функцией $X^{r+1} = f^{r+1}(X^r)$. Предположим, что мы как-то посчитали производную $frac{partialmathcal{L}}{partial X^{r+1}_{ij}}$ функции потерь $mathcal{L}$, тогда
$$frac{partialmathcal{L}}{partial X^{r}_{st}} = sum_{i,j}frac{partial f^{r+1}_{ij}}{partial X^{r}_{st}}frac{partialmathcal{L}}{partial X^{r+1}_{ij}}$$
И мы видим, что, хотя оба градиента $frac{partialmathcal{L}}{partial X_{ij}^{r+1}}$ и $frac{partialmathcal{L}}{partial X_{st}^{r}}$ являются просто матрицами, в ходе вычислений возникает «четырёхмерный кубик» $frac{partial f_{ij}^{r+1}}{partial X_{st}^{r}}$, даже хранить который весьма болезненно: уж больно много памяти он требует ($N^2MK$ по сравнению с безобидными $NM + NK$, требуемыми для хранения градиентов). Поэтому хочется промежуточные производные $frac{partial f^{r+1}}{partial X^{r}}$ рассматривать не как вычисляемые объекты $frac{partial f_{ij}^{r+1}}{partial X_{st}^{r}}$, а как преобразования, которые превращают $frac{partialmathcal{L}}{partial X_{ij}^{r+1}}$ в $frac{partialmathcal{L}}{partial X_{st}^{r}}$. Целью следующих глав будет именно это: понять, как преобразуется градиент в ходе error backpropagation при переходе через тот или иной слой.
Вы спросите себя: надо ли мне сейчас пойти и прочитать главу учебника про матричное дифференцирование?
Встречный вопрос. Найдите производную функции по вектору $x$:
$$f(x) = x^TAx, Ain Mat_{n}{mathbb{R}}text{ — матрица размера }ntimes n$$
А как всё поменяется, если $A$ тоже зависит от $x$? Чему равен градиент функции, если $A$ является скаляром? Если вы готовы прямо сейчас взять ручку и бумагу и посчитать всё, то вам, вероятно, не надо читать про матричные дифференцирования. Но мы советуем всё-таки заглянуть в эту главу, если обозначения, которые мы будем дальше использовать, покажутся вам непонятными: единой нотации для матричных дифференцирований человечество пока, увы, не изобрело, и переводить с одной на другую не всегда легко.
Мы же сразу перейдём к интересующей нас вещи: к вычислению градиентов сложных функций.
Градиент сложной функции
Напомним, что формула производной сложной функции выглядит следующим образом:
$$left[D_{x_0} (color{#5002A7}{u} circ color{#4CB9C0}{v}) right](h) = color{#5002A7}{left[D_{v(x_0)} u right]} left( color{#4CB9C0}{left[D_{x_0} vright]} (h)right)$$
Теперь разберёмся с градиентами. Пусть $f(x) = g(h(x))$ – скалярная функция. Тогда
$$left[D_{x_0} f right] (x-x_0) = langlenabla_{x_0} f, x-x_0rangle.$$
С другой стороны,
$$left[D_{h(x_0)} g right] left(left[D_{x_0}h right] (x-x_0)right) = langlenabla_{h_{x_0}} g, left[D_{x_0} hright] (x-x_0)rangle = langleleft[D_{x_0} hright]^* nabla_{h(x_0)} g, x-x_0rangle.$$
То есть $color{#FFC100}{nabla_{x_0} f} = color{#348FEA}{left[D_{x_0} h right]}^* color{#FFC100}{nabla_{h(x_0)}}g$ — применение сопряжённого к $D_{x_0} h$ линейного отображения к вектору $nabla_{h(x_0)} g$.
Эта формула — сердце механизма обратного распространения ошибки. Она говорит следующее: если мы каким-то образом получили градиент функции потерь по переменным из некоторого промежуточного представления $X^k$ нейронной сети и при этом знаем, как преобразуется градиент при проходе через слой $f^k$ между $X^{k-1}$ и $X^k$ (то есть как выглядит сопряжённое к дифференциалу слоя между ними отображение), то мы сразу же находим градиент и по переменным из $X^{k-1}$:
Таким образом слой за слоем мы посчитаем градиенты по всем $X^i$ вплоть до самых первых слоёв.
Далее мы разберёмся, как именно преобразуются градиенты при переходе через некоторые распространённые слои.
Градиенты для типичных слоёв
Рассмотрим несколько важных примеров.
Примеры
-
$f(x) = u(v(x))$, где $x$ — вектор, а $v(x)$ – поэлементное применение $v$:
$$vbegin{pmatrix}
x_1 \
vdots\
x_N
end{pmatrix}
= begin{pmatrix}
v(x_1)\
vdots\
v(x_N)
end{pmatrix}$$Тогда, как мы знаем,
$$left[D_{x_0} fright] (h) = langlenabla_{x_0} f, hrangle = left[nabla_{x_0} fright]^T h.$$
Следовательно,
$$
left[D_{v(x_0)} uright] left( left[ D_{x_0} vright] (h)right) = left[nabla_{v(x_0)} uright]^T left(v'(x_0) odot hright) =\
$$$$
= sumlimits_i left[nabla_{v(x_0)} uright]_i v'(x_{0i})h_i
= langleleft[nabla_{v(x_0)} uright] odot v'(x_0), hrangle.
,$$где $odot$ означает поэлементное перемножение. Окончательно получаем
$$color{#348FEA}{nabla_{x_0} f = left[nabla_{v(x_0)}uright] odot v'(x_0) = v'(x_0) odot left[nabla_{v(x_0)} uright]}$$
Отметим, что если $x$ и $h(x)$ — это просто векторы, то мы могли бы вычислять всё и по формуле $frac{partial f}{partial x_i} = sum_jbig(frac{partial z_j}{partial x_i}big)cdotbig(frac{partial h}{partial z_j}big)$. В этом случае матрица $big(frac{partial z_j}{partial x_i}big)$ была бы диагональной (так как $z_j$ зависит только от $x_j$: ведь $h$ берётся поэлементно), и матричное умножение приводило бы к тому же результату. Однако если $x$ и $h(x)$ — матрицы, то $big(frac{partial z_j}{partial x_i}big)$ представлялась бы уже «четырёхмерным кубиком», и работать с ним было бы ужасно неудобно.
-
$f(X) = g(XW)$, где $X$ и $W$ — матрицы. Как мы знаем,
$$left[D_{X_0} f right] (X-X_0) = text{tr}, left(left[nabla_{X_0} fright]^T (X-X_0)right).$$
Тогда
$$
left[ D_{X_0W} g right] left(left[D_{X_0} left( ast Wright)right] (H)right) =
left[ D_{X_0W} g right] left(HWright)=\
$$ $$
= text{tr}, left( left[nabla_{X_0W} g right]^T cdot (H) W right) =\
$$ $$
=
text{tr} , left(W left[nabla_{X_0W} (g) right]^T cdot (H)right) = text{tr} , left( left[left[nabla_{X_0W} gright] W^Tright]^T (H)right)
$$Здесь через $ast W$ мы обозначили отображение $Y hookrightarrow YW$, а в предпоследнем переходе использовалось следующее свойство следа:
$$
text{tr} , (A B C) = text{tr} , (C A B),
$$где $A, B, C$ — произвольные матрицы подходящих размеров (то есть допускающие перемножение в обоих приведённых порядках). Следовательно, получаем
$$color{#348FEA}{nabla_{X_0} f = left[nabla_{X_0W} (g) right] cdot W^T}$$
-
$f(W) = g(XW)$, где $W$ и $X$ — матрицы. Для приращения $H = W — W_0$ имеем
$$
left[D_{W_0} f right] (H) = text{tr} , left( left[nabla_{W_0} f right]^T (H)right)
$$Тогда
$$
left[D_{XW_0} g right] left( left[D_{W_0} left(X astright) right] (H)right) = left[D_{XW_0} g right] left( XH right) =
$$ $$
= text{tr} , left( left[nabla_{XW_0} g right]^T cdot X (H)right) =
text{tr}, left(left[X^T left[nabla_{XW_0} g right] right]^T (H)right)
$$Здесь через $X ast$ обозначено отображение $Y hookrightarrow XY$. Значит,
$$color{#348FEA}{nabla_{X_0} f = X^T cdot left[nabla_{XW_0} (g)right]}$$
-
$f(X) = g(softmax(X))$, где $X$ — матрица $Ntimes K$, а $softmax$ — функция, которая вычисляется построчно, причём для каждой строки $x$
$$softmax(x) = left(frac{e^{x_1}}{sum_te^{x_t}},ldots,frac{e^{x_K}}{sum_te^{x_t}}right)$$
В этом примере нам будет удобно воспользоваться формализмом с частными производными. Сначала вычислим $frac{partial s_l}{partial x_j}$ для одной строки $x$, где через $s_l$ мы для краткости обозначим $softmax(x)_l = frac{e^{x_l}} {sum_te^{x_t}}$. Нетрудно проверить, что
$$frac{partial s_l}{partial x_j} = begin{cases}
s_j(1 — s_j), & j = l,
-s_ls_j, & jne l
end{cases}$$Так как softmax вычисляется независимо от каждой строчки, то
$$frac{partial s_{rl}}{partial x_{ij}} = begin{cases}
s_{ij}(1 — s_{ij}), & r=i, j = l,
-s_{il}s_{ij}, & r = i, jne l,
0, & rne i
end{cases},$$где через $s_{rl}$ мы обозначили для краткости $softmax(X)_{rl}$.
Теперь пусть $nabla_{rl} = nabla g = frac{partialmathcal{L}}{partial s_{rl}}$ (пришедший со следующего слоя, уже известный градиент). Тогда
$$frac{partialmathcal{L}}{partial x_{ij}} = sum_{r,l}frac{partial s_{rl}}{partial x_{ij}} nabla_{rl}$$
Так как $frac{partial s_{rl}}{partial x_{ij}} = 0$ при $rne i$, мы можем убрать суммирование по $r$:
$$ldots = sum_{l}frac{partial s_{il}}{partial x_{ij}} nabla_{il} = -s_{i1}s_{ij}nabla_{i1} — ldots + s_{ij}(1 — s_{ij})nabla_{ij}-ldots — s_{iK}s_{ij}nabla_{iK} =$$
$$= -s_{ij}sum_t s_{it}nabla_{it} + s_{ij}nabla_{ij}$$
Таким образом, если мы хотим продифференцировать $f$ в какой-то конкретной точке $X_0$, то, смешивая математические обозначения с нотацией Python, мы можем записать:
$$begin{multline*}
color{#348FEA}{nabla_{X_0}f =}\
color{#348FEA}{= -softmax(X_0) odot text{sum}left(
softmax(X_0)odotnabla_{softmax(X_0)}g, text{ axis = 1}
right) +}\
color{#348FEA}{softmax(X_0)odot nabla_{softmax(X_0)}g}
end{multline*}
$$
Backpropagation в общем виде
Подытожим предыдущее обсуждение, описав алгоритм error backpropagation (алгоритм обратного распространения ошибки). Допустим, у нас есть текущие значения весов $W^i_0$ и мы хотим совершить шаг SGD по мини-батчу $X$. Мы должны сделать следующее:
- Совершить forward pass, вычислив и запомнив все промежуточные представления $X = X^0, X^1, ldots, X^m = widehat{y}$.
- Вычислить все градиенты с помощью backward pass.
- С помощью полученных градиентов совершить шаг SGD.
Проиллюстрируем алгоритм на примере двуслойной нейронной сети со скалярным output’ом. Для простоты опустим свободные члены в линейных слоях.
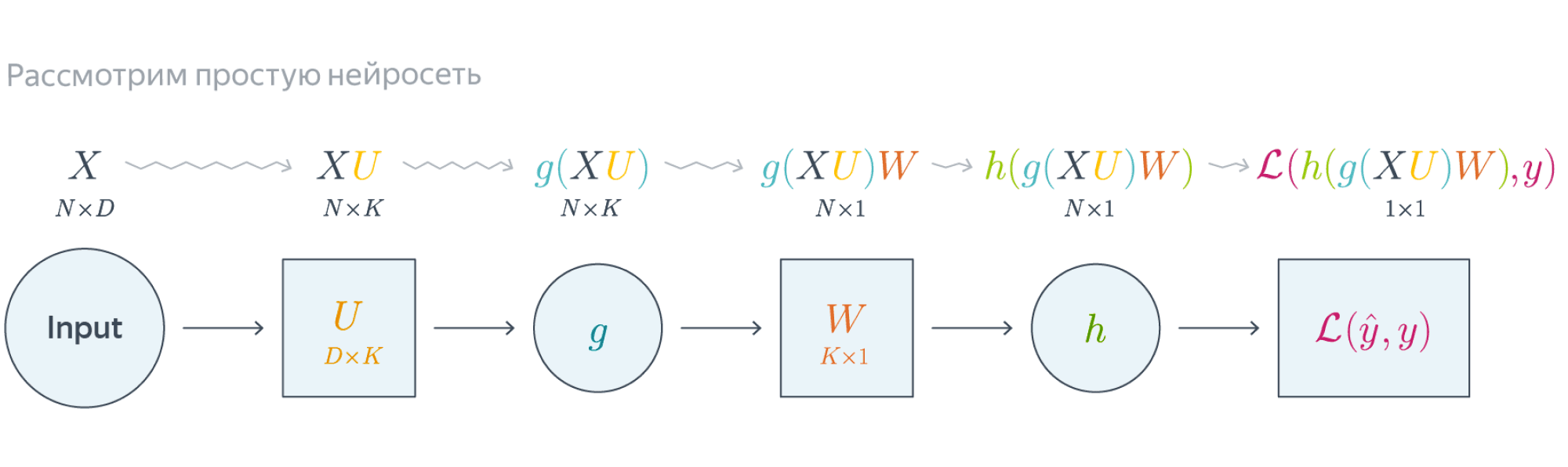
$$nabla_{W_0}mathcal{L} = nabla_{W_0}{left({vphantom{frac12}mathcal{L}circ hcircleft[Wmapsto g(XU_0)Wright]}right)}=$$
$$=g(XU_0)^Tnabla_{g(XU_0)W_0}(mathcal{L}circ h) = underbrace{g(XU_0)^T}_{ktimes N}cdot
left[vphantom{frac12}underbrace{h’left(vphantom{int_0^1}g(XU_0)W_0right)}_{Ntimes 1}odot
underbrace{nabla_{hleft(vphantom{int_0^1}g(XU_0)W_0right)}mathcal{L}}_{Ntimes 1}right]$$
Итого матрица $ktimes 1$, как и $W_0$
$$nabla_{U_0}mathcal{L} = nabla_{U_0}left(vphantom{frac12}
mathcal{L}circ hcircleft[Ymapsto YW_0right]circ gcircleft[ Umapsto XUright]
right)=$$
$$=X^Tcdotnabla_{XU^0}left(vphantom{frac12}mathcal{L}circ hcirc [Ymapsto YW_0]circ gright) =$$
$$=X^Tcdotleft(vphantom{frac12}g'(XU_0)odot
nabla_{g(XU_0)}left[vphantom{in_0^1}mathcal{L}circ hcirc[Ymapsto YW_0right]
right)$$
$$=ldots = underset{Dtimes N}{X^T}cdotleft(vphantom{frac12}
underbrace{g'(XU_0)}_{Ntimes K}odot
underbrace{left[vphantom{int_0^1}left(
underbrace{h’left(vphantom{int_0^1}g(XU_0)W_0right)}_{Ntimes1}odotunderbrace{nabla_{h(vphantom{int_0^1}gleft(XU_0right)W_0)}mathcal{L}}_{Ntimes 1}
right)cdot underbrace{W^T}_{1times K}right]}_{Ntimes K}
right)$$
Итого $Dtimes K$, как и $U_0$
Схематически это можно представить следующим образом:
Backpropagation для двуслойной нейронной сети
Подробнее о предыдущих вычисленияхЕсли вы не уследили за вычислениями в предыдущем примере, давайте более подробно разберём его чуть более конкретную версию (для $g = h = sigma$).
Рассмотрим двуслойную нейронную сеть для классификации. Мы уже встречали ее ранее при рассмотрении линейно неразделимой выборки. Предсказания получаются следующим образом:
$$
widehat{y} = sigma(X^1 W^2) = sigmaBig(big(sigma(X^0 W^1 )big) W^2 Big).
$$
Пусть $W^1_0$ и $W^2_0$ — текущее приближение матриц весов. Мы хотим совершить шаг по градиенту функции потерь, и для этого мы должны вычислить её градиенты по $W^1$ и $W^2$ в точке $(W^1_0, W^2_0)$.
Прежде всего мы совершаем forward pass, в ходе которого мы должны запомнить все промежуточные представления: $X^1 = X^0 W^1_0$, $X^2 = sigma(X^0 W^1_0)$, $X^3 = sigma(X^0 W^1_0) W^2_0$, $X^4 = sigma(sigma(X^0 W^1_0) W^2_0) = widehat{y}$. Они понадобятся нам дальше.
Для полученных предсказаний вычисляется значение функции потерь:
$$
l = mathcal{L}(y, widehat{y}) = y log(widehat{y}) + (1-y) log(1-widehat{y}).
$$
Дальше мы шаг за шагом будем находить производные по переменным из всё более глубоких слоёв.
-
Градиент $mathcal{L}$ по предсказаниям имеет вид
$$
nabla_{widehat{y}}l = frac{y}{widehat{y}} — frac{1 — y}{1 — widehat{y}} = frac{y — widehat{y}}{widehat{y} (1 — widehat{y})},
$$где, напомним, $ widehat{y} = sigma(X^3) = sigmaBig(big(sigma(X^0 W^1_0 )big) W^2_0 Big)$ (обратите внимание на то, что $W^1_0$ и $W^2_0$ тут именно те, из которых мы делаем градиентный шаг).
-
Следующий слой — поэлементное взятие $sigma$. Как мы помним, при переходе через него градиент поэлементно умножается на производную $sigma$, в которую подставлено предыдущее промежуточное представление:
$$
nabla_{X^3}l = sigma'(X^3)odotnabla_{widehat{y}}l = sigma(X^3)left( 1 — sigma(X^3) right) odot frac{y — widehat{y}}{widehat{y} (1 — widehat{y})} =
$$$$
= sigma(X^3)left( 1 — sigma(X^3) right) odot frac{y — sigma(X^3)}{sigma(X^3) (1 — sigma(X^3))} =
y — sigma(X^3)
$$ -
Следующий слой — умножение на $W^2_0$. В этот момент мы найдём градиент как по $W^2$, так и по $X^2$. При переходе через умножение на матрицу градиент, как мы помним, умножается с той же стороны на транспонированную матрицу, а значит:
$$
color{blue}{nabla_{W^2_0}l} = (X^2)^Tcdot nabla_{X^3}l = (X^2)^Tcdot(y — sigma(X^3)) =
$$$$
= color{blue}{left( sigma(X^0W^1_0) right)^T cdot (y — sigma(sigma(X^0W^1_0)W^2_0))}
$$Аналогичным образом
$$
nabla_{X^2}l = nabla_{X^3}lcdot (W^2_0)^T = (y — sigma(X^3))cdot (W^2_0)^T =
$$$$
= (y — sigma(X^2W_0^2))cdot (W^2_0)^T
$$ -
Следующий слой — снова взятие $sigma$.
$$
nabla_{X^1}l = sigma'(X^1)odotnabla_{X^2}l = sigma(X^1)left( 1 — sigma(X^1) right) odot left( (y — sigma(X^2W_0^2))cdot (W^2_0)^T right) =
$$$$
= sigma(X^1)left( 1 — sigma(X^1) right) odotleft( (y — sigma(sigma(X^1)W_0^2))cdot (W^2_0)^T right)
$$ -
Наконец, последний слой — это умножение $X^0$ на $W^1_0$. Тут мы дифференцируем только по $W^1$:
$$
color{blue}{nabla_{W^1_0}l} = (X^0)^Tcdot nabla_{X^1}l = (X^0)^Tcdot big( sigma(X^1) left( 1 — sigma(X^1) right) odot (y — sigma(sigma(X^1)W_0^2))cdot (W^2_0)^Tbig) =
$$$$
= color{blue}{(X^0)^Tcdotbig(sigma(X^0W^1_0)left( 1 — sigma(X^0W^1_0) right) odot (y — sigma(sigma(X^0W^1_0)W_0^2))cdot (W^2_0)^Tbig) }
$$
Итоговые формулы для градиентов получились страшноватыми, но они были получены друг из друга итеративно с помощью очень простых операций: матричного и поэлементного умножения, в которые порой подставлялись значения заранее вычисленных промежуточных представлений.
Автоматизация и autograd
Итак, чтобы нейросеть обучалась, достаточно для любого слоя $f^k: X^{k-1}mapsto X^k$ с параметрами $W^k$ уметь:
- превращать $nabla_{X^k_0}mathcal{L}$ в $nabla_{X^{k-1}_0}mathcal{L}$ (градиент по выходу в градиент по входу);
- считать градиент по его параметрам $nabla_{W^k_0}mathcal{L}$.
При этом слою совершенно не надо знать, что происходит вокруг. То есть слой действительно может быть запрограммирован как отдельная сущность, умеющая внутри себя делать forward pass и backward pass, после чего слои механически, как кубики в конструкторе, собираются в большую сеть, которая сможет работать как одно целое.
Более того, во многих случаях авторы библиотек для глубинного обучения уже о вас позаботились и создали средства для автоматического дифференцирования выражений (autograd). Поэтому, программируя нейросеть, вы почти всегда можете думать только о forward-проходе, прямом преобразовании данных, предоставив библиотеке дифференцировать всё самостоятельно. Это делает код нейросетей весьма понятным и выразительным (да, в реальности он тоже бывает большим и страшным, но сравните на досуге код какой-нибудь разухабистой нейросети и код градиентного бустинга на решающих деревьях и почувствуйте разницу).
Но это лишь начало
Метод обратного распространения ошибки позволяет удобно посчитать градиенты, но дальше с ними что-то надо делать, и старый добрый SGD едва ли справится с обучением современной сетки. Так что же делать? О некоторых приёмах мы расскажем в следующей главе.
Время на прочтение
5 мин
Количество просмотров 82K
В первой части были рассмотрены: структура, топология, функции активации и обучающее множество. В этой части попробую объяснить как происходит обучение сверточной нейронной сети.
Обучение сверточной нейронной сети
На начальном этапе нейронная сеть является необученной (ненастроенной). В общем смысле под обучением понимают последовательное предъявление образа на вход нейросети, из обучающего набора, затем полученный ответ сравнивается с желаемым выходом, в нашем случае это 1 – образ представляет лицо, минус 1 – образ представляет фон (не лицо), полученная разница между ожидаемым ответом и полученным является результат функции ошибки (дельта ошибки). Затем эту дельту ошибки необходимо распространить на все связанные нейроны сети.
Таким образом обучение нейронной сети сводится к минимизации функции ошибки, путем корректировки весовых коэффициентов синаптических связей между нейронами. Под функцией ошибки понимается разность между полученным ответом и желаемым. Например, на вход был подан образ лица, предположим, что выход нейросети был 0.73, а желаемый результат 1 (т.к. образ лица), получим, что ошибка сети является разницей, то есть 0.27. Затем веса выходного слоя нейронов корректируются в соответствии с ошибкой. Для нейронов выходного слоя известны их фактические и желаемые значения выходов. Поэтому настройка весов связей для таких нейронов является относительно простой. Однако для нейронов предыдущих слоев настройка не столь очевидна. Долгое время не было известно алгоритма распространения ошибки по скрытым слоям.
Алгоритм обратного распространения ошибки
Для обучения описанной нейронной сети был использован алгоритм обратного распространения ошибки (backpropagation). Этот метод обучения многослойной нейронной сети называется обобщенным дельта-правилом. Метод был предложен в 1986 г. Румельхартом, Макклеландом и Вильямсом. Это ознаменовало возрождение интереса к нейронным сетям, который стал угасать в начале 70-х годов. Данный алгоритм является первым и основным практически применимым для обучения многослойных нейронных сетей.
Для выходного слоя корректировка весов интуитивна понятна, но для скрытых слоев долгое время не было известно алгоритма. Веса скрытого нейрона должны изменяться прямо пропорционально ошибке тех нейронов, с которыми данный нейрон связан. Вот почему обратное распространение этих ошибок через сеть позволяет корректно настраивать веса связей между всеми слоями. В этом случае величина функции ошибки уменьшается и сеть обучается.
Основные соотношения метода обратного распространения ошибки получены при следующих обозначениях:
Величина ошибки определяется по формуле 2.8 среднеквадратичная ошибка:
Неактивированное состояние каждого нейрона j для образа p записывается в виде взвешенной суммы по формуле 2.9:
Выход каждого нейрона j является значением активационной функции
В качестве метода минимизации ошибки используется метод градиентного спуска, суть этого метода сводится к поиску минимума (или максимума) функции за счет движения вдоль вектора градиента. Для поиска минимума движение должно быть осуществляться в направлении антиградиента. Метод градиентного спуска в соответствии с рисунком 2.7.
Градиент функции потери представляет из себя вектор частных производных, вычисляющийся по формуле 2.11:
Производную функции ошибки по конкретному образу можно записать по правилу цепочки, формула 2.12:
Ошибка нейрона 
Ошибка δ для скрытого слоя рассчитывается по формуле 2.13:
Алгоритм распространения ошибки сводится к следующим этапам:
- прямое распространение сигнала по сети, вычисления состояния нейронов;
- вычисление значения ошибки δ для выходного слоя;
- обратное распространение: последовательно от конца к началу для всех скрытых слоев вычисляем δ по формуле 2.13;
- обновление весов сети на вычисленную ранее δ ошибки.
Алгоритм обратного распространения ошибки в многослойном персептроне продемонстрирован ниже:
До этого момента были рассмотрены случаи распространения ошибки по слоям персептрона, то есть по выходному и скрытому, но помимо них, в сверточной нейросети имеются подвыборочный и сверточный.
Расчет ошибки на подвыборочном слое
Расчет ошибки на подвыборочном слое представляется в нескольких вариантах. Первый случай, когда подвыборочный слой находится перед полносвязным, тогда он имеет нейроны и связи такого же типа, как в полносвязном слое, соответственно вычисление δ ошибки ничем не отличается от вычисления δ скрытого слоя. Второй случай, когда подвыборочный слой находится перед сверточным, вычисление δ происходит путем обратной свертки. Для понимания обратно свертки, необходимо сперва понять обычную свертку и то, что скользящее окно по карте признаков (во время прямого распространения сигнала) можно интерпретировать, как обычный скрытый слой со связями между нейронами, но главное отличие — это то, что эти связи разделяемы, то есть одна связь с конкретным значением веса может быть у нескольких пар нейронов, а не только одной. Интерпретация операции свертки в привычном многослойном виде в соответствии с рисунком 2.8.
Рисунок 2.8 — Интерпретация операции свертки в многослойный вид, где связи с одинаковым цветом имеют один и тот же вес. Синим цветом обозначена подвыборочная карта, разноцветным – синаптическое ядро, оранжевым – получившаяся свертка
Теперь, когда операция свертки представлена в привычном многослойном виде, можно интуитивно понять, что вычисление дельт происходит таким же образом, как и в скрытом слое полносвязной сети. Соответственно имея вычисленные ранее дельты сверточного слоя можно вычислить дельты подвыборочного, в соответствии с рисунком 2.9.
Рисунок 2.9 — Вычисление δ подвыборочного слоя за счет δ сверточного слоя и ядра
Обратная свертка – это тот же самый способ вычисления дельт, только немного хитрым способом, заключающийся в повороте ядра на 180 градусов и скользящем процессе сканирования сверточной карты дельт с измененными краевыми эффектами. Простыми словами, нам необходимо взять ядро сверточной карты (следующего за подвыборочным слоем) повернуть его на 180 градусов и сделать обычную свертку по вычисленным ранее дельтам сверточной карты, но так чтобы окно сканирования выходило за пределы карты. Результат операции обратной свертки в соответствии с рисунком 2.10, цикл прохода обратной свертки в соответствии с рисунком 2.11.
Рисунок 2.10 — Результат операции обратной свертки
Рисунок 2.11 — Повернутое ядро на 180 градусов сканирует сверточную карту
Расчет ошибки на сверточном слое
Обычно впередиидущий слой после сверточного это подвыборочный, соответственно наша задача вычислить дельты текущего слоя (сверточного) за счет знаний о дельтах подвыборочного слоя. На самом деле дельта ошибка не вычисляется, а копируется. При прямом распространении сигнала нейроны подвыборочного слоя формировались за счет неперекрывающегося окна сканирования по сверточному слою, в процессе которого выбирались нейроны с максимальным значением, при обратном распространении, мы возвращаем дельту ошибки тому ранее выбранному максимальному нейрону, остальные же получают нулевую дельту ошибки.
Заключение
Представив операцию свертки в привычном многослойном виде (рисунок 2.8), можно интуитивно понять, что вычисление дельт происходит таким же образом, как и в скрытом слое полносвязной сети.
Источники
Алгоритм обратного распространения ошибки для сверточной нейронной сети
Обратное распространение ошибки в сверточных слоях
раз и два
Обратное распространение ошибки в персептроне
Еще можно почитать в РГБ диссертацию Макаренко: АЛГОРИТМЫ И ПРОГРАММНАЯ СИСТЕМА КЛАССИФИКАЦИИ
Обратное распространение ошибки — это способ обучения нейронной сети. Цели обратного распространения просты: отрегулировать каждый вес пропорционально тому, насколько он способствует общей ошибке. Если мы будем итеративно уменьшать ошибку каждого веса, в конце концов у нас будет ряд весов, которые дают хорошие прогнозы.
Обновление правила цепочки
Прямое распространение можно рассматривать как длинный ряд вложенных уравнений. Если вы так думаете о прямом распространении, то обратное распространение — это просто приложение правила цепочки (дифференцирования сложной функции) для поиска производных потерь по любой переменной во вложенном уравнении. С учётом функции прямого распространения:
f(x)=A(B(C(x)))
A, B, и C — функции активации на различных слоях. Пользуясь правилом цепочки, мы легко вычисляем производную f(x) по x:
f′(x)=f′(A)⋅A′(B)⋅B′(C)⋅C′(x)
Что насчёт производной относительно B? Чтобы найти производную по B, вы можете сделать вид, что B (C(x)) является константой, заменить ее переменной-заполнителем B, и продолжить поиск производной по B стандартно.
f′(B)=f′(A)⋅A′(B)
Этот простой метод распространяется на любую переменную внутри функции, и позволяет нам в точности определить влияние каждой переменной на общий результат.
Применение правила цепочки
Давайте используем правило цепочки для вычисления производной потерь по любому весу в сети. Правило цепочки поможет нам определить, какой вклад каждый вес вносит в нашу общую ошибку и направление обновления каждого веса, чтобы уменьшить ошибку. Вот уравнения, которые нужны, чтобы сделать прогноз и рассчитать общую ошибку или потерю:
Учитывая сеть, состоящую из одного нейрона, общая потеря нейросети может быть рассчитана как:
Cost=C(R(Z(XW)))
Используя правило цепочки, мы легко можем найти производную потери относительно веса W.
C′(W)=C′(R)⋅R′(Z)⋅Z′(W)=(y^−y)⋅R′(Z)⋅X
Теперь, когда у нас есть уравнение для вычисления производной потери по любому весу, давайте обратимся к примеру с нейронной сетью:
Какова производная от потери по Wo?
C′(WO)=C′(y^)⋅y^′(ZO)⋅Z′O(WO)=(y^−y)⋅R′(ZO)⋅H
А что насчет Wh? Чтобы узнать это, мы просто продолжаем возвращаться в нашу функцию, рекурсивно применяя правило цепочки, пока не доберемся до функции, которая имеет элемент Wh.
C′(Wh)=C′(y^)⋅O′(Zo)⋅Z′o(H)⋅H′(Zh)⋅Z′h(Wh)=(y^−y)⋅R′(Zo)⋅Wo⋅R′(Zh)⋅X
И просто забавы ради, что, если в нашей сети было бы 10 скрытых слоев. Что такое производная потери для первого веса w1?
C(w1)=(dC/dy^)⋅(dy^/dZ11)⋅(dZ11/dH10)⋅(dH10/dZ10)⋅(dZ10/dH9)⋅(dH9/dZ9)⋅(dZ9/dH8)⋅(dH8/dZ8)⋅(dZ8/dH7)⋅(dH7/dZ7)⋅(dZ7/dH6)⋅(dH6/dZ6)⋅(dZ6/dH5)⋅(dH5/dZ5)⋅(dZ5/dH4)⋅(dH4/dZ4)⋅(dZ4/dH3)⋅(dH3/dZ3)⋅(dZ3/dH2)⋅(dH2/dZ2)⋅(dZ2/dH1)⋅(dH1/dZ1)⋅(dZ1/dW1)
Заметили закономерность? Количество вычислений, необходимых для расчёта производных потерь, увеличивается по мере углубления нашей сети. Также обратите внимание на избыточность в наших расчетах производных. Производная потерь каждого слоя добавляет два новых элемента к элементам, которые уже были вычислены слоями над ним. Что, если бы был какой-то способ сохранить нашу работу и избежать этих повторяющихся вычислений?
Сохранение работы с мемоизацией
Мемоизация — это термин в информатике, имеющий простое значение: не пересчитывать одно и то же снова и снова. В мемоизации мы сохраняем ранее вычисленные результаты, чтобы избежать пересчета одной и той же функции. Это удобно для ускорения рекурсивных функций, одной из которых является обратное распространение. Обратите внимание на закономерность в уравнениях производных приведённых ниже.
Каждый из этих слоев пересчитывает одни и те же производные! Вместо того, чтобы выписывать длинные уравнения производных для каждого веса, можно использовать мемоизацию, чтобы сохранить нашу работу, так как мы возвращаем ошибку через сеть. Для этого мы определяем 3 уравнения (ниже), которые вместе выражают в краткой форме все вычисления, необходимые для обратного распространения. Математика та же, но уравнения дают хорошее сокращение, которое мы можем использовать, чтобы отслеживать те вычисления, которые мы уже выполнили, и сохранять нашу работу по мере продвижения назад по сети.
Для начала мы вычисляем ошибку выходного слоя и передаем результат на скрытый слой перед ним. После вычисления ошибки скрытого слоя мы передаем ее значение обратно на предыдущий скрытый слой. И так далее и тому подобное. Возвращаясь назад по сети, мы применяем 3-ю формулу на каждом слое, чтобы вычислить производную потерь по весам этого слоя. Эта производная говорит нам, в каком направлении регулировать наши веса, чтобы уменьшить общие потери.
Примечание: термин ошибка слоя относится к производной потерь по входу в слой. Он отвечает на вопрос: как изменяется выход функции потерь при изменении входа в этот слой?
Ошибка выходного слоя
Для расчета ошибки выходного слоя необходимо найти производную потерь по входу выходному слою, Zo. Это отвечает на вопрос: как веса последнего слоя влияют на общую ошибку в сети? Тогда производная такова:
C′(Zo)=(y^−y)⋅R′(Zo)
Чтобы упростить запись, практикующие МО обычно заменяют последовательность (y^−y)∗R'(Zo) термином Eo. Итак, наша формула для ошибки выходного слоя равна:
Eo=(y^−y)⋅R′(Zo)
Ошибка скрытого слоя
Для вычисления ошибки скрытого слоя нужно найти производную потерь по входу скрытого слоя, Zh.
C′(Zh)=(y^−y)⋅R′(Zo)⋅Wo⋅R′(Zh)
Далее мы можем поменять местами элемент Eo выше, чтобы избежать дублирования и создать новое упрощенное уравнение для ошибки скрытого слоя:
Eh=Eo⋅Wo⋅R′(Zh)
Эта формула лежит в основе обратного распространения. Мы вычисляем ошибку текущего слоя и передаем взвешенную ошибку обратно на предыдущий слой, продолжая процесс, пока не достигнем нашего первого скрытого слоя. Попутно мы обновляем веса, используя производную потерь по каждому весу.
Производная потерь по любому весу
Вернемся к нашей формуле для производной потерь по весу выходного слоя Wo.
C′(WO)=(y^−y)⋅R′(ZO)⋅H
Мы знаем, что можем заменить первую часть уравнением для ошибки выходного слоя Eh. H представляет собой активацию скрытого слоя.
C′(Wo)=Eo⋅H
Таким образом, чтобы найти производную потерь по любому весу в нашей сети, мы просто умножаем ошибку соответствующего слоя на его вход (выход предыдущего слоя).
C′(w)=CurrentLayerError⋅CurrentLayerInput
Примечание: вход относится к активации с предыдущего слоя, а не к взвешенному входу, Z.
Подводя итог
Вот последние 3 уравнения, которые вместе образуют основу обратного распространения.
Вот процесс, визуализированный с использованием нашего примера нейронной сети выше:
Обратное распространение: пример кода
def relu_prime(z): if z > 0: return 1 return 0 def cost(yHat, y): return 0.5 * (yHat - y)**2 def cost_prime(yHat, y): return yHat - y def backprop(x, y, Wh, Wo, lr): yHat = feed_forward(x, Wh, Wo) # Layer Error Eo = (yHat - y) * relu_prime(Zo) Eh = Eo * Wo * relu_prime(Zh) # Cost derivative for weights dWo = Eo * H dWh = Eh * x # Update weights Wh -= lr * dWh Wo -= lr * dWo
Рад снова всех приветствовать, и сегодня продолжим планомерно двигаться в выбранном направлении. Речь, конечно, о масштабном разборе искусственных нейронных сетей для решения широкого спектра задач. Продолжим ровно с того момента, на котором остановились в предыдущей части, и это означает, что героем данного поста будет ключевой процесс — обучение нейронных сетей.
- Градиентный спуск
- Функция ошибки
- Метод обратного распространения ошибки
- Пример расчета
Тема эта крайне важна, поскольку именно процесс обучения позволяет сети начать выполнять задачу, для которой она, собственно, и предназначена. То есть нейронная сеть функционирует не по какому-либо жестко заданному на этапе проектирования алгоритму, она совершенствуется в процессе анализа имеющихся данных. Этот процесс и называется обучением нейронной сети. Математически суть процесса обучения заключается в корректировке значений весов синапсов (связей между имеющимися нейронами). Изначально значения весов задаются случайно, затем производится обучение, результатом которого будут новые значения синаптических весов. Это все мы максимально подробно разберем как раз в этой статье.
На своем сайте я всегда придерживаюсь концепции, при которой теоретические выкладки по максимуму сопровождаются практическими примерами для максимальной наглядности. Так мы поступим и сейчас 👍
Итак, суть заключается в следующем. Пусть у нас есть простейшая нейронная сеть, которую мы хотим обучить (продолжаем рассматривать сети прямого распространения):

То есть на входы нейронов I1 и I2 мы подаем какие-либо числа, а на выходе сети получаем соответственно новое значение. При этом нам необходима некая выборка данных, включающая в себя значения входов и соответствующее им, правильное, значение на выходе:
| bold{I_1} | bold{I_2} | bold{O_{net}} |
|---|---|---|
| x_{11} | x_{12} | y_{1} |
| x_{21} | x_{22} | y_{2} |
| x_{31} | x_{32} | y_{3} |
| … | … | … |
| x_{N1} | x_{N2} | y_{N} |
Допустим, сеть выполняет суммирование значений на входе, тогда данный набор данных может быть таким:
| bold{I_1} | bold{I_2} | bold{O_{net}} |
|---|---|---|
| 1 | 4 | 5 |
| 2 | 7 | 9 |
| 3 | 5 | 8 |
| … | … | … |
| 1000 | 1500 | 2500 |
Эти значения и используются для обучения сети. Как именно — рассмотрим чуть ниже, пока сконцентрируемся на идее процесса в целом. Для того, чтобы иметь возможность тестировать работу сети в процессе обучения, исходную выборку данных делят на две части — обучающую и тестовую. Пусть имеется 1000 образцов, тогда можно 900 использовать для обучения, а оставшиеся 100 — для тестирования. Эти величины взяты исключительно ради наглядности и демонстрации логики выполнения операций, на практике все зависит от задачи, размер обучающей выборки может спокойно достигать и сотен тысяч образцов.
Итак, итог имеем следующий — обучающая выборка прогоняется через сеть, в результате чего происходит настройка значений синаптических весов. Один полный проход по всей выборке называется эпохой. И опять же, обучение нейронной сети — это процесс, требующий многократных экспериментов, анализа результатов и творческого подхода. Все перечисленные параметры (размер выборки, количество эпох обучения) могут иметь абсолютно разные значения для разных задач и сетей. Четкого правила тут просто нет, в этом и кроется дополнительный шарм и изящность )
Возвращаемся к разбору, и в результате прохода обучающей выборки через сеть мы получаем сеть с новыми значениями весов синапсов.
Далее мы через эту, уже обученную в той или иной степени, сеть прогоняем тестовую выборку, которая не участвовала в обучении. При этом сеть выдает нам выходные значения для каждого образца, которые мы сравниваем с теми верными значениями, которые имеем.
Анализируем нашу гипотетическую выборку:

Таким образом, для тестирования подаем на вход сети значения x_{(M+1)1}, x_{(M+1)2} и проверяем, чему равен выход, ожидаем очевидно значение y_{(M+1)}. Аналогично поступаем и для оставшихся тестовых образцов. После чего мы можем сделать вывод, успешно или нет работает сеть. Например, сеть дает правильный ответ для 90% тестовых данных, дальше уже встает вопрос — устраивает ли нас данная точность или процесс обучения необходимо повторить, либо провести заново, изменив какие-либо параметры сети.
В этом и заключается суть обучения нейронных сетей, теперь перейдем к деталям и конкретным действиям, которые необходимо осуществить для выполнения данного процесса. Двигаться снова будем поэтапно, чтобы сформировать максимально четкую и полную картину. Поэтому начнем с понятия градиентного спуска, который используется при обучении по методу обратного распространения ошибки. Обо всем этом далее…
Обучение нейронных сетей. Градиентный спуск.
Рассмотрев идею процесса обучения в целом, на данном этапе мы можем однозначно сформулировать текущую цель — необходимо определить математический алгоритм, который позволит рассчитать значения весовых коэффициентов таким образом, чтобы ошибка сети была минимальна. То есть грубо говоря нам необходима конкретная формула для вычисления:
Здесь Delta w_{ij} — величина, на которую необходимо изменить вес синапса, связывающего нейроны i и j нашей сети. Соответственно, зная это, необходимо на каждом этапе обучения производить корректировку весов связей между всеми элементами нейронной сети. Задача ясна, переходим к делу.
Пусть функция ошибки от веса имеет следующий вид:
Для удобства рассмотрим зависимость функции ошибки от одного конкретного веса:

В начальный момент мы находимся в некоторой точке кривой, а для минимизации ошибки попасть мы хотим в точку глобального минимума функции:
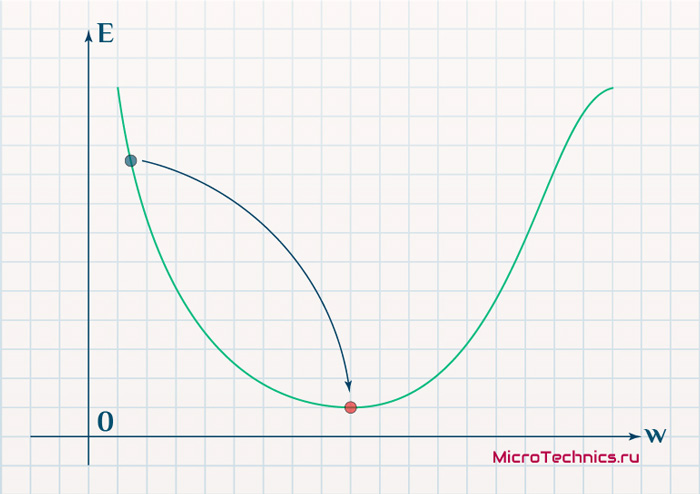
Нанесем на график вектора градиентов в разных точках. Длина векторов численно равна скорости роста функции в данной точке, что в свою очередь соответствует значению производной функции по данной точке. Исходя из этого, делаем вывод, что длина вектора градиента определяется крутизной функции в данной точке:
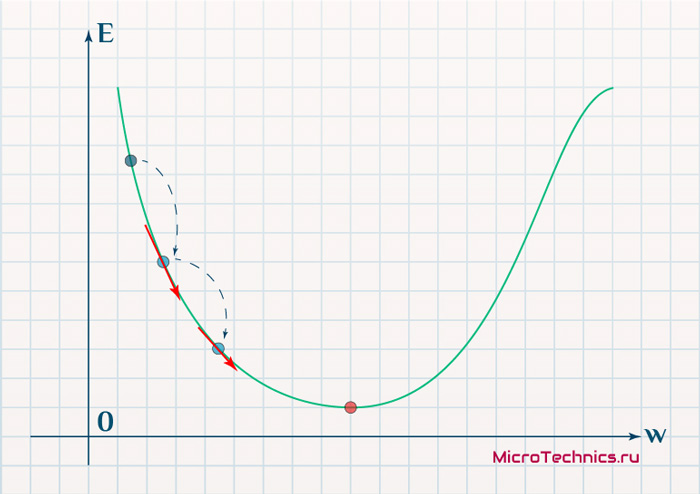
Вывод прост — величина градиента будет уменьшаться по мере приближения к минимуму функции. Это важный вывод, к которому мы еще вернемся. А тем временем разберемся с направлением вектора, для чего рассмотрим еще несколько возможных точек:
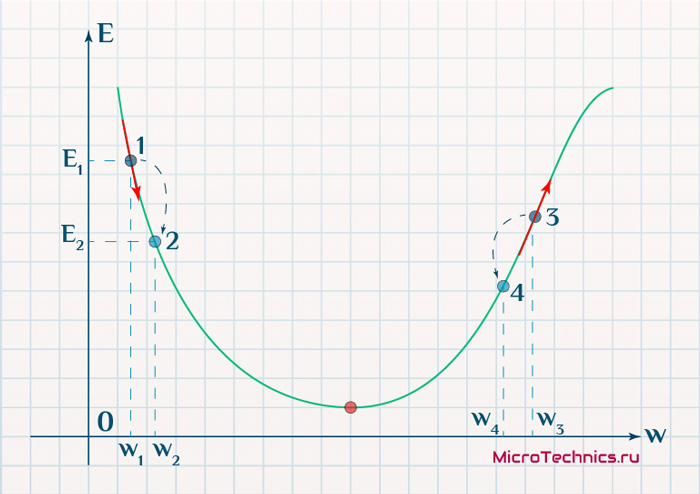
Находясь в точке 1, целью является перейти в точку 2, поскольку в ней значение ошибки меньше (E_2 < E_1), а глобальная задача по-прежнему заключается в ее минимизации. Для этого необходимо изменить величину w на некое значение Delta w (Delta w = w_2 — w_1 > 0). При всем при этом в точке 1 градиент отрицательный. Фиксируем данные факты и переходим к точке 3, предположим, что мы находимся именно в ней.
Тогда для уменьшения ошибки наш путь лежит в точку 4, а необходимое изменение значения: Delta w = w_4 — w_3 < 0. Градиент же в точке 3 положителен. Этот факт также фиксируем.
А теперь соберем воедино эту информацию в виде следующей иллюстрации:
| Переход | bold{Delta w} | Знак bold{Delta w} | Градиент |
|---|---|---|---|
| 1 rArr 2 | w_2 — w_1 | + | — |
| 3 rArr 4 | w_4 — w_3 | — | + |
Вывод напрашивается сам собой — величина, на которую необходимо изменить значение w, в любой точке противоположна по знаку градиенту. И, таким образом, представим эту самую величину в виде:
Delta w = -alpha cdot frac{dE}{dw}
Имеем в наличии:
- Delta w — величина, на которую необходимо изменить значение w.
- frac{dE}{dw} — градиент в этой точке.
- alpha — скорость обучения.
Собственно, логика метода градиентного спуска и заключается в данном математическом выражении, а именно в том, что для минимизации ошибки необходимо изменять w в направлении противоположном градиенту. В контексте нейронных сетей имеем искомый закон для корректировки весов синаптических связей (для синапса между нейронами i и j):
Delta w_{ij} = -alpha cdot frac{dE}{dw_{ij}}
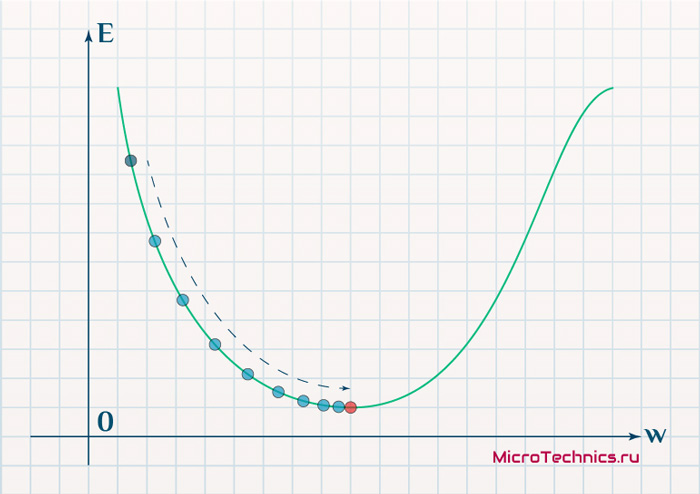
Более того, вспомним о важном свойстве, которое мы отдельно пометили. И заключается оно в том, что величина градиента будет уменьшаться по мере приближения к минимуму функции. Что это нам дает? А то, что в том случае, если наша текущая дислокация далека от места назначения, то величина, корректирующая вес связи, будет больше. А это обеспечит скорейшее приближение к цели. При приближении к целевому пункту, величина frac{dE}{dw_{ij}} будет уменьшаться, что поможет нам точнее попасть в нужную точку, а кроме того, не позволит нам ее проскочить. Визуализируем вышеописанное:
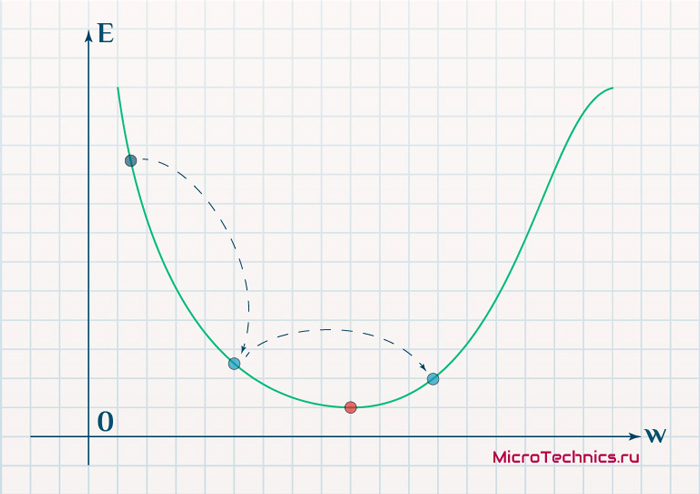
Скорость же обучения несет в себе следующий смысл. Она определяет величину каждого шага при поиске минимума ошибки. Слишком большое значение приводит к тому, что точка может «перепрыгнуть» через нужное значение и оказаться по другую сторону от цели:
Если же величина будет мала, то это приведет к тому, что спуск будет осуществляться очень медленно, что также является нежелательным эффектом. Поэтому скорость обучения, как и многие другие параметры нейронной сети, является очень важной величиной, для которой нет единственно верного значения. Все снова зависит от конкретного случая и оптимальная величина определяется исключительно исходя из текущих условий.
И даже на этом еще не все, здесь присутствует один важный нюанс, который в большинстве статей опускается, либо вовсе не упоминается. Реальная зависимость может иметь совсем другой вид:
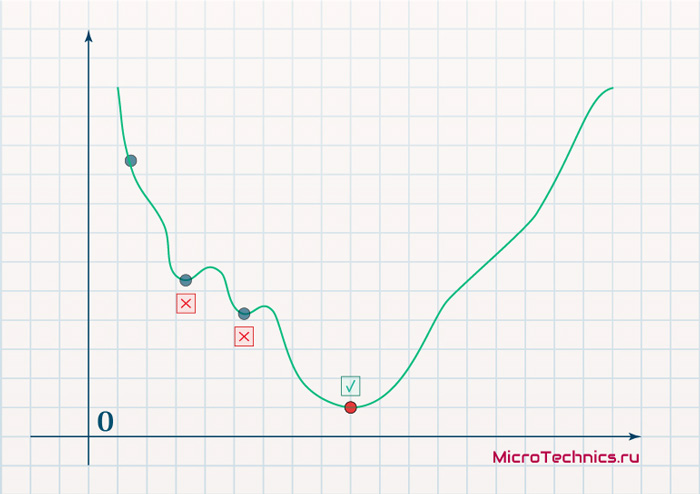
Из чего вытекает потенциальная возможность попадания в локальный минимум, вместо глобального, что является большой проблемой. Для предотвращения данного эффекта вводится понятие момента обучения и формула принимает следующий вид:
Delta w_{ij} = -alpha cdot frac{dE}{dw_{ij}} + gamma cdot Delta w_{ij}^{t - 1}
То есть добавляется второе слагаемое, которое представляет из себя произведение момента на величину корректировки веса на предыдущем шаге.
Итого, резюмируем продвижение к цели:
- Нашей задачей было найти закон, по которому необходимо изменять величину весов связей между нейронами.
- Наш результат — Delta w_{ij} = -alpha cdot frac{dE}{dw_{ij}} + gamma cdot Delta w_{ij}^{t — 1} — именно то, что и требовалось 👍
И опять же, полученный результат логичным образом перенаправляет нас на следующий этап, ставя вопросы — что из себя представляет функция ошибки, и как определить ее градиент.
Обучение нейронных сетей. Функция ошибки.
Начнем с того, что определимся с тем, что у нас в наличии, для этого вернемся к конкретной нейронной сети. Пусть вид ее таков:
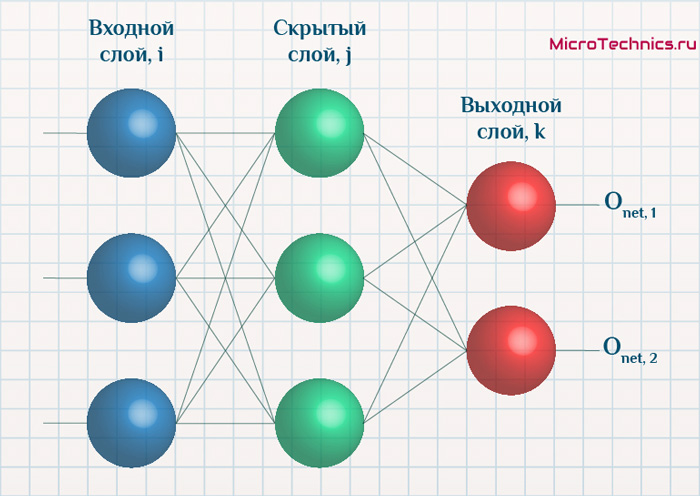
Интересует нас, в первую очередь, часть, относящаяся к нейронам выходного слоя. Подав на вход определенные значения, получаем значения на выходе сети: O_{net, 1} и O_{net, 2}. Кроме того, поскольку мы ведем речь о процессе обучения нейронной сети, то нам известны целевые значения: O_{correct, 1} и O_{correct, 2}. И именно этот набор данных на этом этапе является для нас исходным:
- Известно: O_{net, 1}, O_{net, 2}, O_{correct, 1} и O_{correct, 2}.
- Необходимо определить величины Delta w_{ij} для корректировки весов, для этого нужно вычислить градиенты (frac{dE}{dw_{ij}}) для каждого из синапсов.
Полдела сделано — задача четко сформулирована, начинаем деятельность по поиску решения.
В плане того, как определять ошибку, первым и самым очевидным вариантом кажется простая алгебраическая разность. Для каждого из выходных нейронов:
E_k = O_{correct, k} - O_{net, k}
Дополним пример числовыми значениями:
| Нейрон | bold{O_{net}} | bold{O_{correct}} | bold{E} |
|---|---|---|---|
| 1 | 0.9 | 0.5 | -0.4 |
| 2 | 0.2 | 0.6 | 0.4 |
Недостатком данного варианта является то, что в том случае, если мы попытаемся просуммировать ошибки нейронов, то получим:
E_{sum} = e_1 + e_2 = -0.4 + 0.4 = 0
Что не соответствует действительности (нулевая ошибка, говорит об идеальной работе нейронной сети, по факту оба нейрона дали неверный результат). Так что вариант с разностью откидываем за несостоятельностью.
Вторым, традиционно упоминаемым, методом вычисления ошибки является использование модуля разности:
E_k = | O_{correct, k} - O_{net, k} |
Тут в действие вступает уже проблема иного рода:
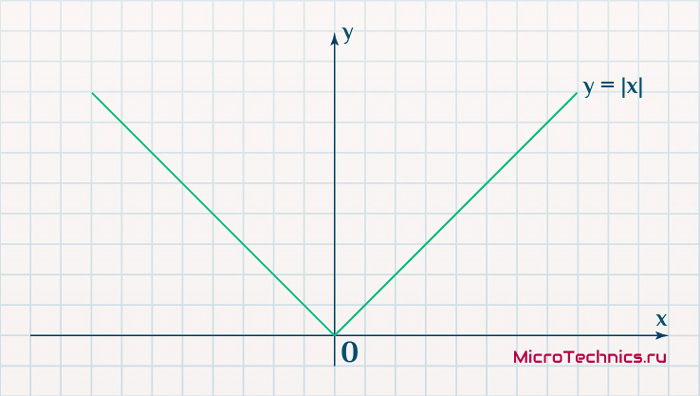
Функция, бесспорно, симпатична, но при приближении к минимуму ее градиент является постоянной величиной, скачкообразно меняясь при переходе через точку минимума. Это нас также не устраивает, поскольку, как мы обсуждали, концепция заключалась в том числе в том, чтобы по мере приближения к минимуму значение градиента уменьшалось.
В итоге хороший результат дает зависимость (для выходного нейрона под номером k):
E_k = (O_{correct, k} - O_{net, k})^2
Функция по многим своим свойствам идеально удовлетворяет нуждам обучения нейронной сети, так что выбор сделан, остановимся на ней. Хотя, как и во многих аспектах, качающихся нейронных сетей, данное решение не является единственно и неоспоримо верным. В каких-то случаях лучше себя могут проявить другие зависимости, возможно, что какой-то вариант даст большую точность, но неоправданно высокие затраты производительности при обучении. В общем, непаханное поле для экспериментов и исследований, это и привлекательно.
Краткий вывод промежуточного шага, на который мы вышли:
- Имеющееся: frac{dE}{dw_{jk}} = frac{d}{d w_{jk}}(O_{correct, k} — O_{net, k})^2.
- Искомое по-прежнему: Delta w_{jk}.
Несложные диффернциально-математические изыскания выводят на следующий результат:
frac{dE}{d w_{jk}} = -(O_{correct, k} - O_{net, k}) cdot f{Large{prime}}(sum_{j}w_{jk}O_j) cdot O_j
Здесь эти самые изыскания я все-таки решил не вставлять, дабы не перегружать статью, которая и так выходит объемной. Но в случае необходимости и интереса, отпишите в комментарии, я добавлю вычисления и закину их под спойлер, как вариант.
Освежим в памяти структуру сети:
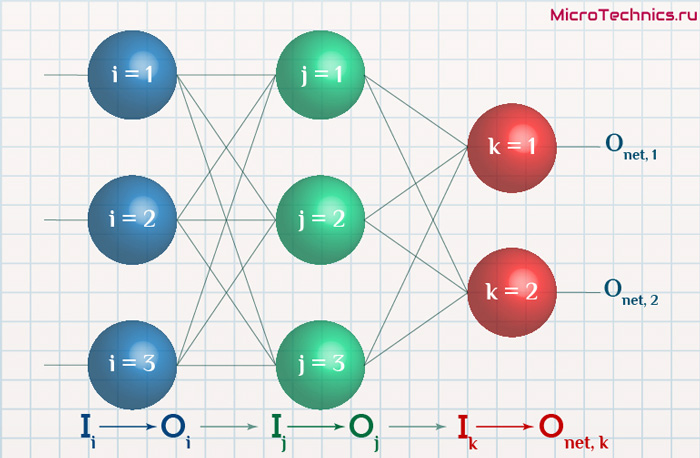
Формулу можно упростить, сгруппировав отдельные ее части:
- (O_{correct, k} — O_{net, k}) cdot f{Large{prime}}(sum_{j}w_{jk}O_j) — ошибка нейрона k.
- O_j — тут все понятно, выходной сигнал нейрона j.
f{Large{prime}}(sum_{j}w_{jk}O_j) — значение производной функции активации. Причем, обратите внимание, что sum_{j}w_{jk}O_j — это не что иное, как сигнал на входе нейрона k (I_{k}). Тогда для расчета ошибки выходного нейрона: delta_k = (O_{correct, k} — O_{net, k}) cdot f{Large{prime}}(I_k).
Итог: frac{dE}{d w_{jk}} = -delta_k cdot O_j.
Одной из причин популярности сигмоидальной функции активности является то, что ее производная очень просто выражается через саму функцию:
f{'}(x) = f(x)medspace (1medspace-medspace f(x))
Данные алгебраические вычисления справедливы для корректировки весов между скрытым и выходным слоем, поскольку для расчета ошибки мы используем просто разность между целевым и полученным результатом, умноженную на производную.
Для других слоев будут незначительные изменения, касающиеся исключительно первого множителя в формуле:
frac{dE}{d w_{ij}} = -delta_j cdot O_i
Который примет следующий вид:
delta_j = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_j)
То есть ошибка для элемента слоя j получается путем взвешенного суммирования ошибок, «приходящих» к нему от нейронов следующего слоя и умножения на производную функции активации. В результате:
frac{dE}{d w_{ij}} = -(sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_j) cdot O_i
Снова подводим промежуточный итог, чтобы иметь максимально полную и структурированную картину происходящего. Вот результаты, полученные нами на двух этапах, которые мы успешно миновали:
- Ошибка:
- выходной слой: delta_k = (O_{correct, k} — O_{net, k}) cdot f{Large{prime}}(I_k)
- скрытые слои: delta_j = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_j)
- Градиент: frac{dE}{d w_{ij}} = -delta_j cdot O_i
- Корректировка весовых коэффициентов: Delta w_{ij} = -alpha cdot frac{dE}{dw_{ij}} + gamma cdot Delta w_{ij}^{t — 1}
Преобразуем последнюю формулу:
Delta w_{ij} = alpha cdot delta_j cdot O_i + gamma cdot Delta w_{ij}^{t - 1}
Из этого мы делаем вывод, что на данный момент у нас есть все, что необходимо для того, чтобы произвести обучение нейронной сети. И героем следующего подраздела будет алгоритм обратного распространения ошибки.
Метод обратного распространения ошибки.
Данный метод является одним из наиболее распространенных и популярных, чем и продиктован его выбор для анализа и разбора. Алгоритм обратного распространения ошибки относится к методам обучение с учителем, что на деле означает необходимость наличия целевых значений в обучающих сетах.
Суть же метода подразумевает наличие двух этапов:
- Прямой проход — входные сигналы двигаются в прямом направлении, в результате чего мы получаем выходной сигнал, из которого в дальнейшем рассчитываем значение ошибки.
- Обратный проход — обратное распространение ошибки — величина ошибки двигается в обратном направлении, в результате происходит корректировка весовых коэффициентов связей сети.
Начальные значения весов (перед обучением) задаются случайными, есть ряд методик для выбора этих значений, я опишу в отдельном материале максимально подробно. Пока вот можно полистать — ссылка.
Вернемся к конкретному примеру для явной демонстрации этих принципов:
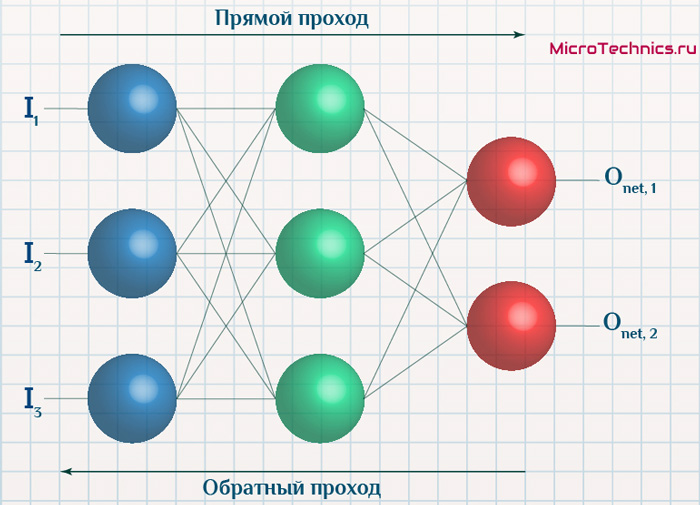
Итак, имеется нейронная сеть, также имеется набор данных обучающей выборки. Как уже обсудили в начале статьи — обучающая выборка представляет из себя набор образцов (сетов), каждый из которых состоит из значений входных сигналов и соответствующих им «правильных» значений выходных величин.
Процесс обучения нейронной сети для алгоритма обратного распространения ошибки будет таким:
- Прямой проход. Подаем на вход значения I_1, I_2, I_3 из обучающей выборки. В результате работы сети получаем выходные значения O_{net, 1}, O_{net, 2}. Этому целиком и полностью был посвящен предыдущий манускрипт.
- Рассчитываем величины ошибок для всех слоев:
- для выходного: delta_k = (O_{correct, k} — O_{net, k}) cdot f{Large{prime}}(I_k)
- для скрытых: delta_j = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_j)
- Далее используем полученные значения для расчета Delta w_{ij} = alpha cdot delta_j cdot O_i + gamma cdot Delta w_{ij}^{t — 1}
- И финишируем, рассчитывая новые значения весов: w_{ij medspace new} = w_{ij} + Delta w_{ij}
- На этом один цикл обучения закончен, данные шаги 1 — 4 повторяются для других образцов из обучающей выборки.
Обратный проход завершен, а вместе с ним и одна итерация процесса обучения нейронной сети по данному методу. Собственно, обучение в целом заключается в многократном повторении этих шагов для разных образцов из обучающей выборки. Логику мы полностью разобрали, при повторном проведении операций она остается в точности такой же.
Таким образом, максимально подробно концентрируясь именно на сути и логике процессов, мы в деталях разобрали метод обратного распространения ошибки. Поэтому переходим к завершающей части статьи, в которой разберем практический пример, произведя полностью все вычисления для конкретных числовых величин. Все в рамках продвигаемой мной концепции, что любая теоретическая информация на порядок лучше может быть осознана при применении ее на практике.
Пример расчетов для метода обратного распространения ошибки.
Возьмем нейронную сеть и зададим начальные значения весов:
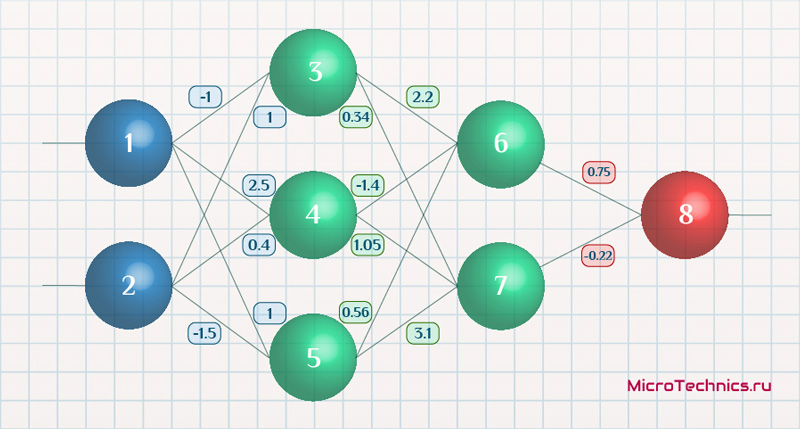
Здесь я задал значения не в соответствии с существующими на сегодняшний день методами, а просто случайным образом для наглядности примера.
В качестве функции активации используем сигмоиду:
f(x) = frac{1}{1 + e^{-x}}
И ее производная:
f{Large{prime}}(x) = f(x)medspace (1medspace-medspace f(x))
Берем один образец из обучающей выборки, пусть будут такие значения:
- Входные: I_1 = 0.6, I_1 = 0.7.
- Выходное: O_{correct} = 0.9.
Скорость обучения alpha пусть будет равна 0.3, момент — gamma = 0.1. Все готово, теперь проведем полный цикл для метода обратного распространения ошибки, то есть прямой проход и обратный.
Прямой проход.
Начинаем с выходных значений нейронов 1 и 2, поскольку они являются входными, то:
O_1 = I_1 = 0.6 \ O_2 = I_2 = 0.7
Значения на входе нейронов 3, 4 и 5:
I_3 = O_1 cdot w_{13} + O_2 cdot w_{23} = 0.6 cdot (-1medspace) + 0.7 cdot 1 = 0.1 \
I_4 = 0.6 cdot 2.5 + 0.7 cdot 0.4 = 1.78 \
I_5 = 0.6 cdot 1 + 0.7 cdot (-1.5medspace) = -0.45
На выходе этих же нейронов первого скрытого слоя:
O_3 = f(I3medspace) = 0.52 \ O_4 = 0.86\ O_5 = 0.39
Продолжаем аналогично для следующего скрытого слоя:
I_6 = O_3 cdot w_{36} + O_4 cdot w_{46} + O_5 cdot w_{56} = 0.52 cdot 2.2 + 0.86 cdot (-1.4medspace) + 0.39 cdot 0.56 = 0.158 \
I_7 = 0.52 cdot 0.34 + 0.86 cdot 1.05 + 0.39 cdot 3.1 = 2.288 \
O_6 = f(I_6) = 0.54 \
O_7 = 0.908
Добрались до выходного нейрона:
I_8 = O_6 cdot w_{68} + O_7 cdot w_{78} = 0.54 cdot 0.75 + 0.908 cdot (-0.22medspace) = 0.205 \
O_8 = O_{net} = f(I_8) = 0.551
Получили значение на выходе сети, кроме того, у нас есть целевое значение O_{correct} = 0.9. То есть все, что необходимо для обратного прохода, имеется.
Обратный проход.
Как мы и обсуждали, первым этапом будет вычисление ошибок всех нейронов, действуем:
delta_8 = (O_{correct} - O_{net}) cdot f{Large{prime}}(I_8) = (O_{correct} - O_{net}) cdot f(I_8) cdot (1-f(I_8)) = (0.9 - 0.551medspace) cdot 0.551 cdot (1-0.551medspace) = 0.0863 \
delta_7 = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_7) = (delta_8 cdot w_{78}) cdot f{Large{prime}}(I_7) = 0.0863 cdot (-0.22medspace) cdot 0.908 cdot (1 - 0.908medspace) = -0.0016 \
delta_6 = 0.086 cdot 0.75 cdot 0.54 cdot (1 - 0.54medspace) = 0.016 \
delta_5 = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_5) = (delta_7 cdot w_{57} + delta_6 cdot w_{56}) cdot f{Large{prime}}(I_7) = (-0.0016 cdot 3.1 + 0.016 cdot 0.56) cdot 0.39 cdot (1 - 0.39medspace) = 0.001 \
delta_4 = (-0.0016 cdot 1.05 + 0.016 cdot (-1.4)) cdot 0.86 cdot (1 - 0.86medspace) = -0.003 \
delta_3 = (-0.0016 cdot 0.34 + 0.016 cdot 2.2) cdot 0.52 cdot (1 - 0.52medspace) = -0.0087
С расчетом ошибок закончили, следующий этап — расчет корректировочных величин для весов всех связей. Для этого мы вывели формулу:
Delta w_{ij} = alpha cdot delta_j cdot O_i + gamma cdot Delta w_{ij}^{t - 1}
Как вы помните, Delta w_{ij}^{t — 1} — это величина поправки для данного веса на предыдущей итерации. Но поскольку у нас это первый проход, то данное значение будет нулевым, соответственно, в данном случае второе слагаемое отпадает. Но забывать о нем нельзя. Продолжаем калькулировать:
Delta w_{78} = alpha cdot delta_8 cdot O_7 = 0.3 cdot 0.0863 cdot 0.908 = 0.0235 \
Delta w_{68} = 0.3 cdot 0.0863 cdot 0.54= 0.014 \
Delta w_{57} = alpha cdot delta_7 cdot O_5 = 0.3 cdot (−0.0016medspace) cdot 0.39= -0.00019 \
Delta w_{47} = 0.3 cdot (−0.0016medspace) cdot 0.86= -0.0004 \
Delta w_{37} = 0.3 cdot (−0.0016medspace) cdot 0.52= -0.00025 \
Delta w_{56} = alpha cdot delta_6 cdot O_5 = 0.3 cdot 0.016 cdot 0.39= 0.0019 \
Delta w_{46} = 0.3 cdot 0.016 cdot 0.86= 0.0041 \
Delta w_{36} = 0.3 cdot 0.016 cdot 0.52= 0.0025 \
Delta w_{25} = alpha cdot delta_5 cdot O_2 = 0.3 cdot 0.001 cdot 0.7= 0.00021 \
Delta w_{15} = 0.3 cdot 0.001 cdot 0.6= 0.00018 \
Delta w_{24} = alpha cdot delta_4 cdot O_2 = 0.3 cdot (-0.003medspace) cdot 0.7= -0.00063 \
Delta w_{14} = 0.3 cdot (-0.003medspace) cdot 0.6= -0.00054 \
Delta w_{23} = alpha cdot delta_3 cdot O_2 = 0.3 cdot (−0.0087medspace) cdot 0.7= -0.00183 \
Delta w_{13} = 0.3 cdot (−0.0087medspace) cdot 0.6= -0.00157
И самый что ни на есть заключительный этап — непосредственно изменение значений весовых коэффициентов:
w_{78 medspace new} = w_{78} + Delta w_{78} = -0.22 + 0.0235 = -0.1965 \
w_{68 medspace new} = 0.75+ 0.014 = 0.764 \
w_{57 medspace new} = 3.1 + (−0.00019medspace) = 3.0998\
w_{47 medspace new} = 1.05 + (−0.0004medspace) = 1.0496\
w_{37 medspace new} = 0.34 + (−0.00025medspace) = 0.3398\
w_{56 medspace new} = 0.56 + 0.0019 = 0.5619 \
w_{46 medspace new} = -1.4 + 0.0041 = -1.3959 \
w_{36 medspace new} = 2.2 + 0.0025 = 2.2025 \
w_{25 medspace new} = -1.5 + 0.00021 = -1.4998 \
w_{15 medspace new} = 1 + 0.00018 = 1.00018 \
w_{24 medspace new} = 0.4 + (−0.00063medspace) = 0.39937 \
w_{14 medspace new} = 2.5 + (−0.00054medspace) = 2.49946 \
w_{23 medspace new} = 1 + (−0.00183medspace) = 0.99817 \
w_{13 medspace new} = -1 + (−0.00157medspace) = -1.00157\
И на этом данную масштабную статью завершаем, конечно же, не завершая на этом деятельность по использованию нейронных сетей. Так что всем спасибо за прочтение, любые вопросы пишите в комментариях и на форуме, ну и обязательно следите за обновлениями и новыми материалами, до встречи!
Метод обратного распространения ошибок (англ. backpropagation) — метод вычисления градиента, который используется при обновлении весов в нейронной сети.
Содержание
- 1 Обучение как задача оптимизации
- 2 Дифференцирование для однослойной сети
- 2.1 Находим производную ошибки
- 3 Алгоритм
- 4 Недостатки алгоритма
- 4.1 Паралич сети
- 4.2 Локальные минимумы
- 5 Примечания
- 6 См. также
- 7 Источники информации
Обучение как задача оптимизации
Рассмотрим простую нейронную сеть без скрытых слоев, с двумя входными вершинами и одной выходной, в которых каждый нейрон использует линейную функцию активации, (обычно, многослойные нейронные сети используют нелинейные функции активации, линейные функции используются для упрощения понимания) которая является взвешенной суммой входных данных.
Простая нейронная сеть с двумя входными вершинами и одной выходной
Изначально веса задаются случайно. Затем, нейрон обучается с помощью тренировочного множества, которое в этом случае состоит из множества троек где и — это входные данные сети и — правильный ответ. Начальная сеть, приняв на вход и , вычислит ответ , который вероятно отличается от . Общепринятый метод вычисления несоответствия между ожидаемым и получившимся ответом — квадратичная функция потерь:
- где ошибка.
В качестве примера, обучим сеть на объекте , таким образом, значения и равны 1, а равно 0. Построим график зависимости ошибки от действительного ответа , его результатом будет парабола. Минимум параболы соответствует ответу , минимизирующему . Если тренировочный объект один, минимум касается горизонтальной оси, следовательно ошибка будет нулевая и сеть может выдать ответ равный ожидаемому ответу . Следовательно, задача преобразования входных значений в выходные может быть сведена к задаче оптимизации, заключающейся в поиске функции, которая даст минимальную ошибку.
График ошибки для нейрона с линейной функцией активации и одним тренировочным объектом
В таком случае, выходное значение нейрона — взвешенная сумма всех его входных значений:
где и — веса на ребрах, соединяющих входные вершины с выходной. Следовательно, ошибка зависит от весов ребер, входящих в нейрон. И именно это нужно менять в процессе обучения. Распространенный алгоритм для поиска набора весов, минимизирующего ошибку — градиентный спуск. Метод обратного распространения ошибки используется для вычисления самого «крутого» направления для спуска.
Дифференцирование для однослойной сети
Метод градиентного спуска включает в себя вычисление дифференциала квадратичной функции ошибки относительно весов сети. Обычно это делается с помощью метода обратного распространения ошибки. Предположим, что выходной нейрон один, (их может быть несколько, тогда ошибка — это квадратичная норма вектора разницы) тогда квадратичная функция ошибки:
- где — квадратичная ошибка, — требуемый ответ для обучающего образца, — действительный ответ сети.
Множитель добавлен чтобы предотвратить возникновение экспоненты во время дифференцирования. На результат это не повлияет, потому что позже выражение будет умножено на произвольную величину скорости обучения (англ. learning rate).
Для каждого нейрона , его выходное значение определено как
Входные значения нейрона — это взвешенная сумма выходных значений предыдущих нейронов. Если нейрон в первом слое после входного, то входного слоя — это просто входные значения сети. Количество входных значений нейрона . Переменная обозначает вес на ребре между нейроном предыдущего слоя и нейроном текущего слоя.
Функция активации нелинейна и дифференцируема. Одна из распространенных функций активации — сигмоида:
у нее удобная производная:
Находим производную ошибки
Вычисление частной производной ошибки по весам выполняется с помощью цепного правила:
Только одно слагаемое в зависит от , так что
Если нейрон в первом слое после входного, то — это просто .
Производная выходного значения нейрона по его входному значению — это просто частная производная функции активации (предполагается что в качестве функции активации используется сигмоида):
По этой причине данный метод требует дифференцируемой функции активации. (Тем не менее, функция ReLU стала достаточно популярной в последнее время, хоть и не дифференцируема в 0)
Первый множитель легко вычислим, если нейрон находится в выходном слое, ведь в таком случае и
Тем не менее, если произвольный внутренний слой сети, нахождение производной по менее очевидно.
Если рассмотреть как функцию, берущую на вход все нейроны получающие на вход значение нейрона ,
и взять полную производную по , то получим рекурсивное выражение для производной:
Следовательно, производная по может быть вычислена если все производные по выходным значениям следующего слоя известны.
Если собрать все месте:
и
Чтобы обновить вес используя градиентный спуск, нужно выбрать скорость обучения, . Изменение в весах должно отражать влияние на увеличение или уменьшение в . Если , увеличение увеличивает ; наоборот, если , увеличение уменьшает . Новый добавлен к старым весам, и произведение скорости обучения на градиент, умноженный на , гарантирует, что изменения будут всегда уменьшать . Другими словами, в следующем уравнении, всегда изменяет в такую сторону, что уменьшается:
Алгоритм
- — скорость обучения
- — коэффициент инерциальности для сглаживания резких скачков при перемещении по поверхности целевой функции
- — обучающее множество
- — количество повторений
- — функция, подающая x на вход сети и возвращающая выходные значения всех ее узлов
- — количество слоев в сети
- — множество нейронов в слое i
- — множество нейронов в выходном слое
fun BackPropagation:
init
repeat :
for = to :
=
for :
=
for = to :
for :
=
for :
=
=
return
Недостатки алгоритма
Несмотря на многочисленные успешные применения обратного распространения, оно не является универсальным решением. Больше всего неприятностей приносит неопределённо долгий процесс обучения. В сложных задачах для обучения сети могут потребоваться дни или даже недели, она может и вообще не обучиться. Причиной может быть одна из описанных ниже.
Градиентный спуск может найти локальный минимум вместо глобального
Паралич сети
В процессе обучения сети значения весов могут в результате коррекции стать очень большими величинами. Это может привести к тому, что все или большинство нейронов будут функционировать при очень больших выходных значениях, а производная активирующей функции будет очень мала. Так как посылаемая обратно в процессе обучения ошибка пропорциональна этой производной, то процесс обучения может практически замереть.
Локальные минимумы
Градиентный спуск с обратным распространением ошибок гарантирует нахождение только локального минимума функции; также, возникают проблемы с пересечением плато на поверхности функции ошибки.
Примечания
- Алгоритм обучения многослойной нейронной сети методом обратного распространения ошибки
- Neural Nets
- Understanding backpropagation
См. также
- Нейронные сети, перцептрон
- Стохастический градиентный спуск
- Настройка глубокой сети
- Практики реализации нейронных сетей
Источники информации
- https://en.wikipedia.org/wiki/Backpropagation
- https://ru.wikipedia.org/wiki/Метод_обратного_распространения_ошибки
Метод обратного распространения ошибки — метод обучения многослойной нейронной сети, математической и компьютерной модели восприятия информации мозгом.
Искусственная нейронная сеть состоит из трёх типов элементов: сенсоры принимающие информацию из вне – входы сети (input units); промежуточные нейроны – ассоциативные, обрабатывающие элементы (hidden units); реагирующие элементы – выходы сети (output units).
Впервые метод был описан в 1974 г. А. И. Галушкиным
Метод был создан с целью минимализации ошибок в искусственных нейронных сетях, и получение желаемых, прогнозируемых выходов (результатов), тем самым строя процесс обучения.
Метод заключается в том, что сигнал об ошибке из выходов сети (output units), передается в обратном направлении, передачи сигналов в сети, к входам (input units)
Для возможности применения этого метода, передаточная функция нейронов должна быть дифференцируема.
Алгоритм обратного распространения это метод позволяющий вычислять частные производные функций в нейронных сетях.
Обзор[]
Существует 2 типа сетей: состоящие из одного слоя, и многослойные, в которой каждый нейрон произвольного слоя связан со всеми окончаниями нейронов предыдущего слоя или, в случае первого слоя, со всеми входами НС
Многослойная сеть
Нейронные сети не программируются в привычном смысле этого слова, они обучаются. Возможность обучения — одно из главных преимуществ нейронных сетей перед традиционными алгоритмами. Технически обучение заключается в нахождении коэффициентов связей между нейронами. В процессе обучения нейронная сеть способна выявлять сложные зависимости между входными данными и выходными, а также выполнять обобщение. Это значит, что, в случае успешного обучения, сеть сможет вернуть верный результат на основании данных, которые отсутствовали в обучающей выборке.
Наиболее приемлемый вариант обучения многослойной нейронной сети – метод обратного распространения ошибки (error backpropagation). Метод был создан с целью минимализации ошибок в искусственных нейронных сетях, и получение желаемых, прогнозируемых выходов (результатов), тем самым строя процесс обучения.
Искусственная нейронная сеть состоит из трёх типов элементов: сенсоры принимающие информацию из вне – входы сети (input units); промежуточные нейроны – ассоциативные, обрабатывающие элементы (hidden units – внутренний слой); реагирующие элементы – выходы сети (output units).
Метод заключается в том, что сигнал об ошибке из выходов сети (output units), передается в обратном направлении, передачи сигналов в сети, к входам (input units).
Метод обратного распространения[]
Для простоты, предположим что у нас сеть состоит из трех слоев. Входы, промежуточные, выходы. Перенумеруем их все.
И возьмем некоторый образ, который должна распознать сеть. Пускай это будет функция на регрессию, и результатом будет на выходе y(t), измененная версия функции на входе x(t):
где 
Обучение сети начинается с предъявления образа и вычисления соответствующей реакции. Когда мы предъявляем ненастроенной сети входной образы Невозможно разобрать выражение (синтаксическая ошибка): {displaystyle x(t) (t=1,…n)}
, она будет выдавать некоторый случайный выход 
И чтобы определить, на сколько хорошо сеть работает, для этого строится функция оценки. Простейший и самый распространенный пример оценки — сумма квадратов расстояний от выходных сигналов сети до их идеальным значений 

Где t – пробегает значения всех распознаваемых образов, i – принимает значения всех выходов.
(i – это индекс рассматриваемого слоя n, а j – слоя n-1)
Мы хотим посчитать производную возможной функции с учетом весов сети.
Будем считать, что мы проводим серию обучений, считая, что весы остаются постоянными в течении эпохи (проходят через все образы), но изменяются между эпохами.
Эпоха – цикл обучения, необходимый для обработки задаваемых образов.
Для простоты в обозначениях введем два индекса времени: n — индекс эпохи , 
Используя структуру сети, вычисление производной можно представить, в три этапа. Это легко осуществить, если мы будем рассматривать выходы и скрытые уровни по отдельности. Для выходов, этапы представлены на три частных производных.



Для скрытого слоя, формула будет

где мы определим активность i – скрытого уровня на шаге 



Сначала рассмотрим выходы. В случаи, который рассматривается здесь имеем

Для задачи регресса(?), выходы используют линейной активности функции

где j – индекс скрытых юнитов. Тогда

и

Для скрытого юнита вычисление производной возможной функции с учетом активности скрытого слоя будет следующая

Где k индекс выходов (K – количество всех выходов, 

Для нашей задачи, уравнение может быть переписано следующим образом:
![{displaystyle {frac {partial E(t)}{partial h_{i}(t)}}=sum limits _{k=1}^{K}[y*_{k}(t)-y_{k}(t)]omega _{ki}(n)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/57627e55bd3cbc02c298c86c3549f37b22fc578d)
Для скрытого слоя как правило используется функция сигмонда


где j индекс входа.
![{displaystyle {frac {partial h_{i}(t)}{partial s_{i}(t)}}=h_{i}(t)[1-h_{i}(t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c42358cba572ea36ee38fc8c519b0d115aa35627)
и

Литература[]
- Jacobs, Robert. Backpropagation Algorithm / Department of Brain & Cognitive Sciences. — 2008
- Короткий, С. Нейронные сети: алгоритм обратного распространения
См.также[]
- Нейронные сети
- Искусственная нейронная сеть
Среди инструментов трейдера уже довольно давно присутствуют машинное обучение и, в частности, нейронные сети. В свою очередь, среди нейронных сетей, в той части их классификации, которая объединяет так называемые методы «обучения с учителем», особое место занимают сети с обратным распространением ошибки (backpropagation neural network, BPNN). Существует множество различных модификаций подобных алгоритмов. На их основе построены, например, глубокие, рекуррентные и сверточные нейронные сети. Так что, нас не должно удивлять обилие материалов на данную тему (как и статей на данном сайте). Сегодня мы разовьем её в относительно новом для MQL5 направлении. Дело в том, что некоторое время назад в MQL5 появились новые возможности API, предназначенные для работы с матрицами и векторами. Они позволяют реализовать расчеты в нейронной сети в пакетном режиме, когда данные обрабатываются целиком (или блоками), а не поэлементно.
Благодаря матричным операциям существенно упрощаются программные инструкции, воплощающие формулы прямого и обратного распространения сигналов в сети. Фактически они преобразуются в однострочные выражения. За счет этого мы сможем уделить внимание другим важным аспектам по усовершенствованию алгоритма.
В данной статье мы напомним вкратце теорию сетей с обратным распространением ошибки и создадим на её основе универсальные классы для построения сетей: приведенные формулы будут почти «зеркально» отражены в исходном коде. Таким образом, новички смогут пройти полный «путь» по освоению данной технологии, не ища сторонние публикации.
Если же вы знакомы с теорией, то можете смело переходить ко второй части статьи, где рассматриваются примеры использования классов на практике — в скрипте, индикаторе и эксперте.
Введение в теорию нейронных сетей
Напомним, что нейронные сети (НС) состоят из простых вычислительных элементов — нейронов, как правило, логически объединенных в слои и соединенных связями (синапсами), по которым «проходит сигнал». Сигнал является математической абстракцией, с помощью которой можно представить ситуации из любой прикладной области, не исключая и трейдинг.
Синапс соединяет выход одного нейрона со входом другого и характеризуется величиной, называемой весом wi. Текущее состоянием нейрона получается, как взвешенная сумма сигналов, поступивших на его связи (входы).
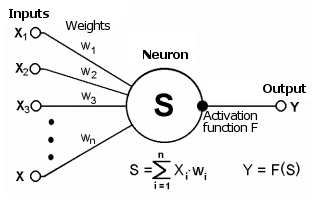
Схема нейрона
Это состояние дополнительно обрабатывается с помощью нелинейной активационной функции, формирующей выходное значение конкретного нейрона, откуда сигнал пойдет далее по синапсам следующих подключенных нейронов (если они есть) или станет компонентой в «ответе» нейронной сети (если текущий нейрон расположен в последнем слое).
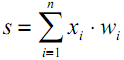 |
(1) |
| |
(2) |
Наличие нелинейности усиливает вычислительные возможности сети. В качестве активационных функций может использоваться, например, гиперболический тангенс или логистическая (обе относятся к так называемым S-образным или сигмоидальным функциям):
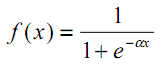 |
(3) |
Как мы увидим далее, MQL5 предоставляет большой набор встроенных активационных функций. Выбор конкретной функции следует делать на основе специфики задачи (регрессия, классификация). Как правило, для любой задачи можно подобрать несколько функций и далее экспериментальным путем найти оптимальную из них.
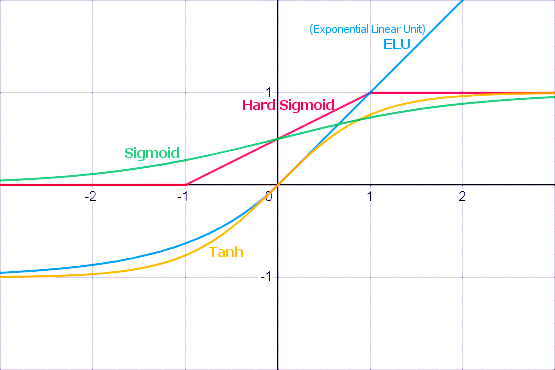
Популярные функции активации
Активационные функции могут иметь различные диапазоны значений — ограниченные или неограниченные. В частности, сигмоида (3) отображает данные в диапазон [0,+1] (лучше подходит для задач классификации), а гиперболический тангенс — в диапазон [-1,+1] (лучше подходит для задач регрессии и прогнозирования).
Одно из важных свойств функции активации — то, как определена её производная на всей оси. Наличие конечной, ненулевой производной является критически необходимым для алгоритма обратного распространения ошибки, который будет рассмотрен в дальнейшем. В частности, S-образные функции удовлетворяют этому требованию. Более того, стандартные функции активации, как правило, имеют довольно простую аналитическую запись производной, что гарантирует их эффективный расчет. Например, для сигмоиды (3) получим:
| |
(4) |
Нейронная сеть из одного слоя представлена на следующем рисунке.
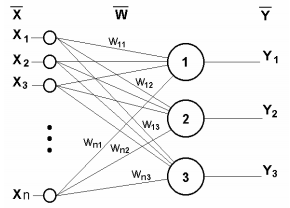
Однослойная нейронная сеть
Принцип её работы математически описывает такое уравнение:
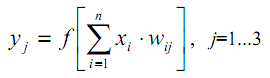 |
(5) |
Очевидно, что все весовые коэффициенты одного слоя можно свести в матрицу W, в которой каждый элемент wij задает величину i-ой связи j-ого нейрона. Таким образом, процесс, происходящий в НС, может быть записан в матричной форме:
| Y = F(X W) | (6) |
где X и Y — соответственно входной и выходной сигнальные векторы, F(V) — активационная функция, применяемая поэлементно к компонентам вектора V.
Число слоев и число нейронов в каждом слое сети зависит от входных данных: их размерности, объема выборки, закона распределения и многих других факторов. Как правило, конфигурацию сети выбирают методом проб.
Для иллюстрации приведем схему сети из двух слоев.
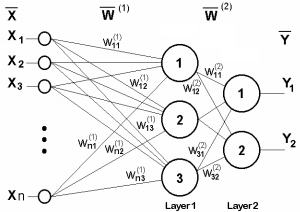
Двухслойная нейронная сеть
Теперь рассмотрим один нюанс, опущенный ранее. Из рисунка активационных функций очевидно, что существует некое значение T, где S-образные функции имеют максимальный наклон и хорошо передают сигналы, а прочие функции имеют характерную точку перелома (или несколько таких точек). Поэтому основная работа каждого нейрона происходит в окрестности T. Обычно T=0 или лежит возле 0, а потому желательно иметь средство для автоматического сдвига аргумента активационной функции к T.
Данное явление не было отражено в формуле (1), которая должна была бы выглядеть так:
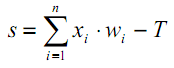 |
(7) |
Такое смещение обычно вводится путем добавления к слою нейронов еще одного псевдо-входа, значение которого всегда равно 1. Присвоим этому входу номер 0. Тогда:
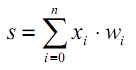 |
(8) |
где w0 = –T, x0 = 1.
Обучение НС с «учителем» предполагает наличие обучающих данных, заранее подготовленных и «размеченных» человеком-экспертом. В этих данных входным векторам сопоставлены желаемые выходные.
Само обучение производится по следующим этапам.
1. Проинициализировать элементы весовой матрицы (обычно небольшими случайными значениями);
2. Подать на входы один из векторов и вычислить реакцию сети; это фаза прямого распространения сигнала, которая будет использоваться и при штатной эксплуатации уже обученной сети;
3. Вычислить разницу между идеальным и полученным значениями выхода, то есть ошибку сети, после чего подстроить веса по некоторой формуле (см. далее) в зависимости от этой ошибки;
4. Продолжать в цикле с пункта 2 для всех входных векторов набора данных, пока ошибка не станет меньше заданного минимального уровня (успешное завершение обучения) или не будет достигнуто предопределенное максимальное количество циклов обучения (НС не справилась с задачей).
Для случая однослойной НС формула для модификации весов довольно очевидна:
| |
(9) |
| |
(10) |
где δ — ошибка сети (разница между полученным ответом сети и идеалом), t и t+1 — номера соответственно текущей и следующей итераций; ν — коэффициент скорости обучения, 0<ν<1; i — номер входа; j — номер нейрона в слое.
Однако, что делать, когда сеть многослойная? Здесь мы и подходим к идее обратного распространения ошибки.
Алгоритм обратного распространения ошибки
Среди различных структур нейронных сетей одной из наиболее известных является многослойная структура, в которой каждый нейрон конкретного слоя связан со всеми нейронами предыдущего слоя или, в случае первого слоя, со всеми входами НС. Такие НС называются полносвязными, и именно для их структуры приводится дальнейшее изложение. Во многих других типах НС, в частности, в сверточных, связи устанавливаются между ограниченными областями слоев, так называемыми ядрами, что несколько усложняет адресацию элементов сети, но не сказывается на применимости метода обратного распространения.
Интуитивно понятно, что информацию об ошибке следует передавать неким образом от выходов нейронной сети к её входам, постепенно «размазывая» по всем слоям, с учетом «проводимости» связей, то есть весов.
Согласно методу наименьших квадратов, минимизируемой целевой функцией ошибки НС является величина:
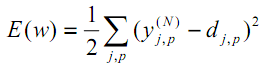 |
(11) |
где yjpᴺ — реальное выходное состояние нейрона j выходного слоя N нейронной сети при подаче на ее входы p-го образа; djp — идеальное (желаемое) выходное состояние этого нейрона.
Суммирование ведется по всем нейронам выходного слоя и по всем обрабатываемым образам. Коэффициент 1/2 вставлен только для получения «красивой» производной от E (двойки сокращаются), которая будет использоваться далее для обучения (см. формулу (12)) и в любом случае «взвешивается» важным параметром алгоритма — скоростью (которую можно увеличить в 2 раза или даже менять динамически по некоторым условиям).
Один из наиболее эффективных способов минимизации функции основывается на том, что наилучшие локальные направления к экстремумам указывают производные от этой функции в конкретной её точке. Производная со знаком плюс приведет нас к максимуму, а производная со знаком минус — к минимуму. Конечно, максимумы и минимумы могут оказаться локальными, и для «перепрыгивания» в глобальный минимум могут потребоваться дополнительные приемы, но мы здесь пока оставим данную проблему за кадром.
Описанный метод называется методом градиентного спуска, и означает подстройку весовых коэффициентов на основе производной E, следующим образом:
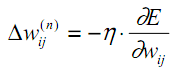 |
(12) |
Здесь wij — весовой коэффициент связи, соединяющей i-ый нейрон слоя n-1 с j-ым нейроном слоя n, η — коэффициент скорости обучения.
Вспомним внутреннее устройство нейрона и на его основе выделим в формуле (12) каждый этап вычислений в частную производную:
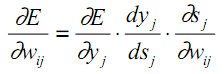 |
(13) |
Здесь под yj, как и раньше, подразумевается выход нейрона j, а под sj — взвешенная сумма его входных сигналов, то есть аргумент активационной функции. Так как множитель dyj/dsj является производной этой функции, из этого следует требование дифференцируемости активационной функции на всей оси абсцисс для использования в рассматриваемом алгоритме обратного распространения ошибки.
Например, в случае гиперболического тангенса:
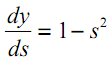 |
(14) |
Третий множитель в (13) ∂sj/∂wij равен выходу нейрона yi предыдущего слоя (n-1). Почему это так? Напомним, что в многослойной сети сигнал попадает с выхода нейрона предыдущего слоя на вход нейрона текущего слоя. Поэтому формулу (1) для sj можно в более общем виде переписать так:
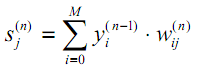 |
(15) |
где M — число нейронов в слое n-1 с учетом нейрона с постоянным выходным состоянием +1, задающего смещение; yi(n-1)=xij(n) — i-ый вход нейрона j слоя n, связанный с выходом i-го нейрона (n-1)-го слоя;
Что касается первого множителя в (13), его логично разложить по приращениям ошибок в соседнем, более старшем слое (ведь значения ошибок распространяются в обратную сторону):
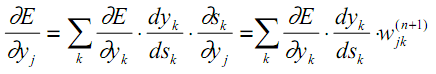 |
(16) |
Здесь суммирование по k выполняется среди нейронов слоя n+1.
Нетрудно заметить, что первые два множителя в (13) для одного слоя (с индексами j при нейронах) повторяются в (16) для следующего слоя (с индексами k) в виде коэффициента перед весом wjk.
Введем промежуточную переменную, включающую эти два множителя:
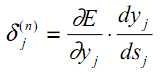 |
(17) |
В результате мы получим рекурсивную формулу для расчетов величин δj(n) слоя n из величин δk(n+1) более старшего слоя n+1.
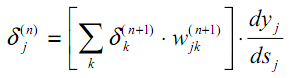 |
(18) |
Для выходного же слоя новая переменная, как и раньше, вычисляется на основе разницы между полученным и желаемым результатом сети.
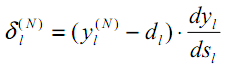 |
(19) |
По сравнению с (9) здесь, формально более строго, добавлена производная активационной функции. Правда, в выходном слое НС, в зависимости от задачи, АФ может и отсутствовать.
Теперь мы можем записать формулу (12) для коррекции весов в процессе обучения в раскрытом виде:
| |
(20) |
Иногда для придания процессу коррекции весов некоторой инерционности, сглаживающей резкие скачки производной при перемещении по поверхности целевой функции, формула (20) дополняется значением изменения веса на предыдущей итерации:
| |
(21) |
где µ — коэффициент инерционности, t — номер текущей итерации.
Таким образом, полный алгоритм обучения НС с помощью процедуры обратного распространения строится так:
1. Проинициализировать весовые матрицы малыми случайными числами.
2. Подать на входы сети один из векторов данных и в режиме обычного функционирования, когда сигналы распространяются от входов к выходам, рассчитать послойно общий результат НС по формулам взвешенного суммирования (15) и активации f:
| |
(22) |
Причем нейроны 0-го, входного слоя используются только для подачи входных сигналов и не имеют синапсов и активационных функций.
| |
(23) |
Iq — q-ая компонента входного вектора, поданная на 0-ой слой.
3. Если ошибка сети меньше заданной малой величины, останавливаем процесс с признаком успеха. Если ошибка существенна, продолжаем следующие шаги.
4. Рассчитать для выходного слоя N: δ по формуле (19), а также изменения весов Δw по формулам (20) или (21).
5. Для всех остальных слоев, в обратном порядке, n=N-1,…1 рассчитать δ и Δw по формулам (18) и (20) (или (18) и (21)) соответственно.
6. Скорректировать все веса в НС, для итерации t на основе предыдущей итерации t-1.
| |
(24) |
7. Повторяем процесс в цикле с шага 2.
Диаграмма сигналов в сети при обучении по алгоритму обратного распространения приведена на следующем рисунке.
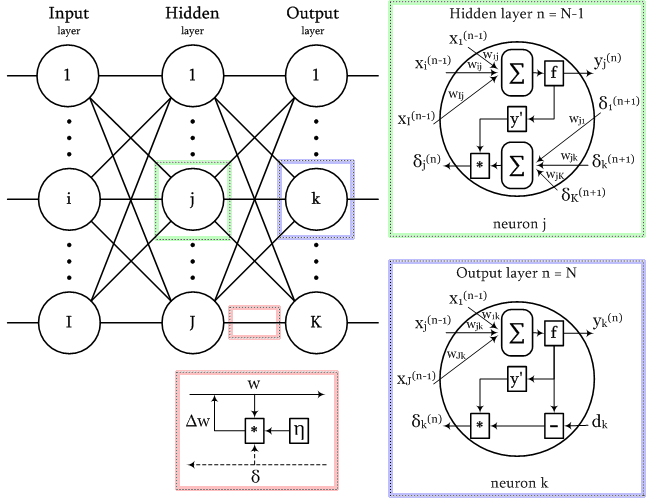
Схема сигналов в алгоритме обратного распространения ошибки
На вход сети попеременно предъявляются все тренировочные образы, чтобы она, образно говоря, не забывала одни по мере запоминания других. Обычно это делается в случайном порядке, но из-за того, что у нас данные будут помещены в матрицы и обсчитываться целиком как единый набор, в нашей реализации мы введем другой элемент случайности, но обсудим его чуть позднее.
Использование матриц означает, что веса всех слоев, а также входные и целевые обучающие данные будут представлены матрицами, а вышеприведенные формулы, и соответственно, алгоритмы получат матричную форму. Другими словами, мы не сможем оперировать отдельными векторами входных и обучающих данных, и весь цикл со 2-го по 7-ой шаги будет рассчитываться сразу для всего набора данных. Один такой цикл называется эпохой обучения.
Обзор активационных функций
К статье прилагается скрипт AF.mq5, который выводит на график миниатюрные изображения всех поддерживаемых в MQL5 активационных функций (синим цветом) и их производных (красным цветом). Скрипт автоматически масштабирует миниатюры так, чтобы в окно уместились все функции, поэтому для получения более детальных изображений рекомендуется предварительно увеличить или максимизировать окно. Пример изображения, полученного с помощью скрипта, приведен ниже.
Правильный выбор активационной функции зависит от типа нейронной сети и решаемой задачи. Более того, в одной сети может применяться несколько разных АФ. Например, SoftMax отличается от прочих функций тем, что обрабатывает выходные значения слоя не поэлементно, а во взаимной увязке — нормализует их таким образом, что величины можно интерпретировать как вероятности (их сумма равна 1), что используется для множественной классификации.
Данная тема настолько обширна, что потребовала отдельной статьи или цикла статей. Здесь мы лишь ограничимся предупреждением, что все функции имеют как положительные, так и отрицательные стороны, которые потенциально могут приводить к неработоспособности сети. В частности, для S-образных функций характерна так называемая проблема обнуления градиента («vanishing gradient», когда сигналы начинают попадать на участки «насыщения» S-кривой и потому подстройка весов стремится к нулю), а для монотонно возрастающих — проблема взрывного роста градиента («exploding gradient», то есть постоянно увеличивающиеся веса, вплоть до численного переполнения и получения NaN (Not A Number)). Обе упомянутые проблемы становятся тем более вероятны, чем больше количество слоев в сети. Для их решения можно использовать различные приемы, такие как нормализация данных (в том числе, не только на входе, но и в промежуточных слоях), алгоритмы прореживания сетей (выбрасывание нейронов («dropout»), пропуск связей), обучение пакетами данных, зашумление и прочие варианты регуляризации — некоторые из них мы рассмотрим и реализуем далее.
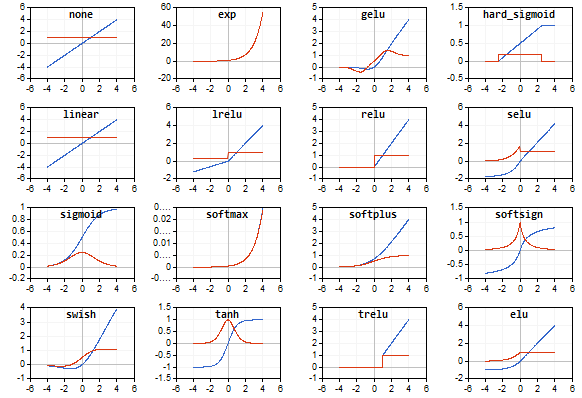
Демо-скрипт со всеми функциями активации
Реализация нейронной сети в классе MatrixNet
Приступим к написанию класса нейронной сети на основе матриц MQL5. Поскольку сеть состоит из слоев, опишем массивы весовых коэффициентов и выходных значений нейронов каждого слоя. Количество слоев будет храниться в переменной n, а веса нейронов в слоях и сигналы на выходе каждого слоя — в матрицах weights и outputs, соответственно. Обратите внимание, что термин outputs обозначает сигналы на выходах нейронов любого слоя, а не только на выходе сети. Так что outputs[i] описывают и промежуточные слои, и даже 0-й слой, куда подаются входные данные.
Индексация массивов weights и outputs иллюстрируется следующей схемой (связи каждого нейрона с источником смещения +1 не показаны для упрощения):
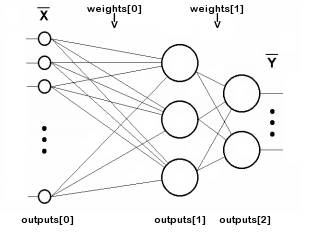
Схема индексации массивов матриц в двухслойной сети
Количество n не включает входной слой, потому что он не требует весов.
class MatrixNet { protected: const int n; matrix weights[]; matrix outputs[]; ENUM_ACTIVATION_FUNCTION af; ENUM_ACTIVATION_FUNCTION of; double speed; bool ready; ...
В нашей сети будут поддерживаться 2 типа активационных функций (на выбор пользователя): один — для всех слоев, кроме выходного (хранится в af), и отдельный — для выходного слоя (в переменной of). В переменной speed хранится скорость обучения (коэффициент η из формулы (20)).
Переменная ready содержит признак успешной инициализации объекта сети.
Конструктор сети принимает целочисленный массив layers, который определяет количество и размеры всех слоев. 0-й элемент задает размер входного псевдо-слоя, то есть количество признаков в каждом векторе входных данных. Последний элемент определяет размер выходного слоя, все остальные — промежуточных скрытых слоев. Количество слоев не может быть меньше двух. Для выделения памяти под массивы матриц написан вспомогательный метод allocate (мы будем его далее дополнять по мере расширения самого класса).
public: MatrixNet(const int &layers[], const ENUM_ACTIVATION_FUNCTION f1 = AF_TANH, const ENUM_ACTIVATION_FUNCTION f2 = AF_NONE): ready(false), af(f1), of(f2), n(ArraySize(layers) - 1) { if(n < 2) return; allocate(); for(int i = 1; i <= n; ++i) { weights[i - 1].Init(layers[i - 1] + 1, layers[i]); } ... } protected: void allocate() { ArrayResize(weights, n); ArrayResize(outputs, n + 1); ... }
Для инициализации каждой матрицы весов в качестве количества строк берется размер предыдущего слоя layers[i — 1] и к нему добавляется один синапс для постоянного регулируемого источника смещения +1. В качестве количества колонок берется размер текущего слоя layers[i]. В каждой матрице весов первый индекс относится к слою слева от матрицы, а второй — к слою справа.
Такая нумерация обеспечивает простую запись умножения векторов сигналов на матрицы слоев при прямом распространении (штатная работа сети). При обратном распространении ошибки (в режиме обучения) потребуется умножать вектор ошибок каждого старшего слоя на его транспонированную матрицу весов, чтобы пересчитать в ошибки для младшего слоя.
Иными словами, из-за того, что информация внутри сети движется в двух противоположных направлениях — рабочие сигналы от входов к выходам, а ошибки от выходов ко входам — весовые матрицы в каком-то из этих двух направлений должны использоваться в обычном виде, а во втором — транспонированными. Мы взяли за нормальную конфигурацию такую разметку матрицы, которая облегчает расчет прямого сигнала.
Матрицы outputs мы будем заполнять непосредственно в процессе прохождения сигнала по сети. А вот веса следует случайным образом инициализировать: для этого в конце конструктора вызывается метод randomize.
public: MatrixNet(const int &layers[], const ENUM_ACTIVATION_FUNCTION f1 = AF_TANH, const ENUM_ACTIVATION_FUNCTION f2 = AF_NONE): ready(false), af(f1), of(f2), n(ArraySize(layers) - 1) { ... ready = true; randomize(); } void randomize(const double from = -0.5, const double to = +0.5) { if(!ready) return; for(int i = 0; i < n; ++i) { weights[i].Random(from, to); } }
Наличия весовых матриц уже достаточно, чтобы реализовать прямой проход сигналов со входа сети на выход. Тот факт, что веса пока не обучены, не принципиален: обучением мы займемся позднее.
bool feedForward(const matrix &data) { if(!ready) return false; if(data.Cols() != weights[0].Rows() - 1) { PrintFormat("Column number in data %d <> Inputs layer size %d", data.Cols(), weights[0].Rows() - 1); return false; } outputs[0] = data; for(int i = 0; i < n; ++i) { if(!outputs[i].Resize(outputs[i].Rows(), weights[i].Rows()) || !outputs[i].Col(vector::Ones(outputs[i].Rows()), weights[i].Rows() - 1)) return false; matrix temp = outputs[i].MatMul(weights[i]); if(!temp.Activation(outputs[i + 1], i < n - 1 ? af : of)) return false; } return true; }
Количество столбцов во входной матрице data должно совпадать с количеством строк в 0-й матрице весов за вычетом 1 (вес к сигналу смещения).
Прочитать результат штатной работы сети позволяет метод getResults. По умолчанию он возвращает матрицу состояний выходного слоя.
matrix getResults(const int layer = -1) const { static const matrix empty = {}; if(!ready) return empty; if(layer == -1) return outputs[n]; if(layer < -1 || layer > n) return empty; return outputs[layer]; }
Оценить текущее качество модели можно методом test: он принимает на вход не только матрицу входных данных, но и матрицу с желаемым откликом сети.
double test(const matrix &data, const matrix &target, const ENUM_LOSS_FUNCTION lf = LOSS_MSE) { if(!ready || !feedForward(data)) return NaN(); return outputs[n].Loss(target, lf); }
После выполнения прямого прохода сигнала с помощью feedForward, мы здесь вычисляем меру «потерь» заданного типа. По умолчанию, это среднеквадратическая ошибка (LOSS_MSE), которая применима для задач регрессии и прогнозирования. Однако если сеть будет использоваться для классификации образов, следует выбрать другой тип оценки, например, кроссэнтропию LOSS_CCE.
В случае ошибки вычислений метод возвращает «не число» (NaN).
Теперь займемся обратным распространением ошибки. Метода backProp также начинается с проверки совпадения размеров целевых данных и выходного слоя. Затем для выходного слоя вычисляется производная активационной функции (если она есть) и «потери» сети на выходе, относительно целевых данных.
bool backProp(const matrix &target) { if(!ready) return false; if(target.Rows() != outputs[n].Rows() || target.Cols() != outputs[n].Cols()) return false; matrix temp; if(!outputs[n].Derivative(temp, of)) return false; matrix loss = (outputs[n] - target) * temp;
Матрица loss содержит величины δ из формулы (19).
Далее для всех слоев кроме выходного выполняется такой цикл:
for(int i = n - 1; i >= 0; --i) { if(i < n - 1) loss.Resize(loss.Rows(), loss.Cols() - 1); matrix delta = speed * outputs[i].Transpose().MatMul(loss);
Здесь мы видим «один в один» формулу (20): получаем приращения весов на основе скорости обучения η, δ текущего слоя и соответствующих выходов предыдущего (младшего) слоя.
Далее для каждого слоя вычисляем формулу (18), рекурсивно получая остальные δ: в ход опять идет производная АФ и умножение более старшей δ на транспонированную весовую матрицу. Следует напомнить, что индекс i в массиве outputs[] соответствует слою с весами в (i-1)-й матрице weights[], потому что входной псевдо-слой (outputs[0]) не имеет весов. Другими словами, при прямом прохождении сигнала матрица weights[0], будучи применена к outputs[0], производит outputs[1], weights[1] производит outputs[2] и так далее, а при обратном распространении ошибки индексы совпадают: например, outputs[2] (после дифференцирования) умножается на транспонированную weights[2].
if(!outputs[i].Derivative(temp, af)) return false; loss = loss.MatMul(weights[i].Transpose()) * temp;
Только после того как мы подсчитали loss δ для младшего слоя, можно подстраивать веса матрицы weights[i], то есть корректировать их на полученную выше delta.
weights[i] -= delta;
}
return true;
}
Теперь у нас почти все готово, чтобы реализовать полный алгоритм обучения с циклом по эпохам и вызовом методов feedForward и backProp. Однако сперва необходимо вновь обратиться к теории, потому что некоторые важные нюансы мы ранее отложили.
Обучение и регуляризация
Обучение НС производится на тренировочных данных, доступных на текущий момент. На основе этих данных выбирается конфигурация сети (количество слоев, количество нейронов по слоям и т.д.), скорость обучения и прочие характеристики. Поэтому, в принципе, всегда можно сконструировать достаточно мощную сеть, чтобы она давала любую достаточно малую ошибку на тренировочных данных. Однако главная сила НС и цель применения НС в том, чтобы она хорошо работала на будущих неизвестных данных (с теми же неявными зависимостями, что и тренировочный набор).
Эффект, когда обученная НС слишком хорошо подстраивается под обучающие данные, но проваливает «форвард-тест», называется переобучением, и должен всячески искореняться. Для этой цели применяют так называемую регуляризацию — добавление в модель или метод обучения неких дополнительных условий, оценивающих обобщающую способность сети. Существует множество различных способов регуляризации, в частности:
- анализ работы обучаемой сети на дополнительном валидационном наборе данных (отличном от обучающего);
- случайное отбрасывание части нейронов или связей во время обучения;
- прореживание (pruning) сети после обучения;
- привнесение шума во входные данные;
- искусственное размножение данных;
- слабое постоянное уменьшение амплитуды весов при обучении;
- экспериментальный подбор объема и конфигурации сети по тонкой грани, когда сеть еще способна обучаться, но уже не переобучается на имеющихся данных;
Мы реализуем некоторые из них в своем классе.
Для начала предусмотрим передачу в метод обучения не только входных и выходных обучающих данных (параметры data и target, соответственно), но также валидационного набора (он тоже состоит из входных и парных им выходных векторов: validation и check).
По мере обучения ошибка сети на обучающих данных, как правило, достаточно монотонно убывает (фраза «как правило» использована, потому что при неверном подборе скорости обучения или емкости сети, процесс может пойти нестабильно). Однако если параллельно подсчитывать ошибку сети на валидационном наборе, она сперва тоже будет уменьшаться (пока сеть выявляет наиболее важные закономерности в данных), а затем начнет расти по мере переобучения (когда сеть адаптируется уже к частным особенностям обучающей выборки, но не валидационной). Таким образом, процесс обучения следует остановить, когда ошибка валидации начнёт расти. Данный подход называется «ранней остановкой».
Помимо двух наборов данных, метод train позволяет задать максимальное количество эпох обучения (epochs), желаемую точность (accuracy, т.е. среднюю минимальную ошибку, которой нам достаточно: при этом обучение также заканчивается с признаком успеха) и способ подсчета ошибки (lf).
Скорость обучения speed устанавливается равной точности accuracy, но для повышения гибкости настроек, их можно при необходимости разнести. Так сделано потому, что далее мы поддержим автоматическую подстройку скорости, и начальное приблизительное значение не столь важно.
double train(const matrix &data, const matrix &target, const matrix &validation, const matrix &check, const int epochs = 1000, const double accuracy = 0.001, const ENUM_LOSS_FUNCTION lf = LOSS_MSE) { if(!ready) return NaN(); speed = accuracy; ...
Величины ошибок сети в текущей эпохе сохраним в переменных mse и msev — для обучающего и валидационного наборов. Но чтобы не реагировать на неизбежные случайные флуктуации, потребуется усреднять ошибки за некоторый период p, рассчитываемый из общего заданного числа эпох. Сглаженные значения ошибок будут храниться в переменных msema и msevma, а их предыдущие значения — в переменных msemap и msevmap.
double mse = DBL_MAX; double msev = DBL_MAX; double msema = 0; double msemap = 0; double msevma = 0; double msevmap = 0; double ema = 0; int p = 0; p = (int)sqrt(epochs); ema = 2.0 / (p + 1); PrintFormat("EMA for early stopping: %d (%f)", p, ema);
Далее запускаем цикл по эпохам обучения. Мы разрешаем не предоставлять валидационные данные, т.к. впоследствии реализуем другой способ регуляризации «dropout». Если валидационная выборка не пуста, рассчитываем msev вызовом метода test на ней. В любом случае рассчитываем mse с помощью вызова test на обучающей выборке. Напоминаем, что test осуществляет вызов метода feedForward и расчет ошибки результата сети относительно целевых значений.
int ep = 0; for(; ep < epochs; ep++) { if(validation.Rows() && check.Rows()) { msev = test(validation, check, lf); msevma = (msevma ? msevma : msev) * (1 - ema) + ema * msev; } mse = test(data, target, lf); msema = (msema ? msema : mse) * (1 - ema) + ema * mse; ...
Прежде всего проверяем, чтобы значение ошибки было валидным числом. В противном случае в сети произошло переполнение или на вход поданы некорректные данные.
if(!MathIsValidNumber(mse)) { PrintFormat("NaN at epoch %d", ep); break; }
Если новая ошибка стала больше прежней с некоторым «запасом», который определяется из соотношения размеров обучающей и валидационной выборок, цикл прерывается.
const int scale = (int)(data.Rows() / (validation.Rows() + 1)) + 1; if(msevmap != 0 && ep > p && msevma > msevmap + scale * (msemap - msema)) { PrintFormat("Stop by validation at %d, v: %f > %f, t: %f vs %f", ep, msevma, msevmap, msema, msemap); break; } msevmap = msevma; msemap = msema; ...
Если же ошибка продолжает уменьшаться или, как минимум не растет, запоминаем новые значения ошибок для сравнения в следующей эпохе.
Если ошибка достигла требуемой точности, считаем обучение завершенным и также выходим из цикла.
if(mse <= accuracy) { PrintFormat("Done by accuracy limit %f at epoch %d", accuracy, ep); break; }
Кроме того, в цикле вызывается виртуальный метод progress, который можно переопределить в производных классах сети, и с помощью него прерывать обучения в ответ на некоторые действия пользователя. Стандартную реализацию progress мы покажем чуть ниже.
if(!progress(ep, epochs, mse, msev, msema, msevma)) { PrintFormat("Interrupted by user at epoch %d", ep); break; }
Наконец, если цикл не был прерван ни по одному из вышеприведенных условий, запускаем обратный проход ошибки по сети с помощью backProp.
if(!backProp(target)) { mse = NaN(); break; } } if(ep == epochs) { PrintFormat("Done by epoch limit %d with accuracy %f", ep, mse); } return mse; }
Предоставленный по умолчанию метод progress выводит в журнал показатели обучения один раз в секунду.
virtual bool progress(const int epoch, const int total, const double error, const double valid = DBL_MAX, const double ma = DBL_MAX, const double mav = DBL_MAX) { static uint trap; if(GetTickCount() > trap) { PrintFormat("Epoch %d of %d, loss %.5f%s%s%s", epoch, total, error, ma == DBL_MAX ? "" : StringFormat(" ma(%.5f)", ma), valid == DBL_MAX ? "" : StringFormat(", validation %.5f", valid), valid == DBL_MAX ? "" : StringFormat(" v.ma(%.5f)", mav)); trap = GetTickCount() + 1000; } return !IsStopped(); }
Возвращаемое значение true продолжает обучение, в то время как false приведет к прерыванию цикла.
Помимо «ранней остановки», класс MatrixNet умеет случайным образом «отключать» часть связей а-ля «dropout».
Канонический метод «dropout» предполагает временное исключение из сети случайно выбранных нейронов. Однако мы не можем это реализовать без больших накладных расходов, поскольку алгоритм использует матричные операции. Для исключения нейронов из слоя потребовалось бы на каждой итерации переформатировать матрицы весов и частично копировать их. Гораздо проще и эффективнее устанавливать случайные веса в 0, то есть обрывать связи. Разумеется, в начале каждой эпохи программа должна восстановить временно отключенные веса до их предыдущего состояния, а потом выбрать несколько новых для отключения в следующей эпохе.
Количество временно обнуляемых связей задается с помощью метода enableDropOut, как процент от общего числа весов сети. По умолчанию, переменная dropOutRate равна 0, и режим отключен.
void enableDropOut(const uint percent = 10) { dropOutRate = (int)percent; }
Принцип работы «dropout» заключается в сохранении текущего состояния весовых матриц в некоем дополнительно хранилище (его реализует класс DropOutState) и обнулении случайно выбранных связей сети. После обучения сети в полученном модифицированном виде на протяжении одной эпохи, обнуленные элементы матриц восстанавливаются из хранилища, и процедура повторяется: выбираются и обнуляются другие случайные веса, сеть обучается с ними, и так далее. С устройством и применением класса DropOutState предлагается разобраться самостоятельно.
Адаптивная скорость обучения
До сих пор подразумевалось, что у нас используется постоянная скорость обучения (переменная speed), но это непрактично (обучение может идти очень медленно при малой скорости или «возбуждаться» при большой).
Одну из разновидностей адаптации скорости обучения можно «подсмотреть» в особой модификации алгоритма обратного распространения, которая называется «rprop» (от resilient propagation, то есть эластичное распространение). Суть заключается в том, чтобы для каждого веса проверять, совпадает ли знак приращений delta на предыдущей и текущей итерации. Совпадение знака означает, что направление градиента сохранилось, и в этом случае скорость можно повысить, причем избирательно для данного веса. Для тех весов, где знак градиента поменялся, имеет смысл, наоборот, «замедлиться».
Поскольку у нас в матрицах на каждой эпохе обсчитываются сразу все данные, значение и знак градиента для каждого веса аккумулируют (и «усредняют») поведение всего пакета данных. Поэтому более точно технология называется «batch rprop».
Все строки кода в классе MatrixNet, которые реализуют это усовершенствование, обложены макросами BATCH_PROP. Перед включением заголовочного файла MatrixNet.mqh в ваш исходный код рекоменуется включать адаптивную скорость с помощью директивы:
#define BATCH_PROP
Для начала обратим внимание, что вместо переменной speed в этом режиме используется массив матриц speed, а также потребуется запоминать приращения весов с прошлой эпохи в массиве матриц deltas.
class MatrixNet { protected: ... #ifdef BATCH_PROP matrix speed[]; matrix deltas[]; #else double speed; #endif
Кроме того, коэффициенты ускорения и торможения, а также максимальная и минимальные скорости задаются выделенными для этого 4-мя переменными.
double plus; double minus; double max; double min;
Выделение памяти под новые массивы и установка значений по умолчанию новым переменным производится в уже знакомом нам методе allocate.
void allocate() { ArrayResize(weights, n); ArrayResize(outputs, n + 1); ArrayResize(bestWeights, n); dropOutRate = 0; #ifdef BATCH_PROP ArrayResize(speed, n); ArrayResize(deltas, n); plus = 1.1; minus = 0.1; max = 50; min = 0.0; #endif }
Для установки других значений этим переменным перед запуском обучения воспользуйтесь методом setupSpeedAdjustment.
В конструкторе MatrixNet массивы матриц speed и deltas инициализируются копированием массива матриц weights — просто так удобнее получить матрицы аналогичных размеров по слоям сети. Заполнение speed и deltas значащими данными происходит на последующих этапах. В частности, в начале метода train вместо простого присваивания точности (accuracy) в скалярную переменную speed теперь производится заполнение этим значением всех матриц в массиве speed.
double train(const matrix &data, const matrix &target, const matrix &validation, const matrix &check, const int epochs = 1000, const double accuracy = 0.001, const ENUM_LOSS_FUNCTION lf = LOSS_MSE) { ... #ifdef BATCH_PROP for(int i = 0; i < n; ++i) { speed[i].Fill(accuracy); deltas[i].Fill(0); } #else speed = accuracy; #endif ... }
Внутри метода backProp выражение с вычислением приращений теперь ссылается на матрицу соответствующего слоя, а не на скаляр. Сразу же после получения приращений delta вызывается метод adjustSpeed (приведен далее), в который для сопоставления прежнего и нового направления передается произведение delta * deltas[i]. Наконец, новые приращения весов сохраняются в deltas[i], чтобы анализировать их на следующей эпохе.
bool backProp(const matrix &target) { ... for(int i = n - 1; i >= 0; --i) { ... #ifdef BATCH_PROP matrix delta = speed[i] * outputs[i].Transpose().MatMul(loss); adjustSpeed(speed[i], delta * deltas[i]); deltas[i] = delta; #else matrix delta = speed * outputs[i].Transpose().MatMul(loss); #endif ... } ... }
Метод adjustSpeed довольно прост. Положительный знак в элементе матричного произведения означает сохранение градиента, и скорость увеличивается в plus раз, но не более чем до величины max. Отрицательный знак означает смену градиента, и скорость уменьшается в minus раз, но не менее величины min.
void adjustSpeed(matrix &subject, const matrix &product) { for(int i = 0; i < (int)product.Rows(); ++i) { for(int j = 0; j < (int)product.Cols(); ++j) { if(product[i][j] > 0) { subject[i][j] *= plus; if(subject[i][j] > max) subject[i][j] = max; } else if(product[i][j] < 0) { subject[i][j] *= minus; if(subject[i][j] < min) subject[i][j] = min; } } } }
Сохранение и восстановление лучшего состояния обученной сети
Итак, обучение сети проводится в цикле по итерациям, называемым эпохами: в каждой эпохе через сеть проходят все вектора обучающего набора, помещенные в матрицу, где по строкам лежат записи, а по колонкам — их признаки. Например, в каждой записи может храниться бар котировок, а по столбцам — цены OHLC и объемы.
Процесс подстройки весов, хотя и выполняется по градиенту, носит случайных характер в том смысле, что из-за неровности целевой функции решаемой задачи и переменной скорости мы можем периодически попадать на более «плохие» настройки, прежде чем «обнаружить» новый минимум ошибки сети. В принципе, у нас нет гарантии, что с увеличением номера эпохи, качество обученной модели будет непременно улучшаться, а ошибка сети — уменьшаться.
В связи с этим имеет смысл постоянно контролировать общую ошибку сети, и если после текущей эпохи ошибка обновляет минимум, найденные веса следует запомнить. Для этих целей определен еще один массив матриц весов, а также структура с показателями обучения Stats.
class MatrixNet { ... public: struct Stats { double bestLoss; int bestEpoch; int epochsDone; }; Stats getStats() const { return stats; } protected: matrix bestWeights[]; Stats stats; ...
Внутри метода train, перед началом цикла по эпохам инициализируем структуру со статистикой.
double train(const matrix &data, const matrix &target, const matrix &validation, const matrix &check, const int epochs = 1000, const double accuracy = 0.001, const ENUM_LOSS_FUNCTION lf = LOSS_MSE) { ... stats.bestLoss = DBL_MAX; stats.bestEpoch = -1; DropOutState state(dropOutRate);
Внутри самого цикла при обнаружении величины ошибки меньше минимальной известной мы запоминаем все весовые матрицы в bestWeights.
int ep = 0; for(; ep < epochs; ep++) { ... const double candidate = (msev != DBL_MAX) ? msev : mse; if(candidate < stats.bestLoss) { stats.bestLoss = candidate; stats.bestEpoch = ep; for(int i = 0; i < n; ++i) { bestWeights[i].Assign(weights[i]); } } } ...
После обучения легко запросить как финальные веса сети, так и лучшие веса.
bool getWeights(matrix &array[]) const { if(!ready) return false; ArrayResize(array, n); for(int i = 0; i < n; ++i) { array[i] = weights[i]; } return true; } bool getBestWeights(matrix &array[]) const { if(!ready) return false; if(!n || !bestWeights[0].Rows()) return false; ArrayResize(array, n); for(int i = 0; i < n; ++i) { array[i] = bestWeights[i]; } return true; }
Эти массивы матриц можно сохранить в файл для последующего восстановления уже обученной и готовой к работе сети. Для этого предусмотрен отдельный конструктор.
MatrixNet(const matrix &w[], const ENUM_ACTIVATION_FUNCTION f1 = AF_TANH, const ENUM_ACTIVATION_FUNCTION f2 = AF_NONE): ready(false), af(f1), of(f2), n(ArraySize(w)) { if(n < 2) return; allocate(); for(int i = 0; i < n; ++i) { weights[i] = w[i]; #ifdef BATCH_PROP speed[i] = weights[i]; deltas[i] = weights[i]; #endif } ready = true; }
Позднее мы покажем сохранение и чтение готовых сетей в одном из практических примеров.
Визуализация прогресса обучения сети
Наличие метода progress, выводящего периодические сообщения в журнал, не особо наглядно. Поэтому в файле MatrixNet.mqh также реализован производный от MatrixNet класс MatrixNetVisual, выводящий в окно график с изменяющимися величинами ошибок обучения по эпохам.
Графическое отображение предоставляет стандартный класс CGraphic (поставляемый с MetaTrader 5), а точнее — небольшой производный от него класс CMyGraphic.
Объект данного класса является частью MatrixNetVisual. Также внутри «визуализируемой» сети описан массив из 5-ти кривых и массивы типа double, предназначенные непосредственно для отображаемых линий.
class MatrixNetVisual: public MatrixNet { CMyGraphic graphic; CCurve *c[5]; double p[], x[], y[], z[], q[], b[]; ...
Здесь:
В методе graph, вызываемом из конструкторов MatrixNetVisual, создается графический объект размером на все окно и добавляются 5 вышеописанных кривых (CCurve).
void graph() { ulong width = ChartGetInteger(0, CHART_WIDTH_IN_PIXELS); ulong height = ChartGetInteger(0, CHART_HEIGHT_IN_PIXELS); bool res = false; const string objname = "BPNNERROR"; if(ObjectFind(0, objname) >= 0) res = graphic.Attach(0, objname); else res = graphic.Create(0, objname, 0, 0, 0, (int)(width - 0), (int)(height - 0)); if(!res) return; c[0] = graphic.CurveAdd(p, x, CURVE_LINES, "Training"); c[1] = graphic.CurveAdd(p, y, CURVE_LINES, "Validation"); c[2] = graphic.CurveAdd(p, z, CURVE_LINES, "Val.EMA"); c[3] = graphic.CurveAdd(p, q, CURVE_LINES, "Train.EMA"); c[4] = graphic.CurveAdd(p, b, CURVE_POINTS, "Best/Minimum"); ... } public: MatrixNetVisual(const int &layers[], const ENUM_ACTIVATION_FUNCTION f1 = AF_TANH, const ENUM_ACTIVATION_FUNCTION f2 = AF_NONE): MatrixNet(layers, f1, f2) { graph(); }
В переопределенном методе progress аргументы добавляются в соответствующие массивы double, а затем вызывается метод plot для актуализации изображения.
virtual bool progress(const int epoch, const int total, const double error, const double valid = DBL_MAX, const double ma = DBL_MAX, const double mav = DBL_MAX) override { PUSH(p, epoch); PUSH(x, error); if(valid != DBL_MAX) PUSH(y, valid); else PUSH(y, nan); if(ma != DBL_MAX) PUSH(q, ma); else PUSH(q, nan); if(mav != DBL_MAX) PUSH(z, mav); else PUSH(z, nan); plot(); return MatrixNet::progress(epoch, total, error, valid, ma, mav); }
Метод plot производит пополнение и отображение кривых.
void plot() { c[0].Update(p, x); c[1].Update(p, y); c[2].Update(p, z); c[3].Update(p, q); double point[1] = {stats.bestEpoch}; b[0] = stats.bestLoss; c[4].Update(point, b); ... graphic.CurvePlotAll(); graphic.Update(); }
С технической стороной визуализации предлагается разобраться самостоятельно. Как это выглядит на экране, мы скоро увидим.
Тестовый скрипт
Классы семейства MatrixNet готовы для первой проверки. Ею станет скрипт MatrixNet.mq5, в котором исходные данные генерируются искусственно на основе известной аналитической записи. Формула взята из раздела справки про машинное обучение, где приведен собственный пример обучения по алгоритму обратного распространения ошибки — не столь универсальный, как наши классы, и потому требующий значительного кодирования (сравните далее количество строк с использованием класса и без).
f = ((x + y + z)^2 / (x^2 + y^2 + z^2)) / 3
Единственное маленькое отличие нашей формулы заключается в делении значения на 3, что дает диапазон функции от 0 до 1.
Форму функции можно оценить с помощью следующего рисунка, где поверхности (x<->y) показаны для трех разных значений z: 0.05, 0.5 и 5.0.
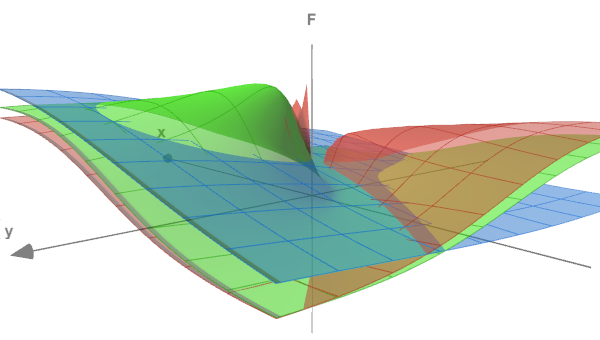
Тестовая функция в 3-х сечениях
Во входных переменных скрипта зададим количество эпох обучения, точность (терминальную ошибку), а также интенсивность шума, которую мы можем по желанию добавить в генерируемые данные (это приблизит эксперимент к реальным задачам и продемонстрирует, как наличие шума усложняет выявлении зависимостей). По умолчанию параметр RandomNoise равен 0, и шум отсутствует.
input int Epochs = 1000; input double Accuracy = 0.001; input double RandomNoise = 0.0;
Генерацией экспериментальных данных «заведует» функция CreateData. Её параметры-матрицы data и target будут заполнены точками описанной выше функции, в количестве count. Один входной вектор (строка матрицы data) имеет 3 колонки (для x, y, z). Выходной вектор (строка матрицы target) — это единственное значение f. Точки (x,y,z) генерируются случайно в диапазоне от -10 до +10.
bool CreateData(matrix &data, matrix &target, const int count) { if(!data.Init(count, 3) || !target.Init(count, 1)) return false; data.Random(-10, 10); vector X1 = MathPow(data.Col(0) + data.Col(1) + data.Col(2), 2); vector X2 = MathPow(data.Col(0), 2) + MathPow(data.Col(1), 2) + MathPow(data.Col(2), 2); if(!target.Col(X1 / X2 / 3.0, 0)) return false; if(RandomNoise > 0) { matrix noise; noise.Init(count, 3); noise.Random(0, RandomNoise); data += noise - RandomNoise / 2; noise.Resize(count, 1); noise.Random(-RandomNoise / 2, RandomNoise / 2); target += noise; } return true; }
Интенсивность шума в RandomNoise задается как амплитуда дополнительного разброса правильных координат и полученного для них значения функции. Учитывая, что функция имеет максимальную величину 1.0, такой уровень шума сделает её практически нераспознаваемой.
Для использования нейронной сети подключим заголовочный файл MatrixNet.mqh и перед этой директивой препроцессора определим макрос BATCH_PROP, чтобы задействовать ускоренное обучения с переменной скоростью.
#define BATCH_PROP #include <MatrixNet.mqh>
В главной функции скрипта определяем конфигурацию сети (количество слоев и их размеры) с помощью массива layers, который передаем в конструктор MatrixNetVisual. Наборы обучающих и валидационных данных генерируем двукратным вызовом CreateData.
void OnStart() { const int layers[] = {3, 11, 7, 1}; MatrixNetVisual net(layers); matrix data, target; CreateData(data, target, 100); matrix valid, test; CreateData(valid, test, 25); ...
На практике исходные данные следует нормализовать, очистить от выбросов, проверить факторы на независимость, прежде чем отправлять в сеть, но в данном случае мы сами генерируем данные.
Обучение выполняется методом train на матрицах data и target. Ранняя остановка произойдет по мере ухудшения показателей на наборе valid/test, однако на незашумленных данных мы, скорее всего, достигнем требуемой точности или же предельного числа циклов, в зависимости от того, что случится быстрее.
Print("Training result: ", net.train(data, target, valid, test, Epochs, Accuracy)); matrix w[]; if(net.getBestWeights(w)) { MatrixNet net2(w); if(net2.isReady()) { Print("Best copy on training data: ", net2.test(data, target)); Print("Best copy on validation data: ", net2.test(valid, test)); } }
После обучения запрашиваем матрицы лучших найденных весов и ради проверки конструируем на их основе другой экземпляр сети — объект net2, после чего выполняем рабочий прогон сети на обоих наборах данных и выводим величины ошибок для них в журнал.
Поскольку в скрипте используется сеть с визуализацией прогресса обучения, запускаем цикл ожидания команды пользователя на завершения скрипта, чтобы пользователь мог ознакомиться с графиком.
while(!IsStopped()) { Sleep(1000); } }
При запуске скрипта с параметрами по умолчанию можем получить примерно следующую картину (каждый запуск будет отличаться от других из-за случайной генерации данных и инициализации сети).
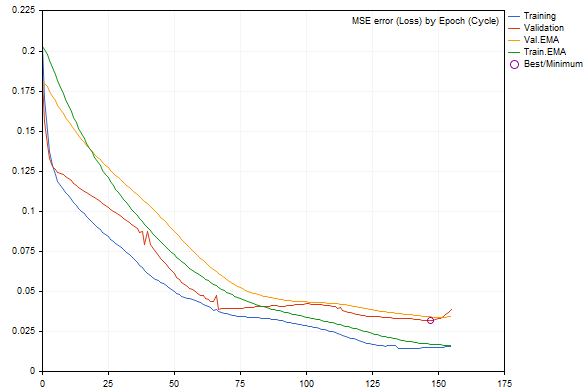
Динамика изменения ошибки сети при обучении
Ошибки на обучающем и валидационном наборе отображены синей и красной линиями, соответственно, а их сглаженные версии — зеленая и желтая. Наглядно видно, что по мере обучения все типы ошибок уменьшаются, но после некоторого момента ошибка валидации становится больше ошибки обучающего набора, а ближе к правому краю графика заметно её возрастание, в результате чего происходит «ранняя остановка». Лучшая конфигурация сети помечена кружком.
В журнале увидим похожие записи:
EMA for early stopping: 31 (0.062500)
Epoch 0 of 1000, loss 0.20296 ma(0.20296), validation 0.18167 v.ma(0.18167)
Epoch 120 of 1000, loss 0.02319 ma(0.02458), validation 0.04566 v.ma(0.04478)
Stop by validation at 155, v: 0.034642 > 0.034371, t: 0.016614 vs 0.016674
Training result: 0.015707719706513287
Best copy on training data: 0.015461956812387292
Best copy on validation data: 0.03211748853774414
Если начать добавлять в данные шум с помощью параметра RandomNoise, темпы обучения заметно снизятся, а при слишком большом шуме ошибка обученной сети возрастет или она вовсе перестанет обучаться.
Вот, например, как выглядит график при добавлении шума 3.0.
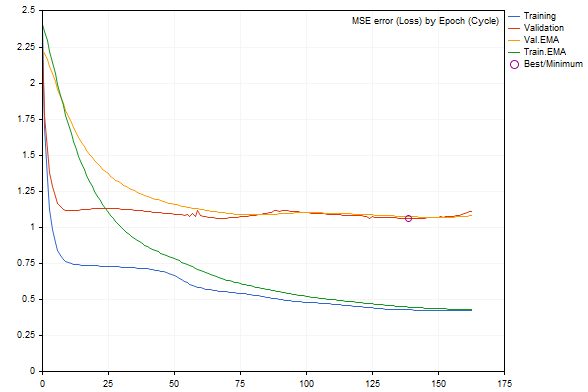
Динамика изменения ошибки сети при обучении с добавленным шумом
Показатель ошибки, согласно журналу, на порядок хуже.
Epoch 0 of 1000, loss 2.40352 ma(2.40352), validation 2.23536 v.ma(2.23536) Stop by validation at 163, v: 1.082419 > 1.080340, t: 0.432023 vs 0.432526 Training result: 0.4244786772678285 Best copy on training data: 0.4300476339855798 Best copy on validation data: 1.062895214094978
Убедившись, что нейросетевой инструментарий работает, перейдем к более практичным примерам: индикатору и эксперту.
Прогнозирующий индикатор
В качестве примера прогнозирующего индикатора на основе НС рассмотрим BPNNMatrixPredictorDemo.mq5 — это модификация готового индикатора из кодовой базы, в котором НС реализована на MQL5 без применения матриц, путем портирования с языка C++ другой, более ранней версии того же индикатора (с подробным описанием, включая релевантные части теории НС).
Принцип работы индикатора заключается в формировании входных векторов заданной длины из прошлых приращений EMA-усредненной цены на отрезках между барами, отстоящими друг от друга по последовательности Фибоначчи (1,2,3,5,8,13,21,34,55,89,144…). По этой информации требуется предсказать приращение цены на следующем баре (справа от исторических баров, попавших в соответствующий вектор). Размер вектора определяется заданным пользователем размером входного слоя НС (_numInputs). Количество слоев (вплоть до 6) и их размеры вводятся в другие входные переменные.
input int _lastBar = 0; input int _futBars = 10; input int _smoothPer = 6; input int _numLayers = 3; input int _numInputs = 12; input int _numNeurons1 = 5; input int _numNeurons2 = 1; input int _numNeurons3 = 0; input int _numNeurons4 = 0; input int _numNeurons5 = 0; input int _ntr = 500; input int _nep = 1000; input int _maxMSEpwr = -7;
Также здесь указывается размер обучающей выборки (_ntr), максимальное количество эпох (_nep) и минимальная MSE-ошибка (_maxMSEpwr).
Период EMA-усреднения цены задается в _smoothPer.
По умолчанию, индикатор берет обучающие данные, начиная с последнего бара (_lastBar равно 0), и делает прогноз на _futBars вперед (очевидно, что имея на выходе сети прогноз на 1 бар, мы можем его поэтапно «задвигать» во входной вектор, чтобы предсказывать несколько последующих баров). Если ввести в _lastBar положительное число, получим прогноз по состоянию на соответствующее количество баров в прошлом, что позволит его визуально оценить (сравнить с уже имеющимися котировками).
Индикатор выводит 3 буфера:
- светло-зеленая линия с целевыми значениями обучающей выборки;
- синяя линия с выходом сети на обучающей выборке;
- красная линия с прогнозом;
Прикладная часть индикатора по формированию наборов данных и визуализации результатов (как исходных данных, так и прогноза) не претерпела изменений.
Основные преобразования произошли в двух функциях Train и Test — теперь они полностью делегируют работу НС объектам класса MatrixNet. Train обучает сеть на основе собранных данных и возвращает массив с весами сети (при запуске в тестере обучение делается лишь однажды, а при запуске онлайн открытие нового бара вызывает повторное обучение — это легко поменять в исходном коде). Test воссоздает сеть по весам и выполняет штатный однократный расчет прогноза. В принципе, более оптимально было бы сохранить объект обученной сети, и эксплуатировать его без воссоздания. Мы сделаем так в следующем примере эксперта, а в случае индикатора специально оставлена исходная структура кода старой версии, чтобы было удобнее сравнивать подходы кодирования с матрицами и без. В частности, можно обратить внимание на то, что в матричной версии мы избавлены от необходимости «прогонять» векторы через сеть в цикле по одному и вручную делать «reshape» массивов с данными, в соответствии с их размерностью.
С настройками по умолчанию индикатор выглядит на графике EURUSD,H1 следующим образом.
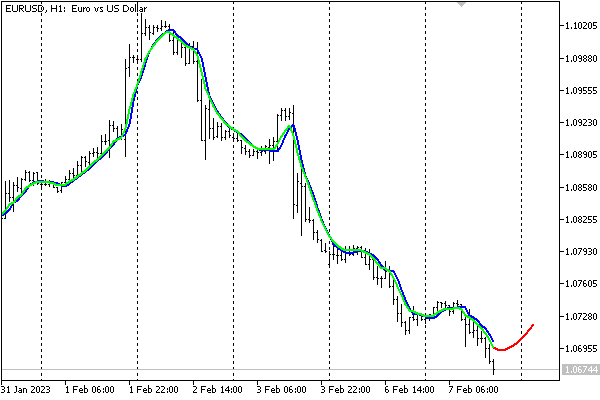
Прогноз нейросетевого индикатора
Следует отметить, что индикатор является лишь демонстрацией работы НС и не рекомендуется в текущем упрощенном виде для принятия торговых решений.
Хранение сетей в файлах
Исходные данные, поступающие с рынка, могут быстро меняться, и некоторые трейдеры считают целесообразным обучать сеть оперативно (каждый день, каждую сессию, и т.д.) на наиболее свежих образцах. Однако это может быть накладно, да и не столь актуально для среднесрочных и долгосрочных торговых систем, оперирующих днями. В подобных случаях обученную сеть желательно сохранить для последующей загрузки и быстрого использования.
Для этой цели в рамках статьи создан класс MatrixNetStore, определенный в заголовочном файле MatrixNetStore.mqh. В классе имеются шаблонные методы save и load, предполагающие в качестве параметра шаблона M любой класс из семейства MatrixNet (пока их у нас только два, с учетом MatrixNetVisual, но желающие могут расширить набор). Оба метода имеют аргумент с именем файла и оперируют стандартными данными НС: количеством слоев, их размером, весовыми матрицами, функциями активации.
Вот как делается сохранения сети.
class MatrixNetStore { static string signature; public: template<typename M> static bool save(const string filename, const M &net, Storage *storage = NULL, const int flags = 0) { matrix w[]; if(!net.getBestWeights(w)) { if(!net.getWeights(w)) { return false; } } int h = FileOpen(filename, FILE_WRITE | FILE_BIN | FILE_SHARE_READ | FILE_SHARE_WRITE | FILE_ANSI | flags); if(h == INVALID_HANDLE) return false; FileWriteString(h, signature); FileWriteInteger(h, net.getActivationFunction()); FileWriteInteger(h, net.getActivationFunction(true)); FileWriteInteger(h, ArraySize(w)); for(int i = 0; i < ArraySize(w); ++i) { matrix m = w[i]; FileWriteInteger(h, (int)m.Rows()); FileWriteInteger(h, (int)m.Cols()); double a[]; m.Swap(a); FileWriteArray(h, a); } if(storage) { if(!storage.store(h)) Print("External info wasn't saved"); } FileClose(h); return true; } ... }; static string MatrixNetStore::signature = "BPNNMS/1.0";
Отметим пару моментов. В начале файла пишется сигнатура, чтобы по ней можно было проверять правильность формата файла (сигнатуру можно менять: для этого в классе предусмотрены методы). Кроме того, метод save позволяет при необходимости дописать к стандартной информации о сети любые дополнительные пользовательские данные: достаточно передать указатель на объект специального интерфейса Storage.
class Storage { public: virtual bool store(const int h) = 0; virtual bool restore(const int h) = 0; };
«Зеркальным» образом сеть можно восстановить из файла.
class MatrixNetStore { ... template<typename M> static M *load(const string filename, Storage *storage = NULL, const int flags = 0) { int h = FileOpen(filename, FILE_READ | FILE_BIN | FILE_SHARE_READ | FILE_SHARE_WRITE | FILE_ANSI | flags); if(h == INVALID_HANDLE) return NULL; const string header = FileReadString(h, StringLen(signature)); if(header != signature) { FileClose(h); Print("Incorrect file header"); return NULL; } const ENUM_ACTIVATION_FUNCTION f1 = (ENUM_ACTIVATION_FUNCTION)FileReadInteger(h); const ENUM_ACTIVATION_FUNCTION f2 = (ENUM_ACTIVATION_FUNCTION)FileReadInteger(h); const int size = FileReadInteger(h); matrix w[]; ArrayResize(w, size); for(int i = 0; i < size; ++i) { const int rows = FileReadInteger(h); const int cols = FileReadInteger(h); double a[]; FileReadArray(h, a, 0, rows * cols); w[i].Swap(a); w[i].Reshape(rows, cols); } if(storage) { if(!storage.restore(h)) Print("External info wasn't read"); } M *m = new M(w, f1, f2); FileClose(h); return m; }
Теперь у нас все готово, чтобы обратиться к завершающему примеру статьи — торговому роботу.
Прогнозирующий эксперт
В качестве стратегии для прогнозирующего эксперта TradeNN.mq5 возьмем достаточно простой принцип: торговать в предсказанном направлении следующего бара. Нам важно продемонстрировать нейросетевые технологии в действии, а не исследовать все обозримые факторы на применимость в контексте прибыльности.
Исходными данными станут приращения цен на заданном количестве баров, причем опционально можно анализировать не только текущий символ, но и дополнительные, что теоретически позволит выявить взаимозависимости (например, если один тикер опосредованно «следует» за другим или их комбинациями). Единственный выход сети не будет интерпретироваться как целевая цена, а вместо этого, с целью упрощения системы, будет анализироваться знак: положительный — покупка, отрицательный — продажа.
Иными словами, схема работы сети в некотором смысле гибридная: с одной стороны сеть будет решать задачу регрессии, но с другой стороны торговое действие выбирается из двух, как при классификации. В перспективе можно увеличить число нейронов в выходном слое до количества торговых ситуаций и применить активационную функцию SoftMax — правда, чтобы обучать такую сеть, потребуется автоматически или вручную разметить котировки согласно ситуациям.
Выбор стратегии специально сделан максимально простым, чтобы сосредоточиться на параметрах сети, а не стратегии.
Перечень анализируемых инструментов вводится во входной параметр Symbols через запятую. Первым должен идти символ текущего графика — именно на этом символе ведется торговля.
input string Symbols = "XAGUSD,XAUUSD,EURUSD"; input int Depth = 5; input int Reserve = 250;
Выбор символов по умолчанию обусловлен тем, что серебро и золото считаются коррелированными активами, и по ним относительно мало возмутительных новостей (по сравнению с валютами), так что, в принципе, можно пробовать анализировать как серебро по золоту (как сейчас), так и золото по серебру. Что же касается EURUSD, то эта пара добавлена в качестве основы всего рынка, и в данном случае наличие новостей по ней не важно, так как она работает как предиктор, а не прогнозируемая переменная.
Среди других наиболее важных параметров — количество баров (Depth) по каждому инструменту, формирующих вектор. Например, если в строке Symbols задано 3 тикера, а в Depth стоит 5 (по умолчанию), значит общий размер входного вектора НС равен 15.
Параметр Reserve позволяет задать длину выборки (количество векторов, формируемых из ближайшей истории котировок). Значение 250 выбрано по умолчанию, потому что в нашем тесте будет использоваться дневной таймфрейм, и 250 составляет примерно 1 год. Соответственно, Depth, равный 5 — это неделя.
Разумеется, все настройки можно менять, как и таймфрейм, но на старших таймфремах, вроде D1, предположительно, более выражены фундаментальные закономерности, нежели спонтанные реакции рынка на сиюминутные обстоятельства.
Важно также напомнить, что при запуске в тестере заранее подгружается примерно 1 год котировок, поэтому увеличение объема запрашиваемых обучающих данных на D1+ потребует пропускать некоторое количество начальных баров, ожидая накопления их достаточного количества.
По аналогии с предыдущими примерами, в параметрах следует задать количество эпох обучения и точность (по совместительству, начальную скорость, а далее скорость будет динамически выбираться для каждого синапса по «rprop»).
input int Epochs = 1000; input double Accuracy = 0.0001;
В данном эксперте НС получит 5 слоев: один входной, 3 скрытых и выходной. Размер входного слоя определяет входной вектор, а второй и третий слои выделяются с коэффициентом HiddenLayerFactor. Для предпоследнего слоя будет использована эмпирическая формула (см. далее исходный код), чтобы его размер лежал между предыдущим и выходным (единичным).
input double HiddenLayerFactor = 2.0; input int DropOutPercentage = 0;
Также на примере данной НС мы испытаем способ регуляризации «dropout»: процент случайно выбираемых для обнуления весов задается в параметре DropOutPercentage. Валидационная выборка здесь не предусморена, хотя желающие смогут совмещать оба метода: класс это позволяет.
Для загрузки сети из файла предназначен параметр NetBinFileName. Файлы всегда ищутся относительно общей папки терминалов, поскольку иначе для тестирования эксперта в тестере потребовалось бы указывать заранее имена всех нужных сетей в исходном коде, в директиве #property tester_file — только так они отправились бы на агент.
Когда параметр NetBinFileName пуст, эксперт обучает новую сеть и сохраняет её в файле с уникальным временным именем. Это делается даже в процессе оптимизации, что позволяет генерировать большое количество конфигураций сети (для разных размеров векторов, слоев, «dropout»-а, глубины истории).
input string NetBinFileName = ""; input int Randomizer = 0;
Более того, параметр Randomizer дает возможность по-разному инициализировать случайный генератор и тем самым обучать много экземпляров сетей для одних и тех же прочих настроек. Напомним, что каждая сеть уникальна за счет рандомизации. Потенциально, использование комитетов НС, из которых считывается консолидированное решение или по принципу большинства, является еще одной разновидностью регуляризации.
Вместе с тем, установка конкретного значения в Randomizer позволит воспроизводить один и тот же процесс обучения в целях отладки.
Хранение ценовой информации по символам организовано с помощью структуры Closes и массива таких структур CC: в результате получим что-то вроде массива массивов.
struct Closes { double C[]; }; Closes CC[];
Под рабочие инструменты и их количество зарезервированы глобальный массив S и переменная Q: они заполняются в OnInit.
string S[]; int Q; int OnInit() { Q = StringSplit(StringLen(Symbols) ? Symbols : _Symbol, ',', S); ArrayResize(CC, Q); MathSrand(Randomizer); ... return INIT_SUCCEEDED; }
Запросить котировки на заданную глубину Depth от конкретного бара offset позволяет функция Calc: именно в ней заполняется массив CC. Как эта функция вызывается, мы увидим чуть дальше.
bool Calc(const int offset) { const datetime dt = iTime(_Symbol, _Period, offset); for(int i = 0; i < Q; ++i) { const int bar = iBarShift(S[i], PERIOD_CURRENT, dt); const int n = CopyClose(S[i], PERIOD_CURRENT, bar, Depth + 2, CC[i].C); for(int j = 0; j < n - 1; ++j) { CC[i].C[j] = (CC[i].C[j + 1] - CC[i].C[j]) / SymbolInfoDouble(S[i], SYMBOL_TRADE_TICK_SIZE) * SymbolInfoDouble(S[i], SYMBOL_TRADE_TICK_VALUE); } ArrayResize(CC[i].C, n - 1); } return true; }
Затем для конкретного массива CC[i].C специальная функция Diff сможет рассчитать приращения цен, которые и попадут во входные векторы для сети. Особенностью функции является то, что все приращения, кроме последнего, она записывает в переданный по ссылке массив d, а последнее приращение, которое будет выступать целевым значением прогноза, возвращается напрямую.
double Diff(const double &a[], double &d[]) { const int n = ArraySize(a); ArrayResize(d, n - 1); double overall = 0; for(int j = 0; j < n - 1; ++j) { int k = n - 2 - j; overall += a[k]; d[j] = overall / sqrt(j + 1); } ... return a[n - 1]; }
Здесь следует отметить, что в соответствии с теорией «случайного блуждания» временных рядов, мы нормируем разницы квадратным корнем расстояния в барах (пропорционально доверительному интервалу, если рассматривать прошлое, как уже отработанный прогноз). Это не является каноническим приемом, но работа с НС зачастую сродни исследовательской.
Вся процедура выбора факторов (например, не только цен, но индикаторов, объемов) и подготовки данных для сети (нормализация, кодирование) — это отдельная обширная тема. Важно максимально облегчить для НС вычислительную работу, в противном случае она может не справиться с задачей.
В главной функции эксперта OnTick все операции выполняются только по открытию бара. Учитывая, что эксперт анализирует котировки разных инструментов, требуется синхронизировать их бары, прежде чем продолжать штатную работу. Синхронизацию выполняет функция Sync, здесь не показанная. Однако интересно отметить, что примененная синхронизация на базе функции Sleep, подходит даже для тестирования в режиме цен открытия. И мы позднее воспользуемся этим режимом из соображений эффективности.
void OnTick() { ... static datetime last = 0; if(last == iTime(_Symbol, _Period, 0)) return; ...
Экземпляр сети хранится в переменной run типа авто-указателя (заголовочный файл AutoPtr.mqh), что избавляет нас от необходимости контролировать освобождение памяти. Переменная std предназначена для хранения дисперсии, рассчитываемой на наборе данных, полученном из рассмотренных выше функций Calc и Diff. Дисперсия потребуется для нормализации данных.
static AutoPtr<MatrixNet> run; static double std;
Если пользователь задал в NetBinFileName имя файла для загрузки, программа попытается загрузить сеть с помощью LoadNet (см. далее). Эта функция в случае успеха возвращает указатель на объект сети.
if(NetBinFileName != "") { if(!run[]) { run = LoadNet(NetBinFileName, std); if(!run[]) { ExpertRemove(); return; } } }
При наличии сети выполняем прогнозирование и осуществляем торговлю: за всё это отвечает TradeTest (см. далее).
if(run[]) { TradeTest(run[], std); } else { run = TrainNet(std); } last = iTime(_Symbol, _Period, 0); }
Если сети еще нет, формируем обучающую выборку и обучаем на ней сеть с помощью вызова TrainNet: эта функция также возвращает указатель на новый объект сети, а кроме того, заполняет переданную по ссылке переменную std рассчитанной дисперсией данных.
Обратите внимание, что сеть сможет обучаться только после того, как в истории по всем рабочим символам окажется как минимум запрошенное количество баров. Для онлайн-графика это произойдет, скорее всего, сразу после размещения эксперта (если только пользователь не ввел запредельное число), а в тестере предзагруженная история, как правило, ограничена одним годом, и потому может потребоваться сдвинуть старт прохода в прошлое, чтобы к интересующему вас моменту накопить нужное количество баров для обучения.
Проверка на достаточное количество баров вставлена в начало OnTick, но в статье не приводится (см. полные исходные коды).
После того как сеть обучена, эксперт начнет торговать. Для тестера это означает, что мы получим своего рода форвард-тест обученной сети. Полученные финансовые показатели можно использовать для оптимизации с целью выбора наиболее подходящей конфигурации сети или селекции комитета сетей (одинаковых по конфигурации).
А вот и сама функция TrainNet (обратите внимание на вызовы Calc и Diff).
MatrixNet *TrainNet(double &std) { double coefs[]; matrix sys(Reserve, Q * Depth); vector model(Reserve); vector t; datetime start = 0; for(int j = Reserve - 1; j >= 0; --j) { if(!Calc(j + 1)) { return NULL; } if(start == 0) start = iTime(_Symbol, _Period, j); ArrayResize(coefs, 0); for(int i = 0; i < Q; ++i) { double temp[]; double m = Diff(CC[i].C, temp); if(i == 0) { model[j] = m; } int dest = ArraySize(coefs); ArrayCopy(coefs, temp, dest, 0); } t.Assign(coefs); sys.Row(t, j); } std = sys.Std() * 3; Print("Normalization by 3 std: ", std); sys /= std; matrix target = {}; target.Col(model, 0); target /= std; int layers[] = {0, 0, 0, 0, 1}; layers[0] = (int)sys.Cols(); layers[1] = (int)(sys.Cols() * HiddenLayerFactor); layers[2] = (int)(sys.Cols() * HiddenLayerFactor); layers[3] = (int)fmax(sqrt(sys.Rows()), fmax(sqrt(layers[1] * layers[3]), sys.Cols() * sqrt(HiddenLayerFactor))); ArrayPrint(layers); MatrixNetVisual *net = new MatrixNetVisual(layers); net.setupSpeedAdjustment(SpeedUp, SpeedDown, SpeedHigh, SpeedLow); net.enableDropOut(DropOutPercentage);
Print("Training result: ", net.train(sys, target, Epochs, Accuracy));
...
Мы используем класс сети с визуализацией, в результате чего прогресс обучения будет виден на графике. После обучения вы можете вручную удалить объект-картинку, когда она станет ненужной. При выгрузке эксперта картинка удаляется автоматически.
Далее требуется прочитать из сети лучшие весовые матрицы. Дополнительно мы проверяем возможность успешно воссоздать сеть по этим весам и тестируем её производительность на тех же данных.
matrix w[]; if(net.getBestWeights(w)) { MatrixNet net2(w); if(net2.isReady()) { Print("Best result: ", net2.test(sys, target)); ... } } return net; }
Наконец, сеть сохраняется в файл вместе со специально подготовленной строкой, описывающей условия обучения: интервал истории, список символов и таймфрейм, размер данных, настройки сети.
const string context = StringFormat("rn%s %s %s-%s", _Symbol, EnumToString(_Period),
TimeToString(start), TimeToString(iTime(_Symbol, _Period, 0))) + "rn" +
Symbols + "rn" + (string)Depth + "/" + (string)Reserve + "rn" +
(string)Epochs + "/" + (string)Accuracy + "rn" +
(string)HiddenLayerFactor + "/" + (string)DropOutPercentage + "rn";
const string tempfile = "bpnnmtmp" + (string)GetTickCount64() + ".bpn";
MatrixNetStore store;
BinFileNetStorage writer(context, net.getStats(), std);
store.save(tempfile, *net, &writer);
...
Упомянутый здесь класс BinFileNetStorage является специфическим для нашего эксперта и с помощью переопределенных методов store/restore (родительский интерфейс Storage) обрабатывает наше дополнительное описание, величину нормализации (она потребуется для штатной работы на новых данных), а также статистику обучения в виде структуры MatrixNet::Stats (приводилась выше).
Далее поведение эксперта зависит от того, работает ли он в режиме оптимизации или нет. При оптимизации мы отправим файл сети с агента в терминал с помощью механизма фреймов (см. исходный код). Такие файлы складируются в локальной папке MQL5/Files/, в подпапке с именем эксперта.
if(!MQLInfoInteger(MQL_OPTIMIZATION)) { string filename = "bpnnm" + TimeStamp((datetime)FileGetInteger(tempfile, FILE_MODIFY_DATE)) + StringFormat("(%7g)", net.getStats().bestLoss) + ".bpn"; if(!FileMove(tempfile, 0, filename, FILE_COMMON)) { PrintFormat("Can't rename temp-file: %s [%d]", tempfile, _LastError); } } else { ... }
В остальных случаях (простое тестирование или работа онлайн) файл перемещается в общую папку терминалов. Так сделано, чтобы облегчить последующую загрузку через параметр NetBinFileName. Дело в том, что для работы в тестере нам потребовалось бы в исходном коде указывать директиву #property tester_file с конкретным именем файла, который планируется вводить в параметр NetBinFileName, и перекомпилировать эксперт. Без этих манипуляций файл сети не будет скопирован на агент. Поэтому более практичным является использование общей папки, доступной из всех локальных агентов.
Функция LoadNet реализована следующим образом:
MatrixNet *LoadNet(const string filename, double &std, const int flags = FILE_COMMON) { BinFileNetStorage reader; MatrixNetStore store; MatrixNet *net; std = 1.0; Print("Loading ", filename); ResetLastError(); net = store.load<MatrixNet>(filename, &reader, flags); if(net == NULL) { Print("Failed: ", _LastError); return NULL; } MatrixNet::Stats s[1]; s[0] = reader.getStats(); ArrayPrint(s); std = reader.getScale(); Print(std); Print(reader.getDescription()); return net; }
Функция TradeTest вызывает Calc(0), чтобы затем получить вектор из актуальных приращений цен.
bool TradeTest(MatrixNet *net, const double std) { if(!Calc(0)) return false; double coefs[]; for(int i = 0; i < Q; ++i) { double temp[]; Diff(CC[i].C, temp, true); ArrayCopy(coefs, temp, ArraySize(coefs), 0); } vector t; t.Assign(coefs); matrix data = {}; data.Row(t, 0); data /= std; ...
На основании вектора сеть должна сделать прогноз, но прежде принудительно закрывается имеющаяся открытая позиция — анализ совпадения прежнего и нового направлений здесь не производится. Используемый для закрытия метод ClosePosition будет показан ниже. Затем, по результатам прямого прогона сети, открываем новую позицию в предполагаемом направлении.
ClosePosition();
if(net.feedForward(data))
{
matrix y = net.getResults();
Print("Prediction: ", y[0][0] * std);
OpenPosition((y[0][0] > 0) ? ORDER_TYPE_BUY : ORDER_TYPE_SELL);
return true;
}
return false;
}
Функции OpenPosition и ClosePosition реализованы схожим образом. Приведем только ClosePosition.
bool ClosePosition() { MqlTradeRequest request = {}; if(!PositionSelect(_Symbol)) return false; const string pl = StringFormat("%+.2f", PositionGetDouble(POSITION_PROFIT)); request.action = TRADE_ACTION_DEAL; request.position = PositionGetInteger(POSITION_TICKET); const ENUM_ORDER_TYPE type = (ENUM_ORDER_TYPE)(PositionGetInteger(POSITION_TYPE) ^ 1); request.type = type; request.price = SymbolInfoDouble(_Symbol, type == ORDER_TYPE_BUY ? SYMBOL_ASK : SYMBOL_BID); request.volume = PositionGetDouble(POSITION_VOLUME); request.deviation = 5; request.comment = pl; ResetLastError(); MqlTradeResult result[1]; const bool ok = OrderSend(request, result[0]); Print("Status: ", _LastError, ", P/L: ", pl); ArrayPrint(result); if(ok && (result[0].retcode == TRADE_RETCODE_DONE || result[0].retcode == TRADE_RETCODE_PLACED)) { return true; } return false; }
Настало время для практических исследований. Запустим эксперт в тестере с настройками по умолчанию, на графике XAGUSD,D1, в режиме по ценам открытия. Начальной датой теста поставим 2022.01.01. Это означает, что сразу после старта эксперта сеть начнет обучаться на ценах предыдущего 2021-го года и затем по её сигналам будет торговать. Чтобы видеть график изменения ошибки по эпохам, тестер следует запускать в визуальном режиме.
В журнале появятся записи следующего вида, связанные с обучением НС.
Sufficient bars at: 2022.01.04 00:00:00 Normalization by 3 std: 1.3415995381755823 15 30 30 21 1 EMA for early stopping: 31 (0.062500) Epoch 0 of 1000, loss 2.04525 ma(2.04525) Epoch 121 of 1000, loss 0.31818 ma(0.36230) Epoch 243 of 1000, loss 0.16857 ma(0.18029) Epoch 367 of 1000, loss 0.09157 ma(0.09709) Epoch 479 of 1000, loss 0.06454 ma(0.06888) Epoch 590 of 1000, loss 0.04875 ma(0.05092) Epoch 706 of 1000, loss 0.03659 ma(0.03806) Epoch 821 of 1000, loss 0.03043 ma(0.03138) Epoch 935 of 1000, loss 0.02721 ma(0.02697) Done by epoch limit 1000 with accuracy 0.024416 Training result: 0.024416206367547762 Best result: 0.024416206367547762 Check-up of saved and restored copy: bpnnm202302121707(0.0244162).bpn Loading bpnnm202302121707(0.0244162).bpn [bestLoss] [bestEpoch] [trainingSet] [validationSet] [epochsDone] [0] 0.024 999 250 0 1000 1.3415995381755823 XAGUSD PERIOD_D1 2021.01.18 00:00-2022.01.04 00:00 XAGUSD,XAUUSD,EURUSD 5/250 1000/0.0001 2.0/0 Best result restored: 0.024416206367547762
Пока обратите внимание на величину финальной ошибки. Позднее мы повторим тест с включенным режимом «dropout» разной интенсивности и сравним результаты.
Торговый отчет выглядит таким образом.
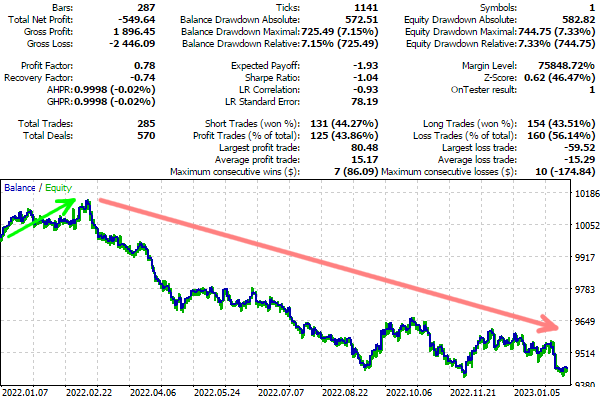
Пример отчета торговли по прогнозу
Очевидно, что на большей части 2022 года торговля пошла неудовлетворительно. Однако в левой части, непосредственно после 2021 года, который предоставил обучающую выборку, заметен непродолжительный прибыльный период. Вероятно, закономерности, найденные сетью, продолжали действовать некоторое время. Так ли это, и не следует ли каким-либо образом изменить настройки сети или обучающего набора, чтобы улучшить показатели, — можно выяснить для каждой конкретной торговой системы только в ходе разносторонних исследований. Это большая кропотливая работа, не связанная с внутренней реализацией нейросетевых алгоритмов. Здесь мы ограничимся минимальным анализом.
В журнале нам сообщается название файла с обученной сетью. Введем его в тестере в параметр NetBinFileName, а время тестирования расширим, начав с 2021 года. В таком режиме все входные параметры, кроме двух первых (Symbols и Depth), не имеют значения.
Тестовая торговля на увеличенном интервале показывает следующую динамику баланса (желтым подсвечена обучающая выборка).
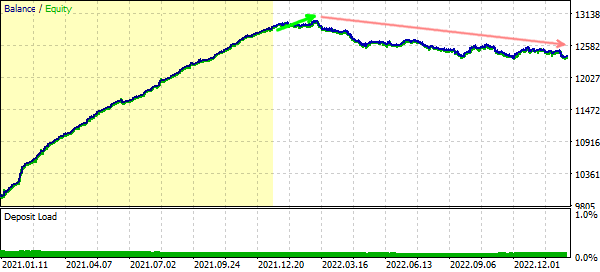
Кривая баланса при торговле на расширенном интервале, включая обучающую выборку
Как и следовало ожидать, сеть «научилась» специфике конкретного интервала, но вскоре после его завершения перестает приносить прибыль.
Давайте повторим обучение сети дважды: с «dropout»-ом в размере 25% и 50% (параметр DropOutPercentage должен быть последовательно выставлен в 25, а потом — в 50). Для инициирования обучения новых сетей очистим параметр NetBinFileName, а начало теста вернем на дату 2022.01.01.
При «dropout» 25% получим ошибку заметно больше, чем в первом случае. Но это ожидаемо, так как мы пытаемся за счет огрубления модели расширить её применимость на данные вне выборки (out-of-sample).
Epoch 0 of 1000, loss 2.04525 ma(2.04525) Epoch 125 of 1000, loss 0.46777 ma(0.48644) Epoch 251 of 1000, loss 0.36113 ma(0.36982) Epoch 381 of 1000, loss 0.30045 ma(0.30557) Epoch 503 of 1000, loss 0.27245 ma(0.27566) Epoch 624 of 1000, loss 0.24399 ma(0.24698) Epoch 744 of 1000, loss 0.22291 ma(0.22590) Epoch 840 of 1000, loss 0.19507 ma(0.20062) Epoch 930 of 1000, loss 0.18931 ma(0.19018) Done by epoch limit 1000 with accuracy 0.182581 Training result: 0.18258059873803228
При «dropout» 50% ошибка еще больше увеличивается.
Epoch 0 of 1000, loss 2.04525 ma(2.04525) Epoch 118 of 1000, loss 0.54929 ma(0.55782) Epoch 242 of 1000, loss 0.43541 ma(0.45008) Epoch 367 of 1000, loss 0.38081 ma(0.38477) Epoch 491 of 1000, loss 0.34920 ma(0.35316) Epoch 611 of 1000, loss 0.30940 ma(0.31467) Epoch 729 of 1000, loss 0.29559 ma(0.29751) Epoch 842 of 1000, loss 0.27465 ma(0.27760) Epoch 956 of 1000, loss 0.25901 ma(0.26199) Done by epoch limit 1000 with accuracy 0.251914 Training result: 0.25191436104184456
На следующем изображении совмещены графики обучения в 3-х вариантах.
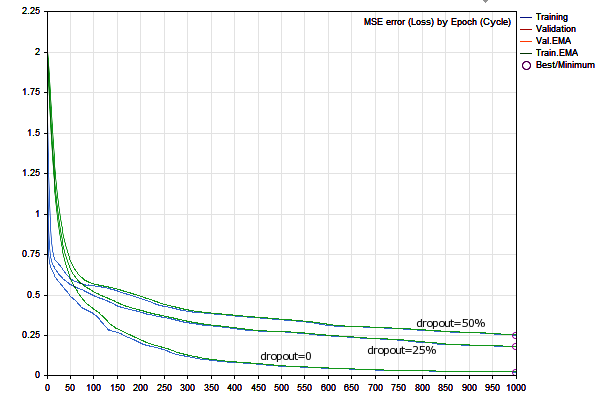
Динамика обучения при различной величине dropout
А вот каковы кривые балансов (желтым подсвечена обучающая выборка).
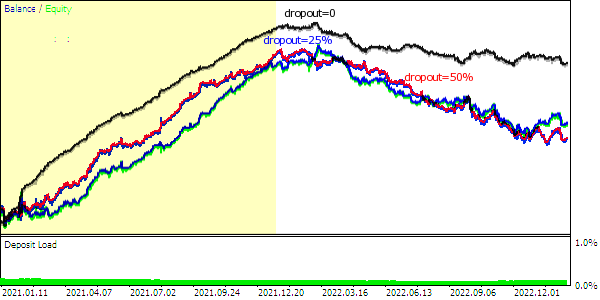
Кривые балансов торговли по прогнозам сетей с разным dropout
Из-за случайного отключения весов при «dropout» линия баланса на обучающем периоде становится не такой гладкой, как на полной сети, и общая прибыль, разумеется, уменьшается.
В данном эксперименте все варианты довольно быстро (в течение месяца-двух) теряют связь с рынком, но суть эксперимента была в проверке созданного нейросетевого инструментария, а не в выработке законченной системы.
В целом, средняя величина «dropout» 25% кажется более оптимальной, потому что меньшая степень регуляризации возвращает нас к переобучению, а бОльшая степень — разрушает вычислительные способности сети. Однако, основной вывод, который мы можем предварительно сделать — нейросетевой подход не является панацеей, способной «вытянуть» любую торговую систему. Причиной неудач могут быть как неверные предположения о наличии конкретных зависимостей, так и в параметрах разных модулей алгоритма и подготовки данных.
Прежде чем отбросить эту (или любую другую ТС) следует попробовать различные способы поиска лучших настроек для сети, как мы обычно делаем для настроек экспертов без ИИ. Для хорошо обусловленных выводов потребуется собрать гораздо больше статистики.
В частности, мы можем искать другие кластеры символов или таймфреймов, запустить оптимизацию по доступным сейчас публичным переменным или расширить их перечень (например, активационными функциями, способами формирования векторов, фильтрацией по дням недели и т.д.).
В этом плане использование НС никоим образом не освобождает трейдера от задачи выдвижения гипотез, проверки идей и значащих факторов. Единственное отличие заключается в том, что оптимизация настроек торговой системы дополняется мета-параметрами НС.
В качестве эксперимента запустим оптимизацию по размеру вектора, количеству векторов, фактору размера скрытых слоев и «dropout». Кроме того, включим в оптимизацию и параметр Randomizer — это позволит для каждого сочетания прочих настроек сгенерировать несколько экземпляров сетей.
- Vector size (Depth) — с 1 по 5
- Training set (Reserve) — с 50 по 400 с шагом 50
- Hidden Layer Factor — с 1 по 5
- DropOut — 0, 25%, 50%
- Randomizer — с 0 по 9
set-файл с настройками прилагается. Интервал дат от 2022.01.01 до 2023.02.15.
Критерием оптимизации выберем, например, Profit Factor, хотя с учетом малого количества сочетаний (6000) и их полного перебора (в отличие от генетики), это не важно.
Анализ результатов оптимизации можно проводить, экспортировав в файл XML или непосредственно из opt-файла, например, как это предлагается в OLAP-программе из статьи Количественный и визуальный анализ отчетов тестера или другими скриптами (opt-формат открыт).
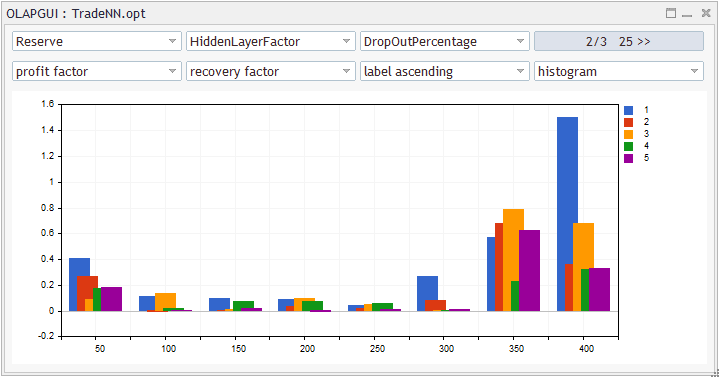
Статистический анализ отчета оптимизации
Для этого скриншота агрегирование показателей в запрошенных разбивках (Reserve по X (горизонтальная ось) относительно HiddenLayerFactor по Y (помечено цветом) при DropOutPercentage 25% по Z) осуществлялось с помощью специфического расчета профит-фактора (по ячейкам в осях X/Y/Z) от фактора восстановления (из каждого прохода тестера в рамках оптимизации). Такая искусственная мера добротности не идеальна, но зато доступна «из коробки».
Аналогичные или более привычные статистики можно рассчитать в Excel.
Статистически более выигрышным является фактор скрытых слоев, равный 1 (а не 2, как было по умолчанию), а размер вектора — равный 4 (вместо 5). При этом рекомендуемая величина «dropout» — 25% или 50%, но не 0%.
Также ожидаемо, более глубокая история предпочтительнее (350 или 400 отсчетов и, вероятно, дальнейшее увеличение оправдано).
Подытожим найденные рабочие настройки:
- Vector size = 4
- Training set = 400
- Hidden Layer Factor = 1
Поскольку в оптимизации был задействован параметр Randomizer, у нас есть 30 экземпляров сетей, обученных в данной конфигурации, — по 10 сетей для каждого уровня «dropout» (0%, 25%, 50%). Нам нужны 25% и 50%. Выгрузив отчет оптимизации в XML, мы можем отфильтровать нужные записи и получим таблицу (сортировка по прибыльности с фильтром больше 1):
Pass Result Profit Expected Profit Recovery Sharpe Custom Equity Trades Depth Reserve Hidden DropOut Randomizer Payoff Factor Factor Ratio DD % LayerF Perc 3838 1.35 336.02 2.41741 1.34991 1.98582 1.20187 1 1.61 139 4 400 1 25 6 838 1.23 234.40 1.68633 1.23117 0.81474 0.86474 1 2.77 139 4 400 1 25 1 3438 1.20 209.34 1.50604 1.20481 0.81329 0.78140 1 2.47 139 4 400 1 50 5 5838 1.17 173.88 1.25094 1.16758 0.61594 0.62326 1 2.76 139 4 400 1 50 9 5038 1.16 167.98 1.20849 1.16070 0.51542 0.60483 1 3.18 139 4 400 1 25 8 3238 1.13 141.35 1.01691 1.13314 0.46758 0.48160 1 2.95 139 4 400 1 25 5 2038 1.11 118.49 0.85245 1.11088 0.38826 0.41380 1 2.96 139 4 400 1 25 3 4038 1.10 107.46 0.77309 1.09951 0.49377 0.38716 1 2.12 139 4 400 1 50 6 1438 1.10 104.52 0.75194 1.09700 0.51681 0.37404 1 1.99 139 4 400 1 25 2 238 1.07 73.33 0.52755 1.06721 0.19040 0.26499 1 3.69 139 4 400 1 25 0 2838 1.03 34.62 0.24907 1.03111 0.10290 0.13053 1 3.29 139 4 400 1 50 4 2238 1.02 21.62 0.15554 1.01927 0.05130 0.07578 1 4.12 139 4 400 1 50 3
Возьмем лучшую, первую строку.
Напомним, что в ходе оптимизации все обученные сети сохраняются в папке MQL5/Files/<имя эксперта>/<дата оптимизации>. В принципе, этого можно не делать, учитывая, что по значению Randomizer можно вновь обучить аналогичную сеть, но только при условии полного соответствия входных данных. Если же история котировок изменится (например, другой брокер), воспроизвести сеть именно с такими характеристиками не получится.
Файлы в указанной папке имеют имена, состоящие из названий и значений оптимизируемых параметров. Поэтому достаточно выполнить поиск в файловой системе:
Depth=4-Reserve=400-HiddenLayerFactor=1-DropOutPercentage=25-Randomizer=6
Допустим, файл имеет имя:
Depth=4-Reserve=400-HiddenLayerFactor=1-DropOutPercentage=25-Randomizer=6-3838(0.428079).bpn
где число в круглых скобках — ошибка сети, число перед скобками — номер прохода.
Заглянем внутрь файла: несмотря на то, что файл бинарный, в его концовке сохранены в виде текста наши мета-данные обучения, в частности указано, что интервал обучения составил 2021.01.12 00:00-2022.07.28 00:00 (400 баров D1).
Скопируем файл под более кратким именем, например, test3838.bpn, в общую папку терминалов.
Введем имя test3838.bpn в параметр NetBinFileName, а в параметр Vector size (Depth) — 4 (все остальные параметры неважны, если работа ведется исключительно в режиме прогнозирования).
Проверим торговлю эксперта на еще более увеличенном периоде: поскольку 2022—2023 год выступил в роли валидационного форвард-теста, захватим 2020 в качестве неизвестного периода.
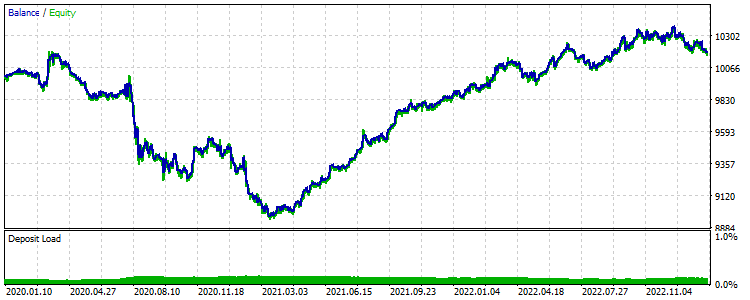
Пример неудачного теста торговли по прогнозам вне обучающей выборки
Чуда не случилось — система убыточна на «новых» данных. Нетрудно убедиться, что подобная картина характерна и для других настроек.
Итак, у нас две новости: хорошая и плохая.
Плохая заключается в том, что предложенная идея не работает — может быть, не работает вообще, а может быть это артефакт ограниченности обследованного пространства факторов в нашем демо-примере (все-таки мы не запускали супер-мега-оптимизацию на миллиарды сочетаний и сотни символов).
А хорошая новость — в том, что предложенный нейросетевой инструментарий позволяет оценивать идеи и выдает ожидаемые (с технической точки зрения) результаты.
Заключение
В данной статье представлены классы нейронных сетей с обратным распространением ошибки на матрицах MQL5. Реализация не требует зависимости от внешних программ, таких как Python, и специальных программно-аппаратных средств (графических ускорителей с поддержкой OpenCL). Помимо штатных режимов обучения и последующей эксплуатации сетей, классы обеспечивают визуализацию процесса, сохранение и восстановление сетей в файлах.
Благодаря подобным классам использование НС довольно легко интегрируется в любую программу, однако следует помнить, что сеть — это лишь инструмент, применяемый к некоторому материалу (в нашем случае: финансовым данным). Если материал не содержит достаточно информации, сильно зашумлен или нерелевантен, никакая нейронная сеть, не сможет найти в нем грааль.
Алгоритм обратного распространения ошибки является одним из наиболее распространенных базовых методов обучения, на основе которого можно конструировать более сложные нейросетевые технологии: рекуррентные сети, сверточные сети, обучение с подкреплением.

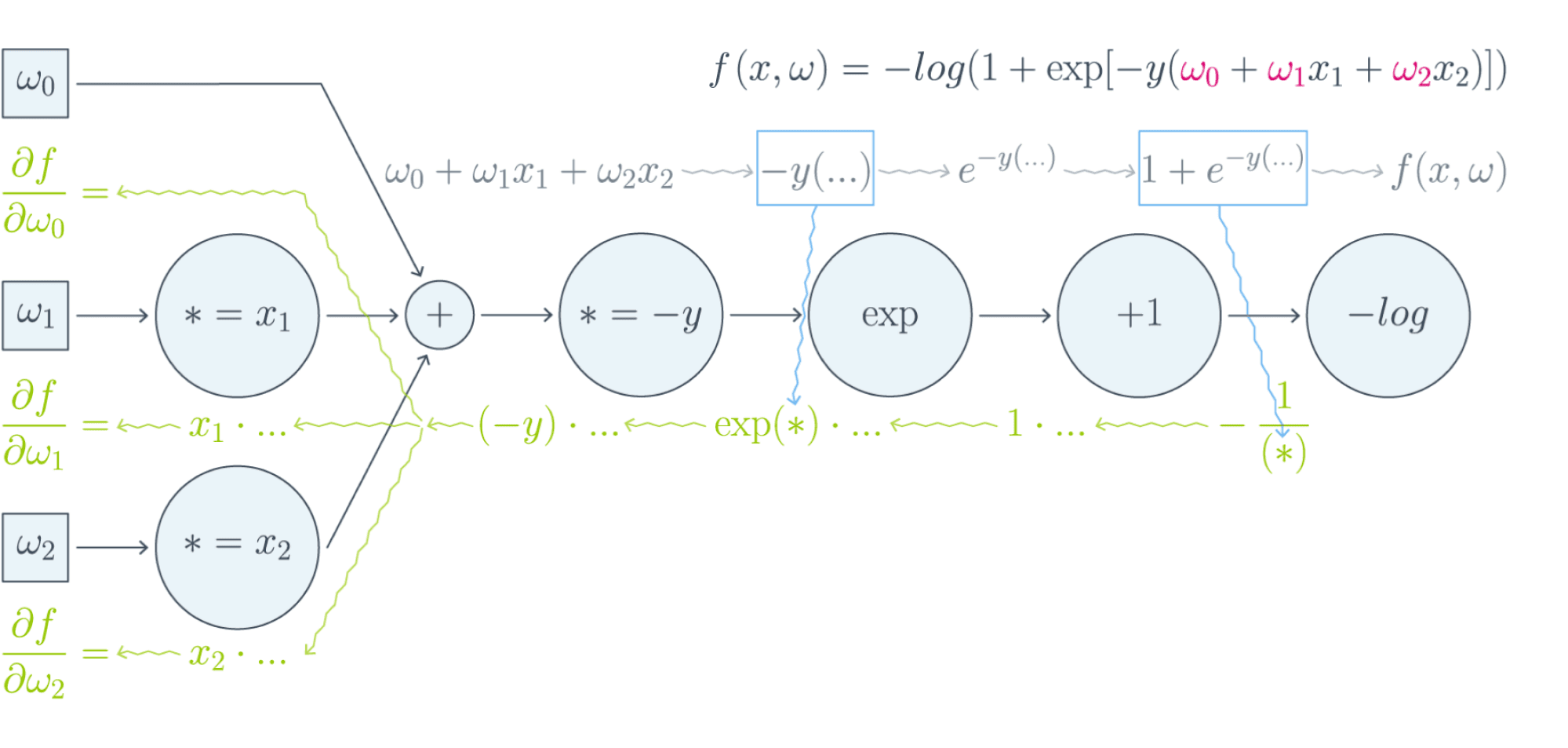
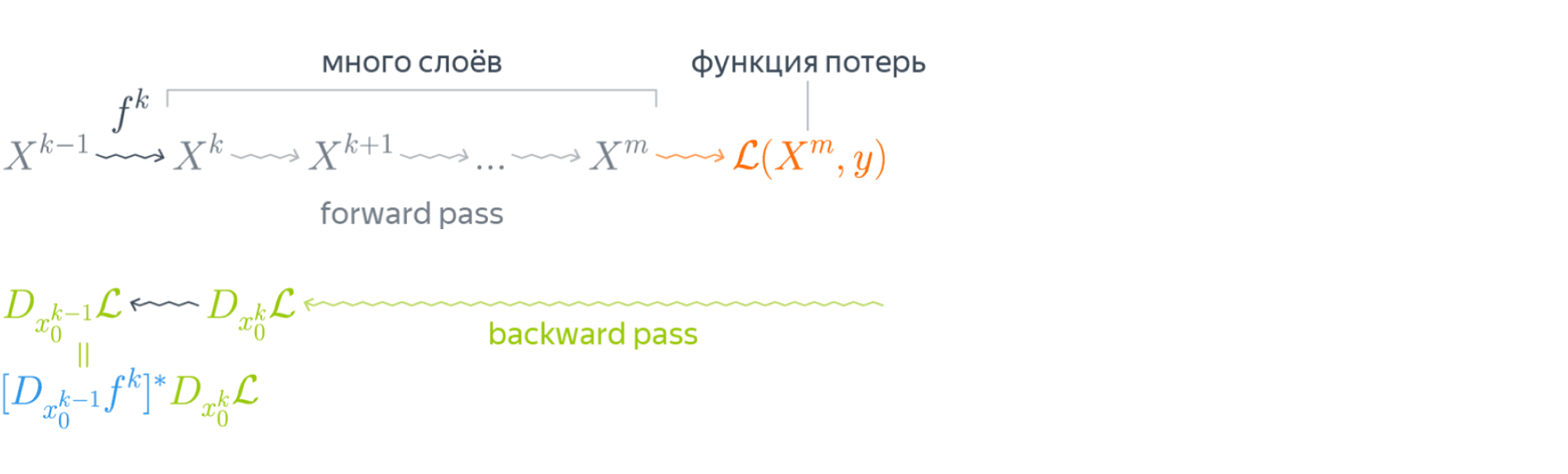
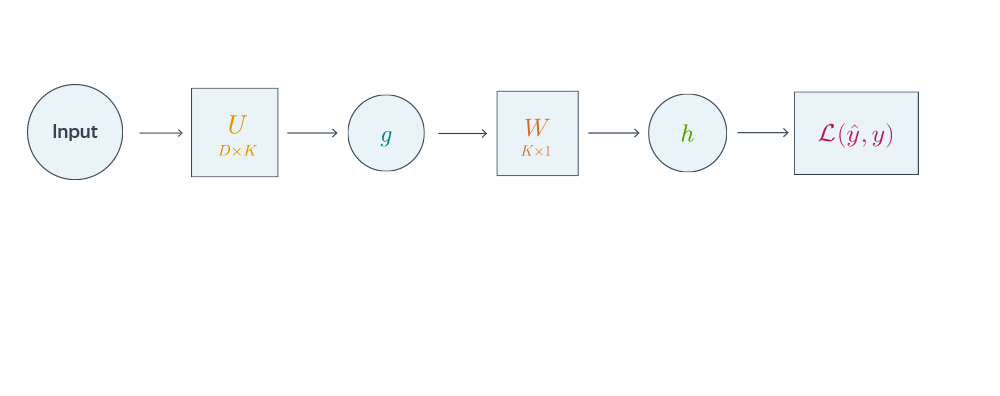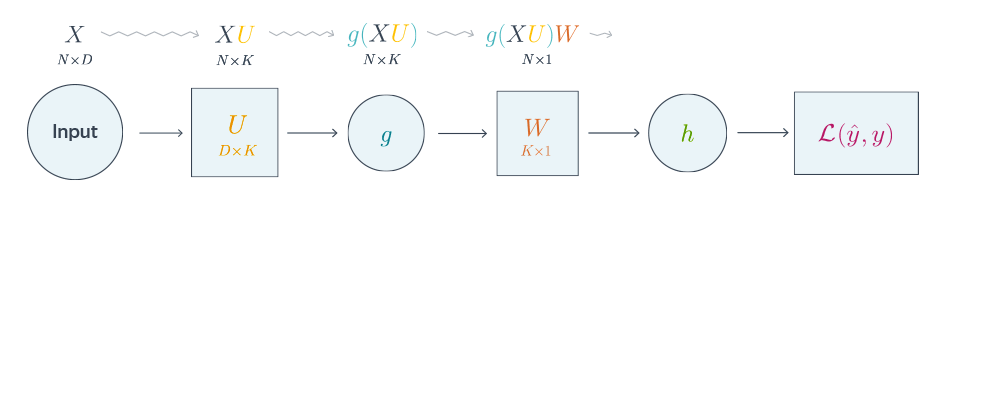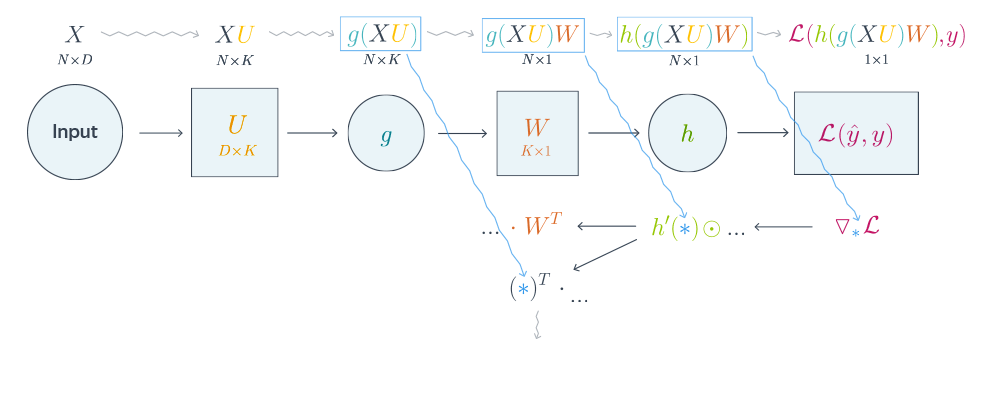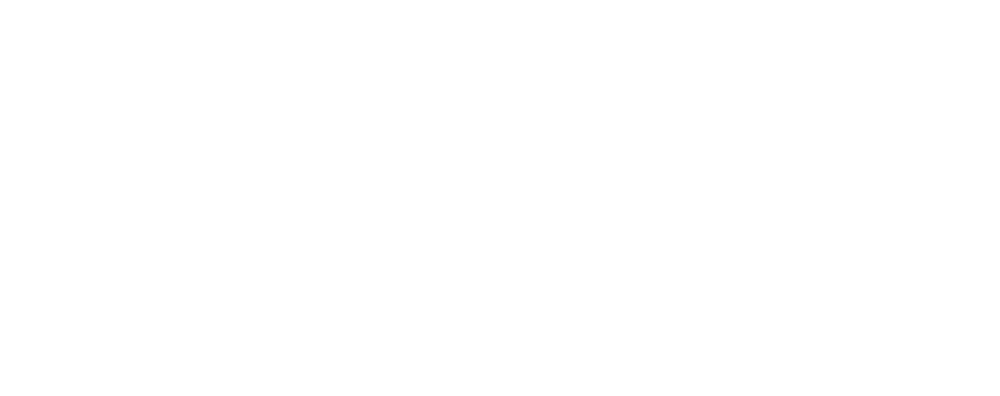




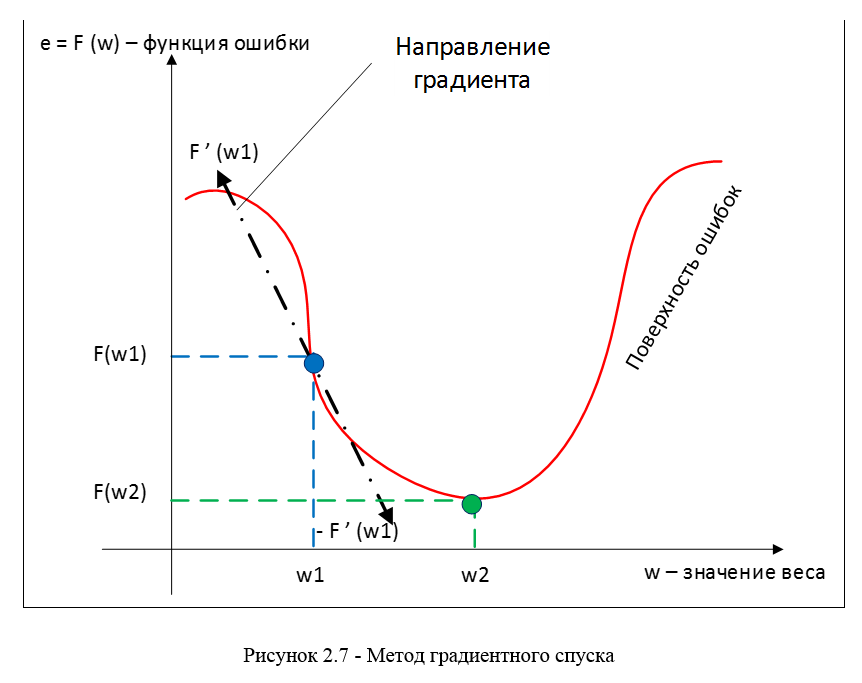



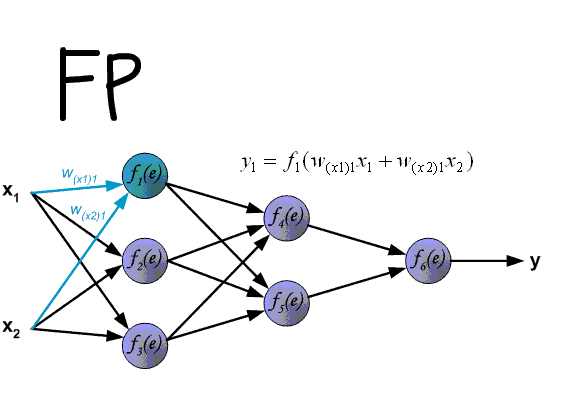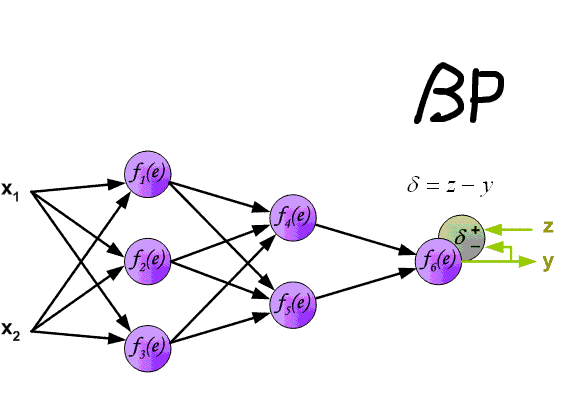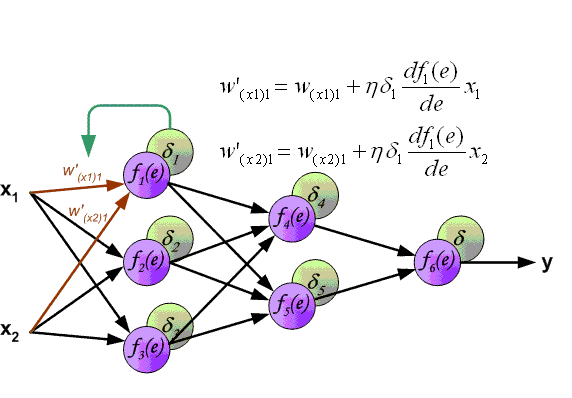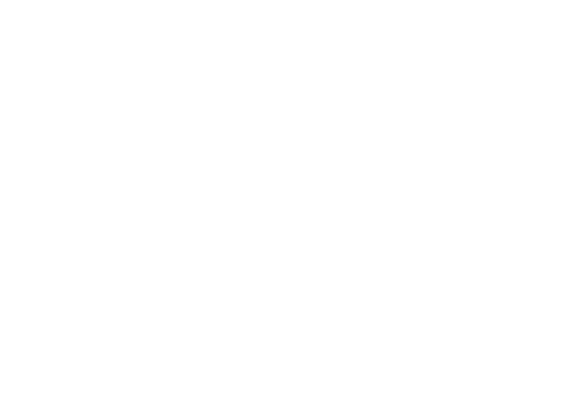
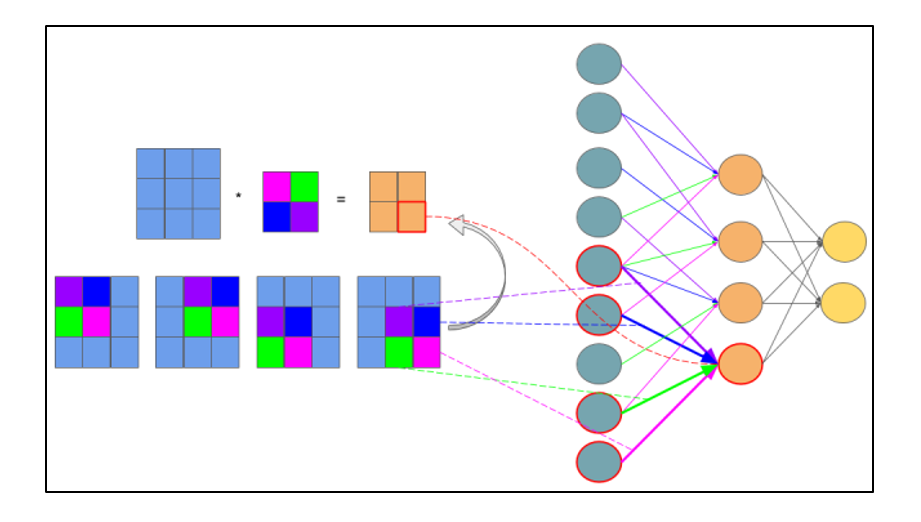


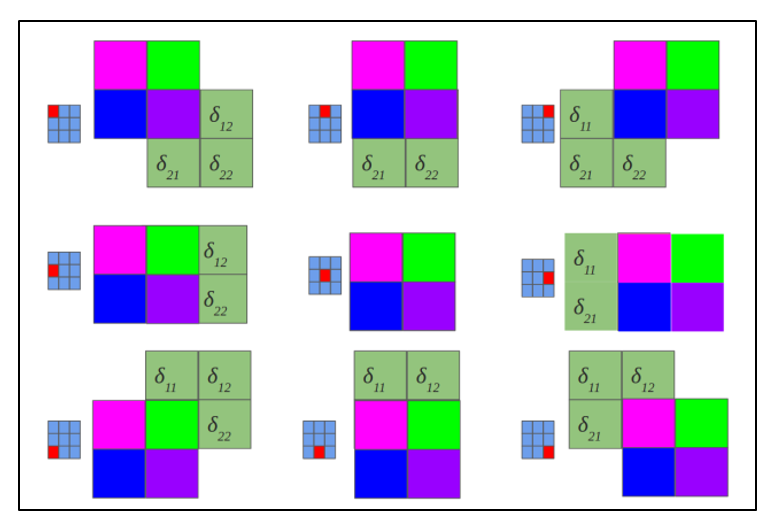
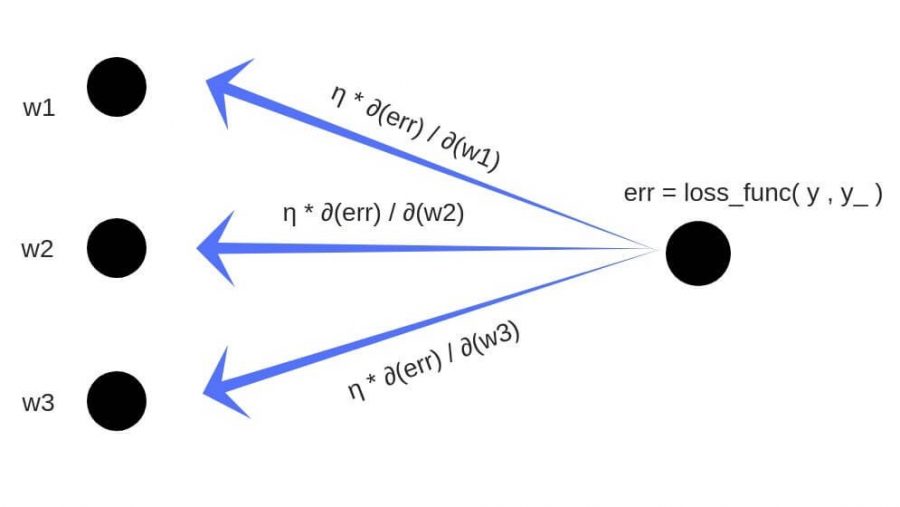
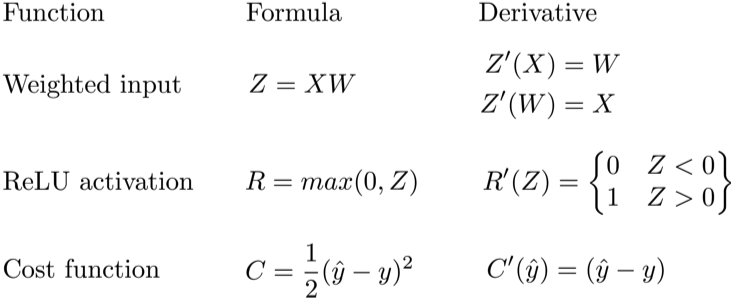
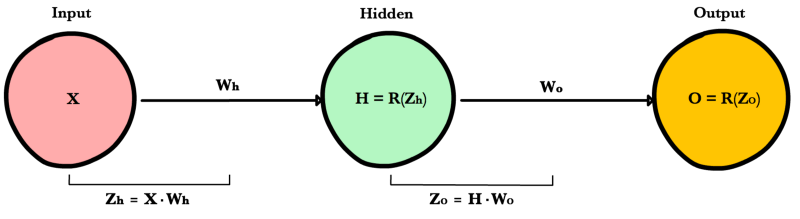
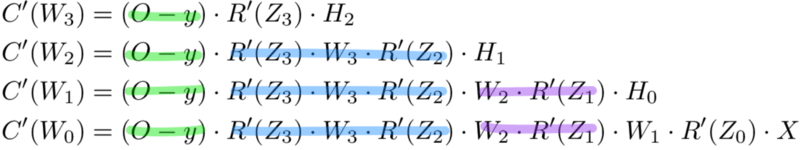
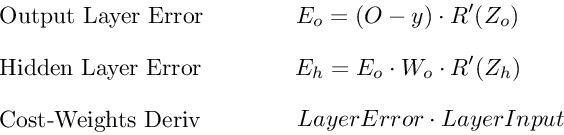
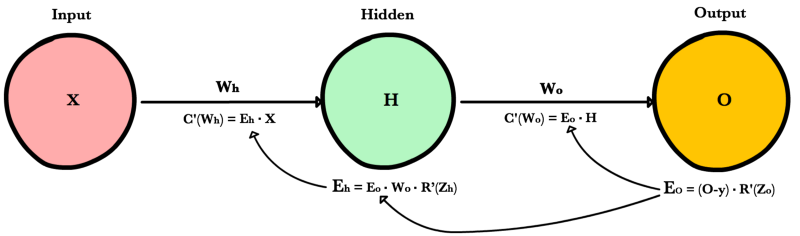
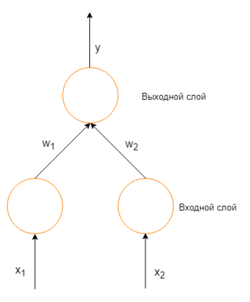
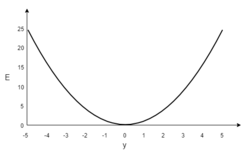
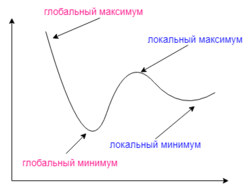
![{displaystyle x(t)=f[x(t)]+epsilon }](https://wikimedia.org/api/rest_v1/media/math/render/svg/c0c181d84db667811cae5651c5300b35991be4f6)
