| Error function | |
|---|---|

Plot of the error function |
|
| General information | |
| General definition |  |
| Fields of application | Probability, thermodynamics |
| Domain, Codomain and Image | |
| Domain |  |
| Image |  |
| Basic features | |
| Parity | Odd |
| Specific features | |
| Root | 0 |
| Derivative |  |
| Antiderivative |  |
| Series definition | |
| Taylor series |  |
In mathematics, the error function (also called the Gauss error function), often denoted by erf, is a complex function of a complex variable defined as:[1]
Some authors define 

This integral is a special (non-elementary) sigmoid function that occurs often in probability, statistics, and partial differential equations. In many of these applications, the function argument is a real number. If the function argument is real, then the function value is also real.
In statistics, for non-negative values of x, the error function has the following interpretation: for a random variable Y that is normally distributed with mean 0 and standard deviation 1/√2, erf x is the probability that Y falls in the range [−x, x].
Two closely related functions are the complementary error function (erfc) defined as
and the imaginary error function (erfi) defined as
where i is the imaginary unit.
Name[edit]
The name «error function» and its abbreviation erf were proposed by J. W. L. Glaisher in 1871 on account of its connection with «the theory of Probability, and notably the theory of Errors.»[3] The error function complement was also discussed by Glaisher in a separate publication in the same year.[4]
For the «law of facility» of errors whose density is given by
(the normal distribution), Glaisher calculates the probability of an error lying between p and q as:
Plot of the error function Erf(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D
Applications[edit]
When the results of a series of measurements are described by a normal distribution with standard deviation σ and expected value 0, then erf (a/σ √2) is the probability that the error of a single measurement lies between −a and +a, for positive a. This is useful, for example, in determining the bit error rate of a digital communication system.
The error and complementary error functions occur, for example, in solutions of the heat equation when boundary conditions are given by the Heaviside step function.
The error function and its approximations can be used to estimate results that hold with high probability or with low probability. Given a random variable X ~ Norm[μ,σ] (a normal distribution with mean μ and standard deviation σ) and a constant L < μ:
where A and B are certain numeric constants. If L is sufficiently far from the mean, specifically μ − L ≥ σ√ln k, then:
so the probability goes to 0 as k → ∞.
The probability for X being in the interval [La, Lb] can be derived as
Properties[edit]
Integrand exp(−z2)
erf z
The property erf (−z) = −erf z means that the error function is an odd function. This directly results from the fact that the integrand e−t2 is an even function (the antiderivative of an even function which is zero at the origin is an odd function and vice versa).
Since the error function is an entire function which takes real numbers to real numbers, for any complex number z:
where z is the complex conjugate of z.
The integrand f = exp(−z2) and f = erf z are shown in the complex z-plane in the figures at right with domain coloring.
The error function at +∞ is exactly 1 (see Gaussian integral). At the real axis, erf z approaches unity at z → +∞ and −1 at z → −∞. At the imaginary axis, it tends to ±i∞.
Taylor series[edit]
The error function is an entire function; it has no singularities (except that at infinity) and its Taylor expansion always converges, but is famously known «[…] for its bad convergence if x > 1.»[5]
The defining integral cannot be evaluated in closed form in terms of elementary functions (see Liouville’s theorem), but by expanding the integrand e−z2 into its Maclaurin series and integrating term by term, one obtains the error function’s Maclaurin series as:
which holds for every complex number z. The denominator terms are sequence A007680 in the OEIS.
For iterative calculation of the above series, the following alternative formulation may be useful:
because −(2k − 1)z2/k(2k + 1) expresses the multiplier to turn the kth term into the (k + 1)th term (considering z as the first term).
The imaginary error function has a very similar Maclaurin series, which is:
which holds for every complex number z.
Derivative and integral[edit]
The derivative of the error function follows immediately from its definition:
From this, the derivative of the imaginary error function is also immediate:
An antiderivative of the error function, obtainable by integration by parts, is
An antiderivative of the imaginary error function, also obtainable by integration by parts, is
Higher order derivatives are given by
where H are the physicists’ Hermite polynomials.[6]
Bürmann series[edit]
An expansion,[7] which converges more rapidly for all real values of x than a Taylor expansion, is obtained by using Hans Heinrich Bürmann’s theorem:[8]
where sgn is the sign function. By keeping only the first two coefficients and choosing c1 = 31/200 and c2 = −341/8000, the resulting approximation shows its largest relative error at x = ±1.3796, where it is less than 0.0036127:
Inverse functions[edit]
Given a complex number z, there is not a unique complex number w satisfying erf w = z, so a true inverse function would be multivalued. However, for −1 < x < 1, there is a unique real number denoted erf−1 x satisfying
The inverse error function is usually defined with domain (−1,1), and it is restricted to this domain in many computer algebra systems. However, it can be extended to the disk |z| < 1 of the complex plane, using the Maclaurin series[9]
where c0 = 1 and
So we have the series expansion (common factors have been canceled from numerators and denominators):
(After cancellation the numerator/denominator fractions are entries OEIS: A092676/OEIS: A092677 in the OEIS; without cancellation the numerator terms are given in entry OEIS: A002067.) The error function’s value at ±∞ is equal to ±1.
For |z| < 1, we have erf(erf−1 z) = z.
The inverse complementary error function is defined as
For real x, there is a unique real number erfi−1 x satisfying erfi(erfi−1 x) = x. The inverse imaginary error function is defined as erfi−1 x.[10]
For any real x, Newton’s method can be used to compute erfi−1 x, and for −1 ≤ x ≤ 1, the following Maclaurin series converges:
where ck is defined as above.
Asymptotic expansion[edit]
A useful asymptotic expansion of the complementary error function (and therefore also of the error function) for large real x is
where (2n − 1)!! is the double factorial of (2n − 1), which is the product of all odd numbers up to (2n − 1). This series diverges for every finite x, and its meaning as asymptotic expansion is that for any integer N ≥ 1 one has
where the remainder is
which follows easily by induction, writing
and integrating by parts.
The asymptotic behavior of the remainder term, in Landau notation, is
as x → ∞. This can be found by
For large enough values of x, only the first few terms of this asymptotic expansion are needed to obtain a good approximation of erfc x (while for not too large values of x, the above Taylor expansion at 0 provides a very fast convergence).
Continued fraction expansion[edit]
A continued fraction expansion of the complementary error function is:[11]
Integral of error function with Gaussian density function[edit]
which appears related to Ng and Geller, formula 13 in section 4.3[12] with a change of variables.
Factorial series[edit]
The inverse factorial series:
converges for Re(z2) > 0. Here
zn denotes the rising factorial, and s(n,k) denotes a signed Stirling number of the first kind.[13][14]
There also exists a representation by an infinite sum containing the double factorial:
Numerical approximations[edit]
Approximation with elementary functions[edit]
- Abramowitz and Stegun give several approximations of varying accuracy (equations 7.1.25–28). This allows one to choose the fastest approximation suitable for a given application. In order of increasing accuracy, they are:
(maximum error: 5×10−4)
where a1 = 0.278393, a2 = 0.230389, a3 = 0.000972, a4 = 0.078108
(maximum error: 2.5×10−5)
where p = 0.47047, a1 = 0.3480242, a2 = −0.0958798, a3 = 0.7478556
(maximum error: 3×10−7)
where a1 = 0.0705230784, a2 = 0.0422820123, a3 = 0.0092705272, a4 = 0.0001520143, a5 = 0.0002765672, a6 = 0.0000430638
(maximum error: 1.5×10−7)
where p = 0.3275911, a1 = 0.254829592, a2 = −0.284496736, a3 = 1.421413741, a4 = −1.453152027, a5 = 1.061405429
All of these approximations are valid for x ≥ 0. To use these approximations for negative x, use the fact that erf x is an odd function, so erf x = −erf(−x).
- Exponential bounds and a pure exponential approximation for the complementary error function are given by[15]
- The above have been generalized to sums of N exponentials[16] with increasing accuracy in terms of N so that erfc x can be accurately approximated or bounded by 2Q̃(√2x), where
In particular, there is a systematic methodology to solve the numerical coefficients {(an,bn)}N
n = 1 that yield a minimax approximation or bound for the closely related Q-function: Q(x) ≈ Q̃(x), Q(x) ≤ Q̃(x), or Q(x) ≥ Q̃(x) for x ≥ 0. The coefficients {(an,bn)}N
n = 1 for many variations of the exponential approximations and bounds up to N = 25 have been released to open access as a comprehensive dataset.[17] - A tight approximation of the complementary error function for x ∈ [0,∞) is given by Karagiannidis & Lioumpas (2007)[18] who showed for the appropriate choice of parameters {A,B} that
They determined {A,B} = {1.98,1.135}, which gave a good approximation for all x ≥ 0. Alternative coefficients are also available for tailoring accuracy for a specific application or transforming the expression into a tight bound.[19]
- A single-term lower bound is[20]
where the parameter β can be picked to minimize error on the desired interval of approximation.
-
- Another approximation is given by Sergei Winitzki using his «global Padé approximations»:[21][22]: 2–3
where
This is designed to be very accurate in a neighborhood of 0 and a neighborhood of infinity, and the relative error is less than 0.00035 for all real x. Using the alternate value a ≈ 0.147 reduces the maximum relative error to about 0.00013.[23]
This approximation can be inverted to obtain an approximation for the inverse error function:
- An approximation with a maximal error of 1.2×10−7 for any real argument is:[24]
with
and
Table of values[edit]
| x | erf x | 1 − erf x |
|---|---|---|
| 0 | 0 | 1 |
| 0.02 | 0.022564575 | 0.977435425 |
| 0.04 | 0.045111106 | 0.954888894 |
| 0.06 | 0.067621594 | 0.932378406 |
| 0.08 | 0.090078126 | 0.909921874 |
| 0.1 | 0.112462916 | 0.887537084 |
| 0.2 | 0.222702589 | 0.777297411 |
| 0.3 | 0.328626759 | 0.671373241 |
| 0.4 | 0.428392355 | 0.571607645 |
| 0.5 | 0.520499878 | 0.479500122 |
| 0.6 | 0.603856091 | 0.396143909 |
| 0.7 | 0.677801194 | 0.322198806 |
| 0.8 | 0.742100965 | 0.257899035 |
| 0.9 | 0.796908212 | 0.203091788 |
| 1 | 0.842700793 | 0.157299207 |
| 1.1 | 0.880205070 | 0.119794930 |
| 1.2 | 0.910313978 | 0.089686022 |
| 1.3 | 0.934007945 | 0.065992055 |
| 1.4 | 0.952285120 | 0.047714880 |
| 1.5 | 0.966105146 | 0.033894854 |
| 1.6 | 0.976348383 | 0.023651617 |
| 1.7 | 0.983790459 | 0.016209541 |
| 1.8 | 0.989090502 | 0.010909498 |
| 1.9 | 0.992790429 | 0.007209571 |
| 2 | 0.995322265 | 0.004677735 |
| 2.1 | 0.997020533 | 0.002979467 |
| 2.2 | 0.998137154 | 0.001862846 |
| 2.3 | 0.998856823 | 0.001143177 |
| 2.4 | 0.999311486 | 0.000688514 |
| 2.5 | 0.999593048 | 0.000406952 |
| 3 | 0.999977910 | 0.000022090 |
| 3.5 | 0.999999257 | 0.000000743 |
[edit]
Complementary error function[edit]
The complementary error function, denoted erfc, is defined as
-
Plot of the complementary error function Erfc(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D
which also defines erfcx, the scaled complementary error function[25] (which can be used instead of erfc to avoid arithmetic underflow[25][26]). Another form of erfc x for x ≥ 0 is known as Craig’s formula, after its discoverer:[27]
This expression is valid only for positive values of x, but it can be used in conjunction with erfc x = 2 − erfc(−x) to obtain erfc(x) for negative values. This form is advantageous in that the range of integration is fixed and finite. An extension of this expression for the erfc of the sum of two non-negative variables is as follows:[28]
Imaginary error function[edit]
The imaginary error function, denoted erfi, is defined as
Plot of the imaginary error function Erfi(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D
where D(x) is the Dawson function (which can be used instead of erfi to avoid arithmetic overflow[25]).
Despite the name «imaginary error function», erfi x is real when x is real.
When the error function is evaluated for arbitrary complex arguments z, the resulting complex error function is usually discussed in scaled form as the Faddeeva function:
Cumulative distribution function[edit]
The error function is essentially identical to the standard normal cumulative distribution function, denoted Φ, also named norm(x) by some software languages[citation needed], as they differ only by scaling and translation. Indeed,
-
the normal cumulative distribution function plotted in the complex plane
or rearranged for erf and erfc:
Consequently, the error function is also closely related to the Q-function, which is the tail probability of the standard normal distribution. The Q-function can be expressed in terms of the error function as
The inverse of Φ is known as the normal quantile function, or probit function and may be expressed in terms of the inverse error function as
The standard normal cdf is used more often in probability and statistics, and the error function is used more often in other branches of mathematics.
The error function is a special case of the Mittag-Leffler function, and can also be expressed as a confluent hypergeometric function (Kummer’s function):
It has a simple expression in terms of the Fresnel integral.[further explanation needed]
In terms of the regularized gamma function P and the incomplete gamma function,
sgn x is the sign function.
Generalized error functions[edit]
Graph of generalised error functions En(x):
grey curve: E1(x) = 1 − e−x/√π
red curve: E2(x) = erf(x)
green curve: E3(x)
blue curve: E4(x)
gold curve: E5(x).
Some authors discuss the more general functions:[citation needed]
Notable cases are:
- E0(x) is a straight line through the origin: E0(x) = x/e√π
- E2(x) is the error function, erf x.
After division by n!, all the En for odd n look similar (but not identical) to each other. Similarly, the En for even n look similar (but not identical) to each other after a simple division by n!. All generalised error functions for n > 0 look similar on the positive x side of the graph.
These generalised functions can equivalently be expressed for x > 0 using the gamma function and incomplete gamma function:
Therefore, we can define the error function in terms of the incomplete gamma function:
Iterated integrals of the complementary error function[edit]
The iterated integrals of the complementary error function are defined by[29]
The general recurrence formula is
They have the power series
from which follow the symmetry properties
and
Implementations[edit]
As real function of a real argument[edit]
- In POSIX-compliant operating systems, the header
math.hshall declare and the mathematical librarylibmshall provide the functionserfanderfc(double precision) as well as their single precision and extended precision counterpartserff,erflanderfcf,erfcl.[30]
- The GNU Scientific Library provides
erf,erfc,log(erf), and scaled error functions.[31]
As complex function of a complex argument[edit]
libcerf, numeric C library for complex error functions, provides the complex functionscerf,cerfc,cerfcxand the real functionserfi,erfcxwith approximately 13–14 digits precision, based on the Faddeeva function as implemented in the MIT Faddeeva Package
See also[edit]
[edit]
- Gaussian integral, over the whole real line
- Gaussian function, derivative
- Dawson function, renormalized imaginary error function
- Goodwin–Staton integral
In probability[edit]
- Normal distribution
- Normal cumulative distribution function, a scaled and shifted form of error function
- Probit, the inverse or quantile function of the normal CDF
- Q-function, the tail probability of the normal distribution
- Standard score
References[edit]
- ^ Andrews, Larry C. (1998). Special functions of mathematics for engineers. SPIE Press. p. 110. ISBN 9780819426161.
- ^ Whittaker, E. T.; Watson, G. N. (1927). A Course of Modern Analysis. Cambridge University Press. p. 341. ISBN 978-0-521-58807-2.
- ^ Glaisher, James Whitbread Lee (July 1871). «On a class of definite integrals». London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 4. 42 (277): 294–302. doi:10.1080/14786447108640568. Retrieved 6 December 2017.
- ^ Glaisher, James Whitbread Lee (September 1871). «On a class of definite integrals. Part II». London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 4. 42 (279): 421–436. doi:10.1080/14786447108640600. Retrieved 6 December 2017.
- ^ «A007680 – OEIS». oeis.org. Retrieved 2 April 2020.
- ^ Weisstein, Eric W. «Erf». MathWorld.
- ^ Schöpf, H. M.; Supancic, P. H. (2014). «On Bürmann’s Theorem and Its Application to Problems of Linear and Nonlinear Heat Transfer and Diffusion». The Mathematica Journal. 16. doi:10.3888/tmj.16-11.
- ^ Weisstein, Eric W. «Bürmann’s Theorem». MathWorld.
- ^ Dominici, Diego (2006). «Asymptotic analysis of the derivatives of the inverse error function». arXiv:math/0607230.
- ^ Bergsma, Wicher (2006). «On a new correlation coefficient, its orthogonal decomposition and associated tests of independence». arXiv:math/0604627.
- ^ Cuyt, Annie A. M.; Petersen, Vigdis B.; Verdonk, Brigitte; Waadeland, Haakon; Jones, William B. (2008). Handbook of Continued Fractions for Special Functions. Springer-Verlag. ISBN 978-1-4020-6948-2.
- ^ Ng, Edward W.; Geller, Murray (January 1969). «A table of integrals of the Error functions». Journal of Research of the National Bureau of Standards Section B. 73B (1): 1. doi:10.6028/jres.073B.001.
- ^ Schlömilch, Oskar Xavier (1859). «Ueber facultätenreihen». Zeitschrift für Mathematik und Physik (in German). 4: 390–415.
- ^ Nielson, Niels (1906). Handbuch der Theorie der Gammafunktion (in German). Leipzig: B. G. Teubner. p. 283 Eq. 3. Retrieved 4 December 2017.
- ^ Chiani, M.; Dardari, D.; Simon, M.K. (2003). «New Exponential Bounds and Approximations for the Computation of Error Probability in Fading Channels» (PDF). IEEE Transactions on Wireless Communications. 2 (4): 840–845. CiteSeerX 10.1.1.190.6761. doi:10.1109/TWC.2003.814350.
- ^ Tanash, I.M.; Riihonen, T. (2020). «Global minimax approximations and bounds for the Gaussian Q-function by sums of exponentials». IEEE Transactions on Communications. 68 (10): 6514–6524. arXiv:2007.06939. doi:10.1109/TCOMM.2020.3006902. S2CID 220514754.
- ^ Tanash, I.M.; Riihonen, T. (2020). «Coefficients for Global Minimax Approximations and Bounds for the Gaussian Q-Function by Sums of Exponentials [Data set]». Zenodo. doi:10.5281/zenodo.4112978.
- ^ Karagiannidis, G. K.; Lioumpas, A. S. (2007). «An improved approximation for the Gaussian Q-function» (PDF). IEEE Communications Letters. 11 (8): 644–646. doi:10.1109/LCOMM.2007.070470. S2CID 4043576.
- ^ Tanash, I.M.; Riihonen, T. (2021). «Improved coefficients for the Karagiannidis–Lioumpas approximations and bounds to the Gaussian Q-function». IEEE Communications Letters. 25 (5): 1468–1471. arXiv:2101.07631. doi:10.1109/LCOMM.2021.3052257. S2CID 231639206.
- ^ Chang, Seok-Ho; Cosman, Pamela C.; Milstein, Laurence B. (November 2011). «Chernoff-Type Bounds for the Gaussian Error Function». IEEE Transactions on Communications. 59 (11): 2939–2944. doi:10.1109/TCOMM.2011.072011.100049. S2CID 13636638.
- ^ Winitzki, Sergei (2003). «Uniform approximations for transcendental functions». Computational Science and Its Applications – ICCSA 2003. Lecture Notes in Computer Science. Vol. 2667. Springer, Berlin. pp. 780–789. doi:10.1007/3-540-44839-X_82. ISBN 978-3-540-40155-1.
- ^ Zeng, Caibin; Chen, Yang Cuan (2015). «Global Padé approximations of the generalized Mittag-Leffler function and its inverse». Fractional Calculus and Applied Analysis. 18 (6): 1492–1506. arXiv:1310.5592. doi:10.1515/fca-2015-0086. S2CID 118148950.
Indeed, Winitzki [32] provided the so-called global Padé approximation
- ^ Winitzki, Sergei (6 February 2008). «A handy approximation for the error function and its inverse».
- ^ Numerical Recipes in Fortran 77: The Art of Scientific Computing (ISBN 0-521-43064-X), 1992, page 214, Cambridge University Press.
- ^ a b c Cody, W. J. (March 1993), «Algorithm 715: SPECFUN—A portable FORTRAN package of special function routines and test drivers» (PDF), ACM Trans. Math. Softw., 19 (1): 22–32, CiteSeerX 10.1.1.643.4394, doi:10.1145/151271.151273, S2CID 5621105
- ^ Zaghloul, M. R. (1 March 2007), «On the calculation of the Voigt line profile: a single proper integral with a damped sine integrand», Monthly Notices of the Royal Astronomical Society, 375 (3): 1043–1048, Bibcode:2007MNRAS.375.1043Z, doi:10.1111/j.1365-2966.2006.11377.x
- ^ John W. Craig, A new, simple and exact result for calculating the probability of error for two-dimensional signal constellations Archived 3 April 2012 at the Wayback Machine, Proceedings of the 1991 IEEE Military Communication Conference, vol. 2, pp. 571–575.
- ^ Behnad, Aydin (2020). «A Novel Extension to Craig’s Q-Function Formula and Its Application in Dual-Branch EGC Performance Analysis». IEEE Transactions on Communications. 68 (7): 4117–4125. doi:10.1109/TCOMM.2020.2986209. S2CID 216500014.
- ^ Carslaw, H. S.; Jaeger, J. C. (1959), Conduction of Heat in Solids (2nd ed.), Oxford University Press, ISBN 978-0-19-853368-9, p 484
- ^ «math.h — mathematical declarations». opengroup.org. 2018. Retrieved 21 April 2023.
- ^ «Special Functions – GSL 2.7 documentation».
Further reading[edit]
- Abramowitz, Milton; Stegun, Irene Ann, eds. (1983) [June 1964]. «Chapter 7». Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Applied Mathematics Series. Vol. 55 (Ninth reprint with additional corrections of tenth original printing with corrections (December 1972); first ed.). Washington D.C.; New York: United States Department of Commerce, National Bureau of Standards; Dover Publications. p. 297. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253.
- Press, William H.; Teukolsky, Saul A.; Vetterling, William T.; Flannery, Brian P. (2007), «Section 6.2. Incomplete Gamma Function and Error Function», Numerical Recipes: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8
- Temme, Nico M. (2010), «Error Functions, Dawson’s and Fresnel Integrals», in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248
External links[edit]
- A Table of Integrals of the Error Functions
| Error function | |
|---|---|

Plot of the error function |
|
| General information | |
| General definition |  |
| Fields of application | Probability, thermodynamics |
| Domain, Codomain and Image | |
| Domain |  |
| Image |  |
| Basic features | |
| Parity | Odd |
| Specific features | |
| Root | 0 |
| Derivative |  |
| Antiderivative |  |
| Series definition | |
| Taylor series |  |
In mathematics, the error function (also called the Gauss error function), often denoted by erf, is a complex function of a complex variable defined as:[1]
This integral is a special (non-elementary) sigmoid function that occurs often in probability, statistics, and partial differential equations. In many of these applications, the function argument is a real number. If the function argument is real, then the function value is also real.
In statistics, for non-negative values of x, the error function has the following interpretation: for a random variable Y that is normally distributed with mean 0 and standard deviation 1/√2, erf x is the probability that Y falls in the range [−x, x].
Two closely related functions are the complementary error function (erfc) defined as
and the imaginary error function (erfi) defined as
where i is the imaginary unit
Name[edit]
The name «error function» and its abbreviation erf were proposed by J. W. L. Glaisher in 1871 on account of its connection with «the theory of Probability, and notably the theory of Errors.»[2] The error function complement was also discussed by Glaisher in a separate publication in the same year.[3]
For the «law of facility» of errors whose density is given by
(the normal distribution), Glaisher calculates the probability of an error lying between p and q as:
Plot of the error function Erf(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D
Applications[edit]
When the results of a series of measurements are described by a normal distribution with standard deviation σ and expected value 0, then erf (a/σ √2) is the probability that the error of a single measurement lies between −a and +a, for positive a. This is useful, for example, in determining the bit error rate of a digital communication system.
The error and complementary error functions occur, for example, in solutions of the heat equation when boundary conditions are given by the Heaviside step function.
The error function and its approximations can be used to estimate results that hold with high probability or with low probability. Given a random variable X ~ Norm[μ,σ] (a normal distribution with mean μ and standard deviation σ) and a constant L < μ:
where A and B are certain numeric constants. If L is sufficiently far from the mean, specifically μ − L ≥ σ√ln k, then:
so the probability goes to 0 as k → ∞.
The probability for X being in the interval [La, Lb] can be derived as
Properties[edit]
Integrand exp(−z2)
erf z
The property erf (−z) = −erf z means that the error function is an odd function. This directly results from the fact that the integrand e−t2 is an even function (the antiderivative of an even function which is zero at the origin is an odd function and vice versa).
Since the error function is an entire function which takes real numbers to real numbers, for any complex number z:
where z is the complex conjugate of z.
The integrand f = exp(−z2) and f = erf z are shown in the complex z-plane in the figures at right with domain coloring.
The error function at +∞ is exactly 1 (see Gaussian integral). At the real axis, erf z approaches unity at z → +∞ and −1 at z → −∞. At the imaginary axis, it tends to ±i∞.
Taylor series[edit]
The error function is an entire function; it has no singularities (except that at infinity) and its Taylor expansion always converges, but is famously known «[…] for its bad convergence if x > 1.»[4]
The defining integral cannot be evaluated in closed form in terms of elementary functions, but by expanding the integrand e−z2 into its Maclaurin series and integrating term by term, one obtains the error function’s Maclaurin series as:
which holds for every complex number z. The denominator terms are sequence A007680 in the OEIS.
For iterative calculation of the above series, the following alternative formulation may be useful:
because −(2k − 1)z2/k(2k + 1) expresses the multiplier to turn the kth term into the (k + 1)th term (considering z as the first term).
The imaginary error function has a very similar Maclaurin series, which is:
which holds for every complex number z.
Derivative and integral[edit]
The derivative of the error function follows immediately from its definition:
From this, the derivative of the imaginary error function is also immediate:
An antiderivative of the error function, obtainable by integration by parts, is
An antiderivative of the imaginary error function, also obtainable by integration by parts, is
Higher order derivatives are given by
where H are the physicists’ Hermite polynomials.[5]
Bürmann series[edit]
An expansion,[6] which converges more rapidly for all real values of x than a Taylor expansion, is obtained by using Hans Heinrich Bürmann’s theorem:[7]
where sgn is the sign function. By keeping only the first two coefficients and choosing c1 = 31/200 and c2 = −341/8000, the resulting approximation shows its largest relative error at x = ±1.3796, where it is less than 0.0036127:
Inverse functions[edit]
Given a complex number z, there is not a unique complex number w satisfying erf w = z, so a true inverse function would be multivalued. However, for −1 < x < 1, there is a unique real number denoted erf−1 x satisfying
The inverse error function is usually defined with domain (−1,1), and it is restricted to this domain in many computer algebra systems. However, it can be extended to the disk |z| < 1 of the complex plane, using the Maclaurin series
where c0 = 1 and
So we have the series expansion (common factors have been canceled from numerators and denominators):
(After cancellation the numerator/denominator fractions are entries OEIS: A092676/OEIS: A092677 in the OEIS; without cancellation the numerator terms are given in entry OEIS: A002067.) The error function’s value at ±∞ is equal to ±1.
For |z| < 1, we have erf(erf−1 z) = z.
The inverse complementary error function is defined as
For real x, there is a unique real number erfi−1 x satisfying erfi(erfi−1 x) = x. The inverse imaginary error function is defined as erfi−1 x.[8]
For any real x, Newton’s method can be used to compute erfi−1 x, and for −1 ≤ x ≤ 1, the following Maclaurin series converges:
where ck is defined as above.
Asymptotic expansion[edit]
A useful asymptotic expansion of the complementary error function (and therefore also of the error function) for large real x is
where (2n − 1)!! is the double factorial of (2n − 1), which is the product of all odd numbers up to (2n − 1). This series diverges for every finite x, and its meaning as asymptotic expansion is that for any integer N ≥ 1 one has
where the remainder, in Landau notation, is
as x → ∞.
Indeed, the exact value of the remainder is
which follows easily by induction, writing
and integrating by parts.
For large enough values of x, only the first few terms of this asymptotic expansion are needed to obtain a good approximation of erfc x (while for not too large values of x, the above Taylor expansion at 0 provides a very fast convergence).
Continued fraction expansion[edit]
A continued fraction expansion of the complementary error function is:[9]
Integral of error function with Gaussian density function[edit]
which appears related to Ng and Geller, formula 13 in section 4.3[10] with a change of variables.
Factorial series[edit]
The inverse factorial series:
converges for Re(z2) > 0. Here
zn denotes the rising factorial, and s(n,k) denotes a signed Stirling number of the first kind.[11][12]
There also exists a representation by an infinite sum containing the double factorial:
Numerical approximations[edit]
Approximation with elementary functions[edit]
- Abramowitz and Stegun give several approximations of varying accuracy (equations 7.1.25–28). This allows one to choose the fastest approximation suitable for a given application. In order of increasing accuracy, they are:
(maximum error: 5×10−4)
where a1 = 0.278393, a2 = 0.230389, a3 = 0.000972, a4 = 0.078108
(maximum error: 2.5×10−5)
where p = 0.47047, a1 = 0.3480242, a2 = −0.0958798, a3 = 0.7478556
(maximum error: 3×10−7)
where a1 = 0.0705230784, a2 = 0.0422820123, a3 = 0.0092705272, a4 = 0.0001520143, a5 = 0.0002765672, a6 = 0.0000430638
(maximum error: 1.5×10−7)
where p = 0.3275911, a1 = 0.254829592, a2 = −0.284496736, a3 = 1.421413741, a4 = −1.453152027, a5 = 1.061405429
All of these approximations are valid for x ≥ 0. To use these approximations for negative x, use the fact that erf x is an odd function, so erf x = −erf(−x).
- Exponential bounds and a pure exponential approximation for the complementary error function are given by[13]
- The above have been generalized to sums of N exponentials[14] with increasing accuracy in terms of N so that erfc x can be accurately approximated or bounded by 2Q̃(√2x), where
In particular, there is a systematic methodology to solve the numerical coefficients {(an,bn)}N
n = 1 that yield a minimax approximation or bound for the closely related Q-function: Q(x) ≈ Q̃(x), Q(x) ≤ Q̃(x), or Q(x) ≥ Q̃(x) for x ≥ 0. The coefficients {(an,bn)}N
n = 1 for many variations of the exponential approximations and bounds up to N = 25 have been released to open access as a comprehensive dataset.[15] - A tight approximation of the complementary error function for x ∈ [0,∞) is given by Karagiannidis & Lioumpas (2007)[16] who showed for the appropriate choice of parameters {A,B} that
They determined {A,B} = {1.98,1.135}, which gave a good approximation for all x ≥ 0. Alternative coefficients are also available for tailoring accuracy for a specific application or transforming the expression into a tight bound.[17]
- A single-term lower bound is[18]
where the parameter β can be picked to minimize error on the desired interval of approximation.
-
- Another approximation is given by Sergei Winitzki using his «global Padé approximations»:[19][20]: 2–3
where
This is designed to be very accurate in a neighborhood of 0 and a neighborhood of infinity, and the relative error is less than 0.00035 for all real x. Using the alternate value a ≈ 0.147 reduces the maximum relative error to about 0.00013.[21]
This approximation can be inverted to obtain an approximation for the inverse error function:
- An approximation with a maximal error of 1.2×10−7 for any real argument is:[22]
with
and
Table of values[edit]
| x | erf x | 1 − erf x |
|---|---|---|
| 0 | 0 | 1 |
| 0.02 | 0.022564575 | 0.977435425 |
| 0.04 | 0.045111106 | 0.954888894 |
| 0.06 | 0.067621594 | 0.932378406 |
| 0.08 | 0.090078126 | 0.909921874 |
| 0.1 | 0.112462916 | 0.887537084 |
| 0.2 | 0.222702589 | 0.777297411 |
| 0.3 | 0.328626759 | 0.671373241 |
| 0.4 | 0.428392355 | 0.571607645 |
| 0.5 | 0.520499878 | 0.479500122 |
| 0.6 | 0.603856091 | 0.396143909 |
| 0.7 | 0.677801194 | 0.322198806 |
| 0.8 | 0.742100965 | 0.257899035 |
| 0.9 | 0.796908212 | 0.203091788 |
| 1 | 0.842700793 | 0.157299207 |
| 1.1 | 0.880205070 | 0.119794930 |
| 1.2 | 0.910313978 | 0.089686022 |
| 1.3 | 0.934007945 | 0.065992055 |
| 1.4 | 0.952285120 | 0.047714880 |
| 1.5 | 0.966105146 | 0.033894854 |
| 1.6 | 0.976348383 | 0.023651617 |
| 1.7 | 0.983790459 | 0.016209541 |
| 1.8 | 0.989090502 | 0.010909498 |
| 1.9 | 0.992790429 | 0.007209571 |
| 2 | 0.995322265 | 0.004677735 |
| 2.1 | 0.997020533 | 0.002979467 |
| 2.2 | 0.998137154 | 0.001862846 |
| 2.3 | 0.998856823 | 0.001143177 |
| 2.4 | 0.999311486 | 0.000688514 |
| 2.5 | 0.999593048 | 0.000406952 |
| 3 | 0.999977910 | 0.000022090 |
| 3.5 | 0.999999257 | 0.000000743 |
[edit]
Complementary error function[edit]
The complementary error function, denoted erfc, is defined as
-
Plot of the complementary error function Erfc(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D
which also defines erfcx, the scaled complementary error function[23] (which can be used instead of erfc to avoid arithmetic underflow[23][24]). Another form of erfc x for x ≥ 0 is known as Craig’s formula, after its discoverer:[25]
This expression is valid only for positive values of x, but it can be used in conjunction with erfc x = 2 − erfc(−x) to obtain erfc(x) for negative values. This form is advantageous in that the range of integration is fixed and finite. An extension of this expression for the erfc of the sum of two non-negative variables is as follows:[26]
Imaginary error function[edit]
The imaginary error function, denoted erfi, is defined as
Plot of the imaginary error function Erfi(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D
where D(x) is the Dawson function (which can be used instead of erfi to avoid arithmetic overflow[23]).
Despite the name «imaginary error function», erfi x is real when x is real.
When the error function is evaluated for arbitrary complex arguments z, the resulting complex error function is usually discussed in scaled form as the Faddeeva function:
Cumulative distribution function[edit]
The error function is essentially identical to the standard normal cumulative distribution function, denoted Φ, also named norm(x) by some software languages[citation needed], as they differ only by scaling and translation. Indeed,
-
the normal cumulative distribution function plotted in the complex plane
or rearranged for erf and erfc:
Consequently, the error function is also closely related to the Q-function, which is the tail probability of the standard normal distribution. The Q-function can be expressed in terms of the error function as
The inverse of Φ is known as the normal quantile function, or probit function and may be expressed in terms of the inverse error function as
The standard normal cdf is used more often in probability and statistics, and the error function is used more often in other branches of mathematics.
The error function is a special case of the Mittag-Leffler function, and can also be expressed as a confluent hypergeometric function (Kummer’s function):
It has a simple expression in terms of the Fresnel integral.[further explanation needed]
In terms of the regularized gamma function P and the incomplete gamma function,
sgn x is the sign function.
Generalized error functions[edit]
Graph of generalised error functions En(x):
grey curve: E1(x) = 1 − e−x/√π
red curve: E2(x) = erf(x)
green curve: E3(x)
blue curve: E4(x)
gold curve: E5(x).
Some authors discuss the more general functions:[citation needed]
Notable cases are:
- E0(x) is a straight line through the origin: E0(x) = x/e√π
- E2(x) is the error function, erf x.
After division by n!, all the En for odd n look similar (but not identical) to each other. Similarly, the En for even n look similar (but not identical) to each other after a simple division by n!. All generalised error functions for n > 0 look similar on the positive x side of the graph.
These generalised functions can equivalently be expressed for x > 0 using the gamma function and incomplete gamma function:
Therefore, we can define the error function in terms of the incomplete gamma function:
Iterated integrals of the complementary error function[edit]
The iterated integrals of the complementary error function are defined by[27]
The general recurrence formula is
They have the power series
from which follow the symmetry properties
and
Implementations[edit]
As real function of a real argument[edit]
- In Posix-compliant operating systems, the header
math.hshall declare and the mathematical librarylibmshall provide the functionserfanderfc(double precision) as well as their single precision and extended precision counterpartserff,erflanderfcf,erfcl.[28] - The GNU Scientific Library provides
erf,erfc,log(erf), and scaled error functions.[29]
As complex function of a complex argument[edit]
libcerf, numeric C library for complex error functions, provides the complex functionscerf,cerfc,cerfcxand the real functionserfi,erfcxwith approximately 13–14 digits precision, based on the Faddeeva function as implemented in the MIT Faddeeva Package
See also[edit]
[edit]
- Gaussian integral, over the whole real line
- Gaussian function, derivative
- Dawson function, renormalized imaginary error function
- Goodwin–Staton integral
In probability[edit]
- Normal distribution
- Normal cumulative distribution function, a scaled and shifted form of error function
- Probit, the inverse or quantile function of the normal CDF
- Q-function, the tail probability of the normal distribution
References[edit]
- ^ Andrews, Larry C. (1998). Special functions of mathematics for engineers. SPIE Press. p. 110. ISBN 9780819426161.
- ^ Glaisher, James Whitbread Lee (July 1871). «On a class of definite integrals». London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 4. 42 (277): 294–302. doi:10.1080/14786447108640568. Retrieved 6 December 2017.
- ^ Glaisher, James Whitbread Lee (September 1871). «On a class of definite integrals. Part II». London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 4. 42 (279): 421–436. doi:10.1080/14786447108640600. Retrieved 6 December 2017.
- ^ «A007680 – OEIS». oeis.org. Retrieved 2 April 2020.
- ^ Weisstein, Eric W. «Erf». MathWorld.
- ^ Schöpf, H. M.; Supancic, P. H. (2014). «On Bürmann’s Theorem and Its Application to Problems of Linear and Nonlinear Heat Transfer and Diffusion». The Mathematica Journal. 16. doi:10.3888/tmj.16-11.
- ^ Weisstein, Eric W. «Bürmann’s Theorem». MathWorld.
- ^ Bergsma, Wicher (2006). «On a new correlation coefficient, its orthogonal decomposition and associated tests of independence». arXiv:math/0604627.
- ^ Cuyt, Annie A. M.; Petersen, Vigdis B.; Verdonk, Brigitte; Waadeland, Haakon; Jones, William B. (2008). Handbook of Continued Fractions for Special Functions. Springer-Verlag. ISBN 978-1-4020-6948-2.
- ^ Ng, Edward W.; Geller, Murray (January 1969). «A table of integrals of the Error functions». Journal of Research of the National Bureau of Standards Section B. 73B (1): 1. doi:10.6028/jres.073B.001.
- ^ Schlömilch, Oskar Xavier (1859). «Ueber facultätenreihen». Zeitschrift für Mathematik und Physik (in German). 4: 390–415. Retrieved 4 December 2017.
- ^ Nielson, Niels (1906). Handbuch der Theorie der Gammafunktion (in German). Leipzig: B. G. Teubner. p. 283 Eq. 3. Retrieved 4 December 2017.
- ^ Chiani, M.; Dardari, D.; Simon, M.K. (2003). «New Exponential Bounds and Approximations for the Computation of Error Probability in Fading Channels» (PDF). IEEE Transactions on Wireless Communications. 2 (4): 840–845. CiteSeerX 10.1.1.190.6761. doi:10.1109/TWC.2003.814350.
- ^ Tanash, I.M.; Riihonen, T. (2020). «Global minimax approximations and bounds for the Gaussian Q-function by sums of exponentials». IEEE Transactions on Communications. 68 (10): 6514–6524. arXiv:2007.06939. doi:10.1109/TCOMM.2020.3006902. S2CID 220514754.
- ^ Tanash, I.M.; Riihonen, T. (2020). «Coefficients for Global Minimax Approximations and Bounds for the Gaussian Q-Function by Sums of Exponentials [Data set]». Zenodo. doi:10.5281/zenodo.4112978.
- ^ Karagiannidis, G. K.; Lioumpas, A. S. (2007). «An improved approximation for the Gaussian Q-function» (PDF). IEEE Communications Letters. 11 (8): 644–646. doi:10.1109/LCOMM.2007.070470. S2CID 4043576.
- ^ Tanash, I.M.; Riihonen, T. (2021). «Improved coefficients for the Karagiannidis–Lioumpas approximations and bounds to the Gaussian Q-function». IEEE Communications Letters. 25 (5): 1468–1471. arXiv:2101.07631. doi:10.1109/LCOMM.2021.3052257. S2CID 231639206.
- ^ Chang, Seok-Ho; Cosman, Pamela C.; Milstein, Laurence B. (November 2011). «Chernoff-Type Bounds for the Gaussian Error Function». IEEE Transactions on Communications. 59 (11): 2939–2944. doi:10.1109/TCOMM.2011.072011.100049. S2CID 13636638.
- ^ Winitzki, Sergei (2003). «Uniform approximations for transcendental functions». Computational Science and Its Applications – ICCSA 2003. Lecture Notes in Computer Science. Vol. 2667. Springer, Berlin. pp. 780–789. doi:10.1007/3-540-44839-X_82. ISBN 978-3-540-40155-1.
- ^ Zeng, Caibin; Chen, Yang Cuan (2015). «Global Padé approximations of the generalized Mittag-Leffler function and its inverse». Fractional Calculus and Applied Analysis. 18 (6): 1492–1506. arXiv:1310.5592. doi:10.1515/fca-2015-0086. S2CID 118148950.
Indeed, Winitzki [32] provided the so-called global Padé approximation
- ^ Winitzki, Sergei (6 February 2008). «A handy approximation for the error function and its inverse».
- ^ Numerical Recipes in Fortran 77: The Art of Scientific Computing (ISBN 0-521-43064-X), 1992, page 214, Cambridge University Press.
- ^ a b c Cody, W. J. (March 1993), «Algorithm 715: SPECFUN—A portable FORTRAN package of special function routines and test drivers» (PDF), ACM Trans. Math. Softw., 19 (1): 22–32, CiteSeerX 10.1.1.643.4394, doi:10.1145/151271.151273, S2CID 5621105
- ^ Zaghloul, M. R. (1 March 2007), «On the calculation of the Voigt line profile: a single proper integral with a damped sine integrand», Monthly Notices of the Royal Astronomical Society, 375 (3): 1043–1048, Bibcode:2007MNRAS.375.1043Z, doi:10.1111/j.1365-2966.2006.11377.x
- ^ John W. Craig, A new, simple and exact result for calculating the probability of error for two-dimensional signal constellations Archived 3 April 2012 at the Wayback Machine, Proceedings of the 1991 IEEE Military Communication Conference, vol. 2, pp. 571–575.
- ^ Behnad, Aydin (2020). «A Novel Extension to Craig’s Q-Function Formula and Its Application in Dual-Branch EGC Performance Analysis». IEEE Transactions on Communications. 68 (7): 4117–4125. doi:10.1109/TCOMM.2020.2986209. S2CID 216500014.
- ^ Carslaw, H. S.; Jaeger, J. C. (1959), Conduction of Heat in Solids (2nd ed.), Oxford University Press, ISBN 978-0-19-853368-9, p 484
- ^ https://pubs.opengroup.org/onlinepubs/9699919799/basedefs/math.h.html
- ^ «Special Functions – GSL 2.7 documentation».
Further reading[edit]
- Abramowitz, Milton; Stegun, Irene Ann, eds. (1983) [June 1964]. «Chapter 7». Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Applied Mathematics Series. Vol. 55 (Ninth reprint with additional corrections of tenth original printing with corrections (December 1972); first ed.). Washington D.C.; New York: United States Department of Commerce, National Bureau of Standards; Dover Publications. p. 297. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253.
- Press, William H.; Teukolsky, Saul A.; Vetterling, William T.; Flannery, Brian P. (2007), «Section 6.2. Incomplete Gamma Function and Error Function», Numerical Recipes: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8
- Temme, Nico M. (2010), «Error Functions, Dawson’s and Fresnel Integrals», in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248
External links[edit]
- A Table of Integrals of the Error Functions
| Error function | |
|---|---|

Plot of the error function |
|
| General information | |
| General definition |  |
| Fields of application | Probability, thermodynamics |
| Domain, Codomain and Image | |
| Domain |  |
| Image |  |
| Basic features | |
| Parity | Odd |
| Specific features | |
| Root | 0 |
| Derivative |  |
| Antiderivative |  |
| Series definition | |
| Taylor series |  |
In mathematics, the error function (also called the Gauss error function), often denoted by erf, is a complex function of a complex variable defined as:[1]
This integral is a special (non-elementary) sigmoid function that occurs often in probability, statistics, and partial differential equations. In many of these applications, the function argument is a real number. If the function argument is real, then the function value is also real.
In statistics, for non-negative values of x, the error function has the following interpretation: for a random variable Y that is normally distributed with mean 0 and standard deviation 1/√2, erf x is the probability that Y falls in the range [−x, x].
Two closely related functions are the complementary error function (erfc) defined as
and the imaginary error function (erfi) defined as
where i is the imaginary unit
Name[edit]
The name «error function» and its abbreviation erf were proposed by J. W. L. Glaisher in 1871 on account of its connection with «the theory of Probability, and notably the theory of Errors.»[2] The error function complement was also discussed by Glaisher in a separate publication in the same year.[3]
For the «law of facility» of errors whose density is given by
(the normal distribution), Glaisher calculates the probability of an error lying between p and q as:
Plot of the error function Erf(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D
Applications[edit]
When the results of a series of measurements are described by a normal distribution with standard deviation σ and expected value 0, then erf (a/σ √2) is the probability that the error of a single measurement lies between −a and +a, for positive a. This is useful, for example, in determining the bit error rate of a digital communication system.
The error and complementary error functions occur, for example, in solutions of the heat equation when boundary conditions are given by the Heaviside step function.
The error function and its approximations can be used to estimate results that hold with high probability or with low probability. Given a random variable X ~ Norm[μ,σ] (a normal distribution with mean μ and standard deviation σ) and a constant L < μ:
where A and B are certain numeric constants. If L is sufficiently far from the mean, specifically μ − L ≥ σ√ln k, then:
so the probability goes to 0 as k → ∞.
The probability for X being in the interval [La, Lb] can be derived as
Properties[edit]
Integrand exp(−z2)
erf z
The property erf (−z) = −erf z means that the error function is an odd function. This directly results from the fact that the integrand e−t2 is an even function (the antiderivative of an even function which is zero at the origin is an odd function and vice versa).
Since the error function is an entire function which takes real numbers to real numbers, for any complex number z:
where z is the complex conjugate of z.
The integrand f = exp(−z2) and f = erf z are shown in the complex z-plane in the figures at right with domain coloring.
The error function at +∞ is exactly 1 (see Gaussian integral). At the real axis, erf z approaches unity at z → +∞ and −1 at z → −∞. At the imaginary axis, it tends to ±i∞.
Taylor series[edit]
The error function is an entire function; it has no singularities (except that at infinity) and its Taylor expansion always converges, but is famously known «[…] for its bad convergence if x > 1.»[4]
The defining integral cannot be evaluated in closed form in terms of elementary functions, but by expanding the integrand e−z2 into its Maclaurin series and integrating term by term, one obtains the error function’s Maclaurin series as:
which holds for every complex number z. The denominator terms are sequence A007680 in the OEIS.
For iterative calculation of the above series, the following alternative formulation may be useful:
because −(2k − 1)z2/k(2k + 1) expresses the multiplier to turn the kth term into the (k + 1)th term (considering z as the first term).
The imaginary error function has a very similar Maclaurin series, which is:
which holds for every complex number z.
Derivative and integral[edit]
The derivative of the error function follows immediately from its definition:
From this, the derivative of the imaginary error function is also immediate:
An antiderivative of the error function, obtainable by integration by parts, is
An antiderivative of the imaginary error function, also obtainable by integration by parts, is
Higher order derivatives are given by
where H are the physicists’ Hermite polynomials.[5]
Bürmann series[edit]
An expansion,[6] which converges more rapidly for all real values of x than a Taylor expansion, is obtained by using Hans Heinrich Bürmann’s theorem:[7]
where sgn is the sign function. By keeping only the first two coefficients and choosing c1 = 31/200 and c2 = −341/8000, the resulting approximation shows its largest relative error at x = ±1.3796, where it is less than 0.0036127:
Inverse functions[edit]
Given a complex number z, there is not a unique complex number w satisfying erf w = z, so a true inverse function would be multivalued. However, for −1 < x < 1, there is a unique real number denoted erf−1 x satisfying
The inverse error function is usually defined with domain (−1,1), and it is restricted to this domain in many computer algebra systems. However, it can be extended to the disk |z| < 1 of the complex plane, using the Maclaurin series
where c0 = 1 and
So we have the series expansion (common factors have been canceled from numerators and denominators):
(After cancellation the numerator/denominator fractions are entries OEIS: A092676/OEIS: A092677 in the OEIS; without cancellation the numerator terms are given in entry OEIS: A002067.) The error function’s value at ±∞ is equal to ±1.
For |z| < 1, we have erf(erf−1 z) = z.
The inverse complementary error function is defined as
For real x, there is a unique real number erfi−1 x satisfying erfi(erfi−1 x) = x. The inverse imaginary error function is defined as erfi−1 x.[8]
For any real x, Newton’s method can be used to compute erfi−1 x, and for −1 ≤ x ≤ 1, the following Maclaurin series converges:
where ck is defined as above.
Asymptotic expansion[edit]
A useful asymptotic expansion of the complementary error function (and therefore also of the error function) for large real x is
where (2n − 1)!! is the double factorial of (2n − 1), which is the product of all odd numbers up to (2n − 1). This series diverges for every finite x, and its meaning as asymptotic expansion is that for any integer N ≥ 1 one has
where the remainder, in Landau notation, is
as x → ∞.
Indeed, the exact value of the remainder is
which follows easily by induction, writing
and integrating by parts.
For large enough values of x, only the first few terms of this asymptotic expansion are needed to obtain a good approximation of erfc x (while for not too large values of x, the above Taylor expansion at 0 provides a very fast convergence).
Continued fraction expansion[edit]
A continued fraction expansion of the complementary error function is:[9]
Integral of error function with Gaussian density function[edit]
which appears related to Ng and Geller, formula 13 in section 4.3[10] with a change of variables.
Factorial series[edit]
The inverse factorial series:
converges for Re(z2) > 0. Here
zn denotes the rising factorial, and s(n,k) denotes a signed Stirling number of the first kind.[11][12]
There also exists a representation by an infinite sum containing the double factorial:
Numerical approximations[edit]
Approximation with elementary functions[edit]
- Abramowitz and Stegun give several approximations of varying accuracy (equations 7.1.25–28). This allows one to choose the fastest approximation suitable for a given application. In order of increasing accuracy, they are:
(maximum error: 5×10−4)
where a1 = 0.278393, a2 = 0.230389, a3 = 0.000972, a4 = 0.078108
(maximum error: 2.5×10−5)
where p = 0.47047, a1 = 0.3480242, a2 = −0.0958798, a3 = 0.7478556
(maximum error: 3×10−7)
where a1 = 0.0705230784, a2 = 0.0422820123, a3 = 0.0092705272, a4 = 0.0001520143, a5 = 0.0002765672, a6 = 0.0000430638
(maximum error: 1.5×10−7)
where p = 0.3275911, a1 = 0.254829592, a2 = −0.284496736, a3 = 1.421413741, a4 = −1.453152027, a5 = 1.061405429
All of these approximations are valid for x ≥ 0. To use these approximations for negative x, use the fact that erf x is an odd function, so erf x = −erf(−x).
- Exponential bounds and a pure exponential approximation for the complementary error function are given by[13]
- The above have been generalized to sums of N exponentials[14] with increasing accuracy in terms of N so that erfc x can be accurately approximated or bounded by 2Q̃(√2x), where
In particular, there is a systematic methodology to solve the numerical coefficients {(an,bn)}N
n = 1 that yield a minimax approximation or bound for the closely related Q-function: Q(x) ≈ Q̃(x), Q(x) ≤ Q̃(x), or Q(x) ≥ Q̃(x) for x ≥ 0. The coefficients {(an,bn)}N
n = 1 for many variations of the exponential approximations and bounds up to N = 25 have been released to open access as a comprehensive dataset.[15] - A tight approximation of the complementary error function for x ∈ [0,∞) is given by Karagiannidis & Lioumpas (2007)[16] who showed for the appropriate choice of parameters {A,B} that
They determined {A,B} = {1.98,1.135}, which gave a good approximation for all x ≥ 0. Alternative coefficients are also available for tailoring accuracy for a specific application or transforming the expression into a tight bound.[17]
- A single-term lower bound is[18]
where the parameter β can be picked to minimize error on the desired interval of approximation.
-
- Another approximation is given by Sergei Winitzki using his «global Padé approximations»:[19][20]: 2–3
where
This is designed to be very accurate in a neighborhood of 0 and a neighborhood of infinity, and the relative error is less than 0.00035 for all real x. Using the alternate value a ≈ 0.147 reduces the maximum relative error to about 0.00013.[21]
This approximation can be inverted to obtain an approximation for the inverse error function:
- An approximation with a maximal error of 1.2×10−7 for any real argument is:[22]
with
and
Table of values[edit]
| x | erf x | 1 − erf x |
|---|---|---|
| 0 | 0 | 1 |
| 0.02 | 0.022564575 | 0.977435425 |
| 0.04 | 0.045111106 | 0.954888894 |
| 0.06 | 0.067621594 | 0.932378406 |
| 0.08 | 0.090078126 | 0.909921874 |
| 0.1 | 0.112462916 | 0.887537084 |
| 0.2 | 0.222702589 | 0.777297411 |
| 0.3 | 0.328626759 | 0.671373241 |
| 0.4 | 0.428392355 | 0.571607645 |
| 0.5 | 0.520499878 | 0.479500122 |
| 0.6 | 0.603856091 | 0.396143909 |
| 0.7 | 0.677801194 | 0.322198806 |
| 0.8 | 0.742100965 | 0.257899035 |
| 0.9 | 0.796908212 | 0.203091788 |
| 1 | 0.842700793 | 0.157299207 |
| 1.1 | 0.880205070 | 0.119794930 |
| 1.2 | 0.910313978 | 0.089686022 |
| 1.3 | 0.934007945 | 0.065992055 |
| 1.4 | 0.952285120 | 0.047714880 |
| 1.5 | 0.966105146 | 0.033894854 |
| 1.6 | 0.976348383 | 0.023651617 |
| 1.7 | 0.983790459 | 0.016209541 |
| 1.8 | 0.989090502 | 0.010909498 |
| 1.9 | 0.992790429 | 0.007209571 |
| 2 | 0.995322265 | 0.004677735 |
| 2.1 | 0.997020533 | 0.002979467 |
| 2.2 | 0.998137154 | 0.001862846 |
| 2.3 | 0.998856823 | 0.001143177 |
| 2.4 | 0.999311486 | 0.000688514 |
| 2.5 | 0.999593048 | 0.000406952 |
| 3 | 0.999977910 | 0.000022090 |
| 3.5 | 0.999999257 | 0.000000743 |
[edit]
Complementary error function[edit]
The complementary error function, denoted erfc, is defined as
-
Plot of the complementary error function Erfc(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D
which also defines erfcx, the scaled complementary error function[23] (which can be used instead of erfc to avoid arithmetic underflow[23][24]). Another form of erfc x for x ≥ 0 is known as Craig’s formula, after its discoverer:[25]
This expression is valid only for positive values of x, but it can be used in conjunction with erfc x = 2 − erfc(−x) to obtain erfc(x) for negative values. This form is advantageous in that the range of integration is fixed and finite. An extension of this expression for the erfc of the sum of two non-negative variables is as follows:[26]
Imaginary error function[edit]
The imaginary error function, denoted erfi, is defined as
Plot of the imaginary error function Erfi(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D
where D(x) is the Dawson function (which can be used instead of erfi to avoid arithmetic overflow[23]).
Despite the name «imaginary error function», erfi x is real when x is real.
When the error function is evaluated for arbitrary complex arguments z, the resulting complex error function is usually discussed in scaled form as the Faddeeva function:
Cumulative distribution function[edit]
The error function is essentially identical to the standard normal cumulative distribution function, denoted Φ, also named norm(x) by some software languages[citation needed], as they differ only by scaling and translation. Indeed,
-
the normal cumulative distribution function plotted in the complex plane
or rearranged for erf and erfc:
Consequently, the error function is also closely related to the Q-function, which is the tail probability of the standard normal distribution. The Q-function can be expressed in terms of the error function as
The inverse of Φ is known as the normal quantile function, or probit function and may be expressed in terms of the inverse error function as
The standard normal cdf is used more often in probability and statistics, and the error function is used more often in other branches of mathematics.
The error function is a special case of the Mittag-Leffler function, and can also be expressed as a confluent hypergeometric function (Kummer’s function):
It has a simple expression in terms of the Fresnel integral.[further explanation needed]
In terms of the regularized gamma function P and the incomplete gamma function,
sgn x is the sign function.
Generalized error functions[edit]
Graph of generalised error functions En(x):
grey curve: E1(x) = 1 − e−x/√π
red curve: E2(x) = erf(x)
green curve: E3(x)
blue curve: E4(x)
gold curve: E5(x).
Some authors discuss the more general functions:[citation needed]
Notable cases are:
- E0(x) is a straight line through the origin: E0(x) = x/e√π
- E2(x) is the error function, erf x.
After division by n!, all the En for odd n look similar (but not identical) to each other. Similarly, the En for even n look similar (but not identical) to each other after a simple division by n!. All generalised error functions for n > 0 look similar on the positive x side of the graph.
These generalised functions can equivalently be expressed for x > 0 using the gamma function and incomplete gamma function:
Therefore, we can define the error function in terms of the incomplete gamma function:
Iterated integrals of the complementary error function[edit]
The iterated integrals of the complementary error function are defined by[27]
The general recurrence formula is
They have the power series
from which follow the symmetry properties
and
Implementations[edit]
As real function of a real argument[edit]
- In Posix-compliant operating systems, the header
math.hshall declare and the mathematical librarylibmshall provide the functionserfanderfc(double precision) as well as their single precision and extended precision counterpartserff,erflanderfcf,erfcl.[28] - The GNU Scientific Library provides
erf,erfc,log(erf), and scaled error functions.[29]
As complex function of a complex argument[edit]
libcerf, numeric C library for complex error functions, provides the complex functionscerf,cerfc,cerfcxand the real functionserfi,erfcxwith approximately 13–14 digits precision, based on the Faddeeva function as implemented in the MIT Faddeeva Package
See also[edit]
[edit]
- Gaussian integral, over the whole real line
- Gaussian function, derivative
- Dawson function, renormalized imaginary error function
- Goodwin–Staton integral
In probability[edit]
- Normal distribution
- Normal cumulative distribution function, a scaled and shifted form of error function
- Probit, the inverse or quantile function of the normal CDF
- Q-function, the tail probability of the normal distribution
References[edit]
- ^ Andrews, Larry C. (1998). Special functions of mathematics for engineers. SPIE Press. p. 110. ISBN 9780819426161.
- ^ Glaisher, James Whitbread Lee (July 1871). «On a class of definite integrals». London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 4. 42 (277): 294–302. doi:10.1080/14786447108640568. Retrieved 6 December 2017.
- ^ Glaisher, James Whitbread Lee (September 1871). «On a class of definite integrals. Part II». London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 4. 42 (279): 421–436. doi:10.1080/14786447108640600. Retrieved 6 December 2017.
- ^ «A007680 – OEIS». oeis.org. Retrieved 2 April 2020.
- ^ Weisstein, Eric W. «Erf». MathWorld.
- ^ Schöpf, H. M.; Supancic, P. H. (2014). «On Bürmann’s Theorem and Its Application to Problems of Linear and Nonlinear Heat Transfer and Diffusion». The Mathematica Journal. 16. doi:10.3888/tmj.16-11.
- ^ Weisstein, Eric W. «Bürmann’s Theorem». MathWorld.
- ^ Bergsma, Wicher (2006). «On a new correlation coefficient, its orthogonal decomposition and associated tests of independence». arXiv:math/0604627.
- ^ Cuyt, Annie A. M.; Petersen, Vigdis B.; Verdonk, Brigitte; Waadeland, Haakon; Jones, William B. (2008). Handbook of Continued Fractions for Special Functions. Springer-Verlag. ISBN 978-1-4020-6948-2.
- ^ Ng, Edward W.; Geller, Murray (January 1969). «A table of integrals of the Error functions». Journal of Research of the National Bureau of Standards Section B. 73B (1): 1. doi:10.6028/jres.073B.001.
- ^ Schlömilch, Oskar Xavier (1859). «Ueber facultätenreihen». Zeitschrift für Mathematik und Physik (in German). 4: 390–415. Retrieved 4 December 2017.
- ^ Nielson, Niels (1906). Handbuch der Theorie der Gammafunktion (in German). Leipzig: B. G. Teubner. p. 283 Eq. 3. Retrieved 4 December 2017.
- ^ Chiani, M.; Dardari, D.; Simon, M.K. (2003). «New Exponential Bounds and Approximations for the Computation of Error Probability in Fading Channels» (PDF). IEEE Transactions on Wireless Communications. 2 (4): 840–845. CiteSeerX 10.1.1.190.6761. doi:10.1109/TWC.2003.814350.
- ^ Tanash, I.M.; Riihonen, T. (2020). «Global minimax approximations and bounds for the Gaussian Q-function by sums of exponentials». IEEE Transactions on Communications. 68 (10): 6514–6524. arXiv:2007.06939. doi:10.1109/TCOMM.2020.3006902. S2CID 220514754.
- ^ Tanash, I.M.; Riihonen, T. (2020). «Coefficients for Global Minimax Approximations and Bounds for the Gaussian Q-Function by Sums of Exponentials [Data set]». Zenodo. doi:10.5281/zenodo.4112978.
- ^ Karagiannidis, G. K.; Lioumpas, A. S. (2007). «An improved approximation for the Gaussian Q-function» (PDF). IEEE Communications Letters. 11 (8): 644–646. doi:10.1109/LCOMM.2007.070470. S2CID 4043576.
- ^ Tanash, I.M.; Riihonen, T. (2021). «Improved coefficients for the Karagiannidis–Lioumpas approximations and bounds to the Gaussian Q-function». IEEE Communications Letters. 25 (5): 1468–1471. arXiv:2101.07631. doi:10.1109/LCOMM.2021.3052257. S2CID 231639206.
- ^ Chang, Seok-Ho; Cosman, Pamela C.; Milstein, Laurence B. (November 2011). «Chernoff-Type Bounds for the Gaussian Error Function». IEEE Transactions on Communications. 59 (11): 2939–2944. doi:10.1109/TCOMM.2011.072011.100049. S2CID 13636638.
- ^ Winitzki, Sergei (2003). «Uniform approximations for transcendental functions». Computational Science and Its Applications – ICCSA 2003. Lecture Notes in Computer Science. Vol. 2667. Springer, Berlin. pp. 780–789. doi:10.1007/3-540-44839-X_82. ISBN 978-3-540-40155-1.
- ^ Zeng, Caibin; Chen, Yang Cuan (2015). «Global Padé approximations of the generalized Mittag-Leffler function and its inverse». Fractional Calculus and Applied Analysis. 18 (6): 1492–1506. arXiv:1310.5592. doi:10.1515/fca-2015-0086. S2CID 118148950.
Indeed, Winitzki [32] provided the so-called global Padé approximation
- ^ Winitzki, Sergei (6 February 2008). «A handy approximation for the error function and its inverse».
- ^ Numerical Recipes in Fortran 77: The Art of Scientific Computing (ISBN 0-521-43064-X), 1992, page 214, Cambridge University Press.
- ^ a b c Cody, W. J. (March 1993), «Algorithm 715: SPECFUN—A portable FORTRAN package of special function routines and test drivers» (PDF), ACM Trans. Math. Softw., 19 (1): 22–32, CiteSeerX 10.1.1.643.4394, doi:10.1145/151271.151273, S2CID 5621105
- ^ Zaghloul, M. R. (1 March 2007), «On the calculation of the Voigt line profile: a single proper integral with a damped sine integrand», Monthly Notices of the Royal Astronomical Society, 375 (3): 1043–1048, Bibcode:2007MNRAS.375.1043Z, doi:10.1111/j.1365-2966.2006.11377.x
- ^ John W. Craig, A new, simple and exact result for calculating the probability of error for two-dimensional signal constellations Archived 3 April 2012 at the Wayback Machine, Proceedings of the 1991 IEEE Military Communication Conference, vol. 2, pp. 571–575.
- ^ Behnad, Aydin (2020). «A Novel Extension to Craig’s Q-Function Formula and Its Application in Dual-Branch EGC Performance Analysis». IEEE Transactions on Communications. 68 (7): 4117–4125. doi:10.1109/TCOMM.2020.2986209. S2CID 216500014.
- ^ Carslaw, H. S.; Jaeger, J. C. (1959), Conduction of Heat in Solids (2nd ed.), Oxford University Press, ISBN 978-0-19-853368-9, p 484
- ^ https://pubs.opengroup.org/onlinepubs/9699919799/basedefs/math.h.html
- ^ «Special Functions – GSL 2.7 documentation».
Further reading[edit]
- Abramowitz, Milton; Stegun, Irene Ann, eds. (1983) [June 1964]. «Chapter 7». Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Applied Mathematics Series. Vol. 55 (Ninth reprint with additional corrections of tenth original printing with corrections (December 1972); first ed.). Washington D.C.; New York: United States Department of Commerce, National Bureau of Standards; Dover Publications. p. 297. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253.
- Press, William H.; Teukolsky, Saul A.; Vetterling, William T.; Flannery, Brian P. (2007), «Section 6.2. Incomplete Gamma Function and Error Function», Numerical Recipes: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8
- Temme, Nico M. (2010), «Error Functions, Dawson’s and Fresnel Integrals», in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248
External links[edit]
- A Table of Integrals of the Error Functions
Функция ошибок (также называемая функция ошибок Гаусса) — не элементарная функция, возникающая в теории вероятностей, статистике и теории дифференциальных уравнений в частных производных. Она определяется как
- [math]displaystyle{ operatorname{erf},x = frac{2}{sqrt{pi}}intlimits_0^x e^{-t^2},mathrm dt }[/math].
Дополнительная функция ошибок, обозначаемая [math]displaystyle{ operatorname{erfc},x }[/math] (иногда применяется обозначение [math]displaystyle{ operatorname{Erf},x }[/math]), определяется через функцию ошибок:
- [math]displaystyle{ operatorname{erfc},x = 1-operatorname{erf},x = frac{2}{sqrt{pi}} intlimits_x^{infty} e^{-t^2},mathrm dt }[/math].
Комплексная функция ошибок, обозначаемая [math]displaystyle{ w(x) }[/math], также определяется через функцию ошибок:
- [math]displaystyle{ w(x) = e^{-x^2}operatorname{erfc},(-ix) }[/math].
Свойства
- Функция ошибок нечётна:
-
- [math]displaystyle{ operatorname{erf},(-x) = -operatorname{erf},x. }[/math]
- Для любого комплексного [math]displaystyle{ x }[/math] выполняется
-
- [math]displaystyle{ operatorname{erf},bar{x} = overline{operatorname{erf},x} }[/math]
- где черта обозначает комплексное сопряжение числа [math]displaystyle{ x }[/math].
- Функция ошибок не может быть представлена через элементарные функции, но, разлагая интегрируемое выражение в ряд Тейлора и интегрируя почленно, мы можем получить её представление в виде ряда:
-
- [math]displaystyle{ operatorname{erf},x= frac{2}{sqrt{pi}}sum_{n=0}^infinfrac{(-1)^n x^{2n+1}}{n! (2n+1)} =frac{2}{sqrt{pi}} left(x-frac{x^3}{3}+frac{x^5}{10}-frac{x^7}{42}+frac{x^9}{216}- cdotsright) }[/math]
- Это равенство выполняется (и ряд сходится) как для любого вещественного [math]displaystyle{ x }[/math], так и на всей комплексной плоскости, согласно признаку Д’Аламбера. Последовательность знаменателей образует последовательность A007680 в OEIS.
- Для итеративного вычисления элементов ряда полезно представить его в альтернативном виде:
-
- [math]displaystyle{ operatorname{erf},x= frac{2}{sqrt{pi}}sum_{n=0}^infinleft(x prod_{i=1}^n{frac{-(2i-1) x^2}{i (2i+1)}}right) = frac{2}{sqrt{pi}} sum_{n=0}^infin frac{x}{2n+1} prod_{i=1}^n frac{-x^2}{i} }[/math]
- поскольку [math]displaystyle{ frac{-(2i-1) x^2}{i (2i+1)} }[/math] — сомножитель, превращающий [math]displaystyle{ i }[/math]-й член ряда в [math]displaystyle{ (i+1) }[/math]-й, считая первым членом [math]displaystyle{ x }[/math].
- Функция ошибок на бесконечности равна единице; однако это справедливо только при приближении к бесконечности по вещественной оси, так как:
- При рассмотрении функции ошибок в комплексной плоскости точка [math]displaystyle{ z=infty }[/math] будет для неё существенно особой.
- Производная функции ошибок выводится непосредственно из определения функции:
-
- [math]displaystyle{ frac{d}{dx},operatorname{erf},x=frac{2}{sqrt{pi}},e^{-x^2}. }[/math]
- Первообразная функции ошибок, получаемая способом интегрирования по частям:
-
- [math]displaystyle{ F(x)=xoperatorname{erf}(x) + frac{e^{-x^2}}{sqrt{pi}}. }[/math]
- Обратная функция ошибок представляет собой ряд
-
- [math]displaystyle{ operatorname{erf}^{-1},x=sum_{k=0}^infinfrac{c_k}{2k+1}left (frac{sqrt{pi}}{2}xright )^{2k+1}, }[/math]
- где c0 = 1 и
- [math]displaystyle{ c_k=sum_{m=0}^{k-1}frac{c_m c_{k-1-m}}{(m+1)(2m+1)} = left{1,1,frac{7}{6},frac{127}{90},ldotsright}. }[/math]
- Поэтому ряд можно представить в следующем виде (заметим, что дроби сокращены):
- [math]displaystyle{ operatorname{erf}^{-1},x=frac{1}{2}sqrt{pi}left (x+frac{pi x^3}{12}+frac{7pi^2 x^5}{480}+frac{127pi^3 x^7}{40320}+frac{4369pi^4 x^9}{5806080}+frac{34807pi^5 x^{11}}{182476800}+dotsright ). }[/math][1]
- Последовательности числителей и знаменателей после сокращения — A092676 и A132467 в OEIS; последовательность числителей до сокращения — A002067 в OEIS.
Дополнительная функция ошибок
Применение
Если набор случайных величин подчиняется нормальному распределению со стандартным отклонением [math]displaystyle{ sigma }[/math], то вероятность, что величина отклонится от среднего не более чем на [math]displaystyle{ a }[/math], равна [math]displaystyle{ operatorname{erf},frac{a}{sigma sqrt{2}} }[/math].
Функция ошибок и дополнительная функция ошибок встречаются в решении некоторых дифференциальных уравнений, например, уравнения теплопроводности с начальными условиями, описываемыми функцией Хевисайда («ступенькой»).
В системах цифровой оптической коммуникации, вероятность ошибки на бит также выражается формулой, использующей функцию ошибок.
Асимптотическое разложение
При больших [math]displaystyle{ x }[/math] полезно асимптотическое разложение для дополнительной функции ошибок:
- [math]displaystyle{ operatorname{erfc},x = frac{e^{-x^2}}{xsqrt{pi}}left [1+sum_{n=1}^infty (-1)^n frac{1cdot3cdot5cdots(2n-1)}{(2x^2)^n}right ]=frac{e^{-x^2}}{xsqrt{pi}}sum_{n=0}^infty (-1)^n frac{(2n)!}{n!(2x)^{2n}}. }[/math]
Хотя для любого конечного [math]displaystyle{ x }[/math] этот ряд расходится, на практике первых нескольких членов достаточно для вычисления [math]displaystyle{ operatorname{erfc},x }[/math] с хорошей точностью, в то время как ряд Тейлора сходится очень медленно.
Другое приближение даётся формулой
- [math]displaystyle{ (operatorname{erf},x)^2approx 1-expleft(-x^2frac{4/pi+ax^2}{1+ax^2}right) }[/math]
где
- [math]displaystyle{ a = frac{8}{3pi}frac{pi — 3}{4 — pi}. }[/math]
Родственные функции
С точностью до масштаба и сдвига, функция ошибок совпадает с нормальным интегральным распределением, обозначаемым [math]displaystyle{ Phi(x) }[/math]
- [math]displaystyle{ Phi(x) = frac{1}{2}biggl(1+operatorname{erf},frac{x}{sqrt{2}}biggl). }[/math]
Обратная функция к [math]displaystyle{ Phi }[/math], известная как нормальная квантильная функция, иногда обозначается [math]displaystyle{ operatorname{probit} }[/math] и выражается через нормальную функцию ошибок как
- [math]displaystyle{
operatorname{probit},p = Phi^{-1}(p) = sqrt{2},operatorname{erf}^{-1}(2p-1).
}[/math]
Нормальное интегральное распределение чаще применяется в теории вероятностей и математической статистике, в то время как функция ошибок чаще применяется в других разделах математики.
Функция ошибок является частным случаем функции Миттаг-Леффлера, а также может быть представлена как вырожденная гипергеометрическая функция (функция Куммера):
- [math]displaystyle{ operatorname{erf},x=
frac{2x}{sqrt{pi}},_1F_1left(frac{1}{2},frac{3}{2},-x^2right). }[/math]
Функция ошибок выражается также через интеграл Френеля. В терминах регуляризованной неполной гамма-функции P и неполной гамма-функции,
- [math]displaystyle{ operatorname{erf},x=operatorname{sign},x,Pleft(frac{1}{2}, x^2right)={operatorname{sign},x over sqrt{pi}}gammaleft(frac{1}{2}, x^2right). }[/math]
Обобщённые функции ошибок
График обобщённых функций ошибок [math]displaystyle{ E_n(x) }[/math]:
серая линия: [math]displaystyle{ E_1(x)=(1-e^{-x})/sqrt{pi} }[/math]
красная линия: [math]displaystyle{ E_2(x)=operatorname{erf},x }[/math]
зелёная линия: [math]displaystyle{ E_3(x) }[/math]
синяя линия: [math]displaystyle{ E_4(x) }[/math]
жёлтая линия: [math]displaystyle{ E_5(x) }[/math].
Некоторые авторы обсуждают более общие функции
- [math]displaystyle{ E_n(x) = frac{n!}{sqrt{pi}} intlimits_0^x e^{-t^n},mathrm dt
=frac{n!}{sqrt{pi}}sum_{p=0}^infin(-1)^pfrac{x^{np+1}}{(np+1)p!},. }[/math]
Примечательными частными случаями являются:
- [math]displaystyle{ E_0(x) }[/math] — прямая линия, проходящая через начало координат: [math]displaystyle{ E_0(x)=frac{x}{e sqrt{pi}} }[/math]
- [math]displaystyle{ E_2(x) }[/math] — функция ошибок [math]displaystyle{ operatorname{erf},x }[/math].
После деления на [math]displaystyle{ n! }[/math] все [math]displaystyle{ E_n }[/math] с нечётными [math]displaystyle{ n }[/math] выглядят похоже (но не идентично), это же можно сказать про [math]displaystyle{ E_n }[/math] с чётными [math]displaystyle{ n }[/math]. Все обобщённые функции ошибок с [math]displaystyle{ ngt 0 }[/math] выглядят похоже на полуоси [math]displaystyle{ xgt 0 }[/math].
На полуоси [math]displaystyle{ xgt 0 }[/math] все обобщённые функции могут быть выражены через гамма-функцию:
- [math]displaystyle{ E_n(x) = frac{Gamma(n)left(Gammaleft(frac{1}{n}right)-Gammaleft(frac{1}{n},x^nright)right)}{sqrtpi},
quad quad
xgt 0 }[/math]
Следовательно, мы можем выразить функцию ошибок через гамма-функцию:
- [math]displaystyle{ operatorname{erf},x = 1 — frac{Gammaleft(frac{1}{2},x^2right)}{sqrtpi} }[/math]
Повторные интегралы дополнительной функции ошибок
Повторные интегралы [math]displaystyle{ operatorname{I^n erfc} }[/math] дополнительной функции ошибок определяются как[1]
- [math]displaystyle{ operatorname{I^0 erfc},z = operatorname{erfc},z }[/math],
- [math]displaystyle{ operatorname{I^n erfc},z = intlimits_z^infty operatorname{I^{n-1}erfc},zeta,dzeta, }[/math] для [math]displaystyle{ ngt 0 }[/math].
Их можно разложить в ряд:
- [math]displaystyle{
operatorname{I^nerfc},z
=
sum_{j=0}^infty frac{(-z)^j}{2^{n-j}j!,Gamma left( 1 + frac{n-j}{2}right)},,
}[/math]
откуда следуют свойства симметрии
- [math]displaystyle{
operatorname{I^{2m}erfc},(-z)
= -operatorname{I^{2m}erfc},z
+ sum_{q=0}^m frac{z^{2q}}{2^{2(m-q)-1}(2q)!(m-q)!}
}[/math]
и
- [math]displaystyle{
operatorname{I^{2m+1}erfc},(-z)
=operatorname{I^{2m+1}erfc},z
+ sum_{q=0}^m frac{z^{2q+1}}{2^{2(m-q)-1}(2q+1)! (m-q)!},.
}[/math]
Реализации
В стандарте языка Си (ISO/IEC 9899:1999, пункт 7.12.8) предусмотрены функция ошибок [math]displaystyle{ operatorname{erf} }[/math] и дополнительная функция ошибок [math]displaystyle{ operatorname{erfc} }[/math]. Функции объявлены в заголовочных файлах math.h (для Си) или cmath (для C++). Там же объявлены пары функций erff(), erfcf() и erfl(), erfcl(). Первая пара получает и возвращает значения типа float, а вторая — значения типа long double. Соответствующие функции также содержатся в библиотеке Math проекта «Boost».
В языке Java стандартная библиотека математических функций java.lang.Math не содержит[2] функцию ошибок. Класс Erf можно найти в пакете org.apache.commons.math.special из не стандартной библиотеки, поставляемой[3] Apache Software Foundation.
Системы компьютерной алгебры Maple[2], Matlab[3], Mathematica и Maxima[4] содержат обычную и дополнительную функции ошибок, а также обратные к ним функции.
В языке Python функция ошибок доступна[4] из стандартной библиотеки math, начиная с версии 2.7. Также функция ошибок, дополнительная функция ошибок и многие другие специальные функции определены в модуле Special проекта SciPy[5].
В языке Erlang функция ошибок и дополнительная функция ошибок доступны из стандартного модуля math[5].
В Excel функция ошибок представлена, как ФОШ и ФОШ.ТОЧН[6]
См. также
- Функция Гаусса
- Функция Доусона
- Гауссов интеграл
Примечания
- ↑ Carslaw, H. S. & Jaeger, J. C. (1959), Conduction of Heat in Solids (2nd ed.), Oxford University Press, ISBN 978-0-19-853368-9, p 484
- ↑ Math (Java Platform SE 6). Дата обращения: 28 марта 2008. Архивировано 29 августа 2009 года.
- ↑ Архивированная копия (недоступная ссылка). Дата обращения: 28 марта 2008. Архивировано 9 апреля 2008 года.
- ↑ 9.2. math — Mathematical functions — Python 2.7.10rc0 documentation
- ↑ Язык Erlang. Описание Архивная копия от 20 июня 2012 на Wayback Machine функций стандартного модуля
math. - ↑ Функция ФОШ. support.microsoft.com. Дата обращения: 15 ноября 2021. Архивировано 15 ноября 2021 года.
Литература
- Press, William H.; Teukolsky, Saul A.; Vetterling, William T. & Flannery, Brian P. (2007), Section 6.2. Incomplete Gamma Function and Error Function, Numerical Recipes: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8
- Milton Abramowitz and Irene A. Stegun, eds. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. — New York: Dover, 1972. — Т. 7.
- Nikolai G. Lehtinen. Error functions (April 2010). Дата обращения: 25 мая 2019.
Ссылки
- MathWorld — Erf
- Онлайновый калькулятор Erf и много других специальных функций (до 6 знаков)
- Онлайновый калькулятор, вычисляющий в том числе Erf

В математике функция ошибок (также называемая Функция ошибок Гаусса ), часто обозначаемая erf, является сложной функцией комплексной определяемой как:
- erf z = 2 π ∫ 0 ze — t 2 dt. { displaystyle operatorname {erf} z = { frac {2} { sqrt { pi}}} int _ {0} ^ {z} e ^ {- t ^ {2}} , dt.}
Этот интеграл является особой (не элементарной ) и сигмоидной функцией, которая часто встречается в статистике вероятность, и уравнения в частных производных. Во многих из этих приложений аргумент функции является действительным числом. Если аргумент функции является действительным, значение также является действительным.
В статистике для неотрицательных значений x функция имеет интерпретацию: для случайной величины Y, которая нормально распределена с среднее 0 и дисперсия 1/2, erf x — это вероятность того, что Y попадает в диапазон [-x, x].
Две связанные функции: дополнительные функции ошибок (erfc ), определенная как
- erfc z = 1 — erf z, { displaystyle operatorname {erfc} z = 1- operatorname {erf} z,}
и функция мнимой ошибки (erfi ), определяемая как
- erfi z = — i erf (iz), { displaystyle operatorname {erfi} z = -i operatorname {erf} (iz),}
, где i — мнимая единица.
Содержание
- 1 Имя
- 2 Приложения
- 3 Свойства
- 3.1 Ряд Тейлора
- 3.2 Производная и интеграл
- 3.3 Ряд Бюрмана
- 3.4 Обратные функции
- 3.5 Асимптотическое разложение
- 3.6 Разложение на непрерывную дробь
- 3,7 Интеграл функции ошибок с функцией плотности Гаусса
- 3.8 Факториальный ряд
- 4 Численные приближения
- 4.1 Аппроксимация с элементарными функциями
- 4.2 Полином
- 4.3 Таблица значений
- 5 Связанные функции
- 5.1 функция дополнительных ошибок
- 5.2 Функция мнимой ошибки
- 5.3 Кумулятивная функци я распределения на
- 5.4 Обобщенные функции ошибок
- 5.5 Итерированные интегралы дополнительных функций ошибок
- 6 Реализации
- 6.1 Как действующая функция действительного аргумента
- 6.2 Как комплексная функция комплексного аргумента
- 7 См. Также
- 7.1 Связанные функции
- 7.2 Вероятность
- 8 Ссылки
- 9 Дополнительная литература
- 10 Внешние ссылки
Имя
Название «функция ошибки» и его аббревиатура erf были предложены Дж. В. Л. Глейшер в 1871 г. по причине его связи с «теорией вероятности, и особенно теорией ошибок ». Дополнение функции ошибок также обсуждалось Глейшером в отдельной публикации в том же году. Для «закона удобства» ошибок плотность задана как
- f (x) = (c π) 1 2 e — cx 2 { displaystyle f (x) = left ({ frac {c } { pi}} right) ^ { tfrac {1} {2}} e ^ {- cx ^ {2}}}
(нормальное распределение ), Глейшер вычисляет вероятность ошибки, лежащей между p { displaystyle p}

- (c π) 1 2 ∫ pqe — cx 2 dx = 1 2 (erf (qc) — erf (pc)). { displaystyle left ({ frac {c} { pi}} right) ^ { tfrac {1} {2}} int _ {p} ^ {q} e ^ {- cx ^ {2} } dx = { tfrac {1} {2}} left ( operatorname {erf} (q { sqrt {c}}) — operatorname {erf} (p { sqrt {c}}) right).}
Приложения
Когда результаты серии измерений описываются нормальным распределением со стандартным отклонением σ { displaystyle sigma}

Функции и дополнительные функции ошибок возникают, например, в решениях уравнения теплопроводности, когда граничные ошибки задаются ступенчатой функцией Хевисайда.
Функция ошибок и ее приближения Программу присвоили себе преподавателей, которые получили с высокой вероятностью или с низкой вероятностью. Дана случайная величина X ∼ Norm [μ, σ] { displaystyle X sim operatorname {Norm} [ mu, sigma]}![X sim operatorname {Norm} [ му, sigma]](https://wikimedia.org/api/rest_v1/media/math/render/svg/84024bc6827355ec6d23a062283a26d54b29698d)

- Pr [X ≤ L ] = 1 2 + 1 2 erf (L — μ 2 σ) ≈ A ехр (- B (L — μ σ) 2) { Displaystyle Pr [X Leq L] = { frac {1} {2 }} + { frac {1} {2}} operatorname {erf} left ({ frac {L- mu} {{ sqrt {2}} sigma}} right) приблизительно A exp left (-B left ({ frac {L- mu} { sigma}} right) ^ {2} right)}
где A и B — верх числовые константы. Если L достаточно далеко от среднего, то есть μ — L ≥ σ ln k { displaystyle mu -L geq sigma { sqrt { ln {k}}}}
- Pr [X ≤ L] ≤ A exp (- B ln k) = A К B { displaystyle Pr [X leq L] leq A exp (-B ln {k}) = { frac {A} {k ^ {B}}}}
, поэтому становится вероятность 0 при k → ∞ { displaystyle k to infty}
Свойства
Графики на комплексной плоскости 

Свойство erf (- z) = — erf (z) { displaystyle operatorname {erf} (-z) = — operatorname {erf} (z)}

Для любого комплексное число z:
- erf (z ¯) = erf (z) ¯ { displaystyle operatorname {erf} ({ overline {z}}) = { overline { operatorname {erf} (z)}}}
где z ¯ { displaystyle { overline {z}}}
Подынтегральное выражение f = exp (−z) и f = erf (z) показано в комплексной плоскости z на рисунках 2 и 3. Уровень Im (f) = 0 показан жирным зеленым цветом. линия. Отрицательные целые значения Im (f) показаны жирными красными линиями. Положительные целые значения Im (f) показаны толстыми синими линиями. Промежуточные уровни Im (f) = проявляются тонкими зелеными линиями. Промежуточные уровни Re (f) = показаны тонкими красными линиями для отрицательных значений и тонкими синими линиями для положительных значений.
Функция ошибок при + ∞ равна 1 (см. интеграл Гаусса ). На действительной оси erf (z) стремится к единице при z → + ∞ и к −1 при z → −∞. На мнимой оси он стремится к ± i∞.
Серия Тейлора
Функция ошибок — это целая функция ; у него нет сингулярностей (кроме бесконечности), и его разложение Тейлора всегда сходится, но, как известно, «[…] его плохая сходимость, если x>1».
определяющий интеграл нельзя вычислить в закрытой форме в терминах элементарных функций, но путем расширения подынтегрального выражения e в его ряд Маклорена и интегрирована почленно, можно получить ряд Маклорена функции ошибок как:
- erf (z) = 2 π ∑ n = 0 ∞ (- 1) nz 2 n + 1 n! (2 n + 1) знак равно 2 π (z — z 3 3 + z 5 10 — z 7 42 + z 9 216 — ⋯) { displaystyle operatorname {erf} (z) = { frac {2} { sqrt { pi}}} sum _ {n = 0} ^ { infty} { frac {(-1) ^ {n} z ^ {2n + 1}} {n! (2n + 1)}} = { frac {2} { sqrt { pi}}} left (z — { frac {z ^ {3}} {3}} + { frac {z ^ { 5}} {10}} — { frac {z ^ {7}} {42}} + { frac {z ^ {9}} {216}} — cdots right)}
, которое выполняется для каждого комплексного числа г. Члены знаменателя представляют собой последовательность A007680 в OEIS.
Для итеративного вычисления нового ряда может быть полезна следующая альтернативная формулировка:
- erf (z) = 2 π ∑ n = 0 ∞ (z ∏ К знак равно 1 N — (2 К — 1) Z 2 К (2 К + 1)) знак равно 2 π ∑ N = 0 ∞ Z 2 N + 1 ∏ К = 1 N — Z 2 К { Displaystyle OperatorName { erf} (z) = { frac {2} { sqrt { pi}}} sum _ {n = 0} ^ { infty} left (z prod _ {k = 1} ^ {n} { frac {- (2k-1) z ^ {2}} {k (2k + 1)}} right) = { frac {2} { sqrt { pi}}} sum _ {n = 0} ^ { infty} { frac {z} {2n + 1}} prod _ {k = 1} ^ {n} { frac {-z ^ {2}} {k}}}
потому что что — (2 k — 1) z 2 k (2 k + 1) { displaystyle { frac {- (2k-1) z ^ {2}} {k (2k + 1))}} }
Функция мнимой ошибки имеет очень похожий ряд Маклорена:
- erfi (z) = 2 π ∑ n = 0 ∞ z 2 n + 1 n! (2 n + 1) знак равно 2 π (z + z 3 3 + z 5 10 + z 7 42 + z 9 216 + ⋯) { displaystyle operatorname {erfi} (z) = { frac {2} { sqrt { pi}}} sum _ {n = 0} ^ { infty} { frac {z ^ {2n + 1}} {n! (2n + 1)}} = { frac {2} { sqrt { pi}}} left (z + { frac {z ^ {3}} {3}} + { frac {z ^ { 5}} {10}} + { frac {z ^ {7}} {42}} + { frac {z ^ {9}} {216}} + cdots right)}
, которое выполняется для любого комплексного числа z.
Производная и интеграл
Производная функция ошибок сразу следует из ее определения:
- ddz erf (z) = 2 π e — z 2. { displaystyle { frac {d} {dz}} operatorname {erf} (z) = { frac {2} { sqrt { pi}}} e ^ {- z ^ {2}}.}
Отсюда немедленно вычисляется производная функция мнимой ошибки :
- ddz erfi (z) = 2 π ez 2. { displaystyle { frac {d} {dz}} operatorname {erfi} (z) = { frac {2} { sqrt { pi }}} e ^ {z ^ {2}}.}
первообразная функции ошибок, которые можно получить посредством интегрирования по частям, составляет
- z erf (z) + е — z 2 π. { displaystyle z operatorname {erf} (z) + { frac {e ^ {- z ^ {2}}} { sqrt { pi}}}.}
Первообразная мнимой функции ошибок, также можно получить интегрированием по частям:
- z erfi (z) — ez 2 π. { displaystyle z operatorname {erfi} (z) — { frac {e ^ {z ^ {2}}} { sqrt { pi}}}.}
Производные высшего порядка задаются как
- erf (k) (z) = 2 (- 1) k — 1 π H k — 1 (z) e — z 2 = 2 π dk — 1 dzk — 1 (e — z 2), k = 1, 2, … { Displaystyle operatorname {erf} ^ {(k)} (z) = { frac {2 (-1) ^ {k-1}} { sqrt { pi}}} { mathit {H} } _ {k-1} (z) e ^ {- z ^ {2}} = { frac {2} { sqrt { pi}}} { frac {d ^ {k-1}} {dz ^ {k-1}}} left (e ^ {- z ^ {2}} right), qquad k = 1,2, dots}
где H { displaystyle { mathit {H}}}
ряд Бюрмана
Расширение, которое сходится быстрее для всех реальных значений x { displaystyle x}
- erf (x) = 2 π sgn (x) 1 — e — x 2 (1 — 1 12 ( 1 — e — x 2) — 7 480 (1 — e — x 2) 2 — 5 896 (1 — e — x 2) 3 — 787 276480 (1 — e — x 2)) 4 — ⋯) знак равно 2 π знак (x) 1 — e — x 2 (π 2 + ∑ k = 1 ∞ cke — kx 2). { displaystyle { begin {align} operatorname {erf} (x) = { frac {2} { sqrt { pi}}} operatorname {sgn} (x) { sqrt {1-e ^ {-x ^ {2}}}} left (1 — { frac {1} {12}} left (1-e ^ {- x ^ {2}} right) — { frac {7} {480}} left (1-e ^ {- x ^ {2}} right) ^ {2} — { frac {5} {896}} left (1-e ^ {- x ^ {2 }} right) ^ {3} — { frac {787} {276480}} left (1-e ^ {- x ^ {2}} right) ^ {4} — cdots right) [10pt] = { frac {2} { sqrt { pi}}} operatorname {sgn} (x) { sqrt {1-e ^ {- x ^ {2}}}} left ({ frac { sqrt { pi}} {2}} + sum _ {k = 1} ^ { infty} c_ {k} e ^ {- kx ^ {2}} right). end {выровнено}}
Сохраняя только первые два коэффициента и выбирая c 1 = 31 200 { displaystyle c_ {1} = { frac {31} {200}}}



- erf (x) ≈ 2 π sign (x) 1 — e — x 2 (π 2 + 31 200 e — x 2 — 341 8000 e — 2 х 2). { displaystyle operatorname {erf} (x) приблизительно { frac {2} { sqrt { pi}}} operatorname {sgn} (x) { sqrt {1-e ^ {- x ^ {2 }}}} left ({ frac { sqrt { pi}} {2}} + { frac {31} {200}} e ^ {- x ^ {2}} — { frac {341} {8000}} e ^ {- 2x ^ {2}} right).}
Обратные функции
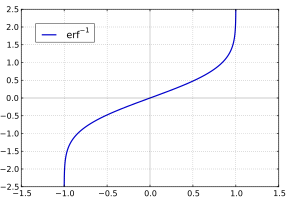
Учитывая комплексное число z, не существует уникального комплексного числа w, удовлетворяющего erf (w) = z { displaystyle operatorname {erf} (w) = z}

- erf (erf — 1 ( х)) = х. { displaystyle operatorname {erf} left ( operatorname {erf} ^ {- 1} (x) right) = x.}
Обратная функция ошибок обычно определяется с помощью домена (- 1,1), и он ограничен этой областью многих систем компьютерной алгебры. Однако его можно продолжить и на диск | z | < 1 of the complex plane, using the Maclaurin series
- erf — 1 (z) знак равно ∑ К знак равно 0 ∞ ck 2 k + 1 (π 2 z) 2 k + 1, { displaystyle operatorname {erf} ^ {- 1} (z) = sum _ {k = 0} ^ { infty} { frac {c_ {k}} {2k + 1}} left ({ frac { sqrt { pi}} {2}} z right) ^ {2k + 1},}
где c 0 = 1 и
- ck = ∑ m = 0 k — 1 cmck — 1 — m (m + 1) (2 m + 1) = {1, 1, 7 6, 127 90, 4369 2520, 34807 16200,…}. { displaystyle c_ {k} = sum _ {m = 0} ^ {k-1} { frac {c_ {m} c_ {k-1-m}} {(m + 1) (2m + 1) }} = left {1,1, { frac {7} {6}}, { frac {127} {90}}, { frac {4369} {2520}}, { frac {34807} {16200}}, ldots right }.}
Итак, у нас есть разложение в ряд (общие множители были удалены из числителей и знаменателей):
- erf — 1 (z) = 1 2 π ( z + π 12 z 3 + 7 π 2 480 z 5 + 127 π 3 40320 z 7 + 4369 π 4 5806080 z 9 + 34807 π 5 182476800 z 11 + ⋯). { displaystyle operatorname {erf} ^ {- 1} (z) = { tfrac {1} {2}} { sqrt { pi}} left (z + { frac { pi} {12} } z ^ {3} + { frac {7 pi ^ {2}} {480}} z ^ {5} + { frac {127 pi ^ {3}} {40320}} z ^ {7} + { frac {4369 pi ^ {4}} {5806080}} z ^ {9} + { frac {34807 pi ^ {5}} {182476800}} z ^ {11} + cdots right). }
(После отмены дроби числителя / знаменателя характерми OEIS : A092676 / OEIS : A092677 в OEIS ; без отмены членов числителя в записи OEIS : A002067.) Значение функции ошибок при ± ∞ равно ± 1.
Для | z | < 1, we have erf (erf — 1 (z)) = z { displaystyle operatorname {erf} left ( operatorname {erf} ^ {- 1} (z) right) = z}
обратная дополнительная функция ошибок определяется как
- erfc — 1 (1 — z) = erf — 1 (z). { displaystyle operatorname {erfc} ^ {- 1} (1-z) = operatorname {erf} ^ {- 1} (z).}
Для действительного x существует уникальное действительное число erfi — 1 (x) { displaystyle operatorname {erfi} ^ {- 1} (x)}


Для любого действительного x, Метод Ньютона можно использовать для вычислений erfi — 1 (x) { displaystyle operatorname {erfi} ^ {- 1} (x)}

- erfi — 1 (z) = ∑ k = 0 ∞ (- 1) ККК 2 К + 1 (π 2 Z) 2 К + 1, { Displaystyle OperatorName {erfi} ^ {- 1} (г) = сумма _ {к = 0} ^ { infty} { гидроразрыва {(-1) ^ {k} c_ {k}} {2k + 1}} left ({ frac { sqrt { pi}} {2}} z right) ^ {2k + 1},}
, где c k определено, как указано выше.
Асимптотическое разложение
Полезным асимптотическим разложением дополнительные функции (и, следовательно, также и функции ошибок) для больших вещественных x
- erfc (x) = e — x 2 x π [1 + ∑ n = 1 ∞ (- 1) n 1 ⋅ 3 ⋅ 5 ⋯ (2 n — 1) (2 x 2) n] = e — x 2 x π ∑ n = 0 ∞ (- 1) п (2 п — 1)! ! (2 х 2) n, { displaystyle operatorname {erfc} (x) = { frac {e ^ {- x ^ {2}}} {x { sqrt { pi}}}} left [1 + sum _ {n = 1} ^ { infty} (- 1) ^ {n} { frac {1 cdot 3 cdot 5 cdots (2n-1)} {(2x ^ {2}) ^ {n}}} right] = { frac {e ^ {- x ^ {2}}} {x { sqrt { pi}}}} sum _ {n = 0} ^ { infty} ( -1) ^ {n} { frac {(2n-1) !!} {(2x ^ {2}) ^ {n}}},}
где (2n — 1) !! — это двойной факториал числа (2n — 1), которое является произведением всех нечетных чисел до (2n — 1). Этот ряд расходуется для любого конечного x, и его значение как асимптотического разложения состоит в том, что для любого N ∈ N { displaystyle N in mathbb {N}}
- erfc (Икс) знак равно е — Икс 2 Икс π ∑ N знак равно 0 N — 1 (- 1) N (2 N — 1)! ! (2 х 2) n + RN (x) { displaystyle operatorname {erfc} (x) = { frac {e ^ {- x ^ {2}}} {x { sqrt { pi}}}} sum _ {n = 0} ^ {N-1} (- 1) ^ {n} { frac {(2n-1) !!} {(2x ^ {2}) ^ {n}}} + R_ {N} (x)}
где остаток в нотации Ландау равен
- RN (x) = O (x 1 — 2 N e — x 2) { displaystyle R_ {N} ( x) = O left (x ^ {1-2N} e ^ {- x ^ {2}} right)}
при x → ∞. { displaystyle x to infty.}
Действительно, точное значение остатка равно
- R N (x): = (- 1) N π 2 1 — 2 N (2 N)! N! ∫ Икс ∞ T — 2 N e — T 2 dt, { Displaystyle R_ {N} (x): = { frac {(-1) ^ {N}} { sqrt { pi}}} 2 ^ { 1-2N} { frac {(2N)!} {N!}} Int _ {x} ^ { infty} t ^ {- 2N} e ^ {- t ^ {2}} , dt,}
который легко следует по индукции, записывая
- e — t 2 = — (2 t) — 1 (e — t 2) ′ { displaystyle e ^ {- t ^ {2}} = — (2t) ^ {- 1} left (e ^ {- t ^ {2}} right) ‘}
и интегрирование по частям.
Для достаточно больших значений x, только первые несколько этих асимптотических разностей необходимы, чтобы получить хорошее приближение erfc (x) (в то время как для не слишком больших значений x приведенное выше разложение Тейлора при 0 обеспечивает очень быструю сходимость).
Расширение непрерывной дроби
A Разложение непрерывной дроби дополнительные функции ошибок:
- erfc (z) = z π e — z 2 1 z 2 + a 1 1 + a 2 z 2 + a 3 1 + ⋯ am = м 2. { displaystyle operatorname {erfc} (z) = { frac {z} { sqrt { pi}}} e ^ {- z ^ {2}} { cfrac {1} {z ^ {2} + { cfrac {a_ {1}} {1 + { cfrac {a_ {2}} {z ^ {2} + { cfrac {a_ {3}} {1+) dotsb}}}}}}}} qquad a_ {m} = { frac {m} {2}}.}
Интеграл функции ошибок с функцией плотности Гаусса
- ∫ — ∞ ∞ erf (ax + б) 1 2 π σ 2 е — (Икс — μ) 2 2 σ 2 dx знак равно erf [a μ + b 1 + 2 a 2 σ 2], a, b, μ, σ ∈ R { displaystyle int _ {- infty} ^ { infty} operatorname {erf} left (ax + b right) { frac {1} { sqrt {2 pi sigma ^ {2}}}} e ^ {- { frac {(x- mu) ^ {2}} {2 sigma ^ {2}}}} , dx = operatorname {erf} left [{ frac {a mu + b } { sqrt {1 + 2a ^ {2} sigma ^ {2}}} right], qquad a, b, mu, sigma in mathbb {R}}
Факториальный ряд
- Обратное:
-
- erfc z = e — z 2 π z ∑ n = 0 ∞ (- 1) n Q n (z 2 + 1) n ¯ = e — z 2 π z (1 — 1 2 1 (z 2 + 1) + 1 4 1 (z 2 + 1) (z 2 + 2) — ⋯) { displaystyle { begin {align} operatorname {erfc} z = { frac {e ^ {- z ^ {2}}} {{ sqrt { pi}} , z}} sum _ {n = 0} ^ { infty} { frac {(-1) ^ {n} Q_ {n}} {{(z ^ {2} + 1)} ^ { ba r {n}}}} = { frac {e ^ {- z ^ {2}}} {{ sqrt { pi}} , z}} left ( 1 — { frac {1} {2}} { frac {1} {(z ^ {2} +1)}} + { frac {1} {4}} { frac {1} {(z ^ {2} +1) (z ^ {2} +2)}} — cdots right) end {align}}}
- erfc z = e — z 2 π z ∑ n = 0 ∞ (- 1) n Q n (z 2 + 1) n ¯ = e — z 2 π z (1 — 1 2 1 (z 2 + 1) + 1 4 1 (z 2 + 1) (z 2 + 2) — ⋯) { displaystyle { begin {align} operatorname {erfc} z = { frac {e ^ {- z ^ {2}}} {{ sqrt { pi}} , z}} sum _ {n = 0} ^ { infty} { frac {(-1) ^ {n} Q_ {n}} {{(z ^ {2} + 1)} ^ { ba r {n}}}} = { frac {e ^ {- z ^ {2}}} {{ sqrt { pi}} , z}} left ( 1 — { frac {1} {2}} { frac {1} {(z ^ {2} +1)}} + { frac {1} {4}} { frac {1} {(z ^ {2} +1) (z ^ {2} +2)}} — cdots right) end {align}}}
- сходится для Re (z 2)>0. { displaystyle operatorname {Re} (z ^ {2})>0.}
Здесь
- Q n = def 1 Γ (1/2) ∫ 0 ∞ τ (τ — 1) ⋯ ( τ — n + 1) τ — 1/2 е — τ d τ знак равно ∑ К знак равно 0 N (1 2) к ¯ s (n, k), { displaystyle Q_ {n} { stackrel { text {def}} {=}} { frac {1} { Gamma (1/2)}} int _ {0} ^ { infty} tau ( tau -1) cdots ( tau -n + 1) tau ^ {-1/2} e ^ {- tau} d tau = sum _ {k = 0} ^ {n} left ({ frac {1} {2}} right) ^ { bar {k}} s (n, k),}
- Q n = def 1 Γ (1/2) ∫ 0 ∞ τ (τ — 1) ⋯ ( τ — n + 1) τ — 1/2 е — τ d τ знак равно ∑ К знак равно 0 N (1 2) к ¯ s (n, k), { displaystyle Q_ {n} { stackrel { text {def}} {=}} { frac {1} { Gamma (1/2)}} int _ {0} ^ { infty} tau ( tau -1) cdots ( tau -n + 1) tau ^ {-1/2} e ^ {- tau} d tau = sum _ {k = 0} ^ {n} left ({ frac {1} {2}} right) ^ { bar {k}} s (n, k),}
- zn ¯ { displaystyle z ^ { bar {n}}}
обозначает возрастающий факториал, а s (n, k) { displaystyle s (n, k)}
обозначает знаковое число Стирлинга первого рода.
- Представление бесконечной суммой, составляющей двойной факториал :
-
- ERF (Z) знак равно 2 π ∑ N знак равно 0 ∞ (- 2) N (2 N — 1)! (2 N + 1)! Z 2 N + 1 { Displaystyle OperatorName {ERF} (г) = { frac {2} { sqrt { pi}}} sum _ {n = 0} ^ { infty} { frac {( -2) ^ {n} (2n-1) !!} {(2n + 1)!}} Z ^ {2n + 1}}
- ERF (Z) знак равно 2 π ∑ N знак равно 0 ∞ (- 2) N (2 N — 1)! (2 N + 1)! Z 2 N + 1 { Displaystyle OperatorName {ERF} (г) = { frac {2} { sqrt { pi}}} sum _ {n = 0} ^ { infty} { frac {( -2) ^ {n} (2n-1) !!} {(2n + 1)!}} Z ^ {2n + 1}}
Численные приближения
Приближение элементов сарными функциями
- Абрамовиц и Стегун дают несколько приближений с точностью (уравнения 7.1.25–28). Это позволяет выбрать наиболее быстрое приближение, подходящее для данного приложения. В порядке увеличения точности они следующие:
-
- erf (x) ≈ 1 — 1 (1 + a 1 x + a 2 x 2 + a 3 x 3 + a 4 x 4) 4, x ≥ 0 { displaystyle имя оператора {erf} (x) приблизительно 1 — { frac {1} {(1 + a_ {1} x + a_ {2} x ^ {2} + a_ {3} x ^ {3} + a_ { 4} x ^ {4}) ^ {4}}}, qquad x geq 0}
- erf (x) ≈ 1 — 1 (1 + a 1 x + a 2 x 2 + a 3 x 3 + a 4 x 4) 4, x ≥ 0 { displaystyle имя оператора {erf} (x) приблизительно 1 — { frac {1} {(1 + a_ {1} x + a_ {2} x ^ {2} + a_ {3} x ^ {3} + a_ { 4} x ^ {4}) ^ {4}}}, qquad x geq 0}
- (максимальная ошибка: 5 × 10)
- , где a 1 = 0,278393, a 2 = 0,230389, a 3 = 0,000972, a 4 = 0,078108
-
- erf (x) ≈ 1 — (a 1 t + a 2 t 2 + a 3 t 3) e — x 2, t = 1 1 + px, x ≥ 0 { displaystyle operatorname {erf} (x) приблизительно 1- (a_ {1} t + a_ {2} t ^ {2} + a_ {3} t ^ {3}) e ^ {- x ^ {2}}, quad t = { frac {1} {1 + px}}, qquad x geq 0}
(максимальная ошибка: 2,5 × 10)
- erf (x) ≈ 1 — (a 1 t + a 2 t 2 + a 3 t 3) e — x 2, t = 1 1 + px, x ≥ 0 { displaystyle operatorname {erf} (x) приблизительно 1- (a_ {1} t + a_ {2} t ^ {2} + a_ {3} t ^ {3}) e ^ {- x ^ {2}}, quad t = { frac {1} {1 + px}}, qquad x geq 0}
- где p = 0,47047, a 1 = 0,3480242, a 2 = -0,0958798, a 3 = 0,7478556
-
- erf (x) ≈ 1 — 1 (1 + a 1 x + a 2 x 2 + ⋯ + a 6 x 6) 16, x ≥ 0 { displaystyle operatorname {erf} (x) приблизительно 1 — { frac {1} {(1 + a_ {1} x + a _ {2} x ^ {2} + cdots + a_ {6} x ^ {6}) ^ {16}}}, qquad x geq 0}
(максимальная ошибка: 3 × 10)
- erf (x) ≈ 1 — 1 (1 + a 1 x + a 2 x 2 + ⋯ + a 6 x 6) 16, x ≥ 0 { displaystyle operatorname {erf} (x) приблизительно 1 — { frac {1} {(1 + a_ {1} x + a _ {2} x ^ {2} + cdots + a_ {6} x ^ {6}) ^ {16}}}, qquad x geq 0}
- , где a 1 = 0,0705230784, a 2 = 0,0422820123, a 3 = 0,0092705272, a 4 = 0,0001520143, a 5 = 0,0002765672, a 6 = 0,0000430638
-
- erf (x) ≈ 1 — (a 1 t + a 2 t 2 + ⋯ + a 5 t 5) e — x 2, t = 1 1 + px { displaystyle operatorname {erf} (x) приблизительно 1- (a_ {1} t + a_ {2} t ^ {2} + cdots + a_ {5} t ^ {5}) e ^ {- x ^ {2}}, quad t = { frac {1} {1 + px}}}
(максимальная ошибка: 1,5 × 10)
- erf (x) ≈ 1 — (a 1 t + a 2 t 2 + ⋯ + a 5 t 5) e — x 2, t = 1 1 + px { displaystyle operatorname {erf} (x) приблизительно 1- (a_ {1} t + a_ {2} t ^ {2} + cdots + a_ {5} t ^ {5}) e ^ {- x ^ {2}}, quad t = { frac {1} {1 + px}}}
- , где p = 0,3275911, a 1 = 0,254829592, a 2 = −0,284496736, a 3 = 1,421413741, a 4 = −1,453152027, a 5 = 1,061405429
- Все эти приближения действительны для x ≥ 0 Чтобы использовать эти приближения для отрицательного x, викорируйте тот факт, что erf (x) — нечетная функция, поэтому erf (x) = −erf (−x).
- Экспоненциальные границы и чисто экспоненциальное приближение для дополнительных функций задаются как
-
- erfc (x) ≤ 1 2 e — 2 x 2 + 1 2 e — x 2 ≤ e — x 2, x>0 erfc ( х) ≈ 1 6 е — х 2 + 1 2 е — 4 3 х 2, х>0. { displaystyle { begin {align} operatorname {erfc} (x) leq { frac {1} {2}} e ^ {- 2x ^ {2}} + { frac {1} {2} } e ^ {- x ^ {2}} leq e ^ {- x ^ {2}}, qquad x>0 имя оператора {erfc} (x) приблизительно { frac {1} { 6}} e ^ {- x ^ {2}} + { frac {1} {2}} e ^ {- { frac {4} {3}} x ^ {2}}, qquad x>0. end {align}}}
- erfc (x) ≤ 1 2 e — 2 x 2 + 1 2 e — x 2 ≤ e — x 2, x>0 erfc ( х) ≈ 1 6 е — х 2 + 1 2 е — 4 3 х 2, х>0. { displaystyle { begin {align} operatorname {erfc} (x) leq { frac {1} {2}} e ^ {- 2x ^ {2}} + { frac {1} {2} } e ^ {- x ^ {2}} leq e ^ {- x ^ {2}}, qquad x>0 имя оператора {erfc} (x) приблизительно { frac {1} { 6}} e ^ {- x ^ {2}} + { frac {1} {2}} e ^ {- { frac {4} {3}} x ^ {2}}, qquad x>0. end {align}}}
-
- erfc (x) ≈ (1 — e — A x) e — x 2 B π х. { displaystyle operatorname {erfc} left (x right) приблизительно { frac { left (1-e ^ {- Ax} right) e ^ {- x ^ {2}}} {B { sqrt { pi}} x}}.}
- erfc (x) ≈ (1 — e — A x) e — x 2 B π х. { displaystyle operatorname {erfc} left (x right) приблизительно { frac { left (1-e ^ {- Ax} right) e ^ {- x ^ {2}}} {B { sqrt { pi}} x}}.}
- Они определили {A, B} = {1.98, 1.135}, { displaystyle {A, B } = {1.98,1.135 },}
, что дает хорошее приближение для всех x ≥ 0. { displaystyle x geq 0.}
- Одноканальная нижняя граница:
-
- erfc (x) ≥ 2 e π β — 1 β е — β Икс 2, Икс ≥ 0, β>1, { Displaystyle OperatorName {erfc} (x) geq { sqrt { frac {2e} { pi}}} { frac { sqrt { beta -1}} { beta}} e ^ {- beta x ^ {2}}, qquad x geq 0, beta>1,}
- erfc (x) ≥ 2 e π β — 1 β е — β Икс 2, Икс ≥ 0, β>1, { Displaystyle OperatorName {erfc} (x) geq { sqrt { frac {2e} { pi}}} { frac { sqrt { beta -1}} { beta}} e ^ {- beta x ^ {2}}, qquad x geq 0, beta>1,}
- где параметр β может быть выбран, чтобы минимизировать ошибку на желаемом интервале приближения.
- Другое приближение дано Сергеем Виницким с использованием его «глобальных приближений Паде»:
-
- erf (x) ≈ sgn (x) 1 — exp (- x 2 4 π + ax 2 1 + ax 2) { displaystyle operatorname {erf} (x) приблизительно Operatorname {sgn} (x) { sqrt {1- exp left (-x ^ {2} { frac {{ frac {4} { pi) })} + ax ^ {2}} {1 + ax ^ {2}}} right)}}}
- erf (x) ≈ sgn (x) 1 — exp (- x 2 4 π + ax 2 1 + ax 2) { displaystyle operatorname {erf} (x) приблизительно Operatorname {sgn} (x) { sqrt {1- exp left (-x ^ {2} { frac {{ frac {4} { pi) })} + ax ^ {2}} {1 + ax ^ {2}}} right)}}}
- где
-
- a = 8 (π — 3) 3 π (4 — π) ≈ 0, 140012. { displaystyle a = { frac {8 ( pi -3)} {3 pi (4- pi)}} приблизительно 0,140012.}
- a = 8 (π — 3) 3 π (4 — π) ≈ 0, 140012. { displaystyle a = { frac {8 ( pi -3)} {3 pi (4- pi)}} приблизительно 0,140012.}
- Это сделано так, чтобы быть очень точным в окрестностях 0 и добавление бесконечности, а относительная погрешность меньше 0,00035 для всех действительных x. Использование альтернативного значения ≈ 0,147 снижает максимальную относительную ошибку примерно до 0,00013.
- Это приближение можно инвертировать, чтобы получить приближение для других функций ошибок:
-
- erf — 1 (x) ≈ sgn (x) (2 π a + ln (1 — x 2) 2) 2 — ln (1 — x 2) a — (2 π a + ln (1 — x 2) 2). { displaystyle operatorname {erf} ^ {- 1} (x) приблизительно operatorname {sgn} (x) { sqrt {{ sqrt { left ({ frac {2} { pi a}} + { frac { ln (1-x ^ {2})} {2}} right) ^ {2} — { frac { ln (1-x ^ {2})} {a}}}} — left ({ frac {2} { pi a}} + { frac { ln (1-x ^ {2})} {2}} right)}}.}
- erf — 1 (x) ≈ sgn (x) (2 π a + ln (1 — x 2) 2) 2 — ln (1 — x 2) a — (2 π a + ln (1 — x 2) 2). { displaystyle operatorname {erf} ^ {- 1} (x) приблизительно operatorname {sgn} (x) { sqrt {{ sqrt { left ({ frac {2} { pi a}} + { frac { ln (1-x ^ {2})} {2}} right) ^ {2} — { frac { ln (1-x ^ {2})} {a}}}} — left ({ frac {2} { pi a}} + { frac { ln (1-x ^ {2})} {2}} right)}}.}
Многочлен
Приближение с максимальной ошибкой 1,2 × 10-7 { displaystyle 1,2 times 10 ^ {- 7}}
- erf ( x) = {1 — τ x ≥ 0 τ — 1 x < 0 {displaystyle operatorname {erf} (x)={begin{cases}1-tau xgeq 0tau -1x<0end{cases}}}
с
- τ = t ⋅ exp (- x 2 — 1,26551223 + 1,00002368 t + 0,37409196 t 2 + 0,09678418 t 3 — 0,18628806 t 4 + 0,27886807 t 5 — 1,13520398 t 6 + 1,48851587 t 7 — 0,82215223 t 8 + 0,17087277 t 9) { displaystyle { begin {align} tau = t cdot exp left (-x ^ {2} -1,26551223 + 1,00002368 t + 0,37409196t ^ {2} + 0,09678418t ^ {3} -0,18628806t ^ {4} вправо. left. qquad qquad qquad + 0,27886807t ^ {5} -1,13520398t ^ {6} + 1,48851587t ^ {7} -0,82215223t ^ {8} + 0,17087 277t ^ {9} right) end {align}}}
и
- t = 1 1 + 0,5 | х |. { displaystyle t = { frac {1} {1 + 0,5 | x |}}.}
Таблица значений
| x | erf(x) | 1-erf (x) |
|---|---|---|
| 0 | 0 | 1 |
| 0,02 | 0,022564575 | 0,977435425 |
| 0,04 | 0,045111106 | 0,954888894 |
| 0,06 | 0,067621594 | 0, 932378406 |
| 0,08 | 0.090078126 | 0,909921874 |
| 0,1 | 0,112462916 | 0,887537084 |
| 0,2 | 0,222702589 | 0,777297411 |
| 0,3 | 0,328626759 | 0,671373241 |
| 0, 4 | 0,428392355 | 0,571607645 |
| 0,5 | 0,520499878 | 0,479500122 |
| 0,6 | 0.603856091 | 0,396143909 |
| 0,7 | 0,677801194 | 0,322198806 |
| 0,8 257> | 0,742100965 | 0,257899035 |
| 0,9 | 0,796908212 | 0,203091788 |
| 1 | 0,842700793 | 0, 157299207 |
| 1,1 | 0,88020507 | 0,11979493 |
| 1,2 | 0,910313978 | 0,089686022 |
| 1,3 | 0,934007945 | 0,065992055 |
| 1,4 | 0.95228512 | 0,04771488 |
| 1,5 | 0, 966105146 | 0,033894854 |
| 1,6 | 0,976348383 | 0,023651617 |
| 1,7 | 0,983790459 | 0,016209541 |
| 1,8 | 0,989090502 | 0,010909498 |
| 1,9 | 0,992790429 | 0,007209571 |
| 2 | 0,995322265<25767> | 0,00477 |
| 2.1 | 0.997020533 | 0.002979467 |
| 2.2 | 0.998137154 | 0,001862846 |
| 2,3 | 0,998856823 | 0,001143177 |
| 2,4 | 0,999311486 | 0,000688514 |
| 2,5 | 0.999593048 | 0.000406952 |
| 3 | 0.99997791 | 0,00002209 |
| 3,5 | 0,999999257 | 0,000000743 |
Связанные функции
Дополнительная функция
дополнительная функция ошибок, обозначается erfc { displaystyle mathrm {erfc}}
- erfc (x) = 1 — erf (x) = 2 π ∫ x ∞ e — t 2 dt знак равно е — Икс 2 erfcx (х), { displaystyle { begin {выровнено} OperatorName {erfc} (x) = 1- operatorname {erf} (x) [5p t] = { frac {2} { sqrt { pi}}} int _ {x} ^ { infty} e ^ {- t ^ {2}} , dt [5pt] = e ^ {- x ^ {2}} operatorname {erfcx} (x), end {align}}}
, который также определяет erfcx { displaystyle mathrm {erfcx} }


- erfc (x ∣ x ≥ 0) = 2 π ∫ 0 π / 2 exp (- x 2 sin 2 θ) d θ. { displaystyle operatorname {erfc} (x mid x geq 0) = { frac {2} { pi}} int _ {0} ^ { pi / 2} exp left (- { frac {x ^ {2}} { sin ^ {2} theta}} right) , d theta.}
Это выражение действительно только для положительных значений x, но его можно использовать вместе с erfc (x) = 2 — erfc (−x), чтобы получить erfc (x) для отрицательных значений. Эта форма выгодна тем, что диапазон интегрирования является фиксированным и конечным. Расширение этого выражения для erfc { displaystyle mathrm {erfc}}
- erfc (x + y ∣ x, y ≥ 0) = 2 π ∫ 0 π / 2 ехр (- x 2 sin 2 θ — y 2 cos 2 θ) d θ. { displaystyle operatorname {erfc} (x + y mid x, y geq 0) = { frac {2} { pi}} int _ {0} ^ { pi / 2} exp left (- { frac {x ^ {2}} { sin ^ {2} theta}} — { frac {y ^ {2}} { cos ^ {2} theta}} right) , d theta.}
Функция мнимой ошибки
мнимой ошибки, обозначаемая erfi, обозначает ошибки как
- erfi (x) = — i erf (ix) Знак равно 2 π ∫ 0 xet 2 dt знак равно 2 π ex 2 D (x), { displaystyle { begin {align} operatorname {erfi} (x) = — i operatorname {erf} (ix) [ 5pt] = { frac {2} { sqrt { pi}}} int _ {0} ^ {x} e ^ {t ^ {2}} , dt [5pt] = { frac {2} { sqrt { pi}}} e ^ {x ^ {2}} D (x), end {align}}}
где D (x) — функция Доусона (который можно использовать вместо erfi, чтобы избежать арифметического переполнения ).
Несмотря на название «функция мнимой ошибки», erfi (x) { displaystyle operatorname {erfi} (x)}
Функция Когда ошибки оценивается для произвольных сложных аргументов z, результирующая комплексная функция ошибок обычно обсуждается в масштабированной форме как функция Фаддеева :
- w (z) = e — z 2 erfc (- iz) = erfcx (- iz). { displaystyle w (z) = e ^ {- z ^ {2}} operatorname {erfc} (-iz) = operatorname {erfcx} (-iz).}
Кумулятивная функция распределения
Функция ошибок по существующей стандартной стандартной функции нормального кумулятивного распределения, обозначаемой нормой (x) в некоторых языках программного обеспечения, поскольку они отличаются только масштабированием и переводом. Действительно,
- Φ (x) = 1 2 π ∫ — ∞ xe — t 2 2 dt = 1 2 [1 + erf (x 2)] = 1 2 erfc (- x 2) { displaystyle Phi (x) = { frac {1} { sqrt {2 pi}}} int _ {- infty} ^ {x} e ^ { tfrac {-t ^ {2}} {2}} , dt = { frac {1} {2}} left [1+ operatorname {erf} left ({ frac {x} { sqrt {2}}} right) right] = { frac {1} {2}} operatorname {erfc} left (- { frac {x} { sqrt {2}}} right)}
или переставлен для erf и erfc:
- erf ( x) = 2 Φ (x 2) — 1 erfc (x) = 2 Φ (- x 2) = 2 (1 — Φ (x 2)). { displaystyle { begin {align} operatorname {erf} (x) = 2 Phi left (x { sqrt {2}} right) -1 operatorname {erfc} (x) = 2 Phi left (-x { sqrt {2}} right) = 2 left (1- Phi left (x { sqrt {2}} right) right). End {выравнивается} }}
Следовательно, функция ошибок также тесно связана с Q-функцией, которая является вероятностью хвоста стандартного нормального распределения. Q-функция может быть выражена через функцию ошибок как
- Q (x) = 1 2 — 1 2 erf (x 2) = 1 2 erfc (x 2). { displaystyle Q (x) = { frac {1} {2}} — { frac {1} {2}} operatorname {erf} left ({ frac {x} { sqrt {2}}) } right) = { frac {1} {2}} operatorname {erfc} left ({ frac {x} { sqrt {2}}} right).}
Обратное значение из Φ { displaystyle Phi}
- пробит (p) = Φ — 1 (p) = 2 erf — 1 (2 p — 1) = — 2 erfc — 1 (2 p). { displaystyle operatorname {probit} (p) = Phi ^ {- 1} (p) = { sqrt {2}} operatorname {erf} ^ {- 1} (2p-1) = — { sqrt {2}} operatorname {erfc} ^ {- 1} (2p).}
Стандартный нормальный cdf чаще используется в вероятности и статистике, а функция ошибок чаще используется в других разделах математики.
Функция ошибки является частным случаем функции Миттаг-Леффлера и может также быть выражена как сливающаяся гипергеометрическая функция (функция Куммера):
- erf (х) знак равно 2 х π M (1 2, 3 2, — х 2). { displaystyle operatorname {erf} (x) = { frac {2x} { sqrt { pi}}} M left ({ frac {1} {2}}, { frac {3} {2 }}, — x ^ {2} right).}
Он имеет простое выражение в терминах интеграла Френеля.
В терминах регуляризованной гамма-функции P и неполная гамма-функция,
- erf (x) = sgn (x) P (1 2, x 2) = sgn (x) π γ (1 2, x 2). { displaystyle operatorname {erf} (x) = operatorname {sgn} (x) P left ({ frac {1} {2}}, x ^ {2} right) = { frac { operatorname {sgn} (x)} { sqrt { pi}}} gamma left ({ frac {1} {2}}, x ^ {2} right).}
sgn (x) { displaystyle operatorname {sgn} (x)}
Обобщенные функции ошибок

π { displaystyle scriptstyle { sqrt { pi}}}

Некоторые авторы обсуждают более общие функции:
- E n (x) = n! π ∫ 0 Икс е — Т N д т знак равно N! π ∑ п знак равно 0 ∞ (- 1) п Икс N п + 1 (N п + 1) п!. { displaystyle E_ {n} (x) = { frac {n!} { sqrt { pi}}} int _ {0} ^ {x} e ^ {- t ^ {n}} , dt = { frac {n!} { sqrt { pi}}} sum _ {p = 0} ^ { infty} (- 1) ^ {p} { frac {x ^ {np + 1}} {(np + 1) p!}}.}
Примечательные случаи:
- E0(x) — прямая линия, проходящая через начало координат: E 0 (x) = xe π { displaystyle textstyle E_ {0} (x) = { dfrac {x} {e { sqrt { pi}}}}}
- E2(x) — функция, erf (x) ошибки.
После деления на n!, все E n для нечетных n выглядят похожими (но не идентичными) друг на друга. Аналогично, E n для четного n выглядят похожими (но не идентичными) друг другу после простого деления на n!. Все обобщенные функции ошибок для n>0 выглядят одинаково на положительной стороне x графика.
Эти обобщенные функции могут быть эквивалентно выражены для x>0 с помощью гамма-функции и неполной гамма-функции :
- E n (x) = 1 π Γ (n) (Γ (1 n) — Γ (1 n, xn)), x>0. { displaystyle E_ {n} (x) = { frac {1} { sqrt { pi}}} Gamma (n) left ( Gamma left ({ frac {1} {n}} right) — Gamma left ({ frac {1} {n}}, x ^ {n} right) right), quad quad x>0.}
Следовательно, мы можем определить ошибку функция в терминах неполной гамма-функции:
- erf (x) = 1 — 1 π Γ (1 2, x 2). { displaystyle operatorname {erf} (x) = 1 — { frac {1} { sqrt { pi}}} Gamma left ({ frac {1} {2}}, x ^ {2} right).}
Итерированные интегралы дополнительных функций
Повторные интегралы дополнительные функции ошибок определения как
- inerfc (z) = ∫ z ∞ in — 1 erfc (ζ) d ζ i 0 erfc (z) = erfc (z) i 1 erfc (z) = ierfc (z) знак равно 1 π е — z 2 — z erfc (z) я 2 erfc (z) = 1 4 [erfc (z) — 2 z ierfc (z)] { displaystyle { begin {align } operatorname {i ^ {n} erfc} (z) = int _ {z} ^ { infty} operatorname {i ^ {n-1} erfc} ( zeta) , d zeta имя оператора {i ^ {0} erfc} (z) = operatorname {erfc} (z) operatorname {i ^ {1} erfc} (z) = operat orname {ierfc} (z) = { frac { 1} { sqrt { pi}}} e ^ {- z ^ {2}} — z operatorname {erfc} (z) operatorname {i ^ {2} erfc} (z) = { frac {1} {4}} left [ operatorname {erfc} (z) -2z operatorname {ierfc} (z) right] end {выровнено}}
Общая рекуррентная формула:
- 2 ninerfc (z) = in — 2 erfc (z) — 2 цинк — 1 erfc (z) { displaystyle 2n operatorname {i ^ {n} erfc} (z) = operatorname {i ^ { n-2} erfc} (z) -2z operatorname {i ^ {n-1} erfc} (z)}
У них есть степенной ряд
- в erfc (z) = ∑ j = 0 ∞ (- Z) J 2 N — JJ! Γ (1 + N — J 2), { displaystyle i ^ {n} operatorname {erfc} (z) = sum _ {j = 0} ^ { infty} { frac {(-z) ^ { j}} {2 ^ {nj} j! Gamma left (1 + { frac {nj} {2}} right)}},}
из следуют свойства симметрии
- i 2 m ERFC (- Z) знак равно — я 2 m ERFC (Z) + ∑ Q знак равно 0 мZ 2 д 2 2 (м — д) — 1 (2 д)! (м — д)! { displaystyle i ^ {2m} operatorname {erfc} (-z) = — i ^ {2m} operatorname {erfc} (z) + sum _ {q = 0} ^ {m} { frac {z ^ {2q}} {2 ^ {2 (mq) -1} (2q)! (Mq)!}}}
и
- i 2 m + 1 erfc (- z) = i 2 m + 1 erfc (г) + ∑ ä знак равно 0 ìZ 2 ä + 1 2 2 ( м — д) — 1 (2 д + 1)! (м — д)!. { displaystyle i ^ {2m + 1} operatorname {erfc} (-z) = i ^ {2m + 1} operatorname {erfc} (z) + sum _ {q = 0} ^ {m} { гидроразрыва {z ^ {2q + 1}} {2 ^ {2 (mq) -1} (2q + 1)! (mq)!}}.}
Реализации
Как действительная функция вещественного аргумента
- В операционных системах, совместимых с Posix, заголовок math.h должен являть, а математическая библиотека libm должна быть функция erf и erfc (двойная точность ), а также их одинарная точность и расширенная точность аналоги erff, erfl и erfc, erfcl.
- Библиотека GNU Scientific предоставляет функции erf, erfc, log (erf) и масштабируемые функции ошибок.
Как сложная функция комплексного аргумента
- libcerf, числовая библиотека C для сложных функций, предоставляет комплексные функции cerf, cerfc, cerfcx и реальные функции erfi, erfcx с точностью 13–14 цифр на основе функции Фаддеева, реализованной в пакете MIT Faddeeva Package
См. также
Связанные ции
- интеграл Гаусса, по всей действительной прямой
- функция Гаусса, производная
- функция Доусона, перенормированная функция мнимой ошибки
- интеграл Гудвина — Стона
по вероятности
- Нормальное распределение
- Нормальная кумулятивная функция распределения, масштабированная и сдвинутая форма функций ошибок
- Пробит, обратная или квантильная функция нормального CDF
- Q-функция, вероятность хвоста нормального распределения
Ссылки
Дополнительная литература
- Abramowitz, Milton ; Стегун, Ирен Энн, ред. (1983) [июнь 1964]. «Глава 7». Справочник по математическим функциям с формулами, графики и математическими таблицами. Прикладная математика. 55 (Девятое переиздание с дополнительными исправлениями; десятое оригинальное издание с исправлениями (декабрь 1972 г.); первое изд.). Вашингтон.; Нью-Йорк: Министерство торговли США, Национальное бюро стандартов; Dover Publications. п. 297. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253.
- Press, William H.; Теукольский, Саул А.; Веттерлинг, Уильям Т.; Фланнери, Брайан П. (2007), «Раздел 6.2. Неполная гамма-функция и функция ошибок », Числовые рецепты: Искусство научных вычислений (3-е изд.), Нью-Йорк: Cambridge University Press, ISBN 978-0-521- 88068-8
- Темме, Нико М. (2010), «Функции ошибок, интегралы Доусона и Френеля», в Олвер, Фрэнк У. Дж. ; Лозье, Даниэль М.; Бойсверт, Рональд Ф.; Кларк, Чарльз В. (ред.), Справочник NIST по математическим функциям, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248
Внешние ссылки
- MathWorld — Erf
- Таблица интегралов функций ошибок
График функции ошибок
В математике функция ошибок (функция Лапласа) — это неэлементарная функция, возникающая в теории вероятностей, статистике и теории дифференциальных уравнений в частных производных. Она определяется как
.
Дополнительная функция ошибок, обозначаемая 

.
Комплексная функция ошибок, обозначаемая 
.
Содержание
- 1 Свойства
- 2 Применение
- 3 Асимптотическое разложение
- 4 Родственные функции
- 4.1 Обобщённые функции ошибок
- 4.2 Итерированные интегралы дополнительной функции ошибок
- 5 Реализация
- 6 См. также
- 7 Литература
- 8 Ссылки
Свойства
- Функция ошибок нечётна:
- Для любого комплексного
выполняется
где черта обозначает комплексное сопряжение числа 
- Функция ошибок не может быть представлена через элементарные функции, но, разлагая интегрируемое выражение в ряд Тейлора и интегрируя почленно, мы можем получить её представление в виде ряда:
Это равенство выполняется (и ряд сходится) как для любого вещественного 
- Для итеративного вычисления элементов ряда полезно представить его в альтернативном виде:
поскольку 



- Функция ошибок на бесконечности равна единице; однако это справедливо только при приближении к бесконечности по вещественной оси, так как:
- При рассмотрении функции ошибок в комплексной плоскости точка
будет для неё существенно особой.
- Производная функции ошибок выводится непосредственно из определения функции:
- Обратная функция ошибок представляет собой ряд
где c0 = 1 и
Поэтому ряд можно представить в следующем виде (заметим, что дроби сокращены):
[1]
Последовательности числителей и знаменателей после сокращения — A092676 и A132467 в OEIS; последовательность числителей до сокращения — A002067 в OEIS.
Дополнительная функция ошибок
Применение
Если набор случайных чисел подчиняется нормальному распределению со стандартным отклонением 


Функция ошибок и дополнительная функция ошибок встречаются в решении некоторых дифференциальных уравнений, например, уравнения теплопроводности с граничными условиями описываемыми функцией Хевисайда («ступенькой»).
В системах цифровой оптической коммуникации, вероятность ошибки на бит также выражается формулой, использующей функцию ошибок.
Асимптотическое разложение
При больших 
Хотя для любого конечного 

Другое приближение даётся формулой
где
Родственные функции
С точностью до масштаба и сдвига, функция ошибок совпадает с нормальным интегральным распределением, обозначаемым
Обратная функция к 

Нормальное интегральное распределение чаще применяется в теории вероятностей и математической статистике, в то время как функция ошибок чаще применяется в других разделах математики.
Функция ошибок является частным случаем функции Миттаг-Леффлера, а также может быть представлена как вырожденная гипергеометрическая функция (функция Куммера):
Функция ошибок выражается также через интеграл Френеля. В терминах регуляризованной неполной гамма-функции P и неполной гамма-функции,
Обобщённые функции ошибок
Некоторые авторы обсуждают более общие функции
Примечательными частными случаями являются:
После деления на 







На полуоси 
Следовательно, мы можем выразить функцию ошибок через гамма-функцию:
Итерированные интегралы дополнительной функции ошибок
Итерированные интегралы дополнительной функции ошибок определяются как
Их можно разложить в ряд:
откуда следуют свойства симметрии
и
Реализация
В стандарте языка Си (ISO/IEC 9899:1999, 7.12.8) предусмотрены функция ошибок 

math.h или cmath. Там же есть пары функций erff(),erfcf() и erfl(),erfcl(). Первая пара получает и возвращает значения типа float, а вторая — значения типа long double. Соответствующие функции также содержатся в библиотеке Math проекта Boost.
В языке Java функции ошибок нет в стандартной библиотеке математических функций java.lang.Math [2]. Класс Erf есть в пакете org.apache.commons.math.special от Apache [3]. Однако эта библиотека не является одной из стандартных библиотек Java 6.
Matlab[4], Mathematica и Maxima[5] содержат обычную и дополнительную функцию ошибок, а также обратные к ним функции.
В языке Python функция ошибок доступна из стандартной библиотеки math, начиная с версии 2.7. [6] Также функция ошибок, дополнительная функция ошибок и многие другие специальные функции определены в модуле Special проекта SciPy [7].
В языке Erlang функция ошибок и дополнительная функция ошибок доступны из стандартного модуля math, [8].
См. также
- Функция Гаусса
- Функция Доусона
Литература
- Milton Abramowitz and Irene A. Stegun, eds. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. New York: Dover, 1972. (См. часть 7)
- Nikolai G. Lehtinen «Error functions», April 2010 [9]
Ссылки
- MathWorld — Erf
- Онлайновый калькулятор Erf и много других специальных функций (до 6 знаков)
- Онлайновый калькулятор, вычисляющий в том числе Erf
В математике функция ошибок (также называемая функцией ошибок Гаусса ), часто обозначаемая erf , является сложной функцией комплексной переменной, определяемой как: [1]
Этот интеграл представляет собой специальную ( неэлементарную ) сигмовидную функцию, которая часто встречается в уравнениях вероятности , статистики и дифференциальных уравнений в частных производных . Во многих из этих приложений аргумент функции является действительным числом. Если аргумент функции является действительным, то значение функции также является действительным.
В статистике для неотрицательных значений x функция ошибок имеет следующую интерпретацию: для случайной величины Y, которая нормально распределена со средним значением 0 и стандартным отклонением 1/√ 2, erf x — вероятность того, что Y попадает в диапазон [- x , x ] .
Две тесно связанные функции — это дополнительная функция ошибок ( erfc ), определяемая как
и функция мнимой ошибки ( erfi ), определяемая как
где i — мнимая единица .
Имя
Название «функция ошибок» и ее сокращение erf были предложены Дж. В. Л. Глейшером в 1871 г. в связи с его связью с «теорией вероятности и, в частности, теорией ошибок ». [2] Дополнение к функции ошибок также обсуждалось Глейшером в отдельной публикации в том же году. [3]
Для «закона легкости» ошибок, плотность которых определяется как
( нормальное распределение ), Глейшер вычисляет вероятность ошибки, лежащей между p и q, как:
Приложения
Когда результаты серии измерений описываются нормальным распределением со стандартным отклонением σ и ожидаемым значением 0, тогда erf (а/σ √ 2) — вероятность того, что ошибка единичного измерения находится между — a и + a для положительного a . Это полезно, например, при определении частоты ошибок по битам в цифровой системе связи.
Ошибки и дополнительные функции ошибок возникают, например, в решениях уравнения теплопроводности, когда граничные условия задаются ступенчатой функцией Хевисайда .
Функция ошибок и ее приближения могут использоваться для оценки результатов, которые имеют высокую или низкую вероятность. Дана случайная величина X ~ Norm [ μ , σ ] (нормальное распределение со средним μ и стандартным отклонением σ ) и константа L < μ :
где A и B — некоторые числовые константы. Если L достаточно далеко от среднего, а именно μ — L ≥ σ √ ln k , то:
поэтому вероятность стремится к 0 при k → ∞ .
Вероятность того, что X находится в интервале [ L a , L b ], может быть получена как
Свойства
Интегрируем exp (- z 2 )
erf z
Свойство erf (- z ) = −erf z означает, что функция ошибок является нечетной функцией . Это напрямую связано с тем, что подынтегральное выражение e — t 2 является четной функцией (интегрирование четной функции дает нечетную функцию и наоборот).
Для любого комплексного числа z :
где г представляет собой комплексно сопряженное из г .
Подынтегральное выражение f = exp (- z 2 ) и f = erf z показано на комплексной плоскости z на рисунках справа. Уровень Im ( f ) = 0 показан жирной зеленой линией. Отрицательные целые значения Im ( f ) показаны толстыми красными линиями. Положительные целые значения Im ( f ) показаны толстыми синими линиями. Промежуточные уровни Im ( f ) = constant показаны тонкими зелеными линиями. Промежуточные уровни Re ( f ) =константы показаны тонкими красными линиями для отрицательных значений и тонкими синими линиями для положительных значений.
Функция ошибок при + ∞ равна 1 (см. Интеграл Гаусса ). На действительной оси erf z стремится к единице при z → + ∞ и −1 при z → −∞ . На мнимой оси он стремится к ± i ∞ .
Серия Тейлор
Функция ошибок — это целая функция ; у него нет сингулярностей (кроме бесконечности), и его разложение Тейлора всегда сходится, но, как известно, «[…] его плохая сходимость, если x > 1 ». [4]
Определяющий интеграл не может быть вычислен в замкнутой форме в терминах элементарных функций , но, раскладывая подынтегральное выражение e — z 2 в его ряд Маклорена и интегрируя член за членом, можно получить ряд Маклорена функции ошибок как:
которое выполняется для любого комплексного числа z . Члены знаменателя — это последовательность (последовательность A007680 в OEIS ) в OEIS .
Для итеративного расчета вышеуказанного ряда может быть полезна следующая альтернативная формулировка:
потому что — (2 к — 1) z 2/к (2 к + 1)выражает множитель для превращения k- го члена в ( k + 1) -й член (считая z первым членом).
Функция мнимой ошибки имеет очень похожий ряд Маклорена, а именно:
которое выполняется для любого комплексного числа z .
Производная и интеграл
Производная функции ошибок сразу следует из ее определения:
Отсюда немедленно вычисляется производная мнимой функции ошибок:
Первообразная функции ошибки, получаемый путем интегрирования по частям , является
Первообразной функции мнимой ошибки, которую также можно получить интегрированием по частям, является
Производные высшего порядка даются формулами
где H — полиномы Эрмита физиков . [5]
Серия Bürmann
Разложение [6], которое сходится быстрее для всех действительных значений x, чем разложение Тейлора, получается с помощью теоремы Ганса Генриха Бюрмана : [7]
где sgn — знаковая функция . Сохраняя только первые два коэффициента и выбирая c 1 =31 год/200и c 2 = —341/8000, полученное приближение показывает свою наибольшую относительную ошибку при x = ± 1,3796 , где она меньше 0,0036127:
Обратные функции
Учитывая комплексное число z , не существует уникального комплексного числа w, удовлетворяющего erf w = z , поэтому истинная обратная функция будет многозначной. Однако для −1 < x <1 существует уникальное действительное число, обозначенное erf −1 x, удовлетворяющее
Функция обратной ошибки обычно определяется с помощью области (-1,1) , и она ограничена этой областью во многих системах компьютерной алгебры. Однако его можно распространить на диск | z | <1 комплексной плоскости, используя ряд Маклорена
где c 0 = 1 и
Итак, у нас есть расширение в ряд (общие множители из числителей и знаменателей удалены):
(После отмены дроби числителя / знаменателя являются записями OEIS : A092676 / OEIS : A092677 в OEIS ; без отмены члены числителя приведены в записи OEIS : A002067 .) Значение функции ошибок при ± ∞ равно ± 1 .
Для | z | <1 , имеем erf (erf −1 z ) = z .
Обратная дополнительная функция ошибок определяются как
Для действительного x существует единственное действительное число erfi −1 x, удовлетворяющее erfi (erfi −1 x ) = x . Функция обратной мнимой ошибки определяется как erfi −1 x . [8]
Для любого вещественного х , метод Ньютона может быть использован для вычисления ЕрФИ -1 х , а для -1 ≤ х ≤ 1 , следующие сходится ряд Маклорена:
где c k определено, как указано выше.
Асимптотическое разложение
Полезное асимптотическое разложение дополнительной функции ошибок (и, следовательно, также функции ошибок) для больших вещественных x :
где (2 n — 1) !! — двойной факториал числа (2 n — 1) , который является произведением всех нечетных чисел до (2 n — 1) . Этот ряд расходится для любого конечного x , и его смысл как асимптотического разложения состоит в том, что для любого целого числа N ≥ 1 выполняется
где остаток в обозначениях Ландау равен
при x → ∞ .
Действительно, точное значение остатка равно
что легко следует по индукции, записывая
и интеграция по частям.
Для достаточно больших значений x необходимы только первые несколько членов этого асимптотического разложения, чтобы получить хорошее приближение erfc x (в то время как для не слишком больших значений x приведенное выше разложение Тейлора при 0 обеспечивает очень быструю сходимость).
Продолжение дроби
Цепная дробь расширение дополнительной функции ошибок является следующим : [9]
Интеграл функции ошибок с функцией плотности Гаусса
которая, по-видимому, связана с Нг и Геллером, формула 13 в разделе 4.3 [10] с заменой переменных.
Факториальная серия
Обратный факторный ряд :
сходится при Re ( z 2 )> 0 . Здесь
z n обозначает возрастающий факториал , а s ( n , k ) обозначает число Стирлинга первого рода со знаком . [11] [12]
Также существует представление бесконечной суммой, содержащее двойной факториал :
Численные приближения
Аппроксимация с элементарными функциями
- Абрамовиц и Стегун дают несколько приближений с различной точностью (уравнения 7.1.25–28). Это позволяет выбрать наиболее быстрое приближение, подходящее для данного приложения. В порядке увеличения точности это:
(максимальная ошибка: 5 × 10 −4 )
где a 1 = 0,278393 , a 2 = 0,230389 , a 3 = 0,000972 , a 4 = 0,078108
(максимальная ошибка: 2,5 × 10 −5 )
где p = 0,47047 , a 1 = 0,3480242 , a 2 = −0,0958798 , a 3 = 0,7478556
(максимальная ошибка: 3 × 10 −7 )
где a 1 = 0,0705230784 , a 2 = 0,0422820123 , a 3 = 0,0092705272 , a 4 = 0,0001520143 , a 5 = 0,0002765672 , a 6 = 0,0000430638
(максимальная ошибка: 1,5 × 10 −7 )
где p = 0,3275911 , a 1 = 0,254829592 , a 2 = −0,284496736 , a 3 = 1,421413741 , a 4 = −1,453152027 , a 5 = 1,061405429.
Все эти приближения верны для x ≥ 0 . Чтобы использовать эти приближения для отрицательного x , используйте тот факт, что erf x — нечетная функция, поэтому erf x = −erf (- x ) . - Экспоненциальные границы и чисто экспоненциальное приближение для дополнительной функции ошибок даны в [13]
- Вышеупомянутое было обобщено до сумм из N экспонент [14] с возрастающей точностью в терминах N, так что erfc x может быть точно аппроксимирован или ограничен величиной 2 Q̃ ( √ 2 x ) , где
В частности, существует систематическая методология решения числовых коэффициентов {( a n , b n )}N
n = 1которые дают минимаксное приближение или оценку для тесно связанной Q-функции : Q ( x ) ≈ Q̃ ( x ) , Q ( x ) ≤ Q̃ ( x ) или Q ( x ) ≥ Q̃ ( x ) для x ≥ 0 . Коэффициенты {( a n , b n )}N
n = 1для многих вариаций экспоненциальных приближений и границ до N = 25 были выпущены в открытый доступ в виде исчерпывающего набора данных. [15] - Точная аппроксимация дополнительной функции ошибок для x ∈ [0, ∞) дана Karagiannidis & Lioumpas (2007) [16], которые показали для соответствующего выбора параметров { A , B }, что
Они определили { A , B } = {1.98,1.135} , что дает хорошее приближение для всех x ≥ 0 . Также доступны альтернативные коэффициенты для настройки точности для конкретного приложения или преобразования выражения в жесткую границу. [17] - Одноканальная нижняя граница [18]
где параметр β может быть выбран так, чтобы минимизировать ошибку на желаемом интервале аппроксимации.
- Другое приближение дано Сергеем Виницким с использованием его «глобальных приближений Паде»: [19] [20] : 2–3
куда
Это сделано так, чтобы быть очень точным в окрестности 0 и в окрестности бесконечности, а относительная ошибка меньше 0,00035 для всех действительных x . Использование альтернативного значения a ≈ 0,147 снижает максимальную относительную ошибку примерно до 0,00013. [21]Это приближение можно инвертировать, чтобы получить приближение для обратной функции ошибок:
- Приближение с максимальной погрешностью 1,2 × 10 −7 для любого действительного аргумента: [22]
с участием
а также
Таблица значений
| Икс | erf x | 1 — эрф х |
|---|---|---|
| 0 | 0 | 1 |
| 0,02 | 0,022 564 575 | 0,977 435 425 |
| 0,04 | 0,045 111 106 | 0,954 888 894 |
| 0,06 | 0,067 621 594 | 0,932 378 406 |
| 0,08 | 0,090 078 126 | 0,909 921 874 |
| 0,1 | 0,112 462 916 | 0,887 537 084 |
| 0,2 | 0,222 702 589 | 0,777 297 411 |
| 0,3 | 0,328 626 759 | 0,671 373 241 |
| 0,4 | 0,428 392 355 | 0,571 607 645 |
| 0,5 | 0,520 499 878 | 0,479 500 122 |
| 0,6 | 0,603 856 091 | 0,396 143 909 |
| 0,7 | 0,677 801 194 | 0,322 198 806 |
| 0,8 | 0,742 100 965 | 0,257 899 035 |
| 0,9 | 0,796 908 212 | 0,203 091 788 |
| 1 | 0,842 700 793 | 0,157 299 207 |
| 1.1 | 0,880 205 070 | 0,119 794 930 |
| 1.2 | 0,910 313 978 | 0,089 686 022 |
| 1.3 | 0,934 007 945 | 0,065 992 055 |
| 1.4 | 0,952 285 120 | 0,047 714 880 |
| 1.5 | 0,966 105 146 | 0,033 894 854 |
| 1.6 | 0,976 348 383 | 0,023 651 617 |
| 1,7 | 0,983 790 459 | 0,016 209 541 |
| 1,8 | 0,989 090 502 | 0,010 909 498 |
| 1.9 | 0,992 790 429 | 0,007 209 571 |
| 2 | 0,995 322 265 | 0,004 677 735 |
| 2.1 | 0,997 020 533 | 0,002 979 467 |
| 2.2 | 0,998 137 154 | 0,001 862 846 |
| 2.3 | 0,998 856 823 | 0,001 143 177 |
| 2,4 | 0,999 311 486 | 0,000 688 514 |
| 2,5 | 0,999 593 048 | 0,000 406 952 |
| 3 | 0,999 977 910 | 0,000 022 090 |
| 3.5 | 0,999 999 257 | 0,000 000 743 |
Дополнительная функция ошибки
Дополнительная функция ошибок , обозначаемая ERFC , определяется как
который также определяет erfcx , масштабированную дополнительную функцию ошибок [23] (которую можно использовать вместо erfc, чтобы избежать арифметического переполнения [23] [24] ). Другая форма erfc x для x ≥ 0 известна как формула Крейга по имени ее первооткрывателя: [25]
Это выражение действительно только для положительных значений x , но его можно использовать вместе с erfc x = 2 — erfc (- x ) для получения erfc ( x ) для отрицательных значений. Эта форма выгодна тем, что диапазон интегрирования является фиксированным и конечным. Расширение этого выражения для erfc суммы двух неотрицательных переменных выглядит следующим образом: [26]
Функция мнимой ошибки
Функция мнимой ошибки , обозначаемая erfi , определяется как
где D ( x ) — функция Доусона (которую можно использовать вместо erfi, чтобы избежать арифметического переполнения [23] ).
Несмотря на название «мнимая функция ошибок», erfi x реально, когда x реально.
Когда функция ошибок оценивается для произвольных комплексных аргументов z , результирующая комплексная функция ошибок обычно обсуждается в масштабированной форме как функция Фаддеева :
Кумулятивная функция распределения
Функция ошибок по существу идентична стандартной нормальной кумулятивной функции распределения , обозначаемой Φ , также называемой нормой ( x ) в некоторых языках программного обеспечения [ необходима цитата ] , поскольку они различаются только масштабированием и переводом. Действительно,
или переставил для erf и erfc :
Следовательно, функция ошибок также тесно связана с Q-функцией , которая представляет собой вероятность хвоста стандартного нормального распределения. Q-функция может быть выражена через функцию ошибок как
Обратное из Ф называется нормальной функции квантиль , или пробит функции и могут быть выражены в терминах функции обратной ошибки как
Стандартный нормальный cdf чаще используется в вероятностях и статистике, а функция ошибок чаще используется в других разделах математики.
Функция ошибок является частным случаем функции Миттаг-Леффлера и также может быть выражена как конфлюэнтная гипергеометрическая функция ( функция Куммера):
Он имеет простое выражение в терминах интеграла Френеля . [ требуется дальнейшее объяснение ]
С точки зрения регуляризованном гамма — функции P и неполной гамма — функции ,
sgn x — знаковая функция .
Обобщенные функции ошибок
График обобщенных функций ошибок E n ( x ) :
серая кривая: E 1 ( x ) =1 — е — х/√ π
красная кривая: E 2 ( x ) = erf ( x )
зеленая кривая: E 3 ( x )
синяя кривая: E 4 ( x )
золотая кривая: E 5 ( x ) .
Некоторые авторы обсуждают более общие функции: [ необходима цитата ]
Известные случаи:
- E 0 ( x ) — прямая линия, проходящая через начало координат: E 0 ( x ) =Икс/е √ π
- E 2 ( x ) — функция ошибок, erf x .
После деления на п ! , все E n для нечетных n похожи (но не идентичны) друг на друга. Точно так же E n для четного n выглядят похожими (но не идентичными) друг на друга после простого деления на n ! . Все обобщенные функции ошибок для n > 0 выглядят одинаково на положительной стороне x графика.
Эти обобщенные функции могут быть эквивалентно выражены для x > 0 с использованием гамма-функции и неполной гамма-функции :
Следовательно, мы можем определить функцию ошибок в терминах неполной гамма-функции:
Итерированные интегралы дополнительной функции ошибок
Повторные интегралы дополнительной функции ошибок определены в [27]
Общая рекуррентная формула
У них есть степенной ряд
откуда следуют свойства симметрии
а также
Реализации
Как реальная функция реального аргумента
- В Posix -совместимый операционных систем, заголовок math.h возвестят и математическая библиотека libm должна обеспечивать функции
erfиerfc( двойной точности ), а также их одинарной точности и повышенной точности аналоговerff,erflиerfcf,erfcl. [28] - GNU Scientific Library предоставляет
erf,erfc,log(erf), и масштабируемые функции ошибок. [29]
Как сложная функция сложного аргумента
- libcerf , цифровая библиотека C для сложных функций ошибок, обеспечивает комплексные функции
cerf,cerfc,cerfcxи реальные функцииerfi,erfcxпримерно с 13-14 точностью цифр, на основе функции Фаддеева , как реализовано в MIT Фаддеевого пакете
См. Также
- Гауссовский интеграл по всей действительной прямой
- Функция Гаусса , производная
- Функция Доусона , перенормированная функция мнимой ошибки
- Интеграл Гудвина – Стэтона
По вероятности
- Нормальное распределение
- Нормальная кумулятивная функция распределения , масштабированная и сдвинутая форма функции ошибок
- Пробит , обратная или квантильная функция нормального CDF
- Q-функция , хвостовая вероятность нормального распределения
Ссылки
- ^ Эндрюс, Ларри С. (1998). Специальные функции математики для инженеров . SPIE Press. п. 110. ISBN 9780819426161.
- ^ Glaisher, Джеймс Уайтбрид Ли (июль 1871). «Об одном классе определенных интегралов» . Лондонский, Эдинбургский и Дублинский философский журнал и научный журнал . 4. 42 (277): 294–302. DOI : 10.1080 / 14786447108640568 . Проверено 6 декабря 2017 года .
- ^ Glaisher, Джеймс Уайтбрид Ли (сентябрь 1871). «Об одном классе определенных интегралов. Часть II» . Лондонский, Эдинбургский и Дублинский философский журнал и научный журнал . 4. 42 (279): 421–436. DOI : 10.1080 / 14786447108640600 . Проверено 6 декабря 2017 года .
- ^ «A007680 — OEIS» . oeis.org . Проверено 2 апреля 2020 .
- ^ Вайсштейн, Эрик В. «Эрф» . MathWorld . Вольфрам.
- ^ Шёпф, HM; Supancic, PH (2014). «О теореме Бюрмана и ее приложении к задачам линейного и нелинейного теплообмена и диффузии» . Журнал Mathematica . DOI : 10.3888 / tmj.16-11 .
- ^ Вайсштейн , EW «Теорема Бюрмана» . Wolfram MathWorld — Интернет-ресурс Wolfram .
- ^ Бергсм, Wicher (2006). «О новом коэффициенте корреляции, его ортогональном разложении и связанных с ним тестах на независимость». arXiv : math / 0604627 .
- ^ Кейт, Энни AM ; Petersen, Vigdis B .; Вердонк, Бриджит; Ваадленд, Хокон; Джонс, Уильям Б. (2008). Справочник по непрерывным дробям для специальных функций . Springer-Verlag. ISBN 978-1-4020-6948-2.
- ^ Ng, Эдвард У .; Геллер, Мюррей (январь 1969). «Таблица интегралов функций ошибок». Журнал исследований Национального бюро стандартов Раздел B . 73B (1): 1. DOI : 10,6028 / jres.073B.001 .
- ^ Schlömilch, Oskar Xavier (1859). «Ueber facultätenreihen» . Zeitschrift für Mathematik und Physik (на немецком языке). 4 : 390–415 . Проверено 4 декабря 2017 года .
- ^ Нильсон, Нильс (1906). Handbuch der Theorie der Gammafunktion (на немецком языке). Лейпциг: BG Teubner. п. 283 Ур. 3 . Проверено 4 декабря 2017 года .
- ^ Chiani, M .; Дардари, Д .; Саймон, МК (2003). «Новые экспоненциальные границы и приближения для вычисления вероятности ошибки в каналах с замираниями» (PDF) . Транзакции IEEE по беспроводной связи . 2 (4): 840–845. CiteSeerX 10.1.1.190.6761 . DOI : 10.1109 / TWC.2003.814350 .
- ^ Танаш, IM; Риихонен, Т. (2020). «Глобальные минимаксные приближения и оценки гауссовой Q-функции суммами экспонент». Транзакции IEEE по коммуникациям . 68 (10): 6514–6524. arXiv : 2007.06939 . DOI : 10.1109 / TCOMM.2020.3006902 . S2CID 220514754 .
- ^ Танаш, IM; Риихонен, Т. (2020). «Коэффициенты для глобального минимаксного приближения и границы для гауссовой Q-функции суммами экспонент [набор данных]» . Зенодо . DOI : 10.5281 / zenodo.4112978 .
- ^ Карагианнидис, GK; Лиумпас, А.С. (2007). «Улучшенное приближение для гауссовой Q-функции» (PDF) . Письма связи IEEE . 11 (8): 644–646.
- ^ Танаш, IM; Риихонен, Т. (2021). «Улучшенные коэффициенты для приближений Карагианнидиса – Лиумпаса и оценки гауссовой Q-функции». Письма связи IEEE . 25 . arXiv : 2101.07631 . DOI : 10,1109 / LCOMM.2021.3052257 .
- ^ Чанг, Сок-Хо; Cosman, Pamela C .; Мильштейн, Лоуренс Б. (ноябрь 2011 г.). «Границы типа Чернова для гауссовской функции ошибок» . Транзакции IEEE по коммуникациям . 59 (11): 2939–2944. DOI : 10.1109 / TCOMM.2011.072011.100049 . S2CID 13636638 .
- ^ Winitzki, Сергей (2003). «Раздел 3.1« Функция ошибок действительного аргумента erf x »» . Равномерные приближения трансцендентных функций . Конспект лекций по информатике. 2667 . Спрингер, Берлин. С. 780–789 . DOI : 10.1007 / 3-540-44839-X_82 . ISBN 978-3-540-40155-1.
- ^ Цзэн, Кайбин; Чен, Ян Цуань (2015). «Глобальные аппроксимации Паде обобщенной функции Миттаг-Леффлера и ее обратной». Дробное исчисление и прикладной анализ . 18 (6): 1492–1506. arXiv : 1310,5592 . DOI : 10,1515 / FCA-2015-0086 . S2CID 118148950 .
Действительно, Виницки [32] представил так называемое глобальное приближение Паде
- ^ Winitzki Сергей (6 февраля 2008). «Удобное приближение для функции ошибок и ее обратной».
- ^ Числовые рецепты в Fortran 77: Искусство научных вычислений ( ISBN 0-521-43064-X ), 1992, стр. 214, Cambridge University Press.
- ^ a b c Cody, WJ (март 1993 г.), «Алгоритм 715: SPECFUN — переносимый пакет FORTRAN, включающий специальные функции и тестовые драйверы» (PDF) , ACM Trans. Математика. Софтв. , 19 (1): 22-32, CiteSeerX 10.1.1.643.4394 , DOI : 10,1145 / 151271,151273 , S2CID 5621105
- ^ Zaghloul, MR (1 марта 2007), «О вычислении профиля Фойгта линии: один собственный интеграл с затухающей синусоиды подынтегральной» , Monthly Notices Королевского астрономического общества , 375 (3): 1043-1048, DOI : 10.1111 / j.1365-2966.2006.11377.x , архивировано с оригинала 6 января 2015 г.
- ^ Джон В. Крейг, Новый, простой и точный результат для расчета вероятности ошибки для двумерных сигнальных созвездий. Архивировано 3 апреля 2012 г. в Wayback Machine , Proceedings of the 1991 IEEE Military Communication Conference, vol. 2. С. 571–575.
- ^ Behnad, Айдын (2020). «Новое расширение формулы Q-функции Крейга и ее применение в анализе производительности EGC с двумя ветвями». Транзакции IEEE по коммуникациям . 68 (7): 4117–4125. DOI : 10.1109 / TCOMM.2020.2986209 . S2CID 216500014 .
- ^ Карслав, HS ; Jaeger, JC (1959), Проводимость тепла в твердых телах (2-е изд.), Oxford University Press, ISBN 978-0-19-853368-9, стр 484
- ^ https://pubs.opengroup.org/onlinepubs/9699919799/basedefs/math.h.html
- ^ https://www.gnu.org/software/gsl/doc/html/specfunc.html#error-functions
Дальнейшее чтение
- Абрамовиц, Милтон ; Стегун, Ирен Энн , ред. (1983) [июнь 1964]. «Глава 7» . Справочник по математическим функциям с формулами, графиками и математическими таблицами . Прикладная математика. 55 (Девятое переиздание с дополнительными исправлениями, десятое оригинальное издание с исправлениями (декабрь 1972 г.); первое изд.). Вашингтон; Нью-Йорк: Министерство торговли США, Национальное бюро стандартов; Dover Publications. п. 297. ISBN. 978-0-486-61272-0. LCCN 64-60036 . Руководство по ремонту 0167642 . LCCN 65-12253 .
- Press, William H .; Teukolsky, Saul A .; Веттерлинг, Уильям Т .; Фланнери, Брайан П. (2007), «Раздел 6.2. Неполная гамма-функция и функция ошибок» , Численные рецепты: Искусство научных вычислений (3-е изд.), Нью-Йорк: Cambridge University Press, ISBN 978-0-521-88068-8
- Темме, Нико М. (2010), «Функции ошибок, интегралы Доусона и Френеля» , в Olver, Frank WJ ; Lozier, Daniel M .; Бойсверт, Рональд Ф .; Кларк, Чарльз В. (ред.), Справочник по математическим функциям NIST , Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248
Внешние ссылки
- MathWorld — Эрф
- Таблица интегралов функций ошибок
Функция ошибок
| Аргумент функции ошибок erf(x) |
| Функция ошибок |
| Дополнительная функция ошибок |
Функция ошибок, она же функция Лапласа, он же интеграл вероятности — все это одна и та же сущность, которая выражается функцией
и используется в статистике и теории вероятностей.
Функция неэлементарная, то есть её нельзя представить в виде элементарных (тригонометрических и алгебраических) функций.
Для расчета в нашем калькуляторе, мы используем связь с неполной гамма функцией
Кроме этого мы сможем здесь же вычислить, дополнительную функцию ошибок, обозначаемую 

В приницпе это все, что можно сказать о ней.
Калькулятор высчитывает результат как в вещественном так и комплексном поле.
Замечание: Функция прекрасно работает на всем поле комплексных чисел при условии если аргумент ( фаза) меньше 180 градусов. Это связано с особенностью вычисления этой функции, неполной гамма функции, интегральной показательной функцией через непрерывные дроби.
Отсюда следует вывод, что при отрицательных вещественных аргументах, функция будет выдавать неверные решения. Но при всех положительных, а также отрицательных комплексных аргументах функция ошибок выдает верный ответ.
Несколько примеров:

В математике функция ошибок (также называемая Функция ошибок Гаусса ), часто обозначаемая erf, является сложной функцией комплексной определяемой как:
- erf z = 2 π ∫ 0 ze — t 2 dt. { displaystyle operatorname {erf} z = { frac {2} { sqrt { pi}}} int _ {0} ^ {z} e ^ {- t ^ {2}} , dt.}
Этот интеграл является особой (не элементарной ) и сигмоидной функцией, которая часто встречается в статистике вероятность, и уравнения в частных производных. Во многих из этих приложений аргумент функции является действительным числом. Если аргумент функции является действительным, значение также является действительным.
В статистике для неотрицательных значений x функция имеет интерпретацию: для случайной величины Y, которая нормально распределена с среднее 0 и дисперсия 1/2, erf x — это вероятность того, что Y попадает в диапазон [-x, x].
Две связанные функции: дополнительные функции ошибок (erfc ), определенная как
- erfc z = 1 — erf z, { displaystyle operatorname {erfc} z = 1- operatorname {erf} z,}
и функция мнимой ошибки (erfi ), определяемая как
- erfi z = — i erf (iz), { displaystyle operatorname {erfi} z = -i operatorname {erf} (iz),}
, где i — мнимая единица.
Содержание
- 1 Имя
- 2 Приложения
- 3 Свойства
- 3.1 Ряд Тейлора
- 3.2 Производная и интеграл
- 3.3 Ряд Бюрмана
- 3.4 Обратные функции
- 3.5 Асимптотическое разложение
- 3.6 Разложение на непрерывную дробь
- 3,7 Интеграл функции ошибок с функцией плотности Гаусса
- 3.8 Факториальный ряд
- 4 Численные приближения
- 4.1 Аппроксимация с элементарными функциями
- 4.2 Полином
- 4.3 Таблица значений
- 5 Связанные функции
- 5.1 функция дополнительных ошибок
- 5.2 Функция мнимой ошибки
- 5.3 Кумулятивная функци я распределения на
- 5.4 Обобщенные функции ошибок
- 5.5 Итерированные интегралы дополнительных функций ошибок
- 6 Реализации
- 6.1 Как действующая функция действительного аргумента
- 6.2 Как комплексная функция комплексного аргумента
- 7 См. Также
- 7.1 Связанные функции
- 7.2 Вероятность
- 8 Ссылки
- 9 Дополнительная литература
- 10 Внешние ссылки
Имя
Название «функция ошибки» и его аббревиатура erf были предложены Дж. В. Л. Глейшер в 1871 г. по причине его связи с «теорией вероятности, и особенно теорией ошибок ». Дополнение функции ошибок также обсуждалось Глейшером в отдельной публикации в том же году. Для «закона удобства» ошибок плотность задана как
- f (x) = (c π) 1 2 e — cx 2 { displaystyle f (x) = left ({ frac {c } { pi}} right) ^ { tfrac {1} {2}} e ^ {- cx ^ {2}}}
(нормальное распределение ), Глейшер вычисляет вероятность ошибки, лежащей между p { displaystyle p}

- (c π) 1 2 ∫ pqe — cx 2 dx = 1 2 (erf (qc) — erf (pc)). { displaystyle left ({ frac {c} { pi}} right) ^ { tfrac {1} {2}} int _ {p} ^ {q} e ^ {- cx ^ {2} } dx = { tfrac {1} {2}} left ( operatorname {erf} (q { sqrt {c}}) — operatorname {erf} (p { sqrt {c}}) right).}
Приложения
Когда результаты серии измерений описываются нормальным распределением со стандартным отклонением σ { displaystyle sigma}

Функции и дополнительные функции ошибок возникают, например, в решениях уравнения теплопроводности, когда граничные ошибки задаются ступенчатой функцией Хевисайда.
Функция ошибок и ее приближения Программу присвоили себе преподавателей, которые получили с высокой вероятностью или с низкой вероятностью. Дана случайная величина X ∼ Norm [μ, σ] { displaystyle X sim operatorname {Norm} [ mu, sigma]}![X sim operatorname {Norm} [ му, sigma]](https://wikimedia.org/api/rest_v1/media/math/render/svg/84024bc6827355ec6d23a062283a26d54b29698d)

- Pr [X ≤ L ] = 1 2 + 1 2 erf (L — μ 2 σ) ≈ A ехр (- B (L — μ σ) 2) { Displaystyle Pr [X Leq L] = { frac {1} {2 }} + { frac {1} {2}} operatorname {erf} left ({ frac {L- mu} {{ sqrt {2}} sigma}} right) приблизительно A exp left (-B left ({ frac {L- mu} { sigma}} right) ^ {2} right)}
где A и B — верх числовые константы. Если L достаточно далеко от среднего, то есть μ — L ≥ σ ln k { displaystyle mu -L geq sigma { sqrt { ln {k}}}}
- Pr [X ≤ L] ≤ A exp (- B ln k) = A К B { displaystyle Pr [X leq L] leq A exp (-B ln {k}) = { frac {A} {k ^ {B}}}}
, поэтому становится вероятность 0 при k → ∞ { displaystyle k to infty}
Свойства
Графики на комплексной плоскости 

Свойство erf (- z) = — erf (z) { displaystyle operatorname {erf} (-z) = — operatorname {erf} (z)}

Для любого комплексное число z:
- erf (z ¯) = erf (z) ¯ { displaystyle operatorname {erf} ({ overline {z}}) = { overline { operatorname {erf} (z)}}}
где z ¯ { displaystyle { overline {z}}}
Подынтегральное выражение f = exp (−z) и f = erf (z) показано в комплексной плоскости z на рисунках 2 и 3. Уровень Im (f) = 0 показан жирным зеленым цветом. линия. Отрицательные целые значения Im (f) показаны жирными красными линиями. Положительные целые значения Im (f) показаны толстыми синими линиями. Промежуточные уровни Im (f) = проявляются тонкими зелеными линиями. Промежуточные уровни Re (f) = показаны тонкими красными линиями для отрицательных значений и тонкими синими линиями для положительных значений.
Функция ошибок при + ∞ равна 1 (см. интеграл Гаусса ). На действительной оси erf (z) стремится к единице при z → + ∞ и к −1 при z → −∞. На мнимой оси он стремится к ± i∞.
Серия Тейлора
Функция ошибок — это целая функция ; у него нет сингулярностей (кроме бесконечности), и его разложение Тейлора всегда сходится, но, как известно, «[…] его плохая сходимость, если x>1».
определяющий интеграл нельзя вычислить в закрытой форме в терминах элементарных функций, но путем расширения подынтегрального выражения e в его ряд Маклорена и интегрирована почленно, можно получить ряд Маклорена функции ошибок как:
- erf (z) = 2 π ∑ n = 0 ∞ (- 1) nz 2 n + 1 n! (2 n + 1) знак равно 2 π (z — z 3 3 + z 5 10 — z 7 42 + z 9 216 — ⋯) { displaystyle operatorname {erf} (z) = { frac {2} { sqrt { pi}}} sum _ {n = 0} ^ { infty} { frac {(-1) ^ {n} z ^ {2n + 1}} {n! (2n + 1)}} = { frac {2} { sqrt { pi}}} left (z — { frac {z ^ {3}} {3}} + { frac {z ^ { 5}} {10}} — { frac {z ^ {7}} {42}} + { frac {z ^ {9}} {216}} — cdots right)}
, которое выполняется для каждого комплексного числа г. Члены знаменателя представляют собой последовательность A007680 в OEIS.
Для итеративного вычисления нового ряда может быть полезна следующая альтернативная формулировка:
- erf (z) = 2 π ∑ n = 0 ∞ (z ∏ К знак равно 1 N — (2 К — 1) Z 2 К (2 К + 1)) знак равно 2 π ∑ N = 0 ∞ Z 2 N + 1 ∏ К = 1 N — Z 2 К { Displaystyle OperatorName { erf} (z) = { frac {2} { sqrt { pi}}} sum _ {n = 0} ^ { infty} left (z prod _ {k = 1} ^ {n} { frac {- (2k-1) z ^ {2}} {k (2k + 1)}} right) = { frac {2} { sqrt { pi}}} sum _ {n = 0} ^ { infty} { frac {z} {2n + 1}} prod _ {k = 1} ^ {n} { frac {-z ^ {2}} {k}}}
потому что что — (2 k — 1) z 2 k (2 k + 1) { displaystyle { frac {- (2k-1) z ^ {2}} {k (2k + 1))}} }
Функция мнимой ошибки имеет очень похожий ряд Маклорена:
- erfi (z) = 2 π ∑ n = 0 ∞ z 2 n + 1 n! (2 n + 1) знак равно 2 π (z + z 3 3 + z 5 10 + z 7 42 + z 9 216 + ⋯) { displaystyle operatorname {erfi} (z) = { frac {2} { sqrt { pi}}} sum _ {n = 0} ^ { infty} { frac {z ^ {2n + 1}} {n! (2n + 1)}} = { frac {2} { sqrt { pi}}} left (z + { frac {z ^ {3}} {3}} + { frac {z ^ { 5}} {10}} + { frac {z ^ {7}} {42}} + { frac {z ^ {9}} {216}} + cdots right)}
, которое выполняется для любого комплексного числа z.
Производная и интеграл
Производная функция ошибок сразу следует из ее определения:
- ddz erf (z) = 2 π e — z 2. { displaystyle { frac {d} {dz}} operatorname {erf} (z) = { frac {2} { sqrt { pi}}} e ^ {- z ^ {2}}.}
Отсюда немедленно вычисляется производная функция мнимой ошибки :
- ddz erfi (z) = 2 π ez 2. { displaystyle { frac {d} {dz}} operatorname {erfi} (z) = { frac {2} { sqrt { pi }}} e ^ {z ^ {2}}.}
первообразная функции ошибок, которые можно получить посредством интегрирования по частям, составляет
- z erf (z) + е — z 2 π. { displaystyle z operatorname {erf} (z) + { frac {e ^ {- z ^ {2}}} { sqrt { pi}}}.}
Первообразная мнимой функции ошибок, также можно получить интегрированием по частям:
- z erfi (z) — ez 2 π. { displaystyle z operatorname {erfi} (z) — { frac {e ^ {z ^ {2}}} { sqrt { pi}}}.}
Производные высшего порядка задаются как
- erf (k) (z) = 2 (- 1) k — 1 π H k — 1 (z) e — z 2 = 2 π dk — 1 dzk — 1 (e — z 2), k = 1, 2, … { Displaystyle operatorname {erf} ^ {(k)} (z) = { frac {2 (-1) ^ {k-1}} { sqrt { pi}}} { mathit {H} } _ {k-1} (z) e ^ {- z ^ {2}} = { frac {2} { sqrt { pi}}} { frac {d ^ {k-1}} {dz ^ {k-1}}} left (e ^ {- z ^ {2}} right), qquad k = 1,2, dots}
где H { displaystyle { mathit {H}}}
ряд Бюрмана
Расширение, которое сходится быстрее для всех реальных значений x { displaystyle x}
- erf (x) = 2 π sgn (x) 1 — e — x 2 (1 — 1 12 ( 1 — e — x 2) — 7 480 (1 — e — x 2) 2 — 5 896 (1 — e — x 2) 3 — 787 276480 (1 — e — x 2)) 4 — ⋯) знак равно 2 π знак (x) 1 — e — x 2 (π 2 + ∑ k = 1 ∞ cke — kx 2). { displaystyle { begin {align} operatorname {erf} (x) = { frac {2} { sqrt { pi}}} operatorname {sgn} (x) { sqrt {1-e ^ {-x ^ {2}}}} left (1 — { frac {1} {12}} left (1-e ^ {- x ^ {2}} right) — { frac {7} {480}} left (1-e ^ {- x ^ {2}} right) ^ {2} — { frac {5} {896}} left (1-e ^ {- x ^ {2 }} right) ^ {3} — { frac {787} {276480}} left (1-e ^ {- x ^ {2}} right) ^ {4} — cdots right) \ [10pt] = { frac {2} { sqrt { pi}}} operatorname {sgn} (x) { sqrt {1-e ^ {- x ^ {2}}}} left ({ frac { sqrt { pi}} {2}} + sum _ {k = 1} ^ { infty} c_ {k} e ^ {- kx ^ {2}} right). end {выровнено}}
Сохраняя только первые два коэффициента и выбирая c 1 = 31 200 { displaystyle c_ {1} = { frac {31} {200}}}



- erf (x) ≈ 2 π sign (x) 1 — e — x 2 (π 2 + 31 200 e — x 2 — 341 8000 e — 2 х 2). { displaystyle operatorname {erf} (x) приблизительно { frac {2} { sqrt { pi}}} operatorname {sgn} (x) { sqrt {1-e ^ {- x ^ {2 }}}} left ({ frac { sqrt { pi}} {2}} + { frac {31} {200}} e ^ {- x ^ {2}} — { frac {341} {8000}} e ^ {- 2x ^ {2}} right).}
Обратные функции

Учитывая комплексное число z, не существует уникального комплексного числа w, удовлетворяющего erf (w) = z { displaystyle operatorname {erf} (w) = z}

- erf (erf — 1 ( х)) = х. { displaystyle operatorname {erf} left ( operatorname {erf} ^ {- 1} (x) right) = x.}
Обратная функция ошибок обычно определяется с помощью домена (- 1,1), и он ограничен этой областью многих систем компьютерной алгебры. Однако его можно продолжить и на диск | z | < 1 of the complex plane, using the Maclaurin series
- erf — 1 (z) знак равно ∑ К знак равно 0 ∞ ck 2 k + 1 (π 2 z) 2 k + 1, { displaystyle operatorname {erf} ^ {- 1} (z) = sum _ {k = 0} ^ { infty} { frac {c_ {k}} {2k + 1}} left ({ frac { sqrt { pi}} {2}} z right) ^ {2k + 1},}
где c 0 = 1 и
- ck = ∑ m = 0 k — 1 cmck — 1 — m (m + 1) (2 m + 1) = {1, 1, 7 6, 127 90, 4369 2520, 34807 16200,…}. { displaystyle c_ {k} = sum _ {m = 0} ^ {k-1} { frac {c_ {m} c_ {k-1-m}} {(m + 1) (2m + 1) }} = left {1,1, { frac {7} {6}}, { frac {127} {90}}, { frac {4369} {2520}}, { frac {34807} {16200}}, ldots right }.}
Итак, у нас есть разложение в ряд (общие множители были удалены из числителей и знаменателей):
- erf — 1 (z) = 1 2 π ( z + π 12 z 3 + 7 π 2 480 z 5 + 127 π 3 40320 z 7 + 4369 π 4 5806080 z 9 + 34807 π 5 182476800 z 11 + ⋯). { displaystyle operatorname {erf} ^ {- 1} (z) = { tfrac {1} {2}} { sqrt { pi}} left (z + { frac { pi} {12} } z ^ {3} + { frac {7 pi ^ {2}} {480}} z ^ {5} + { frac {127 pi ^ {3}} {40320}} z ^ {7} + { frac {4369 pi ^ {4}} {5806080}} z ^ {9} + { frac {34807 pi ^ {5}} {182476800}} z ^ {11} + cdots right). }
(После отмены дроби числителя / знаменателя характерми OEIS : A092676 / OEIS : A092677 в OEIS ; без отмены членов числителя в записи OEIS : A002067.) Значение функции ошибок при ± ∞ равно ± 1.
Для | z | < 1, we have erf (erf — 1 (z)) = z { displaystyle operatorname {erf} left ( operatorname {erf} ^ {- 1} (z) right) = z}
обратная дополнительная функция ошибок определяется как
- erfc — 1 (1 — z) = erf — 1 (z). { displaystyle operatorname {erfc} ^ {- 1} (1-z) = operatorname {erf} ^ {- 1} (z).}
Для действительного x существует уникальное действительное число erfi — 1 (x) { displaystyle operatorname {erfi} ^ {- 1} (x)}


Для любого действительного x, Метод Ньютона можно использовать для вычислений erfi — 1 (x) { displaystyle operatorname {erfi} ^ {- 1} (x)}

- erfi — 1 (z) = ∑ k = 0 ∞ (- 1) ККК 2 К + 1 (π 2 Z) 2 К + 1, { Displaystyle OperatorName {erfi} ^ {- 1} (г) = сумма _ {к = 0} ^ { infty} { гидроразрыва {(-1) ^ {k} c_ {k}} {2k + 1}} left ({ frac { sqrt { pi}} {2}} z right) ^ {2k + 1},}
, где c k определено, как указано выше.
Асимптотическое разложение
Полезным асимптотическим разложением дополнительные функции (и, следовательно, также и функции ошибок) для больших вещественных x
- erfc (x) = e — x 2 x π [1 + ∑ n = 1 ∞ (- 1) n 1 ⋅ 3 ⋅ 5 ⋯ (2 n — 1) (2 x 2) n] = e — x 2 x π ∑ n = 0 ∞ (- 1) п (2 п — 1)! ! (2 х 2) n, { displaystyle operatorname {erfc} (x) = { frac {e ^ {- x ^ {2}}} {x { sqrt { pi}}}} left [1 + sum _ {n = 1} ^ { infty} (- 1) ^ {n} { frac {1 cdot 3 cdot 5 cdots (2n-1)} {(2x ^ {2}) ^ {n}}} right] = { frac {e ^ {- x ^ {2}}} {x { sqrt { pi}}}} sum _ {n = 0} ^ { infty} ( -1) ^ {n} { frac {(2n-1) !!} {(2x ^ {2}) ^ {n}}},}
где (2n — 1) !! — это двойной факториал числа (2n — 1), которое является произведением всех нечетных чисел до (2n — 1). Этот ряд расходуется для любого конечного x, и его значение как асимптотического разложения состоит в том, что для любого N ∈ N { displaystyle N in mathbb {N}}
- erfc (Икс) знак равно е — Икс 2 Икс π ∑ N знак равно 0 N — 1 (- 1) N (2 N — 1)! ! (2 х 2) n + RN (x) { displaystyle operatorname {erfc} (x) = { frac {e ^ {- x ^ {2}}} {x { sqrt { pi}}}} sum _ {n = 0} ^ {N-1} (- 1) ^ {n} { frac {(2n-1) !!} {(2x ^ {2}) ^ {n}}} + R_ {N} (x)}
где остаток в нотации Ландау равен
- RN (x) = O (x 1 — 2 N e — x 2) { displaystyle R_ {N} ( x) = O left (x ^ {1-2N} e ^ {- x ^ {2}} right)}
при x → ∞. { displaystyle x to infty.}
Действительно, точное значение остатка равно
- R N (x): = (- 1) N π 2 1 — 2 N (2 N)! N! ∫ Икс ∞ T — 2 N e — T 2 dt, { Displaystyle R_ {N} (x): = { frac {(-1) ^ {N}} { sqrt { pi}}} 2 ^ { 1-2N} { frac {(2N)!} {N!}} Int _ {x} ^ { infty} t ^ {- 2N} e ^ {- t ^ {2}} , dt,}
который легко следует по индукции, записывая
- e — t 2 = — (2 t) — 1 (e — t 2) ′ { displaystyle e ^ {- t ^ {2}} = — (2t) ^ {- 1} left (e ^ {- t ^ {2}} right) ‘}
и интегрирование по частям.
Для достаточно больших значений x, только первые несколько этих асимптотических разностей необходимы, чтобы получить хорошее приближение erfc (x) (в то время как для не слишком больших значений x приведенное выше разложение Тейлора при 0 обеспечивает очень быструю сходимость).
Расширение непрерывной дроби
A Разложение непрерывной дроби дополнительные функции ошибок:
- erfc (z) = z π e — z 2 1 z 2 + a 1 1 + a 2 z 2 + a 3 1 + ⋯ am = м 2. { displaystyle operatorname {erfc} (z) = { frac {z} { sqrt { pi}}} e ^ {- z ^ {2}} { cfrac {1} {z ^ {2} + { cfrac {a_ {1}} {1 + { cfrac {a_ {2}} {z ^ {2} + { cfrac {a_ {3}} {1+) dotsb}}}}}}}} qquad a_ {m} = { frac {m} {2}}.}
Интеграл функции ошибок с функцией плотности Гаусса
- ∫ — ∞ ∞ erf (ax + б) 1 2 π σ 2 е — (Икс — μ) 2 2 σ 2 dx знак равно erf [a μ + b 1 + 2 a 2 σ 2], a, b, μ, σ ∈ R { displaystyle int _ {- infty} ^ { infty} operatorname {erf} left (ax + b right) { frac {1} { sqrt {2 pi sigma ^ {2}}}} e ^ {- { frac {(x- mu) ^ {2}} {2 sigma ^ {2}}}} , dx = operatorname {erf} left [{ frac {a mu + b } { sqrt {1 + 2a ^ {2} sigma ^ {2}}} right], qquad a, b, mu, sigma in mathbb {R}}
Факториальный ряд
- Обратное:
-
- erfc z = e — z 2 π z ∑ n = 0 ∞ (- 1) n Q n (z 2 + 1) n ¯ = e — z 2 π z (1 — 1 2 1 (z 2 + 1) + 1 4 1 (z 2 + 1) (z 2 + 2) — ⋯) { displaystyle { begin {align} operatorname {erfc} z = { frac {e ^ {- z ^ {2}}} {{ sqrt { pi}} , z}} sum _ {n = 0} ^ { infty} { frac {(-1) ^ {n} Q_ {n}} {{(z ^ {2} + 1)} ^ { ba r {n}}}} \ = { frac {e ^ {- z ^ {2}}} {{ sqrt { pi}} , z}} left ( 1 — { frac {1} {2}} { frac {1} {(z ^ {2} +1)}} + { frac {1} {4}} { frac {1} {(z ^ {2} +1) (z ^ {2} +2)}} — cdots right) end {align}}}
- erfc z = e — z 2 π z ∑ n = 0 ∞ (- 1) n Q n (z 2 + 1) n ¯ = e — z 2 π z (1 — 1 2 1 (z 2 + 1) + 1 4 1 (z 2 + 1) (z 2 + 2) — ⋯) { displaystyle { begin {align} operatorname {erfc} z = { frac {e ^ {- z ^ {2}}} {{ sqrt { pi}} , z}} sum _ {n = 0} ^ { infty} { frac {(-1) ^ {n} Q_ {n}} {{(z ^ {2} + 1)} ^ { ba r {n}}}} \ = { frac {e ^ {- z ^ {2}}} {{ sqrt { pi}} , z}} left ( 1 — { frac {1} {2}} { frac {1} {(z ^ {2} +1)}} + { frac {1} {4}} { frac {1} {(z ^ {2} +1) (z ^ {2} +2)}} — cdots right) end {align}}}
- сходится для Re (z 2)>0. { displaystyle operatorname {Re} (z ^ {2})>0.}
Здесь
- Q n = def 1 Γ (1/2) ∫ 0 ∞ τ (τ — 1) ⋯ ( τ — n + 1) τ — 1/2 е — τ d τ знак равно ∑ К знак равно 0 N (1 2) к ¯ s (n, k), { displaystyle Q_ {n} { stackrel { text {def}} {=}} { frac {1} { Gamma (1/2)}} int _ {0} ^ { infty} tau ( tau -1) cdots ( tau -n + 1) tau ^ {-1/2} e ^ {- tau} d tau = sum _ {k = 0} ^ {n} left ({ frac {1} {2}} right) ^ { bar {k}} s (n, k),}
- Q n = def 1 Γ (1/2) ∫ 0 ∞ τ (τ — 1) ⋯ ( τ — n + 1) τ — 1/2 е — τ d τ знак равно ∑ К знак равно 0 N (1 2) к ¯ s (n, k), { displaystyle Q_ {n} { stackrel { text {def}} {=}} { frac {1} { Gamma (1/2)}} int _ {0} ^ { infty} tau ( tau -1) cdots ( tau -n + 1) tau ^ {-1/2} e ^ {- tau} d tau = sum _ {k = 0} ^ {n} left ({ frac {1} {2}} right) ^ { bar {k}} s (n, k),}
- zn ¯ { displaystyle z ^ { bar {n}}}
обозначает возрастающий факториал, а s (n, k) { displaystyle s (n, k)}
обозначает знаковое число Стирлинга первого рода.
- Представление бесконечной суммой, составляющей двойной факториал :
-
- ERF (Z) знак равно 2 π ∑ N знак равно 0 ∞ (- 2) N (2 N — 1)! (2 N + 1)! Z 2 N + 1 { Displaystyle OperatorName {ERF} (г) = { frac {2} { sqrt { pi}}} sum _ {n = 0} ^ { infty} { frac {( -2) ^ {n} (2n-1) !!} {(2n + 1)!}} Z ^ {2n + 1}}
- ERF (Z) знак равно 2 π ∑ N знак равно 0 ∞ (- 2) N (2 N — 1)! (2 N + 1)! Z 2 N + 1 { Displaystyle OperatorName {ERF} (г) = { frac {2} { sqrt { pi}}} sum _ {n = 0} ^ { infty} { frac {( -2) ^ {n} (2n-1) !!} {(2n + 1)!}} Z ^ {2n + 1}}
Численные приближения
Приближение элементов сарными функциями
- Абрамовиц и Стегун дают несколько приближений с точностью (уравнения 7.1.25–28). Это позволяет выбрать наиболее быстрое приближение, подходящее для данного приложения. В порядке увеличения точности они следующие:
-
- erf (x) ≈ 1 — 1 (1 + a 1 x + a 2 x 2 + a 3 x 3 + a 4 x 4) 4, x ≥ 0 { displaystyle имя оператора {erf} (x) приблизительно 1 — { frac {1} {(1 + a_ {1} x + a_ {2} x ^ {2} + a_ {3} x ^ {3} + a_ { 4} x ^ {4}) ^ {4}}}, qquad x geq 0}
- erf (x) ≈ 1 — 1 (1 + a 1 x + a 2 x 2 + a 3 x 3 + a 4 x 4) 4, x ≥ 0 { displaystyle имя оператора {erf} (x) приблизительно 1 — { frac {1} {(1 + a_ {1} x + a_ {2} x ^ {2} + a_ {3} x ^ {3} + a_ { 4} x ^ {4}) ^ {4}}}, qquad x geq 0}
- (максимальная ошибка: 5 × 10)
- , где a 1 = 0,278393, a 2 = 0,230389, a 3 = 0,000972, a 4 = 0,078108
-
- erf (x) ≈ 1 — (a 1 t + a 2 t 2 + a 3 t 3) e — x 2, t = 1 1 + px, x ≥ 0 { displaystyle operatorname {erf} (x) приблизительно 1- (a_ {1} t + a_ {2} t ^ {2} + a_ {3} t ^ {3}) e ^ {- x ^ {2}}, quad t = { frac {1} {1 + px}}, qquad x geq 0}
(максимальная ошибка: 2,5 × 10)
- erf (x) ≈ 1 — (a 1 t + a 2 t 2 + a 3 t 3) e — x 2, t = 1 1 + px, x ≥ 0 { displaystyle operatorname {erf} (x) приблизительно 1- (a_ {1} t + a_ {2} t ^ {2} + a_ {3} t ^ {3}) e ^ {- x ^ {2}}, quad t = { frac {1} {1 + px}}, qquad x geq 0}
- где p = 0,47047, a 1 = 0,3480242, a 2 = -0,0958798, a 3 = 0,7478556
-
- erf (x) ≈ 1 — 1 (1 + a 1 x + a 2 x 2 + ⋯ + a 6 x 6) 16, x ≥ 0 { displaystyle operatorname {erf} (x) приблизительно 1 — { frac {1} {(1 + a_ {1} x + a _ {2} x ^ {2} + cdots + a_ {6} x ^ {6}) ^ {16}}}, qquad x geq 0}
(максимальная ошибка: 3 × 10)
- erf (x) ≈ 1 — 1 (1 + a 1 x + a 2 x 2 + ⋯ + a 6 x 6) 16, x ≥ 0 { displaystyle operatorname {erf} (x) приблизительно 1 — { frac {1} {(1 + a_ {1} x + a _ {2} x ^ {2} + cdots + a_ {6} x ^ {6}) ^ {16}}}, qquad x geq 0}
- , где a 1 = 0,0705230784, a 2 = 0,0422820123, a 3 = 0,0092705272, a 4 = 0,0001520143, a 5 = 0,0002765672, a 6 = 0,0000430638
-
- erf (x) ≈ 1 — (a 1 t + a 2 t 2 + ⋯ + a 5 t 5) e — x 2, t = 1 1 + px { displaystyle operatorname {erf} (x) приблизительно 1- (a_ {1} t + a_ {2} t ^ {2} + cdots + a_ {5} t ^ {5}) e ^ {- x ^ {2}}, quad t = { frac {1} {1 + px}}}
(максимальная ошибка: 1,5 × 10)
- erf (x) ≈ 1 — (a 1 t + a 2 t 2 + ⋯ + a 5 t 5) e — x 2, t = 1 1 + px { displaystyle operatorname {erf} (x) приблизительно 1- (a_ {1} t + a_ {2} t ^ {2} + cdots + a_ {5} t ^ {5}) e ^ {- x ^ {2}}, quad t = { frac {1} {1 + px}}}
- , где p = 0,3275911, a 1 = 0,254829592, a 2 = −0,284496736, a 3 = 1,421413741, a 4 = −1,453152027, a 5 = 1,061405429
- Все эти приближения действительны для x ≥ 0 Чтобы использовать эти приближения для отрицательного x, викорируйте тот факт, что erf (x) — нечетная функция, поэтому erf (x) = −erf (−x).
- Экспоненциальные границы и чисто экспоненциальное приближение для дополнительных функций задаются как
-
- erfc (x) ≤ 1 2 e — 2 x 2 + 1 2 e — x 2 ≤ e — x 2, x>0 erfc ( х) ≈ 1 6 е — х 2 + 1 2 е — 4 3 х 2, х>0. { displaystyle { begin {align} operatorname {erfc} (x) leq { frac {1} {2}} e ^ {- 2x ^ {2}} + { frac {1} {2} } e ^ {- x ^ {2}} leq e ^ {- x ^ {2}}, qquad x>0 \ имя оператора {erfc} (x) приблизительно { frac {1} { 6}} e ^ {- x ^ {2}} + { frac {1} {2}} e ^ {- { frac {4} {3}} x ^ {2}}, qquad x>0. end {align}}}
- erfc (x) ≤ 1 2 e — 2 x 2 + 1 2 e — x 2 ≤ e — x 2, x>0 erfc ( х) ≈ 1 6 е — х 2 + 1 2 е — 4 3 х 2, х>0. { displaystyle { begin {align} operatorname {erfc} (x) leq { frac {1} {2}} e ^ {- 2x ^ {2}} + { frac {1} {2} } e ^ {- x ^ {2}} leq e ^ {- x ^ {2}}, qquad x>0 \ имя оператора {erfc} (x) приблизительно { frac {1} { 6}} e ^ {- x ^ {2}} + { frac {1} {2}} e ^ {- { frac {4} {3}} x ^ {2}}, qquad x>0. end {align}}}
-
- erfc (x) ≈ (1 — e — A x) e — x 2 B π х. { displaystyle operatorname {erfc} left (x right) приблизительно { frac { left (1-e ^ {- Ax} right) e ^ {- x ^ {2}}} {B { sqrt { pi}} x}}.}
- erfc (x) ≈ (1 — e — A x) e — x 2 B π х. { displaystyle operatorname {erfc} left (x right) приблизительно { frac { left (1-e ^ {- Ax} right) e ^ {- x ^ {2}}} {B { sqrt { pi}} x}}.}
- Они определили {A, B} = {1.98, 1.135}, { displaystyle {A, B } = {1.98,1.135 },}
, что дает хорошее приближение для всех x ≥ 0. { displaystyle x geq 0.}
- Одноканальная нижняя граница:
-
- erfc (x) ≥ 2 e π β — 1 β е — β Икс 2, Икс ≥ 0, β>1, { Displaystyle OperatorName {erfc} (x) geq { sqrt { frac {2e} { pi}}} { frac { sqrt { beta -1}} { beta}} e ^ {- beta x ^ {2}}, qquad x geq 0, beta>1,}
- erfc (x) ≥ 2 e π β — 1 β е — β Икс 2, Икс ≥ 0, β>1, { Displaystyle OperatorName {erfc} (x) geq { sqrt { frac {2e} { pi}}} { frac { sqrt { beta -1}} { beta}} e ^ {- beta x ^ {2}}, qquad x geq 0, beta>1,}
- где параметр β может быть выбран, чтобы минимизировать ошибку на желаемом интервале приближения.
- Другое приближение дано Сергеем Виницким с использованием его «глобальных приближений Паде»:
-
- erf (x) ≈ sgn (x) 1 — exp (- x 2 4 π + ax 2 1 + ax 2) { displaystyle operatorname {erf} (x) приблизительно Operatorname {sgn} (x) { sqrt {1- exp left (-x ^ {2} { frac {{ frac {4} { pi) })} + ax ^ {2}} {1 + ax ^ {2}}} right)}}}
- erf (x) ≈ sgn (x) 1 — exp (- x 2 4 π + ax 2 1 + ax 2) { displaystyle operatorname {erf} (x) приблизительно Operatorname {sgn} (x) { sqrt {1- exp left (-x ^ {2} { frac {{ frac {4} { pi) })} + ax ^ {2}} {1 + ax ^ {2}}} right)}}}
- где
-
- a = 8 (π — 3) 3 π (4 — π) ≈ 0, 140012. { displaystyle a = { frac {8 ( pi -3)} {3 pi (4- pi)}} приблизительно 0,140012.}
- a = 8 (π — 3) 3 π (4 — π) ≈ 0, 140012. { displaystyle a = { frac {8 ( pi -3)} {3 pi (4- pi)}} приблизительно 0,140012.}
- Это сделано так, чтобы быть очень точным в окрестностях 0 и добавление бесконечности, а относительная погрешность меньше 0,00035 для всех действительных x. Использование альтернативного значения ≈ 0,147 снижает максимальную относительную ошибку примерно до 0,00013.
- Это приближение можно инвертировать, чтобы получить приближение для других функций ошибок:
-
- erf — 1 (x) ≈ sgn (x) (2 π a + ln (1 — x 2) 2) 2 — ln (1 — x 2) a — (2 π a + ln (1 — x 2) 2). { displaystyle operatorname {erf} ^ {- 1} (x) приблизительно operatorname {sgn} (x) { sqrt {{ sqrt { left ({ frac {2} { pi a}} + { frac { ln (1-x ^ {2})} {2}} right) ^ {2} — { frac { ln (1-x ^ {2})} {a}}}} — left ({ frac {2} { pi a}} + { frac { ln (1-x ^ {2})} {2}} right)}}.}
- erf — 1 (x) ≈ sgn (x) (2 π a + ln (1 — x 2) 2) 2 — ln (1 — x 2) a — (2 π a + ln (1 — x 2) 2). { displaystyle operatorname {erf} ^ {- 1} (x) приблизительно operatorname {sgn} (x) { sqrt {{ sqrt { left ({ frac {2} { pi a}} + { frac { ln (1-x ^ {2})} {2}} right) ^ {2} — { frac { ln (1-x ^ {2})} {a}}}} — left ({ frac {2} { pi a}} + { frac { ln (1-x ^ {2})} {2}} right)}}.}
Многочлен
Приближение с максимальной ошибкой 1,2 × 10-7 { displaystyle 1,2 times 10 ^ {- 7}}
- erf ( x) = {1 — τ x ≥ 0 τ — 1 x < 0 {displaystyle operatorname {erf} (x)={begin{cases}1-tau xgeq 0\tau -1x<0end{cases}}}
с
- τ = t ⋅ exp (- x 2 — 1,26551223 + 1,00002368 t + 0,37409196 t 2 + 0,09678418 t 3 — 0,18628806 t 4 + 0,27886807 t 5 — 1,13520398 t 6 + 1,48851587 t 7 — 0,82215223 t 8 + 0,17087277 t 9) { displaystyle { begin {align} tau = t cdot exp left (-x ^ {2} -1,26551223 + 1,00002368 t + 0,37409196t ^ {2} + 0,09678418t ^ {3} -0,18628806t ^ {4} вправо. \ left. qquad qquad qquad + 0,27886807t ^ {5} -1,13520398t ^ {6} + 1,48851587t ^ {7} -0,82215223t ^ {8} + 0,17087 277t ^ {9} right) end {align}}}
и
- t = 1 1 + 0,5 | х |. { displaystyle t = { frac {1} {1 + 0,5 | x |}}.}
Таблица значений
| x | erf(x) | 1-erf (x) |
|---|---|---|
| 0 | 0 | 1 |
| 0,02 | 0,022564575 | 0,977435425 |
| 0,04 | 0,045111106 | 0,954888894 |
| 0,06 | 0,067621594 | 0, 932378406 |
| 0,08 | 0.090078126 | 0,909921874 |
| 0,1 | 0,112462916 | 0,887537084 |
| 0,2 | 0,222702589 | 0,777297411 |
| 0,3 | 0,328626759 | 0,671373241 |
| 0, 4 | 0,428392355 | 0,571607645 |
| 0,5 | 0,520499878 | 0,479500122 |
| 0,6 | 0.603856091 | 0,396143909 |
| 0,7 | 0,677801194 | 0,322198806 |
| 0,8 257> | 0,742100965 | 0,257899035 |
| 0,9 | 0,796908212 | 0,203091788 |
| 1 | 0,842700793 | 0, 157299207 |
| 1,1 | 0,88020507 | 0,11979493 |
| 1,2 | 0,910313978 | 0,089686022 |
| 1,3 | 0,934007945 | 0,065992055 |
| 1,4 | 0.95228512 | 0,04771488 |
| 1,5 | 0, 966105146 | 0,033894854 |
| 1,6 | 0,976348383 | 0,023651617 |
| 1,7 | 0,983790459 | 0,016209541 |
| 1,8 | 0,989090502 | 0,010909498 |
| 1,9 | 0,992790429 | 0,007209571 |
| 2 | 0,995322265<25767> | 0,00477 |
| 2.1 | 0.997020533 | 0.002979467 |
| 2.2 | 0.998137154 | 0,001862846 |
| 2,3 | 0,998856823 | 0,001143177 |
| 2,4 | 0,999311486 | 0,000688514 |
| 2,5 | 0.999593048 | 0.000406952 |
| 3 | 0.99997791 | 0,00002209 |
| 3,5 | 0,999999257 | 0,000000743 |
Связанные функции
Дополнительная функция
дополнительная функция ошибок, обозначается erfc { displaystyle mathrm {erfc}}
- erfc (x) = 1 — erf (x) = 2 π ∫ x ∞ e — t 2 dt знак равно е — Икс 2 erfcx (х), { displaystyle { begin {выровнено} OperatorName {erfc} (x) = 1- operatorname {erf} (x) \ [5p t] = { frac {2} { sqrt { pi}}} int _ {x} ^ { infty} e ^ {- t ^ {2}} , dt \ [5pt] = e ^ {- x ^ {2}} operatorname {erfcx} (x), end {align}}}
, который также определяет erfcx { displaystyle mathrm {erfcx} }


- erfc (x ∣ x ≥ 0) = 2 π ∫ 0 π / 2 exp (- x 2 sin 2 θ) d θ. { displaystyle operatorname {erfc} (x mid x geq 0) = { frac {2} { pi}} int _ {0} ^ { pi / 2} exp left (- { frac {x ^ {2}} { sin ^ {2} theta}} right) , d theta.}
Это выражение действительно только для положительных значений x, но его можно использовать вместе с erfc (x) = 2 — erfc (−x), чтобы получить erfc (x) для отрицательных значений. Эта форма выгодна тем, что диапазон интегрирования является фиксированным и конечным. Расширение этого выражения для erfc { displaystyle mathrm {erfc}}
- erfc (x + y ∣ x, y ≥ 0) = 2 π ∫ 0 π / 2 ехр (- x 2 sin 2 θ — y 2 cos 2 θ) d θ. { displaystyle operatorname {erfc} (x + y mid x, y geq 0) = { frac {2} { pi}} int _ {0} ^ { pi / 2} exp left (- { frac {x ^ {2}} { sin ^ {2} theta}} — { frac {y ^ {2}} { cos ^ {2} theta}} right) , d theta.}
Функция мнимой ошибки
мнимой ошибки, обозначаемая erfi, обозначает ошибки как
- erfi (x) = — i erf (ix) Знак равно 2 π ∫ 0 xet 2 dt знак равно 2 π ex 2 D (x), { displaystyle { begin {align} operatorname {erfi} (x) = — i operatorname {erf} (ix) \ [ 5pt] = { frac {2} { sqrt { pi}}} int _ {0} ^ {x} e ^ {t ^ {2}} , dt \ [5pt] = { frac {2} { sqrt { pi}}} e ^ {x ^ {2}} D (x), end {align}}}
где D (x) — функция Доусона (который можно использовать вместо erfi, чтобы избежать арифметического переполнения ).
Несмотря на название «функция мнимой ошибки», erfi (x) { displaystyle operatorname {erfi} (x)}
Функция Когда ошибки оценивается для произвольных сложных аргументов z, результирующая комплексная функция ошибок обычно обсуждается в масштабированной форме как функция Фаддеева :
- w (z) = e — z 2 erfc (- iz) = erfcx (- iz). { displaystyle w (z) = e ^ {- z ^ {2}} operatorname {erfc} (-iz) = operatorname {erfcx} (-iz).}
Кумулятивная функция распределения
Функция ошибок по существующей стандартной стандартной функции нормального кумулятивного распределения, обозначаемой нормой (x) в некоторых языках программного обеспечения, поскольку они отличаются только масштабированием и переводом. Действительно,
- Φ (x) = 1 2 π ∫ — ∞ xe — t 2 2 dt = 1 2 [1 + erf (x 2)] = 1 2 erfc (- x 2) { displaystyle Phi (x) = { frac {1} { sqrt {2 pi}}} int _ {- infty} ^ {x} e ^ { tfrac {-t ^ {2}} {2}} , dt = { frac {1} {2}} left [1+ operatorname {erf} left ({ frac {x} { sqrt {2}}} right) right] = { frac {1} {2}} operatorname {erfc} left (- { frac {x} { sqrt {2}}} right)}
или переставлен для erf и erfc:
- erf ( x) = 2 Φ (x 2) — 1 erfc (x) = 2 Φ (- x 2) = 2 (1 — Φ (x 2)). { displaystyle { begin {align} operatorname {erf} (x) = 2 Phi left (x { sqrt {2}} right) -1 \ operatorname {erfc} (x) = 2 Phi left (-x { sqrt {2}} right) = 2 left (1- Phi left (x { sqrt {2}} right) right). End {выравнивается} }}
Следовательно, функция ошибок также тесно связана с Q-функцией, которая является вероятностью хвоста стандартного нормального распределения. Q-функция может быть выражена через функцию ошибок как
- Q (x) = 1 2 — 1 2 erf (x 2) = 1 2 erfc (x 2). { displaystyle Q (x) = { frac {1} {2}} — { frac {1} {2}} operatorname {erf} left ({ frac {x} { sqrt {2}}) } right) = { frac {1} {2}} operatorname {erfc} left ({ frac {x} { sqrt {2}}} right).}
Обратное значение из Φ { displaystyle Phi}
- пробит (p) = Φ — 1 (p) = 2 erf — 1 (2 p — 1) = — 2 erfc — 1 (2 p). { displaystyle operatorname {probit} (p) = Phi ^ {- 1} (p) = { sqrt {2}} operatorname {erf} ^ {- 1} (2p-1) = — { sqrt {2}} operatorname {erfc} ^ {- 1} (2p).}
Стандартный нормальный cdf чаще используется в вероятности и статистике, а функция ошибок чаще используется в других разделах математики.
Функция ошибки является частным случаем функции Миттаг-Леффлера и может также быть выражена как сливающаяся гипергеометрическая функция (функция Куммера):
- erf (х) знак равно 2 х π M (1 2, 3 2, — х 2). { displaystyle operatorname {erf} (x) = { frac {2x} { sqrt { pi}}} M left ({ frac {1} {2}}, { frac {3} {2 }}, — x ^ {2} right).}
Он имеет простое выражение в терминах интеграла Френеля.
В терминах регуляризованной гамма-функции P и неполная гамма-функция,
- erf (x) = sgn (x) P (1 2, x 2) = sgn (x) π γ (1 2, x 2). { displaystyle operatorname {erf} (x) = operatorname {sgn} (x) P left ({ frac {1} {2}}, x ^ {2} right) = { frac { operatorname {sgn} (x)} { sqrt { pi}}} gamma left ({ frac {1} {2}}, x ^ {2} right).}
sgn (x) { displaystyle operatorname {sgn} (x)}
Обобщенные функции ошибок

π { displaystyle scriptstyle { sqrt { pi}}}

Некоторые авторы обсуждают более общие функции:
- E n (x) = n! π ∫ 0 Икс е — Т N д т знак равно N! π ∑ п знак равно 0 ∞ (- 1) п Икс N п + 1 (N п + 1) п!. { displaystyle E_ {n} (x) = { frac {n!} { sqrt { pi}}} int _ {0} ^ {x} e ^ {- t ^ {n}} , dt = { frac {n!} { sqrt { pi}}} sum _ {p = 0} ^ { infty} (- 1) ^ {p} { frac {x ^ {np + 1}} {(np + 1) p!}}.}
Примечательные случаи:
- E0(x) — прямая линия, проходящая через начало координат: E 0 (x) = xe π { displaystyle textstyle E_ {0} (x) = { dfrac {x} {e { sqrt { pi}}}}}
- E2(x) — функция, erf (x) ошибки.
После деления на n!, все E n для нечетных n выглядят похожими (но не идентичными) друг на друга. Аналогично, E n для четного n выглядят похожими (но не идентичными) друг другу после простого деления на n!. Все обобщенные функции ошибок для n>0 выглядят одинаково на положительной стороне x графика.
Эти обобщенные функции могут быть эквивалентно выражены для x>0 с помощью гамма-функции и неполной гамма-функции :
- E n (x) = 1 π Γ (n) (Γ (1 n) — Γ (1 n, xn)), x>0. { displaystyle E_ {n} (x) = { frac {1} { sqrt { pi}}} Gamma (n) left ( Gamma left ({ frac {1} {n}} right) — Gamma left ({ frac {1} {n}}, x ^ {n} right) right), quad quad x>0.}
Следовательно, мы можем определить ошибку функция в терминах неполной гамма-функции:
- erf (x) = 1 — 1 π Γ (1 2, x 2). { displaystyle operatorname {erf} (x) = 1 — { frac {1} { sqrt { pi}}} Gamma left ({ frac {1} {2}}, x ^ {2} right).}
Итерированные интегралы дополнительных функций
Повторные интегралы дополнительные функции ошибок определения как
- inerfc (z) = ∫ z ∞ in — 1 erfc (ζ) d ζ i 0 erfc (z) = erfc (z) i 1 erfc (z) = ierfc (z) знак равно 1 π е — z 2 — z erfc (z) я 2 erfc (z) = 1 4 [erfc (z) — 2 z ierfc (z)] { displaystyle { begin {align } operatorname {i ^ {n} erfc} (z) = int _ {z} ^ { infty} operatorname {i ^ {n-1} erfc} ( zeta) , d zeta \ имя оператора {i ^ {0} erfc} (z) = operatorname {erfc} (z) \ operatorname {i ^ {1} erfc} (z) = operat orname {ierfc} (z) = { frac { 1} { sqrt { pi}}} e ^ {- z ^ {2}} — z operatorname {erfc} (z) \ operatorname {i ^ {2} erfc} (z) = { frac {1} {4}} left [ operatorname {erfc} (z) -2z operatorname {ierfc} (z) right] \ end {выровнено}}
Общая рекуррентная формула:
- 2 ninerfc (z) = in — 2 erfc (z) — 2 цинк — 1 erfc (z) { displaystyle 2n operatorname {i ^ {n} erfc} (z) = operatorname {i ^ { n-2} erfc} (z) -2z operatorname {i ^ {n-1} erfc} (z)}
У них есть степенной ряд
- в erfc (z) = ∑ j = 0 ∞ (- Z) J 2 N — JJ! Γ (1 + N — J 2), { displaystyle i ^ {n} operatorname {erfc} (z) = sum _ {j = 0} ^ { infty} { frac {(-z) ^ { j}} {2 ^ {nj} j! Gamma left (1 + { frac {nj} {2}} right)}},}
из следуют свойства симметрии
- i 2 m ERFC (- Z) знак равно — я 2 m ERFC (Z) + ∑ Q знак равно 0 мZ 2 д 2 2 (м — д) — 1 (2 д)! (м — д)! { displaystyle i ^ {2m} operatorname {erfc} (-z) = — i ^ {2m} operatorname {erfc} (z) + sum _ {q = 0} ^ {m} { frac {z ^ {2q}} {2 ^ {2 (mq) -1} (2q)! (Mq)!}}}
и
- i 2 m + 1 erfc (- z) = i 2 m + 1 erfc (г) + ∑ ä знак равно 0 ìZ 2 ä + 1 2 2 ( м — д) — 1 (2 д + 1)! (м — д)!. { displaystyle i ^ {2m + 1} operatorname {erfc} (-z) = i ^ {2m + 1} operatorname {erfc} (z) + sum _ {q = 0} ^ {m} { гидроразрыва {z ^ {2q + 1}} {2 ^ {2 (mq) -1} (2q + 1)! (mq)!}}.}
Реализации
Как действительная функция вещественного аргумента
- В операционных системах, совместимых с Posix, заголовок math.h должен являть, а математическая библиотека libm должна быть функция erf и erfc (двойная точность ), а также их одинарная точность и расширенная точность аналоги erff, erfl и erfc, erfcl.
- Библиотека GNU Scientific предоставляет функции erf, erfc, log (erf) и масштабируемые функции ошибок.
Как сложная функция комплексного аргумента
- libcerf, числовая библиотека C для сложных функций, предоставляет комплексные функции cerf, cerfc, cerfcx и реальные функции erfi, erfcx с точностью 13–14 цифр на основе функции Фаддеева, реализованной в пакете MIT Faddeeva Package
См. также
Связанные ции
- интеграл Гаусса, по всей действительной прямой
- функция Гаусса, производная
- функция Доусона, перенормированная функция мнимой ошибки
- интеграл Гудвина — Стона
по вероятности
- Нормальное распределение
- Нормальная кумулятивная функция распределения, масштабированная и сдвинутая форма функций ошибок
- Пробит, обратная или квантильная функция нормального CDF
- Q-функция, вероятность хвоста нормального распределения
Ссылки
Дополнительная литература
- Abramowitz, Milton ; Стегун, Ирен Энн, ред. (1983) [июнь 1964]. «Глава 7». Справочник по математическим функциям с формулами, графики и математическими таблицами. Прикладная математика. 55 (Девятое переиздание с дополнительными исправлениями; десятое оригинальное издание с исправлениями (декабрь 1972 г.); первое изд.). Вашингтон.; Нью-Йорк: Министерство торговли США, Национальное бюро стандартов; Dover Publications. п. 297. ISBN 978-0-486-61272-0 . LCCN 64-60036. MR 0167642. LCCN 65-12253.
- Press, William H.; Теукольский, Саул А.; Веттерлинг, Уильям Т.; Фланнери, Брайан П. (2007), «Раздел 6.2. Неполная гамма-функция и функция ошибок », Числовые рецепты: Искусство научных вычислений (3-е изд.), Нью-Йорк: Cambridge University Press, ISBN 978-0-521- 88068-8
- Темме, Нико М. (2010), «Функции ошибок, интегралы Доусона и Френеля», в Олвер, Фрэнк У. Дж. ; Лозье, Даниэль М.; Бойсверт, Рональд Ф.; Кларк, Чарльз В. (ред.), Справочник NIST по математическим функциям, Cambridge University Press, ISBN 978-0-521-19225-5 , MR 2723248
Внешние ссылки
- MathWorld — Erf
- Таблица интегралов функций ошибок
1. Что такое объект, целевая переменная, признак, модель, функционал ошибки и обучение?
Объект – некая абстрактная сущность, с которой мы хотим работать и для которой хотим делать предсказания.
Пространство объектов – множество всех возможных объектов в данной задаче.
Целевая переменная – некая характеристика объекта, которую мы хотим научиться предсказывать с помощью методов машинного обучения. Обычно объект обозначается (x), пространство объектов — (mathbb{X}). Целевая переменная обозначается — (y), пространство ответов — (mathbb{Y}).
Объекты описываются с помощью своих характеристик, называемых признаками (т.е. признак – некая характеристика объекта), вектор признаков является признаковым описанием объекта. Мы будем отождествлять объект и его признаковое описание.
Модель – некоторый алгоритм, позволяющий предсказывать целевую переменную по признаковому описанию объекта. По сути, это функция (a: mathbb{X} to mathbb{Y}).
Функционал качества позволяет оценить качество работы такого алгоритма, при этом, если функционал устроен так, что его нужно минимизировать, будем называть его функционалом ошибки. Функционал обозначается (Q(a, X)) и чаще всего представляет собой сумму ошибок на отдельных объектах, а функция, измеряющая ошибку на одном объекте, называется функцией потерь.
Пусть нам дано множество объектов (mathbb{X}) — матрица объекты-признаки — с известными ответами (mathbb{Y}). Назовем совокупность ((mathbb{X}), (mathbb{Y})) обучающей выборкой. Обучением будем называть процесс построения оптимального с точки зрения функционала ошибки на обучающей выборке алгоритма (a).
2. Запишите формулы для линейной модели регрессии и для среднеквадратичной ошибки. Запишите среднеквадратичную ошибку в матричном виде.
Линейная модель:
[
mathbb{A}
=
{
a(x) = w_0 + w_1 x_1 + dots + w_d x_d|w_0, w_1, dots, w_d in mathbb{R}
}
], где через (x_i) обозначается значение (i) -го признака у объекта (x), a (d) – количество объектов, (w_{i}) – вес для $i$-го признака.
MSE:
В общем виде
[
Q(a,X)=frac{1}{ell}sum_{i=1}^{ell}(a(x_{i})-y_{i})^{2}
], где (a(x)) – модель, (l) – количество объектов.
Для некой модели (a(x)) описанной выше
[
frac{1}{ell}sum_{i = 1}^{ell} left(w_0+sum_{j = 1}^{d}w_j x_{ij}-y_iright)^2tomin_{w_0, w_1,dots, w_d}.
]
В матричном виде
[
frac{1}{ell}||Xw-y||^{2}_{2}to min_{w}
]
[
Q(w)=(y-Xw)^{T}(y-Xw)
]
где (X) — матрица объекты-признаки, (w) — вектор весов, (y) — вектор целевых значений,(||x||^{2}_{2}) — L2 норма (квадратный корень из суммы квадратов значений вектора)
3. Что такое коэффициент детерминации? Как интерпретировать его значения?
[
R^{2}(a,X)=1-frac{sum_{i=1}^{l}(a(x_{i}-y_{i})^{2})}{sum_{i=1}^{l}(y_{i}-hat{y})^{2}}
]
Коэффициент детерминации измеряет долю дисперсии, объяснённую моделью, в общей дисперсии целевой переменной. Фактически, данная мера качества это нормированная среднеквадратичная ошибка. Если она близка к единице, то модель хорошо объясняет данные, если же она близка к нулю, то прогнозы сопоставимы по качеству с константным предсказанием.
4. Чем отличаются функционалы MSE и MAE?
- MAE более устойчива к выбросам (но гораздо менее точна при приближении к минимуму (произв не содержит инф о близости к экстремуму (в 0 вообще ее нет)) и большим значениям
- MSE увеличит ошибку из-за возведения в квадрат из-за чего появится некоторое искажение реальной ошибки. Если выбросов больше чем нормальных объектов, то устойчивость MAE пропадает.
5. Как устроены робастные функции потерь (Huber loss, log-cosh)? Чем log-cosh лучше функции потерь Хубера?
Huber loss
Huber Loss объединяет в себе MSE и MAE с параметром дельта, этот параметр определяет, что мы считаем за выброс. При (deltarightarrow0) функция потерь Хубера вырождается в абсолютную функцию (MAE) потерь, а при (deltarightarrowinfty) — в квадратичную (MSE). Не имеет вторую производную
[
L_delta(y, a)=
left{begin{aligned}
½ (y — a)^2, quad |y — a| < delta \
&delta left(|y — a| — frac12 delta
right), quad |y — a| geq delta
end{aligned}
right.
]
Log Cosh
Log Cosh (логарифм от гиперболического косинуса) имеет вторую производную. Как и в случае с функцией потерь Хубера, для маленьких отклонений здесь имеет место квадратичное поведение, а для больших — линейное.
[
L(y,a)=log(cosh(a-y))
]
Сравнение
Log Cosh > Huber Loss т.к. Вторая производная в Хубере имеет разрывы, Log Cosh же без разрывов, не нужно подбирать параметр дельта.
6. Что такое градиент? Какое его свойство используется при минимизации функций?
Градиент — направление наискорейшего роста функции, а антиградиент (т.е. (−nabla f) ) направлением наискорейшего убывания функции. Это ключевое свойство градиента, обосновывающее его использование в методах оптимизации.
7. Как устроен градиентный спуск?
Пусть (w^0) начальный набор параметров (например, нулевой или сгенерированный из некоторого случайного распределения). Тогда градиентный спуск состоит в повторении следующих шагов до сходимости:
[
w^{(k)}=w^{(k — 1)}-eta_knabla Q(w^{(k — 1)})
]
Здесь под (Q(w)) понимается значение функционала ошибки для набора параметров (w).
Через (eta_k) обозначается длина шага, которая нужна для контроля скорости движения.
Можно делать её константной: (eta_k = c). При этом если длина шага слишком большая, то есть риск постоянно <перепрыгивать> через точку минимума, а если шаг слишком маленький, то движение к минимуму может занять слишком много итераций. Иногда длину шага монотонно уменьшают по мере движения — например, по простой формуле ((frac{1}{k})).
8. Почему не всегда можно использовать полный градиентный спуск? Какие способы оценивания градиента вы знаете? Почему в стохастическом градиентном спуске важно менять длину шага по мере итераций? Какие стратегии изменения шага вы знаете?
Использование полного градиентного спуска может быть очень трудоёмко при больших размерах выборки. В то же время точное вычисление градиента может быть не так уж необходимо — как правило, мы делаем не очень большие шаги в сторону антиградиента, и наличие в нём неточностей не должно сильно сказаться на общей траектории. Опишем несколько способов оценивания полного градиента.
SGD
[
w^{(k)}=w^{(k — 1)}-eta_knabla q_{ik}(w^{(k — 1)})
] где (i_k) – случайно выбранный номер слагаемого из функционала.
Параметры, оптимальные для средней ошибки на всей выборке, не обязаны являться оптимальными для ошибки на одном из объектов. Поэтому SGD метод запросто может отдаляться от минимума, даже оказавшись рядом с ним. Чтобы исправить эту проблему, важно в SGD делать длину шага убывающей – тогда в окрестности оптимума мы уже не сможем делать длинные шаги и, как следствие, не сможем из этой окрестности выйти. Разумеется, потребуется выбирать формулу для длины шага аккуратно, чтобы не остановиться слишком рано и не уйти от минимума. В частности, сходимость для выпуклых дифференцируемых функций гарантируется (с вероятностью 1), если функционал удовлетворяет ряду условий (как правило, это выпуклость, дифференцируемость и липшицевость градиента) и длина шага удовлетворяет условиям Роббинса-Монро:
[
sum_{k = 1}^{infty} eta_k = infty; quad
sum_{k = 1}^{infty} eta_k^2 < infty.
]
Этим условиям, например, удовлетворяет шаг (eta_k = frac{1}{k}).
Примеры использования
(eta_{k}=frac{1}{k})
(eta_{k}=lambda(frac{s_{0}}{s_{0}+k})^{p})
SAG
На (k) -й итерации выбирается случайное слагаемое (i_{k}) и обновляются вспомогательные переменные:
[
z_i^{(k)}
=
begin{cases}
nabla q_i(w^{(k — 1)}),
quad
&text{если} i = i_k;\
z_i^{(k — 1)}
quad
&text{иначе}.
end{cases}]
[
w^{(k)}=w^{(k — 1)}-eta_kfrac{1}{ell}sum_{i = 1}^{ell}z_i^{(k)}
]
9. В чём заключаются метод инерции и AdaGrad/RMSProp?
Adagrad
В методе AdaGrad предлагается сделать свою длину шага для каждой компоненты вектора параметров. При этом шаг будет тем меньше, чем более длинные шаги мы делали на предыдущих итерациях
[
G_{kj} = G_{k-1,j} + (nabla_w Q(w^{(k-1)}))_j^2
]
[
w_j^{(k)} = w_j^{(k-1)} — frac{eta_t}{sqrt{G_{kj} + varepsilon}} (nabla_w Q(w^{(k-1)}))_j
]
недостаток: переменная (G_{kj}) монотонно растёт, из-за чего шаги становятся всё медленнее и могут остановиться ещё до того, как достигнут минимум функционала
RMSprop
Улучшение над AdaGrad. В этом случае размер шага по координате зависит в основном от того, насколько быстро мы двигались по ней на последних итерациях
[G_{kj} = alpha G_{k-1,j} + (1 — alpha) (nabla_w Q(w^{(k-1)}))_j^2.]
10. Что такое кросс-валидация? На что влияет количество блоков в кросс-валидации? Как построить итоговую модель после того, как по кросс-валидации подобраны оптимальные гиперпараметры?
- CV – размеченные данные разбиваются на (k) блоков примерно одинакового размера. Затем обучается (k) моделей (a_1(x), dots, a_k(x)) причём (i) -я модель обучается на объектах из всех блоков, кроме блока (i).
После этого качество каждой модели оценивается по тому блоку, который не участвовал в её обучении, и результаты усредняются:
[text{CV}
=
frac{1}{k}
sum_{i = 1}^{k}
Qleft( a_i(x), X_i right).] - можно построить композицию из моделей (a_1(x), dots, a_k(x)), полученных в процессе кросс-валидации. Под композицией может пониматься, например, усреднение прогнозов этих моделей, если мы решаем задачу регрессии.
11. Чем гиперпараметры отличаются от параметров? Что является параметрами и гиперпараметрами в линейных моделях и в решающих деревьях?
- Параметры — величины, которые настраиваются по обучающей выборке
- Гиперпараметры — относят величины, которые контролируют сам процесс обучения и не могут быть подобраны по обучающей выборке
- Параметры для линейных моделей:
- Веса
- Гиперпараметр для линейных моделей:
- Коэффициент регуляризации
- Размер шага градиента
- Параметр для деревьев:
- Разбиение
- Гиперпараметр для деревьев:
- Глубина дерева
- Минимальное количество элементов в листьях
- Минимальное количество элементов для разбиения
12. Что такое регуляризация? Запишите L1- и L2-регуляризаторы.
Регуляризация – способ штрафовать модель за высокую норму весов с помощью коэффициента регуляризации для предотвращения переобучения.
Наиболее распространенными являются (L_2) и (L_1) -регуляризаторы:
[
R(w) = |w|_2 = sum_{i = 1}^d w_i^2,
]
[
R(w) = |w|_1 = sum_{i = 1}^d |w_i|.
]
13. Почему L1-регуляризация отбирает признаки?
Зануление весов
Можно показать, что если функционал (Q(w)) является выпуклым, то задача безусловной минимизации функции (Q(w) + alpha |w|_1) эквивалентна задаче условной оптимизации [Q(w) to min_{w}] [|w|_1 leq C] для некоторого (C). Изображены линии уровня функционала (Q(w)), а также множество, определяемое ограничением (|w|_1 leq C). Решение определяется точкой пересечения допустимого множества с линией уровня, ближайшей к безусловному минимуму. Из изображения можно предположить, что в большинстве случаев эта точка будет лежать на одной из вершин ромба, что соответствует решению с одной зануленной компонентой.
Штрафы при малых весах
Предположим, что текущий вектор весов состоит из двух элементов (w = (1, varepsilon)), где (varepsilon) близко к нулю, и мы хотим немного изменить данный вектор по одной из координат. Найдём изменение (L_2) — и (L_1) -норм вектора при уменьшении первой компоненты на некоторое положительное число (delta < varepsilon):
[|w — (delta, 0)|_2^2=1 — 2 delta + delta^2 + varepsilon^2]
[|w — (delta, 0)|_1=1 — delta + varepsilon]
Вычислим то же самое для изменения второй компоненты:
[|w — (0, delta)|_2^2=1 — 2 varepsilon delta + delta^2 + varepsilon^2]
[|w — (0, delta)|_1 =1 — delta + varepsilon]
Видно, что с точки зрения (L_2) -нормы выгоднее уменьшать первую компоненту, а для (L_1) -нормы оба изменения равноценны. Таким образом, при выборе (L_2) -регуляризации гораздо меньше шансов, что маленькие веса будут окончательно обнулены.
Проксимальный шаг
Проксимальные методы – это класс методов оптимизации, которые хорошо подходят для функционалов с негладкими слагаемыми. Формула для шага проксимального метода в применении к линейной регрессии с квадратичным функционалом ошибки и (L_1) -регуляризатором:
[w^{(k)}=S_{eta alpha} left(w^{(k — 1)}-etanabla_w F(w^{(k — 1)})right),]
где (F(w) = |Xw — y|^2) – функционал ошибки без регуляризатора, (eta) – длина шага, (alpha) – коэффициент регуляризации, а функция (S_{eta alpha}(w)) применяется к вектору весов покомпонентно, и для одного элемента выглядит как
[S_{eta alpha} (w_i)=
begin{cases}
w_i — eta alpha, quad &w_i > eta alpha\
0, qquad &|w_i| < eta alpha\
w_i + eta alpha, quad &w_i < -eta alpha
end{cases}]
Из формулы видно, что если на данном шаге значение некоторого веса не очень большое, то на следующем шаге этот вес будет обнулён, причём чем больше коэффициент регуляризации, тем больше весов будут обнуляться.
14. Почему плохо накладывать регуляризацию на свободный коэффициент? Почему регуляризация может странно работать на немасштабированных данных?
-
Отметим, что свободный коэффициент (w_0) нет смысла регуляризовывать — если мы будем штрафовать за его величину, то получится, что мы учитываем некие априорные представления о близости целевой переменной к нулю и отсутствии необходимости в учёте её смещения. Такое предположение является достаточно странным. Особенно об этом следует помнить, если в выборке есть константный признак и коэффициент (w_0) обучается наряду с остальными весами; в этом случае следует исключить слагаемое, соответствующее константному признаку, из регуляризатора.
-
Может быть большой разброс порядков весов.
15. Запишите формулу для линейной модели классификации. Что такое отступ? Как обучаются линейные классификаторы и для чего нужны верхние оценки пороговой функции потерь?
Формула
[
a(x) = text{sign}left(
langle w, x rangle + w_0
right)
=
text{sign} left(
sum_{j = 1}^{d} w_j x_j + w_0
right)
]
Отступ
[
M_i = y<w,x_i>
]
Знак отступа говорит о корректности ответа классификатора (положительный отступ соответствует правильному ответу, отрицательный неправильному), а его абсолютная величина характеризует степень уверенности классификатора в своём ответе. Напомним, что скалярное произведение (<w,x_i>) пропорционально расстоянию от разделяющей гиперплоскости до объекта; соответственно, чем ближе отступ к нулю, тем ближе объект к границе классов, тем ниже уверенность в его принадлежности.
Обучение линейных классификаторов
Нам будет удобнее решать задачу минимизации, поэтому будем вместо этого использовать долю неправильных ответов
[
Q(a, X)=
frac{1}{ell}
sum_{i = 1}^{ell}
[a(x_i) neq y_i]
=
frac{1}{ell}
sum_{i = 1}^{ell}
[mathop{rm sign}limits langle w, x_i rangle neq y_i]
to
min_w
]
Этот функционал является дискретным относительно весов, и поэтому искать его минимум с помощью градиентных методов мы не сможем. Более того, у данного функционала может быть много глобальных минимумов вполне может оказаться, что существует много способов добиться оптимального количества ошибок. Чтобы не пытаться решать все эти проблемы, попытаемся свести задачу к минимизации гладкого функционала (верхней оценки).
Верхние оценки
Функционал оценивает ошибку алгоритма на объекте (x) с помощью пороговой функции потерь (L(M) = [M < 0]),
где аргументом функции является отступ (M = y langle w, x rangle). Оценим эту функцию сверху во всех точках (M) кроме, может быть, небольшой полуокрестности левее нуля:[
L(M) leq tilde L(M).
]
После этого можно получить верхнюю оценку на функционал:
[
Q(a, X)
leq
frac{1}{ell}
sum_{i = 1}^{ell}
tilde L(y_i langle w, x_i rangle)
to
min_w
]
Если верхняя оценка (tilde L(M)) является гладкой, то и данная верхняя оценка будет гладкой. В этом случае её можно будет минимизировать с помощью, например, градиентного спуска. Если верхнюю оценку удастся приблизить к нулю, то и доля неправильных ответов тоже будет близка к нулю.
Приведём несколько примеров верхних оценок:
- (tilde L(M) = log left(1 + e^{-M} right)) – логистическая функция потерь
- (tilde L(M) = (1 — M)_+ = max(0, 1 — M)) – кусочно-линейная функция потерь (используется в методе опорных векторов)
- (tilde L(M) = (-M)_+ = max(0, -M)) – кусочно-линейная функция потерь (соответствует персептрону Розенблатта)
- (tilde L(M) = e^{-M}) – экспоненциальная функция потерь
- (tilde L(M) = 2/(1 + e^M)) – сигмоидная функция потерь
Любая из них подойдёт для обучения линейного классификатора.
16. Что такое точность, полнота и F-мера? Почему F-мера лучше арифметического среднего и минимума?
| y=1 | y=-1 | |
|---|---|---|
| a(x)=1 | True Positive (TP) | False Positive (FP) |
| a(x)=-1 | False Negative (FN) | True Negative (TN) |
Точность
Точность (которая не accuracy (которой точный перевод — доля верных ответов), а precision) — метрика того, насколько можно доверять модели если она сказала что объект относится к положительному классу.
[
text{precision}=frac{text{TP}}{text{TP} + text{FP}}
]
Полнота
Полнота (recall) — метрика того, насколько хорошо модель покрыла положительный класс
[
text{recall}=frac{text{TP}}{text{TP} + text{FN}}
]
F-мера
F — мера — гармоническое среднее точности и полноты, (сохраняет хорошее от ариф. минимума, но более гладкая. Близко к 0 если хотя бы 1 из аргументов близок к нулю). В отличие от геометрического среднего — гармоническое среднее гораздо устойчивее к выбросам.
[
F=frac{2 * text{precision} * text{recall}}{text{precision} + text{recall}}
]
17. Для чего нужен порог в линейном классификаторе? Из каких соображений он может выбираться?
- Для определения класса объекта
- Может выбираться:
- из цен ошибок
- из требуемого количества
- из требований к recall и precision
18. Что такое AUC-ROC? Опишите алгоритм построения ROC-кривой.
AUC ROC-area under ROC (receiving operating characteristic) curve, — площадь под ROC-кривой.
Сортируем объекты (b(x)), по размеру порога; размер шага для объектов с ([y = 0] =frac{1}{L_{-}}) отрицательных (шаги по FPR (горизонт ось)), шаги для ([y = 1] =frac{1}{L_+}) положительных (шаги по TPR (верт ось) )
19. Что такое AUC-PRC? Опишите алгоритм построения PR-кривой.
Она определяется аналогично ROC-кривой, только по осям откладываются не FPR и TPR, а полнота (по оси абсцисс) и точность (по оси ординат). Критерием качества семейства алгоритмов выступает площадь под PR-кривой (AUC-PR).
Описание алгоритма
Стартуем из точки (0, 1). Будем идти по ранжированной выборке, начиная с первого объекта; пусть текущий объект находится на позиции (k). Если он относится к классу −1, то полнота не меняется, точность падает соответственно, кривая опускается строго вниз на (frac{1}{l_{-}}). Если же объект относится к классу 1, то полнота увеличивается на (frac{1}{l_+}), точность растет, и кривая поднимается вправо и вверх. Площадь под этим участком можно аппроксимировать площадью прямоугольника с высотой, равной precision@k и шириной (frac{1}{l_{+}}).
20. Что означает “модель оценивает вероятность положительного класса”? Как можно внедрить это требование в процедуру обучения модели?
Рассмотрим точку (x) пространства объектов. Как мы договорились, в ней имеется распределение на ответах (p(y = +1 | x)). Допустим, алгоритм (b(x)) возвращает числа из отрезка ([0, 1]). Наша задача – выбрать для него такую процедуру обучения, что в точке (x) ему будет оптимально выдавать число (p(y = +1 | x)).
Если в выборке объект (x) встречается (n) раз с ответами ({y_1, dots, y_n}), то получаем следующее требование:
[
mathop{rm arg,min}limits_{b in mathbb{R}}
frac{1}{n}
sum_{i = 1}^{n}
L(y_i, b)
approx
p(y = +1 | x)
]
При стремлении (n) к бесконечности получим, что функционал стремится к матожиданию ошибки:
[
mathop{rm arg,min}limits_{b in mathbb{R}}mathbb{E} left[L(y, b)|xright]
=
p(y = +1 | x)
]
На семинаре будет показано, что этим свойством обладает, например, квадратичная функция потерь (L(y, z) = (y — z)^2), если в ней для положительных объектов использовать истинную метку (y = 1), а для отрицательных брать (y = 0). Если функция потерь (L) удовлетворяет второй формуле, то (b(x)approx p(y=+1|x))
21. Что такое калибровочная кривая? Какие методы калибровки вероятности вы знаете? Почему важно проводить калибровку не на обучающей выборке?
Калибровка вероятностей нужна для того, чтобы заставить модель выдавать корректные вероятности принадлежности к классам. В задаче бинарной классификации откалиброванным алгоритмом называют такой алгоритм, для которого доля положительных примеров (на основе реальных меток классов) для предсказаний в окрестности произвольной вероятности (p) совпадает с этим значением (p).
На этой кривой абсцисса точки соответствуют значению (p) (предсказаний алгоритма), а ордината соответствует доле положительных примеров, для которых алгоритм предсказал вероятность, близкую к (p). В идеальном случае эта кривая совпадает с прямой (y = x).
Есть два подхода к калибровке.
- Масштабирование Платта. Он заключается к подгонке всех предсказаний к логистической кривой (по сути, логистическая регрессия на ответах классификатора) [P(y = 1 | x) = frac{1}{1+exp (af(x) + b)},] где (a, b) – скалярные параметры. Эти параметры настраиваются методом максимума правдоподобия (минимизируя логистическую функцию потерь) на отложенной выборке или с помощью кросс валидации. Также Платт предложил настраивать параметры на обучающей выборке базовой модели, а для избежания переобучения изменить метки объектов на следующие значения:
- [t_{+} = frac{N_{+} + 1}{N_{-} + 2}] для положительных примеров
- [t_{-} = frac{1}{N_{-} + 2}] для отрицательных.
- Изотоническая регрессия. В этом методе также строится отображение из предсказаний модели в откалиброванные вероятности. Для этого используем изотоническую функцию (неубывающая кусочно-постоянная функция), в которой (x) – выходы нашего алгоритма, а (y) – целевая переменная. Мы хотим найти такую функцию (m(t)): (P(y = 1 | x) = m(f(x))). Она настраивается под квадратичную ошибку:
[m = mathop{rm arg,min}limits_{z} sum (y_i — z(f(x_i))^2,] с помощью специального алгоритма (Pool-Adjacent-Violators Algorithm). В результате калибровки получаем надстройку над нашей моделью, которая применяется поверх предсказаний базовой модели.
22. Запишите функционал логистической регрессии. Как он связан с методом максимума правдоподобия?
Модель: [
p(y = 1| x)
=
frac{1}{1 + exp(-langle w, x rangle)}.
]
Подставим трансформированный ответ линейной модели в логарифмическую функцию потерь:
[
-sum_{i = 1}^{ell}left([y_i = +1]
log frac{1}{1 + exp(-langle w, x_i rangle)}
+[y_i = -1]log frac{exp(-langle w, x_i rangle)}{1 + exp(-langle w, x_i rangle)}
right)
=
-sum_{i = 1}^{ell} left(
[y_i = +1]log frac{1}{1 + exp(-langle w, x_i rangle)}
+[y_i = -1]log frac{1}{1 + exp(langle w, x_i rangle)}
right)
=
sum_{i = 1}^{ell}
log left(
1 + exp(-y_i langle w, x_i rangle)
right).
]
Попробуем сконструировать функцию потерь из других соображений. Если алгоритм (b(x) in [0, 1]) действительно выдает вероятности, то они должны согласовываться с выборкой. С точки зрения алгоритма вероятность того, что в выборке встретится объект (x_i) с классом (y_i), равна (b(x_i)^{[y_i = +1]} (1 — b(x_i))^{[y_i = -1]}).
Исходя из этого, можно записать правдоподобие выборки (т.е. вероятность получить такую выборку с точки зрения алгоритма):
[
Q(a, X)=
prod_{i = 1}^{ell}
b(x_i)^{[y_i = +1]} (1 — b(x_i))^{[y_i = -1]}.
]
Данное правдоподобие можно использовать как функционал для обучения алгоритма – с той лишь оговоркой, что удобнее оптимизировать его логарифм:[-sum_{i = 1}^{ell} left([y_i = +1] log b(x_i) + [y_i = -1] log (1 — b(x_i))right)
tomin
]
23. Запишите задачу метода опорных векторов для линейно неразделимого случая. Как функционал этой задачи связан с отступом классификатора? Как выглядит задача безусловной оптимизации в SVM?
Условный
[
left{begin{aligned}
& frac{1}{2} |w|^2 + C sum_{i = 1}^{ell} xi_i to min_{w, b, xi} \
& y_i left(
langle w, x_i rangle + b
right) geq 1 — xi_i, quad i = 1, dots, ell, \
& xi_i geq 0, quad i = 1, dots, ell.
end{aligned}
right.
]
Безусловный
[
frac12 |w|^2+
C
sum_{i = 1}^{ell}
max(0,
1 — y_i (langle w, x_i rangle + b))
to
min_{w, b}
]
Величина (frac{1}{|w|}) в данном случае называется мягким отступом (soft margin). С одной стороны, мы хотим максимизировать отступ, с другой – минимизировать штраф за неидеальное разделение выборки (sum_{i = 1}^{ell} xi_i).
24. В чём заключаются one-vs-all и all-vs-all подходы в многоклассовой классификации?
One-vs-all
Обучим (K) линейных классификаторов (b_1(x), dots, b_K(x)), выдающих оценки принадлежности классам (1, dots, K) соответственно. Например, в случае с линейными моделями эти модели будут иметь вид (b_k(x) = langle w_k, x rangle + w_{0k}). Классификатор с номером (k) будем обучать по выборке (left(x_i, 2 [y_i = k] — 1right)_{i = 1}^{ell}); иными словами, мы учим классификатор отличать (k) -й класс от всех остальных.
Итоговый классификатор будет выдавать класс, соответствующий самому уверенному из бинарных алгоритмов:
[
a(x)
=
mathop{rm arg,max}limits_{k in {1, dots, K}}
b_k(x).
]
Проблема данного подхода заключается в том, что каждый из классификаторов (b_1(x), dots, b_K(x)) обучается на своей выборке, и выходы этих классификаторов могут иметь разные масштабы, из-за чего сравнивать их будет неправильно. Нормировать вектора весов, чтобы они выдавали ответы в одной и той же шкале, не всегда может быть разумным решением – так, в случае с SVM веса перестанут являться решением задачи, поскольку нормировка изменит норму весов.
All-vs-all
Обучим (C_K^2) классификаторов (a_{ij}(x)), (i, j = 1, dots, K), (i neq j).
Например, в случае с линейными моделями эти модели будут иметь вид
[
b_k(x) = mathop{rm sign}limits(langle w_k, x rangle + w_{0k} ).
]
Классификатор (a_{ij}(x)) будем настраивать по подвыборк (X_{ij} subset X), содержащей только объекты классов (i) и (j):
[
X_{ij} = {(x_n, y_n) in X | [y_n = i] = 1 text{или} [y_n = j] = 1 }.
]
Соответственно, классификатор (a_{ij}(x)) будет выдавать для любого объекта либо класс (i), либо класс (j).
Чтобы классифицировать новый объект, подадим его на вход каждого из построенных бинарных классификаторов. Каждый из них проголосует за своей класс; в качестве ответа выберем тот класс, за который наберется больше всего голосов:
[
a(x) = mathop{rm arg,max}limits_{k in {1, dots, K}}
sum_{i = 1}^{K} sum_{j neq i}
[a_{ij}(x) = k].
]
25. Как измеряется качество в задаче многоклассовой классификации? Что такое микро- и макро-усреднение?
В многоклассовых задачах, как правило, стараются свести подсчет качества к вычислению одной из двухклассовых метрик. Выделяют два подхода к такому сведению: микро- и макро-усреднение.
Пусть выборка состоит из (K) классов. Рассмотрим (K) двухклассовых задач, каждая из которых заключается в отделении своего класса от остальных, то есть целевые значения для (k) -й задаче вычисляются как (y_i^k = [y_i = k]). Для каждой из них можно вычислить различные характеристики (TP, FP, и т.д.) алгоритма (a^k(x) = [a(x) = k]); будем обозначать эти величины как (text{TP}_k, text{FP}_k, text{FN}_k, text{TN}_k). Заметим, что в двухклассовом случае все метрики качества, которые мы изучали, выражались через эти элементы матрицы ошибок.
Микро-усренднение
При микро-усреднении сначала эти характеристики усредняются по всем классам, а затем вычисляется итоговая двухклассовая метрика – например, точность, полнота или F-мера. Например, точность будет вычисляться по формуле
[
text{precision}(a, X)
=
frac{overline{text{TP}}}{overline{text{TP}}+overline{text{FP}}},
] где, например, (overline{text{TP}}) вычисляется по формуле [
overline{text{TP}}
=
frac{1}{K}
sum_{k = 1}^{K}
text{TP}_k.
]
Макро-усреднение
При макро-усреднении сначала вычисляется итоговая метрика для каждого класса, а затем результаты усредняются по всем классам. Например, точность будет вычислена как [text{precision}(a, X)=frac{1}{K}sum_{k = 1}^{K}text{precision}_k(a, X);qquad]
[
text{precision}_k(a, X)=frac{text{TP}_k}{text{TP}_k+text{FP}_k}.
]
Сравнение
Если какой-то класс имеет очень маленькую мощность, то при микро-усреднении он практически никак не будет влиять на результат, поскольку его вклад в средние TP, FP, FN и TN будет незначителен. В случае же с макро-вариантом усреднение проводится для величин, которые уже не чувствительны к соотношению размеров классов (если мы используем, например, точность или полноту), и поэтому каждый класс внесет равный вклад в итоговую метрику.
26. В чём заключается преобразование категориальных признаков в вещественные с помощью mean-target encoding? Почему использование этого способа кодирования может привести к переобучению? Какие методы борьбы с этой проблемой вам известны?
Mean target encoding
Более сложный метод кодирования категориальных признаков – через целевую переменную. Идея в том, что алгоритму для предсказания цены необходимо знать не конкретный цвет автомобиля, а то, как этот цвет сказывается на цене. Разберём сначала базовый подход – mean target encoding (иногда его называют ).
Заменим каждую категорию на среднее значение целевой переменной по всем объектам этой категории. Пусть (j) -й признак является категориальным. Для бинарной классификации новый признак будет выглядеть следующим образом:
[
g_j(x, X)
=
frac{
sum_{i=1}^{ell}
[f_j(x) = f_j(x_i)][y_i = +1]
}{
sum_{i=1}^{ell}
[f_j(x) = f_j(x_i)]
},
]
где (f_j(x_i)) – (j) -й признак (i) -го объекта, (y_i) – класс (i) -го объекта.
Отметим, что эту формулу легко перенести как на случай многоклассовой классификации (в этом случае будем считать (K) признаков, по одному для каждого класса, и в числителе будет подсчитывать долю объектов с заданной категорией и с заданным классом), так и на случай регрессии (будем вычислять среднее значение целевой переменной среди объектов данной категории).
Вернёмся к бинарной классификации. Можно заметить, что для редких категорий мы получим некорректные средние значения целевой переменной. Например, в выборке было только три золотистых автомобиля, которые оказались старыми и дешёвыми. Из-за этого наш алгоритм начнёт считать золотистый цвет дешёвым. Для исправления этой проблемы можно регуляризировать признак средним значением целевой переменной по всем категориям так, чтобы у редких категорий значение было близко к среднему по всей выборке, а для популярных к среднему значению по категории.
Формально для задачи бинарной классификации это выражается так:
[
g_j(x, X)
=
frac{
sum_{i=1}^{ell}[f_j(x) = f_j(x_i)][y_i = +1]+
frac{C}{ell}sum_{i=1}^{ell}[y_i = +1]
}{
sum_{i=1}^{ell}
[f_j(x) = f_j(x_i)] + C
},
]
где (C) – коэффициент, отвечающий за баланс между средним значением по категории и глобальным средним значением.
Однако если мы вычислим значения (g_j(x, X)) по всей выборке, то столкнёмся с переобучением, так как мы внесли информацию о целевой переменной в признаки (новый признак слабая, но модель, предсказывающая целевое значение). Поэтому вычисление таких признаков следует производить по блокам, то есть вычислять средние значения на основе одних фолдов для заполнения на другом блоке (аналогично процессу кросс-валидации). Если же ещё планируется оценка качества модели с помощью кросс-валидации по блокам, то придётся применить для подсчёта признаков. Этот подход заключается в кодировании категориальных признаков по блокам внутри блоков, по которым оценивается качество модели.
Разберём этот процесс. Представим, что хотим посчитать качество модели на 3-м блоке. Для этого:
- Разбиваем все внешние блоки, кроме 3-го, на внутренние блоки. Количество внутренних блоков может не совпадать с количеством внешних.
- Рассмотрим конкретный внешний
Для каждого из его внутренних блоков считаем значение (g(x, X)) на основе средних значений целевой переменной по блокам, исключая текущий. Для 3-го внешнего блока (который сейчас играет роль тестовой выборки) вычисляем (g(x, X)) как среднее вычисленных признаков по каждому из внутренних фолдов. - Обучаем модель на всех блоках, кроме 3-го, делаем предсказание на 3-м и считаем на нём качество.
Существуют альтернативы кодированию категориальных признаков по блокам.
Зашумление
Можно посчитать новые признаки по базовой формуле, а затем просто добавить к каждому значению случайный шум (например, нормальный). Это действительно снизит уровень корреляции счётчиков с целевой переменной. Проблема в том, что это делается за счёт снижения силы такого признака, а значит, мы ухудшаем итоговое качество модели. Поэтому важно подбирать дисперсию шума, чтобы соблюсти баланс между борьбой с переобучением и предсказательной силой счётчиков.
Сглаживание
Можно немного модифицировать формулу, чтобы сила регуляризации зависела от объёма данных по конкретной категории:
[
g_j(x, X)
=
lambda left( n(f_j(x)) right)
frac{
sum_{i=1}^{ell}[f_j(x) = f_j(x_i)][y_i = +1]
}{
sum_{i=1}^{ell}[f_j(x) = f_j(x_i)]
}
+left( 1 — lambda left( n(f_j(x)) right) right)
frac{1}{ell}
sum_{i = 1}^{ell}
[y_i = +1]
,
]
где (n(z) = sum_{i = 1}^{ell} [f_j(x_i) = z]) – число объектов категории (z), (lambda(n)) – некоторая монотонно возрастающая функция, дающая значения из отрезка ([0, 1]).
Примером может служить (lambda(n) = frac{1}{1 + exp(-n)}). Если грамотно подобрать эту функцию, то она будет вычищать значение целевой переменной из редких категорий и мешать переобучению.
Кодирование по времени.
Можно отсортировать выборку некоторым образом и для (i) -го объекта вычислять статистики только по предыдущим объектам:
[
g_j(x_k, X)
=
frac{
sum_{i=1}^{k — 1}
[f_j(x) = f_j(x_i)][y_i = +1]
}{
sum_{i=1}^{k — 1}
[f_j(x) = f_j(x_i)]
}.
]
Для хорошего качества имеет смысл отсортировать выборку случайным образом несколько раз, и для каждого такого порядка посчитать свои счётчики.
Это даёт улучшение качества, например, потому что для объектов, находящихся в начале выборки, признаки будут считаться по очень небольшой подвыборке, и поэтому вряд ли будут хорошо предсказывать целевую переменную. При наличии нескольких перестановок хотя бы один из новых признаков будет вычислен по подвыборке достаточного размера. Такой подход, например, используется в библиотеке CatBoost.
Weight of Evidence
Существует альтернативный способ кодирования категориальных признаков, основанный на подсчёте соотношения положительных и отрицательных объектов среди объектов данной категории. Этот подход, в отличие от других, сложнее обобщить на многоклассовый случай или для регрессии.
Введём обозначение для доли объектов класса (b) внутри заданной категории (c) среди всех объектов данного класса в выборке:
[
P(c | y = b)=
frac{
sum_{i = 1}^{ell}[y_i = b] [f_j(x_i) = c]+alpha
}{
sum_{i = 1}^{ell}[y_i = b]+2 alpha
},
]
где (alpha) – параметр сглаживания.
Вычислим новое значение признака как
[
g_j(x, X)
=
logleft(
frac{
P(f_j(x) | y = +1)
}{
P(f_j(x) | y = -1)
}
right).
]
Если (g_j(x, X)) близко к нулю, то данная категория примерно с одинаковой вероятностью встречается в обоих классах, и поэтому вряд ли будет хорошо предсказывать значение целевой переменной. Чем сильнее отличие от нуля, тем сильнее категория характеризует один из классов.
Разумеется, в конкретной задаче лучше всего может себя проявлять любой из этих подходов, поэтому имеет смысл сравнивать их и выбирать лучший – или использовать все сразу.
27. Как определить для линейной модели, какие признаки являются самыми важными?
- наибольшим модулем соответствующего параметра линейной модели
- (t) -статистика
[
t(j) = frac{|mu_+ — mu_-|}{sqrt{frac{n_+ sigma^2_+ + n_- sigma^2_-}{n_+ + n_-}}}
] - исключаем по очереди один из признаков и смотрим, как это влияет на качество. Удаляем признаки таким жадным способом, пока не окажется выполненным некоторое условие (количество признаков или ухудшение качества).
- Можно использовать L1-регуляризацию, которая занулит веса на самых бесполезных признаках.
- Можно, в конце концов, посчитать корреляцию таргета и признака.
28. Опишите жадный алгоритм обучения решающего дерева.
Опишем базовый жадный алгоритм построения бинарного решающего дерева. Начнем со всей обучающей выборки (X) и найдем наилучшее ее разбиение на две части (R_1(j, t) = {x | x_j < t}) и (R_2(j, t) = {x | x_j geq t})
с точки зрения заранее заданного функционала качества (Q(X, j, t)). Найдя наилучшие значения (j) и (t), создадим корневую вершину дерева, поставив ей в соответствие предикат ([x_j < t]).
Объекты разобьются на две части – одни попадут в левое поддерево, другие в правое. Для каждой из этих подвыборок рекурсивно повторим процедуру, построив дочерние вершины для корневой, и так далее. В каждой вершине мы проверяем, не выполнилось ли некоторое условие останова – и если выполнилось, то прекращаем рекурсию и объявляем эту вершину листом. Когда дерево построено, каждому листу ставится в соответствие ответ. В случае с классификацией это может быть класс, к которому относится больше всего объектов в листе, или вектор вероятностей (скажем, вероятность класса может быть равна доле его объектов в листе). Для регрессии это может быть среднее значение, медиана или другая функция от целевых переменных объектов в листе. Выбор конкретной функции зависит от функционала качества в исходной задаче.
29. Почему с помощью бинарного решающего дерева можно достичь нулевой ошибки на обучающей выборке без повторяющихся объектов?
Для выборки без повторяющихся объектов мы можем построить такое дерево, что количество листов в нем будет равно количеству объектов в выборке, и в каждом листе будет стоять отдельный объект. У каждого объекта будет уникальное признаковое описание, а значит, мы можем построить дерево предикатов так, чтобы оно делило выборку идеально. Само собой, обобщающая способность такого дерева будет не очень хорошей.
30. Как в общем случае выглядит критерий хаотичности? Как он используется для выбора предиката во внутренней вершине решающего дерева? Как вывести критерий Джини и энтропийный критерий?
Общий случай
[
H( R)
=
min_{c in mathbb{Y}}
frac{1}{|R|}
sum_{(x_i, y_i) in R}
L(y_i, c),
]
Т.е. критерий показывает, насколько хорошо целевая переменная в данном множестве приближается константой.
Чем менее разнообразно значение целевой переменной среди объектов, тем меньше значение критерия — поэтому мы пытаемся его минимизировать. При этом в процессе разбиения мы пытаемся максимизировать такой функционал:
[
Q(R_m, j, s)=H(R_m)-frac{|R_ell|}{|R_m|}H(R_ell)-frac{|R_r|}{|R_m|}H(R_r)
]
Джини
Рассмотрим ситуацию, в которой мы выдаём в вершине не один класс, а распределение на всех классах (c = (c_1, dots, c_K)), (sum_{k = 1}^{K} c_k = 1). Качество такого распределения можно измерять, например, с помощью критерия Бриера (Brier score):
[
H( R)
=
min_{sum_k c_k = 1}
frac{1}{|R|}
sum_{(x_i, y_i) in R}
sum_{k = 1}^{K}
(c_k — [y_i = k])^2.
]
Легко заметить, что здесь мы, по сути, ищем каждый (c_k) как оптимальную с точки зрения MSE константу, приближающую индикаторы попадания объектов выборки в класс (k). Это означает, что оптимальный вектор вероятностей состоит из долей классов (p_k): [c_* = (p_1, dots, p_K)]
Если подставить эти вероятности в исходный критерий информативности и провести ряд преобразований, то мы получим критерий Джини: [H( R)=sum_{k = 1}^{K}p_k (1 — p_k).]
Энтропийный
Мы уже знакомы с более популярным способом оценивания качества вероятностей – логарифмическими потерями, или логарифмом правдоподобия:
[
H( R)=min_{sum_k c_k = 1} left(-frac{1}{|R|}sum_{(x_i, y_i) in R}sum_{k = 1}^{K}[y_i = k]log c_kright)
]
Для вывода оптимальных значений (c_k) вспомним, что все значения (c_k) должны суммироваться в единицу.
Как известного из методов оптимизации, для учёта этого ограничения необходимо искать минимум лагранжиана:
[
L(c, lambda)=-frac{1}{|R|}sum_{(x_i, y_i) in R}sum_{k = 1}^{K}[y_i = k]log c_k+lambdasum_{k = 1}^{K}c_ktomin_{c_k}
]
Дифференцируя, получаем:
[
frac{partial}{partial c_k}L(c, lambda)=-frac{1}{|R|}sum_{(x_i, y_i) in R}[y_i = k]frac{1}{c_k}+lambda=-frac{p_k}{c_k}+lambda=0
]
откуда выражаем (c_k = p_k / lambda).
Суммируя эти равенства по (k), получим
[
1 = sum_{k = 1}^{K} c_k = frac{1}{lambda} sum_{k = 1}^{K} p_k = frac{1}{lambda},
] откуда (lambda = 1).
Значит, минимум достигается при (c_k = p_k), как и в предыдущем случае. Подставляя эти выражения в критерий, получим, что он будет представлять собой энтропию распределения классов:
[H( R)=-sum_{k = 1}^{K}p_klog p_k.]
Из теории вероятностей известно, что энтропия ограничена снизу нулем, причем минимум достигается на вырожденных распределениях ((p_i = 1), (p_j = 0) для (i neq j)). Максимальное же значение энтропия принимает для равномерного распределения. Отсюда видно, что энтропийный критерий отдает предпочтение более распределениям классов в вершине.
31. Для какой ошибки строится разложение на шум, смещение и разброс? Запишите формулу этой ошибки.
Разложение ошибки на три компоненты, которое мы только что вывели, верно только для квадратичной функции потерь. Существуют более общие формы этого разложения, которые состоят из трёх компонент с аналогичным смыслом, поэтому можно утверждать, что для большинства распространённых функций потерь ошибка метода обучения складывается из шума, смещения и разброса; значит, и дальнейшие рассуждения про изменение этих компонент в композициях также можно обобщить на другие функции потерь (например, на индикатор ошибки классификации).
BVD для среднеквадратичного риска метода (mu) (обученного на выборке (X)), усредненного по всем возможным выборкам.
[
L(mu)=
mathbb{E}_{X} Bigl[
mathbb{E}_{x, y} Bigl[
bigl(
y — mu(X)(x)
bigr)^2
Bigr]
Bigr]
]
[
L(mu)=
underbrace{mathbb{E}_{x, y}Bigl[bigl(y — mathbb{E}[y | x]bigr)^2Bigr]}_{text{шум}}+
underbrace{mathbb{E}_{x} Bigl[bigl(mathbb{E}_{X} bigl[ mu(X) bigr]-mathbb{E}[y | x]bigr)^2Bigr]}_{text{смещение}}
+underbrace{mathbb{E}_{x} Bigl[mathbb{E}_{X} Bigl[bigl(mu(X)-mathbb{E}_{X} bigl[ mu(X) bigr]bigr)^2Bigr]Bigr]}_{text{разброс}}.
]
32. Запишите формулы для шума, смещения и разброса метода обучения для случая квадратичной функции потерь.
[
L(mu)=
underbrace{mathbb{E}_{x, y}Bigl[bigl(y — mathbb{E}[y | x]bigr)^2Bigr]}_{text{шум}}+
underbrace{mathbb{E}_{x} Bigl[bigl(mathbb{E}_{X} bigl[ mu(X) bigr]-mathbb{E}[y | x]bigr)^2Bigr]}_{text{смещение}}
+underbrace{mathbb{E}_{x} Bigl[mathbb{E}_{X} Bigl[bigl(mu(X)-mathbb{E}_{X} bigl[ mu(X) bigr]bigr)^2Bigr]Bigr]}_{text{разброс}}.
]
33. Приведите пример семейства алгоритмов с низким смещением и большим разбросом; семейства алгоритмов с большим смещением и низким разбросом. Поясните примеры.
Смещение показывает, насколько хорошо с помощью данных метода обучения и семейства алгоритмов можно приблизить оптимальный алгоритм. Как правило, смещение маленькое у сложных (precision) семейств (например, у деревьев) и большое у простых семейств (например, линейных классификаторов). Дисперсия показывает, насколько сильно может изменяться ответ обученного алгоритма в зависимости от выборки иными словами, она характеризует чувствительность метода обучения к изменениям в выборке. Как правило, простые семейства имеют маленькую дисперсию (variance), а сложные семейства большую дисперсию.
34. Что такое бэггинг? Как его смещение и разброс связаны со смещением и разбросом базовых моделей?
Для начала, бутстрап – способ ресэмплинга. По имеющейся выборке (X) создадим (N) новых выборок путем взятия элементов из (X) с повторениями.
Пусть имеется некоторый метод обучения (mu(X)). Построим на его основе метод (tilde mu(X)), который генерирует случайную подвыборку (tilde X) с помощью бутстрапа и подает ее на вход метода (mu): (tilde mu(X) = mu(tilde X)). Напомним, что бутстрап представляет собой сэмплирование (ell) объектов из выборки с возвращением, в результате чего некоторые объекты выбираются несколько раз, а некоторые – ни разу.
Помещение нескольких копий одного объекта в бутстрапированную выборку соответствует выставлению веса при данном объекте – соответствующее ему слагаемое несколько раз войдет в функционал, и поэтому штраф за ошибку на нем будет больше.
В бэггинге (bagging, bootstrap aggregation) предлагается обучить некоторое число алгоритмов (b_n(x)) с помощью метода (tilde mu), и построить итоговую композицию как среднее данных базовых алгоритмов:
[
a_N(x)
=
frac{1}{N}
sum_{n = 1}^{N}
b_n(x)
=
frac{1}{N}
sum_{n = 1}^{N}
tilde mu(X)(x).
]
Такая композиция и называется бэггингом. Он позволяет объединить базовые алгоритмы с низким смещением, но высоким разбросом, в композицию с низким смещением и разбросом, причем, в идеальном случае (модели совсем не коррелируют) разброс падает в N раз. Если же корреляция имеет место, то уменьшение дисперсии может быть гораздо менее существенным.
Помещение нескольких копий одного объекта в бутстрапированную выборку соответствует выставлению веса при данном объекте соответствующее ему слагаемое несколько раз войдет в функционал, и поэтому штраф за ошибку на нем будет больше.
35. Что такое случайный лес? Чем он отличается от бэггинга над решающими деревьями?
Случайный лес — метод построения композиции, основанный на бэггинге над деревьями. Т.к. Бэггинг сильнее понижает разброс при слабой корреляции моделей, в RF предлагается специально ее понижать с помощью
- рандомизации по признакам (для каждого базового алгоритма используется некое подмножество признаков вместо всех) (это отличие от бэггинга над деревьями)
- рандомизации по объектам (для каждого базового алгоритма в бутстрапе используется не вся выборка X, а какая-то подвыборка)
36. Что такое out-of-bag оценка в бэггинге?
Мы можем для каждого объекта (x_{i}) найти деревья, которые были обучены без него, и вычислить по их ответам out-of-bag-ошибку
Каждое дерево в случайном лесе обучается по подмножеству объектов. Это значит, что те объекты, которые не вошли в бутстрапированную выборку (X_n) дерева (b_n), по сути являются контрольными для данного дерева.
Значит, мы можем для каждого объекта (x_i) найти деревья, которые были обучены без него, и вычислить по их ответам out-of-bag-ошибку:
[
text{OOB}
=
sum_{i = 1}^{ell}
L left(
y_i,
frac{1}{sum_{n = 1}^{N} [x_i notin X_n]}
sum_{n = 1}^{N}
[x_i notin X_n] b_n(x_i)
right),
] где (L(y, z)) – функция потерь.
Можно показать, что по мере увеличения числа деревьев (N) данная оценка стремится к leave-one-out-оценке, но при этом существенно проще для вычисления.
37. Запишите вид композиции, которая обучается в градиентном бустинге. Как выбирают количество базовых алгоритмов в ней?
(a_{N}(x)=sumlimits_{n=0}^{N}gamma_{n}b_{n}(x))
В такой композиции каждый следующий базовый алгоритм исправляет ошибки предыдущего.
При большом их числе мы начинаем переобучаться — можем использовать валидационную выборку для подбора (это просто гиперпараметр).
38. Что такое сдвиги в градиентном бустинге? Как они вычисляются и для чего используются?
Сдвиг (остаток) — расстояния от ответа нашего алгоритма до истинного ответа.
[
s_i^{(N)}=y_i — sum_{n = 1}^{N — 1} b_n(x_i)=y_i- a_{N — 1}(x_i),qquad i = 1, dots, ell
]
Или
[
s_i=-left.frac{partial L}{partial z}right|_{z = a_{N — 1}(x_i)}
]
С помощью сдвига мы настраиваем очередной базовой алгоритм:
[
b_N(x)
:=
mathop{rm arg,min}limits_{b in mathbb{A}}
frac12
sum_{i = 1}^{ell}
(b(x_i) — s_i^{(N)})^2
]
39. Как обучается очередной базовый алгоритм в градиентном бустинге? Что такое сокращение шага?
Пусть мы построили композицию (a_{N-1}(x)) из (N-1) базовых алгоритмов. Хотим выбрать такой алгоритм следующим, чтобы как можно сильнее уменьшить ошибку
Допустим, мы построили композицию (a_{N — 1}(x)) из (N — 1) алгоритма, и хотим выбрать следующий базовый алгоритм (b_N(x)) так, чтобы как можно сильнее уменьшить ошибку:
[
sum_{i = 1}^{ell}L(y_i, a_{N — 1}(x_i) + gamma_N b_N(x_i))tomin_{b_N, gamma_N}
]
Ответим в первую очередь на следующий вопрос: если бы в качестве алгоритма (b_{N}(x)) мы могли выбрать совершенно любую функцию, то какие значения ей следовало бы принимать на объектах обучающей выборки? Иными словами, нам нужно понять, какие числа (s_1, dots, s_ell) надо выбрать для решения следующей задачи:
[
sum_{i = 1}^{ell}L(y_i, a_{N — 1}(x_i) + s_i)tomin_{s_1, dots, s_ell}
]
Понятно, что можно требовать (s_i = y_i — a_{N — 1}(x_i)), но такой подход никак не учитывает особенностей функции потерь (L(y, z)) и требует лишь точного совпадения предсказаний и истинных ответов. Более разумно потребовать, чтобы сдвиг (s_i) был противоположен производной функции потерь в точке (z = a_{N — 1}(x_i)):
[
s_i=-left.frac{partial L}{partial z}right|_{z = a_{N — 1}(x_i)}
]
В этом случае мы сдвинемся в сторону скорейшего убывания функции потерь. Заметим, что вектор сдвигов (s = (s_1, dots, s_ell)) совпадает с антиградиентом:
[
left(-left.frac{partial L}{partial z}right|_{z = a_{N — 1}(x_i)}right)_{i = 1}^{ell}=-nabla_zsum_{i = 1}^{ell}L(y_i, z_i)big|_{z_i = a_{N — 1}(x_i)}
]
При таком выборе сдвигов (s_i) мы, по сути, сделаем один шаг градиентного спуска, двигаясь в сторону наискорейшего убывания ошибки на обучающей выборке. Отметим, что речь идет о градиентном спуске в (ell) -мерном пространстве предсказаний алгоритма на объектах обучающей выборки. Поскольку вектор сдвига будет свой на каждой итерации, правильнее обозначать его как (s_i^{(N)}), но для простоты будем иногда опускать верхний индекс. Итак, мы поняли, какие значения новый алгоритм должен принимать на объектах обучающей выборки. По данным значениям в конечном числе точек необходимо построить функцию, заданную на всем пространстве объектов. Это классическая задача обучения с учителем, которую мы уже хорошо умеем решать. Один из самых простых функционалов – среднеквадратичная ошибка. Воспользуемся им для поиска базового алгоритма, приближающего градиент функции потерь на обучающей выборке:
[
b_N(x)=mathop{rm arg,min}limits_{b in mathbb{A}}sum_{i = 1}^{ell}left(b(x_i) — s_iright)^2
]
Отметим, что здесь мы оптимизируем квадратичную функцию потерь независимо от функционала исходной задачи – вся информация о функции потерь (L) находится в антиградиенте (s_i), а на данном шаге лишь решается задача аппроксимации функции по (ell) точкам. Разумеется, можно использовать и другие функционалы, но среднеквадратичной ошибки, как правило, оказывается достаточно.
Ещё одна причина для использования среднеквадратичной ошибки состоит в том, что от алгоритма требуется как можно точнее приблизить направление наискорейшего убывания функционала (то есть направление ((s_i)_i)); совпадение направлений вполне логично оценивать через косинус угла между ними, который напрямую связан со среднеквадратичной ошибкой.
После того, как новый базовый алгоритм найден, можно подобрать коэффициент при нем по аналогии с наискорейшим градиентным спуском:
[
gamma_N=mathop{rm arg,min}limits_{gamma in mathbb{R}}sum_{i = 1}^{ell}L(y_i, a_{N — 1}(x_i) + gamma b_N(x_i))
]
Описанный подход с аппроксимацией антиградиента базовыми алгоритмами и называется градиентным бустингом. Данный метод представляет собой поиск лучшей функции, восстанавливающей истинную зависимость ответов от объектов, в пространстве всех возможных функций. Ищем мы данную функцию с помощью спуска – каждый шаг делается вдоль направления, задаваемого некоторым базовым алгоритмом. При этом сам базовый алгоритм выбирается так, чтобы как можно лучше приближать антиградиент ошибки на обучающей выборке.
Сокращение шага — вместо перехода в оптимальную точку делаем укороченный шаг. По сути, мы снижаем доверие к каждому базовому алгоритму. (eta in (0, 1]) (a_{N}(x)=a_{N-1}(x)+etagamma_{N}b_{N}(x))
40. В чём заключается переподбор прогнозов в листьях решающих деревьев в градиентном бустинге?
Вспомним, что решающее дерево разбивает все пространство на непересекающиеся области,в каждой из которых его ответ равен константе:
[
b_n(x)=sum_{j = 1}^{J_n}b_{nj}[x in R_j],
]
где (j = 1, dots, J_n) – индексы листьев, (R_j) – соответствующие области разбиения, (b_{nj}) – значения в листьях.
Значит, на (N) -й итерации бустинга композиция обновляется как
[
a_N(x)=a_{N — 1}(x)+gamma_Nsum_{j = 1}^{J_N}b_{Nj}[x in R_j]=a_{N — 1}(x)+sum_{j = 1}^{J_N}gamma_Nb_{Nj}[x in R_j].
]
Видно, что добавление в композицию одного дерева с (J_N) листьями равносильно добавлению (J_N) базовых алгоритмов, представляющих собой предикаты вида ([x in R_j]). Если бы вместо общего коэффициента (gamma_N) был свой коэффициент (gamma_{Nj}) при каждом предикате, то мы могли бы его подобрать так, чтобы повысить качество композиции. Если подбирать свой коэффициент (gamma_{Nj}) при каждом слагаемом, то потребность в (b_{Nj}) отпадает, его можно просто убрать:
[
sum_{i = 1}^{ell}Lleft(y_i,a_{N — 1}(x_i)+sum_{j = 1}^{J_N}gamma_{Nj}[x in R_j]right)tomin_{{gamma_{Nj}}_{j = 1}^{J_N}}.
]
Поскольку области разбиения (R_j) не пересекаются, данная задача распадается на (J_N) независимых подзадач:
[
gamma_{Nj}=mathop{rm arg,min}limits_gammasum_{x_i in R_j}L(y_i, a_{N — 1}(x_i) + gamma),qquad j = 1, dots, J_N.
]
41. Как в xgboost выводится функционал ошибки с помощью разложения в ряд Тейлора?
Мы хотим найти алгоритм (b(x)), решающий следующую задачу:
[
sum_{i = 1}^{ell}
L(y_i, a_{N — 1}(x_i) + b(x_i))
to
min_{b}
]
Разложим функцию (L) в каждом слагаемом в ряд Тейлора до второго члена с центром в ответе композиции (a_{N — 1}(x_i)):
[
sum_{i = 1}^{ell}L(y_i, a_{N — 1}(x_i) + b(x_i))approx
sum_{i = 1}^{ell} left(L(y_i, a_{N — 1}(x_i))-s_i b(x_i)+frac12h_i b^2(x_i)right),
]
где через (h_i) обозначены вторые производные по сдвигам:
[
h_i
=
left.
frac{partial^2}{partial z^2}
L(y_i, z)
right|_{a_{N — 1}(x_i)}
]
Первое слагаемое не зависит от нового базового алгоритма, и поэтому его можно выкинуть. Получаем функционал:
[
sum_{i = 1}^{ell} left(-s_i b(x_i)+frac{1}{2}h_i b^2(x_i)right)tomin_{b}
]
Покажем, что он очень похож на среднеквадратичный из формулы. Преобразуем его:
[
sum_{i = 1}^{ell}left(b(x_i) — s_iright)^2\
=
sum_{i = 1}^{ell} left(b^2(x_i)-2 s_i b(x_i)+s_i^2right) = {text{последнее слагаемое не зависит от $b$}} \
=
sum_{i = 1}^{ell} left(b^2(x_i)-2 s_i b(x_i)right)\
=
2sum_{i = 1}^{ell}left(-s_ib(x_i)+frac{1}{2}b^2(x_i)right)
tomin_{b}
]
Видно, что последняя формула совпадает с точностью до константы, если положить (h_i = 1). Таким образом, в обычном градиентном бустинге мы используем аппроксимацию второго порядка при обучении очередного базового алгоритма, и при этом отбрасываем информацию о вторых производных (то есть считаем, что функция имеет одинаковую кривизну по всем направлениям).
42. Какие регуляризации используются в xgboost?
Будем далее работать с функционалом. Он измеряет лишь ошибку композиции после добавления нового алгоритма, никак при этом не штрафуя за излишнюю сложность этого алгоритма. Ранее мы решали проблему переобучения путем ограничения глубины деревьев, но можно подойти к вопросу и более гибко. Мы выясняли, что дерево (b(x)) можно описать формулой
[
b(x)
=
sum_{j = 1}^{J}
b_{j}
[x in R_{j}]
]
Его сложность зависит от двух показателей:
- Число листьев (J). Чем больше листьев имеет дерево, тем сложнее его разделяющая поверхность, тем больше у него параметров и тем выше риск переобучения.
- Норма коэффициентов в листьях (|b|_2^2 = sum_{j = 1}^{J} b_j^2). Чем сильнее коэффициенты отличаются от нуля, тем сильнее данный базовый алгоритм будет влиять на итоговый ответ композиции.
Добавляя регуляризаторы, штрафующие за оба этих вида сложности, получаем следующую задачу:
[
sum_{i = 1}^{ell} left(-s_i b(x_i)+frac{1}{2}h_i b^2(x_i)right)
+gamma J
+frac{lambda}{2}sum_{j = 1}^{J}b_j^2
tomin_{b}
]
Если вспомнить, что дерево (b(x)) дает одинаковые ответы на объектах, попадающих в один лист, то можно упростить функционал:
[
sum_{j = 1}^{J} Biggl{
underbrace{
Biggl(-sum_{i in R_j} s_iBiggr)
}_{=-S_j}
b_j+frac12
Biggl(lambda+
underbrace{sum_{i in R_j} h_i}_{=H_j}
Biggr)
b_j^2+gamma
Biggr}
to
min_{b}
]
Каждое слагаемое здесь можно минимизировать по (b_j) независимо. Заметим, что отдельное слагаемое представляет собой параболу относительно (b_j), благодаря чему можно аналитически найти оптимальные коэффициенты в листьях:
[
b_j
=
frac{S_j}{H_j + lambda}
]
Подставляя данное выражение обратно в функционал, получаем, что ошибка дерева с оптимальными коэффициентами в листьях вычисляется по формуле
[
H(b)=
-frac12sum_{j = 1}^{J}
frac{S_j^2}{H_j + lambda}+gamma J
]
43. Задача кластеризации. Метрики качества.
Приведём несколько примеров внутренних метрик качества. Будем считать, что каждый кластер характеризуется своим центром (c_k).
Внутрикластерное расстояние
[
sum_{k = 1}^{K}sum_{i = 1}^{ell}[a(x_i) = k]rho(x_i, c_k),
]
где (rho(x, z)) – некоторая функция расстояния. Данный функционал требуется минимизировать, поскольку в идеале все объекты кластера должны быть одинаковыми.
Межкластерное расстояние
[
sum_{i, j = 1}^{ell}[a(x_i) neq a(x_j)]rho(x_i, x_j).
]
Данный функционал нужно максимизировать, поскольку объекты из разных кластеров должны быть как можно менее похожими друг на друга.
Индекс Данна (Dunn Index)
[
frac{
min_{1 leq k < k^prime leq K}d(k, k^prime)
}{
max_{1 leq k leq K}d(k)
},
]
где (d(k, k^prime)) – расстояние между кластерами (k) и (k^prime) (например, евклидово расстояние между их центрами), а (d(k)) – внутрикластерное расстояние для (k) -го кластера (например, сумма расстояний от всех объектов этого кластера до его центра). Данный индекс необходимо максимизировать.
44. Метод K-Means, вывод его шагов.
Одним из наиболее популярных методов кластеризации является, который оптимизирует внутрикластерное расстояние, в котором используется квадрат евклидовой метрики.
Заметим, что в данном функционале имеется две степени свободы: центры кластеров (c_k) и распределение объектов по кластерам (a(x_i)). Выберем для этих величин произвольные начальные приближения, а затем будем оптимизировать их по очереди:
- Зафиксируем центры кластеров.
В этом случае внутрикластерное расстояние будет минимальным, если каждый объект будет относиться к тому кластеру, чей центр является ближайшим:
[
a(x_i)=mathop{rm arg,min}limits_{1 leq k leq K}rho(x_i, c_k).
] - Зафиксируем распределение объектов по кластерам. В этом случае внутрикластерное расстояние с квадратом евклидовой метрики можно продифференцировать по центрам кластеров и вывести аналитические формулы для них:
[
c_k=frac{1}{sum_{i = 1}^{ell} [a(x_i) = k]}sum_{i = 1}^{ell}[a(x_i) = k] x_i.
]
Повторяя эти шаги до сходимости, мы получим некоторое распределение объектов по кластерам. Новый объект относится к тому кластеру, чей центр является ближайшим.
Результат работы метода K-Means существенно зависит от начального приблжения. Существует большое количество подходов к инициализации; одним из наиболее успешных считается k-means++.
Линейная регрессия
Сегодня пойдет речь о регрессии, как обучать и какие проблемы могут вам попасться при использовании таких моделей.
Для начала давайте введем удобные обозначения.
$mathbb{X} — text{пространство объектов}$
$mathbb{Y} — text{пространство ответов}$
$ x = (x^1, … x^n) — text{признаковое описание объекта}$
$ X = (x_i,y_i)^l_{i=1} — text{обучающая выборка} $
$ a(x) — text{алгоритм, модель} $
$ Q(a,X) — text{функция ошибки алгоритма a на выборке X} $
$ text{Обучение} — a(x) = text{argmin}_{a in mathbb{A}} Q(a,X)$
Но этого мало, давайте разберем, что такое функционал ошибки, семейство алгоритмов, метод обучения.
- Функционал ошибки Q: способ измерения того, хорошо или плохо работает алгоритм на конкретной выборке
- Семейство алгоритмов $mathbb{A}$: как выглядит множество алгоритмов, из которых выбирается лучший
- Метод обучения: как именно выбирается лучший алгоритм из семейства алгоритмов.
Пример задачи регрессии: предсказание количества заказов магазина
Пусть известен один признак — расстояние кафе от метро, а предсказать необходимо количество заказов. Поскольку количество заказов — вещественное число $mathbb{R}$, здесь идет речь о задаче регрессии.
По графику можно сделать вывод о существование зависимости между расстоянием от метро и количеством заказов. Можно предположить, что зависимость линейна, ее можно представить в видео прямой на графике. По этой прямой и можно будет предсказывать количество заказов, если известно расстояние от метро.
В целом такая модель угадывает тенденцию, то есть описывает зависимость между ответом и признаком.
При этом, разумеется ,она делает это не идеально, с некоторой ошибкой. Истинный ответ на каждом объекте несколько отклоняется от прогноза.
Один признак — это несерьезно. Гораздо сложнее и интереснее работать с многомерными выборками, которые описываются большим количеством признаков. В этом случае отобразить выборку и понять, подходит ли модель или нет, нельзя. Можно лишь оценить ее качество и по нему уже понять, подходит ли эта модель.
Описание линейной модели
Давайте обсудим, как выглядит семейство алгоритмов в случае с линейными моделями. Линейный алгоритм в задачах регрессии выглядит следующим образом
$$ a(x)=w_0 + sumlimits_{j=1}^d w_j x^j $$
где $w_0$ — свободный коэффициент, $x^j$ — признаки, а $w_j$ — их веса.
Если у нашего набора данных есть только один признак, то алгоритм выглядит так
$$ a(x)=w_0 + w x $$
Ничего не напоминает? Да, действительно это обычная линейная функция, известная с 7 класса.
$$ y = kx+b $$
В качестве меры ошибки мы не может быть выбрано отклонение от прогноза $Q(a,y)=a(x)-y$, так как в этом случае минимум функционала не будет достигаться при правильном ответе $a(x)=y$. Самый простой способ — считать модуль отклонения.
$$ |a(x)-y| $$
Но функция модуля не является гладкой функцией, и для оптимизации такого функционала неудобно использовать градиентные методы. Поэтому в качестве меры ошибки часто используют квадрат отклонения:
$$ (a(x)-y)^2 $$
Функционал ошибки, именуемый среднеквадратичной ошибкой алгоритма, задается следующим образом:
$$ Q(a,x) = frac{1}{l} sumlimits_{i=1}^l (a(x_i)- y_i)^2 $$
В случае линейной модели его можно переписать в виде функции (поскольку теперь Q зависит от вектора, а не от функции) ошибок:
$$ Q(omega,x) = frac{1}{l} sumlimits_{i=1}^l ( langle w_i,x_irangle- y_i) ^2 $$
Обучение модели линейной регрессии
Разберем том, как обучать модель линейной регрессии, то есть как настраивать ее параметры.
$$ Q(w,x) = frac{1}{l} sumlimits_{i=1}^l ( langle w_i,x_irangle- y_i) ^2 to min_{w}$$
То есть нам необходимо подобрать $w$, что бы линия могла описать наши данные. Или же задача состоит в нахождение таких $w$, что бы была минимальна ошибка $ Q(w,x)$
Матричная форма записи
Прежде, чем рассмотрим задачу о оптимизации этой функции, имеет смысл используемые соотношения в матричной форме. Матрица «объекты-признаки» $X$ составлена из признаков описаний все объектов выборки
$$ X = begin{pmatrix} x_{11} & … & x_{1d} … & … & … x_{l1} & … & x_{ld} end{pmatrix} $$
Таким образом, в $ij$ элементе матрицы $X$ записано значение $j$-го признака на i объекте обучающей выборки. Или короче говоря, каждая строчка — это объект, а каждый столбец — это признак.Так же понадобится вектор ответов y, который составлен из истинных ответов для всех объектов.
$$ y = begin{pmatrix} y_{1} … y_{l} end{pmatrix} $$
В этом случае среднеквадратичная шибка может быть переписана в матричном виде:
$$ Q(w,X) = frac{1}{l} || Xw-y ||^2 to min_{w}$$
Оптимизационный метод решения
Самый лучший метод — это численный метод оптимизации.
Не сложно показать, что среднеквадратичная ошибка — это выпуклая и гладкая функция. Выпуклость гарантирует существование лишь одного минимумам, а гладкость — существование вектора градиента в каждой точке. Это позволяет использовать метод градиентного спуска.
При использовании метода градиентного спуска необходимо указать начальное приближение. Есть много
подходов к тому, как это сделать, в том числе инициализировать случайными числами (не очень большими). Самый простой способ это сделать — инициализировать значения всех весов равными нулю:
$$ w^0=0 $$
На каждой следующей итерации, $t = 1, 2, 3, …,$ из приближения, полученного в предыдущей итерации $w^{t−1}$, вычитается вектор градиента в соответствующей точке $w^{t−1}$, умноженный на некоторый коэффициент $eta_t$, называемый шагом:
$$ w^t = w^{t-1} — eta_t Delta Q(w^{t-1},X) $$
Остановить итерации следует , когда наступает сходимость. Сходимость можно определять по-разному .В данном случае разумно определить сходимость следующим образом: итерации следует завершить, если разница
двух последовательных приближений не слишком велика:
$$ ||w^t — w^{t-1} ||<epsilon $$
Случай парной регрессии
В случае парной регрессии признак всего один, а линейная модель выглядит следующим образом:
$$ a(x)=w_0 + w x $$
где $w_1$ и $w_0$ — два параметра.
Среднеквадратичная ошибка принимает вид:
$$ Q(w_0,w_1,X) = frac{1}{l} sumlimits_{i=1}^l (w_1x_i+w_0 -y_i) ^2$$
Для нахождения оптимальных параметров будет применяться метод градиентного спуска, про который уже было сказано ранее. Чтобы это сделать, необходимо сначала вычислить частные производные функции ошибки:
$$frac{partial Q}{partial w_1} = frac{2}{l} sumlimits_{i=1}^l (w_1x_i+w_0-y_i)x_i$$
$$frac{partial Q}{partial w_0} = frac{2}{l} sumlimits_{i=1}^l (w_1x_i+w_0-y_i)$$
Следующие два графика демонстрируют применение метода градиентного спуска в случае парной регрессии. Справа изображены точки выборки, а слева — пространство параметров. Точка в этом пространстве обозначает конкретную модель (кафе)
График зависимости функции ошибки от числа произведенных операции выглядит следующим образом:
Выбор размера шага в методе градиентного спуска
Очень важно при использовании метода градиентного спуска правильно подбирать шаг. Каких-либо концерт- иных правил подбора шага не существует, выбор шага — это искусство, но существует несколько полезных закономерностей.
Если длина шага слишком мала, то метод будет неспешна, но верно шагать в сторону минимума. Если же
взять размер шага очень большим, появляется риск, что метод будет перепрыгивать через минимум. Более
того, есть риск того, что градиентный спуск не сойдется.
Имеет смысл использовать переменный размер шага: сначала, когда точка минимума находится еще да-
легко, двигаться быстро, а позже, спустя некоторое количество итерации — делать более аккуратные шаги.
Один из способов задать размер шага следующий:
$$ eta_t = frac{k}{t} $$
где $k$-константа, которую необходимо подобрать, а $t$ — номер шага.
import matplotlib.pyplot as plt # библиотека для отрисовки графиков import numpy as np # импортируем numpy для создания своего датасета from sklearn import linear_model, model_selection # импортируем линейную модель для обучения и библиотеку для разделения нашей выборки X = np.random.randint(100,size=(500, 1)) # создаем вектор признаков, вектора так как у нас один признак y = np.random.normal(np.random.randint(300,360,size=(500, 1))-X) # создаем вектор ответом plt.scatter(X, y) # рисуем график точек plt.xlabel('Расстояние до кафе в метрах') # добавляем описание для оси x plt.ylabel('Количество заказов')# добавляем описание для оси y plt.show()
# Делим созданную нами выборку на тестовую и обучающую X_train, X_test, y_train, y_test = model_selection.train_test_split(X, y)
Давайте посмотрим какие параметры принимает LinearRegression.
fit_intercept — подбирать ли значения для свободного член $w_0$. True или False. Если ваши данные центрированны, то можете указать False. По умолчанию — True
normalize— нормализация данных перед обучением. Если fit_intercept=False то параметр будет проигнорирован. Если True — то данные перед обучением будут нормализованы при помощи L^2-Norm нормализации. По умолчанию — False
copy_X — True — копировать матрицу признаков. False — не копировать. **По умолчанию — **True
n_jobs — количество ядер используемых для сборки. Скорость будет существенно выше n_targets>1. По умолчанию — None
Параметры которые можно у модели:
coef_ — коэффициенты $w$, количество возвращаемых коэффициентов зависит от количества признаков. смотри пункт Описание линейной модели
intercept_ — свободный член $w_0$
Что бы предсказать значения необходимо вызвать функцию:
predict и передать массив из признаков.
Example: regr.predict([[40]])
regr = linear_model.LinearRegression() # создаем линейную регрессию #Обучаем модель regr.fit(X_train, y_train)
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
После выполнения кода, вам вернется ответ с установленными параметрами
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
# Посмотрим какие коэффициенты установила модель print('Коэфициент: n', regr.coef_) # Средний квадрат ошибки print("Средний квадрат ошибки: %.2f" % np.mean((regr.predict(X_test) - y_test) ** 2)) # Оценка дисперсии: 1 - идеальное предсказание. Качество предсказания. print('Оценка дисперсии:: %.2f' % regr.score(X_test, y_test))
Коэфициент:
[[-1.03950324]]
Средний квадрат ошибки: 325.63
Оценка дисперсии:: 0.70
# Посмотрим на получившуюся функцию print ("y = {:.2f}*x + {:.2f}".format(regr.coef_[0][0], regr.intercept_[0]))
# Посмотрим, как предскажет наша модель тестовые данные. plt.scatter(X_test, y_test, color='black')# рисуем график точек plt.plot(X_test, regr.predict(X_test), color='blue') # рисуем график линейной регрессии plt.show() # Покажем график
Давайте предскажем количество заказов, для нашего потенциального магазина. Скажем, что мы планируем построить магазин в 40 метрах от метро
290 заказов мы получим если построим магазин в 40 метрах от метро, но при этом качество предсказания всего лишь 71%, думаю не стоит доверять.
А что если, мы увеличим количество признаков?
Для этого воспользуемся встроенным датасетом make_regression из sklearn.
n_features — отвечает за количество признаков один нормальный другой избыточный
n_informative — отвечает за количество информативных признаков
n_targets — отвечает за размер ответов
noise — шум накладываемый на признаки
соef — возвращать ли коэффициенты
random_state — определяет генерацию случайных чисел для создания набора данных.
# Импортируем библиотеки для валидация, создания датасетов, и метрик качества from sklearn import cross_validation, datasets, metrics # Создаем датасет с избыточной информацией X, y, coef = datasets.make_regression(n_features = 2, n_informative = 1, n_targets = 1, noise = 5., coef = True, random_state = 2)
# Поскольку у нас есть два признака,для отрисовки надо их разделить на две части data_1, data_2 = [],[] for x in X: data_1.append(x[0]) data_2.append(x[1]) plt.scatter(data_1, y, color = 'r') plt.scatter(data_2, y, color = 'b')
<matplotlib.collections.PathCollection at 0x1134a6e10>
Можно заметить, что признак отмеченный красным цветом имеет явную линейную зависимость, а признак отмеченный синим, никакой информативность нам не дает.
# Разделение выборку для обучения и тестирования # test_size - отвечает за размер тестовой выборки X_train, X_test, y_train, y_test = cross_validation.train_test_split(X, y, test_size = 0.3)
# Создаем линейную регрессию linear_regressor = linear_model.LinearRegression() # Тренируем ее linear_regressor.fit(X_train, y_train) # Делаем предсказания predictions = linear_regressor.predict(X_test)
# Выводим массив для просмотра наших ответов (меток) print (y_test)
[ 28.15553021 38.36241814 -24.77820218 -61.47026695 13.02656201
23.87701013 12.74038341 -70.11132234 27.83791274 -14.97110322
-80.80239408 24.82763821 58.26281761 -45.27502383 10.33267887
-48.28700118 -21.48288019 -32.71074998 -21.47606913 -15.01435792
78.24817537 19.66406455 5.86887774 -42.44469577 -12.0017312
14.76930132 -16.65927231 -13.99339669 4.45578287 22.13032804]
# Смотрим и сравниваем предсказания print (predictions)
[ 22.32670386 40.26305989 -27.69502682 -56.5548183 18.47241345
31.86585663 6.08896992 -66.15105402 22.99937016 -12.65174022
-78.50894588 30.90311195 56.21877707 -47.81097232 8.98196478
-56.41188567 -24.46096716 -43.55445698 -17.99670898 -9.09225523
65.49657633 26.50900527 4.74114126 -39.28939851 -6.80665816
8.30372903 -15.27594937 -15.15598987 8.34469779 19.45159738]
# Средняя ошибка предсказания metrics.mean_absolute_error(y_test, predictions)
Для валидации можем выполнить перекрестную проверкую cross_val_score.
http://scikit-learn.org/stable/modules/generated/sklearn.model_selection.cross_val_score.html
Передадим, нашу линейную модель, признаки, ответы, количество разделений кросс-валидация
linear_scoring = cross_validation.cross_val_score(linear_regressor, X, y, cv=10) print ('Средняя ошибка: {}, Отклонение: {}'.format(linear_scoring.mean(), linear_scoring.std()))
Средняя ошибка: 0.9792410447209384, Отклонение: 0.020331171766276405
# Создаем свое тестирование на основе абсолютной средней ошибкой scorer = metrics.make_scorer(metrics.mean_absolute_error)
linear_scoring = cross_validation.cross_val_score(linear_regressor, X, y, scoring=scorer, cv=10) print ('Средняя ошибка: {}, Отклонение: {}'.format(linear_scoring.mean(), linear_scoring.std()))
Средняя ошибка: 4.0700714987797, Отклонение: 1.0737104492890193
# Коэффициенты который дал обучающий датасет coef
array([38.07925837, 0. ])
# Коэффициент полученный при обучении linear_regressor.coef_
array([38.18191713, 0.81751244])
# обученная модель так же дает свободный член linear_regressor.intercept_
print ("y = {:.2f}*x1 + {:.2f}*x2".format(coef[0], coef[1]))
print ("y = {:.2f}*x1 + {:.2f}*x2 + {:.2f}".format(linear_regressor.coef_[0], linear_regressor.coef_[1], linear_regressor.intercept_))
y = 37.76*x1 + 0.17*x2 + -0.86
# Посмотрим качество обучения print('Оценка дисперсии:: %.2f' % linear_regressor.score(X_test, y_test))
Домашнее задание
Вы уже знаете как создать модель линейной регрессии, можете создать датасет.
Давайте посмотрим как влияет количество признаков на качество обучения линейной модели.
Скачайте этот файл, можете редактировать этот ноутбук, да бы уменьшить/увеличить количество признаков.
Будут вопросы пишите нам в Slack канал #machine_learning






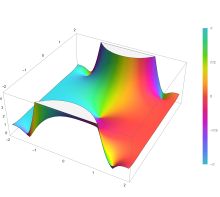
![{displaystyle {begin{aligned}Pr[Xleq L]&={frac {1}{2}}+{frac {1}{2}}operatorname {erf} {frac {L-mu }{{sqrt {2}}sigma }}\&approx Aexp left(-Bleft({frac {L-mu }{sigma }}right)^{2}right)end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f3cb760eaf336393db9fd0bb12c4465655a27de8)
![{displaystyle Pr[Xleq L]leq Aexp(-Bln {k})={frac {A}{k^{B}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2baadea015e20a45d1034fd88eed861e7fcce178)
![{displaystyle {begin{aligned}Pr[L_{a}leq Xleq L_{b}]&=int _{L_{a}}^{L_{b}}{frac {1}{{sqrt {2pi }}sigma }}exp left(-{frac {(x-mu )^{2}}{2sigma ^{2}}}right),mathrm {d} x\&={frac {1}{2}}left(operatorname {erf} {frac {L_{b}-mu }{{sqrt {2}}sigma }}-operatorname {erf} {frac {L_{a}-mu }{{sqrt {2}}sigma }}right).end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd2214f0db2c1d36075815825b616501175c6283)
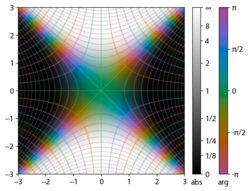


![{displaystyle {begin{aligned}operatorname {erf} z&={frac {2}{sqrt {pi }}}sum _{n=0}^{infty }{frac {(-1)^{n}z^{2n+1}}{n!(2n+1)}}\[6pt]&={frac {2}{sqrt {pi }}}left(z-{frac {z^{3}}{3}}+{frac {z^{5}}{10}}-{frac {z^{7}}{42}}+{frac {z^{9}}{216}}-cdots right)end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c80541f305af070bb0510625c584fe1559a0cd2c)
![{displaystyle {begin{aligned}operatorname {erf} z&={frac {2}{sqrt {pi }}}sum _{n=0}^{infty }left(zprod _{k=1}^{n}{frac {-(2k-1)z^{2}}{k(2k+1)}}right)\[6pt]&={frac {2}{sqrt {pi }}}sum _{n=0}^{infty }{frac {z}{2n+1}}prod _{k=1}^{n}{frac {-z^{2}}{k}}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dca22e8e7dee0297e87a455249c282c6b92fedcb)
![{displaystyle {begin{aligned}operatorname {erfi} z&={frac {2}{sqrt {pi }}}sum _{n=0}^{infty }{frac {z^{2n+1}}{n!(2n+1)}}\[6pt]&={frac {2}{sqrt {pi }}}left(z+{frac {z^{3}}{3}}+{frac {z^{5}}{10}}+{frac {z^{7}}{42}}+{frac {z^{9}}{216}}+cdots right)end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ff91095cd6825137cc951ec0a786db0b7f68fac)





![{displaystyle {begin{aligned}operatorname {erf} x&={frac {2}{sqrt {pi }}}operatorname {sgn} xcdot {sqrt {1-e^{-x^{2}}}}left(1-{frac {1}{12}}left(1-e^{-x^{2}}right)-{frac {7}{480}}left(1-e^{-x^{2}}right)^{2}-{frac {5}{896}}left(1-e^{-x^{2}}right)^{3}-{frac {787}{276480}}left(1-e^{-x^{2}}right)^{4}-cdots right)\[10pt]&={frac {2}{sqrt {pi }}}operatorname {sgn} xcdot {sqrt {1-e^{-x^{2}}}}left({frac {sqrt {pi }}{2}}+sum _{k=1}^{infty }c_{k}e^{-kx^{2}}right).end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/164e7f029977edb47c83845b04abfe5b2d28b837)







![{displaystyle {begin{aligned}operatorname {erfc} x&={frac {e^{-x^{2}}}{x{sqrt {pi }}}}left(1+sum _{n=1}^{infty }(-1)^{n}{frac {1cdot 3cdot 5cdots (2n-1)}{left(2x^{2}right)^{n}}}right)\[6pt]&={frac {e^{-x^{2}}}{x{sqrt {pi }}}}sum _{n=0}^{infty }(-1)^{n}{frac {(2n-1)!!}{left(2x^{2}right)^{n}}},end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/35a11e2e5b22ca898c74f2e913d276c9ac11124a)
























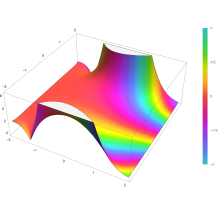
![{displaystyle {begin{aligned}operatorname {erfc} x&=1-operatorname {erf} x\[5pt]&={frac {2}{sqrt {pi }}}int _{x}^{infty }e^{-t^{2}},mathrm {d} t\[5pt]&=e^{-x^{2}}operatorname {erfcx} x,end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4acd0062271e2a19c209a02c8cc33d44a28af7cc)



![{displaystyle {begin{aligned}operatorname {erfi} x&=-ioperatorname {erf} ix\[5pt]&={frac {2}{sqrt {pi }}}int _{0}^{x}e^{t^{2}},mathrm {d} t\[5pt]&={frac {2}{sqrt {pi }}}e^{x^{2}}D(x),end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bfd2dd94cd6d0325224d412f6b5e5ed63ca81d4a)

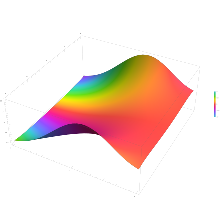
![{displaystyle {begin{aligned}Phi (x)&={frac {1}{sqrt {2pi }}}int _{-infty }^{x}e^{tfrac {-t^{2}}{2}},mathrm {d} t\[6pt]&={frac {1}{2}}left(1+operatorname {erf} {frac {x}{sqrt {2}}}right)\[6pt]&={frac {1}{2}}operatorname {erfc} left(-{frac {x}{sqrt {2}}}right)end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/89a9e9eaaddcd7a91ade15a41b8d1e272d437559)
![{displaystyle {begin{aligned}operatorname {erf} (x)&=2Phi left(x{sqrt {2}}right)-1\[6pt]operatorname {erfc} (x)&=2Phi left(-x{sqrt {2}}right)\&=2left(1-Phi left(x{sqrt {2}}right)right).end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86c84a4d2d79631fe9996e30f1d6c0da3089bfe2)







![{displaystyle {begin{aligned}operatorname {i} ^{n}!operatorname {erfc} z&=int _{z}^{infty }operatorname {i} ^{n-1}!operatorname {erfc} zeta ,mathrm {d} zeta \[6pt]operatorname {i} ^{0}!operatorname {erfc} z&=operatorname {erfc} z\operatorname {i} ^{1}!operatorname {erfc} z&=operatorname {ierfc} z={frac {1}{sqrt {pi }}}e^{-z^{2}}-zoperatorname {erfc} z\operatorname {i} ^{2}!operatorname {erfc} z&={tfrac {1}{4}}left(operatorname {erfc} z-2zoperatorname {ierfc} zright)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c3e7b953efaa4d730a5479bd61a2c378c8f761dc)









![{ displaystyle Pr [X leq L ] = { frac {1} {2}} + { frac {1} {2}} operatorname {erf} left ({ frac {L- mu} {{ sqrt {2}} sigma }} right) приблизительно A exp left (-B left ({ frac {L- mu} { sigma}} right) ^ {2} right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a72302c46832449e128a4d4e1adb28b514131270)









![{ displaystyle { begin {align} operatorname {erf} (x) = { frac {2} { sqrt { pi}}} operatorname {sgn} (x) { sqrt {1-e ^ {- x ^ {2}}}} left (1 - { frac {1} {12}} left (1 -e ^ {- x ^ {2}} right) - { frac {7} {480}} left (1-e ^ {- x ^ {2}} right) ^ {2} - { frac {5} {896}} left (1-e ^ {- x ^ {2}} right) ^ {3} - { frac {787} {276480}} left (1-e ^ {- x ^ {2 }} right) ^ {4} - cdots right) [10pt] = { frac {2} { sqrt { pi}}} operatorname {sgn} (x) { sqrt {1 -e ^ {- x ^ {2}}}} left ({ frac { sqrt { pi}} {2}} + sum _ {k = 1} ^ { infty} c_ {k} e ^ {- kx ^ {2}} right). end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24ddba05e595a553fee25644a3542188281bd844)







![{ displaystyle operatorname {erfc} (x) = { frac {e ^ {- x ^ {2}}} {x { sqrt { pi}}}} left [1+ sum _ {n = 1} ^ { infty} (-1) ^ {n} { frac {1 cdot 3 cdot 5 cdots (2n-1)} {(2x ^ {2}) ^ { n}}} right] = { frac {e ^ {-x ^ {2}}} {x { sqrt { pi}}}} sum _ {n = 0} ^ { infty} (- 1) ^ {n} { frac {(2n-1) !!} {(2x ^ {2}) ^ {n}}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fc8c3aefff3ba787b080c5186dd3aec8ec76ef9)





![{ displaystyle int _ {- infty} ^ { infty} operatorname {erf} left (ax + b right) { frac {1} { sqrt {2 pi sigma ^ {2}}}} e ^ {- { frac {(x- mu) ^ {2}} {2 sigma ^ {2}}}} , dx = operatorname {erf} left [{ frac {a mu + b} { sqrt {1 + 2a ^ {2} sigma ^ {2}}} right], qquad a, b, му, sigma in mathbb {R}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9b6adc2c661b24b44dc1e3d7e16be70023daacd8)

 обозначает возрастающий факториал, а s (n, k) { displaystyle s (n, k)}
обозначает возрастающий факториал, а s (n, k) { displaystyle s (n, k)} обозначает знаковое число Стирлинга первого рода.
обозначает знаковое число Стирлинга первого рода.

 (максимальная ошибка: 2,5 × 10)
(максимальная ошибка: 2,5 × 10) (максимальная ошибка: 3 × 10)
(максимальная ошибка: 3 × 10) (максимальная ошибка: 1,5 × 10)
(максимальная ошибка: 1,5 × 10)

 , что дает хорошее приближение для всех x ≥ 0. { displaystyle x geq 0.}
, что дает хорошее приближение для всех x ≥ 0. { displaystyle x geq 0.}





![{ displaystyle { begin {align} operatorname {erfc} (x) = 1- operatorname {erf} (x) [5pt ] = { frac {2} { sqrt { pi}}} int _ {x} ^ { infty} e ^ {- t ^ {2}} , dt [5pt] = e ^ {- x ^ {2}} operatorname {erfcx} (x), end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8808e6f3ad9aab23f14d55db707a39388d256788)


![{ displaystyle { begin {align} operatorname {erfi} (x) = - i operatorname {erf} (ix) [5pt] = { frac {2} { sqrt { pi}}} int _ {0} ^ {x} e ^ {t ^ {2 }} , dt [5pt] = { frac {2} { sqrt { pi}}} e ^ {x ^ {2}} D (x), end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4480a8ec17e274a7ad6b8ef25cc76234d48c0433)
![{ displaystyle Phi (x) = { frac {1} { sqrt {2 pi}}} int _ {- infty} ^ {x } e ^ { tfrac {-t ^ {2}} {2}} , dt = { frac {1} {2}} left [1+ operatorname {erf} left ({ frac {x } { sqrt {2}}} right) right] = { frac {1} {2}} operatorname {erfc} left (- { frac {x} { sqrt {2}}} справа)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e19dc7206f8b3b571e81153816c478abd91a679e)








![{ displaystyle { begin {align} operatorname { i ^ {n} erfc} (z) = int _ {z} ^ { infty} operatorname {i ^ {n-1} erfc} ( zeta) , d zeta имя оператора {i ^ {0} erfc} (z) = operatorname {erfc} (z) operatorname {i ^ {1} erfc} (z) = operatorname {ierfc} (z) = { frac {1} { sqrt { pi}}} e ^ {- z ^ {2}} - z operatorname {erfc} (z) operatorname {i ^ {2} erfc} (z) = { frac { 1} {4}} left [ operatorname {erfc} (z) -2z operatorname {ierfc} (z) right] конец {выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/66b57abb0a01139b31a14f5a8d651e4aa2e5f4f2)




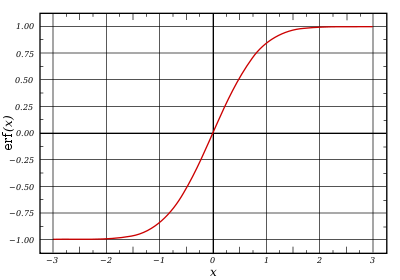
 .
. .
. .
.



 будет для неё существенно особой.
будет для неё существенно особой.


 [1]
[1]
![operatorname{erfc},x = frac{e^{-x^2}}{xsqrt{pi}}left [1+sum_{n=1}^infty (-1)^n frac{1cdot3cdot5cdots(2n-1)}{(2x^2)^n}right ]=frac{e^{-x^2}}{xsqrt{pi}}sum_{n=0}^infty (-1)^n frac{(2n)!}{n!(2x)^{2n}}.,](https://dic.academic.ru/dic.nsf/ruwiki/32769b5d42152b6b316dfca7a42e23eb.png)







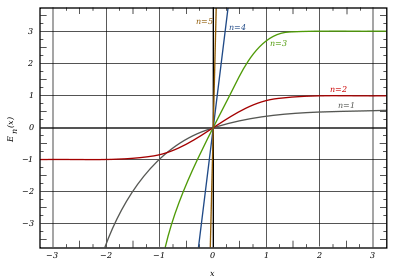













}{{sqrt%20%20pi%20}}})