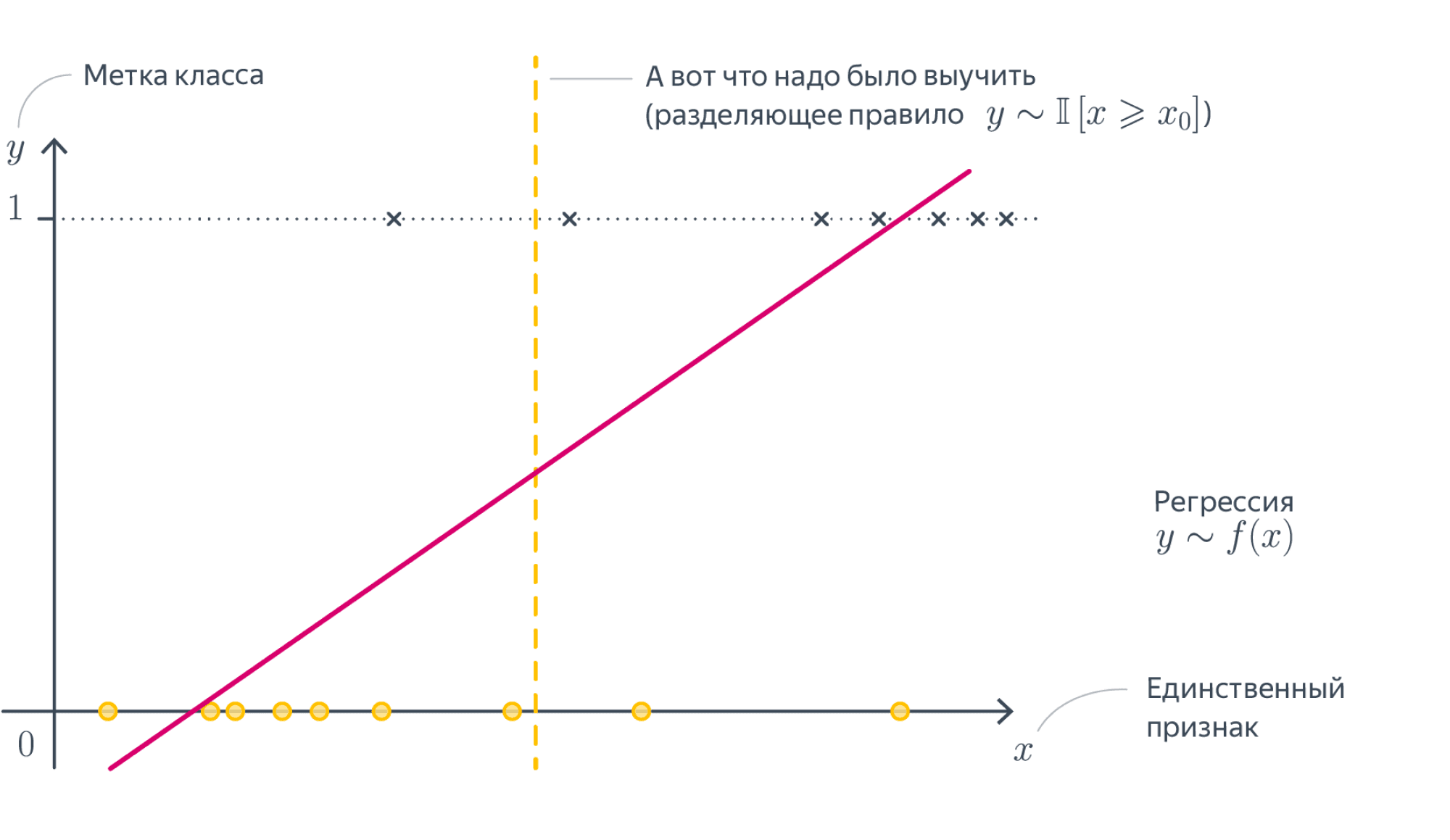Эту функцию называют также «логлосс» (logloss / log_loss), перекрёстной / кросс-энтропией (Cross Entropy) и часто используют в задачах классификации. Разберёмся, почему её используют и какой смысл она имеет. Для чтения поста нужна неплохая ML-математическая подготовка, но даже новичкам я бы рекомендовал почитать (хотя я не очень заботился, чтобы «всё объяснялось на пальцах»).
Начнём издалека…
Вспомним, как решается задача линейной регрессии. Итак, мы хотим получить линейную функцию (т.е. веса w), которая приближает целевое значение с точностью до ошибки:
Здесь мы предположили, что ошибка нормально распределена, x – признаковое описание объекта (возможно, в нём есть и фиктивный константный признак, чтобы в линейной функции был свободный член). Тогда мы знаем как распределены ответы нашей функции и можем записать функцию правдоподобия выборки (т.е. произведение плотностей, в которые подставлены значения из обучающей выборки) и воспользоваться методом максимального правдоподобия (в котором для определения значений параметров берётся максимум правдоподобия, а чаще – его логарифма):
В итоге оказывается, что максимизация правдоподобия эквивалентна минимизации среднеквадратичной ошибки (MSE), т.е. эта функция ошибки не зря широко используется в задачах регрессии. Кроме того, что она вполне логична, легко дифференцируема по параметрам и легко минимизируется, она ещё и теоретически обосновывается с помощью метода максимального правдоподобия в случае, если линейная модель соответствует данным с точностью до нормального шума.
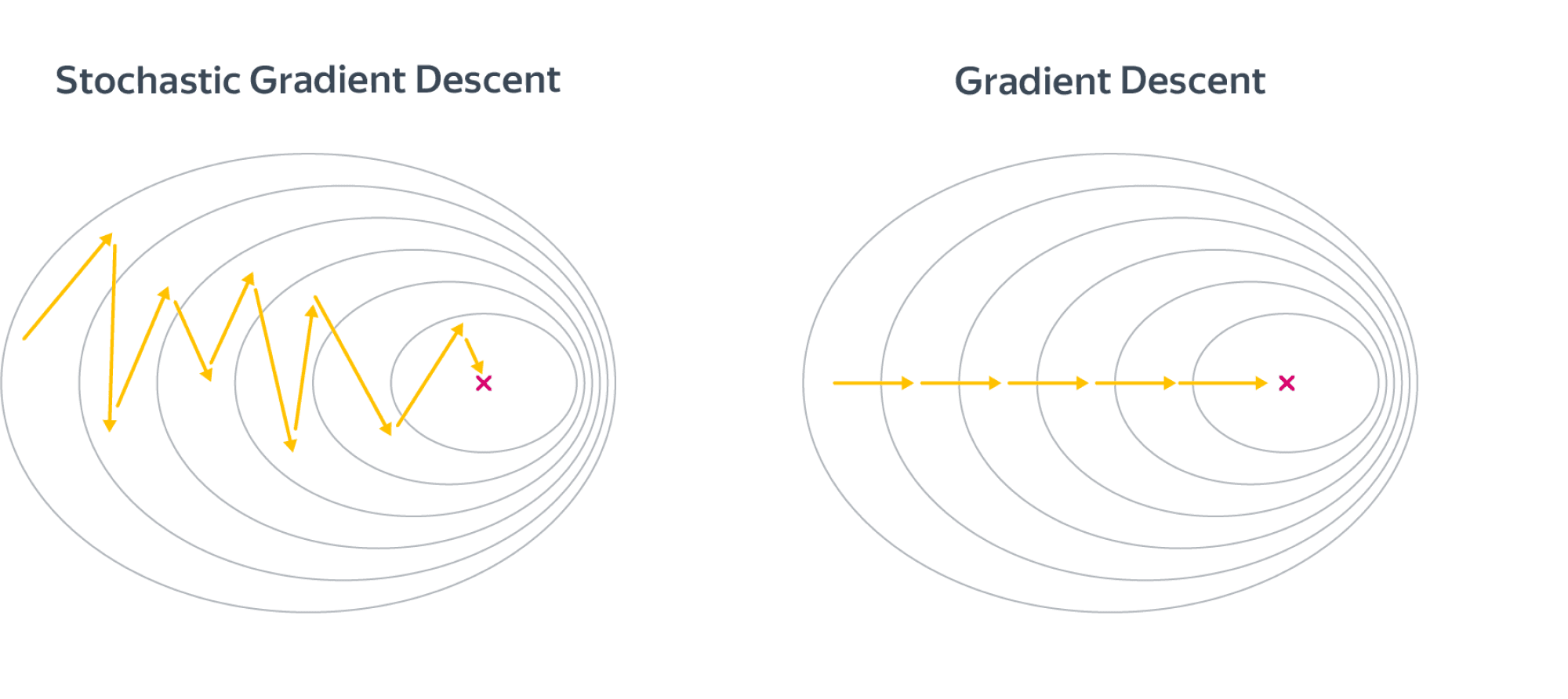
Давайте ещё посмотрим, как реализуется метод стохастического градиента (SGD) для минимизации MSE: надо взять производную функции ошибки для конкретного объекта и записать формулу коррекции весов в виде «шага в сторону антиградиента»:
Получили, что веса линейной модели при её обучении методом SGD корректируются с помощью добавки вектора признаков. Коэффициент, с которым добавляют, зависит от «агрессивности алгоритма» (параметр альфа, который называют темпом обучения) и разности «ответ алгоритма – правильный ответ». Кстати, если разница нулевая (т.е. на данном объекте алгоритм выдаёт точный ответ), то коррекция весов не производится.
Log Loss
Теперь давайте, наконец, поговорим о «логлоссе». Рассматриваем задачу классификации с двумя классами: 0 и 1. Обучающую выборку можно рассматривать, как реализацию обобщённой схемы Бернулли: для каждого объекта генерируется случайная величина, которая с вероятностью p (своей для каждого объекта) принимает значение 1 и с вероятностью (1–p) – 0. Предположим, что мы как раз и строим нашу модель так, чтобы она генерировала правильные вероятности, но тогда можно записать функцию правдоподобия:
После логарифмирования правдоподобия получили, что его максимизация эквивалентна минимизации последнего записанного выражения. Именно его и называют «логистической функции ошибки». Для задачи бинарной классификации, в которой алгоритм должен выдать вероятность принадлежности классу 1, она логична ровно настолько, насколько логична MSE в задаче линейной регрессии с нормальным шумом (поскольку обе функции ошибки выводятся из метода максимального правдоподобия).
Часто гораздо более понятна такая запись logloss-ошибки на одном объекте:
Отметим неприятное свойство логосса: если для объекта 1го класса мы предсказываем нулевую вероятность принадлежности к этому классу или, наоборот, для объекта 0го – единичную вероятность принадлежности к классу 1, то ошибка равна бесконечности! Таким образом, грубая ошибка на одном объекте сразу делает алгоритм бесполезным. На практике часто логлосс ограничивают каким-то большим числом (чтобы не связываться с бесконечностями).
Если задаться вопросом, какой константный алгоритм оптимален для выборки из q_1 представителей класса 1 и q_0 представителей класса 0, q_1 + q_0 = q , то получим
Последний ответ получается взятием производной и приравниванием её к нулю. Описанную задачу приходится решать, например, при построении решающих деревьев (какую метку приписывать листу, если в него попали представители разных классов). На рис. 2 изображён график log_loss-ошибки константного алгоритма для выборки из четырёх объектов класса 0 и 6 объектов класса 1.
Представим теперь, что мы знаем, что объект принадлежит к классу 1 вероятностью p, посмотрим, какой ответ оптимален на этом объекте с точки зрения log_loss: матожидание нашей ошибки
Для минимизации ошибки мы опять взяли производную и приравняли к нулю. Мы получили, что оптимально для каждого объекта выдавать его вероятность принадлежности к классу 1! Таким образом, для минимизации log_loss надо уметь вычислять (оценивать) вероятности принадлежности классам!
Если подставить полученное оптимальное решение в минимизируемый функционал, то получим энтропию:
Это объясняет, почему при построении решающих деревьев в задачах классификации (а также случайных лесов и деревьях в бустингах) применяют энтропийный критерий расщепления (ветвления). Дело в том, что оценка принадлежности к классу 1 часто производится с помощью среднего арифметического меток в листе. В любом случае, для конкретного дерева эта вероятность будет одинакова для всех объектов в листе, т.е. константой. Таким образом, энтропия в листе примерно равна логлосс-ошибке константного решения. Используя энтропийный критерий мы неявно оптимизируем логлосс!
В каких пределах может варьироваться logloss? Ясно, что минимальное значение 0, максимальное – +∞, но эффективным максимальным можно считать ошибку при использовании константного алгоритма (вряд же мы в итоге решения задачи придумаем алгоритм хуже константы?!), т.е.
Интересно, что если брать логарифм по основанию 2, то на сбалансированной выборке это отрезок [0, 1].
Связь с логистической регрессией
Слово «логистическая» в названии ошибки намекает на связь с логистической регрессией – это как раз метод для решения задачи бинарной классификации, который получает вероятность принадлежности к классу 1. Но пока мы исходили из общих предположений, что наш алгоритм генерирует эту вероятность (алгоритмом может быть, например, случайный лес или бустинг над деревьями). Покажем, что тесная связь с логистической регрессией всё-таки есть… посмотрим, как настраивается логистическая регрессия (т.е. сигмоида от линейной комбинации) на эту функцию ошибки методом SGD.
Как видим, корректировка весов точно такая же, как и при настройке линейной регрессии! На самом деле, это говорит о родстве разных регрессий: линейной и логистической, а точнее, о родстве распределений: нормального и Бернулли. Желающие могут внимательно почитать лекцию Эндрю Ына.
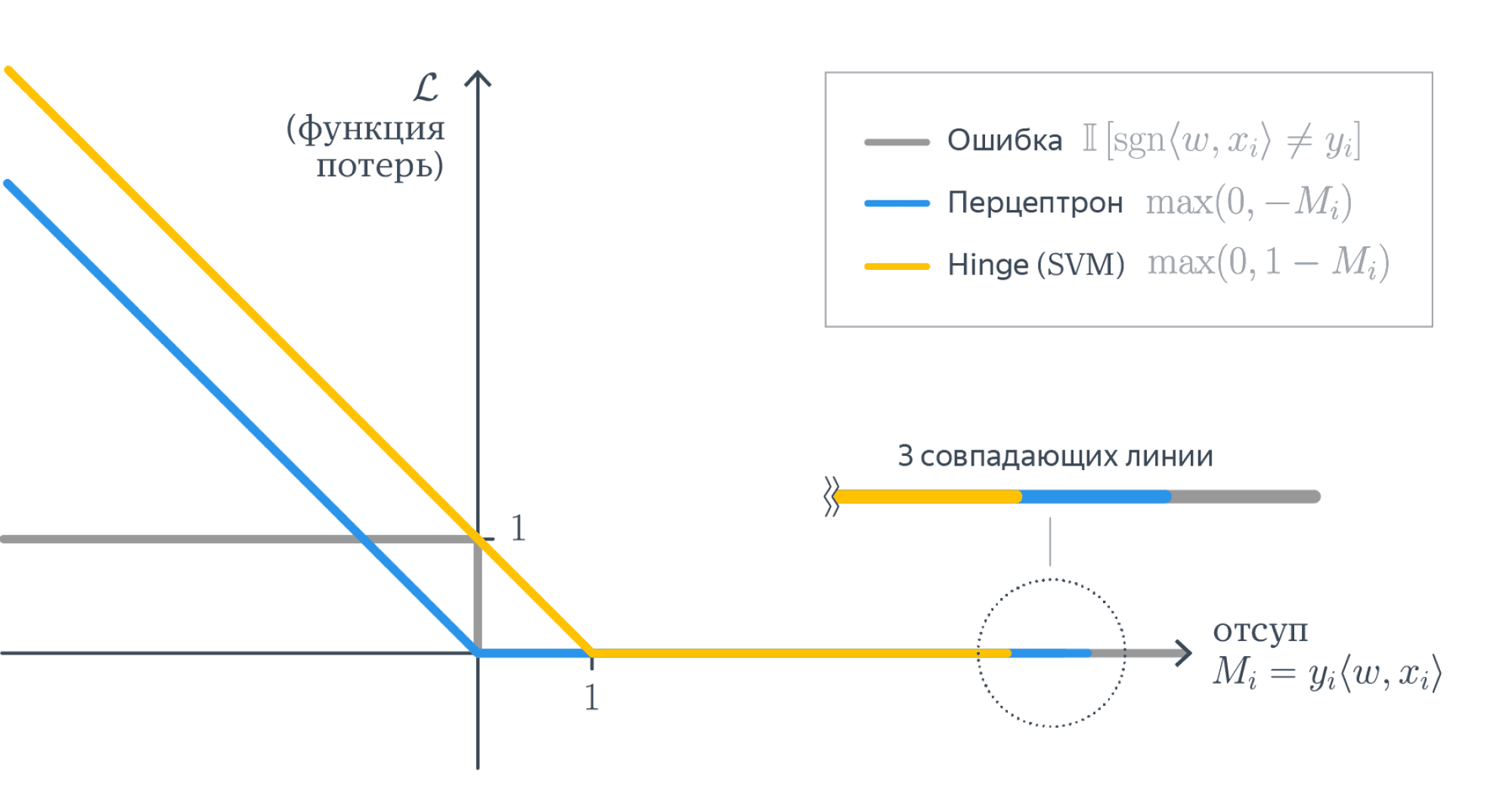
Во многих книгах логистической функцией ошибки (т.е. именно «logistic loss») называется другое выражение, которое мы сейчас получим, подставив выражение для сигмоиды в logloss и сделав переобозначение: считаем, что метки классов теперь –1 и +1, тогда
Полезно посмотреть на график функции, центральной в этом представлении:
Как видно, это сглаженный (всюду дифференцируемый) аналог функции max(0, x), которую в глубоком обучении принято называть ReLu (Rectified Linear Unit). Если при настройке весов минимизировать logloss, то таким образом мы настраиваем классическую логистическую регрессию, если же использовать ReLu, чуть-чуть подправить аргумент и добавить регуляризацию, то получаем классическую настройку SVM:
выражение под знаком суммы принято называть Hinge loss. Как видим, часто с виду совсем разные методы можно получать «немного подправив» оптимизируемые функции на похожие. Между прочим, при обучении RVM (Relevance vector machine) используется тоже очень похожий функционал:
Связь с расхождением Кульбака-Лейблера
Расхождение (дивергенцию) Кульбака-Лейблера (KL, Kullback–Leibler divergence) часто используют (особенно в машинном обучении, байесовском подходе и теории информации) для вычисления непохожести двух распределений. Оно определяется по следующей формуле:
где P и Q – распределения (первое обычно «истинное», а второе – то, про которое нам интересно, насколько оно похоже на истинное), p и q – плотности этих распределений. Часто KL-расхождение называют расстоянием, хотя оно не является симметричным и не удовлетворяет неравенству треугольника. Для дискретных распределений формулу записывают так:
P_i, Q_i – вероятности дискретных событий. Давайте рассмотрим конкретный объект x с меткой y. Если алгоритм выдаёт вероятность принадлежности первому классу – a, то предполагаемое распределение на событиях «класс 0», «класс 1» – (1–a, a), а истинное – (1–y, y), поэтому расхождение Кульбака-Лейблера между ними
что в точности совпадает с logloss.
Настройка на logloss
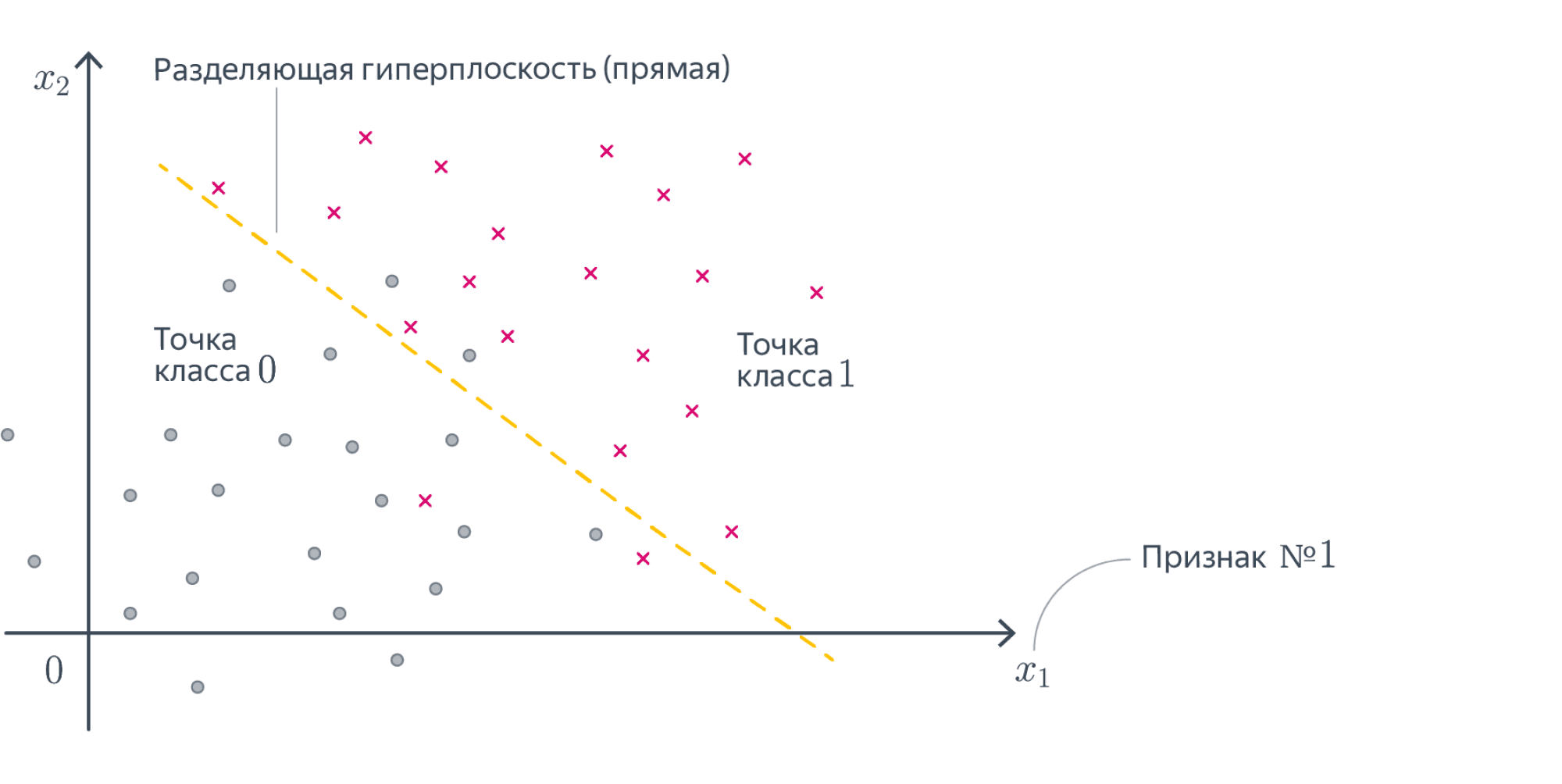
Один из методов «подгонки» ответов алгоритма под logloss – калибровка Платта (Platt calibration). Идея очень простая. Пусть алгоритм порождает некоторые оценки принадлежности к 1му классу – a. Метод изначально разрабатывался для калибровки ответов алгоритма опорных векторов (SVM), этот алгоритм в простейшей реализации разделяет объекты гиперплоскостью и просто выдаёт номер класса 0 или 1, в зависимости от того, с какой стороны гиперплоскости объект расположен. Но если мы построили гиперплоскость, то для любого объекта можем вычислить расстояние до неё (со знаком минус, если объект лежит в полуплоскости нулевого класса). Именно эти расстояния со знаком r мы будем превращать в вероятности по следующей формуле:
неизвестные параметры α, β обычно определяются методом максимального правдоподобия на отложенной выборке (calibration set).
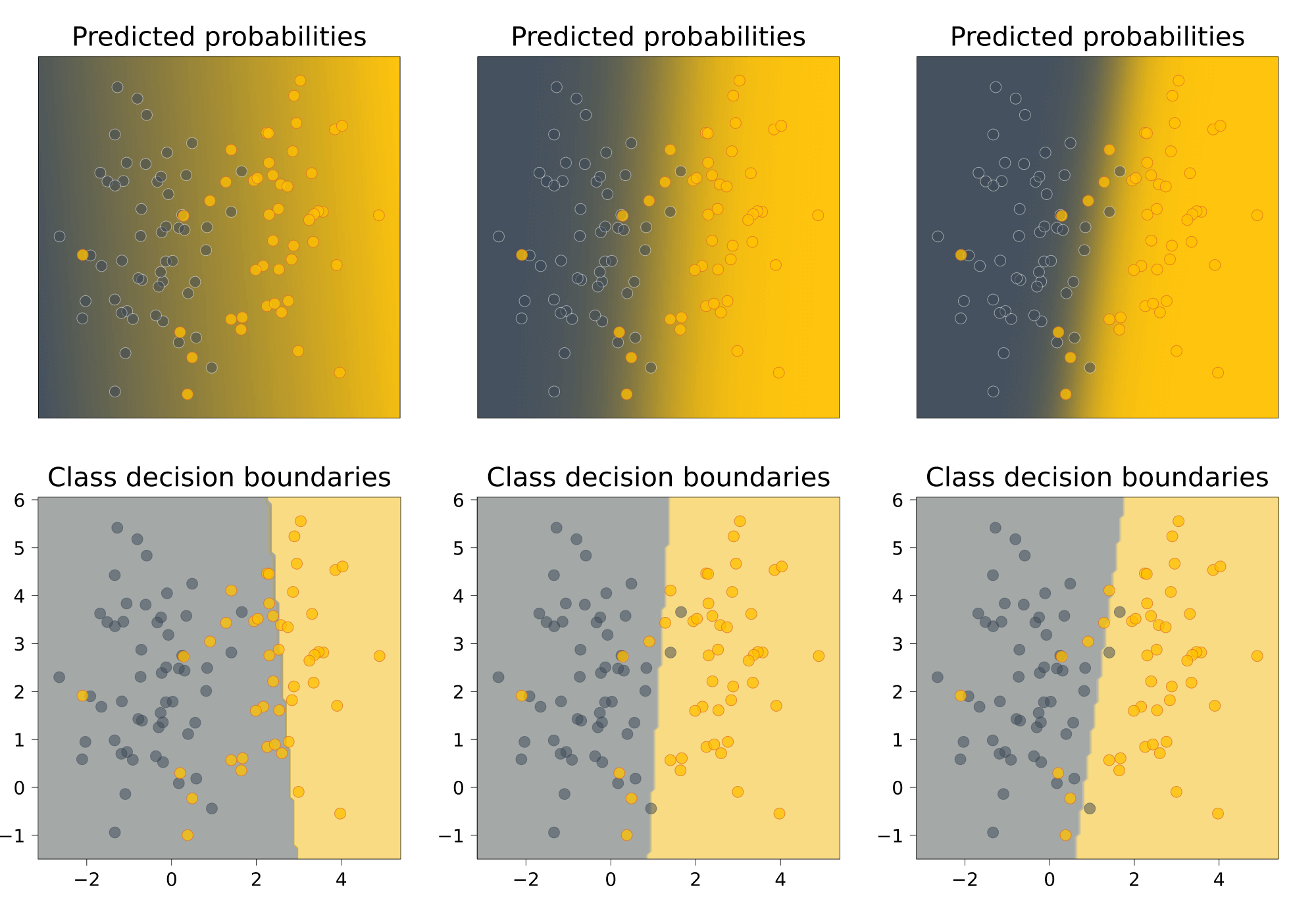
Проиллюстрируем применение метода на реальной задаче, которую автор решал недавно. На рис. показаны ответы (в виде вероятностей) двух алгоритмов: градиентного бустинга (lightgbm) и случайного леса (random forest).
Видно, что качество леса намного ниже и он довольно осторожен: занижает вероятности у объектов класса 1 и завышает у объектов класса 0. Упорядочим все объекты по возрастанию вероятностей (RF), разобьем на k равных частей и для каждой части вычислим среднее всех ответов алгоритма и среднее всех правильных ответов. Результат показан на рис. 5 – точки изображены как раз в этих двух координатах.
Нетрудно видеть, что точки располагаются на линии, похожей на сигмоиду – можно оценить параметр сжатия-растяжения в ней, см. рис. 6. Оптимальная сигмоида показана розовым цветом на рис. 5. Если подвергать ответы такой сигмоидной деформации, то логлосс-ошибка случайного леса снижается с 0.37 до 0.33.
Обратите внимание, что здесь мы деформировали ответы случайного леса (это были оценки вероятности – и все они лежали на отрезке [0, 1]), но из рис. 5 видно, что для деформации нужна именно сигмоида. Практика показывает, что в 80% ситуаций для улучшения logloss-ошибки надо деформировать ответы именно с помощью сигмоиды (для меня это также часть объяснения, почему именно такие функции успешно используются в качестве функций активаций в нейронных сетях).
Ещё один вариант калибровки – монотонная регрессия (Isotonic regression).
Многоклассовый logloss
Для полноты картины отметим, что logloss обобщается и на случай нескольких классов естественным образом:
здесь q – число элементов в выборке, l – число классов, a_ij – ответ (вероятность) алгоритма на i-м объекте на вопрос принадлежности его к j-му классу, y_ij=1 если i-й объект принадлежит j-му классу, в противном случае y_ij=0.
На посошок…
В каждом подобном посте я стараюсь написать что-то из мира машинного обучения, что, с одной стороны, просто и понятно, а с другой – изложение этого не встречается больше нигде. Например, есть такой естественный вопрос: почему в задачах классификации при построении решающих деревьев используют энтропийный критерий расщепления? Во всех курсах его (критерий) преподносят либо как эвристику, которую «вполне естественно использовать», либо говорят, что «энтропия похожа на кросс-энтропию». Сейчас стоимость некоторых курсов по машинному обучению достигает нескольких сотен тысяч рублей, но «профессиональные инструкторы» не могут донести простую цепочку:
- в статистической теории обучения настройка алгоритма производится максимизацией правдоподобия,
- в задаче бинарной классификации это эквивалентно минимизации логлосса, а сам минимум как раз равен энтропии,
- поэтому использование энтропийного критерия фактически эквивалентно выбору расщепления, минимизирующего логлосс.
Если Вы всё-таки отдали несколько сотен тысяч рублей, то можете проверить «профессиональность инструктора» следующими вопросами:
- Энтропия в листе примерно равна logloss-ошибке константного решения. Почему не использовать саму ошибку, а не приближённое значение? Или, как часто происходит в задачах оптимизации, её верхнюю оценку?
- Минимизации какой ошибки соответствует критерий расщепления Джини?
- Можно показать, что если в задаче бинарной классификации использовать в качестве функции ошибки среднеквадратичное отклонение, то также, как и для логлосса, оптимальным ответом на объекте будет вероятность его принадлежности к классу 1. Почему тогда не использовать такую функцию ошибки?
Ответы типа «так принято», «такой функции не существует», «это только для регрессии», естественно, заведомо неправильные. Если Вам не ответят с такой же степенью подробности, как в этом посте, то Вы точно переплатили;)
П.С. Что ещё почитать…
В этом блоге я публиковал уже несколько постов по метрикам качества…
- AUC ROC (площадь под кривой ошибок)
- Задачки про AUC (ROC)
- Знакомьтесь, Джини
И буквально на днях вышла классная статья Дмитрия Петухова про коэффициент Джини, читать обязательно:
- Коэффициент Джини. Из экономики в машинное обучение
Все курсы > Оптимизация > Занятие 5
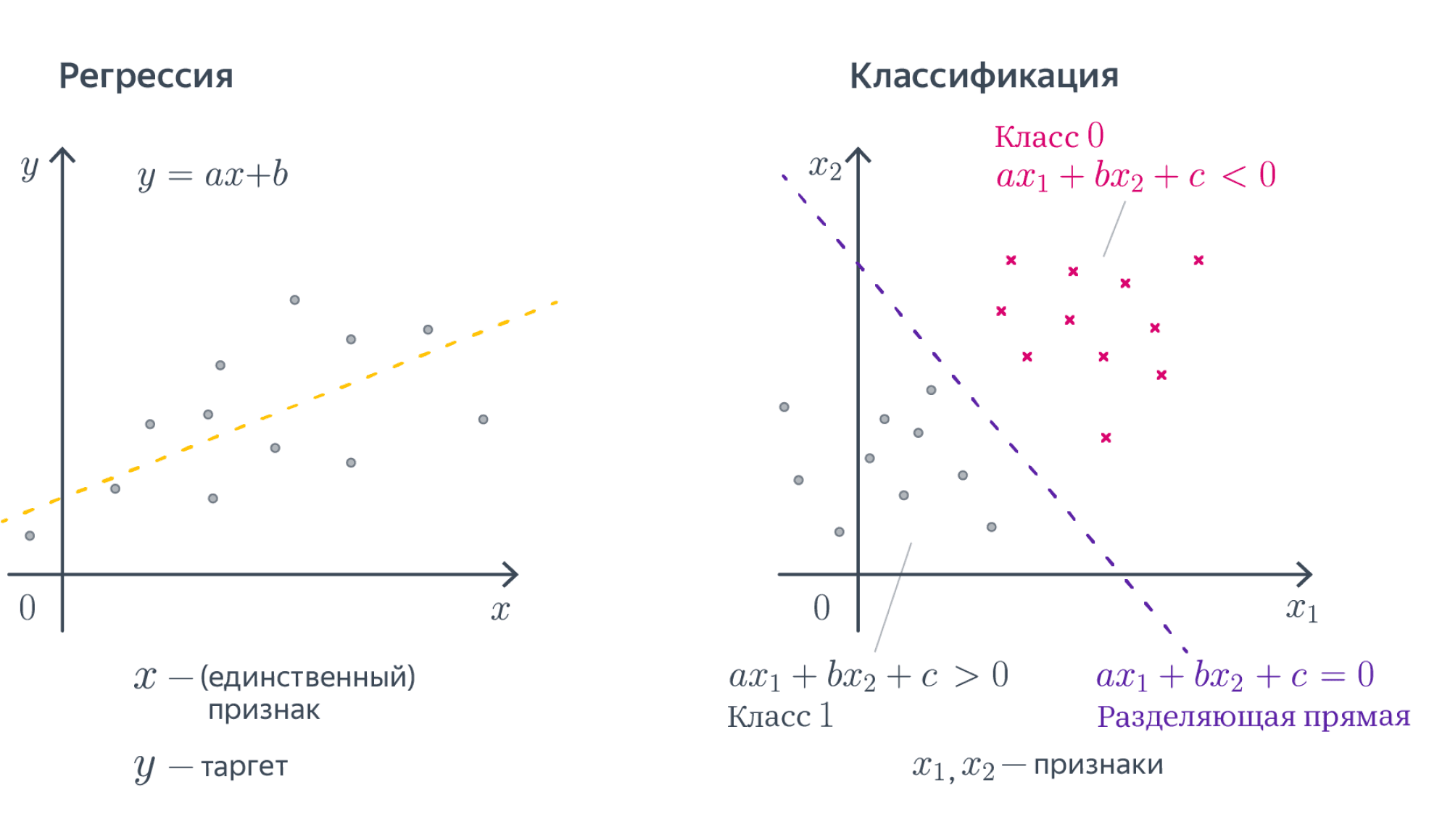
Как мы уже знаем, несмотря на название, логистическая регрессия решает задачу классификации. Сегодня мы подробно разберем принцип работы и составные части алгоритма логистической регрессии, а также построим модели с одной и несколькими независимыми переменными.
Бинарная логистическая регрессия
Задача бинарной классификации
Вернемся к задаче кредитного скоринга, про которую мы говорили, когда обсуждали принцип машинного обучения. Предположим, что мы собрали данные и выявили зависимость возвращения кредита (ось y) от возраста заемщика (ось x).
Как мы видим, в среднем более молодые заемщики реже возвращают кредит. Возникает вопрос, с помощью какой модели можно описать эту зависимость? Казалось бы, можно построить линейную регрессию таким образом, чтобы она выдавала некоторое значение и, если это значение окажется ниже 0,5 — отнести наблюдение к классу 0, если выше — к классу 1.
- Если $ f_w(x) < 0,5 rightarrow hat{y} = 0 $
- Если $ f_w(x) geq 0,5 rightarrow hat{y} = 1 $
Однако, даже если предположить, что мы удачно провели линию регрессии (а на графике выше мы действительно провели ее вполне удачно), и наша модель может делать качественный прогноз, появление новых данных сместит эту границу, и, как следствие, ничего не добавит, а только ухудшит точность модели.
Теперь часть наблюдений, принадлежащих к классу 1, будет ошибочно отнесено моделью к классу 0.
Кроме этого, линейная регрессия по оси y выдает значения, сильно выходящие за пределы интересующего нас интервала от нуля до единицы.
Откроем ноутбук к этому занятию⧉
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
# помимо стандартных библиотек мы также импортируем библиотеку warnings # она позволит скрыть предупреждения об ошибках import numpy as np import pandas as pd import matplotlib.pyplot as plt import seaborn as sns import warnings # кроме того, импортируем датасеты библиотеки sklearn from sklearn import datasets # а также функции для расчета метрики accuracy и построения матрицы ошибок from sklearn.metrics import accuracy_score, confusion_matrix # построенные нами модели мы будем сравнивать с результатом # класса LogisticRegression библиотеки sklearn from sklearn.linear_model import LogisticRegression # среди прочего, мы построим модели полиномиальной логистической регрессии from sklearn.preprocessing import PolynomialFeatures |
Функция логистической регрессии
Сигмоида
Возможное решение упомянутых выше сложностей — пропустить значение линейной регрессии через сигмоиду (sigmoid function), которая при любом значении X не выйдет из необходимого нам диапазона $0 leq h(x) leq 1 $. Напомню формулу и график сигмоиды.
$$ g(z) = frac{1}{1+e^{-z}} $$

Примечание: обратие внимание, когда z представляет собой большое отрицательное число, знаменатель становится очень большим $ 1 + e^{-(-5)} approx 148, 413 $ и значение сигмоиды стремится к нулю; когда z является большим положительным числом, знаменатель, а вместе с ним и все выражение стремятся к единице $ 1 + e^{-(5)} approx 0,0067 $.
Тогда мы можем построить линейную модель, значение которой будет подаваться в сигмоиду.
$$ z = Xtheta rightarrow h_{theta}(x) = frac{1}{1+e^{-(Xtheta)}} $$
В этом смысле никакой ошибки в названии «логистическая регрессия» нет. Этот алгоритм решает задачу классификации через модель линейной регрессии.
Если вы не помните, почему мы записали множественную линейную функцию как $theta x$, посмотрите предыдущую лекцию.
Приведем код на Питоне.
|
def h(x, thetas): z = np.dot(x, thetas) return 1.0 / (1 + np.exp(—z)) |
Теперь посмотрим, как интерпретировать коэффициенты.
Интерпретация коэффициентов
Для любого значения x через $ h_{theta}(x) $ мы будем получать вероятность от 0 до 1, что объект принадлежит к классу y = 1. Например, если класс 1 означает, что заемщик вернул кредит, то $ h_{theta}(x) = 0,8 $ говорит о том, что согласно нашей модели (с параметрами $theta$), для данного заемщика (x) вероятность возвращения кредита состаляет 80 процентов.
В общем случае мы можем записать вероятность вот так.
$$ h_{theta}(x) = P(y = 1 | x; theta) $$
Это выражение можно прочитать как вероятность принадлежности к классу 1 при условии x с параметрами $theta$ (probability of y = 1 given x, parameterized by $theta$).
Поскольку, как мы помним, сумма вероятностей событий, образующих полную группу, всегда равна единице, вероятность принадлежности к классу 0 будет равна
$$ P(y = 0 | x; theta) = 1-P(y = 1 | x; theta) $$
Решающая граница
Решающая граница (decision boundary) — это порог, который определяет к какому классу отнести то или иное наблюдение. Если выбрать порог на уровне 0,5, то все что выше или равно этому порогу мы отнесем к классу 1, все что ниже — к классу 0.
$$ y = 1, h_{theta}(x) geq 0,5 $$
$$ y = 0, h_{theta}(x) < 0,5 $$
Теперь обратите внимание на сигмоиду. Сигмоида $ g(z) $ принимает значения больше 0,5, если $ z geq 0 $, а так как $ z = Xtheta $, то можно сказать, что
- $h_{theta}(x) geq 0,5$ и $ y = 1$, когда $ Xtheta geq 0 $, и соответственно
- $h_{theta}(x) < 0,5 $ и $ y = 0$, когда $ Xtheta < 0 $.
Уравнение решающей границы
Предположим, что у нас есть два признака $x_1$ и $x_2$. Вместе они образуют так называемое пространство ввода (input space), то есть все имеющиеся у нас наблюдения. Мы можем представить это пространство на координатной плоскости, дополнительно выделив цветом наблюдения, относящиеся к разным классам.
Кроме того, представим, что мы уже построили модель логистической регрессии, и она провела для нас соответствующую границу между двумя классами.

Возникает вопрос. Как, зная коэффициенты $theta_0$, $theta_1$ и $theta_2$ модели, найти уравнение линии решающей границы? Для начала договоримся, что уравнение решающией границы будет иметь вид $x_2 = mx_1 + c$, где m — наклон прямой, а c — сдвиг.
Теперь вспомним, что модель с двумя признаками (до подачи в сигмоиду) имеет вид
$$ z = theta_0 + theta_1 x_1 + theta_2 x_2 $$
Также не забудем, что граница проходит там, где $ h_{theta}(x) = 0,5 $, а значит z = 0. Значит,
$$ 0 = theta_0 + theta_1 x_1 + theta_2 x_2 $$
Чтобы найти с (то есть сдвиг линии решающей границы вдоль оси $x_2$) приравняем $x_1$ к нулю и решим для $x_2$ (именно эта точка и будет сдвигом c).
$$ 0 = theta_0 + 0 + theta_2 x_2 rightarrow x_2 = -frac{theta_0}{theta_2} rightarrow c = -frac{theta_0}{theta_2} $$
Теперь займемся наклоном m. Возьмем некоторую точку на линии решающей границы с координатами $(x_1^a, x_2^a)$, $(x_1^b, x_2^b)$. Тогда наклон m будет равен
$$ m = frac{x_2^b-x_2^a}{x_1^b-x_1^a} $$
Так как эти точки расположены на решающей границе, то справедливо, что
$$ 0 = theta_1x_1^b + theta_2x_2^b + theta_0-(theta_1x_1^a + theta_2x_2^a + theta_0) $$
$$ -theta_2(x_2^b-x_2^a) = theta_1(x_1^b-x_1^a) $$
А значит,
$$ frac{x_2^b-x_2^a}{x_1^b-x_1^a} = -frac{theta_1}{theta_2} rightarrow m = -frac{theta_1}{theta_2} $$
Вычислительная устойчивость сигмоиды
При очень больших отрицательных или положительных значениях z может возникнуть переполнение памяти (overflow).
|
# возьмем большое отрицательное значение z = —999 1 / (1 + np.exp(—z)) |
|
RuntimeWarning: overflow encountered in exp 0.0 |
Преодолеть это ограничение и добиться вычислительной устойчивости (numerical stability) алгоритма можно с помощью следующего тождества.
$$ g(z) = frac{1}{1+e^{-z}} = frac{1}{1+e^{-z}} times frac{e^z}{e^z} = frac{e^z}{e^z(1+e^{-z})} = frac {e^z}{e^z + 1} $$
Что интересно, первая часть тождества устойчива при очень больших положительных значениях z.
|
z = 999 1 / (1 + np.exp(—z)) |
При этом вторая стабильна при очень больших отрицательных значениях.
|
z = —999 np.exp(z) / (np.exp(z) + 1) |
Объединим обе части с помощью условия.
|
def stable_sigmoid(z): if z >= 0: return 1 / (1 + np.exp(—z)) else: return np.exp(z) / (np.exp(z) + 1) |
Примечание. Мы не использовали более лаконичный код, например, функцию np.where(), потому что эта функция прежде чем применить условие рассчитывает оба сценария (в данном случае обе части тождества), а это ровно то, чего мы хотим избежать, чтобы не возникло ошибки. Простое условие с if препятствует выполнению той части кода, которая нам не нужна.
Можно также использовать функцию expit() библиотеки scipy.
|
from scipy.special import expit expit(999), expit(—999) |
Остается написать линейную функцию и подать ее результат в сигмоиду.
|
def h(x, thetas): z = np.dot(x, thetas) return np.array([stable_sigmoid(value) for value in z]) |
Протестируем код. Предположим, что в нашем датасете четыре наблюдения и три коэффициента. Схематично расчеты будут выглядеть следующим образом.
Пропишем это на Питоне.
|
# возьмем массив наблюдений 4 х 3 с числами от 1 до 12 x = np.arange(1, 13).reshape(4, 3) # и трехмерный вектор коэффициентов thetas = np.array([—3, 1, 1]) # подадим их в модель h(x, thetas) |
|
array([0.88079708, 0.26894142, 0.01798621, 0.00091105]) |
Модель работает корректно. Теперь обсудим, как ее обучать, то есть какую функцию потерь использовать для оптимизации параметров $theta$.
Logistic loss или функция кросс-энтропии
В модели логистической регрессии мы не можем использовать MSE. Дело в том, что если мы поместим результат сигмоиды (представляющей собою нелинейную функцию) в MSE, то на выходе получим невыпуклую функцию (non-convex), глобальный минимум которой довольно сложно найти.

Вместо MSE мы будем использовать функцию логистической ошибки, которую еще называют функцией бинарной кросс-энтропии (log loss, binary cross-entropy loss).
График и формула функции логистической ошибки
Вначале посмотрим на нее на графике.

Разберемся, как она работает. Наша модель $h_{theta}(x)$ может выдавать вероятность от 0 до 1, фактические значения $y$ только 0 и 1.
Сценарий 1. Предположим, что для конкретного заемщика в обучающем датасете истинное значение/ целевой класс записан как 1 (то есть заемщик вернул кредит). Тогда «срабатывает» синяя ветвь графика и ошибка измеряется по ней. Соответственно, чем ближе выдаваемая моделью вероятность к единице, тем меньше ошибка.
$$ -log(P(y = 1 | x; theta)) = -log(h_{theta}(x)), y = 1 $$
Сценарий 2. Заемщик не вернул кредит и его целевая переменная записана как 0. Тогда срабатывает оранжевая ветвь. Ошибка модели будет минимальна при значениях, близких к нулю.
$$ -log(1-P(y = 1 | x; theta)) = -log(1-h_{theta}(x)), y = 0 $$
Добавлю, что минус логарифм в данном случае очень удачно отвечает нашему желанию иметь нулевую ошибку при правильном прогнозе и наказать алгоритм высокой ошибкой (асимптотически стремящейся к бесконечности) в случае неправильного прогноза.
В итоге нам нужно будет найти сумму вероятностей принадлежности к классу 1 для сценария 1 и сценария 2.
$$ J(theta) = begin{cases} -log(h_{theta}(x)) | y=1 \ -log(1-h_{theta}(x)) | y=0 end{cases} $$
Однако, для каждого наблюдения нам нужно учитывать только одну из вероятностей (либо $y=1$, либо $y=0$). Как нам переключаться между ними? На самом деле очень просто.
В качестве переключателя можно использовать целевую переменную. В частности, умножим левую часть функции на $y$, а правую на $1-y$. Тогда, если речь идет о классе 1, первая часть умножится на единицу, вторая на ноль и исчезнет. Если речь идет о классе 0, произойдет обратное, исчезнет левая часть, а правая останется. Получается
$$ J(theta) = -frac{1}{n} sum y cdot log(h_{theta}(x)) + (1-y) cdot log(1-h_{theta}(x)) $$
Рассмотрим ее работу на учебном примере.
Расчет логистической ошибки
Предположим, мы построили модель и для каждого наблюдения получили некоторый прогноз (вероятность).
|
# выведем результат работы модели (вероятности) y_pred и целевую переменную y output = pd.DataFrame({ ‘y’ :[1, 1, 1, 0, 0, 1, 1, 0], ‘y_pred’ :[0.93, 0.81, 0.78, 0.43, 0.54, 0.49, 0.22, 0.1] }) output |
Найдем вероятность принадлежности к классу 1.
|
# оставим вероятность, если y = 1, и вычтем вероятность из единицы, если y = 0 output[‘y=1 prob’] = np.where(output[‘y’] == 0, 1 — output[‘y_pred’], output[‘y_pred’]) output |
Возьмем отрицательный логарифм из каждой вероятности.
|
output[‘-log’] = —np.log(output[‘y=1 prob’]) output |
Выведем каждое из получившихся значений на графике.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
plt.figure(figsize = (10, 8)) # создадим точки по оси x в промежутке от 0 до 1 x_vals = np.linspace(0, 1) # выведем кривую функции логистической ошибки plt.plot(x_vals, —np.log(x_vals), label = ‘-log(h(x)) | y = 1’) # выведем каждое из значений отрицательного логарифма plt.scatter(output[‘y=1 prob’], output[‘-log’], color = ‘r’) # зададим заголовок, подписи к осям, легенду и сетку plt.xlabel(‘h(x)’, fontsize = 16) plt.ylabel(‘loss’, fontsize = 16) plt.title(‘Функция логистической ошибки’, fontsize = 18) plt.legend(loc = ‘upper right’, prop = {‘size’: 15}) plt.grid() plt.show() |
Как мы видим, так как мы всегда выражаем вероятность принадлежности к классу 1, графически нам будет достаточно одной ветви. Остается сложить результаты и разделить на количество наблюдений.
Окончательный вариант
Напишем функцию логистической ошибки, которую будем использовать в нашем алгоритме.
|
def objective(y, y_pred): # рассчитаем функцию потерь для y = 1, добавив 1e-9, чтобы избежать ошибки при log(0) y_one_loss = y * np.log(y_pred + 1e—9) # также рассчитаем функцию потерь для y = 0 y_zero_loss = (1 — y) * np.log(1 — y_pred + 1e—9) # сложим и разделим на количество наблюдений return —np.mean(y_zero_loss + y_one_loss) |
Проверим ее работу на учебных данных.
|
objective(output[‘y’], output[‘y_pred’]) |
Теперь займемся поиском производной.
Производная функции логистической ошибки
Предположим, что $G(theta)$ — одна из частных производных описанной выше функции логистической ошибки $J(theta)$,
$$ G = y cdot log(h) + (1-y) cdot log(1-h) $$
где h — это сигмоида $1/1+e^{-z}$, а $z(theta)$ — линейная функция $xtheta$. Тогда по chain rule нам нужно найти производные следующих функций
$$ frac{partial G}{partial theta} = frac{partial G}{partial h} cdot frac{partial h}{partial z} cdot frac{partial z}{partial theta} $$
Производная логарифмической функции
Начнем с производной логарифмической функции.
$$ frac{partial}{partial x} ln f(x) = frac{1}{f(x)} $$
Теперь, помня, что x и y — это константы, найдем первую производную.
$$ frac{partial G}{partial h} left[ y cdot log(h) + (1-y) cdot log(1-h) right] $$
$$ = y cdot frac{partial G}{partial h} [log(h)] + (1-y) cdot frac{partial G}{partial h} [log(1-h)] $$
$$ = frac{1}{h}y + frac{1}{1-h} cdot frac{partial G}{partial h} [1-h] cdot (1-y) $$
Упростим выражение (не забыв про производную разности).
$$ = frac{h}{y} + frac{frac{partial G}{partial h} (1-h) (1-y)}{1-h} = frac{h}{y}+frac{(0-1)(1-y)}{1-h} $$
$$ = frac{y}{h}-frac{1-y}{1-h} = frac{y-h}{h(1-h)} $$
Теперь займемся производной сигмоиды.
Производная сигмоиды
Вначале упростим выражение.
$$ frac{partial h}{partial z} left[ frac{1}{1+e^{-z}} right] = frac{partial h}{partial z} left[ (1+e^{-z})^{-1}) right] $$
Теперь перейдем к нахождению производной
$$ = -(1+e^{-z})^{-2}) cdot (-e^{-z}) = frac{e^{-z}}{(1+e^{-z})^2} $$
$$ = frac{1}{1+e^{-z}} cdot frac{e^{-z}}{1+e^{-z}} = frac{1}{1+e^{-z}} cdot frac{(1+e^{-z})-1}{1+e^{-z}} $$
$$ = frac{1}{1+e^{-z}} cdot left( frac{1+e^{-z}}{1+e^{-z}}-frac{1}{1+e^{-z}} right) $$
$$ = frac{1}{1+e^{-z}} cdot left( 1-frac{1}{1+e^{-z}} right) $$
В терминах предложенной выше нотации получается
$$ h(1-h) $$
Производная линейной функции
Наконец найдем производную линейной функции.
$$ frac{partial z}{partial theta} = x $$
Перемножим производные и найдем градиент по каждому из признаков j для n наблюдений.
$$ frac{partial J}{partial theta} = frac{y-h}{h(1-h)} cdot h(1-h) cdot x_j cdot frac{1}{n} = x_j cdot (y-h) cdot frac{1}{n} $$
Замечу, что хотя производная похожа на градиент функции линейной регрессии, на самом деле это разные функции, $h$ в данном случае сигмоида.
Для нахождения градиента (всех частных производных одновременно) перепишем формулу в векторной нотации.
$$ nabla_{theta} J = X^T(h(Xtheta)-y) times frac{1}{n} $$
Схематично для четырех наблюдений и трех коэффициентов нахождение градиента будет выглядеть следующим образом.
Объявим соответствующую функцию.
|
def gradient(x, y, y_pred, n): return np.dot(x.T, (y_pred — y)) / n |
На всякий случай напомню, что прогнозные значения (y_pred) мы получаем с помощью объявленной ранее функции $h(x, thetas)$.
Подготовка данных
В качестве примера возьмем встроенный в sklearn датасет, в котором нам предлагается определить класс вина по его характеристикам.
|
# импортируем датасет о вине из модуля datasets data = datasets.load_wine() # превратим его в датафрейм df = pd.DataFrame(data.data, columns = data.feature_names) # добавим целевую переменную df[‘target’] = data.target # посмотрим на первые три строки df.head(3) |
Целевая переменная
Посмотрим на количество наблюдений и признаков (размерность матрицы), а также уникальные значения (классы) в целевой переменной.
|
df.shape, np.unique(df.target) |
|
((178, 14), array([0, 1, 2])) |
Как мы видим, у нас три класса, а должно быть два, потому что пока что мы создаем алгоритм бинарной классификации. Отфильтруем значения так, чтобы осталось только два класса.
|
# применим маску датафрейма и удалим класс 2 df = df[df.target != 2] # посмотрим на результат df.shape, df.target.unique() |
|
((130, 14), array([0, 1])) |
Отбор признаков
Наша целевая переменная выражена бинарной категорией или, как еще говорят, находится на дихотомической шкале (dichotomous variable). В этом случае применять коэффициент корреляции Пирсона не стоит и можно использовать точечно-бисериальную корреляцию (point-biserial correlation). Рассчитаем корреляцию признаков и целевой переменной нашего датасета.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# импортируем модуль stats из библиотеки scipy from scipy import stats # создадим два списка, один для названий признаков, второй для корреляций columns, correlations = [], [] # пройдемся по всем столбцам датафрейма кроме целевой переменной for col in df.drop(‘target’, axis = 1).columns: # поместим название признака в список columns columns.append(col) # рассчитаем корреляцию этого признака с целевой переменной # и поместим результат в список корреляций correlations.append(stats.pointbiserialr(df[col], df[‘target’])[0]) # создадим датафрейм на основе заполненных списков # и применим градиентную цветовую схему pd.DataFrame({‘column’: columns, ‘correlation’: correlations}).style.background_gradient() |
Наиболее коррелирующим с целевой переменной признаком является пролин (proline). Визуально оценим насколько сильно отличается этот показатель для классов вина 0 и 1.
|
# зададим размер графика plt.figure(figsize = (10, 8)) # на точечной диаграмме выведем пролин по оси x, а класс вина по оси y sns.scatterplot(x = df.proline, y = df.target, s = 80); |
Теперь посмотрим на зависимость двух признаков (спирт и пролин) от целевой переменной.
|
# зададим размер графика plt.figure(figsize = (10, 8)) # на точечной диаграмме по осям x и y выведем признаки, # с помощью параметра hue разделим соответствующие классы целевой переменной sns.scatterplot(x = df.alcohol, y = df.proline, hue = df.target, s = 80) # добавим легенду, зададим ее расположение и размер plt.legend(loc = ‘upper left’, prop = {‘size’: 15}) # выведем результат plt.show() |
В целом можно сказать, что классы линейно разделимы (другими словами, мы можем провести прямую между ними). Поместим признаки в переменную X, а целевую переменную — в y.
|
X = df[[‘alcohol’, ‘proline’]] y = df[‘target’] |
Масштабирование признаков
Как и в случае с линейной регрессией, для алгоритма логистической регрессии важно, чтобы признаки были приведены к одному масштабу. Для этого используем стандартизацию.
|
# т.е. приведем данные к нулевому среднему и единичному СКО X = (X — X.mean()) / X.std() X.head() |
Проверим результат.
|
X.alcohol.mean(), X.alcohol.std(), X.proline.mean(), X.proline.std() |
|
(6.8321416900009635e-15, 1.0, -5.465713352000771e-17, 1.0) |
Теперь мы готовы к созданию и обучению модели.
Обучение модели
Вначале объявим уже знакомую нам функцию, которая добавит в датафрейм столбец под названием x0, заполненный единицами.
|
def add_ones(x): # важно! метод .insert() изменяет исходный датафрейм return x.insert(0,‘x0’, np.ones(x.shape[0])) |
Применим ее к нашему датафрейму с признаками.
|
# добавим столбец с единицами add_ones(X) # и посмотрим на результат X.head() |
Создадим вектор начальных весов (он будет состоять из нулей), а также переменную n, в которой будет храниться количество наблюдений.
|
thetas, n = np.zeros(X.shape[1]), X.shape[0] thetas, n |
|
(array([0., 0., 0.]), 130) |
Кроме того, создадим список, в который будем записывать размер ошибки функции потерь.
Теперь выполним основную работу по минимизации функции потерь и поиску оптимальных весов (выполнение кода ниже у меня заняло около 30 секунд).
|
# в цикле из 20000 итераций for i in range(20000): # рассчитаем прогнозное значение с текущими весами y_pred = h(X, thetas) # посчитаем уровень ошибки при текущем прогнозе loss_history.append(objective(y, y_pred)) # рассчитаем градиент grad = gradient(X, y, y_pred, n) # используем градиент для улучшения весов модели # коэффициент скорости обучения будет равен 0,001 thetas = thetas — 0.001 * grad |
Посмотрим на получившиеся веса и финальный уровень ошибки.
|
# чтобы посмотреть финальный уровень ошибки, # достаточно взять последний элемент списка loss_history thetas, loss_history[—1] |
|
(array([ 0.23234188, -1.73394252, -1.89350543]), 0.12282503517421262) |
Модель обучена. Теперь мы можем сделать прогноз и оценить результат.
Прогноз и оценка качества
Прогноз модели
Объявим функцию predict(), которая будет предсказывать к какому классу относится то или иное наблюдение. От функции $h(x, thetas)$ эта функция будет отличаться тем, что выдаст не только вероятность принадлежности к тому или иному классу, но и непосредственно сам предполагаемый класс (0 или 1).
|
def predict(x, thetas): # найдем значение линейной функции z = np.dot(x, thetas) # проведем его через устойчивую сигмоиду probs = np.array([stable_sigmoid(value) for value in z]) # если вероятность больше или равна 0,5 — отнесем наблюдение к классу 1, # в противном случае к классу 0 # дополнительно выведем значение вероятности return np.where(probs >= 0.5, 1, 0), probs |
Вызовем функцию predict() и запишем прогноз класса и вероятность принадлежности к этому классу в переменные y_pred и probs соответственно.
|
# запишем прогноз класса и вероятность этого прогноза в переменные y_pred и probs y_pred, probs = predict(X, thetas) # посмотрим на прогноз и вероятность для первого наблюдения y_pred[0], probs[0] |
|
(0, 0.022908352078195617) |
Здесь важно напомнить, что вероятность, близкая к нулю, говорит о пренадлжености к классу 0. В качестве упражнения выведите класс последнего наблюдения и соответствующую вероятность.
Метрика accuracy и матрица ошибок
Оценим результат с помощью метрики accuracy и матрицы ошибок.
|
# функцию accuracy_score() мы импортировали в начале ноутбука accuracy_score(y, y_pred) |
|
# функцию confusion_matrix() мы импортировали в начале ноутбука # столбцами будут прогнозные значения (Forecast), # строками — фактические (Actual) pd.DataFrame(confusion_matrix(y, y_pred), columns = [‘Forecast 0’, ‘Forecast 1’], index = [‘Actual 0’, ‘Actual 1’]) |
Как мы видим, алгоритм ошибся пять раз. Дважды он посчитал, что наблюдение относится к классу 1, хотя на самом деле это был класс 0, и трижды, наоборот, неверно отнес класс 1 к классу 0.
Решающая граница
Выше мы уже вывели уравнение решающей границы. Воспользуемся им, чтобы визуально оценить насколько удачно классификатор справился с поставленной задачей.
|
# рассчитаем сдвиг (c) и наклон (m) линии границы c, m = —thetas[0]/thetas[2], —thetas[1]/thetas[2] c, m |
|
(0.1227046263531282, -0.915731474695505) |
|
# найдем минимальное и максимальное значения для спирта (ось x) xmin, xmax = min(X[‘alcohol’]), max(X[‘alcohol’]) # найдем минимальное и максимальное значения для пролина (ось y) ymin, ymax = min(X[‘proline’]), max(X[‘proline’]) # запишем значения оси x в переменную xd xd = np.array([xmin, xmax]) xd |
|
array([-2.15362589, 2.12194856]) |
|
# подставим эти значения, а также значения сдвига и наклона в уравнение линии yd = m * xd + c # в результате мы получим координаты двух точек, через которые проходит линия границы (xd[0], yd[0]), (xd[1], yd[1]) |
|
((-2.1536258890738247, 2.0948476376971197), (2.1219485561396647, -1.8204304541886445)) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
# зададим размер графика plt.figure(figsize = (11, 9)) # построим пунктирную линию по двум точкам, найденным выше plt.plot(xd, yd, ‘k’, lw = 1, ls = ‘—‘) # дополнительно отобразим наши данные, sns.scatterplot(x = X[‘alcohol’], y = X[‘proline’], hue = y, s = 70) # которые снова снабдим легендой plt.legend(loc = ‘upper left’, prop = {‘size’: 15}) # минимальные и максимальные значения по обеим осям будут границами графика plt.xlim(xmin, xmax) plt.ylim(ymin, ymax) # по желанию, разделенные границей половинки можно закрасить # tab: означает, что цвета берутся из палитры Tableau # plt.fill_between(xd, yd, ymin, color=’tab:blue’, alpha = 0.2) # plt.fill_between(xd, yd, ymax, color=’tab:orange’, alpha = 0.2) # а также добавить обозначения переменных в качестве подписей к осям # plt.xlabel(‘x_1’) # plt.ylabel(‘x_2’) plt.show() |
На графике хорошо видны те пять значений, в которых ошибся наш классификатор.
Написание класса
Остается написать класс бинарной логистической регрессии.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 |
class LogReg(): # в методе .__init__() объявим переменные для весов и уровня ошибки def __init__(self): self.thetas = None self.loss_history = [] # метод .fit() необходим для обучения модели # этому методу мы передадим признаки и целевую переменную # кроме того, мы зададим значения по умолчанию # для количества итераций и скорости обучения def fit(self, x, y, iter = 20000, learning_rate = 0.001): # метод создаст «правильные» копии датафрейма x, y = x.copy(), y.copy() # добавит столбец из единиц self.add_ones(x) # инициализирует веса и запишет в переменную n количество наблюдений thetas, n = np.zeros(x.shape[1]), x.shape[0] # создадим список для записи уровня ошибки loss_history = [] # в цикле равном количеству итераций for i in range(iter): # метод сделает прогноз с текущими весами y_pred = self.h(x, thetas) # найдет и запишет уровень ошибки loss_history.append(self.objective(y, y_pred)) # рассчитает градиент grad = self.gradient(x, y, y_pred, n) # и обновит веса thetas -= learning_rate * grad # метод выдаст веса и список с историей ошибок self.thetas = thetas self.loss_history = loss_history # метод .predict() делает прогноз с помощью обученной модели def predict(self, x): # метод создаст «правильную» копию модели x = x.copy() # добавит столбец из единиц self.add_ones(x) # рассчитает значения линейной функции z = np.dot(x, self.thetas) # передаст эти значения в сигмоиду probs = np.array([self.stable_sigmoid(value) for value in z]) # выдаст принадлежность к определенному классу и соответствующую вероятность return np.where(probs >= 0.5, 1, 0), probs # ниже приводятся служебные методы, смысл которых был разобран ранее def add_ones(self, x): return x.insert(0,‘x0’, np.ones(x.shape[0])) def h(self, x, thetas): z = np.dot(x, thetas) return np.array([self.stable_sigmoid(value) for value in z]) def objective(self, y, y_pred): y_one_loss = y * np.log(y_pred + 1e—9) y_zero_loss = (1 — y) * np.log(1 — y_pred + 1e—9) return —np.mean(y_zero_loss + y_one_loss) def gradient(self, x, y, y_pred, n): return np.dot(x.T, (y_pred — y)) / n def stable_sigmoid(self, z): if z >= 0: return 1 / (1 + np.exp(—z)) else: return np.exp(z) / (np.exp(z) + 1) |
Проверим работу написанного нами класса. Вначале подготовим данные и обучим модель.
|
# проверим работу написанного нами класса # поместим признаки и целевую переменную в X и y X = df[[‘alcohol’, ‘proline’]] y = df[‘target’] # приведем признаки к одному масштабу X = (X — X.mean())/X.std() # создадим объект класса LogReg model = LogReg() # и обучим модель model.fit(X, y) # посмотрим на атрибуты весов и финального уровня ошибки model.thetas, model.loss_history[—1] |
|
(array([ 0.23234188, —1.73394252, —1.89350543]), 0.12282503517421262) |
Затем сделаем прогноз и оценим качество модели.
|
# сделаем прогноз y_pred, probs = model.predict(X) # и посмотрим на класс первого наблюдения и вероятность y_pred[0], probs[0] |
|
(0, 0.022908352078195617) |
|
# рассчитаем accuracy accuracy_score(y, y_pred) |
|
# создадим матрицу ошибок pd.DataFrame(confusion_matrix(y, y_pred), columns = [‘Forecast 0’, ‘Forecast 1’], index = [‘Actual 0’, ‘Actual 1’]) |
Модель показала точно такой же результат. Методы класса LogReg работают. Теперь давайте сравним работу нашего класса с классом LogisticRegression библиотеки sklearn.
Сравнение с sklearn
Обучение модели
Вначале обучим модель.
|
# подготовим данные X = df[[‘alcohol’, ‘proline’]] y = df[‘target’] X = (X — X.mean())/X.std() # создадим объект класса LogisticRegression и запишем его в переменную model model = LogisticRegression() # обучим модель model.fit(X, y) # посмотрим на получившиеся веса модели model.intercept_, model.coef_ |
|
(array([0.30838852]), array([[-2.09622008, -2.45991159]])) |
Прогноз
Теперь необходимо сделать прогноз и найти соответствующие вероятности. В классе LogisticRegression библиотеки sklearn метод .predict() отвечает за предсказание принадлежности к определенному классу, а метод .predict_proba() отвечает за вероятность такого прогноза.
|
# выполним предсказание класса y_pred = model.predict(X) # и найдем вероятности probs = model.predict_proba(X) # посмотрим на класс и вероятность первого наблюдения y_pred[0], probs[0] |
|
(0, array([0.9904622, 0.0095378])) |
Модель предсказала для первого наблюдения класс 0. При этом, обратите внимание, что метод .predict_proba() для каждого наблюдения выдает две вероятности, первая — это вероятность принадлежности к классу 0, вторая — к классу 1.
Оценка качества
Рассчитаем метрику accuracy.
|
accuracy_score(y, y_pred) |
И построим матрицу ошибок.
|
pd.DataFrame(confusion_matrix(y, y_pred), columns = [‘Forecast 0’, ‘Forecast 1’], index = [‘Actual 0’, ‘Actual 1’]) |
Как мы видим, хотя веса модели и предсказанные вероятности немного отличаются, ее точность осталась неизменной.
Решающая граница
Построим решающую границу.
|
# найдем сдвиг и наклон для уравнения решающей границы c, m = —model.intercept_ / model.coef_[0][1], —model.coef_[0][0] / model.coef_[0][1] c, m |
|
(array([0.12536569]), -0.8521526076691505) |
|
# посмотрим на линию решающей границы plt.figure(figsize = (11, 9)) xmin, xmax = min(X[‘alcohol’]), max(X[‘alcohol’]) ymin, ymax = min(X[‘proline’]), max(X[‘proline’]) xd = np.array([xmin, xmax]) yd = m*xd + c plt.plot(xd, yd, ‘k’, lw=1, ls=‘—‘) sns.scatterplot(x = X[‘alcohol’], y = X[‘proline’], hue = y, s = 70) plt.legend(loc = ‘upper left’, prop = {‘size’: 15}) plt.xlim(xmin, xmax) plt.ylim(ymin, ymax) plt.show() |
Бинарная полиномиальная регрессия
Идея бинарной полиномиальной логистической регрессии (binary polynomial logistic regression) заключается в том, чтобы использовать полином внутри сигмоиды и соответственно создать нелинейную границу между двумя классами.
Полиномиальные признаки
Уравнение полинома на основе двух признаков будет выглядеть следующим образом.
$$ y = theta_{0}x_0 + theta_{1}x_1 + theta_{2}x_2 + theta_{3} x_1^2 + theta_{4} x_1x_2 + theta_{5} x_2^2 $$
Реализуем этот алгоритм на практике и посмотрим, улучшатся ли результаты. Вначале, подготовим и масштабируем данные.
|
X = df[[‘alcohol’, ‘proline’]] y = df[‘target’] X = (X — X.mean())/X.std() |
Теперь преобразуем наши данные так, как если бы мы использовали полином второй степени.
Смысл создания полиномиальных признаков мы детально разобрали на занятии по множественной линейной регрессии.
|
# создадим объект класса PolynomialFeatures # укажем, что мы хотим создать полином второй степени polynomial_features = PolynomialFeatures(degree = 2) # преобразуем данные с помощью метода .fit_transform() X_poly = polynomial_features.fit_transform(X) |
Сравним исходные признаки с полиномиальными.
|
# посмотрим на первое наблюдение X.head(1) |
|
# должно получиться шесть признаков X_poly[:1] |
|
array([[1. , 1.44685785, 0.77985116, 2.09339765, 1.12833378, 0.60816783]]) |
Моделирование и оценка качества
Обучим модель, сделаем прогноз и оценим результат.
|
# создадим объект класса LogisticRegression poly_model = LogisticRegression() # обучим модель на полиномиальных признаках poly_model = poly_model.fit(X_poly, y) # сделаем прогноз y_pred = poly_model.predict(X_poly) # рассчитаем accuracy accuracy_score(y_pred, y) |
Построим матрицу ошибок.
|
pd.DataFrame(confusion_matrix(y, y_pred), columns = [‘Forecast 0’, ‘Forecast 1’], index = [‘Actual 0’, ‘Actual 1’]) |
Для того чтобы визуально оценить качество модели, построим два графика: фактических классов и прогнозных. Вначале создадим датасет, в котором будут исходные признаки (alcohol, proline) и прогнозные значения (y_pred).
|
# сделаем копию исходного датафрейма с нужными признаками predictions = df[[‘alcohol’, ‘proline’]].copy() # и добавим новый столбец с прогнозными значениями predictions[‘y_pred’] = y_pred # посмотрим на результат predictions.head(3) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
# создадим два подграфика с помощью функции plt.subplots() # расположим подграфики на одной строке fig, (ax1, ax2) = plt.subplots(1, 2, # пропишем размер, figsize = (14, 6), # а также расстояние между подграфиками по горизонтали gridspec_kw = {‘wspace’ : 0.2}) # на левом подграфике выведем фактические классы sns.scatterplot(data = df, x = ‘alcohol’, y = ‘proline’, hue = ‘target’, palette = ‘bright’, s = 50, ax = ax1) ax1.set_title(‘Фактические классы’, fontsize = 14) # на правом — прогнозные sns.scatterplot(data = predictions, x = ‘alcohol’, y = ‘proline’, hue = ‘y_pred’, palette = ‘bright’, s = 50, ax = ax2) ax2.set_title(‘Прогноз’, fontsize = 14) # зададим общий заголовок fig.suptitle(‘Бинарная полиномиальная регрессия’, fontsize = 16) plt.show() |
Как вы видите, нам не удалось добиться улучшения по сравнению с обычной полиномиальной регрессией.
Напомню, что создание подграфиков мы подробно разобрали на занятии по исследовательскому анализу данных.
В качестве упражнения предлагаю вам выяснить, какая степень полинома позволит улучшить результат прогноза на этих данных и насколько, таким образом, улучшится качество предсказаний.
Перейдем ко второй части нашего занятия.
Мультиклассовая логистическая регрессия
Как поступить, если нужно предсказать не два класса, а больше? Сегодня мы рассмотрим два подхода: one-vs-rest и кросс-энтропию. Начнем с того, что подготовим данные.
Подготовка данных
Вернем исходный датасет с тремя классами.
|
# вновь импортируем датасет о вине data = datasets.load_wine() # превратим его в датафрейм df = pd.DataFrame(data.data, columns = data.feature_names) # приведем признаки к одному масштабу df = (df — df.mean())/df.std() # добавим целевую переменную df[‘target’] = data.target # убедимся, что у нас присутствуют все три класса df.target.value_counts() |
|
1 71 0 59 2 48 Name: target, dtype: int64 |
В целевой переменной большое двух классов, а значит точечно-бисериальный коэффициент корреляции мы использовать не можем. Воспользуемся корреляционным отношением (correlation ratio).
|
# код ниже был подробно разобран на предыдущем занятии def correlation_ratio(numerical, categorical): values = np.array(numerical) ss_total = np.sum((values.mean() — values) ** 2) cats = np.unique(categorical, return_inverse = True)[1] ss_betweengroups = 0 for c in np.unique(cats): group = values[np.argwhere(cats == c).flatten()] ss_betweengroups += len(group) * (group.mean() — values.mean()) ** 2 return np.sqrt(ss_betweengroups/ss_total) |
|
# создадим два списка, один для названий признаков, второй для значений корреляционного отношения columns, correlations = [], [] # пройдемся по всем столбцам датафрейма кроме целевой переменной for col in df.drop(‘target’, axis = 1).columns: # поместим название признака в список columns columns.append(col) # рассчитаем взаимосвязь этого признака с целевой переменной # и поместим результат в список значений корреляционного отношения correlations.append(correlation_ratio(df[col], df[‘target’])) # создадим датафрейм на основе заполненных списков # и применим градиентную цветовую схему pd.DataFrame({‘column’: columns, ‘correlation’: correlations}).style.background_gradient() |
Теперь наибольшую корреляцию с целевой переменной показывают флавоноиды (flavanoids) и пролин (proline). Их и оставим.
|
df = df[[‘flavanoids’, ‘proline’, ‘target’]].copy() df.head(3) |
Посмотрим, насколько легко можно разделить эти классы.
|
# зададим размер графика plt.figure(figsize = (10, 8)) # построим точечную диаграмму с двумя признаками, разделяющей категориальной переменной будет класс вина sns.scatterplot(x = df.flavanoids, y = df.proline, hue = df.target, palette = ‘bright’, s = 100) # добавим легенду plt.legend(loc = ‘upper left’, prop = {‘size’: 15}) plt.show() |
Перейдем непосредственно к алгоритмам мультиклассовой логистической регрессии. Начнем с подхода one-vs-rest.
Подход one-vs-rest
Подход one-vs-rest или one-vs-all предполагает, что мы отделяем один класс, а остальные наоборот объединяем. Так мы поступаем с каждым классом и строим по одной модели логистической регрессии относительно каждого из класса. Например, если у нас три класса, то у нас будет три модели логистической регрессии. Далее мы смотрим на получившиеся вероятности и выбираем наибольшую.
$$ h_theta^{(i)}(x) = P(y = i | x; theta), i in {0, 1, 2} $$
При таком подходе сам по себе алгоритм логистической регрессии претерпевает лишь несущественные изменения, главное правильно подготовить данные для обучения модели.
Подготовка датасетов
|
# поместим признаки и данные в соответствующие переменные x1, x2 = df.columns[0], df.columns[1] target = df.target.unique() target |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
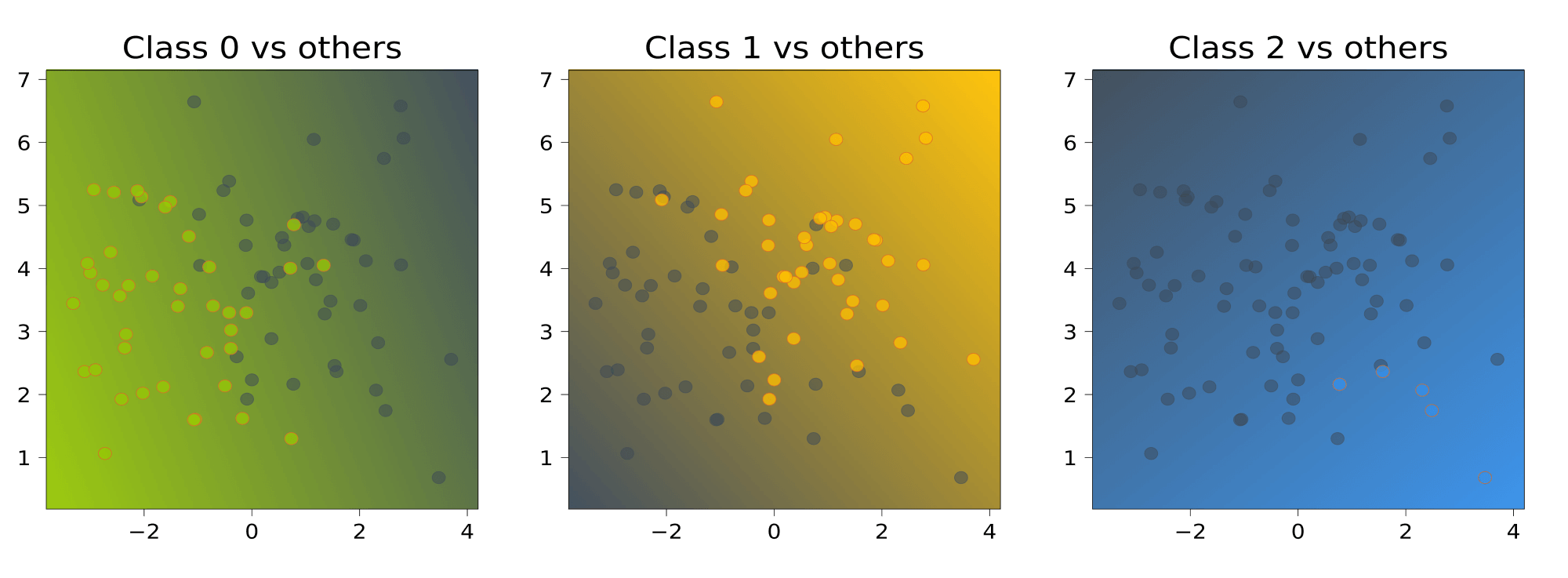
# сделаем копии датафреймов ovr_0, ovr_1, ovr_2 = df.copy(), df.copy(), df.copy() # в каждом из них сделаем целевым классом 0-й, 1-й или 2-й классы # например, в ovr_0 первым классом будет класс 0, а классы 1 и 2 — нулевым ovr_0[‘target’] = np.where(df[‘target’] == target[0], 1, 0) ovr_1[‘target’] = np.where(df[‘target’] == target[1], 1, 0) ovr_2[‘target’] = np.where(df[‘target’] == target[2], 1, 0) # выведем разделение на классы на графике fig, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize = (16, 4), gridspec_kw = {‘wspace’: 0.2, ‘hspace’: 0.08}) sns.scatterplot(data = ovr_0, x = x1, y = x2, hue = ‘target’, s = 50, ax = ax1) ax1.set_title(‘Прогнозирование класса 0’, fontsize = 14) sns.scatterplot(data = ovr_1, x = x1, y = x2, hue = ‘target’, s = 50, ax = ax2) ax2.set_title(‘Прогнозирование класса 1’, fontsize = 14) sns.scatterplot(data = ovr_2, x = x1, y = x2, hue = ‘target’, s = 50, ax = ax3) ax3.set_title(‘Прогнозирование класса 2’, fontsize = 14) plt.show() |
Обучение моделей
|
models = [] # поочередно обучим каждую из моделей for ova_n in [ovr_0, ovr_1, ovr_2]: X = ova_n[[‘flavanoids’, ‘proline’]] y = ova_n[‘target’] model = LogReg() model.fit(X, y) # каждую обученную модель поместим в список models.append(model) |
|
# убедимся, что все работает # например, выведем коэффициенты модели 1 models[0].thetas |
|
array([-0.99971466, 1.280398 , 2.04834457]) |
Прогноз и оценка качества
|
# вновь перенесем данные из исходного датафрейма X = df[[‘flavanoids’, ‘proline’]] y = df[‘target’] # в список probs будем записывать результат каждой модели # для каждого наблюдения probs = [] for model in models: _, prob = model.predict(X) probs.append(prob) |
|
# очевидно, для каждого наблюдения у нас будет три вероятности # принадлежности к целевому классу probs[0][0], probs[1][0], probs[2][0] |
|
(0.9161148288779738, 0.1540913395345091, 0.026621132600103174) |
|
# склеим и изменим размерность массива таким образом, чтобы # строки были наблюдениями, а столбцы вероятностями all_probs = np.concatenate(probs, axis = 0).reshape(len(probs), —1).T all_probs.shape |
|
# каждая из 178 строк — это вероятность одного наблюдения # принадлежать к классу 0, 1, 2 all_probs[0] |
|
array([0.91611483, 0.15409134, 0.02662113]) |
Обратите внимание, при использовании подхода one-vs-rest вероятности в сумме не дают единицу.
|
# например, первое наблюдение вероятнее всего принадлежит к классу 0 np.argmax(all_probs[0]) |
|
# найдем максимальную вероятность в каждой строке, # индекс вероятности [0, 1, 2] и будет прогнозом y_pred = np.argmax(all_probs, axis = 1) # рассчитаем accuracy accuracy_score(y, y_pred) |
|
# выведем матрицу ошибок pd.DataFrame(confusion_matrix(y, y_pred), columns = [‘Forecast 0’, ‘Forecast 1’, ‘Forecast 2’], index = [‘Actual 0’, ‘Actual 1’, ‘Actual 2’]) |
Сравним фактическое и прогнозное распределение классов на точечной диаграмме.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
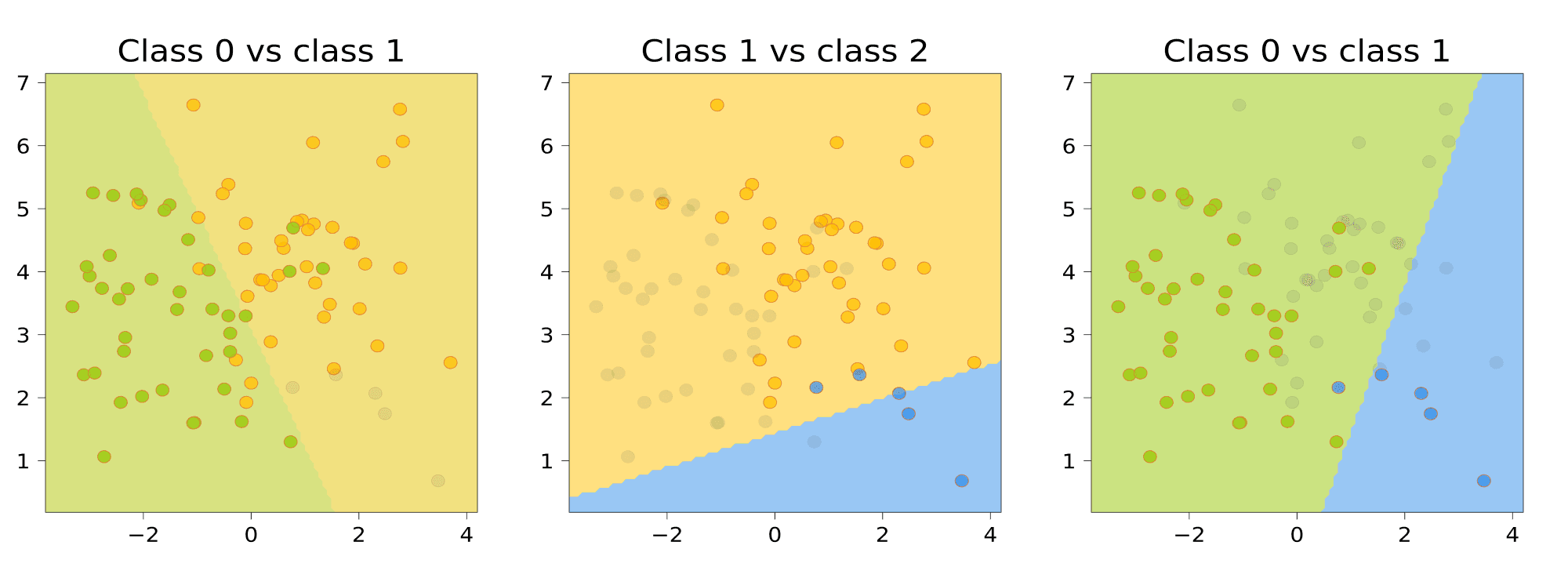
predictions = df[[‘flavanoids’, ‘proline’]].copy() predictions[‘y_pred’] = y_pred fig, (ax1, ax2) = plt.subplots(1, 2, figsize = (14, 6), gridspec_kw = {‘wspace’: 0.2, ‘hspace’: 0.08}) sns.scatterplot(data = df, x = ‘flavanoids’, y = ‘proline’, hue = ‘target’, palette = ‘bright’, s = 50, ax = ax1) ax1.set_title(‘Фактические классы’, fontsize = 14) sns.scatterplot(data = predictions, x = ‘flavanoids’, y = ‘proline’, hue = ‘y_pred’, palette = ‘bright’, s = 50, ax = ax2) ax2.set_title(‘Прогноз one-vs-rest’, fontsize = 14) plt.show() |
Написание класса
Поместим достигнутый выше результат в класс.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 |
class OVR_LogReg(): def __init__(self): self.models_thetas = [] self.models_loss = [] def fit(self, x, y, iter = 20000, learning_rate = 0.001): dfs = self.preprocess(x, y) models_thetas, models_loss = [], [] for ovr_df in dfs: x = ovr_df.drop(‘target’, axis = 1).copy() y = ovr_df.target.copy() self.add_ones(x) loss_history = [] thetas, n = np.zeros(x.shape[1]), x.shape[0] for i in range(iter): y_pred = self.h(x, thetas) loss_history.append(self.objective(y, y_pred)) grad = self.gradient(x, y, y_pred, n) thetas -= learning_rate * grad models_thetas.append(thetas) models_loss.append(loss_history) self.models_thetas = models_thetas self.models_loss = models_loss def predict(self, x): x = x.copy() probs = [] self.add_ones(x) for t in self.models_thetas: z = np.dot(x, t) prob = np.array([self.stable_sigmoid(value) for value in z]) probs.append(prob) all_probs = np.concatenate(probs, axis = 0).reshape(len(probs), —1).T y_pred = np.argmax(all_probs, axis = 1) return y_pred, all_probs def preprocess(self, x, y): x, y = x.copy(), y.copy() x[‘target’] = y classes = x.target.unique() dfs = [] ovr_df = None for c in classes: ovr_df = x.drop(‘target’, axis = 1).copy() ovr_df[‘target’] = np.where(x[‘target’] == classes[c], 1, 0) dfs.append(ovr_df) return dfs def add_ones(self, x): return x.insert(0,‘x0’, np.ones(x.shape[0])) def h(self, x, thetas): z = np.dot(x, thetas) return np.array([self.stable_sigmoid(value) for value in z]) def objective(self, y, y_pred): y_one_loss = y * np.log(y_pred + 1e—9) y_zero_loss = (1 — y) * np.log(1 — y_pred + 1e—9) return —np.mean(y_zero_loss + y_one_loss) def gradient(self, x, y, y_pred, n): return np.dot(x.T, (y_pred — y)) / n def stable_sigmoid(self, z): if z >= 0: return 1 / (1 + np.exp(—z)) else: return np.exp(z) / (np.exp(z) + 1) |
Проверим класс в работе.
|
X = df[[‘flavanoids’, ‘proline’]] y = df[‘target’] model = OVR_LogReg() model.fit(X, y) y_pred, probs = model.predict(X) accuracy_score(y_pred, y) |
Сравнение с sklearn
Для того чтобы применить подход one-vs-rest в классе LogisticRegression, необходимо использовать значение параметра multi_class = ‘ovr’.
|
X = df[[‘flavanoids’, ‘proline’]] y = df[‘target’] ovr_model = LogisticRegression(multi_class = ‘ovr’) ovr_model = ovr_model.fit(X, y) y_pred = ovr_model.predict(X) accuracy_score(y_pred, y) |
Мультиклассовая полиномиальная регрессия
Как мы увидели в предыдущем разделе, линейная решающая граница допустила некоторое количество ошибок. Попробуем улучшить результат, применив мультиклассовую полиномиальную логистическую регрессию.
|
X = df[[‘flavanoids’, ‘proline’]] y = df[‘target’] polynomial_features = PolynomialFeatures(degree = 7) X_poly = polynomial_features.fit_transform(X) poly_ovr_model = LogisticRegression(multi_class = ‘ovr’) poly_ovr_model = poly_ovr_model.fit(X_poly, y) y_pred = poly_ovr_model.predict(X_poly) accuracy_score(y_pred, y) |
Результат, по сравнению с моделью sklearn без полиномиальных признаков, стал чуть лучше. Однако это было достигнуто за счет полинома достаточно высокой степени (degree = 7), что неэффективно с точки зрения временной сложности алгоритма.
Посмотрим, какие нелинейные решающие границы удалось построить алгоритму.
|
predictions = df[[‘flavanoids’, ‘proline’]].copy() predictions[‘y_pred’] = y_pred fig, (ax1, ax2) = plt.subplots(1, 2, figsize = (14, 6), gridspec_kw = {‘wspace’: 0.2, ‘hspace’: 0.08}) sns.scatterplot(data = df, x = ‘flavanoids’, y = ‘proline’, hue = ‘target’, palette = ‘bright’, s = 50, ax = ax1) ax1.set_title(‘Фактические классы’, fontsize = 14) sns.scatterplot(data = predictions, x = ‘flavanoids’, y = ‘proline’, hue = ‘y_pred’, palette = ‘bright’, s = 50, ax = ax2) ax2.set_title(‘Полиномиальная регрессия’, fontsize = 14) plt.show() |
Softmax Regression
Еще один подход при создании мультиклассовой логистической регрессии заключается в том, чтобы не разбивать многоклассовые данные на несколько датасетов и использовать бинарный классификатор, а сразу применять функции, которые подходят для работы с множеством классов.
Такую регрессию часто называют Softmax Regression из-за того, что в ней используется уже знакомая нам по занятию об основах нейросетей функция softmax. Вначале подготовим данные.
Подготовка признаков
Возьмем признаки flavanoids и proline и добавим столбец из единиц.
|
def add_ones(x): # важно! метод .insert() изменяет исходный датафрейм return x.insert(0,‘x0’, np.ones(x.shape[0])) |
|
X = df[[‘flavanoids’, ‘proline’]] add_ones(X) X.head(3) |
Кодирование целевой переменной
Напишем собственную функцию для one-hot encoding.
|
def ohe(y): # количество примеров и количество классов examples, features = y.shape[0], len(np.unique(y)) # нулевая матрица: количество наблюдений x количество признаков zeros_matrix = np.zeros((examples, features)) # построчно проходимся по нулевой матрице и с помощью индекса заполняем соответствующее значение единицей for i, (row, digit) in enumerate(zip(zeros_matrix, y)): zeros_matrix[i][digit] = 1 return zeros_matrix |
|
y = df[‘target’] y_enc = ohe(df[‘target’]) y_enc[:3] |
|
array([[1., 0., 0.], [1., 0., 0.], [1., 0., 0.]]) |
Такой же результат можно получить с помощью класса LabelBinarizer.
|
lb = LabelBinarizer() lb.fit(y) lb.classes_ |
|
y_lb = lb.transform(y) y_lb[:5] |
|
array([[1, 0, 0], [1, 0, 0], [1, 0, 0], [1, 0, 0], [1, 0, 0]]) |
Инициализация весов
Создадим нулевую матрицу весов. Она будет иметь размерность: количество признаков (строки) х количество классов (столбцы). Приведем схематичный пример для четырех наблюдений, трех признаков (включая сдвиг $theta_0$) и трех классов.
Инициализируем веса.
|
thetas = np.zeros((3, 3)) thetas |
|
array([[0., 0., 0.], [0., 0., 0.], [0., 0., 0.]]) |
Функция softmax
Подробнее изучим функцию softmax. Приведем формулу.
$$ text{softmax}(z)_{i} = frac{e^{z_i}}{sum_{k=1}^N e^{z_k}} $$
Рассмотрим ее реализацию на Питоне.
Напомню, что $ z = (-Xtheta) $. Соответственно в нашем случае мы будем умножать матрицу 178 x 3 на 3 x 3.
В результате получим матрицу 178 x 3, где каждая строка — это прогнозные значения принадлежности одного наблюдения к каждому из трех классов.
|
z = np.dot(—X, thetas) z.shape |
Так как мы умножаем на ноль, при первой итерации эти значения будут равны нулю.
|
array([[0., 0., 0.], [0., 0., 0.], [0., 0., 0.], [0., 0., 0.], [0., 0., 0.]]) |
Для того чтобы обеспечить вычислительную устойчивость softmax мы можем вычесть из z максимальное значение в каждой из 178 строк (пока что, опять же на первой итерации, оно равно нулю).
$$ text{softmax}(z)_{i} = frac{e^{z_i-max(z)}}{sum_{k=1}^N e^{z_k-max(z)}} $$
|
# axis = -1 — это последняя ось # keepdims = True сохраняет размерность (в данном случае двумерный массив) np.max(z, axis = —1, keepdims = True)[:5] |
|
array([[0.], [0.], [0.], [0.], [0.]]) |
|
z = z — np.max(z, axis = —1, keepdims = True) z[:5] |
|
array([[0., 0., 0.], [0., 0., 0.], [0., 0., 0.], [0., 0., 0.], [0., 0., 0.]]) |
Смысл такого преобразования⧉ в том, что оно делает значения z нулевыми или отрицательными.
|
arr = np.array([—2, 3, 0, —7, 6]) arr — max(arr) |
|
array([ -8, -3, -6, -13, 0]) |
Далее, число возводимое в увеличивающуюся отрицательную степень стремится к нулю, а не к бесконечности и, таким образом, не вызывает переполнения памяти. Найдем числитель и знаменатель из формулы softmax.
|
numerator = np.exp(z) numerator[:5] |
|
array([[1., 1., 1.], [1., 1., 1.], [1., 1., 1.], [1., 1., 1.], [1., 1., 1.]]) |
|
denominator = np.sum(numerator, axis = —1, keepdims = True) denominator[:5] |
|
array([[3.], [3.], [3.], [3.], [3.]]) |
Разделим числитель и знаменатель и, таким образом, вычислим вероятность принадлежности каждого из наблюдений (строки результата) к одному из трех классов (столбцы).
|
softmax = numerator / denominator softmax[:5] |
|
array([[0.33333333, 0.33333333, 0.33333333], [0.33333333, 0.33333333, 0.33333333], [0.33333333, 0.33333333, 0.33333333], [0.33333333, 0.33333333, 0.33333333], [0.33333333, 0.33333333, 0.33333333]]) |
На первой итерации при одинаковых $theta$ мы получаем, что логично, одинаковые вероятности принадлежности к каждому из классов. Напишем функцию.
|
def stable_softmax(x, thetas): z = np.dot(—x, thetas) z = z — np.max(z, axis = —1, keepdims = True) numerator = np.exp(z) denominator = np.sum(numerator, axis = —1, keepdims = True) softmax = numerator / denominator return softmax |
|
probs = stable_softmax(X, thetas) probs[:3] |
|
array([[0.33333333, 0.33333333, 0.33333333], [0.33333333, 0.33333333, 0.33333333], [0.33333333, 0.33333333, 0.33333333]]) |
Примечание. Обратите внимание, что сигмоида — это частный случай функции softmax для двух классов $[z_1, 0]$. Вероятность класса $z_1$ будет равна
$$ softmax(z_1) = frac{e^{z_1}}{e^{z_1}+e^0} = frac{e^{z_1}}{e^{z_1}+1} $$
Если разделить и числитель, и знаменатель на $e^{z_1}$, то получим
$$ sigmoid(z_1) = frac{e^{z_1}}{1 + e^{-z_1}} $$
Вычислять вероятность принадлежности ко второму классу нет необходимости, достаточно вычесть результат сигмоиды из единицы.
Теперь нужно понять, насколько сильно при таких весах ошибается наш алгоритм.
Функция потерь
Вспомним функцию бинарной кросс-энтропии. То есть функции ошибки для двух классов.
$$ L(y, theta) = -frac{1}{n} sum y cdot log(h_{theta}(x)) + (1-y) cdot log(1-h_{theta}(x)) $$
Напомню, что y выступает в роли своего рода переключателя, сохраняющего одну из частей выражения, и обнуляющего другую. Теперь посмотрите на функцию категориальной (многоклассовой) кросс-энтропии (categorical cross-entropy).
$$ L(y_{ohe}, softmax) = -sum y_{ohe} log(softmax) $$
Разберемся, что здесь происходит. $y_{ohe}$ содержит закодированную целевую переменную, например, для наблюдения класса 0 [1, 0, 0], softmax содержит вектор вероятностей принадлежности наблюдения к каждому из классов, например, [0,3 0,4 0,3] (мы видим, что алгоритм ошибается).
В данном случае закодированная целевая переменная также выступает в виде переключателя. Здесь при умножении «срабатывает» только первая вероятность $1 times 0,3 + 0 times 0,4 + 0 times 0,4 $. Если подставить в формулу, то получаем (np.sum() добавлена для сохранения единообразия с формулой выше, в данном случае у нас одно наблюдение и сумма не нужна).
|
y_ohe = np.array([1, 0, 0]) softmax = np.array([0.3, 0.4, 0.4]) —np.sum(y_ohe * np.log(softmax)) |
Если бы модель в своих вероятностях ошибалась меньше, то и общая ошибка была бы меньше.
|
y_ohe = np.array([1, 0, 0]) softmax = np.array([0.4, 0.3, 0.4]) —np.sum(y_ohe * np.log(softmax)) |
Функция $-log$ позволяет снижать ошибку при увеличении вероятности верного (сохраненного переключателем) класса.
|
x_arr = np.linspace(0.001,1, 100) sns.lineplot(x=x_arr,y=—np.log(x_arr)) plt.title(‘Plot of -log(x)’) plt.xlabel(‘x’) plt.ylabel(‘-log(x)’); |
Напишем функцию.
|
# добавим константу в логарифм для вычислительной устойчивости def cross_entropy(probs, y_enc, epsilon = 1e—9): n = probs.shape[0] ce = —np.sum(y_enc * np.log(probs + epsilon)) / n return ce |
Рассчитаем ошибку для нулевых весов.
|
ce = cross_entropy(probs, y_enc) ce |
Для снижения ошибки нужно найти градиент.
Градиент
Приведем формулу градиента без дифференцирования.
$$ nabla_{theta}J = frac{1}{n} times X^T cdot (y_{ohe}-softmax) $$
По сути, мы умножаем транспонированную матрицу признаков (3 x 178) на разницу между закодированной целевой переменной и вероятностями функции softmax (178 x 3).
|
def gradient_softmax(X, probs, y_enc): # если не добавить функцию np.array(), будет выводиться датафрейм return np.array(1 / probs.shape[0] * np.dot(X.T, (y_enc — probs))) |
|
gradient_softmax(X, probs, y_enc) |
|
array([[-0.00187266, 0.06554307, -0.06367041], [ 0.31627721, 0.02059572, -0.33687293], [ 0.38820566, -0.28801792, -0.10018774]]) |
Обучение модели, прогноз и оценка качества
Выполним обучение модели.
|
loss_history = [] # в цикле for i in range(30000): # рассчитаем прогнозное значение с текущими весами probs = stable_softmax(X, thetas) # посчитаем уровень ошибки при текущем прогнозе loss_history.append(cross_entropy(probs, y_enc, epsilon = 1e—9)) # рассчитаем градиент grad = gradient_softmax(X, probs, y_enc) # используем градиент для улучшения весов модели thetas = thetas — 0.002 * grad |
Посмотрим на получившиеся коэффициенты (напомню, что первая строка матрицы это сдвиг (intercept, $theta_0$)) и достигнутый уровень ошибки.
|
array([[ 0.11290134, -0.90399727, 0.79109593], [-1.7550965 , -0.7857371 , 2.5408336 ], [-1.93839311, 1.77140542, 0.16698769]]) |
|
loss_history[0], loss_history[—1] |
|
(1.0986122856681098, 0.2569641080523888) |
Сделаем прогноз и оценим качество.
|
y_pred = np.argmax(stable_softmax(X, thetas), axis = 1) |
|
accuracy_score(y, y_pred) |
|
pd.DataFrame(confusion_matrix(y, y_pred), columns = [‘Forecast 0’, ‘Forecast 1’, ‘Forecast 2’], index = [‘Actual 0’, ‘Actual 1’, ‘Actual 2’]) |
Написание класса
Объединим созданные выше компоненты в класс.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 |
class SoftmaxLogReg(): def __init__(self): self.loss_ = None self.thetas_ = None def fit(self, x, y, iter = 30000, learning_rate = 0.002): loss_history = [] self.add_ones(x) y_enc = self.ohe(y) thetas = np.zeros((x.shape[1], y_enc.shape[1])) for i in range(iter): probs = self.stable_softmax(x, thetas) loss_history.append(self.cross_entropy(probs, y_enc, epsilon = 1e—9)) grad = self.gradient_softmax(x, probs, y_enc) thetas = thetas — 0.002 * grad self.thetas_ = thetas self.loss_ = loss_history def predict(self, x, y): return np.argmax(self.stable_softmax(x, thetas), axis = 1) def stable_softmax(self, x, thetas): z = np.dot(—x, thetas) z = z — np.max(z, axis = —1, keepdims = True) numerator = np.exp(z) denominator = np.sum(numerator, axis = —1, keepdims = True) softmax = numerator / denominator return softmax def cross_entropy(self, probs, y_enc, epsilon = 1e—9): n = probs.shape[0] ce = —np.sum(y_enc * np.log(probs + epsilon)) / n return ce def gradient_softmax(self, x, probs, y_enc): return np.array(1 / probs.shape[0] * np.dot(x.T, (y_enc — probs))) def add_ones(self, x): return x.insert(0,‘x0’, np.ones(x.shape[0])) def ohe(self, y): examples, features = y.shape[0], len(np.unique(y)) zeros_matrix = np.zeros((examples, features)) for i, (row, digit) in enumerate(zip(zeros_matrix, y)): zeros_matrix[i][digit] = 1 return zeros_matrix |
Обучим модель, сделаем прогноз и оценим качество.
|
X = df[[‘flavanoids’, ‘proline’]] y = df[‘target’] model = SoftmaxLogReg() model.fit(X, y) model.thetas_, model.loss_[—1] |
|
(array([[ 0.11290134, -0.90399727, 0.79109593], [-1.7550965 , -0.7857371 , 2.5408336 ], [-1.93839311, 1.77140542, 0.16698769]]), 0.2569641080523888) |
|
y_pred = model.predict(X, y) accuracy_score(y, y_pred) |
Сравнение с sklearn
Для того чтобы использовать softmax логистическую регрессию в sklearn, соответствующему классу нужно передать параметр multi_class = ‘multinomial’.
|
X = df[[‘flavanoids’, ‘proline’]] y = df[‘target’] # создадим объект класса LogisticRegression и запишем его в переменную model model = LogisticRegression(multi_class = ‘multinomial’) # обучим нашу модель model.fit(X, y) # посмотрим на получившиеся веса модели model.intercept_, model.coef_ |
|
(array([ 0.09046097, 1.12593099, -1.21639196]), array([[ 1.86357908, 1.89698292], [ 0.86696131, -1.43973164], [-2.73054039, -0.45725129]])) |
|
y_pred = model.predict(X) accuracy_score(y, y_pred) |
Подведем итог
Сегодня мы разобрали множество разновидностей и подходов к использованию логистической регрессии. Давайте систематизируем изученный материал с помощью следующей схемы.
Рассмотрим обучение нейронных сетей.
Классификация — одна из наиболее популярных технологий интеллектуального анализа данных. С необходимостью построения классификаторов рано или поздно сталкивается любой аналитик. Но даже построив модель, необходимо прежде всего убедиться в ее работоспособности. Для этого разработано большое количество мер качества. Наиболее популярные из них рассматриваются в данной статье.
Для классификационных моделей, как и для моделей регрессии, актуальна задача оценки их качества для определения работоспособности моделей и их сравнения. Однако решение этой задачи для моделей классификации вообще, и бинарной классификации в частности, сложнее, чем для регрессии. Связано это с тем, что целевая переменная (метка класса) является категориальным (дискретным) значением, и, следовательно, ошибка классификации не может быть выражена числовым значением.
Поэтому в основе оценки качества классификационных моделей лежит статистика результатов классификации обучающих примеров. С ее помощью вычисляются метрики качества — показатели, которые зависят от результатов классификации и не зависят от внутреннего состояния модели.
Среди наиболее популярных методов оценки качества классификаторов можно выделить следующие:
- Матрица ошибок (Сonfusion matrix).
- Меткость (Accuracy).
- Точность (Precision).
- Полнота (Recall).
- Специфичность (Specificity).
- F1-мера (F1-score).
- Метрика P4 .
- Площадь под ROC-кривой (Area under ROC-curve, AUC-ROC).
- Площадь под кривой полнота-точность (Area under precision-recall curve, AUC-PR).
- Коэффициент корреляции Мэтьюса (Matthews correlation coefficient, MCC).
- Функция потерь логистической регрессии (Logistic loss function, Log Loss).
Матрица ошибок
Прежде чем переходить к описанию собственно метрик качества бинарных классификаторов, рассмотрим методику описания этих метрик в терминах ошибок классификации. Пусть заданы два класса y=left { 0,1 right } и алгоритм, предсказывающий принадлежность каждого объекта одному из классов. Эта задача анализа известна как бинарная классификация.
Приведем пример. Пусть в страховой компании используется аналитическая платформа для поддержки принятия решений о целесообразности страхования того или иного объекта. Если риск наступления страхового события выше определенного порога, то такие объекты страховать нецелесообразно. Именно выявление таких объектов и является целью анализа. Тогда для объектов, страхование которых целесообразно, система должна установить класс 0, а объектам, в страховании которых отказано, — класс 1.
Любой реальный классификатор совершает ошибки. В нашем случае таких ошибок может быть две:
- класс 0 распознается классификатором как класс 1, что можно интерпретировать как «ложную тревогу»;
- класс 1 распознается как класс 0, что можно трактовать как «пропуск цели».
Очевидно, что приведенные ошибки неравноценны по связанным с ними издержкам классификации. В случае «ложной тревоги» компания потеряет только потенциальную страховую премию, т.е. будет иметь место всего лишь упущенная выгода. В случае «пропуска цели» возможна потеря значительной суммы из-за наступления страхового случая. Поэтому важнее не допустить «пропуск цели», чем «ложную тревогу».
Иными словами, важнее правильно определить объект, нежелательный для страхования из-за высокого риска, чем ошибиться в распознавании желательного. Будем называть соответствующий исход классификации положительным (объект не подлежит страхованию y=1), а противоположный — отрицательным (объект подлежит страхованию y=0). Тогда возможны следующие исходы классификации:
- Объект, нежелательный для страхования, классифицирован как нежелательный, т.е. «положительный» класс распознан как положительный. Такой исход классификации (а также пример, для которого он получен) называют истинноположительным.
- Объект, желательный для страхования, распознан как желательный, т.е. «отрицательный» класс распознан как отрицательный. Такой исход классификации называют истинноотрицательными.
- Объект, желаемый для страхования, классифицирован как не желаемый, т.е. имела место ошибка, в результате которой отрицательный класс был распознан как положительный. Данный исход классификации называют ложноположительным, а ошибка классификации называется ошибкой I рода.
- Нежелательный объект распознан как желательный, т.е. имела место ошибка, в результате которой положительный класс был распознан как отрицательный. Такой исход классификации называется ложноотрицательным, а ошибка классификации — ошибкой II рода.
Таким образом, ошибка I рода, или ложноположительный исход классификации, имеет место, когда пример, с которым связано отрицательное событие распознан моделью как положительный. Ошибкой II рода, или ложноотрицательным исходом классификации, называют случай, когда пример, с которым связано положительное событие, распознан как отрицательный. Поясним это с помощью матрицы ошибок классификации, называемой также таблицей сопряженности:
| y=0 | y=1 | |
|---|---|---|
| widehat{y}=0 | Истинноположительный (True Positive — TP) | Ложноположительный (False Positive — FP) |
| widehat{y}=1 | Ложноотрицательный (False Negative — FN) | Истинноотрицательный (True Negative — TN) |
Здесь widehat{y} — отклик модели, а y — фактическое значение. Таким образом, ошибки классификации бывают двух видов: False Negative (FN) и False Positive (FP). В данном случае P означает, что классификатор определяет класс объекта как положительный, а N как — отрицательный. T значит, что класс предсказан правильно, соответственно, F — неправильно. Каждая строка в матрице ошибок представляет предсказанный класс, а каждый столбец — фактически наблюдаемый класс.
Идеальный классификатор, если бы он существовал, выдавал бы только истинноположительные и истинноотрицательные классификации, и его матрица ошибок содержала бы значения, отличные от нуля, только на главной диагонали.
Меткость
Представляет собой долю правильных классификаций модели:
ACC=frac{TP+TN}{TP+TN+FP+FN}.
Несложно увидеть, что сумма в знаменателе формулы представляет собой общее число классифицируемых примеров. Графически это можно интерпретировать следующим образом:
Рисунок 1. Меткость
В английском языке этот термин обозначается как «accuracy», поэтому в интернете он часто упоминается как «аккуратность», хотя это слово и не передает смыслового значения данной величины.
Несмотря на то, что эта мера хорошо интерпретируется, на практике она используется достаточно редко, поскольку плохо работает в случае дисбаланса классов в обучающей выборке.
Поясним это на примере кредитного скоринга. Пусть требуется классифицировать заемщиков на добросовестных (не допустивших просрочку) и недобросовестных (допустивших просрочку). Целью является выявление недобросовестных заемщиков, поскольку связанные с ними издержки выше. Следовательно, классификация заемщика как недобросовестного является положительным событием, а как добросовестного — отрицательным.
Выборка содержит 1000 добросовестных заемщиков, 900 из которых классификатор предсказал правильно (TN=900, FP=100), и 100 недобросовестных, 50 из которых классификатор также определил верно (TP=50, FN=50).
Несложно вычислить, что:
ACC=frac{50+900}{50+900+100+50}=0.866.
Однако, если построить «наивную» модель, которая просто будет классифицировать всех клиентов, как добросовестных (на основании того, что таковых большинство), то меткость такой модели окажется:
ACC=frac{0+1000}{0+1000+0+100}=0.909.
Таким образом, оказалось, что меткость «бесполезной» модели, не имеющей предсказательной силы, выше, чем «рабочей» модели. Это противоречит здравому смыслу. Поэтому на практике стараются использовать альтернативные меры качества.
Точность
Точность равна доле истинноположительных классификаций к общему числу положительных классификаций. Данная величина часто упоминается как positive predictive value (PPV) или положительное прогностическое значение:
Pr=PPV=frac{TP}{TP+FP}.
Поясним данное выражение с помощью рисунка:
Рисунок 2. Точность
Несложно увидеть, что попытка отнести все объекты к одному классу неизбежно приведет к росту FP и уменьшению значения точности.
Полнота
Полнота, известная еще как чувствительность или доля истинноположительных примеров (TPR — true positive rate), определяется как число истинноположительных классификаций относительно общего числа положительных наблюдений:
Re=TPR=frac{TP}{TP+FN}.
Таким образом, полноту можно рассматривать как способность классификатора обнаруживать определенный класс. Графически полноту можно проиллюстрировать с помощью рисунка:
Рисунок 3. Полнота
Точность и полноту для каждого класса легко определять с помощью матрицы ошибок. Точность равна отношению соответствующего диагонального элемента матрицы и суммы элементов всей строки класса, а полнота — отношению диагонального элемента матрицы и суммы элементов всего столбца класса.
PPV_{c}=frac{A_{cc}}{sumlimits_{i=1}^{n}A_{ci}},
TPR_{c}=frac{A_{cc}}{sumlimits_{i=1}^{n}A_{ic}},
где c — класс, n — число элементов столбца (равно числу классов), i — номер элемента в столбце, A — элемент матрицы ошибок.
Специфичность
Специфичность классификатора — это доля истинноотрицательных (True Negative Rate — TNR) классификаций в общем числе отрицательных классификаций:
Sp=TNR=frac{TN}{TN+FP}.
TNR показывает, насколько хорошо модель классифицирует отрицательные примеры. Поясним это с помощью рисунка.
Рисунок 4. Специфичность
Очевидно, что если все отрицательные примеры классифицированы правильно (т.е. число ложноположительных случаев равно 0), то TPR=1.
F1-мера
Точность и полнота, в отличие от меткости, не зависят от соотношения классов и, следовательно, могут применяться в условиях несбалансированных выборок. На практике часто встречается задача поиска оптимального баланса между точностью и полнотой. Действительно, улучшая настройку модели на один класс, например, путем изменения дискриминационного порога, мы тем самым ухудшаем настройку на другой.
Чем выше точность и полнота, тем лучше модель. Но на практике их максимальные значения одновременно недостижимы, поэтому приходится искать баланс между ними. Для этого используется метрика, объединяющая в себе информацию о точности и полноте. Она называется F1-мера и вычисляется следующим образом:
F1=frac{2cdot PPVcdot TPR}{PPV+TPR}=frac{2cdot TP}{2cdot TP+FP+FN}.
В данном выражении точность PPV и полнота TPR имеют одинаковый вес, поэтому при их уменьшении F1-мера сокращается пропорционально.
Однако на практике чаще используется сбалансированная F1-мера, в которой точности и полноте присваиваются разные веса с целью найти оптимальный баланс между данными метриками. Для этого в формулу для F1-меры вводится дополнительный балансировочный параметр, обозначаемый β. Сбалансированная F1-мера вычисляется следующим образом:
F1=frac{(1-beta ^{2})cdot PPVcdot TPR}{beta ^{2}cdot PPV+TPR}.
Если параметр принимает значения из диапазона 0< beta < 1, то приоритет имеет точность, а если beta> 1, то полнота.
Еще одним источником критики F1-меры является отсутствие симметрии. Это означает, что она может изменить свое значение при инверсии положительного и отрицательного классов.
Метрика P4
Метрика P_{4} была разработана как расширение F1-меры, обладающее симметрией относительно инверсии классов. Вычисляется по формуле:
P_{4}=frac{4cdot TPcdot TN}{4cdot TPcdot TN+(TP+TN)cdot (FP+FN)}.
Метрика P_{4} изменяется в диапазоне от 0 до 1. Чем ближе значение метрики к 1, тем лучше работает модель. Очевидно, что значение меры стремится к 0, если хотя бы один из множителей в числителе становится равным нулю, т.е. когда модель теряет способность правильно распознавать положительные или отрицательные примеры.
AUC-ROC
ROC-кривая, или кривая рабочих характеристик приемника (Receiver Operating Characteristics curve), позволяет не только оценить качество работы классификатора, но и исследовать его поведение при различных значениях дискриминационного порога. Технология оценки качества моделей бинарной классификации с помощью ROC-кривых известна как ROC-анализ.
Рассмотрим совместно TPR и TNR классификатора. TPR показывает, насколько хорошо модель классифицирует положительные примеры. Очевидно, что если все положительные примеры классифицированы правильно (т.е. число ложноотрицательных случаев равно 0), то TPR=1. TNR показывает, насколько хорошо модель классифицирует отрицательные примеры. Очевидно, что если все отрицательные примеры классифицированы правильно (т.е. число ложноположительных случаев равно 0), то TPR=1.
Таким образом, по отдельности TPR и TNR характеризуют способность модели распознавать только один из классов. Но их совместное использование помогает создать метрику, которая позволяет выбирать значение дискриминационного порога, который оптимально балансирует модель между способностью распознавать положительные и отрицательные примеры. Именно эта задача и решается с помощью ROC-кривой.
Действительно, если изменять дискриминационный порог от 0 до 1 и наносить по оси абсцисс точки 1−TNR, а по оси ординат TPR, то полученный график и будет ROC-кривой. Величину 1−TNR называют долей ложноположительных классификаций (false positive rate) или показателем ложной тревоги. Она вычисляется следующим образом:
1-TNR=FPR=frac{FP}{FP+TN}.
При пороге, равном 1, все примеры будут классифицированы как отрицательные (FPR=1, TPR=1), а при пороге, равном 0, — как положительные (FPR=0, TPR=0). Поэтому ROC-кривая всегда идет от точки (0,0) до точки (1,1).
Рисунок 5. ROC-кривая
Несложно увидеть, что для идеальной модели ROC-кривая превращается в ломаную, проходящую через точки (0,0), (0,1) и (1,1). При этом площадь под ROC-кривой (AUC — Area Under Curve) окажется равной 1. Площадь под кривой выделена на рисунке светло-серым цветом.
Точка (0,1) соответствует идеальному состоянию модели, в котором и TPR, и TNR одновременно равны 1. Т.е. модель одинаково хорошо «научилась» работать как с положительными, так и с отрицательными примерами при существующем в обучающей выборке балансе классов.
Идеальная модель является скорее гипотетической и на практике, как правило, недостижима. Поэтому обычно приходится иметь дело с ROC-кривыми, которые не проходят через точку (0,1), а приближаются к ней на определенное расстояние. Соответственно и AUC−ROC оказывается меньше 1.
Таким образом показатель AUC−ROC является удобной мерой качества классификатора относительно идеального. Принята следующая шкала оценки качества.
| AUC | Оценка |
|---|---|
| 0.9 — 1 | Отличное |
| 0.8 — 0.9 | Очень хорошее |
| 0.7 — 0.8 | Хорошее |
| 0.6 — 0.7 | Удовлетворительное |
| 0.5 — 0.7 | Плохое |
Если AUC-ROC=0.5, то ROC-кривая превращается в линию, проходящую через точки (0,0) и (1,1), которая соответствует бесполезному классификатору, работающему как случайный предсказатель. Если AUC-ROC< 0.5, то получается модель, которая работает хуже случайного предсказателя и от ее использования следует отказаться.
AUC-PR
PR-кривые определяются аналогично ROC-кривым, но только по оси абсцисс у них откладываются значения полноты, а по оси ординат — точности.
Точность и полнота — две наиболее важные метрики, на которые следует обращать внимание при оценке качества модели бинарной классификации в условиях несбалансированности классов. Они помогают увидеть, какая часть фактически положительных наблюдений была классифицирована правильно, и какие среди классифицированных как положительные, были истинноположительными.
Если точность равна 1, то ложноположительные классификации отсутствуют. Но это ничего не говорит о том, были ли распознаны все положительные примеры. Если полнота равна 1, то все положительные объекты были распознаны правильно, а ложноотрицательные классификации отсутствуют. При этом ничего не говорится о том, сколько было допущено ложноположительных классификаций.
Таким образом, точность и полнота не особенно полезны для оценки качества классификатора, если их использовать по отдельности. В задаче классификации оценка точности, равная 1 для класса C, означает, что каждый элемент, помеченный как принадлежащий классу C, действительно принадлежит к классу C, но ничего не говорит о количестве элементов из класса
C, которые не были правильно классифицированы. Тогда как полнота, равная 1, означает, что каждый элемент из класса C был помечен как принадлежащий к классу C, но ничего не говорит о том, сколько элементов из других классов были также неправильно классифицированы как принадлежащие к классу C.
Обычно показатели точности и полноты не используются по отдельности. Вместо этого либо значения одной меры сравниваются с фиксированным уровнем другой (например, точность на уровне полноты 0.75), либо обе меры объединяются в один показатель. Примерами такой комбинации и является F1-мера — взвешенное гармоническое среднее точности и полноты.
Еще одним способом комбинирования точности и полноты в задаче оценки качества классификации являются так называемые кривые полнота-точность, которые строятся в системе координат, где по оси абсцисс откладывается полнота, а по оси ординат — точность. Кривая точность-полнота показывает, как выбор порога влияет на точность классификатора, а также помогает выбрать лучшее значение дискриминационного порога для определенного баланса классов.
Рисунок 6. Кривая точность-полнота
Каждая точка PR-кривой представляет определенное значение дискриминационного порога, а ее расположение соответствует результирующей точности и полноте, когда этот порог выбран. Точка 1 на рисунке соответствует значению дискриминационного порога, равному 1, а точка 3 — значению порога 0. Точка 2 соответствует идеальному классификатору и совпадает с координатами (1,1), а точка 4 — оптимальному значению порога (точка кривой, наиболее близкая к идеальной точке (1,1)).
Преимущества PR-кривой по сравнению с ROC:
- ROC-кривая, как правило, дает чрезмерно оптимистичную картину в условиях несбалансированности классов.
- При изменении распределения классов ROC-кривая не меняется, а PR-кривая отражает изменение.
Аналогично ROC-кривой, площадь под PR-кривой (для отличия от ROC ее часто называют PR−AUC) отражает качество классификатора и позволяет сравнивать кривые, соответствующие различным балансам классов и значениям порога. Чем выше площадь, тем лучше работает модель.
Пунктирная линия внизу графика соответствует бесполезному классификатору (no-skill model — модель без навыков, или базовая модель), уровень которой изменяется при изменении баланса классов. Такая модель будет присваивать рейтинг 0.5 для любого примера.
На рисунке ниже представлена линия, соответствующая балансу классов, когда положительные примеры составляют 10% от обучающей выборки.
Рисунок 7. Кривая точность-полнота при фиксированном балансе классов
На рисунке точка 1 соответствует порогу 0.5, точка 2 соответствует порогу [0, 0.5). Для порогов (0.5, 1] точность не определена из-за деления на ноль. Можно увидеть, что точность здесь является константой, то есть PPV=0.1 (соответствует доле положительного класса), PR−AUC=0.1.
Таким образом, полнота базовой модели лежит в диапазоне (0.5, 1] независимо от дисбаланса классов, а точность равна доле положительного класса в обучающей выборке.
На следующем рисунке представлена PR-кривая для идеальной модели. На ней точка 1 соответствует порогу (0, 1], точка 2 соответствует порогу 0. Очевидно, что PR−AUC=1.
Рисунок 8. Кривая точность-полнота для идеальной модели
И, наконец, на рисунке ниже отображена PR-кривая (красная линия) для модели, которая работает хуже, чем базовая модель «без навыков» (синяя пунктирная линия). Она расположена ниже линии базовой модели.
Рисунок 9. Кривая точность-полнота для модели хуже бесполезной
Очевидный способ повысить качество «плохой» модели без каких-либо настроек — просто инвертировать классы (класс 0 изменить на класс 1). Это автоматически приведет к повышению точности по сравнению с базовой моделью.
Обычно «плохая» PR-кривая классификатора указывает на то, что в обучающих данных присутствуют проблемы: они содержат шум или классы в них плохо выражены (модель не может выявить закономерность, в соответствии с которой один класс отличается от другого). В этом случае PR−AUC не превышает доли положительных примеров обучающей выборке.
Возможен гибридный случай, когда «плохая» модель работает лучше, чем модель «без навыков», но для определенных пороговых значений.
Коэффициент корреляции Мэтьюса
Коэффициент используется в качестве показателя качества бинарных классификаторов. Он учитывает истинные и ложные классификации и обычно рассматривается как сбалансированная мера, которую можно использовать даже в условиях сильного дисбаланса классов.
MCC, по сути, коэффициент корреляции между фактическими и предсказанными моделью бинарными классификациями. Он изменяется в диапазоне от -1 до 1. MCC=1 указывает на идеальную классификацию, когда фактические и предсказанные классы совпадают для всех обучающих примеров (т.е. ложноположительные и ложноотрицательные классификации отсутствуют). Модель, для которой MCC=0, соответствует случайному предсказателю. MCC=−1 указывает на полное расхождение между фактом и предсказанием (т.е. вместо положительного класса модель всегда предсказывает отрицательный, и наоборот), следовательно, истинноположительные и истинноотрицательные классификации отсутствуют.
Формула для расчета MCC имеет вид:
MCC=frac{TPcdot TN-FPcdot FN}{sqrt{(TP+FP)(TP+FN)(TN+FP)(TN+FN)}}.
Несложно увидеть, что если в этой формуле обнулить все ложные классификации, то MCC=1, что соответствует ранее сделанным заключениям. Если число истинных и ложных классификаций равны, то числитель формулы становится равным 0 и MCC=0. И, наконец, если число истинных классификаций равно нулю, то числитель становится отрицательным, и делает таковым результат формулы.
Если какая-либо из четырех сумм в знаменателе равна нулю, знаменатель можно произвольно установить равным единице, это приводит к нулевому коэффициенту корреляции Мэтьюса.
Функция потерь логистической регрессии (Logistic loss function, Log Loss).
Функция потерь в задачах классификации показывает, какую «цену» придется заплатить за неточность предсказаний классификационной модели. Для логистической регрессии, решающей задачу бинарной классификации, она может быть вычислена следующим образом:
Log Loss=-frac{1}{l}sumlimits_{i=1}^{l}(y_{i}cdot log(widehat{y_{i}})+(1-y_{i})cdot log(1-widehat{y_{i}})),
где l — размер выборки, y_{i}=left { 0,1 right } — бинарная метка класса, заданная в примере, widehat{y_{i}} — предсказание модели.
Несложно увидеть, что функция потерь получается путем суммирования логарифма потерь на каждом примере. Потери на каждом примере определяются следующим образом: если предсказанный класс совпадает с фактическим, то потери равны 0, в противном случае потери равны 1. Очевидно, чем больше будет неправильных классификаций, тем больше будет значение LogLoss и тем хуже будет модель. Таким образом, чтобы получить лучшую модель, нужно минимизировать функцию потерь.
Преимуществом метрики LogLoss является устойчивость к выбросам и аномальным значениям в данных и простота вычисления. Недостатком — сложность интерпретации из-за нелинейного характера.
Сравнение метрик
Подведем итоги, кратко резюмируя преимущества и недостатки рассмотренных мер качества классификационных моделей.
| Мера | Преимущества | Недостатки |
|---|---|---|
| Меткость | Хорошо интерпретируется. | Чувствительна к дисбалансу классов. Неадекватно отражает точность классификации. |
| Точность | Не чувствительна к дисбалансу классов. | Отражает качество классификации только для положительного класса. |
| Полнота | Не чувствительна к дисбалансу классов. | Не учитывает отрицательные классификации. |
| Специфичность | Просто вычисляется и интерпретируется. | Характеризует способность модели распознавать только один класс. |
| F1-мера | Позволяет найти баланс между точностью и полнотой. | Чувствительность к дисбалансу, отсутствие симметрии. |
| P4 | Симметрична относительно инверсии классов. | Чувствительность к дисбалансу классов. |
| AUC-ROC | Наглядна, хорошо интерпретируется. | В условиях дисбаланса классов завышает качество модели. Не отражает изменения баланса классов. |
| AUC-PR | Наглядна, хорошо интерпретируется. | Не учитывает отрицательные классификации. |
| Коэффициент Мэтьюса | Более информативен, поскольку использует все типы результатов классификации. | Не может применяться, если один из множителей в знаменателе обращается в 0. |
| LogLoss | Устойчивость к выбросам в данных, простота вычисления. | Сложность интерпретации из-за нелинейного характера. |
В статье рассмотрены наиболее общие меры оценки качества моделей бинарной классификации, отмечены их преимущества и недостатки. Однако в литературе авторы предлагают и другие подходы, которые показали хорошие результаты при решении конкретных задач и не претендующие на универсальность.
Другие материалы по теме:
Метрики качества линейных регрессионных моделей
Отбор переменных в моделях линейной регрессии
Репрезентативность выборочных данных
«Logit model» redirects here. Not to be confused with Logit function.
Example graph of a logistic regression curve fitted to data. The curve shows the probability of passing an exam (binary dependent variable) versus hours studying (scalar independent variable). See § Example for worked details.
In statistics, the logistic model (or logit model) is a statistical model that models the probability of an event taking place by having the log-odds for the event be a linear combination of one or more independent variables. In regression analysis, logistic regression[1] (or logit regression) is estimating the parameters of a logistic model (the coefficients in the linear combination). Formally, in binary logistic regression there is a single binary dependent variable, coded by an indicator variable, where the two values are labeled «0» and «1», while the independent variables can each be a binary variable (two classes, coded by an indicator variable) or a continuous variable (any real value). The corresponding probability of the value labeled «1» can vary between 0 (certainly the value «0») and 1 (certainly the value «1»), hence the labeling;[2] the function that converts log-odds to probability is the logistic function, hence the name. The unit of measurement for the log-odds scale is called a logit, from logistic unit, hence the alternative names. See § Background and § Definition for formal mathematics, and § Example for a worked example.
Binary variables are widely used in statistics to model the probability of a certain class or event taking place, such as the probability of a team winning, of a patient being healthy, etc. (see § Applications), and the logistic model has been the most commonly used model for binary regression since about 1970.[3] Binary variables can be generalized to categorical variables when there are more than two possible values (e.g. whether an image is of a cat, dog, lion, etc.), and the binary logistic regression generalized to multinomial logistic regression. If the multiple categories are ordered, one can use the ordinal logistic regression (for example the proportional odds ordinal logistic model[4]). See § Extensions for further extensions. The logistic regression model itself simply models probability of output in terms of input and does not perform statistical classification (it is not a classifier), though it can be used to make a classifier, for instance by choosing a cutoff value and classifying inputs with probability greater than the cutoff as one class, below the cutoff as the other; this is a common way to make a binary classifier.
Analogous linear models for binary variables with a different sigmoid function instead of the logistic function (to convert the linear combination to a probability) can also be used, most notably the probit model; see § Alternatives. The defining characteristic of the logistic model is that increasing one of the independent variables multiplicatively scales the odds of the given outcome at a constant rate, with each independent variable having its own parameter; for a binary dependent variable this generalizes the odds ratio. More abstractly, the logistic function is the natural parameter for the Bernoulli distribution, and in this sense is the «simplest» way to convert a real number to a probability. In particular, it maximizes entropy (minimizes added information), and in this sense makes the fewest assumptions of the data being modeled; see § Maximum entropy.
The parameters of a logistic regression are most commonly estimated by maximum-likelihood estimation (MLE). This does not have a closed-form expression, unlike linear least squares; see § Model fitting. Logistic regression by MLE plays a similarly basic role for binary or categorical responses as linear regression by ordinary least squares (OLS) plays for scalar responses: it is a simple, well-analyzed baseline model; see § Comparison with linear regression for discussion. The logistic regression as a general statistical model was originally developed and popularized primarily by Joseph Berkson,[5] beginning in Berkson (1944), where he coined «logit»; see § History.
Applications[edit]
Logistic regression is used in various fields, including machine learning, most medical fields, and social sciences. For example, the Trauma and Injury Severity Score (TRISS), which is widely used to predict mortality in injured patients, was originally developed by Boyd et al. using logistic regression.[6] Many other medical scales used to assess severity of a patient have been developed using logistic regression.[7][8][9][10] Logistic regression may be used to predict the risk of developing a given disease (e.g. diabetes; coronary heart disease), based on observed characteristics of the patient (age, sex, body mass index, results of various blood tests, etc.).[11][12] Another example might be to predict whether a Nepalese voter will vote Nepali Congress or Communist Party of Nepal or Any Other Party, based on age, income, sex, race, state of residence, votes in previous elections, etc.[13] The technique can also be used in engineering, especially for predicting the probability of failure of a given process, system or product.[14][15] It is also used in marketing applications such as prediction of a customer’s propensity to purchase a product or halt a subscription, etc.[16] In economics, it can be used to predict the likelihood of a person ending up in the labor force, and a business application would be to predict the likelihood of a homeowner defaulting on a mortgage. Conditional random fields, an extension of logistic regression to sequential data, are used in natural language processing.
Example[edit]
Problem[edit]
As a simple example, we can use a logistic regression with one explanatory variable and two categories to answer the following question:
A group of 20 students spends between 0 and 6 hours studying for an exam. How does the number of hours spent studying affect the probability of the student passing the exam?
The reason for using logistic regression for this problem is that the values of the dependent variable, pass and fail, while represented by «1» and «0», are not cardinal numbers. If the problem was changed so that pass/fail was replaced with the grade 0–100 (cardinal numbers), then simple regression analysis could be used.
The table shows the number of hours each student spent studying, and whether they passed (1) or failed (0).
| Hours (xk) | 0.50 | 0.75 | 1.00 | 1.25 | 1.50 | 1.75 | 1.75 | 2.00 | 2.25 | 2.50 | 2.75 | 3.00 | 3.25 | 3.50 | 4.00 | 4.25 | 4.50 | 4.75 | 5.00 | 5.50 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Pass (yk) | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
We wish to fit a logistic function to the data consisting of the hours studied (xk) and the outcome of the test (yk =1 for pass, 0 for fail). The data points are indexed by the subscript k which runs from 

Model[edit]
Graph of a logistic regression curve fitted to the (xm,ym) data. The curve shows the probability of passing an exam versus hours studying.
The logistic function is of the form:
where μ is a location parameter (the midpoint of the curve, where 
where 




Fit[edit]
The usual measure of goodness of fit for a logistic regression uses logistic loss (or log loss), the negative log-likelihood. For a given xk and yk, write 





The log loss for the k-th point is:
The log loss can be interpreted as the «surprisal» of the actual outcome 











These can be combined into a single expression:
This expression is more formally known as the cross entropy of the predicted distribution 

The sum of these, the total loss, is the overall negative log-likelihood 



Alternatively, instead of minimizing the loss, one can maximize its inverse, the (positive) log-likelihood:
or equivalently maximize the likelihood function itself, which is the probability that the given data set is produced by a particular logistic function:
This method is known as maximum likelihood estimation.
Parameter estimation[edit]
Since ℓ is nonlinear in 



and the maximization procedure can be accomplished by solving the above two equations for 

The values of 

which yields a value for μ and s of:
Predictions[edit]
The 

For example, for a student who studies 2 hours, entering the value 
Similarly, for a student who studies 4 hours, the estimated probability of passing the exam is 0.87:
This table shows the estimated probability of passing the exam for several values of hours studying.
| Hours of study (x) |
Passing exam | ||
|---|---|---|---|
| Log-odds (t) | Odds (et) | Probability (p) | |
| 1 | −2.57 | 0.076 ≈ 1:13.1 | 0.07 |
| 2 | −1.07 | 0.34 ≈ 1:2.91 | 0.26 |
 |
0 | 1 |  = 0.50 = 0.50
|
| 3 | 0.44 | 1.55 | 0.61 |
| 4 | 1.94 | 6.96 | 0.87 |
| 5 | 3.45 | 31.4 | 0.97 |
Model evaluation[edit]
The logistic regression analysis gives the following output.
| Coefficient | Std. Error | z-value | p-value (Wald) | |
|---|---|---|---|---|
| Intercept (β0) | −4.1 | 1.8 | −2.3 | 0.021 |
| Hours (β1) | 1.5 | 0.6 | 2.4 | 0.017 |
By the Wald test, the output indicates that hours studying is significantly associated with the probability of passing the exam (

Generalizations[edit]
This simple model is an example of binary logistic regression, and has one explanatory variable and a binary categorical variable which can assume one of two categorical values. Multinomial logistic regression is the generalization of binary logistic regression to include any number of explanatory variables and any number of categories.
Background[edit]
Figure 1. The standard logistic function 


Definition of the logistic function[edit]
An explanation of logistic regression can begin with an explanation of the standard logistic function. The logistic function is a sigmoid function, which takes any real input 

A graph of the logistic function on the t-interval (−6,6) is shown in Figure 1.
Let us assume that 



And the general logistic function 
In the logistic model, 






Definition of the inverse of the logistic function[edit]
We can now define the logit (log odds) function as the inverse 
and equivalently, after exponentiating both sides we have the odds:
Interpretation of these terms[edit]
In the above equations, the terms are as follows:
Definition of the odds[edit]
The odds of the dependent variable equaling a case (given some linear combination 
So we define odds of the dependent variable equaling a case (given some linear combination 
The odds ratio[edit]
For a continuous independent variable the odds ratio can be defined as:
-
The image represents an outline of what an odds ratio looks like in writing, through a template in addition to the test score example in the «Example» section of the contents. In simple terms, if we hypothetically get an odds ratio of 2 to 1, we can say… «For every one-unit increase in hours studied, the odds of passing (group 1) or failing (group 0) are (expectedly) 2 to 1 (Denis, 2019).
This exponential relationship provides an interpretation for 

For a binary independent variable the odds ratio is defined as 
Multiple explanatory variables[edit]
If there are multiple explanatory variables, the above expression 



Again, the more traditional equations are:
and
where usually 
Definition[edit]
The basic setup of logistic regression is as follows. We are given a dataset containing N points. Each point i consists of a set of m input variables x1,i … xm,i (also called independent variables, explanatory variables, predictor variables, features, or attributes), and a binary outcome variable Yi (also known as a dependent variable, response variable, output variable, or class), i.e. it can assume only the two possible values 0 (often meaning «no» or «failure») or 1 (often meaning «yes» or «success»). The goal of logistic regression is to use the dataset to create a predictive model of the outcome variable.
As in linear regression, the outcome variables Yi are assumed to depend on the explanatory variables x1,i … xm,i.
- Explanatory variables
The explanatory variables may be of any type: real-valued, binary, categorical, etc. The main distinction is between continuous variables and discrete variables.
(Discrete variables referring to more than two possible choices are typically coded using dummy variables (or indicator variables), that is, separate explanatory variables taking the value 0 or 1 are created for each possible value of the discrete variable, with a 1 meaning «variable does have the given value» and a 0 meaning «variable does not have that value».)
- Outcome variables
Formally, the outcomes Yi are described as being Bernoulli-distributed data, where each outcome is determined by an unobserved probability pi that is specific to the outcome at hand, but related to the explanatory variables. This can be expressed in any of the following equivalent forms:
The meanings of these four lines are:
- The first line expresses the probability distribution of each Yi : conditioned on the explanatory variables, it follows a Bernoulli distribution with parameters pi, the probability of the outcome of 1 for trial i. As noted above, each separate trial has its own probability of success, just as each trial has its own explanatory variables. The probability of success pi is not observed, only the outcome of an individual Bernoulli trial using that probability.
- The second line expresses the fact that the expected value of each Yi is equal to the probability of success pi, which is a general property of the Bernoulli distribution. In other words, if we run a large number of Bernoulli trials using the same probability of success pi, then take the average of all the 1 and 0 outcomes, then the result would be close to pi. This is because doing an average this way simply computes the proportion of successes seen, which we expect to converge to the underlying probability of success.
- The third line writes out the probability mass function of the Bernoulli distribution, specifying the probability of seeing each of the two possible outcomes.
- The fourth line is another way of writing the probability mass function, which avoids having to write separate cases and is more convenient for certain types of calculations. This relies on the fact that Yi can take only the value 0 or 1. In each case, one of the exponents will be 1, «choosing» the value under it, while the other is 0, «canceling out» the value under it. Hence, the outcome is either pi or 1 − pi, as in the previous line.
- Linear predictor function
The basic idea of logistic regression is to use the mechanism already developed for linear regression by modeling the probability pi using a linear predictor function, i.e. a linear combination of the explanatory variables and a set of regression coefficients that are specific to the model at hand but the same for all trials. The linear predictor function 
where 
The model is usually put into a more compact form as follows:
- The regression coefficients β0, β1, …, βm are grouped into a single vector β of size m + 1.
- For each data point i, an additional explanatory pseudo-variable x0,i is added, with a fixed value of 1, corresponding to the intercept coefficient β0.
- The resulting explanatory variables x0,i, x1,i, …, xm,i are then grouped into a single vector Xi of size m + 1.
This makes it possible to write the linear predictor function as follows:
using the notation for a dot product between two vectors.
This is an example of an SPSS output for a logistic regression model using three explanatory variables (coffee use per week, energy drink use per week, and soda use per week) and two categories (male and female).
Many explanatory variables, two categories[edit]
The above example of binary logistic regression on one explanatory variable can be generalized to binary logistic regression on any number of explanatory variables x1, x2,… and any number of categorical values 
To begin with, we may consider a logistic model with M explanatory variables, x1, x2 … xM and, as in the example above, two categorical values (y = 0 and 1). For the simple binary logistic regression model, we assumed a linear relationship between the predictor variable and the log-odds (also called logit) of the event that 
where t is the log-odds and 

For a more compact notation, we will specify the explanatory variables and the β coefficients as 
with an added explanatory variable x0 =1. The logit may now be written as:
Solving for the probability p that 
,
where 










As in the simple example above, finding the optimum β parameters will require numerical methods. One useful technique is to equate the derivatives of the log likelihood with respect to each of the β parameters to zero yielding a set of equations which will hold at the maximum of the log likelihood:
where xmk is the value of the xm explanatory variable from the k-th measurement.
Consider an example with 




,
where p is the probability of the event that 
Multinomial logistic regression: Many explanatory variables and many categories[edit]
In the above cases of two categories (binomial logistic regression), the categories were indexed by «0» and «1», and we had two probability distributions: The probability that the outcome was in category 1 was given by 

In general, if we have 


for
Each of the probabilities except 



Note also that for the simple case of 


The log-likelihood that a particular set of K measurements or data points will be generated by the above probabilities can now be calculated. Indexing each measurement by k, let the k-th set of measured explanatory variables be denoted by 

where 
where 


Interpretations[edit]
There are various equivalent specifications and interpretations of logistic regression, which fit into different types of more general models, and allow different generalizations.
As a generalized linear model[edit]
The particular model used by logistic regression, which distinguishes it from standard linear regression and from other types of regression analysis used for binary-valued outcomes, is the way the probability of a particular outcome is linked to the linear predictor function:
Written using the more compact notation described above, this is:
This formulation expresses logistic regression as a type of generalized linear model, which predicts variables with various types of probability distributions by fitting a linear predictor function of the above form to some sort of arbitrary transformation of the expected value of the variable.
The intuition for transforming using the logit function (the natural log of the odds) was explained above[clarification needed]. It also has the practical effect of converting the probability (which is bounded to be between 0 and 1) to a variable that ranges over 
Note that both the probabilities pi and the regression coefficients are unobserved, and the means of determining them is not part of the model itself. They are typically determined by some sort of optimization procedure, e.g. maximum likelihood estimation, that finds values that best fit the observed data (i.e. that give the most accurate predictions for the data already observed), usually subject to regularization conditions that seek to exclude unlikely values, e.g. extremely large values for any of the regression coefficients. The use of a regularization condition is equivalent to doing maximum a posteriori (MAP) estimation, an extension of maximum likelihood. (Regularization is most commonly done using a squared regularizing function, which is equivalent to placing a zero-mean Gaussian prior distribution on the coefficients, but other regularizers are also possible.) Whether or not regularization is used, it is usually not possible to find a closed-form solution; instead, an iterative numerical method must be used, such as iteratively reweighted least squares (IRLS) or, more commonly these days, a quasi-Newton method such as the L-BFGS method.[20]
The interpretation of the βj parameter estimates is as the additive effect on the log of the odds for a unit change in the j the explanatory variable. In the case of a dichotomous explanatory variable, for instance, gender 
An equivalent formula uses the inverse of the logit function, which is the logistic function, i.e.:
The formula can also be written as a probability distribution (specifically, using a probability mass function):
As a latent-variable model[edit]
The logistic model has an equivalent formulation as a latent-variable model. This formulation is common in the theory of discrete choice models and makes it easier to extend to certain more complicated models with multiple, correlated choices, as well as to compare logistic regression to the closely related probit model.
Imagine that, for each trial i, there is a continuous latent variable Yi* (i.e. an unobserved random variable) that is distributed as follows:
where
i.e. the latent variable can be written directly in terms of the linear predictor function and an additive random error variable that is distributed according to a standard logistic distribution.
Then Yi can be viewed as an indicator for whether this latent variable is positive:
The choice of modeling the error variable specifically with a standard logistic distribution, rather than a general logistic distribution with the location and scale set to arbitrary values, seems restrictive, but in fact, it is not. It must be kept in mind that we can choose the regression coefficients ourselves, and very often can use them to offset changes in the parameters of the error variable’s distribution. For example, a logistic error-variable distribution with a non-zero location parameter μ (which sets the mean) is equivalent to a distribution with a zero location parameter, where μ has been added to the intercept coefficient. Both situations produce the same value for Yi* regardless of settings of explanatory variables. Similarly, an arbitrary scale parameter s is equivalent to setting the scale parameter to 1 and then dividing all regression coefficients by s. In the latter case, the resulting value of Yi* will be smaller by a factor of s than in the former case, for all sets of explanatory variables — but critically, it will always remain on the same side of 0, and hence lead to the same Yi choice.
(Note that this predicts that the irrelevancy of the scale parameter may not carry over into more complex models where more than two choices are available.)
It turns out that this formulation is exactly equivalent to the preceding one, phrased in terms of the generalized linear model and without any latent variables. This can be shown as follows, using the fact that the cumulative distribution function (CDF) of the standard logistic distribution is the logistic function, which is the inverse of the logit function, i.e.
Then:
This formulation—which is standard in discrete choice models—makes clear the relationship between logistic regression (the «logit model») and the probit model, which uses an error variable distributed according to a standard normal distribution instead of a standard logistic distribution. Both the logistic and normal distributions are symmetric with a basic unimodal, «bell curve» shape. The only difference is that the logistic distribution has somewhat heavier tails, which means that it is less sensitive to outlying data (and hence somewhat more robust to model mis-specifications or erroneous data).
Two-way latent-variable model[edit]
Yet another formulation uses two separate latent variables:
where
where EV1(0,1) is a standard type-1 extreme value distribution: i.e.
Then
This model has a separate latent variable and a separate set of regression coefficients for each possible outcome of the dependent variable. The reason for this separation is that it makes it easy to extend logistic regression to multi-outcome categorical variables, as in the multinomial logit model. In such a model, it is natural to model each possible outcome using a different set of regression coefficients. It is also possible to motivate each of the separate latent variables as the theoretical utility associated with making the associated choice, and thus motivate logistic regression in terms of utility theory. (In terms of utility theory, a rational actor always chooses the choice with the greatest associated utility.) This is the approach taken by economists when formulating discrete choice models, because it both provides a theoretically strong foundation and facilitates intuitions about the model, which in turn makes it easy to consider various sorts of extensions. (See the example below.)
The choice of the type-1 extreme value distribution seems fairly arbitrary, but it makes the mathematics work out, and it may be possible to justify its use through rational choice theory.
It turns out that this model is equivalent to the previous model, although this seems non-obvious, since there are now two sets of regression coefficients and error variables, and the error variables have a different distribution. In fact, this model reduces directly to the previous one with the following substitutions:
An intuition for this comes from the fact that, since we choose based on the maximum of two values, only their difference matters, not the exact values — and this effectively removes one degree of freedom. Another critical fact is that the difference of two type-1 extreme-value-distributed variables is a logistic distribution, i.e. 
Example[edit]
As an example, consider a province-level election where the choice is between a right-of-center party, a left-of-center party, and a secessionist party (e.g. the Parti Québécois, which wants Quebec to secede from Canada). We would then use three latent variables, one for each choice. Then, in accordance with utility theory, we can then interpret the latent variables as expressing the utility that results from making each of the choices. We can also interpret the regression coefficients as indicating the strength that the associated factor (i.e. explanatory variable) has in contributing to the utility — or more correctly, the amount by which a unit change in an explanatory variable changes the utility of a given choice. A voter might expect that the right-of-center party would lower taxes, especially on rich people. This would give low-income people no benefit, i.e. no change in utility (since they usually don’t pay taxes); would cause moderate benefit (i.e. somewhat more money, or moderate utility increase) for middle-incoming people; would cause significant benefits for high-income people. On the other hand, the left-of-center party might be expected to raise taxes and offset it with increased welfare and other assistance for the lower and middle classes. This would cause significant positive benefit to low-income people, perhaps a weak benefit to middle-income people, and significant negative benefit to high-income people. Finally, the secessionist party would take no direct actions on the economy, but simply secede. A low-income or middle-income voter might expect basically no clear utility gain or loss from this, but a high-income voter might expect negative utility since he/she is likely to own companies, which will have a harder time doing business in such an environment and probably lose money.
These intuitions can be expressed as follows:
| Center-right | Center-left | Secessionist | |
|---|---|---|---|
| High-income | strong + | strong − | strong − |
| Middle-income | moderate + | weak + | none |
| Low-income | none | strong + | none |
This clearly shows that
- Separate sets of regression coefficients need to exist for each choice. When phrased in terms of utility, this can be seen very easily. Different choices have different effects on net utility; furthermore, the effects vary in complex ways that depend on the characteristics of each individual, so there need to be separate sets of coefficients for each characteristic, not simply a single extra per-choice characteristic.
- Even though income is a continuous variable, its effect on utility is too complex for it to be treated as a single variable. Either it needs to be directly split up into ranges, or higher powers of income need to be added so that polynomial regression on income is effectively done.
As a «log-linear» model[edit]
Yet another formulation combines the two-way latent variable formulation above with the original formulation higher up without latent variables, and in the process provides a link to one of the standard formulations of the multinomial logit.
Here, instead of writing the logit of the probabilities pi as a linear predictor, we separate the linear predictor into two, one for each of the two outcomes:
Two separate sets of regression coefficients have been introduced, just as in the two-way latent variable model, and the two equations appear a form that writes the logarithm of the associated probability as a linear predictor, with an extra term 
In this form it is clear that the purpose of Z is to ensure that the resulting distribution over Yi is in fact a probability distribution, i.e. it sums to 1. This means that Z is simply the sum of all un-normalized probabilities, and by dividing each probability by Z, the probabilities become «normalized». That is:
and the resulting equations are
Or generally:
This shows clearly how to generalize this formulation to more than two outcomes, as in multinomial logit.
Note that this general formulation is exactly the softmax function as in
In order to prove that this is equivalent to the previous model, note that the above model is overspecified, in that 


As a result, we can simplify matters, and restore identifiability, by picking an arbitrary value for one of the two vectors. We choose to set 
and so
which shows that this formulation is indeed equivalent to the previous formulation. (As in the two-way latent variable formulation, any settings where 
Note that most treatments of the multinomial logit model start out either by extending the «log-linear» formulation presented here or the two-way latent variable formulation presented above, since both clearly show the way that the model could be extended to multi-way outcomes. In general, the presentation with latent variables is more common in econometrics and political science, where discrete choice models and utility theory reign, while the «log-linear» formulation here is more common in computer science, e.g. machine learning and natural language processing.
As a single-layer perceptron[edit]
The model has an equivalent formulation
This functional form is commonly called a single-layer perceptron or single-layer artificial neural network. A single-layer neural network computes a continuous output instead of a step function. The derivative of pi with respect to X = (x1, …, xk) is computed from the general form:
where f(X) is an analytic function in X. With this choice, the single-layer neural network is identical to the logistic regression model. This function has a continuous derivative, which allows it to be used in backpropagation. This function is also preferred because its derivative is easily calculated:
In terms of binomial data[edit]
A closely related model assumes that each i is associated not with a single Bernoulli trial but with ni independent identically distributed trials, where the observation Yi is the number of successes observed (the sum of the individual Bernoulli-distributed random variables), and hence follows a binomial distribution:
An example of this distribution is the fraction of seeds (pi) that germinate after ni are planted.
In terms of expected values, this model is expressed as follows:
so that
Or equivalently:
This model can be fit using the same sorts of methods as the above more basic model.
Model fitting[edit]
|
This section needs expansion. You can help by adding to it. (October 2016) |
Maximum likelihood estimation (MLE)[edit]
The regression coefficients are usually estimated using maximum likelihood estimation.[21][22] Unlike linear regression with normally distributed residuals, it is not possible to find a closed-form expression for the coefficient values that maximize the likelihood function, so that an iterative process must be used instead; for example Newton’s method. This process begins with a tentative solution, revises it slightly to see if it can be improved, and repeats this revision until no more improvement is made, at which point the process is said to have converged.[21]
In some instances, the model may not reach convergence. Non-convergence of a model indicates that the coefficients are not meaningful because the iterative process was unable to find appropriate solutions. A failure to converge may occur for a number of reasons: having a large ratio of predictors to cases, multicollinearity, sparseness, or complete separation.
- Having a large ratio of variables to cases results in an overly conservative Wald statistic (discussed below) and can lead to non-convergence. Regularized logistic regression is specifically intended to be used in this situation.
- Multicollinearity refers to unacceptably high correlations between predictors. As multicollinearity increases, coefficients remain unbiased but standard errors increase and the likelihood of model convergence decreases.[21] To detect multicollinearity amongst the predictors, one can conduct a linear regression analysis with the predictors of interest for the sole purpose of examining the tolerance statistic [21] used to assess whether multicollinearity is unacceptably high.
- Sparseness in the data refers to having a large proportion of empty cells (cells with zero counts). Zero cell counts are particularly problematic with categorical predictors. With continuous predictors, the model can infer values for the zero cell counts, but this is not the case with categorical predictors. The model will not converge with zero cell counts for categorical predictors because the natural logarithm of zero is an undefined value so that the final solution to the model cannot be reached. To remedy this problem, researchers may collapse categories in a theoretically meaningful way or add a constant to all cells.[21]
- Another numerical problem that may lead to a lack of convergence is complete separation, which refers to the instance in which the predictors perfectly predict the criterion – all cases are accurately classified and the likelihood maximized with infinite coefficients. In such instances, one should re-examine the data, as there may be some kind of error.[2][further explanation needed]
- One can also take semi-parametric or non-parametric approaches, e.g., via local-likelihood or nonparametric quasi-likelihood methods, which avoid assumptions of a parametric form for the index function and is robust to the choice of the link function (e.g., probit or logit).[23]
Iteratively reweighted least squares (IRLS)[edit]
Binary logistic regression (

![{displaystyle mathbf {w} ^{T}=[beta _{0},beta _{1},beta _{2},ldots ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/daccbf84c2c936e0559016491efe98eaf0eca430)
![{displaystyle mathbf {x} (i)=[1,x_{1}(i),x_{2}(i),ldots ]^{T}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8fc5f11bdd42f672417a3f4e44b3a4e5be28faa)


where 
![{displaystyle {boldsymbol {mu }}=[mu (1),mu (2),ldots ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/800927e9be36f4cac166a68862c04234cffd67b8)
The regressor matrix and ![{displaystyle mathbf {y} (i)=[y(1),y(2),ldots ]^{T}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33cbd315328b6ccfc7f216d65e39f92a8ec48694)
Bayesian[edit]
In a Bayesian statistics context, prior distributions are normally placed on the regression coefficients, for example in the form of Gaussian distributions. There is no conjugate prior of the likelihood function in logistic regression. When Bayesian inference was performed analytically, this made the posterior distribution difficult to calculate except in very low dimensions. Now, though, automatic software such as OpenBUGS, JAGS, PyMC3, Stan or Turing.jl allows these posteriors to be computed using simulation, so lack of conjugacy is not a concern. However, when the sample size or the number of parameters is large, full Bayesian simulation can be slow, and people often use approximate methods such as variational Bayesian methods and expectation propagation.
«Rule of ten»[edit]
A widely used rule of thumb, the «one in ten rule», states that logistic regression models give stable values for the explanatory variables if based on a minimum of about 10 events per explanatory variable (EPV); where event denotes the cases belonging to the less frequent category in the dependent variable. Thus a study designed to use 


Others have found results that are not consistent with the above, using different criteria. A useful criterion is whether the fitted model will be expected to achieve the same predictive discrimination in a new sample as it appeared to achieve in the model development sample. For that criterion, 20 events per candidate variable may be required.[28] Also, one can argue that 96 observations are needed only to estimate the model’s intercept precisely enough that the margin of error in predicted probabilities is ±0.1 with a 0.95 confidence level.[29]
Error and significance of fit[edit]
Deviance and likelihood ratio test ─ a simple case[edit]
In any fitting procedure, the addition of another fitting parameter to a model (e.g. the beta parameters in a logistic regression model) will almost always improve the ability of the model to predict the measured outcomes. This will be true even if the additional term has no predictive value, since the model will simply be «overfitting» to the noise in the data. The question arises as to whether the improvement gained by the addition of another fitting parameter is significant enough to recommend the inclusion of the additional term, or whether the improvement is simply that which may be expected from overfitting.
In short, for logistic regression, a statistic known as the deviance is defined which is a measure of the error between the logistic model fit and the outcome data. In the limit of a large number of data points, the deviance is chi-squared distributed, which allows a chi-squared test to be implemented in order to determine the significance of the explanatory variables.
Linear regression and logistic regression have many similarities. For example, in simple linear regression, a set of K data points (xk, yk) are fitted to a proposed model function of the form 
The minimum value which constitutes the fit will be denoted by 
The idea of a null model may be introduced, in which it is assumed that the x variable is of no use in predicting the yk outcomes: The data points are fitted to a null model function of the form y=b0 with a squared error term:
The fitting process consists of choosing a value of b0 which minimizes 





which is proportional to the square of the (uncorrected) sample standard deviation of the yk data points.
We can imagine a case where the yk data points are randomly assigned to the various xk, and then fitted using the proposed model. Specifically, we can consider the fits of the proposed model to every permutation of the yk outcomes. It can be shown that the optimized error of any of these fits will never be less than the optimum error of the null model, and that the difference between these minimum error will follow a chi-squared distribution, with degrees of freedom equal those of the proposed model minus those of the null model which, in this case, will be 2-1=1. Using the chi-squared test, we may then estimate how many of these permuted sets of yk will yield an minimum error less than or equal to the minimum error using the original yk, and so we can estimate how significant an improvement is given by the inclusion of the x variable in the proposed model.
For logistic regression, the measure of goodness-of-fit is the likelihood function L, or its logarithm, the log-likelihood ℓ. The likelihood function L is analogous to the 

In the case of simple binary logistic regression, the set of K data points are fitted in a probabilistic sense to a function of the form:
where 

and the log-likelihood is:
For the null model, the probability that 
The log-odds for the null model are given by:
and the log-likelihood is:
Since we have 
The optimum 
where 
Also, as an analog to the error of the linear regression case, we may define the deviance of a logistic regression fit as:
which will always be positive or zero. The reason for this choice is that not only is the deviance a good measure of the goodness of fit, it is also approximately chi-squared distributed, with the approximation improving as the number of data points (K) increases, becoming exactly chi-square distributed in the limit of an infinite number of data points. As in the case of linear regression, we may use this fact to estimate the probability that a random set of data points will give a better fit than the fit obtained by the proposed model, and so have an estimate how significantly the model is improved by including the xk data points in the proposed model.
For the simple model of student test scores described above, the maximum value of the log-likelihood of the null model is 


Using the chi-squared test of significance, the integral of the chi-squared distribution with one degree of freedom from 11.6661… to infinity is equal to 0.00063649…
This effectively means that about 6 out of a 10,000 fits to random yk can be expected to have a better fit (smaller deviance) than the given yk and so we can conclude that the inclusion of the x variable and data in the proposed model is a very significant improvement over the null model. In other words, we reject the null hypothesis with 
Goodness of fit summary[edit]
Goodness of fit in linear regression models is generally measured using R2. Since this has no direct analog in logistic regression, various methods[30]: ch.21 including the following can be used instead.
Deviance and likelihood ratio tests[edit]
In linear regression analysis, one is concerned with partitioning variance via the sum of squares calculations – variance in the criterion is essentially divided into variance accounted for by the predictors and residual variance. In logistic regression analysis, deviance is used in lieu of a sum of squares calculations.[31] Deviance is analogous to the sum of squares calculations in linear regression[2] and is a measure of the lack of fit to the data in a logistic regression model.[31] When a «saturated» model is available (a model with a theoretically perfect fit), deviance is calculated by comparing a given model with the saturated model.[2] This computation gives the likelihood-ratio test:[2]
In the above equation, D represents the deviance and ln represents the natural logarithm. The log of this likelihood ratio (the ratio of the fitted model to the saturated model) will produce a negative value, hence the need for a negative sign. D can be shown to follow an approximate chi-squared distribution.[2] Smaller values indicate better fit as the fitted model deviates less from the saturated model. When assessed upon a chi-square distribution, nonsignificant chi-square values indicate very little unexplained variance and thus, good model fit. Conversely, a significant chi-square value indicates that a significant amount of the variance is unexplained.
When the saturated model is not available (a common case), deviance is calculated simply as −2·(log likelihood of the fitted model), and the reference to the saturated model’s log likelihood can be removed from all that follows without harm.
Two measures of deviance are particularly important in logistic regression: null deviance and model deviance. The null deviance represents the difference between a model with only the intercept (which means «no predictors») and the saturated model. The model deviance represents the difference between a model with at least one predictor and the saturated model.[31] In this respect, the null model provides a baseline upon which to compare predictor models. Given that deviance is a measure of the difference between a given model and the saturated model, smaller values indicate better fit. Thus, to assess the contribution of a predictor or set of predictors, one can subtract the model deviance from the null deviance and assess the difference on a 
Let
Then the difference of both is:
If the model deviance is significantly smaller than the null deviance then one can conclude that the predictor or set of predictors significantly improve the model’s fit. This is analogous to the F-test used in linear regression analysis to assess the significance of prediction.[31]
Pseudo-R-squared[edit]
In linear regression the squared multiple correlation, R2 is used to assess goodness of fit as it represents the proportion of variance in the criterion that is explained by the predictors.[31] In logistic regression analysis, there is no agreed upon analogous measure, but there are several competing measures each with limitations.[31][32]
Four of the most commonly used indices and one less commonly used one are examined on this page:
- Likelihood ratio R2L
- Cox and Snell R2CS
- Nagelkerke R2N
- McFadden R2McF
- Tjur R2T
Hosmer–Lemeshow test[edit]
The Hosmer–Lemeshow test uses a test statistic that asymptotically follows a 
Coefficient significance[edit]
After fitting the model, it is likely that researchers will want to examine the contribution of individual predictors. To do so, they will want to examine the regression coefficients. In linear regression, the regression coefficients represent the change in the criterion for each unit change in the predictor.[31] In logistic regression, however, the regression coefficients represent the change in the logit for each unit change in the predictor. Given that the logit is not intuitive, researchers are likely to focus on a predictor’s effect on the exponential function of the regression coefficient – the odds ratio (see definition). In linear regression, the significance of a regression coefficient is assessed by computing a t test. In logistic regression, there are several different tests designed to assess the significance of an individual predictor, most notably the likelihood ratio test and the Wald statistic.
Likelihood ratio test[edit]
The likelihood-ratio test discussed above to assess model fit is also the recommended procedure to assess the contribution of individual «predictors» to a given model.[2][21][31] In the case of a single predictor model, one simply compares the deviance of the predictor model with that of the null model on a chi-square distribution with a single degree of freedom. If the predictor model has significantly smaller deviance (c.f. chi-square using the difference in degrees of freedom of the two models), then one can conclude that there is a significant association between the «predictor» and the outcome. Although some common statistical packages (e.g. SPSS) do provide likelihood ratio test statistics, without this computationally intensive test it would be more difficult to assess the contribution of individual predictors in the multiple logistic regression case.[citation needed] To assess the contribution of individual predictors one can enter the predictors hierarchically, comparing each new model with the previous to determine the contribution of each predictor.[31] There is some debate among statisticians about the appropriateness of so-called «stepwise» procedures.[weasel words] The fear is that they may not preserve nominal statistical properties and may become misleading.[34]
Wald statistic[edit]
Alternatively, when assessing the contribution of individual predictors in a given model, one may examine the significance of the Wald statistic. The Wald statistic, analogous to the t-test in linear regression, is used to assess the significance of coefficients. The Wald statistic is the ratio of the square of the regression coefficient to the square of the standard error of the coefficient and is asymptotically distributed as a chi-square distribution.[21]
Although several statistical packages (e.g., SPSS, SAS) report the Wald statistic to assess the contribution of individual predictors, the Wald statistic has limitations. When the regression coefficient is large, the standard error of the regression coefficient also tends to be larger increasing the probability of Type-II error. The Wald statistic also tends to be biased when data are sparse.[31]
Case-control sampling[edit]
Suppose cases are rare. Then we might wish to sample them more frequently than their prevalence in the population. For example, suppose there is a disease that affects 1 person in 10,000 and to collect our data we need to do a complete physical. It may be too expensive to do thousands of physicals of healthy people in order to obtain data for only a few diseased individuals. Thus, we may evaluate more diseased individuals, perhaps all of the rare outcomes. This is also retrospective sampling, or equivalently it is called unbalanced data. As a rule of thumb, sampling controls at a rate of five times the number of cases will produce sufficient control data.[35]
Logistic regression is unique in that it may be estimated on unbalanced data, rather than randomly sampled data, and still yield correct coefficient estimates of the effects of each independent variable on the outcome. That is to say, if we form a logistic model from such data, if the model is correct in the general population, the 


where 

Discussion[edit]
Like other forms of regression analysis, logistic regression makes use of one or more predictor variables that may be either continuous or categorical. Unlike ordinary linear regression, however, logistic regression is used for predicting dependent variables that take membership in one of a limited number of categories (treating the dependent variable in the binomial case as the outcome of a Bernoulli trial) rather than a continuous outcome. Given this difference, the assumptions of linear regression are violated. In particular, the residuals cannot be normally distributed. In addition, linear regression may make nonsensical predictions for a binary dependent variable. What is needed is a way to convert a binary variable into a continuous one that can take on any real value (negative or positive). To do that, binomial logistic regression first calculates the odds of the event happening for different levels of each independent variable, and then takes its logarithm to create a continuous criterion as a transformed version of the dependent variable. The logarithm of the odds is the logit of the probability, the logit is defined as follows:
Although the dependent variable in logistic regression is Bernoulli, the logit is on an unrestricted scale.[2] The logit function is the link function in this kind of generalized linear model, i.e.
Y is the Bernoulli-distributed response variable and x is the predictor variable; the β values are the linear parameters.
The logit of the probability of success is then fitted to the predictors. The predicted value of the logit is converted back into predicted odds, via the inverse of the natural logarithm – the exponential function. Thus, although the observed dependent variable in binary logistic regression is a 0-or-1 variable, the logistic regression estimates the odds, as a continuous variable, that the dependent variable is a ‘success’. In some applications, the odds are all that is needed. In others, a specific yes-or-no prediction is needed for whether the dependent variable is or is not a ‘success’; this categorical prediction can be based on the computed odds of success, with predicted odds above some chosen cutoff value being translated into a prediction of success.
Maximum entropy[edit]
Of all the functional forms used for estimating the probabilities of a particular categorical outcome which optimize the fit by maximizing the likelihood function (e.g. probit regression, Poisson regression, etc.), the logistic regression solution is unique in that it is a maximum entropy solution.[36] This is a case of a general property: an exponential family of distributions maximizes entropy, given an expected value. In the case of the logistic model, the logistic function is the natural parameter of the Bernoulli distribution (it is in «canonical form», and the logistic function is the canonical link function), while other sigmoid functions are non-canonical link functions; this underlies its mathematical elegance and ease of optimization. See Exponential family § Maximum entropy derivation for details.
Proof[edit]
In order to show this, we use the method of Lagrange multipliers. The Lagrangian is equal to the entropy plus the sum of the products of Lagrange multipliers times various constraint expressions. The general multinomial case will be considered, since the proof is not made that much simpler by considering simpler cases. Equating the derivative of the Lagrangian with respect to the various probabilities to zero yields a functional form for those probabilities which corresponds to those used in logistic regression.[36]
As in the above section on multinomial logistic regression, we will consider 








Let pn(x) be the probability, given explanatory variable vector x, that the outcome will be 

The Lagrangian will be expressed as a function of the probabilities pnk and will minimized by equating the derivatives of the Lagrangian with respect to these probabilities to zero. An important point is that the probabilities are treated equally and the fact that they sum to unity is part of the Lagrangian formulation, rather than being assumed from the beginning.
The first contribution to the Lagrangian is the entropy:
The log-likelihood is:
Assuming the multinomial logistic function, the derivative of the log-likelihood with respect the beta coefficients was found to be:
A very important point here is that this expression is (remarkably) not an explicit function of the beta coefficients. It is only a function of the probabilities pnk and the data. Rather than being specific to the assumed multinomial logistic case, it is taken to be a general statement of the condition at which the log-likelihood is maximized and makes no reference to the functional form of pnk. There are then (M+1)(N+1) fitting constraints and the fitting constraint term in the Lagrangian is then:
where the λnm are the appropriate Lagrange multipliers. There are K normalization constraints which may be written:
so that the normalization term in the Lagrangian is:
where the αk are the appropriate Lagrange multipliers. The Lagrangian is then the sum of the above three terms:
Setting the derivative of the Lagrangian with respect to one of the probabilities to zero yields:
Using the more condensed vector notation:
and dropping the primes on the n and k indices, and then solving for 
where:
Imposing the normalization constraint, we can solve for the Zk and write the probabilities as:
The 









Other approaches[edit]
In machine learning applications where logistic regression is used for binary classification, the MLE minimises the Cross entropy loss function.
Logistic regression is an important machine learning algorithm. The goal is to model the probability of a random variable 
Consider a generalized linear model function parameterized by 
Therefore,
and since 


Typically, the log likelihood is maximized,
which is maximized using optimization techniques such as gradient descent.
Assuming the 
where 

Comparison with linear regression[edit]
Logistic regression can be seen as a special case of the generalized linear model and thus analogous to linear regression. The model of logistic regression, however, is based on quite different assumptions (about the relationship between the dependent and independent variables) from those of linear regression. In particular, the key differences between these two models can be seen in the following two features of logistic regression. First, the conditional distribution 
Alternatives[edit]
A common alternative to the logistic model (logit model) is the probit model, as the related names suggest. From the perspective of generalized linear models, these differ in the choice of link function: the logistic model uses the logit function (inverse logistic function), while the probit model uses the probit function (inverse error function). Equivalently, in the latent variable interpretations of these two methods, the first assumes a standard logistic distribution of errors and the second a standard normal distribution of errors.[38] Other sigmoid functions or error distributions can be used instead.
Logistic regression is an alternative to Fisher’s 1936 method, linear discriminant analysis.[39] If the assumptions of linear discriminant analysis hold, the conditioning can be reversed to produce logistic regression. The converse is not true, however, because logistic regression does not require the multivariate normal assumption of discriminant analysis.[40]
The assumption of linear predictor effects can easily be relaxed using techniques such as spline functions.[29]
History[edit]
A detailed history of the logistic regression is given in Cramer (2002). The logistic function was developed as a model of population growth and named «logistic» by Pierre François Verhulst in the 1830s and 1840s, under the guidance of Adolphe Quetelet; see Logistic function § History for details.[41] In his earliest paper (1838), Verhulst did not specify how he fit the curves to the data.[42][43] In his more detailed paper (1845), Verhulst determined the three parameters of the model by making the curve pass through three observed points, which yielded poor predictions.[44][45]
The logistic function was independently developed in chemistry as a model of autocatalysis (Wilhelm Ostwald, 1883).[46] An autocatalytic reaction is one in which one of the products is itself a catalyst for the same reaction, while the supply of one of the reactants is fixed. This naturally gives rise to the logistic equation for the same reason as population growth: the reaction is self-reinforcing but constrained.
The logistic function was independently rediscovered as a model of population growth in 1920 by Raymond Pearl and Lowell Reed, published as Pearl & Reed (1920), which led to its use in modern statistics. They were initially unaware of Verhulst’s work and presumably learned about it from L. Gustave du Pasquier, but they gave him little credit and did not adopt his terminology.[47] Verhulst’s priority was acknowledged and the term «logistic» revived by Udny Yule in 1925 and has been followed since.[48] Pearl and Reed first applied the model to the population of the United States, and also initially fitted the curve by making it pass through three points; as with Verhulst, this again yielded poor results.[49]
In the 1930s, the probit model was developed and systematized by Chester Ittner Bliss, who coined the term «probit» in Bliss (1934), and by John Gaddum in Gaddum (1933), and the model fit by maximum likelihood estimation by Ronald A. Fisher in Fisher (1935), as an addendum to Bliss’s work. The probit model was principally used in bioassay, and had been preceded by earlier work dating to 1860; see Probit model § History. The probit model influenced the subsequent development of the logit model and these models competed with each other.[50]
The logistic model was likely first used as an alternative to the probit model in bioassay by Edwin Bidwell Wilson and his student Jane Worcester in Wilson & Worcester (1943).[51] However, the development of the logistic model as a general alternative to the probit model was principally due to the work of Joseph Berkson over many decades, beginning in Berkson (1944), where he coined «logit», by analogy with «probit», and continuing through Berkson (1951) and following years.[52] The logit model was initially dismissed as inferior to the probit model, but «gradually achieved an equal footing with the logit»,[53] particularly between 1960 and 1970. By 1970, the logit model achieved parity with the probit model in use in statistics journals and thereafter surpassed it. This relative popularity was due to the adoption of the logit outside of bioassay, rather than displacing the probit within bioassay, and its informal use in practice; the logit’s popularity is credited to the logit model’s computational simplicity, mathematical properties, and generality, allowing its use in varied fields.[3]
Various refinements occurred during that time, notably by David Cox, as in Cox (1958).[4]
The multinomial logit model was introduced independently in Cox (1966) and Theil (1969), which greatly increased the scope of application and the popularity of the logit model.[54] In 1973 Daniel McFadden linked the multinomial logit to the theory of discrete choice, specifically Luce’s choice axiom, showing that the multinomial logit followed from the assumption of independence of irrelevant alternatives and interpreting odds of alternatives as relative preferences;[55] this gave a theoretical foundation for the logistic regression.[54]
Extensions[edit]
There are large numbers of extensions:
- Multinomial logistic regression (or multinomial logit) handles the case of a multi-way categorical dependent variable (with unordered values, also called «classification»). Note that the general case of having dependent variables with more than two values is termed polytomous regression.
- Ordered logistic regression (or ordered logit) handles ordinal dependent variables (ordered values).
- Mixed logit is an extension of multinomial logit that allows for correlations among the choices of the dependent variable.
- An extension of the logistic model to sets of interdependent variables is the conditional random field.
- Conditional logistic regression handles matched or stratified data when the strata are small. It is mostly used in the analysis of observational studies.
Software[edit]
Most statistical software can do binary logistic regression.
- SPSS
- [1] for basic logistic regression.
- Stata
- SAS
- PROC LOGISTIC for basic logistic regression.
- PROC CATMOD when all the variables are categorical.
- PROC GLIMMIX for multilevel model logistic regression.
- R
glmin the stats package (using family = binomial)[56]lrmin the rms package- GLMNET package for an efficient implementation regularized logistic regression
- lmer for mixed effects logistic regression
- Rfast package command
gm_logisticfor fast and heavy calculations involving large scale data. - arm package for bayesian logistic regression
- Python
Logitin the Statsmodels module.LogisticRegressionin the scikit-learn module.LogisticRegressorin the TensorFlow module.- Full example of logistic regression in the Theano tutorial [2]
- Bayesian Logistic Regression with ARD prior code, tutorial
- Variational Bayes Logistic Regression with ARD prior code , tutorial
- Bayesian Logistic Regression code, tutorial
- NCSS
- Logistic Regression in NCSS
- Matlab
mnrfitin the Statistics and Machine Learning Toolbox (with «incorrect» coded as 2 instead of 0)fminunc/fmincon, fitglm, mnrfit, fitclinear, mlecan all do logistic regression.
- Java (JVM)
- LibLinear
- Apache Flink
- Apache Spark
- SparkML supports Logistic Regression
- FPGA
Logistic Regresesion IP corein HLS for FPGA.
Notably, Microsoft Excel’s statistics extension package does not include it.
See also[edit]
- Logistic function
- Discrete choice
- Jarrow–Turnbull model
- Limited dependent variable
- Multinomial logit model
- Ordered logit
- Hosmer–Lemeshow test
- Brier score
- mlpack — contains a C++ implementation of logistic regression
- Local case-control sampling
- Logistic model tree
References[edit]
- ^ Tolles, Juliana; Meurer, William J (2016). «Logistic Regression Relating Patient Characteristics to Outcomes». JAMA. 316 (5): 533–4. doi:10.1001/jama.2016.7653. ISSN 0098-7484. OCLC 6823603312. PMID 27483067.
- ^ a b c d e f g h i j k Hosmer, David W.; Lemeshow, Stanley (2000). Applied Logistic Regression (2nd ed.). Wiley. ISBN 978-0-471-35632-5.[page needed]
- ^ a b Cramer 2002, p. 10–11.
- ^ a b Walker, SH; Duncan, DB (1967). «Estimation of the probability of an event as a function of several independent variables». Biometrika. 54 (1/2): 167–178. doi:10.2307/2333860. JSTOR 2333860.
- ^ Cramer 2002, p. 8.
- ^ Boyd, C. R.; Tolson, M. A.; Copes, W. S. (1987). «Evaluating trauma care: The TRISS method. Trauma Score and the Injury Severity Score». The Journal of Trauma. 27 (4): 370–378. doi:10.1097/00005373-198704000-00005. PMID 3106646.
- ^ Kologlu, M.; Elker, D.; Altun, H.; Sayek, I. (2001). «Validation of MPI and PIA II in two different groups of patients with secondary peritonitis». Hepato-Gastroenterology. 48 (37): 147–51. PMID 11268952.
- ^ Biondo, S.; Ramos, E.; Deiros, M.; Ragué, J. M.; De Oca, J.; Moreno, P.; Farran, L.; Jaurrieta, E. (2000). «Prognostic factors for mortality in left colonic peritonitis: A new scoring system». Journal of the American College of Surgeons. 191 (6): 635–42. doi:10.1016/S1072-7515(00)00758-4. PMID 11129812.
- ^ Marshall, J. C.; Cook, D. J.; Christou, N. V.; Bernard, G. R.; Sprung, C. L.; Sibbald, W. J. (1995). «Multiple organ dysfunction score: A reliable descriptor of a complex clinical outcome». Critical Care Medicine. 23 (10): 1638–52. doi:10.1097/00003246-199510000-00007. PMID 7587228.
- ^ Le Gall, J. R.; Lemeshow, S.; Saulnier, F. (1993). «A new Simplified Acute Physiology Score (SAPS II) based on a European/North American multicenter study». JAMA. 270 (24): 2957–63. doi:10.1001/jama.1993.03510240069035. PMID 8254858.
- ^ a b David A. Freedman (2009). Statistical Models: Theory and Practice. Cambridge University Press. p. 128.
- ^ Truett, J; Cornfield, J; Kannel, W (1967). «A multivariate analysis of the risk of coronary heart disease in Framingham». Journal of Chronic Diseases. 20 (7): 511–24. doi:10.1016/0021-9681(67)90082-3. PMID 6028270.
- ^ Harrell, Frank E. (2001). Regression Modeling Strategies (2nd ed.). Springer-Verlag. ISBN 978-0-387-95232-1.
- ^ M. Strano; B.M. Colosimo (2006). «Logistic regression analysis for experimental determination of forming limit diagrams». International Journal of Machine Tools and Manufacture. 46 (6): 673–682. doi:10.1016/j.ijmachtools.2005.07.005.
- ^ Palei, S. K.; Das, S. K. (2009). «Logistic regression model for prediction of roof fall risks in bord and pillar workings in coal mines: An approach». Safety Science. 47: 88–96. doi:10.1016/j.ssci.2008.01.002.
- ^ Berry, Michael J.A (1997). Data Mining Techniques For Marketing, Sales and Customer Support. Wiley. p. 10.
- ^ «How to Interpret Odds Ratio in Logistic Regression?». Institute for Digital Research and Education.
- ^ Everitt, Brian (1998). The Cambridge Dictionary of Statistics. Cambridge, UK New York: Cambridge University Press. ISBN 978-0521593465.
- ^ For example, the indicator function in this case could be defined as
- ^ Malouf, Robert (2002). «A comparison of algorithms for maximum entropy parameter estimation». Proceedings of the Sixth Conference on Natural Language Learning (CoNLL-2002). pp. 49–55. doi:10.3115/1118853.1118871.
- ^ a b c d e f g Menard, Scott W. (2002). Applied Logistic Regression (2nd ed.). SAGE. ISBN 978-0-7619-2208-7.[page needed]
- ^ Gourieroux, Christian; Monfort, Alain (1981). «Asymptotic Properties of the Maximum Likelihood Estimator in Dichotomous Logit Models». Journal of Econometrics. 17 (1): 83–97. doi:10.1016/0304-4076(81)90060-9.
- ^ Park, Byeong U.; Simar, Léopold; Zelenyuk, Valentin (2017). «Nonparametric estimation of dynamic discrete choice models for time series data» (PDF). Computational Statistics & Data Analysis. 108: 97–120. doi:10.1016/j.csda.2016.10.024.
- ^ See e.g.. Murphy, Kevin P. (2012). Machine Learning – A Probabilistic Perspective. The MIT Press. pp. 245pp. ISBN 978-0-262-01802-9.
- ^ Van Smeden, M.; De Groot, J. A.; Moons, K. G.; Collins, G. S.; Altman, D. G.; Eijkemans, M. J.; Reitsma, J. B. (2016). «No rationale for 1 variable per 10 events criterion for binary logistic regression analysis». BMC Medical Research Methodology. 16 (1): 163. doi:10.1186/s12874-016-0267-3. PMC 5122171. PMID 27881078.
- ^ Peduzzi, P; Concato, J; Kemper, E; Holford, TR; Feinstein, AR (December 1996). «A simulation study of the number of events per variable in logistic regression analysis». Journal of Clinical Epidemiology. 49 (12): 1373–9. doi:10.1016/s0895-4356(96)00236-3. PMID 8970487.
- ^ Vittinghoff, E.; McCulloch, C. E. (12 January 2007). «Relaxing the Rule of Ten Events per Variable in Logistic and Cox Regression». American Journal of Epidemiology. 165 (6): 710–718. doi:10.1093/aje/kwk052. PMID 17182981.
- ^ van der Ploeg, Tjeerd; Austin, Peter C.; Steyerberg, Ewout W. (2014). «Modern modelling techniques are data hungry: a simulation study for predicting dichotomous endpoints». BMC Medical Research Methodology. 14: 137. doi:10.1186/1471-2288-14-137. PMC 4289553. PMID 25532820.
- ^ a b Harrell, Frank E. (2015). Regression Modeling Strategies. Springer Series in Statistics (2nd ed.). New York; Springer. doi:10.1007/978-3-319-19425-7. ISBN 978-3-319-19424-0.
- ^ Greene, William N. (2003). Econometric Analysis (Fifth ed.). Prentice-Hall. ISBN 978-0-13-066189-0.
- ^ a b c d e f g h i j Cohen, Jacob; Cohen, Patricia; West, Steven G.; Aiken, Leona S. (2002). Applied Multiple Regression/Correlation Analysis for the Behavioral Sciences (3rd ed.). Routledge. ISBN 978-0-8058-2223-6.[page needed]
- ^ Allison, Paul D. «Measures of fit for logistic regression» (PDF). Statistical Horizons LLC and the University of Pennsylvania.
- ^ Hosmer, D.W. (1997). «A comparison of goodness-of-fit tests for the logistic regression model». Stat Med. 16 (9): 965–980. doi:10.1002/(sici)1097-0258(19970515)16:9<965::aid-sim509>3.3.co;2-f. PMID 9160492.
- ^ Harrell, Frank E. (2010). Regression Modeling Strategies: With Applications to Linear Models, Logistic Regression, and Survival Analysis. New York: Springer. ISBN 978-1-4419-2918-1.[page needed]
- ^ a b https://class.stanford.edu/c4x/HumanitiesScience/StatLearning/asset/classification.pdf slide 16
- ^ a b Mount, J. (2011). «The Equivalence of Logistic Regression and Maximum Entropy models» (PDF). Retrieved Feb 23, 2022.
- ^ Ng, Andrew (2000). «CS229 Lecture Notes» (PDF). CS229 Lecture Notes: 16–19.
- ^ Rodríguez, G. (2007). Lecture Notes on Generalized Linear Models. pp. Chapter 3, page 45.
- ^ Gareth James; Daniela Witten; Trevor Hastie; Robert Tibshirani (2013). An Introduction to Statistical Learning. Springer. p. 6.
- ^ Pohar, Maja; Blas, Mateja; Turk, Sandra (2004). «Comparison of Logistic Regression and Linear Discriminant Analysis: A Simulation Study». Metodološki Zvezki. 1 (1).
- ^ Cramer 2002, pp. 3–5.
- ^ Verhulst, Pierre-François (1838). «Notice sur la loi que la population poursuit dans son accroissement» (PDF). Correspondance Mathématique et Physique. 10: 113–121. Retrieved 3 December 2014.
- ^ Cramer 2002, p. 4, «He did not say how he fitted the curves.»
- ^ Verhulst, Pierre-François (1845). «Recherches mathématiques sur la loi d’accroissement de la population» [Mathematical Researches into the Law of Population Growth Increase]. Nouveaux Mémoires de l’Académie Royale des Sciences et Belles-Lettres de Bruxelles. 18. Retrieved 2013-02-18.
- ^ Cramer 2002, p. 4.
- ^ Cramer 2002, p. 7.
- ^ Cramer 2002, p. 6.
- ^ Cramer 2002, p. 6–7.
- ^ Cramer 2002, p. 5.
- ^ Cramer 2002, p. 7–9.
- ^ Cramer 2002, p. 9.
- ^ Cramer 2002, p. 8, «As far as I can see the introduction of the logistics as an alternative to the normal probability function is the work of a single person, Joseph Berkson (1899–1982), …»
- ^ Cramer 2002, p. 11.
- ^ a b Cramer 2002, p. 13.
- ^ McFadden, Daniel (1973). «Conditional Logit Analysis of Qualitative Choice Behavior» (PDF). In P. Zarembka (ed.). Frontiers in Econometrics. New York: Academic Press. pp. 105–142. Archived from the original (PDF) on 2018-11-27. Retrieved 2019-04-20.
- ^ Gelman, Andrew; Hill, Jennifer (2007). Data Analysis Using Regression and Multilevel/Hierarchical Models. New York: Cambridge University Press. pp. 79–108. ISBN 978-0-521-68689-1.
Further reading[edit]
- Berkson, Joseph (1944). «Application of the Logistic Function to Bio-Assay». Journal of the American Statistical Association. 39 (227): 357–365. doi:10.1080/01621459.1944.10500699. JSTOR 2280041.
- Cox, David R. (1958). «The regression analysis of binary sequences (with discussion)». J R Stat Soc B. 20 (2): 215–242. JSTOR 2983890.
- Cox, David R. (1966). «Some procedures connected with the logistic qualitative response curve». In F. N. David (1966) (ed.). Research Papers in Probability and Statistics (Festschrift for J. Neyman). London: Wiley. pp. 55–71.
- Cramer, J. S. (2002). The origins of logistic regression (PDF) (Technical report). Vol. 119. Tinbergen Institute. pp. 167–178. doi:10.2139/ssrn.360300.
- Published in: Cramer, J. S. (2004). «The early origins of the logit model». Studies in History and Philosophy of Science Part C: Studies in History and Philosophy of Biological and Biomedical Sciences. 35 (4): 613–626. doi:10.1016/j.shpsc.2004.09.003.
- Theil, Henri (1969). «A Multinomial Extension of the Linear Logit Model». International Economic Review. 10 (3): 251–59. doi:10.2307/2525642. JSTOR 2525642.
- Pearl, Raymond; Reed, Lowell J. (June 1920). «On the Rate of Growth of the Population of the United States since 1790 and Its Mathematical Representation». Proceedings of the National Academy of Sciences. 6 (6): 275–288. doi:10.1073/pnas.6.6.275. PMC 1084522.
- Wilson, E.B.; Worcester, J. (1943). «The Determination of L.D.50 and Its Sampling Error in Bio-Assay». Proceedings of the National Academy of Sciences of the United States of America. 29 (2): 79–85. Bibcode:1943PNAS…29…79W. doi:10.1073/pnas.29.2.79. PMC 1078563. PMID 16588606.
- Agresti, Alan. (2002). Categorical Data Analysis. New York: Wiley-Interscience. ISBN 978-0-471-36093-3.
- Amemiya, Takeshi (1985). «Qualitative Response Models». Advanced Econometrics. Oxford: Basil Blackwell. pp. 267–359. ISBN 978-0-631-13345-2.
- Balakrishnan, N. (1991). Handbook of the Logistic Distribution. Marcel Dekker, Inc. ISBN 978-0-8247-8587-1.
- Gouriéroux, Christian (2000). «The Simple Dichotomy». Econometrics of Qualitative Dependent Variables. New York: Cambridge University Press. pp. 6–37. ISBN 978-0-521-58985-7.
- Greene, William H. (2003). Econometric Analysis, fifth edition. Prentice Hall. ISBN 978-0-13-066189-0.
- Hilbe, Joseph M. (2009). Logistic Regression Models. Chapman & Hall/CRC Press. ISBN 978-1-4200-7575-5.
- Hosmer, David (2013). Applied logistic regression. Hoboken, New Jersey: Wiley. ISBN 978-0470582473.
- Howell, David C. (2010). Statistical Methods for Psychology, 7th ed. Belmont, CA; Thomson Wadsworth. ISBN 978-0-495-59786-5.
- Peduzzi, P.; J. Concato; E. Kemper; T.R. Holford; A.R. Feinstein (1996). «A simulation study of the number of events per variable in logistic regression analysis». Journal of Clinical Epidemiology. 49 (12): 1373–1379. doi:10.1016/s0895-4356(96)00236-3. PMID 8970487.
- Berry, Michael J.A.; Linoff, Gordon (1997). Data Mining Techniques For Marketing, Sales and Customer Support. Wiley.
External links[edit]
Media related to Logistic regression at Wikimedia Commons
- Econometrics Lecture (topic: Logit model) on YouTube by Mark Thoma
- Logistic Regression tutorial
- mlelr: software in C for teaching purposes
Мы начнем с самых простых и понятных моделей машинного обучения: линейных. В этой главе мы разберёмся, что это такое, почему они работают и в каких случаях их стоит использовать. Так как это первый класс моделей, с которым вы столкнётесь, мы постараемся подробно проговорить все важные моменты. Заодно объясним, как работает машинное обучение, на сравнительно простых примерах.
Почему модели линейные?
Представьте, что у вас есть множество объектов $mathbb{X}$, а вы хотели бы каждому объекту сопоставить какое-то значение. К примеру, у вас есть набор операций по банковской карте, а вы бы хотели, понять, какие из этих операций сделали мошенники. Если вы разделите все операции на два класса и нулём обозначите законные действия, а единицей мошеннические, то у вас получится простейшая задача классификации. Представьте другую ситуацию: у вас есть данные геологоразведки, по которым вы хотели бы оценить перспективы разных месторождений. В данном случае по набору геологических данных ваша модель будет, к примеру, оценивать потенциальную годовую доходность шахты. Это пример задачи регрессии. Числа, которым мы хотим сопоставить объекты из нашего множества иногда называют таргетами (от английского target).
Таким образом, задачи классификации и регрессии можно сформулировать как поиск отображения из множества объектов $mathbb{X}$ в множество возможных таргетов.
Математически задачи можно описать так:
- классификация: $mathbb{X} to {0,1,ldots,K}$, где $0, ldots, K$ – номера классов,
- регрессия: $mathbb{X} to mathbb{R}$.
Очевидно, что просто сопоставить какие-то объекты каким-то числам — дело довольно бессмысленное. Мы же хотим быстро обнаруживать мошенников или принимать решение, где строить шахту. Значит нам нужен какой-то критерий качества. Мы бы хотели найти такое отображение, которое лучше всего приближает истинное соответствие между объектами и таргетами. Что значит «лучше всего» – вопрос сложный. Мы к нему будем много раз возвращаться. Однако, есть более простой вопрос: среди каких отображений мы будем искать самое лучшее? Возможных отображений может быть много, но мы можем упростить себе задачу и договориться, что хотим искать решение только в каком-то заранее заданном параметризированном семействе функций. Вся эта глава будет посвящена самому простому такому семейству — линейным функциям вида
$$
y = w_1 x_1 + ldots + w_D x_D + w_0,
$$
где $y$ – целевая переменная (таргет), $(x_1, ldots, x_D)$ – вектор, соответствующий объекту выборки (вектор признаков), а $w_1, ldots, w_D, w_0$ – параметры модели. Признаки ещё называют фичами (от английского features). Вектор $w = (w_1,ldots,w_D)$ часто называют вектором весов, так как на предсказание модели можно смотреть как на взвешенную сумму признаков объекта, а число $w_0$ – свободным коэффициентом, или сдвигом (bias). Более компактно линейную модель можно записать в виде
$$y = langle x, wrangle + w_0$$
Теперь, когда мы выбрали семейство функций, в котором будем искать решение, задача стала существенно проще. Мы теперь ищем не какое-то абстрактное отображение, а конкретный вектор $(w_0,w_1,ldots,w_D)inmathbb{R}^{D+1}$.
Замечание. Чтобы применять линейную модель, нужно, чтобы каждый объект уже был представлен вектором численных признаков $x_1,ldots,x_D$. Конечно, просто текст или граф в линейную модель не положить, придётся сначала придумать для него численные фичи. Модель называют линейной, если она является линейной по этим численным признакам.
Разберёмся, как будет работать такая модель в случае, если $D = 1$. То есть у наших объектов есть ровно один численный признак, по которому они отличаются. Теперь наша линейная модель будет выглядеть совсем просто: $y = w_1 x_1 + w_0$. Для задачи регрессии мы теперь пытаемся приблизить значение игрек какой-то линейной функцией от переменной икс. А что будет значить линейность для задачи классификации? Давайте вспомним про пример с поиском мошеннических транзакций по картам. Допустим, нам известна ровно одна численная переменная — объём транзакции. Для бинарной классификации транзакций на законные и потенциально мошеннические мы будем искать так называемое разделяющее правило: там, где значение функции положительно, мы будем предсказывать один класс, где отрицательно – другой. В нашем примере простейшим правилом будет какое-то пороговое значение объёма транзакций, после которого есть смысл пометить транзакцию как подозрительную.
В случае более высоких размерностей вместо прямой будет гиперплоскость с аналогичным смыслом.
Вопрос на подумать. Если вы посмотрите содержание учебника, то не найдёте в нём ни «полиномиальных» моделей, ни каких-нибудь «логарифмических», хотя, казалось бы, зависимости бывают довольно сложными. Почему так?
Ответ (не открывайте сразу; сначала подумайте сами!)Линейные зависимости не так просты, как кажется. Пусть мы решаем задачу регрессии. Если мы подозреваем, что целевая переменная $y$ не выражается через $x_1, x_2$ как линейная функция, а зависит ещё от логарифма $x_1$ и ещё как-нибудь от того, разные ли знаки у признаков, то мы можем ввести дополнительные слагаемые в нашу линейную зависимость, просто объявим эти слагаемые новыми переменными и добавив перед ними соответствующие регрессионные коэффициенты
$$y approx w_1 x_1 + w_2 x_2 + w_3log{x_1} + w_4text{sgn}(x_1x_2) + w_0,$$
и в итоге из двумерной нелинейной задачи мы получили четырёхмерную линейную регрессию.
Вопрос на подумать. А как быть, если одна из фичей является категориальной, то есть принимает значения из (обычно конечного числа) значений, не являющихся числами? Например, это может быть время года, уровень образования, марка машины и так далее. Как правило, с такими значениями невозможно производить арифметические операции или же результаты их применения не имеют смысла.
Ответ (не открывайте сразу; сначала подумайте сами!)В линейную модель можно подать только численные признаки, так что категориальную фичу придётся как-то закодировать. Рассмотрим для примера вот такой датасет
Здесь два категориальных признака – pet_type и color. Первый принимает четыре различных значения, второй – пять.
Самый простой способ – использовать one-hot кодирование (one-hot encoding). Пусть исходный признак мог принимать $M$ значений $c_1,ldots, c_M$. Давайте заменим категориальный признак на $M$ признаков, которые принимают значения $0$ и $1$: $i$-й будет отвечать на вопрос «принимает ли признак значение $c_i$?». Иными словами, вместо ячейки со значением $c_i$ у объекта появляется строка нулей и единиц, в которой единица стоит только на $i$-м месте.
В нашем примере получится вот такая табличка:
Можно было бы на этом остановиться, но добавленные признаки обладают одним неприятным свойством: в каждом из них ровно одна единица, так что сумма соответствующих столбцов равна столбцу из единиц. А это уже плохо. Представьте, что у нас есть линейная модель
$$y sim w_1x_1 + ldots + w_{D-1}x_{d-1} + w_{c_1}x_{c_1} + ldots + w_{c_M}x_{c_M} + w_0$$
Преобразуем немного правую часть:
$$ysim w_1x_1 + ldots + w_{D-1}x_{d-1} + underbrace{(w_{c_1} — w_{c_M})}_{=:w’_{c_1}}x_{c_1} + ldots + underbrace{(w_{c_{M-1}} — w_{c_M})}_{=:w’_{C_{M-1}}}x_{c_{M-1}} + w_{c_M}underbrace{(x_{c_1} + ldots + x_{c_M})}_{=1} + w_0 = $$
$$ = w_1x_1 + ldots + w_{D-1}x_{d-1} + w’_{c_1}x_{c_1} + ldots + w’_{c_{M-1}}x_{c_{M-1}} + underbrace{(w_{c_M} + w_0)}_{=w’_{0}}$$
Как видим, от одного из новых признаков можно избавиться, не меняя модель. Больше того, это стоит сделать, потому что наличие «лишних» признаков ведёт к переобучению или вовсе ломает модель – подробнее об этом мы поговорим в разделе про регуляризацию. Поэтому при использовании one-hot-encoding обычно выкидывают признак, соответствующий одному из значений. Например, в нашем примере итоговая матрица объекты-признаки будет иметь вид:
Конечно, one-hot кодирование – это самый наивный способ работы с категориальными признаками, и для более сложных фичей или фичей с большим количеством значений оно плохо подходит. С рядом более продвинутых техник вы познакомитесь в разделе про обучение представлений.
Помимо простоты, у линейных моделей есть несколько других достоинств. К примеру, мы можем достаточно легко судить, как влияют на результат те или иные признаки. Скажем, если вес $w_i$ положителен, то с ростом $i$-го признака таргет в случае регрессии будет увеличиваться, а в случае классификации наш выбор будет сдвигаться в пользу одного из классов. Значение весов тоже имеет прозрачную интерпретацию: чем вес $w_i$ больше, тем «важнее» $i$-й признак для итогового предсказания. То есть, если вы построили линейную модель, вы неплохо можете объяснить заказчику те или иные её результаты. Это качество моделей называют интерпретируемостью. Оно особенно ценится в индустриальных задачах, цена ошибки в которых высока. Если от работы вашей модели может зависеть жизнь человека, то очень важно понимать, как модель принимает те или иные решения и какими принципами руководствуется. При этом не все методы машинного обучения хорошо интерпретируемы, к примеру, поведение искусственных нейронных сетей или градиентного бустинга интерпретировать довольно сложно.
В то же время слепо доверять весам линейных моделей тоже не стоит по целому ряду причин:
- Линейные модели всё-таки довольно узкий класс функций, они неплохо работают для небольших датасетов и простых задач. Однако, если вы решаете линейной моделью более сложную задачу, то вам, скорее всего, придётся выдумывать дополнительные признаки, являющиеся сложными функциями от исходных. Поиск таких дополнительных признаков называется feature engineering, технически он устроен примерно так, как мы описали в вопросе про «полиномиальные модели». Вот только поиском таких искусственных фичей можно сильно увлечься, так что осмысленность интерпретации будет сильно зависеть от здравого смысла эксперта, строившего модель.
- Если между признаками есть приближённая линейная зависимость, коэффициенты в линейной модели могут совершенно потерять физический смысл (об этой проблеме и о том, как с ней бороться, мы поговорим дальше, когда будем обсуждать регуляризацию).
- Особенно осторожно стоит верить в утверждения вида «этот коэффициент маленький, значит, этот признак не важен». Во-первых, всё зависит от масштаба признака: вдруг коэффициент мал, чтобы скомпенсировать его. Во-вторых, зависимость действительно может быть слабой, но кто знает, в какой ситуации она окажется важна. Такие решения принимаются на основе данных, например, путём проверки статистического критерия (об этом мы коротко упомянем в разделе про вероятностные модели).
- Конкретные значения весов могут меняться в зависимости от обучающей выборки, хотя с ростом её размера они будут потихоньку сходиться к весам «наилучшей» линейной модели, которую можно было бы построить по всем-всем-всем данным на свете.
Обсудив немного общие свойства линейных моделей, перейдём к тому, как их всё-таки обучать. Сначала разберёмся с регрессией, а затем настанет черёд классификации.
Линейная регрессия и метод наименьших квадратов (МНК)
Мы начнём с использования линейных моделей для решения задачи регрессии. Простейшим примером постановки задачи линейной регрессии является метод наименьших квадратов (Ordinary least squares).
Пусть у нас задан датасет $(X, y)$, где $y=(y_i)_{i=1}^N in mathbb{R}^N$ – вектор значений целевой переменной, а $X=(x_i)_{i = 1}^N in mathbb{R}^{N times D}, x_i in mathbb{R}^D$ – матрица объекты-признаки, в которой $i$-я строка – это вектор признаков $i$-го объекта выборки. Мы хотим моделировать зависимость $y_i$ от $x_i$ как линейную функцию со свободным членом. Общий вид такой функции из $mathbb{R}^D$ в $mathbb{R}$ выглядит следующим образом:
$$color{#348FEA}{f_w(x_i) = langle w, x_i rangle + w_0}$$
Свободный член $w_0$ часто опускают, потому что такого же результата можно добиться, добавив ко всем $x_i$ признак, тождественно равный единице; тогда роль свободного члена будет играть соответствующий ему вес:
$$begin{pmatrix}x_{i1} & ldots & x_{iD} end{pmatrix}cdotbegin{pmatrix}w_1\ vdots \ w_Dend{pmatrix} + w_0 =
begin{pmatrix}1 & x_{i1} & ldots & x_{iD} end{pmatrix}cdotbegin{pmatrix}w_0 \ w_1\ vdots \ w_D end{pmatrix}$$
Поскольку это сильно упрощает запись, в дальнейшем мы будем считать, что это уже сделано и зависимость имеет вид просто $f_w(x_i) = langle w, x_i rangle$.
Сведение к задаче оптимизации
Мы хотим, чтобы на нашем датасете (то есть на парах $(x_i, y_i)$ из обучающей выборки) функция $f_w$ как можно лучше приближала нашу зависимость.
Для того, чтобы чётко сформулировать задачу, нам осталось только одно: на математическом языке выразить желание «приблизить $f_w(x)$ к $y$». Говоря простым языком, мы должны научиться измерять качество модели и минимизировать её ошибку, как-то меняя обучаемые параметры. В нашем примере обучаемые параметры — это веса $w$. Функция, оценивающая то, как часто модель ошибается, традиционно называется функцией потерь, функционалом качества или просто лоссом (loss function). Важно, чтобы её было легко оптимизировать: скажем, гладкая функция потерь – это хорошо, а кусочно постоянная – просто ужасно.
Функции потерь бывают разными. От их выбора зависит то, насколько задачу в дальнейшем легко решать, и то, в каком смысле у нас получится приблизить предсказание модели к целевым значениям. Интуитивно понятно, что для нашей текущей задачи нам нужно взять вектор $y$ и вектор предсказаний модели и как-то сравнить, насколько они похожи. Так как эти вектора «живут» в одном векторном пространстве, расстояние между ними вполне может быть функцией потерь. Более того, положительная непрерывная функция от этого расстояния тоже подойдёт в качестве функции потерь. При этом способов задать расстояние между векторами тоже довольно много. От всего этого разнообразия глаза разбегаются, но мы обязательно поговорим про это позже. Сейчас давайте в качестве лосса возьмём квадрат $L^2$-нормы вектора разницы предсказаний модели и $y$. Во-первых, как мы увидим дальше, так задачу будет нетрудно решить, а во-вторых, у этого лосса есть ещё несколько дополнительных свойств:
-
$L^2$-норма разницы – это евклидово расстояние $|y — f_w(x)|_2$ между вектором таргетов и вектором ответов модели, то есть мы их приближаем в смысле самого простого и понятного «расстояния».
-
Как мы увидим в разделе про вероятностные модели, с точки зрения статистики это соответствует гипотезе о том, что наши данные состоят из линейного «сигнала» и нормально распределенного «шума».
Так вот, наша функция потерь выглядит так:
$$L(f, X, y) = |y — f(X)|_2^2 = $$
$$= |y — Xw|_2^2 = sum_{i=1}^N(y_i — langle x_i, w rangle)^2$$
Такой функционал ошибки не очень хорош для сравнения поведения моделей на выборках разного размера. Представьте, что вы хотите понять, насколько качество модели на тестовой выборке из $2500$ объектов хуже, чем на обучающей из $5000$ объектов. Вы измерили $L^2$-норму ошибки и получили в одном случае $300$, а в другом $500$. Эти числа не очень интерпретируемы. Гораздо лучше посмотреть на среднеквадратичное отклонение
$$L(f, X, y) = frac1Nsum_{i=1}^N(y_i — langle x_i, w rangle)^2$$
По этой метрике на тестовой выборке получаем $0,12$, а на обучающей $0,1$.
Функция потерь $frac1Nsum_{i=1}^N(y_i — langle x_i, w rangle)^2$ называется Mean Squared Error, MSE или среднеквадратическим отклонением. Разница с $L^2$-нормой чисто косметическая, на алгоритм решения задачи она не влияет:
$$color{#348FEA}{text{MSE}(f, X, y) = frac{1}{N}|y — X w|_2^2}$$
В самом широком смысле, функции работают с объектами множеств: берут какой-то входящий объект из одного множества и выдают на выходе соответствующий ему объект из другого. Если мы имеем дело с отображением, которое на вход принимает функции, а на выходе выдаёт число, то такое отображение называют функционалом. Если вы посмотрите на нашу функцию потерь, то увидите, что это именно функционал. Для каждой конкретной линейной функции, которую задают веса $w_i$, мы получаем число, которое оценивает, насколько точно эта функция приближает наши значения $y$. Чем меньше это число, тем точнее наше решение, значит для того, чтобы найти лучшую модель, этот функционал нам надо минимизировать по $w$:
$$color{#348FEA}{|y — Xw|_2^2 longrightarrow min_w}$$
Эту задачу можно решать разными способами. В этой главе мы сначала решим эту задачу аналитически, а потом приближенно. Сравнение двух этих решений позволит нам проиллюстрировать преимущества того подхода, которому посвящена эта книга. На наш взгляд, это самый простой способ «на пальцах» показать суть машинного обучения.
МНК: точный аналитический метод
Точку минимума можно найти разными способами. Если вам интересно аналитическое решение, вы можете найти его в главе про матричные дифференцирования (раздел «Примеры вычисления производных сложных функций»). Здесь же мы воспользуемся геометрическим подходом.
Пусть $x^{(1)},ldots,x^{(D)}$ – столбцы матрицы $X$, то есть столбцы признаков. Тогда
$$Xw = w_1x^{(1)}+ldots+w_Dx^{(D)},$$
и задачу регрессии можно сформулировать следующим образом: найти линейную комбинацию столбцов $x^{(1)},ldots,x^{(D)}$, которая наилучшим способом приближает столбец $y$ по евклидовой норме – то есть найти проекцию вектора $y$ на подпространство, образованное векторами $x^{(1)},ldots,x^{(D)}$.
Разложим $y = y_{parallel} + y_{perp}$, где $y_{parallel} = Xw$ – та самая проекция, а $y_{perp}$ – ортогональная составляющая, то есть $y_{perp} = y — Xwperp x^{(1)},ldots,x^{(D)}$. Как это можно выразить в матричном виде? Оказывается, очень просто:
$$X^T(y — Xw) = 0$$
В самом деле, каждый элемент столбца $X^T(y — Xw)$ – это скалярное произведение строки $X^T$ (=столбца $X$ = одного из $x^{(i)}$) на $y — Xw$. Из уравнения $X^T(y — Xw) = 0$ уже очень легко выразить $w$:
$$w = (X^TX)^{-1}X^Ty$$
Вопрос на подумать Для вычисления $w_{ast}$ нам приходится обращать (квадратную) матрицу $X^TX$, что возможно, только если она невырожденна. Что это значит с точки зрения анализа данных? Почему мы верим, что это выполняется во всех разумных ситуациях?
Ответ (не открывайте сразу; сначала подумайте сами!)Как известно из линейной алгебры, для вещественной матрицы $X$ ранги матриц $X$ и $X^TX$ совпадают. Матрица $X^TX$ невырожденна тогда и только тогда, когда её ранг равен числу её столбцов, что равно числу столбцов матрицы $X$. Иными словами, формула регрессии поломается, только если столбцы матрицы $X$ линейно зависимы. Столбцы матрицы $X$ – это признаки. А если наши признаки линейно зависимы, то, наверное, что-то идёт не так и мы должны выкинуть часть из них, чтобы остались только линейно независимые.
Другое дело, что зачастую признаки могут быть приближённо линейно зависимы, особенно если их много. Тогда матрица $X^TX$ будет близка к вырожденной, и это, как мы дальше увидим, будет вести к разным, в том числе вычислительным проблемам.
Вычислительная сложность аналитического решения — $O(N^2D + D^3)$, где $N$ — длина выборки, $D$ — число признаков у одного объекта. Слагаемое $N^2D$ отвечает за сложность перемножения матриц $X^T$ и $X$, а слагаемое $D^3$ — за сложность обращения их произведения. Перемножать матрицы $(X^TX)^{-1}$ и $X^T$ не стоит. Гораздо лучше сначала умножить $y$ на $X^T$, а затем полученный вектор на $(X^TX)^{-1}$: так будет быстрее и, кроме того, не нужно будет хранить матрицу $(X^TX)^{-1}X^T$.
Вычисление можно ускорить, используя продвинутые алгоритмы перемножения матриц или итерационные методы поиска обратной матрицы.
Проблемы «точного» решения
Заметим, что для получения ответа нам нужно обратить матрицу $X^TX$. Это создает множество проблем:
- Основная проблема в обращении матрицы — это то, что вычислительно обращать большие матрицы дело сложное, а мы бы хотели работать с датасетами, в которых у нас могут быть миллионы точек,
- Матрица $X^TX$, хотя почти всегда обратима в разумных задачах машинного обучения, зачастую плохо обусловлена. Особенно если признаков много, между ними может появляться приближённая линейная зависимость, которую мы можем упустить на этапе формулировки задачи. В подобных случаях погрешность нахождения $w$ будет зависеть от квадрата числа обусловленности матрицы $X$, что очень плохо. Это делает полученное таким образом решение численно неустойчивым: малые возмущения $y$ могут приводить к катастрофическим изменениям $w$.
Пара слов про число обусловленности.Пожертвовав математической строгостью, мы можем считать, что число обусловленности матрицы $X$ – это корень из отношения наибольшего и наименьшего из собственных чисел матрицы $X^TX$. Грубо говоря, оно показывает, насколько разного масштаба бывают собственные значения $X^TX$. Если рассмотреть $L^2$-норму ошибки предсказания, как функцию от $w$, то её линии уровня будут эллипсоидами, форма которых определяется квадратичной формой с матрицей $X^TX$ (проверьте это!). Таким образом, число обусловленности говорит о том, насколько вытянутыми являются эти эллипсоиды.ПодробнееДанные проблемы не являются поводом выбросить решение на помойку. Существует как минимум два способа улучшить его численные свойства, однако если вы не знаете про сингулярное разложение, то лучше вернитесь сюда, когда узнаете.
-
Построим $QR$-разложение матрицы $X$. Напомним, что это разложение, в котором матрица $Q$ ортогональна по столбцам (то есть её столбцы ортогональны и имеют длину 1; в частности, $Q^TQ=E$), а $R$ квадратная и верхнетреугольная. Подставив его в формулу, получим
$$w = ((QR)^TQR)^{-1}(QR)^T y = (R^Tunderbrace{Q^TQ}_{=E}R)^{-1}R^TQ^Ty = R^{-1}R^{-T}R^TQ^Ty = R^{-1}Q^Ty$$
Отметим, что написать $(R^TR)^{-1} = R^{-1}R^{-T}$ мы имеем право благодаря тому, что $R$ квадратная. Полученная формула намного проще, обращение верхнетреугольной матрицы (=решение системы с верхнетреугольной левой частью) производится быстро и хорошо, погрешность вычисления $w$ будет зависеть просто от числа обусловленности матрицы $X$, а поскольку нахождение $QR$-разложения является достаточно стабильной операцией, мы получаем решение с более хорошими, чем у исходной формулы, численными свойствами.
-
Также можно использовать псевдообратную матрицу, построенную с помощью сингулярного разложения, о котором подробно написано в разделе про матричные разложения. А именно, пусть
$$A = Uunderbrace{mathrm{diag}(sigma_1,ldots,sigma_r)}_{=Sigma}V^T$$
– это усечённое сингулярное разложение, где $r$ – это ранг $A$. В таком случае диагональная матрица посередине является квадратной, $U$ и $V$ ортогональны по столбцам: $U^TU = E$, $V^TV = E$. Тогда
$$w = (VSigma underbrace{U^TU}_{=E}Sigma V^T)^{-1}VSigma U^Ty$$
Заметим, что $VSigma^{-2}V^Tcdot VSigma^2V^T = E = VSigma^2V^Tcdot VSigma^{-2}V^T$, так что $(VSigma^2 V^T)^{-1} = VSigma^{-2}V^T$, откуда
$$w = VSigma^{-2}underbrace{V^TV}_{=E}Sigma U^Ty = VSigma^{-1}Uy$$
Хорошие численные свойства сингулярного разложения позволяют утверждать, что и это решение ведёт себя довольно неплохо.
Тем не менее, вычисление всё равно остаётся довольно долгим и будет по-прежнему страдать (хоть и не так сильно) в случае плохой обусловленности матрицы $X$.
Полностью вылечить проблемы мы не сможем, но никто и не обязывает нас останавливаться на «точном» решении (которое всё равно никогда не будет вполне точным). Поэтому ниже мы познакомим вас с совершенно другим методом.
МНК: приближенный численный метод
Минимизируемый функционал является гладким и выпуклым, а это значит, что можно эффективно искать точку его минимума с помощью итеративных градиентных методов. Более подробно вы можете прочитать о них в разделе про методы оптимизации, а здесь мы лишь коротко расскажем об одном самом базовом подходе.
Как известно, градиент функции в точке направлен в сторону её наискорейшего роста, а антиградиент (противоположный градиенту вектор) в сторону наискорейшего убывания. То есть имея какое-то приближение оптимального значения параметра $w$, мы можем его улучшить, посчитав градиент функции потерь в точке и немного сдвинув вектор весов в направлении антиградиента:
$$w_j mapsto w_j — alpha frac{d}{d{w_j}} L(f_w, X, y) $$
где $alpha$ – это параметр алгоритма («темп обучения»), который контролирует величину шага в направлении антиградиента. Описанный алгоритм называется градиентным спуском.
Посмотрим, как будет выглядеть градиентный спуск для функции потерь $L(f_w, X, y) = frac1Nvertvert Xw — yvertvert^2$. Градиент квадрата евклидовой нормы мы уже считали; соответственно,
$$
nabla_wL = frac2{N} X^T (Xw — y)
$$
Следовательно, стартовав из какого-то начального приближения, мы можем итеративно уменьшать значение функции, пока не сойдёмся (по крайней мере в теории) к минимуму (вообще говоря, локальному, но в данном случае глобальному).
Алгоритм градиентного спуска
w = random_normal() # можно пробовать и другие виды инициализации
repeat S times: # другой вариант: while abs(err) > tolerance
f = X.dot(w) # посчитать предсказание
err = f - y # посчитать ошибку
grad = 2 * X.T.dot(err) / N # посчитать градиент
w -= alpha * grad # обновить веса
С теоретическими результатами о скорости и гарантиях сходимости градиентного спуска вы можете познакомиться в главе про методы оптимизации. Мы позволим себе лишь несколько общих замечаний:
- Поскольку задача выпуклая, выбор начальной точки влияет на скорость сходимости, но не настолько сильно, чтобы на практике нельзя было стартовать всегда из нуля или из любой другой приятной вам точки;
- Число обусловленности матрицы $X$ существенно влияет на скорость сходимости градиентного спуска: чем более вытянуты эллипсоиды уровня функции потерь, тем хуже;
- Темп обучения $alpha$ тоже сильно влияет на поведение градиентного спуска; вообще говоря, он является гиперпараметром алгоритма, и его, возможно, придётся подбирать отдельно. Другими гиперпараметрами являются максимальное число итераций $S$ и/или порог tolerance.
Иллюстрация.Рассмотрим три задачи регрессии, для которых матрица $X$ имеет соответственно маленькое, среднее и большое числа обусловленности. Будем строить для них модели вида $y=w_1x_1 + w_2x_2$. Раскрасим плоскость $(w_1, w_2)$ в соответствии со значениями $|X_{text{train}}w — y_{text{train}}|^2$. Тёмная область содержит минимум этой функции – оптимальное значение $w_{ast}$. Также запустим из из двух точек градиентный спуск с разными значениями темпа обучения $alpha$ и посмотрим, что получится:
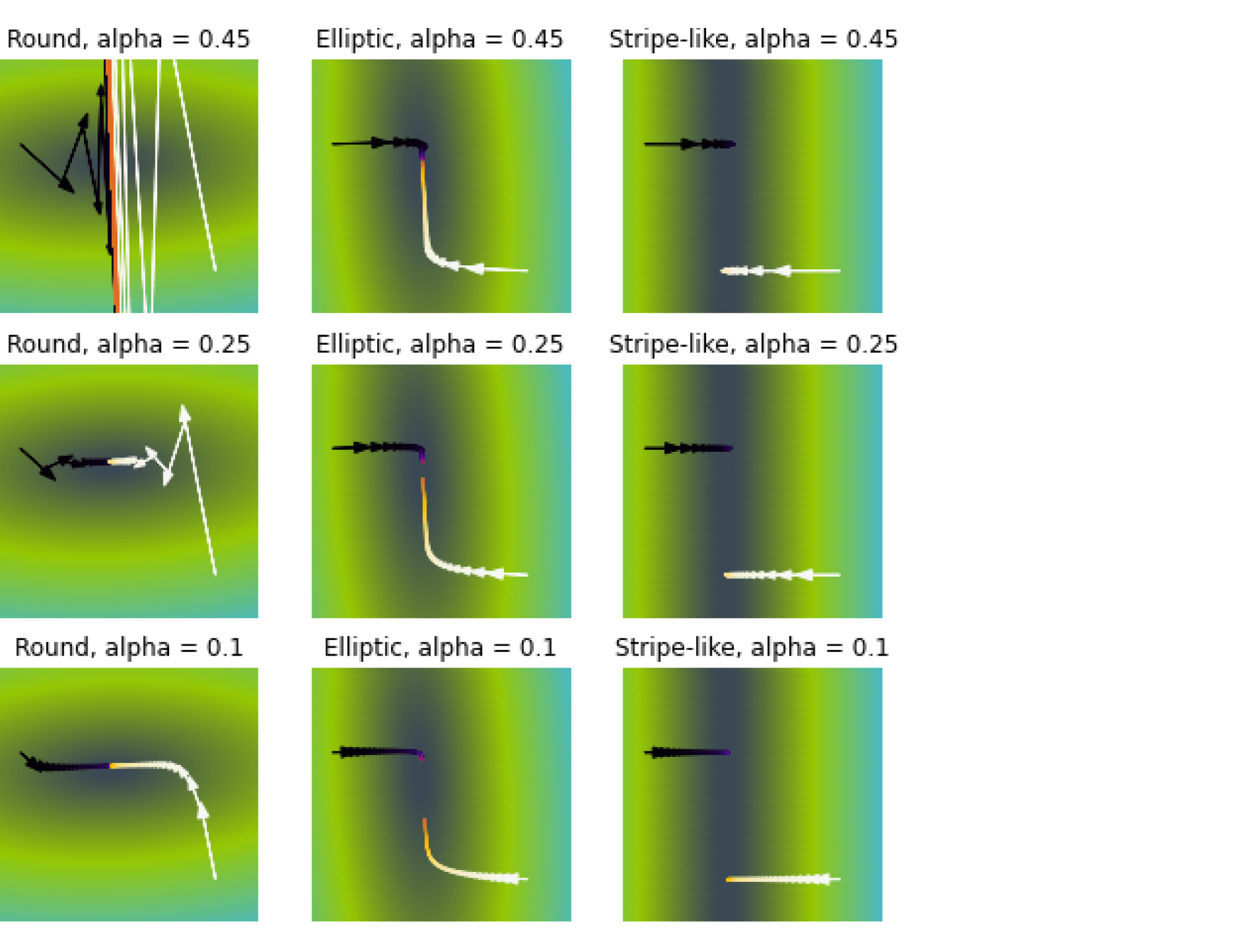
Итог: при неудачном выборе $alpha$ алгоритм не сходится или идёт вразнос, а для плохо обусловленной задачи он сходится абы куда.
Вычислительная сложность градиентного спуска – $O(NDS)$, где, как и выше, $N$ – длина выборки, $D$ – число признаков у одного объекта. Сравните с оценкой $O(N^2D + D^3)$ для «наивного» вычисления аналитического решения.
Сложность по памяти – $O(ND)$ на хранение выборки. В памяти мы держим и выборку, и градиент, но в большинстве реалистичных сценариев доминирует выборка.
Стохастический градиентный спуск
На каждом шаге градиентного спуска нам требуется выполнить потенциально дорогую операцию вычисления градиента по всей выборке (сложность $O(ND)$). Возникает идея заменить градиент его оценкой на подвыборке (в английской литературе такую подвыборку обычно именуют batch или mini-batch; в русской разговорной терминологии тоже часто встречается слово батч или мини-батч).
А именно, если функция потерь имеет вид суммы по отдельным парам объект-таргет
$$L(w, X, y) = frac1Nsum_{i=1}^NL(w, x_i, y_i),$$
а градиент, соответственно, записывается в виде
$$nabla_wL(w, X, y) = frac1Nsum_{i=1}^Nnabla_wL(w, x_i, y_i),$$
то предлагается брать оценку
$$nabla_wL(w, X, y) approx frac1Bsum_{t=1}^Bnabla_wL(w, x_{i_t}, y_{i_t})$$
для некоторого подмножества этих пар $(x_{i_t}, y_{i_t})_{t=1}^B$. Обратите внимание на множители $frac1N$ и $frac1B$ перед суммами. Почему они нужны? Полный градиент $nabla_wL(w, X, y)$ можно воспринимать как среднее градиентов по всем объектам, то есть как оценку матожидания $mathbb{E}nabla_wL(w, x, y)$; тогда, конечно, оценка матожидания по меньшей подвыборке тоже будет иметь вид среднего градиентов по объектам этой подвыборки.
Как делить выборку на батчи? Ясно, что можно было бы случайным образом сэмплировать их из полного датасета, но даже если использовать быстрый алгоритм вроде резервуарного сэмплирования, сложность этой операции не самая оптимальная. Поэтому используют линейный проход по выборке (которую перед этим лучше всё-таки случайным образом перемешать). Давайте введём ещё один параметр нашего алгоритма: размер батча, который мы обозначим $B$. Теперь на $B$ очередных примерах вычислим градиент и обновим веса модели. При этом вместо количества шагов алгоритма обычно задают количество эпох $E$. Это ещё один гиперпараметр. Одна эпоха – это один полный проход нашего сэмплера по выборке. Заметим, что если выборка очень большая, а модель компактная, то даже первый проход бывает можно не заканчивать.
Алгоритм:
w = normal(0, 1)
repeat E times:
for i = B, i <= n, i += B
X_batch = X[i-B : i]
y_batch = y[i-B : i]
f = X_batch.dot(w) # посчитать предсказание
err = f - y_batch # посчитать ошибку
grad = 2 * X_batch.T.dot(err) / B # посчитать градиент
w -= alpha * grad
Сложность по времени – $O(NDE)$. На первый взгляд, она такая же, как и у обычного градиентного спуска, но заметим, что мы сделали в $N / B$ раз больше шагов, то есть веса модели претерпели намного больше обновлений.
Сложность по памяти можно довести до $O(BD)$: ведь теперь всю выборку не надо держать в памяти, а достаточно загружать лишь текущий батч (а остальная выборка может лежать на диске, что удобно, так как в реальности задачи, в которых выборка целиком не влезает в оперативную память, встречаются сплошь и рядом). Заметим, впрочем, что при этом лучше бы $B$ взять побольше: ведь чтение с диска – намного более затратная по времени операция, чем чтение из оперативной памяти.
В целом, разницу между алгоритмами можно представлять как-то так:
Шаги стохастического градиентного спуска заметно более шумные, но считать их получается значительно быстрее. В итоге они тоже сходятся к оптимальному значению из-за того, что матожидание оценки градиента на батче равно самому градиенту. По крайней мере, сходимость можно получить при хорошо подобранных коэффициентах темпа обучения в случае выпуклого функционала качества. Подробнее мы об этом поговорим в главе про оптимизацию. Для сложных моделей и лоссов стохастический градиентный спуск может сходиться плохо или застревать в локальных минимумах, поэтому придумано множество его улучшений. О некоторых из них также рассказано в главе про оптимизацию.
Существует определённая терминологическая путаница, иногда стохастическим градиентным спуском называют версию алгоритма, в которой размер батча равен единице (то есть максимально шумная и быстрая версия алгоритма), а версии с бОльшим размером батча называют batch gradient descent. В книгах, которые, возможно, старше вас, такая процедура иногда ещё называется incremental gradient descent. Это не очень принципиально, но вы будьте готовы, если что.
Вопрос на подумать. Вообще говоря, если объём данных не слишком велик и позволяет это сделать, объекты лучше случайным образом перемешивать перед тем, как подавать их в алгоритм стохастического градиентного спуска. Как вам кажется, почему?
Также можно использовать различные стратегии отбора объектов. Например, чаще брать объекты, на которых ошибка больше. Какие ещё стратегии вы могли бы придумать?
Ответ (не открывайте сразу; сначала подумайте сами!)Легко представить себе ситуацию, в которой объекты как-нибудь неудачно упорядочены, скажем, по возрастанию таргета. Тогда модель будет попеременно то запоминать, что все таргеты маленькие, то – что все таргеты большие. Это может и не повлиять на качество итоговой модели, но может привести и к довольно печальным последствиям. И вообще, чем более разнообразные батчи модель увидит в процессе обучения, тем лучше.
Стратегий можно придумать много. Например, не брать объекты, на которых ошибка слишком большая (возможно, это выбросы – зачем на них учиться), или вообще не брать те, на которых ошибка достаточно мала (они «ничему не учат»). Рекомендуем, впрочем, прибегать к этим эвристикам, только если вы понимаете, зачем они вам нужны и почему есть надежда, что они помогут.
Неградиентные методы
После прочтения этой главы у вас может сложиться ощущение, что приближённые способы решения ML задач и градиентные методы – это одно и тоже, но вы будете правы в этом только на 98%. В принципе, существуют и другие способы численно решать эти задачи, но в общем случае они работают гораздо хуже, чем градиентный спуск, и не обладают таким хорошим теоретическим обоснованием. Мы не будем рассказывать про них подробно, но можете на досуге почитать, скажем, про Stepwise regression, Orthogonal matching pursuit или LARS. У LARS, кстати, есть довольно интересное свойство: он может эффективно работать на выборках, в которых число признаков больше числа примеров. С алгоритмом LARS вы можете познакомиться в главе про оптимизацию.
Регуляризация
Всегда ли решение задачи регрессии единственно? Вообще говоря, нет. Так, если в выборке два признака будут линейно зависимы (и следовательно, ранг матрицы будет меньше $D$), то гарантировано найдётся такой вектор весов $nu$ что $langlenu, x_irangle = 0 forall x_i$. В этом случае, если какой-то $w$ является решением оптимизационной задачи, то и $w + alpha nu $ тоже является решением для любого $alpha$. То есть решение не только не обязано быть уникальным, так ещё может быть сколь угодно большим по модулю. Это создаёт вычислительные трудности. Малые погрешности признаков сильно возрастают при предсказании ответа, а в градиентном спуске накапливается погрешность из-за операций со слишком большими числами.
Конечно, в жизни редко бывает так, что признаки строго линейно зависимы, а вот быть приближённо линейно зависимыми они вполне могут быть. Такая ситуация называется мультиколлинеарностью. В этом случае у нас, всё равно, возникают проблемы, близкие к описанным выше. Дело в том, что $Xnusim 0$ для вектора $nu$, состоящего из коэффициентов приближённой линейной зависимости, и, соответственно, $X^TXnuapprox 0$, то есть матрица $X^TX$ снова будет близка к вырожденной. Как и любая симметричная матрица, она диагонализуется в некотором ортонормированном базисе, и некоторые из собственных значений $lambda_i$ близки к нулю. Если вектор $X^Ty$ в выражении $(X^TX)^{-1}X^Ty$ будет близким к соответствующему собственному вектору, то он будет умножаться на $1 /{lambda_i}$, что опять же приведёт к появлению у $w$ очень больших по модулю компонент (при этом $w$ ещё и будет вычислен с большой погрешностью из-за деления на маленькое число). И, конечно же, все ошибки и весь шум, которые имелись в матрице $X$, при вычислении $ysim Xw$ будут умножаться на эти большие и неточные числа и возрастать во много-много раз, что приведёт к проблемам, от которых нас не спасёт никакое сингулярное разложение.
Важно ещё отметить, что в случае, когда несколько признаков линейно зависимы, веса $w_i$ при них теряют физический смысл. Может даже оказаться, что вес признака, с ростом которого таргет, казалось бы, должен увеличиваться, станет отрицательным. Это делает модель не только неточной, но и принципиально не интерпретируемой. Вообще, неадекватность знаков или величины весов – хорошее указание на мультиколлинеарность.
Для того, чтобы справиться с этой проблемой, задачу обычно регуляризуют, то есть добавляют к ней дополнительное ограничение на вектор весов. Это ограничение можно, как и исходный лосс, задавать по-разному, но, как правило, ничего сложнее, чем $L^1$- и $L^2$-нормы, не требуется.
Вместо исходной задачи теперь предлагается решить такую:
$$color{#348FEA}{min_w L(f, X, y) = min_w(|X w — y|_2^2 + lambda |w|^k_k )}$$
$lambda$ – это очередной параметр, а $|w|^k_k $ – это один из двух вариантов:
$$color{#348FEA}{|w|^2_2 = w^2_1 + ldots + w^2_D}$$
или
$$color{#348FEA}{|w|_1^1 = vert w_1 vert + ldots + vert w_D vert}$$
Добавка $lambda|w|^k_k$ называется регуляризационным членом или регуляризатором, а число $lambda$ – коэффициентом регуляризации.
Коэффициент $lambda$ является гиперпараметром модели и достаточно сильно влияет на качество итогового решения. Его подбирают по логарифмической шкале (скажем, от 1e-2 до 1e+2), используя для сравнения моделей с разными значениями $lambda$ дополнительную валидационную выборку. При этом качество модели с подобранным коэффициентом регуляризации уже проверяют на тестовой выборке, чтобы исключить переобучение. Более подробно о том, как нужно подбирать гиперпараметры, вы можете почитать в соответствующей главе.
Отдельно надо договориться о том, что вес $w_0$, соответствующий отступу от начала координат (то есть признаку из всех единичек), мы регуляризовать не будем, потому что это не имеет смысла: если даже все значения $y$ равномерно велики, это не должно портить качество обучения. Обычно это не отображают в формулах, но если придираться к деталям, то стоило бы написать сумму по всем весам, кроме $w_0$:
$$|w|^2_2 = sum_{color{red}{j=1}}^{D}w_j^2,$$
$$|w|_1 = sum_{color{red}{j=1}}^{D} vert w_j vert$$
В случае $L^2$-регуляризации решение задачи изменяется не очень сильно. Например, продифференцировав новый лосс по $w$, легко получить, что «точное» решение имеет вид:
$$w = (X^TX + lambda I)^{-1}X^Ty$$
Отметим, что за этой формулой стоит и понятная численная интуиция: раз матрица $X^TX$ близка к вырожденной, то обращать её сродни самоубийству. Мы лучше слегка исказим её добавкой $lambda I$, которая увеличит все собственные значения на $lambda$, отодвинув их от нуля. Да, аналитическое решение перестаёт быть «точным», но за счёт снижения численных проблем мы получим более качественное решение, чем при использовании «точной» формулы.
В свою очередь, градиент функции потерь
$$L(f_w, X, y) = |Xw — y|^2 + lambda|w|^2$$
по весам теперь выглядит так:
$$
nabla_wL(f_w, X, y) = 2X^T(Xw — y) + 2lambda w
$$
Подставив этот градиент в алгоритм стохастического градиентного спуска, мы получаем обновлённую версию приближенного алгоритма, отличающуюся от старой только наличием дополнительного слагаемого.
Вопрос на подумать. Рассмотрим стохастический градиентный спуск для $L^2$-регуляризованной линейной регрессии с батчами размера $1$. Выберите правильный вариант шага SGD:
(а) $w_imapsto w_i — 2alpha(langle w, x_jrangle — y_j)x_{ji} — frac{2alphalambda}N w_i,quad i=1,ldots,D$;
(б) $w_imapsto w_i — 2alpha(langle w, x_jrangle — y_j)x_{ji} — 2alphalambda w_i,quad i=1,ldots,D$;
(в) $w_imapsto w_i — 2alpha(langle w, x_jrangle — y_j)x_{ji} — 2lambda N w_i,quad i=1,ldots D$.
Ответ (не открывайте сразу; сначала подумайте сами!)Не регуляризованная функция потерь имеет вид $mathcal{L}(X, y, w) = frac1Nsum_{i=1}^Nmathcal{L}(x_i, y_i, w)$, и её можно воспринимать, как оценку по выборке $(x_i, y_i)_{i=1}^N$ идеальной функции потерь
$$mathcal{L}(w) = mathbb{E}_{x, y}mathcal{L}(x, y, w)$$
Регуляризационный член не зависит от выборки и добавляется отдельно:
$$mathcal{L}_{text{reg}}(w) = mathbb{E}_{x, y}mathcal{L}(x, y, w) + lambda|w|^2$$
Соответственно, идеальный градиент регуляризованной функции потерь имеет вид
$$nabla_wmathcal{L}_{text{reg}}(w) = mathbb{E}_{x, y}nabla_wmathcal{L}(x, y, w) + 2lambda w,$$
Градиент по батчу – это тоже оценка градиента идеальной функции потерь, только не на выборке $(X, y)$, а на батче $(x_{t_i}, y_{t_i})_{i=1}^B$ размера $B$. Он будет выглядеть так:
$$nabla_wmathcal{L}_{text{reg}}(w) = frac1Bsum_{i=1}^Bnabla_wmathcal{L}(x_{t_i}, y_{t_i}, w) + 2lambda w.$$
Как видите, коэффициентов, связанных с числом объектов в батче или в исходной выборке, во втором слагаемом нет. Так что верным является второй вариант. Кстати, обратите внимание, что в третьем ещё и нет коэффициента $alpha$ перед производной регуляризационного слагаемого, это тоже ошибка.
Вопрос на подумать. Распишите процедуру стохастического градиентного спуска для $L^1$-регуляризованной линейной регрессии. Как вам кажется, почему никого не волнует, что функция потерь, строго говоря, не дифференцируема?
Ответ (не открывайте сразу; сначала подумайте сами!)Распишем для случая батча размера 1:
$$w_imapsto w_i — alpha(langle w, x_jrangle — y_j)x_{ji} — frac{lambda}alpha text{sign}(w_i),quad i=1,ldots,D$$
Функция потерь не дифференцируема лишь в одной точке. Так как в машинном обучении чаще всего мы имеем дело с данными вероятностного характера, это не влечёт каких-то особых проблем. Дело в том, что попадание прямо в ноль очень маловероятно из-за численных погрешностей в данных, так что мы можем просто доопределить производную в одной точке, а если даже пару раз попадём в неё за время обучения, это не приведёт к каким-то значительным изменениям результатов.
Отметим, что $L^1$- и $L^2$-регуляризацию можно определять для любой функции потерь $L(w, X, y)$ (и не только в задаче регрессии, а и, например, в задаче классификации тоже). Новая функция потерь будет соответственно равна
$$widetilde{L}(w, X, y) = L(w, X, y) + lambda|w|_1$$
или
$$widetilde{L}(w, X, y) = L(w, X, y) + lambda|w|_2^2$$
Разреживание весов в $L^1$-регуляризации
$L^2$-регуляризация работает прекрасно и используется в большинстве случаев, но есть одна полезная особенность $L^1$-регуляризации: её применение приводит к тому, что у признаков, которые не оказывают большого влияния на ответ, вес в результате оптимизации получается равным $0$. Это позволяет удобным образом удалять признаки, слабо влияющие на таргет. Кроме того, это даёт возможность автоматически избавляться от признаков, которые участвуют в соотношениях приближённой линейной зависимости, соответственно, спасает от проблем, связанных с мультиколлинеарностью, о которых мы писали выше.
Не очень строгим, но довольно интуитивным образом это можно объяснить так:
- В точке оптимума линии уровня регуляризационного члена касаются линий уровня основного лосса, потому что, во-первых, и те, и другие выпуклые, а во-вторых, если они пересекаются трансверсально, то существует более оптимальная точка:
- Линии уровня $L^1$-нормы – это $N$-мерные октаэдры. Точки их касания с линиями уровня лосса, скорее всего, лежат на грани размерности, меньшей $N-1$, то есть как раз в области, где часть координат равна нулю:
Заметим, что данное построение говорит о том, как выглядит оптимальное решение задачи, но ничего не говорит о способе, которым это решение можно найти. На самом деле, найти такой оптимум непросто: у $L^1$ меры довольно плохая производная. Однако, способы есть. Можете на досуге прочитать, например, вот эту статью о том, как работало предсказание CTR в google в 2012 году. Там этой теме посвящается довольно много места. Кроме того, рекомендуем посмотреть про проксимальные методы в разделе этой книги про оптимизацию в ML.
Заметим также, что вообще-то оптимизация любой нормы $L_x, 0 < x leq 1$, приведёт к появлению разреженных векторов весов, просто если c $L^1$ ещё хоть как-то можно работать, то с остальными всё будет ещё сложнее.
Другие лоссы
Стохастический градиентный спуск можно очевидным образом обобщить для решения задачи линейной регрессии с любой другой функцией потерь, не только квадратичной: ведь всё, что нам нужно от неё, – это чтобы у функции потерь был градиент. На практике это делают редко, но тем не менее рассмотрим ещё пару вариантов.
MAE
Mean absolute error, абсолютная ошибка, появляется при замене $L^2$ нормы в MSE на $L^1$:
$$color{#348FEA}{MAE(y, widehat{y}) = frac1Nsum_{i=1}^N vert y_i — widehat{y}_ivert}$$
Можно заметить, что в MAE по сравнению с MSE существенно меньший вклад в ошибку будут вносить примеры, сильно удалённые от ответов модели. Дело тут в том, что в MAE мы считаем модуль расстояния, а не квадрат, соответственно, вклад больших ошибок в MSE получается существенно больше. Такая функция потерь уместна в случаях, когда вы пытаетесь обучить регрессию на данных с большим количеством выбросов в таргете.
Иначе на эту разницу можно посмотреть так: MSE приближает матожидание условного распределения $y mid x$, а MAE – медиану.
MAPE
Mean absolute percentage error, относительная ошибка.
$$MAPE(y, widehat{y}) = frac1Nsum_{i=1}^N left|frac{widehat{y}_i-y_i}{y_i}right|$$
Часто используется в задачах прогнозирования (например, погоды, загруженности дорог, кассовых сборов фильмов, цен), когда ответы могут быть различными по порядку величины, и при этом мы бы хотели верно угадать порядок, то есть мы не хотим штрафовать модель за предсказание 2000 вместо 1000 в разы сильней, чем за предсказание 2 вместо 1.
Вопрос на подумать. Кроме описанных выше в задаче линейной регрессии можно использовать и другие функции потерь, например, Huber loss:
$$mathcal{L}(f, X, y) = sum_{i=1}^Nh_{delta}(y_i — langle w_i, xrangle),mbox{ где }h_{delta}(z) = begin{cases}
frac12z^2, |z|leqslantdelta,\
delta(|z| — frac12delta), |z| > delta
end{cases}$$
Число $delta$ является гиперпараметром. Сложная формула при $vert zvert > delta$ нужна, чтобы функция $h_{delta}(z)$ была непрерывной. Попробуйте объяснить, зачем может быть нужна такая функция потерь.
Ответ (не открывайте сразу; сначала подумайте сами!)Часто требования формулируют в духе «функция потерь должна слабее штрафовать то-то и сильней штрафовать вот это». Например, $L^2$-регуляризованный лосс штрафует за большие по модулю веса. В данном случае можно заметить, что при небольших значениях ошибки берётся просто MSE, а при больших мы начинаем штрафовать нашу модель менее сурово. Например, это может быть полезно для того, чтобы выбросы не так сильно влияли на результат обучения.
Линейная классификация
Теперь давайте поговорим про задачу классификации. Для начала будем говорить про бинарную классификацию на два класса. Обобщить эту задачу до задачи классификации на $K$ классов не составит большого труда. Пусть теперь наши таргеты $y$ кодируют принадлежность к положительному или отрицательному классу, то есть принадлежность множеству ${-1,1}$ (в этой главе договоримся именно так обозначать классы, хотя в жизни вам будут нередко встречаться и метки ${0,1}$), а $x$ – по-прежнему векторы из $mathbb{R}^D$. Мы хотим обучить линейную модель так, чтобы плоскость, которую она задаёт, как можно лучше отделяла объекты одного класса от другого.
В идеальной ситуации найдётся плоскость, которая разделит классы: положительный окажется с одной стороны от неё, а отрицательный с другой. Выборка, для которой это возможно, называется линейно разделимой. Увы, в реальной жизни такое встречается крайне редко.
Как обучить линейную модель классификации, нам ещё предстоит понять, но уже ясно, что итоговое предсказание можно будет вычислить по формуле
$$y = text{sign} langle w, x_irangle$$
Почему бы не решать, как задачу регрессии?Мы можем попробовать предсказывать числа $-1$ и $1$, минимизируя для этого, например, MSE с последующим взятием знака, но ничего хорошего не получится. Во-первых, регрессия почти не штрафует за ошибки на объектах, которые лежат близко к *разделяющей плоскости*, но не с той стороны. Во вторых, ошибкой будет считаться предсказание, например, $5$ вместо $1$, хотя нам-то на самом деле не важно, какой у числа модуль, лишь бы знак был правильным. Если визуализировать такое решение, то проблемы тоже вполне заметны:
Нам нужна прямая, которая разделяет эти точки, а не проходит через них!
Сконструируем теперь функционал ошибки так, чтобы он вышеперечисленными проблемами не обладал. Мы хотим минимизировать число ошибок классификатора, то есть
$$sum_i mathbb{I}[y_i neq sign langle w, x_irangle]longrightarrow min_w$$
Домножим обе части на $$y_i$$ и немного упростим
$$sum_i mathbb{I}[y_i langle w, x_irangle < 0]longrightarrow min_w$$
Величина $M = y_i langle w, x_irangle$ называется отступом (margin) классификатора. Такая фунция потерь называется misclassification loss. Легко видеть, что
-
отступ положителен, когда $sign(y_i) = sign(langle w, x_irangle)$, то есть класс угадан верно; при этом чем больше отступ, тем больше расстояние от $x_i$ до разделяющей гиперплоскости, то есть «уверенность классификатора»;
-
отступ отрицателен, когда $sign(y_i) ne sign(langle w, x_irangle)$, то есть класс угадан неверно; при этом чем больше по модулю отступ, тем более сокрушительно ошибается классификатор.
От каждого из отступов мы вычисляем функцию
$$F(M) = mathbb{I}[M < 0] = begin{cases}1, M < 0,\ 0, Mgeqslant 0end{cases}$$
Она кусочно-постоянная, и из-за этого всю сумму невозможно оптимизировать градиентными методами: ведь её производная равна нулю во всех точках, где она существует. Но мы можем мажорировать её какой-нибудь более гладкой функцией, и тогда задачу можно будет решить. Функции можно использовать разные, у них свои достоинства и недостатки, давайте рассмотрим несколько примеров:
Вопрос на подумать. Допустим, мы как-то обучили классификатор, и подавляющее большинство отступов оказались отрицательными. Правда ли нас постигла катастрофа?
Ответ (не открывайте сразу; сначала подумайте сами!)Наверное, мы что-то сделали не так, но ситуацию можно локально выправить, если предсказывать классы, противоположные тем, которые выдаёт наша модель.
Вопрос на подумать. Предположим, что у нас есть два классификатора с примерно одинаковыми и достаточно приемлемыми значениями интересующей нас метрики. При этом одна почти всегда выдаёт предсказания с большими по модулю отступами, а вторая – с относительно маленькими. Верно ли, что первая модель лучше, чем вторая?
Ответ (не открывайте сразу; сначала подумайте сами!)На первый взгляд кажется, что первая модель действительно лучше: ведь она предсказывает «увереннее», но на самом деле всё не так однозначно: во многих случаях модель, которая умеет «честно признать, что не очень уверена в ответе», может быть предпочтительней модели, которая врёт с той же непотопляемой уверенностью, что и говорит правду. В некоторых случаях лучше может оказаться модель, которая, по сути, просто отказывается от классификации на каких-то объектах.
Ошибка перцептрона
Реализуем простейшую идею: давайте считать отступы только на неправильно классифицированных объектах и учитывать их не бинарно, а линейно, пропорционально их размеру. Получается такая функция:
$$F(M) = max(0, -M)$$
Давайте запишем такой лосс с $L^2$-регуляризацией:
$$L(w, x, y) = lambdavertvert wvertvert^2_2 + sum_i max(0, -y_i langle w, x_irangle)$$
Найдём градиент:
$$
nabla_w L(w, x, y) = 2 lambda w + sum_i
begin{cases}
0, & y_i langle w, x_i rangle > 0 \
— y_i x_i, & y_i langle w, x_i rangle leq 0
end{cases}
$$
Имея аналитическую формулу для градиента, мы теперь можем так же, как и раньше, применить стохастический градиентный спуск, и задача будет решена.
Данная функция потерь впервые была предложена для перцептрона Розенблатта, первой вычислительной модели нейросети, которая в итоге привела к появлению глубокого обучения.
Она решает задачу линейной классификации, но у неё есть одна особенность: её решение не единственно и сильно зависит от начальных параметров. Например, все изображённые ниже классификаторы имеют одинаковый нулевой лосс:
Hinge loss, SVM
Для таких случаев, как на картинке выше, возникает логичное желание не только найти разделяющую прямую, но и постараться провести её на одинаковом удалении от обоих классов, то есть максимизировать минимальный отступ:
Это можно сделать, слегка поменяв функцию ошибки, а именно положив её равной:
$$F(M) = max(0, 1-M)$$
$$L(w, x, y) = lambda||w||^2_2 + sum_i max(0, 1-y_i langle w, x_irangle)$$
$$
nabla_w L(w, x, y) = 2 lambda w + sum_i
begin{cases}
0, & 1 — y_i langle w, x_i rangle leq 0 \
— y_i x_i, & 1 — y_i langle w, x_i rangle > 0
end{cases}
$$
Почему же добавленная единичка приводит к желаемому результату?
Интуитивно это можно объяснить так: объекты, которые проклассифицированы правильно, но не очень «уверенно» (то есть $0 leq y_i langle w, x_irangle < 1$), продолжают вносить свой вклад в градиент и пытаются «отодвинуть» от себя разделяющую плоскость как можно дальше.
К данному выводу можно прийти и чуть более строго; для этого надо совершенно по-другому взглянуть на выражение, которое мы минимизируем. Поможет вот эта картинка:
Если мы максимизируем минимальный отступ, то надо максимизировать $frac{2}{|w|_2}$, то есть ширину полосы при условии того, что большинство объектов лежат с правильной стороны, что эквивалентно решению нашей исходной задачи:
$$lambda|w|^2_2 + sum_i max(0, 1-y_i langle w, x_irangle) longrightarrowminlimits_{w}$$
Отметим, что первое слагаемое у нас обратно пропорционально ширине полосы, но мы и максимизацию заменили на минимизацию, так что тут всё в порядке. Второе слагаемое – это штраф за то, что некоторые объекты неправильно расположены относительно разделительной полосы. В конце концов, никто нам не обещал, что классы наши линейно разделимы и можно провести оптимальную плоскость вообще без ошибок.
Итоговое положение плоскости задаётся всего несколькими обучающими примерами. Это ближайшие к плоскости правильно классифицированные объекты, которые называют опорными векторами или support vectors. Весь метод, соответственно, зовётся методом опорных векторов, или support vector machine, или сокращённо SVM. Начиная с шестидесятых годов это был сильнейший из известных методов машинного обучения. В девяностые его сменили методы, основанные на деревьях решений, которые, в свою очередь, недавно передали «пальму первенства» нейросетям.
Почему же SVM был столь популярен? Из-за небольшого количества параметров и доказуемой оптимальности. Сейчас для нас нормально выбирать специальный алгоритм под задачу и подбирать оптимальные гиперпараметры для этого алгоритма перебором, а когда-то трава была зеленее, а компьютеры медленнее, и такой роскоши у людей не было. Поэтому им нужны были модели, которые гарантированно неплохо работали бы в любой ситуации. Такой моделью и был SVM.
Другие замечательные свойства SVM: существование уникального решения и доказуемо минимальная склонность к переобучению среди всех популярных классов линейных классификаторов. Кроме того, несложная модификация алгоритма, ядровый SVM, позволяет проводить нелинейные разделяющие поверхности.
Строгий вывод постановки задачи SVM можно прочитать тут или в лекции К.В. Воронцова.
Логистическая регрессия
В этом параграфе мы будем обозначать классы нулём и единицей.
Ещё один интересный метод появляется из желания посмотреть на классификацию как на задачу предсказания вероятностей. Хороший пример – предсказание кликов в интернете (например, в рекламе и поиске). Наличие клика в обучающем логе не означает, что, если повторить полностью условия эксперимента, пользователь обязательно кликнет по объекту опять. Скорее у объектов есть какая-то «кликабельность», то есть истинная вероятность клика по данному объекту. Клик на каждом обучающем примере является реализацией этой случайной величины, и мы считаем, что в пределе в каждой точке отношение положительных и отрицательных примеров должно сходиться к этой вероятности.
Проблема состоит в том, что вероятность, по определению, величина от 0 до 1, а простого способа обучить линейную модель так, чтобы это ограничение соблюдалось, нет. Из этой ситуации можно выйти так: научить линейную модель правильно предсказывать какой-то объект, связанный с вероятностью, но с диапазоном значений $(-infty,infty)$, и преобразовать ответы модели в вероятность. Таким объектом является logit или log odds – логарифм отношения вероятности положительного события к отрицательному $logleft(frac{p}{1-p}right)$.
Если ответом нашей модели является $logleft(frac{p}{1-p}right)$, то искомую вероятность посчитать не трудно:
$$langle w, x_irangle = logleft(frac{p}{1-p}right)$$
$$e^{langle w, x_irangle} = frac{p}{1-p}$$
$$p=frac{1}{1 + e^{-langle w, x_irangle}}$$
Функция в правой части называется сигмоидой и обозначается
$$color{#348FEA}{sigma(z) = frac1{1 + e^{-z}}}$$
Таким образом, $p = sigma(langle w, x_irangle)$
Как теперь научиться оптимизировать $w$ так, чтобы модель как можно лучше предсказывала логиты? Нужно применить метод максимума правдоподобия для распределения Бернулли. Это самое простое распределение, которое возникает, к примеру, при бросках монетки, которая орлом выпадает с вероятностью $p$. У нас только событием будет не орёл, а то, что пользователь кликнул на объект с такой вероятностью. Если хотите больше подробностей, почитайте про распределение Бернулли в теоретическом минимуме.
Правдоподобие позволяет понять, насколько вероятно получить данные значения таргета $y$ при данных $X$ и весах $w$. Оно имеет вид
$$ p(ymid X, w) =prod_i p(y_imid x_i, w) $$
и для распределения Бернулли его можно выписать следующим образом:
$$ p(ymid X, w) =prod_i p_i^{y_i} (1-p_i)^{1-y_i} $$
где $p_i$ – это вероятность, посчитанная из ответов модели. Оптимизировать произведение неудобно, хочется иметь дело с суммой, так что мы перейдём к логарифмическому правдоподобию и подставим формулу для вероятности, которую мы получили выше:
$$ ell(w, X, y) = sum_i big( y_i log(p_i) + (1-y_i)log(1-p_i) big) =$$
$$ =sum_i big( y_i log(sigma(langle w, x_i rangle)) + (1-y_i)log(1 — sigma(langle w, x_i rangle)) big) $$
Если заметить, что
$$
sigma(-z) = frac{1}{1 + e^z} = frac{e^{-z}}{e^{-z} + 1} = 1 — sigma(z),
$$
то выражение можно переписать проще:
$$
ell(w, X, y)=sum_i big( y_i log(sigma(langle w, x_i rangle)) + (1 — y_i) log(sigma(-langle w, x_i rangle)) big)
$$
Нас интересует $w$, для которого правдоподобие максимально. Чтобы получить функцию потерь, которую мы будем минимизировать, умножим его на минус один:
$$color{#348FEA}{L(w, X, y) = -sum_i big( y_i log(sigma(langle w, x_i rangle)) + (1 — y_i) log(sigma(-langle w, x_i rangle)) big)}$$
В отличие от линейной регрессии, для логистической нет явной формулы решения. Деваться некуда, будем использовать градиентный спуск. К счастью, градиент устроен очень просто:
$$
nabla_w L(y, X, w) = -sum_i x_i big( y_i — sigma(langle w, x_i rangle)) big)
$$
Вывод формулы градиентаНам окажется полезным ещё одно свойство сигмоиды:
$$
frac{d log sigma(z)}{d z} = left( log left( frac{1}{1 + e^{-z}} right) right)’ = frac{e^{-z}}{1 + e^{-z}} = sigma(-z)
$$ $$
frac{d log sigma(-z)}{d z} = -sigma(z)
$$
Отсюда:
$$
nabla_w log sigma(langle w, x_i rangle) = sigma(-langle w, x_i rangle) x_i
$$ $$
nabla_w log sigma(-langle w, x_i rangle) = -sigma(langle w, x_i rangle) x_i
$$
и градиент оказывается равным
$$
nabla_w L(y, X, w) = -sum_i big( y_i x_i sigma(-langle w, x_i rangle) — (1 — y_i) x_i sigma(langle w, x_i rangle)) big) =
$$ $$
= -sum_i big( y_i x_i (1 — sigma(langle w, x_i rangle)) — (1 — y_i) x_i sigma(langle w, x_i rangle)) big) =
$$ $$
= -sum_i big( y_i x_i — y_i x_i sigma(langle w, x_i rangle) — x_i sigma(langle w, x_i rangle) + y_i x_i sigma(langle w, x_i rangle)) big) =
$$ $$
= -sum_i big( y_i x_i — x_i sigma(langle w, x_i rangle)) big)
$$
Предсказание модели будет вычисляться, как мы договаривались, следующим образом:
$$p=sigma(langle w, x_irangle)$$
Это вероятность положительного класса, а как от неё перейти к предсказанию самого класса? В других методах нам достаточно было посчитать знак предсказания, но теперь все наши предсказания положительные и находятся в диапазоне от 0 до 1. Что же делать? Интуитивным и не совсем (и даже совсем не) правильным является ответ «взять порог 0.5». Более корректным будет подобрать этот порог отдельно, для уже построенной регрессии минимизируя нужную вам метрику на отложенной тестовой выборке. Например, сделать так, чтобы доля положительных и отрицательных классов примерно совпадала с реальной.
Отдельно заметим, что метод называется логистической регрессией, а не логистической классификацией именно потому, что предсказываем мы не классы, а вещественные числа – логиты.
Вопрос на подумать. Проверьте, что, если метки классов – это $pm1$, а не $0$ и $1$, то функцию потерь для логистической регрессии можно записать в более компактном виде:
$$mathcal{L}(w, X, y) = sum_{i=1}^Nlog(1 + e^{-y_ilangle w, x_irangle})$$
Вопрос на подумать. Правда ли разделяющая поверхность модели логистической регрессии является гиперплоскостью?
Ответ (не открывайте сразу; сначала подумайте сами!)Разделяющая поверхность отделяет множество точек, которым мы присваиваем класс $0$ (или $-1$), и множество точек, которым мы присваиваем класс $1$. Представляется логичным провести отсечку по какому-либо значению предсказанной вероятности. Однако, выбор этого значения — дело не очевидное. Как мы увидим в главе про калибровку классификаторов, это может быть не настоящая вероятность. Допустим, мы решили провести границу по значению $frac12$. Тогда разделяющая поверхность как раз задаётся равенством $p = frac12$, что равносильно $langle w, xrangle = 0$. А это гиперплоскость.
Вопрос на подумать. Допустим, что матрица объекты-признаки $X$ имеет полный ранг по столбцам (то есть все её столбцы линейно независимы). Верно ли, что решение задачи восстановления логистической регрессии единственно?
Ответ (не открывайте сразу; сначала подумайте сами!)В этот раз хорошего геометрического доказательства, как было для линейной регрессии, пожалуй, нет; нам придётся честно посчитать вторую производную и доказать, что она является положительно определённой. Сделаем это для случая, когда метки классов – это $pm1$. Формулы так получатся немного попроще. Напомним, что в этом случае
$$L(w, X, y) = -sum_{i=1}^Nlog(1 + e^{-y_ilangle w, x_irangle})$$
Следовательно,
$$frac{partial}{partial w_{j}}L(w, X, y) = sum_{i=1}^Nfrac{y_ix_{ij}e^{-y_ilangle w, x_irangle}}{1 + e^{-y_ilangle w, x_irangle}} = sum_{i=1}^Ny_ix_{ij}left(1 — frac1{1 + e^{-y_ilangle w, x_irangle}}right)$$
$$frac{partial^2L}{partial w_jpartial w_k}(w, X, y) = sum_{i=1}^Ny^2_ix_{ij}x_{ik}frac{e^{-y_ilangle w, x_irangle}}{(1 + e^{-y_ilangle w, x_irangle})^2} =$$
$$ = sum_{i=1}^Ny^2_ix_{ij}x_{ik}sigma(y_ilangle w, x_irangle)(1 — sigma(y_ilangle w, x_irangle))$$
Теперь заметим, что $y_i^2 = 1$ и что, если обозначить через $D$ диагональную матрицу с элементами $sigma(y_ilangle w, x_irangle)(1 — sigma(y_ilangle w, x_irangle))$ на диагонали, матрицу вторых производных можно представить в виде:
$$nabla^2L = left(frac{partial^2mathcal{L}}{partial w_jpartial w_k}right) = X^TDX$$
Так как $0 < sigma(y_ilangle w, x_irangle) < 1$, у матрицы $D$ на диагонали стоят положительные числа, из которых можно извлечь квадратные корни, представив $D$ в виде $D = D^{1/2}D^{1/2}$. В свою очередь, матрица $X$ имеет полный ранг по столбцам. Стало быть, для любого вектора приращения $une 0$ имеем
$$u^TX^TDXu = u^TX^T(D^{1/2})^TD^{1/2}Xu = vert D^{1/2}Xu vert^2 > 0$$
Таким образом, функция $L$ выпукла вниз как функция от $w$, и, соответственно, точка её экстремума непременно будет точкой минимума.
А теперь – почему это не совсем правда. Дело в том, что, говоря «точка её экстремума непременно будет точкой минимума», мы уже подразумеваем существование этой самой точки экстремума. Только вот существует этот экстремум не всегда. Можно показать, что для линейно разделимой выборки функция потерь логистической регрессии не ограничена снизу, и, соответственно, никакого экстремума нет. Доказательство мы оставляем читателю.
Вопрос на подумать. На картинке ниже представлены результаты работы на одном и том же датасете трёх моделей логистической регрессии с разными коэффициентами $L^2$-регуляризации:
Наверху показаны предсказанные вероятности положительного класса, внизу – вид разделяющей поверхности.
Как вам кажется, какие картинки соответствуют самому большому коэффициенту регуляризации, а какие – самому маленькому? Почему?
Ответ (не открывайте сразу; сначала подумайте сами!)Коэффициент регуляризации максимален у левой модели. На это нас могут натолкнуть два соображения. Во-первых, разделяющая прямая проведена достаточно странно, то есть можно заподозрить, что регуляризационный член в лосс-функции перевесил функцию потерь исходной задачи. Во-вторых, модель предсказывает довольно близкие к $frac12$ вероятности – это значит, что значения $langle w, xrangle$ близки к нулю, то есть сам вектор $w$ близок к нулевому. Это также свидетельствует о том, что регуляризационный член играет слишком важную роль при оптимизации.
Наименьший коэффициент регуляризации у правой модели. Её предсказания достаточно «уверенные» (цвета на верхнем графике сочные, то есть вероятности быстро приближаются к $0$ или $1$). Это может свидетельствовать о том, что числа $langle w, xrangle$ достаточно велики по модулю, то есть $vertvert w vertvert$ достаточно велик.
Многоклассовая классификация
В этом разделе мы будем следовать изложению из лекций Евгения Соколова.
Пусть каждый объект нашей выборки относится к одному из $K$ классов: $mathbb{Y} = {1, ldots, K}$. Чтобы предсказывать эти классы с помощью линейных моделей, нам придётся свести задачу многоклассовой классификации к набору бинарных, которые мы уже хорошо умеем решать. Мы разберём два самых популярных способа это сделать – one-vs-all и all-vs-all, а проиллюстрировать их нам поможет вот такой игрушечный датасет
Один против всех (one-versus-all)
Обучим $K$ линейных классификаторов $b_1(x), ldots, b_K(x)$, выдающих оценки принадлежности классам $1, ldots, K$ соответственно. В случае с линейными моделями эти классификаторы будут иметь вид
$$b_k(x) = text{sgn}left(langle w_k, x rangle + w_{0k}right)$$
Классификатор с номером $k$ будем обучать по выборке $left(x_i, 2mathbb{I}[y_i = k] — 1right)_{i = 1}^{N}$; иными словами, мы учим классификатор отличать $k$-й класс от всех остальных.
Логично, чтобы итоговый классификатор выдавал класс, соответствующий самому уверенному из бинарных алгоритмов. Уверенность можно в каком-то смысле измерить с помощью значений линейных функций:
$$a(x) = text{argmax}_k left(langle w_k, x rangle + w_{0k}right) $$
Давайте посмотрим, что даст этот подход применительно к нашему датасету. Обучим три линейных модели, отличающих один класс от остальных:
Теперь сравним значения линейных функций
и для каждой точки выберем тот класс, которому соответствует большее значение, то есть самый «уверенный» классификатор:
Хочется сказать, что самый маленький класс «обидели».
Проблема данного подхода заключается в том, что каждый из классификаторов $b_1(x), dots, b_K(x)$ обучается на своей выборке, и значения линейных функций $langle w_k, x rangle + w_{0k}$ или, проще говоря, «выходы» классификаторов могут иметь разные масштабы. Из-за этого сравнивать их будет неправильно. Нормировать вектора весов, чтобы они выдавали ответы в одной и той же шкале, не всегда может быть разумным решением: так, в случае с SVM веса перестанут являться решением задачи, поскольку нормировка изменит норму весов.
Все против всех (all-versus-all)
Обучим $C_K^2$ классификаторов $a_{ij}(x)$, $i, j = 1, dots, K$, $i neq j$. Например, в случае с линейными моделями эти модели будут иметь вид
$$b_{ij}(x) = text{sgn}left( langle w_{ij}, x rangle + w_{0,ij} right)$$
Классификатор $a_{ij}(x)$ будем настраивать по подвыборке $X_{ij} subset X$, содержащей только объекты классов $i$ и $j$. Соответственно, классификатор $a_{ij}(x)$ будет выдавать для любого объекта либо класс $i$, либо класс $j$. Проиллюстрируем это для нашей выборки:
Чтобы классифицировать новый объект, подадим его на вход каждого из построенных бинарных классификаторов. Каждый из них проголосует за своей класс; в качестве ответа выберем тот класс, за который наберется больше всего голосов:
$$a(x) = text{argmax}_ksum_{i = 1}^{K} sum_{j neq i}mathbb{I}[a_{ij}(x) = k]$$
Для нашего датасета получается следующая картинка:
Обратите внимание на серый треугольник на стыке областей. Это точки, для которых голоса разделились (в данном случае каждый классификатор выдал какой-то свой класс, то есть у каждого класса было по одному голосу). Для этих точек нет явного способа выдать обоснованное предсказание.
Многоклассовая логистическая регрессия
Некоторые методы бинарной классификации можно напрямую обобщить на случай многих классов. Выясним, как это можно проделать с логистической регрессией.
В логистической регрессии для двух классов мы строили линейную модель
$$b(x) = langle w, x rangle + w_0,$$
а затем переводили её прогноз в вероятность с помощью сигмоидной функции $sigma(z) = frac{1}{1 + exp(-z)}$. Допустим, что мы теперь решаем многоклассовую задачу и построили $K$ линейных моделей
$$b_k(x) = langle w_k, x rangle + w_{0k},$$
каждая из которых даёт оценку принадлежности объекта одному из классов. Как преобразовать вектор оценок $(b_1(x), ldots, b_K(x))$ в вероятности? Для этого можно воспользоваться оператором $text{softmax}(z_1, ldots, z_K)$, который производит «нормировку» вектора:
$$text{softmax}(z_1, ldots, z_K) = left(frac{exp(z_1)}{sum_{k = 1}^{K} exp(z_k)},
dots, frac{exp(z_K)}{sum_{k = 1}^{K} exp(z_k)}right).$$
В этом случае вероятность $k$-го класса будет выражаться как
$$P(y = k vert x, w) = frac{
exp{(langle w_k, x rangle + w_{0k})}}{ sum_{j = 1}^{K} exp{(langle w_j, x rangle + w_{0j})}}.$$
Обучать эти веса предлагается с помощью метода максимального правдоподобия: так же, как и в случае с двухклассовой логистической регрессией:
$$sum_{i = 1}^{N} log P(y = y_i vert x_i, w) to max_{w_1, dots, w_K}$$
Масштабируемость линейных моделей
Мы уже обсуждали, что SGD позволяет обучению хорошо масштабироваться по числу объектов, так как мы можем не загружать их целиком в оперативную память. А что делать, если признаков очень много, или мы не знаем заранее, сколько их будет? Такое может быть актуально, например, в следующих ситуациях:
- Классификация текстов: мы можем представить текст в формате «мешка слов», то есть неупорядоченного набора слов, встретившихся в данном тексте, и обучить на нём, например, определение тональности отзыва в интернете. Наличие каждого слова из языка в тексте у нас будет кодироваться отдельной фичой. Тогда размерность каждого элемента обучающей выборки будет порядка нескольких сотен тысяч.
- В задаче предсказания кликов по рекламе можно получить выборку любой размерности, например, так: в качестве фичи закодируем индикатор того, что пользователь X побывал на веб-странице Y. Суммарная размерность тогда будет порядка $10^9 cdot 10^7 = 10^{16}$. Кроме того, всё время появляются новые пользователи и веб-страницы, так что на этапе применения нас ждут сюрпризы.
Есть несколько хаков, которые позволяют бороться с такими проблемами:
- Несмотря на то, что полная размерность объекта в выборке огромна, количество ненулевых элементов в нём невелико. Значит, можно использовать разреженное кодирование, то есть вместо плотного вектора хранить словарь, в котором будут перечислены индексы и значения ненулевых элементов вектора.
- Даже хранить все веса не обязательно! Можно хранить их в хэш-таблице и вычислять индекс по формуле
hash(feature) % tablesize. Хэш может вычисляться прямо от слова или id пользователя. Таким образом, несколько фичей будут иметь общий вес, который тем не менее обучится оптимальным образом. Такой подход называется hashing trick. Ясно, что сжатие вектора весов приводит к потерям в качестве, но, как правило, ценой совсем небольших потерь можно сжать этот вектор на много порядков.
Примером открытой библиотеки, в которой реализованы эти возможности, является vowpal wabbit.
Parameter server
Если при решении задачи ставки столь высоки, что мы не можем разменивать качество на сжатие вектора весов, а признаков всё-таки очень много, то задачу можно решать распределённо, храня все признаки в шардированной хеш-таблице
Кружки здесь означают отдельные сервера. Жёлтые загружают данные, а серые хранят части модели. Для обучения жёлтый кружок запрашивает у серого нужные ему для предсказания веса, считает градиент и отправляет его обратно, где тот потом применяется. Схема обладает бесконечной масштабируемостью, но задач, где это оправдано, не очень много.
Подытожим
На линейную модель можно смотреть как на однослойную нейросеть, поэтому многие методы, которые были изначально разработаны для них, сейчас переиспользуются в задачах глубокого обучения, а базовые подходы к регрессии, классификации и оптимизации вообще выглядят абсолютно так же. Так что несмотря на то, что в целом линейные модели на сегодня применяются редко, то, из чего они состоят и как строятся, знать очень и очень полезно.
Надеемся также, что главным итогом прочтения этой главы для вас будет осознание того, что решение любой ML-задачи состоит из выбора функции потерь, параметризованного класса моделей и способа оптимизации. В следующих главах мы познакомимся с другими моделями и оптимизаторами, но эти базовые принципы не изменятся.

























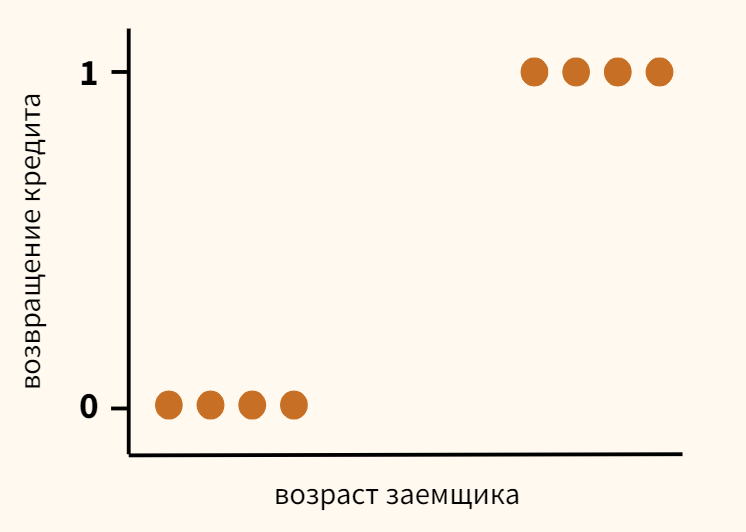

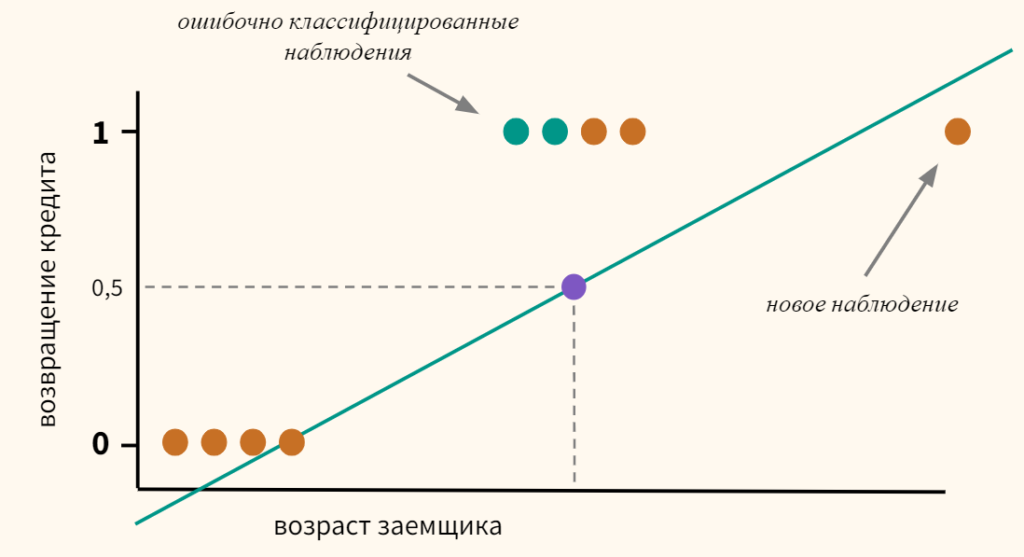
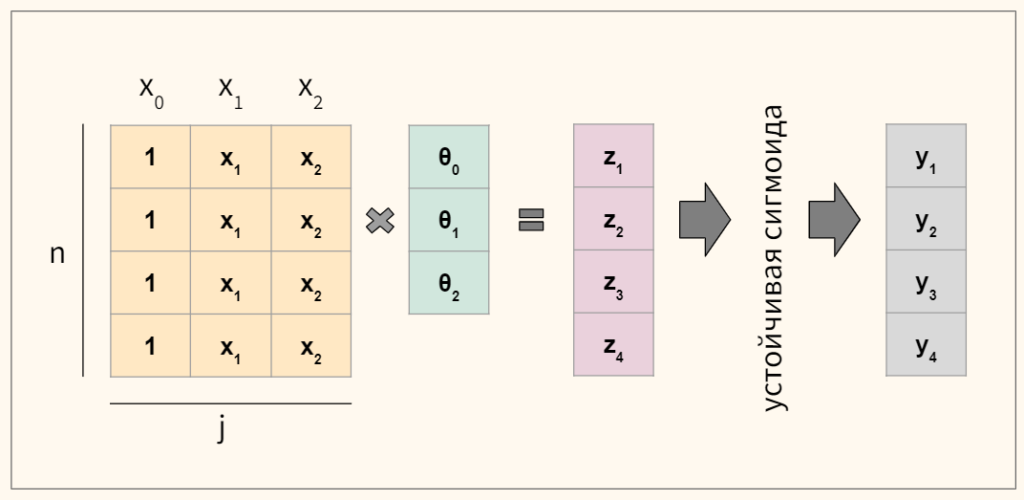



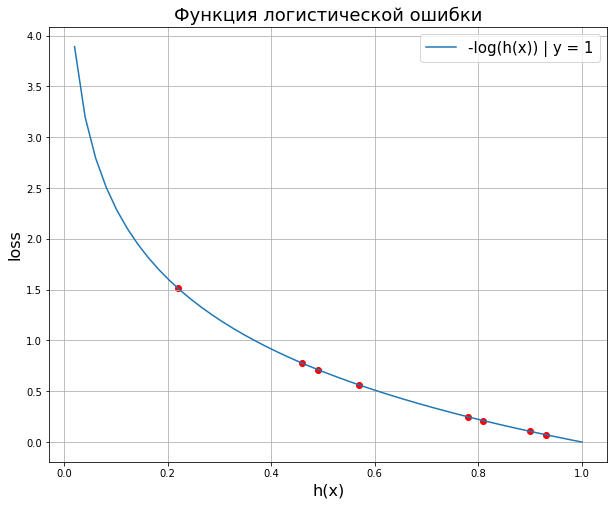




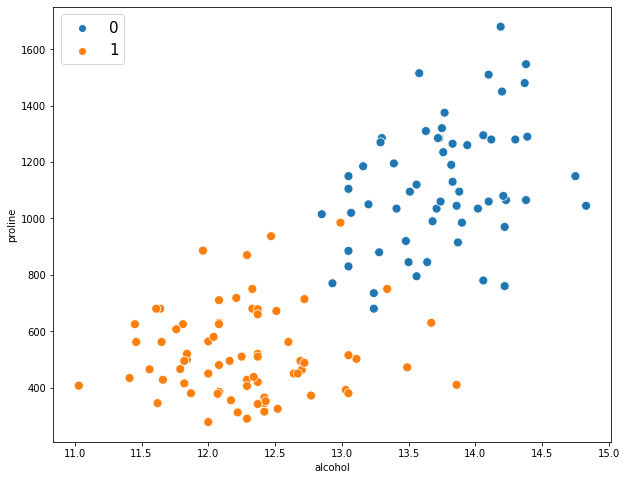









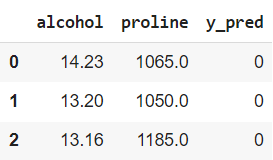
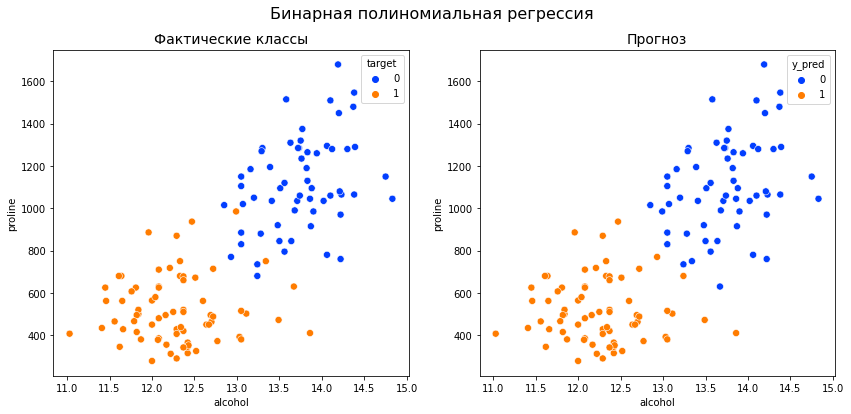

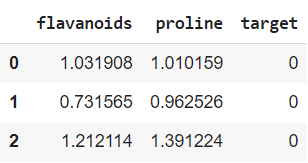

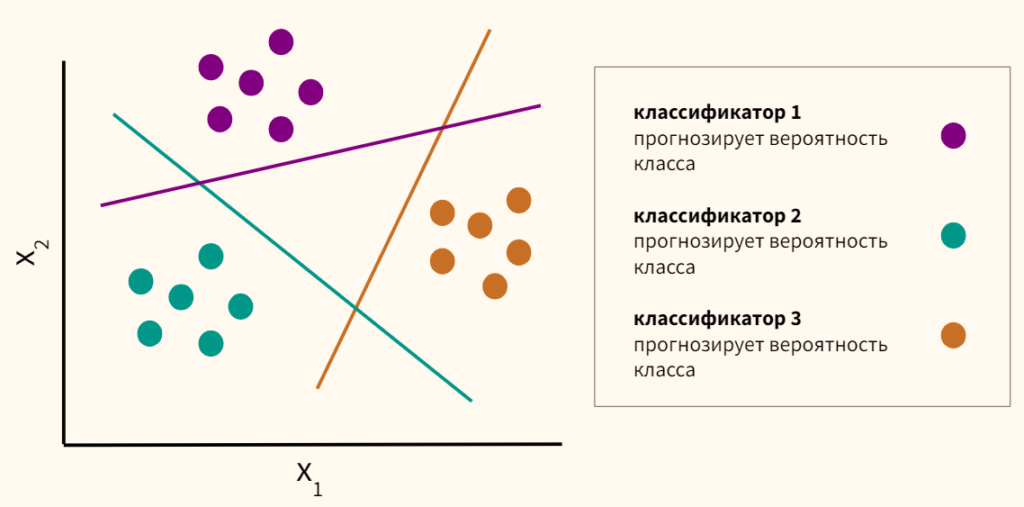


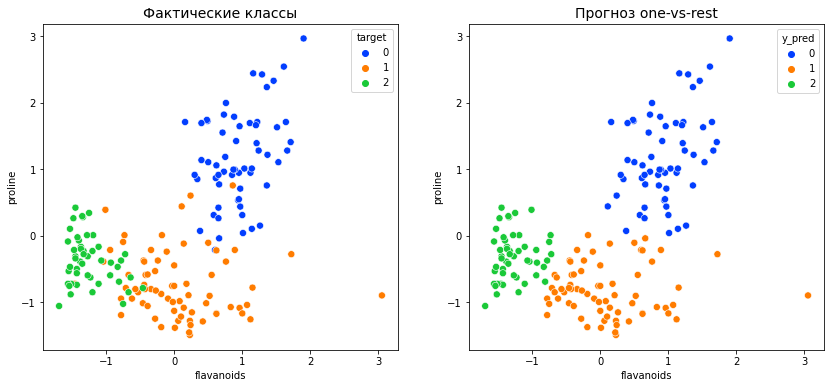






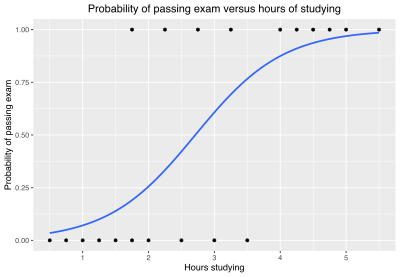























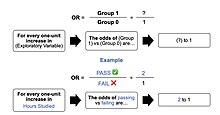



![{displaystyle {begin{aligned}Y_{i}mid x_{1,i},ldots ,x_{m,i} &sim operatorname {Bernoulli} (p_{i})\operatorname {mathbb {E} } [Y_{i}mid x_{1,i},ldots ,x_{m,i}]&=p_{i}\Pr(Y_{i}=ymid x_{1,i},ldots ,x_{m,i})&={begin{cases}p_{i}&{text{if }}y=1\1-p_{i}&{text{if }}y=0end{cases}}\Pr(Y_{i}=ymid x_{1,i},ldots ,x_{m,i})&=p_{i}^{y}(1-p_{i})^{(1-y)}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/49627157ac00e729a38538029505c210f99955d7)


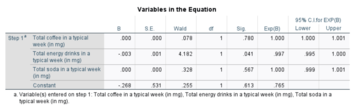















![{displaystyle operatorname {logit} (operatorname {mathbb {E} } [Y_{i}mid x_{1,i},ldots ,x_{m,i}])=operatorname {logit} (p_{i})=ln left({frac {p_{i}}{1-p_{i}}}right)=beta _{0}+beta _{1}x_{1,i}+cdots +beta _{m}x_{m,i}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/be13d1b675b8fb6e9db4835cd151b5fc9076e282)
![{displaystyle operatorname {logit} (operatorname {mathbb {E} } [Y_{i}mid mathbf {X} _{i}])=operatorname {logit} (p_{i})=ln left({frac {p_{i}}{1-p_{i}}}right)={boldsymbol {beta }}cdot mathbf {X} _{i}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55adb25231d3cea8f63c4fe56a8677f6eb59415f)
![{displaystyle operatorname {mathbb {E} } [Y_{i}mid mathbf {X} _{i}]=p_{i}=operatorname {logit} ^{-1}({boldsymbol {beta }}cdot mathbf {X} _{i})={frac {1}{1+e^{-{boldsymbol {beta }}cdot mathbf {X} _{i}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/337230f2ea410541cdcf94442ce37b92515dd364)





![{displaystyle {begin{aligned}Pr(Y_{i}=1mid mathbf {X} _{i})&=Pr(Y_{i}^{ast }>0mid mathbf {X} _{i})\[5pt]&=Pr({boldsymbol {beta }}cdot mathbf {X} _{i}+varepsilon _{i}>0)\[5pt]&=Pr(varepsilon _{i}>-{boldsymbol {beta }}cdot mathbf {X} _{i})\[5pt]&=Pr(varepsilon _{i}<{boldsymbol {beta }}cdot mathbf {X} _{i})&&{text{(because the logistic distribution is symmetric)}}\[5pt]&=operatorname {logit} ^{-1}({boldsymbol {beta }}cdot mathbf {X} _{i})&\[5pt]&=p_{i}&&{text{(see above)}}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/67ce399af3b2241cc7121b48c60ceaf626e430c5)





![{displaystyle {begin{aligned}Pr(Y_{i}=1mid mathbf {X} _{i})={}&Pr left(Y_{i}^{1ast }>Y_{i}^{0ast }mid mathbf {X} _{i}right)&\[5pt]={}&Pr left(Y_{i}^{1ast }-Y_{i}^{0ast }>0mid mathbf {X} _{i}right)&\[5pt]={}&Pr left({boldsymbol {beta }}_{1}cdot mathbf {X} _{i}+varepsilon _{1}-left({boldsymbol {beta }}_{0}cdot mathbf {X} _{i}+varepsilon _{0}right)>0right)&\[5pt]={}&Pr left(({boldsymbol {beta }}_{1}cdot mathbf {X} _{i}-{boldsymbol {beta }}_{0}cdot mathbf {X} _{i})+(varepsilon _{1}-varepsilon _{0})>0right)&\[5pt]={}&Pr(({boldsymbol {beta }}_{1}-{boldsymbol {beta }}_{0})cdot mathbf {X} _{i}+(varepsilon _{1}-varepsilon _{0})>0)&\[5pt]={}&Pr(({boldsymbol {beta }}_{1}-{boldsymbol {beta }}_{0})cdot mathbf {X} _{i}+varepsilon >0)&&{text{(substitute }}varepsilon {text{ as above)}}\[5pt]={}&Pr({boldsymbol {beta }}cdot mathbf {X} _{i}+varepsilon >0)&&{text{(substitute }}{boldsymbol {beta }}{text{ as above)}}\[5pt]={}&Pr(varepsilon >-{boldsymbol {beta }}cdot mathbf {X} _{i})&&{text{(now, same as above model)}}\[5pt]={}&Pr(varepsilon <{boldsymbol {beta }}cdot mathbf {X} _{i})&\[5pt]={}&operatorname {logit} ^{-1}({boldsymbol {beta }}cdot mathbf {X} _{i})\[5pt]={}&p_{i}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/be3b57ca6773ef745cdfd82367611e9394215f9e)

![{displaystyle {begin{aligned}Pr(Y_{i}=0)&={frac {1}{Z}}e^{{boldsymbol {beta }}_{0}cdot mathbf {X} _{i}}\[5pt]Pr(Y_{i}=1)&={frac {1}{Z}}e^{{boldsymbol {beta }}_{1}cdot mathbf {X} _{i}}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e1e2a04fd15f2e5617c0606a7644fe719823960)

![{displaystyle {begin{aligned}Pr(Y_{i}=0)&={frac {e^{{boldsymbol {beta }}_{0}cdot mathbf {X} _{i}}}{e^{{boldsymbol {beta }}_{0}cdot mathbf {X} _{i}}+e^{{boldsymbol {beta }}_{1}cdot mathbf {X} _{i}}}}\[5pt]Pr(Y_{i}=1)&={frac {e^{{boldsymbol {beta }}_{1}cdot mathbf {X} _{i}}}{e^{{boldsymbol {beta }}_{0}cdot mathbf {X} _{i}}+e^{{boldsymbol {beta }}_{1}cdot mathbf {X} _{i}}}}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1fa489d73be139142872ddccccecd567635525d5)


![{displaystyle {begin{aligned}Pr(Y_{i}=1)&={frac {e^{({boldsymbol {beta }}_{1}+mathbf {C} )cdot mathbf {X} _{i}}}{e^{({boldsymbol {beta }}_{0}+mathbf {C} )cdot mathbf {X} _{i}}+e^{({boldsymbol {beta }}_{1}+mathbf {C} )cdot mathbf {X} _{i}}}}\[5pt]&={frac {e^{{boldsymbol {beta }}_{1}cdot mathbf {X} _{i}}e^{mathbf {C} cdot mathbf {X} _{i}}}{e^{{boldsymbol {beta }}_{0}cdot mathbf {X} _{i}}e^{mathbf {C} cdot mathbf {X} _{i}}+e^{{boldsymbol {beta }}_{1}cdot mathbf {X} _{i}}e^{mathbf {C} cdot mathbf {X} _{i}}}}\[5pt]&={frac {e^{mathbf {C} cdot mathbf {X} _{i}}e^{{boldsymbol {beta }}_{1}cdot mathbf {X} _{i}}}{e^{mathbf {C} cdot mathbf {X} _{i}}(e^{{boldsymbol {beta }}_{0}cdot mathbf {X} _{i}}+e^{{boldsymbol {beta }}_{1}cdot mathbf {X} _{i}})}}\[5pt]&={frac {e^{{boldsymbol {beta }}_{1}cdot mathbf {X} _{i}}}{e^{{boldsymbol {beta }}_{0}cdot mathbf {X} _{i}}+e^{{boldsymbol {beta }}_{1}cdot mathbf {X} _{i}}}}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f545a36890435f35e006242acda552c8f62dcd0)






![{displaystyle p_{i}=operatorname {mathbb {E} } left[left.{frac {Y_{i}}{n_{i}}},right|,mathbf {X} _{i}right],,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2b159f2ac064c09122cc087d3d9e8d3bbb415f9)
![{displaystyle operatorname {logit} left(operatorname {mathbb {E} } left[left.{frac {Y_{i}}{n_{i}}},right|,mathbf {X} _{i}right]right)=operatorname {logit} (p_{i})=ln left({frac {p_{i}}{1-p_{i}}}right)={boldsymbol {beta }}cdot mathbf {X} _{i},,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4629c0d5675907b48d10f5173bbc338f262e540a)

















![{displaystyle {begin{aligned}D_{text{null}}&=-2ln {frac {text{likelihood of null model}}{text{likelihood of the saturated model}}}\[6pt]D_{text{fitted}}&=-2ln {frac {text{likelihood of fitted model}}{text{likelihood of the saturated model}}}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d85ab8f60a3e7685815b132b3a80d03d26d9745a)
![{displaystyle {begin{aligned}D_{text{null}}-D_{text{fitted}}&=-2left(ln {frac {text{likelihood of null model}}{text{likelihood of the saturated model}}}-ln {frac {text{likelihood of fitted model}}{text{likelihood of the saturated model}}}right)\[6pt]&=-2ln {frac {left({dfrac {text{likelihood of null model}}{text{likelihood of the saturated model}}}right)}{left({dfrac {text{likelihood of fitted model}}{text{likelihood of the saturated model}}}right)}}\[6pt]&=-2ln {frac {text{likelihood of the null model}}{text{likelihood of fitted model}}}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd851b7e234a5483dbb21da9fff7d9d2419e3e3e)




















![{displaystyle {begin{aligned}&lim limits _{Nrightarrow +infty }N^{-1}sum _{i=1}^{N}log Pr(y_{i}mid x_{i};theta )=sum _{xin {mathcal {X}}}sum _{yin {mathcal {Y}}}Pr(X=x,Y=y)log Pr(Y=ymid X=x;theta )\[6pt]={}&sum _{xin {mathcal {X}}}sum _{yin {mathcal {Y}}}Pr(X=x,Y=y)left(-log {frac {Pr(Y=ymid X=x)}{Pr(Y=ymid X=x;theta )}}+log Pr(Y=ymid X=x)right)\[6pt]={}&-D_{text{KL}}(Yparallel Y_{theta })-H(Ymid X)end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9b300972d40831096c1ab7bdf34338a71eca96d9)