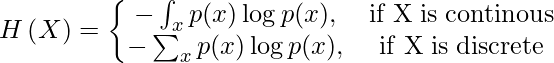При работе с машинным обучением или проблемой глубокого обучения функции потерь / затрат используются для оптимизации модели во время обучения. Цель почти всегда состоит в том, чтобы минимизировать функцию потерь. Чем меньше потери, тем лучше модель. Потери перекрестной энтропии — наиболее важная функция затрат. Он используется для оптимизации моделей классификации. Понимание кросс-энтропии зависит от понимания функции активации Softmax. Я разместил еще одну статью ниже, чтобы осветить это предварительное условие.
Рассмотрим задачу классификации 4 классов, в которой изображение классифицируется как собака, кошка, лошадь или гепард.
На приведенном выше рисунке Softmax преобразует логиты в вероятности. Цель кросс-энтропии — взять выходные вероятности (P) и измерить расстояние от истинных значений (как показано на рисунке ниже).
В приведенном выше примере желаемый результат — [1,0,0,0] для класса dog, но модель выводит [0.775, 0.116, 0.039, 0.070].
Цель состоит в том, чтобы выходные данные модели были как можно ближе к желаемым выходным данным (значениям истинности). Во время обучения модели веса модели итеративно корректируются соответственно с целью минимизации потерь кросс-энтропии. Процесс корректировки весов — это то, что определяет обучение модели, и поскольку модель продолжает обучение, а потери минимизируются, мы говорим, что модель обучается.
Концепция кросс-энтропии восходит к области теории информации, где Клод Шеннон ввел понятие энтропии в 1948 году. Прежде чем погрузиться в функцию стоимости кросс-энтропии, давайте введем энтропию.
Энтропия
Энтропия случайной величины X — это уровень неопределенности, присущий переменным возможного результата.
Для p(x) — распределения вероятностей и случайной величины X энтропия определяется следующим образом
Причина отрицательного знака: log(p(x))<0 для всех p(x) в (0,1). p (x) — это распределение вероятностей, поэтому значения должны находиться в диапазоне от 0 до 1.
Чем больше значение энтропии, H(x), тем больше неопределенность для распределения вероятностей и чем меньше значение, тем меньше неопределенность.
Пример
Рассмотрим следующие 3 «контейнера» с фигурами: треугольники и круги.
Контейнер 1: вероятность выбрать треугольник — 26/30, а вероятность выбрать круг — 4/30. По этой причине вероятность выбрать одну форму и / или не выбрать другую более определена.
Контейнер 2: вероятность выбора треугольной формы составляет 14/30 и 16/30 в противном случае. Есть почти 50–50 шансов выбрать любую конкретную форму. Меньшая уверенность в выборе данной формы, чем в 1.
Контейнер 3. Форма, выбранная из контейнера 3, скорее всего, будет кругом. Вероятность выбрать круг — 29/30, а вероятность выбрать треугольник — 1/30. Совершенно очевидно, что выбранная форма будет круглой.
Давайте вычислим энтропию, чтобы удостовериться в наших утверждениях о достоверности выбора данной формы.
Как и ожидалось, энтропия для первого и третьего контейнера меньше, чем для второго. Это связано с тем, что вероятность выбора данной формы более определена в контейнерах 1 и 3, чем в контейнере 2. Функция кросс-энтропии потерь.
Также называется логарифмической потерей, потерей журнала или логистической потерей. Вероятность каждого прогнозируемого класса сравнивается с фактическим желаемым выходом класса 0 или 1, и вычисляется оценка / потеря, которая штрафует вероятность на основе того, насколько далеко она от фактического ожидаемого значения. Штраф является логарифмическим по своей природе, давая большой балл за большие различия, близкие к 1, и малый балл за небольшие различия, стремящиеся к 0.
Кросс-энтропийная потеря используется при корректировке весов модели во время обучения. Цель состоит в том, чтобы минимизировать потери, т. Е. Чем меньше потери, тем лучше модель. У идеальной модели потеря кросс-энтропии равна 0.
Кросс-энтропия определяется как
Потеря бинарной кросс-энтропии
Для бинарной классификации у нас есть бинарная кросс-энтропия, определяемая как
Бинарная кросс-энтропия часто рассчитывается как средняя кросс-энтропия по всем примерам данных.
Пример
Рассмотрим проблему классификации со следующими вероятностями Softmax (S) и метками (T). Цель состоит в том, чтобы рассчитать потерю кросс-энтропии с учетом этой информации.
Категориальная кросс-энтропия вычисляется следующим образом
Softmax — это непрерывно дифференцируемая функция. Это позволяет вычислить производную функции потерь по каждому весу в нейронной сети. Это свойство позволяет модели соответствующим образом корректировать веса, чтобы минимизировать функцию потерь (выходные данные модели близки к истинным значениям).
Предположим, что после нескольких итераций обучения модели модель выводит следующий вектор логитов
0.095 меньше, чем предыдущие потери, то есть 0.3677, что означает, что модель обучается. Процесс оптимизации (корректировка весов так, чтобы выходные данные были близки к истинным значениям) продолжается до завершения обучения.
Keras предоставляет следующие функции кросс-энтропийных потерь: бинарные, категориальные, разреженные категориальные функции кросс-энтропийных потерь.
Категориальная кросс-энтропия и разреженная категориальная кросс-энтропия
И категориальная кросс-энтропия, и разреженная категориальная кросс-энтропия имеют одну и ту же функцию потерь, как определено в уравнении 2. Единственная разница между ними заключается в том, как определяются метки истинности.
- Категориальная кросс-энтропия используется, когда истинные метки закодированы горячим способом, например, у нас есть следующие истинные значения для задачи классификации 3 классов
[1,0,0],[0,1,0]и[0,0,1]. - В разреженной категориальной кросс-энтропии метки истинности кодируются целыми числами, например,
[1],[2]и[3]для задачи 3 классов.
Надеюсь, эта статья помогла вам более четко понять функцию потерь кросс-энтропии.
Спасибо за прочтение 
В предыдущей части мы рассматривали вероятностную постановку задачи машинного обучения, статистические модели, модель регрессии как частный случай и ее обучение методом максимизации правдоподобия.
В данной части рассмотрим метод максимизации правдоподобия в классификации: в чем роль кроссэнтропии, функций сигмоиды и softmax, как кроссэнтропия связана с «расстоянием» между распределениями вероятностей и почему модель регрессии тоже обучается через минимизацию кроссэнтропии. Данная часть содержит много отсылок к формулам и понятиям, введенным в первой части, поэтому рекомендуется читать их последовательно.
В третьей части (статья планируется) перейдем от метода максимизации правдоподобия к байесовскому выводу и его различным приближениям.
Данная серия статей не является введением в машинное обучение и предполагает знакомство читателя с основными понятиями. Задача статей — рассмотреть машинное обучение с точки зрения теории вероятностей, что позволит по новому взглянуть на проблему, понять связь машинного обучения со статистикой и лучше понимать формулы из научных статей. Также на описанном материале строятся более сложные темы, такие как вариационные автокодировщики (Kingma and Welling, 2013), нейробайесовские методы (Müller et al., 2021) и даже некоторые теории сознания (Friston et al., 2022).
Содержание текущей части
-
В первом разделе мы рассмотрим модель классификации, кроссэнтропию и ее связь с методом максимизации правдоподобия, а также ряд несколько фактов про функции softmax и sigmoid.
-
Во втором разделе поговорим о связи минимизации кроссэнтропии с минимизацией расхождения Кульбака-Лейблера, и как минимизация расхождения Кульбака-Лейблера может помочь в более сложных случаях, чем обычная классификация и регрессия.
Звездочкой* отмечены дополнительные разделы, которые не повлияют на понимание дальнейшего материала.
1. Вероятностная модель классификации
1.1. Модель классификации и функция потерь
1.2. Функция softmax в классификации
1.3. Температура softmax и операция hardmax*
1.4. Функция sigmoid в классификации
2. Кроссэнтропия в вероятностных моделях
2.1. Разметка с неуверенностью
2.2. Кроссэнтропия и расхождение Кульбака-Лейблера
2.3. Кроссэнтропия как максимизация правдоподобия*
2.4. Кроссэнтропия в задаче регрессии*
2.5. Кроссэнтропия с точки зрения оптимизации*
1. Вероятностная модель классификации
1.1. Модель классификации и функция потерь
Чтобы задать вероятностную модель, нам нужно определить, в какой форме она будет предсказывать распределение . Если задаче регрессии мы ограничивали распределения
только нормальными распределениями, то в задаче классификации это будет не оптимальным решением, так как классы по сути представляют собой неупорядоченное множество (хотя на них есть порядок, но лишь технически, и он может быть выбран произвольно). В задаче классификации мы можем предсказывать вероятность для каждого класса, и тогда модель будет выдавать столько чисел, сколько есть классов в
.
Пусть мы имеем датасет и предполагаем, что все примеры независимы и взяты и одного и того же распределения (i.i.d., см. предыдущую часть, раздел 3.4). Для обучения модели снова применим метод максимизации правдоподобия, то есть будем искать такие параметры
, которые максимизируют
. В разделе 2.3 мы уже расписывали формулу, которая получается в результате, но ввиду ее важности повторим ее еще раз. Первое равенство ниже следует из i.i.d.-гипотезы, второе по правилам математики:
Таким образом, для максимизации вероятности выборки данных нам нужно минимизировать сумму величин
для всех обучающих примеров .
В модели регрессии эта величина была сведена к квадрату разности предсказания и верного ответа (часть 1, формула 7). Но в задаче классификации на данном этапе считать больше ничего не нужно. Нашей задачей было задать вероятностную модель, определить с ее помощью функцию потерь и таким образом свести обучение к задаче оптимизации, то есть минимизации функции потерь, и мы это уже сделали. Функция потерь (2) называется кроссэнтропией (также перекрестной энтропией, или logloss). Она равна минус логарифму предсказанной вероятности для верного класса .
Категориальная кроссэнтропия
Возьмем произвольный пример и выданные моделью вероятности обозначим за , где
— количество классов. К метке класса (эталонному ответу) применим one-hot кодирование, получив вектор
, в котором лишь один элемент равен единице, а остальные равны нулю. Тогда выражение (2) можно рассчитать таким образом:
Лишь один элемент суммы будет не равен нулю — тот, который соответствует верному классу. Для него первый множитель будет равен единице, а второй будет логарифмом предсказанной вероятности для верного класса, что соответствует выражению (2).
Примечание. На самом деле формула (3) является определением кроссэнтропии, а формула (2) ее частным случаем, когда вырождено и назначает вероятность 1 классу с индексом
. О случае, когда это не так, подробнее поговорим во втором разделе.
Бинарная кроссэнтропия
Если класса всего два, то как правило делают следующим образом: модель выдает лишь одно число от 0 до 1, оно рассматривается как вероятность второго класса, а
рассматривается как вероятность первого класса. Пусть
равно единице, если первый класс верен, иначе равно нулю. Тогда выражение (3) технически можно вычислить следующим образом:
Снова лишь одно слагаемое будет ненулевым, и таким образом мы посчитаем логарифм предсказанной вероятности для верного класса. Формулы (18) и (19) называются категориальной кроссэнтропией (они эквивалентны если для одного из классов), формула (18) называется бинарной кроссэнтропией.
В этом разделе мы рассмотрели обучение модели классификации. Часто в классификации упоминают о функции softmax, но почему-то мы о ней ничего не говорили. Складывается ощущение, что мы что-то упустили. В следующем разделе мы поговорим о роли функции softmax в классификации.
1.2. Функция softmax в классификации
В предыдущем разделе мы определили, что модель классификации должна выдавать вероятности для всех классов. Но модель — это не только формат входных и выходных данных, а еще и внутренняя архитектура. Она может быть совершенно разной: для классификации применяются либо нейронные сети, либо решающие деревья, либо машины опорных векторов и так далее.
Рассмотрим для примера нейронную сеть. Пусть мы имеем классов, и выходной слой нейронной сети выдает
чисел от
до
. Чтобы вектор из
чисел являлся распределением вероятностей, он должен удовлетворять двум ограничениям:
-
Вероятность каждого класса не может быть ниже нуля
-
Сумма вероятностей должна быть равна единице
Для удовлетворения первого ограничения лучше чтобы модель выдавала не вероятности, а их логарифмы: если логарифм некой величины меняется от до
, то сама величина меняется от
до
. Чтобы удовлетворялось второе ограничение, каждую предсказанную вероятность мы можем делить на сумму всех предсказанных вероятностей. Такая операция называется
-нормализацией вектора вероятностей.
Отсюда мы можем вывести формулу для операции softmax. Эта операция принимает на вход набор из чисел от
до
(они называются логитами, англ. logits)
и возвращает распределение вероятностей из
чисел
. Softmax является последовательностью двух операций: взятия экспоненты и
-нормализации:
Таким образом, softmax — это векторная операция, принимающая вектор из произвольных чисел (логитов) и возвращающая вектор вероятностей, удовлетворяющий свойствам 1 и 2. Она применяется как завершающая операция во многих моделях классификации — таким образом мы можем быть уверены, что выданные моделью числа будут именно распределением вероятностей (т. е. удовлетворять свойствам 1 и 2). Существуют и различные альтернативы функции softmax, например sparsemax (Martins and Astudillo, 2016).
Модель, предсказывающая логитов, к которым применяется операция softmax, будет обладать только одним ограничением: она не может предсказывать строго нулевые или строго единичные вероятности. Зато такую модель можно обучать градиентным спуском, так как функция softmax дифференцируема.
Технически иногда функция softmax рассматривается как часть модели, иногда как часть функции потерь. Например, в библиотеке Keras мы можем добавить функцию активации 'softmax' в последний слой сети и использовать функцию потерь CategoricalCrossentropy(), а можем наоборот не добавлять функцию активации в последний слой и использовать функцию потерь CategoricalCrossentropy (from_logits=True), которая включает в себя расчет softmax (и ее производной при обратном проходе). С математической точки зрения разницы между этими двумя способами не будет, но погрешность расчета функции потерь и производной во втором случае будет меньше. В PyTorch мы можем применить LogSoftmax вместе с NLLLoss (negative log-likelihood), а можем вместо этого применить torch.nn.functional.cross_entropy, который включает в себя расчет LogSoftmax.
1.3. Температура softmax и операция hardmax*
У функции softmax (5) есть важное свойство: если ко всем логитам прибавить одну и ту же константу
, то вероятности
никак не изменятся, так как после применения экспоненты константа из слагаемого превратится в множитель, и множители в числителе и знаменателе сократятся. Однако если все логиты
умножить на некую константу
, то тогда вероятности
изменятся: если
, то вероятности
станут ближе друг к другу, что означает меньшую уверенность в предсказании, если же
, то наоборот мы получим большую уверенность в предсказании. Этот дополнительный множитель, если он используется, называется «температурой» softmax.
При тот класс, логит которого был наибольшим, получит вероятность 1, остальные классы — вероятность 0, такую операцию по аналогии часто называют hardmax. Иногда ее упоминают как argmax, потому что hardmax можно считать one-hot кодированием индекса, который возвращает операция argmax.
На этом примере видно то, как употребляются понятия soft и hard в машинном обучении: hard-операции (hardmax, argmax, hard attention, hard labeling, sign) связаны с выбором некоего элемента в множестве, а soft-операции (softmax, soft attention, soft labeling, soft sign) являются их дифференцируемыми аналогами. Например, в softmax можно рассчитать производную каждого выходного элемента по каждому входному. В hardmax или argmax это не имеет смысла: производные всегда будут равны нулю.
Это можно понять даже не прибегая к расчетам, поскольку у дифференцируемости есть очень простая наглядная интерпретация: операция дифференцируема если плавное изменение
приводит к плавному изменению
. Это верно для операции softmax, и благодаря этому мы можем применять градиентный спуск или градиентный бустинг. Но в операции hardmax плавное изменение логитов приводит к тому, что выходные вероятности либо остаются такими же, либо меняются скачкообразно, поэтому (без дополнительных ухищрений) градиентный спуск и градиентный бустинг оказываются неприменимы.
1.4. Функция sigmoid в классификации
Рассмотрим случай бинарной классификации. Представим, что у нас есть 2 класса, и модель выдает 2 логита , из которых с помощью softmax получаем вероятности
, сумма которых равна единице. Но прибавление одной и той же константы к
не меняет вероятности, поэтому иметь две «степени свободы» излишне, и имеет смысл зафиксировать
в значении 0. Теперь меняя
модель будет менять вероятности классов
. Значения
и
, согласно (21), будут связаны следующим образом:
Такая функция носит название сигмоиды:
Примечание. В более широком смысле, сигмоидами называют и другие функции одной переменной, график которых выглядит похожим образом. Для преобразования логита в вероятность вместо можно использовать любую и этих функций, разница между ними не принципиальна. Также сигмоида иногда используется в промежуточных слоях нейронных сетей.
К чему мы в итоге пришли? К тому, что если класса всего два, то иметь два логита в модели не обязательно, достаточно всего одного, к которому применяется сигмоида вместо softmax. Функция потерь при этом становится бинарной кроссэнтропией (4). На самом деле то же рассуждение можно применить и к мультиклассовой классификации: если классов , то достаточно иметь
логитов, но так обычно не делают.
Теперь запишем функцию, обратную сигмоиде. Эта функция преобразует вероятность обратно в логит и называется logit function:
Если — это вероятность второго класса, а
— вероятность первого класса, то выражение
означает то, во сколько раз второй класс вероятнее первого. Это выражение называется odds ratio. Логит является его логарифмом и называется log odds ratio.
Если мы используем в обучении сигмоиду, то модель непосредственно предсказывает логит , то есть логарифм того, во сколько раз второй класс вероятнее первого.
2. Кроссэнтропия в вероятностных моделях
2.1. Разметка с неуверенностью
В выражениях для функции потерь в классификации (2) и регрессии (часть 1, формула 7) мы предполагали наличие для каждого примера эталонного ответа
, к которому модель должна стремиться. Но в более общем случае эталонный ответ
может быть не конкретным значением, а распределением вероятностей на множестве
, так же как и предсказание модели. То есть в разметке датасета значения
указаны с определенной степенью неуверенности: если это классификация, то могут быть указаны вероятности для всех классов, если регрессия — то может быть указана погрешность.
Ситуация, когда разметка датасета содержит некую степень неуверенности, не такая уж редкая. Например, в пусть в задаче классификации эмоций по видеозаписи датасет размечен сразу несколькими людьми-аннотаторами, которые иногда дают разные ответы. Например, одно из видео в датасете может быть размечено как «happiness» 11 аннотаторами и как «sadness» 9 аннотаторами. Оставив только «happiness» мы потеряем часть информации. Вместо этого мы можем оставить обе эмоции, считать их распределением вероятностей: ,
и обучать модель выдавать для данного примера такое же распределение вероятностей.
Благодаря разметке с неуверенностью сохраняется больше информации: есть явно выраженные эмоции, а есть сложно определяемые.
Но с другой стороны для каждого видео есть какая-то истинная эмоция: либо «happiness», либо «sadness» — человек не может испытывать обе эти эмоции одновременно. В теории модель могла бы обучиться определять эмоции точнее, чем человек, и разметка с неуверенностью может помешать модели выучиться точнее человека: если человек дает 50% вероятности обоим классам, и мы используем это как эталонный ответ, то модель будет стремиться к нему, даже если она способна определить эмоцию точнее.
2.2. Кроссэнтропия и расхождение Кульбака-Лейблера
Пусть мы имеем датасет из пар , в котором эталонный ответ
является не конкретным значением признака
, а распределением вероятностей на множестве
. Нам каким-то образом нужно «подогнать» предсказанное распределение
под эталонное распределение
.
Пример 1. Если в задаче классификации в эталонном распределении вероятности классов равны 0.7 и 0.3, то мы хотели бы, чтобы в предсказании они тоже были бы равны 0.7 и 0.3.
Пример 2. Если в задаче регрессии эталонное распределение имеет две моды в значениях 0.5 и 1.5, то нам хотелось бы, чтобы предсказанное распределение вероятностей тоже имело моды в этих точках. Но если мы моделируем
нормальным распределением (как в разделе 2.3 первой части), тогда в нем в любом случае будет только одна мода, и чтобы хоть как-то приблизить предсказание к эталонному ответу, можно расположить моду посередине между точками 0.5 и 1.5 — тогда мат. ожидание ошибки предсказания будет наименьшим.
Как видим, второй пример получился сложнее первого. Если множество непрерывно, то задача приближения предсказанного распределения к эталонному означает задачу сближения функций плотности вероятности.
Такая постановка задачи неоднозначна: сблизить функции можно по-разному, так как «расстояние» между функциями можно определять по-разному. Чаще всего для этого используют расхождение Кульбака-Лейблера (относительную энтропию) — несимметричную метрику сходства между двумя распределениями вероятностей
и
. Расхождение Кульбака-Лейблера можно расписать как сумму в дискретном случае и как интеграл в непрерывном случае.
Дискретный случай (,
— функции вероятности):
Непрерывный случай (,
— функции плотности вероятности):
Пользуясь тем, что , мы можем расписать расхождение Кульбака-Лейблера как разность двух величин. Для дискретного случая:
Первое слагаемое со знаком минус называется энтропией распределения (или дифференциальной энтропией в непрерывном случае) и обозначается как
, а второе слагаемое (включая минус) называется кроссэнтропией
между распределениями
и
. Эти величины можно расписать через мат. ожидание:
В машинном обучении первым аргументом в обычно ставят эталонное распределение, вторым аргументом — предсказанное. Как видно из формулы (9), первое слагаемое не зависит от
, поэтому минимизация
по
равносильно минимизации кроссэнтропии между
и
.
Резюме. Если значения целевого признака в датасете даны как распределения вероятностей, то для обучения модели мы можем минимизировать кроссэнтропию между предсказанными и эталонными распределениями. Мы так уже делали в модели классификации, но там эталонное распределение было вырожденным назначало вероятность 1 одному из классов, поэтому в формуле (3) лишь одно слагаемое было ненулевым. В этом разделе мы рассмотрели более общий случай, когда эталонное распределение невырождено и в (3) может быть много ненулевых слагаемых.
2.3. Кроссэнтропия как максимизация правдоподобия*
Является ли «подгонка» предсказанного распределения под эталонное распределение
применением метода максимизации правдоподобия? Для ответа на этот вопрос нужно понять что такое «правдоподобие» в том случае, когда вместо эталонного ответа мы имеем распределение.
Мы можем сделать таким образом. Пусть для -го примера мы имеем значение
и распределение
. Мысленно сгенерируем из этого примера очень большое (стремящееся к бесконечности) количество примеров (обозначим его
), в которых исходные признаки равны
, а целевой признак взят из распределения
:
Объединение нельзя рассматривать как i.i.d.-выборку, потому что при бесконечном количестве примеров мы имеем лишь
уникальных значений
. Но поскольку мы не моделируем распределение
, это не является проблемой. Поскольку все
независимы:
В итоге при минус логарифм правдоподобия
оказался равен кроссэнтропии между эталонным распределением
и предсказанным моделью распределением
. Отсюда получается, что минимизация кроссэнтропии (или, что эквивалентно, минимизация расхождения Кульбака-Лейблера) максимизирует правдоподобие.
2.4. Кроссэнтропия в задаче регрессии*
Вернемся к случаю регрессии. Если для обучающей пары точно известен ответ
, то его можно представить как распределение вероятностей на
, имеющее лишь одно возможное значение
с вероятностью 1 (такое распределение называют вырожденным, в данном случае его еще называют «эмпирическим»).
Для таких случаев математики придумали специальную функцию, называемую дельта-функцией Дирака . Она равна нулю во всех точках кроме нуля, в нуле равна бесконечности, а ее интеграл равен единице. Например, если мы возьмем функцию плотности вероятности нормального распределения (часть 1, формула 4) с
и устремим
к нулю, то в пределе получим дельта-функцию.
В случае регрессии эмпирическое распределение можно записать как . Попробуем, по аналогии с классификацией, минимизировать кроссэнтропию между эталонным и предсказанным распределениями. Пусть модель выдает для
нормальное распределение
. Распишем кроссэнтропию между эмпирическим и предсказанным распределением:
Обратите внимание, что оба аргумента являются не числами, а функциями от
, и подынтегральное выражение не равно нулю только в одной точке
. С помощью формулы (10) мы пришли к тому, что минимизация кроссэнтропии означает минимизацию
, что эквивалентно максимизации
. Именно это мы и делали в разделе 2. Получается, что модель регрессии тоже обучается с помощью кроссэнтропии, которая по формуле (10) превращается в минимизацию
и далее в минимизацию среднеквадратичного отклонения (часть1, формула 7), если
моделируется нормальным распределением.
Как видим, мы получаем максимально унифицированный и при этом гибкий подход, который можно применять для задания функции потерь в сложных случаях.
Кроссэнтропия с точки зрения оптимизации*
В задаче регрессии мы рассматривали два подхода к выбору функции потерь: первый подход опирается на здравый смысл, наши представления о метрике сходства на множестве и легкость оптимизации. Второй подход опирается на теорию вероятностей и наши представления об условном распределении
, из которого следует формула для функции потерь (статья 1, формулы 5-7).
Теперь вернемся к задаче классификации. Есть ли здесь аналогичные два подхода? Вероятностный подход, который приводит к кроссэнтропии, мы уже рассматривали. Но хороша ли кроссэнтропия с точки зрения оптимизации, или есть более удобная функция потерь? Например, вместо кроссэнтропии мы могли бы минимизировать среднеквадратичную ошибку между предсказанным распределением вероятностей и эталонным распределением вероятностей
, в котором вероятность 1 назначается верному классу:
Смысл такого выражения с точки зрения теории вероятностей не совсем ясен, но видно, что чем ближе предсказание к истине, тем меньше будет функция потерь. А это и есть то свойство, которое требуется от функции потерь.
Что же лучше: кроссэнтропия или среднеквадратичная ошибка? Чтобы понять, какая из функций потерь лучше подходит для оптимизации градиентным спуском, давайте рассчитаем градиенты этих функций потерь по логитам (то есть тем значениям, которые выдаются до операции softmax или sigmoid). Пусть классификация является бинарной, верный ответом является второй класс, и модель выдала значение логита, равное . Отсюда вероятность второго класса равна
, где
— операция сигмоиды (6). Рассчитаем производную функции потерь по логиту
.
В случае бинарной кроссэнтропии:
В случае среднеквадратичной ошибки:
При (то есть когда модель выдает уверенный неправильный ответ) при бинарной кроссэнтропии производная стремится к 1, а при среднеквадратичной ошибке производная стремится к нулю. Это означает, что при сочетении сигмоиды и среднеквадратичной ошибки уверенные неправильные ответы практически не корректируются градиентным спуском (градиент близок к нулю), что может негативно сказаться на качестве обучения. Это аргумент в пользу того, чтобы при использовании сигмоиды выбирать бинарную кроссэнтропию, а не среднеквадратичную ошибку.
Хотя, с другой стороны, этот аргумент не окончательный, ведь уверенные неправильные ответы модели могут на самом деле быть выбросами в данных или ошибками разметки, которые модель не должна выучивать. Поэтому, возможно, в некоторых случаях имеет смысл использовать среднеквадратичную ошибку вместо кроссэнтропии.
Конец части 2. Часть 3, посвященная байесовскому выводу, планируется к публикации. Спасибо@ivankomarovи @yorkoза ценные комментарии, которые были учтены при подготовке статьи.
Cost functions play a crucial role in improving a Machine Learning model’s performance by being an integrated part of the gradient descent algorithm which helps us optimize the weights of a particular model. In this article, we will learn about one such cost function which is the cross-entropy function which is generally used for classification problems.
What is Entropy?
Entropy is a measure of the randomness or we can say uncertainty in the probability distribution of some specific target. If you have studied entropy in physics in your higher school then you must have encountered that the entropy of gases is higher than that of the solids because of the faster movement of particles in the latter which leads to a higher degree of randomness.
What is the difference between Entropy and Cross-Entropy?
Entropy just gives us the measure of the randomness in a particular probability distribution but the requirement is somewhat different here in machine learning which is to compare the difference between the probability distribution of the predicted probabilities and the true probabilities of the target variable. And for this case, the cross-entropy function comes in handy and serves the purpose.
Due to this only we try to minimize the difference between the predicted and the actual probability distribution of the target variable. And as the value of the cost function decreases the performance of the Machine Learning model improves.
In the above-shown cost functions mathematical formula you must encounter a negative sign the significance of that is to make the values positive to avoid any confusion and better clarity. The original result without the negative sign will be negative because the probability values are between the range 0 to 1 and for these values the value of the logarithm is negative as can be seen from the below graph.
Logarithmic Function Range and Domain
Cross Entropy for Multi-class Classification
Now that we have a basic understanding of the theory and the mathematical formulation of the cross entropy function now let’s try to work on a sample problem to get a feel of how the value for the cross entropy cost function is calculated.
Example 1: Actual Probabilities: [0, 1, 0, 0] Predicted Probabilities: [0.21, 0.68, 0.09, 0.10] Cross Entropy = - 1 * log(0.68) = 0.167
From the above example, we can observe that all the three value for which the actual probabilities was equal to zero becomes zero and the value of the cross entropy depends upon the predicted value for the class whose probability is one.
Example 2: Actual Probabilities: [0, 1, 0, 0] Predicted Probabilities: [0.12, 0.28, 0.34, 0.26] Cross Entropy = - 1 * log(0.28) = 0.558 Example 3: Actual Probabilities: [0, 1, 0, 0] Predicted Probabilities: [0.05, 0.80, 0.09, 0.06] Cross Entropy = - 1 * log(0.80) = 0.096
One may say that all three examples are more or less the same but no there is a subtle difference between all three which is comparable in that as the predicted probability is close to the actual probability the value of the cross entropy decreases but as the predicted probability deviates from the actual probability value of the cross entropy function shoots up.
What is Binary Cross Entropy?
We have learned about the multiclass classification which is when there are more than two classes for which we are predicting probabilities. And hence as the name suggests it is a special case of the multiclass classification when the number of classes is only two so, there is a need to predict only probability for one class and the other one will be 1 – probability predicted.
We can modify the formula for the binary cross entropy as well.
Categorical Cross-Entropy
The error in classification for the complete model is given by the mean of cross-entropy for the complete training dataset. This is the categorical cross-entropy. Categorical cross-entropy is used when the actual-value labels are one-hot encoded. This means that only one ‘bit’ of data is true at a time, like [1, 0, 0], [0, 1, 0], or [0, 0, 1]. The categorical cross-entropy can be mathematically represented as:
Sparse Categorical Cross-Entropy
In sparse categorical cross-entropy, truth labels are labeled with integral values. For example, if a 3-class problem is taken into consideration, the labels would be encoded as [1], [2], [3]. Note that binary cross-entropy cost functions, categorical cross-entropy, and sparse categorical cross-entropy are provided with the Keras API.
Last Updated :
05 May, 2023
Like Article
Save Article
tf.keras.losses.CategoricalCrossentropy
Рассчитывает потерю кроссентропии между этикетками и предсказаниями.
Наследуется от: Loss
View aliases
Совместимые псевдонимы для миграции
Подробнее см. Руководство по миграции .
tf.compat.v1.keras.losses.CategoricalCrossentropy
tf.keras.losses.CategoricalCrossentropy(
from_logits=False,
label_smoothing=0.0,
axis=-1,
reduction=losses_utils.ReductionV2.AUTO,
name=
)
Используйте эту функцию потерь кроссэнтропии, когда существует два или более классов меток. Мы ожидаем, что метки будут предоставлены в представлении one_hot . Если вы хотите предоставить метки как целые числа, используйте потерю SparseCategoricalCrossentropy . Для каждой функции должно быть # classes значений с плавающей запятой.
В приведенном ниже фрагменте есть # classes значений с плавающей точкой для каждого примера. Форма обоих y_pred и y_true являются [batch_size, num_classes] .
Standalone usage:
y_true = [[0, 1, 0], [0, 0, 1]] y_pred = [[0.05, 0.95, 0], [0.1, 0.8, 0.1]] # Using 'auto'/'sum_over_batch_size' reduction type. cce = tf.keras.losses.CategoricalCrossentropy() cce(y_true, y_pred).numpy() 1.177
# Calling with 'sample_weight'. cce(y_true, y_pred, sample_weight=tf.constant([0.3, 0.7])).numpy() 0.814
# Using 'sum' reduction type. cce = tf.keras.losses.CategoricalCrossentropy( reduction=tf.keras.losses.Reduction.SUM) cce(y_true, y_pred).numpy() 2.354
# Using 'none' reduction type. cce = tf.keras.losses.CategoricalCrossentropy( reduction=tf.keras.losses.Reduction.NONE) cce(y_true, y_pred).numpy() array([0.0513, 2.303], dtype=float32)
Использование с API compile() :
model.compile(optimizer='sgd', loss=tf.keras.losses.CategoricalCrossentropy())
| Args | |
|---|---|
from_logits |
Независимо от того y_pred , как ожидается , будет тензором логит — анализ. По умолчанию мы предполагаем, что y_pred кодирует распределение вероятностей. |
label_smoothing |
Плавающая в [0, 1]. Когда > 0, значения меток сглаживаются, что означает ослабление достоверности значений меток. Например, если 0.1 , используйте 0.1 / num_classes для нецелевых меток и 0.9 + 0.1 / num_classes для целевых меток. |
axis |
Ось,по которой вычисляется кроссэнтропия (ось признаков).По умолчанию равно -1. |
reduction |
Тип tf.keras.losses.Reduction для применения к потерям. Значение по умолчанию — AUTO . AUTO указывает, что вариант сокращения будет определяться контекстом использования. Почти во всех случаях по умолчанию используется значение SUM_OVER_BATCH_SIZE . При использовании с tf.distribute.Strategy вне встроенных обучающих циклов, таких как compile и fit tf.keras , использование AUTO или SUM_OVER_BATCH_SIZE вызовет ошибку. Пожалуйста, ознакомьтесь с этим пользовательским учебным пособием для получения более подробной информации. compile fit AUTO SUM_OVER_BATCH_SIZE |
name |
Необязательное имя для экземпляра.По умолчанию ‘categorical_crossentropy’. |
Methods
from_config
View source
@classmethod from_config( config )
Создает экземпляр Loss из своей конфигурации (вывод get_config() ).
| Args | |
|---|---|
config |
Вывод get_config() . |
get_config
View source
get_config()
Возвращает словарь конфигурации для экземпляра Loss .
__call__
View source
__call__( y_true, y_pred, sample_weight=None )
Вызывает экземпляр Loss .
| Args | |
|---|---|
y_true |
Значения истинности земли. shape = [batch_size, d0, .. dN] , за исключением функций разреженных потерь, таких как разреженная кроссэнтропия по категориям, где shape = [batch_size, d0, .. dN-1] |
y_pred |
Прогнозируемые значения. shape = [batch_size, d0, .. dN] |
sample_weight |
Необязательный параметр sample_weight действует как коэффициент потерь. Если предоставляется скаляр, тогда потери просто масштабируются по заданному значению. Если sample_weight является тензором размера [batch_size] , то общие потери для каждой выборки пакета масштабируются с помощью соответствующего элемента в векторе sample_weight . Если форма sample_weight равна [batch_size, d0, .. dN-1] (или может транслироваться в эту форму), то каждый элемент потерь y_pred масштабируется на соответствующее значение sample_weight . (Примечание к dN-1 : все функции потерь уменьшаются на 1 измерение, обычно ось = -1.) |
| Returns |
|---|
Взвешенный убыток с плавающей запятой Tensor . Если reduction не будет NONE , это имеет форму [batch_size, d0, .. dN-1] ; в противном случае — скаляр. (Обратите внимание на dN-1 , потому что все функции потерь уменьшаются на 1 измерение, обычно ось = -1.) |
| Raises | |
|---|---|
ValueError |
Если форма sample_weight недействительна. |
TensorFlow
2.9
-
tf.keras.losses.BinaryFocalCrossentropy
Вычисляет фокальную потерю перекрестной энтропии между истинными метками и предсказаниями.
-
tf.keras.losses.categorical_hinge
Вычисляет категориальную потерю петли между y_true и y_pred.
-
tf.keras.losses.CategoricalHinge
Вычисляет категориальную потерю петли между y_true и y_pred.
-
tf.keras.losses.cosine_similarity
Вычисляет косинусное сходство между этикетками и предсказаниями.
Computes the crossentropy loss between the labels and predictions.
Inherits From: Loss
View aliases
Main aliases
tf.losses.CategoricalCrossentropy
Compat aliases for migration
See
Migration guide for
more details.
tf.compat.v1.keras.losses.CategoricalCrossentropy
tf.keras.losses.CategoricalCrossentropy(
from_logits=False,
label_smoothing=0.0,
axis=-1,
reduction=losses_utils.ReductionV2.AUTO,
name='categorical_crossentropy'
)
Used in the notebooks
| Used in the guide | Used in the tutorials |
|---|---|
|
|
Use this crossentropy loss function when there are two or more label
classes. We expect labels to be provided in a one_hot representation. If
you want to provide labels as integers, please use
SparseCategoricalCrossentropy loss. There should be # classes floating
point values per feature.
In the snippet below, there is # classes floating pointing values per
example. The shape of both y_pred and y_true are
[batch_size, num_classes].
Standalone usage:
y_true = [[0, 1, 0], [0, 0, 1]]y_pred = [[0.05, 0.95, 0], [0.1, 0.8, 0.1]]# Using 'auto'/'sum_over_batch_size' reduction type.cce = tf.keras.losses.CategoricalCrossentropy()cce(y_true, y_pred).numpy()1.177
# Calling with 'sample_weight'.cce(y_true, y_pred, sample_weight=tf.constant([0.3, 0.7])).numpy()0.814
# Using 'sum' reduction type.cce = tf.keras.losses.CategoricalCrossentropy(reduction=tf.keras.losses.Reduction.SUM)cce(y_true, y_pred).numpy()2.354
# Using 'none' reduction type.cce = tf.keras.losses.CategoricalCrossentropy(reduction=tf.keras.losses.Reduction.NONE)cce(y_true, y_pred).numpy()array([0.0513, 2.303], dtype=float32)
Usage with the compile() API:
model.compile(optimizer='sgd',
loss=tf.keras.losses.CategoricalCrossentropy())
Args |
|
|---|---|
from_logits
|
Whether y_pred is expected to be a logits tensor. Bydefault, we assume that y_pred encodes a probability distribution.
|
label_smoothing
|
Float in [0, 1]. When > 0, label values are smoothed, meaning the confidence on label values are relaxed. For example, if 0.1, use 0.1 / num_classes for non-target labels and0.9 + 0.1 / num_classes for target labels.
|
axis
|
The axis along which to compute crossentropy (the features axis). Defaults to -1. |
reduction
|
Type of tf.keras.losses.Reduction to apply toloss. Default value is AUTO. AUTO indicates that the reductionoption will be determined by the usage context. For almost all cases this defaults to SUM_OVER_BATCH_SIZE. When used under atf.distribute.Strategy, except via Model.compile() andModel.fit(), using AUTO or SUM_OVER_BATCH_SIZEwill raise an error. Please see this custom training tutorial for more details. |
name
|
Optional name for the instance. Defaults to ‘categorical_crossentropy’. |
Methods
from_config
View source
@classmethodfrom_config( config )
Instantiates a Loss from its config (output of get_config()).
| Args | |
|---|---|
config
|
Output of get_config().
|
| Returns |
|---|
A keras.losses.Loss instance.
|
get_config
View source
get_config()
Returns the config dictionary for a Loss instance.
__call__
View source
__call__(
y_true, y_pred, sample_weight=None
)
Invokes the Loss instance.
| Args | |
|---|---|
y_true
|
Ground truth values. shape = [batch_size, d0, .. dN], exceptsparse loss functions such as sparse categorical crossentropy where shape = [batch_size, d0, .. dN-1]
|
y_pred
|
The predicted values. shape = [batch_size, d0, .. dN]
|
sample_weight
|
Optional sample_weight acts as a coefficient for theloss. If a scalar is provided, then the loss is simply scaled by the given value. If sample_weight is a tensor of size [batch_size],then the total loss for each sample of the batch is rescaled by the corresponding element in the sample_weight vector. If the shape ofsample_weight is [batch_size, d0, .. dN-1] (or can bebroadcasted to this shape), then each loss element of y_pred isscaled by the corresponding value of sample_weight. (Noteon dN-1: all loss functions reduce by 1 dimension, usuallyaxis=-1.) |
| Returns |
|---|
Weighted loss float Tensor. If reduction is NONE, this hasshape [batch_size, d0, .. dN-1]; otherwise, it is scalar. (NotedN-1 because all loss functions reduce by 1 dimension, usuallyaxis=-1.) |
| Raises | |
|---|---|
ValueError
|
If the shape of sample_weight is invalid.
|