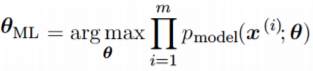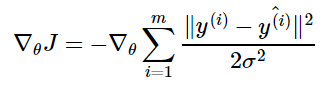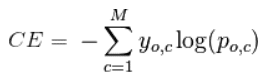Функция ошибки кросс энтропия - Не ошибается лишь тот, кто ничего не делает!

Адаптированный перевод прекрасной статьи энтузиаста технологий машинного обучения Javaid Nabi.

Чтобы понимать как алгоритм машинного обучения учится предсказывать результаты на основе данных, важно разобраться в основных концепциях и понятиях, используемых при обучении алгоритма.

Функции оценки

В контексте технологии машинного обучения, оценка – это
статистический термин для нахождения некоторого приближения неизвестного
параметра на основе некоторых данных. Точечная
оценка – это попытка найти единственное лучшее приближение некоторого
количества интересующих нас параметров. Или на более формальном языке математической статистики — точечная оценка это число, оцениваемое на основе наблюдений,
предположительно близкое к оцениваемому параметру.

Под количеством
интересующих параметров обычно подразумевается:
• Один параметр
• Вектор параметров – например, веса в линейной
регрессии
• Целая функция

Точечная оценка

Чтобы отличать оценки параметров от их истинного значения, представим точечную оценку параметра θ как θˆ. Пусть {x(1), x(2), .. x(m)} будут m независимыми и одинаково распределенными величинами. Тогда точечная оценка может быть записана как некоторая функция этих величин:

Такое определение точечной оценки является очень общим и предоставляет разработчику большую свободу действий. Почти любая функция, таким образом, может рассматриваться как оценщик, но хороший оценщик – это функция, значения которой близки к истинному базовому значению θ, которое сгенерированно обучающими данными.

Точечная оценка также может относиться к оценке взаимосвязи между
входными и целевыми переменными, в этом случае чаще называемой функцией оценки.

Функция оценки

Задача, решаемая машинным обучением, заключается в попытке
предсказать переменную y по
заданному входному вектору x. Мы
предполагаем, что существует функция f(x), которая описывает приблизительную
связь между y и x. Например, можно предположить, что y = f(x) + ε, где ε обозначает
часть y, которая явно не
предсказывается входным вектором x.
При оценке функций нас интересует приближение f с помощью модели или оценки fˆ.
Функция оценки в действительности это тоже самое, что оценка параметра θ; функция оценки f это просто точечная
оценка в функциональном пространстве. Пример: в полиномиальной регрессии мы
либо оцениваем параметр w, либо оцениваем функцию отображения из x в y.

Смещение и дисперсия

Смещение и дисперсия измеряют два разных источника ошибки функции оценки.
Смещение измеряет ожидаемое отклонение от истинного значения функции или
параметра. Дисперсия, с другой стороны, показывает меру отклонения от
ожидаемого значения оценки, которую может вызвать любая конкретная выборка
данных.

Смещение

Смещение определяется следующим
образом:

где ожидаемое значение E(θˆ_m) для данных (рассматриваемых как выборки из случайной величины) и
θ является истинным базовым значением, используемым для определения
распределения, генерирующего данные.

Оценщик θˆ_m называется несмещенным, если bias(θˆ_m)=0, что подразумевает что E(θˆ_m) = θ.

Дисперсия и Стандартная ошибка

Дисперсия оценки обозначается как Var(θˆ), где случайная величина
является обучающим множеством. Альтернативно, квадратный корень дисперсии
называется стандартной ошибкой, обозначаемой как SE(θˆ). Дисперсия или стандартная ошибка
оценщика показывает меру ожидания того, как оценка, которую мы вычисляем, будет
изменяться по мере того, как мы меняем выборки из базового набора данных,
генерирующих процесс.

Точно так же, как мы хотели бы, чтобы функция оценки имела малое
смещение, мы также стремимся, чтобы у нее была относительно низкая дисперсия.

Давайте теперь рассмотрим некоторые обычно используемые функции оценки.

Оценка Максимального Правдоподобия (MLE)

Оценка максимального правдоподобия может быть определена как метод
оценки параметров (таких как среднее значение или дисперсия) из выборки данных,
так что вероятность получения наблюдаемых данных максимальна.

Рассмотрим набор из m примеров X={x(1),… , x(m)} взятых независимо из неизвестного набора данных,
генерирующих распределение P_data(x). Пусть P_model(x;θ) –
параметрическое семейство распределений вероятностей над тем же пространством,
индексированное параметром θ.
Другими словами, P_model(x;θ) отображает любую конфигурацию x в значение, оценивающее истинную
вероятность P_data(x).

Оценка максимального правдоподобия для θ определяется как:

Поскольку мы предположили, что примеры являются независимыми выборками, приведенное выше
уравнение можно записать в виде:

Эта произведение многих вероятностей может быть неудобным по ряду
причин. В частности, оно склонно к числовой недооценке. Кроме того, чтобы найти
максимумы/минимумы этой функции, мы должны взять производную этой функции от θ и приравнять ее к 0. Поскольку это
произведение членов, нам нужно применить правило цепочки, которое довольно
громоздко. Чтобы получить более удобную, но эквивалентную задачу оптимизации,
можно использовать логарифм вероятности, который не меняет его argmax, но
удобно превращает произведение в сумму, и поскольку логарифм – строго
возрастающая функция (функция натурального логарифма – монотонное
преобразование), это не повлияет на итоговое значение θ.

В итоге, получаем:

Два важных свойства: сходимость и
эффективность

Сходимость. По мере того, как число обучающих выборок приближается к
бесконечности, оценка максимального правдоподобия сходится к истинному значению
параметра.

Эффективность. Способ измерения того, насколько мы близки к истинному
параметру, – это ожидаемая средняя квадратичная ошибка, вычисление квадратичной
разницы между оценочными и истинными значениями параметров, где математическое
ожидание вычисляется над m обучающими выборками из данных, генерирующих
распределение. Эта параметрическая среднеквадратичная ошибка уменьшается с
увеличением m, и для
больших m нижняя
граница неравенства Крамера-Рао показывает, что ни у одной сходящейся функции оценки нет
среднеквадратичной ошибки меньше, чем у оценки максимального правдоподобия.

Именно по причине
сходимости и эффективности, оценка максимального правдоподобия часто считается
предпочтительным оценщиком для машинного обучения.

Когда количество примеров достаточно мало, чтобы привести к
переобучению, стратегии регуляризации, такие как понижающие веса, могут
использоваться для получения смещенной версии оценки максимального
правдоподобия, которая имеет меньшую дисперсию, когда данные обучения
ограничены.

Максимальная апостериорная (MAP) оценка

Согласно байесовскому подходу, можно учесть влияние предварительных
данных на выбор точечной оценки. MAP может использоваться для получения
точечной оценки ненаблюдаемой величины на основе эмпирических данных. Оценка
MAP выбирает точку максимальной апостериорной вероятности (или максимальной
плотности вероятности в более распространенном случае непрерывного θ):

где с правой стороны, log(p(x|θ)) – стандартный член
логарифмической вероятности и log(p(θ)) соответствует изначальному
распределению.

Как и при полном байесовском методе, байесовский MAP имеет преимущество
использования изначальной информации, которой нет
в обучающих данных. Эта дополнительная информация помогает уменьшить дисперсию
для точечной оценки MAP (по сравнению с оценкой MLE). Однако, это происходит ценой повышенного смещения.

Функции потерь

В большинстве обучающих сетей ошибка рассчитывается как разница
между фактическим выходным значением y и прогнозируемым выходным значением ŷ.
Функция, используемая для вычисления этой ошибки, известна как функция потерь,
также часто называемая функцией ошибки или затрат.

До сих пор наше основное внимание уделялось оценке параметров с
помощью MLE или MAP. Причина, по которой мы обсуждали это раньше, заключается в
том, что и MLE, и MAP предоставляют механизм для получения функции потерь.

Давайте рассмотрим некоторые часто используемые функции потерь.

Средняя
квадратичная ошибка (MSE): средняя
квадратичная ошибка является наиболее распространенной функцией потерь. Функция
потерь MSE широко используется в линейной регрессии в качестве показателя
эффективности. Чтобы рассчитать MSE, надо взять разницу между предсказанными
значениями и истинными, возвести ее в квадрат и усреднить по всему набору
данных.

где y⁽ⁱ⁾ – фактический ожидаемый результат, а ŷ⁽ⁱ⁾ – прогноз модели.

Многие функции потерь (затрат), используемые в машинном обучении,
включая MSE, могут быть получены из метода максимального правдоподобия.

Чтобы увидеть, как мы можем вывести функции потерь из MLE или MAP,
требуется некоторая математика. Вы можете пропустить ее и перейти к следующему
разделу.

Получение MSE из MLE

Алгоритм линейной регрессии учится принимать входные данные x и получать выходные значения ŷ. Отображение x в ŷ делается так,
чтобы минимизировать среднеквадратичную ошибку. Но как мы выбрали MSE в
качестве критерия для линейной регрессии? Придем к этому решению с точки зрения
оценки максимального правдоподобия. Вместо того, чтобы производить одно
предсказание ŷ , давайте рассмотрим
модель условного распределения p(y|x).

Можно смоделировать модель
линейной регрессии следующим образом:

мы предполагаем, что у имеет
нормальное распределение с ŷ в качестве
среднего значения распределения и некоторой постоянной σ² в качестве дисперсии, выбранной пользователем. Нормальное
распределения являются разумным выбором во многих случаях. В отсутствие
предварительных данных о том, какое распределение в действительности
соответствует рассматриваемым данным, нормальное распределение является хорошим
выбором по умолчанию.

Вернемся к логарифмической вероятности, определенной ранее:

где ŷ(i) – результат
линейной регрессии на i-м входе, а m – количество обучающих примеров. Мы видим,
что две первые величины являются постоянными, поэтому максимизация
логарифмической вероятности сводится к минимизации MSE:

Таким образом, максимизация логарифмического правдоподобия
относительно θ дает такую же оценку параметров θ, что и минимизация
среднеквадратичной ошибки. Два критерия имеют разные значения, но одинаковое
расположение оптимума. Это оправдывает использование MSE в качестве функции
оценки максимального правдоподобия.

Кросс-энтропия
(или логарифмическая функция потерь – log loss): Кросс-энтропия измеряет расхождение между двумя вероятностными
распределениями. Если кросс-энтропия велика, это означает, что разница между
двумя распределениями велика, а если кросс-энтропия мала, то распределения
похожи друг на друга.

Кросс-энтропия определяется как:

где P – распределение истинных ответов, а Q – распределение
вероятностей прогнозов модели. Можно
показать, что функция кросс-энтропии также получается из MLE, но я не буду
утомлять вас большим количеством математики.

Давайте еще
упростим это для нашей модели с:
• N – количество наблюдений
• M – количество возможных меток класса (собака,
кошка, рыба)
• y – двоичный индикатор (0 или 1) того, является
ли метка класса C правильной классификацией для наблюдения O
• p – прогнозируемая вероятность модели

Бинарная классификация

В случае бинарной классификации (M=2),
формула имеет вид:

При двоичной классификации каждая предсказанная вероятность
сравнивается с фактическим значением класса (0 или 1), и вычисляется оценка,
которая штрафует вероятность на основе расстояния от ожидаемого значения.

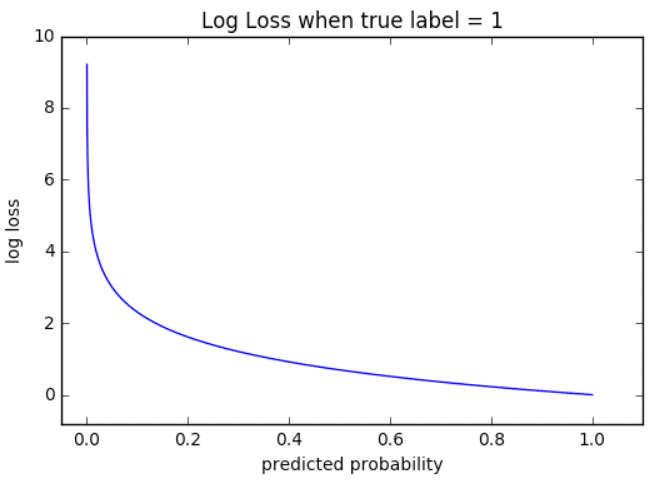
Визуализация

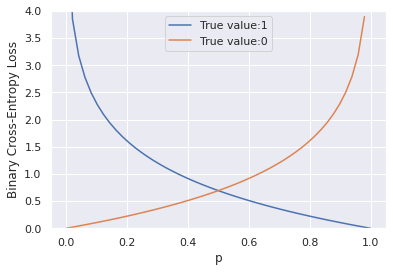
На приведенном ниже графике показан диапазон возможных значений
логистической функции потерь с учетом истинного наблюдения (y = 1). Когда
прогнозируемая вероятность приближается к 1, логистическая функция потерь
медленно уменьшается. Однако при уменьшении прогнозируемой вероятности она быстро возрастает.

Логистическая функция потерь наказывает оба типа ошибок, но
особенно те прогнозы, которые являются достоверными и ошибочными!

Мульти-классовая классификация

В случае мульти-классовой классификации (M>2) мы берем сумму значений логарифмических функций потерь для
каждого прогноза наблюдаемых классов.

Кросс-энтропия для бинарной или двух-классовой задачи
прогнозирования фактически рассчитывается как средняя кросс-энтропия среди всех
примеров. Log loss использует отрицательные
значения логарифма, чтобы обеспечить удобную метрику для сравнения. Этот подход
основан на том, что логарифм чисел <1 возвращает отрицательные значения, что
затрудняет работу при сравнении производительности двух моделей. Вы можете
почитать эту статью, где детально обсуждается функция кросс-энтропии потерь.

Задачи ML и соответствующие функции потерь

Давайте посмотрим, какие обычно используются выходные слои и
функции потерь в задачах машинного обучения:

Задача регрессии

Задача, когда
вы прогнозируете вещественное число.

• Конфигурация выходного уровня: один
узел с линейной единицей активации.
• Функция
потерь: средняя квадратическая ошибка (MSE).

Задача бинарной классификации

Задача состоит в том, чтобы классифицировать пример как
принадлежащий одному из двух классов. Или более точно, задача сформулирована
как предсказание вероятности того, что пример принадлежит первому классу,
например, классу, которому вы присваиваете целочисленное значение 1, тогда как
другому классу присваивается значение 0.

• Конфигурация выходного
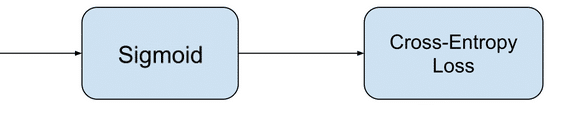
уровня: один узел с сигмовидной активационной функцией.
• Функция
потерь: кросс-энтропия, также называемая логарифмической функцией потерь.

Задача мульти-классовой классификации

Эта задача состоит в том, чтобы классифицировать пример как
принадлежащий одному из нескольких классов. Задача сформулирована как
предсказание вероятности того, что пример принадлежит каждому классу.

• Конфигурация выходного уровня: один
узел для каждого класса, использующий функцию активации softmax.
• Функция потерь: кросс-энтропия, также называемая логарифмической функцией потерь.

Рассмотрев оценку и различные функции потерь, давайте перейдем к
роли оптимизаторов в алгоритмах ML.

Оптимизаторы

Чтобы свести к минимуму ошибку или потерю в прогнозировании,
модель, используя примеры из обучающей выборки, обновляет параметры модели W. Расчеты
ошибок строятся в зависимости от W и также описываются графиком функции затрат
J(w), поскольку она определяет затраты/наказание модели. Таким образом, минимизация
ошибки также часто называется минимизацией функции затрат.

Но как именно это делается? Используя оптимизаторы.

Оптимизаторы используются для обновления весов и смещений, то есть
внутренних параметров модели, чтобы уменьшить ошибку.

Самым важным методом и основой того, как мы обучаем и оптимизируем
нашу модель, является метод Градиентного Спуска.

Градиентный Спуск

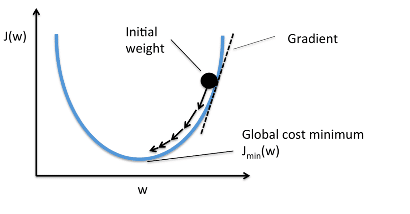
Когда мы строим функцию затрат J(w), это можно представить следующим
образом:

Как видно из кривой, существует значение параметров W, которое
имеет минимальное значение J_min. Нам нужно найти способ достичь
этого минимального значения.

В алгоритме градиентного спуска мы начинаем со случайных
параметров модели и вычисляем ошибку для каждой итерации обучения, продолжая
обновлять параметры, чтобы приблизиться к минимальным значениям.

Повторяем до достижения минимума:

{

}

В приведенном выше уравнении мы обновляем параметры модели после
каждой итерации. Второй член уравнения вычисляет наклон или градиент кривой на
каждой итерации.

Градиент функции затрат вычисляется как частная производная
функции затрат J по каждому параметру модели W_j, где j принимает
значение числа признаков [1, n]. α – альфа, это скорость обучения, определяющий
как быстро мы хотим двигаться к минимуму. Если α слишком велико, мы можем
проскочить минимум. Если α слишком мало, это приведет к небольшим этапам обучения,
поэтому общее время, затрачиваемое моделью для достижения минимума, будет
больше.

Есть три способа сделать градиентный спуск:

Пакетный
градиентный спуск: использует
все обучающие данные для обновления параметров модели в каждой итерации.

Мини-пакетный градиентный спуск: вместо использования всех данных, мини-пакетный градиентный спуск делит тренировочный набор на меньший размер, называемый партией, и обозначаемый буквой «b». Таким образом, мини-пакет «b» используется для обновления параметров модели на каждой итерации.

Вот некоторые другие часто
используемые Оптимизаторы:

Стохастический
Градиентный Спуск (SGD): обновляет
параметры, используя только один обучающий параметр на каждой итерации. Такой
параметр обычно выбирается случайным образом. Стохастический градиентный спуск
часто предпочтителен для оптимизации функций затрат, когда есть сотни тысяч
обучающих или более параметров, поскольку он будет сходиться быстрее, чем
пакетный градиентный спуск.

Адаград

Адаград адаптирует скорость обучения конкретно к индивидуальным
особенностям: это означает, что некоторые веса в вашем наборе данных будут
отличаться от других. Это работает очень хорошо для разреженных наборов данных,
где пропущено много входных значений. Однако, у Адаграда есть одна серьезная
проблема: адаптивная скорость обучения со временем становится очень маленькой.

Некоторые другие оптимизаторы, описанные ниже, пытаются справиться
с этой проблемой.

RMSprop

RMSprop – это специальная версия Adagrad,
разработанная профессором Джеффри Хинтоном в его
классе нейронных сетей. Вместо того,
чтобы вычислять все градиенты, он вычисляет градиенты только в фиксированном
окне. RMSprop похож на Adaprop, это еще один оптимизатор, который пытается
решить некоторые проблемы, которые Адаград оставляет открытыми.

Адам

Адам означает адаптивную оценку момента и является еще одним способом использования
предыдущих градиентов для вычисления текущих градиентов. Адам также использует
концепцию импульса,
добавляя доли предыдущих градиентов к текущему. Этот оптимизатор получил
довольно широкое распространение и практически принят для использования в
обучающих нейронных сетях.

Вы только что ознакомились с кратким обзором
оптимизаторов. Более подробно об этом можно прочитать здесь.

Я надеюсь,
что после прочтения этой статьи, вы будете лучше понимать что происходит, когда
Вы пишите следующий код:

# loss function: Binary Cross-entropy and optimizer: Adam
model.compile(loss='binary_crossentropy', optimizer='adam')

или

# loss function: MSE and optimizer: stochastic gradient descent
model.compile(loss='mean_squared_error', optimizer='sgd')

Спасибо за проявленный интерес!

Ссылки:

[1] https://www.deeplearningbook.org/contents/ml.html

[2] https://machinelearningmastery.com/loss-and-loss-functions-for-training-deep-learning-neural-networks/

[3] https://blog.algorithmia.com/introduction-to-optimizers/

[4] https://jhui.github.io/2017/01/05/Deep-learning-Information-theory/

[5] https://blog.algorithmia.com/introduction-to-loss-functions/

[6] https://gombru.github.io/2018/05/23/cross_entropy_loss/

[7] https://www.kdnuggets.com/2018/04/right-metric-evaluating-machine-learning-models-1.html

[8] https://rohanvarma.me/Loss-Functions/

[9] http://blog.christianperone.com/2019/01/mle/

Источник

Кросс-энтропия (Перекрестная энтропия) – это Функция потерь (Loss Function), которую можно использовать для количественной оценки разницы между двумя Распределениями вероятностей (Probability Distribution).

Лучше всего это можно объяснить на примере. Предположим, у нас есть две модели, A и B, и мы хотели выяснить, какая из них лучше:

Примечание. Цифры рядом с точками данных представляют вероятность того, что Наблюдение (Observation) принадлежит к соответствующему классу – цветовой зоне. Например, вероятность того, что красная точка в левой верхней части графика модели A принадлежит «красному» классу, равна 0,8.
Интуитивно мы знаем, что модель B лучше, поскольку красные точки находятся на красном распределении, а синие точки – в синем. Но как мы передадим модели эти знания?

Один из способов – взять вероятности каждой точки в модели A и перемножить их. Это даст полную вероятность модели, как мы знаем из общего правила умножения вероятностей. Мы можем сделать то же самое для модели B:

Как видно из изображения выше, наилучшей моделью является B, поскольку вероятность выше. Так мы можем выяснить, какая модель лучше, используя вероятность.

С этой последовательностью, однако, есть некоторые проблемы. Как вы, возможно, догадались, чем больше наблюдений, тем меньше результирующая вероятность. Кроме того, если бы мы изменили одну точку данных, результирующая вероятность резко изменилась бы вслед.
Одним словом, использование прозведений – не лучшая идея. Как мы можем это исправить? Один из способов – использовать вместо этого суммы. Если мы вспомним логарифмы, есть способ связать произведение вероятностей с их суммой:

$$ log_{a × b} = log_{a} + log_{b}, где$$

Давайте применим это правило к нашим вероятностям:

Это выглядит неплохо, но давайте избавимся от негативов, сделав записи в журналах отрицательными и посчитаем общее количество:

Использование отрицательных логарифмов вероятностей – это так называемая кросс-энтропия, где большое число означает плохие модели, а маленькое число – хорошую.

Когда мы вычисляем логарифм для каждой точки данных, мы фактически получаем функцию ошибок для нее. Например, функция ошибок для точки 0,2 в модели A равна -ln (0,2), что равно 1,61. Обратите внимание, что неправильно классифицированные точки имеют большие значения, следовательно, имеют большие ошибки.

Итак, давайте еще немного разберемся с перекрестной энтропией. На самом деле она говорит о том, что если у нас есть события и вероятности, насколько вероятно, что события произойдут на основе вероятностей? Если это очень вероятно, у нас малая кросс-энтропия, а если маловероятно, у нас высокая кросс-энтропия. Мы увидим это подробнее на примере.

Например, если мы возьмем вероятность того, что за тремя дверями есть подарок, и у нас есть таблица, которая выглядит следующим образом:

Здесь мы видим, что если кросс-энтропия велика, вероятность того, что событие произойдет, мала, и наоборот.

Предположим, мы возьмем первый случай, когда за дверью № 1 подарок с вероятностью 0,8; за дверью № 2 – 0,7, № 3 – 0,1:

Обратите внимание, что мы описываем третью дверь как 1-p, что означает 1 минус вероятность подарка. Это даст нам вероятность того, что подарка нет. Также обратите внимание, что Y описывает, сколько подарков находится за дверью. Таким образом, кросс-энтропия может быть описана следующей формулой:

$$ -Σp(x) logqx + (1 — p(x)) log (1 — q(x))$$
$$p(x)space{требуемая}space{вероятность,}$$
$$q(x)space{фактическая}space{вероятность,}$$

Эта формула предназначена только для двоичной кросс-энтропии и описывает, насколько близко предсказанное распределение к истинному распределению.

Фото: @hardsurface

Автор оригинальной статьи: Anjali Bhardwaj

Источник

В предыдущей части мы рассматривали вероятностную постановку задачи машинного обучения, статистические модели, модель регрессии как частный случай и ее обучение методом максимизации правдоподобия.

В данной части рассмотрим метод максимизации правдоподобия в классификации: в чем роль кроссэнтропии, функций сигмоиды и softmax, как кроссэнтропия связана с «расстоянием» между распределениями вероятностей и почему модель регрессии тоже обучается через минимизацию кроссэнтропии. Данная часть содержит много отсылок к формулам и понятиям, введенным в первой части, поэтому рекомендуется читать их последовательно.

В третьей части (статья планируется) перейдем от метода максимизации правдоподобия к байесовскому выводу и его различным приближениям.

Данная серия статей не является введением в машинное обучение и предполагает знакомство читателя с основными понятиями. Задача статей — рассмотреть машинное обучение с точки зрения теории вероятностей, что позволит по новому взглянуть на проблему, понять связь машинного обучения со статистикой и лучше понимать формулы из научных статей. Также на описанном материале строятся более сложные темы, такие как вариационные автокодировщики (Kingma and Welling, 2013), нейробайесовские методы (Müller et al., 2021) и даже некоторые теории сознания (Friston et al., 2022).

Содержание текущей части

В первом разделе мы рассмотрим модель классификации, кроссэнтропию и ее связь с методом максимизации правдоподобия, а также ряд несколько фактов про функции softmax и sigmoid.
Во втором разделе поговорим о связи минимизации кроссэнтропии с минимизацией расхождения Кульбака-Лейблера, и как минимизация расхождения Кульбака-Лейблера может помочь в более сложных случаях, чем обычная классификация и регрессия.

Звездочкой* отмечены дополнительные разделы, которые не повлияют на понимание дальнейшего материала.

1. Вероятностная модель классификации
        1.1. Модель классификации и функция потерь
        1.2. Функция softmax в классификации
        1.3. Температура softmax и операция hardmax*
        1.4. Функция sigmoid в классификации
2. Кроссэнтропия в вероятностных моделях
        2.1. Разметка с неуверенностью
        2.2. Кроссэнтропия и расхождение Кульбака-Лейблера
        2.3. Кроссэнтропия как максимизация правдоподобия*
        2.4. Кроссэнтропия в задаче регрессии*
        2.5. Кроссэнтропия с точки зрения оптимизации*

1. Вероятностная модель классификации

1.1. Модель классификации и функция потерь

Чтобы задать вероятностную модель, нам нужно определить, в какой форме она будет предсказывать распределение . Если задаче регрессии мы ограничивали распределения только нормальными распределениями, то в задаче классификации это будет не оптимальным решением, так как классы по сути представляют собой неупорядоченное множество (хотя на них есть порядок, но лишь технически, и он может быть выбран произвольно). В задаче классификации мы можем предсказывать вероятность для каждого класса, и тогда модель будет выдавать столько чисел, сколько есть классов в .

Пусть мы имеем датасет $X = {x_i, y_i}_{i=1}^N$ и предполагаем, что все примеры независимы и взяты и одного и того же распределения (i.i.d., см. предыдущую часть, раздел 3.4). Для обучения модели снова применим метод максимизации правдоподобия, то есть будем искать такие параметры $theta_{best}$ , которые максимизируют . В разделе 2.3 мы уже расписывали формулу, которая получается в результате, но ввиду ее важности повторим ее еще раз. Первое равенство ниже следует из i.i.d.-гипотезы, второе по правилам математики:

$begin{split} theta_{best} &= underset{theta}{text{arg max}} p(X, theta) \ &= underset{theta}{text{arg max}} prodlimits_{i=1}^N p(y_i|x_i, theta) \ &= underset{theta}{text{arg min}} sumlimits_{i=1}^N -log p(y_i|x_i, theta) end{split} tag{1}$

Таким образом, для максимизации вероятности выборки данных нам нужно минимизировать сумму величин

$-log p(y_i|x_i, theta) tag{2}$

для всех обучающих примеров .

В модели регрессии эта величина была сведена к квадрату разности предсказания и верного ответа (часть 1, формула 7). Но в задаче классификации на данном этапе считать больше ничего не нужно. Нашей задачей было задать вероятностную модель, определить с ее помощью функцию потерь и таким образом свести обучение к задаче оптимизации, то есть минимизации функции потерь, и мы это уже сделали. Функция потерь (2) называется кроссэнтропией (также перекрестной энтропией, или logloss). Она равна минус логарифму предсказанной вероятности для верного класса .

Категориальная кроссэнтропия

Возьмем произвольный пример и выданные моделью вероятности обозначим за $p_{pred}[1], dots, p_{pred}[K]$ , где — количество классов. К метке класса (эталонному ответу) применим one-hot кодирование, получив вектор $p_{true}[1], dots, p_{true}[K]$ , в котором лишь один элемент равен единице, а остальные равны нулю. Тогда выражение (2) можно рассчитать таким образом:

$text{CrossEntropy}(p_{true}, p_{pred}) = sumlimits_{i=1}^K p_{true}[i] * ln (p_{pred}[i]) tag{3}$

Лишь один элемент суммы будет не равен нулю — тот, который соответствует верному классу. Для него первый множитель будет равен единице, а второй будет логарифмом предсказанной вероятности для верного класса, что соответствует выражению (2).

Примечание. На самом деле формула (3) является определением кроссэнтропии, а формула (2) ее частным случаем, когда $p_{true}$ вырождено и назначает вероятность 1 классу с индексом . О случае, когда это не так, подробнее поговорим во втором разделе.

Бинарная кроссэнтропия

Если класса всего два, то как правило делают следующим образом: модель выдает лишь одно число $p_{pred}$ от 0 до 1, оно рассматривается как вероятность второго класса, а $1 - p_{pred}$ рассматривается как вероятность первого класса. Пусть $p_{true}$ равно единице, если первый класс верен, иначе равно нулю. Тогда выражение (3) технически можно вычислить следующим образом:

$text{BinaryCrossEntropy}(p_{true}, p_{pred}) = p_{true} * ln (p_{pred}) + (1-p_{true}) * ln (1-p_{pred}) tag{4}$

Снова лишь одно слагаемое будет ненулевым, и таким образом мы посчитаем логарифм предсказанной вероятности для верного класса. Формулы (18) и (19) называются категориальной кроссэнтропией (они эквивалентны если $p_{true}=1$ для одного из классов), формула (18) называется бинарной кроссэнтропией.

В этом разделе мы рассмотрели обучение модели классификации. Часто в классификации упоминают о функции softmax, но почему-то мы о ней ничего не говорили. Складывается ощущение, что мы что-то упустили. В следующем разделе мы поговорим о роли функции softmax в классификации.

1.2. Функция softmax в классификации

В предыдущем разделе мы определили, что модель классификации должна выдавать вероятности для всех классов. Но модель — это не только формат входных и выходных данных, а еще и внутренняя архитектура. Она может быть совершенно разной: для классификации применяются либо нейронные сети, либо решающие деревья, либо машины опорных векторов и так далее.

Рассмотрим для примера нейронную сеть. Пусть мы имеем классов, и выходной слой нейронной сети выдает чисел от до . Чтобы вектор из чисел являлся распределением вероятностей, он должен удовлетворять двум ограничениям:

Вероятность каждого класса не может быть ниже нуля
Сумма вероятностей должна быть равна единице

Для удовлетворения первого ограничения лучше чтобы модель выдавала не вероятности, а их логарифмы: если логарифм некой величины меняется от до , то сама величина меняется от до . Чтобы удовлетворялось второе ограничение, каждую предсказанную вероятность мы можем делить на сумму всех предсказанных вероятностей. Такая операция называется -нормализацией вектора вероятностей.

Отсюда мы можем вывести формулу для операции softmax. Эта операция принимает на вход набор из чисел от до (они называются логитами, англ. logits) ${z_i}_{i=1}^K$ и возвращает распределение вероятностей из чисел ${p_i}_{i=1}^K$ . Softmax является последовательностью двух операций: взятия экспоненты и -нормализации:

${p_i}_{i=1}^K = text{softmax}big(big{z_jbig}_{i=1}^Kbig) = bigg{cfrac{exp (z_i)}{sum_{j=i}^K exp (z_i)}bigg}_{i=1}^K tag{5}$

Таким образом, softmax — это векторная операция, принимающая вектор из произвольных чисел (логитов) и возвращающая вектор вероятностей, удовлетворяющий свойствам 1 и 2. Она применяется как завершающая операция во многих моделях классификации — таким образом мы можем быть уверены, что выданные моделью числа будут именно распределением вероятностей (т. е. удовлетворять свойствам 1 и 2). Существуют и различные альтернативы функции softmax, например sparsemax (Martins and Astudillo, 2016).

Модель, предсказывающая логитов, к которым применяется операция softmax, будет обладать только одним ограничением: она не может предсказывать строго нулевые или строго единичные вероятности. Зато такую модель можно обучать градиентным спуском, так как функция softmax дифференцируема.

Технически иногда функция softmax рассматривается как часть модели, иногда как часть функции потерь. Например, в библиотеке Keras мы можем добавить функцию активации 'softmax' в последний слой сети и использовать функцию потерь CategoricalCrossentropy(), а можем наоборот не добавлять функцию активации в последний слой и использовать функцию потерь CategoricalCrossentropy (from_logits=True), которая включает в себя расчет softmax (и ее производной при обратном проходе). С математической точки зрения разницы между этими двумя способами не будет, но погрешность расчета функции потерь и производной во втором случае будет меньше. В PyTorch мы можем применить LogSoftmax вместе с NLLLoss (negative log-likelihood), а можем вместо этого применить torch.nn.functional.cross_entropy, который включает в себя расчет LogSoftmax.

1.3. Температура softmax и операция hardmax*

У функции softmax (5) есть важное свойство: если ко всем логитам прибавить одну и ту же константу , то вероятности никак не изменятся, так как после применения экспоненты константа из слагаемого превратится в множитель, и множители в числителе и знаменателе сократятся. Однако если все логиты умножить на некую константу , то тогда вероятности изменятся: если , то вероятности станут ближе друг к другу, что означает меньшую уверенность в предсказании, если же , то наоборот мы получим большую уверенность в предсказании. Этот дополнительный множитель, если он используется, называется «температурой» softmax.

При тот класс, логит которого был наибольшим, получит вероятность 1, остальные классы — вероятность 0, такую операцию по аналогии часто называют hardmax. Иногда ее упоминают как argmax, потому что hardmax можно считать one-hot кодированием индекса, который возвращает операция argmax.

На этом примере видно то, как употребляются понятия soft и hard в машинном обучении: hard-операции (hardmax, argmax, hard attention, hard labeling, sign) связаны с выбором некоего элемента в множестве, а soft-операции (softmax, soft attention, soft labeling, soft sign) являются их дифференцируемыми аналогами. Например, в softmax можно рассчитать производную каждого выходного элемента по каждому входному. В hardmax или argmax это не имеет смысла: производные всегда будут равны нулю.

Это можно понять даже не прибегая к расчетам, поскольку у дифференцируемости есть очень простая наглядная интерпретация: операция дифференцируема если плавное изменение приводит к плавному изменению . Это верно для операции softmax, и благодаря этому мы можем применять градиентный спуск или градиентный бустинг. Но в операции hardmax плавное изменение логитов приводит к тому, что выходные вероятности либо остаются такими же, либо меняются скачкообразно, поэтому (без дополнительных ухищрений) градиентный спуск и градиентный бустинг оказываются неприменимы.

1.4. Функция sigmoid в классификации

Рассмотрим случай бинарной классификации. Представим, что у нас есть 2 класса, и модель выдает 2 логита , из которых с помощью softmax получаем вероятности , сумма которых равна единице. Но прибавление одной и той же константы к не меняет вероятности, поэтому иметь две «степени свободы» излишне, и имеет смысл зафиксировать в значении 0. Теперь меняя модель будет менять вероятности классов . Значения и , согласно (21), будут связаны следующим образом:

$p_2 = cfrac{exp(z_2)}{exp(z_1) + exp(z_2)} = cfrac{exp(z_2)}{1 + exp(z_2)}$

Такая функция носит название сигмоиды:

$sigma(x) = cfrac{e^x}{1+e^x} = cfrac{1}{1+e^{-x}} tag{6}$

Примечание. В более широком смысле, сигмоидами называют и другие функции одной переменной, график которых выглядит похожим образом. Для преобразования логита в вероятность вместо можно использовать любую и этих функций, разница между ними не принципиальна. Также сигмоида иногда используется в промежуточных слоях нейронных сетей.

К чему мы в итоге пришли? К тому, что если класса всего два, то иметь два логита в модели не обязательно, достаточно всего одного, к которому применяется сигмоида вместо softmax. Функция потерь при этом становится бинарной кроссэнтропией (4). На самом деле то же рассуждение можно применить и к мультиклассовой классификации: если классов , то достаточно иметь логитов, но так обычно не делают.

Теперь запишем функцию, обратную сигмоиде. Эта функция преобразует вероятность обратно в логит и называется logit function:

$sigma^{-1}(p) = log cfrac{p}{1-p}$

Если — это вероятность второго класса, а — вероятность первого класса, то выражение означает то, во сколько раз второй класс вероятнее первого. Это выражение называется odds ratio. Логит является его логарифмом и называется log odds ratio.

Если мы используем в обучении сигмоиду, то модель непосредственно предсказывает логит $sigma^{-1}(p)$ , то есть логарифм того, во сколько раз второй класс вероятнее первого.

2. Кроссэнтропия в вероятностных моделях

2.1. Разметка с неуверенностью

В выражениях для функции потерь в классификации (2) и регрессии (часть 1, формула 7) мы предполагали наличие для каждого примера эталонного ответа , к которому модель должна стремиться. Но в более общем случае эталонный ответ может быть не конкретным значением, а распределением вероятностей на множестве , так же как и предсказание модели. То есть в разметке датасета значения указаны с определенной степенью неуверенности: если это классификация, то могут быть указаны вероятности для всех классов, если регрессия — то может быть указана погрешность.

Ситуация, когда разметка датасета содержит некую степень неуверенности, не такая уж редкая. Например, в пусть в задаче классификации эмоций по видеозаписи датасет размечен сразу несколькими людьми-аннотаторами, которые иногда дают разные ответы. Например, одно из видео в датасете может быть размечено как «happiness» 11 аннотаторами и как «sadness» 9 аннотаторами. Оставив только «happiness» мы потеряем часть информации. Вместо этого мы можем оставить обе эмоции, считать их распределением вероятностей: , и обучать модель выдавать для данного примера такое же распределение вероятностей.

Благодаря разметке с неуверенностью сохраняется больше информации: есть явно выраженные эмоции, а есть сложно определяемые.

Но с другой стороны для каждого видео есть какая-то истинная эмоция: либо «happiness», либо «sadness» — человек не может испытывать обе эти эмоции одновременно. В теории модель могла бы обучиться определять эмоции точнее, чем человек, и разметка с неуверенностью может помешать модели выучиться точнее человека: если человек дает 50% вероятности обоим классам, и мы используем это как эталонный ответ, то модель будет стремиться к нему, даже если она способна определить эмоцию точнее.

2.2. Кроссэнтропия и расхождение Кульбака-Лейблера

Пусть мы имеем датасет из пар , в котором эталонный ответ является не конкретным значением признака , а распределением вероятностей на множестве . Нам каким-то образом нужно «подогнать» предсказанное распределение под эталонное распределение $p_{true}(y_i|x_i)$ .

Пример 1. Если в задаче классификации в эталонном распределении вероятности классов равны 0.7 и 0.3, то мы хотели бы, чтобы в предсказании они тоже были бы равны 0.7 и 0.3.

Пример 2. Если в задаче регрессии эталонное распределение имеет две моды в значениях 0.5 и 1.5, то нам хотелось бы, чтобы предсказанное распределение вероятностей тоже имело моды в этих точках. Но если мы моделируем нормальным распределением (как в разделе 2.3 первой части), тогда в нем в любом случае будет только одна мода, и чтобы хоть как-то приблизить предсказание к эталонному ответу, можно расположить моду посередине между точками 0.5 и 1.5 — тогда мат. ожидание ошибки предсказания будет наименьшим.

Как видим, второй пример получился сложнее первого. Если множество непрерывно, то задача приближения предсказанного распределения к эталонному означает задачу сближения функций плотности вероятности.

Такая постановка задачи неоднозначна: сблизить функции можно по-разному, так как «расстояние» между функциями можно определять по-разному. Чаще всего для этого используют расхождение Кульбака-Лейблера (относительную энтропию) $D_{KL}(p || q)$ — несимметричную метрику сходства между двумя распределениями вероятностей и . Расхождение Кульбака-Лейблера можно расписать как сумму в дискретном случае и как интеграл в непрерывном случае.

Дискретный случай (, — функции вероятности):

$D_{KL}(P || Q) = mathop{mathbb{E}}limits_{x sim p} log cfrac{P(x)}{Q(x)} = sumlimits_{x in X} P(x) log cfrac{P(x)}{Q(x)} tag{7}$

Непрерывный случай (, — функции плотности вероятности):

$D_{KL}(p || q) = mathop{mathbb{E}}limits_{x sim p} log cfrac{p(x)}{q(x)} = intlimits_{x in X} P(x) log cfrac{p(x)}{q(x)} dx tag{8}$

Пользуясь тем, что , мы можем расписать расхождение Кульбака-Лейблера как разность двух величин. Для дискретного случая:

$D_{KL}(P || Q) = underbrace{sumlimits_{x in X} P(x) log P(x)}_{-H(P)} + underbrace{bigg( - sumlimits_{x in X} P(x) log Q(x) bigg)}_{H(P, Q)} tag{9}$

Первое слагаемое со знаком минус называется энтропией распределения (или дифференциальной энтропией в непрерывном случае) и обозначается как , а второе слагаемое (включая минус) называется кроссэнтропией между распределениями и . Эти величины можно расписать через мат. ожидание:

$H(P) = -mathop{mathbb{E}}limits_{x sim p} log P(x)$ $H(P, Q) = -mathop{mathbb{E}}limits_{x sim p} log Q(x)$ $H(P, Q) = D_{KL}(P || Q) + H(P)$

В машинном обучении первым аргументом в $D_{KL}(P || Q)$ обычно ставят эталонное распределение, вторым аргументом — предсказанное. Как видно из формулы (9), первое слагаемое не зависит от , поэтому минимизация $D_{KL}(P || Q)$ по равносильно минимизации кроссэнтропии между и .

Резюме. Если значения целевого признака в датасете даны как распределения вероятностей, то для обучения модели мы можем минимизировать кроссэнтропию между предсказанными и эталонными распределениями. Мы так уже делали в модели классификации, но там эталонное распределение было вырожденным назначало вероятность 1 одному из классов, поэтому в формуле (3) лишь одно слагаемое было ненулевым. В этом разделе мы рассмотрели более общий случай, когда эталонное распределение невырождено и в (3) может быть много ненулевых слагаемых.

2.3. Кроссэнтропия как максимизация правдоподобия*

Является ли «подгонка» предсказанного распределения под эталонное распределение $p_{true}(y_i|x_i)$ применением метода максимизации правдоподобия? Для ответа на этот вопрос нужно понять что такое «правдоподобие» в том случае, когда вместо эталонного ответа мы имеем распределение.

Мы можем сделать таким образом. Пусть для -го примера мы имеем значение и распределение $p_{true}(y|x_i)$ . Мысленно сгенерируем из этого примера очень большое (стремящееся к бесконечности) количество примеров (обозначим его ), в которых исходные признаки равны , а целевой признак взят из распределения :

$text{Set}_i = { (x_i, y_i^{(k)}) }_{k=1}^K, y_i^{(k)} sim p_{true}(y|x_i)$

Объединение $text{Set}_1 cup dots cup text{Set}_N$ нельзя рассматривать как i.i.d.-выборку, потому что при бесконечном количестве примеров мы имеем лишь уникальных значений . Но поскольку мы не моделируем распределение , это не является проблемой. Поскольку все $y_i^{(k)}$ независимы:

$p(text{Set}_i|x_i, theta) = prodlimits_{k=1}^K p(y_i^{(k)}|x_i, theta)$ $begin{split} -log p(text{Set}_i|x_i, theta) & = -sumlimits_{k=1}^K log p(y_i^{(k)}|x_i, theta) \ & underset{K to infty}{to} -sumlimits_{y in Y} p_{true}(y|x_i) log p(y|x_i, theta) \ & = -mathbb{E}_{y sim p_{true}(y|x_i)} log p(y|x_i, theta) \ & = H(p_{true}(y|x_i), p(y|x_i, theta)) end{split}$

В итоге при минус логарифм правдоподобия $text{Set}_i$ оказался равен кроссэнтропии между эталонным распределением $p_{true}(y|x_i)$ и предсказанным моделью распределением . Отсюда получается, что минимизация кроссэнтропии (или, что эквивалентно, минимизация расхождения Кульбака-Лейблера) максимизирует правдоподобие.

2.4. Кроссэнтропия в задаче регрессии*

Вернемся к случаю регрессии. Если для обучающей пары точно известен ответ , то его можно представить как распределение вероятностей на , имеющее лишь одно возможное значение с вероятностью 1 (такое распределение называют вырожденным, в данном случае его еще называют «эмпирическим»).

Для таких случаев математики придумали специальную функцию, называемую дельта-функцией Дирака . Она равна нулю во всех точках кроме нуля, в нуле равна бесконечности, а ее интеграл равен единице. Например, если мы возьмем функцию плотности вероятности нормального распределения (часть 1, формула 4) с и устремим к нулю, то в пределе получим дельта-функцию.

В случае регрессии эмпирическое распределение можно записать как $delta(y - y_{true})$ . Попробуем, по аналогии с классификацией, минимизировать кроссэнтропию между эталонным и предсказанным распределениями. Пусть модель выдает для нормальное распределение . Распишем кроссэнтропию между эмпирическим и предсказанным распределением:

$begin{split} H(delta(y - y_{true}), p(y|x, theta)) & = -displaystyleint_{-infty}^infty delta(y - y_{true}) log p(y|x, theta) ,dy \ & = -log p(y|x, theta) end{split} tag{10}$

Обратите внимание, что оба аргумента являются не числами, а функциями от , и подынтегральное выражение не равно нулю только в одной точке $y_{true}$ . С помощью формулы (10) мы пришли к тому, что минимизация кроссэнтропии означает минимизацию , что эквивалентно максимизации . Именно это мы и делали в разделе 2. Получается, что модель регрессии тоже обучается с помощью кроссэнтропии, которая по формуле (10) превращается в минимизацию и далее в минимизацию среднеквадратичного отклонения (часть1, формула 7), если моделируется нормальным распределением.

Как видим, мы получаем максимально унифицированный и при этом гибкий подход, который можно применять для задания функции потерь в сложных случаях.

Кроссэнтропия с точки зрения оптимизации*

В задаче регрессии мы рассматривали два подхода к выбору функции потерь: первый подход опирается на здравый смысл, наши представления о метрике сходства на множестве и легкость оптимизации. Второй подход опирается на теорию вероятностей и наши представления об условном распределении , из которого следует формула для функции потерь (статья 1, формулы 5-7).

Теперь вернемся к задаче классификации. Есть ли здесь аналогичные два подхода? Вероятностный подход, который приводит к кроссэнтропии, мы уже рассматривали. Но хороша ли кроссэнтропия с точки зрения оптимизации, или есть более удобная функция потерь? Например, вместо кроссэнтропии мы могли бы минимизировать среднеквадратичную ошибку между предсказанным распределением вероятностей $p_{pred}[1], dots, p_{pred}[K]$ и эталонным распределением вероятностей $p_{true}[1], dots, p_{true}[K]$ , в котором вероятность 1 назначается верному классу:

$loss(p_{true}, p_{pred}) = sumlimits_{i=1}^K (p_{true}[i] - p_{pred}[i])^2$

Смысл такого выражения с точки зрения теории вероятностей не совсем ясен, но видно, что чем ближе предсказание к истине, тем меньше будет функция потерь. А это и есть то свойство, которое требуется от функции потерь.

Что же лучше: кроссэнтропия или среднеквадратичная ошибка? Чтобы понять, какая из функций потерь лучше подходит для оптимизации градиентным спуском, давайте рассчитаем градиенты этих функций потерь по логитам (то есть тем значениям, которые выдаются до операции softmax или sigmoid). Пусть классификация является бинарной, верный ответом является второй класс, и модель выдала значение логита, равное . Отсюда вероятность второго класса равна , где — операция сигмоиды (6). Рассчитаем производную функции потерь по логиту .

В случае бинарной кроссэнтропии:

$cfrac{partial loss}{partial m} = 1 - sigma(m)$

В случае среднеквадратичной ошибки:

$cfrac{partial loss}{partial m} = -2 sigma(m) (1 - sigma(m))^2$

При (то есть когда модель выдает уверенный неправильный ответ) при бинарной кроссэнтропии производная стремится к 1, а при среднеквадратичной ошибке производная стремится к нулю. Это означает, что при сочетении сигмоиды и среднеквадратичной ошибки уверенные неправильные ответы практически не корректируются градиентным спуском (градиент близок к нулю), что может негативно сказаться на качестве обучения. Это аргумент в пользу того, чтобы при использовании сигмоиды выбирать бинарную кроссэнтропию, а не среднеквадратичную ошибку.

Хотя, с другой стороны, этот аргумент не окончательный, ведь уверенные неправильные ответы модели могут на самом деле быть выбросами в данных или ошибками разметки, которые модель не должна выучивать. Поэтому, возможно, в некоторых случаях имеет смысл использовать среднеквадратичную ошибку вместо кроссэнтропии.

Конец части 2. Часть 3, посвященная байесовскому выводу, планируется к публикации. Спасибо@ivankomarovи @yorkoза ценные комментарии, которые были учтены при подготовке статьи.

Источник

Have you ever wondered what happens under the hood when you train a neural network? You’ll run the gradient descent optimization algorithm to find the optimal parameters (weights and biases) of the network. In this process, there’s a loss function that tells the network how good or bad its current prediction is. The goal of optimization is to find those parameters that minimize the loss function: the lower the loss, the better the model.

In classification problems, the model predicts the class label of an input. In such problems, you need metrics beyond accuracy. While accuracy tells the model whether or not a particular prediction is correct, cross-entropy loss gives information on how correct a particular prediction is. When training a classifier neural network, minimizing the cross-entropy loss during training is equivalent to helping the model learn to predict the correct labels with higher confidence.

In this tutorial, we’ll go over binary and categorical cross-entropy losses, used for binary and multiclass classification, respectively. We’ll learn how to interpret cross-entropy loss and implement it in Python. As the loss function’s derivative drives the gradient descent algorithm, we’ll learn to compute the derivative of the cross-entropy loss function.

Let’s begin!

What is Cross Entropy?

Before we proceed to learn about cross-entropy loss, it’d be helpful to review the definition of cross entropy. In the context of information theory, the cross entropy between two discrete probability distributions is related to KL divergence, a metric that captures how close the two distributions are.

Given a true distribution t and a predicted distribution p, the cross entropy between them is given by the following equation.

$$H(textbf{t},textbf{p}) = — sum_{s in S} textbf{t}(s).log(textbf{p}(s))$$

Here, both t and p are distributed on the same support S, but could take potentially different values. For a three-element support S, if t = [t1, t2, t3] and p = [p1, p2, p3], it’s not necessary that t_i = p_i for i in {1,2,3}.

Note: log(x) refers to log to the base e (or natural logarithm), also written as ln(x).

So how is cross entropy relevant in neural networks?

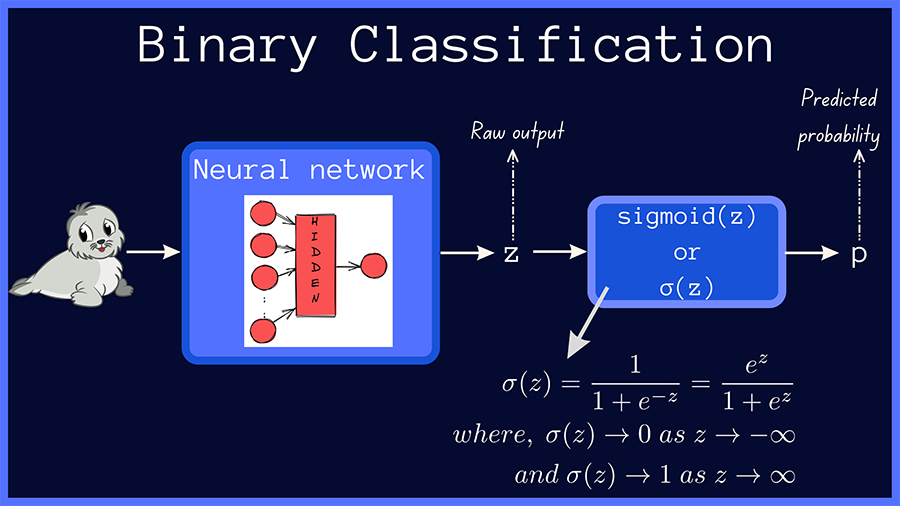
Recall that in binary classification, the sigmoid activation is used in the output layer, and the neural network outputs a probability score (p) between 0 and 1; the true label (t) being one of {0, 1}.

In case of multiclass classification, we use the softmax activation at the output layer to get a vector of predicted probabilities p. The true distribution t contains all of the probability mass (1) at the index of the correct class, and 0 everywhere else. For example, in a classification problem with N classes, the true distribution corresponding to class i is a vector that’s N classes long, with 1 at the index of the class label i and 0 at all other indices.

We’ll discuss this in greater detail in the coming sections.

Cross-Entropy Loss for Binary Classification

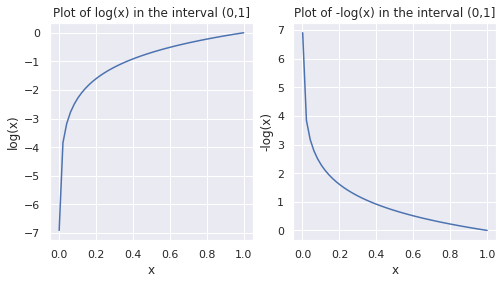
Let’s start this section by reviewing the log function in the interval (0,1].

▶️ Run the following code snippet to plot the values of log(x) and -log(x) in the range 0 to 1. As log(0) is -∞, we add a small offset, and start with 0.001 as the smallest value in the interval.

import numpy as np
import seaborn as sns
from matplotlib import pyplot as plt
sns.set() 
x_arr = np.linspace(0.001,1)
log_x = np.log(x_arr)
fig, axes = plt.subplots(1, 2,figsize=(8,4))
sns.lineplot(ax=axes[0],x=x_arr,y=log_x)
axes[0].set_title('Plot of log(x) in the interval (0,1]')
axes[0].set(xlabel='x', ylabel='log(x)')
sns.lineplot(ax=axes[1],x=x_arr,y=-log_x)
axes[1].set_title('Plot of -log(x) in the interval (0,1]')
axes[1].set(xlabel='x', ylabel='-log(x)')

Plot of log x and -log x in the interval (0,1]

As seen in the plots above, in the interval (0,1], log(x) and -log(x) are negative and positive, respectively. Observe how -log(x) approaches 0 as x approaches 1. This observation will be helpful when we parse the expression for cross-entropy loss.

In binary classification, the raw output of the neural network is passed through the sigmoid function, which outputs a probability score p = σ(z), as shown below.

A Simple Binary Classification Model (Image by the author)

The true value, or the true label, is one of {0, 1} and we’ll call it t. The binary cross-entropy loss, also called the log loss, is given by:

$$mathcal{L}(t,p) = -(t.log(p) + (1-t).log(1-p))$$

As the true label is either 0 or 1, we can rewrite the above equation as two separate equations.

When t = 1, the second term in the above equation goes to zero, and the equation reduces to the following:

$$When text{ } t=1,mathcal{L}(t,p) = -log(p)$$

Therefore, when t =1, the binary cross-entropy loss is equal to the negative logarithm of the predicted probability p.

Similarly, when the true label t=0, the term t.log(p) vanishes, and the expression for binary cross-entropy loss reduces to:

$$When text{ } t=0,mathcal{L}(t,p) = -log(1-p)$$

Now, let’s plot the binary cross-entropy loss for different values of the predicted probability p.

bce_1 = -np.log(p)
bce_0 = -np.log(1-p)
plot1 = sns.lineplot(x=p,y=bce_1,label='True value:1').set(ylim=(0,4))
plot2 = sns.lineplot(x=p,y=bce_0,label='True value:0').set(ylim=(0,4))
plt.xlabel('p')
plt.ylabel('Binary Cross-Entropy Loss')

From the plots above, we can make the following observations:

When the true label t is 1, the cross-entropy loss approaches 0 as the predicted probability p approaches 1 and
When the true label t is 0, the cross-entropy loss approaches 0 as the predicted probability p approaches 0.

In essence, the cross-entropy loss attains its minimum when the predicted probability p is close to the true value and is substantially higher when the predicted probability is far away from the true label.

But which predictions does cross-entropy loss penalize the most?

Recall that log(0) → -∞; so -log(0) → ∞. As seen from the plots of the binary cross-entropy loss, this happens when the network outputs p=1 or a value close to 1 when the true class label is 0, and outputs p=0 or a value close to 0 when the true label is 1.

Putting it all together, cross-entropy loss increases drastically when the network makes incorrect predictions with high confidence.

If there are S samples in the dataset, then the total cross-entropy loss is the sum of the loss values over all the samples in the dataset.

$$mathcal{L}(t,p) = -sum_{i=1}^{S}(t_i.log(p_i) + (1-t_i).log(1-p_i))$$

Binary Cross-Entropy Loss in Python

Let’s define a Python function to compute the binary cross-entropy loss.

def binary_cross_entropy(t,p):
    t = np.float_(t)
    p = np.float_(p)
    # binary cross-entropy loss
    return -np.sum(t * np.log(p) + (1 - t) * np.log(1 - p))

Next, let’s call the function binary_cross_entropywith arrays of true and predicted values as the arguments.

t = [0,1,1,0,0,1,1]
p = [0.07,0.91,0.74,0.23,0.85,0.17,0.94]

binary_cross_entropy(t,p)
4.460303459760249

To get a better idea of how the loss varies with p, let’s modify the function definition to print out the values of the loss for each of the samples, as shown below.

def binary_cross_entropy(t,p):
    t = np.float_(t)
    p = np.float_(p)
    for tt, pp in zip(t,p):
      print(f'true_val = {tt}, predicted_val = {pp}, loss = {-(tt * np.log(pp) + (1 - tt) * np.log(1 - pp))}')
    return -np.sum(t * np.log(p) + (1 - t) * np.log(1 - p))

Now that we’ve modified the function, let’s call the function yet again to check the outputs.

binary_cross_entropy(t,p)

# Output
true_val = 0.0, predicted_val = 0.07, loss = 0.0725706928348355
true_val = 1.0, predicted_val = 0.91, loss = 0.09431067947124129
true_val = 1.0, predicted_val = 0.74, loss = 0.3011050927839216
true_val = 0.0, predicted_val = 0.23, loss = 0.2613647641344075
true_val = 0.0, predicted_val = 0.85, loss = 1.897119984885881
true_val = 1.0, predicted_val = 0.17, loss = 1.7719568419318752
true_val = 1.0, predicted_val = 0.94, loss = 0.06187540371808753
4.460303459760249

In the above output, when the true and predicted values are closer, the cross-entropy loss is lower; the loss increases when the true and predicted values are different.

The highest value of the loss, 1.897, occurs when the network predicts a probability score of 0.85 corresponding to a true value of 0. Suppose the problem is to classify whether the given image is that of a seal or not. The model, in this case, is 85% confident that the image is a seal when it actually isn’t.

Similarly, the second highest value of the binary cross-entropy loss, 1.771 occurs when the network predicts a score of 0.17, significantly lower than the true value of 1. In the image classification example, this means that the model is only about 17% confident of the input image being a seal, when it actually is a seal.

This validates our earlier observation that the loss is higher when the predictions are away from the true values.

In the next section, let’s explore an extension of cross-entropy loss to the multiclass classification case.

Categorical Cross-Entropy Loss for Multiclass Classification

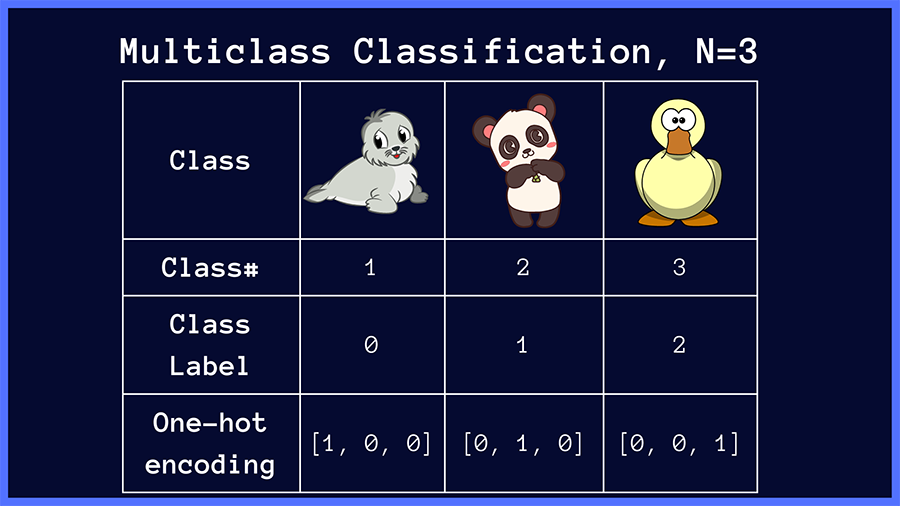
Let’s formalize the setting we’ll consider. In a multiclass classification problem over N classes, the class labels are 0, 1, 2 through N — 1. The labels are one-hot encoded with 1 at the index of the correct label, and 0 everywhere else.

For example, in an image classification problem where the input image is one of {panda, seal, duck}, the class labels and the corresponding one-hot vectors are shown below.

One-hot encoding of class labels in multiclass classification (Image by the author)

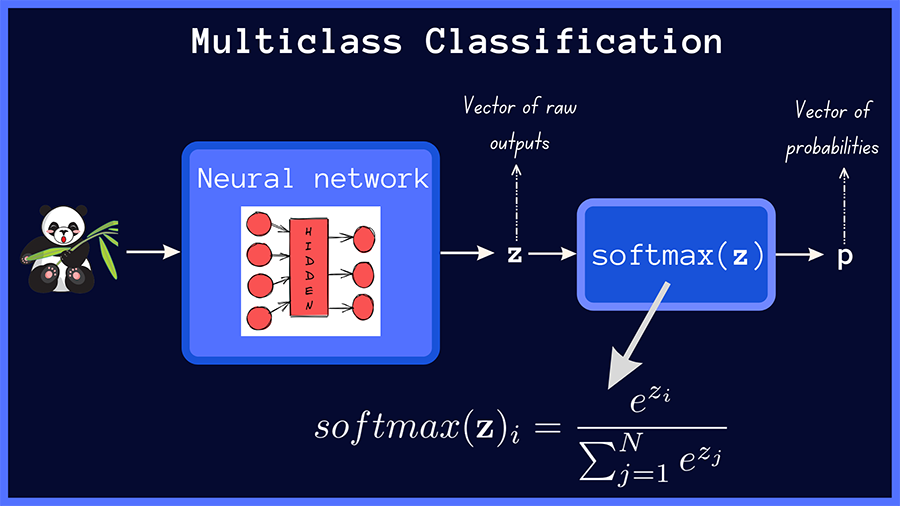
In multiclass classification, the raw outputs of the neural network are passed through the softmax activation, which then outputs a vector of predicted probabilities over the input classes.

A Simple Multiclass Classification Model (Image by the author)

The categorical cross-entropy loss between the true distribution t and the predicted distribution p in a multiclass classification problem with N classes is given by:

$$mathcal{L}(textbf{t},textbf{p}) = — sum_{j=1}^{N}t_j log(p_j)$$

This expression may seem daunting, but we’ll parse this and arrive at a much simpler expression.

Recall that the true distribution t is a one-hot vector that has 1 at one of the indices and zero everywhere else. If a given image belongs to the class k, in the true distribution vector, t_k = 1, and all other indices are zero.

Substituting as follows,
$$t_k=1 text{ } and text{ } t_j = 0 text{ } for text{ } j neq k$$
We see that N - 1 terms in the summation go to zero, and you’ll have the following simplified expression:

$$mathcal{L}(textbf{t},textbf{p}) = — t_k log(p_k) = -log(p_k)\
for text{ } antext{ } input text{ } in text{ } Class text{ }k$$

The loss, therefore, reduces to the negative logarithm of the predicted probability for the correct class. The loss approaches zero, as p_k → 1.

In the figure below, we present some examples of true and predicted distributions. In our image classification example, if the target class is seal, the categorical cross-entropy loss is minimized when the network predicts a probability score close to 1 for the correct class (seal). This works similarly for the other target classes, panda and duck.

Cross-entropy loss decreases as the predicted probability for the target class approaches 1 (Image by the author)

For a dataset with S samples in all, the categorical cross-entropy loss is given by:

$$mathcal{L}(textbf{t},textbf{p}) = — sum_{i=1}^{S}sum_{j=1}^{N}t_{ij} log(p_{ij})$$

In practice, you could also use the average cross-entropy loss across all samples in the dataset. Next, let’s code the categorical cross-entropy loss in Python.

Categorical Cross-Entropy Loss in Python

The code snippet below contains the definition of the function categorical_cross_entropy.The function accepts two lists as arguments: t_list and p_list containing lists of true and predicted distributions, respectively. It then computes the cross-entropy loss over each set of predicted and true values.

def categorical_cross_entropy(t_list,p_list):
    t_list = np.float_(t_list)
    p_list = np.float_(p_list)
    losses = []
    for t,p in zip(t_list,p_list):
      loss = -np.sum(t * np.log(p))
      losses.append(loss)
      print(f't:{t}, p:{p},loss:{loss}n')
    return np.sum(losses)

Now, let’s make a call to the function with the lists of true and predicted distribution vectors as the arguments and check the outputs.

t_list = [[1,0,0],[0,1,0],[0,0,1],[1,0,0]]
p_list = [[0.91,0.04,0.05],[0.11,0.8,0.09],[0.3,0.1,0.6],[0.25,0.4,0.35]]
categorical_cross_entropy(t_list,p_list)

t:[1. 0. 0.], p:[0.91 0.04 0.05],loss:0.09431067947124129

t:[0. 1. 0.], p:[0.11 0.8  0.09],loss:0.2231435513142097

t:[0. 0. 1.], p:[0.3 0.1 0.6],loss:0.5108256237659907

t:[1. 0. 0.], p:[0.25 0.4  0.35],loss:1.3862943611198906

2.214574215671332

From the output above, we see that the loss is lower when the model predicts a higher probability corresponding to the correct class label.

Derivative of the Softmax Cross-Entropy Loss Function

One of the limitations of the argmax function as the output layer activation is that it doesn’t support the backpropagation of gradients through the layers of the neural network. However, when using the softmax function as the output layer activation, along with cross-entropy loss, you can compute gradients that facilitate backpropagation. The gradient evaluates to a simple expression, easy to interpret and intuitive.

If you’d like to know how softmax activation and cross-entropy loss yield a gradient that can be used in backpropagation, please read ahead. The preceding sections do not necessitate the use of the following section but this will provide interesting and potentially helpful insight.

The following subsections assume you have some familiarity with differential calculus. To follow along, you should be able to apply the chain rule for differentiation and compute partial derivatives.

Derivative of the Softmax Function

Recall that if z is the output of the neural network, then softmax(z) outputs a vector p of probabilities. Let’s start with the expression for softmax activation.

$$softmax(textbf{z})_i = p_i = frac{e^{z_i}}{sum_{j = 1}^{N} e^{z_j}}\\
Let text{ } sum_{j = 1}^{N} e^{z_j} = Sigma N \\
softmax(textbf{z})_i = frac{e^{z_i}}{ Sigma N}$$

Now, let’s compute the derivative of the softmax output p_i with respect to the raw output z_i of the neural network.

Here, the computation of derivatives can be handled under two different cases, as shown below.

begin{align}
Casetext{ }1: text{ }Whentext{ } i = j: \
frac{partial p_i}{partial z_i} = frac{partial frac{e^{z_i}}{Sigma N}}{partial z_i}\
= frac{Sigma N.frac{partial e^{z_i}}{partial z_i} — e^{z_i}.frac{partial Sigma N}{partial z_i}}{(Sigma N)^{2}}\
frac{partial Sigma N}{partial z_i} = frac{partial sum_{j neq i} e^{z_j}}{partial z_i} + frac{partial e^{z_i}}{partial z_i} = e^{z_i}\
frac{partial e^{z_i}}{partial z_i} = e^{z_i}\
frac{partial p_i}{partial z_i} = frac{Sigma N.e^{z_i} — e^{z_i}.e^{z_i}}{(Sigma N)^{2}} = frac{e^{z_i}}{Sigma N}left[1- frac{e^{z_i}}{Sigma N}right] = p_i(1-p_i)
end{align}

begin{align}
Casetext{ }2: text{ }Whentext{ } i neq j:\
frac{partial p_i}{partial z_j} = frac{partial frac{e^{z_i}}{Sigma N}}{partial z_j}\
= frac{Sigma N.frac{partial e^{z_i}}{partial z_j} — e^{z_i}.frac{partial Sigma N}{partial z_j}}{(Sigma N)^{2}}\
= 0 — frac{e^{z_i}.e^{z_j}}{(Sigma N)^{2}}\
= 0 — frac{e^{z_i}}{Sigma N}.frac{e^{z_j}}{Sigma N}\
implies frac{partial p_i}{partial z_j} = -p_ip_j
end{align}

Derivative of the Cross-Entropy Loss Function

Next, let’s compute the derivative of the cross-entropy loss function with respect to the output of the neural network. We’ll apply the chain rule and substitute the derivatives of the softmax activation function.

begin{align}frac{partial{L}}{partial{z_i}} = — sum_{j = 1}^{N} frac{partial{(t_j log p_j)}}{partial{z_i}}\
= — sum_{j = 1}^{N} t_jfrac{partial{(log p_j)}}{partial{z_i}}\
= — sum_{j = 1}^{N} t_jfrac{1}{p_j}frac{partial{p_j}}{partial{z_i}}\
= — frac{t_i}{p_i}frac{partial{p_i}}{partial{z_i}} — sum_{j neq i} frac{t_j}{p_j} frac{partial{p_j}}{partial{z_i}}\
= — frac{t_i}{p_i}p_i(1-p_i) — sum_{j neq i} frac{t_j}{p_j} (-p_jp_i)\
= -t_j + t_ip_i + sum_{j neq i} t_jp_i \
= -t_i + sum_{j = 1}^{N} t_jp_i\
= -t_i + p_isum_{j = 1}^{N} t_j\
implies frac{partial{L}}{partial{z_i}} = p_i — t_iend{align}

As seen above, the gradient works out to the difference between the predicted and true probability values.

Wrapping Up

In this tutorial, you’ve learned how binary and categorical cross-entropy losses work. They impose a penalty on predictions that are significantly different from the true value. You’ve learned to implement both the binary and categorical cross-entropy losses from scratch in Python. In addition, we covered how using the cross-entropy loss, in conjunction with the softmax activation, yields a simple gradient expression in backpropagation.

As a next step, you may try spinning up a simple image classification model using softmax activation and cross-entropy loss function. Until the next tutorial!

📚 Resources

[1] Softmax Activation Function, pinecone.io

[2] Essence of Calculus, YouTube playlist by Grant Sanderson of 3Blue1Brown

[3] Gradient Descent Optimization, CS231n

[4] Backpropagation, CS231n

[5] Simple MNIST Convnet, keras.io

[6] Information Theory, Dive into Deep Learning

Источник

People like to use cool names which are often confusing. When I started playing with CNN beyond single label classification, I got confused with the different names and formulations people write in their papers, and even with the loss layer names of the deep learning frameworks such as Caffe, Pytorch or TensorFlow.
In this post I group up the different names and variations people use for Cross-Entropy Loss. I explain their main points, use cases and the implementations in different deep learning frameworks.

First, let’s introduce some concepts:

Tasks

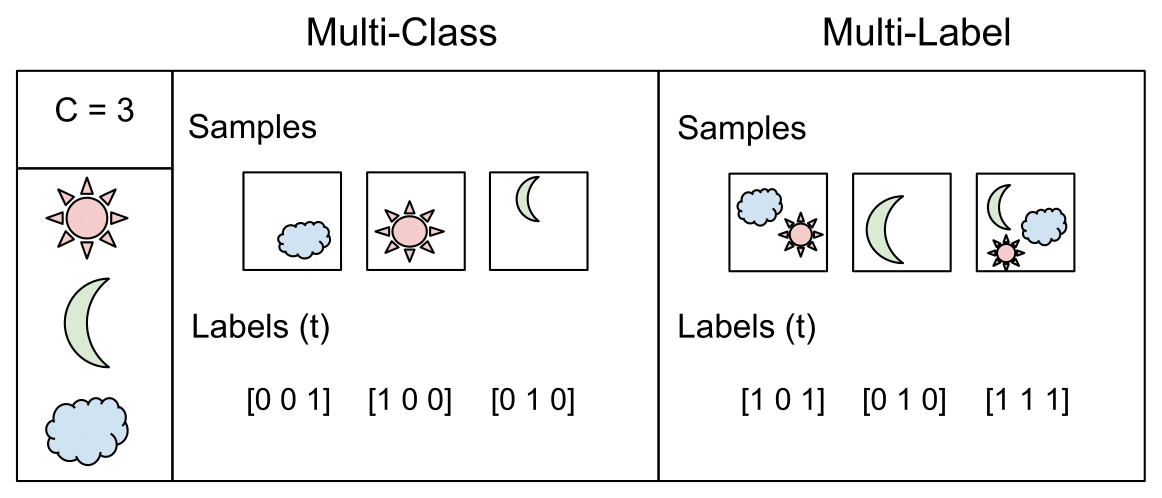
Multi-Class Classification

One-of-many classification. Each sample can belong to ONE of (C) classes. The CNN will have (C) output neurons that can be gathered in a vector (s) (Scores). The target (ground truth) vector (t) will be a one-hot vector with a positive class and (C — 1) negative classes.
This task is treated as a single classification problem of samples in one of (C) classes.

Multi-Label Classification

Each sample can belong to more than one class. The CNN will have as well (C) output neurons. The target vector (t) can have more than a positive class, so it will be a vector of 0s and 1s with (C) dimensionality.
This task is treated as (C) different binary ((C’ = 2, t’ = 0 text{ or } t’ = 1)) and independent classification problems, where each output neuron decides if a sample belongs to a class or not.

Output Activation Functions

These functions are transformations we apply to vectors coming out from CNNs ((s)) before the loss computation.

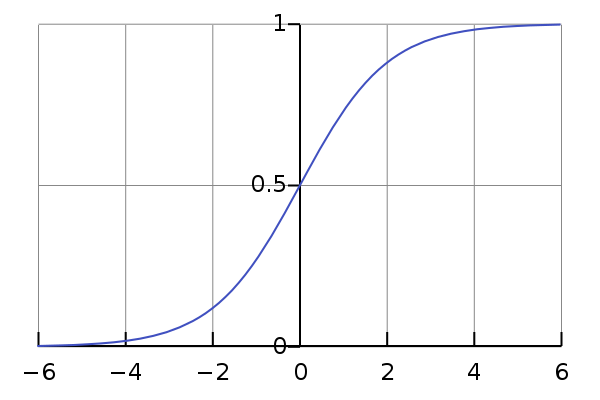
Sigmoid

It squashes a vector in the range (0, 1). It is applied independently to each element of (s) (s_i). It’s also called logistic function.

$f(s_{i}) = frac{1}{1 + e^{-s_{i}}}$

Softmax

Softmax it’s a function, not a loss. It squashes a vector in the range (0, 1) and all the resulting elements add up to 1. It is applied to the output scores (s). As elements represent a class, they can be interpreted as class probabilities.
The Softmax function cannot be applied independently to each (s_i), since it depends on all elements of (s). For a given class (s_i), the Softmax function can be computed as:

$f(s)_{i} = frac{e^{s_{i}}}{sum_{j}^{C} e^{s_{j}}}$

Where (s_j) are the scores inferred by the net for each class in (C). Note that the Softmax activation for a class (s_i) depends on all the scores in (s).

An extense comparison of this two functions can be found here

Activation functions are used to transform vectors before computing the loss in the training phase. In testing, when the loss is no longer applied, activation functions are also used to get the CNN outputs.

If you prefer video format, I made a video out of this post. Also available in Spanish:

Losses

Cross-Entropy loss

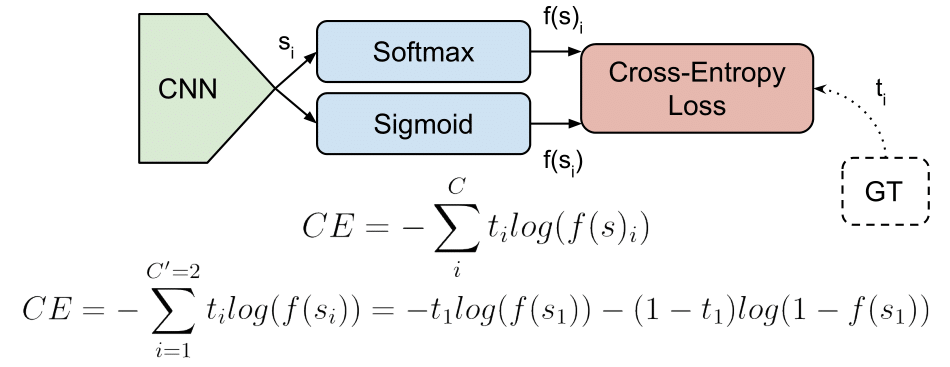
The Cross-Entropy Loss is actually the only loss we are discussing here. The other losses names written in the title are other names or variations of it. The CE Loss is defined as:

$CE = -sum_{i}^{C}t_{i} log (s_{i})$

Where (t_i) and (s_i) are the groundtruth and the CNN score for each class (_i) in (C). As usually an activation function (Sigmoid / Softmax) is applied to the scores before the CE Loss computation, we write (f(s_i)) to refer to the activations.

In a binary classification problem, where (C’ = 2), the Cross Entropy Loss can be defined also as [discussion]:

$CE = -sum_{i=1}^{C'=2}t_{i} log (s_{i}) = -t_{1} log(s_{1}) - (1 - t_{1}) log(1 - s_{1})$

Where it’s assumed that there are two classes: (C_1) and (C_2). (t_1) [0,1] and (s_1) are the groundtruth and the score for (C_1), and (t_2 = 1 — t_1) and (s_2 = 1 — s_1) are the groundtruth and the score for (C_2). That is the case when we split a Multi-Label classification problem in (C) binary classification problems. See next Binary Cross-Entropy Loss section for more details.

Logistic Loss and Multinomial Logistic Loss are other names for Cross-Entropy loss. [Discussion]

The layers of Caffe, Pytorch and Tensorflow than use a Cross-Entropy loss without an embedded activation function are:

Caffe: Multinomial Logistic Loss Layer. Is limited to multi-class classification (does not support multiple labels).
Pytorch: BCELoss. Is limited to binary classification (between two classes).
TensorFlow: log_loss.

Categorical Cross-Entropy loss

Also called Softmax Loss. It is a Softmax activation plus a Cross-Entropy loss. If we use this loss, we will train a CNN to output a probability over the (C) classes for each image. It is used for multi-class classification.

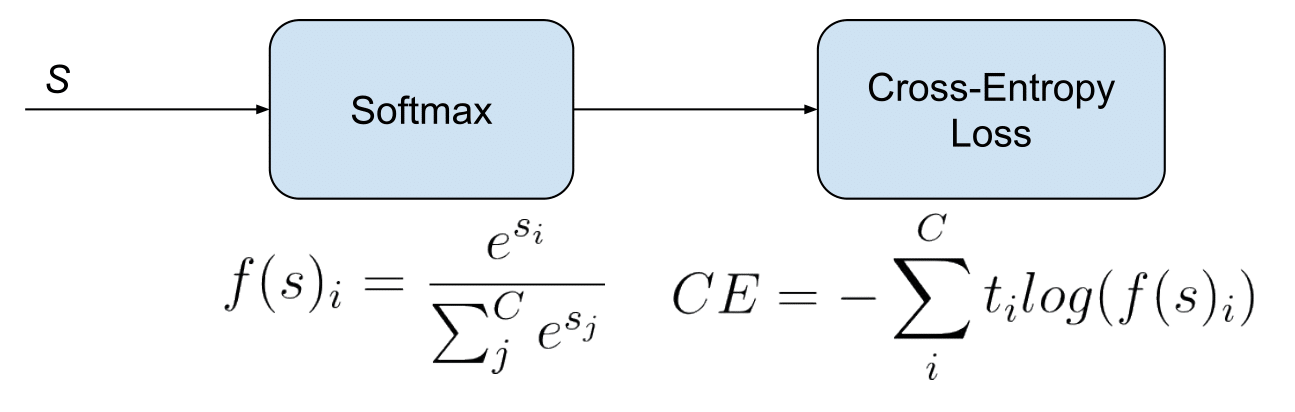
In the specific (and usual) case of Multi-Class classification the labels are one-hot, so only the positive class (C_p) keeps its term in the loss. There is only one element of the Target vector (t) which is not zero (t_i = t_p). So discarding the elements of the summation which are zero due to target labels, we can write:

$CE = -logleft ( frac{e^{s_{p}}}{sum_{j}^{C} e^{s_{j}}} right )$

Where Sp is the CNN score for the positive class.

Defined the loss, now we’ll have to compute its gradient respect to the output neurons of the CNN in order to backpropagate it through the net and optimize the defined loss function tuning the net parameters. So we need to compute the gradient of CE Loss respect each CNN class score in (s).
The loss terms coming from the negative classes are zero. However, the loss gradient respect those negative classes is not cancelled, since the Softmax of the positive class also depends on the negative classes scores.

The gradient expression will be the same for all (C) except for the ground truth class (C_p), because the score of (C_p) ((s_p)) is in the nominator.

After some calculus, the derivative respect to the positive class is:

$frac{partial}{partial s_{p}} left ( -logleft ( frac{e^{s_{p}}}{sum_{j}^{C} e^{s_{j}}} right ) right ) = left ( frac{e^{s_{p}}}{sum_{j}^{C}e^{s_{j}}} - 1 right )$

And the derivative respect to the other (negative) classes is:

$frac{partial}{partial s_{n}} left (-logleft ( frac{e^{s_{p}}}{sum_{j}^{C} e^{s_{j}}} right ) right ) = left ( frac{e^{s_{n}}}{sum_{j}^{C}e^{s_{j}}}right )$

Where (s_n) is the score of any negative class in (C) different from (C_p).

Caffe: SoftmaxWithLoss Layer. Is limited to multi-class classification.
Pytorch: CrossEntropyLoss. Is limited to multi-class classification.
TensorFlow: softmax_cross_entropy. Is limited to multi-class classification.

In this Facebook work they claim that, despite being counter-intuitive, Categorical Cross-Entropy loss, or Softmax loss worked better than Binary Cross-Entropy loss in their multi-label classification problem.

→ Skip this part if you are not interested in Facebook or me using Softmax Loss for multi-label classification, which is not standard.

When Softmax loss is used is a multi-label scenario, the gradients get a bit more complex, since the loss contains an element for each positive class. Consider (M) are the positive classes of a sample. The CE Loss with Softmax activations would be:

$CE = frac{1}{M} sum_{p}^{M} -logleft ( frac{e^{s_{p}}}{sum_{j}^{C} e^{s_{j}}} right )$

Where each (s_p) in (M) is the CNN score for each positive class. As in Facebook paper, I introduce a scaling factor (1/M) to make the loss invariant to the number of positive classes, which may be different per sample.

The gradient has different expressions for positive and negative classes. For positive classes:

$frac{partial}{partial s_{pi}} left ( frac{1}{M} sum_{p}^{M} -logleft ( frac{e^{s_{p}}}{sum_{j}^{C} e^{s_{j}}} right ) right ) = frac{1}{M} left ( left ( frac{e^{s_{pi}}}{sum_{j}^{C}e^{s_{j}}} - 1 right ) + (M - 1) frac{e^{s_{pi}}}{sum_{j}^{C}e^{s_{j}}} right )$

Where (s_pi) is the score of any positive class.

For negative classes:

$frac{partial}{partial s_{n}} left ( frac{1}{M} sum_{p}^{M} -logleft ( frac{e^{s_{p}}}{sum_{j}^{C} e^{s_{j}}} right ) right ) = frac{e^{s_{n}}}{sum_{j}^{C}e^{s_{j}}}$

This expressions are easily inferable from the single-label gradient expressions.

As Caffe Softmax with Loss layer nor Multinomial Logistic Loss Layer accept multi-label targets, I implemented my own PyCaffe Softmax loss layer, following the specifications of the Facebook paper. Caffe python layers let’s us easily customize the operations done in the forward and backward passes of the layer:

Forward pass: Loss computation

def forward(self, bottom, top):
   labels = bottom[1].data
   scores = bottom[0].data
   # Normalizing to avoid instability
   scores -= np.max(scores, axis=1, keepdims=True)  
   # Compute Softmax activations
   exp_scores = np.exp(scores)
   probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True) 
   logprobs = np.zeros([bottom[0].num,1])
   # Compute cross-entropy loss
   for r in range(bottom[0].num): # For each element in the batch
       scale_factor = 1 / float(np.count_nonzero(labels[r, :]))
       for c in range(len(labels[r,:])): # For each class 
           if labels[r,c] != 0:  # Positive classes
               logprobs[r] += -np.log(probs[r,c]) * labels[r,c] * scale_factor # We sum the loss per class for each element of the batch

   data_loss = np.sum(logprobs) / bottom[0].num

   self.diff[...] = probs  # Store softmax activations
   top[0].data[...] = data_loss # Store loss

We first compute Softmax activations for each class and store them in probs. Then we compute the loss for each image in the batch considering there might be more than one positive label. We use an scale_factor ((M)) and we also multiply losses by the labels, which can be binary or real numbers, so they can be used for instance to introduce class balancing.
The batch loss will be the mean loss of the elements in the batch. We then save the data_loss to display it and the probs to use them in the backward pass.

Backward pass: Gradients computation

def backward(self, top, propagate_down, bottom):
   delta = self.diff   # If the class label is 0, the gradient is equal to probs
   labels = bottom[1].data
   for r in range(bottom[0].num):  # For each element in the batch
       scale_factor = 1 / float(np.count_nonzero(labels[r, :]))
       for c in range(len(labels[r,:])):  # For each class
           if labels[r, c] != 0:  # If positive class
               delta[r, c] = scale_factor * (delta[r, c] - 1) + (1 - scale_factor) * delta[r, c]
   bottom[0].diff[...] = delta / bottom[0].num

In the backward pass we need to compute the gradients of each element of the batch respect to each one of the classes scores (s). As the gradient for all the classes (C) except positive classes (M) is equal to probs, we assign probs values to delta. For the positive classes in (M) we subtract 1 to the corresponding probs value and use scale_factor to match the gradient expression. We compute the mean gradients of all the batch to run the backpropagation.

The Caffe Python layer of this Softmax loss supporting a multi-label setup with real numbers labels is available here

Binary Cross-Entropy Loss

Also called Sigmoid Cross-Entropy loss. It is a Sigmoid activation plus a Cross-Entropy loss. Unlike Softmax loss it is independent for each vector component (class), meaning that the loss computed for every CNN output vector component is not affected by other component values. That’s why it is used for multi-label classification, were the insight of an element belonging to a certain class should not influence the decision for another class.
It’s called Binary Cross-Entropy Loss because it sets up a binary classification problem between (C’ = 2) classes for every class in (C), as explained above. So when using this Loss, the formulation of Cross Entroypy Loss for binary problems is often used:

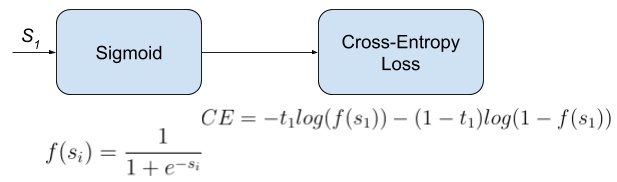
$CE = -sum_{i=1}^{C'=2}t_{i} log (f(s_{i})) = -t_{1} log(f(s_{1})) - (1 - t_{1}) log(1 - f(s_{1}))$

This would be the pipeline for each one of the (C) clases. We set (C) independent binary classification problems ((C’ = 2)). Then we sum up the loss over the different binary problems: We sum up the gradients of every binary problem to backpropagate, and the losses to monitor the global loss. (s_1) and (t_1) are the score and the gorundtruth label for the class (C_1), which is also the class (C_i) in (C). (s_2 = 1 — s_1) and (t_2 = 1 — t_1) are the score and the groundtruth label of the class (C_2), which is not a “class” in our original problem with (C) classes, but a class we create to set up the binary problem with (C_1 = C_i). We can understand it as a background class.

The loss can be expressed as:

$CE = left{begin{matrix} & - log(f(s_{1})) & & if & t_{1} = 1 \ & - log(1 - f(s_{1})) & & if & t_{1} = 0 end{matrix}right.$

Where (t_1 = 1) means that the class (C_1 = C_i) is positive for this sample.

In this case, the activation function does not depend in scores of other classes in (C) more than (C_1 = C_i). So the gradient respect to the each score (s_i) in (s) will only depend on the loss given by its binary problem.

The gradient respect to the score (s_i = s_1) can be written as:

$frac{partial}{partial s_{i}} left ( CE(f(s_{i})right) = t_{1} (f(s_{1}) - 1) + (1 - t_{1}) f(s_{1})$

Where (f()) is the sigmoid function. It can also be written as:

$frac{partial}{partial s_{i}} left ( CE(f(s_{i})right) = begin{Bmatrix} f(s_{i}) - 1 && if & t_{i} = 1\ f(s_{i}) && if & t_{i} = 0 end{Bmatrix}$

Refer here for a detailed loss derivation.

Caffe: Sigmoid Cross-Entropy Loss Layer
Pytorch: BCEWithLogitsLoss
TensorFlow: sigmoid_cross_entropy.

Focal Loss

Focal Loss was introduced by Lin et al., from Facebook, in this paper. They claim to improve one-stage object detectors using Focal Loss to train a detector they name RetinaNet. Focal loss is a Cross-Entropy Loss that weighs the contribution of each sample to the loss based in the classification error. The idea is that, if a sample is already classified correctly by the CNN, its contribution to the loss decreases. With this strategy, they claim to solve the problem of class imbalance by making the loss implicitly focus in those problematic classes.
Moreover, they also weight the contribution of each class to the lose in a more explicit class balancing.
They use Sigmoid activations, so Focal loss could also be considered a Binary Cross-Entropy Loss. We define it for each binary problem as:

$FL = -sum_{i=1}^{C=2}(1 - s_{i})^{gamma }t_{i} log (s_{i})$

Where ((1 — s_i)gamma), with the focusing parameter (gamma >= 0), is a modulating factor to reduce the influence of correctly classified samples in the loss. With (gamma = 0), Focal Loss is equivalent to Binary Cross Entropy Loss.

The loss can be also defined as :

$FL = left{begin{matrix} & - (1 - s_{1})^{gamma }log(s_{1}) & & if & t_{1} = 1 \ & - (1 - (1 - s_{1}))^{gamma } log(1 - s_{1}) & & if & t_{1} = 0 end{matrix}right.$

Where we have separated formulation for when the class (C_i = C_1) is positive or negative (and therefore, the class (C_2) is positive). As before, we have (s_2 = 1 — s_1) and (t2 = 1 — t_1).

The gradient gets a bit more complex due to the inclusion of the modulating factor ((1 — s_i)gamma) in the loss formulation, but it can be deduced using the Binary Cross-Entropy gradient expression.

In case (C_i) is positive ((t_i = 1)), the gradient expression is:

$frac{partial}{partial s_{i}} left ( FL(f(s_{i})) right ) = (1 - f(s_{i}))^{gamma }(gamma f(s_{i}) log(f(s_{i})) + f(s_{i}) - 1) quad if quad t_{1} = 1$

Where (f()) is the sigmoid function. To get the gradient expression for a negative
(C_i (t_i = 0)), we just need to replace (f(s_i)) with ((1 — f(s_i))) in the expression above.

Notice that, if the modulating factor (gamma = 0), the loss is equivalent to the CE Loss, and we end up with the same gradient expression.

I implemented Focal Loss in a PyCaffe layer:

Forward pass: Loss computation

def forward(self, bottom, top):
   labels = bottom[1].data
   scores = bottom[0].data
   scores =  1 / (1 + np.exp(-scores)) # Compute sigmoid activations
   logprobs = np.zeros([bottom[0].num, 1])

   # Compute cross-entropy loss
   for r in range(bottom[0].num):  # For each element in the batch
       for c in range(len(labels[r, :])):
           # For each class we compute the binary cross-entropy loss
           # We sum the loss per class for each element of the batch
           if labels[r, c] == 0: # Loss form for negative classes
               logprobs[r] += self.class_balances[str(c+1)] * -np.log(1-scores[r, c]) * scores[r, c] ** self.focusing_parameter
           else: # Loss form for positive classes
               logprobs[r] += self.class_balances[str(c+1)] * -np.log(scores[r, c]) * (1 - scores[r, c]) ** self.focusing_parameter
               # The class balancing factor can be included in labels by using scaled real values instead of binary labels.

   data_loss = np.sum(logprobs) / bottom[0].num
   top[0].data[...] = data_loss

Where logprobs[r] stores, per each element of the batch, the sum of the binary cross entropy per each class. The focusing_parameter is (gamma), which by default is 2 and should be defined as a layer parameter in the net prototxt. The class_balances can be used to introduce different loss contributions per class, as they do in the Facebook paper.

Backward pass: Gradients computation

def backward(self, top, propagate_down, bottom):
   delta = np.zeros_like(bottom[0].data, dtype=np.float32) 
   labels = bottom[1].data
   scores = bottom[0].data
   # Compute sigmoid activations
   scores =  1 / (1 + np.exp(-scores))

   

   for r in range(bottom[0].num):  # For each element in the batch
       for c in range(len(labels[r, :])):  # For each class
           p = scores[r, c]
           if labels[r, c] == 0:
               delta[r, c] = self.class_balances[str(c+1)] * -(p ** self.focusing_parameter) * ((self.focusing_parameter - p * self.focusing_parameter) * np.log(1-p) - p) # Gradient for classes with negative labels
           else:  # If the class label != 0
               delta[r, c] = self.class_balances[str(c+1)] * (((1 - p) ** self.focusing_parameter) * (
               self.focusing_parameter * p * np.log(
                   p) + p - 1))  # Gradient for classes with positive labels

   bottom[0].diff[...] = delta / bottom[0].num

The Focal Loss Caffe python layer is available here.

Additional Resources

Keras Loss Functions Guide: Keras Loss Functions: Everything You Need To Know

Источник

Функции оценки

Точечная оценка

Функция оценки

Смещение и дисперсия

Смещение

Дисперсия и Стандартная ошибка

Оценка Максимального Правдоподобия (MLE)

Два важных свойства: сходимость и эффективность

Максимальная апостериорная (MAP) оценка

Функции потерь

Получение MSE из MLE

Бинарная классификация

Визуализация

Мульти-классовая классификация

Задачи ML и соответствующие функции потерь

Задача регрессии

Задача бинарной классификации

Задача мульти-классовой классификации

Оптимизаторы

Градиентный Спуск

Адаград

RMSprop

Адам

Ссылки:

Содержание текущей части

1. Вероятностная модель классификации

1.1. Модель классификации и функция потерь

Категориальная кроссэнтропия

Бинарная кроссэнтропия

1.2. Функция softmax в классификации

1.3. Температура softmax и операция hardmax*

1.4. Функция sigmoid в классификации

2. Кроссэнтропия в вероятностных моделях

2.1. Разметка с неуверенностью

2.2. Кроссэнтропия и расхождение Кульбака-Лейблера

2.3. Кроссэнтропия как максимизация правдоподобия*

2.4. Кроссэнтропия в задаче регрессии*

Кроссэнтропия с точки зрения оптимизации*

What is Cross Entropy?

Cross-Entropy Loss for Binary Classification

Binary Cross-Entropy Loss in Python

Categorical Cross-Entropy Loss for Multiclass Classification

Categorical Cross-Entropy Loss in Python

Derivative of the Softmax Cross-Entropy Loss Function

Derivative of the Softmax Function

Derivative of the Cross-Entropy Loss Function

Wrapping Up

📚 Resources

Tasks

Multi-Class Classification

Multi-Label Classification

Output Activation Functions

Sigmoid

Softmax

Losses

Cross-Entropy loss

Categorical Cross-Entropy loss

Forward pass: Loss computation

Backward pass: Gradients computation

Binary Cross-Entropy Loss

Focal Loss

Forward pass: Loss computation

Backward pass: Gradients computation

Additional Resources

Два важных свойства: сходимость и
эффективность