Время на прочтение
15 мин
Количество просмотров 101K
Привет всем, кто выбрал путь ML-самурая!
Введение:
В данной статье рассмотрим метод опорных векторов (англ. SVM, Support Vector Machine) для задачи классификации. Будет представлена основная идея алгоритма, вывод настройки его весов и разобрана простая реализация своими руками. На примере датасета будет продемонстрирована работа написанного алгоритма с линейно разделимыми/неразделимыми данными в пространстве
и визуализация обучения/прогноза. Дополнительно будут озвучены плюсы и минусы алгоритма, его модификации.
Рисунок 1. Фото цветка ириса из открытых источников
Решаемая задача:
Будем решать задачу бинарной (когда класса всего два) классификации. Сначала алгоритм тренируется на объектах из обучающей выборки, для которых заранее известны метки классов. Далее уже обученный алгоритм предсказывает метку класса для каждого объекта из отложенной/тестовой выборки. Метки классов могут принимать значения . Объект — вектор c N признаками
в пространстве
. При обучении алгоритм должен построить функцию
, которая принимает в себя аргумент
— объект из пространства
и выдает метку класса
.
Общие слова об алгоритме:
Задача классификации относится к обучению с учителем. SVM — алгоритм обучения с учителем. Наглядно многие алгоритмы машинного обучения можно посмотреть в этой топовой статье (см. раздел «Карта мира машинного обучения»). Нужно добавить, что SVM может применяться и для задач регрессии, но в данной статье будет разобран SVM-классификатор.
Главная цель SVM как классификатора — найти уравнение разделяющей гиперплоскости
в пространстве
, которая бы разделила два класса неким оптимальным образом. Общий вид преобразования
объекта
в метку класса
:
. Будем помнить, что мы обозначили
. После настройки весов алгоритма
и
(обучения), все объекты, попадающие по одну сторону от построенной гиперплоскости, будут предсказываться как первый класс, а объекты, попадающие по другую сторону — второй класс.
Внутри функции стоит линейная комбинация признаков объекта с весами алгоритма, именно поэтому SVM относится к линейным алгоритмам. Разделяющую гиперплоскость можно построить разными способами, но в SVM веса
и
настраиваются таким образом, чтобы объекты классов лежали как можно дальше от разделяющей гиперплоскости. Другими словами, алгоритм максимизирует зазор (англ. margin) между гиперплоскостью и объектами классов, которые расположены ближе всего к ней. Такие объекты и называют опорными векторами (см. рис.2). Отсюда и название алгоритма.
Рисунок 2. SVM (основа рисунка отсюда)
Подробный вывод правил настройки весов SVM:
Чтобы разделяющая гиперплоскость как можно дальше отстояла от точек выборки, ширина полосы должна быть максимальной. Вектор — вектор нормали к разделяющей гиперплоскости. Здесь и далее будем обозначать скалярное произведение двух векторов как
или
. Давайте найдем проекцию вектора, концами которого являются опорные вектора разных классов, на вектор
. Эта проекция и будет показывать ширину разделяющий полосы (см. рис.3):
Рисунок 3. Вывод правил настройки весов (основа рисунка отсюда)
Отступом (англ. margin) объекта x от границы классов называется величина . Алгоритм допускает ошибку на объекте тогда и только тогда, когда отступ
отрицателен (когда
и
разных знаков). Если
, то объект попадает внутрь разделяющей полосы. Если
, то объект x классифицируется правильно, и находится на некотором удалении от разделяющей полосы. Т.е. алгоритм будет правильно классифицировать объекты, если выполняется условие:
Если объединить два выведенных выражения, то получим дефолтную настройку SVM с жестким зазором (hard-margin SVM), когда никакому объекту не разрешается попадать на полосу разделения. Решается аналитически через теорему Куна-Таккера. Получаемая задача эквивалентна двойственной задаче поиска седловой точки функции Лагранжа.
Всё это хорошо до тех пор, пока у нас классы линейно разделимы. Чтобы алгоритм смог работать и с линейно неразделимых данными, давайте немного преобразуем нашу систему. Позволим алгоритму допускать ошибки на обучающих объектах, но при этом постараемся, чтобы ошибок было поменьше. Введём набор дополнительных переменных , характеризующих величину ошибки на каждом объекте
. Введём в минимизируемый функционал штраф за суммарную ошибку:
Будем считать количество ошибок алгоритма (когда M<0). Назовем это штрафом (Penalty). Тогда штраф для всех объектов будет равен сумме штрафов для каждого объекта , где
— пороговая функция (см. рис.4):
Далее сделаем штраф чувствительным к величине ошибки (чем сильнее «уходит в минус» — тем больше штраф) и заодно введем штраф за приближение объекта к границе классов. Для этого возьмем функцию, которая ограничивает пороговую функцию ошибки (см. рис.4):
При добавлении к выражению штрафа слагаемое получаем классическую фукцию потерь SVM с мягким зазором (soft-margin SVM) для одного объекта:
— функция потерь, она же loss function. Именно ее мы и будем минимизировать с помощью градиентного спуска в реализации руками. Выведем правила изменения весов, где
– шаг спуска:
Возможные вопросы на собеседованиях (основано на реальных событиях):
После общих вопросов про SVM: Почему именно Hinge_loss максимизирует зазор? – для начала вспомним, что гиперплоскость меняет свое положение тогда, когда изменяются веса и
. Веса алгоритма начинают меняться, когда градиенты лосс-функции не равны нулю (обычно говорят: “градиенты текут”). Поэтому мы специально подобрали такую лосс-функцию, у которой начинают течь градиенты в нужное время.
выглядит следующим образом:
. Помним, что зазор
. Когда зазор
достаточно большой (
или более), выражение
становится меньше нуля и
(поэтому градиенты не текут и веса алгоритма никак не изменяются). Если же зазор m достаточно мал (например, когда объект попадает на полосу разделения и/или отрицательный (при неверном прогнозе классификации), то Hinge_loss становится положительной (
), начинают течь градиенты и веса алгоритма изменяются. Резюмируя: градиенты текут в двух случаях: когда объект выборки попал внутрь полосы разделения и при неправильной классификации объекта.
Для проверки уровня иностранного языка возможны подобные вопросы: What are the similarities and differences between LogisticRegression and SVM? – firstly, we will talk about similarities: both of algorithms are linear classification algorithms in supervised learning. Some similarities are in their arguments of loss functions: for LogReg and
for SVM (look at picture 4). Both of algorithms we can configure using gradient descent. Next let’s talk about differences: SVM return class label of object unlike LogReg, which return probability of class membership. SVM can’t work with class labels
(without renaming classes) unlike LogReg (LogReg loss finction for
:
, where
– real class label,
– algorithm’s return, probability of belonging object
to class
). More than that, we can solve hard-margin SVM problem without gradient descent. The task of searching support vectors is reduced to search saddle point in the Lagrange function – this task refers to quadratic programming only.
Loss function’s code:
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
xx = np.linspace(-4,3,100000)
plt.plot(xx, [(x<0).astype(int) for x in xx], linewidth=2, label='1 if M<0, else 0')
plt.plot(xx, [np.log2(1+2.76**(-x)) for x in xx], linewidth=4, label='logistic = log(1+e^-M)')
plt.plot(xx, [np.max(np.array([0,1-x])) for x in xx], linewidth=4, label='hinge = max(0,1-M)')
plt.title('Loss = F(Margin)')
plt.grid()
plt.legend(prop={'size': 14});
Риcунок 4. Функции потерь
Простая имплементация классического soft-margin SVM:
Внимание! Ссылку на полный код вы найдете в конце статьи. Ниже будут представлены блоки кода, вырванные из контекста. Некоторые блоки можно запускать только после отработки предыдущих блоков. Под многими блоками будут размещены картинки, которые показывают, как отработал код, размещенный над ней.
Сначала подрубим нужные библиотеки и функцию отрисовки линии:
import numpy as np
import warnings
warnings.filterwarnings('ignore')
import matplotlib.pyplot as plt
import matplotlib.lines as mlines
plt.rcParams['figure.figsize'] = (8,6)
%matplotlib inline
from sklearn.datasets import load_iris
from sklearn.decomposition import PCA
from sklearn.model_selection import train_test_split
def newline(p1, p2, color=None): # функция отрисовки линии
#function kredits to: https://fooobar.com/questions/626491/how-to-draw-a-line-with-matplotlib
ax = plt.gca()
xmin, xmax = ax.get_xbound()
if(p2[0] == p1[0]):
xmin = xmax = p1[0]
ymin, ymax = ax.get_ybound()
else:
ymax = p1[1]+(p2[1]-p1[1])/(p2[0]-p1[0])*(xmax-p1[0])
ymin = p1[1]+(p2[1]-p1[1])/(p2[0]-p1[0])*(xmin-p1[0])
l = mlines.Line2D([xmin,xmax], [ymin,ymax], color=color)
ax.add_line(l)
return lPython код реализации soft-margin SVM:
def add_bias_feature(a):
a_extended = np.zeros((a.shape[0],a.shape[1]+1))
a_extended[:,:-1] = a
a_extended[:,-1] = int(1)
return a_extended
class CustomSVM(object):
__class__ = "CustomSVM"
__doc__ = """
This is an implementation of the SVM classification algorithm
Note that it works only for binary classification
#############################################################
###################### PARAMETERS ######################
#############################################################
etha: float(default - 0.01)
Learning rate, gradient step
alpha: float, (default - 0.1)
Regularization parameter in 0.5*alpha*||w||^2
epochs: int, (default - 200)
Number of epochs of training
#############################################################
#############################################################
#############################################################
"""
def __init__(self, etha=0.01, alpha=0.1, epochs=200):
self._epochs = epochs
self._etha = etha
self._alpha = alpha
self._w = None
self.history_w = []
self.train_errors = None
self.val_errors = None
self.train_loss = None
self.val_loss = None
def fit(self, X_train, Y_train, X_val, Y_val, verbose=False): #arrays: X; Y =-1,1
if len(set(Y_train)) != 2 or len(set(Y_val)) != 2:
raise ValueError("Number of classes in Y is not equal 2!")
X_train = add_bias_feature(X_train)
X_val = add_bias_feature(X_val)
self._w = np.random.normal(loc=0, scale=0.05, size=X_train.shape[1])
self.history_w.append(self._w)
train_errors = []
val_errors = []
train_loss_epoch = []
val_loss_epoch = []
for epoch in range(self._epochs):
tr_err = 0
val_err = 0
tr_loss = 0
val_loss = 0
for i,x in enumerate(X_train):
margin = Y_train[i]*np.dot(self._w,X_train[i])
if margin >= 1: # классифицируем верно
self._w = self._w - self._etha*self._alpha*self._w/self._epochs
tr_loss += self.soft_margin_loss(X_train[i],Y_train[i])
else: # классифицируем неверно или попадаем на полосу разделения при 0<m<1
self._w = self._w +
self._etha*(Y_train[i]*X_train[i] - self._alpha*self._w/self._epochs)
tr_err += 1
tr_loss += self.soft_margin_loss(X_train[i],Y_train[i])
self.history_w.append(self._w)
for i,x in enumerate(X_val):
val_loss += self.soft_margin_loss(X_val[i], Y_val[i])
val_err += (Y_val[i]*np.dot(self._w,X_val[i])<1).astype(int)
if verbose:
print('epoch {}. Errors={}. Mean Hinge_loss={}'
.format(epoch,err,loss))
train_errors.append(tr_err)
val_errors.append(val_err)
train_loss_epoch.append(tr_loss)
val_loss_epoch.append(val_loss)
self.history_w = np.array(self.history_w)
self.train_errors = np.array(train_errors)
self.val_errors = np.array(val_errors)
self.train_loss = np.array(train_loss_epoch)
self.val_loss = np.array(val_loss_epoch)
def predict(self, X:np.array) -> np.array:
y_pred = []
X_extended = add_bias_feature(X)
for i in range(len(X_extended)):
y_pred.append(np.sign(np.dot(self._w,X_extended[i])))
return np.array(y_pred)
def hinge_loss(self, x, y):
return max(0,1 - y*np.dot(x, self._w))
def soft_margin_loss(self, x, y):
return self.hinge_loss(x,y)+self._alpha*np.dot(self._w, self._w)Подробно рассмотрим работу каждого блока строчек:
1) создаем функцию add_bias_feature(a), которая автоматически расширяет вектор объектов, добавляя в конец каждого вектора число 1. Это нужно для того, чтобы «забыть» про свободный член b. Выражение эквивалентно выражению
. Мы условно считаем, что единица — это последняя компонента вектора для всех векторов x, а
. Теперь настройку весов
и
будем производить одновременно.
Код функции расширения вектора признаков:
def add_bias_feature(a):
a_extended = np.zeros((a.shape[0],a.shape[1]+1))
a_extended[:,:-1] = a
a_extended[:,-1] = int(1)
return a_extended2) далее опишем сам классификатор. Он имеет внутри себя функции инициализации init(), обучения fit(), предсказания predict(), нахождения лосс функции hinge_loss() и нахождения общей лосс функции классического алгоритма с мягким зазором soft_margin_loss().
3) при инициализации вводятся 3 гиперпараметра: _etha – шаг градиентного спуска (), _alpha – коэффициент быстроты пропорционального уменьшения весов (перед квадратичным слагаемым в функции потерь
), _epochs – количество эпох обучения.
Код функции инициализации:
def __init__(self, etha=0.01, alpha=0.1, epochs=200):
self._epochs = epochs
self._etha = etha
self._alpha = alpha
self._w = None
self.history_w = []
self.train_errors = None
self.val_errors = None
self.train_loss = None
self.val_loss = None4) при обучении для каждой эпохи обучающей выборки (X_train, Y_train) мы будем брать по одному элементу из выборки, вычислять зазор между этим элементом и положением гиперплоскости в данный момент времени. Далее в зависимости от величины этого зазора мы будем изменять веса алгоритма с помощью градиента функции потерь . Заодно будем вычислять значение этой функции на каждой эпохе и сколько раз мы изменяем веса за эпоху. Перед началом обучения убедимся, что в функцию обучения пришло действительно не больше двух разных меток класса. Перед настройкой весов происходит их инициализация с помощью нормального распределения.
Код функции обучения:
def fit(self, X_train, Y_train, X_val, Y_val, verbose=False): #arrays: X; Y =-1,1
if len(set(Y_train)) != 2 or len(set(Y_val)) != 2:
raise ValueError("Number of classes in Y is not equal 2!")
X_train = add_bias_feature(X_train)
X_val = add_bias_feature(X_val)
self._w = np.random.normal(loc=0, scale=0.05, size=X_train.shape[1])
self.history_w.append(self._w)
train_errors = []
val_errors = []
train_loss_epoch = []
val_loss_epoch = []
for epoch in range(self._epochs):
tr_err = 0
val_err = 0
tr_loss = 0
val_loss = 0
for i,x in enumerate(X_train):
margin = Y_train[i]*np.dot(self._w,X_train[i])
if margin >= 1: # классифицируем верно
self._w = self._w - self._etha*self._alpha*self._w/self._epochs
tr_loss += self.soft_margin_loss(X_train[i],Y_train[i])
else: # классифицируем неверно или попадаем на полосу разделения при 0<m<1
self._w = self._w +
self._etha*(Y_train[i]*X_train[i] - self._alpha*self._w/self._epochs)
tr_err += 1
tr_loss += self.soft_margin_loss(X_train[i],Y_train[i])
self.history_w.append(self._w)
for i,x in enumerate(X_val):
val_loss += self.soft_margin_loss(X_val[i], Y_val[i])
val_err += (Y_val[i]*np.dot(self._w,X_val[i])<1).astype(int)
if verbose:
print('epoch {}. Errors={}. Mean Hinge_loss={}'
.format(epoch,err,loss))
train_errors.append(tr_err)
val_errors.append(val_err)
train_loss_epoch.append(tr_loss)
val_loss_epoch.append(val_loss)
self.history_w = np.array(self.history_w)
self.train_errors = np.array(train_errors)
self.val_errors = np.array(val_errors)
self.train_loss = np.array(train_loss_epoch)
self.val_loss = np.array(val_loss_epoch)Проверка работы написанного алгоритма:
Проверим, что наш написанный алгоритм работает на каком-нибудь игрушечном наборе данных. Возьмем датасет Iris. Подготовим данные. Обозначим классы 1 и 2 как , а класс 0 как
. С помощью алгоритма PCA (объяснение и применение тут) оптимальным образом сократим пространство 4-х признаков до 2-х с минимальными потерями данных (нам будет проще наблюдать за обучением и разультатом). Далее разделим на обучающую (трейн) выборку и отложенную (валидационную). Обучим на трейн выборке, прогнозируем и проверяем на отложенной. Подберем коэффициенты обучения таким образом, чтобы лосс функция падала. Во время обучения будем смотреть на лосс функцию обучающей и отложенной выборки.
Блок подготовки данных:
# блок подготовки данных
iris = load_iris()
X = iris.data
Y = iris.target
pca = PCA(n_components=2)
X = pca.fit_transform(X)
Y = (Y > 0).astype(int)*2-1 # [0,1,2] --> [False,True,True] --> [0,1,1] --> [0,2,2] --> [-1,1,1]
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.4, random_state=2020)Блок инициализации и обучения:
# блок инициализиции и обучения
svm = CustomSVM(etha=0.005, alpha=0.006, epochs=150)
svm.fit(X_train, Y_train, X_test, Y_test)
print(svm.train_errors) # numbers of error in each epoch
print(svm._w) # w0*x_i[0]+w1*x_i[1]+w2=0
plt.plot(svm.train_loss, linewidth=2, label='train_loss')
plt.plot(svm.val_loss, linewidth=2, label='test_loss')
plt.grid()
plt.legend(prop={'size': 15})
plt.show()Блок визуализации получившейся разделяющей полосы:
d = {-1:'green', 1:'red'}
plt.scatter(X_train[:,0], X_train[:,1], c=[d[y] for y in Y_train])
newline([0,-svm._w[2]/svm._w[1]],[-svm._w[2]/svm._w[0],0], 'blue') # в w0*x_i[0]+w1*x_i[1]+w2*1=0 поочередно
# подставляем x_i[0]=0, x_i[1]=0
newline([0,1/svm._w[1]-svm._w[2]/svm._w[1]],[1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=1
newline([0,-1/svm._w[1]-svm._w[2]/svm._w[1]],[-1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=-1
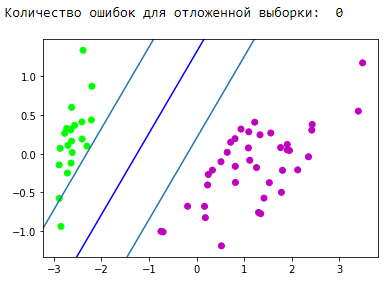
plt.show()Блок визуализации прогноза:
# предсказываем после обучения
y_pred = svm.predict(X_test)
y_pred[y_pred != Y_test] = -100 # find and mark classification error
print('Количество ошибок для отложенной выборки: ', (y_pred == -100).astype(int).sum())
d1 = {-1:'lime', 1:'m', -100: 'black'} # black = classification error
plt.scatter(X_test[:,0], X_test[:,1], c=[d1[y] for y in y_pred])
newline([0,-svm._w[2]/svm._w[1]],[-svm._w[2]/svm._w[0],0], 'blue')
newline([0,1/svm._w[1]-svm._w[2]/svm._w[1]],[1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=1
newline([0,-1/svm._w[1]-svm._w[2]/svm._w[1]],[-1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=-1
plt.show()Отлично! Наш алгоритм справился с линейно разделимыми данными. Теперь заставим его отделить классы 0 и 1 от класса 2:
Блок подготовки данных:
# блок подготовки данных
iris = load_iris()
X = iris.data
Y = iris.target
pca = PCA(n_components=2)
X = pca.fit_transform(X)
Y = (Y == 2).astype(int)*2-1 # [0,1,2] --> [False,False,True] --> [0,1,1] --> [0,0,2] --> [-1,1,1]
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.4, random_state=2020)Блок инициализации и обучения:
# блок инициализиции и обучения
svm = CustomSVM(etha=0.03, alpha=0.0001, epochs=300)
svm.fit(X_train, Y_train, X_test, Y_test)
print(svm.train_errors[:150]) # numbers of error in each epoch
print(svm._w) # w0*x_i[0]+w1*x_i[1]+w2=0
plt.plot(svm.train_loss, linewidth=2, label='train_loss')
plt.plot(svm.val_loss, linewidth=2, label='test_loss')
plt.grid()
plt.legend(prop={'size': 15})
plt.show()Блок визуализации получившейся разделяющей полосы:
d = {-1:'green', 1:'red'}
plt.scatter(X_train[:,0], X_train[:,1], c=[d[y] for y in Y_train])
newline([0,-svm._w[2]/svm._w[1]],[-svm._w[2]/svm._w[0],0], 'blue') # в w0*x_i[0]+w1*x_i[1]+w2*1=0 поочередно
# подставляем x_i[0]=0, x_i[1]=0
newline([0,1/svm._w[1]-svm._w[2]/svm._w[1]],[1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=1
newline([0,-1/svm._w[1]-svm._w[2]/svm._w[1]],[-1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=-1
plt.show()Посмотрим на гифку, которая покажет, как разделяющая прямая изменяла свое положение во время обучения (всего 500 кадров изменения весов. Первые 300 подряд. Далее 200 штук на каждый 130ый кадр):
Код создания анимации:
import matplotlib.animation as animation
from matplotlib.animation import PillowWriter
def one_image(w, X, Y):
axes = plt.gca()
axes.set_xlim([-4,4])
axes.set_ylim([-1.5,1.5])
d1 = {-1:'green', 1:'red'}
im = plt.scatter(X[:,0], X[:,1], c=[d1[y] for y in Y])
im = newline([0,-w[2]/w[1]],[-w[2]/w[0],0], 'blue')
# im = newline([0,1/w[1]-w[2]/w[1]],[1/w[0]-w[2]/w[0],0], 'lime') #w0*x_i[0]+w1*x_i[1]+w2*1=1
# im = newline([0,-1/w[1]-w[2]/w[1]],[-1/w[0]-w[2]/w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=-1
return im
fig = plt.figure()
ims = []
for i in range(500):
if i<=300:
k = i
else:
k = (i-298)*130
im = one_image(svm.history_w[k], X_train, Y_train)
ims.append([im])
ani = animation.ArtistAnimation(fig, ims, interval=20, blit=True,
repeat_delay=500)
writer = PillowWriter(fps=20)
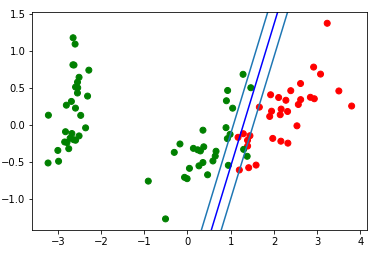
ani.save("my_demo.gif", writer='imagemagick')Блок визуализации прогноза:
# предсказываем после обучения
y_pred = svm.predict(X_test)
y_pred[y_pred != Y_test] = -100 # find and mark classification error
print('Количество ошибок для отложенной выборки: ', (y_pred == -100).astype(int).sum())
d1 = {-1:'lime', 1:'m', -100: 'black'} # black = classification error
plt.scatter(X_test[:,0], X_test[:,1], c=[d1[y] for y in y_pred])
newline([0,-svm._w[2]/svm._w[1]],[-svm._w[2]/svm._w[0],0], 'blue')
newline([0,1/svm._w[1]-svm._w[2]/svm._w[1]],[1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=1
newline([0,-1/svm._w[1]-svm._w[2]/svm._w[1]],[-1/svm._w[0]-svm._w[2]/svm._w[0],0]) #w0*x_i[0]+w1*x_i[1]+w2*1=-1
plt.show()Спрямляющие пространства
Важно понимать, что в реальных задачах не будет простого случая с линейно разделимыми данными. Для работы с подобными данными была предложена идея перехода в другое пространство, где данные будут линейно разделимы. Такое пространство и называется спрямляющим. В данной статье не будут затронуты спрямляющие пространства и ядра. Самую полную математическую теорию Вы сможете найти в 14,15,16 конспектах Е. Соколова и в лекциях К.В.Воронцова.
Применение SVM из sklearn:
В действительности, почти все классические алгоритмы машинного обучения написаны за Вас. Приведем пример кода, алгоритм возьмем из библиотеки sklearn.
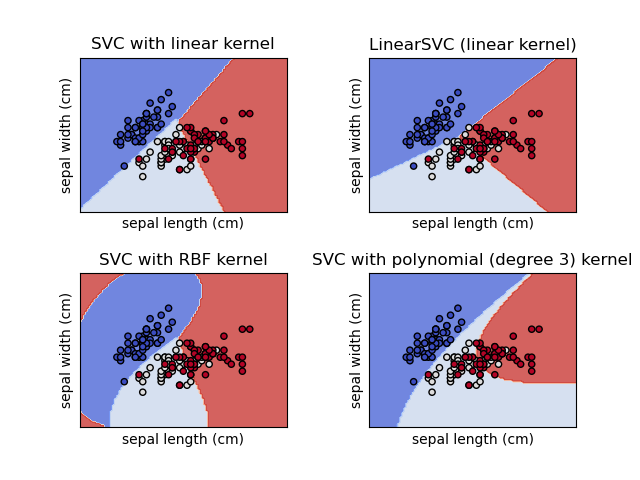
Пример кода
from sklearn import svm
from sklearn.metrics import recall_score
C = 1.0 # = self._alpha in our algorithm
model1 = svm.SVC(kernel='linear', C=C)
#model1 = svm.LinearSVC(C=C, max_iter=10000)
#model1 = svm.SVC(kernel='rbf', gamma=0.7, C=C)
#model1 = svm.SVC(kernel='poly', degree=3, gamma='auto', C=C)
model1.fit(X_train, Y_train)
y_predict = model1.predict(X_test)
print(recall_score(Y_test, y_predict, average=None))Плюсы и минусы классического SVM:
Плюсы:
- хорошо работает с пространством признаков большого размера;
- хорошо работает с данными небольшого объема;
- алгоритм максимизирует разделяющую полосу, которая, как подушка безопасности, позволяет уменьшить количество ошибок классификации;
- так как алгоритм сводится к решению задачи квадратичного программирования в выпуклой области, то такая задача всегда имеет единственное решение (разделяющая гиперплоскость с определенными гиперпараметрами алгоритма всегда одна).
Минусы:
- долгое время обучения (для больших наборов данных);
- неустойчивость к шуму: выбросы в обучающих данных становятся опорными объектами-нарушителями и напрямую влияют на построение разделяющей гиперплоскости;
- не описаны общие методы построения ядер и спрямляющих пространств, наиболее подходящих для конкретной задачи в случае линейной неразделимости классов. Подбирать полезные преобразования данных – искусство.
Применение SVM:
Выбор того или иного алгоритма машинного обучения напрямую зависит от информации, полученной во время исследования данных. Но в общих словах, можно выделить следующие задачи:
- задачи с небольшим набором данных;
- задачи текстовой классификации. SVM дает неплохой baseline ([preprocessing] + [TF-iDF] + [SVM]), получаемая точность прогноза оказывается на уровне некоторых сверточных/рекуррентных нейронных сетей (рекомендую самостоятельно попробовать такой метод для закрепления материала). Отличный пример приведен тут, «Часть 3. Пример одного из трюков, которым мы обучаем»;
- для многих задач со структурированными данными связка [feature engineering] + [SVM] + [kernel] «все еще торт»;
- так как Hinge loss считается довольно быстро, ее можно встретить в Vowpal Wabbit (по умолчанию).
Модификации алгоритма:
Существуют различные дополнения и модификации метода опорных векторов, направленные на устранение определенных недостатков:
- Метод релевантных векторов (Relevance Vector Machine, RVM)
- 1-norm SVM (LASSO SVM)
- Doubly Regularized SVM (ElasticNet SVM)
- Support Features Machine (SFM)
- Relevance Features Machine (RFM)
Дополнительные источники на тему SVM:
- Текстовые лекции К.В.Воронцова
- Конспекты Е.Соколова — 14,15,16
- Крутой источник by Alexandre Kowalczyk
- На хабре есть 2 статьи, посвященные svm:
- 2010 г.
- 2018 г.
- На гитхабе могу выделить 2 крутые реализации SVM по следующим ссылкам:
- MLAlgorithms от отечественного разработчика
- ML-From-Scratch
Заключение:
Большое спасибо за внимание! Буду благодарен за любые комментарии, отзывы и советы.
Полный код из данной статьи найдете на моем гитхабе.
p.s. Благодарю yorko за советы по сглаживанию «углов». Спасибо Алексею Сизых asizykh — физтеху, который частично вложился в код.
Функция потерь SVM
- 1. Что такое SVM
- Во-вторых, функция потерь SVM
- 1. Первое понимание
- вариант
- оптимизация
- 2. Второе понимание
- Конкретный вывод функции потерь SVM
В машинном обучении очень важна SVM (машина опорных векторов). В процессе обработки модели SVM играет большую роль в вычислении эмпирического риска с помощью функции потерь. Далее мы посмотрите на функцию потерь SVM.
1. Что такое SVM
SVM означает машину опорных векторов (машина опорных векторов, SVM) Это тип обобщенного линейного классификатора, который выполняет двоичную классификацию данных в режиме обучения с учителем.Его решающая граница является гиперплоскостью с максимальным запасом для решения обучающей выборки.
Учитывая исходные данные и цели обучения в задаче классификации:
, где каждый образец входных данных содержит несколько функций и, таким образом, составляет пространство функций (пространство функций) :, а цель обучения — это двоичная переменная, которая представляет отрицательный класс и положительный класс ( Положительный класс).
Взглянем на картинку:
Если существует гиперплоскость в качестве границы решения в пространстве функций, где расположены входные данные, цели обучения разделяются на положительные и отрицательные классы, а расстояние между точкой и плоскостью составляет любой образец больше или равен 1:
означает, что проблема классификации линейно разделима, а параметр
w
,
b
w,b
Вектор нормали и точка пересечения гиперплоскости соответственно.
Граница решения, которая удовлетворяет этому условию, фактически создает две параллельные гиперплоскости в качестве границы разделения для определения классификации выборки:
Все выборки выше верхней границы интервала относятся к положительной категории, а все выборки ниже нижней границы интервала относятся к отрицательной категории.
Расстояние между двумя разделительными границами
d
=
2
/
∣
∣
w
∣
∣
d=2/||w||
Он определяется как запас, а положительные и отрицательные отсчеты, расположенные на границе интервала, являются опорным вектором.
Во-вторых, функция потерь SVM
Во-первых, давайте посмотрим, что такое функция потерь:
определение: Он используется для измерения качества предсказателя при классификации и прогнозировании входных данных. Чем меньше значение потерь, тем лучше эффект классификатора и тем лучше он может отражать взаимосвязь между входными данными и меткой выходной категории; напротив, чем больше значение потерь, нам нужно потратить больше энергии на улучшение точность модели.
1. Первое понимание
Hinge Loss — это функция потерь в области машинного обучения, которая можетИспользуется для классификации «максимальной маржи», Его самое известное приложение — это целевая функция SVM.
В случае двух классификаций формула выглядит следующим образом:
L(y) = max(0 , 1 – t⋅y)
Среди них y — это прогнозируемое значение (от -1 до 1), а t — целевое значение (1 или -1). Это означает, что значение y может находиться в диапазоне от -1 до 1, и | y |> 1 не приветствуется, то есть этого достаточно, чтобы позволить выборке быть правильно классифицированной, а классификатору не рекомендуется быть слишком самоуверенным. Когда образец и разделительная линия Нет награды, когда расстояние превышает 1. Цель состоит в том, чтобы сконцентрировать внимание классификатора на общей ошибке классификации.
вариант
В практических приложениях, с одной стороны, прогнозируемое значение y не всегда принадлежит [-1,1], но также может принадлежать другим диапазонам значений; с другой стороны, много раз мы хотим обучаться между двумя элементами Отношение подобия , а не оценка категории образца.
Чаще может использоваться следующая формула:
- L( y, y′) = max( 0, margin – (y–y′) )
-
= max( 0, margin + (y′–y) ) -
= max( 0, margin + y′ – y)
Среди них y — оценка правильного предсказания, y — оценка неверного предсказания, и разница между ними может использоваться для обозначения аналогичной взаимосвязи между двумя результатами предсказания.
Маржа — это запас прочности, определяемый им самим. Мы надеемся, что оценка правильного предсказания выше, чем оценка ошибки в предсказании, и больше, чем предел запаса. Другими словами, чем выше y, тем лучше, чем меньше y ‘, тем лучше и чем больше (yy ′), тем лучше, (y ′ –Y) Чем меньше, тем лучше, но разница между двумя оценками является в лучшем случае достаточной маржей, и за большую разницу не будет вознаграждения. Цель этого плана состоит в том, чтобы иметь определенный запас для правильной классификации отдельной выборки, и в большей уверенности нет необходимости.Слишком большое внимание классификационному эффекту отдельной выборки может ухудшить общий эффект классификации. Классификатор должен уделять больше внимания общей ошибке классификации.
оптимизация
Функция потерь в шарнирах является выпуклой функцией, поэтому многие методы выпуклой оптимизации в машинном обучении также применимы к потерям в шарнирах.
Однако,Поскольку производная потерь на шарнире неопределенная, когда t⋅y = 1, Таким образом, для оптимизации будет более полезна плавная версия функции потерь петли.Она была предложена Ренни и Сребро:
На рисунке выше показаны три версии функции потери подсказки для z = t⋅y. Синяя линия — исходная версия, зеленая линия — квадратичное сглаживание, а красная линия — кусочное сглаживание. ., Который является версией, предложенной Ренни и Сребро.
2. Второе понимание
В процессе обучения опорных векторных машин мы знаемФункция потерь — это функция потерь шарнира.. Что касается того, почему она называется, «Статистический метод обучения» учителя Ли Хана гласит следующее: поскольку функция имеет форму петли, функция потерь петли названа. На следующем рисунке показано изображение функции потерь петли (взято из «Статистического метода обучения»):
Горизонтальная ось представляет интервал функции. Мы понимаем интервал функции с двух сторон.
- Положительный и отрицательный
Если образец классифицирован правильно,y
(
w
T
x
+
b
)
>
0
y(w^Tx+b)>0
; Если образец неправильно классифицирован,y
(
w
T
x
+
b
)
<
0
y(w^Tx+b)<0
. - размер
y
(
w
T
x
+
b
)
y(w^Tx+b)
Абсолютное значение показывает, насколько далеко образец находится от границы решения.
y
(
w
T
x
+
b
)
y(w^Tx+b)
Чем больше абсолютное значение, тем дальше выборка от границы решения.
Итак, мы можем получить:
- когда
y
(
w
T
x
+
b
)
>
0
y(w^Tx+b)>0
Время,y
(
w
T
x
+
b
)
y(w^Tx+b)
Чем больше абсолютное значение, тем лучше различение между границей решения и выборкой. - когда
y
(
w
T
x
+
b
)
<
0
y(w^Tx+b)<0
Время,y
(
w
T
x
+
b
)
y(w^Tx+b)
Чем больше абсолютное значение, тем хуже граница решения различает образец
Как видно из рисунка выше,
- 0-1 проигрыш
Если образец правильно классифицирован, потери равны 0; если образец классифицирован неправильно, потери равны 1. - Функция потерь персептрона
Если образец классифицирован правильно, потери равны 0; если образец классифицирован неправильно, потери составляют−
y
(
w
T
x
+
b
)
-y(w^Tx+b)
。 - Функция потери шарнира
Если образец правильно классифицирован и интервал функции больше 1, потеря на шарнире равна 0, в противном случае потеря1
−
y
(
w
T
x
+
b
)
1-y(w^Tx+b)
Таким образом, функция потерь шарнира, напротив, должна быть не только правильно классифицирована, но и потеря равна 0, когда степень достоверности достаточно высока. Другими словами, функция потери шарнира предъявляет более высокие требования к обучению.
Конкретный вывод функции потерь SVM
Есть много подробных вводных сведений о выводе процесса, и я здесь, чтобы взять его из «Статистических методов обучения»:
Оригинальная ссылка от:
- 1、https://blog.csdn.net/qq_35290785/article/details/97309985
- 2、https://blog.csdn.net/super_jackchen/article/details/103014348#SVM_45
Support vector machines (SVMs) are a set of supervised learning
methods used for classification,
regression and outliers detection.
The advantages of support vector machines are:
Effective in high dimensional spaces.
Still effective in cases where number of dimensions is greater
than the number of samples.Uses a subset of training points in the decision function (called
support vectors), so it is also memory efficient.Versatile: different Kernel functions can be
specified for the decision function. Common kernels are
provided, but it is also possible to specify custom kernels.
The disadvantages of support vector machines include:
If the number of features is much greater than the number of
samples, avoid over-fitting in choosing Kernel functions and regularization
term is crucial.SVMs do not directly provide probability estimates, these are
calculated using an expensive five-fold cross-validation
(see Scores and probabilities, below).
The support vector machines in scikit-learn support both dense
(numpy.ndarray and convertible to that by numpy.asarray) and
sparse (any scipy.sparse) sample vectors as input. However, to use
an SVM to make predictions for sparse data, it must have been fit on such
data. For optimal performance, use C-ordered numpy.ndarray (dense) or
scipy.sparse.csr_matrix (sparse) with dtype=float64.
1.4.1. Classification¶
SVC, NuSVC and LinearSVC are classes
capable of performing binary and multi-class classification on a dataset.
SVC and NuSVC are similar methods, but accept
slightly different sets of parameters and have different mathematical
formulations (see section Mathematical formulation). On the
other hand, LinearSVC is another (faster) implementation of Support
Vector Classification for the case of a linear kernel. Note that
LinearSVC does not accept parameter kernel, as this is
assumed to be linear. It also lacks some of the attributes of
SVC and NuSVC, like support_.
As other classifiers, SVC, NuSVC and
LinearSVC take as input two arrays: an array X of shape
(n_samples, n_features) holding the training samples, and an array y of
class labels (strings or integers), of shape (n_samples):
>>> from sklearn import svm >>> X = [[0, 0], [1, 1]] >>> y = [0, 1] >>> clf = svm.SVC() >>> clf.fit(X, y) SVC()
After being fitted, the model can then be used to predict new values:
>>> clf.predict([[2., 2.]]) array([1])
SVMs decision function (detailed in the Mathematical formulation)
depends on some subset of the training data, called the support vectors. Some
properties of these support vectors can be found in attributes
support_vectors_, support_ and n_support_:
>>> # get support vectors >>> clf.support_vectors_ array([[0., 0.], [1., 1.]]) >>> # get indices of support vectors >>> clf.support_ array([0, 1]...) >>> # get number of support vectors for each class >>> clf.n_support_ array([1, 1]...)
1.4.1.1. Multi-class classification¶
SVC and NuSVC implement the “one-versus-one”
approach for multi-class classification. In total,
n_classes * (n_classes - 1) / 2
classifiers are constructed and each one trains data from two classes.
To provide a consistent interface with other classifiers, the
decision_function_shape option allows to monotonically transform the
results of the “one-versus-one” classifiers to a “one-vs-rest” decision
function of shape (n_samples, n_classes).
>>> X = [[0], [1], [2], [3]] >>> Y = [0, 1, 2, 3] >>> clf = svm.SVC(decision_function_shape='ovo') >>> clf.fit(X, Y) SVC(decision_function_shape='ovo') >>> dec = clf.decision_function([[1]]) >>> dec.shape[1] # 4 classes: 4*3/2 = 6 6 >>> clf.decision_function_shape = "ovr" >>> dec = clf.decision_function([[1]]) >>> dec.shape[1] # 4 classes 4
On the other hand, LinearSVC implements “one-vs-the-rest”
multi-class strategy, thus training n_classes models.
>>> lin_clf = svm.LinearSVC() >>> lin_clf.fit(X, Y) LinearSVC() >>> dec = lin_clf.decision_function([[1]]) >>> dec.shape[1] 4
See Mathematical formulation for a complete description of
the decision function.
Note that the LinearSVC also implements an alternative multi-class
strategy, the so-called multi-class SVM formulated by Crammer and Singer
[16], by using the option multi_class='crammer_singer'. In practice,
one-vs-rest classification is usually preferred, since the results are mostly
similar, but the runtime is significantly less.
For “one-vs-rest” LinearSVC the attributes coef_ and intercept_
have the shape (n_classes, n_features) and (n_classes,) respectively.
Each row of the coefficients corresponds to one of the n_classes
“one-vs-rest” classifiers and similar for the intercepts, in the
order of the “one” class.
In the case of “one-vs-one” SVC and NuSVC, the layout of
the attributes is a little more involved. In the case of a linear
kernel, the attributes coef_ and intercept_ have the shape
(n_classes * (n_classes - 1) / 2, n_features) and (n_classes * respectively. This is similar to the layout for
(n_classes - 1) / 2)
LinearSVC described above, with each row now corresponding
to a binary classifier. The order for classes
0 to n is “0 vs 1”, “0 vs 2” , … “0 vs n”, “1 vs 2”, “1 vs 3”, “1 vs n”, . .
. “n-1 vs n”.
The shape of dual_coef_ is (n_classes-1, n_SV) with
a somewhat hard to grasp layout.
The columns correspond to the support vectors involved in any
of the n_classes * (n_classes - 1) / 2 “one-vs-one” classifiers.
Each support vector v has a dual coefficient in each of the
n_classes - 1 classifiers comparing the class of v against another class.
Note that some, but not all, of these dual coefficients, may be zero.
The n_classes - 1 entries in each column are these dual coefficients,
ordered by the opposing class.
This might be clearer with an example: consider a three class problem with
class 0 having three support vectors
(v^{0}_0, v^{1}_0, v^{2}_0) and class 1 and 2 having two support vectors
(v^{0}_1, v^{1}_1) and (v^{0}_2, v^{1}_2) respectively. For each
support vector (v^{j}_i), there are two dual coefficients. Let’s call
the coefficient of support vector (v^{j}_i) in the classifier between
classes (i) and (k) (alpha^{j}_{i,k}).
Then dual_coef_ looks like this:
|
(alpha^{0}_{0,1}) |
(alpha^{1}_{0,1}) |
(alpha^{2}_{0,1}) |
(alpha^{0}_{1,0}) |
(alpha^{1}_{1,0}) |
(alpha^{0}_{2,0}) |
(alpha^{1}_{2,0}) |
|
(alpha^{0}_{0,2}) |
(alpha^{1}_{0,2}) |
(alpha^{2}_{0,2}) |
(alpha^{0}_{1,2}) |
(alpha^{1}_{1,2}) |
(alpha^{0}_{2,1}) |
(alpha^{1}_{2,1}) |
|
Coefficients |
Coefficients |
Coefficients |
1.4.1.2. Scores and probabilities¶
The decision_function method of SVC and NuSVC gives
per-class scores for each sample (or a single score per sample in the binary
case). When the constructor option probability is set to True,
class membership probability estimates (from the methods predict_proba and
predict_log_proba) are enabled. In the binary case, the probabilities are
calibrated using Platt scaling [9]: logistic regression on the SVM’s scores,
fit by an additional cross-validation on the training data.
In the multiclass case, this is extended as per [10].
The cross-validation involved in Platt scaling
is an expensive operation for large datasets.
In addition, the probability estimates may be inconsistent with the scores:
-
the “argmax” of the scores may not be the argmax of the probabilities
-
in binary classification, a sample may be labeled by
predictas
belonging to the positive class even if the output ofpredict_probais
less than 0.5; and similarly, it could be labeled as negative even if the
output ofpredict_probais more than 0.5.
Platt’s method is also known to have theoretical issues.
If confidence scores are required, but these do not have to be probabilities,
then it is advisable to set probability=False
and use decision_function instead of predict_proba.
Please note that when decision_function_shape='ovr' and n_classes > 2,
unlike decision_function, the predict method does not try to break ties
by default. You can set break_ties=True for the output of predict to be
the same as np.argmax(clf.decision_function(...), axis=1), otherwise the
first class among the tied classes will always be returned; but have in mind
that it comes with a computational cost. See
SVM Tie Breaking Example for an example on
tie breaking.
1.4.1.3. Unbalanced problems¶
In problems where it is desired to give more importance to certain
classes or certain individual samples, the parameters class_weight and
sample_weight can be used.
SVC (but not NuSVC) implements the parameter
class_weight in the fit method. It’s a dictionary of the form
{class_label : value}, where value is a floating point number > 0
that sets the parameter C of class class_label to C * value.
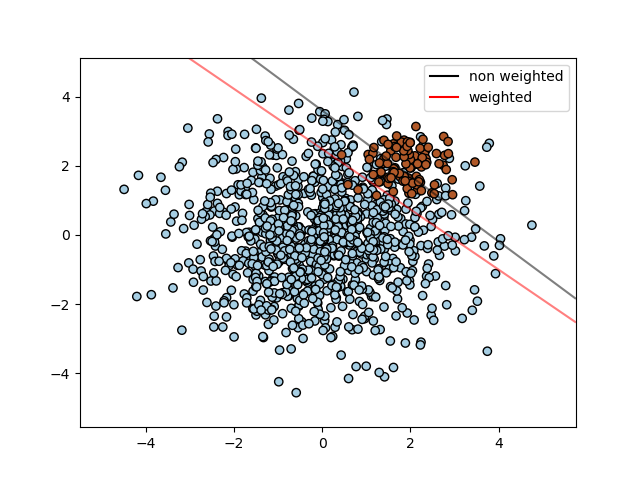
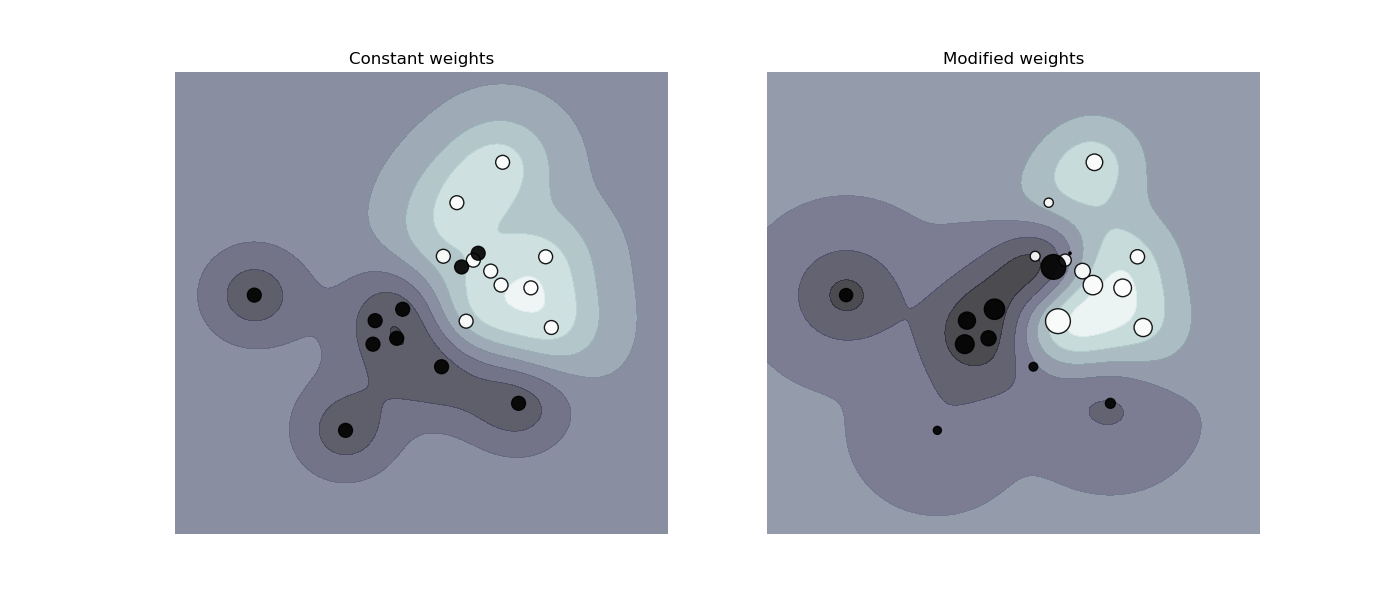
The figure below illustrates the decision boundary of an unbalanced problem,
with and without weight correction.
SVC, NuSVC, SVR, NuSVR, LinearSVC,
LinearSVR and OneClassSVM implement also weights for
individual samples in the fit method through the sample_weight parameter.
Similar to class_weight, this sets the parameter C for the i-th
example to C * sample_weight[i], which will encourage the classifier to
get these samples right. The figure below illustrates the effect of sample
weighting on the decision boundary. The size of the circles is proportional
to the sample weights:
1.4.2. Regression¶
The method of Support Vector Classification can be extended to solve
regression problems. This method is called Support Vector Regression.
The model produced by support vector classification (as described
above) depends only on a subset of the training data, because the cost
function for building the model does not care about training points
that lie beyond the margin. Analogously, the model produced by Support
Vector Regression depends only on a subset of the training data,
because the cost function ignores samples whose prediction is close to their
target.
There are three different implementations of Support Vector Regression:
SVR, NuSVR and LinearSVR. LinearSVR
provides a faster implementation than SVR but only considers
the linear kernel, while NuSVR implements a slightly different
formulation than SVR and LinearSVR. See
Implementation details for further details.
As with classification classes, the fit method will take as
argument vectors X, y, only that in this case y is expected to have
floating point values instead of integer values:
>>> from sklearn import svm >>> X = [[0, 0], [2, 2]] >>> y = [0.5, 2.5] >>> regr = svm.SVR() >>> regr.fit(X, y) SVR() >>> regr.predict([[1, 1]]) array([1.5])
1.4.3. Density estimation, novelty detection¶
The class OneClassSVM implements a One-Class SVM which is used in
outlier detection.
See Novelty and Outlier Detection for the description and usage of OneClassSVM.
1.4.4. Complexity¶
Support Vector Machines are powerful tools, but their compute and
storage requirements increase rapidly with the number of training
vectors. The core of an SVM is a quadratic programming problem (QP),
separating support vectors from the rest of the training data. The QP
solver used by the libsvm-based implementation scales between
(O(n_{features} times n_{samples}^2)) and
(O(n_{features} times n_{samples}^3)) depending on how efficiently
the libsvm cache is used in practice (dataset dependent). If the data
is very sparse (n_{features}) should be replaced by the average number
of non-zero features in a sample vector.
For the linear case, the algorithm used in
LinearSVC by the liblinear implementation is much more
efficient than its libsvm-based SVC counterpart and can
scale almost linearly to millions of samples and/or features.
1.4.5. Tips on Practical Use¶
Avoiding data copy: For
SVC,SVR,NuSVCand
NuSVR, if the data passed to certain methods is not C-ordered
contiguous and double precision, it will be copied before calling the
underlying C implementation. You can check whether a given numpy array is
C-contiguous by inspecting itsflagsattribute.For
LinearSVC(andLogisticRegression) any input passed as a numpy
array will be copied and converted to the liblinear internal sparse data
representation (double precision floats and int32 indices of non-zero
components). If you want to fit a large-scale linear classifier without
copying a dense numpy C-contiguous double precision array as input, we
suggest to use theSGDClassifierclass instead. The objective
function can be configured to be almost the same as theLinearSVC
model.Kernel cache size: For
SVC,SVR,NuSVCand
NuSVR, the size of the kernel cache has a strong impact on run
times for larger problems. If you have enough RAM available, it is
recommended to setcache_sizeto a higher value than the default of
200(MB), such as 500(MB) or 1000(MB).Setting C:
Cis1by default and it’s a reasonable default
choice. If you have a lot of noisy observations you should decrease it:
decreasing C corresponds to more regularization.
LinearSVCandLinearSVRare less sensitive toCwhen
it becomes large, and prediction results stop improving after a certain
threshold. Meanwhile, largerCvalues will take more time to train,
sometimes up to 10 times longer, as shown in [11].Support Vector Machine algorithms are not scale invariant, so it
is highly recommended to scale your data. For example, scale each
attribute on the input vector X to [0,1] or [-1,+1], or standardize it
to have mean 0 and variance 1. Note that the same scaling must be
applied to the test vector to obtain meaningful results. This can be done
easily by using aPipeline:>>> from sklearn.pipeline import make_pipeline >>> from sklearn.preprocessing import StandardScaler >>> from sklearn.svm import SVC >>> clf = make_pipeline(StandardScaler(), SVC())See section Preprocessing data for more details on scaling and
normalization.
Regarding the
shrinkingparameter, quoting [12]: We found that if the
number of iterations is large, then shrinking can shorten the training
time. However, if we loosely solve the optimization problem (e.g., by
using a large stopping tolerance), the code without using shrinking may
be much fasterParameter
nuinNuSVC/OneClassSVM/NuSVR
approximates the fraction of training errors and support vectors.In
SVC, if the data is unbalanced (e.g. many
positive and few negative), setclass_weight='balanced'and/or try
different penalty parametersC.Randomness of the underlying implementations: The underlying
implementations ofSVCandNuSVCuse a random number
generator only to shuffle the data for probability estimation (when
probabilityis set toTrue). This randomness can be controlled
with therandom_stateparameter. Ifprobabilityis set toFalse
these estimators are not random andrandom_statehas no effect on the
results. The underlyingOneClassSVMimplementation is similar to
the ones ofSVCandNuSVC. As no probability estimation
is provided forOneClassSVM, it is not random.The underlying
LinearSVCimplementation uses a random number
generator to select features when fitting the model with a dual coordinate
descent (i.e whendualis set toTrue). It is thus not uncommon
to have slightly different results for the same input data. If that
happens, try with a smallertolparameter. This randomness can also be
controlled with therandom_stateparameter. Whendualis
set toFalsethe underlying implementation ofLinearSVCis
not random andrandom_statehas no effect on the results.Using L1 penalization as provided by
LinearSVC(penalty='l1',yields a sparse solution, i.e. only a subset of feature
dual=False)
weights is different from zero and contribute to the decision function.
IncreasingCyields a more complex model (more features are selected).
TheCvalue that yields a “null” model (all weights equal to zero) can
be calculated usingl1_min_c.
1.4.6. Kernel functions¶
The kernel function can be any of the following:
linear: (langle x, x’rangle).
polynomial: ((gamma langle x, x’rangle + r)^d), where
(d) is specified by parameterdegree, (r) bycoef0.rbf: (exp(-gamma |x-x’|^2)), where (gamma) is
specified by parametergamma, must be greater than 0.sigmoid (tanh(gamma langle x,x’rangle + r)),
where (r) is specified bycoef0.
Different kernels are specified by the kernel parameter:
>>> linear_svc = svm.SVC(kernel='linear') >>> linear_svc.kernel 'linear' >>> rbf_svc = svm.SVC(kernel='rbf') >>> rbf_svc.kernel 'rbf'
See also Kernel Approximation for a solution to use RBF kernels that is much faster and more scalable.
1.4.6.1. Parameters of the RBF Kernel¶
When training an SVM with the Radial Basis Function (RBF) kernel, two
parameters must be considered: C and gamma. The parameter C,
common to all SVM kernels, trades off misclassification of training examples
against simplicity of the decision surface. A low C makes the decision
surface smooth, while a high C aims at classifying all training examples
correctly. gamma defines how much influence a single training example has.
The larger gamma is, the closer other examples must be to be affected.
Proper choice of C and gamma is critical to the SVM’s performance. One
is advised to use GridSearchCV with
C and gamma spaced exponentially far apart to choose good values.
1.4.6.2. Custom Kernels¶
You can define your own kernels by either giving the kernel as a
python function or by precomputing the Gram matrix.
Classifiers with custom kernels behave the same way as any other
classifiers, except that:
Field
support_vectors_is now empty, only indices of support
vectors are stored insupport_A reference (and not a copy) of the first argument in the
fit()
method is stored for future reference. If that array changes between the
use offit()andpredict()you will have unexpected results.
1.4.6.2.1. Using Python functions as kernels¶
You can use your own defined kernels by passing a function to the
kernel parameter.
Your kernel must take as arguments two matrices of shape
(n_samples_1, n_features), (n_samples_2, n_features)
and return a kernel matrix of shape (n_samples_1, n_samples_2).
The following code defines a linear kernel and creates a classifier
instance that will use that kernel:
>>> import numpy as np >>> from sklearn import svm >>> def my_kernel(X, Y): ... return np.dot(X, Y.T) ... >>> clf = svm.SVC(kernel=my_kernel)
1.4.6.2.2. Using the Gram matrix¶
You can pass pre-computed kernels by using the kernel='precomputed'
option. You should then pass Gram matrix instead of X to the fit and
predict methods. The kernel values between all training vectors and the
test vectors must be provided:
>>> import numpy as np >>> from sklearn.datasets import make_classification >>> from sklearn.model_selection import train_test_split >>> from sklearn import svm >>> X, y = make_classification(n_samples=10, random_state=0) >>> X_train , X_test , y_train, y_test = train_test_split(X, y, random_state=0) >>> clf = svm.SVC(kernel='precomputed') >>> # linear kernel computation >>> gram_train = np.dot(X_train, X_train.T) >>> clf.fit(gram_train, y_train) SVC(kernel='precomputed') >>> # predict on training examples >>> gram_test = np.dot(X_test, X_train.T) >>> clf.predict(gram_test) array([0, 1, 0])
1.4.7. Mathematical formulation¶
A support vector machine constructs a hyper-plane or set of hyper-planes in a
high or infinite dimensional space, which can be used for
classification, regression or other tasks. Intuitively, a good
separation is achieved by the hyper-plane that has the largest distance
to the nearest training data points of any class (so-called functional
margin), since in general the larger the margin the lower the
generalization error of the classifier. The figure below shows the decision
function for a linearly separable problem, with three samples on the
margin boundaries, called “support vectors”:
In general, when the problem isn’t linearly separable, the support vectors
are the samples within the margin boundaries.
We recommend [13] and [14] as good references for the theory and
practicalities of SVMs.
1.4.7.1. SVC¶
Given training vectors (x_i in mathbb{R}^p), i=1,…, n, in two classes, and a
vector (y in {1, -1}^n), our goal is to find (w in
mathbb{R}^p) and (b in mathbb{R}) such that the prediction given by
(text{sign} (w^Tphi(x) + b)) is correct for most samples.
SVC solves the following primal problem:
[ begin{align}begin{aligned}min_ {w, b, zeta} frac{1}{2} w^T w + C sum_{i=1}^{n} zeta_i\begin{split}textrm {subject to } & y_i (w^T phi (x_i) + b) geq 1 — zeta_i,\
& zeta_i geq 0, i=1, …, nend{split}end{aligned}end{align} ]
Intuitively, we’re trying to maximize the margin (by minimizing
(||w||^2 = w^Tw)), while incurring a penalty when a sample is
misclassified or within the margin boundary. Ideally, the value (y_i
(w^T phi (x_i) + b)) would be (geq 1) for all samples, which
indicates a perfect prediction. But problems are usually not always perfectly
separable with a hyperplane, so we allow some samples to be at a distance (zeta_i) from
their correct margin boundary. The penalty term C controls the strength of
this penalty, and as a result, acts as an inverse regularization parameter
(see note below).
The dual problem to the primal is
[ begin{align}begin{aligned}min_{alpha} frac{1}{2} alpha^T Q alpha — e^T alpha\begin{split}
textrm {subject to } & y^T alpha = 0\
& 0 leq alpha_i leq C, i=1, …, nend{split}end{aligned}end{align} ]
where (e) is the vector of all ones,
and (Q) is an (n) by (n) positive semidefinite matrix,
(Q_{ij} equiv y_i y_j K(x_i, x_j)), where (K(x_i, x_j) = phi (x_i)^T phi (x_j))
is the kernel. The terms (alpha_i) are called the dual coefficients,
and they are upper-bounded by (C).
This dual representation highlights the fact that training vectors are
implicitly mapped into a higher (maybe infinite)
dimensional space by the function (phi): see kernel trick.
Once the optimization problem is solved, the output of
decision_function for a given sample (x) becomes:
[sum_{iin SV} y_i alpha_i K(x_i, x) + b,]
and the predicted class correspond to its sign. We only need to sum over the
support vectors (i.e. the samples that lie within the margin) because the
dual coefficients (alpha_i) are zero for the other samples.
These parameters can be accessed through the attributes dual_coef_
which holds the product (y_i alpha_i), support_vectors_ which
holds the support vectors, and intercept_ which holds the independent
term (b)
Note
While SVM models derived from libsvm and liblinear use C as
regularization parameter, most other estimators use alpha. The exact
equivalence between the amount of regularization of two models depends on
the exact objective function optimized by the model. For example, when the
estimator used is Ridge regression,
the relation between them is given as (C = frac{1}{alpha}).
1.4.7.2. LinearSVC¶
The primal problem can be equivalently formulated as
[min_ {w, b} frac{1}{2} w^T w + C sum_{i=1}^{n}max(0, 1 — y_i (w^T phi(x_i) + b)),]
where we make use of the hinge loss. This is the form that is
directly optimized by LinearSVC, but unlike the dual form, this one
does not involve inner products between samples, so the famous kernel trick
cannot be applied. This is why only the linear kernel is supported by
LinearSVC ((phi) is the identity function).
1.4.7.3. NuSVC¶
The (nu)-SVC formulation [15] is a reparameterization of the
(C)-SVC and therefore mathematically equivalent.
We introduce a new parameter (nu) (instead of (C)) which
controls the number of support vectors and margin errors:
(nu in (0, 1]) is an upper bound on the fraction of margin errors and
a lower bound of the fraction of support vectors. A margin error corresponds
to a sample that lies on the wrong side of its margin boundary: it is either
misclassified, or it is correctly classified but does not lie beyond the
margin.
1.4.7.4. SVR¶
Given training vectors (x_i in mathbb{R}^p), i=1,…, n, and a
vector (y in mathbb{R}^n) (varepsilon)-SVR solves the following primal problem:
[ begin{align}begin{aligned}min_ {w, b, zeta, zeta^*} frac{1}{2} w^T w + C sum_{i=1}^{n} (zeta_i + zeta_i^*)\begin{split}textrm {subject to } & y_i — w^T phi (x_i) — b leq varepsilon + zeta_i,\
& w^T phi (x_i) + b — y_i leq varepsilon + zeta_i^*,\
& zeta_i, zeta_i^* geq 0, i=1, …, nend{split}end{aligned}end{align} ]
Here, we are penalizing samples whose prediction is at least (varepsilon)
away from their true target. These samples penalize the objective by
(zeta_i) or (zeta_i^*), depending on whether their predictions
lie above or below the (varepsilon) tube.
The dual problem is
[ begin{align}begin{aligned}min_{alpha, alpha^*} frac{1}{2} (alpha — alpha^*)^T Q (alpha — alpha^*) + varepsilon e^T (alpha + alpha^*) — y^T (alpha — alpha^*)\begin{split}
textrm {subject to } & e^T (alpha — alpha^*) = 0\
& 0 leq alpha_i, alpha_i^* leq C, i=1, …, nend{split}end{aligned}end{align} ]
where (e) is the vector of all ones,
(Q) is an (n) by (n) positive semidefinite matrix,
(Q_{ij} equiv K(x_i, x_j) = phi (x_i)^T phi (x_j))
is the kernel. Here training vectors are implicitly mapped into a higher
(maybe infinite) dimensional space by the function (phi).
The prediction is:
[sum_{i in SV}(alpha_i — alpha_i^*) K(x_i, x) + b]
These parameters can be accessed through the attributes dual_coef_
which holds the difference (alpha_i — alpha_i^*), support_vectors_ which
holds the support vectors, and intercept_ which holds the independent
term (b)
1.4.7.5. LinearSVR¶
The primal problem can be equivalently formulated as
[min_ {w, b} frac{1}{2} w^T w + C sum_{i=1}^{n}max(0, |y_i — (w^T phi(x_i) + b)| — varepsilon),]
where we make use of the epsilon-insensitive loss, i.e. errors of less than
(varepsilon) are ignored. This is the form that is directly optimized
by LinearSVR.
1.4.8. Implementation details¶
Internally, we use libsvm [12] and liblinear [11] to handle all
computations. These libraries are wrapped using C and Cython.
For a description of the implementation and details of the algorithms
used, please refer to their respective papers.
Линейно разделимый случай SVM[]
Пусть дана выборка 
Линейный классификатор:

Какой геометрический смысл у линейного классификатора? Он строит гиперплоскость, которая задается уравнением:

И объекты лежащие по разные стороны от разделяющей поверхности классификатор относит к разным классам. Возьмем из обучающий выборки объект, лежащий ближе всего к разделяющей поверхности. И пусть для него выполнено следующее равенство:

Найдем расстояние от него до гиперплоскости. Известно, что расстояние может быть посчитано по формуле: 

Таким образом ширина разделяющей полосы будет равна 


Итак, перейдем к математической постановке задачи:

Заметим, что второе и третье уравнение можно переписать в виде одного:

Если точка 



Итого получим следующую задачу:

Выделяют два типа объектов:
Но все это не имеет отношения к жизни, потому что линейно разделимых выборок не бывает.
Линейно неразделимый случай SVM[]
Теперь рассмотрим случай, когда не удается линейно разделить выборку на два класса. Решать задачу по новой не хочется, поэтому ослабим условие предыдущей задачи. Т.е. разрешим объектам из одного класса попадать в область второго класса.



Параметр 

Классификация типов объектов[]
Выделяют несколько типов объектов:
Какой функции потерь и регуляризатору соответствует SVM?[]
Рассмотрим еще раз линейно неразделимый случай SVM.

Постараемся избавиться от 

Или иначе это можно записать: 
И тогда нашу задачу можно переписать в виде:

Это и есть функция потерь, которую мы пытаемся минимизировать. Видно, что в данном случае используется 
Вывод решения[]
Запишем еще раз условия задачи:

Запишем Лагранжиан:
![{displaystyle L(w,b,xi ,lambda ,mu )={frac {1}{2}}|w|^{2}+Csum _{i=1}^{N}xi _{i}-sum _{i=1}^{N}lambda _{i}[y_{i}(w^{T}x_{i}+b)-1+xi _{i}]-sum _{i=1}^{N}mu _{i}xi _{i}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fe62bafe3fa500c2728f0c50c851c77c820d5cb0)
Выпишем Условия Куна-Таккера:
![{displaystyle {begin{cases}bigtriangledown _{w}L=w-sum _{i=1}^{l}lambda _{i}y_{i}x_{i}=0Longrightarrow w=sum _{i=1}^{l}lambda _{i}y_{i}x_{i}\bigtriangledown _{b}L=-sum _{i=1}^{l}lambda _{i}y_{i}=0Longrightarrow sum _{i=1}^{l}lambda _{i}y_{i}=0\bigtriangledown _{xi _{i}}L=C-lambda _{i}-mu _{i}Longrightarrow mu _{i}+lambda _{i}=C\lambda _{i}[y_{i}(w^{T}x_{i}+b)-1+xi _{i}]=0Longrightarrow (lambda _{i}=0) or (y_{i}(w^{T}x_{i}+b)=1-xi _{i})\mu _{i}xi _{i}=0Longrightarrow (mu _{i}=0) or (xi _{i}=0)\xi _{i}geq 0, lambda _{i}geq 0, mu _{i}geq 0end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb026dab3a470eae7b354cc189a5614fee2fd804)
Воспользуемся этими условиями и перепишем Лагранжиан:


Таким образом мы перешли к двойственной задаче:

Обобщение через ядра[]
Вместо скалярного произведения можно использовать ядра:

В этом случае классификатор будет иметь вид:

Гораздо легче что-то измерить, чем понять, что именно вы измеряете
Джон Уильям Салливан
Задачи машинного обучения с учителем как правило состоят в восстановлении зависимости между парами (признаковое описание, целевая переменная) по данным, доступным нам для анализа. Алгоритмы машинного обучения (learning algorithm), со многими из которых вы уже успели познакомиться, позволяют построить модель, аппроксимирующую эту зависимость. Но как понять, насколько качественной получилась аппроксимация?
Почти наверняка наша модель будет ошибаться на некоторых объектах: будь она даже идеальной, шум или выбросы в тестовых данных всё испортят. При этом разные модели будут ошибаться на разных объектах и в разной степени. Задача специалиста по машинному обучению – подобрать подходящий критерий, который позволит сравнивать различные модели.
Перед чтением этой главы мы хотели бы ещё раз напомнить, что качество модели нельзя оценивать на обучающей выборке. Как минимум, это стоит делать на отложенной (тестовой) выборке, но, если вам это позволяют время и вычислительные ресурсы, стоит прибегнуть и к более надёжным способам проверки – например, кросс-валидации (о ней вы узнаете в отдельной главе).
Выбор метрик в реальных задачах
Возможно, вы уже участвовали в соревнованиях по анализу данных. На таких соревнованиях метрику (критерий качества модели) организатор выбирает за вас, и она, как правило, довольно понятным образом связана с результатами предсказаний. Но на практике всё бывает намного сложнее.
Например, мы хотим:
- решить, сколько коробок с бананами нужно завтра привезти в конкретный магазин, чтобы минимизировать количество товара, который не будет выкуплен и минимизировать ситуацию, когда покупатель к концу дня не находит желаемый продукт на полке;
- увеличить счастье пользователя от работы с нашим сервисом, чтобы он стал лояльным и обеспечивал тем самым стабильный прогнозируемый доход;
- решить, нужно ли направить человека на дополнительное обследование.
В каждом конкретном случае может возникать целая иерархия метрик. Представим, например, что речь идёт о стриминговом музыкальном сервисе, пользователей которого мы решили порадовать сгенерированными самодельной нейросетью треками – не защищёнными авторским правом, а потому совершенно бесплатными. Иерархия метрик могла бы иметь такой вид:
- Самый верхний уровень: будущий доход сервиса – невозможно измерить в моменте, сложным образом зависит от совокупности всех наших усилий;
- Медианная длина сессии, возможно, служащая оценкой радости пользователей, которая, как мы надеемся, повлияет на их желание продолжать платить за подписку – её нам придётся измерять в продакшене, ведь нас интересует реакция настоящих пользователей на новшество;
- Доля удовлетворённых качеством сгенерированной музыки асессоров, на которых мы потестируем её до того, как выставить на суд пользователей;
- Функция потерь, на которую мы будем обучать генеративную сеть.
На этом примере мы можем заметить сразу несколько общих закономерностей. Во-первых, метрики бывают offline и online (оффлайновыми и онлайновыми). Online метрики вычисляются по данным, собираемым с работающей системы (например, медианная длина сессии). Offline метрики могут быть измерены до введения модели в эксплуатацию, например, по историческим данным или с привлечением специальных людей, асессоров. Последнее часто применяется, когда метрикой является реакция живого человека: скажем, так поступают поисковые компании, которые предлагают людям оценить качество ранжирования экспериментальной системы еще до того, как рядовые пользователи увидят эти результаты в обычном порядке. На самом же нижнем этаже иерархии лежат оптимизируемые в ходе обучения функции потерь.
В данном разделе нас будут интересовать offline метрики, которые могут быть измерены без привлечения людей.
Функция потерь $neq$ метрика качества
Как мы узнали ранее, методы обучения реализуют разные подходы к обучению:
- обучение на основе прироста информации (как в деревьях решений)
- обучение на основе сходства (как в методах ближайших соседей)
- обучение на основе вероятностной модели данных (например, максимизацией правдоподобия)
- обучение на основе ошибок (минимизация эмпирического риска)
И в рамках обучения на основе минимизации ошибок мы уже отвечали на вопрос: как можно штрафовать модель за предсказание на обучающем объекте.
Во время сведения задачи о построении решающего правила к задаче численной оптимизации, мы вводили понятие функции потерь и, обычно, объявляли целевой функцией сумму потерь от предсказаний на всех объектах обучающей выборке.
Важно понимать разницу между функцией потерь и метрикой качества. Её можно сформулировать следующим образом:
-
Функция потерь возникает в тот момент, когда мы сводим задачу построения модели к задаче оптимизации. Обычно требуется, чтобы она обладала хорошими свойствами (например, дифференцируемостью).
-
Метрика – внешний, объективный критерий качества, обычно зависящий не от параметров модели, а только от предсказанных меток.
В некоторых случаях метрика может совпадать с функцией потерь. Например, в задаче регрессии MSE играет роль как функции потерь, так и метрики. Но, скажем, в задаче бинарной классификации они почти всегда различаются: в качестве функции потерь может выступать кросс-энтропия, а в качестве метрики – число верно угаданных меток (accuracy). Отметим, что в последнем примере у них различные аргументы: на вход кросс-энтропии нужно подавать логиты, а на вход accuracy – предсказанные метки (то есть по сути argmax логитов).
Бинарная классификация: метки классов
Перейдём к обзору метрик и начнём с самой простой разновидности классификации – бинарной, а затем постепенно будем наращивать сложность.
Напомним постановку задачи бинарной классификации: нам нужно по обучающей выборке ${(x_i, y_i)}_{i=1}^N$, где $y_iin{0, 1}$ построить модель, которая по объекту $x$ предсказывает метку класса $f(x)in{0, 1}$.
Первым критерием качества, который приходит в голову, является accuracy – доля объектов, для которых мы правильно предсказали класс:
$$ color{#348FEA}{text{Accuracy}(y, y^{pred}) = frac{1}{N} sum_{i=1}^N mathbb{I}[y_i = f(x_i)]} $$
Или же сопряженная ей метрика – доля ошибочных классификаций (error rate):
$$text{Error rate} = 1 — text{Accuracy}$$
Познакомившись чуть внимательнее с этой метрикой, можно заметить, что у неё есть несколько недостатков:
- она не учитывает дисбаланс классов. Например, в задаче диагностики редких заболеваний классификатор, предсказывающий всем пациентам отсутствие болезни будет иметь достаточно высокую accuracy просто потому, что больных людей в выборке намного меньше;
- она также не учитывает цену ошибки на объектах разных классов. Для примера снова можно привести задачу медицинской диагностики: если ошибочный положительный диагноз для здорового больного обернётся лишь ещё одним обследованием, то ошибочно отрицательный вердикт может повлечь роковые последствия.
Confusion matrix (матрица ошибок)
Исторически задача бинарной классификации – это задача об обнаружении чего-то редкого в большом потоке объектов, например, поиск человека, больного туберкулёзом, по флюорографии. Или задача признания пятна на экране приёмника радиолокационной станции бомбардировщиком, представляющем угрозу охраняемому объекту (в противовес стае гусей).
Поэтому класс, который представляет для нас интерес, называется «положительным», а оставшийся – «отрицательным».
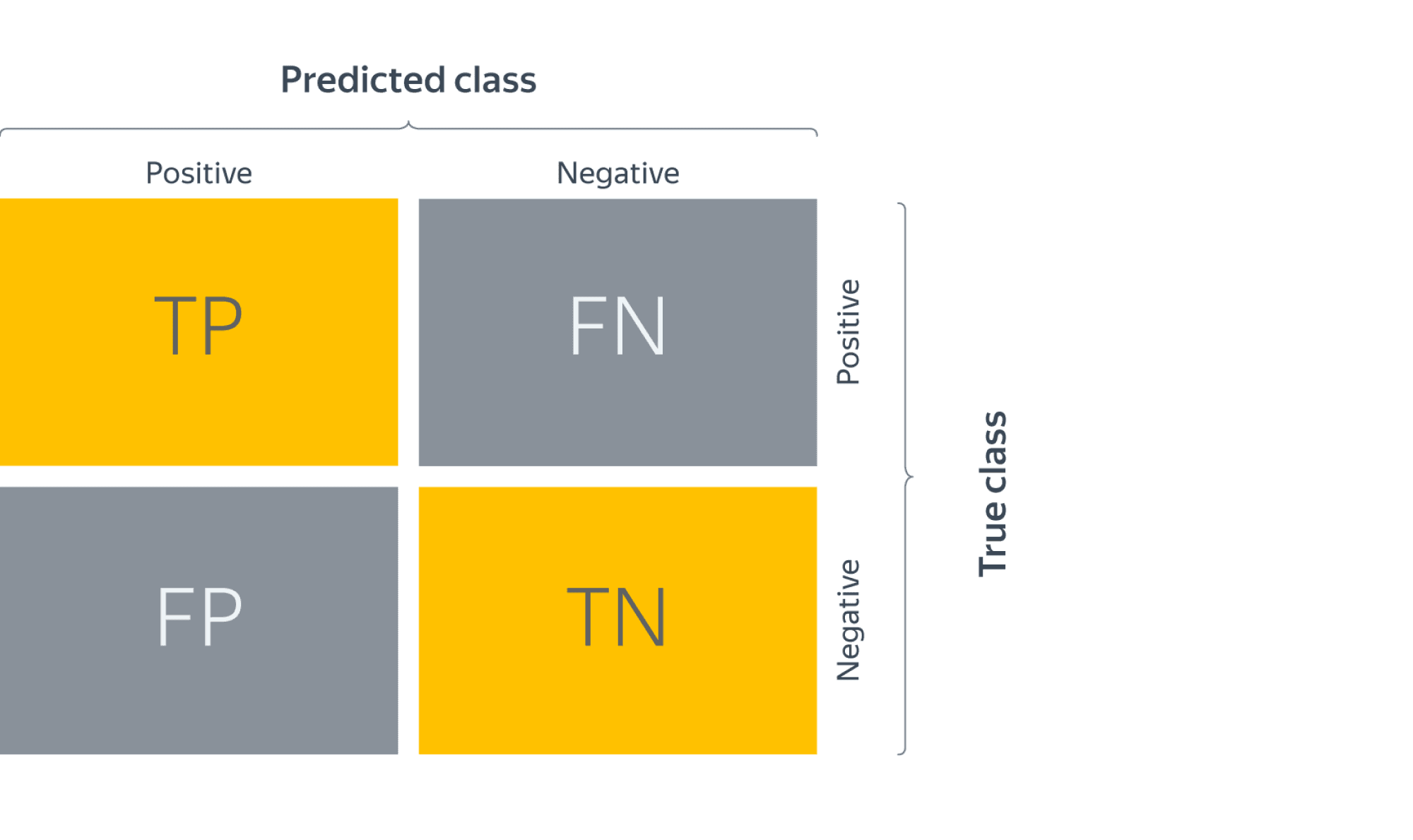
Заметим, что для каждого объекта в выборке возможно 4 ситуации:
- мы предсказали положительную метку и угадали. Будет относить такие объекты к true positive (TP) группе (true – потому что предсказали мы правильно, а positive – потому что предсказали положительную метку);
- мы предсказали положительную метку, но ошиблись в своём предсказании – false positive (FP) (false, потому что предсказание было неправильным);
- мы предсказали отрицательную метку и угадали – true negative (TN);
- и наконец, мы предсказали отрицательную метку, но ошиблись – false negative (FN). Для удобства все эти 4 числа изображают в виде таблицы, которую называют confusion matrix (матрицей ошибок):
Не волнуйтесь, если первое время эти обозначения будут сводить вас с ума (будем откровенны, даже профи со стажем в них порой путаются), однако логика за ними достаточно простая: первая часть названия группы показывает угадали ли мы с классом, а вторая – какой класс мы предсказали.
Пример
Попробуем воспользоваться введёнными метриками в боевом примере: сравним работу нескольких моделей классификации на Breast cancer wisconsin (diagnostic) dataset.
Объектами выборки являются фотографии биопсии грудных опухолей. С их помощью было сформировано признаковое описание, которое заключается в характеристиках ядер клеток (таких как радиус ядра, его текстура, симметричность). Положительным классом в такой постановке будут злокачественные опухоли, а отрицательным – доброкачественные.
Модель 1. Константное предсказание.
Решение задачи начнём с самого простого классификатора, который выдаёт на каждом объекте константное предсказание – самый часто встречающийся класс.
Зачем вообще замерять качество на такой модели?При разработке модели машинного обучения для проекта всегда желательно иметь некоторую baseline модель. Так нам будет легче проконтролировать, что наша более сложная модель действительно дает нам прирост качества.
from sklearn.datasets
import load_breast_cancer
the_data = load_breast_cancer()
# 0 – "доброкачественный"
# 1 – "злокачественный"
relabeled_target = 1 - the_data["target"]
from sklearn.model_selection import train_test_split
X = the_data["data"]
y = relabeled_target
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
from sklearn.dummy import DummyClassifier
dc_mf = DummyClassifier(strategy="most_frequent")
dc_mf.fit(X_train, y_train)
from sklearn.metrics import confusion_matrix
y_true = y_test y_pred = dc_mf.predict(X_test)
dc_mf_tn, dc_mf_fp, dc_mf_fn, dc_mf_tp = confusion_matrix(y_true, y_pred, labels = [0, 1]).ravel()
| Прогнозируемый класс + | Прогнозируемый класс — | |
|---|---|---|
| Истинный класс + | TP = 0 | FN = 53 |
| Истинный класс — | FP = 0 | TN = 90 |
Обучающие данные таковы, что наш dummy-классификатор все объекты записывает в отрицательный класс, то есть признаёт все опухоли доброкачественными. Такой наивный подход позволяет нам получить минимальный штраф за FP (действительно, нельзя ошибиться в предсказании, если положительный класс вообще не предсказывается), но и максимальный штраф за FN (в эту группу попадут все злокачественные опухоли).
Модель 2. Случайный лес.
Настало время воспользоваться всем арсеналом моделей машинного обучения, и начнём мы со случайного леса.
from sklearn.ensemble import RandomForestClassifier
rfc = RandomForestClassifier()
rfc.fit(X_train, y_train)
y_true = y_test
y_pred = rfc.predict(X_test)
rfc_tn, rfc_fp, rfc_fn, rfc_tp = confusion_matrix(y_true, y_pred, labels = [0, 1]).ravel()
| Прогнозируемый класс + | Прогнозируемый класс — | |
|---|---|---|
| Истинный класс + | TP = 52 | FN = 1 |
| Истинный класс — | FP = 4 | TN = 86 |
Можно сказать, что этот классификатор чему-то научился, т.к. главная диагональ матрицы стала содержать все объекты из отложенной выборки, за исключением 4 + 1 = 5 объектов (сравните с 0 + 53 объектами dummy-классификатора, все опухоли объявляющего доброкачественными).
Отметим, что вычисляя долю недиагональных элементов, мы приходим к метрике error rate, о которой мы говорили в самом начале:
$$text{Error rate} = frac{FP + FN}{ TP + TN + FP + FN}$$
тогда как доля объектов, попавших на главную диагональ – это как раз таки accuracy:
$$text{Accuracy} = frac{TP + TN}{ TP + TN + FP + FN}$$
Модель 3. Метод опорных векторов.
Давайте построим еще один классификатор на основе линейного метода опорных векторов.
Не забудьте привести признаки к единому масштабу, иначе численный алгоритм не сойдется к решению и мы получим гораздо более плохо работающее решающее правило. Попробуйте проделать это упражнение.
from sklearn.svm import LinearSVC
from sklearn.preprocessing import StandardScaler
ss = StandardScaler() ss.fit(X_train)
scaled_linsvc = LinearSVC(C=0.01,random_state=42)
scaled_linsvc.fit(ss.transform(X_train), y_train)
y_true = y_test
y_pred = scaled_linsvc.predict(ss.transform(X_test))
tn, fp, fn, tp = confusion_matrix(y_true, y_pred, labels = [0, 1]).ravel()
| Прогнозируемый класс + | Прогнозируемый класс — | |
|---|---|---|
| Истинный класс + | TP = 50 | FN = 3 |
| Истинный класс — | FP = 1 | TN = 89 |
Сравним результаты
Легко заметить, что каждая из двух моделей лучше классификатора-пустышки, однако давайте попробуем сравнить их между собой. С точки зрения error rate модели практически одинаковы: 5/143 для леса против 4/143 для SVM.
Посмотрим на структуру ошибок чуть более внимательно: лес – (FP = 4, FN = 1), SVM – (FP = 1, FN = 3). Какая из моделей предпочтительнее?
Замечание: Мы сравниваем несколько классификаторов на основании их предсказаний на отложенной выборке. Насколько ошибки данных классификаторов зависят от разбиения исходного набора данных? Иногда в процессе оценки качества мы будем получать модели, чьи показатели эффективности будут статистически неразличимыми.
Пусть мы учли предыдущее замечание и эти модели действительно статистически значимо ошибаются в разную сторону. Мы встретились с очевидной вещью: на матрицах нет отношения порядка. Когда мы сравнивали dummy-классификатор и случайный лес с помощью Accuracy, мы всю сложную структуру ошибок свели к одному числу, т.к. на вещественных числах отношение порядка есть. Сводить оценку модели к одному числу очень удобно, однако не стоит забывать, что у вашей модели есть много аспектов качества.
Что же всё-таки важнее уменьшить: FP или FN? Вернёмся к задаче: FP – доля доброкачественных опухолей, которым ошибочно присваивается метка злокачественной, а FN – доля злокачественных опухолей, которые классификатор пропускает. В такой постановке становится понятно, что при сравнении выиграет модель с меньшим FN (то есть лес в нашем примере), ведь каждая не обнаруженная опухоль может стоить человеческой жизни.
Рассмотрим теперь другую задачу: по данным о погоде предсказать, будет ли успешным запуск спутника. FN в такой постановке – это ошибочное предсказание неуспеха, то есть не более, чем упущенный шанс (если вас, конечно не уволят за срыв сроков). С FP всё серьёзней: если вы предскажете удачный запуск спутника, а на деле он потерпит крушение из-за погодных условий, то ваши потери будут в разы существеннее.
Итак, из примеров мы видим, что в текущем виде введенная нами доля ошибочных классификаций не даст нам возможности учесть неравную важность FP и FN. Поэтому введем две новые метрики: точность и полноту.
Точность и полнота
Accuracy — это метрика, которая характеризует качество модели, агрегированное по всем классам. Это полезно, когда классы для нас имеют одинаковое значение. В случае, если это не так, accuracy может быть обманчивой.
Рассмотрим ситуацию, когда положительный класс это событие редкое. Возьмем в качестве примера поисковую систему — в нашем хранилище хранятся миллиарды документов, а релевантных к конкретному поисковому запросу на несколько порядков меньше.
Пусть мы хотим решить задачу бинарной классификации «документ d релевантен по запросу q». Благодаря большому дисбалансу, Accuracy dummy-классификатора, объявляющего все документы нерелевантными, будет близка к единице. Напомним, что $text{Accuracy} = frac{TP + TN}{TP + TN + FP + FN}$, и в нашем случае высокое значение метрики будет обеспечено членом TN, в то время для пользователей более важен высокий TP.
Поэтому в случае ассиметрии классов, можно использовать метрики, которые не учитывают TN и ориентируются на TP.
Если мы рассмотрим долю правильно предсказанных положительных объектов среди всех объектов, предсказанных положительным классом, то мы получим метрику, которая называется точностью (precision)
$$color{#348FEA}{text{Precision} = frac{TP}{TP + FP}}$$
Интуитивно метрика показывает долю релевантных документов среди всех найденных классификатором. Чем меньше ложноположительных срабатываний будет допускать модель, тем больше будет её Precision.
Если же мы рассмотрим долю правильно найденных положительных объектов среди всех объектов положительного класса, то мы получим метрику, которая называется полнотой (recall)
$$color{#348FEA}{text{Recall} = frac{TP}{TP + FN}}$$
Интуитивно метрика показывает долю найденных документов из всех релевантных. Чем меньше ложно отрицательных срабатываний, тем выше recall модели.
Например, в задаче предсказания злокачественности опухоли точность показывает, сколько из определённых нами как злокачественные опухолей действительно являются злокачественными, а полнота – какую долю злокачественных опухолей нам удалось выявить.
Хорошее понимание происходящего даёт следующая картинка: 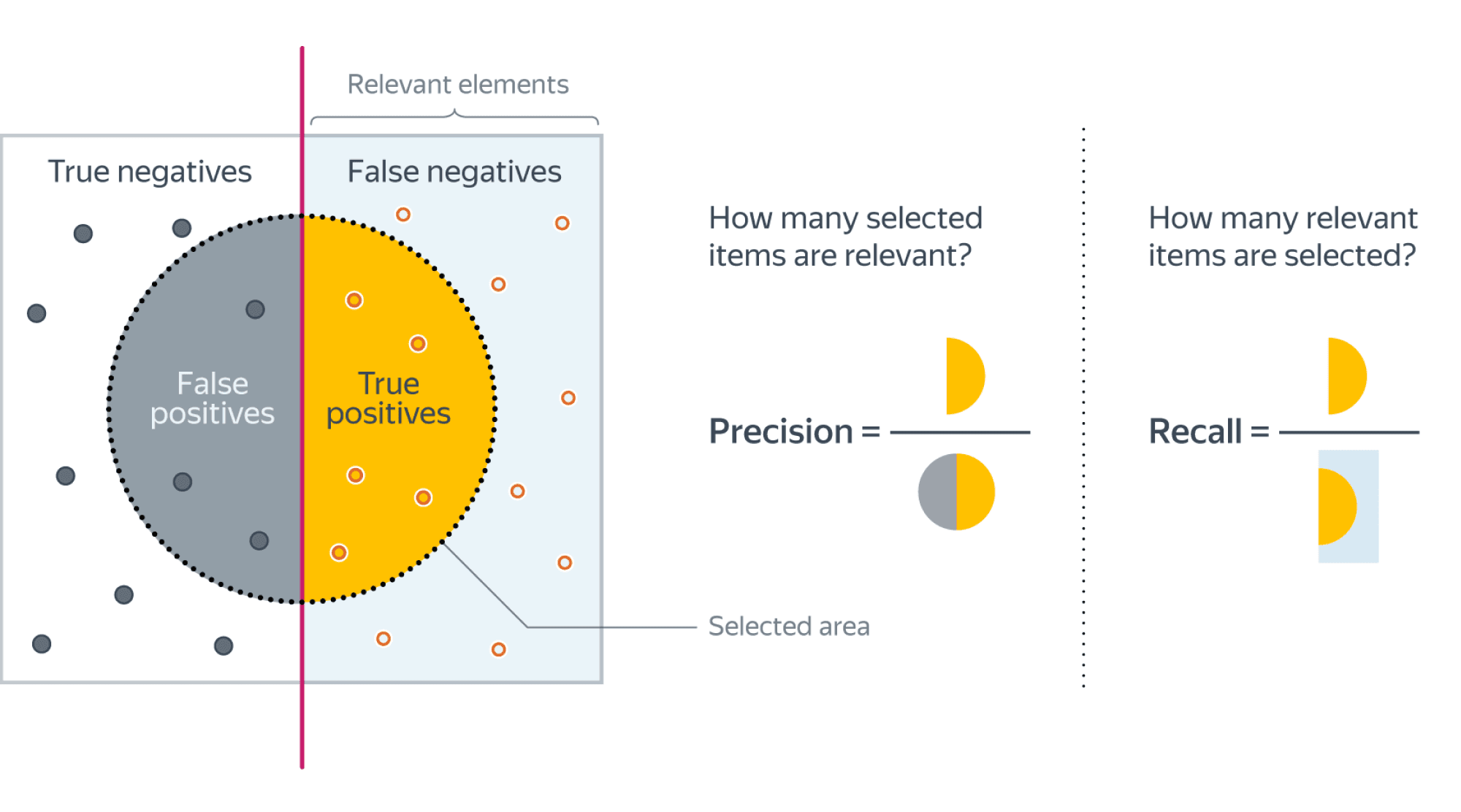
Recall@k, Precision@k
Метрики Recall и Precision хорошо подходят для задачи поиска «документ d релевантен запросу q», когда из списка рекомендованных алгоритмом документов нас интересует только первый. Но не всегда алгоритм машинного обучения вынужден работать в таких жестких условиях. Может быть такое, что вполне достаточно, что релевантный документ попал в первые k рекомендованных. Например, в интерфейсе выдачи первые три подсказки видны всегда одновременно и вообще не очень понятно, какой у них порядок. Тогда более честной оценкой качества алгоритма будет «в выдаче D размера k по запросу q нашлись релевантные документы». Для расчёта метрики по всей выборке объединим все выдачи и рассчитаем precision, recall как обычно подокументно.
F1-мера
Как мы уже отмечали ранее, модели очень удобно сравнивать, когда их качество выражено одним числом. В случае пары Precision-Recall существует популярный способ скомпоновать их в одну метрику — взять их среднее гармоническое. Данный показатель эффективности исторически носит название F1-меры (F1-measure).
$$
color{#348FEA}{F_1 = frac{2}{frac{1}{Recall} + frac{1}{Precision}}} = $$
$$ = 2 frac{Recall cdot Precision }{Recall + Precision} = frac
{TP} {TP + frac{FP + FN}{2}}
$$
Стоит иметь в виду, что F1-мера предполагает одинаковую важность Precision и Recall, если одна из этих метрик для вас приоритетнее, то можно воспользоваться $F_{beta}$ мерой:
$$
F_{beta} = (beta^2 + 1) frac{Recall cdot Precision }{Recall + beta^2Precision}
$$
Бинарная классификация: вероятности классов
Многие модели бинарной классификации устроены так, что класс объекта получается бинаризацией выхода классификатора по некоторому фиксированному порогу:
$$fleft(x ; w, w_{0}right)=mathbb{I}left[g(x, w) > w_{0}right].$$
Например, модель логистической регрессии возвращает оценку вероятности принадлежности примера к положительному классу. Другие модели бинарной классификации обычно возвращают произвольные вещественные значения, но существуют техники, называемые калибровкой классификатора, которые позволяют преобразовать предсказания в более или менее корректную оценку вероятности принадлежности к положительному классу.
Как оценить качество предсказываемых вероятностей, если именно они являются нашей конечной целью? Общепринятой мерой является логистическая функция потерь, которую мы изучали раньше, когда говорили об устройстве некоторых методов классификации (например уже упоминавшейся логистической регрессии).
Если же нашей целью является построение прогноза в терминах метки класса, то нам нужно учесть, что в зависимости от порога мы будем получать разные предсказания и разное качество на отложенной выборке. Так, чем ниже порог отсечения, тем больше объектов модель будет относить к положительному классу. Как в этом случае оценить качество модели?
AUC
Пусть мы хотим учитывать ошибки на объектах обоих классов. При уменьшении порога отсечения мы будем находить (правильно предсказывать) всё большее число положительных объектов, но также и неправильно предсказывать положительную метку на всё большем числе отрицательных объектов. Естественным кажется ввести две метрики TPR и FPR:
TPR (true positive rate) – это полнота, доля положительных объектов, правильно предсказанных положительными:
$$ TPR = frac{TP}{P} = frac{TP}{TP + FN} $$
FPR (false positive rate) – это доля отрицательных объектов, неправильно предсказанных положительными:
$$FPR = frac{FP}{N} = frac{FP}{FP + TN}$$
Обе эти величины растут при уменьшении порога. Кривая в осях TPR/FPR, которая получается при варьировании порога, исторически называется ROC-кривой (receiver operating characteristics curve, сокращённо ROC curve). Следующий график поможет вам понять поведение ROC-кривой.
Желтая и синяя кривые показывают распределение предсказаний классификатора на объектах положительного и отрицательного классов соответственно. То есть значения на оси X (на графике с двумя гауссианами) мы получаем из классификатора. Если классификатор идеальный (две кривые разделимы по оси X), то на правом графике мы получаем ROC-кривую (0,0)->(0,1)->(1,1) (убедитесь сами!), площадь под которой равна 1. Если классификатор случайный (предсказывает одинаковые метки положительным и отрицательным объектам), то мы получаем ROC-кривую (0,0)->(1,1), площадь под которой равна 0.5. Поэкспериментируйте с разными вариантами распределения предсказаний по классам и посмотрите, как меняется ROC-кривая.
Чем лучше классификатор разделяет два класса, тем больше площадь (area under curve) под ROC-кривой – и мы можем использовать её в качестве метрики. Эта метрика называется AUC и она работает благодаря следующему свойству ROC-кривой:
AUC равен доле пар объектов вида (объект класса 1, объект класса 0), которые алгоритм верно упорядочил, т.е. предсказание классификатора на первом объекте больше:
$$
color{#348FEA}{operatorname{AUC} = frac{sumlimits_{i = 1}^{N} sumlimits_{j = 1}^{N}mathbb{I}[y_i < y_j] I^{prime}[f(x_{i}) < f(x_{j})]}{sumlimits_{i = 1}^{N} sumlimits_{j = 1}^{N}mathbb{I}[y_i < y_j]}}
$$
$$
I^{prime}left[f(x_{i}) < f(x_{j})right]=
left{
begin{array}{ll}
0, & f(x_{i}) > f(x_{j}) \
0.5 & f(x_{i}) = f(x_{j}) \
1, & f(x_{i}) < f(x_{j})
end{array}
right.
$$
$$
Ileft[y_{i}< y_{j}right]=
left{
begin{array}{ll}
0, & y_{i} geq y_{j} \
1, & y_{i} < y_{j}
end{array}
right.
$$
Чтобы детальнее разобраться, почему это так, советуем вам обратиться к материалам А.Г.Дьяконова.
В каких случаях лучше отдать предпочтение этой метрике? Рассмотрим следующую задачу: некоторый сотовый оператор хочет научиться предсказывать, будет ли клиент пользоваться его услугами через месяц. На первый взгляд кажется, что задача сводится к бинарной классификации с метками 1, если клиент останется с компанией и $0$ – иначе.
Однако если копнуть глубже в процессы компании, то окажется, что такие метки практически бесполезны. Компании скорее интересно упорядочить клиентов по вероятности прекращения обслуживания и в зависимости от этого применять разные варианты удержания: кому-то прислать скидочный купон от партнёра, кому-то предложить скидку на следующий месяц, а кому-то и новый тариф на особых условиях.
Таким образом, в любой задаче, где нам важна не метка сама по себе, а правильный порядок на объектах, имеет смысл применять AUC.
Утверждение выше может вызывать у вас желание использовать AUC в качестве метрики в задачах ранжирования, но мы призываем вас быть аккуратными.
ПодробнееУтверждение выше может вызывать у вас желание использовать AUC в качестве метрики в задачах ранжирования, но мы призываем вас быть аккуратными.» details=»Продемонстрируем это на следующем примере: пусть наша выборка состоит из $9100$ объектов класса $0$ и $10$ объектов класса $1$, и модель расположила их следующим образом:
$$underbrace{0 dots 0}_{9000} ~ underbrace{1 dots 1}_{10} ~ underbrace{0 dots 0}_{100}$$
Тогда AUC будет близка к единице: количество пар правильно расположенных объектов будет порядка $90000$, в то время как общее количество пар порядка $91000$.
Однако самыми высокими по вероятности положительного класса будут совсем не те объекты, которые мы ожидаем.
Average Precision
Будем постепенно уменьшать порог бинаризации. При этом полнота будет расти от $0$ до $1$, так как будет увеличиваться количество объектов, которым мы приписываем положительный класс (а количество объектов, на самом деле относящихся к положительному классу, очевидно, меняться не будет). Про точность же нельзя сказать ничего определённого, но мы понимаем, что скорее всего она будет выше при более высоком пороге отсечения (мы оставим только объекты, в которых модель «уверена» больше всего). Варьируя порог и пересчитывая значения Precision и Recall на каждом пороге, мы получим некоторую кривую примерно следующего вида:
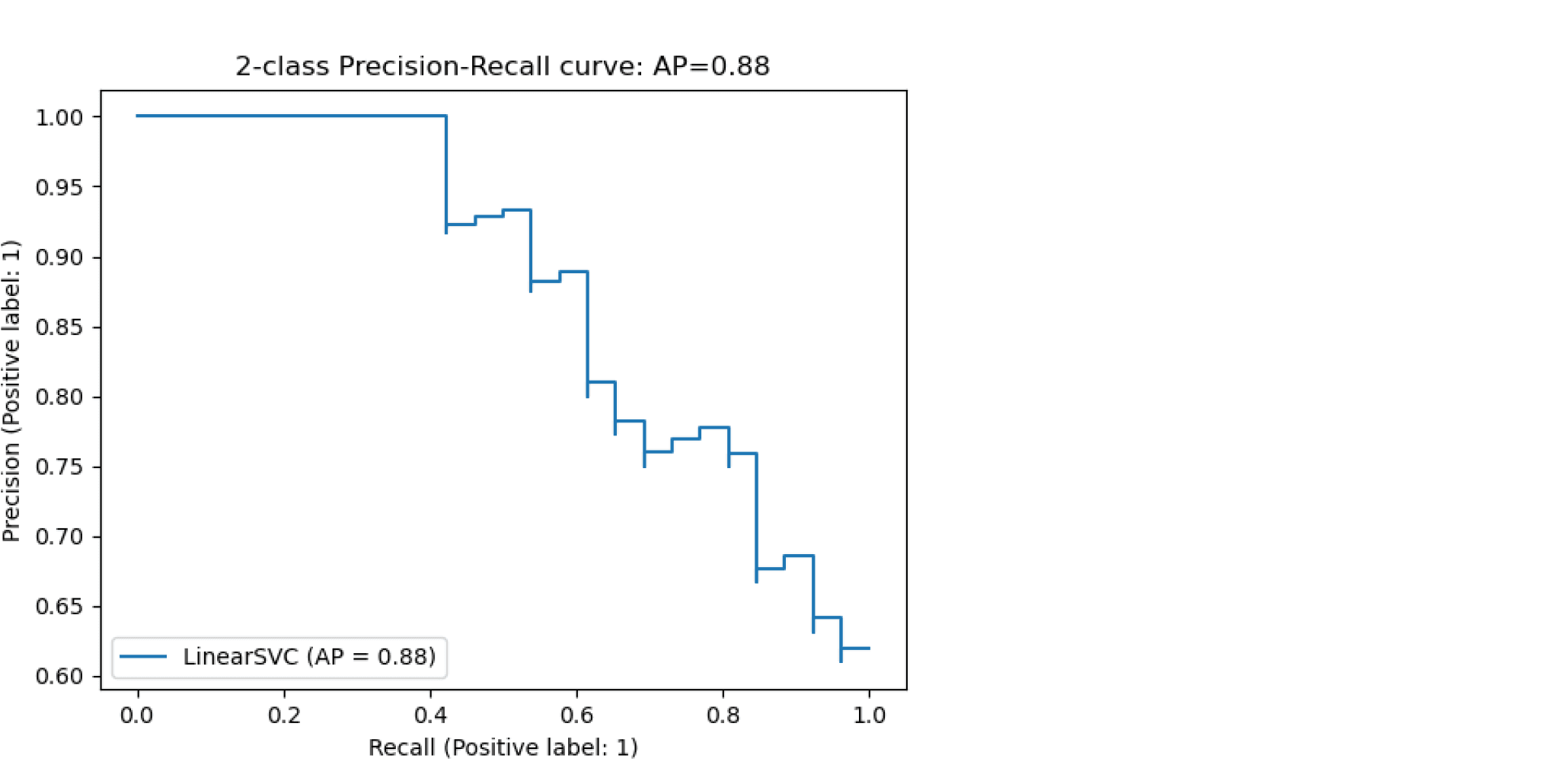
Рассмотрим среднее значение точности (оно равно площади под кривой точность-полнота):
$$ text { AP }=int_{0}^{1} p(r) d r$$
Получим показатель эффективности, который называется average precision. Как в случае матрицы ошибок мы переходили к скалярным показателям эффективности, так и в случае с кривой точность-полнота мы охарактеризовали ее в виде числа.
Многоклассовая классификация
Если классов становится больше двух, расчёт метрик усложняется. Если задача классификации на $K$ классов ставится как $K$ задач об отделении класса $i$ от остальных ($i=1,ldots,K$), то для каждой из них можно посчитать свою матрицу ошибок. Затем есть два варианта получения итогового значения метрики из $K$ матриц ошибок:
- Усредняем элементы матрицы ошибок (TP, FP, TN, FN) между бинарными классификаторами, например $TP = frac{1}{K}sum_{i=1}^{K}TP_i$. Затем по одной усреднённой матрице ошибок считаем Precision, Recall, F-меру. Это называют микроусреднением.
- Считаем Precision, Recall для каждого классификатора отдельно, а потом усредняем. Это называют макроусреднением.
Порядок усреднения влияет на результат в случае дисбаланса классов. Показатели TP, FP, FN — это счётчики объектов. Пусть некоторый класс обладает маленькой мощностью (обозначим её $M$). Тогда значения TP и FN при классификации этого класса против остальных будут не больше $M$, то есть тоже маленькие. Про FP мы ничего уверенно сказать не можем, но скорее всего при дисбалансе классов классификатор не будет предсказывать редкий класс слишком часто, потому что есть большая вероятность ошибиться. Так что FP тоже мало. Поэтому усреднение первым способом сделает вклад маленького класса в общую метрику незаметным. А при усреднении вторым способом среднее считается уже для нормированных величин, так что вклад каждого класса будет одинаковым.
Рассмотрим пример. Пусть есть датасет из объектов трёх цветов: желтого, зелёного и синего. Желтого и зелёного цветов почти поровну — 21 и 20 объектов соответственно, а синих объектов всего 4.
Модель по очереди для каждого цвета пытается отделить объекты этого цвета от объектов оставшихся двух цветов. Результаты классификации проиллюстрированы матрицей ошибок. Модель «покрасила» в жёлтый 25 объектов, 20 из которых были действительно жёлтыми (левый столбец матрицы). В синий был «покрашен» только один объект, который на самом деле жёлтый (средний столбец матрицы). В зелёный — 19 объектов, все на самом деле зелёные (правый столбец матрицы).
Посчитаем Precision классификации двумя способами:
- С помощью микроусреднения получаем $$
text{Precision} = frac{dfrac{1}{3}left(20 + 0 + 19right)}{dfrac{1}{3}left(20 + 0 + 19right) + dfrac{1}{3}left(5 + 1 + 0right)} = 0.87
$$ - С помощью макроусреднения получаем $$
text{Precision} = dfrac{1}{3}left( frac{20}{20 + 5} + frac{0}{0 + 1} + frac{19}{19 + 0}right) = 0.6
$$
Видим, что макроусреднение лучше отражает тот факт, что синий цвет, которого в датасете было совсем мало, модель практически игнорирует.
Как оптимизировать метрики классификации?
Пусть мы выбрали, что метрика качества алгоритма будет $F(a(X), Y)$. Тогда мы хотим обучить модель так, чтобы $F$ на валидационной выборке была минимальная/максимальная. Лучший способ добиться минимизации метрики $F$ — оптимизировать её напрямую, то есть выбрать в качестве функции потерь ту же $F(a(X), Y)$. К сожалению, это не всегда возможно. Рассмотрим, как оптимизировать метрики иначе.
Метрики precision и recall невозможно оптимизировать напрямую, потому что эти метрики нельзя рассчитать на одном объекте, а затем усреднить. Они зависят от того, какими были правильная метка класса и ответ алгоритма на всех объектах. Чтобы понять, как оптимизировать precision, recall, рассмотрим, как расчитать эти метрики на отложенной выборке. Пусть модель обучена на стандартную для классификации функцию потерь (LogLoss). Для получения меток класса специалист по машинному обучению сначала применяет на объектах модель и получает вещественные предсказания модели ($p_i in left(0, 1right)$). Затем предсказания бинаризуются по порогу, выбранному специалистом: если предсказание на объекте больше порога, то метка класса 1 (или «положительная»), если меньше — 0 (или «отрицательная»). Рассмотрим, что будет с метриками precision, recall в крайних положениях порога.
- Пусть порог равен нулю. Тогда всем объектам будет присвоена положительная метка. Следовательно, все объекты будут либо TP, либо FP, потому что отрицательных предсказаний нет, $TP + FP = N$, где $N$ — размер выборки. Также все объекты, у которых метка на самом деле 1, попадут в TP. По формуле точность $text{Precision} = frac{TP}{TP + FP} = frac1N sum_{i = 1}^N mathbb{I} left[ y_i = 1 right]$ равна среднему таргету в выборке. А полнота $text{Recall} = frac{TP}{TP + FN} = frac{TP}{TP + 0} = 1$ равна единице.
- Пусть теперь порог равен единице. Тогда ни один объект не будет назван положительным, $TP = FP = 0$. Все объекты с меткой класса 1 попадут в FN. Если есть хотя бы один такой объект, то есть $FN ne 0$, будет верна формула $text{Recall} = frac{TP}{TP + FN} = frac{0}{0+ FN} = 0$. То есть при пороге единица, полнота равна нулю. Теперь посмотрим на точность. Формула для Precision состоит только из счётчиков положительных ответов модели (TP, FP). При единичном пороге они оба равны нулю, $text{Precision} = frac{TP}{TP + FP} = frac{0}{0 + 0}$то есть при единичном пороге точность неопределена. Пусть мы отступили чуть-чуть назад по порогу, чтобы хотя бы несколько объектов были названы моделью положительными. Скорее всего это будут самые «простые» объекты, которые модель распознает хорошо, потому что её предсказание близко к единице. В этом предположении $FP approx 0$. Тогда точность $text{Precision} = frac{TP}{TP + FP} approx frac{TP}{TP + 0} approx 1$ будет близка к единице.
Изменяя порог, между крайними положениями, получим графики Precision и Recall, которые выглядят как-то так:
Recall меняется от единицы до нуля, а Precision от среднего тагрета до какого-то другого значения (нет гарантий, что график монотонный).
Итого оптимизация precision и recall происходит так:
- Модель обучается на стандартную функцию потерь (например, LogLoss).
- Используя вещественные предсказания на валидационной выборке, перебирая разные пороги от 0 до 1, получаем графики метрик в зависимости от порога.
- Выбираем нужное сочетание точности и полноты.
Пусть теперь мы хотим максимизировать метрику AUC. Стандартный метод оптимизации, градиентный спуск, предполагает, что функция потерь дифференцируема. AUC этим качеством не обладает, то есть мы не можем оптимизировать её напрямую. Поэтому для метрики AUC приходится изменять оптимизационную задачу. Метрика AUC считает долю верно упорядоченных пар. Значит от исходной выборки можно перейти к выборке упорядоченных пар объектов. На этой выборке ставится задача классификации: метка класса 1 соответствует правильно упорядоченной паре, 0 — неправильно. Новой метрикой становится accuracy — доля правильно классифицированных объектов, то есть доля правильно упорядоченных пар. Оптимизировать accuracy можно по той же схеме, что и precision, recall: обучаем модель на LogLoss и предсказываем вероятности положительной метки у объекта выборки, считаем accuracy для разных порогов по вероятности и выбираем понравившийся.
Регрессия
В задачах регрессии целевая метка у нас имеет потенциально бесконечное число значений. И природа этих значений, обычно, связана с каким-то процессом измерений:
- величина температуры в определенный момент времени на метеостанции
- количество прочтений статьи на сайте
- количество проданных бананов в конкретном магазине, сети магазинов или стране
- дебит добывающей скважины на нефтегазовом месторождении за месяц и т.п.
Мы видим, что иногда метка это целое число, а иногда произвольное вещественное число. Обычно случаи целочисленных меток моделируют так, словно это просто обычное вещественное число. При таком подходе может оказаться так, что модель A лучше модели B по некоторой метрике, но при этом предсказания у модели A могут быть не целыми. Если в бизнес-задаче ожидается именно целочисленный ответ, то и оценивать нужно огрубление.
Общая рекомендация такова: оценивайте весь каскад решающих правил: и те «внутренние», которые вы получаете в результате обучения, и те «итоговые», которые вы отдаёте бизнес-заказчику.
Например, вы можете быть удовлетворены, что стали ошибаться не во втором, а только в третьем знаке после запятой при предсказании погоды. Но сами погодные данные измеряются с точностью до десятых долей градуса, а пользователь и вовсе может интересоваться лишь целым числом градусов.
Итак, напомним постановку задачи регрессии: нам нужно по обучающей выборке ${(x_i, y_i)}_{i=1}^N$, где $y_i in mathbb{R}$ построить модель f(x).
Величину $ e_i = f(x_i) — y_i $ называют ошибкой на объекте i или регрессионным остатком.
Весь набор ошибок на отложенной выборке может служить аналогом матрицы ошибок из задачи классификации. А именно, когда мы рассматриваем две разные модели, то, глядя на то, как и на каких объектах они ошиблись, мы можем прийти к выводу, что для решения бизнес-задачи нам выгоднее взять ту или иную модель. И, аналогично со случаем бинарной классификации, мы можем начать строить агрегаты от вектора ошибок, получая тем самым разные метрики.
MSE, RMSE, $R^2$
MSE – одна из самых популярных метрик в задаче регрессии. Она уже знакома вам, т.к. применяется в качестве функции потерь (или входит в ее состав) во многих ранее рассмотренных методах.
$$ MSE(y^{true}, y^{pred}) = frac1Nsum_{i=1}^{N} (y_i — f(x_i))^2 $$
Иногда для того, чтобы показатель эффективности MSE имел размерность исходных данных, из него извлекают квадратный корень и получают показатель эффективности RMSE.
MSE неограничен сверху, и может быть нелегко понять, насколько «хорошим» или «плохим» является то или иное его значение. Чтобы появились какие-то ориентиры, делают следующее:
-
Берут наилучшее константное предсказание с точки зрения MSE — среднее арифметическое меток $bar{y}$. При этом чтобы не было подглядывания в test, среднее нужно вычислять по обучающей выборке
-
Рассматривают в качестве показателя ошибки:
$$ R^2 = 1 — frac{sum_{i=1}^{N} (y_i — f(x_i))^2}{sum_{i=1}^{N} (y_i — bar{y})^2}.$$
У идеального решающего правила $R^2$ равен $1$, у наилучшего константного предсказания он равен $0$ на обучающей выборке. Можно заметить, что $R^2$ показывает, какая доля дисперсии таргетов (знаменатель) объяснена моделью.
MSE квадратично штрафует за большие ошибки на объектах. Мы уже видели проявление этого при обучении моделей методом минимизации квадратичных ошибок – там это проявлялось в том, что модель старалась хорошо подстроиться под выбросы.
Пусть теперь мы хотим использовать MSE для оценки наших регрессионных моделей. Если большие ошибки для нас действительно неприемлемы, то квадратичный штраф за них — очень полезное свойство (и его даже можно усиливать, повышая степень, в которую мы возводим ошибку на объекте). Однако если в наших тестовых данных присутствуют выбросы, то нам будет сложно объективно сравнить модели между собой: ошибки на выбросах будет маскировать различия в ошибках на основном множестве объектов.
Таким образом, если мы будем сравнивать две модели при помощи MSE, у нас будет выигрывать та модель, у которой меньше ошибка на объектах-выбросах, а это, скорее всего, не то, чего требует от нас наша бизнес-задача.
История из жизни про бананы и квадратичный штраф за ошибкуИз-за неверно введенных данных метка одного из объектов оказалась в 100 раз больше реального значения. Моделировалась величина при помощи градиентного бустинга над деревьями решений. Функция потерь была MSE.
Однажды уже во время эксплуатации случилось ч.п.: у нас появились предсказания, в 100 раз превышающие допустимые из соображений физического смысла значения. Представьте себе, например, что вместо обычных 4 ящиков бананов система предлагала поставить в магазин 400. Были распечатаны все деревья из ансамбля, и мы увидели, что постепенно число ящиков действительно увеличивалось до прогнозных 400.
Было решено проверить гипотезу, что был выброс в данных для обучения. Так оно и оказалось: всего одна точка давала такую потерю на объекте, что алгоритм обучения решил, что лучше переобучиться под этот выброс, чем смириться с большим штрафом на этом объекте. А в эксплуатации у нас возникли точки, которые плюс-минус попадали в такие же листья ансамбля, что и объект-выброс.
Избежать такого рода проблем можно двумя способами: внимательнее контролируя качество данных или адаптировав функцию потерь.
Аналогично, можно поступать и в случае, когда мы разрабатываем метрику качества: менее жёстко штрафовать за большие отклонения от истинного таргета.
MAE
Использовать RMSE для сравнения моделей на выборках с большим количеством выбросов может быть неудобно. В таких случаях прибегают к также знакомой вам в качестве функции потери метрике MAE (mean absolute error):
$$ MAE(y^{true}, y^{pred}) = frac{1}{N}sum_{i=1}^{N} left|y_i — f(x_i)right| $$
Метрики, учитывающие относительные ошибки
И MSE и MAE считаются как сумма абсолютных ошибок на объектах.
Рассмотрим следующую задачу: мы хотим спрогнозировать спрос товаров на следующий месяц. Пусть у нас есть два продукта: продукт A продаётся в количестве 100 штук, а продукт В в количестве 10 штук. И пусть базовая модель предсказывает количество продаж продукта A как 98 штук, а продукта B как 8 штук. Ошибки на этих объектах добавляют 4 штрафных единицы в MAE.
И есть 2 модели-кандидата на улучшение. Первая предсказывает товар А 99 штук, а товар B 8 штук. Вторая предсказывает товар А 98 штук, а товар B 9 штук.
Обе модели улучшают MAE базовой модели на 1 единицу. Однако, с точки зрения бизнес-заказчика вторая модель может оказаться предпочтительнее, т.к. предсказание продажи редких товаров может быть приоритетнее. Один из способов учесть такое требование – рассматривать не абсолютную, а относительную ошибку на объектах.
MAPE, SMAPE
Когда речь заходит об относительных ошибках, сразу возникает вопрос: что мы будем ставить в знаменатель?
В метрике MAPE (mean absolute percentage error) в знаменатель помещают целевое значение:
$$ MAPE(y^{true}, y^{pred}) = frac{1}{N} sum_{i=1}^{N} frac{ left|y_i — f(x_i)right|}{left|y_iright|} $$
С особым случаем, когда в знаменателе оказывается $0$, обычно поступают «инженерным» способом: или выдают за непредсказание $0$ на таком объекте большой, но фиксированный штраф, или пытаются застраховаться от подобного на уровне формулы и переходят к метрике SMAPE (symmetric mean absolute percentage error):
$$ SMAPE(y^{true}, y^{pred}) = frac{1}{N} sum_{i=1}^{N} frac{ 2 left|y_i — f(x_i)right|}{y_i + f(x_i)} $$
Если же предсказывается ноль, штраф считаем нулевым.
Таким переходом от абсолютных ошибок на объекте к относительным мы сделали объекты в тестовой выборке равнозначными: даже если мы делаем абсурдно большое предсказание, на фоне которого истинная метка теряется, мы получаем штраф за этот объект порядка 1 в случае MAPE и 2 в случае SMAPE.
WAPE
Как и любая другая метрика, MAPE имеет свои границы применимости: например, она плохо справляется с прогнозом спроса на товары с прерывистыми продажами. Рассмотрим такой пример:
| Понедельник | Вторник | Среда | |
|---|---|---|---|
| Прогноз | 55 | 2 | 50 |
| Продажи | 50 | 1 | 50 |
| MAPE | 10% | 100% | 0% |
Среднее MAPE – 36.7%, что не очень отражает реальную ситуацию, ведь два дня мы предсказывали с хорошей точностью. В таких ситуациях помогает WAPE (weighted average percentage error):
$$ WAPE(y^{true}, y^{pred}) = frac{sum_{i=1}^{N} left|y_i — f(x_i)right|}{sum_{i=1}^{N} left|y_iright|} $$
Если мы предсказываем идеально, то WAPE = 0, если все предсказания отдаём нулевыми, то WAPE = 1.
В нашем примере получим WAPE = 5.9%
RMSLE
Альтернативный способ уйти от абсолютных ошибок к относительным предлагает метрика RMSLE (root mean squared logarithmic error):
$$ RMSLE(y^{true}, y^{pred}| c) = sqrt{ frac{1}{N} sum_{i=1}^N left(vphantom{frac12}log{left(y_i + c right)} — log{left(f(x_i) + c right)}right)^2 } $$
где нормировочная константа $c$ вводится искусственно, чтобы не брать логарифм от нуля. Также по построению видно, что метрика пригодна лишь для неотрицательных меток.
Веса в метриках
Все вышеописанные метрики легко допускают введение весов для объектов. Если мы из каких-то соображений можем определить стоимость ошибки на объекте, можно брать эту величину в качестве веса. Например, в задаче предсказания спроса в качестве веса можно использовать стоимость объекта.
Доля предсказаний с абсолютными ошибками больше, чем d
Еще одним способом охарактеризовать качество модели в задаче регрессии является доля предсказаний с абсолютными ошибками больше заданного порога $d$:
$$frac{1}{N} sum_{i=1}^{N} mathbb{I}left[ left| y_i — f(x_i) right| > d right] $$
Например, можно считать, что прогноз погоды сбылся, если ошибка предсказания составила меньше 1/2/3 градусов. Тогда рассматриваемая метрика покажет, в какой доле случаев прогноз не сбылся.
Как оптимизировать метрики регрессии?
Пусть мы выбрали, что метрика качества алгоритма будет $F(a(X), Y)$. Тогда мы хотим обучить модель так, чтобы F на валидационной выборке была минимальная/максимальная. Аналогично задачам классификации лучший способ добиться минимизации метрики $F$ — выбрать в качестве функции потерь ту же $F(a(X), Y)$. К счастью, основные метрики для регрессии: MSE, RMSE, MAE можно оптимизировать напрямую. С формальной точки зрения MAE не дифференцируема, так как там присутствует модуль, чья производная не определена в нуле. На практике для этого выколотого случая в коде можно возвращать ноль.
Для оптимизации MAPE придётся изменять оптимизационную задачу. Оптимизацию MAPE можно представить как оптимизацию MAE, где объектам выборки присвоен вес $frac{1}{vert y_ivert}$.