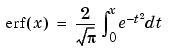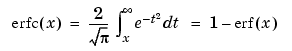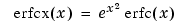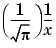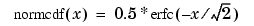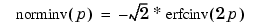Функция ошибок matlab

Main Content

Syntax

Description

Examples

collapse all

Find Error Function

Find the error function of a value.

Find the error function of the elements of a vector.

V = [-0.5 0 1 0.72];
erf(V)
ans = 1×4

   -0.5205         0    0.8427    0.6914

Find the error function of the elements of a matrix.

M = [0.29 -0.11; 3.1 -2.9];
erf(M)
ans = 2×2

    0.3183   -0.1236
    1.0000   -1.0000

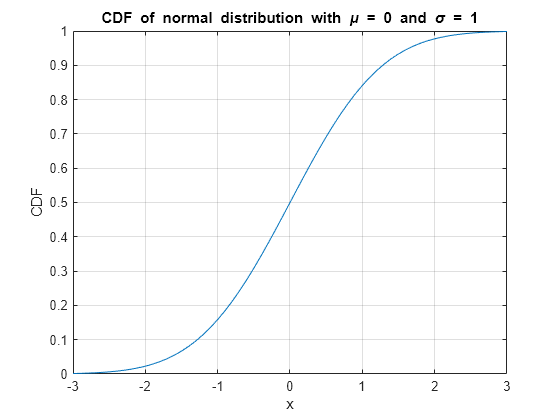
Find Cumulative Distribution Function of Normal Distribution

The cumulative distribution function (CDF) of the normal, or Gaussian, distribution with standard deviation σ and mean μ is

ϕ(x)=12(1+erf(x-μσ2)).

Note that for increased computational accuracy, you can rewrite the formula in terms of erfc . For details, see Tips.

Plot the CDF of the normal distribution with μ=0 and σ=1.

x = -3:0.1:3;
y = (1/2)*(1+erf(x/sqrt(2)));
plot(x,y)
grid on
title('CDF of normal distribution with mu = 0 and sigma = 1')
xlabel('x')
ylabel('CDF')

Figure contains an axes object. The axes object with title CDF of normal distribution with mu blank = blank 0 blank a n d blank sigma blank = blank 1, xlabel x, ylabel CDF contains an object of type line.

Calculate Solution of Heat Equation with Initial Condition

Where u(x,t) represents the temperature at position x and time t, the heat equation is

∂u∂t=c∂2u∂x2,

where c is a constant.

For a material with heat coefficient k, and for the initial condition u(x,0)=a for x>b and u(x,0)=0 elsewhere, the solution to the heat equation is

u(x,t)=a2(erf(x-b4kt)).

For k = 2, a = 5, and b = 1, plot the solution of the heat equation at times t = 0.1, 5, and 100. 

x = -4:0.01:6;
t = [0.1 5 100];
a = 5;
k = 2;
b = 1;
figure(1)
hold on
for i = 1:3
    u(i,:) = (a/2)*(erf((x-b)/sqrt(4*k*t(i))));
    plot(x,u(i,:))
end
grid on
xlabel('x')
ylabel('Temperature')
legend('t = 0.1','t = 5','t = 100','Location','best')
title('Temperatures across material at t = 0.1, t = 5, and t = 100')

Figure contains an axes object. The axes object with title Temperatures across material at t = 0.1, t = 5, and t = 100, xlabel x, ylabel Temperature contains 3 objects of type line. These objects represent t = 0.1, t = 5, t = 100.

Input Arguments

collapse all

x — Input
real number | vector of real numbers | matrix of real numbers | multidimensional array of real numbers

Input, specified as a real number, or a vector, matrix, or multidimensional
array of real numbers. x cannot be sparse.

Data Types: single | double

More About

collapse all

Error Function

The error function erf of x is

Tips

  • You can also find the standard normal probability
    distribution using the function normcdf (Statistics and Machine Learning Toolbox). The relationship between the error
    function erf and normcdf is

  • For expressions of the form 1 - erf(x),
    use the complementary error function erfc instead.
    This substitution maintains accuracy. When erf(x) is
    close to 1, then 1 - erf(x) is
    a small number and might be rounded down to 0.
    Instead, replace 1 - erf(x) with erfc(x).

Extended Capabilities

Tall Arrays
Calculate with arrays that have more rows than fit in memory.

This function fully supports tall arrays. For
more information, see Tall Arrays.

C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.

Usage notes and limitations:

  • Strict single-precision calculations are not supported. In the
    generated code, single-precision inputs produce single-precision
    outputs. However, variables inside the function might be
    double-precision.

Thread-Based Environment
Run code in the background using MATLAB® backgroundPool or accelerate code with Parallel Computing Toolbox™ ThreadPool.

This function fully supports thread-based environments. For
more information, see Run MATLAB Functions in Thread-Based Environment.

GPU Arrays
Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.

This function fully supports GPU arrays. For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).

Distributed Arrays
Partition large arrays across the combined memory of your cluster using Parallel Computing Toolbox™.

This function fully supports distributed arrays. For more
information, see Run MATLAB Functions with Distributed Arrays (Parallel Computing Toolbox).

Version History

Introduced before R2006a

  • Trial Software
  • Trial Software
  • Product Updates
  • Product Updates
Источник

Main Content

Syntax

Description

example

erf(X) represents
the error function of X.
If X is a vector or a matrix, erf(X) computes
the error function of each element of X.

Examples

Error Function for Floating-Point and Symbolic Numbers

Depending on its arguments, erf can
return floating-point or exact symbolic results.

Compute the error function for these numbers. Because these
numbers are not symbolic objects, you get the floating-point results:

A = [erf(1/2), erf(1.41), erf(sqrt(2))]

Compute the error function for the same numbers converted to
symbolic objects. For most symbolic (exact) numbers, erf returns
unresolved symbolic calls:

symA = [erf(sym(1/2)), erf(sym(1.41)), erf(sqrt(sym(2)))]
symA =
[ erf(1/2), erf(141/100), erf(2^(1/2))]

Use vpa to approximate symbolic results
with the required number of digits:

d = digits(10);
vpa(symA)
digits(d)
ans =
[ 0.5204998778, 0.9538524394, 0.9544997361]

Error Function for Variables and Expressions

For most symbolic variables and expressions, erf returns
unresolved symbolic calls.

Compute the error function for x and sin(x)
+ x*exp(x):

syms x
f = sin(x) + x*exp(x);
erf(x)
erf(f)
ans =
erf(x)
 
ans =
erf(sin(x) + x*exp(x))

Error Function for Vectors and Matrices

If the input argument is a vector or a matrix, erf returns
the error function for each element of that vector or matrix.

Compute the error function for elements of matrix M and
vector V:

M = sym([0 inf; 1/3 -inf]);
V = sym([1; -i*inf]);
erf(M)
erf(V)
ans =
[        0,  1]
[ erf(1/3), -1]
 
ans =
 erf(1)
 -Inf*1i

Special Values of Error Function

erf returns special values
for particular parameters.

Compute the error function for x =
0, x =
∞, and x =
–∞. Use sym to convert 0 and
infinities to symbolic objects. The error function has special values
for these parameters:

[erf(sym(0)), erf(sym(Inf)), erf(sym(-Inf))]

Compute the error function for complex infinities. Use sym to
convert complex infinities to symbolic objects:

[erf(sym(i*Inf)), erf(sym(-i*Inf))]

Handling Expressions That Contain Error Function

Many functions, such as diff and int,
can handle expressions containing erf.

Compute the first and second derivatives of the error function:

syms x
diff(erf(x), x)
diff(erf(x), x, 2)
ans =
(2*exp(-x^2))/pi^(1/2)
 
ans =
-(4*x*exp(-x^2))/pi^(1/2)

Compute the integrals of these expressions:

int(erf(x), x)
int(erf(log(x)), x)
ans =
exp(-x^2)/pi^(1/2) + x*erf(x)
 
ans =
x*erf(log(x)) - int((2*exp(-log(x)^2))/pi^(1/2), x)

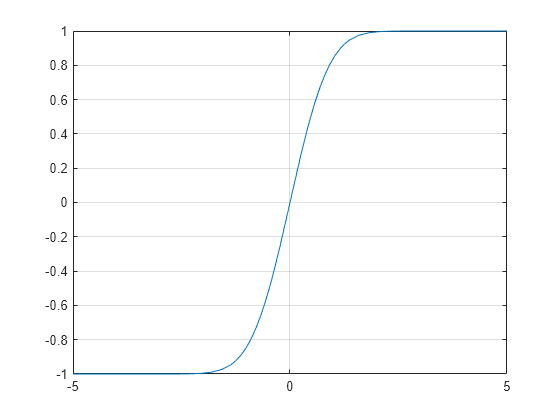
Plot Error Function

Plot the error function on the interval from -5 to 5.

syms x
fplot(erf(x),[-5 5])
grid on

Figure contains an axes object. The axes object contains an object of type functionline.

Input Arguments

collapse all

X — Input
symbolic number | symbolic variable | symbolic expression | symbolic function | symbolic vector | symbolic matrix

Input, specified as a symbolic number, variable, expression,
or function, or as a vector or matrix of symbolic numbers, variables,
expressions, or functions.

More About

collapse all

Error Function

The following integral defines the error function:

Tips

  • Calling erf for a number that
    is not a symbolic object invokes the MATLAB® erf function. This function accepts real
    arguments only. If you want to compute the error function for a complex
    number, use sym to convert
    that number to a symbolic object, and then call erf for
    that symbolic object.

  • For most symbolic (exact) numbers, erf returns
    unresolved symbolic calls. You can approximate such results with floating-point
    numbers using vpa.

Algorithms

The toolbox can simplify expressions that contain error functions
and their inverses. For real values x, the toolbox
applies these simplification rules:

  • erfinv(erf(x)) = erfinv(1 - erfc(x)) = erfcinv(1
    - erf(x)) = erfcinv(erfc(x)) = x

  • erfinv(-erf(x)) = erfinv(erfc(x) - 1) = erfcinv(1
    + erf(x)) = erfcinv(2 - erfc(x)) = -x

For any value x, the system applies these
simplification rules:

  • erfcinv(x) = erfinv(1 - x)

  • erfinv(-x) = -erfinv(x)

  • erfcinv(2 - x) = -erfcinv(x)

  • erf(erfinv(x)) = erfc(erfcinv(x)) = x

  • erf(erfcinv(x)) = erfc(erfinv(x)) = 1 - x

References

[1] Gautschi, W. “Error Function and Fresnel Integrals.” Handbook
of Mathematical Functions with Formulas, Graphs, and Mathematical
Tables. (M. Abramowitz and I. A. Stegun, eds.). New York:
Dover, 1972.

Version History

Introduced before R2006a

  • Trial Software
  • Trial Software
  • Product Updates
  • Product Updates
Источник

Указания и ограничения по применению:

  • Строгие вычисления с одинарной точностью не поддерживаются. В сгенерированном коде входные параметры с одинарной точностью производят выходные параметры с одинарной точностью. Однако переменные в функциональной силе быть с двойной точностью.

Эта функция полностью поддерживает основанные на потоке среды. Для получения дополнительной информации смотрите функции MATLAB Запуска в Основанной на потоке Среде.

Эта функция полностью поддерживает массивы графического процессора. Для получения дополнительной информации смотрите функции MATLAB Запуска на графическом процессоре (Parallel Computing Toolbox).

Эта функция полностью поддерживает распределенные массивы. Для получения дополнительной информации смотрите функции MATLAB Запуска с Распределенными Массивами (Parallel Computing Toolbox).

Источник

erf, erfc, erfcx, erfinv, erfcinv

Error functions

Syntax 

  • Y = erf(X)             Error function
Y = erfc(X)            Complementary error function
Y = erfcx(X)           Scaled complementary error function
X = erfinv(Y)          Inverse error function
X = erfcinv(Y)         Inverse complementary error function

Definition

The error function erf(X) is twice the integral of the Gaussian distribution with 0 mean and variance of .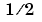

The complementary error function erfc(X) is defined as

The scaled complementary error function erfcx(X) is defined as

For large X, erfcx(X) is approximately

Description

Y = erf(X)
 returns the value of the error function for each element of real array X.

Y = erfc(X)
 computes the value of the complementary error function.

Y = erfcx(X)
 computes the value of the scaled complementary error function.

X = erfinv(Y)
 returns the value of the inverse error function for each element of Y. Elements of Y must be in the interval [-1 1]. The function erfinv satisfies for and .

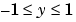
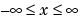
X = erfcinv(Y)
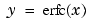
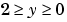
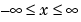
 returns the value of the inverse of the complementary error function for each element of Y. Elements of Y must be in the interval [0 2]. The function erfcinv satisfies for and .

Remarks

The relationship between the complementary error function erfc and the standard normal probability distribution returned by the Statistics Toolbox function normcdf is

The relationship between the inverse complementary error function erfcinv and the inverse standard normal probability distribution returned by the Statistics Toolbox function norminv is

Examples

erfinv(1) is Inf

erfinv(-1) is -Inf.

For abs(Y) > 1, erfinv(Y) is NaN.

Algorithms

For the error functions, the MATLAB code is a translation of a Fortran program by W. J. Cody, Argonne National Laboratory, NETLIB/SPECFUN, March 19, 1990. The main computation evaluates near-minimax rational approximations from [1].

For the inverse of the error function, rational approximations accurate to approximately six significant digits are used to generate an initial approximation, which is then improved to full accuracy by one step of Halley’s method.

References

[1]  Cody, W. J., «Rational Chebyshev Approximations for the Error Function,»
Math. Comp., pgs. 631-638, 1969

   eps   error 

Источник

Tall Arrays
Calculate with arrays that have more rows than fit in memory.

This function fully supports tall arrays. For
more information, see Tall Arrays.

C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.

Usage notes and limitations:

  • Strict single-precision calculations are not supported. In the generated code,
    single-precision inputs produce single-precision outputs. However, variables inside the
    function might be double-precision.

Thread-Based Environment
Run code in the background using MATLAB® backgroundPool or accelerate code with Parallel Computing Toolbox™ ThreadPool.

GPU Arrays
Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.

This function fully supports GPU arrays. For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).

Distributed Arrays
Partition large arrays across the combined memory of your cluster using Parallel Computing Toolbox™.

Источник

Понравилась статья? Поделить с друзьями:
  • Функция ошибок erf эксель
  • Фф ошибки системы автор велзи
  • Функция ошибки нейронной сети это
  • Фф глупая ошибка бтс
  • Функция ошибки машинное обучение