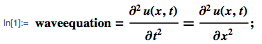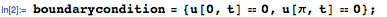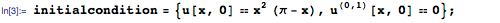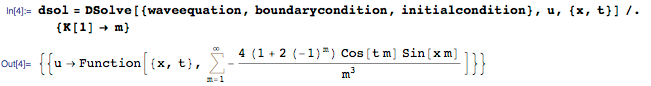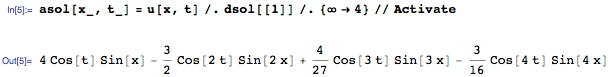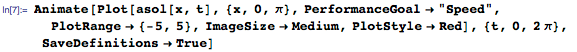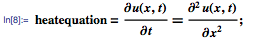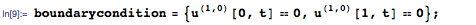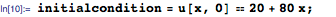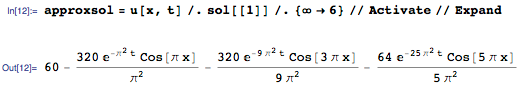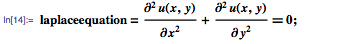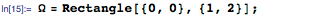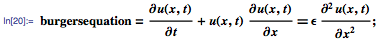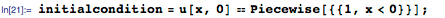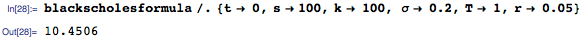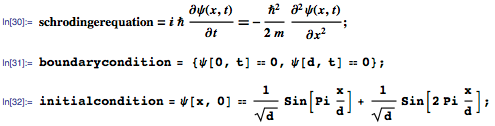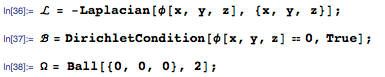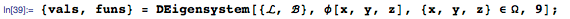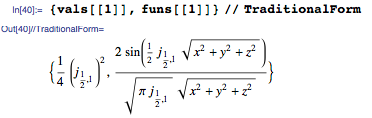Функция ошибок вольфрам - Не ошибается лишь тот, кто ничего не делает!

erf

График функции ошибок

В математике функция ошибки (также называемый Функция ошибок Гаусса), часто обозначаемый Эрф, является сложной функцией комплексной переменной, определяемой как:^[1]

${ displaystyle operatorname {erf} z = { frac {2} { sqrt { pi}}} int _ {0} ^ {z} e ^ {- t ^ {2}} , dt.}$

Этот интеграл является специальный (неэлементарный ) и сигмовидный функция, которая часто встречается в вероятность, статистика, и уравнения в частных производных. Во многих из этих приложений аргумент функции является действительным числом. Если аргумент функции является действительным, значение функции также является действительным.

В статистике при неотрицательных значениях Икс, функция ошибки имеет следующую интерпретацию: для случайная переменная Y это нормально распределенный с иметь в виду 0 и отклонение 1/2, Эрф Икс вероятность того, что Y попадает в диапазон [−Икс, Икс].

Две тесно связанные функции: дополнительная функция ошибок (erfc) определяется как

{ displaystyle operatorname {erfc} z = 1- operatorname {erf} z,}

и функция мнимой ошибки (Эрфи) определяется как

{ displaystyle operatorname {erfi} z = -i operatorname {erf} (iz),}

где я это мнимая единица.

имя

Название «функция ошибки» и его сокращение. Эрф были предложены Дж. У. Л. Глейшер в 1871 г. из-за его связи с «теорией вероятностей, и особенно теорией Ошибки.»^[2] Дополнение функции ошибок также обсуждалось Глейшером в отдельной публикации в том же году.^[3]Для «закона легкости» ошибок, плотность дан кем-то

${ displaystyle f (x) = left ({ frac {c} { pi}} right) ^ { tfrac {1} {2}} e ^ {- cx ^ {2}}}$

(в нормальное распределение ), Глейшер вычисляет вероятность ошибки, лежащей между и в качестве:

${ displaystyle left ({ frac {c} { pi}} right) ^ { tfrac {1} {2}} int _ {p} ^ {q} e ^ {- cx ^ {2} } dx = { tfrac {1} {2}} left ( operatorname {erf} (q { sqrt {c}}) - operatorname {erf} (p { sqrt {c}}) right) .}$

Приложения

Когда результаты серии измерений описываются нормальное распределение с среднеквадратичное отклонение и ожидаемое значение 0, тогда ${ displaystyle textstyle operatorname {erf} left ({ frac {a} { sigma { sqrt {2}}}} right)}$ вероятность того, что ошибка единичного измерения находится между —а и +а, для положительного а. Это полезно, например, при определении частота ошибок по битам цифровой системы связи.

Функции ошибок и дополнительных ошибок встречаются, например, в решениях уравнение теплопроводности когда граничные условия даны Ступенчатая функция Хевисайда.

Функция ошибок и ее приближения могут использоваться для оценки результатов, которые верны. с большой вероятностью или с малой вероятностью. Учитывая случайную величину и постоянный L < mu :

${ displaystyle Pr [X leq L] = { frac {1} {2}} + { frac {1} {2}} operatorname {erf} left ({ frac {L- mu} {{ sqrt {2}} sigma}} right) приблизительно A exp left (-B left ({ frac {L- mu} { sigma}} right) ^ {2} верно)}$

где А и B — определенные числовые константы. Если L достаточно далеко от среднего, т.е. , тогда:

${ Displaystyle Pr [Икс Leq L] Leq A ехр (-B ln {k}) = { frac {A} {k ^ {B}}}}$

так что вероятность стремится к 0 как .

Характеристики

Интегрируем exp (-z²)

эрф (z)

Недвижимость означает, что функция ошибок является нечетная функция. Это напрямую связано с тем, что подынтегральное выражение $е ^ {- т ^ {2}}$ является даже функция.

Для любого комплексное число z:

operatorname {erf} ({ overline {z}}) = { overline { operatorname {erf} (z)}}

где это комплексно сопряженный из z.

Подынтегральное выражение ж = ехр (-z²) и ж = erf (z) показаны в комплексе z-плоскость на рисунках 2 и 3. Уровень Im (ж) = 0 отображается толстой зеленой линией. Отрицательные целые значения Im (ж) показаны толстыми красными линиями. Положительные целочисленные значения Im (ж) показаны толстыми синими линиями. Промежуточные уровни Im (ж) = constant показаны тонкими зелеными линиями. Промежуточные уровни Re (ж) = constant показаны тонкими красными линиями для отрицательных значений и тонкими синими линиями для положительных значений.

Функция ошибок при + ∞ равна 1 (см. Гауссов интеграл ). На действительной оси erf (z) приближается к единице при z → + ∞ и −1 при z → −∞. На мнимой оси он стремится к ±я∞.

Серия Тейлор

Функция ошибок — это вся функция; он не имеет особенностей (кроме бесконечности) и его Расширение Тейлора всегда сходится, но, как известно, «[…] плохая сходимость, если x> 1».^[4]

Определяющий интеграл нельзя вычислить в закрытая форма с точки зрения элементарные функции, но за счет расширения интегрировать е^−z² в его Серия Маклорена и интегрируя почленно, можно получить ряд Маклорена функции ошибок как:

${ displaystyle operatorname {erf} (z) = { frac {2} { sqrt { pi}}} sum _ {n = 0} ^ { infty} { frac {(-1) ^ { n} z ^ {2n + 1}} {n! (2n + 1)}} = { frac {2} { sqrt { pi}}} left (z - { frac {z ^ {3}) } {3}} + { frac {z ^ {5}} {10}} - { frac {z ^ {7}} {42}} + { frac {z ^ {9}} {216}} - cdots right)}$

которое справедливо для каждого комплексное число z. Члены знаменателя — это последовательность A007680 в OEIS.

Для итеративного расчета вышеуказанного ряда может быть полезна следующая альтернативная формулировка:

$operatorname {erf} (z) = { frac {2} { sqrt { pi}}} sum _ {n = 0} ^ { infty} left (z prod _ {k = 1} ^ {n} { frac {- (2k-1) z ^ {2}} {k (2k + 1)}} right) = { frac {2} { sqrt { pi}}} sum _ {n = 0} ^ { infty} { frac {z} {2n + 1}} prod _ {k = 1} ^ {n} { frac {-z ^ {2}} {k}}$

потому что ${ frac {- (2k-1) z ^ {2}} {k (2k + 1)}}$ выражает множитель, чтобы повернуть k^th член в (k + 1)^ул срок (учитывая z как первый член).

Функция мнимой ошибки имеет очень похожий ряд Маклорена, а именно:

${ displaystyle operatorname {erfi} (z) = { frac {2} { sqrt { pi}}} sum _ {n = 0} ^ { infty} { frac {z ^ {2n + 1 }} {n! (2n + 1)}} = { frac {2} { sqrt { pi}}} left (z + { frac {z ^ {3}} {3}} + { frac {z ^ {5}} {10}} + { frac {z ^ {7}} {42}} + { frac {z ^ {9}} {216}} + cdots right)}$

которое справедливо для каждого комплексное число z.

Производная и интеграл

Производная функции ошибок сразу следует из ее определения:

${ displaystyle { frac {d} {dz}} operatorname {erf} (z) = { frac {2} { sqrt { pi}}} e ^ {- z ^ {2}}.}$

Отсюда немедленно вычисляется производная мнимой функции ошибок:

${ displaystyle { frac {d} {dz}} operatorname {erfi} (z) = { frac {2} { sqrt { pi}}} e ^ {z ^ {2}}.}$

An первообразный функции ошибок, которую можно получить интеграция по частям, является

${ displaystyle z operatorname {erf} (z) + { frac {e ^ {- z ^ {2}}} { sqrt { pi}}}.}.$

Первообразной функции мнимой ошибки, также получаемой интегрированием по частям, является

${ displaystyle z operatorname {erfi} (z) - { frac {e ^ {z ^ {2}}} { sqrt { pi}}}.}$

Производные высшего порядка даются формулами

${ displaystyle operatorname {erf} ^ {(k)} (z) = { frac {2 (-1) ^ {k-1}} { sqrt { pi}}} { mathit {H}} _ {k-1} (z) e ^ {- z ^ {2}} = { frac {2} { sqrt { pi}}} { frac {d ^ {k-1}} {dz ^ {k-1}}} left (e ^ {- z ^ {2}} right), qquad k = 1,2, dots}$

где физики Полиномы Эрмита.^[5]

Bürmann серии

Расширение,^[6] который сходится быстрее для всех реальных значений Икс чем разложение Тейлора, получается с помощью Ганс Генрих Бюрманн Теорема:^[7]

${ displaystyle { begin {align} operatorname {erf} (x) & = { frac {2} { sqrt { pi}}} operatorname {sgn} (x) { sqrt {1-e ^ {-x ^ {2}}}} left (1 - { frac {1} {12}} left (1-e ^ {- x ^ {2}} right) - { frac {7} {480}} left (1-e ^ {- x ^ {2}} right) ^ {2} - { frac {5} {896}} left (1-e ^ {- x ^ {2 }} right) ^ {3} - { frac {787} {276480}} left (1-e ^ {- x ^ {2}} right) ^ {4} - cdots right) [10pt] & = { frac {2} { sqrt { pi}}} operatorname {sgn} (x) { sqrt {1-e ^ {- x ^ {2}}}} left ({ frac { sqrt { pi}} {2}} + sum _ {k = 1} ^ { infty} c_ {k} e ^ {- kx ^ {2}} right). end {выровнено }}}$

Сохраняя только первые два коэффициента и выбирая $c_ {1} = { frac {31} {200}}$ и ${ displaystyle c_ {2} = - { frac {341} {8000}},}$ полученное приближение показывает наибольшую относительную ошибку при где меньше чем ${ displaystyle 3.6127 cdot 10 ^ {- 3}}$ :

${ displaystyle operatorname {erf} (x) приблизительно { frac {2} { sqrt { pi}}} operatorname {sgn} (x) { sqrt {1-e ^ {- x ^ {2 }}}} left ({ frac { sqrt { pi}} {2}} + { frac {31} {200}} e ^ {- x ^ {2}} - { frac {341} {8000}} e ^ {- 2x ^ {2}} right).}$

Обратные функции

Функция обратной ошибки

Учитывая комплексное число z, это не уникальный комплексное число ш удовлетворение , поэтому истинная обратная функция будет многозначной. Однако для −1 < Икс < 1, есть уникальный настоящий число обозначено $operatorname {erf} ^ {- 1} (х)$ удовлетворение

${ displaystyle operatorname {erf} left ( operatorname {erf} ^ {- 1} (x) right) = x.}$

В функция обратной ошибки обычно определяется с помощью области (−1,1), и она ограничена этой областью во многих системах компьютерной алгебры. Однако его можно расширить на диск |z| < 1 комплексной плоскости, используя ряд Маклорена

${ displaystyle operatorname {erf} ^ {- 1} (z) = sum _ {k = 0} ^ { infty} { frac {c_ {k}} {2k + 1}} left ({ frac { sqrt { pi}} {2}} z right) ^ {2k + 1},}$

где c₀ = 1 и

$c_ {k} = sum _ {m = 0} ^ {k-1} { frac {c_ {m} c_ {k-1-m}} {(m + 1) (2m + 1)}} = left {1,1, { frac {7} {6}}, { frac {127} {90}}, { frac {4369} {2520}}, { frac {34807} {16200} }, ldots right }.$

Итак, у нас есть разложение в ряд (общие множители из числителей и знаменателей удалены):

${ displaystyle operatorname {erf} ^ {- 1} (z) = { tfrac {1} {2}} { sqrt { pi}} left (z + { frac { pi} {12}} z ^ {3} + { frac {7 pi ^ {2}} {480}} z ^ {5} + { frac {127 pi ^ {3}} {40320}} z ^ {7} + { frac {4369 pi ^ {4}} {5806080}} z ^ {9} + { frac {34807 pi ^ {5}} {182476800}} z ^ {11} + cdots right). }$

(После отмены дроби числителя / знаменателя являются записями OEIS: A092676/OEIS: A092677 в OEIS; без отмены условия в числителе приведены в записи OEIS: A002067.) Значение функции ошибок при ± ∞ равно ± 1.

За |z| < 1, у нас есть $operatorname {erf} left ( operatorname {erf} ^ {- 1} (z) right) = z$ .

В обратная дополнительная функция ошибок определяется как

$operatorname {erfc} ^ {- 1} (1-z) = operatorname {erf} ^ {- 1} (z).$

За настоящий Икс, есть уникальный настоящий количество $operatorname {erfi} ^ {- 1} (х)$ удовлетворение $operatorname {erfi} left ( operatorname {erfi} ^ {- 1} (x) right) = x$ . В функция обратной мнимой ошибки определяется как $operatorname {erfi} ^ {- 1} (х)$ .^[8]

Для любого реального Икс, Метод Ньютона можно использовать для вычисления $operatorname {erfi} ^ {- 1} (х)$ , и для сходится следующий ряд Маклорена:

${ displaystyle operatorname {erfi} ^ {- 1} (z) = sum _ {k = 0} ^ { infty} { frac {(-1) ^ {k} c_ {k}} {2k + 1}} left ({ frac { sqrt { pi}} {2}} z right) ^ {2k + 1},}$

где c_k определяется, как указано выше.

Асимптотическое разложение

Полезный асимптотическое разложение дополнительной функции ошибок (а, следовательно, и функции ошибок) для больших вещественных Икс является

${ displaystyle operatorname {erfc} (x) = { frac {e ^ {- x ^ {2}}} {x { sqrt { pi}}}} left [1+ sum _ {n = 1} ^ { infty} (- 1) ^ {n} { frac {1 cdot 3 cdot 5 cdots (2n-1)} {(2x ^ {2}) ^ {n}}} right ] = { frac {e ^ {- x ^ {2}}} {x { sqrt { pi}}}} sum _ {n = 0} ^ { infty} (- 1) ^ {n} { frac {(2n-1) !!} {(2x ^ {2}) ^ {n}}},}$

где (2п — 1) !! это двойной факториал из (2п — 1), который является произведением всех нечетных чисел до (2п — 1). Этот ряд расходится для каждого конечного Икс, и его смысл как асимптотического разложения состоит в том, что для любого N in N надо

${ displaystyle operatorname {erfc} (x) = { frac {e ^ {- x ^ {2}}} {x { sqrt { pi}}}} sum _ {n = 0} ^ {N -1} (- 1) ^ {n} { frac {(2n-1) !!} {(2x ^ {2}) ^ {n}}} + R_ {N} (x)}$

где остаток, в Обозначения Ландау, является

${ displaystyle R_ {N} (x) = O left (x ^ {1-2N} e ^ {- x ^ {2}} right)}$

так как

Действительно, точное значение остатка равно

${ displaystyle R_ {N} (x): = { frac {(-1) ^ {N}} { sqrt { pi}}} 2 ^ {1-2N} { frac {(2N)!} {N!}} Int _ {x} ^ { infty} t ^ {- 2N} e ^ {- t ^ {2}} , dt,}$

что легко следует по индукции, записывая

${ displaystyle e ^ {- t ^ {2}} = - (2t) ^ {- 1} left (e ^ {- t ^ {2}} right) '}$

и интеграция по частям.

Для достаточно больших значений x нужны только первые несколько членов этого асимптотического разложения, чтобы получить хорошее приближение erfc (Икс) (при не слишком больших значениях Икс, приведенное выше разложение Тейлора в 0 обеспечивает очень быструю сходимость).

Непрерывное расширение фракции

А непрерывная дробь расширение дополнительной функции ошибок:^[9]

${ displaystyle operatorname {erfc} (z) = { frac {z} { sqrt { pi}}} e ^ {- z ^ {2}} { cfrac {1} {z ^ {2} + { cfrac {a_ {1}} {1 + { cfrac {a_ {2}} {z ^ {2} + { cfrac {a_ {3}} {1+ dotsb}}}}}}}} qquad a_ {m} = { frac {m} {2}}.}$

Интеграл функции ошибок с функцией плотности Гаусса

${ displaystyle int _ {- infty} ^ { infty} operatorname {erf} left (ax + b right) { frac {1} { sqrt {2 pi sigma ^ {2}} }} e ^ {- { frac {(x- mu) ^ {2}} {2 sigma ^ {2}}}} , dx = operatorname {erf} left [{ frac {a mu + b} { sqrt {1 + 2a ^ {2} sigma ^ {2}}} right], qquad a, b, mu, sigma in mathbb {R}}$

Факторный ряд

Обратное факториальный ряд:

${ displaystyle { begin {align} operatorname {erfc} z & = { frac {e ^ {- z ^ {2}}} {{ sqrt { pi}} , z}} sum _ {n = 0} ^ { infty} { frac {(-1) ^ {n} Q_ {n}} {{(z ^ {2} +1)} ^ { bar {n}}}} & = { frac {e ^ {- z ^ {2}}} {{ sqrt { pi}} , z}} left (1 - { frac {1} {2}} { frac {1 } {(z ^ {2} +1)}} + { frac {1} {4}} { frac {1} {(z ^ {2} +1) (z ^ {2} +2)} } - cdots right) end {выравнивается}}}$

сходится для ${ displaystyle operatorname {Re} (z ^ {2})> 0.}$ Здесь

${ displaystyle Q_ {n} { stackrel { text {def}} {=}} { frac {1} { Gamma (1/2)}} int _ {0} ^ { infty} tau ( tau -1) cdots ( tau -n + 1) tau ^ {- 1/2} e ^ {- tau} d tau = sum _ {k = 0} ^ {n} left ({ frac {1} {2}} right) ^ { bar {k}} s (n, k),}$

${ Displaystyle г ^ { бар {п}}}$ обозначает возрастающий факториал, и

обозначает подписанный Число Стирлинга первого рода.^[10]^[11]

Представление бесконечной суммой, содержащей двойной факториал:

${ displaystyle operatorname {erf} (z) = { frac {2} { sqrt { pi}}} sum _ {n = 0} ^ { infty} { frac {(-2) ^ { n} (2n-1) !!} {(2n + 1)!}} z ^ {2n + 1}}$

Численные приближения

Приближение с элементарными функциями

Абрамовиц и Стегун дают несколько приближений с различной точностью (уравнения 7.1.25–28). Это позволяет выбрать наиболее быстрое приближение, подходящее для данного приложения. В порядке увеличения точности это:

${ displaystyle operatorname {erf} (x) приблизительно 1 - { frac {1} {(1 + a_ {1} x + a_ {2} x ^ {2} + a_ {3} x ^ {3}) + a_ {4} x ^ {4}) ^ {4}}}, qquad x geq 0}$

(максимальная ошибка: 5 × 10⁻⁴)

где а₁ = 0.278393, а₂ = 0.230389, а₃ = 0.000972, а₄ = 0.078108

${ displaystyle operatorname {erf} (x) приблизительно 1- (a_ {1} t + a_ {2} t ^ {2} + a_ {3} t ^ {3}) e ^ {- x ^ {2 }}, quad t = { frac {1} {1 + px}}, qquad x geq 0}$

(максимальная ошибка: 2,5 × 10⁻⁵)

где п = 0.47047, а₁ = 0.3480242, а₂ = −0.0958798, а₃ = 0.7478556

${ displaystyle operatorname {erf} (x) приблизительно 1 - { frac {1} {(1 + a_ {1} x + a_ {2} x ^ {2} + cdots + a_ {6} x ^ {6}) ^ {16}}}, qquad x geq 0}$

(максимальная ошибка: 3 × 10⁻⁷)

где а₁ = 0.0705230784, а₂ = 0.0422820123, а₃ = 0.0092705272, а₄ = 0.0001520143, а₅ = 0.0002765672, а₆ = 0.0000430638

${ displaystyle operatorname {erf} (x) приблизительно 1- (a_ {1} t + a_ {2} t ^ {2} + cdots + a_ {5} t ^ {5}) e ^ {- x ^ {2}}, quad t = { frac {1} {1 + px}}}$

(максимальная погрешность: 1,5 × 10⁻⁷)

где п = 0.3275911, а₁ = 0.254829592, а₂ = −0.284496736, а₃ = 1.421413741, а₄ = −1.453152027, а₅ = 1.061405429

Все эти приближения справедливы для Икс ≥ 0. Чтобы использовать эти приближения для отрицательных Икс, используйте тот факт, что erf (x) — нечетная функция, поэтому erf (Икс) = −erf (-Икс).

Экспоненциальные границы и чисто экспоненциальное приближение для дополнительной функции ошибок даются формулами ^[12]

${ displaystyle { begin {align} operatorname {erfc} (x) & leq { frac {1} {2}} e ^ {- 2x ^ {2}} + { frac {1} {2} } e ^ {- x ^ {2}} leq e ^ {- x ^ {2}}, qquad x> 0 имя оператора {erfc} (x) & приблизительно { frac {1} {6 }} e ^ {- x ^ {2}} + { frac {1} {2}} e ^ {- { frac {4} {3}} x ^ {2}}, qquad x> 0. конец {выровнено}}}$

${ displaystyle { tilde {Q}} (x) = sum _ {n = 1} ^ {N} a_ {n} e ^ {- b_ {n} x ^ {2}}.}$

В частности, существует систематическая методология решения числовых коэффициентов ${ displaystyle {(a_ {n}, b_ {n}) } _ {n = 1} ^ {N}}$ что дает минимакс приближение или оценка тесно связанных Q-функция:

{ Displaystyle Q (х) приблизительно { тильда {Q}} (х)}

{ Displaystyle Q (х) leq { тильда {Q}} (х)}

, или

{ Displaystyle Q (х) geq { тильда {Q}} (х)}

за

. Коэффициенты ${ displaystyle {(a_ {n}, b_ {n}) } _ {n = 1} ^ {N}}$ для многих вариаций экспоненциальных приближений и оценок вплоть до

были выпущены в открытый доступ в виде исчерпывающего набора данных.^[14]

${ displaystyle operatorname {erfc} left (x right) приблизительно { frac { left (1-e ^ {- Ax} right) e ^ {- x ^ {2}}} {B { sqrt { pi}} x}}.}$

Они определили

{ Displaystyle {А, В } = {1.98,1.135 },}

что дало хорошее приближение для всех

Одноканальная нижняя граница^[16]

${ displaystyle operatorname {erfc} (x) geq { sqrt { frac {2e} { pi}}} { frac { sqrt { beta -1}} { beta}} e ^ {- beta x ^ {2}}, qquad x geq 0, beta> 1,}$

где параметр β можно выбрать, чтобы минимизировать ошибку на желаемом интервале приближения.

Другое приближение дано Сергеем Виницким с использованием его «глобальных приближений Паде»:^[17]^[18]^:2–3

${ displaystyle operatorname {erf} (x) приблизительно operatorname {sgn} (x) { sqrt {1- exp left (-x ^ {2} { frac {{ frac {4} {) pi}} + ax ^ {2}} {1 + ax ^ {2}}} right)}}}$

где

${ displaystyle a = { frac {8 ( pi -3)} {3 pi (4- pi)}} приблизительно 0,140012.}$

Это сделано так, чтобы быть очень точным в окрестности 0 и в окрестности бесконечности, а родственник ошибка меньше 0,00035 для всех реальных Икс. Использование альтернативного значения а ≈ 0,147 снижает максимальную относительную погрешность примерно до 0,00013.^[19]

Это приближение можно инвертировать, чтобы получить приближение обратной функции ошибок:

${ displaystyle operatorname {erf} ^ {- 1} (x) приблизительно operatorname {sgn} (x) { sqrt {{ sqrt { left ({ frac {2} { pi a}} + { frac { ln (1-x ^ {2})} {2}} right) ^ {2} - { frac { ln (1-x ^ {2})} {a}}}} - left ({ frac {2} { pi a}} + { frac { ln (1-x ^ {2})} {2}} right)}}.}$

Полиномиальный

Приближение с максимальной ошибкой $1,2 раз 10 ^ {- 7}$ для любого реального аргумента это:^[20]

{ displaystyle operatorname {erf} (x) = { begin {cases} 1- tau & x geq 0 tau -1 & x <0 end {cases}}}

${ displaystyle { begin {align} tau & = t cdot exp left (-x ^ {2} -1.26551223 + 1.00002368t + 0.37409196t ^ {2} + 0,09678418t ^ {3} -0.18628806t ^ {4} right. & left. Qquad qquad qquad + 0,27886807t ^ {5} -1,13520398t ^ {6} + 1,48851587t ^ {7} -0,82215223t ^ {8} + 0,17087277t ^ {9} right) end {align}}}$

$t = { frac {1} {1 + 0,5 | x |}}.$

Таблица значений

Икс	erf (x)	1-эрф (х)
0	0	1
0.02	0.022564575	0.977435425
0.04	0.045111106	0.954888894
0.06	0.067621594	0.932378406
0.08	0.090078126	0.909921874
0.1	0.112462916	0.887537084
0.2	0.222702589	0.777297411
0.3	0.328626759	0.671373241
0.4	0.428392355	0.571607645
0.5	0.520499878	0.479500122
0.6	0.603856091	0.396143909
0.7	0.677801194	0.322198806
0.8	0.742100965	0.257899035
0.9	0.796908212	0.203091788
1	0.842700793	0.157299207
1.1	0.88020507	0.11979493
1.2	0.910313978	0.089686022
1.3	0.934007945	0.065992055
1.4	0.95228512	0.04771488
1.5	0.966105146	0.033894854
1.6	0.976348383	0.023651617
1.7	0.983790459	0.016209541
1.8	0.989090502	0.010909498
1.9	0.992790429	0.007209571
2	0.995322265	0.004677735
2.1	0.997020533	0.002979467
2.2	0.998137154	0.001862846
2.3	0.998856823	0.001143177
2.4	0.999311486	0.000688514
2.5	0.999593048	0.000406952
3	0.99997791	0.00002209
3.5	0.999999257	0.000000743

Дополнительная функция ошибок

В дополнительная функция ошибок, обозначенный , определяется как

${ displaystyle { begin {align} operatorname {erfc} (x) & = 1- operatorname {erf} (x) [5pt] & = { frac {2} { sqrt { pi}} } int _ {x} ^ { infty} e ^ {- t ^ {2}} , dt [5pt] & = e ^ {- x ^ {2}} operatorname {erfcx} (x) , end {align}}}$

который также определяет , то масштабированная дополнительная функция ошибок^[21] (который можно использовать вместо erfc, чтобы избежать арифметическое истощение^[21]^[22]). Другая форма для неотрицательных Икс известна как формула Крейга в честь ее первооткрывателя:^[23]

${ displaystyle operatorname {erfc} (x mid x geq 0) = { frac {2} { pi}} int _ {0} ^ { pi / 2} exp left (- { frac {x ^ {2}} { sin ^ {2} theta}} right) , d theta.}$

Это выражение действительно только для положительных значений Икс, но его можно использовать вместе с erfc (Икс) = 2 — erfc (-Икс) для получения erfc (Икс) для отрицательных значений. Эта форма выгодна тем, что диапазон интегрирования является фиксированным и конечным. Расширение этого выражения для суммы двух неотрицательных переменных выглядит следующим образом:^[24]

${ displaystyle operatorname {erfc} (x + y mid x, y geq 0) = { frac {2} { pi}} int _ {0} ^ { pi / 2} exp left (- { frac {x ^ {2}} { sin ^ {2} theta}} - { frac {y ^ {2}} { cos ^ {2} theta}} right) , d theta.}$

Функция мнимой ошибки

В функция мнимой ошибки, обозначенный Эрфи, определяется как

${ displaystyle { begin {align} operatorname {erfi} (x) & = - i operatorname {erf} (ix) [5pt] & = { frac {2} { sqrt { pi}} } int _ {0} ^ {x} e ^ {t ^ {2}} , dt [5pt] & = { frac {2} { sqrt { pi}}} e ^ {x ^ {2}} D (x), end {align}}}$

где D(Икс) это Функция Доусона (который можно использовать вместо erfi, чтобы избежать арифметическое переполнение^[21]).

Несмотря на название «функция мнимой ошибки», реально, когда Икс реально.

Когда функция ошибок оценивается для произвольного сложный аргументы z, результирующий сложная функция ошибок обычно обсуждается в масштабированной форме как Функция Фаддеева:

$w (z) = e ^ {- z ^ {2}} operatorname {erfc} (-iz) = operatorname {erfcx} (-iz).$

Кумулятивная функция распределения

Функция ошибок практически идентична стандартной. нормальная кумулятивная функция распределения, обозначаемый Φ, также называемый нормой (Икс) некоторыми языками программного обеспечения^{[нужна цитата ]}, так как они отличаются только масштабированием и переводом. Действительно,

${ displaystyle Phi (x) = { frac {1} { sqrt {2 pi}}} int _ {- infty} ^ {x} e ^ { tfrac {-t ^ {2}} {2}} , dt = { frac {1} {2}} left [1+ operatorname {erf} left ({ frac {x} { sqrt {2}}} right) right ] = { frac {1} {2}} operatorname {erfc} left (- { frac {x} { sqrt {2}}} right)}$

или переставил для erf и erfc:

{ displaystyle { begin {align} operatorname {erf} (x) & = 2 Phi left (x { sqrt {2}} right) -1 operatorname {erfc} (x) & = 2 Phi left (-x { sqrt {2}} right) = 2 left (1- Phi left (x { sqrt {2}} right) right). End {выравнивается} }}

Следовательно, функция ошибок также тесно связана с Q-функция, которая представляет собой хвостовую вероятность стандартного нормального распределения. Q-функция может быть выражена через функцию ошибок как

${ displaystyle Q (x) = { frac {1} {2}} - { frac {1} {2}} operatorname {erf} left ({ frac {x} { sqrt {2}}) } right) = { frac {1} {2}} operatorname {erfc} left ({ frac {x} { sqrt {2}}} right).}$

В обратный из Phi известен как нормальная квантильная функция, или пробит функция и может быть выражена через обратную функцию ошибок как

${ displaystyle operatorname {probit} (p) = Phi ^ {- 1} (p) = { sqrt {2}} operatorname {erf} ^ {- 1} (2p-1) = - { sqrt {2}} operatorname {erfc} ^ {- 1} (2p).}$

Стандартный нормальный cdf чаще используется в вероятностях и статистике, а функция ошибок чаще используется в других разделах математики.

Функция ошибок — это частный случай Функция Миттаг-Леффлера, а также может быть выражено как конфлюэнтная гипергеометрическая функция (Функция Куммера):

${ displaystyle operatorname {erf} (x) = { frac {2x} { sqrt { pi}}} M left ({ frac {1} {2}}, { frac {3} {2 }}, - x ^ {2} right).}$

Он имеет простое выражение в терминах Интеграл Френеля.^{[требуется дальнейшее объяснение ]}

Что касается регуляризованная гамма-функция P и неполная гамма-функция,

${ displaystyle operatorname {erf} (x) = operatorname {sgn} (x) P left ({ frac {1} {2}}, x ^ {2} right) = { frac { operatorname {sgn} (x)} { sqrt { pi}}} gamma left ({ frac {1} {2}}, x ^ {2} right).}$

это функция знака.

Обобщенные функции ошибок

График обобщенных функций ошибок E_п(Икс):
серая кривая: E₁(Икс) = (1 — e^−Икс)/
красная кривая: E₂(Икс) = erf (Икс)
зеленая кривая: E₃(Икс)
синяя кривая: E₄(Икс)
золотая кривая: E₅(Икс).

Некоторые авторы обсуждают более общие функции:^{[нужна цитата ]}

${ displaystyle E_ {n} (x) = { frac {n!} { sqrt { pi}}} int _ {0} ^ {x} e ^ {- t ^ {n}} , dt = { frac {n!} { sqrt { pi}}} sum _ {p = 0} ^ { infty} (- 1) ^ {p} { frac {x ^ {np + 1}} {(np + 1) p!}}.}$

Известные случаи:

E₀(Икс) — прямая линия, проходящая через начало координат: ${ displaystyle textstyle E_ {0} (x) = { dfrac {x} {e { sqrt { pi}}}}}$
E₂(Икс) — функция ошибок, erf (Икс).

После деления на п!, все E_п для нечетных п похожи (но не идентичны) друг на друга. Точно так же E_п даже для п похожи (но не идентичны) друг на друга после простого деления на п!. Все обобщенные функции ошибок для п > 0 похожи на положительные Икс сторона графика.

Эти обобщенные функции могут быть эквивалентно выражены для Икс > 0 с помощью гамма-функция и неполная гамма-функция:

${ displaystyle E_ {n} (x) = { frac {1} { sqrt { pi}}} Gamma (n) left ( Gamma left ({ frac {1} {n}} right) - Gamma left ({ frac {1} {n}}, x ^ {n} right) right), quad quad x> 0.}$

Следовательно, мы можем определить функцию ошибок в терминах неполной гамма-функции:

${ displaystyle operatorname {erf} (x) = 1 - { frac {1} { sqrt { pi}}} Gamma left ({ frac {1} {2}}, x ^ {2} верно).}$

Итерированные интегралы дополнительной функции ошибок

Повторные интегралы дополнительной функции ошибок определяются как^[25]

${ displaystyle { begin {align} operatorname {i ^ {n} erfc} (z) & = int _ {z} ^ { infty} operatorname {i ^ {n-1} erfc} ( zeta ) , d zeta operatorname {i ^ {0} erfc} (z) & = operatorname {erfc} (z) OperatorName {i ^ {1} erfc} (z) & = operatorname {ierfc} (z) = { frac {1} { sqrt { pi}}} e ^ {- z ^ {2}} - z operatorname {erfc} (z) operatorname {i ^ { 2} erfc} (z) & = { frac {1} {4}} left [ operatorname {erfc} (z) -2z operatorname {ierfc} (z) right] конец {выровнено} }}$

Общая рекуррентная формула

${ displaystyle 2n operatorname {я ^ {n} erfc} (z) = operatorname {i ^ {n-2} erfc} (z) -2z operatorname {i ^ {n-1} erfc} (z) }$

У них есть степенной ряд

${ displaystyle i ^ {n} operatorname {erfc} (z) = sum _ {j = 0} ^ { infty} { frac {(-z) ^ {j}} {2 ^ {nj} j ! Gamma left (1 + { frac {nj} {2}} right)}},}$

откуда следуют свойства симметрии

${ displaystyle i ^ {2m} operatorname {erfc} (-z) = - i ^ {2m} operatorname {erfc} (z) + sum _ {q = 0} ^ {m} { frac {z ^ {2q}} {2 ^ {2 (mq) -1} (2q)! (Mq)!}}}$

${ displaystyle i ^ {2m + 1} operatorname {erfc} (-z) = i ^ {2m + 1} operatorname {erfc} (z) + sum _ {q = 0} ^ {m} { гидроразрыв {z ^ {2q + 1}} {2 ^ {2 (mq) -1} (2q + 1)! (mq)!}}.}$

Реализации

Как реальная функция реального аргумента

В Posix совместимые операционные системы, заголовок math.h объявляет и математическая библиотека libm обеспечивает функции Эрф и erfc (двойная точность ) а также их одинарная точность и повышенная точность аналоги эрфф, эрфл и erfc, erfcl.^[26]
В Научная библиотека GNU обеспечивает Эрф, erfc, журнал (erf), и масштабированные функции ошибок.^[27]

Как сложная функция сложного аргумента

libcerf, числовая библиотека C для сложных функций ошибок, предоставляет сложные функции Cerf, Cerfc, Cerfcx и реальные функции Эрфи, erfcx с точностью примерно 13–14 цифр, в зависимости от Функция Фаддеева как реализовано в Пакет МИТ Фаддеева

Смотрите также

Гауссов интеграл, по всей реальной линии
Функция Гаусса, производная
Функция Доусона, перенормированная функция мнимой ошибки
Интеграл Гудвина – Стэтона

По вероятности

Нормальное распределение
Нормальная кумулятивная функция распределения, масштабированная и сдвинутая форма функции ошибок
Пробит, обратное или квантильная функция нормального CDF
Q-функция, хвостовая вероятность нормального распределения

дальнейшее чтение

Абрамовиц, Милтон; Стегун, Ирен Энн, ред. (1983) [июнь 1964]. «Глава 7». Справочник по математическим функциям с формулами, графиками и математическими таблицами. Прикладная математика. 55 (Девятое переиздание с дополнительными исправлениями, десятое оригинальное издание с исправлениями (декабрь 1972 г.); первое изд.). Вашингтон.; Нью-Йорк: Министерство торговли США, Национальное бюро стандартов; Dover Publications. п. 297. ISBN 978-0-486-61272-0. LCCN 64-60036. Г-Н 0167642. LCCN 65-12253.
Press, William H .; Teukolsky, Saul A .; Веттерлинг, Уильям Т .; Фланнери, Брайан П. (2007), «Раздел 6.2. Неполная гамма-функция и функция ошибок», Числовые рецепты: искусство научных вычислений (3-е изд.), Нью-Йорк: Издательство Кембриджского университета, ISBN 978-0-521-88068-8
Темме, Нико М. (2010), «Функции ошибок, интегралы Доусона и Френеля», в Олвер, Фрэнк В. Дж.; Lozier, Daniel M .; Бойсверт, Рональд Ф .; Кларк, Чарльз В. (ред.), Справочник NIST по математическим функциям, Издательство Кембриджского университета, ISBN 978-0-521-19225-5, Г-Н 2723248

внешняя ссылка

MathWorld — Эрф
Таблица интегралов функций ошибок

Источник

Как решать дифференциальные уравнения в wolfram mathematica

WolframAlpha по-русски

Математика с WolframAlpha ® . Объяснения с примерами.

Решение обыкновенных дифференциальных уравнений в Wolfram|Alpha

Решение дифференциальных уравнений с выводом результатов в пошаговом представлении (функция «Show steps» — Показать шаги) является одной из важных особенностей Wolfram|Alpha.

Wolfram|Alpha в большинстве случаев может помочь в решении дифференциальных уравнений различного уровня сложности, начиная от простейших дифференциальных уравнений первого порядка с разделяющимися переменными (separable equations ) и включая более сложные уравнения, для решения которых служат, например, методы операционного исчисления, использующие преобразование Лапласа.

Как видим, Wolfram|Alpha сначала определяет (классифицирует) этот пример, как обыкновенное линейное дифференциальное уравнение первого порядка, затем выводит общее решение данного уравнения, график частного решения, удовлетворяющего условию y(1)=1, а также семейство интегральных кривых данного уравнения.

Чтобы получить детальное пошаговое решение, используйте кнопку «Show steps»:

Новое в Wolfram Language | Аналитическое решение уравнений в частных производных

Перевод поста Devendra Kapadia «New in the Wolfram Language: Symbolic PDEs».
Код, приведенный в статье, можно скачать здесь.
Выражаю огромную благодарность Кириллу Гузенко KirillGuzenko за помощь в переводе и подготовке публикации. Уравнения в частных производных (УрЧП) играют очень важную роль в математике и ее приложениях. Их можно использовать для моделирования реальных явлений, таких как колебания натянутой струны, распространения потока тепла в стержне, в финансовых областях. Цель этой статьи — приоткрыть завесу в мир УрЧП (тем кто еще с ним не знаком) и ознакомить читателя с тем, как можно эффективно решать УрЧП в Wolfram Language, используя новый функционал для решения краевых задач в DSolve, а так же новую функцию DEigensystem, которая появилась в версии 10.3.

История УрЧП восходит к работам известных математиков восемнадцатого века — Эйлера, Даламбера, Лапласа, однако развитие этой области в последние три столетия так и не остановилось. И потому в статье я приведу как классические, так и современные примеры УрЧП, что позволит рассмотреть эту область знаний под разными углами.

Давайте начнем с рассмотрения колебаний натянутой струны с длиной π, закрепленной на обоих концах. Колебания струны можно смоделировать с помощью одномерного волнового уравнения, приведённого ниже. Здесь u(x,t) — вертикальное смещение точки струны с координатой х в момент времени t:

Затем мы задаём граничные условия, указав тем самым, что концы струны при колебаниях сохраняют свои положения.

Зададим теперь начальные условия для движения струны, указав смещения и скорости различных точек струны в момент времени t=0:

Теперь мы можем использовать DSolve для решения волнового уравнения с начальными и краевыми условиями:

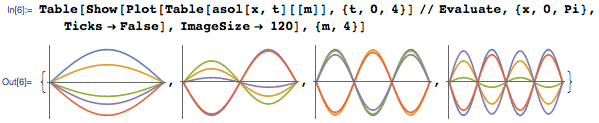
Как указано выше, решение есть бесконечная сумма тригонометрических функций. Сумма возвращается в невычисленной форме (Inactive), поскольку каждый отдельный член разложения имеет физическую интерпретацию, и зачастую даже небольшое количество членов может являться хорошим приближением. К примеру, мы можем взять первые четыре члена для получения приближенного решения asol(x,t)

Каждый член в сумме представляет собой стоячую волну, которые могут быть представлены следующим образом:

И все эти стоячие волны складываются воедино, образуя гладкую кривую, как показано на анимации ниже:

Волновое уравнение относится к классу линейных гиперболических уравнений в частных производных, описывающих распространение сигналов с конечными скоростями. Это УрЧП представляет собой удобный способ для моделирования колебаний в струне или в каком-то другом деформирумом теле, однако ещё более важную роль оно играет в современной физике и инженерных приложениях, т.к. оно описывает распространение света и электромагнитных волн.

Давайте теперь смоделируем поток тепла в стержне единичной длины, изолированном с обоих концов, с помощью представленного ниже уравнения теплопроводности:

Поскольку стержень изолирован с обоих концов, то через них проходит нулевой поток тепла, что можно выразить как граничные условия вида х = 0 и х = 1:

Теперь нужно указать начальное температурное распределение в стержне. В этом примере мы будем использовать приведённую ниже линейную функцию. В левом конце (х = 0) начальная температура — 20 градусов, в правом (х = 1) — 100:

И теперь мы можем решить уравнение теплопроводности с заданными условиями:

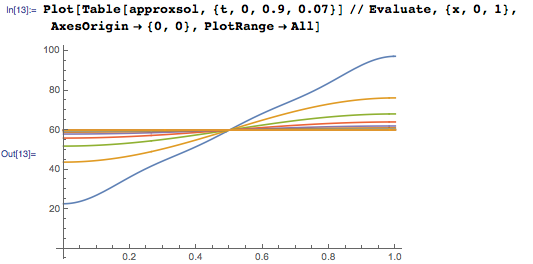
Как и в приведённом выше примере с волновым уравнением, мы можем извлечь несколько членов суммы и получить приближенное решение:

Первый член приближенного решения — 60 — среднее от температур на границах стержня, и она является стационарной температурой для этого стержня. Как показано на графике функции температуры от длины, представленном ниже, температура стержня быстро достигает стационарного значения в 60 градусов:

Уравнение теплопроводности относится к классу линейных параболических уравнений в частных производных, которые описывают процессы диффузии. Это простое на вид уравнение часто можно встретить в самых различных, а иногда и весьма неожиданных областях. Далее в статье мы рассмотрим два примера этого явления.

Рассмотрим теперь уравнение Лапласа, которое используется для моделирования стационарного состояния систем, т. е. поведения после некоторых зависящих от времени уже законченных переходных процессов. В двумерном случае это уравнение можно представить следующим образом:

Ограничим координаты х и у прямоугольной областью Ω, как показано ниже:

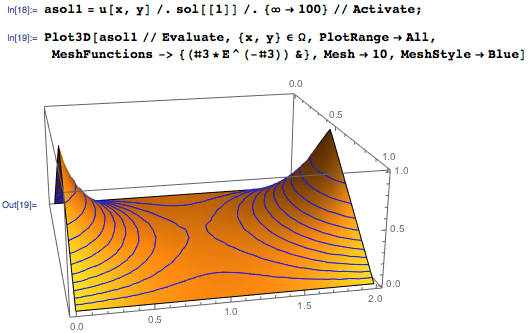
Классическая задача Дирихле — найти функцию u(x,y), удовлетворяющую уравнению Лапласа внутри области Ω с заданным условием Дирихле (DirichletCondition), которое определяет значения на границах области Ω, как показано ниже:

Задачу Дирихле можно решить с помощью функции DSolve, весьма изящно задав при этом область:

Как и в примерах ранее, мы можем извлечь некоторое количество членов (скажем, 100) из суммы и визуализировать решение:

Следует заметить, что решение u(x,y) задачи Дирихле представляется гладким в Ω, несмотря на то, что граничные условия имеют резкие черты. Помимо этого, u(x,y) достигает экстремальных значений на границах, в то время как в центре прямоугольника находится седловая точка. Эти черты характерны для линейных эллиптических уравнений — класса уравнений в частных производных, к которым и принадлежит уравнение Лапласа.

Волновое уравнение, уравнение теплопроводности, уравнение Лапласа — самые известные примеры классических УрЧП. Теперь мы рассмотрим три примера типичных современных УрЧП, первым среди которых будет уравнение Бюргерса для вязкой жидкости, которое может быть представлено следующим образом:

Это нелинейное УрЧП было введено Иоханнесом Бюргерсом в сороковых годах в качестве простой модели для турбулентных потоков (параметр ϵ в уравнении представляет собой вязкость жидкости). Однако, десять лет спустя, Э. Хопф и Д. Коул показали, что уравнение Бюргерса сводится к уравнению теплопроводности, а это значит, что данное уравнение не может проявлять хаотического поведения. Преобразование Коула-Хопфа позволяет решать уравнения Бюргерса в замкнутой форме для начального условия, заданного, к примеру, так:

В этом примере мы будем использовать функцию DSolveValue, которая возвращает только выражение для решения. Члены с функцией ошибок (Erf) в формуле ниже возникают из решения соответствующей граничной задачи теплового уравнения:

Представленный ниже график демонстрирует изменение во времени гипотетического одномерного поля скоростей потока. Решение представляется гладким для положительного ϵ, при том что начальное условие есть кусочно заданная функция:

Как можно заметить на нижепреведённых графиках, решение стремится к разрывному при сремлении вязкости ϵ к нулю. Подобные решения с резким переходом (shock solutions) — известная особенность уравнений Бюргерса для невязкой (ϵ = 0) среды.

В качестве второго примера современных УрЧП рассмотрим уравнение Блэка-Шоулза, используемое в финансовых расчётах. Это уравнение впервые представили Фишер Блэк и Майрон Шоулз в 1973 году в качестве модели для определения теоретической цены на европейские опционы, и формулируется оно следующим образом:

где:
c — цена опциона как функция от стоимости акций s и времени t,
r — процентная ставка без риска,
σ — волатильность акций.

В их эпохальной статье (которая была процитирована более 28000 раз), Блэк и Шоулз отметили, что их уравнения с помощью преобразования переменных могут быть сведены к уравнению теплопроводности. Это резкое упрощение приводит к знаменитой формуле Блэка-Шоулза для европейских опционов с конечными условиями, основанными на цене исполнения (strike price) k актива в момент времени t=Т:

Вооружившись этой формулой, мы можем вычислить значения финансовых опционов для типичных значений параметров:

Ответ согласуется со значением, полученным с помощью встроенной функции FinancialDerivative:

В качестве третьего примера современных УрЧП рассмотрим уравнение Шредингера для электрона в одномерной потенциальной яме с глубиной d и соответствующим начальным условием. Уравнение и условия можно сформулировать следующим образом:

Этот пример имеет элементарное решение, которое принимает мнимые значения из-за наличия I в уравнении Шредингера:

Функция плотности вероятности для электрона ρ = Ψ ⊹ Ψ, с использованием подходящих значений параметров в задаче, может быть вычислена следующим образом:

Мы можем создать анимацию изменения плотности вероятности во времени, которая показывает, что «центр» электрона в яме движется из стороны в сторону:

Собственные значения и собственные функции играют важную роль как в решении уравнения Шрёдингера, так и в других УрЧП. В частности, они предоставляют «строительные блоки» для решений волновых уравнений и уравнений теплопроводности в виде бесконечных сумм, которые приводились ранее в статье. Поэтому, в качестве нашего последнего примера рассмотрим задачу о нахождении девяти наименьших собственных значений и собственных функций для оператора Лапласа с однородным (нулевым) условием Дирихле для трехмерной сферической области. Найдем девять наименьших значений λ и соответствующих им функций ϕ, удовлетворяющих Λϕ = λ ϕ, которые определяются следующим образом:

Новая функция DEigensystem в версии 10.3 позволяет вычислить требуемые собственные значения и функции следующим образом:

Собственные значения в этой задаче выражаются через BesselJZero. Вот пример:

Собственные значения можно визуализировать с помощью функции DensityPlot3D, которая возвращает красивые графики, как показано ниже:

УрЧП являются важным инструментом во многих отраслях науки и техники, в статистике и финансах. На более фундаментальном уровне они предоставляют точные математические формулировки некоторых самых глубоких и тонких вопросов о нашей Вселенной, скажем, о возможности существования голых сингулярностей. По моему опыту, изучение УрЧП награждает редким сочетанием из практических идей и интеллектуального удовлетворения.

Рекомендую изучить документацию по DSolve, NDSolve, DEigensystem, NDEigensystem и методу конечных элементов, чтобы узнать больше о различных подходах к решению УрЧП в Wolfram Language.

УрЧП в символьной форме поддерживаются в Wolfram Mathematica и Wolfram Language с версии 10.3, а в ближайшее время будут представлены и во всех остальных программных продуктах Wolfram.

Иллюстрированный самоучитель по Mathematica 3/4

Дифференциальные уравнения. Решение дифференциальных уравнений в символьном виде.

Дифференциальными принято называть уравнения, в состав которых входят производные функции у(х), представляющей решение уравнения. Дифференциальные уравнения могут быть представлены в различной форме, например в общеизвестной форме Коши:

Несколько дифференциальных уравнений образуют систему дифференциальных уравнений. Решение таких систем также возможно средствами Mathematica и подробно описано в ряде книг по использованию системы. Дифференциальные уравнения и системы дифференциальных уравнений могут быть линейными и нелинейными. Для линейных уравнений обычно существуют решения в аналитическом виде. Нелинейные дифференциальные уравнения в общем случае аналитических решений не имеют, но могут решаться приближенными численными методами.

Дифференциальные уравнения широко используются в практике математических вычислений. Они являются основой при решении задач моделирования – особенно в динамике. Немногие математические системы имеют реализации численных методов решения систем дифференциальных уравнений. Но система Mathematica имеет средства как для символьного, так и для численного решения дифференциальных уравнений и их систем.

Для решения дифференциальных уравнений в символьном виде используются следующие средства:

DSolve[eqn, y[x], х] – решает дифференциальное уравнение относительно функций у [ х ] с независимой переменной х;
DSolve[, , ] – решает систему дифференциальных уравнений.

У функции DSolve и ее численного варианта NDSolve есть пара опций, на которые следует обратить внимание:

DSolveConstants – опция к DSolve, определяющая постоянные интегрирования, которые будут использованы в результате;
StartingStepSize – опция к NDSolve, определяющая величину начального шага.

В решении дифференциальных уравнений встречаются постоянные интегрирования. По умолчанию они обозначаются как С [ i ].

Уравнения в частных производных wolfram mathematica

Достаточно войти на страницу wolframalpha набрать в текстовом поле свой запрос и нажать на кнопку «=»

(имеет всплывающую подсказку вычислить ) или просто нажать Enter .
Функционал Wolfram Alpha не ограничивается лишь поиском ответов на поставленные вопросы. С помощью этой системы можно, например, строить графики и сопоставлять различные данные, что намного наглядней и лучше воспринимается, чем просто текст. Кроме того, с помощью Wolfram Alpha можно производить математические операции, как элементарные (которые без проблем выполняет и Google), так и решать уравнения различной сложности. Также Wolfram Alpha умеет строить графики функций, вычислять значения синуса или косинуса и так далее.

Например можно решить вот такое уравнение :

а чтобы узнать, какое расстояние между Москвой и Тель-Авивом, нужно ввести в поле

и вот вам результат:

Один из минусов сервиса Wolfram Alpha – это его англоязычность…так что если хотите задать вопрос системе придется писать его на английском языке. Даже неизвестно, появится ли русскоязычная версия этой поисково-вычислительной системы.

Основные команды для Вольфрам Альфа

(Команды вводятся в строку Вольфрама — например выше. Все команды заканчиваются нажатием Enter)

1. Решение уравнений, построение графиков

Арифметические знаки плюс, минус, умножить, поделить +, — , *, / Примеры: 3*2, x*y, (a+b)/c
Возведение в степень «x в степени а» x^a. Примеры x^a, x**a, (a+b)^2, (a+b)**2, (a+b)^(2x+1)
Скобки. Действия в скобках ведутся первыми
Функции .sin(x), cos(x), tan(x)=sin(x)/cos(x), cotan(x)=cos(x)/sin(x), sec(x)=1/cos(x), cosec(x)=1/sin(x)
Функции log(x), exp(x), sinh(x), cosh(x), tanh(x), cotanh(x)
Корень квадратный из «х» sqrt(x) или x^(1/2)

Чтобы вычислить выражение, нужно его просто ввести. Например корень из 2 будет выглядеть как sqrt(2) или же 2^(1/2).

2. Чтобы решить уравнение, нужно просто его ввести

3. Чтобы построить график, нужно использовать команду plot

Например нарисуем с помощью Вольфрама функцию 2^(-x) cos(x). Это делается командой plot (график).

Чтобы построить несколько графиков на одной координатной плоскости (например для визуализации решения систем уравнений), при значении переменной x в интервале (A,B), нужно использовать команду

4. Чтобы собрать множители из двучлена (многочлена) f, наберите factor[f]

5. Чтобы развалить произведение f на слагаемые, используйте команду expand[f]

6. Чтобы упростить выражение f[x], наберите команду Simplify[f[x]]

Например упростить «е в степени догарифм х»:

Simplify[ exp[ log[x] ] ]

Вольфрам альфа: интегралы

Как работать с Wolfram Alpha

Основные операции

Сложение : a+b
Вычитание : a-b
Умножение : a*b
Деление : a/b
Возведение в степень : a^b

Примеры

314+278; 314—278; 314*278; 314^278;
(a^2+b^2)+(a^2-b^2); (a^2+b^2)/(a^2-b^2); (a+b)^(2+2/3).

Знаки сравнения

Меньше : : >
Равно : = или ==
Меньше или равно : =

Логические символы

И : &&
ИЛИ : ||
НЕ : !

Основные константы

Число : Pi
Число : E
Бесконечность : Infinity, inf или oo

Основные функции

: x^a

: Sqrt[x]
: x^(1/n)
: a^x
: Log[a, x]
: Log[x]
: cos[x] или Cos[x]
: sin[x] или Sin[x]
: tan[x] или Tan[x]
: cot[x] или Cot[x]
: sec[x] или Sec[x]
: csc[x] или Csc[x]
: ArcCos[x]
: ArcSin[x]
: ArcTan[x]
: ArcCot[x]
: ArcSec[x]
: ArcCsc[x]
: cosh[x] или Cosh[x]
: sinh[x] или Sinh[x]
: tanh[x] или Tanh[x]
: coth[x] или Coth[x]
: sech[x] или Sech[x]
: csch[x] или Csch[е]
: ArcCosh[x]
: ArcSinh[x]
: ArcTanh[x]
: ArcCoth[x]
: ArcSech[x]
: ArcCsch[x]

Решение уравнений

Чтобы получить решение уравнения вида достаточно записать в строке Wolfram|Alpha: f[x]=0, при этом Вы получите некоторую дополнительную информацию, которая генерируется автоматически. Если же Вам необходимо только решение, то необходимо ввести: Solve[f[x]=0, x].

Примеры

Solve[Cos[x]+Cos[2x]+Sin[4x]=0,x] или Cos[x]+Cos[2x]+Sin[4x]=0;
Solve[x^5+x^4+x+1=0,x] или x^5+x^4+x+1=0;
Solve[Log[3,x^2+x+1]-Log[9,x^2]=0,x] или Log[3,x^2+x+1]-Log[9,x^2]=0.

Если Ваше уравнение содержит несколько переменных, то запись: f[x, y,…,z]=0 даст весьма разнообразный набор сведений, таких как решение в целых числах, частные производные функции и т. д. Чтобы получить решение уравнения вида по какой-либо одной из переменных, нужно написать в строке: Solve[f[x, y, …, z]=0, j], где — интересующая Вас переменная.

Примеры

Cos[x+y]=0 или Solve[Cos[x+y]=0,x] или Solve[Cos[x+y]=0,y];
x^2+y^2-5=0 или Solve[x^2+y^2-5=0,x] или Solve[x^2+y^2-5=0,y];
x+y+z+t+p+q=9.

Решение неравенств

Решение в Wolfram Alpha неравенств типа 0″ src=»http://upload.wikimedia.org/math/3/d/9/3d97eb56e02c2889dd20a89529548180.png» />, полностью аналогично решению уравнения . Нужно написать в строке WolframAlpha: f[x]>0 или f[x]>=0 или Solve[f[x]>0, x] или Solve[f[x]>=0,x].

Примеры

Cos[10x]-1/2>0 или Solve[Cos[10x]-1/2>0,x];
x^2+5x+10>=0 или Solve[x^2+5x+10>=0,x].

Если Ваше неравенство содержит несколько переменных, то запись: f[x, y,…,z]>0 или f[x, y,…,z]>=0 даст весьма разнообразный набор сведений, как и в случае соответствующих уравнений. Чтобы получить решение такого неравенства по какой-либо одной из переменных нужно написать в строке: Solve[f[x, y,…,z]>0,j] или Solve[f[x, y,…,z]>=0,j], где — интересующая Вас переменная.

Примеры

Cos[x+y]>0 или Solve[Cos[x+y]>0,x] или Solve[Cos[x+y]>0,y];
x^2+y^3-5 =9.

Решение различных систем уравнений, неравенств и уравнений

Решение систем различного вида в Wolfram Alpha крайне просто. Достаточно набрать уравнения и неравенства Вашей системы, точно так, как это описано выше в пунктах 7. и 8., соединяя их союзом «И», который в Wolfram Alpha имеет вид &&.

Сервис Wolfram Alpha поддерживает возможность построения графиков функций как вида , так и вида . Для того, чтобы построить график функции на отрезке нужно написать в строке Wolfram Alpha: Plot[f[x],]. Если Вы хотите, чтобы диапазон изменения ординаты был конкретным, например , нужно ввести: Plot[f[x],,].

Если Вам требуется построить сразу несколько графиков на одном рисунке, то перечислите их, используя союз «И»:Plot[f[x]&&g[x]&&h[x]&&…&&t[x],].

Для того, чтобы построить график функции на прямоугольнике , нужно написать в строке Wolfram Alpha: Plot[f[x, y],,]. К сожалению, диапазон изменения аппликаты пока что нельзя сделать конкретным. Тем не менее, интересно отметить, что при построении графика функции Вы получите не только поверхность, которую она определяет, но и «контурную карту» поверхности (линии уровня).

Математический анализ

Wolfram Alpha способен находить пределы функций, последовательностей, различные производные, определенные и неопределенные интегралы, решать дифференциальные уравнения и их системы и многое многое другое.

Пределы

Для того, чтобы найти предел последовательности нужно написать в строке Wolfram Alpha: Limit[x_n, n -> Infinity].

Примеры

Limit[n^3/(n^4 + 2*n), n -> Infinity];
Limit[(1+1/n)^n, n -> Infinity].

Найти предел функции при можно совершенно аналогично: Limit[f[x], x -> a].

Производные

Для того, чтобы найти производную функции нужно написать в строке WolframAlpha: D[f[x], x]. Если Вам требуется найти производную n-го порядка, то следует написать: D[f[x], ]. В том случае, если Вам требуется найти частную производную функции напишите в окне гаджета: D[f[x, y, z,…,t], j], где — интересующая Вас переменная. Если нужно найти частную производную по некоторой переменной порядка n, то следует ввести: D[f[x, y, z,…,t], ], где означает тоже, что и Выше.

Важно подчеркнуть, что Wolfram Alpha выдает пошаговое нахождение производной при нажатии на «Show Steps» в правом верхнем углу выдаваемого ей ответа.

Интегралы

Для того, чтобы найти неопределенный интеграл от функции нужно написать в строке WolframAlpha: Integrate f[x], x. Найти определенный интеграл так же просто: Integrate[f[x], ] либо Integrate f(x), x=a..b.

Важно подчеркнуть, что Wolfram Alpha выдает пошаговое нахождение интеграла при нажатии на «Show Steps» в правом верхнем углу выдаваемого ей ответа.

Дифференциальные уравнения и их системы

Чтобы найти общее решение дифференциального уравнения нужно написать в строке WolframAlpha: F[x, y, y’,y»,…] (при k-й производной y ставится k штрихов).

Если Вам требуется решить задачу Коши, то впишите: F[x, y, y’,y»,…], y[s]==A,y'[s]==B, …. Если нужно получить решение краевой задачи, что краевые условия, так же перечисляются через запятую, причем они должны иметь вид y[s]==S.

Решение систем дифференциальных уравнений также просто, достаточно вписать: , где f_1, f_2, …, f_n — дифференциальные уравнения, входящие в систему. К сожалению, решение задач Коши и краевых задач для систем дифференциальных уравнений пока-что не поддерживается.

Ошибки при работе с системой

Система может допускать некоторые ошибки при решении сложных задач [1] . К примеру, если попытаться решить неравенство , для чего ввести запрос solve (3x^2-18x+24)/(2x-2)-(3x-12)/(2x^2-6x+4) Примечания

Использование Wolfram Mathematica в решении дифференциальных уравнений

Саратовский национальный исследовательский государственный университет имени Н.Г. Чернышевского

NovaInfo55, с. 5-9
Опубликовано 20 ноября 2016
Раздел: Физико-математические науки
Просмотров за месяц: 49
CC BY-NC

Аннотация

В статье рассматриваются примеры решения обыкновенных дифференциальных уравнений в системе Wolfram Mathematica.

Ключевые слова

Текст научной работы

Системы компьютерной математики (Maple, Mathematica, MatLab, Derive и др.) применяются в различных областях науки. Они содержат процедуры для численных и аналитических расчетов, средства программирования, визуализации. В настоящее время пакеты прикладных программ используются не только при решении численных задач, но и при доказательстве теорем. Системы компьютерной математики используются в решении математических проблем в работах Д.С. Воронова, О.П. Гладуновой, Е.С. Корнева, М.В. Куркиной, Е.Д. Родионова, Я.В. Славолюбовой, В.В. Славского, Н.К. Смоленцева, Л.Н. Чибриковой и др.

Система компьютерной математики Wolfram Mathematica является одним из наиболее распространенных программных средств, которое позволяет выполнять численные, символьные вычисления, имеет развитую двумерную и трехмерную графику, а также встроенный язык программирования высокого уровня. Для знакомства с языком программирования Wolfram Language рекомендуется интернет-ресурс Wolfram Language & System «Documentation Center» (http://reference.wolfram.com/language/). Выбирая раздел, можно познакомиться с имеющимися командами для решения задач и с примерами их использования. Примеры использования Mathematica в решении геометрических задач приведены в 5.

Система Mathematica обладает обширными возможностями решения обыкновенных дифференциальных уравнений и их систем в символьном виде. Для этого используется функция DSolve, в алгоритме которой реализовано большинство известных на сегодняшний день аналитических методов.

Пример 1. Решим дифференциальное уравнение и построим график решений при различных значениях постоянной.

Пример 2. Решим уравнение y’=frac

Попытаемся решить уравнение с помощью функции DSolve:

В данном случае функция DSolve не может решить нелинейное уравнение. Поэтому запишем уравнение в виде:

и будем интегрировать обе части уравнения:

Следовательно, общее решение уравнения примет вид

-(-2+y^2)cos y+2ysin y=x-10ln (1-x)+13ln(2-x)+C

Пример 3. Решим дифференциальное уравнение и построим поле направлений и график решения уравнения при различных значениях константы.

Построим таблицу решений, заменив С[1] на a, где a изменяется от -2 до 2 с шагом 0,5:

Отобразим два графика одновременно и покажем, что векторы поля направлений являются касательными к решениям дифференциального уравнения:

Система Wolfram Mathematica используется для решения дифференциальных уравнений не только в математике, но и актуальна в других научных областях. Ее можно применять и в механике, в частности, для решения различных постановок задач, где в качестве математических объектов используются дифференциальные уравнения. В работах [6,7] рассмотрены уравнения движения мембран и акустических сред в виде обыкновенных дифференциальных уравнений. Для их решения может быть использована система компьютерной математики Wolfram Mathematica.

Список литературы

Букушева А.В. Использование Mathematica для описания геометрии динамических систем // Математика и ее приложения: фундаментальные проблемы науки и техники : сборник трудов всероссийской конференции, Барнаул, 24 — 26 ноября 2015. — Барнаул : Изд-во Алт. ун-та, 2015. С. 248-249.
Букушева А.В. Применение Wolfram Language для выделения специальных классов почти контактных метрических структур // Компьютерные науки и информационные технологии : Материалы Междунар. науч. конф. — Саратов : Издат. центр.»Наука», 2016. С. 105-107.
Букушева А.В. Использование систем компьютерной математики для решения геометрических задач сложного уровня // Информационные технологии в образовании: Материалы VI Всероссийской научно-практической конференции. – Саратов: ООО «Издательский центр «Наука»». 2014. – С. 76-77.
Букушева А.В. Решение учебно-исследовательских задач с использованием систем компьютерной математики // Информационные технологии в образовании: Материалы VII Всеросс. научно-практ. конф. – Саратов: ООО «Издательский центр «Наука»», 2015. С.185-187.
Букушева А.В. Учебно-исследовательские задачи в продуктивном обучении будущих бакалавров-математиков // Образовательные технологии. 2016. №2. С. 16-26.
Вельмисова А.И. Распространение и отражение гармонических волн в плоском акустическом слое с гибкими стенками в случае разрыва упругих свойств на одной из стенок // Математика. Механика: Сб. науч. тр. Саратов: Изд-во Сарат. ун-та, 2010. Вып.12. С. 136-140.
Вельмисова А.И., Вильде М.В., Кириллова И.В. Распространение и отражение гармонических волн в плоском акустическом слое с кусочно-неоднородными гибкими стенками // Известия Саратовского университета. Новая серия. Серия: Математика. Механика. Информатика. 2011. Т.11. №4. С. 68-73.

Цитировать

Зинина, А.И. Использование Wolfram Mathematica в решении дифференциальных уравнений / А.И. Зинина. — Текст : электронный // NovaInfo, 2016. — № 55. — С. 5-9. — URL: https://novainfo.ru/article/8754 (дата обращения: 23.02.2022).

Электронное периодическое издание зарегистрировано в Федеральной службе по надзору в сфере связи, информационных технологий и массовых коммуникаций (Роскомнадзор), свидетельство о регистрации СМИ — ЭЛ № ФС77-41429 от 23.07.2010 г.

Соучредители СМИ: Долганов А.А., Майоров Е.В.

источники:

http://www.sites.google.com/site/matenatikucozru/wolfram-alpha

http://novainfo.ru/article/8754

Источник

Расширение серии на бесконечности показывает, что действительная и мнимая части имеют очень разные масштабы. Я бы посоветовал вычислять их отдельно, а не добавлять. Ниже я использую первые несколько терминов расширения серии, чтобы получить мнимую часть.

In[186]:= 
w[x_?NumericQ] := {N[Exp[-SetPrecision[x, 25]^2], 20], 
  N[(3 /(4 Sqrt[[Pi]] x^5) + 1/(2 Sqrt[[Pi]] x^3) + 1/(
     Sqrt[[Pi]] x))]}

In[187]:= w[11]

Out[187]= {2.8207700884601354011*10^-53, 0.05150453151309212}

In[188]:= w[1000]

Out[188]= {3.296831478088558579*10^-434295, 0.0005641898656429712}

Не уверен, как сильно вы хотите эту очень маленькую реальную часть. Если вы можете уронить его, это будет держать цифры в разумных пределах. В некоторых диапазонах (или если требуется точность, превышающая точность станка), вы можете использовать больше терминов из расширения этой воображаемой части.

Даниэль Лихтблау Вольфрам Исследования

Источник

Время на прочтение
6 мин

Количество просмотров 22K

Уравнения в частных производных (УрЧП) играют очень важную роль в математике и ее приложениях. Их можно использовать для моделирования реальных явлений, таких как колебания натянутой струны, распространения потока тепла в стержне, в финансовых областях. Цель этой статьи — приоткрыть завесу в мир УрЧП (тем кто еще с ним не знаком) и ознакомить читателя с тем, как можно эффективно решать УрЧП в Wolfram Language, используя новый функционал для решения краевых задач в DSolve, а так же новую функцию DEigensystem, которая появилась в версии 10.3.

Теперь мы можем использовать DSolve для решения волнового уравнения с начальными и краевыми условиями:

Каждый член в сумме представляет собой стоячую волну, которые могут быть представлены следующим образом:

И все эти стоячие волны складываются воедино, образуя гладкую кривую, как показано на анимации ниже:

И теперь мы можем решить уравнение теплопроводности с заданными условиями:

Ограничим координаты х и у прямоугольной областью Ω, как показано ниже:

Задачу Дирихле можно решить с помощью функции DSolve, весьма изящно задав при этом область:

Ответ согласуется со значением, полученным с помощью встроенной функции FinancialDerivative:

Функция плотности вероятности для электрона ρ = Ψ^⊹ Ψ, с использованием подходящих значений параметров в задаче, может быть вычислена следующим образом:

Собственные значения в этой задаче выражаются через BesselJZero. Вот пример:

Источник

имя

Приложения

Характеристики

Серия Тейлор

Производная и интеграл

Bürmann серии

Обратные функции

Асимптотическое разложение

Непрерывное расширение фракции

Интеграл функции ошибок с функцией плотности Гаусса

Факторный ряд

Численные приближения

Приближение с элементарными функциями

Полиномиальный

Таблица значений

Дополнительная функция ошибок

Функция мнимой ошибки

Кумулятивная функция распределения

Обобщенные функции ошибок

Итерированные интегралы дополнительной функции ошибок

Реализации

Как реальная функция реального аргумента

Как сложная функция сложного аргумента

Смотрите также

По вероятности

Рекомендации

дальнейшее чтение

внешняя ссылка

Как решать дифференциальные уравнения в wolfram mathematica

WolframAlpha по-русски

Решение обыкновенных дифференциальных уравнений в Wolfram|Alpha

Новое в Wolfram Language | Аналитическое решение уравнений в частных производных

Иллюстрированный самоучитель по Mathematica 3/4

Дифференциальные уравнения. Решение дифференциальных уравнений в символьном виде.

Уравнения в частных производных wolfram mathematica

Основные операции

Знаки сравнения

Логические символы

Основные константы

Основные функции

Решение уравнений

Решение неравенств

Решение различных систем уравнений, неравенств и уравнений

Математический анализ

Пределы

Производные

Интегралы

Дифференциальные уравнения и их системы

Ошибки при работе с системой

Использование Wolfram Mathematica в решении дифференциальных уравнений

Аннотация

Ключевые слова

Текст научной работы

Читайте также

Математическая подготовка студентов в вузе в контексте будущей профессиональной деятельности

Использование прикладных программ при изучении математической статистики

Применение систем компьютерной математики при изучении комплексного анализа

Организация самостоятельной работы студентов в условиях информационно-образовательной среды вуза

Системы компьютерной математики в решении дифференциальных уравнений

Список литературы

Цитировать

Поделиться