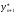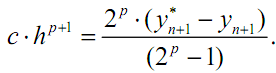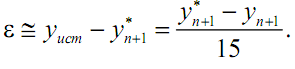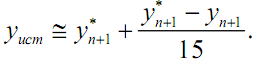Глобальная ошибка это - Не ошибается лишь тот, кто ничего не делает!

Одним
из важнейших практических вопросов,
которые встают перед инженером,
составляющим программы решения
дифференциальных уравнений, является
выбор подходящей величины шага. Если
шаг слишком мал, то расчёт потребует
неоправданно много машинного времени,
а число ошибок на

отдельных
шагах, складывающихся в суммарную
ошибку, будет весьма велико. Если же
наоборот — шаг выбран слишком большим,
то значительной будет погрешность,
обусловленная усечением рядов, и
накопившаяся суммарная ошибка будет
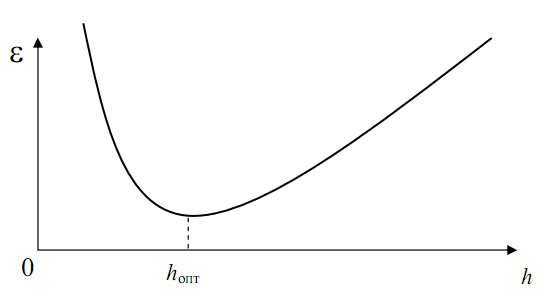
также недопустимо большой (рис.3.6).

Рис.
3.6. Выбор оптимального шага интегрирования

Кроме
того, при больших значениях h
возникает
опасность появления цифровой неустойчивости
решения. Важно различать между собой
две меры погрешностей дискретизации
[9],[10]:

а)
локальная
ошибка — это
погрешность, вносимая в вычислительный
процесс на каждом шаге вычислений.

б)
глобальная
ошибка — это
разность между вычисленным и точным
значениями величины на всем этапе
реализации численного алгоритма,
определяющая
суммарную погрешность,
накопившуюся
с момента начала вычислений.
Обычно,
выбирая величину
шага, стремятся,
чтобы локальная
ошибка на шаге была меньше некоторой
заданной допустимой величины.
Вообще говоря,
если порядок
точности метода Р,
то локальная
ошибка определяется выражением:

L(h)
= c h^p+¹,

где
c — некоторая
постоянная; h
— шаг
интегрирования.

Указанное
выражение с помощью θ-символики может
быть записано более компактно:

L(h)
= θ
(hp+1).

Например,
рассмотрим
метод Эйлера:

Отсюда
заключаем, что
для метода Эйлера p =1,
т.е.
метод имеет
первый порядок точности,
а локальная
ошибка определяется формулой:

L(h)
= θ
(h2
).

Рассмотрим
теперь глобальную ошибку дискретизации
в конечной точке t=t_N.
По мере повышения
требований к точности,
длина шага h
будет убывать,
а общее из
числа N,
необходимое
для достижения t_N,
будет возрастать:

Далее,
глобальная
ошибка E(h) может быть представлена как
сумма N локальных ошибок и поэтому мы
можем, округляя,
записать:

E(h)
= N θ(h^p+¹)
= θ(hp
).

Для
метода Эйлера p =1,
так что
уменьшение длины шага в 2
раза уменьшает
среднюю локальную ошибку примерно в
2^p+¹
= 4
раза.
Но так как для
достижения tN теперь потребуется вдвое
больше шагов,
то глобальная
ошибка ум-еньшится лишь в 2p
= 2 раза.
Если используется
один из методов прогноза и коррекции,
то ошибка на
шаге определяется величиной последнего
члена в формуле коррекции.
При использовании
же одношаговых методов Рунге-Ку-тта,
локальную
ошибку не удается выразить в явной
форме. Один
из методов оценки этой ошибки основан
на двойном счете.
Если для
вычисления значения искомой функции
y_n+₁
в точке t_n+₁
используется
шаг h, то
разность между истинным и вычисленным
значениями на данном шаге равна:

Если
уменьшим шаг вдвое и выполнив два шага
вычислим

в точке t_n+₁,
то получим:

(3.21)

Вычитая
это выражение из предыдущего,
найдем:

Отсюда
можно найти локальную погрешность:

(3.22)

Данная
формула называется правилом Рунге.
Если ошибка
на данном шаге слишком велика,
то шаг делят
пополам и вычисления повторяют вновь.

Запишем
формулу (3.22) в
виде:

Подставляя
полученное выражение в (3.21)
и полагая p=4,
найдём
приближенное значение ошибки на одном
шаге:

(3.23)

Из
(3.23) вытекает
уточнённое решение:

Недостатком
этого метода является то,
что значение
y_n+₁
приходится
вычислять дважды,
причем второй
раз с помощью двух шагов.
Тем не менее,
эта процедура
часто включается в вычислительный
алгоритм для автоматического изменения
шага в процессе вычислений и часто
используется в методах Рунге —
Кутта.
Главное
достоинство методов Рунге —
Кутта —
простота начала
счета и возможность изменения величины
шага в процессе вычисления.
С

другой
стороны, главным
достоинством методов прогноза и коррекции
является простота оценки ошибки на
шаге.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Глобальная ошибка

Cтраница 1

Глобальная ошибка — разность между вычисленным и точным значением величины на каждом этапе реализации численного алгоритма, определяющая суммарную погрешность, накопившуюся с момента начала вычислений.
[1]

Однако глобальная ошибка с уменьшением шага становится меньше.
[2]

Рассмотрим теперь глобальную ошибку дискретизации в фиксированной конечной точке ttf. По мере повышения требований к точности длины шагов hn будут убывать, а общее их число N, необходимое для достижения t1t будет возрастать.
[3]

Далее, глобальная ошибка е может быть представлена как сумма N локальных ошибок с множителями, описывающими устойчивость уравнения.
[4]

Однако это представляется не просто глобальной ошибкой внутреннего ощущения времени, но более тонкой структурной перестройкой временной шкалы восприятия событий. Поскольку в случае стимуляции коры ( учитывая, что она в действительности воспринимается не позднее, чем через полсекунды после ее начала), такая задержка не наблюдается.
[5]

Важно различать между собой две меры ошибок дискретизации: локальную ошибку дискретизации и глобальную ошибку дискретизации. Локальная ошибка дискретизации — это ошибка, сделанная на данном шаге, при условии, что предыдущие значения точны и что нет ошибок округления.
[6]

Если традиционным для теории надежности ( и для обсуждавшихся выше моделей) является представление о том, что система выходит из строя при повреждении элементов, из которых она состоит, то Розен исходит из того, что элементы выходят из строя из-за глобальных ошибок в работе системы при сохранности своих собственных, присущих каждому элементу эксплуатационных качеств. Упреждающая и обратная связи функционально несовершенны, и даже в том случае, если степень их нестабильности не возрастает с течением времени, ее результат становится все более грозным.
[7]

В случае настоящего дифференциального уравнения, где f ( y, t) зависит от у, ошибка на любом интервале зависит от решений, вычисленных для предыдущих интервалов. Вследствие этого глобальная ошибка в общем случае будет больше суммы локальных ошибок, если дифференциальное уравнение неустойчиво, но меньше этой суммы, если дифференциальное уравнение устойчиво. Внимательное изучение рис. 6.4 и 6.5 должно прояснить эти утверждения.
[8]

Ее оценка может производиться на каждом шаге интегрирования, причем она может служить средством косвенного контроля глобальной ошибки дискретизации. Приведенные определения распространяются и на другие методы и задачи.
[9]

Как отмечалось выше, риск при проведении реинжиниринга довольно значителен. Однако необходимо подчеркнуть, что причины неудач заключены не в загадочности реинжиниринга, а в нарушении правил его поведения. Чампи указывают, что с точки зрения риска реинжиниринг подобен игре в шахматы, когда в меру своих знаний и умений играющие могут влиять на результат. Главное — избегать глобальных ошибок.
[10]

Нужно отметить, что при обсуждении численных методов для обыкновенных дифференциальных уравнений слово порядок может иметь несколько различных значений. Порядок дифференциального уравнения — это индекс наивысшей встречающейся в нем производной. Термин порядок системы уравнений иногда относится к числу уравнений системы. Например, y y z, z — у — z есть система второго порядка. Порядок численного метода для решения обыкновенного дифференциального уравнения — это как раз то, что мы здесь обсуждаем. Это степень длины шага, которая появляется в выражении для глобальной ошибки. Например, метод Эйлера имеет первый порядок.
[12]

Страницы:

Источник

глобальная ошибка

глобальная ошибка: Тематики

сети вычислительные

Смотреть что такое «глобальная ошибка» в других словарях:

Звуковые сигналы BIOS — Информация в этой статье или некоторых её разделах устарела. Вы можете помочь проекту … Википедия
отказ — 3.14 отказ: Событие, заключающееся в нарушении работоспособного состояния машины, которое наступает, когда машина утрачивает одну или несколько своих основных функций. Примечание Отказ машины обычно происходит в том случае, когда один или… … Словарь-справочник терминов нормативно-технической документации
целостность — 2.15 целостность (integrity): Свойство сохранения правильности и полноты активов. Источник … Словарь-справочник терминов нормативно-технической документации
целостность ГНСС — 18 целостность ГНСС: Способность глобальной навигационной спутниковой системы за заданный интервал времени и с заданной вероятностью обеспечивать потребителей ГНСС сигналами тревоги о недостоверности навигационных сигналов ГНСС. Источник: ГОСТ Р… … Словарь-справочник терминов нормативно-технической документации
Погрешность — 10. Погрешность По title= РМГ 29 99 ГСИ. Метрология. Основные термины и определения Источник: ГОСТ 12.1.016 79: Система станд … Словарь-справочник терминов нормативно-технической документации
точность — 3.1.1 точность (accuracy): Степень близости результата измерений к принятому опорному значению. Примечание Термин «точность», когда он относится к серии результатов измерений, включает сочетание случайных составляющих и общей систематической… … Словарь-справочник терминов нормативно-технической документации
ГОСТ Р 54119-2010: Глобальные навигационные спутниковые системы. Судовая многосистемная, многоканальная аппаратура потребителей ГНСС ГЛОНАСС/GPS/ГАЛИЛЕО. Технические характеристики, методы и требуемые результаты испытаний — Терминология ГОСТ Р 54119 2010: Глобальные навигационные спутниковые системы. Судовая многосистемная, многоканальная аппаратура потребителей ГНСС ГЛОНАСС/GPS/ГАЛИЛЕО. Технические характеристики, методы и требуемые результаты испытаний оригинал… … Словарь-справочник терминов нормативно-технической документации
Новая хронология (Фоменко) — У этого термина существуют и другие значения, см. Новая хронология. «Новая хронология» (сокращённо НХ[1]) псевдонаучная[2][3][4][5] теория радикального пересмотра истории, созданная группой под руководством академика РАН математика… … Википедия
«Новая хронология» Фоменко — «Новая хронология» неакадемическая теория, утверждающая, что общепризнанная хронология исторических событий в целом неверна, и предлагающая свой вариант хронологии и вообще истории человечества. Согласно утверждениям её авторов, основана на… … Википедия
Критика естественно-научных методов в «Новой хронологии» Фоменко — «Новая хронология» неакадемическая теория, утверждающая, что общепризнанная хронология исторических событий в целом неверна, и предлагающая свой вариант хронологии и вообще истории человечества. Согласно утверждениям её авторов, основана на… … Википедия

Источник

Глобальная ошибка: определение, значение, предложения

Предложения с «глобальная ошибка»

Другие результаты

Не может быть ошибки, что нынешнее глобальное выздоровление носит, несомненно, слабый характер.

Глобальная система позиционирования вносит поправки на ошибки часов приемника и другие эффекты, но есть еще остаточные ошибки, которые не исправляются.

Алгоритм CRBP может свести к минимуму срок глобальной ошибки.

Пытаться сделать это втихаря было глобальной ошибкой.

Действительно, эта организация, действуя методом проб и ошибок, стремится решать глобальные проблемы газовых рынков. И в довольно короткий промежуток времени ей удалось добиться в этом деле существенного прогресса.

Глобальное уничтожение в результате ошибок или неправильных решений сегодня также легко себе представить, как и в разгар холодной войны.

У США намного больше ресурсов для решения глобальных проблем, а их удобное геополитическое положение помогает им в большой степени избегать последствий их собственных ошибок.

Глобальный критерий состоит в том, что сумма ошибок на всех интервалах должна быть меньше t.

Многие китайцы ошибочно заключили, что это представляет собой сдвиг в балансе глобальных сил и что США пришли в упадок.

Ошибочно полагать, что существует единый глобальный принцип, охватывающий различные предметы.

По мнению американцев и немцев, такой трайбализм и самоизоляция в ответ на глобализацию явно ошибочны.

Это ошибочный подход к глобальной экономике, поскольку существует много примеров, когда во время экономических операций выигрывали или же проигрывали все заинтересованные стороны.

Решение игнорировать добрые намерения международного сообщества является ошибочным и не учитывает нашу глобальную ответственность в качестве партнера во имя мира.

На данной странице приводится толкование (значение) фразы / выражения «глобальная ошибка», а также синонимы, антонимы и предложения, при наличии их в нашей базе данных.
Мы стремимся сделать толковый словарь English-Grammar.Biz, в том числе и толкование фразы / выражения «глобальная ошибка», максимально корректным и информативным. Если у вас есть предложения или замечания по поводу корректности определения «глобальная ошибка», просим написать нам в разделе «Обратная связь».

Источник

При рассмотрении численных методов решения задачи Коши выделяют следующие погрешности

1) локальную (ошибку);

2) глобальную (ошибку);

3) вычислений на ЭВМ;

4) общую.

Локальная погрешность – это погрешность, допущенная на данном шаге , при условии, что предыдущие значения вычислены точно и отсутствуют ошибки округления. Другими словами, решается задача Коши:

где известно точное значение . Тогда локальная погрешность равна:

где – решение разностной задачи в отсутствие ошибок округления, а – значение точного решения дифференциальной задачи в точке .

Глобальная погрешность – это разность между вычисленным решением разностной задачи в отсутствии ошибок округления и точным решением. То есть, решается задача Коши:

Глобальная погрешность R равна:

где – вычисленное в отсутствие ошибок округления решение разностной задачи в точке ; – точное решение задачи Коши в этой же точке.

Для частного случая, когда функция не зависит от y, то есть , глобальная погрешность равна сумме локальных погрешностей.

В общем случае для устойчивых дифференциальных задач Коши глобальная погрешность будет меньше суммы локальных погрешностей, но для неустойчивых дифференциальных задач Коши глобальная погрешность больше суммы локальных погрешностей.

Общая погрешность – это сумма глобальной погрешности и погрешности вычислений на ЭВМ. Другими словами, общая погрешность – это разность между вычисленным и точным решениями с учетом ошибок округления на ЭВМ.

При оценке точности численного метода решения задачи Коши важной характеристикой является порядок метода. Разностная задача имеет порядок k по h, если для глобальной погрешности справедливо: . Для локальной погрешности в этом случае справедливо равенство . Условия для глобальной и локальной погрешности можно записать в эквивалентном виде: