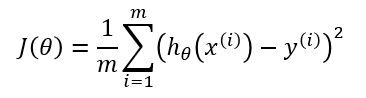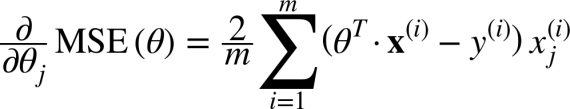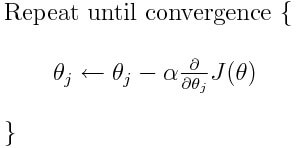Знакомимся с методом обратного распространения ошибки
Время на прочтение
6 мин
Количество просмотров 44K
Всем привет! Новогодние праздники подошли к концу, а это значит, что мы вновь готовы делиться с вами полезным материалом. Перевод данной статьи подготовлен в преддверии запуска нового потока по курсу «Алгоритмы для разработчиков».
Поехали!
Метод обратного распространения ошибки – вероятно самая фундаментальная составляющая нейронной сети. Впервые он был описан в 1960-е и почти 30 лет спустя его популяризировали Румельхарт, Хинтон и Уильямс в статье под названием «Learning representations by back-propagating errors».
Метод используется для эффективного обучения нейронной сети с помощью так называемого цепного правила (правила дифференцирования сложной функции). Проще говоря, после каждого прохода по сети обратное распространение выполняет проход в обратную сторону и регулирует параметры модели (веса и смещения).
В этой статья я хотел бы подробно рассмотреть с точки зрения математики процесс обучения и оптимизации простой 4-х слойной нейронной сети. Я считаю, что это поможет читателю понять, как работает обратное распространение, а также осознать его значимость.
Определяем модель нейронной сети
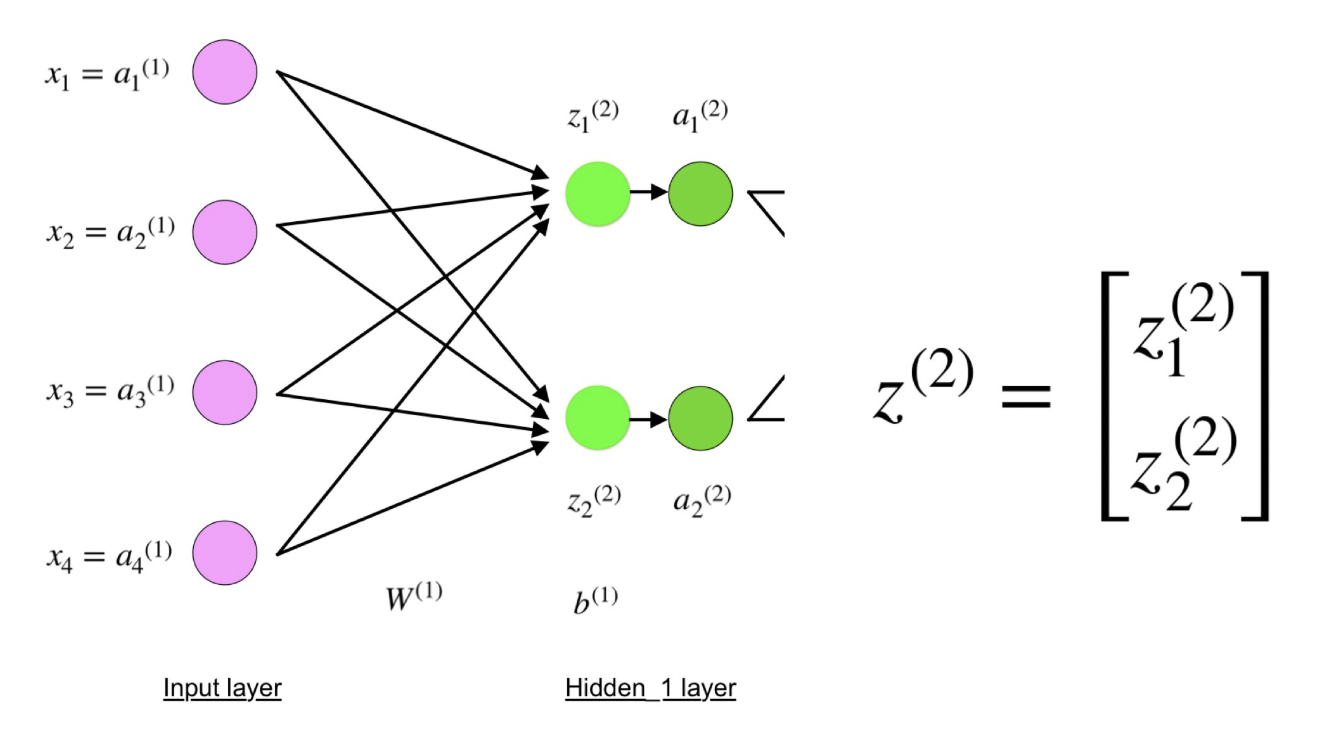
Четырехслойная нейронная сеть состоит из четырех нейронов входного слоя, четырех нейронов на скрытых слоях и 1 нейрона на выходном слое.
Простое изображение четырехслойной нейронной сети.
Входной слой
На рисунке нейроны фиолетового цвета представляют собой входные данные. Они могут быть простыми скалярными величинами или более сложными – векторами или многомерными матрицами.
Уравнение, описывающее входы xi.
Первый набор активаций (а) равен входным значениям. «Активация» — это значение нейрона после применения функции активации. Подробнее смотрите ниже.
Скрытые слои
Конечные значения в скрытых нейронах (на рисунке зеленого цвета) вычисляются с использованием zl – взвешенных входов в слое I и aI активаций в слое L. Для слоев 2 и 3 уравнения будут следующими:
Для l = 2:
Для l = 3:
W2 и W3 – это веса на слоях 2 и 3, а b2 и b3 – смещения на этих слоях.
Активации a2 и a3 вычисляются с помощью функции активации f. Например, эта функция f является нелинейной (как сигмоид, ReLU и гиперболический тангенс) и позволяет сети изучать сложные паттерны в данных. Мы не будем подробно останавливаться на том, как работают функции активации, но, если вам интересно, я настоятельно рекомендую прочитать эту замечательную статью.
Присмотревшись внимательно, вы увидите, что все x, z2, a2, z3, a3, W1, W2, b1 и b2 не имеют нижних индексов, представленных на рисунке четырехслойной нейронной сети. Дело в том, что мы объединили все значения параметров в матрицы, сгруппированные по слоям. Это стандартный способ работы с нейронными сетями, и он довольно комфортный. Однако я пройдусь по уравнениям, чтобы не возникло путаницы.
Давайте возьмем слой 2 и его параметры в качестве примера. Те же самые операции можно применить к любому слою нейронной сети.
W1 – это матрица весов размерности (n, m), где n – это количество выходных нейронов (нейронов на следующем слое), а m – число входных нейронов (нейронов в предыдущем слое). В нашем случае n = 2 и m = 4.
Здесь первое число в нижнем индексе любого из весов соответствует индексу нейрона в следующем слое (в нашем случае – это второй скрытый слой), а второе число соответствует индексу нейрона в предыдущем слое (в нашем случае – это входной слой).
x – входной вектор размерностью (m, 1), где m – число входных нейронов. В нашем случае m = 4.
b1 – это вектор смещения размерности (n, 1), где n – число нейронов на текущем слое. В нашем случае n = 2.
Следуя уравнению для z2 мы можем использовать приведенные выше определения W1, x и b1 для получения уравнения z2:
Теперь внимательно посмотрите на иллюстрацию нейронной сети выше:
Как видите, z2 можно выразить через z12 и z22, где z12 и z22 – суммы произведений каждого входного значения xi на соответствующий вес Wij1.
Это приводит к тому же самому уравнению для z2 и доказывает, что матричные представления z2, a2, z3 и a3 – верны.
Выходной слой
Последняя часть нейронной сети – это выходной слой, который выдает прогнозируемое значение. В нашем простом примере он представлен в виде одного нейрона, окрашенного в синий цвет и рассчитываемого следующим образом:
И снова мы используем матричное представление для упрощения уравнения. Можно использовать вышеприведенные методы, чтобы понять лежащую в их основе логику.
Прямое распространение и оценка
Приведенные выше уравнения формируют прямое распространение по нейронной сети. Вот краткий обзор:
(1) – входной слой
(2) – значение нейрона на первом скрытом слое
(3) – значение активации на первом скрытом слое
(4) – значение нейрона на втором скрытом слое
(5) – значение активации на втором скрытом уровне
(6) – выходной слой
Заключительным шагом в прямом проходе является оценка прогнозируемого выходного значения s относительно ожидаемого выходного значения y.
Выходные данные y являются частью обучающего набора данных (x, y), где x – входные данные (как мы помним из предыдущего раздела).
Оценка между s и y происходит через функцию потерь. Она может быть простой как среднеквадратичная ошибка или более сложной как перекрестная энтропия.
Мы назовем эту функцию потерь С и обозначим ее следующим образом:
Где cost может равняться среднеквадратичной ошибке, перекрестной энтропии или любой другой функции потерь.
Основываясь на значении С, модель «знает», насколько нужно скорректировать ее параметры, чтобы приблизиться к ожидаемому выходному значению y. Это происходит с помощью метода обратного распространения ошибки.
Обратное распространение ошибки и вычисление градиентов
Опираясь на статью 1989 года, метод обратного распространения ошибки:
Постоянно настраивает веса соединений в сети, чтобы минимизировать меру разности между фактическим выходным вектором сети и желаемым выходным вектором.
и
…дает возможность создавать полезные новые функции, что отличает обратное распространение от более ранних и простых методов…
Другими словами, обратное распространение направлено на минимизацию функции потерь путем корректировки весов и смещений сети. Степень корректировки определяется градиентами функции потерь по отношению к этим параметрам.
Возникает один вопрос: Зачем вычислять градиенты?
Чтобы ответить на этот вопрос, нам сначала нужно пересмотреть некоторые понятия вычислений:
Градиентом функции С(x1, x2, …, xm) в точке x называется вектор частных производных С по x.
Производная функции С отражает чувствительность к изменению значения функции (выходного значения) относительно изменения ее аргумента х (входного значения). Другими словами, производная говорит нам в каком направлении движется С.
Градиент показывает, насколько необходимо изменить параметр x (в положительную или отрицательную сторону), чтобы минимизировать С.
Вычисление этих градиентов происходит с помощью метода, называемого цепным правилом.
Для одного веса (wjk)l градиент равен:
(1) Цепное правило
(2) По определению m – количество нейронов на l – 1 слое
(3) Вычисление производной
(4) Окончательное значение
Аналогичный набор уравнений можно применить к (bj)l:
(1) Цепное правило
(2) Вычисление производной
(3) Окончательное значение
Общая часть в обоих уравнениях часто называется «локальным градиентом» и выражается следующим образом:
«Локальный градиент» можно легко определить с помощью правила цепи. Этот процесс я не буду сейчас расписывать.
Градиенты позволяют оптимизировать параметры модели:
Пока не будет достигнут критерий остановки выполняется следующее:
Алгоритм оптимизации весов и смещений (также называемый градиентным спуском)
- Начальные значения w и b выбираются случайным образом.
- Эпсилон (e) – это скорость обучения. Он определяет влияние градиента.
- w и b – матричные представления весов и смещений.
- Производная C по w или b может быть вычислена с использованием частных производных С по отдельным весам или смещениям.
- Условие завершение выполняется, как только функция потерь минимизируется.
Заключительную часть этого раздела я хочу посвятить простому примеру, в котором мы рассчитаем градиент С относительно одного веса (w22)2.
Давайте увеличим масштаб нижней части вышеупомянутой нейронной сети:
Визуальное представление обратного распространения в нейронной сети
Вес (w22)2 соединяет (a2)2 и (z2)2, поэтому вычисление градиента требует применения цепного правила на (z3)2 и (a3)2:
Вычисление конечного значения производной С по (a2)3 требует знания функции С. Поскольку С зависит от (a2)3, вычисление производной должно быть простым.
Я надеюсь, что этот пример сумел пролить немного света на математику, стоящую за вычислением градиентов. Если захотите узнать больше, я настоятельно рекомендую вам посмотреть Стэндфордскую серию статей по NLP, где Ричард Сочер дает 4 замечательных объяснения обратного распространения.
Заключительное замечание
В этой статье я подробно объяснил, как обратное распространение ошибки работает под капотом с помощью математических методов, таких как вычисление градиентов, цепное правило и т.д. Знание механизмов этого алгоритма укрепит ваши знания о нейронных сетях и позволит вам чувствовать себя комфортно при работе с более сложными моделями. Удачи вам в путешествии по глубокому обучению!
На этом все. Приглашаем всех на бесплатный вебинар по теме «Дерево отрезков: просто и быстро».
Градиентный спуск — самый используемый алгоритм обучения нейронных сетей, он применяется почти в каждой модели машинного обучения. Метод градиентного спуска с некоторой модификацией широко используется для обучения персептрона и глубоких нейронных сетей, и известен как метод обратного распространения ошибки.
В этом посте вы найдете объяснение градиентного спуска с небольшим количеством математики. Краткое содержание:
- Смысл ГС — объяснение всего алгоритма;
- Различные вариации алгоритма;
- Реализация кода: написание кода на языке Python.
Что такое градиентный спуск
Градиентный спуск — метод нахождения минимального значения функции потерь (существует множество видов этой функции). Минимизация любой функции означает поиск самой глубокой впадины в этой функции. Имейте в виду, что функция используется, чтобы контролировать ошибку в прогнозах модели машинного обучения. Поиск минимума означает получение наименьшей возможной ошибки или повышение точности модели. Мы увеличиваем точность, перебирая набор учебных данных при настройке параметров нашей модели (весов и смещений).
Итак, градиентный спуск нужен для минимизации функции потерь.
Суть алгоритма – процесс получения наименьшего значения ошибки. Аналогично это можно рассматривать как спуск во впадину в попытке найти золото на дне ущелья (самое низкое значение ошибки).
В дальнейшем, чтобы найти самую низкую ошибку (глубочайшую впадину) в функции потерь (по отношению к одному весу), нужно настроить параметры модели. Как мы их настраиваем? В этом поможет математический анализ. Благодаря анализу мы знаем, что наклон графика функции – производная от функции по переменной. Это наклон всегда указывает на ближайшую впадину!
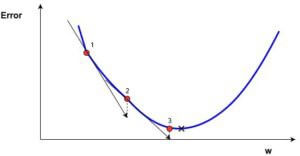
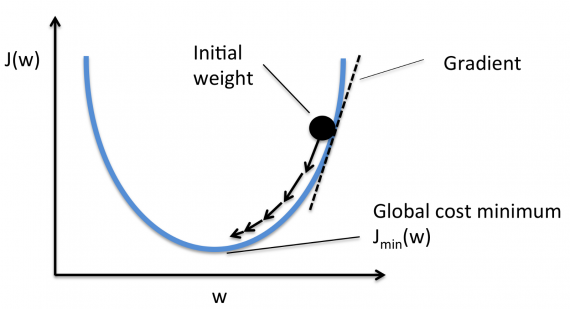
На рисунке мы видим график функции потерь (названный «Ошибка» с символом «J») с одним весом. Теперь, если мы вычислим наклон (обозначим это dJ/dw) функции потерь относительно одного веса, то получим направление, в котором нужно двигаться, чтобы достичь локальных минимумов. Давайте пока представим, что наша модель имеет только один вес.
- Функция потерь
Важно: когда мы перебираем все учебные данные, мы продолжаем добавлять значения dJ/dw для каждого веса. Так как потери зависят от примера обучения, dJ/dw также продолжает меняться. Затем делим собранные значения на количество примеров обучения для получения среднего. Потом мы используем это среднее значение (каждого веса) для настройки каждого веса.
Также обратите внимание: Функция потерь предназначена для отслеживания ошибки с каждым примером обучениям, в то время как производная функции относительного одного веса – это то, куда нужно сместить вес, чтобы минимизировать ее для этого примера обучения. Вы можете создавать модели даже без применения функции потерь. Но вам придется использовать производную относительно каждого веса (dJ/dw).
Теперь, когда мы определили направление, в котором нужно подтолкнуть вес, нам нужно понять, как это сделать. Тут мы используем коэффициент скорости обучения, его называют гипер-параметром. Гипер-параметр – значение, требуемое вашей моделью, о котором мы действительно имеем очень смутное представление. Обычно эти значения могут быть изучены методом проб и ошибок. Здесь не так: одно подходит для всех гипер-параметров. Коэффициент скорости обучения можно рассматривать как «шаг в правильном направлении», где направление происходит от dJ/dw.
Это была функция потерь построенная на один вес. В реальной модели мы делаем всё перечисленное выше для всех весов, перебирая все примеры обучения. Даже в относительно небольшой модели машинного обучения у вас будет более чем 1 или 2 веса. Это затрудняет визуализацию, поскольку график будет обладать размерами, которые разум не может себе представить.
Подробнее о градиентах
Кроме функции потерь градиентный спуск также требует градиент, который является dJ/dw (производная функции потерь относительно одного веса, выполненная для всех весов). dJ/dw зависит от вашего выбора функции потерь. Наиболее распространена функция потерь среднеквадратичной ошибки.
Производная этой функции относительно любого веса (эта формула показывает вычисление градиента для линейной регрессии):
Это – вся математика в ГС. Глядя на это можно сказать, что по сути, ГС не содержит много математики. Единственная математика, которую он содержит в себе – умножение и деление, до которых мы доберемся. Это означает, что ваш выбор функции повлияет на вычисление градиента каждого веса.
Коэффициент скорости обучения
Всё, о чём написано выше, есть в учебнике. Вы можете открыть любую книгу о градиентном спуске, там будет написано то же самое. Формулы градиентов для каждой функции потерь можно найти в интернете, не зная как вывести их самостоятельно.
Однако проблема у большинства моделей возникает с коэффициентом скорости обучения. Давайте взглянем на обновленное выражение для каждого веса (j лежит в диапазоне от 0 до количества весов, а Theta-j это j-й вес в векторе весов, k лежит в диапазоне от 0 до количества смещений, где B-k — это k-е смещение в векторе смещений). Здесь alpha – коэффициент скорости обучения. Из этого можно сказать, что мы вычисляем dJ/dTheta-j ( градиент веса Theta-j), и затем шаг размера alpha в этом направлении. Следовательно, мы спускаемся по градиенту. Чтобы обновить смещение, замените Theta-j на B-k.
Если этот размера шага alpha слишком велик, мы преодолеем минимум: то есть промахнемся мимо минимума. Если alpha слишком мала, мы используем слишком много итераций, чтобы добраться до минимума. Итак, alpha должна быть подходящей.
Использование градиентного спуска
Что ж, вот и всё. Это всё, что нужно знать про градиентный спуск. Давайте подытожим всё в псевдокоде.
Примечание: Весы здесь представлены в векторах. В более крупных моделях они, наверное, будут матрицами.
От i = 0 до «количество примеров обучения»
1. Вычислите градиент функции потерь для i-го примера обучения по каждому весу и смещению. Теперь у вас есть вектор, который полон градиентами для каждого веса и переменной, содержащей градиент смещения.
2. Добавьте градиенты весов, вычисленные для отдельного аккумулятивного вектора, который после того, как вы выполнили итерацию по каждому учебному примеру, должен содержать сумму градиентов каждого веса за несколько итераций.
3. Подобно ситуации с весами, добавьте градиент смещения к аккумулятивной переменной.
Теперь, ПОСЛЕ перебирания всех примеров обучения, выполните следующие действия:
1. Поделите аккумулятивные переменные весов и смещения на количество примеров обучения. Это даст нам средние градиенты для всех весов и средний градиент для смещения. Будем называть их обновленными аккумуляторами (ОА).
2. Затем, используя приведенную ниже формулу, обновите все веса и смещение. Вместо dJ / dTheta-j вы будете подставлять ОА (обновленный аккумулятор) для весов и ОА для смещения. Проделайте то же самое для смещения.
Это была только одна итерация градиентного спуска.
Повторите этот процесс от начала до конца для некоторого количества итераций. Это означает, что для 1-й итерации ГС вы перебираете все примеры обучения, вычисляете градиенты, потом обновляете веса и смещения. Затем вы проделываете это для некоторого количества итераций ГС.
Различные типы градиентного спуска
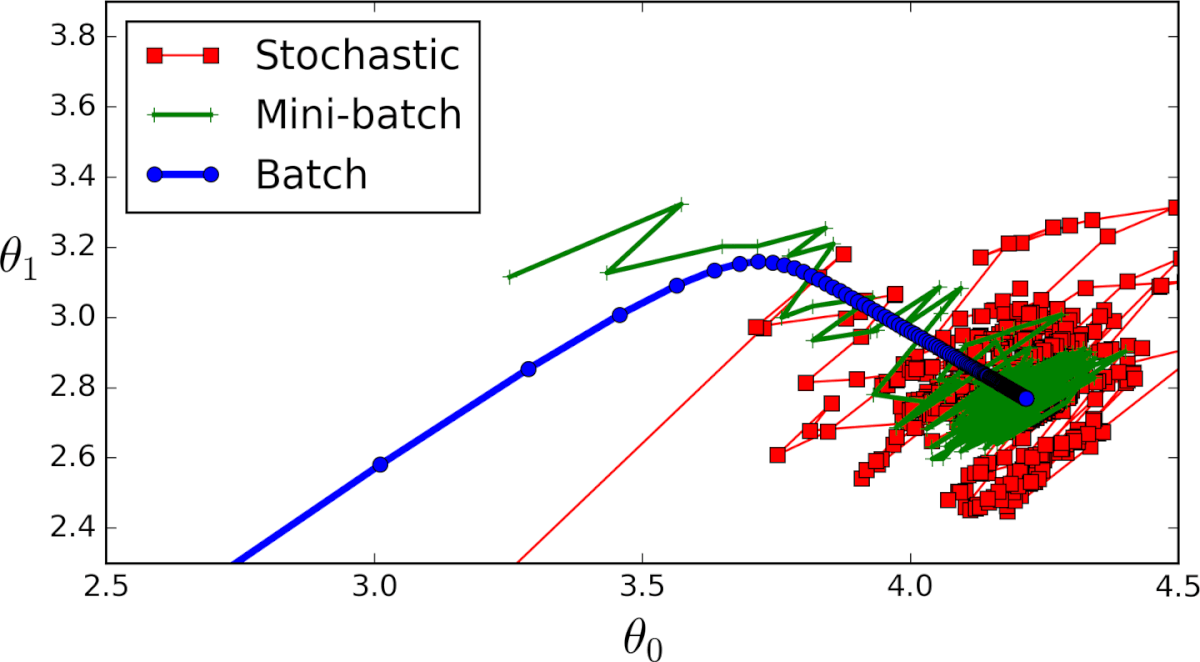
Существует 3 варианта градиентного спуска:
1. Мini-batch: тут, вместо поочерёдного перебора всех примеров обучения и произведения необходимых вычислений для каждого из них, мы производим вычисления для n примеров обучения сразу. Этот выбор подходит для очень больших наборов данных.
2. Стохастический градиентный спуск: в этом случае вместо перебора и использования всего набора примеров обучения мы применяем подход “используй только один”. Здесь нужно отметить несколько моментов:
- Набор примеров обучения необходимо перемешать перед каждым его проходом в ГС, чтобы перебирать их каждый раз в случайном порядке.
- Поскольку каждый раз используется только один пример обучения, то ваш путь к локальному минимуму будет очень неоптимальным;
- С каждой итерацией ГС вам нужно перемешать набор обучения и выбрать случайный пример обучения;
- Поскольку вы используете только один пример обучения, ваш путь к локальным минимумам будет очень шумным.
3. Серия ГС: это то, о чем написано в предыдущих разделах. Цикл на каждом примере обучения.
Пример кода на python
Применимо к cерии ГС, так будет выглядеть блок учебного кода на Python.
def train(X, y, W, B, alpha, max_iters):
'''
Performs GD on all training examples,
X: Training data set,
y: Labels for training data,
W: Weights vector,
B: Bias variable,
alpha: The learning rate,
max_iters: Maximum GD iterations.
'''
dW = 0 # Weights gradient accumulator
dB = 0 # Bias gradient accumulator
m = X.shape[0] # No. of training examples
for i in range(max_iters):
dW = 0 # Reseting the accumulators
dB = 0
for j in range(m):
# 1. Iterate over all examples,
# 2. Compute gradients of the weights and biases in w_grad and b_grad,
# 3. Update dW by adding w_grad and dB by adding b_grad,
W = W - alpha * (dW / m) # Update the weights
B = B - alpha * (dB / m) # Update the bias return W, B # Return the updated weights and bias.Вот и всё. Теперь вы должны хорошо понимать, что такое метод градиентного спуска.
Нейронные сети обучаются с помощью тех или иных модификаций градиентного спуска, а чтобы применять его, нужно уметь эффективно вычислять градиенты функции потерь по всем обучающим параметрам. Казалось бы, для какого-нибудь запутанного вычислительного графа это может быть очень сложной задачей, но на помощь спешит метод обратного распространения ошибки.
Открытие метода обратного распространения ошибки стало одним из наиболее значимых событий в области искусственного интеллекта. В актуальном виде он был предложен в 1986 году Дэвидом Э. Румельхартом, Джеффри Э. Хинтоном и Рональдом Дж. Вильямсом и независимо и одновременно красноярскими математиками С. И. Барцевым и В. А. Охониным. С тех пор для нахождения градиентов параметров нейронной сети используется метод вычисления производной сложной функции, и оценка градиентов параметров сети стала хоть сложной инженерной задачей, но уже не искусством. Несмотря на простоту используемого математического аппарата, появление этого метода привело к значительному скачку в развитии искусственных нейронных сетей.
Суть метода можно записать одной формулой, тривиально следующей из формулы производной сложной функции: если $f(x) = g_m(g_{m-1}(ldots (g_1(x)) ldots))$, то $frac{partial f}{partial x} = frac{partial g_m}{partial g_{m-1}}frac{partial g_{m-1}}{partial g_{m-2}}ldots frac{partial g_2}{partial g_1}frac{partial g_1}{partial x}$. Уже сейчас мы видим, что градиенты можно вычислять последовательно, в ходе одного обратного прохода, начиная с $frac{partial g_m}{partial g_{m-1}}$ и умножая каждый раз на частные производные предыдущего слоя.
Backpropagation в одномерном случае
В одномерном случае всё выглядит особенно просто. Пусть $w_0$ — переменная, по которой мы хотим продифференцировать, причём сложная функция имеет вид
$$f(w_0) = g_m(g_{m-1}(ldots g_1(w_0)ldots)),$$
где все $g_i$ скалярные. Тогда
$$f'(w_0) = g_m'(g_{m-1}(ldots g_1(w_0)ldots))cdot g’_{m-1}(g_{m-2}(ldots g_1(w_0)ldots))cdotldots cdot g’_1(w_0)$$
Суть этой формулы такова. Если мы уже совершили forward pass, то есть уже знаем
$$g_1(w_0), g_2(g_1(w_0)),ldots,g_{m-1}(ldots g_1(w_0)ldots),$$
то мы действуем следующим образом:
-
берём производную $g_m$ в точке $g_{m-1}(ldots g_1(w_0)ldots)$;
-
умножаем на производную $g_{m-1}$ в точке $g_{m-2}(ldots g_1(w_0)ldots)$;
-
и так далее, пока не дойдём до производной $g_1$ в точке $w_0$.
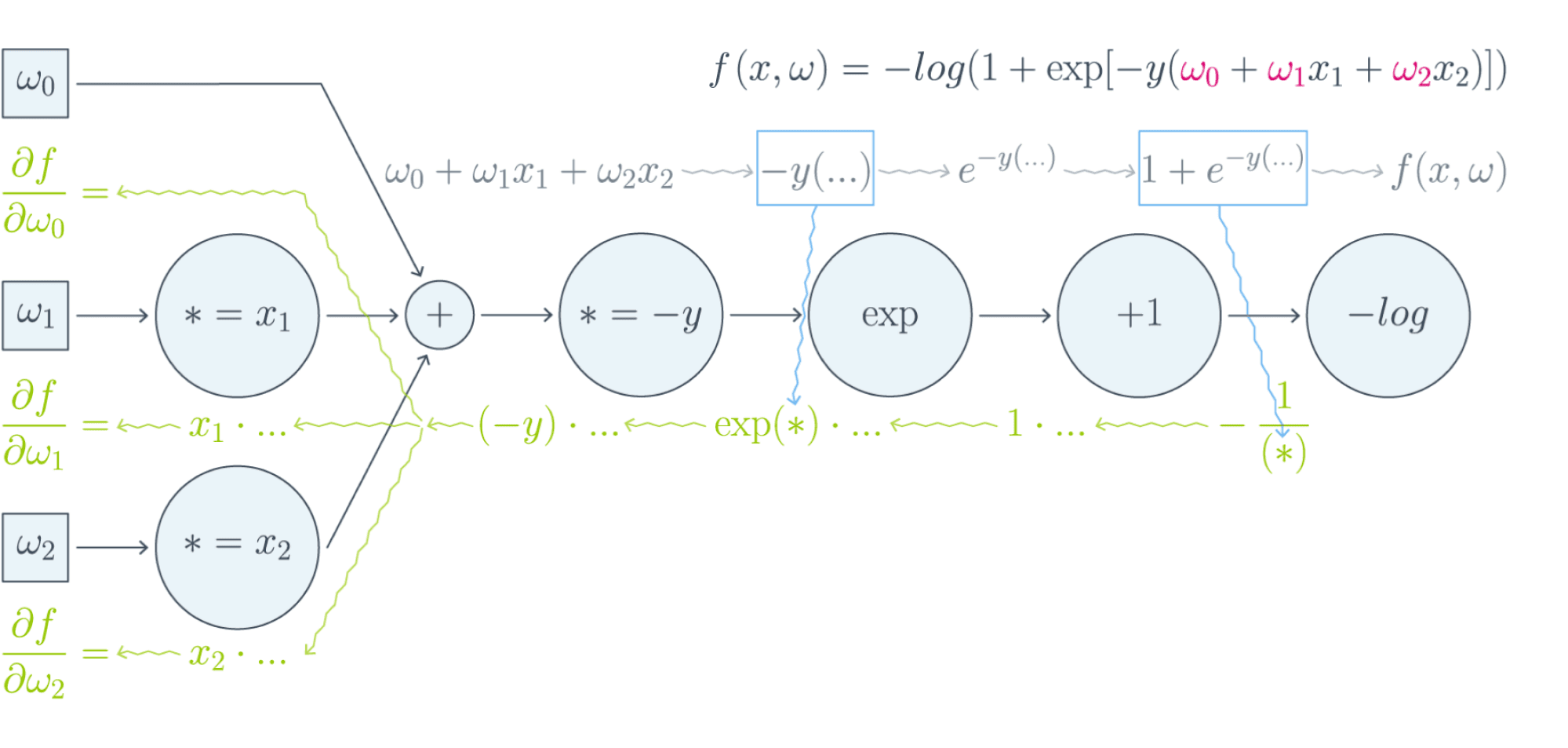
Проиллюстрируем это на картинке, расписав по шагам дифференцирование по весам $w_i$ функции потерь логистической регрессии на одном объекте (то есть для батча размера 1):
Собирая все множители вместе, получаем:
$$frac{partial f}{partial w_0} = (-y)cdot e^{-y(w_0 + w_1x_1 + w_2x_2)}cdotfrac{-1}{1 + e^{-y(w_0 + w_1x_1 + w_2x_2)}}$$
$$frac{partial f}{partial w_1} = x_1cdot(-y)cdot e^{-y(w_0 + w_1x_1 + w_2x_2)}cdotfrac{-1}{1 + e^{-y(w_0 + w_1x_1 + w_2x_2)}}$$
$$frac{partial f}{partial w_2} = x_2cdot(-y)cdot e^{-y(w_0 + w_1x_1 + w_2x_2)}cdotfrac{-1}{1 + e^{-y(w_0 + w_1x_1 + w_2x_2)}}$$
Таким образом, мы видим, что сперва совершается forward pass для вычисления всех промежуточных значений (и да, все промежуточные представления нужно будет хранить в памяти), а потом запускается backward pass, на котором в один проход вычисляются все градиенты.
Почему же нельзя просто пойти и начать везде вычислять производные?
В главе, посвящённой матричным дифференцированиям, мы поднимаем вопрос о том, что вычислять частные производные по отдельности — это зло, лучше пользоваться матричными вычислениями. Но есть и ещё одна причина: даже и с матричной производной в принципе не всегда хочется иметь дело. Рассмотрим простой пример. Допустим, что $X^r$ и $X^{r+1}$ — два последовательных промежуточных представления $Ntimes M$ и $Ntimes K$, связанных функцией $X^{r+1} = f^{r+1}(X^r)$. Предположим, что мы как-то посчитали производную $frac{partialmathcal{L}}{partial X^{r+1}_{ij}}$ функции потерь $mathcal{L}$, тогда
$$frac{partialmathcal{L}}{partial X^{r}_{st}} = sum_{i,j}frac{partial f^{r+1}_{ij}}{partial X^{r}_{st}}frac{partialmathcal{L}}{partial X^{r+1}_{ij}}$$
И мы видим, что, хотя оба градиента $frac{partialmathcal{L}}{partial X_{ij}^{r+1}}$ и $frac{partialmathcal{L}}{partial X_{st}^{r}}$ являются просто матрицами, в ходе вычислений возникает «четырёхмерный кубик» $frac{partial f_{ij}^{r+1}}{partial X_{st}^{r}}$, даже хранить который весьма болезненно: уж больно много памяти он требует ($N^2MK$ по сравнению с безобидными $NM + NK$, требуемыми для хранения градиентов). Поэтому хочется промежуточные производные $frac{partial f^{r+1}}{partial X^{r}}$ рассматривать не как вычисляемые объекты $frac{partial f_{ij}^{r+1}}{partial X_{st}^{r}}$, а как преобразования, которые превращают $frac{partialmathcal{L}}{partial X_{ij}^{r+1}}$ в $frac{partialmathcal{L}}{partial X_{st}^{r}}$. Целью следующих глав будет именно это: понять, как преобразуется градиент в ходе error backpropagation при переходе через тот или иной слой.
Вы спросите себя: надо ли мне сейчас пойти и прочитать главу учебника про матричное дифференцирование?
Встречный вопрос. Найдите производную функции по вектору $x$:
$$f(x) = x^TAx, Ain Mat_{n}{mathbb{R}}text{ — матрица размера }ntimes n$$
А как всё поменяется, если $A$ тоже зависит от $x$? Чему равен градиент функции, если $A$ является скаляром? Если вы готовы прямо сейчас взять ручку и бумагу и посчитать всё, то вам, вероятно, не надо читать про матричные дифференцирования. Но мы советуем всё-таки заглянуть в эту главу, если обозначения, которые мы будем дальше использовать, покажутся вам непонятными: единой нотации для матричных дифференцирований человечество пока, увы, не изобрело, и переводить с одной на другую не всегда легко.
Мы же сразу перейдём к интересующей нас вещи: к вычислению градиентов сложных функций.
Градиент сложной функции
Напомним, что формула производной сложной функции выглядит следующим образом:
$$left[D_{x_0} (color{#5002A7}{u} circ color{#4CB9C0}{v}) right](h) = color{#5002A7}{left[D_{v(x_0)} u right]} left( color{#4CB9C0}{left[D_{x_0} vright]} (h)right)$$
Теперь разберёмся с градиентами. Пусть $f(x) = g(h(x))$ – скалярная функция. Тогда
$$left[D_{x_0} f right] (x-x_0) = langlenabla_{x_0} f, x-x_0rangle.$$
С другой стороны,
$$left[D_{h(x_0)} g right] left(left[D_{x_0}h right] (x-x_0)right) = langlenabla_{h_{x_0}} g, left[D_{x_0} hright] (x-x_0)rangle = langleleft[D_{x_0} hright]^* nabla_{h(x_0)} g, x-x_0rangle.$$
То есть $color{#FFC100}{nabla_{x_0} f} = color{#348FEA}{left[D_{x_0} h right]}^* color{#FFC100}{nabla_{h(x_0)}}g$ — применение сопряжённого к $D_{x_0} h$ линейного отображения к вектору $nabla_{h(x_0)} g$.
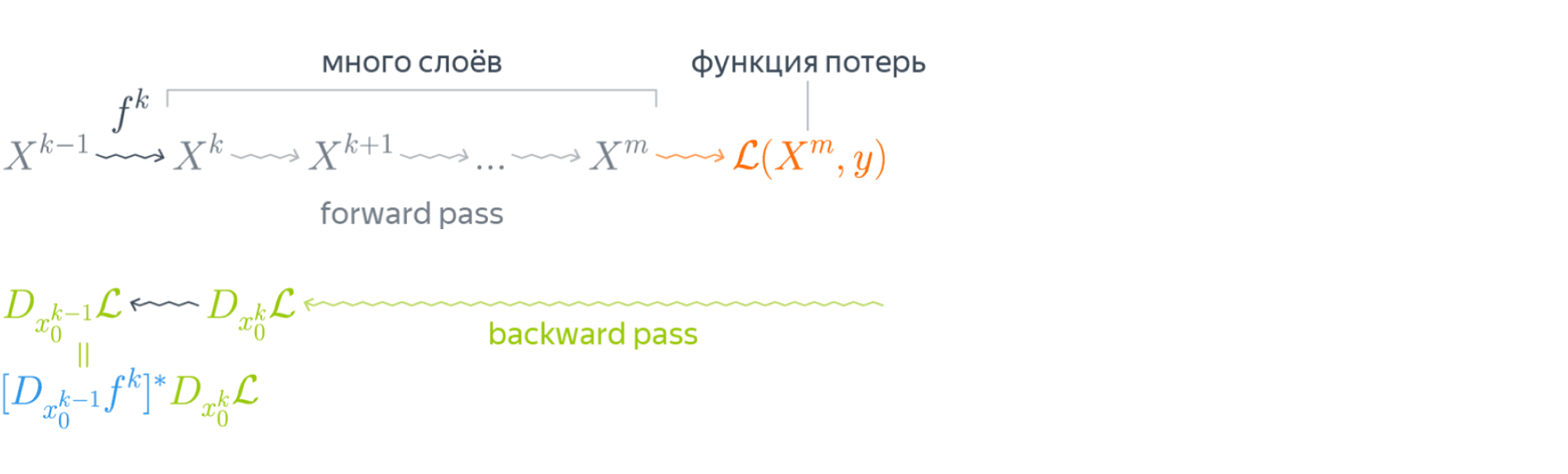
Эта формула — сердце механизма обратного распространения ошибки. Она говорит следующее: если мы каким-то образом получили градиент функции потерь по переменным из некоторого промежуточного представления $X^k$ нейронной сети и при этом знаем, как преобразуется градиент при проходе через слой $f^k$ между $X^{k-1}$ и $X^k$ (то есть как выглядит сопряжённое к дифференциалу слоя между ними отображение), то мы сразу же находим градиент и по переменным из $X^{k-1}$:
Таким образом слой за слоем мы посчитаем градиенты по всем $X^i$ вплоть до самых первых слоёв.
Далее мы разберёмся, как именно преобразуются градиенты при переходе через некоторые распространённые слои.
Градиенты для типичных слоёв
Рассмотрим несколько важных примеров.
Примеры
-
$f(x) = u(v(x))$, где $x$ — вектор, а $v(x)$ – поэлементное применение $v$:
$$vbegin{pmatrix}
x_1 \
vdots\
x_N
end{pmatrix}
= begin{pmatrix}
v(x_1)\
vdots\
v(x_N)
end{pmatrix}$$Тогда, как мы знаем,
$$left[D_{x_0} fright] (h) = langlenabla_{x_0} f, hrangle = left[nabla_{x_0} fright]^T h.$$
Следовательно,
$$
left[D_{v(x_0)} uright] left( left[ D_{x_0} vright] (h)right) = left[nabla_{v(x_0)} uright]^T left(v'(x_0) odot hright) =\
$$$$
= sumlimits_i left[nabla_{v(x_0)} uright]_i v'(x_{0i})h_i
= langleleft[nabla_{v(x_0)} uright] odot v'(x_0), hrangle.
,$$где $odot$ означает поэлементное перемножение. Окончательно получаем
$$color{#348FEA}{nabla_{x_0} f = left[nabla_{v(x_0)}uright] odot v'(x_0) = v'(x_0) odot left[nabla_{v(x_0)} uright]}$$
Отметим, что если $x$ и $h(x)$ — это просто векторы, то мы могли бы вычислять всё и по формуле $frac{partial f}{partial x_i} = sum_jbig(frac{partial z_j}{partial x_i}big)cdotbig(frac{partial h}{partial z_j}big)$. В этом случае матрица $big(frac{partial z_j}{partial x_i}big)$ была бы диагональной (так как $z_j$ зависит только от $x_j$: ведь $h$ берётся поэлементно), и матричное умножение приводило бы к тому же результату. Однако если $x$ и $h(x)$ — матрицы, то $big(frac{partial z_j}{partial x_i}big)$ представлялась бы уже «четырёхмерным кубиком», и работать с ним было бы ужасно неудобно.
-
$f(X) = g(XW)$, где $X$ и $W$ — матрицы. Как мы знаем,
$$left[D_{X_0} f right] (X-X_0) = text{tr}, left(left[nabla_{X_0} fright]^T (X-X_0)right).$$
Тогда
$$
left[ D_{X_0W} g right] left(left[D_{X_0} left( ast Wright)right] (H)right) =
left[ D_{X_0W} g right] left(HWright)=\
$$ $$
= text{tr}, left( left[nabla_{X_0W} g right]^T cdot (H) W right) =\
$$ $$
=
text{tr} , left(W left[nabla_{X_0W} (g) right]^T cdot (H)right) = text{tr} , left( left[left[nabla_{X_0W} gright] W^Tright]^T (H)right)
$$Здесь через $ast W$ мы обозначили отображение $Y hookrightarrow YW$, а в предпоследнем переходе использовалось следующее свойство следа:
$$
text{tr} , (A B C) = text{tr} , (C A B),
$$где $A, B, C$ — произвольные матрицы подходящих размеров (то есть допускающие перемножение в обоих приведённых порядках). Следовательно, получаем
$$color{#348FEA}{nabla_{X_0} f = left[nabla_{X_0W} (g) right] cdot W^T}$$
-
$f(W) = g(XW)$, где $W$ и $X$ — матрицы. Для приращения $H = W — W_0$ имеем
$$
left[D_{W_0} f right] (H) = text{tr} , left( left[nabla_{W_0} f right]^T (H)right)
$$Тогда
$$
left[D_{XW_0} g right] left( left[D_{W_0} left(X astright) right] (H)right) = left[D_{XW_0} g right] left( XH right) =
$$ $$
= text{tr} , left( left[nabla_{XW_0} g right]^T cdot X (H)right) =
text{tr}, left(left[X^T left[nabla_{XW_0} g right] right]^T (H)right)
$$Здесь через $X ast$ обозначено отображение $Y hookrightarrow XY$. Значит,
$$color{#348FEA}{nabla_{X_0} f = X^T cdot left[nabla_{XW_0} (g)right]}$$
-
$f(X) = g(softmax(X))$, где $X$ — матрица $Ntimes K$, а $softmax$ — функция, которая вычисляется построчно, причём для каждой строки $x$
$$softmax(x) = left(frac{e^{x_1}}{sum_te^{x_t}},ldots,frac{e^{x_K}}{sum_te^{x_t}}right)$$
В этом примере нам будет удобно воспользоваться формализмом с частными производными. Сначала вычислим $frac{partial s_l}{partial x_j}$ для одной строки $x$, где через $s_l$ мы для краткости обозначим $softmax(x)_l = frac{e^{x_l}} {sum_te^{x_t}}$. Нетрудно проверить, что
$$frac{partial s_l}{partial x_j} = begin{cases}
s_j(1 — s_j), & j = l,
-s_ls_j, & jne l
end{cases}$$Так как softmax вычисляется независимо от каждой строчки, то
$$frac{partial s_{rl}}{partial x_{ij}} = begin{cases}
s_{ij}(1 — s_{ij}), & r=i, j = l,
-s_{il}s_{ij}, & r = i, jne l,
0, & rne i
end{cases},$$где через $s_{rl}$ мы обозначили для краткости $softmax(X)_{rl}$.
Теперь пусть $nabla_{rl} = nabla g = frac{partialmathcal{L}}{partial s_{rl}}$ (пришедший со следующего слоя, уже известный градиент). Тогда
$$frac{partialmathcal{L}}{partial x_{ij}} = sum_{r,l}frac{partial s_{rl}}{partial x_{ij}} nabla_{rl}$$
Так как $frac{partial s_{rl}}{partial x_{ij}} = 0$ при $rne i$, мы можем убрать суммирование по $r$:
$$ldots = sum_{l}frac{partial s_{il}}{partial x_{ij}} nabla_{il} = -s_{i1}s_{ij}nabla_{i1} — ldots + s_{ij}(1 — s_{ij})nabla_{ij}-ldots — s_{iK}s_{ij}nabla_{iK} =$$
$$= -s_{ij}sum_t s_{it}nabla_{it} + s_{ij}nabla_{ij}$$
Таким образом, если мы хотим продифференцировать $f$ в какой-то конкретной точке $X_0$, то, смешивая математические обозначения с нотацией Python, мы можем записать:
$$begin{multline*}
color{#348FEA}{nabla_{X_0}f =}\
color{#348FEA}{= -softmax(X_0) odot text{sum}left(
softmax(X_0)odotnabla_{softmax(X_0)}g, text{ axis = 1}
right) +}\
color{#348FEA}{softmax(X_0)odot nabla_{softmax(X_0)}g}
end{multline*}
$$
Backpropagation в общем виде
Подытожим предыдущее обсуждение, описав алгоритм error backpropagation (алгоритм обратного распространения ошибки). Допустим, у нас есть текущие значения весов $W^i_0$ и мы хотим совершить шаг SGD по мини-батчу $X$. Мы должны сделать следующее:
- Совершить forward pass, вычислив и запомнив все промежуточные представления $X = X^0, X^1, ldots, X^m = widehat{y}$.
- Вычислить все градиенты с помощью backward pass.
- С помощью полученных градиентов совершить шаг SGD.
Проиллюстрируем алгоритм на примере двуслойной нейронной сети со скалярным output’ом. Для простоты опустим свободные члены в линейных слоях.
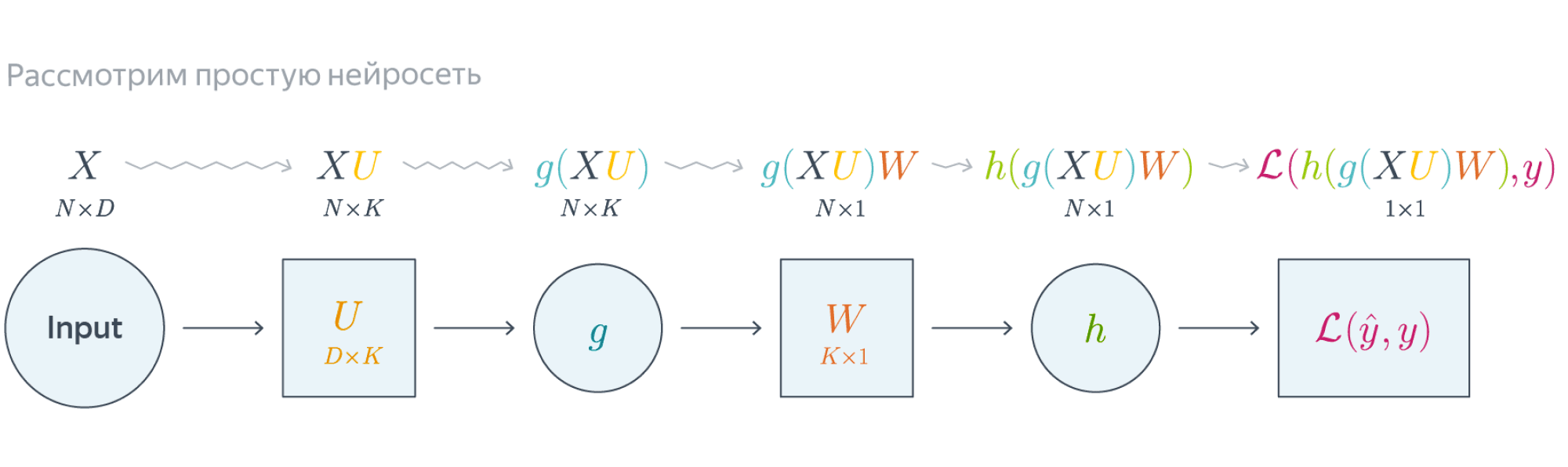
$$nabla_{W_0}mathcal{L} = nabla_{W_0}{left({vphantom{frac12}mathcal{L}circ hcircleft[Wmapsto g(XU_0)Wright]}right)}=$$
$$=g(XU_0)^Tnabla_{g(XU_0)W_0}(mathcal{L}circ h) = underbrace{g(XU_0)^T}_{ktimes N}cdot
left[vphantom{frac12}underbrace{h’left(vphantom{int_0^1}g(XU_0)W_0right)}_{Ntimes 1}odot
underbrace{nabla_{hleft(vphantom{int_0^1}g(XU_0)W_0right)}mathcal{L}}_{Ntimes 1}right]$$
Итого матрица $ktimes 1$, как и $W_0$
$$nabla_{U_0}mathcal{L} = nabla_{U_0}left(vphantom{frac12}
mathcal{L}circ hcircleft[Ymapsto YW_0right]circ gcircleft[ Umapsto XUright]
right)=$$
$$=X^Tcdotnabla_{XU^0}left(vphantom{frac12}mathcal{L}circ hcirc [Ymapsto YW_0]circ gright) =$$
$$=X^Tcdotleft(vphantom{frac12}g'(XU_0)odot
nabla_{g(XU_0)}left[vphantom{in_0^1}mathcal{L}circ hcirc[Ymapsto YW_0right]
right)$$
$$=ldots = underset{Dtimes N}{X^T}cdotleft(vphantom{frac12}
underbrace{g'(XU_0)}_{Ntimes K}odot
underbrace{left[vphantom{int_0^1}left(
underbrace{h’left(vphantom{int_0^1}g(XU_0)W_0right)}_{Ntimes1}odotunderbrace{nabla_{h(vphantom{int_0^1}gleft(XU_0right)W_0)}mathcal{L}}_{Ntimes 1}
right)cdot underbrace{W^T}_{1times K}right]}_{Ntimes K}
right)$$
Итого $Dtimes K$, как и $U_0$
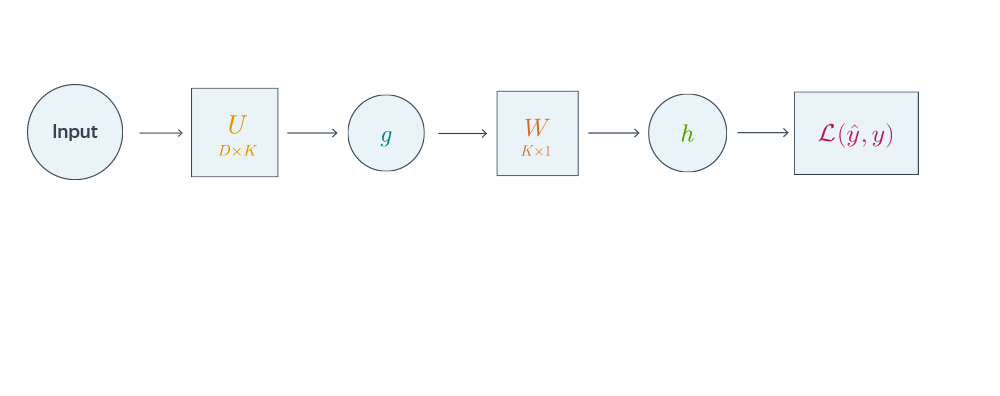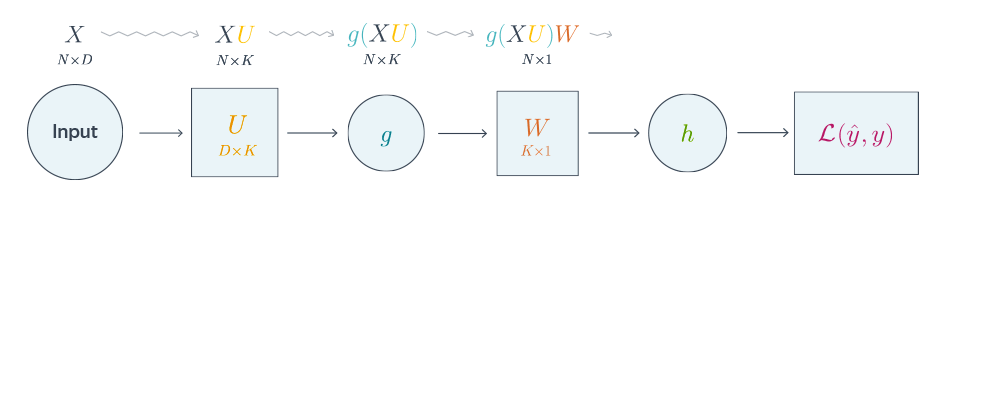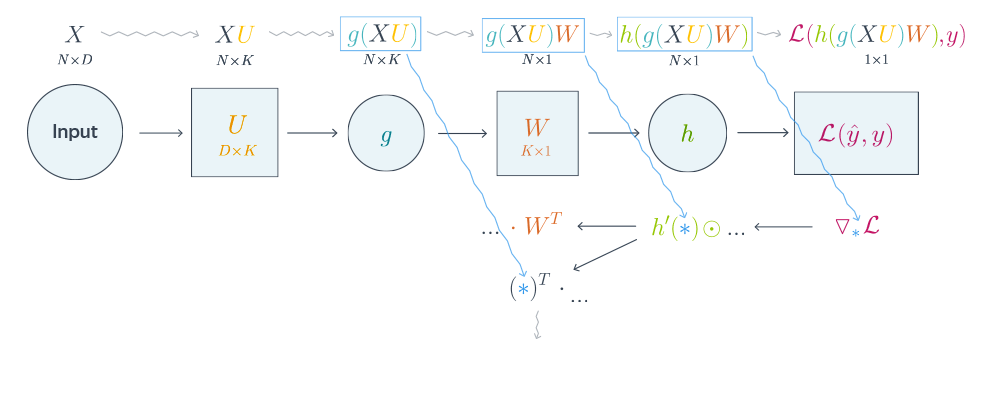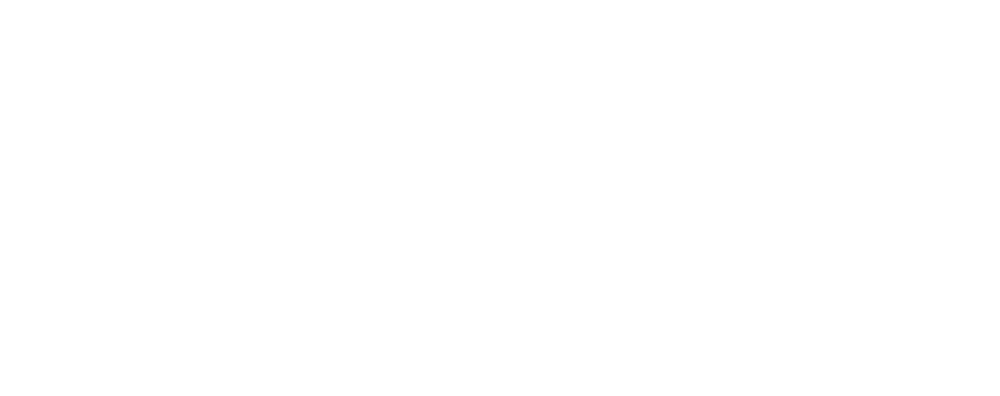
Схематически это можно представить следующим образом:
Backpropagation для двуслойной нейронной сети
Подробнее о предыдущих вычисленияхЕсли вы не уследили за вычислениями в предыдущем примере, давайте более подробно разберём его чуть более конкретную версию (для $g = h = sigma$).
Рассмотрим двуслойную нейронную сеть для классификации. Мы уже встречали ее ранее при рассмотрении линейно неразделимой выборки. Предсказания получаются следующим образом:
$$
widehat{y} = sigma(X^1 W^2) = sigmaBig(big(sigma(X^0 W^1 )big) W^2 Big).
$$
Пусть $W^1_0$ и $W^2_0$ — текущее приближение матриц весов. Мы хотим совершить шаг по градиенту функции потерь, и для этого мы должны вычислить её градиенты по $W^1$ и $W^2$ в точке $(W^1_0, W^2_0)$.
Прежде всего мы совершаем forward pass, в ходе которого мы должны запомнить все промежуточные представления: $X^1 = X^0 W^1_0$, $X^2 = sigma(X^0 W^1_0)$, $X^3 = sigma(X^0 W^1_0) W^2_0$, $X^4 = sigma(sigma(X^0 W^1_0) W^2_0) = widehat{y}$. Они понадобятся нам дальше.
Для полученных предсказаний вычисляется значение функции потерь:
$$
l = mathcal{L}(y, widehat{y}) = y log(widehat{y}) + (1-y) log(1-widehat{y}).
$$
Дальше мы шаг за шагом будем находить производные по переменным из всё более глубоких слоёв.
-
Градиент $mathcal{L}$ по предсказаниям имеет вид
$$
nabla_{widehat{y}}l = frac{y}{widehat{y}} — frac{1 — y}{1 — widehat{y}} = frac{y — widehat{y}}{widehat{y} (1 — widehat{y})},
$$где, напомним, $ widehat{y} = sigma(X^3) = sigmaBig(big(sigma(X^0 W^1_0 )big) W^2_0 Big)$ (обратите внимание на то, что $W^1_0$ и $W^2_0$ тут именно те, из которых мы делаем градиентный шаг).
-
Следующий слой — поэлементное взятие $sigma$. Как мы помним, при переходе через него градиент поэлементно умножается на производную $sigma$, в которую подставлено предыдущее промежуточное представление:
$$
nabla_{X^3}l = sigma'(X^3)odotnabla_{widehat{y}}l = sigma(X^3)left( 1 — sigma(X^3) right) odot frac{y — widehat{y}}{widehat{y} (1 — widehat{y})} =
$$$$
= sigma(X^3)left( 1 — sigma(X^3) right) odot frac{y — sigma(X^3)}{sigma(X^3) (1 — sigma(X^3))} =
y — sigma(X^3)
$$ -
Следующий слой — умножение на $W^2_0$. В этот момент мы найдём градиент как по $W^2$, так и по $X^2$. При переходе через умножение на матрицу градиент, как мы помним, умножается с той же стороны на транспонированную матрицу, а значит:
$$
color{blue}{nabla_{W^2_0}l} = (X^2)^Tcdot nabla_{X^3}l = (X^2)^Tcdot(y — sigma(X^3)) =
$$$$
= color{blue}{left( sigma(X^0W^1_0) right)^T cdot (y — sigma(sigma(X^0W^1_0)W^2_0))}
$$Аналогичным образом
$$
nabla_{X^2}l = nabla_{X^3}lcdot (W^2_0)^T = (y — sigma(X^3))cdot (W^2_0)^T =
$$$$
= (y — sigma(X^2W_0^2))cdot (W^2_0)^T
$$ -
Следующий слой — снова взятие $sigma$.
$$
nabla_{X^1}l = sigma'(X^1)odotnabla_{X^2}l = sigma(X^1)left( 1 — sigma(X^1) right) odot left( (y — sigma(X^2W_0^2))cdot (W^2_0)^T right) =
$$$$
= sigma(X^1)left( 1 — sigma(X^1) right) odotleft( (y — sigma(sigma(X^1)W_0^2))cdot (W^2_0)^T right)
$$ -
Наконец, последний слой — это умножение $X^0$ на $W^1_0$. Тут мы дифференцируем только по $W^1$:
$$
color{blue}{nabla_{W^1_0}l} = (X^0)^Tcdot nabla_{X^1}l = (X^0)^Tcdot big( sigma(X^1) left( 1 — sigma(X^1) right) odot (y — sigma(sigma(X^1)W_0^2))cdot (W^2_0)^Tbig) =
$$$$
= color{blue}{(X^0)^Tcdotbig(sigma(X^0W^1_0)left( 1 — sigma(X^0W^1_0) right) odot (y — sigma(sigma(X^0W^1_0)W_0^2))cdot (W^2_0)^Tbig) }
$$
Итоговые формулы для градиентов получились страшноватыми, но они были получены друг из друга итеративно с помощью очень простых операций: матричного и поэлементного умножения, в которые порой подставлялись значения заранее вычисленных промежуточных представлений.
Автоматизация и autograd
Итак, чтобы нейросеть обучалась, достаточно для любого слоя $f^k: X^{k-1}mapsto X^k$ с параметрами $W^k$ уметь:
- превращать $nabla_{X^k_0}mathcal{L}$ в $nabla_{X^{k-1}_0}mathcal{L}$ (градиент по выходу в градиент по входу);
- считать градиент по его параметрам $nabla_{W^k_0}mathcal{L}$.
При этом слою совершенно не надо знать, что происходит вокруг. То есть слой действительно может быть запрограммирован как отдельная сущность, умеющая внутри себя делать forward pass и backward pass, после чего слои механически, как кубики в конструкторе, собираются в большую сеть, которая сможет работать как одно целое.
Более того, во многих случаях авторы библиотек для глубинного обучения уже о вас позаботились и создали средства для автоматического дифференцирования выражений (autograd). Поэтому, программируя нейросеть, вы почти всегда можете думать только о forward-проходе, прямом преобразовании данных, предоставив библиотеке дифференцировать всё самостоятельно. Это делает код нейросетей весьма понятным и выразительным (да, в реальности он тоже бывает большим и страшным, но сравните на досуге код какой-нибудь разухабистой нейросети и код градиентного бустинга на решающих деревьях и почувствуйте разницу).
Но это лишь начало
Метод обратного распространения ошибки позволяет удобно посчитать градиенты, но дальше с ними что-то надо делать, и старый добрый SGD едва ли справится с обучением современной сетки. Так что же делать? О некоторых приёмах мы расскажем в следующей главе.
Рад снова всех приветствовать, и сегодня продолжим планомерно двигаться в выбранном направлении. Речь, конечно, о масштабном разборе искусственных нейронных сетей для решения широкого спектра задач. Продолжим ровно с того момента, на котором остановились в предыдущей части, и это означает, что героем данного поста будет ключевой процесс — обучение нейронных сетей.
- Градиентный спуск
- Функция ошибки
- Метод обратного распространения ошибки
- Пример расчета
Тема эта крайне важна, поскольку именно процесс обучения позволяет сети начать выполнять задачу, для которой она, собственно, и предназначена. То есть нейронная сеть функционирует не по какому-либо жестко заданному на этапе проектирования алгоритму, она совершенствуется в процессе анализа имеющихся данных. Этот процесс и называется обучением нейронной сети. Математически суть процесса обучения заключается в корректировке значений весов синапсов (связей между имеющимися нейронами). Изначально значения весов задаются случайно, затем производится обучение, результатом которого будут новые значения синаптических весов. Это все мы максимально подробно разберем как раз в этой статье.
На своем сайте я всегда придерживаюсь концепции, при которой теоретические выкладки по максимуму сопровождаются практическими примерами для максимальной наглядности. Так мы поступим и сейчас 👍
Итак, суть заключается в следующем. Пусть у нас есть простейшая нейронная сеть, которую мы хотим обучить (продолжаем рассматривать сети прямого распространения):

То есть на входы нейронов I1 и I2 мы подаем какие-либо числа, а на выходе сети получаем соответственно новое значение. При этом нам необходима некая выборка данных, включающая в себя значения входов и соответствующее им, правильное, значение на выходе:
| bold{I_1} | bold{I_2} | bold{O_{net}} |
|---|---|---|
| x_{11} | x_{12} | y_{1} |
| x_{21} | x_{22} | y_{2} |
| x_{31} | x_{32} | y_{3} |
| … | … | … |
| x_{N1} | x_{N2} | y_{N} |
Допустим, сеть выполняет суммирование значений на входе, тогда данный набор данных может быть таким:
| bold{I_1} | bold{I_2} | bold{O_{net}} |
|---|---|---|
| 1 | 4 | 5 |
| 2 | 7 | 9 |
| 3 | 5 | 8 |
| … | … | … |
| 1000 | 1500 | 2500 |
Эти значения и используются для обучения сети. Как именно — рассмотрим чуть ниже, пока сконцентрируемся на идее процесса в целом. Для того, чтобы иметь возможность тестировать работу сети в процессе обучения, исходную выборку данных делят на две части — обучающую и тестовую. Пусть имеется 1000 образцов, тогда можно 900 использовать для обучения, а оставшиеся 100 — для тестирования. Эти величины взяты исключительно ради наглядности и демонстрации логики выполнения операций, на практике все зависит от задачи, размер обучающей выборки может спокойно достигать и сотен тысяч образцов.
Итак, итог имеем следующий — обучающая выборка прогоняется через сеть, в результате чего происходит настройка значений синаптических весов. Один полный проход по всей выборке называется эпохой. И опять же, обучение нейронной сети — это процесс, требующий многократных экспериментов, анализа результатов и творческого подхода. Все перечисленные параметры (размер выборки, количество эпох обучения) могут иметь абсолютно разные значения для разных задач и сетей. Четкого правила тут просто нет, в этом и кроется дополнительный шарм и изящность )
Возвращаемся к разбору, и в результате прохода обучающей выборки через сеть мы получаем сеть с новыми значениями весов синапсов.
Далее мы через эту, уже обученную в той или иной степени, сеть прогоняем тестовую выборку, которая не участвовала в обучении. При этом сеть выдает нам выходные значения для каждого образца, которые мы сравниваем с теми верными значениями, которые имеем.
Анализируем нашу гипотетическую выборку:

Таким образом, для тестирования подаем на вход сети значения x_{(M+1)1}, x_{(M+1)2} и проверяем, чему равен выход, ожидаем очевидно значение y_{(M+1)}. Аналогично поступаем и для оставшихся тестовых образцов. После чего мы можем сделать вывод, успешно или нет работает сеть. Например, сеть дает правильный ответ для 90% тестовых данных, дальше уже встает вопрос — устраивает ли нас данная точность или процесс обучения необходимо повторить, либо провести заново, изменив какие-либо параметры сети.
В этом и заключается суть обучения нейронных сетей, теперь перейдем к деталям и конкретным действиям, которые необходимо осуществить для выполнения данного процесса. Двигаться снова будем поэтапно, чтобы сформировать максимально четкую и полную картину. Поэтому начнем с понятия градиентного спуска, который используется при обучении по методу обратного распространения ошибки. Обо всем этом далее…
Обучение нейронных сетей. Градиентный спуск.
Рассмотрев идею процесса обучения в целом, на данном этапе мы можем однозначно сформулировать текущую цель — необходимо определить математический алгоритм, который позволит рассчитать значения весовых коэффициентов таким образом, чтобы ошибка сети была минимальна. То есть грубо говоря нам необходима конкретная формула для вычисления:
Здесь Delta w_{ij} — величина, на которую необходимо изменить вес синапса, связывающего нейроны i и j нашей сети. Соответственно, зная это, необходимо на каждом этапе обучения производить корректировку весов связей между всеми элементами нейронной сети. Задача ясна, переходим к делу.
Пусть функция ошибки от веса имеет следующий вид:
Для удобства рассмотрим зависимость функции ошибки от одного конкретного веса:

В начальный момент мы находимся в некоторой точке кривой, а для минимизации ошибки попасть мы хотим в точку глобального минимума функции:
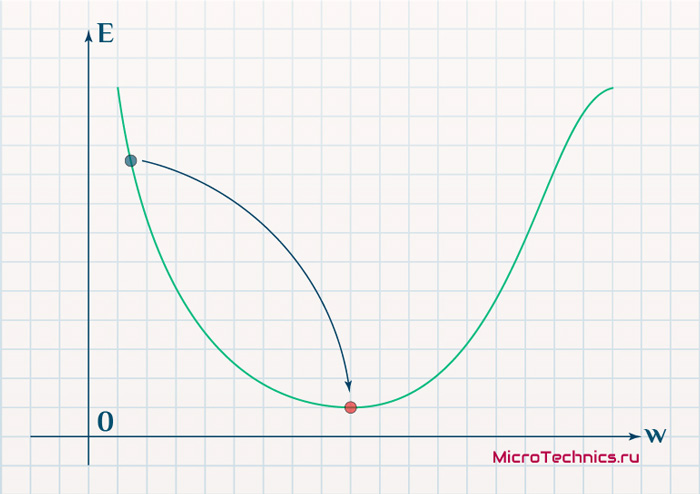
Нанесем на график вектора градиентов в разных точках. Длина векторов численно равна скорости роста функции в данной точке, что в свою очередь соответствует значению производной функции по данной точке. Исходя из этого, делаем вывод, что длина вектора градиента определяется крутизной функции в данной точке:
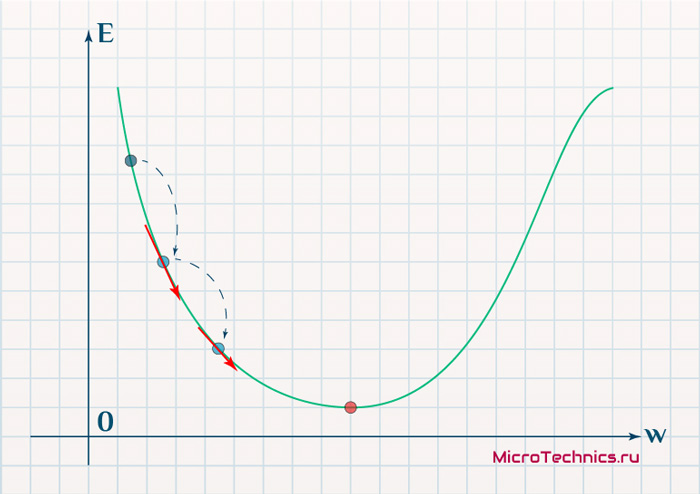
Вывод прост — величина градиента будет уменьшаться по мере приближения к минимуму функции. Это важный вывод, к которому мы еще вернемся. А тем временем разберемся с направлением вектора, для чего рассмотрим еще несколько возможных точек:
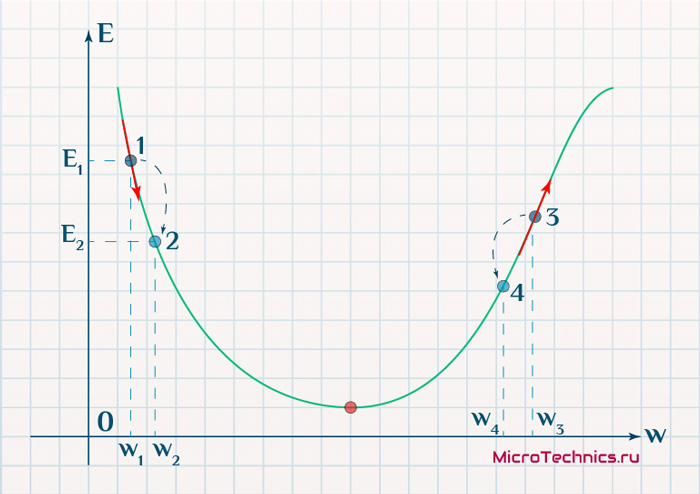
Находясь в точке 1, целью является перейти в точку 2, поскольку в ней значение ошибки меньше (E_2 < E_1), а глобальная задача по-прежнему заключается в ее минимизации. Для этого необходимо изменить величину w на некое значение Delta w (Delta w = w_2 — w_1 > 0). При всем при этом в точке 1 градиент отрицательный. Фиксируем данные факты и переходим к точке 3, предположим, что мы находимся именно в ней.
Тогда для уменьшения ошибки наш путь лежит в точку 4, а необходимое изменение значения: Delta w = w_4 — w_3 < 0. Градиент же в точке 3 положителен. Этот факт также фиксируем.
А теперь соберем воедино эту информацию в виде следующей иллюстрации:
| Переход | bold{Delta w} | Знак bold{Delta w} | Градиент |
|---|---|---|---|
| 1 rArr 2 | w_2 — w_1 | + | — |
| 3 rArr 4 | w_4 — w_3 | — | + |
Вывод напрашивается сам собой — величина, на которую необходимо изменить значение w, в любой точке противоположна по знаку градиенту. И, таким образом, представим эту самую величину в виде:
Delta w = -alpha cdot frac{dE}{dw}
Имеем в наличии:
- Delta w — величина, на которую необходимо изменить значение w.
- frac{dE}{dw} — градиент в этой точке.
- alpha — скорость обучения.
Собственно, логика метода градиентного спуска и заключается в данном математическом выражении, а именно в том, что для минимизации ошибки необходимо изменять w в направлении противоположном градиенту. В контексте нейронных сетей имеем искомый закон для корректировки весов синаптических связей (для синапса между нейронами i и j):
Delta w_{ij} = -alpha cdot frac{dE}{dw_{ij}}
Более того, вспомним о важном свойстве, которое мы отдельно пометили. И заключается оно в том, что величина градиента будет уменьшаться по мере приближения к минимуму функции. Что это нам дает? А то, что в том случае, если наша текущая дислокация далека от места назначения, то величина, корректирующая вес связи, будет больше. А это обеспечит скорейшее приближение к цели. При приближении к целевому пункту, величина frac{dE}{dw_{ij}} будет уменьшаться, что поможет нам точнее попасть в нужную точку, а кроме того, не позволит нам ее проскочить. Визуализируем вышеописанное:
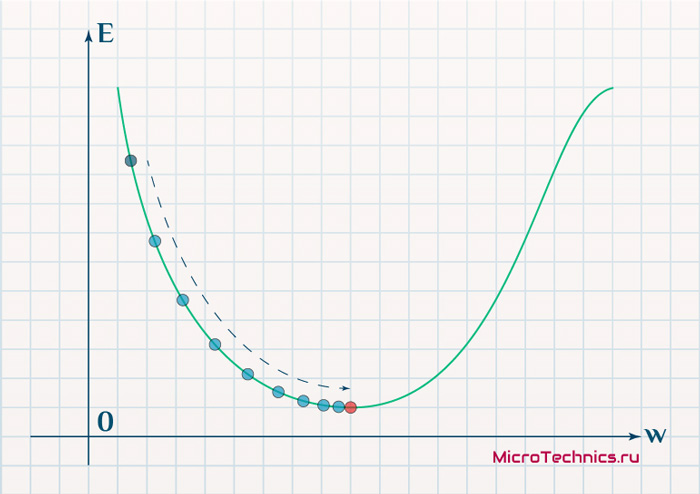
Скорость же обучения несет в себе следующий смысл. Она определяет величину каждого шага при поиске минимума ошибки. Слишком большое значение приводит к тому, что точка может «перепрыгнуть» через нужное значение и оказаться по другую сторону от цели:
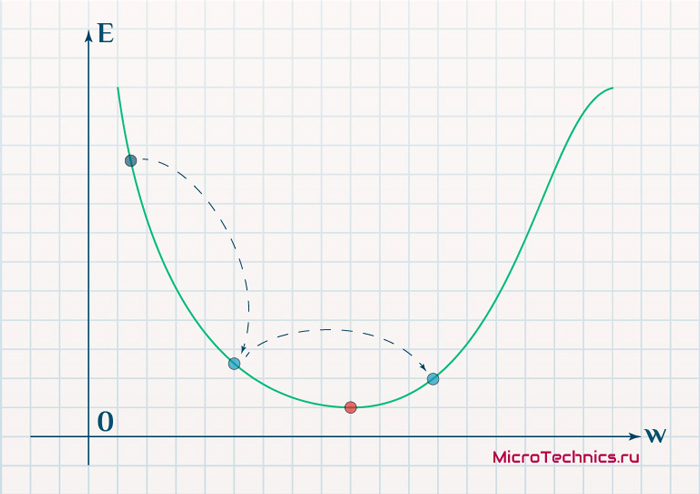
Если же величина будет мала, то это приведет к тому, что спуск будет осуществляться очень медленно, что также является нежелательным эффектом. Поэтому скорость обучения, как и многие другие параметры нейронной сети, является очень важной величиной, для которой нет единственно верного значения. Все снова зависит от конкретного случая и оптимальная величина определяется исключительно исходя из текущих условий.
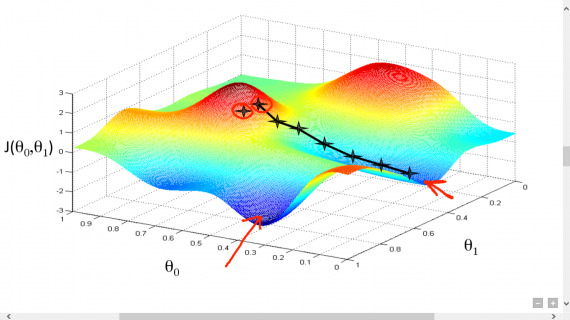
И даже на этом еще не все, здесь присутствует один важный нюанс, который в большинстве статей опускается, либо вовсе не упоминается. Реальная зависимость может иметь совсем другой вид:
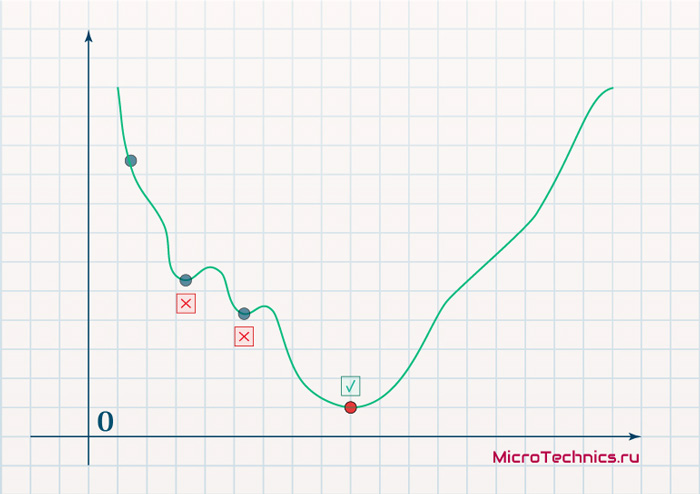
Из чего вытекает потенциальная возможность попадания в локальный минимум, вместо глобального, что является большой проблемой. Для предотвращения данного эффекта вводится понятие момента обучения и формула принимает следующий вид:
Delta w_{ij} = -alpha cdot frac{dE}{dw_{ij}} + gamma cdot Delta w_{ij}^{t - 1}
То есть добавляется второе слагаемое, которое представляет из себя произведение момента на величину корректировки веса на предыдущем шаге.
Итого, резюмируем продвижение к цели:
- Нашей задачей было найти закон, по которому необходимо изменять величину весов связей между нейронами.
- Наш результат — Delta w_{ij} = -alpha cdot frac{dE}{dw_{ij}} + gamma cdot Delta w_{ij}^{t — 1} — именно то, что и требовалось 👍
И опять же, полученный результат логичным образом перенаправляет нас на следующий этап, ставя вопросы — что из себя представляет функция ошибки, и как определить ее градиент.
Обучение нейронных сетей. Функция ошибки.
Начнем с того, что определимся с тем, что у нас в наличии, для этого вернемся к конкретной нейронной сети. Пусть вид ее таков:
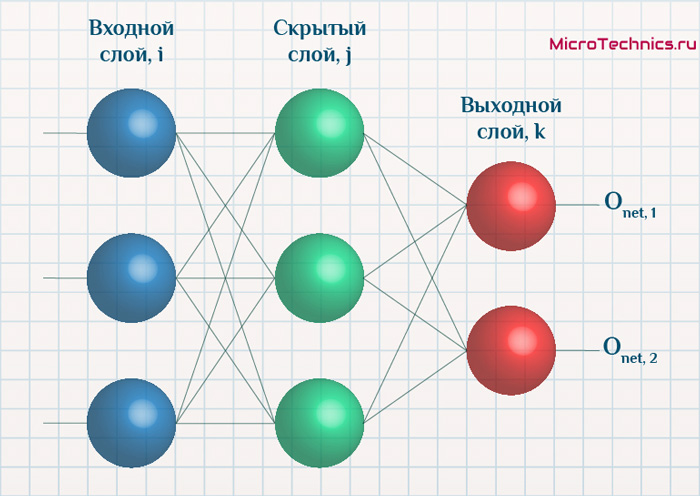
Интересует нас, в первую очередь, часть, относящаяся к нейронам выходного слоя. Подав на вход определенные значения, получаем значения на выходе сети: O_{net, 1} и O_{net, 2}. Кроме того, поскольку мы ведем речь о процессе обучения нейронной сети, то нам известны целевые значения: O_{correct, 1} и O_{correct, 2}. И именно этот набор данных на этом этапе является для нас исходным:
- Известно: O_{net, 1}, O_{net, 2}, O_{correct, 1} и O_{correct, 2}.
- Необходимо определить величины Delta w_{ij} для корректировки весов, для этого нужно вычислить градиенты (frac{dE}{dw_{ij}}) для каждого из синапсов.
Полдела сделано — задача четко сформулирована, начинаем деятельность по поиску решения.
В плане того, как определять ошибку, первым и самым очевидным вариантом кажется простая алгебраическая разность. Для каждого из выходных нейронов:
E_k = O_{correct, k} - O_{net, k}
Дополним пример числовыми значениями:
| Нейрон | bold{O_{net}} | bold{O_{correct}} | bold{E} |
|---|---|---|---|
| 1 | 0.9 | 0.5 | -0.4 |
| 2 | 0.2 | 0.6 | 0.4 |
Недостатком данного варианта является то, что в том случае, если мы попытаемся просуммировать ошибки нейронов, то получим:
E_{sum} = e_1 + e_2 = -0.4 + 0.4 = 0
Что не соответствует действительности (нулевая ошибка, говорит об идеальной работе нейронной сети, по факту оба нейрона дали неверный результат). Так что вариант с разностью откидываем за несостоятельностью.
Вторым, традиционно упоминаемым, методом вычисления ошибки является использование модуля разности:
E_k = | O_{correct, k} - O_{net, k} |
Тут в действие вступает уже проблема иного рода:
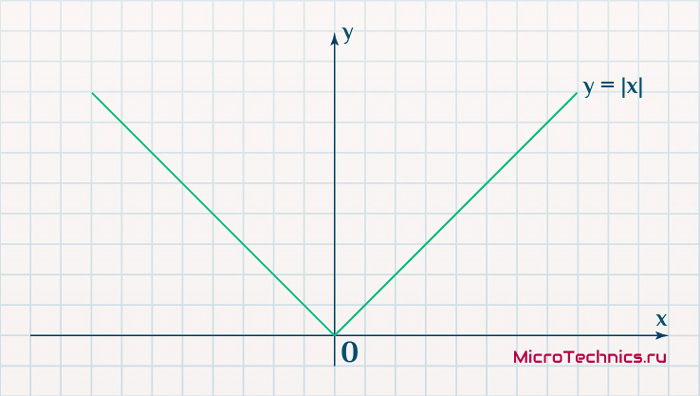
Функция, бесспорно, симпатична, но при приближении к минимуму ее градиент является постоянной величиной, скачкообразно меняясь при переходе через точку минимума. Это нас также не устраивает, поскольку, как мы обсуждали, концепция заключалась в том числе в том, чтобы по мере приближения к минимуму значение градиента уменьшалось.
В итоге хороший результат дает зависимость (для выходного нейрона под номером k):
E_k = (O_{correct, k} - O_{net, k})^2
Функция по многим своим свойствам идеально удовлетворяет нуждам обучения нейронной сети, так что выбор сделан, остановимся на ней. Хотя, как и во многих аспектах, качающихся нейронных сетей, данное решение не является единственно и неоспоримо верным. В каких-то случаях лучше себя могут проявить другие зависимости, возможно, что какой-то вариант даст большую точность, но неоправданно высокие затраты производительности при обучении. В общем, непаханное поле для экспериментов и исследований, это и привлекательно.
Краткий вывод промежуточного шага, на который мы вышли:
- Имеющееся: frac{dE}{dw_{jk}} = frac{d}{d w_{jk}}(O_{correct, k} — O_{net, k})^2.
- Искомое по-прежнему: Delta w_{jk}.
Несложные диффернциально-математические изыскания выводят на следующий результат:
frac{dE}{d w_{jk}} = -(O_{correct, k} - O_{net, k}) cdot f{Large{prime}}(sum_{j}w_{jk}O_j) cdot O_j
Здесь эти самые изыскания я все-таки решил не вставлять, дабы не перегружать статью, которая и так выходит объемной. Но в случае необходимости и интереса, отпишите в комментарии, я добавлю вычисления и закину их под спойлер, как вариант.
Освежим в памяти структуру сети:
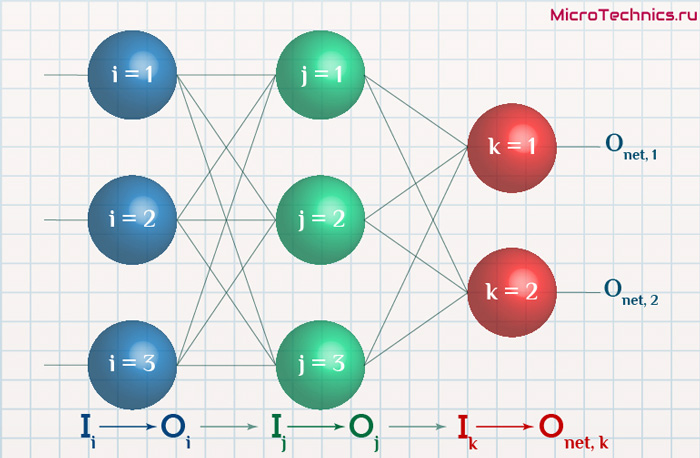
Формулу можно упростить, сгруппировав отдельные ее части:
- (O_{correct, k} — O_{net, k}) cdot f{Large{prime}}(sum_{j}w_{jk}O_j) — ошибка нейрона k.
- O_j — тут все понятно, выходной сигнал нейрона j.
f{Large{prime}}(sum_{j}w_{jk}O_j) — значение производной функции активации. Причем, обратите внимание, что sum_{j}w_{jk}O_j — это не что иное, как сигнал на входе нейрона k (I_{k}). Тогда для расчета ошибки выходного нейрона: delta_k = (O_{correct, k} — O_{net, k}) cdot f{Large{prime}}(I_k).
Итог: frac{dE}{d w_{jk}} = -delta_k cdot O_j.
Одной из причин популярности сигмоидальной функции активности является то, что ее производная очень просто выражается через саму функцию:
f{'}(x) = f(x)medspace (1medspace-medspace f(x))
Данные алгебраические вычисления справедливы для корректировки весов между скрытым и выходным слоем, поскольку для расчета ошибки мы используем просто разность между целевым и полученным результатом, умноженную на производную.
Для других слоев будут незначительные изменения, касающиеся исключительно первого множителя в формуле:
frac{dE}{d w_{ij}} = -delta_j cdot O_i
Который примет следующий вид:
delta_j = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_j)
То есть ошибка для элемента слоя j получается путем взвешенного суммирования ошибок, «приходящих» к нему от нейронов следующего слоя и умножения на производную функции активации. В результате:
frac{dE}{d w_{ij}} = -(sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_j) cdot O_i
Снова подводим промежуточный итог, чтобы иметь максимально полную и структурированную картину происходящего. Вот результаты, полученные нами на двух этапах, которые мы успешно миновали:
- Ошибка:
- выходной слой: delta_k = (O_{correct, k} — O_{net, k}) cdot f{Large{prime}}(I_k)
- скрытые слои: delta_j = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_j)
- Градиент: frac{dE}{d w_{ij}} = -delta_j cdot O_i
- Корректировка весовых коэффициентов: Delta w_{ij} = -alpha cdot frac{dE}{dw_{ij}} + gamma cdot Delta w_{ij}^{t — 1}
Преобразуем последнюю формулу:
Delta w_{ij} = alpha cdot delta_j cdot O_i + gamma cdot Delta w_{ij}^{t - 1}
Из этого мы делаем вывод, что на данный момент у нас есть все, что необходимо для того, чтобы произвести обучение нейронной сети. И героем следующего подраздела будет алгоритм обратного распространения ошибки.
Метод обратного распространения ошибки.
Данный метод является одним из наиболее распространенных и популярных, чем и продиктован его выбор для анализа и разбора. Алгоритм обратного распространения ошибки относится к методам обучение с учителем, что на деле означает необходимость наличия целевых значений в обучающих сетах.
Суть же метода подразумевает наличие двух этапов:
- Прямой проход — входные сигналы двигаются в прямом направлении, в результате чего мы получаем выходной сигнал, из которого в дальнейшем рассчитываем значение ошибки.
- Обратный проход — обратное распространение ошибки — величина ошибки двигается в обратном направлении, в результате происходит корректировка весовых коэффициентов связей сети.
Начальные значения весов (перед обучением) задаются случайными, есть ряд методик для выбора этих значений, я опишу в отдельном материале максимально подробно. Пока вот можно полистать — ссылка.
Вернемся к конкретному примеру для явной демонстрации этих принципов:
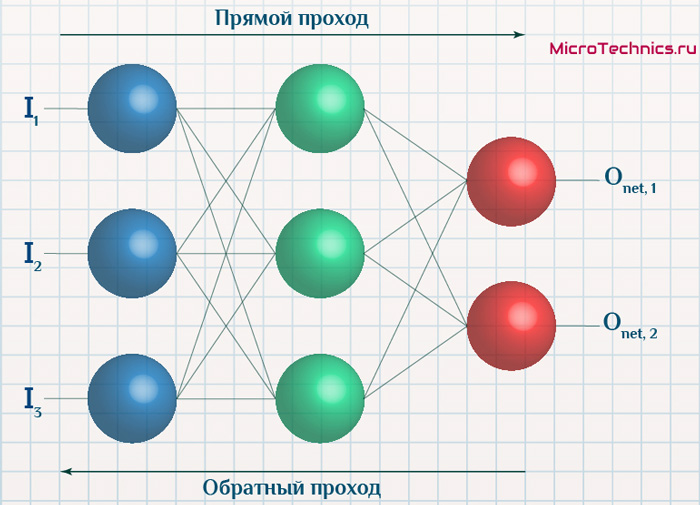
Итак, имеется нейронная сеть, также имеется набор данных обучающей выборки. Как уже обсудили в начале статьи — обучающая выборка представляет из себя набор образцов (сетов), каждый из которых состоит из значений входных сигналов и соответствующих им «правильных» значений выходных величин.
Процесс обучения нейронной сети для алгоритма обратного распространения ошибки будет таким:
- Прямой проход. Подаем на вход значения I_1, I_2, I_3 из обучающей выборки. В результате работы сети получаем выходные значения O_{net, 1}, O_{net, 2}. Этому целиком и полностью был посвящен предыдущий манускрипт.
- Рассчитываем величины ошибок для всех слоев:
- для выходного: delta_k = (O_{correct, k} — O_{net, k}) cdot f{Large{prime}}(I_k)
- для скрытых: delta_j = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_j)
- Далее используем полученные значения для расчета Delta w_{ij} = alpha cdot delta_j cdot O_i + gamma cdot Delta w_{ij}^{t — 1}
- И финишируем, рассчитывая новые значения весов: w_{ij medspace new} = w_{ij} + Delta w_{ij}
- На этом один цикл обучения закончен, данные шаги 1 — 4 повторяются для других образцов из обучающей выборки.
Обратный проход завершен, а вместе с ним и одна итерация процесса обучения нейронной сети по данному методу. Собственно, обучение в целом заключается в многократном повторении этих шагов для разных образцов из обучающей выборки. Логику мы полностью разобрали, при повторном проведении операций она остается в точности такой же.
Таким образом, максимально подробно концентрируясь именно на сути и логике процессов, мы в деталях разобрали метод обратного распространения ошибки. Поэтому переходим к завершающей части статьи, в которой разберем практический пример, произведя полностью все вычисления для конкретных числовых величин. Все в рамках продвигаемой мной концепции, что любая теоретическая информация на порядок лучше может быть осознана при применении ее на практике.
Пример расчетов для метода обратного распространения ошибки.
Возьмем нейронную сеть и зададим начальные значения весов:
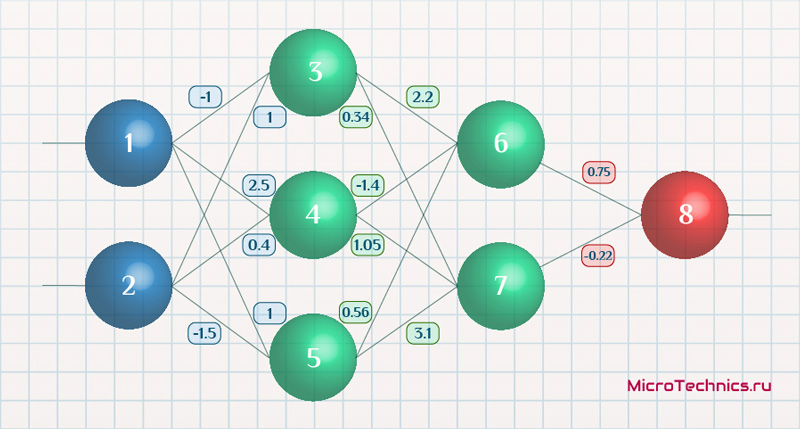
Здесь я задал значения не в соответствии с существующими на сегодняшний день методами, а просто случайным образом для наглядности примера.
В качестве функции активации используем сигмоиду:
f(x) = frac{1}{1 + e^{-x}}
И ее производная:
f{Large{prime}}(x) = f(x)medspace (1medspace-medspace f(x))
Берем один образец из обучающей выборки, пусть будут такие значения:
- Входные: I_1 = 0.6, I_1 = 0.7.
- Выходное: O_{correct} = 0.9.
Скорость обучения alpha пусть будет равна 0.3, момент — gamma = 0.1. Все готово, теперь проведем полный цикл для метода обратного распространения ошибки, то есть прямой проход и обратный.
Прямой проход.
Начинаем с выходных значений нейронов 1 и 2, поскольку они являются входными, то:
O_1 = I_1 = 0.6 \ O_2 = I_2 = 0.7
Значения на входе нейронов 3, 4 и 5:
I_3 = O_1 cdot w_{13} + O_2 cdot w_{23} = 0.6 cdot (-1medspace) + 0.7 cdot 1 = 0.1 \
I_4 = 0.6 cdot 2.5 + 0.7 cdot 0.4 = 1.78 \
I_5 = 0.6 cdot 1 + 0.7 cdot (-1.5medspace) = -0.45
На выходе этих же нейронов первого скрытого слоя:
O_3 = f(I3medspace) = 0.52 \ O_4 = 0.86\ O_5 = 0.39
Продолжаем аналогично для следующего скрытого слоя:
I_6 = O_3 cdot w_{36} + O_4 cdot w_{46} + O_5 cdot w_{56} = 0.52 cdot 2.2 + 0.86 cdot (-1.4medspace) + 0.39 cdot 0.56 = 0.158 \
I_7 = 0.52 cdot 0.34 + 0.86 cdot 1.05 + 0.39 cdot 3.1 = 2.288 \
O_6 = f(I_6) = 0.54 \
O_7 = 0.908
Добрались до выходного нейрона:
I_8 = O_6 cdot w_{68} + O_7 cdot w_{78} = 0.54 cdot 0.75 + 0.908 cdot (-0.22medspace) = 0.205 \
O_8 = O_{net} = f(I_8) = 0.551
Получили значение на выходе сети, кроме того, у нас есть целевое значение O_{correct} = 0.9. То есть все, что необходимо для обратного прохода, имеется.
Обратный проход.
Как мы и обсуждали, первым этапом будет вычисление ошибок всех нейронов, действуем:
delta_8 = (O_{correct} - O_{net}) cdot f{Large{prime}}(I_8) = (O_{correct} - O_{net}) cdot f(I_8) cdot (1-f(I_8)) = (0.9 - 0.551medspace) cdot 0.551 cdot (1-0.551medspace) = 0.0863 \
delta_7 = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_7) = (delta_8 cdot w_{78}) cdot f{Large{prime}}(I_7) = 0.0863 cdot (-0.22medspace) cdot 0.908 cdot (1 - 0.908medspace) = -0.0016 \
delta_6 = 0.086 cdot 0.75 cdot 0.54 cdot (1 - 0.54medspace) = 0.016 \
delta_5 = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_5) = (delta_7 cdot w_{57} + delta_6 cdot w_{56}) cdot f{Large{prime}}(I_7) = (-0.0016 cdot 3.1 + 0.016 cdot 0.56) cdot 0.39 cdot (1 - 0.39medspace) = 0.001 \
delta_4 = (-0.0016 cdot 1.05 + 0.016 cdot (-1.4)) cdot 0.86 cdot (1 - 0.86medspace) = -0.003 \
delta_3 = (-0.0016 cdot 0.34 + 0.016 cdot 2.2) cdot 0.52 cdot (1 - 0.52medspace) = -0.0087
С расчетом ошибок закончили, следующий этап — расчет корректировочных величин для весов всех связей. Для этого мы вывели формулу:
Delta w_{ij} = alpha cdot delta_j cdot O_i + gamma cdot Delta w_{ij}^{t - 1}
Как вы помните, Delta w_{ij}^{t — 1} — это величина поправки для данного веса на предыдущей итерации. Но поскольку у нас это первый проход, то данное значение будет нулевым, соответственно, в данном случае второе слагаемое отпадает. Но забывать о нем нельзя. Продолжаем калькулировать:
Delta w_{78} = alpha cdot delta_8 cdot O_7 = 0.3 cdot 0.0863 cdot 0.908 = 0.0235 \
Delta w_{68} = 0.3 cdot 0.0863 cdot 0.54= 0.014 \
Delta w_{57} = alpha cdot delta_7 cdot O_5 = 0.3 cdot (−0.0016medspace) cdot 0.39= -0.00019 \
Delta w_{47} = 0.3 cdot (−0.0016medspace) cdot 0.86= -0.0004 \
Delta w_{37} = 0.3 cdot (−0.0016medspace) cdot 0.52= -0.00025 \
Delta w_{56} = alpha cdot delta_6 cdot O_5 = 0.3 cdot 0.016 cdot 0.39= 0.0019 \
Delta w_{46} = 0.3 cdot 0.016 cdot 0.86= 0.0041 \
Delta w_{36} = 0.3 cdot 0.016 cdot 0.52= 0.0025 \
Delta w_{25} = alpha cdot delta_5 cdot O_2 = 0.3 cdot 0.001 cdot 0.7= 0.00021 \
Delta w_{15} = 0.3 cdot 0.001 cdot 0.6= 0.00018 \
Delta w_{24} = alpha cdot delta_4 cdot O_2 = 0.3 cdot (-0.003medspace) cdot 0.7= -0.00063 \
Delta w_{14} = 0.3 cdot (-0.003medspace) cdot 0.6= -0.00054 \
Delta w_{23} = alpha cdot delta_3 cdot O_2 = 0.3 cdot (−0.0087medspace) cdot 0.7= -0.00183 \
Delta w_{13} = 0.3 cdot (−0.0087medspace) cdot 0.6= -0.00157
И самый что ни на есть заключительный этап — непосредственно изменение значений весовых коэффициентов:
w_{78 medspace new} = w_{78} + Delta w_{78} = -0.22 + 0.0235 = -0.1965 \
w_{68 medspace new} = 0.75+ 0.014 = 0.764 \
w_{57 medspace new} = 3.1 + (−0.00019medspace) = 3.0998\
w_{47 medspace new} = 1.05 + (−0.0004medspace) = 1.0496\
w_{37 medspace new} = 0.34 + (−0.00025medspace) = 0.3398\
w_{56 medspace new} = 0.56 + 0.0019 = 0.5619 \
w_{46 medspace new} = -1.4 + 0.0041 = -1.3959 \
w_{36 medspace new} = 2.2 + 0.0025 = 2.2025 \
w_{25 medspace new} = -1.5 + 0.00021 = -1.4998 \
w_{15 medspace new} = 1 + 0.00018 = 1.00018 \
w_{24 medspace new} = 0.4 + (−0.00063medspace) = 0.39937 \
w_{14 medspace new} = 2.5 + (−0.00054medspace) = 2.49946 \
w_{23 medspace new} = 1 + (−0.00183medspace) = 0.99817 \
w_{13 medspace new} = -1 + (−0.00157medspace) = -1.00157\
И на этом данную масштабную статью завершаем, конечно же, не завершая на этом деятельность по использованию нейронных сетей. Так что всем спасибо за прочтение, любые вопросы пишите в комментариях и на форуме, ну и обязательно следите за обновлениями и новыми материалами, до встречи!
Среднеквадратичная ошибка в PyTorch рассчитывается почти так же, как и общее уравнение потерь, приведенное ранее. Мы также рассмотрим значение смещения, поскольку это также параметр, который необходимо обновлять в процессе обучения.
(y-Ax+b)2
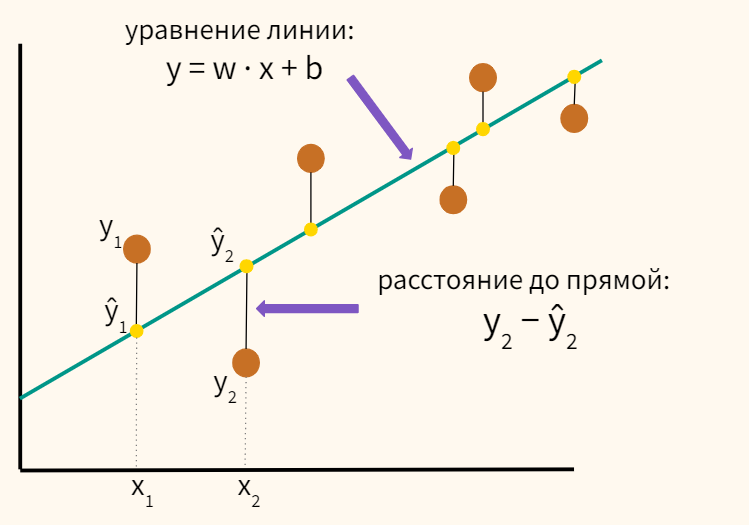
Среднеквадратичная ошибка лучше всего поясняется иллюстрацией.
Предположим, у нас есть набор значений, и мы начинаем с рисования некоторого параметра линии регрессии, размер которого определяется случайным набором веса и значения смещения, как и раньше.
Ошибка соответствует тому, как далеко фактическое значение от прогнозируемого значения – фактическое расстояние между ними.
Для каждой точки ошибка рассчитывается путем сравнения прогнозируемых значений, сделанных нашей линейной моделью, с фактическим значением по следующей формуле.
Каждая точка связана с ошибкой, что означает, что мы должны выполнить суммирование ошибки для каждой точки. Мы знаем, что прогноз можно переписать как:
Поскольку мы вычисляем среднеквадратичную ошибку, мы должны взять среднее значение, разделив его на количество точек данных. Упомянутый ранее градиент функции ошибки должен вести нас в направлении наибольшего увеличения ошибки.
Двигаясь к отрицательному градиенту нашей функции стоимости, мы движемся в направлении наименьшей ошибки. Мы будем использовать этот градиент как компас, который всегда ведет нас вниз. В градиентном спуске мы игнорируем наличие смещения, но для ошибки требуется определить оба параметра A и b.
Теперь мы вычисляем частные производные для каждого, и, как и раньше, мы начинаем с любой пары значений A и b.
Мы используем алгоритм градиентного спуска для обновления A и b в направлении наименьшей ошибки на основе двух частных производных, упомянутых выше. Для каждой отдельной итерации новый вес равен:
A1=A0-∝ f'(A).
И новое значение смещения равно
b1=b0-∝ f'(b).
Основная идея написания кода в том, что мы начинаем с некоторой случайной модели со случайным набором параметров веса и значения смещения. Эта случайная модель будет иметь большую функцию ошибки, большую функцию стоимости, и затем мы используем градиентный спуск, чтобы обновить вес нашей модели в направлении наименьшей ошибки. Минимизация этой ошибки возвращает оптимизированный результат.

Изучаю Python вместе с вами, читаю, собираю и записываю информацию опытных программистов.
Все курсы > Оптимизация > Занятие 2
На прошлом занятии мы познакомились с понятием производной и нашли минимум функции с одной переменной. При этом, мы отказались от использования второй переменной сдвига.
$$ y = w cdot x $$
Сегодня мы научимся находить минимум функции с двумя переменными w и b и построим полноценную модель простой линейной регрессии (Simple Linear Regression).
$$ y = w cdot x + b $$
Для этого мы напишем алгоритм, который называется методом градиентного спуска (gradient descent method). Однако перед этим мы возьмем более простую функцию и на ее примере изучим, как работает этот метод.
Градиент и метод градиентного спуска
Функция нескольких переменных
Возьмем вот такую функцию потерь.
$$ f(w_1, w_2) = w_1^2 + w_2^2 $$
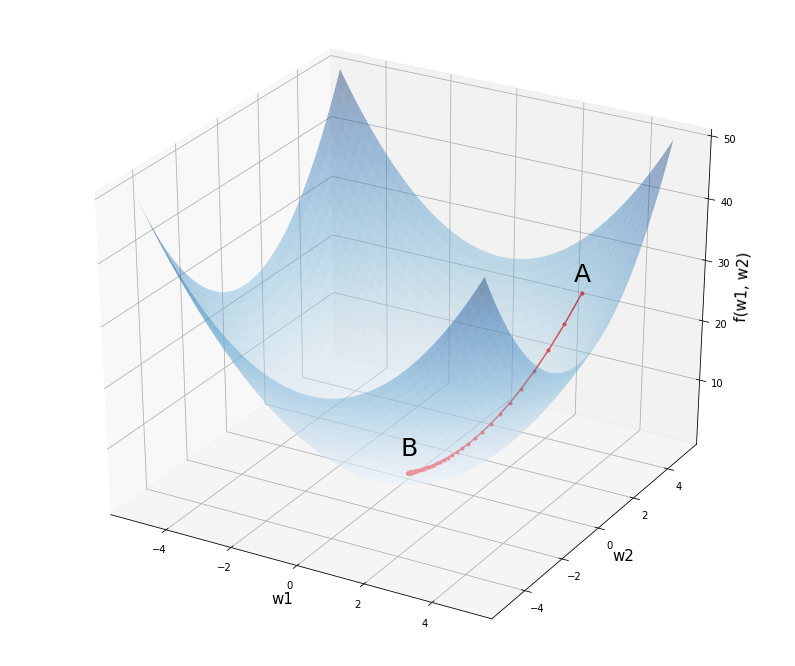
График этой функции можно представить в трехмерном пространстве, где по осям w1 и w2 отложены веса исходной модели, а по оси f(w1, w2) — уровень потерь при заданных весах.
Откроем ноутбук к этому занятию⧉
Посмотрим на график этой функции.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
# установим размер графика fig = plt.figure(figsize = (12,10)) # создадим последовательность из 1000 точек в интервале от -5 до 5 # для осей w1 и w2 w1 = np.linspace(—5, 5, 1000) w2 = np.linspace(—5, 5, 1000) # создадим координатную плоскость из осей w1 и w2 w1, w2 = np.meshgrid(w1, w2) # пропишем функцию f = w1 ** 2 + w2 ** 2 # создадим трехмерное пространство ax = fig.add_subplot(projection = ‘3d’) # выведем график функции, alpha задает прозрачность ax.plot_surface(w1, w2, f, alpha = 0.4, cmap = ‘Blues’) # выведем точку A с координатами (3, 4, 25) и подпись к ней ax.scatter(3, 4, 25, c = ‘red’, marker = ‘^’, s = 100) ax.text(3, 3.5, 28, ‘A’, size = 25) # аналогично выведем точку B с координатами (0, 0, 0) ax.scatter(0, 0, 0, c = ‘red’, marker = ‘^’, s = 100) ax.text(0, —0.4, 4, ‘B’, size = 25) # укажем подписи к осям ax.set_xlabel(‘w1’, fontsize = 15) ax.set_ylabel(‘w2’, fontsize = 15) ax.set_zlabel(‘f(w1, w2)’, fontsize = 15) # выведем результат plt.show() |

Предположим мы начали с весов в точке A с координатами (3, 4, 25). Как нам спуститься в минимум функции в точке B (0, 0, 0)? Просто двигаться в направлении обратном производной мы не можем. Ведь единственной производной, которая бы описывала все изменения нашей функции, просто не существует.
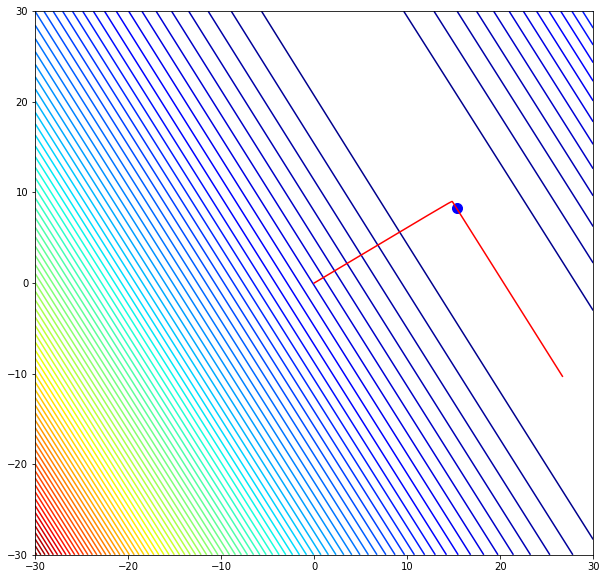
Все дело в том, что если смотреть на нашу функцию «сверху» (то есть на график изолиний или линий уровня, contour lines), то в каждой точке у нас теперь два направления, по оси w1 и по оси w2.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 |
# установим размер графика fig, ax = plt.subplots(figsize = (10,10)) # создадим последовательность из 100 точек в интервале от -5 до 5 # для осей w1 и w2 w1 = np.linspace(—5.0, 5.0, 100) w2 = np.linspace(—5.0, 5.0, 100) # создадим координатную плоскость из осей w1 и w2 w1, w2 = np.meshgrid(w1, w2) # пропишем функцию C = w1 ** 2 + w2 ** 2 # построим изолинии (линии уровня) plt.contourf(w1, w2, C, cmap = ‘Blues’) # выведем точку А с координатами на плоскости (3, 4) ax.scatter(3, 4, c = ‘red’, marker = ‘^’, s = 200) ax.text(2.85, 4.3, ‘A’, size = 25) # и точку B с координатами (0, 0) ax.scatter(0, 0, c = ‘red’, marker = ‘^’, s = 200) ax.text(—0.15, 0.3, ‘B’, size = 25) # укажем подписи к осям ax.set_xlabel(‘w1’, fontsize = 15) ax.set_ylabel(‘w2’, fontsize = 15) # а также стрелки направления изменений вдоль w1 и w2 ax.arrow(2.7, 4, —2, 0, width = 0.1, head_length = 0.3) ax.arrow(3.005, 3.6, 0, —2, width = 0.1, head_length = 0.3) # создадим сетку в виде прерывистой черты plt.grid(linestyle = ‘—‘) # выведем результат plt.show() |

Как понять куда нам двигаться?
Частная производная
Если «заморозить» одну из переменных (то есть представить, что это константа), пусть это будет w2, мы можем найти производную по первой переменной w1.
$$ f_{w_1} = frac{partial f}{partial w_1} = 2w_1 $$
Такая производная называется частной (partial derivative), потому что она описывает изменение только в первой переменной w1.
Графически, мы как бы убираем переменную w2 (получается сечение, представленное параболой) и ищем производную функции, в которой есть только переменная w1.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 |
# зададим размер графика в дюймах plt.figure(figsize = (10, 8)) # объявим функцию параболы def f(x): return x ** 2 # объявим ее производную def der(x): return 2 * x # пропишем уравнение через point-slope form # y — y1 = m * (x — x1) —> y = m * (x — x1) + y1 def line(x, x1, y1): return der(x1) * (x — x1) + y1 # создадим последовательность координат x для параболы x = np.linspace(—4, 4, 100) # построим график параболы plt.plot(x, f(x)) # и заполним ее по умолчанию синим цветом с прозрачностью 0,5 plt.fill_between(x, f(x), 16, alpha = 0.5) # в цикле пройдемся по точкам -2, 0, 2 на оси х for x1 in range(—2, 3, 2): # рассчитаем соответствующие им координаты y y1 = f(x1) # определим пространство по оси x для касательных линий xrange = np.linspace(x1 — 3, x1 + 3, 9) # построим касательные линии plt.plot(xrange, line(xrange, x1, y1), ‘C1—‘, linewidth = 2) # и точки соприкосновения с графиком параболы plt.scatter(x1, y1, color = ‘C1’, s = 50) # укажем подписи к осям plt.xlabel(‘w1’, fontsize = 15) plt.ylabel(‘f(w1, w2)’, fontsize = 15) # выведем результат plt.show() |

Точно таким же образом мы поступаем со второй переменной w2. Мы замораживаем первую переменную w1 и вычисляем частную производную.
$$ f_{w_2} = frac{partial f}{partial w_2} = 2w_2 $$
Теперь, взяв точку на плоскости (w1, w2), мы будем точно знать скорость изменения функции f(w1, w2) в этой точке в каждом из направлений.
Например, возьмем ту же точку A с координатами w1 = 3, w2 = 4, скорость изменения функции в первом измерении будет равна 2 x 3 = 6, во втором 2 x 4 = 8.
Нотация анализа
Вы вероятно заметили, что мы использовали две нотации (записи) частной производной. С первой мы уже знакомы по предыдущему занятию, это нотация Лагранжа.
$$ f(w) rightarrow f'(w) $$
Вторую нотацию, нотацию Лейбница, удобнее использовать для записи частных производных.
$$ f(w_1, w_2) rightarrow frac{partial f}{partial w_1}, frac{partial f}{partial w_2} $$
Она позволяет сразу увидеть, по какой переменной происходит дифференцирование.
Напомню, что запись формул (и, в частности, производной) в текстовых ячейках ноутбуков с помощью LaTeX мы изучили, когда говорили про Jupyter Notebook.
Взятие частных производных
Пошагово рассмотрим, как мы пришли к результату (2w1, 2w2). Вначале найдем производную по первой переменой w1. Вторую переменную, w2, мы будем считать константой, то есть некоторым числом.
$$ frac{partial f}{partial w_1} (w_1^2 + w_2^2) $$
Первое, что бросается в глаза, это то, что у нас производная суммы, а она, как известно, равна сумме производных.
$$ frac{partial f}{partial w_1} (w_1^2 + w_2^2) = frac{partial f}{partial w_1} (w_1^2) + frac{partial f}{partial w_1} (w_2^2) $$
Производную первого слагаемого мы найдем по правилу производной степенной функции. Второе слагаемое мы решили считать константой, а производная константы равна нулю.
$$ frac{partial f}{partial w_1} (w_1^2) + frac{partial f}{partial w_1} (w_2^2) = 2w_1 + 0 = 2w_1 $$
Частная производная по второй переменной находится аналогично.
Использование SymPy
Функцию diff() библиотеки SymPy можно также использовать для взятия частных производных. Вначале импортируем функцию diff() и символы x и y (мы их используем вместо w1 и w2).
|
from sympy import diff from sympy.abc import x, y |
Напишем функцию, которую хотим дифференцировать.
После этого мы можем находить частные производные, передав в diff() функцию для дифференцирования, а затем либо первую, либо вторую переменную.
|
# найдем частную производную по первой переменной diff(f, x) |
|
# найдем частную производную по второй переменной diff(f, y) |
Градиент
Градиент (gradient) — есть не что иное, как совокупность частных производных по каждой из независимых переменных. Его можно назвать «полной производной».
Он обозначается через греческую букву набла ∇ или оператор Гамильтона.
$$ nabla f(w_1, w_2) = begin{bmatrix} frac{partial f}{partial w_1} \ frac{partial f}{partial w_1} end{bmatrix} = begin{bmatrix} 2w_1 \ 2w_2 end{bmatrix} $$
Еще раз посмотрим, чему равен градиент в точке (3, 4), но уже в новой записи.
$$ nabla f(3, 4) = begin{bmatrix} 2 cdot 3 \ 2 cdot 4 end{bmatrix} = begin{bmatrix} 6 \ 8 end{bmatrix} $$
Как вы видите, такая функция на входе принимает два числа, а на выходе выдает вектор, также состоящий из двух чисел. В этом случае говорят о вектор-функции (vector-valued function).
Метод градиентного спуска
Градиент, который мы только что нашли, показывает направление скорейшего подъема (возрастания) функции. Нам же, если мы хотим найти минимум функции, нужно двигаться вниз в направлении, обратном направлению градиента (еще говорят про направление антиградиента, negative gradient).
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 |
# установим размер графика fig, ax = plt.subplots(figsize = (10,10)) # создадим последовательность из 100 точек в интервале от -10 до 10 # для осей w1 и w2 w1 = np.linspace(—10.0, 10.0, 100) w2 = np.linspace(—10.0, 10.0, 100) # создадим координатную плоскость из осей w1 и w2 w1, w2 = np.meshgrid(w1, w2) # пропишем функцию C = w1 ** 2 + w2 ** 2 # построим изолинии (линии уровня) plt.contourf(w1, w2, C, cmap = ‘Blues’) # выведем точку А с координатами на плоскости (3, 4) ax.scatter(3, 4, c = ‘red’, marker = ‘^’, s = 200) ax.text(2.5, 4.5, ‘A’, size = 25) # и точку B с координатами (0, 0) ax.scatter(0, 0, c = ‘red’, marker = ‘^’, s = 200) ax.text(—1, 0.3, ‘B’, size = 25) # укажем подписи к осям ax.set_xlabel(‘w1’, fontsize = 15) ax.set_ylabel(‘w2’, fontsize = 15) # а также стрелки направления изменений вдоль w1 и w2 ax.arrow(2.7, 4, —2, 0, width = 0.1, head_length = 0.3) ax.arrow(3, 3.5, 0, —2, width = 0.1, head_length = 0.3) # выведем вектор антиградиента с направлением (-6, -8) ax.arrow(3, 4, —6, —8, width = 0.05, head_length = 0.3) ax.text(—2.8, —4.5, ‘Антиградиент’, rotation = 53, size = 16) # создадим сетку в виде прерывистой черты plt.grid(linestyle = ‘—‘) # выведем результат plt.show() |

Если мы сдвинемся на −6 по оси w1 и на −8 по оси w2, то обязательно пройдем через минимум функции. При этом, если мы сдвинемся на всю величину градиента, то «перескочим» через минимум. Именно поэтому нам нужен коэффициент скорости обучения (learning rate).
Теперь мы готовы дать определение:
Метод градиентного спуска — это способ нахождения локального минимума функции в процессе движения в направлении антиградиента. Он был предложен Огюстеном Луи Коши еще в 1847 году.
Воспользуемся этим методом для нахождения минимума приведенной выше функции. Другими словами, проделаем путь из точки А в точку B.
Метод градиентного спуска на Питоне
Вначале объявим необходимые функции.
|
# пропишем функцию потерь def objective(w1, w2): return w1 ** 2 + w2 ** 2 # а также производную по первой def partial_1(w1): return 2.0 * w1 # и второй переменной def partial_2(w2): return 2.0 * w2 |
Зададим исходные параметры модели.
|
# пропишем изначальные веса w1, w2 = 3, 4 # количество итераций iter = 100 # и скорость обучения learning_rate = 0.05 |
Теперь создадим списки для учета обновления весов w1 и w2 и изменения уровня ошибки.
|
w1_list, w2_list, l_list = [], [], [] |
Найдем минимум функции потерь.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
# в цикле с заданным количеством итераций for i in range(iter): # будем добавлять текущие веса в соответствующие списки w1_list.append(w1) w2_list.append(w2) # и рассчитывать и добавлять в список текущий уровень ошибки l_list.append(objective(w1, w2)) # также рассчитаем значение частных производных при текущих весах par_1 = partial_1(w1) par_2 = partial_2(w2) # будем обновлять веса в направлении, # обратном направлению градиента, умноженному на скорость обучения w1 = w1 — learning_rate * par_1 w2 = w2 — learning_rate * par_2 # выведем итоговые веса модели и значение функции потерь w1, w2, objective(w1, w2) |
|
(7.968419666276241e-05, 0.00010624559555034984, 1.7637697771638315e-08) |
Как мы видим, уже после ста итераций, как веса модели, так и уровень ошибки приблизились к нулю.
Разумеется, более сложные функции потерь потребуют большего количества итераций и более тонкой настройки коэффициента скорости обучения.
Остается посмотреть на графике, какой путь проделал наш алгоритм градиентного спуска.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
fig = plt.figure(figsize = (14,12)) w1 = np.linspace(—5, 5, 1000) w2 = np.linspace(—5, 5, 1000) w1, w2 = np.meshgrid(w1, w2) f = w1 ** 2 + w2 ** 2 ax = fig.add_subplot(projection = ‘3d’) ax.plot_surface(w1, w2, f, alpha = 0.4, cmap = ‘Blues’) ax.text(3, 3.5, 28, ‘A’, size = 25) ax.text(0, —0.4, 4, ‘B’, size = 25) ax.set_xlabel(‘w1’, fontsize = 15) ax.set_ylabel(‘w2’, fontsize = 15) ax.set_zlabel(‘f(w1, w2)’, fontsize = 15) # выведем путь алгоритма оптимизации ax.plot(w1_list, w2_list, l_list, ‘.-‘, c = ‘red’) plt.show() |
Промежуточные выводы
Давайте еще раз проговорим основные идеи пройденного материала.
- Градиент показывает скорость изменения многомерной функции по каждому из измерений (по каждой из переменных)
- Если «заморозить» все независимые переменные кроме одной и сделать срез, то наклон касательной к кривой среза будет значением частной производной по этому измерению.
- И самое важное для нас: градиент показывает направление скорейшего подъёма (возрастания) функции. Двигаясь в обратном направлении, мы придем к минимуму функции.
Простая линейная регрессия
А теперь давайте с нуля напишем нашу первую модель машинного обучения. Мы наконец-то приобрели для этого все необходимые знания. Наша модель будет по-прежнему иметь только один признак, но при этом будет учитываться не только наклон, но и сдвиг прямой.
$$ hat{y} = w cdot x + b $$
Данные и постановка задачи
Сегодня мы возьмем хорошо известные нам данные роста и обхвата шеи и сразу преобразуем их в массив Numpy.
|
X = np.array([1.48, 1.49, 1.49, 1.50, 1.51, 1.52, 1.52, 1.53, 1.53, 1.54, 1.55, 1.56, 1.57, 1.57, 1.58, 1.58, 1.59, 1.60, 1.61, 1.62, 1.63, 1.64, 1.65, 1.65, 1.66, 1.67, 1.67, 1.68, 1.68, 1.69, 1.70, 1.70, 1.71, 1.71, 1.71, 1.74, 1.75, 1.76, 1.77, 1.77, 1.78]) y = np.array([29.1, 30.0, 30.1, 30.2, 30.4, 30.6, 30.8, 30.9, 31.0, 30.6, 30.7, 30.9, 31.0, 31.2, 31.3, 32.0, 31.4, 31.9, 32.4, 32.8, 32.8, 33.3, 33.6, 33.0, 33.9, 33.8, 35.0, 34.5, 34.7, 34.6, 34.2, 34.8, 35.5, 36.0, 36.2, 36.3, 36.6, 36.8, 36.8, 37.0, 38.5]) |
Выведем эти данные на графике с помощью диаграммы рассеяния или точечной диаграммы.
|
# построим точечную диаграмму plt.figure(figsize = (10,6)) plt.scatter(X, y) # добавим подписи plt.xlabel(‘Рост, см’, fontsize = 16) plt.ylabel(‘Обхват шеи, см’, fontsize = 16) plt.title(‘Зависимость роста и окружности шеи у женщин в России’, fontsize = 18) plt.show() |
Как мы помним, нашей задачей является минимизация средней суммы квадрата расстояний между нашими данными и линией регрессии.
Также приведу формулу.
$$ MSE = frac {1}{n} sum^{n}_{i=1} (y_i-hat{y}_i) ^2 $$
Решение методом наименьшних квадратов
Прежде чем использовать алгоритм градиентного спуска найдем аналитическое решение с помощью метода наименьших квадратов (МНК, least squares method). Для уравнения с одной независимой переменной, напомню, используется следующая формула.
$$ w = frac {sum_{i = 1}^{n} (x_i-bar{x})(y_i-bar{y})} {sum_{i = 1}^{n} (x_i-bar{x})^2} $$
$$ b = bar{y}-wbar{x} $$
Собственная модель
Давайте вычислим наклон и сдвиг прямой с помощью этой формулы на Питоне.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
# найдем среднее значение X и y X_mean = np.mean(X) y_mean = np.mean(y) # объявим переменные для числителя и знаменателя numerator, denominator = 0, 0 # в цикле пройдемся по данным for i in range(len(X)): # вычислим значения числителя и знаменателя по формуле выше numerator += (X[i] — X_mean) * (y[i] — y_mean) denominator += (X[i] — X_mean) ** 2 # найдем наклон и сдвиг w = numerator / denominator b = y_mean — w * X_mean w, b |
|
(26.861812005569753, -10.570936299787313) |
Также давайте реализуем этот алгоритм с помощью векторизованного кода.
|
w = np.sum((X — X_mean) * (y — y_mean)) / np.sum((X — X_mean) ** 2) b = y_mean — w * X_mean w, b |
|
(26.861812005569757, -10.57093629978732) |
Модель LinearRegression библиотеки sklearn
Надо сказать, что модель LinearRegression, которую мы использовали на вводном занятии по оптимизации и затем на занятии по линейной регрессии применяет именно МНК для минимизации MSE.
Давайте еще раз применим класс LinearRegression, чтобы убедиться в получении одинаковых результатов.
|
# из набора линейных моделей библиотеки sklearn импортируем линейную регрессию from sklearn.linear_model import LinearRegression # создадим объект этого класса и запишем в переменную model model = LinearRegression() # обучим модель (для X используем двумерный массив) model.fit(X.reshape(—1, 1), y) # выведем коэффициенты model.coef_, model.intercept_ |
|
(array([26.86181201]), -10.570936299787334) |
Как вы видите, результаты одинаковы. Теперь сделаем прогноз и рассчитаем среднеквадратическую ошибку.
|
# сделаем прогноз y_pred_least_squares = model.predict(X.reshape(—1, 1)) # импортируем модуль метрик from sklearn import metrics # выведем среднеквадратическую ошибку (MSE) metrics.mean_squared_error(y, y_pred_least_squares) |
Позднее мы сравним этот результат с аналогичным показателем алгоритма градиентного спуска.
МНК и метод градиентного спуска
Одна из причин использования алгоритма градиентного спуска вместо МНК заключается в том, что этот алгоритм менее требователен к вычислительным ресурсам при большом объеме (количество наблюдений) и размерности (количество признаков) данных.
Кроме того, метод градиентного спуска может применяться не только в задачах линейной регрессии, но и в других алгоритмах (например, в логистической регрессии, SVM или нейросетях).
Решение методом градиентного спуска
Модель линейной регрессии и функция потерь
Начнем с того, что объявим функцию линейной модели.
|
def regression(X, w, b): return w * X + b |
Теперь давайте немного модифицируем функцию потерь и найдем половину среднеквадратической ошибки (half MSE). Обозначим нашу функцию буквой J.
$$ J_{MSE} = frac{1}{2n} sum_{i=1}^{n} (y_i-(wx_i+b))^2 $$
Число два в знаменателе удачно сократится с двойкой, полученной при дифференцировании степенной функции. При этом точка минимума функции не изменится.
|
def objective(X, y, w, b, n): return np.sum((y — regression(X, w, b)) ** 2) / (2 * n) |
Дополнительно замечу, что использование именно среднеквадратической, то есть усредненной на количество наблюдений, ошибки (MSE) вместо «простой» суммы квадратов отклонений (Sum of Squared Errors, SSE)
$$ J_{SSE} = sum_{i=1} (y_i-(wx_i+b))^2 $$
может быть предпочтительнее, поскольку позволяет сравнивать результаты модели на выборках разных размеров.
Частные производные функции потерь
Найдем частные производные этой функции. Их будет две: одна по наклону (w), вторая по сдвигу (b). Начнем с наклона.
$$ frac{partial J}{partial w} left( frac{1}{2n} sum_{i=1}^{n} (y_i-(wx_i+b))^2 right) $$
Шаг 1. Вынесем число 1/2n за скобку по правилу умножения на число. В данном случае n, то есть количество наблюдений, превратится в число, как только мы применим формулу к набору данных.
$$ frac{partial J}{partial w} = frac{1}{2n} frac{partial J}{partial w} sum_{i=1}^{n} left( (y_i-(wx_i+b))^2 right) $$
Шаг 2. Теперь давайте для удобства перепишем выражение в векторизованной форме. Теперь x и y будут не отдельными числами, а векторами.
$$ frac{partial J}{partial w} = frac{1}{2n} frac{partial J}{partial w} left( (y-(wx+b)) ^2 right) $$
Шаг 3. Перед нами композиция из двух функций. Применим chain rule.
$$ frac{partial J}{partial w} = frac{1}{2n} cdot 2(y-(wx+b)) cdot frac{partial J}{partial w} (y-(wx+b)) $$
Шаг 4. К внутренней функции мы можем применить правило суммы и разности производных.
$$ frac{1}{2n} cdot 2(y-(wx+b)) cdot (0-(x+0)) $$
Замечу, что при дифференцировании внутренней функции, y превратился в ноль, потому что это константа. Одновременно переменную b мы «заморозили» и также решили считать константой.
Шаг 5. Упростим выражение.
$$ frac{partial J}{partial w} = frac{1}{cancel{2}n} cdot cancel{2}-x(y-(wx+b)) = frac{1}{n} cdot -x(y-(wx+b)) $$
Аналогично найдем частную производную по сдвигу.
$$ frac{partial J}{partial b} = frac{1}{n} cdot -(y-(wx+b)) $$
Здесь стоит уточнить лишь, что при нахождении производной внутренней функции мы «заморозили» переменную w.
$$ frac{partial J}{partial b} left( (y-(wx+b)) right) = 0-(0+1)$$
В невекторизованной форме производные выглядят следующим образом.
$$ frac{partial J}{partial w} = frac{1}{n} sum_{i=1}^{n} -x_i(y_i-(wx_i+b)) $$
$$ frac{partial J}{partial b} = frac{1}{n} sum_{i=1}^{n} -(y_i-(wx_i+b)) $$
Поменяв слагаемые в скобках местами и умножив на $-1$, частные производные можно записать и так.
$$ frac{partial J}{partial w} = frac{1}{n} sum_{i=1}^{n} ((wx_i+b)-y_i) cdot x_i $$
$$ frac{partial J}{partial b} = frac{1}{n} sum_{i=1}^{n} ((wx_i+b)-y_i) $$
Пропишем эти функции на Питоне.
|
def partial_w(X, y, w, b, n): return np.sum(—X * (y — (w * X + b))) / n def partial_b(X, y, w, b, n): return np.sum(—(y — (w * X + b))) / n |
Алгоритм градиентного спуска
Создадим функцию, которая будет на входе принимать данные, количество итераций и коэффициент скорости обучения, а на выходе выдавать веса модели и уровень ошибки.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
# передадим функции данные, количество итераций и скорость обучения def gradient_descent(X, y, iter, learning_rate): # зададим изначальные веса w, b = 0, 0 # и количество наблюдений n = len(X) # создадим списки для записи весов модели и уровня ошибки w_list, b_list, l_list = [], [], [] # в цикле с заданным количеством итераций for i in range(iter): # добавим в списки текущие веса w_list.append(w) b_list.append(b) # и уровень ошибки l_list.append(objective(X, y, w, b, n)) # рассчитаем текущее значение частных производных par_1 = partial_w(X, y, w, b, n) par_2 = partial_b(X, y, w, b, n) # обновим веса в направлении антиградиента w = w — learning_rate * par_1 b = b — learning_rate * par_2 # выведем списки с уровнями ошибки и весами return w_list, b_list, l_list |
Обучение модели
Применим написанную выше функцию для обучения модели. Используем следующие гиперпараметры модели:
- количество итераций — 200 000
- коэффициент скорости обучения — 0,01
Напомню, что гиперпараметр — это параметр, который мы задаем до обучения модели.
|
# распакуем результат работы функции в три переменные w_list, b_list, l_list = gradient_descent(X, y, iter = 200000, learning_rate = 0.01) # и выведем последние достигнутые значения весов и уровня ошибки print(w_list[—1], b_list[—1], l_list[—1]) |
|
26.6917462520774 -10.293843835595917 0.1137823984153401 |
В целом, как мы видим, веса модели очень близки к результату, найденному с помощью метода наименьших квадратов. Теперь сделаем прогноз.
|
# передадим функции regression() наиболее оптимальные веса y_pred_gd = regression(X, w_list[—1], b_list[—1]) y_pred_gd[:5] |
|
array([29.20994062, 29.47685808, 29.47685808, 29.74377554, 30.01069301]) |
Посмотрим на результат на графике.
|
plt.figure(figsize = (10, 8)) plt.scatter(X, y) plt.plot(X, y_pred_gd, ‘r’) plt.show() |
Кроме того, мы можем посмотреть на то, как снижался уровень ошибки с каждой последующей итерацией.
Как мы видим, в первые итерации уровень ошибки снижался настолько стремительно, что последующие изменения практически незаметны. Давайте попробуем отбросить первые 150 наблюдений.
|
plt.figure(figsize = (8, 6)) plt.plot(l_list[150:]) plt.show() |
И все же кажется, что после 150000 итераций ошибка перестает снижаться и можно было бы обойтись меньшим количеством шагов. На самом деле это не так.
|
# отбросим первые 150 000 наблюдений plt.figure(figsize = (8, 6)) plt.plot(l_list[150000:]) plt.show() |
В целом подбор количества итераций и длины шага (коэффициента скорости обучения) довольно существенно влияют на качество обучения. Ближе к концу занятия мы рассмотрим этот момент более подробно.
Оценка качества модели
Оценим качество модели с помощью встроенной в sklearn метрики.
|
# рассчитаем MSE metrics.mean_squared_error(y, y_pred_gd) |
Результат очень близок к тому, который мы получили, используя МНК.
Визуализация шагов алгоритма оптимизации
Мы также как и раньше, можем посмотреть на путь, пройденный алгоритмом оптимизации.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 |
# создадим последовательности из 500 значений ww = np.linspace(—30, 30, 500) bb = np.linspace(—30, 30, 500) # сформируем координатную плоскость www, bbb = np.meshgrid(ww, bb) # а также матрицу из нулей для заполнения значениями функции J(w, b) JJ = np.zeros([len(ww), len(bb)]) # для каждой комбинации w и b for i in range(len(ww)): for j in range(len(bb)): # рассчитаем соответствующее прогнозное значение yy = www[i, j] * X + bbb[i, j] # и подставим его в функцию потерь (матрицу JJ) JJ[i, j] = 1 / (2 * len(X)) * np.sum((y — yy) ** 2) # зададим размер графика fig = plt.figure(figsize = (14,12)) # создидим трехмерное пространство ax = fig.add_subplot(projection = ‘3d’) # построим функцию потерь ax.plot_surface(www, bbb, JJ, alpha = 0.4, cmap = plt.cm.jet) # а также путь алгоритма оптимизации ax.plot(w_list, b_list, l_list, c = ‘red’) # для наглядности зададим более широкие, чем график # границы пространства ax.set_xlim(—40, 40) ax.set_ylim(—40, 40) plt.show() |
Мы также можем построить график изолиний («вид сверху»).
|
# для этого используем функцию plt.contour() fig, ax = plt.subplots(figsize = (10, 10)) ax.contour(www, bbb, JJ, 100, cmap = plt.cm.jet) ax.plot(w_list, b_list, c = ‘red’) plt.show() |
Как мы видим, алгоритм сначала двигался в одном направлении (очевидно, так ошибка снижалась наиболее стремительно), затем повернул на 90 градусов и продолжил движение.
Про выбор гиперпараметров модели
Давайте посмотрим, как поведет себя алгоритм при изменении гиперпараметров. Вначале попробуем тот же размер шага, но уменьшим количество итераций.
|
w_list_t1, b_list_t1, l_list_t1 = gradient_descent(X, y, iter = 10000, learning_rate = 0.01) w_list_t1[—1], b_list_t1[—1], l_list_t1[—1] |
|
(17.113947076094593, 5.311508333809235, 0.4836593999661288) |
Коэффициенты довольно сильно отличаются от найденных ранее значений. Посмотрим на графике изолиний, где остановился наш алгоритм.
|
fig, ax = plt.subplots(figsize = (10, 10)) ax.contour(www, bbb, JJ, 100, cmap = plt.cm.jet) ax.plot(w_list, b_list, c = ‘red’) # выведем точку, которой достиг новый алгоритм ax.scatter(w_list_t1[—1], b_list_t1[—1], s = 100, c = ‘blue’) plt.show() |
Как мы видим, алгоритм немного не дошел до оптимума. Теперь давайте попробуем уменьшить размер шага. Количество итераций вернем к прежнему значению.
|
w_list_t2, b_list_t2, l_list_t2 = gradient_descent(X, y, iter = 200000, learning_rate = 0.0001) w_list_t2[—1], b_list_t2[—1], l_list_t2[—1] |
|
(15.302448783526573, 8.263028645561734, 0.6339512457580667) |
|
fig, ax = plt.subplots(figsize = (10, 10)) ax.contour(www, bbb, JJ, 100, cmap = plt.cm.jet) ax.plot(w_list, b_list, c = ‘red’) ax.scatter(w_list_t2[—1], b_list_t2[—1], s = 100, c = ‘blue’) plt.show() |
В данном случае, так как мы делали слишком маленькие шаги, то продвинулись еще меньше.
Тема выбора гиперпараметров довольно сложна и выходит за рамки сегодняшнего занятия, однако уже на этих простых примерах видно, что один и тот же алгоритм при разных изначальных параметрах показывает совершенно разные результаты.
Подведем итог
В первой части занятия мы посмотрели как применить понятие производной к многомерной функции, познакомились с понятием градиента и методом градиентного спуска. Во второй части мы построили модель простой линейной регрессии и оптимизировали ее с помощью метода наименьших квадратов и алгоритма градиентного спуска.
Вопросы для закрепления
Вопрос. Что такое градиент?
Посмотреть правильный ответ
Ответ: градиент — это вектор, показывающий направление скорейшего подъема многомерной функции. Градиент состоит из частных производных по каждому из измерений (переменных) функции.
Вопрос. Какие гиперпараметры существенно влияют на качество оптимизации модели линейной регрессии?
Посмотреть правильный ответ
Ответ: количество итераций и коэффициент скорости обучения
Логичным продолжением будет построение модели многомерной или множественной линейной регрессии (multiple linear regression) с несколькими признаками. Однако прежде будет полезно еще раз в деталях изучить взаимосвязь переменных.
Ответы на вопросы
Вопрос. Почему если умножить функцию потерь на число, в частности на 1/2, точка ее минимума не изменится?
Ответ. Давайте посмотрим на график параболы и параболы, умноженной на 1/2.
Как мы видим, точка минимума не изменилась.
При этом обратите внимание на то, что изменился наклон (значение градиента). Эффект умножения функции потерь на число аналогичен измененению коэффициента скорости обучения (learning rate). Чем круче наклон, тем большие по размеру шаги мы будем делать.
Вопрос. Скажите, а как работает функция np.meshgrid()?
Ответ. Функция np.meshgrid() на входе принимает одномерные массивы и создает двумерный массив с привычной прямоугольной (декартовой) системой координат.
|
# создадим простые последовательности xvalues = np.array([0, 1, 2, 3, 4]) yvalues = np.array([0, 1, 2, 3, 4]) # сформируем координатную плоскость xx, yy = np.meshgrid(xvalues, yvalues) # выведем точки плоскости на графике plt.plot(xx, yy, marker = ‘.’, color = ‘r’, linestyle = ‘none’) plt.show() |
Обратите внимание, начало координат находится в левом нижнему углу.
Вопрос. Функция plt.fill_between() заполняет пространство между двумя функциями, но не очень понятно, какие параметры мы ей передаем.
Ответ. Функция np.fill_between(x, y1, y2 = 0) принимает три основных параметра: координаты по оси x, координаты по оси y (первая функция, y1) и координаты по оси y (вторая функция, y2) и заполняет пространство между y1 и y2. Параметр y2 не является обязательным. Если его не указывать, будет заполняться пространство между линией y1 и осью x (то есть функцией y = 0).
В конце ноутбука⧉ я привел два примера, когда параметр y2 не указывается, то есть равен 0, и когда y2 задает отличную от нуля функцию.
Эту функцию называют также «логлосс» (logloss / log_loss), перекрёстной / кросс-энтропией (Cross Entropy) и часто используют в задачах классификации. Разберёмся, почему её используют и какой смысл она имеет. Для чтения поста нужна неплохая ML-математическая подготовка, но даже новичкам я бы рекомендовал почитать (хотя я не очень заботился, чтобы «всё объяснялось на пальцах»).
Начнём издалека…
Вспомним, как решается задача линейной регрессии. Итак, мы хотим получить линейную функцию (т.е. веса w), которая приближает целевое значение с точностью до ошибки:
Здесь мы предположили, что ошибка нормально распределена, x – признаковое описание объекта (возможно, в нём есть и фиктивный константный признак, чтобы в линейной функции был свободный член). Тогда мы знаем как распределены ответы нашей функции и можем записать функцию правдоподобия выборки (т.е. произведение плотностей, в которые подставлены значения из обучающей выборки) и воспользоваться методом максимального правдоподобия (в котором для определения значений параметров берётся максимум правдоподобия, а чаще – его логарифма):
В итоге оказывается, что максимизация правдоподобия эквивалентна минимизации среднеквадратичной ошибки (MSE), т.е. эта функция ошибки не зря широко используется в задачах регрессии. Кроме того, что она вполне логична, легко дифференцируема по параметрам и легко минимизируется, она ещё и теоретически обосновывается с помощью метода максимального правдоподобия в случае, если линейная модель соответствует данным с точностью до нормального шума.
Давайте ещё посмотрим, как реализуется метод стохастического градиента (SGD) для минимизации MSE: надо взять производную функции ошибки для конкретного объекта и записать формулу коррекции весов в виде «шага в сторону антиградиента»:
Получили, что веса линейной модели при её обучении методом SGD корректируются с помощью добавки вектора признаков. Коэффициент, с которым добавляют, зависит от «агрессивности алгоритма» (параметр альфа, который называют темпом обучения) и разности «ответ алгоритма – правильный ответ». Кстати, если разница нулевая (т.е. на данном объекте алгоритм выдаёт точный ответ), то коррекция весов не производится.
Log Loss
Теперь давайте, наконец, поговорим о «логлоссе». Рассматриваем задачу классификации с двумя классами: 0 и 1. Обучающую выборку можно рассматривать, как реализацию обобщённой схемы Бернулли: для каждого объекта генерируется случайная величина, которая с вероятностью p (своей для каждого объекта) принимает значение 1 и с вероятностью (1–p) – 0. Предположим, что мы как раз и строим нашу модель так, чтобы она генерировала правильные вероятности, но тогда можно записать функцию правдоподобия:
После логарифмирования правдоподобия получили, что его максимизация эквивалентна минимизации последнего записанного выражения. Именно его и называют «логистической функции ошибки». Для задачи бинарной классификации, в которой алгоритм должен выдать вероятность принадлежности классу 1, она логична ровно настолько, насколько логична MSE в задаче линейной регрессии с нормальным шумом (поскольку обе функции ошибки выводятся из метода максимального правдоподобия).
Часто гораздо более понятна такая запись logloss-ошибки на одном объекте:
Отметим неприятное свойство логосса: если для объекта 1го класса мы предсказываем нулевую вероятность принадлежности к этому классу или, наоборот, для объекта 0го – единичную вероятность принадлежности к классу 1, то ошибка равна бесконечности! Таким образом, грубая ошибка на одном объекте сразу делает алгоритм бесполезным. На практике часто логлосс ограничивают каким-то большим числом (чтобы не связываться с бесконечностями).
Если задаться вопросом, какой константный алгоритм оптимален для выборки из q_1 представителей класса 1 и q_0 представителей класса 0, q_1 + q_0 = q , то получим
Последний ответ получается взятием производной и приравниванием её к нулю. Описанную задачу приходится решать, например, при построении решающих деревьев (какую метку приписывать листу, если в него попали представители разных классов). На рис. 2 изображён график log_loss-ошибки константного алгоритма для выборки из четырёх объектов класса 0 и 6 объектов класса 1.
Представим теперь, что мы знаем, что объект принадлежит к классу 1 вероятностью p, посмотрим, какой ответ оптимален на этом объекте с точки зрения log_loss: матожидание нашей ошибки
Для минимизации ошибки мы опять взяли производную и приравняли к нулю. Мы получили, что оптимально для каждого объекта выдавать его вероятность принадлежности к классу 1! Таким образом, для минимизации log_loss надо уметь вычислять (оценивать) вероятности принадлежности классам!
Если подставить полученное оптимальное решение в минимизируемый функционал, то получим энтропию:
Это объясняет, почему при построении решающих деревьев в задачах классификации (а также случайных лесов и деревьях в бустингах) применяют энтропийный критерий расщепления (ветвления). Дело в том, что оценка принадлежности к классу 1 часто производится с помощью среднего арифметического меток в листе. В любом случае, для конкретного дерева эта вероятность будет одинакова для всех объектов в листе, т.е. константой. Таким образом, энтропия в листе примерно равна логлосс-ошибке константного решения. Используя энтропийный критерий мы неявно оптимизируем логлосс!
В каких пределах может варьироваться logloss? Ясно, что минимальное значение 0, максимальное – +∞, но эффективным максимальным можно считать ошибку при использовании константного алгоритма (вряд же мы в итоге решения задачи придумаем алгоритм хуже константы?!), т.е.
Интересно, что если брать логарифм по основанию 2, то на сбалансированной выборке это отрезок [0, 1].
Связь с логистической регрессией
Слово «логистическая» в названии ошибки намекает на связь с логистической регрессией – это как раз метод для решения задачи бинарной классификации, который получает вероятность принадлежности к классу 1. Но пока мы исходили из общих предположений, что наш алгоритм генерирует эту вероятность (алгоритмом может быть, например, случайный лес или бустинг над деревьями). Покажем, что тесная связь с логистической регрессией всё-таки есть… посмотрим, как настраивается логистическая регрессия (т.е. сигмоида от линейной комбинации) на эту функцию ошибки методом SGD.
Как видим, корректировка весов точно такая же, как и при настройке линейной регрессии! На самом деле, это говорит о родстве разных регрессий: линейной и логистической, а точнее, о родстве распределений: нормального и Бернулли. Желающие могут внимательно почитать лекцию Эндрю Ына.
Во многих книгах логистической функцией ошибки (т.е. именно «logistic loss») называется другое выражение, которое мы сейчас получим, подставив выражение для сигмоиды в logloss и сделав переобозначение: считаем, что метки классов теперь –1 и +1, тогда
Полезно посмотреть на график функции, центральной в этом представлении:
Как видно, это сглаженный (всюду дифференцируемый) аналог функции max(0, x), которую в глубоком обучении принято называть ReLu (Rectified Linear Unit). Если при настройке весов минимизировать logloss, то таким образом мы настраиваем классическую логистическую регрессию, если же использовать ReLu, чуть-чуть подправить аргумент и добавить регуляризацию, то получаем классическую настройку SVM:
выражение под знаком суммы принято называть Hinge loss. Как видим, часто с виду совсем разные методы можно получать «немного подправив» оптимизируемые функции на похожие. Между прочим, при обучении RVM (Relevance vector machine) используется тоже очень похожий функционал:
Связь с расхождением Кульбака-Лейблера
Расхождение (дивергенцию) Кульбака-Лейблера (KL, Kullback–Leibler divergence) часто используют (особенно в машинном обучении, байесовском подходе и теории информации) для вычисления непохожести двух распределений. Оно определяется по следующей формуле:
где P и Q – распределения (первое обычно «истинное», а второе – то, про которое нам интересно, насколько оно похоже на истинное), p и q – плотности этих распределений. Часто KL-расхождение называют расстоянием, хотя оно не является симметричным и не удовлетворяет неравенству треугольника. Для дискретных распределений формулу записывают так:
P_i, Q_i – вероятности дискретных событий. Давайте рассмотрим конкретный объект x с меткой y. Если алгоритм выдаёт вероятность принадлежности первому классу – a, то предполагаемое распределение на событиях «класс 0», «класс 1» – (1–a, a), а истинное – (1–y, y), поэтому расхождение Кульбака-Лейблера между ними
что в точности совпадает с logloss.
Настройка на logloss
Один из методов «подгонки» ответов алгоритма под logloss – калибровка Платта (Platt calibration). Идея очень простая. Пусть алгоритм порождает некоторые оценки принадлежности к 1му классу – a. Метод изначально разрабатывался для калибровки ответов алгоритма опорных векторов (SVM), этот алгоритм в простейшей реализации разделяет объекты гиперплоскостью и просто выдаёт номер класса 0 или 1, в зависимости от того, с какой стороны гиперплоскости объект расположен. Но если мы построили гиперплоскость, то для любого объекта можем вычислить расстояние до неё (со знаком минус, если объект лежит в полуплоскости нулевого класса). Именно эти расстояния со знаком r мы будем превращать в вероятности по следующей формуле:
неизвестные параметры α, β обычно определяются методом максимального правдоподобия на отложенной выборке (calibration set).
Проиллюстрируем применение метода на реальной задаче, которую автор решал недавно. На рис. показаны ответы (в виде вероятностей) двух алгоритмов: градиентного бустинга (lightgbm) и случайного леса (random forest).
Видно, что качество леса намного ниже и он довольно осторожен: занижает вероятности у объектов класса 1 и завышает у объектов класса 0. Упорядочим все объекты по возрастанию вероятностей (RF), разобьем на k равных частей и для каждой части вычислим среднее всех ответов алгоритма и среднее всех правильных ответов. Результат показан на рис. 5 – точки изображены как раз в этих двух координатах.
Нетрудно видеть, что точки располагаются на линии, похожей на сигмоиду – можно оценить параметр сжатия-растяжения в ней, см. рис. 6. Оптимальная сигмоида показана розовым цветом на рис. 5. Если подвергать ответы такой сигмоидной деформации, то логлосс-ошибка случайного леса снижается с 0.37 до 0.33.
Обратите внимание, что здесь мы деформировали ответы случайного леса (это были оценки вероятности – и все они лежали на отрезке [0, 1]), но из рис. 5 видно, что для деформации нужна именно сигмоида. Практика показывает, что в 80% ситуаций для улучшения logloss-ошибки надо деформировать ответы именно с помощью сигмоиды (для меня это также часть объяснения, почему именно такие функции успешно используются в качестве функций активаций в нейронных сетях).
Ещё один вариант калибровки – монотонная регрессия (Isotonic regression).
Многоклассовый logloss
Для полноты картины отметим, что logloss обобщается и на случай нескольких классов естественным образом:
здесь q – число элементов в выборке, l – число классов, a_ij – ответ (вероятность) алгоритма на i-м объекте на вопрос принадлежности его к j-му классу, y_ij=1 если i-й объект принадлежит j-му классу, в противном случае y_ij=0.
На посошок…
В каждом подобном посте я стараюсь написать что-то из мира машинного обучения, что, с одной стороны, просто и понятно, а с другой – изложение этого не встречается больше нигде. Например, есть такой естественный вопрос: почему в задачах классификации при построении решающих деревьев используют энтропийный критерий расщепления? Во всех курсах его (критерий) преподносят либо как эвристику, которую «вполне естественно использовать», либо говорят, что «энтропия похожа на кросс-энтропию». Сейчас стоимость некоторых курсов по машинному обучению достигает нескольких сотен тысяч рублей, но «профессиональные инструкторы» не могут донести простую цепочку:
- в статистической теории обучения настройка алгоритма производится максимизацией правдоподобия,
- в задаче бинарной классификации это эквивалентно минимизации логлосса, а сам минимум как раз равен энтропии,
- поэтому использование энтропийного критерия фактически эквивалентно выбору расщепления, минимизирующего логлосс.
Если Вы всё-таки отдали несколько сотен тысяч рублей, то можете проверить «профессиональность инструктора» следующими вопросами:
- Энтропия в листе примерно равна logloss-ошибке константного решения. Почему не использовать саму ошибку, а не приближённое значение? Или, как часто происходит в задачах оптимизации, её верхнюю оценку?
- Минимизации какой ошибки соответствует критерий расщепления Джини?
- Можно показать, что если в задаче бинарной классификации использовать в качестве функции ошибки среднеквадратичное отклонение, то также, как и для логлосса, оптимальным ответом на объекте будет вероятность его принадлежности к классу 1. Почему тогда не использовать такую функцию ошибки?
Ответы типа «так принято», «такой функции не существует», «это только для регрессии», естественно, заведомо неправильные. Если Вам не ответят с такой же степенью подробности, как в этом посте, то Вы точно переплатили;)
П.С. Что ещё почитать…
В этом блоге я публиковал уже несколько постов по метрикам качества…
- AUC ROC (площадь под кривой ошибок)
- Задачки про AUC (ROC)
- Знакомьтесь, Джини
И буквально на днях вышла классная статья Дмитрия Петухова про коэффициент Джини, читать обязательно:
- Коэффициент Джини. Из экономики в машинное обучение
Перевод
Ссылка на автора
В этой статье вы узнаете, как можно обучить нейронную сеть с помощью обратного распространения и стохастического градиентного спуска. Теории будут подробно описаны, и приведен подробный пример расчета, где обновляются как веса, так и смещения.
Это вторая часть в серии статей:
- Часть 1: Фонд,
- Часть 2: градиентный спуск и обратное распространение,
- Часть 3: Реализация в Java,
- Часть 4: лучше, быстрее, сильнее,
- Часть 5. Обучение сети чтению рукописных цифр,
- Дополнительный 1: Как я увеличил точность на 1% за счет увеличения данных,
- Дополнительно 2: Детская площадка MNIST,
Я предполагаю, что вы прочитали последнюю статью и что у вас есть хорошее представление о том, как нейронная сеть можетпреобразованиеданные. Если последняя статья требовала хорошего воображения (размышления о подпространствах в нескольких измерениях), эта статья, с другой стороны, будет более требовательной с точки зрения математики. Готовьтесь: бумага и ручка. Тихая комната. Тщательная мысль. Хороший ночной сон. Время, выносливость и усилие. Он утонет.
Контролируемое обучение
В прошлой статье мы пришли к выводу, что нейронную сеть можно использовать в качестве настраиваемой векторной функции. Мы корректируем эту функцию путем изменения весов и смещений, но их трудно изменить вручную. Их часто слишком много, даже если бы их было меньше, тем не менее было бы очень трудно получить хорошие результаты вручную.
Прекрасно то, что мы можем позволить сети настроить это самостоятельно, обучив сеть. Это можно сделать разными способами. Здесь я опишу то, что называетсяконтролируемое обучение, В этом типе обучения у нас есть набор данных, который былпомечены —у нас уже есть ожидаемый результат для каждого входа в этом наборе данных. Это будет наш учебный набор данных. Мы также гарантируем, что у нас есть маркированный набор данных, на котором мы никогда не обучаем сеть. Это будет наш тестовый набор данных, который будет использоваться для проверки того, насколько хорошо классифицируется обученная сеть.невидимые данные,
При обучении нашей нейронной сети мы подаем образец за образцом из набора обучающих данных по сети, и для каждого из них мы проверяем результат. В частности, мы проверяем, насколько результат отличается от того, что мы ожидали (ярлык). Разница между тем, что мы ожидали, и тем, что мы получили, называется стоимостью (иногда это называетсяошибкаилипотеря). Стоимость говорит нам, насколько правильной или неправильной была наша нейронная сеть в конкретном образце. Эту меру можно затем использовать для незначительной настройки сети, чтобы она была менее ошибочной при следующем поступлении этого образца через сеть.
Существует несколько различных функций стоимости, которые можно использовать (см. этот список например).
В этой статье я буду использовать функцию квадратичной стоимости:
(Иногда это также пишется с константой 0,5 впереди, что сделает его немного чище, когда мы его дифференцируем. Мы будем придерживаться версии выше.)
Возвращаясь к нашему примеру из часть 1,
Если бы мы ожидали:
… и получил …
… Стоимость будет:
Поскольку функция стоимости написана выше, размер ошибки явно зависит от выхода сети и ожидаемого значения. Если бы мы вместо этого определяли стоимость в терминах введенного значения (которое, конечно, детерминировано связано с выходными данными, если мы также учитываем все веса, смещения и какие функции активации были использованы), мы могли бы вместо этого написать:
C = C (y, exp) = C (W, b, Sσ, x, exp)— то есть стоимость является функциейWвосьмерокбiases, набор функций активации, входИксиехрectation.
Стоимость — это всего лишь скалярное значение для всего этого ввода. Поскольку функция непрерывна и дифференцируема (иногдакусочно дифференцируемыйНапример, при использовании ReLU-активаций) мы можем представить непрерывный ландшафт холмов и долин для функции стоимости. В более высоких измерениях этот пейзаж трудно визуализировать, но только с двумя весамиW₁ иWMight это может выглядеть примерно так:
Предположим, мы получили именно то значение стоимости, которое указано красной точкой на изображении (на основе толькоW₁ иWThat в этом упрощенном случае). Наша цель сейчас — улучшить нейронную сеть. Если бы мы могли снизить стоимость, нейронная сеть была бы лучше в классификации наших помеченных данных. Желательно, чтобы мы нашлиглобальный минимумфункции стоимости в этом ландшафте. Другими словами:самая глубокая долина из них всех, Это трудно, и нет никаких явных методов для такой сложной функции, как нейронная сеть. Тем не менее, мы можем найтиместный минимумс помощью итеративного процесса под названием градиентный спуск. Локального минимума может быть достаточно для наших нужд, и если нет, мы всегда можем скорректировать дизайн сети, чтобы получить новый ценовой ландшафт для локального и итеративного исследования
Градиентный спуск
Из исчисления с несколькими переменными мы знаем, что градиент функции ∇f в конкретной точке будет касательным к поверхности вектором, указывающим направление, в котором функция увеличивается наиболее быстро. И наоборот, отрицательный градиент -∇f будет указывать в направлении, где функция уменьшается быстрее всего. Этот факт мы можем использовать для расчета новых весовW⁺ от наших текущих весовW:
В уравнении вышеηэто просто небольшая константа, называемая скоростью обучения. Эта константа говорит нам, какую часть вектора градиента мы будем использовать для изменения текущего набора весов на новые. Если выбран слишком маленький, веса будут корректироваться слишком медленно, и наша конвергенция к локальному минимуму займет много времени. Если установлено слишком высокое, мы можем промахнуться и пропустить (или получить бодрое не сходящееся итеративное поведение).
Все вещи в уравнении выше — это просто матричная арифметика. Нам нужно внимательнее рассмотреть градиент функции стоимости относительно весов:
Как вы видите, нас пока не интересует конкретная скалярная стоимость, C, анасколько изменяется функция Costкогда вес меняется (рассчитывается один за другим),
Если мы расширим аккуратную векторную форму (уравнение 1), это будет выглядеть так:
Хорошая вещь об использовании градиента состоит в том, что он будет корректировать те веса, которые больше всего нуждаются в большем изменении, и веса, которые меньше нуждаются в изменении меньше. Это тесно связано с тем, что вектор отрицательного градиента указывает точно в направлении максимального спуска. Чтобы увидеть это, пожалуйста, еще раз взгляните на упрощенное изображение ландшафта функции стоимости выше и попытайтесь визуализировать разделение вектора красного градиента на векторы его компонентов вдоль осей.
Идея градиентного спуска работает так же хорошо в N измерениях, хотя это трудно визуализировать. Градиент покажет, какие компоненты нужно изменить больше, а какие нужно изменить меньше, чтобы уменьшить функцию C.
До сих пор я только что говорил о весах. Как насчет предубеждений? Что ж, те же рассуждения справедливы и для них, но вместо этого мы вычисляем (что проще):
Теперь пришло время посмотреть, как мы можем вычислить все эти частные производные для весов и смещений. Это приведет нас на более волосатую территорию, так что пристегнитесь. Чтобы разобраться во всем этом, сначала нам нужно слово о …
нотация
В остальной части этой статьи интенсивные обозначения. Множество символов и букв, которые вы увидите, это просто индексы, чтобы помочь нам отслеживать, на какой слой и на нейрон я ссылаюсь. Не позволяйте этим индексам делать математические выражения пугающими. Указатели призваны помочь и сделать его более точным. Вот краткое руководство о том, как их читать:
Также обратите внимание на то, что вход в нейрон был названZв прошлой статье (что довольно распространено), но был изменен наяВот. Причина в том, что мне легче запомнить это какядля вводаа такжеодля вывода,
обратное распространение
Самый простой способ описать, как рассчитать частные производные, это посмотреть на один конкретный вес:
Мы также увидим, что есть небольшая разница в том, как обрабатывать частную производную, если этот конкретный вес связан с последним выходным слоем или если он связан с любым из предыдущих скрытых слоев.
Последний слой
Теперь рассмотрим один весвесʟв последнем слое:
Наша задача — найти:
Как описано в прошлой статье, есть несколько шагов между весом и функцией стоимости:
- Мы умножаем вес на результат предыдущего слоя и добавляем смещение. Результатом является входяʟк нейрону.
- этояʟзатем подается через функцию активацииσ, производя выход из нейронаоʟ₁
- Наконец этооʟ₁используется в функции стоимости.
Справедливо сказать, что это трудно рассчитать …
… просто глядя на это.
Однако, если мы разделим его на три этапа, которые я только что описал, все станет намного проще. Поскольку эти три шага являются цепочечными функциями, мы могли бы отделить их производную, используя правило цепочки из исчисления:
На самом деле эти три частных производных оказывается простым для вычисления:
Это означает, что у нас есть все три фактора, необходимые для расчета
Другими словами, теперь мы знаем, как обновить все веса в последнем слое.
Давайте поработаем в обратном направлении отсюда.
Скрытые слои
Теперь рассмотрим один весвесʜв скрытом слое перед последним слоем:
Наша цель — найти:
Мы продолжаем, как мы делали в последнем слое Цепное правило дает нам:
Два первых фактора те же, что и раньше, и решает следующее:
- выход из предыдущего слоя и…
- производная функции активации соответственно.
Тем не менее, фактор …
… немного сложнее. Причина в том, что изменениеоʜочевидно, изменяет вход для всех нейронов в последнем слое и, как следствие, изменяет функцию стоимости в гораздо более широком смысле по сравнению с тем, когда нам просто нужно было заботиться об одном выходе из одного нейрона последнего слоя (я проиллюстрировал это, сделав соединения шире на изображении выше).
Чтобы решить эту проблему, нам нужно разделить частную производную функции общей стоимости на каждый вклад последнего слоя.
… Где каждый термин описывает, насколько изменяется Стоимость, когдаоʜизменяется, но только для той части сигнала, которая направляется через этот определенный выходной нейрон.
Давайте проверим этот единственный термин для первого нейрона. Опять же, это станет немного понятнее, если мы разделим его с помощью правила цепочки:
Давайте посмотрим на каждый из них:
Давайте на мгновение остановимся и позволим всему этому погрузиться.
Подводя итог тому, что мы только что узнали:
- Чтобы узнать, как обновить конкретный вес в скрытом слое, мы берем частную производную стоимости в терминах этого веса.
- Применяя правило цепочки, мы получаем три фактора, два из которых мы уже знаем, как рассчитать.
- Третьим фактором в этой цепочке является взвешенная сумма произведения двух факторов, которые мы уже рассчитали в последнем слое.
- Это означает, что мы можем вычислить все веса в этом скрытом слое так же, как мы делали в последнем слое, с той лишь разницей, что мы используем уже вычисленные данные из предыдущего слоя вместо производной функции стоимости.
С вычислительной точки зрения это очень хорошая новость, поскольку мы зависим только от вычислений, которые мы только что сделали (только последний слой), и нам не нужно проходить глубже, чем это. Это иногда называютдинамическое программированиечто часто является радикальным способом ускорить алгоритм, когда динамический алгоритм найден.
И так как мы зависим только от общих вычислений в последнем слое (в частности, мы не зависим от функции стоимости), мы можем теперь идти назад, слой за слоем. Ни один скрытый слой не отличается от любого другого в плане того, как мы рассчитываем вес обновлений. Мы говорим, что мы даем стоимость (илиошибкаилиубыток)backpropagate. Когда мы достигаем первого слоя, мы готовы. В этот момент мы имеем частные производные для всех весов в уравнении (уравнение 1) и готовы сделать наш шаг градиентного спуска вниз в ландшафте функции стоимости.
И вы знаете, что: это все.
Эй, подождите … Уклоны !?
Хорошо, я вас слышу. На самом деле они следуют той же схеме. Разница лишь в том, чтопервый срокв производной цепочке выражения последнего слоя и скрытого слоя будут иметь вид:
… вместо того
Поскольку вход в нейроноʜ ·весʟ+ бчастная производная этого по отношению кбпросто равно 1. Итак, где мы в весовом случае умножили цепочку на выходные данные последнего слоя, мы просто игнорируем выходные данные в случае смещения и умножаем на единицу.
Все остальные расчеты идентичны. Вы можете думать о смещениях как о более простом подмножестве вычислений веса. Тот факт, что изменение смещений не зависит от выхода из предыдущего нейрона, на самом деле имеет смысл. Смещения добавляются «со стороны» независимо от данных, поступающих по проводам к нейрону.
Пример
Из моего недавнего спуска в страну обратного распространения я могу себе представить, что приведенное выше прочтение может быть довольно полезным. Не будь парализован. На практике это довольно просто, и, вероятно, все становится яснее и проще для понимания, если проиллюстрировать это на примере.
Давайте опираться на пример из Часть 1: Фонд:
Давайте начнем свес₅:
Собирая данные из прямого прохода в часть 1 и используя данные из приведенного выше примера расчета стоимости, мы рассчитаем фактор за фактором. Также давайте предположим, что у нас есть скорость обученияη= 0,1 для этого примера.
Аналогично мы можем вычислить все остальные параметры в последнем слое:
Теперь мы перемещаем один слой назад и фокусируемся навес₁:
Еще раз, выбирая данные из прямого прохода в часть 1 и используя данные сверху, это просто для расчета фактор за фактором.
Из расчетов в последнем слое:
Теперь у нас есть все и, наконец, можно найтивес₁:
Таким же образом мы можем вычислить все остальные параметры в скрытом слое:
Это оно Мы успешно обновили весы и смещения во всей сети!
Санитарная проверка
Давайте проверим, что сеть теперь ведет себя немного лучше на входе
х = [2, 3]
Когда мы в первый раз пропустили этот вектор через сеть, мы получили вывод
у = [0,712257432295742, 0,533097573871501]
… и стоимость+0,19374977898811957,
Теперь, после того, как мы обновили веса, мы получаем вывод
у = [0,7187729999291985 0,523807451860988]
… и стоимость+0,18393989144952877,
Обратите внимание, что оба компонента слегка сместились в сторону того, что мы ожидали [1, 0,2], и что общая стоимость сети теперь ниже.
Повторное обучение сделает его еще лучше!
Следующая статья показывает, как это выглядит в коде Java. Когда вы будете готовы к этому, пожалуйста, погрузитесь в: Часть 3: Реализация в Java,
Обратная связь приветствуется!
Первоначально опубликовано на machinelearning.tobiashill.se 4 декабря 2018 г.
В этой статье мы поговорим о математике градиентного спуска, почему при обучении нейронных сетей применяется стохастический градиентный спуск и о вариации SGD (Stochastic Gradient Descent) с использованием скользящего среднего (SGD с momentum и Nesterov Accelerated Gradient).
Градиентный спуск
Предполагается, что вы знакомы с понятием нейронной сети, вы имеете представление, какие задачи можно решать с помощью этого алгоритма машинного обучения и что такое параметры (веса) нейронной сети. Также, важно понимать, что градиент функции — это направление наискорейшего роста функции, а градиент взятый с минусом это направление наискорейшего убывания. — это антиградиент функционала,
где — параметры функции (веса нейронной сети),
— функционал ошибки.
Обучение нейронной сети — это такой процесс, при котором происходит подбор оптимальных параметров модели, с точки зрения минимизации функционала ошибки. Иными словами, осуществяется поиск параметров функции, на которой достигается минимум функционала ошибки. Происходит это с помощью итеративного метода оптимизации функционала —градиентного спуска. Процесс может быть записан следующим образом:
где — это номер шага,
— размер шага обучения (learning rate). В результате шага оптимизации веса нейронной сети принимают новые значения.
Виды градиентного спуска
- Пакетный градиентный спуск (batch gradient descent).
При этом подходе градиент функционала обычно вычисляется как сумма градиентов, учитывая каждый элемент обучения сразу. Это хорошо работает в случае выпуклых и относительно гладких функционалов, как например в задаче линейной или логистической регрессии, но не так хорошо, когда мы обучаем многослойные нейронные сети. Поверхность, задаваемая функционалом ошибки нейронной сети, зачастую негладкая и имеет множество локальных экстремумов, в которых мы обречены застрять, если двигаться пакетным градиентным спуском. Также обилие обучающих данных, делает задачу поиска градиента по всем примерам затратной по памяти.
- Стохастический градиентный спуск (stochastic gradient descent)
Этот подход подразумевает корректировку весов нейронной сети, используя аппроксимацию градиента функционала, вычисленную только на одном случайном обучающем примере из выборки. Метод привносит «шум» в процесс обучения, что позволяет (иногда) избежать локальных экстремумов. Также в этом варианте шаги обучения происходят чаще, и не требуется держать в памяти градиенты всех обучающих примеров. Под SGD часто понимают подразумевают описанный ниже.
- Mini-batch градиентный спуск
Гибрид двух подходов SGD и BatchGD, в этом варианте изменение параметров происходит, беря в расчет случайное подмножество примеров обучающей выборки. Благодаря более точной аппроксимации полного градиента, процесс оптимизации имеет большую эффективность, не утрачивая при этом преимущества SGD. Поведение трёх описанных варианта хорошо проиллюстрировано на картинке ниже.

В общем случае, при работе с нейронными сетями, веса оптимизируют стохастическим градиентным спуском или его вариацией. Поговорим о двух модификациях, использующих скользящее среднее градиентов.
SGD с импульсом и Nesterov Accelerated Gradient
Следующие две модификации SGD призваны помочь в решении проблемы попадания в локальные минимумы при оптимизации невыпуклого функционала.
Гладкая выпуклая функция
Функция с множеством локальных минимумов (источник)
Первая модификация
При SGD с импульсом (или SGD with momentum) на каждой новой итерации оптимизации используется скользящее среднее градиента. Движение в направлении среднего прошлых градиентов добавляет в алгоритм оптимизации эффект импульса, что позволяет скорректировать направление очередного шага, относительно исторически доминирующего направления. Для этих целей достаточно использовать приближенное скользящее среднее и не хранить все предыдущие значения градиентов, для вычисления «честного среднего».
Запишем формулы, задающие этот подход:
— это накопленное среднее градиентов на шаге
, коэфициент
требуется для сохранения истории значений среднего (обычно выбирается близким к
.
Вторая модификация
Nesterov accelerated gradient отличается от метода с импульсом, его особенностью является вычисление градиента при обновлении в отличной точке. Эта точка берётся впереди по направлению движения накопленного градиента:
На картинке изображены различия этих двух методов.
источник
Красным вектором на первой части изображено направление градиента в текущей точке пространства параметров, такой градиент используется в стандартном SGD. На второй части красный вектор задает градиент сдвинутый на накопленное среднее. Зелеными векторами на обеих частях выделены импульсы, накопленные градиенты.
Заключение
В этой статье мы детально рассмотрели начала градиентного спуска с точки зрения оптимизации нейронных сетей. Поговорили о трёх разновидностях спуска с точки зрения используемых данных, и о двух модификациях SGD, использующих импульс, для достижения лучшего качества оптимизации невыпуклых и негладких функционалов ошибки. Дальнейшее изучение темы предполагает разбор адаптивных к частоте встречающихся признаков подходов таких как Adagrad, RMSProp, ADAM.
Данная статья была написана в преддверии старта курса «Математика для Data Science» от OTUS.
Приглашаю всех желающих записаться на demo day курса, в рамках которого вы сможете подробно узнать о курсе и процессе обучения, а также познакомиться с экспертами OTUS
— ЗАПИСАТЬСЯ НА DEMO DAY