Список литературы
1.Росляков Г.В., Князев Б.А. Методы обработки экспериментальных данных. Новосибирск: НГУ, 1985. 5
2.Князев Б.А., Кругляков Э.П., Воробьев В.В., Капитонов В.А. Постоянная Керра воды ЖПМТФ. 1976. (1):157–160. 7, 9
3.Сквайрс Дж. Практическая физика. М.: Мир, 1971. 31, 32
4.Кунце Х.-И. Методы физических измерений. М.: Мир, 1989. 39
5.Зайдель А.Н. Ошибки измерений физических величин. Л.: Наука, 1974.
6.Худсон Д. Статистика для физиков. М.: Мир, 1967. 30
7.Тейлор Дж. Введение в теорию ошибок. М.: Мир, 1985. 39
8.Румшисский Л.З. Математическая обработка результатов эксперимента. М.: Наука, 1971.
9.Вильямс А., Кэмпион П.Дж., Барнс Д.Е. Практическое руководство по представлению результатов измерений. М.: Атомиздат, 1979.
10.Агекян Т.А. Основы теории ошибок для астрономов и физиков. М.: Наука, 1968.
11.Маркин Н.С. Основы теории обработки результатов измерений. М.: Изд. стандартов, 1991.
12.Секей Г. Парадоксы в теории вероятностей и в математической статистике. М.: Мир, 1990.
13.Мантуров О.В. Курс высшей математики. М.: Выс.школа, 1991. 7, 22
14.Корн Т., Корн Г. Справочник по математике для научных работников и инженеров. М.: Наука, 1968. 16
15.Сирая Т.Н., Грановский В.А. Методы обработки экспериментальных данных при измерениях. Л.: Энергоатомиздат, 1990. 28
16.Дойников А.С., Брянский Л.Н. Краткий справочник метролога. М.: Стандарты, 1991. 28

Таблицы DPVA.ru — Инженерный Справочник
Адрес этой страницы (вложенность) в справочнике dpva.ru: 
Таблица. Интеграл вероятности или интеграл вероятностей. Таблица значений функции Лапласа. Она же функция ошибок erf.Интегральная функция вероятности распределения обычно выражается через специальную функцию erf(z).
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Поиск в инженерном справочнике DPVA. Введите свой запрос: |
Поиск в инженерном справочнике DPVA. Введите свой запрос:
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста.
Вложите в письмо ссылку на страницу с ошибкой, пожалуйста.
Коды баннеров проекта DPVA.ru
Начинка: KJR Publisiers
Консультации и техническая
поддержка сайта: Zavarka Team
Free xml sitemap generator

В математике функция ошибок (также называемая Функция ошибок Гаусса ), часто обозначаемая erf, является сложной функцией комплексной определяемой как:
- erf z = 2 π ∫ 0 ze — t 2 dt. { displaystyle operatorname {erf} z = { frac {2} { sqrt { pi}}} int _ {0} ^ {z} e ^ {- t ^ {2}} , dt.}
Этот интеграл является особой (не элементарной ) и сигмоидной функцией, которая часто встречается в статистике вероятность, и уравнения в частных производных. Во многих из этих приложений аргумент функции является действительным числом. Если аргумент функции является действительным, значение также является действительным.
В статистике для неотрицательных значений x функция имеет интерпретацию: для случайной величины Y, которая нормально распределена с среднее 0 и дисперсия 1/2, erf x — это вероятность того, что Y попадает в диапазон [-x, x].
Две связанные функции: дополнительные функции ошибок (erfc ), определенная как
- erfc z = 1 — erf z, { displaystyle operatorname {erfc} z = 1- operatorname {erf} z,}
и функция мнимой ошибки (erfi ), определяемая как
- erfi z = — i erf (iz), { displaystyle operatorname {erfi} z = -i operatorname {erf} (iz),}
, где i — мнимая единица.
Содержание
- 1 Имя
- 2 Приложения
- 3 Свойства
- 3.1 Ряд Тейлора
- 3.2 Производная и интеграл
- 3.3 Ряд Бюрмана
- 3.4 Обратные функции
- 3.5 Асимптотическое разложение
- 3.6 Разложение на непрерывную дробь
- 3,7 Интеграл функции ошибок с функцией плотности Гаусса
- 3.8 Факториальный ряд
- 4 Численные приближения
- 4.1 Аппроксимация с элементарными функциями
- 4.2 Полином
- 4.3 Таблица значений
- 5 Связанные функции
- 5.1 функция дополнительных ошибок
- 5.2 Функция мнимой ошибки
- 5.3 Кумулятивная функци я распределения на
- 5.4 Обобщенные функции ошибок
- 5.5 Итерированные интегралы дополнительных функций ошибок
- 6 Реализации
- 6.1 Как действующая функция действительного аргумента
- 6.2 Как комплексная функция комплексного аргумента
- 7 См. Также
- 7.1 Связанные функции
- 7.2 Вероятность
- 8 Ссылки
- 9 Дополнительная литература
- 10 Внешние ссылки
Имя
Название «функция ошибки» и его аббревиатура erf были предложены Дж. В. Л. Глейшер в 1871 г. по причине его связи с «теорией вероятности, и особенно теорией ошибок ». Дополнение функции ошибок также обсуждалось Глейшером в отдельной публикации в том же году. Для «закона удобства» ошибок плотность задана как
- f (x) = (c π) 1 2 e — cx 2 { displaystyle f (x) = left ({ frac {c } { pi}} right) ^ { tfrac {1} {2}} e ^ {- cx ^ {2}}}
(нормальное распределение ), Глейшер вычисляет вероятность ошибки, лежащей между p { displaystyle p}

- (c π) 1 2 ∫ pqe — cx 2 dx = 1 2 (erf (qc) — erf (pc)). { displaystyle left ({ frac {c} { pi}} right) ^ { tfrac {1} {2}} int _ {p} ^ {q} e ^ {- cx ^ {2} } dx = { tfrac {1} {2}} left ( operatorname {erf} (q { sqrt {c}}) — operatorname {erf} (p { sqrt {c}}) right).}
Приложения
Когда результаты серии измерений описываются нормальным распределением со стандартным отклонением σ { displaystyle sigma}

Функции и дополнительные функции ошибок возникают, например, в решениях уравнения теплопроводности, когда граничные ошибки задаются ступенчатой функцией Хевисайда.
Функция ошибок и ее приближения Программу присвоили себе преподавателей, которые получили с высокой вероятностью или с низкой вероятностью. Дана случайная величина X ∼ Norm [μ, σ] { displaystyle X sim operatorname {Norm} [ mu, sigma]}![X sim operatorname {Norm} [ му, sigma]](https://wikimedia.org/api/rest_v1/media/math/render/svg/84024bc6827355ec6d23a062283a26d54b29698d)

- Pr [X ≤ L ] = 1 2 + 1 2 erf (L — μ 2 σ) ≈ A ехр (- B (L — μ σ) 2) { Displaystyle Pr [X Leq L] = { frac {1} {2 }} + { frac {1} {2}} operatorname {erf} left ({ frac {L- mu} {{ sqrt {2}} sigma}} right) приблизительно A exp left (-B left ({ frac {L- mu} { sigma}} right) ^ {2} right)}
где A и B — верх числовые константы. Если L достаточно далеко от среднего, то есть μ — L ≥ σ ln k { displaystyle mu -L geq sigma { sqrt { ln {k}}}}
- Pr [X ≤ L] ≤ A exp (- B ln k) = A К B { displaystyle Pr [X leq L] leq A exp (-B ln {k}) = { frac {A} {k ^ {B}}}}
, поэтому становится вероятность 0 при k → ∞ { displaystyle k to infty}
Свойства
Графики на комплексной плоскости 

Свойство erf (- z) = — erf (z) { displaystyle operatorname {erf} (-z) = — operatorname {erf} (z)}

Для любого комплексное число z:
- erf (z ¯) = erf (z) ¯ { displaystyle operatorname {erf} ({ overline {z}}) = { overline { operatorname {erf} (z)}}}
где z ¯ { displaystyle { overline {z}}}
Подынтегральное выражение f = exp (−z) и f = erf (z) показано в комплексной плоскости z на рисунках 2 и 3. Уровень Im (f) = 0 показан жирным зеленым цветом. линия. Отрицательные целые значения Im (f) показаны жирными красными линиями. Положительные целые значения Im (f) показаны толстыми синими линиями. Промежуточные уровни Im (f) = проявляются тонкими зелеными линиями. Промежуточные уровни Re (f) = показаны тонкими красными линиями для отрицательных значений и тонкими синими линиями для положительных значений.
Функция ошибок при + ∞ равна 1 (см. интеграл Гаусса ). На действительной оси erf (z) стремится к единице при z → + ∞ и к −1 при z → −∞. На мнимой оси он стремится к ± i∞.
Серия Тейлора
Функция ошибок — это целая функция ; у него нет сингулярностей (кроме бесконечности), и его разложение Тейлора всегда сходится, но, как известно, «[…] его плохая сходимость, если x>1».
определяющий интеграл нельзя вычислить в закрытой форме в терминах элементарных функций, но путем расширения подынтегрального выражения e в его ряд Маклорена и интегрирована почленно, можно получить ряд Маклорена функции ошибок как:
- erf (z) = 2 π ∑ n = 0 ∞ (- 1) nz 2 n + 1 n! (2 n + 1) знак равно 2 π (z — z 3 3 + z 5 10 — z 7 42 + z 9 216 — ⋯) { displaystyle operatorname {erf} (z) = { frac {2} { sqrt { pi}}} sum _ {n = 0} ^ { infty} { frac {(-1) ^ {n} z ^ {2n + 1}} {n! (2n + 1)}} = { frac {2} { sqrt { pi}}} left (z — { frac {z ^ {3}} {3}} + { frac {z ^ { 5}} {10}} — { frac {z ^ {7}} {42}} + { frac {z ^ {9}} {216}} — cdots right)}
, которое выполняется для каждого комплексного числа г. Члены знаменателя представляют собой последовательность A007680 в OEIS.
Для итеративного вычисления нового ряда может быть полезна следующая альтернативная формулировка:
- erf (z) = 2 π ∑ n = 0 ∞ (z ∏ К знак равно 1 N — (2 К — 1) Z 2 К (2 К + 1)) знак равно 2 π ∑ N = 0 ∞ Z 2 N + 1 ∏ К = 1 N — Z 2 К { Displaystyle OperatorName { erf} (z) = { frac {2} { sqrt { pi}}} sum _ {n = 0} ^ { infty} left (z prod _ {k = 1} ^ {n} { frac {- (2k-1) z ^ {2}} {k (2k + 1)}} right) = { frac {2} { sqrt { pi}}} sum _ {n = 0} ^ { infty} { frac {z} {2n + 1}} prod _ {k = 1} ^ {n} { frac {-z ^ {2}} {k}}}
потому что что — (2 k — 1) z 2 k (2 k + 1) { displaystyle { frac {- (2k-1) z ^ {2}} {k (2k + 1))}} }
Функция мнимой ошибки имеет очень похожий ряд Маклорена:
- erfi (z) = 2 π ∑ n = 0 ∞ z 2 n + 1 n! (2 n + 1) знак равно 2 π (z + z 3 3 + z 5 10 + z 7 42 + z 9 216 + ⋯) { displaystyle operatorname {erfi} (z) = { frac {2} { sqrt { pi}}} sum _ {n = 0} ^ { infty} { frac {z ^ {2n + 1}} {n! (2n + 1)}} = { frac {2} { sqrt { pi}}} left (z + { frac {z ^ {3}} {3}} + { frac {z ^ { 5}} {10}} + { frac {z ^ {7}} {42}} + { frac {z ^ {9}} {216}} + cdots right)}
, которое выполняется для любого комплексного числа z.
Производная и интеграл
Производная функция ошибок сразу следует из ее определения:
- ddz erf (z) = 2 π e — z 2. { displaystyle { frac {d} {dz}} operatorname {erf} (z) = { frac {2} { sqrt { pi}}} e ^ {- z ^ {2}}.}
Отсюда немедленно вычисляется производная функция мнимой ошибки :
- ddz erfi (z) = 2 π ez 2. { displaystyle { frac {d} {dz}} operatorname {erfi} (z) = { frac {2} { sqrt { pi }}} e ^ {z ^ {2}}.}
первообразная функции ошибок, которые можно получить посредством интегрирования по частям, составляет
- z erf (z) + е — z 2 π. { displaystyle z operatorname {erf} (z) + { frac {e ^ {- z ^ {2}}} { sqrt { pi}}}.}
Первообразная мнимой функции ошибок, также можно получить интегрированием по частям:
- z erfi (z) — ez 2 π. { displaystyle z operatorname {erfi} (z) — { frac {e ^ {z ^ {2}}} { sqrt { pi}}}.}
Производные высшего порядка задаются как
- erf (k) (z) = 2 (- 1) k — 1 π H k — 1 (z) e — z 2 = 2 π dk — 1 dzk — 1 (e — z 2), k = 1, 2, … { Displaystyle operatorname {erf} ^ {(k)} (z) = { frac {2 (-1) ^ {k-1}} { sqrt { pi}}} { mathit {H} } _ {k-1} (z) e ^ {- z ^ {2}} = { frac {2} { sqrt { pi}}} { frac {d ^ {k-1}} {dz ^ {k-1}}} left (e ^ {- z ^ {2}} right), qquad k = 1,2, dots}
где H { displaystyle { mathit {H}}}
ряд Бюрмана
Расширение, которое сходится быстрее для всех реальных значений x { displaystyle x}
- erf (x) = 2 π sgn (x) 1 — e — x 2 (1 — 1 12 ( 1 — e — x 2) — 7 480 (1 — e — x 2) 2 — 5 896 (1 — e — x 2) 3 — 787 276480 (1 — e — x 2)) 4 — ⋯) знак равно 2 π знак (x) 1 — e — x 2 (π 2 + ∑ k = 1 ∞ cke — kx 2). { displaystyle { begin {align} operatorname {erf} (x) = { frac {2} { sqrt { pi}}} operatorname {sgn} (x) { sqrt {1-e ^ {-x ^ {2}}}} left (1 — { frac {1} {12}} left (1-e ^ {- x ^ {2}} right) — { frac {7} {480}} left (1-e ^ {- x ^ {2}} right) ^ {2} — { frac {5} {896}} left (1-e ^ {- x ^ {2 }} right) ^ {3} — { frac {787} {276480}} left (1-e ^ {- x ^ {2}} right) ^ {4} — cdots right) \ [10pt] = { frac {2} { sqrt { pi}}} operatorname {sgn} (x) { sqrt {1-e ^ {- x ^ {2}}}} left ({ frac { sqrt { pi}} {2}} + sum _ {k = 1} ^ { infty} c_ {k} e ^ {- kx ^ {2}} right). end {выровнено}}
Сохраняя только первые два коэффициента и выбирая c 1 = 31 200 { displaystyle c_ {1} = { frac {31} {200}}}



- erf (x) ≈ 2 π sign (x) 1 — e — x 2 (π 2 + 31 200 e — x 2 — 341 8000 e — 2 х 2). { displaystyle operatorname {erf} (x) приблизительно { frac {2} { sqrt { pi}}} operatorname {sgn} (x) { sqrt {1-e ^ {- x ^ {2 }}}} left ({ frac { sqrt { pi}} {2}} + { frac {31} {200}} e ^ {- x ^ {2}} — { frac {341} {8000}} e ^ {- 2x ^ {2}} right).}
Обратные функции

Учитывая комплексное число z, не существует уникального комплексного числа w, удовлетворяющего erf (w) = z { displaystyle operatorname {erf} (w) = z}

- erf (erf — 1 ( х)) = х. { displaystyle operatorname {erf} left ( operatorname {erf} ^ {- 1} (x) right) = x.}
Обратная функция ошибок обычно определяется с помощью домена (- 1,1), и он ограничен этой областью многих систем компьютерной алгебры. Однако его можно продолжить и на диск | z | < 1 of the complex plane, using the Maclaurin series
- erf — 1 (z) знак равно ∑ К знак равно 0 ∞ ck 2 k + 1 (π 2 z) 2 k + 1, { displaystyle operatorname {erf} ^ {- 1} (z) = sum _ {k = 0} ^ { infty} { frac {c_ {k}} {2k + 1}} left ({ frac { sqrt { pi}} {2}} z right) ^ {2k + 1},}
где c 0 = 1 и
- ck = ∑ m = 0 k — 1 cmck — 1 — m (m + 1) (2 m + 1) = {1, 1, 7 6, 127 90, 4369 2520, 34807 16200,…}. { displaystyle c_ {k} = sum _ {m = 0} ^ {k-1} { frac {c_ {m} c_ {k-1-m}} {(m + 1) (2m + 1) }} = left {1,1, { frac {7} {6}}, { frac {127} {90}}, { frac {4369} {2520}}, { frac {34807} {16200}}, ldots right }.}
Итак, у нас есть разложение в ряд (общие множители были удалены из числителей и знаменателей):
- erf — 1 (z) = 1 2 π ( z + π 12 z 3 + 7 π 2 480 z 5 + 127 π 3 40320 z 7 + 4369 π 4 5806080 z 9 + 34807 π 5 182476800 z 11 + ⋯). { displaystyle operatorname {erf} ^ {- 1} (z) = { tfrac {1} {2}} { sqrt { pi}} left (z + { frac { pi} {12} } z ^ {3} + { frac {7 pi ^ {2}} {480}} z ^ {5} + { frac {127 pi ^ {3}} {40320}} z ^ {7} + { frac {4369 pi ^ {4}} {5806080}} z ^ {9} + { frac {34807 pi ^ {5}} {182476800}} z ^ {11} + cdots right). }
(После отмены дроби числителя / знаменателя характерми OEIS : A092676 / OEIS : A092677 в OEIS ; без отмены членов числителя в записи OEIS : A002067.) Значение функции ошибок при ± ∞ равно ± 1.
Для | z | < 1, we have erf (erf — 1 (z)) = z { displaystyle operatorname {erf} left ( operatorname {erf} ^ {- 1} (z) right) = z}
обратная дополнительная функция ошибок определяется как
- erfc — 1 (1 — z) = erf — 1 (z). { displaystyle operatorname {erfc} ^ {- 1} (1-z) = operatorname {erf} ^ {- 1} (z).}
Для действительного x существует уникальное действительное число erfi — 1 (x) { displaystyle operatorname {erfi} ^ {- 1} (x)}


Для любого действительного x, Метод Ньютона можно использовать для вычислений erfi — 1 (x) { displaystyle operatorname {erfi} ^ {- 1} (x)}

- erfi — 1 (z) = ∑ k = 0 ∞ (- 1) ККК 2 К + 1 (π 2 Z) 2 К + 1, { Displaystyle OperatorName {erfi} ^ {- 1} (г) = сумма _ {к = 0} ^ { infty} { гидроразрыва {(-1) ^ {k} c_ {k}} {2k + 1}} left ({ frac { sqrt { pi}} {2}} z right) ^ {2k + 1},}
, где c k определено, как указано выше.
Асимптотическое разложение
Полезным асимптотическим разложением дополнительные функции (и, следовательно, также и функции ошибок) для больших вещественных x
- erfc (x) = e — x 2 x π [1 + ∑ n = 1 ∞ (- 1) n 1 ⋅ 3 ⋅ 5 ⋯ (2 n — 1) (2 x 2) n] = e — x 2 x π ∑ n = 0 ∞ (- 1) п (2 п — 1)! ! (2 х 2) n, { displaystyle operatorname {erfc} (x) = { frac {e ^ {- x ^ {2}}} {x { sqrt { pi}}}} left [1 + sum _ {n = 1} ^ { infty} (- 1) ^ {n} { frac {1 cdot 3 cdot 5 cdots (2n-1)} {(2x ^ {2}) ^ {n}}} right] = { frac {e ^ {- x ^ {2}}} {x { sqrt { pi}}}} sum _ {n = 0} ^ { infty} ( -1) ^ {n} { frac {(2n-1) !!} {(2x ^ {2}) ^ {n}}},}
где (2n — 1) !! — это двойной факториал числа (2n — 1), которое является произведением всех нечетных чисел до (2n — 1). Этот ряд расходуется для любого конечного x, и его значение как асимптотического разложения состоит в том, что для любого N ∈ N { displaystyle N in mathbb {N}}
- erfc (Икс) знак равно е — Икс 2 Икс π ∑ N знак равно 0 N — 1 (- 1) N (2 N — 1)! ! (2 х 2) n + RN (x) { displaystyle operatorname {erfc} (x) = { frac {e ^ {- x ^ {2}}} {x { sqrt { pi}}}} sum _ {n = 0} ^ {N-1} (- 1) ^ {n} { frac {(2n-1) !!} {(2x ^ {2}) ^ {n}}} + R_ {N} (x)}
где остаток в нотации Ландау равен
- RN (x) = O (x 1 — 2 N e — x 2) { displaystyle R_ {N} ( x) = O left (x ^ {1-2N} e ^ {- x ^ {2}} right)}
при x → ∞. { displaystyle x to infty.}
Действительно, точное значение остатка равно
- R N (x): = (- 1) N π 2 1 — 2 N (2 N)! N! ∫ Икс ∞ T — 2 N e — T 2 dt, { Displaystyle R_ {N} (x): = { frac {(-1) ^ {N}} { sqrt { pi}}} 2 ^ { 1-2N} { frac {(2N)!} {N!}} Int _ {x} ^ { infty} t ^ {- 2N} e ^ {- t ^ {2}} , dt,}
который легко следует по индукции, записывая
- e — t 2 = — (2 t) — 1 (e — t 2) ′ { displaystyle e ^ {- t ^ {2}} = — (2t) ^ {- 1} left (e ^ {- t ^ {2}} right) ‘}
и интегрирование по частям.
Для достаточно больших значений x, только первые несколько этих асимптотических разностей необходимы, чтобы получить хорошее приближение erfc (x) (в то время как для не слишком больших значений x приведенное выше разложение Тейлора при 0 обеспечивает очень быструю сходимость).
Расширение непрерывной дроби
A Разложение непрерывной дроби дополнительные функции ошибок:
- erfc (z) = z π e — z 2 1 z 2 + a 1 1 + a 2 z 2 + a 3 1 + ⋯ am = м 2. { displaystyle operatorname {erfc} (z) = { frac {z} { sqrt { pi}}} e ^ {- z ^ {2}} { cfrac {1} {z ^ {2} + { cfrac {a_ {1}} {1 + { cfrac {a_ {2}} {z ^ {2} + { cfrac {a_ {3}} {1+) dotsb}}}}}}}} qquad a_ {m} = { frac {m} {2}}.}
Интеграл функции ошибок с функцией плотности Гаусса
- ∫ — ∞ ∞ erf (ax + б) 1 2 π σ 2 е — (Икс — μ) 2 2 σ 2 dx знак равно erf [a μ + b 1 + 2 a 2 σ 2], a, b, μ, σ ∈ R { displaystyle int _ {- infty} ^ { infty} operatorname {erf} left (ax + b right) { frac {1} { sqrt {2 pi sigma ^ {2}}}} e ^ {- { frac {(x- mu) ^ {2}} {2 sigma ^ {2}}}} , dx = operatorname {erf} left [{ frac {a mu + b } { sqrt {1 + 2a ^ {2} sigma ^ {2}}} right], qquad a, b, mu, sigma in mathbb {R}}
Факториальный ряд
- Обратное:
-
- erfc z = e — z 2 π z ∑ n = 0 ∞ (- 1) n Q n (z 2 + 1) n ¯ = e — z 2 π z (1 — 1 2 1 (z 2 + 1) + 1 4 1 (z 2 + 1) (z 2 + 2) — ⋯) { displaystyle { begin {align} operatorname {erfc} z = { frac {e ^ {- z ^ {2}}} {{ sqrt { pi}} , z}} sum _ {n = 0} ^ { infty} { frac {(-1) ^ {n} Q_ {n}} {{(z ^ {2} + 1)} ^ { ba r {n}}}} \ = { frac {e ^ {- z ^ {2}}} {{ sqrt { pi}} , z}} left ( 1 — { frac {1} {2}} { frac {1} {(z ^ {2} +1)}} + { frac {1} {4}} { frac {1} {(z ^ {2} +1) (z ^ {2} +2)}} — cdots right) end {align}}}
- erfc z = e — z 2 π z ∑ n = 0 ∞ (- 1) n Q n (z 2 + 1) n ¯ = e — z 2 π z (1 — 1 2 1 (z 2 + 1) + 1 4 1 (z 2 + 1) (z 2 + 2) — ⋯) { displaystyle { begin {align} operatorname {erfc} z = { frac {e ^ {- z ^ {2}}} {{ sqrt { pi}} , z}} sum _ {n = 0} ^ { infty} { frac {(-1) ^ {n} Q_ {n}} {{(z ^ {2} + 1)} ^ { ba r {n}}}} \ = { frac {e ^ {- z ^ {2}}} {{ sqrt { pi}} , z}} left ( 1 — { frac {1} {2}} { frac {1} {(z ^ {2} +1)}} + { frac {1} {4}} { frac {1} {(z ^ {2} +1) (z ^ {2} +2)}} — cdots right) end {align}}}
- сходится для Re (z 2)>0. { displaystyle operatorname {Re} (z ^ {2})>0.}
Здесь
- Q n = def 1 Γ (1/2) ∫ 0 ∞ τ (τ — 1) ⋯ ( τ — n + 1) τ — 1/2 е — τ d τ знак равно ∑ К знак равно 0 N (1 2) к ¯ s (n, k), { displaystyle Q_ {n} { stackrel { text {def}} {=}} { frac {1} { Gamma (1/2)}} int _ {0} ^ { infty} tau ( tau -1) cdots ( tau -n + 1) tau ^ {-1/2} e ^ {- tau} d tau = sum _ {k = 0} ^ {n} left ({ frac {1} {2}} right) ^ { bar {k}} s (n, k),}
- Q n = def 1 Γ (1/2) ∫ 0 ∞ τ (τ — 1) ⋯ ( τ — n + 1) τ — 1/2 е — τ d τ знак равно ∑ К знак равно 0 N (1 2) к ¯ s (n, k), { displaystyle Q_ {n} { stackrel { text {def}} {=}} { frac {1} { Gamma (1/2)}} int _ {0} ^ { infty} tau ( tau -1) cdots ( tau -n + 1) tau ^ {-1/2} e ^ {- tau} d tau = sum _ {k = 0} ^ {n} left ({ frac {1} {2}} right) ^ { bar {k}} s (n, k),}
- zn ¯ { displaystyle z ^ { bar {n}}}
обозначает возрастающий факториал, а s (n, k) { displaystyle s (n, k)}
обозначает знаковое число Стирлинга первого рода.
- Представление бесконечной суммой, составляющей двойной факториал :
-
- ERF (Z) знак равно 2 π ∑ N знак равно 0 ∞ (- 2) N (2 N — 1)! (2 N + 1)! Z 2 N + 1 { Displaystyle OperatorName {ERF} (г) = { frac {2} { sqrt { pi}}} sum _ {n = 0} ^ { infty} { frac {( -2) ^ {n} (2n-1) !!} {(2n + 1)!}} Z ^ {2n + 1}}
- ERF (Z) знак равно 2 π ∑ N знак равно 0 ∞ (- 2) N (2 N — 1)! (2 N + 1)! Z 2 N + 1 { Displaystyle OperatorName {ERF} (г) = { frac {2} { sqrt { pi}}} sum _ {n = 0} ^ { infty} { frac {( -2) ^ {n} (2n-1) !!} {(2n + 1)!}} Z ^ {2n + 1}}
Численные приближения
Приближение элементов сарными функциями
- Абрамовиц и Стегун дают несколько приближений с точностью (уравнения 7.1.25–28). Это позволяет выбрать наиболее быстрое приближение, подходящее для данного приложения. В порядке увеличения точности они следующие:
-
- erf (x) ≈ 1 — 1 (1 + a 1 x + a 2 x 2 + a 3 x 3 + a 4 x 4) 4, x ≥ 0 { displaystyle имя оператора {erf} (x) приблизительно 1 — { frac {1} {(1 + a_ {1} x + a_ {2} x ^ {2} + a_ {3} x ^ {3} + a_ { 4} x ^ {4}) ^ {4}}}, qquad x geq 0}
- erf (x) ≈ 1 — 1 (1 + a 1 x + a 2 x 2 + a 3 x 3 + a 4 x 4) 4, x ≥ 0 { displaystyle имя оператора {erf} (x) приблизительно 1 — { frac {1} {(1 + a_ {1} x + a_ {2} x ^ {2} + a_ {3} x ^ {3} + a_ { 4} x ^ {4}) ^ {4}}}, qquad x geq 0}
- (максимальная ошибка: 5 × 10)
- , где a 1 = 0,278393, a 2 = 0,230389, a 3 = 0,000972, a 4 = 0,078108
-
- erf (x) ≈ 1 — (a 1 t + a 2 t 2 + a 3 t 3) e — x 2, t = 1 1 + px, x ≥ 0 { displaystyle operatorname {erf} (x) приблизительно 1- (a_ {1} t + a_ {2} t ^ {2} + a_ {3} t ^ {3}) e ^ {- x ^ {2}}, quad t = { frac {1} {1 + px}}, qquad x geq 0}
(максимальная ошибка: 2,5 × 10)
- erf (x) ≈ 1 — (a 1 t + a 2 t 2 + a 3 t 3) e — x 2, t = 1 1 + px, x ≥ 0 { displaystyle operatorname {erf} (x) приблизительно 1- (a_ {1} t + a_ {2} t ^ {2} + a_ {3} t ^ {3}) e ^ {- x ^ {2}}, quad t = { frac {1} {1 + px}}, qquad x geq 0}
- где p = 0,47047, a 1 = 0,3480242, a 2 = -0,0958798, a 3 = 0,7478556
-
- erf (x) ≈ 1 — 1 (1 + a 1 x + a 2 x 2 + ⋯ + a 6 x 6) 16, x ≥ 0 { displaystyle operatorname {erf} (x) приблизительно 1 — { frac {1} {(1 + a_ {1} x + a _ {2} x ^ {2} + cdots + a_ {6} x ^ {6}) ^ {16}}}, qquad x geq 0}
(максимальная ошибка: 3 × 10)
- erf (x) ≈ 1 — 1 (1 + a 1 x + a 2 x 2 + ⋯ + a 6 x 6) 16, x ≥ 0 { displaystyle operatorname {erf} (x) приблизительно 1 — { frac {1} {(1 + a_ {1} x + a _ {2} x ^ {2} + cdots + a_ {6} x ^ {6}) ^ {16}}}, qquad x geq 0}
- , где a 1 = 0,0705230784, a 2 = 0,0422820123, a 3 = 0,0092705272, a 4 = 0,0001520143, a 5 = 0,0002765672, a 6 = 0,0000430638
-
- erf (x) ≈ 1 — (a 1 t + a 2 t 2 + ⋯ + a 5 t 5) e — x 2, t = 1 1 + px { displaystyle operatorname {erf} (x) приблизительно 1- (a_ {1} t + a_ {2} t ^ {2} + cdots + a_ {5} t ^ {5}) e ^ {- x ^ {2}}, quad t = { frac {1} {1 + px}}}
(максимальная ошибка: 1,5 × 10)
- erf (x) ≈ 1 — (a 1 t + a 2 t 2 + ⋯ + a 5 t 5) e — x 2, t = 1 1 + px { displaystyle operatorname {erf} (x) приблизительно 1- (a_ {1} t + a_ {2} t ^ {2} + cdots + a_ {5} t ^ {5}) e ^ {- x ^ {2}}, quad t = { frac {1} {1 + px}}}
- , где p = 0,3275911, a 1 = 0,254829592, a 2 = −0,284496736, a 3 = 1,421413741, a 4 = −1,453152027, a 5 = 1,061405429
- Все эти приближения действительны для x ≥ 0 Чтобы использовать эти приближения для отрицательного x, викорируйте тот факт, что erf (x) — нечетная функция, поэтому erf (x) = −erf (−x).
- Экспоненциальные границы и чисто экспоненциальное приближение для дополнительных функций задаются как
-
- erfc (x) ≤ 1 2 e — 2 x 2 + 1 2 e — x 2 ≤ e — x 2, x>0 erfc ( х) ≈ 1 6 е — х 2 + 1 2 е — 4 3 х 2, х>0. { displaystyle { begin {align} operatorname {erfc} (x) leq { frac {1} {2}} e ^ {- 2x ^ {2}} + { frac {1} {2} } e ^ {- x ^ {2}} leq e ^ {- x ^ {2}}, qquad x>0 \ имя оператора {erfc} (x) приблизительно { frac {1} { 6}} e ^ {- x ^ {2}} + { frac {1} {2}} e ^ {- { frac {4} {3}} x ^ {2}}, qquad x>0. end {align}}}
- erfc (x) ≤ 1 2 e — 2 x 2 + 1 2 e — x 2 ≤ e — x 2, x>0 erfc ( х) ≈ 1 6 е — х 2 + 1 2 е — 4 3 х 2, х>0. { displaystyle { begin {align} operatorname {erfc} (x) leq { frac {1} {2}} e ^ {- 2x ^ {2}} + { frac {1} {2} } e ^ {- x ^ {2}} leq e ^ {- x ^ {2}}, qquad x>0 \ имя оператора {erfc} (x) приблизительно { frac {1} { 6}} e ^ {- x ^ {2}} + { frac {1} {2}} e ^ {- { frac {4} {3}} x ^ {2}}, qquad x>0. end {align}}}
-
- erfc (x) ≈ (1 — e — A x) e — x 2 B π х. { displaystyle operatorname {erfc} left (x right) приблизительно { frac { left (1-e ^ {- Ax} right) e ^ {- x ^ {2}}} {B { sqrt { pi}} x}}.}
- erfc (x) ≈ (1 — e — A x) e — x 2 B π х. { displaystyle operatorname {erfc} left (x right) приблизительно { frac { left (1-e ^ {- Ax} right) e ^ {- x ^ {2}}} {B { sqrt { pi}} x}}.}
- Они определили {A, B} = {1.98, 1.135}, { displaystyle {A, B } = {1.98,1.135 },}
, что дает хорошее приближение для всех x ≥ 0. { displaystyle x geq 0.}
- Одноканальная нижняя граница:
-
- erfc (x) ≥ 2 e π β — 1 β е — β Икс 2, Икс ≥ 0, β>1, { Displaystyle OperatorName {erfc} (x) geq { sqrt { frac {2e} { pi}}} { frac { sqrt { beta -1}} { beta}} e ^ {- beta x ^ {2}}, qquad x geq 0, beta>1,}
- erfc (x) ≥ 2 e π β — 1 β е — β Икс 2, Икс ≥ 0, β>1, { Displaystyle OperatorName {erfc} (x) geq { sqrt { frac {2e} { pi}}} { frac { sqrt { beta -1}} { beta}} e ^ {- beta x ^ {2}}, qquad x geq 0, beta>1,}
- где параметр β может быть выбран, чтобы минимизировать ошибку на желаемом интервале приближения.
- Другое приближение дано Сергеем Виницким с использованием его «глобальных приближений Паде»:
-
- erf (x) ≈ sgn (x) 1 — exp (- x 2 4 π + ax 2 1 + ax 2) { displaystyle operatorname {erf} (x) приблизительно Operatorname {sgn} (x) { sqrt {1- exp left (-x ^ {2} { frac {{ frac {4} { pi) })} + ax ^ {2}} {1 + ax ^ {2}}} right)}}}
- erf (x) ≈ sgn (x) 1 — exp (- x 2 4 π + ax 2 1 + ax 2) { displaystyle operatorname {erf} (x) приблизительно Operatorname {sgn} (x) { sqrt {1- exp left (-x ^ {2} { frac {{ frac {4} { pi) })} + ax ^ {2}} {1 + ax ^ {2}}} right)}}}
- где
-
- a = 8 (π — 3) 3 π (4 — π) ≈ 0, 140012. { displaystyle a = { frac {8 ( pi -3)} {3 pi (4- pi)}} приблизительно 0,140012.}
- a = 8 (π — 3) 3 π (4 — π) ≈ 0, 140012. { displaystyle a = { frac {8 ( pi -3)} {3 pi (4- pi)}} приблизительно 0,140012.}
- Это сделано так, чтобы быть очень точным в окрестностях 0 и добавление бесконечности, а относительная погрешность меньше 0,00035 для всех действительных x. Использование альтернативного значения ≈ 0,147 снижает максимальную относительную ошибку примерно до 0,00013.
- Это приближение можно инвертировать, чтобы получить приближение для других функций ошибок:
-
- erf — 1 (x) ≈ sgn (x) (2 π a + ln (1 — x 2) 2) 2 — ln (1 — x 2) a — (2 π a + ln (1 — x 2) 2). { displaystyle operatorname {erf} ^ {- 1} (x) приблизительно operatorname {sgn} (x) { sqrt {{ sqrt { left ({ frac {2} { pi a}} + { frac { ln (1-x ^ {2})} {2}} right) ^ {2} — { frac { ln (1-x ^ {2})} {a}}}} — left ({ frac {2} { pi a}} + { frac { ln (1-x ^ {2})} {2}} right)}}.}
- erf — 1 (x) ≈ sgn (x) (2 π a + ln (1 — x 2) 2) 2 — ln (1 — x 2) a — (2 π a + ln (1 — x 2) 2). { displaystyle operatorname {erf} ^ {- 1} (x) приблизительно operatorname {sgn} (x) { sqrt {{ sqrt { left ({ frac {2} { pi a}} + { frac { ln (1-x ^ {2})} {2}} right) ^ {2} — { frac { ln (1-x ^ {2})} {a}}}} — left ({ frac {2} { pi a}} + { frac { ln (1-x ^ {2})} {2}} right)}}.}
Многочлен
Приближение с максимальной ошибкой 1,2 × 10-7 { displaystyle 1,2 times 10 ^ {- 7}}
- erf ( x) = {1 — τ x ≥ 0 τ — 1 x < 0 {displaystyle operatorname {erf} (x)={begin{cases}1-tau xgeq 0\tau -1x<0end{cases}}}
с
- τ = t ⋅ exp (- x 2 — 1,26551223 + 1,00002368 t + 0,37409196 t 2 + 0,09678418 t 3 — 0,18628806 t 4 + 0,27886807 t 5 — 1,13520398 t 6 + 1,48851587 t 7 — 0,82215223 t 8 + 0,17087277 t 9) { displaystyle { begin {align} tau = t cdot exp left (-x ^ {2} -1,26551223 + 1,00002368 t + 0,37409196t ^ {2} + 0,09678418t ^ {3} -0,18628806t ^ {4} вправо. \ left. qquad qquad qquad + 0,27886807t ^ {5} -1,13520398t ^ {6} + 1,48851587t ^ {7} -0,82215223t ^ {8} + 0,17087 277t ^ {9} right) end {align}}}
и
- t = 1 1 + 0,5 | х |. { displaystyle t = { frac {1} {1 + 0,5 | x |}}.}
Таблица значений
| x | erf(x) | 1-erf (x) |
|---|---|---|
| 0 | 0 | 1 |
| 0,02 | 0,022564575 | 0,977435425 |
| 0,04 | 0,045111106 | 0,954888894 |
| 0,06 | 0,067621594 | 0, 932378406 |
| 0,08 | 0.090078126 | 0,909921874 |
| 0,1 | 0,112462916 | 0,887537084 |
| 0,2 | 0,222702589 | 0,777297411 |
| 0,3 | 0,328626759 | 0,671373241 |
| 0, 4 | 0,428392355 | 0,571607645 |
| 0,5 | 0,520499878 | 0,479500122 |
| 0,6 | 0.603856091 | 0,396143909 |
| 0,7 | 0,677801194 | 0,322198806 |
| 0,8 257> | 0,742100965 | 0,257899035 |
| 0,9 | 0,796908212 | 0,203091788 |
| 1 | 0,842700793 | 0, 157299207 |
| 1,1 | 0,88020507 | 0,11979493 |
| 1,2 | 0,910313978 | 0,089686022 |
| 1,3 | 0,934007945 | 0,065992055 |
| 1,4 | 0.95228512 | 0,04771488 |
| 1,5 | 0, 966105146 | 0,033894854 |
| 1,6 | 0,976348383 | 0,023651617 |
| 1,7 | 0,983790459 | 0,016209541 |
| 1,8 | 0,989090502 | 0,010909498 |
| 1,9 | 0,992790429 | 0,007209571 |
| 2 | 0,995322265<25767> | 0,00477 |
| 2.1 | 0.997020533 | 0.002979467 |
| 2.2 | 0.998137154 | 0,001862846 |
| 2,3 | 0,998856823 | 0,001143177 |
| 2,4 | 0,999311486 | 0,000688514 |
| 2,5 | 0.999593048 | 0.000406952 |
| 3 | 0.99997791 | 0,00002209 |
| 3,5 | 0,999999257 | 0,000000743 |
Связанные функции
Дополнительная функция
дополнительная функция ошибок, обозначается erfc { displaystyle mathrm {erfc}}
- erfc (x) = 1 — erf (x) = 2 π ∫ x ∞ e — t 2 dt знак равно е — Икс 2 erfcx (х), { displaystyle { begin {выровнено} OperatorName {erfc} (x) = 1- operatorname {erf} (x) \ [5p t] = { frac {2} { sqrt { pi}}} int _ {x} ^ { infty} e ^ {- t ^ {2}} , dt \ [5pt] = e ^ {- x ^ {2}} operatorname {erfcx} (x), end {align}}}
, который также определяет erfcx { displaystyle mathrm {erfcx} }


- erfc (x ∣ x ≥ 0) = 2 π ∫ 0 π / 2 exp (- x 2 sin 2 θ) d θ. { displaystyle operatorname {erfc} (x mid x geq 0) = { frac {2} { pi}} int _ {0} ^ { pi / 2} exp left (- { frac {x ^ {2}} { sin ^ {2} theta}} right) , d theta.}
Это выражение действительно только для положительных значений x, но его можно использовать вместе с erfc (x) = 2 — erfc (−x), чтобы получить erfc (x) для отрицательных значений. Эта форма выгодна тем, что диапазон интегрирования является фиксированным и конечным. Расширение этого выражения для erfc { displaystyle mathrm {erfc}}
- erfc (x + y ∣ x, y ≥ 0) = 2 π ∫ 0 π / 2 ехр (- x 2 sin 2 θ — y 2 cos 2 θ) d θ. { displaystyle operatorname {erfc} (x + y mid x, y geq 0) = { frac {2} { pi}} int _ {0} ^ { pi / 2} exp left (- { frac {x ^ {2}} { sin ^ {2} theta}} — { frac {y ^ {2}} { cos ^ {2} theta}} right) , d theta.}
Функция мнимой ошибки
мнимой ошибки, обозначаемая erfi, обозначает ошибки как
- erfi (x) = — i erf (ix) Знак равно 2 π ∫ 0 xet 2 dt знак равно 2 π ex 2 D (x), { displaystyle { begin {align} operatorname {erfi} (x) = — i operatorname {erf} (ix) \ [ 5pt] = { frac {2} { sqrt { pi}}} int _ {0} ^ {x} e ^ {t ^ {2}} , dt \ [5pt] = { frac {2} { sqrt { pi}}} e ^ {x ^ {2}} D (x), end {align}}}
где D (x) — функция Доусона (который можно использовать вместо erfi, чтобы избежать арифметического переполнения ).
Несмотря на название «функция мнимой ошибки», erfi (x) { displaystyle operatorname {erfi} (x)}
Функция Когда ошибки оценивается для произвольных сложных аргументов z, результирующая комплексная функция ошибок обычно обсуждается в масштабированной форме как функция Фаддеева :
- w (z) = e — z 2 erfc (- iz) = erfcx (- iz). { displaystyle w (z) = e ^ {- z ^ {2}} operatorname {erfc} (-iz) = operatorname {erfcx} (-iz).}
Кумулятивная функция распределения
Функция ошибок по существующей стандартной стандартной функции нормального кумулятивного распределения, обозначаемой нормой (x) в некоторых языках программного обеспечения, поскольку они отличаются только масштабированием и переводом. Действительно,
- Φ (x) = 1 2 π ∫ — ∞ xe — t 2 2 dt = 1 2 [1 + erf (x 2)] = 1 2 erfc (- x 2) { displaystyle Phi (x) = { frac {1} { sqrt {2 pi}}} int _ {- infty} ^ {x} e ^ { tfrac {-t ^ {2}} {2}} , dt = { frac {1} {2}} left [1+ operatorname {erf} left ({ frac {x} { sqrt {2}}} right) right] = { frac {1} {2}} operatorname {erfc} left (- { frac {x} { sqrt {2}}} right)}
или переставлен для erf и erfc:
- erf ( x) = 2 Φ (x 2) — 1 erfc (x) = 2 Φ (- x 2) = 2 (1 — Φ (x 2)). { displaystyle { begin {align} operatorname {erf} (x) = 2 Phi left (x { sqrt {2}} right) -1 \ operatorname {erfc} (x) = 2 Phi left (-x { sqrt {2}} right) = 2 left (1- Phi left (x { sqrt {2}} right) right). End {выравнивается} }}
Следовательно, функция ошибок также тесно связана с Q-функцией, которая является вероятностью хвоста стандартного нормального распределения. Q-функция может быть выражена через функцию ошибок как
- Q (x) = 1 2 — 1 2 erf (x 2) = 1 2 erfc (x 2). { displaystyle Q (x) = { frac {1} {2}} — { frac {1} {2}} operatorname {erf} left ({ frac {x} { sqrt {2}}) } right) = { frac {1} {2}} operatorname {erfc} left ({ frac {x} { sqrt {2}}} right).}
Обратное значение из Φ { displaystyle Phi}
- пробит (p) = Φ — 1 (p) = 2 erf — 1 (2 p — 1) = — 2 erfc — 1 (2 p). { displaystyle operatorname {probit} (p) = Phi ^ {- 1} (p) = { sqrt {2}} operatorname {erf} ^ {- 1} (2p-1) = — { sqrt {2}} operatorname {erfc} ^ {- 1} (2p).}
Стандартный нормальный cdf чаще используется в вероятности и статистике, а функция ошибок чаще используется в других разделах математики.
Функция ошибки является частным случаем функции Миттаг-Леффлера и может также быть выражена как сливающаяся гипергеометрическая функция (функция Куммера):
- erf (х) знак равно 2 х π M (1 2, 3 2, — х 2). { displaystyle operatorname {erf} (x) = { frac {2x} { sqrt { pi}}} M left ({ frac {1} {2}}, { frac {3} {2 }}, — x ^ {2} right).}
Он имеет простое выражение в терминах интеграла Френеля.
В терминах регуляризованной гамма-функции P и неполная гамма-функция,
- erf (x) = sgn (x) P (1 2, x 2) = sgn (x) π γ (1 2, x 2). { displaystyle operatorname {erf} (x) = operatorname {sgn} (x) P left ({ frac {1} {2}}, x ^ {2} right) = { frac { operatorname {sgn} (x)} { sqrt { pi}}} gamma left ({ frac {1} {2}}, x ^ {2} right).}
sgn (x) { displaystyle operatorname {sgn} (x)}
Обобщенные функции ошибок

π { displaystyle scriptstyle { sqrt { pi}}}

Некоторые авторы обсуждают более общие функции:
- E n (x) = n! π ∫ 0 Икс е — Т N д т знак равно N! π ∑ п знак равно 0 ∞ (- 1) п Икс N п + 1 (N п + 1) п!. { displaystyle E_ {n} (x) = { frac {n!} { sqrt { pi}}} int _ {0} ^ {x} e ^ {- t ^ {n}} , dt = { frac {n!} { sqrt { pi}}} sum _ {p = 0} ^ { infty} (- 1) ^ {p} { frac {x ^ {np + 1}} {(np + 1) p!}}.}
Примечательные случаи:
- E0(x) — прямая линия, проходящая через начало координат: E 0 (x) = xe π { displaystyle textstyle E_ {0} (x) = { dfrac {x} {e { sqrt { pi}}}}}
- E2(x) — функция, erf (x) ошибки.
После деления на n!, все E n для нечетных n выглядят похожими (но не идентичными) друг на друга. Аналогично, E n для четного n выглядят похожими (но не идентичными) друг другу после простого деления на n!. Все обобщенные функции ошибок для n>0 выглядят одинаково на положительной стороне x графика.
Эти обобщенные функции могут быть эквивалентно выражены для x>0 с помощью гамма-функции и неполной гамма-функции :
- E n (x) = 1 π Γ (n) (Γ (1 n) — Γ (1 n, xn)), x>0. { displaystyle E_ {n} (x) = { frac {1} { sqrt { pi}}} Gamma (n) left ( Gamma left ({ frac {1} {n}} right) — Gamma left ({ frac {1} {n}}, x ^ {n} right) right), quad quad x>0.}
Следовательно, мы можем определить ошибку функция в терминах неполной гамма-функции:
- erf (x) = 1 — 1 π Γ (1 2, x 2). { displaystyle operatorname {erf} (x) = 1 — { frac {1} { sqrt { pi}}} Gamma left ({ frac {1} {2}}, x ^ {2} right).}
Итерированные интегралы дополнительных функций
Повторные интегралы дополнительные функции ошибок определения как
- inerfc (z) = ∫ z ∞ in — 1 erfc (ζ) d ζ i 0 erfc (z) = erfc (z) i 1 erfc (z) = ierfc (z) знак равно 1 π е — z 2 — z erfc (z) я 2 erfc (z) = 1 4 [erfc (z) — 2 z ierfc (z)] { displaystyle { begin {align } operatorname {i ^ {n} erfc} (z) = int _ {z} ^ { infty} operatorname {i ^ {n-1} erfc} ( zeta) , d zeta \ имя оператора {i ^ {0} erfc} (z) = operatorname {erfc} (z) \ operatorname {i ^ {1} erfc} (z) = operat orname {ierfc} (z) = { frac { 1} { sqrt { pi}}} e ^ {- z ^ {2}} — z operatorname {erfc} (z) \ operatorname {i ^ {2} erfc} (z) = { frac {1} {4}} left [ operatorname {erfc} (z) -2z operatorname {ierfc} (z) right] \ end {выровнено}}
Общая рекуррентная формула:
- 2 ninerfc (z) = in — 2 erfc (z) — 2 цинк — 1 erfc (z) { displaystyle 2n operatorname {i ^ {n} erfc} (z) = operatorname {i ^ { n-2} erfc} (z) -2z operatorname {i ^ {n-1} erfc} (z)}
У них есть степенной ряд
- в erfc (z) = ∑ j = 0 ∞ (- Z) J 2 N — JJ! Γ (1 + N — J 2), { displaystyle i ^ {n} operatorname {erfc} (z) = sum _ {j = 0} ^ { infty} { frac {(-z) ^ { j}} {2 ^ {nj} j! Gamma left (1 + { frac {nj} {2}} right)}},}
из следуют свойства симметрии
- i 2 m ERFC (- Z) знак равно — я 2 m ERFC (Z) + ∑ Q знак равно 0 мZ 2 д 2 2 (м — д) — 1 (2 д)! (м — д)! { displaystyle i ^ {2m} operatorname {erfc} (-z) = — i ^ {2m} operatorname {erfc} (z) + sum _ {q = 0} ^ {m} { frac {z ^ {2q}} {2 ^ {2 (mq) -1} (2q)! (Mq)!}}}
и
- i 2 m + 1 erfc (- z) = i 2 m + 1 erfc (г) + ∑ ä знак равно 0 ìZ 2 ä + 1 2 2 ( м — д) — 1 (2 д + 1)! (м — д)!. { displaystyle i ^ {2m + 1} operatorname {erfc} (-z) = i ^ {2m + 1} operatorname {erfc} (z) + sum _ {q = 0} ^ {m} { гидроразрыва {z ^ {2q + 1}} {2 ^ {2 (mq) -1} (2q + 1)! (mq)!}}.}
Реализации
Как действительная функция вещественного аргумента
- В операционных системах, совместимых с Posix, заголовок math.h должен являть, а математическая библиотека libm должна быть функция erf и erfc (двойная точность ), а также их одинарная точность и расширенная точность аналоги erff, erfl и erfc, erfcl.
- Библиотека GNU Scientific предоставляет функции erf, erfc, log (erf) и масштабируемые функции ошибок.
Как сложная функция комплексного аргумента
- libcerf, числовая библиотека C для сложных функций, предоставляет комплексные функции cerf, cerfc, cerfcx и реальные функции erfi, erfcx с точностью 13–14 цифр на основе функции Фаддеева, реализованной в пакете MIT Faddeeva Package
См. также
Связанные ции
- интеграл Гаусса, по всей действительной прямой
- функция Гаусса, производная
- функция Доусона, перенормированная функция мнимой ошибки
- интеграл Гудвина — Стона
по вероятности
- Нормальное распределение
- Нормальная кумулятивная функция распределения, масштабированная и сдвинутая форма функций ошибок
- Пробит, обратная или квантильная функция нормального CDF
- Q-функция, вероятность хвоста нормального распределения
Ссылки
Дополнительная литература
- Abramowitz, Milton ; Стегун, Ирен Энн, ред. (1983) [июнь 1964]. «Глава 7». Справочник по математическим функциям с формулами, графики и математическими таблицами. Прикладная математика. 55 (Девятое переиздание с дополнительными исправлениями; десятое оригинальное издание с исправлениями (декабрь 1972 г.); первое изд.). Вашингтон.; Нью-Йорк: Министерство торговли США, Национальное бюро стандартов; Dover Publications. п. 297. ISBN 978-0-486-61272-0 . LCCN 64-60036. MR 0167642. LCCN 65-12253.
- Press, William H.; Теукольский, Саул А.; Веттерлинг, Уильям Т.; Фланнери, Брайан П. (2007), «Раздел 6.2. Неполная гамма-функция и функция ошибок », Числовые рецепты: Искусство научных вычислений (3-е изд.), Нью-Йорк: Cambridge University Press, ISBN 978-0-521- 88068-8
- Темме, Нико М. (2010), «Функции ошибок, интегралы Доусона и Френеля», в Олвер, Фрэнк У. Дж. ; Лозье, Даниэль М.; Бойсверт, Рональд Ф.; Кларк, Чарльз В. (ред.), Справочник NIST по математическим функциям, Cambridge University Press, ISBN 978-0-521-19225-5 , MR 2723248
Внешние ссылки
- MathWorld — Erf
- Таблица интегралов функций ошибок
Калькулятор функции ошибки
О Калькулятор функции ошибки
Калькулятор функции ошибки используется для расчета функции ошибки для заданного числа.
Функция ошибки
В математике функция ошибок — это специальная (нефундаментальная) функция сигмовидной формы, которая встречается в теории вероятностей, статистике и уравнениях в частных производных. Она также известна как функция ошибки Гаусса или интеграл вероятности.
Функция ошибки определяется как:
Таблица функций ошибок
Ниже приведена таблица функций ошибок и дополнительных функций ошибок, в которой показаны значения erf(x) и erfc(x) для x в диапазоне от 0 до 3,5 с шагом 0,01.
| X | ЭРФ(х) | ЭРФК(х) |
|---|---|---|
| 0.0 | 0.0 | 1.0 |
| 0.01 | 0.011283416 | 0.988716584 |
| 0.02 | 0.022564575 | 0.977435425 |
| 0.03 | 0.033841222 | 0.966158778 |
| 0.04 | 0.045111106 | 0.954888894 |
| 0.05 | 0.056371978 | 0.943628022 |
| 0.06 | 0.067621594 | 0.932378406 |
| 0.07 | 0.07885772 | 0.92114228 |
| 0.08 | 0.090078126 | 0.909921874 |
| 0.09 | 0.101280594 | 0.898719406 |
| 0.1 | 0.112462916 | 0.887537084 |
| 0.11 | 0.123622896 | 0.876377104 |
| 0.12 | 0.134758352 | 0.865241648 |
| 0.13 | 0.145867115 | 0.854132885 |
| 0.14 | 0.156947033 | 0.843052967 |
| 0.15 | 0.167995971 | 0.832004029 |
| 0.16 | 0.179011813 | 0.820988187 |
| 0.17 | 0.189992461 | 0.810007539 |
| 0.18 | 0.200935839 | 0.799064161 |
| 0.19 | 0.211839892 | 0.788160108 |
| 0.2 | 0.222702589 | 0.777297411 |
| 0.21 | 0.233521923 | 0.766478077 |
| 0.22 | 0.244295912 | 0.755704088 |
| 0.23 | 0.2550226 | 0.7449774 |
| 0.24 | 0.265700059 | 0.734299941 |
| 0.25 | 0.27632639 | 0.72367361 |
| 0.26 | 0.286899723 | 0.713100277 |
| 0.27 | 0.297418219 | 0.702581781 |
| 0.28 | 0.307880068 | 0.692119932 |
| 0.29 | 0.318283496 | 0.681716504 |
| 0.3 | 0.328626759 | 0.671373241 |
| 0.31 | 0.33890815 | 0.66109185 |
| 0.32 | 0.349125995 | 0.650874005 |
| 0.33 | 0.359278655 | 0.640721345 |
| 0.34 | 0.369364529 | 0.630635471 |
| 0.35 | 0.379382054 | 0.620617946 |
| 0.36 | 0.389329701 | 0.610670299 |
| 0.37 | 0.399205984 | 0.600794016 |
| 0.38 | 0.409009453 | 0.590990547 |
| 0.39 | 0.4187387 | 0.5812613 |
| 0.4 | 0.428392355 | 0.571607645 |
| 0.41 | 0.43796909 | 0.56203091 |
| 0.42 | 0.447467618 | 0.552532382 |
| 0.43 | 0.456886695 | 0.543113305 |
| 0.44 | 0.466225115 | 0.533774885 |
| 0.45 | 0.47548172 | 0.52451828 |
| 0.46 | 0.48465539 | 0.51534461 |
| 0.47 | 0.493745051 | 0.506254949 |
| 0.48 | 0.502749671 | 0.497250329 |
| 0.49 | 0.511668261 | 0.488331739 |
| 0.5 | 0.520499878 | 0.479500122 |
| 0.51 | 0.52924362 | 0.47075638 |
| 0.52 | 0.53789863 | 0.46210137 |
| 0.53 | 0.546464097 | 0.453535903 |
| 0.54 | 0.55493925 | 0.44506075 |
| 0.55 | 0.563323366 | 0.436676634 |
| 0.56 | 0.571615764 | 0.428384236 |
| 0.57 | 0.579815806 | 0.420184194 |
| 0.58 | 0.5879229 | 0.4120771 |
| 0.59 | 0.595936497 | 0.404063503 |
| 0.6 | 0.603856091 | 0.396143909 |
| 0.61 | 0.611681219 | 0.388318781 |
| 0.62 | 0.619411462 | 0.380588538 |
| 0.63 | 0.627046443 | 0.372953557 |
| 0.64 | 0.634585829 | 0.365414171 |
| 0.65 | 0.642029327 | 0.357970673 |
| 0.66 | 0.649376688 | 0.350623312 |
| 0.67 | 0.656627702 | 0.343372298 |
| 0.68 | 0.663782203 | 0.336217797 |
| 0.69 | 0.670840062 | 0.329159938 |
| 0.7 | 0.677801194 | 0.322198806 |
| 0.71 | 0.68466555 | 0.31533445 |
| 0.72 | 0.691433123 | 0.308566877 |
| 0.73 | 0.698103943 | 0.301896057 |
| 0.74 | 0.704678078 | 0.295321922 |
| 0.75 | 0.711155634 | 0.288844366 |
| 0.76 | 0.717536753 | 0.282463247 |
| 0.77 | 0.723821614 | 0.276178386 |
| 0.78 | 0.730010431 | 0.269989569 |
| 0.79 | 0.736103454 | 0.263896546 |
| 0.8 | 0.742100965 | 0.257899035 |
| 0.81 | 0.748003281 | 0.251996719 |
| 0.82 | 0.753810751 | 0.246189249 |
| 0.83 | 0.759523757 | 0.240476243 |
| 0.84 | 0.765142711 | 0.234857289 |
| 0.85 | 0.770668058 | 0.229331942 |
| 0.86 | 0.776100268 | 0.223899732 |
| 0.87 | 0.781439845 | 0.218560155 |
| 0.88 | 0.786687319 | 0.213312681 |
| 0.89 | 0.791843247 | 0.208156753 |
| 0.9 | 0.796908212 | 0.203091788 |
| 0.91 | 0.801882826 | 0.198117174 |
| 0.92 | 0.806767722 | 0.193232278 |
| 0.93 | 0.811563559 | 0.188436441 |
| 0.94 | 0.816271019 | 0.183728981 |
| 0.95 | 0.820890807 | 0.179109193 |
| 0.96 | 0.82542365 | 0.17457635 |
| 0.97 | 0.829870293 | 0.170129707 |
| 0.98 | 0.834231504 | 0.165768496 |
| 0.99 | 0.83850807 | 0.16149193 |
| 1.0 | 0.842700793 | 0.157299207 |
| 1.01 | 0.846810496 | 0.153189504 |
| 1.02 | 0.850838018 | 0.149161982 |
| 1.03 | 0.854784211 | 0.145215789 |
| 1.04 | 0.858649947 | 0.141350053 |
| 1.05 | 0.862436106 | 0.137563894 |
| 1.06 | 0.866143587 | 0.133856413 |
| 1.07 | 0.869773297 | 0.130226703 |
| 1.08 | 0.873326158 | 0.126673842 |
| 1.09 | 0.876803102 | 0.123196898 |
| 1.1 | 0.88020507 | 0.11979493 |
| 1.11 | 0.883533012 | 0.116466988 |
| 1.12 | 0.88678789 | 0.11321211 |
| 1.13 | 0.88997067 | 0.11002933 |
| 1.14 | 0.893082328 | 0.106917672 |
| 1.15 | 0.896123843 | 0.103876157 |
| 1.16 | 0.899096203 | 0.100903797 |
| 1.17 | 0.902000399 | 0.097999601 |
| 1.18 | 0.904837427 | 0.095162573 |
| 1.19 | 0.907608286 | 0.092391714 |
| 1.2 | 0.910313978 | 0.089686022 |
| 1.21 | 0.912955508 | 0.087044492 |
| 1.22 | 0.915533881 | 0.084466119 |
| 1.23 | 0.918050104 | 0.081949896 |
| 1.24 | 0.920505184 | 0.079494816 |
| 1.25 | 0.922900128 | 0.077099872 |
| 1.26 | 0.925235942 | 0.074764058 |
| 1.27 | 0.927513629 | 0.072486371 |
| 1.28 | 0.929734193 | 0.070265807 |
| 1.29 | 0.931898633 | 0.068101367 |
| 1.3 | 0.934007945 | 0.065992055 |
| 1.31 | 0.936063123 | 0.063936877 |
| 1.32 | 0.938065155 | 0.061934845 |
| 1.33 | 0.940015026 | 0.059984974 |
| 1.34 | 0.941913715 | 0.058086285 |
| 1.35 | 0.943762196 | 0.056237804 |
| 1.36 | 0.945561437 | 0.054438563 |
| 1.37 | 0.947312398 | 0.052687602 |
| 1.38 | 0.949016035 | 0.050983965 |
| 1.39 | 0.950673296 | 0.049326704 |
| 1.4 | 0.95228512 | 0.04771488 |
| 1.41 | 0.953852439 | 0.046147561 |
| 1.42 | 0.955376179 | 0.044623821 |
| 1.43 | 0.956857253 | 0.043142747 |
| 1.44 | 0.95829657 | 0.04170343 |
| 1.45 | 0.959695026 | 0.040304974 |
| 1.46 | 0.96105351 | 0.03894649 |
| 1.47 | 0.9623729 | 0.0376271 |
| 1.48 | 0.963654065 | 0.036345935 |
| 1.49 | 0.964897865 | 0.035102135 |
| 1.5 | 0.966105146 | 0.033894854 |
| 1.51 | 0.967276748 | 0.032723252 |
| 1.52 | 0.968413497 | 0.031586503 |
| 1.53 | 0.969516209 | 0.030483791 |
| 1.54 | 0.97058569 | 0.02941431 |
| 1.55 | 0.971622733 | 0.028377267 |
| 1.56 | 0.972628122 | 0.027371878 |
| 1.57 | 0.973602627 | 0.026397373 |
| 1.58 | 0.974547009 | 0.025452991 |
| 1.59 | 0.975462016 | 0.024537984 |
| 1.6 | 0.976348383 | 0.023651617 |
| 1.61 | 0.977206837 | 0.022793163 |
| 1.62 | 0.978038088 | 0.021961912 |
| 1.63 | 0.97884284 | 0.02115716 |
| 1.64 | 0.97962178 | 0.02037822 |
| 1.65 | 0.980375585 | 0.019624415 |
| 1.66 | 0.981104921 | 0.018895079 |
| 1.67 | 0.981810442 | 0.018189558 |
| 1.68 | 0.982492787 | 0.017507213 |
| 1.69 | 0.983152587 | 0.016847413 |
| 1.7 | 0.983790459 | 0.016209541 |
| 1.71 | 0.984407008 | 0.015592992 |
| 1.72 | 0.985002827 | 0.014997173 |
| 1.73 | 0.9855785 | 0.0144215 |
| 1.74 | 0.986134595 | 0.013865405 |
| 1.75 | 0.986671671 | 0.013328329 |
| 1.76 | 0.987190275 | 0.012809725 |
| 1.77 | 0.987690942 | 0.012309058 |
| 1.78 | 0.988174196 | 0.011825804 |
| 1.79 | 0.988640549 | 0.011359451 |
| 1.8 | 0.989090502 | 0.010909498 |
| 1.81 | 0.989524545 | 0.010475455 |
| 1.82 | 0.989943156 | 0.010056844 |
| 1.83 | 0.990346805 | 0.009653195 |
| 1.84 | 0.990735948 | 0.009264052 |
| 1.85 | 0.99111103 | 0.00888897 |
| 1.86 | 0.991472488 | 0.008527512 |
| 1.87 | 0.991820748 | 0.008179252 |
| 1.88 | 0.992156223 | 0.007843777 |
| 1.89 | 0.992479318 | 0.007520682 |
| 1.9 | 0.992790429 | 0.007209571 |
| 1.91 | 0.99308994 | 0.00691006 |
| 1.92 | 0.993378225 | 0.006621775 |
| 1.93 | 0.99365565 | 0.00634435 |
| 1.94 | 0.993922571 | 0.006077429 |
| 1.95 | 0.994179334 | 0.005820666 |
| 1.96 | 0.994426275 | 0.005573725 |
| 1.97 | 0.994663725 | 0.005336275 |
| 1.98 | 0.994892 | 0.005108 |
| 1.99 | 0.995111413 | 0.004888587 |
| 2.0 | 0.995322265 | 0.004677735 |
| 2.01 | 0.995524849 | 0.004475151 |
| 2.02 | 0.995719451 | 0.004280549 |
| 2.03 | 0.995906348 | 0.004093652 |
| 2.04 | 0.99608581 | 0.00391419 |
| 2.05 | 0.996258096 | 0.003741904 |
| 2.06 | 0.996423462 | 0.003576538 |
| 2.07 | 0.996582153 | 0.003417847 |
| 2.08 | 0.996734409 | 0.003265591 |
| 2.09 | 0.996880461 | 0.003119539 |
| 2.1 | 0.997020533 | 0.002979467 |
| 2.11 | 0.997154845 | 0.002845155 |
| 2.12 | 0.997283607 | 0.002716393 |
| 2.13 | 0.997407023 | 0.002592977 |
| 2.14 | 0.997525293 | 0.002474707 |
| 2.15 | 0.997638607 | 0.002361393 |
| 2.16 | 0.997747152 | 0.002252848 |
| 2.17 | 0.997851108 | 0.002148892 |
| 2.18 | 0.997950649 | 0.002049351 |
| 2.19 | 0.998045943 | 0.001954057 |
| 2.2 | 0.998137154 | 0.001862846 |
| 2.21 | 0.998224438 | 0.001775562 |
| 2.22 | 0.998307948 | 0.001692052 |
| 2.23 | 0.998387832 | 0.001612168 |
| 2.24 | 0.998464231 | 0.001535769 |
| 2.25 | 0.998537283 | 0.001462717 |
| 2.26 | 0.998607121 | 0.001392879 |
| 2.27 | 0.998673872 | 0.001326128 |
| 2.28 | 0.998737661 | 0.001262339 |
| 2.29 | 0.998798606 | 0.001201394 |
| 2.3 | 0.998856823 | 0.001143177 |
| 2.31 | 0.998912423 | 0.001087577 |
| 2.32 | 0.998965513 | 0.001034487 |
| 2.33 | 0.999016195 | 0.000983805 |
| 2.34 | 0.99906457 | 0.00093543 |
| 2.35 | 0.999110733 | 0.000889267 |
| 2.36 | 0.999154777 | 0.000845223 |
| 2.37 | 0.99919679 | 0.00080321 |
| 2.38 | 0.999236858 | 0.000763142 |
| 2.39 | 0.999275064 | 0.000724936 |
| 2.4 | 0.999311486 | 0.000688514 |
| 2.41 | 0.999346202 | 0.000653798 |
| 2.42 | 0.999379283 | 0.000620717 |
| 2.43 | 0.999410802 | 0.000589198 |
| 2.44 | 0.999440826 | 0.000559174 |
| 2.45 | 0.99946942 | 0.00053058 |
| 2.46 | 0.999496646 | 0.000503354 |
| 2.47 | 0.999522566 | 0.000477434 |
| 2.48 | 0.999547236 | 0.000452764 |
| 2.49 | 0.999570712 | 0.000429288 |
| 2.5 | 0.999593048 | 0.000406952 |
| 2.51 | 0.999614295 | 0.000385705 |
| 2.52 | 0.999634501 | 0.000365499 |
| 2.53 | 0.999653714 | 0.000346286 |
| 2.54 | 0.999671979 | 0.000328021 |
| 2.55 | 0.99968934 | 0.00031066 |
| 2.56 | 0.999705837 | 0.000294163 |
| 2.57 | 0.999721511 | 0.000278489 |
| 2.58 | 0.9997364 | 0.0002636 |
| 2.59 | 0.999750539 | 0.000249461 |
| 2.6 | 0.999763966 | 0.000236034 |
| 2.61 | 0.999776711 | 0.000223289 |
| 2.62 | 0.999788809 | 0.000211191 |
| 2.63 | 0.999800289 | 0.000199711 |
| 2.64 | 0.999811181 | 0.000188819 |
| 2.65 | 0.999821512 | 0.000178488 |
| 2.66 | 0.999831311 | 0.000168689 |
| 2.67 | 0.999840601 | 0.000159399 |
| 2.68 | 0.999849409 | 0.000150591 |
| 2.69 | 0.999857757 | 0.000142243 |
| 2.7 | 0.999865667 | 0.000134333 |
| 2.71 | 0.999873162 | 0.000126838 |
| 2.72 | 0.999880261 | 0.000119739 |
| 2.73 | 0.999886985 | 0.000113015 |
| 2.74 | 0.999893351 | 0.000106649 |
| 2.75 | 0.999899378 | 0.000100622 |
| 2.76 | 0.999905082 | 9.4918e-05 |
| 2.77 | 0.99991048 | 8.952e-05 |
| 2.78 | 0.999915587 | 8.4413e-05 |
| 2.79 | 0.999920418 | 7.9582e-05 |
| 2.8 | 0.999924987 | 7.5013e-05 |
| 2.81 | 0.999929307 | 7.0693e-05 |
| 2.82 | 0.99993339 | 6.661e-05 |
| 2.83 | 0.99993725 | 6.275e-05 |
| 2.84 | 0.999940898 | 5.9102e-05 |
| 2.85 | 0.999944344 | 5.5656e-05 |
| 2.86 | 0.999947599 | 5.2401e-05 |
| 2.87 | 0.999950673 | 4.9327e-05 |
| 2.88 | 0.999953576 | 4.6424e-05 |
| 2.89 | 0.999956316 | 4.3684e-05 |
| 2.9 | 0.999958902 | 4.1098e-05 |
| 2.91 | 0.999961343 | 3.8657e-05 |
| 2.92 | 0.999963645 | 3.6355e-05 |
| 2.93 | 0.999965817 | 3.4183e-05 |
| 2.94 | 0.999967866 | 3.2134e-05 |
| 2.95 | 0.999969797 | 3.0203e-05 |
| 2.96 | 0.999971618 | 2.8382e-05 |
| 2.97 | 0.999973334 | 2.6666e-05 |
| 2.98 | 0.999974951 | 2.5049e-05 |
| 2.99 | 0.999976474 | 2.3526e-05 |
| 3.0 | 0.99997791 | 2.209E-05 |
| 3.01 | 0.999979261 | 2.0739e-05 |
| 3.02 | 0.999980534 | 1.9466e-05 |
| 3.03 | 0.999981732 | 1.8268e-05 |
| 3.04 | 0.999982859 | 1.7141e-05 |
| 3.05 | 0.99998392 | 1.608e-05 |
| 3.06 | 0.999984918 | 1.5082e-05 |
| 3.07 | 0.999985857 | 1.4143e-05 |
| 3.08 | 0.99998674 | 1.326e-05 |
| 3.09 | 0.999987571 | 1.2429e-05 |
| 3.1 | 0.999988351 | 1.1649e-05 |
| 3.11 | 0.999989085 | 1.0915e-05 |
| 3.12 | 0.999989774 | 1.0226e-05 |
| 3.13 | 0.999990422 | 9.578e-06 |
| 3.14 | 0.99999103 | 8.97e-06 |
| 3.15 | 0.999991602 | 8.398e-06 |
| 3.16 | 0.999992138 | 7.862e-06 |
| 3.17 | 0.999992642 | 7.358e-06 |
| 3.18 | 0.999993115 | 6.885e-06 |
| 3.19 | 0.999993558 | 6.442e-06 |
| 3.2 | 0.999993974 | 6.026e-06 |
| 3.21 | 0.999994365 | 5.635e-06 |
| 3.22 | 0.999994731 | 5.269e-06 |
| 3.23 | 0.999995074 | 4.926e-06 |
| 3.24 | 0.999995396 | 4.604e-06 |
| 3.25 | 0.999995697 | 4.303e-06 |
| 3.26 | 0.99999598 | 4.02e-06 |
| 3.27 | 0.999996245 | 3.755e-06 |
| 3.28 | 0.999996493 | 3.507e-06 |
| 3.29 | 0.999996725 | 3.275e-06 |
| 3.3 | 0.999996942 | 3.058e-06 |
| 3.31 | 0.999997146 | 2.854e-06 |
| 3.32 | 0.999997336 | 2.664e-06 |
| 3.33 | 0.999997515 | 2.485e-06 |
| 3.34 | 0.999997681 | 2.319e-06 |
| 3.35 | 0.999997838 | 2.162e-06 |
| 3.36 | 0.999997983 | 2.017e-06 |
| 3.37 | 0.99999812 | 1.88E-06 |
| 3.38 | 0.999998247 | 1.753e-06 |
| 3.39 | 0.999998367 | 1.633e-06 |
| 3.4 | 0.999998478 | 1.522E-06 |
| 3.41 | 0.999998582 | 1.418e-06 |
| 3.42 | 0.999998679 | 1.321e-06 |
| 3.43 | 0.99999877 | 1.23E-06 |
| 3.44 | 0.999998855 | 1.145e-06 |
| 3.45 | 0.999998934 | 1.066e-06 |
| 3.46 | 0.999999008 | 9.92e-07 |
| 3.47 | 0.999999077 | 9.23e-07 |
| 3.48 | 0.999999141 | 8.59e-07 |
| 3.49 | 0.999999201 | 7.99e-07 |
| 3.5 | 0.999999257 | 7.43e-07 |
Общие инструменты
-
Калькулятор среднего балла (GPA)
-
дробь в десятичный калькулятор
-
футы дюймы в сантиметры
-
калькулятор ИМТ
-
инструмент подсчета слов
-
счетчик символов
-
калькулятор времени удвоения
-
конвертер фунтов в кг
-
калькулятор десятичной дроби
-
калькулятор сложных процентов
-
калькулятор даты
-
калькулятор площади параллелограмма
-
Калькулятор комплексных чисел
-
конвертер футов в метры
-
калькулятор натуральных логарифмов
-
Калькулятор Гугл Адсенс
-
калькулятор скидок
-
Калькулятор коэффициента вариации
-
процентный калькулятор
-
Конвертер градусов в радианы
-
двоичный калькулятор
-
Калькулятор числа судьбы
-
Калькулятор площади поверхности цилиндра (Высокая точность)
-
Калькулятор площади равностороннего треугольника
-
калькулятор возраста
-
Калькулятор объема пирамиды (Высокая точность)
-
Калькулятор рентабельности инвестиций
-
калькулятор дисперсии (Высокая точность)
-
Акры в Квадратные ярды Конвертер
-
Калькулятор гамма-функции
В математике функция ошибок (также называемая функцией ошибок Гаусса ), часто обозначаемая erf , является сложной функцией комплексной переменной, определяемой как:
Этот интеграл представляет собой специальную ( неэлементарную ) сигмовидную функцию, которая часто встречается в уравнениях вероятности , статистики и дифференциальных уравнений в частных производных . Во многих из этих приложений аргумент функции является действительным числом. Если аргумент функции является действительным, то значение функции также является действительным.
В статистике для неотрицательных значений x функция ошибок имеет следующую интерпретацию: для случайной величины Y, которая нормально распределена со средним значением 0 и стандартным отклонением
1/√ 2, erf x — вероятность того, что Y попадает в диапазон [- x , x ] .
Две тесно связанные функции — это дополнительная функция ошибок ( erfc ), определяемая как
и функция мнимой ошибки ( erfi ), определяемая как
где i — мнимая единица .
Имя
Название «функция ошибок» и ее сокращение erf были предложены Дж. В. Л. Глейшером в 1871 г. в связи с его связью с «теорией вероятности и, в частности, теорией ошибок ». Дополнение к функции ошибок также обсуждалось Глейшером в отдельной публикации в том же году. Для «закона удобства» ошибок, плотность которых определяется как
( нормальное распределение ), Глейшер вычисляет вероятность ошибки, лежащей между p и q, как:
Приложения
Когда результаты серии измерений описываются нормальным распределением со стандартным отклонением σ и ожидаемым значением 0, тогда erf (а/σ √ 2) — вероятность того, что ошибка единичного измерения находится между — a и + a для положительного a . Это полезно, например, при определении частоты ошибок по битам в цифровой системе связи.
Ошибки и дополнительные функции ошибок возникают, например, в решениях уравнения теплопроводности, когда граничные условия задаются ступенчатой функцией Хевисайда .
Функция ошибок и ее приближения могут использоваться для оценки результатов, которые имеют высокую или низкую вероятность. Дана случайная величина X ~ Norm [ μ , σ ] (нормальное распределение со средним μ и стандартным отклонением σ ) и константа L < μ :
где A и B — некоторые числовые константы. Если L достаточно далеко от среднего, а именно μ — L ≥ σ √ ln k , то:
поэтому вероятность стремится к 0 при k → ∞ .
Вероятность того, что X находится в интервале [ L a , L b ], может быть получена как
Характеристики
Интегрируем exp (- z 2 )
erf z
Свойство erf (- z ) = −erf z означает, что функция ошибок является нечетной функцией . Это напрямую связано с тем, что подынтегральное выражение e — t 2 является четной функцией (интегрирование четной функции дает нечетную функцию и наоборот).
Для любого комплексного числа z :
где г представляет собой комплексно сопряженное из г .
Подынтегральное выражение f = exp (- z 2 ) и f = erf z показано на комплексной плоскости z на рисунках справа с раскраской области .
Функция ошибок при + ∞ равна 1 (см. Интеграл Гаусса ). На действительной оси erf z стремится к единице при z → + ∞ и −1 при z → −∞ . На мнимой оси он стремится к ± i ∞ .
Серия Тейлора
Функция ошибок — это целая функция ; у него нет сингулярностей (кроме бесконечности), и его разложение Тейлора всегда сходится, но, как известно, «[…] его плохая сходимость, если x > 1 ».
Определяющий интеграл не может быть вычислен в замкнутой форме в терминах элементарных функций , но, раскладывая подынтегральное выражение e — z 2 в его ряд Маклорена и интегрируя член за членом, можно получить ряд Маклорена функции ошибок как:
которое выполняется для любого комплексного числа z . Члены знаменателя — это последовательность (последовательность A007680 в OEIS ) в OEIS .
Для итеративного расчета вышеуказанного ряда может быть полезна следующая альтернативная формулировка:
потому что — (2 к — 1) z 2/к (2 к + 1)выражает множитель для превращения k- го члена в ( k + 1) -й член (считая z первым членом).
Функция мнимой ошибки имеет очень похожий ряд Маклорена, а именно:
которое выполняется для любого комплексного числа z .
Производная и интеграл
Производная функции ошибок сразу следует из ее определения:
Отсюда немедленно вычисляется производная мнимой функции ошибок:
Первообразная функции ошибки, получаемый путем интегрирования по частям , является
Первообразной функции мнимой ошибки, которую также можно получить интегрированием по частям, является
Производные высшего порядка даются формулами
где H — полиномы Эрмита физиков .
Серия Bürmann
Разложение, которое сходится быстрее для всех действительных значений x, чем разложение Тейлора, получается с помощью теоремы Ганса Генриха Бюрмана :
где sgn — знаковая функция . Сохраняя только первые два коэффициента и выбирая c 1 =31 год/200и c 2 = —341/8000, полученное приближение показывает свою наибольшую относительную ошибку при x = ± 1,3796 , где она меньше 0,0036127:
Обратные функции
Для комплексного числа z не существует уникального комплексного числа w, удовлетворяющего erf w = z , поэтому истинная обратная функция будет многозначной. Однако для −1 < x <1 существует уникальное действительное число, обозначенное erf −1 x, удовлетворяющее
Функция обратной ошибки обычно определяется с помощью области (-1,1) , и она ограничена этой областью во многих системах компьютерной алгебры. Однако его можно распространить на диск | z | <1 комплексной плоскости, используя ряд Маклорена
где c 0 = 1 и
Итак, у нас есть расширение в ряд (общие множители из числителей и знаменателей удалены):
(После отмены дроби числителя / знаменателя представляют собой записи OEIS : A092676 / OEIS : A092677 в OEIS ; без отмены члены числителя приведены в записи OEIS : A002067 .) Значение функции ошибок при ± ∞ равно ± 1 .
Для | z | <1 , имеем erf (erf −1 z ) = z .
Обратная дополнительная функция ошибок определяются как
Для действительного x существует уникальное действительное число erfi −1 x, удовлетворяющее erfi (erfi −1 x ) = x . Функция обратной мнимой ошибки определяется как erfi −1 x .
Для любого вещественного х , метод Ньютона может быть использован для вычисления ЕрФИ -1 х , а для -1 ≤ х ≤ 1 , следующие сходится ряд Маклорена:
где c k определено, как указано выше.
Асимптотическое разложение
Полезное асимптотическое разложение дополнительной функции ошибок (и, следовательно, также функции ошибок) для больших действительных x :
где (2 n — 1) !! — двойной факториал числа (2 n — 1) , который является произведением всех нечетных чисел до (2 n — 1) . Этот ряд расходится для любого конечного x , и его смысл как асимптотического разложения состоит в том, что для любого целого числа N ≥ 1 выполняется
где остаток в обозначениях Ландау равен
при x → ∞ .
Действительно, точное значение остатка равно
что легко следует по индукции, записывая
и интеграция по частям.
Для достаточно больших значений x необходимы только первые несколько членов этого асимптотического разложения, чтобы получить хорошее приближение erfc x (в то время как для не слишком больших значений x приведенное выше разложение Тейлора при 0 обеспечивает очень быструю сходимость).
Непрерывное расширение фракции
Цепная дробь расширение дополнительной функции ошибок является:
Интеграл функции ошибок с функцией плотности Гаусса
которая, по-видимому, связана с Нг и Геллером, формула 13 в разделе 4.3 с заменой переменных.
Факторный ряд
Обратный факторный ряд :
сходится при Re ( z 2 )> 0 . Здесь
z n обозначает возрастающий факториал , а s ( n , k ) обозначает число Стирлинга первого рода со знаком . Также существует представление бесконечной суммой, содержащее двойной факториал :
Численные приближения
Приближение с элементарными функциями
- Абрамовиц и Стегун дают несколько приближений с различной точностью (уравнения 7.1.25–28). Это позволяет выбрать наиболее быстрое приближение, подходящее для данного приложения. В порядке увеличения точности это:
(максимальная ошибка: 5 × 10 −4 )
где a 1 = 0,278393 , a 2 = 0,230389 , a 3 = 0,000972 , a 4 = 0,078108
(максимальная ошибка: 2,5 × 10 −5 )
где p = 0,47047 , a 1 = 0,3480242 , a 2 = −0,0958798 , a 3 = 0,7478556
(максимальная ошибка: 3 × 10 −7 )
где a 1 = 0,0705230784 , a 2 = 0,0422820123 , a 3 = 0,0092705272 , a 4 = 0,0001520143 , a 5 = 0,0002765672 , a 6 = 0,0000430638
(максимальная ошибка: 1,5 × 10 −7 )
где p = 0,3275911 , a 1 = 0,254829592 , a 2 = −0,284496736 , a 3 = 1,421413741 , a 4 = −1,453152027 , a 5 = 1,061405429.
Все эти приближения верны для x ≥ 0 . Чтобы использовать эти приближения для отрицательного x , используйте тот факт, что erf x — нечетная функция, поэтому erf x = −erf (- x ) .
- Экспоненциальные границы и чисто экспоненциальное приближение для дополнительной функции ошибок даются формулами
- Вышеупомянутое было обобщено до сумм из N экспонент с возрастающей точностью в терминах N, так что erfc x может быть точно аппроксимирован или ограничен величиной 2 Q̃ ( √ 2 x ) , где
В частности, существует систематическая методология решения числовых коэффициентов {( a n , b n )}N
n = 1которые дают минимаксное приближение или оценку для тесно связанной Q-функции : Q ( x ) ≈ Q̃ ( x ) , Q ( x ) ≤ Q̃ ( x ) или Q ( x ) ≥ Q̃ ( x ) для x ≥ 0 . Коэффициенты {( a n , b n )}N
n = 1для многих вариаций экспоненциальных приближений и границ до N = 25 были выпущены в открытый доступ в виде исчерпывающего набора данных. - Точная аппроксимация дополнительной функции ошибок для x ∈ [0, ∞) дана Karagiannidis & Lioumpas (2007), которые показали для соответствующего выбора параметров { A , B }, что
Они определили { A , B } = {1.98,1.135} , что дает хорошее приближение для всех x ≥ 0 . Также доступны альтернативные коэффициенты для настройки точности для конкретного приложения или преобразования выражения в жесткую границу.
- Одноканальная нижняя граница
где параметр β может быть выбран так, чтобы минимизировать ошибку на желаемом интервале аппроксимации.
-
- Другое приближение дает Сергей Виницкий, используя свои «глобальные приближения Паде»:
куда
Это сделано так, чтобы быть очень точным в окрестности 0 и в окрестности бесконечности, а относительная ошибка меньше 0,00035 для всех действительных x . Использование альтернативного значения a ≈ 0,147 снижает максимальную относительную ошибку примерно до 0,00013.
Это приближение можно инвертировать, чтобы получить приближение для обратной функции ошибок:
- Приближение с максимальной погрешностью 1,2 × 10 −7 для любого действительного аргумента:
с участием
а также
Таблица значений
| Икс | erf x | 1 — эрф х |
|---|---|---|
| 0 | 0 | 1 |
| 0,02 | 0,022 564 575 | 0,977 435 425 |
| 0,04 | 0,045 111 106 | 0,954 888 894 |
| 0,06 | 0,067 621 594 | 0,932 378 406 |
| 0,08 | 0,090 078 126 | 0,909 921 874 |
| 0,1 | 0,112 462 916 | 0,887 537 084 |
| 0,2 | 0,222 702 589 | 0,777 297 411 |
| 0,3 | 0,328 626 759 | 0,671 373 241 |
| 0,4 | 0,428 392 355 | 0,571 607 645 |
| 0,5 | 0,520 499 878 | 0,479 500 122 |
| 0,6 | 0,603 856 091 | 0,396 143 909 |
| 0,7 | 0,677 801 194 | 0,322 198 806 |
| 0,8 | 0,742 100 965 | 0,257 899 035 |
| 0,9 | 0,796 908 212 | 0,203 091 788 |
| 1 | 0,842 700 793 | 0,157 299 207 |
| 1.1 | 0,880 205 070 | 0,119 794 930 |
| 1.2 | 0,910 313 978 | 0,089 686 022 |
| 1.3 | 0,934 007 945 | 0,065 992 055 |
| 1.4 | 0,952 285 120 | 0,047 714 880 |
| 1.5 | 0,966 105 146 | 0,033 894 854 |
| 1.6 | 0,976 348 383 | 0,023 651 617 |
| 1,7 | 0,983 790 459 | 0,016 209 541 |
| 1,8 | 0,989 090 502 | 0,010 909 498 |
| 1.9 | 0,992 790 429 | 0,007 209 571 |
| 2 | 0,995 322 265 | 0,004 677 735 |
| 2.1 | 0,997 020 533 | 0,002 979 467 |
| 2.2 | 0,998 137 154 | 0,001 862 846 |
| 2.3 | 0,998 856 823 | 0,001 143 177 |
| 2,4 | 0,999 311 486 | 0,000 688 514 |
| 2,5 | 0,999 593 048 | 0,000 406 952 |
| 3 | 0,999 977 910 | 0,000 022 090 |
| 3.5 | 0,999 999 257 | 0,000 000 743 |
Дополнительная функция ошибок
Дополнительная функция ошибок , обозначаемая ERFC , определяется как
который также определяет erfcx , масштабированную дополнительную функцию ошибок (которую можно использовать вместо erfc, чтобы избежать арифметического переполнения ). Другая форма erfc x для x ≥ 0 известна как формула Крейга в честь ее первооткрывателя:
Это выражение действительно только для положительных значений x , но его можно использовать вместе с erfc x = 2 — erfc (- x ) для получения erfc ( x ) для отрицательных значений. Эта форма выгодна тем, что диапазон интегрирования является фиксированным и конечным. Расширение этого выражения для erfc суммы двух неотрицательных переменных выглядит следующим образом:
Функция мнимой ошибки
Функция мнимой ошибки , обозначаемая erfi , определяется как
где D ( x ) — функция Доусона (которую можно использовать вместо erfi, чтобы избежать арифметического переполнения ).
Несмотря на название «мнимая функция ошибок», erfi x реально, когда x реально.
Когда функция ошибок оценивается для произвольных комплексных аргументов z , результирующая комплексная функция ошибок обычно обсуждается в масштабированной форме как функция Фаддеева :
Кумулятивная функция распределения
Функция ошибок по существу идентична стандартной нормальной кумулятивной функции распределения , обозначаемой Φ , также называемой нормой ( x ) в некоторых языках программного обеспечения, поскольку они различаются только масштабированием и преобразованием. Действительно,
или переставил для erf и erfc :
Следовательно, функция ошибок также тесно связана с Q-функцией , которая является вероятностью хвоста стандартного нормального распределения. Q-функция может быть выражена через функцию ошибок как
Обратное из Ф называется нормальной функции квантиль , или пробит функции и могут быть выражены в терминах функции обратной ошибки как
Стандартный нормальный cdf чаще используется в вероятностях и статистике, а функция ошибок чаще используется в других разделах математики.
Функция ошибок является частным случаем функции Миттаг-Леффлера и также может быть выражена как конфлюэнтная гипергеометрическая функция ( функция Куммера):
Он имеет простое выражение в терминах интеграла Френеля .
С точки зрения регуляризованном гамма — функции P и неполной гамма — функции ,
sgn x — знаковая функция .
Обобщенные функции ошибок
График обобщенных функций ошибок E n ( x ) :
серая кривая: E 1 ( x ) =1 — е — х/√ π
красная кривая: E 2 ( x ) = erf ( x )
зеленая кривая: E 3 ( x )
синяя кривая: E 4 ( x )
золотая кривая: E 5 ( x ) .
Некоторые авторы обсуждают более общие функции:
Известные случаи:
- E 0 ( x ) — прямая линия, проходящая через начало координат: E 0 ( x ) =Икс/е √ π
- E 2 ( x ) — функция ошибок, erf x .
После деления на п ! , все E n для нечетных n похожи (но не идентичны) друг на друга. Точно так же E n для четного n выглядят похожими (но не идентичными) друг на друга после простого деления на n ! . Все обобщенные функции ошибок для n > 0 выглядят одинаково на положительной стороне графика x .
Эти обобщенные функции могут быть эквивалентно выражены для x > 0 с использованием гамма-функции и неполной гамма-функции :
Следовательно, мы можем определить функцию ошибок в терминах неполной гамма-функции:
Итерированные интегралы дополнительной функции ошибок
Повторные интегралы дополнительной функции ошибок определяются как
Общая рекуррентная формула
У них есть степенной ряд
откуда следуют свойства симметрии
а также
Реализации
Как реальная функция реального аргумента
- В Posix -совместимый операционных систем, заголовок math.h возвестят и математическая библиотека libm должна обеспечивать функции
erfиerfc( двойной точности ), а также их одинарной точности и повышенной точности аналоговerff,erflиerfcf,erfcl. - GNU Scientific Library предоставляет
erf,erfc,log(erf), и масштабируемые функции ошибок.
Как сложная функция сложного аргумента
-
libcerf , цифровая библиотека C для сложных функций ошибок, обеспечивает комплексные функции
cerf,cerfc,cerfcxи реальные функцииerfi,erfcxпримерно с 13-14 точностью цифр, на основе функции Фаддеева , как реализовано в MIT Фаддеевого пакете
Смотрите также
- Гауссовский интеграл по всей действительной прямой
- Функция Гаусса , производная
- Функция Доусона , перенормированная функция мнимой ошибки
- Интеграл Гудвина – Стэтона
По вероятности
- Нормальное распределение
- Нормальная кумулятивная функция распределения , масштабированная и сдвинутая форма функции ошибок
- Пробит , обратная или квантильная функция нормального CDF
- Q-функция , хвостовая вероятность нормального распределения
использованная литература
дальнейшее чтение
- Абрамовиц, Милтон ; Стегун, Ирен Энн , ред. (1983) [июнь 1964]. «Глава 7» . Справочник по математическим функциям с формулами, графиками и математическими таблицами . Прикладная математика. 55 (Девятое переиздание с дополнительными исправлениями, десятое оригинальное издание с исправлениями (декабрь 1972 г.); первое изд.). Вашингтон; Нью-Йорк: Министерство торговли США, Национальное бюро стандартов; Dover Publications. п. 297. ISBN. 978-0-486-61272-0. LCCN 64-60036 . Руководство по ремонту 0167642 . LCCN 65-12253 .
- Press, William H .; Teukolsky, Saul A .; Веттерлинг, Уильям Т .; Фланнери, Брайан П. (2007), «Раздел 6.2. Неполная гамма-функция и функция ошибок» , Численные рецепты: Искусство научных вычислений (3-е изд.), Нью-Йорк: Cambridge University Press, ISBN 978-0-521-88068-8
- Темме, Нико М. (2010), «Функции ошибок, интегралы Доусона и Френеля» , в Olver, Frank WJ ; Lozier, Daniel M .; Бойсверт, Рональд Ф .; Кларк, Чарльз В. (ред.), Справочник по математическим функциям NIST , Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248
внешние ссылки
- MathWorld — Эрф
- Таблица интегралов функций ошибок








![{ displaystyle Pr [X leq L ] = { frac {1} {2}} + { frac {1} {2}} operatorname {erf} left ({ frac {L- mu} {{ sqrt {2}} sigma }} right) приблизительно A exp left (-B left ({ frac {L- mu} { sigma}} right) ^ {2} right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a72302c46832449e128a4d4e1adb28b514131270)
![{ displaystyle Pr [X leq L] leq A exp (-B ln {k}) = { frac {A} {k ^ {B}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2baadea015e20a45d1034fd88eed861e7fcce178)









![{ displaystyle { begin {align} operatorname {erf} (x) = { frac {2} { sqrt { pi}}} operatorname {sgn} (x) { sqrt {1-e ^ {- x ^ {2}}}} left (1 - { frac {1} {12}} left (1 -e ^ {- x ^ {2}} right) - { frac {7} {480}} left (1-e ^ {- x ^ {2}} right) ^ {2} - { frac {5} {896}} left (1-e ^ {- x ^ {2}} right) ^ {3} - { frac {787} {276480}} left (1-e ^ {- x ^ {2 }} right) ^ {4} - cdots right) \ [10pt] = { frac {2} { sqrt { pi}}} operatorname {sgn} (x) { sqrt {1 -e ^ {- x ^ {2}}}} left ({ frac { sqrt { pi}} {2}} + sum _ {k = 1} ^ { infty} c_ {k} e ^ {- kx ^ {2}} right). end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24ddba05e595a553fee25644a3542188281bd844)







![{ displaystyle operatorname {erfc} (x) = { frac {e ^ {- x ^ {2}}} {x { sqrt { pi}}}} left [1+ sum _ {n = 1} ^ { infty} (-1) ^ {n} { frac {1 cdot 3 cdot 5 cdots (2n-1)} {(2x ^ {2}) ^ { n}}} right] = { frac {e ^ {-x ^ {2}}} {x { sqrt { pi}}}} sum _ {n = 0} ^ { infty} (- 1) ^ {n} { frac {(2n-1) !!} {(2x ^ {2}) ^ {n}}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fc8c3aefff3ba787b080c5186dd3aec8ec76ef9)






![{ displaystyle int _ {- infty} ^ { infty} operatorname {erf} left (ax + b right) { frac {1} { sqrt {2 pi sigma ^ {2}}}} e ^ {- { frac {(x- mu) ^ {2}} {2 sigma ^ {2}}}} , dx = operatorname {erf} left [{ frac {a mu + b} { sqrt {1 + 2a ^ {2} sigma ^ {2}}} right], qquad a, b, му, sigma in mathbb {R}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9b6adc2c661b24b44dc1e3d7e16be70023daacd8)


 обозначает возрастающий факториал, а s (n, k) { displaystyle s (n, k)}
обозначает возрастающий факториал, а s (n, k) { displaystyle s (n, k)} обозначает знаковое число Стирлинга первого рода.
обозначает знаковое число Стирлинга первого рода.

 (максимальная ошибка: 2,5 × 10)
(максимальная ошибка: 2,5 × 10) (максимальная ошибка: 3 × 10)
(максимальная ошибка: 3 × 10) (максимальная ошибка: 1,5 × 10)
(максимальная ошибка: 1,5 × 10)

 , что дает хорошее приближение для всех x ≥ 0. { displaystyle x geq 0.}
, что дает хорошее приближение для всех x ≥ 0. { displaystyle x geq 0.}







![{ displaystyle { begin {align} operatorname {erfc} (x) = 1- operatorname {erf} (x) \ [5pt ] = { frac {2} { sqrt { pi}}} int _ {x} ^ { infty} e ^ {- t ^ {2}} , dt \ [5pt] = e ^ {- x ^ {2}} operatorname {erfcx} (x), end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8808e6f3ad9aab23f14d55db707a39388d256788)


![{ displaystyle { begin {align} operatorname {erfi} (x) = - i operatorname {erf} (ix) \ [5pt] = { frac {2} { sqrt { pi}}} int _ {0} ^ {x} e ^ {t ^ {2 }} , dt \ [5pt] = { frac {2} { sqrt { pi}}} e ^ {x ^ {2}} D (x), end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4480a8ec17e274a7ad6b8ef25cc76234d48c0433)

![{ displaystyle Phi (x) = { frac {1} { sqrt {2 pi}}} int _ {- infty} ^ {x } e ^ { tfrac {-t ^ {2}} {2}} , dt = { frac {1} {2}} left [1+ operatorname {erf} left ({ frac {x } { sqrt {2}}} right) right] = { frac {1} {2}} operatorname {erfc} left (- { frac {x} { sqrt {2}}} справа)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e19dc7206f8b3b571e81153816c478abd91a679e)









![{ displaystyle { begin {align} operatorname { i ^ {n} erfc} (z) = int _ {z} ^ { infty} operatorname {i ^ {n-1} erfc} ( zeta) , d zeta \ имя оператора {i ^ {0} erfc} (z) = operatorname {erfc} (z) \ operatorname {i ^ {1} erfc} (z) = operatorname {ierfc} (z) = { frac {1} { sqrt { pi}}} e ^ {- z ^ {2}} - z operatorname {erfc} (z) \ operatorname {i ^ {2} erfc} (z) = { frac { 1} {4}} left [ operatorname {erfc} (z) -2z operatorname {ierfc} (z) right] \ конец {выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/66b57abb0a01139b31a14f5a8d651e4aa2e5f4f2)







![{ displaystyle { begin {align} Pr [X leq L] & = { frac {1} {2}} + { frac {1} {2}} operatorname {erf} { frac {L - mu} {{ sqrt {2}} sigma}} \ & приблизительно A exp left (-B left ({ frac {L- mu} { sigma}} right) ^ {2} right) end {выравнивается}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f3cb760eaf336393db9fd0bb12c4465655a27de8)
![{ displaystyle { begin {align} Pr [L_ {a} leq X leq L_ {b}] & = int _ {L_ {a}} ^ {L_ {b}} { frac {1} {{ sqrt {2 pi}} sigma}} exp left (- { frac {(x- mu) ^ {2}} {2 sigma ^ {2}}} right) , dx \ & = { frac {1} {2}} left ( operatorname {erf} { frac {L_ {b} - mu} {{ sqrt {2}} sigma}} - operatorname {erf} { frac {L_ {a} - mu} {{ sqrt {2}} sigma}} right). end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f1b3e43d593e389ed348ff56374118ab644fcec8)
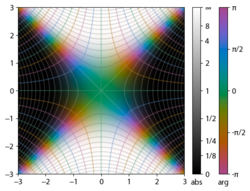


![{ displaystyle { begin {align} operatorname {erf} z & = { frac {2} { sqrt { pi}}} sum _ {n = 0} ^ { infty} { frac {(- 1) ^ {n} z ^ {2n + 1}} {n! (2n + 1)}} \ [6pt] & = { frac {2} { sqrt { pi}}} left (z - { frac {z ^ {3}} {3}} + { frac {z ^ {5}} {10}} - { frac {z ^ {7}} {42}} + { frac { z ^ {9}} {216}} - cdots right) end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c80541f305af070bb0510625c584fe1559a0cd2c)
![{ displaystyle { begin {align} operatorname {erf} z & = { frac {2} { sqrt { pi}}} sum _ {n = 0} ^ { infty} left (z prod _ {k = 1} ^ {n} { frac {- (2k-1) z ^ {2}} {k (2k + 1)}} right) \ [6pt] & = { frac {2 } { sqrt { pi}}} sum _ {n = 0} ^ { infty} { frac {z} {2n + 1}} prod _ {k = 1} ^ {n} { frac {-z ^ {2}} {k}} end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dca22e8e7dee0297e87a455249c282c6b92fedcb)
![{ displaystyle { begin {align} operatorname {erfi} z & = { frac {2} { sqrt { pi}}} sum _ {n = 0} ^ { infty} { frac {z ^ {2n + 1}} {n! (2n + 1)}} \ [6pt] & = { frac {2} { sqrt { pi}}} left (z + { frac {z ^ {3 }} {3}} + { frac {z ^ {5}} {10}} + { frac {z ^ {7}} {42}} + { frac {z ^ {9}} {216} } + cdots right) end {выровнены}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ff91095cd6825137cc951ec0a786db0b7f68fac)





![{ displaystyle { begin {align} operatorname {erf} x & = { frac {2} { sqrt { pi}}} operatorname {sgn} x cdot { sqrt {1-e ^ {- x ^ {2}}}} left (1 - { frac {1} {12}} left (1-e ^ {- x ^ {2}} right) - { frac {7} {480} } left (1-e ^ {- x ^ {2}} right) ^ {2} - { frac {5} {896}} left (1-e ^ {- x ^ {2}} справа) ^ {3} - { frac {787} {276480}} left (1-e ^ {- x ^ {2}} right) ^ {4} - cdots right) \ [10pt] & = { frac {2} { sqrt { pi}}} operatorname {sgn} x cdot { sqrt {1-e ^ {- x ^ {2}}}} left ({ frac { sqrt { pi}} {2}} + sum _ {k = 1} ^ { infty} c_ {k} e ^ {- kx ^ {2}} right). end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/164e7f029977edb47c83845b04abfe5b2d28b837)







![{ displaystyle { begin {align} operatorname {erfc} x & = { frac {e ^ {- x ^ {2}}} {x { sqrt { pi}}}} left (1+ sum _ {n = 1} ^ { infty} (- 1) ^ {n} { frac {1 cdot 3 cdot 5 cdots (2n-1)} { left (2x ^ {2} right) ^ {n}}} right) \ [6pt] & = { frac {e ^ {- x ^ {2}}} {x { sqrt { pi}}}} sum _ {n = 0 } ^ { infty} (- 1) ^ {n} { frac {(2n-1) !!} { left (2x ^ {2} right) ^ {n}}}, end {выровнено} }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/35a11e2e5b22ca898c74f2e913d276c9ac11124a)


















![{ displaystyle { begin {align} operatorname {erfc} x & = 1- operatorname {erf} x \ [5pt] & = { frac {2} { sqrt { pi}}} int _ { x} ^ { infty} e ^ {- t ^ {2}} , dt \ [5pt] & = e ^ {- x ^ {2}} operatorname {erfcx} x, end {выровнено}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/582ae24086ba008f0466a71991c48c405c8248ad)


![{ displaystyle { begin {align} operatorname {erfi} x & = - i operatorname {erf} ix \ [5pt] & = { frac {2} { sqrt { pi}}} int _ { 0} ^ {x} e ^ {t ^ {2}} , dt \ [5pt] & = { frac {2} { sqrt { pi}}} e ^ {x ^ {2}} D (х), конец {выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/937f1aaa2801d245f8056cad15f727ccee0ba1a7)
![{ displaystyle { begin {align} Phi (x) & = { frac {1} { sqrt {2 pi}}} int _ {- infty} ^ {x} e ^ { tfrac { -t ^ {2}} {2}} , dt \ [6pt] & = { frac {1} {2}} left (1+ operatorname {erf} { frac {x} { sqrt {2}}} right) \ [6pt] & = { frac {1} {2}} operatorname {erfc} left (- { frac {x} { sqrt {2}}} right ) конец {выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4c70647a7aa4dea3272cb7d90888444e1928c401)
![{ displaystyle { begin {align} operatorname {erf} (x) & = 2 Phi left (x { sqrt {2}} right) -1 \ [6pt] operatorname {erfc} (x ) & = 2 Phi left (-x { sqrt {2}} right) \ & = 2 left (1- Phi left (x { sqrt {2}} right) right) . end {выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86c84a4d2d79631fe9996e30f1d6c0da3089bfe2)





![{ displaystyle { begin {align} operatorname {i} ^ {n} ! operatorname {erfc} z & = int _ {z} ^ { infty} operatorname {i} ^ {n-1} ! operatorname {erfc} zeta , d zeta \ [6pt] operatorname {i} ^ {0} ! operatorname {erfc} z & = operatorname {erfc} z \ operatorname {i} ^ {1} ! Operatorname {erfc} z & = operatorname {ierfc} z = { frac {1} { sqrt { pi}}} e ^ {- z ^ {2}} - z operatorname {erfc } z \ operatorname {i} ^ {2} ! operatorname {erfc} z & = { tfrac {1} {4}} left ( operatorname {erfc} z-2z operatorname {ierfc} z вправо) \ конец {выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/39d9046debe25c6cb2fa3709a961ac6a9715a37f)



