| Обноружение ошибок | ||||
| Исправление ошибок | ||||
| Коррекция ошибок | ||||
| Назад | ||||
Методы обнаружения ошибок
В обычном равномерном непомехоустойчивом коде число разрядов n в кодовых
комбинациях определяется числом сообщений и основанием кода.
Коды, у которых все кодовые комбинации разрешены, называются простыми или
равнодоступными и являются полностью безызбыточными. Безызбыточные коды обладают
большой «чувствительностью» к помехам. Внесение избыточности при использовании
помехоустойчивых кодов связано с увеличением n – числа разрядов кодовой комбинации. Таким
образом, все множество

подмножество разрешенных комбинаций, обладающих определенными признаками, и
подмножество запрещенных комбинаций, этими признаками не обладающих.
Помехоустойчивый код отличается от обычного кода тем, что в канал передаются не все
кодовые комбинации N, которые можно сформировать из имеющегося числа разрядов n, а только
их часть Nk , которая составляет подмножество разрешенных комбинаций. Если при приеме
выясняется, что кодовая комбинация принадлежит к запрещенным, то это свидетельствует о
наличии ошибок в комбинации, т.е. таким образом решается задача обнаружения ошибок. При
этом принятая комбинация не декодируется (не принимается решение о переданном
сообщении). В связи с этим помехоустойчивые коды называют корректирующими кодами.
Корректирующие свойства избыточных кодов зависят от правила их построения, определяющего
структуру кода, и параметров кода (длительности символов, числа разрядов, избыточности и т. п.).
Первые работы по корректирующим кодам принадлежат Хеммингу, который ввел понятие
минимального кодового расстояния dmin и предложил код, позволяющий однозначно указать ту
позицию в кодовой комбинации, где произошла ошибка. К информационным элементам k в коде
Хемминга добавляется m проверочных элементов для автоматического определения
местоположения ошибочного символа. Таким образом, общая длина кодовой комбинации
составляет: n = k + m.
Метричное представление n,k-кодов
В настоящее время наибольшее внимание с точки зрения технических приложений
уделяется двоичным блочным корректирующим кодам. При использовании блочных кодов
цифровая информация передается в виде отдельных кодовых комбинаций (блоков) равной
длины. Кодирование и декодирование каждого блока осуществляется независимо друг от друга.
Почти все блочные коды относятся к разделимым кодам, кодовые комбинации которых
состоят из двух частей: информационной и проверочной. При общем числе n символов в блоке
число информационных символов равно k, а число проверочных символов:
К основным характеристикам корректирующих кодов относятся:
|
— число разрешенных и запрещенных кодовых комбинаций; |
Для блочных двоичных кодов, с числом символов в блоках, равным n, общее число
возможных кодовых комбинаций определяется значением
Число разрешенных кодовых комбинаций при наличии k информационных разрядов в
первичном коде:
Очевидно, что число запрещенных комбинаций:
а с учетом отношение будет
где m – число избыточных (проверочных) разрядов в блочном коде.
Избыточностью корректирующего кода называют величину
откуда следует:
Эта величина показывает, какую часть общего числа символов кодовой комбинации
составляют информационные символы. В теории кодирования величину Bk называют
относительной скоростью кода. Если производительность источника информации равна H
символов в секунду, то скорость передачи после кодирования этой информации будет
поскольку в закодированной последовательности из каждых n символов только k символов
являются информационными.
Если число ошибок, которые нужно обнаружить или исправить, значительно, то необходимо
иметь код с большим числом проверочных символов. Чтобы при этом скорость передачи
оставалась достаточно высокой, необходимо в каждом кодовом блоке одновременно
увеличивать как общее число символов, так и число информационных символов.
При этом длительность кодовых блоков будет существенно возрастать, что приведет к
задержке информации при передаче и приеме. Чем сложнее кодирование, тем длительнее
временная задержка информации.
Минимальное кодовое расстояние – dmin. Для того чтобы можно было обнаружить и
исправлять ошибки, разрешенная комбинация должна как можно больше отличаться от
запрещенной. Если ошибки в канале связи действуют независимо, то вероятность преобразования
одной кодовой комбинации в другую будет тем меньше, чем большим числом символов они
различаются.
Если интерпретировать кодовые комбинации как точки в пространстве, то отличие
выражается в близости этих точек, т. е. в расстоянии между ними.
Количество разрядов (символов), которыми отличаются две кодовые комбинации, можно
принять за кодовое расстояние между ними. Для определения этого расстояния нужно сложить
две кодовые комбинации «по модулю 2» и подсчитать число единиц в полученной сумме.
Например, две кодовые комбинации xi = 01011 и xj = 10010 имеют расстояние d(xi,xj) , равное 3,
так как:
Здесь под операцией ⊕ понимается сложение «по модулю 2».
Заметим, что кодовое расстояние d(xi,x0) между комбинацией xi и нулевой x0 = 00…0
называют весом W комбинации xi, т.е. вес xi равен числу «1» в ней.
Расстояние между различными комбинациями некоторого конкретного кода могут
существенно отличаться. Так, в частности, в безызбыточном первичном натуральном коде n = k это
расстояние для различных комбинаций может изменяться от единицы до величины n, равной
разрядности кода. Особую важность для характеристики корректирующих свойств кода имеет
минимальное кодовое расстояние dmin, определяемое при попарном сравнении всех кодовых
комбинаций, которое называют расстоянием Хемминга.
В безызбыточном коде все комбинации являются разрешенными и его минимальное
кодовое расстояние равно единице – dmin=1. Поэтому достаточно исказиться одному символу,
чтобы вместо переданной комбинации была принята другая разрешенная комбинация. Чтобы код
обладал корректирующими свойствами, необходимо ввести в него некоторую избыточность,
которая обеспечивала бы минимальное расстояние между любыми двумя разрешенными
комбинациями не менее двух – dmin ≥ 2..
Минимальное кодовое расстояние является важнейшей характеристикой помехоустойчивых
кодов, указывающей на гарантируемое число обнаруживаемых или исправляемых заданным
кодом ошибок.
Число обнаруживаемых или исправляемых ошибок
При применении двоичных кодов учитывают только дискретные искажения, при которых
единица переходит в нуль («1» → «0») или нуль переходит в единицу («0» → «1»). Переход «1» →
«0» или «0» → «1» только в одном элементе кодовой комбинации называют единичной ошибкой
(единичным искажением). В общем случае под кратностью ошибки подразумевают число
позиций кодовой комбинации, на которых под действием помехи одни символы оказались
замененными на другие. Возможны двукратные (g = 2) и многократные (g > 2) искажения
элементов в кодовой комбинации в пределах 0 ≤ g ≤ n.
Минимальное кодовое расстояние является основным параметром, характеризующим
корректирующие способности данного кода. Если код используется только для обнаружения
ошибок кратностью g0, то необходимо и достаточно, чтобы минимальное кодовое расстояние
было равно dmin ≥ g0 + 1.
В этом случае никакая комбинация из go ошибок не может перевести одну разрешенную
кодовую комбинацию в другую разрешенную. Таким образом, условие обнаружения всех ошибок
кратностью g0 можно записать
Чтобы можно было исправить все ошибки кратностью gu и менее, необходимо иметь
минимальное расстояние, удовлетворяющее условию dmin ≥ 2gu
В этом случае любая кодовая комбинация с числом ошибок gu отличается от каждой
разрешенной комбинации не менее чем в gu+1 позициях. Если условие не выполнено,
возможен случай, когда ошибки кратности g исказят переданную комбинацию так, что она станет
ближе к одной из разрешенных комбинаций, чем к переданной или даже перейдет в другую
разрешенную комбинацию. В соответствии с этим, условие исправления всех ошибок кратностью
не более gи можно записать:
Из и
следует, что если код исправляет все ошибки кратностью gu, то число
ошибок, которые он может обнаружить, равно go = 2gu. Следует отметить, что эти соотношения
устанавливают лишь гарантированное минимальное число обнаруживаемых или
исправляемых ошибок при заданном dmin и не ограничивают возможность обнаружения ошибок
большей кратности. Например, простейший код с проверкой на четность с dmin = 2 позволяет
обнаруживать не только одиночные ошибки, но и любое нечетное число ошибок в пределах go < n.
Корректирующие возможности кодов
Вопрос о минимально необходимой избыточности, при которой код обладает нужными
корректирующими свойствами, является одним из важнейших в теории кодирования. Этот вопрос
до сих пор не получил полного решения. В настоящее время получен лишь ряд верхних и нижних
оценок (границ), которые устанавливают связь между максимально возможным минимальным
расстоянием корректирующего кода и его избыточностью.
Коды Хэмминга
Построение кодов Хемминга базируется на принципе проверки на четность веса W (числа
единичных символов «1») в информационной группе кодового блока.
Поясним идею проверки на четность на примере простейшего корректирующего кода,
который так и называется кодом с проверкой на четность или кодом с проверкой по паритету
(равенству).
В таком коде к кодовым комбинациям безызбыточного первичного двоичного k-разрядного
кода добавляется один дополнительный разряд (символ проверки на четность, называемый
проверочным, или контрольным). Если число символов «1» исходной кодовой комбинации
четное, то в дополнительном разряде формируют контрольный символ «0», а если число
символов «1» нечетное, то в дополнительном разряде формируют символ «1». В результате
общее число символов «1» в любой передаваемой кодовой комбинации всегда будет четным.
Таким образом, правило формирования проверочного символа сводится к следующему:
где i – соответствующий информационный символ («0» или «1»); k – общее их число а, под
операцией ⊕ здесь и далее понимается сложение «по модулю 2». Очевидно, что добавление
дополнительного разряда увеличивает общее число возможных комбинаций вдвое по сравнению
с числом комбинаций исходного первичного кода, а условие четности разделяет все комбинации
на разрешенные и неразрешенные. Код с проверкой на четность позволяет обнаруживать
одиночную ошибку при приеме кодовой комбинации, так как такая ошибка нарушает условие
четности, переводя разрешенную комбинацию в запрещенную.
Критерием правильности принятой комбинации является равенство нулю результата S
суммирования «по модулю 2» всех n символов кода, включая проверочный символ m1. При
наличии одиночной ошибки S принимает значение 1:
— ошибок нет,
— однократная ошибка
Этот код является (k+1,k)-кодом, или (n,n–1)-кодом. Минимальное расстояние кода равно
двум (dmin = 2), и, следовательно, никакие ошибки не могут быть исправлены. Простой код с
проверкой на четность может использоваться только для обнаружения (но не исправления)
однократных ошибок.
Увеличивая число дополнительных проверочных разрядов, и формируя по определенным
правилам проверочные символы m, равные «0» или «1», можно усилить корректирующие
свойства кода так, чтобы он позволял не только обнаруживать, но и исправлять ошибки. На этом и
основано построение кодов Хемминга.
Коды Хемминга позволяют исправлять одиночную ошибку, с помощью непосредственного
описания. Для каждого числа проверочных символов m =3, 4, 5… существует классический код
Хемминга с маркировкой
т.е. (7,4), (15,11) (31,26) …
При других значениях числа информационных символов k получаются так называемые
усеченные (укороченные) коды Хемминга. Так для кода имеющего 5 информационных символов,
потребуется использование корректирующего кода (9,5), являющегося усеченным от
классического кода Хемминга (15,11), так как число символов в этом коде уменьшается
(укорачивается) на 6.
Для примера рассмотрим классический код Хемминга (7,4), который можно сформировать и
описать с помощью кодера, представленного на рис. 1 В простейшем варианте при заданных
четырех информационных символах: i1, i2, i3, i4 (k = 4), будем полагать, что они сгруппированы в
начале кодового слова, хотя это и не обязательно. Дополним эти информационные символы
тремя проверочными символами (m = 3), задавая их следующими равенствами проверки на
четность, которые определяются соответствующими алгоритмами, где знак ⊕ означает
сложение «по модулю 2»: r1 = i1 ⊕ i2 ⊕ i3, r2 = i2 ⊕ i3 ⊕ i4, r3 = i1 ⊕ i2 ⊕ i4.
В соответствии с этим алгоритмом определения значений проверочных символов mi, в табл.
1 выписаны все возможные 16 кодовых слов (7,4)-кода Хемминга.
Таблица 1 Кодовые слова (7,4)-кода Хэмминга
|
k=4 |
m=4 |
|
i1 i2 i3 i4 |
r1 r2 r3 |
|
0 0 0 0 |
0 0 0 |
|
0 0 0 1 |
0 1 1 |
|
0 0 1 0 |
1 1 0 |
|
0 0 1 1 |
1 0 1 |
|
0 1 0 0 |
1 1 1 |
|
0 1 0 1 |
1 0 0 |
|
0 1 1 0 |
0 0 1 |
|
0 1 1 1 |
0 1 0 |
|
1 0 0 0 |
1 0 1 |
|
1 0 0 1 |
1 0 0 |
|
1 0 1 0 |
0 1 1 |
|
1 0 1 1 |
0 0 0 |
|
1 1 0 0 |
0 1 0 |
|
1 1 0 1 |
0 0 1 |
|
1 1 1 0 |
1 0 0 |
|
1 1 1 1 |
1 1 1 |
На рис.1 приведена блок-схема кодера – устройства автоматически кодирующего
информационные разряды в кодовые комбинации в соответствии с табл.1

Рис. 1 Кодер для (7,4)-кода Хемминга
На рис. 1.4 приведена схема декодера для (7,4) – кода Хемминга, на вход которого
поступает кодовое слово
. Апостроф означает, что любой символ слова может
быть искажен помехой в телекоммуникационном канале.
В декодере в режиме исправления ошибок строится последовательность:
Трехсимвольная последовательность (s1, s2, s3) называется синдромом. Термин «синдром»
используется и в медицине, где он обозначает сочетание признаков, характерных для
определенного заболевания. В данном случае синдром S = (s1, s2, s3) представляет собой
сочетание результатов проверки на четность соответствующих символов кодовой группы и
характеризует определенную конфигурацию ошибок (шумовой вектор).
Число возможных синдромов определяется выражением:
При числе проверочных символов m =3 имеется восемь возможных синдромов (23 = .
Нулевой синдром (000) указывает на то, что ошибки при приеме отсутствуют или не обнаружены.
Всякому ненулевому синдрому соответствует определенная конфигурация ошибок, которая и
исправляется. Классические коды Хемминга имеют число синдромов, точно равное их
необходимому числу (что позволяет исправить все однократные ошибки в любом информативном
и проверочном символах) и включают один нулевой синдром. Такие коды называются
плотноупакованными.
Усеченные коды являются неплотноупакованными, так как число синдромов у них
превышает необходимое. Так, в коде (9,5) при четырех проверочных символах число синдромов
будет равно 24 =16, в то время как необходимо всего 10. Лишние 6 синдромов свидетельствуют о
неполной упаковке кода (9,5).

Рис. 2 Декодер для (7, 4)-кода Хемминга
Для рассматриваемого кода (7,4) в табл. 2 представлены ненулевые синдромы и
соответствующие конфигурации ошибок.
Таблица 2 Синдромы (7, 4)-кода Хемминга
|
Синдром |
001 |
010 |
011 |
100 |
101 |
110 |
111 |
|
Конфигурация ошибок |
0000001 |
0000010 |
0000100 |
0001000 |
0010000 |
0100000 |
1000000 |
|
Ошибка в символе |
m1 |
m2 |
i4 |
m1 |
i1 |
i3 |
i2 |
Таким образом, (7,4)-код позволяет исправить все одиночные ошибки. Простая проверка
показывает, что каждая из ошибок имеет свой единственный синдром. При этом возможно
создание такого цифрового корректора ошибок (дешифратора синдрома), который по
соответствующему синдрому исправляет соответствующий символ в принятой кодовой группе.
После внесения исправления проверочные символы ri можно на выход декодера (рис. 2) не
выводить. Две или более ошибок превышают возможности корректирующего кода Хемминга, и
декодер будет ошибаться. Это означает, что он будет вносить неправильные исправления и
выдавать искаженные информационные символы.
Идея построения подобного корректирующего кода, естественно, не меняется при
перестановке позиций символов в кодовых словах. Все такие варианты также называются (7,4)-
кодами Хемминга.
Циклические коды
Своим названием эти коды обязаны такому факту, что для них часть комбинаций, либо все
комбинации могут быть получены путем циклическою сдвига одной или нескольких базовых
комбинаций кода.
Построение такого кода основывается на использовании неприводимых многочленов в поле
двоичных чисел. Такие многочлены не могут быть представлены в виде произведения
многочленов низших степеней подобно тому, как простые числа не могут быть представлены
произведением других чисел. Они делятся без остатка только на себя или на единицу.
Для определения неприводимых многочленов раскладывают на простые множители бином
хn -1. Так, для n = 7 это разложение имеет вид:
(x7)=(x-1)(x3+x2)(x3+x-1)
Каждый из полученных множителей разложения может применяться для построения
корректирующего кода.
Неприводимый полином g(x) называют задающим, образующим или порождающим
для корректирующего кода. Длина n (число разрядов) создаваемого кода произвольна.
Кодовая последовательность (комбинация) корректирующего кода состоит из к информационных
разрядов и n — к контрольных (проверочных) разрядов. Степень порождающего полинома
r = n — к равна количеству неинформационных контрольных разрядов.
Если из сделанного выше разложения (при n = 7) взять полипом (х — 1), для которого
r=1, то k=n-r=7-1=6. Соответствующий этому полиному код используется для контроля
на чет/нечет (обнаружение ошибок). Для него минимальное кодовое расстояние D0 = 2
(одна единица от D0 — для исходного двоичного кода, вторая единица — за счет контрольного разряда).
Если же взять полином (x3+x2+1) из указанного разложения, то степень полинома
r=3, а k=n-r=7-3=4.
Контрольным разрядам в комбинации для некоторого кода могут быть четко определено место (номера разрядов).
Тогда код называют систематическим или разделимым. В противном случае код является неразделимым.
Способы построения циклических кодов по заданному полиному.
1) На основе порождающей (задающей) матрицы G, которая имеет n столбцов, k строк, то есть параметры которой
связаны с параметрами комбинаций кода. Порождающую матрицу строят, взяв в качестве ее строк порождающий
полином g(x) и (k — 1) его циклических сдвигов:

Пример; Определить порождающую матрицу, если известно, что n=7, k=4, задающий полином g(x)=x3+х+1.
Решение: Кодовая комбинация, соответствующая задающему полиному g(x)=x3+х+1, имеет вид 1011.
Тогда порождающая матрица G7,4 для кода при n=7, к=4 с учетом того, что k-1=3, имеет вид:

Порождающая матрица содержит k разрешенных кодовых комбинаций. Остальные комбинации кода,
количество которых (2k — k) можно определить суммированием по модулю 2 всевозможных сочетаний
строк матрицы Gn,k. Для матрицы, полученной в приведенном выше примере, суммирование по модулю 2
четырех строк 1-2, 1-3, 1-4, 2-3, 2-4, 3-4 дает следующие кодовые комбинации циклического кода:
001110101001111010011011101010011101110100
Другие комбинации искомого корректирующего кода могут быть получены сложением трех комбинаций, например,
из сочетания строк 1-3-4, что дает комбинацию 1111111, а также сложением четырех строк 1-2-3-4, что
дает комбинацию 1101001 и т.д.
Ряд комбинаций искомого кода может быть получено путем дальнейшего циклического сдвига комбинаций
порождающей матрицы, например, 0110001, 1100010, 1000101. Всего для образования искомого циклического
кода требуется 2k=24=16 комбинаций.
2) Умножение исходных двоичных кодовых комбинаций на задающий полином.
Исходными комбинациями являются все k-разрядные двоичные комбинации. Так, например, для исходной
комбинации 1111 (при k = 4) умножение ее на задающий полином g(x)=x3+х+1=1011 дает 1101001.
Полученные на основе двух рассмотренных способов циклические коды не являются разделимыми.
3) Деление на задающий полином.
Для получения разделимого (систематического) циклического кода необходимо разделить многочлен
xn-k*h(x), где h(x) — исходная двоичная комбинация, на задающий полином g(x) и прибавить полученный
остаток от деления к многочлену xn-k*h(x).
Заметим, что умножение исходной комбинации h(x) на xn-k эквивалентно сдвигу h(x) на (n-к) разрядов влево.
Пример: Требуется определить комбинации циклического разделимого кода, заданного полиномом g(x)=x3+х+1=1011 и
имеющего общее число разрядов 7, число информационных разрядов 4, число контрольных разрядов (n-k)=3.
Решение: Пусть исходная комбинация h(x)=1100. Умножение ее на xn-k=x3=1000 дает
x3*(x3+x2)=1100000, то есть эквивалентно
сдвигу исходной комбинации на 3 разряда влево. Деление комбинации 1100000 на комбинацию 1011, эквивалентно задающему полиному, дает:

Полученный остаток от деления, содержащий xn-k=3 разряда, прибавляем к полиному, в результате чего получаем искомую комбинацию
разделимого циклического кода: 1100010. В ней 4 старших разряда (слева) соответствуют исходной двоичной комбинации, а три младших
разряда являются контрольными.
Следует сделать ряд указаний относительно процедуры деления:
1) При делении задающий полином совмещается старшим разрядом со старшим «единичными разрядом делимого.
2) Вместо вычитания по модулю 2 выполняется эквивалентная ему процедура сложения по модулю 2.
3) Деление продолжается до тех пор, пока степень очередного остатка не будет меньше степени делителя (задающего полинома). При достижении
этого полученный остаток соответствует искомому содержанию контрольных разрядов для данной искомой двоичной комбинации.
Для проверки правильности выполнения процедуры определения комбинации циклического кода необходимо разделить полученную комб1шацию на задающий полином с
учетом сделанных выше замечаний. Получение нулевого остатка от такого деления свидетельствует о правильности определения комбинации.
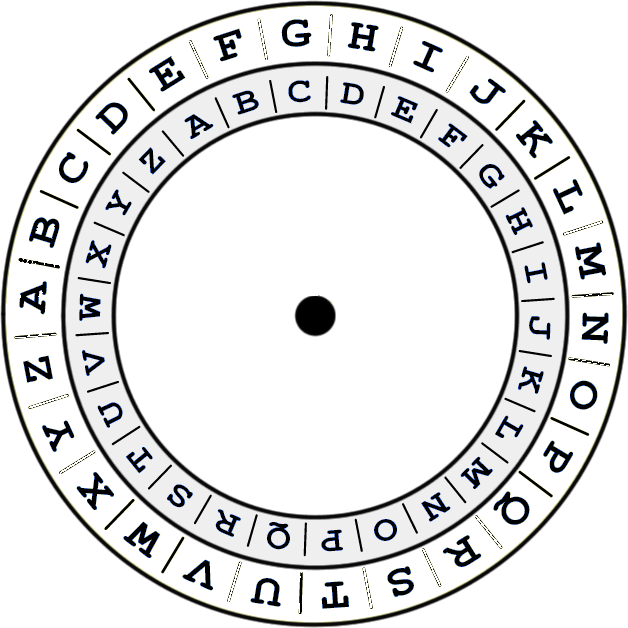
Логический код 4В/5В
Логический код 4В/5В заменяет исходные символы длиной в 4 бита на символы длиной в 5 бит. Так как результирующие символы содержат избыточные биты, то
общее количество битовых комбинаций в них больше, чем в исходных. Таким образом, пяти-битовая схема дает 32 (25) двухразрядных буквенно-цифровых символа,
имеющих значение в десятичном коде от 00 до 31. В то время как исходные данные могут содержать только четыре бита или 16 (24) символов.
Поэтому в результирующем коде можно подобрать 16 таких комбинаций, которые не содержат большого количества нулей, а остальные считать запрещенными кодами
(code violation). В этом случае длинные последовательности нулей прерываются, и код становится самосинхронизирующимся для любых передаваемых данных.
Исчезает также постоянная составляющая, а значит, еще более сужается спектр сигнала. Но этот метод снижает полезную пропускную способность линии,
так как избыточные единицы пользовательской информации не несут, и только «занимают эфирное время». Избыточные коды позволяют приемнику распознавать
искаженные биты. Если приемник принимает запрещенный код, значит, на линии произошло искажение сигнала.
Итак, рассмотрим работу логического кода 4В/5В. Преобразованный сигнал имеет 16 значений для передачи информации и 16 избыточных значений. В декодере
приемника пять битов расшифровываются как информационные и служебные сигналы.
Для служебных сигналов отведены девять символов, семь символов — исключены.
Исключены комбинации, имеющие более трех нулей (01 — 00001, 02 — 00010, 03 — 00011, 08 — 01000, 16 — 10000). Такие сигналы интерпретируются символом
V и командой приемника VIOLATION — сбой. Команда означает наличие ошибки из-за высокого уровня помех или сбоя передатчика. Единственная
комбинация из пяти нулей (00 — 00000) относится к служебным сигналам, означает символ Q и имеет статус QUIET — отсутствие сигнала в линии.
Такое кодирование данных решает две задачи — синхронизации и улучшения помехоустойчивости. Синхронизация происходит за счет исключения
последовательности более трех нулей, а высокая помехоустойчивость достигается приемником данных на пяти-битовом интервале.
Цена за эти достоинства при таком способе кодирования данных — снижение скорости передачи полезной информации.
К примеру, В результате добавления одного избыточного бита на четыре информационных, эффективность использования полосы
частот в протоколах с кодом MLT-3 и кодированием данных 4B/5B уменьшается соответственно на 25%.
Схема кодирования 4В/5В представлена в таблице.
|
Двоичный код 4В |
Результирующий код 5В |
|
0 0 0 0 |
1 1 1 1 0 |
|
0 0 0 1 |
0 1 0 0 1 |
|
0 0 1 0 |
1 0 1 0 0 |
|
0 0 1 1 |
1 0 1 0 1 |
|
0 1 0 0 |
0 1 0 1 0 |
|
0 1 0 1 |
0 1 0 1 1 |
|
0 1 1 0 |
0 1 1 1 0 |
|
0 1 1 1 |
0 1 1 1 1 |
|
1 0 0 0 |
1 0 0 1 0 |
|
1 0 0 1 |
1 0 0 1 1 |
|
1 0 1 0 |
1 0 1 1 0 |
|
1 0 1 1 |
1 0 1 1 1 |
|
1 1 0 0 |
1 1 0 1 0 |
|
1 1 0 1 |
1 1 0 1 1 |
|
1 1 1 0 |
1 1 1 0 0 |
|
1 1 1 1 |
1 1 1 0 1 |
Итак, соответственно этой таблице формируется код 4В/5В, затем передается по линии с помощью физического кодирования по
одному из методов потенциального кодирования, чувствительному только к длинным последовательностям нулей — например, в помощью
цифрового кода NRZI.
Символы кода 4В/5В длиной 5 бит гарантируют, что при любом их сочетании на линии не могут встретиться более трех нулей подряд.
Буква ^ В в названии кода означает, что элементарный сигнал имеет 2 состояния — от английского binary — двоичный. Имеются
также коды и с тремя состояниями сигнала, например, в коде 8В/6Т для кодирования 8 бит исходной информации используется
код из 6 сигналов, каждый из которых имеет три состояния. Избыточность кода 8В/6Т выше, чем кода 4В/5В, так как на 256
исходных кодов приходится 36=729 результирующих символов.
Как мы говорили, логическое кодирование происходит до физического, следовательно, его осуществляют оборудование канального
уровня сети: сетевые адаптеры и интерфейсные блоки коммутаторов и маршрутизаторов. Поскольку, как вы сами убедились,
использование таблицы перекодировки является очень простой операцией, поэтому метод логического кодирования избыточными
кодами не усложняет функциональные требования к этому оборудованию.
Единственное требование — для обеспечения заданной пропускной способности линии передатчик, использующий избыточный код,
должен работать с повышенной тактовой частотой. Так, для передачи кодов 4В/5В со скоростью 100 Мб/с передатчик должен
работать с тактовой частотой 125 МГц. При этом спектр сигнала на линии расширяется по сравнению со случаем, когда по
линии передается чистый, не избыточный код. Тем не менее, спектр избыточного потенциального кода оказывается уже
спектра манчестерского кода, что оправдывает дополнительный этап логического кодирования, а также работу приемника
и передатчика на повышенной тактовой частоте.
В основном для локальных сетей проще, надежней, качественней, быстрей — использовать логическое кодирование данных
с помощью избыточных кодов, которое устранит длительные последовательности нулей и обеспечит синхронизацию
сигнала, потом на физическом уровне использовать для передачи быстрый цифровой код NRZI, нежели без предварительного
логического кодирования использовать для передачи данных медленный, но самосинхронизирующийся манчестерский код.
Например, для передачи данных по линии с пропускной способностью 100М бит/с и полосой пропускания 100 МГц,
кодом NRZI необходимы частоты 25 — 50 МГц, это без кодирования 4В/5В. А если применить для NRZI еще и
кодирование 4В/5В, то теперь полоса частот расширится от 31,25 до 62,5 МГц. Но тем не менее, этот диапазон
еще «влазит» в полосу пропускания линии. А для манчестерского кода без применения всякого дополнительного
кодирования необходимы частоты от 50 до 100 МГц, и это частоты основного сигнала, но они уже не будут пропускаться
линией на 100 МГц.
Скрэмблирование
Другой метод логического кодирования основан на предварительном «перемешивании» исходной информации таким
образом, чтобы вероятность появления единиц и нулей на линии становилась близкой.
Устройства, или блоки, выполняющие такую операцию, называются скрэмблерами (scramble — свалка, беспорядочная сборка) .
При скремблировании данные перемешиваються по определенному алгоритму и приемник, получив двоичные данные, передает
их на дескрэмблер, который восстанавливает исходную последовательность бит.
Избыточные биты при этом по линии не передаются.
Суть скремблирования заключается просто в побитном изменении проходящего через систему потока данных. Практически
единственной операцией, используемой в скремблерах является XOR — «побитное исключающее ИЛИ», или еще говорят —
сложение по модулю 2. При сложении двух единиц исключающим ИЛИ отбрасывается старшая единица и результат записывается — 0.
Метод скрэмблирования очень прост. Сначала придумывают скрэмблер. Другими словами придумывают по какому соотношению
перемешивать биты в исходной последовательности с помощью «исключающего ИЛИ». Затем согласно этому соотношению из текущей
последовательности бит выбираются значения определенных разрядов и складываются по XOR между собой. При этом все разряды
сдвигаются на 1 бит, а только что полученное значение («0» или «1») помещается в освободившийся самый младший разряд.
Значение, находившееся в самом старшем разряде до сдвига, добавляется в кодирующую последовательность, становясь очередным
ее битом. Затем эта последовательность выдается в линию, где с помощью методов физического кодирования передается к
узлу-получателю, на входе которого эта последовательность дескрэмблируется на основе обратного отношения.
Например, скрэмблер может реализовывать следующее соотношение:
где Bi — двоичная цифра результирующего кода, полученная на i-м такте работы скрэмблера, Ai — двоичная цифра исходного
кода, поступающая на i-м такте на вход скрэмблера, Bi-3 и Bi-5 — двоичные цифры результирующего кода, полученные на
предыдущих тактах работы скрэмблера, соответственно на 3 и на 5 тактов ранее текущего такта, ⊕ — операция исключающего
ИЛИ (сложение по модулю 2).
Теперь давайте, определим закодированную последовательность, например, для такой исходной последовательности 110110000001.
Скрэмблер, определенный выше даст следующий результирующий код:
B1=А1=1 (первые три цифры результирующего кода будут совпадать с исходным, так как еще нет нужных предыдущих цифр)

Таким образом, на выходе скрэмблера появится последовательность 110001101111. В которой нет последовательности из шести нулей, п
рисутствовавшей в исходном коде.
После получения результирующей последовательности приемник передает ее дескрэмблеру, который восстанавливает исходную
последовательность на основании обратного соотношения.
Существуют другие различные алгоритмы скрэмблирования, они отличаются количеством слагаемых, дающих цифру
результирующего кода, и сдвигом между слагаемыми.
Главная проблема кодирования на основе скремблеров — синхронизация передающего (кодирующего) и принимающего
(декодирующего) устройств. При пропуске или ошибочном вставлении хотя бы одного бита вся передаваемая информация
необратимо теряется. Поэтому, в системах кодирования на основе скремблеров очень большое внимание уделяется методам синхронизации.
На практике для этих целей обычно применяется комбинация двух методов:
а) добавление в поток информации синхронизирующих битов, заранее известных приемной стороне, что позволяет ей при ненахождении
такого бита активно начать поиск синхронизации с отправителем,
б) использование высокоточных генераторов временных импульсов, что позволяет в моменты потери синхронизации производить
декодирование принимаемых битов информации «по памяти» без синхронизации.
Существуют и более простые методы борьбы с последовательностями единиц, также относимые к классу скрэмблирования.
Для улучшения кода ^ Bipolar AMI используются два метода, основанные на искусственном искажении последовательности нулей запрещенными символами.

Рис. 3 Коды B8ZS и HDB3
На этом рисунке показано использование метода ^ B8ZS (Bipolar with 8-Zeros Substitution) и метода HDB3 (High-Density Bipolar 3-Zeros) для корректировки
кода AMI. Исходный код состоит из двух длинных последовательностей нулей (8- в первом случае и 5 во втором).
Код B8ZS исправляет только последовательности, состоящие из 8 нулей. Для этого он после первых трех нулей вместо оставшихся пяти нулей вставляет пять
цифр: V-1*-0-V-1*. V здесь обозначает сигнал единицы, запрещенной для данного такта полярности, то есть сигнал, не изменяющий полярность предыдущей
единицы, 1* — сигнал единицы корректной полярности, а знак звездочки отмечает тот факт, что в исходном коде в этом такте была не единица, а ноль. В
результате на 8 тактах приемник наблюдает 2 искажения — очень маловероятно, что это случилось из-за шума на линии или других сбоев передачи. Поэтому
приемник считает такие нарушения кодировкой 8 последовательных нулей и после приема заменяет их на исходные 8 нулей.
Код B8ZS построен так, что его постоянная составляющая равна нулю при любых последовательностях двоичных цифр.
Код HDB3 исправляет любые 4 подряд идущих нуля в исходной последовательности. Правила формирования кода HDB3 более сложные, чем кода B8ZS.
Каждые четыре нуля заменяются четырьмя сигналами, в которых имеется один сигнал V. Для подавления постоянной составляющей полярность сигнала
V чередуется при последовательных заменах.
Кроме того, для замены используются два образца четырехтактовых кодов. Если перед заменой исходный код содержал нечетное число единиц, то
используется последовательность 000V, а если число единиц было четным — последовательность 1*00V.
Таким образом, применение логическое кодирование совместно с потенциальным кодированием дает следующие преимущества:
Улучшенные потенциальные коды обладают достаточно узкой полосой пропускания для любых последовательностей единиц и нулей,
которые встречаются в передаваемых данных. В результате коды, полученные из потенциального путем логического кодирования,
обладают более узким спектром, чем манчестерский, даже при повышенной тактовой частоте.
Линейные блочные коды
При передаче информации по каналам связи возможны ошибки вследствие помех и искажений сигналов. Для обнаружения и
исправления возникающих ошибок используются помехоустойчивые коды. Упрощенная схема системы передачи информации
при помехоустойчивом кодировании показана на рис. 4
Кодер служит для преобразования поступающей от источника сообщений последовательности из k информационных
символов в последовательность из n cимволов кодовых комбинаций (или кодовых слов). Совокупность кодовых слов образует код.
Множество символов, из которых составляется кодовое слово, называется алфавитом кода, а число различных символов в
алфавите – основанием кода. В дальнейшем вследствие их простоты и наибольшего распространения рассматриваются главным
образом двоичные коды, алфавит которых содержит два символа: 0 и 1.

Рис. 4 Система передачи дискретных сообщений
Правило, по которому информационной последовательности сопоставляется кодовое слово, называется правилом кодирования.
Если при кодировании каждый раз формируется блок А из k информационных символов, превращаемый затем в n-символьную
кодовую комбинацию S, то код называется блочным. При другом способе кодирования информационная последовательность на
блоки не разбивается, и код называется непрерывным.
С математической точки зрения кодер осуществляет отображение множества из 2k элементов (двоичных информационных
последовательностей) в множество, состоящее из 2n элементов (двоичных последовательностей длины n). Для практики
интересны такие отображения, в результате которых получаются коды, обладающие способностью исправлять часть ошибок
и допускающие простую техническую реализацию кодирующих и декодирующих устройств.
Дискретный канал связи – это совокупность технических средств вместе со средой распространения радиосигналов, включенных
между кодером и декодером для передачи сигналов, принимающих конечное число разных видов. Для описания реальных каналов
предложено много математических моделей, с разной степенью детализации отражающих реальные процессы. Ограничимся рассмотрением
простейшей модели двоичного канала, входные и выходные сигналы которого могут принимать значения 0 и 1.
Наиболее распространено предположение о действии в канале аддитивной помехи. Пусть S=(s1,s2,…,sn)
и Y=(y1,y2,…,yn) соответственно входная и выходная последовательности двоичных символов.
Помехой или вектором ошибки называется последовательность из n символов E=(e1,e2,…,en), которую
надо поразрядно сложить с переданной последовательностью, чтобы получить принятую:
Y=S+E
Таким образом, компонента вектора ошибки ei=0 указывает на то, что 2-й символ принят правильно (yi=si),
а компонента ei=1 указывает на ошибку при приеме (yi≠si).Поэтому важной характеристикой вектора ошибки
является число q ненулевых компонентов, которое называется весом или кратностью ошибки. Кратность ошибки – дискретная случайная величина,
принимающая целочисленные значения от 0 до n.
Классификация двоичных каналов ведется по виду распределения случайного вектора E. Основные результаты теории кодирования получены в
предположении, что вероятность ошибки в одном символе не зависит ни от его номера в последовательности, ни от его значения. Такой
канал называется стационарным и симметричным. В этом канале передаваемые символы искажаются с одинаковой вероятностью
P, т.е. P(ei=1)=P, i=1,2,…,n.
Для симметричного стационарного канала распределение вероятностей векторов ошибки кратности q является биноминальным:
P(Ei)=Pq(1-P)n-q
которая показывает, что при P<0,5 вероятность β2=αj является убывающей функцией q,
т.е. в симметричном стационарном канале более вероятны ошибки меньшей кратности. Этот важный факт используется при построении
помехоустойчивых кодов, т.к. позволяет обосновать тактику обнаружения и исправления в первую очередь ошибок малой кратности.
Конечно, для других моделей канала такая тактика может и не быть оптимальной.
Декодирующее устройство (декодер) предназначено оценить по принятой последовательности Y=(y1,y2,…,yn)
значения информационных символов A‘=(a‘1,a‘2,…,a‘k,).
Из-за действия помех возможны неправильные решения. Процедура декодирования включает решение двух задач: оценивание переданного кодового
слова и формирование оценок информационных символов.
Вторая задача решается относительно просто. При наиболее часто используемых систематических кодах, кодовые слова которых содержат информационные
символы на известных позициях, все сводится к простому их стробированию. Очевидно также, что расположение информационных символов внутри кодового
слова не имеет существенного значения. Удобно считать, что они занимают первые k позиций кодового слова.
Наибольшую трудность представляет первая задача декодирования. При равновероятных информационных последовательностях ее оптимальное решение
дает метод максимального правдоподобия. Функция правдоподобия как вероятность получения данного вектора Y при передаче кодовых слов
Si, i=1,2,…,2k на основании Y=S+E определяется вероятностями появления векторов ошибок:
P(Y/Si)=P(Ei)=Pqi(1-P)n-qi
где qi – вес вектора Ei=Y+Si
Очевидно, вероятность P(Y/Si) максимальна при минимальном qi. На основании принципа максимального правдоподобия оценкой S‘ является кодовое слово,
искажение которого для превращения его в принятое слово Y имеет минимальный вес, т. е. в симметричном канале является наиболее вероятным (НВ):
S‘=Y+EHB
Если несколько векторов ошибок Ei имеют равные минимальные веса, то наивероятнейшая ошибка EHB определяется случайным выбором среди них.
В качестве расстояния между двумя кодовыми комбинациями принимают так называемое расстояние Хэмминга, которое численно равно количеству символов, в которых одна
комбинация отлична от другой, т.е. весу (числу ненулевых компонентов) разностного вектора. Расстояние Хэмминга между принятой последовательностью Y и всеми
возможными кодовыми словами 5, есть функция весов векторов ошибок Ei:

Поэтому декодирование по минимуму расстояния, когда в качестве оценки берется слово, ближайшее к принятой
последовательности, является декодированием по максимуму правдоподобия.
Таким образом, оптимальная процедура декодирования для симметричного канала может быть описана следующей последовательностью операций. По принятому
вектору Y определяется вектор ошибки с минимальным весом EHB, который затем вычитается (в двоичном канале — складывается по модулю 2) из Y:
Y→EHB→S‘=Y+EHB
Наиболее трудоемкой операцией в этой схеме является определение наи-вероятнейшего вектора ошибки, сложность которой
существенно возрастает при увеличении длины кодовых комбинаций. Правила кодирования, которые нацелены на упрощение
процедур декодирования, предполагают придание всем кодовым словам технически легко проверяемых признаков.
Широко распространены линейные коды, называемые так потому, что их кодовые слова образуют линейное
подпространство над конечным полем. Для двоичных кодов естественно использовать поле характеристики p=2.
Принадлежность принятой комбинации Y известному подпространству является тем признаком, по которому
выносится решение об отсутствии ошибок (EHB=0).
Так как по данному коду все пространство последовательностей длины n разбивается на смежные классы,
то для каждого смежного класса можно заранее определить вектор ошибки минимального веса,
называемый лидером смежного класса. Тогда задача декодера состоит в определении номера смежного класса,
которому принадлежит Y, и формировании лидера этого класса.
ФГБОУ ВПО «МОРДОВСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ ИНСТИТУТ ИМЕНИ. М Е. ЕВСЕВЬЕВА»
Физико – математический факультет
Кафедра информатики и вычислительной техники
КУРСОВАЯ РАБОТА
ПРОБЛЕМЫ КОДИРОВАНИЯ ИНФОРМАЦИИ
Автор курсовой работы___________________________________ Д.А. Храмов
Направление подготовки 050100.62 Педагогическое образование
Профиль Математика. Информатика.
Руководитель работы
д.ф.–м.н., проф. каф. ИВТ______________________________ Е.В. Щенникова
Саранск 2013
Содержание
Введение……………………………………………………………………………3
1 Кодирование информации………………………………………………………5
1.1 Кодирование текстовой информации…………………………………5
1.2 Кодирование графической информации……………………….……..6
1.3 Кодирование звуковой информации………………………………….9
2 Шум и защита от шума. Теория кодирования К.Шеннона …………………11
3 Способы обнаружения ошибок с их последующим исправлением…………13
4 Основные понятия корректирующих кодов…………………………………15
4.1 Линейные и групповые коды…………………………………………17
4.2 Код Хэмминга………………………………………………………….21
Заключение……………………………………………………………………… 27
Список литературы………………………………………………………………28
Введение
Кодирование – процесс представления информации в виде кода. Под термином «кодирование», как правило, понимают переход от одной формы представления информации к другой, более удобной для хранения, передачи или обработки. Кодирование в узком смысле – способ сделать сообщение непонятным для всех, кто не владеет ключом кода.
Первым, кто использовал кодирование двух символьной информации, был Готфрид Вильгельм Лейбниц. Он считал: «Вычисление с помощью двоек … является для науки основным и порождает новые открытия. При сведении чисел к простым началам, каковыми являются 0 и 1, везде появляется чудесный порядок». Но, к сожалению, эта система была забыта.
Первым теоретическое решение проблемы передачи данных по зашумленным каналам предложил
Клод Шеннон, основоположник статистической теории информации. Работая в Bell Labs, Шеннон написал работу «Математическая теория передачи сообщений» (1948), где показал, что если пропускная способность канала выше энтропии источника сообщений, то сообщение можно закодировать так, что оно будет передано без излишних задержек.
Переход от теории к практике стал возможен благодаря усилиям Ричарда Хэмминга, коллеги Шеннона по Bell Labs, получившего известность за открытие класса кодов «коды Хэмминга».
Хэмминг первым предложил «коды с исправлением ошибок» (Error-Correcting Code, ECC). Современные модификации этих кодов используются во всех системах хранения данных и для обмена между процессором и оперативной памятью. Один из их вариантов, коды Рида-Соломона применяются в компакт-дисках, позволяя воспроизводить записи без скрипов и шумов, вызванных царапинами и пылинками. Существует множество версий кодов, построенных «по мотивам» Хэмминга, они различаются алгоритмами кодирования и количеством проверочных битов. Особое значение подобные коды приобрели в связи с развитием дальней космической связи с межпланетными станциями.
Цель моей курсовой работы, является ознакомление с методами обнаружения ошибок и защиты информации с помощью корректирующих кодов. Эта проблема в настоящее время относится к числу наиболее актуальных проблем, т.к. при обработке, передачи и хранении информации мы стремимся к повышению ее надежности.
Объект: процесс кодирования информации.
Задачи:
-
Проанализировать пособия по теории информации и информационной безопасности.
-
Выявить формы представления кодирования информации.
-
Обнаружение ошибок (проблем).
-
Методы и способы исправления ошибок.
1 Кодирование информации
Современный ПК может обрабатывать различную информацию (числовую, текстовую, звуковую и видео). Вся информация в компьютере представлена в двоичном коде, т.е. Используется алфавит мощностью два. Это связанно, прежде всего, с тем, что удобно представлять в виде последовательности электрических импульсов (импульс отсутствует — 0, импульс есть — 1). Логическая последовательность нулей и единиц называется, машинным кодом.
1.1 Кодирование текстовой информации
В настоящее время большая часть пользователей при помощи компьютера обрабатывает текстовую информацию, которая состоит из символов: букв, цифр, знаков препинания и др.
Традиционно для того чтобы закодировать один символ используют количество информации равное 1 байту, т. е. I = 1 байт = 8 бит. При помощи формулы, которая связывает между собой количество возможных событий К и количество информации I, можно вычислить сколько различных символов можно закодировать (считая, что символы — это возможные события): К = 2I 28 = 256, т.е. для представления текстовой информации можно использовать алфавит мощностью 256 символов.
Суть кодирования заключается в том, что каждому символу ставят в соответствие двоичный код от 00000000 до 11111111 или соответствующий ему десятичный код от 0 до 255.
Необходимо помнить, что в настоящее время для кодировки русских букв используют пять различных кодовых таблиц (КОИ — 8, СР1251, СР866, Мас, ISO), причем тексты, закодированные, при помощи одной таблицы не будут правильно отображаться в другой кодировке.
В большинстве случаев о перекодировке текстовых документов заботится пользователь, а специальные программы — конвертеры, которые встроены в приложения.
Начиная с 1997г. последние версии Microsoft Windows Office поддерживают новую кодировку Unicode, которая на каждый символ отводит по 2 байта, а поэтому, можно закодировать не 256 символов, а 65536 различных символов.
1.2 Кодирование графической информации
В середине 50-х годов для больших ЭВМ, которые применялись в научных и военных исследованиях, впервые в графическом виде было реализовано представление данных. В настоящее время широко используются технологии обработки графической информации с помощью ПК.
Особенно интенсивно технология обработки графической информации с помощью компьютера стала развиваться в 80-х годах. Графическую информацию можно представлять в двух формах: аналоговой или дискретной. Живописное полотно, цвет которого изменяется непрерывно — это пример аналогового представления, а изображение, напечатанное при помощи струйного принтера и состоящее из отдельных точек разного цвета — это дискретное представление. Чем большее количество цветов используется (т. е. точка изображения может принимать больше возможных состояний), тем больше информации несет каждая точка, а, значит, увеличивается качество кодирования. Создание и хранение графических объектов возможно в нескольких видах — в виде векторного, фрактального или растрового изображения.
Отдельным предметом считается 3D (трехмерная) графика, в которой сочетаются векторный и растровый способы формирования изображений.
Если говорить о кодировании цветных графических изображений, то нужно рассмотреть принцип декомпозиции произвольного цвета на основные составляющие. Применяют несколько систем кодирования: HSB, RGB и CMYK.
1) Модель HSB характеризуется тремя компонентами: оттенок цвета (Hue), насыщенность цвета (Saturation) и яркость цвета (Brightness). Можно получить большое количество произвольных цветов, регулируя эти компоненты.
2) Принцип метода RGB заключается в следующем: известно, что любой цвет можно представить в виде комбинации трех цветов: красного (Red, R), зеленого (Green, G), синего (Blue, B). Другие цвета и их оттенки получаются за счет наличия или отсутствия этих составляющих.
3) Принцип метода CMYK. Эта цветовая модель используется при подготовке публикаций к печати. Каждому из основных цветов ставится в соответствие дополнительный цвет (дополняющий основной до белого).
Различают несколько режимов представления цветной графики:
1) полноцветный (TrueColor);
2) HighColor;
3) индексный.
При полноцветном режиме для кодирования яркости каждой из составляющих используют по 256 значений (восемь двоичных разрядов), то есть на кодирование цвета одного пикселя (в системе RGB) надо затратить 8*3=24 разряда. Это позволяет однозначно определять 16,5 млн цветов. Это довольно близко к чувствительности человеческого глаза. При кодировании с помощью системы CMYK для представления цветной графики надо иметь 8*4=32 двоичных разрядов.
Режим HighColor — это кодирование при помощи 16-разрядных двоичных чисел, то есть уменьшается количество двоичных разрядов при кодировании каждой точки. Но при этом значительно уменьшается диапазон кодируемых цветов.
При индексном кодировании цвета можно передать всего лишь 256 цветовых оттенков. Каждый цвет кодируется при помощи восьми бит данных. Но так как 256 значений не передают весь диапазон цветов, доступный человеческому глазу, то подразумевается, что к графическим данным прилагается палитра (справочная таблица), без которой воспроизведение будет неадекватным: море может получиться красным, а листья — синими. Сам код точки растра в данном случае означает не сам по себе цвет, а только его номер (индекс) в палитре. Отсюда и название режима — индексный.
Соответствие между количеством отображаемых цветов (К) и количеством бит для их кодировки (а) находиться по формуле: К = 2а («Таблица 1») .
«Таблица 1»
|
А |
К |
Достаточно для |
|
4 |
24 = 16 |
|
|
8 |
28 = 256 |
Рисованных изображений типа тех, что видим в мультфильмах, но недостаточно для изображений живой природы |
|
16 (HighColor) |
216 = 65536 |
Изображений, которые на картинках в журналах и на фотографиях |
|
24 (TrueColor) |
224 = 16 777 216 |
Обработки и передачи изображений, не уступающих по качеству наблюдаемым в живой природе |
1.3 Кодирование звуковой информации
С начала 90-х годов персональные компьютеры получили возможность работать со звуковой информацией. Каждый компьютер, имеющий звуковую плату, микрофон и колонки, может записывать, сохранять и воспроизводить звуковую информацию. Звук представляет собой звуковую волну с непрерывно меняющейся амплитудой и частотой. Чем больше амплитуда, тем он громче для человека, чем больше частота сигнала, тем выше тон. Программное обеспечение компьютера в настоящее время позволяет непрерывный звуковой сигнал преобразовывать в последовательность электрических импульсов, которые можно представить в двоичной форме.
Процесс преобразования звуковых волн в двоичный код в памяти компьютера:
Звуковая волна →Микрофон → Переменный электрический ток → Аудиоадаптер →Двоичный код → Память компьютера
Процесс воспроизведения звуковой информации, сохраненной в памяти компьютера:
Память компьютера → Двоичный код → Аудиоадаптер → Переменный электрический ток → Динамик → Звуковая волна
Аудиоадаптер (звуковая плата)– специальное устройство, подключаемое к компьютеру, предназначенное для преобразования электрических колебаний звуковой частоты в числовой двоичный код при вводе звука и для обратного преобразования (из числового кода в электрические колебания) при воспроизведении звука.
В процессе записи звука аудиоадаптер с определенным периодом измеряет амплитуду электрического тока и заносит в регистр двоичный код полученной величины.
Затем полученный код из регистра переписывается в оперативную память компьютера.
Качество компьютерного звука определяется характеристиками аудиоадаптера: частотой дискретизации и разрядностью.
Частота дискретизации – это количество измерений входного сигнала за 1 секунду.
Разрядность регистра– число бит в регистре аудиоадаптера.
2 Шум и защита от шума. Теория кодирования К.Шеннона
Термином «шум» называют разного рода помехи, искажающие передаваемый сигнал и приводящие к потере информации. Такие помехи возникают по техническим причинам: плохое качество линии связи, незащищенность друг от друга различных потоков информации, передаваемых по одним и тем же каналам. Например, при беседе по телефону, мы слышим шум и треск. В таких случаях необходима защита от шума. Способы защиты бывают самыми разными. Использование экранированного кабеля вместо «голого» провода; применение различных фильтров, отделяющих полезный сигнал от шума и т.п.
Клодом Шенноном была разработана специальная теория кодирования, дающая методы борьбы с шумом. Одна из важных идей этой теории состоит в том, что передаваемый по линии связи код должен быть избыточным. За счет этого потеря какой-то части информации при передаче может быть компенсирована. Например, если при разговоре по телефону вас плохо слышно, то, повторяя каждое слово дважды, вы имеете больше шансов на то, что собеседник поймет вас правильно.
Однако нельзя делать избыточность слишком большой. Это приведет к задержкам и удорожанию связи. Теория кодирования К. Шеннона как раз и позволяет получить такой код, который будет оптимальным. При этом избыточность передаваемой информации будет минимально возможной, а достоверность принятой информации — максимальной.
В современных системах цифровой связи часто применяется следующий прием борьбы с потерей информации. Все сообщение разбивается на порции — пакеты. Для каждого пакета вычисляется контрольная сумма (сумма двоичных цифр), которая передается вместе с данным пакетом. В месте приема заново вычисляется контрольная сумма принятого пакета, и если она не совпадает с первоначальной, то передача данного пакета повторяется. Так происходит пока исходная и конечная контрольные суммы не совпадут.
3 Способы обнаружения ошибок с их последующим исправлением
Обнаружение ошибок в технике связи — действие, направленное на контроль целостности данных при записи/воспроизведении информации или при её передаче по линиям связи. Исправление ошибок (коррекция ошибок) — процедура восстановления информации после чтения её из устройства хранения или канала связи.
Для обнаружения ошибок используют коды обнаружения ошибок, для исправления — корректирующие коды (коды, исправляющие ошибки, коды с коррекцией ошибок, помехоустойчивые коды).
В процессе хранения данных и передачи информации по сетям связи неизбежно возникают ошибки. Контроль целостности данных и исправление ошибок — важные задачи на многих уровнях работы с информацией (в частности, физическом, канальном, транспортном уровнях сетевой модели OSI).
В системах связи возможны несколько стратегий борьбы с ошибками:
-
обнаружение ошибок в блоках данных и автоматический запрос повторной передачи поврежденных блоков — этот подход применяется, в основном, на канальном и транспортном уровнях;
-
обнаружение ошибок в блоках данных и отбрасывание поврежденных блоков — такой подход иногда применяется в системах потокового мультимедиа, где важна задержка передачи и нет времени на повторную передачу;
-
Исправление ошибок применяется на физическом уровне.
Корректирующие коды — коды, служащие для обнаружения или исправления ошибок, возникших при передаче информации под влиянием помех, а так же при её хранении.
При записи в данные добавляют специальным образом структурированную избыточную информацию (контрольное число), а при чтении её используют для того, чтобы обнаружить или исправить ошибки. Число ошибок, которое можно исправить, ограничено и зависит от конкретного применяемого кода.
Коды обнаружения ошибок в отличии от кодов исправляющих ошибки, могут только установить факт наличия ошибки.
Фактически любой код, исправляющий ошибки, может быть использован для их обнаружения. При этом он будет способен обнаружить большее число ошибок.
4 Основные понятия корректирующих кодов
Среди корректирующих кодов широко используются циклические коды, в ЭВМ эти коды применяются при последовательной передаче данных между ЭВМ и внешними устройствами, а также при передаче данных по каналам связи. Для исправления двух и более ошибок (d0 5) используются циклические коды БЧХ (Боуза — Чоудхури — Хоквингема), а также Рида-Соломона, которые широко используются в устройствах цифровой записи звука на магнитную ленту или оптические компакт-диски и позволяющие осуществлять коррекцию групповых ошибок. Способность кода обнаруживать и исправлять ошибки достигается за счет введений избыточности в кодовые комбинации, т.е. кодовым комбинациям из к двоичных информационных символов, поступающих на вход кодирующего устройства, соответствует на выходе последовательность из n двоичных символов (такой код называется (n, k) — кодом).
Если N0 = 2n-общее число кодовых комбинаций, а N = 2k — число разрешенных, то число запрещенных кодовых комбинаций равно
N0-N = 2n -2k.
При этом число ошибок, которое приводит к запрещенной кодовой комбинации равно (1).
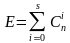
где S — кратность ошибки, т.е. количество искаженных символов в кодовой комбинации S = 0, 1, 2, …
Cni— сочетания из n элементов по i, вычисляемое, по формуле (2)
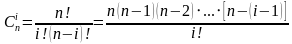
для S = 0; 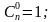
S = 1; 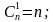
S = 2; 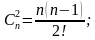
S= 3; 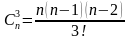
Для исправления S ошибок количество комбинаций кодового слова, составленного из m проверочных разрядов N = 2m, должно быть больше возможного числа ошибок (3), при этом количество обнаруживаемых ошибок в два раза больше, чем исправляемых
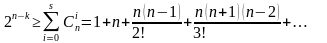
2m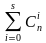
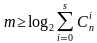
Для одиночной ошибки, как наиболее вероятной 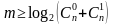
В зависимости от исходных данных кода (n или k) можно использовать
формулы (4).
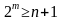
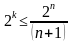
При этом, m = [log2(1+n)] или m = [log2 {(k+1)+ [log2(k+1)]}], где квадратные скобки обозначают округление до большего целого.
В таблице приведены соотношения между длиной кодовой комбинации и количеством информационных и контрольных разрядов для кода исправляющего одиночную ошибку, а также эффективность использования канала связи.
Для исправления двукратной ошибки (5).
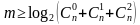
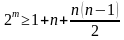
Введение избыточности в кодовые комбинации при использовании корректирующих кодов существенно снижает скорость передачи информации и эффективность использования канала связи.
Например, для кода (31, 26) скорость передачи информации равна
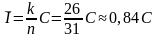
«Таблица 2»
|
n |
7 |
10 |
15 |
31 |
63 |
127 |
255 |
|
k |
4 |
6 |
11 |
26 |
57 |
120 |
247 |
|
m |
3 |
4 |
4 |
5 |
6 |
7 |
8 |
|
|
0,57 |
0,6 |
0,75 |
0,84 |
0,9 |
0,95 |
0,97 |
Как видно из таблицы , чем больше n, тем эффективнее используется канал.
4.1 Линейные и групповые коды
Линейным называется код, в котором проверочные символы представляют собой линейные комбинации информационных.
Групповым называется код, который образует алгебраическую группу по отношению операции сложения по модулю два.
Свойство линейного кода: сумма (разность) кодовых векторов линейного кода дает вектор, принадлежащий этому коду.
Свойство группового кода: минимальное кодовое расстояние между кодовыми векторами равно минимальному весу ненулевых векторов. Вес кодового вектора равен числу единиц в кодовой комбинации.
Групповые коды удобно задавать при помощи матриц, размерность которых определяется параметрами k и n. Число строк равно k, а число столбцов равно n = k+m.(6).
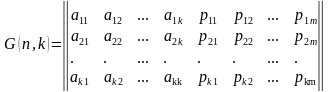
Коды, порождаемые этими матрицами, называются (n, k)-кодами, а соответствующие им матрицы порождающими (образующими, производящими). Порождающая матрица G состоит из информационной Ikk и проверочной Rkm матриц. Она является сжатым описанием линейного кода и может быть представлена в канонической (типовой) форме (7).
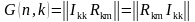
В качестве информационной матрицы удобно использовать единичную матрицу, ранг которой определяется количеством информационных разрядов (8).

Строки единичной матрицы представляют собой линейно-независимые комбинации (базисные вектора), т.е. их по парное суммирование по модулю два не приводит к нулевой строке.
Строки порождающей матрицы представляют собой первые k комбинаций корректирующего кода, а остальные кодовые комбинации могут быть получены в результате суммирования по модулю два всевозможных сочетаний этих строк.
Столбцы добавочной матрицы Rkm определяют правила формирования проверок. Число единиц в каждой строке добавочной матрицы должно удовлетворять условию r1 d0-1, но число единиц определяет число сумматоров по модулю 2 в шифраторе и дешифраторе, и чем их больше, тем сложнее аппаратура.
Производящая матрица кода G(7,4) может иметь вид
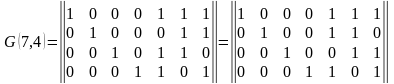
Процесс кодирования состоит во взаимно — однозначном соответствии к-разрядных информационных слов — I и n-разрядных кодовых слов – с(9)
c=IG (9)
Например: информационному слову I=[1 0 1 0] соответствует кодовое слово (10).

При этом, информационная часть остается без изменений, а корректирующие разряды определяются путем суммирования по модулю два тех строк проверочной матрицы, номера которых совпадают с номерами разрядов, содержащих единицу в информационной части кода.
Процесс декодирования состоит в определении соответствия принятого кодового слова, переданному информационному. Это осуществляется с помощью проверочной матрицы H(n, k) (11).
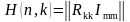
где RmkT -транспонированная проверочная матрица (поменять строки на столбцы); Imm— единичная матрица.
Для (7, 4)- кода проверочная матрица имеет вид (12).
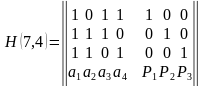
Между G(n ,k) и H(n, k) существует однозначная связь, т.к. они определяются в соответствии с правилами проверки, при этом для любого кодового слова должно выполняться равенство cHT= 0.
Строки проверочной матрицы определяют правила формирования проверок. Для (7, 4)-кода соответствует (13).
p1+a1+a2a4 = S1 ;
p2+a1+a2a3 = S2 ; (13)
p3+a1+a3a4 = S3 .
Полученный синдром сравниваем со столбцами матрицы и определяем разряд, в котором произошла ошибка, номер столбца равен номеру ошибочного разряда. Для исправления ошибки ошибочный бит необходимо проинвертировать.
4.2 Код Хемминга
Код Хэмминга относится к классу линейных кодов и представляет собой систематический код – код, в котором информационные и контрольные биты, расположены на строго определенных местах в кодовой комбинации.
Код Хэмминга, как и любой (n, k)- код, содержит к информационных и m = n-k избыточных (проверочных) бит.
Избыточная часть кода строится т.о. чтобы можно было при декодировании не только установить наличие ошибки но, и указать номер позиции, в которой произошла ошибка, а значит, и исправить ее, инвертировав значение соответствующего бита.
Существуют различные методы реализации кода Хэмминга и кодов которые являются модификацией кода Хэмминга. Рассмотрим алгоритм построения кода для исправления одиночной ошибки.
-
По заданному количеству информационных символов — k, либо информационных комбинаций N = 2k , используя соотношения (14).
n = k+m, 2n (n+1)2k и 2m n+1 (14)
m = [log2 {(k+1)+ [log2(k+1)]}]
вычисляют основные параметры кода n и m.
2. Определяем рабочие и контрольные позиции кодовой комбинации. Номера контрольных позиций определяются по закону 2i,где i=1, 2, 3,… т.е. они равны 1, 2, 4, 8, 16,… а остальные позиции являются рабочими.
3. Определяем значения контрольных разрядов (0 или 1 ) при помощи многократных проверок кодовой комбинации на четность. Количество проверок равно m = n-k. В каждую проверку включается один контрольный и определенные проверочные биты. Если результат проверки дает четное число, то контрольному биту присваивается значение — 0, в противном случае — 1. Номера информационных бит, включаемых в каждую проверку, определяются по двоичному коду натуральных n –чисел разрядностью – m или при помощи проверочной матрицы H(mn), столбцы которой представляют запись в двоичной системе всех целых чисел от 1 до (2k –1) перечисленных в возрастающем порядке. Для m = 3 проверочная матрица имеет вид (15).
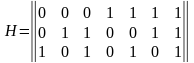
Количество разрядов m — определяет количество проверок («Таблица 3»).
В первую проверку включают коэффициенты, содержащие 1 в младшем (первом) разряде, т.е. b1, b3, b5 и т.д.
Во вторую проверку включают коэффициенты, содержащие 1 во втором разряде, т.е. b2, b3, b6 и т.д.
В третью проверку — коэффициенты которые содержат 1 в третьем разряде и т.д.
«Таблица 3»
|
Десятичные числа (номера разрядов кодовой комбинации) |
Двоичные числа и их разряды |
||
|
3 |
2 |
1 |
|
|
1 2 3 4 5 6 7 |
0 0 0 1 1 1 1 |
0 1 1 0 0 1 1 |
1 0 1 0 1 0 1 |
Для обнаружения и исправления ошибки составляются аналогичные проверки на четность контрольных сумм, результатом которых является двоичное (n-k) -разрядное число, называемое синдромом и указывающим на положение ошибки, т.е. номер ошибочной позиции, который определяется по двоичной записи числа, либо по проверочной матрице.
Для исправления ошибки необходимо проинвертировать бит в ошибочной позиции. Для исправления одиночной ошибки и обнаружения двойной используют дополнительную проверку на четность. Если при исправлении ошибки контроль на четность фиксирует ошибку, то значит в кодовой комбинации две ошибки.
В ЭВМ код Хэмминга чаще всего используется для обнаружения и исправления ошибок в ОП, памяти с обнаружением и исправлением ошибок ECCMemory (ErrorCheckingandCorrecting). Код Хэмминга используется как при параллельной, так и при последовательной записи. В ЭВМ значительная часть интенсивности потока ошибок приходится на ОП. Причинами постоянных неисправностей являются отказы ИС, а случайных изменение содержимого ОП за счет флуктуации питающего напряжения, кратковременных помех и излучений. Неисправность может быть в одном бите, линии выборки разряда, слова либо всей ИС. Сбой может возникнуть при формировании кода (параллельного), адреса или данных, поэтому защищать необходимо и то и др. Обычно дешифратор адреса встроен в микро схему и недоступен для потребителя. Наиболее часто ошибки дают ячейки памяти ЗУ, поэтому главным образом защищают записываемые и считываемые данные.
Наибольшее применение в ЗУ нашли коды Хэмминга с dmin=4, исправляющие одиночные ошибки и обнаруживающие двойные.
Проверочные символы записываются либо в основное, либо специальное ЗУ. Для каждого записываемого информационного слова (а не байта, как при контроле по паритету) по определенным правилам вычисляется функция свертки, результат которой разрядностью в несколько бит также записывается в память. Для 16-ти разрядного информационного слова используется 6 дополнительных бит (32 — 7 бит, 64 – 8 бит). При считывании информации схема контроля («Рис. 1»), используя избыточные биты, позволяет обнаружить ошибки различной кратности или исправить одиночную ошибку. Возможны различные варианты поведения системы:
-
автоматическое исправление ошибки без уведомления системы;
-
исправление однократной ошибки и уведомление системы только о многократных ошибках;
-
не исправление ошибки, а только уведомление системы об ошибках;
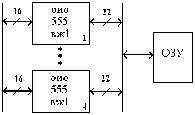
Модуль памяти со встроенной схемой исправления ошибок – EOS 72/64 (ECConSimm). Аналог микросхема к 555 вж 1 -это 16 разрядная схема с обнаружением и исправлением ошибок (ОИО) по коду Хэмминга G(22, 16), использование которой позволяет исправить однократные ошибки и обнаружить все двух кратные ошибки в ЗУ.
Избыточные (контрольные) разряды позволяют обнаружить и исправить ошибки в ЗУ в процессе записи и хранения информации.
В составе ВЖ-1 используются 16 информационных и 6 контрольных разрядов. (DB — информационное слово, CB — контрольное слово).
При записи осуществляется формирование кода, состоящего из 16 информационных и 6 контрольных разрядов, представляющих результат суммирование по модулю 2 восьми информационных разрядов в соответствии с кодом Хэмминга. Сформированные контрольные разряды вместе с информационными поступают на схему и записываются в ЗУ.
«Рис. 1» — схема контроля
При считывании шестнадцатиразрядное слово декодируется, восстанавливаясь вместе с 6 разрядным словом контрольным, поступают на схему сравнения и контроля. Если достигнуто равенство всех контрольных разрядов и двоичных слов, то ошибки нет.
Любая однократная ошибка в 16 разрядном слове данных изменяет 3 байта в 6 разрядном контрольном слове. Обнаруженный ошибочный бит инвертируется.
Заключение
Цель моей работы достигнута: я познакомился с методами обнаружения ошибок и защиты информации с помощью корректирующих кодов. Рассмотрел циклические коды, исправляющие более 2 ошибок (к ним относятся коды БЧХ (Боуза — Чоудхури — Хоквингема) и Рида-Соломона) и линейные коды (коды Хемминга). Все они основываются на избыточности информации.
Научились находить эту избыточность с помощью формул. Узнал, что любой код, исправляющий ошибки, может быть использован для их обнаружения. При этом он будет способен обнаружить большее число ошибок.
Познакомился с различными способами кодирования различных видов информации: текстовой, графической и звуковой.
Список литературы
-
Недвоичные арифметические корректирующие коды, проблемы передачи информации / В.М. Гриценко — 4-е изд. – 1969. – 19 – 27 с.
-
Помехоустойчивые коды в системах связи / Б.М. Золотник — M.: Радио и связь, 1989.—232 c.
-
Информационная безопасность. Лабораторный практикум: учебное пособие / А.В. Бабаш, Е.К. Баранова, Ю.Н. Мельникова. — М.: КНОРУС, 2012. – 136 с.
-
Теория передачи сигналов / Кловский Д.Д. — M.: Cвязь, 1984.
-
Цифровое кодирование звуковых сигналов / Ковалгин Ю.A., Вологдин Э.И. — Изд-во Kорона-принт, 2004. – 240с.
-
Курс теории информации / Колесников B.Д., Полтырев Г.Ш. — M.: Наука, 1982. 416 с.
-
Микропроцессорные кодеры и декодеры / В.М. Муттер, Г.A. Петров и др.—M.: Радио и связь, 1991.—184 с.
-
Экономное кодирование дискретной информации / Семенюк В. В. – СПб: СПбГИТМО (ТУ), 2001. – 115 с.
Муниципальное бюджетное образовательное учреждение
«Школа-гимназия» г. Ярцево Смоленская область
ПРОЕКТ
по информатике
на тему:
«В мире кодов»
Выполнили:
ученицы 5Б класса:
Володина Дарья,
Солдатенкова Екатерина
Руководитель:
учитель информатики,
Слащинина Е.В.
Ярцево,
2016
Содержание
- Введение……………………………………………………………………………………3стр
- Основная часть………………………………………………………………………….5стр
- Коды и шифры………………………………………………………………….5стр
- Язык жестов и поз…………………………………………………………….14стр
- Метод кодирования цвета………………………………………………….17стр
- Метод координат……………………………………………………………….20стр
- Заключение……………………………………………………………………………….22стр
- Список литературы……………………………………………………………………23стр
- Приложение 1………………………………………………………………………….. .24стр
- Приложение 2…………………………………………………………25стр
- Приложение 3…………………………………………………………26стр
Введение
Актуальность: В современной жизни человек сталкивается с различными способами кодирования информации. Чтобы научиться понимать информацию, представленную различными способами, необходимо ориентироваться в многообразии способов кодирования: знать и уметь интерпретировать их. Поэтому мы хотим ответить на вопрос: всё ли мы понимаем из того, что слышим, видим, чувствуем?
Проблемные вопросы:
- Всегда ли мы понимаем друг друга?
- Можно ли говорить, не произнося слова?
- Можно ли прожить без кодов и знаков?
- Чем отличается шифр от кода?
- О чём говорят жесты?
- Можно ли закодировать цветом?
Цель: выяснить, какие методы кодирования существуют?
Задачи: выяснить …
— что такое кодирование и что такое декодирование?
— где используются кодирование информации?
— какие способы кодирования существуют?
— зачем кодировать информацию?
— чем объяснить многообразие окружающих человека кодов?
— к чему приводят ошибки кодирования?
Тип проекта:
по доминирующей деятельности — информационный;
по предметно-содержательной деятельности — монопроект;
по количеству участников — групповой;
по продолжительности выполнения — долгосрочный
Практическая значимость
Вся информация, которую мы получаем из окружающего мира и передаём, закодирована по определенным правилам. Именно этим объясняется то, что человек незнающий правил кодирования, не понимает смысл передаваемого сообщения. Например, не зная языка, сложно понимать иностранную речь и
говорить на этом языке.
Этапы выполнения проекта.
- Подготовительный:
— определение темы проекта;
— уточнение цели и задач;
— определение источников информации.
- Основной этап:
— распределение обязанностей в группе
— определение шагов действий для каждого участника группы
— высказывание возможных путей разрешения спорных вопросов, обсуждения спорных вопросов;
— поиск и сбор информации каждым участником проекта с помощью литературы, средств массовой информации, сети интернета, собственного опыта и исследования.
- Заключительный:
— анализ полученной информации, и её систематизация;
— подведение выводов;
— изготовление буклетов и презентации как продуктов проекта;
— защита проекта
— обсуждение результатов работы
Методы: Онализ литературных источников.
Материалы и ресурсы: ватман, бумага формата А4, клей, карандаши.
Программные средства: веб-браузер, текстовый процессор OpenOfficeWriter, презентация.
Основная часть
Мудр не тот, кто знает много, а тот, чьи знания полезны
Эсхилл
Коды и шифры
Необходимость засекречивать важные послания возникла еще в древности. Со временем люди находили новые, все более сложные способы делать послания недоступными чужим глазам. Вопреки распространенному мнению, код и шифр — это не одно и то же. В коде каждое слово заменяется на какое-то иное кодовое слово, в то время как в шифре заменяются сами символы сообщения. Когда люди говорят «код», они, как правило, имеют в виду «шифр». Древние рукописи и языки были поняты с помощью техник декодирования и дешифрования. Самый известный пример — Розеттский камень Древнего Египта. Фактически коды и шифры определяли исход многих войн и политических интриг на протяжении всей истории человечества. Существуют тысячи типов шифрования сообщений, но в этой статье мы рассмотрим лишь 10 самых известных и значимых из них.
10. Стеганография
Стеганография — это искусство скрытого письма. Этой технике даже больше лет, чем кодам и шифрованию. Например, сообщение может быть написано на бумаге, покрыто ваксой и проглочено с той целью, чтобы незаметно доставить его получателю. Другой способ — нанести сообщение на бритую голову курьера, подождать, пока волосы вырастут заново и скроют послание. Лучше всего для стенографии использовать повседневные объекты. Когда-то в Англии использовался такой метод: под некоторыми буквами на первой странице газеты стояли крохотные точки, почти невидимые невооруженным глазом. Если читать только помеченные буквы, то получится секретное сообщение! Некоторые писали сообщение первыми буквами составлющих его слов или использовали невидимые чернила. Была распространена практика уменьшения целых страниц текста до размера буквально одного пикселя, так что их было легко пропустить при чтении чего-то относительно безобидного. Стенографию лучше всего использовать в сочетании с другими методами шифрования, так как всегда есть шанс, что ваше скрытое послание обнаружат и прочитают.
9. ROT1
Этот шифр известен многим детям. Ключ прост: каждая буква заменяется на следующую за ней в алфавите. Так, A заменяется на B, B на C, и т.д. «ROT1» значит «ROTate 1 letter forward through the alphabet» (англ. «сдвиньте алфавит на одну букву вперед»). Сообщение «I know what you did last summer» станет «J lopx xibu zpv eje mbtu tvnnfs». Этот шифр весело использовать, потому что его легко понять и применять, но его так же легко и расшифровать. Из-за этого его нельзя использовать для серьезных нужд, но дети с радостью «играют» с его помощью. Попробуйте расшифровать сообщение «XBT JU B DBU J TBX?».
8. Транспозиция
В транспозирующих шифрах буквы переставляются по заранее определенному правилу. Например, если каждое слово пишется задом наперед, то из «all the better to see you with» получается «lla eht retteb to ees joy htiw». Другой пример — менять местами каждые две буквы. Таким образом, предыдущее сообщение станет «la tl eh eb tt re to es ye uo iw ht». Подобные шифры использовались в Первую Мировую и Американскую Гражданскую Войну, чтобы посылать важные сообщения. Сложные ключи могут сделать такой шифр довольно сложным на первый взгляд, но многие сообщения, закодированные подобным образом, могут быть расшифрованы простым перебором ключей на компьютере. Попробуйте расшировать «THGINYMROTSDNAKRADASAWTI».
7. Азбука Морзе
В азбуке Морзе каждая буква алфавита, все цифры и наиболее важные знаки препинания имеют свой код, состоящий из череды коротких и длинных сигналов, часто называемых «точками и тире». Так, A — это «•—», B — «—•••», и т.д. В отличие от большинства шифров, азбука Морзе используется не для затруднения чтения сообщений, а наоборот, для облегчения их передачи (с помощью телеграфа). Длинные и короткие сигналы посылаются с помощью включения и выключения электрического тока. Телеграф и азбука Морзе навсегда изменили мир, сделав возможной молниеносную передачу информации между разными странами, а также сильно повлияли на стратегию ведения войны, ведь теперь можно было можно осуществлять почти мгновенную коммуникацию между войсками.
6. Шифр Цезаря
Шифр Цезаря называется так, как ни странно, потому что его использовал сам Юлий Цезарь. На самом деле шифр Цезаря — это не один шифр, а целых двадцать шесть, использующих один и тот же принцип! Так, ROT1 — всего один из них. Получателю нужно сказать, какой из шифров используется. Если используется шифр «G», тогда А заменяется на G, B на H, C на I и т.д. Если используется шифр «Y», тогда А заменяется на Y, B на Z, C на A и т.д. На шифре Цезаря базируется огромное число других, более сложных шифров, но сам по себе он не представляет из себя интереса из-за легкости дешифровки. Перебор 26 возможных ключей не займет много времени. Li bra ghflskhu wklv dqg bra nqrz lw, fods brxu kdqgv.
5. Моноалфавитная замена
ROT1, азбука Морзе, шифр(ы) Цезаря относятся к одному и тому же типу шифров — моноалфавитной замене. Это значит, что каждая буква заменяется на одну и только одну другую букву или символ. Такие шифры очень легко расшифровать даже без знания ключа. Делается это при помощи частотного анализа. Например, наиболее часто встречающаяся буква в английском алфавите — «E». Таким образом, в тексте, зашифрованном моноалфавитным шрифтом, наиболее часто встречающейся буквой будет буква, соответствующая «E». Вторая наиболее часто встречающаяся буква — это «T», а третья — «А». Человек, расшифровывающий моноалфавитный шифр, может смотреть на частоту встречающихся букв и почти законченные слова. Так, «T_E» с большой долей вероятности окажется «ТНЕ». К сожалению, этот принцип работает только для длинных сообщений. Короткие просто не содержат в себе достаточно слов, чтобы с достаточной достоверностью выявить соответствие наиболее часто встречающихся символов буквам из обычного алфавита. Мария Стюарт использовала невероятно сложный моноалфавитный шифр с несколькими вариациями, но когда его наконец-то взломали, прочитанные сообщения дали ее врагам достаточно поводов, чтобы приговорить ее к смерти. Ptbndcb ymdptmq bnw yew, bnwzw raw rkbcriie wrze bd owktxnwa.
4. Шифр Виженера
Этот шифр сложнее, чем моноалфавитные. Представим, что у нас есть таблица, построенная по тому же принципу, что и приведенная выше, и ключевое слово, допустим, «CHAIR». Шифр Виженера использует тот же принцип, что и шифр Цезаря, за тем исключением, что каждая буква меняется в соответствии с кодовым словом. В нашем случае первая буква послания будет зашифрована согласно шифровальному алфавиту для первой буквы кодового слова (в нашем случае «С»), вторая буква — согласно алфавиту для второй буквы кодового слова («H»), и так далее. В случае, если послание длиннее кодового слова, то для (k*n+1)-ой буквы (где n — это длина кодового слова) вновь будет использован алфавит для первой буквы кодового слова, и так далее. Очень долгое время шифр Виженера считался невзламываемым. Чтобы его расшифровать, для начала угадывают длину кодового слова и применяют частотный анализ к каждой n-ной букве послания, где n — предполагаемая длина кодового слова. Если длина была угадана верно, то и сам шифр вскроется с большей или меньшей долей вероятности. Если предполагаемая длина не дает верных результатов, то пробуют другую длину кодового слова, и так далее до победного конца. Eoaqiu hs net hs byg lym tcu smv dot vfv h petrel tw jka.
3. Настоящие коды
В настоящих кодах каждое слово заменяется на другое. Расшифровывается такое послание с помощью кодовой книги, где записано соответствие всех настоящих слов кодовым, прямо как в словаре. Преимущества такого способа в том, что сообщению необходимо быть ЧРЕЗВЫЧАЙНО длинным, чтобы можно было его взломать с помощью частотного анализа, так что коды полезнее некоторых шифров. Многие страны использовали коды, периодически их меняя, чтобы защититься от частотного анализа. Тем не менее, есть и минус: кодовая книга становится критическим предметом, и в случае, если она будет украдена, то с ее помощью больше будет невозможно что-либо зашифровать, и придется придумывать новый код, что требует огромных усилий и затрат времени. Обычно коды используют только богатые и влиятельные люди, которые могут поручить работу по их составлению другим.
2. Шифр Энигмы
Enigma
Энигма — это шифровальная машина, использовавшаяся нацистами во времена Второй Мировой. Принцип ее работы таков: есть несколько колес и клавиатура. На экране оператору показывалась буква, которой шифровалась соответствующая буква на клавиатуре. То, какой будет зашифрованная буква, зависело от начальной конфигурации колес. Соль в том, что существовало более ста триллионов возможных комбинаций колес, и со временем набора текста колеса сдвигались сами, так что шифр менялся на протяжении всего сообщения. Все Энигмы были идентичными, так что при одинаковом начальном положении колес на двух разных машинах и текст выходил одинаковый. У немецкого командования были Энигмы и список положений колес на каждый день, так что они могли с легкостью расшифровывать сообщения друг друга, но враги без знания положений послания прочесть не могли. Когда Энигма попала в руки к союзникам, они все равно сперва не могли ничего с ней сделать, потому что не знали положений-ключей. Дело по взлому шифра Энигмы было начато в польской разведке и доведено до конца в британской с помощью ученых и специальных машин (например, Turing Bombe, чья работа заключалась в том, чтобы моделировать одновременно работу сразу нескольких десятков Энигм). Отслеживание коммуникаций нацистов дало армии союзников важное преимущество в войне, а машины, использовавшиеся для его взлома, стали прообразом современных компьютеров.
Turing Bombe
1. Шифрование публичным ключом
Алгоритм шифрования, применяющийся сегодня в различных модификациях буквально во всех компьютерных системах. Есть два ключа: открытый и секретный. Открытый ключ — это некое очень большое число, имеющее только два делителя, помимо единицы и самого себя. Эти два делителя являются секретным ключом, и при перемножении дают публичный ключ. Например, публичный ключ — это 1961, а секретный — 37 и 53. Открытый ключ используется для того, чтобы зашифровать сообщение, а секретный — чтобы расшифровать. Без секретного ключа расшифровать сообщение невозможно. Когда вы отправляете свои личные данные, допустим, банку, или ваша банковская карточка считывается банкоматом, то все данные шифруются открытым ключом, а расшифровать их может только банк с соотвествующим секретным ключом. Суть в том, что математически очень трудно найти делители очень большого числа. Вот относительно простой пример. Недавно RSA выделила 1000 долларов США в качестве приза тому, кто найдет два пятидесятизначных делителя числа 1522605027922533360535618378132637429718068114961
380688657908494580122963258952897654000350692006139.
Язык жестов и поз
Знаете ли вы, что с помощью жестов, мимики и позы передается примерно 50% информации, в то время, как с помощью слов передается всего 10% информации, а с помощью звуковых средств (тон голоса, интонация) — 40%.
Все жесты делятся на несколько групп.
Первая группа — это жесты-символы.
Это, например, довольно распространенный во многих странах мира американский символ «О.К.». Он означает, что все в порядке и передается с помощью большого и указательного пальца, которые образуют букву «О». Но запомните, что во Франции этот жест может означать ноль, а в Японии — деньги. В Германии такой жест может быть расценен как неприличный намек. Постукивание пальцем по лбу во многих странах означает «ну и дурак», но в Голландии это переводится как «До чего умно!» Помахивание рукой при расставании — обычно пожелание счастливого пути, но в Греции это понимается, как пожелание убираться к черту. В Греции же поднятый вверх большой палец символизирует не высшую оценку, как во многих странах, а просьба «заткнуться», т.е. замолчать. В нашей стране не придается особого значения, какой рукой что-то делается. Но у тех, кто исповедует ислам, левая рука считается «нечистой». Поэтому, если вы протянете подарок или деньги левой рукой, вы можете оскорбить мусульманина.
Вторая группа жестов жесты-иллюстраторы.
Они используются для пояснения сказанного. Именно с помощью этих жестов можно подчеркнуть главные позиции беседы, которые в результате лучше запомнятся. Интенсивность таких жестов зависит от темперамента говорящего.
Третья группа — жесты-регуляторы/
Такие жесты играют важную роль в начале и в конце беседы. Один из таких жестов — рукопожатие. Эти жесты регулируют ход беседы, они могут начать ее, ускорить ход беседы или показать заинтересованность в разговоре, закончить беседу.
Четвёртая группа жестов-жесты — адапторы, которые обычно сопровождают наши чувства и эмоции.
Они напоминают детские непосредственные реакции и проявляются в ситуациях стресса, волнения, являются первыми признаками переживаний.
Значение основных жестов и поз в поведении человека.
1. Раскрытые руки ладонями вверх — Искренность, открытость
2. Человек прикрывает рот рукой во время слушания — Сомнение, недоверие к говорящему
3. Кулаки сжаты (или пальцы вцепились в какой-нибудь предмет так, что побелели суставы) — Защита, оборона
4. Кисти рук расслаблены — Спокойствие
5. Человек опирается подбородком на ладонь, указательный палец вдоль щеки, остальные пальцы ниже рта — Критическая оценка
6. Почесывание подбородка (нередко сопровождается легким прищуриванием глаз) — Обдумывание решения
7. Ладонь захватывает подбородок — Обдумывание решения
8.Человек медленно снимает очки, тщательно протирает стекла — Желание выиграть время, подготовка к решительному сопротивлению
9. Человек сидит на краешке стула, склонившись вперед, голова слегка наклонена и опирается на РУКУ — Заинтересованность
10. Человек прикрывает рот рукой во время своего высказывания — Обман
11. Расстегнут пиджак (или снимается) — Открытость, дружеское расположение
12. Человек старается на вас не смотреть — Скрытность, утаивание своей позиции
13. Говорящий жестикулирует сжатым кулаком — Демонстрация власти, угроза
14. Человек расхаживает по комнате — Обдумывание трудного решения
15. Пощипывание переносицы — Напряженное сопротивление
16. Говорящий слегка касается носа или века (обычно указательным пальцем) — Обман 17. Пиджак застегнут на все пуговицы — Официальность, подчеркивание дистанции
18. Взгляд в сторону от вас — Подозрение, сомнение
19. Руки спрятаны (за спину, в карманы) — Чувство собственной вины или напряженное восприятие ситуации
20. При рукопожатии человек держит свою руку сверху — Превосходство, уверенность
21. При рукопожатии человек держит свою руку снизу — Подчинение
22. Хозяин кабинета начинает собирать бумаги на столе — Разговор окончен
23. Руки скрещены на груди — Защита, оборона
24.Слушающие слегка касаются века, носа или уха — Недоверие к говорящему
25.Человек сидит верхом на стуле— Агрессивное состояние
26. Зрачки расширены — Заинтересованность или возбуждение
27. Зрачки сузились — Скрытность, утаивание позиции. Позы и жесты которых нужно избегать!
Позы. Руки на бёдрах – агрессивная поза; Скрещенные руки на груди – поза зашиты; Ладони соединены ниже талии (поза футболиста) – поза зашиты, слабость; Рука обхватывает вторую руку за спиной – страх, волнение; Руки в карманах – скрытность, нервозность; Откидываетесь на спинку кресла – явное несогласие с мнением собеседника. Жесты. Жесты указательным пальцем — это обвинительный жест; Выставленный большой палец — выражение превосходства, пренебрежительное отношение; Кулак – враждебный жест, агрессивное настроение; Касание рта или других частей лица во время разговора – выдает волнение, люди могут посчитать Вас неискренним. Прикосновения к уху, ко рту или к шее, когда Вы слушаете — это жесты сомнения и несогласия с собеседником.
Методы кодирования цвета
Шифрование – это способ изменения сообщения или другого документа, обеспечивающее искажение (сокрытие) его содержимого.
Кодирование – это преобразование обычного, понятного, текста в код. При этом подразумевается, что существует взаимно однозначное соответствие между символами текста (данных, чисел, слов) и символьного кода – в этом принципиальное отличие кодирования от шифрования.
Кодирование — 1. процесс изменения входящего сообщения из его изначальной формы в некую другую (например, превращение нервных импульсов, исходящих от рецептора в ощущение, феномен психического); 2. трансформация неких данных из одной формы в другую;
ЦВЕТОВОЕ КОДИРОВАНИЕ — способ кодирования зрительной информации, при котором смысл информации заключен в цвете кодового знака. к использованию цветового алфавита состоят в следующем. В алфавите следует отдавать предпочтение зеленому, красному, голубому, желтому и… … Энциклопедический словарь по психологии и педагогике
Человеческий глаз устроен таким образом, что способен раздельно воспринимать три цвета, называемых основными: красный, зеленый и синий.
Каждый цвет воспринимается нашим зрением как определенная комбинация этих основных цветов.
Цветовая модель – это способ разделения цвета на составляющие его компоненты: основные и дополнительные цвета, при смешении которых образуются другие оттенки.
Основным элементом этой цветовой модели является палитра.
Палитрой называется цветовая таблица, сопоставляющая фиксированным образцам цвета порядковые номера в виде натуральных чисел.
Цветова модель (RGB) — Red (Красный) — Green (Зеленый) — Blue(Синий) т.е. три цвета соответствующие модели излучаемого цвета. Рассмотрим смешение в равных пропорциях:
Red (Красный)+Green (Зеленый) =Yellow(Желтый)
Green (Зеленый) + Blue(Синий)=Cyan(Голубой)
Red (Красный) + Blue(Синий)=Magenta(Пурпурный)
Red (Красный) + Green (Зеленый) + Blue(Синий)=Серый
Аддитивной она называется потому, что цвета получаются путём добавления (англ. addition) к чёрному цвету.
Метод кодирования цвета RGB применяется при кодировании изображений, выводимых на экран цветного дисплея.
Цветовая модель CMYK — Cyan(Голубой) — Magenta(Пурпурный)- Yellow(Желтый) – Black(Черный).
Эта цветовая модель используется, когда имеем дело с отраженным цветом. На печатной странице цвета ведут себя иначе. Страница не излучает свет, а отражает его. При воспроизведении цветных изображений на печати мы имеем дело не со светом, а с пигментами (красками, тонером, воском), которые одни цвета поглощают, а другие отражают.
Они называются субтрактивными первичными цветами (от англ. subtract – вычитать).
На практике к базовому набору из трех красок для качественной и более экономичной печати добавляется черный цвет. Такая кодировка называется CMYK-кодировкой (от слова blacK взяли последнюю букву, чтобы не путать с сокращением Blue).
Во многих графических редакторах используется более удобная для человека перцепционная (ориентированная на восприятие) схема кодирования: цветовой фон / насыщенность / яркость. Такая кодировка называется HSB по первым буквам английских слов Hue, Saturation, Brightness. (На рисунке показано окно HSB-конструирования цвета из редактора Paint)
Перемещение движка цвета по горизонтали меняет оттенок (H), по вертикали — контрастность (S). Перемещение треугольного движка по отдельной вертикальной линейке меняет яркость (B).
Оттенок— это цвет на радуге.
Контрастность (насыщенность)— это содержание в цвете серой примеси. Цвет максимальной насыщенности не содержит серого вообще, а при нулевой насыщенности— все цвета серые.
Яркость— это интенсивность, с которой излучается цвет. При максимальной яркости все цвета превращаются в белый цвет, а при нулевой— в черный.
Сначала выбирается цвет в радуге (слева направо), потом устанавливается его контрастность (сверху вниз), а затем отдельным движком задается яркость.
Метод координат
Систе́ма координа́т— комплекс определений, реализующий метод координат, то есть способ определять положение точки или тела с помощью чисел или других символов. Совокупность чисел, определяющих положение конкретной точки, называется координатами этой точки.
В математике координаты—совокупность чисел, сопоставленных точкам многообразия в некоторой карте определённого атласа.
В элементарной геометрии координаты— величины, определяющие положение точки на плоскости и в пространстве. На плоскости положение точки чаще всего определяется расстояниями от двух прямых (координатных осей), пересекающихся в одной точке (начале координат) под прямым углом; одна из координат называетсяординатой, а другая—абсциссой. В пространстве по системе Декарта положение точки определяется расстояниями от трёх плоскостей координат, пересекающихся в одной точке под прямыми углами друг к другу, или сферическими координатами, где начало координат находится в центре сферы.
В географии координаты выбираются как (приближённо) сферическая система координат—широта, долгота и высота над известным общим уровнем (например, океана). См. Географические координаты.
В астрономии небесные координаты—упорядоченная пара угловых величин (например, прямое восхождение и склонение), с помощью которых определяют положение светил и вспомогательных точек на небесной сфере. В астрономии употребляют различные системы небесных координат. Каждая из них по существу представляет собой сферическую систему координат (без радиальной координаты) с соответствующим образом выбранной фундаментальной плоскостью и началом отсчёта. В зависимости от выбора фундаментальной плоскости система небесных координат называется горизонтальной (плоскость горизонта), экваториальной(плоскость экватора), эклиптической (плоскость эклиптики) или галактической (галактическая плоскость).
Наиболее используемая система координат—прямоугольная система координат (также известная как декартова система координат).
Координаты на плоскости и в пространстве можно вводить бесконечным числом разных способов. Решая ту или иную математическую или физическую задачу методом координат, можно использовать различные координатные системы, выбирая ту из них, в которой задача решается проще или удобнее в данном конкретном случае. Известным обобщением системы координат являются системы отсчёта и системы референции.
Метод координат — способ определять положение точки или тела с помощью чисел или других символов (например, положение шахматных фигур на доске определяется с помощью чисел и букв). Числа (символы), определяющие положение точки (тела) на прямой, плоскости, в пространстве, на поверхности и так далее, называются её координатами. В зависимости от целей и характера исследования выбирают различные системы координат
Заключение
Рассмотрев выбранную тему, мы подтвердили гипотезу о том, что без понимания различных способов кодирования информации, человек бы не смог понять то, что видит, слышит, чувствует.
Вся жизнь человека, так или иначе, связана с получением, накоплением и обработкой информации. Чтобы человек ни делал: читает ли он книгу, смотрит ли он телевизор, разговаривает, он постоянно и непрерывно получает и обрабатывает информацию. Для любой операции над информацией (даже такой простой, как сохранение) она должна быть как-то представлена (записана, зафиксирована). Этот процесс имеет специальное название – кодирование информации. Современному человеку невозможно обойтись без кодирования информации. Чтобы мы понимали все из того, что слышим, видим, чувствуем необходимо знать различные способы представления (кодирования) информации. Кодирование информации необычайно разнообразно, множество кодов очень прочно вошло в нашу жизнь.
Выводы:
Знание различных способов кодирования помогает человеку легко ориентироваться в жизненных ситуациях: указания водителю автомобиля кодируются в виде дорожных знаков, музыкальное произведение кодируется с помощью знаков нотной грамоты, для записи шахматных партий и химических формул созданы специальные системы записи, географическая карта кодирует информацию о местности, азбука жестов помогает общаться людям, ограниченным в звуковом общении.
Литературные источники
- infoegehelp.ru. Успешно сдать ЕГЭ по информатике.
URL:http:\oegehelp.ru/index.php?option=com_content&view=article&id=65:kodirovanieizobr&catid=45:2011-12-18-16-49-04&Itemid=66
- Язык жестов URL:http://school.xvatit.com/index.php?title=%D0%AF%D0%B7%D1%8B%D0%BA_%D0%B6%D0%B5%D1%81%D1%82%D0%BE%D0%B2
- https://tproger.ru/translations/10-codes-and-ciphers/
Приложение 1
Азбука Морзе
Приложение 2
Флажковая азбука
Приложение 3
Шифр Цезаря
Муниципальное бюджетное образовательное учреждение средняя общеобразовательная школа села Бичевая муниципального района имени Лазо Хабаровского края.
Индивидуальный проект
Тема: «Кодирования информации» »
Руководитель проекта: Кирсанова Екатерина Владимировна
Выполнила работу ученица 9б класс : Соколова Татьяна Александровна
с. Бичевая
2022 год.
Содержание
-
Введение……………………………………………………………………………………3стр
-
Основная часть………………………………………………………………………….5стр
-
Коды и шифры………………………………………………………………….5стр
-
Язык жестов и поз…………………………………………………………….14стр
-
Метод кодирования цвета………………………………………………….17стр
-
-
Заключение……………………………………………………………………………….22стр
-
Вывод
-
Список литературы……………………………………………………………………23стр
Введение
В современной жизни человек сталкивается с различными способами кодирования информации. Чтобы научиться понимать информацию, представленную различными способами, необходимо ориентироваться в многообразии способов кодирования: знать и уметь интерпретировать их.
Актуальность: В 21 веке, веке цифровых технологий человек сталкивается с различными способами кодирования информации. Чтобы научиться понимать информацию, представленную различными способами, необходимо ориентироваться в многообразии способов кодирования: знать и уметь интерпретировать их. Поэтому я хочу ответить на вопрос: всё ли мы понимаем из того, что слышим, видим, чувствуем?
Проблемные вопросы:
-
Всегда ли мы понимаем друг друга?
-
Можно ли говорить, не произнося слова?
-
Можно ли прожить без кодов и знаков?
-
Чем отличается шифр от кода?
-
О чём говорят жесты?
-
Можно ли закодировать цветом?
Цель: выяснить, какие методы кодирования существуют?
Задачи: выяснить …
— что такое кодирование и что такое декодирование?
— где используются кодирование информации?
— какие способы кодирования существуют?
— зачем кодировать информацию?
— чем объяснить многообразие окружающих человека кодов?
— к чему приводят ошибки кодирования?
Гипотеза: все, кто познакомится с методами кодирования информации, представленными в данном проекте, заинтересуются темой кодирования и шифрования информации и будут использовать их.
2.Основная часть
Мудр не тот, кто знает много, а тот, чьи знания полезны
Эсхилл
2.1 Коды и шифры
Необходимость засекречивать важные послания возникла еще в древности. Со временем люди находили новые, все более сложные способы делать послания недоступными чужим глазам. Вопреки распространенному мнению, код и шифр — это не одно и то же. В коде каждое слово заменяется на какое-то иное кодовое слово, в то время как в шифре заменяются сами символы сообщения. Когда люди говорят «код», они, как правило, имеют в виду «шифр». Древние рукописи и языки были поняты с помощью техник декодирования и дешифрования. Самый известный пример — Розеттский камень Древнего Египта. Фактически коды и шифры определяли исход многих войн и политических интриг на протяжении всей истории человечества. Существуют тысячи типов шифрования сообщений, но в этой статье мы рассмотрим лишь 10 самых известных и значимых из них.
-
Азбука Морзе
-
В
азбуке Морзе каждая буква алфавита, все цифры и наиболее важные знаки препинания имеют свой код, состоящий из череды коротких и длинных сигналов, часто называемых «точками и тире». Так, A — это «•—», B — «—•••», и т.д. В отличие от большинства шифров, азбука Морзе используется не для затруднения чтения сообщений, а наоборот, для облегчения их передачи (с помощью телеграфа). Длинные и короткие сигналы посылаются с помощью включения и выключения электрического тока. Телеграф и азбука Морзе навсегда изменили мир, сделав возможной молниеносную передачу информации между разными странами, а также сильно повлияли на стратегию ведения войны, ведь теперь можно было можно осуществлять почти мгновенную коммуникацию между войсками.1
2. Стеганография
С
Этот шифр известен многим детям. Ключ прост: каждая буква заменяется на следующую за ней в алфавите. Так, A заменяется на B, B на C, и т.д. «ROT1» значит «ROTate 1 letter forward through the alphabet» (англ. «сдвиньте алфавит на одну букву вперед»). Сообщение «I know what you did last summer» станет «J lopx xibu zpv eje mbtu tvnnfs». Этот шифр весело использовать, потому что его легко понять и применять, но его так же легко и расшифровать. Из-за этого его нельзя использовать для серьезных нужд, но дети с радостью «играют» с его помощью. Попробуйте расшифровать сообщение «XBT JU B DBU J TBX?».
4. Транспозиция4
5. Шифр Цезаря
Шифр Цезаря называется так, как ни странно, потому что его использовал сам Юлий Цезарь. На самом деле шифр Цезаря — это не один шифр, а целых 26, использующих один и тот же принцип! Так, ROT1 — всего один из них. Получателю нужно сказать, какой из шифров используется. Если используется шифр «G», тогда А заменяется на G, B на H, C на I и т.д. Если используется шифр «Y», тогда А заменяется на Y, B на Z, C на A и т.д. На шифре Цезаря базируется огромное число других, более сложных шифров, но сам по себе он не представляет из себя интереса из-за легкости дешифровки. Перебор 26 возможных ключей не займет много времени.
6
ROT1, азбука Морзе, шифр(ы) Цезаря относятся к одному и тому же типу шифров — моноалфавитной замене. Это значит, что каждая буква заменяется на одну и только одну другую букву или символ. Такие шифры очень легко расшифровать даже без знания ключа. Делается это при помощи частотного анализа. Например, наиболее часто встречающаяся буква в английском алфавите — «E». Таким образом, в тексте, зашифрованном моноалфавитным шрифтом, наиболее часто встречающейся буквой будет буква, соответствующая «E». Вторая наиболее часто встречающаяся буква — это «T», а третья — «А». Человек, расшифровывающий моноалфавитный шифр, может смотреть на частоту встречающихся букв и почти законченные слова. Так, «T_E» с большой долей вероятности окажется «ТНЕ». К сожалению, этот принцип работает только для длинных сообщений. Короткие просто не содержат в себе достаточно слов, чтобы с достаточной достоверностью выявить соответствие наиболее часто встречающихся символов буквам из обычного алфавита. Мария Стюарт использовала невероятно сложный моноалфавитный шифр с несколькими вариациями, но когда его наконец-то взломали, прочитанные сообщения дали ее врагам достаточно поводов, чтобы приговорить ее к смерти. Ptbndcb ymdptmq bnw yew, bnwzw raw rkbcriie wrze bd owktxnwa.
-
Шифр Виженера6
Этот шифр сложнее, чем моноалфавитные. Представим, что у нас есть таблица, построенная по тому же принципу, что и приведенная выше, и ключевое слово, допустим, «CHAIR». Шифр Виженера использует тот же принцип, что и шифр Цезаря, за тем исключением, что каждая буква меняется в соответствии с кодовым словом. В нашем случае первая буква послания будет зашифрована согласно шифровальному алфавиту для первой буквы кодового слова (в нашем случае «С»), вторая буква — согласно алфавиту для второй буквы кодового слова («H»), и так далее. В случае, если послание длиннее кодового слова, то для (k*n+1)-ой буквы (где n — это длина кодового слова) вновь будет использован алфавит для первой буквы кодового слова, и так далее. Очень долгое время шифр Виженера считался невзламываемым. Чтобы его расшифровать, для начала угадывают длину кодового слова и применяют частотный анализ к каждой n-ной букве послания, где n — предполагаемая длина кодового слова. Если длина была угадана верно, то и сам шифр вскроется с большей или меньшей долей вероятности. Если предполагаемая длина не дает верных результатов, то пробуют другую длину кодового слова, и так далее до победного конца.
8. Настоящие коды7
В
9. Шифр Энигмы8

Enigma
Энигма — это шифровальная машина, использовавшаяся нацистами во времена Второй Мировой. Принцип ее работы таков: есть несколько колес и клавиатура. На экране оператору показывалась буква, которой шифровалась соответствующая буква на клавиатуре. То, какой будет зашифрованная буква, зависело от начальной конфигурации колес. Соль в том, что существовало более ста триллионов возможных комбинаций колес, и со временем набора текста колеса сдвигались сами, так что шифр менялся на протяжении всего сообщения. Все Энигмы были идентичными, так что при одинаковом начальном положении колес на двух разных машинах и текст выходил одинаковый. У немецкого командования были Энигмы и список положений колес на каждый день, так что они могли с легкостью расшифровывать сообщения друг друга, но враги без знания положений послания прочесть не могли. Когда Энигма попала в руки к союзникам, они все равно сперва не могли ничего с ней сделать, потому что не знали положений-ключей. Дело по взлому шифра Энигмы было начато в польской разведке и доведено до конца в британской с помощью ученых и специальных машин (например, Turing Bombe, чья работа заключалась в том, чтобы моделировать одновременно работу сразу нескольких десятков Энигм). Отслеживание коммуникаций нацистов дало армии союзников важное преимущество в войне, а машины, использовавшиеся для его взлома, стали прообразом современных компьютеров.
10. Шифрование публичным ключом
Алгоритм шифрования, применяющийся сегодня в различных модификациях буквально во всех компьютерных системах. Есть два ключа: открытый и секретный. Открытый ключ — это некое очень большое число, имеющее только два делителя, помимо единицы и самого себя. Эти два делителя являются секретным ключом, и при перемножении дают публичный ключ. Например, публичный ключ — это 1961, а секретный — 37 и 53. Открытый ключ используется для того, чтобы зашифровать сообщение, а секретный — чтобы расшифровать. Без секретного ключа расшифровать сообщение невозможно. Когда вы отправляете свои личные данные, допустим, банку, или ваша банковская карточка считывается банкоматом, то все данные шифруются открытым ключом, а расшифровать их может только банк с соотвествующим секретным ключом. Суть в том, что математически очень трудно найти делители очень большого числа. Вот относительно простой пример. Недавно RSA выделила 1000 долларов США в качестве приза тому, кто найдет два пятидесятизначных делителя числа 1522605027922533360535618378132637429718068114961
380688657908494580122963258952897654000350692006139.
2.2 Язык жестов и поз
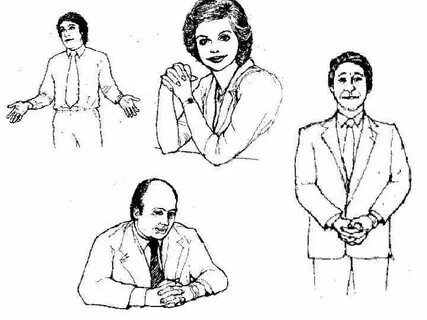
Все жесты делятся на несколько групп.
Первая группа — это жесты-символы.
Это, например, довольно распространенный во многих странах мира американский символ «О.К.». Он означает, что все в порядке и передается с помощью большого и указательного пальца, которые образуют букву «О». Но запомните, что во Франции этот жест может означать ноль, а в Японии — деньги. В Германии такой жест может быть расценен как неприличный намек. Постукивание пальцем по лбу во многих странах означает «ну и дурак», но в Голландии это переводится как «До чего умно!» Помахивание рукой при расставании — обычно пожелание счастливого пути, но в Греции это понимается, как пожелание убираться к черту. В Греции же поднятый вверх большой палец символизирует не высшую оценку, как во многих странах, а просьба «заткнуться», т.е. замолчать. В нашей стране не придается особого значения, какой рукой что-то делается. Но у тех, кто исповедует ислам, левая рука считается «нечистой». Поэтому, если вы протянете подарок или деньги левой рукой, вы можете оскорбить мусульманина.
Вторая группа жестов жесты-иллюстраторы.
Они используются для пояснения сказанного. Именно с помощью этих жестов можно подчеркнуть главные позиции беседы, которые в результате лучше запомнятся. Интенсивность таких жестов зависит от темперамента говорящего.
Третья группа — жесты-регуляторы.
Такие жесты играют важную роль в начале и в конце беседы. Один из таких жестов — рукопожатие. Эти жесты регулируют ход беседы, они могут начать ее, ускорить ход беседы или показать заинтересованность в разговоре, закончить беседу.
Четвёртая группа жестов-жесты — адапторы, которые обычно сопровождают наши чувства и эмоции.
Они напоминают детские непосредственные реакции и проявляются в ситуациях стресса, волнения, являются первыми признаками переживаний.
Значение основных жестов и поз в поведении человека.
1. Раскрытые руки ладонями вверх — Искренность, открытость
2. Человек прикрывает рот рукой во время слушания — Сомнение, недоверие к говорящему
3. Кулаки сжаты (или пальцы вцепились в какой-нибудь предмет так, что побелели суставы) — Защита, оборона
4. Кисти рук расслаблены — Спокойствие
5. Человек опирается подбородком на ладонь, указательный палец вдоль щеки, остальные пальцы ниже рта — Критическая оценка
6. Почесывание подбородка (нередко сопровождается легким прищуриванием глаз) — Обдумывание решения
7. Ладонь захватывает подбородок — Обдумывание решения
8.Человек медленно снимает очки, тщательно протирает стекла — Желание выиграть время, подготовка к решительному сопротивлению
9. Человек сидит на краешке стула, склонившись вперед, голова слегка наклонена и опирается на РУКУ — Заинтересованность
10. Человек прикрывает рот рукой во время своего высказывания — Обман
11. Расстегнут пиджак (или снимается) — Открытость, дружеское расположение
12. Человек старается на вас не смотреть — Скрытность, утаивание своей позиции
13. Говорящий жестикулирует сжатым кулаком — Демонстрация власти, угроза
14. Человек расхаживает по комнате — Обдумывание трудного решения
15. Пощипывание переносицы — Напряженное сопротивление
16. Говорящий слегка касается носа или века (обычно указательным пальцем) — Обман 17. Пиджак застегнут на все пуговицы — Официальность, подчеркивание дистанции
18. Взгляд в сторону от вас — Подозрение, сомнение
19. Руки спрятаны (за спину, в карманы) — Чувство собственной вины или напряженное восприятие ситуации
20. При рукопожатии человек держит свою руку сверху — Превосходство, уверенность
21. При рукопожатии человек держит свою руку снизу — Подчинение
22. Хозяин кабинета начинает собирать бумаги на столе — Разговор окончен
23. Руки скрещены на груди — Защита, оборона
24.Слушающие слегка касаются века, носа или уха — Недоверие к говорящему
25.Человек сидит верхом на стуле— Агрессивное состояние
26. Зрачки расширены — Заинтересованность или возбуждение
27. Зрачки сузились — Скрытность, утаивание позиции. Позы и жесты которых нужно избегать!
Позы. Руки на бёдрах – агрессивная поза; Скрещенные руки на груди – поза зашиты; Ладони соединены ниже талии (поза футболиста) – поза зашиты, слабость; Рука обхватывает вторую руку за спиной – страх, волнение; Руки в карманах – скрытность, нервозность; Откидываетесь на спинку кресла – явное несогласие с мнением собеседника. Жесты. Жесты указательным пальцем — это обвинительный жест; Выставленный большой палец — выражение превосходства, пренебрежительное отношение; Кулак – враждебный жест, агрессивное настроение; Касание рта или других частей лица во время разговора – выдает волнение, люди могут посчитать Вас неискренним. Прикосновения к уху, ко рту или к шее, когда Вы слушаете — это жесты сомнения и несогласия с собеседником.
2.3 Методы кодирования цвета
Шифрование – это способ изменения сообщения или другого документа, обеспечивающее искажение (сокрытие) его содержимого.
Кодирование – это преобразование обычного, понятного, текста в код. При этом подразумевается, что существует взаимно однозначное соответствие между символами текста (данных, чисел, слов) и символьного кода – в этом принципиальное отличие кодирования от шифрования.
Кодирование — 1. процесс изменения входящего сообщения из его изначальной формы в некую другую (например, превращение нервных импульсов, исходящих от рецептора в ощущение, феномен психического); 2. трансформация неких данных из одной формы в другую;
ЦВЕТОВОЕ КОДИРОВАНИЕ9 — способ кодирования зрительной информации, при котором смысл информации заключен в цвете кодового знака. к использованию цветового алфавита состоят в следующем. В алфавите следует отдавать предпочтение зеленому, красному, голубому, желтому и… … Энциклопедический словарь по психологии и педагогике
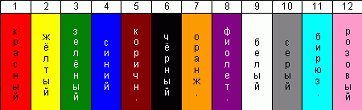
Человеческий глаз устроен таким образом, что способен раздельно воспринимать три цвета, называемых основными: красный, зеленый и синий.
Каждый цвет воспринимается нашим зрением как определенная комбинация этих основных цветов.
Цветовая модель – это способ разделения цвета на составляющие его компоненты: основные и дополнительные цвета, при смешении которых образуются другие оттенки.
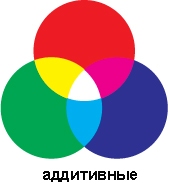
Основным элементом этой цветовой модели является палитра.
Палитрой называется цветовая таблица, сопоставляющая фиксированным образцам цвета порядковые номера в виде натуральных чисел.
Цветова модель (RGB) — Red (Красный) — Green (Зеленый) — Blue(Синий) т.е. три цвета соответствующие модели излучаемого цвета. Рассмотрим смешение в равных пропорциях:
Red (Красный)+Green (Зеленый) =Yellow(Желтый)
Green (Зеленый) + Blue(Синий)=Cyan(Голубой)
Red (Красный) + Blue(Синий)=Magenta(Пурпурный)
Red (Красный) + Green (Зеленый) + Blue(Синий)=Серый
Аддитивной она называется потому, что цвета получаются путём добавления к чёрному цвету.
Метод кодирования цвета RGB применяется при кодировании изображений, выводимых на экран цветного дисплея.
Цветовая модель CMYK — Cyan(Голубой) — Magenta(Пурпурный)- Yellow(Желтый) – Black(Черный).
Эта цветовая модель используется, когда имеем дело с отраженным цветом. На печатной странице цвета ведут себя иначе. Страница не излучает свет, а отражает его. При воспроизведении цветных изображений на печати мы имеем дело не со светом, а с пигментами (красками, тонером, воском), которые одни цвета поглощают, а другие отражают.
Они называются субтрактивными первичными цветами (от англ. subtract – вычитать).
На практике к базовому набору из трех красок для качественной и более экономичной печати добавляется черный цвет. Такая кодировка называется CMYK-кодировкой (от слова blacK взяли последнюю букву, чтобы не путать с сокращением Blue).
Во многих графических редакторах используется более удобная для человека перцепционная (ориентированная на восприятие) схема кодирования: цветовой фон / насыщенность / яркость. Такая кодировка называется HSB по первым буквам английских слов Hue, Saturation, Brightness. (На рисунке показано окно HSB-конструирования цвета из редактора Paint)
Перемещение движка цвета по горизонтали меняет оттенок (H), по вертикали — контрастность (S). Перемещение треугольного движка по отдельной вертикальной линейке меняет яркость (B).
Оттенок— это цвет на радуге.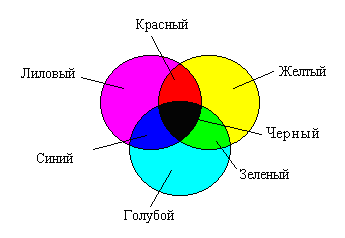
Контрастность (насыщенность)— это содержание в цвете серой примеси. Цвет максимальной насыщенности не содержит серого вообще, а при нулевой насыщенности— все цвета серые.
Яркость— это интенсивность, с которой излучается цвет. При максимальной яркости все цвета превращаются в белый цвет, а при нулевой— в черный.
Сначала выбирается цвет в радуге (слева направо), потом устанавливается его контрастность (сверху вниз), а затем отдельным движком задается яркость.
3. Заключение
Рассмотрев выбранную тему, мы подтвердили гипотезу о том, что без понимания различных способов кодирования информации, человек бы не смог понять то, что видит, слышит, чувствует.
Вся жизнь человека, так или иначе, связана с получением, накоплением и обработкой информации. Чтобы человек ни делал: читает ли он книгу, смотрит ли он телевизор, разговаривает, он постоянно и непрерывно получает и обрабатывает информацию. Для любой операции над информацией (даже такой простой, как сохранение) она должна быть как-то представлена (записана, зафиксирована). Этот процесс имеет специальное название – кодирование информации. Современному человеку невозможно обойтись без кодирования информации. Чтобы мы понимали все из того, что слышим, видим, чувствуем необходимо знать различные способы представления (кодирования) информации. Кодирование информации необычайно разнообразно, множество кодов очень прочно вошло в нашу жизнь.
4.Выводы:
Знание различных способов кодирования помогает человеку легко ориентироваться в жизненных ситуациях: указания водителю автомобиля кодируются в виде дорожных знаков, музыкальное произведение кодируется с помощью знаков нотной грамоты, для записи шахматных партий и химических формул созданы специальные системы записи, географическая карта кодирует информацию о местности, азбука жестов помогает общаться людям, ограниченным в звуковом общении.
5.Литературные источники
-
infoegehelp.ru. Успешно сдать ЕГЭ по информатике.
URL:http:\oegehelp.ru/index.php?option=com_content&view=article&id=65:kodirovanieizobr&catid=45:2011-12-18-16-49-04&Itemid=66
-
Язык жестов URL:http://school.xvatit.com/index.php?title=%D0%AF%D0%B7%D1%8B%D0%BA_%D0%B6%D0%B5%D1%81%D1%82%D0%BE%D0%B2
-
https://tproger.ru/translations/10-codes-and-ciphers
-
Скляр Б. Цифровая связь. Теоретические основы и практическое применение азбуки Морзе. Пер. с англ. — М.: Издательский дом «Вильямс», 2003, 1104 с., С. 39. ISBN 978-5-8459-0497-3
-
А.В. Бабаш. Зарождение криптографии. Материалы к лекции по теме «Криптография в древние времена». — Излагаемый материал входит в двухсеместровый курс «История стенографии», читаемый в ИКСИ Академии ФСБ. Дата обращения: 20 марта 2012.
https://tproger.ru/translations/10-codes-and-ciphers/
-
Саймон Сингх. Глава 2. Нераскрываемый шифр // Книга шифров. Тайная история шифров и их расшифровки = The Code Book by Simon Singh / перевод с английского А. Галыгина. — М.: АСТ, 2007. — Т. 2. — С. 69—74. — 4000 экз. — ISBN 978-5-17-038477-8.
1 ↑ Скляр Б. Цифровая связь. Теоретические основы и практическое применение азбуки Морзе. Пер. с англ. — М.: Издательский дом «Вильямс», 2003, 1104 с., С. 39. ISBN 978-5-8459-0497-3
2 А.В. Бабаш. Зарождение криптографии. Материалы к лекции по теме «Криптография в древние времена». — Излагаемый материал входит в двухсеместровый курс «История стенографии», читаемый в ИКСИ Академии ФСБ. Дата обращения: 20 марта 2012.
3 https://tproger.ru/translations/10-codes-and-ciphers/
-
4 Фред Б. Риксон. Коды, шифры, сигналы и тайная передача информации. — Астрель, 2011. — ISBN 978-5-17-074391-9.
-
5 Саймон Сингх. Глава 2. Нераскрываемый шифр // Книга шифров. Тайная история шифров и их расшифровки = The Code Book by Simon Singh / перевод с английского А. Галыгина. — М.: АСТ, 2007. — Т. 2. — С. 69—74. — 4000 экз. — ISBN 978-5-17-038477-8.
6
-
Саймон Сингх. Глава 2. Нераскрываемый шифр // Книга шифров. Тайная история шифров и их расшифровки = The Code Book by Simon Singh / перевод с английского А. Галыгина. — М.: АСТ, 2007. — Т. 2. — С. 98—105. — 4000 экз. — ISBN 978-5-17-038477-8.
-
7 Фред Б. Риксон. Коды, шифры, сигналы и тайная передача информации. — Астрель, 2011. — ISBN 978-5-17-074391-9.
-
8 Бауэр Ф. Расшифрованные секреты. Методы и принципы криптологии. — Мир, 2007. — ISBN 5-03-003551-6.
-
9 ↑ IEC 60062:2004 Название: «Коды маркировки резисторов и конденсаторов» (Интернет-магазин IEC)
1
Ошибка — кодирование
Cтраница 2
Старший разряд получает положительный знак, а следующие ненулевые — чередующиеся знаки. Это свойство используется в аналого-цифровых преобразователях для уменьшения ошибок кодирования, вызванных механическими или электроннолучевыми рассогласованиями.
[16]
Канонические системы кодирования, предусматривающие взаимнооднозначное соответствие кода и структурной формулы, как правило, весьма сложны. Ручная канонизация неизбежно связана с резким усложнением правил кодирования, что приводит к ошибкам кодирования.
[17]
Существует и еще один подход, при котором отладка частично пересекается с написанием программ. Некоторые программисты предпочитают написать несколько строк кодов и тут же проверить их работу. Этот подход позволяет отыскать ошибки кодирования непосредственно в процессе кодирования. Достоинством такого подхода является и то, что программа свежа в памяти, что позволяет легче выявить ошибки.
[18]
Мы можем полагать, что изображенные выше формы являются более редкими и в обычных условиях неустойчивыми. Однако таутомерные переходы могут происходить, и притом будут зависеть от рН и температуры. Если они являются причиной ошибок кодирования, то ими могут объясняться некоторые типы мутаций.
[19]
Одним из основных требований, предъявляемых к блокам сравнения ЦИП, является высокая перегрузочная способность. Это требование вытекает из того, что сигнал рассогласования на входе блока в процессе преобразования входного напряжения может изменяться в широких пределах, и возникающая при этом перегрузка усилительных каскадов может резко снизить быстродействие всего прибора в целом. Чрезмерная перегрузка УПТ может привести к возникновению ошибок кодирования, например к появлению выходного сигнала неправильной полярности, так как при насыщении усилительного каскада с общим эмиттером сигнал проходит через перегруженный каскад, не меняя фазы. Наконец, перегрузки могут вывести устройство сравнения из строя ввиду превышения допустимых для элементов схемы предельных режимов.
[20]
Сжатие полутоновых изображений обычно происходит не без ошибок. Проводились специальные исследования с целью разработки методов снижения объема данных при сохранении коэффициентов ошибок на возможно более низком уровне. Кодирование двухграда-ционных изображений выполняется без ошибок. Это означает, что ошибки кодирования не допускаются вообще. Исследования в области обработки изображений, распознавания образов, теории кодирования и других смежных областей постоянно пополняют арсенал методов кодирования изображений. В этой области ожидается значительное число интересных достижений.
[21]
Можно решить, что эта трудность полностью преодолевается, если между источником и кодером, использующим неравномерный код, поставить буферное запоминающее устройство, которое будет играть роль управляемого источника. Рассмотрим ситуацию, при которой буферное ЗУ может хранить N сообщений. Имеется отличная от нуля вероятность того, что на выходе источника появится подряд более чем Af / Д блоков длиной п, кодируемых словами длиной m или больше. В случае наступления такого события происходит переполнение буфера и, следовательно, неправильное декодирование. Потеря сообщений или переполнение буфера при неравномерном кодировании и ошибка кодирования или декодирования при равномерном кодировании — явления одного порядка, которые одинаково нежелательны.
[22]
В некоторых случаях при углубленном исследовании отдельного соединения не вся биологическая информация запоминается. Это наблюдается, в частности, в ситуациях, когда имеется семейство родственных соединений, испытанных с помощью одной и той же стандартной методики. В систему вводятся структурные формулы всех новых соединений, которые синтезировались в фирме с целью биологического испытания. Кроме того, в систему вводится структурная информация из литературных источников, представляющая интерес для фирмы. В CCBF применяется поатомная система кодирования типа описанной Горовитцем и Крайнем [34], Вальдо [33] и др. Скорость кодирования в среднем 40 соединений в час. Специальная программа выявляет ошибки кодирования. Для автоматического вывода структурных формул на печать используется высокоскоростное печатающее устройство IBM1403 / N1, в котором применены некоторые дополнительные специальные химические символы.
[23]
Проводоукладчик в виде карандаша, через осевое отверстие которого проходит кодовый провод, перемещают с помощью каретки вдоль ряда П — образных сердечников. С помощью электромагнита, управляемого программным устройством, карандаш отклоняют в тех случаях, когда необходимо проложить провод вне сердечника и записать код О. Отклонение кинематически синхронизировано с продольным перемещением каретки устройства. При записи кода 1 карандаш не отклоняется и прокладывает провод через сердечник. После прохождения одного ряда сердечников продольная каретка с про-водоукладчиком автоматически перемещается поперечной кареткой к другому ряду. Такое устройство в несколько раз повышает производительность прошивки МДЗУ по сравнению с ручным способом и исключает ошибки кодирования информации.
[24]
Страницы:
1
2
Программирование — это умная работа и поиск эффективных способов создания полезного программного обеспечения. При создании программ, веб-приложений или мобильных приложений принципы программирования остаются неизменными.
При первом изучении кода важно понимать хорошие и плохие привычки. Знание ошибок, которые делают программисты, и то, как их избежать, может помочь вам создать лучшую основу для программирования. Вот 10 очень распространенных ошибок, которых следует избегать.
1. Повторяющийся код
Не повторяйте себя — это один из основных принципов программирования. что вы встретите, как вы узнаете. Это часто сокращается до СУХОГО, и код, который написан с использованием этого принципа, называется СУХОЙ код.
Повторение кода — это легкая ловушка, в которую часто попадают, и часто требуется некоторый обзор, чтобы понять, сколько кода повторяется. Как хорошее практическое правило, если вы копируете и вставляете код, он, вероятно, повторяется и должен быть изменен.
Получите удобство, используя циклы и функции, чтобы сделать вашу работу за вас, и эта проблема исчезнет.
2. Неверные имена переменных
Переменные имеют важное значение в программировании независимо от того, на каком языке вы работаете. Поскольку они широко используются, важно иметь хорошие привычки именования переменных.
Переменные должны быть названы точно и аккуратно. Избегайте использования общих терминов, которые ничего не значат. Быстро и легко собрать что-то вместе, но когда вам нужно вернуться к своему коду позже, становится намного сложнее понять, что происходит.
Допустим, вы пишете программу, которая использует процентную ставку для расчета. Вы пишете переменную для использования в программе.
let rate = 0.1; Все, что мы действительно знаем об этой переменной, это то, что это показатель. Какой тариф?
Код будет работать просто отлично, но сложно сказать, что здесь происходит.
Вместо этого назовите ваши переменные более четко.
let interestRate = 0.1;
3. Не используя комментарии
Используйте комментарии! Комментарии — это документация вашего кода. Это лучший способ описать, что именно происходит в вашем коде по мере его роста. Конечно, кажется, немного больше работы, чтобы объяснить ваш код, но вы будете благодарить себя позже.
Написать блестящую функцию? Напишите комментарий о том, что он делает. Создание нового шаблона объекта для объектно-ориентированного программирования? Разбейте это комментарием. Комментарии используются на каждом языке, и они есть по причине.
Комментарии делают ваш код чище, легче ориентироваться и делают вас героем следующего разработчика, который, возможно, должен будет работать над вашим проектом.
4. Языковая перегрузка
Проблема, которая, кажется, перегружает растущих разработчиков, — это заграждение новых языков и технологий. Сообщества разработчиков онлайн полны вопросов о выборе языка.
Должен ли я писать в своем приложении на JavaScript или использовать фреймворк, такой как Node.JS или Express? Должен ли я использовать Python, Scala или Ruby для разработки? C или C ++ или C #? Какие рамки лучше? Должен ли я изучить MongoDB или SQL или SQLite для базы данных? Является ли этот язык устаревшим ??
Не беспокойся об этом.
Шаг назад, сосредоточиться на основах. Языки приходят и уходят, но самые успешные разработчики решают проблемы. Постройте свое программирование на алгоритмическом мышлении, и все остальное станет на свои места.
Эти технологии — всего лишь инструменты, и если вы знаете, в чем заключаются проблемы, вы будете знать, какой инструмент использовать для их решения.
5. Не резервное копирование кода
Неспособность выработать правильные привычки для защиты вашего кода разочаровывает новых разработчиков и губительна для опытных.
Как программисту, очень важно постоянно сохранять и резервировать свою работу. Это ничем не отличается от работы с важным документом или таблицей, которая часто сохраняется.
Узнайте, как управлять файлами с помощью Git. Любой контроль версий на самом деле, программное обеспечение, которое вы используете, не так важно, как умение правильно его использовать. Вы не хотите терять важные изменения, если ваш компьютер выходит из строя или выходит из строя сеть.
6. Сложный код
Кодирование не является тестом IQ. Это не проблема, чтобы увидеть, кто может использовать самые сложные функции или впечатляющие файлы. Код должен быть написан в духе эффективного решения проблем. Простой код легче писать, легче поддерживать и легче управлять.
Чтобы быть понятным, простой код не означает использование ярлыков. Простой код означает понимание сути проблемы, которую вы хотите решить, и эффективное ее решение.
7. Не задавая вопросов
Программирование трудно делать хорошо, а совершенствование означает постоянное изучение новых вещей. Лучшее, что вы можете сделать, — это читать и изучать программирование, чтобы стать лучше, но когда вам нужно какое-то дополнительное руководство, не бойтесь задавать вопросы.
Задавать вопросы могут быть пугающими, но большинство опытных программистов рады поделиться знаниями и идеями.
Просто убедитесь, что вы сделали свое исследование и приложили к нему реальные усилия. Опытные разработчики с большей вероятностью будут наставлять вас, если увидят, что вы посвятили себя обучению. Возможно, ведите журнал программирования, чтобы стать лучше. лучшим , отслеживая важные вопросы и ответы.
8. Не планировать заранее
Написание эффективного программного обеспечения начинается с хорошего планирования и дизайна. Если вы хотите построить дом, вы должны составить план до начала строительства. Программирование ничем не отличается.
Прежде чем написать хотя бы одну строку кода, определите, чего вы на самом деле хотите достичь. Знайте, в чем проблема, как вы хотите ее решить. Если вы попытаетесь выяснить проблемы во время написания кода, вы можете упустить правильные решения.
Отделите решение проблем от кодирования и жизнь хороша.
9. Не делать перерывов
Сделай перерыв, правда! Программирование ментально обременительно, и долгие часы, потянув ваш мозг до предела, в конечном итоге измотают вас. Даже хуже, чем усталость, вы можете страдать от головных болей или болей в шее, которые являются признаками компьютерного напряжения глаз.
Когда вы попали в стену, пришло время сделать перерыв. Отойди от экрана немного и сделай то, что тебе нравится. Прочитайте книгу, отправляйтесь на улицу, отправляйтесь в поход, поужинайте, все, что вас увлекает.
Вы будете морально обновлены, и когда вы вернетесь, вы можете найти новую перспективу в вашем коде.
10. Не веселиться
Программирование может быть сложным, разочаровывающим, а иногда и совершенно бесполезным. Убедитесь, что вам нравятся мелочи, которые вам нравятся в кодировании, и не забудьте немного повеселиться.
Занимаетесь ли вы этим, решая сложные задачи, создавая красивые дизайны или просто изучая новые навыки, используйте то, что вы любите, чтобы продолжать работать. В кодировании есть что любить, так что вдохновляйтесь! Будьте взволнованы, чтобы сделать что-то новое, и доведите это до конца.
Не делайте эти ошибки программирования
Легко попасть в рутину, либо пытаясь понять, что должно быть простым, либо пытаясь вспомнить, что делает какой-то код. В любом случае, избегайте ошибок, и ваш код улучшится.
Все еще борется? Не забывайте, что есть множество увлечений для программистов, которые не связаны с кодом для программистов, которые не привлекают программистов Кодекс для программистов, которые не задействуют код






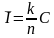
 азбуке Морзе каждая буква алфавита, все цифры и наиболее важные знаки препинания имеют свой код, состоящий из череды коротких и длинных сигналов, часто называемых «точками и тире». Так, A — это «•—», B — «—•••», и т.д. В отличие от большинства шифров, азбука Морзе используется не для затруднения чтения сообщений, а наоборот, для облегчения их передачи (с помощью телеграфа). Длинные и короткие сигналы посылаются с помощью включения и выключения электрического тока. Телеграф и азбука Морзе навсегда изменили мир, сделав возможной молниеносную передачу информации между разными странами, а также сильно повлияли на стратегию ведения войны, ведь теперь можно было можно осуществлять почти мгновенную коммуникацию между войсками.1
азбуке Морзе каждая буква алфавита, все цифры и наиболее важные знаки препинания имеют свой код, состоящий из череды коротких и длинных сигналов, часто называемых «точками и тире». Так, A — это «•—», B — «—•••», и т.д. В отличие от большинства шифров, азбука Морзе используется не для затруднения чтения сообщений, а наоборот, для облегчения их передачи (с помощью телеграфа). Длинные и короткие сигналы посылаются с помощью включения и выключения электрического тока. Телеграф и азбука Морзе навсегда изменили мир, сделав возможной молниеносную передачу информации между разными странами, а также сильно повлияли на стратегию ведения войны, ведь теперь можно было можно осуществлять почти мгновенную коммуникацию между войсками.1