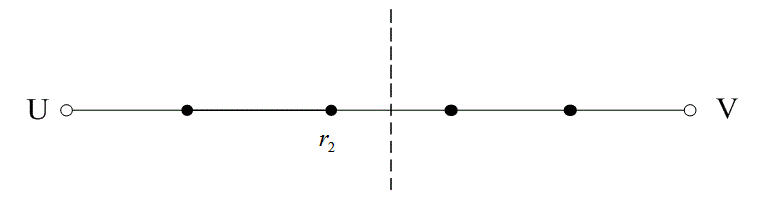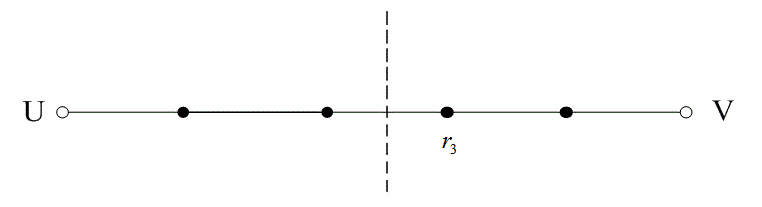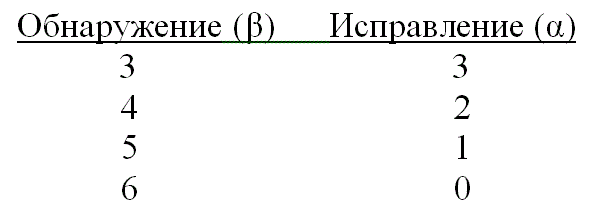Как декодер обнаруживает ошибку

Процедура
декодирования циклического кода с
обнаружением ошибок, по аналогии с
процессом кодирования основана на
использовании свойства делимости без
остатка кодового многочлена Р(x)
циклического (n,m)-кода
на порождающий многочлен g(x).
Поэтому алгоритм декодирования включает
в себя деление принятого кодового слова,
описываемого многочленом F(x)
на g(x),
вычисление и анализ остатка R(x).
Если R(x)=0,
то принятое кодовое слово считается
неискаженным. Если R(x)0,
то принятое кодовое слово стирается и
формируется сигнал «ошибка».

2 Способы декодирования с исправлением ошибок

Декодирование
заключается в определении номера
искаженного разряда и его автоматического
исправления. А также отделения
информационных разрядов от контрольных.

Рассмотрим три
методики декодирования

Определение
искаженного разряда с помощью матрицы
ошибок.

Матрица одиночных
ошибок имеет вид

,
где
—
единичная матрица;— прямоугольная проверочная матрица.

Строки матрицы
определяются из выражений

— остаток от деления
на образующий полином,

где
— значениеi-той
строки матрицы
;

i
— номер строки матрицы
.

Пример. Матрица
для (7,4)-кода на основе порождающего
многочленаимеет вид

.

Единичная матрица
размерности 7х7

.

Рассчитаем
проверочную матрицу
.

При
.

Определим остаток
от деления
на образующий полином.

.

При
.

Определим остаток
от деления
на образующий полином.

.

При
.

Определим остаток
от деления
на образующий полином.

111.

При
.

101.

При
.

100.

При
.

010.

При
.

001.

Тогда матрица
ошибок

Для определения
искаженного разряда необходимо определить
остаток от деления принятой кодовой
комбинации
на порождающий многочлен.

Пример

Внесем искажения
в четвертый разряд

Находим остаток

1 0 1 0 1 0 0
 1 1 0 1
1 1 1 1
 1 1 0 1
0 0 1 0 0 0
 1 1 0 1
1 0 1	— остаток

Находим
строку в матрице ошибок с полученным
остатком (синдромом) 1 0 1

Искаженный разряд
– это разряд в данной строке, в которой
стоит «1».

Искаженный разряд
исправляем посредством сложения строки
в матрице ошибок с полученной комбинацией

.

Сообщение исправлено.

Метод
дополнительного деления первоначального
остатка на образующий многочлен

Метод дополнительного
деления основывается на предыдущем
методе т.к. каждый такт дополнительного
деления (приписывания нуля справа)
соответствует переходу от данной строки
матрицы ошибок (строка с первоначальным
остатком) к строке следующей вверх
матрицы.

Дополнительное
деление продолжается до получения
остатка с «1» в первом разряде и нулями
в остальных разрядах, потому что этот
остаток равен остатку последней строки
матрицы ошибок. Отсчет искаженного
разряда производится от старшего разряда
сообщения, по количеству тактов
дополнительного деления. Такой отсчет
соответствует возвратному движению в
матрице ошибок.

Пример.

Внесем искажения
в четвертый разряд

Находим остаток

1 0 1 0 1 0 0
 1 1 0 1
1 1 1 1
 1 1 0 1
0 0 1 0 0 0
 1 1 0 1
1 0 1	— остаток

Дополниетльное
деление

1 0 1 0	Дополнительное деление 1
 1 1 0 1
1 1 1 0	Дополнительное деление 2
 1 1 0 1
0 0 1 1 0 0	Дополнительное деление 3, 4
 1 1 0 1
0 0 1	— остаток

Понадобилось 4
такта дополнителоного деления. Тогда

.

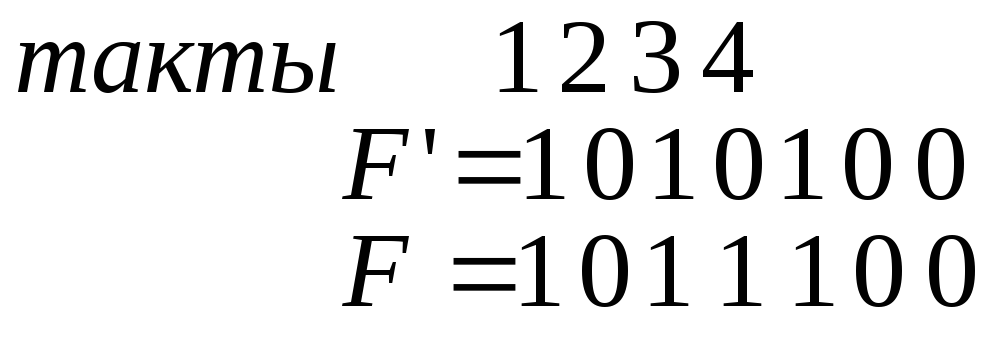
Четвертый такт
указывает номер искаженного разряда,
который исправляем.

Метод циклических
сдвигов

Метод циклических
сдвигов заключается в следующем:

1. Находится
   остаток от деления
   на.
   Если остаток равен нулю, то ошибок нет.

2. Если
   остаток отличен от нуля, определяется
   вес остатка
   и выполнения условия,
   где—
   количество исправляемых ошибок.

Если условие
выполняется, то производится суммирование
по модулю 2 полученного остатка с
комбинацией, из которой он получен.
Затем производятся сдвиги вправо столько
раз сколько было сделано сдвигов влево
В результате получаем исправленной
сообщение.

1. Если
   вес остатка больше кратности исправляемых
   разрядов, то производится сдвиг влево
   полученной комбинации, т.е. умножение
   кодовой комбинации на
   .
   И снова находится остаток от деления
   и переход к п.2.

Пример.

,

.

Внесем искажения
в четвертый разряд

.

Находим остаток
1 0 1.

Вес остатка

.

1-й циклический
сдвиг

Находим остаток

0 1 0 1 0 0 1
 1 1 0 1
0 1 1 1 0
 1 1 0 1
1 1 1	— остаток

Вес остатка
.

2-й циклический
сдвиг

Находим остаток

1 0 1 0 0 1 0
 1 1 0 1
1 1 1 0
 1 1 0 1
1 1 1 0
 1 1 0 1
0 0 1 1	— остаток

Вес остатка
.

3-й циклический
сдвиг

Находим остаток

0 1 0 0 1 0 1
 1 1 0 1
0 1 0 0 0
 1 1 0 1
0 1 0 1 1
 1 1 0 1
0 1 1 0	— остаток

Вес остатка
.

4-й циклический
сдвиг

Находим остаток

1 0 0 1 0 1 0
 1 1 0 1
0 1 0 0 0
 1 1 0 1
0 1 0 1 1
 1 1 0 1
0 1 1 0 0
 1 1 0 1
0 0 0 01	— остаток

Вес остатка
.

Вес равен «1»
поэтому циклические сдвиги закончились.
Теперь необходимо остаток сложить с
той комбинацией, с которой мы его получили

1 0 0 1 0 1 0

 0 0 0 1

1 0 0 1 0 1 1

Затем производятся
сдвиги вправо столько раз, сколько было
сделано сдвигов влево

1 0 0 1 0 1 1

1-й сдвиг

1 1 0 0 1 0 1

2-й сдвиг

1 1 1 0 0 1 0

3-й сдвиг

0 1 1 1 0 0 1

4-й сдвиг

1 0 1 1 1 0 0

Сообщение исправлено

.

Свойства
циклических кодов по обнаружению ошибок

Свойства циклических
кодов полностью определяются выбранным
порождающим (образующим) многочленом
.

I. Если порождающий
многочлен
содержит более одного члена, то циклический
код обнаруживает все одиночные ошибки.
При представлении циклического кода
многочленами одиночная ошибка описывается
одночленом,
где— указывает номер искаженного разряда.
Поскольку одночлен не делится на
многочлен без остатка, то ошибка будет
обнаружена.

2. Циклический код
с порождающим многочленом
обнаруживает все нечетные ошибки.
Используя правила построения проверочной
матрицы для,
получим.
При такой проверочной матрице остаток
определяется суммой по модулю 2 всех
элементов принятой кодовой комбинации
(проверка на четность). Поэтому все
искажения на нечетном количестве позиций
будут обнаружены.

3. Циклический код
обнаруживает все одиночные и двукратные
ошибки, если разрядность кода
не больше длины циклаиспользуемого порождающего многочлена,
т.е..
Под длиной цикла многочлена понимают
минимальный показатель степени двучлена,
при котором этот двучлен делится без
остатка на образующий многочлен.

4. Циклический код
с многочленом
степениобнаруживает все групповые ошибки
длительностью вразрядов и менее. Любая групповая ошибка
вразрядов описывается многочленом
степени,
т.е..
Многочлен же степенина многочлен степенине делится и, таким образом, ошибка
обнаруживается.

5. Циклический код
с порождающим многочленом
степенине обнаруживаетчасть ошибок-й
кратности.

6. Циклический код
с порождающим многочленом
степенине обнаруживаетчасть ошибок более-й
кратности.

Анализируя
перечисленные свойства циклического
кода, можно увидеть, что способности
кода по обнаружению и исправлению ошибок
полностью определяются выбранным
образующим многочленом
.

При обнаружении
ошибок стандартные многочлены имеют
вид:
,при длине кодовой комбинации,

или
,при длине кодовой комбинации;

,
при длине кодовой комбинации.

Разработан ряд
методик по выбору порождающего многочлена
.
В литературе коды называют по фамилиям
ученых, предложивших ту или иную методику.
Так получили свое название коды
Боуза-Чоудхури-Хоквингема (БЧХ), коды
Рида-Соломона, коды Файра и др.

Укороченные
циклические коды

Циклические коды
предполагают равенство разрядности
формируемой кодовой комбинации длине
цикла порождающего
многочлена, т.е.
.
Однако, это требование на практике
трудно выполнимо, поскольку разрядность
комбинаций, выдаваемых источником
информации, зачастую отличается от
целесообразной, в результате чего.
В этих случаях циклический код
преобразуют
и используют так называемый укороченный
циклический код, который получается из
циклического путем исключения в нем
определенного числа разрядов.

При этом число
столбцов проверочной матрицы
уменьшается на величину, равную числу
исключаемых информационных разрядов,
причем исключаются столбцы с наивысшими
номерами. Свойства кода по обнаружению
ошибок при этом не изменяются.

Принципы построения
кодирующих и декодирующих устройств
циклических кодов

Кодирующие и
декодирующие устройства циклических
кодов строятся на основе регистров с
обратными связями. Такие регистры иногда
называют многотактными линейными
переключающими схемами. При кодировании
и декодировании циклических кодов
получаемый остаток содержит число
разрядов, равное показателю степени
порождающего многочлена
.
Поэтому регистр с обратными связями
(ОС) должен содержатьячеек памяти. Как ранее указывалось,
столбцы проверочной матрицыявляются остатками от деления одночленана.
Разделить жепри помощи регистра с ОС это значит
осуществить сдвиг записанной в этот
регистр „1″ натактов после ввода ее в первую ячейку.
Таким образом, при каждом сдвиге
записанной в регистр „1” должен
получаться остаток, соответствующий
делениюна.
Следовательно, содержание регистра при
каждом тактовом сдвиге должно
соответствовать содержанию столбца
проверочной матрицы.

В качестве примера
на рис. 8.15 показаны схема регистра с ОС
для порождающего многочлена
и состояние ячеек этого регистра при
сдвиге «1» записанных в первую ячейку
(табл. 8.19). На конкретном примере покажем,
что данный регистр производит операцию
деления.

Пусть требуется
закодировать кодовую комбинацию вида
1 1 0 1, многочлен которой имеет вид
.

Разделим многочлен
и отметим остатки, полученные перед
каждым следующим тактом деления:

	х 6+ х 5+ х 3	х 3+ х+1
	х 6+ х 4+ х 3
	x5+ х 4
	x5+ х3+ х2
	x4 +х3+х2
	x4 +х2+ x
	х3+ x
	х 3+ х+1
	1	— остаток

Рис. 8.15. Схема
регистра с ОС для порождающего многочлена
.

Табл. 8.19. К пояснению
процесса кодирования

Деление сводится
к последовательному сложению по модулю
2 делителя со старшими разрядами делимого
или полученного остатка. Регистр с
обратными связями производит аналогичные
операции. Определим содержание регистра
перед каждым тактом деления и сравним
их с остатками, полученными путем
обычного деяния.

Процесс деления
в регистре производится только при
поступлении «1» в цепь обратной
связи. Поэтому содержание регистра, при
котором «1» находится в последней
ячейке, будет являться остатком перед
следующим тактом деления. В табл. 8.19
показано содержание ячеек регистра по
тактам. Сравнение остатков, полученных
как при обычном делении, так и при делении
с помощью регистра, показывает, что они
полностью совпадают.

Регистры с обратными
связями в соответствии с выбранным
порождающим многочленом строятся по
следующим правилам:

1. Число ячеек
регистра выбирают равным степени
порождающего многочлена
.

2. Количество
сумматоров по модулю 2 берется на единицу
меньше числа ненулевых членов порождающего
многочлена.

3. Входы всех ячеек
регистра обозначают
.
Выход последней ячейки обозначается, а вход первой —.

Рис 8.16. Схема
регистра с ОС для порождающего многочлена
с обозначением.

4. Сумматоры по
модулю 2 устанавливаются на входе тех
ячеек, для которых в формуле порождающего
многочлена
имеет ненулевое значение. Например, для(рис. 8.16) сумматоры устанавливаются на
входах ячеек 1 и 2 триггеров.

5. Выход последней
ячейки соединяется со входами сумматоров.

6. Выходы предыдущих
ячеек соединяются со входами последующих
через сумматоры или без них, в зависимости
от того, установлены они между ячейками
или нет.

Рис.26.2
Кодирующее устройство

Структурная схема
кодирующего устройства при порождающем
многочлене
показана на рис.8.17. В регистре с обратными
связями передаваемая кодовая комбинация
делится на исходный многочлен. При
помощи линии задержки передаваемая
комбинация смещается наразрядов (в данном случае=4),
что равносильно умножению многочлена,
отображающего передаваемую кодовую
комбинацию, на.

Устройство
функционирует следующим образом.
Передаваемая кодовая комбинация
последовательно подается на вход
регистра и линии задержки. Ключ
находится в положений «1» ключ— в положении «Включено»
(рис.8.18).

После того как
последний импульс с выхода линии задержки
передан в линию связи, ключ
.
переключается в положение ,, 2″— в положение „Выключено» и содержимое
регистра (остаток от деления) передается
в линию связи (рис.8.19).

Приведенная схема
кодирующего устройства обладает одним
существенным недостатком. Кодированное
сообщение задерживается на число тактов,
равное числу ячеек регистра. Устранить
такой недостаток можно при использовании
кодирующего.устройства без линии
задержки. В качестве примера на рис.8.20
изображена структурная схема такого
устройства с
.

Регистры с обратными
связями для таких кодирующих устройств
строятся по правилам, указанным ранее.
Однако один из сумматоров устанавливается
не на входе первой ячейки памяти, а на
выходе последней ячейки.

Декодирующие
устройства также строятся на основе
использования регистров с обратными
связями. На рис.8.21 приведена структурная
схема декодирующего устройства,
предназначенного для обнаружения
ошибок. После приема кодовой комбинации
в регистре с обратными связями образуется
остаток
.
Если этот остаток равен 0, то сигнал
запрета на выдачу принятой кодовой
комбинации потребителю не выдается.

При использовании
циклических кодов в качестве кодов с
исправлением ошибок схема декодирующего
устройства усложняется.

Кратко рассмотрим
методику построения таких декодирующих
устройств для наиболее простого метода
исправления ошибок -последовательного.

Этот метод основан
на следующем свойстве. Если возникшая
в кодовой комбинации ошибка исправляема,
то после введения принятой кодовой
комбинации в регистр с ОС можно
восстановить вектор ошибок. После
поразрядного сложения этого вектора с
вектором, отображающим принятую кодовую
комбинацию, ошибка исправляется.
Структурная схема такого декодирующего
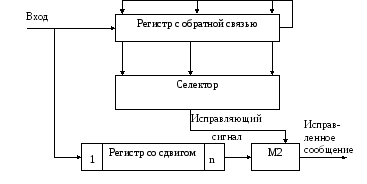
устройства приведена на рис.8.22.

Принятая кодовая
комбинация поразрядно поступает в
регистр со сдвигом и в регистр с ОС.
Затем принятая комбинация последовательным
кодом через сумматор по модулю 2 (М2)
выдается потребителю. В то время, когда
искаженный разряд будет на выходе
регистра со сдвигом, при исправляемых
кодом ошибках содержание регистра с ОС
будет вполне определенным. Селектор
выделяет эту известную кодовую комбинацию
и выдает на сумматор по модулю 2 импульс
для исправления искаженного разряда.
Одновременно в регистр с ОС записывается
кодовая комбинация, при помощи которой
устраняется влияние исправленного
разряда на содержание этого регистра.

Рис 8.22. Декодирующее
устройство с исправлением ошибок

Вероятности
ошибочного декодирования циклических
кодов

Вектором ошибки
называется двоичная последовательность
длины
,
в которой единицы стоят на позициях
символов принятых с ошибкой. Отсюда
вероятность не обнаружения ошибки
заданным кодом равна вероятности
появления в заданном дискретном канале
векторов ошибок, совпадающих с кодовыми
словами

Относительно
просто эти вероятности могут быть
рассчитаны для двоичного симметричного
канала без памяти. В таком канале каждый
двоичный символ с некоторой фиксированной
вероятностью
принимается правильно и с вероятностьюизменяется помехой на обратный.
Передача/прием каждого символа полагается
событием независимым (канал без памяти).

Если по такому
каналу передается кодовое слово длины
,
то вероятность
того, что не произойдет ни одной ошибки,
равна.

Вероятность

того, что
будет одна ошибка в заданном символе,
равна
.

Вероятность того,
что слово на выходе канала будет
отличаться от передан­ного слова в
заданных
разрядах, т.е. вектор ошибок содержитединиц, равна

.

Вероятность того,
что слово на выходе канала будет
отличаться от передан­ного слова в
любых
разрядах, равна

,

где

—
число сочетаний из

по
.

Предположим, что
некоторый линейный код (5,3) содержит
одно нулевое слово (как всякий линейный
код), два слова, вес которых равен 2,
четыре слова — весом 3, одно слово —
весом 4 (всего
слов).

Вероятность
необнаруживаемой этим кодом ошибки
равна вероятности по­явления в ДСК
векторов ошибок, совпадающих с кодовыми
словами, т.е.:

В режиме исправления
ошибок декодер вычисляет остаток

от деления
принятой последовательности

на
.
Этот остаток
называют синдромом.
Принятый
полином

представляет
собой сумму по модулю 2 переданного
слова

и вектора
ошибок
:

.

Тогда синдром
,
так как по
определению циклического кода
.
Некоторому синдрому
может быть
поставлен в соот­ветствие определенный
вектор ошибок
.
Тогда
переданное слово
находят, складывая.

Однако один и тот
же синдром может соответствовать

различным
векто­рам ошибок. Предположим, синдром
соответствует вектору ошибок.
Но и все векторы ошибок, равные сумме,
где— любое кодовое слово, будут давать тот
же синдром. Поэтому, поставив в соответствие
синдромувектор ошибок,
мы будем
осуществлять правильное декодирование
в случае, когда действительно вектор
ошибок равен
,
во всех остальныхслучаях декодирование будет ошибочным.

Для уменьшения
вероятности ошибки декодирования из
всех возможных векторов ошибок, дающих
один и тот же синдром, следует выбирать
в качестве исправляемого наиболее
вероятный в заданном канале.

Например, для
двоичного симметричного канала, в
котором вероятность

ошибочного
приема двоичного символа существенно
меньше вероятности

правильного
приема, вероятность появления векторов
ошибок уменьшается с увеличением их
веса
.
В этом случае следует исправлять в
первую очередь вектор ошибок меньшего
веса.

Если кодом могут
быть исправлены только все векторы
ошибок веса
и меньше, то любой вектор ошибки веса
отдоп будет
приводить к ошибоч­ному декодированию.

Вероятность
ошибочного декодирования будет равна
вероятности

появления
векторов ошибок веса
и больше в заданном канале. Для ДСК эта
вероятность будет равна

Общее число
различных векторов ошибок, которые
может исправлять цик­лический код,
равно числу ненулевых синдромов
.

Соседние файлы в папке Пособие ТЕЗ_рус12

• #
• #
• #
• #
• #
• #
• #
• #
• #

6.5.1. Весовой коэффициент двоичных векторов и расстояние между ними

6.5.2. Минимальное расстояние для линейного кода

6.5.3. Обнаружение и исправление ошибок

6.5.3.1. Распределение весовых коэффициентов кодовых слов

6.5.3.2.Одновременное обнаружение и исправление ошибок

6.5.4. Визуализация пространства 6-кортежей

6.5.5. Коррекция со стиранием ошибок

6.5.1. Весовой коэффициент двоичных векторов и расстояние между ними

Конечно же, понятно, что правильно декодировать можно не все ошибочные комбинации. Возможности кода для исправления ошибок в первую очередь определяются его структурой. Весовой коэффициент Хэмминга (Hamming weight) w(U) кодового слова U определяется как число ненулевых элементов в U. Для двоичного вектора это эквивалентно числу единиц в векторе. Например, если U=100101101, то w(U) = 5. Расстояние Хэмминга (Hamming distance) между двумя кодовыми словами U и V, обозначаемое как d(U, V), определяется как количество элементов, которыми они отличаются.

U=100101101

V=011110100

d(U,V)=6

Согласно свойствам сложения по модулю 2, можно отметить, что сумма двух двоичных векторов является другим двоичным вектором, двоичные единицы которого расположены на тех позициях, которыми эти векторы отличаются.

U + V=111011001

Таким образом, можно видеть, что расстояние Хэмминга между двумя векторами равно весовому коэффициенту Хэмминга их суммы, т.е. d(U, V) = w(U + V). Также видно, что весовой коэффициент Хэмминга кодового слова равен его расстоянию Хэмминга до нулевого вектора.

6.5.2. Минимальное расстояние для линейного кода

Рассмотрим множество расстояний между всеми парами кодовых слой в пространстве Vn. Наименьший элемент этого множества называется минимальным расстоянием кода и обозначается dmin. Как вы думаете, почему нас интересует именно минимальное расстояние, а не максимальное? Минимальное расстояние подобно наиболее слабому звену в цепи, оно дает нам меру минимальных возможностей кода и, следовательно, характеризует его мощность.

Как обсуждалось ранее, сумма двух произвольных кодовых слов дает другой элемент пространства кодовых слов. Это свойство линейных кодов формулируется просто: если U и V — кодовые слова, то и W = U + V тоже должно быть кодовым словом. Следовательно, расстояние между двумя кодовыми словами равно весовому коэффициенту третьего кодового слова, т.е. d(U, V) = w(U + V) = w(W). Таким образом, минимальное расстояние линейного кода можно определить, не прибегая к изучению расстояний между всеми комбинациями пар кодовых слов. Нам нужно лишь определить вес каждого кодового слова (за исключением нулевого вектора) в подпространстве; минимальный вес соответствует минимальному расстоянию dmin. Иными словами, dmin соответствует наименьшему из множества расстояний между нулевым кодовым словом и всеми остальными кодовыми словами.

6.5.3. Обнаружение и исправление ошибок

Задача декодера после приема вектора r заключается в оценке переданного кодового слова Ui. Оптимальная стратегия декодирования может быть выражена в терминах алгоритма максимального правдоподобия (см. приложение Б); считается, что передано было слово Ui, если

(6.41)

Поскольку для двоичного симметричного канала (binary symmetric channel — BSC) правдоподобие Ui относительно r обратно пропорционально расстоянию между r и U, можно сказать, что передано было слово Ui, если

(6.42)

Другими словами, декодер определяет расстояние между r и всеми возможными переданными кодовыми словами Uj, после чего выбирает наиболее правдоподобное Uj, для которого

(6.43)

где М = 2^k — это размер множества кодовых слов. Если минимум не один, выбор между минимальными расстояниями является произвольным. Наше обсуждение метрики расстояний будет продолжено в главе 7.

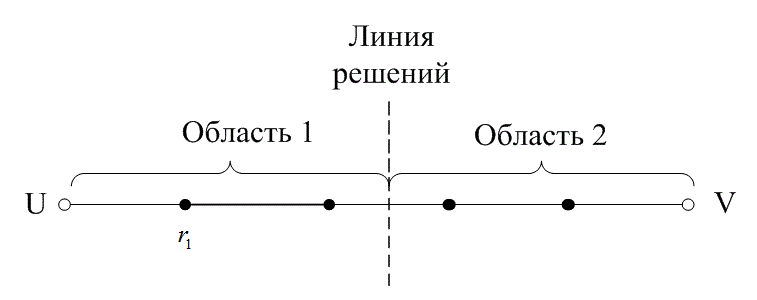
На рис. 6.13 расстояние между двумя кодовыми словами U и V показано как расстояние Хэмминга. Каждая черная точка обозначает искаженное кодовое слово. На рис. 6.13, а проиллюстрирован прием вектора r1 находящегося на расстоянии 1 от кодового слова U и на расстоянии 4 от кодового слова V. Декодер с коррекцией ошибок, следуя стратегии максимального правдоподобия, выберет при принятом векторе r1 кодовое слово U. Если r1 получился в результате появления одного ошибочного бита в переданном векторе кода U, декодер успешно исправит ошибку. Но если же это произошло в результате 4-битовой ошибки в векторе кода V, декодирование будет ошибочным. Точно так же, как показано на рис. 6.13, б, двойная ошибка при передаче U может привести к тому, что в качестве переданного вектора будет ошибочно определен вектор r2, находящийся на расстоянии 2 от вектора U и на расстоянии 3 от вектора кода V. На рис. 6.13 показана ситуация, когда в качестве переданного вектора ошибочно определен вектор r3, который находится на расстоянии 3 от вектора кода U и на расстоянии 2 от вектора V. Из рис. 6.13 видно, что если задача состоит только в обнаружении ошибок, а не в их исправлении, то можно определить искаженный вектор — изображенный черной точкой и представляющий одно-, двух-, трех- и четырехбитовую ошибку. В то же время пять ошибок при передаче могут привести к приему кодового слова V, когда в действительности было передано кодовое слово U; такую ошибку невозможно будет обнаружить.

Из рис. 6.13 можно видеть, что способность кода к обнаружению и исправлению ошибок связана с минимальным расстоянием между кодовыми словами. Линия решения на рисунке служит той же цели, что и в процессе демодуляции, — для разграничения областей решения.

а)

б)

в)

Рис. 6.13. Возможности определения и исправления ошибок: а) принятый вектор r1; б) принятый вектор r2; в) принятый вектор r3

В примере, приведенном на рис. 6.13, критерий принятия решения может быть следующим: выбрать U, если r попадает в область 1, и выбрать V, если r попадает в область 2. Выше показывалось, что такой код (при dmin = 5) может исправить две ошибки. Вообще, способность кода к исправлению ошибок t определяется, как максимальное число гарантированно исправимых ошибок на кодовое слово, и записывается следующим образом [4].

(6.44)

Здесь означает наибольшее целое, не превышающее х. Часто код, который исправляет все искаженные символы, содержащие ошибку в t или меньшем числе бит, также может исправлять символы, содержащие t +1 ошибочных бит. Это можно увидеть на рис. 6.11. В этом случае dmin = 3, поэтому из уравнения (6.44) можно видеть, что исправимы все ошибочные комбинации из t = 1 бит. Также исправима одна ошибочная комбинация, содержащая / +1 (т.е. 2) ошибочных бит. Вообще, линейный код (n, k), способный исправлять все символы, содержащие t ошибочных бит, может исправить всего 2^n—k ошибочных комбинаций. Если блочный код с возможностью исправления символов, имеющих ошибки в t бит, применяется для исправления ошибок в двоичном симметричном канале с вероятностью перехода р, то вероятность ошибки сообщения Рм(вероятность того, что декодер совершит неправильное декодирование и п-битовый блок содержит ошибку) можно оценить сверху, используя уравнение (6.18).

(6.45)

Оценка переходит в равенство, если декодер исправляет все ошибочные комбинации, содержащие до t ошибочных бит включительно, но не комбинации с числом ошибочных бит, большим t. Такие декодеры называются декодерами с ограниченным расстоянием. Вероятность ошибки в декодированном бите РB зависит от конкретного кода и декодера. Приближенно ее можно выразить следующим образом [5].

(6.46)

В блочном коде, прежде чем исправлять ошибки, необходимо их обнаружить. (Или же код может использоваться только для определения наличия ошибок.) Из рис. 6.13 видно, что любой полученный вектор, который изображается черной точкой (искаженное кодовое слово), можно определить как ошибку. Следовательно, возможность определения наличия ошибки дается следующим выражением.

(6.47)

Блочный код с минимальным расстоянием dmin гарантирует обнаружение всех ошибочных комбинаций, содержащих dmin — 1 или меньшее число ошибочных бит. Такой код также способен обнаружить и большую ошибочную комбинацию, содержащую dmin или более ошибок. Фактически код (n, k) может обнаружить 2ⁿ – 2^k ошибочных комбинаций длины п. Объясняется это следующим образом. Всего в пространстве 2ⁿ n-кортежей существует 2ⁿ -1 возможных ненулевых ошибочных комбинаций. Даже правильное кодовое слово — это потенциальная ошибочная комбинация. Поэтому всего существует 2^k -1 ошибочных комбинаций, которые идентичны 2^k -1 ненулевым кодовым словам. При появлении любая из этих 2^k — 1 ошибочных комбинаций изменяет передаваемое кодовое слово Uj на другое кодовое слово Uj. Таким образом, принимается кодовое слово Uj и его синдром равен нулю. Декодер принимает Uj за переданное кодовое слово, и поэтому декодирование дает неверный результат. Следовательно, существует 2^k -1 необнаружимых ошибочных комбинаций. Если ошибочная комбинация не совпадает с одним из 2^k кодовых слов, проверка вектора r с помощью синдромов дает ненулевой синдром и ошибка успешно обнаруживается. Отсюда следует, что существует ровно 2ⁿ-2^k выявляемых ошибочных комбинаций. При больших n, когда 2^k<<2ⁿ, необнаружимой будет только незначительная часть ошибочных комбинаций.

6.5.3.1. Распределение весовых коэффициентов кодовых слов

Пусть Aj — количество кодовых слов с весовым коэффициентом j в линейном коде (п, k). Числа A0,A1,…,An называются распределением весовых коэффициентов этого кода. Если код применяется только для обнаружения ошибок в двоичном симметричном канале, то вероятность того, что декодер не сможет определить ошибку, можно рассчитать, исходя из распределения весовых коэффициентов кода [5].

(6.48)

где р — вероятность перехода в двоичном симметричном канале. Если минимальное расстояние кода равно dmin значения от А1 до , равны нулю.

Пример 6.5. Вероятность необнаруженной ошибки в коде

Пусть код (6,3), введенный в разделе 6.4.3, используется только для обнаружения наличия ошибок. Рассчитайте вероятность необнаруженной ошибки, если применяется двоичный симметричный канал, а вероятность перехода равна 10^-2.

Решение

Распределение весовых коэффициентов этого кода выглядит следующим образом: A0=1, А1= А2 = 0, A3 = 4, A5 = 0, A6 = 0. Следовательно, используя уравнение (6.48), можно записать следующее.

Для р = 10^-2 вероятность необнаруженной ошибки будет равна 3,9 х 10^-6.

6.5.3.2. Одновременное обнаружение и исправление ошибок

Возможностями исправления ошибок с максимальным гарантированным (t), где t определяется уравнением (6.44), можно пожертвовать в пользу определения класса ошибок. Код можно использовать для одновременного исправления α и обнаружения β ошибок, причем , а минимальное расстояние кода дается следующим выражением [4].

(6.49)

При появлении t или меньшего числа ошибок код способен обнаруживать и исправлять их. Если ошибок больше t, но меньше е+1, где е определяется уравнением (6.47), код может определять наличие ошибок, но исправить может только некоторые из них. Например, используя код с dmin = 7. можно выполнить обнаружение и исправление со следующими значениями α и β.

Заметим, что исправление ошибки подразумевает ее предварительное обнаружение. В приведенном выше примере (с тремя ошибками) все ошибки можно обнаружить и исправить. Если имеется пять ошибок, их можно обнаружить, но исправить можно только одну из них.

6.5.4. Визуализация пространства 6-кортежей

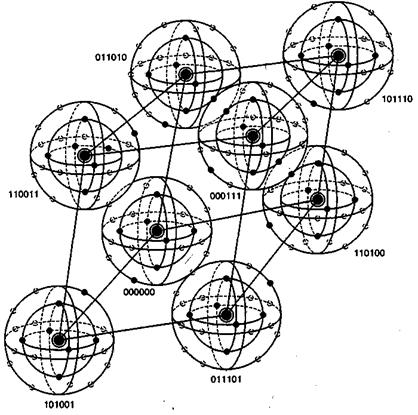
На рис. 6.14 визуально представлено восемь кодовых слов, фигурирующих в примере из раздела 6.4.3. Кодовые слова образованы посредством линейных комбинаций из трех независимых 6-кортежей, приведенных в уравнении (6.26); сами кодовые слова образуют трехмерное подпространство. На рисунке показано, что такое подпространство полностью занято восемью кодовыми словами (большие черные круги); координаты подпространства умышленно выбраны неортогональными. На рис. 6.14 предпринята попытка изобразить все пространство, содержащее шестьдесят четыре 6-кортежей, хотя точно нарисовать или составить такую модель невозможно. Каждое кодовое слово окружают сферические слои или оболочки. Радиус внутренних непересекающихся слоев — это расстояние Хэмминга, равное 1; радиус внешнего слоя — это расстояние Хэмминга, равное 2. Большие расстояния в этом примере не рассматриваются. Для каждого кодового слова два показанных слоя заняты искаженными кодовыми словами. На каждой внутренней сфере существует шесть таких точек (всего 48 точек), представляющих шесть возможных однобитовых ошибок в векторах, соответствующих каждому кодовому слову. Эти кодовые слова с однобитовыми возмущениями могут быть соотнесены только с одним кодовым словом; следовательно, такие ошибки могут быть исправлены. Как видно из нормальной матрицы, приведенной на рис. 6.11, существует также одна двухбитовая ошибочная комбинация, которая также поддается исправлению. Всего существует разных двухбитовых ошибочных комбинаций, которыми может быть искажено любое кодовое слово, но исправить можно только одну из них (в нашем примере это ошибочная комбинация 010001). Остальные четырнадцать двухбитовых ошибочных комбинаций описываются векторами, которые нельзя однозначно сопоставить с каким-либо одним кодовым словом; эти не поддающиеся исправлению ошибочные комбинации дают векторы, которые эквивалентны искаженным векторам двух или большего числа кодовых слов. На рисунке все (56) исправимые кодовые слова с одно- и двухбитовыми искажениями показаны маленькими черными кругами. Искаженные кодовые слова, не поддающиеся исправлению, представлены маленькими прозрачными кругами.

Рис, 6.14. Пример восьми кодовых слов в пространстве 6-кортежей

При представлении свойств класса кодов, известных как совершенные коды (perfect code), рис. 6.14 весьма полезен. Код, исправляющий ошибки в t битах, называется совершенным, если нормальная матрица содержит все ошибочные комбинации из t или меньшего числа ошибок и не содержит иных образующих элементов классов смежности (отсутствует возможность исправления остаточных ошибок). В контексте рис. 6.14 совершенный код с коррекцией ошибок в t битах — это такой код, который (при использовании обнаружения по принципу максимального правдоподобия) может исправить все искаженные кодовые слова, находящиеся на расстоянии Хэмминга t (или ближе) от исходного кодового слова, и не способен исправить ни одну из ошибок, находящихся на расстоянии, превышающем t.

Кроме того, рис. 6.14 способствует пониманию основной цели поиска хороших кодов. Предпочтительным является пространство, максимально заполненное кодовыми словами (эффективное использование введенной избыточности), а также желательно, чтобы кодовые слова были по возможности максимально удалены друг от друга. Очевидно, что эти цели противоречивы.

6.5.5. Коррекция со стиранием ошибок

Приемник можно сконструировать так, чтобы он объявлял символ стертым, если последний принят неоднозначно либо обнаружено наличие помех или кратковременных сбоев. Размер входного алфавита такого канала равен Q, а выходного —Q + 1; лишний выходной символ называется меткой стирания (erasure flag), или просто стиранием (erasure). Если демодулятор допускает символьную ошибку, то для ее исправления необходимы два параметра, определяющие ее расположение и правильное значение символа. В случае двоичных символов эти требования упрощаются — нам необходимо только расположение ошибки. В то же время, если демодулятор объявляет символ стертым (при этом правильное значение символа неизвестно), расположение этого символа известно, поэтому декодирование стертого кодового слова может оказаться проще исправления ошибки. Код защиты от ошибок можно использовать для исправления стертых символов или одновременного исправления ошибок и стертых символов. Если минимальное расстояние кода равно dmin, любая комбинация из ρ или меньшего числа стертых символов может быть исправлена при следующем условии [6].

(6.50)

Предположим, что ошибки появляются вне позиций стирания. Преимущество исправления посредством стираний качественно можно выразить так: если минимальное расстояние кода равно dmin, согласно уравнению (6.50), можно восстановить dmin-1 стирание. Поскольку число ошибок, которые можно исправить без стирания информации, не превышает (dmin-1)/2, то преимущество исправления ошибок посредством стираний очевидно. Далее, любую комбинацию из α ошибок и γ стираний можно исправить одновременно, если, как показано в работе [6],

(6.51)

Одновременное исправление ошибок и стираний можно осуществить следующим образом. Сначала позиции из у стираний замещаются нулями, и получаемое кодовое слово декодируется обычным образом. Затем позиции из у стираний замещаются единицами, и декодирование повторяется для этого варианта кодового слова. После обработки обоих кодовых слов (одно с подставленными нулями, другое — с подставленными единицами) выбирается то из них, которое соответствует наименьшему числу ошибок, исправленных вне позиций стирания. Если удовлетворяется неравенство (6.51), то описанный метод всегда дает верное декодирование.

Пример 6.6. Коррекция со стиранием ошибок

Рассмотрим набор кодовых слов, представленный в разделе 6.4.3.

000000 110100 011010 101110 101001 011101 110011 000111

Пусть передано кодовое слово 110011, в котором два крайних слева разряда приемник объявил стертыми. Проверьте, что поврежденную последовательность хx0011 можно исправить.

Решение

Поскольку , код может исправить = 2 стирания. В этом легко убедиться из рис. 6.11 или приведенного выше перечня кодовых слов, сравнивая 4 крайних правых разряда xx00l1 с каждым из допустимых кодовых слов. Действительно переданное кодовое слово — это ближайшее (с точки зрения расстояния Хэмминга) к искаженной последовательности.

Изобретение относится к технике передачи данных и может использоваться в системах с решающей обратной связью для приема информации, закодированной циклическим кодом, допускающим мажоритарную процедуру декодирования. Технический результат — повышение помехоустойчивости и точности декодирования. Декодер с обнаружением и исправлением ошибок содержит два элемента ИЛИ, регистр сдвига, девять ключей, вычислитель синдрома, сумматоры, мажоритарный элемент, сумматор по модулю два, счетчик исправлений, счетчик сдвигов, блок дискретного интегрирования, счетчик недостоверных символов и буферный регистр сдвига. Новым в декодере является введение блока дискретного интегрирования, счетчика недостоверных символов, второго элемента ИЛИ, двух ключей (восьмого и девятого) и буферного регистра сдвига, а также изменение связей между известными элементами декодера. Все это способствует повышению помехоустойчивости и точности декодирования принимаемых дискретных сигналов за счет использования принципов мажоритарного декодирования. 1 ил.

Изобретение относится к технике передачи данных и может использоваться в системах с решающей обратной связью для приема информации, закодированной циклическим кодом, допускающим мажоритарную процедуру декодирования.

Для многоканальной аппаратуры с временным объединением (разделением) цифровых каналов связи и асинхронным вводом и выводом информации с различными линейными скоростями передачи сигналов очень важным является реализация в ней декодирующего устройства, которое обеспечивало бы защиту от ошибок при передаче информации с переменными параметрами и исправление многократных ошибок. Одним из путей защиты является использование декодеров с обнаружением и исправлением ошибок при помощи корректирующих циклических кодов [1, 2].

Из известных декодеров наиболее близким по технической сущности к предлагаемому изобретению является декодер с обнаружением и исправлением ошибок, описанный в [3].

Известный декодер с обнаружением и исправлением ошибок содержит последовательно соединенные первый элемент ИЛИ, регистр сдвига, первый ключ и вычислитель синдрома, а также сумматор по модулю два, счетчик сдвигов, счетчик исправлений, второй, третий, четвертый, пятый, шестой и седьмой ключи, при этом выходы регистра сдвига через сумматоры подключены к входам мажоритарного элемента, выход которого через второй ключ подсоединен к сигнальному входу третьего ключа, к управляющему входу которого и управляющим входам первого и четвертого ключей подсоединен первый выход счетчика сдвигов, второй и третий выходы которого подключены соответственно к управляющим входам пятого и шестого ключей, причем выход первого ключа соединен с сигнальным входом пятого ключа [3].

Однако известный декодер имеет недостаточную помехоустойчивость и точность.

Целью изобретения является повышение помехоустойчивости и точности декодирования.

Поставленная цель достигается тем, что в декодер с обнаружением и исправлением ошибок, содержащий последовательно соединенные первый элемент ИЛИ, регистр сдвига, первый ключ и вычислитель синдрома, а также сумматор по модулю два, счетчик сдвигов, счетчик исправлений, второй, третий, четвертый, пятый, шестой и седьмой ключи, при этом вторые выходы регистра сдвига через сумматоры подключены к входам мажоритарного элемента, выход которого через второй ключ подсоединен к сигнальному входу третьего ключа, к управляющему входу которого и управляющим входам первого и пятого ключей подсоединен первый выход счетчика сдвигов, второй и третий выходы которого подключены соответственно к управляющим входам пятого и шестого ключей, причем выход первого ключа соединен с сигнальным входом седьмого ключа, введены последовательно соединенные блок дискретного интегрирования, счетчик недостоверных символов и второй элемент ИЛИ, а также буферный регистр сдвига, восьмой и девятый ключи, при этом второй выход счетчика недостоверных символов подключен к управляющим входам второго, четвертого и восьмого ключей, а выход блока дискретного интегрирования через девятый ключ подсоединен к первому входу первого элемента ИЛИ, ко второму входу которого через восьмой ключ подсоединен выход регистра сдвига, а к третьему входу первого элемента ИЛИ и первому входу сумматора по модулю два подключен выход третьего ключа, при этом выход регистра сдвига через последовательно соединенные четвертый и пятый ключи подсоединен к второму входу сумматора по модулю два, выход которого через счетчик исправлений подключен ко второму входу второго элемента ИЛИ, к третьим входам которого подключены выходы вычислителя синдрома, а выход второго элемента ИЛИ подключен к сигнальному входу шестого ключа, выход которого подключен к первому входу буферного регистра сдвига, к второму входу которого подключен выход седьмого ключа, причем первый выход счетчика сдвигов подключен к управляющему входу девятого ключа, при этом вход блока дискретного интегрирования является входом декодера, выходом которого является выход буферного регистра сдвига.

Сопоставительный анализ с прототипом показывает, что предлагаемый декодер с обнаружением и исправлением ошибок отличается наличием новых блоков: блока дискретного интегрирования, счетчика недостоверных символов, второго элемента ИЛИ, восьмого и девятого ключей и буферного регистра сдвига, а также их связями с остальными элементами схемы, что способствовало повышению помехоустойчивости на 10-20% по сравнению с прототипом.

Таким образом, заявляемый декодер с обнаружением и исправлением ошибок соответствует критерию изобретения «новизна». Сравнение заявляемого решения с другими техническими решениями показывает, что вновь введенные в предлагаемый декодер элементы реализуемы, хорошо известны специалистам в данной области техники и дополнительного творчества, учитывая приведенные ниже пояснения, для их воспроизведения не требуется.

Данное решение существенно отличается от известных решений в данной области техники. Заявляемое решение явным образом не следует из уровня техники и имеет изобретательский уровень.

Это позволяет сделать вывод о соответствии технического решения критерию «существенные отличия».

На чертеже представлена структурная электрическая схема предлагаемого декодера.

Декодер с обнаружением и исправлением ошибок содержит первый элемент ИЛИ 1, регистр 2 сдвига, первый ключ 3, вычислитель 4 синдрома, сумматоры 5, мажоритарный элемент 6, второй ключ 7, третий ключ 8, сумматор 9 по модулю два, счетчик 10 исправлений, четвертый ключ 11, пятый ключ 12, шестой ключ 13, счетчик 14 сдвигов, седьмой ключ 15, блок 16 дискретного интегрирования, счетчик 17 недостоверных символов, второй элемент ИЛИ 18, восьмой ключ 19, девятый ключ 20 и буферный регистр 21 сдвига.

Выход первого элемента ИЛИ 1 соединен со входом регистра 2 сдвига, выход которого через первый ключ 3 соединен со входом вычислителя 4 синдрома. Вторые выходы регистра 2 сдвига через сумматоры 5 соединены со входами мажоритарного элемента 6, выход которого через второй ключ 7 соединен с сигнальным входом третьего ключа 8. Выход третьего ключа 8 соединен одновременно с третьим входом первого элемента ИЛИ 1 и со входом сумматора 9 по модулю два, выход которого соединен со входом счетчика 10 исправлений.

Выход регистра 2 сдвига подключен ко входу четвертого ключа 11, выход которого через пятый ключ 12 соединен со вторым входом сумматора 9 по модулю два. Первый выход счетчика 14 сдвигов подключен к управляющим входам первого 3, третьего 8 и пятого 12 ключей, а второй и третий выходы счетчика сдвигов 14 подключены к управляющим входам соответственно шестого 13 и седьмого 15 ключей, к сигнальному входу которого подключен выход первого ключа 3.

Первый выход блока 16 дискретного интегрирования через счетчик 17 недостоверных символов подключен к первому входу второго элемента ИЛИ 18, ко второму входу которого подключен выход счетчика 10 исправлений, третьи входы второго элемента ИЛИ 18 соединены с выходами вычислителя 4 синдрома, а выход второго элемента ИЛИ 18 подключен к сигнальному входу шестого ключа 13, выход которого подключен к первому входу буферного регистра 21 сдвига. Второй выход блока 16 дискретного интегрирования через девятый ключ 20 соединен с первым входом первого элемента ИЛИ 1, к второму входу которого через восьмой ключ 19 подключен выход регистра 2 сдвига. Второй выход счетчика 17 недостоверных символов подключен к управляющим входам второго 7, четвертого 11 и восьмого 19 ключей. Выход седьмого ключа 15 подключен ко второму входу буферного регистра 21 сдвига. При этом вход блока 16 дискретного интегрирования является входом декодера, выходом которого является выход буферного регистра 21 сдвига.

Регистр сдвига 2, сумматоры 5, мажоритарный элемент 6, сумматор 9 по модулю два совместно со вторым 7, третьим 8, четвертым 11 и пятым 12 ключами выполняют функции устройства исправления ошибок мажоритарным способом.

Буферный регистр сдвига 21 содержит элементы памяти для хранения в них информации и выдачи ее потребителю. Одновременно он выполняет функции элемента задержки кодовых слов на время анализа элементов кодового слова, что способствует исключению возможности выдачи искаженной информации потребителю.

Декодер работает следующим образом.

На вход блока 16 дискретного интегрирования поступают элементы кодового слова, при этом каждый принимаемый кодовый элемент стробируется в Е точках, количество которых выбирается исходя из значения, равного нечетному числу, причем Е=b+2m, где b характеризует зону неопределенности блока 16 дискретного интегрирования.

Сигнал о недостоверно принятом элементе кодового слова вырабатывается в том случае, если число импульсов стробирования β находится в пределах m+1≤β≤m+b-1. Число недостоверных кодовых элементов на длине n кодового слова определяется счетчиком 17 недостоверных символов. С выхода блока 16 дискретного интегрирования элементы кодового слова поступают в регистр 2 сдвига через девятый ключ 20, открытый сигналом, поступающим со счетчика 14 сдвигов, и элемент ИЛИ 1. При записи элементов кодового слова в регистр 2 сдвига третий 8 и пятый 12 ключи закрыты сигналом со счетчика 14 сдвигов.

Если число недостоверно принятых элементов кодового слова не превышает t (число ошибок, исправляемых кодом), то начинается процесс исправления ошибок в соответствии с процедурой мажоритарного декодирования циклического кода. При этом ключи 7 и 11 открыты сигналом со счетчика 17, ключи 8 и 12 открыты после приема n элементов, ключи 20 и 3 закрыты на время исправления, равное n тактам, а ключ 19 закрыт. Если в процессе исправления ошибок в кодовом слове счетчик 10 исправлений зарегистрирует число исправлений, не превышающее t, то элементы кодового слова, записанные через ключи 7, 8 и элемент ИЛИ 1 в регистр 2 сдвига, поступают через открытые ключи 3 и 15 в вычислитель 4 синдрома и буферный регистр 21 соответственно, причем ключ 15 открывается на К тактов, а ключ 3 на n тактов.

Если при вычислении синдрома его вес оказался нулевым, то сигналом с выхода ключа 13 разрешается вывод информации из буферного регистра 21, а в случае не нулевого веса синдрома вырабатывается сигнал «ошибка», который поступает на выход ключа 13 и одновременно запрещает вывод информации с буферного регистра 21 сдвига.

Если число исправлений, зарегистрированное счетчиком 10, превышает t, то независимо от результата вычисления синдрома сигнал «ошибка» поступает на выход ключа 13 и запрещает вывод информации из буферного регистра 21.

Если счетчик 17 недостоверных символов зарегистрировал число недостоверно принятых элементов на длине n кодового слова, превышающее t, то сигналом с второго выхода счетчика 17 открывается ключ 19, закрываются ключи 7 и 11, запрещается процесс неисправления ошибок в кодовом слове, записанные в регистр 2 элементы переписываются на его вход через ключ 19 и элемент ИЛИ 1.

При этом независимо от результата вычисления синдрома на выход ключа 13 поступает сигнал «Ошибка» с другого выхода счетчика 17 недостоверных символов через элемент ИЛИ 18 и ключ 13, запрещая выдачу информации потребителю. Изменяя первый порог (второй выход счетчика 17) от 0 до t, второй порог (первый выход счетчика 17) от t до n и ширину b зоны неопределенности от 1 до Е, можно изменять скорость передачи информации и помехоустойчивость декодера в зависимости от качества канала.

Таким образом, при обнаружении числа недостоверно принятых элементов в кодовом слове, превышающего t, процесс неисправления ошибок запрещается, а на выходе декодера появляется сигнал «Ошибка», в результате чего уменьшается вероятность размножения ошибок в процессе мажоритарного декодирования циклического кода, повышается помехоустойчивость декодера.

Использование новых элементов (блока дискретного интегрирования, счетчика недостоверных символов, второго элемента ИЛИ с входами, буферного регистра сдвига, восьмого и девятого ключей) выгодно отличает предлагаемый декодер от известного, так как в соответствии с проведенными по известной методике расчетам повышается на 10-20% по сравнению с прототипом точность исправления ошибок (декодирования) и соответственно увеличивается помехоустойчивость приема дискретной информации. Это достигается тем, что при числе ошибок, превышающем t, осуществляется запрет на исправление ошибок и вырабатывается сигнал «ошибка» независимо от результата вычисления синдрома.

Применение предлагаемого декодера в системах с решающей обратной связью позволяет более эффективно использовать корректирующие свойства кодов, допускающих мажоритарную процедуру декодирования.

Источники информации

1. Колесник В.Д., Мирончиков Е.Г. Декодирование циклических кодов. — М.: Связь, 1968.

2. Элементы теории передачи дискретной информации. Под ред. Л.П.Пуртова. — М.: Связь, 1972.

3. SU авторское свидетельство №563717, кл. H03K 13/32, 1975 (прототип).

Декодер с обнаружением и исправлением ошибок, содержащий последовательно соединенные первый элемент ИЛИ, регистр сдвига, первый ключ и вычислитель синдрома, а также сумматор по модулю два, счетчик сдвигов, счетчик исправлений, второй, третий, четвертый, пятый, шестой и седьмой ключи, при этом вторые выходы регистра сдвига через сумматоры подключены к входам мажоритарного элемента, выход которого через второй ключ подсоединен к сигнальному входу третьего ключа, к управляющему входу которого и управляющим входам первого и пятого ключей подсоединен первый выход счетчика сдвигов, второй и третий выходы которого подключены соответственно к управляющим входам шестого и седьмого ключей, причем выход первого ключа соединен с сигнальным входом седьмого ключа, отличающийся тем, что в него введены последовательно соединенные блок дискретного интегрирования, счетчик недостоверных символов и второй элемент ИЛИ, а также буферный регистр сдвига, восьмой и девятый ключи, при этом второй выход счетчика недостоверных символов подключен к управляющим входам второго, четвертого и восьмого ключей, а второй выход блока дискретного интегрирования через девятый ключ подсоединен к первому входу первого элемента ИЛИ, к второму входу которого через восьмой ключ подсоединен выход регистра сдвига, а к третьему входу первого элемента ИЛИ и первому входу сумматора по модулю два подключен выход третьего ключа, при этом выход регистра сдвига через последовательно соединенные четвертый и пятый ключи подсоединен к второму входу сумматора по модулю два, выход которого через счетчик исправлений подключен ко второму входу второго элемента ИЛИ, к третьим входам которого подключены выходы вычислителя синдрома, а выход второго элемента ИЛИ подключен к сигнальному входу шестого ключа, выход которого подключен к первому входу буферного регистра сдвига, к второму входу которого подключен выход седьмого ключа, причем первый выход счетчика сдвигов подключен к управляющему входу девятого ключа, при этом вход блока дискретного интегрирования является входом декодера, выходом которого является выход буферного регистра сдвига.

Обнаруже́ние оши́бок в технике связи — действие, направленное на контроль целостности данных при записи/воспроизведении информации или при её передаче по линиям связи. Исправление ошибок (коррекция ошибок) — процедура восстановления информации после чтения её из устройства хранения или канала связи.

Для обнаружения ошибок используют коды обнаружения ошибок, для исправления — корректирующие коды (коды, исправляющие ошибки, коды с коррекцией ошибок, помехоустойчивые коды).

Способы борьбы с ошибками

В процессе хранения данных и передачи информации по сетям связи неизбежно возникают ошибки. Контроль целостности данных и исправление ошибок — важные задачи на многих уровнях работы с информацией (в частности, физическом, канальном, транспортном уровнях сетевой модели OSI).

В системах связи возможны несколько стратегий борьбы с ошибками:

• обнаружение ошибок в блоках данных и автоматический запрос повторной передачи повреждённых блоков — этот подход применяется, в основном, на канальном и транспортном уровнях;
• обнаружение ошибок в блоках данных и отбрасывание повреждённых блоков — такой подход иногда применяется в системах потокового мультимедиа, где важна задержка передачи и нет времени на повторную передачу;
• исправление ошибок (англ. forward error correction) применяется на физическом уровне.

Коды обнаружения и исправления ошибок

Корректирующие коды — коды, служащие для обнаружения или исправления ошибок, возникающих при передаче информации под влиянием помех, а также при её хранении.

Для этого при записи (передаче) в полезные данные добавляют специальным образом структурированную избыточную информацию (контрольное число), а при чтении (приёме) её используют для того, чтобы обнаружить или исправить ошибки. Естественно, что число ошибок, которое можно исправить, ограничено и зависит от конкретного применяемого кода.

С кодами, исправляющими ошибки, тесно связаны коды обнаружения ошибок. В отличие от первых, последние могут только установить факт наличия ошибки в переданных данных, но не исправить её.

В действительности используемые коды обнаружения ошибок принадлежат к тем же классам кодов, что и коды, исправляющие ошибки. Фактически любой код, исправляющий ошибки, может быть также использован для обнаружения ошибок (при этом он будет способен обнаружить большее число ошибок, чем был способен исправить).

По способу работы с данными коды, исправляющие ошибки, делятся на блоковые, делящие информацию на фрагменты постоянной длины и обрабатывающие каждый из них в отдельности, и свёрточные, работающие с данными как с непрерывным потоком.

Блоковые коды

Пусть кодируемая информация делится на фрагменты длиной бит, которые преобразуются в кодовые слова длиной бит. Тогда соответствующий блоковый код обычно обозначают . При этом число называется скоростью кода.

Если исходные бит код оставляет неизменными, и добавляет проверочных, такой код называется систематическим, иначе — несистематическим.

Задать блоковый код можно по-разному, в том числе таблицей, где каждой совокупности из информационных бит сопоставляется бит кодового слова. Однако хороший код должен удовлетворять как минимум следующим критериям:

• способность исправлять как можно большее число ошибок,
• как можно меньшая избыточность,
• простота кодирования и декодирования.

Нетрудно видеть, что приведённые требования противоречат друг другу. Именно поэтому существует большое количество кодов, каждый из которых пригоден для своего круга задач.

Практически все используемые коды являются линейными. Это связано с тем, что нелинейные коды значительно сложнее исследовать, и для них трудно обеспечить приемлемую лёгкость кодирования и декодирования.

Линейные коды общего вида

Линейный блоковый код — такой код, что множество его кодовых слов образует -мерное линейное подпространство (назовём его ) в -мерном линейном пространстве, изоморфное пространству -битных векторов.

Это значит, что операция кодирования соответствует умножению исходного -битного вектора на невырожденную матрицу , называемую порождающей матрицей.

Пусть  — ортогональное подпространство по отношению к , а  — матрица, задающая базис этого подпространства. Тогда для любого вектора справедливо:

Минимальное расстояние и корректирующая способность

Расстоянием Хемминга (метрикой Хемминга) между двумя кодовыми словами и называется количество отличных бит на соответствующих позициях:

.

Минимальное расстояние Хемминга является важной характеристикой линейного блокового кода. Она показывает, насколько «далеко» расположены коды друг от друга. Она определяет другую, не менее важную характеристику — корректирующую способность:

.

Корректирующая способность определяет, сколько ошибок передачи кода (типа ) можно гарантированно исправить. То есть вокруг каждого кодового слова имеем -окрестность , которая состоит из всех возможных вариантов передачи кодового слова с числом ошибок () не более . Никакие две окрестности двух любых кодовых слов не пересекаются друг с другом, так как расстояние между кодовыми словами (то есть центрами этих окрестностей) всегда больше двух их радиусов .

Таким образом, получив искажённую кодовую комбинацию из , декодер принимает решение, что исходной была кодовая комбинация , исправляя тем самым не более ошибок.

Поясним на примере. Предположим, что есть два кодовых слова и , расстояние Хемминга между ними равно 3. Если было передано слово , и канал внёс ошибку в одном бите, она может быть исправлена, так как даже в этом случае принятое слово ближе к кодовому слову , чем к любому другому, и, в частности, к . Но если каналом были внесены ошибки в двух битах (в которых отличалось от ), то результат ошибочной передачи окажется ближе к , чем , и декодер примет решение, что передавалось слово .

Коды Хемминга

Коды Хемминга — простейшие линейные коды с минимальным расстоянием 3, то есть способные исправить одну ошибку. Код Хемминга может быть представлен в таком виде, что синдром

, где  — принятый вектор, будет равен номеру позиции, в которой произошла ошибка. Это свойство позволяет сделать декодирование очень простым.

Общий метод декодирования линейных кодов

Любой код (в том числе нелинейный) можно декодировать с помощью обычной таблицы, где каждому значению принятого слова соответствует наиболее вероятное переданное слово . Однако данный метод требует применения огромных таблиц уже для кодовых слов сравнительно небольшой длины.

Для линейных кодов этот метод можно существенно упростить. При этом для каждого принятого вектора вычисляется синдром . Поскольку , где  — кодовое слово, а  — вектор ошибки, то . Затем с помощью таблицы по синдрому определяется вектор ошибки, с помощью которого определяется переданное кодовое слово. При этом таблица получается гораздо меньше, чем при использовании предыдущего метода.

Линейные циклические коды

Несмотря на то, что декодирование линейных кодов значительно проще декодирования большинства нелинейных, для большинства кодов этот процесс всё ещё достаточно сложен. Циклические коды, кроме более простого декодирования, обладают и другими важными свойствами.

Циклическим кодом является линейный код, обладающий следующим свойством: если является кодовым словом, то его циклическая перестановка также является кодовым словом.

Слова циклического кода удобно представлять в виде многочленов. Например, кодовое слово представляется в виде полинома . При этом циклический сдвиг кодового слова эквивалентен умножению многочлена на по модулю .

В дальнейшем, если не указано иное, мы будем считать, что циклический код является двоичным, то есть могут принимать значения 0 или 1.

Порождающий (генераторный) полином

Можно показать, что все кодовые слова конкретного циклического кода кратны определённому порождающему полиному . Порождающий полином является делителем .

С помощью порождающего полинома осуществляется кодирование циклическим кодом. В частности:

Коды CRC

Коды CRC (англ. cyclic redundancy check — циклическая избыточная проверка) являются систематическими кодами, предназначенными не для исправления ошибок, а для их обнаружения. Они используют способ систематического кодирования, изложенный выше: «контрольная сумма» вычисляется путём деления на . Ввиду того, что исправление ошибок не требуется, проверка правильности передачи может производиться точно так же.

Таким образом, вид полинома задаёт конкретный код CRC. Примеры наиболее популярных полиномов:

Название кода	Степень	Полином
CRC-12	12
CRC-16	16
CRC-CCITT	16
CRC-32	32

Коды БЧХ

Коды Боуза — Чоудхури — Хоквингема (БЧХ) являются подклассом циклических кодов. Их отличительное свойство — возможность построения кода БЧХ с минимальным расстоянием не меньше заданного. Это важно, потому что, вообще говоря, определение минимального расстояния кода есть очень сложная задача.

Коды коррекции ошибок Рида — Соломона

Коды Рида — Соломона — недвоичные циклические коды, позволяющие исправлять ошибки в блоках данных. Элементами кодового вектора являются не биты, а группы битов (блоки). Очень распространены коды Рида-Соломона, работающие с байтами (октетами).

Математически коды Рида — Соломона являются кодами БЧХ.

Преимущества и недостатки блоковых кодов

Хотя блоковые коды, как правило, хорошо справляются с редкими, но большими пачками ошибок, их эффективность при частых, но небольших ошибках (например, в канале с АБГШ), менее высока.

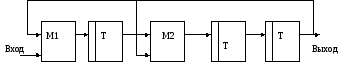
Свёрточные коды

Свёрточные коды, в отличие от блоковых, не делят информацию на фрагменты и работают с ней как со сплошным потоком данных.

Свёрточные коды, как правило, порождаются дискретной линейной инвариантной во времени системой. Поэтому, в отличие от большинства блоковых кодов, свёрточное кодирование — очень простая операция, чего нельзя сказать о декодировании.

Кодирование свёрточным кодом производится с помощью регистра сдвига, отводы от которого суммируются по модулю два. Таких сумм может быть две (чаще всего) или больше.

Декодирование свёрточных кодов, как правило, производится по алгоритму Витерби, который пытается восстановить переданную последовательность согласно критерию максимального правдоподобия.

Преимущества и недостатки свёрточных кодов

Свёрточные коды эффективно работают в канале с белым шумом, но плохо справляются с пакетами ошибок. Более того, если декодер ошибается, на его выходе всегда возникает пакет ошибок.

Каскадное кодирование. Итеративное декодирование

Преимущества разных способов кодирования можно объединить, применив каскадное кодирование. При этом информация сначала кодируется одним кодом, а затем другим, в результате получается код-произведение.

Например, популярной является следующая конструкция: данные кодируются кодом Рида-Соломона, затем перемежаются (при этом символы, расположенные близко, помещаются далеко друг от друга) и кодируются свёрточным кодом. На приёмнике сначала декодируется свёрточный код, затем осуществляется обратное перемежение (при этом пачки ошибок на выходе свёрточного декодера попадают в разные кодовые слова кода Рида — Соломона), и затем осуществляется декодирование кода Рида — Соломона.

Некоторые коды-произведения специально сконструированы для итеративного декодирования, при котором декодирование осуществляется в несколько проходов, каждый из которых использует информацию от предыдущего. Это позволяет добиться большой эффективности, однако декодирование требует больших ресурсов. К таким кодам относят турбо-коды и LDPC-коды (коды Галлагера).

Сетевое кодирование

Оценка эффективности кодов

Эффективность кодов определяется количеством ошибок, которые тот может исправить, количеством избыточной информации, добавление которой требуется, а также сложностью реализации кодирования и декодирования (как аппаратной, так и в виде программы для ЭВМ).

Граница Хемминга и совершенные коды

Пусть имеется двоичный блоковый код с корректирующей способностью . Тогда справедливо неравенство (называемое границей Хемминга):

Коды, удовлетворяющие этой границе с равенством, называются совершенными. К совершенным кодам относятся, например, коды Хемминга. Часто применяемые на практике коды с большой корректирующей способностью (такие, как коды Рида — Соломона) не являются совершенными.

Энергетический выигрыш

При передаче информации по каналу связи вероятность ошибки зависит от отношения сигнал/шум на входе демодулятора, таким образом, при постоянном уровне шума решающее значение имеет мощность передатчика. В системах спутниковой и мобильной, а также других типов связи остро стоит вопрос экономии энергии. Кроме того, в определённых системах связи (например, телефонной) неограниченно повышать мощность сигнала не дают технические ограничения.

Поскольку помехоустойчивое кодирование позволяет исправлять ошибки, при его применении мощность передатчика можно снизить, оставляя скорость передачи информации неизменной. Энергетический выигрыш определяется как разница отношений с/ш при наличии и отсутствии кодирования.

Применение кодов, исправляющих ошибки

Коды, исправляющие ошибки, применяются:

• в системах цифровой связи, в том числе: спутниковой, радиорелейной, сотовой, передаче данных по телефонным каналам.
• в системах хранения информации, в том числе магнитных и оптических.

Коды, обнаруживающие ошибки, применяются в сетевых протоколах различных уровней.

Автоматический запрос повторной передачи

Системы с автоматическим запросом повторной передачи (ARQ — Automatic Repeat reQuest) основаны на технологии обнаружения ошибок. Распространены следующие методы автоматического запроса:

Запрос ARQ с остановками (stop-and-wait ARQ)

Идея этого метода заключается в том, что передатчик ожидает от приемника подтверждения успешного приема предыдущего блока данных перед тем, как начать передачу следующего. В случае, если блок данных был принят с ошибкой, приемник передает отрицательное подтверждение (negative acknowledgement, NAK), и передатчик повторяет передачу блока. Данный метод подходит для полудуплексного канала связи. Его недостатком является низкая скорость из-за высоких накладных расходов на ожидание.

Непрерывный запрос ARQ с возвратом (continuous ARQ with pullback)

Для этого метода необходим полнодуплексный канал. Передача данных от передатчика к приемнику производится одновременно. В случае ошибки передача возобновляется, начиная с ошибочного блока (то есть передается ошибочный блок и все последующие).

Непрерывный запрос ARQ с выборочным повторением (continuous ARQ with selective repeat)

При этом подходе осуществляется передача только ошибочно принятых блоков данных.

См. также

• Цифровая связь
• Код ответа (Код причины завершения)
• Линейный код
• Циклический код
• Код Боуза — Чоудхури — Хоквингема
• Код Рида — Соломона
• LDPC
• Свёрточный код
• Турбо-код

Литература

• Блейхут Р. Теория и практика кодов, контролирующих ошибки = Theory and Practice of Error Control Codes. — М.: Мир, 1986. — 576 с.
• Мак-Вильямс Ф. Дж., Слоэн Н. Дж. А. Теория кодов, исправляющих ошибки. М.: Радио и связь, 1979.
• Морелос-Сарагоса Р. Искусство помехоустойчивого кодирования. Методы, алгоритмы, применение / пер. с англ. В. Б. Афанасьева. — М.: Техносфера, 2006. — 320 с. — (Мир связи). — 2000 экз. — ISBN 5-94836-035-0.

Ссылки

• Помехоустойчивое кодирование (11 ноября 2001). — реферат по проблеме кодирования сообщений с исправлением ошибок. Проверено 25 декабря 2006. Архивировано 25 августа 2011 года.
• Коды Рида-Соломона. Простой пример. Просто, доступно, на конкретных числах. Для начинающих.