Условное
обозначение средней арифметической
величины через М (от латинского слова
Media) чаще применяется в медицинских и
педагогических исследованиях. В
математической статистике предпочитают
обозначение через .
Средняя арифметическая величина является
производной, обобщающей количественные
признаки ряда однородных показателей
(совокупности). Выражая одним числом
определенную совокупность, она как бы
ослабляет влияние случайных индивидуальных
отклонений, и акцентирует некую обобщенную
количественную характеристику, наиболее
типичное свойство изучаемого ряда
показателей.
Определяя
значение средней арифметической
величины, следует придерживаться
некоторых правил.
1.
Средняя арифметическая величина может
характеризовать только те признаки
изучаемого объекта, которые присущи
всей совокупности, но в разной
количественной мере (например, уровень
развития быстроты движений характерен
для каждого человека, хотя и в разной
количественной мере). Средняя арифметическая
величина не может характеризовать
количественную меру тех признаков,
которые одной части совокупности
присущи, а другой нет, т. е. она не может
отражать присутствие или отсутствие
того или иного признака (например, умение
или неумение выполнять то или иное
двигательное действие).
2.
Средняя арифметическая величина должна
включать все показатели, полученные в
данном исследовании. Произвольное
исключение даже некоторых из них
неизбежно приведет к искажению конечного
результата.
3.
Средняя арифметическая величина обязана
отражать только однородную совокупность.
Нельзя, например, определять средний
уровень физического развития школьников,
не разделив их предварительно по возрасту
и полу.
4.
Средняя арифметическая величина должна
вычисляться на достаточно большой
совокупности, размеры которой определяются
в каждом конкретном случае отдельно
(см. «Подбор исследуемых»).
5.
Необходимо стремиться к тому, чтобы
средняя арифметическая величина имела
четкие и простые свойства, позволяющие
легко и быстро ее вычислять.
6.
Средняя арифметическая величина должна
обладать достаточной устойчивостью к
действию случайных факторов. Только в
этом случае она будет отражать
действительное состояние изучаемого
явления, а не его случайные изменения.
7.
Точность вычисления средней арифметической
величины должна соответствовать
содержанию изучаемого педагогического
явления. В некоторых случаях нет
необходимости в расчетах с большой
точностью, в других — большая точность
нужна при вычислениях, но совершенно
не нужна в выводах. Например, при расчете
средних величин числа подтягиваний на
перекладине можно пользоваться и сотыми
долями целого, но представлять и выводах,
что исследуемые в среднем подтянулись
7,83 раза, было бы неграмотна, так как
невозможно измерение с подобной
точностью. В этом случае необходимо в
выводах представлять числа, округленные
до целых единиц.
В
простейшем случае этот показатель
вычисляется путем сложения всех
полученных значений (которые называются
вариантами) и деления суммы на число
вариант:
где
S — знак суммирования;
V
— полученные в исследовании значения
(варианты);
п
— число вариант.
По
этой формуле вычисляется так называемая
простая средняя арифметическая величина.
Применяется она в тех случаях, когда
имеется небольшое число вариант.
При
большом числе вариант прибегают к
вычислению так называемой взвешенной
средней арифметической величины. С этой
целью строят ряд распределения, или
вариационный ряд, который представляет
собой ряд вариант и их частот,
характеризующих какой-нибудь признак
в убывающем или возрастающем порядке.
Например, в нашем случае измерение
точности попадания мячом в цель дало
125 вариант, т. е. в группе I, где применялась
методика обучения «А», одноразово
исследовалось 125 детей с числовым
выражением от 0 (точное попадание в цель)
до 21,5 см (максимальное отклонение от
цели). Каждое числовое выражение
встречалось в исследовании один и более
раз, например «0» встретился 28 раз.
Другими словами, 28 участников эксперимента
точно попали в цель. Этот показатель
называется числом наблюдений или
частотой вариант и условно обозначается
буквой «Р» (число наблюдений составляет
часть числа вариант).
Для
упрощения числовых операций все 125
вариант разбиваются на классы с величиной
интервала 1,9 см. Число классов зависит
от величины колебаний вариант (разности
между максимальной и минимальной
вариантами), наличия вариант для каждого
класса (если, например, для первого
класса — «0 — 1,9» — нет соответствующих
вариант, т.е. ни один исследуемый не имел
точных попаданий или отклонений от цели
в пределах от 0 до 1,9 см, то подобный класс
не вносится в вариационный ряд) и,
наконец, требуемой точности вычисления,
(чем больше классов, тем точность
вычисления выше). Вполне понятно, что
чем больше величина интервала, тем
меньше число классов при одной и той же
величине колебаний вариант.
После
разбивки вариант по классам в каждом
классе определяется срединная варианта
«Vc»,
и для каждой срединной варианты
проставляется число наблюдений. Пример
этих операций, и дальнейший ход вычислений
приведены в следующей таблице:
|
Классы |
Серединные |
Число |
VCP |
VC-M=d |
d2 |
d2P |
|
0 |
1 |
28 |
28 |
-4.6 |
21.16 |
592.48 |
|
2 |
3 |
29 |
87 |
-2.6 |
6.76 |
196.04 |
|
4 |
5 |
22 |
110 |
-0.6 |
0.36 |
7.92 |
|
6 |
7 |
13 |
91 |
1.4 |
1.96 |
25.48 |
|
8 |
9 |
11 |
99 |
3.4 |
11.56 |
127.16 |
|
10 |
11 |
13 |
143 |
5.4 |
29.16 |
379.08 |
|
12 |
13 |
4 |
52 |
7.4 |
54.76 |
219.04 |
|
14 |
15 |
2 |
30 |
9.4 |
88.36 |
176.72 |
|
16 |
17 |
1 |
17 |
11.4 |
130.00 |
130.00 |
|
18 |
19 |
1 |
19 |
13.4 |
179.60 |
179.60 |
|
20 |
21 |
1 |
21 |
15.4 |
237.20 |
237.20 |
|
125 |
697 |
2270.72 |
Очередность
числовых операций:
1)
вычислить сумму числа наблюдений (в
нашем примере она равна 125);
2)
вычислить произведение каждой срединной
варианты на ее частоту (например, 1*28 =
28);
3)
вычислить сумму произведений срединных
вариант на их частоты (в нашем примере
она равна 697);
4)
вычислить взвешенную среднюю арифметическую
величину по формуле:
Средняя
арифметическая величина позволяет
сравнивать и оценивать группы изучаемых
явлений в целом. Однако для характеристики
группы явлений только этой величины
явно недостаточно, так как размер
колебаний вариант, из которых она
складывается, может быть различным.
Поэтому в характеристику группы явлений
необходимо ввести такой показатель,
который давал бы представление о величине
колебаний вариант около их средней
величины.
Вычисление
средней ошибки среднего арифметического.
Условное обозначение средней ошибки
среднего арифметического — т. Следует
помнить, что под «ошибкой» в статистике
понимается не ошибка исследования, а
мера представительства данной величины,
т. е. мера, которой средняя арифметическая
величина, полученная на выборочной
совокупности (в нашем примере — на 125
детях), отличается от истинной средней
арифметической величины, которая была
бы получена на генеральной совокупности
(в нашем примере это были бы все дети
аналогичного возраста, уровня
подготовленности и т. д.). Например, в
приведенном ранее примере определялась
точность попадания малым мячом в цель
у 125 детей и была получена средняя
арифметическая величина примерно равная
5,6 см. Теперь надо установить, в какой
мере эта величина будет характерна,
если взять для исследования 200, 300, 500 и
больше аналогичных детей. Ответ на этот
вопрос и даст вычисление средней ошибки
среднего арифметического, которое
производится по формуле:
Для
приведенного примера величина средней
ошибки среднего арифметического будет
равна:
Следовательно,
M±m = 5,6±0,38. Это означает, что полученная
средняя арифметическая величина (M =
5,6) может иметь в других аналогичных
исследованиях значения от 5,22 (5,6 — 0,38 =
5,22) до 5,98 (5,6+0,38 = 5,98).
Соседние файлы в предмете Ветеринарная генетика
- #
- #
- #
Среднее арифметическое, как известно, используется для получения обобщающей характеристики некоторого набора данных. Если данные более-менее однородны и в них нет аномальных наблюдений (выбросов), то среднее хорошо обобщает данные, сведя к минимуму влияние случайных факторов (они взаимопогашаются при сложении).
Когда анализируемые данные представляют собой выборку (которая состоит из случайных значений), то среднее арифметическое часто (но не всегда) выступает в роли приближенной оценки математического ожидания. Почему приближенной? Потому что среднее арифметическое – это величина, которая зависит от набора случайных чисел, и, следовательно, сама является случайной величиной. При повторных экспериментах (даже в одних и тех же условиях) средние будут отличаться друг от друга.
Для того, чтобы на основе статистического анализа данных делать корректные выводы, необходимо оценить возможный разброс полученного результата. Для этого рассчитываются различные показатели вариации. Но то исходные данные. И как мы только что установили, среднее арифметическое также обладает разбросом, который необходимо оценить и учитывать в дальнейшем (в выводах, в выборе метода анализа и т.д.).
Интуитивно понятно, что разброс средней должен быть как-то связан с разбросом исходных данных. Основной характеристикой разброса средней выступает та же дисперсия.
Дисперсия выборочных данных – это средний квадрат отклонения от средней, и рассчитать ее по исходным данным не составляет труда, например, в Excel предусмотрены специальные функции. Однако, как же рассчитать дисперсию средней, если в распоряжении есть только одна выборка и одно среднее арифметическое?
Расчет дисперсии и стандартной ошибки средней арифметической
Чтобы получить дисперсию средней арифметической нет необходимости проводить множество экспериментов, достаточно иметь только одну выборку. Это легко доказать. Для начала вспомним, что средняя арифметическая (простая) рассчитывается по формуле:
где xi – значения переменной,
n – количество значений.
Теперь учтем два свойства дисперсии, согласно которым, 1) — постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат и 2) — дисперсия суммы независимых случайных величин равняется сумме соответствующих дисперсий. Предполагается, что каждое случайное значение xi обладает одинаковым разбросом, поэтому несложно вывести формулу дисперсии средней арифметической:
Используя более привычные обозначения, формулу записывают как:
где σ2 – это дисперсия, случайной величины, причем генеральная.
На практике же, генеральная дисперсия известна далеко не всегда, точнее совсем редко, поэтому в качестве оной используют выборочную дисперсию:
Стандартное отклонение средней арифметической называется стандартной ошибкой средней и рассчитывается, как квадратный корень из дисперсии.
Формула стандартной ошибки средней при использовании генеральной дисперсии
Формула стандартной ошибки средней при использовании выборочной дисперсии
Последняя формула на практике используется чаще всего, т.к. генеральная дисперсия обычно не известна. Чтобы не вводить новые обозначения, стандартную ошибку средней обычно записывают в виде соотношения стандартного отклонения выборки и корня объема выборки.
Назначение и свойство стандартной ошибки средней арифметической
Стандартная ошибка средней много, где используется. И очень полезно понимать ее свойства. Посмотрим еще раз на формулу стандартной ошибки средней:
Числитель – это стандартное отклонение выборки и здесь все понятно. Чем больше разброс данных, тем больше стандартная ошибка средней – прямо пропорциональная зависимость.
Посмотрим на знаменатель. Здесь находится квадратный корень из объема выборки. Соответственно, чем больше объем выборки, тем меньше стандартная ошибка средней. Для наглядности изобразим на одной диаграмме график нормально распределенной переменной со средней равной 10, сигмой – 3, и второй график – распределение средней арифметической этой же переменной, полученной по 16-ти наблюдениям (которое также будет нормальным).
Судя по формуле, разброс стандартной ошибки средней должен быть в 4 раза (корень из 16) меньше, чем разброс исходных данных, что и видно на рисунке выше. Чем больше наблюдений, тем меньше разброс средней.
Казалось бы, что для получения наиболее точной средней достаточно использовать максимально большую выборку и тогда стандартная ошибка средней будет стремиться к нулю, а сама средняя, соответственно, к математическому ожиданию. Однако квадратный корень объема выборки в знаменателе говорит о том, что связь между точностью выборочной средней и размером выборки не является линейной. Например, увеличение выборки с 20-ти до 50-ти наблюдений, то есть на 30 значений или в 2,5 раза, уменьшает стандартную ошибку средней только на 36%, а со 100-а до 130-ти наблюдений (на те же 30 значений), снижает разброс данных лишь на 12%.
Лучше всего изобразить эту мысль в виде графика зависимости стандартной ошибки средней от размера выборки. Пусть стандартное отклонение равно 10 (на форму графика это не влияет).
Видно, что примерно после 50-ти значений, уменьшение стандартной ошибки средней резко замедляется, после 100-а – наклон постепенно становится почти нулевым.
Таким образом, при достижении некоторого размера выборки ее дальнейшее увеличение уже почти не сказывается на точности средней. Этот факт имеет далеко идущие последствия. Например, при проведении выборочного обследования населения (опроса) чрезмерное увеличение выборки ведет к неоправданным затратам, т.к. точность почти не меняется. Именно поэтому количество опрошенных редко превышает 1,5 тысячи человек. Точность при таком размере выборки часто является достаточной, а дальнейшее увеличение выборки – нецелесообразным.
Подведем итог. Расчет дисперсии и стандартной ошибки средней имеет довольно простую формулу и обладает полезным свойством, связанным с тем, что относительно хорошая точность средней достигается уже при 100 наблюдениях (в этом случае стандартная ошибка средней становится в 10 раз меньше, чем стандартное отклонение выборки). Больше, конечно, лучше, но бесконечно увеличивать объем выборки не имеет практического смысла. Хотя, все зависит от поставленных задач и цены ошибки. В некоторых опросах участие принимают десятки тысяч людей.
Дисперсия и стандартная ошибка средней имеют большое практическое значение. Они используются в проверке гипотез и расчете доверительных интервалов.
Поделиться в социальных сетях:
Среднее арифметическое, как известно, используется для получения обобщающей характеристики некоторого набора данных. Если данные более-менее однородны и в них нет аномальных наблюдений (выбросов), то среднее хорошо обобщает данные, сведя к минимуму влияние случайных факторов (они взаимопогашаются при сложении).
Когда анализируемые данные представляют собой выборку (которая состоит из случайных значений), то среднее арифметическое часто (но не всегда) выступает в роли приближенной оценки математического ожидания. Почему приближенной? Потому что среднее арифметическое – это величина, которая зависит от набора случайных чисел, и, следовательно, сама является случайной величиной. При повторных экспериментах (даже в одних и тех же условиях) средние будут отличаться друг от друга.
Для того, чтобы на основе статистического анализа данных делать корректные выводы, необходимо оценить возможный разброс полученного результата. Для этого рассчитываются различные показатели вариации. Но то исходные данные. И как мы только что установили, среднее арифметическое также обладает разбросом, который необходимо оценить и учитывать в дальнейшем (в выводах, в выборе метода анализа и т.д.).
Интуитивно понятно, что разброс средней должен быть как-то связан с разбросом исходных данных. Основной характеристикой разброса средней выступает та же дисперсия.
Дисперсия выборочных данных – это средний квадрат отклонения от средней, и рассчитать ее по исходным данным не составляет труда, например, в Excel предусмотрены специальные функции. Однако, как же рассчитать дисперсию средней, если в распоряжении есть только одна выборка и одно среднее арифметическое?
Расчет дисперсии и стандартной ошибки средней арифметической
Чтобы получить дисперсию средней арифметической нет необходимости проводить множество экспериментов, достаточно иметь только одну выборку. Это легко доказать. Для начала вспомним, что средняя арифметическая (простая) рассчитывается по формуле:
где xi – значения переменной,
n – количество значений.
Теперь учтем два свойства дисперсии, согласно которым, 1) — постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат и 2) — дисперсия суммы независимых случайных величин равняется сумме соответствующих дисперсий. Предполагается, что каждое случайное значение xi обладает одинаковым разбросом, поэтому несложно вывести формулу дисперсии средней арифметической:
Используя более привычные обозначения, формулу записывают как:
где σ2 – это дисперсия, случайной величины, причем генеральная.
На практике же, генеральная дисперсия известна далеко не всегда, точнее совсем редко, поэтому в качестве оной используют выборочную дисперсию:
Стандартное отклонение средней арифметической называется стандартной ошибкой средней и рассчитывается, как квадратный корень из дисперсии.
Формула стандартной ошибки средней при использовании генеральной дисперсии
Формула стандартной ошибки средней при использовании выборочной дисперсии
Последняя формула на практике используется чаще всего, т.к. генеральная дисперсия обычно не известна. Чтобы не вводить новые обозначения, стандартную ошибку средней обычно записывают в виде соотношения стандартного отклонения выборки и корня объема выборки.
Назначение и свойство стандартной ошибки средней арифметической
Стандартная ошибка средней много, где используется. И очень полезно понимать ее свойства. Посмотрим еще раз на формулу стандартной ошибки средней:
Числитель – это стандартное отклонение выборки и здесь все понятно. Чем больше разброс данных, тем больше стандартная ошибка средней – прямо пропорциональная зависимость.
Посмотрим на знаменатель. Здесь находится квадратный корень из объема выборки. Соответственно, чем больше объем выборки, тем меньше стандартная ошибка средней. Для наглядности изобразим на одной диаграмме график нормально распределенной переменной со средней равной 10, сигмой – 3, и второй график – распределение средней арифметической этой же переменной, полученной по 16-ти наблюдениям (которое также будет нормальным).
Судя по формуле, разброс стандартной ошибки средней должен быть в 4 раза (корень из 16) меньше, чем разброс исходных данных, что и видно на рисунке выше. Чем больше наблюдений, тем меньше разброс средней.
Казалось бы, что для получения наиболее точной средней достаточно использовать максимально большую выборку и тогда стандартная ошибка средней будет стремиться к нулю, а сама средняя, соответственно, к математическому ожиданию. Однако квадратный корень объема выборки в знаменателе говорит о том, что связь между точностью выборочной средней и размером выборки не является линейной. Например, увеличение выборки с 20-ти до 50-ти наблюдений, то есть на 30 значений или в 2,5 раза, уменьшает стандартную ошибку средней только на 36%, а со 100-а до 130-ти наблюдений (на те же 30 значений), снижает разброс данных лишь на 12%.
Лучше всего изобразить эту мысль в виде графика зависимости стандартной ошибки средней от размера выборки. Пусть стандартное отклонение равно 10 (на форму графика это не влияет).
Видно, что примерно после 50-ти значений, уменьшение стандартной ошибки средней резко замедляется, после 100-а – наклон постепенно становится почти нулевым.
Таким образом, при достижении некоторого размера выборки ее дальнейшее увеличение уже почти не сказывается на точности средней. Этот факт имеет далеко идущие последствия. Например, при проведении выборочного обследования населения (опроса) чрезмерное увеличение выборки ведет к неоправданным затратам, т.к. точность почти не меняется. Именно поэтому количество опрошенных редко превышает 1,5 тысячи человек. Точность при таком размере выборки часто является достаточной, а дальнейшее увеличение выборки – нецелесообразным.
Подведем итог. Расчет дисперсии и стандартной ошибки средней имеет довольно простую формулу и обладает полезным свойством, связанным с тем, что относительно хорошая точность средней достигается уже при 100 наблюдениях (в этом случае стандартная ошибка средней становится в 10 раз меньше, чем стандартное отклонение выборки). Больше, конечно, лучше, но бесконечно увеличивать объем выборки не имеет практического смысла. Хотя, все зависит от поставленных задач и цены ошибки. В некоторых опросах участие принимают десятки тысяч людей.
Дисперсия и стандартная ошибка средней имеют большое практическое значение. Они используются в проверке гипотез и расчете доверительных интервалов.
Поделиться в социальных сетях:
Представление результатов исследования
В научных публикациях важно представление результатов исследования. Очень часто окончательный результат приводится в следующем виде: M±m, где M – среднее арифметическое, m –ошибка среднего арифметического. Например, 163,7±0,9 см.
Прежде чем разбираться в правилах представления результатов исследования, давайте точно усвоим, что же такое ошибка среднего арифметического.
Ошибка среднего арифметического
Среднее арифметическое, вычисленное на основе выборочных данных (выборочное среднее), как правило, не совпадает с генеральным средним (средним арифметическим генеральной совокупности). Экспериментально проверить это утверждение невозможно, потому что нам неизвестно генеральное среднее. Но если из одной и той же генеральной совокупности брать повторные выборки и вычислять среднее арифметическое, то окажется, что для разных выборок среднее арифметическое будет разным.
Чтобы оценить, насколько выборочное среднее арифметическое отличается от генерального среднего, вычисляется ошибка среднего арифметического или ошибка репрезентативности.
Ошибка среднего арифметического обозначается как m или
Ошибка среднего арифметического рассчитывается по формуле:
где: S — стандартное отклонение, n – объем выборки; Например, если стандартное отклонение равно S=5 см, объем выборки n=36 человек, то ошибка среднего арифметического равна: m=5/6 = 0,833.
Ошибка среднего арифметического показывает, какая ошибка в среднем допускается, если использовать вместо генерального среднего выборочное среднее.
Так как при небольшом объеме выборки истинное значение генерального среднего не может быть определено сколь угодно точно, поэтому при вычислении выборочного среднего арифметического нет смысла оставлять большое число значащих цифр.
Правила записи результатов исследования
- В записи ошибки среднего арифметического оставляем две значащие цифры, если первые цифры в ошибке «1» или «2».
- В остальных случаях в записи ошибки среднего арифметического оставляем одну значащую цифру.
- В записи среднего арифметического положение последней значащей цифры должно соответствовать положению первой значащей цифры в записи ошибки среднего арифметического.
Представление результатов научных исследований
В своей статье «Осторожно, статистика!», опубликованной в 1989 году В.М. Зациорский указал, какие числовые характеристики должны быть представлены в публикации, чтобы она имела научную ценность. Он писал, что исследователь «…должен назвать: 1) среднюю величину (или другой так называемый показатель положения); 2) среднее квадратическое отклонение (или другой показатель рассеяния) и 3) число испытуемых. Без них его публикация научной ценности иметь не будет “с. 52
В научных публикациях в области физической культуры и спорта очень часто окончательный результат приводится в виде: (М±m) (табл.1).
Таблица 1 — Изменение механических свойств латеральной широкой мышцы бедра под воздействием физической нагрузки (n=34)
| Эффективный модуль
упругости (Е), кПа |
Эффективный модуль
вязкости (V), Па с |
|||
| Этап
эксперимента |
Рассл. | Напряж. | Рассл. | Напряж. |
| До ФН | 7,0±0,3 | 17,1±1,4 | 29,7±1,7 | 46±4 |
| После ФН | 7,7±0,3 | 18,7±1,4 | 30,9±2,0 | 53±6 |
Литература
- Высшая математика и математическая статистика: учебное пособие для вузов / Под общ. ред. Г. И. Попова. – М. Физическая культура, 2007.– 368 с.
- Гласс Дж., Стэнли Дж. Статистические методы в педагогике и психологии. М.: Прогресс. 1976.- 495 с.
- Зациорский В.М. Осторожно — статистика! // Теория и практика физической культуры, 1989.- №2.
- Катранов А.Г. Компьютерная обработка данных экспериментальных исследований: Учебное пособие/ А. Г. Катранов, А. В. Самсонова; СПб ГУФК им. П.Ф. Лесгафта. – СПб.: изд-во СПб ГУФК им. П.Ф. Лесгафта, 2005. – 131 с.
- Основы математической статистики: Учебное пособие для ин-тов физ. культ / Под ред. В.С. Иванова.– М.: Физкультура и спорт, 1990. 176 с.
17 авг. 2022 г.
читать 2 мин
Стандартная ошибка среднего — это способ измерить, насколько разбросаны значения в наборе данных. Он рассчитывается как:
Стандартная ошибка = с / √n
куда:
- s : стандартное отклонение выборки
- n : размер выборки
Вы можете рассчитать стандартную ошибку среднего для любого набора данных в Excel, используя следующую формулу:
= СТАНДОТКЛОН (диапазон значений) / КОРЕНЬ ( СЧЁТ (диапазон значений))
В следующем примере показано, как использовать эту формулу.
Пример: Стандартная ошибка в Excel
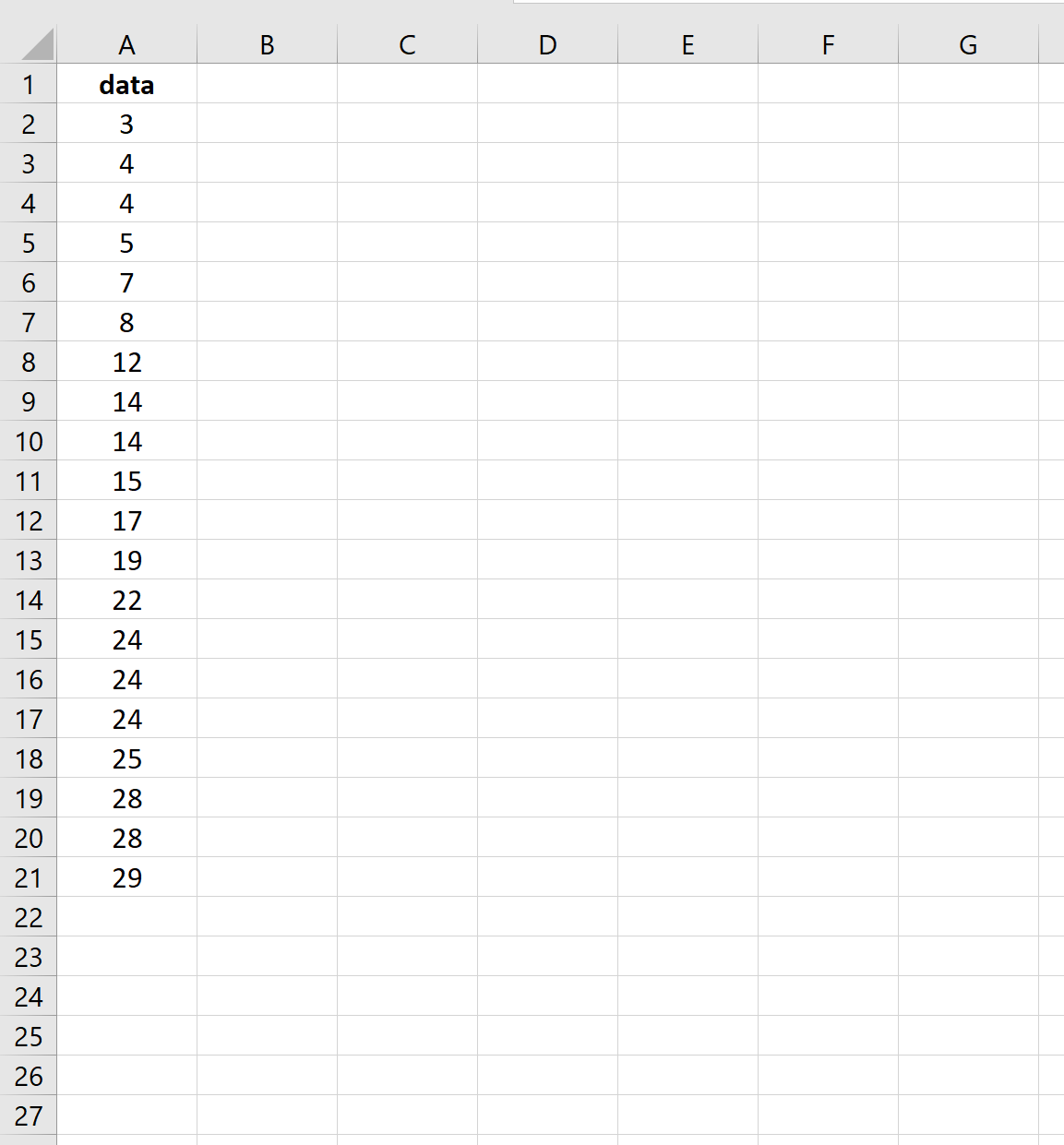
Предположим, у нас есть следующий набор данных:
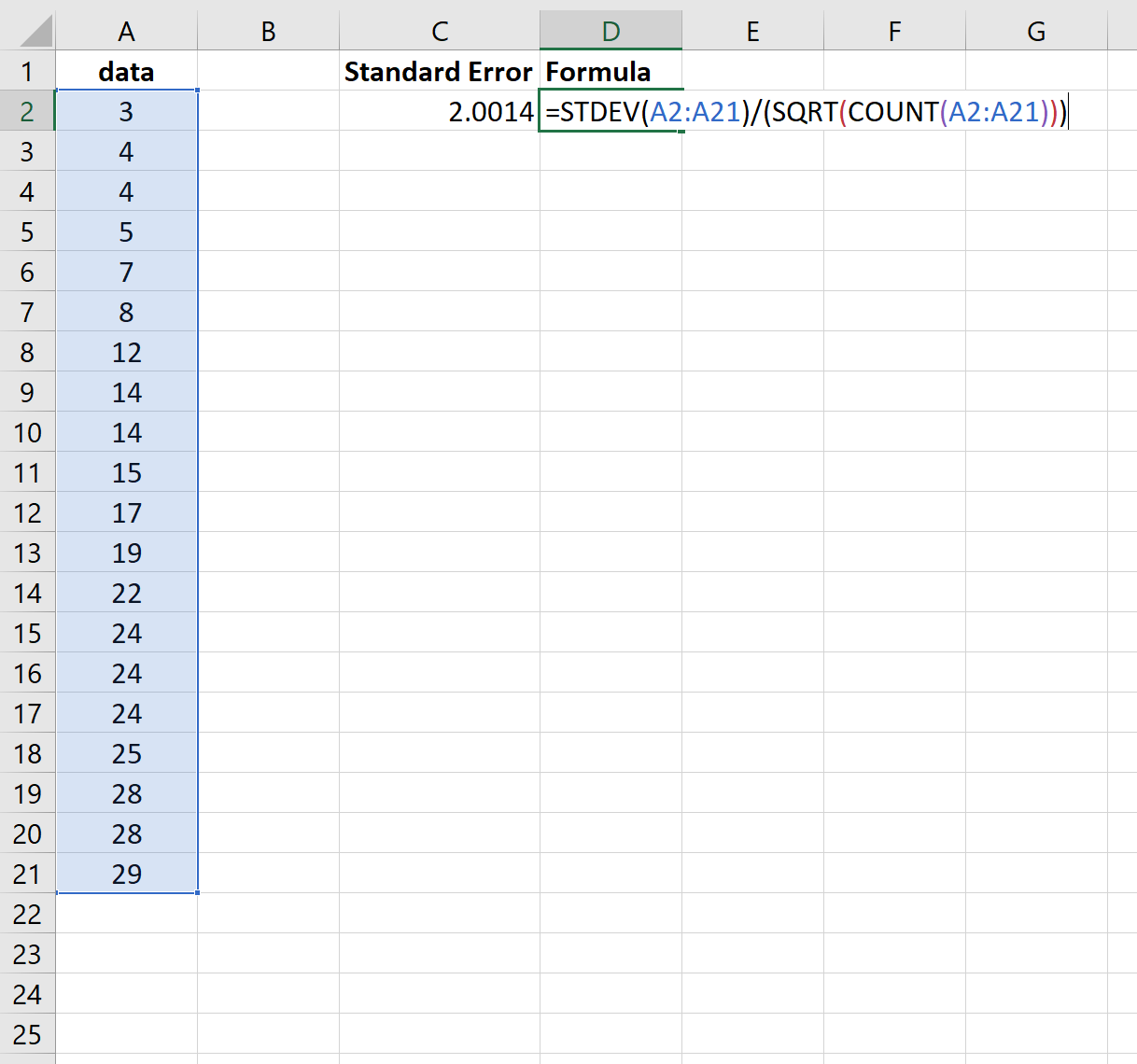
На следующем снимке экрана показано, как рассчитать стандартную ошибку среднего значения для этого набора данных:
Стандартная ошибка оказывается равной 2,0014 .
Обратите внимание, что функция =СТАНДОТКЛОН() вычисляет выборочное среднее, что эквивалентно функции =СТАНДОТКЛОН.С() в Excel.
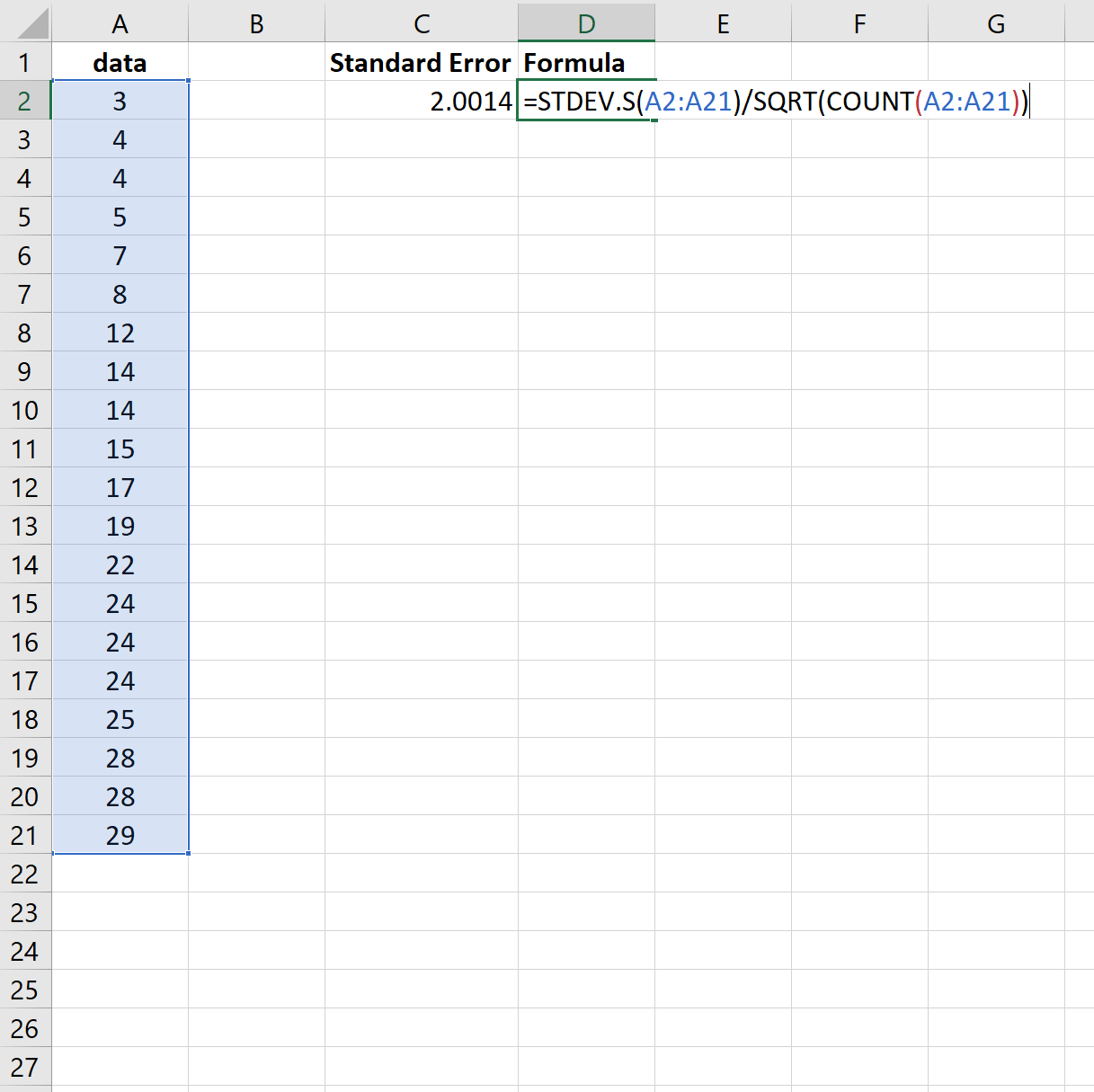
Таким образом, мы могли бы использовать следующую формулу для получения тех же результатов:
И снова стандартная ошибка оказывается равной 2,0014 .
Как интерпретировать стандартную ошибку среднего
Стандартная ошибка среднего — это просто мера того, насколько разбросаны значения вокруг среднего. При интерпретации стандартной ошибки среднего следует помнить о двух вещах:
1. Чем больше стандартная ошибка среднего, тем более разбросаны значения вокруг среднего в наборе данных.
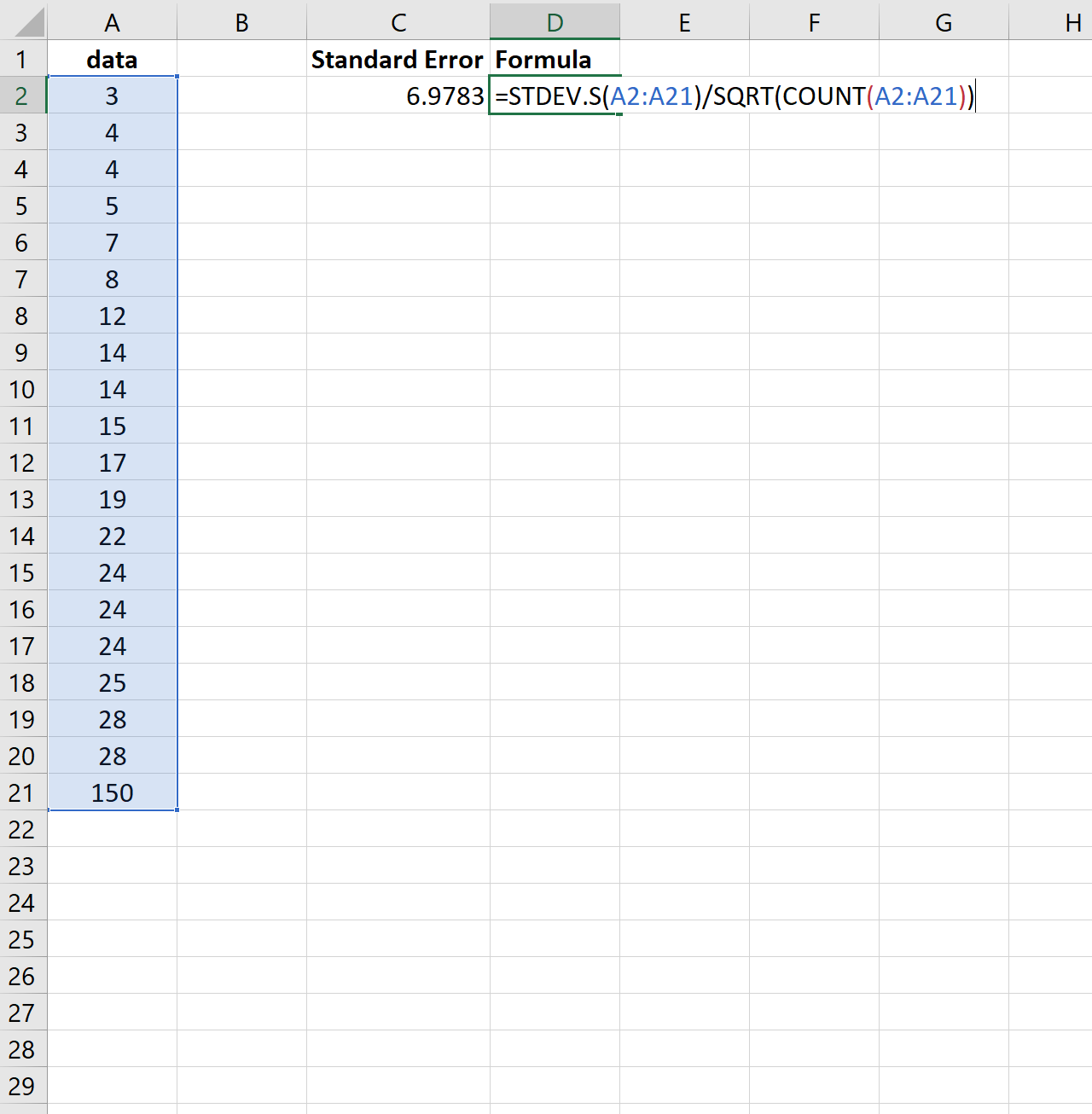
Чтобы проиллюстрировать это, рассмотрим, изменим ли мы последнее значение в предыдущем наборе данных на гораздо большее число:
Обратите внимание на скачок стандартной ошибки с 2,0014 до 6,9783.Это указывает на то, что значения в этом наборе данных более разбросаны вокруг среднего значения по сравнению с предыдущим набором данных.
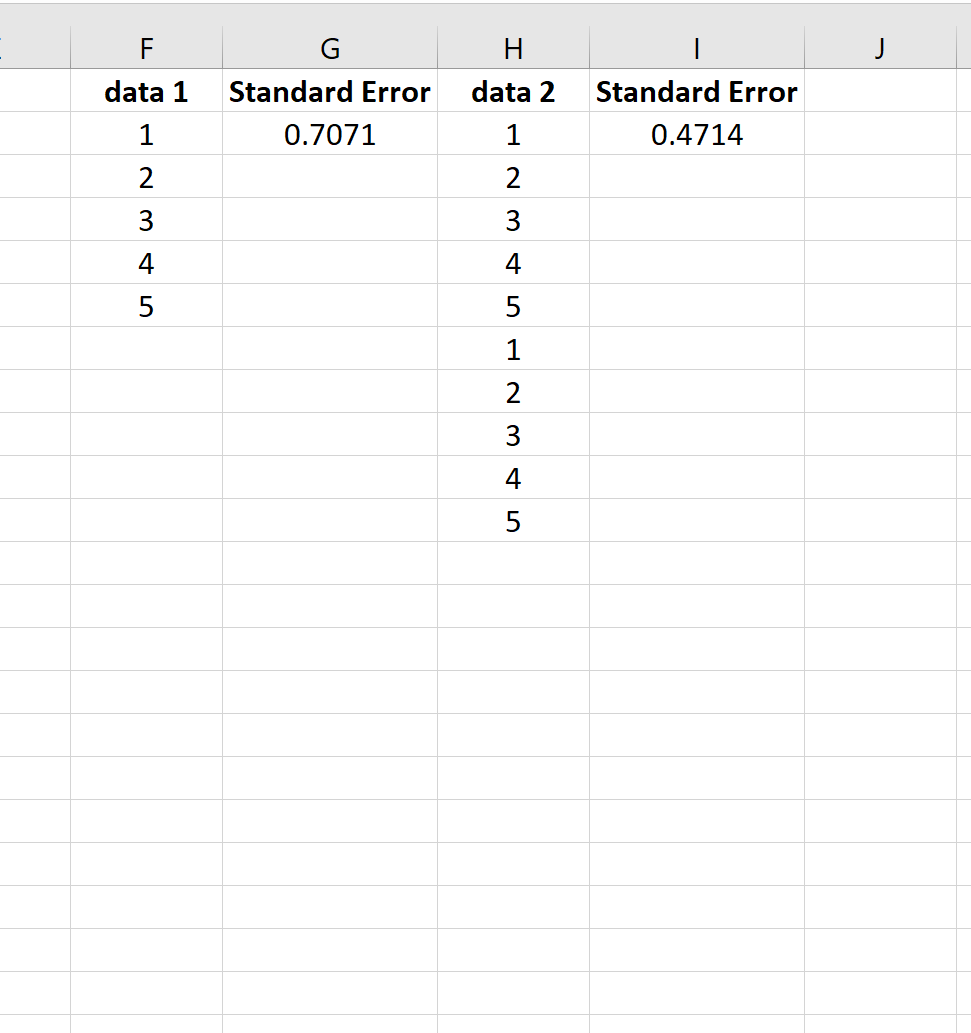
2. По мере увеличения размера выборки стандартная ошибка среднего имеет тенденцию к уменьшению.
Чтобы проиллюстрировать это, рассмотрим стандартную ошибку среднего для следующих двух наборов данных:
Второй набор данных — это просто первый набор данных, повторенный дважды. Таким образом, два набора данных имеют одинаковое среднее значение, но второй набор данных имеет больший размер выборки, поэтому стандартная ошибка меньше.