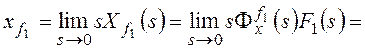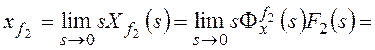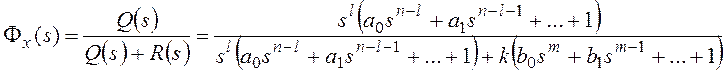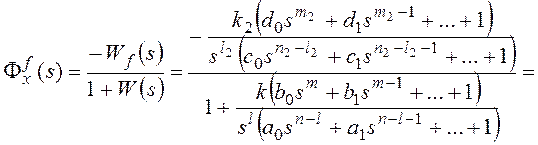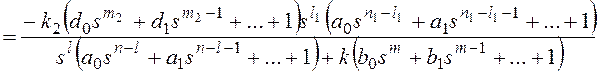Точность системы автоматического управления Статическая ошибка системы
В системах
автоматического управления часто
приходится решать задачу стабилизации
управляемой величины. Точность поддержания
требуемого значения управляемой величины
в такой системе можно оценить как разницу
между заданным значением управляемой
величины и её установившимся значением
в системе после окончания переходного
процесса:
.
Эта величина
получила название статической ошибки
системы. При вычислении статической
ошибки предполагается, что система
находится в статике и все сигналы в ней
имеют постоянные величины. Статическая
ошибка используется для оценки точности
установления в системе заданной
постоянной выходной величины после
окончания переходного процесса.
Используя
передаточную функцию замкнутой системы
по ошибке, для изображения ошибки в
системе можно записать
,
гдепередаточная
функция замкнутой системы по ошибке,изображение
задающего воздействия.
Для статики,
когда все сигналы в системе неизменны,
выражение для ошибки можно перенести
в область оригиналов
.
Поскольку
,
гдеW(p)
– передаточная функция разомкнутой
системы, то статическую ошибку системы
можно вычислить, зная передаточную
функцию разомкнутой системы:
,
где.
Вместо
абсолютного значения статической ошибки
часто используют относительную
статическую ошибку
.
Если система
статическая (т.е. не содержит интегрирующих
звеньев), то передаточную функцию
разомкнутой системы можно представить
в следующем нормированном виде:
,
гдеK– коэффициент
усиления системы,A*(p),B*(p)
– нормированные полиномыA(p)
иB(p).
При этоми
.
Тогдаи статическая ошибка в статической
системе
.
Статическая
ошибка в статической системе уменьшается
с увеличением коэффициента усиления
системы. Статическая система всегда
будет иметь некоторую ошибку. Физический
смысл такой ошибки заключается в
необходимости некоторого рассогласования
между задающей и выходной величинами
системы для получения сигнала управления.
Если в системе
управления имеются интегрирующие
звенья, то система будет астатической.
Для астатической системы первого порядка
(содержащей одно интегрирующее звено)
передаточная функция разомкнутой
системы
и передаточная функция замкнутой системы
по ошибке
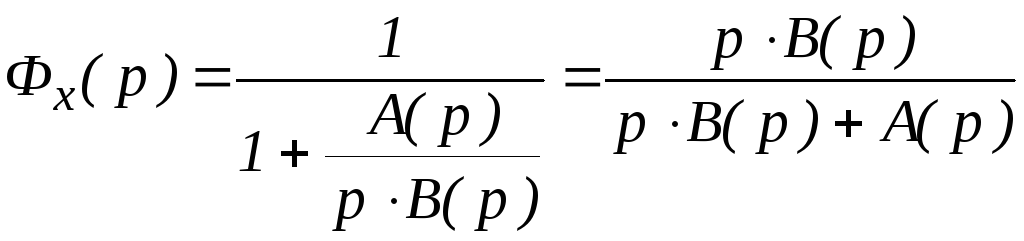
В этом случае всегда
и, следовательно, статическая ошибка
астатической системы будет равна нулю.
Таким образом, статическая ошибка в
астатической системе в принципе
отсутствует, что обуславливает более
высокую точность астатических систем,
по сравнению со статическими системами.
В астатической системе автоматического
управления установившееся значение
управляемой величины равно заданному
значению этой величины.
Вынужденная ошибка системы
Процесс в
системе складывается из свободного
процесса и вынужденного процесса:
.
Для
устойчивой системы свободный процесс
по истечении времениtпзатухает и в системе устанавливается
вынужденный процесс
Точность
поддержания заданного значения
управляемой величины в вынужденном
режиме характеризуется вынужденной
ошибкой системы
.
Вынужденная
ошибка хорошо характеризует работу
системы автоматического управления в
том случае, когда изменения управляющего
воздействия происходят существенно
медленнее собственных переходных
процессов в системе и последними можно
пренебречь.
Рассмотрим
вычисление вынужденной ошибки системы
автоматического управления. Изображение
для вынужденной ошибки
.
В общем случае
является дробно-рациональной функцией
отpи ее можно разложить
в ряд Тейлора по степенямрвблизи, тогда
и
выражение для вынужденной ошибки системы
примет вид
где
постоянные
коэффициенты.
Для полученного
изображения вынужденной ошибки на
основе свойств преобразования Лапласа
легко находится выражение для оригинала
ошибки
где
,
,
…коэффициенты
ошибок, полученные выше (C0– коэффициент статической ошибки,C1
– коэффициент скоростной ошибки и
т. д.).
Коэффициенты
ошибки могут быть также получены делением
числителя передаточной функции на ее
знаменатель. Полученное выражение для
вынужденной ошибки позволяет оценить
точность системы автоматического
управления в установившемся режиме.
Вынужденная ошибка, например, хорошо
характеризует точность работы следящих
систем автоматического управления.
Соседние файлы в папке ТАУ
- #
- #
- #
Лекция 17. Расчет установившейся ошибки в системах управления.
Структурные признаки астатизма
Установившейся (статической) ошибкой называют
постоянное значение сигнала ошибки x(t)=g(t)-y(t),
которое она приобретает по окончании переходного процесса: , рисунок 116.
Очевидно, установившаяся ошибка зависит от законов
изменения и численных характеристик входных сигналов системы. Поэтому при ее
определении принято рассматривать так называемые типовые входные сигналы,
законы изменения которых составляют степенной ряд относительно времени.
Например, для задающего воздействия:
,
,

далее.
При наличии нескольких воздействий на линейную систему
для определения xуст используется
принцип суперпозиции – реакция линейной системы на совокупность входных
сигналов совпадает с алгебраической суммой ее реакций на каждый из сигналов в
отдельности:
каждое слагаемое, или составляющая сигнала ошибки, определяется
для i-го входного сигнала при условии, что остальные
тождественно равны нулю. Такой подход полностью соответствует определению
передаточной функции и позволяет выполнять расчет установившейся ошибки на
основе структурной схемы системы.
Рассмотрим порядок расчета установившейся ошибки на
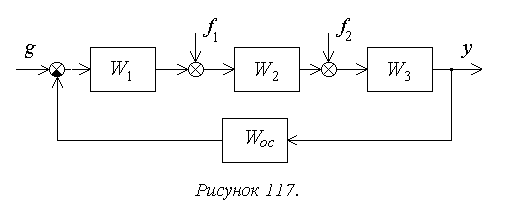
следующем достаточно общем примере (рисунок 117).
В соответствии с принципом суперпозиции установившаяся
ошибка будет определяться здесь в виде суммы трех составляющих .
Изображение по Лапласу ошибки от задающего воздействия
получают через передаточную функцию замкнутой системы по ошибке при известном изображении задающего
воздействия G(s):
, где
F(s) – основная передаточная функция замкнутой системы.
Для структурной схемы на рисунке 117
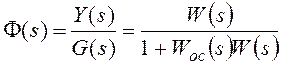
— передаточная функция
разомкнутой системы, или прямой цепи системы, для рассматриваемого примера.
Непосредственно для расчета
установившегося значения ошибки от задающего воздействия используют теорему о
конечном значении для преобразования Лапласа:
В результате:
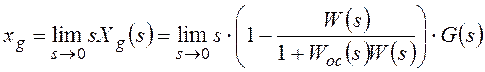
Изображение по Лапласу ошибки от возмущающего
воздействия получают через передаточную функцию замкнутой системы по ошибке от
возмущения при известном изображении возмущающего
воздействия F(s):
, где
Ff(s) –передаточная функция замкнутой системы по
возмущающему воздействию,
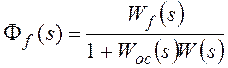
Wf(s)
– передаточная функция разомкнутой системы по возмущению (передаточная функция
участка прямой цепи системы от точки приложения возмущающего воздействия до
выхода системы).
Для структурной схемы на рисунке 8 необходимо
учитывать два возмущающих воздействия, приложенные в различные точки системы.
Для f1:
,
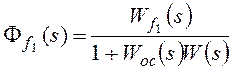
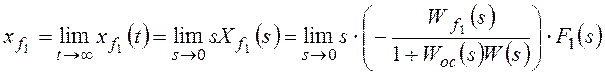
Для f2:
,
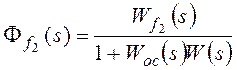
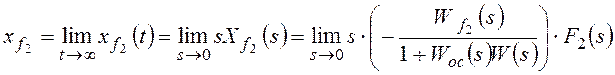
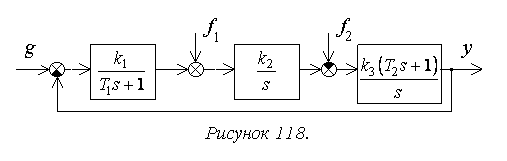
Расчет упрощается для
системы с единичной отрицательной обратной связью (рисунок 118):
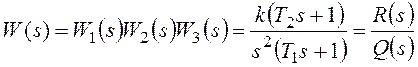
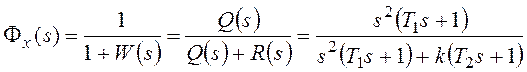
разомкнутой системы.
Найдем установившуюся ошибку
для некоторых типовых вариантов задающего воздействия.
При получим:
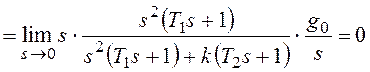
При получим:
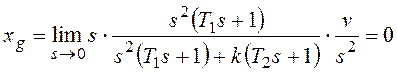
При 
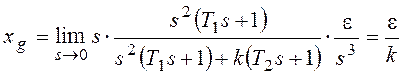
Если установившаяся ошибка
тождественно равна нулю при каком-либо типовом варианте входного сигнала,
независимо от его численных характеристик, систему называют астатической по
рассматриваемому входному сигналу.
Количество типовых вариантов
входного сигнала – членов степенного ряда, при которых установившаяся ошибка
тождественно равна нулю, определяет порядок астатизма.
Рассматриваемая система
обладает свойством астатизма второго порядка по задающему воздействию.
Рассмотрим установившуюся
ошибку от возмущения f1:
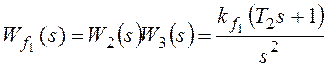
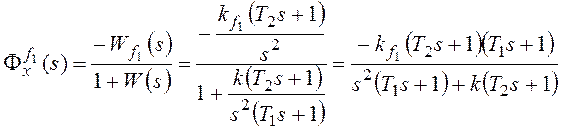
–
коэффициент передачи разомкнутой системы по возмущению f1.
При получим:
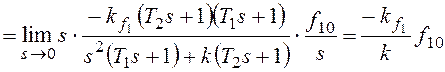
При получим:
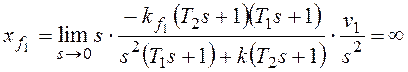
При 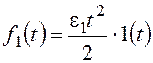
тот же результат.
Отметим, что по возмущению f1 рассматриваемая система
не является астатической. Кроме того, она не в состоянии отработать два последних
варианта входного сигнала.
Рассмотрим установившуюся
ошибку от возмущения f2:
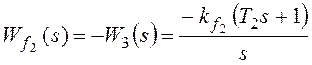
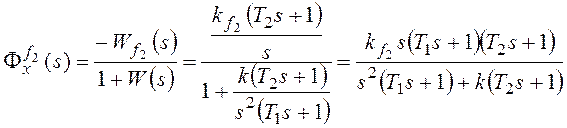
–
коэффициент передачи разомкнутой системы по возмущению f2.
При получим:
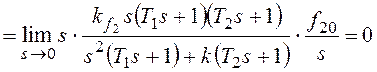
При получим:
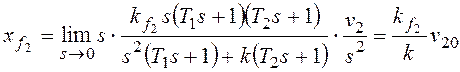
При 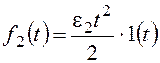
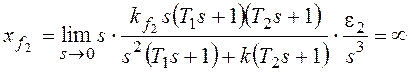
По возмущению f2 рассматриваемая система имеет
астатизм первого порядка. Она не в состоянии отработать возмущающее
воздействие, изменяющееся во времени с постоянным ускорением.
Подведем некоторые итоги:
1. Наличие и глубина
свойства астатизма зависят от точки приложения входного сигнала.
2. Постоянные времени
звеньев системы не влияют на ее точность.
3. Увеличение значения
коэффициента передачи разомкнутой системы приводит к снижению величины
установившейся ошибки.
Для систем с единичной
отрицательной обратной связью существуют достаточно простые структурные
признаки астатизма.
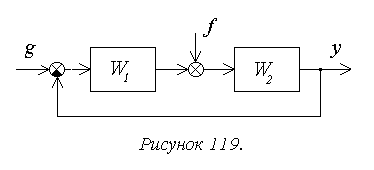
Рассмотрим структуру,
показанную на рисунке 119.
В общем случае передаточная
функция разомкнутой системы может быть представлена в следующей форме:
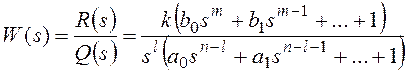
Тогда получим:
и для общего вида задающего воздействия 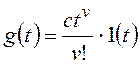
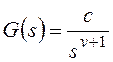
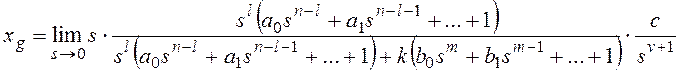
Результат нахождения этого
предела зависит от соотношения показателей степени:
— при l>v установившаяся
ошибка равна нулю независимо от остальных параметров, то есть имеет место
астатизм;
— при l=v получаем
константу;
— при l<v установившаяся
ошибка стремится к бесконечности, то есть система не в состоянии отработать
входной сигнал.
Учитывая, что минимальное
значение v нулевое,
получаем условие астатизма по задающему воздействию: l>0.
Таким образом, структурный
признак астатизма по задающему воздействию в системе с единичной отрицательной
обратной связью состоит в наличии нулевых корней в знаменателе передаточной
функции разомкнутой системы, или интегрирующих звеньев в прямой цепи системы.
Нетрудно также убедиться,
что положительное значение l совпадает
с порядком астатизма.
Для получения признака
астатизма по возмущающему воздействию представим передаточные функции на
рисунке 10 в форме:
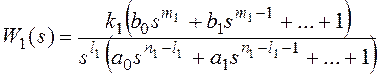
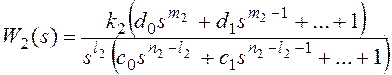
k1k2=k, m1+m2=m,
n1+n2=n,
причем и
.
Тогда получим:
и для общего вида возмущающего воздействия 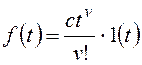
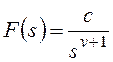
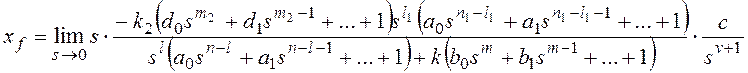
Все вышеприведенные выводы
можно повторить для показателя степени l1.
Таким образом, структурный
признак астатизма по возмущающему воздействию в системе с единичной
отрицательной обратной связью состоит в наличии нулевых корней в знаменателе
передаточной функции участка системы до точки приложения воздействия, или
интегрирующих звеньев на том же участке.
Величина — статическая ошибка
Cтраница 1
Величина статической ошибки зависит как от настройки регулятора, так и от характеристики и режима работы объекта.
[1]
Стремление уменьшить величину статической ошибки иногда неизбежно приводит к увеличению перерегулирования и времени регулирования. Уменьшение перерегулирования иногда приводит к увеличению статической ошибки.
[2]
В статических системах величина статической ошибки зависит от величины ступенчатой нагрузки. Эта зависимость, называемая статической характеристикой, имеет большое значение для анализа работы САР.
[3]
В астатических системах величина статической ошибки определяется значением нечувствительности регулятора.
[4]
При большом числе компрессоров величина статической ошибки может выйти за допустимые пределы.
[5]
Статическая точность передачи характеризуется величиной статической ошибки, определяемой углом рассогласования между осями датчика и приемника при отсутствии вращения. Величина статической ошибки зависит от нагрузки или момента на валу приемника, а также от собственной погрешности сельсинов.
[6]
Статическая точность передачи характеризуется величиной статической ошибки, определяемой углом пяссогласования между осями датчика и приемника при отсутствии вращения. Величина статической ошибки зависит от нагрузки или момента на валу приемника, а также от собственной погрешности сельсинов.
[7]
По мере увеличения коэффициента усиления величина статической ошибки уменьшается. В то же время степень колебания повышается и соответственно увеличивается динамическая ошибка регулирования. Оптимальная величина должна выбираться как с учетом статической, так и динамической ошибки. Причем статическая ошибка регулирования может быть исключена за счет введения интегральной составляющей в закон регулирования.
[8]
Нужно иметь в виду, что величина статической ошибки зависит как от настройки регулятора, так и от характеристики и режима работы объекта.
[9]
Получается противоречие между требованиями обеспечения устойчивости и величиной статической ошибки.
[10]
Определим границу ОНР, исходя из предположения, что величина статической ошибки не должна превышать величины 0 5 % от входного сигнала при полном перемещении исполнительного механизма.
[11]
Таким образом, давление в приемном канале 2 с точностью до величины статической ошибки, определяемой коэффициентом усиления струйного усилителя, поддерживается постоянным. При постоянном сечении потока этим способом измеряют расход вещества, определяемого как произведение скорости на площадь поперечного сечения потока.
[13]
По оси ординат откладывается отношение максимальной динамической ошибки в переходном процессе к величине статической ошибки, которая имела бы место, если бы в системе использовался пропорциональный регулятор, и была бы равна KLI ( K) при единичном ступенчатом изменении нагрузки. Это значение принято считать наилучшим. Нижняя кривая соответствует декременту затухания, равному 0 46, который получается, если коэффициент усиления выбрать близким к максимальному.
[15]
Страницы:
1
2
3
4
В автоматической системе с симметричной нелинейностью могут иметь место несимметричные автоколебания с некоторой постоянной составляющей 
Величина 

Практический интерес представляет также определение зависимости амплитуды и частоты автоколебаний от величины постоянного внешнего воздействия.
Уравнение нелинейной автоматической системы

где 

В статической системе будет 







Решение уравнения 

где 
Вследствие наличия смещения 

постоянную составляющую; при этом выражение для гармонической линеаризации нелинейности приобретает вид

здесь 

где 
В частном случае, когда нелинейность 


Определив по формулам 





Это уравнение можно представить в виде системы двух уравнений соответственно для постоянной и колебательной составляющих решения:

Уравнение 






Из уравнения 

Подставляя найденное выражение 



Решить аналитически уравнения 






Из уравнения 

Полученное уравнение 




Если какая-либо из искомых величин входит только в одно из уравнений 
Поскольку после построения графиков станет известной зависимость амплитуды автоколебаний 






Таким образом определяется величина статической ошибки 


Решение уравнений 


Эти уравнения дают возможность определить амплитуду А и частоту 



которая является характеристикой данного нелинейного звена по отношению к постоянной составляющей 

После определения функции смещения из уравнения 


Возможен случай, когда к нелинейной системе приложено несколько внешних воздействий:
Методика расчетов при этом сохраняется. В отличие от линейных систем в данном случае складывать статические ошибки от отдельных воздействий нельзя. Это обусловлено нелинейной зависимостью 


Для облегчения практических расчетов в табл. 1 и 2 приложения IV приведены значения коэффициентов гармонической линеаризации для некоторых типоб нелинейных звеньев. Более полные сведения по гармонической линеаризации при наличии внешнего воздействия приведены в работе [13].
Несимметричные колебания в нелинейных автоматических системах могут возникать не только при наличии внешнего воздействия, но и при несимметричных характеристиках самого нелинейного элемента 
В этом случае правая часть уравнения 

При несимметричных характеристиках нелинейного звена 

Поэтому решение уравнения 

Уравнения 

Решение уравнений 
Для облегчения использования описанной выше методики в табл. 3 приложения II приведены готовые выражения 
Пример 4. Для иллюстрации описанной выше методики определения установившихся ошибок в автоколебательных нелинейных системах рассмотрим систему, блок-схема которой приведена на рис. Х.20.

Рис. Х.20. Блок-схема релейной системы автоматического регулирования
Уравнения этой системы имеют вид:

Нелинейность представляет собой характеристику идеального симметричного реле

Уравнение системы будет

Предположим, что функция 

которое должна воспроизвести система на выходе. Второе внешнее воздействие 

Необходимо определить установившуюся ошибку на выходе системы. Правая часть характеристического уравнения будет при этом постоянной и установившееся решение для X с учетом автоколебаний следует искать в виде выражений 
Тогда уравнения для постоянных и периодических составляющих будут иметь вид:

В соответствии с изложенной выше методикой из уравнений 

Откуда

или

Для определения амплитуды А периодической составляющей используется уравнение 

Подставив 


Из уравнений 

Исключая из уравнений 


Подставив полученные значения 


Здесь величина

является амплитудой симметричных автоколебаний при отсутствии внешних воздействий 
Подставив полученное значение амплитуды А в формулу 

Из формулы (Х.82) видно, что автоколебания в системе существуют только до тех пор, пока внешние воздействия удовлетворяют условию

причем амплитуда автоколебаний уменьшается 
Так, в результате расчета определена величина смещения на входе реле. Однако практически больший интерес представляет установившаяся ошибка на выходе системы. Поскольку на выходе системы должно воспроизводиться внешнее воздействие 


Из заданных уравнений системы 

Учитывая, что 


В соответствии с характером правой части нужно искать установившееся решение этого линейного уравнения в виде

где 
— периодическая составляющая.
Подставляя выражение 

Из уравнения (X.87) определим

Затем из уравнения 

Наконец, из уравнения 

где 

Итак, в системе содержатся все три составляющие ошибки 


Точность системы автоматического управления Статическая ошибка системы
В системах
автоматического управления часто
приходится решать задачу стабилизации
управляемой величины. Точность поддержания
требуемого значения управляемой величины
в такой системе можно оценить как разницу
между заданным значением управляемой
величины и её установившимся значением
в системе после окончания переходного
процесса:
.
Эта величина
получила название статической ошибки
системы. При вычислении статической
ошибки предполагается, что система
находится в статике и все сигналы в ней
имеют постоянные величины. Статическая
ошибка используется для оценки точности
установления в системе заданной
постоянной выходной величины после
окончания переходного процесса.
Используя
передаточную функцию замкнутой системы
по ошибке, для изображения ошибки в
системе можно записать
,
гдепередаточная
функция замкнутой системы по ошибке,изображение
задающего воздействия.
Для статики,
когда все сигналы в системе неизменны,
выражение для ошибки можно перенести
в область оригиналов
.
Поскольку
,
гдеW(p)
– передаточная функция разомкнутой
системы, то статическую ошибку системы
можно вычислить, зная передаточную
функцию разомкнутой системы:
,
где.
Вместо
абсолютного значения статической ошибки
часто используют относительную
статическую ошибку
.
Если система
статическая (т.е. не содержит интегрирующих
звеньев), то передаточную функцию
разомкнутой системы можно представить
в следующем нормированном виде:
,
гдеK– коэффициент
усиления системы,A*(p),B*(p)
– нормированные полиномыA(p)
иB(p).
При этоми
.
Тогдаи статическая ошибка в статической
системе
.
Статическая
ошибка в статической системе уменьшается
с увеличением коэффициента усиления
системы. Статическая система всегда
будет иметь некоторую ошибку. Физический
смысл такой ошибки заключается в
необходимости некоторого рассогласования
между задающей и выходной величинами
системы для получения сигнала управления.
Если в системе
управления имеются интегрирующие
звенья, то система будет астатической.
Для астатической системы первого порядка
(содержащей одно интегрирующее звено)
передаточная функция разомкнутой
системы
и передаточная функция замкнутой системы
по ошибке
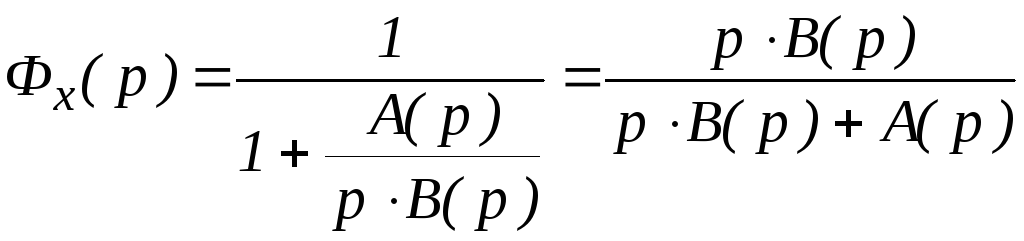
В этом случае всегда
и, следовательно, статическая ошибка
астатической системы будет равна нулю.
Таким образом, статическая ошибка в
астатической системе в принципе
отсутствует, что обуславливает более
высокую точность астатических систем,
по сравнению со статическими системами.
В астатической системе автоматического
управления установившееся значение
управляемой величины равно заданному
значению этой величины.
Вынужденная ошибка системы
Процесс в
системе складывается из свободного
процесса и вынужденного процесса:
.
Для
устойчивой системы свободный процесс
по истечении времениtпзатухает и в системе устанавливается
вынужденный процесс
Точность
поддержания заданного значения
управляемой величины в вынужденном
режиме характеризуется вынужденной
ошибкой системы
.
Вынужденная
ошибка хорошо характеризует работу
системы автоматического управления в
том случае, когда изменения управляющего
воздействия происходят существенно
медленнее собственных переходных
процессов в системе и последними можно
пренебречь.
Рассмотрим
вычисление вынужденной ошибки системы
автоматического управления. Изображение
для вынужденной ошибки
.
В общем случае
является дробно-рациональной функцией
отpи ее можно разложить
в ряд Тейлора по степенямрвблизи, тогда
и
выражение для вынужденной ошибки системы
примет вид
где
постоянные
коэффициенты.
Для полученного
изображения вынужденной ошибки на
основе свойств преобразования Лапласа
легко находится выражение для оригинала
ошибки
где
,
,
…коэффициенты
ошибок, полученные выше (C0– коэффициент статической ошибки,C1
– коэффициент скоростной ошибки и
т. д.).
Коэффициенты
ошибки могут быть также получены делением
числителя передаточной функции на ее
знаменатель. Полученное выражение для
вынужденной ошибки позволяет оценить
точность системы автоматического
управления в установившемся режиме.
Вынужденная ошибка, например, хорошо
характеризует точность работы следящих
систем автоматического управления.
Соседние файлы в папке ТАУ
- #
- #
- #
Лекция 17. Расчет установившейся ошибки в системах управления.
Структурные признаки астатизма
Установившейся (статической) ошибкой называют
постоянное значение сигнала ошибки x(t)=g(t)-y(t),
которое она приобретает по окончании переходного процесса: , рисунок 116.
Очевидно, установившаяся ошибка зависит от законов
изменения и численных характеристик входных сигналов системы. Поэтому при ее
определении принято рассматривать так называемые типовые входные сигналы,
законы изменения которых составляют степенной ряд относительно времени.
Например, для задающего воздействия:
,
,

далее.
При наличии нескольких воздействий на линейную систему
для определения xуст используется
принцип суперпозиции – реакция линейной системы на совокупность входных
сигналов совпадает с алгебраической суммой ее реакций на каждый из сигналов в
отдельности:
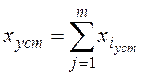
каждое слагаемое, или составляющая сигнала ошибки, определяется
для i-го входного сигнала при условии, что остальные
тождественно равны нулю. Такой подход полностью соответствует определению
передаточной функции и позволяет выполнять расчет установившейся ошибки на
основе структурной схемы системы.
Рассмотрим порядок расчета установившейся ошибки на
следующем достаточно общем примере (рисунок 117).
В соответствии с принципом суперпозиции установившаяся
ошибка будет определяться здесь в виде суммы трех составляющих .
Изображение по Лапласу ошибки от задающего воздействия
получают через передаточную функцию замкнутой системы по ошибке при известном изображении задающего
воздействия G(s):
, где
F(s) – основная передаточная функция замкнутой системы.
Для структурной схемы на рисунке 117
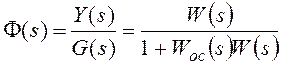
— передаточная функция
разомкнутой системы, или прямой цепи системы, для рассматриваемого примера.
Непосредственно для расчета
установившегося значения ошибки от задающего воздействия используют теорему о
конечном значении для преобразования Лапласа:
В результате:
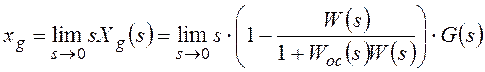
Изображение по Лапласу ошибки от возмущающего
воздействия получают через передаточную функцию замкнутой системы по ошибке от
возмущения при известном изображении возмущающего
воздействия F(s):
, где
Ff(s) –передаточная функция замкнутой системы по
возмущающему воздействию,
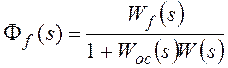
Wf(s)
– передаточная функция разомкнутой системы по возмущению (передаточная функция
участка прямой цепи системы от точки приложения возмущающего воздействия до
выхода системы).
Для структурной схемы на рисунке 8 необходимо
учитывать два возмущающих воздействия, приложенные в различные точки системы.
Для f1:
,
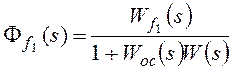
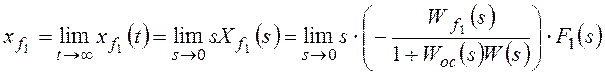
Для f2:
,
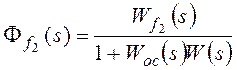
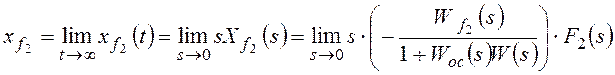
Расчет упрощается для
системы с единичной отрицательной обратной связью (рисунок 118):
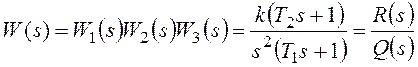
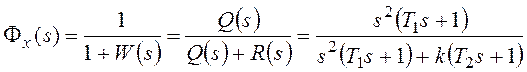
разомкнутой системы.
Найдем установившуюся ошибку
для некоторых типовых вариантов задающего воздействия.
При получим:
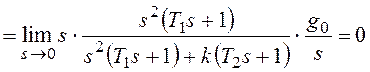
При получим:
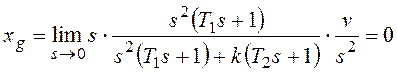
При 
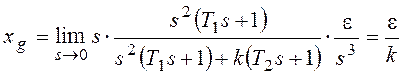
Если установившаяся ошибка
тождественно равна нулю при каком-либо типовом варианте входного сигнала,
независимо от его численных характеристик, систему называют астатической по
рассматриваемому входному сигналу.
Количество типовых вариантов
входного сигнала – членов степенного ряда, при которых установившаяся ошибка
тождественно равна нулю, определяет порядок астатизма.
Рассматриваемая система
обладает свойством астатизма второго порядка по задающему воздействию.
Рассмотрим установившуюся
ошибку от возмущения f1:
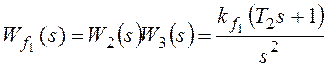
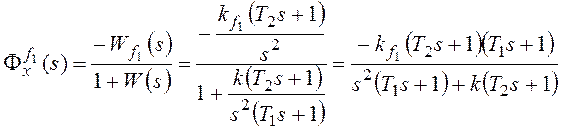
–
коэффициент передачи разомкнутой системы по возмущению f1.
При получим:
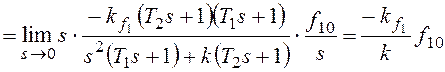
При получим:
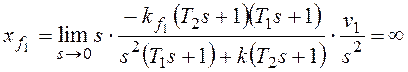
При 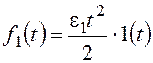
тот же результат.
Отметим, что по возмущению f1 рассматриваемая система
не является астатической. Кроме того, она не в состоянии отработать два последних
варианта входного сигнала.
Рассмотрим установившуюся
ошибку от возмущения f2:
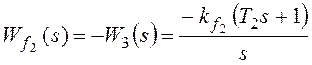
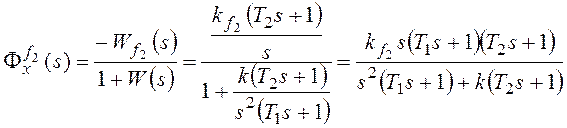
–
коэффициент передачи разомкнутой системы по возмущению f2.
При получим:
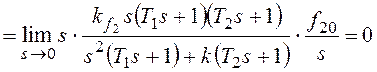
При получим:
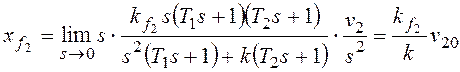
При 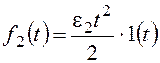
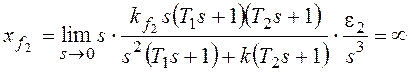
По возмущению f2 рассматриваемая система имеет
астатизм первого порядка. Она не в состоянии отработать возмущающее
воздействие, изменяющееся во времени с постоянным ускорением.
Подведем некоторые итоги:
1. Наличие и глубина
свойства астатизма зависят от точки приложения входного сигнала.
2. Постоянные времени
звеньев системы не влияют на ее точность.
3. Увеличение значения
коэффициента передачи разомкнутой системы приводит к снижению величины
установившейся ошибки.
Для систем с единичной
отрицательной обратной связью существуют достаточно простые структурные
признаки астатизма.
Рассмотрим структуру,
показанную на рисунке 119.
В общем случае передаточная
функция разомкнутой системы может быть представлена в следующей форме:
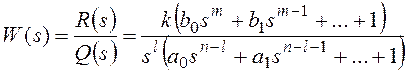
Тогда получим:
и для общего вида задающего воздействия 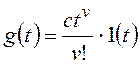
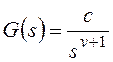
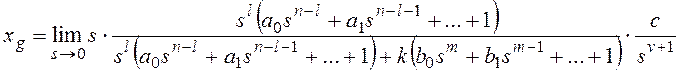
Результат нахождения этого
предела зависит от соотношения показателей степени:
— при l>v установившаяся
ошибка равна нулю независимо от остальных параметров, то есть имеет место
астатизм;
— при l=v получаем
константу;
— при l<v установившаяся
ошибка стремится к бесконечности, то есть система не в состоянии отработать
входной сигнал.
Учитывая, что минимальное
значение v нулевое,
получаем условие астатизма по задающему воздействию: l>0.
Таким образом, структурный
признак астатизма по задающему воздействию в системе с единичной отрицательной
обратной связью состоит в наличии нулевых корней в знаменателе передаточной
функции разомкнутой системы, или интегрирующих звеньев в прямой цепи системы.
Нетрудно также убедиться,
что положительное значение l совпадает
с порядком астатизма.
Для получения признака
астатизма по возмущающему воздействию представим передаточные функции на
рисунке 10 в форме:
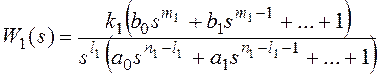
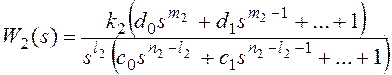
k1k2=k, m1+m2=m,
n1+n2=n,
причем и
.
Тогда получим:
и для общего вида возмущающего воздействия 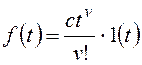
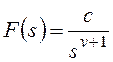
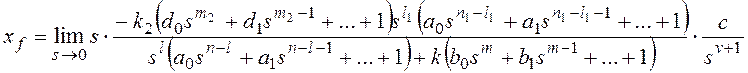
Все вышеприведенные выводы
можно повторить для показателя степени l1.
Таким образом, структурный
признак астатизма по возмущающему воздействию в системе с единичной
отрицательной обратной связью состоит в наличии нулевых корней в знаменателе
передаточной функции участка системы до точки приложения воздействия, или
интегрирующих звеньев на том же участке.
Глава 8. Типовые законы регулирования. Одноконтурные САР
8.1. Основные типы автоматических регуляторов
Регулятор на основе усилительного звена называется П-регулятором (пропорциональный). Его положительной характеристикой является высокое быстродействие: при отклонении регулируемой величины от заданного значения регулятор выдает регулирующее воздействие, пропорциональное величине отклонения x, что обеспечивает быструю компенсацию возмущения. Существенным недостатком П-регулятора является наличие статической ошибки в переходном процессе АСР с П-регулятором (рис. 37). Статическая ошибка возникает потому, что у П-регулятора между регулируемой величиной x и регулирующим воздействием xр существует зависимость, однозначно определяемая коэффициентом K. Поэтому генерировать регулирующее воздействие xр для компенсации возмущения xв П-регулятор может только путем изменения регулируемой величины x, что и создает статическую ошибку.
Регулятор на основе интегрирующего звена (48) называется И‑регулятором:
Если xвых усилительного звена (П-регулятор) однозначно определяется величиной правой части уравнения, что является причиной возникновения статической погрешности в АСР с П-регулятором, то правая часть уравнения (48) интегрирующего звена (И-регулятор) определяет не величину, а скорость изменения xвых. Величина xвых будет изменяться до тех пор, пока правая часть уравнения (48) не станет равна нулю, т. е. пока регулируемая величина x при наличии возмущения xв не вернется к заданному значению. Следовательно, в АСР с И-регулятором не возникает статическая погрешность.
Однако у И-регулятора имеется свой недостаток сравнительно с П-регулятором: в случае возникновения возмущения регулирующее воздействие П-регулятора меняется быстрее, чем у И-регулятора с его конечной скоростью, что замедляет процесс компенсации возмущения и ухудшает критерии качества регулирования (рис. 40).
Рис. 40. Переходные процессы в АСР с П- и И-регуляторами
Таким образом, П-регулятор обеспечивает высокое быстродействие (что уменьшает динамическую ошибку), но не может обеспечить при наличии возмущения заданное значение регулируемой величины (статическая ошибка). И-регулятор, наоборот, не создает статическую ошибку, но вследствие относительно медленного изменения xр имеет большую динамическую ошибку.
Сравнивая характеристики П- и И-регуляторов можно сделать вывод: если включить усилительное и интегрирующие звенья параллельно, то автоматический регулятор будет лишен указанных недостатков. Такой регулятор называется ПИ-регулятором (рис. 41).
Рис. 41. Принципиальная схема АСР с ПИ-регулятором
Действительно, быстродействие ПИ-регулятора обеспечивает усилительное звено, а статическую ошибку снимает интегрирующее звено. Для управления производственными процессами чаще всего используются ПИ-регуляторы.
Кривая разгона идеального ПИ-регулятора показана на рис. 42 .
Уравнение ПИ-регулятора при нулевых начальных условиях имеет вид:

Отношение коэффициентов Kp1/Kp определяет степень влияния интегрирующей части, и его обратная величина называется временем изодрома Tи.

Время изодрома – это время, в течение которого интегрирующее звено изменяет регулирующее воздействие xр ПИ-регулятора на величину Dxр, равную предварительному изменению Dxр усилительного звена (рис. 42). Поэтому иногда время изодрома называют временем удвоения.
Рис. 42. График кривой разгона идеального ПИ-регулятора:
а – скачкообразное изменение входного воздействия x;
б – реакция (кривая разгона) ПИ-регулятора xр
Уравнение ПИ-регулятора можно записать как
откуда передаточная функция
Амплитудно-фазовая характеристика:

В том случае, если рассмотренные регуляторы не обеспечивают требуемое качество регулирования, необходимо увеличить интенсивность процесса компенсации возмущения. Этого можно достигнуть увеличением регулирующего воздействия, которое в свою очередь определяется коэффициентом усиления автоматического регулятора Kp
. Однако ниже будет показано, что увеличение коэффициента усиления регулятора в АСР приводит к тому, что в системе начинают генерироваться незатухающие колебания.
В связи с этим представляет интерес рассмотреть алгоритм, который реализует дифференцирующее звено.
Входной величиной любого регулятора является кривая разгона регулируемой величины (рис. 27), которая определяется величиной возмущения и передаточной функцией объекта регулирования (9). В свою очередь, регулирующее воздействие xp (рис. 27) определяется кривой разгона x и передаточной функцией регулятора.
На рис. 43 показана реакция дифференцирующего звена (Д‑регулятора) на входное воздействие в виде кривой разгона в соответствии с уравнением (51).
Рис. 43. Реакция дифференцирующего звена на кривую разгона
а –изменение входного воздействия x в виде кривой разгона;
б – реакция xр дифференцирующего звена
Из рис. 43,а следует, что дифференцирующее звено обеспечивает большее регулирующее воздействие в начале переходного процесса. Это означает, что дифференцирующий регулятор активно компенсирует возмущение и исключает возникновение незатухающих колебаний.
Если включить дифференцирующее звено параллельно ПИ‑регулятору (рис. 44), то получим ПИД-регулятор, обеспечивающий интенсивную компенсацию возмущений. При этом недостаток дифференцирующего звена (при Хвх = const, Хвых = 0 ) компенсируется усилительным и интегрирующим звеньями.
Рис. 44. Принципиальная схема АСР с ПИД-регулятором
На рис. 45 показана кривая разгона ПИД-регулятора.
Рис. 45. Кривая разгона ПИД-регулятора
На рис. 46 показаны переходные процессы на с различными регуляторами. ПИД-регулятор уменьшает динамическую ошибку сравнительно с ПИ-регулятором на 25–30%. Также можно объединить дифференцирующее звено с усилительным звеном и улучшить показатели П-регулятора, получив ПД-регулятор.

Все пять типов рассмотренных автоматических регуляторов имеют общую особенность своего функционирования – обеспечивают стабилизацию регулируемой величины после окончания переходного процесса.
8.2. Критерии качества регулирования
Качество процесса регулирования в АСР характеризуют следующие показатели (критерии) (рис. 16):
Рис. 16. Показатели качества регулирования:
1 – переходной процесс без статической ошибки;
2 – переходной процесс со статической ошибкой
1. Максимальное отклонение в процессе регулирования от заданного значения (динамическая ошибка) ΔХдин.
2. Статическая ошибка ΔХст — возможные отклонения от заданного значения по окончании переходного процесса при использовании некоторых типов регуляторов (подробнее такие АСР рассмотрены ниже).
3. Длительность переходного процесса Тр – период времени с момента начала отклонения регулируемого параметра от задания до возвращения его к заданному значению с определенной степенью точности регулирования ±Δ.
Например, если ±Δ=±25%, это означает, что для заданного значения температуры в 100 °С процесс регулирования будет завершен при достижении диапазона (100 ± 2,5) °С.
4. Степень затухания показывает характер затухания переходного процесса регулирования:
Для того, чтобы переходный процесс затухал за 2 ¸ 3 периода колебаний, степень затухания должна быть равна

5. Степень колебательности процесса m определяет характер колебательности процесса и равна отношению действительной части корня характеристического уравнения к коэффициенту при его мнимой части. Степень колебательности связана со степенью затухания следующим соотношением:
6. Интегральный квадратичный критерий – критерий, определяющий площадь под кривой переходного процесса, возведенной в квадрат (рис. 17):
Уменьшение интегрального критерия соответствует ускорению процесса регулирования.
Рис. 17. Интегральный квадратичный критерий качества регулирования
Однако все приведенные шесть критериев качества не определяют величину потерь производства при отклонениях регулируемой величины от оптимального значения в переходных процессах регулирования. Для определения таких потерь можно использовать экономический критерий.
7. Экономический критерий рассмотрим на примере, регулирования температуры химического реактора θ, когда степень превращения Q в реакторе определяется температурой (рис. 18а).
Разделим переходной процесс на равные интервалы времени Δt и запишем значения θ
в этих точках по графику (18, б). На графике (18, а) для этих температур определим уменьшение степени превращения вследствие отклонения от оптимального режима, а затем сделаем расчет потерь исходных продуктов для каждого интервала Δθ, суммируем эти потери для всего переходного процесса и представим потери в денежном выражении.
Рис. 18. Экономический критерий качества регулирования:
а – зависимость степени превращения Q от температуры θ;
б – переходный процесс регулирования температуры
Совместно со специалистом по технологии или по его заданию необходимо определить, какой из указанных критериев для рассматриваемой АСР является превалирующим, и задать максимально допустимую величину этого критерия, т. е. определить, какое качество регулирования должна обеспечить проектируемая АСР.
8.3. Выбор закона регулирования
При выборе регулятора следует определиться с группой регулирующих устройств – непрерывного, релейного или импульсного действия. Такой выбор ориентировочно может быть сделан по величине отношения запаздывания к постоянной времени объекта τ/Tоб:
· при отношении τ/Tоб меньше 0.2 целесообразно использовать регулятор релейного действия;
· если отношение τ/Tоб от 0.2 до 1.0, то нужно использовать регулятор непрерывного действия;
· при отношении τ/Tоб больше единицы можно использовать регулятор импульсного действия, или специальные регуляторы, например, регулятор («предиктор») Смита.
Затем необходимо определиться с типом регулятора, т.е. выбрать определенный закон регулирования: П-, И-, ПИ-, ПД- или ПИД-закон
8.4. Методы расчета одноконтурных САР
Как указывалось выше, качество автоматического регулирования определяется свойствами системы в целом, т. е. суммарными свойствами объекта и регулятора. Поскольку объект обычно является неизменяемой частью системы, то обеспечить определенные свойства системы, а следовательно и заданное качество регулирования, можно соответствующим подбором свойств автоматического регулятора, что зависит от параметров его настройки. В свою очередь, параметры настройки являются коэффициентами передачи в уравнении автоматического регулятора.
Таким образом, параметры настройки автоматического регулятора определяются свойствами объекта регулирования, т. е. величинами τоб, Тоб, Коб.
8.4.1. Расчет по «приближенным» формулам
Приближенные формулы для расчета параметров настройки автоматических регуляторов (Kр – коэффициент усиления; Tи – время изодрома; Тд – время дифференцирования) сведены в следующую таблицу:
Таблица 8.1. Формулы для приближенного расчета
параметров настройки регуляторов

Формулы сгруппированы в столбцы в зависимости от характера переходного процесса, который желательно получить, используя рассчитанный таким образом регулятор: апериодический или с перерегулированием в 20 %. В формулы входят следующие свойства объекта регулирования: Коб – коэффициент усиления; Тоб – постоянная времени; τоб – время запаздывания (полного).
Рис. 53. Кривые разгона:
1 – фактическая кривая разгона промышленного объекта;
2 – аппроксимированная (приближенная) кривая разгона
Необходимо отметить, что для пневматических регуляторов требуется определять не Kp, а диапазон дросселирования:
Рассмотрим методику более точного определения параметров настройки на примере расчета наиболее «популярного» регулятора – ПИ-регулятора.
8.4.2. Метод незатухающих колебаний
(метод Циглера-Никольса)
При использовании метода незатухающих колебаний [6], который иногда также называется по именам авторов методом Циглера-Никольса, поиск оптимальных параметров настройки осуществляется по величине критического коэффициента усиления П-регулятора и величине периода автоколебательного процесса.
Рис. 54. К поиску параметров настройки методом Циглера-Никольса
Расчет параметров настройки регуляторов проводится в два этапа.
1. На исследуемом объекте устанавливается П-регулятор и, последовательно увеличивая коэффициент усиления (уменьшая диапазон дросселирования), АСР выводится в режим незатухающих колебаний (автоколебаний на границе устойчивости). При этом фиксируется величина коэффициента усиления П-регулятора Ккрр и период незатухающих автоколебаний Т (рис. 54).
2. На втором этапе по величинам Кркр и Т определяются параметры настройки П-, ПИ- и ПИД-регуляторов:
Метод незатухающих колебаний не требует сложных вычислений, но имеет свои характерные недостатки:
· получить Кркр и Т можно только на действующем объекте, оснащенном АСР с П-регулятором;
· не все объекты химической технологии допускают режим автоколебаний;
· практически трудно уловить момент начала автоколебаний.
Данные недостатки имеют место лишь при настройке регулятора методом Циглера-Никольса непосредственно на действующем объекте. Если заменить реальный объект его математической моделью, данный метод лишается указанных недостатков, кроме того, моделирование позволяет на порядок ускорить процесс поиска параметров настройки. Но для выполнения моделирования требуется достаточно точное математическое описание объекта регулирования, а получить его удается не всегда.
8.4.3. Метод расширенных частотных характеристик
Уравнение ПИ-регулятора (65) или (66):
Передаточная функция ПИ-регулятора:

Знак «минус» указывает, что действие регулятора направлено против возмущения.
Из передаточной функции получаем амплитудно-фазовую характеристику ПИ-регулятора путем замены p на iw:

Так как по формуле Эйлера


с затуханием за три периода
Заменив iw на комплексную переменную (-mw+iw), получаем расширенную амплитудно-фазовую характеристику (РАФХ)Ю

Расширенными такие характеристики называются потому, что они как бы «расширены» по отношению к обычной АФХ (рис. 56).
Предположим, что объект регулирования имеет передаточную функцию второго порядка следующего вида:

Для дальнейшего математического моделирования АСР передаточную функцию необходимо преобразовать:

Рис. 56. АФХ объекта регулирования с самовыравниванием:
1 – обычная; 2 – расширенная
Расширенная амплитудно-фазовая характеристика объекта регулирования при замене p на (-mw+iw) будет иметь вид:



Где Rоб(m,w) -расширенная амплитудно-частотная характеристика объекта; Fоб(m,w) -расширенная фазочастотная харктеристика объекта. Величина 40w в выражении для Fоб (m,w) опеделяет угол в радианах и для пересчета в градусы неоходимо 40w умножить на 57,3
Условием нахождения замкнутой АСР на границе устойчивости является уравнение:

Аналогично, исходным уравнением для получения заданной степени колебательности m, а следовательно, определенной степени затухания y, является соотношение:
Это соотношение двух комплексных чисел возможно в том случае, если произведение модулей РАФХ равно единице, а аргументы (фазы) равны между собой, т. е.

Решая эти уравнения относительно S0 и Kp, получаем:


Обычно принимают степень колебательности m = 0,221, что соответствует степени затухания ψ=0,75 и обеспечивает затухание процесса регулирования примерно за три периода. Тогда

Уравнения для определения параметров настройки ПИ-регулятора можно преобразовать:


Подставляя в приведенные уравнения численные значения частоты w от 0 до значения, когда S0 становится отрицательной величиной, строим на плоскости параметров настройки кривую равной степени колебательности


Пример кривых равной степени колебательности в плоскости параметров настройки ПИ-регулятора показан на рис. 57. Графики процессов регулирования с различными параметрами настройки ПИ-регулятора при m = 0,221 показаны на рис. 58. Все процессы регулирования, показанные на рис. 58, реализованы ПИ-регулятором с параметрами настройки, полученными по кривой равной степени колебательности в точках 1, 2, 3, 4 (рис. 57), и все имеют m = 0,221, т. е. затухают примерно за три периода, но обладают существенно различным характером.
В связи с этим возникает задача определения оптимальных параметров настройки на кривой равной степени колебательности.
Рис. 57. Кривые равной степени колебательности
В качестве критерия оптимальности выбираем продолжительность переходного процесса – время регулирования (т. е. быстродействие АСР) и отсутствие постоянной или врéменной статической ошибки. Это исключает из рассмотрения параметры настройки в точке 4 (параметры настройки П-регулятора) и в точке 3 (врéменная статическая ошибка) (рис. 58).
Рис. 58. Графики процессов регулирования для ПИ-регулятора
с различными параметрами настройки в точках 1, 2, 3 и 4
при степени колебательности m =0,221
Быстродействие автоматического регулятора прежде всего зависит от величины регулирующего воздействия, которое для ПИ-регулятора, как следует из уравнения (65), прямо пропорционально величине коэффициента усиления Kp и обратно пропорционально времени изодрома Tи. Расчеты показывают, что если двигаться по кривой равной степени колебательности вправо, то величина регулирующего воздействия при прочих равных условиях сначала возрастает и достигает максимального значения на кривой равной степени колебательности вблизи ее вершины, когда
а затем начинает уменьшаться в связи с резким увеличением Tи (рис. 57).
Рис. 59. Выбор оптимальных параметров настройки
Таким образом, оптимальные параметры настройки ПИ-регулятора находятся в точке 2 на кривой равной степени колебательности (рис. 59).
Источник
Плютто В. П., Дубровский И. И. Элементы теории управления химико-технологическими процессами и системами. Конспект лекций: Учеб. пособие – М.: РХТУ им. Д. И. Менделеева, 2003. – 127 с.