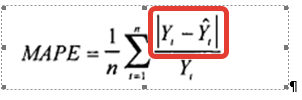17 авг. 2022 г.
читать 2 мин
Одной из наиболее распространенных метрик, используемых для измерения точности прогнозирования модели, является MAPE , что означает среднюю абсолютную ошибку в процентах .
Формула для расчета MAPE выглядит следующим образом:
MAPE = (1/n) * Σ(|факт – прогноз| / |факт|) * 100
куда:
- Σ — причудливый символ, означающий «сумма».
- n – размер выборки
- фактический – фактическое значение данных
- прогноз – прогнозируемое значение данных
MAPE обычно используется, потому что его легко интерпретировать и легко объяснить. Например, значение MAPE, равное 11,5%, означает, что средняя разница между прогнозируемым значением и фактическим значением составляет 11,5%.
Чем ниже значение MAPE, тем лучше модель способна прогнозировать значения. Например, модель с MAPE 2% более точна, чем модель с MAPE 10%.
Как рассчитать MAPE в Excel
Чтобы рассчитать MAPE в Excel, мы можем выполнить следующие шаги:
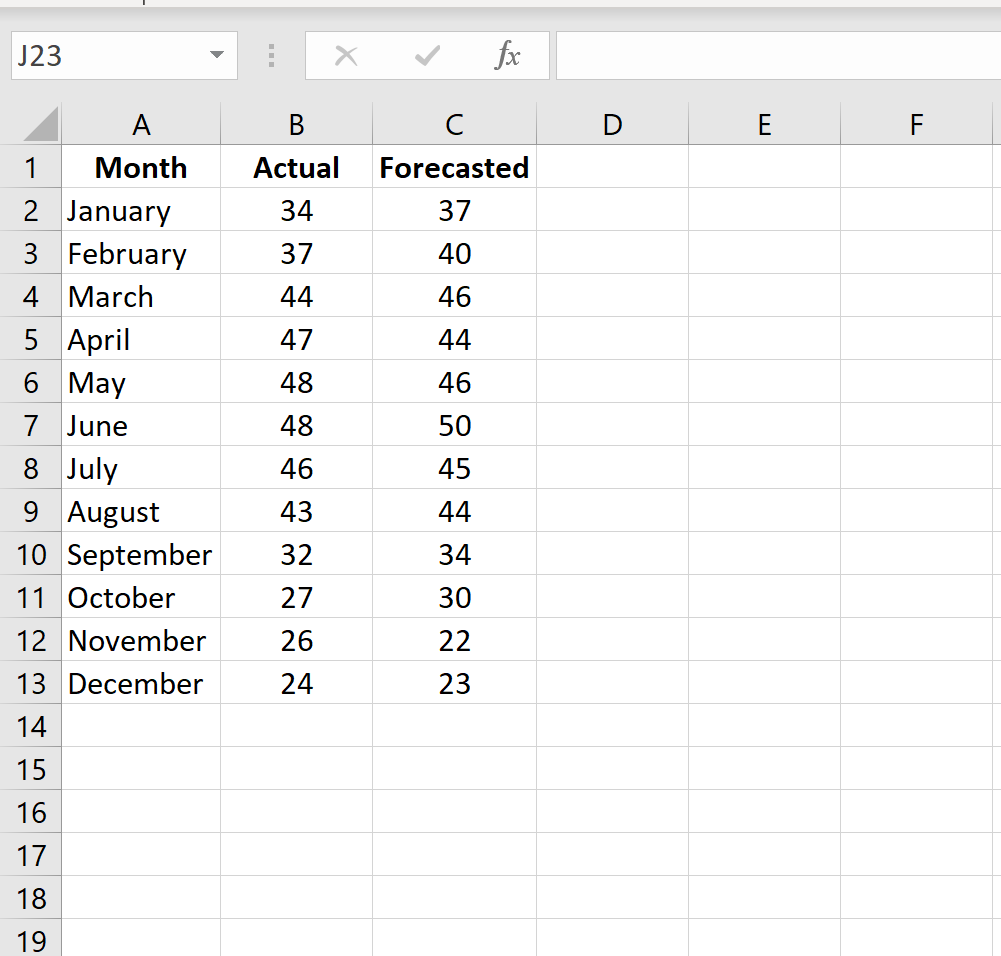
Шаг 1: Введите фактические значения и прогнозируемые значения в два отдельных столбца.
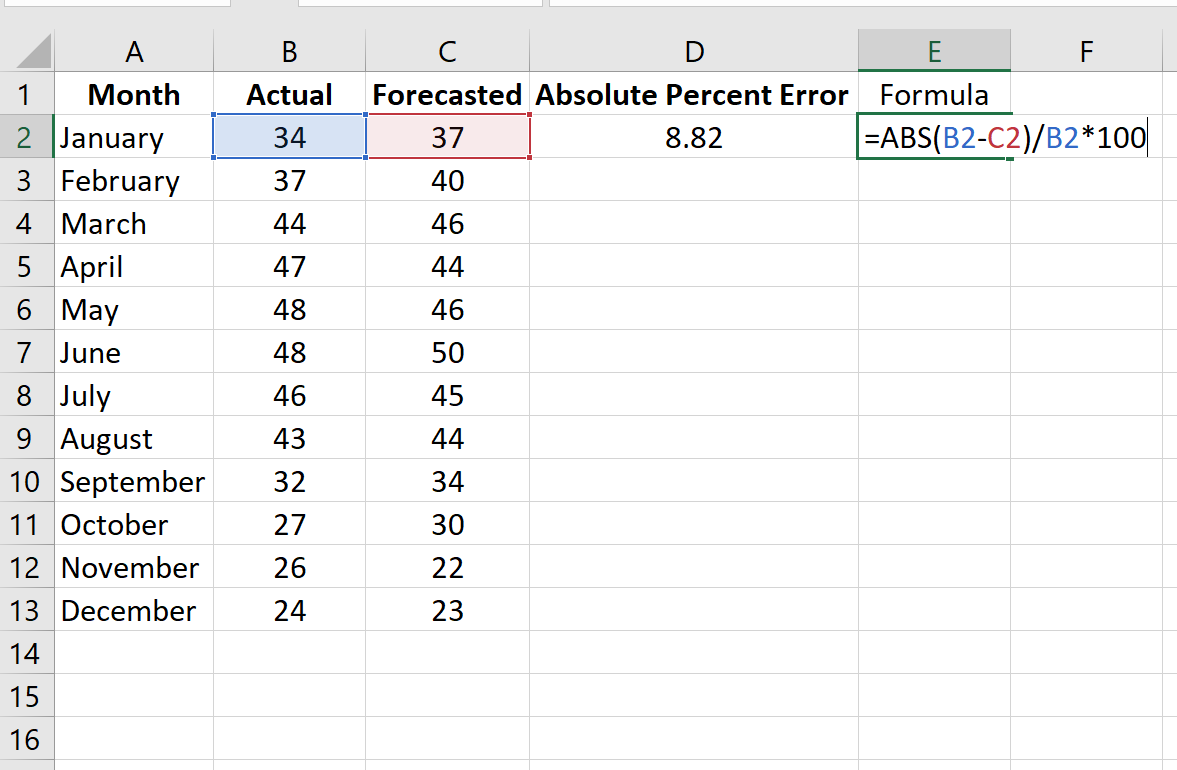
Шаг 2: Рассчитайте абсолютную процентную ошибку для каждой строки.
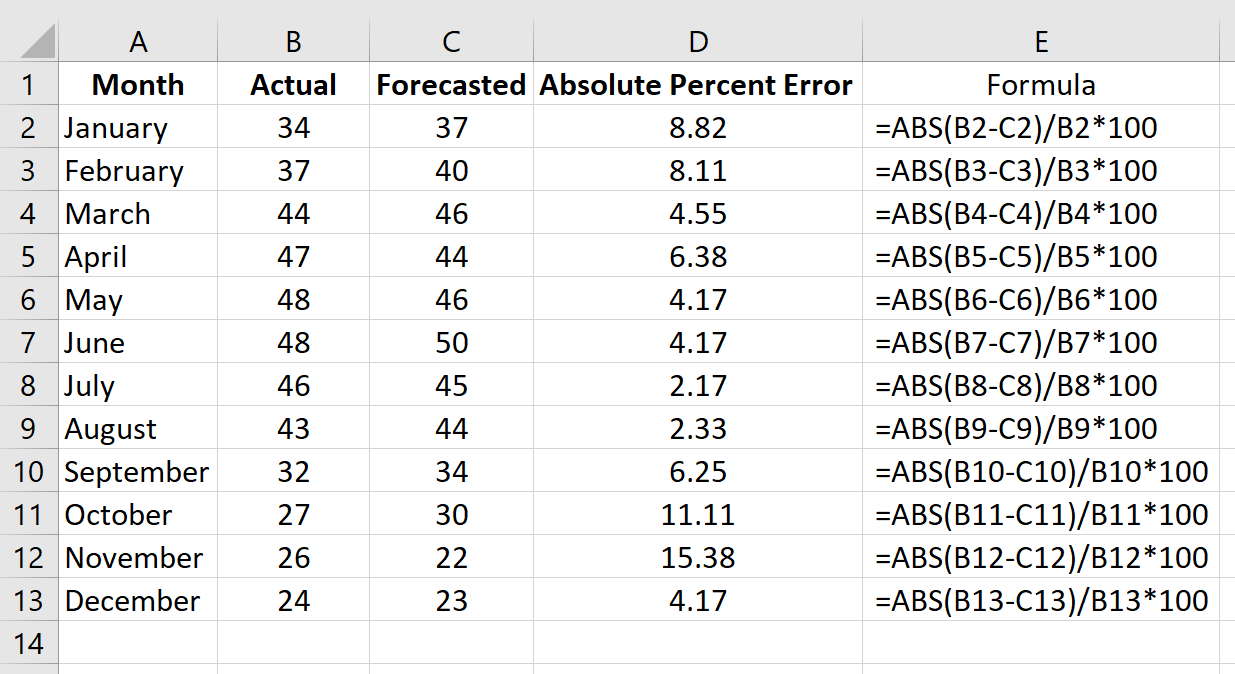
Напомним, что абсолютная процентная ошибка рассчитывается как: |фактический-прогноз| / |фактическое| * 100. Мы будем использовать эту формулу для расчета абсолютной процентной ошибки для каждой строки.
Столбец D отображает абсолютную процентную ошибку, а столбец E показывает формулу, которую мы использовали:
Повторим эту формулу для каждой строки:
Шаг 3: Рассчитайте среднюю абсолютную ошибку в процентах.
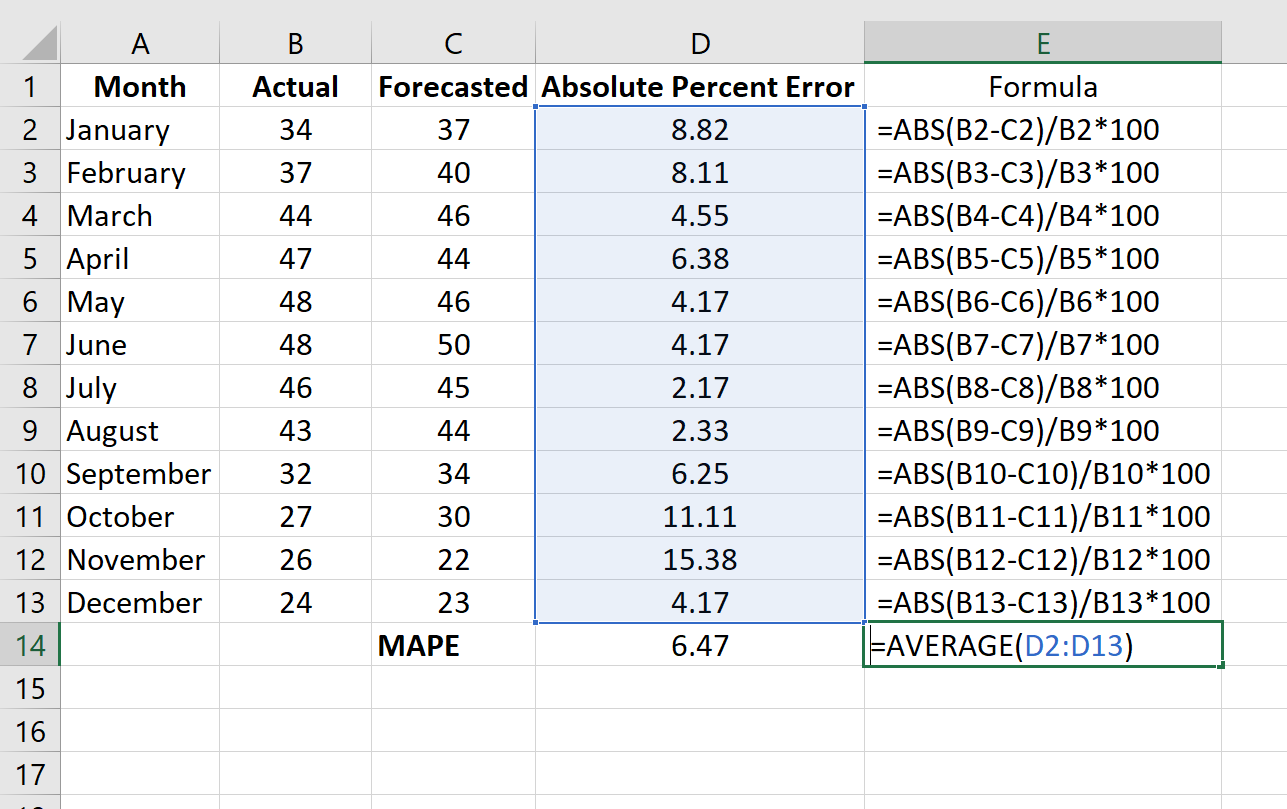
Рассчитайте MAPE, просто найдя среднее значение в столбце D:
MAPE этой модели оказывается равным 6,47% .
Примечание по использованию MAPE
Хотя MAPE легко вычислить и легко интерпретировать, его использование имеет несколько потенциальных недостатков:
1. Поскольку формула для расчета абсолютной процентной ошибки |фактический-прогноз| / |фактическое| это означает, что он будет неопределенным, если какое-либо из фактических значений равно нулю.
2. MAPE не следует использовать с данными небольшого объема. Например, если фактический спрос на какой-либо товар равен 2, а прогноз равен 1, значение абсолютной процентной ошибки будет |2-1| / |2| = 50%, что создает впечатление, что ошибка прогноза довольно высока, несмотря на то, что прогноз отличается всего на одну единицу.
Другим распространенным способом измерения точности прогнозирования модели является MAD — среднее абсолютное отклонение. О том, как посчитать MAD в Excel, читайте здесь .
Дополнительные ресурсы
Что считается хорошей ценностью для MAPE?
Как рассчитать SMAPE в Excel
Как рассчитать MAE в Excel
1 октября 2021 г.
MAPE = (1 / размер выборки) x ∑[( |actual — forecast| ) / |actual| ] х 100
Многие отрасли используют прогнозирование для предсказания будущих событий, таких как спрос и потенциальные продажи. Прогнозирование помогает организациям принимать решения, связанные с такими вопросами, как составление бюджета, планирование и трудовые ресурсы, поэтому важно, чтобы прогнозы были точными. Чтобы помочь проанализировать точность прогнозов и улучшить прогнозы на будущее, организации могут использовать такие показатели, как MAPE, для точного сравнения фактических продаж с прогнозируемыми продажами. В этой статье мы определяем, что такое MAPE, обсуждаем, почему это важно, объясняем, что такое ошибка прогноза, описываем, как рассчитать MAPE, и приводим пример расчета.
Что такое МАПЕ?
Средняя абсолютная процентная ошибка (MAPE) измеряет точность метода прогнозирования, используемого организацией. Он представляет собой среднее значение абсолютных процентных ошибок каждой записи в наборе данных, показывая, в среднем, насколько точными были прогнозируемые количества по сравнению с фактическими количествами. MAPE часто эффективен для анализа больших наборов данных, но невозможно рассчитать MAPE для наборов данных с нулевыми значениями. Это связано с тем, что для расчета потребуется разделить на ноль, что невозможно.
MAPE — это простая метрика, означающая, что MAPE 10% представляет собой среднее отклонение между прогнозируемым значением и фактическими значениями, составляющее 10%, независимо от того, было ли отклонение положительным или отрицательным. Однако не существует отраслевого стандарта для того, что считается хорошим MAPE. Например, организация, которая часто меняет цены или часто предлагает рекламные акции, может иметь более высокий MAPE, чем организация с постоянным ценообразованием. Это связано с тем, что изменения в ценообразовании могут затруднить точное прогнозирование продаж, но обе организации могут по-прежнему добиваться успеха.
MAPE — важный показатель, который легко интерпретировать. Это зависит конкретно от данных, которые вы оцениваете, обеспечивая точную оценку надежности вашего прогноза. На основе MAPE ваша организация может разрабатывать более точные прогнозы для будущих проектов, правильно корректируя затраты на материалы и рабочую силу и гарантируя, что вы сможете наилучшим образом согласовать свое производство и операции с требованиями клиентов.
Что такое ошибка прогноза?
Ошибка прогноза относится к фактическому количеству и тому, как оно отклоняется от прогнозируемого количества. Ошибка может быть больше фактического количества или прогнозируемого количества, но не может быть больше того и другого. Вот формула для расчета ошибки прогноза:
Ошибка прогноза = | факт — прогноз |
В этом уравнении столбцы представляют собой использование абсолютного значения, что означает, что результат уравнения всегда будет положительным независимо от того, действительно ли фактическая сумма меньше прогнозируемой. Ошибка прогноза фокусируется на величине ошибки, а не на том, является ли она положительной или отрицательной. Чтобы рассчитать MAPE, важно рассчитать процент ошибки прогноза. Вот формула для расчета процента ошибки прогноза:
Процент ошибки прогноза = [(| actual — forecast | ) / actual] х 100
Процент ошибки прогноза лучше всего отражает точность прогноза. Если процент ошибки прогноза близок к 100 % или превышает его, это означает, что прогноз полностью или очень неточен. И наоборот, если процент ошибки прогноза близок к 0%, это означает, что прогноз точен.
Как рассчитать MAPE
Вот шаги, которые необходимо выполнить, чтобы рассчитать MAPE:
1. Организуйте свои данные
Соберите и организуйте свои данные, чтобы наилучшим образом визуализировать фактические и прогнозируемые значения в вашем наборе данных. Рассмотрите возможность использования программы для работы с электронными таблицами, которая позволяет создавать столбцы для каждого периода времени, фактические значения и прогнозируемые значения. Размещение каждого значения рядом позволяет легко сравнивать информацию и выполнять вычисления.
2. Рассчитайте абсолютную процентную ошибку
После организации данных рассчитайте абсолютную процентную ошибку фактической суммы по сравнению с прогнозируемой суммой для каждого ввода данных. Повторите для каждой строки в вашем наборе данных. Вот формула, которую вы можете использовать:
Абсолютная ошибка в процентах = [( | actual — forecast | ) / | actual | ] х 100
Столбцы в уравнении представляют определение абсолютного значения разницы между фактической суммой и прогнозируемой величиной. Абсолютное значение означает использование положительного значения числа независимо от результата вычисления, и оно используется для MAPE, потому что проблема заключается в том, насколько значительна разница, а не в том, является ли она положительной или отрицательной. Например, если фактическое количество проданных товаров равно 54, а прогнозируемое количество равно 65, разница составит -11. Однако с абсолютным значением вы должны использовать 11 для завершения вычислений с абсолютной процентной ошибкой 20,37%.
3. Рассчитайте MAPE
Получив абсолютную процентную ошибку для каждой записи данных, вы можете рассчитать MAPE. Сложите все абсолютные проценты ошибок вместе, затем разделите сумму на количество ошибок. Например, если ваш набор данных включает 12 записей, вы должны разделить сумму на 12. Конечным результатом будет MAPE.
Пример расчета MAPE
Вот пример расчета MAPE:
Средняя школа Эдвардса хочет рассчитать MAPE своих заказов на ежегодник за предыдущий учебный год. Они рассчитывали продать 400 ежегодников, но продали только 386. Они используют следующую таблицу, чтобы систематизировать фактическое количество ежегодников, заказываемых в месяц, прогнозируемое количество ежегодников, заказываемых в месяц, и абсолютную процентную ошибку заказов ежегодников за каждый месяц:
Месяц Фактический прогноз Абсолютная ошибка в процентах 17 августа 20 17,65% 23 сентября 25 8,70% 35 октября 30 14,29% 28 ноября 30 7,14% 23 25 декабря 8,70% 18 20 января 11,11% 22 февраля 25 13,64% 45 марта 50 11,11% апрель 66 75 % май 96 100 4,17%
Для определения MAPE определяют сумму абсолютной процентной ошибки за каждый месяц. Получив сумму 100,18, они делят это число на девять на девять месяцев учебного года. В результате MAPE составляет 11,13%.*
 MAPE – средняя абсолютная ошибка в процентах используется:
MAPE – средняя абсолютная ошибка в процентах используется:
- Для оценки точности прогноза;
- Показывает на сколько велики ошибки в сравнении со значениями ряда;
- Хороша для сравнения 1-й модели для разных рядов;
- Используется для сравнения разных моделей для одного ряда;
- Оценки экономического эффекта, за счет повышения точности прогноза.
В данной статье мы рассмотрим, как рассчитать MAPE в Excel и как ее использовать.
Формула расчета MAPE:
Где:
- Yt – фактический объем продаж за анализируемый период;
- Ŷt — значение прогнозной модели за аналазируемый период;
- n — количество периодов.
Для того, чтобы рассчитать среднюю абсолютную ошибку мы:
- Рассчитываем значение модели прогноза — Ŷt;
- Рассчитываем ошибку прогноза;
- Берем ошибку по модулю;
- Определяем абсолютную ошибку;
- Рассчитываем среднюю абсолютную ошибку в процентах — MAPE.
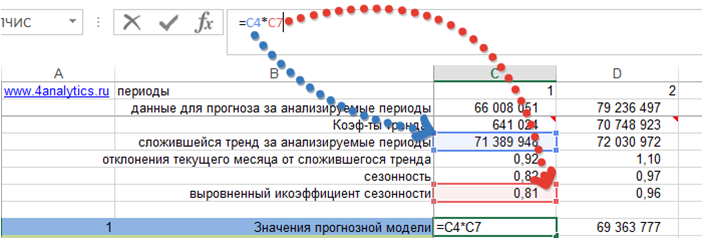
1. Рассчитаем значение модели прогноза — Ŷt
Возьмем модель с трендом и сезонностью. Рассчитаем значение модели для каждого периода, когда нам известны фактические продажи. Для этого сложившийся тренд за анализируемый период умножим на коэффициент сезонности для соответствующего месяца.
Получили значения прогнозной модели для каждого периода времени:
Подробнее о расчете прогноза с помощью тренда и сезонности читайте в статье «Расчет прогноза с помощью тренда и сезонности».
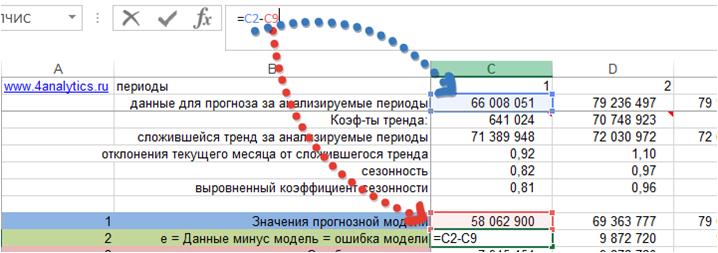
2. Рассчитаем значения ошибки прогноза.
В формуле расчета MAPE – это:
e — Ошибка прогноза — это разность между значениями временного ряда (фактом продаж) и моделью прогноза:
e= Yt — Ŷt
Получили значение ошибки прогноза для каждого момента времени за анализируемый период.
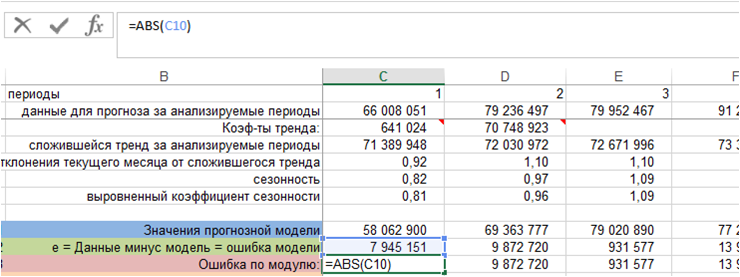
3. Рассчитаем ошибку по модулю.
Для этого воспользуемся функцией Excel =ABC()
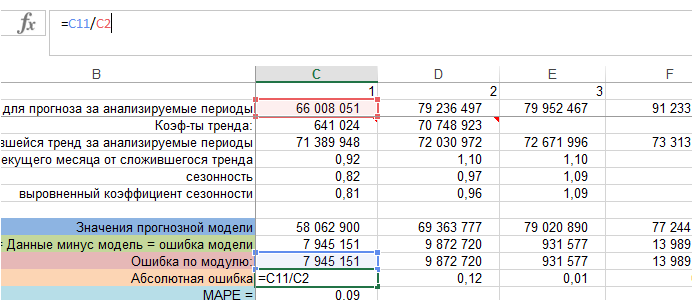
4. Определяем абсолютную ошибку.
Для каждого периода ошибку по модулю делим на фактические значения ряда, т.е. на фактический объем продаж:
Получили абсолютную ошибку для каждого периода фактических продаж. В формуле MAPE — это:
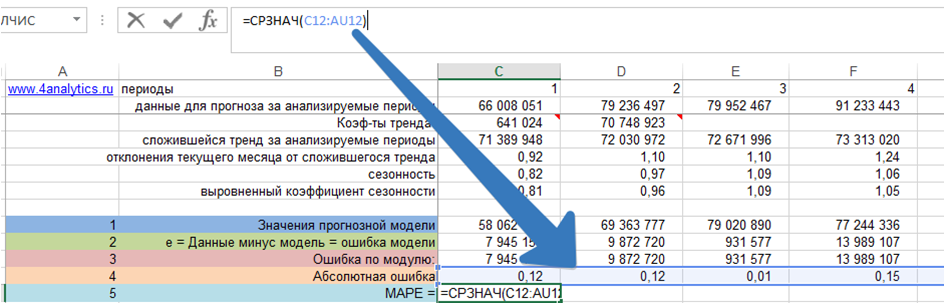
5. Рассчитаем MAPE – среднюю абсолютную ошибку.
Для этого рассчитаем среднее значение абсолютной ошибки за все периоды:
Скачать файл с примером расчета MAPE – средней абсолютной ошибки.
Как рассчитать показатель точность прогноза?
Показатель точность прогноза = 1 –MAPE:
С помощью MAPE вы можете сравнивать различные модели между собой, можете оценивать, как и на сколько модель делает точные прогнозы для разных временных рядов.
А также, что самое главное, можете оценить экономический эффект для компании за счет повышения точности прогноза.
Об этом подробнее можете почитать в нашей статье на сайте http://novoforecast.com/novo-forecast/instruktsiya/item/rost-tochnosti-prognoza-rost-pribyli.html
Если есть вопросы, пожалуйста, пишите в комментариях!
Forecast4AC PRO рассчитает MAPE для каждого временного ряда!
Точных вам прогнозов!
Присоединяйтесь к нам!
Скачивайте бесплатные приложения для прогнозирования и бизнес-анализа:
- Novo Forecast Lite — автоматический расчет прогноза в Excel.
- 4analytics — ABC-XYZ-анализ и анализ выбросов в Excel.
- Qlik Sense Desktop и QlikView Personal Edition — BI-системы для анализа и визуализации данных.
Тестируйте возможности платных решений:
- Novo Forecast PRO — прогнозирование в Excel для больших массивов данных.
Получите 10 рекомендаций по повышению точности прогнозов до 90% и выше.
Зарегистрируйтесь и скачайте решения
Статья полезная? Поделитесь с друзьями
Ошибка прогнозирования: виды, формулы, примеры
Ошибка прогнозирования — это такая величина, которая показывает, как сильно прогнозное значение отклонилось от фактического. Она используется для расчета точности прогнозирования, что в свою очередь помогает нам оценивать как точно и корректно мы сформировали прогноз. В данной статье я расскажу про основные процентные «ошибки прогнозирования» с кратким описанием и формулой для расчета. А в конце статьи я приведу общий пример расчётов в Excel. Напомню, что в своих расчетах я в основном использую ошибку WAPE или MAD-Mean Ratio, о которой подробно я рассказал в статье про точность прогнозирования, здесь она также будет упомянута.
В каждой формуле буквой Ф обозначено фактическое значение, а буквой П — прогнозное. Каждая ошибка прогнозирования (кроме последней!), может использоваться для нахождения общей точности прогнозирования некоторого списка позиций, по типу того, что изображен ниже (либо для любого другого подобной детализации):
Алгоритм для нахождения любой из ошибок прогнозирования для такого списка примерно одинаковый: сначала находим ошибку прогнозирования по одной позиции, а затем рассчитываем общую. Итак, основные ошибки прогнозирования!
MPE — Mean Percent Error
MPE — средняя процентная ошибка прогнозирования. Основная проблема данной ошибки заключается в том, что в нестабильном числовом ряду с большими выбросами любое незначительное колебание факта или прогноза может значительно поменять показатель ошибки и, как следствие, точности прогнозирования. Помимо этого, ошибка является несимметричной: одинаковые отклонения в плюс и в минус по-разному влияют на показатель ошибки.
- Для каждой позиции рассчитывается ошибка прогноза (из факта вычитается прогноз) — Error
- Для каждой позиции рассчитывается процентная ошибка прогноза (ошибка прогноза делится на фактический показатель) — Percent Error
- Находится среднее арифметическое всех процентных ошибок прогноза (процентные ошибки суммируются и делятся на количество) — Mean Percent Error
MAPE — Mean Absolute Percent Error
MAPE — средняя абсолютная процентная ошибка прогнозирования. Основная проблема данной ошибки такая же, как и у MPE — нестабильность.
- Для каждой позиции рассчитывается абсолютная ошибка прогноза (прогноз вычитается из факта по модулю) — Absolute Error
- Для каждой позиции рассчитывается абсолютная процентная ошибка прогноза (абсолютная ошибка прогноза делится на фактический показатель) — Absolute Percent Error
- Находится среднее арифметическое всех абсолютных процентных ошибок прогноза (абсолютные процентные ошибки суммируются и делятся на количество) — Mean Absolute Percent Error
Вместо среднего арифметического всех абсолютных процентных ошибок прогноза можно использовать медиану числового ряда (MdAPE — Median Absolute Percent Error), она наиболее устойчива к выбросам.
WMAPE / MAD-Mean Ratio / WAPE — Weighted Absolute Percent Error
WAPE — взвешенная абсолютная процентная ошибка прогнозирования. Одна из «лучших ошибок» для расчета точности прогнозирования. Часто называется как MAD-Mean Ratio, то есть отношение MAD (Mean Absolute Deviation — среднее абсолютное отклонение/ошибка) к Mean (среднее арифметическое). После упрощения дроби получается искомая формула WAPE, которая очень проста в понимании:
- Для каждой позиции рассчитывается абсолютная ошибка прогноза (прогноз вычитается из факта, по модулю) — Absolute Error
- Находится сумма всех фактов по всем позициям (общий фактический объем)
- Сумма всех абсолютных ошибок делится на сумму всех фактов — WAPE
Данная ошибка прогнозирования является симметричной и наименее чувствительна к искажениям числового ряда.
Рекомендуется к использованию при расчете точности прогнозирования. Более подробно читать здесь.
RMSE (as %) / nRMSE — Root Mean Square Error
RMSE — среднеквадратичная ошибка прогнозирования. Примерно такая же проблема, как и в MPE и MAPE: так как каждое отклонение возводится в квадрат, любое небольшое отклонение может значительно повлиять на показатель ошибки. Стоит отметить, что существует также ошибка MSE, из которой RMSE как раз и получается путем извлечения корня. Но так как MSE дает расчетные единицы измерения в квадрате, то использовать данную ошибку будет немного неправильно.
- Для каждой позиции рассчитывается квадрат отклонений (разница между фактом и прогнозом, возведенная в квадрат) — Square Error
- Затем рассчитывается среднее арифметическое (сумма квадратов отклонений, деленное на количество) — MSE — Mean Square Error
- Извлекаем корень из полученного результат — RMSE
- Для перевода в процентную или в «нормализованную» среднеквадратичную ошибку необходимо:
- Разделить на разницу между максимальным и минимальным значением показателей
- Разделить на разницу между третьим и первым квартилем значений показателей
- Разделить на среднее арифметическое значений показателей (наиболее часто встречающийся вариант)
MASE — Mean Absolute Scaled Error
MASE — средняя абсолютная масштабированная ошибка прогнозирования. Согласно Википедии, является очень хорошим вариантом для расчета точности, так как сама ошибка не зависит от масштабов данных и является симметричной: то есть положительные и отрицательные отклонения от факта рассматриваются в равной степени.
Важно! Если предыдущие ошибки прогнозирования мы могли использовать для нахождения точности прогнозирования некого списка номенклатур, где каждой из которых соответствует фактическое и прогнозное значение (как было в примере в начале статьи), то данная ошибка для этого не предназначена: MASE используется для расчета точности прогнозирования одной единственной позиции, основываясь на предыдущих показателях факта и прогноза, и чем больше этих показателей, тем более точно мы сможем рассчитать показатель точности. Вероятно, из-за этого ошибка не получила широкого распространения.
Здесь данная формула представлена исключительно для ознакомления и не рекомендуется к использованию.
Суть формулы заключается в нахождении среднего арифметического всех масштабированных ошибок, что при упрощении даст нам следующую конечную формулу:
Также, хочу отметить, что существует ошибка RMMSE (Root Mean Square Scaled Error — Среднеквадратичная масштабированная ошибка), которая примерно похожа на MASE, с теми же преимуществами и недостатками.
Это основные ошибки прогнозирования, которые могут использоваться для расчета точности прогнозирования. Но не все! Их очень много и, возможно, чуть позже я добавлю еще немного информации о некоторых из них. А примеры расчетов уже описанных ошибок прогнозирования будут выложены через некоторое время, пока что я подготавливаю пример, ожидайте.
Об авторе
HeinzBr
Автор статей и создатель сайта SHTEM.RU
Для того чтобы модель линейной регрессии можно было применять на практике необходимо сначала оценить её качество. Для этих целей предложен ряд показателей, каждый из которых предназначен для использования в различных ситуациях и имеет свои особенности применения (линейные и нелинейные, устойчивые к аномалиям, абсолютные и относительные, и т.д.). Корректный выбор меры для оценки качества модели является одним из важных факторов успеха в решении задач анализа данных.
«Хорошая» аналитическая модель должна удовлетворять двум, зачастую противоречивым, требованиям — как можно лучше соответствовать данным и при этом быть удобной для интерпретации пользователем. Действительно, повышение соответствия модели данным как правило связано с её усложнением (в случае регрессии — увеличением числа входных переменных модели). А чем сложнее модель, тем ниже её интерпретируемость.
Поэтому при выборе между простой и сложной моделью последняя должна значимо увеличивать соответствие модели данным чтобы оправдать рост сложности и соответствующее снижение интерпретируемости. Если это условие не выполняется, то следует выбрать более простую модель.
Таким образом, чтобы оценить, насколько повышение сложности модели значимо увеличивает её точность, необходимо использовать аппарат оценки качества регрессионных моделей. Он включает в себя следующие меры:
- Среднеквадратичная ошибка (MSE).
- Корень из среднеквадратичной ошибки (RMSE).
- Среднеквадратичная ошибка в процентах (MSPE).
- Средняя абсолютная ошибка (MAE).
- Средняя абсолютная ошибка в процентах (MAPE).
- Cимметричная средняя абсолютная процентная ошибка (SMAPE).
- Средняя абсолютная масштабированная ошибка (MASE)
- Средняя относительная ошибка (MRE).
- Среднеквадратичная логарифмическая ошибка (RMSLE).
- Коэффициент детерминации R-квадрат.
- Скорректированный коэффициент детеминации.
Прежде чем перейти к изучению метрик качества, введём некоторые базовые понятия, которые нам в этом помогут. Для этого рассмотрим рисунок.
Рисунок 1. Линейная регрессия
Наклонная прямая представляет собой линию регрессии с переменной, на которой расположены точки, соответствующие предсказанным значениям выходной переменной widehat{y} (кружки синего цвета). Оранжевые кружки представляют фактические (наблюдаемые) значения y . Расстояния между ними и линией регрессии — это ошибка предсказания модели y-widehat{y} (невязка, остатки). Именно с её использованием вычисляются все приведённые в статье меры качества.
Горизонтальная линия представляет собой модель простого среднего, где коэффициент при независимой переменной x равен нулю, и остаётся только свободный член b, который становится равным среднему арифметическому фактических значений выходной переменной, т.е. b=overline{y}. Очевидно, что такая модель для любого значения входной переменной будет выдавать одно и то же значение выходной — overline{y}.
В линейной регрессии такая модель рассматривается как «бесполезная», хуже которой работает только «случайный угадыватель». Однако, она используется для оценки, насколько дисперсия фактических значений y относительно линии среднего, больше, чем относительно линии регрессии с переменной, т.е. насколько модель с переменной лучше «бесполезной».
MSE
Среднеквадратичная ошибка (Mean Squared Error) применяется в случаях, когда требуется подчеркнуть большие ошибки и выбрать модель, которая дает меньше именно больших ошибок. Большие значения ошибок становятся заметнее за счет квадратичной зависимости.
Действительно, допустим модель допустила на двух примерах ошибки 5 и 10. В абсолютном выражении они отличаются в два раза, но если их возвести в квадрат, получив 25 и 100 соответственно, то отличие будет уже в четыре раза. Таким образом модель, которая обеспечивает меньшее значение MSE допускает меньше именно больших ошибок.
MSE рассчитывается по формуле:
MSE=frac{1}{n}sumlimits_{i=1}^{n}(y_{i}-widehat{y}_{i})^{2},
где n — количество наблюдений по которым строится модель и количество прогнозов, y_{i} — фактические значение зависимой переменной для i-го наблюдения, widehat{y}_{i} — значение зависимой переменной, предсказанное моделью.
Таким образом, можно сделать вывод, что MSE настроена на отражение влияния именно больших ошибок на качество модели.
Недостатком использования MSE является то, что если на одном или нескольких неудачных примерах, возможно, содержащих аномальные значения будет допущена значительная ошибка, то возведение в квадрат приведёт к ложному выводу, что вся модель работает плохо. С другой стороны, если модель даст небольшие ошибки на большом числе примеров, то может возникнуть обратный эффект — недооценка слабости модели.
RMSE
Корень из среднеквадратичной ошибки (Root Mean Squared Error) вычисляется просто как квадратный корень из MSE:
RMSE=sqrt{frac{1}{n}sumlimits_{i=1}^{n}(y_{i}-widehat{y_{i}})^{2}}
MSE и RMSE могут минимизироваться с помощью одного и того же функционала, поскольку квадратный корень является неубывающей функцией. Например, если у нас есть два набора результатов работы модели, A и B, и MSE для A больше, чем MSE для B, то мы можем быть уверены, что RMSE для A больше RMSE для B. Справедливо и обратное: если MSE(A)<MSE(B), то и RMSE(A)<RMSE(B).
Следовательно, сравнение моделей с помощью RMSE даст такой же результат, что и для MSE. Однако с MSE работать несколько проще, поэтому она более популярна у аналитиков. Кроме этого, имеется небольшая разница между этими двумя ошибками при оптимизации с использованием градиента:
frac{partial RMSE}{partial widehat{y}_{i}}=frac{1}{2sqrt{MSE}}frac{partial MSE}{partial widehat{y}_{i}}
Это означает, что перемещение по градиенту MSE эквивалентно перемещению по градиенту RMSE, но с другой скоростью, и скорость зависит от самой оценки MSE. Таким образом, хотя RMSE и MSE близки с точки зрения оценки моделей, они не являются взаимозаменяемыми при использовании градиента для оптимизации.
Влияние каждой ошибки на RMSE пропорционально величине квадрата ошибки. Поэтому большие ошибки оказывают непропорционально большое влияние на RMSE. Следовательно, RMSE можно считать чувствительной к аномальным значениям.
MSPE
Среднеквадратичная ошибка в процентах (Mean Squared Percentage Error) представляет собой относительную ошибку, где разность между наблюдаемым и фактическим значениями делится на наблюдаемое значение и выражается в процентах:
MSPE=frac{100}{n}sumlimits_{i=1}^{n}left ( frac{y_{i}-widehat{y}_{i}}{y_{i}} right )^{2}
Проблемой при использовании MSPE является то, что, если наблюдаемое значение выходной переменной равно 0, значение ошибки становится неопределённым.
MSPE можно рассматривать как взвешенную версию MSE, где вес обратно пропорционален квадрату наблюдаемого значения. Таким образом, при возрастании наблюдаемых значений ошибка имеет тенденцию уменьшаться.
MAE
Cредняя абсолютная ошибка (Mean Absolute Error) вычисляется следующим образом:
MAE=frac{1}{n}sumlimits_{i=1}^{n}left | y_{i}-widehat{y}_{i} right |
Т.е. MAE рассчитывается как среднее абсолютных разностей между наблюдаемым и предсказанным значениями. В отличие от MSE и RMSE она является линейной оценкой, а это значит, что все ошибки в среднем взвешены одинаково. Например, разница между 0 и 10 будет вдвое больше разницы между 0 и 5. Для MSE и RMSE, как отмечено выше, это не так.
Поэтому MAE широко используется, например, в финансовой сфере, где ошибка в 10 долларов должна интерпретироваться как в два раза худшая, чем ошибка в 5 долларов.
MAPE
Средняя абсолютная процентная ошибка (Mean Absolute Percentage Error) вычисляется следующим образом:
MAPE=frac{100}{n}sumlimits_{i=1}^{n}frac{left | y_{i}-widehat{y_{i}} right |}{left | y_{i} right |}
Эта ошибка не имеет размерности и очень проста в интерпретации. Её можно выражать как в долях, так и в процентах. Если получилось, например, что MAPE=11.4, то это говорит о том, что ошибка составила 11.4% от фактического значения.
SMAPE
Cимметричная средняя абсолютная процентная ошибка (Symmetric Mean Absolute Percentage Error) — это мера точности, основанная на процентных (или относительных) ошибках. Обычно определяется следующим образом:
SMAPE=frac{100}{n}sumlimits_{i=1}^{n}frac{left | y_{i}-widehat{y_{i}} right |}{(left | y_{i} right |+left | widehat{y}_{i} right |)/2}
Т.е. абсолютная разность между наблюдаемым и предсказанным значениями делится на полусумму их модулей. В отличие от обычной MAPE, симметричная имеет ограничение на диапазон значений. В приведённой формуле он составляет от 0 до 200%. Однако, поскольку диапазон от 0 до 100% гораздо удобнее интерпретировать, часто используют формулу, где отсутствует деление знаменателя на 2.
Одной из возможных проблем SMAPE является неполная симметрия, поскольку в разных диапазонах ошибка вычисляется неодинаково. Это иллюстрируется следующим примером: если y_{i}=100 и widehat{y}_{i}=110, то SMAPE=4.76, а если y_{i}=100 и widehat{y}_{i}=90, то SMAPE=5.26.
Ограничение SMAPE заключается в том, что, если наблюдаемое или предсказанное значение равно 0, ошибка резко возрастет до верхнего предела (200% или 100%).
MASE
Средняя абсолютная масштабированная ошибка (Mean absolute scaled error) — это показатель, который позволяет сравнивать две модели. Если поместить MAE для новой модели в числитель, а MAE для исходной модели в знаменатель, то полученное отношение и будет равно MASE. Если значение MASE меньше 1, то новая модель работает лучше, если MASE равно 1, то модели работают одинаково, а если значение MASE больше 1, то исходная модель работает лучше, чем новая модель. Формула для расчета MASE имеет вид:
MASE=frac{MAE_{i}}{MAE_{j}}
MASE симметрична и устойчива к выбросам.
MRE
Средняя относительная ошибка (Mean Relative Error) вычисляется по формуле:
MRE=frac{1}{n}sumlimits_{i=1}^{n}frac{left | y_{i}-widehat{y}_{i}right |}{left | y_{i} right |}
Несложно увидеть, что данная мера показывает величину абсолютной ошибки относительно фактического значения выходной переменной (поэтому иногда эту ошибку называют также средней относительной абсолютной ошибкой, MRAE). Действительно, если значение абсолютной ошибки, скажем, равно 10, то сложно сказать много это или мало. Например, относительно значения выходной переменной, равного 20, это составляет 50%, что достаточно много. Однако относительно значения выходной переменной, равного 100, это будет уже 10%, что является вполне нормальным результатом.
Очевидно, что при вычислении MRE нельзя применять наблюдения, в которых y_{i}=0.
Таким образом, MRE позволяет более адекватно оценить величину ошибки, чем абсолютные ошибки. Кроме этого она является безразмерной величиной, что упрощает интерпретацию.
RMSLE
Среднеквадратичная логарифмическая ошибка (Root Mean Squared Logarithmic Error) представляет собой RMSE, вычисленную в логарифмическом масштабе:
RMSLE=sqrt{frac{1}{n}sumlimits_{i=1}^{n}(log(widehat{y}_{i}+1)-log{(y_{i}+1}))^{2}}
Константы, равные 1, добавляемые в скобках, необходимы чтобы не допустить обращения в 0 выражения под логарифмом, поскольку логарифм нуля не существует.
Известно, что логарифмирование приводит к сжатию исходного диапазона изменения значений переменной. Поэтому применение RMSLE целесообразно, если предсказанное и фактическое значения выходной переменной различаются на порядок и больше.
R-квадрат
Перечисленные выше ошибки не так просто интерпретировать. Действительно, просто зная значение средней абсолютной ошибки, скажем, равное 10, мы сразу не можем сказать хорошая это ошибка или плохая, и что нужно сделать чтобы улучшить модель.
В этой связи представляет интерес использование для оценки качества регрессионной модели не значения ошибок, а величину показывающую, насколько данная модель работает лучше, чем модель, в которой присутствует только константа, а входные переменные отсутствуют или коэффициенты регрессии при них равны нулю.
Именно такой мерой и является коэффициент детерминации (Coefficient of determination), который показывает долю дисперсии зависимой переменной, объяснённой с помощью регрессионной модели. Наиболее общей формулой для вычисления коэффициента детерминации является следующая:
R^{2}=1-frac{sumlimits_{i=1}^{n}(widehat{y}_{i}-y_{i})^{2}}{sumlimits_{i=1}^{n}({overline{y}}_{i}-y_{i})^{2}}
Практически, в числителе данного выражения стоит среднеквадратическая ошибка оцениваемой модели, а в знаменателе — модели, в которой присутствует только константа.
Главным преимуществом коэффициента детерминации перед мерами, основанными на ошибках, является его инвариантность к масштабу данных. Кроме того, он всегда изменяется в диапазоне от −∞ до 1. При этом значения близкие к 1 указывают на высокую степень соответствия модели данным. Очевидно, что это имеет место, когда отношение в формуле стремится к 0, т.е. ошибка модели с переменными намного меньше ошибки модели с константой. R^{2}=0 показывает, что между независимой и зависимой переменными модели имеет место функциональная зависимость.
Когда значение коэффициента близко к 0 (т.е. ошибка модели с переменными примерно равна ошибке модели только с константой), это указывает на низкое соответствие модели данным, когда модель с переменными работает не лучше модели с константой.
Кроме этого, бывают ситуации, когда коэффициент R^{2} принимает отрицательные значения (обычно небольшие). Это произойдёт, если ошибка модели среднего становится меньше ошибки модели с переменной. В этом случае оказывается, что добавление в модель с константой некоторой переменной только ухудшает её (т.е. регрессионная модель с переменной работает хуже, чем предсказание с помощью простой средней).
На практике используют следующую шкалу оценок. Модель, для которой R^{2}>0.5, является удовлетворительной. Если R^{2}>0.8, то модель рассматривается как очень хорошая. Значения, меньшие 0.5 говорят о том, что модель плохая.
Скорректированный R-квадрат
Основной проблемой при использовании коэффициента детерминации является то, что он увеличивается (или, по крайней мере, не уменьшается) при добавлении в модель новых переменных, даже если эти переменные никак не связаны с зависимой переменной.
В связи с этим возникают две проблемы. Первая заключается в том, что не все переменные, добавляемые в модель, могут значимо увеличивать её точность, но при этом всегда увеличивают её сложность. Вторая проблема — с помощью коэффициента детерминации нельзя сравнивать модели с разным числом переменных. Чтобы преодолеть эти проблемы используют альтернативные показатели, одним из которых является скорректированный коэффициент детерминации (Adjasted coefficient of determinftion).
Скорректированный коэффициент детерминации даёт возможность сравнивать модели с разным числом переменных так, чтобы их число не влияло на статистику R^{2}, и накладывает штраф за дополнительно включённые в модель переменные. Вычисляется по формуле:
R_{adj}^{2}=1-frac{sumlimits_{i=1}^{n}(widehat{y}_{i}-y_{i})^{2}/(n-k)}{sumlimits_{i=1}^{n}({overline{y}}_{i}-y_{i})^{2}/(n-1)}
где n — число наблюдений, на основе которых строится модель, k — количество переменных в модели.
Скорректированный коэффициент детерминации всегда меньше единицы, но теоретически может принимать значения и меньше нуля только при очень малом значении обычного коэффициента детерминации и большом количестве переменных модели.
Сравнение метрик
Резюмируем преимущества и недостатки каждой приведённой метрики в следующей таблице:
| Мера | Сильные стороны | Слабые стороны |
|---|---|---|
| MSE | Позволяет подчеркнуть большие отклонения, простота вычисления. | Имеет тенденцию занижать качество модели, чувствительна к выбросам. Сложность интерпретации из-за квадратичной зависимости. |
| RMSE | Простота интерпретации, поскольку измеряется в тех же единицах, что и целевая переменная. | Имеет тенденцию занижать качество модели, чувствительна к выбросам. |
| MSPE | Нечувствительна к выбросам. Хорошо интерпретируема, поскольку имеет линейный характер. | Поскольку вклад всех ошибок отдельных наблюдений взвешивается одинаково, не позволяет подчёркивать большие и малые ошибки. |
| MAPE | Является безразмерной величиной, поэтому её интерпретация не зависит от предметной области. | Нельзя использовать для наблюдений, в которых значения выходной переменной равны нулю. |
| SMAPE | Позволяет корректно работать с предсказанными значениями независимо от того больше они фактического, или меньше. | Приближение к нулю фактического или предсказанного значения приводит к резкому росту ошибки, поскольку в знаменателе присутствует как фактическое, так и предсказанное значения. |
| MASE | Не зависит от масштаба данных, является симметричной: положительные и отрицательные отклонения от фактического значения учитываются одинаково. Устойчива к выбросам. Позволяет сравнивать модели. | Сложность интерпретации. |
| MRE | Позволяет оценить величину ошибки относительно значения целевой переменной. | Неприменима для наблюдений с нулевым значением выходной переменной. |
| RMSLE | Логарифмирование позволяет сделать величину ошибки более устойчивой, когда разность между фактическим и предсказанным значениями различается на порядок и выше | Может быть затруднена интерпретация из-за нелинейности. |
| R-квадрат | Универсальность, простота интерпретации. | Возрастает даже при включении в модель бесполезных переменных. Плохо работает когда входные переменные зависимы. |
| R-квадрат скорр. | Корректно отражает вклад каждой переменной в модель. | Плохо работает, когда входные переменные зависимы. |
В данной статье рассмотрены наиболее популярные меры качества регрессионных моделей, которые часто используются в различных аналитических приложениях. Эти меры имеют свои особенности применения, знание которых позволит обоснованно выбирать и корректно применять их на практике.
Однако в литературе можно встретить и другие меры качества моделей регрессии, которые предлагаются различными авторами для решения конкретных задач анализа данных.
Другие материалы по теме:
Отбор переменных в моделях линейной регрессии
Репрезентативность выборочных данных
Логистическая регрессия и ROC-анализ — математический аппарат


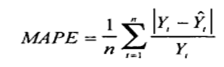 MAPE – средняя абсолютная ошибка в процентах используется:
MAPE – средняя абсолютная ошибка в процентах используется: