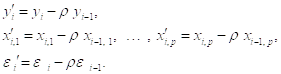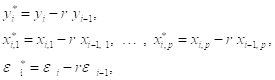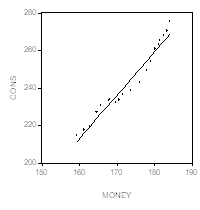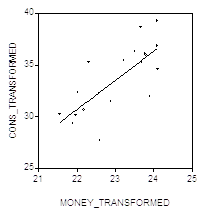Как уменьшить ошибку аппроксимации

Регрессионная сумма квадратов

Рисунок 4 Результат вычисления функции ЛИНЕЙН

Получили уровнение регрессии:

Делаем вывод: С увеличением среднедушевого прожиточного минимума на 1 руб. среднедневная заработная плата возрастает в среднем на 0,92 руб.

Означает, что 52% вариации заработной платы (у) объясняется вариацией фактора х — среднедушевого прожиточного минимума, а 48% — действием других факторов, не включённых в модель.

По вычисленному коэффициенту детерминации можно рассчитать коэффициент корреляции: .

Связь оценивается как тесная.

4. С помощью среднего (общего) коэффициента эластичности определим силу влияния фактора на результат.

Для уравнения прямой средний (общий) коэффициент эластичности определим по формуле:

Средние значения найдём, выделив область ячеек со значениями х, и выберем Формулы / Автосумма / Среднее , и то же самое произведём со значениями у.

Рисунок 5 Расчёт средних значений функции и аргумент

Таким образом, при изменении среднедушевого прожиточного минимума на 1% от своего среднего значения среднедневная заработная плата изменится в среднем на 0,51%.

С помощью инструмента анализа данных Регрессия можно получить:
— результаты регрессионной статистики,
— результаты дисперсионного анализа,
— результаты доверительных интервалов,
— остатки и графики подбора линии регрессии,
— остатки и нормальную вероятность.

Порядок действий следующий:

1) проверьте доступ к Пакету анализа . В главном меню последовательно выберите: Файл/Параметры/Надстройки .

2) В раскрывающемся списке Управление выберите пункт Надстройки Excel и нажмите кнопку Перейти.

3) В окне Надстройки установите флажок Пакет анализа , а затем нажмите кнопку ОК .

Если Пакет анализа отсутствует в списке поля Доступные надстройки , нажмите кнопку Обзор , чтобы выполнить поиск.

Если выводится сообщение о том, что пакет анализа не установлен на компьютере, нажмите кнопку Да , чтобы установить его.

4) В главном меню последовательно выберите: Данные / Анализ данных / Инструменты анализа / Регрессия , а затем нажмите кнопку ОК .

5) Заполните диалоговое окно ввода данных и параметров вывода:

Входной интервал Y — диапазон, содержащий данные результативного признака;

Входной интервал X — диапазон, содержащий данные факторного признака;

Метки — флажок, который указывает, содержит ли первая строка названия столбцов или нет;

Константа — ноль — флажок, указывающий на наличие или отсутствие свободного члена в уравнении;

Выходной интервал — достаточно указать левую верхнюю ячейку будущего диапазона;

6) Новый рабочий лист — можно задать произвольное имя нового листа.

Затем нажмите кнопку ОК .

Рисунок 6 Диалоговое окно ввода параметров инструмента Регрессия

Результаты регрессионного анализа для данных задачи представлены на рисунке 7.

Рисунок 7 Результат применения инструмента регрессия

5. Оценим с помощью средней ошибки аппроксимации качество уравнений. Воспользуемся результатами регрессионного анализа представленного на Рисунке 8.

Рисунок 8 Результат применения инструмента регрессия «Вывод остатка»

Составим новую таблицу как показано на рисунке 9. В графе С рассчитаем относительную ошибку аппроксимации по формуле:

Рисунок 9 Расчёт средней ошибки аппроксимации

Средняя ошибка аппроксимации рассчитывается по формуле:

Качество построенной модели оценивается как хорошее, так как не превышает 8 — 10%.

6. Из таблицы с регрессионной статистикой (Рисунок 4) выпишем фактическое значение F-критерия Фишера:

Поскольку при 5%-ном уровне значимости, то можно сделать вывод о значимости уравнения регрессии (связь доказана).

8. Оценку статистической значимости параметров регрессии проведём с помощью t-статистики Стьюдента и путём расчёта доверительного интервала каждого из показателей.

Выдвигаем гипотезу Н 0 о статистически незначимом отличии показателей от нуля:

.

для числа степеней свободы

На рисунке 7 имеются фактические значения t-статистики:

t-критерий для коэффициента корреляции можно рассчитать двумя способами:

где — случайная ошибка коэффициента корреляции.

Данные для расчёта возьмём из таблицы на Рисунке 7.

Фактические значения t-статистики превосходят табличные значения:

Поэтому гипотеза Н 0 отклоняется, то есть параметры регрессии и коэффициент корреляции не случайно отличаются от нуля, а статистически значимы.

Доверительный интервал для параметра a определяется как

Для параметра a 95%-ные границы как показано на рисунке 7 составили:

Доверительный интервал для коэффициента регрессии определяется как

Для коэффициента регрессии b 95%-ные границы как показано на рисунке 7 составили:

Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью параметры a и b, находясь в указанных границах, не принимают нулевых значений, т.е. не являются статистически незначимыми и существенно отличны от нуля.

7. Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение прожиточного минимума составит:

Тогда прогнозное значение прожиточного минимума составит:

Ошибку прогноза рассчитаем по формуле:

где

Дисперсию посчитаем также с помощью ППП Excel. Для этого:

1) Активизируйте Мастер функций : в главном меню выберете Формулы / Вставить функцию .

3) Заполните диапазон, содержащий числовые данные факторного признака. Нажмите ОК .

Рисунок 10 Расчёт дисперсии

Получили значение дисперсии

Для подсчёта остаточной дисперсии на одну степень свободы воспользуемся результатами дисперсионного анализа как показано на Рисунке 7.

Доверительные интервалы прогноза индивидуальных значений у при с вероятностью 0,95 определяются выражением:

Интервал достаточно широк, прежде всего, за счёт малого объёма наблюдений. В целом выполненный прогноз среднемесячной заработной платы оказался надёжным.

Условие задачи взято из: Практикум по эконометрике: Учеб. пособие / И.И. Елисеева, С.В. Курышева, Н.М. Гордеенко и др.; Под ред. И.И. Елисеевой. — М.: Финансы и статистика, 2003. — 192 с.: ил.

Для общей оценки качества построенной эконометрической определяются такие характеристики как коэффициент детерминации, индекс корреляции, средняя относительная ошибка аппроксимации, а также проверяется значимость уравнения регрессии с помощью F -критерия Фишера. Перечисленные характеристики являются достаточно универсальными и могут применяться как для линейных, так и для нелинейных моделей, а также моделей с двумя и более факторными переменными. Определяющее значение при вычислении всех перечисленных характеристик качества играет ряд остатков ε i , который вычисляется путем вычитания из фактических (полученных по наблюдениям) значений исследуемого признака y i значений, рассчитанных по уравнению модели y рi .

показывает, какая доля изменения исследуемого признака учтена в модели. Другими словами коэффициент детерминации показывает, какая часть изменения исследуемой переменной может быть вычислена, исходя из изменений включённых в модель факторных переменных с помощью выбранного типа функции, связывающей факторные переменные и исследуемый признак в уравнении модели.

Коэффициент детерминации R 2 может принимать значения от 0 до 1. Чем ближе коэффициент детерминации R 2 к единице, тем лучше качество модели.

Индекс корреляции можно легко вычислить, зная коэффициент детерминации:

Индекс корреляции R характеризует тесноту выбранного при построении модели типа связи между учтёнными в модели факторами и исследуемой переменной. В случае линейной парной регрессии его значение по абсолютной величине совпадает с коэффициентом парной корреляции r (x, y) , который мы рассмотрели ранее, и характеризует тесноту линейной связи между x и y . Значения индекса корреляции, очевидно, также лежат в интервале от 0 до 1. Чем ближе величина R к единице, тем теснее выбранный вид функции связывает между собой факторные переменные и исследуемый признак, тем лучше качество модели.

(2.11)

выражается в процентах и характеризует точность модели. Приемлимая точность модели при решении практических задач может определяться, исходя из соображений экономической целесообразности с учётом конкретной ситуации. Широко применяется критерий, в соответствии с которым точность считается удовлетворительной, если средняя относительная погрешность меньше 15%. Если E отн.ср. меньше 5%, то говорят, что модель имеет высокую точность. Не рекомендуется применять для анализа и прогноза модели с неудовлетворительной точностью, то есть, когда E отн.ср. больше 15%.

F-критерий Фишера используется для оценки значимости уравнения регрессии. Расчётное значение F-критерия определяется из соотношения:

. (2.12)

Критическое значение F -критерия определяется по таблицам при заданном уровне значимости α и степенях свободы (можно использовать функцию FРАСПОБР в Excel). Здесь, по-прежнему, m – число факторов, учтённых в модели, n – количество наблюдений. Если расчётное значение больше критического, то уравнение модели признаётся значимым. Чем больше расчётное значение F -критерия, тем лучше качество модели.

Определим характеристики качества построенной нами линейной модели для Примера 1 . Воспользуемся данными Таблицы 2. Коэффициент детерминации :

Следовательно, в рамках линейной модели изменение объёма продаж на 90,1% объясняется изменением температуры воздуха.

.

Значение индекса корреляции в случае парной линейной модели как мы видим, действительно по модулю равно коэффициенту корреляции между соответствующими переменными (объём продаж и температура). Поскольку полученное значение достаточно близко к единице, то можно сделать вывод о наличии тесной линейной связи между исследуемой переменной (объём продаж) и факторной переменноё (температура).

Критическое значение F кр при α = 0,1; ν 1 =1; ν 2 =7-1-1=5 равно 4,06. Расчётное значение F -критерия больше табличного, следовательно, уравнение модели является значимым.

Средняя относительная ошибка аппроксимации

Построенная линейная модель парной регрессии имеет неудовлетворительную точность (>15%), и её не рекомендуется использовать для анализа и прогнозирования.

В итоге, несмотря на то, что большинство статистических характеристик удовлетворяют предъявляемым к ним критериям, линейная модель парной регрессии непригодна для прогнозирования объёма продаж в зависимости от температуры воздуха. Нелинейный характер зависимости между указанными переменными по данным наблюдений достаточно хорошо виден на Рис.1. Проведённый анализ это подтвердил.

Среди различных методов прогнозирования нельзя не выделить аппроксимацию. С её помощью можно производить приблизительные подсчеты и вычислять планируемые показатели, путем замены исходных объектов на более простые. В Экселе тоже существует возможность использования данного метода для прогнозирования и анализа. Давайте рассмотрим, как этот метод можно применить в указанной программе встроенными инструментами.

Наименование данного метода происходит от латинского слова proxima – «ближайшая» Именно приближение путем упрощения и сглаживания известных показателей, выстраивание их в тенденцию и является его основой. Но данный метод можно использовать не только для прогнозирования, но и для исследования уже имеющихся результатов. Ведь аппроксимация является, по сути, упрощением исходных данных, а упрощенный вариант исследовать легче.

Главный инструмент, с помощью которого проводится сглаживания в Excel – это построение линии тренда. Суть состоит в том, что на основе уже имеющихся показателей достраивается график функции на будущие периоды. Основное предназначение линии тренда, как не трудно догадаться, это составление прогнозов или выявление общей тенденции.

Но она может быть построена с применением одного из пяти видов аппроксимации:

• Линейной;
• Экспоненциальной;
• Логарифмической;
• Полиномиальной;
• Степенной.

Рассмотрим каждый из вариантов более подробно в отдельности.

Способ 1: линейное сглаживание

Прежде всего, давайте рассмотрим самый простой вариант аппроксимации, а именно с помощью линейной функции. На нем мы остановимся подробнее всего, так как изложим общие моменты характерные и для других способов, а именно построение графика и некоторые другие нюансы, на которых при рассмотрении последующих вариантов уже останавливаться не будем.

Прежде всего, построим график, на основании которого будем проводить процедуру сглаживания. Для построения графика возьмем таблицу, в которой помесячно указана себестоимость единицы продукции, производимой предприятием, и соответствующая прибыль в данном периоде. Графическая функция, которую мы построим, будет отображать зависимость увеличения прибыли от уменьшения себестоимости продукции.

Сглаживание, которое используется в данном случае, описывается следующей формулой:

В конкретно нашем случае формула принимает такой вид:

Величина достоверности аппроксимации у нас равна 0,9418 , что является довольно приемлемым итогом, характеризующим сглаживание, как достоверное.

Способ 2: экспоненциальная аппроксимация

Теперь давайте рассмотрим экспоненциальный тип аппроксимации в Эксель.

Общий вид функции сглаживания при этом такой:

где e – это основание натурального логарифма.

В конкретно нашем случае формула приняла следующую форму:

Способ 3: логарифмическое сглаживание

Теперь настала очередь рассмотреть метод логарифмической аппроксимации.

В общем виде формула сглаживания выглядит так:

где ln – это величина натурального логарифма. Отсюда и наименование метода.

В нашем случае формула принимает следующий вид:

Способ 4: полиномиальное сглаживание

Настал черед рассмотреть метод полиномиального сглаживания.

Формула, которая описывает данный тип сглаживания, приняла следующий вид:

Способ 5: степенное сглаживание

В завершении рассмотрим метод степенной аппроксимации в Excel.

Данный способ эффективно используется в случаях интенсивного изменения данных функции. Важно учесть, что этот вариант применим только при условии, что функция и аргумент не принимают отрицательных или нулевых значений.

Общая формула, описывающая данный метод имеет такой вид:

В конкретно нашем случае она выглядит так:

Как видим, при использовании конкретных данных, которые мы применяли для примера, наибольший уровень достоверности показал метод полиномиальной аппроксимации с полиномом в шестой степени (0,9844 ), наименьший уровень достоверности у линейного метода (0,9418 ). Но это совсем не значит, что такая же тенденция будет при использовании других примеров. Нет, уровень эффективности у приведенных выше методов может значительно отличаться, в зависимости от конкретного вида функции, для которой будет строиться линия тренда. Поэтому, если для этой функции выбранный метод наиболее эффективен, то это совсем не означает, что он также будет оптимальным и в другой ситуации.

Если вы пока не можете сразу определить, основываясь на вышеприведенных рекомендациях, какой вид аппроксимации подойдет конкретно в вашем случае, то есть смысл попробовать все методы. После построения линии тренда и просмотра её уровня достоверности можно будет выбрать оптимальный вариант.

Контрольная работа: Парная регрессия

Смысл регрессионного анализа – построение функциональных зависимостей между двумя группами переменных величин Х₁ , Х₂ , … Х_р и Y. При этом речь идет о влиянии переменных Х (это будут аргументы функций) на значения переменной Y (значение функции). Переменные Х мы будем называть факторами, а Y – откликом.

Наиболее простой случай – установление зависимости одного отклика y от одного фактора х. Такой случай называется парной (простой) регрессией.

Парная регрессия – уравнение связи двух переменных у иx :

,

где у – зависимая переменная (результативный признак);

х – независимая, объясняющая переменная (признак-фактор).

Различают линейные и нелинейные регрессии.

Линейная регрессия:.

Нелинейные регрессии делятся на два класса: регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам, и регрессии, нелинейные по оцениваемым параметрам.

Регрессии, нелинейные по объясняющим переменным:

• полиномы разных степеней

•равносторонняя гипербола

Регрессии, нелинейные по оцениваемым параметрам:

• степенная ;

• показательная

• экспоненциальная

Построение уравнения регрессии сводится к оценке ее параметров. Для оценки параметров регрессий, линейных по параметрам, используют метод наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака у от теоретических минимальна, т.е.

Для линейных и нелинейных уравнений, приводимых к линейным, решается следующая система относительно а и b :

Можно воспользоваться готовыми формулами, которые вытекают из этой системы:

Тесноту связи изучаемых явлений оценивает линейный коэффициент парной корреляции для линейной регрессии

и индекс корреляции — для нелинейной регрессии ():

Оценку качества построенной модели даст коэффициент (индекс) детерминации, а также средняя ошибка аппроксимации.

Средняя ошибка аппроксимации – среднее отклонение расчетных значений от фактических:

Допустимый предел значений – не более 8 – 10%.

Средний коэффициент эластичности показывает, на сколько процентов в среднем по совокупности изменится результат у от своей средней величины при изменении фактора x на 1% от своего среднего значения:

Задача дисперсионного анализа состоит в анализе дисперсии зависимой переменной:

где – общая сумма квадратов отклонений;

– сумма квадратов отклонений, обусловленная регрессией («объясненная» или «факторная»);

–остаточная сумма квадратов отклонений.

Долю дисперсии, объясняемую регрессией, в общей дисперсии результативного признака у характеризует коэффициент (индекс) детерминации R 2 :

Коэффициент детерминации – квадрат коэффициента или индекса корреляции.

F -тест – оценивание качества уравнения регрессии – состоит в проверке гипотезы Н_о о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического F_факт и критического (табличного) F_табл значений F -критерия Фишера. F _факт определяется из соотношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы:

п – число единиц совокупности;

т – число параметров при переменных х.

F_табл – это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости а. Уровень значимости а – вероятность отвергнуть правильную гипотезу при условии, что она верна. Обычно а принимается равной 0,05 или 0,01.

Если F_табл F_факт , то гипотеза Н₀ не отклоняется и признается статистическая незначимость, ненадежность уравнения регрессии.

Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитываются t -критерий Стьюдента и доверительные интервалы каждого из показателей. Выдвигается гипотеза Н₀ о случайной природе показателей, т.е. о незначимом их отличии от нуля. Оценка значимости коэффициентов регрессии и корреляции с помощью f-критерия Стьюдента проводится путем сопоставления их значений с величиной случайной ошибки:

Случайные ошибки параметров линейной регрессии и коэффициента корреляции определяются по формулам:

Сравнивая фактическое и критическое (табличное) значения t-статистики – t_табл и t_факт – принимаем или отвергаем гипотезу H_о .

Связь между F-критерием Фишера и t-статистикой Стьюдента выражается равенством

Если t_табл t_факт , то гипотеза Н_о не отклоняется и признается случайная природа формирования a , b или .

Для расчета доверительного интервала определяем предельную ошибку ∆ для каждого показателя:

Формулы для расчета доверительных интервалов имеют следующий вид:

Если в границы доверительного интервала попадает ноль, т.е. нижняя граница отрицательна, а верхняя положительна, то оцениваемый параметр принимается нулевым, так как он не может одновременно принимать и положительное, и отрицательное значения.

Прогнозное значение определяется путем подстановки в уравнение регрессии соответствующего (прогнозного) значения . Вычисляется средняя стандартная ошибка прогноза :

где

и строится доверительный интервал прогноза:

где

По 22 регионам страны изучается зависимость розничной продажи телевизоров, y от среднедушевых денежных доходов в месяц, x (табл. 1):

Название: Парная регрессия Раздел: Рефераты по математике Тип: контрольная работа Добавлен 13:41:57 15 апреля 2011 Похожие работы Просмотров: 3780 Комментариев: 22 Оценило: 4 человек Средний балл: 4.5 Оценка: неизвестно Скачать

№ региона	X	Y
1,000	2,800	28,000
2,000	2,400	21,300
3,000	2,100	21,000
4,000	2,600	23,300
5,000	1,700	15,800
6,000	2,500	21,900
7,000	2,400	20,000
8,000	2,600	22,000
9,000	2,800	23,900
10,000	2,600	26,000
11,000	2,600	24,600
12,000	2,500	21,000
13,000	2,900	27,000
14,000	2,600	21,000
15,000	2,200	24,000
16,000	2,600	34,000
17,000	3,300	31,900
19,000	3,900	33,000
20,000	4,600	35,400
21,000	3,700	34,000
22,000	3,400	31,000

1. Постройте поле корреляции и сформулируйте гипотезу о форме связи.

2. Рассчитайте параметры уравнений линейной, степенной, экспоненциальной, полулогарифмической, обратной, гиперболической парной регрессий.

3. Оцените тесноту связи с помощью показателей корреляции и детерминации.

4. С помощью среднего (общего) коэффициента эластичности дайте сравнительную оценку силы связи фактора с результатом.

5. Качество уравнений оцените с помощью средней ошибки аппроксимации.

6. С помощью F-критерия Фишера определите статистическую надежность результатов регрессионного моделирования. Выберите лучшее уравнение регрессии и дайте его обоснование.

7. Рассчитайте прогнозное значение результата по линейному уравнению регрессии, если прогнозное значение фактора увеличится на 7% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости α=0,05.

8. Оцените полученные результаты, выводы оформите в аналитической записке.

1. Поле корреляции для:

· Линейной регрессии y=a+b*x:

Гипотеза о форме связи: чем больше размер среднедушевого денежного дохода в месяц (факторный признак), тем больше при прочих равных условиях розничная продажа телевизоров (результативный признак). В данной модели параметр b называется коэффициентом регрессии и показывает, насколько в среднем отклоняется величина результативного признака у при отклонении величины факторного признаках на одну единицу.

· Степенной регрессии :

Гипотеза о форме связи : степенная функция имеет вид Y=ax b .

Параметр b степенного уравнения называется показателем эластичности и указывает, на сколько процентов изменится у при возрастании х на 1%. При х = 1 a = Y.

· Экспоненциальная регрессия :

· Равносторонняя гипербола :

Гипотеза о форме связи: В ряде случаев обратная связь между факторным и результативным признаками может быть выражена уравнением гиперболы: Y=a+b/x.

· Обратная гипербола :

· Полулогарифмическая регрессия :

2. Рассчитайте параметры уравнений линейной, степенной, экспоненциальной, полулогарифмической, обратной, гиперболической парной регрессий.

· Рассчитаем параметры уравнений линейной парной регрессии. Для расчета параметров a и b линейной регрессии y=a+b*x решаем систему нормальных уравнений относительно a и b:

По исходным данным рассчитываем ∑y, ∑x, ∑yx, ∑x 2 , ∑y 2 (табл. 2):

№ региона	X	Y	XY	X^2	Y^2	Y^cp	Y-Y^cp	Ai
1	2,800	28,000	78,400	7,840	784,000	25,719	2,281	0,081
2	2,400	21,300	51,120	5,760	453,690	22,870	-1,570	0,074
3	2,100	21,000	44,100	4,410	441,000	20,734	0,266	0,013
4	2,600	23,300	60,580	6,760	542,890	24,295	-0,995	0,043
5	1,700	15,800	26,860	2,890	249,640	17,885	-2,085	0,132
6	2,500	21,900	54,750	6,250	479,610	23,582	-1,682	0,077
7	2,400	20,000	48,000	5,760	400,000	22,870	-2,870	0,144
8	2,600	22,000	57,200	6,760	484,000	24,295	-2,295	0,104
9	2,800	23,900	66,920	7,840	571,210	25,719	-1,819	0,076
10	2,600	26,000	67,600	6,760	676,000	24,295	1,705	0,066
11	2,600	24,600	63,960	6,760	605,160	24,295	0,305	0,012
12	2,500	21,000	52,500	6,250	441,000	23,582	-2,582	0,123
13	2,900	27,000	78,300	8,410	729,000	26,431	0,569	0,021
14	2,600	21,000	54,600	6,760	441,000	24,295	-3,295	0,157
15	2,200	24,000	52,800	4,840	576,000	21,446	2,554	0,106
16	2,600	34,000	88,400	6,760	1156,000	24,295	9,705	0,285
17	3,300	31,900	105,270	10,890	1017,610	29,280	2,620	0,082
19	3,900	33,000	128,700	15,210	1089,000	33,553	-0,553	0,017
20	4,600	35,400	162,840	21,160	1253,160	38,539	-3,139	0,089
21	3,700	34,000	125,800	13,690	1156,000	32,129	1,871	0,055
22	3,400	31,000	105,400	11,560	961,000	29,992	1,008	0,033
Итого	58,800	540,100	1574,100	173,320	14506,970	540,100	0,000
сред значение	2,800	25,719	74,957	8,253	690,808	0,085
станд. откл	0,643	5,417

Система нормальных уравнений составит:

Ур-ие регрессии: = 5,777+7,122∙x. Данное уравнение показывает, что с увеличением среднедушевого денежного дохода в месяц на 1 тыс. руб. доля розничных продаж телевизоров повышается в среднем на 7,12%.

· Рассчитаем параметры уравнений степенной парной регрессии. Построению степенной модели предшествует процедура линеаризации переменных. В примере линеаризация производится путем логарифмирования обеих частей уравнения:

где

Для расчетов используем данные табл. 3:

№ рег	X	Y	XY	X^2	Y^2	Yp^cp	y^cp
1	1,030	3,332	3,431	1,060	11,104	3,245	25,67072
2	0,875	3,059	2,678	0,766	9,356	3,116	22,56102
3	0,742	3,045	2,259	0,550	9,269	3,004	20,17348
4	0,956	3,148	3,008	0,913	9,913	3,183	24,12559
5	0,531	2,760	1,465	0,282	7,618	2,827	16,90081
6	0,916	3,086	2,828	0,840	9,526	3,150	23,34585
7	0,875	2,996	2,623	0,766	8,974	3,116	22,56102
8	0,956	3,091	2,954	0,913	9,555	3,183	24,12559
9	1,030	3,174	3,268	1,060	10,074	3,245	25,67072
10	0,956	3,258	3,113	0,913	10,615	3,183	24,12559
11	0,956	3,203	3,060	0,913	10,258	3,183	24,12559
12	0,916	3,045	2,790	0,840	9,269	3,150	23,34585
13	1,065	3,296	3,509	1,134	10,863	3,275	26,4365
14	0,956	3,045	2,909	0,913	9,269	3,183	24,12559
15	0,788	3,178	2,506	0,622	10,100	3,043	20,97512
16	0,956	3,526	3,369	0,913	12,435	3,183	24,12559
17	1,194	3,463	4,134	1,425	11,990	3,383	29,4585
19	1,361	3,497	4,759	1,852	12,226	3,523	33,88317
20	1,526	3,567	5,443	2,329	12,721	3,661	38,90802
21	1,308	3,526	4,614	1,712	12,435	3,479	32,42145
22	1,224	3,434	4,202	1,498	11,792	3,408	30,20445
итого	21,115	67,727	68,921	22,214	219,361	67,727	537,270
сред зн	1,005	3,225	3,282	1,058	10,446	3,225
стан откл	0,216	0,211

Рассчитаем С и b:

Получим линейное уравнение: . Выполнив его потенцирование, получим:

Подставляя в данное уравнение фактические значения х, получаем теоретические значения результата y .

· Рассчитаем параметры уравнений экспоненциальной парной регрессии. Построению экспоненциальной модели предшествует процедура линеаризации переменных. В примере линеаризация производится путем логарифмирования обеих частей уравнения:

где

Для расчетов используем данные табл. 4:

№ региона	X	Y	XY	X^2	Y^2	Yp	y^cp
1	2,800	3,332	9,330	7,840	11,104	3,225	25,156
2	2,400	3,059	7,341	5,760	9,356	3,116	22,552
3	2,100	3,045	6,393	4,410	9,269	3,034	20,777
4	2,600	3,148	8,186	6,760	9,913	3,170	23,818
5	1,700	2,760	4,692	2,890	7,618	2,925	18,625
6	2,500	3,086	7,716	6,250	9,526	3,143	23,176
7	2,400	2,996	7,190	5,760	8,974	3,116	22,552
8	2,600	3,091	8,037	6,760	9,555	3,170	23,818
9	2,800	3,174	8,887	7,840	10,074	3,225	25,156
10	2,600	3,258	8,471	6,760	10,615	3,170	23,818
11	2,600	3,203	8,327	6,760	10,258	3,170	23,818
12	2,500	3,045	7,611	6,250	9,269	3,143	23,176
13	2,900	3,296	9,558	8,410	10,863	3,252	25,853
14	2,600	3,045	7,916	6,760	9,269	3,170	23,818
15	2,200	3,178	6,992	4,840	10,100	3,061	21,352
16	2,600	3,526	9,169	6,760	12,435	3,170	23,818
17	3,300	3,463	11,427	10,890	11,990	3,362	28,839
19	3,900	3,497	13,636	15,210	12,226	3,526	33,978
20	4,600	3,567	16,407	21,160	12,721	3,717	41,140
21	3,700	3,526	13,048	13,690	12,435	3,471	32,170
22	3,400	3,434	11,676	11,560	11,792	3,389	29,638
Итого	58,800	67,727	192,008	173,320	219,361	67,727	537,053
сред зн	2,800	3,225	9,143	8,253	10,446
стан откл	0,643	0,211

Рассчитаем С и b:

Получим линейное уравнение: . Выполнив его потенцирование, получим:

Для расчета теоретических значений y подставим в уравнение значения x .

· Рассчитаем параметры уравнений полулогарифмической парной регрессии. Построению полулогарифмической модели предшествует процедура линеаризации переменных. В примере линеаризация производится путем замены:

где

Для расчетов используем данные табл. 5:

№ региона	X	Y	XY	X^2	Y^2	y^cp
1	1,030	28,000	28,829	1,060	784,000	26,238
2	0,875	21,300	18,647	0,766	453,690	22,928
3	0,742	21,000	15,581	0,550	441,000	20,062
4	0,956	23,300	22,263	0,913	542,890	24,647
5	0,531	15,800	8,384	0,282	249,640	15,525
6	0,916	21,900	20,067	0,840	479,610	23,805
7	0,875	20,000	17,509	0,766	400,000	22,928
8	0,956	22,000	21,021	0,913	484,000	24,647
9	1,030	23,900	24,608	1,060	571,210	26,238
10	0,956	26,000	24,843	0,913	676,000	24,647
11	0,956	24,600	23,506	0,913	605,160	24,647
12	0,916	21,000	19,242	0,840	441,000	23,805
13	1,065	27,000	28,747	1,134	729,000	26,991
14	0,956	21,000	20,066	0,913	441,000	24,647
15	0,788	24,000	18,923	0,622	576,000	21,060
16	0,956	34,000	32,487	0,913	1156,000	24,647
17	1,194	31,900	38,086	1,425	1017,610	29,765
19	1,361	33,000	44,912	1,852	1089,000	33,351
20	1,526	35,400	54,022	2,329	1253,160	36,895
21	1,308	34,000	44,483	1,712	1156,000	32,221
22	1,224	31,000	37,937	1,498	961,000	30,406
Итого	21,115	540,100	564,166	22,214	14506,970	540,100
сред зн	1,005	25,719	26,865	1,058	690,808
стан откл	0,216	5,417

Рассчитаем a и b:

Получим линейное уравнение: .

· Рассчитаем параметры уравнений обратной парной регрессии. Для оценки параметров приведем обратную модель к линейному виду, заменив , тогда

Для расчетов используем данные табл. 6:

№ региона	X	Y	XY	X^2	Y^2	Y^cp
1	2,800	0,036	0,100	7,840	0,001	24,605
2	2,400	0,047	0,113	5,760	0,002	22,230
3	2,100	0,048	0,100	4,410	0,002	20,729
4	2,600	0,043	0,112	6,760	0,002	23,357
5	1,700	0,063	0,108	2,890	0,004	19,017
6	2,500	0,046	0,114	6,250	0,002	22,780
7	2,400	0,050	0,120	5,760	0,003	22,230
8	2,600	0,045	0,118	6,760	0,002	23,357
9	2,800	0,042	0,117	7,840	0,002	24,605
10	2,600	0,038	0,100	6,760	0,001	23,357
11	2,600	0,041	0,106	6,760	0,002	23,357
12	2,500	0,048	0,119	6,250	0,002	22,780
13	2,900	0,037	0,107	8,410	0,001	25,280
14	2,600	0,048	0,124	6,760	0,002	23,357
15	2,200	0,042	0,092	4,840	0,002	21,206
16	2,600	0,029	0,076	6,760	0,001	23,357
17	3,300	0,031	0,103	10,890	0,001	28,398
19	3,900	0,030	0,118	15,210	0,001	34,844
20	4,600	0,028	0,130	21,160	0,001	47,393
21	3,700	0,029	0,109	13,690	0,001	32,393
22	3,400	0,032	0,110	11,560	0,001	29,301
Итого	58,800	0,853	2,296	173,320	0,036	537,933
сред знач	2,800	0,041	0,109	8,253	0,002
стан отклон	0,643	0,009

Рассчитаем a и b:

Получим линейное уравнение: . Выполнив его потенцирование, получим:

Для расчета теоретических значений y подставим в уравнение значения x .

· Рассчитаем параметры уравнений равносторонней гиперболы парной регрессии. Для оценки параметров приведем модель равносторонней гиперболы к линейному виду, заменив , тогда

Для расчетов используем данные табл. 7:

№ региона	X=1/z	Y	XY	X^2	Y^2	Y^cp
1	0,357	28,000	10,000	0,128	784,000	26,715
2	0,417	21,300	8,875	0,174	453,690	23,259
3	0,476	21,000	10,000	0,227	441,000	19,804
4	0,385	23,300	8,962	0,148	542,890	25,120
5	0,588	15,800	9,294	0,346	249,640	13,298
6	0,400	21,900	8,760	0,160	479,610	24,227
7	0,417	20,000	8,333	0,174	400,000	23,259
8	0,385	22,000	8,462	0,148	484,000	25,120
9	0,357	23,900	8,536	0,128	571,210	26,715
10	0,385	26,000	10,000	0,148	676,000	25,120
11	0,385	24,600	9,462	0,148	605,160	25,120
12	0,400	21,000	8,400	0,160	441,000	24,227
13	0,345	27,000	9,310	0,119	729,000	27,430
14	0,385	21,000	8,077	0,148	441,000	25,120
15	0,455	24,000	10,909	0,207	576,000	21,060
16	0,385	34,000	13,077	0,148	1156,000	25,120
17	0,303	31,900	9,667	0,092	1017,610	29,857
19	0,256	33,000	8,462	0,066	1089,000	32,564
20	0,217	35,400	7,696	0,047	1253,160	34,829
21	0,270	34,000	9,189	0,073	1156,000	31,759
22	0,294	31,000	9,118	0,087	961,000	30,374
Итого	7,860	540,100	194,587	3,073	14506,970	540,100
сред знач	0,374	25,719	9,266	0,146	1318,815
стан отклон	0,079	25,639

Рассчитаем a и b:

Получим линейное уравнение: . Получим уравнение регрессии: .

3. Оценка тесноты связи с помощью показателей корреляции и детерминации :

· Линейная модель. Тесноту линейной связи оценит коэффициент корреляции. Был получен следующий коэффициент корреляции r_xy =b=7,122*, что говорит о прямой сильной связи фактора и результата. Коэффициент детерминации r²_xy =(0,845)²=0,715. Это означает, что 71,5% вариации результативного признака (розничнаяпродажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.

· Степенная модель. Тесноту нелинейной связи оценит индекс корреляции. Был получен следующий индекс корреляции =, что говорит о очень сильной тесной связи, но немного больше чем в линейной модели. Коэффициент детерминации r²_xy =0,7175. Это означает, что 71,75% вариации результативного признака (розничнаяпродажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.

· Экспоненциальная модель. Был получен следующий индекс корреляции ρ_xy =0,8124, что говорит о том, что связь прямая и очень сильная, но немного слабее, чем в линейной и степенной моделях. Коэффициент детерминации r²_xy =0,66. Это означает, что 66% вариации результативного признака (розничнаяпродажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.

· Полулогарифмическая модель. Был получен следующий индекс корреляции ρ_xy =0,8578, что говорит о том, что связь прямая и очень сильная, но немного больше чем в предыдущих моделях. Коэффициент детерминации r²_xy =0,7358. Это означает, что 73,58% вариации результативного признака (розничнаяпродажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.

· Гиперболическая модель. Был получен следующий индекс корреляции ρ_xy =0,8448 и коэффициент корреляции r_xy =-0,1784 что говорит о том, что связь обратная очень сильная. Коэффициент детерминации r²_xy =0,7358. Это означает, что 73,5% вариации результативного признака (розничнаяпродажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.

· Обратная модель. Был получен следующий индекс корреляции ρ_xy =0,8114 и коэффициент корреляции r_xy =-0,8120, что говорит о том, что связь обратная очень сильная. Коэффициент детерминации r²_xy =0,6584. Это означает, что 65,84% вариации результативного признака (розничнаяпродажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.

Вывод: по полулогарифмическому уравнению получена наибольшая оценка тесноты связи: ρ_xy =0,8578 (по сравнению с линейной, степенной, экспоненциальной, гиперболической, обратной регрессиями).

4. С помощью среднего (общего) коэффициента эластичности дайте сравнительную оценку силы связи фактора с результатом.

Рассчитаем коэффициент эластичности для линейной модели:

· Для уравнения прямой:y = 5,777+7,122∙x

· Для уравнениястепенноймодели :

· Для уравненияэкспоненциальноймодели :

Для уравненияполулогарифмическоймодели :

· Для уравнения обратной гиперболической модели :

· Для уравнения равносторонней гиперболической модели :

Сравнивая значения , характеризуем оценку силы связи фактора с результатом:

·

·

·

·

·

·

Известно, что коэффициент эластичности показывает связь между фактором и результатом, т.е. на сколько% изменится результат y от своей средней величины при изменении фактора х на 1% от своего среднего значения. В данном примере получилось, что самая большая сила связи между фактором и результатом в полулогарифмической модели, слабая сила связи в обратной гиперболической модели.

5. Оценка качества уравнений с помощью средней ошибки аппроксимации.

Подставляя в уравнение регрессии фактические значения х, определим теоретические (расчетные) значения . Найдем величину средней ошибки аппроксимации :

В среднем расчетные значения отклоняются от фактических на:

· Линейная регрессия. =*100%= 8,5%, что говорит о повышенной ошибке аппроксимации, но в допустимых пределах.

Качество построенной модели оценивается как хорошее, так как не превышает 8 -10%.

· Степенная регрессия. =*100%= 8,2%, что говорит о повышенной ошибке аппроксимации, но в допустимых пределах.

Качество построенной модели оценивается как хорошее, так как не превышает 8 -10%.

· Экспоненциальная регрессия. =*100%= 9%, что говорит о повышенной ошибке аппроксимации, но в допустимых пределах.

Качество построенной модели оценивается как хорошее, так как не превышает 8 -10%.

· Полулогарифмическая регрессия. =*100%= 7,9 что говорит о повышенной ошибке аппроксимации, но в допустимых пределах.

Качество построенной модели оценивается как хорошее, так как не превышает 8 -10%.

· Гиперболическая регрессия. =*100%= 9,3 что говорит о повышенной ошибке аппроксимации, но в допустимых пределах.

Качество построенной модели оценивается как хорошее, так как не превышает 8 -10%.

· Обратная регрессия. =*100%= 9,9 3 что говорит о повышенной ошибке аппроксимации, но в допустимых пределах.

Качество построенной модели оценивается как хорошее, так как не превышает 8 -10%.

6. Рассчитаем F-критерий:

· Линейная регрессия. = *19= 47,579

УДК 004.021, 519.651, 519.654

V

ПОВЫШЕНИЕ ТОЧНОСТИ МОДЕЛЕЙ АППРОКСИМАЦИИ

Д. Л. Петрянин, Н. К. Юрков

Введение

Основу математических моделей многих процессов и явлений в физике, электронике, экономике и других областях составляют уравнения различного вида: нелинейные уравнения, обыкновенные дифференциальные уравнения, дифференциальные уравнения в частных производных и т.д. Для решения подобных уравнений необходимо иметь возможность вычислять значения функций, входящих в описание математической модели рассматриваемого процесса или явления, при произвольном значении аргумента. Для сложных моделей подобные вычисления могут быть трудоемкими даже при использовании компьютера.

Используемые в математических моделях функции могут быть заданы как аналитическим способом (в виде формулы), так и табличным, при котором функция известна только при определенных дискретных значениях аргумента. В частности, если функциональная зависимость получена в результате расчетов, проведенных на ЭВМ, или в процессе измерений, осуществленных в рамках какого-либо эксперимента, то она оказывается заданной именно табличным способом. На практике нам могут понадобиться значения функции и в других точках, отличных от тех, что заданы в таблице. Однако получить эти значения можно только путем сложных расчетов или проведением дорогостоящих экспериментов.

Таким образом, с точки зрения экономии времени и средств мы приходим к задаче вычисления приближенных значений функции /(х) (описывающей экспериментальные данные) при любом значении аргумента на основе имеющихся табличных данных.

Эта задача решается путем приближенной замены функции / (х) более простой функцией ф(х), которую нетрудно вычислять при любом значении аргумента х в заданном интервале его изменения. Приближение функции /(х) более простой функцией ф(х) называется аппроксимацией.

От выбора вида аппроксимации зависит значение погрешности — для одних моделей больше, для других меньше. Аппроксимация с помощью найденной модели осуществляется с погрешностью, которая значительно ухудшает результаты исследования [1-3]. Необходимо снизить погрешность аппроксимации, снижающую погрешность экспериментального исследования.

Выбор модели аппроксимации. Как правило, выбор модели аппроксимации определяется по минимальному значению погрешности, как на всем интервале исходных данных, так и для конкретно взятого промежутка.

Входные данные до уточнения модели аппроксимации представляются в следующем виде:

где п — количество узлов; х1…хп и у1…уп — экспериментальные данные (заданные табличным способом) причем у = Ып (х), здесь Ып (х) — функция экспериментальных данных в п узле.

Для расчетов необходимо использовать несколько видов аппроксимаций, чтобы определить более точное описание зависимости экспериментальных данных у = N(х). Для удобства (записи в формулах) условно принимаем нумерацию видов аппроксимации вместо их названий (1… 1) .

В случае, когда исходное значение у превышает рассчитанное значение 1-го вида аппроксимации (х), т.е. уп > (х) (рис. 1), то уточнение аппроксимации происходит по модели (2):

х б [ х1… хп ], у е[ Л… уп ]

(1)

Рвр1(*) = У1 +| У1 — РА1( Х%

Рвр2(х) = У2 +|У2 — РА2(х^ Рвр3(х) = Уз + Уз -РА3(х)|,

Рвр,(х) = Уп + Уп — Ра, (х%

(2)

где Рвр» (х) — временное значение исходных данных »-го вида аппроксимации; РА» (х) — значение найденной функции »-го вида аппроксимации.

Рис. 1. Графическое представление уточнения аппроксимации

Когда исходное значение у меньше рассчитанного значения ,-го вида аппроксимации РА»(х), т.е. уп < РА»(х), то уточнение аппроксимации происходит по модели (3):

‘ Рвр1( х) = У1 -| У1 — РА1( х %

Рвр2(х) = У2 -|У2 — РА2(х)|,

Рвр3(х) = Уз -|Уз — РА3(х)|, (3)

Рвр,(х) = Уп -|Уп — Ра, (х)|.

В случае равенства исходного значения у и рассчитанного значения ,-го вида аппроксимации РА, (х), т.е. Уп = РА» (х), то уточнение модели аппроксимации в данном случае не происходит (4):

Рвр1( х) = Уь Рвр2( х) = У2, Рвр3( х) = У3′

Рвр i( х) = Уп .

(4)

Для определения точности рассчитывают погрешность (относительная ошибка аппроксимации) в каждой точке по известной формуле

•100%, (5)

п

где У — исходное значение экспериментальных данных; У» — расчетное значение функции; п — количество узлов. Ошибка аппроксимации в пределах 5-7 % свидетельствует о хорошем подборе функции к исходным данным.

Данная модель повышения точности аппроксимации отличается от существующих:

1) возможностью отсутствия дополнительного сбора экспериментальных данных;

2) нахождением временных данных, на основе которых происходит уточнение. Разработана методика снижения погрешности аппроксимации за счет многопроходных расчетов и нахождения случайной ошибки аппроксимации (рис. 2). За основу была взята методика анализа данных Н. Некипелова [4], которая отличается от разработанной следующими свойствами:

1) поиск временных данных и модели по ним;

2) проверкой приемлемости качества найденной модели после каждого расчета;

3) нахождением и расчетом случайной ошибки аппроксимации в каждой точке исходных данных.

А -.

У — У»

Рис. 2. Методика снижения погрешности аппроксимации

Нахождение временных данных происходит по моделям (2)-(4).

Данная модель позволит решать задачи исследования технических направлений, результаты которых будут более точными и близки к исходным данным.

Алгоритм повышения точности модели аппроксимации, представленный на рис. 3, работает следующим образом. Пользователем загружаются экспериментальные данные (х, у) и выбираются используемые виды аппроксимации (^А1, ^А2, FА3… ЕАп). По загруженным данным определяется количество узлов п, рассчитываются аппроксимации с погрешностями и осуществляется выбор оптимальной модели аппроксимации. Пользователь определяет качество полученной модели (по значениям погрешности, по точности в определенных интервалах данных). Если качество не удовлетворяет пользователя, происходит уточнение аппроксимации — определяются временные данные, по которым повторно рассчитываются аппроксимации и погрешности. Здесь погрешности вычисляются на основе исходных данных. Затем происходит проверка на качество новой модели. При отрицательном решении (пользователя) осуществляется расчет случайных ошибок аппроксимации в каждой точке для дальнейшего анализа данных или возможности получения новых экспериментальных данных.

Рис. 3. Алгоритм повышения точности модели аппроксимации

Для расчетов аппроксимации, их относительных ошибок, снижения погрешности и выбора оптимальной модели аппроксимации разработано программное обеспечение «Выбор метода аппроксимации» [5] на основе разработанного алгоритма (рис. 4).

В программе присутствуют два способа ввода данных: ручной ввод или готовый файл с экспериментальными данными. Также реализованы следующие виды аппроксимации: метод наименьших квадратов (функции: линейная, парабола, экспоненциальная, степенная, гипербола, логарифмическая, кубическая парабола), интерполяция (линейная, полином Лагранжа, полином Ньютона).

На рис. 4 представлены результаты расчетов погрешностей аппроксимации «до» и «после» уточнения моделей. В качестве исходных данных использовались экспериментальные значения температуры процессора ЭВМ (при выполнении различных задач: очистка диска, копирование файлов, запуск программ).

Рис. 4. Результат работы программы «Выбор метода аппроксимации»

На рис. 5 представлены графические результаты исходных и временных данных, расчетные значения «до» и «после» уточнения моделей (для степенного вида аппроксимации).

Рис. 5. Графические результаты уточнения степенного вида аппроксимации

Из рис. 4 и 5 видно, что разработанные математическая модель повышения точности метода аппроксимации и методика снижения погрешности работоспособны, актуальны и дают неплохой результат для методов наименьших квадратов. Здесь можно прокомментировать тот факт, что в найденной модели (степенного вида аппроксимации) не удалось повысить точность в некоторых точках (см. рис. 5). Это объясняется двумя причинами:

1) имеются отклонения считывания данных с температурного датчика;

2) найденная модель не соответствует данному процессу — для этого необходимо реализовать в программе намного больше способов аппроксимации, для получения наиболее подходящего решения.

В случае с большим количеством экспериментальных данных (более 100 узлов) в программе предусмотрена возможность разбиения данных на несколько частей. Для каждой части находится оптимальная модель аппроксимации и рассчитывается погрешность. Результаты такого исследования представлены на рис. 6.

5 Выбор метода аппроксимации

Внодные данные 8 ид отображения

Текстовый Файл

X

1 42

2 42

3 42

4 43

5 43

8 42

7 44

8 45

3 48

10 43

11 43

12 43

13 50

14 50

15 50

16 50

Шаг уплотнения: 11 Интервал; [5Т01 |Э131

{X Расчет

Метод наименьших кеадратое Интерполяция Расчет погрешности и выбор метода Уточнение модели Файл

Исходный файл ¡орчгинал|

Сохраняемый файл

X У ш

42

1

2 42

3 42

4 43

5 43

6 42 V

л 0 Разбиение Файла (кол-во точек] [50 Т}

[8701 8750]13038456 981 ВОБЗ’Х -1 ЗБ1Э0В83035564

[8751..3800]СК»2+2.558Х+-11096,755

[8801 ..8850]СК~2-2.02ЭХ*8982.34

18851 8300]1 73Э23873Э07783Е11735422363863

18301. .8350]0!~2-4.484Х»20073.845

[8351..Э000](к’2+4.61Х+-20764.309

13001,3050)213.464″екр((К)

13051., 3100]433252.04/Х*104.336

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

|3101. 3131 ]74387.506/Х+47.833

Погрешность

Промежуток Относит, ошибка аппроксимации, «а Относит, ошибка после ут | Л

[2251..2300] 0.000861048652583333 0.000744714875546667

[2301. .2350] 0.247587570601287 0.138318756126454 Э

[2351..24001 0.233333183900183 0.237200111014127

[2401 .2450] 0 450508836834224 0 364318037525694

1 [2451..2500] 0.68104733167380В 0.64500430685233 V

[[2501..25501 0.235763121266608 0.168513095138436

Рис. 6. Результаты нахождения модели аппроксимации для большого количества экспериментальных данных

Разбиение на части дает более точную выходную модель и низкую погрешность.

Сохраненные экспериментальные данные могут быть обработаны в любое назначенное время или при простое ЭВМ. Это снижает нагрузку на центральный процессор и обеспечивает быстродействие при загрузке экспериментальных данных. Логическая схема данного процесса представлена на рис. 7.

Рис. 7. Логическая схема сохранения и нахождения моделей экспериментальных данных

В связи с вышеизложенным использование уточненной модели аппроксимации позволяет достичь поставленной цели повышения точности.

Заключение

Разработанные математическая модель повышения точности аппроксимации и методика

снижения погрешности аппроксимации позволили повысить точность выходной модели экспериментальных данных до 10 %.

Список литературы

1. Петрянин, Д. Л. Анализ систем защиты информации в базах данных / Д. Л. Петрянин, Н. В. Горячев, Н. К. Юрков // Труды международного симпозиума Надежность и качество. — 2013. — Т. 1. — С. 115-122.

2. Саушев, А. В. Методы назначения допусков на параметры технических систем путем линейной аппроксимации граничных точек / А. В. Саушев // Труды международного симпозиума Надежность и качество. -2015. — Т. 1. — С. 144-147.

3. Петрянин, Д. Л. Структура системы поддержки принятия решений при архивировании данных / Д. Л. Петрянин, Н. К. Юрков // Труды международного симпозиума Надежность и качество. — 2014. -Т. 1. — С. 331-333.

4. Методика анализа данных // Электронные статьи для чтения. — иКЬ: https://basegroup.ru/community/ articles/base (дата обращения: 20.01.2016).

5. Выбор метода аппроксимации / Д. Л. Петрянин, Н. В. Горячев, Н. К. Юрков. — Зарегистрировано в реестре фонда алгоритмов и программ Сибирского отделения Российской академии наук. Регистрационный номер — РЯ15012. — ИРЬ: http://fap.sbras.ru/node/4152

Петрянин Дмитрий Львович аспирант,

Пензенский государственный университет (440026, Россия, г. Пенза, ул. Красная, 40) E-mail: ra4cbh@mail.ru

Юрков Николай Кондратьевич

доктор технических наук, профессор, заведующий кафедрой конструирования и производства радиоаппаратуры, Пензенский государственный университет (440026, Россия, г. Пенза, ул. Красная, 40) E-mail: yurkov_NK@mail.ru

Аннотация. Актуальность и цели. В настоящее время задача аппроксимации является актуальной темой решения в различных технических исследованиях. Целью является нахождение моделей аппроксимации с максимально возможной точностью и низкой погрешностью. Доказана необходимость разработки эффективных методов анализа экспериментальных кривых и построения моделей аппроксимации. Материалы и методы. Дана модель повышения точности аппроксимации. Описана методика снижения погрешности аппроксимации за счет многопроходных расчетов и нахождения случайной ошибки аппроксимации, которая позволяет проводить оценку результатов исследования технических систем и получать результаты, более приближенные к исходным данным. Разработан алгоритм повышения точности модели аппроксимации, на основе которого разработано программное обеспечение, позволяющее загрузить экспериментальные данные и произвести расчеты для нахождения моделей аппроксимации. Приведена методика, позволяющая уточнить модели аппроксимации, а также выявить лучшую с точки зрения погрешности ап-

Petrjanin Dmitry L’vovich

postgraduate student,

Penza State University

(440026, 40 Krasnaya street, Penza, Russia)

Yurkov Nikolay Kondrat’evich

doctor of technical sciences, professor,

head of sub-department of radio equipment

design and production,

Penza State University

(440026, 40 Krasnaya street, Penza, Russia)

Abstract. Background. The challenge now is a hot topic of approximation of solutions to various technical studies. The aim is to find approximations of the models with the greatest possible precision and low error. The necessity of the development of effective methods for the analysis of experimental curves and constructing approximation models. Materials and methods. Dana model increasing accuracy of approximation. A technique for reducing the error of approximation by multipass calculations and finding random approximation error, which allows you to assess the results of the study of technical systems and get the results more close to the original data. An algorithm for improving the accuracy of approximation of the model on which developed software that allows you to download experimental data and make calculations to find the approximation models. The technique, which allows to specify the approximation of the model, and to identify the best in terms of the approximation error. Results. It is shown that the developed mathematical model improve accuracy and reduce error of approximation technique improved the accuracy of the output model of the experimental data up to 10 %. Conclusions. The use of the approximation

проксимации. Результаты. Показано, что разработанная математическая модель повышения точности и методика снижения погрешности аппроксимации позволили повысить точность выходной модели экспериментальных данных до 10 %. Выводы. Применение моделей аппроксимации позволяет оценивать полученные результаты исследования технических систем и получать результаты, более приближенные к исходным данным.

Ключевые слова: аппроксимация, данные, модель, расчет, метод.

model allows to evaluate the results of research and technical systems to obtain results more close to the original data.

Key words: approximation, the data, model, the calculation, method.

УДК 004.021, 519.651, 519.654 Петрянин, Д. Л.

Повышение точности моделей аппроксимации / Д. Л. Петрянин, Н. К. Юрков // Надежность и качество сложных систем. — 2016. — № 2 (14). — С. 59-66.

· 3.5. Коррекция статистических выводов при автокоррелированности ошибок

Пусть мы имеем дело с наблюдениями, производимыми последовательно через равные промежутки времени (ежедневные, еженедельные, ежеквартальные, ежегодные статистические данные) и выявляем по графику зависимости стандартизованных остатков от тенденцию Сохранения знака Соседних наблюдений. В таком случае мы можем подозревать Нарушение условия независимости случайных ошибок в принятой нами модели наблюдений

В форме положительной автокоррелированности ряда ошибок.

Простейшей моделью автокоррелированности ошибок является Модель авторегрессии первого порядка:

Где , а — независимые в совокупности случайные величины, имеющие одинаковое нормальное распределение . Тогда гипотеза

Соответствует (при нашем предположении о нормальности распределения случайных ошибок) Независимости в совокупности случайных величин . В качестве альтернативной используем гипотезу

Соответствующую Положительной автокоррелированности случайных величин (т. е. Тенденции преимущественного сохранения знака случайной ошибки при переходе от — го наблюдения к -му). Если гипотеза Отклоняется критерием Дарбина-Уотсона в пользу альтернативной гипотезы То для получения правильных статистических выводов относительно коэффициентов модели необходима соответствующая коррекция.

Итерационная процедура Кохрейна-Оркатта (Cochrane-Orcutt).

Умножим обе части выражения для -го наблюдения на , так что

И вычтем обе части полученного выражения из соответствующих частей выражения для -го наблюдения:

Тем самым мы приходим к преобразованной модели наблюдений

Где

Поскольку в принятой модели ошибок

То это означает, что ошибки в преобразованной модели — независимые в совокупности случайные величины, имеющие одинаковое нормальное распределение .

Иными словами, Случайные ошибки в преобразованной модели удовлетворяют стандартным предположениям. Следовательно, В рамках преобразованной модели никакой дополнительной коррекции обычных статистических выводов о коэффициентах модели не требуется. Проблема только в том, что используемое в процессе преобразования модели значение коэффициента нам Не известно. Поэтому реально провести указанное преобразование невозможно. Вместо этого можно пытаться заменить указаное преобразование какой-либо его аппроксимацией с заменой неизвестного значения на его оценку по данным наблюдений. Конечно, при использовании такой аппроксимации мы уже не можем гарантировать, что в преобразованной модели будут независимыми в совокупности случайными величинами, однако есть некоторая надежда на то, что эти ошибки все же будут обнаруживать Меньшую автокоррелированность по сравнению с ошибками в исходной модели.

Описываемая здесь процедура Кохрейна-Оркатта использует для получения аппроксимации теоретического преобразования оценку для в виде

Где — остатки, получаемые при оценивании Исходной модели наблюдений. Аппроксимирующее преобразование определяется соотношениями

Которые приводят к преобразованной модели

Если в последней модели автокоррелированность не проявляется, то полученные в рамках этой модели оценки параметров можно принять в качестве Уточненных оценок параметров . Если же в преобразованной модели еще остается выраженная автокоррелированность, то процесс преобразования применяют уже к Преобразованной модели и еще раз уточняют значения параметров и т. д., пока последовательно уточняемые значения параметров не перестанут изменяться в пределах заданной точности.

Заметим, наконец, что обычно мы предполагаем, что. Соответственно, для первой объясняющей переменной получаем

Так что фактически мы имеем преобразованную модель

С . Получив в этой модели оценку для , мы можем оценить параметр исходной модели, просто полагая

Пример. Проанализируем статистические данные о совокупных потребительских расходах (CONS) и денежной массе (MONEY) в США за 1952—1956 г. г. (квартальные данные, в млрд. долларов).

Obs	MONEY	CONS	Obs	MONEY	CONS
1952:1	159.3	214.6	1954:3	173.9	238.7
1952:2	161.2	217.7	1954:4	176.1	243.2
1952:3	162.8	219.6	1955:1	178.0	249.4
1952:4	164.6	227.2	1955:2	179.1	254.3
1953:1	165.9	230.9	1955:3	180.2	260.9
1953:2	167.9	233.3	1955:4	181.2	263.3
1953:3	168.3	234.1	1956:1	181.6	265.6
1953:4	169.7	232.3	1956:2	182.5	268.2
1954:1	170.5	233.7	1956:3	183.3	270.4
1954:2	171.6	236.5	1956:4	184.3	275.6

Результаты оценивания линейной модели наблюдений

В которой — значения объясняемой переменной CONS, а — значения объясняющей переменной MONEY, приведены в следующей таблице:

Variable	Coefficient	Std. Error	T-Statistic	Prob.
1	–154.719	19.850	-7.794	0.0000
X	2.300	0.114	20.080	0.0000
R-squared	0.957	Durbin-Watson stat	0.328

Хотя коэффициент детерминации весьма близок к единице, значение статистики Дарбина-Уотсона достаточно мало, и это дает возможность подозревать наличие положительной автокоррелированности ошибок в принятой модели наблюдений. Два следующих графика дают представление о рассеянии значений переменных и о поведении остатков.

Здесь наблюдаются серии остатков, имеющих одинаковые знаки, что как раз и характерно для моделей, в которых имеется положительная автокоррелированность ошибок.

Для подтверждения положительной автокоррелированности ошибок используем критерий Дарбина-Уотсона. По таблицам находим нижнюю границу для критического значения при : . Полученное при оценивании модели значение существенно меньше этой нижней границы, так что гипотеза Отвергается в пользу альтернативной гипотезы . Для коррекции статистических выводов используем процедуру Кохрейна-Оркатта.

Прежде всего находим оценку для неизвестного значения коэффициента : Основываясь на этой оценке, переходим к преобразованной модели, оценивание которой дает следующие результаты:

Included observations: 19 after adjusting endpoints
Variable	Coefficient	Std. Error	T-Statistic	Prob.
1	-30.777	14.043	-2.192	0.0426
X’	2.795	0.609	4.593	0.0003
R-squared	0.554	Durbin-Watson stat	1.667

Хотя в преобразованной модели коэффициент детерминации существенно ниже, чем в непреобразованной модели, значение статистики Дарбина-Уотсона теперь Превышает верхнюю границу для критического значения , соответствующего . (В преобразованной модели наблюдений на единицу меньше, чем в исходной, так как при преобразовании используются Запаздывающие Значения обеих переменных). Поэтому гипотеза о независимости в совокупности ошибок в преобразованной модели не отвергается (в пользу гипотезы об их положительной автокоррелированности). Два следующих графика дают представление о рассеянии значений преобразованных переменных и о поведении остатков в преобразованной модели.

RESID: TRANSFORMED MODEL

Обратим внимание на существенно более нерегулярное поведение остатков по сравнению с исходной моделью.

Обращаясь к результатам оценивания коэффициентов в преобразованной модели, отметим значительное (более, чем в 5 раз!) возрастание оценки стандартной ошибки , что подтверждает сделанное ранее замечание о Занижении стандартных ошибок при неучете имеющейся в действительности положительной автокорреляции случайных ошибок в модели наблюдений. Столь существенное возрастание значения приводит к возрастанию более, чем в 5 раз, и ширины доверительного интервала Для мультипликатора . Если при оценивании исходной линейной модели 95%-доверительный интервал для этого параметра имел вид , то при оценивании преобразованной модели мы получаем интервал .

Рассмотренный пример ясно демонстрирует опасность пренебрежения возможной неадекватностью построенной модели в отношении стандартных предположений об ошибках и необходимость Обязательного проведения в процессе подбора подходящей модели связи между теми или иными экономическими факторами Анализа остатков, полученных при оценивании выбранной модели.

Более того, используя преобразованную модель, можно получить Улучшенную модель для прогнозирования объемов расходов на потребление при планируемых объемах денежной массы. Поясним это на примере простой линейной модели

Предполагая, что и используя оценку для коэффициента , переходим к преобразованной модели

C и

И получаем в рамках этой модели оценки и параметров и , так что оцененная модель линейной связи между преобразованными переменными имеет вид

В исходных переменных последние соотношения принимают вид

Где , откуда получаем:

Если мы собираемся теперь прогнозировать будущее значение, соответствующее плановому значению объясняющей переменной, то естественно воспользоваться полученным соотношением и предложить в качестве прогнозного дляЗначение

При таком способе вычисления прогнозного значения для Учитывается тенденция сохранения знака остатков: если в последнем наблюдении наблюдавшееся значение Превышало значение предсказываемое линейной моделью связи то и последующее значение Прогнозируется с превышением значения предсказываемого этой линейной моделью связи при . Если же значение Меньше, чем то тогда будущее значение прогнозируется Меньшим значения

Пример. Продолжим рассмотрение предыдущего примера. В этом примере , . Наблюдавшимся значениям можно сопоставить:

· Наблюдавшиеся значения ;

· значения

Получаемые по модели, построенной Без учета автокоррелированности ошибок;

· значения

Получаемые по модели, параметры которой скорректированы С учетом автокоррелированности ошибок;

· значения

Отличающиеся от значений, указанных в предыдущем пункте, Учетом Значения остатка в предшествующем наблюдении.

Ниже приведены графики значений , получаемых указанными тремя методами, и графики соответствующих им расхождений . Индексы 1, 2, 3 указывают на один из трех способов получения значений , в том порядке, в котором они были перечислены выше).

Сравним средние квадраты расхождений При использовании указанных трех методов вычисления значений . Эти средние квадраты равны, соответственно,

Что говорит о большей гибкости прогноза, построенного по последнему (третьему) методу.

Рассмотрим еще одно важное следствие автокоррелированности ошибок в линейной модели

С Преобразование

Приводит к модели наблюдений

На основании которой получаем соотношение

Вспомним теперь о нашем предположении, что , и преобразуем последнее соотношение следующим образом:

Или

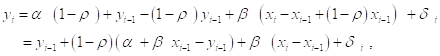
Здесь , и . Второе слагаемое в правой части по-существу поддерживает «долговременную» линейную связь (тенденцию)

Если в момент отклонение от положительно , то второе слагаемое будет Отрицательным, действуя в сторону Уменьшения приращения . Если же отклонение от Отрицательно , то второе слагаемое будет Положительным, действуя в сторону Увеличения приращения .

Указанная модель коррекции приращений переменной использует «истинные» значения параметров . Поскольку эти значения нам не известны, мы в состоянии построить только Аппроксимацию такой модели, использующую оценки параметров. При этом естественно воспользоваться оценкой и уточненными оценками , полученными на базе преобразованной модели.

В рассмотренном примере аппроксимирующая модель коррекции приращений принимает вид

< Предыдущая		Следующая >