Как уменьшить стандартную ошибку - Не ошибается лишь тот, кто ничего не делает!

Автор:
Laura McKinney

Дата создания:
7 Апрель 2021

Дата обновления:
1 Июнь 2023

Видео: Стандартное отклонение vs стандартная ошибка среднего

Содержание

Сравнительная таблица
Определение стандартного отклонения
Определение стандартной ошибки
Ключевые различия между стандартным отклонением и стандартной ошибкой
Вывод

Стандартное отклонение определяется как абсолютная мера дисперсии ряда. Он уточняет стандартную величину отклонения по обе стороны от среднего. Его часто неправильно истолковывают со стандартной ошибкой, поскольку он основан на стандартном отклонении и размере выборки.

Стандартная ошибка используется для измерения статистической точности оценки. Он в основном используется в процессе проверки гипотез и оценки интервала.

Это две важные концепции статистики, которые широко используются в области исследований. Разница между стандартным отклонением и стандартной ошибкой основана на различии между описанием данных и их выводом.

Сравнительная таблица

Основа для сравнения	Стандартное отклонение	Стандартная ошибка
Имея в виду	Стандартное отклонение подразумевает меру отклонения набора значений от их среднего.	Стандартная ошибка означает меру статистической точности оценки.
Статистика	Описательный	Логический
Меры	Насколько наблюдения отличаются друг от друга.	Насколько точно среднее значение выборки соответствует истинному среднему значению генеральной совокупности.
Распределение	Распределение наблюдения относительно нормальной кривой.	Распределение оценки относительно нормальной кривой.
Формула	Корень квадратный из дисперсии	Стандартное отклонение, деленное на квадратный корень из размера выборки.
Увеличение размера выборки	Дает более конкретную меру стандартного отклонения.	Уменьшает стандартную ошибку.

Определение стандартного отклонения

Стандартное отклонение — это мера разброса ряда или расстояния от стандарта. В 1893 году Карл Пирсон ввел понятие стандартного отклонения, которое, несомненно, является наиболее часто используемой мерой в научных исследованиях.

Это квадратный корень из среднего квадрата отклонений от их среднего значения. Другими словами, для данного набора данных стандартное отклонение — это среднеквадратичное отклонение от среднего арифметического. Для всего населения он обозначается греческой буквой «сигма (σ)», а для выборки — латинской буквой «s».

Стандартное отклонение — это мера, которая количественно определяет степень дисперсии набора наблюдений. Чем дальше точки данных от среднего значения, тем больше отклонение в наборе данных, что означает, что точки данных разбросаны по более широкому диапазону значений и наоборот.

Определение стандартной ошибки

Вы могли заметить, что разные выборки одинакового размера, взятые из одной и той же совокупности, дадут разные значения рассматриваемой статистики, т.е. выборочное среднее. Стандартная ошибка (SE) представляет собой стандартное отклонение различных значений выборочного среднего. Он используется для сравнения выборочных средних по совокупности.

Короче говоря, стандартная ошибка статистики — это не что иное, как стандартное отклонение ее выборочного распределения. Он играет большую роль в проверке статистических гипотез и интервальной оценке. Это дает представление о точности и достоверности сметы. Чем меньше стандартная ошибка, тем больше однородность теоретического распределения и наоборот.

Формула: Стандартная ошибка для выборочного среднего = σ / √n
Где, σ — стандартное отклонение совокупности

Ключевые различия между стандартным отклонением и стандартной ошибкой

Приведенные ниже моменты существенны с точки зрения разницы между стандартным отклонением:

Стандартное отклонение — это мера, которая оценивает степень вариации набора наблюдений. Стандартная ошибка измеряет точность оценки, т. Е. Является мерой изменчивости теоретического распределения статистики.
Стандартное отклонение — это описательная статистика, тогда как стандартная ошибка — это выводимая статистика.
Стандартное отклонение измеряет, насколько отдельные значения отличаются от среднего значения. Напротив, насколько близко среднее значение выборки к среднему значению генеральной совокупности.
Стандартное отклонение — это распределение наблюдений относительно нормальной кривой. В отличие от этого, стандартная ошибка — это распределение оценки относительно нормальной кривой.
Стандартное отклонение определяется как квадратный корень из дисперсии. И наоборот, стандартная ошибка описывается как стандартное отклонение, деленное на квадратный корень из размера выборки.
Когда размер выборки увеличивается, это дает более конкретную меру стандартного отклонения. В отличие от стандартной ошибки, когда размер выборки увеличивается, стандартная ошибка имеет тенденцию к уменьшению.

Вывод

В целом стандартное отклонение считается одним из лучших показателей дисперсии, который измеряет отклонение значений от центрального значения. С другой стороны, стандартная ошибка в основном используется для проверки надежности и точности оценки, поэтому чем меньше ошибка, тем выше ее надежность и точность.

Источник

Среднее арифметическое, как известно, используется для получения обобщающей характеристики некоторого набора данных. Если данные более-менее однородны и в них нет аномальных наблюдений (выбросов), то среднее хорошо обобщает данные, сведя к минимуму влияние случайных факторов (они взаимопогашаются при сложении).

Когда анализируемые данные представляют собой выборку (которая состоит из случайных значений), то среднее арифметическое часто (но не всегда) выступает в роли приближенной оценки математического ожидания. Почему приближенной? Потому что среднее арифметическое – это величина, которая зависит от набора случайных чисел, и, следовательно, сама является случайной величиной. При повторных экспериментах (даже в одних и тех же условиях) средние будут отличаться друг от друга.

Для того, чтобы на основе статистического анализа данных делать корректные выводы, необходимо оценить возможный разброс полученного результата. Для этого рассчитываются различные показатели вариации. Но то исходные данные. И как мы только что установили, среднее арифметическое также обладает разбросом, который необходимо оценить и учитывать в дальнейшем (в выводах, в выборе метода анализа и т.д.).

Интуитивно понятно, что разброс средней должен быть как-то связан с разбросом исходных данных. Основной характеристикой разброса средней выступает та же дисперсия.

Дисперсия выборочных данных – это средний квадрат отклонения от средней, и рассчитать ее по исходным данным не составляет труда, например, в Excel предусмотрены специальные функции. Однако, как же рассчитать дисперсию средней, если в распоряжении есть только одна выборка и одно среднее арифметическое?

Расчет дисперсии и стандартной ошибки средней арифметической

Чтобы получить дисперсию средней арифметической нет необходимости проводить множество экспериментов, достаточно иметь только одну выборку. Это легко доказать. Для начала вспомним, что средняя арифметическая (простая) рассчитывается по формуле:

где x_i – значения переменной,
n – количество значений.

Теперь учтем два свойства дисперсии, согласно которым, 1) — постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат и 2) — дисперсия суммы независимых случайных величин равняется сумме соответствующих дисперсий. Предполагается, что каждое случайное значение x_i обладает одинаковым разбросом, поэтому несложно вывести формулу дисперсии средней арифметической:

Используя более привычные обозначения, формулу записывают как:

где σ² – это дисперсия, случайной величины, причем генеральная.

На практике же, генеральная дисперсия известна далеко не всегда, точнее совсем редко, поэтому в качестве оной используют выборочную дисперсию:

Стандартное отклонение средней арифметической называется стандартной ошибкой средней и рассчитывается, как квадратный корень из дисперсии.

Формула стандартной ошибки средней при использовании генеральной дисперсии

Формула стандартной ошибки средней при использовании выборочной дисперсии

Последняя формула на практике используется чаще всего, т.к. генеральная дисперсия обычно не известна. Чтобы не вводить новые обозначения, стандартную ошибку средней обычно записывают в виде соотношения стандартного отклонения выборки и корня объема выборки.

Назначение и свойство стандартной ошибки средней арифметической

Стандартная ошибка средней много, где используется. И очень полезно понимать ее свойства. Посмотрим еще раз на формулу стандартной ошибки средней:

Числитель – это стандартное отклонение выборки и здесь все понятно. Чем больше разброс данных, тем больше стандартная ошибка средней – прямо пропорциональная зависимость.

Посмотрим на знаменатель. Здесь находится квадратный корень из объема выборки. Соответственно, чем больше объем выборки, тем меньше стандартная ошибка средней. Для наглядности изобразим на одной диаграмме график нормально распределенной переменной со средней равной 10, сигмой – 3, и второй график – распределение средней арифметической этой же переменной, полученной по 16-ти наблюдениям (которое также будет нормальным).

Судя по формуле, разброс стандартной ошибки средней должен быть в 4 раза (корень из 16) меньше, чем разброс исходных данных, что и видно на рисунке выше. Чем больше наблюдений, тем меньше разброс средней.

Казалось бы, что для получения наиболее точной средней достаточно использовать максимально большую выборку и тогда стандартная ошибка средней будет стремиться к нулю, а сама средняя, соответственно, к математическому ожиданию. Однако квадратный корень объема выборки в знаменателе говорит о том, что связь между точностью выборочной средней и размером выборки не является линейной. Например, увеличение выборки с 20-ти до 50-ти наблюдений, то есть на 30 значений или в 2,5 раза, уменьшает стандартную ошибку средней только на 36%, а со 100-а до 130-ти наблюдений (на те же 30 значений), снижает разброс данных лишь на 12%.

Лучше всего изобразить эту мысль в виде графика зависимости стандартной ошибки средней от размера выборки. Пусть стандартное отклонение равно 10 (на форму графика это не влияет).

Видно, что примерно после 50-ти значений, уменьшение стандартной ошибки средней резко замедляется, после 100-а – наклон постепенно становится почти нулевым.

Таким образом, при достижении некоторого размера выборки ее дальнейшее увеличение уже почти не сказывается на точности средней. Этот факт имеет далеко идущие последствия. Например, при проведении выборочного обследования населения (опроса) чрезмерное увеличение выборки ведет к неоправданным затратам, т.к. точность почти не меняется. Именно поэтому количество опрошенных редко превышает 1,5 тысячи человек. Точность при таком размере выборки часто является достаточной, а дальнейшее увеличение выборки – нецелесообразным.

Подведем итог. Расчет дисперсии и стандартной ошибки средней имеет довольно простую формулу и обладает полезным свойством, связанным с тем, что относительно хорошая точность средней достигается уже при 100 наблюдениях (в этом случае стандартная ошибка средней становится в 10 раз меньше, чем стандартное отклонение выборки). Больше, конечно, лучше, но бесконечно увеличивать объем выборки не имеет практического смысла. Хотя, все зависит от поставленных задач и цены ошибки. В некоторых опросах участие принимают десятки тысяч людей.

Дисперсия и стандартная ошибка средней имеют большое практическое значение. Они используются в проверке гипотез и расчете доверительных интервалов.

Поделиться в социальных сетях:

Источник

Основные выводы:

Стандартная ошибка среднего указывает, насколько среднее значение генеральной совокупности может отличаться от среднего выборочного.
Вы можете уменьшить стандартную ошибку, увеличив размер выборки.
Стандартная ошибка среднего и стандартное отклонение являются мерами изменчивости, используемыми для обобщения наборов данных.

Если вы собираете данные для научных или статистических целей, стандартная ошибка среднего может помочь вам определить, насколько точно набор данных представляет фактическую совокупность. Проверка точности вашего образца подтверждает ваше клиническое исследование и помогает вам сделать правильные выводы.

В этой статье мы определяем стандартную ошибку среднего, объясняем, как она отличается от стандартного отклонения, и предлагаем формулу для ее расчета.

Какова стандартная ошибка среднего?

Стандартная ошибка среднего (SEM) используется для определения различий между более чем одной выборкой данных. Это помогает вам оценить, насколько хорошо ваши выборочные данные представляют всю совокупность, измеряя точность, с которой выборочные данные представляют совокупность, используя стандартное отклонение.

В статистике, среднеквадратичное отклонение является мерой того, насколько разбросаны числа. Иметь в виду относится к среднему числу. Стандартные функции ошибок используются для проверки точности выборки из нескольких выборок путем анализа отклонений в пределах средних значений.

Высокая стандартная ошибка показывает, что средние значения выборки широко разбросаны по среднему значению генеральной совокупности, поэтому ваша выборка может не точно представлять вашу генеральную совокупность. Низкая стандартная ошибка показывает, что средние значения выборки близко распределены вокруг среднего значения совокупности, что означает, что ваша выборка репрезентативна для вашей совокупности. Вы можете уменьшить стандартную ошибку, увеличив размер выборки.

Например, если вы измерите вес большой выборки мужчин, их вес может варьироваться от 125 до более чем 300 фунтов. Однако, если вы посмотрите на среднее значение выборочных данных, образцы будут различаться всего на несколько фунтов. Затем вы можете использовать стандартную ошибку среднего, чтобы определить, насколько вес отличается от среднего.

Связанный: Как рассчитать стандартную ошибку в Excel (с советами)

Стандартная ошибка среднего по сравнению со стандартным отклонением

Стандартная ошибка среднего и стандартное отклонение являются мерами изменчивости, используемыми для суммирования наборов данных.

Стандартная ошибка среднего значенияСтандартное отклонениеОценивает изменчивость в нескольких выборках генеральной совокупностиОписывает изменчивость в пределах одной выборкиВыводная статистика, которую можно оценитьОписательная статистика, которую можно рассчитатьИзмеряет, насколько вероятно, что среднее значение выборки будет отличаться от фактического среднего значения в популяции. выборка отличается от фактического среднего значенияСтандартная ошибка — это стандартное отклонение, деленное на квадратный корень размера выборкиСтандартное отклонение — это квадратный корень из дисперсии

Стандартная ошибка средней формулы

Формула для стандартной ошибки среднего выражается как:

SE = σ/√n

SE = стандартная ошибка выборки
σ = стандартное отклонение выборки
n = размер выборки

Обратите внимание, что σ — это греческая буква сигма, а √ — символ квадратного корня.

Формула стандартного отклонения выборки выражается следующим образом:

Формула стандартного отклонения выборки.

x̄ = среднее значение выборки, сначала найдите это значение
xᵢ = отдельные значения x
x = значение в наборе данных
n = количество точек данных
Σ — это сигма-обозначение для суммирования

Вот шаги, которые вы можете использовать для расчета стандартной ошибки среднего, используя выборку из пяти результатов теста SAT. Сначала рассчитайте стандартное отклонение, а затем подставьте это значение в формулу SEM.

1. Рассчитайте среднее

Сложите все образцы вместе и разделите общую сумму на количество образцов.

Пример: пять общих баллов SAT: 1000 + 1200 + 820 + 1300 + 680 = 5000.

Среднее (мк) = 5000 / 5 = 1000

2. Рассчитать отклонение от среднего

Рассчитайте отклонение каждого измерения от среднего, вычитая отдельные измерения из среднего.

Пример. Вычтите средний балл SAT, равный 1000, из каждого балла SAT.

хᵢ — мю

1000 — 1000 = 0

1200 — 1000 = 200

820 — 1000 = -180

1300 — 1000 = 300

680 — 1000 = -320

3. Возведите в квадрат каждое отклонение от среднего

Вычислите квадрат отклонения каждого измерения от среднего. Измерения, которые были отрицательными, после возведения в квадрат станут положительными.

Пример: Найдите квадратный корень отклонения каждой оценки от среднего.

(xᵢ — μ)²

0² = 0

200² = 40000

-180² = 32400

300² = 90000

-320² = 102400

4. Рассчитайте сумму квадратов отклонений

Определить сумму квадратов отклонений, сложив все числа из третьего шага.

Пример: 0 + 10 + 40000 + 32400 + 90000 + 102400 = 264810 = Σ

5. Разделите эту сумму на количество точек данных.

Возьмите сумму, которую вы подсчитали на четвертом шаге, и разделите ее на единицу меньше размера выборки. Используя приведенную выше формулу, это будет выглядеть как n-1.

Пример: 264810 / (5-1) = 66202,5

6. Вычислить квадратный корень, чтобы найти стандартное отклонение

Возьмите квадратный корень из числа, которое вы вычислили на пятом шаге. Это даст вам стандартное отклонение.

Пример: σ = √ 66202,5 = 257,298

7. Разделите стандартное отклонение на квадратный корень из размера выборки.

Используя стандартное отклонение, которое вы определили на шестом шаге, разделите это число на квадратный корень из размера выборки. Это позволит вам определить стандартную ошибку.

Пример: SE = σ/√n

SE = 257,298/√5

SE = 115,067

8. Рассчитайте стандартную ошибку среднего

Вычтите из среднего значения стандартную ошибку и запишите это число. Это стандартная ошибка ниже среднего. Затем добавьте стандартную ошибку к среднему значению и запишите число. Это стандартная ошибка выше среднего.

Пример:

SE ниже среднего: 1000 — 115,067 = 884,933

SE выше среднего: 1000 + 115,067 = 1115,067

Стандартная ошибка среднего может быть представлена следующим образом:

Средний балл SAT случайной выборки испытуемых составляет 1000 ± 115,067.

Пример СЭМ

Чтобы понять силу информации, которую вы можете получить из случайной выборки, используя стандартную ошибку среднего, рассмотрим следующий пример.

Вам дан вес при рождении 17 000 детей, рожденных в больницах Нью-Йорка. Средний вес при рождении составлял семь фунтов и три унции, а стандартное отклонение — один фунт три унции. Допустим, вы хотели узнать средний вес при рождении в этом районе, но получили веса только 30 случайных рождений по сравнению с общей численностью населения. Если бы эта выборка была взята только из всего населения, то вам лучше всего было бы предположить, что средний вес при рождении в выборке также будет равен семи фунтам и трем унциям.

Это предположение вряд ли будет точным, поскольку среднее значение выборки из 30 не будет таким точным, как среднее значение выборки из 17 000. Если бы вы продолжали брать случайные выборки из 30, вполне вероятно, что среднее значение каждой из них несколько изменилось бы.

Поскольку стандартное отклонение генеральной совокупности обычно неизвестно, вам необходимо оценить его, используя стандартное отклонение выборки. Чтобы сделать это с некоторой точностью, ваша выборка должна иметь нормальное распределение и состоять как минимум из 20 измерений. Хотя оценка может быть не совсем точной даже при большой выборке, ошибки в выборочной оценке стандартного отклонения генеральной совокупности будут уменьшены, если вы разделите его на квадратный корень из размера выборки.

Допустим, у вас есть шесть случайных выборок из 30 масс при рождении со стандартными отклонениями 1,3 фунта, 1,16 фунта, 1,14 фунта, 1,2 фунта, 1,25 фунта и 1,19 фунта, что на 0,098 фунта отличается от истинного значения стандартного отклонения населения. Эти шесть образцов приводят к оценкам стандартной ошибки, которые находятся в пределах 0,017 фунта от истинного значения. Ошибки стандартной ошибки средних оценок меньше, чем ошибки оценок стандартного отклонения, а значит, они более точные. Если бы размер выборки был больше 30, стандартная ошибка среднего была бы еще больше уменьшена.

Источник

Когда мы подгоняем регрессионную модель к набору данных, нас часто интересует, насколько хорошо регрессионная модель «подходит» к набору данных. Две метрики, обычно используемые для измерения согласия, включают R -квадрат (R2) и стандартную ошибку регрессии , часто обозначаемую как S.

В этом руководстве объясняется, как интерпретировать стандартную ошибку регрессии (S), а также почему она может предоставить более полезную информацию, чем R 2 .

Стандартная ошибка по сравнению с R-квадратом в регрессии

Предположим, у нас есть простой набор данных, который показывает, сколько часов 12 студентов занимались в день в течение месяца, предшествующего важному экзамену, а также их баллы за экзамен:

Если мы подгоним простую модель линейной регрессии к этому набору данных в Excel, мы получим следующий результат:

R-квадрат — это доля дисперсии переменной отклика, которая может быть объяснена предикторной переменной. При этом 65,76% дисперсии экзаменационных баллов можно объяснить количеством часов, потраченных на учебу.

Стандартная ошибка регрессии — это среднее расстояние, на которое наблюдаемые значения отклоняются от линии регрессии. В этом случае наблюдаемые значения отклоняются от линии регрессии в среднем на 4,89 единицы.

Если мы нанесем фактические точки данных вместе с линией регрессии, мы сможем увидеть это более четко:

Обратите внимание, что некоторые наблюдения попадают очень близко к линии регрессии, в то время как другие не так близки. Но в среднем наблюдаемые значения отклоняются от линии регрессии на 4,19 единицы .

Стандартная ошибка регрессии особенно полезна, поскольку ее можно использовать для оценки точности прогнозов. Примерно 95% наблюдений должны находиться в пределах +/- двух стандартных ошибок регрессии, что является быстрым приближением к 95% интервалу прогнозирования.

Если мы заинтересованы в прогнозировании с использованием модели регрессии, стандартная ошибка регрессии может быть более полезной метрикой, чем R-квадрат, потому что она дает нам представление о том, насколько точными будут наши прогнозы в единицах измерения.

Чтобы проиллюстрировать, почему стандартная ошибка регрессии может быть более полезной метрикой для оценки «соответствия» модели, рассмотрим другой пример набора данных, который показывает, сколько часов 12 студентов занимались в день в течение месяца, предшествующего важному экзамену, а также их экзаменационная оценка:

Обратите внимание, что это точно такой же набор данных, как и раньше, за исключением того, что все значения s сокращены вдвое.Таким образом, студенты из этого набора данных учились ровно в два раза дольше, чем студенты из предыдущего набора данных, и получили ровно половину экзаменационного балла.

Обратите внимание, что R-квадрат 65,76% точно такой же, как и в предыдущем примере.

Однако стандартная ошибка регрессии составляет 2,095 , что ровно вдвое меньше стандартной ошибки регрессии в предыдущем примере.

Если мы нанесем фактические точки данных вместе с линией регрессии, мы сможем увидеть это более четко:

Обратите внимание на то, что наблюдения располагаются гораздо плотнее вокруг линии регрессии. В среднем наблюдаемые значения отклоняются от линии регрессии на 2,095 единицы .

Таким образом, несмотря на то, что обе модели регрессии имеют R-квадрат 65,76% , мы знаем, что вторая модель будет давать более точные прогнозы, поскольку она имеет более низкую стандартную ошибку регрессии.

Преимущества использования стандартной ошибки

Стандартную ошибку регрессии (S) часто бывает полезнее знать, чем R-квадрат модели, потому что она дает нам фактические единицы измерения. Если мы заинтересованы в использовании регрессионной модели для получения прогнозов, S может очень легко сказать нам, достаточно ли точна модель для прогнозирования.

Например, предположим, что мы хотим создать 95-процентный интервал прогнозирования, в котором мы можем прогнозировать результаты экзаменов с точностью до 6 баллов от фактической оценки.

Наша первая модель имеет R-квадрат 65,76%, но это ничего не говорит нам о том, насколько точным будет наш интервал прогнозирования. К счастью, мы также знаем, что у первой модели показатель S равен 4,19. Это означает, что 95-процентный интервал прогнозирования будет иметь ширину примерно 2*4,19 = +/- 8,38 единиц, что слишком велико для нашего интервала прогнозирования.

Наша вторая модель также имеет R-квадрат 65,76%, но опять же это ничего не говорит нам о том, насколько точным будет наш интервал прогнозирования. Однако мы знаем, что вторая модель имеет S 2,095. Это означает, что 95-процентный интервал прогнозирования будет иметь ширину примерно 2*2,095= +/- 4,19 единиц, что меньше 6 и, следовательно, будет достаточно точным для использования для создания интервалов прогнозирования.

Дальнейшее чтение

Введение в простую линейную регрессию
Что такое хорошее значение R-квадрата?

Источник

Использование математических функций в Microsoft Excel может облегчить быстрое и точное выполнение сложных математических вычислений. Изучение того, как рассчитать стандартную ошибку в Excel, позволит вам получить точные результаты стандартной ошибки для набора данных. Автоматическое вычисление может снизить риск возможных ошибок и одновременно сэкономить ваше время. В этой статье мы обсудим, что такое расчет стандартной ошибки, почему он важен и как его выполнять в Excel, включая советы, как сделать это более эффективно.

Что такое расчет стандартной ошибки?

Расчет стандартной ошибки показывает, насколько далеко среднее значение выборочного набора данных может быть от общего среднего значения данных, которые вы оцениваете. Например, компания, изучающая рейтинги удовлетворенности клиентов в рамках популяции, может попытаться сделать это, собрав рейтинги от части своих клиентов. Расчет стандартной ошибки позволяет компании определить, насколько информация, которую они собирают с помощью этой выборки, вероятно, близка к общему мнению их клиентов, исходя из размера выборки.

Почему важен расчет стандартной ошибки?

Стандартная ошибка может быть ценным расчетом при использовании выборочных наборов данных, поскольку она позволяет оценить их надежность. По мере увеличения количества выборок, включенных в расчет стандартного отклонения, размер стандартной ошибки уменьшается. Это указывает на то, что вы можете в большей степени доверять точности выборки по отношению к генеральной совокупности, так как вы включили в выборку больший объем.

Как рассчитать стандартную ошибку в Excel

Выполните следующие шаги, чтобы создать формулу в Excel, которая вычисляет стандартную ошибку для набора данных:

1. Введите свои данные

Для того чтобы использовать Microsoft Excel для выполнения расчетов, вы должны сначала предоставить все необходимые данные. Введите каждую точку данных в отдельную ячейку. Хотя вам не обязательно группировать все данные вместе, это может облегчить создание формул на более поздних этапах процесса, если вы сделаете это. Расположение данных в виде вертикальной, горизонтальной или прямоугольной линии позволяет включить все данные в формулы, используя простые обозначения, вместо того, чтобы выбирать каждую ячейку по отдельности.

В этом примере компания использует Microsoft Excel для отслеживания ежедневных продаж за пять будних дней, чтобы найти стандартную ошибку в течение недели.

	A	B
1
2	57
3	45
4	68
5	57
6	46

2. Создайте метки

Использование меток в документе Microsoft Excel может облегчить идентификацию информации на листе. Это не только облегчает понимание листа при просмотре результатов вычислений, но и позволяет правильно вводить формулы и избегать ошибок. Маркировка различных ячеек, в которые вы вводите ключевые фрагменты информации, служит ориентиром при выборе ячеек для включения в формулы.

Для расчета стандартной ошибки, помимо обозначения данных, вы можете включить обозначения для стандартного отклонения, количества оцениваемых элементов и стандартной ошибки.

	A	B
1	Ежедневные продажи	Стандартное отклонение
2	57
3	45	Ежедневный подсчет
4	68
5	57	Стандартная ошибка
6	46

3. Рассчитайте стандартное отклонение

Стандартное отклонение является одной из двух важных переменных при расчете стандартной ошибки набора данных. Microsoft Excel упрощает вычисление стандартного отклонения, автоматически обрабатывая все математические уравнения с помощью функции STDEV() функция. Щелкните по ячейке, которую вы хотите использовать для хранения значения стандартного отклонения, и введите =STDEV([Ячейка 1]:[Ячейка 2]) где ячейка 1 — первая ячейка данных в введенном вами наборе, а ячейка 2 — последняя ячейка данных. Excel автоматически включает данные для всех ячеек между двумя введенными вами ячейками при расчете стандартного отклонения.

В примере пользователь вводит =STDEV(A2:A6) в ячейке под меткой стандартного отклонения. Excel не отображает эту формулу на листе. Вместо этого вычисляется значение стандартного отклонения и выводится результат. На этом и последующих этапах курсивом выделена формула, которую вводит пользователь, а текст без курсива показывает, как ячейки отображаются в электронной таблице.

	A	B
1	Ежедневные продажи	Стандартное отклонение
2	57	=STDEV(A2:A6)
3	45	Ежедневный подсчет
4	68
5	57	Стандартная ошибка
6	46

Похожие: Что такое стандартное отклонение? Как это работает и другие часто задаваемые вопросы

4. Подсчитайте ваши предметы

Второй важной переменной при расчете стандартной ошибки является общее количество элементов, включенных в расчет стандартного отклонения. Как и в случае со стандартным отклонением, Excel включает функцию, которая позволяет автоматически генерировать значение для этой переменной. Щелкните по ячейке, которую вы хотите использовать для хранения значения подсчета, и введите =COUNT([Ячейка 1]:[Ячейка 2]) где ячейка 1 — первая ячейка данных в наборе, который вы ввели, а ячейка 2 — последняя ячейка данных.

В примере пользователь вводит =COUNT(A2:A6) в ячейке под табличкой ежедневных подсчетов. Как и в случае с расчетом стандартного отклонения, хотя формула появляется в строке в верхней части экрана, как только пользователь нажимает клавишу Enter, на листе вместо формулы отображается значение подсчета.

	A	B
1	Ежедневные продажи	Стандартное отклонение
2	57	9.449867
3	45	Ежедневный подсчет
4	68	=COUNT(A2:A6)
5	57	Стандартная ошибка
6	46

Похожие: Основные формулы Excel и как их использовать

5. Рассчитать стандартную ошибку

Теперь, когда вы рассчитали для обеих переменных, вы можете использовать последнюю функцию Microsoft Excel, чтобы легко рассчитать стандартную ошибку для вашего набора данных. Щелкните на ячейке, в которой вы хотите сохранить значение стандартной ошибки, и введите =[Ячейка результата стандартного отклонения]SQRT([Ячейка результата подсчета]) как формула. Деление стандартного отклонения на квадратный корень из количества элементов в расчете отклонения дает стандартную ошибку, которую Excel вычисляет для вас автоматически.

В примере пользователь вводит =B2SQRT(B4) в ячейке под меткой стандартной ошибки. Если пользователь обнаружит ошибку в исходном наборе данных или захочет обновить набор данных с новой неделей чисел, он может изменить значения в ячейках набора данных, а все остальные значения обновятся автоматически.

	A	B
1	Ежедневные продажи	Стандартное отклонение
2	57	9.449867
3	45	Ежедневный подсчет
4	68	5
5	57	Стандартная ошибка
6	46	=B2SQRT(B4)

Советы по расчету стандартной ошибки в Excel

Если вы используете Microsoft Excel для расчета стандартной ошибки, запомните эти советы:

Сократите свои вычисления. Хотя отдельные вычисления для стандартного отклонения и подсчета могут сделать ваш лист более понятным, они не обязательны, и вы можете выбрать только одну формулу для всех вычислений. Для этого замените каждую отдельную ячейку в формуле стандартной ошибки на формулу, которую вы ввели в эти ячейки, например =STDEV(A2:A6)SQRT(COUNT(A2:A6)).
Планирование документа. Перед созданием макета документа электронной таблицы уделите время планированию своих потребностей, чтобы создать более эффективный дизайн. Понимание типа данных, которые вы собираетесь включить, включая количество записей и то, является ли ваш набор данных статичным или тем, который вы планируете пополнять в будущем, может помочь вам выбрать правильное расположение меток и расчетов.
Расширение диапазонов. При создании формул для стандартного отклонения и подсчета вы можете расширить диапазоны за пределы конечной точки данных, если собираетесь в будущем пополнять статистику. Функции, используемые для расчета стандартного отклонения и подсчета, игнорируют пустые ячейки, что означает, что вы можете расширить диапазон за пределы конечной точки и получить правильные результаты сейчас, а в будущем добавить дополнительные точки и попросить Excel рассчитать их без необходимости обновления формул.

Обратите внимание, что ни одна из компаний, упомянутых в этой статье, не связана с Indeed.

Источник

Расчет дисперсии и стандартной ошибки средней арифметической

где x_i – значения переменной,
n – количество значений.

Используя более привычные обозначения, формулу записывают как:

где σ² – это дисперсия, случайной величины, причем генеральная.

Формула стандартной ошибки средней при использовании генеральной дисперсии

Формула стандартной ошибки средней при использовании выборочной дисперсии

Назначение и свойство стандартной ошибки средней арифметической

Поделиться в социальных сетях:

Источник

Стандартная ошибка появляется при прогнозировании каких-либо данных или арифметических вычислениях, поэтому важно научиться находить этот параметр. В этой публикации разбираем, как найти и исправить стандартную ошибку путем использования инструментов Excel.

Расчет средней арифметической ошибки

В Microsoft Excel цельность и однородность выборки определяется при помощи стандартной ошибки. Стандартная ошибка — это квадратный корень из дисперсии. В приложении предусмотрено два варианта поиска стандартной ошибки: при помощи пакетного анализа и расширенных функций программы.
Чтобы найти значение средней арифметической, необходимо выполнить деление суммарной величины выборки на ее количество в электронной книге.

Расчет стандартной ошибки при помощи встроенных функций

Для того, чтобы правильно вычислять, необходимо изучить пошаговую инструкцию. В этом способе подбор результатов будет осуществляться с помощью комбинированных манипуляций.

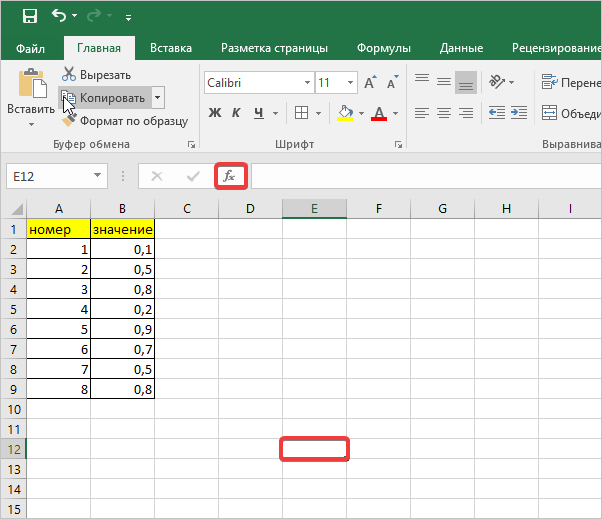
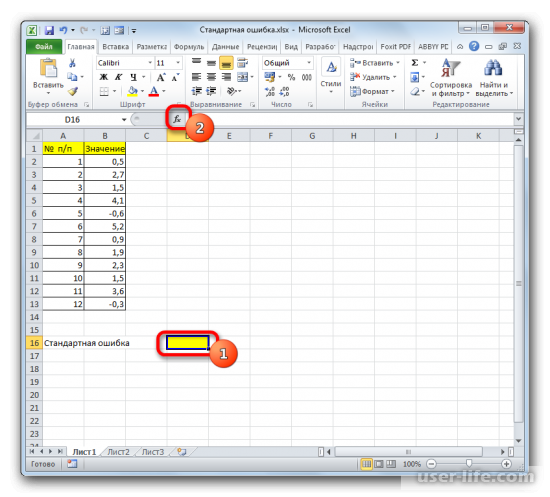
Для расчетов будем использовать таблицу с выборкой чисел. Кликаем на любой пустой ячейке на листе, где будет отображаться результат. Затем нажимаем кнопку «Вставить функцию.

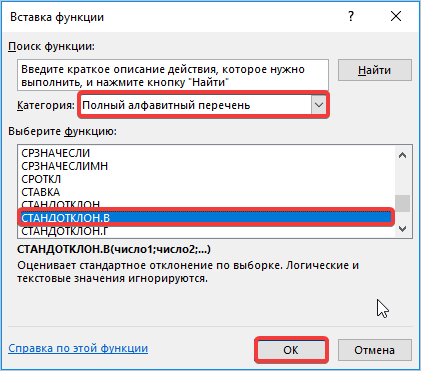
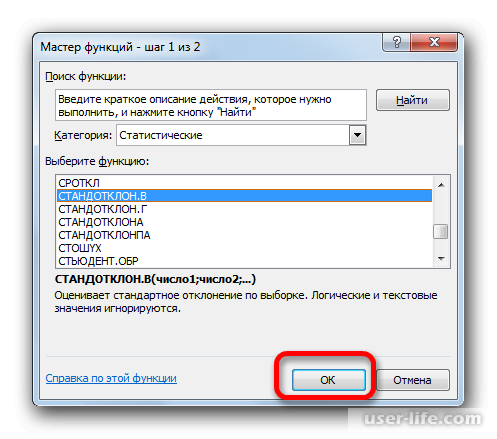
Далее перед вами открывается диалоговое окно, в котором необходимо использовать «СТАНДОТКЛ.В», для этого в поле «Категория» необходимо выбрать «Полный алфавитный перечень». Затем нажмите кнопку «ОК».

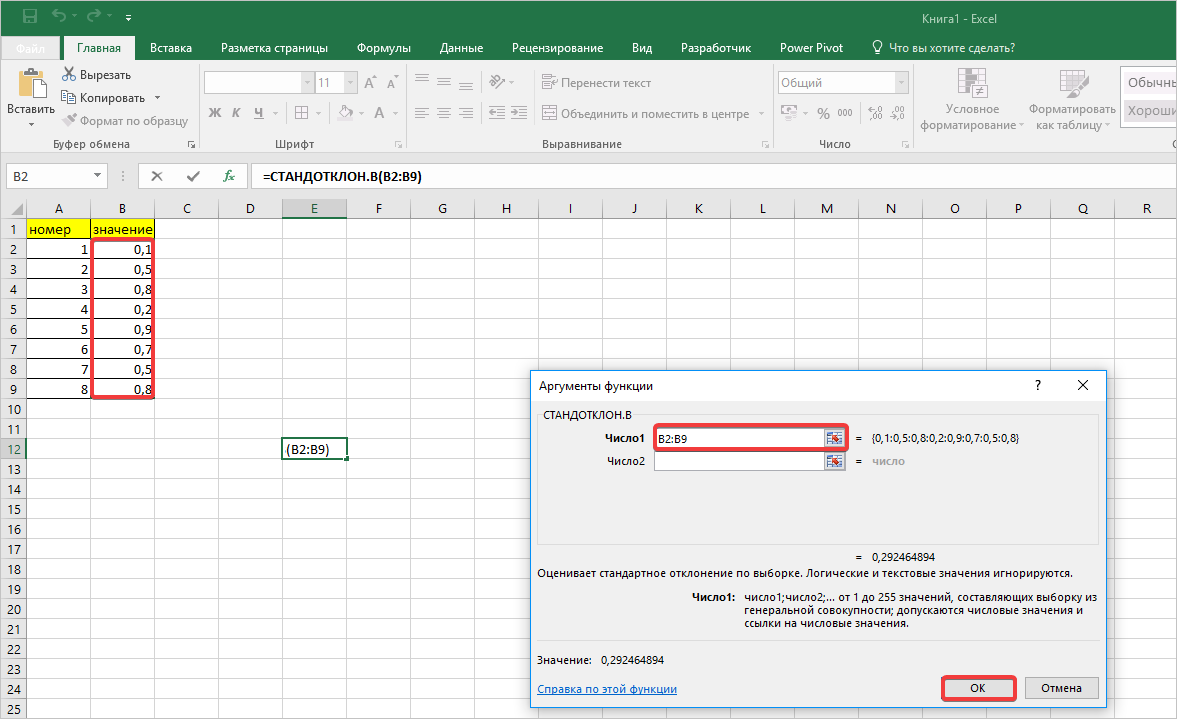
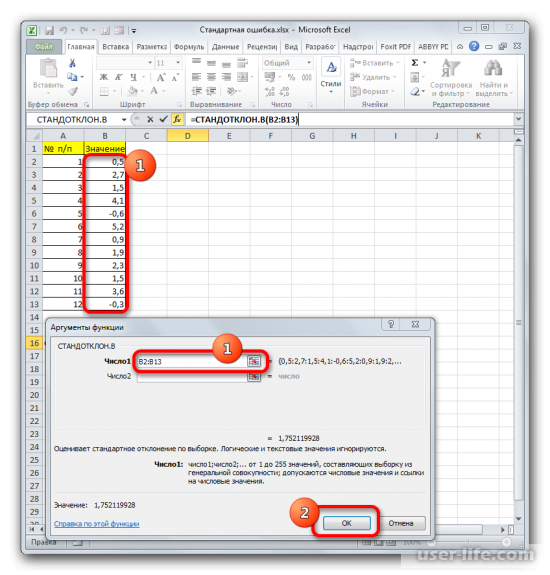
В окне «Аргументы функции» кликаем в первом поле «Число 1», затем выполняем выделение мышью диапазона ячеек со значениями таблицы и нажимаем кнопку «ОК».

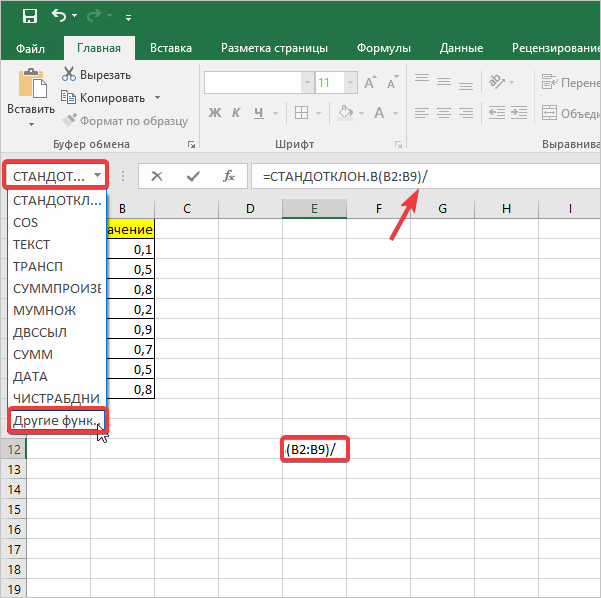
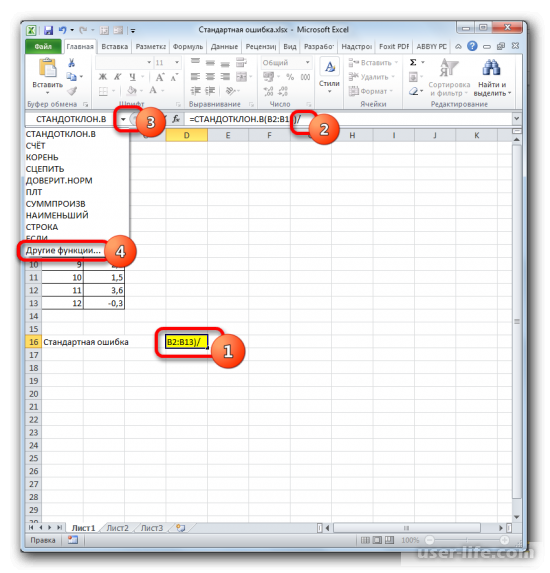
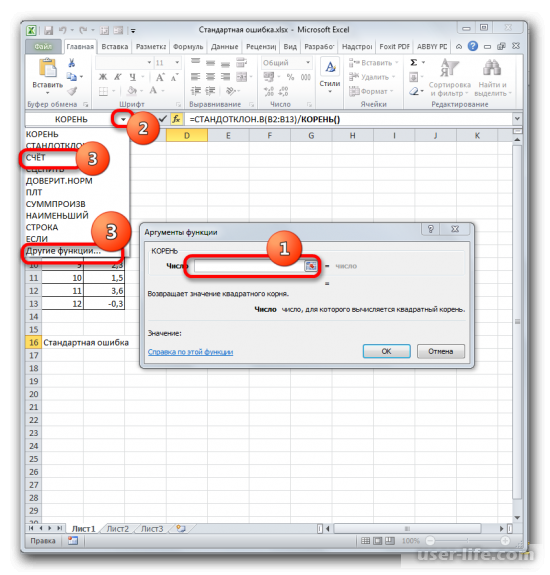
Далее активируем ячейку с нашими значениями, переходим в строку формулы и ставим после значений наклонную линию. Переходим в поле наименования, кликаем на указывающий вниз флажок, где из списка выбираем «Другие функции».

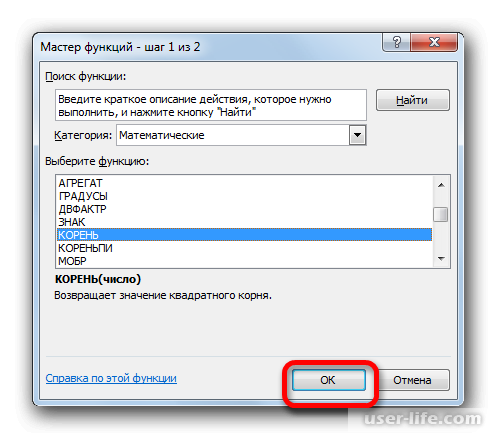
Снова активируется окно с перечнем функций, в котором необходимо выбрать категорию «Математические», затем функцию «Корень». Далее нажмите кнопку «ОК».

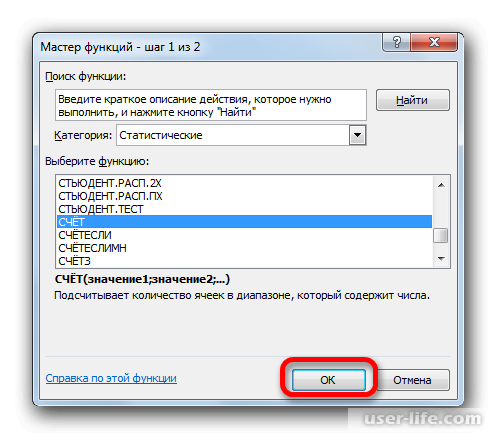
Далее открывается окно, в котором необходимо заполнить поле с числом. Для этого переходим в поле «Имя», где спускаемся к пункту «Счет». Если его нет, ищите в дополнительных функциях.

После выполнения этих шагов, стандартная ошибка высчитывается автоматически, пользователю остается только сверить их и проверить значение на некорректное отображение.

Важно!

Для малых и стандартных выборок необходимо использовать разные формулы. В первом случае (если находится до 30 значений), ее необходимо видоизменить.

Решение задачи с помощью опции «Описательная статистика»

Благодаря опции «Описательная статистика» удается выполнить вычисление по различным критериям. По этим правилам удается найти среднюю арифметическую ошибку. Для использования данного метода предварительно нужно запустить «Пакет анализа».

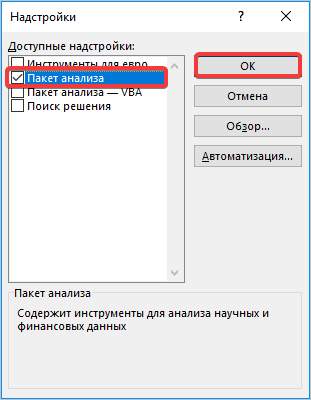
Переходим во вкладку «Файл», где перемещаемся в пункт «Параметры». Далее нажимаем на запись «Надстройки».

Открывается окошко, в нем в графе «Управление» должно быть прописано «Надстройки Excel», затем рядом нажимаем кнопку «Параметры».

В появившемся окне находим «Пакет анализа» и нажимаем кнопку «ОК».

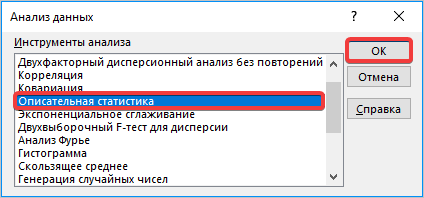
Далее выбираем любую свободную ячейку, переходим во вкладку «Данные» и нажимаем «Анализ данных» в блоке «Анализ».

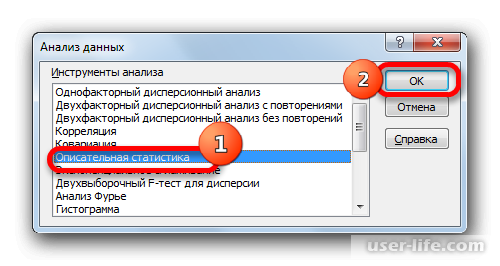
Происходит запуск вспомогательного окошка, в котором необходимо выбрать из всех инструментов «Описательную статистику» и нажать кнопку «ОК».

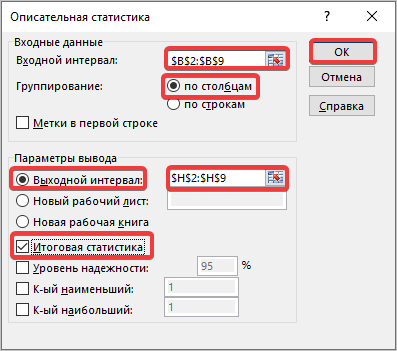
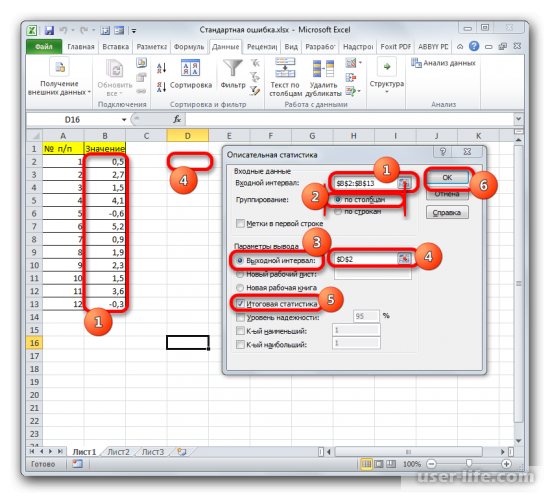
Открывается новый мастер значений. Здесь нужно вводить данные предельно внимательно. В поле «Входной интервал» вносим адрес диапазона ячеек с выборкой. Затем указываем параметр «Группирование» «По столбцам». Затем выбираем место для «выходного интервала», его должно быть столько же, сколько и «входного». Ставим галочку напротив «Итоговая статистика» и нажимаем кнопку «ОК».

В результате вычислений вы получаете небольшую таблицу, в которой указаны все данные с определенной стандартной ошибкой.

Источник

Стандартная ошибка в Excel

Расчет с помощью комбинаций функций

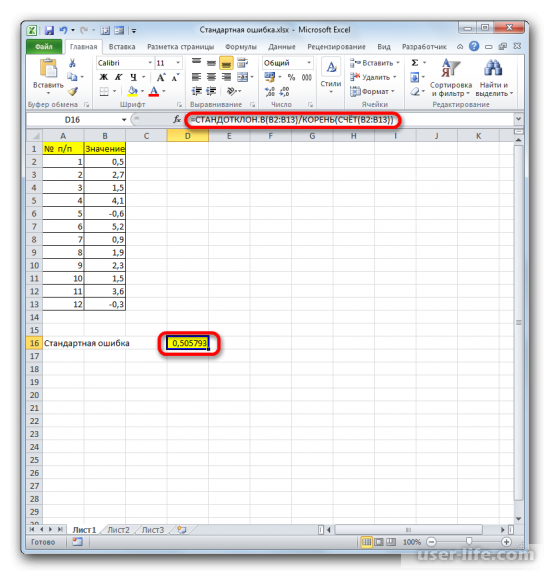
На примере рассмотрим составленный алгоритм действий по расчету ошибки средней арифметической с использованием комбинаций функций. Для того чтобы выполнить задачу, нужно использовать операторы СТАНДОТКЛОН.В, КОРЕНЬ и СЧЁТ. Выборка будет использоваться из 12 чисел, которые представлены в таблице.

Выделите ячейку, в которой отобразится итоговое значение стандартной ошибки. Кликаете на иконку «Вставить функцию».

Появится Мастер функций, в котором нужно произвести перемещение в блок «Статистические». Появится список наименований, выбираете «СТАНДОТКЛОН.В».

Запустится окно аргументов выбранного оператора, предназначенного для оценивания стандартного отклонения при выборке. У него такой синтаксис – =СТАНДОТКЛОН.В(число1;число2;…). Устанавливаете курсор в полу «Число1». Далее, зажав левую кнопку мыши, выделяете курсором весь диапазон выборки, чтобы координаты этого массива отобразились там же в поле окна. Кликаете на ОК.

В ячейке появится проделанный результат, но это еще не то, что мы хотим получить в итоге. Теперь нужно стандартное отклонение разделить на квадратный корень от числа элементов выборки. Выделяете ячейку с нужной функцией и устанавливаете курсор мышки в строку формул. Дописываете выражение, которое там уже существует, знаком деления (/). Далее нажимаете на пиктограмму перевернутого вниз углом треугольника (находится слева от строки формул). Должен открыться список недавно использованных функций. Находите оператора «КОРЕНЬ» и нажимаете на него. Если его нет в списке, то кликайте на «Другие функции…».

Должен снова запуститься Мастер функций, в котором нужно перейти в категорию «Математические». Выделяете там «КОРЕНЬ» и кликаете ОК.

Далее должно открыться окно аргументов функции КОРЕНЬ. Его синтаксис простой – =КОРЕНЬ(число). Устанавливаете курсор в поле «Число» и нажимаете на уже знакомый треугольник, чтобы показался список последних использованных функций. Находите «СЧЕТ» и нажимаете на него. Если в списке его нет, тогда нажимаете на «Другие функции…».

Появится раскрывшееся окно Мастера функций, в котором нужно переместиться в группу «Статистические». В ней выделяете «СЧЕТ» и кликаете ОК.

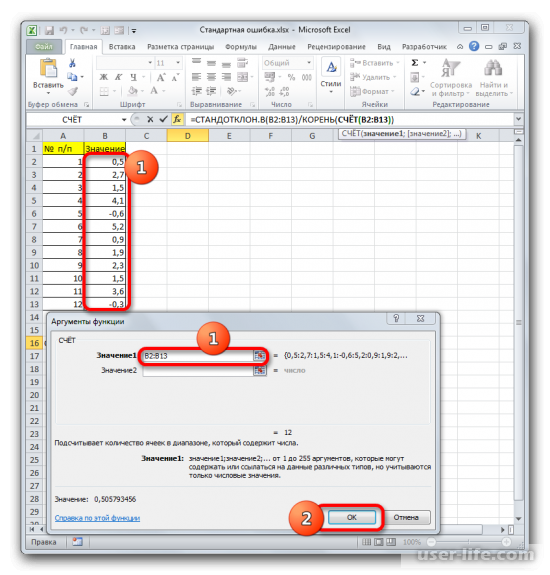
Должно запуститься окно аргументов функции СЧЕТ. Синтаксис функции будет таким – =СЧЁТ(значение1;значение2;…). Ставите курсор в строку «Значение1» и зажимаете левую кнопку мыши, чтобы выделить весь диапазон выборки. Когда координаты отобразятся, жмите ОК.

Когда будет выполнено последнее действие, то не только произведется расчет количества ячеек, которые заполнены числами, но и вычисляется ошибка средней арифметической. Величина будет выведена в ячейку с размещенной сложной формулой, вид которой таков – =СТАНДОТКЛОН.В(B2:B13)/КОРЕНЬ(СЧЁТ(B2:B13)).

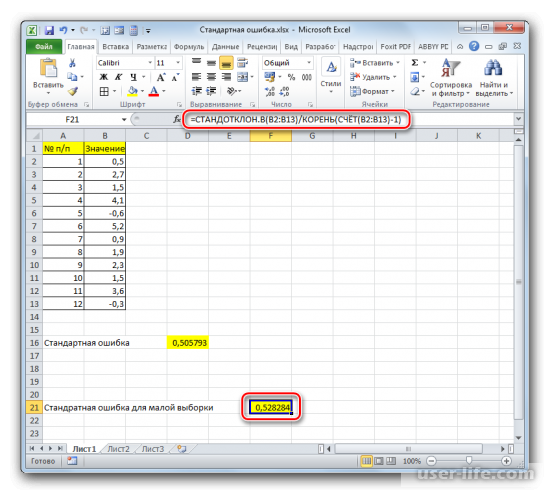
Если выборка до 30 единиц, тогда лучше применять немного другую формулу – =СТАНДОТКЛОН.В(B2:B13)/КОРЕНЬ(СЧЁТ(B2:B13)-1).

Применение инструмента «Описательная статистика»

Когда будет открыт документ с выборкой, нужно перейти во вкладку «Файл».

В левом вертикальном меню заходите в раздел «Параметры».

Должно запуститься окно параметров Excel, в левой части которого нужно перейти в «Надстройки».

В самом низу окна находите «Управление» в выставляете в нем параметр «Надстройки Excel». Кликаете на «Перейти…» справа от него.

В окне надстроек появится список скриптов, которые доступны и нужно отметить галочкой «Пакет анализа», а затем нажать ОК.

Теперь на странице должна появиться новая группа инструментов «Анализ». Для перехода к ней кликаете на вкладку «Данные».

Кликаете на «Анализ данных» в блоке инструментов «Анализ» в самом конце.

Запустится окно выбора инструмента анализа, в котором необходимо выделить «Описательная статистика» и нажать справа на ОК.

Далее запустится окно настроек инструмента комплексного статистического анализа «Описательная статистика». Здесь нужно установить все так, в зависимости от того, что именно вы хотите получить в итоге.

После всех совершенных манипуляций, инструмент «Описательная статистика» должен отобразить результаты обработки выборки на текущем листе. Разноплановых статистических показателей будет немало, но среди них находится и тот, который нам нужен – «Стандартная ошибка».

Microsoft Excel

трюки • приёмы • решения

Какие существуют ошибки в Excel и как их исправлять

Когда вы вводите или редактируете формулу, а также когда меняется одно из входных значений функции, Excel может показать одну из ошибок вместо значения формулы. В программе предусмотрено семь типов ошибок. Давайте рассмотрим их описание и способы устранения.

#ДЕЛ/О! — данная ошибка практически всегда означает, что формула в ячейке пытается разделить какое-то значение на ноль. Чаще всего это происходит из-за того, что в другой ячейке, ссылающейся на данную, находится нулевое значение или значение отсутствует. Вам необходимо проверить все связанные ячейки на предмет наличия таких значений. Также данная ошибка может возникать, когда вы вводите неправильные значения в некоторые функции, например в ОСТАТ() , когда второй аргумент равен 0. Также ошибка деления на ноль может возникать, если вы оставляете пустые ячейки для ввода данных, а какая-либо формула требует некоторые данные. При этом будет выведена ошибка #ДЕЛ/0!, что может смутить конечного пользователя. Для этих случаев вы можете использовать функцию ЕСЛИ() для проверки, например =ЕСЛИ(А1=0;0;В1/А1) . В этом примере функция вернет 0 вместо ошибки, если в ячейке А1 находится нулевое или пустое значение.
#Н/Д — данная ошибка расшифровывается как недоступно, и это означает, что значение недоступно функции или формуле. Вы можете увидеть такую ошибку, если введете неподходящее значение в функцию. Для исправления проверьте прежде всего входные ячейки на предмет ошибок, особенно если в них тоже появляется данная ошибка.
#ИМЯ? — данная ошибка возникает, когда вы неправильно указываете имя в формуле или ошибочно задаете имя самой формулы. Для исправления проверьте еще раз все имена и названия в формуле.
#ПУСТО! — данная ошибка связана с диапазонами в формуле. Чаще всего она возникает, когда в формуле указывается два непересекающихся диапазона, например =СУММ(С4:С6;А1:С1) .
#ЧИСЛО! — ошибка возникает, когда в формуле присутствуют некорректные числовые значения, выходящие за границы допустимого диапазона.
#ССЫЛКА! — ошибка возникает, когда были удалены ячейки, на которые ссылается данная формула.
#ЗНАЧ! — в данном случае речь идет об использовании неправильного типа аргумента для функции.

Если при вводе формулы вы случайно неправильно расставили скобки, Excel выведет на экран предупреждающее сообщение — см. рис. 1. В этом сообщении вы увидите предположение Excel о том, как их необходимо расставить. В случае если вы подтверждаете такую расстановку, нажмите Да. Но зачастую требуется собственное вмешательство. Для этот нажмите Нет и исправьте скобки самостоятельно.

Обработка ошибок с помощью функции ЕОШИБКА()

Перехватить любые ошибки и обработать их можно с помощью функции ЕОШИБКА() . Данная функция возвращает истину или ложь в зависимости от того, появляется ли ошибка при вычислении ее аргумента. Общая формула для перехвата выглядит так: =ЕСЛИ(ЕОШИБКА(выражение);ошибка; выражение) .

Рис. 1. Предупреждающее сообщение о неправильно расставленных скобках

Функция если вернет ошибку (например, сообщение), если при расчете появляется ошибка. Например, рассмотрим следующую формулу: =ЕСЛИ(ЕОШИБКА(А1/А2);””; А1/А2) . При возникновении ошибки (деление на 0) формула возвращает пустую строку. Если же ошибки не возникает, возвращается само выражение А1/А2 .

Существует другая, более удобная функция ЕСЛИОШИБКА() , которая совмещает две предыдущие функции ЕСЛИ() и ЕОШИБКА() : ЕСЛИОШИБКА(значение;значение при ошибке) , где: значение — выражение для расчета, значение при ошибке — возвращаемый результат в случае ошибки. Для нашего примера это будет выглядеть так: =ЕСЛИОШИБКА(А1/А2;””) .

How to dou

Когда вы создаете граф в Excel и ваши данные являются средствами, рекомендуется включить стандартную ошибку каждого значения на вашем графике. Это дает зрителю представление о распространении баллов вокруг каждого среднего.

Вот пример ситуации, когда это возникает. Данные являются (вымышленными) результатами тестов для четырех групп людей. Каждый заголовок столбца указывает количество времени подготовки для восьми человек в группе. Вы можете использовать графические возможности Excel для рисования графика. Поскольку независимая переменная является количественной, граф линии является подходящим.

Четыре группы, их средства, стандартные отклонения и стандартные ошибки. На графике показаны групповые средства.

Для каждой группы вы можете использовать AVERAGE для вычисления среднего и STDEV. S для вычисления стандартного отклонения. Вы можете рассчитать стандартную ошибку каждого среднего. Выберите ячейку B12, поэтому в поле формулы показано, что вы вычислили стандартную ошибку для столбца B по этой формуле:

= B11 / SQRT (COUNT (B2: B9))

Фокус в том, чтобы получить каждую стандартную ошибку в графике. В Excel 2016 это легко сделать, и оно отличается от предыдущих версий Excel. Начните с выбора графика. Это приведет к появлению вкладок Design and Format. Выберите

Дизайн | Добавить элемент диаграммы | Ошибка баров | Дополнительные параметры ошибок.

Путь к вставке баров ошибок.

В меню «Бары ошибок» вы должны быть осторожны. Один из вариантов – стандартная ошибка. Избегай это. Если вы считаете, что этот выбор указывает Excel на стандартную ошибку каждого значения на графике, будьте уверены, что Excel не имеет абсолютно никакого представления о том, о чем вы говорите. Для этого выбора Excel вычисляет стандартную ошибку набора из четырех средств – не стандартную ошибку в каждой группе.

Дополнительные параметры панели ошибок являются подходящим выбором. Откроется панель «Формат ошибок».

Панель «Ошибки формата».

В области «Направление» панели выберите переключатель рядом с «Оба», а в области «Стиль конца» выберите переключатель рядом с «Кап».

Один выбор в области «Сумма ошибки» – это стандартная ошибка. Избегайте этого. Это не означает, что Excel помещает стандартную ошибку каждого среднего на график.

Прокрутите вниз до области «Сумма ошибки» и выберите переключатель рядом с «Пользовательский». Это активирует кнопку «Укажите значение». Нажмите эту кнопку, чтобы открыть диалоговое окно «Пользовательские ошибки». С помощью курсора в поле «Положительное значение ошибки» выберите диапазон ячеек, который содержит стандартные ошибки ($ B $ 12: $ E $ 12). Вставьте вкладку «Отрицательная ошибка» и сделайте то же самое.

Диалоговое окно «Нестандартные ошибки».

Это поле Negative Error Value может дать вам небольшую проблему. Перед тем, как вводить диапазон ячеек, убедитесь, что он очищен от значений по умолчанию.

Нажмите «ОК» в диалоговом окне «Нестандартные ошибки» и закройте диалоговое окно «Формат ошибок», и график будет выглядеть следующим образом.

График группы означает, включая стандартную ошибку каждого среднего.

Стандартная ошибка средней арифметической

Расчет дисперсии и стандартной ошибки средней арифметической

где x_i – значения переменной,
n – количество значений.

Используя более привычные обозначения, формулу записывают как:

где σ 2 – это дисперсия, случайной величины, причем генеральная.

Формула стандартной ошибки средней при использовании генеральной дисперсии

Формула стандартной ошибки средней при использовании выборочной дисперсии

Назначение и свойство стандартной ошибки средней арифметической

Источник

В процессе разработки программного обеспечения, при написании кода, есть риск допустить ошибку. Это нормально и естественно, ведь программисты тоже люди. Но когда ошибка становится «стандартной», это уже может привести к серьезным проблемам.

Стандартная ошибка — это ошибка, которую разработчики часто допускают, из-за чего она получила свое название. Эти ошибки могут быть связаны с использованием неоптимальных алгоритмов, неуместным использованием операторов или библиотек, а также с проблемами в проектировании или тестировании.

Исправление стандартных ошибок может потребовать много времени и усилий. Их избежать, однако, гораздо проще. Прежде всего, необходимо следовать инструкциям и изучать документацию, связанную с использованием определенных функций и методов. Также полезно применять проверенные временем практики и стандарты разработки кода.

Мы рассмотрим несколько наиболее распространенных стандартных ошибок при программировании и важность их правильного решения. Наши советы помогут избежать этих ошибок и повысить качество кода при создании программного обеспечения.

Содержание

Что такое стандартная ошибка и почему она важна
Как избежать и исправить стандартную ошибку
Что такое стандартная ошибка?
Как избежать стандартной ошибки?
Как исправить стандартную ошибку?
Важность предотвращения стандартной ошибки
Вопрос-ответ
Что такое стандартная ошибка и почему она возникает?
Как избежать стандартной ошибки при проведении исследования?
Как исправить стандартную ошибку, если она уже возникла?
Что значит, если стандартная ошибка очень большая?
Важно ли учитывать стандартную ошибку при обработке результатов исследования?

Что такое стандартная ошибка и почему она важна

Стандартная ошибка — это показатель разброса данных вокруг среднего значения. Этот показатель позволяет измерять точность и достоверность статистических данных и исследований. Чем меньше стандартная ошибка, тем более точными и надежными являются полученные результаты.

Обычно стандартная ошибка вычисляется на основе выборочного среднего и дисперсии выборки. Если в выборке много данных, стандартная ошибка будет меньше, чем при небольшой выборке. Также стандартная ошибка может быть снижена путем использования более точных методов измерения и анализа данных.

Как избежать и исправить стандартную ошибку

Увеличивать объем выборки, чтобы снизить вероятность ошибки выборки.
Проводить более точные измерения, чтобы снизить ошибку измерения.
Использовать более точные методы анализа данных.
Проверять и повторять эксперименты, чтобы исключить случайность и снизить вероятность ошибки.
Проводить статистические тесты на значимость полученных результатов.

Важно понимать, что стандартная ошибка может влиять на результаты и их интерпретацию. Поэтому необходимо изучать и контролировать этот показатель при проведении исследований и анализе данных.

Что такое стандартная ошибка?

Стандартная ошибка – это мера разброса статистических данных относительно среднего значения выборки. Она показывает насколько точно среднее значение выборки отражает основную генеральную совокупность. Чем меньше стандартная ошибка, тем более точно выборочное среднее отображает среднее значение генеральной совокупности.

Стандартная ошибка является важной характеристикой статистических данных и используется для проверки гипотез и принятия решений на основе статистических результатов. Она также помогает определить доверительный интервал с заданным уровнем доверия. Рассчитывается она путем деления стандартного отклонения на квадратный корень из размера выборки.

Избежать стандартной ошибки невозможно, так как она обусловлена генеральной совокупностью, но можно уменьшить ее значение путем увеличения размера выборки или улучшения сбора данных. Кроме того, важно выбирать правильный метод расчета стандартной ошибки в зависимости от уровня доверия и характеристик выборки.

Как избежать стандартной ошибки?

Стандартная ошибка может возникнуть по множеству причин, но существуют способы, как ее избежать:

Будьте внимательными. Во время работы над проектом старайтесь не отвлекаться и следите за каждой деталью.
Используйте проверенные инструменты. Экспериментирование может привести к ошибкам, поэтому выбор проверенных инструментов является более безопасным решением.
Тестируйте свой код. После написания кода проводите тестирование, чтобы убедиться, что все работает правильно.
Следуйте стандартам. Соблюдайте стандарты кодирования для того, чтобы избежать ошибок, связанных с несоблюдением стандартов.

Следуя этим советам, вы сможете избежать стандартной ошибки и создать качественный продукт.

Как исправить стандартную ошибку?

Если вы столкнулись с стандартной ошибкой, не отчаивайтесь – возможно, наиболее простое решение находится в вашем распоряжении. Одним из действий может быть перезагрузка компьютера. Это не только поможет исправить ошибку, но и сбросит некорректно работающие программы и память. Кроме того, проверьте, корректно ли установлены все необходимые драйверы и обновления, что может помочь решить проблему.

Если перезагрузка и проверка драйверов не помогли, то можно попробовать воспользоваться отладочной консолью. В большинстве ОС для этого есть специальный инструмент, который позволяет проверять систему на наличие проблем, а также исправлять их. Отладочная консоль также может помочь в случае, когда виноватой проблемы стала плохая установка приложений или же системных настроек.

Если же приведенные меры не помогли, попробуйте обратиться к профессионалам. Специалисты могут определить причину ошибки и понять, что именно требуется для ее решения. Но помните, что решение проблемы может потребовать замены оборудования, и в таком случае нужно будет обратиться в сервисный центр, чтобы компьютер был отремонтирован.

Перезагрузите компьютер
Проверьте установленные драйверы и обновления
Используйте отладочную консоль
Обратитесь за помощью к профессионалам

Важность предотвращения стандартной ошибки

Стандартная ошибка является результатом неправильного выполнения определенных задач. Ее присутствие может привести к недостоверным результатам, неверным выводам и неэффективному решению проблемы.
Предотвращение стандартной ошибки играет ключевую роль в достижении точности и достоверности данных.

Кроме того, стандартная ошибка может повлечь за собой финансовые и временные издержки, так как проведение дополнительных исследований и исправление ошибок может занять много времени и стоит дополнительных денежных средств.
Предотвращение стандартной ошибки является эффективным способом сокращения времени и стоимости проведения исследований и улучшения качества результатов.

В случае отсутствия предотвращения стандартной ошибки могут появиться трудности при повторении исследований и восстановлении данных. Это может привести к недоверию к результатам и неспособности убедить в правильности выводов.
Предотвращение стандартной ошибки не только обеспечит точность и достоверность данных, но и гарантирует их прозрачность и возможность повторения.

Вопрос-ответ

Что такое стандартная ошибка и почему она возникает?

Стандартная ошибка — это показатель распределения значений, полученных из выборки. Она демонстрирует, какое содержательное значение на основании результатов выборки можно приписать исследуемой совокупности. Ошибка возникает из-за того, что выборка не может полностью представлять всю совокупность и включает в себя ряд случайных элементов.

Как избежать стандартной ошибки при проведении исследования?

Чтобы избежать стандартной ошибки, нужно тщательно подходить к выборке и обрабатыванию данных. Необходимо увеличить объём выборки и попытаться сделать её максимально репрезентативной. Также нужно использовать проверенные методы анализа данных и тщательно проверять результаты.

Как исправить стандартную ошибку, если она уже возникла?

Если стандартная ошибка уже возникла, то исправить её можно, во-первых, увеличив объём выборки. Это может снизить показатель ошибки. Во-вторых, можно провести дополнительное исследование и проверить анализ результатов. Также можно использовать другие методы анализа, которые могут дать более точные результаты.

Что значит, если стандартная ошибка очень большая?

Если стандартная ошибка очень большая, то это может говорить о том, что выборка не является репрезентативной или что данные не обработаны должным образом. В этом случае результаты исследования могут быть недостоверными или ошибочными, и нужно проводить дополнительные исследования для получения точных данных.

Важно ли учитывать стандартную ошибку при обработке результатов исследования?

Да, стандартная ошибка очень важна при обработке результатов исследования. Она помогает оценить надёжность полученных результатов и понять, какой доверительный интервал можно приписать исследованной совокупности. Игнорирование стандартной ошибки может привести к неверной оценке рисков и принятию неправильных решений.

Источник