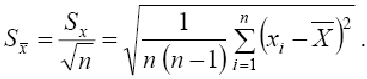Способы уменьшения случайных погрешностей.
1
Метод многократных измерений.
Тогда
2.
Метод комплексирования.
Проводят
измерения одной и той же величины при
следующих условиях:
А)
несколькими однотипными СИ одновременно
Б)
разнотипными
С)
различными методами( разными группами
экспериментаторов)
В
дальнейшем проводится объединение
результатов наблюдений по алгоритму
средневзвешенной оценки, более точным
наблюдениям больший вес. Объединение
может быть только для равноточных
результатов по систематической
погрешности.
3.
Метод косвенных измерений.
В
отдельных случаях позволяет уменьшить
случайную погрешность.
Средства измерений. Характеристики си для определения результатов измерений.
Средство
измерений –
это техническое средство (или комплекс),
предназначенное для измерений, имеющее
нормированные метрологические
характеристики, воспроизводящие и (или)
хранящие единицу физической величины,
размер которой принимается неизменным
(в пределах установленной погрешности)
в течение известного интервала времени
[24].
Данное определение раскрывает
метрологическую
сущность СИ,
заключающуюся
в умении хранить (или воспроизводить)
единицу ФВ
и
в неизменности размера хранимой единицы
во времени.
Первое обуславливает возможность
выполнения измерения, суть которого,
как известно, состоит в сравнении
измеряемой величины с ее единицей.
Второе принципиально необходимо,
поскольку при изменении размера хранимой
единицы ФВ с помощью данного СИ нельзя
получить результат с требуемой точностью.
Под метрологическими характеристиками
(MX)
понимают такие характеристики СИ,
которые позволяют судить об их пригодности
для измерений в известном диапазоне с
известной точностью. В отличие от СИ
приборы или вещества, не имеющие
нормированных MX,
называют индикаторами. СИ — это
техническая основа метрологического
обеспечения.
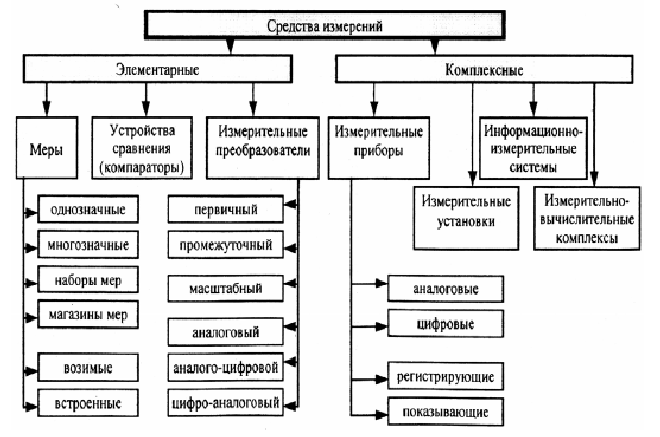
Классификация
средств измерений по их роли в процессе
измерения и
выполняемым
функциям
Эталон
–
средство измерений (или их комплекс),
предназначенное для воспроизведения
и (или) хранения единицы и передачи ее
размера нижестоящим по поверочной схеме
СИ и утвержденное в качестве эталона в
установленном порядке.
Меры
— это СИ, воспроизводящие или хранящие
физическую величину заданного размера.
Меры могут быть однозначными,
воспроизводящими одно значение физической
величины (гиря, калибр на заданный
размер, образцы твердости, шероховатости,
катушка сопротивления, нормальный
элемент, воспроизводящий значение
ЭДС), и
многозначными
— для воспроизведения плавно или
дискретно ряда значений одной и той же
физической величины (измерительный
конденсатор переменной емкости, набор
конечных мер, магазин емкостей,
индуктивности и сопротивления,
измерительные линейки).
Для
ряда областей измерений, и в первую
очередь для физико-химических измерений,
чрезвычайно перспективным средством
повышения эффективности поверочных
работ является применение стандартных
образцов (СО). Правила работы с СО
устанавливает ГОСТ 8.315—97. Согласно
этому документу,
стандартный
образец состава и свойств веществ и
материалов
— это средство измерений в виде вещества
(материала), состав или свойства которого
установлены аттестацией. Можно
дать и другое определение: стандартный
образец
— образец вещества (материала) с
установленными в результате метрологической
аттестации
значениями
одной или более величин, характеризующими
свойство или состав этого вещества
(материала).
Стандартные
образцы предназначены для обеспечения
единства и требуемой точности измерений
посредством:
•
градуировки,
метрологической аттестации и поверки
СИ;
•
метрологической
аттестации методик выполнения измерений;
•
контроля
показателей точности измерений;
•
измерения
ФВ, характеризующих состав или свойства
веществ материалов, методами сравнения.
По
своему назначению СО исполняют роль
мер, однако в отличие от «классических»
мер они имеют ряд особенностей. Например,
образцы состава воспроизводят значения
ФВ,
характеризующих
состав или свойства именно того материала
(вещества), из которого они изготовлены.
Стандартные образцы, как правило не
являются изделиями, они реализованы
обычно в виде части или порции однородного
вещества (материала), причем эта часть
является полноценным носителем
воспроизводимой единицы ФВ, а не ее
части Эта особенность образцов отражена
в требованиях к их однородности по
составу и свойствам. Однородность
материала, из которого сделан образец,
имеет принципиальное значение, в то
время как для меры такая характеристик
часто является второстепенной.
Измерительные
преобразователи
— СИ, предназначенные для выработки
сигнала измерительной информации в
форме, удобной для передачи, дальнейшего
преобразования, обработки и хранения,
но не доступной для непосредственного
восприятия наблюдателем. Это термопары,
измерительные трансформаторы,
усилители,
преобразователи давления. По месту,
занимаемому в измерительной цепи, они
делятся на первичные, промежуточные и
т. п. Конструктивно они выполняются либо
отдельными блоками, либо составной
частью СИ. Не следует отождествлять
измерительные преобразователи с
преобразовательными элементам. Последние
не имеют метрологических характеристик,
как, например, трансформатор тока или
напряжения.
Измерительный
прибор
— СИ, предназначенное для переработки
сигнала измерительной информации в
другие, доступные для непосредственного
восприятия наблюдателем формы. Различают
приборы прямого действия (амперметры,
вольтметры,
манометры)
и приборы сравнения (компараторы). По
способу отсчета измеряемой величины
СИ делятся на показывающие (аналоговые,
цифровые), регистрирующие (на
бумажную
или магнитную ленту) и т. п.
Измерительная
установка
— совокупность функционально объединенных
СИ и вспомогательных устройств,
расположенных в одном месте. Например,
поверочные установки, установки для
испытания электротехнических, магнитных
и других материалов. Измерительная
установка позволяет предусмотреть
определенный
метод
измерения и заранее оценить погрешность
измерения.
Измерительная
система
— это комплекс СИ и вспомогательных
устройств
с компонентами связи (проводные,
предназначенный
для выработки сигналов измерительной
информации в форме, удобной для
автоматической обработки, передачи
и/или
использования в автоматических системах
управления. В отличие от измерительных
установок, предусматривающих изменения
режима и условий функционирования,
измерительная система не воздействует
на режимы работы, а предназначена только
для сбора и/или хранения информации.
Частными случаями измерительной системы
являются информационно-вычислительный
комплекс (ИВК), информационно-измерительные
системы (ИИС). К последним можно отнести
системы автоматического контроля,
системы технического диагностирования,
системы распознавания образов, системы
для передачи неизмерительной информации.
При организации поверки рабочих СИ
используют различные эталоны и образцовые
СИ. СИ, как правило, работают совместно
с датчиками (измерительными
преобразователями), имеющими свои MX.
При
использовании средств измерений
принципиально важно знать степень
соответствия информации об измеряемой
величине, содержащейся в выходном
сигнале, ее истинному значению. С этой
целью для каждого СИ вводятся и нормируются
определенные метрологические
характеристики (МХ).
Метрологическими
называются
характеристики свойств СИ, оказывающие
влияние на результат измерения и его
погрешности. Характеристики, устанавливаемые
нормативными документами, называются
нормируемыми,
а определяемые экспериментально –
действительными.
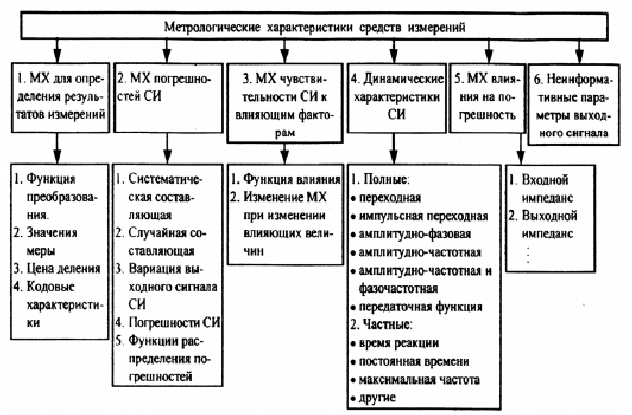
Номенклатура
метрологических характеристик средств
измерений
Неинформативным
называется параметр входного сигнала
СИ,
не связанный функционально с измеряемым
параметром. Например, частота переменного
тока при измерении его амплитуды.
Нормальные метрологические характеристики
(НМХ) устанавливаются документами. MX,
определенные документами, считаются
действительными. На практике наиболее
распространены следующие MX СИ.
Диапазон
измерений
— область значений измеряемой величины,
для которой нормированы допускаемые
пределы погрешности СИ (для преобразователей
— это диапазон преобразования):
Предел
измерения
— наибольшее или наименьшее значение
диапазона измерения. Для мер
— это номинальное значение воспроизводимой
величины.
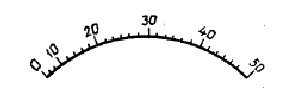
Рис
32 Неравномерная шкала СИ
Например,
у шкалы на рис. 32 начальный участок
(~20%) сжат, потому производить отсчеты
на нем неудобно. Тогда предел измерения
по шкале составляет 50 ед., а диапазон —
10…50 единиц.
Цена
деления шкалы
— разность значений величин,
соответствующих двум соседним
отметкам
шкалы. Приборы с равномерной шкалой
имеют постоянную цену деления, а с
неравномерной — переменную. В этом
случае нормируется минимальная цена
деления.
Чувствительность
— отношение изменения сигнала Δу на
выде СИ к вызвавшему это изменение
изменению Δх сигнала на входе
S=
Δу/Δх.
Например,
для стрелочного СИ — это отношение
перемещения dl
конца стрелки к вызвавшему его изменению
dx
измеряемой величины
S=
dl/dx.
Таким
образом, для неравномерных шкал величина
S=
var,
и степень неравномерности шкалы оценивают
через коэффициент
J=Smax/Smin
Для
равномерных шкал S
= Sср
= const
и Sср
= l/хN
где xN
— диапазон измерений.
Поскольку
х и у могут быть выражены в различных
единицах то величина S
имеет размерность [мм/А], [мм/В], [градус/В]и
т.д. Говоря о чувствительности, указывают
чувствительность тока, напряжения и т.
д. Иногда для оперирования безразмерными
единицами вводят понятие относительной
чувствительности
S0
= (Δy/y0)/(Δx/x0),
где
х0,
у0
— номинальные (или средние) величины.
Чувствительность нельзя отождествлять
с порогом чувствительности — наименьшим
значением измеряемой величины, вызывающим
заметное изменение показаний прибора.
Величину,
обратную чувствительности, называют
постоянной прибора С = 1/S.
Как
правило, выходным сигналом СИ является
отсчет (показание) в единицах величины.
В этом случае постоянная прибора С
равна цене деления. Поэтому для СИ с
неравномерной шкалой чувствительность
— величина переменная.
Вариация
(гистерезис)
— разность между показаниями СИ в данной
точке диапазона измерения при возрастании
и убывании измерений величины и неизменных
внешних условиях:
Н=
|хв
– xу|,
где
хв,
ху
— значения измерений образцовыми СИ
при возрастании и убывании величины
х. Следует иметь в виду, что, хотя вариация
показаний СИ вызывается случайными
факторами, сама она — не случайная
величина.
Зависимость
между выходным и входным сигналом СИ,
полученную экспериментально, называют
градуировочной характеристикой (или
статической характеристикой
преобразования), которая
может быть представлена аналитически,
графически или в виде таблицы.
Градуировочная характеристика может
изменяться под воздей ствием внешних
и внутренних причин. Например, при
быстром изменении тока подвижная часть
СИ, вследствие инерции, не успевает
«следить» за изменением тока.
Градуировочная характеристика в этом
случае должна выражаться дифференциальным
уравнением.
Характеристики
погрешности измерений в статике.
Статический
режим –
это такой режим работы СИ, при котором
изменением измеряемой величины за
время, требуемое для проведения одного
измерения, можно пренебречь. В динамическом
режиме такое
пренебрежение недопустимо, поскольку
указанное изменение превышает допустимую
погрешность.
Все
погрешности СИ в зависимости от внешних
условий делятся на основные и
дополнительные.
Основная
погрешность — это погрешность СИ при
нормальных условиях эксплуатации. Как
правило, нормальными условиями
эксплуатации являются: температура
293±5 К или 20±5 °С, относительная влажность
воздуха 65+15% при 20 °С, напряжение в сети
питания 220 В+10% с частотой 50 Гц±1%,
атмосферное давление от 97,4 до 104 кПа,
отсутствие электрических и магнитных
полей (наводок). В рабочих условиях,
зачастую отличающихся от нормальных
более широким диапазоном влияющих
величин, при необходимости нормируется
дополнительная погрешность СИ.
Классы
точности средств измерений
.
При технических измерениях, когда не
предусмотрено выделение случайных и
систематических составляющих, когда
не существенна динамическая погрешность
СИ, когда не учитываются влияющие
(дестабилизирующие) факторы и т.д., можно
пользоваться более грубым нормированием
— присвоением СИ определенного класса
точности по ГОСТ 8.401—80.
Класс
точности
–это обобщенная характеристика СИ,
выражаемая пределами допускаемых
значений его основной и дополнительной
погрешностей, а также другими
характеристиками,
влияющими на точность. Класс точности
не является непосредственной оценкой
точности измерений, выполняемых этим
СИ, поскольку погрешность зависит еще
от ряда факторов: метода измерений,
условий измерений и т.д. Класс точности
лишь позволяет судить о том, в каких
пределах находится погрешность СИ
данного типа. Общие положения деления
средств измерений по классу точности
устанавливает ГОСТ 8.401–80.года). Класс
точности СИ уже включает систематическую
и случайную погрешности. Однако он не
является непосредственной характеристикой
точности измерений, выполняемых с
помощью этих СИ, поскольку точность
измерения
зависит
и от метода измерения, взаимодействия
СИ с объектом, условий измерения и т.д.
В
связи с большим разнообразием как самих
СИ, так и их MX,
ГОСТ 8.401—80 устанавливает несколько
способов назначения классов точности.
При этом в основу заложены следующие
положения:
•
в
качестве норм служат пределы допускаемых
погрешностей, включающие систематические
и случайные составляющие;
•
основная
δосн
и все виды дополнительных погрешностей
δдоп
нормируются
порознь (см. п. 3.2).
Первое
положение свидетельствует о необходимости
разрабатывать СИ с учетом однократного
отсчета показаний по величине общей
погрешности. Второе положение направлено
на обеспечение максимальной однородности
однотипных СИ. .
Пределы
допускаемых основной и дополнительной
погрешностей выражают
в форме приведенных, относительных или
абсолютных
погрешностей.
Выбор формы представления зависит от
характера
изменения
погрешностей в пределах диапазона
измерений, а также от
условий
применения и назначения СИ.
Пределы
допускаемой абсолютной основной
погрешности
устанавливаются
по одной из формул: Δ
= ±а
или
Δ
= ±(а
+
bx),
где
х
–
значение
измеряемой величины или число делений,
отсчитанное по шкале;
а,
b
–
положительные числа, не зависящие от
х.
Первая формула описывает чисто аддитивную
погрешность (рис. 6.4, а), а вторая – сумму
аддитивной и мультипликативной (рис.
6.4, б) погрешностей (рис. 6.4, в). В технической
документации классы точности,
установленные
в виде абсолютных погрешностей,
обозначают, например, «Класс точности
М», а на приборе – буквой «М». Для
обозначения используются прописные
буквы латинского алфавита или римские
цифры, причём меньшие пределы погрешностей
должны соответствовать буквам, находящимся
ближе к началу алфавита, или меньшим
цифрам. Пределы допускаемой приведенной
основной погрешности определяются по
формуле γ
= Δ
/xN
=
± p
,
где xN
–
нормирующее значение, выраженное в тех
же единицах, что и Δ;
р
–
отвлеченное положительное число,
выбираемое из ряда значений:
(1;
1,5; 2; 2,5; 4; 5; 6)·10n
;
n
=
1;
0; −1;
−
2;…..
.
Рис.
6.4. Аддитивная а), мультипликативная б)
и суммарная в)
погрешности
в абсолютной и относительной формах
Нормирующее
значение xN
устанавливается
равным большему из пределов измерений
(или модулей) для СИ с равномерной,
практически равномерной или степенной
шкалой и для измерительных преобразователей,
для которых нулевое значение выходного
сигнала
находится
на краю или вне диапазона измерений.
Для СИ, шкала которых имеет условный
нуль, xN
равно
модулю разности пределов измерений.
Для приборов с существенно неравномерной
шкалой xN
принимают
равным всей длине шкалы или ее части,
соответствующей диапазону измерении.
В этом случае пределы абсолютной
погрешности выражают, как и длину шкалы,
в единицах длины, а на средстве измерений
класс
точности
условно обозначают, например, в виде
значка 0,5 , где 0,5 –значение числа р
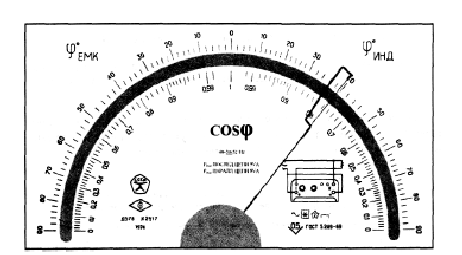
Рис.
6.5.Лицевая панель фазометра класса
точности 0,5 с существенно
неравномерной
нижней шкалой
В
остальных рассмотренных случаях класс
точности обозначают конкретным числом
р,
например 1,5. Обозначение наносится на
циферблат,
щиток или корпус прибора (рис. 6.6).
Рис
6.6. Лицевая панель амперметра класса
точности 1,5
с
равномерной шкалой
В
случае если абсолютная погрешность
задается формулой ±(a
+
bx),
пределы допускаемой относительной
основной погрешности δ
= Δ
x
=
±[c
+
d(
|xk/
x|
−1)],
(6.2)
где
с,
d
–
отвлеченные положительные числа,
выбираемые из ряда:
(1;
1,5; 2; 2,5; 4; 5; 6)·10n
;
n
=
1;
0; −1;
−
2;….
; xk
–
больший (по модулю) из пределов измерений.
При использовании формулы (6.2) класс
точности обозначается в виде «0,02/0,01»,
где числитель – конкретное значение
числа с,
знаменатель – числа d
(рис.
6.7).
Причем,
как правило, c>d.
Например, класс точности 0,02/0,01 означает,
что с = 0,02,
а
d=
0,01, т. е. приведенное значение относительной
погрешности к началу диапазона измерения
γн
= 0,02%, а к концу — γк=
0,01%.
В
обоснованных случаях пределы допускаемой
относительной основной погрешности
определяют по более сложным формулам
либо в виде графика или таблицы.
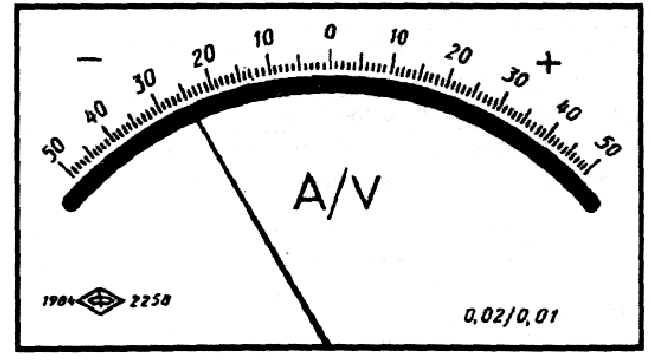
Рис.
6.7. Лицевая панель ампервольтметра
класса точности 0,02/0,01
с
равномерной шкалой
Пределы
допускаемой относительной основной
погрешности определяются по формуле
δ
= Δ /x
=
±q
,
если
Δ
= ±a
.
Значение
постоянного числа q
устанавливается
так же, как и значение числа p.
Класс точности на прибор обозначается
в виде
,
где 0,5 – конкретное значениеq
(рис.
6.8).
Так
обозначают классы точности мостов
переменного тока, счетчик0в электроэнергии,
делителей напряжения, измерительны
трансформаторов и др.
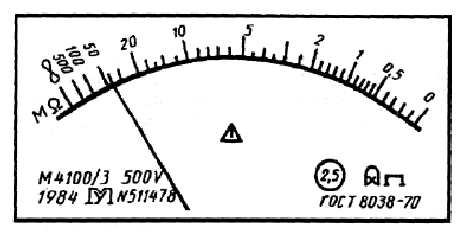
Рис
6.8. Лицевая панель мегаомметра класса
точности 2,5
с
неравномерной шкалой
В
стандартах и технических условиях на
СИ указывается минимальное значение
x0
, начиная с которого применим принятый
способ выражения пределов допускаемой
относительной погрешности. Отношение
xk/
x0
называется динамическим диапазоном
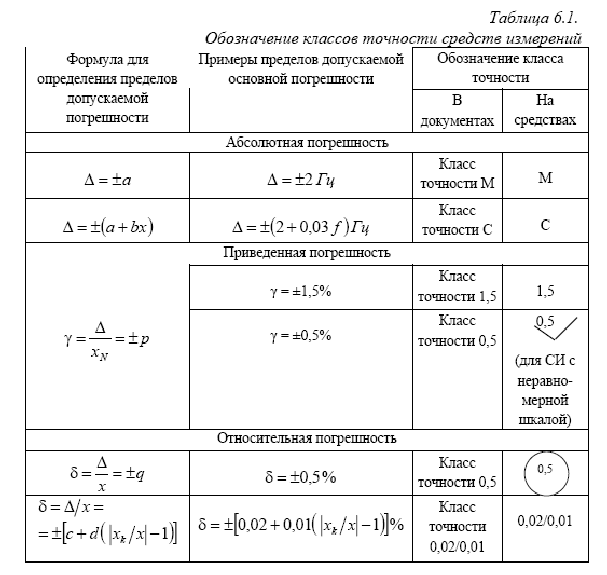
измерения. Правила построения и примеры
обозначения классов точности в
документации
и на средствах измерений приведены в
таблице 6.1.
Наиболее
широкое распространение (особенно для
аналоговых СИ) получило нормирование
класса точности по приведенной
погрешности:
γ=±Δ/xN100%
= ±A·10n.
xN
условное обозначение класса точности
в этом случае зависит от нормирующего
значения хN
т.
е. от шкалы СИ. Если xN
представляется в единицах измеряемой
величины, то класс точности обозначается
числом, совпадающим с пределом допускаемой
приведенной погрешности. Например,
класс 1,5 означает, что γ = 1,5%. Если xN
—
длина шкалы (например, у амперметров),
то класс 1.5 означает, что γ =1,5% длины
шкалы.
Не
всегда число, обозначающее класс
точности, показывает предел допускаемой
погрешности. В частности, у некоторых
однозначных мер электрических величин
оно характеризует нестабильность,
показывая, на сколько процентов значение
меры мо-
ет
изменяться в течение года.
Способы уменьшения случайных погрешностей.
1
Метод многократных измерений.
Тогда
2.
Метод комплексирования.
Проводят
измерения одной и той же величины при
следующих условиях:
А)
несколькими однотипными СИ одновременно
Б)
разнотипными
С)
различными методами( разными группами
экспериментаторов)
В
дальнейшем проводится объединение
результатов наблюдений по алгоритму
средневзвешенной оценки, более точным
наблюдениям больший вес. Объединение
может быть только для равноточных
результатов по систематической
погрешности.
3.
Метод косвенных измерений.
В
отдельных случаях позволяет уменьшить
случайную погрешность.
Средства измерений. Характеристики си для определения результатов измерений.
Средство
измерений –
это техническое средство (или комплекс),
предназначенное для измерений, имеющее
нормированные метрологические
характеристики, воспроизводящие и (или)
хранящие единицу физической величины,
размер которой принимается неизменным
(в пределах установленной погрешности)
в течение известного интервала времени
[24].
Данное определение раскрывает
метрологическую
сущность СИ,
заключающуюся
в умении хранить (или воспроизводить)
единицу ФВ
и
в неизменности размера хранимой единицы
во времени.
Первое обуславливает возможность
выполнения измерения, суть которого,
как известно, состоит в сравнении
измеряемой величины с ее единицей.
Второе принципиально необходимо,
поскольку при изменении размера хранимой
единицы ФВ с помощью данного СИ нельзя
получить результат с требуемой точностью.
Под метрологическими характеристиками
(MX)
понимают такие характеристики СИ,
которые позволяют судить об их пригодности
для измерений в известном диапазоне с
известной точностью. В отличие от СИ
приборы или вещества, не имеющие
нормированных MX,
называют индикаторами. СИ — это
техническая основа метрологического
обеспечения.
Классификация
средств измерений по их роли в процессе
измерения и
выполняемым
функциям
Эталон
–
средство измерений (или их комплекс),
предназначенное для воспроизведения
и (или) хранения единицы и передачи ее
размера нижестоящим по поверочной схеме
СИ и утвержденное в качестве эталона в
установленном порядке.
Меры
— это СИ, воспроизводящие или хранящие
физическую величину заданного размера.
Меры могут быть однозначными,
воспроизводящими одно значение физической
величины (гиря, калибр на заданный
размер, образцы твердости, шероховатости,
катушка сопротивления, нормальный
элемент, воспроизводящий значение
ЭДС), и
многозначными
— для воспроизведения плавно или
дискретно ряда значений одной и той же
физической величины (измерительный
конденсатор переменной емкости, набор
конечных мер, магазин емкостей,
индуктивности и сопротивления,
измерительные линейки).
Для
ряда областей измерений, и в первую
очередь для физико-химических измерений,
чрезвычайно перспективным средством
повышения эффективности поверочных
работ является применение стандартных
образцов (СО). Правила работы с СО
устанавливает ГОСТ 8.315—97. Согласно
этому документу,
стандартный
образец состава и свойств веществ и
материалов
— это средство измерений в виде вещества
(материала), состав или свойства которого
установлены аттестацией. Можно
дать и другое определение: стандартный
образец
— образец вещества (материала) с
установленными в результате метрологической
аттестации
значениями
одной или более величин, характеризующими
свойство или состав этого вещества
(материала).
Стандартные
образцы предназначены для обеспечения
единства и требуемой точности измерений
посредством:
•
градуировки,
метрологической аттестации и поверки
СИ;
•
метрологической
аттестации методик выполнения измерений;
•
контроля
показателей точности измерений;
•
измерения
ФВ, характеризующих состав или свойства
веществ материалов, методами сравнения.
По
своему назначению СО исполняют роль
мер, однако в отличие от «классических»
мер они имеют ряд особенностей. Например,
образцы состава воспроизводят значения
ФВ,
характеризующих
состав или свойства именно того материала
(вещества), из которого они изготовлены.
Стандартные образцы, как правило не
являются изделиями, они реализованы
обычно в виде части или порции однородного
вещества (материала), причем эта часть
является полноценным носителем
воспроизводимой единицы ФВ, а не ее
части Эта особенность образцов отражена
в требованиях к их однородности по
составу и свойствам. Однородность
материала, из которого сделан образец,
имеет принципиальное значение, в то
время как для меры такая характеристик
часто является второстепенной.
Измерительные
преобразователи
— СИ, предназначенные для выработки
сигнала измерительной информации в
форме, удобной для передачи, дальнейшего
преобразования, обработки и хранения,
но не доступной для непосредственного
восприятия наблюдателем. Это термопары,
измерительные трансформаторы,
усилители,
преобразователи давления. По месту,
занимаемому в измерительной цепи, они
делятся на первичные, промежуточные и
т. п. Конструктивно они выполняются либо
отдельными блоками, либо составной
частью СИ. Не следует отождествлять
измерительные преобразователи с
преобразовательными элементам. Последние
не имеют метрологических характеристик,
как, например, трансформатор тока или
напряжения.
Измерительный
прибор
— СИ, предназначенное для переработки
сигнала измерительной информации в
другие, доступные для непосредственного
восприятия наблюдателем формы. Различают
приборы прямого действия (амперметры,
вольтметры,
манометры)
и приборы сравнения (компараторы). По
способу отсчета измеряемой величины
СИ делятся на показывающие (аналоговые,
цифровые), регистрирующие (на
бумажную
или магнитную ленту) и т. п.
Измерительная
установка
— совокупность функционально объединенных
СИ и вспомогательных устройств,
расположенных в одном месте. Например,
поверочные установки, установки для
испытания электротехнических, магнитных
и других материалов. Измерительная
установка позволяет предусмотреть
определенный
метод
измерения и заранее оценить погрешность
измерения.
Измерительная
система
— это комплекс СИ и вспомогательных
устройств
с компонентами связи (проводные,
предназначенный
для выработки сигналов измерительной
информации в форме, удобной для
автоматической обработки, передачи
и/или
использования в автоматических системах
управления. В отличие от измерительных
установок, предусматривающих изменения
режима и условий функционирования,
измерительная система не воздействует
на режимы работы, а предназначена только
для сбора и/или хранения информации.
Частными случаями измерительной системы
являются информационно-вычислительный
комплекс (ИВК), информационно-измерительные
системы (ИИС). К последним можно отнести
системы автоматического контроля,
системы технического диагностирования,
системы распознавания образов, системы
для передачи неизмерительной информации.
При организации поверки рабочих СИ
используют различные эталоны и образцовые
СИ. СИ, как правило, работают совместно
с датчиками (измерительными
преобразователями), имеющими свои MX.
При
использовании средств измерений
принципиально важно знать степень
соответствия информации об измеряемой
величине, содержащейся в выходном
сигнале, ее истинному значению. С этой
целью для каждого СИ вводятся и нормируются
определенные метрологические
характеристики (МХ).
Метрологическими
называются
характеристики свойств СИ, оказывающие
влияние на результат измерения и его
погрешности. Характеристики, устанавливаемые
нормативными документами, называются
нормируемыми,
а определяемые экспериментально –
действительными.
Номенклатура
метрологических характеристик средств
измерений
Неинформативным
называется параметр входного сигнала
СИ,
не связанный функционально с измеряемым
параметром. Например, частота переменного
тока при измерении его амплитуды.
Нормальные метрологические характеристики
(НМХ) устанавливаются документами. MX,
определенные документами, считаются
действительными. На практике наиболее
распространены следующие MX СИ.
Диапазон
измерений
— область значений измеряемой величины,
для которой нормированы допускаемые
пределы погрешности СИ (для преобразователей
— это диапазон преобразования):
Предел
измерения
— наибольшее или наименьшее значение
диапазона измерения. Для мер
— это номинальное значение воспроизводимой
величины.
Рис
32 Неравномерная шкала СИ
Например,
у шкалы на рис. 32 начальный участок
(~20%) сжат, потому производить отсчеты
на нем неудобно. Тогда предел измерения
по шкале составляет 50 ед., а диапазон —
10…50 единиц.
Цена
деления шкалы
— разность значений величин,
соответствующих двум соседним
отметкам
шкалы. Приборы с равномерной шкалой
имеют постоянную цену деления, а с
неравномерной — переменную. В этом
случае нормируется минимальная цена
деления.
Чувствительность
— отношение изменения сигнала Δу на
выде СИ к вызвавшему это изменение
изменению Δх сигнала на входе
S=
Δу/Δх.
Например,
для стрелочного СИ — это отношение
перемещения dl
конца стрелки к вызвавшему его изменению
dx
измеряемой величины
S=
dl/dx.
Таким
образом, для неравномерных шкал величина
S=
var,
и степень неравномерности шкалы оценивают
через коэффициент
J=Smax/Smin
Для
равномерных шкал S
= Sср
= const
и Sср
= l/хN
где xN
— диапазон измерений.
Поскольку
х и у могут быть выражены в различных
единицах то величина S
имеет размерность [мм/А], [мм/В], [градус/В]и
т.д. Говоря о чувствительности, указывают
чувствительность тока, напряжения и т.
д. Иногда для оперирования безразмерными
единицами вводят понятие относительной
чувствительности
S0
= (Δy/y0)/(Δx/x0),
где
х0,
у0
— номинальные (или средние) величины.
Чувствительность нельзя отождествлять
с порогом чувствительности — наименьшим
значением измеряемой величины, вызывающим
заметное изменение показаний прибора.
Величину,
обратную чувствительности, называют
постоянной прибора С = 1/S.
Как
правило, выходным сигналом СИ является
отсчет (показание) в единицах величины.
В этом случае постоянная прибора С
равна цене деления. Поэтому для СИ с
неравномерной шкалой чувствительность
— величина переменная.
Вариация
(гистерезис)
— разность между показаниями СИ в данной
точке диапазона измерения при возрастании
и убывании измерений величины и неизменных
внешних условиях:
Н=
|хв
– xу|,
где
хв,
ху
— значения измерений образцовыми СИ
при возрастании и убывании величины
х. Следует иметь в виду, что, хотя вариация
показаний СИ вызывается случайными
факторами, сама она — не случайная
величина.
Зависимость
между выходным и входным сигналом СИ,
полученную экспериментально, называют
градуировочной характеристикой (или
статической характеристикой
преобразования), которая
может быть представлена аналитически,
графически или в виде таблицы.
Градуировочная характеристика может
изменяться под воздей ствием внешних
и внутренних причин. Например, при
быстром изменении тока подвижная часть
СИ, вследствие инерции, не успевает
«следить» за изменением тока.
Градуировочная характеристика в этом
случае должна выражаться дифференциальным
уравнением.
Характеристики
погрешности измерений в статике.
Статический
режим –
это такой режим работы СИ, при котором
изменением измеряемой величины за
время, требуемое для проведения одного
измерения, можно пренебречь. В динамическом
режиме такое
пренебрежение недопустимо, поскольку
указанное изменение превышает допустимую
погрешность.
Все
погрешности СИ в зависимости от внешних
условий делятся на основные и
дополнительные.
Основная
погрешность — это погрешность СИ при
нормальных условиях эксплуатации. Как
правило, нормальными условиями
эксплуатации являются: температура
293±5 К или 20±5 °С, относительная влажность
воздуха 65+15% при 20 °С, напряжение в сети
питания 220 В+10% с частотой 50 Гц±1%,
атмосферное давление от 97,4 до 104 кПа,
отсутствие электрических и магнитных
полей (наводок). В рабочих условиях,
зачастую отличающихся от нормальных
более широким диапазоном влияющих
величин, при необходимости нормируется
дополнительная погрешность СИ.
Классы
точности средств измерений
.
При технических измерениях, когда не
предусмотрено выделение случайных и
систематических составляющих, когда
не существенна динамическая погрешность
СИ, когда не учитываются влияющие
(дестабилизирующие) факторы и т.д., можно
пользоваться более грубым нормированием
— присвоением СИ определенного класса
точности по ГОСТ 8.401—80.
Класс
точности
–это обобщенная характеристика СИ,
выражаемая пределами допускаемых
значений его основной и дополнительной
погрешностей, а также другими
характеристиками,
влияющими на точность. Класс точности
не является непосредственной оценкой
точности измерений, выполняемых этим
СИ, поскольку погрешность зависит еще
от ряда факторов: метода измерений,
условий измерений и т.д. Класс точности
лишь позволяет судить о том, в каких
пределах находится погрешность СИ
данного типа. Общие положения деления
средств измерений по классу точности
устанавливает ГОСТ 8.401–80.года). Класс
точности СИ уже включает систематическую
и случайную погрешности. Однако он не
является непосредственной характеристикой
точности измерений, выполняемых с
помощью этих СИ, поскольку точность
измерения
зависит
и от метода измерения, взаимодействия
СИ с объектом, условий измерения и т.д.
В
связи с большим разнообразием как самих
СИ, так и их MX,
ГОСТ 8.401—80 устанавливает несколько
способов назначения классов точности.
При этом в основу заложены следующие
положения:
•
в
качестве норм служат пределы допускаемых
погрешностей, включающие систематические
и случайные составляющие;
•
основная
δосн
и все виды дополнительных погрешностей
δдоп
нормируются
порознь (см. п. 3.2).
Первое
положение свидетельствует о необходимости
разрабатывать СИ с учетом однократного
отсчета показаний по величине общей
погрешности. Второе положение направлено
на обеспечение максимальной однородности
однотипных СИ. .
Пределы
допускаемых основной и дополнительной
погрешностей выражают
в форме приведенных, относительных или
абсолютных
погрешностей.
Выбор формы представления зависит от
характера
изменения
погрешностей в пределах диапазона
измерений, а также от
условий
применения и назначения СИ.
Пределы
допускаемой абсолютной основной
погрешности
устанавливаются
по одной из формул: Δ
= ±а
или
Δ
= ±(а
+
bx),
где
х
–
значение
измеряемой величины или число делений,
отсчитанное по шкале;
а,
b
–
положительные числа, не зависящие от
х.
Первая формула описывает чисто аддитивную
погрешность (рис. 6.4, а), а вторая – сумму
аддитивной и мультипликативной (рис.
6.4, б) погрешностей (рис. 6.4, в). В технической
документации классы точности,
установленные
в виде абсолютных погрешностей,
обозначают, например, «Класс точности
М», а на приборе – буквой «М». Для
обозначения используются прописные
буквы латинского алфавита или римские
цифры, причём меньшие пределы погрешностей
должны соответствовать буквам, находящимся
ближе к началу алфавита, или меньшим
цифрам. Пределы допускаемой приведенной
основной погрешности определяются по
формуле γ
= Δ
/xN
=
± p
,
где xN
–
нормирующее значение, выраженное в тех
же единицах, что и Δ;
р
–
отвлеченное положительное число,
выбираемое из ряда значений:
(1;
1,5; 2; 2,5; 4; 5; 6)·10n
;
n
=
1;
0; −1;
−
2;…..
.
Рис.
6.4. Аддитивная а), мультипликативная б)
и суммарная в)
погрешности
в абсолютной и относительной формах
Нормирующее
значение xN
устанавливается
равным большему из пределов измерений
(или модулей) для СИ с равномерной,
практически равномерной или степенной
шкалой и для измерительных преобразователей,
для которых нулевое значение выходного
сигнала
находится
на краю или вне диапазона измерений.
Для СИ, шкала которых имеет условный
нуль, xN
равно
модулю разности пределов измерений.
Для приборов с существенно неравномерной
шкалой xN
принимают
равным всей длине шкалы или ее части,
соответствующей диапазону измерении.
В этом случае пределы абсолютной
погрешности выражают, как и длину шкалы,
в единицах длины, а на средстве измерений
класс
точности
условно обозначают, например, в виде
значка 0,5 , где 0,5 –значение числа р
Рис.
6.5.Лицевая панель фазометра класса
точности 0,5 с существенно
неравномерной
нижней шкалой
В
остальных рассмотренных случаях класс
точности обозначают конкретным числом
р,
например 1,5. Обозначение наносится на
циферблат,
щиток или корпус прибора (рис. 6.6).
Рис
6.6. Лицевая панель амперметра класса
точности 1,5
с
равномерной шкалой
В
случае если абсолютная погрешность
задается формулой ±(a
+
bx),
пределы допускаемой относительной
основной погрешности δ
= Δ
x
=
±[c
+
d(
|xk/
x|
−1)],
(6.2)
где
с,
d
–
отвлеченные положительные числа,
выбираемые из ряда:
(1;
1,5; 2; 2,5; 4; 5; 6)·10n
;
n
=
1;
0; −1;
−
2;….
; xk
–
больший (по модулю) из пределов измерений.
При использовании формулы (6.2) класс
точности обозначается в виде «0,02/0,01»,
где числитель – конкретное значение
числа с,
знаменатель – числа d
(рис.
6.7).
Причем,
как правило, c>d.
Например, класс точности 0,02/0,01 означает,
что с = 0,02,
а
d=
0,01, т. е. приведенное значение относительной
погрешности к началу диапазона измерения
γн
= 0,02%, а к концу — γк=
0,01%.
В
обоснованных случаях пределы допускаемой
относительной основной погрешности
определяют по более сложным формулам
либо в виде графика или таблицы.
Рис.
6.7. Лицевая панель ампервольтметра
класса точности 0,02/0,01
с
равномерной шкалой
Пределы
допускаемой относительной основной
погрешности определяются по формуле
δ
= Δ /x
=
±q
,
если
Δ
= ±a
.
Значение
постоянного числа q
устанавливается
так же, как и значение числа p.
Класс точности на прибор обозначается
в виде
,
где 0,5 – конкретное значениеq
(рис.
6.8).
Так
обозначают классы точности мостов
переменного тока, счетчик0в электроэнергии,
делителей напряжения, измерительны
трансформаторов и др.
Рис
6.8. Лицевая панель мегаомметра класса
точности 2,5
с
неравномерной шкалой
В
стандартах и технических условиях на
СИ указывается минимальное значение
x0
, начиная с которого применим принятый
способ выражения пределов допускаемой
относительной погрешности. Отношение
xk/
x0
называется динамическим диапазоном
измерения. Правила построения и примеры
обозначения классов точности в
документации
и на средствах измерений приведены в
таблице 6.1.
Наиболее
широкое распространение (особенно для
аналоговых СИ) получило нормирование
класса точности по приведенной
погрешности:
γ=±Δ/xN100%
= ±A·10n.
xN
условное обозначение класса точности
в этом случае зависит от нормирующего
значения хN
т.
е. от шкалы СИ. Если xN
представляется в единицах измеряемой
величины, то класс точности обозначается
числом, совпадающим с пределом допускаемой
приведенной погрешности. Например,
класс 1,5 означает, что γ = 1,5%. Если xN
—
длина шкалы (например, у амперметров),
то класс 1.5 означает, что γ =1,5% длины
шкалы.
Не
всегда число, обозначающее класс
точности, показывает предел допускаемой
погрешности. В частности, у некоторых
однозначных мер электрических величин
оно характеризует нестабильность,
показывая, на сколько процентов значение
меры мо-
ет
изменяться в течение года.
Определение качества выборки включает описание ряда условий, позволяющих оценить валидность, надеж-ность и репрезентативность выборочной совокупности по отношению к объекту исследования.
Надежность и валидность. Надежность и валидность — основные параметры определения качества информации, полученной в результате проведения эмпирического исследования. Под надежностью подразумевается определенная гарантия, что полученный результат правильно отражает изучаемую действительность. Валидностью (обоснованностью) информации называется подтверждение (доказательство), что исследовались (измерялись) именно те явления, которые социолог предполагал исследовать.
На качестве информации (надежности и валидиости данных) сказываются особенности различных этапов эмпирического исследования (исходные теоретические пред-посылки, качество инструментария, организация контроля работы интервьюеров и т.д.).
Особую роль в обеспечении надежности и валидное данных играют особенности формирования выборки. В этом разделе мы остановимся на проблеме влияния особенностей выборочного подхода па надежность и валидность получаемой в результате исследования информации. Надежность информации на этапе формирования выборки обеспечивается учетом случайных ошибок.
Случайные ошибки выборки неизбежны вследствие неоднородности исследуемого контингента. Качество исследования определяется способностью социолога вычислить величину случайной ошибки и учесть ее при распространении выводов, полученных на основе опроса части определенной группы людей, на всю ее совокупность.
Если бы все люди по всем своим характеристикам были совершенно идентичными, то достаточно было опросить одного человека для вывода, что именно так считают (или, по крайней мере, ответили бы) все остальные. Но социолог именно потому и проводит опрос, что предполагает у обследуемых людей разные точки зрения.
Характеристик, по которым люди различаются, очень много. Часть таких характеристик формализована и фиксируется в определенных документах (пол, возраст, образование, семейное положение, национальность, специальность, должность, заработная плата и т.д.). Другая, значительно большая часть характеристик (личностные особенности, отношение к различным социальным явлениям, мнения и т.п.) не формализована и не зафиксирована в каких-либо документах.
Систематизацией и обобщением формализованных характеристик населения занимается статистика (государственная и ведомственная). Исследование же социолога направлено на то, чтобы формализовать и систематизировать информацию о тех характеристиках людей, которые исследователю представляются наиболее важными с социальной точки зрения, но о них нет сведений в документальных источниках.
Фактически, каждый пункт анкеты является определенной характеристикой (признаком), и исследователь хочет установить, как и в какой степени люди различаются по этой характеристике. Другими словами, исследователь с самого начала исходит из принципа неоднородности обследуемого контингента.
Когда исследователь отбирает часть людей из их обшей совокупности для обследования (чтобы по избранной части делать вывод обо всех), то в его выборку могут не попасть люди с какими-либо значениями исследуемых характеристик. Менее вероятно, что в выборку попадут люди по какой-либо характеристике «нетипичные». Со статистической точки зрения это означает, что их удельный вес в общей совокупности невысок. Чем меньше удельный вес лиц с определенным значением характеристики в общей совокупности, тем меньше вероятность того, что они попадут в выборочное обследование.
Другой особенностью выборки является то, что в выборочную совокупность могут попасть лица со всеми возможными значениями характеристики, но в выборке они будут представлены не в той пропорции, которая характерна для общей совокупности.
Например, в общей совокупности 13% лиц, имеющих высшее образование, а в выборку попадает 37%; или в общей совокупности 25% лиц, придерживающихся коммунистической ориентации, а в выборку попадет только 4% и т.п. Если из общей совокупности отбирать некоторую ее часть случайным образом, то на основе теории вероятности можно определить величину, на которую может отклоняться значение признака в выборке по отношению к данному значению совокупности в целом.
Эта величина называется случайной ошибкой или ошибкой выборки.
Величина случайной ошибки зависит от двух основных параметров: от объема выборки и степени изменчивости признака (однородности контингента по какой-либо характеристике).
Если исследователь хочет обеспечить представительство в выборке людей, которые по своим характеристикам нетипичны (не распространены в данной совокупности), он должен увеличивать объем выборки.
Таким образом, чем более однородный контингент подлежит обследованию и чем больше объем выборочной совокупности, тем меньше случайная ошибка выборки и, соответственно, выше надежность полученных в результате опроса данных.
Основным эмпирическим критерием надежности является устойчивость результатов, характеризующая свойство получать данные с одним и тем же результатом в разных опросах, проведенных в одинаковых условиях.
Например, если бы исследователь повторил свой опрос по той же анкете, примерно в то же время и по аналогичной (по принципам, процедурам и объему) выборке, но на других людях, и получил такие же данные, как и в первом опросе, то можно считать, что результаты его опроса достаточно надежны.
Конечно, случайные ошибки, снижающие устойчивость данных, могут быть результатом и других особенностей исследования: инструментария или работы интервьюеров. Например, если в вопросах анкеты используются термины, совершенно не знакомые многим респондентам, и они будут скорее «угадывать» их значение, то их ответы в этом случае во многом будут лишь «случайной догадкой», и надежность данных по этому пункту анкеты будет снижена.
При тестировании на устойчивость исследователь может делать ориентировочные предположения — привели ли к снижению надежности погрешности выборки или погрешности инструментария: если данные неустойчивы по нескольким (определенным) пунктам анкеты, то, вероятно, к снижению надежности привели погрешности инструментария; если данные неустойчивы по всем пунктам анкеты, то искажение информации происходит скорее всего из-за случайных ошибок выборки. Чем больше объем выборки, тем в меньшей степени случайные ошибки сказываются на общем результате исследования, так как основное свойство случайных ошибок заключается в том, что они «погашают» друг друга.
Валидность (обоснованность) данных, как отмечалось выше, характеризует, в какой степени было измерено именно то, что предполагалось измерить. К снижению валидности могут привести не только ошибки инструментария (о чем шла речь в соответствующем разделе), но и погрешности выборки, в частности — систематическая ошибка или отклонение выборки. Например, если отбор респондентов будет производиться в районе расположения воинской части, то можно предположить, что в выборке военнослужащих может быть больше, чем это характерно для генеральной совокупности.
При повторном исследовании данные могут быть достаточно устойчивыми, но как в первом, так и во втором случае результаты будут подвержены влиянию данного фактора в большей степени, чем его испытывает генеральная совокупность. То же, вернувшись к приведенному выше примеру, можно сказать и о таких местах опроса, как очередь (в рабочее время суток в очереди значительно больше представителей неработающих категорий населения, чем в структуре населения в целом) или остановка автобуса. Необоснованный выбор точек опроса чаще всего приводит именно к систематической ошибке.
Следует заметить, что надежность и валидность — довольно независимые друг от друга параметры, поэтому при оценке качества информации исследователь должен учитывать обе эти характеристики; данные могут быть валидны, но ненадежны, и наоборот, исследователь может получать достаточно устойчивые (надежные) результаты, но они не валидны по отношению к предмету анализа.
Наглядной иллюстрацией характеристик надежности и валидности, обеспечиваемых особенностями выборки, является аналогия с мишенью, которую приводят в своей работе американские авторы P.Alreck, R.Settle. На рисунке 1 представлены четыре типа результатов выстрелов по мишени.
В качестве центра каждой мишени выступает среднее реальное значение некоторого признака (например, средняя заработная плата) изучаемой генеральной совокупности; точками на рисунке отмечены значения полученных результатов повторных исследований по подготовленным выборочным совокупностям.
В квадрате А результаты сгущены вокруг центра (истинного значения измеряемого признака). При каждом повторном исследовании полученная по результатам опроса выборки величина незначительно отличается от истинного значения признака.
В данном случае можно говорить о высокой надежности и валидности выборки. Чем меньше общая площадь рассеяния, тем меньше величина случайных ошибок и, соответственно, выше надежность. Чем ближе эти значения к истинному результату, тем выше валидность (обоснованность) данных (исследователь измерял именно то, что предполагал измерять).
В квадрате Б точки также группируются вокруг истинного значения, но результаты повторных измерений значительно отстоят друг от друга. В тех случаях, когда проводится только одно исследование (а чаще всего автор проводит одно исследование), результат, полученный на основе опроса выборочной совокупности, может быть достаточно отдален от истинного значения (из-за влияния случайных ошибок). На практике такой тип ошибок чаще всего возникает в случаях недостаточного объема выборки. Квадрат Б иллюстрирует результаты исследования, характеризующиеся высокой валидностью, но низкой надежностью.
В квадрате В представлены результаты, характеризующиеся высокой надежностью и низкой валидностью. Исследователь при повторных опросах будет получать достаточно схожие данные, но они не отражают истинную картину характеристики той совокупности, о которой делаются выводы.
Например, делаются выводы о средней заработной плате всего населения, а опрашивались респонденты в магазине в рабочее время, когда там выше доля людей неработающих, доход которых в среднем значительно ниже, чем у населения в целом; или опрос проводится в районе какого-либо предприятия, средняя зарплата работников которого в среднем выше, чем у населения в целом, о котором исследователь делает выводы. Систематическая ошибка приводит к искаженному, но достаточно устойчивому результату.
И наконец, квадрат Г иллюстрирует результаты исследования с низкой валидностью и низкой надежностью; результаты исследования претерпевают влияние как случайных, так и систематических ошибок.
Чтобы избежать влияния случайных и систематических ошибок (или, по крайней мере, вычислить их величину и учесть ее при интерпретации результатов), необходимо знать основные характеристики генеральной совокупности, на которую исследователь будет распространять выводы, полученные в результате опроса выборочной совокупности.
В принципе, как остроумно заметил социолог В.Шляпентох: «В этом мире нет нерепрезентативных данных — надо только восстановить ту генеральную совокупность, которую эти данные представляют» (В.Шляпентох. Открывая Америку, 1989, с.74).
Другими словами, результаты любого опроса позволяют получить определенную информацию; если исследователь достаточно корректно интерпретирует результаты опроса и делает выводы только относительно той части населения, которую репрезентирует его выборка.
Однако, когда перед социологом стоит достаточно конкретная цель, своей постановкой определяющая объект исследования, модель его выборки по своим основным параметрам должна соответствовать модели генеральной совокупности. Поэтому при формировании выборки он обязан исходить из поставленной цели.
Главная задача исследователя на этапе составления выборки правильно построить модель выборочной совокупности (так, чтобы по своей структуре она соответствовала генеральной совокупности), а на этапе интерпретации результатов — учесть все погрешности, которые были допущены при формировании выборки.
Качество информации в конечном итоге определяется не отсутствием ошибок и погрешностей (избежать которых практически невозможно), а создаваемыми исследователем условиями, позволяющими учесть влияние этих ошибок на конечный результат.
Более строго это положение формулирует В.Паниотто: «Надежной называют информацию, в которой, во-первых, учтенные ошибки не превышают некоторой заданной исследователем величины; во-вторых, отсутствуют неучтенные ошибки, т.е. ошибки, величину которых исследователь не в состоянии оценить».
Решению проблемы учета ошибок построения выборки может помочь технологическая схема перехода от определения объекта исследования (анализировать который предполагает автор на основании данных эмпирического исследования) к определению выборочной совокупности (объема и способов отбора).
Уменьшение — влияние — случайная погрешность
Cтраница 1
Уменьшение влияния случайных погрешностей на результат измерений достигается путем многократных измерений величины в одинаковых условиях.
[1]
Уменьшение влияния случайных погрешностей на результат измерений достигается путем многократных измерений величины в одинаковых условиях. Если принять, что систематические погрешности близки к нулю, то наиболее достоверное значение, которое можно приписать измеряемой величине на основании ряда измерений, есть среднее арифметическое из полученных значений.
[2]
Уменьшение влияния случайных погрешностей на результат измерений достигается путем многократных измерений величины в одинаковых условиях.
[3]
Для уменьшения влияния случайных погрешностей на результат измерения рекомендуется производить измерение данной величины в одинаковых условиях и по возможности большее число раз и из полученных значений брать среднее арифметическое, которое считается наиболее вероятным значением измеренной величины, так как случайные погрешности, одинаковые по абсолютной величине, но разные по знакам, при большом числе измерений встречаются одинаково часто.
[4]
Для уменьшения влияния случайных погрешностей измерения при каждом сочетании пикового ускорения и длительности действия проводят три-четыре измерения.
[5]
Для уменьшения влияния случайных погрешностей показаний индикатор многократно проверяют в каждой точке шкалы и затем вычисляют среднее значение.
[6]
Как уже указывалось ( § 13), для уменьшения влияния случайных погрешностей на результат анализа обычно проводят не одно, а два и более определения интересующего нас элемента в данном веществе. Как правило, ни при одном из этих определений не получается истинного значения определяемой величины, так как все они содержат ошибки. Поэтому задачей анализа является нахождение наиболее вероятного значения определяемой величины и оценка точности полученного результата.
[7]
Как уже указывалось ( § 13), для уменьшения влияния случайных погрешностей на результат анализа обычно проводят не одно, а два или несколько определений интересующего нас элемента в данном веществе. Как правило, ни при одном из этих определений не получается истинного значения определяемой величины, так как все они содержат ошибки. Поэтому задачей анализа является нахождение наиболее вероятного значения определяемой величины и оценка степени точности полученного результата.
[8]
Как уже указывалось ( § 13), для уменьшения влияния случайных погрешностей на результат анализа обычно проводят не одно, а два или несколько определений интересующего нас элемента в данном веществе. Как правило, ни при одном у из этих определений не получается истинного значения определяемой величины, так как все они содержат ошибки. Поэтому задачей анализа является нахождение наиболее вероятного значения определяемой величины и оценка степени точности полученного результата.
[10]
Рассмотрим прежде всего статистические измерения, при которых многократные измерения проводятся для уменьшения влияния случайных погрешностей. Результат каждого измерения при этом дает оценку измеряемой величины.
[11]
Повышение точности результата измерений может быть достигнуто исключением грубых и систематических погрешностей из результатов измерений и уменьшением влияния случайных погрешностей. При этом во всех случаях грубые погрешности ( промахи) следует исключать из результатов измерений. Систематические погрешности следует исключать тогда, когда это обеспечивает заметное повышение точности. Способы уменьшения влияния случайных погрешностей изложены в § 1.4. Необходимо иметь в виду, что, если принять за результат измерений среднее арифметическое из ряда — измерений, точность повышается в У — п раз.
[12]
В ряде случаев — при измерении заведомо постоянной величины — возникает задача повышения точности измерения за счет уменьшения влияния случайных погрешностей, для чего проводят ряд повторных наблюдений. Повторные наблюдения имеет смысл производить в том случае, если систематические погрешности исключены или если они значительно меньше случайных погрешностей, так как систематические погрешности нельзя исключить увеличением числа наблюдений. Кроме того, необходимо также учитывать, что погрешность результата измерения, обусловленная случайными погрешностями, не может быть снижена до значения, меньшего порога чувствительности используемых средств изменений.
[13]
В § 1.3 было показано, что проведение многократных наблюдений с последующим усреднением результатов — эффективный способ уменьшения влияния случайной погрешности на результат измерения.
[14]
Повышение точности измерительных приборов достигается за счет автоматической компенсации ( исключения) систематической погрешности, в частности автоматической установки нуля перед началом измерений, автоматического выполнения градуировочной операции ( самокалибровки), осуществления самоконтроля, уменьшения влияния случайных погрешностей путем проведения многократных измерений с последующим усреднением их результатов, выявления и исключения грубых погрешностей, выведения на дисплей информации о числовых значениях погрешностей по ходу измерений.
[15]
Страницы:
1
2