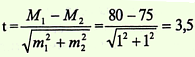Как вычислить ошибку репрезентативности

В практической и научно-практической работе
врачи обобщают результаты, полученные как правило на выборочных
совокупностях.
Для более широкого распространения и применения полученных при изучении
репрезентативной выборочной совокупности данных и выводов
надо уметь по части явления судить о явлении и его закономерностях в
целом.

Учитывая, что врачи, как правило, проводят исследования на
выборочных совокупностях, теория статистики позволяет с помощью
математического аппарата (формул) переносить данные с выборочного
исследования на генеральную совокупность. При этом врач должен
уметь не только воспользоваться математической формулой, но сделать
вывод, соответствующий каждому способу оценки достоверности
полученных данных. С этой целью врач должен знать способы оценки
достоверности.

Применяя метод оценки достоверности результатов исследования для изучения общественного здоровья и деятельности учреждений
здравоохранения, а также в своей научной деятельности, исследователь должен уметь правильно выбрать способ данного метода.
Среди методов оценки достоверности различают параметрические и непараметрические.

Параметрическими называют количественные методы статистической обработки данных, применение которых требует обязательного
знания закона распределения изучаемых признаков в совокупности и вычисления их основных параметров.

Непараметрическими являются количественные методы статистической обработки данных, применение которых не требует знания
закона распределения изучаемых признаков в совокупности и вычисления их основных параметров.

Как параметрические, так и непараметрические методы, используемые
для сравнения результатов исследований, т.е. для сравнения
выборочных совокупностей, заключаются в применении определенных формул и
расчете определенных показателей в соответствии с
предписанными алгоритмами. В конечном результате высчитывается
определенная числовая величина, которую сравнивают с табличными
пороговыми значениями. Критерием достоверности будет результат сравнения
полученной величины и табличного значения при данном числе
наблюдений (или степеней свободы) и при заданном уровне безошибочного
прогноза.

Таким образом, в статистической процедуре оценки основное
значение имеет полученный критерий достоверности, поэтому сам способ
оценки достоверности в целом иногда называют тем или иным критерием по
фамилии автора, предложившего его в качестве основы метода.

---

Применение параметрических методов

При проведении выборочных исследований полученный результат не обязательно совпадает с результатом, который мог бы быть получен
при исследовании всей генеральной совокупности. Между этими величинами существует определенная разница, называемая ошибкой
репрезентативности, т.е. это погрешность, обусловленная переносом результатов выборочного исследования на всю генеральную
совокупность.

Определение доверительных границ средних
и относительных величин

Формулы определения доверительных границ представлены следующим образом:

• для средних величин (М): М_ген = М_выб ± tm
• для относительных показателей (Р): Р_ген = Р_выб ± tm
  
  где М_ген и Р_ген — соответственно, значения средней величины и относительного показателя генеральной
  совокупности;
  
  М_вы6 и Р_вы6 — значения средней величины и относительного показателя выборочной совокупности;
  
  m — ошибка репрезентативности;
  
  t — критерий достоверности (доверительный коэффициент).

Данный способ применяется в тех случаях, когда по результатам выборочной совокупности необходимо судить о размерах изучаемого
явления (или признака) в генеральной совокупности.

Обязательным условием для применения способа является репрезентативность выборочной совокупности. Для переноса результатов,
полученных при выборочных исследованиях, на генеральную совокупность необходима степень вероятности безошибочного прогноза (Р),
показывающая, в каком проценте случаев результаты выборочных исследований по изучаемому признаку (явлению) будут иметь место в
генеральной совокупности.

При определении доверительных границ средней величины или относительного показателя генеральной совокупности, исследователь сам
задает определенную (необходимую) степень вероятности безошибочного прогноза (Р).

Для большинства медико-биологических исследований считается
достаточной степень вероятности безошибочного прогноза, равная 95%,
а число случаев генеральной совокупности, в котором могут наблюдаться
отклонения от закономерностей, установленных при выборочном
исследовании, не будут превышать 5%. При ряде исследований, связанных,
например, с применением высокотоксичных веществ, вакцин,
оперативного лечения и т.п., в результате чего возможны тяжелые
заболевания, осложнения, летальные исходы, применяется степень
вероятности Р = 99,7%, т.е. не более чем у 1% случаев генеральной
совокупности возможны отклонения от закономерностей,
установленных в выборочной совокупности.

Заданной степени вероятности (Р) безошибочного прогноза соответствует определенное, подставляемое в формулу, значение критерия
t, зависящее также и от числа наблюдений.

При n>30 степени вероятности безошибочного прогноза Р = 99,7% — соответствует значение t = 3, а при Р = 95,5% — значение
t = 2.

При п<30 величина t при соответствующей степени вероятности безошибочного прогноза определяется по специальной таблице
(Н.А. Плохинского).

на определение ошибок репрезентативности (m) и доверительных границ средней величины генеральной совокупности (М_ген)
при числе наблюдений больше 30

Условие задачи: при изучении комбинированного воздействия шума и низкочастотной вибрации на организм человека было
установлено, что средняя частота пульса у 36 обследованных водителей сельскохозяйственных машин через 1 ч работы составила 80
ударов в 1 минуту; σ = ± 6 ударов в минуту.

Задание: определить ошибку репрезентативности (m_M) и доверительные границы средней величины генеральной
совокупности (М_ген).

Решение.

1. Вычисление средней ошибки средней арифметической (ошибки репрезентативности) (m):

   m = σ / √n =
   6 / √36 =
   ±1 удар в минуту

2. Вычисление доверительных границ средней величины генеральной совокупности (М_ген). Для этого необходимо:
   • а) задать степень вероятности безошибочного прогноза (Р = 95 %);
   • б) определить величину критерия t. При заданной степени вероятности (Р=95%) и числе наблюдений меньше 30 величина критерия t,
     определяемого по таблице, равна 2 (t = 2). Тогда М_ген = М_выб ± tm = 80 ± 2×1 = 80 ± 2
     удара в минуту.

Вывод. Установлено с вероятностью безошибочного прогноза Р =
95%, что средняя частота пульса в генеральной совокупности,
т.е. у всех водителей сельскохозяйственных машин, через 1 ч работы в
аналогичных условиях будет находиться в пределах от 78 до 82
ударов в минуту, т.е. средняя частота пульса менее 78 и более 82 ударов в
минуту возможна не более, чем у 5% случаев генеральной
совокупности.

на определение ошибок репрезентативности (m) и доверительных границ относительного показателя генеральной совокупности
(Р_ген)

Условие задачи: при медицинском осмотре 164 детей 3 летнего возраста, проживающих в одном из районов городе Н., в 18%
случаев обнаружено нарушение осанки функционального характера.

Задание: определить ошибку репрезентативности (m_p) и доверительные границы относительного показателя
генеральной совокупности (Р_ген).

Решение.

1. Вычисление ошибки репрезентативности относительного показателя:

   m = √P x q / n =
   √18 x (100 — 18) / 164 =
   ± 3%

2. Вычисление доверительных границ средней величины генеральной совокупности (Р_ген) производится следующим образом:
   • необходимо задать степень вероятности безошибочного прогноза (Р=95%);
   • при заданной степени вероятности и числе наблюдений больше 30, величина критерия t равна 2 (t = 2).
     Тогда Р_ген = Р_выб± tm = 18% ± 2 х 3 = 18% ± 6%.

Вывод. Установлено с вероятностью безошибочного прогноза Р=95%, что частота нарушения осанки функционального характера у
детей 3 летнего возраста, проживающих в городе Н., будет находиться в пределах от 12 до 24% случаев.

---

Оценка достоверности разности результатов исследования

Данный способ применяется в тех случаях, когда необходимо определить, случайны или достоверны (существенны), т.е. обусловлены
какой-то причиной, различия между двумя средними величинами или относительными показателями.

Обязательным условием для применения данного способа является репрезентативность выборочных совокупностей, а также наличие
причинно-следственной связи между сравниваемыми величинами (показателями) и факторами, влияющими на них.

Формулы определения достоверности разности представлены следующим образом:

Если вычисленный критерий t более или равен 2 (t ≥ 2), что соответствует вероятности безошибочного прогноза Р равном или
более 95% (Р ≥ 95%), то разность следует считать достоверной (существенной), т.е. обусловленной влиянием какого-то фактора, что
будет иметь место и в генеральной совокупности.

При t < 2, вероятность безошибочного прогноза Р < 95%, это означает, что разность недостоверна, случайна, т.е. не
обусловлена какой-то закономерностью (не обусловлена влиянием какого-то фактора).

на оценку достоверности разности средних величин

Условие задачи: при изучении комбинированного воздействия шума
и низкочастотной вибрации на организм человека было
установлено, что средняя частота пульса у водителей сельскохозяйственных
машин через 1 ч после начала работы составила 80 ударов в
минуту; m = ± 1 удар в мин. Средняя частота пульса у этой же группы
водителей до начала работы равнялась 75 ударам в минуту;
m = ± 1 удар в минуту.

Задание: оценить достоверность различий средних значений пульса у водителей сельскохозяйственных машин до и после 1 ч
работы.

Решение.

Вывод. Значение критерия t = 3,5 соответствует вероятности безошибочного прогноза Р > 99,7%, следовательно можно
утверждать, что различия в средних значениях пульса у водителей сельскохозяйственных машин до и после 1 ч работы не случайно, а
достоверно, существенно, т.е. обусловлено влиянием воздействия шума и низкочастотной вибрации.

на оценку достоверности разности относительных показателей

Условие задачи: при медицинском осмотре детей 3 летнего возраста в 18% (m = ± 3%) случаях обнаружено нарушение
осанки функционального характера. Частота аналогичных нарушений осанки при медосмотре детей 4-летнего возраста составила 24%
(m = ± 2,64%).

Задание: оценить достоверность различий в частоте нарушения осанки у детей 2 возрастных групп.

Решение.

Вывод. Значение критерия t=1,5 соответствует вероятности безошибочного прогноза Р<95%. Следовательно, различие в
частоте нарушений осанки среди детей, сравниваемых возрастных групп случайно, недостоверно, несущественно, т.е. не обусловлено
влиянием возраста детей.

---

Типичные ошибки, допускаемые исследователями при
применении способа оценки достоверности разности результатов исследования

• При оценке достоверности разности результатов исследования по критерию t часто делается вывод о достоверности (или
  недостоверности) самих результатов исследования. В действительности же этот способ позволяет судить только о достоверности
  (существенности) или случайности различий между результатами исследования.

• При полученном значении критерия t<2 часто делается вывод о необходимости увеличения числа наблюдений. Если же
  выборочные совокупности репрезентативны, то нельзя делать вывод о необходимости увеличения числа наблюдений, т.к. в данном
  случае значение критерия t<2 свидетельствует о случайности, недостоверности различия между двумя сравниваемыми результатами
  исследования.

---

Применение методов статистического анализа для изучения общественного здоровья и здравоохранения.
Под ред. чл.-корр. РАМН, проф. В.З.Кучеренко. М., «Гэотар-Медиа», 2007, учебное пособие для вузов

1. Власов В.В. Эпидемиология. — М.: ГЭОТАР-МЕД, 2004. — 464 с.
2. Лисицын Ю.П. Общественное здоровье и здравоохранение. Учебник для вузов. — М.: ГЭОТАР-МЕД, 2007. — 512 с.
3. Медик В.А., Юрьев В.К. Курс лекций по общественному здоровью
   и здравоохранению: Часть 1. Общественное здоровье. — М.: Медицина,
   2003. — 368 с.
4. Миняев В.А., Вишняков Н.И. и др. Социальная медицина и организация здравоохранения (Руководство в 2 томах). — СПб, 1998. -528 с.
5. Кучеренко В.З., Агарков Н.М. и др.Социальная гигиена и организация здравоохранения (Учебное пособие) — Москва, 2000. — 432 с.
6. С. Гланц. Медико-биологическая статистика. Пер с англ. — М., Практика, 1998. — 459 с.